از ویکیپدیا، دانشنامه آزاد
اجازه دهید X یک تنوع تصویری صاف روی یک فیلد عددی K باشد. اصل هاس پیشبینی میکند که اگر X یک نقطه گویا روی تمام تکمیلهای K v از K داشته باشد، آنگاه X یک نقطه گویا K دارد. اصلهاسبرای برخی از کلاس های خاص از انواع صدق می کند، اما نه به طور کلی. مانین از گروه برائر X برای تعریف انسداد برائر-مانین استفاده کرد که میتواند در بسیاری از موارد برای نشان دادن اینکه X هیچ نقطه K ندارد حتی زمانی که X استفادهدر ریاضیات ، گروه برائر یک میدان K یک گروه آبلی است که عناصر آن کلاسهای همارزی موریتا از جبرهای ساده مرکزی بر K هستند که با حاصلضرب تانسور جبرها جمع میشوند. توسط جبرشناس ریچارد برائر تعریف شد .
گروه برائر از تلاش برای طبقه بندی جبرهای تقسیم بر روی یک میدان بوجود آمد. همچنین میتوان آن را بر اساس همشناسی گالوا تعریف کرد . به طور کلی تر، گروه برائر از یک طرح بر اساس جبرهای Azumaya یا به طور معادل با استفاده از بسته های تصویری تعریف می شود .
فهرست
ساخت و ساز [ ویرایش ]
جبر ساده مرکزی (CSA) روی یک میدان K یک جبر K- بعدی محدود است به طوری که A یک حلقه ساده است و مرکز A برابر با K است. توجه داشته باشید که CSAها به طور کلی جبرهای تقسیمی نیستند ، اگرچه از CSAها می توان برای طبقه بندی جبرهای تقسیمی استفاده کرد.
به عنوان مثال، اعداد مختلط C روی خودشان یک CSA تشکیل میدهند، اما نه روی R (مرکز خود C است، بنابراین بزرگتر از آن است که CSA روی R باشد). جبرهای تقسیم بعدی محدود با مرکز R (یعنی بعد روی R متناهی است) اعداد حقیقی و رباعی های یک قضیه فروبنیوس هستند، در حالی که هر حلقه ماتریسی بر روی واقعی ها یا چهارتایی ها - M( n ، R ) یا M هستند. ( n , H ) - یک CSA بر روی واقعی است، اما جبر تقسیم نیست (اگر n > 1).
ما به دست آوردن رابطه هم ارزی در CSAS بیش از K توسط قضیه آرتین-ودربرن به ( ودربرن به بخش نیست، در واقع)، برای بیان هر CSA به عنوان یک م ( N ، D ) برای برخی از بخش جبر D . اگر فقط به D نگاه کنیم ، یعنی اگر یک رابطه هم ارزی را تحمیل کنیم که M( m , D ) را با M( n , D ) برای همه اعداد صحیح مثبت m و n مشخص می کند ، رابطه هم ارزی برائر را بر روی CSA ها روی K می گیریم.. عناصر گروه برائر کلاس های هم ارزی برائر CSA ها روی K هستند.
با توجه به جبرهای ساده مرکزی A و B ، می توان به حاصل ضرب تانسور A ⊗ B آنها به عنوان یک جبر K نگاه کرد (به حاصل ضرب تانسور جبرهای R مراجعه کنید ). به نظر می رسد که این همیشه ساده مرکزی است. یک راه نرم و صاف برای دیدن این است که استفاده از خصوصیات: ساده جبر مرکزی بیش از K است K جبر که تبدیل به یک حلقه ماتریس هنگامی که ما زمینه گسترش بندی به بسته شدن جبری از K . این نتیجه همچنین نشان می دهد که بعد یک جبر ساده مرکزی A به عنوان Kفضای برداری همیشه یک مربع است. درجه از تعریف می شود ریشه دوم بعد آن.
در نتیجه، کلاسهای هممورفیسم CSAها روی K ، یک محصول تانسوری یکنوید را تشکیل میدهند که با معادل برائر سازگار است، و کلاسهای بروئر همگی معکوس هستند : معکوس جبر A توسط جبر مقابل آن A op داده میشود ( حلقه مقابل با همان عمل توسط K زیرا تصویر K → A در مرکز A است). به صراحت، برای یک CSA A ، A ⊗ A op = M( n 2 , K ) داریم که در آن nدرجه A بر K است .
گروه برائر هر میدانی یک گروه پیچشی است . در جزئیات بیشتر، تعریف دوره از ساده جبر مرکزی بیش از K به آن سفارش به عنوان یک عنصر از گروه برائر. تعریف شاخص از به درجه جبر تقسیم است که برائر معادل . سپس دوره شاخص تقسیم (و از این رو محدود است). [1]
- در موارد زیر، هر جبر بخش مرکزی محدود بعدی بیش از یک میدان K است K خود را، به طوری که گروه برائر برزیلی ( K ) است بی اهمیت :
- گروه برائر Br( R ) میدان R از اعداد حقیقی ، گروه چرخه ای مرتبه دو است. فقط دو جبر تقسیم واقعی غیر هم شکل با مرکز R وجود دارد : خود R و جبر چهارتایی H. [4] از آنجایی که H ⊗ H ≅ M(4, R )، کلاس H دارای مرتبه دو در گروه برائر است.
- فرض کنید K یک میدان محلی غیر ارشمیدسی باشد، به این معنی که K تحت یک ارزش گذاری گسسته با میدان باقیمانده محدود کامل است. سپس Br( K ) به Q / Z هم شکل است. [5]
انواع Severi–برائر [ ویرایش ]
یکی دیگر از تفسیر مهم از گروه برائر از یک میدان K است که آن را طبقه بندی کرده است رقم تصویری بیش از K که ریخت برای تبدیل شدن به فضای تصویری بیش از یک بسته شدن جبری از K . چنین گونهای ، واریته سوری-برائر نامیده میشود ، و بین طبقات همشکلی انواع سوری-بروئر با ابعاد n -1 روی K و جبرهای ساده مرکزی درجه n بر K مطابقت یک به یک وجود دارد . [6]
به عنوان مثال، انواع Severi-برائر با بعد 1 دقیقاً مخروط های صاف در صفحه پرتاب کننده روی K هستند. برای یک میدان K با مشخصه نه 2، هر مخروطی روی K به یکی از شکل های ax 2 + با 2 = z 2 برای برخی از عناصر غیر صفر a و b از K هم شکل است. جبر ساده مرکزی مربوطه جبر چهارتایی است [7]

مخروطی با خط پرتابی P 1 روی K هم شکل است اگر و فقط اگر جبر چهارتایی متناظر با جبر ماتریس M(2, K ) هم شکل باشد.
جبرهای چرخه ای [ ویرایش ]
برای یک عدد صحیح مثبت n ، فرض کنید K میدانی باشد که در آن n معکوس باشد، به طوری که K حاوی n ام ابتدایی واحد ز باشد. برای عناصر غیرصفر a و b از K ، جبر حلقوی مرتبط جبر ساده مرکزی با درجه n بر K است که توسط

جبرهای حلقوی بهترین جبرهای ساده مرکزی هستند که به خوبی قابل درک هستند. (زمانی که n در K معکوس نباشد یا K ریشه n ام ابتدایی وحدت نداشته باشد، یک ساختار مشابه جبر حلقوی (χ, a ) مربوط به یک Z / n - پسوند حلقوی χ از K و یک عنصر غیرصفر a را می دهد. از K. [ 8] )
قضیه Merkurjev-Suslin در نظریه K جبری یک نتیجه قوی در مورد گروه برائر دارد. یعنی، برای یک عدد صحیح مثبت n ، اجازه دهید K میدانی باشد که در آن n معکوس باشد به طوری که K حاوی n امین ریشه اولیه وحدت باشد. سپس زیرگروه گروه برائر از K کشته شده توسط n توسط جبرهای حلقوی درجه n تولید می شود. [9] به طور معادل، هر جبر تقسیم دوره ای که n را تقسیم می کند ، برائر معادل حاصل ضرب تانسور جبرهای حلقوی درجه n است. حتی برای عدد اول pمثالهایی وجود دارد که نشان میدهد جبر تقسیمبندی دوره p نیازی به همشکل بودن یک حاصل ضرب تانسور جبرهای حلقوی درجه p ندارد . [10]
این یک مشکل باز اصلی است (که توسط آلبرت مطرح شد ) که آیا هر جبر تقسیم درجه اول بر روی یک میدان چرخه ای است یا خیر. این درست است اگر درجه 2 یا 3 باشد، اما مشکل برای اعداد اول حداقل 5 کاملاً باز است. نتایج شناخته شده فقط برای کلاس های خاصی از فیلدها هستند. به عنوان مثال، اگر K یک میدان جهانی یا میدان محلی باشد ، جبر تقسیم با هر درجه بر K چرخه ای است، توسط Albert– برائر –هاس– Noether . [11] یک نتیجه "بعدی بالاتر" در همین جهت توسط سالتمن ثابت شد: اگر K میدانی با درجه متعالی 1 بر میدان محلی Q باشد.p ، پس هر جبر تقسیم درجه اول l ≠ p روی K حلقوی است. [12]
مشکل شاخص دوره [ ویرایش ]
برای هر جبر ساده مرکزی A بر روی یک میدان K ، دوره A شاخص A را تقسیم می کند و دو عدد دارای عوامل اول یکسان هستند. [13] مشکل شاخص دوره ، محدود کردن شاخص بر حسب دوره، برای فیلدهای K مورد علاقه است. به عنوان مثال، اگر A یک جبر ساده مرکزی بر روی یک میدان محلی یا میدان جهانی باشد، آلبرت-برائر-هاسه-نوتر نشان داد که شاخص A برابر با دوره A است. [11]
برای یک جبر ساده مرکزی A روی یک میدان K با درجه متعالی n بر روی یک میدان بسته جبری، حدس زده می شود که ind( A ) بر ( A ) n -1 تقسیم می شود . این برای n ≤ 2 صدق می کند ، مورد n = 2 پیشرفت مهمی توسط دی یونگ است که توسط دی یونگ استار و لیبلیچ در ویژگی مثبت مشخص شده است. [14]
نظریه میدان کلاس [ ویرایش ]
گروه برائر نقش مهمی در فرمول بندی مدرن نظریه میدان کلاس ایفا می کند . اگر K V یک میدان محلی غیر ارشمیدسی است، کلاس تئوری میدان محلی می دهد متعارف ریخت INV V : BR ( K V ) → Q / Z از ثابت هاس . [5]
مورد یک میدان جهانی K (مانند یک فیلد عددی ) توسط نظریه میدان کلاس جهانی بررسی می شود . اگر D یک جبر ساده مرکزی روی K باشد و v یک مکان K باشد، D ⊗ K v یک جبر ساده مرکزی روی K v است، تکمیل K در v . این یک هممورفیسم از گروه برائر K به گروه برائر K v را تعریف می کند . جبر ساده مرکزی داده شده D برای همه تقسیم می شود، اما تعداد محدودیv ، به طوری که تصویر D در تقریباً همه این هممورفیسم ها 0 است. گروه برائر Br( K ) در یک دنباله دقیق ساخته شده توسطهاسقرار می گیرد: [15] [16]

که در آن S مجموعه همه مکان های K و فلش سمت راست مجموع متغیرهای محلی است. گروه برائر از اعداد واقعی با (1/2) Z / Z شناسایی می شود. تزریقی بودن فلش سمت چپ محتوای قضیه آلبرت-بروئر-هاس-نوتر است .
این واقعیت که مجموع همه متغیرهای محلی یک جبر ساده مرکزی روی K صفر است، یک قانون متقابل معمولی است . به عنوان مثال، اعمال این مورد برای جبر چهارگانه ( a , b ) بر روی Q قانون متقابل درجه دوم را به دست می دهد .
همشناسی گالوا [ ویرایش ]
برای یک میدان دلخواه K ، گروه برائر را میتوان بر حسب همشناسی Galois به صورت زیر بیان کرد: [17]

که در آن G m نشانگر گروه ضربی است که به عنوان یک گروه جبری روی K دیده می شود. به طور دقیق تر، گروه cohomology نشان داده شده به معنی H2 ( Gal(Ks / K ) ، Ks * )، که در آن Ks نشان دهنده بسته شدن قابل جدا شدن K است .
ایزومورفیسم گروه برائر با یک گروه cohomology Galois را می توان به شرح زیر توصیف کرد. گروه خودمورفیسم جبر n × n ماتریس، گروه خطی تصویری PGL( n ) است. از آنجایی که تمام جبرهای ساده مرکزی روی K به جبر ماتریس با بسته شدن قابل تفکیک K هم شکل می شوند ، مجموعه ای از کلاس های هم شکل جبرهای ساده مرکزی با درجه n روی K را می توان با مجموعه همومولوژی Galois H 1 ( K , PGL( n) شناسایی کرد. )). کلاس یک جبر ساده مرکزی در H 2 ( K, G m ) تصویر کلاس آن در H 1 در زیر هممورفیسم مرزی است

مربوط به دنباله دقیق کوتاه 1 → G m → GL(n) → PGL(n) → 1.
گروه برائر از یک طرح [ ویرایش ]
گروه برائر از میدان ها به حلقه های جابجایی توسط اسلاندر و گلدمن تعمیم داده شد . ثانیه گروتندیک بیشتر با تعریف گروه برائر هر رفت طرح .
دو راه برای تعریف گروه برائر از یک طرح وجود دارد X ، با استفاده از جبری آزومایا بیش از X و یا بسته نرم افزاری تصویری بیش از X . تعریف دوم شامل بسته های تصویری است که به صورت محلی در توپولوژی étale بی اهمیت هستند و نه لزوماً در توپولوژی Zariski . به طور خاص، یک بسته تصویری در گروه برائر صفر تعریف میشود، اگر و تنها در صورتی که پروژکتیوسازی برخی از بستههای برداری باشد.
گروه کومولوژی برائر از یک طرح شبه فشرده X به عنوان زیرگروه پیچشی از گروه کومولوژی اتاتH2 ( X , Gm ) تعریف شده است. (کل گروه H 2 ( X , G m ) نیازی به پیچش ندارد، اگرچه برای طرح های منظم X پیچشی است . [18] ) گروه برائر همیشه زیرگروهی از گروه برائر کومولوژی است. گاببر نشان داد که گروه برائر برابر با گروه برائرکومولوژی برای هر طرحی با یک بسته خطی فراوان است (به عنوان مثال، هرطرح شبه فرافکنی بر روی یک حلقه جابجایی). [19]
کل گروه H 2 ( X , G m ) را می توان به عنوان دسته بندی گرب ها بر X با گروه ساختاری G m مشاهده کرد .
برای واریته های پرتابی صاف روی یک مزرعه، گروه برائر یک متغیر دوتایی است. مثمر ثمر بوده است. برای مثال، هنگامی که X نیز به طور منطقی روی اعداد مختلط متصل میشود، گروه برائر X نسبت به زیرگروه پیچشی گروه همومولوژی منفرد H 3 ( X , Z ) همشکل است، که بنابراین یک متغیر دوتایی است. آرتین و مامفورد از این توصیف در مورد گروه برائر استفاده کردند تا اولین مثال از یک نوع غیر منطقی X بر C را ارائه دهند که به طور منطقی پایدار نیست (یعنی هیچ محصولی ازX با فضای تصویری منطقی است). [20]
ارتباط با حدس تیت [ ویرایش ]
آرتین حدس زد که هر طرح مناسب بر روی اعداد صحیح دارای گروه برائر محدود است. [21] این امر حتی در مورد خاص یک نوع تصویری صاف X در یک میدان محدود نیز شناخته شده نیست. در واقع، محدودیت از گروه برائر برای سطوح در آن صورت معادل است حدس تیت برای مقسوم علیه های ان در X ، یکی از مشکلات اصلی در نظریه چرخه جبری . [22]
برای یک طرح انتگرالی منظم با بعد 2 که روی حلقه اعداد صحیح یک میدان اعداد مسطح و مناسب است و دارای یک بخش است، محدود بودن گروه برائر معادل محدود بودن گروه تات-شافرویچ Ш برای ژاکوبین است. تنوع فیبر عمومی (منحنی روی یک فیلد عددی). [23] محدود بودن Ш یک مشکل اصلی در محاسبات منحنی های بیضوی و به طور کلی انواع آبلی است .
انسداد برائر-مانین [ ویرایش ]
منبع
https://en.wikipedia.org/wiki/Brauer_group
و
و
و

![{\displaystyle [a,b]_{+}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/c7289995fc78776166741f2a036fbcfb0e632c02)
![{\displaystyle [a,b]_{-}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/59120bf940c61971319243298b88ebb28f752588)

![{\displaystyle \operatorname {ad} _{A}(B)=[A,B]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/8a40684049019f333e05818bcd1ce5b48f839561)

![{\textstyle e^{A}Be^{-A}\ =\ B+[A,B]+{\frac {1}{2!}}[A,[A,B]]+{\frac {1 {3!}}[A,[A,[A,B]]]+\cdots \ =\ e^{\operatorname {ad} _{A}}(B).}](https://wikimedia.org/api/rest_v1/media/math/render/svg/5e4b0b44677de183969e936bb4cede2bf5515ad4)



![{\displaystyle \operatorname {ad} _{x}\operatorname {ad} _{y}(z)=[x,[y,z]\,]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/8c27f6b58b814f258e43d4529f26e9ec0523b58a)
![{\displaystyle \operatorname {ad} _{x}^{2}\!(z)\ =\ \operatorname {ad} _{x}\!(\operatorname {ad} _{x}\!(z) )\ =\ [x،[x،z]\،].}](https://wikimedia.org/api/rest_v1/media/math/render/svg/856ad01497c91a4c78ba471c5ba199d82744c717)











![{\displaystyle x^{y}=x[x,y].}](https://wikimedia.org/api/rest_v1/media/math/render/svg/dbfda5e3214a078a56860ef1d958532efd6ecc6c)
![{\displaystyle [y,x]=[x,y]^{-1}.}](https://wikimedia.org/api/rest_v1/media/math/render/svg/59c8c7dabf4a3f20a3f9a04a295468426eb22009)
![{\displaystyle [xz,y]=[x,y]^{z}\cdot [z,y].}](https://wikimedia.org/api/rest_v1/media/math/render/svg/51d505bd20b4dfad61942e780f9019f2342a28df)
![{\displaystyle \left[x^{-1},y\right]=[y,x]^{x^{-1}}.}](https://wikimedia.org/api/rest_v1/media/math/render/svg/5ec4802d72362fa5f8b6f440bee17b73b8f9ff48)
![{\displaystyle \left[\left[x,y\right],z^{x}\right]\cdot \left[[z,x],y^{z}\right]\cdot \چپ[[y ,z],x^{y}\right]=1.}](https://wikimedia.org/api/rest_v1/media/math/render/svg/969627eb5e4b01b893d68ba8cb5aefb6fb9dcb4e)
![{\displaystyle (xy)^{2}=x^{2}y^{2}[y,x][[y,x],y].}](https://wikimedia.org/api/rest_v1/media/math/render/svg/9c75b2bcc9c723ec68c6e482e9e1e002b02082d3)
![{\displaystyle (xy)^{n}=x^{n}y^{n}[y,x]^{\binom {n}{2}}.}](https://wikimedia.org/api/rest_v1/media/math/render/svg/128ae0855aada1e122d118d63c2bfa18a08eb603)
![{\displaystyle [a,b]=ab-ba.}](https://wikimedia.org/api/rest_v1/media/math/render/svg/c73ba7fbd6260acd540051cc2c6f9131ff0d7f8e)

![{\displaystyle [A+B,C]=[A,C]+[B,C]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/b3f1c95436e1c9c40871bc7a3704072ae067dc10)
![{\displaystyle [A,A]=0}](https://wikimedia.org/api/rest_v1/media/math/render/svg/7c816c8f8631ef069ad0b1aee64ed996ad8309ed)
![{\displaystyle [A,B]=-[B,A]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/37b04a066443e96c0b27d4b14f7f5d51c7b2b0c3)
![{\displaystyle [A,[B,C]]+[B,[C,A]]+[C,[A,B]]=0}](https://wikimedia.org/api/rest_v1/media/math/render/svg/046dbc0d4387302c8d321afb443e35bc1890fcac)
![{\displaystyle [A,BC]=[A,B]C+B[A,C]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/1c7c96785faa7d6e5ecc7d8ada53830b24338c60)
![{\displaystyle [A,BCD]=[A,B]CD+B[A,C]D+BC[A,D]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/aa03949d714777910e992c14aeed34adf42d9766)
![{\displaystyle [A,BCDE]=[A,B]CDE+B[A,C]DE+BC[A,D]E+BCD[A,E]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/8b79c370dc9984ff5e2720b3e06c6153af7ba572)
![{\displaystyle [AB,C]=A[B,C]+[A,C]B}](https://wikimedia.org/api/rest_v1/media/math/render/svg/71ba3177011b65b292d8dc39dd2e3391f29b0a07)
![{\displaystyle [ABC,D]=AB[C,D]+A[B,D]C+[A,D]BC}](https://wikimedia.org/api/rest_v1/media/math/render/svg/b9e755fd1fe3c26c40e007256c6976b9612e5d9b)
![{\displaystyle [ABCD,E]=ABC[D,E]+AB[C,E]D+A[B,E]CD+[A,E]BCD}](https://wikimedia.org/api/rest_v1/media/math/render/svg/4e00b8c22f5a63ff3dbbcf8a74f0d01f43994afa)
![{\displaystyle [A,B+C]=[A,B]+[A,C]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/7f50e382d516600cfe9f7a34376ebe694bb62177)
![{\displaystyle [A+B,C+D]=[A,C]+[A,D]+[B,C]+[B,D]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/2e47836a02ce95e65488370410a80446b1ae636c)
![{\displaystyle [AB,CD]=A[B,C]D+[A,C]BD+CA[B,D]+C[A,D]B=A[B,C]D+AC[B, D]+[A,C]DB+C[A,D]B}](https://wikimedia.org/api/rest_v1/media/math/render/svg/a8b90ee684250322ac794d8cb193d75c8c1d4db3)
![{\displaystyle [[A,C],[B,D]]=[[[A,B],C],D]+[[[B,C],D],A]+[[[C, D],A],B]+[[[D,A],B],C]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/33e847e641c8d2810846e666be23d2512b08eb2f)
![{\displaystyle [A^{N},B^{M}]=\sum _{n=0}^{N-1}\sum _{m=0}^{M-1}A^{n} B^{m}[A,B]B^{Nn-1}A^{Mm-1}=\sum _{n=0}^{N-1}\sum _{m=0}^{M-1}B^{n}A^{m}[A,B]A^{Nn-1}B^{Mm-1}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/b2a8a7436d26ef75d1023a36ffa1c561597c8506)
![{\displaystyle [AB,C]_{\pm }=A[B,C]_{-}+[A,C]_{\pm }B}](https://wikimedia.org/api/rest_v1/media/math/render/svg/187aaec93ded1a30cd6ad33d9e323c786d4a39fd)
![{\displaystyle [AB,CD]_{\pm }=A[B,C]_{-}D+AC[B,D]_{-}+[A,C]_{-}DB+C[ A,D]_{\pm }B}](https://wikimedia.org/api/rest_v1/media/math/render/svg/2abfd9c204056463779a2541fa7f5bc02930bf9a)
![{\displaystyle [[A,B],[C,D]]=[[[B,C]_{+},A]_{+},D]-[[[B,D]_{+} ,A]_{+},C]+[[[A,D]_{+},B]_{+},C]-[[A,C]_{+},B]_{+ },D]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/6c14c4def5d057ec857052e280d0c27658c3796d)
![{\displaystyle \left[A,[B,C]_{\pm }\right]+\left[B,[C,A]_{\pm }\right]+\left[C,[A,B ]_{\pm }\right]=0}](https://wikimedia.org/api/rest_v1/media/math/render/svg/7fa38c6ec51fd44c85b6a7dd7820d8ebaee4f2cf)
![{\displaystyle [A,BC]_{\pm }=[A,B]_{-}C+B[A,C]_{\pm }=[A,B]_{\pm }C\mp B[A,C]_{-}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/cee7d373e2721aa7ec3c50a8f645785d7da7b804)
![{\displaystyle [A,BC]=[A,B]_{\pm }C\mp B[A,C]_{\pm }}](https://wikimedia.org/api/rest_v1/media/math/render/svg/2f480a46e5c19fea0ae860621b38e69606a71239)
![{\displaystyle e^{A}e^{B}e^{-A}e^{-B}=\exp \!\left([A,B]+{\frac {1}{2!}} [A{+}B,[A,B]]+{\frac {1}{3!}}\left({\frac {1}{2}}[A,[B,[B,A]]]+[A{+}B,[A{+}B,[A,B]]]\right)+\cdots \right )](https://wikimedia.org/api/rest_v1/media/math/render/svg/f104655d91482ecf24b550407ef28112b27bd564)
![{\displaystyle [\omega ,\eta ]_{gr}:=\omega \eta -(-1)^{\deg \omega \deg \eta }\eta \omega .}](https://wikimedia.org/api/rest_v1/media/math/render/svg/4a31537974b529c2386b07f032b0452d7ab70e81)
![{\displaystyle \operatorname {ad} _{x}(y)=[x,y]=xy-yx.}](https://wikimedia.org/api/rest_v1/media/math/render/svg/06e06c88110f66faa14de2b3fba0644b13e96429)

![{\displaystyle \mathrm {ad} _{x}[y,z]\ =\ [\mathrm {ad} _{x}\!(y),z]\,+\,[y,\mathrm {ad} } _{x}\!(z)].}](https://wikimedia.org/api/rest_v1/media/math/render/svg/97e49b2f65e16c28bbcad712a40e4bf680ebf909)
![{\displaystyle \operatorname {ad} _{[x,y]}=\left[\operatorname {ad} _{x},\operatorname {ad} _{y}\right].}](https://wikimedia.org/api/rest_v1/media/math/render/svg/3c43069feeed684198e360f083c3c004bf3cb2f2)



 ).
). که در آن V یکانی است و D قطری است و یکانی.
که در آن V یکانی است و D قطری است و یکانی. . به این معنا که،
. به این معنا که، روی دایره یکانی صفحه مختلط خواهد بود.
روی دایره یکانی صفحه مختلط خواهد بود. یکانی است
یکانی است یکانی است
یکانی است .
. با توجه به ضرب داخلی معمولی. به عبارت دیگر،
با توجه به ضرب داخلی معمولی. به عبارت دیگر، .
. .
. برای همه
برای همه  ، جایی که
، جایی که .
.

 با
با  گروه یکانی ویژه SU(2) نامیده می شود.
گروه یکانی ویژه SU(2) نامیده می شود.
 و ه ،
و ه ، بالا و زوایای
بالا و زوایای  می تواند هر مقداری را بگیرد.
می تواند هر مقداری را بگیرد. و ،
و ، فاکتورسازی زیر را دارد:
فاکتورسازی زیر را دارد:




 (فضای برداری مجهز به این فرم درجه دوم گاهی نوشته می شود
(فضای برداری مجهز به این فرم درجه دوم گاهی نوشته می شود ). این شکل درجه دوم، هنگامی که در فرم ماتریس قرار می گیرد (به
). این شکل درجه دوم، هنگامی که در فرم ماتریس قرار می گیرد (به 
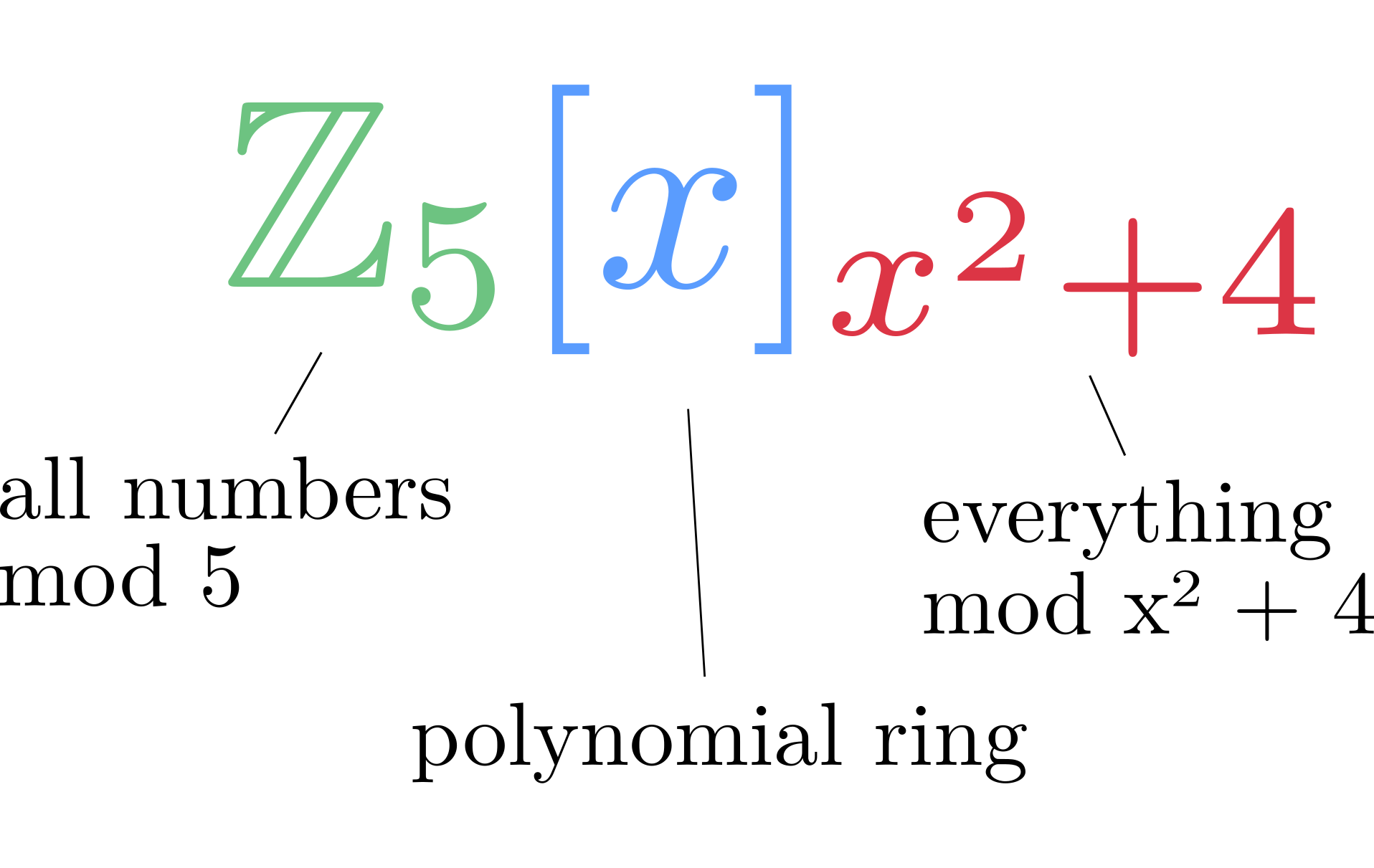
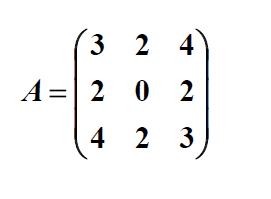
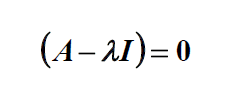
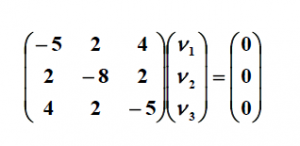
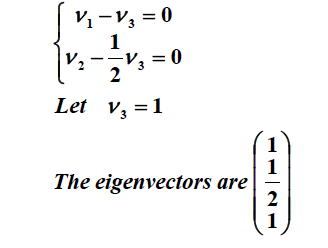
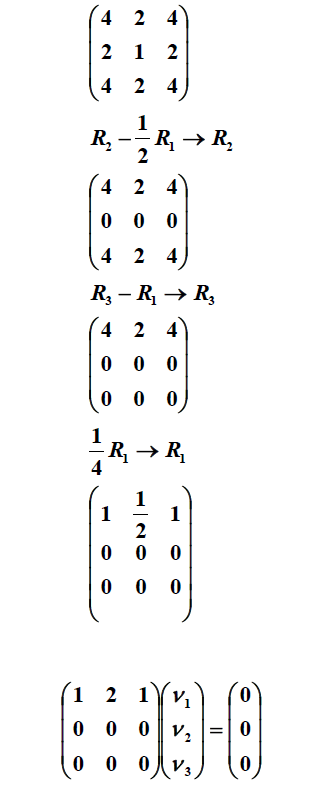
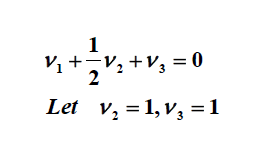
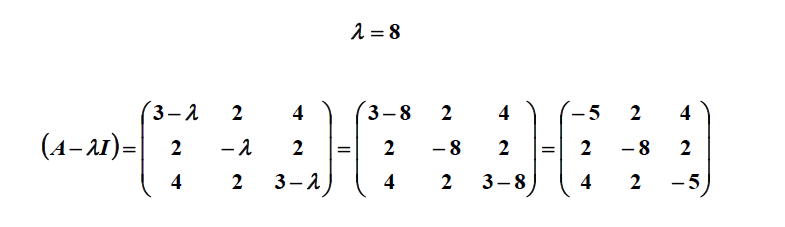








 بر روی
بر روی  یک میدان جبری بسته است، سپس حلقه ماتریس دارای ورودی هایی از است
یک میدان جبری بسته است، سپس حلقه ماتریس دارای ورودی هایی از است جایی که
جایی که  اعداد صحیح مثبت هستند و
اعداد صحیح مثبت هستند و  جبر است
جبر است  ماتریس های بیش از k .
ماتریس های بیش از k . قابل حل است اگر ...
قابل حل است اگر ... که هر کدام در
که هر کدام در  آن
آن  آبلی
آبلی  که هر کدام
که هر کدام  و هر کدام
و هر کدام  آن
آن  و
و ![G^{(i+1)} = [G^{(i)}، G^{(i)}]](https://groupprops.subwiki.org/w/images/math/6/1/8/61821731652d94617999581509cf6397.png)
 یک
یک  گروههای قابل حل هستند . سپس
گروههای قابل حل هستند . سپس  یک
یک  قابل حل باشند،
قابل حل باشند،  نیز قابل حل است.
نیز قابل حل است. همه زیرگروه های
همه زیرگروه های  قابل حل است.
قابل حل است. و
و  ، پس قابل حل است اگر و فقط اگر باشد. علاوه بر این، اگر چنین است، طول مشتق شده برابر است با طول مشتق شده از , مگر اینکه یکی از گروه ها جزئی و دیگری آبلی غیر جزئی باشد.
، پس قابل حل است اگر و فقط اگر باشد. علاوه بر این، اگر چنین است، طول مشتق شده برابر است با طول مشتق شده از , مگر اینکه یکی از گروه ها جزئی و دیگری آبلی غیر جزئی باشد. 




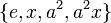 ،
، 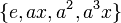


 یا
یا  )
) ; مانند حلقه تولید شده توسط مقادیر کاراکتر
; مانند حلقه تولید شده توسط مقادیر کاراکتر (بنابراین، این یک
(بنابراین، این یک 

 (سایز 1)
(سایز 1) (سایز 2)
(سایز 2) (سایز 2)
(سایز 2) (سایز 2)
(سایز 2) -هسته
-هسته -هسته
-هسته -هسته
-هسته نه صفر است و نه
نه صفر است و نه  مدول
مدول  . این را با مورد فرد مقایسه کنید
. این را با مورد فرد مقایسه کنید  ، درجه
، درجه
 و مرتبه
و مرتبه
 به عنصر چرخش مرتبه چهار و مولد دوم به عنصر انعکاس
به عنصر چرخش مرتبه چهار و مولد دوم به عنصر انعکاس درجه دو نگاشت می شود.
درجه دو نگاشت می شود. گروه دور ای مرتبه چهار را تعریف کنید (با استفاده از
گروه دور ای مرتبه چهار را تعریف کنید (با استفاده از  ،
،  حتی:
حتی: .
.  :
: 
 تعداد زیرگروه ها است
تعداد زیرگروه ها است  ، که در آن
، که در آن  تابع شمارش مقسوم علیه و
تابع شمارش مقسوم علیه و  تابع مجموع مقسوم علیه است. ساختار زیر گروه گروه دو وجهی را ببینید
تابع مجموع مقسوم علیه است. ساختار زیر گروه گروه دو وجهی را ببینید 


 و رفت و
و رفت و  آمد نکنید
آمد نکنید ، که طبیعی است، اما
، که طبیعی است، اما  طبیعی نیست
طبیعی نیست





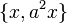

 -- یکی از
-- یکی از 

 -- یکی از
-- یکی از 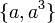


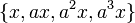

 و
و  : نظم حاصلضرب دستورات
: نظم حاصلضرب دستورات 
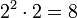
 دارای توانی برابر با
دارای توانی برابر با  .
. ، که گاهی اوقات نامیده می شود
، که گاهی اوقات نامیده می شود  ، همچنین به نام
، همچنین به نام  نشان دادن همانی ، تعریف می شود. عنصر:
نشان دادن همانی ، تعریف می شود. عنصر:
 که توسط:
که توسط:
 این را می توان با در نظر گرفتن رئوس مربع و در نظر گرفتن عنصری از
این را می توان با در نظر گرفتن رئوس مربع و در نظر گرفتن عنصری از  و
و  .
. ، مانند ارائه بالا.
، مانند ارائه بالا.




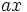
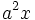

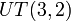 میدان
میدان 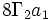

 ) در خلاف جهت عقربه های ساعت
) در خلاف جهت عقربه های ساعت
 نیز نامیده می شود
نیز نامیده می شود

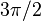 (یعنی
(یعنی  ) در خلاف جهت عقربه های ساعت، یا معادل آن، توسط
) در خلاف جهت عقربه های ساعت، یا معادل آن، توسط 

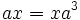





 یک
یک  تنها دو
تنها دو  به این معنی است که یک پوشش دوتایی است (به
به این معنی است که یک پوشش دوتایی است (به  دو گروه شبه ساده متناظر هستند .
دو گروه شبه ساده متناظر هستند . توان 4.
توان 4.







 .
. : 2، 10، 59 ، 501، 3786، 48337، ...
: 2، 10، 59 ، 501، 3786، 48337، ... هال از مرتبه 12 (
هال از مرتبه 12 (  یا زیرگروه -Hall وجود ندارد
یا زیرگروه -Hall وجود ندارد 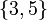 .
.



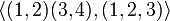



![\mathbb{Z}[(1 + \sqrt{5})/2]](https://groupprops.subwiki.org/w/images/math/9/5/7/9571a637ac52d32af6afc3cdad0a11f2.png) یا
یا ![\mathbb{Z}[2\cos(2\pi/5)]](https://groupprops.subwiki.org/w/images/math/4/a/9/4a95ab6e953d54684480256e2ff0b9b2.png)
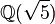 - گسترش درجه دوم میدان اعداد
- گسترش درجه دوم میدان اعداد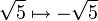 )
) (سایز 12)
(سایز 12)

 نامیده می شود، به روش های زیر تعریف می شود:
نامیده می شود، به روش های زیر تعریف می شود: (گاهی اوقات به مرتبه معکوس به عنوان نوشته می شود
(گاهی اوقات به مرتبه معکوس به عنوان نوشته می شود  ).
). به این صورت مشاهده می شود، یا نشان داده می شود
به این صورت مشاهده می شود، یا نشان داده می شود  . اطلاعات بیشتر:
. اطلاعات بیشتر:  . همچنین
. همچنین  . همچنین
. همچنین  است.
است. است.
است. ،
، 
 ،
، 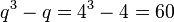
 ،
،  .
. :
: 
 ( بدون
( بدون  ): به
): به 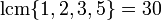

 (فرد):
(فرد):
 .
. (بیشتر
(بیشتر  ,
, 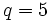 :
:  (
(  ,
,  (زوج):
(زوج):  (اطلاعات بیشتر
(اطلاعات بیشتر  غیر آبلی است،
غیر آبلی است،  .
. ،
، .
. (همانی، اندازه 1)
(همانی، اندازه 1) (اندازه 1)
(اندازه 1) (اندازه 2)
(اندازه 2) (اندازه 2)
(اندازه 2) (اندازه 2)
(اندازه 2) -هسته
-هسته -هسته
-هسته -هسته
-هسته
![\mathbb{Z}[i]](https://groupprops.subwiki.org/w/images/math/2/a/2/2a2fc748028420198e13c31eaadb6939.png) که در آن
که در آن  معادل
معادل ![\mathbb{Z}[t]/(t^2 + 1)](https://groupprops.subwiki.org/w/images/math/b/d/a/bdaaaa61e231878ff94a23bf211e8b51.png) است،
است، ![\mathbb{Z}[\sqrt{-2}]](https://groupprops.subwiki.org/w/images/math/c/b/2/cb2cb15c3160a682927d46e421fa88a6.png) یا
یا ![\mathbb{Z}[t]/(t^2 + 2)](https://groupprops.subwiki.org/w/images/math/f/c/8/fc8ac1bd26f88375919c94a722a2e48e.png) .
.![\mathbb{Z}[\آلفا،\بتا]](https://groupprops.subwiki.org/w/images/math/1/f/0/1f0f6de3f0e97814f330443f7b3ed137.png) که در آن
که در آن  حلقه ای از تحقق برای همه نمایش های کاهش ناپذیر است. به طور خاص،
حلقه ای از تحقق برای همه نمایش های کاهش ناپذیر است. به طور خاص، ![\mathbb{Z}[\sqrt{-m^2 - 1}]](https://groupprops.subwiki.org/w/images/math/d/2/5/d25c5a9bf29af37e54b57b5e72470138.png) برای هر منطقی کار می کند
برای هر منطقی کار می کند  .
. یا
یا ![\mathbb{Q}[t]/(t^2 + 1)](https://groupprops.subwiki.org/w/images/math/2/d/d/2dd8015d50efd0a01e1c014ae0cc8acd.png) کار می کند، همینطور می کند
کار می کند، همینطور می کند  یا
یا ![\mathbb{Q}[t]/(t^2 + 2)](https://groupprops.subwiki.org/w/images/math/2/a/2/2a29bc188f1f177ce72e9c7b6c5eaa7e.png) . به طور کلی تر،
. به طور کلی تر،  جایی
جایی  برای هر منطقی کار می کند
برای هر منطقی کار می کند  شرط کافی: مشخصه دو نیست و در میدان وجود دارد به گونه ای که
شرط کافی: مشخصه دو نیست و در میدان وجود دارد به گونه ای که  . به طور خاص، هر
. به طور خاص، هر 
 هر یک از کلاس های مزدوج عناصر غیر مرکزی هستند.
هر یک از کلاس های مزدوج عناصر غیر مرکزی هستند.
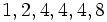
 ها وجود دارد که در آن
ها وجود دارد که در آن  همه
همه  اعداد صحیح مثبت وجود دارد. علاوه بر این،
اعداد صحیح مثبت وجود دارد. علاوه بر این، 
 اول و
اول و  اعداد صحیح مثبت هستند.
اعداد صحیح مثبت هستند.  مستقل از انتخاب بیان است. علاوه بر این، تعداد دفعاتی که هر توان اول
مستقل از انتخاب بیان است. علاوه بر این، تعداد دفعاتی که هر توان اول  در بین آنها رخ می دهد
در بین آنها رخ می دهد  ، مستقل از انتخاب عبارات است.
، مستقل از انتخاب عبارات است.
 . علاوه بر این،
. علاوه بر این، 

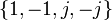



 نشان داده می شود
نشان داده می شود  به
به  ترتیب نشان داده می شوند.
ترتیب نشان داده می شوند. که در آن 1 عنصر هویت است،
که در آن 1 عنصر هویت است،  و همه عناصر دیگر از ریشه مربع هستند
و همه عناصر دیگر از ریشه مربع هستند  و بیشتر،
و بیشتر،  (روابط باقی مانده را می توان از اینها استنباط کرد).
(روابط باقی مانده را می توان از اینها استنباط کرد). .
. .
.















 در این وبلاگ به ریاضیات و کاربردهای آن و تحقیقات در آنها پرداخته می شود. مطالب در این وبلاگ ترجمه سطحی و اولیه است و کامل نیست.در صورتی سوال یا نظری در زمینه ریاضیات دارید مطرح نمایید .در صورت امکان به آن می پردازم. من دوست دارم برای یافتن پاسخ به سوالات و حل پروژه های علمی با دیگران همکاری نمایم.در صورتی که شما هم بامن هم عقیده هستید با من تماس بگیرید.
در این وبلاگ به ریاضیات و کاربردهای آن و تحقیقات در آنها پرداخته می شود. مطالب در این وبلاگ ترجمه سطحی و اولیه است و کامل نیست.در صورتی سوال یا نظری در زمینه ریاضیات دارید مطرح نمایید .در صورت امکان به آن می پردازم. من دوست دارم برای یافتن پاسخ به سوالات و حل پروژه های علمی با دیگران همکاری نمایم.در صورتی که شما هم بامن هم عقیده هستید با من تماس بگیرید.