توسط علی رضا نقش نیلچی
| یکشنبه نهم دی ۱۴۰۳ | 8:3
کلیات
[ ویرایش ]
روابط بین مختصات فضا-زمان اولیه و غیر آغاز شده تبدیلات لورنتس است ، هر مختصات در یک فریم تابع خطی همه مختصات در قاب دیگر است و توابع معکوس تبدیل معکوس هستند. بسته به نحوه حرکت قاب ها نسبت به یکدیگر و نحوه جهت گیری آنها در فضا نسبت به یکدیگر، پارامترهای دیگری که جهت، سرعت و جهت را توصیف می کنند وارد معادلات تبدیل می شوند.
تبدیلهایی که حرکت نسبی را با سرعت ثابت (یکنواخت) و بدون چرخش محورهای مختصات فضا توصیف میکنند، بوستهای لورنتس یا بوستهای ساده نامیده میشوند و سرعت نسبی بین فریمها پارامتر تبدیل است. نوع اصلی دیگر تبدیل لورنتز چرخش در مختصات فضایی است، این بوستها تبدیلهای اینرسی هستند زیرا هیچ حرکت نسبی وجود ندارد، فریمها به سادگی کج میشوند (و به طور پیوسته نمیچرخند)، و در این مورد کمیتهای تعیینکننده چرخش هستند. پارامترهای تبدیل (به عنوان مثال، نمایش محور-زاویه ، یا زوایای اویلر ، و غیره). ترکیبی از چرخش و تقویت یک تبدیل همگن است که مبدا را به مبدا تبدیل می کند.
گروه کامل لورنتس O(3, 1) همچنین شامل دگرگونیهای ویژهای است که نه چرخش هستند و نه تقویت، بلکه انعکاسهایی در یک صفحه از مبدا هستند. دو مورد از این موارد را می توان مشخص کرد. وارونگی مکانی که در آن مختصات مکانی همه رویدادها در علامت معکوس می شود و وارونگی زمانی که در آن مختصات زمانی برای هر رویداد علامت خود را معکوس می کند.
افزایش ها را نباید با جابجایی های صرف در فضازمان ترکیب کرد. در این حالت، سیستم مختصات به سادگی جابجا شده و هیچ حرکت نسبی وجود ندارد. با این حال، اینها همچنین به عنوان تقارن های وادار شده توسط نسبیت خاص به حساب می آیند زیرا بازه فضازمان را ثابت می گذارند. ترکیبی از یک چرخش با یک تقویت، و به دنبال آن یک تغییر در فضازمان، تبدیل ناهمگن لورنتس است ، عنصری از گروه پوانکاره، که گروه ناهمگن لورنتس نیز نامیده میشود.
فرمول فیزیکی لورنتس را تقویت می کند
[ ویرایش ]
اطلاعات بیشتر: مشتقات تبدیلات لورنتس
تحول هماهنگ کنید
[ ویرایش ]

مختصات فضا-زمان یک رویداد، همانطور که توسط هر ناظر در چارچوب مرجع اینرسی اندازه گیری می شود (در پیکربندی استاندارد) در حباب های گفتار نشان داده شده است.
بالا: فریم F با سرعت v در امتداد محور x قاب F حرکت می کند .
پایین: فریم F با سرعت − v در امتداد محور x قاب F حرکت می کند . [ 12 ]
یک ناظر "ایستا" در قاب F رویدادها را با مختصات t , x , y , z تعریف می کند . یک قاب دیگر F ′ با سرعت v نسبت به F حرکت می کند و ناظری در این قاب “متحرک” F ′ رویدادها را با استفاده از مختصات t ′, x ′, y , z ′ تعریف می کند .
محورهای مختصات در هر فریم موازی هستند ( محورهای x و x موازی هستند، محورهای y و y موازی هستند و محورهای z و z موازی هستند)، عمود بر یکدیگر باقی می مانند و حرکت نسبی در امتداد xx منطبق است . " تبرها. در t = t ′ = 0 ، مبدا هر دو سیستم مختصات یکسان است،
( x, y, z ) = ( x ′, y ′, z ′) = (0, 0, 0)
. به عبارت دیگر، زمان و موقعیت در این رویداد همزمان است. اگر همه اینها پابرجا باشند، سیستم مختصات در پیکربندی استاندارد یا همگام میگویند .
اگر ناظری در F یک رویداد t , x , y , z را ثبت کند ، آنگاه ناظری در F همان رویداد را با مختصات ثبت می کند [ 13 ]
تقویت لورنتس ( x جهت )

که در آن v سرعت نسبی بین فریم ها در جهت x است ، c سرعت نور است و

( گامای کوچک ) عامل لورنتس است .
در اینجا، v پارامتر تبدیل است ، برای یک تقویت معین، یک عدد ثابت است، اما می تواند یک محدوده پیوسته از مقادیر را بگیرد. در تنظیمات مورد استفاده در اینجا، سرعت نسبی مثبت v > 0 حرکت در امتداد جهت های مثبت محورهای xx ' است ، سرعت نسبی صفر v = 0 حرکت نسبی نیست، در حالی که سرعت نسبی منفی v <0 حرکت نسبی در امتداد جهات منفی است. محورهای xx . بزرگی سرعت نسبی v نمی تواند برابر یا بیشتر از c باشد ، بنابراین فقط سرعت های زیر نوری - c < v < c مجاز هستند. محدوده مربوط به γ 1 ≤ γ < ∞ است .
اگر v خارج از این محدودیت ها باشد، تبدیل ها تعریف نمی شوند . در سرعت نور ( v = c ) γ نامتناهی است و سریعتر از نور ( v > c ) γ عدد مختلطی است که هر کدام تبدیل ها را غیرفیزیکی می کند. مختصات مکان و زمان کمیت های قابل اندازه گیری هستند و از نظر عددی باید اعداد واقعی باشند.
به عنوان یک تبدیل فعال ، یک ناظر در F' متوجه میشود که مختصات رویداد در جهتهای منفی محورهای xx «تقویت میشوند ، زیرا - v در تبدیلها. این اثر معادل سیستم مختصات F' تقویت شده در جهت های مثبت محورهای xx را دارد ، در حالی که رویداد تغییر نمی کند و به سادگی در یک سیستم مختصات دیگر، یک تبدیل غیرفعال نشان داده می شود .
روابط معکوس ( t , x , y , z بر حسب t ′, x ′, y ′, z ′ ) را می توان با حل جبری مجموعه اصلی معادلات یافت. راه کارآمدتر استفاده از اصول فیزیکی است. در اینجا F قاب "ایستا" است در حالی که F قاب "متحرک" است. طبق اصل نسبیت، هیچ چارچوب مرجع ممتازی وجود ندارد، بنابراین تبدیلهای F به F باید دقیقاً همان شکل تبدیلهای F به F را داشته باشند . تنها تفاوت این است که F با سرعت - v نسبت به F ' حرکت می کند (یعنی سرعت نسبی همان مقدار است اما جهت مخالف است). بنابراین اگر ناظری در F " رویداد t "، x "، y "، z " را یادداشت کند ، آنگاه ناظری در F همان رویداد را با مختصات یادداشت می کند .
تقویت معکوس لورنتس ( جهت x )

و مقدار γ بدون تغییر باقی می ماند. این «ترفند» صرفاً معکوس کردن جهت سرعت نسبی با حفظ بزرگی آن، و مبادله متغیرهای اولیه و غیر آغاز شده، همیشه برای یافتن تبدیل معکوس هر بوست در هر جهتی کاربرد دارد. [ 14 ] [ 15 ]
گاهی اوقات استفاده از β = v / c ( بتا کوچک ) به جای v راحت تر است ، به طوری که

که به وضوح تقارن در تبدیل را نشان می دهد. از محدوده مجاز v و تعریف β ، −1 < β < 1 است . استفاده از β و γ در سراسر ادبیات استاندارد است.
هنگامی که سرعت افزایش در جهت بردار دلخواه با بردار تقویت است
در جهت بردار دلخواه با بردار تقویت است ، سپس تبدیل از یک سیستم مختصات فضازمان بدون پرایم به یک سیستم مختصات اولیه توسط [ 16 ] ، [1] داده می شود.
، سپس تبدیل از یک سیستم مختصات فضازمان بدون پرایم به یک سیستم مختصات اولیه توسط [ 16 ] ، [1] داده می شود.

جایی که عامل لورنتس است
 . تعیین کننده ماتریس تبدیل +1 و ردیابی آن است
. تعیین کننده ماتریس تبدیل +1 و ردیابی آن است . معکوس تبدیل با معکوس کردن علامت داده می شود
. معکوس تبدیل با معکوس کردن علامت داده می شود . مقدار
. مقدار تحت تغییر شکل ثابت است.
تحت تغییر شکل ثابت است.
تبدیلهای لورنتس را میتوان به گونهای مشتق کرد که شبیه چرخشهای دایرهای در فضای سه بعدی با استفاده از توابع هذلولی باشد . برای افزایش در جهت x ، نتایج هستند
تقویت لورنتس ( جهت x با سرعت ζ )

که در آن ζ ( زتا با حروف کوچک ) پارامتری به نام سرعت است (بسیاری از نمادهای دیگر از جمله θ، φ، φ، η، ψ، ξ استفاده میشود ). با توجه به شباهت زیاد به چرخش مختصات فضایی در فضای سه بعدی در صفحات دکارتی xy، yz، و zx، تقویت لورنتس را می توان به عنوان چرخش هذلولی مختصات فضازمان در صفحات زمان دکارتی xt، yt و zt در نظر گرفت . فضای چهار بعدی مینکوفسکی پارامتر ζ زاویه هذلولی چرخش است که مشابه زاویه معمولی برای چرخش های دایره ای است. این تبدیل را می توان با نمودار مینکوفسکی نشان داد .
توابع هذلولی از تفاوت بین مجذورهای زمان و مختصات مکانی در بازه فضازمان به جای مجموع ناشی می شوند. اهمیت هندسی توابع هذلولی را می توان با گرفتن x = 0 یا ct = 0 در تبدیل ها مشاهده کرد. با مربع و تفریق نتایج، می توان منحنی های هذلولی با مقادیر مختصات ثابت اما ز متغیر را استخراج کرد که منحنی ها را بر اساس هویت پارامتری می کند.cosh2ز-گناه2ز=1.
برعکس، محورهای ct و x را میتوان برای مختصات متفاوت اما ζ ثابت ساخت . تعریف

ارتباط بین مقدار ثابت سرعت و شیب محور ct در فضازمان را فراهم می کند. نتیجه این دو فرمول هذلولی، هویتی است که با عامل لورنتس مطابقت دارد

با مقایسه تبدیلهای لورنتس از نظر سرعت و سرعت نسبی یا با استفاده از فرمولهای بالا، ارتباطات بین β ، γ و
.
گرفتن مماس هذلولی معکوس سرعت را می دهد.
از آنجایی که −1 < β < 1 , به دنبال −∞ < ζ < ∞ می آید . از رابطه بین ζ و β ، سرعت مثبت ζ > 0 حرکت در جهت مثبت محورهای xx ' است ، سرعت صفر ζ = 0 حرکت نسبی نیست، در حالی که سرعت منفی ζ < 0 حرکت نسبی در امتداد جهات منفی محور است. محورهای xx .
تبدیلهای معکوس با مبادله مقادیر اولیه و غیر پرایم شده برای تغییر قابهای مختصات، و نفی سرعت ζ → - ζ به دست میآیند زیرا این معادل با نفی سرعت نسبی است. بنابراین،
تقویت معکوس لورنتس ( جهت x با سرعت ζ )

تبدیلهای معکوس را میتوان با در نظر گرفتن مواردی که x '=0 و ct ' = 0 مشاهده کرد .
تاکنون تبدیلات لورنتس در یک رویداد اعمال شده است . اگر دو رویداد وجود داشته باشد، یک جدایی مکانی و فاصله زمانی بین آنها وجود دارد. از خطی بودن تبدیلهای لورنتس به دست میآید که میتوان دو مقدار مختصات مکان و زمان را انتخاب کرد، تبدیلهای لورنتس را میتوان برای هر کدام اعمال کرد، سپس برای بدست آوردن تبدیلهای لورنتس تفاوتها از آن کسر کرد.

با روابط معکوس

که در آن Δ ( دلتای بزرگ ) تفاوت مقادیر را نشان می دهد. به عنوان مثال، Δ x = x 2 - x 1 برای دو مقدار مختصات x و غیره.
این دگرگونیها در تفاوتها به جای نقاط مکانی یا لحظههای زمانی به دلایلی مفید هستند:
- در محاسبات و آزمایشها، طولهای بین دو نقطه یا بازههای زمانی است که اندازهگیری میشوند یا مورد علاقه هستند (مثلاً طول یک وسیله نقلیه در حال حرکت یا مدت زمانی که طول میکشد تا از یک مکان به مکان دیگر سفر کند).
- با کوچک کردن بینهایت اختلاف و تقسیم معادلات و تکرار فرآیند برای تبدیل شتاب، میتوان به آسانی تبدیلهای سرعت را به دست آورد.
- اگر سیستم های مختصات هرگز منطبق نباشند (یعنی در پیکربندی استاندارد نباشند)، و اگر هر دو ناظر بتوانند روی یک رویداد توافق کنند
- t 0 , x 0 , y 0 , z 0 در F و t 0 ′, x 0 , y 0 ′ ، z 0 " در F " ، سپس آنها می توانند از آن رویداد به عنوان مبدأ استفاده کنند، و تفاوت مختصات فضازمان، تفاوت بین مختصات آنها و این مبدا است، به عنوان مثال، Δ x = x − x 0 ، Δ x ′ = x ′ − x 0 ′ و غیره.
پیامدهای فیزیکی
[ ویرایش ]
یکی از الزامات مهم تبدیلهای لورنتس، تغییرناپذیری سرعت نور است، واقعیتی که در اشتقاق آنها استفاده میشود و در خود تبدیلها وجود دارد. اگر در F معادله یک پالس نور در امتداد جهت x x = ct باشد ، در F ′ تبدیلات لورنتس
x ′ = ct ′
را به دست می دهند و بالعکس، برای هر − c < v < c .
برای سرعت های نسبی بسیار کمتر از سرعت نور، تبدیل های لورنتس به تبدیل گالیله کاهش می یابد : [ 17 ] [ 18 ]

مطابق با اصل مطابقت . گاهی گفته می شود که فیزیک غیر نسبیتی فیزیک «کنش آنی در فاصله» است. [ 19 ]
سه پیشبینی نادرست، اما درست از تحولات عبارتند از:
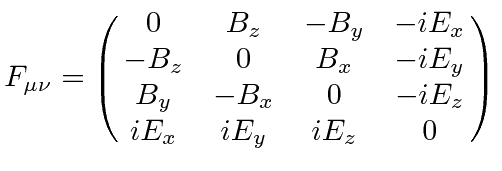
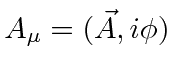
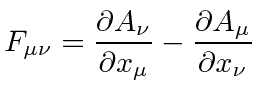
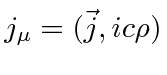
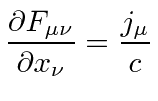
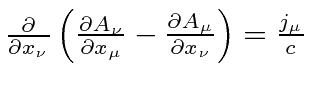
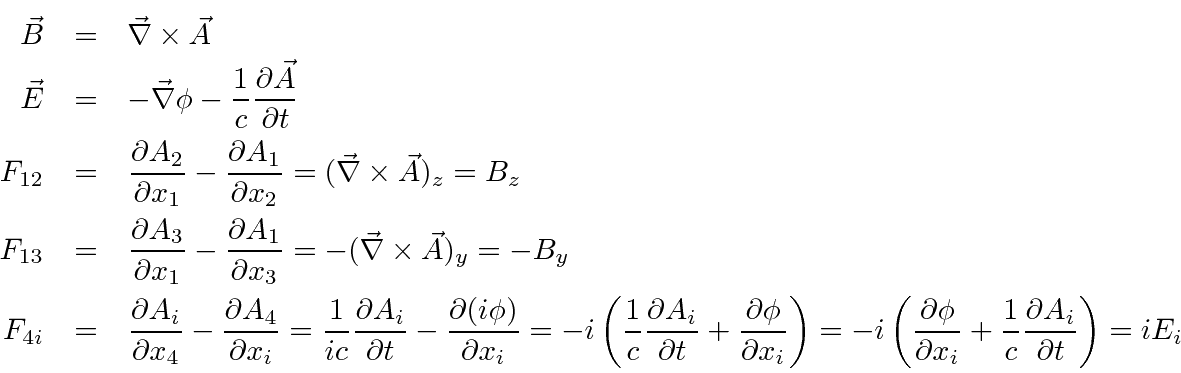
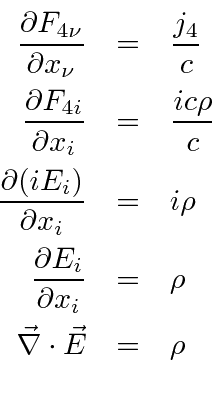

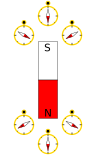



 که در آن جهت
که در آن جهت 


 ; در یک ماده مغناطیسی، مقادیر در هر طرف این معادله با میدان
; در یک ماده مغناطیسی، مقادیر در هر طرف این معادله با میدان 
 که
که بار روی ذره است،
بار روی ذره است، سرعت ذره و F
سرعت ذره و F 




 .
.
![{\displaystyle {\begin{aligned}\mathbf {E} '&=\mathbf {E} +\mathbf {v} \times \mathbf {B} \\[1ex]\mathbf {B} '&=\mathbf {B} -{\frac {1}{c^{2}}}\mathbf {v} \times \mathbf {E} ,\end{تراز شده}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/1a7962757d0368c6a3f4ac952602feedc39adedd)





![{\displaystyle \mathbf {F} =q\left[\mathbf {E} +\mathbf {v} \times \mathbf {B} \راست].}](https://wikimedia.org/api/rest_v1/media/math/render/svg/e464ca1df543d0e3799230f7b9c78c3d980d2734)
 در حالی که در قاب رسانا که آهنربا در حال حرکت است، نیرو نیز در جهت منفی y است و اکنون فقط به دلیل میدان E با مقدار:
در حالی که در قاب رسانا که آهنربا در حال حرکت است، نیرو نیز در جهت منفی y است و اکنون فقط به دلیل میدان E با مقدار:
![{\displaystyle {\begin{aligned}x'&=\gamma \left(x-vt\right),&x&=\gamma \left(x'+vt'\right),\\[1ex]t'&= \gamma \left(t-{\tfrac {vx}{c^{2}}}\right),&t&=\gamma \left(t'+{\tfrac {vx'}{c^{2}}}\right).\end{تراز شده}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/c26eb88c26443a7e159464a8086ba7807f8a5ad0)

 که کاملا موافق است بنابراین نیروی وارد بر بار در هر دو فریم یکسان نیست ، اما مطابق با نسبیت تغییر میکند.
که کاملا موافق است بنابراین نیروی وارد بر بار در هر دو فریم یکسان نیست ، اما مطابق با نسبیت تغییر میکند. ، یا به طور خاص، که سرعت آن با
، یا به طور خاص، که سرعت آن با  .
. 
 انرژی است،
انرژی است،  حرکت است، و
حرکت است، و جرم سکون است، وقتی جرم سکون به صفر میل می کند، مثلاً برای یک فوتون، یا تکانه به بزرگی میل می کند، مثلا برای یک پروتون با سرعت زیاد، این رابطه به یک پراکندگی خطی فرو می ریزد، یعنی
جرم سکون است، وقتی جرم سکون به صفر میل می کند، مثلاً برای یک فوتون، یا تکانه به بزرگی میل می کند، مثلا برای یک پروتون با سرعت زیاد، این رابطه به یک پراکندگی خطی فرو می ریزد، یعنی



 (T4)
(T4)![{\displaystyle {\begin{aligned}&U(\Lambda,a)\Psi _{p_{1}\sigma _{1}n_{1};p_{2}\sigma _{2}n_{2}; \cdots }\\={}&e^{-ia_{\mu }\left[(\Lambda p_{1})^{\mu }+(\Lambda p_{2})^{\mu }+\cdots \right]}{\sqrt {\frac {(\Lambda p_{1})^{0}(\Lambda p_{2})^ {0}\cdots }{p_{1}^{0}p_{2}^{0}\cdots }}}\left(\sum _{\sigma _{1}'\sigma _{2}'\cdots }D_{\sigma _{1}'\sigma _{1}}^{(j_{1})}\left[W(\Lambda ,p_{ 1})\right]D_{\sigma _{2}'\sigma _{2}}^{(j_{2})}\left[W(\Lambda ,p_{2})\right]\cdots \right)\Psi _{\Lambda p_{1}\sigma _{1}'n_{1};\Lambda p_{2}\sigma _{2}'n_ {2};\cdots }،\end{تراز شده}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/f3b8eb18b9a1a818885bf7f841ef3cfae600ebd8)
 ، بنابراین به گفته یک ناظر متحرک، رویدادها دیگر همزمان نیستند.
، بنابراین به گفته یک ناظر متحرک، رویدادها دیگر همزمان نیستند.
 سپس تحولات هستند
سپس تحولات هستند



 و "بردار سرعت" را می توان به صورت تعریف کرد،
و "بردار سرعت" را می توان به صورت تعریف کرد، که هر کدام در برخی زمینه ها به عنوان مخفف مفیدی عمل می کنند. بزرگی ζ قدر مطلق اسکالر سرعت محدود به 0 ≤ ζ < ∞ است که با محدوده 0 ≤ β < 1 مطابقت دارد .
که هر کدام در برخی زمینه ها به عنوان مخفف مفیدی عمل می کنند. بزرگی ζ قدر مطلق اسکالر سرعت محدود به 0 ≤ ζ < ∞ است که با محدوده 0 ≤ β < 1 مطابقت دارد .

![{\displaystyle \mathbf {u} '={\frac {1}{1-{\frac {\mathbf {v} \cdot \mathbf {u} }{c^{2}}}}}\left[{ \frac {\mathbf {u} }{\gamma _{\mathbf {v} }}}-\mathbf {v} +{\frac {1}{c^{2}}}{\frac {\gamma _{\mathbf {v} }}{\gamma _{\mathbf {v} }+1}}\left(\mathbf {u} \ cdot \mathbf {v} \right)\mathbf {v} \right]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/4d9ce52162b9b5960496a83093a8241a3736852c)





 در جهت بردار دلخواه با بردار تقویت است
در جهت بردار دلخواه با بردار تقویت است ، سپس تبدیل از یک سیستم مختصات فضازمان بدون پرایم به یک سیستم مختصات اولیه توسط
، سپس تبدیل از یک سیستم مختصات فضازمان بدون پرایم به یک سیستم مختصات اولیه توسط 
 .
.  . معکوس تبدیل با معکوس کردن علامت داده می شود
. معکوس تبدیل با معکوس کردن علامت داده می شود . مقدار
. مقدار تحت تغییر شکل ثابت است.
تحت تغییر شکل ثابت است.










![{\displaystyle {\begin{تراز شده}&c^{2}(t_{2}-t_{1})^{2}-(x_{2}-x_{1})^{2}-(y_{2}-y_ {1})^{2}-(z_{2}-z_{1})^{2}\\[ 6pt]={}&c^{2}(t_{2}'-t_{1}')^{2}-(x_{2}'-x_{1}')^{2}-(y_{2 }'-y_{1}')^{2}-(z_{2}'-z_{1}')^{2}\quad {\text{(همه رویدادهای 1، 2)}}.\end{تراز شده}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/d685ef5891f02b82c2656cc341f2016d231c4549)
![{\displaystyle {\begin{تراز شده}&c^{2}t^{2}-x^{2}-y^{2}-z^{2}=c^{2}t'^{2}- x'^{2}-y'^{2}-z'^{2}\\[6pt]{\text{یا}}\quad &c^{2}t_{1}t_{2}-x_{1}x_{2}-y_{1}y_{2}-z_{1}z_{2}=c^{2}t'_{ 1}t'_{2}-x'_{1}x'_{2}-y'_{1}y'_{2}-z'_{1}z'_{2}\end{ تراز شده}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/f78e5280c899e10f32769743cf58e272651c33e4)



 نشان دهنده سرعت محدود به جهت
نشان دهنده سرعت محدود به جهت 
 یک شکل معادل از تبدیل
یک شکل معادل از تبدیل 
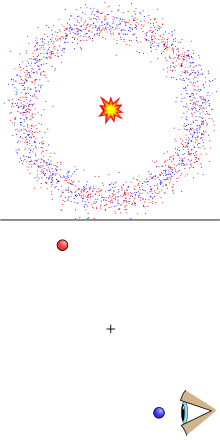

 (همانطور که از نوار مواد مشاهده می شود). دو ناظر A و B را تصور کنید که روی محور x ایستاده اند و با فاصله از هم جدا شده اندL
(همانطور که از نوار مواد مشاهده می شود). دو ناظر A و B را تصور کنید که روی محور x ایستاده اند و با فاصله از هم جدا شده اندL . آنها در کنار نوار ماده می ایستند، که در حال استراحت نیست، بلکه در جهت x منفی با سرعت حرکت می کند.v
. آنها در کنار نوار ماده می ایستند، که در حال استراحت نیست، بلکه در جهت x منفی با سرعت حرکت می کند.v . A از نوار برای ارسال سیگنال به B استفاده می کند . از فرمول ترکیب سرعت، سیگنال از A به B با سرعت منتشر می شود
. A از نوار برای ارسال سیگنال به B استفاده می کند . از فرمول ترکیب سرعت، سیگنال از A به B با سرعت منتشر می شود . زمان
. زمان  برای انتشار سیگنال از A به B مورد نیاز است
برای انتشار سیگنال از A به B مورد نیاز است
 . با توجه به فرض شروع
. با توجه به فرض شروع  ، همیشه می توان حرکت نوار را با سرعت تنظیم کرد
، همیشه می توان حرکت نوار را با سرعت تنظیم کرد .
.

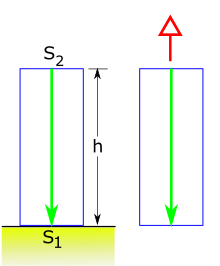
 در امتداد محور z با فاصله از هم جدا می شوندساعت
در امتداد محور z با فاصله از هم جدا می شوندساعت بالای یک گیرنده
بالای یک گیرنده  در یک میدان گرانشی همگن با نیرویی در واحد جرم 1g.
در یک میدان گرانشی همگن با نیرویی در واحد جرم 1g. مقدار معینی از انرژی الکترومغناطیسی
مقدار معینی از انرژی الکترومغناطیسی بر اساس اصل هم ارزی، این سیستم معادل یک سیستم بدون گرانش است که با شتاب یکنواخت حرکت می کند.
بر اساس اصل هم ارزی، این سیستم معادل یک سیستم بدون گرانش است که با شتاب یکنواخت حرکت می کند. در جهت مثبت z -محور، با
در جهت مثبت z -محور، با برای رسیدن به .
برای رسیدن به . از سرعت آن هنگام تابش نور. انرژی رسیده به
از سرعت آن هنگام تابش نور. انرژی رسیده به  اما انرژی بیشتر
اما انرژی بیشتر  داده شده توسط
داده شده توسط
 با اختلاف پتانسیل گرانشی
با اختلاف پتانسیل گرانشی بین
بین 
 منتشر شده توسط
منتشر شده توسط در میدان گرانشی از این رو
در میدان گرانشی از این رو مطابق با جرم گرانشی و همچنین جرم اینرسی یک مقدار انرژی است.
مطابق با جرم گرانشی و همچنین جرم اینرسی یک مقدار انرژی است. 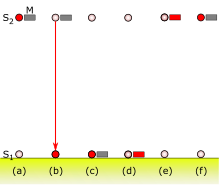
 می تواند شاتل بیناس2
می تواند شاتل بیناس2 جذب می شود
جذب می شود آزاد کردن مقدار کار برابر با .
آزاد کردن مقدار کار برابر با . (د) انرژی جذب شده توسط
(د) انرژی جذب شده توسط  این باعث افزایش جرم گرانشی می شود
این باعث افزایش جرم گرانشی می شود  (ه) جرم به عقب برمی گردد
(ه) جرم به عقب برمی گردد  (ه) سپس انرژی حمل شده توسط جرم به آن منتقل می شود ،
(ه) سپس انرژی حمل شده توسط جرم به آن منتقل می شود ، تکمیل چرخه
تکمیل چرخه ، باید برابر باشد ،
، باید برابر باشد ، یا به طور بالقوه می توان یک
یا به طور بالقوه می توان یک 
 (همانطور که در اندازه گیری شدا
(همانطور که در اندازه گیری شدا  داده شده توسط
داده شده توسط
 غیرممکن است که تاج های موج در مسیر پایین ظاهر شوند
غیرممکن است که تاج های موج در مسیر پایین ظاهر شوند 
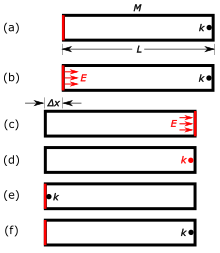
 از آنجایی که تکانه کل سیستم صفر است، سیلندر با سرعتی پس میزند
از آنجایی که تکانه کل سیستم صفر است، سیلندر با سرعتی پس میزند
 (با فرض
(با فرض ، سیلندر را پس از طی مسافتی متوقف می کند
، سیلندر را پس از طی مسافتی متوقف می کند

 در حین انتقال انرژی از راست به چپ نمی تواند بدون جرم باشد. اگر انرژی
در حین انتقال انرژی از راست به چپ نمی تواند بدون جرم باشد. اگر انرژی تناقض از بین می رود
تناقض از بین می رود 
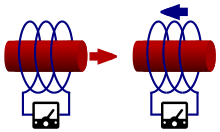
 ،
، زاویه چرخش است، و
زاویه چرخش است، و دوبردار نرمال شده است که صفحه چرخش را نشان می دهد به طوری که
دوبردار نرمال شده است که صفحه چرخش را نشان می دهد به طوری که .
. ، بنابراین فرمول اویلر اعمال می شود، [ 2 ] : 401 که چرخش را می دهد
، بنابراین فرمول اویلر اعمال می شود، [ 2 ] : 401 که چرخش را می دهد .
. بنابراین یک "چرخش در طول زمان" از معادله مشابه برای اعداد مختلط تقسیم می شود :
بنابراین یک "چرخش در طول زمان" از معادله مشابه برای اعداد مختلط تقسیم می شود : .
. با ضرب با شبه مقیاس تبدیل می شود تا عنصر دوگانه آن را تشکیل دهد
با ضرب با شبه مقیاس تبدیل می شود تا عنصر دوگانه آن را تشکیل دهد . [ 12 ] : 114 چرخش دوگانه عنصر فضا-زمان را تبدیل می کند
. [ 12 ] : 114 چرخش دوگانه عنصر فضا-زمان را تبدیل می کند از طریق زاویه
از طریق زاویه با شبه اسکالر
با شبه اسکالر است: [ 1 ] : 13
است: [ 1 ] : 13 
 به r∗
به r∗ : [ 1 ] : 13 [ 16 ]
: [ 1 ] : 13 [ 16 ]
 بازگشت است
بازگشت است  :
:
 : [ 18 ]
: [ 18 ]

 میدان های الکتریکی و مغناطیسی معمولی هستند و
میدان های الکتریکی و مغناطیسی معمولی هستند و شبه STA است. [ 2 ] : 230 متناوباً، در حال گسترش
شبه STA است. [ 2 ] : 230 متناوباً، در حال گسترش از نظر اجزاء
از نظر اجزاء
 و
و میدانها از آن بازیابی می شوند
میدانها از آن بازیابی می شوند
 اصطلاح یک چارچوب مرجع معین را نشان میدهد، و به این ترتیب، استفاده از چارچوبهای مرجع مختلف، منجر به میدانهای نسبی ظاهراً متفاوتی میشود، دقیقاً مانند نسبیت خاص استاندارد. [ 2 ] : 233
اصطلاح یک چارچوب مرجع معین را نشان میدهد، و به این ترتیب، استفاده از چارچوبهای مرجع مختلف، منجر به میدانهای نسبی ظاهراً متفاوتی میشود، دقیقاً مانند نسبیت خاص استاندارد. [ 2 ] : 233 
 توسط [ 22 ] : 26 داده شده است
توسط [ 22 ] : 26 داده شده است
 اجزای چگالی جریان سه بعدی کلاسیک هستند. هنگامی که این مقادیر را به این ترتیب ترکیب می کنیم، به ویژه مشخص می شود که چگالی بار کلاسیک چیزی نیست جز جریانی که در جهت زمانی داده شده توسط
اجزای چگالی جریان سه بعدی کلاسیک هستند. هنگامی که این مقادیر را به این ترتیب ترکیب می کنیم، به ویژه مشخص می شود که چگالی بار کلاسیک چیزی نیست جز جریانی که در جهت زمانی داده شده توسط
 ، می توان دستکاری زیر را انجام داد: [ 23 ] : 231
، می توان دستکاری زیر را انجام داد: [ 23 ] : 231 ![{\displaystyle {\begin{aligned}\nabla \cdot \left[\nabla F\right]&=\nabla \cdot \left[\mu _{0}cJ\right]\\0&=\nabla \cdot J .\end{تراز شده}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/fddaae634e913589d397263ea660f33dbef138b9)

 ، مشابه چهار پتانسیل الکترومغناطیسی در حساب تانسور است. در STA به این صورت تعریف می شود
، مشابه چهار پتانسیل الکترومغناطیسی در حساب تانسور است. در STA به این صورت تعریف می شود
 پتانسیل اسکالر است و
پتانسیل اسکالر است و اجزای پتانسیل مغناطیسی هستند. همانطور که تعریف شد، این میدان دارای واحدهای SI وبر در هر متر است (V⋅s⋅m -1 ).
اجزای پتانسیل مغناطیسی هستند. همانطور که تعریف شد، این میدان دارای واحدهای SI وبر در هر متر است (V⋅s⋅m -1 ).
 ، پتانسیل داده شده توسط
، پتانسیل داده شده توسط

 برای سادهترین مشکل معین به عنوان ثابت کردن سنج شناخته میشود . با این حال، در الکترودینامیک نسبیتی، شرط لورنز اغلب تحمیل می شود، جایی که
برای سادهترین مشکل معین به عنوان ثابت کردن سنج شناخته میشود . با این حال، در الکترودینامیک نسبیتی، شرط لورنز اغلب تحمیل می شود، جایی که . [ 2 ] : 231
. [ 2 ] : 231 




 .
. ، همان معادله حرکتی که در بالا برای میدان پتانسیل وجود دارد
، همان معادله حرکتی که در بالا برای میدان پتانسیل وجود دارد
 اسپینور است ،
اسپینور است ، واحد خیالی بدون تفسیر هندسی است،
واحد خیالی بدون تفسیر هندسی است، ماتریس های پائولی هستند (با نماد "کلاه" نشان دهنده آن است
ماتریس های پائولی هستند (با نماد "کلاه" نشان دهنده آن است یک عملگر ماتریسی است و نه عنصری در جبر هندسی)، و
یک عملگر ماتریسی است و نه عنصری در جبر هندسی)، و شرودینگر همیلتونی است.
شرودینگر همیلتونی است. به نمایندگی STA
به نمایندگی STA با استفاده از عناصر،σ1،σ2،
با استفاده از عناصر،σ1،σ2، ، از زیر جبر فضازمان با درجه زوج و شبه مقیاس
، از زیر جبر فضازمان با درجه زوج و شبه مقیاس : [ 2 ] : 37 [ 27 ] : 270، 271
: [ 2 ] : 37 [ 27 ] : 270، 271 

 یک چند بردار زوج جبر هندسی است و شرودینگر همیلتونی
یک چند بردار زوج جبر هندسی است و شرودینگر همیلتونی  یک بردار ثابت انتخابی دلخواه است. یک چرخش ثابت می تواند هر بردار ثابت انتخابی جایگزینی را ایجاد کند"
یک بردار ثابت انتخابی دلخواه است. یک چرخش ثابت می تواند هر بردار ثابت انتخابی جایگزینی را ایجاد کند" . [ 28 ] : 30
. [ 28 ] : 30  ، یک ضرب برداری (هندسی) وجود دارد
، یک ضرب برداری (هندسی) وجود دارد  ، ضرب درونی (نقطه ای).
، ضرب درونی (نقطه ای).  و ضرب بیرونی (خارجی، گوه ای).
و ضرب بیرونی (خارجی، گوه ای).  . حاصل ضرب برداری مجموع حاصلضرب درونی و بیرونی است: [ 1 ] : 6
. حاصل ضرب برداری مجموع حاصلضرب درونی و بیرونی است: [ 1 ] : 6 
 و
و اگر حاصل ضرب داخلی آنها صفر باشد متعامد هستند. بردارها
اگر حاصل ضرب داخلی آنها صفر باشد متعامد هستند. بردارها و 3 بردار فضایی
و 3 بردار فضایی . جمله های غیر صفر تانسور متریک مینکوفسکی عبارت های قطر هستند،
. جمله های غیر صفر تانسور متریک مینکوفسکی عبارت های قطر هستند، . برای
. برای :
:
 ، چهار بردار
، چهار بردار ، شش دو بردار
، شش دو بردار , چهار شبه بردار ( سه بردار )
, چهار شبه بردار ( سه بردار ) و یک شبه اسکالر
و یک شبه اسکالر  با
با . [ 1 ] : 11 شبه اسکالر با تمام عناصر STA درجه زوج جابجا می کند ، اما با همه عناصر STA درجه فرد ضد جابجا می کند . [ 4 ] : 6
. [ 1 ] : 11 شبه اسکالر با تمام عناصر STA درجه زوج جابجا می کند ، اما با همه عناصر STA درجه فرد ضد جابجا می کند . [ 4 ] : 6 

 به عنوان
به عنوان و دو بردارهای
و دو بردارهای  به عنوان
به عنوان . [ 1 ] : 22 [ 2 ] : 37 ماتریس های پائولی
. [ 1 ] : 22 [ 2 ] : 37 ماتریس های پائولی ، یک نمایش ماتریسی برای هستندσ1،σ2،σ3
، یک نمایش ماتریسی برای هستندσ1،σ2،σ3 . [ 2 ] : 37 برای هر جفتی از
. [ 2 ] : 37 برای هر جفتی از و ضرب خارجی غیر صفر عبارتند از: [ 2 ] : 37 [ 1 ] : 16
و ضرب خارجی غیر صفر عبارتند از: [ 2 ] : 37 [ 1 ] : 16 
 . [ 6 ] : 2 یک مثال است
. [ 6 ] : 2 یک مثال است . بردارهای تهی مماس بر مخروط نور (مخروط پوچ) هستند. [ 6 ] : 4 یک عنصر
. بردارهای تهی مماس بر مخروط نور (مخروط پوچ) هستند. [ 6 ] : 4 یک عنصر . [ 7 ] : 103 دو ناتوان
. [ 7 ] : 103 دو ناتوان  و
و ناتوان متعامد هستند اگر
ناتوان متعامد هستند اگر . [ 7 ] : 103 مثالی از یک جفت ناتوان متعامد است
. [ 7 ] : 103 مثالی از یک جفت ناتوان متعامد است و
و با
با . مقسومکنندههای صفر مناسب، عناصر غیرصفری هستند که حاصلضرب آنها صفر است، مانند بردارهای تهی یا غیر توانای متعامد. [ 8 ] : 191 جبر تقسیم جبری است که شامل عناصر معکوس (مقابل) ضربی برای هر عنصر است، اما این در صورتی رخ می دهد که مقسوم علیه های صفر مناسب وجود نداشته باشد و تنها ناتوان آن 1 باشد. [ 7 ] : 103 [ 9 ] : 211 [ a ] تنها جبرهای تقسیم انجمنی اعداد حقیقی، اعداد مختلط و رباعی ها [ 10 ] : 366 از آنجایی که STA یک جبر تقسیم نیست، برخی از عناصر STA ممکن است فاقد معکوس باشند. با این حال، تقسیم بر بردار غیر تهی
. مقسومکنندههای صفر مناسب، عناصر غیرصفری هستند که حاصلضرب آنها صفر است، مانند بردارهای تهی یا غیر توانای متعامد. [ 8 ] : 191 جبر تقسیم جبری است که شامل عناصر معکوس (مقابل) ضربی برای هر عنصر است، اما این در صورتی رخ می دهد که مقسوم علیه های صفر مناسب وجود نداشته باشد و تنها ناتوان آن 1 باشد. [ 7 ] : 103 [ 9 ] : 211 [ a ] تنها جبرهای تقسیم انجمنی اعداد حقیقی، اعداد مختلط و رباعی ها [ 10 ] : 366 از آنجایی که STA یک جبر تقسیم نیست، برخی از عناصر STA ممکن است فاقد معکوس باشند. با این حال، تقسیم بر بردار غیر تهی ممکن است با ضرب در معکوس آن، که به صورت تعریف شده است
ممکن است با ضرب در معکوس آن، که به صورت تعریف شده است  . [ 11 ] : 14
. [ 11 ] : 14  ارضای این معادلات: [ 1 ] : 63
ارضای این معادلات: [ 1 ] : 63 
 ، اما
، اما .
.





 ، این جزئی ها هستند
، این جزئی ها هستند




 ما داریم
ما داریم
 [ 1 ] : 22-24
[ 1 ] : 22-24  مربع به وحدت، آنها به عنوان یک پایه فضایی خدمت می کنند. با استفاده از نماد ماتریس پائولی ، اینها نوشته شده اند
مربع به وحدت، آنها به عنوان یک پایه فضایی خدمت می کنند. با استفاده از نماد ماتریس پائولی ، اینها نوشته شده اند . بردارهای فضایی در STA با خط پررنگ مشخص می شوند. سپس با
. بردارهای فضایی در STA با خط پررنگ مشخص می شوند. سپس با و
و ،
، و برعکس آن
و برعکس آن عبارتند از:
عبارتند از:
 و
و باید استفاده شود.
باید استفاده شود.
 سپس امواج ساطع شد
سپس امواج ساطع شد ، در حالی که
، در حالی که ; شیب معکوس AB نشان دهنده سرعت انتشار سیگنال (یعنی سرعت صوت) به رویداد B است . بنابراین می توانیم بنویسیم:
; شیب معکوس AB نشان دهنده سرعت انتشار سیگنال (یعنی سرعت صوت) به رویداد B است . بنابراین می توانیم بنویسیم:  (سرعت صدا)
(سرعت صدا)
 (سرعت منبع و گیرنده)
(سرعت منبع و گیرنده)

 و
و کمتر از
کمتر از زیرا در غیر این صورت عبور آنها از محیط باعث ایجاد امواج ضربه ای می شود که محاسبه را باطل می کند. برخی از جبرهای معمولی نسبت فرکانس ها را نشان می دهند:
زیرا در غیر این صورت عبور آنها از محیط باعث ایجاد امواج ضربه ای می شود که محاسبه را باطل می کند. برخی از جبرهای معمولی نسبت فرکانس ها را نشان می دهند:


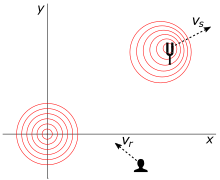
 (در زمان انتشار). سیگنالی را منتشر می کند که با سرعت حرکت می کند
(در زمان انتشار). سیگنالی را منتشر می کند که با سرعت حرکت می کند به سمت گیرنده که با سرعت در حال حرکت است
به سمت گیرنده که با سرعت در حال حرکت است در زمان پذیرایی تجزیه و تحلیل در یک سیستم مختصاتی که در آن سرعت سیگنال انجام می شود
در زمان پذیرایی تجزیه و تحلیل در یک سیستم مختصاتی که در آن سرعت سیگنال انجام می شود مستقل از جهت است
مستقل از جهت است 
 و معادله به
و معادله به  و معادله به
و معادله به 
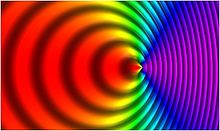











 همانطور که توسط یک ناظر بر روی گیرنده یا منبع اندازه گیری می شود (قرارداد نشانه ای که در اینجا به تصویب رسید این است
همانطور که توسط یک ناظر بر روی گیرنده یا منبع اندازه گیری می شود (قرارداد نشانه ای که در اینجا به تصویب رسید این است دور از گیرنده (جایی که
دور از گیرنده (جایی که




 سرعت گیرنده بر حسب سرعت نور است. مربوطه
سرعت گیرنده بر حسب سرعت نور است. مربوطه فرکانس برخورد جبهههای موج به گیرنده در کادر منبع، برابر است با
فرکانس برخورد جبهههای موج به گیرنده در کادر منبع، برابر است با






 (همچنین
(همچنین یا
یا )،
)، 

 سرعت M نسبت به Earth است ،
سرعت M نسبت به Earth است ، سرعت M نسبت به باران T است ،
سرعت M نسبت به باران T است ، سرعت باران T نسبت به Earth است .
سرعت باران T نسبت به Earth است .


 ، نشان دهنده مکان B همانطور که از A مشاهده می شود.
، نشان دهنده مکان B همانطور که از A مشاهده می شود.

 و
و ، داریم:
، داریم:






 و
و ، که
، که و
و به حرکت A که توسط یک ناظر در قاب پرایم نشده و اولیه دیده می شود، مراجعه کنید. به یاد بیاورید که v حرکت یک جسم ساکن در قاب اولیه است، همانطور که از قاب پرایم نشده مشاهده می شود. بنابراین ما داریم
به حرکت A که توسط یک ناظر در قاب پرایم نشده و اولیه دیده می شود، مراجعه کنید. به یاد بیاورید که v حرکت یک جسم ساکن در قاب اولیه است، همانطور که از قاب پرایم نشده مشاهده می شود. بنابراین ما داریم ،
، 
 سرعت یک جسم یا ناظر B در قاب استراحت جسم دیگر یا ناظر A است . با این حال، بر خلاف مورد مکانیک کلاسیک، در نسبیت خاص، به طور کلی چنین نیست
سرعت یک جسم یا ناظر B در قاب استراحت جسم دیگر یا ناظر A است . با این حال، بر خلاف مورد مکانیک کلاسیک، در نسبیت خاص، به طور کلی چنین نیست






![{\displaystyle \mathbf {v} _{\mathrm {B|A} }={\frac {1}{\gamma _{\mathrm {A} }\left(1-{\frac {\mathbf {v} _{\mathrm {A} }\mathbf {v} _{\mathrm {B} }}{c^{2}}}\right)}}\left[\mathbf {v} _{\mathrm {B} }-\mathbf {v} _{\mathrm {A} }+\mathbf {v} _{\mathrm {A} }(\گاما _{\mathrm {A} }-1)\left({\frac { \mathbf {v} _{\mathrm {A} }\cdot \mathbf {v} _{\mathrm {B} }}{v_{\mathrm {A} }^{2}}}-1\right)\ درست]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/41824d072f371a9f972d7b1f60cb764d1f288d17)


 سپس با
سپس با 

![{\displaystyle \mathbf {u} =\mathbf {u} _{\parallel }+\mathbf {u} _{\perp }={\frac {1}{1+{\frac {\mathbf {v} \ cdot \mathbf {u} '}{c^{2}}}}\left[\alpha _{v}\mathbf {u} '+\mathbf {v} +(1-\alpha _{v}){\frac {(\mathbf {v} \cdot \mathbf {u} ')}{v^{2}}}\mathbf {v } \right]\equiv \mathbf {v} \oplus \mathbf {u} ',}](https://wikimedia.org/api/rest_v1/media/math/render/svg/69619ca3017cfb16ce21f2f2d2e8aea8e3d8cbd5)
 و
و ,
, ![{\displaystyle {\begin{aligned}\mathbf {v} \oplus \mathbf {u} '\equiv \mathbf {u} &={\frac {1}{1+{\frac {\mathbf {u} ' \cdot \mathbf {v} }{c^{2}}}}\left[\mathbf {v} +{\frac {\mathbf {u} '}{\gamma _{v}}}+{\frac {1}{c^{2}}}{\frac {\gamma _{v}}{1+\gamma _{ v}}}(\mathbf {u} '\cdot \mathbf {v} )\mathbf {v} \right]\\&={\frac {1}{1+{\frac {\mathbf {u} '\cdot \mathbf {v} }{c^{2}}}}}\left[\mathbf {v} +\mathbf {u} '+{\frac {1}{c^ {2}}}{\frac {\gamma _{v}}{1+\gamma _{v}}}\mathbf {v} \times (\mathbf {v} \times \mathbf {u} ')\right],\end{تراز شده}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/a4a4626061e5696673bd8548072f1c7b91eb6e5a) z
z![{\displaystyle {\begin{aligned}\mathbf {v} \oplus \mathbf {u} \equiv \mathbf {u} '&={\frac {1}{1-{\frac {\mathbf {u} \ cdot \mathbf {v} }{c^{2}}}}}\left[{\frac {\mathbf {u} }{\gamma _{v}}}-\mathbf {v} +{\frac {1}{c^{2}}}{\frac {\gamma _{v}}{1+\gamma _{v}}}( \mathbf {u} \cdot \mathbf {v} )\mathbf {v} \right]\\&={\frac {1}{1-{\frac {\mathbf {u} \cdot \mathbf {v} }{c^{2}}}}}\left[\mathbf {u} -\mathbf {v} +{\frac {1}{c^{2}}}{\frac {\gamma _{v}}{1+\gamma _{v}}}\mathbf {v} \times (\mathbf {v} \times \mathbf {u} )\راست]\پایان{تراز شده}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/62a3866f450b8fdc5702aed25fb21001564ce506)
 برای
برای 
 نه
نه 
![{\displaystyle |\mathbf {u} |^{2}\equiv |\mathbf {v} \oplus \mathbf {u} '|^{2}={\frac {1}{\left(1+{\ frac {\mathbf {v} \cdot \mathbf {u} '}{c^{2}}}\right)^{2}}}\left[\left(\mathbf {v} +\mathbf {u} '\right)^{2}-{\frac {1}{c^{2}}}\left(\mathbf {v} \times \mathbf {u} '\right)^{2}\right]= |\mathbf {u} '\plus \mathbf {v} |^{2}.}](https://wikimedia.org/api/rest_v1/media/math/render/svg/587953edb063d6ed45750ec75efb725b92a7e837) و
و![{\displaystyle |\mathbf {u} '|^{2}\equiv |\mathbf {v} \oplus \mathbf {u} |^{2}={\frac {1}{\left(1-{\ frac {\mathbf {v} \cdot \mathbf {u} }{c^{2}}}\right)^{2}}}\left[\left(\mathbf {u} -\mathbf {v} \ راست)^{2}-{\frac {1}{c^{2}}}\left(\mathbf {v} \times \mathbf {u} \right)^{2}\right]=|\mathbf {u} \oplus \mathbf {v} |^{2}.}](https://wikimedia.org/api/rest_v1/media/math/render/svg/97d9fe963a64c1c9b62d8142e0cc490f4dc5b6ec)
![{\displaystyle {\begin{aligned}&\left(1+{\frac {\mathbf {v} \cdot \mathbf {u} '}{c^{2}}}\right)^{2}|\ mathbf {v} \oplus \mathbf {u} '|^{2}\\&=\left[\mathbf {v} +\mathbf {u} '+{\frac {1}{c^{2}}}{\frac {\gamma _{v}}{1+\gamma _{v}}}\mathbf {v} \times (\mathbf {v } \times \mathbf {u} ')\right]^{2}\\&=(\mathbf {v} +\mathbf {u} ')^{2}+2{\frac {1}{c^{2}}}{\frac {\gamma _{v}}{\gamma _{v}+1}}\left[(\mathbf {v} \cdot \mathbf {u} ' )^{2}-(\mathbf {v} \cdot \mathbf {v} )(\mathbf {u} '\cdot \mathbf {u} ')\right]+{\frac {1}{c^{4}}}\left({\frac {\gamma _{v}}{\gamma _{v}+1}}\right)^{ 2}\left[(\mathbf {v} \cdot \mathbf {v} )^{2}(\mathbf {u} '\cdot \mathbf {u} ')-(\mathbf {v} \cdot \mathbf {u} ')^{2}(\mathbf {v} \cdot \mathbf {v} )\right]\\&=(\mathbf {v} + \mathbf {u} ')^{2}+2{\frac {1}{c^{2}}}{\frac {\gamma _{v}}{\gamma _{v}+1}}\left[(\mathbf {v} \cdot \mathbf {u} ')^{2}-(\mathbf {v} \cdot \mathbf {v} )(\mathbf {u } '\cdot \mathbf {u} ')\right]+{\frac {v^{2}}{c^{4}}}\left({\frac {\gamma _{v}}{\gamma _{v}+1}}\right)^{2}\left[(\mathbf {v} \cdot \mathbf {v})(\mathbf {u} ' \cdot \mathbf {u} ')-(\mathbf {v} \cdot \mathbf {u} ')^{2}\right]\\&=(\mathbf {v} +\mathbf {u} ')^{2}+2{\frac {1}{c^{2}}}{\frac {\gamma _{v}}{\gamma _{v}+1}}\left[(\mathbf {v} \cdot \mathbf {u} ')^{2}-(\mathbf {v} \cdot \mathbf {v} )(\mathbf {u} '\cdot \mathbf {u} ')\right]+{\frac {(1-\alpha _{v})(1+\alpha _{v})}{c^{2}}}\left({\frac {\gamma _{v}}{\gamma _{v}+1}}\راست)^{2}\left[(\mathbf {v} \cdot \mathbf {v} )(\mathbf {u} '\cdot \mathbf {u} ')-( \mathbf {v} \cdot \mathbf {u} ')^{2}\right]\\&=(\mathbf {v} +\mathbf {u} ')^{2}+2{\frac {1}{c^{2}}}{\frac {\gamma _{v}}{\gamma _{v}+1}}\left[ (\mathbf {v} \cdot \mathbf {u} ')^{2}-(\mathbf {v} \cdot \mathbf {v} )(\mathbf {u} '\cdot \mathbf {u} ')\right]+{\frac {(\gamma _{v}-1)}{c^{2}(\gamma _{v}+1)}}\left[ (\mathbf {v} \cdot \mathbf {v} )(\mathbf {u} '\cdot \mathbf {u} ')-(\mathbf {v} \cdot \mathbf {u} ')^{2}\right]\\&=(\mathbf {v} +\mathbf {u} ')^{2}+2{\frac {1}{c^{ 2}}}{\frac {\gamma _{v}}{\gamma _{v}+1}}\left[(\mathbf {v} \cdot \mathbf {u} ')^{2}-(\mathbf {v} \cdot \mathbf {v} )(\mathbf {u} '\cdot \mathbf {u} ')\right]+{\frac {(1-\gamma _{v})}{c^{2}(\گاما _{v}+1)}}\left[(\mathbf {v} \cdot \mathbf {u} ')^{2}-(\mathbf {v} \cdot \mathbf {v} )(\mathbf {u} '\cdot \mathbf {u} ')\right]\\&=(\mathbf {v} +\mathbf {u} ')^{2}+{\frac {1}{c^{2}}}{\frac {\gamma _{v}+1}{\gamma _{v}+1}}\left[(\mathbf {v} \cdot \mathbf {u} ')^{2}-(\mathbf {v} \cdot \ mathbf {v} )(\mathbf {u} '\cdot \mathbf {u} ')\right]\\&=(\mathbf {v} +\mathbf {u} ')^{2}-{\frac {1}{c^{2}}}|\mathbf {v} \times \mathbf {u} '|^{2}\end{تراز شده }}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/3099c302f1314b31c5c0140eb79ed7954d8b14cc)

 بنابراین
بنابراین




 C نسبت به A (سرعت سقوط جسم همانطور که گالیله آن را می بیند) مجموع سرعت است
C نسبت به A (سرعت سقوط جسم همانطور که گالیله آن را می بیند) مجموع سرعت است  از C نسبت به B (سرعت سقوط جسم نسبت به کشتی) به اضافه سرعت
از C نسبت به B (سرعت سقوط جسم نسبت به کشتی) به اضافه سرعت 
 مثلاً یک گلوله توپ که به صورت افقی به سمت دریا شلیک می شود، همانطور که از کشتی اندازه گیری می شود، با سرعت حرکت می کند
مثلاً یک گلوله توپ که به صورت افقی به سمت دریا شلیک می شود، همانطور که از کشتی اندازه گیری می شود، با سرعت حرکت می کند

 در جهت
در جهت 





 (نگاه کنید
(نگاه کنید 




 ،
، انرژی نسبیتی (استراحت + جنبشی)
انرژی نسبیتی (استراحت + جنبشی) ، و حرکت
، و حرکت ،
، . بنابراین انرژی و تکانه نسبیتی به طور قابل توجهی با سرعت افزایش می یابد، بنابراین سرعت نور توسط ذرات عظیم قابل دستیابی نیست. در برخی از کتاب های درسی نسبیت، به اصطلاح "
. بنابراین انرژی و تکانه نسبیتی به طور قابل توجهی با سرعت افزایش می یابد، بنابراین سرعت نور توسط ذرات عظیم قابل دستیابی نیست. در برخی از کتاب های درسی نسبیت، به اصطلاح "  نیز استفاده می شود. با این حال، این مفهوم توسط بسیاری از نویسندگان مضر تلقی می شود، به جای آن باید از عبارات انرژی و تکانه نسبیتی برای بیان وابستگی سرعت در نسبیت استفاده کرد که همان پیش بینی های تجربی را ارائه می دهد.
نیز استفاده می شود. با این حال، این مفهوم توسط بسیاری از نویسندگان مضر تلقی می شود، به جای آن باید از عبارات انرژی و تکانه نسبیتی برای بیان وابستگی سرعت در نسبیت استفاده کرد که همان پیش بینی های تجربی را ارائه می دهد. معادل "جرم نسبیتی"
معادل "جرم نسبیتی"

 اندازه گیری شد. آنها نسبیت را با حد بالایی برای انحرافات ~0.00037 تایید کردند.
اندازه گیری شد. آنها نسبیت را با حد بالایی برای انحرافات ~0.00037 تایید کردند. 
 .
.  .
.  معتبر بودند، آن پرتوهای گاما باید با سرعت های فوق نوری حرکت می کردند. با این حال، آنها هیچ تفاوتی پیدا نکردند و حد بالایی را ارائه کردند
معتبر بودند، آن پرتوهای گاما باید با سرعت های فوق نوری حرکت می کردند. با این حال، آنها هیچ تفاوتی پیدا نکردند و حد بالایی را ارائه کردند .
.  (
(  (یعنی مجموع انرژی استراحت و انرژی جنبشی آنها) به طور قابل توجهی به حدود 1500 مگا ولت افزایش می یابد. هنگامی که این ذرات با هم برخورد می کنند، ذرات دیگری مانند
(یعنی مجموع انرژی استراحت و انرژی جنبشی آنها) به طور قابل توجهی به حدود 1500 مگا ولت افزایش می یابد. هنگامی که این ذرات با هم برخورد می کنند، ذرات دیگری مانند  و همچنین نسبت
و همچنین نسبت 


 و
و
 توجه داشته باشید که این فرمول فقط برای ذرات یا سیستم هایی با تکانه صفر صادق است.
توجه داشته باشید که این فرمول فقط برای ذرات یا سیستم هایی با تکانه صفر صادق است.
 ، تنها چهار بردار مرتبط با حرکت ذره است، به طوری که اگر چهار تکانه حفظ شده باشد
، تنها چهار بردار مرتبط با حرکت ذره است، به طوری که اگر چهار تکانه حفظ شده باشد ، باید متناسب با این بردار باشد. این اجازه می دهد تا نسبت انرژی به تکانه را بیان کنیم
، باید متناسب با این بردار باشد. این اجازه می دهد تا نسبت انرژی به تکانه را بیان کنیم در نتیجه یک رابطه بین
در نتیجه یک رابطه بین 
 و
و
 جایی که عامل
جایی که عامل

 طول نسبیتی تکانه انرژی
طول نسبیتی تکانه انرژی  از سیستم، یک کمیت برداری نیز میتواند با جمع کردن لحظهای تمام اجزای آن محاسبه شود. با توجه به انرژی کل
از سیستم، یک کمیت برداری نیز میتواند با جمع کردن لحظهای تمام اجزای آن محاسبه شود. با توجه به انرژی کل 

 جرم نسبیتی است. برای ذره ای با جرم سکون غیر صفر
جرم نسبیتی است. برای ذره ای با جرم سکون غیر صفر 
 و جرم نسبیتی برابر با جرم بقیه است. در چارچوب های دیگر، جرم نسبیتی (یک جسم یا سیستم اجسام) شامل سهمی از انرژی جنبشی "خالص" بدن (انرژی جنبشی مرکز
و جرم نسبیتی برابر با جرم بقیه است. در چارچوب های دیگر، جرم نسبیتی (یک جسم یا سیستم اجسام) شامل سهمی از انرژی جنبشی "خالص" بدن (انرژی جنبشی مرکز 

 و طول موج
و طول موج به عنوان یک
به عنوان یک  ، جرم بدن کاهش می یابد
، جرم بدن کاهش می یابد ,
,  . اگرچه برخی از نویسندگان جرم نسبیتی را به عنوان مفهومی بنیادی از نظریه ارائه می کنند، اما استدلال شده است که این اشتباه است زیرا مبانی نظریه مربوط به فضا-زمان است. در مورد اینکه آیا این مفهوم از نظر آموزشی مفید است یا خیر، اختلاف نظر وجود دارد.
. اگرچه برخی از نویسندگان جرم نسبیتی را به عنوان مفهومی بنیادی از نظریه ارائه می کنند، اما استدلال شده است که این اشتباه است زیرا مبانی نظریه مربوط به فضا-زمان است. در مورد اینکه آیا این مفهوم از نظر آموزشی مفید است یا خیر، اختلاف نظر وجود دارد.  ، طول مناسب خود را دارد
، طول مناسب خود را دارد . با این حال، اگر میله ای در آن قرار گیرداس"
. با این حال، اگر میله ای در آن قرار گیرداس"
 در حال حرکت با0.6ج
در حال حرکت با0.6ج در جهت مخالف، در نتیجهالف∗ب∗.
در جهت مخالف، در نتیجهالف∗ب∗. 
 و
و نقطه پایانی یک جسم در حال حرکت را نشان می دهد. در این قاب طول جسمL
نقطه پایانی یک جسم در حال حرکت را نشان می دهد. در این قاب طول جسمL . در همین حال، طول مناسب این جسم، همانط
. در همین حال، طول مناسب این جسم، همانط

 و
و ، طول مناسب در S به دست می آید
، طول مناسب در S به دست می آید



 و همچنین با فرض اندازه گیری زمان همزمان
و همچنین با فرض اندازه گیری زمان همزمان و با اتصال به طول مناسب
و با اتصال به طول مناسب ، به شرح زیر است:
، به شرح زیر است:

 به طول قرارداد تبدیل می شود
به طول قرارداد تبدیل می شود :
: .
. .
. ) نسبت به دو ساعت "استراحت" هماهنگ شده کمتر است (نشان می دهدتی
) نسبت به دو ساعت "استراحت" هماهنگ شده کمتر است (نشان می دهدتی
 در حال استراحت دراس
در حال استراحت دراس در
در در
در و
و . با درج فرمول اتساع زمانی، نسبت بین این طول ها برابر است با:
. با درج فرمول اتساع زمانی، نسبت بین این طول ها برابر است با: .
.



 در قاب استراحت میله یا
در قاب استراحت میله یا در قاب استراحت ساعت
در قاب استراحت ساعت 

 که
که
 در این وبلاگ به ریاضیات و کاربردهای آن و تحقیقات در آنها پرداخته می شود. مطالب در این وبلاگ ترجمه سطحی و اولیه است و کامل نیست.در صورتی سوال یا نظری در زمینه ریاضیات دارید مطرح نمایید .در صورت امکان به آن می پردازم. من دوست دارم برای یافتن پاسخ به سوالات و حل پروژه های علمی با دیگران همکاری نمایم.در صورتی که شما هم بامن هم عقیده هستید با من تماس بگیرید.
در این وبلاگ به ریاضیات و کاربردهای آن و تحقیقات در آنها پرداخته می شود. مطالب در این وبلاگ ترجمه سطحی و اولیه است و کامل نیست.در صورتی سوال یا نظری در زمینه ریاضیات دارید مطرح نمایید .در صورت امکان به آن می پردازم. من دوست دارم برای یافتن پاسخ به سوالات و حل پروژه های علمی با دیگران همکاری نمایم.در صورتی که شما هم بامن هم عقیده هستید با من تماس بگیرید.