ریاضیات | توابع مختلط و کاربردها

مثال 1:بسط مکلورن

Why is the Maclaurin series important? - Quora

+ نوشته شده در چهارشنبه ششم دی ۱۴۰۲ ساعت 19:11 توسط علی رضا نقش نیلچی |

این مقاله شامل فهرستی از مراجع عمومی است ، اما فاقد استنادهای درون خطی متناظر کافی است . لطفا با معرفی نقل قول های دقیق تر به بهبود این مقاله کمک کنید. ( ژانویه 2015 ) ( نحوه و زمان حذف این پیام الگو را بیاموزید )

(مختصات x) دایره های قرمز نقاط ثابت هستند . مربع های آبی نقطه عطف هستند .

نقطه بحرانی اصطلاحی است که در بسیاری از شاخه های ریاضیات استفاده می شود .

وقتی با توابع یک متغیر حقیقی سروکار داریم ، نقطه بحرانی نقطه‌ای در دامنه تابع است که در آن تابع یا مشتق پذیر نیست یا مشتق آن برابر با صفر است. [1] به طور مشابه، هنگام برخورد با متغیرهای مختلط ، یک نقطه بحرانی نقطه‌ای در دامنه تابع است که در آن یا هولومورفیک نیست یا مشتق آن برابر با صفر است. [2] [3] به همین ترتیب، برای تابعی از چندین متغیر حقیقی ، یک نقطه بحرانی مقداری در دامنه آن است که در آن گرادیان تعریف نشده یا برابر با صفر است. [4]

مقدار تابع در یک نقطه بحرانی یک مقدار بحرانی است . [5]

این نوع از تعریف به نقشه های مشتق پذیر بین گسترش می یابد $\mathbb{R} ^{m}$ و $\mathbb {R} ^{n},$ یک نقطه بحرانی ، در این مورد، نقطه ای است که رتبه ماتریس ژاکوبین حداکثر نیست. این به نقشه های مشتق پذیر بین منیفولدهای قابل تفکیک گسترش می یابد ، زیرا نقاطی که رتبه ماتریس ژاکوبین کاهش می یابد. در این حالت به نقاط بحرانی نقاط انشعاب نیز می گویند .

به طور خاص، اگر C یک منحنی مسطح باشد که با یک معادله ضمنی f ( x , y ) = 0 تعریف شده است ، نقاط بحرانی طرح ریزی بر روی محور x ، موازی با محور y ، نقاطی هستند که مماس بر C هستند. موازی با محور y هستند ، این نقاطی است که در آن

${\frac {\partial f}{\partial y}}(x,y)=0$

به عبارت دیگر، نقاط بحرانی نقاطی هستند که قضیه تابع ضمنی در آنها کاربرد ندارد.

مفهوم نقطه بحرانی اجازه توصیف ریاضی یک پدیده نجومی را می دهد که قبل از زمان کوپرنیک توضیح داده نشده بود . نقطه ثابت در مدار یک سیاره، نقطه ای از مسیر سیاره در کره آسمانی است ، جایی که به نظر می رسد حرکت سیاره قبل از شروع مجدد در جهت دیگر متوقف می شود. این به دلیل نقطه بحرانی پرتاب مدار به دایره دایره البروج رخ می دهد .

نقطه بحرانی یک تابع متغیر واحد [ ویرایش ]

نقطه بحرانی یک تابع از یک متغیر حقیقی منفرد ، f ( x ) ، مقدار x 0 در دامنه f است که در آن f مشتق پذیر نیست یا مشتق آن 0 است (یعنی $f'(x_{0})=0$ ). [1] یک مقدار بحرانی تصویر زیر f یک نقطه بحرانی است. این مفاهیم ممکن است از طریق نمودار f تجسم شوند : در یک نقطه بحرانی، اگر اصلاً بتوانید آن را اختصاص دهید، نمودار دارای مماس افقی است.

توجه کنید که چگونه برای یک تابع متمایز ، نقطه بحرانی همان نقطه ثابت است .

اگرچه به راحتی در نمودار (که یک منحنی است) قابل مشاهده است، مفهوم نقطه بحرانی یک تابع نباید با مفهوم نقطه بحرانی، در برخی جهت، یک منحنی اشتباه گرفته شود (برای تعریف دقیق به زیر مراجعه کنید ) . اگر g ( x , y ) یک تابع متمایز از دو متغیر باشد، آنگاه g ( x , y ) = 0 معادله ضمنی یک منحنی است . یک نقطه بحرانی چنین منحنی، برای طرح ریزی موازی با محور y (نقشه ( x , y ) → x )، نقطه ای از منحنی است که در آن. ${\tfrac {\partial g}{\partial y}}(x,y)=0.$ این بدان معناست که مماس منحنی موازی با محور y است ، و در این نقطه، g تابع ضمنی از x به y را تعریف نمی کند (به قضیه تابع ضمنی مراجعه کنید ). اگر ( x 0 , y 0 ) چنین نقطه بحرانی باشد، آنگاه x 0 مقدار بحرانی مربوطه است . به چنین نقطه بحرانی، نقطه انشعاب نیز می گویند ، زیرا به طور کلی، هنگامی که x تغییر می کند، دو شاخه منحنی در یک طرف x 0 و صفر در طرف دیگر وجود دارد.

از این تعاریف نتیجه می شود که یک تابع متمایز f ( x ) دارای یک نقطه بحرانی x 0 با مقدار بحرانی y 0 است ، اگر و فقط اگر ( x 0 , y 0 ) نقطه بحرانی نمودار آن برای طرح ریزی موازی x باشد. محور، با همان مقدار بحرانی y 0 . اگر f در x 0 به دلیل موازی شدن مماس با محور y مشتق پذیر نباشد ، x 0 دوباره نقطه بحرانی f است ، اما اکنون ( x 0 , y 0 ) نقطه بحرانی نمودار آن برای طرح ریزی است. موازی با محور y

به عنوان مثال، نقاط بحرانی دایره واحد معادله $x^{2}+y^{2}-1=0$ (0، 1) و (0، -1) برای برآمدگی موازی با محور x ، و (1، 0) و (-1، 0) برای جهت موازی با محور y هستند . اگر نیم دایره بالایی را نمودار تابع در نظر بگیریم $f(x)={\sqrt {1-x^{2}}}،$ سپس x = 0 یک نقطه بحرانی با مقدار بحرانی 1 است زیرا مشتق برابر با 0 است و x = ± 1 نقاط بحرانی با مقدار بحرانی 0 به دلیل تعریف نشده بودن مشتق هستند.

مثالها [ ویرایش ]

کارکرد $f(x) = x^2 + 2x + 3$ در همه جا با مشتق مشتق پذیر است $f'(x)=2x+2.$ این تابع دارای یک نقطه بحرانی منحصر به فرد −1 است، زیرا عدد یکتایی x 0 برای آن است2. $2x+2=0.$ این نقطه حداقل جهانی f است . مقدار بحرانی مربوطه است. $f(-1)=2.$ نمودار f یک سهمی مقعر به سمت بالا است، نقطه بحرانی آبسیس راس است که در آن خط مماس افقی است، و مقدار بحرانی مربوط به راس است و ممکن است با تقاطع این خط مماس و خط مماس نشان داده شود. محور y .
کارکرد $f(x)=x^{2/3}$ برای همه x تعریف شده و برای x ≠ 0 با مشتق قابل تفکیک است $f'(x)={\tfrac {2x^{-1/3}}{3}}.$ از آنجایی که f در x = 0 و قابل تفکیک نیست $f'(x)\neq 0$ در غیر این صورت، آن نقطه بحرانی منحصر به فرد است. نمودار تابع f در این نقطه یک کاسپ با مماس عمودی دارد . مقدار بحرانی مربوطه است. $f(0)=0.$
تابع مقدار مطلق $f(x)=|x|$ در همه جا مشتق پذیر است به جز در نقطه بحرانی x = 0 ، جایی که یک نقطه حداقل جهانی با مقدار بحرانی 0 دارد.
کارکرد $f(x)={\tfrac {1}{x}}$ نقاط بحرانی ندارد نقطه x = 0 یک نقطه بحرانی نیست زیرا در دامنه تابع گنجانده نشده است.

مکان نقاط بحرانی [ ویرایش ]

طبق قضیه گاوس-لوکاس ، تمام نقاط بحرانی یک تابع چند جمله ای در صفحه مختلط در داخل بدنه محدب ریشه های تابع قرار دارند. بنابراین برای یک تابع چند جمله ای با ریشه های حقیقی، تمام نقاط بحرانی حقیقی هستند و بین بزرگترین و کوچکترین ریشه ها قرار دارند.

حدس سندوف بیان می‌کند که اگر همه ریشه‌های یک تابع در دیسک واحد در صفحه مختلط قرار گیرند، حداقل یک نقطه بحرانی در فاصله واحد از هر ریشه معین وجود دارد.

نقاط بحرانی یک منحنی ضمنی [ ویرایش ]

همچنین ببینید: منحنی جبری

نقاط بحرانی نقش مهمی در مطالعه منحنی های سطحی تعریف شده توسط معادلات ضمنی ایفا می کنند ، به ویژه برای ترسیم آنها و تعیین توپولوژی آنها . مفهوم نقطه بحرانی که در این بخش استفاده می شود، ممکن است متفاوت از قسمت قبلی به نظر برسد. در واقع این تخصص به یک مورد ساده از مفهوم کلی نقطه بحرانی است که در زیر آورده شده است .

بنابراین، منحنی C را در نظر می گیریم که با یک معادله ضمنی تعریف شده است $f(x,y)=0$ ، که در آن f یک تابع متمایز از دو متغیر است که معمولاً یک چند جمله ای دو متغیره است . نقاط منحنی نقاط صفحه اقلیدسی هستند که مختصات دکارتی آن معادله را برآورده می کند. دو پیش بینی استاندارد وجود دارد $\pi _{y}$ و $\pi _{x}$ ، تعریف شده بوسیله ی $\pi _{y}((x،y))=x$ و $\pi _{x}((x,y))=y,$ که منحنی را روی محورهای مختصات ترسیم می کند . آنها را به ترتیب پروجکشن موازی با محور y و برآمدگی موازی با محور x می نامند .

نقطه C برای آن حیاتی است $\pi _{y}$ ، اگر مماس بر C وجود داشته باشد و با محور y موازی باشد . در آن صورت، تصاویر توسط $\pi _{y}$ نقطه بحرانی و مماس همان نقطه محور x هستند که مقدار بحرانی نامیده می شود . بنابراین یک نقطه C برای آن حیاتی است $\pi _{y}$ اگر مختصات آن جوابی برای سیستم معادلات باشد :

$f(x,y)={\frac {\partial f}{\partial y}}(x,y)=0$

این بدان معناست که این تعریف یک مورد خاص از تعریف کلی یک نقطه بحرانی است که در زیر آورده شده است .

تعریف نقطه بحرانی برای $\pi _{x}$ مشابه است. اگر C نمودار یک تابع باشد $y=g(x)$ ، سپس ( x , y ) برای آن حیاتی است $\pi _{x}$ اگر و فقط اگر x نقطه بحرانی g باشد و مقادیر بحرانی یکسان باشند.

برخی از نویسندگان نقاط بحرانی C را به عنوان نقاطی که برای هر یک از آنها حیاتی هستند تعریف می کنند $\pi _{x}$ یا $\pi _{y}$ ، اگرچه آنها نه تنها به C ، بلکه به انتخاب محورهای مختصات نیز بستگی دارند. همچنین به نویسندگان بستگی دارد که آیا نقاط مفرد به عنوان نقاط بحرانی در نظر گرفته شوند. در واقع نقاط مفرد نقاطی هستند که راضی کننده هستند

$f(x,y)={\frac {\partial f}{\partial x}}(x,y)={\frac {\partial f}{\partial y}}(x,y)=0$ ،

و بنابراین راه حل های هر یک از سیستم های معادلات هستند که نقاط بحرانی را مشخص می کنند. با این تعریف کلی تر، نقاط بحرانی برای $\pi _{y}$ دقیقاً نقاطی هستند که قضیه تابع ضمنی در آنها اعمال نمی شود.

استفاده از تمایز [ ویرایش ]

وقتی منحنی C جبری است، یعنی زمانی که با یک چند جمله‌ای دو متغیره f تعریف می‌شود ، آنگاه ممیز ابزار مفیدی برای محاسبه نقاط بحرانی است.

در اینجا ما فقط طرح را در نظر می گیریم $\pi _{y}$ ; نتایج مشابهی برای $\pi _{x}$ با مبادله x و y .

اجازه دهید دیسک $\operatorname {Disc} _{y}(f)$ ممیز f باشد که به عنوان یک چند جمله ای در y با ضرایبی که چند جمله ای در x هستند مشاهده می شود . بنابراین این متمایز یک چند جمله ای در x است که دارای مقادیر بحرانی است $\pi _{y}$ در میان ریشه های آن

به طور دقیق تر، یک ریشه ساده ازدیسک $\operatorname {Disc} _{y}(f)$ یا یک مقدار بحرانی است $\pi _{y}$ نقطه بحرانی متناظر نقطه‌ای است که نه مفرد است و نه نقطه عطف، یا مختصات x مجانبی است که موازی با محور y است و «در بی‌نهایت» بر یک نقطه عطف مماس است (مجاد خمشی).

یک ریشه چندگانه تمایز یا به چندین نقطه بحرانی یا مجانب عطف که دارای ارزش بحرانی یکسان هستند، یا به یک نقطه بحرانی که همچنین یک نقطه عطف است، یا به یک نقطه منفرد مطابقت دارد.

چندین متغیر [ ویرایش ]

برای تابعی از چندین متغیر حقیقی ، یک نقطه P (که مجموعه ای از مقادیر برای متغیرهای ورودی است که به عنوان یک نقطه در نظر گرفته می شود.آر $\mathbb {R} ^{n}$ ) اگر نقطه ای باشد که گرادیان صفر یا تعریف نشده باشد، حیاتی است . [4] مقادیر بحرانی مقادیر تابع در نقاط بحرانی هستند.

یک نقطه بحرانی (جایی که تابع قابل تفکیک است) ممکن است یک حداکثر محلی ، یک حداقل محلی یا یک نقطه زینتی باشد . اگر تابع حداقل دو بار به طور پیوسته مشتق پذیر باشد، موارد مختلف را می توان با در نظر گرفتن مقادیر ویژه ماتریس هسین مشتقات دوم متمایز کرد.

یک نقطه بحرانی که در آن ماتریس هسین غیرمفرد است، گفته می‌شود که غیرمنحط است و نشانه‌های مقادیر ویژه هسین، رفتار محلی تابع را تعیین می‌کنند. در مورد تابعی از یک متغیر منفرد، هسین به سادگی دومین مشتق است که به عنوان یک ماتریس 1×1 در نظر گرفته می‌شود، که اگر و فقط اگر صفر نباشد غیرمفرد است. در این حالت، یک نقطه بحرانی غیر انحطاط، بسته به علامت مشتق دوم، یک ماکزیمم محلی یا یک مینیمم محلی است که برای حداقل محلی مثبت و برای حداکثر محلی منفی است. اگر مشتق دوم صفر باشد، نقطه بحرانی به طور کلی یک نقطه عطف است ، اما ممکن است یک نقطه موجی نیز باشد ، که ممکن است حداقل محلی یا حداکثر محلی باشد.

برای تابعی از n متغیر، تعداد مقادیر ویژه منفی ماتریس هسین در یک نقطه بحرانی را شاخص نقطه بحرانی می نامند. یک نقطه بحرانی غیر منحط یک حداکثر محلی است اگر و فقط اگر شاخص n باشد ، یا به طور معادل، اگر ماتریس هسین منفی قطعی باشد . اگر شاخص صفر باشد، یک حداقل محلی است، یا اگر ماتریس هسین مثبت قطعی باشد . برای سایر مقادیر شاخص، یک نقطه بحرانی غیر انحطاط یک نقطه زینی است ، یعنی نقطه ای که در برخی جهات حداکثر و در برخی دیگر حداقل است.

کاربرد بهینه سازی [ ویرایش ]

مقاله اصلی: بهینه سازی ریاضی

بر اساس قضیه فرما ، همه ماکزیمم ها و مینیمم های محلی یک تابع پیوسته در نقاط بحرانی رخ می دهند. بنابراین، برای یافتن ماکزیمم و مینیمم محلی یک تابع قابل تفکیک، از نظر تئوری، محاسبه صفرهای گرادیان و مقادیر ویژه ماتریس هسین در این صفرها کافی است. این نیاز به حل یک سیستم معادلات دارد که می تواند کار دشواری باشد. الگوریتم‌های عددی معمول برای یافتن اکسترم‌های محلی بسیار کارآمدتر هستند، اما نمی‌توانند تأیید کنند که همه اکستریم‌ها پیدا شده‌اند. به ویژه، در بهینه سازی جهانی ، این روش ها نمی توانند تأیید کنند که خروجی واقعاً بهینه جهانی است.

هنگامی که تابع کمینه سازی یک چند جمله ای چند متغیره است ، نقاط بحرانی و مقادیر بحرانی راه حل های یک سیستم معادلات چند جمله ای هستند و الگوریتم های مدرن برای حل چنین سیستم هایی روش های تایید شده رقابتی را برای یافتن حداقل جهانی ارائه می دهند.

نقطه بحرانی یک نقشه مشتق پذیر [ ویرایش ]

با توجه به یک نقشه متمایز $f:\mathbb {R} ^{m}\to \mathbb {R} ^{n},$ نقاط بحرانی f نقاط بحرانی هستند، $\mathbb {R} ^{m},$ که در آن رتبه ماتریس ژاکوبین f حداکثر نیست. [6] تصویر یک نقطه بحرانی در زیر f مقدار بحرانی نامیده می شود . نقطه ای از مکمل مجموعه مقادیر بحرانی را مقدار منظم می نامند . قضیه سارد بیان می کند که مجموعه مقادیر بحرانی یک نقشه صاف دارای اندازه صفر است .

برخی از نویسندگان [7] تعریف کمی متفاوت ارائه می دهند: نقطه بحرانی f یک نقطه از است $\mathbb{R} ^{m}$ که در آن رتبه ماتریس ژاکوبین f کمتر از n است . با این قرارداد، همه نقاط زمانی که m < n بحرانی هستند .

این تعاریف به نقشه های دیفرانسیل بین منیفولدهای قابل تفکیک به روش زیر گسترش می یابد. اجازه دهید: $f:V\to W$ یک نقشه دیفرانسیل بین دو منیفولد V و W با ابعاد مربوطه m و باشد n باشد . در همسایگی یک نقطه p از V و از f ( p ) ، نمودارها دیفرمورفیسم هستند. :→ $\varphi :V\to \mathbb {R} ^{m}$ و: $\psi :W\to \mathbb {R} ^{n}.$ نقطه p حیاتی است برای f اگر $\varphi (p)$ برای $\psi \circ f\circ \varphi ^{-1}.$ این تعریف به انتخاب نمودارها بستگی ندارد زیرا نقشه‌های انتقال دارای تفاوت هستند، ماتریس‌های ژاکوبین آن‌ها معکوس هستند و ضرب در آنها رتبه ماتریس ژاکوبین را تغییر نمی‌دهد. $\psi \circ f\circ \varphi ^{-1}.$ اگر M یک منیفولد هیلبرت باشد ( الزاماً بعد محدود نیست) و f یک تابع با مقدار حقیقی باشد، می‌گوییم که p یک نقطه بحرانی f است اگر f یک غوطه‌ور در p نباشد . [8]

کاربرد در توپولوژی [ ویرایش ]

نقاط بحرانی برای مطالعه توپولوژی منیفولدها و انواع جبری حقیقی اساسی هستند . [5] به ویژه، آنها ابزار اساسی برای نظریه مورس و نظریه فاجعه هستند هستند .

پیوند بین نقاط بحرانی و توپولوژی در حال حاضر در سطح پایین تری از انتزاع ظاهر می شود. به عنوان مثال، اجازه دهید $V$ یک زیر چندگانه از $\mathbb {R} ^{n}،$ و P یک نقطه بیرون باشد. $V.$ مجذور فاصله تا P نقطه از $V$ یک نقشه دیفرانسیل است به طوری که هر جزء متصل از $V$ حداقل دارای یک نقطه بحرانی است که در آن فاصله حداقل است. نتیجه می شود که تعداد اجزای متصل از $V$ در بالا با تعداد نقاط بحرانی محدود می شود.

در مورد انواع جبری حقیقی، این مشاهدات مرتبط با قضیه بزو به ما اجازه می‌دهد تا تعداد اجزای متصل را با تابعی از درجات چندجمله‌ای که تنوع را تعریف می‌کنند، محدود کنیم.

همچنین ببینید [ ویرایش ]

نقطه مفرد یک منحنی
نظریه تکینگی
قضیه گاوس-لوکاس

https://en.wikipedia.org/wiki/Critical_point_%28mathematics%29

+ نوشته شده در شنبه چهارم آذر ۱۴۰۲ ساعت 20:36 توسط علی رضا نقش نیلچی |

نوسان میانگین محدود

از ویکیپدیا، دانشنامه آزاد

در تجزیه و تحلیل هارمونیک در ریاضیات ، تابعی از نوسان میانگین محدود ، که به عنوان تابع BMO نیز شناخته می‌شود ، تابعی با مقدار واقعی است که نوسان میانگین آن محدود (محدود) است. فضای توابع نوسان میانگین محدود ( BMO )، فضای تابعی است که به تعبیر دقیق، همان نقشی را در نظریه فضاهای هاردی Hp ایفا می کند که فضای L∞ توابع محدود شده اساسا در نظریه L ایفا می کند. p -spaces : به نام فضای John–Nirenberg نیز نامیده می شود ، به نام فریتز جان و لوئیس نیرنبرگ که برای اولین بار آن را معرفی و مطالعه کردند.

یادداشت تاریخی [ ویرایش ]

به گفته نیرنبرگ (1985 ، ص 703 و ص 707)، [1] فضای توابع نوسان میانگین محدود توسط جان (1961 ، صفحات 410-411) در ارتباط با مطالعات خود در مورد نگاشت از یک مجموعه محدود معرفی شد. Ω متعلق به Rn به Rn و مشکلات مربوطه ناشی از تئوری الاستیسیته ، دقیقاً از مفهوم کرنش الاستیک : نماد اصلی در مقاله ای که توسط جان و نیرنبرگ (1961) از نزدیک معرفی شد ، [2] که در آن چندین ویژگی از این فضاهای تابع ثابت شد. گام مهم بعدی در توسعه این نظریه اثبات دوگانگی بین BMO و فضای هاردی H 1 توسط چارلز ففرمن [3] بود، در مقاله یادداشت شده Fefferman & Stein 1972 : اثبات سازنده این نتیجه، معرفی روش های جدید. و شروع توسعه بیشتر این نظریه توسط آکیهیتو اوچیاما ارائه شد . [4]

تعریف [ ویرایش ]

تعریف 1. میانگین نوسان یک تابع قابل انتگرال محلی u بر روی یک ابر مکعب [5] Q در Rn به عنوان مقدار انتگرال زیر تعریف می شود :

${\frac {1}{|Q|}}\int _{Q}|u(y)-u_{Q}|\,\mathrm {d} y$ جایی که

| س | حجم Q است ، یعنی اندازه گیری Lebesgue آن
u Q میانگین مقدار u در مکعب Q است ، یعنی

$u_{Q}={\frac {1}{|Q|}}\int _{Q}u(y)\,\mathrm {d} y.$

تعریف 2. یک تابع BMO یک تابع محلی قابل ادغام u است که میانگین نوسان فوق العاده آن که بر مجموعه تمام مکعب های Q موجود در R n گرفته شده است محدود است.

تبصره 1 . بالاترین نوسان میانگین، هنجار BMO از u نامیده می شود . [6] و با || نشان داده می شود u || BMO (و در برخی موارد با || u || ∗ نیز مشخص می شود ).

تبصره 2 . استفاده از مکعب‌های Q در Rn به‌عنوان حوزه‌های ادغامی که بر روی آنها نوسان میانگین محاسبه می‌شود، اجباری نیست: ویگرینک (2001) به جای آن از توپ‌ها استفاده می‌کند و همانطور که استاین (1993، ص 140) اشاره کرد ، در انجام این کار کاملاً عمل می‌کند. تعریف معادلی از توابع نوسان میانگین محدود به وجود می آید.

نشانه گذاری [ ویرایش ]

نماد جهانی مورد استفاده برای مجموعه توابع BMO در یک دامنه معین Ω BMO ( Ω ) است : وقتی Ω = Rn ، BMO ( Rn ) به سادگی به عنوان BMO نشان داده می شود .
هنجار BMO یک تابع BMO معین u با || نشان داده می شود u || BMO : در برخی موارد به صورت || نیز مشخص می شود u || ∗ .

ویژگی های اساسی [ ویرایش ]

**توابع BMO به صورت محلی قابل ادغام p هستند [ ویرایش ]**

توابع BMO به صورت محلی L p هستند اگر 0 < p <∞، اما لازم نیست به صورت محلی محدود شوند. در واقع، با استفاده از نابرابری جان-نیرنبرگ، می‌توانیم آن را ثابت کنیم

$\|u\|_{\text{BMO}}\simeq \sup _{Q}\left({\frac {1}{|Q|}}\int _{Q}|u-u_{ Q}|^{p}dx\right)^{1/p}.$

BMO یک فضای Banach است [ ویرایش ]

توابع ثابت دارای نوسان میانگین صفر هستند، بنابراین توابع متفاوت برای ثابت c > 0 می توانند مقدار نرمال BMO یکسانی داشته باشند حتی اگر تفاوت آنها تقریباً در همه جا صفر نباشد . بنابراین تابع || u || BMO به درستی یک هنجار در فضای ضریب توابع BMO است و فضای توابع ثابت در دامنه در نظر گرفته شده را مدول می کند .

میانگین مکعب های مجاور قابل مقایسه هستند [ ویرایش ]

همانطور که از نام آن پیداست، میانگین یا میانگین یک تابع در BMO هنگام محاسبه آن بر روی مکعب های نزدیک به یکدیگر در موقعیت و مقیاس، نوسان زیادی ندارد. به طور دقیق، اگر Q و R مکعب های دوتایی هستند به گونه ای که مرزهای آنها با هم تماس داشته باشد و طول ضلع Q کمتر از نصف طول ضلع R نباشد (و بالعکس)

$|f_{R}-f_{Q}|\leq C\|f\|_{\text{BMO}}$

که در آن C > 0 مقداری ثابت جهانی است. این ویژگی در واقع معادل f است که در BMO است، یعنی اگر f یک تابع انتگرال پذیر محلی باشد به طوری که | f R − f Q | ≤ C برای همه مکعب‌های دوتایی Q و R مجاور به معنایی که در بالا توضیح داده شد و f در BMO دوتایی است (که در آن برتری فقط بر مکعب‌های دوتایی Q گرفته می‌شود )، سپس f در BMO است. [7]

BMO فضای برداری دوگانه H 1 است [ ویرایش ]

ففرمن (1971) نشان داد که فضای BMO دو برابر H 1 است ، فضای هاردی با p = 1 است . [8] جفت شدن بین f∈ H 1 و g ∈ BMO توسط

$(f,g)=\int _{\mathbb {R} ^{n}}f(x)g(x)\,\mathrm {d} x$

اگرچه در تعریف این انتگرال کمی دقت لازم است، زیرا به طور کلی مطلقاً همگرا نیست.

نابرابری جان-نیرنبرگ [ ویرایش ]

نابرابری جان -نیرنبرگ تخمینی است که نشان می‌دهد یک تابع نوسان میانگین کران‌دار تا چه حد ممکن است از میانگین خود به میزان معینی منحرف شود.

بیانیه [ ویرایش ]

برای هر $f\in \operatorname {BMO} \left(\mathbb {R} ^{n}\right)$ ، ثابت وجود دارد $c_{1},c_{2}>0$ (مستقل از f)، به طوری که برای هر مکعبس $س$ که درآر $\mathbb {R} ^{n}$ ،

$\left|\left\{x\in Q:|f-f_{Q}|>\lambda \right\}\right|\leq c_{1}\exp \left(-c_{2}{2} \frac {\lambda }{\|f\|_{\text{BMO}}}}\right)|Q|.$

برعکس، اگر این نابرابری روی همه مکعب‌هایی با مقداری C ثابت به جای || برقرار باشد f || BMO ، سپس f در BMO با هنجار حداکثر یک بار ثابت C است .

نتیجه: فاصله در BMO تا L ∞ [ ویرایش ]

نابرابری جان-نیرنبرگ در واقع می تواند اطلاعات بیشتری نسبت به هنجار BMO یک تابع بدهد. برای یک تابع محلی ادغام پذیر f ، اجازه دهید A ( f ) A > 0 غیر رسمی باشد که برای آن

$\sup _{Q\subseteq \mathbb {R} ^{n}}{\frac {1}{|Q|}}\int _{Q}e^{\left|f-f_{Q} \right|/A}\mathrm {d} x<\infty .$

نابرابری جان-نیرنبرگ نشان می‌دهد که A ( f ) ≤ C|| f || BMO برای مقداری ثابت جهانی C. با این حال، برای یک تابع L ∞ ، نابرابری بالا برای همه A > 0 برقرار خواهد بود. به عبارت دیگر، اگر f در L ∞ باشد، A ( f ) = 0 است . از این رو ثابت A ( f ) راهی برای اندازه گیری فاصله یک تابع در BMO از زیرفضای L ∞ به ما می دهد . این عبارت را می توان دقیق تر بیان کرد: [9] یک ثابت C وجود دارد که فقط به بعد n بستگی دارد ، به طوری که برای هر تابع f ∈ BMO( Rn ) نابرابری دو طرفه زیر برقرار است.

${\frac {1}{C}}A(f)\leq \inf _{g\in L^{\infty }}\|fg\|_{\text{BMO}}\leq CA( و)$

تعمیم ها و پسوندها [ ویرایش ]

فضاهای BMOH و BMOA [ ویرایش ]

هنگامی که بعد فضای محیط 1 باشد، فضای BMO را می توان به عنوان یک زیرفضای خطی از توابع هارمونیک روی دیسک واحد مشاهده کرد و نقش اصلی را در نظریه فضاهای هاردی ایفا می کند : با استفاده از تعریف 2 ، می توان آن را تعریف کرد. فضای BMO( T ) روی دایره واحد به عنوان فضای توابع f : T → R به طوری که

${\frac {1}{|I|}}\int _{I}|f(y)-f_{I}|\,\mathrm {d} y<C<+\infty$

یعنی به گونه ای که میانگین نوسان آن بر روی هر کمان I دایره واحد [10] محدود باشد. در اینجا مانند قبل f I مقدار میانگین f روی قوس I است.

تعریف 3. یک تابع تحلیلی روی دیسک واحد به BMO هارمونیک یا در فضای BMOH تعلق دارد اگر و فقط اگر انتگرال پواسون یک تابع BMO( T ) باشد . بنابراین، BMOH فضای تمام توابع u با شکل زیر است:

$u(a)={\frac {1}{2\pi }}\int _{\mathbf {T} }{\frac {1-|a|^{2}}{\left|ae^ {i\theta }\right|^{2}}}f(e^{i\theta })\,\mathrm {d} \theta$

مجهز به هنجار:

$\|u\|_{\text{BMOH}}=\sup _{|a|<1}\left\{{\frac {1}{2\pi }}\int _{\mathbf { T} }{\frac {1-|a|^{2}}{|ae^{i\theta }|^{2}}}\left|f(e^{i\theta })-u(a )\right|\mathrm {d} \theta \right\}$

زیرفضای توابع تحلیلی متعلق به BMOH را فضای تحلیلی BMO یا فضای BMOA می نامند .

BMOA به عنوان فضای دوگانه H 1 ( D ) [ ویرایش ]

چارلز ففرمن در کار اصلی خود ثابت کرد که فضای BMO واقعی دوگانه به فضای هاردی با ارزش واقعی در نیمه فضای بالایی است. [11] در تئوری تحلیل مختلط و هارمونیک بر روی واحد. دیسک، نتیجه‌اش به صورت زیر بیان می‌شود. [12] فرض کنید H p ( D ) فضای هاردی تحلیلی روی دیسک واحد باشد . برای p = 1، ( H 1 )* را با BMOA با جفت کردن f ∈ H 1 ( D ) شناسایی می‌کنیم. و g ∈ BMOA با استفاده از تبدیل ضد خطی Tg

$T_{g}(f)=\lim _{r\to 1}\int _{-\pi }^{\pi }{\bar {g}}(e^{i\theta })f (re^{i\theta })\,\mathrm {d} \theta$

توجه داشته باشید که اگرچه حد همیشه برای یک تابع H1 f وجود دارد و Tg عنصری از فضای دوگانه ( H1 )* است، از آنجایی که تبدیل ضد خطی است ، ما ایزومورفیسم ایزومتریک بین ( H1 ) نداریم . * و BMOA. با این حال، اگر فضایی از توابع مزدوج BMOA را در نظر بگیریم، می توان ایزومتری را به دست آورد .

**فضای VMO [ ویرایش ]**

فضای VMO توابع نوسان میانگین ناپدید شدن، بسته شدن در BMO توابع پیوسته ای است که در بی نهایت ناپدید می شوند. همچنین می‌توان آن را به‌عنوان فضای توابعی تعریف کرد که «نوسان‌های میانگین» آن‌ها روی مکعب‌های Q نه تنها محدود است، بلکه به‌طور یکنواخت به صفر گرایش دارند زیرا شعاع مکعب Q به 0 یا ∞ متمایل می‌شود. فضای VMO نوعی آنالوگ فضای هاردی از فضای توابع پیوسته است که در بی نهایت ناپدید می شوند، و به ویژه فضای هاردی با ارزش واقعی H 1 دوگانه VMO است. [13]

ارتباط با تبدیل هیلبرت [ ویرایش ]

یک تابع محلی ادغام پذیر f در R BMO است اگر و فقط اگر بتوان آن را به صورت نوشتاری کرد

$f=f_{1}+Hf_{2}+\alpha$

که در آن f i ∈ L ∞ ، α یک ثابت و H تبدیل هیلبرت است .

سپس هنجار BMO معادل infimum از است $\|f_{1}\|_{\infty }+\|f_{2}\|_{\infty }$ بیش از همه این نمایندگی ها

به طور مشابه f VMO است اگر و فقط در صورتی که بتوان آن را به شکل بالا با توابع پیوسته یکنواخت با f i در R نشان داد . [14]

فضای دوتایی BMO [ ویرایش ]

اجازه دهید Δ مجموعه ای از مکعب های دوتایی را در R n نشان دهد . BMO دوتایی فضایی که BMO d نوشته می‌شود فضای توابعی است که همان نابرابری را برای توابع BMO برآورده می‌کند، فقط که برتری روی همه مکعب‌های دوتایی است. این برتری گاهی با ||•|| نشان داده می شود BMO d .

این فضا به درستی حاوی BMO است. به طور خاص، تابع log( x ) χ [0،∞) تابعی است که در BMO دوتایی است اما در BMO نیست. اما اگر تابع f به گونه ای باشد که || f (•− x )|| BMO d ≤ C برای همه x در Rn برای برخی C > 0، سپس با یک سوم ترفند f نیز در BMO است . در مورد BMO روی T n به جای R n ، تابع f به گونه ای است که || f (•− x )|| BMO d ≤ C برای n+1 x انتخاب مناسب ، سپس f نیز در BMO است. این بدان معناست که BMO( Tn ) تقاطع n+1 ترجمه BMO دوتایی است. با دوگانگی ، H 1 ( Tn ) مجموع n +1 ترجمه H 1 دوتایی است . [15]

اگرچه BMO دوتایی یک کلاس بسیار محدودتر از BMO است، بسیاری از قضایا که برای BMO صادق هستند، برای BMO دوتایی بسیار ساده‌تر اثبات می‌شوند، و در برخی موارد می‌توان قضایای BMO اصلی را با اثبات آن‌ها ابتدا در حالت دوتایی خاص بازیابی کرد. [16]

مثالها [ ویرایش ]

نمونه هایی از توابع BMO شامل موارد زیر است:

همه توابع محدود (قابل اندازه گیری). اگر f در L ∞ باشد ، آنگاه || f || BMO ≤ 2||f|| ∞ : [17] با این حال، عکس آن همانطور که در مثال زیر نشان می دهد درست نیست.
تابع log(| P |) برای هر چند جمله ای P که به طور یکسان صفر نیست: به ویژه، این برای | P ( x )| = | x |. [17]
اگر w یک وزن A ∞ باشد ، log( w ) BMO است. برعکس، اگر f BMO باشد، e δf یک وزن A ∞ برای δ>0 به اندازه کافی کوچک است: این واقعیت نتیجه نابرابری جان-نیرنبرگ است . [18]

https://en.wikipedia.org/wiki/Bounded_mean_oscillation

+ نوشته شده در یکشنبه سی ام مهر ۱۴۰۲ ساعت 21:51 توسط علی رضا نقش نیلچی |

مزدوج مختلط (پیچیده) یک ماتریس

در این پست توضیح می دهیم که ماتریس مزدوج چیست و چگونه می توان مزدوج مختلط یک ماتریس را پیدا کرد. علاوه بر این، نمونه ای از مزدوج یک ماتریس و تمام ویژگی های این نوع ماتریس را به شما نشان می دهیم.

فهرست مطالب

ماتریس مزدوج چیست؟

تعریف ماتریس مزدوج پیچیده به شرح زیر است.

ماتریس مزدوج ماتریس مختلطی است که تمام عناصر آن با مزدوج های مختلط خود جایگزین شده اند، یعنی علامت قسمت مختلط تمام اعداد مختلط آن تغییر کرده است.

ماتریس مزدوج با یک نوار افقی بالای آن نشان داده می شود: $\overline{A}.$

مثالی از مزدوج یک ماتریس

وقتی معنی ماتریس مزدوج را دیدیم، بیایید مثالی را برای درک کامل مفهوم ببینیم:

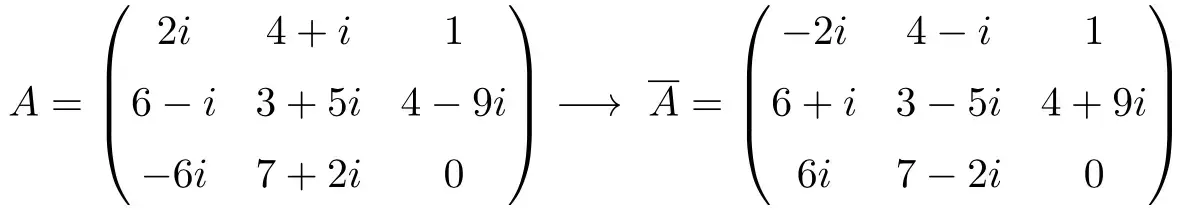
مثالی از یک ماتریس مزدوج 3x3،

ماتریس $\overline{A}$ مزدوج ماتریس A است، زیرا تمام ورودی های ماتریس $\overline{A}$ مزدوج هستند. به عبارت دیگر، اعداد در ماتریس $\overline{A}$ دارای قسمت واقعی یکسان با اعداد در ماتریس A هستند، اما قسمت مختلط آنها دارای علامت مخالف هستند.

خواص ماتریس مزدوج

ویژگی های ماتریس مزدوج به شرح زیر است:

مزدوج یک ماتریس مزدوج منجر به ماتریس اصلی می شود.

$\displaystyle \overline{\bigl( \ \overline{A} \vphantom{A^{9^1}} \ \bigr)} = A$

اضافه کردن (یا تفریق) دو ماتریس و به هم پیوستن نتیجه، مانند این است که ابتدا دو ماتریس را به طور جداگانه به هم متصل کنید و سپس آنها را جمع کنید (یا تفریق کنید).

$\displaystyle \overline{\bigl(A \pm B \bigr)} = \overline{A} \pm \overline{B}$

ببینید: جمع و تفریق ماتریس ها .

حاصلضرب مزدوج دو ماتریس برابر است با مزدوج کردن دو ماتریس به طور جداگانه و سپس محاسبه ضرب ماتریس.

$\displaystyle \overline{\bigl(A \cdot B \bigr)} = \overline{A} \cdot \overline{B}$

نگاه کنید به: ضرب ماتریسی .

ضرب یک ماتریس در یک اسکالر و به هم زدن نتیجه مانند این است که ابتدا مزدوج های اسکالر و ماتریس را انجام داده و سپس حاصل را حل کنیم.

$\displaystyle \overline{\bigl(k \cdot A \bigr)} = \overline{k} \cdot \overline{A}$

جابجایی یک ماتریس و سپس کونژوگه کردن آن مانند این است که ابتدا ماتریس را مزدوج کرده و سپس انتقال آن را محاسبه کنیم.

$\displaystyle \overline{\bigl(A^T \bigr)} = \left( \overline{A}\right)^T$

با محاسبه معکوس یک ماتریس و سپس مزدوج آن، ابتدا ماتریس و سپس معکوس آن یکسان است.

$\displaystyle \overline{\bigl(A^{-1} \bigr)} = \left(\overline{A} \راست)^{-1}$

رتبه یک ماتریس مزدوج برابر با رتبه ماتریس اصلی است

$\displaystyle rk\left(\overline{A}\right) =rk(A)$

محاسبه اثرماتریس مزدوج یا محاسبه رد ماتریس غیر مزدوج و سپس انجام مزدوج نتیجه بی تفاوت است.

$\displaystyle tr\left(\overline{A}\right) =\overline{tr(A)}$

در نهایت، یافتن دترمینان یک ماتریس مزدوج برابر است با محاسبه مزدوج حاصل از دترمینان ماتریس اصلی.

$\displaystyle det\left(\overline{A}\right) = \overline{det(A)}$

منبع

https://www.algebrapracticeproblems.com/complex-conjugate-of-a-matrix/

+ نوشته شده در یکشنبه سیزدهم فروردین ۱۴۰۲ ساعت 11:16 توسط علی رضا نقش نیلچی |

12-تبدیل فوریه

توزیع ها، تک بعدی [ ویرایش ]

تبدیل فوریه در این جدول را می توان در Erdélyi (1954) یا Kammler (2000 ، ضمیمه) یافت.

	عملکرد	تبدیل فوریه فرکانس واحد، معمولی	تبدیل فوریه فرکانس واحد، زاویه ای	تبدیل فوریه فرکانس غیر واحدی و زاویه ای	ملاحظات
	$f(x)\,$	${\begin{aligned}&{\hat {f}}(\xi )\\&=\int _{-\infty }^{\infty }f(x)e^{-2\pi ix \xi }\,dx\end{تراز شده}}$	${\begin{aligned}&{\hat {f}}(\omega )\\&={\frac {1}{\sqrt {2\pi }}}\int _{-\infty }^ {\infty }f(x)e^{-i\omega x}\,dx\end{تراز شده}}$	${\begin{aligned}&{\hat {f}}(\nu )\\&=\int _{-\infty }^{\infty }f(x)e^{-i\nu x }\,dx\end{تراز شده}}$
301	$1$	$\delta (\xi )$	${\sqrt {2\pi }}\cdot \delta (\omega )$	$2\pi \delta (\nu )$	توزیع δ ( ξ ) نشان دهنده تابع دلتای دیراک است .
302	$\delta (x)\,$	$1$	${\frac {1}{\sqrt {2\pi }}}\,$	$1$	قانون دوگانه 301.
303	$e^{iax}$	$\delta \left(\xi -{\frac {a}{2\pi }}\right)$	${\sqrt {2\pi }}\cdot \delta (\omega -a)$	$2\pi \delta (\nu -a)$	این از 103 و 301 به دست می آید.
304	$\cos(ax)$	${\frac {\delta \left(\xi -{\frac {a}{2\pi }}\right)+\delta \left(\xi +{\frac {a}{2\pi } }\راست)}{2}}$	${\sqrt {2\pi }}\cdot {\frac {\delta (\omega -a)+\delta (\omega +a)}{2}}$	$\pi \left(\delta (\nu -a)+\delta (\nu +a)\right)$	این از قوانین 101 و 303 با استفاده از فرمول اویلر نتیجه می گیرد : $\cos(ax)={\frac {e^{iax}+e^{-iax}}{2}}.$
305	$\sin(ax)$	${\frac {\delta \left(\xi -{\frac {a}{2\pi }}\right)-\delta \left(\xi +{\frac {a}{2\pi } }\right)}{2i}}$	${\sqrt {2\pi }}\cdot {\frac {\delta (\omega -a)-\delta (\omega +a)}{2i}}$	$-i\pi {\bigl (}\delta (\nu -a)-\delta (\nu +a){\bigr )}$	این از 101 و 303 استفاده می شود $\sin(ax)={\frac {e^{iax}-e^{-iax}}{2i}}.$
306	$\cos \left(ax^{2}\right)$	${\sqrt {\frac {\pi }{a}}}\cos \left({\frac {\pi ^{2}\xi ^{2}}{a}}-{\frac {\ pi {4}}\راست)$	$\frac{1}{\sqrt{2 a}} \cos \left( \frac{\omega^2}{4 a} - \frac{\pi}{4} \راست)$	${\sqrt {\frac {\pi }{a}}}\cos \left({\frac {\nu ^{2}}{4a}}-{\frac {\pi }{4}} \درست)$	این از 101 و 207 استفاده می شود $\cos(ax^{2})={\frac {e^{iax^{2}}+e^{-iax^{2}}}{2}}.$
307	$\sin \left(ax^{2}\right)$	$-{\sqrt {\frac {\pi }{a}}}\sin \left({\frac {\pi ^{2}\xi ^{2}}{a}}-{\frac { \pi {4}}\راست)$	$\frac{-1}{\sqrt{2 a}} \sin \left( \frac{\omega^2}{4 a} - \frac{\pi}{4} \راست)$	$-{\sqrt {\frac {\pi }{a}}}\sin \left({\frac {\nu ^{2}}{4a}}-{\frac {\pi }{4} }\درست)$	این از 101 و 207 استفاده می شود $\sin(ax^{2})={\frac {e^{iax^{2}}-e^{-iax^{2}}}{2i}}.$
308	$x^{n}\,$	$\left({\frac {i}{2\pi }}\right)^{n}\delta ^{(n)}(\xi )$	$i^{n}{\sqrt {2\pi }}\delta ^{(n)}(\omega )$	$2\pi i^{n}\delta ^{(n)}(\nu )$	در اینجا n یک عدد طبیعی و δ ( n ) ( ξ ) n امین مشتق توزیع تابع دلتای دیراک است. این قانون از قوانین 107 و 301 ناشی می شود. با ترکیب این قانون با 101، می توانیم همه چند جمله ای ها را تبدیل کنیم .
	$\delta ^{(n)}(x)$	$(2\pi i\xi )^{n}$	${\frac {(i\omega )^{n}}{\sqrt {2\pi }}}$	$(i\nu )^{n}$	دوگانه قانون 308. δ ( n ) ( ξ ) N امین مشتق توزیع تابع دلتای دیراک است. این قانون از 106 و 302 پیروی می کند.
309	${\frac {1}{x}}$	$-i\pi \operatorname {sgn}(\xi )$	$-i{\sqrt {\frac {\pi }{2}}}\operatorname {sgn}(\omega )$	$-i\pi \operatorname {sgn}(\nu )$	در اینجا sgn( ξ ) تابع علامت است . توجه داشته باشید که1/ایکستوزیع نیست هنگام آزمایش در برابر توابع شوارتز ، استفاده از مقدار اصلی کوشی ضروری است . این قانون در مطالعه تبدیل هیلبرت مفید است .
310	${\begin{aligned}&{\frac {1}{x^{n}}}}\\&:={\frac {(-1)^{n-1}}{(n-1) !}}{\frac {d^{n}}{dx^{n}}}\log \|x\|\end{تراز شده}}$	$-i\pi {\frac {(-2\pi i\xi )^{n-1}}{(n-1)!}}\operatorname {sgn}(\xi )$	$-i{\sqrt {\frac {\pi }{2}}}\cdot {\frac {(-i\omega )^{n-1}}{(n-1)!}}\operatorname {sgn}(\omega )$	$-i\pi {\frac {(-i\nu )^{n-1}}{(n-1)!}}\operatorname {sgn}(\nu )$	1/x nتوزیع همگنی است که توسط مشتق توزیعی تعریف می شود ${\frac {(-1)^{n-1}}{(n-1)!}}{\frac {d^{n}}{dx^{n}}}\log \|x\|$
311	$\|x\|^{\alpha }$	$-{\frac {2\sin \left({\frac {\pi \alpha }{2}}\right)\Gamma (\alpha +1)}{\|2\pi \xi \|^{\ آلفا +1}}}$	${\frac {-2}{\sqrt {2\pi }}}\cdot {\frac {\sin \left({\frac {\pi \alpha }{2}}\right)\Gamma ( \alpha +1)}{\|\omega \|^{\alpha +1}}}$	$-{\frac {2\sin \left({\frac {\pi \alpha }{2}}\right)\Gamma (\alpha +1)}{\|\nu \|^{\alpha +1 }}}$	این فرمول برای 0 > α > -1 معتبر است . برای α > 0 برخی از اصطلاحات مفرد در مبدأ به وجود می آیند که می توان آنها را با تمایز 318 پیدا کرد. اگر Re α > -1 ، آنگاه \| x \| α یک تابع قابل ادغام محلی است و بنابراین یک توزیع معتدل است. تابع α ↦ \| x \| α یک تابع هولومورفیک از نیم صفحه سمت راست تا فضای توزیع‌های معتدل است. این یک بسط مرومورفیک منحصربه‌فرد را به یک توزیع معتدل می‌پذیرد که با علامت \| نیز مشخص می‌شود x \| α برای α ≠ -1، -3، ... (نگاه کنید بهتوزیع همگن .)
	${\frac {1}{\sqrt {\|x\|}}}$	${\frac {1}{\sqrt {\|\xi \|}}}$	${\frac {1}{\sqrt {\|\omega \|}}}$	${\frac {\sqrt {2\pi }}{\sqrt {\|\nu \|}}}$	مورد ویژه 311.
312	$\operatorname {sgn}(x)$	${\frac {1}{i\pi \xi }}$	${\sqrt {\frac {2}{\pi }}}{\frac {1}{i\omega }}$	${\frac {2}{i\nu }}$	قانون دوگانه 309. این بار تبدیل فوریه باید به عنوان یک مقدار اصلی کوشی در نظر گرفته شود .
313	$u(x)$	${\frac {1}{2}}\left({\frac {1}{i\pi \xi }}+\delta (\xi )\right)$	${\sqrt {\frac {\pi }{2}}}\left({\frac {1}{i\pi \omega }}+\delta (\omega )\right)$	$\pi \left({\frac {1}{i\pi \nu }}+\delta (\nu )\right)$	تابع u ( x ) تابع مرحله واحد Heaviside است . این از قوانین 101، 301 و 312 ناشی می شود.
314	$\sum _{n=-\infty }^{\infty }\delta (x-nT)$	${\frac {1}{T}}\sum _{k=-\infty }^{\infty }\delta \left(\xi -{\frac {k}{T}}\right)$	${\frac {\sqrt {2\pi }}{T}}\sum _{k=-\infty }^{\infty }\delta \left(\omega -{\frac {2\pi k }{T}}\راست)$	${\frac {2\pi }{T}}\sum _{k=-\infty }^{\infty }\delta \left(\nu -{\frac {2\pi k}{T} }\درست)$	این تابع به عنوان تابع شانه دیراک شناخته می شود. این نتیجه را می توان از 302 و 102 به دست آورد، همراه با این واقعیت که ${\begin{aligned}&\sum _{n=-\infty }^{\infty }e^{inx}\\={}&2\pi \sum _{k=-\infty }^{ \infty }\delta (x+2\pi k)\end{تراز شده}}$ به عنوان توزیع
315	$J_{0}(x)$	${\frac {2\,\operatorname {rect} (\pi \xi )}{\sqrt {1-4\pi ^{2}\xi ^{2}}}}$	${\sqrt {\frac {2}{\pi }}}\cdot {\frac {\operatorname {rect} \left({\frac {\omega }{2}}\right)}{\sqrt {1-\omega ^{2}}}}$	${\frac {2\,\operatorname {rect} \left({\frac {\nu }{2}}\right)}{\sqrt {1-\nu ^{2}}}}$	تابع J 0 ( x ) تابع بسل مرتبه صفر از نوع اول است.
316	$J_{n}(x)$	${\frac {2(-i)^{n}T_{n}(2\pi \xi )\operatorname {rect} (\pi \xi )}{\sqrt {1-4\pi ^{ 2}\xi ^{2}}}}$	${\sqrt {\frac {2}{\pi }}}{\frac {(-i)^{n}T_{n}(\omega )\operatorname {rect} \left({\frac { \omega }{2}}\right)}{\sqrt {1-\omega ^{2}}}}$	${\frac {2(-i)^{n}T_{n}(\nu )\operatorname {rect} \left({\frac {\nu }{2}}\right)}{\sqrt {1-\nu ^{2}}}}$	این یک تعمیم 315 است. تابع J n ( x ) تابع بسل مرتبه n از نوع اول است. تابع T n ( x ) چند جمله ای چبیشف از نوع اول است .
317	$\log \چپ\|x\راست\|$	$-{\frac {1}{2}}{\frac {1}{\left\|\xi \right\|}}-\gamma \delta \left(\xi \right)$	$-{\frac {\sqrt {\frac {\pi }{2}}}{\left\|\omega \right\|}}-{\sqrt {2\pi }}\gamma \delta \left( \omega \راست)$	$-{\frac {\pi }{\left\|\nu \right\|}}-2\pi \gamma \delta \left(\nu \right)$	γ ثابت اویلر- ماسکرونی است . استفاده از انتگرال قسمت محدود هنگام آزمایش ضروری است1/\| ξ \|،1/\| ω \|،1/\| ν \|در برابر توابع شوارتز جزئیات این ممکن است ضریب تابع دلتا را تغییر دهد.
318	$\left(\mp ix\right)^{-\alpha }$	${\frac {\left(2\pi \right)^{\alpha }}{\Gamma \left(\alpha \right)}}u\left(\pm \xi \right)\left(\ pm \xi \right)^{\alpha -1}$	${\frac {\sqrt {2\pi }}{\Gamma \left(\alpha \right)}}u\left(\pm \omega \right)\left(\pm \omega \right)^ {\alpha -1}$	${\frac {2\pi }{\Gamma \left(\alpha \right)}}u\left(\pm \nu \right)\left(\pm \nu \right)^{\alpha - 1}$	این فرمول برای 1 > α > 0 معتبر است . از تمایز برای استخراج فرمول برای توان های بالاتر استفاده کنید. u تابع Heaviside است.

منبع

https://en.wikipedia.org/wiki/Fourier_transform

+ نوشته شده در سه شنبه بیست و نهم شهریور ۱۴۰۱ ساعت 7:59 توسط علی رضا نقش نیلچی |

5-تبدیل فوریه

قضیه پلانچرل و قضیه پارسوال [ ویرایش ]

فرض کنید f ( x ) و g ( x ) انتگرال پذیر باشند و f̂ ( ξ ) و ĝ ( ξ ) تبدیل فوریه آنها باشند. اگر f ( x ) و g ( x ) نیز مربع انتگرال پذیر باشند ، فرمول پارسوال به شرح زیر است: [17]

$\langle f,g\rangle _{L^{2}}=\int _{-\infty }^{\infty }f(x){\overline {g(x)}}\,dx= \int _{-\infty }^{\infty }{\hat {f}}(\xi ){\overline {{\hat {g}}(\xi )}}\,d\xi ,$

که در آن نوار نشان دهنده صرف پیچیده است .

قضیه پلانچرل که از مطالب فوق نتیجه می گیرد بیان می کند که [18]

$\|f\|_{L^{2}}=\int _{-\infty }^{\infty }\left|f(x)\right|^{2}\,dx=\int _{-\infty }^{\infty }\left|{\hat {f}}(\xi )\right|^{2}\,d\xi .$

قضیه پلانچرل این امکان را فراهم می‌کند که تبدیل فوریه را با استدلال پیوستگی به یک عملگر واحد در L 2 ( R ) بسط دهیم . در L 1 ( R ) ∩ L 2 ( R ) ، این پسوند با تبدیل فوریه اصلی تعریف شده در L 1 ( R ) مطابقت دارد ، بنابراین دامنه تبدیل فوریه به L 1 ( R ) + L 2 ( R ) بزرگ می شود (و در نتیجه به L p ( R )برای 1 ≤ p ≤ 2 ). قضیه پلانچرل در علوم این تعبیر را دارد که تبدیل فوریه انرژی کمیت اصلی را حفظ می کند. اصطلاحات این فرمول ها کاملاً استاندارد نیست. قضیه پارسوال فقط برای سری فوریه اثبات شد و اولین بار توسط لیاپانوف اثبات شد. اما فرمول پارسوال برای تبدیل فوریه نیز منطقی است، و بنابراین حتی اگر در زمینه تبدیل فوریه توسط پلانچرل ثابت شد، هنوز هم اغلب به عنوان فرمول پارسوال، یا رابطه پارسوال، یا حتی قضیه پارسوال از آن یاد می شود.

دوگانگی Pontryagin را برای فرمول بندی کلی این مفهوم در زمینه گروه های آبلی فشرده محلی ببینید.

فرمول جمع پواسون [ ویرایش ]

مقاله اصلی: فرمول جمع پواسون

فرمول جمع پواسون (PSF) معادله ای است که ضرایب سری فوریه جمع تناوبی یک تابع را به مقادیر تبدیل فوریه پیوسته تابع مرتبط می کند. فرمول جمع پواسون می گوید که برای توابع به اندازه کافی منظم f ،

$\sum _{n}{\hat {f}}(n)=\sum _{n}f(n).$

دارای انواع مختلفی از اشکال مفید است که با استفاده از خواص مقیاس‌پذیری و تغییر زمان تبدیل فوریه از شکل اصلی به دست می‌آیند. این فرمول در مهندسی، فیزیک و نظریه اعداد کاربرد دارد. دو دامنه فرکانس فرمول جمع پواسون استاندارد تبدیل فوریه گسسته زمان نیز نامیده می شود .

جمع پواسون به طور کلی با فیزیک محیط های تناوبی مانند هدایت گرما روی یک دایره مرتبط است. جواب اصلی معادله گرما روی یک دایره تابع تتا نامیده می شود . در تئوری اعداد برای اثبات ویژگی‌های تبدیل توابع تتا استفاده می‌شود، که معلوم می‌شود یک نوع شکل مدولار است ، و به طور کلی به نظریه اشکال اتومورفیک متصل است، جایی که در یک طرف فرمول ردیابی سلبرگ ظاهر می‌شود .

تمایز [ ویرایش ]

فرض کنید f ( x ) یک تابع کاملاً متمایز پیوسته است و هم f و هم مشتق آن f' قابل انتگرال هستند. سپس تبدیل فوریه مشتق به دست می آید

${\widehat {f'\,}}(\xi )={\mathcal {F}}\left\{{\frac {d}{dx}}f(x)\right\}=2\ pi i\xi {\hat {f}}(\xi ).$

به طور کلی تر، تبدیل فوریه n امین مشتق f ( n ) با استفاده از

${\widehat {f^{(n)}}}(\xi )={\mathcal {F}}\left\{{\frac {d^{n}}{dx^{n}}} f(x)\right\}=(2\pi i\xi )^{n}{\hat {f}}(\xi).$

با اعمال تبدیل فوریه و استفاده از این فرمول ها می توان برخی از معادلات دیفرانسیل معمولی را به معادلات جبری تبدیل کرد که حل آنها بسیار آسان تر است. این فرمول‌ها همچنین قاعده کلی را ایجاد می‌کنند که " f ( x ) صاف است اگر و فقط اگر f̂ ( ξ ) به سرعت به 0 برای | ξ | ∞ ∞ بیفتد ." با استفاده از قوانین مشابه برای تبدیل فوریه معکوس، می‌توان گفت: " f ( x ) به سرعت به 0 می‌افتد برای | x | ∞ اگر و فقط اگر f̂ ( ξ )صاف است."

قضیه کانولوشن [ ویرایش ]

مقاله اصلی: قضیه کانولوشن

تبدیل فوریه بین کانولوشن و ضرب توابع ترجمه می شود. اگر f ( x ) و g ( x ) به ترتیب با تبدیل های فوریه f̂ ( ξ ) و ĝ ( ξ ) توابع انتگرال پذیر باشند، تبدیل فوریه کانولوشن از حاصلضرب تبدیل های فوریه f̂ ( ξ ) و ĝ ( به دست می آید. ξ ) (در سایر قراردادها برای تعریف تبدیل فوریه ممکن است یک عامل ثابت ظاهر شود).

این بدان معنی است که اگر:

$h(x)=(f*g)(x)=\int _{-\infty }^{\infty }f(y)g(xy)\,dy,$

که در آن ∗ عملیات پیچیدگی را نشان می دهد، سپس:

${\hat {h}}(\xi )={\hat {f}}(\xi )\cdot {\hat {g}}(\xi ).$

در تئوری سیستم خطی زمان ثابت (LTI) ، معمولاً g ( x ) به عنوان پاسخ ضربه یک سیستم LTI با ورودی f ( x ) و خروجی h ( x ) تفسیر می‌شود ، زیرا تکانه واحد را جایگزین f ( x ) می‌کنیم. h ( x ) = g ( x ) را به دست می دهد . در این حالت ĝ ( ξ ) نشان دهنده پاسخ فرکانسی سیستم است.

برعکس، اگر f ( x ) را بتوان به عنوان حاصلضرب دو تابع مربعی انتگرال پذیر p ( x ) و q ( x ) تجزیه کرد ، آنگاه تبدیل فوریه f ( x ) با کانولوشن تبدیل های فوریه مربوطه p̂ ( ξ ) به دست می آید. ) و q̂ ( ξ ) .

قضیه همبستگی متقابل [ ویرایش ]

مقاله اصلی: همبستگی متقابل

به روشی مشابه، می توان نشان داد که اگر h ( x ) همبستگی متقابل f ( x ) و g ( x ) باشد :

$h(x)=(f\star g)(x)=\int _{-\infty }^{\infty }{\overline {f(y)}}g(x+y)\,dy$

سپس تبدیل فوریه h ( x ) برابر است با:

${\hat {h}}(\xi )={\overline {{\hat {f}}(\xi )}}\cdot {\hat {g}}(\xi ).$

به عنوان یک مورد خاص، خودهمبستگی تابع f ( x ) به صورت زیر است:

$h(x)=(f\star f)(x)=\int _{-\infty }^{\infty }{\overline {f(y)}}f(x+y)\,dy$

برای کدام

${\hat {h}}(\xi )={\overline {{\hat {f}}(\xi )}}{\hat {f}}(\xi )=\left|{\hat {f}}(\xi )\right|^{2}.$

توابع ویژه [ ویرایش ]

یکی از انتخاب های مهم یک پایه متعارف برای L 2 ( R ) توسط توابع Hermite ارائه شده است.

$\psi _{n}(x)={\frac {\sqrt[{4}]{2}}{\sqrt {n!}}}e^{-\pi x^{2}}\ mathrm {He} _{n}\left(2x{\sqrt {\pi }}\right)$

که در آن He n ( x ) چندجمله‌ای هرمیت " احتمال‌گرا" هستند که به صورت تعریف می‌شوند.

$\mathrm {He} _{n}(x)=(-1)^{n}e^{\frac {x^{2}}{2}}\left({\frac {d}{dx}} \راست)^{n}e^{-{\frac {x^{2}}{2}}}$

تحت این قرارداد برای تبدیل فوریه، ما آن را داریم

${\hat {\psi }}_{n}(\xi )=(-i)^{n}\psi _{n}(\xi )$ .

به عبارت دیگر، توابع هرمیت یک سیستم متعارف کامل از توابع ویژه برای تبدیل فوریه در L 2 ( R ) را تشکیل می دهند. [14] با این حال، این انتخاب از توابع ویژه منحصر به فرد نیست. تنها چهار مقدار ویژه مختلف از تبدیل فوریه وجود دارد (±1 و ± i ) و هر ترکیب خطی از توابع ویژه با مقدار ویژه یکسان تابع ویژه دیگری را به دست می دهد. در نتیجه، می توان L 2 ( R ) را به صورت مجموع مستقیم چهار فضای H 0 , H 1 , H تجزیه کرد.2 و H 3 که در آن تبدیل فوریه روی He k به سادگی با ضرب در i k عمل می کند.

از آنجایی که مجموعه کامل توابع هرمیت وضوح هویت را ارائه می‌کند، تبدیل فوریه را می‌توان با چنین مجموع عباراتی که با مقادیر ویژه بالا وزن شده‌اند، نشان داد و این مجموع را می‌توان به صراحت جمع کرد. این رویکرد برای تعریف تبدیل فوریه اولین بار توسط نوربرت وینر انجام شد . [19] در میان ویژگی‌های دیگر، توابع هرمیت به‌طور تصاعدی در حوزه‌های فرکانس و زمان کاهش می‌یابند، و بنابراین از آن‌ها برای تعریف تعمیم تبدیل فوریه، یعنی تبدیل فوریه کسری مورد استفاده در تحلیل زمان-فرکانس استفاده می‌شود. [20] در فیزیک ، این تبدیل توسط ادوارد کاندون معرفی شد . [21]

ارتباط با گروه هایزنبرگ [ ویرایش ]

گروه هایزنبرگ گروه خاصی از عملگرهای واحد در فضای هیلبرت L 2 ( R ) از توابع مجتمع مربعی با ارزش f روی خط واقعی است که توسط ترجمه های ( T y f ) ( x ) = f ( x + y ) ایجاد می شود. و ضرب در e 2π ixξ , ( M ξ f ) ( x ) = e 2π ixξ f (x ) . این اپراتورها مانند جابجایی (گروهی) آنها رفت و آمد نمی کنند

$\left(M_{\xi }^{-1}T_{y}^{-1}M_{\xi }T_{y}f\right)(x)=e^{2\pi iy\ xi }f(x)$

ضرب در ثابت (مستقل از x ) e 2π iyξ ∈ U (1) ( گروه دایره اعداد مختلط مدول واحد). به عنوان یک گروه انتزاعی، گروه هایزنبرگ گروه سه بعدی سه بعدی Lie ( x , ξ , z ) ∈ R 2 × U (1) با قانون گروه است.

$\left(x_{1},\xi _{1},t_{1}\right)\cdot \left(x_{2},\xi _{2},t_{2}\right)= \left(x_{1}+x_{2},\xi _{1}+\xi _{2},t_{1}t_{2}e^{2\pi i\left(x_{1}\ xi _{1}+x_{2}\xi _{2}+x_{1}\xi _{2}\right)}\right).$

گروه هایزنبرگ را با H 1 نشان دهید . روش بالا نه تنها ساختار گروه، بلکه یک نمایش واحد استاندارد از H1 را در فضای هیلبرت توصیف می کند، که ما آن را با ρ نشان می دهیم : H1 → B ( L2 ( R ) ) . اتومورفیسم خطی R 2 را تعریف کنید

$J{\begin{pmatrix}x\\\xi \end{pmatrix}}={\begin{pmatrix}-\xi \\x\end{pmatrix}}$

به طوری که J 2 = − I . این J را می توان به یک اتومورفیسم منحصر به فرد H 1 گسترش داد :

$j\left(x,\xi ,t\right)=\left(-\xi ,x,te^{-2\pi ix\xi }\right).$

طبق قضیه استون-فون نویمان ، نمایش های واحد ρ و ρ ∘j به طور واحد معادل هستند، بنابراین یک درهم تنیده منحصر به فرد W ∈ U ( L 2 ( R ) ) وجود دارد که

$\rho \circ j=W\rho W^{*}.$

این عملگر W تبدیل فوریه است.

بسیاری از خصوصیات استاندارد تبدیل فوریه پیامدهای فوری این چارچوب کلی تر هستند. [22] برای مثال، مربع تبدیل فوریه، W 2 ، یک درهم تنیده مرتبط با J 2 = − I است، و بنابراین داریم ( W 2 f ) ( x ) = f (- x ) بازتابی از تابع اصلی f .

دامنه پیچیده [ ویرایش ]

انتگرال برای تبدیل فوریه

${\hat {f}}(\xi )=\int _{-\infty }^{\infty }e^{-2\pi i\xi t}f(t)\,dt$

می توان مقادیر مختلط آرگومان ξ را مطالعه کرد. بسته به ویژگی‌های f ، این ممکن است اصلاً از محور واقعی همگرا نشود، یا ممکن است به یک تابع تحلیلی پیچیده برای همه مقادیر ξ = σ + iτ یا چیزی در بین آن همگرا شود. [23]

قضیه پیلی-وینر می گوید که f صاف است (یعنی n - بار برای همه اعداد صحیح مثبت n قابل تمایز است ) و به طور فشرده پشتیبانی می شود اگر و فقط اگر f̂ ( σ + iτ ) یک تابع هولومورفیک باشد که برای آن ثابت a > 0 وجود داشته باشد. که برای هر عدد صحیح n ≥ 0 ،

$\left\vert \xi ^{n}{\hat {f}}(\xi )\right\vert \leq Ce^{a\vert \tau \vert }$

برای مقداری C ثابت (در این مورد، f روی [− a , a ] پشتیبانی می‌شود .) این را می‌توان با گفتن اینکه f̂ یک تابع کامل است که به سرعت در σ کاهش می‌یابد (برای τ ثابت ) و رشد نمایی در τ (به طور یکنواخت در σ ) کاهش می‌یابد. ). [24]

(اگر f صاف نباشد، اما فقط L 2 باشد، گزاره همچنان با n = 0 برقرار است. [25] ) فضای چنین توابعی از یک متغیر مختلط ، فضای Paley-Wiener نامیده می شود. این قضیه به گروه های دروغ نیمه ساده تعمیم داده شده است . [26]

اگر f روی نیم خط t ≥ 0 پشتیبانی شود ، آنگاه f را «علت» می گویند زیرا تابع پاسخ ضربه ای یک فیلتر قابل تحقق فیزیکی باید این ویژگی را داشته باشد، زیرا هیچ اثری نمی تواند مقدم بر علت آن باشد. پیلی و وینر نشان دادند که پس از آن ، f به یک تابع هولومورفیک در نیم صفحه پایین پیچیده τ < 0 گسترش می‌یابد که وقتی τ به سمت بی‌نهایت می‌رود ، به صفر می‌رود. [27] عکس آن نادرست است و مشخص نیست که چگونه تبدیل فوریه یک تابع علی را مشخص کنیم. [28]

تبدیل لاپلاس [ ویرایش ]

همچنین ببینید: تبدیل لاپلاس § تبدیل فوریه

تبدیل فوریه f̂ ( ξ ) مربوط به تبدیل لاپلاس F ( s ) است که برای حل معادلات دیفرانسیل و تحلیل فیلترها نیز استفاده می شود .

ممکن است اتفاق بیفتد که تابع f که انتگرال فوریه آن به هیچ وجه روی محور واقعی همگرا نمی شود، با این حال تبدیل فوریه پیچیده ای در ناحیه ای از صفحه مختلط تعریف شده است .

به عنوان مثال، اگر f ( t ) دارای رشد نمایی باشد، به عنوان مثال،

$\vert f(t)\vert <Ce^{a\vert t\vert }$

برای برخی از ثابت های C ، a ≥ 0 ، سپس [29]

${\hat {f}}(i\tau )=\int _{-\infty }^{\infty }e^{2\pi \tau t}f(t)\,dt,$

همگرا برای همه 2π τ < - a ، تبدیل لاپلاس دو طرفه f است.

نسخه معمول تر ("یک طرفه") تبدیل لاپلاس است

$F(s)=\int _{0}^{\infty }f(t)e^{-st}\,dt.$

اگر f نیز علی و تحلیلی باشد، آنگاه: ${\hat {f}}(i\tau )=F(-2\pi \tau).$ بنابراین، گسترش تبدیل فوریه به حوزه مختلط به این معنی است که تبدیل لاپلاس را به عنوان یک مورد خاص در مورد توابع علی - اما با تغییر متغیر s = 2π iξ در بر می گیرد .

از دیدگاهی دیگر، شاید کلاسیک‌تر، تبدیل لاپلاس از نظر شکل شامل یک عبارت تنظیم‌کننده نمایی اضافی است که به آن اجازه می‌دهد خارج از خط خیالی جایی که تبدیل فوریه تعریف می‌شود، همگرا شود. به این ترتیب، می‌تواند برای سری‌ها و انتگرال‌های به‌طور نمایی واگرا همگرا شود، در حالی که تجزیه فوریه اصلی نمی‌تواند، امکان تجزیه و تحلیل سیستم‌های دارای عناصر واگرا یا بحرانی را فراهم می‌کند. دو نمونه خاص از پردازش سیگنال خطی، ساخت شبکه‌های فیلتر همه‌گذر از فیلترهای حساس و کاهش‌دهنده از طریق لغو دقیق قطب صفر در دایره واحد است. چنین طرح‌هایی در پردازش صوتی رایج هستند، جایی که پاسخ فاز بسیار غیرخطی مانند Reverb جستجو می‌شود.

علاوه بر این، زمانی که پاسخ‌های پالس‌مانند تمدید شده برای کار پردازش سیگنال جستجو می‌شوند، ساده‌ترین راه برای تولید آن‌ها داشتن یک مدار است که یک پاسخ زمانی واگرا تولید می‌کند، و سپس لغو واگرایی آن از طریق پاسخ متضاد و جبرانی تاخیری. در آنجا، فقط مدار تأخیر در بین، توصیف فوریه کلاسیک را می پذیرد که بسیار مهم است. هر دو مدار کناری ناپایدار هستند و تجزیه فوریه همگرا را قبول ندارند. با این حال، آن‌ها یک توصیف دامنه لاپلاس را می‌پذیرند، با نیم‌صفحه‌های همگرایی یکسان در صفحه مختلط (یا در مورد گسسته، صفحه Z)، که در آن اثرات آنها لغو می‌شود.

در ریاضیات مدرن، تبدیل لاپلاس به طور معمول تحت روش های فوریه قرار می گیرد. هر دوی آنها با ایده بسیار کلی تر و انتزاعی تر تحلیل هارمونیک جمع می شوند.

منبع

https://en.wikipedia.org/wiki/Fourier_transform

+ نوشته شده در سه شنبه بیست و نهم شهریور ۱۴۰۱ ساعت 7:32 توسط علی رضا نقش نیلچی |

3-تبدیل فوریه

تبدیل فوریه برای توابعی که خارج از یک بازه صفر هستند [ ویرایش ]

ارتباط نزدیکی بین تعریف سری فوریه و تبدیل فوریه برای توابع f که خارج از یک بازه صفر هستند وجود دارد. برای چنین تابعی می‌توانیم سری فوریه آن را در هر بازه‌ای که شامل نقاطی باشد که f صفر نیست محاسبه کنیم. تبدیل فوریه نیز برای چنین تابعی تعریف شده است. با افزایش طول بازه‌ای که در آن سری فوریه را محاسبه می‌کنیم، ضرایب سری فوریه شبیه تبدیل فوریه و مجموع سری فوریه f شبیه تبدیل فوریه معکوس می‌شوند. به طور دقیق تر، فرض کنید T به اندازه کافی بزرگ است که بازه [T/2،T/2-] شامل بازه‌ای است که f صفر نیست. سپس ضریب سری c n به صورت زیر بدست می آید:

$c_{n}={\frac {1}{T}}\int _{-{\frac {T}{2}}}^{\frac {T}{2}}f(x)\ ,e^{-2\pi i\left({\frac {n}{T}}\right)x}\,dx.$

از مقایسه این با تعریف تبدیل فوریه، چنین است که:

$c_{n}={\frac {1}{T}}{\hat {f}}\left({\frac {n}{T}}\right)$

زیرا f ( x ) در خارج از [- صفر استتی/2،تی/2] . بنابراین، ضرایب فوریه برابر با مقادیر تبدیل فوریه نمونه برداری شده در شبکه ای از عرض است.1/تیضرب در عرض شبکه1/تی.

تحت شرایط مناسب، سری فوریه f برابر با تابع f خواهد بود. به عبارت دیگر، f را می توان نوشت:

$f(x)=\sum _{n=-\infty }^{\infty }c_{n}\,e^{2\pi i\left({\frac {n}{T}}\ راست)x}=\sum _{n=-\infty }^{\infty }{\hat {f}}(\xi _{n})\ e^{2\pi i\xi _{n}x }\Delta \xi ,$

که در آن آخرین مجموع به سادگی اولین مجموع است که با استفاده از تعاریف ξ n = بازنویسی شده استn/تیو Δ ξ =n + 1/تی-n/تی=1/تی.

این جمع دوم یک مجموع ریمان است. با اجازه دادن به T → ∞ به انتگرال تبدیل فوریه معکوس همانطور که در بالا بیان شد همگرا می شود. در شرایط مناسب، این استدلال ممکن است دقیق شود. [13]

مثال [ ویرایش ]

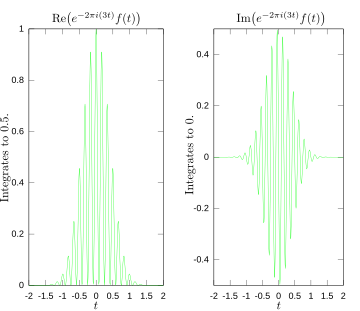
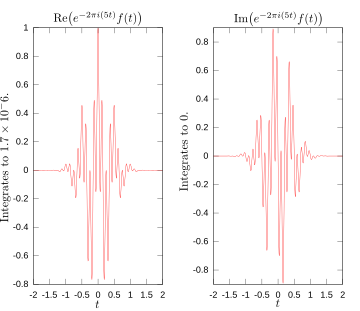
شکل‌های زیر یک تصویر بصری ارائه می‌دهند که چگونه تبدیل فوریه، وجود فرکانس در یک تابع خاص را اندازه‌گیری می‌کند. تابع نشان داده شده f ( t ) = cos(6π t ) e -π t 2 در 3 هرتز نوسان می کند (اگر t ثانیه را اندازه گیری کند) و به سرعت به 0 میل می کند. (فاکتور دوم در این معادله یک تابع پوششی است که سینوسی پیوسته را شکل می دهد. شکل کلی آن یک تابع گاوسی است ). این تابع به طور ویژه برای داشتن یک تبدیل فوریه حقیقی انتخاب شده است که می تواند به راحتی ترسیم شود. تصویر اول شامل نمودار آن است. به منظور محاسبه ${\hat {f}}(3)$ ما باید e - 2π i (3 t ) f ( t ) را ادغام کنیم . تصویر دوم نمودار قسمت های حقیقی و موهومی این تابع را نشان می دهد. بخش حقیقی انتگرال تقریبا همیشه مثبت است، زیرا وقتی f ( t ) منفی است، قسمت حقیقی e - 2π i (3 t ) نیز منفی است. از آنجایی که آنها با سرعت یکسانی نوسان می کنند، وقتی f ( t ) مثبت است، بخش حقیقی e - 2π i (3 t ) نیز مثبت است.. نتیجه این است که وقتی بخش حقیقی انتگرال را ادغام می‌کنید، عدد نسبتاً زیادی به دست می‌آید (در این مورد1/2). از سوی دیگر، هنگامی که شما سعی می کنید فرکانس را اندازه گیری کنید که وجود ندارد، مانند موردی که ما به آن نگاه می کنیم ${\hat {f}}(5)$ ، می بینید که هر دو جزء حقیقی و موهومی این تابع به سرعت بین مقادیر مثبت و منفی تغییر می کنند، همانطور که در تصویر سوم ترسیم شده است. بنابراین، در این حالت، انتگرال به اندازه کافی سریع نوسان می کند به طوری که انتگرال بسیار کوچک است و مقدار تبدیل فوریه برای آن فرکانس تقریباً صفر است.

وضعیت کلی ممکن است کمی پیچیده‌تر از این باشد، اما از نظر روحی، تبدیل فوریه نشان می‌دهد که چقدر از یک فرکانس فردی در تابع f ( t ) وجود دارد.

- تابع اصلی که نوسان 3 هرتز را نشان می دهد.

- بخش های حقیقی و موهومی انتگرال برای تبدیل فوریه در 3 هرتز

- بخش های حقیقی و موهومی انتگرال برای تبدیل فوریه در 5 هرتز

قدر تبدیل فوریه، با 3 و 5 هرتز برچسب زده شده است.

منبع

https://en.wikipedia.org/wiki/Fourier_transform#math_Eq.2

+ نوشته شده در سه شنبه بیست و نهم شهریور ۱۴۰۱ ساعت 7:15 توسط علی رضا نقش نیلچی |

2-تبدیل فوریه

تاریخچه [ ویرایش ]

مقالات اصلی: تحلیل فوریه § تاریخچه و سری فوریه § تاریخ

در سال 1822، فوریه ادعا کرد (نگاه کنید به جوزف فوریه § تئوری تحلیلی گرما ) که هر تابع، خواه پیوسته یا ناپیوسته، می تواند به یک سری سینوس بسط یابد. [10] آن کار مهم توسط دیگران تصحیح و گسترش یافت تا پایه و اساس اشکال مختلف تبدیل فوریه را که از آن زمان استفاده شده است، فراهم کند.

مقدمه [ ویرایش ]

همچنین ببینید: تحلیل فوریه و سری فوریه

تابع f (قرمز) ابتدا به سری فوریه آن تبدیل می شود : مجموع امواج سینوسی (به رنگ آبی). سپس این سینوسی ها در سراسر طیف فرکانس پخش می شوند و به صورت پیک ( توابع دلتای دیراک ) در حوزه فرکانس نشان داده می شوند. نمایش دامنه فرکانس تابع ( f̂ ) مجموعه ای از این پیک ها است.

اگرچه سری فوریه می تواند شکل موج های تناوبی را به عنوان مجموع سینوسی های مرتبط با هارمونیک نشان دهد، سری فوریه نمی تواند شکل موج های غیر تناوبی را نشان دهد. با این حال، تبدیل فوریه قادر است شکل موج های غیر تناوبی را نیز نمایش دهد. این امر با اعمال یک فرآیند محدود کننده برای طولانی کردن دوره هر شکل موج تا بی نهایت و سپس در نظر گرفتن آن به عنوان یک شکل موج دوره ای به دست می آید. [11]

در مطالعه سری فوریه، ضرایب فوریه نشان دهنده دامنه هر سینوسی مرتبط با هماهنگی موجود در سری فوریه تابع تناوبی f است. به طور مشابه، تبدیل فوریه دامنه و فاز هر سینوسی موجود در تابع (احتمالاً غیر تناوبی) f را نشان می‌دهد .

تبدیل فوریه از یک انتگرال (یا "جمع پیوسته") استفاده می کند که از ویژگی های سینوس و کسینوس برای بازیابی دامنه و فاز هر سینوسی در یک سری فوریه استفاده می کند. تبدیل فوریه معکوس این امواج را با استفاده از یک انتگرال مشابه برای بازتولید تابع اصلی دوباره ترکیب می کند.

استفاده از سینوسی های مختلط برای نمایش سینوس های حقیقی [ ویرایش ]

همچنین ببینید: فرکانس منفی § ساده سازی تبدیل فوریه

برای ساده کردن ریاضی، مطلوب است که سری فوریه را به صورت مجموع نمایی های مختلط بنویسیم (به سری فوریه § شکل نمایی مراجعه کنید ). هر سینوسی مختلط نمایی یا مختلط فرکانس ξ را می توان با استفاده از فرمول اویلر به عنوان مجموع موج کسینوس فرکانس ξ برای مولفه حقیقی به اضافه یک موج سینوسی همچنین فرکانس ξ برای مؤلفه موهومی بیان کرد:

${\begin{aligned}e^{2\pi i\xi x}&=\cos(2\pi \xi x)+i\sin(2\pi \xi x)\end{تراز شده}}$

بیان سینوس های حقیقی به صورت سینوسی های مختلط، ضرایب فوریه را ضروری می کند $c_{n}$ مختلط باشد، اما دارای مزیت نمایش فشرده تمام اطلاعات لازم در مورد هر فرکانس است. تعبیر معمول این عدد مختلط این است که $\left\vert c_{n}\right\vert$ ( قدر آن ) دامنه و $\arg(c_{n})$ ( آگومان آن ) فاز سینوسی مختلط را برای آن ضریب نشان می دهد.

نشان دادن نمایی مختلط در سه بعدی. مؤلفه حقیقی یک موج کسینوس است. جزء موهومی یک موج سینوسی است. آنها با هم یک مارپیچ را تشکیل می دهند. نفی فرکانس را می توان به عنوان تغییر دستی مارپیچ درک کرد . چرخش با جهت مخالف اما با همان تعداد چرخش در ثانیه.

این نمایی های مختلط ممکن است فرکانس منفی داشته باشند . برای مثال، هر دو سینوسی مختلط e 2π iξx و e -2π iξx یک چرخه را در هر واحد x کامل می کنند، اما اولی نشان دهنده فرکانس مثبت است در حالی که دومی نشان دهنده فرکانس منفی است. فرکانس مثبت را می توان به عنوان چرخش در خلاف جهت عقربه های ساعت در مورد صفحه مختلط درک کرد در حالی که فرکانس منفی را می توان به عنوان چرخش در جهت عقربه های ساعت در مورد صفحه مختلط درک کرد. هنگامی که سینوسی های مختلط به عنوان یک مارپیچ در سه بعدی تفسیر می شوند (با بعد سوم که جزء موهومی است)، نفی فرکانس به سادگی حالت دستی مارپیچ را تغییر می دهد.. [12]

امواج حقیقی سینوسی و کسینوس را می توان از نمایش نمایی مختلط سینوسی ها بازیابی کرد. به عنوان مثال، نتیجه ای از فرمول اویلر اجازه می دهد تا امواج کسینوس و سینوسی را به عنوان بخش حقیقی یا موهومی یک سینوسی مختلط یا به عنوان مجموع وزنی دو سینوسی مختلط با فرکانس مخالف بیان کنیم:

${\begin{aligned}\cos(2\pi \xi x)&=\operatorname {Re} \left(e^{2\pi i\xi x}\right)={\tfrac {1} {2}}e^{2\pi i\xi x}+{\tfrac {1}{2}}e^{-2\pi i\xi x},\\\sin(2\pi \xi x )&=\operatorname {Im} \left(e^{2\pi i\xi x}\right)={\tfrac {1}{2i}}e^{2\pi i\xi x}-{\ tfrac {1}{2i}}e^{-2\pi i\xi x}.\end{تراز شده}}$

در نتیجه، یک شکل کلی از هر سینوسی حقیقی (با فرکانس ξ ، تغییر فاز θ و دامنه A ) را می توان به صورت مجموع دو سینوسی مختلط با فرکانس مخالف ( ξ و - ξ ) اما قدر مساوی بیان کرد.آ/2) و با تغییر فاز θ که در هر دو ضرایب مختلط آنها تعبیه شده است:

${\begin{aligned}A\cos(2\pi \xi x+\theta )&={\tfrac {A}{2}}e^{2\pi i\xi x+i\theta }+ {\tfrac {A}{2}}e^{-2\pi i\xi xi\theta }={\tfrac {Ae^{i\theta }}{2}}e^{2\pi i\xi x}+{\tfrac {Ae^{-i\theta }}{2}}e^{-2\pi i\xi x}.\end{تراز شده}}$

از این رو، هر سینوسی حقیقی (و سیگنال حقیقی) را می توان متشکل از یک فرکانس مثبت و منفی در نظر گرفت که اجزای موهومی آن خنثی می شوند اما اجزای حقیقی آن به طور مساوی در تشکیل سیگنال حقیقی مشارکت دارند.

برای اجتناب از استفاده از اعداد مختلط و فرکانس های منفی، تبدیل های سینوسی و کسینوس با هم می توانند به عنوان شکل جایگزین معادل تبدیل فوریه استفاده شوند.

منبع

https://en.wikipedia.org/wiki/Fourier_transform

+ نوشته شده در سه شنبه بیست و نهم شهریور ۱۴۰۱ ساعت 6:59 توسط علی رضا نقش نیلچی |

مثال از نگاشت Log z و exp z

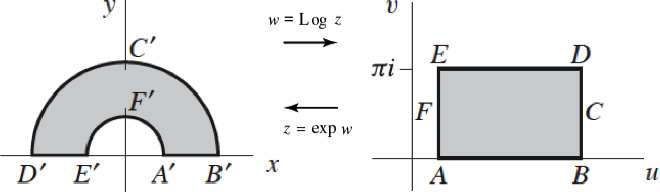
Figure 4 from Numerical Scheme for the Solution to Laplace's Equation using Local Conformal Mapping Techniques | Semantic Scholar

+ نوشته شده در یکشنبه چهارم اردیبهشت ۱۴۰۱ ساعت 13:30 توسط علی رضا نقش نیلچی |

توابع تحلیلی

توابع تحلیلی

(الف) توضیح دهید که منظور از تابعی از دو متغیر x و y تحلیلی چیست و بحث کنید که چرا ممکن است بخواهیم با چنین توابعی کار کنیم.

(ب) سه تابع زیر را از دو متغیر x و y در نظر بگیرید و مشخص کنید که کدام یک از آنها به عنوان توابع z = x + iy در نظر گرفته می شوند.

نتیجه گیری خود را به دو صورت نشان دهید: با استفاده از معادلات کوشی-ریمان و با بازنویسی آنها به عنوان تابعی از z و z*.

(ج) آیا این سه تابع در همه جای صفحه xy تحلیلی هستند؟ اگر نه، مشخص کنید کجا هستند و کجا نیستند.

راه حل

(الف) تابعی از دو متغیر در یک نقطه z=a در صفحه مختلط تحلیلی است اگر مشتق در نقطه ای با قانون مشتق معمولی تعریف شده باشد (اما اکنون از "عدد توسعه یافته"، z = x+iy به عنوان متغیر):

این نسبت به 1 متغیر مشکل‌تر است، زیرا می‌توانیم Δ z را به روش‌های مختلف انتخاب کنیم - با استفاده از Δ z = Δ x یا Δ z = Δ y یا ترکیبی از این دو. ما اصولاً بسته به اینکه چگونه این کار را انجام می دادیم، می توانستیم نتایج متفاوتی بگیریم. نمونه های زیادی از این وجود دارد. اگر Sqrt(z) را در نظر بگیرید و مشتق را در 0 در امتداد محور واقعی که از جهت مثبت نزدیک می شود بگیرید، یک عدد واقعی (-- در واقع یک عدد واقعی بی نهایت) به دست می آورید. اگر مشتق را از جهت منفی نزدیک کنید، یک عدد فرضی (-- دوباره یک نامتناهی) به دست می‌آید.

دلیل ارزشمند بودن این موضوع فراتر از رضایت از عدم نیاز به مشخص کردن جهتی است که هنگام استفاده از یک مشتق، از کدام سمت می آیید. توابعی که این ویژگی را دارند به طور چشمگیری محدود می شوند. به عنوان مثال، اگر یک تابع در هر نقطه از یک منطقه تحلیلی باشد و ما آن را در هر نقطه از یک منحنی بسته در آن منطقه بدانیم، می‌توانیم آن را در هر نقطه داخل منحنی بسته با استفاده از قضیه باقیمانده پیدا کنیم. بسیاری از انتگرال هایی که ارزیابی آنها بسیار دشوار است، به راحتی می توانند به صورت تحلیلی انجام شوند.

دلیل خاصی که ما علاقه مندیم این است که پیامدهای فیزیکی وجود دارد. تابعی که معادلات CR را برآورده می کند، معادله لاپلاس را نیز برآورده می کند و بسیاری از خواص فیزیکی (مثلاً پتانسیل الکتریکی) معادله لاپلاس را برآورده می کند. انتگرال هایی که اغلب از حل معادلات دیفرانسیل معمولی با روش تبدیل فوریه (یا لاپلاس) ظاهر می شوند، اغلب با استفاده از روش های انتگرال کانتور پیچیده ای که از تجزیه و تحلیل می آیند قابل انجام هستند.

(ب) ابتدا f را در نظر بگیرید. آیا قسمت های واقعی و خیالی آن معادلات CR را برآورده می کند؟

جواب منفی. حال اجازه دهید f را تابعی از z و z* بیان کنیم .

پس f تحلیلی نیست.

حالا g را در نظر بگیرید :

معادلات CR را برآورده می کند. آیا می‌توانیم با بیان آن بر حسب z و z* متوجه شویم چرا ؟

از آنجایی که فقط تابعی از z است، تحلیلی است.

در مورد h چطور؟

بنابراین معادله CR اول را برآورده نمی کند. آیا می توانیم با نوشتن آن بر حسب z و z* دلیل آن را بفهمیم؟

این فقط تابعی از z* است بنابراین تحلیلی نیست.

ج) تنها تابعی که تحلیلی است g است. این یک قطب در 0 دارد، بنابراین در آنجا تحلیلی نیست - فقط در هر جای دیگر.

منبع

https://physics.umd.edu/courses/Phys374/fall05/hw/sol_hw12/MP54-S.htm

+ نوشته شده در شنبه سوم اردیبهشت ۱۴۰۱ ساعت 19:38 توسط علی رضا نقش نیلچی |

اثبات رابطه کوشی -ریمان در دستگاه قطبی

complex analysis - Proof of Cauchy Riemann Equations in Polar Coordinates - Mathematics Stack Exchange

+ نوشته شده در شنبه سوم اردیبهشت ۱۴۰۱ ساعت 19:17 توسط علی رضا نقش نیلچی |

مثال20 :بررسی رابطه کوشی - ریمان

برای اثبات تحلیلی بودن تابع می توان از معادلات کوشی -ریمان استفاده کرد یعنی

باید تابع مختلط را ابتدا ت بصورت u+vi نوشت
مشتقu نسبت به x برابر مشتق v نسبت بهy
مشتق u نسبت به y برابر قرینه مشتق v نسبت بهx

برای بررسی تحلیلی بودن تابع می توان از معادلات کوشی -ریمان از دستورالعمل زیر استفاده کنید

تابع مختلط را ابتدا ت بصورت u+vi بنویسید
مشتقu نسبت به x را حساب کنید
مشتق v نسبت بهy را حساب کنید
اگر جواب دوقسمت قبل مساوی نشدند تحلیلی نیست در غیر اینصورت مراحل زیر را انجام دهید
مشتقu نسبت به y را حساب کنید
مشتق v نسبت بهx را حساب کنید
اگر جواب دوقسمت قبل قرینه شدند تحلیلی است در غیر اینصورت تحلیلی نیست

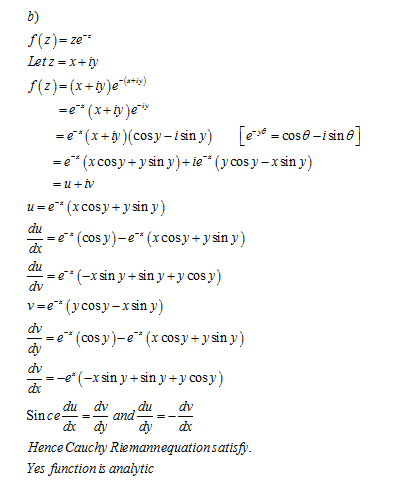
Answered: Verify that the real and imaginary… | bartleby

+ نوشته شده در شنبه سوم اردیبهشت ۱۴۰۱ ساعت 18:32 توسط علی رضا نقش نیلچی |

ثابت کنید sin z = sin x cos hy + i cos x sin hy

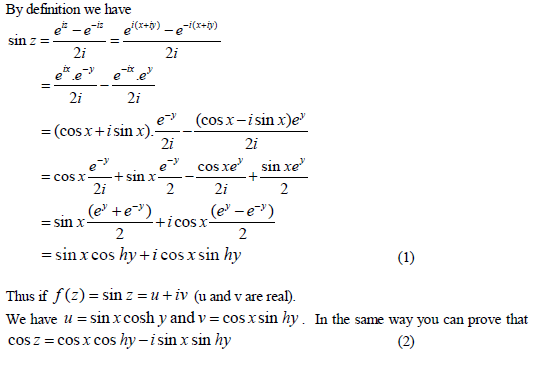
Prove that sin z = sin x cos hy + i cos x sin hy

+ نوشته شده در شنبه سوم اردیبهشت ۱۴۰۱ ساعت 17:52 توسط علی رضا نقش نیلچی |

2-توابع هذلولی

ویژگی های مشخصه [ ویرایش ]

کسینوس هایپربولیک [ ویرایش ]

می توان نشان داد که مساحت زیر منحنی کسینوس هذلولی (در یک بازه محدود) همیشه برابر با طول قوس مربوط به آن بازه است: [15]

${\text{area}}=\int _{a}^{b}\cosh x\,dx=\int _{a}^{b}{\sqrt {1+\left({\frac {d}{dx}}\cosh x\right)^{2}}}\,dx={\text{طول قوس.}}$

مماس هایپربولیک[ ویرایش ]

مماس هذلولی جواب (یکتا) معادله دیفرانسیل f ′ = 1 − f 2 است که f (0) = 0 دارد. [16] [17]

روابط مفید [ ویرایش ]

توابع هذلولی بسیاری از هویت ها را برآورده می کنند که همه آنها از نظر شکل شبیه به هویت های مثلثاتی هستند . در واقع، قانون آزبورن [18] بیان می کند که می توان هر هویت مثلثاتی را برای تبدیل کرد $تتا$ ، $2\ تتا$ ، $3\ تتا$ یا $تتا$ و $\varphi$ به یک هویت هذلولی، با بسط کامل آن بر حسب قدرت های انتگرال سینوس ها و کسینوس ها، تغییر سینوس به سینه و کسینوس به کوش، و تغییر علامت هر عبارت حاوی حاصل ضرب دو سین.

توابع زوج و فرد:

${\begin{aligned}\sinh(-x)&=-\sinh x\\\cosh(-x)&=\cosh x\end{aligned}}$

از این رو:

${\begin{aligned}\tanh(-x)&=-\tanh x\\\coth(-x)&=-\coth x\\\operatorname {sech} (-x)&=\operatorname {sech} x\\\ نام عامل {csch} (-x)&=-\نام اپراتور {csch} x\end{تراز شده}}$

بنابراین، cosh x و sech x توابع زوج هستند . بقیه توابع فرد هستند .

${\begin{aligned}\operatorname {arsech} x&=\operatorname {arcosh} \left({\frac {1}{x}}\right)\\\operatorname {arcsch} x&=\operatorname {arsinh } \left({\frac {1}{x}}\right)\\\operatorname {arcoth} x&=\operatorname {artanh} \left({\frac {1}{x}}\right)\end{ هم راستا}}$

سینوس و کسینوس هایپربولیک:

${\begin{aligned}\cosh x+\sinh x&=e^{x}\\\cosh x-\sinh x&=e^{-x}\\\cosh ^{2}x-\sinh ^ {2}x&=1\end{تراز شده}}$

که آخرین آنها شبیه به هویت مثلثاتی فیثاغورثی است .

یکی هم دارد

${\begin{aligned}\operatorname {sech} ^{2}x&=1-\tanh ^{2}x\\\operatorname {csch} ^{2}x&=\coth ^{2}x- 1\end{تراز شده}}$

برای توابع دیگر

مجموع آرگومان ها [ ویرایش ]

${\begin{aligned}\sinh(x+y)&=\sinh x\cosh y+\cosh x\sinh y\\\cosh(x+y)&=\cosh x\cosh y+\sinh x \sinh y\\[6px]\tanh(x+y)&={\frac {\tanh x+\tanh y}{1+\tanh x\tanh y}}\\\end{تراز شده}}$

به ویژه

${\begin{aligned}\cosh(2x)&=\sinh ^{2}{x}+\cosh ^{2}{x}=2\sinh ^{2}x+1=2\cosh ^{2}x-1\\\sinh(2x)&=2\sinh x\cosh x\\\tanh(2x)&={\frac {2\tanh x}{1+\tanh ^{2} x}}\\\پایان{تراز شده}}$

همچنین:

${\begin{aligned}\sinh x+\sinh y&=2\sinh \left({\frac {x+y}{2}}\right)\cosh \left({\frac {xy}{2 }}\right)\\\cosh x+\cosh y&=2\cosh \left({\frac {x+y}{2}}\right)\cosh \left({\frac {xy}{2}} \راست)\\\پایان{تراز شده}}$

فرمول های تفریق [ ویرایش ]

${\begin{aligned}\sinh(xy)&=\sinh x\cosh y-\cosh x\sinh y\\\cosh(xy)&=\cosh x\cosh y-\sinh x\sinh y\\\tanh(xy)&={\frac {\tanh x-\tanh y}{1-\tanh x\tanh y}}\\\end{تراز شده}}$

همچنین: [19]

${\begin{aligned}\sinh x-\sinh y&=2\cosh \left({\frac {x+y}{2}}\right)\sinh \left({\frac {xy}{ 2}}\right)\\\cosh x-\cosh y&=2\sinh \left({\frac {x+y}{2}}\right)\sinh \left({\frac {xy}{2 }}\راست)\\\end{تراز شده}}$

فرمول های نیم آرگومان [ ویرایش ]

${\begin{aligned}\sinh \left({\frac {x}{2}}\right)&={\frac {\sinh x}{\sqrt {2(\cosh x+1)} }}&&=\operatorname {sgn} x\,{\sqrt {\frac {\cosh x-1}{2}}}\\[6px]\cosh \left({\frac {x}{2}} \right)&={\sqrt {\frac {\cosh x+1}{2}}}\\[6px]\tanh \left({\frac {x}{2}}\right)&={\ frac {\sinh x}{\cosh x+1}}&&=\operatorname {sgn} x\,{\sqrt {\frac {\cosh x-1}{\cosh x+1}}}={\frac {e^{x}-1}{e^{x}+1}}\end{تراز شده}}$

که در آن sgn تابع علامت است .

اگر x ≠ 0 ، سپس [20]

$\tanh \left({\frac {x}{2}}\right)={\frac {\cosh x-1}{\sinh x}}=\coth x-\operatorname {csch} x$

فرمول های مربعی [ ویرایش ]

${\begin{aligned}\sinh ^{2}x&={\frac {1}{2}}(\cosh 2x-1)\\\cosh ^{2}x&={\frac {1} {2}}(\cosh 2x+1)\end{تراز شده}}$

نابرابری ها [ ویرایش ]

نابرابری زیر در آمار مفید است: $\operatorname {cosh} (t)\leq e^{t^{2}/2}$ [21]

این را می توان با مقایسه ترم به ترم سری تیلور دو تابع ثابت کرد.

توابع معکوس به عنوان لگاریتم [ ویرایش ]

مقاله اصلی: تابع هذلولی معکوس

${\begin{aligned}\operatorname {arsinh} (x)&=\ln \left(x+{\sqrt {x^{2}+1}}\right)\\\operatorname {arcosh} (x )&=\ln \left(x+{\sqrt {x^{2}-1}}\right)&&x\geq 1\\\operatorname {artanh} (x)&={\frac {1}{2} }\ln \left({\frac {1+x}{1-x}}\right)&&|x|<1\\\operatorname {arcoth} (x)&={\frac {1}{2} }\ln \left({\frac {x+1}{x-1}}\right)&&|x|>1\\\operatorname {arsech} (x)&=\ln \left({\frac { 1}{x}}+{\sqrt {{\frac {1}{x^{2}}}-1}}\right)=\ln \left({\frac {1+{\sqrt {1- x^{2}}}}{x}}\right)&&0<x\leq 1\\\operatorname {arcsch} (x)&=\ln \left({\frac {1}{x}}+{ \sqrt {{\frac {1}{x^{2}}}+1}}\right)&&x\neq 0\end{تراز شده}}$

+ نوشته شده در شنبه سوم اردیبهشت ۱۴۰۱ ساعت 10:33 توسط علی رضا نقش نیلچی |

1-توابع هذلولی

"منحنی هیپربولیک" به اینجا هدایت می شود. برای منحنی هندسی، Hyperbola را ببینید .

در ریاضیات , توابع هذلولی مشابه توابع مثلثاتی معمولی هستند , اما با استفاده از هذلولی به جای دایره تعریف می شوند . همانطور که نقاط (cost ، sin t ) دایره ای با شعاع واحد تشکیل می دهند ، نقاط (cosh t ، sinh t ) نیمه سمت راست هذلولی واحد را تشکیل می دهند. همچنین، به طور مشابه، مشتقات sin( t ) و cos( t ) cos( t ) هستند .و –sin( t ) ، مشتقات sinh( t ) و cosh( t ) cosh( t ) و +sinh( t ) هستند .

توابع هذلولی در محاسبات زوایا و فواصل در هندسه هذلولی رخ می دهند . آنها همچنین در راه حل های بسیاری از معادلات دیفرانسیل خطی (مانند معادله تعریف یک خطی )، معادلات مکعبی ، و معادله لاپلاس در مختصات دکارتی رخ می دهند. معادلات لاپلاس در بسیاری از زمینه های فیزیک از جمله نظریه الکترومغناطیسی ، انتقال حرارت ، دینامیک سیالات و نسبیت خاص مهم هستند.

توابع هذلولی اساسی عبارتند از: [1]

سینوس هذلولی "sinh" ( / ˈ s ɪ ŋ , ˈ s ɪ n tʃ , ˈ ʃ aɪ n / )، [2]
کسینوس هذلولی "cosh" ( / ˈ k ɒ ʃ , ˈ k oʊ ʃ / )، [3]

که از آن مشتق شده است: [4]

تانژانت هذلولی "tanh" ( / ˈ t æ ŋ , ˈ t æ n tʃ , ˈ θ æ n / )، [5]
کسکانت هذلولی "csch" یا "cosech" ( / ˈ k oʊ s ɛ tʃ , ˈ k oʊ ʃ ɛ k / [3] )
سکانت هذلولی "sech" ( / ˈ s ɛ tʃ , ˈ ʃ ɛ k / )، [6]
هذلولی همتنژانت "coth" ( / ˈ k ɒ θ , ˈ k oʊ θ / )، [7] [8]

مربوط به توابع مثلثاتی مشتق شده است.

توابع هذلولی معکوس عبارتند از:

سینوس هذلولی منطقه "arsinh" (همچنین به "sinh -1 "، "asinh" یا گاهی اوقات "arcsinh" نشان داده می شود) [9] [10] [11]
کسینوس هذلولی ناحیه "arcosh" (همچنین به "cosh -1 "، "acosh" یا گاهی اوقات "arccosh" نشان داده می شود)
و غیره

پرتویی از هذلولی واحد x 2 − y 2 = 1 در نقطه (cosh a , sinh a ) , جایی که a دو برابر مساحت بین پرتو، هذلولی و محور x است. برای نقاط روی هذلولی زیر محور x ، ناحیه منفی در نظر گرفته می شود ( نسخه متحرک با مقایسه با توابع مثلثاتی (دایره ای) را ببینید).

توابع هذلولی یک متغیر حقیقی به نام زاویه هذلولی می گیرند . اندازه یک زاویه هذلولی دو برابر مساحت بخش هذلولی آن است . توابع هذلولی ممکن است برحسب پایه های یک مثلث قائم الزاویه که این بخش را پوشش می دهد، تعریف شوند.

در تحلیل مختلط ، توابع هذلولی به عنوان بخش های مختلط سینوس و کسینوس به وجود می آیند. سینوس هیپربولیک و کسینوس هذلولی توابع کامل هستند . در نتیجه، سایر توابع هذلولی در کل صفحه مختلط مرومورفیک هستند.

بر اساس قضیه لیندمان – وایرشتراس ، توابع هذلولی برای هر مقدار جبری غیرصفری متغیر، یک مقدار ماورایی دارند . [12]

توابع هیپربولیک در دهه 1760 به طور مستقل توسط وینچنزو ریکاتی و یوهان هاینریش لامبرت معرفی شدند. [13] Riccati از Sc. و رونوشت ( sinus/cosinus circulare ) اشاره به توابع حلقوی و Sh. و چ. ( سینوس/کوسینوس هیپربولیکو ) برای اشاره به توابع هذلولی. لامبرت این نام ها را پذیرفت، اما اختصارات را به نام هایی که امروزه استفاده می شود تغییر داد. [14] اختصارات sh , ch , th , cth نیز در حال حاضر بسته به ترجیح شخصی استفاده می شود.

فهرست

1نشانه گذاری
2تعاریف
- 2.1تعاریف نمایی
- 2.2تعاریف معادلات دیفرانسیل
- 2.3تعاریف مختلط مثلثاتی
3ویژگی های مشخص کننده
- 3.1کسینوس هیپربولیک
- 3.2تانژانت هیپربولیک
4روابط مفید
- 4.1مجموع استدلال ها
- 4.2فرمول های تفریق
- 4.3فرمول های نیم متغیر
- 4.4فرمول های مربعی
- 4.5نابرابری ها
5توابع معکوس به عنوان لگاریتم
6مشتقات
7مشتقات دوم
8انتگرال های استاندارد
9عبارات سری تیلور
10ضربهای نامتناهی و کسرهای ادامه دار
11مقایسه با توابع دایره ای
12رابطه با تابع نمایی
13توابع هذلولی برای اعداد مختلط
14همچنین ببینید
15منابع
16لینک های خارجی

نشانه گذاری [ ویرایش ]

مقاله اصلی: توابع مثلثاتی § نمادگذاری

تعاریف [ ویرایش ]

سین ، کوش و تن

csch ، sech و coth

روش های معادل مختلفی برای تعریف توابع هذلولی وجود دارد.

تعاریف نمایی [ ویرایش ]

sinh x نصف اختلاف e x و e - x است

cosh x میانگین e x و e - x است _

از نظر تابع نمایی : [1] [4]

سینوس هیپربولیک: قسمت فرد تابع نمایی، یعنی

$\sinh x={\frac {e^{x}-e^{-x}}{2}}={\frac {e^{2x}-1}{2e^{x}}}= {\frac {1-e^{-2x}}{2e^{-x}}}.$
کسینوس هیپربولیک: قسمت زوج تابع نمایی، یعنی

$\cosh x={\frac {e^{x}+e^{-x}}{2}}={\frac {e^{2x}+1}{2e^{x}}}= {\frac {1+e^{-2x}}{2e^{-x}}}.$
مماس هیپربولیک:

$\tanh x={\frac {\sinh x}{\cosh x}}={\frac {e^{x}-e^{-x}}{e^{x}+e^{- x}}}={\frac {e^{2x}-1}{e^{2x}+1}}.$
کتانژانت هیپربولیک: برای x ≠ 0 ،

$\coth x={\frac {\cosh x}{\sinh x}}={\frac {e^{x}+e^{-x}}{e^{x}-e^{- x}}}={\frac {e^{2x}+1}{e^{2x}-1}}.$
سکانس هیپربولیک:

$\operatorname {sech} x={\frac {1}{\cosh x}}={\frac {2}{e^{x}+e^{-x}}}={\frac {2e ^{x}}{e^{2x}+1}}.$
کسکانت هذلولی: برای x ≠ 0 ،

$\operatorname {csch} x={\frac {1}{\sinh x}}={\frac {2}{e^{x}-e^{-x}}}={\frac {2e ^{x}}{e^{2x}-1}}.$

تعاریف معادلات دیفرانسیل [ ویرایش ]

توابع هذلولی را می توان به عنوان جواب معادلات دیفرانسیل تعریف کرد : سینوس و کسینوس هذلولی حل ( s , c ) یک سیستم هستند.

${\begin{aligned}c'(x)&=s(x),\\s'(x)&=c(x),\\\end{aligned}}$ با شرایط اولیه $s(0)=0,c(0)=1,$ جلوگیری از هر جفت عملکرد{ $(ae^{x}+be^{-x},ae^{x}-be^{-x})$ راه حل باشد

sinh( x ) و cosh( x ) نیز راه‌حل منحصربه‌فرد معادله f ″( x ) = f ( x ) هستند، به طوری که f (0) = 1 ، f ′(0) = 0 برای کسینوس هذلولی، و f (0) = 0 ، f ′(0) = 1 برای سینوس هذلولی.

تعاریف مختلط توابع مثلثاتی [ ویرایش ]

توابع هذلولی نیز ممکن است از توابع مثلثاتی با متغیر های مختلط استنتاج شوند:

سینوس هیپربولیک: [1]

$\sinh x=-i\sin(ix).$
کسینوس هیپربولیک: [1]

$\cosh x=\cos(ix).$
تانژانت هیپربولیک:

$\tanh x=-i\tan(ix).$
کتانژانت هیپربولیک:

$\coth x=i\cot(ix).$
سکانس هیپربولیک:
$\operatorname {sech} x=\sec(ix).$
کسکانت هیپربولیک:
$\operatorname {csch} x=i\csc(ix).$

جایی که i واحد موهومی با i 2 = −1 است.

تعاریف فوق به تعاریف نمایی از طریق فرمول اویلر مرتبط هستند (به § توابع هیپربولیک برای اعداد مختلط زیر مراجعه کنید).

+ نوشته شده در شنبه سوم اردیبهشت ۱۴۰۱ ساعت 10:29 توسط علی رضا نقش نیلچی |

اثبات :cosh(iz) = cos z sinh(iz) = i sin z cos(iz) = cosh z

منبع

https://slideplayer.com/slide/15536512/

+ نوشته شده در شنبه سوم اردیبهشت ۱۴۰۱ ساعت 10:12 توسط علی رضا نقش نیلچی |

بیان Artan(z) بر حسب ln

پس

https://www.arjay.bc.ca/Modula-2/Text/Ch17/Ch17.3.html

+ نوشته شده در شنبه سوم اردیبهشت ۱۴۰۱ ساعت 9:51 توسط علی رضا نقش نیلچی |

بیان Arccos(z) بر حسب ln

منبع

https://www.arjay.bc.ca/Modula-2/Text/Ch17/Ch17.3.html

+ نوشته شده در شنبه سوم اردیبهشت ۱۴۰۱ ساعت 9:45 توسط علی رضا نقش نیلچی |

بیان Arcsin(z) بر حسب ln

+ نوشته شده در شنبه سوم اردیبهشت ۱۴۰۱ ساعت 9:43 توسط علی رضا نقش نیلچی |

انتگرال نوع R

https://www.slideserve.com/xandy/7-calculus-of-residues

+ نوشته شده در شنبه سوم اردیبهشت ۱۴۰۱ ساعت 0:26 توسط علی رضا نقش نیلچی |

شرح ارزیابی انتگرال های معین انتگرال های مثلثاتی

https://www.slideserve.com/xandy/7-calculus-of-residues

+ نوشته شده در شنبه سوم اردیبهشت ۱۴۰۱ ساعت 0:18 توسط علی رضا نقش نیلچی |

ارزیابی انتگرال های معین انتگرال های مثلثاتی

8. ارزیابی انتگرال های معین انتگرال های مثلثاتی،

+ نوشته شده در شنبه سوم اردیبهشت ۱۴۰۱ ساعت 0:14 توسط علی رضا نقش نیلچی |

ادامه مثال باقی مانده

https://www.slideserve.com/xandy/7-calculus-of-residues

+ نوشته شده در جمعه دوم اردیبهشت ۱۴۰۱ ساعت 23:59 توسط علی رضا نقش نیلچی |

مثال از محاسبه باقیمانده توابع

+ نوشته شده در جمعه دوم اردیبهشت ۱۴۰۱ ساعت 23:54 توسط علی رضا نقش نیلچی |

محاسبه باقیمانده توابع

+ نوشته شده در جمعه دوم اردیبهشت ۱۴۰۱ ساعت 23:51 توسط علی رضا نقش نیلچی |

قضیه باقیمانده

7 calculus of residues n.

+ نوشته شده در جمعه دوم اردیبهشت ۱۴۰۱ ساعت 23:49 توسط علی رضا نقش نیلچی |

انواع تکینگی ها

5.2 انواع تکینگی ها

5.2.1. تکینگی جدا شده

یک نقطه z = z 0 می گویند تکینگی جدا شده از f(z) اگر

1. f(z) در z = z 0 تحلیلی نیست

2. همسایگی z = z 0 وجود دارد که هیچ تکینگی دیگری ندارد.

5.2.2. تکینگی قابل جابجایی:

اگر قسمت اصلی f(z) در بسط سری Laurent از f(z) حول نقطه z 0 صفر باشد، نقطه z = z 0 تکینگی قابل جابجایی نامیده می شود.

5.2.3. قطب:

اگر بتوانیم یک عدد صحیح مثبت n را طوری بیابیم که z!a (za) n f(z) 6= 0 باشد، آنگاه z = a قطبی از مرتبه n برای f(z) نامیده می شود.

5.2.4. تکینگی اساسی:

اگر قسمت اصلی f(z) در بسط سری Laurent از f(z) در مورد نقطه z 0 به صورت عددی دارای عبارات غیر صفر باشد، نقطه z = z 0 را تکینگی اساسی می گویند.

5.5.3 نمونه های کار شده

تابع f(z) در z = 0 تعریف نمی شود.

با قانون L'Hospital

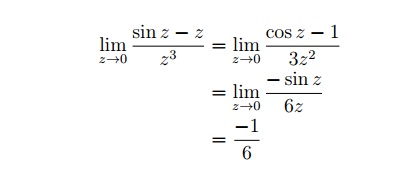
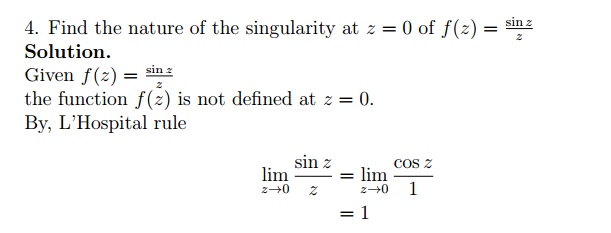
از آنجایی که حد وجود دارد و nite است، تکینگی در z = 0 یک تکینگی قابل جابجایی است.

5.5.4 مشکلات آموزشی

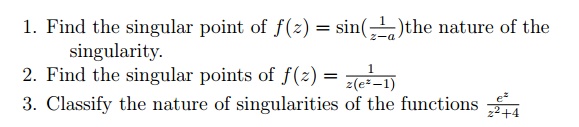
https://www.brainkart.com/article/Complex-Integration_6461/

+ نوشته شده در جمعه دوم اردیبهشت ۱۴۰۱ ساعت 11:48 توسط علی رضا نقش نیلچی |

سری تیلور سینوس در کسینوس

+ نوشته شده در جمعه دوم اردیبهشت ۱۴۰۱ ساعت 0:52 توسط علی رضا نقش نیلچی |

سری تیلور

از آنجا که

انتگرال آن دارای نمایش سری قدرت است

بیایید حد نسبت های مطلق این سری را پیدا کنیم:

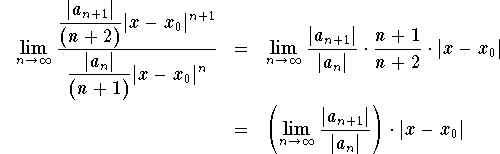
eqnarray14

اما توجه داشته باشید که این دقیقاً همان عبارتی است که هنگام محاسبه حد نسبتهای مطلق سری تیلور از f ( x ) به آن برخورد می کنیم. بنابراین هر دو سری شعاع همگرایی یکسانی دارند!

سری تیلور و چند جمله ای ها

سری تیلور چند جمله ای چیست؟

سری تیلور با مرکز یک چند جمله ای خود چند جمله ای است! (این را با چند جمله ای مورد علاقه خود بررسی کنید و از فرمول سری تیلور با مرکز استفاده کنید!)

اگر مرکز 0 نباشد چه؟ سپس شخص واقعاً چند جمله ای را بازنویسی می کند و به جای استفاده از آن به عنوان "بلوک های سازنده" آن استفاده می کند.

در اینجا یک مثال آورده شده است: سری تیلور را با مرکز چند جمله ای پیدا کنید. بیایید مشتقات آن را بگیریم و وصل کنیم :

بنابراین p (-1)=1+3+5=9.

p '( x )=2 x -3، بنابراین p '(-1)=-2-3=-5.

p ''( x )=2، بنابراین p ''(-1)=2.

تمام مشتقات بالاتر 0 هستند، بنابراین سری تیلور خاتمه می یابد!

با استفاده از فرمول ما به دست می آوریم:

از این رو، فهمیدن اینکه یک تابع دارای سری پایانی تیلور است، سخت نیست، اگر و فقط اگر تابع چند جمله ای باشد.

ضرب سری تیلور در چند جمله ای

بیایید سعی کنیم بسط سری تیلور با مرکز را پیدا کنیم .

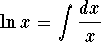برای پیدا کردن سری تیلور برای ، از آن استفاده کنید tex2html_wrap_inline177 . شما بسط را بدست می آورید:

displaymath165

همانطور که در مثال بالا می توانیم بازنویسی کنیم

سپس هر دو عبارت را ضرب می کنیم:

eqnarray60

بدون وارد شدن به جزئیات فنی: اگر اولین عبارت های این سری را بنویسید، می توانید قدرت های مربوط به ( x -1) را با هم ترکیب کنید تا شروع سری تیلور را برای f ( x ) بدست آورید:

خودت آن را امتحان کن!

تقریباً چندان پیچیده نیست: نمایش سری تیلور را با مرکز برای پیدا کنید.

منبع

http://www.sosmath.com/calculus/tayser/tayser05/tayser05.html

+ نوشته شده در پنجشنبه یکم اردیبهشت ۱۴۰۱ ساعت 23:35 توسط علی رضا نقش نیلچی |

بدست آوردن سری تیلور e^x/(1-x) و arctanx /e^x بروش صرب و تقسیم سری ها

می‌توانیم این سری‌ها را طوری ضرب کنیم که انگار سری‌های متناهی هستند. ما ضرایب را جمع آوری می کنیم:

جمله ثابت 1 است .
ترم درجه اول 1 + 1 = 2 است.
ترم درجه دوم 1 + 1 + 1/2 = 5/2 است.
ترم درجه سوم 1 + 1 + 1/2 + 1/6 = 8/3 است
ترم درجه چهارم 1 + 1 + 1/2 + 1/6 + 1/24 = 65/24 است.

ما می‌توانیم این فرآیند را به‌طور نامحدود ادامه دهیم، یا بهتر است از رایانه برای تولید شرایط استفاده کنیم.

سریال است

                      5 8 65
        1 + x +        x 2   +         x 3   +            x 4   + ...
                      2 3 24

تقسیم بندی سری های قدرت

فرض کنید می‌خواهیم نمایش سری توانی را در مخرج ضرب کنیم و ضرایب را برابر کنیم: (c 0 + c 1 x + c 2 x 2 + ...)(1 + x + x 2 /2 + x 3 /6 + x 4 /24 + ...) = (x - x 3 /3 + x 5 /5- x 7/7 + ...)

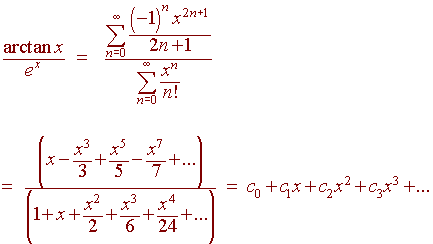
ضریب ثابت به ما c 0 = 0 می دهد .
عبارت درجه اول به ما c 0 + c 1 = 1 می دهد. بنابراین c 1 = 1 .
جمله درجه دوم 1 + c 2 = 0 به ما می دهد . بنابراین c 2 = -1 .
عبارت درجه سوم 1/2 - 1 + c 3 = -1/3 به ما می دهد . بنابراین c 3 = 1 - 1/2 - 1/3 = 1/6 .

و غیره

منبع

https://ltcconline.net/greenl/courses/107/Series/taylrser.htm

+ نوشته شده در پنجشنبه یکم اردیبهشت ۱۴۰۱ ساعت 23:22 توسط علی رضا نقش نیلچی |

مطالب قدیمی‌تر

آموزش ریاضی

نقطه بحرانی یک تابع متغیر واحد [ ویرایش ]

مثالها [ ویرایش ]

مکان نقاط بحرانی [ ویرایش ]

نقاط بحرانی یک منحنی ضمنی [ ویرایش ]

استفاده از تمایز [ ویرایش ]

چندین متغیر [ ویرایش ]

کاربرد بهینه سازی [ ویرایش ]

نقطه بحرانی یک نقشه مشتق پذیر [ ویرایش ]

کاربرد در توپولوژی [ ویرایش ]

همچنین ببینید [ ویرایش ]

یادداشت تاریخی [ ویرایش ]

تعریف [ ویرایش ]

نشانه گذاری [ ویرایش ]

ویژگی های اساسی [ ویرایش ]

توابع BMO به صورت محلی قابل ادغام p هستند [ ویرایش ]

BMO یک فضای Banach است [ ویرایش ]

میانگین مکعب های مجاور قابل مقایسه هستند [ ویرایش ]

BMO فضای برداری دوگانه H 1 است [ ویرایش ]

نابرابری جان-نیرنبرگ [ ویرایش ]

تعمیم ها و پسوندها [ ویرایش ]

فضاهای BMOH و BMOA [ ویرایش ]

فضای VMO [ ویرایش ]

ارتباط با تبدیل هیلبرت [ ویرایش ]

فضای دوتایی BMO [ ویرایش ]

مثالها [ ویرایش ]

ماتریس مزدوج چیست؟

مثالی از مزدوج یک ماتریس

خواص ماتریس مزدوج

توزیع ها، تک بعدی [ ویرایش ]

قضیه پلانچرل و قضیه پارسوال [ ویرایش ]

فرمول جمع پواسون [ ویرایش ]

تمایز [ ویرایش ]

قضیه کانولوشن [ ویرایش ]

قضیه همبستگی متقابل [ ویرایش ]

توابع ویژه [ ویرایش ]

ارتباط با گروه هایزنبرگ [ ویرایش ]

دامنه پیچیده [ ویرایش ]

تبدیل لاپلاس [ ویرایش ]

تبدیل فوریه برای توابعی که خارج از یک بازه صفر هستند [ ویرایش ]

مثال [ ویرایش ]

تاریخچه [ ویرایش ]

مقدمه [ ویرایش ]

استفاده از سینوسی های مختلط برای نمایش سینوس های حقیقی [ ویرایش ]

ویژگی های مشخصه [ ویرایش ]

کسینوس هایپربولیک [ ویرایش ]

مماس هایپربولیک[ ویرایش ]

روابط مفید [ ویرایش ]

مجموع آرگومان ها [ ویرایش ]

فرمول های تفریق [ ویرایش ]

فرمول های نیم آرگومان [ ویرایش ]

فرمول های مربعی [ ویرایش ]

نابرابری ها [ ویرایش ]

توابع معکوس به عنوان لگاریتم [ ویرایش ]

فهرست

نشانه گذاری [ ویرایش ]

تعاریف [ ویرایش ]

تعاریف نمایی [ ویرایش ]

تعاریف معادلات دیفرانسیل [ ویرایش ]

تعاریف مختلط توابع مثلثاتی [ ویرایش ]

سری تیلور و چند جمله ای ها

سری تیلور چند جمله ای چیست؟

ضرب سری تیلور در چند جمله ای

پیوندهای روزانه

نوشته‌های پیشین

آرشیو موضوعی

پیوندها

**توابع BMO به صورت محلی قابل ادغام p هستند [ ویرایش ]**

**فضای VMO [ ویرایش ]**