مثال واقع گرایانه [ ویرایش ]
مثالهای فوق ممکن است طبیعی به نظر نرسد ، اما در واقعیت ، هم جامعه بشری و هم طبیعت می توانند نمونه ای از معضلات زندانی را پیدا کنند و نتایج به همان ماتریس درآمد تقسیم می شود . علوم اجتماعی در اقتصاد ، علوم سیاسی و جامعه شناسی ، و همچنین علوم طبیعی ازرفتارشناسی ، زیست شناسی تکاملی و رشته های دیگر، می توان تجزیه و تحلیل وضعیت دشوار زندانی، شبیه سازی از بازی معضل صورت بیولوژیکی زندانی بی پایان استفاده می شود. معضل زندانی می تواند بسیار مورد استفاده قرار گیرد و این نشانگر اهمیت این بازی است. در زیر نمونه هایی از حلقه های مختلف:
مثال علوم سیاسی: مسابقه تسلیحاتی [ ویرایش ]
در علوم سیاسی ، مسابقه تسلیحاتی بین دو کشور را می توان در معضل زندانی توصیف کرد. هر دو کشور می توانند ادعا کنند که دو گزینه دارند: افزایش تسلیحات (خیانت) یا دستیابی به توافق کاهش سلاح (همکاری). هیچ یک از کشورها اطمینان ندارند که طرف دیگر به توافق نامه عمل کند ، بنابراین دو کشور در نهایت تمایل به افزایش تسلیحات خود خواهند داشت. به نظر می رسد متناقض است که اگرچه افزایش تسلیحات یک عمل "عقلانی" از دو کشور است ، اما نتیجه "غیر منطقی" است (به عنوان مثال آسیب به اقتصاد و غیره). این ممکن است در نظر گرفته می شود که شامل تئوری از استنتاج ، آن را به یک قوی است نیروی نظامی برای مهار حمله دیگر، به منظور دستیابی به صلح است.
مثال اقتصادی: جنگ تعرفه ای [ ویرایش ]
در دو کشور ، دو گزینه برای تعرفه وجود دارد :
- برای محافظت از کالاهای خود تعرفه را افزایش دهید. (خیانت)
- رسیده با دیگر توافقات تعرفه به کاهش تعرفه به منظور تسهیل در خود کالا گردش است. (همکاری)
هنگامی که یک کشور با توجه به برخی از شرایط عوامل تعرفه منطبق نیست، در حالی که بالا بردن تعرفه تنهایی (خیانت)، یک کشور دیگر در حال ساخت همان واکنش (همچنین خیانت) است، که به موجب جنگ تعرفه بین دو کشور در کالاها یکدیگر از دست داده بازار همچنین باعث خسارت به اقتصاد خود (نتیجه خیانت مشترک) می شود. سپس دو کشور توافق نامه تعرفه را دوباره برقرار کردند . ( نتیجه بازی های مکرر این است که مزایای همکاری متقابل بزرگترین آنها خواهد بود.)
مثال تجاری: جنگ تبلیغاتی [ ویرایش ]
نمونه هایی از معضلات زندانیان نیز در فعالیت های تجاری ظاهر می شوند. به عنوان نمونه از رقابت تبلیغاتی استفاده کنید.
این دو شرکت با یکدیگر به رقابت می پردازند و تبلیغات این دو شرکت بر یکدیگر تأثیر می گذارد ، یعنی اگر تبلیغات یک شرکت توسط مشتری پذیرفته شود ، بخشی از درآمد طرف مقابل را به خود جلب می کند. با این حال ، اگر این دو انتشار همزمان تبلیغات مشابه داشته باشند ، افزایش درآمد اندک است اما هزینه افزایش می یابد. اما اگر کیفیت تبلیغات خود را ارتقا ندهید ، تجارت شما توسط طرف دیگر از بین می رود.
این دو شرکت می توانند دو انتخاب داشته باشند:
- توافق نامه های متقابل برای کاهش هزینه های تبلیغات. ( همکاری )
- هزینه تبلیغات را افزایش دهید ، سعی کنید کیفیت تبلیغات را بهبود بخشید ، بر یکدیگر غلبه کنید. ( خیانت )
اگر دو شرکت به یکدیگر اعتماد ندارند ، نمی توانند همکاری کنند ، خیانت به یک استراتژی غالب تبدیل می شود ، شرکت دوم وارد جنگ تبلیغات می شود و افزایش در هزینه های تبلیغاتی به درآمد دو شرکت آسیب می زند ، که این معضل زندانی است. در واقعیت ، دستیابی به توافق نامه همکاری با دو شرکت رقیب دشوارتر است و بیشتر آنها در معضل زندانی قرار می گیرند.
مثال مسابقه دوچرخه [ ویرایش ]
استراتژی رقابت مسابقه دوچرخه سواری نیز یک بازی است و می توان نتایج تحقیقات معضل زندانی را توضیح داد. به عنوان مثال، برگزار می شود هر سال تور دو فرانس در موارد زیر: بازیکنان اغلب "راه رفتن در پایان مقابل تیم های بزرگ " (به فرانسوی: peloton ) راه رو به جلو، آنها را این استراتژی این است که خود را نه در پشت کنید، و بازده متوسط. مهمترین بازیکن در زمین باد پر تلاش ترین است ، بنابراین انتخاب سمت راست بدترین استراتژی است. معمولاً این اتفاق می افتد که در ابتدا همه مایل به پیشروی نیستند ( خیانت رایج ) که باعث می شود سرعت کلی بسیار کند شود و سپس معمولاً دو یا چند بازیکن سوار جبهه می شوند و سپس برای یک دوره زمانی اصلی ترین موقعیت را با یکدیگر مبادله می کنند. به اشتراک گذاشتنمقاومت در برابر باد ( همکاری ) باعث افزایش سرعت کل می شود و اگر یکی از افراد جلوی آن تلاش کند که موقعیت را در جلو نگه دارد ( خیانت ) ، سایر بازیکنان و تیم های بزرگ گیر می آیند ( خیانت مشترک ). و اغلب مورد، بیشترین تعداد بازیکنان در بالا ( همکاری ) معمولا در پشت بازیکن آخرین توان به گرفتن ( خیانت )، به دلیل پشت پخش سواری در مقابل بازیکنان جریان در، گردیده است.
وقایع مربوط به معضل زندانی [ ویرایش ]
ویلیام پوندستون در کتاب خود از مثال نیوزیلند برای نشان دادن معضل زندانی استفاده می کند. یک خواننده صادقانه در نیوزیلند وجود دارد. این کیوسک نه مدیر دارد و نه قفل. افرادی که روزنامه می خرید پول خود را می گذارند و روزنامه را می گیرند. البته ممکن است برخی افراد بدون پرداخت ( خیانت )روزنامه را بگیرند ، اما این بندرت به ندرت اتفاق می افتد زیرا همه می دانند که اگر همه روزنامه را بدزدند ( خیانت مشترک ) در آینده منجر به نتایج ناخوشایند و مضر خواهد شد. آنچه در این مثال خاص است این است که نیوزیلندی ها تحت تأثیر هیچ عامل دیگری نیستند و می توانند از معضل زندانی فرار کنند. هیچ کس توجه خاصی به روزنامه نمی کند مردم برای جلوگیری از عواقب خیانت مشترک از قوانین پیروی می کنند . با این روش معضل زندانی است استدلال و ایده های مشترک به نام " فانتزی (تفکر جادویی)". [3]
"مجازات گناه و کاهش حکم" عملی نیست [ ویرایش ]
نتیجه گیری معضل زندانی یکی از دلایلی است که جنایتکاران گروهی در بسیاری از کشورها نسبت به اعتراف به گناه اعتراف کرده اند (انگلیسی: plea pazgain). نتیجه گیری معضل زندانی این است که اگر دو مجرم وجود داشته باشد ، یکی از آنها مرتکب جرم و دیگری بی گناه می شود ، مرتکب به منظور کاهش حکم ( خیانت فردی ) به همه چیز و حتی بی گناه اعتراف می کند . در بدترین حالت ، اگر هر دوی آنها به زندان محکوم شوند ، متخلفین اعتراف شده احکام کمتری دارند و مجرمان بی گناه احکام بیشتری دارند.
تراژدی کالاهای عمومی [ ویرایش ]
در بازی واقعی بیش از یک مهمانی وجود دارد و معضل زندانی وجود خواهد داشت که شامل چندین مهمانی باشد. تراژدی کالاهای عمومی گارنتجیمز هاردین به عنوان نمونه ای است: "تراژدی کالاهای عمومی به این معنی است که اموال عمومی متعلق به بیشترین تعداد افراد ، اغلب کمترین مراقبت از آنها" ، مانند شیلات ، در دریاهای بلند است . ماهی عمومی است و طبق این عقیده که به طور غیرقابل تفریحی توسط دیگران دستگیر نشود ، صیادان در ماهیگیری بی بند و باری می شوند و در نتیجه محیط زیست دریایی از بین می رود و وضعیت معیشت صیادان تحت تأثیر قرار می گیرد ( نتیجه خیانت مشترک ). با این وجود ، مراجعه به معضل چند زندانی قابل سؤال نیست زیرا همواره می توان آن را به گروهی از زندانیان کلاسیک دو طرفه تقسیم کرد. یعنی فقط زندانیان دو طرف در وضعیت دشواری قرار دارند. معضل زندانی به اصطلاح چند حزبی فقط توهمی است که با اختلاط چندین زندانی دو طرفه ایجاد شده است.
معضل زندانی مکرر (چندین نفر) [ ویرایش ]
دانشمند آمریکایی سیاسی رابرت اکسلراد ( رابرت مارشال اکسلراد ) در کتاب خود " تکامل از همکاری " ( در تکامل از همکاری )، اکتشاف یک صحنه طولانی معمای زندانی های کلاسیک، و آن را "تکرار معضل زندانیان »(IPD). در این بازی ، شرکت کنندگان باید بارها و بارها استراتژی های مربوط به یکدیگر را انتخاب کرده و تقابل قبلی خود را به خاطر بسپارند. Axelrod از همسالان دانشگاهی در سراسر جهان برای طراحی استراتژی های رایانه ای دعوت می کند و در معضل تکراری زندانی ، با یکدیگر رقابت می کند . تفاوت در رویه های شرکت در مسابقه به طور گسترده در این زمینه ها وجود دارد: پیچیدگی الگوریتم ، رویارویی اولیه ، توانایی بخشش و غیره.
آکسلرود دریافت که وقتی این رویارویی ها برای هر یک از شرکت کنندگان که استراتژی های مختلفی را انتخاب می کردند ، مدت طولانی تکرار شد ، با قضاوت از دیدگاه خود علاقه مند ، استراتژی نهایی "حریص" نهایی کاهش می یابد و استراتژی " نوعدوست " مقایسه می شود. بیشتر به تصویب رسید. او از این بازی استفاده می کند تا نشان دهد از طریق انتخاب طبیعی ، مکانیسم رفتار نوع دوستانه ممکن است از مکانیسم خودخواهانه خالص اصلی تکامل یابد.
بهترین استراتژی تعیین کننده " دندان برای دندان " در نظر گرفته می شود ، روشی که توسط روانشناس ریاضی روسی-آمریکایی آناتول رپوپورت طراحی و اعمال شده است. این ساده ترین حالت از تمام ورودی ها است ، فقط شامل چهار خط BASIC است و بازی را به دست آورد. این استراتژی صرفاً همکاری در ابتدای بازی تکراری و سپس اتخاذ استراتژی دور قبلی حریف خود است. استراتژی بهتر این است که "دندان ها را ببخشید". هنگامی که حریف شما خیانت کرد ، به هر حال در دور بعدی با احتمال کمی (حدود 1٪ -5٪) همکاری خواهید کرد. این برای در نظر گرفتن بهبودی گاه به گاه از فریب چرخه خیانت است. وقتی سوءاستفاده وارد بازی شد ، "بخشش بهترین است". این بدان معنی است که گاهی اوقات اقدامات شما به اشتباه به طرف مقابلتان ابلاغ می شود: شما همکاری می کنید اما طرف مقابل شما می شنود که خیانت کرده اید.
Axelrod با تجزیه و تحلیل استراتژی نمره بالا چندین شرط لازم را برای موفقیت استراتژیک مشخص کرده است.
دوستانه: مهمترین شرط این است که استراتژی باید "دوستانه" باشد ، به این معنی که قبل از خیانت به حریف خیانت نکنید. تقریباً همه استراتژی های نمره بالا دوستانه هستند. بنابراین ، یک استراتژی کاملاً خودخواهانه فقط به دلایل خودخواهانه است و هرگز در ابتدا به مخالفان خود نخواهید رسید.
قصاص: با این حال ، اکسلد استدلال می کند که استراتژی موفقیت نباید خوش بینانه کور باشد. همیشه انتقام بگیر. نمونه ای از یک استراتژی غیر انتقام جویانه همیشه در کنار هم کار می کنند. این یک انتخاب بسیار بد است ، زیرا استراتژی "پایین دست" به طرز وحشیانه ای از چنین احمق ها سوءاستفاده می کند.
بخشش: یکی دیگر از کیفیتهای استراتژی موفقیت ، نیاز به بخشش است. اگرچه آنها تلافی نمی کنند ، اگر حریف به خیانت ادامه ندهد ، آنها به همکاری عقب می روند. این امر قصاص طولانی مدت و ضد تلافی را متوقف کرد و امتیازات را به حداکثر رساند.
عجیب نیست: آخرین کیفیت ارزش ندارد ، یعنی تلاش برای گرفتن امتیاز بالاتر از حریف (این نیز برای یک استراتژی "دوستانه" غیرممکن است ، به این معنی که استراتژی "دوستانه" هرگز نمی تواند بالاتر از حریف باشد. امتیاز)
بنابراین ، اکسلرود به این نتیجه رسید که تصورات اتوپیایی را به وجود آورد که نشان می دهد افراد خودخواه برای داشتن منافع خودخواهانه دوستانه ، بخشنده و ناعادلانه هستند. یکی از نتیجه گیری های مهم تحقیقات Axelrod در مورد تکرار معضل زندانی این است که بچه های دوست می توانند ابتدا معامله را انجام دهند.
تجدید معضل زندانی کلاسیک یک داده نژاد مدل: این نتیجه رسیدند که تنها استراتژی عقلانی به منظور افزایش نظامی، به نظر می رسد که این دو کشور ترجیح می دهند به صرف خود تولید ناخالص داخلی در اسلحه به جای کره. جالب توجه است، در واقع، تلاش برای توضیح این کشور در این راه (بین "معضل زندانی تکرار است فرض" در زمان های مختلف هزینه های نظامی در "بالا" و "پایین" در برابر تکرار تلاش برای رقابت)، اما اغلب آن را نشان می دهد که قلمداد مسابقه تسلیحات همانطور که انتظار می رفت ظاهر نمی شد. (به عنوان مثال ، به نظر نمی رسد که مخارج نظامی یونانی ها وترک ها دنبال مسابقه اسلحه معضل زندانی باشند ، اما به احتمال زیاد توسط سیاست های داخلی آنها هدایت می شوند.) این ممکن است یک بازی یک بار و تکرار باشد. نمونه های مختلف رفتار منطقی در بازی های جنسی.
برای یک بازی معضل یک بار زندانی ، بهترین استراتژی (حداکثر امتیاز) صرفاً خیانت است ؛ همانطور که در ابتدا توضیح داده شد ، این مهم است که مهم نیست اقدامات طرف مقابل چیست. اما ، در یک بازی معضل زندانی مکرر ، بهترین استراتژی به استراتژی های مخالفان احتمالی و نحوه واکنش آنها به خیانت و همکاری متکی است. به عنوان مثال ، جمعیتی را در نظر بگیرید که هرکس هر بار به آن خیانت می کند ، به جز اینکه یک نفر از یک راهبرد دندان به انگشتان پا پیروی کند. این فرد به دلیل از دست دادن دور اول در یک نقطه ضعف قرار دارد. در چنین جمعیتی ، بهترین استراتژی برای این شخص خیانت در هر زمان است. در جمعیتی که درصد مشخصی از کل افراد خیانتکار و بقیه افرادی که دندان شیری دارند ، بهترین استراتژی برای افراد به این درصد و طول بازی بستگی دارد.
به طور کلی دو روش برای به دست آوردن بهترین استراتژی وجود دارد:
- تعادل نشانی بیزی: اگر توزیع آماری استراتژی های رویارویی مشخص شود (به عنوان مثال 50٪ دندان ها ، 50٪ با هم کار می کنند) ، بهترین استراتژی نسبی را می توان از لحاظ ریاضی بدست آورد [4] .
- در حال حاضر شبیه سازی مونت کارلو از جمعیت وجود دارد ، که در آن افراد با امتیاز کم ناپدید می شوند و افراد با نمره بالا به طور مکرر تولید می شوند (الگوریتمی نبوغ که بهترین استراتژی را بدست می آورد). سنتز الگوریتم در جمع نهایی معمولاً بستگی به ترکیب الگوریتم در مسابقه مقدماتی دارد.
اگرچه دندان در برابر دندان همواره استراتژی اساسی قابل اطمینان ترین در نظر گرفته شده است، اما معضل زندانی تکرار است سالگرد 20th باشد از مسابقه است، از بریتانیا دانشگاه ساوتهمپتون، یک گروه (از نیکلاس جنینگز رهبری (نیکلاس جنینگز) [1] ، از جمله Rajdeep Dash ، Sarvapali Ramchurn ، الکس راجرز و Perukrishnen Vytelingum ) استراتژی جدیدی را ارائه داد که ثابت کرد که موفقیت بیشتری نسبت به دندان برای دندان دارد. این استراتژی برای دستیابی به بیشترین تعداد امتیاز در یک برنامه واحد ، به همکاری بین برنامه ها متکی است. دانشگاه ساوتهمپتون 60 برنامه برای شرکت در این مسابقه ارسال کرده است.در آغاز این برنامه ها برای شناسایی یکدیگر از طریق مجموعه 5 تا 10 عمل طراحی شده است. پس از شناسایی این شناسنامه ها ، همیشه یک برنامه همکاری خواهد کرد و سایر برنامه ها همیشه خیانت می کنند ، و اطمینان می دهند که خیانتکار حداکثر امتیاز را کسب می کند. اگر برنامه تشخیص دهد كه مشاركت كننده غیر ساوتهمپتون را اجرا می كند ، در تلاش برای به حداقل رساندن نمره فرایند رقابت ، این خیانت ادامه خواهد یافت. نتیجه [5] ، این استراتژی برای به دست آوردن 3 نفر برتر به رقابت پایان داد ، همچنین موقعیتهای بسیاری نزدیک به پایین داشت. اگرچه این استراتژی به طور قابل توجهی نشان داده است که از دندان موثرتر است ، اما به این دلیل است که چندین کانال در این رقابت خاص مجاز است. در مسابقه ای که یک طرف فقط می تواند یک شرکت کننده را کنترل کند ، در واقع یک راه حل بهتر برای ساختن دندان است.
اگر معضل زندانی تکراری دقیقاً N بار تکرار شود ، دانستن اینکه N ثابت است ، پس یک واقعیت جالب دیگر بوجود می آید. تعادل نش هر بار خیانت است. این با القاء آسان است. همچنین می توانید در دور نهایی خیانت کنید ، زیرا حریف شما هیچ فرصتی برای مجازات شما نخواهد داشت. بنابراین ، شما در دور نهایی خیانت خواهید کرد. در این زمان ، شما می توانید در دور مقدماتی خیانت کنید ، زیرا آخرین بار مهم نیست که چه کاری انجام می دهید ، حریف شما خیانت خواهد کرد. و غیره برای همکاری برای حفظ درخواست ، آینده برای هر دو شرکت نامشخص است. یک راه حل این است که تعداد کل بازی های N را نامحدود یا غیرقابل پیش بینی کنید. انتظارات برای آینده باید از پیش تعیین نشده باشد.
مورد جداگانه دیگر معضل زندانی در مورد "هرگز متوقف" نیست. این بازی بارها و بارها تکرار می شود ، و نمره شما به طور متوسط (البته توسط کامپیوتر محاسبه می شود).
بازی معضلات زندانیان اساس برخی از تئوری های همکاری انسانی و اعتماد است. با فرض اینکه معضل زندانی می تواند ارتباطات بین دو نفر را که باید به آنها اعتماد کرد ، شبیه سازی کند ، رفتار مشارکتی این گروه را می توان با انواع مختلفی از بازیکنان با بازی های مکرر مدل کرد. این امر باعث شده است که علاقه مندی پایدار بسیاری از دانشمندان وجود داشته باشد. در سال 1975 ، گروفمن و استول تخمین زدند که بیش از 2،000 مقاله علمی به تحقیقات در این زمینه اختصاص یافته است.
روانشناسی یادگیری و نظریه بازی [ ویرایش ]
هنگامی که شرکت کنندگان در بازی می توانند یاد بگیرند که احتمال خیانت توسط سایر شرکت کنندگان را تخمین بزنند ، رفتار خودشان تحت تأثیر تجربه آنها با دیگران قرار می گیرد. آمارهای ساده نشان می دهد که ، به طور کلی ، تعامل شرکت کنندگان بی تجربه با سایر شرکت کنندگان یا به طور معمول خوب است یا به طور معمول بد است. اگر براساس این تجربیات عمل کنند (از طریق خیانت بیشتر یا همکاری ، در غیر این صورت) ممکن است در معاملات آینده آسیب ببینند. با تجربه به دست آمده ، آنها تصور واقع بینانه تری از احتمال خیانت به دست آوردند و در بازی موفق تر شدند. تأثیر معاملات اولیه که توسط شرکت کنندگان نابالغ در مشارکت آینده آنها تجربه شده ممکن است بسیار بیشتر از تأثیر این معاملات بر شرکت کنندگان بالغ باشد. این اصول تا حدودی توضیح می دهند که چرا تجربیات رشد جوانان اینقدر تأثیرگذار است و چرا به ویژه در مقابل زورگویی آسیب پذیر هستند ، و گاهی خود آنها قلدر می شوند.
احتمال خیانت در گروه می تواند با تجربه همکاری تضعیف شود [6] ، زیرا بازی قبلی اعتماد ایجاد کرد . بنابراین ، رفتار فداکارانه می تواند مثلاً خصوصیات اخلاقی گروه را تقویت کند. اگر گروه كوچك باشد ، رفتار مثبت احتمالاً بازخورد را به روشی مثبت با هم خواهد گرفت - افراد گروه را ترغیب می كنند كه به همكاری خود ادامه دهند. این مربوط به یک معضل مشابه است: به کسانی که از آنها کمک می شود تشویق شوند که از رفتارهایی که ممکن است آنها را در معرض خطر قرار دهد ، راضی شوند. چنین روشهایی در درجه اول در مطالعه نوع دوستی متقابل ، انتخاب گروه ، انتخاب خون و فلسفه اخلاقی نقش دارند .
بازی مرتبط [ ویرایش ]
معامله کیف بسته [ ویرایش ]
هافستادتر 2 سوالاتی مانند معضل زندانی را مطرح کرده است. او پیشنهاد "معامله کیسه ای بسته" را داد که به عقیده وی به افراد کمک می کند تا با این سوال بازی ساده این موضوع را درک کنند.
"معامله کیسه های بسته شده": A و B کیسه های بسته بندی شده رو در رو مبادله می کنند. اجماع هر دو طرف این است که یک کیف پول می گذارد و B کالا را قرار می دهد . هر طرف می تواند صادقانه چیزهایی را در کیسه قرار داده و سپس آنها را مبادله کند ؛ یا آنها می توانند کیسه را به طرف مقابل خالی کنند و خیانت کنند.
در این بازی به دلیل فواید بسیار زیاد خیانت ، افراد زیادی وجود دارند که خیانت را انتخاب می کنند. این به این معنی است که تاجر عقلانی نیست که انجام این معاملات، در نتیجه "بستن یک معامله کیسه" با توجه به انتخاب نامساعد و از دست دادن بازار .
آیا دشمن است یا دوست؟ [ ویرایش ]
"دوست یا دشمن؟" آیا اجرای مسابقه، 2002 تا 2005 در ایالات متحده آمریکا رقابت های شبکه پخش نشان می دهد (بازی نمایش شبکه). این نمونه ای از بازی معضل زندانی با افراد واقعی است ، اما صحنه مصنوعی است. سه جفت نفر در این مسابقه شرکت می کنند. وقتی هر جفت از بین رفت ، آنها بازی معضل زندانی را انجام می دهند و تصمیم می گیرند که چگونه جوایز خود را تقسیم کنند. اگر همه آنها همکاری کنند ("دوستان") ، جوایز آنها به طور مساوی تقسیم می شود. اگر یکی همکاری کند و دیگری خیانت کند ("دشمن") ، خائن همه جوایز را می گیرد ، و همکاران نمی توانند چیزی بدست آورند. اگر دو طرف به یکدیگر خیانت کنند ، آنگاه هردو هیچی ندارند. توجه داشته باشید که این ماتریس پرداخت با ماتریس پرداخت استاندارد فوق الذکر متفاوت است ، زیرا از بین رفتن وضعیت "خیانت متقابل" و پرونده "من با حریف خیانت می کنم همکاری می کنم" یکسان است. در مقایسه با تعادل پایدار معضل زندانی استاندارد ، "خیانت متقابل" یک تعادل ضعیف است. اگر بدانید که حریف شما به "دشمن" تبدیل می شود ، پس انتخاب شما تاثیری در جایزه شما نخواهد داشت. به تعبیری ، "دشمن است یا دوست" الگوی درآمد بین "معضل زندانی" و "مرغ" دارد.
این ماتریس درآمد:
- اگر شرکت کنندگان با هم کار کنند ، هر 1+ می شود.
- اگر به آنها خیانت شود ، هر یک 0 می شود.
- اگر A همکاری کند و B خیانت کند ، A 0 می شود و B +2 می شود.
این دشمن و دوستی است که برای کسانی که می خواهند یک تحلیل واقع بینانه از معضل زندانی انجام دهند ، مفید خواهد بود. خاطرنشان كرد: شركت كنندگان فقط یك بار می توانند این كار را انجام دهند ، بنابراین تمام ایده هایی كه شامل بازی های مكرر هستند كاربردی ندارند و استراتژی "دندان به دندان" قابل توسعه نیست.
در مورد دشمنان و دوستان ، هر یک از شرکت کنندگان مجاز به اظهارنظر هستند ، به طوری که یک رفیق دیگر اطمینان دارد که قبل از اینکه دو طرف مخفیانه تصمیم به همکاری یا خیانت بگیرند ، دوستانه دوست هستند. راه "شکستن سیستم" این خواهد بود که یک شرکت کننده به طرف مقابل خود می گوید: "من دشمن را انتخاب می کنم. اگر فکر می کنید بعدا به شما پاداش می دهم ، دوست را انتخاب می کنم. در غیر اینصورت ، اگر شما دشمن را انتخاب می کنید ، ما این دست خالی خواهد بود. "یک نسخه حریص تر خواهد بود:" من دشمن را انتخاب خواهم کرد. من به شما درصد X را می دهم و درصد باقیمانده (100-X) مال من خواهد بود. بنابراین ، اگر می خواهید یا نه ، یا همه ما مقداری بدست می آوریم ، یا چیزی برای به دست آوردن نداریم. "(در بازی Ultimatum ). این ترفند اکنون تلاش برای کاهش آن X٪ و نگه داشتن رقیب دیگر است که هنوز هم دوست خود را انتخاب می کند. اصولاً این شرکت کننده باید این مرز را بشناسد ، جایی که ابزار حریف وی از دیدن او چیزی بیش از آن چیزی نیست که بتواند در صورت موفقیت ، از پولی که بدست می آورد ، کسب کند.
این روش هرگز در رقابت آزمایش نشده است ؛ ممکن است به این دلیل باشد که داوران اجازه نمی دهند و حتی در صورت اجازه ، نابرابری به دلیل استفاده از این قانون منجر به بازده مورد انتظار کمتر می شود (آخرین بازی تلاش شده در بازی یک شبه ) نتیجه ، رد پیشنهادهای زیاد و نابرابر است ، در بعضی موارد ، معادل دو هفته دستمزد با توجه به اینكه جوایز هر دو شركت كننده در اولویت قرار ندارند ، در اولویت قرار دارد.




 از جانب
از جانب  به
به  به طوری که
به طوری که برای همه
برای همه  و
و  که در
که در پیوند مزدوج است
پیوند مزدوج است  برای همه غیروزارها واقعی و مثبت است
برای همه غیروزارها واقعی و مثبت است  ؛ این در صورتی است که فقط و فقط اگر
؛ این در صورتی است که فقط و فقط اگر ماتریس فرعی به نظر می رسد که اگر همه این عوامل تعیین کننده مثبت باشند ، یک ماتریس مثبت است. این شرط به عنوان
ماتریس فرعی به نظر می رسد که اگر همه این عوامل تعیین کننده مثبت باشند ، یک ماتریس مثبت است. این شرط به عنوان  معیار سیلوستر معادل بررسی اینکه آیا عناصر مورب آن همه مثبت هستند یا خیر. این وضعیت را می توان هر بار که یک ردیف جدید بررسی کرد
معیار سیلوستر معادل بررسی اینکه آیا عناصر مورب آن همه مثبت هستند یا خیر. این وضعیت را می توان هر بار که یک ردیف جدید بررسی کرد مثبت (نیمه) قطعی است.
مثبت (نیمه) قطعی است. به طوری که
به طوری که  برای همه
برای همه .
. به
به  می تواند به عنوان نوشته شود
می تواند به عنوان نوشته شود  جایی که
جایی که  واقعی است
واقعی است -وکتور ، و
-وکتور ، و  یک ثابت واقعی این عملکرد درجه دوم کاملاً محدب است و از این رو حداقل و در صورت محدود بودن حداقل جهانی منحصر به فرد دارد
یک ثابت واقعی این عملکرد درجه دوم کاملاً محدب است و از این رو حداقل و در صورت محدود بودن حداقل جهانی منحصر به فرد دارد یک ماتریس مشخص و متقارن و مثبت. معادله ویژه مقدماتی عمومی را بنویسید
یک ماتریس مشخص و متقارن و مثبت. معادله ویژه مقدماتی عمومی را بنویسید جایی که ما آن را تحمیل می کنیم
جایی که ما آن را تحمیل می کنیم  . اکنون ما برای
. اکنون ما برای  . ضرب توسط
. ضرب توسط و اجازه دادن
و اجازه دادن ، ما گرفتیم
، ما گرفتیم ، که می تواند بازنویسی به عنوان
، که می تواند بازنویسی به عنوان  جایی که
جایی که  . دستکاری اکنون بازده است
. دستکاری اکنون بازده است جایی که
جایی که  یک ماتریس است که به عنوان ستون های ویژه مجرای عمومی و
یک ماتریس است که به عنوان ستون های ویژه مجرای عمومی و یک ماتریس مورب از مقادیر ویژه ای تعمیم یافته است. در حال حاضر نسخه آزمایشی با\
یک ماتریس مورب از مقادیر ویژه ای تعمیم یافته است. در حال حاضر نسخه آزمایشی با\ نتیجه نهایی را می دهد:
نتیجه نهایی را می دهد:  و
و اما توجه داشته باشید که این دیگر یک مورب شدن متعامد با توجه به کالای داخلی است که در آن وجود ندارد
اما توجه داشته باشید که این دیگر یک مورب شدن متعامد با توجه به کالای داخلی است که در آن وجود ندارد  قطعی مثبت است (و به همین ترتیب نیمه مثبت قطعی نیز مثبت است). این یک ماتریس متقارن واقعی است ، و برای هر بردار ستونی غیر صفر z با ورودی های واقعی a و b ،
قطعی مثبت است (و به همین ترتیب نیمه مثبت قطعی نیز مثبت است). این یک ماتریس متقارن واقعی است ، و برای هر بردار ستونی غیر صفر z با ورودی های واقعی a و b ، .
. .
. و
و 

 ، یعنی وقتی z بردار صفر است.
، یعنی وقتی z بردار صفر است. ، ضرب
، ضرب یک ماتریس قطعی مثبت است. اثبات ساده این است که برای هر بردار غیر صفر وجود دارد
یک ماتریس قطعی مثبت است. اثبات ساده این است که برای هر بردار غیر صفر وجود دارد از آنجا که غیرقابل برگشت بودن ماتریس است
از آنجا که غیرقابل برگشت بودن ماتریس است 


 باشد
باشد  یک
یک  یک
یک  نشان میدهد که
نشان میدهد که برای هر بردار پیچیده واقعی و مثبت است
برای هر بردار پیچیده واقعی و مثبت است  برای هر کسی واقعی و مثبت است
برای هر کسی واقعی و مثبت است 







 برخی از ماتریس
برخی از ماتریس  سپس یکی ماتریس را تغییر می دهد
سپس یکی ماتریس را تغییر می دهد ، و یکی می خواهد تجزیه Cholesky ماتریس به روز شده را محاسبه کند:
، و یکی می خواهد تجزیه Cholesky ماتریس به روز شده را محاسبه کند: . حال این سؤال مطرح است که آیا می توان از تجزیه چولسکی استفاده کرد؟
. حال این سؤال مطرح است که آیا می توان از تجزیه چولسکی استفاده کرد؟ ، به عنوان یک به روزرسانی درجه یک شناخته می شود .
، به عنوان یک به روزرسانی درجه یک شناخته می شود . . این تنها در صورت ماتریس جدید کار می کند
. این تنها در صورت ماتریس جدید کار می کند


 بدون محاسبه مستقیم کل تجزیه.
بدون محاسبه مستقیم کل تجزیه.
 برای راه حل
برای راه حل ، که می توان به راحتی برای ماتریس های مثلثی پیدا کرد ، و
، که می توان به راحتی برای ماتریس های مثلثی پیدا کرد ، و برای تجزیه Cholesky از
برای تجزیه Cholesky از  روابط زیر را می توان یافت:
روابط زیر را می توان یافت:




 ، که به آنها اجازه می دهد تا با استفاده از روشهای به روزرسانی و downdate که به تفصیل در قسمت قبلی شرح داده شده ، محاسبه شوند.
، که به آنها اجازه می دهد تا با استفاده از روشهای به روزرسانی و downdate که به تفصیل در قسمت قبلی شرح داده شده ، محاسبه شوند.  متشکل از
متشکل از 
 تجزیه Cholesky است
تجزیه Cholesky است  . براساس ویژگی هنجار اپراتور ،
. براساس ویژگی هنجار اپراتور ،
 یک مجموعه محدود در
یک مجموعه محدود در  . به راحتی قابل بررسی است که این
. به راحتی قابل بررسی است که این
 مثلث پایین با ورودی های مورب غیر منفی است ،
مثلث پایین با ورودی های مورب غیر منفی است ،  . اکنون می توان
. اکنون می توان  ، منجر به
، منجر به ، جایی که
، جایی که واحد است و
واحد است و  مثلث فوقانی است درج تجزیه در بازده اصلی برابری
مثلث فوقانی است درج تجزیه در بازده اصلی برابری . تنظیمات
. تنظیمات اثبات را کامل می کند.
اثبات را کامل می کند. دنباله ای از
دنباله ای از 



 ، سپس یک ماتریس اپراتور مثلثی L پایین وجود دارد به گونه ای که A = LL *. همچنین می توان ورودی های مورب L را مثبت دانست.
، سپس یک ماتریس اپراتور مثلثی L پایین وجود دارد به گونه ای که A = LL *. همچنین می توان ورودی های مورب L را مثبت دانست.


![\ mathbf {J} _ {\ mathbf {f} x (x، y) = {\ آغاز {bmatrix {\ dfrac {\ جزئی f_ {1}} {\ جزئی x}} & {\ dfrac {\ جزئی f_ 1}} {\ part y y}} \\ [1em] {\ dfrac {\ partial f_ {2}} part \ partial x}} & {\ dfrac {\ جزئی f_ {2}} {\ جزئی y}} \ end {bmatrix}} = {\ fill bmatrix} 2xy & x ^ {2} \\ 5 & \ cos y \ end {bmatrix](https://wikimedia.org/api/rest_v1/media/math/render/svg/7fe3958d277972f8ea78a75384d7d4c1ceceb185)


![\ displaystyle \ mathbf {J} _ {\ mathbf {F} r (r، \ varphi) = {\ آغاز {bmatrix} {\ dfrac {\ جزئی x} {\ جزئی جزئی r}} & {\ dfrac {\ جزئی x} {\ partial \ varphi}} \\ [1em] {\ dfrac {\ partial y} {\ partial r}} & {\ dfrac {\ partial y} {\ partial \ varphi} \ end {bmatrix} = {\ fill bmatrix \ cos \ varphi & -r \ sin \ varphi \\\ sin \ varphi & r \ cos \ varphi \ end {bmatrix}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/f7f070cf16746e85af8ccc976cdfa318b7d29212)


![\ displaystyle \ mathbf {J} _ {\ mathbf {F}} (r، \ theta، \ varphi) = {\ آغاز {bmatrix} {\ dfrac {\ جزئی x} {\ جزئی r r} & {\ dfrac \ partial x} {\ partial \ phi}} & {\ dfrac {\ partial x} {\ partial \ vartheta}} \\ [1em] {\ dfrac {\ partial y} {\ جزئی r}} & {\ dfrac {\ partial y} {\ partial \ phi}} & {\ dfrac {\ part y y} {\ partial \ vartheta}} \\ [1em] \ dfrac {\ partial z} {\ جزئی r}} & { \ dfrac {\ partial z {\ partial \ phi}} & {\ dfrac {\ partial z} {\ partial \ vartheta} \ end {bmatrix}} = {\ fill bmatrix} \ sin \ vartheta \ cos \ phi & -r \ sin \ vartheta \ sin \ phi & r \ cos \ vartheta \ cos \ phi \\\ sin \ vartheta \ sin \ phi & r \ sin \ vartheta \ cos \ phi & r \ cos \ vartheta \ sin \ phi \ \\ cos \ vartheta & 0 & -r \ sin \ vartheta \ end {bmatrix}.](https://wikimedia.org/api/rest_v1/media/math/render/svg/52b07633ac88e9456ea078064b551294101aff47)

![\ mathbf {J} _ {\ mathbf {F}} (x_ {1}، x_ {2}، x_ {3}) = {\ آغاز {bmatrix {\ dfrac {\ جزئی y_ {1}} {\ جزئی x_ {1}}} & {\ dfrac {\ part y_ {1}} {\ partial x_ {2}}} & {\ dfrac {\ جزئی y_ {1}} {\ جزئی x_ {3}}} \\ [1em] \ dfrac {\ جزئی y_ {2}} {\ جزئی x_ {1}}} & {\ dfrac {\ جزئی y_ {2}} {\ جزئی x_ {2}}} & {\ dfrac {\ جزئی y_ {2}} part \ جزئی x_ {3}}} \\ [1em] {\ dfrac {\ جزئی y_ {3}} {\ جزئی x_ {1}}} & {\ dfrac {\ جزئی y_ {3 }} {\ partial x_ {2}}} & {\ dfrac {\ part y y {3}} {\ partial x_ {3}}} \\ [1em] \ dfrac {\ جزئی y_ {4}} {\ جزئی x_ {1}}} & {\ dfrac {\ جزئی y_ {4}} {\ جزئی x_ {2}}} & {\ dfrac {\ جزئی y_ {4}} {\ جزئی x_ {3}}} \ end bmatrix}} = {\ fill {bmatrix} 1 & 0 & 0 \\ 0 & 0 & 5 \\ 0 & 8x_ {2} & - 2 \\ x_ {3} \ cos x_ {1} & 0 & \ sin x_ {1} \ end {bmatrix}} .](https://wikimedia.org/api/rest_v1/media/math/render/svg/c8cdd61024fb8153b850520350a6a90648e454a9)


 L(x
L(x (در مقابل ، فضای دوتایی مداوم H با مشخص شده است
(در مقابل ، فضای دوتایی مداوم H با مشخص شده است ) و با تحمل آن با هنجار متعارف (به همان روشی كه هنجار كانونی در فضای دوتایی مداوم H است تعریف می کنیم) به یك
) و با تحمل آن با هنجار متعارف (به همان روشی كه هنجار كانونی در فضای دوتایی مداوم H است تعریف می کنیم) به یك  برای همه X ، Y ∈ H .
برای همه X ، Y ∈ H .  ، تعریف شده توسط x ↦ B ( x ، x ) 1/2 ، در صورتی که اگر B نیز قطعی مثبت باشد ، این نقشه یک
، تعریف شده توسط x ↦ B ( x ، x ) 1/2 ، در صورتی که اگر B نیز قطعی مثبت باشد ، این نقشه یک  تعریف شده توسط
تعریف شده توسط  ، جایی که
، جایی که  نقشه تعریف شده توسط [y ↦ B ( x ، y ).
نقشه تعریف شده توسط [y ↦ B ( x ، y ). 
 ) و R یک
) و R یک  )
)
![{\ displaystyle A = \ left [\ mathbf {a} _ {1}، \ ldots، \ mathbf {a} _ {n} \ Right]](https://wikimedia.org/api/rest_v1/media/math/render/svg/60dd9beb7731c713aa7aeeaa2aeddf6fe992d2fb)
 (یا
(یا برای مورد پیچیده).
برای مورد پیچیده).

 بر اساس مبنای ارتودنسی تازه محاسبه شده ما:
بر اساس مبنای ارتودنسی تازه محاسبه شده ما:
 . این را می توان به شکل ماتریس نوشت:
. این را می توان به شکل ماتریس نوشت:
![{\ displaystyle Q = \ left [\ mathbf {e} _ {1}، \ ldots، \ mathbf {e} _ {n} \ Right]](https://wikimedia.org/api/rest_v1/media/math/render/svg/4870cf012233565bea374e174ab454c41f0cf889)






 . ما می توانیم از یک طرح ریزی متعامد (گرم-اشمیت) استفاده کنیم اما اگر بردارها از نظر عددی ناپایدار باشند.
. ما می توانیم از یک طرح ریزی متعامد (گرم-اشمیت) استفاده کنیم اما اگر بردارها از نظر عددی ناپایدار باشند. یک واقعی خودسرانه متر بردار ستونی بعدی از
یک واقعی خودسرانه متر بردار ستونی بعدی از برای یک اسکالر α . اگر این الگوریتم با استفاده از
برای یک اسکالر α . اگر این الگوریتم با استفاده از  این است که به محور مختصات و پس از آن تمام پست های 0 در ماتریس ، بازدید کنندگان نهایی شکل مثلثی بالا، برای جلوگیری از
این است که به محور مختصات و پس از آن تمام پست های 0 در ماتریس ، بازدید کنندگان نهایی شکل مثلثی بالا، برای جلوگیری از 
 وکتور است (1 0… 0) T ، || · || است
وکتور است (1 0… 0) T ، || · || است  یک IS متر -by- متر ماتریس، مجموعه ای
یک IS متر -by- متر ماتریس، مجموعه ای




 تکرار این روند ،
تکرار این روند ، ،
،





 ، به
، به 


 و
و
 و
و و بعد
و بعد









 و از
و از  -ماتریکس
-ماتریکس به معنای دقیق (همچنین: به شدت یا به شدت) مورب مسلط است ، اگر مقادیر عناصر مورب آنها باشد
به معنای دقیق (همچنین: به شدت یا به شدت) مورب مسلط است ، اگر مقادیر عناصر مورب آنها باشد هر کدام از تعداد مبالغ ورودی های خط مربوطه بیشتر هستند
هر کدام از تعداد مبالغ ورودی های خط مربوطه بیشتر هستند د. یعنی اگر برای همه باشد
د. یعنی اگر برای همه باشد اعمال می شود
اعمال می شود  .
. .
.

 شود
شود  ارضا می کند
ارضا می کند برای همه
برای همه بنابراین یک
بنابراین یک  ارضا می کند
ارضا می کند برای همه
برای همه بنابراین ، این همجنسگرایی است.
بنابراین ، این همجنسگرایی است. و
و  نشان می دهد که
نشان می دهد که 
 می
می  ، اعداد صحیح از 0 به 5 با
، اعداد صحیح از 0 به 5 با  ، جفتهای مرتب شده در جایی كه مختصات x می توانند 0 یا 1 باشند و مختصات y می توانند 0 ، 1 یا 2 باشند ، در حالی كه علاوه بر این در x- coordinate modulo 2 و اضافه شدن در y- koordinate modulo 3 است.
، جفتهای مرتب شده در جایی كه مختصات x می توانند 0 یا 1 باشند و مختصات y می توانند 0 ، 1 یا 2 باشند ، در حالی كه علاوه بر این در x- coordinate modulo 2 و اضافه شدن در y- koordinate modulo 3 است. و
و 
 اگر و فقط اگر m و n
اگر و فقط اگر m و n 
 ، پس از آن ریخت از X به Y یک تابع bijective است ƒ: X → Y به طوری که
، پس از آن ریخت از X به Y یک تابع bijective است ƒ: X → Y به طوری که
 و
و 
 در حالی که دیگری است
در حالی که دیگری است 
 . اگر کسی پایه ای برای V انتخاب کند ، این یک ایزومورفیسم ایجاد می کند: برای همه شما . v ∈ V ،
. اگر کسی پایه ای برای V انتخاب کند ، این یک ایزومورفیسم ایجاد می کند: برای همه شما . v ∈ V ، .
. .
. ، برای هر فضای برداری به روشی مداوم رسمیت این شهود انگیزه ای برای توسعه تئوری مقوله است.
، برای هر فضای برداری به روشی مداوم رسمیت این شهود انگیزه ای برای توسعه تئوری مقوله است. و
و 





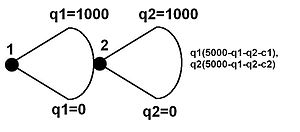
 . از همان روش برای محاسبه عملکرد پاسخ بهینه پیشرو استفاده کنید ، و فرض کنید که اولین حرکت دهنده می داند که پیرو عمل فوق را انتخاب کرده و توسط مشتقات جزئی مرتبه اول آن را حل می کند.
. از همان روش برای محاسبه عملکرد پاسخ بهینه پیشرو استفاده کنید ، و فرض کنید که اولین حرکت دهنده می داند که پیرو عمل فوق را انتخاب کرده و توسط مشتقات جزئی مرتبه اول آن را حل می کند. . جایگزینی q1 * به عملکرد پاسخ بهینه پیروان ،
. جایگزینی q1 * به عملکرد پاسخ بهینه پیروان ، در این زمان (q1 * ، q2 *) فرعی تعادل نش عالی است. اگر فرض کنیم که c1 = c2 = 1000 است ، آنگاه راه حل تعادل کامل نش در زیر نام (2000 ، 1000) است.
در این زمان (q1 * ، q2 *) فرعی تعادل نش عالی است. اگر فرض کنیم که c1 = c2 = 1000 است ، آنگاه راه حل تعادل کامل نش در زیر نام (2000 ، 1000) است.
![\ گاما = \ langle \ mathcal {K}} ، {\ mathbf {H}} ، [({\ mathbf {H}} _ {i}) _ {{i \ in {\ mathcal {I}}} ]، \ {A (H) \} _ {{H \ in {\ mathbf {H}}}}]، a، \ rho، u \ rangle](https://wikimedia.org/api/rest_v1/media/math/render/svg/7339d688679ae2856247b490669c03cabed86a2e) کجا:
کجا: یک درخت محدود را نشان می دهد.
یک درخت محدود را نشان می دهد. همه گره های درخت ،
همه گره های درخت ، یک گره اولیه منحصر به فرد را نشان می دهد ، زیرمجموعه V
یک گره اولیه منحصر به فرد را نشان می دهد ، زیرمجموعه V تمام گره های ترمینال را نشان می دهد (
تمام گره های ترمینال را نشان می دهد ( گره تصمیم گیری است) و عملکرد{\ صفحه نمایش صفحه نمایش:
گره تصمیم گیری است) و عملکرد{\ صفحه نمایش صفحه نمایش:  قوانینی که نمایانگر بازی هستند ،
قوانینی که نمایانگر بازی هستند ، اکسپرس
اکسپرس مجموعه اطلاعات
مجموعه اطلاعات اقدامات ممکن مجاز است. همه اقدامات به صورت بیان شده است
اقدامات ممکن مجاز است. همه اقدامات به صورت بیان شده است .
.
 مجموعه ای از "بازیکنان" است. برای هر "شرکت کننده"
مجموعه ای از "بازیکنان" است. برای هر "شرکت کننده" مجموعه ای از "خط مشی"
مجموعه ای از "خط مشی" بازی (بازی) است
بازی (بازی) است 

 بازی (بازی) از مجموعه نتیجه (مجموعه ای نتیجه). برای هر شرکت کننده
بازی (بازی) از مجموعه نتیجه (مجموعه ای نتیجه). برای هر شرکت کننده .
.![{\displaystyle [x_{1},x_{2}]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/91bdff343d848c2b70c68b5c04a2479b14a9fef0) و
و 
 باشد.
باشد.





 ).
).
 مورچه ها در تصویر
مورچه ها در تصویر  جایی که
جایی که  . ماتریکس فرومون
. ماتریکس فرومون با مقدار تصادفی مقدار دهی اولیه می شوند. چالش اصلی در فرایند آغازین تعیین ماتریس اکتشافی است.
با مقدار تصادفی مقدار دهی اولیه می شوند. چالش اصلی در فرایند آغازین تعیین ماتریس اکتشافی است.

 ، که یک عامل عادی است
، که یک عامل عادی است
 می تواند با استفاده از توابع زیر محاسبه شود:
می تواند با استفاده از توابع زیر محاسبه شود:



 در هر یک از توابع فوق، اشکال مربوط به توابع را تنظیم می کند.
در هر یک از توابع فوق، اشکال مربوط به توابع را تنظیم می کند. 
 ) به روز شده است جایی که در مرحله 5 نرخ تبخیر دنباله به روز شده است که توسط معادله زیر داده شده است.
) به روز شده است جایی که در مرحله 5 نرخ تبخیر دنباله به روز شده است که توسط معادله زیر داده شده است. ، جایی که
، جایی که  ضریب فرونشینی فرومون است
ضریب فرونشینی فرومون است 










 در این وبلاگ به ریاضیات و کاربردهای آن و تحقیقات در آنها پرداخته می شود. مطالب در این وبلاگ ترجمه سطحی و اولیه است و کامل نیست.در صورتی سوال یا نظری در زمینه ریاضیات دارید مطرح نمایید .در صورت امکان به آن می پردازم. من دوست دارم برای یافتن پاسخ به سوالات و حل پروژه های علمی با دیگران همکاری نمایم.در صورتی که شما هم بامن هم عقیده هستید با من تماس بگیرید.
در این وبلاگ به ریاضیات و کاربردهای آن و تحقیقات در آنها پرداخته می شود. مطالب در این وبلاگ ترجمه سطحی و اولیه است و کامل نیست.در صورتی سوال یا نظری در زمینه ریاضیات دارید مطرح نمایید .در صورت امکان به آن می پردازم. من دوست دارم برای یافتن پاسخ به سوالات و حل پروژه های علمی با دیگران همکاری نمایم.در صورتی که شما هم بامن هم عقیده هستید با من تماس بگیرید.