اصل هویگنز-فرنل
از ویکیپدیا، دانشنامه آزاد
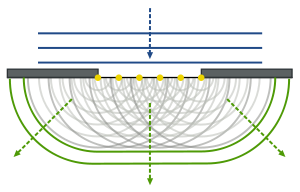
شکست موج به روش هویگنس
پراش موج به روش هویگنس و فرنل
اصل هویگنز-فرنل (به نام فیزیکدان هلندی کریستیان هویگنز و فیزیکدان فرانسوی آگوستین-ژان فرنل نامگذاری شده است) روشی برای تجزیه و تحلیل است که برای مشکلات انتشار موج هم در حد میدان دور و هم در پراش میدان نزدیک و همچنین بازتاب اعمال می شود. بیان میکند که هر نقطه در یک جبهه موج ، خود منبع موجکهای کروی است و موجکهای ثانویه که از نقاط مختلف سرچشمه میگیرند، متقابلاً تداخل دارند. [1] مجموع این موجک های کروی جبهه موج را تشکیل می دهد.
فهرست
تاریخچه [ ویرایش ]
پراش یک موج صفحه زمانی که عرض شکاف برابر با طول موج باشد
در سال 1678، هویگنس [2] پیشنهاد کرد که هر نقطه ای که یک اختلال نورانی به آن می رسد، منبع یک موج کروی می شود. مجموع این امواج ثانویه شکل موج را در هر زمان بعدی تعیین می کند. او فرض کرد که امواج ثانویه فقط در جهت "به جلو" حرکت می کنند و در تئوری توضیح داده نشده است که چرا چنین است. او توانست توضیحی کیفی از انتشار موج خطی و کروی ارائه دهد و قوانین بازتاب و شکست را با استفاده از این اصل استخراج کند، اما نتوانست انحرافات از انتشار مستقیم را که هنگام برخورد نور با لبهها، روزنهها و صفحهها اتفاق میافتد توضیح دهد. به عنوان اثرات پراش [3] حل این خطا در نهایت توسط توضیح داده شددیوید AB میلر در سال 1991. [4] قطعنامه این است که منبع یک دوقطبی است (نه تک قطبی که هویگنز در نظر گرفته است)، که در جهت منعکس شده لغو می شود.
در سال 1818، فرنل [5] نشان داد که اصل هویگنز، همراه با اصل تداخل او می تواند هم انتشار مستقیم نور و هم اثرات پراش را توضیح دهد. برای به دست آوردن توافق با نتایج تجربی، او باید مفروضات دلخواه اضافی در مورد فاز و دامنه امواج ثانویه، و همچنین یک عامل انحراف را شامل می شد. این مفروضات هیچ پایه فیزیکی آشکاری ندارند، اما منجر به پیشبینیهایی شد که با بسیاری از مشاهدات تجربی، از جمله نقطه پواسون ، مطابقت داشت .
پواسون یکی از اعضای آکادمی فرانسه بود که کار فرنل را بررسی می کرد. [6] او از نظریه فرنل برای پیش بینی اینکه یک نقطه روشن باید در مرکز سایه یک دیسک کوچک ظاهر شود، استفاده کرد و از آن نتیجه گرفت که این نظریه نادرست است. با این حال، آراگو، یکی دیگر از اعضای کمیته، آزمایش را انجام داد و نشان داد که پیشبینی درست بوده است. (Lisle این را پنجاه سال قبل مشاهده کرده بود. [3] ) این یکی از تحقیقاتی بود که به پیروزی نظریه موجی نور بر نظریه غالب جسمی در آن زمان انجامید .
در تئوری و مهندسی آنتن ، فرمول بندی مجدد اصل هویگنز-فرنل برای تابش منابع جریان به عنوان اصل هم ارزی سطح شناخته می شود . [7] [8]
اصل هویگنز به عنوان یک مدل میکروسکوپی [ ویرایش ]
اصل هویگنز-فرنل مبنای معقولی برای درک و پیشبینی انتشار موج کلاسیک نور فراهم میکند. با این حال، محدودیتهایی برای این اصل وجود دارد، یعنی همان تقریبهایی که برای استخراج فرمول پراش کیرشهوف و تقریب میدان نزدیک ناشی از فرنل انجام میشود. اینها را می توان در این واقعیت خلاصه کرد که طول موج نور بسیار کوچکتر از ابعاد هر مؤلفه نوری است. [6]
فرمول پراش Kirchhoff یک پایه ریاضی دقیق برای پراش، بر اساس معادله موج فراهم می کند. مفروضات دلخواه فرنل برای رسیدن به معادله هویگنز-فرنل به طور خودکار از ریاضیات در این اشتقاق بیرون میآیند. [9]
یک مثال ساده از عملکرد اصل را می توان زمانی مشاهده کرد که یک درب باز دو اتاق را به هم متصل می کند و در گوشه ای دورافتاده یکی از آنها صدا تولید می شود. شخصی در اتاق دیگر صدا را می شنود که انگار از در ورودی است. تا آنجا که به اتاق دوم مربوط می شود، هوای ارتعاشی در درگاه منبع صدا است.
تفاسیر فیزیک مدرن [ ویرایش ]
همه کارشناسان موافق نیستند که اصل هویگنز نمایش میکروسکوپی دقیق واقعیت است. به عنوان مثال، ملوین شوارتز استدلال کرد که "اصل هویگنز در واقع پاسخ درست را می دهد اما به دلایل اشتباه". [1]
این را می توان در حقایق زیر منعکس کرد:
- مکانیک میکروسکوپی برای ایجاد فوتون و انتشار، به طور کلی، اساساً شتاب الکترون است. [1]
- تجزیه و تحلیل اولیه هویگنس [10] فقط شامل دامنه ها بود. این شامل نه فازها و نه امواجی است که با سرعت های مختلف منتشر می شوند (به دلیل پراش در محیط های پیوسته)، و بنابراین تداخل را در نظر نمی گیرند.
- تجزیه و تحلیل هویگنز همچنین قطبش نور را که دلالت بر پتانسیل برداری دارد را شامل نمی شود، در عوض امواج صوتی را می توان با پتانسیل اسکالر توصیف کرد و هیچ ترجمه منحصر به فرد و طبیعی بین این دو وجود ندارد. [11]
- در توصیف هویگنز ، هیچ توضیحی در مورد اینکه چرا ما فقط موج رو به جلو ( موج عقبافتاده یا پوشش جلویی جبهههای موج) را در مقابل موج پیشرفته انتشار به عقب (پاکت به عقب) انتخاب میکنیم، وجود ندارد. [11]
- در تقریب فرنل، به دلیل مجموع امواج کروی با فازهای مختلف که از نقاط مختلف جبهه موج می آید، مفهوم رفتار غیرمحلی وجود دارد و نظریه های غیرمحلی موضوع بحث های زیادی هستند (مثلاً کواریانت لورنتس نبودن). ) و تحقیق فعال.
- تقریب فرنل را میتوان به روش احتمالی کوانتومی تفسیر کرد، اما مشخص نیست که این مجموع حالتها (یعنی موجکها در جبهه موج) تا چه اندازه فهرست کاملی از حالتهایی است که از نظر فیزیکی معنادار هستند یا بیشتر از یک تقریب بر مبنای عمومی را نشان میدهند . روش ترکیب خطی اوربیتال های اتمی (LCAO).
اصل هویگنز اساساً با نظریه میدان کوانتومی در تقریب میدان دور سازگار است ، با در نظر گرفتن میدانهای مؤثر در مرکز پراکندگی، در نظر گرفتن اغتشاشات کوچک ، و به همان معنا که اپتیک کوانتومی با اپتیک کلاسیک سازگار است ، سایر تفاسیر موضوع بحث است. و تحقیقات فعال
مدل فاینمن که در آن هر نقطه در یک جبهه موج خیالی به بزرگی اتاق موجک تولید میکند، نیز باید در این تقریبها تفسیر شود [12] و در یک زمینه احتمالی، در این زمینه، نقاط دوردست تنها میتوانند حداقل به احتمال کلی کمک کنند. دامنه
نظریه میدان کوانتومی هیچ مدل میکروسکوپی برای ایجاد فوتون را شامل نمی شود و مفهوم تک فوتون نیز در سطح نظری مورد بررسی قرار می گیرد.
بیان ریاضی اصل [ ویرایش ]
آرایش هندسی برای محاسبه فرنل
مورد منبع نقطه ای واقع در نقطه P 0 را در نظر بگیرید که با فرکانس f ارتعاش می کند . اغتشاش ممکن است با یک متغیر مختلط U 0 که به نام دامنه پیچیده شناخته می شود، توصیف شود . یک موج کروی با طول موج λ، عدد موج k = 2 π / λ تولید می کند . در یک ثابت تناسب، دامنه مختلط موج اولیه در نقطه Q واقع در فاصله r 0 از P 0 است:
توجه داشته باشید که قدر به نسبت معکوس مسافت طی شده کاهش می یابد و فاز به صورت k ضربدر مسافت طی شده تغییر می کند.
با استفاده از نظریه هویگنز و اصل برهم نهی امواج، دامنه مختلط در نقطه دیگر P با جمع کردن سهم هر نقطه در کره شعاع r 0 به دست میآید . به منظور توافق با نتایج تجربی، فرنل دریافت که مشارکتهای منفرد از امواج ثانویه روی کره باید در یک ثابت، -i /λ، و با یک عامل تمایل اضافی، K (χ) ضرب شود. فرض اول به این معنی است که امواج ثانویه در یک چهارم سیکل خارج از فاز نسبت به موج اولیه نوسان می کنند و بزرگی امواج ثانویه در نسبت 1:λ به موج اولیه است. او همچنین فرض کرد که K(χ) دارای حداکثر مقدار زمانی که χ = 0 بود، و برابر با صفر بود که χ = π/2، که در آن χ زاویه بین نرمال جبهه موج اولیه و نرمال جبهه موج ثانویه است. دامنه مختلط در P ، به دلیل مشارکت امواج ثانویه، سپس با: [13] داده می شود.
که در آن S سطح کره را توصیف می کند و s فاصله بین Q و P است.
فرنل از یک روش ساخت ناحیه برای یافتن مقادیر تقریبی K برای مناطق مختلف استفاده کرد، [6] که او را قادر ساخت پیشبینیهایی انجام دهد که مطابق با نتایج تجربی بود. قضیه انتگرال کیرشهوف شامل ایده اصلی اصل هویگنز-فرنل است. کیرشهوف نشان داد که در بسیاری از موارد، این قضیه را می توان به شکل ساده تری که معادل شکل گیری فرمول فرنل است، تقریب زد. [6]
برای روشنایی دیافراگم متشکل از یک موج کروی منبسط شونده، اگر شعاع انحنای موج به اندازه کافی بزرگ باشد، کیرشهوف عبارت زیر را برای K (χ) ارائه می دهد: [6]
K دارای حداکثر مقدار در χ = 0 مانند اصل هویگنز-فرنل است. با این حال، K در χ = π/2 برابر با صفر نیست، اما در χ = π است.
در اشتقاق بالای K (χ) فرض می شود که دیافراگم پراش توسط یک موج کروی منفرد با شعاع انحنای به اندازه کافی بزرگ روشن می شود. با این حال، این اصل برای روشنایی های عمومی تر صادق است. [13] یک روشنایی دلخواه را می توان به مجموعه ای از منابع نقطه ای تجزیه کرد و خطی بودن معادله موج را می توان برای اعمال این اصل برای هر منبع نقطه ای به طور جداگانه فراخوانی کرد. K (χ) را می توان به طور کلی به صورت زیر بیان کرد: [13]
در این مورد، K شرایط ذکر شده در بالا را برآورده می کند (حداکثر مقدار در χ = 0 و صفر در χ = π/2).
اصل تعمیم یافته هویگنس [ ویرایش ]
بسیاری از کتاب ها و مراجع به عنوان مثال [14] و [15] به اصل تعمیم یافته هویگنز به عنوان چیزی که توسط فاینمن در این انتشار اشاره شده است اشاره می کنند [16]
فاینمن اصل تعمیم یافته را به صورت زیر تعریف می کند:
"در واقع اصل هویگنز در اپتیک صحیح نیست. با اصلاح کرچوف (sic) جایگزین شده است که مستلزم آن است که هم دامنه و هم مشتق آن در سطح مجاور شناخته شوند. این نتیجه این واقعیت است که معادله موج در اپتیک است. معادله موجی مکانیک کوانتومی مرتبه اول در زمان است، بنابراین اصل هویگنس برای امواج ماده، عمل جایگزین زمان صحیح است.
این واقعیت را روشن می کند که در این زمینه، اصل تعمیم یافته منعکس کننده خطی بودن مکانیک کوانتومی و این واقعیت است که معادلات مکانیک کوانتومی مرتبه اول در زمان هستند. در نهایت فقط در این مورد اصل برهم نهی به طور کامل اعمال می شود، یعنی تابع موج در نقطه P را می توان به صورت برهم نهی امواج بر روی سطح مرزی که P را در بر می گیرد، گسترش داد. فرمالیسم توابع گرین و انتشار دهنده ها اعمال می شود. آنچه شایان توجه است این است که این اصل تعمیم یافته برای «امواج ماده» قابل اجرا است نه دیگر برای امواج نور. فاکتور فاز اکنون همانطور که توسط عمل ارائه شده است روشن می شود و دیگر سردرگمی وجود ندارد که چرا فازهای موجک با موج اصلی متفاوت است و توسط پارامترهای فرنل اضافی اصلاح می شود.
طبق نظر گرینر [14] می توان اصل تعمیم یافته را برای آن بیان کرد
جایی که G تابع سبز معمولی است که در زمان تابع موج را منتشر می کند 
نظریه هویگنز و تابع موج فوتون مدرن [ ویرایش ]
نظریه هویگنز به عنوان یک توضیح اساسی در مورد ماهیت موجی تداخل نور عمل کرد و توسط فرنل و یانگ بیشتر توسعه یافت، اما تمام مشاهدات مانند آزمایش دو شکاف با شدت کم را که اولین بار توسط GI Taylor در سال 1909 انجام شد، به طور کامل حل نکرد. تا اوایل و اواسط دهه 1900 که در مورد نظریه کوانتومی بحث شد، به ویژه بحث های اولیه در کنفرانس سالوی بروکسل در سال 1927 ، جایی که لویی دو بروگلی فرضیه دو بروگلی خود را ارائه کرد که فوتون توسط یک تابع موج هدایت می شود. [17] تابع موج توضیح بسیار متفاوتی از نوارهای روشن و تاریک مشاهده شده در آزمایش دو شکاف ارائه می دهد. در این مفهوم، فوتون مسیری را دنبال میکند که انتخاب تصادفی یکی از مسیرهای ممکن است. این مسیرهای ممکن الگو را تشکیل می دهند: در مناطق تاریک، هیچ فوتونی فرود نمی آید، و در مناطق روشن، فوتون های زیادی فرود می آیند. مجموعه مسیرهای ممکن فوتون توسط محیط اطراف تعیین می شود: نقطه مبدا فوتون (اتم)، شکاف و صفحه. تابع موج راه حلی برای این هندسه است. رویکرد تابع موج بیشتر توسط آزمایشهای دو شکاف اضافی در ایتالیا و ژاپن در دهههای 1970 و 1980 با الکترونها پشتیبانی شد. [18]
اصل هویگنز و نظریه میدان کوانتومی [ ویرایش ]
اصل هویگنس را می توان نتیجه همگنی فضا دانست - فضا در همه مکان ها یکنواخت است. [19] هر گونه اختلال ایجاد شده در یک منطقه به اندازه کافی کوچک از فضای همگن (یا در یک محیط همگن) از آن منطقه در تمام جهات ژئودزیک منتشر می شود. امواج حاصل از این اختلال به نوبه خود باعث ایجاد اختلال در مناطق دیگر و ... می شود. برهم نهی همه امواج منجر به الگوی مشاهده شده انتشار موج می شود.
همگنی فضا برای نظریه میدان کوانتومی (QFT) اساسی است که در آن تابع موج هر جسم در تمام مسیرهای بدون مانع موجود منتشر می شود. هنگامی که در طول تمام مسیرهای ممکن ، با یک فاکتور فاز متناسب با عمل ، تداخل توابع موج به درستی پدیدههای قابل مشاهده را پیشبینی میکند. هر نقطه در جبهه موج به عنوان منبع موجک های ثانویه عمل می کند که در مخروط نور با همان سرعت موج پخش می شوند. جبهه موج جدید با ساختن سطح مماس بر موجک های ثانویه پیدا می شود.
در سایر ابعاد فضایی [ ویرایش ]
در سال 1900، ژاک هادامارد مشاهده کرد که وقتی تعداد ابعاد فضایی زوج باشد، اصل هویگنز شکسته شد. [20] [21] [22] از این رو، او مجموعهای از حدسها را ایجاد کرد که همچنان یک موضوع فعال تحقیقاتی است. [23] [24] به طور خاص، کشف شده است که اصل هویگنز بر کلاس بزرگی از فضاهای همگن مشتق شده از گروه Coxeter (به عنوان مثال، گروه های Weyl از جبرهای ساده Lie ) صادق است. [19] [25]
بیان سنتی اصل هویگنس برای دالامبرتیان باعث ایجاد سلسله مراتب KdV می شود . به طور مشابه، عملگر دیراک باعث ایجاد سلسله مراتب AKNS می شود. [26] [27]
منبع
https://en.wikipedia.org/wiki/Huygens%E2%80%93Fresnel_principle
































![{\displaystyle dE={\frac {A}{r_{1}}}e^{i\omega [t-(r_{1}/c)]}dy={\frac {A}{r_{1} }}e^{i(\omega t-\beta r_{1})}dy}](https://wikimedia.org/api/rest_v1/media/math/render/svg/3e2bba4341965c0b9a84db188c0804be01725000)
 . با این حال
. با این حال و ادغام از
و ادغام از  به
به  ،
،
 .
.
 که در آن طول آرایه بر حسب رادیان است
که در آن طول آرایه بر حسب رادیان است  ، سپس،
، سپس،
 است
است  .
. (شرایط فرانهوفر)
(شرایط فرانهوفر) - بزرگترین اندازه دیافراگم یا شکاف پراش،
- بزرگترین اندازه دیافراگم یا شکاف پراش، - طول موج،
- طول موج، 
 .
.
 ;
; .
. .
. بنابراین
بنابراین  ، سپس اختلاف فاز است
، سپس اختلاف فاز است  . مفهوم هندسی این عبارت این است که مسیرهای r 2 و r 1 تقریباً با یکدیگر موازی هستند. از آنجایی که می تواند مسیر موج پراش صفحه پراش - صفحه مشاهده وجود داشته باشد که زاویه آن نسبت به خط مستقیم موازی با محور نوری نزدیک به 0 باشد، این شرایط تقریب را می توان بیشتر به صورت ساده تر کرد.
. مفهوم هندسی این عبارت این است که مسیرهای r 2 و r 1 تقریباً با یکدیگر موازی هستند. از آنجایی که می تواند مسیر موج پراش صفحه پراش - صفحه مشاهده وجود داشته باشد که زاویه آن نسبت به خط مستقیم موازی با محور نوری نزدیک به 0 باشد، این شرایط تقریب را می توان بیشتر به صورت ساده تر کرد. که در آن L فاصله بین دو صفحه در امتداد محور نوری است. با توجه به این واقعیت که یک موج تابشی در یک صفحه پراش عملاً یک موج صفحه است اگر
که در آن L فاصله بین دو صفحه در امتداد محور نوری است. با توجه به این واقعیت که یک موج تابشی در یک صفحه پراش عملاً یک موج صفحه است اگر


![{\mathcal {S}}[{\mathbf {q}}]\ {\stackrel {{\mathrm {def}}}{=}}\ \int _{{t_{1}}}^{{t_{ 2}}}L({\mathbf {q}}(t)،{\dot {{\mathbf {q}}}}(t),t)\,dt](https://wikimedia.org/api/rest_v1/media/math/render/svg/2ec5865ab1d4f3428b6a2df163d3aba124bd55ae)
 تابع
تابع  . عمل
. عمل

 خواهد بود
خواهد بود![\delta {\mathcal {S}}=\int _{{t_{1}}}^{{t_{2}}}\;\left[L({\mathbf {q}}+{\boldsymbol \varepsilon }،{\dot {{\mathbf {q}}}}+{\dot {{\boldsymbol {\varepsilon }}}})-L({\mathbf {q}}،{\dot {{\mathbf { q}}}})\right]dt=\int _{{t_{1}}}^{{t_{2}}}\;\left({\boldsymbol \varepsilon }\cdot {\frac {\partial L}{\partial {\mathbf {q}}}}+{\dot {{\boldsymbol {\varepsilon }}}}\cdot {\frac {\partial L}{\partial {\dot {{\mathbf { q}}}}}}\right)\,dt](https://wikimedia.org/api/rest_v1/media/math/render/svg/85b5b794ae18521a6283f966fa3bed0766ebb457)
![\delta {\mathcal {S}}=\left[{\boldsymbol \varepsilon }\cdot {\frac {\partial L}{\partial {\dot {{\mathbf {q}}}}}}\right] _{{t_{1}}}^{{t_{2}}}+\int _{{t_{1}}}^{{t_{2}}}\;\left({\boldsymbol \varepsilon } \cdot {\frac {\partial L}{\partial {\mathbf {q}}}}-{\boldsymbol \varepsilon }\cdot {\frac {d}{dt}}{\frac {\partial L}{ \partial {\dot {{\mathbf {q}}}}}}\right)\,dt](https://wikimedia.org/api/rest_v1/media/math/render/svg/2744b1ea64e497406f586fde689c7542515e8b19)


 .
.





 .
.

![{\displaystyle \int _{t_{1}}^{t_{2}}\left[\delta W_{e}+\delta T-\delta U\right]dt=0}](https://wikimedia.org/api/rest_v1/media/math/render/svg/f0f842cc866f991677a6eaec8ca7d6f7785dab00)
![{\displaystyle \delta \int _{t_{1}}^{t_{2}}\left[T-(U+V)\right]dt=0.}](https://wikimedia.org/api/rest_v1/media/math/render/svg/b479c99527f12bab4fc6eaf5b2d14159985f4bfd)

 متناسب با تکانه فوتون، جهت انتشار عرضی است {\displaystyle (k_{x},k_{y},0)}
متناسب با تکانه فوتون، جهت انتشار عرضی است {\displaystyle (k_{x},k_{y},0)} باید در هر دو منطقه یکسان باقی بماند. فرض کنید بدون از دست دادن کلیت، سطحی از وقوع در{\displaystyle z,x}
باید در هر دو منطقه یکسان باقی بماند. فرض کنید بدون از دست دادن کلیت، سطحی از وقوع در{\displaystyle z,x} سطح {\displaystyle k_{x{\text{Region}}_{1}}=k_{x{\text{Region}}_{2}}}
سطح {\displaystyle k_{x{\text{Region}}_{1}}=k_{x{\text{Region}}_{2}}} . با استفاده از وابستگی شناخته شده
. با استفاده از وابستگی شناخته شده 


 عدد موج در خلاء است. اگرچه هیچ سطحی در مقیاس اتمی واقعاً همگن نیست، تقارن انتقالی کامل هر زمان که ناحیه در مقیاس طول موج نور همگن باشد، تقریبی عالی است.
عدد موج در خلاء است. اگرچه هیچ سطحی در مقیاس اتمی واقعاً همگن نیست، تقارن انتقالی کامل هر زمان که ناحیه در مقیاس طول موج نور همگن باشد، تقریبی عالی است. (اشاره از منبع نور به سمت سطح) و یک بردار نرمال صفحه نرمال شده {\displaystyle {\vec {n}}}
(اشاره از منبع نور به سمت سطح) و یک بردار نرمال صفحه نرمال شده {\displaystyle {\vec {n}}} ، می توان از طریق کسینوس های زاویه تابش پرتوهای منعکس شده و منکسر نرمال شده را بررسی کرد. {\displaystyle \theta _{1}}
، می توان از طریق کسینوس های زاویه تابش پرتوهای منعکس شده و منکسر نرمال شده را بررسی کرد. {\displaystyle \theta _{1}} و زاویه شکست {\displaystyle \theta _{2}}
و زاویه شکست {\displaystyle \theta _{2}} ، بدون استفاده صریح از مقادیر سینوسی یا هر تابع مثلثاتی یا زاویه:
، بدون استفاده صریح از مقادیر سینوسی یا هر تابع مثلثاتی یا زاویه: 
 باید مثبت باشد، که اگر باشد {\displaystyle {\vec {n}}}
باید مثبت باشد، که اگر باشد {\displaystyle {\vec {n}}} . اگر{\displaystyle \cos \theta _{1}}
. اگر{\displaystyle \cos \theta _{1}}



 و
و  ، از هرگونه ظاهر شدن نام تابع trig یا نام زاویه اجتناب کنید:
، از هرگونه ظاهر شدن نام تابع trig یا نام زاویه اجتناب کنید:



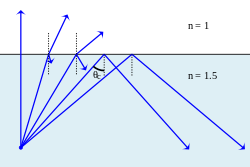
 ، که فقط برای پرتوهایی که به محیطی با چگالی کمتر عبور می کنند اتفاق بیفتد (
، که فقط برای پرتوهایی که به محیطی با چگالی کمتر عبور می کنند اتفاق بیفتد ( ).
).
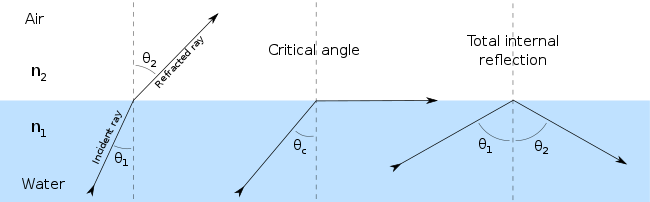



 و غیره، برای نشان دادن عاملی استفاده می شود که توسط آن سرعت پرتو نور در هنگام حرکت از طریق یک محیط انکساری مانند شیشه یا آب، بر خلاف سرعت آن در خلاء کاهش می یابد.
و غیره، برای نشان دادن عاملی استفاده می شود که توسط آن سرعت پرتو نور در هنگام حرکت از طریق یک محیط انکساری مانند شیشه یا آب، بر خلاف سرعت آن در خلاء کاهش می یابد. و
و  :
:


 و
و به ترتیب.
به ترتیب. سرعت نور در خلاء است.
سرعت نور در خلاء است.
 (نقطه ثابت)
(نقطه ثابت)





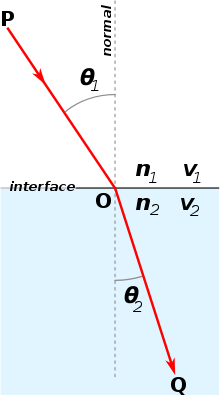

 به عنوان زاویه اندازه گیری شده از نرمال مرز،
به عنوان زاویه اندازه گیری شده از نرمال مرز، به عنوان سرعت نور در محیط مربوطه (واحد SI متر بر ثانیه یا m/s است) و
به عنوان سرعت نور در محیط مربوطه (واحد SI متر بر ثانیه یا m/s است) و به عنوان ضریب شکست (که کمتر از واحد است) محیط مربوطه.
به عنوان ضریب شکست (که کمتر از واحد است) محیط مربوطه.


 قابل حل است اگر ...
قابل حل است اگر ... که هر کدام در
که هر کدام در  آن
آن  آبلی
آبلی  که هر کدام
که هر کدام  و هر کدام
و هر کدام  آن
آن  و
و ![G^{(i+1)} = [G^{(i)}، G^{(i)}]](https://groupprops.subwiki.org/w/images/math/6/1/8/61821731652d94617999581509cf6397.png)
 یک
یک  گروههای قابل حل هستند . سپس
گروههای قابل حل هستند . سپس  یک
یک  قابل حل باشند،
قابل حل باشند،  نیز قابل حل است.
نیز قابل حل است. همه زیرگروه های
همه زیرگروه های  قابل حل است.
قابل حل است. و
و  ، پس قابل حل است اگر و فقط اگر باشد. علاوه بر این، اگر چنین است، طول مشتق شده برابر است با طول مشتق شده از , مگر اینکه یکی از گروه ها جزئی و دیگری آبلی غیر جزئی باشد.
، پس قابل حل است اگر و فقط اگر باشد. علاوه بر این، اگر چنین است، طول مشتق شده برابر است با طول مشتق شده از , مگر اینکه یکی از گروه ها جزئی و دیگری آبلی غیر جزئی باشد. 




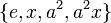 ،
، 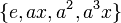


 یا
یا  )
) ; مانند حلقه تولید شده توسط مقادیر کاراکتر
; مانند حلقه تولید شده توسط مقادیر کاراکتر (بنابراین، این یک
(بنابراین، این یک 

 (سایز 1)
(سایز 1) (سایز 2)
(سایز 2) (سایز 2)
(سایز 2) (سایز 2)
(سایز 2) -هسته
-هسته -هسته
-هسته -هسته
-هسته نه صفر است و نه
نه صفر است و نه  مدول
مدول  . این را با مورد فرد مقایسه کنید
. این را با مورد فرد مقایسه کنید  ، درجه
، درجه
 و مرتبه
و مرتبه
 به عنصر چرخش مرتبه چهار و مولد دوم به عنصر انعکاس
به عنصر چرخش مرتبه چهار و مولد دوم به عنصر انعکاس درجه دو نگاشت می شود.
درجه دو نگاشت می شود. گروه دور ای مرتبه چهار را تعریف کنید (با استفاده از
گروه دور ای مرتبه چهار را تعریف کنید (با استفاده از  ،
،  حتی:
حتی: .
.  :
: 
 تعداد زیرگروه ها است
تعداد زیرگروه ها است  ، که در آن
، که در آن  تابع شمارش مقسوم علیه و
تابع شمارش مقسوم علیه و  تابع مجموع مقسوم علیه است. ساختار زیر گروه گروه دو وجهی را ببینید
تابع مجموع مقسوم علیه است. ساختار زیر گروه گروه دو وجهی را ببینید 


 و رفت و
و رفت و  آمد نکنید
آمد نکنید ، که طبیعی است، اما
، که طبیعی است، اما  طبیعی نیست
طبیعی نیست





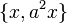

 -- یکی از
-- یکی از 

 -- یکی از
-- یکی از 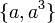


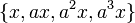

 و
و  : نظم حاصلضرب دستورات
: نظم حاصلضرب دستورات 
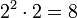
 دارای توانی برابر با
دارای توانی برابر با  .
. ، که گاهی اوقات نامیده می شود
، که گاهی اوقات نامیده می شود  ، همچنین به نام
، همچنین به نام  نشان دادن همانی ، تعریف می شود. عنصر:
نشان دادن همانی ، تعریف می شود. عنصر:
 که توسط:
که توسط:
 این را می توان با در نظر گرفتن رئوس مربع و در نظر گرفتن عنصری از
این را می توان با در نظر گرفتن رئوس مربع و در نظر گرفتن عنصری از  و
و  .
. ، مانند ارائه بالا.
، مانند ارائه بالا.




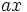
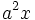

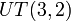 میدان
میدان 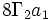

 ) در خلاف جهت عقربه های ساعت
) در خلاف جهت عقربه های ساعت
 نیز نامیده می شود
نیز نامیده می شود

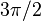 (یعنی
(یعنی  ) در خلاف جهت عقربه های ساعت، یا معادل آن، توسط
) در خلاف جهت عقربه های ساعت، یا معادل آن، توسط 

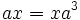





 یک
یک  تنها دو
تنها دو  به این معنی است که یک پوشش دوتایی است (به
به این معنی است که یک پوشش دوتایی است (به  دو گروه شبه ساده متناظر هستند .
دو گروه شبه ساده متناظر هستند . توان 4.
توان 4.







 .
. : 2، 10، 59 ، 501، 3786، 48337، ...
: 2، 10، 59 ، 501، 3786، 48337، ... هال از مرتبه 12 (
هال از مرتبه 12 (  یا زیرگروه -Hall وجود ندارد
یا زیرگروه -Hall وجود ندارد 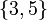 .
.



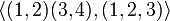



![\mathbb{Z}[(1 + \sqrt{5})/2]](https://groupprops.subwiki.org/w/images/math/9/5/7/9571a637ac52d32af6afc3cdad0a11f2.png) یا
یا ![\mathbb{Z}[2\cos(2\pi/5)]](https://groupprops.subwiki.org/w/images/math/4/a/9/4a95ab6e953d54684480256e2ff0b9b2.png)
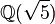 - گسترش درجه دوم میدان اعداد
- گسترش درجه دوم میدان اعداد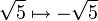 )
) (سایز 12)
(سایز 12)

 نامیده می شود، به روش های زیر تعریف می شود:
نامیده می شود، به روش های زیر تعریف می شود: (گاهی اوقات به مرتبه معکوس به عنوان نوشته می شود
(گاهی اوقات به مرتبه معکوس به عنوان نوشته می شود  ).
). به این صورت مشاهده می شود، یا نشان داده می شود
به این صورت مشاهده می شود، یا نشان داده می شود  . اطلاعات بیشتر:
. اطلاعات بیشتر:  . همچنین
. همچنین  . همچنین
. همچنین  است.
است. است.
است. ،
، 
 ،
، 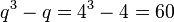
 ،
،  .
. :
: 
 ( بدون
( بدون  ): به
): به 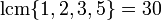

 (فرد):
(فرد):
 .
. (بیشتر
(بیشتر  ,
, 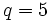 :
:  (
(  ,
,  (زوج):
(زوج):  (اطلاعات بیشتر
(اطلاعات بیشتر  غیر آبلی است،
غیر آبلی است،  .
. ،
، .
. (همانی، اندازه 1)
(همانی، اندازه 1) (اندازه 1)
(اندازه 1) (اندازه 2)
(اندازه 2) (اندازه 2)
(اندازه 2) (اندازه 2)
(اندازه 2) -هسته
-هسته -هسته
-هسته -هسته
-هسته
![\mathbb{Z}[i]](https://groupprops.subwiki.org/w/images/math/2/a/2/2a2fc748028420198e13c31eaadb6939.png) که در آن
که در آن  معادل
معادل ![\mathbb{Z}[t]/(t^2 + 1)](https://groupprops.subwiki.org/w/images/math/b/d/a/bdaaaa61e231878ff94a23bf211e8b51.png) است،
است، ![\mathbb{Z}[\sqrt{-2}]](https://groupprops.subwiki.org/w/images/math/c/b/2/cb2cb15c3160a682927d46e421fa88a6.png) یا
یا ![\mathbb{Z}[t]/(t^2 + 2)](https://groupprops.subwiki.org/w/images/math/f/c/8/fc8ac1bd26f88375919c94a722a2e48e.png) .
.![\mathbb{Z}[\آلفا،\بتا]](https://groupprops.subwiki.org/w/images/math/1/f/0/1f0f6de3f0e97814f330443f7b3ed137.png) که در آن
که در آن  حلقه ای از تحقق برای همه نمایش های کاهش ناپذیر است. به طور خاص،
حلقه ای از تحقق برای همه نمایش های کاهش ناپذیر است. به طور خاص، ![\mathbb{Z}[\sqrt{-m^2 - 1}]](https://groupprops.subwiki.org/w/images/math/d/2/5/d25c5a9bf29af37e54b57b5e72470138.png) برای هر منطقی کار می کند
برای هر منطقی کار می کند  .
. یا
یا ![\mathbb{Q}[t]/(t^2 + 1)](https://groupprops.subwiki.org/w/images/math/2/d/d/2dd8015d50efd0a01e1c014ae0cc8acd.png) کار می کند، همینطور می کند
کار می کند، همینطور می کند  یا
یا ![\mathbb{Q}[t]/(t^2 + 2)](https://groupprops.subwiki.org/w/images/math/2/a/2/2a29bc188f1f177ce72e9c7b6c5eaa7e.png) . به طور کلی تر،
. به طور کلی تر،  جایی
جایی  برای هر منطقی کار می کند
برای هر منطقی کار می کند  شرط کافی: مشخصه دو نیست و در میدان وجود دارد به گونه ای که
شرط کافی: مشخصه دو نیست و در میدان وجود دارد به گونه ای که  . به طور خاص، هر
. به طور خاص، هر 
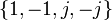



 هر یک از کلاس های مزدوج عناصر غیر مرکزی هستند.
هر یک از کلاس های مزدوج عناصر غیر مرکزی هستند.
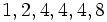

 نشان داده می شود
نشان داده می شود  به ترتیب نشان داده
به ترتیب نشان داده  می شوند.
می شوند. که در آن 1 عنصر هویت است،
که در آن 1 عنصر هویت است،  و همه عناصر دیگر از ریشه مربع هستند
و همه عناصر دیگر از ریشه مربع هستند  و بیشتر،
و بیشتر،  (روابط باقی مانده را می توان از اینها استنباط کرد).
(روابط باقی مانده را می توان از اینها استنباط کرد). .
. است.
است.



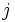









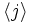



 ها وجود دارد که در آن
ها وجود دارد که در آن  همه
همه  اعداد صحیح مثبت وجود دارد. علاوه بر این،
اعداد صحیح مثبت وجود دارد. علاوه بر این، 
 اول و
اول و  اعداد صحیح مثبت هستند.
اعداد صحیح مثبت هستند.  مستقل از انتخاب بیان است. علاوه بر این، تعداد دفعاتی که هر توان اول
مستقل از انتخاب بیان است. علاوه بر این، تعداد دفعاتی که هر توان اول  در بین آنها رخ می دهد
در بین آنها رخ می دهد  ، مستقل از انتخاب عبارات است.
، مستقل از انتخاب عبارات است.
 . علاوه بر این،
. علاوه بر این،  که در امتداد خط مستقیم بین دو نقطه جزء ندارند. برای تجسم این موضوع، دو نفر را در حال بالا رفتن از یک صخره تصور کنید. یکی تصمیم می گیرد تا صخره را با بالا رفتن عمودی از آن بالا ببرد، و دومی تصمیم می گیرد در امتداد مسیری پرپیچ و خم قدم بزند که طول آن بیشتر از ارتفاع صخره است، اما فقط با زاویه کمی نسبت به افقی. اگرچه این دو کوهنورد مسیرهای مختلفی را برای رسیدن به بالای صخره طی کردهاند، اما در بالای آن، هر دو به یک اندازه انرژی پتانسیل گرانشی به دست آوردهاند. این به این دلیل است که یک میدان گرانشی پایستار است. به عنوان نمونه ای از یک میدان غیر پایستار، فشار دادن یک جعبه را از یک سر اتاق به انتهای دیگر تصور کنید. فشار دادن جعبه در یک خط مستقیم در سراسر اتاق به کار کمتری در برابر اصطکاک نسبت به مسیر منحنی که مسافت بیشتری را پوشش می دهد نیاز دارد.
که در امتداد خط مستقیم بین دو نقطه جزء ندارند. برای تجسم این موضوع، دو نفر را در حال بالا رفتن از یک صخره تصور کنید. یکی تصمیم می گیرد تا صخره را با بالا رفتن عمودی از آن بالا ببرد، و دومی تصمیم می گیرد در امتداد مسیری پرپیچ و خم قدم بزند که طول آن بیشتر از ارتفاع صخره است، اما فقط با زاویه کمی نسبت به افقی. اگرچه این دو کوهنورد مسیرهای مختلفی را برای رسیدن به بالای صخره طی کردهاند، اما در بالای آن، هر دو به یک اندازه انرژی پتانسیل گرانشی به دست آوردهاند. این به این دلیل است که یک میدان گرانشی پایستار است. به عنوان نمونه ای از یک میدان غیر پایستار، فشار دادن یک جعبه را از یک سر اتاق به انتهای دیگر تصور کنید. فشار دادن جعبه در یک خط مستقیم در سراسر اتاق به کار کمتری در برابر اصطکاک نسبت به مسیر منحنی که مسافت بیشتری را پوشش می دهد نیاز دارد.
 ، جایی که
، جایی که  یک زیر مجموعه باز از
یک زیر مجموعه باز از  ، گفته می شود که اگر و فقط در صورت وجود a پایستار است
، گفته می شود که اگر و فقط در صورت وجود a پایستار است
 بر
بر 
 نشان دهنده
نشان دهنده  نامیده می شود.
نامیده می شود. یک مسیر قابل اصلاح در
یک مسیر قابل اصلاح در و نقطه پایانی
و نقطه پایانی  . اگر
. اگر برای برخی
برای برخی 

 که در
که در  ، سپس
، سپس 
 تعریف شده در
تعریف شده در  تقریباً در همه جا پیچش صفر دارد و بنابراین چرخش ندارد. با این حال، نه پایستار است و نه استقلال مسیر دارد.
تقریباً در همه جا پیچش صفر دارد و بنابراین چرخش ندارد. با این حال، نه پایستار است و نه استقلال مسیر دارد. ، و اجازه دهید
، و اجازه دهید  یک
یک 

 میدان اسکالر
میدان اسکالر 
 با
با  -محور حذف شد، به عنوان مثال،
-محور حذف شد، به عنوان مثال، 
 -فضا
-فضا  ، بنابراین انتگرال روی دایره واحد است
، بنابراین انتگرال روی دایره واحد است

 یک تابع (میدان اسکالر)
یک تابع (میدان اسکالر)  بر
بر  به طوری که
به طوری که  . مانند
. مانند ، هر شکل دقیقی بسته است، بنابراین هر میدان برداری پایستار غیر چرخشی است. برعکس، همه بسته است
، هر شکل دقیقی بسته است، بنابراین هر میدان برداری پایستار غیر چرخشی است. برعکس، همه بسته است یک میدان برداری را می توان به صورت زیر تعریف کرد:
یک میدان برداری را می توان به صورت زیر تعریف کرد:

 پایستار است، پس گفته می شود نیرو یک
پایستار است، پس گفته می شود نیرو یک  بر روی یک توده عمل می کند
بر روی یک توده عمل می کند  به دلیل یک توده
به دلیل یک توده  ، که یک فاصله است
، که یک فاصله است  بین آنها، از معادله تبعیت می کند
بین آنها، از معادله تبعیت می کند
 ثابت
ثابت  یک بردار واحد است که از
یک بردار واحد است که از ، جایی که
، جایی که
 پایستار است، مشروط بر اینکه
پایستار است، مشروط بر اینکه  انتگرال پذیر است.
انتگرال پذیر است.
 ، جایی که
، جایی که  ، که دو بار به طور پیوسته قابل تمایز است و اجازه دهید
، که دو بار به طور پیوسته قابل تمایز است و اجازه دهید  سطحی باشد که دامنه را در بر می گیرد
سطحی باشد که دامنه را در بر می گیرد  . سپس
. سپس جایی که
جایی که![{\displaystyle {\begin{aligned}\Phi (\mathbf {r} )&={\frac {1}{4\pi }}\int _{V}{\frac {\nabla '\cdot \mathbf { F} (\mathbf {r} ')}{|\mathbf {r} -\mathbf {r} '|}}\,\mathrm {d} V'-{\frac {1}{4\pi }} \oint _{S}\mathbf {\hat {n}} '\cdot {\frac {\mathbf {F} (\mathbf {r} ')}{|\mathbf {r} -\mathbf {r} ' |}}\,\mathrm {d} S'\\[8pt]\mathbf {A} (\mathbf {r} )&={\frac {1}{4\pi }}\int _{V}{ \frac {\nabla '\times \mathbf {F} (\mathbf {r} ')}{|\mathbf {r} -\mathbf {r} '|}}\,\mathrm {d} V'-{ \frac {1}{4\pi }}\oint _{S}\mathbf {\hat {n}} '\times {\frac {\mathbf {F} (\mathbf {r} ')}{|\ mathbf {r} -\mathbf {r} '|}}\,\mathrm {d} S'\end{تراز شده}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/eac70ccfda5b216df7e6fa4c0b885fca40b60768)
 عملگر nabla با توجه به
عملگر nabla با توجه به  ، نه
، نه  .
. و بنابراین نامتناهی است، و
و بنابراین نامتناهی است، و  مانند
مانند  ، سپس یکی دارد
، سپس یکی دارد ![{\displaystyle {\begin{aligned}\Phi (\mathbf {r} )&={\frac {1}{4\pi }}\int _{\mathbb {R} ^{3}}{\frac { \nabla '\cdot \mathbf {F} (\mathbf {r} ')}{|\mathbf {r} -\mathbf {r} '|}}\,\mathrm {d} V'\\[8pt] \mathbf {A} (\mathbf {r} )&={\frac {1}{4\pi }}\int _{\mathbb {R} ^{3}}{\frac {\nabla '\times \ mathbf {F} (\mathbf {r} ')}{|\mathbf {r} -\mathbf {r} '|}}\,\mathrm {d} V'\end{تراز شده}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/eb7c801c2c724ce19131c2e23e9a6c83eb62afa7)
 که ما چرخش آن را می شناسیم،
که ما چرخش آن را می شناسیم،  و واگرایی،
و واگرایی،  ، در دامنه و میدانهای روی مرز. نوشتن تابع با استفاده از تابع
، در دامنه و میدانهای روی مرز. نوشتن تابع با استفاده از تابع 
 عملگر لاپلاس است، ما داریم
عملگر لاپلاس است، ما داریم![{\displaystyle {\begin{aligned}\mathbf {F} (\mathbf {r})&=\int _{V}\mathbf {F} \left(\mathbf {r} '\right)\delta ^{ 3}(\mathbf {r} -\mathbf {r} ')\mathrm {d} V'\\&=\int _{V}\mathbf {F} (\mathbf {r} ')\left(- {\frac {1}{4\pi }}\nabla ^{2}{\frac {1}{\left|\mathbf {r} -\mathbf {r} '\right|}}\right)\mathrm {d} V'\\&=-{\frac {1}{4\pi }}\nabla ^{2}\int _{V}{\frac {\mathbf {F} (\mathbf {r} ' )}{\left|\mathbf {r} -\mathbf {r} '\right|}}\mathrm {d} V'\\&=-{\frac {1}{4\pi }}\left[ \nabla \left(\nabla \cdot \int _{V}{\frac {\mathbf {F} (\mathbf {r} ')}{\left|\mathbf {r} -\mathbf {r} '\ راست|}}\mathrm {d} V'\right)-\nabla \times \left(\nabla \times \int _{V}{\frac {\mathbf {F} (\mathbf {r} ')} {\left|\mathbf {r} -\mathbf {r} '\right|}}\mathrm {d} V'\right)\right]\\&=-{\frac {1}{4\pi }}\left[\nabla \left(\int _{V}\mathbf {F} (\mathbf {r} ')\cdot \nabla {\frac {1 }{\left|\mathbf {r} -\mathbf {r} '\right|}}\mathrm {d} V'\right)+\nabla \times \left(\int _{V}\mathbf {F } (\mathbf {r} ')\times \nabla {\frac {1}{\left|\mathbf {r} -\mathbf {r} '\right|}}\mathrm {d} V'\right) \right]\\&=-{\frac {1}{4\pi }}\left[-\nabla \left(\int _{V}\mathbf {F} (\mathbf {r} ')\cdot \nabla '{\frac {1}{\left|\mathbf {r} -\mathbf {r} '\right|}}\mathrm {d} V'\right)-\nabla \times \left(\int _{V}\mathbf {F} (\mathbf {r} ')\times \nabla '{\frac {1}{\left|\mathbf {r} -\mathbf {r} '\right|}}\ ریاضی {d} V'\right)\right]\end{تراز شده}}}\right)+\nabla \times \left(\int _{V}\mathbf {F} (\mathbf {r} ')\times \nabla {\frac {1}{\left|\mathbf {r} - \mathbf {r} '\right|}}\mathrm {d} V'\right)\right]\\&=-{\frac {1}{4\pi }}\left[-\nabla \left( \int _{V}\mathbf {F} (\mathbf {r} ')\cdot \nabla '{\frac {1}{\left|\mathbf {r} -\mathbf {r} '\right|} }\mathrm {d} V'\right)-\nabla \times \left(\int _{V}\mathbf {F} (\mathbf {r} ')\times \nabla '{\frac {1}{ \left|\mathbf {r} -\mathbf {r} '\right|}}\mathrm {d} V'\right)\right]\end{تراز شده}}}\right)+\nabla \times \left(\int _{V}\mathbf {F} (\mathbf {r} ')\times \nabla {\frac {1}{\left|\mathbf {r} - \mathbf {r} '\right|}}\mathrm {d} V'\right)\right]\\&=-{\frac {1}{4\pi }}\left[-\nabla \left( \int _{V}\mathbf {F} (\mathbf {r} ')\cdot \nabla '{\frac {1}{\left|\mathbf {r} -\mathbf {r} '\right|} }\mathrm {d} V'\right)-\nabla \times \left(\int _{V}\mathbf {F} (\mathbf {r} ')\times \nabla '{\frac {1}{ \left|\mathbf {r} -\mathbf {r} '\right|}}\mathrm {d} V'\right)\right]\end{تراز شده}}}\right|}}\mathrm {d} V'\right)-\nabla \times \left(\int _{V}\mathbf {F} (\mathbf {r} ')\times \nabla '{\frac {1}{\left|\mathbf {r} -\mathbf {r} '\right|}}\mathrm {d} V'\right)\right]\end{تراز شده}}}\right|}}\mathrm {d} V'\right)-\nabla \times \left(\int _{V}\mathbf {F} (\mathbf {r} ')\times \nabla '{\frac {1}{\left|\mathbf {r} -\mathbf {r} '\right|}}\mathrm {d} V'\right)\right]\end{تراز شده}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/3eeae76841c8576de93f6113dc147a818b15a2d6)

 توسط
توسط  و در خط آخر خطی بودن آرگومان های تابع:
و در خط آخر خطی بودن آرگومان های تابع:

![{\displaystyle {\begin{aligned}\mathbf {F} (\mathbf {r} )=-{\frac {1}{4\pi }}{\bigg [}&-\nabla \left(-\int _{V}{\frac {\nabla '\cdot \mathbf {F} \left(\mathbf {r} '\right)}{\left|\mathbf {r} -\mathbf {r} '\right| }}\mathrm {d} V'+\int _{V}\nabla '\cdot {\frac {\mathbf {F} \left(\mathbf {r} '\right)}{\left|\mathbf { r} -\mathbf {r} '\right|}}\mathrm {d} V'\right)\\&-\nabla \times \left(\int _{V}{\frac {\nabla '\times \mathbf {F} \left(\mathbf {r} '\right)}{\left|\mathbf {r} -\mathbf {r} '\right|}}\mathrm {d} V'-\int _ {V}\nabla '\times {\frac {\mathbf {F} \left(\mathbf {r} '\right)}{\left|\mathbf {r} -\mathbf {r} '\right|} }\mathrm {d} V'\right){\bigg ]}.\end{تراز شده}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/e68ffe47992c705df5dce699d0c1a2d320a418db)
![{\displaystyle {\begin{aligned}\mathbf {F} (\mathbf {r} )&=-{\frac {1}{4\pi }}{\bigg [}-\nabla \left(-\int _{V}{\frac {\nabla '\cdot \mathbf {F} \left(\mathbf {r} '\right)}{\left|\mathbf {r} -\mathbf {r} '\right| }}\mathrm {d} V'+\oint _{S}\mathbf {\hat {n}} '\cdot {\frac {\mathbf {F} \left(\mathbf {r} '\right)} {\left|\mathbf {r} -\mathbf {r} '\right|}}\mathrm {d} S'\right)\\&\qquad \qquad -\nabla \times \left(\int _{ V}{\frac {\nabla '\times \mathbf {F} \left(\mathbf {r} '\right)}{\left|\mathbf {r} -\mathbf {r} '\right|}} \mathrm {d} V'-\oint _{S}\mathbf {\hat {n}} '\times {\frac {\mathbf {F} \left(\mathbf {r} '\right)}{\ چپ|\mathbf {r} -\mathbf {r} '\right|}}\mathrm {d} S'\right){\bigg ]}\\&=-\nabla \left[{\frac {1} {4\pi }}\int _{V}{\frac {\nabla '\cdot \mathbf {F} \left(\mathbf {r} '\right)}{\left|\mathbf {r} -\mathbf {r} '\right|}}\mathrm {d} V'-{ \frac {1}{4\pi }}\oint _{S}\mathbf {\hat {n}} '\cdot {\frac {\mathbf {F} \left(\mathbf {r} '\right) }{\left|\mathbf {r} -\mathbf {r} '\right|}}\mathrm {d} S'\right]\\&\quad +\nabla \times \left[{\frac {1 }{4\pi }}\int _{V}{\frac {\nabla '\times \mathbf {F} \left(\mathbf {r} '\right)}{\left|\mathbf {r} - \mathbf {r} '\right|}}\mathrm {d} V'-{\frac {1}{4\pi }}\oint _{S}\mathbf {\hat {n}} '\times { \frac {\mathbf {F} \left(\mathbf {r} '\right)}{\left|\mathbf {r} -\mathbf {r} '\right|}}\mathrm {d} S'\ راست]\پایان{تراز شده}}}\cdot {\frac {\mathbf {F} \left(\mathbf {r} '\right)}{\left|\mathbf {r} -\mathbf {r} '\right|}}\mathrm {d} S'\right]\\&\quad +\nabla \times \left[{\frac {1}{4\pi }}\int _{V}{\frac {\nabla '\times \mathbf {F} \left(\mathbf {r} '\right)}{\left|\mathbf {r} -\mathbf {r} '\right|}}\mathrm {d} V'-{\frac {1}{4 \pi }}\oint _{S}\mathbf {\hat {n}} '\times {\frac {\mathbf {F} \left(\mathbf {r} '\right)}{\left|\mathbf {r} -\mathbf {r} '\right|}}\mathrm {d} S'\right]\end{تراز شده}}}\cdot {\frac {\mathbf {F} \left(\mathbf {r} '\right)}{\left|\mathbf {r} -\mathbf {r} '\right|}}\mathrm {d} S'\right]\\&\quad +\nabla \times \left[{\frac {1}{4\pi }}\int _{V}{\frac {\nabla '\times \mathbf {F} \left(\mathbf {r} '\right)}{\left|\mathbf {r} -\mathbf {r} '\right|}}\mathrm {d} V'-{\frac {1}{4 \pi }}\oint _{S}\mathbf {\hat {n}} '\times {\frac {\mathbf {F} \left(\mathbf {r} '\right)}{\left|\mathbf {r} -\mathbf {r} '\right|}}\mathrm {d} S'\right]\end{تراز شده}}}-{\frac {1}{4\pi }}\oint _{S}\mathbf {\hat {n}} '\times {\frac {\mathbf {F} \left(\mathbf {r} '\ راست)}{\left|\mathbf {r} -\mathbf {r} '\right|}}\mathrm {d} S'\right]\end{تراز شده}}}-{\frac {1}{4\pi }}\oint _{S}\mathbf {\hat {n}} '\times {\frac {\mathbf {F} \left(\mathbf {r} '\ راست)}{\left|\mathbf {r} -\mathbf {r} '\right|}}\mathrm {d} S'\right]\end{تراز شده}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/40f0b5ca659060eba8fd5a766c0275764c7ab5f7)
 .
.


 تابع
تابع  . برای تعمیم ابعاد بالاتر، بحث
. برای تعمیم ابعاد بالاتر، بحث  ، وجود تضمین شده است. ما کنوانسیون را اعمال می کنیم
، وجود تضمین شده است. ما کنوانسیون را اعمال می کنیم
![{\displaystyle {\begin{aligned}G_{\Phi }(\mathbf {k} )&=i{\frac {\mathbf {k} \cdot \mathbf {G} (\mathbf {k} )}{\ |\mathbf {k} \|^{2}}}\\\mathbf {G} _{\mathbf {A} }(\mathbf {k})&=i{\frac {\mathbf {k} \times \mathbf {G} (\mathbf {k} )}{\|\mathbf {k} \|^{2}}}\\[8pt]\Phi (\mathbf {r} )&=\iiint G_{\ Phi }(\mathbf {k} )e^{i\mathbf {k} \cdot \mathbf {r} }dV_{k}\\\mathbf {A} (\mathbf {r})&=\iiint \mathbf {G} _{\mathbf {A} }(\mathbf {k} )e^{i\mathbf {k} \cdot \mathbf {r} }dV_{k}\end{تراز شده}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/16acf598eb6d627f8977f9486787d2c5032a5456)
![{\displaystyle {\begin{aligned}\mathbf {G} (\mathbf {k} )&=-i\mathbf {k} G_{\Phi }(\mathbf {k})+i\mathbf {k} \ بار \mathbf {G} _{\mathbf {A} }(\mathbf {k} )\\[6pt]\mathbf {F} (\mathbf {r} )&=-\iint i\mathbf {k} G_ {\Phi }(\mathbf {k} )e^{i\mathbf {k} \cdot \mathbf {r} }dV_{k}+\iiint i\mathbf {k} \times \mathbf {G} _{ \mathbf {A} }(\mathbf {k} )e^{i\mathbf {k} \cdot \mathbf {r} }dV_{k}\\&=-\nabla \Phi (\mathbf {r} ) +\nabla \times \mathbf {A} (\mathbf {r} )\end{تراز شده}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/10d9c781899f7a7e818436632e636e7c13806834)


 عملگر
عملگر 

 از زمینه برداری
از زمینه برداری 





 و
و  ،
،

 .
.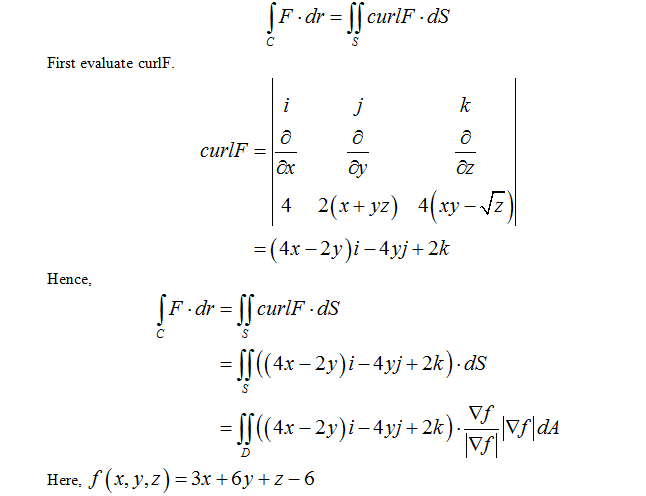

 در این وبلاگ به ریاضیات و کاربردهای آن و تحقیقات در آنها پرداخته می شود. مطالب در این وبلاگ ترجمه سطحی و اولیه است و کامل نیست.در صورتی سوال یا نظری در زمینه ریاضیات دارید مطرح نمایید .در صورت امکان به آن می پردازم. من دوست دارم برای یافتن پاسخ به سوالات و حل پروژه های علمی با دیگران همکاری نمایم.در صورتی که شما هم بامن هم عقیده هستید با من تماس بگیرید.
در این وبلاگ به ریاضیات و کاربردهای آن و تحقیقات در آنها پرداخته می شود. مطالب در این وبلاگ ترجمه سطحی و اولیه است و کامل نیست.در صورتی سوال یا نظری در زمینه ریاضیات دارید مطرح نمایید .در صورت امکان به آن می پردازم. من دوست دارم برای یافتن پاسخ به سوالات و حل پروژه های علمی با دیگران همکاری نمایم.در صورتی که شما هم بامن هم عقیده هستید با من تماس بگیرید.