ماتریس لاپلاسین برای یک گراف بدون جهت از طریق ماتریس تابش جهتدار
[ ویرایش ]
The ماتریس تابش جهتدار B با عنصر B ve برای رأس v و یال e (رئوس متصلکنندهویمن
ماتریس تابش جهتدار B با عنصر B ve برای رأس v و یال e (رئوس متصلکنندهویمن و
و که در آن i ≠ j ) به صورت زیر تعریف میشود
که در آن i ≠ j ) به صورت زیر تعریف میشود
بویای،در غیر این صورت.
اگرچه لبهها در این تعریف از نظر فنی جهتدار هستند، اما جهت آنها میتواند دلخواه باشد و همچنان منجر به همان لاپلاسین متقارن شود. ماتریس L به صورت زیر تعریف میشود
ماتریس L به صورت زیر تعریف میشود

 ترانهاده ماتریس B است .
ترانهاده ماتریس B است .
گراف بدون جهتماتریس بروزماتریس لاپلاسین



یک محصول جایگزین به اصطلاح تعریف میکند
به اصطلاح تعریف میکند لاپلاسین مبتنی بر لبه، برخلاف ماتریس لاپلاسین L که معمولاً مبتنی بر رأس است .
لاپلاسین مبتنی بر لبه، برخلاف ماتریس لاپلاسین L که معمولاً مبتنی بر رأس است .
لاپلاسین متقارن برای یک گراف جهتدار
[ ویرایش ]
ماتریس لاپلاسین یک گراف جهتدار، طبق تعریف، عموماً غیرمتقارن است، در حالی که، مثلاً، خوشهبندی طیفی سنتی در درجه اول برای گرافهای بدون جهت با مجاورت متقارن و ماتریسهای لاپلاسین توسعه داده شده است. یک رویکرد بدیهی برای اعمال تکنیکهایی که نیاز به تقارن دارند، تبدیل گراف جهتدار اصلی به یک گراف بدون جهت و ساخت ماتریس لاپلاسین برای دومی است.
در نمادگذاری ماتریسی، ماتریس مجاورت گراف بدون جهت میتواند، مثلاً، به صورت مجموع بولی ماتریس مجاورت تعریف شود. از گراف جهتدار اصلی و ترانهاده ماتریسی آن
از گراف جهتدار اصلی و ترانهاده ماتریسی آن  که در آن ورودیهای صفر و یک از
که در آن ورودیهای صفر و یک از مانند مثال زیر، به عنوان مقادیر منطقی و نه عددی در نظر گرفته میشوند:
مانند مثال زیر، به عنوان مقادیر منطقی و نه عددی در نظر گرفته میشوند:
ماتریس مجاورت مجاورت متقارن ماتریس لاپلاسین متقارن



نرمالسازی ماتریس لاپلاسین
[ ویرایش ]
یک رأس با درجه بزرگ، که گره سنگین نیز نامیده میشود ، منجر به یک ورودی قطری بزرگ در ماتریس لاپلاس میشود که بر خواص ماتریس غالب است. هدف از نرمالسازی، برابرتر کردن تأثیر چنین رئوسی با سایر رئوس است که با تقسیم ورودیهای ماتریس لاپلاس بر درجه رئوس انجام میشود. برای جلوگیری از تقسیم بر صفر، رئوس ایزوله با درجه صفر از فرآیند نرمالسازی حذف میشوند.
لاپلاسین نرمالشده متقارن
[ ویرایش ]
ماتریس لاپلاسین نرمالشده متقارن به صورت زیر تعریف میشود: [ 1 ]

کجا معکوس مور-پنروز ماتریس درجه است .
معکوس مور-پنروز ماتریس درجه است .
عناصر بنابراین توسط داده میشوند
بنابراین توسط داده میشوند

ماتریس لاپلاسین نرمالشده متقارن، متقارن است اگر و تنها اگر ماتریس مجاورت متقارن باشد.
ماتریس مجاورت ماتریس درجه لاپلاسین نرمال شده



برای یک ماتریس مجاورت نامتقارن از یک گراف جهتدار، میتوان از هر یک از مقادیر indegree و outdegree برای نرمالسازی استفاده کرد:
ماتریس مجاورت ماتریس درجه خروجی لاپلاسین نرمال شده با درجه خارج ازماتریس درجه ورودی لاپلاسین نرمال شده درون درجهای





لاپلاسینهای نرمالشده چپ (با گام تصادفی) و راست
[ ویرایش ]
ماتریس لاپلاسین نرمالشده چپ (گام تصادفی) به صورت زیر تعریف میشود:

کجادی+ معکوس مور-پنروز است . عناصرِلآر دبلیو
معکوس مور-پنروز است . عناصرِلآر دبلیو توسط داده میشوند
توسط داده میشوند

به طور مشابه، ماتریس لاپلاسین نرمال شده راست به صورت زیر تعریف میشود:
 .
.
ماتریس لاپلاسین نرمال شده چپ یا راست متقارن است اگر ماتریس مجاورت متقارن و نمودار منظم باشد. در غیر این صورت، ماتریس لاپلاسین نرمال شده چپ یا راست نامتقارن است. به عنوان مثال،
ماتریس مجاورت ماتریس درجه لاپلاسین نرمال شده چپ لاپلاسین نرمال شده به راست




این مثال همچنین نشان میدهد که اگر هیچ رأس ایزولهای ندارد، آنگاه
هیچ رأس ایزولهای ندارد، آنگاه تصادفی راست و از این رو ماتریس یک گام تصادفی است ، به طوری که لاپلاسین نرمال شده
تصادفی راست و از این رو ماتریس یک گام تصادفی است ، به طوری که لاپلاسین نرمال شده  جمع هر سطر برابر با صفر است. بنابراین گاهی اوقات به طور متناوب فراخوانی میکنیملآر دبلیو
جمع هر سطر برابر با صفر است. بنابراین گاهی اوقات به طور متناوب فراخوانی میکنیملآر دبلیو لاپلاسین نرمالشده با گام تصادفی . در لاپلاسین نرمالشده به راست که کمتر مورد استفاده قرار میگیرد
لاپلاسین نرمالشده با گام تصادفی . در لاپلاسین نرمالشده به راست که کمتر مورد استفاده قرار میگیرد مجموع هر ستون برابر با صفر است، زیرا
مجموع هر ستون برابر با صفر است، زیرا تصادفی چپ است .
تصادفی چپ است .
برای یک ماتریس مجاورت نامتقارن از یک گراف جهتدار، برای نرمالسازی باید indegree یا outdegree را نیز انتخاب کرد :
ماتریس مجاورت ماتریس درجه خروجی لاپلاسین نرمال شده چپ با درجه خروجی ماتریس درجه ورودی لاپلاسین نرمالشدهی همدرجه به راست





لاپلاسین نرمالشده با درجه خروجی چپ با مجموع سطری که همه ۰ است مربوط به تصادفی راست است. در حالی که لاپلاسین نرمال شده درجه راست با مجموع ستونی همه ۰ شامل تصادفی چپ است
در حالی که لاپلاسین نرمال شده درجه راست با مجموع ستونی همه ۰ شامل تصادفی چپ است .
.
تعاریف گرافها با یالهای وزندار
[ ویرایش ]
گرافهای رایج در کاربردها با یالهای وزندار، به راحتی توسط ماتریسهای مجاورت خود تعریف میشوند که در آنها مقادیر ورودیها عددی هستند و دیگر محدود به صفر و یک نیستند. در خوشهبندی طیفی و پردازش سیگنال مبتنی بر گراف ، که در آنها رئوس گراف نشاندهنده نقاط داده هستند، وزنهای یال را میتوان محاسبه کرد، مثلاً به صورت معکوس متناسب با فواصل بین جفت نقاط داده، که منجر به غیرمنفی بودن همه وزنها با مقادیر بزرگتر میشود که به طور غیررسمی مربوط به جفتهای مشابهتر نقاط داده است. استفاده از همبستگی و ضد همبستگی بین نقاط داده به طور طبیعی منجر به وزنهای مثبت و منفی میشود. اکثر تعاریف برای گرافهای ساده به طور جزئی به حالت استاندارد وزنهای غیرمنفی تعمیم داده میشوند، در حالی که وزنهای منفی نیاز به توجه بیشتری دارند، به خصوص در نرمالسازی.
ماتریس لاپلاسین
[ ویرایش ]
ماتریس لاپلاسین به صورت زیر تعریف میشود:

که در آن D ماتریس درجه و A ماتریس مجاورت گراف است .
برای گرافهای جهتدار ، بسته به کاربرد، میتوان از درجه ورودی یا درجه خروجی استفاده کرد، مانند مثال زیر:
ماتریس مجاورت ماتریس درجه ورودی لاپلاسین درون درجهای ماتریس درجه خروجی لاپلاسین خارج از درجه





خود-حلقههای گراف، که خود را با درایههای غیر صفر روی قطر اصلی ماتریس مجاورت نشان میدهند، مجاز هستند اما بر مقادیر لاپلاسین گراف تأثیری ندارند.
لاپلاسین متقارن از طریق ماتریس تابش
[ ویرایش ]
یک سیستم فنر دو بعدی.
برای گرافهایی با یالهای وزندار، میتوان یک ماتریس بروز وزندار B تعریف کرد و از آن برای ساخت لاپلاسین متقارن مربوطه به صورت زیر استفاده کرد: یک رویکرد جایگزین و تمیزتر که در اینجا شرح داده شده است، جداسازی وزنها از اتصال است: استفاده از ماتریس بروز را مانند گرافهای منظم ادامه دهید و ماتریسی را معرفی کنید که فقط مقادیر وزنها را در خود نگه دارد. یک سیستم فنر نمونهای از این مدل است که در مکانیک برای توصیف سیستمی از فنرها با سختیهای داده شده و طول واحد استفاده میشود، که در آن مقادیر سختیها نقش وزنهای یالهای گراف را ایفا میکنند.
یک رویکرد جایگزین و تمیزتر که در اینجا شرح داده شده است، جداسازی وزنها از اتصال است: استفاده از ماتریس بروز را مانند گرافهای منظم ادامه دهید و ماتریسی را معرفی کنید که فقط مقادیر وزنها را در خود نگه دارد. یک سیستم فنر نمونهای از این مدل است که در مکانیک برای توصیف سیستمی از فنرها با سختیهای داده شده و طول واحد استفاده میشود، که در آن مقادیر سختیها نقش وزنهای یالهای گراف را ایفا میکنند.
بنابراین ما از تعریف بیوزنی دوباره استفاده میکنیم ماتریس رخداد B با عنصر B ve برای رأس v و یال e (رئوس متصل کننده
ماتریس رخداد B با عنصر B ve برای رأس v و یال e (رئوس متصل کننده و
و که i > j ) به صورت زیر تعریف میشود
که i > j ) به صورت زیر تعریف میشود

اکنون یک قطر را نیز تعریف میکنیم ماتریس W شامل وزنهای یالها. اگرچه یالها در تعریف B از نظر فنی جهتدار هستند، اما جهت آنها میتواند دلخواه باشد و همچنان منجر به همان لاپلاسین متقارن شود.
ماتریس W شامل وزنهای یالها. اگرچه یالها در تعریف B از نظر فنی جهتدار هستند، اما جهت آنها میتواند دلخواه باشد و همچنان منجر به همان لاپلاسین متقارن شود. ماتریس L به صورت زیر تعریف میشود
ماتریس L به صورت زیر تعریف میشود

 ترانهاده ماتریس B است .
ترانهاده ماتریس B است .
این ساختار در مثال زیر نشان داده شده است، که در آن هر یالای مقدار وزنی i به آن اختصاص داده شده است ، با.
مقدار وزنی i به آن اختصاص داده شده است ، با.
گراف بدون جهت ماتریس بروز وزن لبهها ماتریس لاپلاسین




لاپلاسین متقارن برای یک گراف جهتدار
[ ویرایش ]
درست مانند گرافهای ساده، ماتریس لاپلاسین یک گراف وزندار جهتدار، طبق تعریف عموماً نامتقارن است. تقارن را میتوان با تبدیل گراف جهتدار اصلی به یک گراف بدون جهت، قبل از ساخت لاپلاسین، اعمال کرد. ماتریس مجاورت گراف بدون جهت، به عنوان مثال، میتواند به صورت مجموع ماتریس مجاورت تعریف شود.الف از گراف جهتدار اصلی و ترانهاده ماتریسی آن
از گراف جهتدار اصلی و ترانهاده ماتریسی آن  مانند مثال زیر:
مانند مثال زیر:
ماتریس مجاورت ماتریس مجاورت متقارن ماتریس لاپلاسین متقارن



که در آن ورودیهای صفر و یک از مانند گرافهای ساده، به عنوان مقادیر عددی در نظر گرفته میشوند، نه منطقی، که تفاوت در نتایج را توضیح میدهد - برای گرافهای ساده، گراف متقارن همچنان باید ساده باشد و ماتریس مجاورت متقارن آن فقط مقادیر منطقی و نه عددی داشته باشد، مثلاً مجموع منطقی ۱ در ۱ = ۱ است، در حالی که مجموع عددی ۱ + ۱ = ۲ است.
مانند گرافهای ساده، به عنوان مقادیر عددی در نظر گرفته میشوند، نه منطقی، که تفاوت در نتایج را توضیح میدهد - برای گرافهای ساده، گراف متقارن همچنان باید ساده باشد و ماتریس مجاورت متقارن آن فقط مقادیر منطقی و نه عددی داشته باشد، مثلاً مجموع منطقی ۱ در ۱ = ۱ است، در حالی که مجموع عددی ۱ + ۱ = ۲ است.
به طور جایگزین، ماتریس لاپلاسین متقارن را میتوان از دو لاپلاسین با استفاده از indegree و outdegree محاسبه کرد ، همانطور که در مثال زیر آمده است:
ماتریس مجاورت ماتریس درجه خروجی لاپلاسین خارج از درجه ماتریس درجه ورودی لاپلاسین درون درجهای





مجموع لاپلاسین درجه خروجی و لاپلاسین درجه ورودی برابر با ماتریس لاپلاسین متقارن است.
نرمالسازی ماتریس لاپلاسین
[ ویرایش ]
هدف از نرمالسازی، مانند گرافهای ساده، این است که ورودیهای قطری ماتریس لاپلاسین کاملاً واحد باشند و ورودیهای غیرقطری نیز به طور متناظر مقیاسبندی شوند. در یک گراف وزندار ، یک رأس ممکن است به دلیل تعداد کم یالهای متصل اما با وزنهای بزرگ و همچنین به دلیل تعداد زیاد یالهای متصل با وزن واحد، درجه بزرگی داشته باشد.
خود-حلقههای گراف، یعنی ورودیهای غیر صفر روی قطر اصلی ماتریس مجاورت، بر مقادیر لاپلاسین گراف تأثیری ندارند، اما ممکن است برای محاسبه ضرایب نرمالسازی لازم باشد که شمارش شوند.
لاپلاسین نرمالشده متقارن
[ ویرایش ]
لاپلاسین نرمالشده متقارن به صورت زیر تعریف میشود:

که در آن L لاپلاسین غیر نرمال شده، A ماتریس مجاورت، D ماتریس درجه و معکوس مور-پنروز است . از آنجایی که ماتریس درجه D قطری است، جذر معکوس آن
معکوس مور-پنروز است . از آنجایی که ماتریس درجه D قطری است، جذر معکوس آن فقط ماتریس قطری است که درایههای قطری آن، معکوس جذر درایههای قطری D هستند . اگر همه وزنهای یال غیرمنفی باشند، همه مقادیر درجه نیز به طور خودکار غیرمنفی هستند و بنابراین هر مقدار درجه یک جذر مثبت منحصر به فرد دارد. برای جلوگیری از تقسیم بر صفر، رأسهایی با درجه صفر از فرآیند نرمالسازی حذف میشوند، مانند مثال زیر:
فقط ماتریس قطری است که درایههای قطری آن، معکوس جذر درایههای قطری D هستند . اگر همه وزنهای یال غیرمنفی باشند، همه مقادیر درجه نیز به طور خودکار غیرمنفی هستند و بنابراین هر مقدار درجه یک جذر مثبت منحصر به فرد دارد. برای جلوگیری از تقسیم بر صفر، رأسهایی با درجه صفر از فرآیند نرمالسازی حذف میشوند، مانند مثال زیر:
ماتریس مجاورت ماتریس درجه ورودی لاپلاسین نرمال شده درون درجهای ماتریس درجه خروجی لاپلاسین نرمال شده با درجه خارج از





لاپلاسین نرمالشده متقارن، یک ماتریس متقارن است اگر و تنها اگر ماتریس مجاورت A متقارن و درایههای قطری D غیرمنفی باشند، که در این صورت میتوانیم از اصطلاح لاپلاسین نرمالشده متقارن استفاده کنیم .
ماتریس لاپلاسین نرمالشده متقارن را میتوان به صورت زیر نیز نوشت:

با استفاده از بیوزنی ماتریس بروز B و قطری
ماتریس بروز B و قطری ماتریس W شامل وزنهای یالها و تعریف مقادیر جدید|وی|×|ای|
ماتریس W شامل وزنهای یالها و تعریف مقادیر جدید|وی|×|ای| ماتریس وزنی بروز
ماتریس وزنی بروز که سطرهای آن توسط رئوس و ستونهای آن توسط یالهای G اندیسگذاری شدهاند، به طوری که هر ستون مربوط به یال e = {u, v} یک ورودی دارد.۱
که سطرهای آن توسط رئوس و ستونهای آن توسط یالهای G اندیسگذاری شدهاند، به طوری که هر ستون مربوط به یال e = {u, v} یک ورودی دارد.۱ در ردیف مربوط به u ، یک ورودی−۱
در ردیف مربوط به u ، یک ورودی−۱ در ردیف مربوط به v قرار دارد و در جاهای دیگر 0 ورودی دارد.
در ردیف مربوط به v قرار دارد و در جاهای دیگر 0 ورودی دارد.
لاپلاسین نرمالشده با گام تصادفی
[ ویرایش ]
لاپلاسین نرمالشده با گام تصادفی به صورت زیر تعریف میشود:

که در آن D ماتریس درجه است. از آنجایی که ماتریس درجه D قطری است، معکوس آن  به سادگی به عنوان یک ماتریس قطری تعریف میشود که دارای درایههای قطری است که معکوس درایههای قطری متناظر D هستند . برای رئوس منفرد (آنهایی که درجه 0 دارند)، یک انتخاب رایج، تنظیم عنصر متناظر است.
به سادگی به عنوان یک ماتریس قطری تعریف میشود که دارای درایههای قطری است که معکوس درایههای قطری متناظر D هستند . برای رئوس منفرد (آنهایی که درجه 0 دارند)، یک انتخاب رایج، تنظیم عنصر متناظر است.  به 0. عناصر ماتریس
به 0. عناصر ماتریس  توسط داده میشوند
توسط داده میشوند

نام لاپلاسین نرمالشده با گام تصادفی از این واقعیت گرفته شده است که این ماتریس  ، کجا
، کجا  به سادگی ماتریس انتقال یک فرد تصادفی روی نمودار است، با فرض وزنهای غیر منفی. برای مثال، فرض کنیدایمن
به سادگی ماتریس انتقال یک فرد تصادفی روی نمودار است، با فرض وزنهای غیر منفی. برای مثال، فرض کنیدایمن نشان دهنده بردار پایه استاندارد i ام است . سپس
نشان دهنده بردار پایه استاندارد i ام است . سپس  یک بردار احتمال است که توزیع مکانهای یک راهرونده تصادفی را پس از برداشتن یک گام از رأس نشان میدهد.
یک بردار احتمال است که توزیع مکانهای یک راهرونده تصادفی را پس از برداشتن یک گام از رأس نشان میدهد.  ؛ یعنی،
؛ یعنی،  به طور کلی، اگر بردارایکس
به طور کلی، اگر بردارایکس توزیع احتمال مکان یک راه رونده تصادفی روی رئوس گراف است، آنگاه
توزیع احتمال مکان یک راه رونده تصادفی روی رئوس گراف است، آنگاه  توزیع احتمال واکر پس ازتی
توزیع احتمال واکر پس ازتی مراحل.
مراحل.
لاپلاسین نرمالشده با گام تصادفی را میتوان لاپلاسین نرمالشده با چپ نیز نامید.  از آنجا که نرمالسازی با ضرب لاپلاسین در ماتریس نرمالسازی انجام میشود
از آنجا که نرمالسازی با ضرب لاپلاسین در ماتریس نرمالسازی انجام میشود  در سمت چپ. از آن زمان جمع هر سطر برابر با صفر است
در سمت چپ. از آن زمان جمع هر سطر برابر با صفر است  با فرض اینکه همه وزنها غیر منفی باشند، تصادفی راست است .
با فرض اینکه همه وزنها غیر منفی باشند، تصادفی راست است .
در لاپلاسین نرمال شده به راست که کمتر مورد استفاده قرار میگیردلدی مجموع هر ستون برابر با صفر است، زیراالفدی+
مجموع هر ستون برابر با صفر است، زیراالفدی+ تصادفی چپ است .
تصادفی چپ است .
برای یک ماتریس مجاورت نامتقارن از یک گراف جهتدار، برای نرمالسازی باید indegree یا outdegree را نیز انتخاب کرد :
ماتریس مجاورت ماتریس درجه خروجی لاپلاسین نرمال شده چپ با درجه خروجی ماتریس درجه ورودی لاپلاسین نرمالشدهی همدرجه به راست





لاپلاسین نرمالشده با درجه خروجی چپ با مجموع سطری که همه ۰ است مربوط به تصادفی راست است.  در حالی که لاپلاسین نرمال شده درجه راست با مجموع ستونی همه ۰ شامل تصادفی چپ است +
در حالی که لاپلاسین نرمال شده درجه راست با مجموع ستونی همه ۰ شامل تصادفی چپ است + .
.
وزنهای منفی
[ ویرایش ]
وزنهای منفی چالشهای متعددی را برای نرمالسازی ایجاد میکنند:
- وجود وزنهای منفی میتواند به طور طبیعی منجر به صفر شدن مجموع سطرها و/یا ستونها برای رئوس غیر ایزوله شود. رأسی با مجموع سطرهای بزرگ از وزنهای مثبت و مجموع سطرهای به همان اندازه بزرگ منفی از وزنهای منفی، که مجموع آنها به صفر میرسد، میتواند یک گره سنگین در نظر گرفته شود و هر دو مقادیر بزرگ مقیاسبندی شوند، در حالی که ورودی قطری، مانند یک رأس ایزوله، صفر باقی میماند.
- وزنهای منفی همچنین ممکن است مجموع سطرها و/یا ستونهای منفی ایجاد کنند، به طوری که ورودی قطری مربوطه در ماتریس لاپلاسین غیر نرمال شده منفی خواهد بود و جذر مثبت مورد نیاز برای نرمالسازی متقارن وجود نخواهد داشت.
- میتوان استدلالهایی ارائه داد که برای نرمالسازی، قدر مطلق مجموع سطرها و/یا ستونها در نظر گرفته شود، بنابراین مقدار احتمالی -۱ به عنوان یک واحد ورودی مشروع از قطر اصلی ماتریس لاپلاسین نرمالسازی شده در نظر گرفته میشود.
خواص
[ ویرایش ]
برای یک گراف (بدون جهت) G و ماتریس لاپلاسین L آن با مقادیر ویژه  :
:
- L متقارن است .
- L مثبت-نیمه معین است (یعنی
 برای همه
برای همه  ). این را میتوان از این واقعیت دریافت که لاپلاسین متقارن و قطری غالب است .
). این را میتوان از این واقعیت دریافت که لاپلاسین متقارن و قطری غالب است . - L یک ماتریس M است (درجههای خارج از قطر آن غیرمثبت هستند، اما بخشهای حقیقی مقادیر ویژه آن غیرمنفی هستند).
- مجموع هر سطر و مجموع ستون از L برابر با صفر است. در واقع، در این مجموع، درجه رأس با "-1" برای هر همسایه جمع میشود.
- در نتیجه،
 ، زیرا برداروی
، زیرا برداروی ارضا میکند.
ارضا میکند. این همچنین نشان میدهد که ماتریس لاپلاسین منفرد است.
این همچنین نشان میدهد که ماتریس لاپلاسین منفرد است. - تعداد مؤلفههای متصل در گراف، بُعد فضای تهی لاپلاسین و کثرت جبری مقدار ویژه ۰ است.
- کوچکترین مقدار ویژه غیر صفر L ، شکاف طیفی نامیده میشود .
- دومین کوچکترین مقدار ویژه L (که میتواند صفر باشد) همبندی جبری (یا مقدار فیدلر ) G است و تنکترین برش یک گراف را تقریب میزند.
- لاپلاسین یک عملگر روی فضای برداری n بعدی از توابع است .ف:
 ، کجاپ
، کجاپ مجموعه رئوس G است، و
مجموعه رئوس G است، و  .
. - وقتی G k-منظم باشد ، لاپلاسین نرمالشده برابر است با:
 که در آن A ماتریس مجاورت و I ماتریس همانی است.
که در آن A ماتریس مجاورت و I ماتریس همانی است. - برای گرافی با چندین مؤلفه متصل ، L یک ماتریس قطری بلوکی است که در آن هر بلوک، ماتریس لاپلاسین مربوط به هر مؤلفه است، احتمالاً پس از مرتبسازی مجدد رئوس (یعنی L یک جایگشت است - شبیه به یک ماتریس قطری بلوکی).
- اثر ماتریس لاپلاسین L برابر است با
 کجا
کجا  تعداد یالهای گراف مورد نظر است.
تعداد یالهای گراف مورد نظر است. - اکنون یک تجزیه ویژه از را در نظر بگیریدل
 ، با بردارهای ویژه با نرم واحد
، با بردارهای ویژه با نرم واحد  و مقادیر ویژه مربوطه
و مقادیر ویژه مربوطه  :
:

زیرا  را میتوان به صورت ضرب داخلی بردار نوشت
را میتوان به صورت ضرب داخلی بردار نوشت  با خودش، این نشان میدهد که
با خودش، این نشان میدهد که و بنابراین مقادیر ویژهیل
و بنابراین مقادیر ویژهیل همه غیر منفی هستند.
همه غیر منفی هستند.
- تمام مقادیر ویژه لاپلاسین متقارن نرمالشده در 0 = μ 0 ≤ … ≤ μ n−1 ≤ 2 صدق میکنند. این مقادیر ویژه (که به عنوان طیف لاپلاسین نرمالشده شناخته میشوند) به خوبی با سایر ثابتهای گراف برای گرافهای عمومی مرتبط هستند. [ 1 ]
 ،
،
یعنی، مشابه لاپلاسین نرمال شده است
مشابه لاپلاسین نرمال شده است  به همین دلیل، حتی اگر
به همین دلیل، حتی اگر به طور کلی متقارن نیست، مقادیر ویژه حقیقی دارد — دقیقاً مشابه مقادیر ویژه لاپلاسین متقارن نرمال شده
به طور کلی متقارن نیست، مقادیر ویژه حقیقی دارد — دقیقاً مشابه مقادیر ویژه لاپلاسین متقارن نرمال شده .
.
تفسیر به عنوان عملگر لاپلاس گسسته که لاپلاسین پیوسته را تقریب میزند
[ ویرایش ]
ماتریس لاپلاسین گراف را میتوان به عنوان فرم ماتریسی عملگر لاپلاسین گسسته منفی روی گرافی که عملگر لاپلاسین پیوسته منفی حاصل از روش تفاضل محدود را تقریب میزند، در نظر گرفت . (به معادله پواسون گسسته مراجعه کنید ) [ 2 ] در این تفسیر، هر رأس گراف به عنوان یک نقطه شبکه در نظر گرفته میشود؛ اتصال محلی رأس، الگوی تقریب تفاضل محدود را در این نقطه شبکه تعیین میکند، اندازه شبکه همیشه برای هر یال یکی است و هیچ محدودیتی روی هیچ نقطه شبکهای وجود ندارد، که مربوط به حالت شرط مرزی همگن نیومن ، یعنی مرز آزاد است. چنین تفسیری به عنوان مثال، تعمیم ماتریس لاپلاسین به حالت گرافهایی با تعداد نامحدود رأس و یال را ممکن میسازد که منجر به یک ماتریس لاپلاسین با اندازه نامحدود میشود.
تعمیمها و بسطهای ماتریس لاپلاسین
[ ویرایش ]
لاپلاسین تعمیمیافته
[ ویرایش ]
لاپلاسین تعمیمیافته به صورت زیر تعریف میشود: [ 3 ]
به صورت زیر تعریف میشود: [ 3 ]

توجه داشته باشید که لاپلاسین معمولی، یک لاپلاسین تعمیمیافته است.
ماتریس ادمیتانس یک مدار AC
[ ویرایش ]
لاپلاسین یک گراف برای اولین بار برای مدلسازی شبکههای الکتریکی معرفی شد. در یک شبکه الکتریکی جریان متناوب (AC)، مقاومتهای با مقادیر حقیقی با امپدانسهای با مقادیر مختلط جایگزین میشوند. وزن یال ( i , j ) طبق قرارداد، منهای معکوس امپدانس مستقیماً بین i و j است . در مدلهای چنین شبکههایی، ورودیهای ماتریس مجاورت مختلط هستند، اما ماتریس کیرشهف متقارن باقی میماند، نه هرمیتی . چنین ماتریسی معمولاً " ماتریس ادمیتانس " نامیده میشود که با نشان داده میشود.ی ، به جای یک "لاپلاسین". این یکی از کاربردهای نادری است که منجر به ماتریسهای متقارن مختلط میشود .
، به جای یک "لاپلاسین". این یکی از کاربردهای نادری است که منجر به ماتریسهای متقارن مختلط میشود .
ماتریس مجاورت ماتریس درجه وزنی ماتریس ادمیتانس



لاپلاسین مغناطیسی
[ ویرایش ]
موقعیتهای دیگری نیز وجود دارد که در آنها ورودیهای ماتریس مجاورت، مختلط هستند و لاپلاسین به یک ماتریس هرمیتی تبدیل میشود . لاپلاسین مغناطیسی برای یک گراف جهتدار با وزنهای حقیقی  به عنوان حاصلضرب هادامارد ماتریس متقارن حقیقی لاپلاسین متقارن و ماتریس فاز هرمیتی با ورودیهای مختلط ساخته میشود
به عنوان حاصلضرب هادامارد ماتریس متقارن حقیقی لاپلاسین متقارن و ماتریس فاز هرمیتی با ورودیهای مختلط ساخته میشود

که جهت لبه را در فاز صفحه مختلط کدگذاری میکنند. در زمینه فیزیک کوانتومی، لاپلاسین مغناطیسی را میتوان به عنوان عملگری تفسیر کرد که پدیدهشناسی یک ذره باردار آزاد را روی یک گراف توصیف میکند، که تابع عمل یک میدان مغناطیسی است و پارامترس بار الکتریکی نامیده میشود. [ 4 ] در مثال زیر
بار الکتریکی نامیده میشود. [ 4 ] در مثال زیر :
:
ماتریس مجاورت لاپلاسین متقارن ماتریس فازلاپلاسین مغناطیسی




لاپلاسین تغییر شکل یافته
[ ویرایش ]
لاپلاسین تغییر شکل یافته معمولاً به صورت زیر تعریف میشود:

که در آن I ماتریس همانی، A ماتریس مجاورت، D ماتریس درجه و s یک عدد (مقدار مختلط) است. [ 5 ]
لاپلاسین استاندارد به صورت زیر است:دلتا(۱) ودلتا
ودلتا لاپلاسینِ بدون علامت است.
لاپلاسینِ بدون علامت است.
لاپلاسین بدون علامت
[ ویرایش ]
لاپلاسین بدون علامت به صورت زیر تعریف میشود:

کجا  ماتریس درجه است، و
ماتریس درجه است، و ماتریس مجاورت است. [ 6 ] مانند لاپلاسین علامتدار
ماتریس مجاورت است. [ 6 ] مانند لاپلاسین علامتدار لاپلاسین بیعلامتس
لاپلاسین بیعلامتس همچنین مثبت و نیمه قطعی است زیرا میتوان آن را به صورت زیر فاکتورگیری کرد:
همچنین مثبت و نیمه قطعی است زیرا میتوان آن را به صورت زیر فاکتورگیری کرد:

کجار ماتریس بروز است.
ماتریس بروز است. یک بردار ویژه 0 دارد اگر و تنها اگر یک مؤلفه همبند دوبخشی داشته باشد (رأسهای ایزوله، مؤلفههای همبند دوبخشی هستند). این را میتوان به صورت زیر نشان داد
یک بردار ویژه 0 دارد اگر و تنها اگر یک مؤلفه همبند دوبخشی داشته باشد (رأسهای ایزوله، مؤلفههای همبند دوبخشی هستند). این را میتوان به صورت زیر نشان داد

این یک راه حل دارد که در آن  اگر و تنها اگر گراف دارای یک مؤلفه همبند دوبخشی باشد.
اگر و تنها اگر گراف دارای یک مؤلفه همبند دوبخشی باشد.
گرافهای چندگانه جهتدار
[ ویرایش ]
میتوان معادلی از ماتریس لاپلاسین را برای گرافهای چندگانه جهتدار تعریف کرد. [ 7 ] در این حالت، ماتریس لاپلاسین L به صورت زیر تعریف میشود.

که در آن D یک ماتریس قطری با Di i است که i برابر با درجه خروجی رأس i و A ماتریسی با A i و j برابر با تعداد یالهای i تا j (شامل حلقهها) است.
پیادهسازی نرمافزارهای متنباز
[ ویرایش ]
- سایپای [ 8 ]
- شبکه ایکس [ 9 ]
- جولیا [ 10 ]
نرمافزار کاربردی
[ ویرایش ]
- خوشهبندی طیفی scikit-learn [ 11 ]
- PyGSP: پردازش سیگنال گراف در پایتون [ 12 ]
- مگامن: یادگیری منیفولد برای میلیونها امتیاز [ 13 ]
- صافG [ 14 ]
- تشخیص نقطه تغییر لاپلاسین برای گرافهای پویا (KDD 2020) [ 15 ]
- LaplacianOpt (یک بسته جولیا برای به حداکثر رساندن مقدار ویژه دوم لاپلاسین گرافهای وزندار) [ 16 ]
- LigMG (گراف نامنظم بزرگ چندشبکهای) [ 17 ]
- Laplacians.jl [ 18 ]
همچنین ببینید
[ ویرایش ]
- ماتریس سختی
- فاصله مقاومت
- ماتریس نرخ گذار
- حساب دیفرانسیل و انتگرال روی گرافهای وزندار متناهی
- تبدیل فوریه گراف
https://en.wikipedia.org/wiki/Laplacian_matrix
 ماتریس تابش جهتدار B با عنصر B ve برای رأس v و یال e (رئوس متصلکنندهویمن
ماتریس تابش جهتدار B با عنصر B ve برای رأس v و یال e (رئوس متصلکنندهویمن و
و که در آن i ≠ j ) به صورت زیر تعریف میشود
که در آن i ≠ j ) به صورت زیر تعریف میشود
 ماتریس L به صورت زیر تعریف میشود
ماتریس L به صورت زیر تعریف میشود
 ترانهاده ماتریس B است .
ترانهاده ماتریس B است .


 به اصطلاح تعریف میکند
به اصطلاح تعریف میکند لاپلاسین مبتنی بر لبه، برخلاف ماتریس لاپلاسین L که معمولاً مبتنی بر رأس است .
لاپلاسین مبتنی بر لبه، برخلاف ماتریس لاپلاسین L که معمولاً مبتنی بر رأس است . از گراف جهتدار اصلی و ترانهاده ماتریسی آن
از گراف جهتدار اصلی و ترانهاده ماتریسی آن  که در آن ورودیهای صفر و یک از
که در آن ورودیهای صفر و یک از



 معکوس مور-پنروز ماتریس درجه است .
معکوس مور-پنروز ماتریس درجه است . بنابراین توسط داده میشوند
بنابراین توسط داده میشوند









 توسط داده میشوند
توسط داده میشوند
 .
.

 هیچ رأس ایزولهای ندارد، آنگاه
هیچ رأس ایزولهای ندارد، آنگاه تصادفی راست و از این رو ماتریس یک گام تصادفی است ، به طوری که لاپلاسین نرمال شده
تصادفی راست و از این رو ماتریس یک گام تصادفی است ، به طوری که لاپلاسین نرمال شده  جمع هر سطر برابر با صفر است. بنابراین گاهی اوقات به طور متناوب فراخوانی میکنیملآر دبلیو
جمع هر سطر برابر با صفر است. بنابراین گاهی اوقات به طور متناوب فراخوانی میکنیملآر دبلیو لاپلاسین نرمالشده با گام تصادفی . در لاپلاسین نرمالشده به راست که کمتر مورد استفاده قرار میگیرد
لاپلاسین نرمالشده با گام تصادفی . در لاپلاسین نرمالشده به راست که کمتر مورد استفاده قرار میگیرد تصادفی چپ است .
تصادفی چپ است .

 در حالی که لاپلاسین نرمال شده درجه راست با مجموع ستونی همه ۰ شامل تصادفی چپ است
در حالی که لاپلاسین نرمال شده درجه راست با مجموع ستونی همه ۰ شامل تصادفی چپ است .
.







 مقدار وزنی i به آن اختصاص داده شده است ، با.
مقدار وزنی i به آن اختصاص داده شده است ، با.






 فقط ماتریس قطری است که درایههای قطری آن، معکوس جذر درایههای قطری D هستند . اگر همه وزنهای یال غیرمنفی باشند، همه مقادیر درجه نیز به طور خودکار غیرمنفی هستند و بنابراین هر مقدار درجه یک جذر مثبت منحصر به فرد دارد. برای جلوگیری از تقسیم بر صفر، رأسهایی با درجه صفر از فرآیند نرمالسازی حذف میشوند، مانند مثال زیر:
فقط ماتریس قطری است که درایههای قطری آن، معکوس جذر درایههای قطری D هستند . اگر همه وزنهای یال غیرمنفی باشند، همه مقادیر درجه نیز به طور خودکار غیرمنفی هستند و بنابراین هر مقدار درجه یک جذر مثبت منحصر به فرد دارد. برای جلوگیری از تقسیم بر صفر، رأسهایی با درجه صفر از فرآیند نرمالسازی حذف میشوند، مانند مثال زیر:




 که سطرهای آن توسط رئوس و ستونهای آن توسط یالهای G اندیسگذاری شدهاند، به طوری که هر ستون مربوط به یال e = {u, v} یک ورودی دارد.۱
که سطرهای آن توسط رئوس و ستونهای آن توسط یالهای G اندیسگذاری شدهاند، به طوری که هر ستون مربوط به یال e = {u, v} یک ورودی دارد.۱ در ردیف مربوط به u ، یک ورودی−۱
در ردیف مربوط به u ، یک ورودی−۱ در ردیف مربوط به v قرار دارد و در جاهای دیگر 0 ورودی دارد.
در ردیف مربوط به v قرار دارد و در جاهای دیگر 0 ورودی دارد. به سادگی به عنوان یک ماتریس قطری تعریف میشود که دارای درایههای قطری است که معکوس درایههای قطری متناظر D هستند . برای رئوس منفرد (آنهایی که درجه 0 دارند)، یک انتخاب رایج، تنظیم عنصر متناظر است.
به سادگی به عنوان یک ماتریس قطری تعریف میشود که دارای درایههای قطری است که معکوس درایههای قطری متناظر D هستند . برای رئوس منفرد (آنهایی که درجه 0 دارند)، یک انتخاب رایج، تنظیم عنصر متناظر است.  به 0. عناصر ماتریس
به 0. عناصر ماتریس 
 ، کجا
، کجا  به سادگی ماتریس انتقال یک فرد تصادفی روی نمودار است، با فرض وزنهای غیر منفی. برای مثال، فرض کنیدایمن
به سادگی ماتریس انتقال یک فرد تصادفی روی نمودار است، با فرض وزنهای غیر منفی. برای مثال، فرض کنیدایمن یک بردار احتمال است که توزیع مکانهای یک راهرونده تصادفی را پس از برداشتن یک گام از رأس نشان میدهد.
یک بردار احتمال است که توزیع مکانهای یک راهرونده تصادفی را پس از برداشتن یک گام از رأس نشان میدهد.  ؛ یعنی،
؛ یعنی،  به طور کلی، اگر بردارایکس
به طور کلی، اگر بردارایکس توزیع احتمال مکان یک راه رونده تصادفی روی رئوس گراف است، آنگاه
توزیع احتمال مکان یک راه رونده تصادفی روی رئوس گراف است، آنگاه  توزیع احتمال واکر پس ازتی
توزیع احتمال واکر پس ازتی مراحل.
مراحل. از آنجا که نرمالسازی با ضرب لاپلاسین در ماتریس نرمالسازی انجام میشود
از آنجا که نرمالسازی با ضرب لاپلاسین در ماتریس نرمالسازی انجام میشود  با فرض اینکه همه وزنها غیر منفی باشند، تصادفی راست است .
با فرض اینکه همه وزنها غیر منفی باشند، تصادفی راست است .

 :
: برای همه
برای همه  ، زیرا برداروی
، زیرا برداروی ارضا میکند.
ارضا میکند. این همچنین نشان میدهد که ماتریس لاپلاسین منفرد است.
این همچنین نشان میدهد که ماتریس لاپلاسین منفرد است. ، کجاپ
، کجاپ مجموعه رئوس G است، و
مجموعه رئوس G است، و  .
. که در آن A ماتریس مجاورت و I ماتریس همانی است.
که در آن A ماتریس مجاورت و I ماتریس همانی است. کجا
کجا  تعداد یالهای گراف مورد نظر است.
تعداد یالهای گراف مورد نظر است. ، با بردارهای ویژه با نرم واحد
، با بردارهای ویژه با نرم واحد  و مقادیر ویژه مربوطه
و مقادیر ویژه مربوطه  :
:
 با خودش، این نشان میدهد که
با خودش، این نشان میدهد که ،
، به صورت زیر تعریف میشود: [ 3 ]
به صورت زیر تعریف میشود: [ 3 ]
 ، به جای یک "لاپلاسین". این یکی از کاربردهای نادری است که منجر به ماتریسهای متقارن مختلط میشود .
، به جای یک "لاپلاسین". این یکی از کاربردهای نادری است که منجر به ماتریسهای متقارن مختلط میشود .


 به عنوان حاصلضرب هادامارد ماتریس متقارن حقیقی لاپلاسین متقارن و ماتریس فاز هرمیتی با ورودیهای مختلط ساخته میشود
به عنوان حاصلضرب هادامارد ماتریس متقارن حقیقی لاپلاسین متقارن و ماتریس فاز هرمیتی با ورودیهای مختلط ساخته میشود
 بار الکتریکی نامیده میشود. [ 4 ] در مثال زیر
بار الکتریکی نامیده میشود. [ 4 ] در مثال زیر :
:




 ودلتا
ودلتا لاپلاسینِ بدون علامت است.
لاپلاسینِ بدون علامت است.
 ماتریس درجه است، و
ماتریس درجه است، و لاپلاسین بیعلامتس
لاپلاسین بیعلامتس
 ماتریس بروز است.
ماتریس بروز است.
 اگر و تنها اگر گراف دارای یک مؤلفه همبند دوبخشی باشد.
اگر و تنها اگر گراف دارای یک مؤلفه همبند دوبخشی باشد.
 رأسها
رأسها ، ماتریس لاپلاسین
، ماتریس لاپلاسین 








 که در آن هر بردار
که در آن هر بردار ویژگیهای مربوط به یک سری داده را در یک بازه محلی مشخص توصیف میکند. سپس ماتریس خود-شباهت با محاسبه شباهت جفتهای بردارهای ویژگی تشکیل میشود.
ویژگیهای مربوط به یک سری داده را در یک بازه محلی مشخص توصیف میکند. سپس ماتریس خود-شباهت با محاسبه شباهت جفتهای بردارهای ویژگی تشکیل میشود.
 تابعی است که میزان شباهت دو بردار را اندازهگیری میکند، برای مثال،
تابعی است که میزان شباهت دو بردار را اندازهگیری میکند، برای مثال،  سپس بخشهای مشابه بردارهای ویژگی به صورت مسیری با شباهت بالا در امتداد قطرهای ماتریس نشان داده میشوند.
سپس بخشهای مشابه بردارهای ویژگی به صورت مسیری با شباهت بالا در امتداد قطرهای ماتریس نشان داده میشوند. 

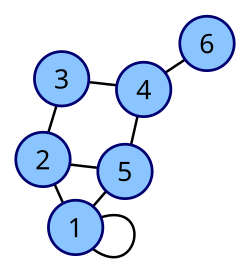






 در بالا توسط حداکثر درجه محدود شده است. این را میتوان به عنوان نتیجه
در بالا توسط حداکثر درجه محدود شده است. این را میتوان به عنوان نتیجه 
 برای گرافهای متصل. میتوان نشان داد که برای هر مقدار ویژه
برای گرافهای متصل. میتوان نشان داد که برای هر مقدار ویژه ، نقطه مقابل آن
، نقطه مقابل آن همچنین اگر
همچنین اگر 
 این عدد محدود به ... است.
این عدد محدود به ... است. این کران در
این کران در 
 در این وبلاگ به ریاضیات و کاربردهای آن و تحقیقات در آنها پرداخته می شود. مطالب در این وبلاگ ترجمه سطحی و اولیه است و کامل نیست.در صورتی سوال یا نظری در زمینه ریاضیات دارید مطرح نمایید .در صورت امکان به آن می پردازم. من دوست دارم برای یافتن پاسخ به سوالات و حل پروژه های علمی با دیگران همکاری نمایم.در صورتی که شما هم بامن هم عقیده هستید با من تماس بگیرید.
در این وبلاگ به ریاضیات و کاربردهای آن و تحقیقات در آنها پرداخته می شود. مطالب در این وبلاگ ترجمه سطحی و اولیه است و کامل نیست.در صورتی سوال یا نظری در زمینه ریاضیات دارید مطرح نمایید .در صورت امکان به آن می پردازم. من دوست دارم برای یافتن پاسخ به سوالات و حل پروژه های علمی با دیگران همکاری نمایم.در صورتی که شما هم بامن هم عقیده هستید با من تماس بگیرید.