اشتراک گذاری را باز کنید
گوارینو گوارینی معمار و ریاضیدان
گوارینو گوارینی معمار و ریاضیدان
کمی تاریخ

گوارینو گوارینی در سال 1624 در مودنا به دنیا آمد.
در جوانی به دستور Theatine پیوست که او را برای تازه کار به رم فرستادند. او هشت سال از سال 1639 تا 1647 را در شهر پاپ گذراند و در این مدت فرصت یافت تا با معماری باروک به ویژه در تفسیر نابغه بورومینی آشنا شود و مطالعه کند. گوارینو جوان از استادان بزرگ باروک وارث سختی سازنده، تخیل فنون ساختاری بی نهایت و ذوق رنگ در انتخاب مواد است. پس از اتمام تحصیلات، به زادگاه خود بازگشت تا به مقام کشیش منصوب شود و کار آکادمیک خود را با تدریس ریاضیات و فیزیک آغاز کند. در این دوره او مطالعات خود را در مورد جنبه های نظری معماری عمیق تر کرد.
در دوره دو ساله 1660-1662، طی اقامتی در مسینا، کلیسای Santissima Annunziata، Casa dei Teatini، کلیسای San Filippo و کلیسای پدران Somaschi را طراحی و ساخت.
این اثر آخر از آنجایی که نوع گنبد باز با طاقهای درهم تنیده برای اولین بار ظاهر میشود و به یکی از نقوش غالب معماری گوارینی تبدیل میشود، اهمیت ویژهای دارد.
مدت کوتاهی پس از بازگشت به مودنا، او به پاریس فرستاده شد تا از ساخت کلیسای سنت آن لا رویال مراقبت کند.
در سال 1666 او به تورین فراخوانده شد و تا سال 1681 به عنوان مهندس و ریاضیدان برای کارلو امانوئل ساووی باقی ماند.
وظیفه ای که به او سپرده شده است به معمار این امکان را می دهد که نبوغ خود را به کامل ترین شکل بیان کند، چه زمانی که امکان طراحی ساختمان ها را از ابتدا داشته باشد و چه زمانی که مجبور به ساختن بر روی ساختمان های از قبل موجود است.
تقریباً تمام سایتهای بزرگ ساختوساز پیمونتز در آن دوره، مداخله گوارینی را بهویژه در منطقه کونئو و در تورینی که او در آنجا ساخت، علاوه بر کلیسای جامع کفن مقدس، و ساختمانهای دیگری مانند Palazzo Carignano که نشاندهنده اوج است، ثبت کردند. از توسعه کاخ ایتالیایی قرن هفدهم، کلیسای سن فیلیپو و کلیسای تئاتین سن لورنزو، که در آن گوارینی به طور قطع بر مفهوم گنبد کلاسیک غلبه کرده و آن را به یک ساختار شفاف بسیار سبک تبدیل می کند که تداعی کننده بی نهایت آسمانی است.
در طول اقامت طولانی خود در تورین، او در پاسخ به درخواستها برای مداخله، سفرهایی به اروپا، به ویژه به پراگ و لیسبون انجام داد.
سالهایی که در دوک نشین ساووی گذرانده به معمار اجازه میدهد تا به موضوعات نظری در مورد ریاضیات و رشتههای برگرفته از آن نیز بپردازد: هندسه، نجوم و معماری.
او در سال 1683 در میلان درگذشت.
نمازخانه کفن در تورین
نام پدر گوارینو گوارینی در راس معماری مذهبی و مدنی قرن هفدهم قرار دارد. از این رو ، اگرچه مطالعات انجام شده در قرن اخیر محدود است، اما مفاهیم بسیاری در مورد آفرینش هنری او روشن شده است . با این حال، سوال بین جامعه مدنی، علم و هنر هنوز حل نشده باقی مانده است، که به طور کامل توسط کلیسای کفن در تورین نشان داده شده است. گوارینی در طول ساخت آن بنای تاریخی خارقالعاده و در نتیجه از طریق معماری، ارتباط عمیق بین الهیات، "regina scientiarum" که توسط اسقف تورین تجسم یافته بود، و عملکرد نذری کلیسای کوچک، نگهبان مقبرههای ساووی، کشف کرد. خانواده (ساکنان کاخ سلطنتی مجاور) و دانش انتزاعی رشته های ریاضی فیزیک.
در کلیسای کوچک، فضای معماری انتزاعی را از طریق عناصر ملموس، قابل مقایسه با چشم، بیان می کند، همانطور که در ساختار پیچیده موسیقایی جی اس باخ اتفاق می افتد که از روابط محدود بین نت ها، هنر فوگ را می سازد .
گوارینی در مسیر زیباییشناسی، فلسفه هنر مدرن که هنوز متولد نشده است ، نمونه جدیدی از زیبایی را طراحی کرد که با اندازهگیریهای دقیق، تناسب اجزا، انسجام فضاها، بر اساس فواصل عددی سه، شش، نه قابل نمایش است. . قبلاً یونانیان در پارتنون (448 قبل از میلاد) یا رنسانس در اوربینو، در اواسط قرن 15، با پیرو دلا فرانچسکا یا فرانچسکو دی جورجیو مارتینی، که برای فدریکو دا مونتفلترو کار میکردند، پیچیدگی بصری بخش طلایی را آزمایش کردند . برای مثال در Palazzo Ducal، با روابط پیچیدهتر بین بخش و ضلع مربع یا بین پایه، درگاه، پنجرهها و ارتفاع.
گوارینو گوارینی محدودیتهای عقل بشری را به چالش کشید و ایده فضایی از قبل موجود در ذهن را تا حد زیادی پیش برد که به خواست خدا شهودی است و به زیربخشهای بینهایت کوچک سطح تقسیم میشود. گنبد كفن تاريخي عذابآور، حيرتانگيز و بدبينانه مانند فلسفه قديس آگوستين دارد: ترديد درباره وجود خدا و معناي زندگي انسان به درون ميخزد تا راه را به سوي معرفت باز كند.
ورق کفن از سال 1452، زمانی که تورین پایتخت دوک نشین ساووی شد، مورد وقف تاریخی قرار گرفت، اما تنها با امانوئل فیلیبرتو تصمیم به ساختن کلیسایی در مکانی باریک، پشت اپسیس قرن شانزدهم گرفته شد. کلیسای جامع قرن، برای بزرگداشت پیروزی مسیحیان در لپانتو (1571). این ساختمان برای نگهداری یادگار مسیح که به طور معجزه آسایی از قرون وسطی جان سالم به در برد و مقبره شاهزاده سلطنتی در نظر گرفته شده بود.
از آن زمان به بعد، سه پروژه یکی دیگر را دنبال کردند: اولی توسط کارلو امانوئل اول به کارلو دی کاستلامونته سفارش داده شد، دومی توسط کارلو امانوئل دوم (1655) به Amedeo di Castellamonte سپرده شد که متعاقباً به دلایلی که مشخص نشده بود و در حال ساخت بود. آغاز شد، به نام گوارینو گوارینی (1667) 5 . تنها در سال 1694، پس از مرگ نویسنده، گنبد کامل شد.
موضوع پیشنهادی مستلزم بالاترین دانش دانش بشری بود. در واقع نمیتوان مرگ خدا را بهطور منطقی نشان داد، بلکه فقط این واقعیت را ممکن بود که خداوند به طور موقت از یک موقعیت مطلق و ماورای زمانی کنارهگیری کرده بود، همانطور که سنت تومیستی میخواست، برای دانستن مرگ فیزیکی و غیر موجه، که با رنج و آبرو مشخص شده بود. از صلیب بخش زمینی نمازخانه به شدت در مورد عدم امکان رد یک جمله ناعادلانه تأمل می کرد و یادگار مردی قربانی را نشان می داد. مطمئناً نمیتوان از راهحلهای آشکار، رقص یا نمایشی با توجه به مواضع بلاغی برنینی استفاده کرد که در ستون سنت پیتر، نظریههای درخشان پیشنهادی کاراموئل را غارت کرده و آنها را از آن خود ساخته بود .
دسترسی به نمازخانه کفن از عناصر ناپایدار و متضاد شروع شد که میتوانست سطح بالایی از مردم را که تمایلی به ارادت مردمی ندارند راضی کند. سه ورودی منظم، در زوایای 120 درجه، نقش ممتاز را به شاهزادگانی که مستقیماً از جناح جدید کاخ وارد میشدند، واگذار میکردند و در همان زمان به زائرانی که کلیسا را شلوغ میکردند، مسیری یک طرفه را نشان میدادند. مانع از عملکرد کلیسای جامع 7 نشد .
Fig.1.a. نمازخانه کفن: پلان، زوایا و نسبتهای عددی (از پاسانتی، 1963)
بر اساس مفهومی که زمان تاریخی را ترجیح میداد، یعنی حد یک فصل کوتاه که در آن هر موجود، حتی موجودات مرتفع، جان خود را از دست میداد، مجبور شد به دور حرم در جهت عقربههای ساعت و خلاف جهت عقربههای ساعت بچرخد (شکل 1).
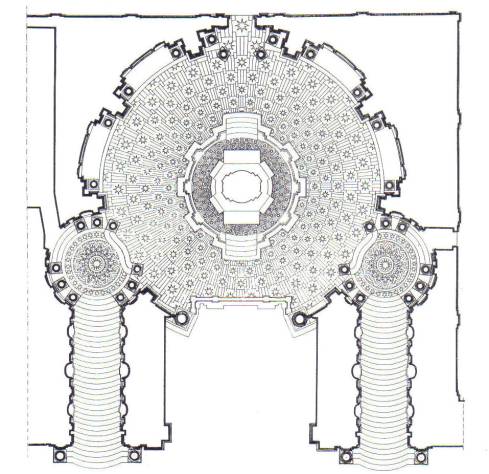
Fig.1.b. نمازخانه کفن: راه پله ها، دهلیزها، کف و نمازخانه (از پاسانتی، 1963)
بدبینی کف سنگ مرمر سیاه با تزئینات سبک، پیشرفت بی رحمانه وجود را با وجود ستاره هشت پر، با وسواس تکراری، ستایش دنباله دار مجوس 8 ، ظهور و باز هم زندگی ابدی، برجسته کرد.
به اتاق مرکزی از طریق راه پله ها و دهلیزهایی می رسید که منظره کلیسای کوچک را از کسانی که بالا می روند و حواس پرتی خروجی 9 را از کسانی که پایین می آیند پنهان می کنند . انسان در چنگال زمینی است که تنها با اراده نمی تواند از آن فرار کند.
هیچ گچ بری، نقاشی، ایدههای طفرهآمیز یا شهوانی چند کرومی وجود ندارد که حتی فرانچسکو بورومینی 10 ، یک فرد بزرگ تنها، در S.Ivo خود در Sapienza نشان داد. پلهها در تورین مقعر یا محدب، پهن هستند که نشاندهنده تلاش برای پا گذاشتن روی آنها، عقب نگهداشتن یا هل دادن مردم به جلو تا دهلیزها است. نرده زاویه دید پرسپکتیو را افزایش می دهد، اما به دیوار فشرده می شود، آزاد نیست و مانع از تسهیل بالا رفتن توسط نرده می شود.
نیم ستون ها (شکل 2) نیروهای داخلی دیوار را با دو انحنای خفیف تقریبا محدب، مخالف جریان راه پله، فشرده می کنند. سقفهای تیره و ظالمانه در عوض مقعر، با دریچههای پوستهای مخروطی شکل کوتاه هستند و به سقف مثلثی دهلیزها میریزند که با یک محیط دوگانه احاطه شدهاند.

شکل 2. نمازخانه کفن: پلکان، رمپ، طاقچه های فرورفته، دهلیزها و سقف ها (از پاسانتی، 1963)
ایده یک فضای جهش یافته و غیرقابل پیش بینی شروع به ظهور می کند که منجر به دکارت می شود، فیلسوفی با اهمیت فوق العاده برای گوارینی که از پاریس بازگشته است. دکارت در «قوانین جهت عقل» که معمار مطمئناً نمیدانست که پس از مرگشان در سال 1701 منتشر شد، گفت که رشتههای ریاضی پاکت حاوی اولین مبانی عقل برای استخراج حقیقت از هر شی هستند . حتی هنری فلسفه برای دکارت مانند درختی است که ریشه های متافیزیکی و تنه ای فیزیکی دارد. برای گوارینی هواپیما مشابه است، موجودی خنثی که یک دانشمند فیلسوف شرایط بصری را برای تمرکز بر زنجیره ای از ارزش های عقلانی از آن ترسیم می کند. پدر گوارینو، به گفته مورخ ماریو پاسانتی، از یک حالت خلاقانه ناخودآگاه یا شاید بهتر از قبل منطقی، یعنی قبل از محاسبه و فرمولبندیهای آن، شروع میکرد .

شکل 3. نمازخانه کفن: پایه مثلثی با دکل، بادبان و درام (از پاسانتی، 1963)
با ورود از دهلیزهای "زانویی"، با عرض محدود، در حال چرخش بر روی محوری از ستونهای کورنتی که به آرامی از دیوار جدا میشوند (شکل 2، 3 و 4)، دایرهای نمازخانه رو به آسمان، هماهنگی درونی، را درک میکنیم. فاصله از راه دور

شکل 4. نمازخانه کفن: بخش گنبد (از پاسانتی، 1963)
در بالای گنبد به شکل گلدسته ای تقریباً گوتیک، کبوتر روح القدس وجود دارد که در هنگام سقوط مرگ بر انسان مسلط است و بر روی کوزه های ساووی ها که نور ایمان به عنوان مدافعان ترک بر آن می تابد. خطر نزدیک به وین (1683) .
انسان به تنهایی نمی تواند به طاق آسمان نزدیک شود مگر با قواعد هندسه و ریاضیات: بنابراین روش دکارتی بر عقل تحمیل می شود.
عمودهای گنبد با قواعد وضوح و شواهد رشد می کنند 13 . هر خط بدون دیوارهای پشتیبان نمایش داده می شود و قوانین استاتیک فیزیک گالیله را نقض می کند. نظم هندسی اعمال شده بر اعداد بسیار مهمتر است، همانطور که توسط بخش سه نشان داده شده است (شکل 3). دکارت بیان می کند که تجزیه و تحلیل هر مسئله پیچیده را به ساده ترین مفاهیم غیرقابل تجزیه کاهش می دهد و چه چیزی ساده تر از یک مثلث متساوی الاضلاع در تکیه گاه است؟
به این صورت اتفاق میافتد: نظم اصلی از سه قوس عظیم بر روی ستونها شروع میشود که قبل از کل پیشروی فوقانی قرار دارند و از ستونها ستونهای مقعر با نه صلیب برمیخیزند که بیطرفی پسزمینه را خنثی میکنند.
صلیب ها نقطه شروعی برای تجزیه و تحلیل هستند و شما را به باز کردن عمودی دعوت می کنند، اما محیط قدرتمند پنجره 14 در حد واسط بین ستون و آرشیترو بالایی قرار می گیرد.
در اصل شما بین آسمان و زمین معلق می مانید. پس در اینجا جهت سنتز است که دکارت به ترتیب عبور از سادگی یک شی به پیچیدگی اشاره می کند.
کل این قسمت از کلیسای کوچک باعث حرکت افقی و عمودی می شود: این حرکت متزلزل کسانی است که روی زمین زندگی می کنند و مجموعه هندسی دقیقاً در جایی که عناصر تکتونیکی مانع یکدیگر می شوند، یعنی در پایین، بزرگتر است.
بخش شش به دنبال یک محیط به دست میآید و با محیط بالایی بسته میشود، اما از برش تمیز و خشونتآمیز آرشیتروها بهدنبال یکدیگر پدید میآید (شکل 4). روی استوانه سرلیاناهایی با ستون های بیرون زده وجود دارد، نه همسطح با قوس که خود به خود می چرخد. پنجره شیشه ای دورتر و خارج از سطوح قرار دارد، در حالی که در فضاهای مفصلی، طاقچه های محدب با ظاهری رفتاری شایسته پالاتزو مارینو وجود دارد (شکل 4-2).
این جنبه زمانی متوسط است که با راه حل های ارائه شده در ارتفاعات بالا برای انتقال حس دست نیافتنی از دنیای بی اعتمادی و خطر دائمی ما با وجود تضمین مسیحی مقایسه شود.
ایده مخروط همگرا در چشم ما بسیار زیاد به نظر می رسد، ذهن انسان فقیر جذب شده توسط بی نهایت را باطل می کند. چند ضلعی ها شش بار با قوس هایی که گاوهای نر را نشان می دهند، اکنون نزدیک، اکنون دور، بدون لمس کردن، در مفهومی موسیقایی شبیه به فوگ باخ تکرار می شوند.
عقل تلاش زیادی می کند تا به خدا برسد. نور در یک وضعیت تقریباً اسلامی از شیشه نامحسوس می شکند و به طور مداوم در طول ساعت ها یا فصول تغییر می کند (شکل 5).

شکل 5. نمازخانه کفن: طرح گرافیکی گنبد (از پاسانتی، 1963، اصلاح شده)
پایان سفر، سخنان پاسکال را به یاد می آورد: روح هندسه ای که خصوصیات شکل ها و عناصر را غیرقابل انکار می کند، کافی نیست. آنچه لازم است نه تنها روحیه تهذیب است که در همه مشترک است، بلکه با قلب صحبت می کند، شگفت زده می شود و با خودانگیختگی می بیند 16 . ظرافت شهود است، هندسه هوشمندی است: بنابراین لازم است که هر دو را یکپارچه کنیم. پرتوها و کبوتر روح القدس در مورد حضور خدا در جایی که عقل متوقف شده است هشدار می دهد. از سوی دیگر، روش ریاضی برای امر ناگفتنی آماده می شود و آگاهی از وجود خدا را اعلام می کند. بنابراین در اینجا فیرینگ از راه دور راه خود را به جلو خیره می کند. هر عنصر معماری باروک به دلیل جسارت فضاها حذف می شود، همانطور که الساندرو آنتونلی در قرن نوزدهم در مول معروف خود انجام داد: ما یک قدم با حدس های معاصر در مورد فضا فاصله داریم.
یادداشت های کتابشناختی
1. کتابشناسی اساسی در مورد G. Guarini شامل سه مشارکت مهم است: M. Passanti, "In the Magical World of G. Guarini", Turin, 1963; AAVV، «G. گوارینی و بین المللی بودن باروک، مجموعه مقالات کنگره بین المللی، تورین، 1970; H. Meek، "Guarini"، میلان، 1991، کار کامل بر روی تمام مراحل نویسنده.
2. در مورد JSBach تک نگاری مفید برای مورد ما در C.Wolff، "JSBach، علم موسیقی"، میلان، 2003، جایی که باخ از طریق درگذشت فردریش آگریکولا به عنوان یک موسیقیدان با توسعه پیچیده یک موزیکال جدی تعریف شده است. موضوع (صص 12-13).
3. زیبایی شناسی در قرن 18 در انگلستان به عنوان مستقل از مفهوم اخلاقی با شفتسبری و هاچسون (1694-1746) متولد شد.
4. در مورد نسبت طلایی، مقاله A. Marcolli را در مورد رشد ارگانیک و نسبت طلایی در "نظریه میدان"، فلورانس، 2001 مقایسه کنید.
5. رجوع کنید به M. Passersby, op.cit. صفحه 165.
6. کامل ترین تک نگاری ها در مورد برنینی، آنهایی هستند که وی. ماریان، «GLBernini»، ناپل، 1974، و F.Borsi، «Bernini architettura»، میلان، 1980.
7. م. پاسانتی، پیشینه، صفحه 189.
8. O. Beigbeder, “Lexicon of Medieval symbols”, Milan, 1997, pp.69 and 229, منشا دور دنباله دار را در رابطه با نقش برجسته ها بررسی می کند.
9. م. پاسانتی، پیشینه، صفحه 189.
10. در مورد Borromini رجوع کنید به: P.Portoghesi, “Borromini in European Culture”, Rome, 1982. برای رابطه گوارینی-بورومینی رجوع کنید به A. Griseri, Le metamorfosi del Barocco, Turin, 1967.
11. گزارش شده در E. Balducci، "تاریخ اندیشه بشر"، میلان، 1986، II، صفحه. 109.
12. M. Passanti، پیشینه، صفحه 189.
13. در R. Descartes، "گفتمان در مورد روش" ویرایش G. De Ruggiero، فلورانس، 1938.
14. ما در مورد چشم ها یا پنجره های کاذب صحبت می کنیم، بلکه در مورد پنجره های واقعی در مناطق متناوب صحبت می کنیم.
15. تحلیل استادانه مسیر در R.Wittkower، "هنر و معماری در ایتالیا"، تورین، 1972.
16. تصادفی نیست که پاسکال شامل فیزیک، موسیقی و معماری در رشتههایی است که به تجربه و استدلال بستگی دارد. M. Dal Pra, “Profile of history of philosophy”, Florence, 1971, II, pp. 115-116.
نقش ریاضیات و علوم در کار گوارینی
گوارینی با تجزیه و تحلیل رابطه هنر و ریاضیات با جزئیات بیشتر، بدون شک یکی از جالب ترین چهره های تمام دوران را نشان می دهد. او که به سنت گره خورده است، اما عمیقاً توسط اکتشافات علمی عصر خود جذب شده است، روشنفکری چند وجهی است: او خود را به عنوان الهیات، فیلسوف، ریاضیدان و همچنین معمار تعریف می کند و به نظر می رسد که دقیقاً ریاضیات، که مطالعه آن را در رم شروع می کند. ، جایی که در سال 1639 پس از ورود به نظمیه Theatine به آنجا می رود، او را با معماری آشنا کرد.
بنابراین اولین سوالی که از خود می پرسیم این است که آیا می توان گوارینی را از همه نظر یک ریاضیدان در نظر گرفت؟ سهم او در مقایسه با دیگر شخصیت های ایتالیایی آن زمان، مانند بوناونتورا کاوالیری (1598-1647) یا اوانجلیستا توریچلی (1608-1647)، تعیین کننده به نظر نمی رسد و به همین دلیل است که نام او توسط تعداد کمی از مورخان ذکر شده است. ریاضیات از جمله Chasles (1793-1880) در "Aperçu historique sur l'origine et le developpement des methodes en geometrie" (1837)، در مورد مطالعات بر روی مقاطع مخروطی و هندسه توصیفی، و Gino Loria (1862-1954) که در "تاریخ" هندسه توصیفی» (1921)، آثار گوارینی را در مراحل اولیه ساخت این شاخه قرار می دهد.
برای پرداختن به موضوع، لازم است به اثر دایرهالمعارفی (اولین اثری که در نوع خود در ایتالیا منتشر شد) "Euclides adauctus et methodicus mathematicaeque universalis" که توسط گوارینی به کارلو امانوئل دوم، دوک ساووی تقدیم شده و در تورین منتشر شده است، مراجعه کرد. در سال 1671. این کتاب برای اهداف آموزشی نوشته شده است، نوعی "جمع" بیش از هفتصد صفحه است که از سی و پنج رساله مشتمل بر مقدمه مختصر، نظرات، تعاریف، قضایا، مسائل، ساختارهای هندسی و نشانه های صریح و به موقع تشکیل شده است. بر روی منابع
حدود نیمی از کار به موضوعات کاملاً هندسی اختصاص دارد، از جمله تجزیه و تحلیل دوازده کتاب اقلیدس: مشاهده چگونگی گوارینی، در قرنی که نقش جبر به طور فزایندهای مرتبط میشود (به کاربرد دکارت و حتی تلاش والیس برای رهایی حساب و جبر از نمایش هندسی)، هندسه را برتر از شاخه های دیگر ریاضیات می داند. بقیه کتاب اقلیدس مربوط به محاسبه لگاریتم است که در آغاز قرن هفدهم توسط بریگز و نپر توسعه یافت، مثلثات و استفاده از آن در تفکیک مثلث های مسطح و کروی، نجوم و با یک سری جداول عددی به پایان می رسد.
از منظر ارجاعات معماری، رساله هجدهم جالب توجه است که به مسئله اندازه گیری دایره و منحنی های خاص مانند مارپیچ، چهارگوش، بیضی، پوسته، سیکلوئید برگرفته از یونانیان و موضوع تجزیه و تحلیل بسیاری از ریاضیدانان و دانشمندان آن زمان، رساله XXIV، که مربوط به مقاطع مخروطی است، از اهمیت اساسی هم برای کاربردهای آنها در زمینه نجوم و هم برای توسعه هندسه تصویری دسارگ، و رساله XXXII، که به توسعه در صفحه ای از خطوط منحنی و سطوح سه بعدی مربوط می شود و توسط برخی از منتقدان به عنوان تصویری نظری از نتایج به دست آمده در ایجاد طاق ها تفسیر می شود. در مورد مقاطع مخروطی، جالب است بدانیم که در «اقلیدس»، با ارجاع نسبتاً صریح به قانون اول کپلر، از سودمندی بیضی برای توضیح حرکت سیارات پشتیبانی می شود: شاید گوارینی، در حالی که از سیستم زمین مرکزی در برابر نظریه کوپرنیک، شروع به شک و تردید در مورد پایداری خود می کند.
Un altro trattato legato all'architettura è il XXVI, sul tema delle proiezioni, riprese qualche anno più tardi nei capitoli di ”Architettura Civile” dedicati all' ortografia elevata e all' ortografia gettata . از مقدمه او، l'attenzione dell'autore nei confrontai delle applicazione delle techniche descritte پدیدار می شود: " گسترده ترین استفاده از برجستگی ها، هم ساعت ها و هم ابزارهای ریاضی، مانند اسطرلاب و ربع: سپس کیهان شناسی در یک صفحه برای نمایش دایره های طول و عرض جغرافیایی و در نهایت و به ویژه در معماری برای برآمدگی بدنه ها و طرح های خاص دشت ها مفید است. و از این نظر، از آنجایی که ابتدا آن چیزی که با کاهش پرسپکتیو چشمی نشان داده می شود، باید آن را به داخل صفحه امتداد داد، و همچنین اجسام و سطوح را به داخل صفحه نمایش داد.
می دانیم که گوارینی در طول اقامت خود در پاریس (از 1662 تا 1666) این فرصت را داشت که نظریه های دزارگ، پاسکال، دکارت و فرما را بیاموزد و علاقه ای را در خود پرورش دهد که او را با اکثریت ریاضی دانان قرن هفدهم متحد کرد. برای حساب بی نهایت و بی نهایت کوچک (به استفاده از روش های درون یابی و مطالعه برخی سری ها توسط استوینو، کپلر، گالیله، کاوالیری، روبروال، توریچلی، والیس، فرما فکر کنید). بنابراین، استفاده از هندسه تصویری دزارگ همچنان منبع بحث در میان منتقدان است: برخی ادعا میکنند که این در واقع مبانی نظری ساختهای جسورانه گوارینی (به ویژه گنبدها) را نشان میدهد، در حالی که برخی دیگر بر تمایز بین مفاهیم فرافکنی و فرافکنی تأکید میکنند. هندسه ، استدلال می کند که نقشه ها یا چشم اندازهای ترسیم شده توسط گوارینی برای درک اینکه او واقعاً تا چه حد از هندسه اقلیدسی فراتر رفته است با آگاهی از معنای عمیق تر هندسه تصویری، یعنی از این واقعیت که تمام ویژگی های یک شکل سه- ابعاد را می توان از نمایش مناسب آن استنباط کرد 1 .
سبک «اقلیدس» نسبتاً سنگین است، اگرچه نویسنده قصد دارد تظاهرات و استدلال را ساده کند. این امر بیش از حد قابل درک و توجیه است، زیرا فقدان محاسبه تحت اللفظی و زبان جبری به ناچار حتی پیش پا افتاده ترین روابط بین کمیت های هندسی ابتدایی را پیچیده و خواندنی دشوار می کند (سعی کنید رساله XXI در مورد لگاریتم ها را بخوانید: بیان مفاهیم نسبتاً ساده مانند برابری بین لگاریتم مربع یک عدد و دو برابر لگاریتم خود عدد چندین صفحه طول می کشد).
گوارینی آثار دیگری با ماهیت ریاضی و نجومی مانند کتابچه راهنمای gnomonics "Leges temporum et planetarum" که در سال 1678 در تورین منتشر شد، و دایره المعارف دو جلدی "Coelestis mathematica" که در سال 1683 در میلان منتشر شد و به اندازه گیری اختصاص داشت نوشت. از زمان، طراحی و ساخت ساعت های آفتابی و قوانین حاکم بر حرکت اجرام آسمانی. با این حال، قابل توجه ترین متن شاید «معماری عمران» باشد. پس از مرگش در سال 1737 توسط برادران تئاتین در تورین منتشر شد و به پنج رساله تقسیم می شود: در مورد معماری به طور کلی، در مورد آیکونوگرافی (مشکلات اندازه گیری، تسطیح، نمایش های پلان سنجی)، در مورد املای عالی (نظام های معماری و نماها)، در مورد " املاح پرتاب شده" (پیشبینی استوانهها، کرهها و اجسام بیضوی روی صفحات)، در مورد ژئودزی (روشهای تجزیه و تبدیل شکلها و محاسبه مساحتها). اگرچه رویه ای که در ارائه استدلال های هندسی دنبال می شود همیشه دقیق نیست - برای مثال در رساله املای پرتاب شده ، هم در مواردی که در آن ایجاد یک جامد به روشی دقیق (مخروط و استوانه) امکان پذیر است و هم مواردی که در آن تنها با توسل به تقریب ها (کره و چنبره) امکان پذیر است – کار گوارینی بدون شک قابل قدردانی است و به صراحت تمام اشتیاق او به ریاضیات را نشان می دهد.
در مورد استفاده از محاسبه در خلق آثار معماری، در هیچ نوشته ای از محاسبات ثابت یا ملاحظاتی در مورد تلاش و مقاومت مصالح اثری دیده نمی شود و به نظر می رسد کاربرد ریاضیات محدود به نمایش گیاهان و ساختمان ها باشد. از سوی دیگر، علم ساخت و ساز یک رشته جدید است، اگرچه برخی آن را به گالیله برمیگردانند که در «گفتگوهایی درباره دو علم جدید» (1638) به برخی مشکلات در خمش تیرها میپردازد.
بنابراین جسارت ساختمان های گوارینی ثمره شهود و تجربه است تا کاربرد عینی محاسبه، اما هندسه توسعه یک ذهنیت خاص را تعیین کرده است و با مراجعه مجدد به نوشته ها، می توان تلاش کرد تا بفهمیم چگونه و تا چه حد. مفهوم جهان و هنر، معنای منسوب به چهره ها و شمایل نگاری به کار رفته نتیجه آن است.
ما قبلاً به این واقعیت اشاره کردیم که از نیمه اول قرن 16، متون هندسی استثنایی تولید می شد (مثلاً متون هندسی که توسط روشنفکران حلقه گالیله، مانند Guidobaldo del Monte و Bonaventura Cavalieri، یا در ایتالیا منتشر می شد. فرانسه توسط گروه دکارتی) و بسیاری از مشکلات پیش روی از نیازهای عملی ناشی می شود. در این رابطه جمله ای از دزارگ را نقل می کنیم: « باید صراحتا اعتراف کنم که هیچ گاه ذوق مطالعه و تحقیق در هندسه و فیزیک نداشته ام مگر تا آنجا که می توانستم به عنوان وسیله ای برای رسیدن به نوعی مورد استفاده قرار بگیرم. آگاهی از علل تقریبی (...) برای حسن و آسایش زندگی (...) در تمرین برخی از هنرها (...) با مشاهده این که بخش خوبی از هنرها مبتنی بر هندسه است، مانند از جمله تراش سنگ در معماری ، هنر ساعت آفتابی و به ویژه هنر پرسپکتیو. .
علاقه به هندسه نیز از رساله های معماری سرچشمه می گیرد و گوارینی با پیروی از این گرایش، علاوه بر نوشتن اثری کاملاً ریاضی مانند اقلیدس، «معماری مدنی» را با یک سری اصول هندسه آغاز می کند و بدین ترتیب انتخاب خود را توجیه می کند: « معماری. به عنوان دانشکده ای که در تمام عملیات خود از اندازه گیری استفاده می کند، به هندسه وابسته است و می خواهد حداقل عناصر اولیه آن را بشناسد . به گفته گریسری 4 ، قصد نویسنده این است که به صورت گرافیکی ایده منحنی های مورد استفاده را نیز تأیید کند و در عین حال یک پردازش هندسی را در پایه هر حجم معماری-تجسمی، در جستجوی واضح و قابل اثبات قرار دهد. پیدایش
روش طراحی گوارینی، در زمینهای باروک، که در آن کثرت دیدگاهها با هدف برانگیختن دیدی متمرکز و چندگانه از فضای معماری به طور همزمان، میتواند در پرتو اکتشافات جدید در زمینه نجوم و نقش جدیدی که بر عهده گرفته است تفسیر شود. ریاضیات شکل ساختمان، بر اساس اصول هندسی، به یک مفهوم کلی از تکامل پایبند است که از اجزای اصلی پروژه شروع می شود و در آن جزئیات پلان و ارتفاعات در زمان بعدی، در مرحله پایان، تقریباً به عنوان توسعه یافته است. عناصر مکمل علاوه بر این، به لطف تسلط کامل بر ابزارهای فنی و شاید به لطف دانش هندسه برتر، طرح کلی اغلب با آزادی کامل تفسیر می شود. خود گوارینی مینویسد : « معماری، اگرچه وابسته به ریاضیات است، اما چیزی کمتر از هنر چاپلوسی نیست، که به دلایلی نمیخواهد این حس را منزجر کند: بنابراین، اگرچه بسیاری از قوانین آن از دستوراتش پیروی میکنند، اما وقتی صحبت از تظاهرات مشاهدهشده او به میان میآید. قصد آزار دید را دارد، آنها را تغییر می دهد، آنها را رها می کند و در نهایت با آنها مخالفت می کند... ».
اگر برنینی اقدامات سادهای را برای ساختمانهای خود اتخاذ کند، معمار مودنا در ابتدا فقط ابعاد فضاهای اصلی را تعیین میکند، سپس با ساختارهای هندسی، ابعاد کوچکتر را تعیین میکند که بسیاری از آنها ناگزیر قابل مقایسه نیستند.
در آثار او ماهیت روابط فضای درونی-جرمی خارجی، نور-فضا، فضا-سازه عموماً به راحتی قابل خواندن نیست و در کنار پیچیدگی طرح، فرم های معماری همپوشانی دارند تا تنش مداوم ایجاد کنند و همچنین تا راه غلبه بر آن را پیشنهاد کند.
هر نمازخانه، دیوار یا ستون تابع توسعه یک ایده واحد است، بنابراین جزئیات تزئینی، تناسبات و هر عنصر دیگری را می توان تغییر داد و یا حتی حذف کرد تا نیازهای فضایی تصور شده از طریق یک فرآیند بسط هندسی را برآورده کند. آرگان 2 بیان می کند که گوارینی عناصر تزئینی را به عناصر کاربردی تبدیل می کند و بالعکس، به منظور دستیابی به یک نتیجه فیگوراتیو که رابطه بین جرم و فضا، بین عناصر مختلف و بین عناصر و نور را برجسته می کند، که به طور نمادین به عنوان یک مولد زندگی درک می شود.
از آنجایی که « هیچ چیزی در هنر یا علم وجود ندارد که قبلاً در هندسه نبوده است »، هندسه به نوعی Weltanschauung ، شکل نمادین، ایده ناب، ماتریس همه علوم و هنرها تبدیل می شود و برای برجسته کردن دامنه این «فلسفه هندسه» یا « هندسه فلسفی» برای تعریف سیستم فکری که کار گوارینی بر آن استوار است با اصطلاح geosophy پیشنهاد شد . در زمینشناسی ، فلسفه، نجوم، فیزیک، الهیات، رسالهها، معماری، مهندسی و حتی شعر همگرا میشوند: اساس عدد است و هندسه نشاندهنده بالاترین ارزشها است (در این قرار دادن هندسه در پایه روش فلسفی میتوانیم تشخیص دهیم. نفوذ گالیله). خود رساله «Placita philosophica» که در سال 1666 در پاریس منتشر شد، ساختاری هندسی دارد. این کتاب که به شش بخش تقسیم شده است، تلاشی برای درک همه دانش بشری، از منطق گرفته تا فیزیک، نجوم و متافیزیک است. گوارینی در آن اعلام میکند که میخواهد موضوعات « فیزیک، تجربیات، شکلهای ریاضی » را افشا کند و در این فرآیند عقلانیسازی، تا آنجا پیش میرود که فصل «De arte» را در بخش فیزیک وارد میکند و معتقد است که همه هنرها به ریاضیات وابسته هستند، از فلسفه یا پزشکی، علومی که به تشبیهات بین چیزها، نسبت آنها و روابط طبیعی آنها می پردازند.
ریاضیات در هر زمینه ای مداخله می کند: "روش اندازه گیری کارخانه ها" (1674) چیزی نیست جز یک دوره در ریاضیات ابتدایی، نسخه ای عملی از "اقلیدس". "پیمان استحکامات" (1676) حتی تجزیه و تحلیل استراتژی های محاصره و نبرد را بر اساس اصول ریاضی پایه ریزی می کند. پیشگفتار «اقلیدس» رمزگذاری ریاضیات و اعداد را به عنوان نمادهای هنر الهی ارائه می دهد. "mathematicae luces" حوزه معماری را فرا می گیرد که اغلب به محلی تبدیل می شود که قضایای هندسی در آن نمایش داده می شود و با مقایسه تصاویر ساختمان ها با تصاویر گزارش شده در رساله ها می توان اسمز بین هنر و علم را درک کرد.
هر عدد به یک شکل هندسی مرتبط است: به عنوان مثال، ترکیب عدد سه با مثلث متساوی الاضلاع که به شدت در نمازخانه کفن به دلیل معنای ریاضی، زیبایی شناختی و مهمتر از همه باطنی آن، به عنوان نمادی از کمال تثلیثی استفاده می شود. حکمت کافی است هر پارتیشن نمازخانه کفن، هم از نظر پلان و هم از نظر ارتفاع، بر اساس اعداد 3، 6، 12، 36 است: سه دهلیز مدور به مدت یک سوم محیط خود در فضای اصلی قرار داده شده است که ستون ها به صورت مرتب شده اند. سه ضلعی و توسط قوس های قطعه ای به هم متصل می شوند که به نوبه خود یک مثلث متساوی الاضلاع را روی سقف می کشند. سه طاق بر روی جفت ستونهایی که در کنار دهلیزها قرار گرفتهاند و سه اسپندل بین یک طاق و طاق دیگر قرار گرفتهاند. شش پنجره قوسی در قسمت میانی وجود دارد. شش حلقه با ارتفاعات رو به کاهش وجود دارد که گنبد به آنها تقسیم شده و یک "لانه" متشکل از سی و شش طاق ایجاد می کند. دوازده نقطه از ستاره در بالای گنبد و همچنین تکیه های خارجی وجود دارد. بیضی های درام و گلدسته به اندازه یک سی و ششم محیط نسبت به پنجره ها می چرخند (شکل 5، بالا، و 8).

شکل 8. نمازخانه کفن: داخلی (از پاسانتی، 1963)
مثلث اولین چند ضلعی، تقسیم ناپذیر، اتم هندسه را تشکیل می دهد، شکلی که هر چند ضلعی دیگر را می توان به آن تقسیم کرد.
گوارینی، در ساختمان های خود، ارقام منظم را ترجیح می دهد، از مثلث متساوی الاضلاع تا شش ضلعی، به هشت ضلعی، تا دایره، مکانی از کمال، نماد جهانی بودن الهی (برای تأیید این موضوع، توجه داشته باشید که بیضی عمدتاً در جانبی استفاده می شود. یا جزئی یا در عناصر تزئینی).
پاسانتی 9 اشاره می کند که چگونه گوارینی، در گنبد کفن، بر صعود از ناحیه زمینی به ناحیه آسمانی تأکید می کند و در اول با استفاده از چند ضلعی هایی با تعداد اضلاع فرد و در دومی یک حس بی قراری ایجاد می کند. احساس استراحت و آرامش از طریق استفاده از چند ضلعی با تعداد اضلاع زوج و دایره.
ریاضیات فیزیک را نیز فراگرفته است (در "Placita" می توانیم بخوانیم که همه چیز عدد است، از جمله حرکت و نور) و برعکس، ریاضیات موجودیت فیزیکی خاص خود را دارد.
گالیله می گوید که در کتاب کیهان فلسفه به زبان ریاضی نوشته شده است « و شخصیت ها مثلث ها، دایره ها و دیگر اشکال هندسی هستند (...) بدون این ها سرگردانی بیهوده در هزارتوی تاریک است » و گوارینی در کتاب خود کار می کند، هزارتوی ریاضی جذابی را ایجاد می کند که در آن هر نماد معنایی دارد.
یکی از تکراری ترین موضوعات گوارینی دقیقاً در هم تنیدگی ساختارها با ارزش هندسی و نجومی آن است. برای مثال، ابتداییترین طاقها، مانند تالار Palazzo di Racconigi، در تصاویر مربوط به مشکلات مربوط به تقاطع طبقات مطابقت دارند، در حالی که طاقهای پیچیدهتر، مانند طاقهای S. Anna Reale و S. لورنزو، در تصاویر مربوط به مدارهای آسمانی (شکل 9).
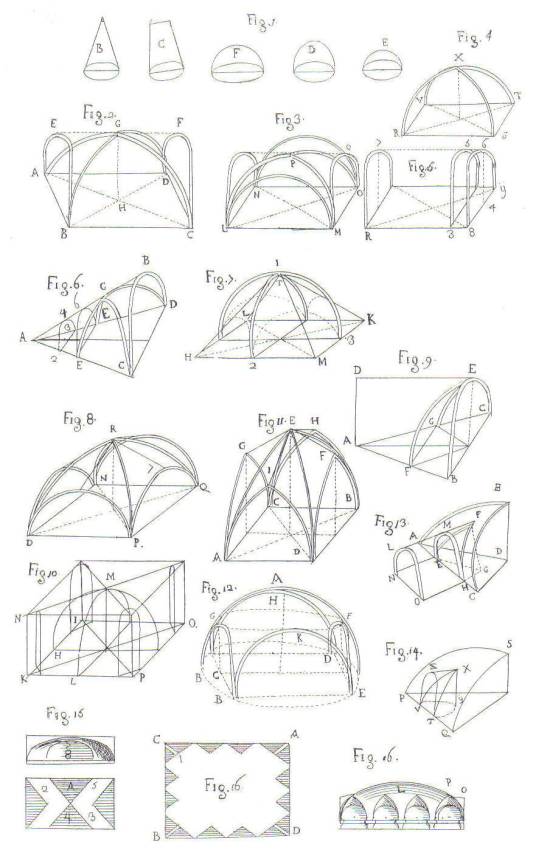
شکل 9. از «معماری مدنی» (1968): برگه. XXVII
گنبد نماد آسمان است و گوارینی در آن به دنبال کمال نیست، بلکه حرکت است، زیرا در پشت آن خدا، خدای اتفاق گرایان، عامل همه چیز و همه حرکات است.
در گنبدها به پایان نامه های رساله های ریاضی در مورد مخروط ها و مقاطع مخروطی اشاره شده است: گنبد خود کفن که شکل آن توسط استوانه های متوالی با ابعاد تدریجی کاهش می یابد، برخی از چهره های «اقلیدس» را به یاد می آورد.
با بازگشت به نجوم، گوارینی، در حالی که انسان را معیار همه چیز و زمین را در مرکز جهان می داند، به بررسی حرکت کرات سماوی، وابستگی های متقابل بین ستارگان می پردازد. در زمینه معماری، این از اهمیتی که نه چندان به یک مرکز مطلق، که به روابط میان مرکز و پیرامون نسبت داده میشود، سرچشمه میگیرد: به نفوذ متقابل محیطهای جانبی فکر کنید، همانطور که در دهلیزهای نمازخانه کفن اتفاق میافتد.
علاقه به ستاره شناسی نیز از استفاده از ستاره ها به عنوان یک عنصر تزئینی پدیدار می شود. در کف نمازخانه کفن، دایره های متحدالمرکز ستارگان به تصویر کشیده شده است (شکل 1b) که یادآور تصاویر نیمکره قطب شمال و قطب جنوب از "Coelestis mathematica" است. اما این همه ماجرا نیست: ستارگان در شبکه لونت های زیر طبل یافت می شوند، ستاره ها صلیب هایی در ستون ها هستند و یک ستاره بزرگ دوازده پر در بالای گنبد ظاهر می شود.
موضوع دیگری که گوارینی را مجذوب خود می کند و در بسیاری از نوشته های او فضای زیادی به آن اختصاص داده شده است، اندازه گیری زمان است. برخی از محققان گنبد S. Lorenzo را به یک ساعت آفتابی بزرگ و طبل آن را به عنوان نمایشی از مراحل ماه تعبیر می کنند. به همین ترتیب، شباهتهایی (شاید کمی اجباری) بین صفحهنمایش کلیسای کفن و نقاشیهای رسالههای «Placita» و «Leges temporum et planetarum» که مراحل خسوفها را نشان میدهند برجسته شده است: به گفته حامیان این تز 1 موقعیت های ماه می تواند با موقعیت دهلیزها مطابقت داشته باشد و این مطابقت تصادفی نخواهد بود زیرا موضوع نجومی با عملکرد نمادین نمازخانه مرتبط است.
برای گوارینی، ستارگان در آسمان به دنبال مسیری موجدار، سینوسی و مارپیچی حرکت میکنند (او تلاش میکند تا سیستم بطلمیوسی را با جایگزینی منحنیهای مارپیچی به جای مجموعه پیچیده چرخهها و اپیکچرها اصلاح کند): بار دیگر با اشکال هندسی غنیشده با ارزش کیهانی مواجه میشویم. به عنوان عناصر معماری در تمام سطوح، از دکوراسیون گرفته تا سیستم های پلان متری استفاده می شود.

شکل 10. نمازخانه کفن: نمای بیرونی گنبد (از پاسانتی، 1963)
در نمازخانه کفن، سینوسی هم در بیرون، در نمای طبل (شکل 10)، و هم در داخل گنبد، در توری مارپیچ که به صورت زیگزاگ برای اتصال دهانههای شیشهای بالا میآیند، استفاده میشود. علاوه بر این، در اولین پروژه گزارش شده در "معماری عمران" یک پایان مارپیچی برای مناره در نظر گرفته شده است، خطی که بهتر از بقیه می تواند نمادی از مسیر بینهایت کوچک به بی نهایت بزرگ باشد و مفهوم گوارینی را خلاصه کند.
به عنوان تأییدی دیگر بر رابطه نزدیک بین هندسه و معماری، به نظر می رسد گنبد کفن یکی از مشکلات متعدد «املای پرتاب شده» را نشان می دهد که در «معماری مدنی» (شکل 11)، مطالعه ای در مورد نحوه « ریخت گذاری » پیشنهاد شده است. از یک سطح کروی که توسط دایره های موازی اره شده است ، " برای توزیع یک کره در بسیاری از سطوح حلقوی ": در تحقق معماری به نظر می رسد که این کره باز می شود، متلاشی می شود، به تکه تکه می شود.
در گوارینی، «غیر منتظره» و «شگفتانگیز» 5 با قواعدی برگرفته از هندسه اقلیدسی پشتیبانی میشوند و به شیوهای کاملاً شخصی اعمال میشوند.
نمی توان معمار را از ریاضیدان جدا کرد، زیرا عناصر خارق العاده و عقلانی آنقدر به هم مرتبط و وابسته هستند که به طور همزمان به عنوان کنترل و تحریک بر یکدیگر عمل می کنند . در بینش فلسفی معمار مدنی، متاثر از اقبال گرایی (گوارینی «Traité de l'homme» دکارت را می خواند)، خدا تنها خالق و تنها علت واقعی و هنرمند در نظر گرفته می شود که ظرفیت خلاقیت خود را از محرک های ریاضیات می گیرد. و به ویژه هندسه اعمال بر عقل، آزادی فرد را از طریق انتخاب وسایل، مواد، فنون، قواعد ریاضی برای خلق آثار خود بیان می کند.
بنابراین، استفاده از هندسه، در هم تنیدگی خطوط، تضاد فضاها جلوه ای از عرفان گوارینی است، تجلی اندیشه ای که تجرید ریاضی و گمانه زنی الهیاتی را به نام یک مخرج مشترک در هم می آمیزد: مفاهیم مطلق و بی نهایت.
یادداشت های کتابشناختی:
1. AAVV، " گوارینو گوارینی و بین المللی بودن باروک "، مجموعه مقالات کنفرانس بین المللی ، آکادمی علوم تورین، 1968.
2. آرگان جی سی، « معماری باروک در ایتالیا »، گارزانتی، 1957.
3. بویر، « تاریخ ریاضیات »، اسکار مونداتوری، 1980.4. De Bernardi Ferrero D.، " طراحی های معماری مدنی و کلیسایی گوارینو گوارینی و هنر استاد "، آلبرا، 1966.
5. Griseri A., “ The Metamorphoses of the Baroque ”, Einaudi, 1967.
6. Guarini G., “ Civil architecture ”, Il Polifilo, 1968.
7. Guarini G., “ Euclides adauctus et methodicus ”, Augustae Taurinorum, 1671 8.
Kline M., “ تاریخ اندیشه ریاضی ”, Einaudi, 1991, vol.1.
9. Meek HQ، " Guarini Guarini "، Electa، 1991.
10. Passanti، " در دنیای جادویی گوارینو گوارینی "، Toso، 1963.
11. Wittkower R.، " هنر و معماری در ایتالیا: 1600-1750 "، عینودی، 1972.
https://matematica.unibocconi.eu/articoli/guarino-guarini-architetto-e-matematico


















































 در این وبلاگ به ریاضیات و کاربردهای آن و تحقیقات در آنها پرداخته می شود. مطالب در این وبلاگ ترجمه سطحی و اولیه است و کامل نیست.در صورتی سوال یا نظری در زمینه ریاضیات دارید مطرح نمایید .در صورت امکان به آن می پردازم. من دوست دارم برای یافتن پاسخ به سوالات و حل پروژه های علمی با دیگران همکاری نمایم.در صورتی که شما هم بامن هم عقیده هستید با من تماس بگیرید.
در این وبلاگ به ریاضیات و کاربردهای آن و تحقیقات در آنها پرداخته می شود. مطالب در این وبلاگ ترجمه سطحی و اولیه است و کامل نیست.در صورتی سوال یا نظری در زمینه ریاضیات دارید مطرح نمایید .در صورت امکان به آن می پردازم. من دوست دارم برای یافتن پاسخ به سوالات و حل پروژه های علمی با دیگران همکاری نمایم.در صورتی که شما هم بامن هم عقیده هستید با من تماس بگیرید.