ابزار
از ویکیپدیا، دانشنامه آزاد
| ترمودینامیک |
|---|
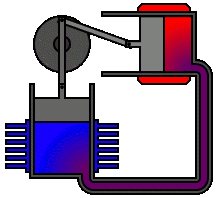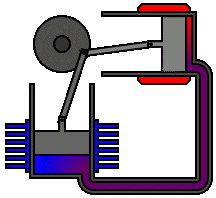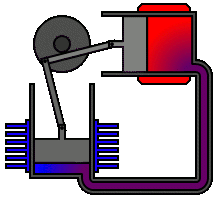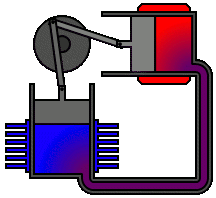
 موتور حرارتی کلاسیک کارنو |
| نشان می دهد شاخه ها |
| نشان می دهد |
| نشان می دهد |
| نشان می دهد |
| نشان می دهد |
| نشان می دهد |
| نشان می دهد |
نشان می دهد
|
| نشان می دهد دانشمندان |
| نشان می دهد دیگر |
چرخه کارنو یک چرخه ترمودینامیکی ایده آل است که توسط فیزیکدان فرانسوی سادی کارنو در سال 1824 پیشنهاد شد و توسط دیگران در دهه های 1830 و 1840 گسترش یافت. با قضیه کارنو ، حد بالایی را برای بازده هر موتور ترمودینامیکی کلاسیک در طول تبدیل گرما به کار ، یا برعکس، کارایی یک سیستم تبرید در ایجاد اختلاف دما از طریق اعمال کار بر روی سیستم، فراهم میکند.
در چرخه کارنو، یک سیستم یا موتور انرژی را به شکل گرما بین دو مخزن حرارتی در دماها منتقل می کند.





| ویدیوهای خارجی | |
|---|---|
مراحل [ ویرایش ]
چرخه کارنو به عنوان یک چرخه ترمودینامیکی ایده آل که توسط موتور حرارتی کارنو انجام می شود ، شامل مراحل زیر است:
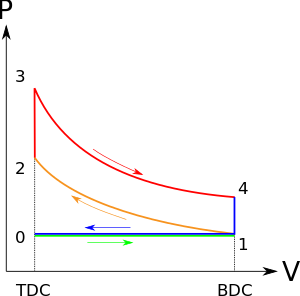
انبساط همدما . گرما (به عنوان یک انرژی) به طور برگشت پذیر از مخزن دمای داغ در دمای ثابت TH به گاز در دمای بینهایت کمتر از TH منتقل می شود (تا امکان انتقال گرما به گاز بدون تغییر عملاً دمای گاز بنابراین اضافه یا جذب گرمای همدما فراهم شود ). در طی این مرحله (1 تا 2 در شکل 1 ، A تا B در شکل 2 )، گاز از نظر حرارتی با مخزن دمای داغ در تماس است (در حالی که از نظر حرارتی از مخزن دمای سرد جدا شده است) و گاز اجازه انبساط داده و کار را انجام می دهد. روی محیط اطراف با فشار دادن گاز پیستون به سمت بالا (شکل مرحله 1، سمت راست). اگرچه فشار از نقاط 1 تا 2 کاهش می یابد (شکل 1) دمای گاز در طول فرآیند تغییر نمی کند زیرا گرمای منتقل شده از مخزن دمای داغ به گاز دقیقاً برای انجام کار بر روی محیط اطراف توسط گاز استفاده می شود. بدون تغییر انرژی داخلی گاز (بدون تغییر دمای گاز برای یک گاز ایده آل). گرمای QH > 0 از مخزن دمای داغ جذب می شود و در نتیجه آنتروپی افزایش می یابد .
گاز بر حسب مقدار
.
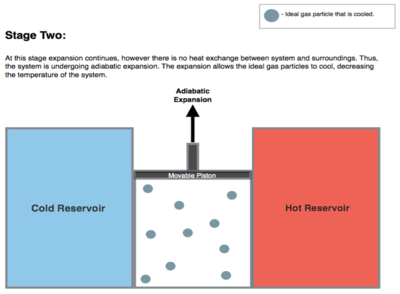
انبساط ایزنتروپیک ( آدیاباتیک برگشت پذیر ) گاز (خروجی کار ایسنتروپیک). برای این مرحله (2 تا 3 در شکل 1 ، B تا C در شکل 2 ) گاز موتور از نظر حرارتی از مخازن سرد و گرم عایق می شود، بنابراین آنها نه گرما را دریافت می کنند و نه از دست می دهند، یک فرآیند " آدیاباتیک ". گاز با کاهش فشار خود به انبساط ادامه می دهد، کار روی محیط اطراف انجام می دهد (بالا بردن پیستون؛ مرحله 2 شکل، سمت راست)، و مقداری از انرژی داخلی را از دست می دهد که برابر با کار انجام شده است. انبساط گاز بدون ورودی گرما باعث سرد شدن گاز به دمای "سرد" می شود (با از دست دادن انرژی داخلی خود) که بی نهایت بالاتر از دمای مخزن سرد T C است . آنتروپی بدون تغییر باقی میماند زیرا هیچ گرمایی Q بین سیستم (گاز) و محیط اطراف آن منتقل نمیشود، بنابراین یک فرآیند ایزنتروپیک، به معنی عدم تغییر آنتروپی در فرآیند).
فشرده سازی ایزوترمال. گرما به طور برگشت پذیر به مخزن دمای پایین در دمای ثابت T C (دفع حرارت همدما) منتقل می شود. در این مرحله (3 تا 4 در شکل 1 ، C تا D در شکل 2 )، گاز موتور در تماس حرارتی با مخزن سرد در دمای T C (در حالی که از نظر حرارتی از مخزن دمای داغ جدا شده است) و دمای گاز است. بی نهایت بالاتر از این دما است (برای انتقال حرارت از گاز به مخزن سرد بدون تغییر عملا دمای گاز). محیط اطراف روی گاز کار می کند و پیستون را به پایین فشار می دهد (شکل مرحله 3، سمت راست). مقداری از انرژی که توسط گاز حاصل از این کار به دست میآید دقیقاً به عنوان انرژی گرمایی QC < 0 (منفی خروج از سیستم، طبق قرارداد جهانی در ترمودینامیک) به مخزن سرد منتقل میشود ، بنابراین آنتروپی سیستم کاهش مییابد. میزان
. [1]
زیرا فشردگی همدما باعث کاهش تعدد گاز می شود.
فشرده سازی ایزنتروپیک. (4 به 1 در شکل 1 ، D تا A در شکل 2 ) یک بار دیگر گاز موجود در موتور از مخازن سرد و گرم عایق حرارتی می شود، و موتور بدون اصطکاک فرض می شود و فرآیند به اندازه کافی کند است، بنابراین برگشت پذیر است. در طی این مرحله، محیط اطراف روی گاز کار می کند، پیستون را بیشتر به سمت پایین فشار می دهد (مرحله 4 شکل، سمت راست)، انرژی داخلی آن را افزایش می دهد، آن را فشرده می کند و باعث می شود که دمای آن به دمای بی نهایت کمتر از TH برگردد . به کار اضافه شده به سیستم، اما آنتروپی بدون تغییر باقی می ماند. در این مرحله گاز در همان حالت ابتدای مرحله 1 قرار دارد.
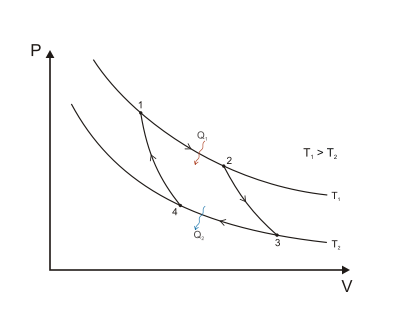
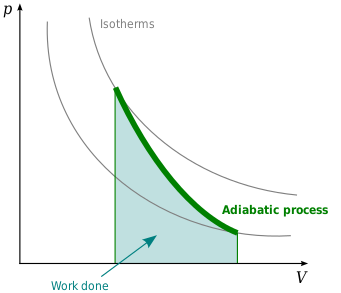
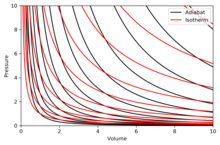
شکل 1 : چرخه کارنو که بر روی یک نمودار PV برای نشان دادن کار انجام شده نشان داده شده است. 1-به-2 (انبساط همدما)، 2-به-3 (انبساط ایسنتروپیک)، 3-به-4 (فشرده سازی همدما)، 4-به-1 (فشرده سازی ایسنتروپیک).
در این حالت، از آنجایی که یک چرخه ترمودینامیکی برگشت پذیر است (بدون تغییر خالص در سیستم و محیط اطراف آن در هر سیکل) [2] [1]

این درست است به عنوان


نمودار فشار-حجم [ ویرایش ]
هنگامی که یک چرخه کارنو بر روی نمودار فشار-حجم ترسیم می شود ( شکل 1 )، مراحل همدما از خطوط همدما برای سیال عامل پیروی می کنند، مراحل آدیاباتیک بین ایزوترم ها حرکت می کنند و ناحیه محدود شده توسط مسیر چرخه کامل، کل کار را نشان می دهد. را می توان در یک چرخه انجام داد. از نقطه 1 تا 2 و نقطه 3 تا 4 دما ثابت است (فرایند همدما). انتقال حرارت از نقطه 4 به 1 و نقطه 2 به 3 برابر با صفر است (فرایند آدیاباتیک).
خواص و اهمیت [ ویرایش ]
نمودار دما – آنتروپی [ ویرایش ]
مقاله اصلی: نمودار دما – آنتروپی
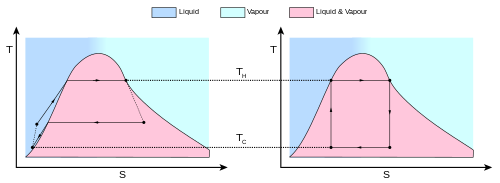
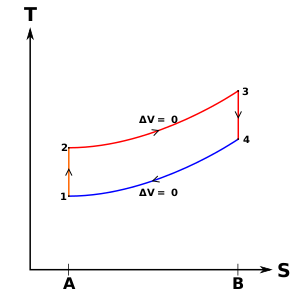
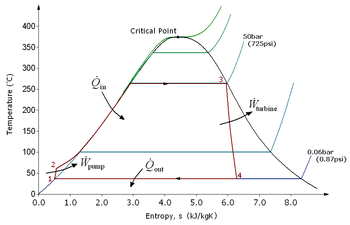
شکل 2 : یک چرخه کارنو به عنوان یک چرخه ترمودینامیکی ایده آل که توسط یک موتور حرارتی کارنو انجام می شود ، که بر روی نمودار TS (دما آنتروپی T-S) نشان داده شده است. چرخه بین یک مخزن گرم در دمای T H و یک مخزن سرد در دمای T C انجام می شود . محور عمودی دمای سیستم و محور افقی آنتروپی سیستم است. A-to-B (انبساط همدما)، B-to-C (انبساط ایسنتروپیک)، C-to-D (فشرده سازی همدما)، D-to-A (فشرده سازی ایسنتروپیک).
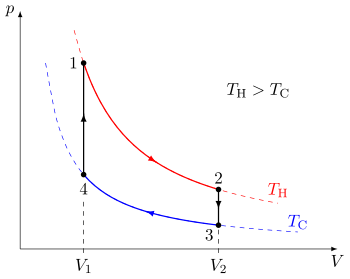
شکل 3 : یک چرخه ترمودینامیکی تعمیم یافته که بین یک مخزن داغ در دمای TH و یک مخزن سرد در دمای TC انجام می شود . طبق قانون دوم ترمودینامیک ، چرخه نمی تواند در خارج از باند دما از TC تا TH گسترش یابد . منطقه به رنگ قرمز، | Q C |، مقدار انرژی مبادله شده بین سیستم و مخزن سرد است. مساحت سفید W مقدار انرژی کاری است که سیستم با محیط اطرافش مبادله می کند. مقدار حرارت مبادله شده با مخزن داغ مجموع این دو است. اگر سیستم مانند یک موتور رفتار کند، فرآیند در جهت عقربههای ساعت در اطراف حلقه حرکت میکند و اگر مانند یک یخچال رفتار کند در خلاف جهت عقربههای ساعت حرکت میکند. بازده به چرخه، نسبت ناحیه سفید (کار) تقسیم بر مجموع نواحی سفید و قرمز (گرمای جذب شده از مخزن داغ) است. Q C (انرژی از دست رفته به مخزن سرد) را می توان به عنوان یک تفریق مستقیم یا به صورت مجموع یک کمیت منفی بیان کرد که می تواند به قراردادهای مختلفی منجر شود.
رفتار موتور یا یخچال کارنو با استفاده از نمودار دما- آنتروپی ( نمودار T - S ) که در آن حالت ترمودینامیکی با نقطه ای از نمودار با آنتروپی ( S ) به عنوان محور افقی و دما مشخص می شود، بهتر درک می شود. T ) به عنوان محور عمودی ( شکل 2 ). برای یک سیستم بسته ساده (تجزیه و تحلیل جرم کنترل)، هر نقطه در نمودار نشان دهنده وضعیت خاصی از سیستم است. یک فرآیند ترمودینامیکی با یک منحنی نشان داده می شود که حالت اولیه (A) و حالت نهایی (B) را به هم متصل می کند. مساحت زیر منحنی عبارت است از:
| ( 1 ) |
که مقدار گرمای منتقل شده در فرآیند است. اگر فرآیند سیستم را به سمت آنتروپی بیشتر سوق دهد، سطح زیر منحنی مقدار گرمای جذب شده توسط سیستم در آن فرآیند است. در غیر این صورت، مقدار گرمایی است که از سیستم خارج می شود یا از آن خارج می شود. برای هر فرآیند چرخه ای، یک بخش بالایی از چرخه و یک بخش پایین تر وجود دارد. در نمودارهای T - S برای یک چرخه جهت عقربه های ساعت، ناحیه زیر قسمت بالایی انرژی جذب شده توسط سیستم در طول چرخه خواهد بود، در حالی که ناحیه زیر قسمت پایین انرژی حذف شده از سیستم در طول چرخه خواهد بود. سپس مساحت داخل چرخه تفاوت بین این دو (انرژی گرمای خالص جذب شده) است، اما از آنجایی که انرژی داخلی سیستم باید به مقدار اولیه خود بازگشته باشد، این تفاوت باید مقدار کار انجام شده توسط سیستم در هر چرخه باشد. . با مراجعه به شکل 1 ، از نظر ریاضی، برای یک فرآیند برگشت پذیر، ممکن است مقدار کار انجام شده در یک فرآیند چرخه ای را به صورت زیر بنویسیم:
| ( 2 ) |
از آنجایی که dU یک دیفرانسیل دقیق است ، انتگرال آن بر روی هر حلقه بسته صفر است و نتیجه آن این است که سطح داخل حلقه در نمودار T - S برابر است با کل کار انجام شده توسط سیستم بر روی محیط اطراف اگر حلقه باشد. در جهت عقربههای ساعت پیمایش میشود، و (ب) برابر است با کل کار انجام شده بر روی سیستم توسط محیط اطراف هنگامی که حلقه در جهت خلاف جهت عقربههای ساعت پیمایش میشود.
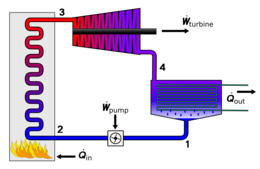
شکل 4 : چرخه کارنو که بین یک مخزن گرم در دمای TH و یک مخزن سرد در دمای TC انجام می شود .
چرخه کارنو [ ویرایش ]
شکل 5 : تجسم یک چرخه کارنو
ارزیابی انتگرال فوق به ویژه برای یک چرخه کارنو ساده است. مقدار انرژی منتقل شده به عنوان کار است
مقدار کل گرمای منتقل شده از مخزن گرم به سیستم (در انبساط همدما) خواهد بود.

به دلیل حفظ انرژی، گرمای خالص منتقل شده،س
کارایی
| ( 3 ) |
جایی که
- W کار انجام شده توسط سیستم است (انرژی خروجی از سیستم به عنوان کار)،
<0 گرمای گرفته شده از سیستم (انرژی گرمایی خروجی از سیستم) است.
> 0 گرمای وارد شده به سیستم (انرژی گرمایی ورودی به سیستم) است.
دمای مطلق مخزن سرد است و
دمای مطلق مخزن گرم است.
حداکثر آنتروپی سیستم است
حداقل آنتروپی سیستم است
بیان با دما




این تعریف راندمان کار موتور حرارتی کارنو به عنوان کسری از کار انجام شده توسط سیستم به انرژی حرارتی دریافتی سیستم از مخزن داغ در هر سیکل است. این انرژی حرارتی آغازگر چرخه است.
چرخه کارنو معکوس [ ویرایش ]
یک چرخه موتور حرارتی کارنو که شرح داده شد یک چرخه کاملاً برگشت پذیر است. یعنی تمام فرآیندهای تشکیل دهنده آن را می توان معکوس کرد که در این صورت تبدیل به پمپ حرارتی و چرخه تبرید کارنو می شود . این بار، چرخه دقیقاً یکسان می ماند با این تفاوت که جهت هر گونه فعل و انفعالات حرارتی و کاری معکوس می شود. گرما از مخزن با دمای پایین جذب میشود، گرما به مخزن با دمای بالا دفع میشود و برای انجام همه اینها یک ورودی کاری لازم است. نمودار P - V چرخه معکوس کارنو مانند چرخه موتور حرارتی کارنو است با این تفاوت که جهت فرآیندها معکوس است. [3]
قضیه کارنو [ ویرایش ]
مقاله اصلی: قضیه کارنو (ترمودینامیک)
از نمودار بالا می توان دریافت که برای هر چرخه ای که بین دماها کار می کند

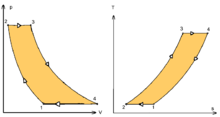
شکل 6 : یک موتور واقعی (سمت چپ) در مقایسه با چرخه کارنو (راست). آنتروپی یک ماده واقعی با دما تغییر می کند. این تغییر با منحنی در نمودار T - S نشان داده می شود . برای این شکل، منحنی یک تعادل بخار-مایع را نشان می دهد ( به چرخه رانکین مراجعه کنید ). سیستم های برگشت ناپذیر و تلفات انرژی (مثلاً کار در اثر اصطکاک و تلفات حرارتی) مانع از تحقق ایده آل در هر مرحله می شود.
قضیه کارنو بیانیه رسمی این واقعیت است: هیچ موتوری که بین دو مخزن حرارتی کار می کند نمی تواند کارآمدتر از موتور کارنو بین همان مخازن باشد. بنابراین، معادله 3 حداکثر بازده ممکن را برای هر موتوری با استفاده از دماهای مربوطه نشان می دهد. نتیجهای از قضیه کارنو بیان میکند که: همه موتورهای برگشتپذیر که بین مخازن حرارتی یکسانی کار میکنند به یک اندازه کارآمد هستند. تنظیم مجدد سمت راست معادله شکل سادهتری از معادله را به دست میدهد، یعنی اینکه حداکثر بازده نظری یک موتور حرارتی برابر است با اختلاف دمای بین مخزن سرد و گرم تقسیم بر دمای مطلق مخزن گرم. . با نگاهی به این فرمول یک واقعیت جالب آشکار می شود: کاهش دمای مخزن سرد تاثیر بیشتری بر بازده سقف یک موتور حرارتی خواهد داشت تا اینکه دمای مخزن داغ را به همان میزان افزایش دهد. در دنیای واقعی، دستیابی به این امر ممکن است دشوار باشد زیرا مخزن سرد اغلب دمای محیط موجود است.
به عبارت دیگر، حداکثر بازده در صورتی به دست می آید که آنتروپی در هر چرخه تغییر نکند. تغییر آنتروپی در هر چرخه ایجاد می شود، برای مثال، اگر اصطکاک وجود داشته باشد که منجر به اتلاف کار به گرما شود. در این صورت، چرخه برگشت پذیر نیست و قضیه کلازیوس به جای برابری تبدیل به نابرابری می شود. در غیر این صورت، از آنجایی که آنتروپی یک تابع حالت است ، تخلیه گرمای مورد نیاز به محیط برای دفع آنتروپی اضافی منجر به کاهش (حداقل) راندمان می شود. بنابراین معادله 3 کارایی هر موتور حرارتی برگشت پذیر را نشان می دهد .
در موتورهای حرارتی مزوسکوپی، کار در هر چرخه عملیات به طور کلی به دلیل نویز حرارتی در نوسان است. اگر چرخه به صورت شبه ایستا انجام شود، نوسانات حتی در مقیاس مزو مقیاس ناپدید می شوند. [4] با این حال، اگر چرخه سریعتر از زمان استراحت محیط کار انجام شود، نوسانات کار اجتناب ناپذیر است. با این وجود، هنگامی که نوسانات کار و گرما شمارش می شود، یک برابری دقیق میانگین نمایی کار انجام شده توسط هر موتور حرارتی را به انتقال حرارت از حمام حرارتی گرمتر مرتبط می کند. [5]
کارایی موتورهای حرارتی واقعی [ ویرایش ]
همچنین ببینید: موتور حرارتی § راندمان
کارنو متوجه شد که در واقعیت، ساخت یک موتور ترمودینامیکی برگشت پذیر امکان پذیر نیست . بنابراین، موتورهای حرارتی واقعی حتی کمتر از آنچه در معادله 3 نشان داده شده است، کارآمد هستند . علاوه بر این، موتورهای واقعی که در امتداد سبک چرخه کارنو (انبساط همدما / انبساط ایزوتروپیک / تراکم همدما / تراکم ایزنتروپیک) کار می کنند نادر هستند. با این وجود، معادله 3 برای تعیین حداکثر بازدهی که میتوان برای مجموعه معینی از مخازن حرارتی انتظار داشت، بسیار مفید است.
اگرچه چرخه کارنو یک ایده آل سازی است، اما رابطه 3 به عنوان بیان کارایی کارنو هنوز مفید است. دمای متوسط را در نظر بگیرید ،

برای چرخه کارنو یا معادل آن، مقدار متوسط 〈 T H 〉 برابر با بالاترین دمای موجود، یعنی T H و 〈 T C 〉 کمترین، یعنی T C خواهد بود . برای سایر چرخههای ترمودینامیکی کمتر کارآمد، 〈 T H 〉 کمتر از T H و 〈 T C 〉 بالاتر از T C خواهد بود . به عنوان مثال، این می تواند نشان دهد که چرا یک گرم کننده یا احیاء کننده می تواند بازده حرارتی نیروگاه های بخار را بهبود بخشد و چرا راندمان حرارتی نیروگاه های سیکل ترکیبی (که دارای توربین های گازی هستند که در دماهای بالاتر کار می کنند) از بخار معمولی فراتر می رود. گیاهان اولین نمونه اولیه موتور دیزل بر اساس اصول چرخه کارنو بود.
به عنوان یک ساختار ماکروسکوپی [ ویرایش ]
مقاله اصلی: موتور حرارتی کارنو § به عنوان یک ساختار ماکروسکوپی
موتور حرارتی کارنو ، در نهایت، یک ساختار نظری است که بر اساس یک سیستم ترمودینامیکی ایده آل است . در سطح عملی در مقیاس انسانی، چرخه کارنو یک مدل با ارزش است، مانند پیشرفت در توسعه موتور دیزل . با این حال، در مقیاس ماکروسکوپی، محدودیتهای اعمال شده توسط مفروضات مدل، غیرعملی بودن و در نهایت ناتوانی در انجام هر کاری را ثابت میکند . [6] به این ترتیب، طبق قضیه کارنو ، موتور کارنو ممکن است به عنوان حد نظری موتورهای حرارتی در مقیاس ماکروسکوپی در نظر گرفته شود تا هر وسیله عملی که میتوان ساخت. [7]
همچنین ببینید [ ویرایش ]
منبع
https://en.wikipedia.org/wiki/Carnot_cycle















 "نسبت انفجار" نامیده می شود.
"نسبت انفجار" نامیده می شود. "نسبت انبساط ایسنتروپیک" نامیده می شود. (برای چرخه اتو همان نسبت تراکم است
"نسبت انبساط ایسنتروپیک" نامیده می شود. (برای چرخه اتو همان نسبت تراکم است ). از نظر مکانیکی، این انبساط مخلوط گاز داغ در سیلندر است که به عنوان ضربه انبساط (قدرت) شناخته می شود.
). از نظر مکانیکی، این انبساط مخلوط گاز داغ در سیلندر است که به عنوان ضربه انبساط (قدرت) شناخته می شود.
 انرژی از 1-2-3 و به سیستم اضافه می شود
انرژی از 1-2-3 و به سیستم اضافه می شود انرژی از سیستم 3-4-1 حذف می شود. از نظر کار و حرارت اضافه شده به سیستم
انرژی از سیستم 3-4-1 حذف می شود. از نظر کار و حرارت اضافه شده به سیستم
























 (به
(به 



 نسبت گرمای ویژه است
نسبت گرمای ویژه است




 نسبت تراکم است
نسبت تراکم است :
:

 برای هوا 1.4 است، افزایش در
برای هوا 1.4 است، افزایش در



 به
به در نمودار زیر). این یک مدل ریاضی ایدهآل است: دیزلهای فیزیکی واقعی در این دوره افزایش فشار دارند، اما نسبت به چرخه اتو کمتر مشخص است. در مقابل، چرخه اتوی ایده آل موتور بنزینی به یک فرآیند حجم ثابت در طول آن فاز تقریب می زند.
در نمودار زیر). این یک مدل ریاضی ایدهآل است: دیزلهای فیزیکی واقعی در این دوره افزایش فشار دارند، اما نسبت به چرخه اتو کمتر مشخص است. در مقابل، چرخه اتوی ایده آل موتور بنزینی به یک فرآیند حجم ثابت در طول آن فاز تقریب می زند.
 فشار و V حجم یا
فشار و V حجم یا اگر فرآیند بر اساس جرم واحد قرار گیرد، حجم خاص است. چرخه دیزل ایده آل گاز ایده آل را در نظر می گیرد و شیمی احتراق ، اگزوز و فرآیندهای شارژ مجدد را نادیده می گیرد و به سادگی چهار فرآیند متمایز را دنبال می کند:
اگر فرآیند بر اساس جرم واحد قرار گیرد، حجم خاص است. چرخه دیزل ایده آل گاز ایده آل را در نظر می گیرد و شیمی احتراق ، اگزوز و فرآیندهای شارژ مجدد را نادیده می گیرد و به سادگی چهار فرآیند متمایز را دنبال می کند: ، اما طبق تعریف (ایسنتروپیک) هیچ انرژی به صورت گرما به داخل یا خارج سیستم منتقل نمی شود. در طی فرآیند فشار ثابت (قرمز، ایزوباریک )، انرژی به صورت گرما وارد سیستم می شود
، اما طبق تعریف (ایسنتروپیک) هیچ انرژی به صورت گرما به داخل یا خارج سیستم منتقل نمی شود. در طی فرآیند فشار ثابت (قرمز، ایزوباریک )، انرژی به صورت گرما وارد سیستم می شود . در طی فرآیندهای ایزنتروپیک بالا (زرد)، انرژی به شکل به خارج از سیستم منتقل می شود
. در طی فرآیندهای ایزنتروپیک بالا (زرد)، انرژی به شکل به خارج از سیستم منتقل می شود ، اما طبق تعریف (ایسنتروپیک) هیچ انرژی به صورت گرما به داخل یا خارج سیستم منتقل نمی شود. در طول فرآیند حجم ثابت (سبز، ایزوکوریک )، مقداری از انرژی به عنوان گرما از طریق فرآیند کاهش فشار مناسب از سیستم خارج می شود.
، اما طبق تعریف (ایسنتروپیک) هیچ انرژی به صورت گرما به داخل یا خارج سیستم منتقل نمی شود. در طول فرآیند حجم ثابت (سبز، ایزوکوریک )، مقداری از انرژی به عنوان گرما از طریق فرآیند کاهش فشار مناسب از سیستم خارج می شود. . کاری که از سیستم خارج می شود برابر است با کاری که وارد سیستم می شود به اضافه تفاوت بین گرمای اضافه شده به سیستم و حرارتی که از سیستم خارج می شود. به عبارت دیگر، سود خالص کار برابر است با تفاوت بین گرمای اضافه شده به سیستم و گرمایی که از سیستم خارج می شود.
. کاری که از سیستم خارج می شود برابر است با کاری که وارد سیستم می شود به اضافه تفاوت بین گرمای اضافه شده به سیستم و حرارتی که از سیستم خارج می شود. به عبارت دیگر، سود خالص کار برابر است با تفاوت بین گرمای اضافه شده به سیستم و گرمایی که از سیستم خارج می شود.
 بازده حرارتی است
بازده حرارتی است نسبت برش است
نسبت برش است (نسبت بین حجم پایان و شروع برای فاز احتراق)
(نسبت بین حجم پایان و شروع برای فاز احتراق)




 را می توان به دمای شعله سوخت مورد استفاده تقریب زد. دمای شعله را می توان به دمای شعله آدیاباتیک سوخت با نسبت هوا به سوخت و فشار تراکم مربوطه تقریب زد.
را می توان به دمای شعله سوخت مورد استفاده تقریب زد. دمای شعله را می توان به دمای شعله آدیاباتیک سوخت با نسبت هوا به سوخت و فشار تراکم مربوطه تقریب زد. .
.  را می توان به دمای هوای ورودی تقریب زد.
را می توان به دمای هوای ورودی تقریب زد.











 ، جایی که
، جایی که




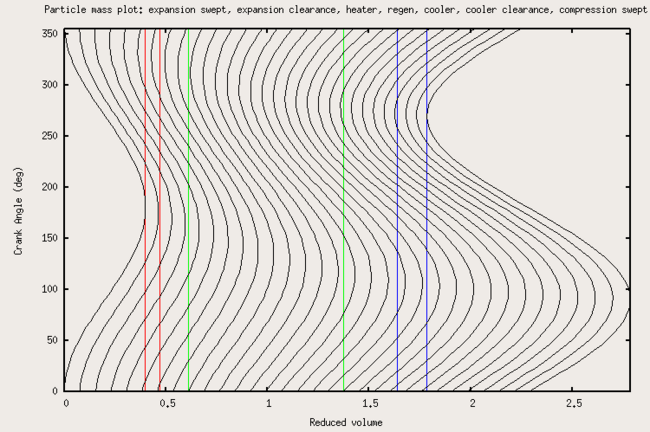









































 حاضر است)؛
حاضر است)؛


























































 پس باید این باشد
پس باید این باشد
 ،
، .
.
 مقدار انرژی است که سیستم با گرم کردن به دست می آورد،
مقدار انرژی است که سیستم با گرم کردن به دست می آورد،
 تغییر در آنتروپی است. علامت برابر به یک
تغییر در آنتروپی است. علامت برابر به یک 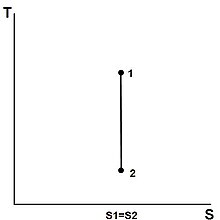
 یا
یا .
. 



 آنتالپی خاص در حالت خروج برای فرآیند واقعی است،
آنتالپی خاص در حالت خروج برای فرآیند واقعی است، آنتالپی خاص در حالت خروج برای فرآیند ایزنتروپیک است.
آنتالپی خاص در حالت خروج برای فرآیند ایزنتروپیک است.


 ) از رابطه زیر بدست می آید
) از رابطه زیر بدست می آید
 ، و غیره
، و غیره تمام فرآیندهای برگشت پذیر آدیاباتیک ایزنتروپیک هستند. این منجر به دو مشاهدات مهم می شود:
تمام فرآیندهای برگشت پذیر آدیاباتیک ایزنتروپیک هستند. این منجر به دو مشاهدات مهم می شود:

 ، و
، و
 و
و ، سپس
، سپس




 ،
، اما nR = خود ثابت است، بنابراین
اما nR = خود ثابت است، بنابراین .)
.)
 (در هر خال)،
(در هر خال)، و
و


 یا
یا


















 = فشار،
= فشار، ،
، = دما،
= دما، = ثابت گاز برای گاز خاص =
= ثابت گاز برای گاز خاص = ،
، = وزن مولکولی گاز مخصوص،
= وزن مولکولی گاز مخصوص، = تراکم،
= تراکم، = گرمای ویژه در فشار ثابت،
= گرمای ویژه در فشار ثابت، = گرمای ویژه در حجم ثابت.
= گرمای ویژه در حجم ثابت.

















 پتانسیل
پتانسیل  تعداد ذرات در سیستم، و
تعداد ذرات در سیستم، و تعداد انواع ذرات در سیستم است.
تعداد انواع ذرات در سیستم است.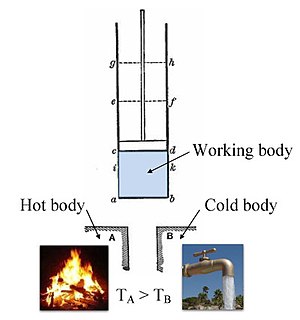

 جایی که
جایی که جایی که
جایی که جایی که
جایی که


 و ضرایب دیفرانسیل متغیر طبیعی
و ضرایب دیفرانسیل متغیر طبیعی فقط متغیرهای منفرد هستند
فقط متغیرهای منفرد هستند

 زیرا T یک متغیر طبیعی برای آنتالپی H نیست.
زیرا T یک متغیر طبیعی برای آنتالپی H نیست. به طوری که
به طوری که برای یک
برای یک 




 جایی که
جایی که





















 به طوری که
به طوری که
 . آنتروپی شانون (در
. آنتروپی شانون (در  و اگر آنتروپی با واحد اندازه گیری شود
و اگر آنتروپی با واحد اندازه گیری شود در هر nat، سپس آنتروپی با:
در هر nat، سپس آنتروپی با:
 ).
).
 در دمای معینی وارد سیستم می شود
در دمای معینی وارد سیستم می شود 

 و
و به طوری که دومی به طور آدیاباتیک از اولی قابل دسترسی است اما بالعکس نیست. تعریف آنتروپی حالت های مرجع به ترتیب 0 و 1 آنتروپی یک حالت
به طوری که دومی به طور آدیاباتیک از اولی قابل دسترسی است اما بالعکس نیست. تعریف آنتروپی حالت های مرجع به ترتیب 0 و 1 آنتروپی یک حالت به عنوان بزرگترین عدد تعریف می شود
به عنوان بزرگترین عدد تعریف می شود به طوری که
به طوری که ، در ایالت
، در ایالت


 (
(  (کار فشار-حجم)، در سراسر مرزهای سیستم، به طور کلی باعث تغییر در آنتروپی سیستم می شود. انتقال به عنوان گرما مستلزم انتقال آنتروپی است
(کار فشار-حجم)، در سراسر مرزهای سیستم، به طور کلی باعث تغییر در آنتروپی سیستم می شود. انتقال به عنوان گرما مستلزم انتقال آنتروپی است ، جایی که
، جایی که در یک
در یک  ، یعنی میزان تغییر
، یعنی میزان تغییر از آنتروپی کمیت گسترده
از آنتروپی کمیت گسترده
 نرخ خالص جریان آنتروپی ناشی از جریان جرم به داخل و خارج از سیستم است (که در آن
نرخ خالص جریان آنتروپی ناشی از جریان جرم به داخل و خارج از سیستم است (که در آن آنتروپی در واحد جرم است).
آنتروپی در واحد جرم است). نرخ جریان آنتروپی ناشی از جریان گرما در سراسر مرز سیستم است.
نرخ جریان آنتروپی ناشی از جریان گرما در سراسر مرز سیستم است. نرخ
نرخ  جایی که
جایی که جریان گرما است و
جریان گرما است و درجه حرارت در است
درجه حرارت در است پورت جریان گرما به سیستم.
پورت جریان گرما به سیستم. هرگز یک کمیت شناخته شده نیست، بلکه همیشه بر اساس عبارت بالا مشتق شده است. بنابراین، نسخه سیستم باز قانون دوم به طور مناسب تر به عنوان "معادله تولید آنتروپی" توصیف می شود زیرا مشخص می کند که
هرگز یک کمیت شناخته شده نیست، بلکه همیشه بر اساس عبارت بالا مشتق شده است. بنابراین، نسخه سیستم باز قانون دوم به طور مناسب تر به عنوان "معادله تولید آنتروپی" توصیف می شود زیرا مشخص می کند که ، با صفر برای فرآیندهای برگشت پذیر یا بزرگتر از صفر برای فرآیندهای برگشت ناپذیر.
، با صفر برای فرآیندهای برگشت پذیر یا بزرگتر از صفر برای فرآیندهای برگشت ناپذیر. و فشار
و فشار تا یک جلد نهایی
تا یک جلد نهایی
 تا دمای نهایی
تا دمای نهایی






 اندازه گیری تغییر آنتروپی را معرفی می کند،
اندازه گیری تغییر آنتروپی را معرفی می کند، آنتروپی مولی استاندارد هر عنصر یا ترکیب را تشکیل می دهد، نشانگر مقدار انرژی ذخیره شده توسط یک ماده در298 K.
آنتروپی مولی استاندارد هر عنصر یا ترکیب را تشکیل می دهد، نشانگر مقدار انرژی ذخیره شده توسط یک ماده در298 K.  . این عبارت از طریق برخی مراحل به معادله
. این عبارت از طریق برخی مراحل به معادله  [تغییر انرژی آزاد گیبس سیستم]
[تغییر انرژی آزاد گیبس سیستم] [تغییر آنتالپی]
[تغییر آنتالپی] [تغییر آنتروپی].
[تغییر آنتروپی]. 


 ماتریس
ماتریس 



 ) و در ترمودینامیک کلاسیک (
) و در ترمودینامیک کلاسیک ( همراه با
همراه با  .
.  جذب بی نهایت گرما
جذب بی نهایت گرما به صورت برگشت پذیر، توسط داده می شود
به صورت برگشت پذیر، توسط داده می شود . به طور واضح تر، یک انرژی
. به طور واضح تر، یک انرژی در دسترس نیست برای انجام کار مفید، که در آن
در دسترس نیست برای انجام کار مفید، که در آن دمای سردترین مخزن در دسترس یا سینک حرارتی خارج از سیستم است. برای بحث بیشتر،
دمای سردترین مخزن در دسترس یا سینک حرارتی خارج از سیستم است. برای بحث بیشتر،  . این به معنای انتگرال خط است
. این به معنای انتگرال خط است
 سیستم (بدون احتساب محیط اطراف) به خوبی به عنوان گرما تعریف شده است
سیستم (بدون احتساب محیط اطراف) به خوبی به عنوان گرما تعریف شده است به سیستم تقسیم بر دمای سیستم منتقل می شود
به سیستم تقسیم بر دمای سیستم منتقل می شود
 گرمای موتور از مخزن داغ است و
گرمای موتور از مخزن داغ است و  گرما به مخزن سرد موتور است. برای به دست آوردن راندمان کارنو که 1 - T C / T H است (عددی کمتر از یک)، کلوین مجبور شد نسبت خروجی کار به گرمای جذب شده در طول انبساط همدما را با کمک معادله کارنو-کلاپیرون ارزیابی کند. که حاوی یک تابع ناشناخته به نام تابع کارنو بود. این احتمال که تابع کارنو می تواند دمایی باشد که از نقطه صفر دما اندازه گیری می شود توسط
گرما به مخزن سرد موتور است. برای به دست آوردن راندمان کارنو که 1 - T C / T H است (عددی کمتر از یک)، کلوین مجبور شد نسبت خروجی کار به گرمای جذب شده در طول انبساط همدما را با کمک معادله کارنو-کلاپیرون ارزیابی کند. که حاوی یک تابع ناشناخته به نام تابع کارنو بود. این احتمال که تابع کارنو می تواند دمایی باشد که از نقطه صفر دما اندازه گیری می شود توسط 


 هنگامی که از معادله (
هنگامی که از معادله (  یا
یا با در نظر گرفتن قرارداد علامت گرما که در آن QH > 0 گرمایی است که از مخزن داغ است و توسط موتور جذب می شود و Q C < 0 گرمای تلف شده ای است که از موتور به مخزن سرد منتقل می شود. بنابراین، گرمای بیشتری نسبت به چرخه کارنو به مخزن سرد داده می شود. نابرابری فوق
با در نظر گرفتن قرارداد علامت گرما که در آن QH > 0 گرمایی است که از مخزن داغ است و توسط موتور جذب می شود و Q C < 0 گرمای تلف شده ای است که از موتور به مخزن سرد منتقل می شود. بنابراین، گرمای بیشتری نسبت به چرخه کارنو به مخزن سرد داده می شود. نابرابری فوق اگر مجدداً تغییر آنتروپی یک مخزن حرارتی را با ΔS r,i = - Q i / T i نشان دهیم ، برای i به عنوان H (مخزن گرم) یا C (مخزن سرد)، با در نظر گرفتن قرارداد سیگنال فوق الذکر پس از آن گرمای موتور
اگر مجدداً تغییر آنتروپی یک مخزن حرارتی را با ΔS r,i = - Q i / T i نشان دهیم ، برای i به عنوان H (مخزن گرم) یا C (مخزن سرد)، با در نظر گرفتن قرارداد سیگنال فوق الذکر پس از آن گرمای موتور یا
یا
 در این وبلاگ به ریاضیات و کاربردهای آن و تحقیقات در آنها پرداخته می شود. مطالب در این وبلاگ ترجمه سطحی و اولیه است و کامل نیست.در صورتی سوال یا نظری در زمینه ریاضیات دارید مطرح نمایید .در صورت امکان به آن می پردازم. من دوست دارم برای یافتن پاسخ به سوالات و حل پروژه های علمی با دیگران همکاری نمایم.در صورتی که شما هم بامن هم عقیده هستید با من تماس بگیرید.
در این وبلاگ به ریاضیات و کاربردهای آن و تحقیقات در آنها پرداخته می شود. مطالب در این وبلاگ ترجمه سطحی و اولیه است و کامل نیست.در صورتی سوال یا نظری در زمینه ریاضیات دارید مطرح نمایید .در صورت امکان به آن می پردازم. من دوست دارم برای یافتن پاسخ به سوالات و حل پروژه های علمی با دیگران همکاری نمایم.در صورتی که شما هم بامن هم عقیده هستید با من تماس بگیرید.