2-نیروی کوریولیس

تاریخچه نیروی کوریولیس به شکل زیر است:

تصاویر از Cursus seu Mundus Mathematicus (1674) توسط C.F.M. Dechales:

  • تصویری که نشان می‌دهد چگونه یک توپ توپخانه باید به سمت راست هدف خود در یک زمین چرخان منحرف شود، زیرا حرکت به سمت راست توپ سریع‌تر از برج است.

  • تصویری که نشان می‌دهد چگونه یک توپ از یک برج در یک زمین چرخان سقوط می‌کند. توپ از نقطه F رها می‌شود. بالای برج سریع‌تر از پایه آن حرکت می‌کند، بنابراین وقتی توپ سقوط می‌کند، پایه برج به نقطه I حرکت می‌کند، اما توپ که سرعت شرقی بالای برج را دارد، پایه برج را پشت سر می‌گذارد و به سمت شرق در نقطه L فرود می‌آید.

دانشمندان ایتالیایی Giovanni Battista Riccioli و دستیارش Francesco Maria Grimaldi:

  • در سال ۱۶۵۱ در کتاب Almagestum Novum، تأثیر نیروی کوریولیس را در ارتباط با توپخانه توصیف کردند و نوشتند که چرخش زمین باید باعث انحراف توپ‌های شلیک شده به سمت شمال به سمت شرق شود.

Claude François Milliet Dechales (1674):

  • در کتاب Cursus seu Mundus Mathematicus توضیح داد که چگونه چرخش زمین باعث انحراف در مسیرهای جسم‌های سقوطی و پرتابه‌های هدف‌گیری شده به سمت یکی از قطب‌های سیاره می‌شود.

برهان علیه سیستم هلیوسنتریکی کوپرنیکوس:

  • Riccioli، Grimaldi، و Dechales همه این اثر را به عنوان بخشی از یک استدلال علیه سیستم هلیوسنتریکی کوپرنیکوس توصیف کردند و معتقد بودند که چرخش زمین باید این اثر را ایجاد کند و بنابراین عدم مشاهده این اثر دلیلی برای یک زمین غیرمتحرک است.

معادله شتاب کوریولیس:

  • توسط اویلر در سال ۱۷۴۹ استخراج شد.

  • در معادلات جزر و مدی Pierre-Simon Laplace در سال ۱۷۷۸ توصیف شد.

Gaspard-Gustave de Coriolis (1835):

  • مقاله‌ای در مورد بازده انرژی ماشین‌های با قطعات چرخان منتشر کرد.

  • این مقاله نیروهای اضافی که در یک چارچوب مرجع چرخان تشخیص داده می‌شوند را در نظر گرفت. کوریولیس این نیروهای اضافی را به دو دسته تقسیم کرد. دسته دوم حاوی نیرویی بود که از حاصل‌ضرب برداری سرعت زاویه‌ای یک سیستم مختصات و تصویر سرعت ذره در یک صفحه عمود بر محور چرخش سیستم ایجاد می‌شود. کوریولیس این نیرو را به عنوان "نیروی مرکب گریز از مرکز" به دلیل شباهت‌هایش با نیروی گریز از مرکز در دسته اول توصیف کرد.

پیشنهاد ویلیام فرل (1856):

  • وجود یک سلول گردش در عرض‌های میانی با هوایی که توسط نیروی کوریولیس منحرف می‌شود تا بادهای غربی غالب را ایجاد کند.

کامل شدن درک کینماتیک چرخش زمین و تأثیر آن بر جریان هوا در اواخر قرن نوزدهم:

  • تعامل بزرگ‌مقیاس نیروی گرادیان فشار و نیروی انحرافی که در نهایت باعث حرکت توده‌های هوا در امتداد خطوط ایزوبار می‌شود.

در مکانیک نیوتونی، معادله حرکت برای یک جسم در یک چارچوب مرجع لخت به صورت زیر است:

{\displaystyle {\begin{aligned}\mathbf {F'} &=\mathbf {F} -m{\frac {\mathrm {d} {\boldsymbol {\omega }}}{\mathrm {d} t}}\times \mathbf {r} '-2m{\boldsymbol {\omega }}\times \mathbf {v} '-m{\boldsymbol {\omega }}\times ({\boldsymbol {\omega }}\times \mathbf {r} ')\\&=m\mathbf {a} '\end{aligned}}}

این توضیحات متغیرهای موجود در معادله حرکت نیوتونی در چارچوب مرجع چرخان هستند:

  • 𝑭: مجموع برداری نیروهای فیزیکی اعمال شده بر جسم.

  • 𝜔: سرعت زاویه‌ای چارچوب مرجع چرخان نسبت به چارچوب مرجع لخت.

  • 𝒓': بردار موقعیت جسم نسبت به چارچوب مرجع چرخان.

  • 𝒗': سرعت جسم نسبت به چارچوب مرجع چرخان.

  • 𝒂': شتاب جسم نسبت به چارچوب مرجع چرخان.

در معادله کامل، نیروهای مجازی مانند نیروی کوریولیس و نیروی گریز از مرکز در چارچوب مرجع چرخان به عنوان نیروهای اضافی عمل می‌کنند که به شتاب ظاهری جسم کمک می‌کنند.

در چارچوب مرجع چرخان، نیروهای مجازی به عنوان نیروهای اضافی عمل می‌کنند که مانند نیروهای خارجی واقعی به شتاب ظاهری کمک می‌کنند. اصطلاحات نیروی مجازی در معادله از چپ به راست به شرح زیر هستند:

  • نیروی اویلر (Euler force) یک نیروی مجازی است که در چارچوب‌های مرجع چرخان ظاهر می‌شود. این نیرو ناشی از تغییرات سرعت زاویه‌ای چارچوب مرجع چرخان نسبت به چارچوب مرجع لخت است. نیروی اویلر به صورت زیر بیان می‌شود:

    {\displaystyle -m{\frac {\mathrm {d} {\boldsymbol {\omega }}}{\mathrm {d} t}}\times \mathbf {r} '}

  • Coriolis force

    نیروی کوریولیس یک نیروی مجازی است که بر روی اجسام متحرک در یک چارچوب مرجع چرخان اثر می‌گذارد و باعث می‌شود که مسیر حرکت آنها منحرف شود. این نیرو به علت چرخش زمین ایجاد می‌شود و تأثیرات مهمی در الگوهای جوی، اقیانوسی و حرکت پرتابه‌ها دارد.

    برخی از تأثیرات نیروی کوریولیس عبارتند از:

  • جریان‌های هوا و اقیانوس: نیروی کوریولیس باعث انحراف جریان‌های بزرگ هوا و اقیانوس به سمت راست در نیم‌کره شمالی و به سمت چپ در نیم‌کره جنوبی می‌شود.

  • شکل‌گیری سیکلون‌ها: این نیرو باعث چرخش و شکل‌گیری سیکلون‌ها و طوفان‌ها می‌شود. در نیم‌کره شمالی، سیکلون‌ها به صورت پادساعت‌گرد می‌چرخند و در نیم‌کره جنوبی به صورت ساعت‌گرد.

  • پرتابه‌ها: نیروی کوریولیس باعث انحراف مسیر پرتابه‌ها و موشک‌های دوربرد می‌شود.

  • نیروی کوریولیس در جهت عمود بر سرعت زاویه‌ای چارچوب مرجع چرخان و سرعت جسم نسبت به چارچوب مرجع چرخان عمل می‌کند. اندازه این نیرو متناسب با سرعت جسم در چارچوب مرجع چرخان است.

    {\displaystyle -2m({\boldsymbol {\omega }}\times \mathbf {v} ')}

  • نیروی گریز از مرکز (Centrifugal force) یک نیروی مجازی است که در یک چارچوب مرجع چرخان ظاهر می‌شود و باعث می‌شود که اجسام به سمت بیرون از محور چرخش هدایت شوند. این نیرو نتیجه تمایل ذرات به حفظ حرکت مستقیم‌الخط خود در یک چارچوب مرجع چرخان است و به صورت زیر بیان می‌شود:

    {\displaystyle -m{\boldsymbol {\omega }}\times ({\boldsymbol {\omega }}\times \mathbf {r} ')}
+ نوشته شده در پنجشنبه هجدهم بهمن ۱۴۰۳ ساعت 1:50 توسط علی رضا نقش نیلچی  | 

-1-نیروی کوریولیس

نیروی کوریولیس یک نیروی مجازی است که بر روی اجسام متحرک در یک چارچوب مرجع چرخان اثر می‌گذارد و باعث می‌شود که مسیر حرکت آنها منحرف شود. این نیرو به علت چرخش زمین ایجاد می‌شود و تأثیرات مهمی در الگوهای جوی، اقیانوسی و حرکت پرتابه‌ها دارد.

برخی از تأثیرات نیروی کوریولیس عبارتند از:

  • جریان‌های هوا و اقیانوس: نیروی کوریولیس باعث انحراف جریان‌های بزرگ هوا و اقیانوس به سمت راست در نیم‌کره شمالی و به سمت چپ در نیم‌کره جنوبی می‌شود.

  • شکل‌گیری سیکلون‌ها: این نیرو باعث چرخش و شکل‌گیری سیکلون‌ها و طوفان‌ها می‌شود. در نیم‌کره شمالی، سیکلون‌ها به صورت پادساعت‌گرد می‌چرخند و در نیم‌کره جنوبی به صورت ساعت‌گرد.

  • پرتابه‌ها: نیروی کوریولیس باعث انحراف مسیر پرتابه‌ها و موشک‌های دوربرد می‌شود.

به طور کلی، نیروی کوریولیس یکی از نیروهای مهم و تأثیرگذار در فیزیک و دینامیک‌های جوی و اقیانوسی است.

در فیزیک، نیروی کوریولیس یک نیروی مجازی است که بر اجسام متحرک در یک چارچوب مرجع چرخان اثر می‌گذارد و باعث می‌شود مسیر حرکت آنها منحرف شود. در چارچوب مرجعی که ساعت‌گرد می‌چرخد، نیروی کوریولیس به سمت چپ حرکت جسم اثر می‌گذارد و در چارچوبی که پادساعت‌گرد می‌چرخد، نیروی کوریولیس به سمت راست حرکت جسم اثر می‌گذارد. انحراف یک جسم به دلیل نیروی کوریولیس به عنوان اثر کوریولیس شناخته می‌شود.

اگرچه این نیرو پیش از این توسط دیگران شناخته شده بود، ولی بیان ریاضی آن در سال ۱۸۳۵ توسط دانشمند فرانسوی گاسپار-گوستاو دو کوریولیس در ارتباط با نظریه چرخ‌های آبی منتشر شد. اوایل قرن بیستم، اصطلاح نیروی کوریولیس در ارتباط با هواشناسی مورد استفاده قرار گرفت.

تصویر به این صورت است که در چارچوب مرجع لخت (قسمت بالای تصویر)، توپ سیاه در خط مستقیمی حرکت می‌کند. اما ناظری که در چارچوب مرجع چرخان/غیرلخت (نقطه قرمز در قسمت پایین تصویر) قرار دارد، مشاهده می‌کند که جسم به دلیل حضور نیروهای کوریولیس و گریز از مرکز در این چارچوب، مسیر منحنی را دنبال می‌کند. در چارچوب مرجع لخت، حرکت جسم به صورت خط مستقیم است، اما در چارچوب مرجع چرخان، نیروهای مجازی مانند نیروی کوریولیس و نیروی گریز از مرکز باعث انحراف مسیر جسم می‌شوند و آن را به صورت منحنی مشاهده می‌کنند. این پدیده توضیح می‌دهد که چگونه نیروی کوریولیس بر حرکت اجسام در یک چارچوب مرجع چرخان تأثیر می‌گذارد و باعث انحراف مسیر آنها می‌شود.

قوانین حرکت نیوتون حرکت یک جسم در یک چارچوب مرجع لخت (غیر شتاب‌دار) را توصیف می‌کنند. وقتی این قوانین به چارچوب مرجع چرخان تبدیل می‌شوند، شتاب‌های کوریولیس و گریز از مرکز ظاهر می‌شوند. وقتی این نیروها به اجسام با جرم اعمال می‌شوند، نیروهای مربوطه متناسب با جرم‌های آن‌ها هستند. اندازه نیروی کوریولیس متناسب با نرخ چرخش است و اندازه نیروی گریز از مرکز متناسب با مربع نرخ چرخش است.

نیروی کوریولیس در جهتی عمود بر دو کمیت عمل می‌کند: سرعت زاویه‌ای چارچوب مرجع چرخان نسبت به چارچوب مرجع لخت و سرعت جسم نسبت به چارچوب مرجع چرخان. اندازه این نیرو متناسب با سرعت جسم در چارچوب مرجع چرخان است (به طور دقیق‌تر، به جزء سرعت که عمود بر محور چرخش است). نیروی گریز از مرکز به سمت بیرون در جهت شعاعی عمل می‌کند و متناسب با فاصله جسم از محور چارچوب مرجع چرخان است.

این نیروهای اضافی به عنوان نیروهای اینرسی، نیروهای مجازی یا نیروهای شبه‌ای شناخته می‌شوند. با معرفی این نیروهای مجازی به یک چارچوب مرجع چرخان، قوانین حرکت نیوتون می‌توانند به سیستم چرخان اعمال شوند به گونه‌ای که گویی یک سیستم لخت است؛ این نیروها به عنوان عوامل تصحیحی هستند که در یک سیستم غیر چرخان لازم نیستند.

در استفاده عمومی (غیر فنی) از اصطلاح "اثر کوریولیس"، چارچوب مرجع چرخان تقریباً همیشه زمین است. به دلیل چرخش زمین، ناظران زمینی برای تحلیل صحیح حرکت اجسام باید نیروی کوریولیس را در نظر بگیرند. زمین هر روز یک چرخش کامل انجام می‌دهد، بنابراین برای حرکت اجسام روزمره، نیروی کوریولیس محسوس نیست؛ تأثیرات آن فقط برای حرکات در فواصل بزرگ و مدت زمان طولانی مانند حرکت بزرگ‌مقیاس هوا در جو یا آب در اقیانوس، یا جایی که دقت بالا مهم است، مانند مسیر پرتاب گلوله‌ها و موشک‌ها قابل توجه است.

این حرکات به سطح زمین محدود می‌شوند، بنابراین تنها جزء افقی نیروی کوریولیس به طور کلی مهم است. این نیرو باعث می‌شود که اجسام متحرک روی سطح زمین در نیم‌کره شمالی به سمت راست (با توجه به جهت حرکت) و در نیم‌کره جنوبی به سمت چپ منحرف شوند. اثر انحراف افقی در نزدیکی قطب‌ها بزرگ‌تر است، زیرا نرخ چرخش مؤثر در اطراف محور عمودی محلی در آنجا بزرگ‌تر است و در استوا به صفر کاهش می‌یابد.

به جای جریان مستقیم از مناطق با فشار بالا به مناطق با فشار پایین، همان‌طور که در یک سیستم غیر چرخان رخ می‌دهد، بادها و جریان‌ها به سمت راست این جهت در شمال استوا (ساعت‌گرد) و به سمت چپ این جهت در جنوب آن (پادساعت‌گرد) تمایل دارند. این اثر مسئول چرخش و در نتیجه تشکیل سیکلون‌ها است.

+ نوشته شده در پنجشنبه هجدهم بهمن ۱۴۰۳ ساعت 1:39 توسط علی رضا نقش نیلچی  | 

اثر موسی

از ویکی پدیا، دانشنامه آزاد

(برگرفته از موسی افکت )

مستقیم (A) و معکوس (B) جلوه های موسی به تصویر کشیده شده است.

مستقیم (A) و معکوس (B) اثرات موسی.

در فیزیک ، اثر موسی پدیده تغییر شکل سطح یک مایع دیامغناطیسی توسط یک میدان مغناطیسی است . [ 1 ] [ 2 ] این اثر به نام شخصیت کتاب مقدس موسی نامگذاری شد که از عبور اسطوره ای از دریای سرخ در عهد عتیق الهام گرفته شده است . [ 2 ]

پیشرفت سریع در توسعه آهنرباهای نئودیمیم ، تامین میدان های مغناطیسی به اندازه c. 1 T ، آزمایش های ساده و ارزانی را در رابطه با اثر موسی و تجسم آن امکان پذیر می کند. [ 3 ] [ 4 ] [ 5 ] اعمال میدان های مغناطیسی در مرتبه قدر 0.5-1 T منجر به تشکیل "چاه" نزدیک به سطح با عمق ده ها میکرومتر می شود. در مقابل، سطح یک مایع پارامغناطیس توسط میدان مغناطیسی بالا می رود. این اثر را اثر موسی معکوس می نامند. [ 1 ] معمولاً به طور پنهان پیشنهاد می شود که شکل چاه از تأثیر متقابل نیروی مغناطیسی و گرانش ناشی می شود و شکل چاه نزدیک به سطح با معادله زیر به دست می آید:

{\displaystyle h(r)={\frac {\chi |\mathbf {B} (r)|^{2}}{2\rho g\mu _{0}}}}

که در آن χ و ρ به ترتیب حساسیت و چگالی مغناطیسی مایع هستند ، B میدان مغناطیسی، g شتاب گرانش ، و μ0 گذردهی مغناطیسی خلاء است . [ 6 ] در واقع، شکل چاه سطح نزدیک به کشش سطحی مایع نیز بستگی دارد. اثر موسی امکان به دام انداختن ذرات دیامغناطیس شناور و تشکیل الگوهای ریز را می دهد . [ 7 ] [ 8 ] اعمال میدان مغناطیسی ( B ≅0.5 T) روی سطح مشترک مایع/بخار دیا مغناطیسی ، حرکت اجسام دیامغناطیسی شناور و حباب های صابون را امکان پذیر می کند. [ 9 ]

https://en.wikipedia.org/wiki/Moses_effect

+ نوشته شده در دوشنبه هشتم بهمن ۱۴۰۳ ساعت 19:54 توسط علی رضا نقش نیلچی  | 

تپانچه مغناطیسی

از ویکی پدیا، دانشنامه آزاد

نباید با تفنگ ریلی یا مارپیچ اشتباه شود .

تپانچه مغناطیسی اصطلاحی است برای دستگاهی روی اژدر یا مین دریایی که هدف خود را با میدان مغناطیسی خود تشخیص می دهد و فیوز را برای انفجار فعال می کند. وسیله ای برای منفجر کردن اژدر یا مین در تماس با کشتی یا زیردریایی به عنوان تپانچه تماسی شناخته می شود .

یک تپانچه مغناطیسی روی یک مین به مین اجازه می دهد تا در نزدیکی یک هدف، به جای تماس واقعی، منفجر شود و به مین اجازه می دهد منطقه موثر بزرگتری را پوشش دهد.

یک تپانچه مغناطیسی روی یک اژدر به اژدر اجازه می دهد تا به جای برخورد با پهلوی کشتی، در زیر کشتی منفجر شود. از آنجایی که یک انفجار در زیر یک کشتی بین آب و کشتی قرار می گیرد، آسیب بسیار بیشتری به کشتی وارد می شود. انفجار کشتی را از آب خارج می کند و ممکن است کیل کشتی را بشکند و آن را به دو نیم کند. هر سوراخی که در اثر انفجار ایجاد شود در قسمت پایینی آن قرار می گیرد و باعث سیل بیشتر می شود.

یک تپانچه تماسی روی یک اژدر به اژدر نیاز دارد تا به پهلوی کشتی ضربه بزند. هر سوراخی که در اثر انفجار ایجاد شود به خط آب نزدیک‌تر می‌شود و سیل را کاهش می‌دهد. انفجار همچنین در هوا پخش می شود و آسیب را کاهش می دهد. اگر اژدر خیلی عمیق شلیک شود، اژدر به کشتی برخورد نمی کند. اگر کشتی دارای کف گرد یا شیب دار باشد، اژدر ممکن است به پایین نگاه کند و منفجر نشود.

تاریخچه

[ ویرایش ]

در جنگ جهانی اول ، یوبوت‌های آلمانی تا سال 1917 از تپانچه‌های مغناطیسی استفاده می‌کردند، اما تا سال 1918 بریتانیا نمونه‌هایی از این تپانچه‌ها را در حین نجات یوبوت SM UB-110 پیدا کرد . آنها ثابت کردند که مشکل ساز هستند و اغلب شلیک های زودهنگام داشتند. [ 1 ]

در طول جنگ جهانی دوم ، تپانچه های مغناطیسی اغلب زودتر از موعد منفجر می شدند یا اصلاً منفجر نمی شدند. دلیل آن این بود که خطوط مغناطیسی بیشتر افقی نزدیک به استوا هستند تا به سمت قطب ها. به عنوان مثال، تپانچه مغناطیسی US Mark 6 تنها یک بار در عرض جغرافیایی 41 درجه ( عرض جغرافیایی 60 درجه ژئومغناطیسی ) در خلیج ناراگانست طراحی و آزمایش شد ، اما عمدتاً در عرض های جغرافیایی استوایی استفاده می شد. [ 2 ] در خط استوا، قدرت سیگنال به تپانچه مغناطیسی Mark 6 تنها تقریباً نصف قدرت سیگنال مورد آزمایش Mark 6 بود. علاوه بر این، سرعت نسبی (یعنی زمانی که یک اژدر از پشت یا از جلوی کشتی شلیک می شود) علاوه بر این، ناگهانی سیگنال مغناطیسی را تغییر می دهد و در نتیجه تپانچه مغناطیسی زودتر از موعد فعال می شود یا اصلاً فعال نمی شود.

در نهایت، تپانچه مغناطیسی مارک 6 آمریکا با تپانچه های تماسی جایگزین شد (که در مورد اژدر زیردریایی مارک 14 آمریکا و اژدر کشتی مارک 15 نیز غیرقابل اعتماد بودن آنها ثابت شد).

برخی از کشتی ها برای کاهش سیگنال شناسایی شده توسط یک تپانچه مغناطیسی، تجهیزات ضد گاز را حمل می کنند.

در طول جنگ جهانی دوم، ژاپن از یک چاشنی مکانیکی از راه دور استفاده کرد تا عملکرد فیوزهای مجاورتی مغناطیسی را که توسط اژدرهای نیروی دریایی دیگر مانند آلمان و ایالات متحده استفاده می شد، تکرار کند. با استفاده از یک دستگاه مکانیکی، مشکلات ذاتی حسگر تأثیر مغناطیسی دور زد. این دستگاه که چاشنی تی-دستگاه نوع 1 نامیده می شود (، ایشیکی کیباکو سوچی T-Sōchi )، دارای یک بادبادک زیر آب متصل شده (凧) بود که پس از پرتاب از سر اژدر مستقر می شد، بدون اینکه خم شود. تنش این دستگاه شبیه یک اژدر بالدار کوچک بود. بادبادک به طور فیزیکی با بدنه یک کشتی سطح هدف برخورد می‌کند و در نتیجه آن را قطع می‌کند. یک مکانیسم عقب نشینی در اژدر، سستی ناگهانی در افسار را حس می‌کند و سرجنگی اژدر را منفجر می‌کند، که در آن نقطه زیر کیل کشتی هدف قرار می‌گیرد. [ 3 ]

همچنین ببینید

[ ویرایش ]

https://en.wikipedia.org/wiki/Magnetic_pistol

+ نوشته شده در دوشنبه هشتم بهمن ۱۴۰۳ ساعت 19:52 توسط علی رضا نقش نیلچی  | 

تئوری دینامو

از ویکی پدیا، دانشنامه آزاد

این مقاله در مورد یک نظریه پیشنهادی برای منبع میدان مغناطیسی یک سیاره است. برای توضیح عملکرد یک دینام مکانیکی، دینامو را ببینید .

تصویری از مکانیسم دینام که میدان مغناطیسی زمین را تولید می کند: جریان های همرفتی فلز سیال در هسته بیرونی زمین ، که توسط جریان گرما از هسته داخلی هدایت می شود و توسط نیروی کوریولیس به شکل غلتک ها سازماندهی می شود ، جریان های الکتریکی در گردش را تولید می کند که از میدان مغناطیسی پشتیبانی می کند. . [ 1 ]

در فیزیک ، نظریه دینام مکانیزمی را پیشنهاد می کند که توسط آن یک جرم آسمانی مانند زمین یا یک ستاره ، میدان مغناطیسی ایجاد می کند . نظریه دینام فرآیندی را توصیف می کند که از طریق آن یک سیال در حال چرخش، همرفت و رسانای الکتریکی می تواند یک میدان مغناطیسی را در مقیاس های زمانی نجومی حفظ کند. تصور می‌شود که یک دینام منبع میدان مغناطیسی زمین و میدان‌های مغناطیسی عطارد و سیارات جووین باشد .

تاریخچه نظریه

[ ویرایش ]

هنگامی که ویلیام گیلبرت کتاب مگنت را در سال 1600 منتشر کرد ، به این نتیجه رسید که زمین مغناطیسی است و اولین فرضیه را برای منشأ این مغناطیس ارائه کرد: مغناطیس دائمی مانند مغناطیس موجود در لودستون . در سال 1822، آندره ماری آمپر پیشنهاد کرد که جریان های داخلی مسئول مغناطیس زمین هستند. [ 2 ] در سال 1919، جوزف لارمور پیشنهاد کرد که یک دینام ممکن است این میدان را تولید کند. [ 3 ] [ 4 ] با این حال، حتی پس از اینکه او فرضیه خود را مطرح کرد، برخی از دانشمندان برجسته توضیحات جایگزین را ارائه کردند. پاتریک بلکت، برنده جایزه نوبل، مجموعه‌ای از آزمایش‌ها را انجام داد که به دنبال رابطه‌ای اساسی بین تکانه زاویه‌ای و گشتاور مغناطیسی بودند ، اما هیچ‌یک را نیافتند. [ 5 ] [ 6 ]

والتر ام. الساسر ، که به عنوان "پدر" نظریه دینام پذیرفته شده در حال حاضر به عنوان توضیحی از مغناطیس زمین در نظر گرفته می شود، پیشنهاد کرد که این میدان مغناطیسی ناشی از جریان های الکتریکی القا شده در هسته بیرونی سیال زمین است. او تاریخچه میدان مغناطیسی زمین را با پیشگامی در مطالعه جهت گیری مغناطیسی کانی ها در سنگ ها فاش کرد.

به منظور حفظ میدان مغناطیسی در برابر واپاشی اهمی (که برای میدان دوقطبی در 20000 سال رخ می دهد)، هسته خارجی باید همرفت باشد. همرفت احتمالاً ترکیبی از همرفت حرارتی و ترکیبی است . گوشته سرعت استخراج گرما از هسته را کنترل می کند. منابع حرارتی شامل انرژی گرانشی آزاد شده توسط فشرده سازی هسته، انرژی گرانشی آزاد شده توسط رد عناصر سبک (احتمالا گوگرد ، اکسیژن یا سیلیکون ) در مرز هسته داخلی در حین رشد، گرمای نهان تبلور در مرز هسته داخلی، و رادیواکتیویته پتاسیم , اورانیوم و توریم . [ 7 ]

در طلوع قرن بیست و یکم، مدل‌سازی عددی میدان مغناطیسی زمین با موفقیت نشان داده نشده است. مدل‌های اولیه بر تولید میدان از طریق همرفت در هسته سیال بیرونی سیاره متمرکز شده‌اند. زمانی که مدل دمای سطح هسته یکنواخت و ویسکوزیته فوق‌العاده بالایی را برای سیال هسته در نظر گرفت، می‌توان یک میدان قوی و زمین مانند را نشان داد. محاسباتی که مقادیر پارامترهای واقعی‌تری را در بر می‌گرفت، میدان‌های مغناطیسی کمتری شبیه زمین به دست می‌داد، اما نشان می‌داد که اصلاحات مدل [ کدام؟ ] ممکن است در نهایت منجر به یک مدل تحلیلی دقیق شود. تغییرات جزئی در دمای سطح هسته، در محدوده چند میلی‌کلوین، منجر به افزایش قابل‌توجهی در جریان همرفتی و تولید میدان‌های مغناطیسی واقعی‌تر می‌شود. [ 8 ] [ 9 ]

تعریف رسمی

[ ویرایش ]

تئوری دینامو فرآیندی را توصیف می کند که از طریق آن یک سیال در حال چرخش، همرفت و رسانای الکتریکی برای حفظ یک میدان مغناطیسی عمل می کند. این نظریه برای توضیح وجود میدان های مغناطیسی با عمر غیرعادی در اجسام اخترفیزیکی استفاده می شود. سیال رسانا در ژئودینامو آهن مایع در هسته بیرونی است و در دینام خورشیدی گاز یونیزه شده در تاکوکلین است . نظریه دینامو اجسام اخترفیزیکی از معادلات مغناطیسی هیدرودینامیکی برای بررسی این موضوع استفاده می کند که چگونه سیال می تواند به طور مداوم میدان مغناطیسی را بازسازی کند. [ 10 ]

زمانی اعتقاد بر این بود که دوقطبی که بیشتر میدان مغناطیسی زمین را در بر می گیرد و در امتداد محور چرخش به میزان 11.3 درجه ناهماهنگ است، ناشی از مغناطش دائمی مواد در زمین است. این بدان معنی است که نظریه دینام در ابتدا برای توضیح میدان مغناطیسی خورشید در رابطه آن با زمین استفاده می شد. با این حال، این فرضیه که در ابتدا توسط جوزف لارمور در سال 1919 ارائه شد ، به دلیل مطالعات گسترده تغییرات سکولار مغناطیسی ، دیرینه مغناطیس (شامل وارونگی قطبی )، لرزه شناسی و فراوانی عناصر منظومه شمسی اصلاح شده است. همچنین، کاربرد نظریه های کارل فردریش گاوس در مشاهدات مغناطیسی نشان داد که میدان مغناطیسی زمین منشأ داخلی دارد نه خارجی.

سه شرط لازم برای کارکرد دینام وجود دارد:

  • یک محیط سیال رسانای الکتریکی
  • انرژی جنبشی حاصل از چرخش سیاره
  • منبع انرژی داخلی برای به حرکت درآوردن حرکات همرفتی در سیال. [ 11 ]

در مورد زمین، میدان مغناطیسی توسط جابجایی آهن مایع در هسته بیرونی القا شده و دائماً حفظ می شود. لازمه القای میدان یک سیال دوار است. چرخش در هسته بیرونی توسط اثر کوریولیس ناشی از چرخش زمین تامین می شود. نیروی کوریولیس تمایل دارد تا حرکات سیال و جریان های الکتریکی را در ستون هایی سازماندهی کند (همچنین به ستون های تیلور مراجعه کنید ) که با محور چرخش هم تراز هستند. القاء یا تولید میدان مغناطیسی با معادله القایی توصیف می شود :{\displaystyle {\frac {\partial \mathbf {B} }{\partial t}}=\eta \nabla ^{2}\mathbf {B} +\nabla \times (\mathbf {u} \times \mathbf {B} )}

که در آن u سرعت، B میدان مغناطیسی، t زمان، و{\displaystyle \eta =1/(\sigma \mu )}انتشار مغناطیسی با است{\displaystyle \sigma }هدایت الکتریکی و{\displaystyle \mu } نفوذپذیری . نسبت جمله دوم در سمت راست به جمله اول عدد رینولدز مغناطیسی را نشان می‌دهد ، نسبتی بی‌بعد از فرارفت میدان مغناطیسی به انتشار.

گرمایش جزر و مدی که از دینام پشتیبانی می کند

[ ویرایش ]

نیروهای جزر و مدی بین اجرام آسمانی در حال چرخش باعث اصطکاک می شود که فضای داخلی آنها را گرم می کند. این به عنوان گرمایش جزر و مدی شناخته می شود و به حفظ فضای داخلی در حالت مایع کمک می کند. برای تولید دینام به یک فضای داخلی مایع که می تواند الکتریسیته را هدایت کند نیاز است. انسلادوس زحل و یو مشتری گرمای جزر و مدی کافی برای مایع شدن هسته داخلی خود دارند، اما ممکن است دینام ایجاد نکنند زیرا نمی توانند الکتریسیته را هدایت کنند. [ 12 ] [ 13 ] عطارد، علیرغم اندازه کوچکش، دارای میدان مغناطیسی است، زیرا دارای یک هسته مایع رسانا است که از ترکیب آهن و اصطکاک ناشی از مدار بسیار بیضوی آن ایجاد شده است. [ 14 ] بر اساس شواهد به دست آمده از سنگ های ماه مغناطیسی شده، به دلیل فاصله کوتاه تر آن از زمین که باعث گرمایش جزر و مدی می شود، نظریه ای وجود دارد که زمانی ماه دارای میدان مغناطیسی بوده است. [ 15 ] یک مدار و چرخش یک سیاره به ایجاد یک هسته مایع کمک می کند و انرژی جنبشی را تکمیل می کند که از عمل دینام پشتیبانی می کند.

نظریه دینام حرکتی

[ ویرایش ]

در تئوری دینام حرکتی، میدان سرعت به جای اینکه یک متغیر دینامیکی باشد، تجویز می‌شود : این مدل هیچ پیش‌بینی‌ای برای اعوجاج جریان در پاسخ به میدان مغناطیسی ندارد. این روش نمی‌تواند رفتار متغیر زمانی یک دینام پر هرج و مرج غیرخطی را ارائه دهد، اما می‌تواند برای مطالعه چگونگی تغییر قدرت میدان مغناطیسی با ساختار جریان و سرعت استفاده شود.

با استفاده از معادلات ماکسول به طور همزمان با کرل قانون اهم ، می‌توان معادله‌ای را که اساساً یک معادله ارزش ویژه خطی برای میدان‌های مغناطیسی ( B ) است استخراج کرد، که با فرض مستقل بودن میدان مغناطیسی از میدان سرعت می‌توان انجام داد. یک عدد به عدد رینولدز مغناطیسی بحرانی می رسد ، که در بالای آن قدرت جریان برای تقویت میدان مغناطیسی تحمیلی کافی است و در زیر آن میدان مغناطیسی از بین می رود.

اندازه گیری عملی دینام های ممکن

[ ویرایش ]

کاربردی ترین ویژگی تئوری دینام کینماتیکی این است که می توان از آن برای آزمایش اینکه آیا میدان سرعت قادر به عمل دینام است یا نه استفاده کرد. با اعمال تجربی یک میدان با سرعت معین به یک میدان مغناطیسی کوچک، می توان مشاهده کرد که آیا میدان مغناطیسی در پاسخ به جریان اعمال شده تمایل به رشد دارد (یا نه). اگر میدان مغناطیسی رشد کند، آنگاه سیستم یا قادر به عمل دینام است یا دینام است، اما اگر میدان مغناطیسی رشد نکند، آنگاه به سادگی به عنوان "نه دینام" نامیده می شود.

روش مشابهی به نام پارادایم غشایی ، روشی برای مشاهده سیاهچاله ها است که اجازه می دهد تا مواد نزدیک به سطح آنها به زبان تئوری دینام بیان شود.

شکست خود به خودی یک ابر تقارن توپولوژیکی

[ ویرایش ]

دینام سینماتیکی را می توان به عنوان پدیده شکست خود به خودی ابرتقارن توپولوژیکی معادله دیفرانسیل تصادفی مرتبط با جریان ماده زمینه مشاهده کرد. [ 16 ] در نظریه فوق متقارن تصادفی ، این ابرتقارن یک ویژگی ذاتی تمام معادلات دیفرانسیل تصادفی است ، تفسیر آن این است که فضای فاز مدل، تداوم را از طریق جریان‌های زمانی پیوسته حفظ می‌کند. هنگامی که تداوم آن جریان به طور خود به خود از بین می رود، سیستم در حالت تصادفی هرج و مرج قطعی قرار می گیرد . [ 17 ] به عبارت دیگر، دینام کینماتیکی به دلیل جریان آشفته در ماده پس زمینه ایجاد می شود.

تئوری دینام غیرخطی

[ ویرایش ]

تقریب سینماتیک زمانی نامعتبر می شود که میدان مغناطیسی به اندازه کافی قوی شود که بر حرکات سیال تأثیر بگذارد. در این صورت میدان سرعت تحت تأثیر نیروی لورنتس قرار می گیرد و بنابراین معادله القایی دیگر در میدان مغناطیسی خطی نیست. در بیشتر موارد این منجر به خاموش شدن دامنه دینام می شود. این دینام ها گاهی اوقات به عنوان دینام های هیدرومغناطیسی نیز شناخته می شوند . [ 18 ] تقریباً همه دینام ها در اخترفیزیک و ژئوفیزیک دینام های هیدرومغناطیسی هستند.

ایده اصلی این تئوری این است که هر میدان مغناطیسی کوچکی که در هسته بیرونی وجود داشته باشد، به دلیل نیروی لورنتس، جریان هایی را در سیال متحرک آنجا ایجاد می کند. این جریان ها به دلیل قانون آمپر میدان مغناطیسی بیشتری ایجاد می کنند . با حرکت سیال، جریان ها به گونه ای منتقل می شوند که میدان مغناطیسی قوی تر می شود (تا زمانی که {\displaystyle \;\mathbf {u} \cdot (\mathbf {J} \times \mathbf {B} )\;}منفی است [ 19 ] ). بنابراین یک میدان مغناطیسی "دانه" می تواند قوی تر و قوی تر شود تا زمانی که به مقداری برسد که مربوط به نیروهای غیر مغناطیسی موجود است.

مدل‌های عددی برای شبیه‌سازی دینام‌های کاملاً غیرخطی استفاده می‌شوند. از معادلات زیر استفاده می شود:

  • معادله القایی، ارائه شده در بالا.
  • معادلات ماکسول برای میدان الکتریکی ناچیز:{\displaystyle {\begin{aligned}&\nabla \cdot \mathbf {B} =0\\[1ex]&\nabla \times \mathbf {B} =\mu _{0}\mathbf {J} \end {تراز شده}}}
  • معادله پیوستگی برای بقای جرم ، که اغلب از تقریب بوسینسک برای آن استفاده می شود:{\displaystyle \nabla \cdot \mathbf {u} =0،}
  • معادله ناویر-استوکس برای بقای تکانه ، دوباره با همان تقریب، با نیروی مغناطیسی و نیروی گرانش به عنوان نیروهای خارجی:{\displaystyle {\frac {D\mathbf {u} }{Dt}}=-{\frac {1}{\rho _{0}}}\nabla p+\nu \nabla ^{2}\mathbf {u } +\rho '\mathbf {g} +2{\boldsymbol {\Omega }}\times \mathbf {u} +{\boldsymbol {\Omega }}\times {\boldsymbol {\Omega }}\times \mathbf {R} +{\frac {1}{\rho _{0}}}\mathbf {J} \times \mathbf {B} ~،}که{\displaystyle \,\nu \,}ویسکوزیته سینماتیکی است ،{\displaystyle \,\rho _{0}\,}میانگین چگالی است و{\displaystyle \rho '}اغتشاش چگالی نسبی است که شناوری را فراهم می کند (برای همرفت حرارتی{\displaystyle \;\rho '=\alpha \Delta T\;}که{\displaystyle \,\alpha \,}ضریب انبساط حرارتی است ){\displaystyle \,\Omega \,}سرعت چرخش زمین است و{\displaystyle \,\mathbf {J} \,}چگالی جریان الکتریکی است.
  • یک معادله انتقال، معمولاً گرما (گاهی اوقات غلظت عنصر سبک):{\displaystyle {\frac {\,\partial T\,}{\partial t}}=\kappa \nabla ^{2}T+\varepsilon }جایی که T دما است،ρ{\displaystyle \;\kappa =k/\rho c_{p}\;}انتشار حرارتی با k هدایت حرارتی است،{\displaystyle \,c_{p}\,}ظرفیت گرمایی و{\displaystyle \rho }تراکم، وε{\displaystyle \varepsilon }یک منبع حرارتی اختیاری است. اغلب فشار، فشار دینامیکی است که فشار هیدرواستاتیک و پتانسیل مرکزگرا حذف می شود.

سپس این معادلات غیربعدی می شوند و پارامترهای غیر بعدی را معرفی می کنند.{\displaystyle R_{\mathsf {a}}={\frac {\,g\alpha TD^{3}\,}{\nu \kappa }}\;,\quad E={\frac {\nu } {\,\Omega D^{2}\,}}\;,\quad P_{\mathsf {r}}={\frac {\,\nu \,}{\kappa }}\;,\quad P_{\mathsf {m}}={\frac {\,\nu \,}{\eta }}}که در آن R a عدد ریلی ، E عدد اکمن ، Pr و P m عدد پراندتل و مغناطیسی پراندتل است . مقیاس میدان مغناطیسی اغلب در واحدهای عددی الساسر است{\displaystyle B=(\rho \Omega /\sigma )^{1/2}.}

تبدیل انرژی بین انرژی مغناطیسی و سینماتیکی

[ ویرایش ]

حاصل ضرب اسکالر شکل فوق معادله ناویر-استوکس با{\displaystyle \;\rho _{0}\mathbf {u} \;}نرخ افزایش چگالی انرژی جنبشی را نشان می دهد،{\displaystyle \;{\tfrac {1}{2}}\rho _{0}u^{2}c\;}، در سمت چپ. آخرین عبارت در سمت راست پس از آن است {\displaystyle \;\mathbf {u} \cdot (\mathbf {J} \times \mathbf {B} )\;}سهم محلی در انرژی جنبشی ناشی از نیروی لورنتس .

حاصل ضرب اسکالر معادله القایی با{\textstyle {\tfrac {1}{\mu _{0}}}\mathbf {B} }نرخ افزایش چگالی انرژی مغناطیسی را نشان می دهد،{\displaystyle \;{\tfrac {1}{2}}\mu _{0}B^{2}\;}، در سمت چپ. آخرین عبارت در سمت راست پس از آن است{\textstyle {\tfrac {1}{\mu _{0}}}\mathbf {B} \cdot \left(\nabla \times \left(\mathbf {u} \times \mathbf {B} \right) \راست)\;.}از آنجایی که معادله یکپارچه حجمی است، این عبارت معادل یک ترم مرزی است (و با استفاده مضاعف از هویت ضرب سه گانه اسکالر )-{\textstyle \;-\mathbf {u} \cdot \left({\tfrac {1}{\mu _{0}}}\left(\nabla \times \mathbf {B} \right)\times \mathbf {B} \right)=-\mathbf {u} \cdot \left(\mathbf {J} \times \mathbf {B} \راست)~}(جایی که یکی از معادلات ماکسول استفاده شده است). این سهم محلی در انرژی مغناطیسی ناشی از حرکت سیال است.

بنابراین اصطلاح{\displaystyle \;-\mathbf {u} \cdot (\mathbf {J} \times \mathbf {B} )\;}سرعت تبدیل انرژی جنبشی به انرژی مغناطیسی است. حداقل در بخشی از حجم باید غیرمنفی باشد تا دینام میدان مغناطیسی تولید کند. [ 19 ]

از نمودار بالا، مشخص نیست که چرا این عبارت باید مثبت باشد. یک استدلال ساده می تواند بر اساس در نظر گرفتن اثرات خالص باشد. برای ایجاد میدان مغناطیسی، جریان الکتریکی خالص باید به دور محور چرخش سیاره بپیچد. در آن صورت، برای مثبت بودن عبارت، جریان خالص ماده رسانا باید به سمت محور چرخش باشد. نمودار فقط یک جریان خالص از قطب ها به استوا را نشان می دهد. با این حال، حفظ جرم نیاز به یک جریان اضافی از استوا به سمت قطب ها دارد. اگر آن جریان در امتداد محور چرخش بود، به این معنی است که گردش با جریانی از جریان‌های نشان‌داده‌شده به سمت محور چرخش تکمیل می‌شود و اثر مورد نظر را ایجاد می‌کند.

ترتیب قدر میدان مغناطیسی ایجاد شده توسط دینام زمین

[ ویرایش ]

فرمول فوق برای سرعت تبدیل انرژی جنبشی به انرژی مغناطیسی، معادل نرخ کاری است که توسط نیرویی از{\displaystyle \;\mathbf {J} \times \mathbf {B} \;}روی ماده هسته بیرونی که سرعت آن است {\displaystyle \mathbf {u} }. این کار نتیجه نیروهای غیر مغناطیسی است که بر سیال وارد می شود.

از میان آنها، نیروی گرانش و نیروی گریز از مرکز محافظه کار هستند و بنابراین هیچ سهمی در حرکت سیال در حلقه های بسته ندارند. عدد اکمن (تعریف شده در بالا)، که نسبت بین دو نیروی باقیمانده، یعنی ویسکوزیته و نیروی کوریولیس است، در داخل هسته خارجی زمین بسیار کم است، زیرا ویسکوزیته آن کم است (1.2-1.5×10-2 پاسکال -ثانیه [ 20 ] ] ) به دلیل نقدینگی آن.

بنابراین سهم اصلی میانگین زمان در کار از نیروی کوریولیس است که اندازه آن است{\displaystyle \;-2\rho \,\mathbf {\Omega } \times \mathbf {u} \;,}هر چند این مقدار و{\displaystyle \mathbf {J} \times \mathbf {B} }فقط به طور غیرمستقیم مرتبط هستند و به طور کلی به صورت محلی برابر نیستند (بنابراین آنها بر یکدیگر تأثیر می گذارند اما نه در یک مکان و زمان).

چگالی جریان J خود نتیجه میدان مغناطیسی طبق قانون اهم است . باز هم به دلیل حرکت ماده و جریان جریان، این میدان لزوماً در همان مکان و زمان نیست. با این حال، هنوز هم می توان از این روابط برای استنباط مرتبه های بزرگی از مقادیر مورد نظر استفاده کرد.

از نظر ترتیب بزرگی،{\displaystyle \;J\,B\sim \rho \,\Omega \,u\;}و{\displaystyle \;J\sim \sigma uB\;}، دادن،{\displaystyle \;\sigma \,u\,B^{2}\sim \rho \,\Omega \,u\;,}یا:{\displaystyle B\sim {\sqrt {{\frac {\,\rho \,\Omega \,}{\sigma }}\;}}}

نسبت دقیق بین هر دو طرف جذر عدد الساسر است .

توجه داشته باشید که جهت میدان مغناطیسی را نمی توان از این تقریب (حداقل نه علامت آن) استنتاج کرد زیرا مربع به نظر می رسد، و در واقع، گاهی اوقات معکوس می شود ، اگرچه به طور کلی بر روی یک محور مشابه با محور قرار دارد.{\displaystyle \mathbf {\Omega } }.

برای هسته بیرونی زمین، ρ تقریباً 10 4 کیلوگرم بر متر مکعب است ، [ 20 ] Ω = 2 π / روز = 7.3×10-5 / ثانیه و σ تقریباً 10 7 Ω -1 m -1 است . [ 21 ] این تسلا 2.7×10-4 است .

میدان مغناطیسی یک دوقطبی مغناطیسی از نظر فاصله وابستگی مکعبی معکوس دارد، بنابراین ترتیب قدر آن در سطح زمین را می‌توان با ضرب نتیجه بالا در ( R هسته بیرونی ⁄ R زمین ) 3 = ( 2890 ⁄ 6370 ) 3 = تقریب زد. 0.093، 2.5×10-5 تسلا ، نه چندان دور از مقدار اندازه گیری شده 3×10-5 تسلا در خط استوا .

مدل های عددی

[ ویرایش ]

یک نمایش بصری از مدل گلاتزمایر قبل از معکوس دوقطبی

به طور کلی، مدل‌های ژئودینامو برای تولید میدان‌های مغناطیسی مطابق با داده‌های مشاهده‌شده با توجه به شرایط و معادلات خاصی که در بخش‌های بالا ذکر شد، تلاش می‌کنند. اجرای موفقیت آمیز معادلات مغناطیسی هیدرودینامیکی از اهمیت ویژه ای برخوردار بود زیرا آنها مدل های دینام را به سمت خود سازگاری سوق دادند. اگرچه مدل‌های ژئودینامو بسیار رایج هستند، مدل‌های دینام لزوماً محدود به ژئودینامو نیستند. مدل های دینام خورشیدی و عمومی نیز مورد توجه هستند. مطالعه مدل‌های دینام در زمینه ژئوفیزیک کاربرد دارد، زیرا انجام این کار می‌تواند تشخیص دهد که چگونه مکانیسم‌های مختلف میدان‌های مغناطیسی مانند آنچه توسط اجسام اخترفیزیکی مانند زمین تولید می‌شوند را تشکیل می‌دهند و چگونه باعث می‌شوند که میدان‌های مغناطیسی ویژگی‌های خاصی مانند وارونگی قطب‌ها را نشان دهند.

معادلات مورد استفاده در مدل های عددی دینام بسیار پیچیده است. برای دهه‌ها، نظریه‌پردازان به مدل‌های دینام سینماتیک دو بعدی که در بالا توضیح داده شد، محدود می‌شدند ، که در آن‌ها حرکت سیال از قبل انتخاب می‌شد و تأثیر آن بر میدان مغناطیسی محاسبه می‌شد. پیشرفت از مدل‌های سه‌بعدی دینام خطی به غیرخطی تا حد زیادی با جستجوی راه‌حل‌های معادلات مغناطیسی هیدرودینامیکی که نیاز به بسیاری از مفروضات ساخته شده در مدل‌های سینماتیکی را از بین می‌برد و امکان خودسازگاری را فراهم می‌کند، مانع شد.

یک نمایش بصری از مدل گلاتزمایر در طول معکوس دوقطبی

اولین مدل‌های دینام خودسازگار ، مدل‌هایی که هم حرکت سیال و هم میدان مغناطیسی را تعیین می‌کنند، توسط دو گروه در سال 1995 توسعه یافتند، یکی در ژاپن [ 22 ] و دیگری در ایالات متحده. [ 23 ] [ 24 ] دومی به عنوان یک مدل با توجه به ژئودینامو ساخته شد و مورد توجه قابل توجهی قرار گرفت زیرا با موفقیت برخی از ویژگی های میدان زمین را بازتولید کرد. [ 19 ] به دنبال این پیشرفت، رشد زیادی در توسعه مدل‌های دینام سه بعدی معقول وجود داشت. [ 19 ]

اگرچه بسیاری از مدل‌های خودسازگار در حال حاضر وجود دارد، اما تفاوت‌های قابل توجهی بین مدل‌ها وجود دارد، هم در نتایجی که تولید می‌کنند و هم در روش توسعه آن‌ها. [ 19 ] با توجه به پیچیدگی توسعه یک مدل ژئودینامو، مکان‌های زیادی وجود دارد که می‌تواند در آن‌ها مغایرت‌ها رخ دهد، مانند مفروضات مربوط به مکانیسم‌هایی که انرژی را برای دینام فراهم می‌کنند، هنگام انتخاب مقادیر برای پارامترهای مورد استفاده در معادلات، یا هنگام عادی‌سازی معادلات. با وجود تفاوت‌های زیادی که ممکن است رخ دهد، اکثر مدل‌ها ویژگی‌های مشترکی مانند دوقطبی‌های محوری واضح دارند. در بسیاری از این مدل‌ها، پدیده‌هایی مانند تغییرات سکولار و وارونگی قطبیت ژئومغناطیسی نیز با موفقیت بازسازی شده‌اند. [ 19 ]

مشاهدات

[ ویرایش ]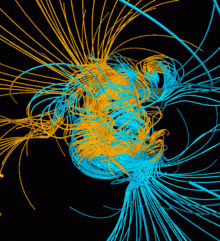

یک نمایش بصری از مدل گلاتزمایر پس از معکوس دوقطبی

مشاهدات زیادی را می توان از مدل های دینام انجام داد. می توان از مدل ها برای تخمین چگونگی تغییر میدان های مغناطیسی با زمان استفاده کرد و می تواند با داده های دیرینه مغناطیسی مشاهده شده مقایسه شود تا شباهت هایی بین مدل و زمین پیدا شود. با این حال، به دلیل عدم قطعیت مشاهدات دیرینه مغناطیسی، مقایسه ها ممکن است کاملا معتبر یا مفید نباشند. [ 19 ] مدل‌های ژئودینامو ساده شده روابط بین عدد دینام (تعیین شده توسط واریانس در نرخ‌های چرخشی در هسته خارجی و همرفت نامتقارن آینه‌ای (مثلا زمانی که همرفت به نفع یک جهت در شمال و دیگری در جنوب باشد)) و قطب مغناطیسی نشان داده‌اند. واژگونی ها و همچنین شباهت هایی بین ژئودینامو و دینام خورشید یافت شد. [ 19 ] در بسیاری از مدل‌ها، به نظر می‌رسد که میدان‌های مغناطیسی دارای قدرهای تصادفی هستند که از روند عادی پیروی می‌کنند که میانگین آن صفر است. [ 19 ] علاوه بر این مشاهدات، مشاهدات کلی در مورد مکانیسم‌های نیروبخش ژئودینامو را می‌توان بر اساس میزان دقت مدل منعکس‌کننده داده‌های واقعی جمع‌آوری‌شده از زمین انجام داد.

مدلسازی مدرن

[ ویرایش ]

پیچیدگی مدل‌سازی دینام به قدری زیاد است که مدل‌های ژئودینامو توسط قدرت فعلی ابررایانه‌ها محدود می‌شوند ، به ویژه به این دلیل که محاسبه عدد اکمن و ریلی هسته بیرونی بسیار دشوار است و به تعداد زیادی محاسبات نیاز دارد.

پیشرفت‌های زیادی در مدل‌سازی دینام از زمان پیشرفت خودسازگار در سال 1995 ارائه شده است. یک پیشنهاد در مطالعه تغییرات پیچیده میدان مغناطیسی، استفاده از روش‌های طیفی برای ساده‌سازی محاسبات است. [ 25 ] در نهایت، تا زمانی که پیشرفت‌های قابل‌توجهی در قدرت کامپیوتر ایجاد نشود، روش‌های محاسبه مدل‌های دینام واقعی باید کارآمدتر شوند، بنابراین ایجاد بهبود در روش‌های محاسبه مدل برای پیشرفت مدل‌سازی دینام عددی از اهمیت بالایی برخوردار است.

https://en.wikipedia.org/wiki/Dynamo_theory

+ نوشته شده در دوشنبه هشتم بهمن ۱۴۰۳ ساعت 19:50 توسط علی رضا نقش نیلچی  | 

مارپیچ مغناطیسی

از ویکی پدیا، دانشنامه آزاد

لحن یا سبک این مقاله ممکن است منعکس کننده لحن دایره المعارفی مورد استفاده در ویکی پدیا نباشد . راهنمای ویکی‌پدیا برای نوشتن مقالات بهتر برای پیشنهادات را ببینید. ( دسامبر 2022 ) ( با نحوه و زمان حذف این پیام آشنا شوید )

در فیزیک پلاسما ، مارپیچ مغناطیسی معیاری برای سنجش پیوند، پیچش و پیچش میدان مغناطیسی است . [ 1 ] [ 2 ]

مارپیچ مغناطیسی یک مفهوم مفید در تجزیه و تحلیل سیستم هایی با مقاومت بسیار کم مانند سیستم های اخترفیزیکی است. هنگامی که مقاومت کم است، مارپیچ مغناطیسی در بازه های زمانی طولانی تر حفظ می شود، تا به یک تقریب خوب. دینامیک مارپیچ مغناطیسی به ویژه در تجزیه و تحلیل شعله های خورشیدی و پرتاب جرم تاج مهم است . [ 3 ] مارپیچ مغناطیسی در دینامیک باد خورشیدی مرتبط است . [ 4 ] حفاظت از آن در فرآیندهای دینام قابل توجه است ، و همچنین نقشی در تحقیقات همجوشی ، مانند آزمایش‌های پینچ میدانی معکوس دارد. [ 5 ] [ 6 ] [ 7 ] [ 8 ] [ 9 ]

هنگامی که یک میدان مغناطیسی دارای مارپیچ مغناطیسی باشد، تمایل دارد ساختارهای مقیاس بزرگ را از ساختارهای کوچک تشکیل دهد. [ 10 ] این فرآیند را می توان به عنوان یک انتقال معکوس در فضای فوریه نام برد . این خاصیت افزایش مقیاس سازه ها مارپیچ مغناطیسی را در سه بعدی خاص می کند، زیرا سایر جریان های سه بعدی در مکانیک سیالات معمولی برعکس هستند، متلاطم هستند و تمایل به "تخریب" سازه دارند، به این معنا که گرداب های بزرگ مقیاس به قطعات کوچکتر تقسیم می شوند ، تا زمانی که از طریق اثرات چسبناک به گرما پراکنده شوند. از طریق یک فرآیند موازی اما معکوس، برعکس برای گردابه‌های مغناطیسی اتفاق می‌افتد، جایی که ساختارهای مارپیچی کوچک با مارپیچ مغناطیسی غیرصفر ترکیب شده و میدان‌های مغناطیسی در مقیاس بزرگ را تشکیل می‌دهند. این در دینامیک ورق جریان هلیوسفر ، [ 11 ] یک ساختار مغناطیسی بزرگ در منظومه شمسی قابل مشاهده است .

تعریف ریاضی

[ ویرایش ]

به طور کلی، مارپیچ بودن {\displaystyle H^{\mathbf {f} }}یک میدان برداری صاف {\displaystyle \mathbf {f} }محدود به یک حجم{\displaystyle V}معیار استاندارد میزان پیچیدگی و پیچیدن خطوط میدان به دور یکدیگر است. [ 12 ] [ 2 ] به عنوان انتگرال حجم تعریف می شود{\displaystyle V}حاصل ضرب اسکالر از{\displaystyle \mathbf {f} }و پیچش آن ،{\displaystyle \nabla \times {\mathbf {f} }}:

{\displaystyle H^{\mathbf {f} }=\int _{V}{\mathbf {f} }\cdot \left(\nabla \times {\mathbf {f} }\right)\ dV.}

مارپیچ مغناطیسی

[ ویرایش ]

مارپیچ مغناطیسی {\displaystyle H^{\mathbf {M} }}مارپیچ بودن پتانسیل بردار مغناطیسی است {\displaystyle {\mathbf {A} }}که{\displaystyle \nabla \times {\mathbf {A} }={\mathbf {B} }}میدان مغناطیسی مرتبط محدود به یک حجم است{\displaystyle V}. سپس مارپیچ مغناطیسی را می توان به صورت [ 5 ] بیان کرد.

{\displaystyle H^{\mathbf {M} }=\int _{V}{\mathbf {A} }\cdot {\mathbf {B} }\ dV.}

از آنجایی که پتانسیل بردار مغناطیسی ثابت سنج نیست ، مارپیچ مغناطیسی نیز به طور کلی ثابت نیست. در نتیجه، مارپیچ مغناطیسی یک سیستم فیزیکی را نمی توان به طور مستقیم اندازه گیری کرد. در شرایط معین و در مفروضات معین، می‌توان مارپیچ فعلی یک سیستم را اندازه‌گیری کرد و در صورت تحقق شرایط بیشتر و تحت فرضیات بیشتر، مارپیچ مغناطیسی را از آن استنتاج کرد. [ 13 ]

مارپیچ مغناطیسی دارای واحدهای شار مغناطیسی مربع است: Wb 2 ( مربع وبر ) در واحدهای SI و Mx 2 ( معادل ماکسولز ) در واحدهای گاوسی . [ 14 ]

مارپیچ فعلی

[ ویرایش ]

مارپیچ فعلی یا مارپیچ بودن{\displaystyle M^{\mathbf {J} }}از میدان مغناطیسی {\displaystyle \mathbf {B} }محدود به یک حجم{\displaystyle V}، می تواند به صورت بیان شود

{\displaystyle H^{\mathbf {J} }=\int _{V}{\mathbf {B} }\cdot {\mathbf {J} }\ dV}

که{\displaystyle {\mathbf {J} }=\nabla \times {\mathbf {B} }}

چگالی جریان است . [ 15 ] برخلاف مارپیچ مغناطیسی، مارپیچ جریان یک متغیر ثابت ایده‌آل نیست (حتی زمانی که مقاومت الکتریکی صفر باشد ، حفظ نمی‌شود ).

ملاحظات را اندازه گیری کنید

[ ویرایش ]

مارپیچ مغناطیسی یک کمیت وابسته به سنج است، زیرا{\displaystyle \mathbf {A} }می توان با افزودن یک گرادیان به آن ( انتخاب سنج ) دوباره تعریف کرد. با این حال، برای رسانایی کامل مرزها یا سیستم های تناوبی بدون شار مغناطیسی خالص، مارپیچ مغناطیسی موجود در کل دامنه ثابت است، [ 15 ] ، یعنی مستقل از انتخاب گیج. یک مارپیچ نسبی ثابت سنج برای احجام با شار مغناطیسی غیر صفر در سطوح مرزی آنها تعریف شده است. [ 11 ]

تفسیر توپولوژیکی

[ ویرایش ]

نام "مارپیچ" به این دلیل است که مسیر حرکت یک ذره سیال در یک سیال با سرعت است{\displaystyle {\boldsymbol {v}}}و گردابی {\displaystyle {\boldsymbol {\omega }}=\nabla \times {\boldsymbol {v}}}در مناطقی که مارپیچ جنبشی دارد ، یک مارپیچ تشکیل می دهد {\displaystyle \textstyle H^{K}=\int \mathbf {v} \cdot {\boldsymbol {\omega }}\neq 0}. چه زمانی {\displaystyle \textstyle H^{K}>0}، مارپیچ به دست آمده راست دست است و که{\displaystyle \textstyle H^{K}<0}چپ دست است این رفتار بسیار شبیه به آنچه در مورد خطوط میدان مغناطیسی یافت می شود.

مناطقی که مارپیچ مغناطیسی در آنها صفر نیست همچنین می توانند دارای انواع دیگر ساختارهای مغناطیسی مانند خطوط میدان مغناطیسی مارپیچ باشند. مارپیچ مغناطیسی تعمیم مداوم مفهوم توپولوژیکی پیوند عدد به کمیت های دیفرانسیل مورد نیاز برای توصیف میدان مغناطیسی است. [ 11 ] در جایی که اعداد پیوند دهنده تعداد دفعاتی که منحنی ها به هم مرتبط هستند را توصیف می کند، مارپیچ مغناطیسی تعداد خطوط میدان مغناطیسی را توصیف می کند که به هم پیوسته اند. [ 5 ]

نمونه هایی از منحنی ها با مقادیر متغیر پیچ خوردگی و پیچش . مارپیچ مغناطیسی مجموع این دو کمیت را برای خطوط میدان مغناطیسی اندازه گیری می کند. مجموع تحت تمام تبدیل هایی که منحنی ها قطع یا به هم متصل نمی شوند، حفظ می شود.

مارپیچ مغناطیسی متناسب با مجموع کمیت های توپولوژیکی است که برای خطوط میدان مغناطیسی می پیچند و می پیچند . پیچش چرخش لوله شار حول محور آن است و پیچش چرخش خود محور لوله شار است. تبدیل های توپولوژیکی می توانند پیچ ​​و تاب اعداد را تغییر دهند، اما مجموع آنها را حفظ کنند. از آنجایی که لوله های شار مغناطیسی (مجموعه حلقه های خط میدان مغناطیسی بسته) تمایل به مقاومت در برابر عبور از یکدیگر در سیالات مغناطیسی هیدرودینامیکی دارند، مارپیچ مغناطیسی به خوبی حفظ می شود.

مانند بسیاری از کمیت ها در الکترومغناطیس، مارپیچ مغناطیسی ارتباط نزدیکی با مارپیچ مکانیکی سیال دارد ، کمیت مربوط به خطوط جریان سیال و دینامیک آنها به هم مرتبط است. [ 10 ] [ 16 ]

خواص

[ ویرایش ]

عدم تغییر درجه دوم ایده آل

[ ویرایش ]

در اواخر دهه 1950، Lodewijk Woltjer و Walter M. Elsässer به طور مستقل تغییر ناپذیری ایده آل مارپیچ مغناطیسی، [ 17 ] [ 18 ] را کشف کردند ، یعنی بقای آن در زمانی که مقاومت صفر است. اثبات Woltjer، معتبر برای یک سیستم بسته، در موارد زیر تکرار می شود:

در مگنتوهیدرودینامیک ایده آل ، تکامل زمانی میدان مغناطیسی و پتانسیل بردار مغناطیسی را می توان با استفاده از معادله القایی بیان کرد .

{\displaystyle {\frac {\partial {\mathbf {B} }}{\partial t}}=\nabla \times ({\mathbf {v} }\times {\mathbf {B} }),\quad { \frac {\partial {\mathbf {A} }}{\partial t}}={\mathbf {v} }\times {\mathbf {B} }+\nabla \Phi,}

به ترتیب، در که{\displaystyle \nabla \Phi }یک پتانسیل اسکالر داده شده توسط شرط سنج است (به § ملاحظات گیج مراجعه کنید ). انتخاب گیج به گونه ای که پتانسیل اسکالر ناپدید شود،{\displaystyle \nabla \Phi =\mathbf {0} }، تکامل زمانی مارپیچ مغناطیسی در یک حجم{\displaystyle V}توسط:

{\displaystyle {\begin{aligned}{\frac {\partial H^{\mathbf {M} }}{\partial t}}&=\int _{V}\left({\frac {\partial {\ mathbf {A} }}{\ t جزئی}}\cdot {\mathbf {B} }+{\mathbf {A} }\cdot {\frac {\partial {\mathbf {B}}}{\partial t}}\right)dV\\&=\int _{V}({\mathbf {v} }\times {\mathbf {B} })\ cdot {\mathbf {B} }\ dV+\int _{V}{\mathbf {A} }\cdot \left(\nabla \times {\frac {\partial {\mathbf {A} }}{\partial t}}\right)dV.\end{aligned}}}

حاصل ضرب نقطه در انتگرال جمله اول صفر است{\displaystyle {\mathbf {B} }}متعامد به ضرب متقاطع است{\displaystyle {\mathbf {v} }\times {\mathbf {B} }}، و عبارت دوم را می توان با بخش هایی برای دادن یکپارچه کرد

{\displaystyle {\frac {\partial H^{\mathbf {M} }}{\partial t}}=\int _{V}\left(\nabla \times {\mathbf {A} }\right)\ cdot {\frac {\partial {\mathbf {A} }}{\partial t}}\ dV+\int _{\partial V}\left({\mathbf {A} }\times {\frac {\partial {\mathbf {A} }}{\partial t}}\right)\cdot d\mathbf {S} }

که در آن جمله دوم یک سطح انتگرال بر روی سطح مرزی است{\displaystyle \partial V}از سیستم بسته حاصل ضرب نقطه در انتگرال جمله اول صفر است زیرا{\displaystyle \nabla \times {\mathbf {A} }={\mathbf {B} }}متعامد به است.{\displaystyle \partial {\mathbf {A} }/\partial t.}عبارت دوم نیز ناپدید می شود زیرا حرکات در داخل سیستم بسته نمی توانند بر پتانسیل برداری خارج تأثیر بگذارند، به طوری که در سطح مرزی{\displaystyle \partial {\mathbf {A} }/\partial t=\mathbf {0} }از آنجایی که پتانسیل بردار مغناطیسی یک تابع پیوسته است. بنابراین،

{\displaystyle {\frac {\partial H^{\mathbf {M} }}{\partial t}}=0,}

و مارپیچ مغناطیسی به طور ایده آل حفظ می شود. در تمام شرایطی که مارپیچ مغناطیسی ثابت است، مارپیچ مغناطیسی به طور ایده آل بدون نیاز به انتخاب سنج خاص حفظ می شود.{\displaystyle \nabla \Phi =\mathbf {0}.}

مارپیچ مغناطیسی در تقریبی خوب حتی با یک مقاومت کوچک اما محدود حفظ می شود، در این صورت اتصال مجدد مغناطیسی انرژی را تلف می کند . [ 11 ] [ 5 ]

انتقال معکوس

[ ویرایش ]

ساختارهای مارپیچ در مقیاس کوچک تمایل به تشکیل ساختارهای مغناطیسی بزرگتر و بزرگتر دارند. این را می توان انتقال معکوس در فضای فوریه نامید ، برخلاف آبشار انرژی (مستقیم) در جریان های هیدرودینامیکی آشفته سه بعدی. امکان چنین انتقال معکوس برای اولین بار توسط اوریل فریش و همکاران [ 10 ] پیشنهاد شد و از طریق بسیاری از آزمایشات عددی تأیید شده است. [ 19 ] [ 20 ] [ 21 ] [ 22 ] [ 23 ] [ 24 ] در نتیجه، وجود مارپیچ مغناطیسی امکانی برای توضیح وجود و پایداری ساختارهای مغناطیسی در مقیاس بزرگ در جهان است.

استدلالی برای این انتقال معکوس که از [ 10 ] گرفته شده است ، در اینجا تکرار می شود، که بر اساس به اصطلاح "شرط تحقق پذیری" در طیف فوریه مارپیچ مغناطیسی است.{\displaystyle {\hat {H}}_{\mathbf {k} }^{M}={\hat {\mathbf {A} }}_{\mathbf {k} }^{*}\cdot {\ کلاه {\mathbf {B} }}_{\mathbf {k} }}({\displaystyle {\hat {\mathbf {B} }}_{\mathbf {k} }}ضریب فوریه در بردار موج است {\displaystyle {\mathbf {k} }}از میدان مغناطیسی {\displaystyle {\mathbf {B} }}، و به طور مشابه برای{\displaystyle {\hat {\mathbf {A} }}}، ستاره ای که مزدوج مختلط را نشان می دهد ). "شرط تحقق پذیری" با کاربرد نابرابری کوشی-شوارتز مطابقت دارد که به دست می آید:،{\displaystyle \left|{\hat {H}}_{\mathbf {k} }^{M}\right|\leq {\frac {2E_{\mathbf {k} }^{M}}{|{ \mathbf {k} }|}}،}با{\textstyle E_{\mathbf {k} }^{M}={\frac {1}{2}}{\hat {\mathbf {B} }}_{\mathbf {k} }^{*}\ cdot {\hat {\mathbf {B} }}_{\mathbf {k} }}طیف انرژی مغناطیسی برای به دست آوردن این نابرابری، این واقعیت است که{\displaystyle |{\hat {\mathbf {B} }}_{\mathbf {k} }|=|{\mathbf {k} }||{\hat {\mathbf {A} }}_{\mathbf {k} ^{\perp }|}(با⊥{\displaystyle {\hat {\mathbf {A} }}_{\mathbf {k} }^{\perp }}بخش شیر برقی پتانسیل بردار مغناطیسی تبدیل شده فوریه، متعامد بر بردار موج در فضای فوریه) استفاده شده است.{\displaystyle {\hat {\mathbf {B} }}_{\mathbf {k} }=i{\mathbf {k} }\times {\hat {\mathbf {A} }}_{\mathbf {k } }}. ضریب 2 در مقاله [ 10 ] وجود ندارد زیرا مارپیچ مغناطیسی به صورت متناوب در آنجا تعریف شده است.{\displaystyle {\frac {1}{2}}\int _{V}{\mathbf {A} }\cdot {\mathbf {B} }\ dV}.

سپس می توان یک موقعیت اولیه را بدون میدان سرعت و میدان مغناطیسی فقط در دو بردار موج تصور کرد{\displaystyle \mathbf {p} }و{\displaystyle \mathbf {q} }. میدان مغناطیسی کاملاً مارپیچی را فرض می کنیم، به این معنی که شرایط تحقق پذیری را اشباع می کند

{\displaystyle \left|{\hat {H}}_{\mathbf {p} }^{M}\right|={\frac {2E_{\mathbf {p} }^{M}}{|{\ mathbf {p} }|}}}و{\displaystyle \left|{\hat {H}}_{\mathbf {q} }^{M}\right|={\frac {2E_{\mathbf {q} }^{M}}{|{\ mathbf {q} }|}}}.

با فرض اینکه تمام انتقال انرژی و مارپیچ مغناطیسی به بردار موج دیگری انجام شودک{\displaystyle \mathbf {k} }حفظ مارپیچ مغناطیسی از یک طرف و کل انرژی{\displaystyle E^{T}=E^{M}+E^{K}}(مجموع انرژی مغناطیسی و جنبشی) از طرف دیگر به دست می آید:

{\displaystyle H_{\mathbf {k} }^{M}=H_{\mathbf {p} }^{M}+H_{\mathbf {q}}^{M},}

{\displaystyle E_{\mathbf {k} }^{T}=E_{\mathbf {p} }^{T}+E_{\mathbf {q} }^{T}=E_{\mathbf {p} } ^{M}+E_{\mathbf {q} }^{M}.}

برابری دوم برای انرژی از این واقعیت ناشی می شود که ما یک حالت اولیه را بدون انرژی جنبشی در نظر می گیریم. سپس ما باید لزوما{\displaystyle |\mathbf {k} |\leq \max(|\mathbf {p} |,|\mathbf {q} |)}. در واقع، اگر ما داشته باشیم{\displaystyle |\mathbf {k} |>\max(|\mathbf {p} |,|\mathbf {q} |)}، سپس:

{\displaystyle H_{\mathbf {k} }^{M}=H_{\mathbf {p} }^{M}+H_{\mathbf {q} }^{M}={\frac {2E_{\mathbf {p} }^{M}}{|\mathbf {p} |}}+{\frac {2E_{\mathbf {q} }^{M}}{|\mathbf {q} |}}>{\frac {2\left(E_{\mathbf {p} }^{M}+E_{\mathbf {q} }^{M} \right)}{|\mathbf {k} |}}={\frac {2E_{\mathbf {k} }^{T}}{|\mathbf {k} |}}\geq {\frac {2E_{\mathbf {k} }^{M}}{|\mathbf {k} |}}،}

که شرط تحقق پذیری را می شکند. این به این معنی است که{\displaystyle |\mathbf {k} |\leq \max(|\mathbf {p} |,|\mathbf {q} |)}. به طور خاص، برای{\displaystyle |{\mathbf {p} }|=|{\mathbf {q} }|}، مارپیچ مغناطیسی به یک بردار موج کوچکتر منتقل می شود که به معنای به مقیاس های بزرگتر است.

https://en.wikipedia.org/wiki/Magnetic_helicity

+ نوشته شده در دوشنبه هشتم بهمن ۱۴۰۳ ساعت 19:42 توسط علی رضا نقش نیلچی  |