چگونه می توانم این را حل کنم: اگر G یک گروه ساده از مرتبه 168 است، پس زیرگروه های sylow-2 از G دو وجهی هستند و زیر گروه های sylow-3 و sylow-7 چرخه ای هستند؟
از آنجا که [ریاضی]168=2^3*3*7[/math]، تنها عبارت غیر واضح این است که زیر گروه های Sylow-2 هم شکل هستند. [ریاضی]D_8[/math]. بدیهی است که سایر زیرگروه های Sylow چرخه ای هستند، زیرا از مرتبه اول برخوردار هستند.
ارزش آن را ذکر در این نقطه است که در واقع وجود دارد است یک گروه ساده از سفارش 168. (من نمی خواهد زحمت به نوشتن این پاسخ غیر این صورت.). برای طبقهبندی کاملتر، به یک متن جبر انتزاعی مانند Dummit و Foote مراجعه کنید، که حاوی اثبات کاملی است مبنی بر اینکه یک گروه ساده از مرتبه 168 باید با گروه اتومورفیسم هواپیمای فانو همشکل باشد - و در واقع، این یک ساده است. گروه سفارش 168.
با این حال، در زیر ما این حقایق را بدیهی نمی دانیم. در عوض، من فقط شروع اثبات را در Dummit و Foote خلاصه می کنم، حداقل تا جایی که بتوانیم دو وجهی بودن زیرگروه های Sylow-2 را ثابت کنیم.
قبل از شروع، برای مرجع، برخی از حقایق کلی در مورد زیرگروه های Sylow را فهرست می کنم که برای خواننده آشنا فرض می شود. اجازه دهید[ریاضی]p[/math] اول تقسیم ترتیب باشد [ریاضی]G[/math] و اجازه دهید [ریاضی]n_p[/math] تعداد زیرگروه های Sylow-p را نشان می دهد [ریاضی]G[/math]. سپس:
- [ریاضی]n_p\equiv 1\mod p[/math].
- همه زیرگروه های Sylow-p به صورت مزدوج هستند [ریاضی]G[/math].
- [ریاضی]n_p[/math]شاخص نرمال ساز هر زیرگروه Sylow-p است. به ویژه، اگر[ریاضی]|G|=p^km[/math] جایی که [ریاضی]p \nاواسط متر[/math]، سپس زیرگروه های Sylow-p دارای نظم هستند [ریاضی]p^k[/math] و [ریاضی]n_p|m[/math].
- نرمال سازهای زیرگروه های Sylow-p نیز به صورت مزدوج هستند[ریاضی]G[/math].
با آن، اجازه دهید [ریاضی]G[/math] یک گروه ساده از مرتبه 168 باشد. اولین قدم این است که توجه داشته باشید [ریاضی]n_7=8[/math]، زیرا این تنها امکان است. این بدان معناست که همه نرمال سازهای Sylow-7 دارای سفارش 21 هستند.
بعد، توجه داشته باشید که [ریاضی]G[/math] نمی توان زیر گروه مناسبی از شاخص کمتر از 7 داشت. این یک آرگومان استاندارد با گروه های ساده است: اگر [ریاضی]ح[/ریاضی] زیر گروهی از شاخص است [ریاضی]k[/math] سپس [ریاضی]G[/math] با ضرب چپ بر روی همزاد عمل می کند [ریاضی]ح[/ریاضی]، که هممورفیسمی از [ریاضی]G[/math] به [ریاضی]S_k[/math] که هسته آن در [ریاضی]ح[/ریاضی]. از آنجا که[ریاضی]G[/math] ساده است، هسته 1 و است [ریاضی]G[/math] به زیرگروه ای هم شکل است [ریاضی]S_k[/math]. این کار نمی کند اگر[math]k\le 6[/math] زیرا 168 تقسیم نمی کند [ریاضی]6!=720[/math].
این امر منتفی است [ریاضی]n_3=4[/math]، بنابراین [ریاضی]n_3[/math]7 یا 28 است. توجه داشته باشید که در هر دو مورد، هیچ عنصری از مرتبه 7 یک زیر گروه Sylow-3 را عادی نمی کند. از این رو[ریاضی]G[/math] هیچ عنصری از نظم 21 ندارد.
بعد، می توانیم از این برای اثبات استفاده کنیم [math]n_3\ne 7[/math]. اجازه دهید[ریاضی] K[/math]یکی از نرمال سازهای Sylow-7 باشد. ما فقط این را ثابت کردیم[ریاضی] K[/math] گروه غیرآبلی مرتبه 21 است که به معنی [ریاضی] K[/math] دقیقا شامل 7 زیر گروه از مرتبه 3. اما اگر [ریاضی]n_3=7[/math] که در [ریاضی]G[/math]، سپس [ریاضی] K[/math]شامل تمام زیر گروه های Sylow-3 از[ریاضی]G[/math]، که تناقض است: هر مزدوج از [ریاضی] K[/math]همچنین یک نرمال ساز Sylow-7 است، از این رو شامل تمام زیر گروه های Sylow-3 نیز می شود. بنابراین تقاطع همه مزدوج های[ریاضی] K[/math] بی اهمیت است، به این معناست که [ریاضی]G[/math] یک گروه ساده نیست
بنابراین ما اکنون داریم [ریاضی]n_3=28[/math]و نرمال سازهای Sylow-3 دارای مرتبه 6 هستند. در حالی که ما در حال کار هستیم، اجازه دهید ثابت کنیم که دو وجهی هستند، یعنی چرخه ای نیستند. اگر آنها چرخه ای بودند، پس[ریاضی]G[/math]دارای 28*2 عنصر مرتبه 3 و 28*2=56 عنصر از مرتبه 6 خواهد بود. (هیچ دو مورد از این زیرگروه ها نمی توانند عنصری با درجه 3 یا 6 مشترک داشته باشند.) به آن عناصر 8*6=48 را اضافه کنید. سفارش 7، و این در حال حاضر 160 عنصر است. این خوب نیست زیرا تنها برای یک زیرگروه Sylow-2 جا می گذارد که در نتیجه طبیعی است.
تا اینجا، ما نوع ایزومورفیسم نرمالکنندههای Sylow-3 و Sylow-7 را میدانیم، و به ویژه هیچ عنصری از مرتبه 6، 14 یا 21 وجود ندارد، بنابراین همه عناصر دارای ترتیب قدرت اول هستند. 56 عنصر از مرتبه 3، 48 عنصر از مرتبه 7، و 1 هویت وجود دارد که 63 عنصر از مرتبه 2، 4، یا احتمالاً 8 باقی می ماند.[ریاضی]n_2=7[/math]: در آن صورت حداکثر می تواند 49 عنصر از این دست وجود داشته باشد، حتی اگر زیرگروه های Sylow-2 دارای تقاطع های بی اهمیت باشند.
نتیجه می شود که [ریاضی]n_2=21[/math] و تقاطع های غیر ضروری بین زیر گروه های Sylow-2 وجود دارد.
اکنون می توانیم در نهایت ثابت کنیم که زیرگروه های Sylow-2 دو وجهی هستند. اجازه دهید[ریاضی]x[/math] عنصری از درجه 2 باشد که در بیش از یک زیرگروه Sylow-2 وجود دارد.
اگر زیرگروههای Sylow-2 abelian بودند، پس مرکزیکننده از [ریاضی]x[/math] زیر گروهی از [ریاضی]G[/math] حاوی بیش از یک زیرگروه از مرتبه 8. بنابراین، باید حاوی عنصری از مرتبه 3 یا 7 باشد که با آن جابجا می شود. [ریاضی]x[/math]، که می دانیم وجود ندارد.
اگر زیرگروه های Sylow-2 گروه کواترنیون بودند [ریاضی]Q_8[/math]، پس دقیقاً با همان مشکل مواجه خواهیم شد، زیرا تنها عنصر [ریاضی]Q_8[/math]دستور 2 در مرکز آن موجود است. بنابراین، از آنجایی که تنها گروههای غیرآبلی مرتبه 8 هستند[ریاضی]D_8[/math] و [ریاضی]Q_8[/math]، زیر گروه های Sylow-2 باید ایزومورف باشند [ریاضی]D_8[/math] با فرآیند حذف [ریاضی]\blacksquare[/math]
در این مرحله ما همه اعداد Sylow و نوع ایزومورفیسم همه زیرگروه های Sylow-p و نرمال سازهای Sylow-p را می دانیم. این شروع خوبی است. اگر بخواهیم ادامه دهیم، میتوانیم ساختار زیرگروه داخلی را تحلیل کنیم[ریاضی]G[/math]و نشان دهید که چگونه "هندسه" یکسانی با صفحه فانو ایجاد می کند. این برای نشان دادن این کافی است.[ریاضی]G[/math]به گروه اتومورفیسم همان هم شکل است.
How do I solve this: if G is a simple group of order 168, then the sylow-2 subgroups of G are dihedral, and the sylow-3 and sylow-7 subgroups are cyclic?
1 Answer

Alex Eustis
, Ph.D. Mathematics, University of California, San Diego (2013)
Answered 6 months ago · Author has 2.4K answers and 10M answer views
Since 168=23∗3∗7168=23∗3∗7, the only non-obvious statement is that the Sylow-2 subgroups are isomorphic to D8D8. Evidently the other Sylow subgroups are cyclic because they're of prime order.
It's worth mentioning at this point that there actually is a simple group of order 168. (I wouldn't bother to write this answer otherwise.). For a more complete classification, see an Abstract Algebra text such as Dummit and Foote, which contains a full proof that a simple group of order 168 must be isomorphic to the automorphism group of the Fano plane — and that, indeed, this is a simple group of order 168.
However, below we won't take for granted these facts. Instead I'll just summarize the start of the proof in Dummit and Foote, at least to the point where we can prove the Sylow-2 subgroups are dihedral.
Before we begin, for reference I'll list some general facts about Sylow subgroups which will be assumed familiar to the reader. Let pp be a prime dividing the order of GG and let npnp denote the number of Sylow-p subgroups of GG. Then:
- np≡1modpnp≡1modp.
- All Sylow-p subgroups are conjugate in GG.
- npnp is the index of the normalizer of any Sylow-p subgroup. In particular, if |G|=pkm|G|=pkm where p∤mp∤m, then Sylow-p subgroups have order pkpk and np|mnp|m.
- The normalizers of the Sylow-p subgroups are also conjugate in GG.
With that, let GG be a simple group of order 168. The first step is to note that n7=8n7=8, because it's the only possibility. This means all Sylow-7 normalizers have order 21.
Next, note that GG can't have a proper subgroup of index less than 7. This is a standard argument with simple groups: if HH is a subgroup of index kk then GG acts by left multiplication on the cosets of HH, which gives a homomorphism of GG into SkSk whose kernel is contained in HH. Since GG is simple, the kernel is 1 and GG is isomorphic to a subgroup of SkSk. That won't work if k≤6k≤6 because 168 doesn't divide 6!=7206!=720.
This rules out n3=4n3=4, so n3n3 is 7 or 28. Note that in both cases, no element of order 7 normalizes a Sylow-3 subgroup. Therefore GG has no element of order 21.
Next, we can use this to prove n3≠7n3≠7. Let KK be one of the Sylow-7 normalizers. We just proved that KK is the non-abelian group of order 21, which means KK contains exactly 7 subgroups of order 3. But if n3=7n3=7 in GG, then KK contains all the Sylow-3 subgroups of GG, which is a contradiction: each conjugate of KK is also a Sylow-7 normalizer, hence it contains all the Sylow-3 subgroups too. Therefore the intersection of all conjugates of KK is nontrivial, implying that GG is not a simple group.
Therefore we now have n3=28n3=28, and the Sylow-3 normalizers have order 6. While we're at it, let's prove they're dihedral, i.e. not cyclic. If they were cyclic, then GG would have 28*2 elements of order 3 and 28*2=56 elements of order 6. (No two of these subgroups can have an element of order 3 or 6 in common.) Add to that the 8*6=48 elements of order 7, and that's already 160 elements. That's no good because it leaves room for only a single Sylow-2 subgroup, which would therefore be normal.
So far, we know the isomorphism type of the Sylow-3 and Sylow-7 normalizers, and in particular no element of order 6, 14, or 21 exists, so all elements have prime power order. There are 56 elements of order 3, 48 elements of order 7, and 1 identity, which leaves 63 elements of order 2, 4, or possibly 8. This rules out n2=7n2=7: in that case there could be at most 49 such elements, even if the Sylow-2 subgroups had trivial intersections.
It follows that n2=21n2=21 and there are nontrivial intersections among the Sylow-2 subgroups.
We can now finally prove that the Sylow-2 subgroups are dihedral. Let xx be some element of order 2 contained in more than one Sylow-2 subgroup.
If Sylow-2 subgroups were abelian, then the centralizer of xx would be a subgroup of GG containing more than one subgroup of order 8. Hence, it would have to contain an element of order 3 or 7 that commutes with xx, which we know doesn't exist.
If the Sylow-2 subgroups were the quaternion group Q8Q8, then we would run into the exact same problem, because the only element of Q8Q8 order 2 is contained in its center. Therefore, since the only non-abelian groups of order 8 are D8D8 and Q8Q8, the Sylow-2 subgroups must be isomorphic to D8D8 by process of elimination. ■◼
At this point we know all the Sylow numbers, and the isomorphism type of all Sylow-p subgroups and Sylow-p normalizers. That's a good start. If we wanted to continue, we could keep analyzing the internal subgroup structure of GG and show how it gives rise to a “geometry" identical to that of the Fano plane. This would be sufficient to show that GG is isomorphic to the automorphism group of same.
578 views
View upvotes
7
Related Answers
Related Answer

Alon Amit
, Ph.D. in Mathematics.Answered 1 year ago · Upvoted by
Vance Faber
, Ph. D. Mathematics and
Ali Taghavi
, Ph.D Mathematics, Sharif University of Technology (2002) · Author has 6.9K answers and 99.5M answer views
How can I prove that if G is a group of order 91, then every proper subgroup of G is cyclic?
There are good answers here already so I won’t repeat them, but I do wish to point out that the restriction “proper” in the question is unnecessary: if GG is a group of order 9191 then GG itself must be cyclic (it then follows immediately that its subgroups are cyclic as well.)
In fact, if p>qp>q are primes and qq does not divide p−1p−1 then any group of order pqpq is cyclic. To show this, first prove that GG has unique Sylow subgroups, and then count the number of elements of order pp and qq. You’ll see that there must be other (nontrivial) elements, and the only possible order of such elements is pqpq.
6.4K views
View upvotes
View 6 shares
Answer requested by
Zehra Akhan
85
6
Related Answer

Darrah Chavey
, Professor, Math & Comp. Sci. at Beloit College (1987-present)Answered 7 months ago · Upvoted by
Alon Amit
, Ph.D. in Mathematics. · Author has 867 answers and 546.8K answer views
If G is a group of order 385, show that both sylow 7-subgroup and sylow 11-subgroup are normal in G and sylow 7-subgroup is in the center of G?
By Sylow’s 3rd theorem, the number of subgroups of size 11 must be ≡1mod11≡1mod11, and it must be a divisor of 385. The only number that satisfies those conditions is 1, so there is a unique 11-subgroup. Being unique, it must be normal. The same statement applies to 7, so there is a unique 7-subgroup, which is then also normal.
If we conjugate the 7-subgroup S by an element g of the group, the action is an automorphism on the six non-identity elements of S. The order of that action, d, must then be a divisor of 6. Consequently, the order of g must be a multiple of d, and of course is also a d
Continue Reading
6
Related Answer

Alon Amit
, PhD in Mathematics; Mathcircler.Answered 4 years ago · Upvoted by
Yair Livne
, Master's Mathematics, Hebrew University of Jerusalem (2007) and
Alex Sadovsky
, Ph.D. Mathematics & Biomechanics, University of California, Irvine · Author has 6.9K answers and 99.5M answer views
Suppose that a cyclic group G has exactly 3 subgroups: G itself, {e}, and subgroup of order 7. What is |G|? What can you say if 7 is replaced with p where p is a prime?
Consider this: the group has order nn, for some nn. It is cyclic, so it has a generator aa of order nn. The given prime pp must divide nn. If nn were divisible by any proper divisor mm other than pp then an/man/m would generate a subgroup of order mm, but there are no such subgroups. So pp is the only proper divisor of nn.
Which numbers have a single proper prime divisor?
(By “proper divisor” I mean a divisor which is neither 11 nor the number itself).
5.2K views
View upvotes
44
2
Related Answer

Amitabha Tripathi
, teaching Group Theory for almost three decades
Answered 4 years ago · Author has 3.8K answers and 7.6M answer views
How many distinct subgroups does the cyclic group of order 6 have?
Theorem. Let GG be a cyclic group of order nn. For each d∣nd∣n, there exists a unique subgroup of order dd.
Proof. (sketch) Let G=G=, and let Hd=Hd=. Then |G|=o(a)=n|G|=o(a)=n and |H|=o(an/d)=d|H|=o(an/d)=d. Thus there is at least one subgroup of order dd.
Let HH be a subgroup of GG of order dd. Since every subgroup of a cyclic group is cyclic, H=H= for some k∈{1,2,3,…,n}k∈{1,2,3,…,n}. From
d=|H|=o(ak)=ngcd(k,n)d=|H|=o(ak)=ngcd(k,n)
we have gcd(k,n)=ndgcd(k,n)=nd. Hence nd∣knd∣k, so that ak∈Hdak∈Hd. Thus H⊆HdH⊆Hd, and since they are of the same order, H=HdH=Hd. T
Continue Reading
22
Related Answer

Amitabha Tripathi
, teaching abstract Algebra for almost three decades
Answered 9 months ago · Author has 3.8K answers and 7.6M answer views
What are the elements of the cyclic subgroup generated by R270 in the dihedral group D4 of order 8?
The dihedral group D4D4 is the group of symmetries on a square. There are four rotations and four reflections ((two each with respect to lines joining midpoints of opposite sides and lines joining opposite vertices, or diagonals)).
The four rotations may be denoted by the angle by which each vertex is transformed: R0R0, R90R90, R180R180, R270R270. The first is the identity mapping, the second is the mapping (1234)(1234), the third is (13)(24)(13)(24), and the fourth is (1432)(1432). The second and fourth mappings are inverses of one another, and each has order 44 ((because the length of the permutation is 4)4). The third ma
Continue Reading
2
1
Related Answer

Richard Goldstone
, PhD Mathematics, The Graduate Center, CUNY (1995)
Answered 1 year ago · Author has 915 answers and 473.3K answer views
If d is divisor of the order of a finite cyclic group G, how can you prove that G contains a subgroup of order d?
Let G be a finite cyclic group of order nn, let gg be a generator of GG, and let dd be a divisor of n.n. suppose that
(gnd)k=1G.(gnd)k=1G.
By a corollary to Lagrange’s theorem, (nd)k≡0(modn).(nd)k≡0(modn).
Then, dividing both terms and the modulus of this congruence by n/d,n/d,
(nd)k≡0(modn)⟹k≡0(modd).(nd)k≡0(modn)⟹k≡0(modd).
This shows not only the obvious fact that
(gnd)d=1G,(gnd)d=1G,
but also the more essential fact that no non-zero integer k∈{0,1,2,…,d−1}k∈{0,1,2,…,d−1} produces
(nd)k≡0(modn)(nd)k≡0(modn)
Continue Reading
3
Related Answer

Wes Browning
, PhD Geometry and Topology, Cornell University (1979)
Answered 1 year ago · Author has 3.1K answers and 1.1M answer views
How do I find the number of sylow subgroups of D10D10, dihedral group of order 20, and which groups do they represent?
The group is represented by
A 5-Sylow subgroup is {1, a^2, a^4, a^6, a^8}. This is cyclic of order 5 generated by any nontrivial element. It’s the only 2-Sylow group and it’s normal.
A 2-Sylow subgroup has to have order 4. One such is {1, b, a^5, ba^5} This is closed and therefore a subgroup. Since all three nontrivial elements have order two, it is isomophic to (Z/2Z)^2, the Klein four-group. By Sylow’s theory there has to be an odd number of 2-Sylow groups, and the number must divide 20. Therefore the number is 1 or 5. I can in fact find five:
{1, b, a
Continue Reading
3
Related Answer

Swetha Dandibhotla
, B. SC Mathematics & Statistics (2021)
Answered 1 year ago · Author has 375 answers and 45.6K answer views
How many subgroups are there for a group of order 19?
Given, the order of group is 19 , that is, the group is of prime order.
From, a known theorem, a group of prime order has no proper subgroups.
If G is the group, the subgroups of G are G, {e} where ‘e' is the identity element of G. Therefore, the number of subgroups of group G of order 19 is 2.
1.2K views
View upvotes
2
Related Answer

Amitabha Tripathi
, teaching abstract Algebra for almost three decades
Answered 3 years ago · Author has 3.8K answers and 7.6M answer views
Suppose that a cyclic group G has exactly 3 subgroups: G itself, {e}, and subgroup of order 11. What is |G|?
Every cyclic group of order nn has a unique subgroup of order dd, for each d∣nd∣n. So a cyclic group of order nn has as as many subgroups as nn has positive divisors.
If d(n)d(n) denotes the number of positive divisors of nn, then
d⎛⎝∏p∣npα⎞⎠=∏p∣n(1+α)d(∏p∣npα)=∏p∣n(1+α).
Thus, d(n)=3⇔n=p2d(n)=3⇔n=p2, where pp is a prime. Since 11∣n11∣n, p=11p=11, and so n=112=121n=112=121. ■◼
1.2K views
View upvotes
Answer requested by
Lipsa Priyadarshini Behera
7
Related Answer

Vance Faber
, Ph. D. Mathematics
Answered 2 years ago · Author has 1.9K answers and 606.3K answer views
A group is super-solvable if it is the product of two super-solvable normal subgroups of co-prime indices, so what if the subgroups are not normal?
How are you defining the product of two subgroups? Is it the group generated by the product of elements, one from each? I think in that case, the group might not even be solvable.
منبع
https://www.quora.com/How-do-I-solve-this-if-G-is-a-simple-group-of-order-168-then-the-sylow-2-subgroups-of-G-are-dihedral-and-the-sylow-3-and-sylow-7-subgroups-are-cyclic













 یک فضای توپولوژیکی
یک فضای توپولوژیکی  بسته نامیده می شود اگر مکمل ن باشد
بسته نامیده می شود اگر مکمل ن باشد زیر مجموعه باز است
زیر مجموعه باز است یک مجموعه در بسته است
یک مجموعه در بسته است اگر و تنها در صورتی که برابر با بسته شدن ن باشد.
اگر و تنها در صورتی که برابر با بسته شدن ن باشد. به همین ترتیب، یک مجموعه بسته می شود اگر و تنها در صورتی که تمام نقاط حد خود را داشته باشد . تعریف مشابه دیگر این است که یک مجموعه بسته است اگر و فقط در صورتی که تمام نقاط مرزی خود را داشته باشد . هر زیر مجموعه
به همین ترتیب، یک مجموعه بسته می شود اگر و تنها در صورتی که تمام نقاط حد خود را داشته باشد . تعریف مشابه دیگر این است که یک مجموعه بسته است اگر و فقط در صورتی که تمام نقاط مرزی خود را داشته باشد . هر زیر مجموعه  همیشه در بسته شدن ( توپولوژیکی) ن وجود دارد،
همیشه در بسته شدن ( توپولوژیکی) ن وجود دارد، که با نشان داده می شود;
که با نشان داده می شود; یعنی اگر
یعنی اگر علاوه بر این،
علاوه بر این،
 در یک فضای قابل شمارش اول (مانند فضای متریک)، به جای همه شبکه ها، فقط دنباله های همگرا را در نظر بگیرید. یکی از ارزش های این خصوصیات این است که ممکن است به عنوان یک تعریف در زمینه فضاهای همگرایی که کلی تر از فضاهای توپولوژیکی هستند، استفاده شود. توجه داشته باشید که این شخصیت پردازی به فضای اطراف نیز بستگی دارد،
در یک فضای قابل شمارش اول (مانند فضای متریک)، به جای همه شبکه ها، فقط دنباله های همگرا را در نظر بگیرید. یکی از ارزش های این خصوصیات این است که ممکن است به عنوان یک تعریف در زمینه فضاهای همگرایی که کلی تر از فضاهای توپولوژیکی هستند، استفاده شود. توجه داشته باشید که این شخصیت پردازی به فضای اطراف نیز بستگی دارد، که در
که در س( یا به طور معادل، اگر
س( یا به طور معادل، اگر معنی
معنی جایی که
جایی که دارای توپولوژی زیرفضایی است که توسط ن القا شده است
دارای توپولوژی زیرفضایی است که توسط ن القا شده است این اصطلاح به توضیح انگلیسی ساده زیر مجموعه های بسته اجازه می دهد:
این اصطلاح به توضیح انگلیسی ساده زیر مجموعه های بسته اجازه می دهد: نزدیک به یک زیر مجموعه است
نزدیک به یک زیر مجموعه است اگر
اگر که در این صورت
که در این صورت ابر فضای توپولوژیکی نامیده می شود،
ابر فضای توپولوژیکی نامیده می شود، که نزدیک است
که نزدیک است اگر
اگر که نشان دهنده بسته شدن است
که نشان دهنده بسته شدن است در واقع، حتی اگر
در واقع، حتی اگر ، با این حال هنوز هم برای ن امکان پذیر است
، با این حال هنوز هم برای ن امکان پذیر است با این حال،
با این حال، برای برخی (یا به طور معادل، برای هر) ابر فضای توپولوژیکی
برای برخی (یا به طور معادل، برای هر) ابر فضای توپولوژیکی اگر و فقط اگر پیوسته است
اگر و فقط اگر پیوسته است برای هر زیر مجموعه
برای هر زیر مجموعه  اگر و فقط اگر برای هر زیر مجموعه پیوسته است،
اگر و فقط اگر برای هر زیر مجموعه پیوسته است،
 به همین ترتیب،
به همین ترتیب، نزدیک است به
نزدیک است به در یک فضای هاسدورف دلخواه،
در یک فضای هاسدورف دلخواه، از
از
 از زیر مجموعه های
از زیر مجموعه های ویژگی های ذکر شده در بالا را داشته باشید، پس یک توپولوژی منحصر به فرد وجود دارد
ویژگی های ذکر شده در بالا را داشته باشید، پس یک توپولوژی منحصر به فرد وجود دارد بر
بر ویژگی اشتراک همچنین به فرد اجازه می دهد تا بسته شدن یک مجموعه را تعریف کند
ویژگی اشتراک همچنین به فرد اجازه می دهد تا بسته شدن یک مجموعه را تعریف کند![[الف، ب]](https://wikimedia.org/api/rest_v1/media/math/render/svg/9c4b788fc5c637e26ee98b45f89a5c08c85f7935) اعداد واقعی بسته است. ( برای توضیح نماد مجموعه براکت و پرانتز به فاصله (ریاضیات) مراجعه کنید.)
اعداد واقعی بسته است. ( برای توضیح نماد مجموعه براکت و پرانتز به فاصله (ریاضیات) مراجعه کنید.)![[0,1]](https://wikimedia.org/api/rest_v1/media/math/render/svg/738f7d23bb2d9642bab520020873cccbef49768d) در فضای متریک اعداد حقیقی و مجموعه بسته شده است
در فضای متریک اعداد حقیقی و مجموعه بسته شده است![{\displaystyle [0,1]\cap \mathbb {Q} }](https://wikimedia.org/api/rest_v1/media/math/render/svg/b97119403d3148dbf45f6e697c559c2e44fce8a9) از اعداد گویا بین
از اعداد گویا بین و1
و1 (شامل) در فضای اعداد گویا بسته است اما
(شامل) در فضای اعداد گویا بسته است اما در اعداد واقعی
در اعداد واقعی بسته است.
بسته است. یک مجموعه بسته نامحدود و نامحدود در اعداد حقیقی است.
یک مجموعه بسته نامحدود و نامحدود در اعداد حقیقی است. با
با و
و ، یعنی
، یعنی برای به دست آوردن راه حل نرمال شده منحصر به فرد، باید شرط را اضافه کنیم
برای به دست آوردن راه حل نرمال شده منحصر به فرد، باید شرط را اضافه کنیم . بنابراین مختصات باریسنتریک حل
. بنابراین مختصات باریسنتریک حل  که هست
که هست

 سه خطی دارد
سه خطی دارد


 و
و است
است 
 بین
بین و
و ، یا طول بردار جابجایی
، یا طول بردار جابجایی است
است ![{\displaystyle d^{2}=\left|PQ\right|^{2}=-a^{2}yz-b^{2}zx-c^{2}xy={\frac {1}{ 2}}[x^{2}(b^{2}+c^{2}-a^{2})+y^{2}(c^{2}+a^{2}-b^{ 2})+z^{2}(a^{2}+b^{2}-c^{2})].}](https://wikimedia.org/api/rest_v1/media/math/render/svg/dc8615c8fe62884423e5e671a2b1a4cf5cd145ad)
 که نگه می دارد زیرا
که نگه می دارد زیرا


 . در واقع، با توجه به هر نقطه ای در مختصات دکارتی، می توانیم از این واقعیت برای تعیین اینکه این نقطه نسبت به مثلث کجاست استفاده کنیم.
. در واقع، با توجه به هر نقطه ای در مختصات دکارتی، می توانیم از این واقعیت برای تعیین اینکه این نقطه نسبت به مثلث کجاست استفاده کنیم. اگر نقطه ای روی یک یال مثلث قرار داشته باشد اما در یک راس نباشد، یکی از ناحیه ها مختصات
اگر نقطه ای روی یک یال مثلث قرار داشته باشد اما در یک راس نباشد، یکی از ناحیه ها مختصات (یکی که با راس مخالف مرتبط است) صفر است، در حالی که دو مورد دیگر در بازه باز قرار دارند
(یکی که با راس مخالف مرتبط است) صفر است، در حالی که دو مورد دیگر در بازه باز قرار دارند
 .
. و
و .
.
 مقادیر شناخته شده هستند، اما مقادیر
مقادیر شناخته شده هستند، اما مقادیر ناشناخته است، آنها را می توان با استفاده از
ناشناخته است، آنها را می توان با استفاده از  ،
، ،
، ، سپس
، سپس
 ، سپس نقطه در آن مثلث یا لبه آن قرار دارد (در قسمت قبل توضیح داده شد). سپس ارزش
، سپس نقطه در آن مثلث یا لبه آن قرار دارد (در قسمت قبل توضیح داده شد). سپس ارزش همانطور که در بالا توضیح داده شد می توان درون یابی کرد.
همانطور که در بالا توضیح داده شد می توان درون یابی کرد. . تحت این تغییر متغیرها،
. تحت این تغییر متغیرها،
 . به طور مشابه، برای ادغام بر روی یک چهار وجهی، به جای شکستن انتگرال به دو یا سه قطعه جداگانه، می توان به مختصات چهار وجهی سه بعدی تحت تغییر متغیرها تغییر داد.
. به طور مشابه، برای ادغام بر روی یک چهار وجهی، به جای شکستن انتگرال به دو یا سه قطعه جداگانه، می توان به مختصات چهار وجهی سه بعدی تحت تغییر متغیرها تغییر داد. جایی که
جایی که حجم چهار وجهی است.
حجم چهار وجهی است. ،
، ، و
، و .
. 







![{\displaystyle =[a^{2}(b^{2}+c^{2})-(b^{2}-c^{2})^{2}]:[b^{2}( c^{2}+a^{2})-(c^{2}-a^{2})^{2}]:[c^{2}(a^{2}+b^{2} )-(a^{2}-b^{2})^{2}].}](https://wikimedia.org/api/rest_v1/media/math/render/svg/f089d53cef3483e79aa1e2c5214b4c1744867c70)
 .
. .
. در سیستم مختصات باریسنتریک یک مثلث.
در سیستم مختصات باریسنتریک یک مثلث.  نقشه به مختصات باریسنتریک
نقشه به مختصات باریسنتریک ،
، ، و غیره.
، و غیره.
 اکنون یک ماتریس 3×3 است:
اکنون یک ماتریس 3×3 است:
 با مختصات دکارتی مربوطه:
با مختصات دکارتی مربوطه:
 یک نقطه
یک نقطه که با توجه به مجموعه ای محدود از k نقطه تعریف می شوند
که با توجه به مجموعه ای محدود از k نقطه تعریف می شوند به جای یک
به جای یک 
 . در مورد یک سیمپلکس، نقاط با مختصات تعمیم یافته نرمال شده غیر منفی (
. در مورد یک سیمپلکس، نقاط با مختصات تعمیم یافته نرمال شده غیر منفی ( ) بدنه
) بدنه  ) مختصات باریسنتریک تعمیم یافته یک نقطه منحصر به فرد نیستند ، به عنوان سیستم خطی تعیین کننده (در اینجا برای n=2)
) مختصات باریسنتریک تعمیم یافته یک نقطه منحصر به فرد نیستند ، به عنوان سیستم خطی تعیین کننده (در اینجا برای n=2)
 -simplex، که دارای n رأس است - نقشه بر روی:
-simplex، که دارای n رأس است - نقشه بر روی: نقشه یک به یک است اگر و فقط اگر پلی توپ یک سیمپلکس باشد، در این صورت نقشه یک هم شکل است. این مربوط به نقطهای است که مختصات باریسنتریک تعمیمیافته منحصربهفرد ندارد مگر زمانی که P یک سیمپلکس باشد.
نقشه یک به یک است اگر و فقط اگر پلی توپ یک سیمپلکس باشد، در این صورت نقشه یک هم شکل است. این مربوط به نقطهای است که مختصات باریسنتریک تعمیمیافته منحصربهفرد ندارد مگر زمانی که P یک سیمپلکس باشد. به f -
به f -  به عنوان شی استاندارد برای فضاهای برداری، و
به عنوان شی استاندارد برای فضاهای برداری، و  به عنوان شی استاندارد برای فضاهای وابسته، که در هر مورد، انتخاب یک
به عنوان شی استاندارد برای فضاهای وابسته، که در هر مورد، انتخاب یک 

 n + 1 نقطه در یک
n + 1 نقطه در یک  از بعد n که
از بعد n که 
 که همه صفر نیستند، به طوری که
که همه صفر نیستند، به طوری که
 نشان دهنده
نشان دهنده  که این معادله را برآورده می کند، مختصات باریسنتریک P نسبت به
که این معادله را برآورده می کند، مختصات باریسنتریک P نسبت به استفاده از دو نقطه در علامت گذاری تاپل به این معنی است که مختصات باریسنتریک نوعی
استفاده از دو نقطه در علامت گذاری تاپل به این معنی است که مختصات باریسنتریک نوعی  مختصات باریسنتریک یک نقطه هستند
مختصات باریسنتریک یک نقطه هستند  به طوری که
به طوری که برای هر من .
برای هر من .
 با مجموع همه
با مجموع همه این مختصات باریسنتریک خاص، مختصات باریسنتریک نرمال شده یا مطلق نامیده می شوند .
این مختصات باریسنتریک خاص، مختصات باریسنتریک نرمال شده یا مطلق نامیده می شوند .  که
که  به طوری که
به طوری که

 که مختصات آن صفر است به جز مختصات شاخص i که برابر با یک است.
که مختصات آن صفر است به جز مختصات شاخص i که برابر با یک است.


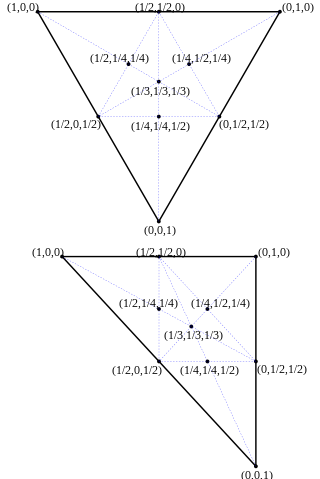
 روی مثلث متساوی الاضلاع و مثلث قائم الزاویه.
روی مثلث متساوی الاضلاع و مثلث قائم الزاویه. با سه رأس آن تعریف می شود،
با سه رأس آن تعریف می شود، و
و . هر نقطه
. هر نقطه به طوری که
به طوری که
 مختصات "باری مرکزی" یا "منطقه" نقطه را نشان می دهد
مختصات "باری مرکزی" یا "منطقه" نقطه را نشان می دهد بجای
بجای . در اینجا،
. در اینجا،  و
و  .
.  دراز کشیده در
دراز کشیده در
 از
از یکی دارد
یکی دارد ![{\displaystyle \mathbf {h} ={\frac {1}{(\mathbf {e} ,\mathbf {f} ,\mathbf {g} )}}\cdot \left[(\mathbf {h} ,\ mathbf {f} ,\mathbf {g} )\mathbf {e} +(\mathbf {e} ,\mathbf {h} ,\mathbf {g} )\mathbf {f} +(\mathbf {e} ,\ mathbf {f}،\mathbf {h})\mathbf {g} \راست]،}](https://wikimedia.org/api/rest_v1/media/math/render/svg/2b1318f42d7c5bac15a253331f26a3a18a519e45)
 مخفف
مخفف  ، جایی که
، جایی که
 در واقع،
در واقع،  .
.
 و
و دقیقاً دو برابر
دقیقاً دو برابر 
 و به ترتیبب
و به ترتیبب .
.
 ،
،
 -نشان نویسی مختصات باریسنتریک از این واقعیت ناشی می شود که نقطه
-نشان نویسی مختصات باریسنتریک از این واقعیت ناشی می شود که نقطه ،
، .
. یا برعکس.
یا برعکس. و از نظر مختصات باریسنتریک از
و از نظر مختصات باریسنتریک از
 به موارد فوق برای به دست آوردن
به موارد فوق برای به دست آوردن



 و
و






 را می توان به یک نقطه قرارداد: یک نقشه پیوسته وجود دارد
را می توان به یک نقطه قرارداد: یک نقشه پیوسته وجود دارد  به طوری که
به طوری که  محدود به
محدود به  است
است  اینجا،
اینجا،  به ترتیب
به ترتیب ![{\displaystyle p:[0,1]\to X}](https://wikimedia.org/api/rest_v1/media/math/render/svg/b6b80282e47ebd79e3d481bb8338a956446ce551) و
و ![{\displaystyle q:[0,1]\to X}](https://wikimedia.org/api/rest_v1/media/math/render/svg/8fdfdce571cc9c14cdf115476670c4a20a6b194f) دو مسیر (یعنی نقشه های پیوسته) با نقطه شروع و پایان یکسان هستند (
دو مسیر (یعنی نقشه های پیوسته) با نقطه شروع و پایان یکسان هستند ( و
و  )، سپس
)، سپس می تواند به طور مداوم تغییر شکل دهد
می تواند به طور مداوم تغییر شکل دهد در حالی که هر دو نقطه پایانی ثابت هستند.
در حالی که هر دو نقطه پایانی ثابت هستند. ![{\displaystyle F:[0,1]\times [0,1]\to X}](https://wikimedia.org/api/rest_v1/media/math/render/svg/8935dc7cebf2aa3d676da7e02082cfd94ea5f10e) به طوری که
به طوری که  و
و 
 مجموعه
مجموعه  در
در  به سادگی همبند است اگر و فقط اگر هر دو
به سادگی همبند است اگر و فقط اگر هر دو 

 به سادگی همبند است، اما
به سادگی همبند است، اما نیست. اگر
نیست. اگر سپس هر دو
سپس هر دو و
و  به سادگی همبند است اگر و فقط اگر
به سادگی همبند است اگر و فقط اگر
 گروه
گروه  به سادگی همبند نیست و
به سادگی همبند نیست و  به سادگی همبند است.
به سادگی همبند است. به سادگی همبند نیست (حتی
به سادگی همبند نیست (حتی به سادگی همبند است، اما فشرده سازی آن، خط طولانی طولانی است
به سادگی همبند است، اما فشرده سازی آن، خط طولانی طولانی است نیست (زیرا حتی مسیر همبند نیست).
نیست (زیرا حتی مسیر همبند نیست). که به سادگی همبند نیست.
که به سادگی همبند نیست. یک زیرمجموعه باز همبند ساده از
یک زیرمجموعه باز همبند ساده از  و
و  پس یک
پس یک  و مقدار هر
و مقدار هر  و
و  از مسیر، و می تواند به عنوان محاسبه شود
از مسیر، و می تواند به عنوان محاسبه شود بنابراین انتگرال به مسیر خاص اتصال بستگی ندارد
بنابراین انتگرال به مسیر خاص اتصال بستگی ندارد
 (بجز
(بجز  از فرم است
از فرم است  با
با  یک ایده آل از
یک ایده آل از  ) اما دارای ایده آل های چپ غیر پیش پا افتاده است (مثلا مجموعه ماتریس هایی که تعدادی ستون صفر ثابت دارند).
) اما دارای ایده آل های چپ غیر پیش پا افتاده است (مثلا مجموعه ماتریس هایی که تعدادی ستون صفر ثابت دارند). ماتریس با ورودی در
ماتریس با ورودی در 
 حلقه ای از ماتریس ها با ورودی های داخل باشد
حلقه ای از ماتریس ها با ورودی های داخل باشد  ،
، . بنابراین یک ایده آل مینیمال در
. بنابراین یک ایده آل مینیمال در ،
، . به عبارت دیگر، اگر
. به عبارت دیگر، اگر ، جایی که
، جایی که  ماتریس
ماتریس  ورود و صفر در جای دیگر. همچنین،
ورود و صفر در جای دیگر. همچنین، . ایده آل چپ
. ایده آل چپ . اجازه دهید
. اجازه دهید ، به عنوان یک ماژول سمت راست در نظر گرفته شده است
، به عنوان یک ماژول سمت راست در نظر گرفته شده است  . سپس
. سپس .
. توسط
توسط  برای
برای  . سپس
. سپس
 ، سپس
، سپس  ، که دلالت بر آن دارد
، که دلالت بر آن دارد  .
. . از آنجا که
. از آنجا که . بنابراین
. بنابراین .
. بستگی ندارد
بستگی ندارد ، و سپس آن را نشان دهید
، و سپس آن را نشان دهید از
از 









 .
.
 ضریب H با
ضریب H با 
 و جفت نهایی مورفیسم
و جفت نهایی مورفیسم  . اگر شیئی وجود دارد
. اگر شیئی وجود دارد و مورفیسم
و مورفیسم  به طوری که }
به طوری که } دقیق است، سپس دقت
دقیق است، سپس دقت  تضمین شده است. مجدداً مقوله گروهها را مثال میزنیم، این واقعیت که im( f ) هسته برخی هممورفیسمها در H است، نشان میدهد که آن یک
تضمین شده است. مجدداً مقوله گروهها را مثال میزنیم، این واقعیت که im( f ) هسته برخی هممورفیسمها در H است، نشان میدهد که آن یک 
 اگر
اگر  . دنباله اگر در هر یک دقیق باشد دقیق نامیده می شود
. دنباله اگر در هر یک دقیق باشد دقیق نامیده می شود ، یعنی اگر تصویر هر هم شکلی با هسته بعدی برابر باشد.
، یعنی اگر تصویر هر هم شکلی با هسته بعدی برابر باشد.



 (1)
(1) (2)
(2) برای هر
برای هر  . از نظر ساخت، دنبالههای (2) دقیقاً در سطح هستند
. از نظر ساخت، دنبالههای (2) دقیقاً در سطح هستند 's (صرف نظر از دقت (1) ). علاوه بر این، (1) یک دنباله دقیق طولانی است اگر و فقط اگر (2) همه دنباله های دقیق کوتاه باشند.
's (صرف نظر از دقت (1) ). علاوه بر این، (1) یک دنباله دقیق طولانی است اگر و فقط اگر (2) همه دنباله های دقیق کوتاه باشند.
 نشان می دهد که نقشه 2× از Z تا Z یک تک شکلی است و فلش دو سر است
نشان می دهد که نقشه 2× از Z تا Z یک تک شکلی است و فلش دو سر است یک epiریخت را نشان می دهد (نقشه mod 2). این یک دنباله دقیق است زیرا تصویر 2 Z از تک شکلی هسته اپیمورفیسم است. اساساً "همان" دنباله را می توان به صورت نوشتاری نیز نوشت
یک epiریخت را نشان می دهد (نقشه mod 2). این یک دنباله دقیق است زیرا تصویر 2 Z از تک شکلی هسته اپیمورفیسم است. اساساً "همان" دنباله را می توان به صورت نوشتاری نیز نوشت



 است که
است که  است
است 
 نقشه هر عنصر X از
نقشه هر عنصر X از به عنصر
به عنصر  از
از  و هممورفسیم
و هممورفسیم  هر عنصر را ترسیم می کند
هر عنصر را ترسیم می کند  .
.









![8: چهار مرحله ایجاد مثلث چند ضلعی یک شش ضلعی مربوط به پیکربندی [0، 1، 2، 2]. (الف) چندضلعی بدون مثلث. (ب) بعد از مرحله 1. (ج) بعد از مرحله 2. (د) بعد از مرحله 3.](https://www.researchgate.net/profile/Phillip-Kirlin/publication/261252216/figure/fig5/AS:669378915880965@1536603778207/The-four-steps-of-creating-the-polygon-triangulation-of-a-hexagon-corresponding-to.png)








 نقاط شامل یک مسیر چند ضلعی حداقل است
نقاط شامل یک مسیر چند ضلعی حداقل است  لبه هایی که در آنها همه شیب ها علامت یکسانی دارند. این نتیجه ای از
لبه هایی که در آنها همه شیب ها علامت یکسانی دارند. این نتیجه ای از 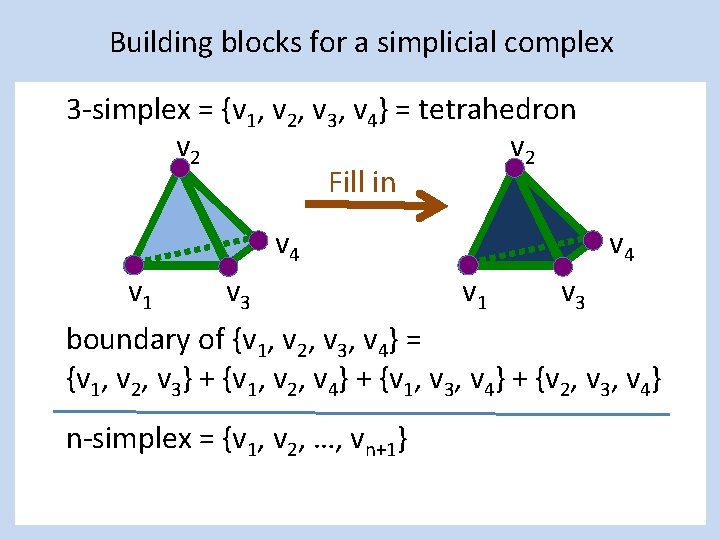
 در این وبلاگ به ریاضیات و کاربردهای آن و تحقیقات در آنها پرداخته می شود. مطالب در این وبلاگ ترجمه سطحی و اولیه است و کامل نیست.در صورتی سوال یا نظری در زمینه ریاضیات دارید مطرح نمایید .در صورت امکان به آن می پردازم. من دوست دارم برای یافتن پاسخ به سوالات و حل پروژه های علمی با دیگران همکاری نمایم.در صورتی که شما هم بامن هم عقیده هستید با من تماس بگیرید.
در این وبلاگ به ریاضیات و کاربردهای آن و تحقیقات در آنها پرداخته می شود. مطالب در این وبلاگ ترجمه سطحی و اولیه است و کامل نیست.در صورتی سوال یا نظری در زمینه ریاضیات دارید مطرح نمایید .در صورت امکان به آن می پردازم. من دوست دارم برای یافتن پاسخ به سوالات و حل پروژه های علمی با دیگران همکاری نمایم.در صورتی که شما هم بامن هم عقیده هستید با من تماس بگیرید.