توسط علی رضا نقش نیلچی
| دوشنبه ششم فروردین ۱۴۰۳ | 1:15
خاص، لاگرانژ شکل دیگری به خود می گیرد، که می توانید در اینجا اطلاعات بیشتری درباره آن بخوانید .
اصل عمل ثابت، به طور شهودی چیست؟
پیش از این، من توضیح دادم که عمل چیست (کمیتی که یک مسیر خاص را در فضا و زمان توصیف می کند). اکنون می خواهم بررسی کنم که اصل عمل ثابت در واقع به چه معناست.
بعداً خواهیم دید که چگونه به معادلات اویلر-لاگرانژ منتهی می شود ، که اساساً معادل قانون دوم نیوتن، F=ma است.
اول از همه، عمل به عنوان این انتگرال در طول زمان تعریف میشود، که به طور شهودی میتوان با «تقسیم» مسیر به قطعات کوچک به شکل Ldt (مقدار L لاگرانژی در یک بازه زمانی کوچک dt؛ این Ldt-) به دست آورد. قطعات اساساً عمل را در یک بازه کوچک dt از مسیر نشان می دهند).
سپس عمل مسیر کامل مجموع تمام این قطعات کوچک Ldt، یا به طور دقیق تر، انتگرال Ldt به شرح زیر است (از آنجایی که زمان یک متغیر پیوسته است، در اینجا باید از انتگرال استفاده کنیم):

گاهی اوقات عملی را می بینید که با حرف S مشخص شده است.
مسیر فیزیکی واقعی یک شی یا یک سیستم همیشه مسیری است که در آن عمل ثابت است. این به عنوان اصل عمل ثابت شناخته می شود .
اکنون، این ممکن است یکباره قابل هضم باشد، بنابراین اجازه دهید کمی آن را بررسی کنیم. اولاً، حتی ثابت بودن چیزی به چه معناست؟
پاسخ به این در واقع بسیار ساده است و شما حتی ممکن است آن را از ریاضی ابتدایی دبیرستان بدانید. یک نقطه ثابت برای یک تابع به سادگی نقطه ای است که در آن خط مماس افقی است (یعنی مشتق در این نقطه صفر است) :

اکنون، همان ایده نقاط ثابت در مورد عمل نیز صدق می کند، اما با کمی ریاضی بیشتر.
این به این دلیل است که عمل در واقع یک تابع است ، نه فقط یک تابع. اگر میخواهید در مورد توابع و به طور کلیتر، حساب تغییرات - که حوزهای از مکانیک لاگرانژی ریاضی است - بیشتر بدانید، میتوانید این مقاله را بررسی کنید .
ایده اصلی این است که یک نقطه ثابت در عمل به عنوان دیفرانسیل عملکردی برابر با صفر تعریف می شود (که با δA=0 نشان داده می شود). این اساساً فقط به این معنی است که یک تغییر جزئی (دیفرانسیل) در عمل باید صفر باشد.
اصل عمل ثابت از نظر ریاضی:

مسیری که یک سیستم طی می کند مسیری است که در آن عمل این معادله را برآورده می کند.

دیفرانسیل عملکردی اساساً به معنای تغییر مقدار عمل کمی (بی نهایت کوچک) است. سپس نقاط ثابت نقاطی هستند که در آنها یک واریانس جزئی بر ارزش عمل تأثیر نمی گذارد.
این اساساً اصل عمل ثابت است که به ساده ترین شکل ممکن توضیح داده شده است.
اکنون، ممکن است فکر کنید که این جالب است و همه چیز، اما چرا سیستم های فیزیکی دقیقاً باید از این اصل پیروی کنند ؟ چرا یک شی باید به جای مسیر دیگری، مسیر عمل ساکن را طی کند؟
اساساً هیچ کس واقعاً پاسخ واقعی این را نمی داند . این کاملاً خنده دار است که چگونه اصل عمل ثابت اساس تقریباً تمام فیزیک مدرن است، اما هیچ کس نمی داند که چرا اتفاقاً درست است.
بهترین چیزی که در اینجا می توانم به شما بدهم نوعی انگیزه است که چرا ممکن است منطقی باشد که جهان از چنین اصلی پیروی کند.
برای من، حداقل، منطقی است که چرا جهان بخواهد (نه اینکه جهان به معنای واقعی کلمه هر چیزی را «خواهد» میخواهد، اما فکر میکنم شما متوجه موضوع شدهاید) چیزها را بهگونهای بهینهسازی کند که چیزی ثابت بماند.
شما می توانید آن را به عنوان سیستم های فیزیکی در نظر بگیرید که تمایل به تکامل به سمت یک حالت تعادل دارند ، درست مانند سیستم های ترمودینامیک که همیشه به گونه ای تکامل می یابند که در آن به حالت تعادل حرارتی می رسد.
همین نوع فرآیند را میتوان به عنوان کاربرد در حرکت نیز در نظر گرفت، اما دقیقاً به عنوان یک مفهوم سطح بالاتر.
خط سیر خاصی که عمل را ثابت می کند، می تواند به عنوان نوعی حالت تعادل کنش در نظر گرفته شود ، زیرا عمل تغییر نمی کند (یعنی در یک نقطه ساکن یا یک حالت تعادل است).
حال، اگر این خیلی انتزاعی به نظر میرسد، نکته اینجا واقعاً این است که هر چیزی که ما میتوانیم در جهان مشاهده کنیم، از اصل کنش ثابت تبعیت میکند ، بنابراین معقولترین چیز این است که آن را به عنوان یک اصل در نظر بگیریم و با آن کار کنیم.
در واقع، درک فعلی از اصل عمل ساکن این است که از تقریب کلاسیک مکانیک کوانتومی ناشی میشود . در مکانیک کوانتومی، ما میتوانیم به ذرات فکر کنیم که تمام مسیرهای ممکن را با تمام مقادیر ممکن عمل میکنند (به طور رسمی، این در فرمول انتگرال مسیر فاینمن ثبت شده است). محتمل ترین مسیر، مسیری است که مقدار ثابتی از کنش دارد - مسیر کلاسیک. این چیزی است که من در کتاب کامل خود مکانیک لاگرانژی برای غیرفیزیکدان (لینک به صفحه کتاب) بیشتر در مورد آن صحبت می کنم.
شهود پشت معادله اویلر-لاگرانژ (+ مشتق گام به گام)
اکنون که اصل عمل ثابت چیست، نکته بعدی یافتن راهی عملی برای استفاده واقعی از آن است.
برای انجام این کار، بیایید دوباره به معنی اصل عمل ثابت از نظر ریاضی فکر کنیم:

این در واقع فقط یک معادله است که باید حل شود و اگر کمی حساب دیفرانسیل و انتگرال بلد باشید انجام آن خیلی سخت نیست (در زیر اشتقاق را پیدا خواهید کرد).
حال، چیزی که به دست می آورید این است که برای ثابت ماندن عمل، لاگرانژ باید چیزی به نام معادله اویلر-لاگرانژ را برآورده کند .
معادله اویلر-لاگرانژ:

معادله فوق مسلماً مهمترین معادله ای است که در مکانیک لاگرانژی به آن نیاز خواهید داشت . این اساساً نسخه لاگرانژی قانون دوم نیوتن است ، همانطور که بعدا خواهیم دید.
استخراج معادله اویلر-لاگرانژ (برای مشاهده بیشتر کلیک کنید)
حال، معادله اویلر-لاگرانژ واقعا چیست؟
به طور خلاصه، معادله اویلر-لاگرانژ شرطی است که لاگرانژ باید آن را برآورده کند تا اصل کنش ثابت صادق باشد. این اساساً همان چیزی است که معادلات حرکت یک سیستم را با یک لاگرانژی خاص ایجاد می کند، درست همانطور که قانون دوم نیوتن برای یک نیروی معین انجام می دهد .
یکی از جزئیات مهم این است که معادله اویلر-لاگرانژ را می توان در واقع تنها با دانستن اینکه لاگرانژ به موقعیت و سرعت بستگی دارد ، بدست آورد، نه چیز بیشتر.
به عبارت دیگر، ما نیازی به دانستن شکل خاص لاگرانژی (TV) نداریم. هر لاگرانژی که تابعی از موقعیت و سرعت است، باید معادله اویلر-لاگرانژ را صرفاً در نتیجه اصل کنش ساکن برآورده کند.
بنابراین، معادله EL در واقع بسیار کلی است، نه فقط نتیجه لاگرانژی که به طور دلخواه انتخاب شده است (در واقع یک معادله بسیار کلی است که برای محاسبه مینیمم و ماکزیمم توابع در یک حوزه ریاضی به نام حساب تغییرات استفاده می شود ).
اگر بخواهیم حرکت را بر حسب انرژی جنبشی و پتانسیل بیان کنیم، لاگرانژ وارد می شود. اینجاست که تلویزیون برای توصیف حرکت به عنوان یک فرآیند پویا ضروری است.
اگر لاگرانژ (L=TV) را به معادله اویلر-لاگرانژ وصل کنیم، به دست می آید:
%7D%7B%5Cpartial%20%5Cdot%20x%7D%3D%5Cfrac%7B%5Cpartial%5Cleft(T-V%5Cright)%7D%7B%5Cpartial%20x%7D)
از آنجایی که انرژی جنبشی به موقعیت و انرژی پتانسیل به سرعت (x با یک نقطه بالای آن) بستگی ندارد، ما با این موارد روبرو هستیم:

علامت منهای در اینجا از علامت منهای در لاگرانژی، L=TV می آید.
این دقیقاً همان چیزی است که قبلاً با مفهوم یک فرآیند بهینهسازی دینامیکی بین انرژی جنبشی و پتانسیل منظور میکردم و دقیقاً به دلیل علامت منفی در اینجا است که از شکل لاگرانژی تلویزیون میآید.
بگذار توضیح بدهم. به دلیل علامت منفی، می توانید تغییرات انرژی پتانسیل را به نوعی مخالف تغییرات انرژی جنبشی در نظر بگیرید .
برای من این کاملا منطقی است. به عنوان مثال، جسمی را در نظر بگیرید که در یک میدان گرانشی سقوط می کند.
وقتی جسم می افتد، به سمت پایین شتاب می گیرد و با افزایش سرعت، انرژی جنبشی آن افزایش می یابد. از سوی دیگر، انرژی پتانسیل آن با نزدیکتر شدن به زمین کاهش مییابد (بر اساس فرمول V=mgh).
بنابراین، یک فرآیند دینامیکی واضح بین انرژی جنبشی و پتانسیل وجود دارد که به ما امکان می دهد حرکت را با استفاده از آنها توصیف کنیم! این زیبایی مکانیک لاگرانژی است. همه چیز به سادگی با تغییرات انرژی توصیف می شود .
همه چیز در مکانیک لاگرانژ به عنوان تغییرات در انرژی های جنبشی و پتانسیل توصیف می شود و رابطه دینامیکی بین این تغییرات توسط معادله اویلر-لاگرانژ ارائه می شود.
حال، نکته بسیار مفید در مورد معادله EL این است که اگر انرژی جنبشی و پتانسیل را بدانیم، معادلات حرکت یک سیستم را به ما می دهد . این درست مانند قانون دوم نیوتن است که اگر هر یک از اجزای نیروها را بدانیم، معادلات حرکت را به ما می دهد.
در واقع یک ارتباط بسیار نزدیک (و به نظر من، بسیار زیبا) بین معادله نیوتن، F=ma، و معادله اویلر-لاگرانژ وجود دارد.
رابطه اویلر-لاگرانژ با قانون دوم نیوتن چگونه است؟
اولاً، می دانیم که قانون دوم نیوتن را می توان بر حسب تکانه به صورت زیر بیان کرد:

جرم را ثابت فرض کردهایم، بنابراین میتوان آن را درون مشتق حرکت داد و سپس از فرمول معمول برای تکانه (p=mv) استفاده کرد.
همچنین، یک ویژگی کلیدی نیروها این است که هر نیروی محافظه کارانه را می توان بر حسب انرژی پتانسیل بیان کرد (همانطور که در این مقاله توضیح داده شد ):

به طور کلی، این گرادیان منفی انرژی پتانسیل است ، اما این فقط در جهت x است.
سپس می توانیم F=ma را به صورت زیر بیان کنیم:

اکنون بیایید این را با معادله اویلر-لاگرانژ مقایسه کنیم و مشخص خواهد شد که در واقع چقدر شبیه هستند:


در واقع، اگر بخواهیم انرژی جنبشی را به سادگی 1/2mv 2 انتخاب کنیم ، معادله اویلر-لاگرانژ دقیقاً F=ma را تولید خواهد کرد.
استخراج F=ma از معادله اویلر-لاگرانژ (برای مشاهده بیشتر کلیک کنید)
بعداً در مقاله، من همچنین چند مثال عملی از چگونگی استفاده از معادله اویلر-لاگرانژ و دلیل مفید بودن آن (و نه فقط مکانیک نیوتنی با مراحل اضافی پیچیده تر) را پوشش خواهم داد.
نحوه حل مسائل با استفاده از مکانیک لاگرانژی (روش گام به گام)
به طور کلی، حل هر مشکلی در مکانیک حول محور یافتن معادلات حرکت برای یک سیستم خاص مورد علاقه است.
یکی از کاربردها و مزایای اصلی مکانیک لاگرانژی این است که یک روش سیستماتیک برای استخراج معادلات حرکت با تلاش بسیار کم (در مقایسه با چیزی مانند استفاده از F=ma) حتی برای سیستم های بسیار پیچیده وجود دارد.
اساساً، نحوه ساخت لاگرانژی (اصطلاح انرژی جنبشی و پتانسیل) برای یک سیستم مشخص می کند که چه نوع فرمول هایی را از آن استخراج خواهید کرد. به طور کلی، این به شکل L=TV خواهد بود.
مکانیک لاگرانژی به ویژه برای سیستم های پیچیده تر مفید است، زیرا تنها کاری که باید انجام دهید این است که انرژی های جنبشی و پتانسیل را برای هر جسم در سیستم تعریف کنید. بقیه فقط معادله اویلر-لاگرانژ را اعمال می کنند.
روند کلی گام به گام برای یافتن معادلات حرکت یک سیستم کم و بیش به این صورت است:
- مجموعه ای از مختصات مناسب (= مختصات تعمیم یافته ) را برای مسئله خاص پیدا کنید. اینها ممکن است مختصات دکارتی معمولی (x، y، z) باشند، اما میتوان از سیستمهای مختصاتی مانند مختصات کروی (r، θ، φ) نیز استفاده کرد.
- لاگرانژ را از طریق مختصات تعمیم یافته تعریف کنید . برای اجسام متعدد در یک سیستم، لاگرانژی مجموع تفاوت بین انرژی جنبشی و انرژی بالقوه هر جسم خواهد بود:

معمولا ساده تر است که ابتدا لاگرانژ را در مختصات دکارتی تعریف کنید و سپس به هر مختصات تعمیم یافته ای که استفاده می کنید تبدیل کنید!
- معادلات اویلر-لاگرانژ را بر روی لاگرانژ اعمال کنید . برای هر مختصاتی که برای سیستم انتخاب کرده اید، یک معادله اویلر-لاگرانژ خواهید داشت.
- معادلات حرکت را ساده و حل کنید . در این مرحله، شما باید برای هر مختصاتی که دارید یک معادله دیفرانسیل مرتبه دوم داشته باشید.
در اینجا، من به استفاده از مختصات تعمیم یافته اشاره کرده ام . اینها یکی از مزیت های کلیدی مکانیک لاگرانژی است که چنین روش های ظریف و ساده ای را برای حل مسئله امکان پذیر می کند. بعداً همه چیز را در مورد اینها توضیح خواهم داد.
مثال عملی: حرکت پرتابه با مکانیک لاگرانژی (برای مشاهده بیشتر کلیک کنید)
شایان ذکر است که برای حل انواع مشکلاتی که می توانید با استفاده از مکانیک لاگرانژی حل کنید، محدودیت هایی نیز وجود دارد.
برای مثال، نیروهای غیرمحافظهکار را نمیتوان مستقیماً از لاگرانژی استخراج کرد ، زیرا آنها بر حسب انرژی پتانسیل تعریف نشدهاند.
نمونه ای از آنها نیروهای اصطکاک هستند، مانند نیروی ویسکوز در یک سیال و برای این نوع نیروهای غیر محافظه کار، معمولاً بازگشت به مکانیک نیوتنی آسان تر است (این در این مقاله توضیح داده شده است ).
با این حال، هنوز راههایی برای اصلاح مکانیک لاگرانژی وجود دارد که این نیروها را شامل شود، اما آنها نمیتوانند مستقیماً از اصل کمترین عمل ناشی شوند.

اگر میخواهید درک عمیقتری از مکانیک لاگرانژی به دست آورید، توصیه میکنم کتاب مکانیک لاگرانژی من برای غیرفیزیکدان (لینک به صفحه کتاب) را بررسی کنید. این کتاب همه چیزهایی را که باید در مورد مکانیک لاگرانژی بدانید - و بیشتر به شما آموزش می دهد.
نمونه های بیشتری از استفاده از مکانیک لاگرانژی!
شاید هنوز مشخص نباشد که مکانیک لاگرانژی واقعاً چگونه در موقعیتهای پیچیدهتر استفاده میشود. بهترین راه برای درک این موضوع از طریق مثال هایی است که در ادامه بیشتر آنها را خواهید یافت.
آونگ ساده
آونگ ساده سیستمی متشکل از جرمی در انتهای یک میله صلب است که تحت تأثیر گرانش اجازه دارد در یک صفحه تاب بخورد. طول میله L، جرم «باب آونگ» m و شتاب گرانشی به سمت پایین g (ثابت) است.
هدف ما در اینجا با مکانیک لاگرانژی بدست آوردن معادلات حرکت برای این سیستم است .
راههای زیادی برای انجام این کار وجود دارد – یکی از این راهها توصیف چگونگی تغییر مختصات x و y باب با زمان است، اما این لزوما سادهترین راه نیست. ساده ترین راه استفاده از یک زاویه است، زیرا برای توصیف موقعیت باب در هر زمان کافی است.
در اینجا راه اندازی است - ما با قرار دادن آونگ در یک سیستم مختصات x،y به طوری که میله به مبدا متصل شود، شروع می کنیم. من همچنین زاویه نسبت به عمود (محور y) را با θ نشان خواهم داد.

کاری که می خواهیم انجام دهیم این است که توضیح دهیم که چگونه زاویه θ با زمان تغییر می کند - بنابراین، در اینجا تابع θ(t) است - با ساختن یک لاگرانژ برای این سیستم و اعمال معادلات اویلر-لاگرانژ ، درست مانند آنچه قبلا در مورد یک پرتابه در زیر متوجه خواهید شد که دقیقا چگونه این کار را انجام دهید.
حل کامل آونگ ساده
هواپیمای شیبدار متحرک
صفحه شیبدار متحرک شامل بلوکی به جرم m است که روی شیبدار شیبدار جرمی M قرار دارد. شتاب گرانشی قدر g به سمت پایین وجود دارد.
صفحه با زاویه α نسبت به زمین کج می شود، به طوری که بلوک شروع به لغزش به پایین سطح شیب دار می کند. طول کل رمپ L است. علاوه بر این، خود سطح شیب دار مجاز است در جهت افقی حرکت کند.
هدف ما این است که بفهمیم چگونه بلوک و سطح شیب دار با گذشت زمان شروع به حرکت می کنند - به عبارت دیگر، معادلات حرکت را برای سیستم کامل پیدا کنیم .
ما با قرار دادن سیستم در یک سیستم مختصات دکارتی که سطح شیبدار در ابتدا در مبدا قرار دارد، شروع می کنیم. برای مختصاتی که مایل به توصیف آن هستیم، مختصات x سطح شیب دار و جابجایی s بلوک اندازه گیری شده از بالای سطح شیب دار را انتخاب می کنیم:

بنابراین، ما می خواهیم معادلات حرکت مختصات x و s را به عنوان تابعی از زمان پیدا کنیم. راه حل کامل را در زیر پیدا خواهید کرد.
حل کامل صفحه مایل متحرک
ویژگی های کلیدی مکانیک لاگرانژی
در ادامه، نگاهی به برخی از جنبه های مهم مکانیک لاگرانژ خواهیم انداخت که آن را منحصر به فرد و قدرتمند می کند.
همه چیزهایی که در اینجا مورد بحث قرار می گیرد با جزئیات بسیار بیشتری در کتاب کامل مکانیک لاگرانژی من پوشش داده شده است، که می توانید در اینجا اطلاعات بیشتری در مورد آن بیابید . در آنجا، ما همچنین به برخی از مسائل مربوط به مکانیک نیوتنی و اینکه چگونه مکانیک لاگرانژی به طور طبیعی آنها را برطرف می کند، نگاه می کنیم.
مختصات تعمیم یافته
معمولاً معادله اویلر-لاگرانژ بر حسب چیزی به نام مختصات تعمیم یافته نوشته میشود که با q نشان داده میشوند (شاخص i در اینجا به سادگی نشاندهنده تعداد مختصات شماست؛ برای مثال، با چند مختصات مختلف، یک EL دارید. معادله برای q 1 ، دیگری برای q 2 و غیره):

اما این مختصات تعمیم یافته دقیقاً چیست؟ اینها (همانطور که از نام ممکن است نشان دهد) انواع کلی تری از مختصات هستند، آنهایی که آزادی بسیار بیشتری را در انتخاب مختصات و سیستم مختصات ما اجازه می دهند .
ببینید، در مکانیک لاگرانژی، ما محدود به مجموعه خاصی از مختصات مانند سیستم مختصات x، y، z - نیستیم.
در عوض، میتوانید برای مثال، زاویه θ را به عنوان مختصات خود در مسئلهای که شامل حرکت چرخشی است، داشته باشید.
نکته زیبا در مورد مکانیک لاگرانژی این است که روشهای حل مسئله (که قبلاً در مورد آن صحبت شد) دقیقاً یکسان عمل میکنند، صرف نظر از اینکه از چه مختصاتی میخواهید استفاده کنید .
این مختصات تعمیم یافته مزایای بسیار مفیدی برای مختصات دکارتی معمولی دارند (البته در صورت تمایل می توانید از مختصات دکارتی استفاده کنید):
- مختصات تعمیم یافته به ما این امکان را می دهد که به طور ضمنی شامل تمام اطلاعات در مورد نحوه رفتار یک سیستم باشیم (به عنوان مثال، انتخاب مختصات قطبی (r و θ) برای یک آونگ قبلاً شامل این واقعیت است که آونگ در یک دایره حرکت می کند؛ فقط با استفاده از مختصات دکارتی، شما می توانید باید محدودیت های خاصی را بر سیستم تحمیل کند).
- انتخاب درست مختصات تعمیم یافته می تواند یک محاسبه را بسیار ساده کند .
- مختصات تعمیم یافته می تواند تعداد متغیرها/معادلات مورد نیاز برای حل یک مسئله خاص را کاهش دهد (به عنوان مثال، انتخاب تنها زاویه θ برای یک آونگ برای یافتن معادلات حرکت کافی است، در حالی که در مختصات دکارتی، شما به هر دو مورد نیاز دارید. مختصات x و y).
- مختصات تعمیم یافته اجازه می دهد تا کمیت های مختلف به راحتی به شکل کلی تر بیان شوند (سرعت تعمیم یافته، تکانه تعمیم یافته، نیروهای تعمیم یافته و غیره).
من در واقع یک مقاله کامل در مورد مختصات تعمیم یافته و نحوه استفاده از آنها (و همچنین نمونه هایی از آن) دارم که در اینجا خواهید یافت. من به شدت توصیه می کنم آن را بررسی کنید، زیرا مختصات تعمیم یافته یکی از مهم ترین بخش های مکانیک لاگرانژی است.
تکانه تعمیم یافته
همانطور که شروع به استفاده از معادله اویلر-لاگرانژ می کنید، الگوهای واضحی وجود دارد که ظاهر می شوند.
جالب ترین آنها یکی از اصطلاحات معادله اویلر-لاگرانژ است که همیشه به نوعی کمیتی شبیه به تکانه می دهد. این اصطلاح، در واقع، تعریف حرکت تعمیم یافته است :

تکانه تعمیم یافته گاهی اوقات تکانه متعارف نیز نامیده می شود.
وقتی وارد مکانیک پیشرفتهتر میشوید، تکانه منظم (که گاهی اوقات تکانه جنبشی نیز نامیده میشود ) دیگر کافی نخواهد بود.
در عوض، ما این چیز را داریم به نام تکانه تعمیم یافته ، که با p i نشان داده می شود (در اینجا i نشان دهنده این واقعیت است که هر تکانه تعمیم یافته p i همیشه با مختصات تعمیم یافته خاصی q i در سیستم همراه است):

با این حال، این حرکت تعمیم یافته واقعاً برای چه چیزی مفید است؟ خوب، اولین دلیل این است که به ما امکان می دهد به سرعت لحظه های مختلف را در یک سیستم شناسایی کنیم ، تقریباً با عبارت زیر:
اگر لاگرانژی مشتق زمانی از مقداری مختصات تعمیم یافته q i داشته باشد ، باید یک تکانه تعمیم یافته p i مرتبط با مختصات q i وجود داشته باشد .
در زیر نمونههایی از این که این لحظههای تعمیمیافته چگونه به نظر میرسند و چگونه از لاگرانژی به دست میآیند را آوردهام (توجه داشته باشید که این تعریف حتی در خارج از مکانیک کلاسیک نیز معتبر است).
نمونه هایی از مومنتای تعمیم یافته (برای مشاهده بیشتر کلیک کنید)
نکته مفید دیگر در مورد تکانه تعمیم یافته این است که به ما امکان می دهد مفهوم تکانه را به بسیاری از موارد مختلف تعمیم دهیم که در آن p=mv معمولی دیگر کار نمی کند.
من قبلاً نمونهای از بالا را نشان دادم، که به ما امکان داد به راحتی فرمول حرکت نسبیتی را استخراج کنیم (همچنین اطلاعات بیشتری در مورد آن در این مقاله خواهید یافت ).
نیروهای تعمیم یافته
همانطور که اینها لحظه های تعمیم یافته هستند، چیزهایی نیز وجود دارد که به آنها نیروهای تعمیم یافته می گویند .
اکنون، اینها مستقیماً از طریق لاگرانژ بیان نمیشوند، بلکه با استفاده از مختصات تعمیمیافته بیان میشوند . برای بیان قوانین حرکت با استفاده از آنها.
نیروهای تعمیم یافته به این صورت تعریف می شوند (که با Q مشخص می شود و شاخص i با مختصات تعمیم یافته خاص q i مرتبط است ):

نیروهای تعمیم یافته در واقع فقط نیروهای نیوتنی معمولی هستند، اما به مختصات تعمیم یافته تبدیل شده اند، که مایلیم در مکانیک لاگرانژی از آنها استفاده کنیم.
حال، ممکن است در حال حاضر کمی انتزاعی به نظر برسد و همچنین ممکن است بپرسید؛ چرا ما حتی به این نیروهای تعمیم یافته نیاز داریم اگر مکانیک لاگرانژی تماماً در مورد استفاده از انرژی است؟
خوب، پاسخ این است که ما این کار را نمی کنیم - معمولا. استثناهای این مورد شامل ترکیب اصطکاک و سایر نیروهای وابسته به سرعت در مکانیک لاگرانژی است.
برای نیروهای اصطکاک و غیر محافظه کار به طور کلی، باید آنها را به صورت دستی در معادلات اویلر-لاگرانژ به عنوان نیروهای تعمیم یافته اضافه کنیم (نیروهای اصطکاک تعمیم یافته که با Q i f نشان می دهم ) مانند این:

اکنون، نحوه برخورد با این نیروهای اصطکاک در مکانیک لاگرانژی با استفاده از چیزی به نام تابع اتلاف است که اساساً انرژی «از دست رفته» ناشی از اصطکاک را محاسبه میکند.
من همه چیز را در مورد نحوه ترکیب اصطکاک در مکانیک لاگرانژی توضیح می دهم و همچنین مجموعه ای از مثال های مفید را در این مقاله نشان می دهم .
کاربرد مفید دیگر نیروهای تعمیم یافته برای یافتن نیروهای محدودیت (مانند کشش یا نیروی نرمال یک سطح) است که از روش ضرب کننده لاگرانژ استفاده می کند . در اینجا شما میتوانید اطلاعات بیشتری راجع به آن بخوانید .
همچنین، نیروهای تعمیم یافته در واقع امکان فرمول بندی دیگری از مکانیک لاگرانژی را فراهم می کنند (این عملاً فقط یک روش متفاوت برای استخراج معادله اویلر-لاگرانژ است) که از اصل کنش ساکن استفاده نمی کند.
در عوض، از چیزی به نام اصل کار مجازی و اصل دالامبر استفاده می کند تا اساساً مکانیک لاگرانژی را استخراج کند.
ریاضیات این کمی انتزاعیتر است و در حال حاضر واقعاً مهم نیست، بنابراین من فقط بیان میکنم که این فرمول وجود دارد و آن را رها میکنم.
با این حال، اگر می خواهید درباره نیروهای تعمیم یافته، اصطکاک و نیروهای غیر محافظه کار در مکانیک لاگرانژی اطلاعات بیشتری کسب کنید ، من یک فصل کامل دارم که دقیقاً این موضوعات را با جزئیات کتابم مکانیک لاگرانژی برای غیرفیزیکدان را پوشش می دهد (لینک به صفحه کتاب ).
اینها موضوعاتی هستند که حتی بسیاری از دروس دانشگاهی در مورد مکانیک لاگرانژی پوشش نمی دهند، به همین دلیل است که من به طور خاص می خواستم آنها را در دوره خود لحاظ کنم. بنابراین، آن را بررسی کنید!
اسکالرها در مقابل بردارها
در فرمول لاگرانژی مکانیک کلاسیک، همه چیز فقط با انرژی جنبشی و پتانسیل توصیف میشود و هر دو را میتوان به خوبی در یک معادله، لاگرانژی، جای داد.
سودمندی این به صراحت زمانی مشخص می شود که آن را با فرمول های نیروهای مختلف مقایسه کنید، جایی که شما فقط یک سری چیزهای مختلف دارید که در نگاه اول، حتی به نظر نمی رسد که به هیچ وجه واضح به هم متصل باشند.
در مکانیک لاگرانژی، این موضوع متفاوت است، زیرا همه چیز به وضوح فقط به چند مفهوم مرتبط است. یعنی مفاهیم انرژی و کنش , لاگرانژی و اصل کنش ساکن . سپس همه اینها با معادله اویلر-لاگرانژ جمع می شوند .
نکته جالب دیگر در مورد مکانیک لاگرانژ و این واقعیت که ما فقط از انرژی به جای نیرو استفاده می کنیم، این واقعیت است که نیروها کمیت های برداری هستند ، در حالی که انرژی ها کمیت های اسکالر هستند .
این بدان معنی است که نیروها همیشه جهت و مقدار دارند ، در حالی که انرژی ها فقط یک مقدار دارند (به معنای ابتدایی؛ در نسبیت، این به عنوان یک تعریف کافی نخواهد بود).
این یک مزیت آشکار استفاده از انرژی به جای نیرو است، زیرا فقط بسیاری از مشکلات را از بین می برد، مانند تجزیه نیروها به اجزای برداری آنها یا نگرانی در مورد محاسبه نقطه ای نیروها، زوایای بین بردارها و غیره.
همچنین، بردارها در مختصات به اصطلاح منحنی (به عنوان مثال، سیستم مختصات قطبی که دارای خطوط مختصات منحنی است) بسیار دردسرساز هستند . نکته خوب این است که مکانیک لاگرانژی طبیعتاً تمام مشکلات مربوط به این موضوع را از بین می برد.
چرا به مکانیک لاگرانژی نیاز داریم؟
ما قبلاً در مورد مزایای مکانیک لاگرانژی صحبت کردهایم، اما در صورتی که هنوز کاملاً مشخص نیست، در اینجا فهرستی از مهمترین جنبههای مکانیک لاگرانژی وجود دارد که آن را بسیار مفید میکند:
- محدودیتها : معمولاً وقتی میخواهیم یک سیستم را به نحوی محدود کنیم - مثلاً یک جسم در امتداد یک سطح حرکت میکند - باید نیروهای محدودیتی را اضافه کنیم که کار کردن با آنها دشوار است. مکانیک لاگرانژی همه اینها را با معرفی مختصات تعمیم یافته حذف می کند .
- مختصات منحنی : در سیستم های مختصاتی که بردارهای پایه می توانند از نقطه ای به نقطه دیگر تغییر کنند - برای مثال مختصات قطبی - توصیف حرکت با استفاده از بردارها بسیار پیچیده تر است. مکانیک لاگرانژی این را بسیار ساده می کند، زیرا ما فقط باید با اسکالرها کار کنیم .
- تقارن ها و قوانین بقا : مکانیک لاگرانژی راهی مستقیم برای تجزیه و تحلیل تقارن های سیستم های فیزیکی و شناسایی قوانین بقا در آنها ارائه می دهد. این قضیه قضیه نوتر نامیده می شود که می توانید در اینجا اطلاعات بیشتری درباره آن بخوانید .
- کاربردها در فیزیک مدرن : تقریباً همه چیز در مکانیک لاگرانژی به سایر حوزه های فیزیک مدرن منتقل می شود. این موضوع مکانیک لاگرانژی را به یکی از با ارزش ترین ابزارها در درک و به طور کلی انجام فیزیک مدرن تبدیل می کند.
مکانیک لاگرانژی در فیزیک مدرن و نظریه میدان
در حال حاضر، استفاده از مکانیک لاگرانژی برای یافتن معادلات حرکت برای سیستمهای مختلف بسیار جالب است، اما واقعاً اهمیت این فرمولبندی در زمینه کلاسیک به اندازه کافی عدالت داده نمیشود.
فرمول لاگرانژی در واقع سنگ بنای بسیاری از فیزیک مدرن است و در واقع زیربنای هر نظریه ای است که تاکنون می دانیم (این حتی یک اغراق هم نیست).
دلیل واقعی این امر این است که اصل کنش ثابت به طور اتفاقی در زمینهها نیز صدق میکند، بنابراین اساس اکثر نظریههای میدانی را تشکیل میدهد.
از سوی دیگر، تقریباً تمام نظریههای مدرن فیزیک نوعی نظریه میدان هستند (نسبیت عام، نظریه میدان کوانتومی، الکترومغناطیس و غیره همگی نظریههای میدان هستند). این اصل عمل را برای تقریباً همه چیز اساسی می کند.
حال، فرمول لاگرانژی نظریه میدان واقعاً کاملاً انتزاعی است و نمی توان در اینجا به تفصیل آن را پوشش داد. در صورتی که مایلید در مورد آن بیشتر بدانید، می توانید این کار را از کتاب دوم من نظریه میدان برای غیرفیزیکدان که در اینجا یافت شده است انجام دهید .
بیایید فقط به اصول اولیه در اینجا بپردازیم. اساساً، بیشتر مواردی که در مورد مکانیک لاگرانژی در این مقاله در مورد آن صحبت کردیم، به شکلی در مورد نظریه میدان نیز کاربرد دارد.
اول، به جای اینکه یک لاگرانژی ساده برای میدان ها وجود داشته باشد، چیزی به نام چگالی لاگرانژی (که با یک L مجعد مشخص می شود) وجود دارد . چگالی لاگرانژی تابعی از میدان و اولین مشتقات آن است (درست مانند لاگرانژی معمولی تابعی از موقعیت و سرعت است):
)
این ∂ µ را 4-gradient (یعنی معادل نسبیتی یک گرادیان منظم) می نامند، که به سادگی یک مشتق wrt هم مکان و هم زمان است (زیرا میدان به فضا و زمان بستگی دارد).
عمل برای یک میدان این است که چگالی لاگرانژی یکپارچه است، نه در طول زمان، بلکه در فضازمان (این را با d 4 x نشان میدهیم ). این عمل نیز باید ثابت باشد (یعنی δA=0):
d%5E4x%3D0)
این اصل عمل ثابت است، اما در یک میدان اعمال می شود.
نتیجه این شرط معادله اویلر-لاگرانژ را برای میدان ϕ به دست میدهد که دینامیک آن را به طور کامل توصیف میکند. سپس معادله میدان را می توان حل کرد تا نحوه رفتار میدان به عنوان تابعی از فضا و زمان را دریابیم.
حالا، اگر این موضوع از سر شما گذشت، نگران نباشید. نکته اصلی در اینجا این است که اصل عمل ثابت در سراسر فیزیک مدرن استفاده می شود.
شاید مهمترین کاربرد فرمول لاگرانژی نظریه میدان برای نظریه میدان کوانتومی باشد. برای مثال، شاید قبلاً مدل استاندارد لاگرانژی معروف را دیده باشید که درک فعلی ما از فیزیک ذرات را توضیح میدهد:
)
این در واقع یک نسخه واقعا فشرده از مدل کامل استاندارد لاگرانژی است که در شکل کامل آن بسیار بد به نظر می رسد.
با این حال، نکته این است که این لاگرانژی دینامیک دسته ای از فیلدها را در مدل استاندارد (ψ و φ، میدان اسپینور دیراک و فیلد هیگز، برای نام بردن یک زوج) رمزگذاری می کند و سپس می تواند برای به دست آوردن دینامیک کامل استفاده شود. از هر زمینه
یکی دیگر از کاربردهای مهم لاگرانژی مرتبط با فیزیک مدرن از نسبیت عام می آید، جایی که معادلات میدان انیشتین را می توان از چیزی به نام کنش اینشتین-هیلبرت استخراج کرد . من در واقع مشتق کامل را در این مقاله ارائه می کنم .
اگر میخواهید مدل استاندارد لاگرانژی و نظریه میدان کوانتومی را بهتر درک کنید، مطمئناً باید کتاب کامل نظریه میدان برای غیرفیزیکدان (لینک به صفحه کتاب) را بررسی کنید . این کتاب عمدتاً به توصیف لاگرانژی نظریههای میدان اختصاص دارد - همه چیز از اینکه چرا ما از لاگرانژی استفاده میکنیم تا اینکه این لاگرانژیها چگونه ساخته میشوند و چگونه همه چیز را در مورد میدانها و ذرات و همچنین خواص و پویایی آنها توصیف میکنند. سپس هر آنچه را که بحث می کنیم برای درک نظریه های میدان کوانتومی ، فیزیک ذرات ، نسبیت و فیزیک مدرن به طور کلی اعمال می شود!
قضیه نوتر و قوانین حفاظت
یک ایده بسیار مهم که ارتباط نزدیکی با مکانیک لاگرانژی دارد، قضیه نوتر است.
به بیان ساده، قضیه نوتر راهی کلی برای استخراج قوانین بقای هر سیستم فیزیکی به ما می دهد. این کار با تجزیه و تحلیل تقارن های موجود در سیستم انجام می شود و می توان به راحتی با استفاده از لاگرانژ به صورت ریاضی فرموله کرد.
در حال حاضر، چیزهای زیادی برای تعریف منظور ما از تقارن در فیزیک و همچنین ارتباط دقیق آنها با قوانین حفاظت وجود دارد، بنابراین ما در اینجا به جزئیات بیشتر نخواهیم پرداخت.
برای درک دقیق این ایده ها، توصیه می کنم راهنمای کامل من در مورد قضیه نوتر را بخوانید . همه چیزهایی را که باید بدانید به روشی مبتدی به شما می آموزد و همچنین مثال های زیادی را به شما نشان می دهد (و اکنون باید پیش نیازهای لازم را در مورد مکانیک لاگرانژی برای درک آن داشته باشید!).
همچنین یک فصل کامل در مورد قضیه نوتر در کتاب کامل من مکانیک لاگرانژی برای غیرفیزیکدان وجود دارد ، در صورتی که واقعاً بخواهید درک خود را به سطح بعدی ببرید.
مثالها و کاربردهای مکانیک لاگرانژی (PDF رایگان)
در زیر، نمونههایی را خواهید یافت که امیدواریم کاربردهای مکانیک لاگرانژی را در عمل نشان دهند (این یک PDF رایگان است، خودتان آن را دانلود کنید).
PDF رایگان را از اینجا دریافت کنید .
در PDF، ما به عنوان مثال، به دنبال یافتن لاگرانژ و معادلات حرکت برای سیستمهایی مانند آونگ ساده و آونگ کروی هستیم. ما همچنین رفتار این سیستم ها را تجزیه و تحلیل می کنیم.
با این حال، جالب ترین مثالی که به آن پرداخته شد، مسئله کپلر با استفاده از مکانیک لاگرانژی است.
مسئله کپلر یکی از اساسی ترین مسائل فیزیک است، شاید در تمام دوران ها و با حل حرکت دو جرم عظیم (مانند سیارات) که تحت تأثیر گرانش به دور یکدیگر می چرخند، مربوط می شود.
کجا می توان درباره مکانیک لاگرانژ بیشتر بدانید؟ (منابع پیشنهادی)
اگر این مقاله جالب بود و میخواهید در مورد مکانیک لاگرانژی و عمق واقعی این فرمولبندی اطلاعات بیشتری کسب کنید، قدم بعدی این است که به دنبال منابع دیگر باشید.
اکنون، قبل از مطالعه مکانیک لاگرانژی، شایان ذکر است که مکانیک لاگرانژی آسان نیست . این مقاله فقط سطح مکانیک لاگرانژی را نشان می دهد.
در گذشته، من فقط به مردم می گفتم که می توانند مکانیک لاگرانژی را فقط با خواندن مقالات اینترنتی یا تماشای ویدیوهای یوتیوب در آن یاد بگیرند. در حالی که این برای برخی افراد ممکن است، من متوجه شده ام که این بهترین راه برای انجام آن نیست.
برای اکثر مردم، اگر منبع اختصاصی و کاملی برای آن داشته باشند، در واقع میتوانند مکانیک لاگرانژی (و همیلتونی) را بسیار سریعتر و عمیقتر بیاموزند .
البته، شما آزادید هر منبعی را که می خواهید انتخاب کنید، اما اگر توصیه من را می خواهید، کتاب جدید من، مکانیک لاگرانژی برای غیرفیزیکدان (پیوند به صفحه کتاب)، چیزی است که کاملاً دوست خواهید داشت. این همان کتابی است که من شخصاً آرزو داشتم در هنگام شروع یادگیری فیزیک داشته باشم.
این کتاب ابتدا مکانیک نیوتنی پایه را پوشش می دهد و همچنین برخی از مسائل مربوط به قوانین نیوتن را به عنوان انگیزه ای برای معرفی مکانیک لاگرانژی مورد بررسی قرار می دهد. سپس حساب تغییرات را مورد بحث قرار میدهیم ، حوزه مکانیک لاگرانژی ریاضی مبتنی بر آن است.
پس از این، فصلهای زیر به جنبههای مختلف مکانیک لاگرانژی مانند مختصات تعمیمیافته، لحظهها و نیروها، پتانسیلهای وابسته به سرعت، دینامیک محدود، توابع اتلاف، تقارنها، قوانین حفاظت و همچنین نحوه حل مسائل مکانیک لاگرانژی در کارآمدترین روشها میپردازند. مسیر.

اگر میخواهید درک عمیقتری از مکانیک لاگرانژی به دست آورید، توصیه میکنم کتاب مکانیک لاگرانژی من برای غیرفیزیکدان (لینک به صفحه کتاب) را بررسی کنید. این کتاب همه چیزهایی را که باید در مورد مکانیک لاگرانژی بدانید - و بیشتر به شما آموزش می دهد.
من همچنین یک "بخش دوم" از کتاب مکانیک لاگرانژی دارم که کاملاً به نظریه میدان اختصاص دارد . این کتاب نظریه میدان برای غیرفیزیکدان نام دارد (لینک به صفحه آمازون آن) و اساساً ادامه مستقیم کتاب مکانیک لاگرانژی است که در بالا ذکر شد.
ما همه چیز را پوشش می دهیم، از چرایی و چگونگی ساخت نظریه های میدان نسبیتی گرفته تا کاربردها و پیش بینی های فیزیکی آنها و همچنین اینکه چگونه همه اینها به ما اجازه می دهد تا بسیاری از حوزه های فیزیک مدرن را توصیف کنیم (مانند مدل استاندارد و فیزیک ذرات).

ویل هیروونن
من بنیانگذار فیزیک عمیق هستم، وبسایتی که برای کمک به کسانی که سعی در خودآموزی فیزیک دارند، ایجاد کردم، زیرا این همان کاری است که من خودم به آن علاقه دارم. من دوست دارم آنچه را که آموخته ام به روشی قابل فهم و آرام توضیح دهم و تا زمانی که در مورد شگفتی های فیزیک بیشتر بدانم به این کار ادامه خواهم داد.
https://profoundphysics.com/lagrangian-mechanics-for-beginners/






یک مبنای گسسته را تشکیل می دهد، بنابراین هر حالتی یک جمع است
که در آن c i اعداد مختلط هستند به طوری که | c i | 2 = c i * c i احتمال اندازه گیری حالت است
، و مجموعه مربوط به مقادیر ویژه a i نیز گسسته است - یا متناهی یا قابل شمارش نامتناهی . در این حالت، حاصل ضرب درونی دو حالت ویژه توسط
، کجا
دلتای کرونکر را نشان می دهد . با این حال،
هر حالتی که یک پایه پیوسته را تشکیل می دهد، یک انتگرال است
که در آن c ( φ ) یک تابع پیچیده است به طوری که | ج (φ)| 2 = c (φ) * c (φ) احتمال اندازه گیری حالت است
، و مجموعه ای نامتناهی از مقادیر ویژه a وجود دارد . در این حالت، حاصلضرب داخلی دو حالت ویژه به صورت تعریف می شود
، اینجا کجاست
دلتای دیراک را نشان می دهد .

























![{\displaystyle \left[{\hat {A}},{\hat {B}}\right]={\hat {A}}{\hat {B}}-{\hat {B}}{\hat {A}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/fa7917e45fa532ccc9cfd210a2ac545e0b60b093)
![{\displaystyle \left[{\hat {A}},{\hat {B}}\right]\psi ={\hat {A}}{\hat {B}}\psi -{\hat {B} }{\hat {A}}\psi .}](https://wikimedia.org/api/rest_v1/media/math/render/svg/7967ebafc93ebd938b2cac7691d783e42e8e67c6)
![{\displaystyle \left[{\hat {A}},{\hat {B}}\right]\psi =0,}](https://wikimedia.org/api/rest_v1/media/math/render/svg/02d5d62427be967a2826edc5f9cf45ea1d2c25d3)
![{\displaystyle {\begin{aligned}\left[{\hat {A}},{\hat {B}}\right]\psi &={\hat {A}}{\hat {B}}\psi -{\hat {B}}{\hat {A}}\psi \\&=a(b\psi )-b(a\psi )\\&=0.\\\end{تراز شده}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/185fc76a611137a886e1661f483db74dd073084d)
![{\displaystyle \left[{\hat {A}},{\hat {B}}\right]\psi \neq 0,}](https://wikimedia.org/api/rest_v1/media/math/render/svg/b87d66f7edae65001f4b897bc0184bdc896709a0)
![{\displaystyle \Delta A\Delta B\geq \left|{\frac {1}{2}}\langle [A,B]\rangle \right|}](https://wikimedia.org/api/rest_v1/media/math/render/svg/815d659c43d441760fba8fb8c923b4831b78c06e)




 .
.


















 و زاویه θ .
و زاویه θ .
 اپراتور هویت است،
اپراتور هویت است، یک پارامتر با مقدار کمی است و
یک پارامتر با مقدار کمی است و به تبدیل در دست بستگی دارد و
به تبدیل در دست بستگی دارد و  . اگر
. اگر بی نهایت کوچک است، پس ممکن است بنویسیم
بی نهایت کوچک است، پس ممکن است بنویسیم

 مولد گروه ترجمه است که در این مورد عملگر مشتق است . بنابراین گفته می شود که مولد ترجمه ها مشتق است.
مولد گروه ترجمه است که در این مورد عملگر مشتق است . بنابراین گفته می شود که مولد ترجمه ها مشتق است.













 ،
، .
. به طوری که یک یادگاری آشناتر "BAC - CAB" به دست می آید، مانند "پشت کابین".
به طوری که یک یادگاری آشناتر "BAC - CAB" به دست می آید، مانند "پشت کابین".



 .
. جزئی از
جزئی از  از رابطه زیر بدست می آید:
از رابطه زیر بدست می آید:
 و
و اجزای
اجزای 
 [5]
[5]
![{\displaystyle \mathbf {a} \cdot [\mathbf {b} \times \mathbf {c} ]=\varepsilon _{ijk}a^{i}b^{j}c^{k}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/1f5abca130937a2012b0f42bf0a587074f8f08d6)
![{\displaystyle (\mathbf {a} \times [\mathbf {b} \times \mathbf {c} ])_{i}=\varepsilon _{ijk}a^{j}\varepsilon ^{k\ell m }b_{\ell }c_{m}=\varepsilon _{ijk}\varepsilon ^{k\ell m}a^{j}b_{\ell }c_{m},}](https://wikimedia.org/api/rest_v1/media/math/render/svg/d4b9001d4ed44c60bef2063869e9f9f04f79a66f)
 -امین جزء بردار حاصل. این را می توان با انجام یک انقباض بر روی نمادهای لوی-سویتا ساده کرد .
-امین جزء بردار حاصل. این را می توان با انجام یک انقباض بر روی نمادهای لوی-سویتا ساده کرد . جایی که
جایی که تابع دلتای کرونکر است (
تابع دلتای کرونکر است ( چه زمانی
چه زمانی و
و چه زمانی
چه زمانی  ) و
) و تابع دلتای کرونکر تعمیم یافته است . ما میتوانیم این اتحاد را با تشخیص این شاخص مشخص کنیم
تابع دلتای کرونکر تعمیم یافته است . ما میتوانیم این اتحاد را با تشخیص این شاخص مشخص کنیم  صرفا خروج خلاصه خواهد شد
صرفا خروج خلاصه خواهد شد . در ترم اول تعمیر می کنیم
. در ترم اول تعمیر می کنیم و بنابراین
و بنابراین . به همین ترتیب در ترم دوم اصلاح می کنیممن
. به همین ترتیب در ترم دوم اصلاح می کنیممن و بنابراین
و بنابراین .
.![{\displaystyle (\mathbf {a} \times [\mathbf {b} \times \mathbf {c} ])_{i}=(\delta _{i}^{\ell }\delta _{j}^ {m}-\delta _{i}^{m}\delta _{j}^{\ell })a^{j}b_{\ell }c_{m}=a^{j}b_{i} c_{j}-a^{j}b_{j}c_{i}=b_{i}(\mathbf {a} \cdot \mathbf {c} )-c_{i}(\mathbf {a} \cdot \mathbf {b} )\,.}](https://wikimedia.org/api/rest_v1/media/math/render/svg/bf362b74fdd08b44a8d0da1a117b4cad3d07b7b9)
 در سراسر سطح پارامتریک تعریف شده است
در سراسر سطح پارامتریک تعریف شده است :
: . بردار واحد نرمال
. بردار واحد نرمال به سطح داده شده توسط
به سطح داده شده توسط بنابراین انتگرال
بنابراین انتگرال یک ضرب سه گانه اسکالر است.
یک ضرب سه گانه اسکالر است.


















 ,
,  ,
,  )
) ،
،  ،
،  ,
,  ,
, 









































 و
و ، به ترتیب، زاویه
، به ترتیب، زاویه بین آنها توسط رابطه داده می شود
بین آنها توسط رابطه داده می شود


 مضرب ثابت درجه هارمونیک کروی ناحیه ای است . از این منظر، تعمیم زیر به ابعاد بالاتر وجود دارد. فرض کنید Y j یک مبنای متعامد دلخواه فضای H از هارمونیک های کروی درجه روی کره n باشد . سپس
مضرب ثابت درجه هارمونیک کروی ناحیه ای است . از این منظر، تعمیم زیر به ابعاد بالاتر وجود دارد. فرض کنید Y j یک مبنای متعامد دلخواه فضای H از هارمونیک های کروی درجه روی کره n باشد . سپس  ، درجه هارمونیک ناحیه ای مربوط به بردار واحد x ، به صورت [21] تجزیه می شود.
، درجه هارمونیک ناحیه ای مربوط به بردار واحد x ، به صورت [21] تجزیه می شود.
 به عنوان مضرب ثابت چند جمله ای جیگنبوئر مناسب داده می شود :
به عنوان مضرب ثابت چند جمله ای جیگنبوئر مناسب داده می شود :


 و
و
 روی واحد کره و خطوط گره ای آن.
روی واحد کره و خطوط گره ای آن.![{\displaystyle \Re [Y_{\ell m}]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/fe4514a0a6a49a33432a4bf36efe1f6fa05cb3dc) برابر است با 0 در امتداد دایره های بزرگی که از قطب ها می گذرند و در امتداد دایره های − m با عرض جغرافیایی مساوی. تابع هر بار که از یکی از این خطوط عبور می کند علامت تغییر می دهد.
برابر است با 0 در امتداد دایره های بزرگی که از قطب ها می گذرند و در امتداد دایره های − m با عرض جغرافیایی مساوی. تابع هر بار که از یکی از این خطوط عبور می کند علامت تغییر می دهد.
 می توان با در نظر گرفتن " خطوط گره " آنها، یعنی مجموعه نقاط روی کره ای که در آن قرار دارد، تجسم کرد
می توان با در نظر گرفتن " خطوط گره " آنها، یعنی مجموعه نقاط روی کره ای که در آن قرار دارد، تجسم کرد![{\displaystyle \Re [Y_{\ell }^{m}]=0}](https://wikimedia.org/api/rest_v1/media/math/render/svg/26617636b368a6d09ed57405f1fb8652eb51e617) ، یا به جای آن که
، یا به جای آن که![{\displaystyle \Im [Y_{\ell }^{m}]=0}](https://wikimedia.org/api/rest_v1/media/math/render/svg/2b2fb51f4ee139b5891db76afaa139113a04982d) . خطوط گره ای از
. خطوط گره ای از و
و جهت ها به ترتیب. با توجه به
جهت ها به ترتیب. با توجه به که از قرارداد فاز کاندون-شورتلی استفاده می کنند:
که از قرارداد فاز کاندون-شورتلی استفاده می کنند:


 در فضای سه بعدی اقلیدسی
در فضای سه بعدی اقلیدسی . هارمونیک های کروی را می توان به فضای اقلیدسی با ابعاد بالاتر تعمیم دادآر
. هارمونیک های کروی را می توان به فضای اقلیدسی با ابعاد بالاتر تعمیم دادآر به شرح زیر منجر به توابع می شود
به شرح زیر منجر به توابع می شود . [24] اجازه دهید P فضای چندجملهای همگن با مقدار مختلط درجه را در n متغیر حقیقی نشان دهد که در اینجا به عنوان تابع در نظر گرفته میشود.
. [24] اجازه دهید P فضای چندجملهای همگن با مقدار مختلط درجه را در n متغیر حقیقی نشان دهد که در اینجا به عنوان تابع در نظر گرفته میشود. . یعنی یک p چند جمله ای در P است به شرطی که برای هر حقیقی باشد
. یعنی یک p چند جمله ای در P است به شرطی که برای هر حقیقی باشد ، یک نفر دارد
، یک نفر دارد



 از توابع پیوسته در
از توابع پیوسته در با توجه به توپولوژی یکنواخت ، توسط قضیه استون-وایرشتراس . در نتیجه، مجموع این فضاها در فضای L 2 ( Sn - 1 ) از توابع انتگرال پذیر مربع روی کره نیز اکم است. بنابراین هر تابع مربع انتگرال پذیر در کره به طور منحصر به فردی به یک سری هارمونیک های کروی تجزیه می شود، جایی که سری به معنای L 2 همگرا می شوند .
با توجه به توپولوژی یکنواخت ، توسط قضیه استون-وایرشتراس . در نتیجه، مجموع این فضاها در فضای L 2 ( Sn - 1 ) از توابع انتگرال پذیر مربع روی کره نیز اکم است. بنابراین هر تابع مربع انتگرال پذیر در کره به طور منحصر به فردی به یک سری هارمونیک های کروی تجزیه می شود، جایی که سری به معنای L 2 همگرا می شوند .

 اثبات دیگری می دهد که فضاهای H به صورت زوجی متعامد و در L 2 کامل هستند ( Sn - 1 ) .
اثبات دیگری می دهد که فضاهای H به صورت زوجی متعامد و در L 2 کامل هستند ( Sn - 1 ) .



 متقارن بر روی شاخص ها، به طور منحصر به فرد توسط نیاز تعیین می شود
متقارن بر روی شاخص ها، به طور منحصر به فرد توسط نیاز تعیین می شود









 . سپس، همانطور که از بسیاری جهات می توان دید (شاید به سادگی از تابع تولید هرگلوتز)، با
. سپس، همانطور که از بسیاری جهات می توان دید (شاید به سادگی از تابع تولید هرگلوتز)، با بردار واحد بودن
بردار واحد بودن
 به
به . بیانیه برابری هارمونیک های کروی پس از آن است
. بیانیه برابری هارمونیک های کروی پس از آن است

 در مورد مبدایی که بردار واحد را ارسال می کند
در مورد مبدایی که بردار واحد را ارسال می کند . تحت این عملیات، هارمونیک کروی درجه
. تحت این عملیات، هارمونیک کروی درجه و سفارش دهید
و سفارش دهید تبدیل به یک ترکیب خطی از هارمونیک های کروی با همان درجه می شود. به این معنا که،
تبدیل به یک ترکیب خطی از هارمونیک های کروی با همان درجه می شود. به این معنا که،
 یک ماتریس از نظم است
یک ماتریس از نظم است که به چرخش بستگی داردآر
که به چرخش بستگی داردآر![{\displaystyle Y_{\ell }^{m}({\mathbf {r} }')=\sum _{m'=-\ell }^{\ell [D_{mm'}^{(\ell )}({\mathcal {R}})]^{*}Y_{\ell }^{m'}({\mathbf {r} })،}](https://wikimedia.org/api/rest_v1/media/math/render/svg/d90f021b19abdcb67fe194dea9981c6473be594a)
 مزدوج مختلط یک عنصر از ماتریس D ویگنر است . به ویژه زمانی که"
مزدوج مختلط یک عنصر از ماتریس D ویگنر است . به ویژه زمانی که" با چرخش آزیموت ما اتحاد را بدست می آوریم،
با چرخش آزیموت ما اتحاد را بدست می آوریم،
 . در کره واحداس2
. در کره واحداس2 بنابراین می توان به عنوان یک ترکیب خطی از این موارد گسترش داد:
بنابراین می توان به عنوان یک ترکیب خطی از این موارد گسترش داد:


 همچنین می تواند از نظر هارمونیک های حقیقی گسترش یابد:
همچنین می تواند از نظر هارمونیک های حقیقی گسترش یابد: در بالا به عنوان جمع
در بالا به عنوان جمع
 . مزایای بسط از نظر توابع هارمونیک حقیقی
. مزایای بسط از نظر توابع هارمونیک حقیقی تضمین شده است که حقیقی هستند، در حالی که ضرایب آنها
تضمین شده است که حقیقی هستند، در حالی که ضرایب آنها در گسترش آنها از نظر
در گسترش آنها از نظر ) آن خاصیت را ندارند.
) آن خاصیت را ندارند.
 مبنای فضای چندجمله ای های هارمونیک و همگن درجه است
مبنای فضای چندجمله ای های هارمونیک و همگن درجه است و یک فرمول صریح برای
و یک فرمول صریح برای
 ،
، ، و
، و
 بردار با مختصات مختلط است:
بردار با مختصات مختلط است:![{\displaystyle \mathbf {a} =[{\frac {1}{2}}({\frac {1}{\lambda }}-\lambda ),-{\frac {i}{2}}({ \frac {1}{\lambda }}+\lambda ),1].}](https://wikimedia.org/api/rest_v1/media/math/render/svg/9d5d338cb35165858d91d7076b25277522143951)

 و
و به عنوان پاراهای حقیقی در نامگذاری این تابع مولد به نام هرگلوتز ، ما از کورانت-هیلبرت 1962 ، §VII.7 پیروی میکنیم که یادداشتهای منتشر نشده او را برای کشف آن اعتبار میدانند.
به عنوان پاراهای حقیقی در نامگذاری این تابع مولد به نام هرگلوتز ، ما از کورانت-هیلبرت 1962 ، §VII.7 پیروی میکنیم که یادداشتهای منتشر نشده او را برای کشف آن اعتبار میدانند. ، به طوری که
، به طوری که آنالوگ عملگر هارمونیک جامد است (/)
آنالوگ عملگر هارمونیک جامد است (/) ، [16] یک تابع تولید کننده برای مجموعه استاندارد شده ای از عملگرهای تانسور کروی بدست می آید .
، [16] یک تابع تولید کننده برای مجموعه استاندارد شده ای از عملگرهای تانسور کروی بدست می آید .
 تبدیل تحت چرخش ها (به زیر مراجعه کنید) به همان شیوه ای است
تبدیل تحت چرخش ها (به زیر مراجعه کنید) به همان شیوه ای است ، با
، با
 با رعایت تمام خصوصیات این عملگرها، مانند قضیه ترکیب کلبش-گوردان و قضیه ویگنر-اکارت . علاوه بر این، آنها یک مجموعه استاندارد شده با مقیاس یا عادی سازی ثابت هستند.
با رعایت تمام خصوصیات این عملگرها، مانند قضیه ترکیب کلبش-گوردان و قضیه ویگنر-اکارت . علاوه بر این، آنها یک مجموعه استاندارد شده با مقیاس یا عادی سازی ثابت هستند.![{\displaystyle r^{\ell }\,{\begin{pmatrix}Y_{\ell }^{m}\\Y_{\ell }^{-m}\end{pmatrix}}=\left[{\ frac {2\ell +1}{4\pi }}\right]^{1/2}{\bar {\Pi }}_{\ell }^{m}(z){\begin{pmatrix}\ چپ(-1\راست)^{m}(A_{m}+iB_{m})\\(A_{m}-iB_{m})\end{pmatrix}}،\qquad m>0.}](https://wikimedia.org/api/rest_v1/media/math/render/svg/066f9cfa96f2c4550337a93bf73d61517362c834)



![{\displaystyle {\bar {\Pi }}_{\ell }^{m}(z)=\left[{\frac {(\ell -m)!}{(\ell +m)!}}\ راست]^{1/2}\sum _{k=0}^{\left\lطبقه (\ell -m)/2\right\rfloor }(-1)^{k}2^{-\ell } {\binom {\ell }{k}}{\binom {2\ell -2k}{\ell }}{\frac {(\ell -2k)!}{(\ell -2k-m)!}} \;r^{2k}\;z^{\ell -2k-m}.}](https://wikimedia.org/api/rest_v1/media/math/render/svg/7e4c8fef579a7f234ae71d6ed82da1013e72c592)
 این کاهش می یابد
این کاهش می یابد
 اساساً چند جمله ای لژاندر مرتبط است
اساساً چند جمله ای لژاندر مرتبط است ، و عوامل
، و عوامل اساسا هستند
اساسا هستند .
. ، و
، و که به صراحت در بالا ذکر شده است، به دست می آوریم:
که به صراحت در بالا ذکر شده است، به دست می آوریم:![{\displaystyle Y_{3}^{1}=-{\frac {1}{r^{3}}}\left[{\tfrac {7}{4\pi }}\cdot {\tfrac {3} {16}}\right]^{1/2}\left(5z^{2}-r^{2}\right)\left(x+iy\right)=-\left[{\tfrac {7} {4\pi }}\cdot {\tfrac {3}{16}}\right]^{1/2}\left(5\cos ^{2}\theta -1\right)\left(\sin \ تتا e^{i\varphi }\right)}](https://wikimedia.org/api/rest_v1/media/math/render/svg/ed582e41ffef571704b11f0ad0dee2d0c0f40858)
![{\displaystyle Y_{4}^{-2}={\frac {1}{r^{4}}}\left[{\tfrac {9}{4\pi }}\cdot {\tfrac {5} {32}}\right]^{1/2}\left(7z^{2}-r^{2}\right)\left(x-iy\right)^{2}=\left[{\tfrac {9}{4\pi }}\cdot {\tfrac {5}{32}}\right]^{1/2}\left(7\cos ^{2}\theta -1\right)\left( \sin ^{2}\theta e^{-2i\varphi }\right)}](https://wikimedia.org/api/rest_v1/media/math/render/svg/4bcad8b6882705b752928a0c469aa0ef2f9e306f)
 فقطآ
فقطآ شرایط (کسینوس) گنجانده شده است، و برای<0
شرایط (کسینوس) گنجانده شده است، و برای<0 فقطب
فقطب اصطلاحات (سینوس ها) شامل می شوند:
اصطلاحات (سینوس ها) شامل می شوند:

 م،
م، یا ساده تر در مختصات دکارتی،
یا ساده تر در مختصات دکارتی،
 ، و
، و


 فرض کنید که هر موج الکترومغناطیسی باید یک موج عرضی باشد ، جایی که میدان الکتریکی E و میدان مغناطیسی B هر دو عمود بر جهت انتشار موج هستند.
فرض کنید که هر موج الکترومغناطیسی باید یک موج عرضی باشد ، جایی که میدان الکتریکی E و میدان مغناطیسی B هر دو عمود بر جهت انتشار موج هستند.












 تانسور انحنای ریچی است و نقطه ویرگول نشان دهنده تمایز کوواریانت است.
تانسور انحنای ریچی است و نقطه ویرگول نشان دهنده تمایز کوواریانت است.



 فرمول اویلر است .
فرمول اویلر است .



 ، اگر از معادلات ماکسول برای حذف B استفاده شود ، معادله موج الکترومغناطیسی به معادله هلمهولتز برای E کاهش می یابد :
، اگر از معادلات ماکسول برای حذف B استفاده شود ، معادله موج الکترومغناطیسی به معادله هلمهولتز برای E کاهش می یابد :

![{\displaystyle {\begin{aligned}\mathbf {E} &=e^{-i\omega t}\sum _{l,m}{\sqrt {l(l+1)}}\left[a_{ E}(l,m)\mathbf {E} _{l,m}^{(E)}+a_{M}(l,m)\mathbf {E} _{l,m}^{(M) }\right]\\\mathbf {B} &=e^{-i\omega t}\sum _{l,m}{\sqrt {l(l+1)}}\left[a_{E}( l,m)\mathbf {B} _{l,m}^{(E)}+a_{M}(l,m)\mathbf {B} _{l,m}^{(M)}\راست ]\,,\end{تراز شده}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/f9bd81bcc18094a00580fc693e40fb49125e668f)
 و
و میدان های چند قطبی الکتریکی مرتبه (l, m) و
میدان های چند قطبی الکتریکی مرتبه (l, m) و و
و میدان های مغناطیسی چند قطبی متناظر هستند و یک E ( l ، m ) و یک M ( l ، m ) ضرایب انبساط هستند. فیلدهای چندقطبی توسط
میدان های مغناطیسی چند قطبی متناظر هستند و یک E ( l ، m ) و یک M ( l ، m ) ضرایب انبساط هستند. فیلدهای چندقطبی توسط![{\displaystyle {\begin{aligned}\mathbf {B} _{l,m}^{(E)}&={\sqrt {l(l+1)}}\left[B_{l}^{( 1)}h_{l}^{(1)}(kr)+B_{l}^{(2)}h_{l}^{(2)}(kr)\right]\mathbf {\Phi } _ {l,m}\\\mathbf {E} _{l,m}^{(E)}&={\frac {i}{k}}\nabla \times \mathbf {B} _{l,m }^{(E)}\\\mathbf {E} _{l,m}^{(M)}&={\sqrt {l(l+1)}}\left[E_{l}^{( 1)}h_{l}^{(1)}(kr)+E_{l}^{(2)}h_{l}^{(2)}(kr)\right]\mathbf {\Phi } _ {l,m}\\\mathbf {B} _{l,m}^{(M)}&=-{\frac {i}{k}}\nabla \times \mathbf {E} _{l, m}^{(M)}\,,\end{تراز شده}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/d938769bfe8f5eb7ff3222338801c2fb4928bb8f)


![{\displaystyle {\begin{aligned}\mathbf {B} &\approx {\frac {e^{i(kr-\omega t)}}{kr}}\sum _{l,m}(-i) ^{l+1}\left[a_{E}(l,m)\mathbf {\Phi } _{l,m}+a_{M}(l,m)\mathbf {\hat {r}} \ بار \mathbf {\Phi } _{l,m}\right]\\\mathbf {E} &\approx \mathbf {B} \times \mathbf {\hat {r}} .\end{تراز شده}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/830a465252ce6bd6118c1fc45adbb4836d93d7a3)
![{\displaystyle {\frac {dP}{d\Omega }}\approx {\frac {1}{2k^{2}}}\left|\sum _{l,m}(-i)^{l+ 1}\left[a_{E}(l,m)\mathbf {\Phi } _{l,m}\times \mathbf {\hat {r}} +a_{M}(l,m)\mathbf { \Phi } _{l,m}\right]\right|^{2}.}](https://wikimedia.org/api/rest_v1/media/math/render/svg/d1ffd55668cb3d7afe8d6887c3d25d55e722f160)























 انرژی سیستم مکانیکی مربوطه، طبق تعریف ،
انرژی سیستم مکانیکی مربوطه، طبق تعریف ،
 انرژی تحت تغییرات مختصات فضای پیکربندی ثابت است
انرژی تحت تغییرات مختصات فضای پیکربندی ثابت است ، یعنی
، یعنی
 به عنوان ضرایب یک فرم خطی تغییر می کند.
به عنوان ضرایب یک فرم خطی تغییر می کند. یک سیستم بسته یک انتگرال حرکت است .
یک سیستم بسته یک انتگرال حرکت است . افراطی بودن . (به عبارت دیگر،
افراطی بودن . (به عبارت دیگر، معادلات اویلر-لاگرانژ را برآورده می کند). در نظر گرفتن کل مشتق زمانی از
معادلات اویلر-لاگرانژ را برآورده می کند). در نظر گرفتن کل مشتق زمانی از![{\displaystyle -{\frac {\partial L}{\partial t}}{\biggl |}_{\mathbf {q} (t)}={\frac {\mathrm {d} }{\mathrm {d } t}}\left[E{\biggl |}_{\mathbf {q} (t)}\راست].}](https://wikimedia.org/api/rest_v1/media/math/render/svg/97d8bb04875cb2c57a1ce578378edae29d1f1797)
 بنابراین
بنابراین






















![{\displaystyle {\begin{array}{rcl}L&=&T-V\\&=&{\frac {1}{2}}M{\dot {x}}^{2}+{\frac {1 {2}}m\left[\left({\dot {x}}+\ell {\dot {\theta }}\cos \theta \right)^{2}+\left(\ell {\dot {\theta }}\sin \theta \right)^{2}\right]+mg\ell \cos \theta \\&=&{\frac {1}{2}}\left(M+m\right ){\dot {x}}^{2}+m{\dot {x}}\ell {\dot {\theta }}\cos \theta +{\frac {1}{2}}m\ell ^ {2}{\dot {\theta }}^{2}+mg\ell \cos \theta \,.\end{آرایه}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/fcea9ca5dd9452880b94f4315f2430d4f9c88684)


![\frac{\mathrm{d}}{\mathrm{d}t}\left[ m( \dot x \ell \cos\theta + \ell^2 \dot\theta ) \right] + m \ell (\ نقطه x \dot \theta + g) \sin\theta = 0;](https://wikimedia.org/api/rest_v1/media/math/render/svg/27ef95240aa335e09f85c8c7ef67a7301547c588)

 باید معادلات حرکت یک آونگ ساده را که در یک قاب اینرسی ساکن است ، ارائه دهد ، در حالی که¨→0
باید معادلات حرکت یک آونگ ساده را که در یک قاب اینرسی ساکن است ، ارائه دهد ، در حالی که¨→0 باید معادلات یک آونگ در یک سیستم دائماً شتابدهنده و غیره را ارائه دهد. علاوه بر این، با توجه به شرایط شروع مناسب و یک گام زمانی انتخابی، با گام برداشتن از نتایج به صورت تکراری، به دست آوردن نتایج به صورت عددی امری بیاهمیت است .
باید معادلات یک آونگ در یک سیستم دائماً شتابدهنده و غیره را ارائه دهد. علاوه بر این، با توجه به شرایط شروع مناسب و یک گام زمانی انتخابی، با گام برداشتن از نتایج به صورت تکراری، به دست آوردن نتایج به صورت عددی امری بیاهمیت است .



![{\displaystyle \int _{t_{1}}^{t_{2}}\delta L\,\mathrm {d} t=\int _{t_{1}}^{t_{2}}\sum _ {j=1}^{n}\left({\frac {\partial L}{\partial q_{j}}}\delta q_{j}+{\frac {\mathrm {d} }{\mathrm { d} t}}\left({\frac {\partial L}{\partial {\dot {q}}_{j}}}\delta q_{j}\right)-{\frac {\mathrm {d } }{\mathrm {d} t}}{\frac {\partial L}{\partial {\dot {q}}_{j}}}\delta q_{j}\right)\,\mathrm {d } t\,=\sum _{j=1}^{n}\left[{\frac {\partial L}{\partial {\dot {q}}_{j}}}\delta q_{j} \right]_{t_{1}}^{t_{2}}+\int _{t_{1}}^{t_{2}}\sum _{j=1}^{n}\left({ \frac {\partial L}{\partial q_{j}}}-{\frac {\mathrm {d} }{\mathrm {d} t}}{\frac {\partial L}{\partial {\dot {q}}_{j}}}\right)\delta q_{j}\,\mathrm {d} t\,.}](https://wikimedia.org/api/rest_v1/media/math/render/svg/54a48053647f191bd378c62f02e1dc5e53fdfb4e)













![{\displaystyle \sum _{j=1}^{n}\left[Q_{j}-\left({\frac {\mathrm {d} }{\mathrm {d} t}}{\frac {\ T جزئی {\ جزئی {\dot {q}}_{j}}}-{\frac {\partial T}{\partial q_{j}}}\right)\right]\delta q_{j}= 0\,,}](https://wikimedia.org/api/rest_v1/media/math/render/svg/cf81ebf14cb6b43779228e274d39444e1a4d7787)


 انرژی جنبشی کل سیستم، برابر با مجموع Σ انرژی جنبشی ذرات است، [5] و V انرژی پتانسیل سیستم است .
انرژی جنبشی کل سیستم، برابر با مجموع Σ انرژی جنبشی ذرات است، [5] و V انرژی پتانسیل سیستم است .

 ، فقط است
، فقط است ; برای ارتباط دادن مولفه سرعت به مختصات مربوطه z 2 نیازی به استفاده از قوانین زنجیره نامناسب یا مشتقات کل نیست .
; برای ارتباط دادن مولفه سرعت به مختصات مربوطه z 2 نیازی به استفاده از قوانین زنجیره نامناسب یا مشتقات کل نیست .

 .
.







 متشکل از یک فضای پیکربندی
متشکل از یک فضای پیکربندی  و عملکرد صاف
و عملکرد صاف درون آن فضایی که لاگرانژی نامیده می شود . برای بسیاری از سیستم
درون آن فضایی که لاگرانژی نامیده می شود . برای بسیاری از سیستم  جایی که
جایی که و
و به ترتیب انرژی جنبشی و پتانسیل سیستم هستند . [2]
به ترتیب انرژی جنبشی و پتانسیل سیستم هستند . [2]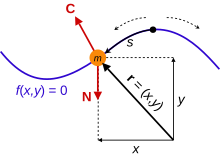

 در مکانیک نیوتنی، معادلات حرکت با قوانین نیوتن ارائه می شود . قانون دوم " نیروی خالص برابر است با جرم ضربدر شتاب ".
در مکانیک نیوتنی، معادلات حرکت با قوانین نیوتن ارائه می شود . قانون دوم " نیروی خالص برابر است با جرم ضربدر شتاب ". برای هر ذره اعمال می شود. برای یک سیستم ذرات N در 3 بعد، معادلات دیفرانسیل معمولی 3 N مرتبه دوم در موقعیتهای ذرات وجود دارد که باید حل شوند.
برای هر ذره اعمال می شود. برای یک سیستم ذرات N در 3 بعد، معادلات دیفرانسیل معمولی 3 N مرتبه دوم در موقعیتهای ذرات وجود دارد که باید حل شوند.






 (برعکس کردن ترتیب بردارها در
(برعکس کردن ترتیب بردارها در معادل تغییر علامت آن است).
معادل تغییر علامت آن است).












 که در آن محور یک بردار واحد است که جهت محور روتور را مشخص می کند. از مبدا، در هر جهت، همان محور چرخش است، با مقیاس زاویه معادل فاصله از مبدا. از هر نقطه دیگری در فضا، به طور مشابه همان بردار جهت اعمال شده نسبت به جهت نشان داده شده توسط نقطه شروع به جای مبدا، همان تغییر را در اطراف همان محورهایی اعمال می کند که بردار واحد مشخص می کند. اینزاویه∗محور
که در آن محور یک بردار واحد است که جهت محور روتور را مشخص می کند. از مبدا، در هر جهت، همان محور چرخش است، با مقیاس زاویه معادل فاصله از مبدا. از هر نقطه دیگری در فضا، به طور مشابه همان بردار جهت اعمال شده نسبت به جهت نشان داده شده توسط نقطه شروع به جای مبدا، همان تغییر را در اطراف همان محورهایی اعمال می کند که بردار واحد مشخص می کند. اینزاویه∗محور مقیاس گذاری هر نقطه یک مختصات منحصر به فرد در نماد Angle-Angle-Angle می دهد. تفاوت بین دو مختصات بلافاصله یک محور چرخش و زاویه بین دو جهت را ایجاد می کند.
مقیاس گذاری هر نقطه یک مختصات منحصر به فرد در نماد Angle-Angle-Angle می دهد. تفاوت بین دو مختصات بلافاصله یک محور چرخش و زاویه بین دو جهت را ایجاد می کند. تبرها این چرخش ها ممکن است به سادگی اضافه و کم شوند، به خصوص زمانی که فریم های در حال چرخش مانند زنجیره های IK به یکدیگر ثابت می شوند. تفاوت بین دو شی که در یک چارچوب مرجع قرار دارند به سادگی با کم کردن جهت آنها پیدا می شود. چرخش هایی که از منابع خارجی اعمال می شوند، یا از منابعی نسبت به چرخش فعلی هستند، همچنان نیاز به ضرب دارند، استفاده از فرمول رودریگز ارائه شده است.
تبرها این چرخش ها ممکن است به سادگی اضافه و کم شوند، به خصوص زمانی که فریم های در حال چرخش مانند زنجیره های IK به یکدیگر ثابت می شوند. تفاوت بین دو شی که در یک چارچوب مرجع قرار دارند به سادگی با کم کردن جهت آنها پیدا می شود. چرخش هایی که از منابع خارجی اعمال می شوند، یا از منابعی نسبت به چرخش فعلی هستند، همچنان نیاز به ضرب دارند، استفاده از فرمول رودریگز ارائه شده است. منحنی های مرتبط دارند. به نظر می رسد انحنای چیزهایی که به این مرز نزدیک می شوند، به طور آشفته ای به مدارها می پرند.
منحنی های مرتبط دارند. به نظر می رسد انحنای چیزهایی که به این مرز نزدیک می شوند، به طور آشفته ای به مدارها می پرند.




![{\displaystyle {Q}=[{X}،{Y}،{Z}]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/cc821ccb9da7c1120e95a8253301474e3ae7b2a1) ،
،

![{\displaystyle {A}=[X,Y,Z]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/b732043aabcf7a1d454138c502433313f8e32bb0)

![{\displaystyle [x,y,z]={\frac {A}{\|A\|}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/7becd9c40f0aec3b4d3762fd18f06833957010c4)



 حول
حول  .
. .
.
 و یک بردار چرخشی دیگر
و یک بردار چرخشی دیگر برای چرخاندن قاب به اطراف
برای چرخاندن قاب به اطراف









 نشان دهنده سه محور است. اینها میتوانند بهعنوان خلاصهنویسی برای چرخاندن چرخش به دور با استفاده از «چرخش یک بردار چرخشی» بالا استفاده شوند. این عبارات به بهترین شکل به عنوان قطعات کد نمایش داده می شوند.
نشان دهنده سه محور است. اینها میتوانند بهعنوان خلاصهنویسی برای چرخاندن چرخش به دور با استفاده از «چرخش یک بردار چرخشی» بالا استفاده شوند. این عبارات به بهترین شکل به عنوان قطعات کد نمایش داده می شوند.
![{\displaystyle {\text{x-axis}}=\left[x=cn_{x}^{2}+c_{1},\;y=cn_{x}n_{y}+sn_{z}، \;z=cn_{x}n_{z}-sn_{y}\right]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/f2d5d60e7e381e1f0ebc934f68aee30c3fc56f06)
![{\displaystyle {\text{y-axis}}=\left[x=cn_{y}n_{x}-sn_{z},\;y=cn_{y}^{2}+c_{1}، \;z=cn_{y}n_{z}+sn_{x}\right]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/ea4b603b0e87094cfb7487811077cc18530a606d)
![{\displaystyle {\text{z-axis}}=\left[x=cn_{z}n_{x}+sn_{y},\;y=cn_{z}n_{y}-sn_{x}، \;z=cn_{z}^{2}+c_{1}\right]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/57b034a19855bc69fd1cce3daf8d67de13379c21)








 "بالا" است. اگر یک محور دیگر اصلی در نظر گرفته شود، مختصات را می توان به سادگی تعویض کرد.
"بالا" است. اگر یک محور دیگر اصلی در نظر گرفته شود، مختصات را می توان به سادگی تعویض کرد.













![{\displaystyle {a}=[{X}،{Y}،{Z}]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/fa710dbd1ad69bcb2ba16caf65d0ab0f6c4fa297) عادی شده است. اگر 0 چرخش وجود دارد، نتیجه را با
عادی شده است. اگر 0 چرخش وجود دارد، نتیجه را با





















 نسبت به طرح کواترنیون اصلی q . با مقایسه مولفه ها به آن می رسیم
نسبت به طرح کواترنیون اصلی q . با مقایسه مولفه ها به آن می رسیم
 ،
، ,
, ، که پایه چرخشی را تشکیل می دهند که هر کدام از 3 مختصات تشکیل شده است که در مجموع 9 پارامتر را به دست می دهند.
، که پایه چرخشی را تشکیل می دهند که هر کدام از 3 مختصات تشکیل شده است که در مجموع 9 پارامتر را به دست می دهند.
 جایی که
جایی که 
 یک
یک  (به ترتیب توجه کنید، زیرا بردار در حال چرخش از سمت راست ضرب می شود).
(به ترتیب توجه کنید، زیرا بردار در حال چرخش از سمت راست ضرب می شود).

 ،
،  پارامتر کردن
پارامتر کردن![{\displaystyle \mathbf {R} =[\cos(\theta /2)-Iu\sin(\theta /2)]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/ccaf9643d65a54a5bd1b4d962d07f605c9c67648) جایی که
جایی که
 محور چرخش (بردار واحد) است و
محور چرخش (بردار واحد) است و شبه اسکالر (سه بردار در
شبه اسکالر (سه بردار در


 (
( 











 .
. 

























 ما داریم
ما داریم
 طرح دوگانه یک بردار واحد است،
طرح دوگانه یک بردار واحد است،

 ، ابتدا آن را بر روی صفحه تعریف شده توسط محور z و خط گره ها پخش می کند. همانطور که زاویه بین صفحات است
، ابتدا آن را بر روی صفحه تعریف شده توسط محور z و خط گره ها پخش می کند. همانطور که زاویه بین صفحات است و
و ، این منجر به:
، این منجر به:







 ما داریم
ما داریم







 در این وبلاگ به ریاضیات و کاربردهای آن و تحقیقات در آنها پرداخته می شود. مطالب در این وبلاگ ترجمه سطحی و اولیه است و کامل نیست.در صورتی سوال یا نظری در زمینه ریاضیات دارید مطرح نمایید .در صورت امکان به آن می پردازم. من دوست دارم برای یافتن پاسخ به سوالات و حل پروژه های علمی با دیگران همکاری نمایم.در صورتی که شما هم بامن هم عقیده هستید با من تماس بگیرید.
در این وبلاگ به ریاضیات و کاربردهای آن و تحقیقات در آنها پرداخته می شود. مطالب در این وبلاگ ترجمه سطحی و اولیه است و کامل نیست.در صورتی سوال یا نظری در زمینه ریاضیات دارید مطرح نمایید .در صورت امکان به آن می پردازم. من دوست دارم برای یافتن پاسخ به سوالات و حل پروژه های علمی با دیگران همکاری نمایم.در صورتی که شما هم بامن هم عقیده هستید با من تماس بگیرید.