از ویکیپدیا، دانشنامه آزاد
برای تحلیل استاتیکی در اقتصاد، استاتیک مقایسه ای را ببینید . برای تکنیک تصحیح استاتیکی مورد استفاده در ژئوفیزیک اکتشافی، به لرزهشناسی بازتابی مراجعه کنید . برای سایر کاربردها، تجزیه و تحلیل استاتیک را ببینید .
| بخشی از یک سریال در |
| مکانیک کلاسیک |
|---|
 |
| پنهان شدن شاخه ها |
| نشان دادن مبانی |
| نشان دادن فرمولاسیون |
| نشان دادن موضوعات اصلی |
| نشان دادن |
| نشان دادن دانشمندان |
استاتیک شاخه ای از مکانیک است که به تجزیه و تحلیل ( نیرو و گشتاور یا "لحظه" ) اثر بر روی سیستم های فیزیکی که شتاب ( a =0) را تجربه نمی کنند، می پردازد ، بلکه در تعادل ایستا با محیط خود هستند. استفاده از قانون دوم نیوتن در یک سیستم به دست می دهد:
جایی که فونت پررنگ بردار را نشان میدهد که بزرگی و جهت دارد .



مجموع نیروها، که ممکن است یکی از آنها ناشناخته باشد، به یافتن آن مجهول اجازه می دهد. بنابراین هنگامی که در تعادل استاتیکی است، شتاب سیستم صفر است و سیستم یا در حال سکون است یا مرکز جرم آن با سرعت ثابت حرکت می کند. به همین ترتیب، استفاده از فرض شتاب صفر در مجموع گشتاورهای تأثیرگذار بر روی سیستم منجر به موارد زیر می شود:
اینجا،


مجموع لحظاتی که ممکن است یکی از آنها ناشناخته باشد، امکان یافتن آن مجهول را فراهم می کند. این دو معادله با هم، می توانند برای حل دو بار (نیروها و گشتاورها) وارد بر سیستم اعمال شوند.
از قانون اول نیوتن ، این نشان می دهد که نیروی خالص و گشتاور خالص در هر قسمت از سیستم صفر است. نیروهای خالص برابر با صفر به عنوان شرط اول برای تعادل و گشتاور خالص برابر با صفر به عنوان شرط دوم برای تعادل شناخته می شوند. رجوع به استاتیک نامعین شود.
فهرست
- 1تاریخ
- 2بردارها
- 3زور
- 4لحظه یک نیرو
- 5معادلات تعادل
- 6ممان اینرسی
- 7مواد جامد
- 8مایعات
- 9همچنین ببینید
- 10یادداشت
- 11منابع
- 12لینک های خارجی
تاریخچه [ ویرایش ]
ارشمیدس (حدود 287 - حدود 212 قبل از میلاد) کارهای پیشگامانه ای در استاتیک انجام داد. [1] [2] تحولات بعدی در زمینه استاتیک در آثار Thebit یافت می شود. [3]
بردارها [ ویرایش ]
مثالی از یک تیر در تعادل استاتیکی. مجموع نیرو و گشتاور صفر است.
اسکالر کمیتی است که فقط مقداری مانند جرم یا دما دارد . بردار دارای قدر و جهت است. چندین نماد برای شناسایی یک بردار وجود دارد ، از جمله:
- شخصیتی با چهره جسور V
- یک شخصیت V
- شخصیتی با یک فلش بر روی آن
.
بردارها با استفاده از قانون متوازی الاضلاع یا قانون مثلث اضافه می شوند . بردارها شامل اجزایی در پایه های متعامد هستند. بردارهای واحد i , j , و k طبق قرارداد به ترتیب در امتداد محورهای x، y و z هستند.
اجباری [ ویرایش ]
نیرو عمل یک جسم بر جسم دیگر است. نیرو یا فشار یا کشش است و تمایل دارد جسم را در جهت حرکت خود حرکت دهد. عملکرد یک نیرو با بزرگی، جهت حرکت و نقطه کاربرد آن مشخص می شود. بنابراین، نیرو یک کمیت برداری است، زیرا تأثیر آن به جهت و همچنین به بزرگی عمل بستگی دارد. [4]
نیروها به دو دسته نیروهای تماسی یا بدنی طبقه بندی می شوند. نیروی تماس با تماس فیزیکی مستقیم تولید می شود. به عنوان مثال نیرویی است که توسط یک سطح نگهدارنده بر جسم وارد می شود. نیروی بدن به واسطه موقعیت جسم در یک میدان نیرو مانند میدان گرانشی، الکتریکی یا مغناطیسی ایجاد می شود و مستقل از تماس با هر جسم دیگری است. نمونه ای از نیروی بدن، وزن جسم در میدان گرانشی زمین است. [5]
لحظه یک نیرو [ ویرایش ]
علاوه بر تمایل به حرکت جسم در جهت اعمال آن، یک نیرو می تواند جسم را حول یک محور نیز بچرخاند. محور ممکن است هر خطی باشد که نه قطع می کند و نه موازی با خط عمل نیرو است. این گرایش چرخشی به ممان ( M ) نیرو معروف است. به لحظه به عنوان گشتاور نیز گفته می شود .
لحظه ای در مورد یک نقطه [ ویرایش ]
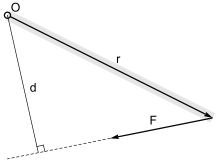
نمودار بازوی لحظه ای نیروی F.
بزرگی گشتاور یک نیرو در نقطه O برابر است با فاصله عمود از O تا خط عمل F ضرب در بزرگی نیرو: M = F · d ، که در آن
F = نیروی اعمال شده
d = فاصله عمود از محور تا خط عمل نیرو. این فاصله عمود بر بازوی لحظه ای نامیده می شود.
جهت لحظه توسط قانون دست راست داده می شود، جایی که خلاف جهت عقربه های ساعت (CCW) خارج از صفحه است و در جهت عقربه های ساعت (CW) داخل صفحه است. جهت گشتاور ممکن است با استفاده از یک قرارداد علامت مشخص شده، مانند علامت مثبت (+) برای گشتاورهای خلاف جهت عقربه های ساعت و علامت منفی (-) برای ممان های عقربه های ساعت، یا برعکس، محاسبه شود. لحظه ها را می توان به عنوان بردار با هم جمع کرد.
در قالب برداری، ممان را می توان به عنوان حاصل ضرب بین بردار شعاع r (بردار نقطه O تا خط عمل) و بردار نیرو، F تعریف کرد : [6]
قضیه واریگنون [ ویرایش ]
قضیه وارینیون بیان می کند که گشتاور یک نیرو در مورد هر نقطه برابر است با مجموع گشتاورهای اجزای نیرو در مورد همان نقطه.
معادلات تعادل [ ویرایش ]
تعادل استاتیکی یک ذره یک مفهوم مهم در استاتیک است. یک ذره فقط در حالت تعادل است که حاصل تمام نیروهای وارد بر ذره برابر با صفر باشد. در یک سیستم مختصات مستطیلی، معادلات تعادل را می توان با سه معادله اسکالر نشان داد، که در آن مجموع نیروها در هر سه جهت برابر با صفر است. یکی از کاربردهای مهندسی این مفهوم، تعیین کشش حداکثر سه کابل تحت بار است، برای مثال نیروهای وارد شده بر هر کابل بالابر که یک جسم را بالا میبرد یا سیمهایی که یک بالون هوای داغ را به زمین مهار میکنند . [7]
لحظه اینرسی [ ویرایش ]
در مکانیک کلاسیک، ممان اینرسی که به آن گشتاور جرمی، اینرسی چرخشی، گشتاور قطبی اینرسی جرم یا جرم زاویهای نیز گفته میشود، اندازهگیری مقاومت جسم در برابر تغییرات چرخش آن است. اینرسی یک جسم دوار نسبت به چرخش آن است. ممان اینرسی تقریباً همان نقشی را در دینامیک دورانی ایفا می کند که جرم در دینامیک خطی انجام می دهد و رابطه بین تکانه زاویه ای و سرعت زاویه ای، گشتاور و شتاب زاویه ای و چندین کمیت دیگر را توصیف می کند. نمادهای I و J معمولاً برای اشاره به ممان اینرسی یا گشتاور قطبی اینرسی استفاده می شوند.
در حالی که یک درمان اسکالر ساده ممان اینرسی برای بسیاری از موقعیتها کافی است، یک درمان تانسور پیشرفتهتر امکان تجزیه و تحلیل سیستمهای پیچیدهای مانند فرهای چرخشی و حرکت ژیروسکوپی را فراهم میکند.
این مفهوم توسط لئونارد اویلر در کتاب خود Theoria motus corporum solidorum seu rigidorum در سال 1765 معرفی شد . او ممان اینرسی و بسیاری از مفاهیم مرتبط مانند محور اصلی اینرسی را مورد بحث قرار داد.
جامدات [ ویرایش ]
استاتیک در تجزیه و تحلیل سازه ها استفاده می شود، به عنوان مثال در مهندسی معماری و سازه . استحکام مواد یک رشته مرتبط از مکانیک است که به شدت بر استفاده از تعادل استاتیکی متکی است. یک مفهوم کلیدی مرکز ثقل جسم در حال سکون است: این یک نقطه خیالی را نشان می دهد که تمام جرم یک جسم در آن قرار دارد. موقعیت نقطه نسبت به پایه هایی که جسم روی آن قرار دارد، پایداری آن را تعیین می کنددر پاسخ به نیروهای خارجی اگر مرکز ثقل خارج از شالوده ها وجود داشته باشد، بدن ناپایدار است زیرا یک گشتاور در آن اثر می کند: هر اختلال کوچکی باعث سقوط یا واژگونی بدن می شود. اگر مرکز ثقل درون پایه ها وجود داشته باشد، بدنه پایدار است زیرا هیچ گشتاور خالصی روی بدنه اثر نمی گذارد. اگر مرکز ثقل با پایهها منطبق باشد، گفته میشود که بدن ناپایدار است.
سیالات [ ویرایش ]
هیدرواستاتیک ، همچنین به عنوان استاتیک سیالات شناخته می شود ، مطالعه سیالات در حالت سکون (یعنی در تعادل ایستا) است. ویژگی هر سیال در حالت سکون این است که نیروی وارد شده بر هر ذره سیال در تمام نقاط در همان عمق (یا ارتفاع) درون سیال یکسان است. اگر نیروی خالص بزرگتر از صفر باشد، سیال در جهت نیروی حاصل حرکت می کند. این مفهوم برای اولین بار توسط ریاضیدان و فیلسوف فرانسوی بلز پاسکال در سال 1647 به شکل کمی توسعه یافته فرموله شد و به قانون پاسکال معروف شد . کاربردهای بسیار مهمی در هیدرولیک دارد. ارشمیدس ، ابوریحان بیرونی ، الخازینی [8] و گالیله گالیله نیز از چهره های اصلی در توسعه هیدرواستاتیک بودند.
همچنین مشاهده کنید [ ویرایش ]
منبع
https://en.wikipedia.org/wiki/Statics










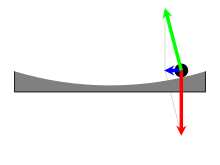
 تنها تحت تأثیر نیروی کوریولیس در یک مسیر دایره ای به نام "دایره اینرسی" حرکت می کند. از آنجایی که نیرو در زوایای قائم به حرکت ذره هدایت می شود، با سرعت ثابتی به دور دایره ای حرکت می کند که شعاع آن
تنها تحت تأثیر نیروی کوریولیس در یک مسیر دایره ای به نام "دایره اینرسی" حرکت می کند. از آنجایی که نیرو در زوایای قائم به حرکت ذره هدایت می شود، با سرعت ثابتی به دور دایره ای حرکت می کند که شعاع آن از رابطه زیر بدست می آید:
از رابطه زیر بدست می آید:
 پارامتر کوریولیس است
پارامتر کوریولیس است ، معرفی شده در بالا (جایی که
، معرفی شده در بالا (جایی که عرض جغرافیایی است). بنابراین زمان صرف شده برای تکمیل یک دایره کامل جرم است
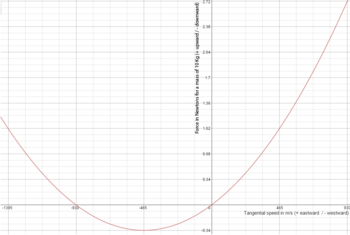
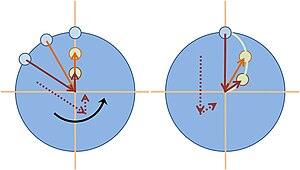
عرض جغرافیایی است). بنابراین زمان صرف شده برای تکمیل یک دایره کامل جرم است . پارامتر Coriolis معمولاً دارای مقدار عرض جغرافیایی میانه حدود 10-4 s -1 است. بنابراین برای سرعت معمولی جوی 10 متر بر ثانیه (22 مایل در ساعت)، شعاع 100 کیلومتر (62 مایل) با دوره زمانی حدود 17 ساعت است. برای یک جریان اقیانوسی با سرعت معمولی 10 سانتی متر بر ثانیه (0.22 مایل در ساعت)، شعاع یک دایره اینرسی 1 کیلومتر (0.6 مایل) است. این دایره های اینرسی در نیمکره شمالی (جایی که مسیرها به سمت راست خم می شوند) در جهت عقربه های ساعت و در نیمکره جنوبی در خلاف جهت عقربه های ساعت هستند.
. پارامتر Coriolis معمولاً دارای مقدار عرض جغرافیایی میانه حدود 10-4 s -1 است. بنابراین برای سرعت معمولی جوی 10 متر بر ثانیه (22 مایل در ساعت)، شعاع 100 کیلومتر (62 مایل) با دوره زمانی حدود 17 ساعت است. برای یک جریان اقیانوسی با سرعت معمولی 10 سانتی متر بر ثانیه (0.22 مایل در ساعت)، شعاع یک دایره اینرسی 1 کیلومتر (0.6 مایل) است. این دایره های اینرسی در نیمکره شمالی (جایی که مسیرها به سمت راست خم می شوند) در جهت عقربه های ساعت و در نیمکره جنوبی در خلاف جهت عقربه های ساعت هستند.

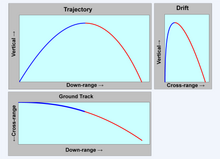



 = شتاب پایین برد.
= شتاب پایین برد. = شتاب عمودی با شتاب مثبت به سمت بالا.
= شتاب عمودی با شتاب مثبت به سمت بالا. = شتاب متقابل با شتاب مثبت به سمت راست.
= شتاب متقابل با شتاب مثبت به سمت راست. = سرعت پایین برد
= سرعت پایین برد = سرعت عمودی با نشان دهنده مثبت به سمت بالا.
= سرعت عمودی با نشان دهنده مثبت به سمت بالا. = سرعت متقاطع با سرعت نشان دهنده مثبت به سمت راست.
= سرعت متقاطع با سرعت نشان دهنده مثبت به سمت راست. = سرعت زاویه ای زمین = 0.00007292 راد در ثانیه (بر اساس یک
= سرعت زاویه ای زمین = 0.00007292 راد در ثانیه (بر اساس یک  = عرض جغرافیایی با نشانگر مثبت نیمکره شمالی.
= عرض جغرافیایی با نشانگر مثبت نیمکره شمالی. = آزیموت در جهت عقربه های ساعت از شمال اندازه گیری می شود.
= آزیموت در جهت عقربه های ساعت از شمال اندازه گیری می شود.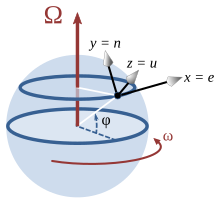



 ) در مقایسه با شتاب ناشی از گرانش (گرم، تقریباً 9.81 m/s 2 (32.2 ft/s 2 ) در نزدیکی سطح زمین) کوچک است. برای چنین مواردی فقط اجزای افقی (شرق و شمال) اهمیت دارند. محدودیت موارد فوق به صفحه افقی است (تنظیم v u = 0):
) در مقایسه با شتاب ناشی از گرانش (گرم، تقریباً 9.81 m/s 2 (32.2 ft/s 2 ) در نزدیکی سطح زمین) کوچک است. برای چنین مواردی فقط اجزای افقی (شرق و شمال) اهمیت دارند. محدودیت موارد فوق به صفحه افقی است (تنظیم v u = 0):

 پارامتر کوریولیس نامیده می شود.
پارامتر کوریولیس نامیده می شود.






 مجموع بردار نیروهای فیزیکی وارد بر جسم است،
مجموع بردار نیروهای فیزیکی وارد بر جسم است، شتاب جسم نسبت به قاب مرجع اینرسی است.
شتاب جسم نسبت به قاب مرجع اینرسی است. با داشتن نرخ چرخش متغیر، معادله شکل می گیرد
با داشتن نرخ چرخش متغیر، معادله شکل می گیرد

 سرعت نسبت به قاب مرجع چرخان است
سرعت نسبت به قاب مرجع چرخان است بردار موقعیت جسم نسبت به قاب مرجع در حال چرخش است
بردار موقعیت جسم نسبت به قاب مرجع در حال چرخش است شتاب نسبت به قاب مرجع چرخان است
شتاب نسبت به قاب مرجع چرخان است


 نیروی کوریولیس و تمام نیروهای ساختگی دیگر ناپدید می شوند.
نیروی کوریولیس و تمام نیروهای ساختگی دیگر ناپدید می شوند.  .
.



 عرض جغرافیایی است که در
عرض جغرافیایی است که در 


 برش های محوری و
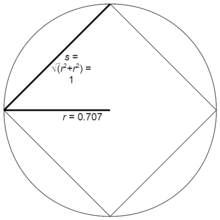
برش های محوری و رئوس شعاعی حد منطقه به عنوان
رئوس شعاعی حد منطقه به عنوان


















 = معادله برداری پارامتریک سطح
= معادله برداری پارامتریک سطح = مشتق جزئی از
= مشتق جزئی از
 = مشتق جزئی از
= مشتق جزئی از
 = منطقه سایه
= منطقه سایه




 مساحت هر قطعه با فرمول مشخص می شود
مساحت هر قطعه با فرمول مشخص می شود
 به سطح روی ناحیه مناسب D در صفحه پارامتریک UV . سپس مساحت کل سطح با جمع کردن نواحی قطعات با هم، با استفاده از افزایش سطح به دست می آید. فرمول اصلی را می توان به کلاس های مختلف سطوح اختصاص داد، به ویژه فرمول هایی را برای مناطق نمودار z = f ( x , y ) و
به سطح روی ناحیه مناسب D در صفحه پارامتریک UV . سپس مساحت کل سطح با جمع کردن نواحی قطعات با هم، با استفاده از افزایش سطح به دست می آید. فرمول اصلی را می توان به کلاس های مختلف سطوح اختصاص داد، به ویژه فرمول هایی را برای مناطق نمودار z = f ( x , y ) و 





![{\displaystyle r={\frac {\sqrt {[(x_{2}-x_{1})^{2}+(y_{2}-y_{1})^{2}][(x_{2) }-x_{3})^{2}+(y_{2}-y_{3})^{2}][(x_{3}-x_{1})^{2}+(y_{3} -y_{1})^{2}]}}{2|x_{1}y_{2}+x_{2}y_{3}+x_{3}y_{1}-x_{1}y_{3 }-x_{2}y_{1}-x_{3}y_{2}|}}.}](https://wikimedia.org/api/rest_v1/media/math/render/svg/caffb954e8c39a26dcc5e4ad4f66494edd313008)
 مقادیر
مقادیر 


























![{\displaystyle X^{(n)}(t)={\begin{cases}\displaystyle -\int _{a}^{x}X^{(n-1)}(t)p(t)^ {-1}y_{0}(t)^{-2}\,dt&n{\text{ odd}},\\[6pt]\displaystyle \quad \int _{a}^{x}X^{( n-1)}(t)y_{0}(t)^{2}w(t)\,dt&n{\text{ even}}\end{موارد}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/a0bbcf22a1e2cff3b5d2f18877a2fdc973729e83)
![{\displaystyle {\tilde {X}}^{(n)}(t)={\begin{cases}\displaystyle \quad \int _{a}^{x}{\tilde {X}}^{( n-1)}(t)y_{0}(t)^{2}w(t)\,dt&n{\text{ odd}},\\[6pt]\displaystyle -\int _{a}^{ x}{\tilde {X}}^{(n-1)}(t)p(t)^{-1}y_{0}(t)^{-2}\,dt&n{\text{ حتی. }}\end{موارد}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/1bf8a21cadd3a1412985dc53c37ddc1dafcb431b)



















![{\displaystyle Lu=-{\frac {1}{w(x)}}\left({\frac {d}{dx}}\left[p(x)\,{\frac {du}{dx} }\right]+q(x)u\right)}](https://wikimedia.org/api/rest_v1/media/math/render/svg/b6bfdef3bf2aabb27385d96d5f2a6f6f4fb151b2)

![{\displaystyle L^{2}([a,b],w(x)\,dx)}](https://wikimedia.org/api/rest_v1/media/math/render/svg/558fef7efc0f815d4240e19891a1342e6c5f321c)





![{\displaystyle {\frac {d}{dx}}\!\!\left[\,p(x){\frac {dy}{dx}}\right]+q(x)y=-\lambda \ ,w(x)y,}](https://wikimedia.org/api/rest_v1/media/math/render/svg/b7ed22ff2571ca9f5bc6f1236c5f57aea09ec786)



 جایی که δ mn
جایی که δ mn که می توان آن را به شکل Sturm–Liouville (ابتدا با تقسیم بر x و سپس با جمع کردن دو جمله اول سمت چپ به یک جمله) نوشت.
که می توان آن را به شکل Sturm–Liouville (ابتدا با تقسیم بر x و سپس با جمع کردن دو جمله اول سمت چپ به یک جمله) نوشت.
 که به راحتی می توان آن را به شکل Sturm–Liouville قرار داد، زیراد/dx(1 − x 2 ) = −2 x ، بنابراین معادله لژاندر معادل است با
که به راحتی می توان آن را به شکل Sturm–Liouville قرار داد، زیراد/dx(1 − x 2 ) = −2 x ، بنابراین معادله لژاندر معادل است با


 می دهد
می دهد که به راحتی می توان آن را به شکل Sturm–Liouville قرار داد
که به راحتی می توان آن را به شکل Sturm–Liouville قرار داد بنابراین معادله دیفرانسیل معادل است
بنابراین معادله دیفرانسیل معادل است

 و سپس جمع آوری شکل Sturm–Liouville را می دهد:
و سپس جمع آوری شکل Sturm–Liouville را می دهد: یا به صراحت:
یا به صراحت:
![{\displaystyle J[f]=\int _{a}^{b}L(\,x,f(x),f\,'(x)\,)\,dx\ ,}](https://wikimedia.org/api/rest_v1/media/math/render/svg/68be973ffd7b1b84391c61f2dcacd0ecf74ca766) که در آن f ′( x ) ≡ df/dx . اگر f با اضافه کردن یک تابع δf به آن تغییر کند و انتگرال L ( x, f δf, f' δf ') در توانهای δf بسط داده شود ، آنگاه تغییر در مقدار J به مرتبه اول در δf را می توان به صورت زیر بیان کرد:
که در آن f ′( x ) ≡ df/dx . اگر f با اضافه کردن یک تابع δf به آن تغییر کند و انتگرال L ( x, f δf, f' δf ') در توانهای δf بسط داده شود ، آنگاه تغییر در مقدار J به مرتبه اول در δf را می توان به صورت زیر بیان کرد:  که در آن تغییر در مشتق، δf " به عنوان مشتق تغییر ( δf ) " بازنویسی شد و
که در آن تغییر در مشتق، δf " به عنوان مشتق تغییر ( δf ) " بازنویسی شد و  مشتق عملکردی F [ ρ ] که به δF / δρ نشان داده می شود، از طریق
مشتق عملکردی F [ ρ ] که به δF / δρ نشان داده می شود، از طریق ![{\displaystyle {\begin{aligned}\int {\frac {\delta F}{\delta \rho }}(x)\phi (x)\;dx&=\lim _{\varepsilon \to 0}{\ frac {F[\rho +\varepsilon \phi ]-F[\rho ]}{\varepsilon }}\\&=\left[{\frac {d}{d\varepsilon }}F[\rho +\varepsilon \phi ]\right]_{\varepsilon =0}،\end{تراز شده}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/132e1da8f763ed918cb58f7d83cd4c108acc888f) جایی که
جایی که تغییر ρ نامیده می شود .
تغییر ρ نامیده می شود .![{\displaystyle \phi \mapsto \left[{\frac {d}{d\varepsilon }}F[\rho +\varepsilon \phi ]\right]_{\varepsilon =0}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/8b1ada65ccea3070c2f498355c7e01f1a82b1fb7) یک تابع خطی است، بنابراین می توان
یک تابع خطی است، بنابراین می توان  به عنوان مشتق جهت در نقطه ρ در جهت ϕ . سپس مشابه حساب برداری، حاصل ضرب درونی با گرادیان مشتق جهت را می دهد.
به عنوان مشتق جهت در نقطه ρ در جهت ϕ . سپس مشابه حساب برداری، حاصل ضرب درونی با گرادیان مشتق جهت را می دهد.![{\displaystyle F\left[\rho \right]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/b5f2b97341e91c7e096b9fdb0cfa2cd7294b2afc)
![{\displaystyle \delta F[\rho ;\phi ]=\int {\frac {\delta F}{\delta \rho }}(x)\ \phi (x)\ dx\ .}](https://wikimedia.org/api/rest_v1/media/math/render/svg/1d7e377793bd3f8a8deb912eb0199638f4c2975a) از نظر اکتشافی،
از نظر اکتشافی، ، بنابراین ما "رسما" داریم
، بنابراین ما "رسما" داریم ، و سپس این از نظر شکل مشابه
، و سپس این از نظر شکل مشابه  ،
، جایی که
جایی که متغیرهای مستقل هستند مقایسه دو معادله آخر، مشتق تابعی
متغیرهای مستقل هستند مقایسه دو معادله آخر، مشتق تابعی نقشی مشابه نقش مشتق جزئی دارد
نقشی مشابه نقش مشتق جزئی دارد ، که در آن متغیر ادغام
، که در آن متغیر ادغام مانند نسخه پیوسته شاخص جمع است
مانند نسخه پیوسته شاخص جمع است .
. ![{\displaystyle {\frac {\delta (\lambda F+\mu G)[\rho ]}{\delta \rho (x)}}=\lambda {\frac {\delta F[\rho ]}{\delta \rho (x)}}+\mu {\frac {\delta G[\rho ]}{\delta \rho (x)}}،}](https://wikimedia.org/api/rest_v1/media/math/render/svg/a3855d2be1b75c59c9da233cf9c8c71eeed66eaf) که در آن λ ، μ ثابت هستند.
که در آن λ ، μ ثابت هستند.![{\displaystyle {\frac {\delta (FG)[\rho ]}{\delta \rho (x)}}={\frac {\delta F[\rho ]}{\delta \rho (x)}} G[\rho ]+F[\rho ]{\frac {\delta G[\rho ]}{\delta \rho (x)}}\,,}](https://wikimedia.org/api/rest_v1/media/math/render/svg/ee0421ecdfb105f4b62dcbd729c20e8ca587bda2)
![{\displaystyle {\frac {\delta F[G[\rho ]]}{\delta \rho (y)}}=\int dx{\frac {\delta F[G]}{\delta G(x) }}_{G=G[\rho ]}\cdot {\frac {\delta G[\rho ](x)}{\delta \rho (y)}}\ .}](https://wikimedia.org/api/rest_v1/media/math/render/svg/f89c5a56528b98b95ed70e2011242b78e9cadf91)
![{\displaystyle {\frac {\delta F[g(\rho )]}{\delta \rho (y)}}={\frac {\delta F[g(\rho )]}{\delta g[\ rho (y)]}}\ {\frac {dg(\rho )}{d\rho (y)}}\ .}](https://wikimedia.org/api/rest_v1/media/math/render/svg/68fbcc664f79881c08549ade9a45a74d13db3dce)
![{\displaystyle F[\rho ]=\int f({\boldsymbol {r}},\rho ({\boldsymbol {r}}),\nabla \rho ({\boldsymbol {r}}))\,d {\boldsymbol {r}}،}](https://wikimedia.org/api/rest_v1/media/math/render/svg/984500e18fa20fadb9f03147b92b046a166aafc7) و یک تابع ϕ ( r ) که در مرز ناحیه ادغام ناپدید می شود، از قسمت قبلی
و یک تابع ϕ ( r ) که در مرز ناحیه ادغام ناپدید می شود، از قسمت قبلی ![{\displaystyle {\begin{aligned}\int {\frac {\delta F}{\delta \rho ({\boldsymbol {r}})}}\,\phi ({\boldsymbol {r}})\, d{\boldsymbol {r}}&=\left[{\frac {d}{d\varepsilon }}\int f({\boldsymbol {r}},\rho +\varepsilon \phi ,\nabla \rho + \varepsilon \nabla \phi )\,d{\boldsymbol {r}}\right]_{\varepsilon =0}\\&=\int \left({\frac {\partial f}{\partial \rho } }\,\phi +{\frac {\partial f}{\partial \nabla \rho }}\cdot \nabla \phi \right)d{\boldsymbol {r}}\\&=\int \nabla \rho[{ \frac {\partial f}{\partial \rho }}\,\phi +\nabla \cdot \left({\frac {\partial f}{\partial \nabla \rho }}\,\phi \right) -\left(\nabla \cdot {\frac {\partial f}{\partial \nabla \rho }}\right)\phi \right]d{\boldsymbol {r}}\\&=\int \left[ {\frac {\partial f}{\partial \rho }}\,\phi -\left(\nabla \cdot {\frac {\partial f}{\partial \nabla \rho }}\right)\phi \ راست]d{\boldsymbol {r}}\\&=\int \left({\frac {\partial f}{\partial \rho }}-\nabla \cdot {\frac {\partial f}{\partial \nabla \rho }}\right)\phi ({ \boldsymbol {r}})\ d{\boldsymbol {r}}\,.\end{تراز شده}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/364480cb1cb7bbad967750d4f4c2b2baa061f134)

![{\displaystyle F[\rho ({\boldsymbol {r}})]=\int f({\boldsymbol {r}},\rho ({\boldsymbol {r}}),\nabla \rho ({\boldsymbol {r}})،\nabla ^{(2)}\rho ({\boldsymbol {r}}),\dots ,\nabla ^{(N)}\rho ({\boldsymbol {r}}))\ ,d{\boldsymbol {r}},}](https://wikimedia.org/api/rest_v1/media/math/render/svg/e8d2a74e6ffc8d130e6540ae052afa4431152535)
![{\displaystyle \left[\nabla ^{(i)}\right]_{\alpha _{1}\alpha _{2}\cdots \alpha _{i}}={\frac {\partial ^{\ ,i}}{\partial r_{\alpha _{1}}\partial r_{\alpha _{2}}\cdots \partial r_{\alpha _{i}}}}\qquad \qquad {\text{ where}}\quad \alpha _{1},\alpha _{2},\cdots ,\alpha _{i}=1,2,\cdots ,n\ .}](https://wikimedia.org/api/rest_v1/media/math/render/svg/56d037aa2a7b100d82e701c7c784e8fc1c4db99f)
![{\displaystyle {\begin{aligned}{\frac {\delta F[\rho ]}{\delta \rho }}&{}={\frac {\partial f}{\partial \rho }}-\nabla \cdot {\frac {\partial f}{\partial (\nabla \rho )}}+\nabla ^{(2)}\cdot {\frac {\partial f}{\partial \left(\nabla ^{ (2)}\rho \right)}}+\dots +(-1)^{N}\nabla ^{(N)}\cdot {\frac {\partial f}{\partial \left(\nabla ^ {(N)}\rho \right)}}\\&{}={\frac {\partial f}{\partial \rho }}+\sum _{i=1}^{N}(-1) ^{i}\nabla ^{(i)}\cdot {\frac {\partial f}{\partial \left(\nabla ^{(i)}\rho \right)}}\ .\end{تراز شده} }}](https://wikimedia.org/api/rest_v1/media/math/render/svg/5e309ee6857a3699070ebbbb3e9380ededa6572d)
 مشتقات جزئی f نسبت به مشتقات جزئی ρ هستند،
مشتقات جزئی f نسبت به مشتقات جزئی ρ هستند،![{\displaystyle \left[{\frac {\partial f}{\partial \left(\nabla ^{(i)}\rho \right)}}\right]_{\alpha _{1}\alpha _{ 2}\cdots \alpha _{i}}={\frac {\partial f}{\partial \rho _{\alpha _{1}\alpha _{2}\cdots \alpha _{i}}}} \qquad \qquad {\text{where}}\quad \rho _{\alpha _{1}\alpha _{2}\cdots \alpha _{i}}\equiv {\frac {\partial ^{\, i}\rho }{\partial r_{\alpha _{1}}\,\partial r_{\alpha _{2}}\cdots \partial r_{\alpha _{i}}}}\ ,}](https://wikimedia.org/api/rest_v1/media/math/render/svg/75a055a108cb726caf3543357d6e379254a09dbf) و حاصل ضرب اسکالر تانسور است،
و حاصل ضرب اسکالر تانسور است،
![{\displaystyle T_{\mathrm {TF} }[\rho ]=C_{\mathrm {F} }\int \rho ^{5/3}(\mathbf {r} )\,d\mathbf {r} \ ،.}](https://wikimedia.org/api/rest_v1/media/math/render/svg/805e085a9d15321704c17fcea9c5c2f3a1f8924b) از آنجایی که انتگرال TTF [ ρ ] مشتقات ρ ( r ) را شامل نمی شود ، مشتق عملکردی TTF [ ρ ] است،
از آنجایی که انتگرال TTF [ ρ ] مشتقات ρ ( r ) را شامل نمی شود ، مشتق عملکردی TTF [ ρ ] است، 
![{\displaystyle V[\rho ]=\int {\frac {\rho ({\boldsymbol {r}})}{|{\boldsymbol {r}}|}}\ d{\boldsymbol {r}}.}](https://wikimedia.org/api/rest_v1/media/math/render/svg/2c1593ae52b426aa72244fda7d98ac6aab5a6fd4)
![{\displaystyle {\begin{aligned}\int {\frac {\delta V}{\delta \rho ({\boldsymbol {r}})}}\ \phi ({\boldsymbol {r}})\ d{ \boldsymbol {r}}&{}=\left[{\frac {d}{d\varepsilon }}\int {\frac {\rho ({\boldsymbol {r}})+\varepsilon \phi ({\ boldsymbol {r}})}{|{\boldsymbol {r}}|}}\ d{\boldsymbol {r}}\right]_{\varepsilon =0}\\&{}=\int {\frac { 1}{|{\boldsymbol {r}}|}}\,\phi ({\boldsymbol {r}})\ d{\boldsymbol {r}}\,.\end{تراز شده}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/c5feda7981e551ab3ef736601c97d676b5c93eeb) بنابراین،
بنابراین،
![{\displaystyle J[\rho ]={\frac {1}{2}}\iint {\frac {\rho (\mathbf {r} )\rho (\mathbf {r} ')}{|\mathbf { r} -\mathbf {r} '|}}\,d\mathbf {r} d\mathbf {r} '\,.}](https://wikimedia.org/api/rest_v1/media/math/render/svg/30ff0a58eecdab9b69e1da85dc506f029c9b65b3) از
از ![{\displaystyle {\begin{aligned}\int {\frac {\delta J}{\delta \rho ({\boldsymbol {r}})}}\phi ({\boldsymbol {r}})d{\boldsymbol {r}}&{}=\left[{\frac {d\ }{d\epsilon }}\,J[\rho +\epsilon \phi ]\right]_{\epsilon =0}\\&{ }=\left[{\frac {d\ }{d\epsilon }}\,\left({\frac {1}{2}}\iint {\frac {[\rho ({\boldsymbol {r}} )+\epsilon \phi ({\boldsymbol {r}})]\,[\rho ({\boldsymbol {r}}')+\epsilon \phi ({\boldsymbol {r}}')]}{| {\boldsymbol {r}}-{\boldsymbol {r}}'|}}\,d{\boldsymbol {r}}d{\boldsymbol {r}}'\right)\right]_{\epsilon =0 }\\&{}={\frac {1}{2}}\iint {\frac {\rho ({\boldsymbol {r}}')\phi ({\boldsymbol {r}})}{|{ \boldsymbol {r}}-{\boldsymbol {r}}'|}}\,d{\boldsymbol {r}}d{\boldsymbol {r}}'+{\frac {1}{2}}\iint {\frac {\rho ({\boldsymbol {r}})\phi ({\boldsymbol {r}}')}{|{\boldsymbol {r}}-{\boldsymbol {r}}'|}}\ ،d{\boldsymbol {r}}d{\boldsymbol {r}}'\\\end{تراز شده}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/e5ea4497d6c3471c141f5882e3e91e4c80e36c5f) جمله اول و دوم در سمت راست آخرین معادله با هم برابر هستند، زیرا r و r در جمله دوم را می توان بدون تغییر مقدار انتگرال با هم عوض کرد. از این رو،
جمله اول و دوم در سمت راست آخرین معادله با هم برابر هستند، زیرا r و r در جمله دوم را می توان بدون تغییر مقدار انتگرال با هم عوض کرد. از این رو، و مشتق عملکردی انرژی پتانسیل الکترون-الکترون کولن تابعی J [ ρ ] است،
و مشتق عملکردی انرژی پتانسیل الکترون-الکترون کولن تابعی J [ ρ ] است، 
![{\displaystyle {\frac {\delta ^{2}J[\rho ]}{\delta \rho (\mathbf {r} ')\delta \rho (\mathbf {r} )}}={\frac { \partial }{\partial \rho (\mathbf {r} ')}}\left({\frac {\rho (\mathbf {r} ')}{|\mathbf {r} -\mathbf {r} ' |}}\right)={\frac {1}{|\mathbf {r} -\mathbf {r} '|}}.}](https://wikimedia.org/api/rest_v1/media/math/render/svg/b6863a6705ea4606b99eda69a687aacb21964bc2)
![{\displaystyle T_{\mathrm {W} }[\rho ]={\frac {1}{8}}\int {\frac {\nabla \rho (\mathbf {r} )\cdot \nabla \rho ( \mathbf {r} )}{\rho (\mathbf {r} )}}d\mathbf {r} =\int t_{\mathrm {W} }\ d\mathbf {r} \,,}](https://wikimedia.org/api/rest_v1/media/math/render/svg/0eafe31ae78208f4c75df2c3147f18c61ed02e29) جایی که
جایی که
 و نتیجه این است،
و نتیجه این است، 
![{\displaystyle H[p(x)]=-\sum _{x}p(x)\log p(x)}](https://wikimedia.org/api/rest_v1/media/math/render/svg/5badc001355f04544f4992a05020910fadf0d19d) بدین ترتیب،
بدین ترتیب،![{\displaystyle {\begin{aligned}\sum _{x}{\frac {\delta H}{\delta p(x)}}\,\phi (x)&{}=\left[{\frac { d}{d\epsilon }}H[p(x)+\epsilon \phi (x)]\right]_{\epsilon =0}\\&{}=\left[-\,{\frac {d }{d\varepsilon }}\sum _{x}\,[p(x)+\varepsilon \phi (x)]\ \log[p(x)+\varepsilon \phi (x)]\right]_ {\varepsilon =0}\\&{}=-\sum _{x}\,[1+\log p(x)]\ \phi (x)\,.\end{تراز شده}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/3a3d7804d80847c74e11341f823e94d5f1176333) بدین ترتیب،
بدین ترتیب،
![{\displaystyle F[\varphi (x)]=e^{\int \varphi (x)g(x)dx}.}](https://wikimedia.org/api/rest_v1/media/math/render/svg/8cf62da868a4878d3d5c56043e0e7947d1a3789f)
![{\displaystyle {\begin{aligned}{\frac {\delta F[\varphi (x)]}{\delta \varphi (y)}}&{}=\lim _{\varepsilon \to 0}{\ frac {F[\varphi (x)+\varepsilon \delta (xy)]-F[\varphi (x)]}{\varepsilon }}\\&{}=\lim _{\varepsilon \to 0}{ \frac {e^{\int (\varphi (x)+\varepsilon \delta (xy))g(x)dx}-e^{\int \varphi (x)g(x)dx}}{\varepsilon }}\\&{}=e^{\int \varphi (x)g(x)dx}\lim _{\varepsilon \to 0}{\frac {e^{\varepsilon \int \delta (xy) g(x)dx}-1}{\varepsilon }}\\&{}=e^{\int \varphi (x)g(x)dx}\lim _{\varepsilon \to 0}{\frac { e^{\varepsilon g(y)}-1}{\varepsilon }}\\&{}=e^{\int \varphi (x)g(x)dx}g(y).\end{تراز شده} }}](https://wikimedia.org/api/rest_v1/media/math/render/svg/ec4bb807430d52bf84582815526969c5182132bb)
![{\displaystyle {\frac {\delta F[\varphi (x)]}{\delta \varphi (y)}}=g(y)F[\varphi (x)].}](https://wikimedia.org/api/rest_v1/media/math/render/svg/e78f30af55466f2e117b3dc25af74e86a2db308c)
![{\displaystyle \rho ({\boldsymbol {r}})=F[\rho ]=\int \rho ({\boldsymbol {r}}')\delta ({\boldsymbol {r}}-{\boldsymbol { r}}')\,d{\boldsymbol {r}}'.}](https://wikimedia.org/api/rest_v1/media/math/render/svg/d4a462a8d7648c751791e624f6bb5abdfa985733) از آنجایی که انتگرال به مشتقات ρ وابسته نیست ، مشتق تابعی ρ ( r ) است،
از آنجایی که انتگرال به مشتقات ρ وابسته نیست ، مشتق تابعی ρ ( r ) است،![{\displaystyle {\begin{aligned}{\frac {\delta \rho ({\boldsymbol {r}})}{\delta \rho ({\boldsymbol {r}}')}}\equiv {\frac { \delta F}{\delta \rho ({\boldsymbol {r}}')}}&={\frac {\partial \ \ }{\partial \rho ({\boldsymbol {r}}')}}\ ,[\rho ({\boldsymbol {r}}')\delta ({\boldsymbol {r}}-{\boldsymbol {r}}')]\\&=\delta ({\boldsymbol {r}}- {\boldsymbol {r}}').\end{تراز شده}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/1583fde0b7d6e164506aced9aa3781e502395d53)
 از رابطه زیر بدست می آید:
از رابطه زیر بدست می آید: و
و


 به جای یک تابع تست عمومی
به جای یک تابع تست عمومی ، برای به دست آوردن مشتق عملکردی در نقطه
، برای به دست آوردن مشتق عملکردی در نقطه (این یک نقطه از کل مشتق عملکردی است زیرا
(این یک نقطه از کل مشتق عملکردی است زیرا ![{\displaystyle {\frac {\delta F[\rho (x)]}{\delta \rho (y)}}=\lim _{\varepsilon \to 0}{\frac {F[\rho (x) +\varepsilon \delta (xy)]-F[\rho (x)]}{\varepsilon }}.}](https://wikimedia.org/api/rest_v1/media/math/render/svg/b01a2033e8c8afc08ec56de9981c0e29042885f6)
![F[\rho(x)+\varepsilon f(x)]](https://wikimedia.org/api/rest_v1/media/math/render/svg/b979a338aa9020b6c02e0bcae441aaa605ec2a20) به طور رسمی می توان به صورت یک سری (یا حداقل تا مرتبه اول) گسترش داد
به طور رسمی می توان به صورت یک سری (یا حداقل تا مرتبه اول) گسترش داد . با این حال، فرمول از نظر ریاضی دقیق نیست، زیرا
. با این حال، فرمول از نظر ریاضی دقیق نیست، زیرا![F[\rho(x)+\varepsilon\delta(xy)]](https://wikimedia.org/api/rest_v1/media/math/render/svg/659a52b75b432c570f6c2a7415fc5b4334bf3618) معمولاً حتی تعریف نمی شود.
معمولاً حتی تعریف نمی شود.![{\displaystyle F[\rho (x)]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/c7fab43f9b14ba7f5581e7767857988b966692be) در نتیجه یک تغییر کوچک در کل عملکرد تغییر می کند
در نتیجه یک تغییر کوچک در کل عملکرد تغییر می کند . شکل خاص تغییر در
. شکل خاص تغییر در معرفی می شود.
معرفی می شود. جایی که
جایی که و
و ،
، ،
، بردارهای واحد در امتداد محورهای x، y، z هستند.
بردارهای واحد در امتداد محورهای x، y، z هستند.![{\displaystyle \left[\nabla ^{(2)}\right]_{\alpha \beta }={\frac {\partial ^{\,2}}{\partial r_{\alpha }\,\partial r_{\beta }}}\qquad \qquad {\text{where}}\quad \alpha ,\beta =1,2,3\,.}](https://wikimedia.org/api/rest_v1/media/math/render/svg/78cbff2c145d8b1d793a8318a07d6f72883d2f3d)



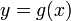 و z به عنوان تابع داده شده است
و z به عنوان تابع داده شده است 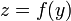 . میزان تغییر z بر حسب y توسط مشتق داده می شود
. میزان تغییر z بر حسب y توسط مشتق داده می شود 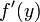 و نرخی که در آن y بر حسب x تغییر می کند توسط مشتق داده می شود
و نرخی که در آن y بر حسب x تغییر می کند توسط مشتق داده می شود 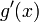 . بنابراین نرخی که z بر حسب x تغییر میکند، حاصلضرب است
. بنابراین نرخی که z بر حسب x تغییر میکند، حاصلضرب است 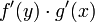 ، و با جایگزین
، و با جایگزین 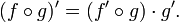
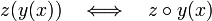
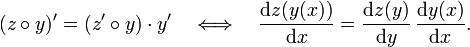 .
.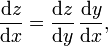
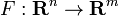 و
و 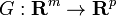 تابع هایی با F دارای مشتق
تابع هایی با F دارای مشتق 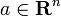 و G دارای مشتق
و G دارای مشتق 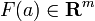 . بنابراین
. بنابراین 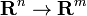 و
و 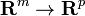 . سپس
. سپس 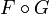 در
در 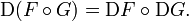
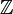
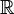
![\sum_{i=m}^n \; f_i\; \delta_{ia} = \begin{cases} f_a & \quad\hbox{if}\quad a\in[m,n] \sub\mathbb{Z} \\ 0 & \quad \hbox{if}\quad a \notin [m,n]. \پایان{موارد}](https://www.theochem.ru.nl/~pwormer/Knowino/knowino.org/w/images/math/f/9/0/f904dcdb548b7a8d7c9049a207e07f94.png)
![\int_{a_0}^{a_1} f(x) \delta(xa) \mathrm{d}x = \begin{موارد} f(a) & \quad\hbox{if}\quad a\in[a_0، a_1] \sub\mathbb{R}، \\ 0 و \quad \hbox{if}\quad a \notin [a_0,a_1]. \پایان{موارد}](https://www.theochem.ru.nl/~pwormer/Knowino/knowino.org/w/images/math/e/2/8/e28c2a00a29b294b1ce1e0390b4cfdc6.png)
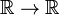 ، بلکه یک
، بلکه یک 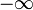 و
و  میگیریم. از اینجا به بعد این کار انجام خواهد شد.
میگیریم. از اینجا به بعد این کار انجام خواهد شد.
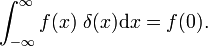
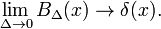
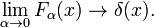
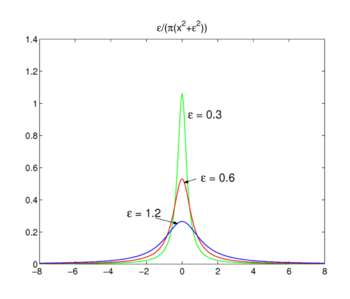
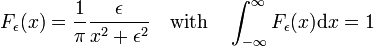
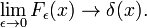
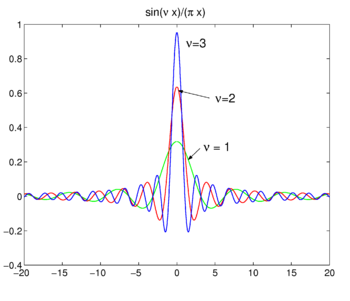
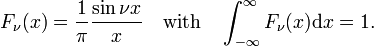
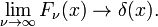
![\int^\nu_{-\nu} e^{ikx} \mathrm{d}k = \frac{1}{ix} \left[ e^{ikx} \right]_{-\nu}^{\ nu} = \frac{2\sin \nu x}{x}،](https://www.theochem.ru.nl/~pwormer/Knowino/knowino.org/w/images/math/2/6/3/2630d795bd1c75bb357a8e9a124e4803.png)
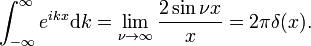
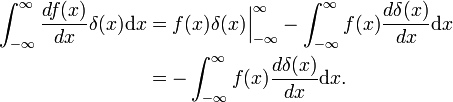
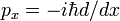 کنیم، در اینجا نشان دادیم که d/d x ضد هرمیتی است.
کنیم، در اینجا نشان دادیم که d/d x ضد هرمیتی است.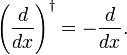
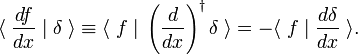
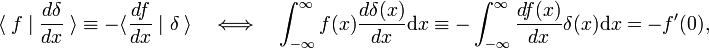
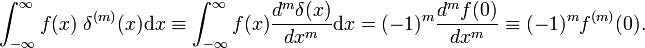
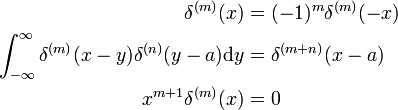

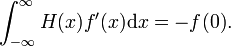
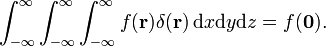
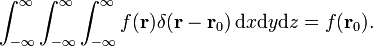
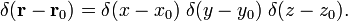
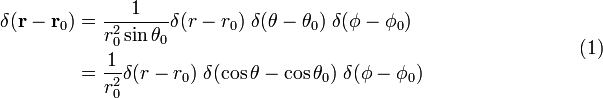
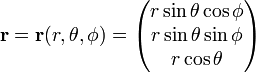
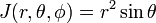
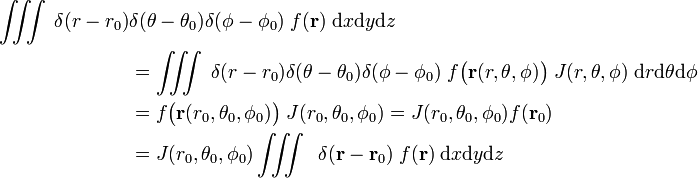
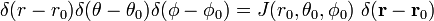
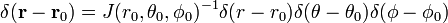
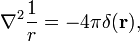





 . سپس،
. سپس، ![{\displaystyle {\begin{aligned}G(x,y,x_{0},y_{0})={\dfrac {1}{2\pi }}&\left[\ln {\sqrt {(x -x_{0})^{2}+(y-y_{0})^{2}}}-\ln {\sqrt {(x+x_{0})^{2}+(y-y_{ 0})^{2}}}\right.\\[5pt]&\left.{}+\ln {\sqrt {(x-x_{0})^{2}+(y+y_{0} )^{2}}}-\ln {\sqrt {(x+x_{0})^{2}+(y+y_{0})^{2}}}\,\right].\end{ هم راستا}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/13fbf122af36e07bc209fd6fa423687e8d8f63c1)
 ، و هر سه عناصر اعداد حقیقی هستند. سپس، برای هر عملکرد {R} }
، و هر سه عناصر اعداد حقیقی هستند. سپس، برای هر عملکرد {R} } با یک
با یک -ام مشتق است که در طول بازه قابل انتگرال گیری است
-ام مشتق است که در طول بازه قابل انتگرال گیری است![[الف، ب]](https://wikimedia.org/api/rest_v1/media/math/render/svg/9c4b788fc5c637e26ee98b45f89a5c08c85f7935) :
:![{\displaystyle {\begin{aligned}f(x)&=\sum _{m=0}^{n-1}{\frac {(xa)^{m}}{m!}}\left[{ \frac {d^{m}f}{dx^{m}}}\right]_{x=a}+\int _{a}^{b}\left[{\frac {(xs)^{ n-1}}{(n-1)!}}\Theta (xs)\right]\left[{\frac {d^{n}f}{dx^{n}}}\right]_{x =s}ds\end{تراز شده}}~.}](https://wikimedia.org/api/rest_v1/media/math/render/svg/fc9ecbd68e5ee3907569c9d36bb93634bef1aaf4) تابع گرین در معادله بالا،
تابع گرین در معادله بالا، ، منحصر به فرد نیست. چگونه معادله اصلاح می شود اگر
، منحصر به فرد نیست. چگونه معادله اصلاح می شود اگر به اضافه می شود
به اضافه می شود ، جایی که
، جایی که راضی می کند
راضی می کند برای همه
برای همه![{\displaystyle x\in [a,b]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/026357b404ee584c475579fb2302a4e9881b8cce) (مثلا،
(مثلا، با
با )؟ همچنین معادله فوق را با شکل یک
)؟ همچنین معادله فوق را با شکل یک  .
.

 ، سپس تابع دلتا صفر می دهد و جواب کلی است
، سپس تابع دلتا صفر می دهد و جواب کلی است
 ، شرایط مرزی در
، شرایط مرزی در دلالت دارد
دلالت دارد
 .
. ، شرایط مرزی در
، شرایط مرزی در دلالت دارد
دلالت دارد
 به دلایل مشابه نادیده گرفته می شود.
به دلایل مشابه نادیده گرفته می شود.
 و
و .
. دلالت دارد
دلالت دارد
 به
به و حد را به عنوان
و حد را به عنوان



 و جایگزین قانون گاوس شود.
و جایگزین قانون گاوس شود. و قانون ضرب را برای عملگر ∇ اعمال کنید،
و قانون ضرب را برای عملگر ∇ اعمال کنید،


 در اتحاد دوم
در اتحاد دوم ![{\displaystyle \int _{V}\left[\varphi (x')\delta (xx')-G(x,x')\,{\nabla '}^{2}\,\varphi (x' )\right]\ d^{3}x'=\int _{S}\left[\varphi (x')\,{\nabla '}G(x,x')-G(x,x') \,{\nabla '}\varphi (x')\right]\cdot d{\widehat {\sigma }}'.}](https://wikimedia.org/api/rest_v1/media/math/render/svg/2a6deb7207fd88c9f116a786927a3b2410821523)

![{\displaystyle \varphi (x)=-\int _{V}G(x,x')\rho (x')\ d^{3}x'+\int _{S}\left[\varphi ( x')\,\nabla 'G(x,x')-G(x,x')\,\nabla '\varphi (x')\right]\cdot d{\widehat {\sigma }}'. }](https://wikimedia.org/api/rest_v1/media/math/render/svg/527d0f78422408b1f342eedff063e16a96162e26)
 به عنوان جزء طبیعی میدان الکتریکی.
به عنوان جزء طبیعی میدان الکتریکی.

 مقدار متوسط پتانسیل روی سطح است. این عدد به طور کلی شناخته شده نیست، اما اغلب بی اهمیت است، زیرا هدف اغلب بدست آوردن میدان الکتریکی داده شده توسط گرادیان پتانسیل است، نه خود پتانسیل.
مقدار متوسط پتانسیل روی سطح است. این عدد به طور کلی شناخته شده نیست، اما اغلب بی اهمیت است، زیرا هدف اغلب بدست آوردن میدان الکتریکی داده شده توسط گرادیان پتانسیل است، نه خود پتانسیل.

 در این وبلاگ به ریاضیات و کاربردهای آن و تحقیقات در آنها پرداخته می شود. مطالب در این وبلاگ ترجمه سطحی و اولیه است و کامل نیست.در صورتی سوال یا نظری در زمینه ریاضیات دارید مطرح نمایید .در صورت امکان به آن می پردازم. من دوست دارم برای یافتن پاسخ به سوالات و حل پروژه های علمی با دیگران همکاری نمایم.در صورتی که شما هم بامن هم عقیده هستید با من تماس بگیرید.
در این وبلاگ به ریاضیات و کاربردهای آن و تحقیقات در آنها پرداخته می شود. مطالب در این وبلاگ ترجمه سطحی و اولیه است و کامل نیست.در صورتی سوال یا نظری در زمینه ریاضیات دارید مطرح نمایید .در صورت امکان به آن می پردازم. من دوست دارم برای یافتن پاسخ به سوالات و حل پروژه های علمی با دیگران همکاری نمایم.در صورتی که شما هم بامن هم عقیده هستید با من تماس بگیرید.