ادامه گروه کواترنیون
خواص گروهی
می خواهم به مقایسه و خواص گروه مقابل با گروه های دیگر از همان سفارش ؟ اتمام گروه از سفارش 8 # خواص گروه
خواص مهم
| ویژگی | راضی | توضیح | اظهار نظر |
|---|---|---|---|
| گروه نظم قدرت اول | آره | ||
| گروه nilpotent | آره | نظم قدرت اول دلالت بر nilpotent دارد | |
| گروه فوق حل پذیر | آره | از طریق nilpotent: nilpotent متناهی به معنای فوق حل پذیر است | |
| گروه قابل حل | آره | از طریق nilpotent: nilpotent به معنی قابل حل است | |
| گروه آبلیان | خیر |  و  رفت و آمد نکنید | کوچکترین گروه غیرآبلی نظم قدرت اول |
| گروه متاسیکلیک | آره | زیر گروه نرمال چرخه ای مرتبه چهار، ضریب چرخه ای مرتبه دو | |
| گروه ددکیند | آره | هر زیرگروه طبیعی است | کوچکترین گروه ددکیند غیرآبلی |
| گروه تی | آره | ددکیند به معنای گروه T است |
سایر خواص
زیر گروه ها
اطلاعات بیشتر: ساختار زیرگروهی گروه کواترنیون 
| کلاس اتومورفیسم از زیر گروه ها | لیست زیر گروه ها | کلاس ایزومورفیسم | ترتیب زیر گروه ها | فهرست زیر گروه ها | تعداد کلاس های مزدوج (=1 اگر زیرگروه automorph-conjugate ) | اندازه هر کلاس conjugacy (=1 اگر زیر گروه نرمال ) | تعداد کل زیر گروه ها (=1 زیر گروه مشخصه اگر ) | کلاس ضریب ایزومورفیسم (در صورت وجود) | کلاس Nilpotency |
|---|---|---|---|---|---|---|---|---|---|
| زیر گروه بی اهمیت |  | زیر گروه بی اهمیت | 1 | 8 | 1 | 1 | 1 | گروه کواترنیون | 0 |
| مرکز گروه کواترنیون |  | گروه چرخه ای: Z2 | 2 | 4 | 1 | 1 | 1 | کلاین چهار گروه | 1 |
| زیرگروه های حداکثر چرخه ای گروه کواترنیون |  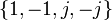  | گروه چرخه ای: Z4 | 4 | 2 | 3 | 1 | 3 | گروه چرخه ای: Z2 | 1 |
| کل گروه |  | گروه کواترنیون | 8 | 1 | 1 | 1 | 1 | گروه بی اهمیت | 2 |
| مجموع (4 ردیف) | -- | -- | -- | -- | 6 | -- | 6 | -- | -- |
+ نوشته شده در شنبه هجدهم دی ۱۴۰۰ ساعت 13:11 توسط علی رضا نقش نیلچی
|
در این وبلاگ به ریاضیات و کاربردهای آن و تحقیقات در آنها پرداخته می شود. مطالب در این وبلاگ ترجمه سطحی و اولیه است و کامل نیست.در صورتی سوال یا نظری در زمینه ریاضیات دارید مطرح نمایید .در صورت امکان به آن می پردازم. من دوست دارم برای یافتن پاسخ به سوالات و حل پروژه های علمی با دیگران همکاری نمایم.در صورتی که شما هم بامن هم عقیده هستید با من تماس بگیرید.