شکل جهان ، در کیهان شناسی فیزیکی ، است محلی و هندسه جهانی از جهان . ویژگی های محلی هندسه جهان در درجه اول توسط انحنای آن توصیف می شود ، در حالی که توپولوژی جهان ویژگی های کلی جهانی شکل آن را به عنوان یک شی مداوم توصیف می کند. انحنای مکانی مربوط به نسبیت عام است ، و توضیح می دهد که چگونه فاصله زمانی توسط انبوه و انرژی منحنی و خم می شود ، در حالی که توپولوژی فضایی را نمی توان از انحنای آن مشخص کرد. فضاهای غیر قابل تشخیص محلی با توپولوژی های مختلف از نظر ریاضی وجود دارد. [1]
کیهان شناسان بین جهان مشاهده شده و کل جهان تمایز قائل هستند ، که بخش اول بخش کروی از دومی است که در اصل با مشاهدات نجومی قابل دسترسی است. با فرض اصل کیهان شناختی ، جهان قابل مشاهده برای همه نقاط برتری معاصر مشابه است ، که به کیهان شناسان این امکان را می دهد که درباره کیهان شناسان درباره خصوصیات کل جهان تنها اطلاعات موجود در جهان قابل مشاهده خود بحث کنند.
شکل کل جهان را می توان با سه ویژگی توصیف کرد: [2]
- محدود یا نامتناهی است
- تخت ( انحنای صفر ) ، باز (انحنای منفی) یا بسته (انحنای مثبت)
- اتصال ، نحوه تشکیل جهان ، یعنی فضای ساده متصل شده یا چند برابر شده است.
بین این خصوصیات اتصالات منطقی خاصی وجود دارد. به عنوان مثال ، جهان با انحنای مثبت لزوما محدود است. [3] اگرچه معمولاً در ادبیات فرض بر این است که یک جهان مسطح یا منفی منحنی بی نهایت است ، اما اگر توپولوژی یک چیز مهم نیست بی اهمیت نیست: برای مثال ، یک سه توروس مسطح اما محدود است. [3]
شکل دقیق هنوز هم در کیهان شناسی فیزیکی مورد بحث است ، اما داده های تجربی از منابع مختلف مستقل ( WMAP ، BOOMERanG و Planck ) به عنوان مثال تأیید می کنند که جهان مسطح است و تنها حاشیه 0.4 درصد خطا دارد. [4] [5] [6] نظریه پردازان در تلاشند تا یک الگوی ریاضی رسمی از شکل جهان را بسازند. به طور رسمی ، این یک مدل 3 مانیفولد است که مربوط به بخش مکانی (در مختصات متحرک ) از زمان فضایی 4 بعدی جهان است. مدلی که بیشتر نظریه پردازان در حال حاضر از آن استفاده می کنند Friedmann – Lemaître – Robertson – Walker است(FLRW) مدل. استدلال مطرح شده است که داده های مشاهده به بهترین وجه منطبق با این نتیجه هستند که شکل جهان جهانی نامتناهی و مسطح است ، [7] اما داده ها با دیگر اشکال ممکن ، مانند به اصطلاح فضای dodecahedral Poincaré همخوانی دارند . 8] [9] و فضای سوکولوف-استاروبینسکی (بخشی از مدل نیم فضای فوقانی فضای چربی با شبکه مشبک 2 بعدی). [10]
فهرست
شکل جهان قابل مشاهده [ ویرایش ]
مقاله اصلی: جهان قابل مشاهده
همچنین مشاهده کنید: اقدامات از راه دور (کیهان شناسی)
همانطور که در مقدمه بیان شد ، دو جنبه قابل بررسی است:
- هندسه محلی آن ، که عمدتا مربوط به انحنای جهان ، به ویژه جهان قابل مشاهده است ، و
- هندسه جهانی آن ، که مربوط به توپولوژی جهان به عنوان یک کل است.
جهان قابل مشاهده می توان به عنوان یک کره که به سمت خارج گسترش از هر نقطه مشاهده برای 46500000000 سال نوری، رفتن دورتر در زمان و بیشتر فکر انتقال سرخ در فاصله بسیار دور به دور یکی به نظر می رسد. در حالت ایده آل ، می توان همه راه را به Big Bang نگاه کرد . با این حال ، در عمل ، دورترین فاصله ممکن است با استفاده از نور به نظر برسد و تابش الکترومغناطیسی دیگر ، پس زمینه مایکروویو کیهانی (CMB) است ، مانند گذشته های مات. تحقیقات تجربی نشان می دهد که جهان مشاهده بسیار نزدیک به ایزوتروپیک و همگن است .
اگر عالم قابل مشاهده کل عالم را در بر می گیرد ، ممکن است بتوانیم با مشاهده ، ساختار کل جهان را تعیین کنیم. با این حال ، اگر جهان قابل مشاهده از کل جهان کوچکتر باشد ، مشاهدات ما فقط به بخشی از کل محدود خواهد شد و ممکن است ما نتوانیم هندسه جهانی آن را از طریق اندازه گیری مشخص کنیم. از آزمایشها می توان مدلهای مختلف ریاضی از هندسه جهانی کل جهان را ساخت ، که همگی مطابق با داده های مشاهده فعلی هستند. بنابراین در حال حاضر مشخص نیست که آیا جهان مشاهده با جهان جهانی یکسان است یا در عوض بسیاری از مرتبه های قدر کوچکتر هستند. جهان ممکن است در بعضی ابعاد کوچک باشد و در بعضی دیگر (مشابه آن با یک مکعب) نیستدر ابعاد طول بیشتر از ابعاد عرض و عمق است). برای بررسی اینکه آیا یک مدل ریاضی معین ، جهان را به طور دقیق توصیف می کند ، دانشمندان به دنبال پیامدهای جدید این مدل هستند - پدیده هایی در جهان چیست که ما هنوز آنها را مشاهده نکرده ایم ، اما اگر این مدل صحیح باشد باید وجود داشته باشد - و آنها آزمایش هایی را برای آزمایش طراحی می کنند. خواه آن پدیده ها رخ دهند یا نه. به عنوان مثال ، اگر جهان یک حلقه بسته کوچک باشد ، انتظار می رود چندین تصویر از یک شی را در آسمان مشاهده کند ، گرچه لزوماً تصاویر در همان سن نیستند.
کیهان شناسان بطور معمول با یک قطعه فضایی مانند فضای مختصر به نام مختصات دوست داشتنی کار می کنند ، وجود یک مجموعه ترجیحی که در کیهان شناسی جسمی امروزی امکان پذیر است و به طور گسترده ای پذیرفته شده است. بخش فاصله زمانی فضایی که می توان مشاهده کرد مخروط نوری عقب (همه نقاط درون افق نور کیهانی ، با توجه به زمان رسیدن به یک مشاهده گر معین) می باشد ، در حالی که از اصطلاح مربوط به حجم هابل می توان برای توصیف یا مخروط نوری گذشته یا فضای خنک کننده استفاده کرد. تا سطح آخرین پراکندگی سخن گفتن از "شکل جهان (در یک مقطع زمانی)" از نظر نسبیت خاص تنها از نظر هستی شناسانه ساده است : به دلیلنسبیت هم زمان بودن ما نمی توانیم از نقاط مختلف فضا به عنوان "در همان نقطه در زمان" صحبت کنیم و نه ، بنابراین ، از "شکل جهان در یک نقطه از زمان". با این حال ، مختصات دلپذیر (اگر به خوبی تعریف شده باشند) با استفاده از زمان از Big Bang (اندازه گیری در مرجع CMB) به عنوان یک زمان جهانی برجسته ، یک حس دقیق را برای کسانی فراهم می کنند.
انحنای جهان [ ویرایش ]
مقاله اصلی: انحنای فضای
انحنای یک مقدار توصیف چگونه هندسه فضا در سطح محلی از یکی از متفاوت است فضای هموار و تخت . انحنای هر فضای ایزوتروپی محلی (و از این رو یک جهان به صورت محلی ایزوتروپی) در یکی از سه مورد زیر قرار می گیرد:
- انحنای صفر (صاف)؛ زاویه های مثلث رسم شده تا 180 درجه می افزاید و قضیه Pythagorean در آن نگه می دارد. چنین فضای 3 بعدی به صورت محلی توسط فضای Euclidean E 3 مدل سازی شده است .
- انحنای مثبت؛ زاویه های مثلث کشیده شده بیش از 180 درجه اضافه می کنند. چنین فضای 3 بعدی به صورت محلی توسط منطقه ای از 3 کره S 3 مدل سازی شده است .
- انحنای منفی؛ زاویه های مثلث کشیده شده تا کمتر از 180 درجه اضافه می شوند. چنین فضای 3 بعدی به صورت محلی توسط یک منطقه از یک مدل فضای هذلولی H 3 .
هندسه های منحنی در حوزه هندسه غیر اقلیدسی قرار دارند . نمونه ای از فضای خمیده مثبت می تواند سطح کره ای مانند زمین باشد. مثلثی که از استوا به قطب کشیده می شود حداقل دو زاویه برابر 90 درجه دارد ، که باعث می شود جمع 3 زاویه از 180 درجه بیشتر شود. نمونه ای از یک سطح منحنی منفی شکل می تواند شکل زین یا گذر کوه باشد. مثلثی که روی سطح زین کشیده شده است ، تعداد زاویه هایی خواهد داشت که کمتر از 180 درجه است.
هندسه محلی از جهان است که آیا تعیین چگالی پارامتر Ω بیشتر از، کمتر از است، و یا به 1. برابر
از بالا به پایین: یک جهان کروی با Ω> 1 ، یک جهان هذلولی با Ω <1 و تخت جهان با Ω = 1 . این تصویر از سطوح دو بعدی صرفاً آنالوگهایی که به راحتی قابل مشاهده است با ساختار 3 بعدی فضای (محلی) قابل مشاهده است.
نسبیت عام توضیح می دهد که جرم و انرژی انحنای فضا را خم می کند و برای تعیین اینکه انحنای جهان با استفاده از مقداری به نام پارامتر چگالی ، که با امگا ( Ω ) نشان داده شده است ، تعیین می شود. پارامتر چگالی میانگین چگالی جهان است که بر اساس چگالی انرژی بحرانی تقسیم می شود ، یعنی انرژی جرم مورد نیاز برای یک جهان صاف است. راه دیگری بگذار ،
- اگر Ω = 1 ، جهان مسطح است
- اگر Ω> 1 ، انحنای مثبت وجود دارد
- اگر Ω <1 انحنای منفی وجود دارد
برای تعیین انحنای دو روش می توان این Ω را به صورت تجربی محاسبه کرد . یکی این است که شمارش تمام انرژی جرم در جهان و گرفتن چگالی متوسط آن و سپس تقسیم آن به طور متوسط با چگالی انرژی بحرانی. داده های مربوط به مایکروویو ویلکینسون ناهمسانگردی پروب (WMAP) و همچنین فضاپیمای پلانک برای سه ماده تشکیل دهنده کل انرژی جرم در جهان مقادیر می دهد - جرم طبیعی ( ماده باریونی و ماده تاریک ) ، ذرات نسبیتی ( فوتون و نوترینو ) و انرژی تاریک یا ثابت کیهان شناسی : [11] [12]
جرم Ω 0.018 ≈ 0.315
نسبیت گرایانه Ω 9.24 × 10 − 5
Ω Λ ≈ 0.6817 ± 0.0018
Ω کل = Ω توده ای + Ω نسبیت گرایانه + Ω Λ = 0.02 00 1.00
ارزش واقعی برای ارزش چگالی بحرانی به عنوان ρ اندازه گیری انتقادی = 9.47 × 10 -27 کیلوگرم بر متر مربع -3 . از این مقادیر ، در خلال خطای آزمایشی ، جهان مسطح به نظر می رسد.
روش دیگر برای اندازه گیری Ω ، انجام این کار از لحاظ هندسی با اندازه گیری یک زاویه در سراسر جهان قابل مشاهده است. ما می توانیم این کار را با استفاده از CMB و اندازه گیری طیف توان و ناهمسانگردی دما انجام دهیم. برای یک شهود می توان تصور کرد که یک ابر گازی که به دلیل بزرگ بودن در تعادل حرارتی قرار ندارد ، پیدا کند که سرعت نور نتواند اطلاعات حرارتی را پخش کند. با دانستن این سرعت انتشار ، اندازه ابر گاز و همچنین فاصله تا ابر گاز را می دانیم ، سپس دو طرف مثلث داریم و بعد می توانیم زاویه ها را تعیین کنیم. با استفاده از روشی مشابه با این ، آزمایش BOOMERanG مشخص کرده است که مقدار زاویه ها تا 180 درجه در خطای آزمایشی ، مربوط به Ω 12 total 1.00 ≈ کل . [13]
این و سایر اندازه گیری های نجومی ، انحنای مکانی را نزدیک به صفر می کنند ، گرچه نشانه های آن را محدود نمی کنند. این بدان معناست که اگرچه هندسه های محلی فضا با تئوری نسبیت مبتنی بر فواصل زمانی فضایی ایجاد می شوند ، اما می توانیم با هندسه اقلیدسی آشنا ، 3 فضا را تقریبی کنیم .
مدل Friedmann-Lemaître-Robertson-Walker (FLRW) با استفاده از معادلات فریدمن معمولاً برای مدل سازی جهان استفاده می شود. مدل FLRW یک خمیدگی از جهان را بر اساس ریاضیات دینامیک سیال ارائه می دهد ، یعنی مدل کردن ماده درون جهان به عنوان یک سیال کامل. اگرچه ستارگان و ساختارهای جرم را می توان در یک مدل "تقریبا FLRW" معرفی کرد ، از یک مدل FLRW کاملاً برای تقریب هندسه محلی جهان قابل مشاهده استفاده می شود. روش دیگر گفتن این امر این است که اگر همه اشکال انرژی تاریک باشدنادیده گرفته می شوند ، سپس انحنای جهان را می توان با اندازه گیری چگالی متوسط ماده در درون آن تعیین کرد ، با فرض اینکه تمام ماده به طور مساوی توزیع می شود (به جای تحریفات ناشی از اشیاء متراکم مانند کهکشانها). این فرض با مشاهدات توجیه می شود که ، در حالی که جهان "ضعیف" ناهمگن و ناهمسانگرد است ( ساختار بزرگ کیهان را ببینید ) ، اما به طور متوسط یکدست و همسان است .
ساختار جهان جهانی [ ویرایش ]
ساختار جهانی هندسه و توپولوژی کل جهان را شامل می شود - هم جهان قابل مشاهده و هم فراتر از آن. در حالی که هندسه محلی هندسه جهانی را به طور کامل تعیین نمی کند ، اما امکانات ، به ویژه هندسه انحنای ثابت را محدود می کند. جهان اغلب به عنوان یک منیفولد ژئودزیکی ، عاری از نقایص توپولوژیکی در نظر گرفته می شود . آرامش هر یک از این موارد تجزیه و تحلیل را بطور چشمگیری پیچیده می کند. هندسه جهانی یک هندسه محلی به علاوه توپولوژی است. از این رو نتیجه می گیرد که یک توپولوژی به تنهایی هندسه جهانی ندارد: به عنوان مثال ، 3-فضای اقلیدسی و 3-فضای بدون قوز دارای توپولوژی یکسان اما هندسه های مختلف جهانی است.
همانطور که در مقدمه گفته شد ، تحقیقات در مورد مطالعه ساختار جهانی جهان شامل موارد زیر است:
- خواه جهان به اندازه نامحدود باشد یا محدود
- این که هندسه جهان جهانی صاف باشد ، دارای انحنا مثبت یا منحنی منفی باشد
- این که آیا توپولوژی به سادگی مانند یک کره متصل است یا چند برابر به هم وصل می شود ، مانند یک توروس [14]
نامتناهی یا محدود [ ویرایش ]
یكی از سؤالهای بی پاسخ در مورد جهان ، این است كه آیا از نظر ابعادی نامتناهی است یا محدود. برای شهود می توان فهمید که یک جهان محدود دارای یک حجم محدود است که به عنوان مثال می تواند از نظر تئوری با یک ماده محدود از مواد پر شود ، در حالی که یک جهان نامتناهی بی حد و مرز است و هیچ حجم عددی نمی تواند آن را پر کند. از نظر ریاضی ، این سؤال که آیا جهان نامحدود است یا محدود ، محدودیت نامیده می شود . یک جهان بی نهایت (فضای متریک نامحدود) بدان معنی است که نقاط وجود دارد خودسرانه دور از هم: برای هر فاصله د ، نقاط که از یک فاصله حداقل وجود دارد د از هم جدا. جهان محدود یک فضای متریک محدود است ، جایی که در آن فاصله d وجود داردبه گونه ای که همه نقاط در فاصله d از یکدیگر قرار دارند. کوچکترین چنین d را قطر جهان می نامند که در این صورت جهان دارای یک "حجم" یا "مقیاس" تعریف شده است.
با یا بدون مرز [ ویرایش ]
با فرض یک جهان محدود ، جهان می تواند یک لبه یا بدون لبه داشته باشد. بسیاری از فضاهای ریاضی محدود ، به عنوان مثال ، یک دیسک ، حاشیه یا مرز دارند. جاهایی که دارای یک لبه هستند ، چه از نظر مفهومی و چه از لحاظ ریاضی قابل درمان هستند. یعنی ، بیان اینکه چه اتفاقی می افتد در حاشیه چنین جهانی است. به همین دلیل ، فضاهایی که دارای لبه هستند ، معمولاً از ملاحظه خارج می شوند.
با این حال ، بسیاری از فضای محدود ، مانند 3-کره و 3-torus وجود دارد ، که هیچ لبه ای ندارند. ریاضی، این فضاها، به عنوان اشاره فشرده بدون مرز. اصطلاح جمع و جور اساساً به معنای محدود بودن محدود ("محدود") و کامل است . اصطلاح "بدون مرز" به این معنی است که فضا بدون حاشیه است. علاوه بر این ، به منظور استفاده از حساب ، جهان به طور معمول فرض می شود منیفولد متفاوت باشد . یک موضوع ریاضی که تمام این خصوصیات را داشته باشد ، فشرده و بدون مرز و قابل تمایز است ، یک منیفولد بسته گفته می شود . 3-کره و 3-torus هر دو منیفولد بسته هستند.
انحنای جهان محدودیت هایی را بر روی توپولوژی قرار می دهد. اگر هندسه فضایی کروی باشد ، یعنی دارای انحنای مثبت باشد ، توپولوژی جمع و جور است. برای یک هندسه فضایی مسطح (انحنای صفر) یا یک ابرقابل (انحنای منفی) ، توپولوژی می تواند کامپکت یا بی نهایت باشد. [15] بسیاری از کتب درسی به اشتباه بیان می کنند که یک جهان مسطح دلالت بر یک جهان بی نهایت دارد. با این حال ، جمله صحیح این است که یک جهان مسطح که به سادگی به هم پیوسته است ، دلالت بر یک جهان بیکران دارد. [15] به عنوان مثال، فضای اقلیدسی صاف، متصل به سادگی و بی نهایت است، اما چنبره صاف، اتصال ضرب، محدود، و جمع و جور است.
به طور کلی ، قضایای محلی به جهانی در هندسه ریمانی هندسه محلی را به هندسه جهانی مربوط می کنند. اگر هندسه محلی دارای انحنای ثابت باشد ، هندسه جهانی بسیار محدود است ، همانطور که در هندسه Fiveton توضیح داده شده است .
آخرین تحقیقات نشان می دهد که حتی اغلب آزمایش های آینده قدرتمند (مانند SKA ) نخواهد بود قادر به تمایز بین تخت، جهان باز و بسته اگر ارزش واقعی پارامتر انحنای کیهانی کوچکتر از 10 است -4 . اگر مقدار واقعی پارامتر انحنای کیهانی بزرگتر از 10 است -3 ما قادر به تمایز بین این سه مدل حتی در حال حاضر خواهد بود. [16]
نتایج ماموریت پلانک منتشر شده در سال 2015 نشان می دهد که پارامتر انحنای کیهان شناسی ، Ω K ، برابر با 0.005 0. 000/0 ، مطابق با جهان مسطح است. [17]
جهان با انحنای صفر [ ویرایش ]
در جهانی با انحنای صفر ، هندسه محلی صاف است . بارزترین ساختار جهانی ، فضای اقلیدسی است که از نظر ابعادی بی نهایت است. جهان های مسطح که به طور محدود محدود هستند شامل بطری توروس و کلاین است . علاوه بر این ، در سه بعد ، 10 منیفولد مسطح محدود بسته وجود دارد ، که 6 نوع آن دارای جهت گیری و 4 نوع غیرمستقیم هستند. اینها منیفولدهای بیبرباخ است . مشهورترین جهان فوق الذکر 3 توروس است .
در صورت عدم وجود انرژی تاریک ، یک جهان مسطح برای همیشه گسترش می یابد اما با سرعت مداوم کاهش می یابد ، با انبساط انبساط به صفر نزدیک می شود. با انرژی تاریک ، سرعت انبساط جهان به دلیل اثر گرانش در ابتدا کند می شود ، اما در نهایت افزایش می یابد. سرانجام کیهان همان است که از یک جهان باز است.
یک جهان مسطح می تواند انرژی کل صفر داشته باشد .
جهان با انحنای مثبت [ ویرایش ]
یک جهان منحنی مثبت با هندسه بیضوی توصیف می شود ، و می توان آن را به عنوان یک ابرشهر سه بعدی یا برخی مانیفولد کروی دیگر (مانند فضای dodecahedral Poincaré ) تصور کرد که همه اینها کمیته 3-کره هستند.
فضای Dodecahedral Poincaré یک فضای خمیده مثبت است که به صورت محاوره ای از آن به عنوان "فوتبال شکل" یاد می شود ، زیرا به عنوان سهمیه 3 کره توسط گروه دوتایی آیکادواس دودویی ، که بسیار نزدیک به تقارن ایکوزا متال ، تقارن یک توپ فوتبال است. این کار توسط ژان پیر لومینت و همکارانش در سال 2003 پیشنهاد شد [8] [18] و جهت گیری بهینه برای این مدل در سال 2008 تخمین زده شد. [9]
جهان با انحنای منفی [ ویرایش ]
جهان کربن ، یکی از انحنای مکانی منفی ، توسط هندسه هایپربولیک توصیف شده است ، و می توان از نظر محلی به عنوان یک آنالوگ سه بعدی از یک شکل زین بی نهایت گسترده فکر کرد. انواع زیادی از مانیفولد هایپربولیک 3 وجود دارد و طبقه بندی آنها کاملاً مشخص نیست. مواردی از حجم محدود را می توان از طریق قضیه سفتی Mostow درک کرد . برای هندسه محلی هایپربولیک ، بسیاری از فضاهای سه بعدی ممکن به طور غیررسمی "توپولوژی شاخ" نامیده می شوند ، به اصطلاح به دلیل شکل شبه قشر ، یک مدل معمولی از هندسه هایپربولیک نامیده می شود . به عنوان مثال شاخ پیكارد ، فضایی با خمیدگی منفی ، كه به صورت محاوره ای به عنوان "قیف شكل" توصیف می شود. [10]
انحنا: باز یا بسته [ ویرایش ]
وقتی کیهان شناسان از جهان به عنوان "باز" یا "بسته" سخن می گویند ، آنها معمولاً به این واقعیت اشاره می کنند که آیا انحنای آن منفی است یا مثبت. این معانی باز و بسته با معنای ریاضی معنای باز و بسته استفاده شده برای مجموعه ها در فضاهای توپولوژیکی و برای معنای ریاضی منیفولد های باز و بسته متفاوت است ، که باعث ابهام و سردرگمی می شود. در ریاضیات تعاریفی برای یک منیفولد بسته (به عنوان مثال ، جمع و جور بدون مرز) و منیفولد باز (به عنوان مثال ، فشرده و بدون مرز) وجود دارد. "جهان بسته" لزوماً منیفولد بسته است. "جهان باز" می تواند یک منیفولد بسته یا باز باشد. به عنوان مثال ، در Friedmann-Lemaître – Robertson – Walker (FLRW) مدل جهان بدون مرز در نظر گرفته می شود ، در این صورت "جهان جمع و جور" می تواند جهانی را توصیف کند که یک مانیفولد بسته است.
مدل میلن ("کروی" در حال گسترش) [ ویرایش ]
مقاله اصلی: مدل میلن
اگر کسی از نسبیت ویژه مبتنی بر فضای Minkowski برای گسترش جهان استفاده کند ، بدون آنکه به مفهوم فاصله زمانی خمیده متوسل شود ، مدل Milne را بدست می آورد. هر بخش مکانی جهان از یک عصر ثابت ( زمان مناسب سپری شده از Big Bang) انحنای منفی خواهد داشت. این صرفاً یک واقعیت هندسی شبه اقلیدسی است که مشابه آن با حوزه های متحدالمرکز در فضای مسطح اقلیدسی منحنی است. هندسه فضایی این مدل یک فضای بی حد و حصر بی حد و مرز است . کل جهان درون یک مخروط نور قرار دارد ، یعنی مخروط آینده Big Bang. برای هر لحظه t > 0 از زمان مختصات (با فرض اینکه Big Bang دارای t = 0 باشد ) ، کل جهان توسط یک کره شعاع دقیقاً c t محدود شده است . پارادوکس ظاهری جهان بیکران موجود در یک کره با انقباض طول توضیح داده شده است : کهکشانهای دورتر ، که سریعتر از بیننده دور می شوند ، نازک تر به نظر می رسند.
این مدل در اصل FLRW انحطاطی برای Ω = 0 است . با مشاهدات ناسازگار است که قطعاً چنین انحنای مکانی بزرگ منفی را رد می کند. با این حال ، به عنوان پیش زمینه ای که در آن می توانید زمینه های گرانشی (یا گراویتون ها) فعالیت کنند ، به دلیل عدم وجود دیفئورمورفیسم ، فضای موجود در مقیاس ماکروسکوپی ، معادل هر راه حل دیگر (باز) معادلات میدانی انیشتین است.
منبع
https://en.wikipedia.org/wiki/Shape_of_the_universe
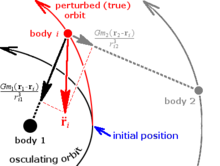
اجسام متقابل متقابل ، این روش از نظر ریاضی برای نیروهای 
با جمع بندی تعاملات فردی از طرف دیگر
بدن:
است 
است 
است 
و
هستند 
فاصله از جسم است 
، 
و 
و اینها بصورت عددی یکپارچه شده اند تا بردارهای سرعت و موقعیت جدید شکل بگیرند این روند هر چند بار که لازم باشد تکرار می شود. مزیت روش Cowell سهولت کاربرد و برنامه نویسی است. یک نقطه ضعف این است که وقتی آشفتگی ها به بزرگی بزرگ می شوند (مثل وقتی که یک شیء به دیگری نزدیک می شود) خطاهای روش نیز بزرگ می شوند. 
شود 
وکتور شعاع مدار آشفته ، و
تغییر از مدار نوسان کننده ،
، و 
.
فقط معادلات حرکت است
برای مدار آشفته و
برای مدار غیر قابل کنترل ،
است 
و
و
بزرگی هستند 
، تفاوت دو بردار تقریبا مساوی است ، و برای جلوگیری از نیاز به 
) که همراه با زمان خود ( 
) منحصر به فرد مسیر حرکت بدن در مدار را در فضا مشخص کنید. 
سپس 
می توان از بردار موقعیت مشتق شد 
با 
.
![\ displaystyle {\ شروع {تراز وسط} \ برنزه \ چپ (\ لامبدا \ سمت راست) و = {\ sin \ چپ (\ alpha \ سمت راست) \ cos \ چپ (\ varepsilon \ راست) + \ برنزه / سمت چپ (\ دلتا) \ right] \ sin \ left (\ varepsilon \ right) \ over \ cos \ left (\ alpha \ Right)}؛ \ qquad {\ شروع {موارد} \ cos \ سمت چپ (\ بتا \ راست) \ sin \ left ( \ lambda \ right) = \ cos \ left (\ delta \ Right) \ sin \ left (\ alpha \ Right) \ cos \ left (\ varepsilon \ Right) + \ gun = left (\ delta \ Right) \ sin \ سمت چپ (\ varepsilon \ سمت راست)؛ \\\ cos \ چپ (\ بتا \ سمت راست) \ cos \ چپ (\ لامبدا \ راست) = \ کوس \ سمت چپ (\ دلتا \ راست) \ cos \ چپ (\ آلفا \ راست ). \ end {موارد}} \\\ گناه \ چپ (\ بتا \ راست) و= \ sin \ left (\ delta \ Right) \ cos \ left (\ varepsilon \ Right) - \ cos \ left (\ delta \ Right) \ gun \ left (\ varepsilon \ Right) \ gun \ left (\ alpha \ راست) \\ [3pt] \ شروع {bmatrix} \ cos \ چپ (\ بتا \ راست) \ cos \ چپ (\ لامبدا \ راست) \\\ cos \ چپ (\ بتا \ راست) \ گناه \ چپ ( \ lambda \ right) \\\ sin \ left (\ beta \ Right) \ end {bmatrix}} & = {\ fill bmatrix} 1 & 0 & 0 & 0 \\ 0 & \ cos \ left (\ varepsilon \ Right) & \ sin \ left (\ varepsilon \ right) \\ 0 & - \ sin \ left (\ varepsilon \ Right) & \ cos \ left (\ varepsilon \ Right) \ end bmatrix}} {\ fill {bmatrix} \ cos \ left (\ delta \ راست) \ کوس \ چپ (\ آلفا \ راست) \\\ کوس \ چپ (\ دلتا \ راست) \ گناه \ چپ (\ آلفا \ راست) \\\ گناه \ چپ (\ دلتا \ راست) \ پایان { bmatrix} \ \\ [6pt] \ tan \ left (\ alpha \ right) & = {\ sin \ left (\ lambda \ Right) \ cos \ left (\ varepsilon \ right) - \ برنزه سمت چپ (\ بتا \ سمت راست) \ sin \ left (\ varepsilon \ Right) \ over \ cos \ left (\ lambda \ right)}؛\ qquad {\ شروع {موارد} \ cos \ چپ (\ دلتا \ راست) \ گناه \ سمت چپ (\ alpha \ راست) = \ cos \ سمت چپ (\ بتا \ راست) \ گناه \ چپ (\ لامبدا \ راست) \ cos \ left (\ varepsilon \ Right) - \ gun \ left (\ beta \ right) \ sin \ left (\ varepsilon \ Right)؛ \\\ cos \ left (\ delta \ Right) \ cos \ left (\ alpha \ right] = \ cos \ چپ (\ بتا \ راست) \ cos \ چپ (\ لامبدا \ راست). \ end {موارد}} \\ [3pt] \ sin \ left (\ delta \ Right) & = \ sin \ سمت چپ (\ بتا \ راست) \ cos \ چپ (\ وارسسیلون \ راست) + \ کوس \ سمت چپ (\ بتا \ راست) \ گناه \ چپ (\ وارپسیلون \ راست) \ گناه \ سمت چپ (\ لامبدا \ راست). \\ [6pt] {\ start bmatrix} \ cos \ left (\ delta \ Right) \ cos \ left (\ alpha \ right) \\\ cos \ left (\ delta \ Right) \ sin \ left (\ alpha \ سمت راست \ \ گناه \ سمت چپ (\ دلتا \ راست) \ پایان {bmatrix}} & = {\ آغاز {bmatrix} 1 & 0 & 0 \\ 0 & \ cos \ left (\ varepsilon \ Right) & - \ sin \ left ( \ varepsilon \ Right) \\ 0 & \ sin \ left (\ varepsilon \ Right) &\ cos \ left (\ varepsilon \ Right) \ end {bmatrix}} {\ fill {bmatrix} \ cos \ left (\ beta Right) \ cos \ left (\ lambda \ right) \\\ cos \ left (\ بتا \ راست) \ گناه \ چپ (\ لامبدا \ راست) \\\ گناه \ چپ (\ بتا \ راست) \ پایان {bmatrix}}. \ end {تراز وسط}](https://wikimedia.org/api/rest_v1/media/math/render/svg/32e64f7f6ef1f8a0eda9cf775fa41f0023c54d4d)
![{\ displaystyle {\ شروع {تراز وسط} \ برنزه \ چپ (A \ راست) و = {\ sin \ چپ (h \ راست) \ بالای \ cos \ چپ (h \ راست) \ sin \ left (\ phi _ {) \ text {o} right \ Right) - \ tan \ left (\ delta \ Right) \ cos \ left (\ phi _ {\ text {o}} \ Right)}؛ \ qquad {\ fill {موارد} \ cos \ چپ (یک \ راست) \ گناه \ چپ (A \ راست) = \ cos \ چپ (\ دلتا \ راست) \ گناه \ چپ (h \ راست) ؛ \\\ cos \ چپ (یک راست) \ cos \ سمت چپ (A \ راست) = \ cos \ چپ (\ دلتا \ راست) \ cos \ چپ (h \ راست) \ sin \ left (\ phi _ {\ text {o}} \ Right) - \ sin \ left (\ delta \ Right) \ cos \ left (\ phi _ {\ text {o}} \ Right) \ end {موارد}} \\ [3pt] \ sin \ left (یک \ راست) و = = گناه \ چپ (\ phi _ {\ text {o}} \ Right) \ sin \ left (\ delta \ Right) + \ cos \ left (\ phi _ {\ text {o}} \ Right) \ cos \ left (\ delta \ سمت راست \ cos \ سمت چپ (h \ راست) ؛ \ end {تراز شده}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/24591754e1a4d05bbcb52fd2b752ad2fa281ad42){kind=small}
،
.![{\ displaystyle {\ شروع {تراز وسط} {\ شروع {bmatrix} \ cos \ چپ (یک \ راست) \ cos \ چپ (A \ راست) \\\ cos \ چپ (یک \ راست) \ sin \ left (A \ سمت راست \ \ گناه \ سمت چپ (یک \ راست) \ پایان {bmatrix}} & = {\ آغاز {bmatrix} \ sin \ left (\ phi _ {\ text {o}} \ Right) & 0 & - cos \ left (\ phi _ {\ text {o}} \ Right) \\ 0 & 1 & 0 \\\ cos \ left (\ phi _ {\ text {o}} \ Right) & 0 & \ sin \ left (\ phi _ {\ متن {o}} \ درست) \ end {bmatrix}} {\ fill {bmatrix} \ cos \ left (\ delta \ Right) \ cos \ left (h \ Right) \\\ cos \ left (\ delta \ Right ) \ sin \ left (h \ Right) \\\ sin \ left (\ delta \ Right) \ end {bmatrix}} \\ & = {\ fill bmatrix \ sin \ left (\ phi _ {\ text o}} \ right) & 0 & - \ cos \ left (\ phi _ {\ text {o}} \ Right) \\ 0 & 1 & 0 \\\ cos \ left (\ phi _ {\ text {o}} \ Right) & 0 & \ sin \ left (\ phi _ {\ text {o}} \ right) \ end {bmatrix}} {\ fill {bmatrix} \ cos \ left (\ theta _ {L} \ Right) & \ sin \ left ( \ تتا _ {ل} \ راست) و 0 \\\ گناه \ سمت چپ (\ تتا _ {ل} \ راست) و- \ cos \ left (\ theta _ {L} \ right) & 0 \\ 0 & 0 & 1 \ end {bmatrix}} {\ fill bmatrix} \ cos \ left (\ delta \ Right) \ cos \ left (\ alpha \ right ) \\\ cos \ left (\ delta \ Right) \ gun \ left (\ alpha \ Right) \\\ gun \ left (\ delta \ Right) \ end {bmatrix}}؛ \\ [6pt] \ tan \ سمت چپ (h \ راست) و = {\ sin \ left (A \ راست) \ over \ cos \ left (A \ راست) \ sin \ left (\ phi _ {\ text {o}} \ Right) + \ tan \ left (a \ Right) \ cos \ left (\ phi _ {\ text {o}} \ right)}؛ \ qquad {\ شروع {موارد} \ cos \ سمت چپ (\ دلتا \ راست) \ گناه \ چپ ( h \ Right) = \ cos \ left (a \ Right) \ sin \ left (A \ Right)؛ \\\ cos \ left (\ delta \ Right) \ cos \ left (h \ Right) = \ sin gun (a \ Right) \ cos \ left (\ phi _ {\ text {o}} \ Right) + \ cos \ left (یک \ سمت راست) \ cos \ چپ (A \ راست) \ sin \ left (\ phi _ {\ text {o} right \ Right) \ end {موارد}} \\ [3pt] \ sin \ left (\ delta \ Right) & = \ sin \ left (\ phi _ {\ text {o}} \ Right ) \ sin \ left (a \ Right) - \ cos \ left (\ phi _ {\ text {o}} \ right) \ cos \ left (a \ Right) \ cos \ left (A \ Right)؛\ end {تراز شده}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/d0b38b9e388153fa974a286f72be3bf6906a5fe3)
،![{\ displaystyle {\ شروع {تراز شده} x & = \ sin \ left (\ phi _ {\ text {o}} \ Right) \ cos \ left (یک \ سمت راست) \ cos \ چپ (A \ راست) + \ cos \ چپ (\ phi _ {\ متن {o}} \ سمت راست) \ sin \ left (یک \ راست) \\ y & = \ cos \ چپ (یک \ راست) \ گناه \ چپ (A \ راست) \\ [ 3pt] {\ start bmatrix} \ cos \ left (\ delta \ Right) \ cos \ left (h \ Right) \\\ cos \ left (\ delta \ Right) \ sin \ left (h \ Right) \\ \ sin \ left (\ delta \ right) \ end {bmatrix}} & = {\ fill {bmatrix} \ sin \ left (\ phi _ {\ text {o}} \ right) & 0 & \ cos \ left (\ phi _ {\ text {o}} \ Right) \\ 0 & 1 & 0 \\ - \ cos \ left (\ phi _ {\ text {o}} \ Right) & 0 &\ sin \ left (\ phi _ {\ text {o}} \ right) \ end {bmatrix}} {\ fill {bmatrix} \ cos \ چپ (یک \ راست) \ cos \ چپ (A \ راست) \\ \ cos \ left (یک \ راست) \ gun \ left (A \ Right) \\\ sin \ left (a \ Right) \ end {bmatrix}} \\ {\ fill bmatrix \ cos \ left (\ delta \ راست) \ کوس \ چپ (\ آلفا \ راست) \\\ کوس \ چپ (\ دلتا \ راست) \ گناه \ چپ (\ آلفا \ راست) \\\ گناه \ چپ (\ دلتا \ راست) \ پایان { bmatrix}} & = {\ fill bmatrix} \ cos \ left (\ theta _ {L} \ Right) & \ sin \ left (\ theta _ {L} \ Right) & 0 \\\ sin \ left (\ theta _ {L} \ right) & - \ cos \ left (\ theta _ {L} \ Right) & 0 \\ 0 & 0 & 1 \ end {bmatrix}} {\ fill bmatrix} \ sin \ left (\ phi _ {\ متن {o}} \ Right) & 0 & \ cos \ left (\ phi _ {\ text {o}} \ Right) \\ 0 & 1 & 0 \\ - \ cos \ left (\ phi _ {\ text {o}} \ Right) و 0 و\ sin \ left (\ phi _ {\ text {o}} \ right) \ end {bmatrix}} {\ fill {bmatrix} \ cos \ چپ (یک \ راست) \ cos \ چپ (A \ راست) \\ \ cos \ سمت چپ (یک \ راست) \ گناه \ چپ (A \ راست) \\\ گناه \ چپ (یک \ راست) \ پایان {bmatrix}}. \ end {تراز وسط}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/e80cd665d08444dadd652d53b0f1bfd9bb35e9c5)
مختصات استوایی قطب شمال کهکشانی و
طول جغرافیایی قطب آسمانی شمالی است. مقادیر این مقادیر به 
.jpg)
.png)
![\ displaystyle S_2 = \ frac {1} {4 \ pi \ alpha '} \ int d ^ 2z \ sqrt {\ gamma} \ left [\ gamma ^ {ab} G _ {\ mu \ nu} (X) \ partial_aX ^ \ mu \ partial_bX ^ \ nu + \ alpha '\ ^ {(2)} R \ Phi (X) \ Right]،}](https://wikimedia.org/api/rest_v1/media/math/render/svg/30b41c2bbb31905c125c1fafcdcddc42972cc785)
است 
ثابت رشته. شاخص ها
دامنه بیش از 1،2 ، و
بر فراز 
، جایی که D بعد از فضای هدف. می توان یک میدان ضد تقارن دیگری اضافه کرد. این امر معمولاً در نظر گرفته می شود که شخص بخواهد این اقدام پتانسیل تورم را ایجاد کند. 
فقط ناهنجاری 
، و از این مدل های کیهانی می توان سناریوی بنگ قبل از بزرگ را ساخت. در واقع ، این معادلات کم مصرف را می توان از اقدامات زیر بدست آورد:![\ displaystyle S = \ frac {1} {2 \ kappa_0 ^ 2} \ int d ^ Dx \ sqrt {-G} e ^ {- 2 \ Phi} \ left [- \ frac {2 (D-26) {3 \ alpha '+ R + 4 \ partial_ \ mu \ Ph \ partial ^ \ mu \ Phi + O (\ alpha') \ درست] ،](https://wikimedia.org/api/rest_v1/media/math/render/svg/47c063f4cc57a882846e139f56a5b544827bb6c7)
ثابت است که همیشه می تواند با تعریف دوباره میدان dilaton تغییر کند. همچنین با تعریف مجدد فیلدها (قاب انیشتین) نیز می توانید این اقدام را به شکلی آشناتر بازنویسی کنید
می توان نوشت![\ displaystyle S = \ frac {1} {2 \ kappa ^ 2} \ int d ^ Dx \ sqrt {-g} \ left [- \ frac {2 (D-26)} 3 \ alpha '} e ^ \ frac {4 \ tilde \ Phi} {D-2}} + \ tilde R- \ frac {4} {D-2} \ partial_ \ mu \ tilde \ Phi \ partial ^ \ mu \ tilde \ Phi + O (\ alpha ') \ درست] ،}](https://wikimedia.org/api/rest_v1/media/math/render/svg/6f1253d4ee32d42a41ac00fed0dc76786e6d11c3){kind=small}
![\ displaystyle \ tilde R = e ^ {- 2 \ omega} [R- (D-1) \ nabla ^ 2 \ omega- (D-2) (D-1) \ partial_ \ mu \ omega \ partial ^ \ mu \ omega].](https://wikimedia.org/api/rest_v1/media/math/render/svg/2622a14c33d501411d9d375ac3d2b987e46659ef)
ثابت نیوتن در ابعاد D و
توده مربوط به پلانک هنگام تنظیم
در این اقدام ، شرایط تورم برآورده نمی شود مگر اینکه اصطلاح بالقوه یا ضد متقارنی به عملکرد رشته اضافه شود ، 
با 
بودن 
توسط،
.
.
با سرعت نور
و حل مسافت مناسب 
شعاع کره هابل را به دست می آوریم
.
،
.
مختصات زمانی پایان جهان است که در مورد جهانی که برای همیشه گسترش می یابد نامتناهی خواهد بود.
.
به عنوان سیگنال های از حوادث آینده تبدیل 
در این وبلاگ به ریاضیات و کاربردهای آن و تحقیقات در آنها پرداخته می شود. مطالب در این وبلاگ ترجمه سطحی و اولیه است و کامل نیست.در صورتی سوال یا نظری در زمینه ریاضیات دارید مطرح نمایید .در صورت امکان به آن می پردازم. من دوست دارم برای یافتن پاسخ به سوالات و حل پروژه های علمی با دیگران همکاری نمایم.در صورتی که شما هم بامن هم عقیده هستید با من تماس بگیرید.