توسط علی رضا نقش نیلچی
| یکشنبه سی و یکم اردیبهشت ۱۴۰۲ | 15:8
-تصحیح سرعت نویز هوابرد D v a : 30log(v/v o )
(معادله 1)
-تصحیح سرعت نویز تابش شده از ساختار D v s : 25log (v/v o )
(معادله 2)
-تضعیف ناشی از گسترش هندسی D s:
(معادله 3)
-اصلاح زاویه دید Dq : 10log ( q /180)
(معادله 4)
-تضعیف مانع برای شرایطی که در آن جذب صوت کافی در سمت منبع قرار می گیرد با استفاده از معادله زیر برای منابع نقطه ای محاسبه شد:
(معادله 5)
که در آن N، عدد فرنل، تابعی از اختلاف طول مسیر است.
تضعیف صدا از یک منبع خط موازی با لبه مانع با ادغام در زاویه قطعه محاسبه می شود. ادغام عددی برای تصحیح منبع خط در فرآیند مدلسازی انجام میشود.
-تبدیل حداکثر سطح فشار صدا، L max ، به سطح نویز معادل، L eq :

(معادله 6)
که در آن R = تعداد قطار در ساعت .
d = فاصله گیرنده از خط مرکزی مسیر (m) ;
l = طول قطار (m) ;
v = سرعت قطار (km/h) ;
q = زاویه دید بخش راه آهن .
d o = فاصله مرجع = 25 متر ;
v o = سرعت قطار مرجع = 100 کیلومتر در ساعت.
-تصحیح برای جلوه نما = 2.5dB(A)
-اصلاحات برای نقاط و گذرگاه ها:
شرایط آهنگ | در مقطع تحصیلی | پل راهاهن |
نقاط و گذرگاه ها | +7.0dB(A) | +7dB(A) |
در ویاداکت و پلنوم در سطح، در متقاطع هایی که نمی توان پلنوم را تهیه کرد، سطح نویز منبع عبارت منبع نویز + 7dB(A) است.
II. نمونه محاسبه نویز راه آهن
برای نشان دادن روش محاسبه اتخاذ شده در ارزیابی تاثیر نویز عملیاتی، پیشبینی سطح نویز کاهش نیافته برای گیرنده حساس به نویز نماینده 13-2 به شرح زیر است.
RNSR 13-2 در 15 متری خط مرکزی بخش مسیر و 10.8 متر زیر بالای ریل قرار دارد. از مشخصات سرعت ارائه شده توسط KCRC، میانگین سرعت قطار تعیین شده برای این بخش 86.3 کیلومتر در ساعت است.
-موقعیت های گیرنده و بخش آهنگ با سهم عمده نویز
| ایستینگ | شمالی شدن | ارتفاع (mPD) |
بخش آهنگ صعودی شماره 84 | 830057.6 | 840939.7 | 17.8 |
RNSR 13-2 | 830061.5 | 840926.5 | 7.1 |
در پیشبینی نویز راهآهن، اجزای اصلی نویز، یعنی نویز هوا، نویز تابش شده از سازه و نویز تهویه مطبوع (A/C)، بهطور جداگانه مدلسازی شدند و برای به دست آوردن نویز کل ترکیب شدند.
الف) نویز هوا
-سطح نویز هوابرد در 25 متر از خط مرکزی مسیر با اعمال تصحیح سرعت در سطح نویز منبع محاسبه شد.
سطح نویز منبع (Airborne) برای سیستم تک پلنوم = 75.3dB(A)
L max، A/B، 25m = 75.3 + 30log (86.3/100) = 73.4dB(A) (با استفاده از معادله 1)
-تضعیف ناشی از گسترش هندسی D s:
فاصله عقبگرد از شکاف پلنوم = 13.5 متر
فاصله عمودی از شکاف پلنوم = 11.6 متر
فاصله شیب از شکاف پلنوم = 17.9 متر
فاصله مرجع، d o ، 25 متر و طول یک قطار 12 واگنی، l، 300 متر است.
Ds = 1.5 dB(A) (با استفاده از رابطه 3)
-تصحیح زاویه دید Dq :
زاویه دید قطعه = 65 درجه
Dq = -4.4dB(A) (با استفاده از رابطه 4)
-تضعیف سد:
اختلاف طول مسیر تخمین زده شده برای دیوار جان پناه 1.2 متری در سازه ویاداکت استاندارد 1.6 متر است.
طیف نویز راه آهن مرجع اتخاذ شده در مطالعه غرب ریل EIA در محاسبه تضعیف مانع استفاده شد.
تضعیف مانع منبع نقطه ای D b = -20.9dB(A) (با استفاده از رابطه 5)
-حداکثر سطح نویز هوا در RNSR13-2 به دلیل بخش #84،
L max، A/B = L max، A/B، 25m + Dq + D s + D b = 73.4 + 1.5 - 4.4 -20.9 = 49.5dB(A)
-سهم نویز هوابرد از بخش #84 با تبدیل L max به L eq و با اعمال تصحیح اثر نما به دست آمد:
برای شرایط پایه، فرکانس قطار 12 قطار در ساعت در هر جهت در نظر گرفته می شود.
L eq، A/B = 49.5 + 10log (12(1.5 ´ 17.9+300)/86.3) -30 + 2.5 = 38.6dB(A)
(با استفاده از معادله 6)
ب) نویز تابش شده از سازه
-سطح نویز تابشی سازه در 25 متر از خط مرکزی مسیر با اعمال تصحیح سرعت در سطح نویز منبع محاسبه شد.
سطح نویز منبع (تابش ساختار) برای مسیر با لرزش کم = 66.5dB(A)
L max، S/R، 25m = 66.5 + 25log (86.3/100) = 64.9dB(A) (با استفاده از معادله 2)
-تضعیف ناشی از گسترش هندسی D s:
فاصله عقبگرد از سازه ویاداکت = 15.0 متر
فاصله عمودی از سازه ویاداکت = 8.7 متر
فاصله شیب از سازه ویاداکت = 17.3 متر
فاصله مرجع، d o ، 25 متر و طول یک قطار 12 واگنی، l، 300 متر است.
Ds = 1.6 dB(A) (با استفاده از رابطه 3)
-تصحیح زاویه دید Dq :
زاویه دید قطعه = 65 درجه
Dq = -4.4dB(A) (با استفاده از رابطه 4)
-حداکثر سطح نویز تابش شده از ساختار در RNSR13-2 به دلیل بخش #84،
L max، S/R = L max، S/R، 25m + Dq + D s = 64.9 + 1.6 - 4.4 = 62.1dB(A)
-سهم نویز تابشی ساختار از بخش #84 با تبدیل L max به L eq و با اعمال تصحیح اثر نما به دست آمد:
برای شرایط پایه، فرکانس قطار 12 قطار در ساعت در هر جهت در نظر گرفته می شود.
L eq، S/R = 62.1 + 10log (12(1.5 ´ 17.3+300)/86.3) -30 + 2.5 = 51.1dB(A)
(با استفاده از معادله 6)
ج) صدای تهویه مطبوع (A/C).
-سطح صدای تهویه مطبوع در 25 متر از خط مرکزی مسیر برای قطار بازسازی شده ریل شرقی:
حداکثر L ، تهویه مطبوع، 25 متر = 62.8dB(A)
-تضعیف ناشی از گسترش هندسی D s:
فاصله عقبگرد از شکاف پلنوم = 15.0 متر
فاصله عمودی از شکاف پلنوم = 14.4 متر
فاصله شیب از شکاف پلنوم = 20.8 متر
فاصله مرجع، d o ، 25 متر و طول یک قطار 12 واگنی، l، 300 متر است.
Ds = 0.8 dB(A) (با استفاده از رابطه 3)
-تصحیح زاویه دید Dq :
زاویه دید قطعه = 65 درجه
Dq = -4.4dB(A) (با استفاده از رابطه 4)
-تضعیف سد:
تفاوت طول مسیر تخمین زده شده برای دیوار جان پناه 1.2 متری در سازه ویاداکت استاندارد 0.3 متر است.
طیف نویز راه آهن مرجع اتخاذ شده در مطالعه غرب ریل EIA در محاسبه تضعیف مانع استفاده شد.
تضعیف مانع منبع نقطه ای Db = -16.8dB(A) (با استفاده از رابطه 5)
-حداکثر سطح نویز A/C در RNSR13-2 به دلیل بخش #84،
L max، A/C = L max، A/C، 25m + Dq + D s + D b = 62.8 + 0.8 - 4.4 -16.8 = 42.4dB(A)
-سهم نویز A/C از بخش #84 با تبدیل L max به L eq و با اعمال تصحیح اثر نما به دست آمد:
برای شرایط پایه، فرکانس قطار 12 قطار در ساعت در هر جهت در نظر گرفته می شود.
L eq، A/C = 42.4 + 10log (12(1.5 ´ 20.8+300)/86.3) -30 + 2.5 = 31.5dB(A)
(با استفاده از معادله 6)
د) سر و صدای کل
سهم کل نویز از بخش #84 با جمع کردن سهم نویز از سه مولفه نویز کنار راه به دست آمد.
-حداکثر سطح نویز در RNSR13-2 به دلیل بخش #84،
L max، کل = مجموع گزارش (L max، A/B، L max، S/R ، L max، A/C ) = 62.4dB(A)
-سهم کل نویز از بخش #84،
L eq، کل = مجموع log (L eq، A/B، L eq، S/R ، L eq، A/C ) = 51.4dB(A)
به طور مشابه، سهم نویز از هر بخش از مسیر جنوب و شمال خط Spur محاسبه شد. برای بخش مسیر که نقاط و گذرگاهها در آن قرار دارند، فاکتورهای اصلاحی برای افزایش سطح صدای غلتش در هنگام عبور قطار از روی این بخشهای مسیر اعمال شد.
حداکثر سطح نویز ناشی از عبور قطار و سطح نویز پیشبینیشده در RNSR13-2 با جمعکردن سطوح نویز از تمام بخشهای مسیر بالا و پایین خط خار بهدست آمد. نتایج پیشبینی، با تفکیک سهم از اجزای اصلی نویز، در پیوست E آورده شده است.
https://www.epd.gov.hk/eia/register/report/eiareport/eia_0442000/Append/Ap-D.htm































































































![{\displaystyle {\begin{aligned}x(t)&=R\left[(1-k)\cos t+lk\cos {\frac {1-k}{k}}t\right],\\ y(t)&=R\left[(1-k)\sin t-lk\sin {\frac {1-k}{k}}t\right].\\\end{تراز شده}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/5f1b39a37ec7e9d19341c5424fd55323f5e94a40)






















 یک سیستم مختصات در U است، سپس هر فیلد برداری e j را می توان به صورت ترکیبی خطی از فیلدهای برداری مختصات بیان کرد.
یک سیستم مختصات در U است، سپس هر فیلد برداری e j را می توان به صورت ترکیبی خطی از فیلدهای برداری مختصات بیان کرد. :
: جایی که هر کدام
جایی که هر کدام تابعی در U است. اینها را می توان به عنوان اجزای یک ماتریس دید
تابعی در U است. اینها را می توان به عنوان اجزای یک ماتریس دید :
: جایی که هر کدام
جایی که هر کدام یک تابع در U. از آنجا که
یک تابع در U. از آنجا که  ، دو عبارت مختصات بالا با هم ترکیب می شوند و به دست می آیند
، دو عبارت مختصات بالا با هم ترکیب می شوند و به دست می آیند ; از نظر ماتریس، این فقط این را می گوید
; از نظر ماتریس، این فقط این را می گوید
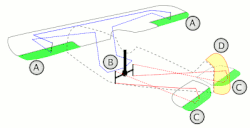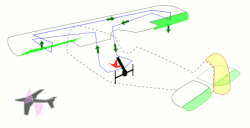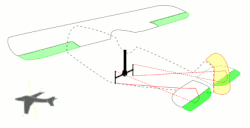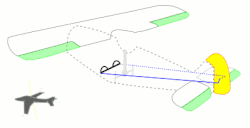
 (لغزش کناری)، r (سرعت انحراف) و p (نرخ چرخش)، با گشتاورهای N (انحراف) و L (لغزش)، و نیروی Y (به طرفین). 9 مشتق پایداری مربوط به این حرکت وجود دارد که در زیر نحوه ایجاد آنها توضیح داده شده است. با این حال، با بازی کردن با هواپیمای مدل، و در نظر گرفتن اینکه چگونه نیروهای وارد بر هر جزء تحت تأثیر تغییرات در لغزش کناری و سرعت زاویهای قرار میگیرند، میتوان درک شهودی بهتری به دست آورد:
(لغزش کناری)، r (سرعت انحراف) و p (نرخ چرخش)، با گشتاورهای N (انحراف) و L (لغزش)، و نیروی Y (به طرفین). 9 مشتق پایداری مربوط به این حرکت وجود دارد که در زیر نحوه ایجاد آنها توضیح داده شده است. با این حال، با بازی کردن با هواپیمای مدل، و در نظر گرفتن اینکه چگونه نیروهای وارد بر هر جزء تحت تأثیر تغییرات در لغزش کناری و سرعت زاویهای قرار میگیرند، میتوان درک شهودی بهتری به دست آورد: 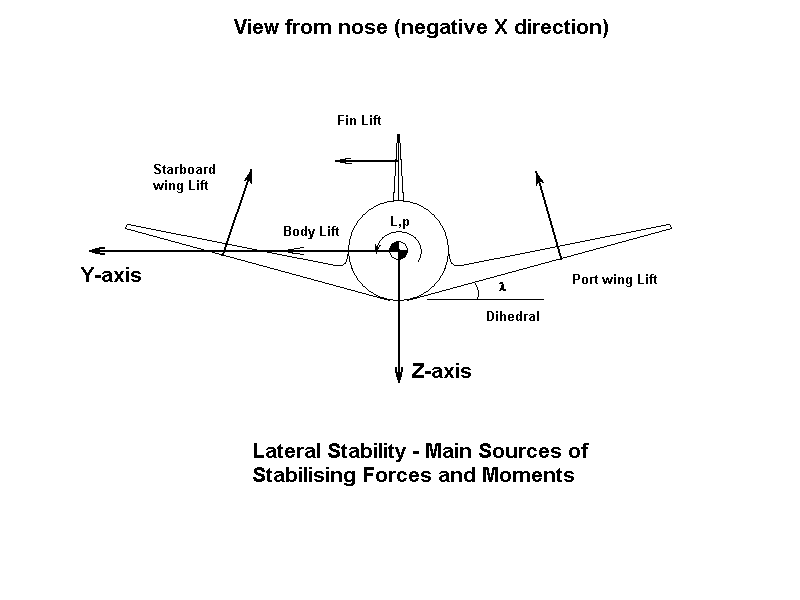
 نیروی جانبی ناشی از لغزش جانبی (در صورت عدم انحراف).
نیروی جانبی ناشی از لغزش جانبی (در صورت عدم انحراف). نیروی جانبی ناشی از سرعت چرخش.
نیروی جانبی ناشی از سرعت چرخش. نیروی جانبی ناشی از سرعت انحراف.
نیروی جانبی ناشی از سرعت انحراف. لحظه خمیازه کشیدن به دلیل نیروهای لغزش کناری.
لحظه خمیازه کشیدن به دلیل نیروهای لغزش کناری. لحظه خمیازه کشیدن به دلیل نرخ چرخش.
لحظه خمیازه کشیدن به دلیل نرخ چرخش. لحظه خمیازه به دلیل نرخ انحراف.
لحظه خمیازه به دلیل نرخ انحراف. لحظه چرخش به دلیل لغزش کناری.
لحظه چرخش به دلیل لغزش کناری.
 لحظه چرخش به دلیل نرخ انحراف.
لحظه چرخش به دلیل نرخ انحراف. لحظه چرخش به دلیل نرخ رول.
لحظه چرخش به دلیل نرخ رول.
 (اوه)
(اوه) (رول)
(رول)


 (phi) توسط:
(phi) توسط:
 (میرایی)
(میرایی) (سفتی، سختی)
(سفتی، سختی) مثبت خواهد بود زیرا
مثبت خواهد بود زیرا
 (
(  (psi). معادله نیروی حرکت شامل یک جزء وزن است: [
(psi). معادله نیروی حرکت شامل یک جزء وزن است: [ 

 (اوه)
(اوه) (رول)
(رول)


 (هر دو محصول مثبت هستند). این در تضاد مستقیم با الزامات پایداری رول هلندی است، و طراحی هواپیمایی که هر دو حالت رول هلندی و مارپیچی ذاتاً پایدار باشند، دشوار است. [
(هر دو محصول مثبت هستند). این در تضاد مستقیم با الزامات پایداری رول هلندی است، و طراحی هواپیمایی که هر دو حالت رول هلندی و مارپیچی ذاتاً پایدار باشند، دشوار است. [  (گاما) و سرعت. معادلات اغتشاش کوچک حرکت عبارتند از:
(گاما) و سرعت. معادلات اغتشاش کوچک حرکت عبارتند از:

 و
و باید در نظر گرفته شود.
باید در نظر گرفته شود.



 مساحت بال، W وزن و
مساحت بال، W وزن و ضریب افزایش است (ثابت فرض می شود زیرا بروز ثابت است)، تقریباً داریم:
ضریب افزایش است (ثابت فرض می شود زیرا بروز ثابت است)، تقریباً داریم:











 (تتا) و بروز
(تتا) و بروز (آلفا). جهت بردار سرعت نسبت به محورهای اینرسی است
(آلفا). جهت بردار سرعت نسبت به محورهای اینرسی است . بردار سرعت:
. بردار سرعت: 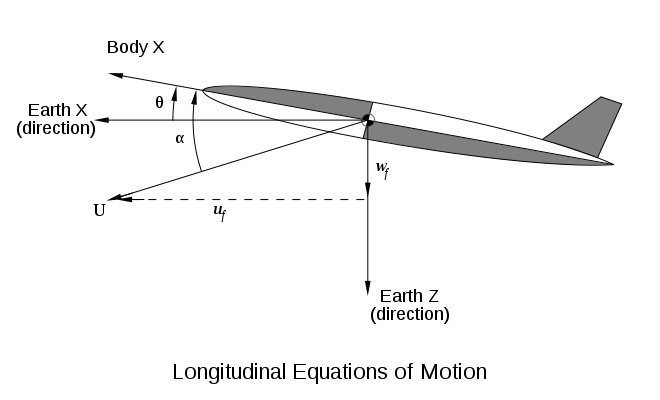


 ،
، مولفه های محورهای اینرسی سرعت هستند. طبق
مولفه های محورهای اینرسی سرعت هستند. طبق 

 در طول دوره نوسان ناچیز است، بنابراین:
در طول دوره نوسان ناچیز است، بنابراین:




 ، نرخ زمین. بنابراین، معادلات حرکت با تمام نیروها و گشتاورهای محور باد عبارتند از:
، نرخ زمین. بنابراین، معادلات حرکت با تمام نیروها و گشتاورهای محور باد عبارتند از:

 بالا بردن به دلیل وقوع، این منفی است زیرا محور z رو به پایین است در حالی که برخورد مثبت باعث نیروی رو به بالا می شود.
بالا بردن به دلیل وقوع، این منفی است زیرا محور z رو به پایین است در حالی که برخورد مثبت باعث نیروی رو به بالا می شود. لیفت به دلیل نرخ گام، از افزایش بروز دم ناشی می شود، از این رو نیز منفی است، اما در مقایسه با
لیفت به دلیل نرخ گام، از افزایش بروز دم ناشی می شود، از این رو نیز منفی است، اما در مقایسه با
 لحظه شیب به دلیل نرخ زمین - اصطلاح میرایی زمین، این همیشه منفی است.
لحظه شیب به دلیل نرخ زمین - اصطلاح میرایی زمین، این همیشه منفی است.



 در مقایسه با وحدت کوچک باشد، بنابراین ضریب
در مقایسه با وحدت کوچک باشد، بنابراین ضریب . این عبارت تحت سلطه است
. این عبارت تحت سلطه است


















 در این وبلاگ به ریاضیات و کاربردهای آن و تحقیقات در آنها پرداخته می شود. مطالب در این وبلاگ ترجمه سطحی و اولیه است و کامل نیست.در صورتی سوال یا نظری در زمینه ریاضیات دارید مطرح نمایید .در صورت امکان به آن می پردازم. من دوست دارم برای یافتن پاسخ به سوالات و حل پروژه های علمی با دیگران همکاری نمایم.در صورتی که شما هم بامن هم عقیده هستید با من تماس بگیرید.
در این وبلاگ به ریاضیات و کاربردهای آن و تحقیقات در آنها پرداخته می شود. مطالب در این وبلاگ ترجمه سطحی و اولیه است و کامل نیست.در صورتی سوال یا نظری در زمینه ریاضیات دارید مطرح نمایید .در صورت امکان به آن می پردازم. من دوست دارم برای یافتن پاسخ به سوالات و حل پروژه های علمی با دیگران همکاری نمایم.در صورتی که شما هم بامن هم عقیده هستید با من تماس بگیرید.