نقطه بحرانی

این مقاله شامل فهرستی از مراجع عمومی است ، اما فاقد استنادهای درون خطی متناظر کافی است . لطفا با معرفی نقل قول های دقیق تر به بهبود این مقاله کمک کنید. ( ژانویه 2015 ) ( نحوه و زمان حذف این پیام الگو را بیاموزید )

(مختصات x) دایره های قرمز نقاط ثابت هستند . مربع های آبی نقطه عطف هستند .

نقطه بحرانی اصطلاحی است که در بسیاری از شاخه های ریاضیات استفاده می شود .

وقتی با توابع یک متغیر حقیقی سروکار داریم ، نقطه بحرانی نقطه‌ای در دامنه تابع است که در آن تابع یا مشتق پذیر نیست یا مشتق آن برابر با صفر است. [1] به طور مشابه، هنگام برخورد با متغیرهای مختلط ، یک نقطه بحرانی نقطه‌ای در دامنه تابع است که در آن یا هولومورفیک نیست یا مشتق آن برابر با صفر است. [2] [3] به همین ترتیب، برای تابعی از چندین متغیر حقیقی ، یک نقطه بحرانی مقداری در دامنه آن است که در آن گرادیان تعریف نشده یا برابر با صفر است. [4]

مقدار تابع در یک نقطه بحرانی یک مقدار بحرانی است . [5]

این نوع از تعریف به نقشه های مشتق پذیر بین گسترش می یابد $\mathbb{R} ^{m}$ و $\mathbb {R} ^{n},$ یک نقطه بحرانی ، در این مورد، نقطه ای است که رتبه ماتریس ژاکوبین حداکثر نیست. این به نقشه های مشتق پذیر بین منیفولدهای قابل تفکیک گسترش می یابد ، زیرا نقاطی که رتبه ماتریس ژاکوبین کاهش می یابد. در این حالت به نقاط بحرانی نقاط انشعاب نیز می گویند .

به طور خاص، اگر C یک منحنی مسطح باشد که با یک معادله ضمنی f ( x , y ) = 0 تعریف شده است ، نقاط بحرانی طرح ریزی بر روی محور x ، موازی با محور y ، نقاطی هستند که مماس بر C هستند. موازی با محور y هستند ، این نقاطی است که در آن

${\frac {\partial f}{\partial y}}(x,y)=0$

به عبارت دیگر، نقاط بحرانی نقاطی هستند که قضیه تابع ضمنی در آنها کاربرد ندارد.

مفهوم نقطه بحرانی اجازه توصیف ریاضی یک پدیده نجومی را می دهد که قبل از زمان کوپرنیک توضیح داده نشده بود . نقطه ثابت در مدار یک سیاره، نقطه ای از مسیر سیاره در کره آسمانی است ، جایی که به نظر می رسد حرکت سیاره قبل از شروع مجدد در جهت دیگر متوقف می شود. این به دلیل نقطه بحرانی پرتاب مدار به دایره دایره البروج رخ می دهد .

نقطه بحرانی یک تابع متغیر واحد [ ویرایش ]

نقطه بحرانی یک تابع از یک متغیر حقیقی منفرد ، f ( x ) ، مقدار x 0 در دامنه f است که در آن f مشتق پذیر نیست یا مشتق آن 0 است (یعنی $f'(x_{0})=0$ ). [1] یک مقدار بحرانی تصویر زیر f یک نقطه بحرانی است. این مفاهیم ممکن است از طریق نمودار f تجسم شوند : در یک نقطه بحرانی، اگر اصلاً بتوانید آن را اختصاص دهید، نمودار دارای مماس افقی است.

توجه کنید که چگونه برای یک تابع متمایز ، نقطه بحرانی همان نقطه ثابت است .

اگرچه به راحتی در نمودار (که یک منحنی است) قابل مشاهده است، مفهوم نقطه بحرانی یک تابع نباید با مفهوم نقطه بحرانی، در برخی جهت، یک منحنی اشتباه گرفته شود (برای تعریف دقیق به زیر مراجعه کنید ) . اگر g ( x , y ) یک تابع متمایز از دو متغیر باشد، آنگاه g ( x , y ) = 0 معادله ضمنی یک منحنی است . یک نقطه بحرانی چنین منحنی، برای طرح ریزی موازی با محور y (نقشه ( x , y ) → x )، نقطه ای از منحنی است که در آن. ${\tfrac {\partial g}{\partial y}}(x,y)=0.$ این بدان معناست که مماس منحنی موازی با محور y است ، و در این نقطه، g تابع ضمنی از x به y را تعریف نمی کند (به قضیه تابع ضمنی مراجعه کنید ). اگر ( x 0 , y 0 ) چنین نقطه بحرانی باشد، آنگاه x 0 مقدار بحرانی مربوطه است . به چنین نقطه بحرانی، نقطه انشعاب نیز می گویند ، زیرا به طور کلی، هنگامی که x تغییر می کند، دو شاخه منحنی در یک طرف x 0 و صفر در طرف دیگر وجود دارد.

از این تعاریف نتیجه می شود که یک تابع متمایز f ( x ) دارای یک نقطه بحرانی x 0 با مقدار بحرانی y 0 است ، اگر و فقط اگر ( x 0 , y 0 ) نقطه بحرانی نمودار آن برای طرح ریزی موازی x باشد. محور، با همان مقدار بحرانی y 0 . اگر f در x 0 به دلیل موازی شدن مماس با محور y مشتق پذیر نباشد ، x 0 دوباره نقطه بحرانی f است ، اما اکنون ( x 0 , y 0 ) نقطه بحرانی نمودار آن برای طرح ریزی است. موازی با محور y

به عنوان مثال، نقاط بحرانی دایره واحد معادله $x^{2}+y^{2}-1=0$ (0، 1) و (0، -1) برای برآمدگی موازی با محور x ، و (1، 0) و (-1، 0) برای جهت موازی با محور y هستند . اگر نیم دایره بالایی را نمودار تابع در نظر بگیریم $f(x)={\sqrt {1-x^{2}}}،$ سپس x = 0 یک نقطه بحرانی با مقدار بحرانی 1 است زیرا مشتق برابر با 0 است و x = ± 1 نقاط بحرانی با مقدار بحرانی 0 به دلیل تعریف نشده بودن مشتق هستند.

مثالها [ ویرایش ]

کارکرد $f(x) = x^2 + 2x + 3$ در همه جا با مشتق مشتق پذیر است $f'(x)=2x+2.$ این تابع دارای یک نقطه بحرانی منحصر به فرد −1 است، زیرا عدد یکتایی x 0 برای آن است2. $2x+2=0.$ این نقطه حداقل جهانی f است . مقدار بحرانی مربوطه است. $f(-1)=2.$ نمودار f یک سهمی مقعر به سمت بالا است، نقطه بحرانی آبسیس راس است که در آن خط مماس افقی است، و مقدار بحرانی مربوط به راس است و ممکن است با تقاطع این خط مماس و خط مماس نشان داده شود. محور y .
کارکرد $f(x)=x^{2/3}$ برای همه x تعریف شده و برای x ≠ 0 با مشتق قابل تفکیک است $f'(x)={\tfrac {2x^{-1/3}}{3}}.$ از آنجایی که f در x = 0 و قابل تفکیک نیست $f'(x)\neq 0$ در غیر این صورت، آن نقطه بحرانی منحصر به فرد است. نمودار تابع f در این نقطه یک کاسپ با مماس عمودی دارد . مقدار بحرانی مربوطه است. $f(0)=0.$
تابع مقدار مطلق $f(x)=|x|$ در همه جا مشتق پذیر است به جز در نقطه بحرانی x = 0 ، جایی که یک نقطه حداقل جهانی با مقدار بحرانی 0 دارد.
کارکرد $f(x)={\tfrac {1}{x}}$ نقاط بحرانی ندارد نقطه x = 0 یک نقطه بحرانی نیست زیرا در دامنه تابع گنجانده نشده است.

مکان نقاط بحرانی [ ویرایش ]

طبق قضیه گاوس-لوکاس ، تمام نقاط بحرانی یک تابع چند جمله ای در صفحه مختلط در داخل بدنه محدب ریشه های تابع قرار دارند. بنابراین برای یک تابع چند جمله ای با ریشه های حقیقی، تمام نقاط بحرانی حقیقی هستند و بین بزرگترین و کوچکترین ریشه ها قرار دارند.

حدس سندوف بیان می‌کند که اگر همه ریشه‌های یک تابع در دیسک واحد در صفحه مختلط قرار گیرند، حداقل یک نقطه بحرانی در فاصله واحد از هر ریشه معین وجود دارد.

نقاط بحرانی یک منحنی ضمنی [ ویرایش ]

همچنین ببینید: منحنی جبری

نقاط بحرانی نقش مهمی در مطالعه منحنی های سطحی تعریف شده توسط معادلات ضمنی ایفا می کنند ، به ویژه برای ترسیم آنها و تعیین توپولوژی آنها . مفهوم نقطه بحرانی که در این بخش استفاده می شود، ممکن است متفاوت از قسمت قبلی به نظر برسد. در واقع این تخصص به یک مورد ساده از مفهوم کلی نقطه بحرانی است که در زیر آورده شده است .

بنابراین، منحنی C را در نظر می گیریم که با یک معادله ضمنی تعریف شده است $f(x,y)=0$ ، که در آن f یک تابع متمایز از دو متغیر است که معمولاً یک چند جمله ای دو متغیره است . نقاط منحنی نقاط صفحه اقلیدسی هستند که مختصات دکارتی آن معادله را برآورده می کند. دو پیش بینی استاندارد وجود دارد $\pi _{y}$ و $\pi _{x}$ ، تعریف شده بوسیله ی $\pi _{y}((x،y))=x$ و $\pi _{x}((x,y))=y,$ که منحنی را روی محورهای مختصات ترسیم می کند . آنها را به ترتیب پروجکشن موازی با محور y و برآمدگی موازی با محور x می نامند .

نقطه C برای آن حیاتی است $\pi _{y}$ ، اگر مماس بر C وجود داشته باشد و با محور y موازی باشد . در آن صورت، تصاویر توسط $\pi _{y}$ نقطه بحرانی و مماس همان نقطه محور x هستند که مقدار بحرانی نامیده می شود . بنابراین یک نقطه C برای آن حیاتی است $\pi _{y}$ اگر مختصات آن جوابی برای سیستم معادلات باشد :

$f(x,y)={\frac {\partial f}{\partial y}}(x,y)=0$

این بدان معناست که این تعریف یک مورد خاص از تعریف کلی یک نقطه بحرانی است که در زیر آورده شده است .

تعریف نقطه بحرانی برای $\pi _{x}$ مشابه است. اگر C نمودار یک تابع باشد $y=g(x)$ ، سپس ( x , y ) برای آن حیاتی است $\pi _{x}$ اگر و فقط اگر x نقطه بحرانی g باشد و مقادیر بحرانی یکسان باشند.

برخی از نویسندگان نقاط بحرانی C را به عنوان نقاطی که برای هر یک از آنها حیاتی هستند تعریف می کنند $\pi _{x}$ یا $\pi _{y}$ ، اگرچه آنها نه تنها به C ، بلکه به انتخاب محورهای مختصات نیز بستگی دارند. همچنین به نویسندگان بستگی دارد که آیا نقاط مفرد به عنوان نقاط بحرانی در نظر گرفته شوند. در واقع نقاط مفرد نقاطی هستند که راضی کننده هستند

$f(x,y)={\frac {\partial f}{\partial x}}(x,y)={\frac {\partial f}{\partial y}}(x,y)=0$ ،

و بنابراین راه حل های هر یک از سیستم های معادلات هستند که نقاط بحرانی را مشخص می کنند. با این تعریف کلی تر، نقاط بحرانی برای $\pi _{y}$ دقیقاً نقاطی هستند که قضیه تابع ضمنی در آنها اعمال نمی شود.

استفاده از تمایز [ ویرایش ]

وقتی منحنی C جبری است، یعنی زمانی که با یک چند جمله‌ای دو متغیره f تعریف می‌شود ، آنگاه ممیز ابزار مفیدی برای محاسبه نقاط بحرانی است.

در اینجا ما فقط طرح را در نظر می گیریم $\pi _{y}$ ; نتایج مشابهی برای $\pi _{x}$ با مبادله x و y .

اجازه دهید دیسک $\operatorname {Disc} _{y}(f)$ ممیز f باشد که به عنوان یک چند جمله ای در y با ضرایبی که چند جمله ای در x هستند مشاهده می شود . بنابراین این متمایز یک چند جمله ای در x است که دارای مقادیر بحرانی است $\pi _{y}$ در میان ریشه های آن

به طور دقیق تر، یک ریشه ساده ازدیسک $\operatorname {Disc} _{y}(f)$ یا یک مقدار بحرانی است $\pi _{y}$ نقطه بحرانی متناظر نقطه‌ای است که نه مفرد است و نه نقطه عطف، یا مختصات x مجانبی است که موازی با محور y است و «در بی‌نهایت» بر یک نقطه عطف مماس است (مجاد خمشی).

یک ریشه چندگانه تمایز یا به چندین نقطه بحرانی یا مجانب عطف که دارای ارزش بحرانی یکسان هستند، یا به یک نقطه بحرانی که همچنین یک نقطه عطف است، یا به یک نقطه منفرد مطابقت دارد.

چندین متغیر [ ویرایش ]

برای تابعی از چندین متغیر حقیقی ، یک نقطه P (که مجموعه ای از مقادیر برای متغیرهای ورودی است که به عنوان یک نقطه در نظر گرفته می شود.آر $\mathbb {R} ^{n}$ ) اگر نقطه ای باشد که گرادیان صفر یا تعریف نشده باشد، حیاتی است . [4] مقادیر بحرانی مقادیر تابع در نقاط بحرانی هستند.

یک نقطه بحرانی (جایی که تابع قابل تفکیک است) ممکن است یک حداکثر محلی ، یک حداقل محلی یا یک نقطه زینتی باشد . اگر تابع حداقل دو بار به طور پیوسته مشتق پذیر باشد، موارد مختلف را می توان با در نظر گرفتن مقادیر ویژه ماتریس هسین مشتقات دوم متمایز کرد.

یک نقطه بحرانی که در آن ماتریس هسین غیرمفرد است، گفته می‌شود که غیرمنحط است و نشانه‌های مقادیر ویژه هسین، رفتار محلی تابع را تعیین می‌کنند. در مورد تابعی از یک متغیر منفرد، هسین به سادگی دومین مشتق است که به عنوان یک ماتریس 1×1 در نظر گرفته می‌شود، که اگر و فقط اگر صفر نباشد غیرمفرد است. در این حالت، یک نقطه بحرانی غیر انحطاط، بسته به علامت مشتق دوم، یک ماکزیمم محلی یا یک مینیمم محلی است که برای حداقل محلی مثبت و برای حداکثر محلی منفی است. اگر مشتق دوم صفر باشد، نقطه بحرانی به طور کلی یک نقطه عطف است ، اما ممکن است یک نقطه موجی نیز باشد ، که ممکن است حداقل محلی یا حداکثر محلی باشد.

برای تابعی از n متغیر، تعداد مقادیر ویژه منفی ماتریس هسین در یک نقطه بحرانی را شاخص نقطه بحرانی می نامند. یک نقطه بحرانی غیر منحط یک حداکثر محلی است اگر و فقط اگر شاخص n باشد ، یا به طور معادل، اگر ماتریس هسین منفی قطعی باشد . اگر شاخص صفر باشد، یک حداقل محلی است، یا اگر ماتریس هسین مثبت قطعی باشد . برای سایر مقادیر شاخص، یک نقطه بحرانی غیر انحطاط یک نقطه زینی است ، یعنی نقطه ای که در برخی جهات حداکثر و در برخی دیگر حداقل است.

کاربرد بهینه سازی [ ویرایش ]

مقاله اصلی: بهینه سازی ریاضی

بر اساس قضیه فرما ، همه ماکزیمم ها و مینیمم های محلی یک تابع پیوسته در نقاط بحرانی رخ می دهند. بنابراین، برای یافتن ماکزیمم و مینیمم محلی یک تابع قابل تفکیک، از نظر تئوری، محاسبه صفرهای گرادیان و مقادیر ویژه ماتریس هسین در این صفرها کافی است. این نیاز به حل یک سیستم معادلات دارد که می تواند کار دشواری باشد. الگوریتم‌های عددی معمول برای یافتن اکسترم‌های محلی بسیار کارآمدتر هستند، اما نمی‌توانند تأیید کنند که همه اکستریم‌ها پیدا شده‌اند. به ویژه، در بهینه سازی جهانی ، این روش ها نمی توانند تأیید کنند که خروجی واقعاً بهینه جهانی است.

هنگامی که تابع کمینه سازی یک چند جمله ای چند متغیره است ، نقاط بحرانی و مقادیر بحرانی راه حل های یک سیستم معادلات چند جمله ای هستند و الگوریتم های مدرن برای حل چنین سیستم هایی روش های تایید شده رقابتی را برای یافتن حداقل جهانی ارائه می دهند.

نقطه بحرانی یک نقشه مشتق پذیر [ ویرایش ]

با توجه به یک نقشه متمایز $f:\mathbb {R} ^{m}\to \mathbb {R} ^{n},$ نقاط بحرانی f نقاط بحرانی هستند، $\mathbb {R} ^{m},$ که در آن رتبه ماتریس ژاکوبین f حداکثر نیست. [6] تصویر یک نقطه بحرانی در زیر f مقدار بحرانی نامیده می شود . نقطه ای از مکمل مجموعه مقادیر بحرانی را مقدار منظم می نامند . قضیه سارد بیان می کند که مجموعه مقادیر بحرانی یک نقشه صاف دارای اندازه صفر است .

برخی از نویسندگان [7] تعریف کمی متفاوت ارائه می دهند: نقطه بحرانی f یک نقطه از است $\mathbb{R} ^{m}$ که در آن رتبه ماتریس ژاکوبین f کمتر از n است . با این قرارداد، همه نقاط زمانی که m < n بحرانی هستند .

این تعاریف به نقشه های دیفرانسیل بین منیفولدهای قابل تفکیک به روش زیر گسترش می یابد. اجازه دهید: $f:V\to W$ یک نقشه دیفرانسیل بین دو منیفولد V و W با ابعاد مربوطه m و باشد n باشد . در همسایگی یک نقطه p از V و از f ( p ) ، نمودارها دیفرمورفیسم هستند. :→ $\varphi :V\to \mathbb {R} ^{m}$ و: $\psi :W\to \mathbb {R} ^{n}.$ نقطه p حیاتی است برای f اگر $\varphi (p)$ برای $\psi \circ f\circ \varphi ^{-1}.$ این تعریف به انتخاب نمودارها بستگی ندارد زیرا نقشه‌های انتقال دارای تفاوت هستند، ماتریس‌های ژاکوبین آن‌ها معکوس هستند و ضرب در آنها رتبه ماتریس ژاکوبین را تغییر نمی‌دهد. $\psi \circ f\circ \varphi ^{-1}.$ اگر M یک منیفولد هیلبرت باشد ( الزاماً بعد محدود نیست) و f یک تابع با مقدار حقیقی باشد، می‌گوییم که p یک نقطه بحرانی f است اگر f یک غوطه‌ور در p نباشد . [8]

کاربرد در توپولوژی [ ویرایش ]

نقاط بحرانی برای مطالعه توپولوژی منیفولدها و انواع جبری حقیقی اساسی هستند . [5] به ویژه، آنها ابزار اساسی برای نظریه مورس و نظریه فاجعه هستند هستند .

پیوند بین نقاط بحرانی و توپولوژی در حال حاضر در سطح پایین تری از انتزاع ظاهر می شود. به عنوان مثال، اجازه دهید $V$ یک زیر چندگانه از $\mathbb {R} ^{n}،$ و P یک نقطه بیرون باشد. $V.$ مجذور فاصله تا P نقطه از $V$ یک نقشه دیفرانسیل است به طوری که هر جزء متصل از $V$ حداقل دارای یک نقطه بحرانی است که در آن فاصله حداقل است. نتیجه می شود که تعداد اجزای متصل از $V$ در بالا با تعداد نقاط بحرانی محدود می شود.

در مورد انواع جبری حقیقی، این مشاهدات مرتبط با قضیه بزو به ما اجازه می‌دهد تا تعداد اجزای متصل را با تابعی از درجات چندجمله‌ای که تنوع را تعریف می‌کنند، محدود کنیم.

همچنین ببینید [ ویرایش ]

نقطه مفرد یک منحنی
نظریه تکینگی
قضیه گاوس-لوکاس

https://en.wikipedia.org/wiki/Critical_point_%28mathematics%29

+ نوشته شده در شنبه چهارم آذر ۱۴۰۲ ساعت 20:36 توسط علی رضا نقش نیلچی |

11-تبدیل فوریه

جداول تبدیل فوریه مهم [ ویرایش ]

جداول زیر برخی از تبدیل های فوریه به شکل بسته را ثبت می کنند. برای توابع f ( x ) ، g ( x ) و h ( x ) تبدیل فوریه خود را به ترتیب با f̂ ، ĝ و ĥ نشان می دهند. فقط سه قرارداد متداول گنجانده شده است. توجه به این نکته ممکن است مفید باشد که مدخل 105 رابطه ای بین تبدیل فوریه یک تابع و تابع اصلی به دست می دهد که می تواند به عنوان ارتباط بین تبدیل فوریه و معکوس آن دیده شود.

روابط عملکردی، تک بعدی [ ویرایش ]

تبدیل فوریه در این جدول را می توان در Erdélyi (1954) یا Kammler (2000 ، ضمیمه) یافت.

	عملکرد	تبدیل فوریه فرکانس واحد، معمولی	تبدیل فوریه فرکانس واحد، زاویه ای	تبدیل فوریه فرکانس غیر واحدی و زاویه ای	ملاحظات
	$f(x)\,$	${\begin{aligned}&{\hat {f}}(\xi )\\&=\int _{-\infty }^{\infty }f(x)e^{-2\pi ix \xi }\,dx\end{تراز شده}}$	${\begin{aligned}&{\hat {f}}(\omega )\\&={\frac {1}{\sqrt {2\pi }}}\int _{-\infty }^ {\infty }f(x)e^{-i\omega x}\,dx\end{تراز شده}}$	${\begin{aligned}&{\hat {f}}(\nu )\\&=\int _{-\infty }^{\infty }f(x)e^{-i\nu x }\,dx\end{تراز شده}}$	تعریف
101	$a\cdot f(x)+b\cdot g(x)\,$	$a\cdot {\hat {f}}(\xi )+b\cdot {\hat {g}}(\xi )\,$	$a\cdot {\hat {f}}(\omega )+b\cdot {\hat {g}}(\omega )\,$	$a\cdot {\hat {f}}(\nu )+b\cdot {\hat {g}}(\nu )\,$	خطی بودن
102	$f(xa)\,$	$e^{-2\pi ia\xi }{\hat {f}}(\xi )\,$	$e^{-ia\omega }{\hat {f}}(\omega )\,$	$e^{-ia\nu }{\hat {f}}(\nu )\,$	تغییر در حوزه زمانی
103	$f(x)e^{iax}\,$	${\hat {f}}\left(\xi -{\frac {a}{2\pi }}\right)\,$	${\hat {f}}(\omega -a)\,$	${\hat {f}}(\nu -a)\,$	تغییر در حوزه فرکانس، دوتایی 102
104	$f(ax)\,$	${\frac {1}{\|a\|}}{\hat {f}}\left({\frac {\xi }{a}}\right)\,$	${\frac {1}{\|a\|}}{\hat {f}}\left({\frac {\omega }{a}}\right)\,$	${\frac {1}{\|a\|}}{\hat {f}}\left({\frac {\nu }{a}}\right)\,$	مقیاس بندی در حوزه زمان اگر \| یک \| بزرگ است، سپس f ( ax ) در اطراف 0 متمرکز شده است و ${\frac {1}{\|a\|}}{\hat {f}}\left({\frac {\omega }{a}}\right)\,$ پخش می شود و صاف می شود.
105	${\hat {f}}(x)\,$	$f(-\xi )\,$	$f(-\omega )\,$	$2\pi f(-\nu )\,$	ثنویت. در اینجا f̂ باید با استفاده از همان روش ستون تبدیل فوریه محاسبه شود. نتایج حاصل از تعویض متغیرهای "ساختگی" x و ξ یا ω یا ν .
106	${\frac {d^{n}f(x)}{dx^{n}}}\,$	$(2\pi i\xi )^{n}{\hat {f}}(\xi )\,$	$(i\omega )^{n}{\hat {f}}(\omega )\,$	$(i\nu )^{n}{\hat {f}}(\nu )\,$	زیرا f تابع شوارتز است
107	$x^{n}f(x)\,$	$\left({\frac {i}{2\pi }}\right)^{n}{\frac {d^{n}{\hat {f}}(\xi )}{d\xi ^{n}}}\,$	$i^{n}{\frac {d^{n}{\hat {f}}(\omega )}{d\omega ^{n}}}$	$i^{n}{\frac {d^{n}{\hat {f}}(\nu )}{d\nu ^{n}}}$	این دوگانه 106 است
108	${\splaystyle (f*g)(x)\,}$	${\hat {f}}(\xi ){\hat {g}}(\xi )\,$	${\sqrt {2\pi }}{\hat {f}}(\omega ){\hat {g}}(\omega )\,$	${\hat {f}}(\nu ){\hat {g}}(\nu )\,$	نماد f ∗ g نشان دهنده انحراف f و g است - این قاعده قضیه کانولوشن است
109	$f(x)g(x)\,$	$\left({\hat {f}}*{\hat {g}}\right)(\xi )\,$	${\frac {1}{\sqrt {2\pi }}}\left({\hat {f}}*{\hat {g}}\right)(\omega )\,$	${\frac {1}{2\pi }}\left({\hat {f}}*{\hat {g}}\right)(\nu )\,$	این دوگانه 108 است
110	برای f ( x ) کاملا واقعی	${\hat {f}}(-\xi )={\overline {{\hat {f}}(\xi )}}\,$	${\hat {f}}(-\omega )={\overline {{\hat {f}}(\omega )}}\,$	${\hat {f}}(-\nu )={\overline {{\hat {f}}(\nu )}}\,$	تقارن هرمیتی z مزدوج مختلط را نشان می دهد .
111	برای f ( x ) کاملا واقعی و زوج	f̂ ( ξ ) , f̂ ( ω ) و f̂ ( ν ) توابع زوج کاملا واقعی.
112	برای f ( x ) کاملا واقعی و فرد	f̂ ( ξ ) , f̂ ( ω ) و f̂ ( ν ) توابع فرد کاملاً خیالی هستند .
113	برای f ( x ) کاملاً خیالی	${\hat {f}}(-\xi )=-{\overline {{\hat {f}}(\xi )}}\,$	${\hat {f}}(-\omega )=-{\overline {{\hat {f}}(\omega )}}\,$	${\hat {f}}(-\nu )=-{\overline {{\hat {f}}(\nu )}}\,$	z مزدوج مختلطرا نشان می دهد.
114	${\overline {f(x)}}$	${\overline {{\hat {f}}(-\xi )}}$	${\overline {{\hat {f}}(-\omega )}}$	${\overline {{\hat {f}}(-\nu )}}$	صرف مختلط ، تعمیم 110 و 113
115	$f(x)\cos(ax)$	${\frac {{\hat {f}}\left(\xi -{\frac {a}{2\pi }}\right)+{\hat {f}}\left(\xi +{ \frac {a}{2\pi }}\right)}{2}}$	${\frac {{\hat {f}}(\omega -a)+{\hat {f}}(\omega +a)}{2}}\,$	${\frac {{\hat {f}}(\nu -a)+{\hat {f}}(\nu +a)}{2}}$	این از قوانین 101 و 103 با استفاده از فرمول اویلر نتیجه می گیرد : $\cos(ax)={\frac {e^{iax}+e^{-iax}}{2}}.$
116	$f(x)\sin(ax)$	${\frac {{\hat {f}}\left(\xi -{\frac {a}{2\pi }}\right)-{\hat {f}}\left(\xi +{ \frac {a}{2\pi }}\right)}{2i}}$	${\frac {{\hat {f}}(\omega -a)-{\hat {f}}(\omega +a)}{2i}}$	${\frac {{\hat {f}}(\nu -a)-{\hat {f}}(\nu +a)}{2i}}$	این از 101 و 103 با استفاده از فرمول اویلر به دست می آید : $\sin(ax)={\frac {e^{iax}-e^{-iax}}{2i}}.$

توابع ادغام‌پذیر مربع، تک بعدی [ ویرایش ]

تبدیل فوریه در این جدول را می توان در Campbell & Foster (1948) ، Erdélyi (1954) یا Kammler (2000 ، ضمیمه) یافت.

	عملکرد	تبدیل فوریه فرکانس واحد، معمولی	تبدیل فوریه فرکانس واحد، زاویه ای	تبدیل فوریه فرکانس غیر واحدی و زاویه ای	ملاحظات
	$f(x)\,$	${\begin{aligned}&{\hat {f}}(\xi )\\&=\int _{-\infty }^{\infty }f(x)e^{-2\pi ix \xi }\,dx\end{تراز شده}}$	${\begin{aligned}&{\hat {f}}(\omega )\\&={\frac {1}{\sqrt {2\pi }}}\int _{-\infty }^ {\infty }f(x)e^{-i\omega x}\,dx\end{تراز شده}}$	${\begin{aligned}&{\hat {f}}(\nu )\\&=\int _{-\infty }^{\infty }f(x)e^{-i\nu x }\,dx\end{تراز شده}}$
201	$\operatorname {rect} (ax)\,$	${\frac {1}{\|a\|}}\cdot \operatorname {sinc} \left({\frac {\xi }{a}}\right)$	${\frac {1}{\sqrt {2\pi a^{2}}}}\cdot \operatorname {sinc} \left({\frac {\omega }{2\pi a}}\right )$	${\frac {1}{\|a\|}}\cdot \operatorname {sinc} \left({\frac {\nu }{2\pi a}}\right)$	پالس مستطیلی و تابع sinc نرمال شده که در اینجا به صورت sinc( x ) = تعریف می شودگناه (π x )/π x
202	$\operatorname {sinc} (ax)\,$	${\frac {1}{\|a\|}}\cdot \operatorname {rect} \left({\frac {\xi }{a}}\right)\,$	${\frac {1}{\sqrt {2\pi a^{2}}}}\cdot \operatorname {rect} \left({\frac {\omega }{2\pi a}}\right )$	${\frac {1}{\|a\|}}\cdot \operatorname {rect} \left({\frac {\nu }{2\pi a}}\right)$	قانون دوگانه 201. تابع مستطیل شکل یک فیلتر پایین گذر ایده آل است و تابع sinc پاسخ ضربه غیر علّی چنین فیلتری است. تابع sinc در اینجا به صورت sinc( x ) = تعریف می شود sin (π x )/π x
203	$\operatorname {sinc} ^{2}(ax)$	${\frac {1}{\|a\|}}\cdot \operatorname {tri} \left({\frac {\xi }{a}}\right)$	${\frac {1}{\sqrt {2\pi a^{2}}}}\cdot \operatorname {tri} \left({\frac {\omega }{2\pi a}}\right )$	${\frac {1}{\|a\|}}\cdot \operatorname {tri} \left({\frac {\nu }{2\pi a}}\right)$	تابع tri( x ) تابع مثلثی است
204	$\operatorname {tri} (ax)$	${\frac {1}{\|a\|}}\cdot \operatorname {sinc} ^{2}\left({\frac {\xi }{a}}\right)\,$	${\frac {1}{\sqrt {2\pi a^{2}}}}\cdot \operatorname {sinc} ^{2}\left({\frac {\omega }{2\pi a }}\درست)$	${\frac {1}{\|a\|}}\cdot \operatorname {sinc} ^{2}\left({\frac {\nu }{2\pi a}}\right)$	قانون دوگانه 203.
205	$e^{-ax}u(x)\,$	${\frac {1}{a+2\pi i\xi }}$	${\frac {1}{{\sqrt {2\pi }}(a+i\omega )}}$	${\frac {1}{a+i\nu }}$	تابع u ( x ) تابع مرحله واحد Heaviside و a > 0 است.
206	$e^{-\alpha x^{2}}\,$	${\sqrt {\frac {\pi }{\alpha }}}\cdot e^{-{\frac {(\pi \xi )^{2}}{\alpha }}}$	${\frac {1}{\sqrt {2\alpha }}}\cdot e^{-{\frac {\omega ^{2}}{4\alpha }}}$	${\sqrt {\frac {\pi }{\alpha }}}\cdot e^{-{\frac {\nu ^{2}}{4\alpha }}}$	این نشان می‌دهد که برای تبدیل‌های فوریه واحد، تابع گاوسی e - αx 2 تبدیل فوریه خودش برای انتخابی از α است. برای انتگرال پذیری آن باید Re( α ) > 0 داشته باشیم .
207	$e^{-i\alpha x^{2}}\,$	${\sqrt {\frac {\pi }{\alpha }}}\cdot e^{i({\frac {(\pi \xi )^{2}}{\alpha }}-{\frac {\pi }{4}})}$	${\frac {1}{\sqrt {2\alpha }}}\cdot e^{i({\frac {\omega ^{2}}{4\alpha }}-{\frac {\pi {4}})}$	${\sqrt {\frac {\pi }{\alpha }}}\cdot e^{i({\frac {\nu ^{2}}{4\alpha }}-{\frac {\pi {4}})}$	این به عنوان سینوسی فاز دوم پیچیده یا تابع "چیپ" شناخته می شود. [53]
208	$e^{-a\|x\|}\,$	${\frac {2a}{a^{2}+4\pi ^{2}\xi ^{2}}}$	$\sqrt{\frac{2}{\pi}} \cdot \frac{a}{a^2 + \omega^2}$	${\frac {2a}{a^{2}+\nu ^{2}}}$	برای Re( a ) > 0 . یعنی تبدیل فوریه یک تابع نمایی در حال فروپاشی دو طرفه یک تابع لورنتسی است .
209	$\operatorname {sech} (ax)\,$	${\frac {\pi }{a}}\operatorname {sech} \left({\frac {\pi ^{2}}{a}}\xi \right)$	${\frac {1}{a}}{\sqrt {\frac {\pi }{2}}}\operatorname {sech} \left({\frac {\pi }{2a}}\omega \ درست)$	${\frac {\pi }{a}}\operatorname {sech} \left({\frac {\pi }{2a}}\nu \راست)$	سکانت هایپربولیک تبدیل فوریه خودش است
210	$e^{-{\frac {a^{2}x^{2}}{2}}}H_{n}(ax)\,$	${\frac {{\sqrt {2\pi }}(-i)^{n}}{a}}e^{-{\frac {2\pi ^{2}\xi ^{2} {a^{2}}}}H_{n}\left({\frac {2\pi \xi }{a}}\right)$	${\frac {(-i)^{n}}{a}}e^{-{\frac {\omega ^{2}}{2a^{2}}}}H_{n}\left ({\frac {\omega }{a}}\right)$	${\frac {(-i)^{n}{\sqrt {2\pi }}}{a}}e^{-{\frac {\nu ^{2}}{2a^{2} }}}H_{n}\left({\frac {\nu }{a}}\right)$	H n چند جمله ای مرتبهn هرمیت است . اگر a = 1 باشد، توابع گاوس-هرمیت، توابع ویژه عملگر تبدیل فوریه هستند. برای اشتقاق، به چند جمله ای هرمیت مراجعه کنید . فرمول برای n = 0 به 206 کاهش می یابد .

+ نوشته شده در سه شنبه بیست و نهم شهریور ۱۴۰۱ ساعت 7:50 توسط علی رضا نقش نیلچی |

2-توابع هذلولی

ویژگی های مشخصه [ ویرایش ]

کسینوس هایپربولیک [ ویرایش ]

می توان نشان داد که مساحت زیر منحنی کسینوس هذلولی (در یک بازه محدود) همیشه برابر با طول قوس مربوط به آن بازه است: [15]

${\text{area}}=\int _{a}^{b}\cosh x\,dx=\int _{a}^{b}{\sqrt {1+\left({\frac {d}{dx}}\cosh x\right)^{2}}}\,dx={\text{طول قوس.}}$

مماس هایپربولیک[ ویرایش ]

مماس هذلولی جواب (یکتا) معادله دیفرانسیل f ′ = 1 − f 2 است که f (0) = 0 دارد. [16] [17]

روابط مفید [ ویرایش ]

توابع هذلولی بسیاری از هویت ها را برآورده می کنند که همه آنها از نظر شکل شبیه به هویت های مثلثاتی هستند . در واقع، قانون آزبورن [18] بیان می کند که می توان هر هویت مثلثاتی را برای تبدیل کرد $تتا$ ، $2\ تتا$ ، $3\ تتا$ یا $تتا$ و $\varphi$ به یک هویت هذلولی، با بسط کامل آن بر حسب قدرت های انتگرال سینوس ها و کسینوس ها، تغییر سینوس به سینه و کسینوس به کوش، و تغییر علامت هر عبارت حاوی حاصل ضرب دو سین.

توابع زوج و فرد:

${\begin{aligned}\sinh(-x)&=-\sinh x\\\cosh(-x)&=\cosh x\end{aligned}}$

از این رو:

${\begin{aligned}\tanh(-x)&=-\tanh x\\\coth(-x)&=-\coth x\\\operatorname {sech} (-x)&=\operatorname {sech} x\\\ نام عامل {csch} (-x)&=-\نام اپراتور {csch} x\end{تراز شده}}$

بنابراین، cosh x و sech x توابع زوج هستند . بقیه توابع فرد هستند .

${\begin{aligned}\operatorname {arsech} x&=\operatorname {arcosh} \left({\frac {1}{x}}\right)\\\operatorname {arcsch} x&=\operatorname {arsinh } \left({\frac {1}{x}}\right)\\\operatorname {arcoth} x&=\operatorname {artanh} \left({\frac {1}{x}}\right)\end{ هم راستا}}$

سینوس و کسینوس هایپربولیک:

${\begin{aligned}\cosh x+\sinh x&=e^{x}\\\cosh x-\sinh x&=e^{-x}\\\cosh ^{2}x-\sinh ^ {2}x&=1\end{تراز شده}}$

که آخرین آنها شبیه به هویت مثلثاتی فیثاغورثی است .

یکی هم دارد

${\begin{aligned}\operatorname {sech} ^{2}x&=1-\tanh ^{2}x\\\operatorname {csch} ^{2}x&=\coth ^{2}x- 1\end{تراز شده}}$

برای توابع دیگر

مجموع آرگومان ها [ ویرایش ]

${\begin{aligned}\sinh(x+y)&=\sinh x\cosh y+\cosh x\sinh y\\\cosh(x+y)&=\cosh x\cosh y+\sinh x \sinh y\\[6px]\tanh(x+y)&={\frac {\tanh x+\tanh y}{1+\tanh x\tanh y}}\\\end{تراز شده}}$

به ویژه

${\begin{aligned}\cosh(2x)&=\sinh ^{2}{x}+\cosh ^{2}{x}=2\sinh ^{2}x+1=2\cosh ^{2}x-1\\\sinh(2x)&=2\sinh x\cosh x\\\tanh(2x)&={\frac {2\tanh x}{1+\tanh ^{2} x}}\\\پایان{تراز شده}}$

همچنین:

${\begin{aligned}\sinh x+\sinh y&=2\sinh \left({\frac {x+y}{2}}\right)\cosh \left({\frac {xy}{2 }}\right)\\\cosh x+\cosh y&=2\cosh \left({\frac {x+y}{2}}\right)\cosh \left({\frac {xy}{2}} \راست)\\\پایان{تراز شده}}$

فرمول های تفریق [ ویرایش ]

${\begin{aligned}\sinh(xy)&=\sinh x\cosh y-\cosh x\sinh y\\\cosh(xy)&=\cosh x\cosh y-\sinh x\sinh y\\\tanh(xy)&={\frac {\tanh x-\tanh y}{1-\tanh x\tanh y}}\\\end{تراز شده}}$

همچنین: [19]

${\begin{aligned}\sinh x-\sinh y&=2\cosh \left({\frac {x+y}{2}}\right)\sinh \left({\frac {xy}{ 2}}\right)\\\cosh x-\cosh y&=2\sinh \left({\frac {x+y}{2}}\right)\sinh \left({\frac {xy}{2 }}\راست)\\\end{تراز شده}}$

فرمول های نیم آرگومان [ ویرایش ]

${\begin{aligned}\sinh \left({\frac {x}{2}}\right)&={\frac {\sinh x}{\sqrt {2(\cosh x+1)} }}&&=\operatorname {sgn} x\,{\sqrt {\frac {\cosh x-1}{2}}}\\[6px]\cosh \left({\frac {x}{2}} \right)&={\sqrt {\frac {\cosh x+1}{2}}}\\[6px]\tanh \left({\frac {x}{2}}\right)&={\ frac {\sinh x}{\cosh x+1}}&&=\operatorname {sgn} x\,{\sqrt {\frac {\cosh x-1}{\cosh x+1}}}={\frac {e^{x}-1}{e^{x}+1}}\end{تراز شده}}$

که در آن sgn تابع علامت است .

اگر x ≠ 0 ، سپس [20]

$\tanh \left({\frac {x}{2}}\right)={\frac {\cosh x-1}{\sinh x}}=\coth x-\operatorname {csch} x$

فرمول های مربعی [ ویرایش ]

${\begin{aligned}\sinh ^{2}x&={\frac {1}{2}}(\cosh 2x-1)\\\cosh ^{2}x&={\frac {1} {2}}(\cosh 2x+1)\end{تراز شده}}$

نابرابری ها [ ویرایش ]

نابرابری زیر در آمار مفید است: $\operatorname {cosh} (t)\leq e^{t^{2}/2}$ [21]

این را می توان با مقایسه ترم به ترم سری تیلور دو تابع ثابت کرد.

توابع معکوس به عنوان لگاریتم [ ویرایش ]

مقاله اصلی: تابع هذلولی معکوس

${\begin{aligned}\operatorname {arsinh} (x)&=\ln \left(x+{\sqrt {x^{2}+1}}\right)\\\operatorname {arcosh} (x )&=\ln \left(x+{\sqrt {x^{2}-1}}\right)&&x\geq 1\\\operatorname {artanh} (x)&={\frac {1}{2} }\ln \left({\frac {1+x}{1-x}}\right)&&|x|<1\\\operatorname {arcoth} (x)&={\frac {1}{2} }\ln \left({\frac {x+1}{x-1}}\right)&&|x|>1\\\operatorname {arsech} (x)&=\ln \left({\frac { 1}{x}}+{\sqrt {{\frac {1}{x^{2}}}-1}}\right)=\ln \left({\frac {1+{\sqrt {1- x^{2}}}}{x}}\right)&&0<x\leq 1\\\operatorname {arcsch} (x)&=\ln \left({\frac {1}{x}}+{ \sqrt {{\frac {1}{x^{2}}}+1}}\right)&&x\neq 0\end{تراز شده}}$

+ نوشته شده در شنبه سوم اردیبهشت ۱۴۰۱ ساعت 10:33 توسط علی رضا نقش نیلچی |

1-توابع هذلولی

"منحنی هیپربولیک" به اینجا هدایت می شود. برای منحنی هندسی، Hyperbola را ببینید .

در ریاضیات , توابع هذلولی مشابه توابع مثلثاتی معمولی هستند , اما با استفاده از هذلولی به جای دایره تعریف می شوند . همانطور که نقاط (cost ، sin t ) دایره ای با شعاع واحد تشکیل می دهند ، نقاط (cosh t ، sinh t ) نیمه سمت راست هذلولی واحد را تشکیل می دهند. همچنین، به طور مشابه، مشتقات sin( t ) و cos( t ) cos( t ) هستند .و –sin( t ) ، مشتقات sinh( t ) و cosh( t ) cosh( t ) و +sinh( t ) هستند .

توابع هذلولی در محاسبات زوایا و فواصل در هندسه هذلولی رخ می دهند . آنها همچنین در راه حل های بسیاری از معادلات دیفرانسیل خطی (مانند معادله تعریف یک خطی )، معادلات مکعبی ، و معادله لاپلاس در مختصات دکارتی رخ می دهند. معادلات لاپلاس در بسیاری از زمینه های فیزیک از جمله نظریه الکترومغناطیسی ، انتقال حرارت ، دینامیک سیالات و نسبیت خاص مهم هستند.

توابع هذلولی اساسی عبارتند از: [1]

سینوس هذلولی "sinh" ( / ˈ s ɪ ŋ , ˈ s ɪ n tʃ , ˈ ʃ aɪ n / )، [2]
کسینوس هذلولی "cosh" ( / ˈ k ɒ ʃ , ˈ k oʊ ʃ / )، [3]

که از آن مشتق شده است: [4]

تانژانت هذلولی "tanh" ( / ˈ t æ ŋ , ˈ t æ n tʃ , ˈ θ æ n / )، [5]
کسکانت هذلولی "csch" یا "cosech" ( / ˈ k oʊ s ɛ tʃ , ˈ k oʊ ʃ ɛ k / [3] )
سکانت هذلولی "sech" ( / ˈ s ɛ tʃ , ˈ ʃ ɛ k / )، [6]
هذلولی همتنژانت "coth" ( / ˈ k ɒ θ , ˈ k oʊ θ / )، [7] [8]

مربوط به توابع مثلثاتی مشتق شده است.

توابع هذلولی معکوس عبارتند از:

سینوس هذلولی منطقه "arsinh" (همچنین به "sinh -1 "، "asinh" یا گاهی اوقات "arcsinh" نشان داده می شود) [9] [10] [11]
کسینوس هذلولی ناحیه "arcosh" (همچنین به "cosh -1 "، "acosh" یا گاهی اوقات "arccosh" نشان داده می شود)
و غیره

پرتویی از هذلولی واحد x 2 − y 2 = 1 در نقطه (cosh a , sinh a ) , جایی که a دو برابر مساحت بین پرتو، هذلولی و محور x است. برای نقاط روی هذلولی زیر محور x ، ناحیه منفی در نظر گرفته می شود ( نسخه متحرک با مقایسه با توابع مثلثاتی (دایره ای) را ببینید).

توابع هذلولی یک متغیر حقیقی به نام زاویه هذلولی می گیرند . اندازه یک زاویه هذلولی دو برابر مساحت بخش هذلولی آن است . توابع هذلولی ممکن است برحسب پایه های یک مثلث قائم الزاویه که این بخش را پوشش می دهد، تعریف شوند.

در تحلیل مختلط ، توابع هذلولی به عنوان بخش های مختلط سینوس و کسینوس به وجود می آیند. سینوس هیپربولیک و کسینوس هذلولی توابع کامل هستند . در نتیجه، سایر توابع هذلولی در کل صفحه مختلط مرومورفیک هستند.

بر اساس قضیه لیندمان – وایرشتراس ، توابع هذلولی برای هر مقدار جبری غیرصفری متغیر، یک مقدار ماورایی دارند . [12]

توابع هیپربولیک در دهه 1760 به طور مستقل توسط وینچنزو ریکاتی و یوهان هاینریش لامبرت معرفی شدند. [13] Riccati از Sc. و رونوشت ( sinus/cosinus circulare ) اشاره به توابع حلقوی و Sh. و چ. ( سینوس/کوسینوس هیپربولیکو ) برای اشاره به توابع هذلولی. لامبرت این نام ها را پذیرفت، اما اختصارات را به نام هایی که امروزه استفاده می شود تغییر داد. [14] اختصارات sh , ch , th , cth نیز در حال حاضر بسته به ترجیح شخصی استفاده می شود.

فهرست

1نشانه گذاری
2تعاریف
- 2.1تعاریف نمایی
- 2.2تعاریف معادلات دیفرانسیل
- 2.3تعاریف مختلط مثلثاتی
3ویژگی های مشخص کننده
- 3.1کسینوس هیپربولیک
- 3.2تانژانت هیپربولیک
4روابط مفید
- 4.1مجموع استدلال ها
- 4.2فرمول های تفریق
- 4.3فرمول های نیم متغیر
- 4.4فرمول های مربعی
- 4.5نابرابری ها
5توابع معکوس به عنوان لگاریتم
6مشتقات
7مشتقات دوم
8انتگرال های استاندارد
9عبارات سری تیلور
10ضربهای نامتناهی و کسرهای ادامه دار
11مقایسه با توابع دایره ای
12رابطه با تابع نمایی
13توابع هذلولی برای اعداد مختلط
14همچنین ببینید
15منابع
16لینک های خارجی

نشانه گذاری [ ویرایش ]

مقاله اصلی: توابع مثلثاتی § نمادگذاری

تعاریف [ ویرایش ]

سین ، کوش و تن

csch ، sech و coth

روش های معادل مختلفی برای تعریف توابع هذلولی وجود دارد.

تعاریف نمایی [ ویرایش ]

sinh x نصف اختلاف e x و e - x است

cosh x میانگین e x و e - x است _

از نظر تابع نمایی : [1] [4]

سینوس هیپربولیک: قسمت فرد تابع نمایی، یعنی

$\sinh x={\frac {e^{x}-e^{-x}}{2}}={\frac {e^{2x}-1}{2e^{x}}}= {\frac {1-e^{-2x}}{2e^{-x}}}.$
کسینوس هیپربولیک: قسمت زوج تابع نمایی، یعنی

$\cosh x={\frac {e^{x}+e^{-x}}{2}}={\frac {e^{2x}+1}{2e^{x}}}= {\frac {1+e^{-2x}}{2e^{-x}}}.$
مماس هیپربولیک:

$\tanh x={\frac {\sinh x}{\cosh x}}={\frac {e^{x}-e^{-x}}{e^{x}+e^{- x}}}={\frac {e^{2x}-1}{e^{2x}+1}}.$
کتانژانت هیپربولیک: برای x ≠ 0 ،

$\coth x={\frac {\cosh x}{\sinh x}}={\frac {e^{x}+e^{-x}}{e^{x}-e^{- x}}}={\frac {e^{2x}+1}{e^{2x}-1}}.$
سکانس هیپربولیک:

$\operatorname {sech} x={\frac {1}{\cosh x}}={\frac {2}{e^{x}+e^{-x}}}={\frac {2e ^{x}}{e^{2x}+1}}.$
کسکانت هذلولی: برای x ≠ 0 ،

$\operatorname {csch} x={\frac {1}{\sinh x}}={\frac {2}{e^{x}-e^{-x}}}={\frac {2e ^{x}}{e^{2x}-1}}.$

تعاریف معادلات دیفرانسیل [ ویرایش ]

توابع هذلولی را می توان به عنوان جواب معادلات دیفرانسیل تعریف کرد : سینوس و کسینوس هذلولی حل ( s , c ) یک سیستم هستند.

${\begin{aligned}c'(x)&=s(x),\\s'(x)&=c(x),\\\end{aligned}}$ با شرایط اولیه $s(0)=0,c(0)=1,$ جلوگیری از هر جفت عملکرد{ $(ae^{x}+be^{-x},ae^{x}-be^{-x})$ راه حل باشد

sinh( x ) و cosh( x ) نیز راه‌حل منحصربه‌فرد معادله f ″( x ) = f ( x ) هستند، به طوری که f (0) = 1 ، f ′(0) = 0 برای کسینوس هذلولی، و f (0) = 0 ، f ′(0) = 1 برای سینوس هذلولی.

تعاریف مختلط توابع مثلثاتی [ ویرایش ]

توابع هذلولی نیز ممکن است از توابع مثلثاتی با متغیر های مختلط استنتاج شوند:

سینوس هیپربولیک: [1]

$\sinh x=-i\sin(ix).$
کسینوس هیپربولیک: [1]

$\cosh x=\cos(ix).$
تانژانت هیپربولیک:

$\tanh x=-i\tan(ix).$
کتانژانت هیپربولیک:

$\coth x=i\cot(ix).$
سکانس هیپربولیک:
$\operatorname {sech} x=\sec(ix).$
کسکانت هیپربولیک:
$\operatorname {csch} x=i\csc(ix).$

جایی که i واحد موهومی با i 2 = −1 است.

تعاریف فوق به تعاریف نمایی از طریق فرمول اویلر مرتبط هستند (به § توابع هیپربولیک برای اعداد مختلط زیر مراجعه کنید).

+ نوشته شده در شنبه سوم اردیبهشت ۱۴۰۱ ساعت 10:29 توسط علی رضا نقش نیلچی |

سری تیلور

از آنجا که

انتگرال آن دارای نمایش سری قدرت است

بیایید حد نسبت های مطلق این سری را پیدا کنیم:

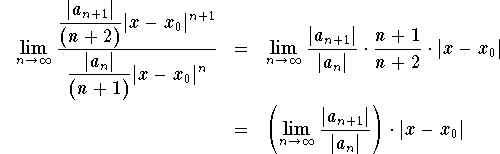
eqnarray14

اما توجه داشته باشید که این دقیقاً همان عبارتی است که هنگام محاسبه حد نسبتهای مطلق سری تیلور از f ( x ) به آن برخورد می کنیم. بنابراین هر دو سری شعاع همگرایی یکسانی دارند!

سری تیلور و چند جمله ای ها

سری تیلور چند جمله ای چیست؟

سری تیلور با مرکز یک چند جمله ای خود چند جمله ای است! (این را با چند جمله ای مورد علاقه خود بررسی کنید و از فرمول سری تیلور با مرکز استفاده کنید!)

اگر مرکز 0 نباشد چه؟ سپس شخص واقعاً چند جمله ای را بازنویسی می کند و به جای استفاده از آن به عنوان "بلوک های سازنده" آن استفاده می کند.

در اینجا یک مثال آورده شده است: سری تیلور را با مرکز چند جمله ای پیدا کنید. بیایید مشتقات آن را بگیریم و وصل کنیم :

بنابراین p (-1)=1+3+5=9.

p '( x )=2 x -3، بنابراین p '(-1)=-2-3=-5.

p ''( x )=2، بنابراین p ''(-1)=2.

تمام مشتقات بالاتر 0 هستند، بنابراین سری تیلور خاتمه می یابد!

با استفاده از فرمول ما به دست می آوریم:

از این رو، فهمیدن اینکه یک تابع دارای سری پایانی تیلور است، سخت نیست، اگر و فقط اگر تابع چند جمله ای باشد.

ضرب سری تیلور در چند جمله ای

بیایید سعی کنیم بسط سری تیلور با مرکز را پیدا کنیم .

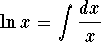برای پیدا کردن سری تیلور برای ، از آن استفاده کنید tex2html_wrap_inline177 . شما بسط را بدست می آورید:

displaymath165

همانطور که در مثال بالا می توانیم بازنویسی کنیم

سپس هر دو عبارت را ضرب می کنیم:

eqnarray60

بدون وارد شدن به جزئیات فنی: اگر اولین عبارت های این سری را بنویسید، می توانید قدرت های مربوط به ( x -1) را با هم ترکیب کنید تا شروع سری تیلور را برای f ( x ) بدست آورید:

خودت آن را امتحان کن!

تقریباً چندان پیچیده نیست: نمایش سری تیلور را با مرکز برای پیدا کنید.

منبع

http://www.sosmath.com/calculus/tayser/tayser05/tayser05.html

+ نوشته شده در پنجشنبه یکم اردیبهشت ۱۴۰۱ ساعت 23:35 توسط علی رضا نقش نیلچی |

بسط تیلور sinx ,x=p/2

+ نوشته شده در پنجشنبه یکم اردیبهشت ۱۴۰۱ ساعت 18:28 توسط علی رضا نقش نیلچی |

جملات سری تیلور f(x)=ln(2x) در 3=x

چهار ترم اول سری تیلور

building terms of the taylor polynomial

منبع

https://www.kristakingmath.com/blog/radius-interval-of-convergence-taylor-series

+ نوشته شده در پنجشنبه یکم اردیبهشت ۱۴۰۱ ساعت 14:22 توسط علی رضا نقش نیلچی |

3-سری تیلور

خطای تقریب و همگرایی [ ویرایش ]

مقاله اصلی: قضیه تیلور

تابع سینوس (آبی) با چند جمله ای تیلور درجه 7 (صورتی) برای یک دوره کامل در مرکز مبدأ تقریباً تقریب دارد.

چند جمله ای های تیلور برای ln(1 + x ) فقط تقریب های دقیقی را در محدوده -1 < x≤ 1 ارائه می دهند. برای x > 1 ، چند جمله ای های تیلور با درجه بالاتر تقریب بدتری ارائه می دهند.

تقریب های تیلور برای ln(1 + x ) (سیاه). برای x > 1 ، تقریب ها واگرا می شوند.

تصویر سمت راست تقریب دقیق sin x در اطراف نقطه x = 0 است. منحنی صورتی یک چند جمله ای درجه هفت است:

$\sin \left(x\right)\approx x-{\frac {x^{3}}{3!}}+{\frac {x^{5}}{5!}}-{\frac {x ^{7}}{7!}}.\!$

خطا در این تقریب بیشتر از | نیست x | 9/9 ! . برای یک چرخه کامل در مرکز مبدا ( -π < x < π ) خطا کمتر از 0.08215 است. به طور خاص، برای -1 < x < 1 ، خطا کمتر از 0.000003 است.

در مقابل، همچنین تصویری از تابع لگاریتم طبیعی ln(1 + x ) و برخی از چندجمله ای های تیلور آن در اطراف a = 0 نشان داده شده است. این تقریب ها فقط در ناحیه -1 < x ≤ 1 به تابع همگرا می شوند . در خارج از این منطقه، چند جمله ای های درجه بالاتر تیلور، تقریب بدتری برای تابع هستند.

خطایی که در تقریب یک تابع با چند جمله ای تیلور درجه n آن رخ می دهد باقیمانده یا باقیمانده نامیده می شود و با تابع Rn ( x ) نشان داده می شود . از قضیه تیلور می توان برای به دست آوردن حدی در اندازه باقیمانده استفاده کرد.

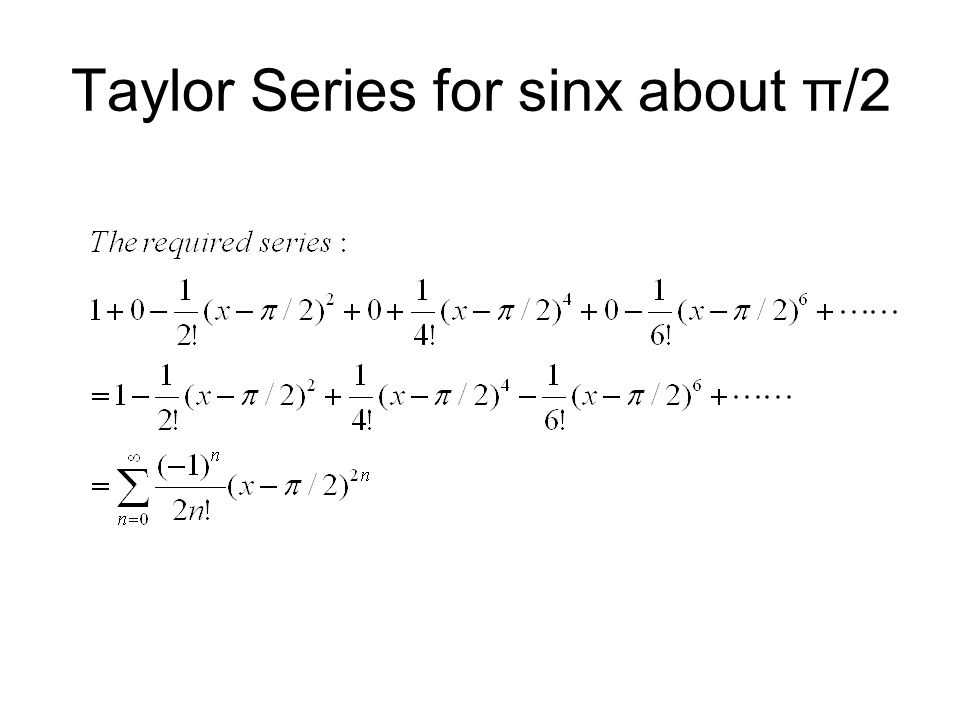
به طور کلی، سری های تیلور به هیچ وجه نیازی به همگرایی ندارند. و در واقع مجموعه توابع با سری تیلور همگرا مجموعه ای ناچیز در فضای فریشه از توابع صاف است . و حتی اگر سری تیلور یک تابع f همگرا شود، نیازی نیست حد آن به طور کلی برابر با مقدار تابع f ( x ) باشد. به عنوان مثال، تابع

$f(x)={\begin{cases}e^{-1/x^{2}}&{\text{if }}x\neq 0\\[3mu]0&{\text{if } }x=0\end{موارد}}$

بی نهایت در x = 0 قابل تمایز است و تمام مشتقات آن صفر است. در نتیجه، سری تیلور از f ( x ) حدود x = 0 به طور یکسان صفر است. با این حال، f ( x ) تابع صفر نیست، بنابراین با سری تیلور آن در اطراف مبدا برابر نیست. بنابراین، f ( x ) مثالی از یک تابع صاف غیر تحلیلی است .

در تجزیه و تحلیل واقعی ، این مثال نشان می دهد که توابع بی نهایت قابل تمایز f ( x ) وجود دارد که سری تیلور آنها با f ( x ) برابر نیستند ، حتی اگر همگرا شوند. در مقابل، توابع هولومورف مورد مطالعه در تحلیل پیچیده همیشه دارای یک سری تیلور همگرا هستند، و حتی سری تیلور از توابع مرومورفیک ، که ممکن است دارای تکینگی باشند، هرگز به مقداری متفاوت از خود تابع همگرا نمی شوند. با این حال، تابع مختلط e −1/ z 2 به 0 نزدیک نمی‌شوددر امتداد محور فرضی به 0 نزدیک می شود، بنابراین در صفحه مختلط پیوسته نیست و سری تیلور آن در 0 تعریف نشده است.

به طور کلی‌تر، هر دنباله‌ای از اعداد حقیقی یا مختلط می‌تواند به‌عنوان ضرایبی در سری تیلور از یک تابع بی‌نهایت متمایز تعریف‌شده بر روی خط واقعی ظاهر شود که نتیجه لم بورل است . در نتیجه، شعاع همگرایی یک سری تیلور می تواند صفر باشد. حتی توابع بی نهایت قابل تمایز نیز بر روی خط واقعی تعریف شده اند که سری های تیلور در همه جا شعاع همگرایی 0 دارند. [8]

یک تابع را نمی توان به عنوان یک سری تیلور با محوریت تکینگی نوشت . در این موارد، اگر قدرت های منفی متغیر x را نیز مجاز بدانیم، اغلب می توان به یک بسط سری دست یافت . سری Laurent را ببینید . برای مثال، f ( x ) = e −1/ x 2 را می توان به صورت سری Laurent نوشت.

تعمیم [ ویرایش ]

با این حال، یک تعمیم [9] [10] از سری تیلور وجود دارد که با استفاده از حساب تفاوت‌های محدود ، به مقدار خود تابع برای هر تابع پیوسته محدود در (0,∞) همگرا می‌شود . به طور خاص، با توجه به Einar Hille ، یک قضیه زیر را دارد که برای هر t > 0 ،

$\lim _{h\to 0^{+}}\sum _{n=0}^{\infty }{\frac {t^{n}}{n!}}{\frac {\Delta _{h }^{n}f(a)}{h^{n}}}=f(a+t).$

اینجا Δn
ساعتn امین عملگر تفاضل محدود با اندازه گام h است. این سری دقیقاً سری تیلور است، با این تفاوت که به جای تمایز، تفاوت‌های تقسیم شده ظاهر می‌شود: این سری از نظر رسمی شبیه به سری‌های نیوتن است . وقتی تابع f در a تحلیلی است ، عبارت‌های سری با عبارت‌های سری تیلور همگرا می‌شوند و از این نظر سری معمول تیلور را تعمیم می‌دهند.

به طور کلی، برای هر دنباله نامتناهی a i ، هویت سری توانی زیر برقرار است:

$\sum _{n=0}^{\infty }{\frac {u^{n}}{n!}}\Delta ^{n}a_{i}=e^{-u}\sum _{j =0}^{\infty }{\frac {u^{j}}{j!}}a_{i+j}.$

بنابراین به طور خاص،

$f(a+t)=\lim _{h\to 0^{+}}e^{-t/h}\sum _{j=0}^{\infty }f(a+jh){\frac {(t/h)^{j}}{j!}}.$

سری سمت راست مقدار انتظاری f ( a + X ) است، که در آن X یک متغیر تصادفی توزیع شده توسط پواسون است که مقدار jh را با احتمال e - t / h می گیرد .( t / h ) j/ج !. از این رو،

$f(a+t)=\lim _{h\to 0^{+}}\int _{-\infty }^{\infty }f(a+x)dP_{t/h,h} (ایکس).$

قانون اعداد بزرگ نشان می دهد که هویت وجود دارد. [11]

فهرستی از سری مکلورن از برخی توابع رایج [ ویرایش ]

همچنین ببینید: لیست سری های ریاضی

چندین بسط مهم سری مکلورن دنبال می شود. [12] همه این بسط ها برای آرگومان های پیچیده x معتبر هستند .

تابع نمایی [ ویرایش ]

تابع نمایی e x (به رنگ آبی)، و مجموع اولین جمله های n + 1 سری تیلور آن در 0 (به رنگ قرمز).

تابع نمایی $e^{x}$ (با پایه e ) دارای سری مکلورن است

$e^{x}=\sum _{n=0}^{\infty }{\frac {x^{n}}{n!}}=1+x+{\frac {x^{2} }{2!}}+{\frac {x^{3}}{3!}}+\cdots$ .

برای همه x همگرا می شود .

لگاریتم طبیعی [ ویرایش ]

نوشتار اصلی: سری مرکاتور

لگاریتم طبیعی (با پایه e ) دارای سری مکلورن است

${\begin{aligned}\ln(1-x)&=-\sum _{n=1}^{\infty }{\frac {x^{n}}{n}}=-x- {\frac {x^{2}}{2}}-{\frac {x^{3}}{3}}-\cdots ,\\\ln(1+x)&=\sum _{n= 1}^{\infty }(-1)^{n+1}{\frac {x^{n}}{n}}=x-{\frac {x^{2}}{2}}+{ \frac {x^{3}}{3}}-\cdots .\end{تراز شده}}$

آنها برای همگرا می شوند $|x|<1$ . (علاوه بر این، سری برای ln(1 - x ) برای x = -1 همگرا می شود ، و سری برای ln(1 + x ) برای x = 1 همگرا می شود .)

سری هندسی [ ویرایش ]

سری هندسی و مشتقات آن دارای سری مکلورن هستند

${\begin{aligned}{\frac {1}{1-x}}&=\sum _{n=0}^{\infty }x^{n}\\{\frac {1}{ (1-x)^{2}}}&=\sum _{n=1}^{\infty }nx^{n-1}\\{\frac {1}{(1-x)^{3 }}}&=\sum _{n=2}^{\infty }{\frac {(n-1)n}{2}}x^{n-2}.\end{تراز شده}}$

همه همگرا هستند برای $|x|<1$ . اینها موارد خاصی از سری دوجمله ای هستند که در بخش بعدی آورده شده است.

سری دو جمله ای [ ویرایش ]

سری دوجمله ای سری توان است

$(1+x)^{\alpha }=\sum _{n=0}^{\infty }{\binom {\alpha }{n}}x^{n}$

که ضرایب آن ضرایب دوجمله ای تعمیم یافته است

${\binom {\alpha }{n}}=\prod _{k=1}^{n}{\frac {\alpha -k+1}{k}}={\frac {\alpha ( \alpha -1)\cdots (\alpha -n+1)}{n!}}.$

(اگر n = 0 باشد، این حاصلضرب یک محصول خالی است و مقدار 1 دارد.) برای همگرا می شود $|x|<1$ برای هر عدد واقعی یا مختلط α .

وقتی α = -1 ، این اساساً سری هندسی نامتناهی است که در بخش قبل ذکر شد. موارد خاص α =1/2و α = -1/2تابع جذر و معکوس آن را بدهید :

${\begin{aligned}(1+x)^{\frac {1}{2}}&=1+{\tfrac {1}{2}}x-{\tfrac {1}{8} }x^{2}+{\tfrac {1}{16}}x^{3}-{\tfrac {5}{128}}x^{4}+{\tfrac {7}{256}}x ^{5}-\cdots &&=\sum _{n=0}^{\infty }{\frac {(-1)^{n-1}(2n)!}{4^{n}(n! )^{2}(2n-1)}}x^{n}،\\(1+x)^{-{\frac {1}{2}}}&=1-{\tfrac {1}{ 2}}x+{\tfrac {3}{8}}x^{2}-{\tfrac {5}{16}}x^{3}+{\tfrac {35}{128}}x^{4 }-{\tfrac {63}{256}}x^{5}+\cdots &&=\sum _{n=0}^{\infty }{\frac {(-1)^{n}(2n) !}{4^{n}(n!)^{2}}}x^{n}.\end{تراز شده}}$

هنگامی که فقط عبارت خطی حفظ می شود، این به تقریب دو جمله ای ساده می شود .

توابع مثلثاتی [ ویرایش ]

توابع مثلثاتی معمول و معکوس آنها دارای سری مکلورن زیر هستند:

${\begin{aligned}\sin x&=\sum _{n=0}^{\infty }{\frac {(-1)^{n}}{(2n+1)!}}x^ {2n+1}&&=x-{\frac {x^{3}}{3!}}+{\frac {x^{5}}{5!}}-\cdots &&{\text{برای همه }}x\\[6pt]\cos x&=\sum _{n=0}^{\infty }{\frac {(-1)^{n}}{(2n)!}}x^{2n} &&=1-{\frac {x^{2}}{2!}}+{\frac {x^{4}}{4!}}-\cdots &&{\text{برای همه }}x\\ [6pt]\tan x&=\sum _{n=1}^{\infty }{\frac {B_{2n}(-4)^{n}\left(1-4^{n}\right)} {(2n)!}}x^{2n-1}&&=x+{\frac {x^{3}}{3}}+{\frac {2x^{5}}{15}}+\cdots && {\text{for }}|x|<{\frac {\pi }{2}}\\[6pt]\sec x&=\sum _{n=0}^{\infty }{\frac {(- 1)^{n}E_{2n}}{(2n)!}}x^{2n}&&=1+{\frac {x^{2}}{2}}+{\frac {5x^{4 }}{24}}+\cdots &&{\text{for }}|x|<{\frac {\pi }{2}}\\[6pt]\arcsin x&=\sum _{n=0}^ {\infty }{\frac {(2n)!}{4^{n}(n!)^{2}(2n+1)}}x^{2n+1}&&=x+{\frac {x^{3}}{6}}+{\frac {3x^{5}}{40}}+\cdots &&{\text{برای }}|x|\leq 1\\ [6pt]\arccos x&={\frac {\pi }{2}}-\arcsin x\\&={\frac {\pi }{2}}-\sum _{n=0}^{\infty }{\frac {(2n)!}{4^{n}(n!)^{2}(2n+1)}}x^{2n+1}&&={\frac {\pi }{2} }-x-{\frac {x^{3}}{6}}-{\frac {3x^{5}}{40}}-\cdots &&{\text{برای }}|x|\leq 1 \\[6pt]\arctan x&=\sum _{n=0}^{\infty }{\frac {(-1)^{n}}{2n+1}}x^{2n+1}&&= x-{\frac {x^{3}}{3}}+{\frac {x^{5}}{5}}-\cdots &&{\text{for }}|x|\leq 1,\ x\neq \pm i\end{تراز شده}}}=\sum _{n=0}^{\infty }{\frac {(-1)^{n}}{2n+1}}x^{2n+1}&&=x-{\frac {x^ {3}}{3}}+{\frac {x^{5}}{5}}-\cdots &&{\text{for }}|x|\leq 1,\ x\neq \pm i\end {هم راستا}}}=\sum _{n=0}^{\infty }{\frac {(-1)^{n}}{2n+1}}x^{2n+1}&&=x-{\frac {x^ {3}}{3}}+{\frac {x^{5}}{5}}-\cdots &&{\text{for }}|x|\leq 1,\ x\neq \pm i\end {هم راستا}}$

همه زوایا بر حسب رادیان بیان می شوند . اعداد B k که در بسط های tan x ظاهر می شوند اعداد برنولی هستند . E k در بسط sec x اعداد اویلر هستند .

توابع هذلولی [ ویرایش ]

توابع هذلولی دارای سری مکلورن هستند که نزدیک به سری برای توابع مثلثاتی مربوطه هستند:

${\begin{aligned}\sinh x&=\sum _{n=0}^{\infty }{\frac {x^{2n+1}}{(2n+1)!}}&&=x+ {\frac {x^{3}}{3!}}+{\frac {x^{5}}{5!}}+\cdots &&{\text{برای همه }}x\\[6pt]\ cosh x&=\sum _{n=0}^{\infty }{\frac {x^{2n}}{(2n)!}}&&=1+{\frac {x^{2}}{2! }}+{\frac {x^{4}}{4!}}+\cdots &&{\text{برای همه }}x\\[6pt]\tanh x&=\sum _{n=1}^{ \infty }{\frac {B_{2n}4^{n}\left(4^{n}-1\right)}{(2n)!}}x^{2n-1}&&=x-{\ frac {x^{3}}{3}}+{\frac {2x^{5}}{15}}-{\frac {17x^{7}}{315}}+\cdots &&{\text{ برای }}|x|<{\frac {\pi }{2}}\\[6pt]\operatorname {arsinh} x&=\sum _{n=0}^{\infty }{\frac {(-1) )^{n}(2n)!}{4^{n}(n!)^{2}(2n+1)}}x^{2n+1}&&=x-{\frac {x^{3 }}{6}}+{\frac {3x^{5}}{40}}-\cdots &&{\text{for }}|x|\leq 1\\[6pt]\operatorname {artanh} x&= \sum _{n=0}^{\infty }{\frac {x^{2n+1}}{2n+1}}&&=x+{\frac {x^{3}}{3}}+{\frac {x^{5}}{5}}+\cdots &&{\text{برای }}|x|\leq 1,\ x\neq \pm 1\end{تراز شده}}$

اعداد B k که در سری برای tanh x ظاهر می شوند اعداد برنولی هستند .

+ نوشته شده در پنجشنبه یکم اردیبهشت ۱۴۰۱ ساعت 13:9 توسط علی رضا نقش نیلچی |

1-سری تیلور

سری تیلور

از ویکیپدیا، دانشنامه آزاد

اپراتور شیفت

با افزایش درجه چند جمله ای تیلور، به تابع صحیح نزدیک می شود. این تصویر sin x و تقریب های تیلور آن را با چند جمله ای های درجه 1 ، 3 ، 5 ، 7 ، 9 ، 11 و 13 در x = 0 نشان می دهد.

بخشی از مجموعه مقالات در مورد

حساب دیفرانسیل و انتگرال

نشان دادن

دیفرانسیل

نشان دادن

انتگرال

پنهان شدن

سلسله

تست های همگرایی
هندسی ( حساب هندسی ) هارمونیک متناوب قدرت دو جمله ای تیلور
حد جمع (آزمون ترم) نسبت ریشه انتگرال مقایسه مستقیم مقایسه محدود سری متناوب تراکم کوشی دیریکله هابیل

نشان دادن

بردار

نشان دادن

چند متغیره

نشان دادن

تخصصی

نشان دادن

متفرقه

در ریاضیات ، سری تیلور یک تابع ، مجموع نامتناهی از عبارت‌هایی است که برحسب مشتقات تابع در یک نقطه بیان می‌شوند. برای اکثر توابع رایج، تابع و مجموع سری تیلور آن در نزدیکی این نقطه برابر است. سری های تیلور به نام بروک تیلور نامگذاری شده اند که آنها را در سال 1715 معرفی کرد. اگر 0 نقطه ای باشد که مشتقات در نظر گرفته می شوند، سری های تیلور به نام کالین مکلارین که از این مورد خاص از سری تیلور استفاده گسترده ای کرده است ، سری مکلارین نیز نامیده می شود. در اواسط 1700.

مجموع جزئی که توسط اولین جمله های n + 1 یک سری تیلور تشکیل می شود، چند جمله ای درجه n است که n امین چند جمله ای تیلور تابع نامیده می شود. چند جمله ای های تیلور تقریبی از یک تابع هستند که با افزایش n به طور کلی بهتر می شوند . قضیه تیلور برآوردهای کمی را در مورد خطای ایجاد شده با استفاده از چنین تقریبی ارائه می دهد. اگر سری تیلور یک تابع همگرا باشد ، مجموع آن حد دنباله نامتناهی است .از چند جمله ای های تیلور یک تابع ممکن است با مجموع سری تیلور خود متفاوت باشد، حتی اگر سری تیلور آن همگرا باشد. یک تابع در نقطه x تحلیلی است اگر برابر مجموع سری تیلور آن در یک بازه باز (یا دیسک باز در صفحه مختلط ) حاوی x باشد. این بدان معناست که تابع در هر نقطه از بازه (یا دیسک) تحلیلی است.

فهرست

تعریف [ ویرایش ]

سری تیلور یک تابع واقعی یا با مقادیر مختلط f ( x ) که در یک عدد واقعی یا مختلط a بی نهایت قابل تفکیک است سری توانی است .

$f(a)+{\frac {f'(a)}{1!}}(xa)+{\frac {f''(a)}{2!}}(xa)^{2} +{\frac {f'''(a)}{3!}}(xa)^{3}+\cdots ,$

کجا n ! فاکتوریل n را نشان می دهد . در نماد سیگما فشرده تر ، این می تواند به صورت نوشته شود

$\sum _{n=0}^{\infty }{\frac {f^{(n)}(a)}{n!}}(xa)^{n}،$

که در آن f ( n ) ( a ) نشان دهنده n امین مشتق f ارزیابی شده در نقطه a است. (مشتق مرتبه صفر f خود f و ( x - a ) 0 و 0! هر دو به 1 تعریف می شوند . )

زمانی که a = 0 باشد، سری نیز سری مکلارین نامیده می شود . [1]

+ نوشته شده در پنجشنبه یکم اردیبهشت ۱۴۰۱ ساعت 12:56 توسط علی رضا نقش نیلچی |

بسط مکلورن sin,cos,sinh,cosh

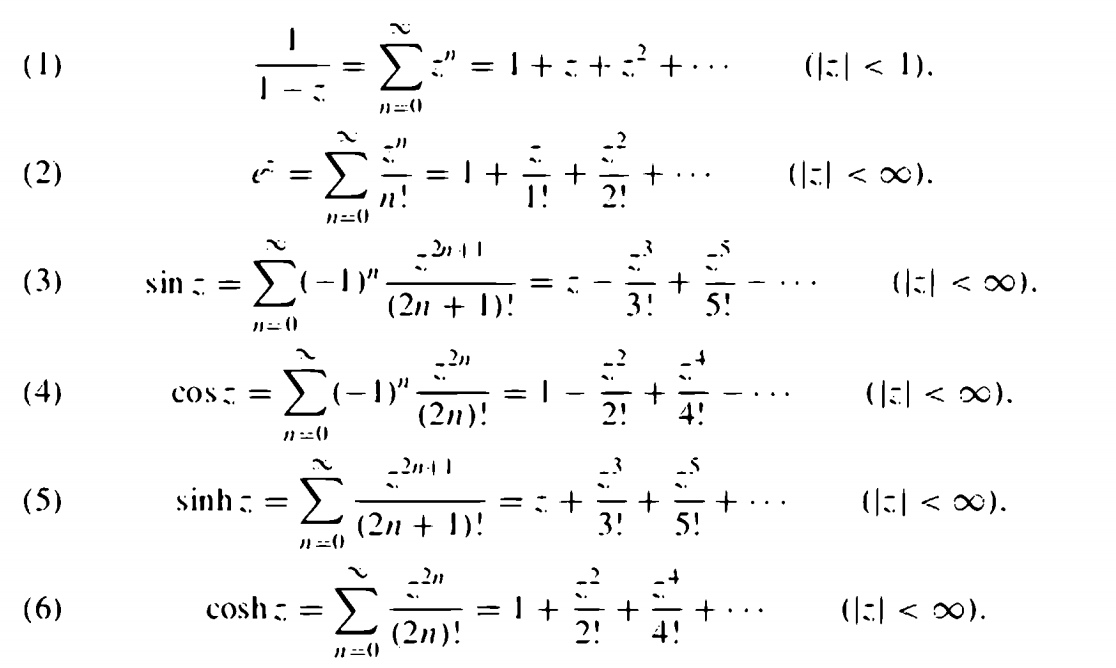
Solved You can use the series for e», sin z, cos z, sinh z, | Chegg.com

+ نوشته شده در چهارشنبه هجدهم اسفند ۱۴۰۰ ساعت 9:28 توسط علی رضا نقش نیلچی |

تقریب استرلینگ(4)

برآورد اثر مرکزی در توزیع دوجمله ای [ ویرایش ]

این بخش نمی استناد هر منابع . لطفاً با افزودن نقل قول ها به منابع معتبر به بهبود این بخش کمک کنید . مواد بدون منبع ممکن است به چالش کشیده و حذف شود . ( مه 2020 ) (با نحوه و زمان حذف این پیام الگو آشنا شوید )

در علوم کامپیوتر ، به ویژه در زمینه الگوریتم های تصادفی ، تولید بردارهای بیت تصادفی که دارای طول دو قدرت هستند ، معمول است. بسیاری از الگوریتم های تولید کننده و مصرف کننده این بردارهای بیتی به تعداد جمعیت بردارهای بیتی تولید شده یا فاصله منهتن بین دو بردار از این دست حساس هستند . غالباً مورد توجه خاص تراکم بردارهای "عادلانه" است ، جایی که تعداد جمعیت یک بردار n- bit دقیقاً است $n / 2$ . این به احتمال زیاد پرتاب یک سکه تکراری در بسیاری از آزمایش ها منجر به بازی تساوی می شود.

تقریب استرلینگ با ${\ displaystyle {n \ n را انتخاب کنید / 2}}$ ، مرکزی و حداکثر ضریب دو جمله ای از توزیع دو جمله ای ، ساده به خصوص به خوبی که در آن $n$ شکل می گیرد ${\ displaystyle 4 ^ {k}}$ ، برای یک عدد صحیح $ک$ . در اینجا ما علاقه مندیم که چگونه تراکم تعداد جمعیت مرکزی در مقایسه با کاهش می یابد $2 ^ {n}$ ، اخذ آخرین شکل در میرایی دسی بل :

${\ displaystyle {\ start {تراز شده} \ log _ {2} {n \ n / 2} را انتخاب کنید -n & = - k - {\ frac {\ log _ {2} (\ pi) -1} {2}} + O (\ log _ {2} n) \\ & \ تقریبی -k-0.3257481 \\ & \ تقریبی -k - {\ frac {1} {3}} \\ & \ تقریبی \ mathbf {3k + 1} ~~ \ mathrm {dB} ({\ text {attenuation}}) \ end {تراز شده}}}$

این تقریب ساده دقت شگفت انگیزی را به نمایش می گذارد:

${\ displaystyle {\ start {تراز شده} 10 \ log _ {10} (2 ^ {- 1024} {1024 \ را انتخاب کنید 512}) و \ تقریبی -16.033159 ~~~ {\ start {موارد} k & = 5 \\ n = 4 ^ {k} & = 1024 \\ 3k + 1 & = \ mathbf {16} \\\ end {موارد}} \\ 10 \ log _ {10} (2 ^ {- 1048576} {1048576 \ انتخاب 524288} ) & \ تقریبی -31.083600 ~~~ {\ شروع {موارد} k & = 10 \\ n = 4 ^ {k} & = 1048576 \\ 3k + 1 & = \ mathbf {31} \\\ پایان {موارد}} \ پایان {تراز شده}}}$

کاهش دودویی از dB در تقسیم بر بدست می آید ${\ displaystyle 10 \ log (2) / \ log (10) \ تقریبی 3.0103 \ تقریبا 3}$ .

به عنوان یک برآورد کسری مستقیم:

${\ displaystyle {\ شروع {تراز شده} {n \ انتخاب n / 2} / 2 ^ {n} & = 2 ^ {{\ frac {1- \ log _ {2} (\ pi)} {2}} - k} + O (n) \\ & \ تقریبی {\ sqrt {\ frac {2} {\ pi}}} ~ 2 ^ {- k} \\ & \ تقریبی 0.7978846 ~ 2 ^ {- k} \\ & \ تقریبی \ mathbf {{\ frac {4} {5}} 2 ^ {- k}} \ پایان {تراز شده}}}$

یک بار دیگر ، هر دو نمونه دقت 1٪ را به راحتی نشان می دهند:

${\ displaystyle {\ شروع {تراز شده} {256 \ انتخاب 128} 2 ^ {- 256} و \ تقریبی 20.072619 ^ {- 1} ~~~ {\ start {موارد} k & = 4 \\ n = 4 ^ {k } & = 256 \\ {\ frac {4} {5}} \ times {\ frac {1} {2 ^ {4}}} & = \ mathbf {20} ^ {- 1} \\\ end {موارد }} \\ {1048576 \ را انتخاب کنید 524288} 2 ^ {- 1048576} و \ تقریبا 1283.3940 ^ {- 1} ~~~ {\ شروع {موارد} k & = 10 \\ n = 4 ^ {k} & = 1048576 \ \ {\ frac {4} {5}} \ times {\ frac {1} {2 ^ {10}}} & = \ mathbf {1280} ^ {- 1} \ end {موارد}} \ end {تراز شده} }}$

در یک پرتاب تکراری سکه ، جلسه ای که شامل کمی بیش از یک میلیون برگرداندن سکه (یک میلیون باینری) است ، تقریباً در 1300 فرصت دارد که به تساوی ختم شود.

هر دو این تقریب ها (یکی در فضای ورود به سیستم ، دیگری در فضای خطی) برای بسیاری از توسعه دهندگان نرم افزار برای دستیابی به تخمین ذهنی ، با دقت استثنایی بر اساس معیارهای تخمین های ذهنی ، به اندازه کافی ساده هستند.

توزیع دوجمله ای توزیع طبیعی را برای بزرگ تقریباً نزدیک می کند $n$ ، بنابراین این برآوردها براساس تقریب استرلینگ نیز به مقدار اوج تابع احتمال توده برای بزرگ مربوط می شود $n$ و $p = 0.5$ ، همانطور که برای توزیع زیر مشخص شده است: ${\ displaystyle {\ mathcal {N}} (np ، \ ، np (1-p))}}$ .

تاریخچه [ ویرایش ]

این فرمول برای اولین بار توسط آبراهام دو موایور [2] در فرم کشف شد

${\ displaystyle n! \ sim [{\ rm {ثابت}}] \ cdot n ^ {n + {\ frac {1} {2}}} e ^ {- n}.}$

دی موایر برای لگاریتم طبیعی ثابت ، عبارتی تقریبی با تعداد منطقی ارائه داد. سهم استرلینگ متشکل از نشان دادن دقیق بودن ثابت است ${\ displaystyle {\ sqrt {2 \ pi}}}$ . [3]

همچنین به [ ویرایش ] مراجعه کنید

https://en.wikipedia.org/wiki/Stirling%27s_approximation

+ نوشته شده در شنبه دوم مرداد ۱۴۰۰ ساعت 11:32 توسط علی رضا نقش نیلچی |

تقریب استرلینگ(3)

فرمول استرلینگ برای عملکرد گاما [ ویرایش ]

برای تمام عددهای صحیح مثبت ،

${\ displaystyle n! = \ Gamma (n + 1)،}$

جایی که Γ تابع گاما را نشان می دهد .

با این حال ، تابع گاما ، برخلاف فاکتوریل ، به طور گسترده تر برای همه اعداد مختلط غیر از اعداد صحیح غیر مثبت تعریف شده است. با این وجود ، فرمول استرلینگ هنوز هم قابل استفاده است. اگر Re ( z )> 0 باشد ، پس

${\ displaystyle \ ln \ Gamma (z) = z \ ln z-z + {\ tfrac {1} {2}} \ ln {\ frac {2 \ pi} {z}} + \ int _ {0} ^ { \ infty} {\ frac {2 \ arctan \ چپ ({\ frac {t} {z}} \ راست)} {e ^ {2 \ pi t} -1}} \ ، {\ rm {d}} t .}$

ادغام مکرر توسط قطعات می دهد

${\ displaystyle \ ln \ Gamma (z) \ sim z \ ln z-z + {\ tfrac {1} {2}} \ ln {\ frac {2 \ pi} {z}} + \ sum _ {n = 1 } ^ {N-1} {\ frac {B_ {2n}} {2n (2n-1) z ^ {2n-1}}} ،}$

که در آن B N است N هفتم تعداد برنولی (توجه داشته باشید که از حد از مجموع عنوان $N \ به \ کمبود$ همگرا نیست ، بنابراین این فرمول فقط یک گسترش مجانبی است ). فرمول برای z بزرگ به اندازه کافی مطلق معتبر است ، هنگامی که | arg ( z ) | <π - ε ، جایی که ε مثبت است ، با یک اصطلاح خطای O ( z- 2 N + 1 ) . تقریب مربوطه اکنون می تواند نوشته شود:

${\ displaystyle \ Gamma (z) = {\ sqrt {\ frac {2 \ pi} {z}}} \ ، {\ چپ ({\ frac {z} {e}} \ راست)} ^ {z} \ چپ (1 + O \ چپ ({\ frac {1} {z}} \ راست) \ راست).}$

که در آن گسترش با سری استرلینگ در بالا برای n یکسان است ! ، با این تفاوت که n با z - 1 جایگزین می شود . [8]

کاربرد بیشتر این گسترش مجانبی برای استدلال پیچیده z با ثابت Re ( z ) است . به عنوان مثال فرمول استرلینگ را که در Im ( z ) = t از تتا ریمان-سیگل در خط مستقیم اعمال شده است ، ببینید1/4+ آن .

حدود خطا [ ویرایش ]

برای هر عدد صحیح مثبت N ، علامت گذاری زیر ارائه می شود:

${\ displaystyle \ ln \ Gamma (z) = z \ ln z-z + {\ tfrac {1} {2}} \ ln {\ frac {2 \ pi} {z}} + \ sum \ limit _ {n = 1} ^ {N-1} {\ frac {B_ {2n}} {2n \ چپ ({2n-1} \ راست) z ^ {2n-1}}} + R_ {N} (z)}$

${\ displaystyle \ Gamma (z) = {\ sqrt {\ frac {2 \ pi} {z}}} \ چپ ({\ frac {z} {e}} \ راست) ^ {z} \ چپ ({\ sum \ حدود _ {n = 0} ^ {N-1} {\ frac {a_ {n}} {z ^ {n}}} + {\ widetilde {R}} _ {N} (z)} \ راست ).}$

سپس [9] [10]

${\ displaystyle {\ start {تراز شده} | R_ {N} (z) | & \ leq {\ frac {| B_ {2N} |} {2N (2N-1) | z | ^ {2N-1}}} {\ start {cases} 1 & {\ text {if}} | \ arg z | \ leq {\ frac {\ pi} {4}} ، \\ | \ csc (\ arg z) | و {\ text {if }} {\ frac {\ pi} {4}} <| \ arg z | <{\ frac {\ pi} {2}} ، \\\ sec ^ {2N} \ سمت چپ ({\ tfrac {\ arg z } {2}} \ راست) و {\ متن {if}} | \ arg z | <\ pi ، \ end {موارد}} \\ [6pt] \ چپ | {\ widetilde {R}} _ {N} (z) \ راست | & \ leq \ چپ ({\ frac {\ چپ | a_ {N} \ راست |} {| z | ^ {N}}} + {\ frac {\ چپ | a_ {N + 1 } \ right |} {| z | ^ {N + 1}}} \ right) {\ start {موارد} 1 & {\ متن {if}} | \ arg z | \ leq {\ frac {\ pi} {4 }} ، \\ | \ csc (2 \ arg z) | & {\ text {if}} {\ frac {\ pi} {4}} <| \ arg z | <{\ frac {\ pi} {2 }}. \ end {موارد}} \ end {تراز شده}}}$

برای کسب اطلاعات بیشتر و سایر محدوده های خطا ، به مقالات ذکر شده مراجعه کنید.

نسخه همگرا از فرمول استرلینگ [ ویرایش ]

توماس بیز در نامه ای به جان كانتون كه توسط انجمن سلطنتی در سال 1763 منتشر شد ، نشان داد كه فرمول استرلینگ سری همگرا ارائه نمی دهد . [11] بدست آوردن نسخه همگرا از فرمول استرلینگ ، ارزیابی فرمول رابه را در پی دارد :

${\ displaystyle \ int _ {0} ^ {\ infty} {\ frac {2 \ arctan \ left ({\ frac {t} {x}} \ right)} {e ^ {2 \ pi t} -1} } \ ، {\ rm {d}} t = \ ln \ Gamma (x) -x \ ln x + x - {\ tfrac {1} {2}} \ ln {\ frac {2 \ pi} {x} }.}$

یکی از راه های انجام این کار استفاده از یک مجموعه همگرا از نماهای معکوس در حال افزایش است . اگر

${\ displaystyle z ^ {\ bar {n}} = z (z + 1) \ cdots (z + n-1)،}$

سپس

${\ displaystyle \ int _ {0} ^ {\ infty} {\ frac {2 \ arctan \ left ({\ frac {t} {x}} \ right)} {e ^ {2 \ pi t} -1} } \، {\ rm {d}} t = \ sum _ {n = 1} ^ {\ infty} {\ frac {c_ {n}} {(x + 1) ^ {\ bar {n}}}} ،}$

جایی که

${\ displaystyle c_ {n} = {\ frac {1} {n}} \ int _ {0} ^ {1} x ^ {\ bar {n}} \ سمت چپ (x - {\ tfrac {1} {2 }} \ راست) \ ، {\ rm {d}} x = {\ frac {1} {2n}} \ sum _ {k = 1} ^ {n} {\ frac {k | s (n، k) |} {(k + 1) (k + 2)}} ،}$

جایی که s ( n ، k ) اعداد استرلینگ را از نوع اول نشان می دهد . از این نسخه نسخه ای از سری استرلینگ را بدست می آورید

${\ displaystyle {\ start {تراز شده} \ ln \ گاما (x) & = x \ ln x-x + {\ tfrac {1} {2}} \ ln {\ frac {2 \ pi} {x}} + { \ frac {1} {12 (x + 1)}} + {\ frac {1} {12 (x + 1) (x + 2)}} + \\ & \ quad + {\ frac {59} {360 (x + 1) (x + 2) (x + 3)}} + {\ frac {29} {60 (x + 1) (x + 2) (x + 3) (x + 4)}} + \ cdots ، \ end {تراز شده}}}$

که وقتی Re ( x )> 0 جمع می شود .

نسخه های مناسب برای ماشین حساب [ ویرایش ]

تقریب

${\ displaystyle \ Gamma (z) \ تقریبی {\ sqrt {\ frac {2 \ pi} {z}}} \ چپ ({\ frac {z} {e}} {\ sqrt {z \ sinh {\ frac { 1} {z}} + {\ frac {1} {810z ^ {6}}}}} \ راست) ^ {z}}$

و شکل معادل آن

${\ displaystyle 2 \ ln \ Gamma (z) \ تقریبی \ ln (2 \ pi) - \ ln z + z \ چپ (2 \ ln z + \ ln \ چپ (z \ sinh {\ frac {1} {z} } + {\ frac {1} {810z ^ {6}}} \ راست) -2 \ راست)}$

با تنظیم مجدد فرمول گسترده استرلینگ و مشاهده همزمانی بین سری قدرت حاصل و گسترش سری تیلور از عملکرد سینوسی هذلولی می توان بدست آورد . این تقریب برای بیش از 8 رقم اعشاری برای z با یک قسمت واقعی بزرگتر از 8 خوب است. رابرت اچ. ویندشیتل آن را در سال 2002 برای محاسبه عملکرد گاما با دقت مناسب روی ماشین حسابهای دارای برنامه محدود یا حافظه ثبت شده پیشنهاد داده است. [12]

Gergő Nemes در سال 2007 تقریب ارائه کرد که تعداد دقیق همان رقم تقریب Windschitl را می دهد اما بسیار ساده تر است: [13]

${\ displaystyle \ Gamma (z) \ تقریبی {\ sqrt {\ frac {2 \ pi} {z}}} \ چپ ({\ frac {1} {e}} \ چپ (z + {\ frac {1} {) 12z - {\ frac {1} {10z}}}} \ right) \ right) ^ {z}،}$

یا معادل آن ،

${\ displaystyle \ ln \ Gamma (z) \ تقریبی {\ tfrac {1} {2}} \ چپ (\ ln (2 \ pi) - \ ln z \ سمت راست) + z \ چپ (\ ln \ چپ (z + {\ frac {1} {12z - {\ frac {1} {10z}}}} \ راست) -1 \ راست).}$

یک تقریب جایگزین برای عملکرد گاما که توسط Srinivasa Ramanujan بیان شده است ( Ramanujan 1988 [ لازم به توضیح ] )

${\ displaystyle \ Gamma (1 + x) \ تقریبی {\ sqrt {\ pi}} \ چپ ({\ frac {x} {e}} \ راست) ^ {x} \ چپ (8x ^ {3} + 4x ^ {2} + x + {\ frac {1} {30}} \ راست) ^ {\ frac {1} {6}}}$

برای x ≥ 0 . تقریب معادل ln n ! دارای یک خطای مجانبی از1/1400 n 3 و توسط

${\ displaystyle \ ln n! \ تقریبی n \ ln n-n + {\ tfrac {1} {6}} \ ln (8n ^ {3} + 4n ^ {2} + n + {\ tfrac {1} {30} }) + {\ tfrac {1} {2}} \ ln \ pi.}$

تقریب ممکن است با دادن مرزهای بالا و پایین جفت شده دقیق شود. یکی از این نابرابری ها [14] [15] [16] [17]

${\ displaystyle {\ sqrt {\ pi}} \ چپ ({\ frac {x} {e}} \ راست) ^ {x} \ چپ (8x ^ {3} + 4x ^ {2} + x + {\ frac {1} {100}} \ راست) ^ {1/6} <\ Gamma (1 + x) <{\ sqrt {\ pi}} \ چپ ({\ frac {x} {e}} \ راست) ^ {x} \ چپ (8x ^ {3} + 4x ^ {2} + x + {\ frac {1} {30}} \ راست) ^ {1/6}.}$

https://en.wikipedia.org/wiki/Stirling%27s_approximation

+ نوشته شده در شنبه دوم مرداد ۱۴۰۰ ساعت 11:29 توسط علی رضا نقش نیلچی |

تقریب استرلینگ(1)

مقایسه تقریب استرلینگ با فاکتوریل

در ریاضیات ، تقریب استرلینگ (یا فرمول استرلینگ ) یک تقریب برای فاکتوریل ها است . این یک تقریب خوب است ، حتی برای مقادیر کوچک n نیز به نتایج دقیق منجر می شود . این نام از جیمز استرلینگ گرفته شده است ، گرچه برای اولین بار توسط آبراهام دو موایر بیان شد . [1] [2] [3]

نسخه فرمولی که معمولاً در برنامه ها استفاده می شود ، می باشد

${\ displaystyle \ ln n! = n \ ln n-n + O (\ ln n)}$

(در بزرگ نماد O ، به عنوان $n \ به \ بی فایده است$ ) ، یا ، با تغییر پایه لگاریتم (به عنوان مثال در بدترین حالت پایین تر برای مرتب سازی مقایسه ) ،

${\ displaystyle \ log _ {2} n! = n \ log _ {2} nn \ log _ {2} e + O (\ log _ {2} n).}$

تعیین ثابت در اصطلاح خطای O (ln n ) نشان می دهد1/2ln (2 πn ) ، فرمول دقیق تر را ارائه می دهد:

${\ displaystyle n! \ sim {\ sqrt {2 \ pi n}} \ چپ ({\ frac {n} {e}} \ راست) ^ {n} ،}$

جایی که علامت ~ به معنای مجانبی بودن دو کمیت است : نسبت آنها به 1 گرایش دارد زیرا n به بی نهایت گرایش دارد.

همچنین ممکن است مرزهای ساده ای برای همه صحیح مثبت n معتبر باشد ، نه فقط برای n بزرگ :

${\ displaystyle {\ sqrt {2 \ pi}} \ n ^ {n + {\ frac {1} {2}}} e ^ {- n} \ leq n! \ leq e \ n ^ {n + {\ frac { 1} {2}}} e ^ {- n}}$

برای $n = 1،2،3 ، \ نقاط$ . این موارد از مرزهای دقیق تر خطایی که در زیر بحث شده است پیروی می کنند .

فهرست

اشتقاق [ ویرایش ]

به طور تقریبی ، ساده ترین نسخه فرمول استرلینگ را می توان با تقریب حاصل از جمع به سرعت بدست آورد

${\ displaystyle \ ln n! = \ sum _ {j = 1} ^ {n} \ ln j}$

با یک انتگرال :

${\ displaystyle \ sum _ {j = 1} ^ {n} \ ln j \ تقریبی \ int _ {1} ^ {n} \ ln x \ ، {\ rm {d}} x = n \ ln n-n 1+.}$

فرمول کامل ، همراه با برآورد دقیق از خطای آن ، می تواند به شرح زیر استخراج شود. به جای تقریب n ! ، یکی لگاریتم طبیعی آن را در نظر می گیرد ، زیرا این یک عملکرد به آرامی متفاوت است :

${\ displaystyle \ ln n! = \ ln 1+ \ ln 2+ \ cdots + \ ln n.}$

سمت راست این معادله منهای

${\ displaystyle {\ tfrac {1} {2}} (\ ln 1+ \ ln n) = {\ tfrac {1} {2}} \ ln n}$

تقریب توسط قاعده ذوزنقه انتگرال است

${\ displaystyle \ ln n! - {\ tfrac {1} {2}} \ ln n \ تقریبی \ int _ {1} ^ {n} \ ln x \ ، {\ rm {d}} x = n \ ln n-n + 1 ،}$

و خطا در این تقریب با فرمول اویلر-ماکلورین آورده شده است :

${\ displaystyle {\ start {تراز شده} \ ln n! - {\ tfrac {1} {2}} \ ln n & = {\ tfrac {1} {2}} \ ln 1+ \ ln 2+ \ ln 3+ \ cdots + \ ln (n-1) + {\ tfrac {1} {2}} \ ln n \\ & = n \ ln n-n + 1 + \ sum _ {k = 2} ^ {m} { \ frac {(-1) ^ {k} B_ {k}} {k (k-1)}} \ چپ ({\ frac {1} {n ^ {k-1}}} - 1 \ راست) + R_ {m ، n} ، \ end {تراز شده}}}$

که در آن B K است تعداد برنولی ، و R متر ، N باقی مانده مدت در فرمول اویلر-Maclaurin است. برای یافتن آن محدودیت هایی را در نظر بگیرید

${\ displaystyle \ lim _ {n \ to \ infty} \ left (\ ln n! -n \ ln n + n - {\ tfrac {1} {2}} \ ln n \ right) = 1- \ sum _ {k = 2} ^ {m} {\ frac {(-1) ^ {k} B_ {k}} {k (k-1)}} + \ lim _ {n \ to \ infty} R_ {m، n}.}$

این حد را به عنوان y نشان دهید . از آنجا که باقی مانده R متر ، N در فرمول اویلر-Maclaurin ارضا

$R_ {m، n} = \ lim _ {n \ to \ infty} R_ {m، n} + O \ left ({\ frac {1} {n ^ {m}}} \ right) ،$

در جایی که از علامت بزرگ استفاده می شود ، ترکیبی از معادلات فوق فرمول تقریب را در فرم لگاریتمی آن بدست می آورد:

${\ displaystyle \ ln n! = n \ ln \ چپ ({\ frac {n} {e}} \ راست) + {\ tfrac {1} {2}} \ ln n + y + \ sum _ {k = 2 } ^ {m} {\ frac {(-1) ^ {k} B_ {k}} {k (k-1) n ^ {k-1}}} + O \ چپ ({\ frac {1} { n ^ {m}}} \ درست).}$

با توجه به نماد هر دو طرف و انتخاب هر عدد صحیح مثبت m ، فرمولی بدست می آید که شامل مقدار ناشناخته e y باشد. برای m = 1 ، فرمول است

${\ displaystyle n! = e ^ {y} {\ sqrt {n}} \ چپ ({\ frac {n} {e}} \ راست) ^ {n} \ چپ (1 + O \ چپ ({\ frac {1} {n}} \ راست) \ درست).}$

مقدار e y را می توان با در نظر گرفتن حد در هر دو طرف در حالی که n به سمت بی نهایت تمایل دارد و با استفاده از محصول والیس پیدا کرد ، که نشان می دهد e y = √ 2 π . بنابراین ، فرمول استرلینگ به دست می آید:

$n! = {\ sqrt {2 \ pi n}} \ چپ ({\ frac {n} {e}} \ راست) ^ {n} \ چپ (1 + O \ چپ ({\ frac {1} {n }} \ راست) \ درست).$

https://en.wikipedia.org/wiki/Stirling%27s_approximation

+ نوشته شده در شنبه دوم مرداد ۱۴۰۰ ساعت 11:23 توسط علی رضا نقش نیلچی |

سری توانی

از ویکیپدیا، دانشنامه آزاد

برای سری نوت‌بوک‌ها، سری IBM ThinkPad Power را ببینید .

در ریاضیات ، یک سری توانی (در یک متغیر ) یک سری نامتناهی از فرم است

$\sum _{n=0}^{\infty }a_{n}\left(xc\right)^{n}=a_{0}+a_{1}(xc)+a_{2}( xc)^{2}+\dots$

که در آن a n نشان دهنده ضریب n ام و c یک ثابت است. سری های توانی در آنالیز ریاضی مفید هستند، جایی که به عنوان سری های تیلور از توابع بی نهایت متمایز به وجود می آیند . در واقع، قضیه بورل نشان می دهد که هر سری توانی، سری تیلور از برخی تابع صاف است.

در بسیاری از موقعیت‌ها، c ( مرکز سری) برابر با صفر است، به عنوان مثال زمانی که یک سری مکلورن را در نظر می‌گیریم . در چنین مواردی، سری پاور شکل ساده تری به خود می گیرد

$\sum _{n=0}^{\infty }a_{n}x^{n}=a_{0}+a_{1}x+a_{2}x^{2}+\dots .$

فراتر از نقش آنها در تحلیل ریاضی، سری های توان در ترکیبات به عنوان توابع مولد (نوعی سری توانی استاندارد ) و در مهندسی الکترونیک (تحت نام تبدیل Z ) نیز دیده می شوند. نماد اعشاری آشنا برای اعداد حقیقی را می‌توان به عنوان نمونه‌ای از سری توانی، با ضرایب صحیح ، اما با آرگومان x ثابت در 1/10 مشاهده کرد . در نظریه اعداد ، مفهوم اعداد p -adic نیز ارتباط نزدیکی با سری توانی دارد.

فهرست

مثالها [ ویرایش ]

تابع نمایی (به رنگ آبی) و مجموع n + 1 جمله اول سری توان مکلورن آن (به رنگ قرمز).

هر چند جمله‌ای را می‌توان به راحتی به عنوان یک سری توان در اطراف هر مرکز c بیان کرد، اگرچه تمام ضرایب به استثنای محدود، صفر خواهند بود زیرا یک سری توانی دارای بی‌نهایت اصطلاحات تعریف شده است. به عنوان مثال، چند جمله ای ${\textstyle f(x)=x^{2}+2x+3}$ را می توان به عنوان یک سری توانی در اطراف مرکز نوشت ${\textstyle c=0}$ مانند

$f(x)=3+2x+1x^{2}+0x^{3}+0x^{4}+\cdots$ یا اطراف مرکز ${\textstyle c=1}$ مانند

$f(x)=6+4(x-1)+1(x-1)^{2}+0(x-1)^{3}+0(x-1)^{4}+ \cdots$ یا در واقع در اطراف هر مرکز دیگری ج . [1] می‌توان سری‌های توانی را مانند «چندجمله‌های درجه بی‌نهایت» دید، اگرچه سری‌های توانی چند جمله‌ای نیستند.

فرمول سری هندسی

${\frac {1}{1-x}}=\sum _{n=0}^{\infty }x^{n}=1+x+x^{2}+x^{3} +\cdots،$ که برای ${\textstyle |x|<1}$ ، یکی از مهم ترین نمونه های سری توانی است، مانند فرمول تابع نمایی

$e^{x}=\sum _{n=0}^{\infty }{\frac {x^{n}}{n!}}=1+x+{\frac {x^{2} }{2!}}+{\frac {x^{3}}{3!}}+\cdots ,$ و فرمول سینوس

$\sin(x)=\sum _{n=0}^{\infty }{\frac {(-1)^{n}x^{2n+1}}{(2n+1)!} }=x-{\frac {x^{3}}{3!}}+{\frac {x^{5}}{5!}}-{\frac {x^{7}}{7!} }+\cdots ,$

برای همه x حقیقی معتبر است.

این سری های پاور نیز نمونه هایی از سری تیلور هستند .

در مجموعه توانها [ ویرایش ]

توانی های منفی در یک سری توانی مجاز نیستند. برای مثال، ${\textstyle 1+x^{-1}+x^{-2}+\cdots }$ به عنوان یک سری توانی در نظر گرفته نمی شود (اگرچه یک سری لرنت است ). به همین ترتیب، توان های کسری مانند ${\textstyle x^{\frac {1}{2}}}$ مجاز نیستند (اما سری Puiseux را ببینید ). ضرایب ${\textstyle a_{n}}$ مجاز به وابستگی نیستند ${\textstyle x}$ ، به عنوان مثال:

$\sin(x)x+\sin(2x)x^{2}+\sin(3x)x^{3}+\cdots$ سری پاور نیست

شعاع همگرایی [ ویرایش ]

یک سری توانی ${\textstyle \sum _{n=0}^{\infty }a_{n}(xc)^{n}}$ برای برخی از مقادیر متغیر x همگرا است که همیشه x = c را شامل می شود (مثلاً، $(xc)^{0}$ به عنوان ارزیابی می کند1 و مجموع سری به این ترتیب است $a_{0}$ برای x = c ). این سری ممکن است برای مقادیر دیگر x واگرا شود . اگر c تنها نقطه همگرایی نباشد، همیشه یک عدد r با 0 < r ≤ ∞ وجود دارد به طوری که هر زمان که | x – c | < r و هر زمان که | x – c | > r _ عدد r شعاع همگرایی سری توان نامیده می شود . به طور کلی به عنوان داده می شود

$r=\liminf _{n\to \infty }\left|a_{n}\right|^{-{\frac {1}{n}}}$ یا به طور معادل

$r^{-1}=\limsup _{n\to \infty }\left|a_{n}\right|^{\frac {1}{n}}$ (این قضیه کوشی-هادامارد است ؛ برای توضیح نماد ، حد برتر و حد پایین را ببینید). ارتباط

$r^{-1}=\lim _{n\to \infty }\left|{a_{n+1} \over a_{n}}\راست|$ در صورت وجود این محدودیت نیز راضی است.

مجموعه ای از اعداد مختلط به گونه ای که | x – c | < r دیسک همگرایی سری نامیده می شود . این سری کاملاً در داخل دیسک همگرایی خود همگرا می شود و به طور یکنواخت در هر زیر مجموعه فشرده از دیسک همگرایی همگرا می شود.

برای | x – c | = r ، هیچ بیانیه کلی در مورد همگرایی سری وجود ندارد. با این حال، قضیه آبل بیان می کند که اگر سری برای مقداری z همگرا باشد به طوری که | z – c | = r ، سپس مجموع سری برای x = z حد مجموع سری برای x = c + t ( z – c ) است که در آن t یک متغیر حقیقی کمتر از1 که تمایل دارد1 .

عملیات روی سری توانی[ ویرایش ]

جمع و تفریق [ ویرایش ]

هنگامی که دو تابع f و g به سری توانی در اطراف یک مرکز c تجزیه می شوند ، سری توان مجموع یا تفاضل توابع را می توان با جمع و تفریق مدتی به دست آورد. یعنی اگر

$f(x)=\sum _{n=0}^{\infty }a_{n}(xc)^{n}$ و

$g(x)=\sum _{n=0}^{\infty }b_{n}(xc)^{n}$ سپس

$f(x)\pm g(x)=\sum _{n=0}^{\infty }(a_{n}\pm b_{n})(xc)^{n}.$

این درست نیست که اگر دو سری توانی ${\textstyle \sum _{n=0}^{\infty }a_{n}x^{n}}$ و ${\textstyle \sum _{n=0}^{\infty }b_{n}x^{n}}$ پس شعاع همگرایی یکسانی دارند ${\textstyle \sum _{n=0}^{\infty }\left(a_{n}+b_{n}\right)x^{n}}$ این شعاع همگرایی را نیز دارد. اگر ${\textstyle a_{n}=(-1)^{n}}$ و ${\textstyle b_{n}=(-1)^{n+1}\left(1-{\frac {1}{3^{n}}}\راست)}$ ، سپس هر دو سری شعاع همگرایی یکسانی دارند اما سری ${\textstyle \sum _{n=0}^{\infty }\left(a_{n}+b_{n}\right)x^{n}=\sum _{n=0}^{\infty } {\frac {(-1)^{n}}{3^{n}}}x^{n}}$ دارای شعاع همگرایی 3 است.

مجموع دو سری توان، حداقل، شعاع همگرایی کوچکتر از دو شعاع همگرایی دو سری خواهد داشت (و ممکن است از هر کدام بیشتر باشد، همانطور که در مثال بالا مشاهده می شود). [2]

ضرب و تقسیم [ ویرایش ]

با همین تعاریف برای $f(x)$ و $g(x)$ سری توان محصول و ضریب توابع را می توان به صورت زیر بدست آورد:

${\begin{aligned}f(x)g(x)&=\left(\sum _{n=0}^{\infty }a_{n}(xc)^{n}\right)\ چپ(\sum _{n=0}^{\infty }b_{n}(xc)^{n}\right)\\&=\sum _{i=0}^{\infty }\sum _{ j=0}^{\infty }a_{i}b_{j}(xc)^{i+j}\\&=\sum _{n=0}^{\infty }\left(\sum _{ i=0}^{n}a_{i}b_{ni}\right)(xc)^{n}.\end{تراز شده}}$

تسلسل و توالی ${\textstyle m_{n}=\sum _{i=0}^{n}a_{i}b_{ni}}$ به عنوان پیچیدگی دنباله ها شناخته می شود $a_{n}$ و $b_{n}$ .

برای تقسیم، اگر یکی دنباله را تعریف کند $d_{n}$ توسط

${\frac {f(x)}{g(x)}}={\frac {\sum _{n=0}^{\infty }a_{n}(xc)^{n}}{ \sum _{n=0}^{\infty }b_{n}(xc)^{n}}}=\sum _{n=0}^{\infty }d_{n}(xc)^{n }$ سپس

$f(x)=\left(\sum _{n=0}^{\infty }b_{n}(xc)^{n}\right)\left(\sum _{n=0}^ {\infty }d_{n}(xc)^{n}\right)$ و می توان به صورت بازگشتی برای عبارت ها حل کرد $d_{n}$ با مقایسه ضرایب

با حل معادلات مربوطه، فرمول هایی بر اساس تعیین کننده های ماتریس های معینی از ضرایب به دست می آید. $f(x)$ و $g(x)$

$d_{0}={\frac {a_{0}}{b_{0}}}$

$d_{n}={\frac {1}{b_{0}^{n+1}}}{\begin{vmatrix}a_{n}&b_{1}&b_{2}&\cdots &b_{ n}\\a_{n-1}&b_{0}&b_{1}&\cdots &b_{n-1}\\a_{n-2}&0&b_{0}&\cdots &b_{n-2}\\ \vdots &\vdots &\vdots &\ddots &\vdots \\a_{0}&0&0&\cdots &b_{0}\end{vmatrix}}$

مشتق و انتگرال[ ویرایش ]

یک بار یک تابع $f(x)$ به عنوان یک سری توانی مانند بالا داده شده است، در داخل حوزه همگرایی قابل مشتق گیری است. با در نظر گرفتن هر اصطلاح به طور جداگانه، می توان آن را به راحتی مشتق و انتگرال گیری کرد:

${\begin{aligned}f'(x)&=\sum _{n=1}^{\infty }a_{n}n(xc)^{n-1}=\sum _{n= 0}^{\infty }a_{n+1}(n+1)(xc)^{n},\\\int f(x)\,dx&=\sum _{n=0}^{\infty }{\frac {a_{n}(xc)^{n+1}}{n+1}}+k=\sum _{n=1}^{\infty }{\frac {a_{n-1 }(xc)^{n}}{n}}+k.\end{aligned}}$

هر دوی این سری ها شعاع همگرایی مشابه سری اصلی دارند.

توابع تحلیلی [ ویرایش ]

مقاله اصلی: تابع تحلیلی

تابع f تعریف شده روی زیرمجموعه باز U از R یا C اگر به صورت محلی توسط یک سری توان همگرا داده شود، تحلیلی نامیده می شود. این بدان معناست که هر a ∈ U یک همسایگی باز V ⊆ U دارد، به طوری که یک سری توان با مرکز a وجود دارد که به ازای هر x ∈ V به f ( x ) همگرا می شود .

هر سری توانی با شعاع همگرایی مثبت، در داخل منطقه همگرایی خود تحلیلی است. همه توابع هولومورفیک مختلط-تحلیلی هستند. مجموع و حاصلضرب توابع تحلیلی و تا زمانی که مخرج غیر صفر باشد، ضرایب تحلیلی هستند.

اگر تابعی تحلیلی باشد، بی نهایت قابل تمایز است، اما در حالت حقیقی عکس آن به طور کلی صادق نیست. برای یک تابع تحلیلی، ضرایب a n را می توان به صورت محاسبه کرد

$a_{n}={\frac {f^{\left(n\right)}\left(c\right)}{n!}}$

جایی که $f^{(n)}(c)$ نشان دهنده n امین مشتق f در c و $f^{(0)}(c) = f(c)$ . این بدان معنی است که هر تابع تحلیلی به صورت محلی با سری تیلور خود نشان داده می شود .

شکل کلی یک تابع تحلیلی کاملاً با رفتار محلی آن به معنای زیر تعیین می شود: اگر f و g دو تابع تحلیلی هستند که روی یک مجموعه باز متصل U تعریف شده اند، و اگر یک عنصر c∈ U وجود داشته باشد به طوری که f ( n ) ( c ) = g ( n ) ( c ) برای همه n ≥ 0 , سپس f ( x ) = g ( x ) برای همه x ∈ U.

اگر یک سری توان با شعاع همگرایی r داده شود، می توان ادامه های تحلیلی سری را در نظر گرفت، یعنی توابع تحلیلی f که روی مجموعه های بزرگتر از { x | | x − c | < r } و با سری توانی داده شده در این مجموعه موافقت کنید. عدد r به معنای زیر حداکثر است: همیشه یک عدد مختلط x با | وجود دارد x − c | = r به گونه ای که هیچ ادامه تحلیلی سری را نمی توان در x تعریف کرد .

بسط سری توان تابع معکوس یک تابع تحلیلی را می توان با استفاده از قضیه وارونگی لاگرانژ تعیین کرد .

رفتار نزدیک به مرز [ ویرایش ]

مجموع یک سری توان با شعاع همگرایی مثبت یک تابع تحلیلی در هر نقطه از داخل دیسک همگرایی است. با این حال، رفتارهای متفاوتی می تواند در نقاطی در مرز آن دیسک رخ دهد. مثلا:

واگرایی در حالی که مجموع به یک تابع تحلیلی گسترش می یابد : ${\textstyle \sum _{n=0}^{\infty }z^{n}}$ دارای شعاع همگرایی برابر است $1$ و در هر نقطه از $|z|=1$ . با این وجود، مجموع در $|z|<1$ ${\textstyle {\frac {1}{1-z}}}$ ، که در هر نقطه از هواپیما به جز برای $z=1$ .
همگرا در برخی نقاط واگرا در برخی دیگر : ${\textstyle \sum _{n=1}^{\infty }(-1)^{n+1}{\frac {z^{n}}{n}}}$ شعاع همگرایی دارد $1$ . برای همگرا می شود $z=1$ ، در حالی که برای $z=-1$
همگرایی مطلق در هر نقطه از مرز : ${\textstyle \sum _{n=1}^{\infty }{\frac {z^{n}}{n^{2}}}}$ شعاع همگرایی دارد $1$ ، در حالی که به طور مطلق و یکنواخت در هر نقطه از همگرا می شود $|z|=1$ به دلیل استفاده از آزمون ام واشتراس با سری همگرای هایپر هارمونیک ${\textstyle \sum _{n=1}^{\infty }{\frac {1}{n^{2}}}}$ .
همگرا در بسته شدن دیسک همگرایی اما مجموع پیوسته نیست : سرپینسکی مثالی [3] از یک سری توان با شعاع همگرایی ارائه کرد. $1$ ، همگرا در تمام نقاط با $|z|=1$ ، اما مجموع یک تابع نامحدود و به ویژه ناپیوسته است. یک شرط کافی برای تداوم یک طرفه در یک نقطه مرزی توسط قضیه آبل ارائه شده است .

سری استاندارد توانی [ ویرایش ]

مقاله اصلی: سری استاندارد توانی

در جبر انتزاعی ، شخص تلاش می‌کند تا ماهیت سری‌های توانی را بدون محدود شدن به میدان‌های اعداد حقیقی و مختلط، و بدون نیاز به صحبت در مورد همگرایی، به تصویر بکشد. این منجر به مفهوم سری توان استاندارد می شود ، مفهومی که در ترکیبات جبری کاربرد زیادی دارد .

سری توانی در چندین متغیر [ ویرایش ]

بسط نظریه برای اهداف حساب چند متغیره ضروری است . یک سری توان در اینجا به عنوان یک سری نامتناهی از فرم تعریف می شود

$f(x_{1},\dots,x_{n})=\sum _{j_{1},\dots ,j_{n}=0}^{\infty }a_{j_{1}, \dots ,j_{n}}\prod _{k=1}^{n}(x_{k}-c_{k})^{j_{k}},$ که در آن j = ( j 1 ، …، jn) بردار اعداد طبیعی است، ضرایب a (j 1 , …, j n ) معمولاً اعداد حقیقی یا مختلط هستند و مرکز c = ( c 1 , …, c n ) و آرگومان x = ( x 1 , …, x n ) معمولا بردارهای حقیقی یا مختلط هستند. نماد $\ پی$ نماد حاصل ضرب است. در نماد چند شاخصی راحت تر ، این را می توان نوشت

$f(x)=\sum _{\alpha \in \mathbb {N} ^{n}}a_{\alpha }(xc)^{\alpha }.$ جایی که $\mathbb {N}$ مجموعه اعداد طبیعی است و غیره $\mathbb {N} ^{n}$ مجموعه ای از n مرتبه - چند تایی اعداد طبیعی است.

تئوری چنین سری هایی مختلط تر از سری های تک متغیری با مناطق همگرایی مختلط تر است. به عنوان مثال، سری توانی ${\textstyle \sum _{n=0}^{\infty }x_{1}^{n}x_{2}^{n}}$ در مجموعه کاملاً همگرا است $\{(x_{1},x_{2}):|x_{1}x_{2}|<1\}$ بین دو هذلولی (این نمونه ای از یک مجموعه log-convex است ، به این معنا که مجموعه نقاط $(\log |x_1|، \log |x_2|)$ ، جایی که $(x_{1}،x_{2})$ در ناحیه فوق قرار دارد، مجموعه ای محدب است. به طور کلی تر، می توان نشان داد که وقتی c=0، فضای داخلی ناحیه همگرایی مطلق همیشه یک مجموعه لگ محدب است به این معنا.) از طرف دیگر، در داخل این ناحیه همگرایی می توان متمایز و ادغام کرد. در زیر علامت سری، درست مانند یک سری توانی معمولی. [4]

سفارش یک سری توانی [ ویرایش ]

فرض کنید α یک شاخص چندگانه برای یک سری توانی f ( x 1 , x 2 , …, x n ) باشد. ترتیب سری توان f به عنوان حداقل مقدار تعریف شده است $r$ به طوری که α ≠ 0 با وجود دارد $r=|\alpha |=\alpha _{1}+\alpha _{2}+\cdots +\alpha _{n}$ ، یا $\کوچک$ اگر f ≡ 0. به ویژه، برای یک سری توانی f ( x ) در یک متغیر منفرد x ، مرتبه f کوچکترین توان x با ضریب غیر صفر است. این تعریف به راحتی به سری لرنت گسترش می یابد .

منبع

https://en.wikipedia.org/wiki/Power_series

+ نوشته شده در جمعه نوزدهم دی ۱۳۹۹ ساعت 23:58 توسط علی رضا نقش نیلچی |

حدس زدن

حدس زدن غیررسمی است انگلیسی واژه مرکب از حدس و برآورد ، برای اولین بار توسط آمریکا مورد استفاده قرار آمار در سال 1934 [1] و یا سال 1935. [2] آن را به عنوان یک برآورد شده بدون استفاده از اطلاعات کافی و یا کامل تعریف شده است، [3] [4] و یا، در به شدت ، به عنوان تخمینی که با حدس یا حدس به دست می آید . [2] [5] [6] مانند کلمات تخمین و حدس می زنیم ، ممکن است از guesstimate به عنوان فعل یا اسم استفاده شود (با همان تغییر در تلفظبه عنوان تخمین) ارزیابی دقیق ممکن است اولین تقریب خشن در انتظار تخمین دقیق تر باشد ، یا ممکن است یک حدس تحصیل کرده در مورد چیزی باشد که اطلاعات بهتری برای آن در دسترس نباشد.

اگر اطلاعات برای تخمین بهتر در دسترس است اما نادیده گرفته می شود ، ممکن است این کلمه را به معنای مزاحمت بکار برد . [7] [8]

تکنیک های Guesstimation استفاده می شوند:

در فیزیک ، که در آن استفاده از تکنیک های guesstimation برای حل مشکلات Fermi به عنوان یک مهارت مفید برای دانشجویان علوم تدریس می شود. [9]
در کیهان شناسی ، جایی که معادله دریک یک روش مشهور به دست آمده است. [10]
در اقتصاد ، جایی که پیش بینی ها و آمارهای اقتصادی غالباً بر اساس معیارهای سنجش استوار است. [11]
در مهندسی نرم افزار ، که در آن توسعه جدید از ویژگی ها و زمان بندی انتشار بر اساس شاخص های تلاش وظایف است.

کتاب لورنس وینشتین و جان آدامز Guesstimation: حل مشکلات جهان در پشت یک دستمال کوکتل ، بر اساس دوره "فیزیک در پشت یک پاکت" در دانشگاه Old Dominion ، تکنیک های guesstimation را به عنوان یک مهارت مفید در زندگی ترویج می کند. این شامل بسیاری از نمونه های کار شده از guesstimation ، از جمله مشکلات زیر است:

چند آمریکایی مایل در طی سال چند مایل رانندگی می کنند؟

پاسخ: حدود 2 تریلیون (2x10 12 ). [12]

یک نیروگاه هسته ای با ظرفیت 1 گیگاوات در سال تولید چقدر زباله هسته ای سطح بالایی را تولید می کند؟

جواب: حدود 60 تن. [13]

همچنین مشاهده کنید [ ویرایش ]

منابع

https://en.wikipedia.org/wiki/Guesstimate

+ نوشته شده در جمعه بیست و نهم فروردین ۱۳۹۹ ساعت 6:45 توسط علی رضا نقش نیلچی |

آزمون فرمی ، سوال فرمی ، برآورد فرمی

در آموزش فیزیک یا مهندسی ، یک مشکل فرمی ، آزمون فرمی ، سوال فرمی ، برآورد فرمی یا تخمین سفارش یک مسئله تخمین است که برای آموزش تجزیه و تحلیل ابعادی یا تقریب محاسبات شدید علمی طراحی شده است و چنین مشکلی معمولاً پشتیبان است. محاسبه پاکت . این روش تخمین نام فیزیکدان Enrico Fermi نامگذاری شده استاز آنجا که او به دلیل توانایی خود در انجام محاسبات تقریبی خوب با داده های کم یا بدون واقعی شناخته شده بود. مشکلات فرمی معمولاً شامل حدس و گمان های موجه در مورد کمیت ها و واریانس آنها یا مرزهای پایین و بالا است.

فهرست

پیشینه تاریخی [ ویرایش ]

نمونه ای از تخمین انریکو فرمی از قدرت بمب اتمی است که در آزمایش Trinity منفجر شده است ، بر اساس مسافت طی شده توسط تکه های کاغذی که وی هنگام انفجار از دستش کاسته است. [1] تخمین Fermi از 10 کیلوتن TNT به میزان بزرگی از ارزش اکنون پذیرفته شده 21 کیلوتن بود.

مثالها [ ویرایش ]

نمونه هایی از سؤالات فرمی اغلب از نظر ماهیت بسیار افراطی هستند و معمولاً با استفاده از اطلاعات رایج ریاضی یا علمی قابل حل نیست.

نمونه سوالات ارائه شده توسط مسابقات رسمی فرمی:

"اگر جرم یک قاشق چایخوری آب به صورت گرما کاملاً به انرژی تبدیل شود ، چه حجم آب ، در ابتدا در دمای اتاق ، می تواند آن را به جوش آورد؟ (لیتر)."
"رودخانه تیمز چقدر در عبور از سد Fanshawe گرم می شود؟" (درجه سانتیگراد). "
"این توده تمام اتومبیل های ضبط شده در آمریکای شمالی در این ماه چقدر است؟" (کیلوگرم) " [2] [3]

احتمالاً مشهورترین سؤال فرمی معادله دریک است که درصدد تخمین تعداد تمدنهای هوشمند در کهکشان است. سوال اساسی که چرا ، اگر تعداد قابل توجهی از چنین تمدن ها وجود داشته باشد ، ما هرگز با دیگران روبرو نشده ایم ، پارادوکس فرمی نامیده می شود . [4]

مزایا و دامنه [ ویرایش ]

دانشمندان اغلب قبل از مراجعه به روشهای پیچیده تر برای محاسبه پاسخی دقیق ، به دنبال تخمین پاسخی برای یک مشکل هستند. این یک بررسی مفید در مورد نتایج است. در حالی که تخمین تقریباً صحیح نادرست است ، این یک محاسبه ساده است که امکان بررسی آسان خطا را نیز فراهم می آورد ، و اگر رقم تولید شده بسیار فراتر از چیزی باشد که ما انتظار داشتیم معقولات را پیدا کنیم. در مقابل ، محاسبات دقیق می تواند بسیار پیچیده باشد اما با این انتظار که پاسخ آنها تولید صحیح باشد. تعداد بسیار بیشتری از عوامل و عملیات درگیر می توانند خطای بسیار مهمی را چه در فرآیند ریاضی و چه در فرضیات براساس معادله ایجاد کنند. انتظار می رود نتایج خوبی داشته باشد. بدون داشتن یک مرجع منطقی برای کار از آن ، به ندرت مشخص است که آیا یک نتیجه از نظر قابل قبولی دقیق است یا درجه های بزرگی (ده ها یا صدها برابر) خیلی بزرگ یا خیلی کوچک است. برآورد فرمی راهی سریع و ساده برای به دست آوردن این چارچوب مرجع برای آنچه می توان پاسخ منطقی را انتظار داشت ارائه می دهد.

تا زمانی که فرضیات اولیه در برآورد مقادیر معقول باشد ، نتیجه بدست آمده پاسخی را در همان مقیاس به عنوان نتیجه صحیح می دهد ، و اگر نتواند پایه ای برای درک دلیل این امر فراهم کند. به عنوان مثال فرض کنید از شما خواسته شده است که تعداد تیونرهای پیانو را در شیکاگو تعیین کنید. اگر برآورد اولیه شما به شما گفته باشد باید صدها مورد وجود داشته باشد ، اما پاسخ دقیق به شما می گوید هزاران نفر وجود دارد ، پس می دانید که باید بدانید که چرا این واگرایی از نتیجه مورد انتظار وجود دارد. ابتدا به دنبال خطا ، سپس در عواملی که تخمین در نظر گرفته نشده است - آیا شیکاگو تعدادی از آموزشگاه های موسیقی یا مکانهای دیگر با نسبت نامناسب پیانوی به مردم را دارد؟ خواه نزدیک به نتایج بسیار مشاهده شده باشد ،

برآورد فرمی همچنین برای نزدیک شدن به مشکلاتی که انتخاب بهینه روش محاسبه به اندازه مورد انتظار پاسخ بستگی دارد نیز مفید است. به عنوان مثال ، یک برآورد فرمی ممکن است نشان دهد که آیا تنش های داخلی یک ساختار به اندازه کافی کم است که می توان آنرا با کشش خطی دقیق توصیف کرد . یا اگر تخمین قبلاً در مقیاس نسبت به برخی از مقادیر دیگر دارای رابطه معنی داری باشد ، به عنوان مثال ، اگر یک سازه بیش از حد مهندسی شده باشد که در برابر بارها چندین برابر بیشتر از تخمین باشد. [ نیاز به استناد ]

اگرچه محاسبات فرمی غالباً دقیق نیستند ، زیرا ممکن است مشکلات زیادی در مورد فرضیات آنها وجود داشته باشد ، اما این نوع تحلیل به ما می گوید که برای به دست آوردن پاسخ بهتر ، باید به دنبال چه چیزی باشیم. برای مثال فوق ، ممکن است سعی کنیم تخمین بهتری از تعداد پیانوهای تنظیم شده توسط یک تنظیم کننده پیانو در یک روز معمولی پیدا کنیم ، یا تعداد دقیقی را برای جمعیت شیکاگو جستجو کنیم. همچنین تخمین تقریباً خوبی را برای ما به ارمغان می آورد که ممکن است برای برخی از اهداف به اندازه کافی خوب باشد: اگر می خواهیم فروشگاهی را در شیکاگو راه اندازی کنیم که تجهیزات تنظیم پیانو را بفروشد ، و محاسبه کنیم که برای ماندن در تجارت نیاز به 10،000 مشتری بالقوه داریم ، می توانیم منطقی تصور کنیم. برآورد فوق به مراتب کمتر از 10،000 است که باید یک برنامه تجاری متفاوت را در نظر بگیریم (و با کمی کار بیشتر ، می توانیم با در نظر گرفتن شدیدترین موارد ، تعداد بالایی را در تعداد تنظیم کننده پیانو محاسبه کنیم.مقادیر معقولی که می تواند در هر یک از فرضیات ما ظاهر شود).

توضیح [ ویرایش ]

تخمین های فرمی به طور کلی کار می کنند زیرا تخمین های اصطلاحات فردی اغلب نزدیک به صحیح است ، و دست کم گرفتن و دست کم گرفتن آنها به لغو یکدیگر کمک می کند. به این معنا که ، اگر تعصب مداوم وجود نداشته باشد ، یک محاسبه فرمی که شامل ضرب چندین فاکتور تخمین زده شده (مانند تعداد تنظیم کننده پیانو در شیکاگو) باشد ، احتمالاً دقیق تر از آن چیزی است که پیش بینی می شد.

به طور جزئی ، برآورد های چند برابر با اضافه کردن لگاریتم های آنها مطابقت دارد. بنابراین فرد نوعی فرایند وینر یا پیاده روی تصادفی را در مقیاس لگاریتمی بدست می آورد ، که به صورت پراکنده پخش می شود\ displaystyle {\ sqrt {n}} $\ sqrt {n$ (به تعداد اصطلاحات n ). به تعبیر گسسته ، تعداد دستاوردهای منهای دست کم یک توزیع دو جمله ای خواهد داشت . به طور مداوم ، اگر یک تخمین Fermi از n مراحل را ایجاد کند ، با واحدهای انحراف استاندارد σ در مقیاس log از مقدار واقعی ، آنگاه تخمین کلی انحراف استاندارد σ را خواهد داشت\ displaystyle {\ sqrt {n}} $\ sqrt {n$ ، از آنجا که انحراف استاندارد مقیاس مبلغ است \ displaystyle {\ sqrt {n}} $\ sqrt {n$ در تعداد اجاره.

به عنوان مثال ، اگر کسی تخمین Fermi 9 مرحله ای را انجام دهد ، در هر مرحله با غلبه بر عدد صحیح توسط یک عدد 2 (یا با یک انحراف استاندارد 2) عدد صحیح را دست کم می گیرد ، سپس بعد از 9 مرحله خطای استاندارد توسط یک فاکتور لگاریتمی رشد می کند. از \ displaystyle {\ sqrt {9}}} $\ displaystyle {\ sqrt {9}}}$ = 3، پس از 2 3 = 8. بنابراین انتظار می رود تا در شود 1 / 8 تا 8 برابر مقدار صحیح - در یک منظور از قدر ، و خیلی کمتر از بدترین حالت از گمراه با ضریب 2 9 = 512 (حدود 2.71 سفارش از بزرگی). اگر کسی زنجیره کوتاه تری داشته باشد یا دقیق تر تخمین بزند ، برآورد کلی مطابق با آن بهتر خواهد بود.

همچنین مشاهده کنید [ ویرایش ]

منابع

https://en.wikipedia.org/wiki/Fermi_problem

+ نوشته شده در جمعه بیست و نهم فروردین ۱۳۹۹ ساعت 6:43 توسط علی رضا نقش نیلچی |

درون یابی کنید.

ØªØµÙÛØ± ÙØ±ØªØ¨Ø·

چند جمله ای لاگرانژ برای درون یابی یک نقطه از یک تابع جدولی از نقاط معین استفاده میشود با استفاده از برنامه نویسی برنامه ای را آماده کنید که در آن ابتدا تعداد نقاط مشخص موجود را از کاربر گرفته و سپس x و y های مشخص را از کاربر گرفته و در انتها مقدار x نقطه ای که میخواهیم مقدار تابع را در ان نقطه درون یابی کنیم از کاربر گرفته شود و سپس چند جمله ای لاگراژ مربوط به این نقاط بدست آورید و در خروجی برنامه مقدار تابع در x مورد نظر چاپ شود

+ نوشته شده در چهارشنبه دوازدهم تیر ۱۳۹۸ ساعت 2:9 توسط علی رضا نقش نیلچی |

روش نویل

The example uses problem 1. a. from the same page:
int i, j;
int n = 4;
double X; //X will be used to approximate f(X).
double x[n]; //The x values.
double y[n]; //The y or f(x) values.
double Q[n][n]; //The output table.
for (i = 0; i < n; i++)
for (j = 0; j < n; j++)
Q[i][j] = 0.0; //Initializing the Q matrix to 0.
//Hardcoding the x and y values from problem 1. a.
x[0] = 8.1;
x[1] = 8.3;
x[2] = 8.6;
x[3] = 8.7;
y[0] = 16.94410;
y[1] = 17.56492;
y[2] = 18.50515;
y[3] = 18.82091;
X = 8.4; //Want to approximate f(X), or f(8.4).
for (i = 0; i < n; i++)
Q[i][0] = y[i]; //Setting the first column of Q to y[0] through y[3].
//Neville's method.
for (i = 1; i < n; i++) {
for (j = 1; j <= i; j++) {
Q[i][j] = ((X ‐ x[i ‐ j])*(Q[i][j ‐ 1])
‐ (X ‐ x[i])*(Q[i ‐ 1][j ‐ 1]))/(x[i] ‐ x[i ‐ j]);
}
}
printf("Resultant Q matrix:\n");
for (i = 0; i < n; i++) {
for (j = 0; j < n; j++) {
printf("%9f ", Q[i][j]);
}
printf("\n");
}

+ نوشته شده در پنجشنبه چهارم آبان ۱۳۹۶ ساعت 10:8 توسط علی رضا نقش نیلچی |

آموزش ریاضی

نقطه بحرانی یک تابع متغیر واحد [ ویرایش ]

مثالها [ ویرایش ]

مکان نقاط بحرانی [ ویرایش ]

نقاط بحرانی یک منحنی ضمنی [ ویرایش ]

استفاده از تمایز [ ویرایش ]

چندین متغیر [ ویرایش ]

کاربرد بهینه سازی [ ویرایش ]

نقطه بحرانی یک نقشه مشتق پذیر [ ویرایش ]

کاربرد در توپولوژی [ ویرایش ]

همچنین ببینید [ ویرایش ]

جداول تبدیل فوریه مهم [ ویرایش ]

روابط عملکردی، تک بعدی [ ویرایش ]

توابع ادغام‌پذیر مربع، تک بعدی [ ویرایش ]

ویژگی های مشخصه [ ویرایش ]

کسینوس هایپربولیک [ ویرایش ]

مماس هایپربولیک[ ویرایش ]

روابط مفید [ ویرایش ]

مجموع آرگومان ها [ ویرایش ]

فرمول های تفریق [ ویرایش ]

فرمول های نیم آرگومان [ ویرایش ]

فرمول های مربعی [ ویرایش ]

نابرابری ها [ ویرایش ]

توابع معکوس به عنوان لگاریتم [ ویرایش ]

فهرست

نشانه گذاری [ ویرایش ]

تعاریف [ ویرایش ]

تعاریف نمایی [ ویرایش ]

تعاریف معادلات دیفرانسیل [ ویرایش ]

تعاریف مختلط توابع مثلثاتی [ ویرایش ]

سری تیلور و چند جمله ای ها

سری تیلور چند جمله ای چیست؟

ضرب سری تیلور در چند جمله ای

خطای تقریب و همگرایی [ ویرایش ]

تعمیم [ ویرایش ]

فهرستی از سری مکلورن از برخی توابع رایج [ ویرایش ]

تابع نمایی [ ویرایش ]

لگاریتم طبیعی [ ویرایش ]

سری هندسی [ ویرایش ]

سری دو جمله ای [ ویرایش ]

توابع مثلثاتی [ ویرایش ]

توابع هذلولی [ ویرایش ]

سری تیلور

فهرست

تعریف [ ویرایش ]

برآورد اثر مرکزی در توزیع دوجمله ای [ ویرایش ]

تاریخچه [ ویرایش ]

همچنین به [ ویرایش ] مراجعه کنید

فرمول استرلینگ برای عملکرد گاما [ ویرایش ]

حدود خطا [ ویرایش ]

نسخه همگرا از فرمول استرلینگ [ ویرایش ]

نسخه های مناسب برای ماشین حساب [ ویرایش ]

فهرست

اشتقاق [ ویرایش ]

فهرست

مثالها [ ویرایش ]

در مجموعه توانها [ ویرایش ]

شعاع همگرایی [ ویرایش ]

عملیات روی سری توانی[ ویرایش ]

جمع و تفریق [ ویرایش ]

ضرب و تقسیم [ ویرایش ]

مشتق و انتگرال[ ویرایش ]

توابع تحلیلی [ ویرایش ]

رفتار نزدیک به مرز [ ویرایش ]

سری استاندارد توانی [ ویرایش ]

سری توانی در چندین متغیر [ ویرایش ]

سفارش یک سری توانی [ ویرایش ]

همچنین مشاهده کنید [ ویرایش ]

منابع

فهرست

پیشینه تاریخی [ ویرایش ]

مثالها [ ویرایش ]

مزایا و دامنه [ ویرایش ]

توضیح [ ویرایش ]

همچنین مشاهده کنید [ ویرایش ]

منابع

پیوندهای روزانه

نوشته‌های پیشین

آرشیو موضوعی

پیوندها