|
https://functions.wolfram.com/ElementaryFunctions/Sinh/introductions/Hyperbolics/ShowAll.html
|
https://functions.wolfram.com/ElementaryFunctions/Sinh/introductions/Hyperbolics/ShowAll.html
سینوس و سینوس هذلولی.
Y = sin(X)
Y = sinh (X)
توابع مثلثاتی از نظر عنصر بر روی ماتریس ها عمل می کنند. دامنه ها و محدوده های آنها شامل مقادیر پیچیده است. تمام زوایا بر حسب رادیان اندازه گیری می شوند.
sin(X)سینوس دایره ای عناصر X.
sinh(X)سینوس هذلولی عناصر X.
sin(pi)دقیقاً صفر نیست، بلکه مقداری به اندازه دقت نقطه شناور است، epsزیرا piدقیقاً برابر با pi نیست.
acos, asin, atan, cos, exp, expm, funm_tan
منبع
https://www.math.clemson.edu/~warner/M360/Matlab/sinh.html
ما چند روزی است که با تار می نوازیم. بیایید به یک رسانه دیگر، و یک نوع اختلال کمی متفاوت تغییر دهیم. ما رفتار امواج طولی را که از میان یک میله بلند و نازک حرکت می کنند، بررسی خواهیم کرد. برخلاف امواج عرضی روی یک رشته، امواج طولی شامل نوسان مواد در امتداد (و خلاف) جهت حرکت اختلال است.
شما باید ببینید که دوست جدید ما معادله موج نشان داده می شود همانطور که ما پاسخ بخش کوچکی از میله را به یک نیروی مزاحم بررسی می کنیم ...
بر بخش کوچکی از میله نیرو وارد می کند
ما قصد داریم از دو متغیر مختلف در بحث زیر استفاده کنیم، که هر دو به نوعی موقعیت بخش کوچکی از میله را در امتداد محور x توصیف میکنند. بنابراین اجازه دهید قبل از شروع، معنای هر یک را به وضوح تعریف کنیم.

یک میله بلند و نازک از مواد، با سطح مقطع A و چگالی ρ را در نظر بگیرید . ما روی خصوصیات بخش کوچکی از میله که از موقعیت x به (x + Δ x) کشیده می شود تمرکز خواهیم کرد .

س: جرم این بخش کوچک چقدر است؟
درست.

حالا به یک سر میله نیرو وارد می کنیم. چگونه پاسخ می دهد؟

میله در پاسخ به نیرو کشیده می شود. میزان کشش میله بستگی به این دارد که فرد از انتهای آن چقدر دور به نظر می رسد: هر چه نیرو به انتهای آن نزدیکتر باشد، تغییر طول بیشتر می شود.

اجازه دهید تغییر موقعیت هر نقطه روی میله را z بنامیم . هر چه به انتهای سمت راست میله نزدیکتر باشد، z بزرگتر است. در موقعیت لبه سمت چپ بخش ما، x ، ماده با z تغییر شکل می دهد . اما در لبه سمت راست بخش، ماده به مقدار کمی بیشتر تغییر شکل می دهد (z + Δ z) .
به عبارت دیگر، بخش کوچک ما نه تنها به سمت راست ترجمه می شود، بلکه کمی طولانی تر نیز می شود.
چرا بخش کشیده می شود؟ زیرا نیرویی که به سمت راست آن وارد می شود کمی بزرگتر از نیرویی است که در سمت چپ آن وارد می شود. به عبارت دیگر، F 2 > F 1 .

استرس و واکنش به آن: فشار
ممکن است به یاد داشته باشید که فیزیکدانان از اصطلاح استرس برای توصیف نیروی دیفرانسیل وارد بر دو انتهای بخش کوچکی از یک جسم استفاده می کنند.

در پاسخ به استرس روی یک جسم، ممکن است شکل آن تغییر کند. این پاسخ فشار نامیده می شود.

برای بسیاری از اجسام، این دو پدیده - استرس روی یک جسم و کرنش ناشی از آن - به شیوهای ساده با هم مرتبط هستند، حداقل زمانی که تغییرات شکل در مقایسه با اندازه اصلی جسم بسیار کوچک است. به طور کلی، تنش برابر است با مقداری مدول الاستیک ضرب در کرنش. هنگامی که جسم بلند و نازک است و در طول آن کشیده می شود، این ضریب مدول یانگ نامیده می شود . معمولاً با Y یا E برچسب گذاری می شود .


سمت چپ این معادله جعبه ای دارای نیروی خالص بر بخش کوچک تقسیم بر مساحت است. آن نیروی خالص، طبق قانون دوم نیوتن، فقط جرم مقطع ضربدر شتاب آن در جهت طول میله است. به عبارت دیگر، شتاب در جهت z .

بنابراین سمت چپ می شود
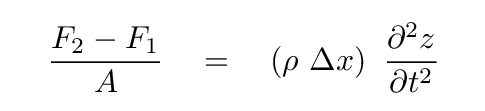
در حال حاضر، در اینجا قسمت مشکل است. در سمت راست معادله کادر، عبارتی برای تغییر z تقسیم بر تغییر x وجود دارد . تغییر در فاصله کشیده، Δ z ، در طول بخش کوچک ما چقدر است؟ یکی از راههای محاسبه، نرخ تغییر z با x ضرب در عرض بخش کوچک ما است:
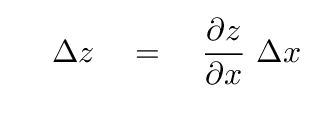
این باید شما را به یاد تکنیک ریاضی مشابهی بیاندازد که در جلسه قبلی کلاس خود، هنگام بحث در مورد تغییر شیب یک رشته ارتعاشی، از آن استفاده کردیم.
هنگامی که همه فواصل درگیر بسیار کوچک هستند، و ما خود را به یک لحظه ثابت در زمان محدود می کنیم، می توانیم این را با استفاده از مشتق دوم z نسبت به x بنویسیم .

معادله دیفرانسیل حرکت
بنابراین، اگر از این روابط استفاده کنیم، قانون دوم نیوتن برای حرکت این بخش کوچک از میله تبدیل به

با قرار دادن این به شکل استاندارد، با مشتق دوم SPATIAL در سمت چپ و دومین مشتق TEMPORAL در سمت راست، با معادله موج برای امواج طولی که از یک میله بلند و نازک حرکت می کنند، پایان می دهیم. به یاد داشته باشید، z به عنوان جابجایی قطعه کوچکی از میله از موقعیت تعادل آن تعریف می شود. به موازات جهت x اجرا می شود .

س: سرعت این امواج چقدر است؟
بله، سرعت امواج توسط داده می شود

حالت های معمولی میله ای که در یک انتها بسته شده است
همانطور که ممکن است حدس بزنید، حالت های خاص خاصی وجود دارد - حالت های معمولی - ارتعاش که در آن تمام قسمت های میله با فرکانس یکسان ω نوسان می کنند . فرکانس های مربوط به این حالت ها چیست؟
در این مورد، ساده ترین راه برای یافتن آنها این است که از ریاضیات صرف نظر کنید و به وضعیت فیزیکی نگاه کنید. فرض کنید که یک سر میله را با گیره محکم می کنیم، آن را کاملاً ثابت نگه می داریم و از لرزش آن جلوگیری می کنیم. مواد در سرتاسر بقیه میله ممکن است ارتعاش کنند، و مواد در انتهای سمت راست میله نیز آزاد است که ارتعاش کنند.

در این حالت، هر نوسانی باید دامنه صفر در انتهای سمت چپ میله (گیره دار) و حداکثر دامنه در انتهای سمت راست (بدون گیره) میله داشته باشد. پایینترین حالت نرمال، با نام مستعار حالت اساسی، باید دامنهای داشته باشد که شبیه به این باشد. در شکل زیر، موقعیت عمودی خط سبز به دور از نقطه وسط میله نشان دهنده دامنه حرکات افقی است . بله، تلاش برای ترسیم ارتعاشات طولی ناخوشایند است.
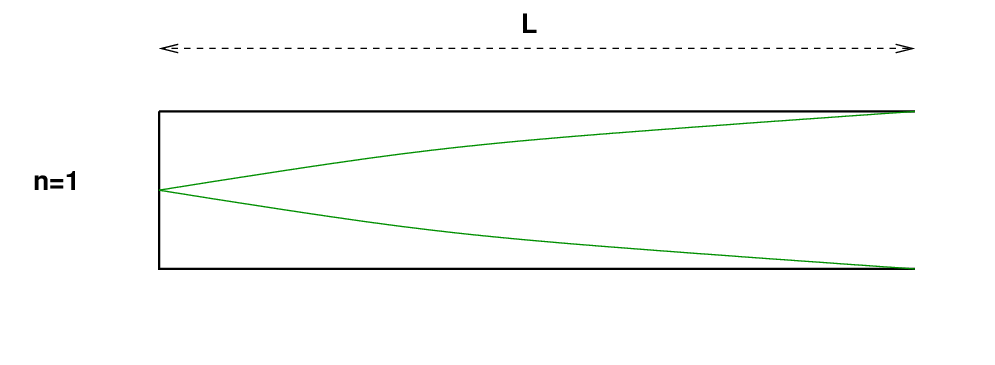
س: طول موج حالت n=1 چقدر است ؟
در حالت n=2 ، دامنه در هر انتها یکسان است -- صفر در چپ، حداکثر در راست -- اما اکنون یک گره اضافی در بین آن وجود دارد.
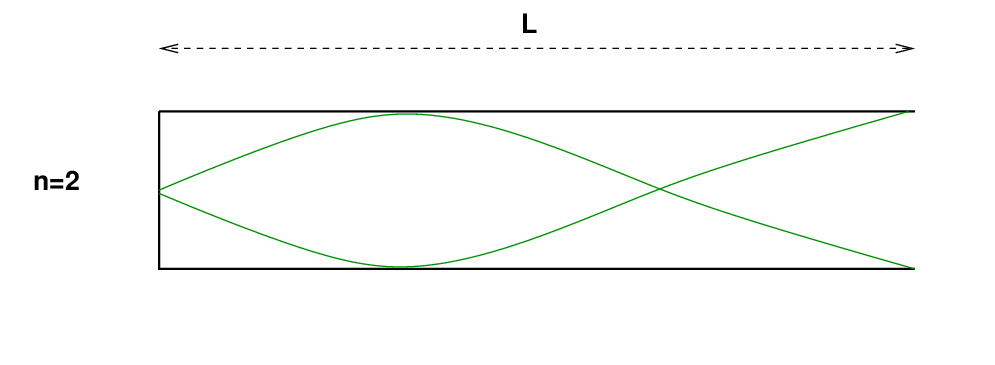
س: طول موج حالت n=2 چقدر است ؟
در حالت n=3 یک گره دیگر در وسط وجود دارد.
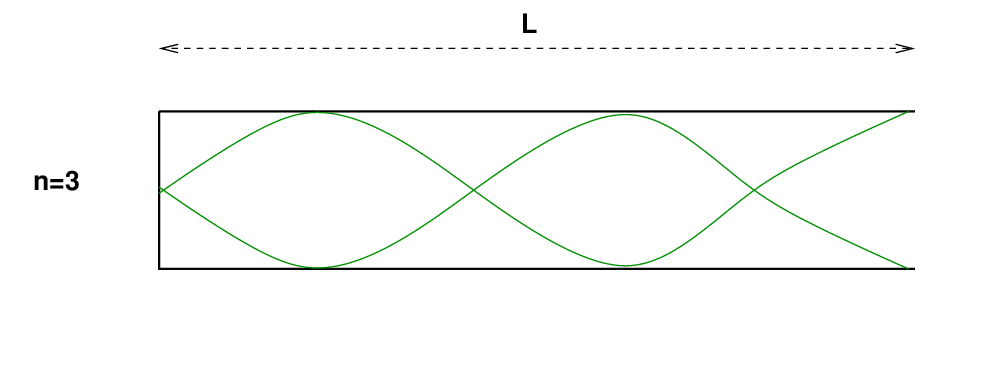
س: طول موج حالت n=3 چقدر است ؟
س: آیا می توانید معادله ای برای طول موج آن استخراج کنید؟
حالت عادی؟
س: آیا می توانید معادله ای برای فرکانس بدست آورید؟
حالت عادی؟
شما باید در نهایت با
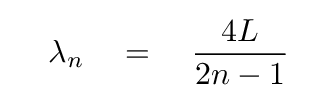
و
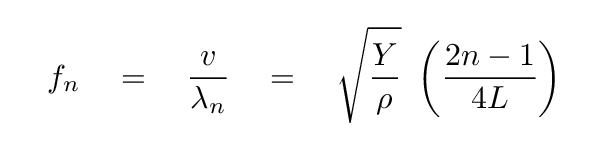
حالت های معمولی از یک میله گیره در وسط
این بار، اجازه دهید میله را در وسط آن نگه داریم، نه در یک انتها. حال، دامنه نوسان باید در مرکز میله صفر باشد، اما در هر دو انتها باید حداکثر باشد.
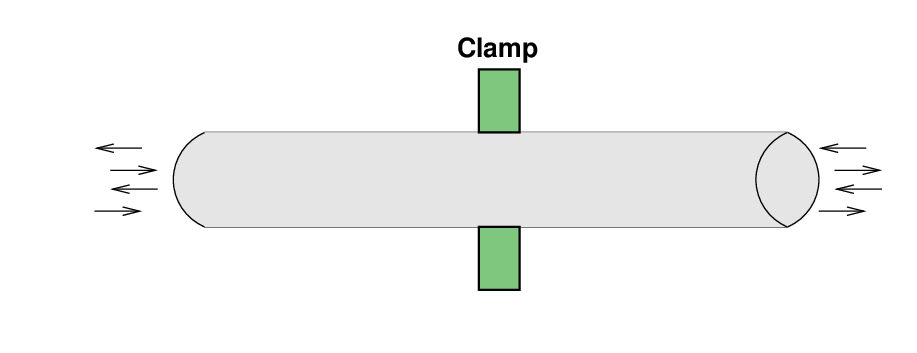
این بدان معنی است که حالت اساسی ارتعاش به نظر می رسد:
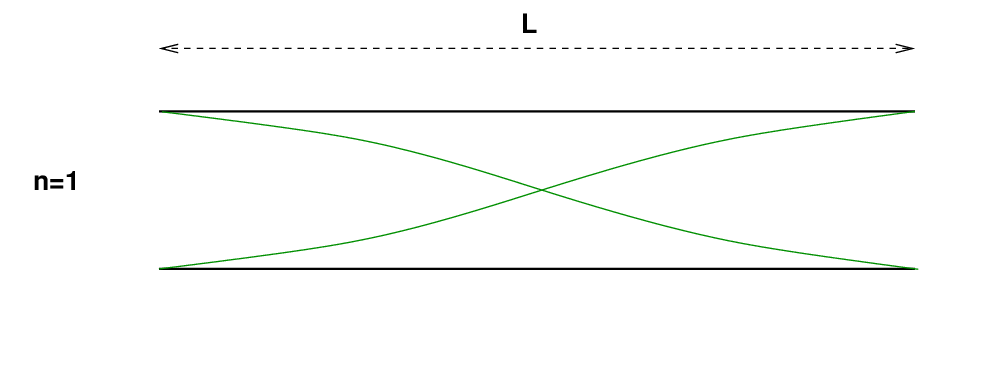
س: طول موج حالت n=1 چقدر است ؟
در حالت n=2 ، دامنه در هر انتها یکسان است -- صفر در چپ، حداکثر در راست -- اما اکنون یک گره اضافی بین هر انتها و وسط وجود دارد.
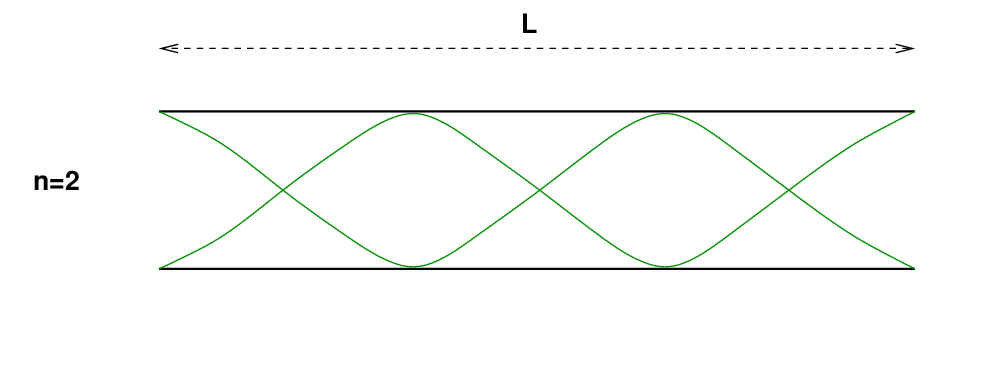
س: طول موج حالت n=2 چقدر است ؟
در حالت n=3 به هر نیمه میله گره دیگری اضافه می کنیم.

س: طول موج حالت n=3 چقدر است ؟
س: آیا می توانید معادله ای برای طول موج آن استخراج کنید؟
حالت عادی؟
س: آیا می توانید معادله ای برای فرکانس بدست آورید؟
حالت عادی؟
شما باید در نهایت با
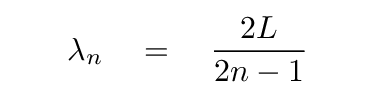
و
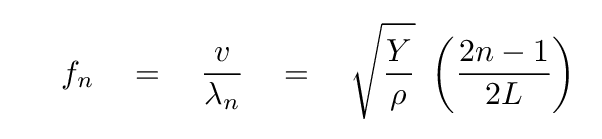
مثال: میله را حلقه کنید
من در کلاس یک میله بلند و نازک از آلومینیوم دارم. خواص این میله عبارتند از:
طول L = 91.1 سانتی متر
چگالی ρ = 2700 kg/m^3
مدول یانگ Y = 69 x 10 9 N/m^2
آیا می توانید پاسخ سوالات زیر را بیابید؟
س: سرعت امواجی که از میله عبور می کنند چقدر است؟
س: اگر میله را در وسط نگه دارم و آن را حلقه کنم،
چه فرکانس صدا را خواهیم شنید؟
س: اگر میله را در 1/4 فاصله از سمت چپ نگه دارم
به سمت راست، و زنگ آن، چه فرکانس
صدا را خواهیم شنید؟
س: اگر میله را در 1/3 فاصله از سمت چپ نگه دارم
به سمت راست، و زنگ آن، چه فرکانس
صدا را خواهیم شنید؟
منبع
http://spiff.rit.edu/classes/phys283/lectures/long/long.html
4.3. پارامترهای پیزوالکتریک
علاوه بر تأثیر پارامترهای ساختاری و مواد، پارامترهای پیزوالکتریک نیز می توانند بر باند توقف تأثیر بگذارند. در این بخش، جهت قطبی پیزوالکتریک، مورد مدار باز الکتریکی و مورد اتصال کوتاه الکتریکی در اینجا به عنوان مثال در نظر گرفته شده است تا قانون تغییر باندهای توقف را آشکار کند.
سفتی خمشی ماده پیزوالکتریک PZT4 برای مورد اتصال کوتاه الکتریکی و مورد مدار باز الکتریکی در معادلات ( 21 ) و ( 22 ) به دست آمده است . با استفاده از نرم افزار MATLAB برای برنامه ریزی و جایگزینی در معادله ماتریس انتقال کل ( 32 )، منحنی های پاسخ انتقال فیبوناچی RPCAP پیزوالکتریک همانطور که در شکل 9 نشان داده شده است ترسیم شده است . . این منحنی ها نشان می دهد که مورد اتصال کوتاه الکتریکی و مورد مدار باز می توانند به طور قابل توجهی بر باندهای توقف موج عرضی تأثیر بگذارند. همچنین مکان باندهای توقف موج عرضی به سمت فرکانس پایین حرکت می کند. پدیده فوق همچنین نشان می دهد که سفتی خمشی مواد پیزوالکتریک PZT4 به دلیل اثر پیزوالکتریک تغییر می کند. به عبارت دیگر، مقادیر سفتی خمشی توسط مورد اتصال کوتاه الکتریکی و مورد مدار باز تعیین میشود که منجر به تغییر مکان و عرض باند میشود.
شکل 9
منحنی های باند برای اتصال باز و کوتاه.
با اتخاذ رویکرد شبیهسازی المان محدود، ماده پیزوالکتریک PZT4 در امتداد جهتهای قطبش X ، Y و Z در مختصات استوانهای انتخاب میشود. شکل 10 اثر جهت قطبش را بر پاسخ انتقال موج عرضی برای فیبوناچی RPCAP نشان می دهد. از شکل 10 می توان دریافت که باندهای توقف به طور قابل توجهی در ناحیه فرکانس بالا ضعیف می شوند، اما در ناحیه فرکانس پایین واضح نیست. این پدیده نشان می دهد که جهت پلاریزاسیون نیز یکی از دلایل اصلی ایجاد تغییر باند توقف است.
شکل 10
اثر جهت قطبی
به طور خلاصه، مطالعات پاسخ انتقال فوق نشان می دهد که پارامترهای ساختاری، پارامترهای مواد و پارامترهای پیزوالکتریک برای فیبوناچی RPCAP می توانند به طور قابل توجهی بر باندهای توقف موج عرضی تأثیر بگذارند. از طریق طراحی مناسب این پارامترها، می توان به نوارهای توقف موج الاستیک بزرگ و گسترده برای کاهش ارتعاشات مهندسی دست یافت.
5. نتیجه گیری
این مقاله یک مدل فیبوناچی RPCAP پیزوالکتریک را برای به دست آوردن باندهای توقف موج عرضی ارائه میکند. ابتدا بر اساس حل معادله مواد همگن و معادله حاکم پیزوالکتریک، عبارات زاویه چرخش، نیروی برشی و لنگر خمشی به دست میآیند. سپس، این پارامترها در مختصات استوانه ای برای استخراج ماتریس انتقال ترکیب می شوند. رفتارهای باند توقف موج عرضی برای مدل فیبوناچی RPCAP تجزیه و تحلیل میشوند. شبیه سازی المان محدود در اینجا با نرم افزار ANSYS 14.0 انجام می شود تا موقعیت و عرض باندهای توقف را تأیید کند.
تجزیه و تحلیل بیشتر برای تأثیر پارامترهای ساختاری و پارامترهای مواد بر روی باند توقف مورد بحث قرار گرفته است. می توان دریافت که این پارامترها برای فیبوناچی RPCAP می توانند به طور قابل توجهی بر باندهای توقف موج عرضی تأثیر بگذارند. علاوه بر این، نتایج همچنین نشان میدهد که عملکردهای پیزوالکتریک مانند اتصال کوتاه الکتریکی، مدار باز الکتریکی و جهت قطبش PZT4 نیز دلیل اصلی تغییر باند توقف موج عرضی هستند.
در نهایت، رفتارهای باند توقف موج عرضی به تفصیل بررسی شده است. این کار برای جلوگیری از انتشار موج اهمیت زیادی دارد، به ویژه برای آن دسته از سیستم های روتور پیچشی همراه با ارتعاش عرضی.
در دسترس بودن داده ها
داده های مورد استفاده برای حمایت از یافته های این مطالعه در مقاله گنجانده شده است.
تضاد علاقه
نویسندگان اعلام می کنند که در مورد انتشار این مقاله تضاد منافع وجود ندارد.
قدردانی
این مطالعه توسط صندوق های تحقیقات بنیادی برای دانشگاه های مرکزی (گرنت شماره 2572020BG01)، برنامه ملی تحقیق و توسعه کلیدی چین (شماره کمک مالی 2020YFB2006400)، و پروژه های علمی و فناوری عمده استان هیلونگجیانگ (گرنت شماره 20203X0) حمایت شد. نویسندگان مایلند از دانشکده مهندسی مکاترونیک، موسسه فناوری هاربین، هاربین، چین برای ارائه پشتیبانی فنی تشکر کنند.
منابع
S. Asiri, A. Baz, and D. Pines, “Active periodic struts for a gearbox support system” Smart Materials and Structures , vol. 15، نه 6، صفحات 1707-1714، 2006.
مشاهده در: سایت ناشر | Google ScholarD. Wang، S. Zhijun، و L. WeiC. Meilong، L. Siyuan، و L. Shidan، "تجزیه و تحلیل ارتعاش درون صفحه پرتوهای منحنی کریستال صوتی،" Noise Control Engineering Journal ، جلد. 64، شماره 5، صفحات 658-667، 2016.
مشاهده در: سایت ناشر | Google ScholarD. Qian, J. Wu, and F. He, "شکافهای باند کوپلینگ الکترومکانیکی نانوپرتو تیموشنکو کریستال فونیک پیزوالکتریک با اثرات سطحی" Ultrasonics , vol. 109، شناسه مقاله 106225، 2021.
مشاهده در: سایت ناشر | Google ScholarL. Yao، D. Zhang، K. Xu، L. Dong، و X. Chen، "صفحات کریستالی آوایی توپولوژیکی با سیستمهای موج الاستیک رزونانس محلی،" Applied Acoustics ، جلد. 177، شناسه مقاله 107931، 2021.
مشاهده در: سایت ناشر | Google ScholarD. Yu، J. Wen، H. Zhao، Y. Liu، و X. Wen، "کاهش ارتعاش با استفاده از ایده کریستال های آوایی در یک سیال انتقال دهنده لوله،" Journal of Sound and Vibration، جلد . 318، شماره 1-2، صص 193-205، 2008.
مشاهده در: سایت ناشر | Google ScholarM. Mazzotti، M. Miniaci، و I. Bartoli، "تجزیه و تحلیل ساختار نواری امواج بلوخ نشتی در صفحات کریستالی فونونیک دوبعدی،" Ultrasonics ، جلد. 74، صص 140-143، 2017.
مشاهده در: سایت ناشر | Google ScholarP. Chen, Y.-Z. وانگ و Y.-S. وانگ، "کنترل فعال امواج خمشی در یک پرتو کریستالی آوایی با ویژگیهای متناوب متناوب،" Wave Motion ، جلد. 93، شناسه مقاله 102481، 2020.
مشاهده در: سایت ناشر | Google ScholarAM Goto، ED Nóbrega، FN Pereira، و JMC Dos Santos، "تحقیق عددی و تجربی بلورهای آوایی از طریق مدلهای میلهای مرتبه بالاتر مبتنی بر موج،" مجله بینالمللی علوم مکانیکی ، جلد. 181، شناسه مقاله 105776، 2020.
مشاهده در: سایت ناشر | Google ScholarA. Zak، M. Krawczuk، G. Redlarski و همکاران، "یک پرتو تناوبی سه بعدی برای اهداف جداسازی ارتعاشی،" Mechanical Systems and Signal Processing ، جلد. 130، صفحات 524-544، 2019.
مشاهده در: سایت ناشر | Google ScholarX. Guo، P. Wei و L. Li، "روابط پراکندگی امواج الاستیک در کریستال آوایی پیزوالکتریک تک بعدی با رابط های مکانیکی و دی الکتریکی ناقص،" Mechanics of Materials ، جلد. 93، صفحات 168-183، 2016.
مشاهده در: سایت ناشر | Google ScholarHS Shu، LQ Dong، SD Li و همکاران، "انتشار موج پیچشی در یک صفحه حلقوی نازک از کریستال های آوایی تعمیم یافته،" Journal of Applied Physics D ، جلد. 47، صفحات 1-11، 2014.
مشاهده در: Google ScholarH. Shu، W. Liu، S. Li و همکاران، "تحقیق در مورد شکاف باند موج خمشی یک صفحه دایره ای نازک از کریستال های صوتی شعاعی پیزوالکتریک،" مجله ارتعاش و کنترل ، جلد. 22، شماره 7، صفحات 1777-1789، 2016.
مشاهده در: سایت ناشر | Google ScholarZ. Chai، D. Wang، W. Liu، و D. Kong، "انتشار موج پیچشی در کریستال های صوتی شعاعی پیزوالکتریک،" Noise Control Engineering Journal ، جلد. 64، شماره 1، صفحات 75-84، 2016.
مشاهده در: سایت ناشر | Google ScholarZ. Xu، F. Wu و Z. Guo، "ساختارهای باند آوایی فرکانس پایین در بلورهای آوایی دوبعدی قوسی شکل،" Physics Letters A ، جلد. 376، شماره 33، صفحات 2256-2263، 2012.
مشاهده در: سایت ناشر | Google ScholarD. Torrent و J. Sánchez-Dehesa، "رزونانس های صوتی در پوسته های کریستالی شعاعی شعاعی دو بعدی،" New Journal of Physics ، جلد. 12، شماره 7، شناسه مقاله 073034، 2010.
مشاهده در: سایت ناشر | Google ScholarD. Torrent و J. Sánchez-Dehesa، "کریستالهای موج شعاعی: ساختارهای دوره ای شعاعی از فرامواد ناهمسانگرد برای مهندسی امواج صوتی یا الکترومغناطیسی،" Physical Review Letters ، جلد. 103، شناسه مقاله 064301، 2009.
مشاهده در: سایت ناشر | Google ScholarJ. Carbonell، D. Torrent و J. Sanchez-Dehesa، "پوسته های کریستالی فوتونی شعاعی و کاربرد آنها به عنوان عناصر تشدید کننده و تابشی،" IEEE Transactions on Antennas and Propagation ، جلد. 61، شماره 2، صفحات 755-767، 2013.
مشاهده در: سایت ناشر | Google ScholarHS Shu، L. Zhao، XN Shi، و W. Liu، "انتشار موج پیچشی در یک صفحه دایره ای از کریستال های صوتی شعاعی پیزوالکتریک،" Journal of Applied Physics ، جلد. 118، شماره 2، شناسه مقاله 184904، 2015.
مشاهده در: Google Scholaمنبع
https://www.hindawi.com/journals/sv/2021/3905426/
4. عوامل تأثیرگذار
اندازه سازه، مشخصه مواد و عملکرد پیزوالکتریک پارامترهای اصلی هستند که بر پاسخ انتقال ارتعاش سازههای مرکب تأثیر میگذارند. همچنین، این پارامترها معمولاً برای تجزیه و تحلیل رفتارهای باند توقف موج الاستیک استفاده میشوند. بر این اساس، در این بخش به طور مفصل به تأثیر این پارامترها بر روی باندهای توقف پرداخته شده است.
4.1. پارامترهای ساختاری
با توجه به فیبوناچی پیزوالکتریک RPCAP، اثر نسبت دهانه بر باندهای توقف موج عرضی مورد مطالعه قرار گرفته است. نگه داشتنو سایر پارامترهای ساختاری بدون تغییر، ما فقط نسبت دهانه شعاعی را تغییر می دهیم. شکل 6(a) اثر نسبت دهانه بر فرکانس های شروع و قطع برای باندهای توقف اول و دوم را شرح می دهد. مشاهده می شود که با افزایش نسبت دهانه، فرکانس شروع و قطع به تدریج کاهش می یابد. به طور مشابه، با اتخاذ یک رویکرد مشابه، شکل 6(b) اثر نسبت ضخامت را بر فرکانس های شروع و قطع برای باند اول و دوم نشان می دهد. با افزایش نسبت ضخامت، فرکانس شروع و قطع به سرعت افزایش می یابد و همزمان پهنای باند بزرگتر می شود.

(ب)

(آ)

(ب)

(آ)

(ب)

(آ)

(ب)
شکل 6
تأثیر نسبت دهانه و نسبت ضخامت بر باندهای توقف: (الف) نسبت دهانه. ب) نسبت ضخامت
اثر قدر شعاع داخلی بر باندهای توقف موج عرضی در شکل 7 نشان داده شده است . از شکل 7 می بینیم که با افزایش شعاع داخلی، پاسخ انتقال برای این فیبوناچی RPCAP بسیار کوچک تغییر می کند. به عبارت دیگر، مکان و عرض باندهای توقف تقریباً تغییری ندارند، اما باندهای توقف به شدت ضعیف می شوند.
شکل 7
تأثیر شعاع داخلی بر باندهای توقف.
4.2. پارامترهای مواد
مشابه مطالعه بر روی تأثیر پارامترهای سازه، شکل 8 تأثیر مدول و چگالی را بر باندهای توقف موج عرضی نشان می دهد. با ثابت نگه داشتن سایر پارامترها، در اینجا چگالی به عنوان پارامتر متغیر انتخاب می شود. چگالی مواد به عنوان پلکسی گلاس، آل، آلیاژ تیتانیوم، PZT4 و Plumbum انتخاب شده است. از شکل 8 (الف) می توان دید که با افزایش چگالی، فرکانس های شروع و قطع اولین باند موج عرضی به تدریج کاهش می یابد، اما پهنای باند تقریباً تغییری نمی کند. فرکانس های شروع و قطع باند توقف موج عرضی دوم ابتدا کوچکتر و سپس به تدریج بزرگتر می شوند. شکل 8 (ب)اثر مدول را بر باندهای توقف موج عرضی نشان می دهد، که نشان می دهد مدول می تواند به طور قابل توجهی بر این باندها تأثیر بگذارد. هر دو فرکانس شروع باند توقف اول و دوم کاهش می یابد و هر دو فرکانس قطع به تدریج با افزایش مدول افزایش می یابند. در همین حال، این پهنای باند گسترده تر می شود.

(ب)

(آ)

(ب)

(آ)

(ب)

(آ)

(ب)
شکل 8
اثر مدول و چگالی بر باندهای توقف: (الف) اثر چگالی. (ب) اثر مدول.
2.3. ماتریس انتقال
در این بخش، ماتریس انتقال ارتعاش عرضی برای فیبوناچی RPCAP پیزوالکتریک به تفصیل استنباط می شود. ماتریس انتقال بهدستآمده در مختصات استوانهای برای محاسبه باند توقف توصیفشده در منحنیهای پاسخ انتقال مفید است.
همانطور که در شکل 1 نشان داده شده است، یک فیبوناچی RPCAP پیزوالکتریک با هشت لایه مربوط به مدل غیر تناوبی ABAABABA را در نظر بگیرید . در امتداد جهت شعاعی، بخشهای فیبوناچی پیزوالکتریک RPCAP به هفت رابط تقسیم میشوند که به صورت b ، c ، d ، e ، f ، m و n مشخص شدهاند . اتصالات بین دو ماده برای اتصال مکانیکی اتخاذ شده است. برای برجسته کردن ماهیت، در اینجا، انواع اتصال به عنوان ایده آل تلقی می شوند. برای مواد رزینی که در لایه های 1، 3، 4، 6، 8 شرح داده شده در شکل 1 (ب) منتشر می شود، مدول یانگ، چگالی و ضریب پواسون عبارتند از ، و . به طور مشابه، برای مواد پیزوالکتریک PZT4 که در 2 ، 5، 7 لایه منتشر می شوند، آنها ، و . تعداد موج رزین و PZT4 را می توان به صورت بیان کرد و. سختی را می توان به صورت محاسبه کردو.
در حالی که موج عرضی در فیبوناچی RPCAP پیزوالکتریک منتشر می شود، پارامترهای فیزیکی مانند جابجایی، زاویه، گشتاور و نیروی برشی باید شرایط پیوستگی زیر را در فصل مشترک مواد مختلف برآورده کنند. با توجه به مواد رزین، عبارات خاصی از این پارامترهای فیزیکی را می توان به صورت نوشتاری نوشت
برای ماده پیزوالکتریک PZT4، این پارامترهای فیزیکی هستند
با توجه به شرایط تداوم در رابط، رابطه است
در اینجا، معادله ( 25 ) را می توان به صورت ماتریسی بازنویسی کرد:جایی کهو.
به طور مشابه، با توجه به شرایط تداوم در رابط، می توان رابطه زیر را بدست آورد:
سپس معادله ( 27 ) به کاهش می یابد
با ترکیب معادلات ( 26 ) و ( 28 )، یک می شودجایی کهماتریس انتقال از لایه 1 به لایه 3 است.
با توجه به لایه سوم و چهارم، موارد زیر را می توان به راحتی به دست آورد:. مشابه روش اشتقاق، با توجه به پیوستگی رابط در e و f ، یکی دارد
به طور مشابه، ماتریس انتقال از لایه 6 به لایه 8 را می توان به عنوان به دست آورد
در نهایت، ترکیب معادلات ( 29 )–( 31 ) به کاهش می یابدجایی کهماتریس انتقال کل از لایه 1 به لایه هشتم فیبوناچی پیزوالکتریک RPCAP است.
در اینجا، مرز داخلی با جابجایی عرضی بارگذاری می شود و مرز بیرونی آزاد می شود. بنابراین، شرایط مرزی در لبه داخلی است
شرایط مرزی در لبه بیرونی است
ترکیب معادلات ( 33 ) – ( 36 ) به دست می آیدجایی که
با در نظر گرفتن معادلات ( 35 )-( 37 )، جابجایی عرضی در بیرونی ترین لایه را می توان به صورت محاسبه کرد.
بنابراین، قابلیت انتقال ارتعاش را می توان به صورت نوشتاری نوشتکه نشان دهنده دامنه جابجایی قابلیت انتقال ارتعاش است که در بیرونی ترین مرز لایه انتخاب شده است .
3. تجزیه و تحلیل و بحث
در این بخش، پاسخ انتقال برای فیبوناچی پیزوالکتریک RPCAP برای به دست آوردن رفتارهای نواری موج عرضی ارائه شده است. از طریق استفاده از نرم افزار MATLAB، قابلیت انتقال ارتعاش و ماتریس انتقال مشتق شده برای ارائه یک رویکرد عددی برای تجزیه و تحلیل باند موج عرضی این فیبوناچی RPCAP ترکیب میشوند. در اینجا، طول شعاعی رزین و PZT4 1 = 0.01 متر، a 2 = 0.01 متر است. شعاع داخلی r 1 = 0.005 متر است. ضخامت h = 0.001 متر است. پارامترهای مواد به شرح زیر است: رزین: مدول، تراکم، و نسبت پواسون. PZT4: ضریب الاستیک، ضریب جفت شدنثابت پیزوالکتریک، ثابت دی الکتریک، ، مدول، تراکم، و نسبت پواسون.
مانند انواع دیگر کریستال های دکارتی، مقابله با ساختار کامپیوتر بی نهایت غیرممکن است. در اینجا، یک فیبوناچی RPCAP پیزوالکتریک متشکل از هشت لایه در امتداد جهت شعاعی، مربوط به مدل غیر تناوبی ABAABABA، برای بررسی رفتارهای باند توقف در نظر گرفته شده است. پس از آن، مثالهای عددی برای سه مورد: رزین منفرد، رزین/Al، و رزین/PZT4، مقایسه میشوند تا ویژگیهای دینامیکی منحصربهفرد فیبوناچی RPCAP، همانطور که در شکل 2 نشان داده شده است، آشکار شود . می توان دریافت که ارتعاش عرضی تقریباً 10- دسی بل کاهش می یابد در حالی که موج عرضی در یک رزین منفرد منتشر می شود. در واقع، به طور کلی، هیچ کاهش ارتعاشی برای یک مورد ماده وجود ندارد. بنابراین، تضعیف ارتعاش 10- دسی بل در نظر گرفته می شود که ناشی از جبهه موج شعاعی است [12 ]. در مقایسه با کیس تک رزین، یک نوار تضعیف ارتعاش تازه در حال ظهور را می توان برای مورد رزین/Al در حالی که نظم شعاعی فیبوناچی به مدل RPCAP معرفی شده است، گرفت. این ناحیه تضعیف ارتعاش مربوط به باندهای توقف III (9.4 کیلوهرتز-19.2 کیلوهرتز) و IV (2.56 کیلوهرتز-3.75 کیلوهرتز) است که حدود -30 دسی بل ضعیف می شوند. بدیهی است که تضعیف ارتعاش انتشار موج عرضی در مدل فیبوناچی RPCAP بسیار مؤثرتر از یک مورد رزینی است که ناشی از تناوب شعاعی است.
شکل 2
منحنی های نظری
علاوه بر این، منحنیهای پاسخ انتقال، باندهای توقف موج عرضی قابل توجهی، I (7.6 کیلوهرتز-17.8 کیلوهرتز) و II (22.4 کیلوهرتز-32.5 کیلوهرتز) را نشان میدهند که در حدود -40 دسیبل ضعیف شدهاند که از آن میتوان به این نتیجه رسید که تضعیف ارتعاش در رزین/ PZT4 RPCAP بسیار سنگین تر از آن در مورد رزین/Al است. پس از وارد کردن ماده پیزوالکتریک PZT4 به فیبوناچی RPCAP، مکان باند توقف به تدریج به سمت فرکانس پایین حرکت می کند. علاوه بر تضعیف ارتعاش ناشی از گسترش جبهه موج، تضعیف زیر خطوط چین نشان داده شده در شکل 2 به دلیل نظم فیبوناچی RPCAP ایجاد می شود. نتایج عددی همچنین نشان می دهد که بسیاری از باندهای توقف تضعیف کوچک دیگر برای این فیبوناچی RPCAP وجود دارد.
به منظور نشان دادن اعتبار محاسبات نظری، شبیه سازی اجزای محدود با نرم افزار ANSYS 14.0 برای نشان دادن مکان و عرض باندهای توقف انجام شده است. در این حالت، ماده رزین با عنصر solid45 مشبک میشود در حالی که عنصر solid226 برای مشبندی مواد پیزوالکتریک استفاده میشود. تعداد کل عناصر 3145 است. جابجایی عرضی بر روی سطح شعاعی داخلی فیبوناچی RPCAP بارگذاری می شود و سپس جابجایی در بیرونی ترین سطح شعاعی انتخاب می شود. در اینجا، تجزیه و تحلیل پاسخ هارمونیک برای انجام باندهای توقف انجام می شود. شکل 3 منحنیهای پاسخ انتقال شبیهسازی شده را نشان میدهد که از آنها میتوان دید که مکان و عرض باندهای عرضی با نتایج نظری نشاندادهشده در شکل 2 منطبق است.خیلی خوب. بنابراین، منحنی های شبیه سازی شده صحت نتایج نظری را تایید می کنند.
شکل 3
منحنی های FEM
به منظور بهتر نشان دادن رفتارهای باند توقف پس از معرفی نظم فیبوناچی، منحنی های پاسخ انتقال موج عرضی منتشر شده در مدل پیزوالکتریک فیبوناچی RPCAP و مدل RPCAP دوره ای مطابق شکل 4 ترسیم شده است . دو منحنی نشان داده شده در شکل 4 برای مقایسه نشان داده شده است. از این منحنیها، میتوانیم ببینیم که در مقایسه با مدل RPCAP تناوبی، مدل فیبوناچی RPCAP دو فرکانس تشدید تازه در حال ظهور مربوط به نقاط A و B را ارائه میکند.. ما در نظر می گیریم که دو نقطه رزونانس توسط نظم فیبوناچی شعاعی ایجاد می شوند. به عبارت دیگر، نظم شعاعی فیبوناچی تناوب شعاعی قبلی را می شکند. همچنین نتایج نشان می دهد که پس از معرفی نظم شعاعی فیبوناچی، مکان و عرض باندهای توقف به سمت فرکانس بالا حرکت می کند. علاوه بر این، نتایج شبیهسازی المان محدود که در شکل 5 نشان داده شده است ، صحت منحنیهای نظری مربوط به شکل 4 را تأیید میکند .
شکل 4
منحنی های نظری
شکل 5
منحنی های FEM
2. مبانی نظری فیبوناچی پیزوالکتریک RPCAP
2.1. مدل فیبوناچی RPCAP
یک مدل فیبوناچی RPCAP متشکل از دو ماده متناوب مختلف که در شکل 1 نشان داده شده است را در نظر بگیرید . شکل 1(a) یک مدل پایه و شکل 1(b) مدل یک چهارم را نشان می دهد. حالت RPCAP به شکل نظم فیبوناچی که به صورت نوع ABAABABA ساخته شده است مرتب شده است. در اینجا ماده اول به عنوان رزین و ماده دوم به عنوان PZT4 انتخاب می شود. ماده پیزوالکتریک PZT4 که در امتداد جهت ضخامت قطبیده شده است به مدل فیبوناچی RPCAP وارد می شود. برای این مدل فیبوناچی RPCAP، شعاع داخلی و شعاع بیرونی هستند و . طول شعاعی دو ماده و . علاوه بر این، ضخامت رزین با PZT4 مطابقت دارد. ضخامت است .

(ب)

(آ)

(ب)

(آ)

(ب)

(آ)

(ب)
شکل 1
نمودار شماتیک مدل فیبوناچی RPCAP: (الف) مدل پایه. (ب) مدل یک چهارم.
2.2. معادله حاکم بر ارتعاش عرضی
2.2.1. معادله حاکم همگن
در مختصات استوانه ای، معادلات حاکم بر ارتعاش عرضی برای مواد همگن به صورت [ 12 ] تعریف می شود.که در آن ، ممان خمشی شعاعی و محیطی را مشخص کنید، برش عرضی است، نیروی بیرونی است (برای ارتعاش آزاد، ) جهت شعاعی،جهت محیطی،جهت محور وجابجایی عرضی است.
از آنجایی که ارتعاش عرضی متقارن است، تنش را می توان به صورت بیان کردکه در آن تنش شعاعی، تنش محیطی، مدول یانگ و ضریب پواسون است.
عبارات کرنش و تغییر شکل عرضی با هم مرتبط هستندکه در آن ، کرنش های شعاعی و محیطی هستند.
در این حالت، ترکیب معادلات ( 1 )–( 7 ) به کاهش می یابدکجا تغییر شکل عرضی و عدد موج است (). سفتی خمشی عرضی است. فرکانس است.
با توجه به رابطه ( 8 )، جواب کلی زیر ایجاد می شود:که در آن , , , ثابت هایی هستند که می توان با مرزها تعیین کرد , توابع بسل نوع اول و دوم و , به ترتیب توابع بسل اصلاح شده نوع اول و دوم هستند.
2.2.2. معادله حاکم پیزوالکتریک
از آنجایی که جهت پلاریزاسیون مواد پیزوالکتریک PZT4 در امتداد محور Z است، نوع معادلات حاکم بر پیزوالکتریک با [ 12 ] ارائه میشود.
در اینجا معادلات ( 10 )–( 12 ) را می توان به صورت مجدد مرتب کردجایی که.
مشابه با مواد همگن، با جایگزینی معادلات ( 13 ) و ( 14 ) به معادلات ( 3 ) و ( 4 )، بیان تنش عرضی در معادله ( 1 ) با یک مشتق ساده ایجاد میشود:
معادله ارتعاش عرضی بدون حالت بار را می توان به شرح زیر توصیف کرد
ادغام را می توان برای معادله سازنده پیزوالکتریک ( 15 ) در بازه فرکانس انجام داد.که از آن به دست می آید
میدان الکتریکی استکه مربوط به مورد اتصال کوتاه الکتریکی است و سپس شارژ رابطه را برآورده می کند. جایگزینی معادلات ( 16 ) و ( 18 ) به معادله ( 17 ) منجر به
برای ماده پیزوالکتریک PZT4، راه حل کلی ارتعاش عرضی از معادله ( 19 ) ایجاد می شود:
بنابراین، سفتی خمشی ماده پیزوالکتریک PZT4 برای مورد اتصال کوتاه الکتریکی را می توان به صورت محاسبه کرد.
به طور مشابه، در حالی که اتهام استکه مربوط به مورد مدار باز الکتریکی است، میدان الکتریکی را برآورده می کند. سفتی خمشی مواد پیزوالکتریک PZT4 برای مورد مدار باز الکتریکی را می توان به صورت سادهr
وی لیو1 و گوانگبین یو2
بیشتر نشان بده، اطلاعات بیشتر
ویراستار آکادمیک: Ömer Cívalek
اخذ شده06 مه 2021
تجدید نظر شده است20 ژوئیه 2021
پذیرفته شده22 ژوئیه 2021
منتشر شده31 ژوئیه 2021
خلاصه
این مقاله بر اساس ساختارهای کریستال آوایی مرسوم قبلی (PC) بینهایت تناوبی در مختصات دکارتی، به یک صفحه حلقوی کریستالی آوایی شعاعی جدید (RPCAP) مدلسازی شده در نظم فیبوناچی در امتداد جهت شعاعی میپردازد. در این مطالعه، ماده پیزوالکتریک PZT4 به طور همزمان در مدل RPCAP برای بررسی رفتارهای باند توقف قرار میگیرد. برای نشان دادن واضح ویژگیهای انتقال موج عرضی، در مختصات استوانهای، ماتریس انتقال از طریق ترکیب جوابهای کلی، معادلات حاکم پیزوالکتریک و شرایط پیوستگی استنتاج میشود. در مقایسه با ساختارهای PC معمولی، پاسخ انتقال ارتعاش عرضی برای مدل فیبوناچی RPCAP به صورت تئوری برای تجزیه و تحلیل پدیده باند توقف محاسبه میشود. روش شبیهسازی المان محدود (FEM) در اینجا برای تأیید نتایج نظری انجام میشود. نتایج نشان میدهد که مدل فیبوناچی RPCAP دو فرکانس تشدید تازه در حال ظهور را ارائه میکند در حالی که نظم تناوبی شعاعی به هم ریخته است. برای درک کامل RPCAP، اثرات پارامترهای ساختاری، پارامترهای مواد و پارامترهای پیزوالکتریک بر روی باند توقف به تفصیل مورد بحث قرار گرفته است. فیبوناچی RPCAP پیشنهادی را می توان در بسیاری از کاربردهای مهندسی، از جمله در قطعات چرخشی که اغلب با ارتعاش عرضی همراه هستند (مانند سیستم های چرخ دنده) استفاده کرد. پارامترهای مواد و پارامترهای پیزوالکتریک در باند توقف به تفصیل مورد بحث قرار میگیرند. فیبوناچی RPCAP پیشنهادی را می توان در بسیاری از کاربردهای مهندسی، از جمله در قطعات چرخشی که اغلب با ارتعاش عرضی همراه هستند (مانند سیستم های چرخ دنده) استفاده کرد. پارامترهای مواد و پارامترهای پیزوالکتریک در باند توقف به تفصیل مورد بحث قرار میگیرند. فیبوناچی RPCAP پیشنهادی را می توان در بسیاری از کاربردهای مهندسی، از جمله در قطعات چرخشی که اغلب با ارتعاش عرضی همراه هستند (مانند سیستم های چرخ دنده) استفاده کرد.
1. معرفی
PC نوع جدیدی از ساختارهای کامپوزیت دوره ای مصنوعی است. این ساختارهای مرکب رفتارهای دینامیکی منحصر به فردی از خود نشان می دهند، مانند فیلترهای موجی که می توانند برخی از امواج الاستیک را در محدوده فرکانسی مشخصی به نام «باند توقف» کاملاً مسدود کنند. بر این اساس، تلاشهای گستردهای به مطالعه ساختارهای مختلف رایانه شخصی در تلاش برای توقف انتشار موج الاستیک از طریق طراحی مناسب این ساختارها اختصاص یافته است. عسیری و همکاران [ 1 ] یک کلاس از ساختارهای PC فعال متشکل از دو ماده همگن متناوب و مواد پیزوالکتریک را برای نشان دادن قابلیت های فیلترینگ منحصر به فرد ایجاد کرد. نتایج تجربی آنها نشان می دهد که باند توقف طراحی شده را می توان برای کنترل انتشار موج از جعبه دنده به بدنه هواپیما در محدوده فرکانس پایین استفاده کرد. وانگ و همکاران [2 ] یک مدل پرتو منحنی کامپیوتر جدید برای بررسی باند موج الاستیک درون صفحه با استفاده از روش ماتریس انتقال ساخت. باندهای توقف شعاعی و مماسی بدست آمده توسط نرم افزار اجزای محدود تایید می شوند. با استفاده از اثر سطحی و نظریه تیر تیموشنکو، کیان و همکاران. [ 3 ] یک نانوپرتو PC پیزوالکتریک برای تجزیه و تحلیل رفتارهای باند جفت الکترومکانیکی پیشنهاد کرد. اثرات میدانهای جفت الکترومکانیکی، تنشهای سطحی پسماند و پارامترهای هندسی بر روی نوارهای توقف به تفصیل مورد بحث قرار گرفتهاند. یائو و همکاران [ 4 ] از روش اجزای محدود برای محاسبه ویژگی های باند توقف موج الاستیک صفحات PC توپولوژیکی با تشدیدگرهای محلی استفاده کرد. یو و همکاران [ 5] ویژگیهای باند توقف خمشی پیچیده سیستم لوله PC انتقال مایع را بررسی کرد. و خواص باند توقف عمیقاً توسط مکانیسم های پراکندگی براگ و رزونانس محلی با استفاده از ماتریس انتقال آشکار شد. مازوتی و همکاران [ 6 ] تجزیه و تحلیل بیشتری برای رفتار نواری امواج بلوخ نشتی در صفحات PC 2 بعدی با استفاده از روش بسط موج المان محدود-صفحه هیبریدی انجام داد. چن و همکاران [ 7 ] بر کنترل فعال موج خمشی پرتو پیزوالکتریک PC با خواص متناوب متناوب تأکید کرد. اثر درجه درهم آمیختگی و مدارهای خازن منفی بر باند توقف ارزیابی شد. گوتو و همکاران [ 8] باندهای پراکندگی براگ و پاسخ های اجباری میله PC را از طریق مدل میله مرتبه بالاتر مبتنی بر موج و روش المان محدود موج محاسبه کرد. آزمایش تجربی برای تایید نتایج عددی انجام می شود. زک و همکاران [ 9 ] رفتارهای باند موج طولی، خمشی و پیچشی یک پرتو PC همسانگرد سه بعدی را برای دستیابی به اهداف جداسازی ارتعاشی بررسی کرد. گوو و همکاران [ 10 ] نوعی ساختار پیزوالکتریک PC تک بعدی با رابط های ناقص را در نظر گرفت و دریافت که رابط مکانیکی و دی الکتریکی ناقص تأثیر آشکاری بر باندهای توقف دارد.
علاوه بر ساختارهای مرسوم PC [ 1-10 ] با تناوب ترجمه ای، مطالعات تحقیقاتی در حال حاضر به طور گسترده به یک کلاس از ساختارهای کریستال صوتی شعاعی (RPC) با تناوب شعاعی گسترش یافته است . در کار قبلی ما [ 11 ]، پدیده نوار پیچشی موج تنش PC تعمیم یافته با تناوب شعاعی تایید شده است، و نتایج نشان می دهد که پدیده باند توقف مشابه PC موجود است. به طور همزمان، رفتارهای نواری انتشار موج خمشی در RPC پیزوالکتریک مورد بررسی قرار گرفت. اثرات پارامترهای ساختاری و کنترل فعال بیرونی بر روی باندهای توقف تجزیه و تحلیل شد [ 12 ]. به منظور کنترل انتشار موج پیچشی در صفحه دایره ای، چای و همکاران. [13 ] پراکندگی براگ و باندهای تشدید محلی موج پیچشی در RPC پیزوالکتریک را مورد مطالعه قرار دادند و دریافتند که باندهای توقف می توانند به طور موثری از طریق تنظیم پارامترهای مدار خارجی تغییر کنند. خو و همکاران [ 14 ] از روش ماتریس انتقال برای تجزیه و تحلیل باندهای آوایی فرکانس پایین یک کامپیوتر کمانی شکل دوبعدی در مختصات استوانه ای استفاده کرد. به طور مشابه، تورنت و همکاران با معرفی فرامواد آکوستیک با طراحی خاص. [ 15-17 ] یک تحقیق جامع برای کریستال صوتی شعاعی انجام داد تا مکانیسم نوار توقف را آشکار کند .
طبق دانش نویسندگان، مطالعات رایانه شخصی موجود عمدتاً در مورد ساختارهای طراحی شده ویژه با تناوب ترجمه یا تناوب شعاعی است در حالی که مطالعات تحقیقاتی در مورد RPC فیبوناچی نادر است. در واقع، در مقایسه با ساختارهای تناوبی، ساختارهای فیبوناچی (غیر دوره ای) می توانند بسیاری از رفتارهای دینامیکی منحصر به فرد را از خود نشان دهند. در کار قبلی ما، نوار توقف موج پیچشی برای فیبوناچی RPC [ 18 ] به طور بدوی بررسی شده است. با این حال، مطالعات کمی در مورد باند توقف موج عرضی را می توان یافت. این اولین بار است که ماده پیزوالکتریک PZT4 برای دستیابی به باند توقف موج عرضی به فیبوناچی RPCAP وارد می شود.
در این مقاله، یک فیبوناچی RPCAP شامل مواد پیزوالکتریک برای تحلیل رفتارهای باند توقف با استفاده از روش ماتریس انتقال پیشنهاد شده است. باندهای توقف محاسبه شده توسط فیبوناچی RPCAP با آنهایی که توسط RPCAP دوره ای به دست می آیند مقایسه می شوند. پس از آن، شبیه سازی اجزای محدود برای تایید نتایج نظری انجام می شود. در نهایت، پارامترهای ساختاری و اثرات پیزوالکتریک بر روی باند توقف به تفصیل مورد بحث قرار میگیرند. تاکید این مطالعه نشان دادن رفتارهای نواری فیبوناچی RPCAP است که برای کاهش ارتعاش سازههای ماشین روتور همراه با ارتعاش عرضی بسیار مهم است.
تبدیل لاپلاس تکنیکی برای حل معادلات دیفرانسیل است. در اینجا ابتدا معادله دیفرانسیل فرم حوزه زمان به یک معادله جبری فرم حوزه فرکانس تبدیل می شود. پس از حل معادله جبری در حوزه فرکانس، نتیجه در نهایت به فرم حوزه زمان تبدیل می شود تا جواب نهایی معادله دیفرانسیل به دست آید. به عبارت دیگر می توان گفت تبدیل لاپلاس فقط یک روش میانبر برای حل معادلات دیفرانسیل است. در این مقاله به تبدیل لاپلاس
خواهیم پرداختو نحوه استفاده از آنها برای حل معادلات دیفرانسیل. آنها همچنین روشی را برای تشکیل یک تابع انتقال برای یک سیستم ورودی ارائه می دهند، اما در اینجا مورد بحث قرار نخواهد گرفت. آنها بلوک های اصلی مهندسی کنترل را با استفاده از نمودارهای بلوکی و غیره ارائه می دهند.
شکلهای بسیاری از تبدیلها در حال حاضر وجود دارد، اما تبدیلهای لاپلاس و تبدیل فوریه معروفترین آنها هستند. تبدیل لاپلاس معمولاً برای ساده کردن یک معادله دیفرانسیل به یک مسئله جبری ساده و قابل حل استفاده می شود. حتی زمانی که جبر کمی پیچیده می شود، باز هم حل آن آسان تر از حل یک معادله دیفرانسیل است.
یک قیاس جالب که می تواند به درک لاپلاس کمک کند این است. تصور کنید که با یک شعر انگلیسی روبرو می شوید که متوجه نمی شوید. اما شما یک دوست اسپانیایی دارید که در بیان این اشعار عالی است. بنابراین شما این شعر را به اسپانیایی ترجمه می کنید و برای او می فرستید، سپس او این شعر را به زبان اسپانیایی توضیح می دهد و برای شما باز می فرستد. شما توضیح اسپانیایی را درک می کنید و سپس می توانید معنای شعر را به انگلیسی منتقل کنید و در نتیجه شعر انگلیسی را درک کنید.
تبدیل لاپلاس از قانون لغو لرچ گرفته شده است. در روش تبدیل لاپلاس، تابع در حوزه زمان به تابع لاپلاس در حوزه فرکانس تبدیل می شود. این تابع لاپلاس به شکل یک معادله جبری خواهد بود و به راحتی قابل حل است. راه حل دوباره می تواند با استفاده از تبدیل لاپلاس معکوس به حوزه زمان تبدیل شود.
این تبدیل بیشتر برای سیستم های کنترلی استفاده می شود، همانطور که در بالا به اختصار اشاره شد. تبدیل ها برای مطالعه و تجزیه و تحلیل سیستم هایی مانند تهویه، گرمایش و شرایط هوا و غیره استفاده می شوند. این سیستم ها در هر ساختمان و ساختمان مدرن استفاده می شود.
تبدیل لاپلاس نیز برای کنترل فرآیند مهم است. به تجزیه و تحلیل متغیر کمک می کند که وقتی تغییر می کند نتایج مورد نیاز را می دهد. نمونه ای از این را می توان در آزمایشات با گرما یافت.
جدای از این دو مثال، تبدیل های لاپلاس در بسیاری از کاربردهای مهندسی مورد استفاده قرار می گیرند و روش بسیار مفیدی هستند. هم در مهندسی الکترونیک و هم در مهندسی مکانیک مفید است.
کنترل یک سیستم کنترل دینامیکی اعم از الکتریکی، مکانیکی، حرارتی، هیدرولیک و غیره را می توان با یک معادله دیفرانسیل نشان داد. معادله دیفرانسیل سیستم بر اساس قوانین فیزیکی حاکم بر یک سیستم به دست می آید. برای تسهیل حل یک معادله دیفرانسیل که یک سیستم کنترل را توصیف می کند، معادله به شکل جبری تبدیل می شود. این تبدیل با استفاده از تکنیک تبدیل لاپلاس انجام می شود ، یعنی معادله دیفرانسیل حوزه زمان به یک ضریب فرکانس الفبایی جبری تبدیل می شود.
فرض کنید f (t) تابع t باشد، زمان برای همه t ≥ 0
سپس تبدیل لاپلاس f (t)، F (s) را می توان به صورت تعریف کرد.

با فرض وجود انتگرال. که در آن اپراتور لاپلاس، s = σ + jω; واقعی یا مختلط خواهد بود j = √ (-1)
از تبدیل لاپلاس فقط می توان برای حل معادلات دیفرانسیل پیچیده استفاده کرد و مانند همه روش های خوب، یک ایراد دارد که ممکن است چندان بزرگ به نظر نرسد. یعنی فقط می توانید از این روش برای حل معادلات دیفرانسیل با ثابت های شناخته شده استفاده کنید. اگر معادله ای بدون ثابت شناخته شده دارید، این روش بی فایده است و باید روش دیگری پیدا کنید.
تبدیل در ریاضیات شامل تبدیل یک تابع به تابع دیگری است که ممکن است در همان حوزه نباشد. روش تبدیل در آن دسته از مسائلی که به طور مستقیم قابل حل نیستند کاربرد خود را پیدا می کند. این دگرگونی به نام ریاضیدان و ستاره شناس معروف پیر سیمون لاپلاس که در فرانسه زندگی می کرد نامگذاری شده است.
او تغییری مشابه را برای اضافات خود به نظریه احتمال اعمال کرد. پس از جنگ جهانی دوم رایج شد. این تحول توسط الیور هیوساید، مهندس برق انگلیسی رایج شد. دانشمندان مشهور دیگری مانند نیلز آبل، ماتیاس لرچ و توماس برومویچ در قرن نوزدهم از آن استفاده کردند.
تاریخ کامل تبدیل لاپلاس را می توان کمی بیشتر در گذشته دنبال کرد، به ویژه در سال 1744. این زمانی است که ریاضیدان بزرگ دیگری به نام لئونارد اویلر در مورد انواع دیگر انتگرال ها تحقیق کرد. با این حال، اویلر آن را چندان دنبال نکرد و آن را رها کرد. یکی از ستایشگران اویلر به نام جوزف لاگرانژ. تغییراتی در کار اویلر ایجاد کرد و کار را ادامه داد. کار لاگرانژ 38 سال بعد توجه لاپلاس را به خود جلب کرد، در سال 1782، جایی که او از جایی که اویلر متوقف شد ادامه داد. اما 3 سال بعد نبود. در سال 1785، جایی که لاپلاس نبوغی داشت و روش حل معادلات دیفرانسیل را برای همیشه تغییر داد. او به کار بر روی آن ادامه داد و تا سال 1809 به باز کردن قدرت واقعی تبدیل لاپلاس ادامه داد، زمانی که شروع به استفاده از بی نهایت به عنوان یک شرط جدایی ناپذیر کرد.
تبدیل لاپلاس بخش مهمی از مهندسی سیستم کنترل است. برای مطالعه یا تجزیه و تحلیل یک سیستم کنترل، باید تبدیل لاپلاس توابع مختلف (تابع زمان) را انجام دهیم. لاپلاس معکوس نیز ابزار مهمی برای یافتن تابع f(t) از فرم لاپلاس است. هر دو تبدیل لاپلاس معکوس و لاپلاس دارای ویژگی های خاصی در تجزیه و تحلیل سیستم های کنترل دینامیکی هستند. ترانسفورماتور لاپلاس دارای چندین ویژگی برای سیستم های خطی است. ویژگی های مختلف عبارتند از:
خطی بودن، تمایز، ادغام، ضرب، تغییر فرکانس، مقیاس بندی زمانی، جابجایی زمانی، کانولوشن، صرف، تابع تناوبی. دو قضیه بسیار مهم در رابطه با سیستم های کنترل وجود دارد. اینها هستند :
تبدیل لاپلاس بر روی تعدادی از توابع انجام می شود که عبارتند از - ضربه، تکانه واحد، گام، گام واحد، گام واحد جابجا شده، رمپ، واپاشی نمایی، سینوس، کسینوس، سینوس هذلولی، کسینوس هذلولی، لگاریتم طبیعی، تابع بسل. اما مزیت اصلی استفاده از تبدیل لاپلاس حل آسان معادلات دیفرانسیل مرتبه بالاتر با تبدیل به معادلات جبری است.
برای انجام تبدیل لاپلاس یک تابع زمان، مراحل خاصی باید دنبال شود. برای تبدیل یک تابع معین از زمان f (t) به تبدیل لاپلاس مربوطه، باید مراحل زیر را دنبال کنیم:

تابع زمان f (t) از تبدیل لاپلاس توسط فرآیندی به نام تبدیل لاپلاس معکوس بدست می آید و با £ -1 نشان داده می شود.

خصوصیات اصلی تبدیل لاپلاس را می توان به صورت زیر خلاصه کرد:
خطی بودن: فرض کنید C 1 و C 2 ثابت باشند. f (t)، g (t) توابع زمان، t، سپس

اولین جمله تغییر دهنده:

ویژگی ارزش مقیاس:

تفکیک:

ادغام:

تغییر زمان:
اگر L {f (t)} = F (s)، تبدیل لاپلاس f (t) پس از تاخیر زمانی، T برابر است با حاصلضرب تبدیل لاپلاس f (t) و e -St آن است

در جایی که u (tT) تابع گام واحد را نشان می دهد.
حاصل ضرب:
اگر L {f (t)} = F (s)، حاصل ضرب دو تابع f 1 (t) و f 2 (t) است.

قضیه ارزش نهایی:

این قضیه در تجزیه و تحلیل و طراحی سیستم کنترل بازخورد مرتبط است، زیرا تبدیل لاپلاس یک راه حل برای شرایط اولیه
قضیه ارزش اولیه ارائه می دهد:

اجازه دهید روش های تبدیل لاپلاس را برای یک تابع ساده f (t) = e αt بررسی کنیم تا موضوع را بهتر درک کنیم.

با مقایسه راه حل فوق می توانیم بنویسیم،

به طور مشابه، با تنظیم α = 0، به دست می آوریم،

به طور مشابه، با تنظیم α = jω، دریافت می کنیم


بدین ترتیب،

بیایید نمونه دیگری از روش های تبدیل لاپلاس را برای تابع بررسی کنیم


دوباره شکل تبدیل لاپلاس e t است،

این فرم لاپلاس را می توان به صورت بازنویسی کرد

حال از تعریف سری توان دریافت می کنیم،


همیشه جدولی در دسترس مهندس است که حاوی اطلاعاتی در مورد تبدیل های لاپلاس است. نمونه ای از جدول تبدیل لاپلاس در زیر انجام شده است. از جدول زیر با تبدیل لاپلاس توابع رایج مختلف آشنا می شویم.

















معادله را با تبدیل لاپلاس حل کنید

با استفاده از جدول بالا، معادله را می توان به شکل لاپلاس تبدیل کرد:

با استفاده از داده های داده شده در سوال، فرم لاپلاس را می توان ساده کرد.

قسمت هایی از (s 2 + 3s + 2) می دهد

این را می توان با استفاده از کسرهای جزئی حل کرد که راحت تر از حل آن در شکل قبلی است. ابتدا باید مخرج را فاکتور گرفت.

ضرب متقاطع به دست می دهد:

سپس باید ضرایب A و B را پیدا کرد

با جایگزینی در معادله:

با استفاده از جدول بالا می توان این معادله را به حالت عادی تبدیل کرد.
مثال هایی برای امتحان کردن
تبدیل لاپلاس معکوس موارد زیر را محاسبه و چاپ کنید، توصیه می شود جدولی از تبدیل های لاپلاس را به صورت آنلاین پیدا کنید:

پاسخ

نمونه های بیشتری از تبدیل لاپلاس
منبع
https://riverglennapts.com/no/laplace/503-laplace-transforms-table-method-examples-history-of-laplace-transform.html
تبدیل لاپلاس تکنیکی برای حل معادلات دیفرانسیل است. در اینجا ابتدا معادله دیفرانسیل فرم حوزه زمان به یک معادله جبری فرم حوزه فرکانس تبدیل می شود. پس از حل معادله جبری در حوزه فرکانس، نتیجه در نهایت به فرم حوزه زمان تبدیل می شود تا جواب نهایی معادله دیفرانسیل به دست آید. به عبارت دیگر می توان گفت تبدیل لاپلاس فقط یک روش میانبر برای حل معادلات دیفرانسیل است. در این مقاله به تبدیل لاپلاس
خواهیم پرداختو نحوه استفاده از آنها برای حل معادلات دیفرانسیل. آنها همچنین روشی را برای تشکیل یک تابع انتقال برای یک سیستم ورودی ارائه می دهند، اما در اینجا مورد بحث قرار نخواهد گرفت. آنها بلوک های اصلی مهندسی کنترل را با استفاده از نمودارهای بلوکی و غیره ارائه می دهند.
شکلهای بسیاری از تبدیلها در حال حاضر وجود دارد، اما تبدیلهای لاپلاس و تبدیل فوریه معروفترین آنها هستند. تبدیل لاپلاس معمولاً برای ساده کردن یک معادله دیفرانسیل به یک مسئله جبری ساده و قابل حل استفاده می شود. حتی زمانی که جبر کمی پیچیده می شود، باز هم حل آن آسان تر از حل یک معادله دیفرانسیل است.
یک قیاس جالب که می تواند به درک لاپلاس کمک کند این است. تصور کنید که با یک شعر انگلیسی روبرو می شوید که متوجه نمی شوید. اما شما یک دوست اسپانیایی دارید که در بیان این اشعار عالی است. بنابراین شما این شعر را به اسپانیایی ترجمه می کنید و برای او می فرستید، سپس او این شعر را به زبان اسپانیایی توضیح می دهد و برای شما باز می فرستد. شما توضیح اسپانیایی را درک می کنید و سپس می توانید معنای شعر را به انگلیسی منتقل کنید و در نتیجه شعر انگلیسی را درک کنید.
تبدیل لاپلاس از قانون لغو لرچ گرفته شده است. در روش تبدیل لاپلاس، تابع در حوزه زمان به تابع لاپلاس در حوزه فرکانس تبدیل می شود. این تابع لاپلاس به شکل یک معادله جبری خواهد بود و به راحتی قابل حل است. راه حل دوباره می تواند با استفاده از تبدیل لاپلاس معکوس به حوزه زمان تبدیل شود.
این تبدیل بیشتر برای سیستم های کنترلی استفاده می شود، همانطور که در بالا به اختصار اشاره شد. تبدیل ها برای مطالعه و تجزیه و تحلیل سیستم هایی مانند تهویه، گرمایش و شرایط هوا و غیره استفاده می شوند. این سیستم ها در هر ساختمان و ساختمان مدرن استفاده می شود.
تبدیل لاپلاس نیز برای کنترل فرآیند مهم است. به تجزیه و تحلیل متغیر کمک می کند که وقتی تغییر می کند نتایج مورد نیاز را می دهد. نمونه ای از این را می توان در آزمایشات با گرما یافت.
جدای از این دو مثال، تبدیل های لاپلاس در بسیاری از کاربردهای مهندسی مورد استفاده قرار می گیرند و روش بسیار مفیدی هستند. هم در مهندسی الکترونیک و هم در مهندسی مکانیک مفید است.
کنترل یک سیستم کنترل دینامیکی اعم از الکتریکی، مکانیکی، حرارتی، هیدرولیک و غیره را می توان با یک معادله دیفرانسیل نشان داد. معادله دیفرانسیل سیستم بر اساس قوانین فیزیکی حاکم بر یک سیستم به دست می آید. برای تسهیل حل یک معادله دیفرانسیل که یک سیستم کنترل را توصیف می کند، معادله به شکل جبری تبدیل می شود. این تبدیل با استفاده از تکنیک تبدیل لاپلاس انجام می شود ، یعنی معادله دیفرانسیل حوزه زمان به یک ضریب فرکانس الفبایی جبری تبدیل می شود.
فرض کنید f (t) تابع t باشد، زمان برای همه t ≥ 0
سپس تبدیل لاپلاس f (t)، F (s) را می توان به صورت تعریف کرد.

با فرض وجود انتگرال. که در آن اپراتور لاپلاس، s = σ + jω; واقعی یا مختلط خواهد بود j = √ (-1)
از تبدیل لاپلاس فقط می توان برای حل معادلات دیفرانسیل پیچیده استفاده کرد و مانند همه روش های خوب، یک ایراد دارد که ممکن است چندان بزرگ به نظر نرسد. یعنی فقط می توانید از این روش برای حل معادلات دیفرانسیل با ثابت های شناخته شده استفاده کنید. اگر معادله ای بدون ثابت شناخته شده دارید، این روش بی فایده است و باید روش دیگری پیدا کنید.
تبدیل در ریاضیات شامل تبدیل یک تابع به تابع دیگری است که ممکن است در همان حوزه نباشد. روش تبدیل در آن دسته از مسائلی که به طور مستقیم قابل حل نیستند کاربرد خود را پیدا می کند. این دگرگونی به نام ریاضیدان و ستاره شناس معروف پیر سیمون لاپلاس که در فرانسه زندگی می کرد نامگذاری شده است.
او تغییری مشابه را برای اضافات خود به نظریه احتمال اعمال کرد. پس از جنگ جهانی دوم رایج شد. این تحول توسط الیور هیوساید، مهندس برق انگلیسی رایج شد. دانشمندان مشهور دیگری مانند نیلز آبل، ماتیاس لرچ و توماس برومویچ در قرن نوزدهم از آن استفاده کردند.
تاریخ کامل تبدیل لاپلاس را می توان کمی بیشتر در گذشته دنبال کرد، به ویژه در سال 1744. این زمانی است که ریاضیدان بزرگ دیگری به نام لئونارد اویلر در مورد انواع دیگر انتگرال ها تحقیق کرد. با این حال، اویلر آن را چندان دنبال نکرد و آن را رها کرد. یکی از ستایشگران اویلر به نام جوزف لاگرانژ. تغییراتی در کار اویلر ایجاد کرد و کار را ادامه داد. کار لاگرانژ 38 سال بعد توجه لاپلاس را به خود جلب کرد، در سال 1782، جایی که او از جایی که اویلر متوقف شد ادامه داد. اما 3 سال بعد نبود. در سال 1785، جایی که لاپلاس نبوغی داشت و روش حل معادلات دیفرانسیل را برای همیشه تغییر داد. او به کار بر روی آن ادامه داد و تا سال 1809 به باز کردن قدرت واقعی تبدیل لاپلاس ادامه داد، زمانی که شروع به استفاده از بی نهایت به عنوان یک شرط جدایی ناپذیر کرد.
تبدیل لاپلاس بخش مهمی از مهندسی سیستم کنترل است. برای مطالعه یا تجزیه و تحلیل یک سیستم کنترل، باید تبدیل لاپلاس توابع مختلف (تابع زمان) را انجام دهیم. لاپلاس معکوس نیز ابزار مهمی برای یافتن تابع f(t) از فرم لاپلاس است. هر دو تبدیل لاپلاس معکوس و لاپلاس دارای ویژگی های خاصی در تجزیه و تحلیل سیستم های کنترل دینامیکی هستند. ترانسفورماتور لاپلاس دارای چندین ویژگی برای سیستم های خطی است. ویژگی های مختلف عبارتند از:
خطی بودن، تمایز، ادغام، ضرب، تغییر فرکانس، مقیاس بندی زمانی، جابجایی زمانی، کانولوشن، صرف، تابع تناوبی. دو قضیه بسیار مهم در رابطه با سیستم های کنترل وجود دارد. اینها هستند :
تبدیل لاپلاس بر روی تعدادی از توابع انجام می شود که عبارتند از - ضربه، تکانه واحد، گام، گام واحد، گام واحد جابجا شده، رمپ، واپاشی نمایی، سینوس، کسینوس، سینوس هذلولی، کسینوس هذلولی، لگاریتم طبیعی، تابع بسل. اما مزیت اصلی استفاده از تبدیل لاپلاس حل آسان معادلات دیفرانسیل مرتبه بالاتر با تبدیل به معادلات جبری است.
برای انجام تبدیل لاپلاس یک تابع زمان، مراحل خاصی باید دنبال شود. برای تبدیل یک تابع معین از زمان f (t) به تبدیل لاپلاس مربوطه، باید مراحل زیر را دنبال کنیم:

تابع زمان f (t) از تبدیل لاپلاس توسط فرآیندی به نام تبدیل لاپلاس معکوس بدست می آید و با £ -1 نشان داده می شود.

خصوصیات اصلی تبدیل لاپلاس را می توان به صورت زیر خلاصه کرد:
خطی بودن: فرض کنید C 1 و C 2 ثابت باشند. f (t)، g (t) توابع زمان، t، سپس

اولین جمله تغییر دهنده:

ویژگی ارزش مقیاس:

تفکیک:

ادغام:

تغییر زمان:
اگر L {f (t)} = F (s)، تبدیل لاپلاس f (t) پس از تاخیر زمانی، T برابر است با حاصلضرب تبدیل لاپلاس f (t) و e -St آن است

در جایی که u (tT) تابع گام واحد را نشان می دهد.
حاصل ضرب:
اگر L {f (t)} = F (s)، حاصل ضرب دو تابع f 1 (t) و f 2 (t) است.

قضیه ارزش نهایی:

این قضیه در تجزیه و تحلیل و طراحی سیستم کنترل بازخورد مرتبط است، زیرا تبدیل لاپلاس یک راه حل برای شرایط اولیه
قضیه ارزش اولیه ارائه می دهد:

اجازه دهید روش های تبدیل لاپلاس را برای یک تابع ساده f (t) = e αt بررسی کنیم تا موضوع را بهتر درک کنیم.

با مقایسه راه حل فوق می توانیم بنویسیم،

به طور مشابه، با تنظیم α = 0، به دست می آوریم،

به طور مشابه، با تنظیم α = jω، دریافت می کنیم


بدین ترتیب،

بیایید نمونه دیگری از روش های تبدیل لاپلاس را برای تابع بررسی کنیم


دوباره شکل تبدیل لاپلاس e t است،

این فرم لاپلاس را می توان به صورت بازنویسی کرد

حال از تعریف سری توان دریافت می کنیم،


همیشه جدولی در دسترس مهندس است که حاوی اطلاعاتی در مورد تبدیل های لاپلاس است. نمونه ای از جدول تبدیل لاپلاس در زیر انجام شده است. از جدول زیر با تبدیل لاپلاس توابع رایج مختلف آشنا می شویم.

















معادله را با تبدیل لاپلاس حل کنید

با استفاده از جدول بالا، معادله را می توان به شکل لاپلاس تبدیل کرد:

با استفاده از داده های داده شده در سوال، فرم لاپلاس را می توان ساده کرد.

قسمت هایی از (s 2 + 3s + 2) می دهد

این را می توان با استفاده از کسرهای جزئی حل کرد که راحت تر از حل آن در شکل قبلی است. ابتدا باید مخرج را فاکتور گرفت.

ضرب متقاطع به دست می دهد:

سپس باید ضرایب A و B را پیدا کرد

با جایگزینی در معادله:

با استفاده از جدول بالا می توان این معادله را به حالت عادی تبدیل کرد.
مثال هایی برای امتحان کردن
تبدیل لاپلاس معکوس موارد زیر را محاسبه و چاپ کنید، توصیه می شود جدولی از تبدیل های لاپلاس را به صورت آنلاین پیدا کنید:

پاسخ

نمونه های بیشتری از تبدیل لاپلاس
منبع
https://riverglennapts.com/no/laplace/503-laplace-transforms-table-method-examples-history-of-laplace-transform.html
با توسعه ادغام در مقیاس بزرگ در اواخر دهه 1970، آشکار شد که بهینه سازی فرآیندهای تولید نیمه هادی صرفاً بر اساس تجربی مورد تردید است. شبیهسازی عددی فرآیند ساخت و ویژگیهای الکتریکی دستگاههای نیمهرسانا، راهی سریع و ارزان برای بررسی طرحها و فرآیندهای دستگاه ارائه میدهد. ابزارهای شبیه سازی عددی را می توان به سه دسته تقسیم کرد (شکل 2.11 را ببینید.): شبیه سازی فرآیند، شبیه سازی دستگاه و شبیه سازی مدار. شبیهسازی فرآیند بر اساس اندازهگیریهایی مانند پروفایلهای دوپینگ ارائه شده توسط SIMS (طیفسنجی جرمی یونی ثانویه)، توپوگرافی ارائهشده توسط TEM (میکروسکوپ الکترونی عبوری)، دستور فرآیند و ماسکهای لیتوگرافی است. فرآیندهایی مانند انتشار، اکسیداسیون، اچینگ، لیتوگرافی و کاشت یون شبیه سازی می شوند. شبیهسازی دستگاه از هندسه دستگاه و نمایه دوپینگ بهدستآمده برای بازتولید و پیشبینی دادههای الکتریکی مانند منحنیهای جریان-ولتاژ (IV)، منحنیهای خازن-ولتاژ (CV) یا فرکانسهای انتقال استفاده میکند. خروجی شبیه سازهای دستگاه می تواند برای کالیبره کردن مدل های فشرده برنامه های شبیه سازی مدار مفید باشد. برای انجام خودکار این مراحل می توان از بسته های شبیه سازی یکپارچه استفاده کرد.
|
شبیه سازی دستگاه های نیمه هادی بر اساس فرمول های نیمه کلاسیک یا مکانیکی کوانتومی است. بر اساس معادلات اساسی -- P OISSON 2 . 3 , B OLTZMANN 2 . 4 , W IGNER 2 . 5 یا S CHRÖDINGER 2 . معادله 6 -- چندین مدل را می توان استخراج کرد. در بخش های بعدی به اختصار توضیح داده خواهد شد.
زیر بخش ها
همانطور که در شکل 2.11 نشان داده شده است، می توان مدل های افزایش پیچیدگی را برای شبیه سازی انتقال بار در دستگاه های نیمه هادی به دست آورد . مهمترین معادله ای که در همه مدل ها مشترک است، معادله P OISSON برای تعیین پتانسیل الکترواستاتیک است.
| ( 2. 1 ) _ |
که در آن ![]() پتانسیل الکترواستاتیک،
پتانسیل الکترواستاتیک، ![]() گذردهی دی الکتریک،
گذردهی دی الکتریک، ![]() و
و ![]() غلظت الکترون و حفره، و غلظت خالص ناخالصی ها را نشان می دهد. حمل و نقل حامل ها توسط معادله حمل و نقل B OLTZMANN (BTE) که یک فرمول نیمه کلاسیک از انتقال بار است، توصیف می شود.
غلظت الکترون و حفره، و غلظت خالص ناخالصی ها را نشان می دهد. حمل و نقل حامل ها توسط معادله حمل و نقل B OLTZMANN (BTE) که یک فرمول نیمه کلاسیک از انتقال بار است، توصیف می شود. ![]()
اثرات مکانیکی کوانتومی با معادله S CHRÖDINGER توصیف می شود . برای گنجاندن اثرات مکانیکی کوانتومی در شبیهسازی دستگاه کلاسیک، معادله انتقال B OLTZMANN را میتوان با معادله S CHRÖDINGER جفت کرد ، یا معادله W IGNER را میتوان اعمال کرد [ 39 ، 40 ، 41 ، 42 ]. مدل های حمل و نقل مبتنی بر حل معادله انتقال B OLTZMANN را می توان با استفاده از روش گشتاور [ 43 ، 44 ، 45 ] که مدل رانش- انتشار [ 46 ]، انتقال انرژی یا مدل هیدرودینامیکی را به دست می آورد [47 ]، یا مدلهای حمل و نقل مرتبه بالاتر [ 48 ]. علاوه بر این، یک راه حل تقریبی را می توان با بیان تابع توزیع به عنوان یک بسط سری که به رویکرد هارمونیک های کروی منجر می شود، به دست آورد [ 49 ، 50 ، 51 ، 52 ، 53 ].
همانطور که در شکل 2.11 نشان داده شده است، می توان مدل های افزایش پیچیدگی را برای شبیه سازی انتقال بار در دستگاه های نیمه هادی به دست آورد . مهمترین معادله ای که در همه مدل ها مشترک است، معادله P OISSON برای تعیین پتانسیل الکترواستاتیک است.
| ( 2. 1 ) _ |
که در آن ![]() پتانسیل الکترواستاتیک،
پتانسیل الکترواستاتیک، ![]() گذردهی دی الکتریک،
گذردهی دی الکتریک، ![]() و
و ![]() غلظت الکترون و حفره، و غلظت خالص ناخالصی ها را نشان می دهد. حمل و نقل حامل ها توسط معادله حمل و نقل B OLTZMANN (BTE) که یک فرمول نیمه کلاسیک از انتقال بار است، توصیف می شود.
غلظت الکترون و حفره، و غلظت خالص ناخالصی ها را نشان می دهد. حمل و نقل حامل ها توسط معادله حمل و نقل B OLTZMANN (BTE) که یک فرمول نیمه کلاسیک از انتقال بار است، توصیف می شود. ![]()
اثرات مکانیکی کوانتومی با معادله S CHRÖDINGER توصیف می شود . برای گنجاندن اثرات مکانیکی کوانتومی در شبیهسازی دستگاه کلاسیک، معادله انتقال B OLTZMANN را میتوان با معادله S CHRÖDINGER جفت کرد ، یا معادله W IGNER را میتوان اعمال کرد [ 39 ، 40 ، 41 ، 42 ]. مدل های حمل و نقل مبتنی بر حل معادله انتقال B OLTZMANN را می توان با استفاده از روش گشتاور [ 43 ، 44 ، 45 ] که مدل رانش- انتشار [ 46 ]، انتقال انرژی یا مدل هیدرودینامیکی را به دست می آورد [47 ]، یا مدلهای حمل و نقل مرتبه بالاتر [ 48 ]. علاوه بر این، یک راه حل تقریبی را می توان با بیان تابع توزیع به عنوان یک بسط سری که به رویکرد هارمونیک های کروی منجر می شود، به دست آورد [ 49 ، 50 ، 51 ، 52 ، 53 ].
همانطور که در شکل 2.11 نشان داده شده است، می توان مدل های افزایش پیچیدگی را برای شبیه سازی انتقال بار در دستگاه های نیمه هادی به دست آورد . مهمترین معادله ای که در همه مدل ها مشترک است، معادله P OISSON برای تعیین پتانسیل الکترواستاتیک است.
| ( 2. 1 ) _ |
که در آن ![]() پتانسیل الکترواستاتیک،
پتانسیل الکترواستاتیک، ![]() گذردهی دی الکتریک،
گذردهی دی الکتریک، ![]() و
و ![]() غلظت الکترون و حفره، و غلظت خالص ناخالصی ها را نشان می دهد. حمل و نقل حامل ها توسط معادله حمل و نقل B OLTZMANN (BTE) که یک فرمول نیمه کلاسیک از انتقال بار است، توصیف می شود.
غلظت الکترون و حفره، و غلظت خالص ناخالصی ها را نشان می دهد. حمل و نقل حامل ها توسط معادله حمل و نقل B OLTZMANN (BTE) که یک فرمول نیمه کلاسیک از انتقال بار است، توصیف می شود. ![]()
اثرات مکانیکی کوانتومی با معادله S CHRÖDINGER توصیف می شود . برای گنجاندن اثرات مکانیکی کوانتومی در شبیهسازی دستگاه کلاسیک، معادله انتقال B OLTZMANN را میتوان با معادله S CHRÖDINGER جفت کرد ، یا معادله W IGNER را میتوان اعمال کرد [ 39 ، 40 ، 41 ، 42 ]. مدل های حمل و نقل مبتنی بر حل معادله انتقال B OLTZMANN را می توان با استفاده از روش گشتاور [ 43 ، 44 ، 45 ] که مدل رانش- انتشار [ 46 ]، انتقال انرژی یا مدل هیدرودینامیکی را به دست می آورد [47 ]، یا مدلهای حمل و نقل مرتبه بالاتر [ 48 ]. علاوه بر این، یک راه حل تقریبی را می توان با بیان تابع توزیع به عنوان یک بسط سری که به رویکرد هارمونیک های کروی منجر می شود، به دست آورد [ 49 ، 50 ، 51 ، 52 ، 53 ].
اگر ماهیت مکانیکی کوانتومی الکترون ها نادیده گرفته شود، انتقال حامل در یک دستگاه را می توان با معادله انتقال B OLTZMANN که یک معادله انتگرو دیفرانسیل هفت بعدی در فضای فاز است، توصیف کرد [ 46 ]. برای الکترون ها می خواند
| ( 2. 2 ) _ |
در اینجا، توزیع حامل ها در فضا ( )، تکانه ( ) و زمان است. در سمت راست این معادله دیفرانسیل جزئی، عملگر برخورد قرار دارد که پراکندگی ذرات به دلیل فونون ها، ناخالصی ها، رابط ها یا سایر منابع پراکندگی را توصیف می کند. با این حال، حل مستقیم این معادله از نظر محاسباتی بازدارنده است . 7 . بلکه با استفاده از روش لحظه ها یا با استفاده از روش های تقریبی حل می شود. در روش گشتاورها، هر جمله از ( 2.2 ) با یک تابع وزن ضرب میشود و روی فضا یکپارچه میشود. این مجموعه ای از معادلات دیفرانسیل را در فضای () به دست می دهد. گشتاورهای تابع توزیع با [ ![]()
![]()
![]()
![]()
![]()
![]() 54 ]
54 ]
| ( 2. 3 ) _ |
زیر بخش ها
مشخصات دوپینگ منبع و منطقه تخلیه تأثیر مهمی بر ویژگی های دستگاه دارد. از یک طرف، داشتن اتصالات کم عمق برای کاهش نفوذ زهکشی بر کانال و بهبود کنترل گیت بر شارژ وارونگی مطلوب است. از طرف دیگر، یک منبع عمیق و به شدت دوپ شده و منطقه تخلیه مقاومت سری را کاهش می دهد. یکی از امکانهای دستیابی به هر دو، معرفی نواحی درن با دوپ کم (LDD) است ، جایی که یک ایمپلنت عمیق در محل تماس استفاده میشود و از طریق یک ایمپلنت کم عمق به کانال متصل میشود. رویکرد دیگر استفاده از کنتاکتهای منبع/زهکشی است که در ارتفاع بالاتری نسبت به کانال ایجاد میشوند [ 22 ].
طبق نظریه مقیاس بندی که در بخش 2.1 بیان شده است، ضخامت دی الکتریک گیت باید با هر نسل جدید دستگاه کوچک شود و به مقادیر 2.2 نانومتر، 1.9 نانومتر و 1.4 نانومتر برای دستگاه های طول دروازه 180 نانومتر، 150 نانومتر و 100 نانومتر برسد [23 ] . با این حال، اگر سد انرژی بین گیت و نیمه هادی کوچک شود، اثر تونل مکانیکی کوانتومی وارد عمل می شود. یک راه حل برای مقابله با این اثر استفاده از مواد دی الکتریک است که دارای گذردهی دی الکتریک بالاتری هستند. این مواد امکان دستیابی به ضخامت فیزیکی بالا همراه با ضخامت اکسید موثر کوچک (EOT) را فراهم می کنند. EOT به عنوان ضخامت یک ![]() لایه SiO با ظرفیت برابر تعریف می شود. برای لایه ای از SiO
لایه SiO با ظرفیت برابر تعریف می شود. برای لایه ای از SiO ![]() و یک دی الکتریک بالا
و یک دی الکتریک بالا ![]() ، EOT است
، EOT است
که در آن و نشان دهنده ضخامت SiO و لایه بالا، و و و ضریب مربوطه هستند. با دی الکتریک بالا می توان کنترل خوبی بر بار وارونگی حتی با دی الکتریک های ضخیم فیزیکی برای مسدود کردن جریان های تونل زنی حفظ کرد. این موضوع با جزئیات بیشتر در بخش 5.1.5 بررسی خواهد شد . ![]()
![]()
![]()
![]()
![]()
![]()
![]()
با این حال، قابلیت اطمینان دی الکتریک دروازه ، به ویژه در مورد مواد جدید، یک مسئله حیاتی است. جریان تونل زنی انگلی که از طریق دی الکتریک می گذرد باعث فرسودگی می شود که به این معنی است که قابلیت انسداد دی الکتریک کاهش می یابد و حتی شکست دی الکتریک که یک افزایش رسانایی ناگهانی است. معمولاً فرض بر این است که این شکست ناشی از تجمع تدریجی نقص در لایه دی الکتریک است که ممکن است در اثر تزریق سوراخ آند یا آزاد شدن هیدروژن از رابط Si-SiO ایجاد شود ![]() [ 24 ]. این به ویژه برای
[ 24 ]. این به ویژه برای ![]() دی الکتریک های بالا که یک لایه بومی روی سیلیکون تشکیل نمی دهند بسیار مهم است.
دی الکتریک های بالا که یک لایه بومی روی سیلیکون تشکیل نمی دهند بسیار مهم است.
علاوه بر فرآیند مقیاسبندی مداوم، مفاهیم طراحی جدید به وجود آمده است تا امکان افزایش بیشتر در چگالی یکپارچهسازی را فراهم کند. این مفاهیم از دستگاههای MOS سیلیکونی کرنششده که در آن کانال سیلیکونی با سیلیکون کرنششده برای بهبود تحرک جایگزین میشود، تا دستگاههای با بستر تخلیهشده مانند سیلیکون تک دروازهای یا دو دروازهای روی دستگاههای عایق (SOI)، FinFETها، ترانزیستورهای عمودی، گسترش مییابد. و حتی نانولولههای کربنی (CNT) که ساختار دستگاه کاملاً جدیدی را نشان میدهند.
زیر بخش ها
تحرک حامل ها در سیلیکون افزایش می یابد اگر کرنش کششی دو محوره اعمال شود [ 25 ]، زیرا تحت کرنش کششی در سیلیکون (001)، بیضی های نوار هدایت منحط چهار برابر با جرم موثر بالاتر بلند می شوند. بنابراین، حامل های بیشتری در بیضی های منحط دو برابر با جرم موثر کمتر باقی می مانند. علاوه بر این، پراکندگی بین دره کاهش می یابد. کانال های سیلیکونی کشیده شده را می توان با رشد یک لایه نازک از سیلیکون بر روی ماده ای با ثابت شبکه کمی بزرگتر مانند سیلیکون-ژرمانیوم محقق کرد. لایه سیلیکون باید به اندازه کافی نازک باشد تا از آرامش و تسکین فشار جلوگیری کند.
همانطور که در بالا ذکر شد، punchthrough یکی از مشکلات اصلی در دستگاه های MOS است. یک اقدام متقابل ساده استفاده از وسایلی است که در آن بستر به طور جزئی یا کامل تخلیه شده است [ 13 ]. از آنجایی که هیچ اپراتور رایگانی به جز در کانال وجود ندارد، انجام پانچ نمی تواند اتفاق بیفتد. دستگاه های با لایه خالی شده را می توان با استفاده از سیلیکون بر روی بسترهای عایق به وجود آورد. ساختار و لبه نوار هدایت یک دستگاه SOI تک دروازه کاملاً تخلیه شده در قسمت سمت چپ شکل 2.9 نشان داده شده است . این شامل یک ماسفت استاندارد با بستری است که توسط لایه ای از SiO از ویفر عایق شده است ![]() . گیت می تواند کنترل بهتری بر شارژ وارونگی داشته باشد اگر SOI دو دروازه ای باشدترانزیستور در نظر گرفته شده است، همانطور که در قسمت سمت راست شکل 2.9 نشان داده شده است . ماسفت های دو یا حتی سه گیت را می توان با استفاده از FinFET بدست آورد . این دستگاهی است که در آن یک کانال سیلیکونی کوچک - باله - از دو یا سه طرف توسط الکترود دروازه احاطه شده است [ 25 ، 26 ، 27 ]. ضخامت باله تا 6.5 نانومتر گزارش شده است [ 28 ] که به این معنی است که کانال بین منبع و تخلیه تنها از حدود 15 لایه اتمی سیلیکون تشکیل شده است.
. گیت می تواند کنترل بهتری بر شارژ وارونگی داشته باشد اگر SOI دو دروازه ای باشدترانزیستور در نظر گرفته شده است، همانطور که در قسمت سمت راست شکل 2.9 نشان داده شده است . ماسفت های دو یا حتی سه گیت را می توان با استفاده از FinFET بدست آورد . این دستگاهی است که در آن یک کانال سیلیکونی کوچک - باله - از دو یا سه طرف توسط الکترود دروازه احاطه شده است [ 25 ، 26 ، 27 ]. ضخامت باله تا 6.5 نانومتر گزارش شده است [ 28 ] که به این معنی است که کانال بین منبع و تخلیه تنها از حدود 15 لایه اتمی سیلیکون تشکیل شده است.
|
ماسفتهایی که به عنوان ترانزیستورهای دسترسی در سلولهای DRAM استفاده میشوند، به یک ردپای مخصوصاً کوچک برای اجازه دادن به تراکم یکپارچهسازی بالا نیاز دارند [ 29 ]. خازن DRAM که به ظرفیت تقریباً 50fF نیاز دارد تا زمانهای ماندگاری عملی را فراهم کند، معمولاً به عنوان خازن ترانشه ساخته میشود. یکی از روش هایی که توسط آن ردپای به شدت کاهش می یابد، تبدیل ترانزیستور دسترسی به جهت عمودی مستقیماً بالای خازن ترانشه است [ 30 ، 31 ، 32 ، 33 ، 34 ، 35 ].
نانولوله های کربنی ورقه های استوانه ای از یک یا چند لایه متحدالمرکز اتم های کربن هستند. آزمایشات نشان داده است که لوله ها می توانند خواص فلزی یا نیمه رسانایی داشته باشند. ساختار نوار آنها بستگی به موقعیت اتم های کربن تشکیل دهنده لوله دارد. به ویژه نانولولههای کربنی تک جداره، خواص الکتریکی برتری را نشان میدهند و کاندیدهای امیدوارکنندهای برای کاربردهای نانوالکترونیکی آینده، چه بهعنوان اتصالدهنده یا دستگاههای فعال در نظر گرفته میشوند. نانولوله های نیمه رسانا می توانند به عنوان عناصر فعال در طرح های ترانزیستور اثر میدانی (FET) استفاده شوند. دو کاربرد احتمالی نانولوله های کربنی به عنوان دستگاه های ترانزیستوری در شکل 2.10 نشان داده شده است [ 36 ، 37 ]. نانولوله های کربنی تک جداره رسانای بالستیک هستند، بنابراین جریان توسط L کنترل می شودمعادله آندوئر با این حال، این نشان می دهد که حداقل مقاومت یک نانولوله فلزی k است . در حال حاضر به طور کلی پذیرفته شده است که حمل و نقل در لوله ها تحت سلطه موانع S CHOTKY در تماس های فلزی است [ 38 ]. ![]()
![]()
|
برای تحقق مدارهای CMOS لازم است دستگاه های nMOS و pMOS از نزدیک با هم ادغام شوند. دروازههای پلی سیلیکونی امکان تنظیم عملکرد کار را با دوپینگ فراهم میکنند و بنابراین برای یکپارچهسازی در مقیاس بزرگ [ 18 ] ایدهآل هستند ، برخلاف فلزاتی که در آنها یافتن مواد با عملکردهای کار مکمل دشوار است. با این حال، اگر ولتاژی روی گیت پلی سیلیکونی اعمال شود، یک لایه تخلیه در رابط به دی الکتریک گیت تشکیل می شود. در این لایه یک افت ولتاژ رخ می دهد که تقریباً با [ 19 ] داده می شود.
که در آن و نشان دهنده گذردهی دی الکتریک دی الکتریک دروازه و زیرلایه، میدان الکتریکی در دی الکتریک و دوپینگ پلی سیلیکون است. این اثر تخلیه پلی سیلیکون نامیده می شود . منجر به کاهش غلظت الکترون در سطح مشترک می شود و باعث افزایش موثر ضخامت دی الکتریک و افزایش ولتاژ آستانه می شود. اثر تخلیه پلی سیلیکون را می توان با استفاده از دروازه های فلزی مانند مولیبدن دوپ شده با نیتروژن [ 20 ]، که، با این حال، از نقطه نظر فرآیندی نیاز دارد، اجتناب کرد. ![]()
![]()
![]()
![]()
علاوه بر این، گیت های پلی سیلیکونی باید دوپ شوند و ماده بور به عنوان ناخالصی برای دستگاه های pMOS استفاده می شود. با این حال، در طی مراحل بعدی فرآیند، بور تمایل دارد از طریق دروازه پلی سیلیکونی پخش شود و به لایه دی الکتریک و حتی کانال ( نفوذ بور ) نفوذ کند [ 21 ]. این امر نه تنها در کیفیت و قابلیت اطمینان دی الکتریک بلکه به ویژه در عملکرد دستگاه باعث ایجاد مشکلاتی می شود: نفوذ بور ولتاژ آستانه دستگاه های MOS را افزایش می دهد و رسانایی ترانس ماسفت و شیب زیرآستانه آن را کاهش می دهد.
در لایه وارونگی یک ماسفت، خم شدن باند قوی عمود بر کانال منجر به کوانتیزه شدن انرژی می شود . در حالی که انرژی لبه باند در امتداد کانال فقط کمی تغییر می کند، یک گرادیان قوی عمود بر کانال وجود دارد. حامل های وارونگی به یک چاه کوانتومی باریک در زیر دی الکتریک گیت محدود می شوند که به آن گاز الکترونی دو بعدی می گویند. این در شکل 2.5 نشان داده شده است ، جایی که غلظت حامل در کانال برای یک شبیه سازی کلاسیک با و بدون تصحیح کوانتومی نشان داده شده است.
|
اگر فرض شود که تابع موج حامل در دی الکتریک دروازه مسدود شده است - یعنی نفوذ تابع موج نادیده گرفته شده است - سطوح انرژی گسسته تشکیل می شوند [ 16 ]. حداکثر غلظت الکترون، مرکز بار، در رابط به دی الکتریک گیت قرار ندارد، اما همانطور که در قسمت سمت چپ شکل 2.6 نشان داده شده است، در داخل کانال شکل می گیرد . این اثر همانطور که در قسمت سمت راست شکل 2.6 نشان داده شده است به صورت کاهش جریان خروجی ظاهر می شود و می تواند تا حدی به عنوان یک تغییر ولتاژ آستانه مدل شود. علاوه بر این، ظرفیت گیت با این اثر کاهش می یابد.
|
مشکلات اضافی پوسته پوسته شدن دستگاه مربوط به اثرات حامل داغ است : هنگامی که حامل ها در یک ماسفت روشن از منبع به سمت تخلیه حرکت می کنند، سرعت و انرژی به دست می آورند. در نزدیکی زهکش دمای بالایی دارند که باعث افزایش تونل زنی نوار به باند، تونل زنی دی الکتریک دروازه و یونیزاسیون ضربه ای می شود (پدیده تونل زنی با حامل گرم در بخش 5.1.4 مجدداً منتشر خواهد شد.) حامل های اضافی ایجاد شده توسط این فرآیندها به جریان بستر و در نتیجه به نشتی دستگاه اضافه کنید. علاوه بر این، جریان تونل زنی الکترون داغ منجر به کاهش قابلیت اطمینان دی الکتریک گیت می شود.
Punchthrough یک مشکل جدی برای دستگاه های کوچک ایجاد می کند. زمانی اتفاق میافتد که یک مسیر کاذب بین منبع و تخلیه ماسفت خاموش در ناحیه تودهای شکل میگیرد که گیت کنترلی بر شارژ ندارد. این منجر به افزایش شدید جریان نشتی می شود. شکل 2.7 چگالی جریان را در ماسفت خاموش 90 نانومتری در = 0.0 ولت، = 1.2 ولت با چاه رتروگراد (چپ) و بدون (راست) نشان می دهد. به دلیل سوراخ شدن، چگالی جریان در دستگاه مناسب بسیار زیاد است. مشاهده می شود که جریان از کانال عبور نمی کند بلکه به عمق زیرلایه می رود. اقدامات انجام شده برای کاهش این اثر چاه های رتروگراد، ایمپلنت های هاله ای، یا ایمپلنت های جیبی است [ 17 ]. ![]()
![]()
برای دستگاه هایی با کانال های بسیار کوتاه، یک اثر اضافی رخ می دهد که منجر به افزایش جریان نشتی می شود. به دلیل فاصله کوتاه بین منبع و تخلیه، پتانسیل در کنتاکت تخلیه، مقدار پیک سد انرژی در کانال را کاهش می دهد. این در قسمت سمت چپ شکل 2.8 برای طول دروازه 250 نانومتر تا 50 نانومتر نشان داده شده است. مشاهده می شود که اوج سد انرژی در نزدیکی تماس منبع به شدت کاهش می یابد، اثری که به آن کاهش سد ناشی از تخلیه (DIBL) می گویند . این منجر به کاهش ولتاژ آستانه با کاهش طول کانال می شود. مقادیر حاصل از ولتاژ آستانه برای کاهش طول کانال، همانطور که در قسمت سمت راست شکل 2.8 نشان داده شده است ، به اصطلاح منحنی "roll-off" را نشان می دهد.
|
|
چندین موضوع را می توان شناسایی کرد که نشان دهنده نقص های شدید برای مقیاس بندی بیشتر دستگاه های CMOS است. شکل 2.4 برش یک اینورتر معمولی CMOS را نشان می دهد که از یک دستگاه nMOS و یک دستگاه pMOS تشکیل شده است که توسط جداسازی ترانشه کم عمق (STI) از هم جدا شده اند [ 14 ، 13 ]. موضوعات مهمی که باید در نظر گرفته شوند تا امکان انقباض بیشتر دستگاه وجود داشته باشد، برجسته شده اند [ 15 ]. در بخش های بعدی به اختصار مورد بحث قرار خواهند گرفت.
|
زیر بخش ها
ترانزیستور اثر میدانی (FET) اولین بار توسط L ILIENFELD در سال 1926 پیشنهاد شد و در سال 1930 به ثبت رسید [ 1 ]. با این حال، اجرای عملی به دلیل مشکلات مربوط به مواد غیرممکن بود. در 23 دسامبر 1947، B ARDEEN و B RATTAIN ، دانشمندان آزمایشگاه AT&T Bell که در گروه S HOCKLEY کار می کردند ، اثر ترانزیستور [ 2 , 3 , 4 ] را کشف کردند که برای آن جایزه N OBEL را در سال 1956 دریافت کردند. مدار مجتمع توسط K ILBY در Texas Instruments در سال 1959 نشان داده شد. در همان سال N OYCE و M OORE ![]() که با S HOCKLEY کار می کرد، شرکت Fairchild Semiconductor را تأسیس کرد، جایی که آنها اولین ترانزیستورهای نیمه هادی تجاری مورد استفاده را معرفی کردند . 2 . اولین ترانزیستور اثر میدانی مبتنی بر فناوری MOS توسط K AHNG و A TALLA در سال 1960 توسعه یافت [ 5 ]. M OORE ، N OYCE و G ROVE Fairchild Semiconductor را ترک کردند و شرکت اینتل را در سال 1968 تأسیس کردند. به زودی، این شرکت به تولید کننده پیشرو در ریزپردازنده ها تبدیل شد. در سال 1965، M OOREتخمین زد که تعداد ترانزیستورها در هر مدار مجتمع تقریباً هر سال دو برابر می شود، و او این را در سه اثر اصلی کمک کرد: بهبود در لیتوگرافی، افزایش اندازه تراشه، و سود حاصل از نوآوری در مدار و طراحی [6 ] . در سال 1975 او بیانیه خود را به روز کرد و پیش بینی کرد که تعداد ترانزیستورها هر هجده ماه تا دو سال دو برابر می شود [ 7 ]. این بیانیه به طور گسترده ای به عنوان قانون M OORE شناخته شد و در دهه های بعد به پارادایم اصلی صنعت میکروالکترونیک تبدیل شد.
که با S HOCKLEY کار می کرد، شرکت Fairchild Semiconductor را تأسیس کرد، جایی که آنها اولین ترانزیستورهای نیمه هادی تجاری مورد استفاده را معرفی کردند . 2 . اولین ترانزیستور اثر میدانی مبتنی بر فناوری MOS توسط K AHNG و A TALLA در سال 1960 توسعه یافت [ 5 ]. M OORE ، N OYCE و G ROVE Fairchild Semiconductor را ترک کردند و شرکت اینتل را در سال 1968 تأسیس کردند. به زودی، این شرکت به تولید کننده پیشرو در ریزپردازنده ها تبدیل شد. در سال 1965، M OOREتخمین زد که تعداد ترانزیستورها در هر مدار مجتمع تقریباً هر سال دو برابر می شود، و او این را در سه اثر اصلی کمک کرد: بهبود در لیتوگرافی، افزایش اندازه تراشه، و سود حاصل از نوآوری در مدار و طراحی [6 ] . در سال 1975 او بیانیه خود را به روز کرد و پیش بینی کرد که تعداد ترانزیستورها هر هجده ماه تا دو سال دو برابر می شود [ 7 ]. این بیانیه به طور گسترده ای به عنوان قانون M OORE شناخته شد و در دهه های بعد به پارادایم اصلی صنعت میکروالکترونیک تبدیل شد.
کاهش پیوسته ابعاد دستگاه ماسفت و چگالی ادغام یک مبنای نظری در سال 1974 پیدا کرد، زمانی که D ENNARD قانون مقیاس بندی میدان ثابت را ارائه کرد [ 8] .] که بر اساس آن می توان ابعاد دستگاه را بدون تغییر مشخصات الکتریکی کاهش داد اگر همه ابعاد، ولتاژها و غلظت دوپینگ به گونه ای مقیاس شوند که میدان الکتریکی در دستگاه ثابت بماند. بنابراین، طول و ولتاژ با یک عامل کاهش می یابد ![]() ، در حالی که غلظت دوپینگ با همان عامل افزایش می یابد. این به صورت شماتیک در شکل 2.2 برای یک ضریب مقیاس
، در حالی که غلظت دوپینگ با همان عامل افزایش می یابد. این به صورت شماتیک در شکل 2.2 برای یک ضریب مقیاس ![]() [ 9 ] نشان داده شده است. B ACCARANI و همکاران. یک قانون مقیاس بندی تعمیم یافته [ 10 ] ارائه کرد که در نظر می گیرد که ولتاژها را نمی توان با همان فاکتور طول کاهش داد. در عوض، اگر ولتاژها با ضریب
[ 9 ] نشان داده شده است. B ACCARANI و همکاران. یک قانون مقیاس بندی تعمیم یافته [ 10 ] ارائه کرد که در نظر می گیرد که ولتاژها را نمی توان با همان فاکتور طول کاهش داد. در عوض، اگر ولتاژها با ضریب ![]() و طول ها با ضریب مقیاس شوند
و طول ها با ضریب مقیاس شوند![]() ، غلظت دوپینگ باید بر اساس مقیاس شود
، غلظت دوپینگ باید بر اساس مقیاس شود ![]() .
.
|
در سال 1992، انجمن صنایع نیمه هادی (SIA) نقشه راه فناوری ملی برای نیمه هادی ها (NTRS) را منتشر کرد که بعداً با نقشه راه فناوری بین المللی برای نیمه هادی ها (ITRS) جایگزین شد. این سند نشان دهنده تلاش مشترک برای شناسایی موضوعات مهم در توسعه نیمه هادی است. هر دو سال یک بار، پیشبینیهای جامع پارامترهای تکنولوژیکی اصلی فناوری نیمهرسانا منتشر میشود.
دو مورد از مهمترین پارامترها برای تعیین کمیت مقیاس دستگاه عبارتند از: DRAM (حافظه با دسترسی تصادفی دینامیکی) نیم گام و MPU (واحد ریزپردازنده) نیم گام، که به عنوان نیمی از فاصله دو خط فلزی متصل تعریف شده است. پارامتر مهم دیگر طول دروازه ماسفت ها است که باید بین طول گیت چاپی و فیزیکی تمایز قائل شد. جدول ![]() 2.1 پیش بینی های نسخه 2001 ITRS [ 11 ] را در مقایسه با مقادیر نسخه 1999 و 1997 نشان می دهد.
2.1 پیش بینی های نسخه 2001 ITRS [ 11 ] را در مقایسه با مقادیر نسخه 1999 و 1997 نشان می دهد.
| ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
مشاهده میشود که پیشبینیهای هر نقشه راه از پیشبینیهای قبلی فراتر میرود، مشاهدهای که شتاب نقشه راه نامیده میشود: در حالی که در سال 1997 نیمپیچ DRAM 70 نانومتری برای سال 2009 پیشبینی شده بود، برای سال 2008 در سال 1999 پیشبینی شد. و نقشه راه 2001 آن را در سال 2006 می بیند.
|
این مقیاس گذاری مداوم منجر به توسعه ترانزیستورهایی با طول گیت به کوچکی 60 نانومتر یا حتی 10 نانومتر در دستگاه های آزمایشی شده است، همانطور که در شکل 2.3 نشان داده شده است [ 12 ، 13 ] . با این حال، هنگامی که دستگاهها تا این اندازه کوچک مقیاس شوند، موانع بزرگی به وجود میآیند.
سوئیچ ها بلوک های اصلی هر پیاده سازی منطق سخت افزاری هستند. کامپیوتر به معنای امروزی 2 . 1با استفاده از کلیدهای مکانیکی و بعدی الکترومکانیکی ساخته شده اند. کاستی های اصلی این گونه قطعات سرعت کم و مصرف برق زیاد آنهاست. لوله های خلاء، که سوئیچ هایی بدون قطعات متحرک هستند، به عنوان جایگزین استفاده شده اند، اما از قابلیت اطمینان ضعیف رنج می برند. اختراع سوئیچ های نیمه هادی یک جایگزین سریع و قابل اعتماد ارائه کرد. ترانزیستورهای دوقطبی سرعت سوئیچینگ بالا و تقویت زیاد را امکان پذیر می کنند، با این حال، جریان جریان در تماس پایه باید حفظ شود تا کلید باز بماند. در ترانزیستورهای اثر میدانی فلز-اکسید-نیمه هادی جریان جریان توسط یک ولتاژ کنترل می شود. در حالت ایده آل، هیچ برقی برای کنترل حالت روشن و خاموش مورد نیاز نیست. فناوری MOS مکمل مبتنی بر ترانزیستورهای نوع مکمل است که در آن جریان فقط در طول فرآیند سوئیچینگ جریان دارد. این دستگاهها اجرای منطق سختافزاری را با قدرت آماده به کار بسیار کم، سرعت بالا و ردپای کوچک امکانپذیر میسازند. شکل. 2.1 یک طرح شماتیک و یک طرح ساده از یک اینورتر CMOS را نشان می دهد، که نیروی کار همه رایانه های مدرن است. یک دستگاه MOS نوع n (nMOS) و یک دستگاه MOS نوع p (pMOS) بر روی یک ویفر دوپ شده p ساخته میشوند و دستگاه pMOS در یک چاه دوپ شده n تعبیه شده است. ردپای این سازه ها بسیار کوچک است و امکان تراکم یکپارچه سازی بالایی را فراهم می کند.
|
زیر بخش ها
افزایش تقاضا برای قدرت محاسباتی بالاتر، ابعاد کوچکتر و مصرف انرژی کمتر دستگاه های الکترونیکی منجر به نیاز مبرم به کاهش مقیاس اجزای نیمه هادی می شود. این فرآیند قبلاً منجر به مقیاسهای طولی شده است که در آن ویژگیهای دستگاه الکتریکی تحت تأثیر اثرات مکانیکی کوانتومی است. یکی از جالبترین این اثرات، تونلزنی مکانیکی کوانتومی حاملهای بار در مناطق کلاسیک ممنوع است.
این اثر برای بسیاری از جنبه های فناوری میکروالکترونیک مهم است. از یک طرف، جریان های تونل زنی در سلول های حافظه غیر فرار مانند EEPROM (حافظه فقط خواندنی قابل برنامه ریزی با قابلیت پاک شدن الکتریکی) یا دستگاه های Flash برای انتقال شارژ به یک دروازه شناور ایزوله با اعمال ولتاژهای بالا در یک کنتاکت کوپل شده خازنی مورد استفاده قرار می گیرند. از طرف دیگر، جریان های تونل زنی انگلی از طریق دی الکتریک دروازه فوق نازک باعث افزایش مصرف انرژی ترانزیستورهای MOS با عمق زیر میکرون (فلز-اکسید-نیمه هادی) می شود. سلولهای DRAM (حافظه دسترسی تصادفی پویا) و SRAM شبه غیرفرار (حافظه با دسترسی تصادفی استاتیک) به دلیل نشت از طریق جداسازی گره حافظه، زمانهای ماندگاری کمتری دارند. دیودهای تونل زنی رزونانس بر اساس مکانیسم تونل زنی برای دستیابی به مقاومت تفاضلی منفی هستند.
بنابراین لازم است اثرات تونل زنی در طراحی دستگاه های نیمه هادی در نظر گرفته شود. این را می توان با استفاده از شبیه سازی عددی به دست آورد. در زمینه میکروالکترونیک، اصطلاح TCAD (تکنولوژی طراحی به کمک کامپیوتر) برای توصیف شبیهسازی عددی فرآیند تولید نیمهرسانا و پیشبینی ویژگیهای الکتریکی دستگاههای حاصل استفاده میشود. فصل 2 اصول فناوری CMOS (MOS مکمل) معاصر را تشریح میکند، مروری مختصر در مورد موضوعات مهمی که در مقیاسبندی دستگاه با آن مواجه میشوند، ارائه میکند و سلسله مراتب رویکردهای شبیهسازی TCAD را تشریح میکند.
چندین مدل با پیچیدگی و دقت متفاوت را می توان برای توصیف چگالی جریان تونل در دستگاه های نیمه هادی به دست آورد. مدلها به دو کمیت مرکزی، یعنی تابع عرضه، که عرضه الکترونهای موجود را توصیف میکند، و ضریب انتقال، که احتمال عبور یک الکترون از مانع را توصیف میکند، بستگی دارند. تابع عرضه توسط توزیع انرژی الکترون ها تعیین می شود. در حالت تعادل، این توزیع را می توان با توزیع ian M AXWELL تقریب زد .
با این حال، میدان الکتریکی در دستگاههای کوچک شده آنقدر زیاد است که مدلهای غیر M AXWELL باید برای توصیف دقیق شکل تابع توزیع و بهویژه شکل دم پرانرژی توزیع در نظر گرفته شوند.
برای محاسبه ضریب انتقال یک لایه دی الکتریک، معادله S CHRÖDINGER باید حل شود. یکی از متداولترین روشها، تقریب W ENTZEL -K RAMERS -B RILLOUIN (WKB) است که با این حال، نوسانات ضریب انتقال را همانطور که در دیالکتریکهای دروازه نازک مشاهده میشود، بازتولید نمیکند. برای توصیف دقیق تونل زدن از طریق پشته های دی الکتریک، لازم است اثرات تداخل تابع موج را حل کنیم. این را می توان با استفاده از روش ماتریس انتقال با قطعات پتانسیل ثابت یا خطی به دست آورد. با این حال، این روش از نظر عددی فقط برای ضخامت لایه تا چند نانومتر پایدار است. بنابراین به سختی برای شبیه سازی بالا قابل استفاده است.![]() پشته های دی الکتریک، که ممکن است ضخامت آنها تا 10 نانومتر باشد. یک رویکرد امیدوارکننده تر، روش مرزی انتقال کوانتومی است که امکان ارزیابی پایدار و قابل اعتماد ضریب انتقال را فراهم می کند.
پشته های دی الکتریک، که ممکن است ضخامت آنها تا 10 نانومتر باشد. یک رویکرد امیدوارکننده تر، روش مرزی انتقال کوانتومی است که امکان ارزیابی پایدار و قابل اعتماد ضریب انتقال را فراهم می کند.
بر خلاف فرض در مدل های ایده آل، لایه های دی الکتریک عایق ایده آل نیستند. ناشی از تنش الکتریکی یا شرایط پردازش، نقص هایی در دی الکتریک ایجاد می شود که باعث ایجاد تونل به کمک تله می شود. این منجر به افزایش جریان تونل زنی در بایاس کم می شود که به آن SILC (جریان نشتی ناشی از استرس) می گویند. فرآیند تونل زنی به کمک تله توسط انتقال غیرکشسان حامل ها که توسط انتشار فونون ها پشتیبانی می شود ایجاد می شود. از آنجایی که این یک فرآیند گذرا است، لازم است ایجاد و نابودی تله ها در دی الکتریک بر اساس معادله سرعت تله ها در نظر گرفته شود.
همه این اثرات در فصل 3 مورد بحث قرار گرفته است که به بررسی نظریه تونل زنی در نیمه هادی ها می پردازد. این شامل مدلسازی تابع عرضه، ضریب انتقال و تونلسازی به کمک تله است.
شبیهسازهای دستگاه مدرن بستههای نرمافزاری پیچیدهای هستند و ادغام رابطها برای اجازه دادن به تونلسازی حاملهای شارژ بین مکانهای دلخواه در یک دستگاه، کار سادهای نیست. فصل 4 شرح کوتاهی از شبیه ساز دستگاه M INIMOS- NT ارائه می دهد و اجرای مدل های تونل زنی را خلاصه می کند. علاوه بر این، حل کننده S CHRÖDINGER که برای محاسبه ضریب انتقال استفاده می شود به طور خلاصه ترسیم شده است.
در فصل 5 چندین برنامه کاربردی ارائه شده است. M INIMOS- NT برای شبیهسازی جریانهای نشتی گیت در خازنهای MOS و MOSFET (ترانزیستورهای اثر میدانی MOS) استفاده میشود. تاکید بر مدلسازی مسیرهای تونلزنی مختلف در ترانزیستورهای MOS و ارزیابی ![]() مواد جایگزین با دیالکتریک بالا است. علاوه بر این، چندین دستگاه NVM (حافظه غیر فرار) مانند دستگاههای EEPROM، دیالکتریک غنی از تله، یا دستگاههای مبتنی بر تونل زنی چند مانع بررسی میشوند.
مواد جایگزین با دیالکتریک بالا است. علاوه بر این، چندین دستگاه NVM (حافظه غیر فرار) مانند دستگاههای EEPROM، دیالکتریک غنی از تله، یا دستگاههای مبتنی بر تونل زنی چند مانع بررسی میشوند.
در نهایت، فصل ششم به اختصار پایان نامه را با چند نتیجه گیری خلاصه می کند.
| ... | ثابت P LANCK | ||
| ... | ثابت P LANCK را کاهش داد | ||
| ... | ثابت B OLTZMANN | ||
| ... | شارژ ابتدایی | ||
| ... | جرم سکون الکترون | ||
| ... | ثابت دی الکتریک | ||
| ... |
| سمبل | واحد | شرح | ||
| 1 | کشیدگی الکترون | |||
| 1 | کشیدگی الکترون در حجم | |||
| eV | میل الکترونی در نیمه هادی | |||
| m | ضریب انتشار الکترون | |||
| m | ضریب انتشار سوراخ | |||
| Vm | میدان الکتریکی | |||
| Vm | میدان الکتریکی در دی الکتریک | |||
| eV | انرژی | |||
| eV | انرژی F ERMI | |||
| eV | انرژی لبه نوار هدایت | |||
| eV | انرژی لبه باند ظرفیت | |||
| eV | انرژی لبه نوار رسانایی در مورد باند تخت | |||
| eV | انرژی لبه باند ظرفیت در مورد باند تخت | |||
| eV | انرژی شکاف باند | |||
| eV | انرژی ذاتی | |||
| eV | انرژی تصحیح نیروی تصویر | |||
| eV | جزء انرژی در جهت تونل زنی | |||
| eV | جزء انرژی عمود بر جهت تونل زنی | |||
| eV | ارزش ویژه انرژی | |||
| eV | بخشی خیالی از ارزش ویژه انرژی | |||
| eV | بخش واقعی ارزش ویژه انرژی | |||
| eV | سطح انرژی را در زیر نوار هدایت دی الکتریک به دام بیندازید | |||
| eV | به دام انداختن انرژی | |||
| V | پتانسیل الکترواستاتیک | |||
| V | پتانسیل سطحی | |||
| V | پتانسیل F ERMI | |||
| eV | ارتفاع مانع | |||
| eV | عملکرد کار | |||
| eV | عملکرد کار نیمه هادی | |||
| eV | عملکرد کار فلز | |||
| eV | تفاوت عملکرد کار بین فلز و نیمه هادی | |||
| eV | لبه بالایی یک مانع انرژی مثلثی شکل | |||
| eV | لبه پایینی یک مانع انرژی مثلثی شکل | |||
| eV | سد انرژی الکترونی | |||
| eV | مانع انرژی سوراخ | |||
| 1 | توزیع فونون ها در انرژی | |||
| 1 | اشغال تله | |||
| m | تراکم حالت ها | |||
| eV | انرژی فونون | |||
| صبح | چگالی جریان |
| سمبل | واحد | شرح | ||
| صبح | چگالی جریان الکترون | |||
| صبح | چگالی جریان سوراخ | |||
| متر | عدد موج | |||
| متر | بردار عدد موج | |||
| متر | جزء عددی موج در جهت تونل زنی | |||
| متر | جزء عددی موج عمود بر جهت تونل زنی | |||
| متر | شعاع کره F ERMI | |||
| AsV | گذردهی دی الکتریک | |||
| AsV | گذردهی دی الکتریک لایه دی الکتریک | |||
| AsV | گذردهی دی الکتریک در سیلیکون | |||
| AsV | گذردهی دی الکتریک در دی اکسید سیلیکون | |||
| AsV | ||||
| m | تحرک الکترون | |||
| m | تحرک سوراخ | |||
| m | تحرک شار انرژی | |||
| کیلوگرم | جرم | |||
| کیلوگرم | جرم حامل در دی الکتریک | |||
| کیلوگرم | جرم موثر حامل در نیمه هادی | |||
| متر | غلظت الکترون | |||
| متر | غلظت ذاتی | |||
| eV | عملکرد تامین | |||
| متر | تمرکز اهداکنندگان | |||
| متر | تمرکز پذیرندگان | |||
| متر | غلظت مواد ناخالص در پلی سیلیکون | |||
| متر | چگالی موثر حالت های نوار هدایت | |||
| متر | تله تمرکز | |||
| متر | غلظت سوراخ | |||
| 1 | تعداد فونون ها | |||
| متر | تابع موج | |||
| مانند | وضعیت شارژ دام | |||
| متر | وکتور فضا | |||
| 1 | چگالی احتمالی | |||
| s | نرخ خالص نوترکیبی | |||
| 1 | ضریب بازتاب | |||
| m | دوره نوترکیبی اضافی به دلیل جریان تونل سازی | |||
| J m | چگالی شار انرژی الکترون | |||
| 1 | فاکتور H UANG -R HYS | |||
| س | زمان | |||
| س | زمان آرامش انرژی | |||
| س | زمان آرامش تکانه | |||
| س | زمان استراحت شار انرژی | |||
| س | زمان استراحت کورتوز |
| سمبل | واحد | شرح | ||
| س | طول عمر یک حالت شبه محدود | |||
| س | زمان ضبط | |||
| س | زمان انتشار | |||
| س | ضبط زمان به آند | |||
| س | ضبط زمان به کاتد | |||
| س | زمان انتشار به آند | |||
| س | زمان انتشار به کاتد | |||
| متر | ضخامت دی الکتریک | |||
| متر | ضخامت | |||
| متر | ضخامت | |||
| ک | درجه حرارت | |||
| ک | دمای شبکه | |||
| ک | دمای الکترون | |||
| 1 | ضریب انتقال | |||
| اماس | سرعت | |||
| اماس | بردار سرعت | |||
| اماس | جزء سرعت در جهت تونل زنی | |||
| اماس | مولفه سرعت عمود بر جهت تونل زنی | |||
| V | افت ولتاژ در پلی سیلیکون | |||
| V | ولتاژ منبع دروازه | |||
| V | ولتاژ منبع تخلیه | |||
| V | کنترل ولتاژ گیت | |||
| V | ولتاژ دروازه شناور | |||
| V | افت ولتاژ در دی الکتریک | |||
| جیم | انتگرال همپوشانی | |||
| eV | انرژی پتانسیل | |||
| m | نرخ ضبط | |||
| m | میزان انتشار | |||
| متر | طول سمت مکعب را تله کنید |
| ... | اسکالر | |
| ... | مزدوج پیچیده از | |
| ... | بردار | |
| ... | ماتریس | |
| ... | عناصر ماتریس | |
| ... | ماتریس انتقال مزدوج: | |
| ... | بردار وحدت در جهت x | |
| ... | محصول اسکالر (در) | |
| ... | مشتق جزئی نسبت به | |
| ... | اپراتور نابله | |
| ... | گرادیان از | |
| ... | واگرایی از | |
| ... | اپراتور L APLACE | |
| ... | تابع گاما | |
| ... | تابع گاما ناقص | |
| ... | میانگین آماری | |
| ... | تابع توزیع | |
| ... | اپراتور برخورد | |
| ... | اپراتور H AMILTON ian | |
| ... | عملکرد G REEN | |
| ... | ماتریس وحدت | |
| ... | ماتریس انتقال | |
| ... | تعیین کننده یک ماتریس | |
| ... | F ERMI انتگرال نظم | |
| ... | A IRY کار می کند | |
| ... | مشتق توابع A IRY |
| nMOS | ... | MOS نوع n |
| pMOS | ... | MOS نوع p |
| BTE | ... | معادله حمل و نقل B OLTZMANN |
| CMOS | ... | MOS مکمل |
| CNT | ... | نانولوله کربنی |
| CSB | ... | مانع کرکره مرکزی |
| رزومه | ... | ظرفیت-ولتاژ |
| DIBL | ... | کاهش سد ناشی از زهکشی |
| DRAM | ... | رم دینامیک |
| بانک مرکزی اروپا | ... | الکترون از باند هدایت |
| EED | ... | توزیع انرژی الکترون |
| EEPROM | ... | حافظه فقط خواندنی قابل برنامه ریزی با قابلیت پاک کردن الکتریکی |
| EOT | ... | ضخامت اکسید موثر |
| EVB | ... | الکترون ها از باند ظرفیت |
| FET | ... | ترانزیستور اثر میدانی |
| FN | ... | F OWLER -N ORDHEIM |
| FWHM | ... | عرض کامل نصف حداکثر |
| HED | ... | توزیع انرژی حفره |
| HVB | ... | سوراخ هایی از نوار ظرفیت |
| ITRS | ... | نقشه راه فناوری بین المللی برای نیمه هادی ها |
| IV | ... | جریان-ولتاژ |
| LDD | ... | زهکش کمی دوپ شده |
| MOCVD | ... | رسوب بخار شیمیایی فلز آلی |
| MOS | ... | فلز-اکسید-نیمه هادی |
| MPU | ... | واحد ریزپردازنده |
| ماسفت | ... | ترانزیستور اثر میدانی MOS |
| NEGF | ... | تابع غیرتعادلی G REEN |
| NTRS | ... | نقشه راه فناوری ملی برای نیمه هادی ها |
| NVM | ... | حافظه غیر فرار |
| PIF | ... | پروفیل I ORMAT را تغییر می دهم |
| PLEDM | ... | حافظه دستگاه الکترون موضعی مسطح |
| PLEDTR | ... | ترانزیستور دستگاه الکترونی موضعی مسطح |
| QTBM | ... | روش مرز انتقال کوانتومی |
| QBS | ... | حالت شبه مقید |
| رم | ... | حافظه دسترسی تصادفی |
| RTA | ... | تقریب آرامش-زمان |
| SIA | ... | انجمن صنایع نیمه هادی |
| SILC | ... | جریان نشتی ناشی از استرس |
| SIMS | ... | طیف سنجی جرمی یون ثانویه |
| SOI | ... | سیلیکون روی عایق |
| SONOS | ... | سیلیکون-اکسید-نیترید-اکسید-سیلیکون |
| SRAM | ... | حافظه با دسترسی تصادفی استاتیک |
| STI | ... | جداسازی ترانشه کم عمق |
| TAT | ... | تونل سازی با کمک تله |
| TCAD | ... | فناوری طراحی به کمک کامپیوتر |
| TEM | ... | میکروسکوپ الکترونی عبوری |
| TM | ... | ماتریس انتقال |
| WKB | ... | W ENTZEL -K RAMERS -B RILLOUIN |
| WSS | ... | W AFER -S TATE S ERVER |
قبل از هر چیز میخواهم از پروفسور S IEGFRIED S ELBERHERR تشکر کنم که به من این فرصت را داد تا به گروه تحقیقاتیاش ملحق شوم، زیرساختهای عالی در مؤسسه میکروالکترونیک فراهم کرده است، و برای شبکه صنعتی قوی که به دانشجویانش اجازه میدهد تجربه بینالمللی کسب کنند.
من از پروفسور E MMERICH B ERTAGNOLLI ، که در واقع یکی از اولین کسانی بود که علاقه من به میکروالکترونیک را برانگیخت، تشکر می کنم که مایل بود در کمیته آزمون من خدمت کند. علاوه بر این، من به شدت مدیون پروفسور E RASMUS L ANGER ، رئیس مؤسسه میکروالکترونیک هستم، که رئیسی سختگیر اما بسیار همکاری و کمک کننده بود.
من از شانس همکاری نزدیک با دو مشاور بزرگ لذت بردم: پروفسور H ANS K OSINA و پروفسور T IBOR G RASSER . پروفسور K OSINA من را از همان اولین برخورد با دانش عمیق خود در مورد مدل سازی دستگاه های نیمه هادی و به طور کلی فیزیک تحت تأثیر قرار داد. روش واضح و قابل فهم او برای نوشتن حتی انتزاعی ترین و پیچیده ترین موضوعات، که گاهی اوقات فقط فضای محدود یک دستمال سفره را مصرف می کند، زمینه کار من را فراهم کرد.
پروفسور جی راسر ، رئیس M INIMOS-خدمه توسعه NT، خیلی زود مرا متقاعد کردند که برنامه نویسی صرفاً یک هنر نیست، بلکه یک هنر استادانه است. سبک کدنویسی مبتکرانه او و دانش صحیح او در مورد معماری نرم افزار الهام بخش من شد تا دانش خود را در این جهت بهبود بخشم.
R OBERT K LIMA من را در مؤسسه بوت استرپ کرد و او همیشه مایل بود در مورد موضوعات برنامه نویسی با من بحث کند. تصحیح متون او در مورد برنامه نویسی در C به من اجازه داد تا درک عمیق او از برنامه نویسی را به اشتراک بگذارم.
من همچنین مدیون S TEPHAN W AGNER ، یک متخصص واقعی C++ هستم، که جنبه های متعدد برنامه نویسی شی گرا را به من توضیح داد، به من در حل مشکلات کامپایل کمک کرد، و مرتباً کدم را بهبود بخشید.
من از M ARKUS G RITSCH که هم اتاقی بسیار دلپذیر و باهوشی بود سپاسگزارم. دانش جامع او در مورد سیستم حروفچینی L A T E X در موارد بی شماری به من کمک کرد. S ERGEY S MIRNOV دومین هم اتاقی من شد و بلافاصله با دانش قوی خود در فیزیک نیمه هادی ها و اشتیاق باورنکردنی اش برای کار مرا تحت تأثیر قرار داد. اخیراً، S TEPHAN H OLZER به دفتر ما پیوست و در آنجا به دلیل شیرینی های شکلاتی که توزیع می کرد بسیار محبوب شد.
K LAUS D RAGOSITS منبعی بی پایان از داستان های خنده دار در مورد انواع موضوعات بود، و من از او برای پشتیبانی مکرر و بحث در مورد شبیه سازی CV و مدل سازی مکانیکی کوانتومی تشکر می کنم. هم اتاقی او V ASSIL P ALANKOVSKI با ساعات کاری طولانی و فهرست انتشاراتش و با دانش جامعش در مورد دستگاه های دوقطبی مرا تحت تأثیر قرار داد. همچنین P ETER F LEISCHMANN را به یاد دارم که در سفر ما به ژاپن اطلاعات عمیقی در مورد فرهنگ ژاپن و جدول زمانی راه آهن به من داد. علاوه بر این، من از J ONG- M UN P ARK سپاسگزارمکه تجربه قوی خود را با بسته های شبیه سازی تجاری TCAD و T ESFAYE A YALEW برای بحث های متعدد در مورد دستگاه های پرقدرت به اشتراک گذاشت. R AINER S ABELKA ، J OHANNES C ERVENKA ، C HRISTIAN H ARLANDER ، E NZO U NGERSBÖCK ، و R OBERT E NTNER از شبکه و زیرساخت رایانه مراقبت کردند که می خواهم از آنها نیز تشکر کنم.
E WALD H ASLINGER ، M ANFred K ATTERBAUER ، و RENATE W INKLER کار پس زمینه ای را در موسسه ارائه کردند، که اغلب به طور کامل مورد ارزیابی قرار نمی گیرد. همه اعضای دیگر مؤسسه میکروالکترونیک برای کمک و فضای کاری محرکی که ایجاد می کنند سزاوار قدردانی هستند.
B YOUNG H O C HEONG از مؤسسه فناوری پیشرفته سامسونگ یک رهبر پروژه بسیار مهربان و صبور بود که من سالها در چندین موضوع با او همکاری کردم. او همچنین مرا با فرهنگ، عادات و غذاهای کره ای آشنا کرد که از این بابت بسیار سپاسگزارم.
F RANCISCO J IMÉNEZ- M OLINOS دو ماه بسیار پربار را در موسسه ما گذراند و من از او برای همکاری خوب در مورد مدل تونل زنی با کمک تله تشکر می کنم.
S TEFAN H ARASEK اطلاعاتی در مورد دنیای واقعی در اختیار من قرار داد.![]() مواد دی الکتریک و من از او برای اندازه گیری ها و بحث در مورد مکانیسم های تونل زنی به کمک تله تشکر می کنم.
مواد دی الکتریک و من از او برای اندازه گیری ها و بحث در مورد مکانیسم های تونل زنی به کمک تله تشکر می کنم.
H ELMUT P UCHNER کارآموزی در Cypress Semiconductor را در مدت زمان کوتاهی فعال کرد. او با دانش جامع خود در مورد دستگاه و فناوری فرآیند CMOS و سطح بالای حرفه ای خود مرا تحت تأثیر قرار داد.
مهمتر از هر حمایت دیگری، همسرم E LISABETH برای من عشق و درک فراهم کرد و به من احساسی نسبت به چیزهای واقعاً مهم در زندگی داد. در نهایت، هیچ یک از تحصیلات من بدون حمایت مداوم والدینم امکان پذیر نبود.
میکروالکترونیک به نقطه ای رسیده است که اثرات کوانتومی تأثیر عمده ای بر ویژگی های الکتریکی دستگاه های نیمه هادی دارد. یکی از مهمترین اثرات در این رژیم، تونل زدن کوانتومی مکانیکی حامل ها از طریق لایه های نازک دی الکتریک است. از یک طرف، این منجر به افزایش مصرف برق و در نتیجه محدود کردن ضخامت دی الکتریک دروازه می شود. از سوی دیگر، اثرات تونل زنی در دستگاه های حافظه غیر فرار برای انتقال بار به یک دروازه شناور ایزوله استفاده می شود.
جریان تونل زنی در اثر انتقال حامل ها از یک الکترود از طریق یک ناحیه ایزوله کلاسیک به الکترود دیگر ایجاد می شود. سه عامل اصلی بر این فرآیند تأثیر میگذارند: توزیع انرژی حامل در هر دو الکترود، ضریب انتقال مکانیکی کوانتومی سد انرژی بین الکترودها، و وجود تلهها در لایه عایق که ممکن است به فرآیند تونلزنی کمک کند.
توزیع انرژی حامل برای فرآیند تونل زنی اهمیت زیادی دارد. توزیع F ERMI -D IRAC یا M AXWELL -B OLTZMANN اغلب برای تقریب این توزیع استفاده می شود. با این حال، این عبارات فقط در حد تعادل معتبر هستند و توزیع حامل های داغ را توصیف نمی کنند. در این کار یک عبارت جایگزین برای تابع توزیع، که بر اساس غلظت حامل، دما، و کشیدگی است، استفاده شد. این توزیع تطابق خوبی با نتایج شبیهسازیها نشان میدهد و دم پر انرژی توزیع را با دقت بازتولید میکند. گرمکن M AXWELLتوزیع ian که فقط غلظت و دما الکترون را در نظر می گیرد، به طور کامل در بازتولید دم پرانرژی شکست خورده و چگالی جریان تونل زنی را بسیار بیش از حد تخمین می زند.
ضریب انتقال مکانیکی کوانتومی با حل معادله ثابت S CHRÖDINGER در منطقه در نظر گرفته شده برای تونل سازی محاسبه می شود. ضریب به شکل سد انرژی در لایه دی الکتریک بستگی دارد. دیالکتریکهایی که از یک لایه تشکیل شدهاند، یک تغییر پتانسیل خطی در سد ایجاد میکنند که نمودار نواری ذوزنقهای یا مثلثی را ایجاد میکند. مدل های تحلیلی را می توان برای محاسبه تقریبی ضریب انتقال در این موارد، بر اساس تقریب W ENTZEL -K RAMERS -B RILLOUIN یا بر اساس فرمول G UNDLACH استخراج کرد.
با این حال، با کاهش ابعاد دستگاه، دیالکتریک گیت در دستگاههای MOS باید بر این اساس مقیاسبندی شود که برای مواد معمول استفادهشده SiO ![]() ، منجر به چگالی جریان گیت غیرقابل تحملی میشود. برای غلبه بر این مشکل، پشته های دی الکتریک گیت شامل
، منجر به چگالی جریان گیت غیرقابل تحملی میشود. برای غلبه بر این مشکل، پشته های دی الکتریک گیت شامل ![]() دی الکتریک بالا پیشنهاد شده است.
دی الکتریک بالا پیشنهاد شده است.
در چنین پشته های دی الکتریک، پروفیل نواری شکل غیر خطی دارد و مدل های مبتنی بر موانع مثلثی یا ذوزنقه ای دیگر معتبر نیستند. در عوض، معادله S CHRODINGER باید با استفاده از ماتریس انتقال یا روش مرز ارسال کوانتومی حل شود. این روشها مورد مطالعه قرار گرفتهاند و روش مرزی انتقال کوانتومی به دلیل پایداری عددی بهتر و امکان اعمال آن در مسائل دو بعدی و سه بعدی برتری یافته است.
![]() دستگاه های حافظه غیر فرار برای نوشتن و پاک کردن چرخه ها در ولتاژ 8-12 ولت باید تحمل کنند . این تنش مکرر میدان زیاد باعث ایجاد نقص در دی الکتریک تونل زنی می شود که منجر به جریان تونل زنی به کمک تله در میدان های الکتریکی کم می شود. این تولید تله دلیل اصلی تخریب دستگاه در نظر گرفته می شود. در این کار، تونلسازی به کمک تله به عنوان یک فرآیند دو مرحلهای مدلسازی میشود که طی آن آرامش انرژی توسط انتشار فونون صورت میگیرد. اشغال تله در دی الکتریک با یک معادله نرخ وابسته به زمان توصیف می شود. برای حل این معادله از یک روش تکراری استفاده می شود.
دستگاه های حافظه غیر فرار برای نوشتن و پاک کردن چرخه ها در ولتاژ 8-12 ولت باید تحمل کنند . این تنش مکرر میدان زیاد باعث ایجاد نقص در دی الکتریک تونل زنی می شود که منجر به جریان تونل زنی به کمک تله در میدان های الکتریکی کم می شود. این تولید تله دلیل اصلی تخریب دستگاه در نظر گرفته می شود. در این کار، تونلسازی به کمک تله به عنوان یک فرآیند دو مرحلهای مدلسازی میشود که طی آن آرامش انرژی توسط انتشار فونون صورت میگیرد. اشغال تله در دی الکتریک با یک معادله نرخ وابسته به زمان توصیف می شود. برای حل این معادله از یک روش تکراری استفاده می شود.
مدلهایی برای توصیف فرآیندهای مشخص شده در شبیهساز دستگاه همه منظوره M INIMOS- NT پیادهسازی شدهاند . چندین برنامه مورد بررسی قرار می گیرند که در آن تمایز بین ترانزیستورهای MOS و دستگاه های حافظه غیر فرار ایجاد می شود. کاربرد مواد دی الکتریک جایگزین بررسی شده و به عنوان مثال، یک خازن MOS با ![]() دی الکتریک ZrO شبیه سازی شده و با اندازه گیری ها مقایسه می شود. دستگاههای حافظه غیرفرار مانند دستگاههای EEPROM معمولی، دستگاههای دی الکتریک غنی از تله، دستگاههای تونل زنی چند مانع، و دستگاههایی که از موانع تونل لایهای برای بهبود زمان نگهداری استفاده میکنند، مورد بررسی قرار میگیرند. با مدل های پیاده سازی شده، M INIMOS-NT را می توان برای ارزیابی جریان های تونل زنی در سازه های دستگاه با پیچیدگی دلخواه استفاده کرد.
دی الکتریک ZrO شبیه سازی شده و با اندازه گیری ها مقایسه می شود. دستگاههای حافظه غیرفرار مانند دستگاههای EEPROM معمولی، دستگاههای دی الکتریک غنی از تله، دستگاههای تونل زنی چند مانع، و دستگاههایی که از موانع تونل لایهای برای بهبود زمان نگهداری استفاده میکنند، مورد بررسی قرار میگیرند. با مدل های پیاده سازی شده، M INIMOS-NT را می توان برای ارزیابی جریان های تونل زنی در سازه های دستگاه با پیچیدگی دلخواه استفاده کرد.
MICROELECTRONICS به نقطه ای رسیده است که اثرات مکانیکی کوانتومی تأثیر قابل توجهی بر خواص الکتریکی دستگاه های نیمه هادی دارد. یکی از مهم ترین این اثرات، تونل زدن مکانیکی کوانتومی حامل های بار از طریق لایه هایی از دی الکتریک های نازک است. از یک طرف، این منجر به افزایش مصرف برق اجزای نیمه هادی می شود و در نتیجه ضخامت دی الکتریک گیت را محدود می کند. از سوی دیگر، اثرات تونل زنی در دستگاه های حافظه غیر فرار برای انتقال شارژ به یک گره ذخیره سازی ایزوله استفاده می شود.
اثر تونل بر اساس انتقال حامل های بار از یک الکترود از طریق یک منطقه عایق کلاسیک به الکترود دیگر است. این فرآیند تحت تأثیر سه عامل است: توزیع انرژی حاملهای بار در هر دو الکترود، ضریب انتقال مکانیکی کوانتومی سد انرژی، و هرگونه نقص در دی الکتریک که بر فرآیند تونلزنی تأثیر میگذارد.
توزیع انرژی حامل های بار در الکترودها برای جریان تونل اهمیت اساسی دارد. توزیع F ERMI -D IRAC یا M AXWELL -B OLTZMANN معمولاً در نظر گرفته می شود. با این حال، این توابع توزیع تنها در نزدیکی حالت تعادل معتبر هستند و نمی توانند رفتار حامل های بار داغ را توصیف کنند. در این کار از یک تابع توزیع جدید بر اساس غلظت، دما و کشش حامل های بار استفاده شده است. این تابع توزیع مطابقت خوبی با نتایج شبیهسازی مونت کارلو نشان میدهد و توزیع حاملهای بار پرانرژی را با دقت بالا بازتولید میکند. M AXWELL داغتوزیع تنها بر اساس غلظت حامل و دما نمی تواند توزیع حامل های پرانرژی را بازتولید کند و منجر به چگالی جریان تونل زنی بسیار زیاد می شود.
ضریب انتقال مکانیکی کوانتومی با حل معادله شرودینگر تعیین می شود و به شکل سد انرژی در دی الکتریک بستگی دارد. دی الکتریک های تک لایه یک تغییر پتانسیل خطی در مانع را نشان می دهند که منجر به نمودار نواری مثلثی یا ذوزنقه ای می شود. در این مورد می توان مدل های تحلیلی را برای محاسبه ضریب انتقال استخراج کرد که بر اساس تقریب W ENTZEL -K RAMERS -B RILLOUIN یا فرمول G UNDLACH هستند .
![]() با این حال، فرآیند کوچک سازی ثابت قطعات الکترونیکی منجر به کاهش ضخامت دی الکتریک دروازه در اجزای MOS می شود که منجر به جریان های نشتی غیرمجاز برای ماده SiO می شود که تقریباً به طور انحصاری استفاده می شود . دی الکتریک های لایه ای ساخته شده از مواد با ثابت دی الکتریک بالاتر به عنوان یک درمان پیشنهاد شده اند.
با این حال، فرآیند کوچک سازی ثابت قطعات الکترونیکی منجر به کاهش ضخامت دی الکتریک دروازه در اجزای MOS می شود که منجر به جریان های نشتی غیرمجاز برای ماده SiO می شود که تقریباً به طور انحصاری استفاده می شود . دی الکتریک های لایه ای ساخته شده از مواد با ثابت دی الکتریک بالاتر به عنوان یک درمان پیشنهاد شده اند.
در چنین دی الکتریک های لایه ای، نمودار نواری غیرخطی است و مدل های مبتنی بر یک سد انرژی مثلثی یا ذوزنقه ای دیگر معتبر نیستند. در عوض، معادله شرودینگر باید با استفاده از ماتریس انتقال یا روش مرز انتقال کوانتومی حل شود. این روشها مورد بررسی قرار گرفتند که به موجب آن روش مرز انتقال کوانتومی به دلیل پایداری عددی بالاتر و مناسب بودن برای مسائل چند بعدی سودمند بود.
اجزای حافظه غیر فرار باید حداکثر 10 ![]() فرآیند نوشتن و پاک کردن را بدون خطا در ولتاژهای 8-12 ولت انجام دهند. این تنش مکرر دی الکتریک منجر به تشکیل عیوب می شود که تونل زنی به کمک ناخالصی را در قدرت های میدان کم امکان پذیر می کند. این تولید ناخالصی یکی از دلایل اصلی تخریب خواص عایق دی الکتریک در نظر گرفته می شود. تونل زنی به کمک ناخالصی در این کار به عنوان یک فرآیند دو مرحله ای مدل سازی شده است که در آن انرژی از طریق انتشار فونون ها آزاد می شود. تراکم جمعیت نقص ها با یک معادله نرخ توصیف می شود. برای حل این معادله از مدل تکراری استفاده شده است.
فرآیند نوشتن و پاک کردن را بدون خطا در ولتاژهای 8-12 ولت انجام دهند. این تنش مکرر دی الکتریک منجر به تشکیل عیوب می شود که تونل زنی به کمک ناخالصی را در قدرت های میدان کم امکان پذیر می کند. این تولید ناخالصی یکی از دلایل اصلی تخریب خواص عایق دی الکتریک در نظر گرفته می شود. تونل زنی به کمک ناخالصی در این کار به عنوان یک فرآیند دو مرحله ای مدل سازی شده است که در آن انرژی از طریق انتشار فونون ها آزاد می شود. تراکم جمعیت نقص ها با یک معادله نرخ توصیف می شود. برای حل این معادله از مدل تکراری استفاده شده است.
مدل های توصیف شده در شبیه ساز مؤلفه M INIMOS- NT پیاده سازی شدند. کاربردهای متعددی برای تمایز بین ترانزیستورهای MOS و دستگاه های حافظه غیر فرار مورد مطالعه قرار گرفته است. کاربرد دی الکتریک های جایگزین بررسی و با اندازه گیری ها با استفاده از خازن MOS با ![]() دی الکتریک ZrO مقایسه شد. علاوه بر این، اجزای حافظه غیر فرار مانند EEPROM و ساختارهای جایگزین مورد بررسی قرار گرفتند. با کمک مدل های پیاده سازی شده می توان از M INIMOS- NT برای مدل سازی جریان تونل در هر جزء نیمه هادی استفاده کرد.
دی الکتریک ZrO مقایسه شد. علاوه بر این، اجزای حافظه غیر فرار مانند EEPROM و ساختارهای جایگزین مورد بررسی قرار گرفتند. با کمک مدل های پیاده سازی شده می توان از M INIMOS- NT برای مدل سازی جریان تونل در هر جزء نیمه هادی استفاده کرد.
پایان نامه شبیه سازی تونل زنی در دستگاه های نیمه هادی
ausgeführt zum Zwecke der Erlangung des akademischen Grades
eines Doktors der technischen Wissenschaften
eingereicht an der Technischen Universität Wien
Fakultät für Geektrotechdssenik /7 A-1180 Wien, Österreich
Matr . شماره 9525275 geboren am 5. فوریه 1975 در Mistelbach
Wien, im نوامبر 2003
راه عقل؟ خوب
بیان آن ساده و ساده است:
اشتباه
و خطا
و دوباره اشتباه
، اما کمتر
و کمتر
و کمتر
پیت هاین
https://www.iue.tuwien.ac.at/phd/gehring/diss.html
برای فرض یک چاه انرژی مثلثی، تابع موج تقریباً به صورت داده شده است (به بخش 3.6.1 مراجعه کنید ).
| (ج. 1 ) |
با
| (ج. 2 ) |
مربع تابع موج یک احتمال است، بنابراین نرمال سازی را می توان به صورت [ 156 ] نوشت.
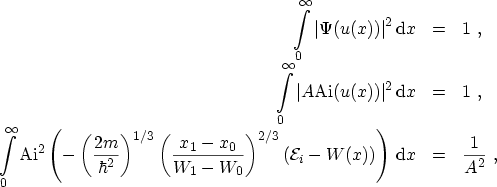 | (ج. 3 ) |
که در آن یک مانع بی نهایت برای ![]() . با
. با ![]() ،
، ![]() و میدان الکتریکی
و میدان الکتریکی
| (ج 4 ) |
انتگرال می شود
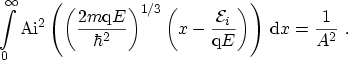 | (ج 5 ) |
جایگزین کردن
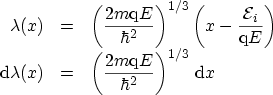 | (ج 6 ) |
بازده - محصول
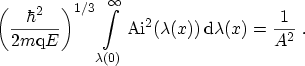 | (ج 7 ) |
با استفاده از عبارت [ 157 ]
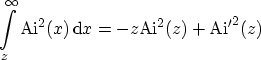 | (ج 8 ) |
و ثابت عادی سازی می شود ![]()
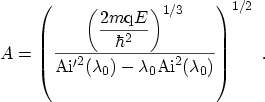 | (ج 9 ) |
در این پست سعی خواهم کرد دو روش محاسباتی را که معمولا برای تجزیه و تحلیل سیستم های کوانتومی استفاده می شود به خواننده آموزش دهم. این روش ها به روش تطبیق و روش مونت کارلو معروف هستند. این روش ها هر کدام مزایا و معایب خاص خود را در سناریوهای مختلف دارند، به همین دلیل است که معتقدم برای خواننده مفید است که هر دوی این روش ها را در کمربند ابزار خود داشته باشند.
اساس همه محاسبات ما در یک سیستم کوانتومی معمولاً بر اساس معادله شرودینگر مستقل از زمان است، بنابراین اجازه دهید ابتدا این معادله را تجزیه و تحلیل کنیم تا ببینیم چگونه می توان از آن در محاسبات استفاده کرد.
ما می توانیم مشتق جزئی دو تابع موج را به صورت تقریبی تقریبی کنیم:
اکنون که معادله ای برای مشتق جزئی دوگانه داریم، می توانیم آن را دوباره وارد معادله شرودینگر کرده و عبارت ها را به صورت زیر مرتب کنیم:
اکنون معادله ای داریم که به ما امکان می دهد هر تابع موجی را با توجه به انرژی و پتانسیل محاسبه کنیم.
روش تطبیق
اکنون که میتوانیم یک تابع موج را محاسبه کنیم، باید انرژیهای ویژه مرتبط با یک سیستم را پیدا کنیم تا حالت ویژه را تعیین کنیم. راه های متعددی برای انجام این کار وجود دارد، یکی از آن ها روش تطبیق است که به ویژه برای سیستم های پتانسیل نامتقارن مفید است. هدف تابع تطبیق ایجاد یک تابع موج صاف و پیوسته با ترکیب دو تابع موج است که از گوشه های چپ و راست آرایه پتانسیل تولید می شوند.
شکل (1) - روش تطبیق در داخل یک چاه مربع بی نهایت.
ورودی های تابع روش تطبیق عبارتند از حدس اولیه انرژی، آرایه پتانسیل، اندازه گام فضایی و یک نقطه نمایه سازی که برای بررسی شیب هر تابع موج از آن استفاده خواهیم کرد. برای محاسبه هر تابع موج، شرایط اولیه منحصر به فرد برای جواب های برابری زوج و فرد وجود دارد:
با استفاده از معادله 3 و شرایط اولیه، می توانیم تابع موج اول را با استفاده از حدس انرژی اولیه خود محاسبه کنیم. سپس، این فرآیند را با برگرداندن آرایه پتانسیل و ایجاد تابع موج دوم با همان شرایط اولیه تکرار می کنیم. سپس این تابع موج دوم را برمیگردانیم تا به طور موثر یک آرایه از چپ به راست و یک آرایه دوم از راست به چپ ایجاد کنیم. سپس هر تابع موج را در نقطه نمایه شده نرمال می کنیم تا آنها را قطع کنند.
اکنون ممکن است شیب هر تابع موج را در شاخص محاسبه کنیم. سپس یک تابع تطبیق ثانویه را فراخوانی می کنیم که جهت شیب ها را پیگیری می کند. اگر جهت گیری نسبی هر شیب ثابت باقی بماند، آنگاه مقدار «تغییر در انرژی» ما، که در ادامه اضافه خواهیم کرد، ثابت می ماند. اگر جهت گیری نسبی هر شیب تغییر کند، آنگاه مقدار «تغییر انرژی» ما نصف و نفی می شود. در هر صورت، مقدار «تغییر در انرژی» را به حدس اولیه انرژی اضافه میکنیم، توابع موج چپ و راست را دوباره محاسبه میکنیم و فرآیند را تکرار میکنیم.
این تابع به ما امکان می دهد حالت های ویژه را پیدا کنیم و انرژی های ویژه یک سیستم را بررسی کنیم. زمانی که به حد معینی رسیدیم، مقدار «تغییر انرژی» آنقدر کم خواهد بود که میتوانیم برنامه را متوقف کرده و دو تابع را در نقطه شاخص ادغام کنیم.
کاربردهای بسیار مفیدی از این روش وجود دارد که یکی از آنها نوسان ساز هارمونیک کوانتومی است. نوسان ساز هارمونیک کوانتومی یک آنالوگ مفید برای بسیاری از پتانسیل های دلخواه است که دارای نقاط تعادل پایدار هستند.
شکل (2) - بالا روش تطبیقی را نشان می دهد که روی 6 سطح انرژی اول یک نوسان ساز هارمونیک کوانتومی اجرا می شود. پایین نتیجه نهایی را نشان می دهد.
شکل (3) - توزیع احتمال 100 سطح انرژی در نتیجه روش تطبیق.
شکل (4) - یکی دیگر از پتانسیل های مفید برای مطالعه، پتانسیل لنارد جونز است. این پتانسیل برای مدل سازی نیروهای واندروالس بین اتم های بی اثر استفاده می شود.
روش مونت کارلو
یکی دیگر از روش های محاسباتی مفید، روش مونت کارلو است. به جای حدس زدن انرژی مانند روش تطبیق، در این روش تابع موج را حدس زده و بر اساس این حدس تکرار میکنیم. ایده روش مونت کارلو این است که ما به طور تصادفی یک سیستم را تغییر می دهیم و فقط تغییراتی را حفظ می کنیم که ما را به راه حلی که انتظارش را داریم نزدیکتر می کند. در مورد مکانیک کوانتومی، این برای تغییر تصادفی تابع موج و حفظ تغییراتی که انرژی سیستم را کاهش می دهد، استفاده می شود.
برای اجرای این رویکرد، ابتدا باید نحوه محاسبه انرژی را با استفاده از رابطه 4 زیر درک کنیم:
برای پیشفرم کردن این انتگرالها در فضای گسسته، میتوانیم از چندین روش مختلف استفاده کنیم، اما برای این فرآیند من از روش انتگرال ذوزنقهای استفاده کردم:
با اعمال این روش بر ضریب و مخرج معادله 4، معادلات زیر به دست می آید:
حال معادله 4 می شود:
اما اکنون در هر دو طرف معادله انرژی داریم. برای حل این مشکل، باید معادله شرودینگر مستقل از زمان (معادله 1) را جایگزین کنیم.
در نهایت برای خلاص شدن از مشتقات جزئی دوگانه، معادله 2 را جایگزین می کنیم و پیدا می کنیم:
این راه حل نهایی است که به ما امکان می دهد انرژی را در هر سیستمی با تابع موج و آرایه پتانسیل محاسبه کنیم.
اکنون که می توانیم انرژی را محاسبه کنیم، می توانیم از روش مونت کارلو استفاده کنیم. این روش در واقع بسیار ساده است. تابعی ایجاد می کنیم که تابع موج را به صورت دلخواه حدس می زند و انرژی این حدس را محاسبه می کند. سپس به طور تصادفی نقطه ای از تابع موج را انتخاب می کنیم و آن را به مقدار تصادفی تغییر می دهیم. سپس انرژی سیستم را دوباره محاسبه می کنیم و اگر انرژی کاهش یافته است، می توانیم آن تغییر تصادفی را حفظ کنیم، در غیر این صورت تغییر را کنار گذاشته و به تابع موج قبلی بر می گردیم. این فرآیند را بارها و بارها تکرار می کنیم تا به نقطه ای برسیم که پس از تعداد مشخصی تلاش، انرژی تغییر نکند. در این مرحله می توانیم فرض کنیم که به وضعیت پایه سیستم بالقوه خود رسیده ایم.
شکل (5) - روش مونت کارلو در چاه مربع بی نهایت. این انیمیشن بیش از 5 میلیون بار تکرار می شود.
شکل (6) - روش مونت کارلو در پتانسیل لنارد جونز. این انیمیشن بیش از 50 میلیون بار تکرار می شود.
معمولاً هنگام استفاده از روش مونت کارلو در یک سیستم پتانسیل جدید، تشخیص اینکه چه زمانی به حالت پایه رسیدهایم بسیار دشوار است، مگر اینکه واقعاً تکرارها را هنگام وقوع تماشا کنیم. همانطور که تابع موج شروع به تغییر کمتر و کمتر می کند، می توانیم فرض کنیم که به حالت پایه نزدیک می شویم. این هنوز یک فرآیند بسیار کند است و بسته به حدس اولیه تابع موج و اندازه گام تغییرات تصادفی شما، ممکن است زمانهای بسیار متفاوتی طول بکشد تا به حالت پایه برسد.
در حالی که روش مونت کارلو به طور قابل توجهی کندتر از روش تطبیق است، اما همچنان در یافتن انرژی حالت پایه یک سیستم دلخواه بسیار مفید است. ما معمولاً به شهود کمی نیاز داریم که هنگام حدس زدن تابع موج اولیه، حالت پایه چگونه به نظر می رسد. تا زمانی که روش مونت کارلو برای مدت زمان کافی اجرا شود، تابع به حالت پایه نزدیک می شود. یکی دیگر از نکات منفی روش مونت کارلو این است که فقط حالت پایه را جستجو می کند. با این حال، روش تطبیق در یافتن سطوح انرژی چندگانه مفید است. این روش در اطراف هر حالت ویژه طنین انداز خواهد شد تا زمانی که حدس انرژی اولیه و مقدار "تغییر انرژی" ما اجازه دهد. به طور کلی، هر دو عملکرد کاربردهای خود را دارند و می توانند در کنار هم بسیار مفید باشند.
به عنوان یک کنار، همچنین باید بگویم که هر دوی این روشها تنها زمانی مفید هستند که ما قبلاً نحوه توصیف پتانسیل یک سیستم را درک کرده باشیم و فقط به دنبال انرژیهای ویژه سیستم مذکور باشیم. در دنیای واقعی، اکثر محققان معمولاً از مشکل معکوس رنج می برند، که در آن ما انرژی های سیستم را می شناسیم اما باید از این اطلاعات برای ساختن پتانسیلی که با این انرژی ها منطبق است استفاده کنیم. اگرچه این روشها ممکن است برای آن محققان مفید نباشند، من هنوز فکر میکنم این روشها ارزشمند هستند، بهویژه برای دانشآموزانی که میخواهند سیستمهایی را مطالعه کنند که ممکن است از قبل بدانیم چگونه توصیف کنیم.
https://pages.vassar.edu/magnes/2019/05/10/computational-methods-in-quantum-mechanics/
https://www.physicsforums.com/threads/normalization-of-the-wave-function-for-the-electron-in-a-hydrogen-atom.993874/
 در این وبلاگ به ریاضیات و کاربردهای آن و تحقیقات در آنها پرداخته می شود. مطالب در این وبلاگ ترجمه سطحی و اولیه است و کامل نیست.در صورتی سوال یا نظری در زمینه ریاضیات دارید مطرح نمایید .در صورت امکان به آن می پردازم. من دوست دارم برای یافتن پاسخ به سوالات و حل پروژه های علمی با دیگران همکاری نمایم.در صورتی که شما هم بامن هم عقیده هستید با من تماس بگیرید.
در این وبلاگ به ریاضیات و کاربردهای آن و تحقیقات در آنها پرداخته می شود. مطالب در این وبلاگ ترجمه سطحی و اولیه است و کامل نیست.در صورتی سوال یا نظری در زمینه ریاضیات دارید مطرح نمایید .در صورت امکان به آن می پردازم. من دوست دارم برای یافتن پاسخ به سوالات و حل پروژه های علمی با دیگران همکاری نمایم.در صورتی که شما هم بامن هم عقیده هستید با من تماس بگیرید.