توسط علی رضا نقش نیلچی
| دوشنبه نهم آبان ۱۴۰۱ | 6:12
پس از جنگ [ ویرایش ]
در اکتبر 1947، بل X-1 اولین هواپیمایی بود که از سرعت صوت فراتر رفت. [21]
در سالهای 1948-1949، هواپیماها در طی محاصره برلین ، تدارکات را حمل کردند . انواع هواپیماهای جدید مانند B-52 در طول جنگ سرد تولید شدند .
اولین هواپیمای جت ، De Havilland Comet ، در سال 1952 معرفی شد و به دنبال آن توپولف Tu-104 شوروی در سال 1956 معرفی شد. بوئینگ 707 ، اولین جت تجاری بسیار موفق، برای بیش از 50 سال، از سال 1958 تا 1958 در خدمت تجاری بود. 2010. بوئینگ 747 از سال 1970 تا زمانی که ایرباس A380 در سال 2005 از آن پیشی گرفت، بزرگترین هواپیمای مسافربری جهان بود .
کلاس هواپیماهای بال ثابت [ ویرایش ]
هواپیما/هواپیما [ ویرایش ]
نوشتار اصلی: هواپیما

هواپیما در افغانستان روی زمین پارک شده است
هواپیما (همچنین به عنوان هواپیما یا به سادگی یک هواپیما نیز شناخته می شود ) یک هواپیمای بال ثابت نیرودار است که با رانش موتور جت یا ملخ به جلو رانده می شود. هواپیماها در اندازهها، شکلها و پیکربندیهای بالهای مختلف هستند. طیف وسیع استفاده از هواپیماها شامل تفریح، حمل و نقل کالا و افراد، نظامی و تحقیقاتی است.
هواپیمای دریایی [ ویرایش ]
نوشتار اصلی: هواپیمای دریایی
هواپیمای دریایی یک هواپیمای بال ثابت است که قادر به بلند شدن و فرود (فرود) روی آب است. هواپیماهای دریایی که می توانند از خشکی نیز کار کنند، زیر کلاسی به نام هواپیماهای دوزیستان هستند. گاهی اوقات به این هواپیماها هواپیماهای آبی می گفتند . [22] هواپیماهای دریایی و دوزیستان معمولاً بر اساس ویژگی های فنی خود به دو دسته تقسیم می شوند: هواپیماهای شناور و قایق های پرنده .
- یک هواپیمای شناور از نظر طراحی کلی شبیه به هواپیمای زمینی است و بدنه آن در مقایسه با هواپیمای زمینی آن به طور کلی تغییر نیافته است، با این تفاوت که چرخهای پایه زیرشاخه با شناورها جایگزین میشوند و به هواپیما اجازه میدهند تا از آب کار کند. از خشکی
- قایق پرنده یک هواپیمای دریایی با بدنه ای ضد آب است که قسمت های پایینی (شکمی) بدنه آن را تشکیل می دهد و مستقیماً روی سطح آب قرار می گیرد. این هواپیما با هواپیمای شناور متفاوت است زیرا برای شناوری نیازی به شناورهای اضافی ندارد، اگرچه ممکن است شناورهای کوچک زیر بال یا اسپون های روی بدنه برای تثبیت آن روی آب داشته باشد. هواپیماهای دریایی بزرگ معمولاً قایق های پرنده هستند، با اکثر طرح های کلاسیک هواپیماهای دوزیستانی از نوعی طراحی قایق پرنده برای بدنه/بدنه خود استفاده می کنند.
گلایدرهای قدرتمند [ ویرایش ]
بسیاری از اشکال گلایدر (به زیر مراجعه کنید) ممکن است با افزودن یک نیروگاه کوچک اصلاح شوند. این شامل:
وسیله نقلیه اثر زمینی [ ویرایش ]
مقاله اصلی: وسیله نقلیه اثر زمینی
وسیله نقلیه اثر زمینی (GEV) کشتیای است که در نزدیکی سطح زمین به پرواز در میآید و از اثر زمینی استفاده میکند - یک تعامل آیرودینامیکی بین بالها و سطح زمین. برخی از GEVها در صورت لزوم قادر به پرواز بالاتر از اثر زمینی (OGE) هستند - اینها به عنوان هواپیماهای بال ثابت نیرودار طبقه بندی می شوند. [23]

یک گلایدر (هواپیمای بادبانی) که با وینچ پرتاب می شود
نوشتار اصلی: گلایدر (هواپیما)
گلایدر کشتی سنگین تر از هوا است که در هنگام پرواز توسط واکنش دینامیکی هوا در برابر سطوح بالابر آن پشتیبانی می شود و پرواز آزاد آن به موتور بستگی ندارد. هواپیمای بادبانی یک گلایدر بال ثابت است که برای اوج گرفتن طراحی شده است - توانایی افزایش ارتفاع در جریان هوا و پرواز برای مدت طولانی.
گلایدرها عمدتاً برای تفریح مورد استفاده قرار می گیرند، اما برای اهداف دیگری مانند تحقیقات آیرودینامیک، جنگ و بازیابی فضاپیماها نیز استفاده شده است.
موتور گلایدر دارای موتوری برای افزایش عملکرد خود است و برخی موتورهای آنقدر قوی برای بلند شدن دارند، اما موتور در پروازهای معمولی استفاده نمی شود.
همانطور که در مورد هواپیماها وجود دارد، انواع مختلفی از گلایدرها وجود دارد که از نظر ساختار بال، کارایی آیرودینامیکی، مکان خلبان و کنترلها متفاوت هستند. شاید آشناترین نوع هواپیمای کاغذی اسباب بازی باشد .
گلایدرهای بزرگ معمولاً توسط هواپیمای یدککش یا وینچ پرتاب میشوند. از گلایدرهای نظامی در جنگ برای تحویل نیروهای تهاجمی و از گلایدرهای تخصصی در تحقیقات اتمسفر و آیرودینامیکی استفاده شده است. هواپیماهای راکتی و هواپیماهای فضایی نیز فرودهای بدون نیرو داشته اند.
گلایدرها و هواپیماهای بادبانی که برای ورزش گلایدینگ استفاده می شوند دارای راندمان آیرودینامیکی بالایی هستند. بالاترین نسبت بالابر به درگ 70:1 است، اگرچه 50:1 رایج تر است. پس از پرتاب، انرژی بیشتری از طریق بهره برداری ماهرانه از افزایش هوا در جو به دست می آید. پروازهای هزاران کیلومتری با سرعت متوسط بیش از 200 کیلومتر در ساعت انجام شده است.
پرشمارترین هواپیماهای بدون نیرو، هواپیماهای کاغذی هستند که نوعی گلایدر دست ساز هستند. مانند هنگ گلایدر و پاراگلایدر، آنها با پا پرتاب می شوند و به طور کلی کندتر، کوچکتر و ارزان تر از هواپیماهای بادبانی هستند. گلایدرهای آویزان اغلب دارای بالهای انعطافپذیر هستند که توسط یک قاب شکل میگیرند، اگرچه برخی بالهای سفت و سخت دارند. پاراگلایدرها و هواپیماهای کاغذی هیچ قاب در بال های خود ندارند.
گلایدرها و هواپیماهای بادبانی می توانند تعدادی ویژگی مشترک با هواپیماهای برقی داشته باشند، از جمله بسیاری از انواع مشابه بدنه و ساختار بال. برای مثال، Horten H.IV یک گلایدر بال پرنده بدون دم بود و مدارگرد شاتل فضایی به شکل بال دلتا بسیار شبیه یک گلایدر معمولی در پایین جو پرواز می کرد. بسیاری از گلایدرها نیز از کنترل ها و ابزارهای مشابه به عنوان کشتی های موتوردار استفاده می کنند.
انواع گلایدر [ ویرایش ]
0:21
(ویدئو) یک گلایدر بر فراز گونما ، ژاپن حرکت می کند
امروزه کاربرد اصلی هواپیماهای گلایدر ورزش و تفریح است.
هواپیمای بادبانی [ ویرایش ]
نوشتار اصلی: گلایدر (هواپیما)
گلایدرها از دهه 1920 برای اهداف تفریحی ساخته شدند. هنگامی که خلبانان شروع به درک نحوه استفاده از هوای بالارونده کردند، گلایدرهای هواپیمای بادبانی با نسبت بالابر به درگ بالا توسعه یافتند . اینها به سر خوردن های طولانی تری به منبع بعدی " بالابر " اجازه می دهد و بنابراین شانس آنها را برای پرواز در مسافت های طولانی افزایش می دهد. این باعث ایجاد ورزش محبوب گلایدر شد.
گلایدرهای اولیه عمدتاً از چوب و فلز ساخته می شدند، اما اکثر هواپیماهای بادبانی اکنون از مواد کامپوزیتی شامل الیاف شیشه، کربن یا آرامید استفاده می کنند. برای به حداقل رساندن درگ ، این تیپها دارای بدنه ساده و بالهای باریک بلند با نسبت تصویر بالا هستند . گلایدرهای تک سرنشین و دو سرنشینه در دسترس هستند.
در ابتدا آموزش توسط "هاپ" کوتاه در گلایدرهای اولیه انجام می شد که هواپیماهای بسیار ابتدایی و بدون کابین خلبان و ابزار حداقلی هستند. [24] از زمان کوتاهی پس از جنگ جهانی دوم ، آموزش همیشه در گلایدرهای کنترلی دو سرنشینه انجام می شود، اما از هواپیماهای دو سرنشینه با کارایی بالا نیز برای به اشتراک گذاشتن حجم کار و لذت بردن از پروازهای طولانی استفاده می شود. در ابتدا از اسکیت ها برای فرود استفاده می شد، اما اکثریت آنها اکنون روی چرخ هایی قرار می گیرند که اغلب قابل جمع شدن هستند. برخی از گلایدرها که به عنوان موتور گلایدر شناخته می شوند ، برای پرواز بدون نیرو طراحی شده اند، اما می توانند موتورهای پیستونی ، چرخشی ، جت یا الکتریکی را به کار گیرند . [25]گلایدرها توسط FAI برای مسابقات به کلاس های مسابقه گلایدر عمدتاً بر اساس دهانه و فلپ طبقه بندی می شوند.

فوق سبک "صندلی بادی" گلایدر بز 1
دسته ای از هواپیماهای بادبانی فوق سبک، از جمله برخی از آنها به عنوان گلایدر میکرولیفت و برخی به عنوان "صندلی بادی" شناخته می شوند، توسط FAI بر اساس حداکثر وزن تعریف شده اند. آنها به اندازه کافی سبک هستند تا به راحتی حمل شوند و در برخی کشورها می توان آنها را بدون مجوز پرواز کرد. گلایدرهای فوق سبک عملکردی مشابه گلایدرهای آویزان دارند ، اما ایمنی بیشتری را در هنگام تصادف ارائه می دهند، زیرا خلبان را می توان در یک صندلی عمودی در یک سازه قابل تغییر شکل بست. فرود معمولاً روی یک یا دو چرخ است که این کاردستی را از گلایدرهای آویزان متمایز می کند. چندین گلایدر فوق سبک تجاری آمده و رفته اند، اما بیشتر توسعه های فعلی توسط طراحان و سازندگان خانه انجام می شود.
گلایدرهای نظامی [ ویرایش ]

یک USAAF Waco CG-4 A 1943
گلایدرهای نظامی در طول جنگ جهانی دوم برای حمل نیرو ( پیاده نظام گلایدر ) و تجهیزات سنگین به مناطق جنگی مورد استفاده قرار گرفتند. گلایدرها توسط هواپیماهای ترابری نظامی، به عنوان مثال C-47 داکوتا ، یا توسط بمب افکن هایی که به فعالیت های ثانویه منتقل شده بودند، مانند شورت استرلینگ ، به هوا و بیشتر مسیر به سمت هدف خود کشیده می شدند.. پس از رها شدن از یدک کش در نزدیکی هدف، تا حد امکان نزدیک به هدف فرود آمدند. مزیت آن نسبت به چتربازان این بود که تجهیزات سنگین را میتوانستند فرود بیاورند و نیروها بهجای پراکنده شدن در یک منطقه به سرعت جمعآوری میشدند. گلایدرها به عنوان یک بار مصرف در نظر گرفته شدند، که منجر به ساخت و ساز از مواد معمول و ارزان قیمت مانند چوب شد، اگرچه تعداد کمی از آنها بازیابی و دوباره استفاده شد. در زمان جنگ کره ، هواپیماهای ترابری نیز بزرگتر و کارآمدتر شده بودند، به طوری که حتی تانکهای سبک را میتوان با چتر نجات انداخت و باعث از بین رفتن گلایدرها شد.
گلایدرهای تحقیقاتی [ ویرایش ]
حتی پس از توسعه هواپیماهای موتوری، گلایدرها همچنان برای تحقیقات هوانوردی مورد استفاده قرار می گرفتند . بال انعطاف پذیر Paresev Rogallo ناسا در ابتدا برای بررسی روش های جایگزین برای بازیابی فضاپیما ساخته شد. اگرچه این برنامه کنار گذاشته شد، اما تبلیغات الهام بخش علاقه مندان به تطبیق ایرفویل بال انعطاف پذیر برای گلایدرهای آویزان مدرن شد.
تحقیقات اولیه در مورد بسیاری از انواع هواپیماهای بال ثابت، از جمله بال های پرنده و بدنه های بالابر نیز با استفاده از نمونه های اولیه بدون نیرو انجام شد.
گلایدر آویزان [ ویرایش ]

پرواز آویزان
هنگ گلایدر هواپیمای گلایدری است که در آن خلبان در یک مهار آویزان شده از بدنه هواپیما قرار می گیرد و با تغییر وزن بدن در مقابل قاب کنترل، کنترل را اعمال می کند. اکثر هنگ گلایدرهای مدرن از آلیاژ آلومینیوم یا بال پارچه ای با قاب کامپوزیت ساخته می شوند. خلبانان این توانایی را دارند که ساعتها اوج بگیرند، هزاران متر ارتفاع را در جریانهای حرارتی بالا ببرند، ورزشهای هوازی انجام دهند و صدها کیلومتر را از روی کانتری سر بخورند.
پاراگلایدر [ ویرایش ]
پاراگلایدر یک هواپیمای گلایدر سبک وزن با پرواز آزاد و با پا و بدون ساختار اولیه سفت و سخت است. [26] خلبان در یک مهار آویزان شده در زیر یک بال پارچه توخالی که شکل آن توسط خطوط تعلیق آن، فشار هوای ورودی به دریچههای جلوی بال و نیروهای آیرودینامیکی هوا در خارج از آن شکل میگیرد، مینشیند. پاراگلایدر اغلب یک فعالیت تفریحی است.
گلایدرهای بدون سرنشین [ ویرایش ]
هواپیمای کاغذی یک هواپیمای اسباب بازی (معمولا یک گلایدر) است که از کاغذ یا مقوا ساخته شده است.
هواپیماهای مدل گلایدر مدل هایی از هواپیماهایی هستند که از مواد سبک وزن مانند پلی استایرن و چوب بالسا استفاده می کنند. طرحها از هواپیماهای گلایدر ساده تا مدلهای مقیاس دقیق را شامل میشود که برخی از آنها میتوانند بسیار بزرگ باشند.
بمبهای گلاید بمبهایی با سطوح آیرودینامیکی هستند که به جای پرواز بالستیک، مسیر پروازی را امکانپذیر میکنند. این امر هواپیمای حامل را قادر می سازد تا از فاصله دور به یک هدف با دفاع سنگین حمله کند.

بادبادک در حال پرواز
مقاله اصلی: بادبادک
بادبادک هواپیمای است که به یک نقطه ثابت بسته می شود تا باد از روی بال های آن می وزد. [27] بالابر زمانی ایجاد می شود که هوا بر روی بال بادبادک جریان می یابد و فشار کم در بالای بال و فشار زیاد در زیر آن ایجاد می شود و جریان هوا را به سمت پایین منحرف می کند. این انحراف همچنین باعث ایجاد کشش افقی در جهت باد می شود. بردار نیروی حاصل از اجزای نیروی بالابر و کشش با کشش یک یا چند خط طناب یا بند متصل به بال مخالف است.
بادبادک ها بیشتر برای اهداف تفریحی پرواز می کنند، اما کاربردهای بسیار دیگری نیز دارند. پیشگامان اولیه مانند برادران رایت و جی دبلیو دان گاهی اوقات یک هواپیما را به عنوان بادبادک پرواز می کردند تا آن را توسعه دهند و ویژگی های پروازی آن را تأیید کنند، قبل از اضافه کردن موتور و کنترل پرواز و پرواز با آن به عنوان یک هواپیما.
همچنین ببینید: بادبادک روتور
استفاده می کند [ ویرایش ]

بادبادک اژدهای چینی بیش از صد فوت طول دارد که در جشنواره بادبادک برکلی کالیفرنیا در سال 2000 پرواز کرد.
برنامه های نظامی [ ویرایش ]
بادبادکها برای سیگنالدهی، ارسال مهمات و رصد ، با بلند کردن ناظر از بالای میدان نبرد و با استفاده از عکسبرداری هوایی از بادبادک استفاده میشوند .
علم و هواشناسی [ ویرایش ]
بادبادک ها برای اهداف علمی مورد استفاده قرار گرفته اند، مانند آزمایش معروف بنجامین فرانکلین که ثابت کرد صاعقه الکتریسیته است . بادبادک ها پیش ساز هواپیماهای سنتی بودند و در توسعه هواپیماهای پرنده اولیه نقش مهمی داشتند. الکساندر گراهام بل مانند برادران رایت و لارنس هارگریو بادبادک های بسیار بزرگی را آزمایش کرد . بادبادک ها نقش تاریخی در بلند کردن ابزارهای علمی برای اندازه گیری شرایط جوی برای پیش بینی آب و هوا داشتند.
آنتن های رادیویی و چراغ های نور [ ویرایش ]
از بادبادک ها می توان برای حمل آنتن های رادیویی استفاده کرد. این روش برای ایستگاه دریافت اولین انتقال از اقیانوس اطلس توسط مارکونی استفاده شد . بالنهای اسیر ممکن است برای چنین آزمایشهایی راحتتر باشند، زیرا آنتنهای حمل بادبادک به باد زیادی نیاز دارند، که ممکن است همیشه با تجهیزات سنگین و هادی زمین امکانپذیر نباشد.
بادبادک ها را می توان برای حمل جلوه های نوری مانند چراغ های برقی یا چراغ های باتری دار استفاده کرد.
کشش بادبادک [ ویرایش ]

بادبادک کششی چهار خطی که معمولاً به عنوان منبع انرژی برای کایت موج سواری استفاده می شود
بادبادک ها را می توان برای کشیدن افراد و وسایل نقلیه به سمت باد استفاده کرد. بادبادک های کارآمد از نوع فویل مانند بادبادک های قدرتی نیز می توانند برای بادبانی در جهت باد با همان اصولی که توسط سایر کشتی های بادبانی استفاده می شود استفاده شوند، مشروط بر اینکه نیروهای جانبی روی زمین یا در آب مانند کیل ها، تخته های مرکزی، چرخ ها و چرخ ها هدایت شوند. تیغه های یخی کشتی های قایقرانی سنتی. در دو دهه اخیر، چندین ورزش بادبادکی مانند بادبادک باگینگ، کایت لندبوردینگ، کایت قایق و کایت موج سواری رایج شده اند. کیتینگ برفی نیز رایج شده است.
بادبادک بادبانی چندین امکان را میگشاید که در قایقرانی سنتی موجود نیست:
- سرعت باد در ارتفاعات بیشتر است
- بادبادک ها ممکن است به صورت دینامیکی مانور داده شوند که به طور چشمگیری نیروی موجود را افزایش می دهد
- نیازی به سازه های مکانیکی برای مقاومت در برابر نیروهای خمشی وجود ندارد. وسایل نقلیه یا بدنه ها می توانند بسیار سبک باشند یا به طور کلی از آنها صرف نظر شود
تولید برق [ ویرایش ]
همچنین ببینید: نردبان و نیروی باد در ارتفاع بالا
پروژههای تحقیق و توسعه مفهومی توسط بیش از صد شرکتکننده برای بررسی استفاده از بادبادکها در مهار جریانهای باد در ارتفاعات بالا برای تولید برق انجام میشود. [28]
کاربردهای فرهنگی [ ویرایش ]
جشنواره بادبادک ها یک نوع سرگرمی محبوب در سراسر جهان است. آنها شامل رویدادهای محلی، جشنواره های سنتی و جشنواره های بزرگ بین المللی می شوند.
طرح ها [ ویرایش ]

بادبادک دلتا (مثلثی شکل).

قطار بادبادک های متصل
انواع [ ویرایش ]
مقاله اصلی: انواع بادبادک
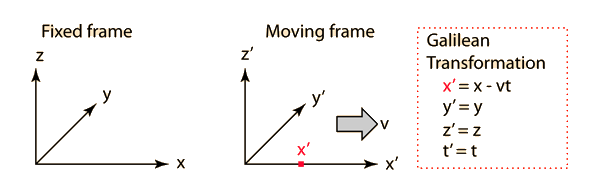
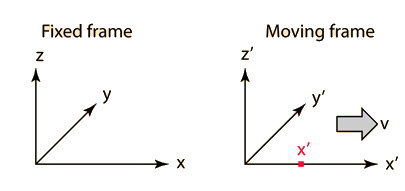
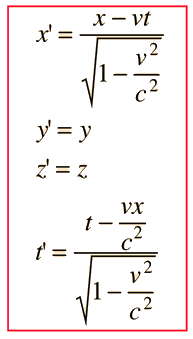
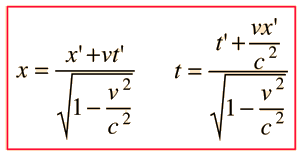
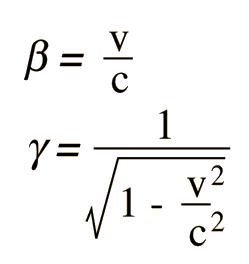

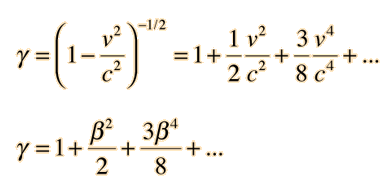
 در جدول بالا آورده شده است.
در جدول بالا آورده شده است. یک جبر فرعی یک پارامتری از سهمی های SO(0,1) ایجاد می کند.
یک جبر فرعی یک پارامتری از سهمی های SO(0,1) ایجاد می کند. یک جبر فرعی یک پارامتری از SO(1, 1) را ایجاد می کند.
یک جبر فرعی یک پارامتری از SO(1, 1) را ایجاد می کند. یک پارامتر چرخش SO(2) ایجاد می کند،
یک پارامتر چرخش SO(2) ایجاد می کند، (برای هرچی
(برای هرچی ) یک زیر جبر یک پارامتری از تبدیلات لوکسودرومی را ایجاد می کند.
) یک زیر جبر یک پارامتری از تبدیلات لوکسودرومی را ایجاد می کند. کلاس های مختلف بدهید.) جبرهای فرعی دو بعدی عبارتند از:
کلاس های مختلف بدهید.) جبرهای فرعی دو بعدی عبارتند از: ایجاد یک زیر جبر آبلی که تماماً از سهمیها تشکیل شده است،
ایجاد یک زیر جبر آبلی که تماماً از سهمیها تشکیل شده است، ایجاد یک جبر غیرآبلی هم شکل با جبر لی از
ایجاد یک جبر غیرآبلی هم شکل با جبر لی از  ایجاد یک جبر آبلی متشکل از تقویتها، چرخشها و لوکسودرومیکها که همگی یک جفت نقطه ثابت را به اشتراک میگذارند.
ایجاد یک جبر آبلی متشکل از تقویتها، چرخشها و لوکسودرومیکها که همگی یک جفت نقطه ثابت را به اشتراک میگذارند. ایجاد یک زیر جبر بیانچی V ، هم شکل با جبر لی Hom(2)، گروه همتاهای اقلیدسی ،
ایجاد یک زیر جبر بیانچی V ، هم شکل با جبر لی Hom(2)، گروه همتاهای اقلیدسی ، ایجاد یک زیر جبر بیانچی VII 0 ، هم شکل با جبر لی از E(2)،
ایجاد یک زیر جبر بیانچی VII 0 ، هم شکل با جبر لی از E(2)،  ، جایی که
، جایی که ایجاد یک زیر جبر بیانچی VIII ، هم شکل با جبر لی SL(2, R )، گروه ایزومتریک
ایجاد یک زیر جبر بیانچی VIII ، هم شکل با جبر لی SL(2, R )، گروه ایزومتریک  یک زیر جبر بیانچی IX ، هم شکل با جبر لی از SO(3)، گروه چرخش ایجاد کنید.
یک زیر جبر بیانچی IX ، هم شکل با جبر لی از SO(3)، گروه چرخش ایجاد کنید. ایجاد یک جبر فرعی هم شکل با جبر لی Sim(2)، گروه
ایجاد یک جبر فرعی هم شکل با جبر لی Sim(2)، گروه 


 ، مجهز به این انتخاب فرم درجه دوم است
، مجهز به این انتخاب فرم درجه دوم است .
.






![{\displaystyle {\begin{aligned}Q_{4}&={\begin{bmatrix}1+{\frac {1}{2}}\vert \alpha \vert ^{2}&\operatorname {Re} ( \alpha )&\operatorname {Im} (\alpha)&-{\frac {1}{2}}\vert \alpha \vert ^{2}\\\operatorname {Re} (\alpha)&1&0&-\operatorname {Re} (\alpha )\\-\operatorname {Im} (\alpha)&0&1&\operatorname {Im} (\alpha)\\{\frac {1}{2}}\vert \alpha \vert ^{2 }&\operatorname {Re} (\alpha)&\operatorname {Im} (\alpha)&1-{\frac {1}{2}}\vert \alpha \vert ^{2}\end{bmatrix}}\ \[6pt]&=\exp {\begin{bmatrix}0&\operatorname {Re} (\alpha )&\operatorname {Im} (\alpha)&0\\\operatorname {Re} (\alpha)&0&0&-\operatorname {Re} (\alpha)\\-\operatorname {Im} (\alpha)&0&0&\operatorname {Im} (\alpha)\\0&\operatorname {Re} (\alpha)&\operatorname {Im} (\alpha )&0\end{bmatrix}}~.\end{تراز شده}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/ccdadcadc9f056de764c57e9649d9e7d283c55eb)







 تحت ضریب داده شده برای فضاهای تصویری:
تحت ضریب داده شده برای فضاهای تصویری: اگر
اگر برای
برای . این به عنوان کره سماوی شناخته می شود زیرا به ما امکان می دهد مختصات زمانی را مجدداً اندازه گیری کنیم
. این به عنوان کره سماوی شناخته می شود زیرا به ما امکان می دهد مختصات زمانی را مجدداً اندازه گیری کنیم به 1 پس از عمل با استفاده از تبدیل لورنتس، اطمینان حاصل شود که قسمت فضا مانند روی کره واحد قرار می گیرد.
به 1 پس از عمل با استفاده از تبدیل لورنتس، اطمینان حاصل شود که قسمت فضا مانند روی کره واحد قرار می گیرد. در فضای پیچیده تصویری عمل می کند
در فضای پیچیده تصویری عمل می کند ، که می توان نشان داد که به کره 2 تفاوت دارد - گاهی اوقات به آن
، که می توان نشان داد که به کره 2 تفاوت دارد - گاهی اوقات به آن  هست یک
هست یک ماتریس هرمیتی از جاهای دیگر این مقاله می دانیم که این فضای ماتریس ها را می توان به صورت 4 بردار مشاهده کرد. فضای ماتریس هایی که از تبدیل هر بردار تصویری در کره ریمان به یک ماتریس به دست می آیند، به عنوان
ماتریس هرمیتی از جاهای دیگر این مقاله می دانیم که این فضای ماتریس ها را می توان به صورت 4 بردار مشاهده کرد. فضای ماتریس هایی که از تبدیل هر بردار تصویری در کره ریمان به یک ماتریس به دست می آیند، به عنوان  جزء
جزء 



 عبارتند از:
عبارتند از:  ، با توجه به
، با توجه به 



 بر روی فضای ماتریس های هرمیتی از طریق
بر روی فضای ماتریس های هرمیتی از طریق
 انتقال
انتقال  . این عمل تعیین کننده را حفظ می کند و بنابراین SL(2, C ) بر روی فضازمان مینکوفسکی توسط ایزومتریک (خطی) عمل می کند. شکل برابری معکوس در بالا است
. این عمل تعیین کننده را حفظ می کند و بنابراین SL(2, C ) بر روی فضازمان مینکوفسکی توسط ایزومتریک (خطی) عمل می کند. شکل برابری معکوس در بالا است


 این دو پوشش متمایز با دو عمل
این دو پوشش متمایز با دو عمل  در حالی که شکل روی خط مربوط به اسپینورهای چپ دست است که به عنوان تبدیل می شوند
در حالی که شکل روی خط مربوط به اسپینورهای چپ دست است که به عنوان تبدیل می شوند
 مانند
مانند بنابراین ماتریس را با شاخص های فضازمان نشان می دهد
بنابراین ماتریس را با شاخص های فضازمان نشان می دهد یک چهار بردار را می توان از ماتریس های پائولی به دو روش مختلف ایجاد کرد: به عنوان
یک چهار بردار را می توان از ماتریس های پائولی به دو روش مختلف ایجاد کرد: به عنوان و به عنوان
و به عنوان این دو شکل با
این دو شکل با 
 پوشش دوگانه گروه لورنتز متعامد توسط
پوشش دوگانه گروه لورنتز متعامد توسط
 این شکل می گیرد
این شکل می گیرد

 وقتی به شکل نمایه شده نوشته می شود، تشخیص آن دشوار است. تبدیل های لورنتس تحت تبدیل های لورنتس تانسور نیستند ! بنابراین اثبات مستقیم این هویت برای اثبات درستی آن مفید است. با شروع از هویت می توان آن را نشان داد
وقتی به شکل نمایه شده نوشته می شود، تشخیص آن دشوار است. تبدیل های لورنتس تحت تبدیل های لورنتس تانسور نیستند ! بنابراین اثبات مستقیم این هویت برای اثبات درستی آن مفید است. با شروع از هویت می توان آن را نشان داد
 به طوری که موارد فوق فقط ماتریس های معمولی پائولی هستند و
به طوری که موارد فوق فقط ماتریس های معمولی پائولی هستند و انتقال ماتریس است، و
انتقال ماتریس است، و صرف پیچیده است ماتریکس
صرف پیچیده است ماتریکس است
است


 یعنی فرم را تحت تبدیل های لورنتس ثابت بگذاریم. این ممکن است به صورت زیر بیان شود. گروه سمپلتیک به این صورت تعریف می شود
یعنی فرم را تحت تبدیل های لورنتس ثابت بگذاریم. این ممکن است به صورت زیر بیان شود. گروه سمپلتیک به این صورت تعریف می شود
 برای این عنصر؛ گاهی
برای این عنصر؛ گاهی استفاده می شود، اما این باعث سردرگمی با ایده
استفاده می شود، اما این باعث سردرگمی با ایده 


 و غیره
و غیره


 تانسور
تانسور  مثل قبل.
مثل قبل.

 (فضای برداری مجهز به این فرم درجه دوم گاهی نوشته می شود
(فضای برداری مجهز به این فرم درجه دوم گاهی نوشته می شود

 موقعیت ذره ای که x 0 در زمان t نشان داده شده است.
موقعیت ذره ای که x 0 در زمان t نشان داده شده است. زیرا هر دو طرف سرعت ذره ای را که x 0 نشان داده شده در زمان t توصیف می کنند.
زیرا هر دو طرف سرعت ذره ای را که x 0 نشان داده شده در زمان t توصیف می کنند. که در آن ∇ عملگر
که در آن ∇ عملگر 









 تبدیلات ناهمسانگرد
تبدیلات ناهمسانگرد تبدیل های هم زمان
تبدیل های هم زمان تحولات اقلیدسی فضایی
تحولات اقلیدسی فضایی تبدیلهای ویژه یکنواخت / تبدیلهای همگن، تبدیلهای هم شکل به اقلیدسی.
تبدیلهای ویژه یکنواخت / تبدیلهای همگن، تبدیلهای هم شکل به اقلیدسی. تغییرات مبدأ / ترجمه در فضازمان نیوتنی.
تغییرات مبدأ / ترجمه در فضازمان نیوتنی. چرخش (قاب مرجع) (به
چرخش (قاب مرجع) (به  حرکات یکنواخت قاب / تقویت.
حرکات یکنواخت قاب / تقویت. ) از گروه ها مورد نیاز است.
) از گروه ها مورد نیاز است. (
( 



![[H,P_{i}]=0](https://wikimedia.org/api/rest_v1/media/math/render/svg/62b718a50d9bbc524206f938d4094000fdd5f02a)
![[P_{i}،P_{j}]=0](https://wikimedia.org/api/rest_v1/media/math/render/svg/98fc7c4a468ce7fa72d4ce1a447632324337ff52)
![[L_{{ij}}،H]=0](https://wikimedia.org/api/rest_v1/media/math/render/svg/01b7aa61bc2856d4e3cfc6ce5f3d72564535f1f5)
![[C_{i}،C_{j}]=0](https://wikimedia.org/api/rest_v1/media/math/render/svg/ade86ef409f8f767be149b605b2a76127684a3dc)
![[L_{{ij}}،L_{{kl}}]=i[\delta _{{ik}}L_{{jl}}-\delta _{{il}}L_{{jk}}-\delta _{{jk}}L_{{il}}+\delta _{{jl}}L_{{ik}}]](https://wikimedia.org/api/rest_v1/media/math/render/svg/285a4d16555cfca4c80d963f36f2925c64d7037d)
![[L_{{ij}}،P_{k}]=i[\delta _{{ik}}P_{j}-\delta _{{jk}}P_{i}]](https://wikimedia.org/api/rest_v1/media/math/render/svg/7337d08fee8d9be08a2969bb16b578504d9182b1)
![[L_{{ij}}،C_{k}]=i[\delta _{{ik}}C_{j}-\delta _{{jk}}C_{i}]](https://wikimedia.org/api/rest_v1/media/math/render/svg/61e8488de4717b3e616094f5b8b3d8ab464aa502)
![[C_i,H]=i P_i \,\!](https://wikimedia.org/api/rest_v1/media/math/render/svg/ca5972e950d30691dba2fafc2e58977300b6ad69)
![[C_i,P_j]=0 ~.](https://wikimedia.org/api/rest_v1/media/math/render/svg/2c57b7e93beefa09f215b05f16f8f2a309ba7775)





![{\displaystyle [C'_{i},P'_{j}]=iM\delta _{ij}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/564a2c4dc04101feac5a35d8633bfd432d5bf059) ، به طوری که
، به طوری که ![[H',P'_i]=0 \,\!](https://wikimedia.org/api/rest_v1/media/math/render/svg/c5de574832089c79e6f579c52ef4de1f1f950c13)
![[P'_i,P'_j]=0 \,\!](https://wikimedia.org/api/rest_v1/media/math/render/svg/8e56cbe7fc5ad8aaa4b5e99bd208e961edcbb242)
![[L'_{ij},H']=0 \,\!](https://wikimedia.org/api/rest_v1/media/math/render/svg/334b98de717fad3a286c171163b52e65222e72a5)
![[C'_i,C'_j]=0 \,\!](https://wikimedia.org/api/rest_v1/media/math/render/svg/7c93f26d28dda58f1c60e3938f66753530cd0fec)
![[L'_{ij},L'_{kl}]=i [\delta_{ik}L'_{jl}-\delta_{il}L'_{jk}-\delta_{jk}L'_ {il}+\delta_{jl}L'_{ik}] \,\!](https://wikimedia.org/api/rest_v1/media/math/render/svg/627522438a338d0623fe653177fbf778892aa7d3)
![[L'_{ij},P'_k]=i[\delta_{ik}P'_j-\delta_{jk}P'_i] \,\!](https://wikimedia.org/api/rest_v1/media/math/render/svg/bc33032edd56c7309ae548c711c86071e157dc0b)
![[L'_{ij},C'_k]=i[\delta_{ik}C'_j-\delta_{jk}C'_i] \,\!](https://wikimedia.org/api/rest_v1/media/math/render/svg/8f774a5b5348649053a05ecb9349301f2f659c5e)
![[C'_i,H']=i P'_i \,\!](https://wikimedia.org/api/rest_v1/media/math/render/svg/eaa99e5eac46bb60b94276b49313baea2e8dabc3)
![[C'_i,P'_j]=i M\delta_{ij} ~.](https://wikimedia.org/api/rest_v1/media/math/render/svg/235c0adc062f85c03c8d1263d159233b1c483f23)
 نشان می دهد. این بسط و
نشان می دهد. این بسط و 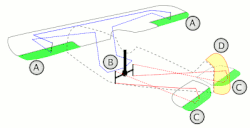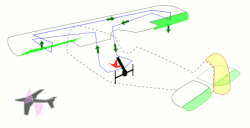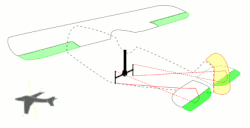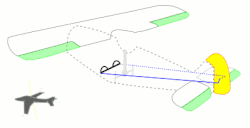






 یک سیستم مختصات در U است، سپس هر فیلد برداری e j را می توان به صورت ترکیبی خطی از فیلدهای برداری مختصات بیان کرد.
یک سیستم مختصات در U است، سپس هر فیلد برداری e j را می توان به صورت ترکیبی خطی از فیلدهای برداری مختصات بیان کرد. :
: جایی که هر کدام
جایی که هر کدام تابعی در U است. اینها را می توان به عنوان اجزای یک ماتریس دید
تابعی در U است. اینها را می توان به عنوان اجزای یک ماتریس دید . همانطور که در بخش بعدی توضیح داده شد، این ماتریس برای یافتن بیان مختصات همفریم دوگانه مفید است.
. همانطور که در بخش بعدی توضیح داده شد، این ماتریس برای یافتن بیان مختصات همفریم دوگانه مفید است. :
: جایی که هر کدام
جایی که هر کدام یک تابع در U. از آنجا که
یک تابع در U. از آنجا که  ، دو عبارت مختصات بالا با هم ترکیب می شوند و به دست می آیند
، دو عبارت مختصات بالا با هم ترکیب می شوند و به دست می آیند ; از نظر ماتریس، این فقط این را می گوید
; از نظر ماتریس، این فقط این را می گوید

 (لغزش کناری)، r (سرعت انحراف) و p (نرخ چرخش)، با گشتاورهای N (انحراف) و L (لغزش)، و نیروی Y (به طرفین). 9 مشتق پایداری مربوط به این حرکت وجود دارد که در زیر نحوه ایجاد آنها توضیح داده شده است. با این حال، با بازی کردن با هواپیمای مدل، و در نظر گرفتن اینکه چگونه نیروهای وارد بر هر جزء تحت تأثیر تغییرات در لغزش کناری و سرعت زاویهای قرار میگیرند، میتوان درک شهودی بهتری به دست آورد:
(لغزش کناری)، r (سرعت انحراف) و p (نرخ چرخش)، با گشتاورهای N (انحراف) و L (لغزش)، و نیروی Y (به طرفین). 9 مشتق پایداری مربوط به این حرکت وجود دارد که در زیر نحوه ایجاد آنها توضیح داده شده است. با این حال، با بازی کردن با هواپیمای مدل، و در نظر گرفتن اینکه چگونه نیروهای وارد بر هر جزء تحت تأثیر تغییرات در لغزش کناری و سرعت زاویهای قرار میگیرند، میتوان درک شهودی بهتری به دست آورد: 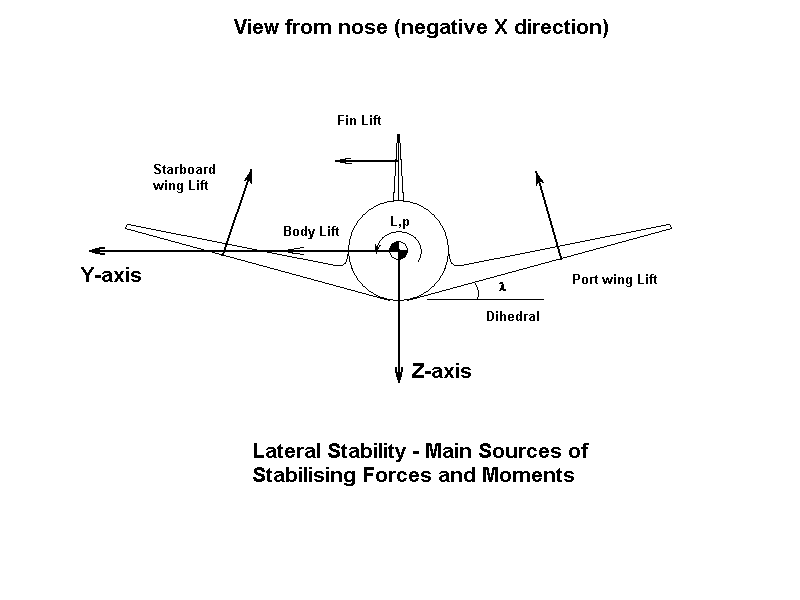
 نیروی جانبی ناشی از لغزش جانبی (در صورت عدم انحراف).
نیروی جانبی ناشی از لغزش جانبی (در صورت عدم انحراف). نیروی جانبی ناشی از سرعت چرخش.
نیروی جانبی ناشی از سرعت چرخش. نیروی جانبی ناشی از سرعت انحراف.
نیروی جانبی ناشی از سرعت انحراف. لحظه خمیازه کشیدن به دلیل نیروهای لغزش کناری.
لحظه خمیازه کشیدن به دلیل نیروهای لغزش کناری. لحظه خمیازه کشیدن به دلیل نرخ چرخش.
لحظه خمیازه کشیدن به دلیل نرخ چرخش. لحظه خمیازه به دلیل نرخ انحراف.
لحظه خمیازه به دلیل نرخ انحراف. لحظه چرخش به دلیل لغزش کناری.
لحظه چرخش به دلیل لغزش کناری.
 لحظه چرخش به دلیل نرخ انحراف.
لحظه چرخش به دلیل نرخ انحراف. لحظه چرخش به دلیل نرخ رول.
لحظه چرخش به دلیل نرخ رول.
 (اوه)
(اوه) (رول)
(رول)


 (phi) توسط:
(phi) توسط:
 (میرایی)
(میرایی) (سفتی، سختی)
(سفتی، سختی) مثبت خواهد بود زیرا
مثبت خواهد بود زیرا
 (
(  (psi). معادله نیروی حرکت شامل یک جزء وزن است: [
(psi). معادله نیروی حرکت شامل یک جزء وزن است: [ 

 (اوه)
(اوه) (رول)
(رول)


 (هر دو محصول مثبت هستند). این در تضاد مستقیم با الزامات پایداری رول هلندی است، و طراحی هواپیمایی که هر دو حالت رول هلندی و مارپیچی ذاتاً پایدار باشند، دشوار است. [
(هر دو محصول مثبت هستند). این در تضاد مستقیم با الزامات پایداری رول هلندی است، و طراحی هواپیمایی که هر دو حالت رول هلندی و مارپیچی ذاتاً پایدار باشند، دشوار است. [  (گاما) و سرعت. معادلات اغتشاش کوچک حرکت عبارتند از:
(گاما) و سرعت. معادلات اغتشاش کوچک حرکت عبارتند از:

 و
و باید در نظر گرفته شود.
باید در نظر گرفته شود.



 چگالی هوا است،
چگالی هوا است، مساحت بال، W وزن و
مساحت بال، W وزن و ضریب افزایش است (ثابت فرض می شود زیرا بروز ثابت است)، تقریباً داریم:
ضریب افزایش است (ثابت فرض می شود زیرا بروز ثابت است)، تقریباً داریم:











 (تتا) و بروز
(تتا) و بروز (آلفا). جهت بردار سرعت نسبت به محورهای اینرسی است
(آلفا). جهت بردار سرعت نسبت به محورهای اینرسی است . بردار سرعت:
. بردار سرعت: 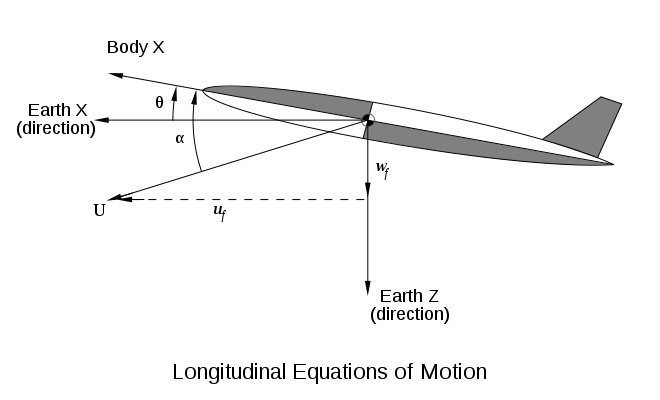


 ،
، مولفه های محورهای اینرسی سرعت هستند. طبق
مولفه های محورهای اینرسی سرعت هستند. طبق 

 در طول دوره نوسان ناچیز است، بنابراین:
در طول دوره نوسان ناچیز است، بنابراین:




 ، نرخ زمین. بنابراین، معادلات حرکت با تمام نیروها و گشتاورهای محور باد عبارتند از:
، نرخ زمین. بنابراین، معادلات حرکت با تمام نیروها و گشتاورهای محور باد عبارتند از:

 بالا بردن به دلیل وقوع، این منفی است زیرا محور z رو به پایین است در حالی که برخورد مثبت باعث نیروی رو به بالا می شود.
بالا بردن به دلیل وقوع، این منفی است زیرا محور z رو به پایین است در حالی که برخورد مثبت باعث نیروی رو به بالا می شود. لیفت به دلیل نرخ گام، از افزایش بروز دم ناشی می شود، از این رو نیز منفی است، اما در مقایسه با
لیفت به دلیل نرخ گام، از افزایش بروز دم ناشی می شود، از این رو نیز منفی است، اما در مقایسه با
 لحظه شیب به دلیل نرخ زمین - اصطلاح میرایی زمین، این همیشه منفی است.
لحظه شیب به دلیل نرخ زمین - اصطلاح میرایی زمین، این همیشه منفی است.



 در مقایسه با وحدت کوچک باشد، بنابراین ضریب
در مقایسه با وحدت کوچک باشد، بنابراین ضریب . این عبارت تحت سلطه است
. این عبارت تحت سلطه است






 تفاوت فشار استاتیک و فشار جریان آزاد
تفاوت فشار استاتیک و فشار جریان آزاد بردار نرمال بیرونی عنصر مساحت
بردار نرمال بیرونی عنصر مساحت بردار تنش مماسی که توسط هوا روی بدن اعمال می شود
بردار تنش مماسی که توسط هوا روی بدن اعمال می شود سطح مرجع مناسب
سطح مرجع مناسب
 بکشید
بکشید نیروی جانبی
نیروی جانبی بلند کردن
بلند کردن



![\ equiv C_{d}={\dfrac {D}{qS}}=-{\dfrac {1}{S}}\int _{\Sigma }[(-C_{p}){\mathbf {n} }\bullet {\mathbf {i_{w}}}+C_{f}{\mathbf {t}}\bullet {\mathbf {i_{w}}}]\,d\sigma](https://wikimedia.org/api/rest_v1/media/math/render/svg/b16598ab4310bdfb79e62c3b3ffa8fb3d7356bea)
![\ equiv C_{Q}={\dfrac {Q}{qS}}=-{\dfrac {1}{S}}\int _{\Sigma }[(-C_{p}){\mathbf {n} }\bullet {\mathbf {j_{w}}}+C_{f}{\mathbf {t}}\bullet {\mathbf {j_{w}}}]\,d\sigma](https://wikimedia.org/api/rest_v1/media/math/render/svg/058ae7bf706024c1943fc8d36eb6ca9a35653039)
![\ equiv C_{L}={\dfrac {L}{qS}}=-{\dfrac {1}{S}}\int _{\Sigma }[(-C_{p}){\mathbf {n} }\bullet {\mathbf {k_{w}}}+C_{f}{\mathbf {t}}\bullet {\mathbf {k_{w}}}]\,d\sigma](https://wikimedia.org/api/rest_v1/media/math/render/svg/a92e802e0eb8cad0e69f7849d35e2b6dbec96a1b)



 سرعت
سرعت 














 نقطه در نظر گرفته سطح
نقطه در نظر گرفته سطح
 معادله ضریب درگ
معادله ضریب درگ










































 در این وبلاگ به ریاضیات و کاربردهای آن و تحقیقات در آنها پرداخته می شود. مطالب در این وبلاگ ترجمه سطحی و اولیه است و کامل نیست.در صورتی سوال یا نظری در زمینه ریاضیات دارید مطرح نمایید .در صورت امکان به آن می پردازم. من دوست دارم برای یافتن پاسخ به سوالات و حل پروژه های علمی با دیگران همکاری نمایم.در صورتی که شما هم بامن هم عقیده هستید با من تماس بگیرید.
در این وبلاگ به ریاضیات و کاربردهای آن و تحقیقات در آنها پرداخته می شود. مطالب در این وبلاگ ترجمه سطحی و اولیه است و کامل نیست.در صورتی سوال یا نظری در زمینه ریاضیات دارید مطرح نمایید .در صورت امکان به آن می پردازم. من دوست دارم برای یافتن پاسخ به سوالات و حل پروژه های علمی با دیگران همکاری نمایم.در صورتی که شما هم بامن هم عقیده هستید با من تماس بگیرید.