از ویکی پدیا، دانشنامه آزاد
"پتانسیل گرانش" به اینجا هدایت می شود. برای پتانسیل گرانشی زمین، پتانسیل ژئوپتانسیل را ببینید . برای میدان پتانسیل های گرانشی، میدان گرانشی را ببینید .
در مکانیک کلاسیک ، پتانسیل گرانشی یک پتانسیل اسکالر است که با هر نقطه در فضا، کار ( انرژی منتقل شده) در واحد جرم را که برای حرکت یک جسم به آن نقطه از یک نقطه مرجع ثابت در میدان گرانشی محافظه کار لازم است، مرتبط می کند . مشابه پتانسیل الکتریکی با جرمی است که نقش بار را ایفا می کند . نقطه مرجع، که در آن پتانسیل صفر است، طبق قرارداد بی نهایت از هر جرمی دور است، که در نتیجه در هر فاصله محدود ، پتانسیل منفی ایجاد می شود . شباهت آنها با هر دو زمینه مرتبط با نیروهای محافظه کار مرتبط است .
از نظر ریاضی، پتانسیل گرانشی به عنوان پتانسیل نیوتنی نیز شناخته می شود و در مطالعه نظریه پتانسیل اساسی است . همچنین ممکن است برای حل میدان های الکترواستاتیک و مغناطیس استاتیک تولید شده توسط اجسام بیضی دارای بار یکنواخت یا قطبی شده استفاده شود. [ 1 ]
انرژی بالقوه
[ ویرایش ]
مقاله اصلی: انرژی پتانسیل گرانشی
پتانسیل گرانشی ( V ) در یک مکان، انرژی پتانسیل گرانشی ( U ) در آن مکان در واحد جرم است:
که در آن m جرم جسم است. انرژی بالقوه برابر (از نظر بزرگی، اما منفی) با کاری است که میدان گرانشی جسم را از بی نهایت به موقعیت معین خود در فضا می برد. اگر جرم جسم 1 کیلوگرم باشد، انرژی پتانسیلی که باید به آن جسم نسبت داده شود برابر با پتانسیل گرانشی است. بنابراین پتانسیل را می توان به عنوان منفی کار انجام شده توسط میدان گرانشی که یک واحد جرم را از بی نهایت به داخل منتقل می کند تفسیر کرد.
در برخی شرایط، معادلات را می توان با فرض میدانی که تقریباً مستقل از موقعیت است، ساده کرد. به عنوان مثال ، در ناحیه ای نزدیک به سطح زمین، شتاب گرانشی g را می توان ثابت در نظر گرفت. در آن صورت، تفاوت انرژی پتانسیل از یک ارتفاع به ارتفاع دیگر، به یک تقریب خوب، به طور خطی با اختلاف ارتفاع مرتبط است:
فرم ریاضی
[ ویرایش ]
پتانسیل گرانشی V در فاصله x از یک نقطه جرم با جرم M را می توان به عنوان کار W که باید توسط یک عامل خارجی انجام شود تا یک واحد جرم را از بینهایت به آن نقطه وارد کند تعریف کرد: [ 2 ] [ 3 ] [ 4 ] [ 5 ]
که در آن G ثابت گرانشی و F نیروی گرانشی است. محصول GM پارامتر گرانشی استاندارد است و اغلب با دقت بالاتری نسبت به G یا M به طور جداگانه شناخته می شود. پتانسیل دارای واحدهای انرژی در هر جرم است، به عنوان مثال، J/kg در سیستم MKS . طبق قرارداد، در جایی که تعریف می شود همیشه منفی است و وقتی x به بی نهایت میل می کند، به صفر نزدیک می شود.
میدان گرانشی ، و در نتیجه شتاب یک جسم کوچک در فضای اطراف جسم عظیم، شیب منفی پتانسیل گرانشی است. بنابراین، منفی یک گرادیان منفی، شتاب مثبتی را به سمت یک جسم عظیم ایجاد می کند. چون پتانسیل هیچ مولفه زاویه ای ندارد، گرادیان آن است
که در آن x بردار طول x است که از جرم نقطه به سمت جسم کوچک وx^
پتانسیل مرتبط با توزیع جرم، برهم نهی پتانسیل های جرم های نقطه ای است. اگر توزیع جرم مجموعهای محدود از جرمهای نقطهای باشد، و اگر جرمهای نقطهای در نقاط x 1 ، ...، x n قرار داشته باشند و دارای جرمهای m 1 ، ...، m n باشند ، پس پتانسیل توزیع وجود دارد. در نقطه x است
نقاط x و r ، با r موجود در جرم توزیع شده (خاکستری) و جرم تفاضلی dm ( r ) واقع در نقطه r .
اگر توزیع جرم به عنوان یک اندازه گیری جرم dm در فضای سه بعدی اقلیدسی R 3 داده شود ، آنگاه پتانسیل انحراف
−G / | r |
با dm [ نیاز به نقل قول ] در موارد خوب [ توضیح لازم است ] این برابر با انتگرال است
که | x − r | فاصله بین نقاط x و r است . اگر تابع ρ ( r ) نشان دهنده چگالی توزیع در r وجود داشته باشد ، به طوری که dm ( r ) = ρ ( r ) dv ( r ) ، که در آن dv ( r ) عنصر حجم اقلیدسی است ، آنگاه پتانسیل گرانشی برابر است با انتگرال حجمی
اگر V یک تابع بالقوه است که از توزیع جرم پیوسته ρ ( r ) به دست میآید، میتوان ρ را با استفاده از عملگر لاپلاس ، Δ بازیابی کرد :.
انتگرال ممکن است بر حسب توابع ماورایی شناخته شده برای همه اشکال بیضی، از جمله شکل های متقارن و منحط بیان شود. [ 6 ] اینها شامل کره است که در آن سه نیمه محور برابر هستند. کروی شکل (به بیضی مرجع مراجعه کنید ) و پرولات، که در آن دو نیمه محور برابر هستند. ورق های منحط که در آن یک نیم محور بی نهایت است (استوانه بیضوی و دایره ای) و ورق نامحدود که در آن دو نیمه محور بی نهایت هستند. همه این اشکال به طور گسترده در کاربردهای انتگرال پتانسیل گرانشی (به غیر از ثابت G ، با چگالی بار ثابت ) برای الکترومغناطیس استفاده می شود.
تقارن کروی
[ ویرایش ]
یک توزیع جرم کروی متقارن برای یک ناظر کاملاً خارج از توزیع رفتار می کند، به گونه ای که انگار تمام جرم در مرکز متمرکز شده است، و بنابراین به طور مؤثر به عنوان یک جرم نقطه ای ، توسط قضیه پوسته . در سطح زمین، شتاب به اصطلاح با گرانش استاندارد g ، تقریباً 9.8 m/s2 داده میشود ، اگرچه این مقدار با عرض جغرافیایی و ارتفاع کمی متفاوت است. قدر شتاب در قطب ها کمی بیشتر از استوا است زیرا زمین یک کروی مایل است .
در یک توزیع جرم کروی متقارن، می توان معادله پواسون را در مختصات کروی حل کرد . در یک جسم کروی یکنواخت با شعاع R ، چگالی ρ و جرم m ، نیروی گرانشی g در داخل کره با فاصله r از مرکز بهطور خطی تغییر میکند و پتانسیل گرانشی درون کره را میدهد که [ 7 ] [ 8 ] است.![{\displaystyle V(r)={\frac {2}{3}}\pi G\rho \left[r^{2}-3R^{2}\right]={\frac {Gm}{2R^ {3}}}\left[r^{2}-3R^{2}\right],\qquad r\leq R,}](https://wikimedia.org/api/rest_v1/media/math/render/svg/9edacd57f6ef05612224090a38b674c9e164ccab)
نسبیت عام
[ ویرایش ]
همچنین ببینید: شتاب گرانشی § نسبیت عام و میدان گرانشی § نسبیت عام
در نسبیت عام ، پتانسیل گرانشی با تانسور متریک جایگزین می شود . هنگامی که میدان گرانشی ضعیف است و منابع در مقایسه با سرعت نور بسیار آهسته حرکت می کنند، نسبیت عام به گرانش نیوتنی کاهش می یابد و تانسور متریک را می توان از نظر پتانسیل گرانشی منبسط کرد. [ 9 ]
انبساط چند قطبی
[ ویرایش ]
مقالات اصلی: گشتاورهای چند قطبی کروی و انبساط چند قطبی
پتانسیل در یک نقطه x توسط
تصویری از توزیع جرم (خاکستری) با مرکز جرم به عنوان مبدأ بردارهای x و r و نقطه ای که در آن پتانسیل در سر بردار x محاسبه می شود .
که در آخرین انتگرال
r = | r |
و θ زاویه بین x و r است .
(به "فرم ریاضی" مراجعه کنید.) انتگرال را می توان به عنوان یک سری تیلور در
Z = r /| x |
، با محاسبه صریح ضرایب. یک راه کم زحمت برای دستیابی به نتیجه مشابه استفاده از قضیه دو جمله ای تعمیم یافته است . [ 10 ] سری حاصل تابع تولید چند جملهای لژاندر است:
| X | ≤ 1
و
| Z | < 1
. ضرایب P n چند جمله ای های لژاندر درجه n هستند . بنابراین، ضرایب تیلور انتگرال توسط چندجملهای لژاندر در X = cos θ داده میشود . بنابراین پتانسیل را می توان در یک سری همگرا برای موقعیت های x گسترش داد به طوری که r < | x | برای تمام عناصر جرمی سیستم (یعنی خارج از یک کره، در مرکز جرم، که سیستم را در بر می گیرد):


این نشان می دهد که ازدیاد طول بدن باعث پتانسیل کمتری در جهت ازدیاد طول و پتانسیل بالاتر در جهات عمودی نسبت به پتانسیل ناشی از یک جرم کروی می شود، اگر مواردی را با فاصله یکسان با مرکز جرم مقایسه کنیم. (اگر مواردی را با فاصله یکسان با سطح مقایسه کنیم ، عکس آن صادق است.)
مقادیر عددی
[ ویرایش ]
قدر مطلق پتانسیل گرانشی در تعدادی از مکان ها با توجه به گرانش زمین ، خورشید و کهکشان راه شیری در جدول زیر آورده شده است. به عنوان مثال، یک جسم در سطح زمین به 60 MJ/kg برای "ترک" میدان گرانشی زمین، 900 MJ/kg دیگر برای خروج از میدان گرانش خورشید و بیش از 130 GJ/kg برای خروج از میدان گرانشی کهکشان راه شیری نیاز دارد. پتانسیل نصف مربع سرعت فرار است .
| مکان | با توجه به | ||
|---|---|---|---|
| زمین | خورشید | راه شیری | |
| سطح زمین | 60 MJ/kg | 900 MJ/kg | ≥ 130 GJ/kg |
| لئو | 57 MJ/kg | 900 MJ/kg | ≥ 130 GJ/kg |
| وویجر 1 (17000 میلیون کیلومتر از زمین) | 23 ژول بر کیلوگرم | 8 مگاژول بر کیلوگرم | ≥ 130 GJ/kg |
| 0.1 سال نوری از زمین فاصله دارد | 0.4 ژول بر کیلوگرم | 140 کیلوژول بر کیلوگرم | ≥ 130 GJ/kg |
گرانش را در این مکان ها مقایسه کنید .
https://en.wikipedia.org/wiki/Gravitational_potential














 سپس امواج ساطع شد
سپس امواج ساطع شد ، در حالی که
، در حالی که ; شیب معکوس AB نشان دهنده سرعت انتشار سیگنال (یعنی سرعت صوت) به رویداد B است . بنابراین می توانیم بنویسیم:
; شیب معکوس AB نشان دهنده سرعت انتشار سیگنال (یعنی سرعت صوت) به رویداد B است . بنابراین می توانیم بنویسیم:  (سرعت صدا)
(سرعت صدا)
 (سرعت منبع و گیرنده)
(سرعت منبع و گیرنده)

 و
و کمتر از
کمتر از زیرا در غیر این صورت عبور آنها از محیط باعث ایجاد امواج ضربه ای می شود که محاسبه را باطل می کند. برخی از جبرهای معمولی نسبت فرکانس ها را نشان می دهند:
زیرا در غیر این صورت عبور آنها از محیط باعث ایجاد امواج ضربه ای می شود که محاسبه را باطل می کند. برخی از جبرهای معمولی نسبت فرکانس ها را نشان می دهند:

 ، معادله بالا به فرمول کلاسیک داپلر برای صدا کاهش می یابد.
، معادله بالا به فرمول کلاسیک داپلر برای صدا کاهش می یابد.
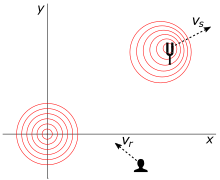
 (در زمان انتشار). سیگنالی را منتشر می کند که با سرعت حرکت می کند
(در زمان انتشار). سیگنالی را منتشر می کند که با سرعت حرکت می کند به سمت گیرنده که با سرعت در حال حرکت است
به سمت گیرنده که با سرعت در حال حرکت است در زمان پذیرایی تجزیه و تحلیل در یک سیستم مختصاتی که در آن سرعت سیگنال انجام می شود
در زمان پذیرایی تجزیه و تحلیل در یک سیستم مختصاتی که در آن سرعت سیگنال انجام می شود مستقل از جهت است
مستقل از جهت است 
 و معادله به
و معادله به  و معادله به
و معادله به 

 دمای منبع است و
دمای منبع است و فرکانس)، میتوانیم به این نتیجه برسیم که طیف جسم سیاهی که از طریق تغییر داپلر دیده میشود (با جهت دلخواه) همچنان یک طیف جسم سیاه است که دمای آن در همان ضریب داپلر به عنوان فرکانس ضرب میشود.
فرکانس)، میتوانیم به این نتیجه برسیم که طیف جسم سیاهی که از طریق تغییر داپلر دیده میشود (با جهت دلخواه) همچنان یک طیف جسم سیاه است که دمای آن در همان ضریب داپلر به عنوان فرکانس ضرب میشود.








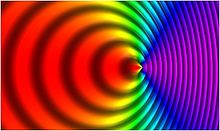
 . شکل 5b اساساً معادل سناریویی است که در شکل 3 توضیح داده شده است و نور به قرمز منتقل شده است.
. شکل 5b اساساً معادل سناریویی است که در شکل 3 توضیح داده شده است و نور به قرمز منتقل شده است.

 در هر نقطه
در هر نقطه


 سرعت زاویه ای روتور است. منبع و امیتر لازم نیست 180 درجه از هم فاصله داشته باشند، اما می توانند در هر زاویه ای نسبت به مرکز باشند.
سرعت زاویه ای روتور است. منبع و امیتر لازم نیست 180 درجه از هم فاصله داشته باشند، اما می توانند در هر زاویه ای نسبت به مرکز باشند. 
 در یک زاویه
در یک زاویه در قاب گیرنده اندازه گیری می شود. جزء شعاعی حرکت منبع در طول خط دید برابر است با
در قاب گیرنده اندازه گیری می شود. جزء شعاعی حرکت منبع در طول خط دید برابر است با


 ،
، 

 با توجه به قاب استراحت منبع به جای قاب استراحت گیرنده.
با توجه به قاب استراحت منبع به جای قاب استراحت گیرنده.
 در
در  در
در 










 همانطور که توسط یک ناظر بر روی گیرنده یا منبع اندازه گیری می شود (قرارداد نشانه ای که در اینجا به تصویب رسید این است
همانطور که توسط یک ناظر بر روی گیرنده یا منبع اندازه گیری می شود (قرارداد نشانه ای که در اینجا به تصویب رسید این است دور از گیرنده (جایی که
دور از گیرنده (جایی که




 سرعت گیرنده بر حسب سرعت نور است. مربوطه
سرعت گیرنده بر حسب سرعت نور است. مربوطه فرکانس برخورد جبهههای موج به گیرنده در کادر منبع، برابر است با
فرکانس برخورد جبهههای موج به گیرنده در کادر منبع، برابر است با






 (همچنین
(همچنین یا
یا )،
)، 

 سرعت M نسبت به Earth است ،
سرعت M نسبت به Earth است ، سرعت M نسبت به باران T است ،
سرعت M نسبت به باران T است ، سرعت باران T نسبت به Earth است .
سرعت باران T نسبت به Earth است .


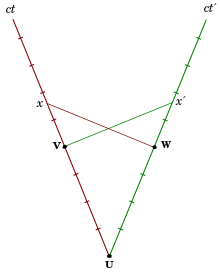
 ، نشان دهنده مکان B همانطور که از A مشاهده می شود.
، نشان دهنده مکان B همانطور که از A مشاهده می شود.

 و
و ، داریم:
، داریم:






 و
و ، که
، که و
و به حرکت A که توسط یک ناظر در قاب پرایم نشده و اولیه دیده می شود، مراجعه کنید. به یاد بیاورید که v حرکت یک جسم ساکن در قاب اولیه است، همانطور که از قاب پرایم نشده مشاهده می شود. بنابراین ما داریم
به حرکت A که توسط یک ناظر در قاب پرایم نشده و اولیه دیده می شود، مراجعه کنید. به یاد بیاورید که v حرکت یک جسم ساکن در قاب اولیه است، همانطور که از قاب پرایم نشده مشاهده می شود. بنابراین ما داریم ،
، 
 سرعت یک جسم یا ناظر B در قاب استراحت جسم دیگر یا ناظر A است . با این حال، بر خلاف مورد مکانیک کلاسیک، در نسبیت خاص، به طور کلی چنین نیست
سرعت یک جسم یا ناظر B در قاب استراحت جسم دیگر یا ناظر A است . با این حال، بر خلاف مورد مکانیک کلاسیک، در نسبیت خاص، به طور کلی چنین نیست






![{\displaystyle \mathbf {v} _{\mathrm {B|A} }={\frac {1}{\gamma _{\mathrm {A} }\left(1-{\frac {\mathbf {v} _{\mathrm {A} }\mathbf {v} _{\mathrm {B} }}{c^{2}}}\right)}}\left[\mathbf {v} _{\mathrm {B} }-\mathbf {v} _{\mathrm {A} }+\mathbf {v} _{\mathrm {A} }(\گاما _{\mathrm {A} }-1)\left({\frac { \mathbf {v} _{\mathrm {A} }\cdot \mathbf {v} _{\mathrm {B} }}{v_{\mathrm {A} }^{2}}}-1\right)\ درست]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/41824d072f371a9f972d7b1f60cb764d1f288d17)








 درست برای
درست برای 
 زاویه انحراف کلاسیک ، در حد
زاویه انحراف کلاسیک ، در حد 
 به عنوان فاصله فضایی، یا
به عنوان فاصله فضایی، یا  و فرکانس مشاهده شده
و فرکانس مشاهده شده 







 جایی که بردار
جایی که بردار از گروه لورنتس که توسط
از گروه لورنتس که توسط  . این فضا، که آن را فضای سرعت می نامند ، به عنوان یک فضای برداری به
. این فضا، که آن را فضای سرعت می نامند ، به عنوان یک فضای برداری به  , فضای سرعت , از طریق رابطه بالا.
, فضای سرعت , از طریق رابطه بالا.  با
با












 یا در اکثر کتاب های درسی،
یا در اکثر کتاب های درسی، که
که حجم فضازمان است. این یک تغییر ناپذیر تحت تحولات لورنتس است.
حجم فضازمان است. این یک تغییر ناپذیر تحت تحولات لورنتس است. تعداد کل واکنش هایی است که منجر به حالت نهایی می شود
تعداد کل واکنش هایی است که منجر به حالت نهایی می شود تعداد واکنش هایی است که منجر به حالت نهایی می شود
تعداد واکنش هایی است که منجر به حالت نهایی می شود شار حادثه نامیده می شود . این لازم است که ثابت باشد، اما در عمومی ترین تنظیمات نیست.
شار حادثه نامیده می شود . این لازم است که ثابت باشد، اما در عمومی ترین تنظیمات نیست. مقطع پراکندگی است. لازم است که ثابت باشد.
مقطع پراکندگی است. لازم است که ثابت باشد. چگالی ذرات در پرتوهای فرودی است. اینها به دلیل
چگالی ذرات در پرتوهای فرودی است. اینها به دلیل  سرعت نسبی دو پرتو فرودی است . از آنجایی که این نمی تواند ثابت باشد
سرعت نسبی دو پرتو فرودی است . از آنجایی که این نمی تواند ثابت باشد و یک عبارت ثابت برای شار حادثه.
و یک عبارت ثابت برای شار حادثه. ، لازم است که
، لازم است که تنظیم سرعت نور
تنظیم سرعت نور ، عبارت برای
، عبارت برای
 همانطور که باید، و نتیجه صحیح را در قاب های باقیمانده ذرات می دهد. سرعت نسبی در بیشتر، شاید همه کتابهای فیزیک ذرات و نظریه میدان کوانتومی به اشتباه آورده شده است.
همانطور که باید، و نتیجه صحیح را در قاب های باقیمانده ذرات می دهد. سرعت نسبی در بیشتر، شاید همه کتابهای فیزیک ذرات و نظریه میدان کوانتومی به اشتباه آورده شده است. 

 . برای به دست آوردن یک عبارت ثابت لورنتس می نویسد
. برای به دست آوردن یک عبارت ثابت لورنتس می نویسد با
با ، که
، که چگالی در قاب استراحت است، برای ذرات منفرد شار می شود و به
چگالی در قاب استراحت است، برای ذرات منفرد شار می شود و به 
 و همچنین
و همچنین![{\displaystyle \gamma _{u}=\gamma _{\mathbf {v} \oplus \mathbf {u} '}=\left[1-{\frac {1}{c^{2}}}{\ frac {1}{(1+{\frac {\mathbf {v} \cdot \mathbf {u} '}{c^{2}}})^{2}}}\left((\mathbf {v} +\mathbf {u} ')^{2}-{\frac {1}{c^{2}}}(v^{2}u'^{2}-(\mathbf {v} \cdot \mathbf {u} ')^{2})\right)\right]^{-{\frac {1}{2}}}=\gamma _{v}\gamma _{u}'\left(1+{ \frac {\mathbf {v} \cdot \mathbf {u} '}{c^{2}}}\right),\quad \quad \gamma _{u}'=\gamma _{v}\gamma _ {u}\left(1-{\frac {\mathbf {v} \cdot \mathbf {u} }{c^{2}}}\right)}](https://wikimedia.org/api/rest_v1/media/math/render/svg/0ead10fe6c4bab9de282a04b882f05ef2cacee8d)
![{\displaystyle {\begin{aligned}\gamma _{\mathbf {v} \oplus \mathbf {u} '}&=\left[{\frac {c^{3}(1+{\frac {\mathbf {v} \cdot \mathbf {u} '}{c^{2}}})^{2}}{c^{2}(1+{\frac {\mathbf {v} \cdot \mathbf {u } '}{c^{2}}})^{2}}}-{\frac {1}{c^{2}}}{\frac {(\mathbf {v} +\mathbf {u} ' )^{2}-{\frac {1}{c^{2}}}(v^{2}u'^{2}-(\mathbf {v} \cdot \mathbf {u} ')^{ 2})}{(1+{\frac {\mathbf {v} \cdot \mathbf {u} '}{c^{2}}})^{2}}}\right]^{-{\frac {1}{2}}}\\&=\left[{\frac {c^{2}(1+{\frac {\mathbf {v} \cdot \mathbf {u} '}{c^{2 }}})^{2}-(\mathbf {v} +\mathbf {u} ')^{2}+{\frac {1}{c^{2}}}(v^{2}u' ^{2}-(\mathbf {v} \cdot \mathbf {u} ')^{2})}{c^{2}(1+{\frac {\mathbf {v} \cdot \mathbf {u } '}{c^{2}}})^{2}}}\right]^{-{\frac {1}{2}}}\\&=\left[{\frac {c^{2 }(1+2{\frac {\mathbf {v} \cdot \mathbf {u} '}{c^{2}}}+{\frac {(\mathbf {v} \cdot \mathbf {u} ' )^{2}}{c^{4}}})-v^{2}-u'^{2}-2(\mathbf {v} \cdot \mathbf {u} ')+{\frac { 1}{c^{2}}}(v^{2}u'^{2}-(\mathbf {v} \cdot \mathbf {u} ')^{2})}{c^{2} (1+{\frac {\mathbf {v} \cdot \mathbf {u} '}{c^{2}}})^{2}}}\right]^{-{\frac {1}{2 }}}\\&=\left[{\frac {1+2{\frac {\mathbf {v} \cdot \mathbf {u} '}{c^{2}}}+{\frac {(\ mathbf {v} \cdot \mathbf {u} ')^{2}}{c^{4}}}-{\frac {v^{2}}{c^{2}}}-{\frac { u'^{2}}{c^{2}}}-{\frac {2}{c^{2}}}(\mathbf {v} \cdot \mathbf {u} ')+{\frac { 1}{c^{4}}}(v^{2}u'^{2}-(\mathbf {v} \cdot \mathbf {u} ')^{2})}{(1+{\ frac {\mathbf {v} \cdot \mathbf {u} '}{c^{2}}})^{2}}}\right]^{-{\frac {1}{2}}}\\ &=\left[{\frac {1+{\frac {(\mathbf {v} \cdot \mathbf {u} ')^{2}}{c^{4}}}-{\frac {v^ {2}}{c^{2}}}-{\frac {u'^{2}}{c^{2}}}+{\frac {1}{c^{4}}}(v^ {2}u'^{2}-(\mathbf {v} \cdot \mathbf {u} ')^{2})}{(1+{\frac {\mathbf {v} \cdot \mathbf {u } '}{c^{2}}})^{2}}}\right]^{-{\frac {1}{2}}}\\&=\left[{\frac {\left(1 -{\frac {v^{2}}{c^{2}}}\right)\left(1-{\frac {u'^{2}}{c^{2}}}\right)} {\left(1+{\frac {\mathbf {v} \cdot \mathbf {u} '}{c^{2}}}\right)^{2}}}\right]^{-{\frac {1}{2}}}=\left[{\frac {1}{\gamma _{v}^{2}\gamma _{u}'^{2}\left(1+{\frac {\ mathbf {v} \cdot \mathbf {u} '}{c^{2}}}\right)^{2}}}\right]^{-{\frac {1}{2}}}\\& =\gamma _{v}\gamma _{u}'\left(1+{\frac {\mathbf {v} \cdot \mathbf {u} '}{c^{2}}}\راست)\end {تراز شده}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/517c984a1cefc97c3c7ebf655a34dd629258ea59)
![{\displaystyle |\mathbf {v_{rel}} |^{2}={\frac {1}{(1-\mathbf {v_{1}} \cdot \mathbf {v_{2}} )^{2 }}}\left[(\mathbf {v_{1}} -\mathbf {v_{2}} )^{2}-(\mathbf {v_{1}} \times \mathbf {v_{2}} )^{2}\right]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/d4efaec0156c44dd14c38fd97c5fa40a01a1d1ea)
![{\displaystyle \mathbf {u} \oplus \mathbf {v} ={\frac {1}{1+{\frac {\mathbf {u} \cdot \mathbf {v} }{c^{2}}} }}\left[\mathbf {v} +\mathbf {u} +{\frac {1}{c^{2}}}{\frac {\gamma _{\mathbf {u} }}{\gamma _{\mathbf {u} }+1}}\mathbf {u} \times (\mathbf {u} \times \mathbf {v} )\right]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/d52e347b81ede2da9516baed88d841e4000f12b8)
![{\displaystyle \mathbf {u} *\mathbf {v} ={\frac {1}{1+{\frac {\mathbf {u} \cdot \mathbf {v} }{c^{2}}}} }\left[\mathbf {v} +\mathbf {u} +{\frac {1}{c^{2}}}{\frac {\gamma _{\mathbf {u} }}{\gamma _{\mathbf {u} }+1}}\mathbf {u} \times (\mathbf {u} \times \mathbf {v} )\right]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/f80cd2300be17c80aba4bee954569eb8a76c0d50)
![{\displaystyle \mathbf {w} \circ \mathbf {v} ={\frac {1}{1+{\frac {\mathbf {v} \cdot \mathbf {w} {c^{2}}} }}\left[{\frac {\mathbf {w} }{\gamma _{\mathbf {v} }}}+\mathbf {v} +{\frac {1}{c^{2}}}{\frac {\gamma _{\mathbf {v} }}{\gamma _{\mathbf {v} }+1}}(\mathbf {w } \cdot \mathbf {v} )\mathbf {v} \right]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/1f3e418672bf02f2bee8088bb044a9589d0bd47c)

 سپس با
سپس با 

![{\displaystyle \mathbf {u} =\mathbf {u} _{\parallel }+\mathbf {u} _{\perp }={\frac {1}{1+{\frac {\mathbf {v} \ cdot \mathbf {u} '}{c^{2}}}}\left[\alpha _{v}\mathbf {u} '+\mathbf {v} +(1-\alpha _{v}){\frac {(\mathbf {v} \cdot \mathbf {u} ')}{v^{2}}}\mathbf {v } \right]\equiv \mathbf {v} \oplus \mathbf {u} ',}](https://wikimedia.org/api/rest_v1/media/math/render/svg/69619ca3017cfb16ce21f2f2d2e8aea8e3d8cbd5)
 و
و ,
, ![{\displaystyle {\begin{aligned}\mathbf {v} \oplus \mathbf {u} '\equiv \mathbf {u} &={\frac {1}{1+{\frac {\mathbf {u} ' \cdot \mathbf {v} }{c^{2}}}}\left[\mathbf {v} +{\frac {\mathbf {u} '}{\gamma _{v}}}+{\frac {1}{c^{2}}}{\frac {\gamma _{v}}{1+\gamma _{ v}}}(\mathbf {u} '\cdot \mathbf {v} )\mathbf {v} \right]\\&={\frac {1}{1+{\frac {\mathbf {u} '\cdot \mathbf {v} }{c^{2}}}}}\left[\mathbf {v} +\mathbf {u} '+{\frac {1}{c^ {2}}}{\frac {\gamma _{v}}{1+\gamma _{v}}}\mathbf {v} \times (\mathbf {v} \times \mathbf {u} ')\right],\end{تراز شده}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/a4a4626061e5696673bd8548072f1c7b91eb6e5a) z
z![{\displaystyle {\begin{aligned}\mathbf {v} \oplus \mathbf {u} \equiv \mathbf {u} '&={\frac {1}{1-{\frac {\mathbf {u} \ cdot \mathbf {v} }{c^{2}}}}}\left[{\frac {\mathbf {u} }{\gamma _{v}}}-\mathbf {v} +{\frac {1}{c^{2}}}{\frac {\gamma _{v}}{1+\gamma _{v}}}( \mathbf {u} \cdot \mathbf {v} )\mathbf {v} \right]\\&={\frac {1}{1-{\frac {\mathbf {u} \cdot \mathbf {v} }{c^{2}}}}}\left[\mathbf {u} -\mathbf {v} +{\frac {1}{c^{2}}}{\frac {\gamma _{v}}{1+\gamma _{v}}}\mathbf {v} \times (\mathbf {v} \times \mathbf {u} )\راست]\پایان{تراز شده}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/62a3866f450b8fdc5702aed25fb21001564ce506)
 برای
برای 
 نه
نه 
![{\displaystyle |\mathbf {u} |^{2}\equiv |\mathbf {v} \oplus \mathbf {u} '|^{2}={\frac {1}{\left(1+{\ frac {\mathbf {v} \cdot \mathbf {u} '}{c^{2}}}\right)^{2}}}\left[\left(\mathbf {v} +\mathbf {u} '\right)^{2}-{\frac {1}{c^{2}}}\left(\mathbf {v} \times \mathbf {u} '\right)^{2}\right]= |\mathbf {u} '\plus \mathbf {v} |^{2}.}](https://wikimedia.org/api/rest_v1/media/math/render/svg/587953edb063d6ed45750ec75efb725b92a7e837) و
و![{\displaystyle |\mathbf {u} '|^{2}\equiv |\mathbf {v} \oplus \mathbf {u} |^{2}={\frac {1}{\left(1-{\ frac {\mathbf {v} \cdot \mathbf {u} }{c^{2}}}\right)^{2}}}\left[\left(\mathbf {u} -\mathbf {v} \ راست)^{2}-{\frac {1}{c^{2}}}\left(\mathbf {v} \times \mathbf {u} \right)^{2}\right]=|\mathbf {u} \oplus \mathbf {v} |^{2}.}](https://wikimedia.org/api/rest_v1/media/math/render/svg/97d9fe963a64c1c9b62d8142e0cc490f4dc5b6ec)
![{\displaystyle {\begin{aligned}&\left(1+{\frac {\mathbf {v} \cdot \mathbf {u} '}{c^{2}}}\right)^{2}|\ mathbf {v} \oplus \mathbf {u} '|^{2}\\&=\left[\mathbf {v} +\mathbf {u} '+{\frac {1}{c^{2}}}{\frac {\gamma _{v}}{1+\gamma _{v}}}\mathbf {v} \times (\mathbf {v } \times \mathbf {u} ')\right]^{2}\\&=(\mathbf {v} +\mathbf {u} ')^{2}+2{\frac {1}{c^{2}}}{\frac {\gamma _{v}}{\gamma _{v}+1}}\left[(\mathbf {v} \cdot \mathbf {u} ' )^{2}-(\mathbf {v} \cdot \mathbf {v} )(\mathbf {u} '\cdot \mathbf {u} ')\right]+{\frac {1}{c^{4}}}\left({\frac {\gamma _{v}}{\gamma _{v}+1}}\right)^{ 2}\left[(\mathbf {v} \cdot \mathbf {v} )^{2}(\mathbf {u} '\cdot \mathbf {u} ')-(\mathbf {v} \cdot \mathbf {u} ')^{2}(\mathbf {v} \cdot \mathbf {v} )\right]\\&=(\mathbf {v} + \mathbf {u} ')^{2}+2{\frac {1}{c^{2}}}{\frac {\gamma _{v}}{\gamma _{v}+1}}\left[(\mathbf {v} \cdot \mathbf {u} ')^{2}-(\mathbf {v} \cdot \mathbf {v} )(\mathbf {u } '\cdot \mathbf {u} ')\right]+{\frac {v^{2}}{c^{4}}}\left({\frac {\gamma _{v}}{\gamma _{v}+1}}\right)^{2}\left[(\mathbf {v} \cdot \mathbf {v})(\mathbf {u} ' \cdot \mathbf {u} ')-(\mathbf {v} \cdot \mathbf {u} ')^{2}\right]\\&=(\mathbf {v} +\mathbf {u} ')^{2}+2{\frac {1}{c^{2}}}{\frac {\gamma _{v}}{\gamma _{v}+1}}\left[(\mathbf {v} \cdot \mathbf {u} ')^{2}-(\mathbf {v} \cdot \mathbf {v} )(\mathbf {u} '\cdot \mathbf {u} ')\right]+{\frac {(1-\alpha _{v})(1+\alpha _{v})}{c^{2}}}\left({\frac {\gamma _{v}}{\gamma _{v}+1}}\راست)^{2}\left[(\mathbf {v} \cdot \mathbf {v} )(\mathbf {u} '\cdot \mathbf {u} ')-( \mathbf {v} \cdot \mathbf {u} ')^{2}\right]\\&=(\mathbf {v} +\mathbf {u} ')^{2}+2{\frac {1}{c^{2}}}{\frac {\gamma _{v}}{\gamma _{v}+1}}\left[ (\mathbf {v} \cdot \mathbf {u} ')^{2}-(\mathbf {v} \cdot \mathbf {v} )(\mathbf {u} '\cdot \mathbf {u} ')\right]+{\frac {(\gamma _{v}-1)}{c^{2}(\gamma _{v}+1)}}\left[ (\mathbf {v} \cdot \mathbf {v} )(\mathbf {u} '\cdot \mathbf {u} ')-(\mathbf {v} \cdot \mathbf {u} ')^{2}\right]\\&=(\mathbf {v} +\mathbf {u} ')^{2}+2{\frac {1}{c^{ 2}}}{\frac {\gamma _{v}}{\gamma _{v}+1}}\left[(\mathbf {v} \cdot \mathbf {u} ')^{2}-(\mathbf {v} \cdot \mathbf {v} )(\mathbf {u} '\cdot \mathbf {u} ')\right]+{\frac {(1-\gamma _{v})}{c^{2}(\گاما _{v}+1)}}\left[(\mathbf {v} \cdot \mathbf {u} ')^{2}-(\mathbf {v} \cdot \mathbf {v} )(\mathbf {u} '\cdot \mathbf {u} ')\right]\\&=(\mathbf {v} +\mathbf {u} ')^{2}+{\frac {1}{c^{2}}}{\frac {\gamma _{v}+1}{\gamma _{v}+1}}\left[(\mathbf {v} \cdot \mathbf {u} ')^{2}-(\mathbf {v} \cdot \ mathbf {v} )(\mathbf {u} '\cdot \mathbf {u} ')\right]\\&=(\mathbf {v} +\mathbf {u} ')^{2}-{\frac {1}{c^{2}}}|\mathbf {v} \times \mathbf {u} '|^{2}\end{تراز شده }}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/3099c302f1314b31c5c0140eb79ed7954d8b14cc)

 بنابراین
بنابراین




 C نسبت به A (سرعت سقوط جسم همانطور که گالیله آن را می بیند) مجموع سرعت است
C نسبت به A (سرعت سقوط جسم همانطور که گالیله آن را می بیند) مجموع سرعت است  از C نسبت به B (سرعت سقوط جسم نسبت به کشتی) به اضافه سرعت
از C نسبت به B (سرعت سقوط جسم نسبت به کشتی) به اضافه سرعت 
 مثلاً یک گلوله توپ که به صورت افقی به سمت دریا شلیک می شود، همانطور که از کشتی اندازه گیری می شود، با سرعت حرکت می کند
مثلاً یک گلوله توپ که به صورت افقی به سمت دریا شلیک می شود، همانطور که از کشتی اندازه گیری می شود، با سرعت حرکت می کند

 در جهت
در جهت 





 (نگاه کنید
(نگاه کنید 




 ،
، انرژی نسبیتی (استراحت + جنبشی)
انرژی نسبیتی (استراحت + جنبشی) ، انرژی جنبشی
، انرژی جنبشی ، و حرکت
، و حرکت ذرات عظیم به شرح زیر
ذرات عظیم به شرح زیر  ،
، . بنابراین انرژی و تکانه نسبیتی به طور قابل توجهی با سرعت افزایش می یابد، بنابراین سرعت نور توسط ذرات عظیم قابل دستیابی نیست. در برخی از کتاب های درسی نسبیت، به اصطلاح "
. بنابراین انرژی و تکانه نسبیتی به طور قابل توجهی با سرعت افزایش می یابد، بنابراین سرعت نور توسط ذرات عظیم قابل دستیابی نیست. در برخی از کتاب های درسی نسبیت، به اصطلاح "  نیز استفاده می شود. با این حال، این مفهوم توسط بسیاری از نویسندگان مضر تلقی می شود، به جای آن باید از عبارات انرژی و تکانه نسبیتی برای بیان وابستگی سرعت در نسبیت استفاده کرد که همان پیش بینی های تجربی را ارائه می دهد.
نیز استفاده می شود. با این حال، این مفهوم توسط بسیاری از نویسندگان مضر تلقی می شود، به جای آن باید از عبارات انرژی و تکانه نسبیتی برای بیان وابستگی سرعت در نسبیت استفاده کرد که همان پیش بینی های تجربی را ارائه می دهد. معادل "جرم نسبیتی"
معادل "جرم نسبیتی" همانطور که در بالا ذکر شد). از آنجایی که جرم نسبیتی دیگر اغلب در کتابهای درسی مدرن استفاده نمیشود، میتوان آن آزمونها را از اندازهگیری تکانه یا انرژی نسبیتی توصیف کرد، زیرا رابطه زیر اعمال میشود:
همانطور که در بالا ذکر شد). از آنجایی که جرم نسبیتی دیگر اغلب در کتابهای درسی مدرن استفاده نمیشود، میتوان آن آزمونها را از اندازهگیری تکانه یا انرژی نسبیتی توصیف کرد، زیرا رابطه زیر اعمال میشود:

 اندازه گیری شد. آنها نسبیت را با حد بالایی برای انحرافات ~0.00037 تایید کردند.
اندازه گیری شد. آنها نسبیت را با حد بالایی برای انحرافات ~0.00037 تایید کردند. 
 .
.  .
.  معتبر بودند، آن پرتوهای گاما باید با سرعت های فوق نوری حرکت می کردند. با این حال، آنها هیچ تفاوتی پیدا نکردند و حد بالایی را ارائه کردند
معتبر بودند، آن پرتوهای گاما باید با سرعت های فوق نوری حرکت می کردند. با این حال، آنها هیچ تفاوتی پیدا نکردند و حد بالایی را ارائه کردند .
.  (
(  (یعنی مجموع انرژی استراحت و انرژی جنبشی آنها) به طور قابل توجهی به حدود 1500 مگا ولت افزایش می یابد. هنگامی که این ذرات با هم برخورد می کنند، ذرات دیگری مانند
(یعنی مجموع انرژی استراحت و انرژی جنبشی آنها) به طور قابل توجهی به حدود 1500 مگا ولت افزایش می یابد. هنگامی که این ذرات با هم برخورد می کنند، ذرات دیگری مانند  ، که می تواند جرم مکانیکی طبیعی اجسام را افزایش دهد.
، که می تواند جرم مکانیکی طبیعی اجسام را افزایش دهد.  به موازات جهت حرکت و جرم
به موازات جهت حرکت و جرم عمود بر جهت حرکت (جایی که
عمود بر جهت حرکت (جایی که ضریب
ضریب  جرم طولی و
جرم طولی و
 حرکت در جهت x با سرعت v و عامل لورنتس مرتبط
حرکت در جهت x با سرعت v و عامل لورنتس مرتبط
 و بدن در حال است
و بدن در حال است با نسبت
با نسبت
 برای همه ذرات، از جمله آنهایی که با سرعت نور حرکت می کنند، صادق است، در حالی که فرمول
برای همه ذرات، از جمله آنهایی که با سرعت نور حرکت می کنند، صادق است، در حالی که فرمول فقط برای یک ذره کندتر از نور (ذره ای با جرم سکون غیر صفر) کاربرد دارد. تولمن در مورد این رابطه خاطرنشان کرد که "علاوه بر این، ما البته تأیید تجربی بیان را در مورد الکترون های متحرک داریم... بنابراین ما هیچ تردیدی در پذیرش این بیان به طور کلی برای جرم یک ذره متحرک نداریم. "
فقط برای یک ذره کندتر از نور (ذره ای با جرم سکون غیر صفر) کاربرد دارد. تولمن در مورد این رابطه خاطرنشان کرد که "علاوه بر این، ما البته تأیید تجربی بیان را در مورد الکترون های متحرک داریم... بنابراین ما هیچ تردیدی در پذیرش این بیان به طور کلی برای جرم یک ذره متحرک نداریم. "  شکل مشتق شده
شکل مشتق شده معتبر نیست زیرا
معتبر نیست زیرا در
در به طور کلی ثابت نیست
به طور کلی ثابت نیست  (1905) او با
(1905) او با  جسم متحرکی که نمی توان برای آن تعریف روشنی ارائه داد. بهتر است مفهوم جرم دیگری به جز «جرم باقیمانده» m معرفی نشود . به جای معرفی M بهتر است به بیان تکانه و انرژی جسم در حال حرکت اشاره شود.
جسم متحرکی که نمی توان برای آن تعریف روشنی ارائه داد. بهتر است مفهوم جرم دیگری به جز «جرم باقیمانده» m معرفی نشود . به جای معرفی M بهتر است به بیان تکانه و انرژی جسم در حال حرکت اشاره شود. به جای توده نسبیتی.
به جای توده نسبیتی. و همچنین نسبت
و همچنین نسبت 


 و
و
 توجه داشته باشید که این فرمول فقط برای ذرات یا سیستم هایی با تکانه صفر صادق است.
توجه داشته باشید که این فرمول فقط برای ذرات یا سیستم هایی با تکانه صفر صادق است.
 ، تنها چهار بردار مرتبط با حرکت ذره است، به طوری که اگر چهار تکانه حفظ شده باشد
، تنها چهار بردار مرتبط با حرکت ذره است، به طوری که اگر چهار تکانه حفظ شده باشد ، باید متناسب با این بردار باشد. این اجازه می دهد تا نسبت انرژی به تکانه را بیان کنیم
، باید متناسب با این بردار باشد. این اجازه می دهد تا نسبت انرژی به تکانه را بیان کنیم در نتیجه یک رابطه بین
در نتیجه یک رابطه بین 
 و
و
 جایی که عامل
جایی که عامل

 طول نسبیتی تکانه انرژی
طول نسبیتی تکانه انرژی  از سیستم، یک کمیت برداری نیز میتواند با جمع کردن لحظهای تمام اجزای آن محاسبه شود. با توجه به انرژی کل
از سیستم، یک کمیت برداری نیز میتواند با جمع کردن لحظهای تمام اجزای آن محاسبه شود. با توجه به انرژی کل 

 جرم نسبیتی است. برای ذره ای با جرم سکون غیر صفر
جرم نسبیتی است. برای ذره ای با جرم سکون غیر صفر 
 و جرم نسبیتی برابر با جرم بقیه است. در چارچوب های دیگر، جرم نسبیتی (یک جسم یا سیستم اجسام) شامل سهمی از انرژی جنبشی "خالص" بدن (انرژی جنبشی مرکز
و جرم نسبیتی برابر با جرم بقیه است. در چارچوب های دیگر، جرم نسبیتی (یک جسم یا سیستم اجسام) شامل سهمی از انرژی جنبشی "خالص" بدن (انرژی جنبشی مرکز 

 و طول موج
و طول موج به عنوان یک
به عنوان یک  ، جرم بدن کاهش می یابد
، جرم بدن کاهش می یابد ,
,  . اگرچه برخی از نویسندگان جرم نسبیتی را به عنوان مفهومی بنیادی از نظریه ارائه می کنند، اما استدلال شده است که این اشتباه است زیرا مبانی نظریه مربوط به فضا-زمان است. در مورد اینکه آیا این مفهوم از نظر آموزشی مفید است یا خیر، اختلاف نظر وجود دارد.
. اگرچه برخی از نویسندگان جرم نسبیتی را به عنوان مفهومی بنیادی از نظریه ارائه می کنند، اما استدلال شده است که این اشتباه است زیرا مبانی نظریه مربوط به فضا-زمان است. در مورد اینکه آیا این مفهوم از نظر آموزشی مفید است یا خیر، اختلاف نظر وجود دارد.  ، طول مناسب خود را دارد
، طول مناسب خود را دارد . با این حال، اگر میله ای در آن قرار گیرداس"
. با این حال، اگر میله ای در آن قرار گیرداس"
 در حال حرکت با0.6ج
در حال حرکت با0.6ج در جهت مخالف، در نتیجهالف∗ب∗.
در جهت مخالف، در نتیجهالف∗ب∗. 
 و
و نقطه پایانی یک جسم در حال حرکت را نشان می دهد. در این قاب طول جسمL
نقطه پایانی یک جسم در حال حرکت را نشان می دهد. در این قاب طول جسمL با توجه به قراردادهای فوق، با تعیین موقعیت همزمان نقاط انتهایی آن در
با توجه به قراردادهای فوق، با تعیین موقعیت همزمان نقاط انتهایی آن در . در همین حال، طول مناسب این جسم، همانط
. در همین حال، طول مناسب این جسم، همانط

 و
و ، طول مناسب در S به دست می آید
، طول مناسب در S به دست می آید



 و همچنین با فرض اندازه گیری زمان همزمان
و همچنین با فرض اندازه گیری زمان همزمان و با اتصال به طول مناسب
و با اتصال به طول مناسب ، به شرح زیر است:
، به شرح زیر است:

 به طول قرارداد تبدیل می شود
به طول قرارداد تبدیل می شود :
: .
. .
. ) نسبت به دو ساعت "استراحت" هماهنگ شده کمتر است (نشان می دهدتی
) نسبت به دو ساعت "استراحت" هماهنگ شده کمتر است (نشان می دهدتی
 در حال استراحت دراس
در حال استراحت دراس در
در در
در و
و . با درج فرمول اتساع زمانی، نسبت بین این طول ها برابر است با:
. با درج فرمول اتساع زمانی، نسبت بین این طول ها برابر است با: .
.



 در قاب استراحت میله یا
در قاب استراحت میله یا در قاب استراحت ساعت
در قاب استراحت ساعت 

 که
که
 و
و ، بدین ترتیب:
، بدین ترتیب:
 ، بنابراین فاصله
، بنابراین فاصله توسط:
توسط:






 از کشتی، فرمول های زیر برقرار است:
از کشتی، فرمول های زیر برقرار است: 







 فرکانس های بالا و پایین تابش از منابع متحرک به صورت زیر اندازه گیری شد:
فرکانس های بالا و پایین تابش از منابع متحرک به صورت زیر اندازه گیری شد:  همانطور که انیشتین (1905) از
همانطور که انیشتین (1905) از  همانطور که انیشتین (1905) استنباط کرد.
همانطور که انیشتین (1905) استنباط کرد. 

 .
. 

 برابر است با
برابر است با 
 از دید ناظر متحرک یعنی همانطور که در یک قاب در حال حرکت نسبت به ساعت محلی اندازه گیری می شود، این ساعت آهسته تر اجرا می شود (که در حال تیک تیک است) زیرا نرخ تیک برابر با یک در بازه زمانی بین تیک
از دید ناظر متحرک یعنی همانطور که در یک قاب در حال حرکت نسبت به ساعت محلی اندازه گیری می شود، این ساعت آهسته تر اجرا می شود (که در حال تیک تیک است) زیرا نرخ تیک برابر با یک در بازه زمانی بین تیک



 سپس یک تابع ماتریس
سپس یک تابع ماتریس  را می توان با جایگزینی
را می توان با جایگزینی  ، سپس سری ماتریس مربوطه برای ماتریس های
، سپس سری ماتریس مربوطه برای ماتریس های  برای برخی از
برای برخی از  .
. یک
یک 


 برای.
برای.
 برای .
برای .


 ، که در آن ماتریس J از
، که در آن ماتریس J از 
 برای همه مقادیر ویژه
برای همه مقادیر ویژه 


 که در آن
که در آن 
 با ماتریس جایگزین شود. این به طور کلی در هنگام گسترش از نظر درست نیست
با ماتریس جایگزین شود. این به طور کلی در هنگام گسترش از نظر درست نیست  در مورد
در مورد مگر اینکه
مگر اینکه![{\displaystyle [A,B]=0}](https://wikimedia.org/api/rest_v1/media/math/render/svg/0a47e750fbc5133ba2297852549b52797d18f908) . یک مثال متقابل است
. یک مثال متقابل است که دارای یک
که دارای یک 

![{\displaystyle {\begin{aligned}f(a+\eta b)&=f(a)+f'(a){\frac {\eta b}{1!}}+f''(a){\ frac {(\eta b)^{2}}{2!}}+f'''(a){\frac {(\eta b)^{3}}{3!}}\\[.5em] &=a^{3}+3a^{2}(\eta b)+3a(\eta b)^{2}+(\eta b)^{3}\\[.5em]&\to A^ {3}=+3A^{2}(\eta B)+3A(\eta B)^{2}+(\eta B)^{3}\end{تراز شده}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/7008f78a7002b12b1a5148da2c49e6c8e20fe423)
 . اگر
. اگر در آن زمان وجود دارد
در آن زمان وجود دارد . سپس بسط اولین ترم از سری توان ارائه شده در بالا پیروی می کند.
. سپس بسط اولین ترم از سری توان ارائه شده در بالا پیروی می کند.
 تحت هنجار ماتریس مناسب به اندازه کافی کوچک باشد. برای مسائل کلیتر، که نمیتوان آنها را به گونهای بازنویسی کرد که دو ماتریس جابجا شوند، ترتیب محصولات ماتریسی تولید شده با استفاده مکرر از قانون لایبنیتس باید ردیابی شود.
تحت هنجار ماتریس مناسب به اندازه کافی کوچک باشد. برای مسائل کلیتر، که نمیتوان آنها را به گونهای بازنویسی کرد که دو ماتریس جابجا شوند، ترتیب محصولات ماتریسی تولید شده با استفاده مکرر از قانون لایبنیتس باید ردیابی شود. که
که مقادیر ویژه معادله مشخصه آن است،
مقادیر ویژه معادله مشخصه آن است،  با این حال، اگر انحطاط وجود داشته باشد، از فرمول زیر استفاده می شود، که در آن f' مشتق f است.
با این حال، اگر انحطاط وجود داشته باشد، از فرمول زیر استفاده می شود، که در آن f' مشتق f است.

 برای همه ماتریس های خود الحاقی
برای همه ماتریس های خود الحاقی  برای همه ماتریس های خود الحاقی
برای همه ماتریس های خود الحاقی ![{\displaystyle \tau \در [0,1]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/2ebb0822357169cac2d073719e50b660e8074cbd) . این تعریف مشابه تابع
. این تعریف مشابه تابع  به
به در تعریف بالا
در تعریف بالا .
. اعداد می توانند چندین لگاریتم پیچیده داشته باشند و در نتیجه برخی از ماتریس ها ممکن است بیش از یک لگاریتم داشته باشند، همانطور که در زیر توضیح داده شده است. اگر لگاریتم ماتریس از
اعداد می توانند چندین لگاریتم پیچیده داشته باشند و در نتیجه برخی از ماتریس ها ممکن است بیش از یک لگاریتم داشته باشند، همانطور که در زیر توضیح داده شده است. اگر لگاریتم ماتریس از وجود دارد و منحصر به فرد است، سپس به صورت نوشته می شود
وجود دارد و منحصر به فرد است، سپس به صورت نوشته می شود در این صورت
در این صورت
 ،
، .
. ، سپس سری قبل همگرا می شود و
، سپس سری قبل همگرا می شود و .
. 


 . این لگاریتم به لگاریتم اصلی معروف است .
. این لگاریتم به لگاریتم اصلی معروف است . 

![{\displaystyle \operatorname {arg} (\mu _{j})+\operatorname {arg} (\nu _{j})\in (-\pi ,\pi ]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/9e95cd05d009dcc65ab09780baf426a840161fbe) ، که
، که یک
یک 
 وقتی A و B رفت و آمد دارند و هر دو
وقتی A و B رفت و آمد دارند و هر دو 




 و
و در حد
در حد .
. 3 توسط یک
3 توسط یک 

 .
.






 به گروه لی مربوطه G
به گروه لی مربوطه G
 چند ارزشی است و با لگاریتم ماتریسی که در اینجا مورد بحث قرار گرفته است، منطبق است. لگاریتم از گروه لی G به جبر دروغ نگاشت می شود
چند ارزشی است و با لگاریتم ماتریسی که در اینجا مورد بحث قرار گرفته است، منطبق است. لگاریتم از گروه لی G به جبر دروغ نگاشت می شود و یک همسایگی V از ماتریس هویت
و یک همسایگی V از ماتریس هویت .
. 

 .
. .
. .
.
 .
. .
.
 ،
،






 (به
(به 

 با مقدار ویژه +1، از این رو مانند یک
با مقدار ویژه +1، از این رو مانند یک  ،
،

 جبر واقعی سه بعدی است که توسط مجموعه
جبر واقعی سه بعدی است که توسط مجموعه 

 نسبت به جبر لی
نسبت به جبر لی  ، که مربوط به گروه Lie
، که مربوط به گروه Lie  ، با گستره بردارهای پایه نشان داده می شود
، با گستره بردارهای پایه نشان داده می شود ایزومورفیسم از
ایزومورفیسم از

 یک نقطه در فضا بر اساس ماتریس برداری پائولی بالا تعریف می شود،
یک نقطه در فضا بر اساس ماتریس برداری پائولی بالا تعریف می شود،


 ماتریس ها دارای خواص جبری مشابه با ماتریس
ماتریس ها دارای خواص جبری مشابه با ماتریس  سه باقی مانده
سه باقی مانده

![{\displaystyle \Sigma _{\mu \nu }={\frac {i}{2}}{\bigl [}\gamma _{\mu },\gamma _{\nu }{\bigr ]}.}](https://wikimedia.org/api/rest_v1/media/math/render/svg/f60c6c46fcdcfb3c1e1d1a2921742c92cd1b4031)
![{\displaystyle {\begin{aligned}\left[\sigma _{j},\sigma _{k}\right]+\{\sigma _{j},\sigma _{k}\}&=(\ سیگما _{j}\سیگما _{k}-\سیگما _{k}\سیگما _{j})+(\سیگما _{j}\سیگما _{k}+\sigma _{k}\sigma _{j})\\2i\varepsilon _{jk\ell }\,\sigma _{\ell }+2\delta _{jk}I&=2\ سیگما _{j}\سیگما _{k}\end{تراز شده}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/610aa4fbda5736e477bd004340dee1c6e95fac5c)



 که تعریف حاصلضرب دو بردار در جبر هندسی نیز می باشد.
که تعریف حاصلضرب دو بردار در جبر هندسی نیز می باشد. یا به طور معادل، بردار پائولی را برآورده می کند:
یا به طور معادل، بردار پائولی را برآورده می کند:


 برای نشان دادن مجموع روی
برای نشان دادن مجموع روی 


![{\displaystyle {\begin{aligned}e^{ia\left({\hat {n}}\cdot {\vec {\sigma }}\right)}&=\sum _{k=0}^{\ infty }{\frac {i^{k}\left[a\left({\hat {n}}\cdot {\vec {\sigma }}\right)\right]^{k}}{k!}}\\&=\sum _{p=0}^{\infty }{\frac {(-1)^{p}(a{ \hat {n}}\cdot {\vec {\sigma }})^{2p}}{(2p)!}}+i\sum _{q=0}^{\infty }{\frac {(-1)^{q}(a{\hat {n}}\cdot {\vec {\sigma }})^{2q+1}}{(2q+1)!}}\\&=I \sum _{p=0}^{\infty }{\frac {(-1)^{p}a^{2p}}{(2p)!}}+i({\hat {n}}\cdot {\vec {\sigma }})\sum _{q=0}^{\infty }{\frac {(-1)^{q}a^{2q+1}}{(2q+1)!}}\\ \end{تراز شده}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/d72e640e54da92d32160753e65de29076aaf8b3c) .
.
![{\displaystyle \det[ia({\hat {n}}\cdot {\vec {\sigma }})]=a^{2}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/6101197de6277f0051a565f637da03e4068d40b8) ،
،

 قانون
قانون 

 به موازات است
به موازات است ، همینطور است
، همینطور است و
و  در امتداد هر محوری
در امتداد هر محوری
 .
.
 که در آن
که در آن  که در آن "
که در آن " ![{\displaystyle {\begin{aligned}c&={}{\tfrac {1}{2}}\,\operatorname {tr} \,M\,,{\begin{aligned}&&a_{k}&={\ tfrac {1}{2}}\,\operatorname {tr} \,\sigma ^{k}\,M.\end{aligned}}\\[3pt]\ بنابراین ~~2\,M&=I\, \operatorname {tr} \,M+\sum _{k}\sigma ^{k}\,\operatorname {tr} \,\sigma ^{k}M~,\end{تراز شده}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/2a7c5374079c6f3a527ea62b424778f58d6a770e) که می تواند بر حسب شاخص های ماتریسی به صورت بازنویسی شود
که می تواند بر حسب شاخص های ماتریسی به صورت بازنویسی شود که در آن جمع بر روی شاخص های مکرر
که در آن جمع بر روی شاخص های مکرر 


 به عنوان تعریف شده است
به عنوان تعریف شده است و
و  نشان داده شده است
نشان داده شده است 
![{\displaystyle \sigma _{jk}={\tfrac {1}{4}}[\sigma _{j},\sigma _{k}]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/4b7b378067295cb76cab0ec92a8da0591b2fc842) از
از![{\displaystyle {\begin{aligned}\left[\sigma _{1},\sigma _{1}\right]&=0\\\left[\sigma _{1},\sigma _{2}\ راست]&=2i\سیگما _{3}\\\چپ[\سیگما _{2}،\سیگما _{3}\راست]&=2i\سیگما _{1}\\\چپ[\سیگما _{ 3}،\sigma _{1}\right]&=2i\sigma _{2}\end{تراز شده}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/7ed3380088107fcd3ea3b2a603c43931e2aa7165)


 کجا
کجا ،
، ، و
، و نمادی معادل برای آشناتر هستند
نمادی معادل برای آشناتر هستند ،
، ، و
، و .
.

 که نقشه ها
که نقشه ها
 را می توان از ماتریس بازیابی کرد (به
را می توان از ماتریس بازیابی کرد (به  این یک معکوس نسبت به نقشه است
این یک معکوس نسبت به نقشه است  ، نشان می دهد که نقشه یک bijection است.
، نشان می دهد که نقشه یک bijection است. سپس با در نظر گرفتن عمل صرف یک
سپس با در نظر گرفتن عمل صرف یک ماتریس
ماتریس در این فضای ماتریس،
در این فضای ماتریس،
 و آن
و آن هرمیت و بی ردی است. سپس تعریف کردن منطقی است
هرمیت و بی ردی است. سپس تعریف کردن منطقی است کجا
کجا همان هنجار را دارد
همان هنجار را دارد و بنابراین تفسیر کنید
و بنابراین تفسیر کنید داده شده توسط
داده شده توسط






 )⋅
)⋅![{\displaystyle [{\vec {a}}\cdot {\vec {\sigma }},{\vec {b}}\cdot {\vec {\sigma }}]=2i\,({\vec {a }}\times {\vec {b}})\cdot {\vec {\sigma }}.}](https://wikimedia.org/api/rest_v1/media/math/render/svg/253faefdd11b5ceac1a081c537f8cdb3533aa228) در واقع وجود هنجار از آنجا ناشی می شود که
در واقع وجود هنجار از آنجا ناشی می شود که هستند
هستند این بلافاصله از بی ردیابی و محاسبه صریح تعیین کننده ناشی می شود.
این بلافاصله از بی ردیابی و محاسبه صریح تعیین کننده ناشی می شود. از آنجایی که می توان آن را فاکتورسازی کرد
از آنجایی که می توان آن را فاکتورسازی کرد یک نتیجه استاندارد در جبر خطی (نقشه خطی که معادله چند جمله ای نوشته شده در فاکتورهای خطی متمایز را برآورده می کند، مورب است) به این معنی است که
یک نتیجه استاندارد در جبر خطی (نقشه خطی که معادله چند جمله ای نوشته شده در فاکتورهای خطی متمایز را برآورده می کند، مورب است) به این معنی است که




 برای به دست آوردن بردارهای ویژه
برای به دست آوردن بردارهای ویژه و
و .
. با اجزای
با اجزای
 به فضای برداری ماتریس های هرمیتی
به فضای برداری ماتریس های هرمیتی



 در این مورد گروه ماتریس است
در این مورد گروه ماتریس است و این نشان می دهد
و این نشان می دهد به طور مشابه با بالا، این را می توان به صراحت متوجه شد
به طور مشابه با بالا، این را می توان به صراحت متوجه شد با اجزای
با اجزای
 برای
برای ماتریس ها، هویت زیر برقرار است
ماتریس ها، هویت زیر برقرار است


 از آنجایی که ماتریس ها هستند
از آنجایی که ماتریس ها هستند این برابر است با
این برابر است با
















 از
از  از همه ماتریس های
از همه ماتریس های  .
.![{\displaystyle [\sigma _{j},\sigma _{k}]=2i\sum _{l}\varepsilon _{jkl}\,\sigma _{l},}](https://wikimedia.org/api/rest_v1/media/math/render/svg/6c795add56c0a214dfee1fac28e09133254e1ccb)












![{\displaystyle R(M,x)\in \left[\lambda _{\min },\lambda _{\max }\right]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/3367126b01f5e7829818dc7726de621c12767dd3)














 غیر منفی هستند:.
غیر منفی هستند:.
 اگر مقادیر ویژه متفاوت باشند - در مورد تعدد، اساس را می توان متعامد کرد.
اگر مقادیر ویژه متفاوت باشند - در مورد تعدد، اساس را می توان متعامد کرد. که
که مختصات است
مختصات است که با
که با 
 را نیز به حداکثر می رساند
را نیز به حداکثر می رساند تحت این محدودیت که
تحت این محدودیت که .
.



 ،
، 
 . مشکل پیدا کردن
. مشکل پیدا کردن  مشمول محدودیت
مشمول محدودیت به عبارت دیگر، یافتن نقاط بحرانی است
به عبارت دیگر، یافتن نقاط بحرانی است که
که رخ می دهد درد (با برداشت از جابجایی هر دو طرف و توجه به آن م هرمیتی است
رخ می دهد درد (با برداشت از جابجایی هر دو طرف و توجه به آن م هرمیتی است و
و
 از
از مقادیر ثابت هستند
مقادیر ثابت هستند . این ویژگی مبنایی برای
. این ویژگی مبنایی برای ![{\displaystyle L(y)={\frac {1}{w(x)}}\left(-{\frac {d}{dx}}\left[p(x){\frac {dy}{dx }}\right]+q(x)y\right)}](https://wikimedia.org/api/rest_v1/media/math/render/svg/371147c6e1ef449ffd33e67888014e4866665d32) در
در  از توابعی که برخی
از توابعی که برخی ![{\displaystyle {\frac {\langle {y,Ly}\rangle }{\langle {y,y}\rangle }}={\frac {\int _{a}^{b}y(x)\left (-{\frac {d}{dx}}\left[p(x){\frac {dy}{dx}}\right]+q(x)y(x)\right)dx}{\int _{a}^{b}{w(x)y(x)^{2}}dx}}.}](https://wikimedia.org/api/rest_v1/media/math/render/svg/cbc74991eb4219cc9d071797b1c76c086a0f6509)
![{\displaystyle {\begin{aligned}{\frac {\langle {y,Ly}\rangle }{\langle {y,y}\rangle }}&={\frac {\left\{\int _{a }^{b}y(x)\left(-{\frac {d}{dx}}\left[p(x)y'(x)\right]\right)dx\right\}+\left\{\int _{a}^{b}{q(x) y(x)^{2}}\,dx\right\}}{\int _{a}^{b}{w(x)y(x)^{2}}\,dx}}\\& ={\frac {\left\{\left.-y(x)\left[p(x)y'(x)\right]\right|_{a}^{b}\right\}+\left\{\int _{a}^{b}y'(x)\left[p(x)y'(x)\right]\,dx\right\}+\left\{\int _{a}^{b}{q(x)y(x)^{2}}\,dx\right\}}{\int _{a}^{b}w(x)y(x)^ {2}\,dx}}\\&={\frac {\left\{\left.-p(x)y(x)y'(x)\right|_{a}^{b}\right \}+\چپ\{\int _{a}^{b}\left[p(x)y'(x)^{2}+q(x)y(x)^{2}\right]\,dx\right\}}{\ int _{a}^{b}{w(x)y(x)^{2}}\,dx}}.\end{تراز شده}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/8c68f876aa4dd809977dfd4ff2ce4a2cc3bcf852)
 ضریب ریلی تعمیم یافته را می توان به ضریب ریلی کاهش داد
ضریب ریلی تعمیم یافته را می توان به ضریب ریلی کاهش داد از طریق تحول
از طریق تحول که
که
 زمانی که x = y با R ( H , x ) منطبق است . در مکانیک کوانتومی به این کمیت «عنصر ماتریس» یا گاهی «دامنه انتقال» می گویند.
زمانی که x = y با R ( H , x ) منطبق است . در مکانیک کوانتومی به این کمیت «عنصر ماتریس» یا گاهی «دامنه انتقال» می گویند. در
در  یک بردار حالت
یک بردار حالت  .
. در فضای هیلبرت ارزش انتظاری از
در فضای هیلبرت ارزش انتظاری از
 ، با
، با  سپس (
سپس ( 
 نتایج احتمالی آزمایش،
نتایج احتمالی آزمایش،  احتمال وقوع این نتیجه است. اغلب به آن احتمال انتقال می گویند .
احتمال وقوع این نتیجه است. اغلب به آن احتمال انتقال می گویند .
 در مکانیک کوانتومی این عملگر دارای یک
در مکانیک کوانتومی این عملگر دارای یک  به عنوان
به عنوان .
.  در طیف
در طیف . این اتفاق می افتد که بردارهای ویژه عملگر موقعیت یک مبنای کامل برای فضای برداری حالت ها تشکیل می دهند و بنابراین از یک
. این اتفاق می افتد که بردارهای ویژه عملگر موقعیت یک مبنای کامل برای فضای برداری حالت ها تشکیل می دهند و بنابراین از یک 

 ، انتگرال دوگانه را به یک انتگرال منفرد کاهش می دهد. خط آخر
، انتگرال دوگانه را به یک انتگرال منفرد کاهش می دهد. خط آخر  با
با ، که یک جایگزین رایج در انتگرال های مکانیکی کوانتومی است.
، که یک جایگزین رایج در انتگرال های مکانیکی کوانتومی است.
 , عملگر آماری یا
, عملگر آماری یا 

 با اپراتور
با اپراتور  از ردیابی 1. این فرمول (
از ردیابی 1. این فرمول (  یک
یک  ، که فرمول (
، که فرمول (  با یک
با یک  ، این یعنی
، این یعنی که ممکن است به عنوان تعمیم رایج فرمول های (
که ممکن است به عنوان تعمیم رایج فرمول های (  ، فضای توابع قابل انتگرالگیری مربع روی خط واقعی. بردارها
، فضای توابع قابل انتگرالگیری مربع روی خط واقعی. بردارها توسط توابع نشان داده می شوند
توسط توابع نشان داده می شوند . توابع موج یک تفسیر مستقیم به عنوان توزیع احتمال دارند:
. توابع موج یک تفسیر مستقیم به عنوان توزیع احتمال دارند:
 در مورد یک نقطه
در مورد یک نقطه ، که بر روی توابع موج عمل می کند
، که بر روی توابع موج عمل می کند

 . به صراحت، ارزش انتظاری آن است
. به صراحت، ارزش انتظاری آن است
 در این وبلاگ به ریاضیات و کاربردهای آن و تحقیقات در آنها پرداخته می شود. مطالب در این وبلاگ ترجمه سطحی و اولیه است و کامل نیست.در صورتی سوال یا نظری در زمینه ریاضیات دارید مطرح نمایید .در صورت امکان به آن می پردازم. من دوست دارم برای یافتن پاسخ به سوالات و حل پروژه های علمی با دیگران همکاری نمایم.در صورتی که شما هم بامن هم عقیده هستید با من تماس بگیرید.
در این وبلاگ به ریاضیات و کاربردهای آن و تحقیقات در آنها پرداخته می شود. مطالب در این وبلاگ ترجمه سطحی و اولیه است و کامل نیست.در صورتی سوال یا نظری در زمینه ریاضیات دارید مطرح نمایید .در صورت امکان به آن می پردازم. من دوست دارم برای یافتن پاسخ به سوالات و حل پروژه های علمی با دیگران همکاری نمایم.در صورتی که شما هم بامن هم عقیده هستید با من تماس بگیرید.