معادله دیفرانسیل معمولی
از ویکیپدیا، دانشنامه آزاد

مسیر پرتابه ای که از یک توپ پرتاب می شود از منحنی تعیین شده توسط یک معادله دیفرانسیل معمولی که از قانون دوم نیوتن مشتق شده است، پیروی می کند.
معادلات دیفرانسیل
محدوده
نشان می دهد
زمینه های
طبقه بندی
نشان می دهد
انواع
نشان می دهد
ارتباط با فرآیندها
راه حل
نشان می دهد
وجود و منحصر به فرد بودن
نشان می دهد
مباحث عمومی
نشان می دهد
روش های حل
مردم
نشان می دهد
فهرست کنید
- v
- تی
- ه
در ریاضیات ، یک معادله دیفرانسیل معمولی ( ODE ) یک معادله دیفرانسیل (DE) است که تنها به یک متغیر مستقل وابسته است . مانند سایر DE، مجهول(های) آن از یک (یا چند تابع) تشکیل شده و مشتقات آن توابع را شامل می شود. [1] اصطلاح "معمولی" در مقابل معادلات دیفرانسیل جزئی استفاده می شود که ممکن است با توجه به بیش از یک متغیر مستقل باشد. [2]
معادلات دیفرانسیل [ ویرایش ]
معادله دیفرانسیل خطی یک معادله دیفرانسیل است که توسط یک چند جمله ای خطی در تابع مجهول و مشتقات آن تعریف می شود که معادله ای از شکل است.
،
جایی که 


در بین معادلات دیفرانسیل معمولی، معادلات دیفرانسیل خطی به چند دلیل نقش برجسته ای دارند. اکثر توابع ابتدایی و ویژه ای که در فیزیک و ریاضیات کاربردی با آنها مواجه می شوند ، حل معادلات دیفرانسیل خطی هستند (به تابع هولونومی مراجعه کنید ). هنگامی که پدیده های فیزیکی با معادلات غیر خطی مدل می شوند، معمولاً با معادلات دیفرانسیل خطی برای حل آسان تر تقریب می شوند. معدود ODE های غیر خطی که می توانند به طور صریح حل شوند، عموماً با تبدیل معادله به یک ODE خطی معادل حل می شوند (به عنوان مثال معادله Riccati را ببینید ).
برخی از ODE ها را می توان به صراحت از نظر توابع و انتگرال های شناخته شده حل کرد . هنگامی که این امکان پذیر نیست، معادله محاسبه سری تیلور از راه حل ها ممکن است مفید باشد. برای مسائل کاربردی، روشهای عددی برای معادلات دیفرانسیل معمولی میتوانند تقریبی از جواب را ارائه کنند.
پس زمینه [ ویرایش ]
معادلات دیفرانسیل معمولی (ODE) در بسیاری از زمینه های ریاضیات و علوم اجتماعی و طبیعی به وجود می آیند . در توصیف های ریاضی تغییر از دیفرانسیل ها و مشتقات استفاده می شود. دیفرانسیل ها، مشتقات و توابع مختلف از طریق معادلات به هم مرتبط می شوند، به طوری که یک معادله دیفرانسیل نتیجه ای است که پدیده ها، تکامل و تغییرات به طور پویا در حال تغییر را توصیف می کند. غالباً کمیت ها به عنوان نرخ تغییر کمیت های دیگر (مثلاً مشتقات جابجایی نسبت به زمان) یا شیب کمیت ها تعریف می شوند که نحوه ورود آنها به معادلات دیفرانسیل است. [ نیازمند منبع ]
رشته های ریاضی خاص شامل هندسه و مکانیک تحلیلی است . زمینه های علمی شامل بسیاری از فیزیک و ستاره شناسی (مکانیک آسمان)، هواشناسی (مدل سازی آب و هوا)، شیمی (نرخ واکنش)، [3] زیست شناسی (بیماری های عفونی، تنوع ژنتیکی)، بوم شناسی و مدل سازی جمعیت (رقابت جمعیت)، اقتصاد (روند سهام). ، نرخ بهره و تغییرات قیمت تعادلی بازار).
بسیاری از ریاضیدانان معادلات دیفرانسیل را مطالعه کرده اند و در این زمینه مشارکت داشته اند، از جمله نیوتن ، لایبنیتس ، خانواده برنولی ، ریکاتی ، کلراوت ، دالامبر و اویلر .
یک مثال ساده قانون دوم حرکت نیوتن است - رابطه بین جابجایی x و زمان t یک جسم تحت نیروی F توسط معادله دیفرانسیل به دست میآید.
که حرکت ذره ای با جرم ثابت m را محدود می کند . به طور کلی، F تابعی از موقعیت x ( t ) ذره در زمان t است . تابع مجهول x ( t ) در دو طرف معادله دیفرانسیل ظاهر می شود و در نماد F ( x ( t ) نشان داده می شود. [4] [5] [6] [7]
تعاریف [ ویرایش ]
در ادامه، y یک متغیر وابسته است که نشان دهنده یک تابع مجهول y = f ( x ) از متغیر مستقل x است . نماد تمایز بسته به نویسنده و اینکه کدام نماد برای کار مورد نظر مفیدتر است متفاوت است. در این زمینه، نماد لایب نیتس (dx،d 2 y/dx 2,…,d n y/dx n) برای تمایز و انتکرال مفیدتر است ، در حالی که علامت لاگرانژ برای نمایش مشتقات مرتبه بالاتر به صورت فشرده و نماد نیوتن مفیدتر است. 
تعریف کلی [ ویرایش ]
همچنین ببینید: ترتیب معادلات دیفرانسیل
با در نظر گرفتن F ، تابعی از x ، y ، و مشتقات y . سپس یک معادله از فرم
معادله دیفرانسیل معمولی صریح از مرتبه n نامیده می شود . [8] [9]
به طور کلی، یک معادله دیفرانسیل معمولی ضمنی از مرتبه n شکل زیر را دارد: [10]
طبقه بندی های دیگری نیز وجود دارد:
خود مختار
دیفرانسیل اگر به متغیر x وابسته نباشد مستقل است .
خطی
یک معادله دیفرانسیل خطی است اگراف
که در آن i ( x ) و r ( x ) توابع پیوسته x هستند . [8] [11] [12] تابع r ( x ) اصطلاح منبع نامیده می شود که منجر به طبقه بندی بیشتر می شود. [11] [13]
همگن
یک معادله دیفرانسیل خطی همگن است اگر r ( x ) = 0 . در این مورد، همیشه " راه حل بی اهمیت " y = 0 وجود دارد .
ناهمگن (یا ناهمگن)
یک معادله دیفرانسیل خطی ناهمگن است اگر r ( x ) ≠ 0 .
غیر خطی
معادله دیفرانسیل که خطی نیست.
سیستم ODE ها [ ویرایش ]
مقاله اصلی: سیستم معادلات دیفرانسیل
تعدادی از معادلات دیفرانسیل جفت شده یک سیستم معادلات را تشکیل می دهند. اگر y برداری است که عناصر آن توابع هستند. y ( x ) = [ y 1 ( x )، y 2 ( x )،...، y m ( x )] و F تابعی با مقدار برداری از y و مشتقات آن است ، سپس
یک سیستم صریح از معادلات دیفرانسیل معمولی مرتبه n و بعد m است . در شکل بردار ستونی :
اینها لزوما خطی نیستند. آنالوگ ضمنی این است:
اف
که در آن 0 = (0، 0، ...، 0) بردار صفر است . به صورت ماتریسی
برای یک سیستم از فرم

رفتار یک سیستم از ODE ها را می توان از طریق استفاده از پرتره فاز مشاهده کرد .
راه حل ها [ ویرایش ]
معادله دیفرانسیل داده می شود
ا
یک تابع u : I ⊂ R → R ، جایی که I یک بازه است، منحنی راه حل یا انتگرال برای F نامیده می شود ، اگر u n بار در I قابل تفکیک باشد ، و
با توجه به دو راه حل u : J ⊂ R → R و v : I ⊂ R → R ، u پسوند v نامیده می شود اگر I ⊂ J و
راه حلی که پسوندی ندارد راه حل حداکثری نامیده می شود . راه حلی که روی تمام R تعریف شده است راه حل جهانی نامیده می شود .
راه حل کلی یک معادله مرتبه n راه حلی است که حاوی n ثابت مستقل دلخواه انتگرال گیری باشد . یک راهحل خاص از راهحل عمومی با تنظیم ثابتها به مقادیر خاص، که اغلب برای انجام مجموعه « شرایط اولیه یا شرایط مرزی » انتخاب میشوند، مشتق میشود. [18] راه حل منفرد راه حلی است که نمی توان آن را با اختصاص مقادیر معین به ثابت های دلخواه در جواب کلی به دست آورد. [19]
در زمینه ODE خطی، راه حل خاص اصطلاحی همچنین می تواند به هر راه حل ODE اشاره کند (الزاماً شرایط اولیه را برآورده نمی کند)، که سپس به محلول همگن اضافه می شود (راه حل کلی ODE همگن)، که سپس تشکیل می شود. یک راه حل کلی از ODE اصلی. این اصطلاحی است که در بخش روش حدس زدن در این مقاله استفاده میشود و اغلب هنگام بحث در مورد روش ضرایب نامشخص و تغییرات پارامترها استفاده میشود .
راه حل های مدت زمان محدود [ ویرایش ]
برای ODEهای مستقل غیرخطی، تحت برخی شرایط ممکن است راهحلهایی با مدت زمان محدود ایجاد شود، [20] به این معنی که در اینجا از دینامیک خود، سیستم در یک زمان پایانی به مقدار صفر میرسد و برای همیشه در آن صفر باقی میماند. این راه حل های مدت زمان محدود نمی توانند توابع تحلیلی در کل خط حقیقی باشند، و چون در زمان پایان خود توابع غیر لیپشیتز خواهند بود، در قضیه منحصر به فرد بودن جواب های معادلات دیفرانسیل لیپشیتز گنجانده نمی شوند.
به عنوان مثال، معادله:
راه حل مدت زمان محدود را می پذیرد:
نظریه ها [ ویرایش ]
راه حل های مفرد [ ویرایش ]
تئوری جوابهای منفرد معادلات دیفرانسیل معمولی و جزئی موضوع تحقیق از زمان لایب نیتس بود، اما تنها از اواسط قرن نوزدهم مورد توجه ویژه قرار گرفت. یک اثر ارزشمند اما کمتر شناخته شده در این زمینه، اثر فوشیان (1854) است. داربوکس (از سال 1873) در نظریه پیشرو بود و در تفسیر هندسی این راه حل ها زمینه ای را گشود که توسط نویسندگان مختلف، به ویژه کاسوراتی و کیلی کار شده بود . به دلیل دومی (1872) تئوری حل های منفرد معادلات دیفرانسیل مرتبه اول است که در حدود سال 1900 پذیرفته شده است.
کاهش به ربع [ ویرایش ]
تلاش اولیه در برخورد با معادلات دیفرانسیل کاهش به ربع بود . همانطور که جبر گرایان قرن هجدهم امید داشتند روشی برای حل معادله کلی درجه n بیابند ، تحلیلگران نیز امیدوار بودند که روشی کلی برای انتکرال هر معادله دیفرانسیل بیابند. با این حال، گاوس (1799) نشان داد که معادلات دیفرانسیل پیچیده به اعداد مختلط نیاز دارند . از این رو، تحلیلگران شروع به جایگزینی مطالعه توابع کردند و بدین ترتیب میدانی جدید و حاصلخیز باز کردند. کوشی اولین کسی بود که به اهمیت این دیدگاه پی برد. پس از آن، سؤال حقیقی دیگر این نبود که آیا یک راه حل با استفاده از توابع شناخته شده یا انتگرال آنها امکان پذیر است یا خیر، بلکه این بود که آیا یک معادله دیفرانسیل معین برای تعریف تابعی از متغیر یا متغیرهای مستقل کافی است، و اگر چنین است، چه هستند. خواص مشخصه
نظریه فوشیان [ ویرایش ]
مقاله اصلی: روش فروبنیوس
دو خاطرات فوکس [21] الهام بخش رویکردی بدیع بود که متعاقباً توسط توم و فروبنیوس شرح داده شد . کولت از سال 1869 شروع به کار کرد. روش او برای انتکرال یک سیستم غیر خطی در سال 1868 به برتراند ابلاغ شد. کلبش (1873) این نظریه را در امتداد خطوط موازی با نظریه انتگرال های آبلی خود مورد حمله قرار داد . از آنجایی که میتوان دومی را بر اساس ویژگیهای منحنی بنیادی طبقهبندی کرد که تحت یک تبدیل منطقی بدون تغییر باقی میماند، کلبش پیشنهاد کرد که توابع متعالی تعریف شده توسط معادلات دیفرانسیل را بر اساس ویژگیهای ثابت سطوح متناظر f = 0 در زیر منطقی یک به طبقهبندی کند. یک تحول.
نظریه لی [ ویرایش ]
از سال 1870، سوفوس لی 'ثانیه کار نظریه معادلات دیفرانسیل را بر اساس بهتر قرار داده است. او نشان داد که نظریههای یکپارچهسازی ریاضیدانان قدیمیتر را میتوان با استفاده از گروههای لی به یک منبع مشترک ارجاع داد، و معادلات دیفرانسیل معمولی که همان تبدیلهای بینهایت کوچک را پذیرفتهاند ، مشکلات انتگرالگیری قابل مقایسهای دارند. او همچنین بر موضوع تحولات تماس تأکید کرد .
نظریه گروهی Lie در مورد معادلات دیفرانسیل تایید شده است، یعنی: (1) که بسیاری از روش های موردی شناخته شده برای حل معادلات دیفرانسیل را متحد می کند، و (2) که راه های جدید قدرتمندی برای یافتن راه حل ها ارائه می دهد. این نظریه برای معادلات دیفرانسیل معمولی و جزئی کاربرد دارد. [22]
یک رویکرد حل کلی از خاصیت تقارن معادلات دیفرانسیل استفاده می کند، تبدیل بی نهایت کوچک پیوسته راه حل ها به راه حل ها ( نظریه لی ). تئوری گروه پیوسته ، جبرهای لی ، و هندسه دیفرانسیل برای درک ساختار معادلات دیفرانسیل خطی و غیرخطی (جزئی) برای تولید معادلات انتگرالپذیر، یافتن جفتهای Lax ، عملگرهای بازگشتی، تبدیل بکلوند و در نهایت یافتن راهحلهای تحلیلی دقیق استفاده میشوند. به DE.
روشهای تقارن برای معادلات دیفرانسیل که در ریاضیات، فیزیک، مهندسی و سایر رشتهها به وجود میآیند، استفاده شدهاند.
نظریه استورم-لیوویل [ ویرایش ]
مقاله اصلی: نظریه اشتورم لیوویل
نظریه اشتورم لیوویل نظریه ای از نوع خاصی از معادلات دیفرانسیل معمولی خطی مرتبه دوم است. راه حل های آنها بر اساس مقادیر ویژه و توابع ویژه مربوط به عملگرهای خطی است که از طریق معادلات خطی همگن مرتبه دوم تعریف شده اند . این مشکلات به عنوان مشکلات اشتورم-لیوویل (SLP) شناخته می شوند و به نام JCF Sturm و جی لیوویل که آنها را در اواسط دهه 1800 مطالعه کردند، نامگذاری شده اند . SLP ها دارای تعداد نامتناهی مقادیر ویژه هستند و توابع ویژه مربوطه یک مجموعه کامل و متعامد را تشکیل می دهند که بسط های متعامد را ممکن می کند. این یک ایده کلیدی در ریاضیات کاربردی، فیزیک و مهندسی است. [23] SLP ها همچنین در تجزیه و تحلیل برخی معادلات دیفرانسیل جزئی مفید هستند.
وجود و منحصر به فرد بودن راه حل ها [ ویرایش ]
چندین قضیه وجود دارد که وجود و منحصربهفرد بودن راهحلها را برای مسائل ارزش اولیه که شامل ODEها هم در سطح محلی و هم در سطح جهانی است، ایجاد میکنند. دو قضیه اصلی عبارتند از
قضیهفرضنتیجه
قضیه وجود پینوF پیوستهفقط وجود محلی
قضیه پیکارد-لیندلوفF لیپشیتس پیوستهوجود و منحصر به فرد بودن محلی
در شکل اصلی خود، هر دوی این قضیهها فقط نتایج محلی را تضمین میکنند، اگرچه دومی را میتوان برای به دست آوردن یک نتیجه کلی، برای مثال، اگر شرایط نابرابری گرونوال برآورده شود، گسترش داد.
همچنین، قضایای منحصربهفرد مانند لیپشیتس در بالا برای سیستمهای DAE ، که ممکن است راهحلهای متعددی داشته باشند که از بخش جبری (غیر خطی) آنها به تنهایی ناشی میشوند، اعمال نمیشوند . [24]
وجود محلی و قضیه یگانگی ساده شده [ ویرایش ]
قضیه را می توان به سادگی به صورت زیر بیان کرد. [25] برای معادله و مسئله مقدار اولیه:

![{\displaystyle R=[x_{0}-a,x_{0}+a]\times [y_{0}-b,y_{0}+b]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/dfa448c4a13705b1df4c401c5ca9d11fc7c10735)
![{\displaystyle I=[x_{0}-h,x_{0}+h]\subset [x_{0}-a,x_{0}+a]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/b231b296413a91fd03243fa6b0b15a1fc58684c1)
منحصر به فرد بودن جهانی و حداکثر دامنه راه حل [ ویرایش ]
هنگامی که فرضیه های قضیه پیکارد-لیندلوف برآورده شود، وجود محلی و منحصر به فرد را می توان به یک نتیجه جهانی تعمیم داد. دقیق تر: [26]
برای هر شرط اولیه ( x 0 , y 0 ) یک بازه باز حداکثر (احتمالا بی نهایت) منحصر به فرد وجود دارد.
به طوری که هر راه حلی که این شرط اولیه را برآورده کند، محدودیت راه حلی است که این شرط اولیه را با دامنه برآورده می کند.
در صورتی که 
- انفجار در زمان محدود:
- دامنه تعریف را ترک می کند:
که در آن Ω مجموعه باز است که در آن F تعریف شده است، و¯
توجه داشته باشید که حداکثر دامنه راه حل
- همیشه یک فاصله است (برای داشتن منحصر به فرد بودن)
- ممکن است کوچکتر ازآر
- ممکن است به انتخاب خاص ( x 0 ، y 0 ) بستگی داشته باشد.
مثال.
این بدان معنی است که F ( x, y ) = y 2 است که C 1 است و بنابراین به صورت محلی لیپشیتس پیوسته است و قضیه پیکارد-لیندلوف را برآورده می کند.
حتی در چنین تنظیمات ساده ای، حداکثر دامنه راه حل نمی تواند همه باشدآر
که دارای حداکثر دامنه است:
این به وضوح نشان می دهد که حداکثر فاصله ممکن است به شرایط اولیه بستگی داشته باشد. دامنه y را می توان به عنوان موجود در نظر گرفتآر
حداکثر دامنه نیست
که با توجه به قضیه فوق یکی از دو حالت ممکن است.
کاهش مرتبه [ ویرایش ]
اگر بتوان ترتیب معادله را کاهش داد معمولا حل معادلات دیفرانسیل آسانتر است .
کاهش به یک سیستم مرتبه اول [ ویرایش ]
هر معادله دیفرانسیل صریح از مرتبه n ،
می توان با تعریف یک خانواده جدید از توابع مجهول به صورت سیستمی از n معادله دیفرانسیل مرتبه اول نوشت.
برای i = 1، 2، ...، n . سپس سیستم n بعدی معادلات دیفرانسیل جفت شده مرتبه اول است
در نماد برداری فشرده تر:
جایی که
خلاصه راه حل های دقیق [ ویرایش ]
برخی معادلات دیفرانسیل راه حل هایی دارند که می توان آنها را به صورت دقیق و بسته نوشت. چندین کلاس مهم در اینجا برگزار می شود.
در جدول زیر، P ( x ) ، Q ( x ) ، P ( y ) ، Q ( y ) و M ( x ، y ) ، N ( x ، y ) هر توابع انتگرال پذیر x ، y هستند . b و c ثابت داده شده حقیقی هستند. C 1 , C 2 , ... ثابت دلخواه هستند ( به طور کلی پیچیده ). معادلات دیفرانسیل در اشکال معادل و جایگزین خود هستند که از طریق یکپارچه سازی به حل منتهی می شوند.
در راه حل های انتگرالی، λ و ε متغیرهای ساختگی انتگرال گیری هستند (آنالوگ های پیوسته شاخص ها در مجموع )، و نماد ∫ x F ( λ ) dλ فقط به معنای انتکرال F ( λ ) با توجه به λ ، سپس پس از انتکرال است. جایگزین λ = x ، بدون اضافه کردن ثابت (به صراحت بیان شده است).
معادلات قابل تفکیک [ ویرایش ]
معادله دیفرانسیلروش حلراه حل کلی
مرتبه اول، قابل تفکیک در x و y (حالت عمومی، برای موارد خاص به زیر مراجعه کنید) [27]
جداسازی متغیرها (تقسیم بر P 2 Q 1 ).
انتکرال مستقیم
جداسازی متغیرها (تقسیم بر F ).
انتکرال در سراسر.
معادلات مرتبه اول عمومی [ ویرایش ]
معادله دیفرانسیلروش حلراه حل کلی
مرتبه اول، همگن [25]
y = ux را تنظیم کنید ، سپس با جداسازی متغیرهای u و x حل کنید .
جداسازی متغیرها (تقسیم بر xy ).
اگر N = M جواب xy = C است .
دیفرانسیل دقیق ، مرتبه اول [25]
جایی که
انتکرال در سراسر.
جایی که

دیفرانسیل غیر دقیق ، مرتبه اول [25]
جایی که
عامل انتکرال μ ( x , y ) راضی کننده است
اگر μ ( x , y ) را بتوان به روشی مناسب پیدا کرد، پس
ا
جایی که

معادلات مرتبه دوم عمومی [ ویرایش ]
معادله دیفرانسیلروش حلراه حل کلی
مرتبه دوم، خودمختار [28]
هر دو طرف معادله را در 2 dy / dx ضرب کنید ، جایگزین کنید2
معادلات خطی تا مرتبه n [ ویرایش ]
معادله دیفرانسیلروش حلراه حل کلی
ضرایب تابعی مرتبه اول، خطی، ناهمگن [25]
عامل یکپارچه سازی:.
ضرایب تابع مرتبه دوم، خطی، ناهمگن
عامل یکپارچه سازی:![{\displaystyle y=e^{-\int ^{x}P(\lambda )\,d\lambda }\left[\int ^{x}\left(\int ^{\xi }e^{\int ^{\lambda }P(\varepsilon )\,d\varepsilon }Q(\lambda )\,d\lambda \right)d\xi +C_{1}x+C_{2}\right]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/b111803be7ae071250bbfd01eaf62f114e454aae)
تابع مکمل y c : y c = e α x را در نظر بگیرید ، چند جمله ای را در α جایگزین کرده و حل کنید تا توابع مستقل خطی را پیدا کنید.ه
انتگرال خاص y p : به طور کلی روش تغییر پارامترها ، اگرچه برای بازرسی r ( x ) بسیار ساده ممکن است کار کند. [25]
اگر b 2 > 4 c , پس
اگر b 2 = 4 c ، پس
اگر b 2 < 4 c ، پس
ضرایب مرتبه n ، خطی، ناهمگن، ثابت [29]
تابع مکمل y c : y c = e α x را در نظر بگیرید ، چند جمله ای را در α جایگزین کرده و حل کنید تا توابع مستقل خطی را پیدا کنید.ه
انتگرال خاص y p : به طور کلی روش تغییر پارامترها ، اگرچه برای بازرسی r ( x ) بسیار ساده ممکن است کار کند. [25]
از آنجایی که α j حل های چند جمله ای درجه n هستند :



روش حدس زدن [ ویرایش ]

در این بخش هیچ منبعی ذکر نشده است . لطفاً با افزودن نقل قول به منابع معتبر به بهبود این بخش کمک کنید . اطلاعات بدون مرجع ممکن است مشکل ایجاد کرده و پاک شوند . ( ژانويه 2020 ) ( با نحوه و زمان حذف اين پيام الگو آشنا شويد )
هنگامی که همه روشهای دیگر برای حل یک ODE با شکست مواجه میشوند، یا در مواردی که ما شهودی در مورد اینکه راهحل یک DE ممکن است شبیه باشد، داریم، گاهی اوقات میتوان یک DE را به سادگی با حدس زدن راهحل و تأیید صحت آن حل کرد. برای استفاده از این روش، ما به سادگی یک راه حل برای معادله دیفرانسیل را حدس می زنیم، و سپس راه حل را به معادله دیفرانسیل متصل می کنیم تا اگر معادله را برآورده می کند، اعتبار سنجی کنیم. اگر اینطور شد، راه حل خاصی برای DE داریم، در غیر این صورت دوباره از نو شروع می کنیم و حدس دیگری را امتحان می کنیم. برای مثال میتوانیم حدس بزنیم که راهحل یک DE به شکل زیر است:�=آه�تی
در مورد یک ODE مرتبه اول که ناهمگن است، ابتدا باید یک راه حل DE برای بخش همگن DE پیدا کنیم، که در غیر این صورت معادله مشخصه نامیده می شود، و سپس با حدس زدن، راه حلی برای کل معادله ناهمگن پیدا کنیم. . در نهایت، ما هر دوی این راهحلها را با هم اضافه میکنیم تا جواب کل به ODE به دست آید، یعنی:
راه حل کلی=محلول همگن+راه حل خاص
نرم افزار برای حل ODE [ ویرایش ]
- ماکسیما ، یک سیستم جبر کامپیوتری منبع باز .
- COPASI ، یک بسته نرم افزاری رایگان ( Artistic License 2.0 ) برای انتکرال و تجزیه و تحلیل ODE ها.
- MATLAB ، یک برنامه محاسباتی فنی (MATrix LABoratory)
- GNU Octave ، یک زبان سطح بالا، که عمدتاً برای محاسبات عددی در نظر گرفته شده است.
- Scilab ، یک برنامه منبع باز برای محاسبات عددی.
- Maple ، یک برنامه اختصاصی برای محاسبات نمادین.
- Mathematica ، یک برنامه اختصاصی است که در درجه اول برای محاسبات نمادین در نظر گرفته شده است.
- SymPy ، یک بسته پایتون است که می تواند ODE ها را به صورت نمادین حل کند
- جولیا (زبان برنامه نویسی) ، یک زبان سطح بالا که در درجه اول برای محاسبات عددی در نظر گرفته شده است.
- SageMath ، یک برنامه متن باز است که از نحوی شبیه پایتون با طیف گسترده ای از قابلیت ها که چندین شاخه از ریاضیات را در بر می گیرد، استفاده می کند.
- SciPy ، یک بسته پایتون که شامل یک ماژول انتکرال ODE است.
- Chebfun ، یک بسته منبع باز، نوشته شده در MATLAB ، برای محاسبه توابع با دقت 15 رقمی.
- گنو R ، یک محیط محاسباتی منبع باز که در درجه اول برای آمار در نظر گرفته شده است، که شامل بسته هایی برای حل ODE است.
همچنین ببینید [ ویرایش ]
- مشکل ارزش مرزی
- نمونه هایی از معادلات دیفرانسیل
- تبدیل لاپلاس برای معادلات دیفرانسیل اعمال می شود
- فهرست مباحث سیستم های دینامیکی و معادلات دیفرانسیل
- معادله دیفرانسیل ماتریسی
- روش ضرایب نامشخص
- رابطه عود
یادداشت ها [ ویرایش ]
- ↑ Dennis G. Zill (15 مارس 2012). اولین دوره معادلات دیفرانسیل با کاربردهای مدلسازی . Cengage Learning. شابک 978-1-285-40110-2. بایگانی شده از نسخه اصلی در 17 ژانویه 2020 . بازیابی شده در 11 جولای 2019 .
- ↑ "منشأ اصطلاح "معادلات دیفرانسیل معمولی" چیست؟" . hsm.stackexchange.com . صرافی پشته . بازیابی شده در 2016-07-28 .
- ↑ Mathematics for Chemists, DM Hirst, Macmillan Press , 1976, (بدون ISBN) SBN: 333-18172-7
- ↑ کریزیگ (1972 ، ص 64)
- ^ سیمونز (1972 ، صفحات 1، 2)
- ↑ هالیدی و رسنیک (1977 ، ص 78)
- ^ تیپلر (1991 ، صفحات 78-83)
- ^ a bپرش به بالا: هارپر (1976 ، ص 127)
- ↑ کریزیگ (1972 ، ص 2)
- ^ سیمونز (1972 ، ص 3)
- ^ a bپرش به بالا: Kreyszig (1972 ، ص 24)
- ^ سیمونز (1972 ، ص 47)
- ↑ هارپر (1976 ، ص 128)
- ↑ کریزیگ (1972 ، ص 12)
- ↑ Ascher (1998 ، ص 12)
- ^ آخیم ایلچمن؛ تیمو ریس (2014). بررسی در معادلات دیفرانسیل جبری II . اسپرینگر. صص 104-105. شابک 978-3-319-11050-9.
- ↑ Ascher (1998 ، ص 5)
- ↑ کریزیگ (1972 ، ص 78)
- ↑ کریزیگ (1972 ، ص 4)
- ↑ واردیا تی هایمو (1985). "معادلات دیفرانسیل زمان محدود" . 1985 بیست و چهارمین کنفرانس IEEE در مورد تصمیم گیری و کنترل . صفحات 1729-1733. doi : 10.1109/CDC.1985.268832 . S2CID 45426376 .
- ↑ کرل ، 1866، 1868
- ^ لارنس (1999 ، ص 9)
- ^ لوگان، جی (2013). ریاضیات کاربردی (ویرایش چهارم).
- ↑ Ascher (1998 ، ص 13)
- ^ a b c d e f g h i jپرش به بالا: معادلات دیفرانسیل ابتدایی و مسائل ارزش مرزی (ویرایش چهارم)، WE Boyce، RC Diprima، Wiley International، John Wiley & Sons، 1986، ISBN 0-471-83824-1
- ^ بوسکاین؛ چیتور 2011، ص. 21
- ^ a bپرش به بالا: Mathematical Handbook of Formulas and Tables (ویرایش سوم)، S. Lipschutz, MR Spiegel, J. Liu, Schaum's Outline Series, 2009, ISC_2N 978-0-07-154855-7
- ↑ تحلیل ابتدایی بیشتر، R. Porter، G.Bell & Sons (لندن)، 1978، ISBN 0-7135-1594-5
- ^ a bپرش به بالا: روش های ریاضی برای فیزیک و مهندسی، KF Riley، MP Hobson، SJ Bence، انتشارات دانشگاه کمبریج، 2010، ISC_2N 978-0-521-86153-3
منابع [ ویرایش ]
- هالیدی، دیوید ؛ رسنیک، رابرت (1977)، فیزیک (ویرایش سوم)، نیویورک: وایلی ، شابک 0-471-71716-9
- هارپر، چارلی (1976)، مقدمه ای بر فیزیک ریاضی ، نیوجرسی: پرنتیس هال ، شابک 0-13-487538-9
- کریزیگ، اروین (1972)، ریاضیات مهندسی پیشرفته (ویرایش سوم)، نیویورک: وایلی ، ISBN 0-471-50728-8.
- Polyanin, AD and VF Zaitsev, Handbook of Exact Solutions for Ordinary Differential Equations (ویرایش دوم)، چاپمن و هال/CRC Press, Boca Raton, 2003. ISBN 1-58488-297-2
- سیمونز، جورج اف (1972)، معادلات دیفرانسیل با کاربردها و یادداشت های تاریخی ، نیویورک: مک گراو-هیل ، LCCN 75173716
- تیپلر، پل ای. (1991)، فیزیک برای دانشمندان و مهندسان: نسخه توسعه یافته (ویرایش سوم)، نیویورک: ناشران ورث ، شابک 0-87901-432-6
- بوسکاین، اوگو؛ Chitour، Yacine (2011)، Introduction à l'automatique (PDF) (به زبان فرانسوی)
- درزنر، لارنس (1999)، کاربردهای نظریه لی معادلات دیفرانسیل معمولی و جزئی ، بریستول و فیلادلفیا: موسسه انتشارات فیزیک ، شابک 978-0750305303
- اشر، اوری؛ پتزولد، لیندا (1998)، روشهای کامپیوتری برای معادلات دیفرانسیل معمولی و معادلات دیفرانسیل-جبری ، SIAM، ISBN 978-1-61197-139-2
کتابشناسی [ ویرایش ]
- کدینگتون، ارل ا. لوینسون، نورمن (1955). نظریه معادلات دیفرانسیل معمولی . نیویورک: مک گراو هیل .
- هارتمن، فیلیپ (2002) [1964]، معادلات دیفرانسیل معمولی ، کلاسیک در ریاضیات کاربردی، جلد. 38, Philadelphia: Society for Industrial and Applied Mathematics , doi : 10.1137/1.9780898719222 , ISBN 978-0-89871-510-1، MR 1929104
- دبلیو جانسون، رساله ای بر معادلات دیفرانسیل معمولی و جزئی ، جان وایلی و پسران، 1913، در مجموعه ریاضیات تاریخی دانشگاه میشیگان
- اینس، ادوارد ال. (1944) [1926]، معادلات دیفرانسیل معمولی ، انتشارات دوور، نیویورک، شابک 978-0-486-60349-0، MR 0010757
- ویتولد هورویچ ، سخنرانیهایی درباره معادلات دیفرانسیل معمولی ، انتشارات دوور، شابک 0-486-49510-8
- ابراگیموف، نایل اچ. (1993). CRC Handbook of Lie Group Analysis of Differential Equations Vol. 1-3 . Providence: CRC-Press. شابک 0-8493-4488-3..
- تسچل، جرالد (2012). معادلات دیفرانسیل معمولی و سیستم های دینامیکی . Providence : انجمن ریاضی آمریکا . شابک 978-0-8218-8328-0.
- AD Polyanin , VF Zaitsev, and A. Moussiaux, Handbook of First Order Partial Differential Equations , Taylor & Francis, London, 2002. ISBN 0-415-27267-X
- D. Zwillinger، Handbook of Differential Equations (ویرایش سوم) ، انتشارات دانشگاهی، بوستون، 1997.
پیوندهای خارجی [ ویرایش ]

Wikibooks کتابی با موضوع: حساب دیفرانسیل و انتگرال/معادلات دیفرانسیل معمولی دارد

در ویکیانبار رسانههای مربوط به معادلات دیفرانسیل معمولی موجود است .
- "معادله دیفرانسیل، معمولی" ، دایره المعارف ریاضیات ، انتشارات EMS ، 2001 [1994]
- EqWorld: دنیای معادلات ریاضی ، حاوی لیستی از معادلات دیفرانسیل معمولی با حل آنها.
- یادداشت های آنلاین / معادلات دیفرانسیل توسط پل داوکینز، دانشگاه لامار .
- معادلات دیفرانسیل ، SOS ریاضیات.
- آغازگر حل تحلیلی معادلات دیفرانسیل از موسسه روشهای عددی جامع، دانشگاه فلوریدا جنوبی.
- یادداشت های سخنرانی معادلات دیفرانسیل معمولی و سیستم های دینامیکی توسط جرالد تسل .
- یادداشتهایی درباره Diffy Qs: Differential Equations for Engineers کتاب درسی مقدماتی در مورد معادلات دیفرانسیل توسط Jiri Lebl از UIUC .
- مدل سازی با ODE ها با استفاده از Scilab آموزش نحوه مدل سازی یک سیستم فیزیکی که توسط ODE با استفاده از زبان برنامه نویسی استاندارد Scilab توسط تیم Openeering توضیح داده شده است.
- حل یک معادله دیفرانسیل معمولی در Wolfram|Alpha




















![{\displaystyle {\begin{cases}\mathbb {R} &y_{0}=0\\[4pt]\left(-\infty,x_{0}+{\frac {1}{y_{0}}} \right)&y_{0}>0\\[4pt]\left(x_{0}+{\frac {1}{y_{0}}},+\infty \right)&y_{0}<0\end {موارد}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/8142f4985f0a70e5b2d7db31af3f8a6546c7b621)













![{\displaystyle \ln(Cx)=\int ^{xy}{\frac {N(\lambda )\,d\lambda }{\lambda [N(\lambda )-M(\lambda )]}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/ef860b95a78299857b7025649deb3e6e30504c74)











![{\displaystyle y=e^{-\int ^{x}P(\lambda )\,d\lambda }\left[\int ^{x}e^{\int ^{\lambda }P(\varepsilon ) \,d\varepsilon }Q(\lambda )\,d\lambda +C\right]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/0161923c3b281e7f5d6d2c5c61e51e6c61f3e67d)






![{\displaystyle y_{c}=e^{-{\frac {bx}{2}}}\left[C_{1}\sin \left(x\,{\frac {\sqrt {4c-b^{ 2}}}{2}}\right)+C_{2}\cos \left(x\,{\frac {\sqrt {4c-b^{2}}}{2}}\right)\right] }](https://wikimedia.org/api/rest_v1/media/math/render/svg/5e53e6e17d2d3b8ca6aef9f6aacaae372efe9c3d)


 و
و ، به ترتیب، زاویه
، به ترتیب، زاویه بین آنها توسط رابطه داده می شود
بین آنها توسط رابطه داده می شود


 مضرب ثابت درجه هارمونیک کروی ناحیه ای است . از این منظر، تعمیم زیر به ابعاد بالاتر وجود دارد. فرض کنید Y j یک مبنای متعامد دلخواه فضای H از هارمونیک های کروی درجه روی کره n باشد . سپس
مضرب ثابت درجه هارمونیک کروی ناحیه ای است . از این منظر، تعمیم زیر به ابعاد بالاتر وجود دارد. فرض کنید Y j یک مبنای متعامد دلخواه فضای H از هارمونیک های کروی درجه روی کره n باشد . سپس  ، درجه هارمونیک ناحیه ای مربوط به بردار واحد x ، به صورت [21] تجزیه می شود.
، درجه هارمونیک ناحیه ای مربوط به بردار واحد x ، به صورت [21] تجزیه می شود.
 به عنوان مضرب ثابت چند جمله ای جیگنبوئر مناسب داده می شود :
به عنوان مضرب ثابت چند جمله ای جیگنبوئر مناسب داده می شود :


 و
و
 روی واحد کره و خطوط گره ای آن.
روی واحد کره و خطوط گره ای آن.![{\displaystyle \Re [Y_{\ell m}]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/fe4514a0a6a49a33432a4bf36efe1f6fa05cb3dc) برابر است با 0 در امتداد دایره های بزرگی که از قطب ها می گذرند و در امتداد دایره های − m با عرض جغرافیایی مساوی. تابع هر بار که از یکی از این خطوط عبور می کند علامت تغییر می دهد.
برابر است با 0 در امتداد دایره های بزرگی که از قطب ها می گذرند و در امتداد دایره های − m با عرض جغرافیایی مساوی. تابع هر بار که از یکی از این خطوط عبور می کند علامت تغییر می دهد.
 می توان با در نظر گرفتن " خطوط گره " آنها، یعنی مجموعه نقاط روی کره ای که در آن قرار دارد، تجسم کرد
می توان با در نظر گرفتن " خطوط گره " آنها، یعنی مجموعه نقاط روی کره ای که در آن قرار دارد، تجسم کرد![{\displaystyle \Re [Y_{\ell }^{m}]=0}](https://wikimedia.org/api/rest_v1/media/math/render/svg/26617636b368a6d09ed57405f1fb8652eb51e617) ، یا به جای آن که
، یا به جای آن که![{\displaystyle \Im [Y_{\ell }^{m}]=0}](https://wikimedia.org/api/rest_v1/media/math/render/svg/2b2fb51f4ee139b5891db76afaa139113a04982d) . خطوط گره ای از
. خطوط گره ای از و
و جهت ها به ترتیب. با توجه به
جهت ها به ترتیب. با توجه به که از قرارداد فاز کاندون-شورتلی استفاده می کنند:
که از قرارداد فاز کاندون-شورتلی استفاده می کنند:


 در فضای سه بعدی اقلیدسی
در فضای سه بعدی اقلیدسی . هارمونیک های کروی را می توان به فضای اقلیدسی با ابعاد بالاتر تعمیم دادآر
. هارمونیک های کروی را می توان به فضای اقلیدسی با ابعاد بالاتر تعمیم دادآر به شرح زیر منجر به توابع می شود
به شرح زیر منجر به توابع می شود . [24] اجازه دهید P فضای چندجملهای همگن با مقدار مختلط درجه را در n متغیر حقیقی نشان دهد که در اینجا به عنوان تابع در نظر گرفته میشود.
. [24] اجازه دهید P فضای چندجملهای همگن با مقدار مختلط درجه را در n متغیر حقیقی نشان دهد که در اینجا به عنوان تابع در نظر گرفته میشود. . یعنی یک p چند جمله ای در P است به شرطی که برای هر حقیقی باشد
. یعنی یک p چند جمله ای در P است به شرطی که برای هر حقیقی باشد ، یک نفر دارد
، یک نفر دارد



 از توابع پیوسته در
از توابع پیوسته در با توجه به توپولوژی یکنواخت ، توسط قضیه استون-وایرشتراس . در نتیجه، مجموع این فضاها در فضای L 2 ( Sn - 1 ) از توابع انتگرال پذیر مربع روی کره نیز اکم است. بنابراین هر تابع مربع انتگرال پذیر در کره به طور منحصر به فردی به یک سری هارمونیک های کروی تجزیه می شود، جایی که سری به معنای L 2 همگرا می شوند .
با توجه به توپولوژی یکنواخت ، توسط قضیه استون-وایرشتراس . در نتیجه، مجموع این فضاها در فضای L 2 ( Sn - 1 ) از توابع انتگرال پذیر مربع روی کره نیز اکم است. بنابراین هر تابع مربع انتگرال پذیر در کره به طور منحصر به فردی به یک سری هارمونیک های کروی تجزیه می شود، جایی که سری به معنای L 2 همگرا می شوند .

 اثبات دیگری می دهد که فضاهای H به صورت زوجی متعامد و در L 2 کامل هستند ( Sn - 1 ) .
اثبات دیگری می دهد که فضاهای H به صورت زوجی متعامد و در L 2 کامل هستند ( Sn - 1 ) .



 متقارن بر روی شاخص ها، به طور منحصر به فرد توسط نیاز تعیین می شود
متقارن بر روی شاخص ها، به طور منحصر به فرد توسط نیاز تعیین می شود







 . سپس، همانطور که از بسیاری جهات می توان دید (شاید به سادگی از تابع تولید هرگلوتز)، با
. سپس، همانطور که از بسیاری جهات می توان دید (شاید به سادگی از تابع تولید هرگلوتز)، با بردار واحد بودن
بردار واحد بودن
 به
به . بیانیه برابری هارمونیک های کروی پس از آن است
. بیانیه برابری هارمونیک های کروی پس از آن است

 در مورد مبدایی که بردار واحد را ارسال می کند
در مورد مبدایی که بردار واحد را ارسال می کند . تحت این عملیات، هارمونیک کروی درجه
. تحت این عملیات، هارمونیک کروی درجه و سفارش دهید
و سفارش دهید تبدیل به یک ترکیب خطی از هارمونیک های کروی با همان درجه می شود. به این معنا که،
تبدیل به یک ترکیب خطی از هارمونیک های کروی با همان درجه می شود. به این معنا که،
 یک ماتریس از نظم است
یک ماتریس از نظم است که به چرخش بستگی داردآر
که به چرخش بستگی داردآر![{\displaystyle Y_{\ell }^{m}({\mathbf {r} }')=\sum _{m'=-\ell }^{\ell [D_{mm'}^{(\ell )}({\mathcal {R}})]^{*}Y_{\ell }^{m'}({\mathbf {r} })،}](https://wikimedia.org/api/rest_v1/media/math/render/svg/d90f021b19abdcb67fe194dea9981c6473be594a)
 مزدوج مختلط یک عنصر از ماتریس D ویگنر است . به ویژه زمانی که"
مزدوج مختلط یک عنصر از ماتریس D ویگنر است . به ویژه زمانی که" با چرخش آزیموت ما اتحاد را بدست می آوریم،
با چرخش آزیموت ما اتحاد را بدست می آوریم،
 . در کره واحداس2
. در کره واحداس2 بنابراین می توان به عنوان یک ترکیب خطی از این موارد گسترش داد:
بنابراین می توان به عنوان یک ترکیب خطی از این موارد گسترش داد:


 همچنین می تواند از نظر هارمونیک های حقیقی گسترش یابد:
همچنین می تواند از نظر هارمونیک های حقیقی گسترش یابد: در بالا به عنوان جمع
در بالا به عنوان جمع
 . مزایای بسط از نظر توابع هارمونیک حقیقی
. مزایای بسط از نظر توابع هارمونیک حقیقی تضمین شده است که حقیقی هستند، در حالی که ضرایب آنها
تضمین شده است که حقیقی هستند، در حالی که ضرایب آنها در گسترش آنها از نظر
در گسترش آنها از نظر ) آن خاصیت را ندارند.
) آن خاصیت را ندارند.
 مبنای فضای چندجمله ای های هارمونیک و همگن درجه است
مبنای فضای چندجمله ای های هارمونیک و همگن درجه است و یک فرمول صریح برای
و یک فرمول صریح برای
 ،
، ، و
، و
 بردار با مختصات مختلط است:
بردار با مختصات مختلط است:![{\displaystyle \mathbf {a} =[{\frac {1}{2}}({\frac {1}{\lambda }}-\lambda ),-{\frac {i}{2}}({ \frac {1}{\lambda }}+\lambda ),1].}](https://wikimedia.org/api/rest_v1/media/math/render/svg/9d5d338cb35165858d91d7076b25277522143951)

 و
و به عنوان پاراهای حقیقی در نامگذاری این تابع مولد به نام هرگلوتز ، ما از کورانت-هیلبرت 1962 ، §VII.7 پیروی میکنیم که یادداشتهای منتشر نشده او را برای کشف آن اعتبار میدانند.
به عنوان پاراهای حقیقی در نامگذاری این تابع مولد به نام هرگلوتز ، ما از کورانت-هیلبرت 1962 ، §VII.7 پیروی میکنیم که یادداشتهای منتشر نشده او را برای کشف آن اعتبار میدانند. ، به طوری که
، به طوری که آنالوگ عملگر هارمونیک جامد است (/)
آنالوگ عملگر هارمونیک جامد است (/) ، [16] یک تابع تولید کننده برای مجموعه استاندارد شده ای از عملگرهای تانسور کروی بدست می آید .
، [16] یک تابع تولید کننده برای مجموعه استاندارد شده ای از عملگرهای تانسور کروی بدست می آید .
 تبدیل تحت چرخش ها (به زیر مراجعه کنید) به همان شیوه ای است
تبدیل تحت چرخش ها (به زیر مراجعه کنید) به همان شیوه ای است ، با
، با
 با رعایت تمام خصوصیات این عملگرها، مانند قضیه ترکیب کلبش-گوردان و قضیه ویگنر-اکارت . علاوه بر این، آنها یک مجموعه استاندارد شده با مقیاس یا عادی سازی ثابت هستند.
با رعایت تمام خصوصیات این عملگرها، مانند قضیه ترکیب کلبش-گوردان و قضیه ویگنر-اکارت . علاوه بر این، آنها یک مجموعه استاندارد شده با مقیاس یا عادی سازی ثابت هستند. و دیگری از
و دیگری از و
و ، به شرح زیر (فاز کاندون – شورتلی):
، به شرح زیر (فاز کاندون – شورتلی):![{\displaystyle r^{\ell }\,{\begin{pmatrix}Y_{\ell }^{m}\\Y_{\ell }^{-m}\end{pmatrix}}=\left[{\ frac {2\ell +1}{4\pi }}\right]^{1/2}{\bar {\Pi }}_{\ell }^{m}(z){\begin{pmatrix}\ چپ(-1\راست)^{m}(A_{m}+iB_{m})\\(A_{m}-iB_{m})\end{pmatrix}}،\qquad m>0.}](https://wikimedia.org/api/rest_v1/media/math/render/svg/066f9cfa96f2c4550337a93bf73d61517362c834)



![{\displaystyle {\bar {\Pi }}_{\ell }^{m}(z)=\left[{\frac {(\ell -m)!}{(\ell +m)!}}\ راست]^{1/2}\sum _{k=0}^{\left\lطبقه (\ell -m)/2\right\rfloor }(-1)^{k}2^{-\ell } {\binom {\ell }{k}}{\binom {2\ell -2k}{\ell }}{\frac {(\ell -2k)!}{(\ell -2k-m)!}} \;r^{2k}\;z^{\ell -2k-m}.}](https://wikimedia.org/api/rest_v1/media/math/render/svg/7e4c8fef579a7f234ae71d6ed82da1013e72c592)
 این کاهش می یابد
این کاهش می یابد
 اساساً چند جمله ای لژاندر مرتبط است
اساساً چند جمله ای لژاندر مرتبط است ، و عوامل
، و عوامل اساسا هستند
اساسا هستند .
. ، و
، و که به صراحت در بالا ذکر شده است، به دست می آوریم:
که به صراحت در بالا ذکر شده است، به دست می آوریم:![{\displaystyle Y_{3}^{1}=-{\frac {1}{r^{3}}}\left[{\tfrac {7}{4\pi }}\cdot {\tfrac {3} {16}}\right]^{1/2}\left(5z^{2}-r^{2}\right)\left(x+iy\right)=-\left[{\tfrac {7} {4\pi }}\cdot {\tfrac {3}{16}}\right]^{1/2}\left(5\cos ^{2}\theta -1\right)\left(\sin \ تتا e^{i\varphi }\right)}](https://wikimedia.org/api/rest_v1/media/math/render/svg/ed582e41ffef571704b11f0ad0dee2d0c0f40858)
![{\displaystyle Y_{4}^{-2}={\frac {1}{r^{4}}}\left[{\tfrac {9}{4\pi }}\cdot {\tfrac {5} {32}}\right]^{1/2}\left(7z^{2}-r^{2}\right)\left(x-iy\right)^{2}=\left[{\tfrac {9}{4\pi }}\cdot {\tfrac {5}{32}}\right]^{1/2}\left(7\cos ^{2}\theta -1\right)\left( \sin ^{2}\theta e^{-2i\varphi }\right)}](https://wikimedia.org/api/rest_v1/media/math/render/svg/4bcad8b6882705b752928a0c469aa0ef2f9e306f)
 فقطآ
فقطآ شرایط (کسینوس) گنجانده شده است، و برای<0
شرایط (کسینوس) گنجانده شده است، و برای<0 فقطب
فقطب اصطلاحات (سینوس ها) شامل می شوند:
اصطلاحات (سینوس ها) شامل می شوند:

 م،
م، یا ساده تر در مختصات دکارتی،
یا ساده تر در مختصات دکارتی،
 ، و
، و
 ، در مختصات استوانه ای ρ (مختصات شعاعی)، φ (زاویه قطبی) و z ( ارتفاع) بیان می شود. هر تابع V n ( k ) حاصل ضرب سه جمله است که هر کدام به تنهایی به یک مختصات بستگی دارد. عبارت وابسته به ρ توسط توابع بسل (که گاهی به آنها هارمونیک استوانه ای نیز گفته می شود) داده می شود.
، در مختصات استوانه ای ρ (مختصات شعاعی)، φ (زاویه قطبی) و z ( ارتفاع) بیان می شود. هر تابع V n ( k ) حاصل ضرب سه جمله است که هر کدام به تنهایی به یک مختصات بستگی دارد. عبارت وابسته به ρ توسط توابع بسل (که گاهی به آنها هارمونیک استوانه ای نیز گفته می شود) داده می شود. این مبنا از حاصل ضرب سه تابع تشکیل شده است:
این مبنا از حاصل ضرب سه تابع تشکیل شده است:
 مختصات استوانهای و ثابتهای n و k هستند که اعضای مجموعه را متمایز میکنند. در نتیجه اصل برهم نهی اعمال شده در معادله لاپلاس، راه حل های بسیار کلی برای معادله لاپلاس را می توان با ترکیب خطی این توابع به دست آورد.
مختصات استوانهای و ثابتهای n و k هستند که اعضای مجموعه را متمایز میکنند. در نتیجه اصل برهم نهی اعمال شده در معادله لاپلاس، راه حل های بسیار کلی برای معادله لاپلاس را می توان با ترکیب خطی این توابع به دست آورد.






 برای
برای  ، معادله لاپلاس اکنون می تواند نوشته شود:
، معادله لاپلاس اکنون می تواند نوشته شود:
 ، اکنون می توانیم توابع P و Φ را از هم جدا کنیم و یک ثابت دیگر ( n ) معرفی کنیم تا به دست آوریم:
، اکنون می توانیم توابع P و Φ را از هم جدا کنیم و یک ثابت دیگر ( n ) معرفی کنیم تا به دست آوریم:

 ثابت ها مشترک هستند. راه حل های حقیقی برای
ثابت ها مشترک هستند. راه حل های حقیقی برای

 شکلی از معادله بسل است.
شکلی از معادله بسل است.


 و
و توابع معمولی بسل هستند .
توابع معمولی بسل هستند .
 و
و )توابع بسل اصلاح شده اند .
)توابع بسل اصلاح شده اند .
 با توجه به مختصات استوانه ای ثابت هستند و حدود جمع و انتگرالبا شرایط مرزی مسئله تعیین می شود. توجه داشته باشید که انتگرال ممکن است با یک جمع برای شرایط مرزی مناسب جایگزین شود. متعامد بودن
با توجه به مختصات استوانه ای ثابت هستند و حدود جمع و انتگرالبا شرایط مرزی مسئله تعیین می شود. توجه داشته باشید که انتگرال ممکن است با یک جمع برای شرایط مرزی مناسب جایگزین شود. متعامد بودن اغلب هنگام یافتن راه حلی برای یک مشکل خاص بسیار مفید است. این
اغلب هنگام یافتن راه حلی برای یک مشکل خاص بسیار مفید است. این و
و توابع اساساً بسط های فوریه یا لاپلاس هستند و مجموعه ای از توابع متعامد را تشکیل می دهند. چه زمانی
توابع اساساً بسط های فوریه یا لاپلاس هستند و مجموعه ای از توابع متعامد را تشکیل می دهند. چه زمانی  ساده است
ساده است  ، متعامد بود
، متعامد بود ، همراه با روابط متعامد از
، همراه با روابط متعامد از دنباله ای از صفرهای مثبت است
دنباله ای از صفرهای مثبت است [2]
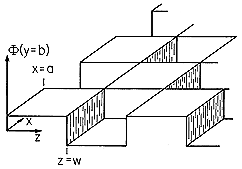
[2] داخل یک لوله استوانه ای رسانا (به عنوان مثال یک قوطی حلبی خالی) که از بالا و پایین توسط صفحات محدود شده است.
داخل یک لوله استوانه ای رسانا (به عنوان مثال یک قوطی حلبی خالی) که از بالا و پایین توسط صفحات محدود شده است. و
و و در طرفین توسط استولنه
و در طرفین توسط استولنه . [3] (در واحدهای MKS، فرض خواهیم کرد1
. [3] (در واحدهای MKS، فرض خواهیم کرد1 ). از آنجایی که پتانسیل توسط صفحات روی محور z محدود می شود ، تابع Z(k,z) را می توان تناوبی در نظر گرفت. از آنجایی که پتانسیل باید در مبدا صفر باشد، مقدار را می گیریم
). از آنجایی که پتانسیل توسط صفحات روی محور z محدود می شود ، تابع Z(k,z) را می توان تناوبی در نظر گرفت. از آنجایی که پتانسیل باید در مبدا صفر باشد، مقدار را می گیریم
 r-امین صفر است
r-امین صفر است![A_{{nr}}={\frac {4(2-\delta _{{n0}})}{a^{2}}}\,\,{\frac {\sinh k_{{nr}} L-z_{0})}{\sinh 2k_{{nr}}L}}\,\,{\frac {J_{n}(k_{{nr}}\rho _{0})}{k_{ {nr}}[J_{{n+1}}(k_{{nr}}a)]^{2}}}\,](https://wikimedia.org/api/rest_v1/media/math/render/svg/4b4eb5e3569947e4b1f824713a44baee89017cf6)

![A_{{nr}}={\frac {4(2-\delta _{{n0}})}{a^{2}}}\,\,{\frac {\sinh k_{{nr}} L+z_{0})}{\sinh 2k_{{nr}}L}}\,\,{\frac {J_{n}(k_{{nr}}\rho _{0})}{k_{ {nr}}[J_{{n+1}}(k_{{nr}}a)]^{2}}}.\,](https://wikimedia.org/api/rest_v1/media/math/render/svg/2ba17c88a547a517467acec9b9a0ea8eb6078143)
 ، تابع فوق صفر است. همچنین می توان به راحتی نشان داد که این دو تابع از نظر مقدار و مقدار اولین مشتقات خود در مطابقت دارند
، تابع فوق صفر است. همچنین می توان به راحتی نشان داد که این دو تابع از نظر مقدار و مقدار اولین مشتقات خود در مطابقت دارند .
.
![A_{{nr}}={\frac {2(2-\delta _{{n0}})}{a^{2}}}\,\,{\frac {J_{n}(k_{{nr }}\rho _{0})}{k_{{nr}}[J_{{n+1}}(k_{{nr}}a)]^{2}}}.\,](https://wikimedia.org/api/rest_v1/media/math/render/svg/f38faa25590cacb01d1bf458be2ffc81bd43f3bd)






 اگر پتانسیل الکتریکی با چگالی بار
اگر پتانسیل الکتریکی با چگالی بار  توسط معادله پواسون مرتبط باشد ، قانون گاوس برآورده می شود.
توسط معادله پواسون مرتبط باشد ، قانون گاوس برآورده می شود.
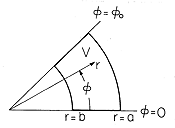
 = 0 یا
= 0 یا 
 نگه داشته شوند ، فقط مقادیر صحیح ثابت جداسازی m مجاز هستند، یعنی فقط راه حل هایی که در ادواری هستند
نگه داشته شوند ، فقط مقادیر صحیح ثابت جداسازی m مجاز هستند، یعنی فقط راه حل هایی که در ادواری هستند 
 به صفر میرسد و از این رو پتانسیل را در بینهایتی که قبلاً با (1) داده شده، مختل نمیکند. با یک ضریب دلخواه A ، راه حل است
به صفر میرسد و از این رو پتانسیل را در بینهایتی که قبلاً با (1) داده شده، مختل نمیکند. با یک ضریب دلخواه A ، راه حل است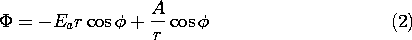

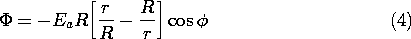
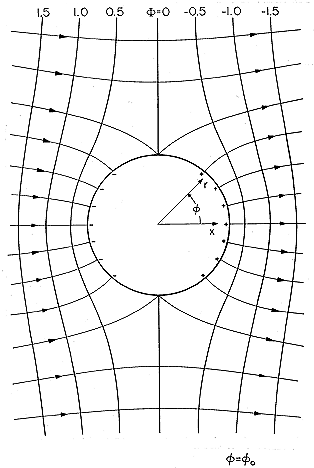
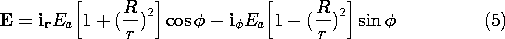
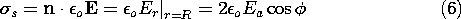
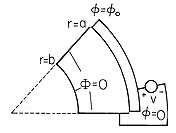
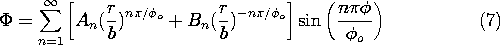
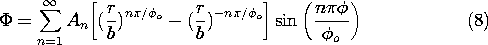
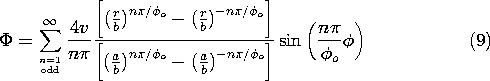
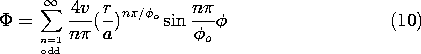
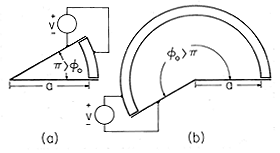
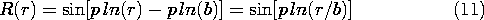
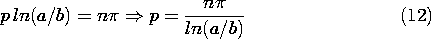
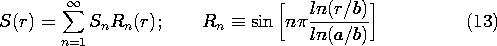
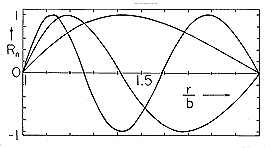
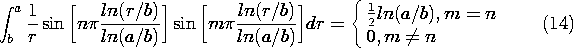
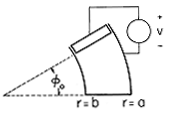
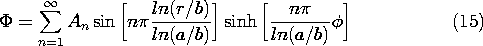
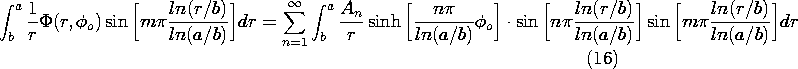
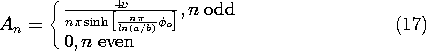

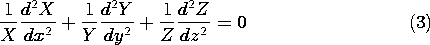
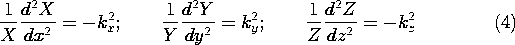

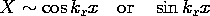
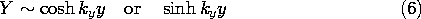

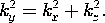
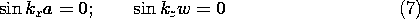
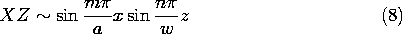
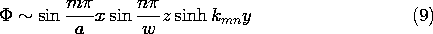
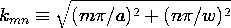
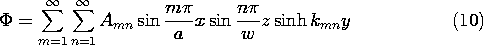
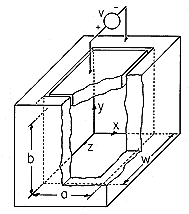
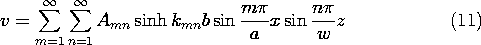
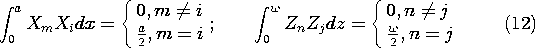
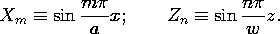
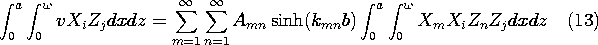
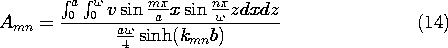
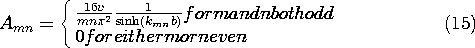
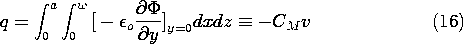
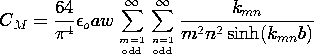
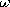 t ، در می یابیم که v o = V o cos
t ، در می یابیم که v o = V o cos 
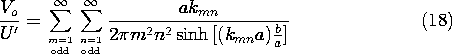
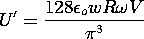
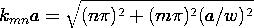
 a مقایسه می کنیم . در این حد، سینوس هذلولی تحت تسلط یکی از نمایی های آن قرار می گیرد و اولین جمله در این سری به دست می دهد.
a مقایسه می کنیم . در این حد، سینوس هذلولی تحت تسلط یکی از نمایی های آن قرار می گیرد و اولین جمله در این سری به دست می دهد.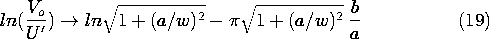

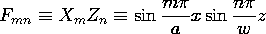
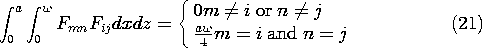


 وابستگی توسط توابع لژاندر توصیف شده است. برخلاف توابع بسل که با سری های چند جمله ای نامتناهی توصیف می شوند، توابع لژاندر چند جمله ای های محدودی در cos (
وابستگی توسط توابع لژاندر توصیف شده است. برخلاف توابع بسل که با سری های چند جمله ای نامتناهی توصیف می شوند، توابع لژاندر چند جمله ای های محدودی در cos ( 
 (جایی که
(جایی که عملگر nabla است )، یا
عملگر nabla است )، یا . در یک سیستم مختصات دکارتی , لاپلاسین با مجموع مشتقات جزئی دوم تابع نسبت به هر متغیر مستقل داده می شود . در سایر سیستم های مختصات ، مانند مختصات استوانه ای و کروی ، لاپلاسین نیز شکل مفیدی دارد. به طور غیررسمی، f ( p ) لاپلاسی تابع f در یک نقطه p اندازه میگیرد که مقدار میانگین f روی کرههای کوچک یا توپهایی که در مرکز p هستند، از f ( p ) چقدر انحراف دارد .
. در یک سیستم مختصات دکارتی , لاپلاسین با مجموع مشتقات جزئی دوم تابع نسبت به هر متغیر مستقل داده می شود . در سایر سیستم های مختصات ، مانند مختصات استوانه ای و کروی ، لاپلاسین نیز شکل مفیدی دارد. به طور غیررسمی، f ( p ) لاپلاسی تابع f در یک نقطه p اندازه میگیرد که مقدار میانگین f روی کرههای کوچک یا توپهایی که در مرکز p هستند، از f ( p ) چقدر انحراف دارد . ) از گرادیان (
) از گرادیان ( ). بنابراین اگر
). بنابراین اگر یک تابع با ارزش حقیقی دو بار متمایز است ، سپس لاپلاسی از
یک تابع با ارزش حقیقی دو بار متمایز است ، سپس لاپلاسی از




 سمت چپ این معادله عملگر لاپلاس است و کل معادله u = 0 به عنوان معادله لاپلاس شناخته می شود . راه حل های معادله لاپلاس، یعنی توابعی که لاپلاسین آنها یکسان صفر است، بنابراین چگالی های تعادلی ممکن را تحت نفوذ نشان می دهند.
سمت چپ این معادله عملگر لاپلاس است و کل معادله u = 0 به عنوان معادله لاپلاس شناخته می شود . راه حل های معادله لاپلاس، یعنی توابعی که لاپلاسین آنها یکسان صفر است، بنابراین چگالی های تعادلی ممکن را تحت نفوذ نشان می دهند. و یک نکته
و یک نکته  . سپس، مقدار متوسط از
. سپس، مقدار متوسط از متمرکز در
متمرکز در است: [2]
است: [2]







 که در آن x و y مختصات دکارتی استاندارد صفحه xy هستند .
که در آن x و y مختصات دکارتی استاندارد صفحه xy هستند .


 یا
یا


 :
: از فرمول ووس-ویل [3] برای واگرایی .
از فرمول ووس-ویل [3] برای واگرایی .


 هر گاه ρ یک چرخش باشد و به همین ترتیب:
هر گاه ρ یک چرخش باشد و به همین ترتیب: هر زمان که τ ترجمه باشد. (به طور کلی، زمانی که ρ یک تبدیل متعامد مانند بازتاب است، این موضوع صادق است .)
هر زمان که τ ترجمه باشد. (به طور کلی، زمانی که ρ یک تبدیل متعامد مانند بازتاب است، این موضوع صادق است .)
 به عنوان ... تعریف شده است
به عنوان ... تعریف شده است

 ،
، ، و
، و اجزای میدان برداری هستند
اجزای میدان برداری هستند ("تانسور " شامل اسکالر و برداری است) به عنوان واگرایی گرادیان تانسور تعریف می شود :
("تانسور " شامل اسکالر و برداری است) به عنوان واگرایی گرادیان تانسور تعریف می شود :


 که در آن عبارت با بردار لاپلاسی میدان سرعت است
که در آن عبارت با بردار لاپلاسی میدان سرعت است نشان دهنده تنش های چسبناک در سیال است.
نشان دهنده تنش های چسبناک در سیال است.
 جایی که
جایی که دلامبرتی است که در معادله کلاین-گوردون استفاده می شود .
دلامبرتی است که در معادله کلاین-گوردون استفاده می شود .


 یا دالامبرتین:
یا دالامبرتین:


 و
و یک نقطه بحرانی ، در این مورد، نقطه ای است که رتبه ماتریس ژاکوبین حداکثر نیست. این به نقشه های مشتق پذیر بین منیفولدهای قابل تفکیک گسترش می یابد ، زیرا نقاطی که رتبه ماتریس ژاکوبین کاهش می یابد. در این حالت به نقاط بحرانی نقاط انشعاب نیز می گویند .
یک نقطه بحرانی ، در این مورد، نقطه ای است که رتبه ماتریس ژاکوبین حداکثر نیست. این به نقشه های مشتق پذیر بین منیفولدهای قابل تفکیک گسترش می یابد ، زیرا نقاطی که رتبه ماتریس ژاکوبین کاهش می یابد. در این حالت به نقاط بحرانی نقاط انشعاب نیز می گویند .
 ). [1] یک مقدار بحرانی تصویر زیر f یک نقطه بحرانی است. این مفاهیم ممکن است از طریق نمودار f تجسم شوند : در یک نقطه بحرانی، اگر اصلاً بتوانید آن را اختصاص دهید، نمودار دارای مماس افقی است.
). [1] یک مقدار بحرانی تصویر زیر f یک نقطه بحرانی است. این مفاهیم ممکن است از طریق نمودار f تجسم شوند : در یک نقطه بحرانی، اگر اصلاً بتوانید آن را اختصاص دهید، نمودار دارای مماس افقی است. این بدان معناست که مماس منحنی موازی با محور y است ، و در این نقطه، g تابع ضمنی از x به y را تعریف نمی کند (به قضیه تابع ضمنی مراجعه کنید ). اگر ( x 0 , y 0 ) چنین نقطه بحرانی باشد، آنگاه x 0 مقدار بحرانی مربوطه است . به چنین نقطه بحرانی، نقطه انشعاب نیز می گویند ، زیرا به طور کلی، هنگامی که x تغییر می کند، دو شاخه منحنی در یک طرف x 0 و صفر در طرف دیگر وجود دارد.
این بدان معناست که مماس منحنی موازی با محور y است ، و در این نقطه، g تابع ضمنی از x به y را تعریف نمی کند (به قضیه تابع ضمنی مراجعه کنید ). اگر ( x 0 , y 0 ) چنین نقطه بحرانی باشد، آنگاه x 0 مقدار بحرانی مربوطه است . به چنین نقطه بحرانی، نقطه انشعاب نیز می گویند ، زیرا به طور کلی، هنگامی که x تغییر می کند، دو شاخه منحنی در یک طرف x 0 و صفر در طرف دیگر وجود دارد. (0، 1) و (0، -1) برای برآمدگی موازی با محور x ، و (1، 0) و (-1، 0) برای جهت موازی با محور y هستند . اگر نیم دایره بالایی را نمودار تابع در نظر بگیریم
(0، 1) و (0، -1) برای برآمدگی موازی با محور x ، و (1، 0) و (-1، 0) برای جهت موازی با محور y هستند . اگر نیم دایره بالایی را نمودار تابع در نظر بگیریم سپس x = 0 یک نقطه بحرانی با مقدار بحرانی 1 است زیرا مشتق برابر با 0 است و x = ± 1 نقاط بحرانی با مقدار بحرانی 0 به دلیل تعریف نشده بودن مشتق هستند.
سپس x = 0 یک نقطه بحرانی با مقدار بحرانی 1 است زیرا مشتق برابر با 0 است و x = ± 1 نقاط بحرانی با مقدار بحرانی 0 به دلیل تعریف نشده بودن مشتق هستند. در همه جا با مشتق مشتق پذیر است
در همه جا با مشتق مشتق پذیر است این تابع دارای یک نقطه بحرانی منحصر به فرد −1 است، زیرا عدد یکتایی x 0 برای آن است2.
این تابع دارای یک نقطه بحرانی منحصر به فرد −1 است، زیرا عدد یکتایی x 0 برای آن است2. این نقطه حداقل جهانی f است . مقدار بحرانی مربوطه است.
این نقطه حداقل جهانی f است . مقدار بحرانی مربوطه است. نمودار f یک سهمی مقعر به سمت بالا است، نقطه بحرانی آبسیس راس است که در آن خط مماس افقی است، و مقدار بحرانی مربوط به راس است و ممکن است با تقاطع این خط مماس و خط مماس نشان داده شود. محور y .
نمودار f یک سهمی مقعر به سمت بالا است، نقطه بحرانی آبسیس راس است که در آن خط مماس افقی است، و مقدار بحرانی مربوط به راس است و ممکن است با تقاطع این خط مماس و خط مماس نشان داده شود. محور y . برای همه x تعریف شده و برای x ≠ 0 با مشتق قابل تفکیک است
برای همه x تعریف شده و برای x ≠ 0 با مشتق قابل تفکیک است از آنجایی که f در x = 0 و قابل تفکیک نیست
از آنجایی که f در x = 0 و قابل تفکیک نیست در غیر این صورت، آن نقطه بحرانی منحصر به فرد است. نمودار تابع f در این نقطه یک کاسپ با مماس عمودی دارد . مقدار بحرانی مربوطه است.
در غیر این صورت، آن نقطه بحرانی منحصر به فرد است. نمودار تابع f در این نقطه یک کاسپ با مماس عمودی دارد . مقدار بحرانی مربوطه است.
 در همه جا مشتق پذیر است به جز در نقطه بحرانی x = 0 ، جایی که یک نقطه حداقل جهانی با مقدار بحرانی 0 دارد.
در همه جا مشتق پذیر است به جز در نقطه بحرانی x = 0 ، جایی که یک نقطه حداقل جهانی با مقدار بحرانی 0 دارد. نقاط بحرانی ندارد نقطه x = 0 یک نقطه بحرانی نیست زیرا در دامنه تابع گنجانده نشده است.
نقاط بحرانی ندارد نقطه x = 0 یک نقطه بحرانی نیست زیرا در دامنه تابع گنجانده نشده است. ، که در آن f یک تابع متمایز از دو متغیر است که معمولاً یک چند جمله ای دو متغیره است . نقاط منحنی نقاط صفحه اقلیدسی هستند که مختصات دکارتی آن معادله را برآورده می کند. دو پیش بینی استاندارد وجود دارد
، که در آن f یک تابع متمایز از دو متغیر است که معمولاً یک چند جمله ای دو متغیره است . نقاط منحنی نقاط صفحه اقلیدسی هستند که مختصات دکارتی آن معادله را برآورده می کند. دو پیش بینی استاندارد وجود دارد  و
و ، تعریف شده بوسیله ی
، تعریف شده بوسیله ی و
و که منحنی را روی محورهای مختصات ترسیم می کند . آنها را به ترتیب پروجکشن موازی با محور y و برآمدگی موازی با محور x می نامند .
که منحنی را روی محورهای مختصات ترسیم می کند . آنها را به ترتیب پروجکشن موازی با محور y و برآمدگی موازی با محور x می نامند .
 ، سپس ( x , y ) برای آن حیاتی است
، سپس ( x , y ) برای آن حیاتی است ،
، ممیز f باشد که به عنوان یک چند جمله ای در y با ضرایبی که چند جمله ای در x هستند مشاهده می شود . بنابراین این متمایز یک چند جمله ای در x است که دارای مقادیر بحرانی است
ممیز f باشد که به عنوان یک چند جمله ای در y با ضرایبی که چند جمله ای در x هستند مشاهده می شود . بنابراین این متمایز یک چند جمله ای در x است که دارای مقادیر بحرانی است نقاط بحرانی f نقاط بحرانی هستند،
نقاط بحرانی f نقاط بحرانی هستند، که در آن رتبه ماتریس ژاکوبین f حداکثر نیست. [6] تصویر یک نقطه بحرانی در زیر f مقدار بحرانی نامیده می شود . نقطه ای از مکمل مجموعه مقادیر بحرانی را مقدار منظم می نامند . قضیه سارد بیان می کند که مجموعه مقادیر بحرانی یک نقشه صاف دارای اندازه صفر است .
که در آن رتبه ماتریس ژاکوبین f حداکثر نیست. [6] تصویر یک نقطه بحرانی در زیر f مقدار بحرانی نامیده می شود . نقطه ای از مکمل مجموعه مقادیر بحرانی را مقدار منظم می نامند . قضیه سارد بیان می کند که مجموعه مقادیر بحرانی یک نقشه صاف دارای اندازه صفر است . یک نقشه دیفرانسیل بین دو منیفولد V و W با ابعاد مربوطه m و باشد n باشد . در همسایگی یک نقطه p از V و از f ( p ) ، نمودارها دیفرمورفیسم هستند. :→
یک نقشه دیفرانسیل بین دو منیفولد V و W با ابعاد مربوطه m و باشد n باشد . در همسایگی یک نقطه p از V و از f ( p ) ، نمودارها دیفرمورفیسم هستند. :→ و:
و: نقطه p حیاتی است برای f اگر
نقطه p حیاتی است برای f اگر برای
برای این تعریف به انتخاب نمودارها بستگی ندارد زیرا نقشههای انتقال دارای تفاوت هستند، ماتریسهای ژاکوبین آنها معکوس هستند و ضرب در آنها رتبه ماتریس ژاکوبین را تغییر نمیدهد.
این تعریف به انتخاب نمودارها بستگی ندارد زیرا نقشههای انتقال دارای تفاوت هستند، ماتریسهای ژاکوبین آنها معکوس هستند و ضرب در آنها رتبه ماتریس ژاکوبین را تغییر نمیدهد. یک زیر چندگانه از
یک زیر چندگانه از مجذور فاصله تا P نقطه از
مجذور فاصله تا P نقطه از![[-1،1]](https://wikimedia.org/api/rest_v1/media/math/render/svg/51e3b7f14a6f70e614728c583409a0b9a8b9de01) قرار دارند.یک سیستم
قرار دارند.یک سیستم 
![{\displaystyle {\frac {\mathrm {d} }{\mathrm {d} x}}\left[\left(1-x^{2}\right)\,y'(x)\right]+n (n+1)\,y(x)=0}](https://wikimedia.org/api/rest_v1/media/math/render/svg/1d8d5660d19479dff340689f286576cb5d0aaf67)
![x \ در [-1,1]](https://wikimedia.org/api/rest_v1/media/math/render/svg/1f9d0dda56ce3e01e14570ac9aef0021c6125722) و
و در حال نمایندگی
در حال نمایندگی

 و
و . یکی چند جمله ای های لژاندر را می نامد
. یکی چند جمله ای های لژاندر را می نامد







 چند جمله ای -te Legendre
چند جمله ای -te Legendre

![{\mathbb Q}[x]](https://wikimedia.org/api/rest_v1/media/math/render/svg/da33ddef34ad0c677b6eb7e042f574ee0e7553f7) ، یعنی یعنی ضرایب
، یعنی یعنی ضرایب ![I = [a,b]](https://wikimedia.org/api/rest_v1/media/math/render/svg/6d6214bb3ce7f00e496c0706edd1464ac60b73b5) و یک تابع وزن بر روی آن داده شده است
و یک تابع وزن بر روی آن داده شده است یک نتیجه است
یک نتیجه است از چند جمله ای های واقعی
از چند جمله ای های واقعی![P_n\in\R[X]](https://wikimedia.org/api/rest_v1/media/math/render/svg/ee840442661e2d073eadbb276082fbb8b4b361e9)

 با
با برآورده می کند.
برآورده می کند.![I = [-1,1]](https://wikimedia.org/api/rest_v1/media/math/render/svg/7edb704e6cad4f0d3828511af70f70be8861ccab) همراه با ساده ترین توابع وزن
همراه با ساده ترین توابع وزن چنین چندجملهای متعامد را میتوان با استفاده از
چنین چندجملهای متعامد را میتوان با استفاده از  به صورت تکراری تولید شود. چند جمله ای های لژاندر هنگام انجام کارهای اضافی به دست می آیند
به صورت تکراری تولید شود. چند جمله ای های لژاندر هنگام انجام کارهای اضافی به دست می آیند مورد نیاز است.
مورد نیاز است.
 قابل اجرا است
قابل اجرا است

 به روش زیر که معمولاً یافت می شود:
به روش زیر که معمولاً یافت می شود:
 با
با ، به ترتیب.
، به ترتیب.  نمایش بازگشتی زیر از چند جملهایهای لژاندر نتیجه میگیرد که مشتقات این چند جملهای را نیز در نظر میگیرد:
نمایش بازگشتی زیر از چند جملهایهای لژاندر نتیجه میگیرد که مشتقات این چند جملهای را نیز در نظر میگیرد:
 و.
و.![V:= L^2([-1,1]؛ \R)](https://wikimedia.org/api/rest_v1/media/math/render/svg/8fb95919b12ba38e52bb364a5093cc0b0364657d)
 .
. چند جمله ای لژاندر تشکیل می شود
چند جمله ای لژاندر تشکیل می شود یک سیستم متعامد کامل، بنابراین آنها یک مورد خاص از
یک سیستم متعامد کامل، بنابراین آنها یک مورد خاص از  ،
، به نام
به نام  در از
در از


 ،
،
 در، بنابراین شما دریافت کنید
در، بنابراین شما دریافت کنید . برای استفاده از سمت چپ باید طبق تعریف با
. برای استفاده از سمت چپ باید طبق تعریف با ضرب و سپس دوباره
ضرب و سپس دوباره بجای
بجای برای
برای برای همه
برای همه![f\in L^2 ([-1,1]; \R)](https://wikimedia.org/api/rest_v1/media/math/render/svg/d85daf21c61d8c5dac8a5c524c19de9e27cc4f2c) (به معنای
(به معنای -همگرایی).
-همگرایی). . در چه نسبتی صفر از
. در چه نسبتی صفر از -صفر
-صفر از جانب
از جانب
 بنابراین همه صفرها حداقل تا دو رقم اعشار با خطاهای بین تخمین زده می شوند
بنابراین همه صفرها حداقل تا دو رقم اعشار با خطاهای بین تخمین زده می شوند و
و ، در حالی که کوچکترین فاصله صفر از
، در حالی که کوچکترین فاصله صفر از فقط
فقط است. در
است. در در حال حاضر سه رقم اعشار امن هستند، با خطاهای بین
در حال حاضر سه رقم اعشار امن هستند، با خطاهای بین و
و ، در حالی که بهترین تودرتو از طریق
، در حالی که بهترین تودرتو از طریق فقط
فقط است. حداکثر خطای تخمین برای
است. حداکثر خطای تخمین برای تنهاست
تنهاست برای دو پنجم صفر از خارج، مقدار دقیق آنها با
برای دو پنجم صفر از خارج، مقدار دقیق آنها با آغاز می شود.
آغاز می شود. ، سپس بالا
، سپس بالا و
و .
. و هر کدام
و هر کدام
 ،
، ،
، قابل اجرا است
قابل اجرا است
 شعاع
شعاع  بنابراین به عنوان
بنابراین به عنوان  تعیین شده است.
تعیین شده است. (به عنوان مثال در
(به عنوان مثال در  :
:





 و در امتداد برش های شاخه
و در امتداد برش های شاخه  و
و

 تابع با ارزش حقیقی، مختلط یا
تابع با ارزش حقیقی، مختلط یا  را
را برابر با
برابر با  ثابت، در کاملا
ثابت، در کاملا تابع حل در مورد خاص مهم که
تابع حل در مورد خاص مهم که معادله با ناهمگن
معادله با ناهمگن و
و با ناهمگونی
با ناهمگونی
 معادله با ناهمگن
معادله با ناهمگن به ویژه، در حالت همگن، مجموع و مضرب راه حل ها همیشه راه حل هستند. دلیلش این است که یک مشتق بالاتر
به ویژه، در حالت همگن، مجموع و مضرب راه حل ها همیشه راه حل هستند. دلیلش این است که یک مشتق بالاتر به
به  بستگی دارد.
بستگی دارد.
 و
و توابع پیوسته هستند. سیستم همگن مربوطه است
توابع پیوسته هستند. سیستم همگن مربوطه است

 توابع پیوسته هستند. معادله همگن مربوطه است
توابع پیوسته هستند. معادله همگن مربوطه است

 .
.


 .
.
















 و
و هر سپس
هر سپس 
 .
. برای تعیین مجموع راه حل های مسئله ناهمگن کافی است. چون هست
برای تعیین مجموع راه حل های مسئله ناهمگن کافی است. چون هست
 مسئله ناهمگن با روش
مسئله ناهمگن با روش  نقشه با ارزش ماتریس پیوسته و
نقشه با ارزش ماتریس پیوسته و ناهمگونی سیستم
ناهمگونی سیستم
 و
و همچنین
همچنین  ، یعنی اعمال می شود
، یعنی اعمال می شود و
و . اگرچه به طور کلی نمی توان به طور صریح یک سیستم اساسی از مسئله همگن مرتبط را ساخت، ساختار آن
. اگرچه به طور کلی نمی توان به طور صریح یک سیستم اساسی از مسئله همگن مرتبط را ساخت، ساختار آن  . ابتدا در فضای راه حل هستید
. ابتدا در فضای راه حل هستید
 یک
یک  . سپس
. سپس  ضرب کننده های فلوکه یا ضرایب مشخصه از
ضرب کننده های فلوکه یا ضرایب مشخصه از

 درست پس از آن یکی
درست پس از آن یکی
 قابل اجرا است.
قابل اجرا است. . بنابراین صاحب
. بنابراین صاحب
 و
و .
.
 و
و .
. .
. تقسیم کرد یک معادله دیفرانسیل از فرم
تقسیم کرد یک معادله دیفرانسیل از فرم



![{\displaystyle {\begin{تراز شده}&z^{2}\sum _{k=0}^{\infty }(k+r-1)(k+r)A_{k}z^{k+r- 2}+zp(z)\sum _{k=0}^{\infty }(k+r)A_{k}z^{k+r-1}+q(z)\sum _{k=0 }^{\infty }A_{k}z^{k+r}\\&=\sum _{k=0}^{\infty }(k+r-1)(k+r)A_{k} z^{k+r}+p(z)\sum _{k=0}^{\infty }(k+r)A_{k}z^{k+r}+q(z)\sum _{ k=0}^{\infty }A_{k}z^{k+r}\\&=\sum _{k=0}^{\infty }[(k+r-1)(k+r) A_{k}z^{k+r}+p(z)(k+r)A_{k}z^{k+r}+q(z)A_{k}z^{k+r}]\ \&=\sum _{k=0}^{\infty }\left[(k+r-1)(k+r)+p(z)(k+r)+q(z)\right]A_ {k}z^{k+r}\\&=\left[r(r-1)+p(z)r+q(z)\right]A_{0}z^{r}+\sum _ {k=1}^{\infty }\left[(k+r-1)(k+r)+p(z)(k+r)+q(z)\right]A_{k}z^{ k+r}=0\end{تراز شده}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/0bfb90bb4fb997990a819416abd04660202641d3)











 یک
یک 
 اولین راه حل است (بر اساس ریشه بزرگتر در مورد ریشه های نابرابر)،
اولین راه حل است (بر اساس ریشه بزرگتر در مورد ریشه های نابرابر)، ریشه کوچکتر و ثابت
ریشه کوچکتر و ثابت  قرار است تعیین شود. یک بار
قرار است تعیین شود. یک بار انتخاب می شود (مثلاً با تنظیم آن بر روی 1) سپس
انتخاب می شود (مثلاً با تنظیم آن بر روی 1) سپس  ، که می تواند خودسرانه تنظیم شود. سپس بقیه موارد را مشخص می کند
، که می تواند خودسرانه تنظیم شود. سپس بقیه موارد را مشخص می کند در برخی موارد ثابت
در برخی موارد ثابت 
 و
و بنابراین می بینیم که لگاریتم در هیچ راه حلی ظاهر نمی شود. راه حل
بنابراین می بینیم که لگاریتم در هیچ راه حلی ظاهر نمی شود. راه حل دارای یک سری توان است که با توان صفر شروع می شود. در یک سری قدرت شروع با
دارای یک سری توان است که با توان صفر شروع می شود. در یک سری قدرت شروع با رابطه عود هیچ محدودیتی در ضریب برای مدت ایجاد نمی کند
رابطه عود هیچ محدودیتی در ضریب برای مدت ایجاد نمی کند که می تواند خودسرانه تنظیم شود. اگر روی صفر تنظیم شود، با این معادله دیفرانسیل، تمام ضرایب دیگر صفر می شوند و جواب
که می تواند خودسرانه تنظیم شود. اگر روی صفر تنظیم شود، با این معادله دیفرانسیل، تمام ضرایب دیگر صفر می شوند و جواب 


![{\displaystyle {\begin{aligned}f(x)&={\frac {1}{2\pi }}\int _{-\infty }^{\infty }e^{ipx}\left(\int _{-\infty }^{\infty }e^{-ip\alpha }f(\alpha )\,d\alpha \right)\,dp\\[4pt]&={\frac {1}{2 \pi }}\int _{-\infty }^{\infty }\left(\int _{-\infty }^{\infty }e^{ipx}e^{-ip\alpha }\,dp\ راست)f(\alpha )\,d\alpha =\int _{-\infty }^{\infty }\delta (x-\alpha )f(\alpha )\,d\alpha ,\end{aligned} }}](https://wikimedia.org/api/rest_v1/media/math/render/svg/656c821d528199232d832d301bbec290a815fe63)






![{\displaystyle H(x)=\int _{\mathbf {R} }\mathbf {1} _{(-\infty,x]}(t)\,\delta \{dt\}=\delta (- \infty,x],}](https://wikimedia.org/api/rest_v1/media/math/render/svg/da5a86fa6be3d9b9a19be89442b5a319085ad13d)

![{\displaystyle \delta [\varphi ]=\varphi (0)}](https://wikimedia.org/api/rest_v1/media/math/render/svg/df9006764a21dbc1593891d76b94e4a6c13cdd06)
![{\displaystyle \left|S[\varphi ]\right|\leq C_{N}\sum _{k=0}^{M_{N}}\sup _{x\in [-N,N]}\ چپ|\varphi ^{(k)}(x)\right|.}](https://wikimedia.org/api/rest_v1/media/math/render/svg/78f0622892eeb300dc23be96814b3078cc00f96f)
![\delta [\varphi ]=-\int _{-\infty }^{\infty }\varphi '(x)H(x)\,dx.](https://wikimedia.org/api/rest_v1/media/math/render/svg/461ad001cf1f108fdd65fcd3ed84702f91e4cdef)





![\delta _{x_{0}}[\varphi ]=\varphi (x_{0})](https://wikimedia.org/api/rest_v1/media/math/render/svg/9219b75c2a59f85c4a495187a42b9f997c7547a9)
 تعبیه مداوم X در فضای اندازه گیری های محدود رادون روی X است که مجهز به
تعبیه مداوم X در فضای اندازه گیری های محدود رادون روی X است که مجهز به  توپ دیگری به آن اصابت می کند و آن را با
توپ دیگری به آن اصابت می کند و آن را با  ، که در
، که در . مبادله تکانه در واقع آنی نیست و توسط فرآیندهای الاستیک در سطح مولکولی و زیر اتمی انجام می شود، اما برای اهداف عملی، راحت است که انتقال انرژی را به طور موثر آنی در نظر بگیریم. بنابراین
. مبادله تکانه در واقع آنی نیست و توسط فرآیندهای الاستیک در سطح مولکولی و زیر اتمی انجام می شود، اما برای اهداف عملی، راحت است که انتقال انرژی را به طور موثر آنی در نظر بگیریم. بنابراین  . (واحدهای
. (واحدهای هستند
هستند .)
.)![{\displaystyle \Delta t=[0,T]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/f9e2d96fc8758cc490227383eb4eadb234578795) . به این معنا که،
. به این معنا که،

 ، دادن
، دادن
 به عنوان تقریب های مفیدی برای ایده انتقال لحظه ای تکانه در نظر گرفته می شوند.
به عنوان تقریب های مفیدی برای ایده انتقال لحظه ای تکانه در نظر گرفته می شوند. در همه جا صفر است به جز یک نقطه، که در آن بی نهایت است. برای درک درست دلتای دیراک، در عوض باید اصرار داشته باشیم که این ویژگی
در همه جا صفر است به جز یک نقطه، که در آن بی نهایت است. برای درک درست دلتای دیراک، در عوض باید اصرار داشته باشیم که این ویژگی
 ، باید همچنان در حد باقی بماند. بنابراین، در معادله
، باید همچنان در حد باقی بماند. بنابراین، در معادله ، قابل درک است که حد همیشه خارج از انتگرال گرفته می شود .
، قابل درک است که حد همیشه خارج از انتگرال گرفته می شود .


 یک سطح صاف گرا در R 3 با مرز
یک سطح صاف گرا در R 3 با مرز . اگر یک فیلد برداری
. اگر یک فیلد برداری تعریف شده است و دارای
تعریف شده است و دارای  به طور واضح تر، برابری این را می گوید
به طور واضح تر، برابری این را می گوید

 :
:

 ، که می توان آن را به صورت پارامتری نشان داد:
، که می توان آن را به صورت پارامتری نشان داد:
 جایی که
جایی که  واحد طول قوس از نقطه است
واحد طول قوس از نقطه است  به نقطه
به نقطه 


 ، می توانیم ارزیابی کنیم
، می توانیم ارزیابی کنیم  ، و به دلیل
، و به دلیل ،
، .
. 
 محدود به نابرابری های زیر:
محدود به نابرابری های زیر:



 . اگر
. اگر یک میدان برداری سه بعدی است، سپس واگرایی از
یک میدان برداری سه بعدی است، سپس واگرایی از  .
.


![{\displaystyle {\begin{aligned}I&=\iiint _{V}\nabla \cdot \mathbf {F} \,\mathrm {d} V\\[6pt]&=\iiint _{V}\left( {\frac {\partial \mathbf {F_{x}} }{\partial x}}+{\frac {\partial \mathbf {F_{y}} }{\partial y}}+{\frac {\partial \mathbf {F_{z}} }{\partial z}}\right)\mathrm {d} V\\[6pt]&=\iiint _{V}(4x+4y+4z)\,\mathrm {d } V\\[6pt]&=\int _{0}^{3}\int _{-2}^{2}\int _{0}^{2\pi }(4x+4y+4z)\ ,\mathrm {d} V\end{تراز شده}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/d474d797d9611bde7396b5ad3c477fc3954e40fb)
![{\displaystyle {\begin{aligned}\int _{0}^{3}\int _{-2}^{2}\int _{0}^{2\pi }(4x+4y+4z)\ ,\mathrm {d} V&=\int _{-2}^{2}\int _{0}^{2\pi }(12y+12z+18)\,\mathrm {d} y\,\mathrm {d} z\\[6pt]&=\int _{0}^{2\pi }24(2z+3)\,\mathrm {d} z\\[6pt]&=48\pi (2\ pi +3)\end{تراز شده}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/620b3ddd2e22372f036668159bdb83c2be45446e)






 زاویه بین طرح بردار شعاع بر روی صفحه xy و محور x است. تعاریف متعدد دیگری نیز در حال استفاده است، بنابراین باید در مقایسه منابع مختلف دقت کرد.
زاویه بین طرح بردار شعاع بر روی صفحه xy و محور x است. تعاریف متعدد دیگری نیز در حال استفاده است، بنابراین باید در مقایسه منابع مختلف دقت کرد. 




 ). در مختصات دکارتی این به سادگی است:
). در مختصات دکارتی این به سادگی است:




 .
.
























 ؟ بطور دقیقتر، یک روش چند مرحله ای است سازگار اگر
؟ بطور دقیقتر، یک روش چند مرحله ای است سازگار اگر  از این روش ، با فرض اینکه تمام مقادیر قبلی
از این روش ، با فرض اینکه تمام مقادیر قبلی  دقیق هستند ، و حل دقیق معادله در زمان
دقیق هستند ، و حل دقیق معادله در زمان  . یک محاسبه با استفاده از
. یک محاسبه با استفاده از 
 همانطور که h به صفر می رود. این معادل شرط زیر در ضرایب روشها است:
همانطور که h به صفر می رود. این معادل شرط زیر در ضرایب روشها است:
 (
( 

 و
و .
. ، اما راه حل عددی بازدید کنندگان روش گام در همه بستگی ها ارزش شروع،
، اما راه حل عددی بازدید کنندگان روش گام در همه بستگی ها ارزش شروع، . بنابراین جالب است که آیا محلول عددی با توجه به اغتشاشات در مقادیر شروع پایدار است. یک روش چند مرحله ای خطی برای یک معادله دیفرانسیل خاص در یک بازه زمانی معین صفر است ، اگر اغتشاش در مقادیر شروع اندازه ε باعث شود که مقدار عددی K در آن فاصله زمانی بیش از K ε تغییر نکند برای مقادیر K که به اندازه گام h بستگی ندارد . این "ثبات صفر" نامیده می شود زیرا برای بررسی شرایط معادله دیفرانسیل کافی است
. بنابراین جالب است که آیا محلول عددی با توجه به اغتشاشات در مقادیر شروع پایدار است. یک روش چند مرحله ای خطی برای یک معادله دیفرانسیل خاص در یک بازه زمانی معین صفر است ، اگر اغتشاش در مقادیر شروع اندازه ε باعث شود که مقدار عددی K در آن فاصله زمانی بیش از K ε تغییر نکند برای مقادیر K که به اندازه گام h بستگی ندارد . این "ثبات صفر" نامیده می شود زیرا برای بررسی شرایط معادله دیفرانسیل کافی است (
(  همه به مقدار اولیه جمع می شوند
همه به مقدار اولیه جمع می شوند . سپس ، حل عددی به همان اندازه حل می شود که دقیقاً حل می شود
. سپس ، حل عددی به همان اندازه حل می شود که دقیقاً حل می شود (
(  تنها ریشه مدول 1 است. اگر همگرا باشد و همه ریشه های مدول 1 تکرار نشوند ، اما بیش از یک ریشه وجود دارد ، گفته می شود که نسبتاً پایدار است . توجه داشته باشید که 1 باید ریشه ای برای همگرایی روش باشد. بنابراین روشهای همگرا همیشه یکی از این دو روش هستند.
تنها ریشه مدول 1 است. اگر همگرا باشد و همه ریشه های مدول 1 تکرار نشوند ، اما بیش از یک ریشه وجود دارد ، گفته می شود که نسبتاً پایدار است . توجه داشته باشید که 1 باید ریشه ای برای همگرایی روش باشد. بنابراین روشهای همگرا همیشه یکی از این دو روش هستند.


 ، و شرایط فوق راضی است. مانند
، و شرایط فوق راضی است. مانند
 و
و . باز هم ضرایب b برای بدست آوردن بالاترین مرتبه ممکن انتخاب می شوند. با این حال ، روشهای آدامز-مولتون روشهای ضمنی است. با برداشتن محدودیتی که
. باز هم ضرایب b برای بدست آوردن بالاترین مرتبه ممکن انتخاب می شوند. با این حال ، روشهای آدامز-مولتون روشهای ضمنی است. با برداشتن محدودیتی که ، یک بازدید کنندگان روش آدامز-مولتون -Step می توانید سفارش رسیدن
، یک بازدید کنندگان روش آدامز-مولتون -Step می توانید سفارش رسیدن این
این  این
این 
 ، همانطور که در بالا ، بلکه
، همانطور که در بالا ، بلکه  . ضرایب توسط داده می شود
. ضرایب توسط داده می شود
 و ضرایب دیگر به گونه ای انتخاب شده اند که روش به ترتیب s (حداکثر ممکن) برسد. این روش ها به ویژه برای حل
و ضرایب دیگر به گونه ای انتخاب شده اند که روش به ترتیب s (حداکثر ممکن) برسد. این روش ها به ویژه برای حل  به گونه ای انتخاب می شوند که روش ها دارای نظم s باشند (این روش ها را به طور منحصر به فرد تعیین می کند).
به گونه ای انتخاب می شوند که روش ها دارای نظم s باشند (این روش ها را به طور منحصر به فرد تعیین می کند).
 به طوری که
به طوری که

 بجای. این معادله دقیقاً قابل حل است. راه حل به سادگی انتگرال p است . این نشان می دهد که گرفتن
بجای. این معادله دقیقاً قابل حل است. راه حل به سادگی انتگرال p است . این نشان می دهد که گرفتن

 توسط p intolant خود دچار خطای سفارش h s می شود ، و از این رو نتیجه می گیرد که روش s -
توسط p intolant خود دچار خطای سفارش h s می شود ، و از این رو نتیجه می گیرد که روش s - 
 در زمان های گسسته
در زمان های گسسته  :
:
 ) و
) و  یک عدد صحیح است
یک عدد صحیح است و
و  برای محاسبه مقدار
برای محاسبه مقدار 
 . ضرایب
. ضرایب و
و  روش را تعیین کنید. طراح این روش ضرایب را انتخاب کرده و نیاز به تقریب مناسب با راه حل واقعی را در برابر تمایل به دستیابی به روشی که کاربرد آن آسان است ، متعادل می کند. غالباً ، بسیاری از ضرایب برای ساده سازی روش صفر هستند.
روش را تعیین کنید. طراح این روش ضرایب را انتخاب کرده و نیاز به تقریب مناسب با راه حل واقعی را در برابر تمایل به دستیابی به روشی که کاربرد آن آسان است ، متعادل می کند. غالباً ، بسیاری از ضرایب برای ساده سازی روش صفر هستند. پس از آن روش "ضمنی" نامیده می شود ، زیرا مقدار
پس از آن روش "ضمنی" نامیده می شود ، زیرا مقدار  ، و باید معادله برای حل شود
، و باید معادله برای حل شود 
 .
.
 در مورد مشکل
در مورد مشکل ، نتایج زیر را می دهد:
، نتایج زیر را می دهد:

 و
و  ، برای محاسبه مقدار بعدی ،
، برای محاسبه مقدار بعدی ،  . با این حال ، مشکل مقدار اولیه فقط یک مقدار را فراهم می کند ،
. با این حال ، مشکل مقدار اولیه فقط یک مقدار را فراهم می کند ، . یک امکان برای حل این مسئله استفاده از
. یک امکان برای حل این مسئله استفاده از با روش اولر به عنوان مقدار دوم محاسبه می شود. با این انتخاب ، روش Adams – Bashforth بازده می شود (گرد شده به چهار رقم):
با روش اولر به عنوان مقدار دوم محاسبه می شود. با این انتخاب ، روش Adams – Bashforth بازده می شود (گرد شده به چهار رقم):
 است
است  ، بنابراین روش دو مرحله ای آدامز-باشفورث دقیق تر از روش اولر است. اگر اندازه گام به اندازه کافی کوچک باشد ، این همیشه وجود دارد.
، بنابراین روش دو مرحله ای آدامز-باشفورث دقیق تر از روش اولر است. اگر اندازه گام به اندازه کافی کوچک باشد ، این همیشه وجود دارد.

















![\ displaystyle (5) \ qquad \ qquad X ^ {(n) (t) = {\ آغاز {موارد} \ displaystyle - \ int _ {a} ^ {x} X ^ {(n-1)} ( t) p (t) ^ {- 1} y_ {0} (t) ^ {- 2} \، \ mathrm {d} t & n {\ text {عجیب}} ، \\ [6pt] \ displaystyle \ quad \ int _ {a} ^ {x} X ^ {(n-1)} (t) y_ {0} (t) ^ {2} w (t) \، \ mathrm {d} t & n {\ متن {حتی} \ end {موارد}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/a935431ccded6399b6b5cf5e77be5f37b850e119)
![\ displaystyle (6) \ qquad \ qquad {\ tilde {X}} ^ {(n) (t) = {\ آغاز {موارد} \ displaystyle \ quad \ int _ {a} ^ {x} {\ tilde {X}} ^ {(n-1)} (t) y_ {0} (t) ^ {2} w (t) \، \ mathrm {d} t & n {\ text {عجیب}} ، \\ [6pt ] \ displaystyle - \ int _ {a} ^ {x} {\ tilde {X}} ^ {(n-1) (t) p (t) ^ {- 1} y_ {0} (t) ^ -2} \، \ mathrm {d} t & n text \ text {حتی.}} \ end {موارد}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/f06583997b843e2112524e851d2ddd1ae6976e04)


![{\ displaystyle Lu = - {\ frac {1} {w (x)}} سمت چپ ({\ frac {\ mathrm {d}} {\ mathrm {d} x}} \ left [p (x) \، \ frac {\ mathrm {d} u} {\ mathrm {d} x}} \ Right] + q (x) u \ Right)](https://wikimedia.org/api/rest_v1/media/math/render/svg/695fea81795a5e4762471531b9b6b7708ce48550)

![\ displaystyle L ^ {2} ([a، b]، w (x) \، dx)](https://wikimedia.org/api/rest_v1/media/math/render/svg/558fef7efc0f815d4240e19891a1342e6c5f321c)




 با همان عملکردهای ویژه
با همان عملکردهای ویژه
 . مانند گذشته ، این می تواند به شکل SL کاهش یابد
. مانند گذشته ، این می تواند به شکل SL کاهش یابد : نوشتن یک اپراتور SL به عنوان:
: نوشتن یک اپراتور SL به عنوان:










 . در این حالت ، ما باید
. در این حالت ، ما باید 

 جایی که
جایی که  نماینده
نماینده 
 پیوسته است
پیوسته است جایی که
جایی که  نمایانگر
نمایانگر  فضاهای متریک، و N است
فضاهای متریک، و N است  یک فضای متریک است ، جایی که
یک فضای متریک است ، جایی که 

 است
است  ، نقشه مسافت
، نقشه مسافت (از
(از  ، و به طور خاص با توجه به توپولوژی محصول از پیوسته است
، و به طور خاص با توجه به توپولوژی محصول از پیوسته است  .
.![d '([x] ، [y]) = \ inf \ {d (p_1 ، q_1) + d (p_2، q_2) + \ dotsb + d (p_ {n ، q_ {n}) \](https://wikimedia.org/api/rest_v1/media/math/render/svg/b76c4134b02163411e4c3529bd699762f1e35911)
 و
و  با
با ![[p_1] = [x]](https://wikimedia.org/api/rest_v1/media/math/render/svg/a1d73570f663c6c3b07374f267f5fa4bc1135445) ،
، ![[q_n] = [y]](https://wikimedia.org/api/rest_v1/media/math/render/svg/ced6b87b086042c63417641c63edb4cfc5c3d0a1) ،
، ![[q_i] = [p_ {i + 1}]، i = 1،2، \ dots، n-1](https://wikimedia.org/api/rest_v1/media/math/render/svg/aa921d9eb1c7739ebdea8b30697d4376b5236ea9) . به طور کلی ، این فقط یک
. به طور کلی ، این فقط یک ![d '([x] ، [y]) = 0](https://wikimedia.org/api/rest_v1/media/math/render/svg/4f0686af91a21fdf1ed41059fa39ffbbe883bd4f) لزوماً دلالت بر این امر ندارد
لزوماً دلالت بر این امر ندارد ![[x] = [y]](https://wikimedia.org/api/rest_v1/media/math/render/svg/9c34866e2a1216182b168dc1e272b0b02f1aab3a) . با این حال ، برای برخی از روابط هم ارزی (به عنوان مثال ، آنهایی که با چسباندن چند لایه در کنار صورت) ، d ' یک معیار است.
. با این حال ، برای برخی از روابط هم ارزی (به عنوان مثال ، آنهایی که با چسباندن چند لایه در کنار صورت) ، d ' یک معیار است. یک
یک  برای همه x ، y ) رضایت بخش f ( x ) = f ( y ) هر زمان
برای همه x ، y ) رضایت بخش f ( x ) = f ( y ) هر زمان سپس عملکرد القایی
سپس عملکرد القایی  داده شده توسط
داده شده توسط![\ overline {f} ([x]) = f (x)](https://wikimedia.org/api/rest_v1/media/math/render/svg/aa40e344823d6033e5b82eaf6f31f3a562c6c9c6) ، یک نقشه متریک است
، یک نقشه متریک است 
 فضای -metric . اگر تابع فاصله مقادیر را در برخی از مجموعه های مناسب (مناسب) (و نابرابری مثلث براساس آن تنظیم شود) طول می کشد ، سپس به مفهوم اولتراسنج عمومی تعمیم می دهیم .
فضای -metric . اگر تابع فاصله مقادیر را در برخی از مجموعه های مناسب (مناسب) (و نابرابری مثلث براساس آن تنظیم شود) طول می کشد ، سپس به مفهوم اولتراسنج عمومی تعمیم می دهیم .  با درخواست دقیقاً یک
با درخواست دقیقاً یک  اگر
اگر  و هیچ کس دیگری نیست. با استفاده از
و هیچ کس دیگری نیست. با استفاده از به عنوان
به عنوان  به عنوان
به عنوان  . هر فضای متریک
. هر فضای متریک

 تنظیم
تنظیم 
 خواهد بود مورفیسم منحصر به فرد در
خواهد بود مورفیسم منحصر به فرد در
 خواهد بود مورفیسم منحصر به فرد داده شده از این واقعیت است
خواهد بود مورفیسم منحصر به فرد داده شده از این واقعیت است  .
. در این وبلاگ به ریاضیات و کاربردهای آن و تحقیقات در آنها پرداخته می شود. مطالب در این وبلاگ ترجمه سطحی و اولیه است و کامل نیست.در صورتی سوال یا نظری در زمینه ریاضیات دارید مطرح نمایید .در صورت امکان به آن می پردازم. من دوست دارم برای یافتن پاسخ به سوالات و حل پروژه های علمی با دیگران همکاری نمایم.در صورتی که شما هم بامن هم عقیده هستید با من تماس بگیرید.
در این وبلاگ به ریاضیات و کاربردهای آن و تحقیقات در آنها پرداخته می شود. مطالب در این وبلاگ ترجمه سطحی و اولیه است و کامل نیست.در صورتی سوال یا نظری در زمینه ریاضیات دارید مطرح نمایید .در صورت امکان به آن می پردازم. من دوست دارم برای یافتن پاسخ به سوالات و حل پروژه های علمی با دیگران همکاری نمایم.در صورتی که شما هم بامن هم عقیده هستید با من تماس بگیرید.