گراف ها
[ ویرایش ]
در نظریه گراف طیفی ، مقدار ویژه یک گراف به عنوان مقدار ویژه ماتریس مجاورت گراف تعریف می شود. 



برابر با درجه راس







بردار ویژه اصلی برای اندازه گیری مرکزیت رئوس آن استفاده می شود. به عنوان مثال الگوریتم مرتبه صفحه گوگل است . بردار ویژه اصلی یک ماتریس مجاورت اصلاح شده گراف وب جهانی، رتبه های صفحه را به عنوان اجزای آن نشان می دهد. این بردار مربوط به توزیع ثابت زنجیره مارکوف است که با ماتریس مجاورت نرمال شده ردیفی نشان داده شده است. با این حال، ماتریس مجاورت ابتدا باید برای اطمینان از وجود توزیع ثابت اصلاح شود. دومین بردار ویژه کوچکترین میتواند برای تقسیمبندی گراف به خوشهها از طریق خوشهبندی طیفی استفاده شود . روش های دیگری نیز برای خوشه بندی موجود است.
زنجیر مارکوف
[ ویرایش ]
یک زنجیره مارکوف با ماتریسی نشان داده می شود که مبنا های آن احتمالات انتقال بین حالت های یک سیستم هستند. به ویژه مبنا ها غیر منفی هستند و هر ردیف از ماتریس به یک جمع می شود، که مجموع احتمالات انتقال از یک حالت به حالت دیگر سیستم است. قضیه پرون-فروبنیوس شرایط کافی را برای یک زنجیره مارکوف فراهم میکند تا یک مقدار ویژه غالب منحصربهفرد داشته باشد، که بر همگرایی سیستم به حالت پایدار حاکم است.
تجزیه و تحلیل ارتعاش
شکل حالت یک چنگال تنظیم در فرکانس ویژه 440.09 هرتز
مقاله اصلی: لرزش
مسئلهات ارزش ویژه به طور طبیعی در تحلیل ارتعاش سازه های مکانیکی با درجات آزادی زیاد رخ می دهد . مقادیر ویژه، فرکانسهای طبیعی (یا فرکانسهای ویژه ) ارتعاش هستند و بردارهای ویژه شکلهای این حالتهای ارتعاشی هستند. به طور خاص، ارتعاش بدون میرا کنترل می شود

یعنی شتاب متناسب با موقعیت است (یعنی ما انتظار داریم
در







این را می توان به یک مسئله ارزش ویژه تعمیم یافته با دستکاری جبری به قیمت حل یک سیستم بزرگتر کاهش داد.
ویژگیهای متعامد بردارهای ویژه اجازه جداسازی معادلات دیفرانسیل را میدهد تا سیستم را بتوان به صورت جمع خطی بردارهای ویژه نشان داد. مسئله ارزش ویژه ساختارهای مختلط اغلب با استفاده از تحلیل اجزای محدود حل میشود ، اما راهحل را برای مسائل ارتعاشی با ارزش اسکالر تعمیم میدهد.
تانسور ممان اینرسی
[ ویرایش ]
در مکانیک ، بردارهای ویژه تانسور ممان اینرسی، محورهای اصلی یک جسم صلب را مشخص می کنند . تانسور گشتاور اینرسی یک کمیت کلیدی است که برای تعیین چرخش جسم صلب به دور مرکز جرمش لازم است .
تانسور استرس
[ ویرایش ]
در مکانیک جامدات ، تانسور تنش متقارن است و بنابراین میتوان آن را به یک تانسور مورب با مقادیر ویژه روی قطر و بردارهای ویژه تجزیه کرد. از آنجایی که مورب است، در این جهت، تانسور تنش دارای اجزای برشی نیست. اجزایی که دارد اجزای اصلی هستند.
معادله شرودینگر
توابع موج مرتبط با حالت های محدود یک الکترون در اتم هیدروژن را می توان به عنوان بردارهای ویژه اتم هیدروژن هامیلتونی و همچنین عملگر تکانه زاویه ای مشاهده کرد . آنها با مقادیر ویژه مرتبط هستند که به عنوان انرژی آنها تفسیر می شود (افزایش به سمت پایین
مثالی از یک معادله مقدار ویژه که در آن تبدیل 
که


با این حال، در موردی که فرد فقط به راه حل های حالت مقید معادله شرودینگر علاقه مند است، به دنبال


نماد bra-ket اغلب در این زمینه استفاده می شود. یک بردار، که حالتی از سیستم را نشان می دهد، در فضای هیلبرت از توابع انتگرال پذیر مربع با نشان داده می شود.

که






حمل و نقل موج
[ ویرایش ]
نور ، امواج صوتی ، و امواج مایکروویو به طور تصادفی چندین بار در هنگام عبور از یک سیستم بی نظم ساکن پراکنده می شوند . حتی اگر پراکندگی چندگانه به طور مکرر امواج را تصادفی کند، در نهایت انتقال موج منسجم از طریق سیستم یک فرآیند قطعی است که می تواند توسط یک ماتریس انتقال میدان توصیف شود





اوربیتال های مولکولی
[ ویرایش ]
در مکانیک کوانتومی ، و به ویژه در فیزیک اتمی و مولکولی ، در نظریه هارتری-فوک ، اوربیتال های اتمی و مولکولی را می توان با بردارهای ویژه عملگر فوک تعریف کرد . مقادیر ویژه مربوطه به عنوان پتانسیل یونیزاسیون از طریق قضیه کوپمنز تفسیر می شوند . در این مورد، اصطلاح بردار ویژه به معنای کمی کلی تر استفاده می شود، زیرا عملگر فوک به صراحت به اوربیتال ها و مقادیر ویژه آنها وابسته است. بنابراین، اگر کسی بخواهد زیر این جنبه خط بکشد، از مسائل ارزش ویژه غیرخطی صحبت می کند. چنین معادلاتی معمولاً با یک روش تکرار حل می شوند که در این مورد روش میدان خودسازگار نامیده می شود. در شیمی کوانتومی ، اغلب معادله هارتری-فوک را در یک مجموعه پایه غیر متعامد نشان میدهد . این نمایش خاص یک مسئله ارزش ویژه تعمیم یافته به نام معادلات روثان است .
زمین شناسی و یخچال شناسی
[ ویرایش ]
![]()
این بخش ممکن است برای اکثر خوانندگان برای درک آن بسیار فنی باشد . لطفاً بدون حذف جزئیات فنی، به بهبود آن کمک کنید تا برای افراد غیر متخصص قابل درک باشد . ( دسامبر 2023 ) ( با نحوه و زمان حذف این پیام آشنا شوید )
در زمینشناسی ، بهویژه در مطالعه یخبندان ، بردارهای ویژه و مقادیر ویژه بهعنوان روشی استفاده میشود که با آن میتوان انبوهی از اطلاعات جهت گیری و شیب اجزای یک پارچه کلاسست را در یک فضای سه بعدی با شش عدد خلاصه کرد. در این زمینه، یک زمینشناس ممکن است چنین دادههایی را برای صدها یا هزاران کلاس در یک نمونه خاک جمعآوری کند، که فقط میتوان آنها را به صورت گرافیکی مقایسه کرد، مانند گراف Tri-Plot (اسنید-فولک)، [ 47 ] [ 48 ] یا به عنوان یک گراف استریونت در یک شبکه ولف. [ 49 ]
خروجی تانسور جهت گیری در سه محور متعامد (عمود) فضا است. سه بردار ویژه مرتب شده اند










شماره تکثیر پایه
[ ویرایش ]
مقاله اصلی: شماره تکثیر پایه
شماره تولید مثل اصلی (




صورتهای ویژه
صورتهای ویژه به عنوان نمونه هایی از بردارهای ویژه
مقاله اصلی: صورتهای ویژه
در پردازش تصویر ، تصاویر پردازش شده از چهره ها را می توان به عنوان بردارهایی دید که اجزای آن روشنایی هر پیکسل است . [ 54 ] بعد این فضای برداری تعداد پیکسل ها است. بردارهای ویژه ماتریس کوواریانس مرتبط با مجموعه بزرگی از تصاویر نرمال شده از چهره ها ، صورتهای ویژه نامیده می شوند . این نمونه ای از تحلیل مؤلفه های اصلی است . آنها برای بیان هر تصویر چهره به صورت ترکیبی خطی از برخی از آنها بسیار مفید هستند. در شاخه تشخیص چهره بیومتریک ، چهره های ویژه ابزاری برای اعمال فشرده سازی داده ها بر روی چهره ها برای اهداف شناسایی فراهم می کنند . تحقیقات مربوط به سیستم های بینایی ویژه که حرکات دست را تعیین می کنند نیز انجام شده است.
مشابه این مفهوم، صداهای ویژه نشان دهنده جهت کلی تغییرپذیری در تلفظ های انسانی یک گفته خاص، مانند یک کلمه در یک زبان است. بر اساس یک ترکیب خطی از این صداهای ویژه، می توان یک تلفظ صوتی جدید از کلمه ایجاد کرد. این مفاهیم در سیستمهای تشخیص خودکار گفتار برای سازگاری با سخنران مفید بوده است.
همچنین ببینید
[ ویرایش ]
- نظریه ضد ارزش ویژه
- اپراتور ویژه
- فضا ی خاص
- لحظات ویژه
- الگوریتم ارزش ویژه
- حالات کوانتومی
- فرم معمولی جردن
- لیست نرم افزارهای تحلیل عددی
- مسئله ویژه غیرخطی
- مقدار ویژه معمولی
- مسئله ارزش ویژه درجه دوم
- ارزش مفرد
- طیف یک ماتریس
https://en.wikipeia.org/wiki/Eigenvalues_an_eigenvectors








 با معادله ارزش ویژه
با معادله ارزش ویژه
 تابع ویژه عملگر مشتق است. در این مورد، تابع ویژه خود تابعی از مقدار ویژه مرتبط با آن است. به طور خاص، برای λ = 0، تابع ویژه f ( t ) یک ثابت است.
تابع ویژه عملگر مشتق است. در این مورد، تابع ویژه خود تابعی از مقدار ویژه مرتبط با آن است. به طور خاص، برای λ = 0، تابع ویژه f ( t ) یک ثابت است.
 ( 5 )
( 5 )




 یک سیستم k بعدی مرتبه اول در بردار متغیر انباشته داده می شود
یک سیستم k بعدی مرتبه اول در بردار متغیر انباشته داده می شود بر حسب مقدار یک بار تاخیر آن و با در نظر گرفتن معادله مشخصه ماتریس این سیستم. این معادله k ریشه مشخصه می دهدλ1،…،λک،
بر حسب مقدار یک بار تاخیر آن و با در نظر گرفتن معادله مشخصه ماتریس این سیستم. این معادله k ریشه مشخصه می دهدλ1،…،λک، برای استفاده در معادله حل
برای استفاده در معادله حل

 ماتریس مجموع است
ماتریس مجموع است ضربهای مختلف [ e ]
ضربهای مختلف [ e ]
 ، یعنی
، یعنی
 یعنی
یعنی
 . بنابراین، هر بردار از فرم
. بنابراین، هر بردار از فرم ، برای هر عدد حقیقی غیر صفر
، برای هر عدد حقیقی غیر صفر ، بردار ویژه ای از
، بردار ویژه ای از .
. . یک محاسبه مشابه نشان می دهد که بردارهای ویژه مربوطه، راه حل های غیر صفر هستند
. یک محاسبه مشابه نشان می دهد که بردارهای ویژه مربوطه، راه حل های غیر صفر هستند ، یعنی هر بردار فرم
، یعنی هر بردار فرم ، برای هر عدد حقیقی غیر صفر
، برای هر عدد حقیقی غیر صفر  .
. ; این باعث می شود که به بردار ویژه نزدیکترین مقدار ویژه همگرا شود
; این باعث می شود که به بردار ویژه نزدیکترین مقدار ویژه همگرا شود .
. (تقریبی خوب از) بردار ویژه است
(تقریبی خوب از) بردار ویژه است
 نشان دهنده جابجایی مزدوج است
نشان دهنده جابجایی مزدوج است
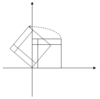




























 ، که هرگاه θ مضرب صحیح 180 درجه نباشد یک عدد منفی است . بنابراین، به جز این موارد خاص، دو مقدار ویژه اعداد مختلط هستند.
، که هرگاه θ مضرب صحیح 180 درجه نباشد یک عدد منفی است . بنابراین، به جز این موارد خاص، دو مقدار ویژه اعداد مختلط هستند. ; و همه بردارهای ویژه دارای ورودی های غیر حقیقی هستند. در واقع، به جز موارد خاص، یک چرخش جهت هر بردار غیر صفر را در صفحه تغییر می دهد.
; و همه بردارهای ویژه دارای ورودی های غیر حقیقی هستند. در واقع، به جز موارد خاص، یک چرخش جهت هر بردار غیر صفر را در صفحه تغییر می دهد.
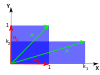
 با انحراف استاندارد 3 در تقریبا
با انحراف استاندارد 3 در تقریبا جهت و از 1 در جهت متعامد. بردارهای نشان داده شده بردارهای ویژه واحدی از ماتریس کوواریانس (متقارن، مثبت-نیمه معین) هستند که با جذر مقدار ویژه مربوطه مقیاس شده اند. همانطور که در حالت تک بعدی، جذر گرفته می شود زیرا انحراف معیار به راحتی قابل مشاهده است تا واریانس .
جهت و از 1 در جهت متعامد. بردارهای نشان داده شده بردارهای ویژه واحدی از ماتریس کوواریانس (متقارن، مثبت-نیمه معین) هستند که با جذر مقدار ویژه مربوطه مقیاس شده اند. همانطور که در حالت تک بعدی، جذر گرفته می شود زیرا انحراف معیار به راحتی قابل مشاهده است تا واریانس . ( 3 )
( 3 ) ( 4 )
( 4 )

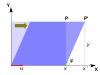
 . در این مثال، بردارهای ویژه هر مضرب اسکالر غیر صفر هستند
. در این مثال، بردارهای ویژه هر مضرب اسکالر غیر صفر هستند



 .
. . از آنجایی که E نیز فضای تهی ( A - λI ) است، چندگانگی هندسی λ بعد فضای خالی ( A - λI ) است، که به آن تهی ( A - λI ) نیز می گویند ، که به بعد و رتبه مربوط می شود. ( A − λI ) به عنوان
. از آنجایی که E نیز فضای تهی ( A - λI ) است، چندگانگی هندسی λ بعد فضای خالی ( A - λI ) است، که به آن تهی ( A - λI ) نیز می گویند ، که به بعد و رتبه مربوط می شود. ( A − λI ) به عنوان

 ، در نظر بگیرید که چگونه تعریف چندگانگی هندسی دلالت بر وجود دارد
، در نظر بگیرید که چگونه تعریف چندگانگی هندسی دلالت بر وجود دارد ، طوری که
، طوری که . بنابراین ما می توانیم یک ماتریس (یونیتی) پیدا کنیمV
. بنابراین ما می توانیم یک ماتریس (یونیتی) پیدا کنیمV اولین کسی که
اولین کسی که بردارهای متعامد به این بردارهای ویژه از
بردارهای متعامد به این بردارهای ویژه از ، ماتریسی به دست می آوریم که بلوک بالای سمت چپ آن ماتریس مورب است
، ماتریسی به دست می آوریم که بلوک بالای سمت چپ آن ماتریس مورب است . این را می توان با ارزیابی عملکرد سمت چپ با بردارهای پایه ستون اول مشاهده کرد. با سازماندهی مجدد و اضافه کردن
. این را می توان با ارزیابی عملکرد سمت چپ با بردارهای پایه ستون اول مشاهده کرد. با سازماندهی مجدد و اضافه کردن در هر دو طرف، ما دریافت می کنیم
در هر دو طرف، ما دریافت می کنیم از آنجایی که
از آنجایی که رفت و آمد با
رفت و آمد با  شبیه
شبیه  ، است و
، است و . اما از تعریف
. اما از تعریف  حاوی یک عامل
حاوی یک عامل ، به این معنی که چندگانگی جبری از
، به این معنی که چندگانگی جبری از  باید راضی کند
باید راضی کند .
. مقادیر ویژه متمایز
مقادیر ویژه متمایز ، که در آن چندگانگی هندسی از
، که در آن چندگانگی هندسی از . چندگانگی هندسی
. چندگانگی هندسی
 ، سپس
، سپس . مقدار ویژه مربوطه ، مقدار مشخصه یا ریشه مشخصه عامل ضرب است
. مقدار ویژه مربوطه ، مقدار مشخصه یا ریشه مشخصه عامل ضرب است ماتریس A و یک بردار غیر صفر
ماتریس A و یک بردار غیر صفر اگر A را در ضرب کنیم
اگر A را در ضرب کنیم ) به سادگی ترازو
) به سادگی ترازو . [ 2 ]
. [ 2 ] به عنوان معادله ارزش ویژه یا معادله ویژه شناخته می شود . به طور کلی، λ ممکن است هر اسکالر باشد . برای مثال، λ ممکن است منفی باشد، در این صورت بردار ویژه به عنوان بخشی از مقیاس بندی جهت معکوس می کند، یا ممکن است صفر یا مختلط باشد .
به عنوان معادله ارزش ویژه یا معادله ویژه شناخته می شود . به طور کلی، λ ممکن است هر اسکالر باشد . برای مثال، λ ممکن است منفی باشد، در این صورت بردار ویژه به عنوان بخشی از مقیاس بندی جهت معکوس می کند، یا ممکن است صفر یا مختلط باشد .
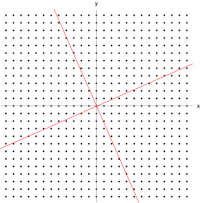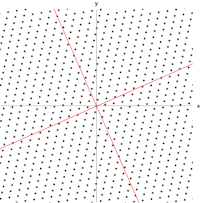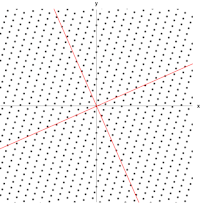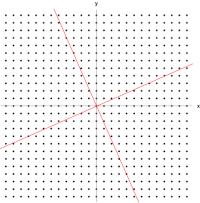
 ، در این صورت بردارهای ویژه توابعی هستند به نام توابع ویژه که توسط آن عملگر دیفرانسیل مقیاس بندی می شوند، ماننددد.
، در این صورت بردارهای ویژه توابعی هستند به نام توابع ویژه که توسط آن عملگر دیفرانسیل مقیاس بندی می شوند، ماننددد. از طرف دیگر، تبدیل خطی می تواند به شکل یک ماتریس n در n باشد ، در این صورت بردارهای ویژه n در 1 ماتریس هستند. اگر تبدیل خطی به شکل n با n ماتریس A بیان شود ، معادله مقدار ویژه برای تبدیل خطی بالا می تواند به صورت ضرب ماتریس بازنویسی شود.،
از طرف دیگر، تبدیل خطی می تواند به شکل یک ماتریس n در n باشد ، در این صورت بردارهای ویژه n در 1 ماتریس هستند. اگر تبدیل خطی به شکل n با n ماتریس A بیان شود ، معادله مقدار ویژه برای تبدیل خطی بالا می تواند به صورت ضرب ماتریس بازنویسی شود.، که در آن بردار ویژه v یک ماتریس n در 1 است. برای یک ماتریس، مقادیر ویژه و بردارهای ویژه را می توان برای تجزیه ماتریس استفاده کرد - برای مثال با قطری کردن آن.
که در آن بردار ویژه v یک ماتریس n در 1 است. برای یک ماتریس، مقادیر ویژه و بردارهای ویژه را می توان برای تجزیه ماتریس استفاده کرد - برای مثال با قطری کردن آن.


 .
.
 جایی که برای هر ردیف
جایی که برای هر ردیف
 ( 1 )
( 1 ) ( 2 )
( 2 )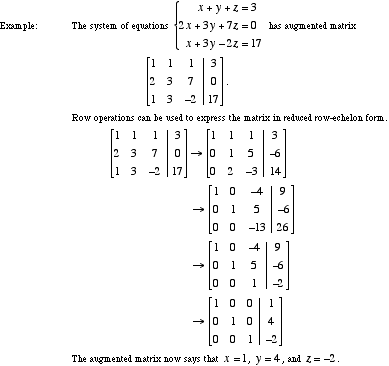

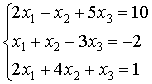
 .
.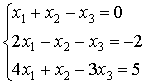

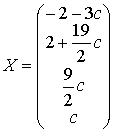 .
.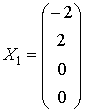 .
.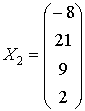 .
.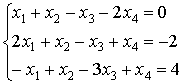
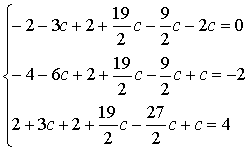
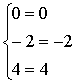


 ).
). که در آن V یکانی است و D قطری است و یکانی.
که در آن V یکانی است و D قطری است و یکانی. . به این معنا که،
. به این معنا که، روی دایره یکانی صفحه مختلط خواهد بود.
روی دایره یکانی صفحه مختلط خواهد بود. یکانی است
یکانی است یکانی است
یکانی است .
. .
. .
. برای همه
برای همه  ، جایی که
، جایی که .
.

 با
با  گروه یکانی ویژه SU(2) نامیده می شود.
گروه یکانی ویژه SU(2) نامیده می شود.
 و ه ،
و ه ، بالا و زوایای
بالا و زوایای  می تواند هر مقداری را بگیرد.
می تواند هر مقداری را بگیرد. و ،
و ، فاکتورسازی زیر را دارد:
فاکتورسازی زیر را دارد:

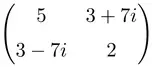
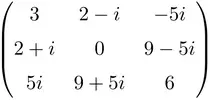
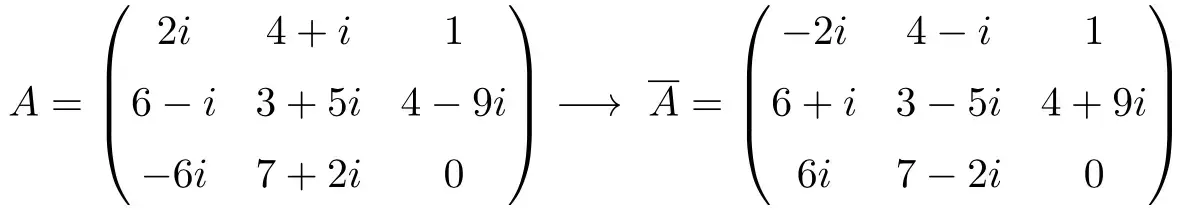











![{\displaystyle \psi _{n}(x)={\frac {\sqrt[{4}]{2}}{\sqrt {n!}}}e^{-\pi x^{2}}\ mathrm {He} _{n}\left(2x{\sqrt {\pi }}\right)}](https://wikimedia.org/api/rest_v1/media/math/render/svg/a9121f54a3fdbb0eedecf2aef5a379bdfae414b7)

 .
.









 بنابراین، گسترش تبدیل فوریه به حوزه مختلط به این معنی است که تبدیل لاپلاس را به عنوان یک مورد خاص در مورد توابع علی - اما با تغییر متغیر
بنابراین، گسترش تبدیل فوریه به حوزه مختلط به این معنی است که تبدیل لاپلاس را به عنوان یک مورد خاص در مورد توابع علی - اما با تغییر متغیر 

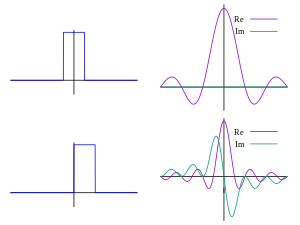
 مختلط باشد، اما دارای مزیت نمایش فشرده تمام اطلاعات لازم در مورد هر فرکانس است. تعبیر معمول این عدد مختلط این است که
مختلط باشد، اما دارای مزیت نمایش فشرده تمام اطلاعات لازم در مورد هر فرکانس است. تعبیر معمول این عدد مختلط این است که (
(  (
( 











 .
. 
 در فرکانس
در فرکانس با عدد مختلط داده می شود
با عدد مختلط داده می شود . ارزیابی
. ارزیابی  بجای
بجای بجای
بجای 
 بنابراین می توان آن را به موارد زیر کاهش داد:
بنابراین می توان آن را به موارد زیر کاهش داد:
 در این زمینه غیر ضروری هستند.
در این زمینه غیر ضروری هستند.

 اغلب به عنوان جفت انتگرال فوریه یا جفت تبدیل فوریه نامیده می شود .
اغلب به عنوان جفت انتگرال فوریه یا جفت تبدیل فوریه نامیده می شود .  .
.








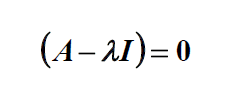
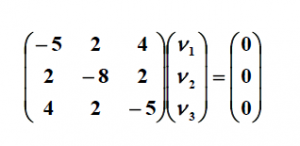
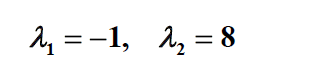
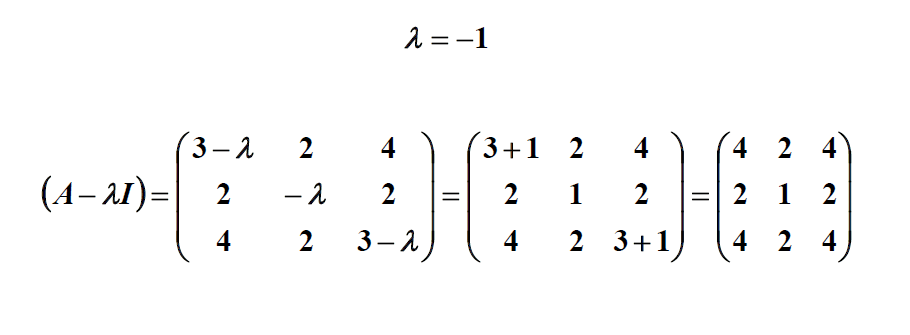
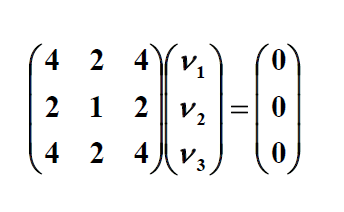
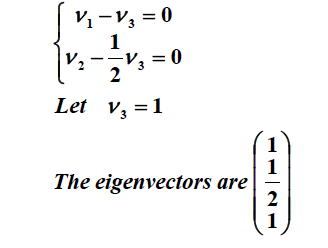
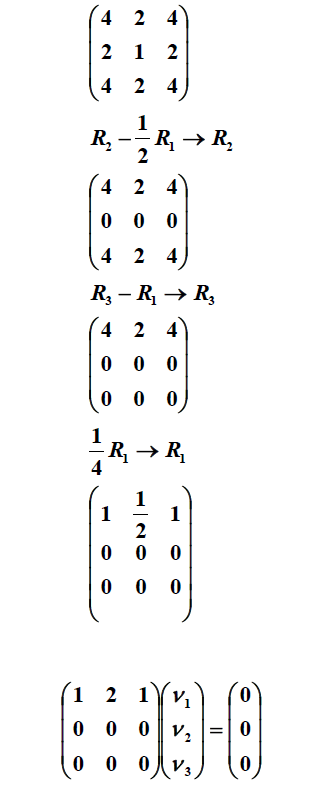
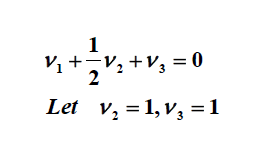
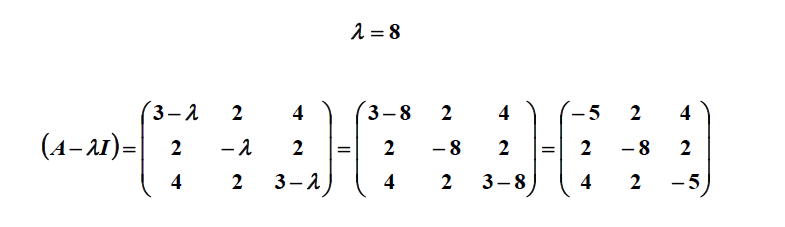























 در این وبلاگ به ریاضیات و کاربردهای آن و تحقیقات در آنها پرداخته می شود. مطالب در این وبلاگ ترجمه سطحی و اولیه است و کامل نیست.در صورتی سوال یا نظری در زمینه ریاضیات دارید مطرح نمایید .در صورت امکان به آن می پردازم. من دوست دارم برای یافتن پاسخ به سوالات و حل پروژه های علمی با دیگران همکاری نمایم.در صورتی که شما هم بامن هم عقیده هستید با من تماس بگیرید.
در این وبلاگ به ریاضیات و کاربردهای آن و تحقیقات در آنها پرداخته می شود. مطالب در این وبلاگ ترجمه سطحی و اولیه است و کامل نیست.در صورتی سوال یا نظری در زمینه ریاضیات دارید مطرح نمایید .در صورت امکان به آن می پردازم. من دوست دارم برای یافتن پاسخ به سوالات و حل پروژه های علمی با دیگران همکاری نمایم.در صورتی که شما هم بامن هم عقیده هستید با من تماس بگیرید.