ضرب سه گانه

از ویکیپدیا، دانشنامه آزاد

این مقاله در مورد عملیات سه تایی بردار است. برای کاربردهای دیگر، ضرب سه گانه (ابهام‌زدایی) را ببینید .

"حجم امضا شده" به اینجا هدایت می شود. برای کتاب‌های امضا شده، به Bibliophilia مراجعه کنید .

در هندسه و جبر ، حاصل ضرب سه گانه حاصلضرب سه بردار 3 بعدی ، معمولاً بردارهای اقلیدسی است . نام "ضرب سه گانه" برای دو ضرب مختلف استفاده می شود، حاصل ضرب سه گانه اسکالر با ارزش و در موارد کمتر، حاصلضرب سه گانه برداری با ارزش برداری .

ضرب سه گانه اسکالر [ ویرایش ]

سه بردار که یک متوازی الاضلاع را تعریف می کنند

حاصل ضرب سه گانه اسکالر ( همچنین به نام ضرب مخلوط ، ضرب جعبه یا حاصل ضرب اسکالر سه گانه ) به عنوان حاصل ضرب نقطه ای یکی از بردارها با ضرب ضربدر دو بردار دیگر تعریف می شود .

تفسیر هندسی

از نظر هندسی، حاصل ضرب سه گانه اسکالر

$\mathbf {a} \cdot (\mathbf {b} \times \mathbf {c} )$

حجم (نشانه دار) متوازی الاضلاع است که توسط سه بردار داده شده تعریف شده است.

خواص

حاصل ضرب سه گانه اسکالر تحت یک جابجایی دایره ای از سه عملوند آن ( a , b , c ) بدون تغییر است:
$\mathbf {a} \cdot (\mathbf {b} \times \mathbf {c} )=\mathbf {c} \cdot (\mathbf {a} \times \mathbf {b} )=\mathbf { b} \cdot (\mathbf {c} \times \mathbf {a} )$
تعویض موقعیت عملگرها بدون مرتب کردن مجدد عملوندها، ضرب سه گانه را بدون تغییر باقی می گذارد. این از ویژگی قبلی و ویژگی جابجایی حاصلضرب نقطه است:
$\mathbf {a} \cdot (\mathbf {b} \times \mathbf {c} )=(\mathbf {a} \times \mathbf {b} )\cdot \mathbf {c}$
مبادله هر دو از سه عملوند، حاصلضرب سه گانه را نفی می کند . این از خاصیت جابجایی دایره ای و ضد جابجایی ضرب متقاطع به دست می آید:
${\begin{aligned}\mathbf {a} \cdot (\mathbf {b} \times \mathbf {c} )&=-\mathbf {a} \cdot (\mathbf {c} \times \mathbf {b} )\\&=-\mathbf {b} \cdot (\mathbf {a} \times \mathbf {c} )\\&=-\mathbf {c} \cdot (\mathbf {b} \times \mathbf {a} )\end{تراز شده}}$
حاصلضرب سه‌گانه اسکالر را می‌توان به‌عنوان دترمینان ماتریس 3 × 3 که دارای سه بردار یا به‌عنوان ردیف‌ها یا ستون‌هایش است، درک کرد (یک ماتریس همان تدترمینانی دارد که جابه‌جایی آن است ):
$\mathbf {a} \cdot (\mathbf {b} \times \mathbf {c} )=\det {\begin{bmatrix}a_{1}&a_{2}&a_{3}\\b_{1 }&b_{2}&b_{3}\\c_{1}&c_{2}&c_{3}\\\end{bmatrix}}=\det {\begin{bmatrix}a_{1}&b_{1}&c_{ 1}\\a_{2}&b_{2}&c_{2}\\a_{3}&b_{3}&c_{3}\end{bmatrix}}=\det {\begin{bmatrix}\mathbf {a} &\mathbf {b} &\mathbf {c} \end{bmatrix}}.$
اگر حاصل ضرب سه گانه اسکالر برابر با صفر باشد، سه بردار a ، b و c همسطح هستند ، زیرا متوازی الاضلاع تعریف شده توسط آنها مسطح است و حجم ندارد.
اگر هر دو بردار در حاصل ضرب سه گانه اسکالر برابر باشند، مقدار آن صفر است:
$\mathbf {a} \cdot (\mathbf {a} \times \mathbf {b} )=\mathbf {a} \cdot (\mathbf {b} \times \mathbf {a} )=\mathbf { b} \cdot (\mathbf {a} \times \mathbf {a} )=0$
همچنین:
$(\mathbf {a} \cdot (\mathbf {b} \times \mathbf {c} ))\,\mathbf {a} =(\mathbf {a} \times \mathbf {b} )\times (\mathbf {a} \times \mathbf {c} )$
حاصل ضرب ساده دو ضرب سه گانه (یا مربع حاصلضرب سه گانه)، ممکن است برحسب حاصلضرب نقطه بسط داده شود: [1]

$((\mathbf {a} \times \mathbf {b} )\cdot \mathbf {c} )\;((\mathbf {d} \times \mathbf {e} )\cdot \mathbf {f} )=\det {\begin{bmatrix}\mathbf {a} \cdot \mathbf {d} &\mathbf {a} \cdot \mathbf {e} &\mathbf {a} \cdot \mathbf {f} \\ \mathbf {b} \cdot \mathbf {d} &\mathbf {b} \cdot \mathbf {e} &\mathbf {b} \cdot \mathbf {f} \\\mathbf {c} \cdot \mathbf { d} &\mathbf {c} \cdot \mathbf {e} &\mathbf {c} \cdot \mathbf {f} \end{bmatrix}}$

این در نماد برداری دوباره بیان می کند که حاصل ضرب عوامل دترمینان دو ماتریس 3×3 برابر با دترمینان حاصلضرب ماتریس آنها است. به عنوان یک مورد خاص، مربع یک ضرب سه گانه یک دترمینان گرم است .

نسبت حاصلضرب سه گانه و حاصل ضرب سه هنجار بردار به عنوان سینوس قطبی شناخته می شود :

${\frac {\mathbf {a} \cdot (\mathbf {b} \times \mathbf {c} )}{\|{\mathbf {a} }\|\|{\mathbf {b} } \|\|{\mathbf {c} }\|}}=\operatorname {psin} (\mathbf {a} ,\mathbf {b} ,\mathbf {c} )$

که بین ۱- و ۱ متغیر است.

اسکالر یا شبه اسکالر

اگرچه حاصل ضرب سه گانه اسکالر حجم متوازی الاضلاع را می دهد، اما این حجم علامت گذاری شده است، علامت بسته به جهت قاب یا برابری جایگشت بردارها است. این بدان معنی است که اگر جهت گیری معکوس شود، برای مثال با تبدیل برابری ، ضرب نفی می شود ، و بنابراین اگر جهت گیری بتواند تغییر کند، به طور صحیح تر به عنوان یک شبه مقیاس توصیف می شود.

این همچنین به دست بودن ضرب متقاطع مربوط می شود . حاصلضرب متقاطع به عنوان یک شبه بردار تحت تبدیل های برابری تبدیل می شود و بنابراین به درستی به عنوان شبه بردار توصیف می شود. حاصلضرب نقطه ای دو بردار یک عددی است اما حاصلضرب نقطه ای یک بردار کاذب و یک بردار یک شبه مقیاس است، بنابراین حاصلضرب سه گانه اسکالر (بردارها) باید ارزش شبه مقیاسی داشته باشد.

اگر T یک چرخش مناسب است پس

${\displaystyle \mathbf {Ta} \cdot (\mathbf {Tb} \times \mathbf {Tc} )=\mathbf {a} \cdot (\mathbf {b} \times \mathbf {c})$

اما اگر T یک چرخش نامناسب است ، پس

$\mathbf {Ta} \cdot (\mathbf {Tb} \times \mathbf {Tc} )=-\mathbf {a} \cdot (\mathbf {b} \times \mathbf {c}).$

تراکم اسکالر یا اسکالر

به بیان دقیق، یک اسکالر تحت یک تبدیل مختصات به هیچ وجه تغییر نمی کند. (به عنوان مثال، ضریب 2 که برای دو برابر کردن یک بردار استفاده می شود، اگر بردار در مختصات کروی در مقابل مستطیل باشد، تغییر نمی کند.) با این حال، اگر هر بردار توسط یک ماتریس تبدیل شود، حاصل ضرب سه گانه در نهایت در دترمینان ضرب می شود. ماتریس تبدیل، که می تواند برای یک غیر چرخشی کاملاً دلخواه باشد. یعنی ضرب سه گانه به طور صحیح تر به عنوان چگالی اسکالر توصیف می شود .

به عنوان یک ضرب بیرونی

سه بردار که یک متوازی الاضلاع را پوشانده اند، حاصلضرب سه برابری برابر با حجم آن دارند. (اما مراقب باشید جهت فلش های این نمودار نادرست باشد.)

در جبر بیرونی و جبر هندسی حاصلضرب بیرونی دو بردار دو بردار است در حالی که حاصلضرب بیرونی سه بردار یک سه بردار است . یک دوبردار یک عنصر صفحه جهت‌دار و یک سه بردار یک عنصر حجمی جهت‌دار است، همانطور که یک بردار یک عنصر خط جهت‌دار است.

با توجه به بردارهای a ، b و c ، حاصلضرب

$\mathbf {a} \wedge \mathbf {b} \wedge \mathbf {c}$

یک سه بردار با بزرگی برابر با حاصل ضرب سه گانه اسکالر است، یعنی

$|\mathbf {a} \wedge \mathbf {b} \wedge \mathbf {c} |=|\mathbf {a} \cdot (\mathbf {b} \times \mathbf {c})|$ ،

و Hodge دوگانه حاصلضرب سه گانه اسکالر است. از آنجایی که ضرب بیرونی، براکت های ارتباطی است، نیازی نیست، زیرا مهم نیست که کدام یک از a ∧ b یا b ∧ c ابتدا محاسبه می شود، اگرچه ترتیب بردارها در ضرب مهم است. از نظر هندسی سه بردار a ∧ b ∧ c مربوط به متوازی الاضلاع است که توسط a , b و c امتداد یافته است ، با دو بردار a ∧ b , b ∧ c و a ∧ c با وجوه متوازی الاضلاع متوازی الاضلاع مطابقت دارند .

به عنوان یک تابع سه خطی

حاصل ضرب سه گانه با فرم حجمی فضای 3 اقلیدسی که از طریق حاصلضرب داخلی به بردارها اعمال می شود، یکسان است . همچنین می توان آن را به صورت انقباض بردارها با تانسور رتبه-3 معادل شکل (یا شبه تانسور معادل شبه شکل حجمی) بیان کرد. زیر را ببینید .

ضرب سه گانه برداری

حاصلضرب سه گانه برداری به صورت حاصلضرب متقاطع یک بردار با حاصلضرب دو بردار دیگر تعریف می شود . رابطه زیر برقرار است:

$\mathbf {a} \times (\mathbf {b} \times \mathbf {c} )=(\mathbf {a} \cdot \mathbf {c} )\mathbf {b} -(\mathbf {a } \cdot \mathbf {b} )\mathbf {c}$ .

این به عنوان توسعه ضرب سه گانه یا فرمول لاگرانژ شناخته می شود ، [2] [3] اگرچه نام دوم برای چندین فرمول دیگر نیز استفاده می شود . سمت راست آن را می توان با استفاده از یادداشت "ACB - ABC" به خاطر آورد، مشروط بر اینکه در نظر داشته باشید که کدام بردارها با هم نقطه چین شده اند. یک مدرک در زیر ارائه شده است . برخی از کتاب های درسی اتحاد را به عنوان $\mathbf {a} \times (\mathbf {b} \times \mathbf {c} )=\mathbf {b} (\mathbf {a} \cdot \mathbf {c} )-\mathbf {c} (\mathbf {a} \cdot \mathbf {b} )$ به طوری که یک یادگاری آشناتر "BAC - CAB" به دست می آید، مانند "پشت کابین".

از آنجایی که ضرب متقاطع ضد جابجایی است، این فرمول ممکن است (تا جایگشت حروف) نیز به صورت زیر نوشته شود:

$(\mathbf {a} \times \mathbf {b} )\times \mathbf {c} =-\mathbf {c} \times (\mathbf {a} \times \mathbf {b} )=-( \mathbf {c} \cdot \mathbf {b} )\mathbf {a} +(\mathbf {c} \cdot \mathbf {a} )\mathbf {b}$

از فرمول لاگرانژ چنین استنباط می شود که حاصلضرب سه گانه بردار برآورده می شود:

$\mathbf {a} \times (\mathbf {b} \times \mathbf {c} )+\mathbf {b} \times (\mathbf {c} \times \mathbf {a} )+\mathbf { c} \times (\mathbf {a} \times \mathbf {b} )=\mathbf {0}$

که اتحاد ژاکوبی برای ضرب متقاطع است. فرمول مفید دیگری به شرح زیر است:

$(\mathbf {a} \times \mathbf {b} )\times \mathbf {c} =\mathbf {a} \times (\mathbf {b} \times \mathbf {c} )-\mathbf { b} \times (\mathbf {a} \times \mathbf {c} )$

این فرمول ها در ساده کردن محاسبات برداری در فیزیک بسیار مفید هستند . یک اتحاد مرتبط با شیب ها و مفید در محاسبات برداری، فرمول لاگرانژ اتحاد متقابل بردار است: [4]

${\boldsymbol {\nabla }}\times ({\boldsymbol {\nabla }}\times \mathbf {A} )={\boldsymbol {\nabla }}({\boldsymbol {\nabla }}\cdot \mathbf {A} )-({\boldsymbol {\nabla }}\cdot {\boldsymbol {\nabla }})\mathbf {A}$

این را می توان به عنوان یک مورد خاص از عملگر عمومی تر Laplace-de Rham نیز در نظر گرفت $\Delta =d\delta +\delta d$ .

اثبات

را $x$ جزئی از $\mathbf {u} \times (\mathbf {v} \times \mathbf {w} )$ از رابطه زیر بدست می آید:

${\begin{aligned}(\mathbf {u} \times (\mathbf {v} \times \mathbf {w} ))_{x}&=\mathbf {u} _{y}(\mathbf {v} _{x}\mathbf {w} _{y}-\mathbf {v} _{y}\mathbf {w} _{x})-\mathbf {u} _{z}(\mathbf { v} _{z}\mathbf {w} _{x}-\mathbf {v} _{x}\mathbf {w} _{z})\\&=\mathbf {v} _{x}(\ mathbf {u} _{y}\mathbf {w} _{y}+\mathbf {u} _{z}\mathbf {w} _{z})-\mathbf {w} _{x}(\mathbf {u} _{y}\mathbf {v} _{y}+\mathbf {u} _{z}\mathbf {v} _{z})\\&=\mathbf {v} _{x}( \mathbf {u} _{y}\mathbf {w} _{y}+\mathbf {u} _{z}\mathbf {w} _{z})-\mathbf {w} _{x}(\ mathbf {u} _{y}\mathbf {v} _{y}+\mathbf {u} _{z}\mathbf {v} _{z})+(\mathbf {u} _{x}\mathbf {v} _{x}\mathbf {w} _{x}-\mathbf {u} _{x}\mathbf {v} _{x}\mathbf {w} _{x})\\&=\ mathbf {v} _{x}(\mathbf {u} _{x}\mathbf {w} _{x}+\mathbf {u} _{y}\mathbf {w} _{y}+\mathbf { u} _{z}\mathbf {w} _{z})-\mathbf {w} _{x}(\mathbf {u} _{x}\mathbf {v} _{x}+\mathbf {u } _{y}\mathbf {v} _{y}+\mathbf {u} _{z}\mathbf {v} _{z})\\&=(\mathbf {u} \cdot \mathbf {w } )\mathbf {v} _{x}-(\mathbf {u} \cdot \mathbf {v} )\mathbf {w} _{x}\end{تراز شده}}$

به طور مشابه، $y$ و $z$ اجزای $\mathbf {u} \times (\mathbf {v} \times \mathbf {w} )$ توسط:

${\begin{aligned}(\mathbf {u} \times (\mathbf {v} \times \mathbf {w} ))_{y}&=(\mathbf {u} \cdot \mathbf {w } )\mathbf {v} _{y}-(\mathbf {u} \cdot \mathbf {v} )\mathbf {w} _{y}\\(\mathbf {u} \times (\mathbf {v } \times \mathbf {w} ))_{z}&=(\mathbf {u} \cdot \mathbf {w} )\mathbf {v} _{z}-(\mathbf {u} \cdot \mathbf {v} )\mathbf {w} _{z}\end{تراز شده}}$

با ترکیب این سه جزء به دست می آید:

$\mathbf {u} \times (\mathbf {v} \times \mathbf {w} )=(\mathbf {u} \cdot \mathbf {w} )\ \mathbf {v} -(\mathbf { u} \cdot \mathbf {v} )\ \mathbf {w}$ [5]

استفاده از جبر هندسی

اگر از جبر هندسی استفاده شود، حاصل ضرب متقاطع b × c بردارها به صورت حاصلضرب بیرونی b ∧ c ، یک دوبردار بیان می شود . دومین ضرب متقاطع را نمی توان به عنوان یک ضرب بیرونی بیان کرد، در غیر این صورت حاصل ضرب سه گانه اسکالر ایجاد می شود. در عوض می توان از انقباض چپ [6] استفاده کرد، بنابراین فرمول تبدیل به [7] می شود.

${\begin{aligned}-\mathbf {a} \;{\big \lrcorner }\;(\mathbf {b} \wedge \mathbf {c} )&=\mathbf {b} \wedge (\ mathbf {a} \;{\big \lrcorner }\;\mathbf {c} )-(\mathbf {a} \;{\big \lrcorner }\;\mathbf {b} )\wedge \mathbf {c} \\&=(\mathbf {a} \cdot \mathbf {c} )\mathbf {b} -(\mathbf {a} \cdot \mathbf {b} )\mathbf {c} \end{تراز شده}}$

اثبات از خواص انقباض حاصل می شود. [6] نتیجه همان بردار محاسبه شده با استفاده از × ( b × c ) است.

تفاسیر

حساب تانسور

در نماد تانسور ، حاصل ضرب سه گانه با استفاده از نماد لوی-سویتا بیان می شود : [8]

$\mathbf {a} \cdot [\mathbf {b} \times \mathbf {c} ]=\varepsilon _{ijk}a^{i}b^{j}c^{k}$

$(\mathbf {a} \times [\mathbf {b} \times \mathbf {c} ])_{i}=\varepsilon _{ijk}a^{j}\varepsilon ^{k\ell m }b_{\ell }c_{m}=\varepsilon _{ijk}\varepsilon ^{k\ell m}a^{j}b_{\ell }c_{m},$

با اشاره به $i$ -امین جزء بردار حاصل. این را می توان با انجام یک انقباض بر روی نمادهای لوی-سویتا ساده کرد . $\varepsilon _{ijk}\varepsilon ^{k\ell m}=\delta _{ij}^{\ell m}=\delta _{i}^{\ell }\delta _{j}^ {m}-\delta _{i}^{m}\delta _{j}^{\ell }\,,$ جایی که $\delta _{j}^{i}$ تابع دلتای کرونکر است ( $\delta _{j}^{i}=0$ چه زمانی $i\neq j$ و $\delta _{j}^{i}=1$ چه زمانی $i=j$ ) و $\delta _{ij}^{\ell m}$ تابع دلتای کرونکر تعمیم یافته است . ما می‌توانیم این اتحاد را با تشخیص این شاخص مشخص کنیم $k$ صرفا خروج خلاصه خواهد شد $i$ و $j$ . در ترم اول تعمیر می کنیم $i=l$ و بنابراین $j=m$ . به همین ترتیب در ترم دوم اصلاح می کنیممن $i=m$ و بنابراین $l=j$ .

بازگشت به ضرب متقاطع سه گانه،

$(\mathbf {a} \times [\mathbf {b} \times \mathbf {c} ])_{i}=(\delta _{i}^{\ell }\delta _{j}^ {m}-\delta _{i}^{m}\delta _{j}^{\ell })a^{j}b_{\ell }c_{m}=a^{j}b_{i} c_{j}-a^{j}b_{j}c_{i}=b_{i}(\mathbf {a} \cdot \mathbf {c} )-c_{i}(\mathbf {a} \cdot \mathbf {b} )\,.$

حساب برداری

انتگرال شار میدان برداری را در نظر بگیریداف $\mathbf {F}$ در سراسر سطح پارامتریک تعریف شده است $S=\mathbf {r} (u,v)$ : ${\textstyle \iint _{S}\mathbf {F} \cdot {\hat {\mathbf {n} }}\,dS}$ . بردار واحد نرمال ${\hat {\mathbf {n} }}$ به سطح داده شده توسط ${\textstyle {\frac {\mathbf {r} _{u}\times \mathbf {r} _{v}}{|\mathbf {r} _{u}\times \mathbf {r} _{v} |}}}$ بنابراین انتگرال ${\textstyle \mathbf {F} \cdot {\frac {(\mathbf {r} _{u}\times \mathbf {r} _{v})}{|\mathbf {r} _{u}\times \mathbf {r} _{v}|}}}$ یک ضرب سه گانه اسکالر است.

این بخش نیاز به گسترش دارد . می توانید با افزودن به آن کمک کنید . ( ژانویه 2014 )

https://en.wikipedia.org/wiki/Triple_product

+ نوشته شده در جمعه بیست و چهارم فروردین ۱۴۰۳ ساعت 9:10 توسط علی رضا نقش نیلچی |

فرمول استرلینگ، تعریف، مثال های حل شده

فرمول استرلینگ: فرمول استرلینگ یک روش تقریبی برای فاکتوریل ها است که تخمین های نزدیک را برای اعداد بزرگ ارائه می دهد که به صورت n!≈ √2πn (n/e ) n بیان می شود.

مانوج کومار

8 نوامبر 2023

فرمول استرلینگ

فهرست مطالب

فرمول استرلینگ: فرمول استرلینگ که به نام جیمز استرلینگ نامگذاری شده است، به عنوان یک روش تقریبی برای محاسبه فاکتوریل یک عدد معین (n! یا Γ(n) برای مقادیر بزرگ n عمل می کند. این فرمول یک تقریب ارزشمند را ارائه می دهد، به ویژه برای تعیین سریع فاکتوریل های اعداد بزرگ مفید است. در حالی که در ارائه نتایج دقیق برای مقادیر بزرگتر 'n' برتری دارد، اما برای مقادیر کوچکتر نیز قابل اجرا و موثر است.

علاوه بر این، فرمول استرلینگ کاربرد خود را فراتر از فاکتوریل ها گسترش می دهد و در زمینه تابع گاما به کار می رود و در زمینه های مختلف ریاضیات کاربردی ارتباط پیدا می کند. بررسی فرمول استرلینگ از طریق مثال های حل شده می تواند کاربردهای عملی و اثربخشی محاسباتی آن را بیشتر روشن کند.

فرمول استرلینگ یک عبارت ریاضی است که برای تقریب فاکتوریل یک عدد استفاده می‌شود و مقداری را ارائه می‌کند که با مقدار فاکتوریل واقعی، اغلب در حاشیه خطای کمتر از 2% همسو است. این روش تقریبی که به نام جیمز استرلینگ نامگذاری شده است برای تخمین فاکتوریل یک عدد معین 'n' استفاده می شود. این فرمول به عنوان یک ابزار ارزشمند در ریاضیات است و بیانی را ارائه می دهد که به مقدار فاکتوریل واقعی نزدیک می شود و آن را برای اهداف مختلف محاسباتی و تحلیلی بسیار مفید می کند. فرمول استرلینگ به صورت زیر بیان می شود:

فرمول استرلینگ

نمونه های حل شده فرمول استرلینگ

مثال 1: مقدار 5 فاکتوریل را با استفاده از فرمول استرلینگ بیابید.

راه حل:

برای یافتن: 5 فاکتوریل.

با استفاده از فرمول

n! = √(2×π×n)(n/e)^ n

5 ! = √(2×π×5) (5/e) ^5

= 118.019

پاسخ: فرمول استرلینگ مقدار ! 5 را به 118.019 تقریب می زند که حاشیه خطای 1.66 درصد را نشان می دهد.

مثال 2: مقدار !11 را با استفاده از فرمول استرلینگ بیابید.

راه حل:

برای یافتن:! 11 .

استفاده از فرمول استرلینگ

n! = √(2×π×n)(n/e)^ n

11! = √(2×π×11)(11/e) ^11

= 39615625.05

مثال 3: با استفاده از فرمول استرلینگ می توان 9 را تقریب زد! - 7! 9!-7!.

با اعمال فرمول، محاسبه به صورت زیر است:

9!-7!≈

(√(2π×9)× (9/e)^ 9 )−(√(2π×7)× (7/e)^ 7 )

این به سادگی به:

9 ! - 7! ≈ 18107.57 - 1651.73

9!-7!≈18107.57-1651.73

بنابراین،

9! - 7! ≈ 16455.84 .

بنابراین، مقدار تقریبی

9!-7! =16455.84

است.

مثال 4: تقریبی مقدار! 7 با استفاده از فرمول استرلینگ راه حل: با استفاده از فرمول استرلینگ، تقریب 7! به صورت زیر محاسبه می شود:

7!≈ √ 2π×7 ×( 7/e ) 7

= 7! ≈ 19857.17

بنابراین، ارزش تخمینی !7 تقریباً 19857.17 است.

مثال 5: تخمین مقدار! 12 با استفاده از فرمول استرلینگ

راه حل: با استفاده از فرمول، تخمین 12! به صورت زیر محاسبه می شود:

12!≈ √2π×12 ×( 12/e )^ 12

= 12! ≈ 479001600

از این رو، مقدار تقریبی

12!= 479001600

است.

مثال 5: تخمین مقدار

5!+4!

با استفاده از فرمول استرلینگ

راه حل: با استفاده از فرمول، تخمین

12!

به صورت زیر محاسبه می شود:

5!+4! ≈ √2π×5 ×( 5/e )^ 5 + √2π×4 ×( 4/e ) ^4

= 5! + 4! ≈ 146.30

فرمول استرلینگ، که به افتخار ریاضیدان جیمز استرلینگ نامگذاری شده است، به عنوان یک روش تقریبی قدرتمند برای فاکتوریل ها می ایستد، که تخمینی نزدیک به مقادیر واقعی، به ویژه برای اعداد بزرگ، با حاشیه خطا اغلب کمتر از 2٪ ارائه می دهد. این فرمول به صورت n بیان می شود

n! ≈ √(2πn) * (n/e)^n

، نه تنها فاکتوریل ها را به طور دقیق تخمین می زند، بلکه کاربردهای گسترده ای در زمینه های مختلف ریاضیات کاربردی پیدا می کند.

فرمول استرلینگ از طریق مثال‌هایی که کاربرد آن را نشان می‌دهد، کاربرد عملی خود را در تقریب سریع و دقیق مقادیر فاکتوریل نشان می‌دهد و به تلاش‌های محاسباتی و تحلیلی کمک می‌کند. تطبیق پذیری آن به مقادیر کوچک و بزرگ "n" پاسخ می دهد و آن را به ابزاری ارزشمند در محاسبات و تحلیل های ریاضی تبدیل می کند. به طور کلی، فرمول استرلینگ به عنوان سنگ بنای تکنیک های تقریب،تسهیل برآورد کارآمد فاکتوریل ها و یافتن ارتباط در کاربردهای ریاضی متنوع است.

https://www.pw.live/exams/school/stirling-formula/

+ نوشته شده در جمعه چهارم اسفند ۱۴۰۲ ساعت 12:28 توسط علی رضا نقش نیلچی |

مثال قضیه واگرایی

فرض کنید می خواستیم شار میدان برداری زیر را که توسط تعریف شده است، ارزیابی کنیم $\mathbf {F} =2x^{2}{\textbf {i}}+2y^{2}{\textbf {j}}+2z^{2}{\textbf {k}}$ محدود به نابرابری های زیر است:

$\left\{0\leq x\leq 3\right\}\left\{-2\leq y\leq 2\right\}\left\{0\leq z\leq 2\pi \right\ }$

با قضیه واگرایی،

$\iiint _{V}\left(\mathbf {\nabla } \cdot \mathbf {F} \right)\mathrm {d} V=$ $\اینت$ $\scriptstyle S$ . $(\mathbf {F} \cdot \mathbf {n} )\,\mathrm {d} S.$

اکنون باید واگرایی ${\textbf {F}}$ را تعیین کنیم. اگر $\mathbf {F}$ یک میدان برداری سه بعدی است، سپس واگرایی ${\textbf {F}}$ از رابطه زیر بدست می آید⋅

بنابراین، ما می توانیم انتگرال شار زیر را تنظیم کنیم

$من =$ $\اینت$ ${\scriptstyle S}$ $\mathbf {F} \cdot \mathbf {n} \,\mathrm {d} S,$

به شرح زیر است:

${\begin{aligned}I&=\iiint _{V}\nabla \cdot \mathbf {F} \,\mathrm {d} V\\[6pt]&=\iiint _{V}\left( {\frac {\partial \mathbf {F_{x}} }{\partial x}}+{\frac {\partial \mathbf {F_{y}} }{\partial y}}+{\frac {\partial \mathbf {F_{z}} }{\partial z}}\right)\mathrm {d} V\\[6pt]&=\iiint _{V}(4x+4y+4z)\,\mathrm {d } V\\[6pt]&=\int _{0}^{3}\int _{-2}^{2}\int _{0}^{2\pi }(4x+4y+4z)\ ,\mathrm {d} V\end{تراز شده}}$

اکنون که انتگرال را تنظیم کرده ایم، می توانیم آن را ارزیابی کنیم.

${\begin{aligned}\int _{0}^{3}\int _{-2}^{2}\int _{0}^{2\pi }(4x+4y+4z)\ ,\mathrm {d} V&=\int _{-2}^{2}\int _{0}^{2\pi }(12y+12z+18)\,\mathrm {d} y\,\mathrm {d} z\\[6pt]&=\int _{0}^{2\pi }24(2z+3)\,\mathrm {d} z\\[6pt]&=48\pi (2\ pi +3)\end{تراز شده}}$

+ نوشته شده در جمعه بیست و چهارم آذر ۱۴۰۲ ساعت 13:0 توسط علی رضا نقش نیلچی |

عملگر لاپلاس

از ویکیپدیا، دانشنامه آزاد

این مقاله در مورد عملگر ریاضی در زمینه های اسکالر است. برای عملکرد میدانهای برداری، لاپلاس بردار را ببینید . برای توزیع احتمال لاپلاس، توزیع لاپلاس را ببینید . برای مفهوم نظری نمودار، به لاپلاسی ماتریس مراجعه کنید .

بخشی از مجموعه مقالات در مورد

حساب دیفرانسیل و انتگرال

قضیه اساسی

محدودیت ها
تداوم

قضیه رول
قضیه مقدار میانگین
قضیه تابع معکوس

نشان می دهد

دیفرانسیل

نشان می دهد

انتگرال

نشان می دهد

سلسله

پنهان شدن

بردار

شیب
واگرایی
حلقه
لاپلاسی
مشتق جهت دار
اتحاد ها

قضایا

شیب
سبز
استوکس
واگرایی
استوکس تعمیم یافته

نشان می دهد

چند متغیره

نشان می دهد

پیشرفته

نشان می دهد

تخصصی

نشان می دهد

در ریاضیات ، عملگر لاپلاس یا لاپلاسین یک عملگر دیفرانسیل است که از واگرایی گرادیان یک تابع اسکالر در فضای اقلیدسی به دست می‌آید . معمولاً با نمادها نشان داده می شود $\nabla\cdot\nabla$ $\nabla ^{2}$ (جایی که $\nabla$ عملگر nabla است )، یا $\ دلتا$ . در یک سیستم مختصات دکارتی , لاپلاسین با مجموع مشتقات جزئی دوم تابع نسبت به هر متغیر مستقل داده می شود . در سایر سیستم های مختصات ، مانند مختصات استوانه ای و کروی ، لاپلاسین نیز شکل مفیدی دارد. به طور غیررسمی، f ( p ) لاپلاسی تابع f در یک نقطه p اندازه می‌گیرد که مقدار میانگین f روی کره‌های کوچک یا توپ‌هایی که در مرکز p هستند، از f ( p ) چقدر انحراف دارد .

عملگر لاپلاس از نام ریاضیدان فرانسوی پیر سیمون د لاپلاس (1749-1827) نامگذاری شده است، که برای اولین بار این عملگر را برای مطالعه مکانیک سماوی به کار برد : لاپلاسین پتانسیل گرانشی ناشی از توزیع چگالی جرم معین، مضرب ثابتی از آن توزیع چگالی راه حل های معادله لاپلاس f = 0 توابع هارمونیک نامیده می شوند و پتانسیل های گرانشی ممکن را در مناطق خلاء نشان می دهند .

لاپلاسین در بسیاری از معادلات دیفرانسیل که پدیده های فیزیکی را توصیف می کنند، رخ می دهد. معادله پواسون پتانسیل های الکتریکی و گرانشی را توصیف می کند . معادله انتشار گرما و جریان سیال را توصیف می کند . معادله موج انتشار موج را توصیف می کند . و معادله شرودینگر تابع موج را در مکانیک کوانتومی توصیف می کند . در پردازش تصویر و بینایی کامپیوتری ، از اپراتور لاپلاسین برای کارهای مختلفی مانند تشخیص حباب و لبه استفاده شده است . لاپلاسین ساده ترین عملگر بیضوی است و در هسته نظریه هاج و همچنین نتایج کومولوژی د رام قرار دارد .

تعریف [ ویرایش ]

عملگر لاپلاس یک عملگر دیفرانسیل مرتبه دوم در فضای اقلیدسی n بعدی است که به عنوان واگرایی (⋅ $\nabla \cdot$ ) از گرادیان ( $\nabla f$ ). بنابراین اگر $f$ یک تابع با ارزش حقیقی دو بار متمایز است ، سپس لاپلاسی از $f$ تابع با ارزش حقیقی است که توسط:

$\Delta f=\nabla ^{2}f=\nabla \cdot \nabla f$

( 1 )

جایی که نمادهای اخیر از نوشتن رسمی ناشی می شوند:

$\nabla =\left({\frac {\partial }{\partial x_{1}}},\ldots ,{\frac {\partial }{\partial x_{n}}}\right).$

به صراحت، لاپلاسین f حاصل مجموع تمام مشتقات جزئی دوم غیر مخلوط در مختصات دکارتی x i است :

$\Delta f=\sum _{i=1}^{n}{\frac {\partial ^{2}f}{\partial x_{i}^{2}}}$

( 2 )

به عنوان یک عملگر دیفرانسیل مرتبه دوم، عملگر لاپلاس توابع Ck را به توابع Ck - 2 برای k ≥ 2 نگاشت می کند . این یک عملگر خطی : C k ( R n ) → C k −2 ( R n ) یا به طور کلی، یک عملگر : C k (Ω) → C k −2 (Ω) برای هر مجموعه باز Ω است. R n _

انگیزه [ ویرایش ]

انتشار [ ویرایش ]

در تئوری فیزیکی انتشار ، عملگر لاپلاس به طور طبیعی در توصیف ریاضی تعادل به وجود می آید . [1] به طور خاص، اگر u چگالی در تعادل مقداری مانند غلظت شیمیایی باشد، شار خالص u از مرز ∂ V هر ناحیه صاف V صفر است، مشروط بر اینکه هیچ منبع یا فرورفتگی در V وجود نداشته باشد :

$\int _{\partial V}\nabla u\cdot \mathbf {n} \,dS=0,$

که در آن n واحد بیرونی نرمال با مرز V است . با قضیه واگرایی ،

$\int _{V}\operatorname {div} \nabla u\,dV=\int _{\partial V}\nabla u\cdot \mathbf {n} \,dS=0.$

از آنجایی که این برای همه مناطق صاف V صادق است ، می توان نشان داد که به این معنی است:

$\operatorname {div} \nabla u=\Delta u=0.$ سمت چپ این معادله عملگر لاپلاس است و کل معادله u = 0 به عنوان معادله لاپلاس شناخته می شود . راه حل های معادله لاپلاس، یعنی توابعی که لاپلاسین آنها یکسان صفر است، بنابراین چگالی های تعادلی ممکن را تحت نفوذ نشان می دهند.

عملگر لاپلاس خود یک تفسیر فیزیکی برای انتشار غیرتعادلی دارد به عنوان میزانی که یک نقطه نشان دهنده منبع یا سینک غلظت شیمیایی است، به معنایی که معادله انتشار دقیق است . این تفسیر از لاپلاسی نیز با حقیقیت زیر در مورد میانگین ها توضیح داده می شود.

میانگین ها [ ویرایش ]

با توجه به یک تابع دو بار متمایز پیوسته: $f:\mathbb {R} ^{n}\to \mathbb {R}$ و یک نکته $p\in \mathbb {R} ^{n}$ . سپس، مقدار متوسط از $f$ بالای توپ با شعاع $ساعت$ متمرکز در $پ$ است: [2]

${\overline {f}}_{B}(p,h)=f(p)+{\frac {\Delta f(p)}{2(n+2)}}h^{2} +o(h^{2})\quad {\text{for}}\;\;h\to 0$

به طور مشابه، مقدار متوسط از $f$ بر روی کره (مرز یک توپ) با شعاع $ساعت$ متمرکز در $پ$ است:

${\overline {f}}_{S}(p,h)=f(p)+{\frac {\Delta f(p)}{2n}}h^{2}+o(h^ {2})\quad {\text{for}}\;\;h\to 0.$

چگالی مرتبط با پتانسیل [ ویرایش ]

اگر φ نشان دهنده پتانسیل الکترواستاتیک مرتبط با توزیع بار q باشد، خود توزیع بار توسط منفی لاپلاسین φ بدست می آید :

$q=-\varepsilon _{0}\Delta \varphi ,$

جایی که ε 0 ثابت الکتریکی است .

این نتیجه قانون گاوس است . در واقع، اگر V هر ناحیه صاف با مرز ∂ V باشد ، طبق قانون گاوس، شار میدان الکترواستاتیک E در سراسر مرز با بار محصور شده متناسب است:

$\int _{\partial V}\mathbf {E} \cdot \mathbf {n} \,dS=\int _{V}\operatorname {div} \mathbf {E} \,dV={\frac {1}{\varepsilon _{0}}}\int _{V}q\,dV.$

که در آن برابری اول ناشی از قضیه واگرایی است . از آنجایی که میدان الکترواستاتیک شیب (منفی) پتانسیل است، این نشان می دهد:

$-\int _{V}\operatorname {div} (\operatorname {grad} \varphi )\,dV={\frac {1}{\varepsilon _{0}}}\int _{V}q \,dV.$

از آنجایی که این برای همه مناطق V صادق است ، باید داشته باشیم

$\operatorname {div} (\operatorname {grad} \varphi )=-{\frac {1}{\varepsilon _{0}}}q$

همین رویکرد نشان می دهد که منفی لاپلاسین پتانسیل گرانشی توزیع جرم است . اغلب توزیع بار (یا جرم) داده می شود و پتانسیل مرتبط ناشناخته است. یافتن تابع پتانسیل تحت شرایط مرزی مناسب معادل حل معادله پواسون است .

به حداقل رساندن انرژی [ ویرایش ]

انگیزه دیگر برای ظاهر شدن لاپلاسین در فیزیک این است که راه حل های f = 0 در ناحیه U توابعی هستند که انرژی دیریکله را ثابت می کنند :

$E(f)={\frac {1}{2}}\int _{U}\lVert \nabla f\rVert ^{2}\,dx.$

برای مشاهده این، فرض کنید f : U → R یک تابع است و u : U → R تابعی است که در مرز U ناپدید می شود . سپس:

$\left.{\frac {d}{d\varepsilon }}\right|_{\varepsilon =0}E(f+\varepsilon u)=\int _{U}\nabla f\cdot \nabla u \,dx=-\int _{U}u\,\Delta f\,dx$

که در آن آخرین برابری با استفاده از اولین اتحاد گرین دنبال می شود . این محاسبه نشان می دهد که اگر f = 0 باشد ، E در اطراف f ثابت است . برعکس، اگر E حول f ثابت باشد ، آنگاه f = 0 توسط لم اساسی حساب تغییرات .

عبارات مختصات [ ویرایش ]

دو بعدی [ ویرایش ]

عملگر لاپلاس در دو بعد توسط:

در مختصات دکارتی ،

$\Delta f={\frac {\partial ^{2}f}{\partial x^{2}}}+{\frac {\partial ^{2}f}{\partial y^{2} }}$ که در آن x و y مختصات دکارتی استاندارد صفحه xy هستند .

در مختصات قطبی ،

${\begin{aligned}\Delta f&={\frac {1}{r}}{\frac {\partial }{\partial r}}\left(r{\frac {\partial f}{\ r partial r}}\right)+{\frac {1}{r^{2}}}{\frac {\partial ^{2}f}{\partial \theta ^{2}}}\\&={ \frac {\partial ^{2}f}{\partial r^{2}}}+{\frac {1}{r}}{\frac {\partial f}{\partial r}}+{\frac {1}{r^{2}}}{\frac {\partial ^{2}f}{\partial \theta ^{2}}},\end{aligned}}$

که r نشان دهنده فاصله شعاع ی و θ زاویه است.

سه بعدی [ ویرایش ]

همچنین ببینید: دل در مختصات استوانه ای و کروی

در سه بعد، کار با لاپلاسین در انواع سیستم های مختصات مختلف رایج است.

در مختصات دکارتی ،

$\Delta f={\frac {\partial ^{2}f}{\partial x^{2}}}+{\frac {\partial ^{2}f}{\partial y^{2} }}+{\frac {\partial ^{2}f}{\partial z^{2}}}.$

در مختصات استوانه ای ،

$\Delta f={\frac {1}{\rho }}{\frac {\partial }{\partial \rho }}\left(\rho {\frac {\partial f}{\partial \rho }}\right)+{\frac {1}{\rho ^{2}}}{\frac {\partial ^{2}f}{\partial \varphi ^{2}}}+{\frac {\ جزئی ^{2}f}{\جزئی z^{2}}}،$

جایی که $\rho$ نشان دهنده فاصله شعاع ی، φ زاویه آزیموت و z ارتفاع است.

در مختصات کروی :

$\Delta f={\frac {1}{r^{2}}}{\frac {\partial }{\partial r}}\left(r^{2}{\frac {\partial f} {\partial r}}\right)+{\frac {1}{r^{2}\sin \theta }}{\frac {\partial }{\partial \theta }}\left(\sin \theta { \frac {\partial f}{\partial \theta }}\right)+{\frac {1}{r^{2}\sin ^{2}\theta }}{\frac {\partial ^{2} f}{\partial \varphi ^{2}}}،$ یا

$\Delta f={\frac {1}{r}}{\frac {\partial ^{2}}{\partial r^{2}}}(rf)+{\frac {1}{r ^{2}\sin \theta }}{\frac {\partial }{\partial \theta }}\left(\sin \theta {\frac {\partial f}{\partial \theta }}\right)+ {\frac {1}{r^{2}\sin ^{2}\theta }}{\frac {\partial ^{2}f}{\partial \varphi ^{2}}}،$

با گسترش عبارت اول، این عبارات خوانده می شوند

$\Delta f={\frac {\partial ^{2}f}{\partial r^{2}}}+{\frac {2}{r}}{\frac {\partial f}{\ partal r}}+{\frac {1}{r^{2}\sin \theta }}{\frac {\partial }{\partial \theta }}\left(\sin \theta {\frac {\partial f}{\partial \theta }}\right)+{\frac {1}{r^{2}\sin ^{2}\theta }}{\frac {\partial ^{2}f}{\partial \varphi ^{2}}}،$

که در آن φ نشان دهنده زاویه ازیموتال و θ زاویه اوج یا هم عرض جغرافیایی است .

به طور کلی مختصات منحنی ( ξ 1 , ξ 2 , ξ 3 ):

$\Delta =\nabla \xi ^{m}\cdot \nabla \xi ^{n}{\frac {\partial ^{2}}{\partial \xi ^{m}\,\partial \xi ^{n}}}+\nabla ^{2}\xi ^{m}{\frac {\partial }{\partial \xi ^{m}}}=g^{mn}\left({\frac { \partial ^{2}}{\partial \xi ^{m}\,\partial \xi ^{n}}}-\Gamma _{mn}^{l}{\frac {\partial }{\partial \ xi ^{l}}}\راست)،$

جایی که جمع بر روی شاخص های مکرر دلالت دارد ، g mn تانسور معکوس متریک و Γl mn نمادهای کریستوفل برای مختصات انتخاب شده هستند .

ابعاد N [ ویرایش ]

در مختصات منحنی دلخواه در ابعاد N ( ξ 1 ، ...، ξN )، می‌توانیم لاپلاسین را بر حسب تانسور متریک معکوس بنویسیم . $g^{ij}$ :

$\Delta ={\frac {1}{\sqrt {\det g}}}{\frac {\partial }{\partial \xi ^{i}}}\left({\sqrt {\det g }}g^{ij}{\frac {\partial }{\partial \xi ^{j}}}\right),$ از فرمول ووس-ویل [3] برای واگرایی .

در مختصات کروی در ابعاد N ، با پارامترسازی x = rθ ∈ R N با r نشان دهنده یک شعاع حقیقی مثبت و θ عنصری از کره واحد S N -1 ،

$\Delta f={\frac {\partial ^{2}f}{\partial r^{2}}}+{\frac {N-1}{r}}{\frac {\partial f} {\partial r}}+{\frac {1}{r^{2}}}\Delta _{S^{N-1}}f$

که در آن S N -1 عملگر لاپلاس-بلترامی روی ( N -1) -کره است که به عنوان لاپلاسین کروی شناخته می شود. دو عبارت مشتق شعاع ی را می توان به طور معادل به صورت زیر بازنویسی کرد:

${\frac {1}{r^{N-1}}}{\frac {\partial }{\partial r}}\left(r^{N-1}{\frac {\partial f} {\r جزئی}}\راست).$

در نتیجه، لاپلاسین کروی تابعی که بر روی SN - 1 ⊂ RN تعریف شده است را می توان به عنوان لاپلاسی معمولی تابعی که به RN ∖ {0} گسترش یافته محاسبه کرد تا در طول پرتوها ثابت باشد، یعنی درجه همگن باشد . صفر

تغییر ناپذیری اقلیدسی [ ویرایش ]

لاپلاسی تحت تمام دگرگونی های اقلیدسی ثابت است : چرخش ها و ترجمه ها . به عنوان مثال، در دو بعد، به این معنی است که:

$\Delta (f(x\cos \theta -y\sin \theta +a,x\sin \theta +y\cos \theta +b))=(\Delta f)(x\cos \theta - y\sin \theta +a,x\sin \theta +y\cos \theta +b)$

برای همه θ , a , و b . در ابعاد دلخواه،

$\Delta (f\circ \rho )=(\Delta f)\circ \rho$ هر گاه ρ یک چرخش باشد و به همین ترتیب:

$\Delta (f\circ \tau )=(\Delta f)\circ \tau$ هر زمان که τ ترجمه باشد. (به طور کلی، زمانی که ρ یک تبدیل متعامد مانند بازتاب است، این موضوع صادق است .)

در واقع، جبر همه عملگرهای دیفرانسیل خطی اسکالر، با ضرایب ثابت، که با همه تبدیل‌های اقلیدسی جابه‌جا می‌شوند، جبر چند جمله‌ای است که توسط عملگر لاپلاس ایجاد می‌شود.

نظریه طیفی [ ویرایش ]

همچنین ببینید: شنیدن شکل یک درام و مقدار ویژه دیریکله

طیف عملگر لاپلاس از تمام مقادیر ویژه λ تشکیل شده است که برای آنها یک تابع ویژه f با عبارت زیر وجود دارد :

$-\Delta f=\lambda f.$

این معادله به عنوان معادله هلمهولتز شناخته می شود .

اگر Ω یک دامنه محدود در R n باشد ، آنگاه توابع ویژه لاپلاسین یک مبنای متعارف برای فضای هیلبرت L 2 (Ω) هستند . این نتیجه اساساً از قضیه طیفی بر روی عملگرهای فشرده خود الحاقی که به معکوس لاپلاسین (که فشرده است، توسط نابرابری پوانکاره و قضیه رلیش-کوندراخوف ) اعمال می‌شود. [4] همچنین می توان نشان داد که توابع ویژه، توابع بی نهایت قابل تمایز هستند . [5] به طور کلی، این نتایج برای عملگر لاپلاس-بلترامی در هر منیفولد فشرده ریمانی با مرز، یا در واقع برای مسئله مقدار ویژه دیریکله هر عملگر بیضی با ضرایب صاف در یک دامنه محدود، صادق است. وقتی Ω n- کره باشد ، توابع ویژه لاپلاسین هارمونیک های کروی هستند .

لاپلاسی بردار [ ویرایش ]

بردار عملگر لاپلاس که با نشان داده می شود2 $\nabla ^{2}$ ، یک عملگر دیفرانسیل است که روی یک میدان برداری تعریف شده است . [6] لاپلاس بردار شبیه لاپلاسین اسکالر است. در حالی که لاپلاسین اسکالر به یک میدان اسکالر اعمال می شود و یک کمیت اسکالر را برمی گرداند، بردار لاپلاسی برای یک میدان برداری اعمال می شود و یک کمیت برداری را برمی گرداند. هنگامی که در مختصات دکارتی متعامد محاسبه می شود ، میدان برداری برگشتی برابر با میدان برداری لاپلاسین اسکالر اعمال شده برای هر جزء برداری است.

لاپلاسین بردار یک میدان برداری آ $\mathbf {A}$ به عنوان ... تعریف شده است

$\nabla ^{2}\mathbf {A} =\nabla (\nabla \cdot \mathbf {A} )-\nabla \times (\nabla \times \mathbf {A}).$

در مختصات دکارتی ، این به شکل بسیار ساده‌تر کاهش می‌یابد

$\nabla ^{2}\mathbf {A} =(\nabla ^{2}A_{x}،\nabla ^{2}A_{y}،\nabla ^{2}A_{z})،$

جایی که $تبر$ ، $A_y$ ، و $A_z$ اجزای میدان برداری هستند $\mathbf {A}$ ، و $\nabla ^{2}$ فقط در سمت چپ هر جزء بردار عملگر لاپلاس (اسکالار) قرار دارد. می توان مشاهده کرد که این مورد خاصی از فرمول لاگرانژ است. ضرب سه گانه برداری را ببینید .

برای بیان لاپلاس بردار در سایر سیستم های مختصات به دل در مختصات استوانه ای و کروی مراجعه کنید .

تعمیم [ ویرایش ]

لاپلاسین هر میدان تانسوری $\mathbf {T}$ ("تانسور " شامل اسکالر و برداری است) به عنوان واگرایی گرادیان تانسور تعریف می شود :

$\nabla ^{2}\mathbf {T} =(\nabla \cdot \nabla )\mathbf {T} .$

برای مورد خاص که $\mathbf {T}$ یک اسکالر (تانسور درجه صفر) است، لاپلاسی شکل آشنا به خود می گیرد.

اگر $\mathbf {T}$ یک بردار است (تانسور درجه اول)، گرادیان یک مشتق کوواریانت است که منجر به یک تانسور درجه دوم می شود و واگرایی این دوباره یک بردار است. فرمول بردار لاپلاسی بالا ممکن است برای جلوگیری از ریاضیات تانسور استفاده شود و ممکن است معادل واگرایی ماتریس ژاکوبین نشان داده شده در زیر برای گرادیان یک بردار باشد:

$\nabla \mathbf {T} =(\nabla T_{x},\nabla T_{y},\nabla T_{z})={\begin{bmatrix}T_{xx}&T_{xy}&T_{ xz}\\T_{yx}&T_{yy}&T_{yz}\\T_{zx}&T_{zy}&T_{zz}\end{bmatrix}}،{\text{ جایی که }}T_{uv}\equiv {\frac {\partial T_{u}}{\partial v}}.$

و به همین ترتیب، حاصلضرب نقطه‌ای که بردار را با گرادیان بردار دیگر (تانسور درجه 2) به بردار ارزیابی می‌کند، می‌تواند به‌عنوان حاصلضرب ماتریس‌ها دیده شود:

$\mathbf {A} \cdot \nabla \mathbf {B} ={\begin{bmatrix}A_{x}&A_{y}&A_{z}\end{bmatrix}}\nabla \mathbf {B} = {\begin{bmatrix}\mathbf {A} \cdot \nabla B_{x}&\mathbf {A} \cdot \nabla B_{y}&\mathbf {A} \cdot \nabla B_{z}\end{ bmatrix}}.$

این اتحاد یک نتیجه وابسته به مختصات است و کلی نیست.

استفاده در فیزیک [ ویرایش ]

نمونه ای از استفاده از بردار لاپلاسی معادلات ناویر-استوکس برای یک جریان تراکم ناپذیر نیوتنی است :

$\rho \left({\frac {\partial \mathbf {v} }{\partial t}}+(\mathbf {v} \cdot \nabla )\mathbf {v} \right)=\rho \ mathbf {f} -\nabla p+\mu \left(\nabla ^{2}\mathbf {v} \راست)،$ که در آن عبارت با بردار لاپلاسی میدان سرعت است $\mu\left(\nabla ^2 \mathbf{v}\right)$ نشان دهنده تنش های چسبناک در سیال است.

مثال دیگر معادله موج میدان الکتریکی است که می توان از معادلات ماکسول در غیاب بار و جریان بدست آورد:

$\nabla ^{2}\mathbf {E} -\mu _{0}\epsilon _{0}{\frac {\partial ^{2}\mathbf {E} }{\partial t^{2 }}}=0.$

این معادله را می توان به صورت زیر نیز نوشت:

$\Box \,\mathbf {E} =0,$ جایی که

$\Box \equiv {\frac {1}{c^{2}}}{\frac {\partial ^{2}}{\partial t^{2}}}-\nabla ^{2},$ دلامبرتی است که در معادله کلاین-گوردون استفاده می شود .

کلیات [ ویرایش ]

هر جا که عملکرد انرژی دیریکله معنا داشته باشد ، می توان نسخه ای از لاپلاسی را تعریف کرد ، که نظریه اشکال دیریکله است . برای فضاهایی با ساختار اضافی، می توان توضیحات واضح تری از لاپلاسین به شرح زیر ارائه داد.

اپراتور لاپلاس–بلترامی [ ویرایش ]

مقاله اصلی: اپراتور لاپلاس–بلترامی

لاپلاسین همچنین می تواند به یک عملگر بیضوی به نام عملگر لاپلاس-بلترامی تعمیم داده شود که در منیفولد ریمانی تعریف شده است . عملگر لاپلاس-بلترامی، زمانی که به یک تابع اعمال می شود، رد ( tr ) هسین تابع است :

$\Delta f=\operatorname {tr} {\big (}H(f){\big )}$

جایی که ردیابی با توجه به معکوس تانسور متریک گرفته می شود . عملگر لاپلاس-بلترامی را نیز می توان به یک عملگر (که عملگر لاپلاس-بلترامی نیز نامیده می شود) تعمیم داد که بر روی میدان های تانسوری عمل می کند ، با یک فرمول مشابه.

تعمیم دیگری از عملگر لاپلاس که در منیفولدهای شبه ریمانی موجود است از مشتق بیرونی استفاده می کند که بر حسب آن "لاپلاسی هندسه" به صورت بیان می شود.

$\Delta f=\delta df.$

در اینجا کد دیفرانسیل است که می تواند بر حسب ستاره هاج و مشتق بیرونی نیز بیان شود. این عملگر از نظر علامت با "لاپلاسی تحلیلگر" تعریف شده در بالا متفاوت است. به طور کلی، لاپلاسین "Hodge" بر روی اشکال دیفرانسیل α توسط تعریف می شود

$\Delta \alpha =\delta d\alpha +d\delta \alpha .$

این عملگر به عنوان عملگر لاپلاس-د رام شناخته می‌شود ، که با اتحاد Weitzenböck به عملگر لاپلاس-بلترامی مرتبط است .

دلامبرتی [ ویرایش ]

لاپلاسی را می توان به طرق خاصی به فضاهای غیر اقلیدسی تعمیم داد، جایی که ممکن است بیضوی ، هذلولی یا فوق هایپربولیک باشد .

در فضای مینکوفسکی عملگر لاپلاس -بلترامی به عملگر دالامبر تبدیل می‌شود ◻ $\ جعبه$ یا دالامبرتین:

$\square ={\frac {1}{c^{2}}}{\frac {\partial ^{2}}{\partial t^{2}}}-{\frac {\partial ^{ 2}}{\partial x^{2}}}-{\frac {\partial ^{2}}{\partial y^{2}}}-{\frac {\partial ^{2}}{\partial z^{2}}}.$

این تعمیم عملگر لاپلاس است به این معنا که عملگر دیفرانسیل است که تحت گروه ایزومتری فضای زیرین ثابت است و اگر به توابع مستقل از زمان محدود شود به عملگر لاپلاس کاهش می یابد. علامت کلی متریک در اینجا به گونه‌ای انتخاب می‌شود که بخش‌های فضایی عملگر یک علامت منفی را بپذیرد، که قرارداد معمول در فیزیک ذرات پرانرژی است . عملگر دالامبر به عنوان عملگر موج نیز شناخته می شود زیرا عملگر دیفرانسیل است که در معادلات موج ظاهر می شود و همچنین بخشی از معادله کلاین-گوردون است که در حالت بدون جرم به معادله موج کاهش می یابد.

ضریب اضافی c در متریک در فیزیک مورد نیاز است اگر فضا و زمان در واحدهای مختلف اندازه گیری شود. برای مثال، اگر جهت x بر حسب متر و جهت y بر حسب سانتی متر اندازه گیری شود، فاکتور مشابهی لازم است . در واقع، فیزیکدانان نظری معمولاً در واحدهایی کار می کنند که c =1 باشد تا معادله را ساده کنند.

عملگر دی المبرت به یک عملگر هذلولی در منیفولدهای شبه ریمانی تعمیم می دهد .

همچنین ببینید [ ویرایش ]

عملگر لاپلاس-بلترامی ، تعمیم به زیرمنیفولدها در فضای اقلیدسی و منیفولد ریمانی و شبه ریمانی.
عملگر لاپلاسی بردار ، تعمیم میدانهای لاپلاسی به برداری .
لاپلاسی در هندسه دیفرانسیل .
عملگر لاپلاس گسسته یک آنالوگ تفاضل محدود از لاپلاسین پیوسته است که بر روی نمودارها و شبکه ها تعریف شده است.
لاپلاسین یک اپراتور رایج در پردازش تصویر و بینایی کامپیوتری است (به لاپلاسین گاوسی ، آشکارساز حباب و فضای مقیاس مراجعه کنید ).
فهرست فرمول ها در هندسه ریمانی شامل عباراتی برای لاپلاسی بر حسب نمادهای کریستوفل است.
لم ویل (معادله لاپلاس) .
قضیه ارنشاو که نشان می دهد تعلیق گرانشی، الکترواستاتیکی یا مغناطیسی پایدار غیرممکن است.
دل در مختصات استوانه ای و کروی .
موقعیت های دیگری که در آنها یک لاپلاسی تعریف می شود عبارتند از: تجزیه و تحلیل بر روی فراکتال ها ، حساب مقیاس زمانی و حساب خارجی گسسته .

یادداشت ها [ ویرایش ]

^ ایوانز 1998 ، §2.2
↑ Oval, Jeffrey S. (01-03-2016). "لاپلاسی و ارزش های متوسط و افراطی" (PDF) . ماهنامه ریاضی آمریکا . 123 (3): 287-291. doi : 10.4169/amer.math.monthly.123.3.287 . S2CID 124943537 .
↑ بایگانی شده در Ghostarchive and the Wayback Machine : Grinfeld, Pavel. "فرمول Voss-Weyl" . یوتیوب . بازیابی شده در 9 ژانویه 2018 .
↑ گیلبارگ و ترودینگر 2001 ، قضیه 8.6
↑ گیلبارگ و ترودینگر 2001 ، نتیجه 8.11
^ دنیای ریاضی. " لاپلاس بردار " .

منابع [ ویرایش ]

ایوانز، ال. (1998)، معادلات دیفرانسیل جزئی ، انجمن ریاضی آمریکا، شابک 978-0-8218-0772-9
سخنرانی های فاینمن در فیزیک جلد. فصل دوم 12: آنالوگ های الکترواستاتیک
گیلبارگ، دی. ترودینگر، ن. (2001)، معادلات دیفرانسیل جزئی بیضوی مرتبه دوم ، اسپرینگر، شابک 978-3-540-41160-4.
Schey, HM (1996), Div, Grad, Curl, and All That , WW Norton, ISBN 978-0-393-96997-9.

ادامه مطلب [ ویرایش ]

لاپلاسیان - ریچارد فیتزپاتریک 2006

پیوندهای خارجی [ ویرایش ]

"اپراتور لاپلاس" ، دایره المعارف ریاضیات ، انتشارات EMS ، 2001 [1994]
وایستاین، اریک دبلیو. "لاپلاسین" . دنیای ریاضی .
لاپلاسین در اشتقاق مختصات قطبی
معادلات مکعب فراکتال و اثر کازیمیر

https://en.wikipedia.org/wiki/Laplace_operator

+ نوشته شده در چهارشنبه هشتم آذر ۱۴۰۲ ساعت 21:34 توسط علی رضا نقش نیلچی |

5-سیستم مختصات قطبی

حساب انتگرال (طول قوس) [ ویرایش ]

طول قوس (طول یک پاره خط) که توسط یک تابع قطبی تعریف می‌شود، با ادغام روی منحنی r ( φ ) به دست می‌آید. اجازه دهید L این طول را در امتداد منحنی نشان دهد که از نقاط A تا نقطه B شروع می شود ، جایی که این نقاط مطابق با φ = a و φ = b هستند به طوری که 0 < b − a < 2 π . طول L با انتگرال زیر بدست می آید

$L=\int _{a}^{b}{\sqrt {\left[r(\varphi )\right]^{2}+\left[{\tfrac {dr(\varphi )}{d \varphi }}\right]^{2}}}d\varphi$

حساب انتگرال (مساحت) [ ویرایش ]

ناحیه یکپارچه سازی R توسط منحنی r ( φ ) و پرتوهای φ = a و φ = b محدود شده است.

فرض کنید R ناحیه محصور شده توسط یک منحنی r ( φ ) و پرتوهای φ = a و φ = b را نشان می دهد ، که در آن 0 < b − a ≤ 2 π . سپس مساحت R برابر است

${\frac {1}{2}}\int _{a}^{b}\left[r(\varphi )\right]^{2}\,d\varphi .$

منطقه R با n بخش تقریبی می شود (در اینجا n = 5).

یک پلان متر که به صورت مکانیکی انتگرال های قطبی را محاسبه می کند

این نتیجه را می توان به صورت زیر یافت. ابتدا بازه [ a , b ] به n زیر بازه تقسیم می شود که n مقداری صحیح مثبت است. بنابراین Δ φ ، اندازه گیری زاویه هر زیر بازه، برابر است با b - a (میزان اندازه گیری کل زاویه بازه)، تقسیم بر n ، تعداد زیر بازه ها. برای هر زیر بازه i = 1، 2، ...، n ، اجازه دهید φ i نقطه میانی زیر بازه باشد، و یک بخش با مرکز در قطب، شعاع r ( φi) بسازیم .)، زاویه مرکزی Δ φ و طول قوس r ( φ i )Δ φ . بنابراین مساحت هر بخش ساخته شده برابر است با

$\left[r(\varphi _{i})\right]^{2}\pi \cdot {\frac {\Delta \varphi }{2\pi }}={\frac {1}{2 }}\left[r(\varphi _{i})\right]^{2}\Delta \varphi .$

از این رو، مساحت کل همه بخش ها است

$\sum _{i=1}^{n}{\tfrac {1}{2}}r(\varphi _{i})^{2}\,\Delta \varphi .$

با افزایش تعداد زیر بازه های n ، تقریب مساحت بهبود می یابد. با گرفتن n ∞ ∞ ، حاصل جمع ریمان برای انتگرال فوق می شود.

دستگاه مکانیکی که انتگرال‌های مساحت را محاسبه می‌کند پلان‌متر است که مساحت شکل‌های صفحه را با ردیابی آنها اندازه‌گیری می‌کند: این انتگرال را در مختصات قطبی با افزودن یک مفصل تکرار می‌کند به طوری که پیوند دو عنصری قضیه گرین را تحت تأثیر قرار می‌دهد و انتگرال قطبی درجه دوم را به یک انتگرال خطی

تعمیم [ ویرایش ]

با استفاده از مختصات دکارتی ، یک عنصر مساحت بینهایت کوچک را می توان به صورت dA = dx dy محاسبه کرد. قانون جایگزینی برای انتگرال های چندگانه بیان می کند که هنگام استفاده از مختصات دیگر، تعیین کننده ژاکوبین فرمول تبدیل مختصات باید در نظر گرفته شود:

$J=\det {\frac {\partial (x,y)}{\partial (r,\varphi )}}={\begin{vmatrix}{\frac {\partial x}{\partial r} }&{\frac {\partial x}{\partial \varphi }}\\[2pt]{\frac {\partial y}{\partial r}}&{\frac {\partial y}{\partial \varphi }}\end{vmatrix}}={\begin{vmatrix}\cos \varphi &-r\sin \varphi \\\sin \varphi &r\cos \varphi \end{vmatrix}}=r\cos ^{2 }\varphi +r\sin ^{2}\varphi =r.$

بنابراین، یک عنصر مساحت در مختصات قطبی را می توان به صورت نوشتاری نوشت

$dA=dx\,dy\ =J\,dr\,d\varphi =r\,dr\,d\varphi .$

اکنون، یک تابع، که در مختصات قطبی داده شده است، می تواند به صورت زیر یکپارچه شود:

$\iint _{R}f(x,y)\,dA=\int _{a}^{b}\int _{0}^{r(\varphi )}f(r,\varphi ) \,r\,dr\,d\varphi .$

در اینجا، R همان ناحیه فوق است، یعنی ناحیه محصور شده توسط یک منحنی r ( φ ) و پرتوهای φ = a و φ = b . فرمول مساحت R با گرفتن f به طور یکسان برابر با 1 بازیابی می شود.

یک نمودار از $f(x)=e^{-x^{2}}$ و ناحیه بین تابع و $ایکس$ -axis که برابر است با ${\sqrt {\pi }}$ .

یک کاربرد شگفت‌انگیزتر از این نتیجه انتگرال گاوسی را به دست می‌دهد :

$\int _{-\infty }^{\infty }e^{-x^{2}}\,dx={\sqrt {\pi }}.$

حساب برداری [ ویرایش ]

حساب برداری را می توان برای مختصات قطبی نیز اعمال کرد. برای حرکت مسطح، اجازه دهید $\mathbf {r}$ بردار موقعیت ( r cos( φ )، r sin( φ )) باشد ، با r و φ بسته به زمان t .

بردارهای واحد را تعریف می کنیم

${\hat {\mathbf {r} }}=(\cos(\varphi ),\sin(\varphi ))$ در مسیر $\mathbf {r}$ و

${\hat {\boldsymbol {\varphi }}}=(-\sin(\varphi ),\cos(\varphi ))={\hat {\mathbf {k} }}\times {\hat { \mathbf {r} }}\ ,$

در صفحه حرکت عمود بر جهت شعاعی، جایی که ${\hat {\mathbf {k} }}$ یک بردار واحد نرمال با صفحه حرکت است.

سپس

${\begin{aligned}\mathbf {r} &=(x,\ y)=r(\cos \varphi ,\ \sin \varphi )=r{\hat {\mathbf {r} }}\ ,\\{\dot {\mathbf {r} }}&=\left({\dot {x}},\ {\dot {y}}\right)={\dot {r}}(\cos \ varphi ,\ \sin \varphi )+r{\dot {\varphi }}(-\sin \varphi ,\ \cos \varphi )={\dot {r}}{\hat {\mathbf {r} }} +r{\dot {\varphi }}{\hat {\boldsymbol {\varphi }}}\ ,\\{\ddot {\mathbf {r} }}&=\left({\ddot {x}}, \ {\ddot {y}}\right)\\&={\ddot {r}}(\cos \varphi ,\ \sin \varphi )+2{\dot {r}}{\dot {\varphi } }(-\sin \varphi ,\ \cos \varphi )+r{\ddot {\varphi }}(-\sin \varphi ,\ \cos \varphi )-r{\dot {\varphi }}^{2 }(\cos \varphi ,\ \sin \varphi )\\&=\left({\ddot {r}}-r{\dot {\varphi }}^{2}\right){\hat {\mathbf {r} }}+\left(r{\ddot {\varphi }}+2{\dot {r}}{\dot {\varphi }}\right){\hat {\boldsymbol {\varphi }}} \\&=\left({\ddot {r}}-r{\dot {\varphi }}^{2}\right){\hat {\mathbf {r} }}+{\frac {1}{r}} \;{\frac {d}{dt}}\left(r^{2}{\dot {\varphi }}\right){\hat {\boldsymbol {\varphi }}}.\end{تراز شده}}$

اصطلاحات گریز از مرکز و کوریولیس [ ویرایش ]

همچنین ببینید: مکانیک حرکت ذرات مسطح و نیروی گریز از مرکز (قاب مرجع چرخشی)

بردار موقعیت r ، همیشه به صورت شعاعی از مبدا اشاره می کند.

بردار سرعت v ، همیشه مماس بر مسیر حرکت است.

بردار شتاب a ، موازی با حرکت شعاعی نیست، بلکه توسط شتاب‌های زاویه‌ای و کوریولیس جبران می‌شود، و نه مماس بر مسیر، بلکه با شتاب‌های مرکز و شعاعی جبران می‌شود.

بردارهای سینماتیکی در مختصات قطبی مسطح. توجه داشته باشید که راه اندازی به فضای دو بعدی محدود نمی شود، بلکه یک صفحه در هر بعد بالاتر است.

عبارت $r{\dot {\varphi }}^{2}$ گاهی اوقات به عنوان شتاب مرکزگرا و اصطلاح شناخته می شود $2{\dot {r}}{\dot {\varphi }}$ به عنوان شتاب کوریولیس . برای مثال به شانکار مراجعه کنید. [18]

توجه: این عبارات، که هنگام بیان شتاب در مختصات قطبی ظاهر می شوند، یک نتیجه ریاضی تمایز هستند. هر زمان که از مختصات قطبی استفاده می شود ظاهر می شوند. در دینامیک ذرات مسطح، این شتاب ها هنگام تنظیم قانون دوم حرکت نیوتن در یک چارچوب مرجع چرخشی ظاهر می شوند. در اینجا این اصطلاحات اضافی اغلب نیروهای ساختگی نامیده می شوند . ساختگی هستند زیرا آنها صرفاً نتیجه تغییر در چارچوب مختصات هستند. این بدان معنا نیست که آنها وجود ندارند، بلکه فقط در چارچوب چرخان وجود دارند.

قاب اینرسی مرجع S و قاب غیر اینرسی همزمان چرخشی آنی مرجع S' . قاب دوار همزمان با سرعت زاویه ای Ω برابر با سرعت چرخش ذره حول مبدا S' در لحظه خاص t می چرخد . ذره در موقعیت برداری r ( t ) قرار دارد و بردارهای واحد در جهت شعاعی به ذره از مبدأ، و همچنین در جهت افزایش زاویه ϕ نرمال به جهت شعاعی نشان داده می شوند. این بردارهای واحد نیازی به ارتباط با مماس و نرمال مسیر ندارند. همچنین فاصله شعاعی r نیازی به ارتباط با شعاع انحنای مسیر ندارد.

قاب چرخشی همزمان [ ویرایش ]

برای یک ذره در حرکت مسطح، یک رویکرد برای ضمیمه کردن اهمیت فیزیکی به این عبارات مبتنی بر مفهوم چارچوب مرجع همزمان چرخشی آنی است . [19] برای تعریف یک قاب هم چرخان، ابتدا یک مبدا انتخاب می شود که از آن فاصله r ( t ) تا ذره تعریف می شود. یک محور چرخشی عمود بر صفحه حرکت ذره تنظیم می شود و از این مبدا می گذرد. سپس، در لحظه انتخاب شده t ، سرعت چرخش قاب هم‌گردان Ω مطابق با سرعت چرخش ذره حول این محور، dφ / dt ساخته می‌شود.. در مرحله بعد، اصطلاحات موجود در شتاب در قاب اینرسی با موارد موجود در قاب هم چرخش مرتبط هستند. اجازه دهید مکان ذره در قاب اینرسی ( r ( t )، φ ( t )) و در قاب چرخش همزمان ( r ′(t)، φ ′(t) باشد). از آنجایی که قاب دوار هم‌زمان با همان سرعت ذره می‌چرخد، dφ ′/ dt = 0. نیروی گریز از مرکز خیالی در قاب هم‌گردان mr Ω 2 است که به صورت شعاعی به سمت بیرون است. سرعت ذره در قاب هم چرخان نیز به صورت شعاعی به سمت بیرون است، زیرا dφ ′/ dt = 0.بنابراین نیروی ساختگی کوریولیس دارای مقدار -2 m ( d / dt )Ω است که فقط در جهت افزایش φ است. بنابراین، با استفاده از این نیروها در قانون دوم نیوتن متوجه می شویم:

${\boldsymbol {F}}+{\boldsymbol {F}}_{\text{cf}}+{\boldsymbol {F}}_{\text{Cor}}=m{\ddot {\boldsymbol {r}}}\ ,$

که در آن بیش از نقطه نشان دهنده تمایز زمانی است، و F نیروی واقعی خالص است (در مقابل نیروهای ساختگی). از نظر مولفه ها، این معادله برداری به صورت زیر می شود:

${\begin{aligned}F_{r}+mr\Omega ^{2}&=m{\ddot {r}}\\F_{\varphi }-2m{\dot {r}}\Omega & =mr{\ddot {\varphi }}\ ,\end{تراز شده}}$

که می توان آن را با معادلات قاب اینرسی مقایسه کرد:

${\begin{aligned}F_{r}&=m{\ddot {r}}-mr{\dot {\varphi }}^{2}\\F_{\varphi }&=mr{\ddot {\varphi }}+2m{\dot {r}}{\dot {\varphi }}\ .\end{تراز شده}}$

این مقایسه، به علاوه تشخیص اینکه با تعریف قاب دوار در زمان t دارای نرخ چرخش Ω = dφ / dt است، نشان می‌دهد که می‌توانیم اصطلاحات موجود در شتاب (ضرب در جرم ذره) را تفسیر کنیم. همانطور که در قاب اینرسی به عنوان منفی نیروهای گریز از مرکز و کوریولیس یافت می شود که در قاب هم چرخش آنی و غیر اینرسی دیده می شود.

برای حرکت کلی یک ذره (برخلاف حرکت دایره ای ساده)، نیروهای گریز از مرکز و کوریولیس در چارچوب مرجع ذره معمولاً به دایره نوسانی آنی حرکت آن اشاره می کنند، نه به مرکز ثابت مختصات قطبی. برای جزئیات بیشتر، نیروی مرکزگرا را ببینید .

+ نوشته شده در چهارشنبه هشتم تیر ۱۴۰۱ ساعت 20:9 توسط علی رضا نقش نیلچی |

3-سیستم مختصات قطبی

دایره [ ویرایش ]

دایره ای با معادله r ( φ ) = 1

معادله کلی یک دایره با مرکز در $(r_{0},\gamma )$ و شعاع a است

$r^{2}-2rr_{0}\cos(\varphi -\gamma )+r_{0}^{2}=a^{2}.$

این را می توان به روش های مختلفی ساده کرد تا با موارد خاص تر مانند معادله مطابقت داشته باشد

$r(\varphi )=a$ برای دایره ای با مرکز در قطب و شعاع a . [15]

وقتی r 0 = a یا مبدأ روی دایره باشد، معادله تبدیل می شود

$r=2a\cos(\varphi -\gamma).$

در حالت کلی، معادله را می توان برای r حل کرد

$r=r_{0}\cos(\varphi -\gamma )+{\sqrt {a^{2}-r_{0}^{2}\sin ^{2}(\varphi -\gamma) }}$

محلول با علامت منفی جلوی جذر همان منحنی را می دهد.

خط [ ویرایش ]

خطوط شعاعی (آنهایی که از قطب عبور می کنند) با معادله نشان داده می شوند

$\varphi =\gamma ,$ جایی که $\گاما$ زاویه ارتفاع خط است. به این معنا که، $\varphi =\arctan m$ ، جایی که $متر$ شیب خط در دستگاه مختصات دکارتی است. خط غیر شعاعی که از خط شعاعی عبور می کند $\varphi =\gamma$ عمود بر نقطه $(r_{0},\gamma )$ معادله را دارد

$r(\varphi )=r_{0}\sec(\varphi -\gamma).$

در غیر این صورت بیان شده است $(r_{0},\gamma )$ نقطه ای است که در آن مماس دایره فرضی شعاع را قطع می کند $r_{0}$

گل رز قطبی [ ویرایش ]

یک گل رز قطبی با معادله r ( φ ) = 2 sin 4 φ

گل رز قطبی یک منحنی ریاضی است که شبیه یک گل گلبرگ است و می توان آن را به صورت یک معادله قطبی ساده بیان کرد.

$r(\varphi )=a\cos \left(k\varphi +\gamma _{0}\right)$

برای هر ثابت γ 0 (شامل 0). اگر k یک عدد صحیح باشد، اگر k فرد باشد، این معادلات یک گل رز k گلبرگدار و اگر k زوج باشد یک رز 2 k گلبرگ ایجاد می کند. اگر k منطقی باشد، اما یک عدد صحیح نباشد، ممکن است یک شکل گل رز شکل بگیرد، اما با گلبرگ های روی هم قرار گرفته باشد. توجه داشته باشید که این معادلات هرگز گل رز را با گلبرگ های 2، 6، 10، 14 و غیره تعریف نمی کنند. متغیر a مستقیماً طول یا دامنه گلبرگ های گل رز را نشان می دهد، در حالی که k به فرکانس فضایی آنها مربوط می شود. ثابت γ 0 را می توان به عنوان یک زاویه فاز در نظر گرفت.

مارپیچ ارشمیدسی [ ویرایش ]

یک بازوی مارپیچ ارشمیدسی با معادله r ( φ ) = φ / 2 π برای 0 < φ < 6 π پی

مارپیچ ارشمیدسی مارپیچی کشف شده توسط ارشمیدس است که می تواند به عنوان یک معادله قطبی ساده نیز بیان شود. با معادله نشان داده می شود

$r(\varphi )=a+b\varphi .$

تغییر پارامتر a باعث چرخش مارپیچ می شود، در حالی که b فاصله بین بازوها را کنترل می کند که برای یک مارپیچ معین همیشه ثابت است. مارپیچ ارشمیدسی دو بازو دارد، یکی برای φ > 0 و دیگری برای φ < 0 . دو بازو به آرامی در قطب به هم متصل شده اند. اگر a = 0 باشد، گرفتن تصویر آینه ای از یک بازو در سراسر خط 90 درجه/270 درجه، بازوی دیگر را نشان می دهد. این منحنی به عنوان یکی از اولین منحنی ها، پس از مقاطع مخروطی ، قابل توجه است که در یک رساله ریاضی شرح داده شده است، و به عنوان مثال اصلی منحنی است که به بهترین وجه توسط یک معادله قطبی تعریف می شود.

بیضی، رکتوم نیمه لاتوس را نشان می دهد

+ نوشته شده در چهارشنبه هشتم تیر ۱۴۰۱ ساعت 20:6 توسط علی رضا نقش نیلچی |

2-توابع هذلولی

ویژگی های مشخصه [ ویرایش ]

کسینوس هایپربولیک [ ویرایش ]

می توان نشان داد که مساحت زیر منحنی کسینوس هذلولی (در یک بازه محدود) همیشه برابر با طول قوس مربوط به آن بازه است: [15]

${\text{area}}=\int _{a}^{b}\cosh x\,dx=\int _{a}^{b}{\sqrt {1+\left({\frac {d}{dx}}\cosh x\right)^{2}}}\,dx={\text{طول قوس.}}$

مماس هایپربولیک[ ویرایش ]

مماس هذلولی جواب (یکتا) معادله دیفرانسیل f ′ = 1 − f 2 است که f (0) = 0 دارد. [16] [17]

روابط مفید [ ویرایش ]

توابع هذلولی بسیاری از هویت ها را برآورده می کنند که همه آنها از نظر شکل شبیه به هویت های مثلثاتی هستند . در واقع، قانون آزبورن [18] بیان می کند که می توان هر هویت مثلثاتی را برای تبدیل کرد $تتا$ ، $2\ تتا$ ، $3\ تتا$ یا $تتا$ و $\varphi$ به یک هویت هذلولی، با بسط کامل آن بر حسب قدرت های انتگرال سینوس ها و کسینوس ها، تغییر سینوس به سینه و کسینوس به کوش، و تغییر علامت هر عبارت حاوی حاصل ضرب دو سین.

توابع زوج و فرد:

${\begin{aligned}\sinh(-x)&=-\sinh x\\\cosh(-x)&=\cosh x\end{aligned}}$

از این رو:

${\begin{aligned}\tanh(-x)&=-\tanh x\\\coth(-x)&=-\coth x\\\operatorname {sech} (-x)&=\operatorname {sech} x\\\ نام عامل {csch} (-x)&=-\نام اپراتور {csch} x\end{تراز شده}}$

بنابراین، cosh x و sech x توابع زوج هستند . بقیه توابع فرد هستند .

${\begin{aligned}\operatorname {arsech} x&=\operatorname {arcosh} \left({\frac {1}{x}}\right)\\\operatorname {arcsch} x&=\operatorname {arsinh } \left({\frac {1}{x}}\right)\\\operatorname {arcoth} x&=\operatorname {artanh} \left({\frac {1}{x}}\right)\end{ هم راستا}}$

سینوس و کسینوس هایپربولیک:

${\begin{aligned}\cosh x+\sinh x&=e^{x}\\\cosh x-\sinh x&=e^{-x}\\\cosh ^{2}x-\sinh ^ {2}x&=1\end{تراز شده}}$

که آخرین آنها شبیه به هویت مثلثاتی فیثاغورثی است .

یکی هم دارد

${\begin{aligned}\operatorname {sech} ^{2}x&=1-\tanh ^{2}x\\\operatorname {csch} ^{2}x&=\coth ^{2}x- 1\end{تراز شده}}$

برای توابع دیگر

مجموع آرگومان ها [ ویرایش ]

${\begin{aligned}\sinh(x+y)&=\sinh x\cosh y+\cosh x\sinh y\\\cosh(x+y)&=\cosh x\cosh y+\sinh x \sinh y\\[6px]\tanh(x+y)&={\frac {\tanh x+\tanh y}{1+\tanh x\tanh y}}\\\end{تراز شده}}$

به ویژه

${\begin{aligned}\cosh(2x)&=\sinh ^{2}{x}+\cosh ^{2}{x}=2\sinh ^{2}x+1=2\cosh ^{2}x-1\\\sinh(2x)&=2\sinh x\cosh x\\\tanh(2x)&={\frac {2\tanh x}{1+\tanh ^{2} x}}\\\پایان{تراز شده}}$

همچنین:

${\begin{aligned}\sinh x+\sinh y&=2\sinh \left({\frac {x+y}{2}}\right)\cosh \left({\frac {xy}{2 }}\right)\\\cosh x+\cosh y&=2\cosh \left({\frac {x+y}{2}}\right)\cosh \left({\frac {xy}{2}} \راست)\\\پایان{تراز شده}}$

فرمول های تفریق [ ویرایش ]

${\begin{aligned}\sinh(xy)&=\sinh x\cosh y-\cosh x\sinh y\\\cosh(xy)&=\cosh x\cosh y-\sinh x\sinh y\\\tanh(xy)&={\frac {\tanh x-\tanh y}{1-\tanh x\tanh y}}\\\end{تراز شده}}$

همچنین: [19]

${\begin{aligned}\sinh x-\sinh y&=2\cosh \left({\frac {x+y}{2}}\right)\sinh \left({\frac {xy}{ 2}}\right)\\\cosh x-\cosh y&=2\sinh \left({\frac {x+y}{2}}\right)\sinh \left({\frac {xy}{2 }}\راست)\\\end{تراز شده}}$

فرمول های نیم آرگومان [ ویرایش ]

${\begin{aligned}\sinh \left({\frac {x}{2}}\right)&={\frac {\sinh x}{\sqrt {2(\cosh x+1)} }}&&=\operatorname {sgn} x\,{\sqrt {\frac {\cosh x-1}{2}}}\\[6px]\cosh \left({\frac {x}{2}} \right)&={\sqrt {\frac {\cosh x+1}{2}}}\\[6px]\tanh \left({\frac {x}{2}}\right)&={\ frac {\sinh x}{\cosh x+1}}&&=\operatorname {sgn} x\,{\sqrt {\frac {\cosh x-1}{\cosh x+1}}}={\frac {e^{x}-1}{e^{x}+1}}\end{تراز شده}}$

که در آن sgn تابع علامت است .

اگر x ≠ 0 ، سپس [20]

$\tanh \left({\frac {x}{2}}\right)={\frac {\cosh x-1}{\sinh x}}=\coth x-\operatorname {csch} x$

فرمول های مربعی [ ویرایش ]

${\begin{aligned}\sinh ^{2}x&={\frac {1}{2}}(\cosh 2x-1)\\\cosh ^{2}x&={\frac {1} {2}}(\cosh 2x+1)\end{تراز شده}}$

نابرابری ها [ ویرایش ]

نابرابری زیر در آمار مفید است: $\operatorname {cosh} (t)\leq e^{t^{2}/2}$ [21]

این را می توان با مقایسه ترم به ترم سری تیلور دو تابع ثابت کرد.

توابع معکوس به عنوان لگاریتم [ ویرایش ]

مقاله اصلی: تابع هذلولی معکوس

${\begin{aligned}\operatorname {arsinh} (x)&=\ln \left(x+{\sqrt {x^{2}+1}}\right)\\\operatorname {arcosh} (x )&=\ln \left(x+{\sqrt {x^{2}-1}}\right)&&x\geq 1\\\operatorname {artanh} (x)&={\frac {1}{2} }\ln \left({\frac {1+x}{1-x}}\right)&&|x|<1\\\operatorname {arcoth} (x)&={\frac {1}{2} }\ln \left({\frac {x+1}{x-1}}\right)&&|x|>1\\\operatorname {arsech} (x)&=\ln \left({\frac { 1}{x}}+{\sqrt {{\frac {1}{x^{2}}}-1}}\right)=\ln \left({\frac {1+{\sqrt {1- x^{2}}}}{x}}\right)&&0<x\leq 1\\\operatorname {arcsch} (x)&=\ln \left({\frac {1}{x}}+{ \sqrt {{\frac {1}{x^{2}}}+1}}\right)&&x\neq 0\end{تراز شده}}$

+ نوشته شده در شنبه سوم اردیبهشت ۱۴۰۱ ساعت 10:33 توسط علی رضا نقش نیلچی |

1-توابع هذلولی

"منحنی هیپربولیک" به اینجا هدایت می شود. برای منحنی هندسی، Hyperbola را ببینید .

در ریاضیات , توابع هذلولی مشابه توابع مثلثاتی معمولی هستند , اما با استفاده از هذلولی به جای دایره تعریف می شوند . همانطور که نقاط (cost ، sin t ) دایره ای با شعاع واحد تشکیل می دهند ، نقاط (cosh t ، sinh t ) نیمه سمت راست هذلولی واحد را تشکیل می دهند. همچنین، به طور مشابه، مشتقات sin( t ) و cos( t ) cos( t ) هستند .و –sin( t ) ، مشتقات sinh( t ) و cosh( t ) cosh( t ) و +sinh( t ) هستند .

توابع هذلولی در محاسبات زوایا و فواصل در هندسه هذلولی رخ می دهند . آنها همچنین در راه حل های بسیاری از معادلات دیفرانسیل خطی (مانند معادله تعریف یک خطی )، معادلات مکعبی ، و معادله لاپلاس در مختصات دکارتی رخ می دهند. معادلات لاپلاس در بسیاری از زمینه های فیزیک از جمله نظریه الکترومغناطیسی ، انتقال حرارت ، دینامیک سیالات و نسبیت خاص مهم هستند.

توابع هذلولی اساسی عبارتند از: [1]

سینوس هذلولی "sinh" ( / ˈ s ɪ ŋ , ˈ s ɪ n tʃ , ˈ ʃ aɪ n / )، [2]
کسینوس هذلولی "cosh" ( / ˈ k ɒ ʃ , ˈ k oʊ ʃ / )، [3]

که از آن مشتق شده است: [4]

تانژانت هذلولی "tanh" ( / ˈ t æ ŋ , ˈ t æ n tʃ , ˈ θ æ n / )، [5]
کسکانت هذلولی "csch" یا "cosech" ( / ˈ k oʊ s ɛ tʃ , ˈ k oʊ ʃ ɛ k / [3] )
سکانت هذلولی "sech" ( / ˈ s ɛ tʃ , ˈ ʃ ɛ k / )، [6]
هذلولی همتنژانت "coth" ( / ˈ k ɒ θ , ˈ k oʊ θ / )، [7] [8]

مربوط به توابع مثلثاتی مشتق شده است.

توابع هذلولی معکوس عبارتند از:

سینوس هذلولی منطقه "arsinh" (همچنین به "sinh -1 "، "asinh" یا گاهی اوقات "arcsinh" نشان داده می شود) [9] [10] [11]
کسینوس هذلولی ناحیه "arcosh" (همچنین به "cosh -1 "، "acosh" یا گاهی اوقات "arccosh" نشان داده می شود)
و غیره

پرتویی از هذلولی واحد x 2 − y 2 = 1 در نقطه (cosh a , sinh a ) , جایی که a دو برابر مساحت بین پرتو، هذلولی و محور x است. برای نقاط روی هذلولی زیر محور x ، ناحیه منفی در نظر گرفته می شود ( نسخه متحرک با مقایسه با توابع مثلثاتی (دایره ای) را ببینید).

توابع هذلولی یک متغیر حقیقی به نام زاویه هذلولی می گیرند . اندازه یک زاویه هذلولی دو برابر مساحت بخش هذلولی آن است . توابع هذلولی ممکن است برحسب پایه های یک مثلث قائم الزاویه که این بخش را پوشش می دهد، تعریف شوند.

در تحلیل مختلط ، توابع هذلولی به عنوان بخش های مختلط سینوس و کسینوس به وجود می آیند. سینوس هیپربولیک و کسینوس هذلولی توابع کامل هستند . در نتیجه، سایر توابع هذلولی در کل صفحه مختلط مرومورفیک هستند.

بر اساس قضیه لیندمان – وایرشتراس ، توابع هذلولی برای هر مقدار جبری غیرصفری متغیر، یک مقدار ماورایی دارند . [12]

توابع هیپربولیک در دهه 1760 به طور مستقل توسط وینچنزو ریکاتی و یوهان هاینریش لامبرت معرفی شدند. [13] Riccati از Sc. و رونوشت ( sinus/cosinus circulare ) اشاره به توابع حلقوی و Sh. و چ. ( سینوس/کوسینوس هیپربولیکو ) برای اشاره به توابع هذلولی. لامبرت این نام ها را پذیرفت، اما اختصارات را به نام هایی که امروزه استفاده می شود تغییر داد. [14] اختصارات sh , ch , th , cth نیز در حال حاضر بسته به ترجیح شخصی استفاده می شود.

فهرست

1نشانه گذاری
2تعاریف
- 2.1تعاریف نمایی
- 2.2تعاریف معادلات دیفرانسیل
- 2.3تعاریف مختلط مثلثاتی
3ویژگی های مشخص کننده
- 3.1کسینوس هیپربولیک
- 3.2تانژانت هیپربولیک
4روابط مفید
- 4.1مجموع استدلال ها
- 4.2فرمول های تفریق
- 4.3فرمول های نیم متغیر
- 4.4فرمول های مربعی
- 4.5نابرابری ها
5توابع معکوس به عنوان لگاریتم
6مشتقات
7مشتقات دوم
8انتگرال های استاندارد
9عبارات سری تیلور
10ضربهای نامتناهی و کسرهای ادامه دار
11مقایسه با توابع دایره ای
12رابطه با تابع نمایی
13توابع هذلولی برای اعداد مختلط
14همچنین ببینید
15منابع
16لینک های خارجی

نشانه گذاری [ ویرایش ]

مقاله اصلی: توابع مثلثاتی § نمادگذاری

تعاریف [ ویرایش ]

سین ، کوش و تن

csch ، sech و coth

روش های معادل مختلفی برای تعریف توابع هذلولی وجود دارد.

تعاریف نمایی [ ویرایش ]

sinh x نصف اختلاف e x و e - x است

cosh x میانگین e x و e - x است _

از نظر تابع نمایی : [1] [4]

سینوس هیپربولیک: قسمت فرد تابع نمایی، یعنی

$\sinh x={\frac {e^{x}-e^{-x}}{2}}={\frac {e^{2x}-1}{2e^{x}}}= {\frac {1-e^{-2x}}{2e^{-x}}}.$
کسینوس هیپربولیک: قسمت زوج تابع نمایی، یعنی

$\cosh x={\frac {e^{x}+e^{-x}}{2}}={\frac {e^{2x}+1}{2e^{x}}}= {\frac {1+e^{-2x}}{2e^{-x}}}.$
مماس هیپربولیک:

$\tanh x={\frac {\sinh x}{\cosh x}}={\frac {e^{x}-e^{-x}}{e^{x}+e^{- x}}}={\frac {e^{2x}-1}{e^{2x}+1}}.$
کتانژانت هیپربولیک: برای x ≠ 0 ،

$\coth x={\frac {\cosh x}{\sinh x}}={\frac {e^{x}+e^{-x}}{e^{x}-e^{- x}}}={\frac {e^{2x}+1}{e^{2x}-1}}.$
سکانس هیپربولیک:

$\operatorname {sech} x={\frac {1}{\cosh x}}={\frac {2}{e^{x}+e^{-x}}}={\frac {2e ^{x}}{e^{2x}+1}}.$
کسکانت هذلولی: برای x ≠ 0 ،

$\operatorname {csch} x={\frac {1}{\sinh x}}={\frac {2}{e^{x}-e^{-x}}}={\frac {2e ^{x}}{e^{2x}-1}}.$

تعاریف معادلات دیفرانسیل [ ویرایش ]

توابع هذلولی را می توان به عنوان جواب معادلات دیفرانسیل تعریف کرد : سینوس و کسینوس هذلولی حل ( s , c ) یک سیستم هستند.

${\begin{aligned}c'(x)&=s(x),\\s'(x)&=c(x),\\\end{aligned}}$ با شرایط اولیه $s(0)=0,c(0)=1,$ جلوگیری از هر جفت عملکرد{ $(ae^{x}+be^{-x},ae^{x}-be^{-x})$ راه حل باشد

sinh( x ) و cosh( x ) نیز راه‌حل منحصربه‌فرد معادله f ″( x ) = f ( x ) هستند، به طوری که f (0) = 1 ، f ′(0) = 0 برای کسینوس هذلولی، و f (0) = 0 ، f ′(0) = 1 برای سینوس هذلولی.

تعاریف مختلط توابع مثلثاتی [ ویرایش ]

توابع هذلولی نیز ممکن است از توابع مثلثاتی با متغیر های مختلط استنتاج شوند:

سینوس هیپربولیک: [1]

$\sinh x=-i\sin(ix).$
کسینوس هیپربولیک: [1]

$\cosh x=\cos(ix).$
تانژانت هیپربولیک:

$\tanh x=-i\tan(ix).$
کتانژانت هیپربولیک:

$\coth x=i\cot(ix).$
سکانس هیپربولیک:
$\operatorname {sech} x=\sec(ix).$
کسکانت هیپربولیک:
$\operatorname {csch} x=i\csc(ix).$

جایی که i واحد موهومی با i 2 = −1 است.

تعاریف فوق به تعاریف نمایی از طریق فرمول اویلر مرتبط هستند (به § توابع هیپربولیک برای اعداد مختلط زیر مراجعه کنید).

+ نوشته شده در شنبه سوم اردیبهشت ۱۴۰۱ ساعت 10:29 توسط علی رضا نقش نیلچی |

سری تیلور سینوس در کسینوس

+ نوشته شده در جمعه دوم اردیبهشت ۱۴۰۱ ساعت 0:52 توسط علی رضا نقش نیلچی |

سری تیلور

از آنجا که

انتگرال آن دارای نمایش سری قدرت است

بیایید حد نسبت های مطلق این سری را پیدا کنیم:

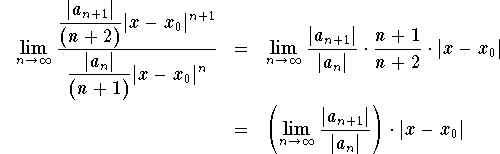
eqnarray14

اما توجه داشته باشید که این دقیقاً همان عبارتی است که هنگام محاسبه حد نسبتهای مطلق سری تیلور از f ( x ) به آن برخورد می کنیم. بنابراین هر دو سری شعاع همگرایی یکسانی دارند!

سری تیلور و چند جمله ای ها

سری تیلور چند جمله ای چیست؟

سری تیلور با مرکز یک چند جمله ای خود چند جمله ای است! (این را با چند جمله ای مورد علاقه خود بررسی کنید و از فرمول سری تیلور با مرکز استفاده کنید!)

اگر مرکز 0 نباشد چه؟ سپس شخص واقعاً چند جمله ای را بازنویسی می کند و به جای استفاده از آن به عنوان "بلوک های سازنده" آن استفاده می کند.

در اینجا یک مثال آورده شده است: سری تیلور را با مرکز چند جمله ای پیدا کنید. بیایید مشتقات آن را بگیریم و وصل کنیم :

بنابراین p (-1)=1+3+5=9.

p '( x )=2 x -3، بنابراین p '(-1)=-2-3=-5.

p ''( x )=2، بنابراین p ''(-1)=2.

تمام مشتقات بالاتر 0 هستند، بنابراین سری تیلور خاتمه می یابد!

با استفاده از فرمول ما به دست می آوریم:

از این رو، فهمیدن اینکه یک تابع دارای سری پایانی تیلور است، سخت نیست، اگر و فقط اگر تابع چند جمله ای باشد.

ضرب سری تیلور در چند جمله ای

بیایید سعی کنیم بسط سری تیلور با مرکز را پیدا کنیم .

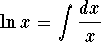برای پیدا کردن سری تیلور برای ، از آن استفاده کنید tex2html_wrap_inline177 . شما بسط را بدست می آورید:

displaymath165

همانطور که در مثال بالا می توانیم بازنویسی کنیم

سپس هر دو عبارت را ضرب می کنیم:

eqnarray60

بدون وارد شدن به جزئیات فنی: اگر اولین عبارت های این سری را بنویسید، می توانید قدرت های مربوط به ( x -1) را با هم ترکیب کنید تا شروع سری تیلور را برای f ( x ) بدست آورید:

خودت آن را امتحان کن!

تقریباً چندان پیچیده نیست: نمایش سری تیلور را با مرکز برای پیدا کنید.

منبع

http://www.sosmath.com/calculus/tayser/tayser05/tayser05.html

+ نوشته شده در پنجشنبه یکم اردیبهشت ۱۴۰۱ ساعت 23:35 توسط علی رضا نقش نیلچی |

مثال از تعیین بسط تیلور e^x cosx به روش ضرب سریها

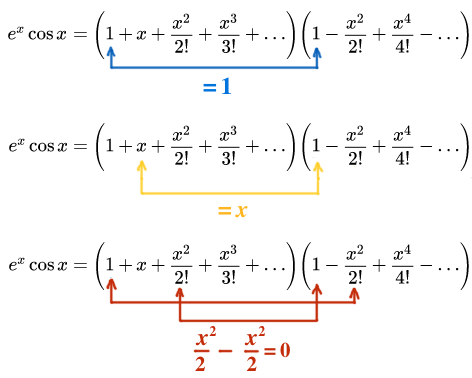
Taylor Series Manipulation | Brilliant Math & Science Wiki

+ نوشته شده در پنجشنبه یکم اردیبهشت ۱۴۰۱ ساعت 23:9 توسط علی رضا نقش نیلچی |

بسط تیلور sinx ,x=p/2

+ نوشته شده در پنجشنبه یکم اردیبهشت ۱۴۰۱ ساعت 18:28 توسط علی رضا نقش نیلچی |

بسط تیلور sinx ,x=p

+ نوشته شده در پنجشنبه یکم اردیبهشت ۱۴۰۱ ساعت 16:53 توسط علی رضا نقش نیلچی |

بسط تیلور e^3x در 5=x

+ نوشته شده در پنجشنبه یکم اردیبهشت ۱۴۰۱ ساعت 16:49 توسط علی رضا نقش نیلچی |

4-سری تیلور

محاسبه سری تیلور [ ویرایش ]

چندین روش برای محاسبه سری تیلور از تعداد زیادی توابع وجود دارد. می توان سعی کرد از تعریف سری تیلور استفاده کرد، اگرچه این اغلب مستلزم تعمیم شکل ضرایب بر اساس یک الگوی آشکار است. به‌علاوه، می‌توان از دستکاری‌هایی مانند جایگزینی، ضرب یا تقسیم، جمع یا تفریق سری‌های استاندارد تیلور برای ساخت سری تیلور یک تابع استفاده کرد، زیرا سری تیلور سری‌های توانی است. در برخی موارد، می توان سری تیلور را با اعمال مکرر ادغام توسط قطعات استخراج کرد. استفاده از سیستم های جبر رایانه ای برای محاسبه سری های تیلور بسیار راحت است .

مثال اول [ ویرایش ]

به منظور محاسبه چند جمله ای ماکلورین درجه 7 برای تابع

$f(x)=\ln(\cos x),\quad x\in \left(-{\frac {\pi }{2}},{\frac {\pi }{2}}\right )$ ،

می توان ابتدا تابع را به صورت بازنویسی کرد

$f(x)=\ln {\bigl (}1+(\cos x-1){\bigr )}\!$ .

سری تیلور برای لگاریتم طبیعی است (با استفاده از نماد O بزرگ )

$\ln(1+x)=x-{\frac {x^{2}}{2}}+{\frac {x^{3}}{3}}+{O}\left(x ^{4}\راست)\!$

و برای تابع کسینوس

$\cos x-1=-{\frac {x^{2}}{2}}+{\frac {x^{4}}{24}}-{\frac {x^{6}} {720}}+{O}\left(x^{8}\right)\!$ .

بسط سری دوم دارای یک جمله ثابت صفر است که ما را قادر می سازد سری دوم را با سری اول جایگزین کنیم و با استفاده از علامت O بزرگ به راحتی از عبارت های مرتبه بالاتر از درجه 7 حذف کنیم :

${\begin{aligned}f(x)&=\ln {\bigl (}1+(\cos x-1){\bigr )}\\&=(\cos x-1)-{\ tfrac {1}{2}}(\cos x-1)^{2}+{\tfrac {1}{3}}(\cos x-1)^{3}+{O}\left((\ cos x-1)^{4}\right)\\&=\left(-{\frac {x^{2}}{2}}+{\frac {x^{4}}{24}}- {\frac {x^{6}}{720}}+{O}\left(x^{8}\right)\right)-{\frac {1}{2}}\left(-{\frac {x^{2}}{2}}+{\frac {x^{4}}{24}}+{O}\left(x^{6}\right)\right)^{2}+{ \frac {1}{3}}\left(-{\frac {x^{2}}{2}}+O\left(x^{4}\right)\right)^{3}+{O }\left(x^{8}\right)\\&=-{\frac {x^{2}}{2}}+{\frac {x^{4}}{24}}-{\frac {x^{6}}{720}}-{\frac {x^{4}}{8}}+{\frac {x^{6}}{48}}-{\frac {x^{6 }}{24}}+O\left(x^{8}\right)\\&=-{\frac {x^{2}}{2}}-{\frac {x^{4}}{ 12}}-{\frac {x^{6}}{45}}+O\left(x^{8}\right).\end{تراز شده}}\!$

از آنجایی که کسینوس یک تابع زوج است، ضرایب برای تمام توان های فرد x , x 3 , x 5 , x 7 , ... باید صفر باشد.

مثال دوم [ ویرایش ]

فرض کنید می خواهیم سری تیلور در 0 تابع باشد

$g(x)={\frac {e^{x}}{\cos x}}.\!$

ما برای تابع نمایی داریم

$e^{x}=\sum _{n=0}^{\infty }{\frac {x^{n}}{n!}}=1+x+{\frac {x^{2} {2!}}+{\frac {x^{3}}{3!}}+{\frac {x^{4}}{4!}}+\cdots \!$

و مانند مثال اول،

$\cos x=1-{\frac {x^{2}}{2!}}+{\frac {x^{4}}{4!}}-\cdots \!$

فرض کنید سری قدرت است

${\frac {e^{x}}{\cos x}}=c_{0}+c_{1}x+c_{2}x^{2}+c_{3}x^{3} +\cdots \!$

سپس ضرب با مخرج و جایگزینی سری کسینوس حاصل می شود

${\begin{aligned}e^{x}&=\left(c_{0}+c_{1}x+c_{2}x^{2}+c_{3}x^{3}+ \cdots \right)\cos x\\&=\left(c_{0}+c_{1}x+c_{2}x^{2}+c_{3}x^{3}+c_{4} x^{4}+\cdots \right)\left(1-{\frac {x^{2}}{2!}}+{\frac {x^{4}}{4!}}-\cdots \right)\\&=c_{0}-{\frac {c_{0}}{2}}x^{2}+{\frac {c_{0}}{4!}}x^{4} +c_{1}x-{\frac {c_{1}}{2}}x^{3}+{\frac {c_{1}}{4!}}x^{5}+c_{2} x^{2}-{\frac {c_{2}}{2}}x^{4}+{\frac {c_{2}}{4!}}x^{6}+c_{3}x ^{3}-{\frac {c_{3}}{2}}x^{5}+{\frac {c_{3}}{4!}}x^{7}+c_{4}x^ {4}+\cdots \end{aligned}}\!$

جمع آوری شرایط تا مرتبه چهارم بازده

$e^{x}=c_{0}+c_{1}x+\left(c_{2}-{\frac {c_{0}}{2}}\right)x^{2}+\ چپ(c_{3}-{\frac {c_{1}}{2}}\right)x^{3}+\left(c_{4}-{\frac {c_{2}}{2}} +{\frac {c_{0}}{4!}}\right)x^{4}+\cdots \!$

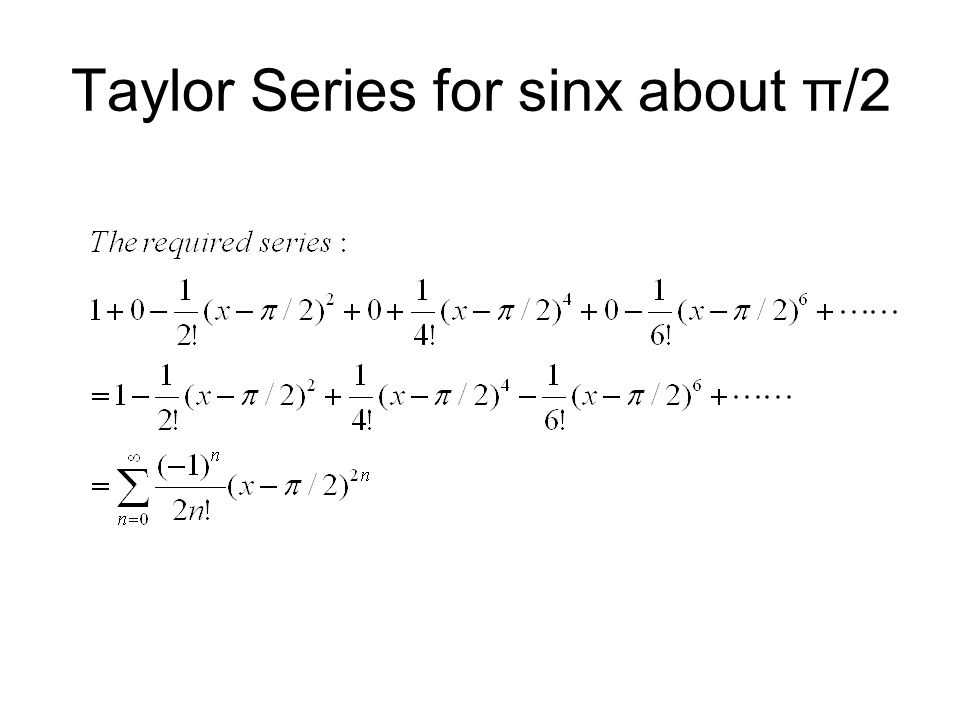
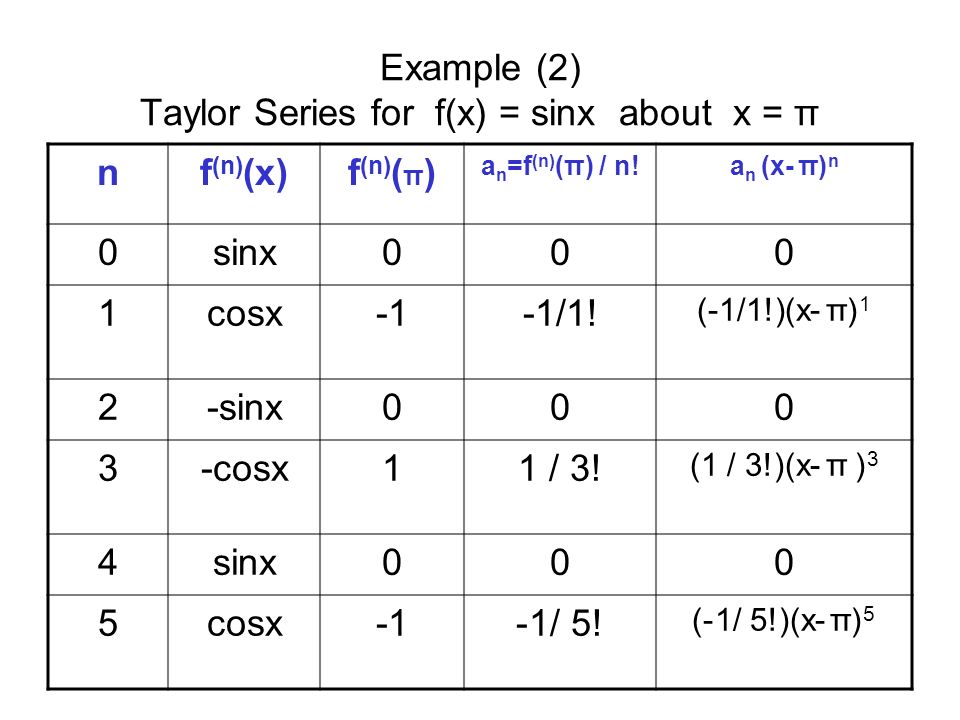
ارزش های $ج_{i}$ می توان با مقایسه ضرایب با عبارت بالا برای یافت $e^{x}$ ، بازده:

${\frac {e^{x}}{\cos x}}=1+x+x^{2}+{\frac {2x^{3}}{3}}+{\frac {x ^{4}}{2}}+\cdots .\!$

مثال سوم [ ویرایش ]

در اینجا ما از روشی به نام "گسترش غیر مستقیم" برای گسترش تابع داده شده استفاده می کنیم. این روش از بسط تیلور شناخته شده تابع نمایی استفاده می کند. برای بسط (1 + x ) e x به عنوان یک سری تیلور در x ، از سری شناخته شده تیلور تابع e x استفاده می کنیم :

$e^{x}=\sum _{n=0}^{\infty }{\frac {x^{n}}{n!}}=1+x+{\frac {x^{2} }{2!}}+{\frac {x^{3}}{3!}}+{\frac {x^{4}}{4!}}+\cdots .$

بدین ترتیب،

${\begin{aligned}(1+x)e^{x}&=e^{x}+xe^{x}=\sum _{n=0}^{\infty }{\frac { x^{n}}{n!}}+\sum _{n=0}^{\infty }{\frac {x^{n+1}}{n!}}=1+\sum _{n =1}^{\infty }{\frac {x^{n}}{n!}}+\sum _{n=0}^{\infty }{\frac {x^{n+1}}{ n!}}\\&=1+\sum _{n=1}^{\infty }{\frac {x^{n}}{n!}}+\sum _{n=1}^{\ infty }{\frac {x^{n}}{(n-1)!}}=1+\sum _{n=1}^{\infty }\left({\frac {1}{n!} }+{\frac {1}{(n-1)!}}\right)x^{n}\\&=1+\sum _{n=1}^{\infty }{\frac {n+ 1}{n!}}x^{n}\\&=\sum _{n=0}^{\infty }{\frac {n+1}{n!}}x^{n}.\end {هم راستا}}$

مجموعه تیلور به عنوان تعاریف [ ویرایش ]

به طور کلاسیک، توابع جبری با یک معادله جبری تعریف می شوند، و توابع ماورایی (از جمله آنهایی که در بالا مورد بحث قرار گرفت) با ویژگی هایی مانند یک معادله دیفرانسیل تعریف می شوند. به عنوان مثال، تابع نمایی تابعی است که در همه جا با مشتق خود برابر است و در مبدا مقدار 1 را در نظر می گیرد. با این حال، می توان به همان اندازه یک تابع تحلیلی را با سری تیلور آن تعریف کرد.

سری تیلور برای تعریف توابع و " عملگرها " در حوزه های مختلف ریاضیات استفاده می شود. به ویژه، این امر در مناطقی که تعاریف کلاسیک توابع شکسته می شوند صادق است. به عنوان مثال، با استفاده از سری تیلور، می‌توان توابع تحلیلی را به مجموعه‌ای از ماتریس‌ها و عملگرها، مانند لگاریتم ماتریس نمایی یا ماتریس تعمیم داد .

در زمینه های دیگر، مانند تجزیه و تحلیل رسمی، راحت تر است که به طور مستقیم با خود سری های قدرت کار کنید. بنابراین می توان راه حل یک معادله دیفرانسیل را به عنوان یک سری توانی تعریف کرد که امیدواریم ثابت شود سری تیلور راه حل مورد نظر است.

سری تیلور در چندین متغیر [ ویرایش ]

سری تیلور همچنین ممکن است به توابع بیش از یک متغیر با [13] [14] تعمیم داده شود.

${\begin{aligned}T(x_{1},\ldots,x_{d})&=\sum _{n_{1}=0}^{\infty }\cdots \sum _{n_{ d}=0}^{\infty }{\frac {(x_{1}-a_{1})^{n_{1}}\cdots (x_{d}-a_{d})^{n_{d }}}{n_{1}!\cdots n_{d}!}}\,\left({\frac {\partial ^{n_{1}+\cdots +n_{d}}f}{\partial x_ {1}^{n_{1}}\cdots \partial x_{d}^{n_{d}}}}\right)(a_{1},\ldots ,a_{d})\\&=f( a_{1},\ldots ,a_{d})+\sum _{j=1}^{d}{\frac {\partial f(a_{1},\ldots ,a_{d})}{\ x_{j}}}(x_{j}-a_{j})+{\frac {1}{2!}}\sum _{j=1}^{d}\sum _{k=1} ^{d}{\frac {\partial ^{2}f(a_{1},\ldots ,a_{d})}{\partial x_{j}\partial x_{k}}}(x_{j} -a_{j})(x_{k}-a_{k})\\&\qquad \qquad +{\frac {1}{3!}}\sum _{j=1}^{d}\sum _{k=1}^{d}\sum _{l=1}^{d}{\frac {\partial ^{3}f(a_{1},\ldots ,a_{d})}{\ x_{j}\جزئی x_{k}\جزئی x_{l}}}(x_{j}-a_{j})(x_{k}-a_{k})(x_{l}-a_{l })+\cdots \end{تراز شده}}$

به عنوان مثال، برای یک تابع $f(x,y)$ که به دو متغیر x و y بستگی دارد ، سری تیلور به مرتبه دوم در مورد نقطه ( a , b ) است.

$f(a,b)+(xa)f_{x}(a,b)+(yb)f_{y}(a,b)+{\frac {1}{2!}}{\Big (}(xa)^{2}f_{xx}(a,b)+2(xa)(yb)f_{xy}(a,b)+(yb)^{2}f_{yy}(a, ب){\بزرگ)}$

که در آن زیرنویس ها مشتقات جزئی مربوطه را نشان می دهند .

یک بسط مرتبه دوم سری تیلور از یک تابع با مقدار اسکالر بیش از یک متغیر را می توان به صورت فشرده نوشت:

$T(\mathbf {x})=f(\mathbf {a})+(\mathbf {x} -\mathbf {a})^{\mathsf {T}}Df(\mathbf {a}) +{\frac {1}{2!}}(\mathbf {x} -\mathbf {a} )^{\mathsf {T}}\left\{D^{2}f(\mathbf {a}) \right\}(\mathbf {x} -\mathbf {a} )+\cdots ,$

که در آن D f ( a ) گرادیان f است که با x = a ارزیابی می شود و D 2 f ( a ) ماتریس هسین است . با اعمال نماد چند شاخص ، سری تیلور برای چندین متغیر تبدیل می شود

${\displaystyle T(\mathbf {x} )=\sum _{|\alpha |\geq 0}{\frac {(\mathbf {x} -\mathbf {a})^{\alpha }}{\alpha !}}\left({\mathrm {\partial } ^{\alpha }}f\right)(\mathbf {a})$

که باید به عنوان یک نسخه اختصاری چند شاخصه از معادله اول این پاراگراف، با تشبیه کامل به حالت تک متغیر درک شود.

مثال [ ویرایش ]

تقریب مرتبه دوم سری تیلور (به رنگ نارنجی) تابع f ( x , y ) = e x ln(1 + y ) در اطراف مبدا.

به منظور محاسبه بسط سری تیلور مرتبه دوم حول نقطه ( a , b ) = (0, 0) تابع

$f(x,y)=e^{x}\ln(1+y),$

ابتدا تمام مشتقات جزئی لازم را محاسبه می کند:

${\begin{aligned}f_{x}&=e^{x}\ln(1+y)\\[6pt]f_{y}&={\frac {e^{x}}{1 +y}}\\[6pt]f_{xx}&=e^{x}\ln(1+y)\\[6pt]f_{yy}&=-{\frac {e^{x}}{ (1+y)^{2}}}\\[6pt]f_{xy}&=f_{yx}={\frac {e^{x}}{1+y}}.\end{تراز شده}}$

ارزیابی این مشتقات در مبدا، ضرایب تیلور را به دست می دهد

${\begin{aligned}f_{x}(0,0)&=0\\f_{y}(0,0)&=1\\f_{xx}(0,0)&=0\ \f_{yy}(0,0)&=-1\\f_{xy}(0,0)&=f_{yx}(0,0)=1.\end{تراز شده}}$

جایگزینی این مقادیر به فرمول کلی

${\begin{aligned}T(x,y)=&f(a,b)+(xa)f_{x}(a,b)+(yb)f_{y}(a,b)\\ &{}+{\frac {1}{2!}}\left((xa)^{2}f_{xx}(a,b)+2(xa)(yb)f_{xy}(a,b )+(yb)^{2}f_{yy}(a,b)\right)+\cdots \end{تراز شده}}$

تولید می کند

${\begin{aligned}T(x,y)&=0+0(x-0)+1(y-0)+{\frac {1}{2}}{\Big (}0( x-0)^{2}+2(x-0)(y-0)+(-1)(y-0)^{2}{\Big )}+\cdots \\&=y+xy- {\frac {y^{2}}{2}}+\cdots \end{aligned}}$

از آنجایی که ln(1 + y ) در | y | < 1 ، ما داریم

$e^{x}\ln(1+y)=y+xy-{\frac {y^{2}}{2}}+\cdots ,\qquad |y|<1.$

مقایسه با سری فوریه [ ویرایش ]

نوشتار اصلی: سری فوریه

سری فوریه مثلثاتی فرد را قادر می سازد تا یک تابع تناوبی (یا تابعی که در بازه بسته [ a , b ] تعریف شده است ) را به عنوان مجموع نامتناهی از توابع مثلثاتی ( سینوس ها و کسینوس ها ) بیان کند. از این نظر، سری فوریه مشابه سری تیلور است، زیرا دومی به فرد اجازه می دهد تا یک تابع را به عنوان مجموع بی نهایت توان بیان کند . با این وجود، این دو سریال در چندین موضوع مرتبط با یکدیگر تفاوت دارند:

برش های محدود سری تیلور از f ( x ) در مورد نقطه x = a همگی دقیقاً برابر با f در a هستند. در مقابل، سری فوریه با ادغام در یک بازه کامل محاسبه می‌شود، بنابراین به طور کلی چنین نقطه‌ای وجود ندارد که تمام برش‌های محدود سری دقیق باشند.
محاسبه سری تیلور به دانش تابع در یک همسایگی کوچک دلخواه یک نقطه نیاز دارد، در حالی که محاسبه سری فوریه مستلزم دانستن تابع در کل بازه دامنه آن است . به تعبیری می توان گفت که سریال تیلور «محلی» و سری فوریه «جهانی» است.
سری تیلور برای تابعی تعریف می شود که مشتقات بی نهایت زیادی در یک نقطه دارد، در حالی که سری فوریه برای هر تابع انتگرال پذیر تعریف می شود . به طور خاص، این تابع هیچ جا قابل تمایز نیست. (به عنوان مثال، f ( x ) می تواند یک تابع وایرشتراس باشد .)
همگرایی هر دو سری خواص بسیار متفاوتی دارد. حتی اگر سری تیلور دارای شعاع همگرایی مثبت باشد، ممکن است سری حاصل با تابع منطبق نباشد. اما اگر تابع تحلیلی باشد، سری به صورت نقطه ای به تابع همگرا می شود، و به طور یکنواخت در هر زیر مجموعه فشرده بازه همگرایی . در مورد سری فوریه، اگر تابع مربع انتگرال پذیر باشد، سری در میانگین درجه دوم همگرا می شود ، اما الزامات اضافی برای اطمینان از همگرایی نقطه ای یا یکنواخت مورد نیاز است (به عنوان مثال، اگر تابع تناوبی و از کلاس C 1 باشد، پس همگرایی لباس فرم).
در نهایت، در عمل می‌خواهیم تابع را با تعداد محدودی از جمله‌ها، مثلاً با چند جمله‌ای تیلور یا مجموع جزئی سری مثلثاتی، تقریب بزنیم. در مورد سری تیلور، خطا در همسایگی نقطه ای که محاسبه می شود بسیار کوچک است، در حالی که ممکن است در یک نقطه دور بسیار بزرگ باشد. در مورد سری فوریه، خطا در امتداد دامنه تابع توزیع می شود.

همچنین مشاهده کنید [ ویرایش ]

منبع

https://en.wikipedia.org/wiki/Taylor_series

+ نوشته شده در پنجشنبه یکم اردیبهشت ۱۴۰۱ ساعت 13:13 توسط علی رضا نقش نیلچی |

3-سری تیلور

خطای تقریب و همگرایی [ ویرایش ]

مقاله اصلی: قضیه تیلور

تابع سینوس (آبی) با چند جمله ای تیلور درجه 7 (صورتی) برای یک دوره کامل در مرکز مبدأ تقریباً تقریب دارد.

چند جمله ای های تیلور برای ln(1 + x ) فقط تقریب های دقیقی را در محدوده -1 < x≤ 1 ارائه می دهند. برای x > 1 ، چند جمله ای های تیلور با درجه بالاتر تقریب بدتری ارائه می دهند.

تقریب های تیلور برای ln(1 + x ) (سیاه). برای x > 1 ، تقریب ها واگرا می شوند.

تصویر سمت راست تقریب دقیق sin x در اطراف نقطه x = 0 است. منحنی صورتی یک چند جمله ای درجه هفت است:

$\sin \left(x\right)\approx x-{\frac {x^{3}}{3!}}+{\frac {x^{5}}{5!}}-{\frac {x ^{7}}{7!}}.\!$

خطا در این تقریب بیشتر از | نیست x | 9/9 ! . برای یک چرخه کامل در مرکز مبدا ( -π < x < π ) خطا کمتر از 0.08215 است. به طور خاص، برای -1 < x < 1 ، خطا کمتر از 0.000003 است.

در مقابل، همچنین تصویری از تابع لگاریتم طبیعی ln(1 + x ) و برخی از چندجمله ای های تیلور آن در اطراف a = 0 نشان داده شده است. این تقریب ها فقط در ناحیه -1 < x ≤ 1 به تابع همگرا می شوند . در خارج از این منطقه، چند جمله ای های درجه بالاتر تیلور، تقریب بدتری برای تابع هستند.

خطایی که در تقریب یک تابع با چند جمله ای تیلور درجه n آن رخ می دهد باقیمانده یا باقیمانده نامیده می شود و با تابع Rn ( x ) نشان داده می شود . از قضیه تیلور می توان برای به دست آوردن حدی در اندازه باقیمانده استفاده کرد.

به طور کلی، سری های تیلور به هیچ وجه نیازی به همگرایی ندارند. و در واقع مجموعه توابع با سری تیلور همگرا مجموعه ای ناچیز در فضای فریشه از توابع صاف است . و حتی اگر سری تیلور یک تابع f همگرا شود، نیازی نیست حد آن به طور کلی برابر با مقدار تابع f ( x ) باشد. به عنوان مثال، تابع

$f(x)={\begin{cases}e^{-1/x^{2}}&{\text{if }}x\neq 0\\[3mu]0&{\text{if } }x=0\end{موارد}}$

بی نهایت در x = 0 قابل تمایز است و تمام مشتقات آن صفر است. در نتیجه، سری تیلور از f ( x ) حدود x = 0 به طور یکسان صفر است. با این حال، f ( x ) تابع صفر نیست، بنابراین با سری تیلور آن در اطراف مبدا برابر نیست. بنابراین، f ( x ) مثالی از یک تابع صاف غیر تحلیلی است .

در تجزیه و تحلیل واقعی ، این مثال نشان می دهد که توابع بی نهایت قابل تمایز f ( x ) وجود دارد که سری تیلور آنها با f ( x ) برابر نیستند ، حتی اگر همگرا شوند. در مقابل، توابع هولومورف مورد مطالعه در تحلیل پیچیده همیشه دارای یک سری تیلور همگرا هستند، و حتی سری تیلور از توابع مرومورفیک ، که ممکن است دارای تکینگی باشند، هرگز به مقداری متفاوت از خود تابع همگرا نمی شوند. با این حال، تابع مختلط e −1/ z 2 به 0 نزدیک نمی‌شوددر امتداد محور فرضی به 0 نزدیک می شود، بنابراین در صفحه مختلط پیوسته نیست و سری تیلور آن در 0 تعریف نشده است.

به طور کلی‌تر، هر دنباله‌ای از اعداد حقیقی یا مختلط می‌تواند به‌عنوان ضرایبی در سری تیلور از یک تابع بی‌نهایت متمایز تعریف‌شده بر روی خط واقعی ظاهر شود که نتیجه لم بورل است . در نتیجه، شعاع همگرایی یک سری تیلور می تواند صفر باشد. حتی توابع بی نهایت قابل تمایز نیز بر روی خط واقعی تعریف شده اند که سری های تیلور در همه جا شعاع همگرایی 0 دارند. [8]

یک تابع را نمی توان به عنوان یک سری تیلور با محوریت تکینگی نوشت . در این موارد، اگر قدرت های منفی متغیر x را نیز مجاز بدانیم، اغلب می توان به یک بسط سری دست یافت . سری Laurent را ببینید . برای مثال، f ( x ) = e −1/ x 2 را می توان به صورت سری Laurent نوشت.

تعمیم [ ویرایش ]

با این حال، یک تعمیم [9] [10] از سری تیلور وجود دارد که با استفاده از حساب تفاوت‌های محدود ، به مقدار خود تابع برای هر تابع پیوسته محدود در (0,∞) همگرا می‌شود . به طور خاص، با توجه به Einar Hille ، یک قضیه زیر را دارد که برای هر t > 0 ،

$\lim _{h\to 0^{+}}\sum _{n=0}^{\infty }{\frac {t^{n}}{n!}}{\frac {\Delta _{h }^{n}f(a)}{h^{n}}}=f(a+t).$

اینجا Δn
ساعتn امین عملگر تفاضل محدود با اندازه گام h است. این سری دقیقاً سری تیلور است، با این تفاوت که به جای تمایز، تفاوت‌های تقسیم شده ظاهر می‌شود: این سری از نظر رسمی شبیه به سری‌های نیوتن است . وقتی تابع f در a تحلیلی است ، عبارت‌های سری با عبارت‌های سری تیلور همگرا می‌شوند و از این نظر سری معمول تیلور را تعمیم می‌دهند.

به طور کلی، برای هر دنباله نامتناهی a i ، هویت سری توانی زیر برقرار است:

$\sum _{n=0}^{\infty }{\frac {u^{n}}{n!}}\Delta ^{n}a_{i}=e^{-u}\sum _{j =0}^{\infty }{\frac {u^{j}}{j!}}a_{i+j}.$

بنابراین به طور خاص،

$f(a+t)=\lim _{h\to 0^{+}}e^{-t/h}\sum _{j=0}^{\infty }f(a+jh){\frac {(t/h)^{j}}{j!}}.$

سری سمت راست مقدار انتظاری f ( a + X ) است، که در آن X یک متغیر تصادفی توزیع شده توسط پواسون است که مقدار jh را با احتمال e - t / h می گیرد .( t / h ) j/ج !. از این رو،

$f(a+t)=\lim _{h\to 0^{+}}\int _{-\infty }^{\infty }f(a+x)dP_{t/h,h} (ایکس).$

قانون اعداد بزرگ نشان می دهد که هویت وجود دارد. [11]

فهرستی از سری مکلورن از برخی توابع رایج [ ویرایش ]

همچنین ببینید: لیست سری های ریاضی

چندین بسط مهم سری مکلورن دنبال می شود. [12] همه این بسط ها برای آرگومان های پیچیده x معتبر هستند .

تابع نمایی [ ویرایش ]

تابع نمایی e x (به رنگ آبی)، و مجموع اولین جمله های n + 1 سری تیلور آن در 0 (به رنگ قرمز).

تابع نمایی $e^{x}$ (با پایه e ) دارای سری مکلورن است

$e^{x}=\sum _{n=0}^{\infty }{\frac {x^{n}}{n!}}=1+x+{\frac {x^{2} }{2!}}+{\frac {x^{3}}{3!}}+\cdots$ .

برای همه x همگرا می شود .

لگاریتم طبیعی [ ویرایش ]

نوشتار اصلی: سری مرکاتور

لگاریتم طبیعی (با پایه e ) دارای سری مکلورن است

${\begin{aligned}\ln(1-x)&=-\sum _{n=1}^{\infty }{\frac {x^{n}}{n}}=-x- {\frac {x^{2}}{2}}-{\frac {x^{3}}{3}}-\cdots ,\\\ln(1+x)&=\sum _{n= 1}^{\infty }(-1)^{n+1}{\frac {x^{n}}{n}}=x-{\frac {x^{2}}{2}}+{ \frac {x^{3}}{3}}-\cdots .\end{تراز شده}}$

آنها برای همگرا می شوند $|x|<1$ . (علاوه بر این، سری برای ln(1 - x ) برای x = -1 همگرا می شود ، و سری برای ln(1 + x ) برای x = 1 همگرا می شود .)

سری هندسی [ ویرایش ]

سری هندسی و مشتقات آن دارای سری مکلورن هستند

${\begin{aligned}{\frac {1}{1-x}}&=\sum _{n=0}^{\infty }x^{n}\\{\frac {1}{ (1-x)^{2}}}&=\sum _{n=1}^{\infty }nx^{n-1}\\{\frac {1}{(1-x)^{3 }}}&=\sum _{n=2}^{\infty }{\frac {(n-1)n}{2}}x^{n-2}.\end{تراز شده}}$

همه همگرا هستند برای $|x|<1$ . اینها موارد خاصی از سری دوجمله ای هستند که در بخش بعدی آورده شده است.

سری دو جمله ای [ ویرایش ]

سری دوجمله ای سری توان است

$(1+x)^{\alpha }=\sum _{n=0}^{\infty }{\binom {\alpha }{n}}x^{n}$

که ضرایب آن ضرایب دوجمله ای تعمیم یافته است

${\binom {\alpha }{n}}=\prod _{k=1}^{n}{\frac {\alpha -k+1}{k}}={\frac {\alpha ( \alpha -1)\cdots (\alpha -n+1)}{n!}}.$

(اگر n = 0 باشد، این حاصلضرب یک محصول خالی است و مقدار 1 دارد.) برای همگرا می شود $|x|<1$ برای هر عدد واقعی یا مختلط α .

وقتی α = -1 ، این اساساً سری هندسی نامتناهی است که در بخش قبل ذکر شد. موارد خاص α =1/2و α = -1/2تابع جذر و معکوس آن را بدهید :

${\begin{aligned}(1+x)^{\frac {1}{2}}&=1+{\tfrac {1}{2}}x-{\tfrac {1}{8} }x^{2}+{\tfrac {1}{16}}x^{3}-{\tfrac {5}{128}}x^{4}+{\tfrac {7}{256}}x ^{5}-\cdots &&=\sum _{n=0}^{\infty }{\frac {(-1)^{n-1}(2n)!}{4^{n}(n! )^{2}(2n-1)}}x^{n}،\\(1+x)^{-{\frac {1}{2}}}&=1-{\tfrac {1}{ 2}}x+{\tfrac {3}{8}}x^{2}-{\tfrac {5}{16}}x^{3}+{\tfrac {35}{128}}x^{4 }-{\tfrac {63}{256}}x^{5}+\cdots &&=\sum _{n=0}^{\infty }{\frac {(-1)^{n}(2n) !}{4^{n}(n!)^{2}}}x^{n}.\end{تراز شده}}$

هنگامی که فقط عبارت خطی حفظ می شود، این به تقریب دو جمله ای ساده می شود .

توابع مثلثاتی [ ویرایش ]

توابع مثلثاتی معمول و معکوس آنها دارای سری مکلورن زیر هستند:

${\begin{aligned}\sin x&=\sum _{n=0}^{\infty }{\frac {(-1)^{n}}{(2n+1)!}}x^ {2n+1}&&=x-{\frac {x^{3}}{3!}}+{\frac {x^{5}}{5!}}-\cdots &&{\text{برای همه }}x\\[6pt]\cos x&=\sum _{n=0}^{\infty }{\frac {(-1)^{n}}{(2n)!}}x^{2n} &&=1-{\frac {x^{2}}{2!}}+{\frac {x^{4}}{4!}}-\cdots &&{\text{برای همه }}x\\ [6pt]\tan x&=\sum _{n=1}^{\infty }{\frac {B_{2n}(-4)^{n}\left(1-4^{n}\right)} {(2n)!}}x^{2n-1}&&=x+{\frac {x^{3}}{3}}+{\frac {2x^{5}}{15}}+\cdots && {\text{for }}|x|<{\frac {\pi }{2}}\\[6pt]\sec x&=\sum _{n=0}^{\infty }{\frac {(- 1)^{n}E_{2n}}{(2n)!}}x^{2n}&&=1+{\frac {x^{2}}{2}}+{\frac {5x^{4 }}{24}}+\cdots &&{\text{for }}|x|<{\frac {\pi }{2}}\\[6pt]\arcsin x&=\sum _{n=0}^ {\infty }{\frac {(2n)!}{4^{n}(n!)^{2}(2n+1)}}x^{2n+1}&&=x+{\frac {x^{3}}{6}}+{\frac {3x^{5}}{40}}+\cdots &&{\text{برای }}|x|\leq 1\\ [6pt]\arccos x&={\frac {\pi }{2}}-\arcsin x\\&={\frac {\pi }{2}}-\sum _{n=0}^{\infty }{\frac {(2n)!}{4^{n}(n!)^{2}(2n+1)}}x^{2n+1}&&={\frac {\pi }{2} }-x-{\frac {x^{3}}{6}}-{\frac {3x^{5}}{40}}-\cdots &&{\text{برای }}|x|\leq 1 \\[6pt]\arctan x&=\sum _{n=0}^{\infty }{\frac {(-1)^{n}}{2n+1}}x^{2n+1}&&= x-{\frac {x^{3}}{3}}+{\frac {x^{5}}{5}}-\cdots &&{\text{for }}|x|\leq 1,\ x\neq \pm i\end{تراز شده}}}=\sum _{n=0}^{\infty }{\frac {(-1)^{n}}{2n+1}}x^{2n+1}&&=x-{\frac {x^ {3}}{3}}+{\frac {x^{5}}{5}}-\cdots &&{\text{for }}|x|\leq 1,\ x\neq \pm i\end {هم راستا}}}=\sum _{n=0}^{\infty }{\frac {(-1)^{n}}{2n+1}}x^{2n+1}&&=x-{\frac {x^ {3}}{3}}+{\frac {x^{5}}{5}}-\cdots &&{\text{for }}|x|\leq 1,\ x\neq \pm i\end {هم راستا}}$

همه زوایا بر حسب رادیان بیان می شوند . اعداد B k که در بسط های tan x ظاهر می شوند اعداد برنولی هستند . E k در بسط sec x اعداد اویلر هستند .

توابع هذلولی [ ویرایش ]

توابع هذلولی دارای سری مکلورن هستند که نزدیک به سری برای توابع مثلثاتی مربوطه هستند:

${\begin{aligned}\sinh x&=\sum _{n=0}^{\infty }{\frac {x^{2n+1}}{(2n+1)!}}&&=x+ {\frac {x^{3}}{3!}}+{\frac {x^{5}}{5!}}+\cdots &&{\text{برای همه }}x\\[6pt]\ cosh x&=\sum _{n=0}^{\infty }{\frac {x^{2n}}{(2n)!}}&&=1+{\frac {x^{2}}{2! }}+{\frac {x^{4}}{4!}}+\cdots &&{\text{برای همه }}x\\[6pt]\tanh x&=\sum _{n=1}^{ \infty }{\frac {B_{2n}4^{n}\left(4^{n}-1\right)}{(2n)!}}x^{2n-1}&&=x-{\ frac {x^{3}}{3}}+{\frac {2x^{5}}{15}}-{\frac {17x^{7}}{315}}+\cdots &&{\text{ برای }}|x|<{\frac {\pi }{2}}\\[6pt]\operatorname {arsinh} x&=\sum _{n=0}^{\infty }{\frac {(-1) )^{n}(2n)!}{4^{n}(n!)^{2}(2n+1)}}x^{2n+1}&&=x-{\frac {x^{3 }}{6}}+{\frac {3x^{5}}{40}}-\cdots &&{\text{for }}|x|\leq 1\\[6pt]\operatorname {artanh} x&= \sum _{n=0}^{\infty }{\frac {x^{2n+1}}{2n+1}}&&=x+{\frac {x^{3}}{3}}+{\frac {x^{5}}{5}}+\cdots &&{\text{برای }}|x|\leq 1,\ x\neq \pm 1\end{تراز شده}}$

اعداد B k که در سری برای tanh x ظاهر می شوند اعداد برنولی هستند .

+ نوشته شده در پنجشنبه یکم اردیبهشت ۱۴۰۱ ساعت 13:9 توسط علی رضا نقش نیلچی |

1-سری تیلور

سری تیلور

از ویکیپدیا، دانشنامه آزاد

اپراتور شیفت

با افزایش درجه چند جمله ای تیلور، به تابع صحیح نزدیک می شود. این تصویر sin x و تقریب های تیلور آن را با چند جمله ای های درجه 1 ، 3 ، 5 ، 7 ، 9 ، 11 و 13 در x = 0 نشان می دهد.

بخشی از مجموعه مقالات در مورد

حساب دیفرانسیل و انتگرال

نشان دادن

دیفرانسیل

نشان دادن

انتگرال

پنهان شدن

سلسله

تست های همگرایی
هندسی ( حساب هندسی ) هارمونیک متناوب قدرت دو جمله ای تیلور
حد جمع (آزمون ترم) نسبت ریشه انتگرال مقایسه مستقیم مقایسه محدود سری متناوب تراکم کوشی دیریکله هابیل

نشان دادن

بردار

نشان دادن

چند متغیره

نشان دادن

تخصصی

نشان دادن

متفرقه

در ریاضیات ، سری تیلور یک تابع ، مجموع نامتناهی از عبارت‌هایی است که برحسب مشتقات تابع در یک نقطه بیان می‌شوند. برای اکثر توابع رایج، تابع و مجموع سری تیلور آن در نزدیکی این نقطه برابر است. سری های تیلور به نام بروک تیلور نامگذاری شده اند که آنها را در سال 1715 معرفی کرد. اگر 0 نقطه ای باشد که مشتقات در نظر گرفته می شوند، سری های تیلور به نام کالین مکلارین که از این مورد خاص از سری تیلور استفاده گسترده ای کرده است ، سری مکلارین نیز نامیده می شود. در اواسط 1700.

مجموع جزئی که توسط اولین جمله های n + 1 یک سری تیلور تشکیل می شود، چند جمله ای درجه n است که n امین چند جمله ای تیلور تابع نامیده می شود. چند جمله ای های تیلور تقریبی از یک تابع هستند که با افزایش n به طور کلی بهتر می شوند . قضیه تیلور برآوردهای کمی را در مورد خطای ایجاد شده با استفاده از چنین تقریبی ارائه می دهد. اگر سری تیلور یک تابع همگرا باشد ، مجموع آن حد دنباله نامتناهی است .از چند جمله ای های تیلور یک تابع ممکن است با مجموع سری تیلور خود متفاوت باشد، حتی اگر سری تیلور آن همگرا باشد. یک تابع در نقطه x تحلیلی است اگر برابر مجموع سری تیلور آن در یک بازه باز (یا دیسک باز در صفحه مختلط ) حاوی x باشد. این بدان معناست که تابع در هر نقطه از بازه (یا دیسک) تحلیلی است.

فهرست

تعریف [ ویرایش ]

سری تیلور یک تابع واقعی یا با مقادیر مختلط f ( x ) که در یک عدد واقعی یا مختلط a بی نهایت قابل تفکیک است سری توانی است .

$f(a)+{\frac {f'(a)}{1!}}(xa)+{\frac {f''(a)}{2!}}(xa)^{2} +{\frac {f'''(a)}{3!}}(xa)^{3}+\cdots ,$

کجا n ! فاکتوریل n را نشان می دهد . در نماد سیگما فشرده تر ، این می تواند به صورت نوشته شود

$\sum _{n=0}^{\infty }{\frac {f^{(n)}(a)}{n!}}(xa)^{n}،$

که در آن f ( n ) ( a ) نشان دهنده n امین مشتق f ارزیابی شده در نقطه a است. (مشتق مرتبه صفر f خود f و ( x - a ) 0 و 0! هر دو به 1 تعریف می شوند . )

زمانی که a = 0 باشد، سری نیز سری مکلارین نامیده می شود . [1]

+ نوشته شده در پنجشنبه یکم اردیبهشت ۱۴۰۱ ساعت 12:56 توسط علی رضا نقش نیلچی |

1-بسط مکلورن

cochranmath / Taylor Series - manipulation to form new series from known series

+ نوشته شده در چهارشنبه هجدهم اسفند ۱۴۰۰ ساعت 10:4 توسط علی رضا نقش نیلچی |

2-بسط مکلورن

Solved Use known power series (from table below... | Chegg.com

+ نوشته شده در چهارشنبه هجدهم اسفند ۱۴۰۰ ساعت 10:4 توسط علی رضا نقش نیلچی |

گرادیان و دیورژانس و کرل و لاپلاسین در مختصات کروی

${\begin{aligned}\nabla f={}&{\partial f \over \partial r}{\hat {\mathbf {r} }}+{1 \over r}{\partial f \over \partial \theta }{\hat {\boldsymbol {\theta }}}+{1 \over r\sin \theta }{\partial f \over \partial \varphi }{\hat {\boldsymbol {\varphi }}},\\[8pt]\nabla \cdot \mathbf {A} ={}&{\frac {1}{r^{2}}}{\partial \over \partial r}\left(r^{2}A_{r}\right)+{\frac {1}{r\sin \theta }}{\partial \over \partial \theta }\left(\sin \theta A_{\theta }\right)+{\frac {1}{r\sin \theta }}{\partial A_{\varphi } \over \partial \varphi },\\[8pt]\nabla \times \mathbf {A} ={}&{\frac {1}{r\sin \theta }}\left({\partial \over \partial \theta }\left(A_{\varphi }\sin \theta \right)-{\partial A_{\theta } \over \partial \varphi }\right){\hat {\mathbf {r} }}\\[8pt]&{}+{\frac {1}{r}}\left({1 \over \sin \theta }{\partial A_{r} \over \partial \varphi }-{\partial \over \partial r}\left(rA_{\varphi }\right)\right){\hat {\boldsymbol {\theta }}}\\[8pt]&{}+{\frac {1}{r}}\left({\partial \over \partial r}\left(rA_{\theta }\right)-{\partial A_{r} \over \partial \theta }\right){\hat {\boldsymbol {\varphi }}},\\[8pt]\nabla ^{2}f={}&{1 \over r^{2}}{\partial \over \partial r}\left(r^{2}{\partial f \over \partial r}\right)+{1 \over r^{2}\sin \theta }{\partial \over \partial \theta }\left(\sin \theta {\partial f \over \partial \theta }\right)+{1 \over r^{2}\sin ^{2}\theta }{\partial ^{2}f \over \partial \varphi ^{2}}\\[8pt]={}&\left({\frac {\partial ^{2}}{\partial r^{2}}}+{\frac {2}{r}}{\frac {\partial }{\partial r}}\right)f+{1 \over r^{2}\sin \theta }{\partial \over \partial \theta }\left(\sin \theta {\frac {\partial }{\partial \theta }}\right)f+{\frac {1}{r^{2}\sin ^{2}\theta }}{\frac {\partial ^{2}}{\partial \varphi ^{2}}}f~.\end{aligned}}$

+ نوشته شده در پنجشنبه دوازدهم اسفند ۱۴۰۰ ساعت 7:22 توسط علی رضا نقش نیلچی |

6-مختصات کروی

عنصر حجمی که از r تا r + d r ، θ تا θ + d θ ، و φ تا φ + d φ را در بر می گیرد، توسط تعیین کننده ماتریس ژاکوبین مشتقات جزئی مشخص می شود .

$J={\frac {\partial (x,y,z)}{\partial (r,\theta ,\varphi )}}={\begin{pmatrix}\sin \theta \cos \varphi &r\ cos \theta \cos \varphi &-r\sin \theta \sin \varphi \\\sin \theta \sin \varphi &r\cos \theta \sin \varphi &r\sin \theta \cos \varphi \\\cos \theta &-r\sin \theta &0\end{pmatrix}}،$

برای مثال

$\mathrm {d} V=\left|{\frac {\partial (x,y,z)}{\partial (r,\theta ,\varphi )}}\right|\,\mathrm {d } r\,\mathrm {d} \theta \,\mathrm {d} \varphi =r^{2}\sin \theta \,\mathrm {d} r\,\mathrm {d} \theta \,\ mathrm {d} \varphi =r^{2}\,\mathrm {d} r\,\mathrm {d} \Omega ~.$

بنابراین، برای مثال، یک تابع f ( r ، θ ، φ ) را می توان بر روی هر نقطه در R3 توسط انتگرال سه گانه ادغام کرد.

$\int \limits _{0}^{2\pi }\int \limits _{0}^{\pi }\int \limits _{0}^{\infty }f(r,\theta , \varphi )r^{2}\sin \theta \,\mathrm {d} r\,\mathrm {d} \theta \,\mathrm {d} \varphi ~.$

عملگر del در این سیستم به عبارات زیر برای گرادیان ، واگرایی ، کرل و (اسکالر) لاپلاسی منجر می شود .

${\begin{aligned}\nabla f={}&{\partial f \over \partial r}{\hat {\mathbf {r} }}+{1 \over r}{\partial f \over \partial \theta }{\hat {\boldsymbol {\theta }}}+{1 \over r\sin \theta }{\partial f \over \partial \varphi }{\hat {\boldsymbol {\varphi }} },\\[8pt]\nabla \cdot \mathbf {A} ={}&{\frac {1}{r^{2}}}{\partial \over \partial r}\left(r^{2 }A_{r}\right)+{\frac {1}{r\sin \theta }}{\partial \over \partial \theta }\left(\sin \theta A_{\theta }\right)+{ \frac {1}{r\sin \theta }}{\partial A_{\varphi } \over \partial \varphi },\\[8pt]\nabla \times \mathbf {A} ={}&{\frac {1}{r\sin \theta }}\left({\partial \over \partial \theta }\left(A_{\varphi }\sin \theta \right)-{\partial A_{\theta } \over \partial \varphi }\right){\hat {\mathbf {r} }}\\[8pt]&{}+{\frac {1}{r}}\left({1 \over \sin \theta }{\partial A_{r} \over \partial \varphi }-{\partial \over \partial r}\ چپ(rA_{\varphi }\right)\right){\hat {\boldsymbol {\theta }}}\\[8pt]&{}+{\frac {1}{r}}\left({\partial \over \partial r}\left(rA_{\theta }\right)-{\partial A_{r} \over \partial \theta }\right){\hat {\boldsymbol {\varphi }}}،\\ [8pt]\nabla ^{2}f={}&{1 \over r^{2}}{\partial \over \partial r}\left(r^{2}{\partial f \over \partial r }\right)+{1 \over r^{2}\sin \theta }{\partial \over \partial \theta }\left(\sin \theta {\partial f \over \partial \theta }\right) +{1 \over r^{2}\sin ^{2}\theta }{\partial ^{2}f \over \partial \varphi ^{2}}\\[8pt]={}&\left({\frac {\partial ^{2}}{\partial r^{2}}}+{\frac {2}{r}}{\frac {\partial }{\partial r}}\right )f+{1 \over r^{2}\sin \theta }{\partial \over \partial \theta }\left(\sin \theta {\frac {\partial }{\partial \theta }}\right) f+{\frac {1}{r^{2}\sin ^{2}\theta }}{\frac {\partial ^{2}}{\partial \varphi ^{2}}}f~.\end {هم راستا}}$

علاوه بر این، ژاکوبین معکوس در مختصات دکارتی است

$J^{-1}={\begin{pmatrix}{\dfrac {x}{r}}&{\dfrac {y}{r}}&{\dfrac {z}{r}}\\ \\{\dfrac {xz}{r^{2}{\sqrt {x^{2}+y^{2}}}}}&{\dfrac {yz}{r^{2}{\sqrt { x^{2}+y^{2}}}}}&{\dfrac {-(x^{2}+y^{2})}{r^{2}{\sqrt {x^{2} +y^{2}}}}}\\\\{\dfrac {-y}{x^{2}+y^{2}}}&{\dfrac {x}{x^{2}+y ^{2}}}&0\end{pmatrix}}.$

تانسور متریک در سیستم مختصات کروی است $g=J^{T}J$ .

فاصله در مختصات کروی [ ویرایش ]

در مختصات کروی، با توجه به دو نقطه که φ مختصات ازیموتال است

${\begin{aligned}{\mathbf {r} }&=(r,\theta ,\varphi ),\\{\mathbf {r} '}&=(r',\theta ',\varphi ')\end{تراز شده}}$

فاصله بین دو نقطه را می توان به صورت بیان کرد

${\begin{aligned}{\mathbf {D} }&={\sqrt {r^{2}+r'^{2}-2rr'(\sin {\theta }\sin {\theta ' }\cos {(\varphi -\varphi ')}+\cos {\theta }\cos {\theta '})}}\end{تراز شده}}$

+ نوشته شده در دوشنبه نهم اسفند ۱۴۰۰ ساعت 12:5 توسط علی رضا نقش نیلچی |

5-مختصات کروی

تعمیم [ ویرایش ]

همچنین ببینید: مختصات بیضی شکل

همچنین می توان با استفاده از نسخه اصلاح شده مختصات کروی با بیضی ها در مختصات دکارتی مقابله کرد.

فرض کنید P یک بیضی مشخص شده توسط مجموعه سطح باشد

$ax^{2}+by^{2}+cz^{2}=d.$

مختصات کروی اصلاح شده یک نقطه در P در کنوانسیون ISO (یعنی برای فیزیک: شعاع r ، تمایل θ ، آزیموت φ ) را می توان از مختصات دکارتی آن ( x ، y ، z ) با فرمول به دست آورد.

${\begin{aligned}x&={\frac {1}{\sqrt {a}}}r\sin \theta \,\cos \varphi ,\\y&={\frac {1}{\sqrt {b}}}r\sin \theta \,\sin \varphi ,\\z&={\frac {1}{\sqrt {c}}}r\cos \theta ,\\r^{2}&= ax^{2}+by^{2}+cz^{2}.\end{aligned}}$

یک عنصر حجم بینهایت کوچک توسط

$\mathrm {d} V=\left|{\frac {\partial (x,y,z)}{\partial (r,\theta ,\varphi )}}\right|\,dr\,d \theta \,d\varphi ={\frac {1}{\sqrt {abc}}}r^{2}\sin \theta \,\mathrm {d} r\,\mathrm {d} \theta \, \mathrm {d} \varphi ={\frac {1}{\sqrt {abc}}}r^{2}\,\mathrm {d} r\,\mathrm {d} \Omega .$

ضریب ریشه مربع از خاصیت دترمینان می آید که اجازه می دهد یک ثابت از یک ستون خارج شود:

${\begin{vmatrix}ka&b&c\\kd&e&f\\kg&h&i\end{vmatrix}}=k{\begin{vmatrix}a&b&c\\d&e&f\\g&h&i\end{vmatrix}}.$

ادغام و تمایز در مختصات کروی [ ویرایش ]

بردارهای واحد در مختصات کروی

معادلات زیر (Iyanaga 1977) فرض می‌کنند که colatitude θ تمایل از محور z (قطبی) است (مبهم است زیرا x ، y ، و z متقابل نرمال هستند)، همانطور که در قرارداد فیزیک مورد بحث قرار گرفت.

عنصر خط برای جابجایی بینهایت کوچک از ( r ، θ ، φ ) به ( r + d r ، θ + d θ ، φ + d φ ) است.

$\mathrm {d} \mathbf {r} =\mathrm {d} r\,{\hat {\mathbf {r} }}+r\,\mathrm {d} \theta \,{\hat { \boldsymbol {\theta }}}+r\sin {\theta }\,\mathrm {d} \varphi \,\mathbf {\hat {\boldsymbol {\varphi }}} ,$

جایی که

${\begin{aligned}{\hat {\mathbf {r} }}&=\sin \theta \cos \varphi \,{\hat {\mathbf {x} }}+\sin \theta \sin \varphi \,{\hat {\mathbf {y} }}+\cos \theta \,{\hat {\mathbf {z} }},\\{\hat {\boldsymbol {\theta }}}&= \cos \theta \cos \varphi \,{\hat {\mathbf {x} }}+\cos \theta \sin \varphi \,{\hat {\mathbf {y} }}-\sin \theta \, {\hat {\mathbf {z} }},\\{\hat {\boldsymbol {\varphi }}}&=-\sin \varphi \,{\hat {\mathbf {x} }}+\cos \ varphi \,{\hat {\mathbf {y} }}\end{تراز شده}}$

بردارهای واحد متعامد محلی به ترتیب در جهت افزایش r , θ , و φ هستند و x̂ , ŷ و ẑ بردارهای واحد در مختصات دکارتی هستند. تبدیل خطی به این سه گانه مختصات راست دست یک ماتریس چرخشی است .

$R={\begin{pmatrix}\sin \theta \cos \varphi &\sin \theta \sin \varphi &\cos \theta \\\cos \theta \cos \varphi &\cos \theta \sin \varphi &-\sin \theta \\-\sin \varphi &\cos \varphi &0\end{pmatrix}}.$

این تبدیل از کروی به دکارتی را می دهد، برعکس آن توسط معکوس آن به دست می آید. نکته: ماتریس یک ماتریس متعامد است، یعنی معکوس آن به سادگی جابجایی آن است.

بنابراین، بردارهای واحد دکارتی با بردارهای واحد کروی مرتبط هستند:

${\begin{bmatrix}\mathbf {\hat {x}} \\\mathbf {\hat {y}} \\\mathbf {\hat {z}} \end{bmatrix}}={\begin {bmatrix}\sin \theta \cos \phi &\cos \theta \cos \phi &-\sin \phi \\\sin \theta \sin \phi &\cos \theta \sin \phi &\cos \phi \\\cos \theta &-\sin \theta &0\end{bmatrix}}{\begin{bmatrix}{\boldsymbol {\hat {r}}}\\{\boldsymbol {\hat {\theta }}} \\{\boldsymbol {\hat {\phi }}}\end{bmatrix}}$

شکل کلی فرمول برای اثبات عنصر خط دیفرانسیل، [5] است.

$\mathrm {d} \mathbf {r} =\sum _{i}{\frac {\partial \mathbf {r} }{\partial x_{i}}}\,\mathrm {d} x_{ i}=\sum _{i}\left|{\frac {\partial \mathbf {r} }{\partial x_{i}}}\right|{\frac {\frac {\partial \mathbf {r} }{\partial x_{i}}}{\left|{\frac {\partial \mathbf {r} }{\partial x_{i}}}\right|}}\,\mathrm {d} x_{i }=\sum _{i}\left|{\frac {\partial \mathbf {r} }{\partial x_{i}}}\right|\,\mathrm {d} x_{i}\,{\ کلاه {\boldsymbol {x}}}_{i}،$

یعنی تغییر در $\mathbf {r}$ به تغییرات فردی مربوط به تغییرات در مختصات فردی تجزیه می شود.

برای اعمال این مورد در مورد حاضر، باید نحوه محاسبه را محاسبه کرد $\mathbf {r}$ با هر یک از مختصات تغییر می کند. در کنوانسیون های مورد استفاده،

$\mathbf {r} ={\begin{bmatrix}r\sin \theta \,\cos \varphi \\r\sin \theta \,\sin \varphi \\r\cos \theta \end{bmatrix }}.$

بدین ترتیب،

${\frac {\partial \mathbf {r} }{\partial r}}={\begin{bmatrix}\sin \theta \,\cos \varphi \\\sin \theta \,\sin \varphi \\\cos \theta \end{bmatrix}},\quad {\frac {\partial \mathbf {r} }{\partial \theta }}={\begin{bmatrix}r\cos \theta \,\cos \varphi \\r\cos \theta \,\sin \varphi \\-r\sin \theta \end{bmatrix}},\quad {\frac {\partial \mathbf {r} }{\partial \varphi } }={\begin{bmatrix}-r\sin \theta \,\sin \varphi \\r\sin \theta \,\cos \varphi \\0\end{bmatrix}}.$

ضرایب مورد نظر، بزرگی این بردارها هستند: [5]

$\left|{\frac {\partial \mathbf {r} }{\partial r}}\right|=1,\quad \left|{\frac {\partial \mathbf {r} }{\partial \theta }}\right|=r,\quad \left|{\frac {\partial \mathbf {r} }{\partial \varphi }}\right|=r\sin \theta .$

عنصر سطحی که از θ تا θ + d θ و φ تا φ + d φ بر روی یک سطح کروی در شعاع r (ثابت) را پوشانده است.

$\mathrm {d} S_{r}=\left\|{\frac {\partial r{\hat {\mathbf {r} }}}{\partial \theta }}\times {\frac {\ جزئی r{\hat {\mathbf {r} }}}{\partial \varphi }}\right\|\mathrm {d} \theta \,\mathrm {d} \varphi =r^{2}\sin \ تتا \,\ mathrm {d} \theta \,\mathrm {d} \varphi ~.$

بنابراین زاویه جامد دیفرانسیل است

$\mathrm {d} \Omega ={\frac {\mathrm {d} S_{r}}{r^{2}}}=\sin \theta \,\mathrm {d} \theta \,\ ریاضی {d} \varphi .$

عنصر سطح در سطحی با زاویه قطبی θ ثابت (یک مخروط با راس مبدأ) است

$\mathrm {d} S_{\theta }=r\sin \theta \,\mathrm {d} \varphi \,\mathrm {d} r.$

عنصر سطح در سطحی با آزیموت φ ثابت (یک نیمه صفحه عمودی) است

$\mathrm {d} S_{\varphi }=r\,\mathrm {d} r\,\mathrm {d} \theta .$

+ نوشته شده در دوشنبه نهم اسفند ۱۴۰۰ ساعت 12:4 توسط علی رضا نقش نیلچی |

4-مختصات کروی

تبدیل سیستم مختصات [ ویرایش ]

همچنین ببینید: فهرست تبدیل مختصات رایج § به مختصات کروی

از آنجایی که سیستم مختصات کروی تنها یکی از بسیاری از سیستم های مختصات سه بعدی است، معادلاتی برای تبدیل مختصات بین سیستم مختصات کروی و سایرین وجود دارد.

مختصات دکارتی [ ویرایش ]

مختصات کروی یک نقطه در کنوانسیون ISO (یعنی برای فیزیک: شعاع r ، تمایل θ ، آزیموت φ ) را می‌توان از مختصات دکارتی آن ( x ، y ، z ) با فرمول‌ها به دست آورد.

${\begin{aligned}r&={\sqrt {x^{2}+y^{2}+z^{2}}}\\\theta &=\arccos {\frac {z}{\ sqrt {x^{2}+y^{2}+z^{2}}}}=\arccos {\frac {z}{r}}=\arctan {\frac {\sqrt {x^{2} +y^{2}}}{z}}\\\varphi &={\begin{cases}\arctan({\frac {y}{x}})&{\text{if }}x>0، \\\arctan({\frac {y}{x}})+\pi &{\text{if }}x<0{\text{ and }}y\geq 0,\\\arctan({\frac {y}{x}})-\pi &{\text{if }}x<0{\text{ و }}y<0,\\+{\frac {\pi }{2}}&{\ text{if }}x=0{\text{ و }}y>0,\\-{\frac {\pi }{2}}&{\text{if }}x=0{\text{ و } }y<0،\\{\text{undefined}}&{\text{if }}x=0{\text{ و }}y=0.\end{cases}}\end{تراز شده}}$

مماس معکوس با φ = آرکتان نشان داده شده استy/ایکسباید با در نظر گرفتن ربع صحیح ( x , y ) به طور مناسب تعریف شود . مقاله atan2 را ببینید.

از طرف دیگر، تبدیل را می توان به عنوان دو تبدیل متوالی مستطیلی به قطبی در نظر گرفت: اولین مورد در صفحه xy دکارتی از ( x , y ) به ( R , φ ) که در آن R طرح ریزی r بر روی صفحه xy است و دوم در صفحه zR دکارتی از ( z , R ) تا ( r , θ ) . ربع صحیح φ و θبا صحت تبدیل مستطیل مسطح به قطبی دلالت دارند.

این فرمول‌ها فرض می‌کنند که دو سیستم منشأ یکسانی دارند، صفحه مرجع کروی صفحه xy دکارتی است، θ از جهت z تمایل دارد، و زوایای آزیموت از محور x دکارتی اندازه‌گیری می‌شوند (به طوری که محور y دارای φ = +90 درجه ). اگر θ ارتفاع را از صفحه مرجع به جای شیب از نقطه اوج اندازه گیری کند، آرکوس بالا به یک کمان تبدیل می شود، و cos θ و sin θ زیر سوئیچ می شوند.

برعکس، مختصات دکارتی ممکن است از مختصات کروی بازیابی شوند ( شعاع r ، تمایل θ ، آزیموت φ )، که در آن r∈ [0، ∞) ، θ∈ [0، π ] ، φ∈ [ 0، 2π ) توسط

${\begin{aligned}x&=r\cos \varphi \,\sin \theta ,\\y&=r\sin \varphi \,\sin \theta ,\\z&=r\cos \theta .\ پایان{تراز شده}}$

مختصات استوانه ای [ ویرایش ]

نوشتار اصلی: سیستم مختصات استوانه‌ای

مختصات استوانه‌ای ( شعاع محوری ρ ، آزیموت φ ، ارتفاع z ) ممکن است با فرمول‌ها به مختصات کروی تبدیل شوند ( شعاع مرکزی r ، تمایل θ ، آزیموت φ ).

${\begin{aligned}r&={\sqrt {\rho ^{2}+z^{2}}},\\\theta &=\arctan {\frac {\rho }{z}}= \arccos {\frac {z}{\sqrt {\rho ^{2}+z^{2}}}}،\\\varphi &=\varphi .\end{تراز شده}}$

برعکس، مختصات کروی ممکن است توسط فرمول ها به مختصات استوانه ای تبدیل شوند

${\begin{aligned}\rho &=r\sin \theta ,\\\varphi &=\varphi ,\\z&=r\cos \theta .\end{aligned}$

این فرمول‌ها فرض می‌کنند که دو سیستم دارای مبدأ یکسان و صفحه مرجع یکسان هستند، زاویه زاویه φ را به همان معنا از یک محور اندازه‌گیری می‌کنند، و زاویه کروی θ از محور استوانه‌ای z تمایل دارد .

+ نوشته شده در دوشنبه نهم اسفند ۱۴۰۰ ساعت 12:3 توسط علی رضا نقش نیلچی |

3-مختصات کروی

طرح ریزی[ ویرایش ]

برای رسم یک نقطه از مختصات کروی آن ( r ، θ ، φ ) ، که در آن θ میل است، r واحدها را از مبدا در جهت اوج حرکت دهید، با θ در مورد مبدا به سمت جهت مرجع آزیموت بچرخانید، و به اندازه φ در حدود اوج در جهت مناسب.

برنامه های کاربردی [ ویرایش ]

همانطور که سیستم مختصات دکارتی دوبعدی در صفحه مفید است، سیستم مختصات کروی دو بعدی نیز بر روی سطح یک کره مفید است. در این سیستم، کره به عنوان یک کره در نظر گرفته می شود ، بنابراین شعاع واحد است و به طور کلی می توان آن را نادیده گرفت. این ساده‌سازی می‌تواند هنگام برخورد با اشیائی مانند ماتریس‌های چرخشی نیز بسیار مفید باشد .

مختصات کروی در تجزیه و تحلیل سیستم هایی که درجاتی از تقارن در مورد یک نقطه دارند، مانند انتگرال های حجمی در داخل یک کره، میدان انرژی پتانسیل اطراف یک جرم یا بار متمرکز، یا شبیه سازی آب و هوای جهانی در جو سیاره مفید هستند. کره ای که معادله دکارتی x 2 + y^ 2 + z^ 2 = c^ 2 دارد، معادله ساده r = c در مختصات کروی دارد.

دو معادله دیفرانسیل جزئی مهم که در بسیاری از مسائل فیزیکی بوجود می آیند، معادله لاپلاس و معادله هلمهولتز ، امکان جداسازی متغیرها را در مختصات کروی فراهم می کنند. بخش های زاویه ای راه حل های چنین معادلاتی به شکل هارمونیک های کروی هستند.

کاربرد دیگر طراحی ارگونومیک است، جایی که r طول بازوی یک فرد ساکن است و زاویه ها جهت بازو را در حین رسیدن به بیرون توصیف می کنند.

الگوی خروجی یک بلندگوی صنعتی با استفاده از نمودارهای قطبی کروی که در شش فرکانس گرفته شده است نشان داده شده است.

از مدل سازی سه بعدی الگوهای خروجی بلندگو می توان برای پیش بینی عملکرد آنها استفاده کرد. تعدادی نمودار قطبی مورد نیاز است که در طیف وسیعی از فرکانس ها گرفته شده است، زیرا الگوی با فرکانس به شدت تغییر می کند. نمودارهای قطبی نشان می دهد که بسیاری از بلندگوها در فرکانس های پایین تر به سمت همه جانبه گرایش دارند.

سیستم مختصات کروی نیز معمولاً در ساخت بازی های سه بعدی برای چرخاندن دوربین در اطراف موقعیت بازیکن استفاده می شود [4]

در جغرافیا [ ویرایش ]

نوشتار اصلی: سیستم مختصات جغرافیایی

همچنین ببینید: ECEF

برای اولین تقریب، سیستم مختصات جغرافیایی به جای شیب، از زاویه ارتفاع ( عرض جغرافیایی ) در درجه شمالی صفحه استوا ، در محدوده -90 درجه ≤ φ ≤ 90 درجه استفاده می کند. عرض جغرافیایی یا عرض جغرافیایی ژئومرکزی است که در مرکز زمین اندازه گیری می شود و با ψ , q , φ ′, φ c , φ g یا عرض جغرافیایی تعیین می شود که با عمود محلی ناظر اندازه گیری می شود و معمولاً φ تعیین می شود.. زاویه قطبی که 90 درجه منهای عرض جغرافیایی است و از 0 تا 180 درجه متغیر است، در جغرافیا هم عرض نامیده می شود .

زاویه آزیموت ( طول جغرافیایی )، که معمولاً با λ نشان داده می‌شود، در درجه‌های شرقی یا غربی برخی از نصف النهار مرجع معمولی (معمولاً نصف النهار مرجع IERS ) اندازه‌گیری می‌شود، بنابراین دامنه آن 180- ≤ λ ≤ 180 درجه است. برای موقعیت های روی زمین یا دیگر جرم های جامد سماوی , صفحه مرجع معمولاً صفحه عمود بر محور چرخش در نظر گرفته می شود .

به جای فاصله شعاعی، جغرافیدانان معمولاً از ارتفاع بالا یا زیر برخی از سطح مرجع ( مقصد عمودی ) استفاده می کنند که ممکن است میانگین سطح دریا باشد . فاصله شعاعی r را می توان از ارتفاع با اضافه کردن شعاع زمین که تقریباً 11 ± 6360 کیلومتر (7 ± 3952 مایل) است محاسبه کرد.

با این حال، سیستم‌های مختصات جغرافیایی مدرن کاملاً پیچیده هستند و موقعیت‌هایی که این فرمول‌های ساده نشان می‌دهند ممکن است چندین کیلومتر اشتباه باشند. معانی استاندارد دقیق عرض جغرافیایی، طول جغرافیایی و ارتفاع در حال حاضر توسط سیستم جهانی ژئودتیک (WGS) تعریف شده است و مسطح شدن زمین در قطب ها (حدود 21 کیلومتر یا 13 مایل) و بسیاری جزئیات دیگر را در نظر می گیرد.

سیستم های مختصات سیاره ای از فرمول های مشابه با سیستم مختصات جغرافیایی استفاده می کنند.

در نجوم [ ویرایش ]

مجموعه ای از سیستم های مختصات نجومی برای اندازه گیری زاویه ارتفاع از سطوح مختلف بنیادی استفاده می شود . این صفحات مرجع عبارتند از: افق ناظر ، استوای سماوی (تعریف شده توسط چرخش زمین)، صفحه دایره البروج (تعریف شده توسط مدار زمین به دور خورشید )، صفحه پایان دهنده زمین (عادی تا جهت آنی خورشید )، و استوای کهکشانی (که با چرخش کهکشان راه شیری تعریف می شود ).

+ نوشته شده در دوشنبه نهم اسفند ۱۴۰۰ ساعت 11:58 توسط علی رضا نقش نیلچی |

2-مختصات کروی

کنوانسیون ها [ ویرایش ]

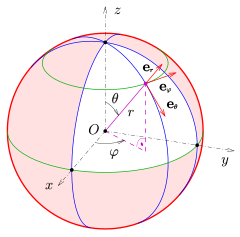
چندین قرارداد مختلف برای نمایش سه مختصات و ترتیبی که باید نوشته شوند وجود دارد. استفاده از $(r,\theta,\varphi)$ نشان دادن فاصله شعاعی، شیب (یا ارتفاع) و آزیموت، به ترتیب، یک روش معمول در فیزیک است و توسط استاندارد ISO 80000-2:2019 ، و قبل از آن در ISO 31-11 (1992) مشخص شده است.

با این حال، برخی از نویسندگان (از جمله ریاضیدانان) ρ را برای فاصله شعاعی، φ را برای شیب (یا ارتفاع) و θ را برای آزیموت، و r را برای شعاع از محور z- استفاده می‌کنند، که "بسط منطقی نماد مختصات قطبی معمولی را ارائه می‌دهد". [3] برخی از نویسندگان همچنین ممکن است آزیموت را قبل از شیب (یا ارتفاع) فهرست کنند. برخی از ترکیبات این انتخاب ها منجر به یک سیستم مختصات چپ دست می شود. کنوانسیون استاندارد $(r,\theta,\varphi)$ با نماد معمول برای مختصات قطبی دو بعدی و مختصات استوانه ای سه بعدی در تضاد است ، جایی که θ اغلب برای آزیموت استفاده می شود. [3]

زاویه ها معمولاً بر حسب درجه (°) یا رادیان (راد) اندازه گیری می شوند که 360 درجه = 2 π راد. مدارک تحصیلی بیشتر در جغرافیا، نجوم و مهندسی رایج است، در حالی که رادیان معمولاً در ریاضیات و فیزیک نظری استفاده می شود. واحد فاصله شعاعی معمولاً توسط زمینه تعیین می شود.

هنگامی که سیستم برای سه فضای فیزیکی استفاده می شود، مرسوم است که از علامت مثبت برای زوایای آزیموت استفاده شود که در جهت خلاف جهت عقربه های ساعت از جهت مرجع در صفحه مرجع اندازه گیری می شوند، همانطور که از سمت اوج صفحه مشاهده می شود. این قرارداد مخصوصاً برای مختصات جغرافیایی استفاده می‌شود، جایی که جهت "اوج" شمال است و زوایای آزیموت (طول جغرافیایی) مثبت به سمت شرق از یک نصف النهار اول اندازه‌گیری می‌شوند .

کنوانسیون های اصلی
مختصات	جهت های جغرافیایی محلی مربوطه ( Z ، X ، Y )	راست / چپ دست
( r ، θ inc ، φ az، راست )	( U , S , E )	درست
( r ، φ az، راست ، θ el )	( U , E , N )	درست
( r ، θ el ، φ az، راست )	( U , N , E )	ترک کرد

توجه: شرق ( E )، شمال ( N )، رو به بالا ( U ). زاویه آزیموت محلی ، به عنوان مثال، در خلاف جهت عقربه های ساعت از S تا E در مورد ( U ، S ، E ) اندازه گیری می شود .

مختصات منحصر به فرد [ ویرایش ]

هر سه گانه مختصات کروی $(r,\theta,\varphi)$ یک نقطه از فضای سه بعدی را مشخص می کند. از سوی دیگر، هر نقطه دارای بی نهایت مختصات کروی معادل است. می توان هر تعداد دور کامل را بدون تغییر خود زوایا و در نتیجه بدون تغییر نقطه به هر یک از معیارهای زاویه ای اضافه یا کم کرد. همچنین در بسیاری از زمینه ها، اجازه دادن فواصل شعاعی منفی با این قرارداد راحت است $(-r,-\theta,\varphi {+}180)$ برابر است با $(r,\theta,\varphi)$ برای هر r ، θ و φ . علاوه بر این، $(r,-\theta,\varphi)$ برابر است با $(r,\theta,\varphi {+}180^{\circ })$ .

اگر لازم باشد برای هر نقطه یک مجموعه منحصر به فرد از مختصات کروی تعریف شود، باید محدوده آنها را محدود کرد. یک انتخاب رایج است

r ≥ 0،

0° ≤ θ ≤ 180° (π rad)،

0° ≤ φ < 360 درجه (2π راد).

با این حال، آزیموت φ اغلب به بازه (-180°، +180°] یا ( -π , + π ] به رادیان، به جای [0، 360°) محدود می‌شود. این قرارداد استاندارد برای طول جغرافیایی است.

برای θ ، محدوده [0°، 180°] برای شیب معادل [90-°، +90°] برای ارتفاع است. در جغرافیا، عرض جغرافیایی ارتفاع است.

حتی با این محدودیت‌ها، اگر θ 0 درجه یا 180 درجه باشد (ارتفاع 90 درجه یا 90- درجه) باشد، زاویه آزیموت دلخواه است. و اگر r صفر باشد، هم آزیموت و هم شیب/ارتفاع دلخواه هستند. برای منحصر به فرد کردن مختصات، می توان از قراردادی استفاده کرد که در این موارد مختصات دلخواه صفر هستند.

+ نوشته شده در دوشنبه نهم اسفند ۱۴۰۰ ساعت 11:54 توسط علی رضا نقش نیلچی |

1-مختصات کروی

از ویکیپدیا، دانشنامه آزاد

مختصات کروی ( r ، θ ، φ ) که معمولاً در فیزیک استفاده می شود ( کنوانسیون ISO 80000-2:2019 ): فاصله شعاعی r (فاصله تا مبدأ)، زاویه قطبی θ ( تتا ) (زاویه نسبت به محور قطبی)، و ازیموتال زاویه φ ( ph ) (زاویه چرخش از صفحه نصف النهار اولیه). نماد ρ ( rho ) اغلب به جای r استفاده می شود .

مختصات کروی ( r , θ , φ ) که اغلب در ریاضیات استفاده می شود : فاصله شعاعی r , زاویه زاویه θ , و زاویه قطبی φ . معانی θ و φ در مقایسه با قرارداد فیزیک عوض شده است. همانطور که در فیزیک، ρ ( rho ) اغلب به جای r استفاده می شود تا از اشتباه گرفتن مقدار r در مختصات قطبی استوانه ای و دو بعدی جلوگیری شود.

کره ای که فاصله شعاعی، زاویه قطبی و زاویه قطبی نقطه P را نسبت به یک کره واحد نشان می دهد ، در قرارداد ریاضیات. در این تصویر r برابر 4/6، θ برابر 90 درجه و φ برابر 30 درجه است.

در ریاضیات ، سیستم مختصات کروی یک سیستم مختصات برای فضای سه بعدی است که در آن موقعیت یک نقطه با سه عدد مشخص می شود: فاصله شعاعی آن نقطه از یک مبدأ ثابت، زاویه قطبی آن اندازه گیری شده از یک جهت اوج ثابت ، و زاویه متعامد برآمدگی متعامد آن بر روی صفحه مرجعی که از مبدا می گذرد و متعامد به نقطه اوج است، از یک جهت مرجع ثابت در آن صفحه اندازه گیری می شود. می توان آن را به عنوان نسخه سه بعدی سیستم مختصات قطبی دید .

فاصله شعاعی را شعاع یا مختصات شعاعی نیز می نامند . زاویه قطبی را می توان زاویه همبستگی ، زاویه اوج ، زاویه معمولی یا زاویه شیب نامید .

استفاده از نمادها و ترتیب مختصات در منابع و رشته ها متفاوت است. این مقاله از کنوانسیون ISO [1] که اغلب در فیزیک با آن مواجه می‌شود، استفاده می‌کند : $(r,\theta,\varphi)$ فاصله شعاعی، زاویه قطبی و زاویه ازیموت را نشان می دهد. در بسیاری از کتاب های ریاضی، $(\rho,\theta,\varphi)$ یا $(r,\theta,\varphi)$ فاصله شعاعی، زاویه ازیموتال و زاویه قطبی را نشان می‌دهد و معانی θ و φ را تغییر می‌دهد . قراردادهای دیگری نیز استفاده می شود، مانند r برای شعاع از محور z ، بنابراین باید دقت زیادی برای بررسی معنای نمادها انجام شود.

طبق قراردادهای سیستم های مختصات جغرافیایی ، موقعیت ها با طول، طول جغرافیایی و ارتفاع (ارتفاع) اندازه گیری می شوند. تعدادی سیستم مختصات آسمانی بر اساس صفحات بنیادی مختلف و با اصطلاحات مختلف برای مختصات مختلف وجود دارد. سیستم های مختصات کروی مورد استفاده در ریاضیات معمولاً به جای درجه از رادیان استفاده می کنند و زاویه آزیموتال را در خلاف جهت عقربه های ساعت از محور x به محور y به جای جهت عقربه های ساعت از شمال (0 درجه) به شرق (90 درجه) مانند سیستم مختصات افقی اندازه گیری می کنند. . [2] زاویه قطبی اغلب با زاویه جایگزین می شودزاویه ارتفاع از صفحه مرجع اندازه گیری می شود، به طوری که زاویه ارتفاع صفر در افق باشد.

سیستم مختصات کروی سیستم مختصات قطبی دو بعدی را تعمیم می دهد. همچنین می توان آن را به فضاهای با ابعاد بالاتر گسترش داد و سپس به عنوان یک سیستم مختصات ابرکره ای نامیده می شود .

فهرست

تعریف [ ویرایش ]

برای تعریف یک سیستم مختصات کروی، باید دو جهت متعامد، نقطه اوج و نقطه مرجع ، و یک نقطه مبدا در فضا را انتخاب کرد. این انتخاب ها صفحه مرجعی را تعیین می کنند که مبدا را در بر می گیرد و بر نقطه اوج عمود است. سپس مختصات کروی یک نقطه P به صورت زیر تعریف می شود:

شعاع یا فاصله شعاعی فاصله اقلیدسی از مبدأ O تا P است.
شیب (یا زاویه قطبی ) زاویه بین جهت اوج و پاره خط OP است.
آزیموت (یا زاویه آزیموت ) زاویه علامتی است که از جهت مرجع آزیموت تا برجستگی متعامد پاره خط OP در صفحه مرجع اندازه گیری می شود.

علامت آزیموت با انتخاب حس مثبت چرخش در اوج تعیین می شود. این انتخاب دلخواه است و بخشی از تعریف سیستم مختصات است.

زاویه ارتفاع 90 درجه (π/2رادیان) منهای زاویه میل.

اگر شیب صفر یا 180 درجه ( رادیان π ) باشد، آزیموت دلخواه است. اگر شعاع صفر باشد، هم آزیموت و هم میل دلخواه هستند.

در جبر خطی ، بردار از مبدأ O تا نقطه P را اغلب بردار موقعیت P می نامند .

+ نوشته شده در دوشنبه نهم اسفند ۱۴۰۰ ساعت 11:51 توسط علی رضا نقش نیلچی |

مثال 10:بررسی قضیه استوکس با یک مثال

Question: Verify Stokes' theorem for A = (2x - y)x - 2yz^2 y - 2zy^2 z on the u - Wegglab

+ نوشته شده در شنبه بیست و پنجم دی ۱۴۰۰ ساعت 7:18 توسط علی رضا نقش نیلچی |

قضیه استوکس

از ویکیپدیا، دانشنامه آزاد

(برگرفته از قضیه کلوین-استوکس )

نباید با قضیه تعمیم یافته استوکس اشتباه شود .

تصویری از قضیه استوکس، با سطح Σ ، مرز آن ∂Σ و بردار نرمال n .

بخشی از مجموعه مقالات در مورد

حساب دیفرانسیل و انتگرال

نشان دادن

نشان دادن

نشان دادن

پنهان شدن

قضایا
شیب واگرایی حلقه لاپلاس مشتق جهت دار هویت ها
شیب سبز استوکس واگرایی استوکس تعمیم یافته

نشان دادن

چند متغیره

نشان دادن

تخصصی

نشان دادن

متفرقه

قضیه استوکس ، [1] همچنین به عنوان قضیه کلوین-استوکس [2] [3] پس از لرد کلوین و جورج استوکس شناخته می شود ، قضیه اساسی برای کرل ها یا به سادگی قضیه کرل ، [4] یک قضیه در محاسبات برداری بر روی $\mathbb {R} ^{3}$ . با توجه به میدان برداری ، قضیه مربوط به جدایی ناپذیر از حلقه میدان برداری در بیش از برخی از سطح، به انتگرال خطی میدان برداری در اطراف مرز از سطح. قضیه کلاسیک استوکس را می توان در یک جمله بیان کرد: انتگرال خط یک میدان برداری روی یک حلقه برابر است با شار پیچش آن در سطح محصور.

قضیه استوکس یک مورد خاص از قضیه تعمیم یافته استوکس است . [5] [6] به طور خاص، یک فیلد برداری روشن است $\mathbb {R} ^{3}$ را می توان به صورت یک شکل در نظر گرفت که در این صورت حلقه آن مشتق بیرونی آن ، یک شکل 2 است.

فهرست

+ نوشته شده در دوشنبه سیزدهم دی ۱۴۰۰ ساعت 15:19 توسط علی رضا نقش نیلچی |

نامساوی مثلثی؟نامساوی کوشی -شواتز؟

Proof: $||u+v||^2≤(||u||+||v||)^2$ Using Cauchy Schwarz Inequality - Mathematics Stack Exchange

+ نوشته شده در دوشنبه سیزدهم دی ۱۴۰۰ ساعت 12:37 توسط علی رضا نقش نیلچی |

تمرین :لاپلاسین توابع زیر را حساب کنید

Solved Problem 3.57 Find the Laplacian of the following | Chegg.com

+ نوشته شده در دوشنبه سیزدهم دی ۱۴۰۰ ساعت 12:20 توسط علی رضا نقش نیلچی |

مطالب قدیمی‌تر

آموزش ریاضی

ضرب سه گانه اسکالر [ ویرایش ]

تفسیر هندسی

خواص

اسکالر یا شبه اسکالر

تراکم اسکالر یا اسکالر

به عنوان یک ضرب بیرونی

به عنوان یک تابع سه خطی

ضرب سه گانه برداری

اثبات

استفاده از جبر هندسی

تفاسیر

حساب تانسور

حساب برداری

https://en.wikipedia.org/wiki/Triple_product

نمونه های حل شده فرمول استرلینگ

تعریف [ ویرایش ]

انگیزه [ ویرایش ]

انتشار [ ویرایش ]

میانگین ها [ ویرایش ]

چگالی مرتبط با پتانسیل [ ویرایش ]

به حداقل رساندن انرژی [ ویرایش ]

عبارات مختصات [ ویرایش ]

دو بعدی [ ویرایش ]

سه بعدی [ ویرایش ]

ابعاد N [ ویرایش ]

تغییر ناپذیری اقلیدسی [ ویرایش ]

نظریه طیفی [ ویرایش ]

لاپلاسی بردار [ ویرایش ]

تعمیم [ ویرایش ]

استفاده در فیزیک [ ویرایش ]

کلیات [ ویرایش ]

اپراتور لاپلاس–بلترامی [ ویرایش ]

دلامبرتی [ ویرایش ]

همچنین ببینید [ ویرایش ]

یادداشت ها [ ویرایش ]

منابع [ ویرایش ]

ادامه مطلب [ ویرایش ]

پیوندهای خارجی [ ویرایش ]

​

حساب انتگرال (طول قوس) [ ویرایش ]

حساب انتگرال (مساحت) [ ویرایش ]

حساب برداری [ ویرایش ]

دایره [ ویرایش ]

خط [ ویرایش ]

گل رز قطبی [ ویرایش ]

مارپیچ ارشمیدسی [ ویرایش ]

ویژگی های مشخصه [ ویرایش ]

کسینوس هایپربولیک [ ویرایش ]

مماس هایپربولیک[ ویرایش ]

روابط مفید [ ویرایش ]

مجموع آرگومان ها [ ویرایش ]

فرمول های تفریق [ ویرایش ]

فرمول های نیم آرگومان [ ویرایش ]

فرمول های مربعی [ ویرایش ]

نابرابری ها [ ویرایش ]

توابع معکوس به عنوان لگاریتم [ ویرایش ]

فهرست

نشانه گذاری [ ویرایش ]

تعاریف [ ویرایش ]

تعاریف نمایی [ ویرایش ]

تعاریف معادلات دیفرانسیل [ ویرایش ]

تعاریف مختلط توابع مثلثاتی [ ویرایش ]

سری تیلور و چند جمله ای ها

سری تیلور چند جمله ای چیست؟

ضرب سری تیلور در چند جمله ای

محاسبه سری تیلور [ ویرایش ]

مثال اول [ ویرایش ]

مثال دوم [ ویرایش ]

مثال سوم [ ویرایش ]

مجموعه تیلور به عنوان تعاریف [ ویرایش ]

سری تیلور در چندین متغیر [ ویرایش ]

مثال [ ویرایش ]

مقایسه با سری فوریه [ ویرایش ]

همچنین مشاهده کنید [ ویرایش ]

خطای تقریب و همگرایی [ ویرایش ]

تعمیم [ ویرایش ]

فهرستی از سری مکلورن از برخی توابع رایج [ ویرایش ]

تابع نمایی [ ویرایش ]

لگاریتم طبیعی [ ویرایش ]