قضیه پایه هیلبرت

14 زبان

از ویکیپدیا، دانشنامه آزاد

در ریاضیات ، به ویژه جبر جابجایی ، قضیه پایه هیلبرت می گوید که یک حلقه چند جمله ای بر روی یک حلقه نوتری ، نوتری است.

بیانیه [ ویرایش ]

اگر $آر$ یک حلقه است ، اجازه دهید $R[X]$ حلقه چند جمله ای ها را در نامتعین نشان دهیدایکس $ایکس$ بر فراز $آر$ . هیلبرت ثابت کرد که اگر $آر$ "خیلی بزرگ نیست"، به این معنا که اگر $آر$ نوتری است، همین امر باید برای آن صادق باشد $R[X]$ . به طور رسمی،

قضیه پایه هیلبرت. اگر $آر$ پس یک حلقه نوتری است $R[X]$ یک حلقه نوتری است.

نتیجه. اگر $آر$ پس یک حلقه نوتری است $R[X_{1}،\dotsc،X_{n}]$ یک حلقه نوتری است.

این را می توان به شکل زیر به هندسه جبری ترجمه کرد: هر مجموعه جبری روی یک میدان را می توان به عنوان مجموعه ریشه های مشترک بسیاری از معادلات چند جمله ای توصیف کرد. هیلبرت این قضیه را (برای مورد خاص حلقه‌های چندجمله‌ای در یک میدان) در طول اثبات نسل محدود حلقه‌های متغیر ثابت کرد . [1]

هیلبرت با استفاده از استقرای ریاضی، اثباتی بدیع از طریق تضاد ارائه کرد . روش او الگوریتمی برای تولید چندجمله‌ای‌های پایه محدود برای یک ایده‌آل ارائه نمی‌دهد : فقط نشان می‌دهد که آنها باید وجود داشته باشند. می توان چند جمله ای های پایه را با استفاده از روش پایه های گروبنر تعیین کرد .

اثبات [ ویرایش ]

قضیه. اگر $آر$ یک حلقه نوترین چپ (مثلاً راست) و سپس حلقه چند جمله ای است $R[X]$ همچنین یک حلقه نوترین چپ (مثلاً راست) است.

تذکر دهید. ما دو دلیل می آوریم که در هر دو فقط حالت «چپ» در نظر گرفته می شود. اثبات مورد درست مشابه است.

اثبات اول [ ویرایش ]

فرض کنیدآ⊆ ${\mathfrak a}\subseteq R[X]$ یک ایده‌آل چپ غیر محدود تولید شده است. سپس با بازگشت (با استفاده از اصل انتخاب وابسته ) دنباله ای از چند جمله ای ها وجود دارد. $\{f_{0},f_{1},\ldots \}$ به گونه ای که اگر ${\mathfrak b}_{n}$ ایده آل چپ تولید شده توسط $f_{0},\ldots,f_{n-1}$ سپس $f_{n}\in {\mathfrak {a}}\setminus {\mathfrak {b}}_{n}$ حداقل درجه است . واضح است که $\{\deg(f_{0})،\deg(f_{1})،\ldots \}$ دنباله ای غیر کاهشی از اعداد طبیعی است . اجازه دهید $a_{n}$ ضریب پیشرو باشد $f_{n}$ و اجازه دهید ${\mathfrak {b}}$ ایده آل چپ در $آر$ تولید شده توسط $a_{0},a_{1},\ldots$ . از آنجا که $آر$ زنجیر مان نوتری است

$(a_{0})\subset (a_{0},a_{1})\subset (a_{0},a_{1},a_{2})\subset \cdots$ ⊂⋯

باید خاتمه یابد. بدین ترتیب ${\mathfrak {b}}=(a_{0},\ldots ,a_{N-1})$ برای تعدادی عدد صحیح $ن$ . بنابراین به طور خاص،

$a_{N}=\sum _{i<N}u_{i}a_{i},\qquad u_{i}\in R.$

حال در نظر بگیرید

$g=\sum _{{i<N}}u_{{i}}X^{{\deg(f_{{N}})-\deg(f_{{i}})}}f_{{i} }،$

که عبارت اصلی آن برابر است با $f_{N}$ ; علاوه بر این، $g\in {\mathfrak b}_{N}$ . با این حال، $f_{N}\notin {\mathfrak b}_{N}$ ، که به این معنی است $f_{N}-g\in {\mathfrak a}\setminus {\mathfrak b}_{N}$ دارای مدرک کمتر از $f_{N}$ ، در تضاد با حداقل است.

اثبات دوم [ ویرایش ]

اجازه دهیدآ⊆ ${\mathfrak a}\subseteq R[X]$ یک ایده آل چپ باشد اجازه دهیدب ${\mathfrak b}$ مجموعه ضرایب پیشرو اعضا باشدآ ${\mathfrak {a}}$ . این بدیهی است که یک ایده آل باقی مانده است $آر$ و بنابراین به طور محدود توسط ضرایب پیشرو تعداد محدودی از اعضای تولید می شود ${\mathfrak {a}}$ ; گفتن $f_{0},\ldots ,f_{N-1}$ . اجازه دهیدد $د$ حداکثر مجموعه باشد $\{\deg(f_{0}),\ldots,\deg(f_{N-1})\}$ ، و اجازه دهیدبک ${\mathfrak b}_{k}$ مجموعه ضرایب پیشرو اعضا باشدآ ${\mathfrak {a}}$ ، که مدرک آن است $\le k$ . مانند قبل، ${\mathfrak b}_{k}$ مان ها باقی مانده اند $آر$ ، و بنابراین به طور محدود توسط ضرایب پیشرو تعداد محدودی از اعضای تولید می شوندآ ${\mathfrak {a}}$ ، گفتن

$f_{0}^{(k)},\ldots ,f_{N^{(k)}-1}^{(k)}$

با $\le k$ . حالا اجازه دهیدآ∗⊆ ${\mathfrak a}^{*}\subseteq R[X]$ ایده آل چپ باشد که توسط:

$\left\{f_{i},f_{j}^{(k)}\,:\ i<N,\,j<N^{(k)},\,k<d\راست\ }\!\!\;.$

ما داریم ${\mathfrak a}^{*}\subseteq {\mathfrak a}$ و همچنین ادعا کنید ${\mathfrak a}\subseteq {\mathfrak a}^{*}$ . فرض کنید برای تناقض اینطور نیست. سپس اجازه دهید $h\in {\mathfrak a}\setminus {\mathfrak a}^{*}$ حداقل درجه باشد و ضریب اصلی آن را با نشان دهید $آ$ .

مورد 1: $\deg(h)\geq d$ . صرف نظر از این شرط، داریم $a\in {\mathfrak b}$ ، یک ترکیب خطی سمت چپ نیز همینطور است

$a=\sum _{j}u_{j}a_{j}$

از ضرایب از $f_{j}$ . در نظر گرفتن

$h_{0}\triangleq \sum _{{j}}u_{{j}}X^{{\deg(h)-\deg(f_{{j}})}}f_{{j}}،$

که همان اصطلاح اصلی را دارد $ساعت$ ; علاوه بر این $h_{0}\در {\mathfrak a}^{*}$ در حالی که $h\notin {\mathfrak a}^{*}$ . از این رو $h-h_{0}\in {\mathfrak a}\setminus {\mathfrak a}^{*}$ و $\deg(h-h_{0})<\deg(h)$ ، که با حداقلی بودن در تضاد است.

مورد 2: $\deg(h)=k<d$ . سپس $a\in {\mathfrak b}_{k}$ بنابراین یک ترکیب خطی سمت چپ است

$a=\sum _{j}u_{j}a_{j}^{{(k)}}$

از ضرایب پیشرو از $f_{j}^{{(k)}}$ . با توجه به

$h_{0}\triangleq \sum _{j}u_{j}X^{{\deg(h)-\deg(f_{{j}}^{{(k)}})}}f_{{j }}^{{(k)}}،$

ما تضاد مشابه مورد 1 را به دست می دهیم.

بنابراین ادعای ما صادق است، و ${\mathfrak a}={\mathfrak a}^{*}$ که به طور متناهی تولید می شود.

توجه داشته باشید که تنها دلیلی که مجبور شدیم به دو پرونده تقسیم شویم، اطمینان از این بود که اختیاراتایکس $ایکس$ ضرب عوامل در ساخت و سازها غیرمنفی بود.

برنامه های کاربردی [ ویرایش ]

اجازه دهید $آر$ یک حلقه جابجایی نوتری باشد . قضیه پایه هیلبرت چند نتیجه فوری دارد .

با استقرا می بینیم که $R[X_{0}،\dotsc،X_{n-1}]$ نوتری نیز خواهد بود.
از آنجا که هر گونه وابسته بیش از $R^{n}$ (یعنی یک مجموعه مکان از مجموعه ای از چند جمله ای ها) ممکن است به عنوان مکان یک ایده آل نوشته شود ${\mathfrak {a}}\subset R[X_{0},\dotsc ,X_{n-1}]$ و علاوه بر این، به عنوان مکان مولدهای آن، نتیجه می‌شود که هر گونه وابسته، مکان چندجمله‌ای محدود بسیاری است - یعنی محل تلاقی تعداد بسیار زیاد ابرسطحی .
اگر $آ$ به طور متناهی تولید شده است $آر$ -جبر ، پس ما آن را می دانیم $A\simeq R[X_{0},\dotsc,X_{n-1}]/{\mathfrak {a}}$ ، جایی که ${\mathfrak {a}}$ یک ایده آل است قضیه مبنا دلالت بر آن دارد ${\mathfrak {a}}$ مثلاً باید به طور متناهی تولید شود ${\mathfrak {a}}=(p_{0},\dotsc ,p_{N-1})$ ، یعنی $آ$ به طور کامل ارائه شده است .

شواهد رسمی [ ویرایش ]

اثبات های رسمی قضیه پایه هیلبرت از طریق پروژه Mizar (به فایل HILBASIS مراجعه کنید ) و Lean (به ring_theory.polynomial مراجعه کنید) تأیید شده است .

منبع

https://en.wikipedia.org/wiki/Hilbert%27s_basis_theorem

+ نوشته شده در چهارشنبه بیست و چهارم اسفند ۱۴۰۱ ساعت 19:1 توسط علی رضا نقش نیلچی |

15-برنامه ها و دوره ها دانشکده ریاضی در دانشگاه اوتاوا

آزمون جامع MAT 9900: Real Analysis I / آزمون جامع: Real Analysis 1

این آزمون محتوای دوره MAT 5125 را پوشش می دهد . این آزمون امتحان نهایی دوره است و توسط اساتیدی که در سال تحصیلی MAT 5125 و MAT 5126 را تدریس می کنند، علامت گذاری می شود. دارای رتبه S (رضایت بخش) یا NS (غیر رضایت بخش). / این آزمون محتوای درس MAT 5125 را در بر می گیرد . این آزمون امتحان نهایی دوره است و توسط اساتیدی که در سال تحصیلی MAT 5125 و MAT 5126 را تدریس می کنند نمره گذاری می شود. درجه S (رضایت بخش) یا NS (راضی کننده نیست).

جزء / جزء درس: تحقیق / پژوهش

آزمون جامع MAT 9901: Real Analysis II / آزمون جامع: Real Analysis II

این آزمون محتوای دوره MAT 5126 را پوشش می دهد . این آزمون امتحان نهایی دوره است و توسط اساتیدی که در سال تحصیلی MAT 5125 و MAT 5126 را تدریس می کنند، علامت گذاری می شود. دارای رتبه S (رضایت بخش) یا NS (غیر رضایت بخش). / این آزمون محتوای درس MAT 5126 را در بر می گیرد . این آزمون امتحان نهایی دوره است و توسط اساتیدی که در سال تحصیلی MAT 5125 و MAT 5126 را تدریس می کنند نمره گذاری می شود. درجه S (رضایت بخش) یا NS (راضی کننده نیست).

جزء / جزء درس: تحقیق / پژوهش

آزمون جامع MAT 9902: جبر I / آزمون جامع: جبر I

این آزمون محتوای دوره MAT 5541 را پوشش می دهد . این آزمون امتحان نهایی دوره است و توسط اساتیدی که در سال تحصیلی MAT 5141 و MAT 5142 را تدریس می کنند تصحیح می شود. دارای رتبه S (رضایت بخش) یا NS (غیر رضایت بخش). / این آزمون محتوای درس MAT 5141 را در بر می گیرد . این آزمون امتحان نهایی دوره است و توسط اساتیدی که در سال تحصیلی MAT 5141 و MAT 5142 را تدریس می کنند نمره گذاری می شود. درجه S (رضایت بخش) یا NS (راضی کننده نیست).

جزء / جزء درس: تحقیق / پژوهش

آزمون جامع MAT 9903: جبر II / آزمون جامع: جبر II

این آزمون محتوای دوره MAT 5142 را پوشش می دهد . این آزمون امتحان نهایی این دوره است و توسط اساتیدی که در سال تحصیلی MAT 5141 و MAT 5142 را تدریس می کنند، علامت گذاری می شود. دارای رتبه S (رضایت بخش) یا NS (غیر رضایت بخش). / این آزمون محتوای درس MAT 5142 را در بر می گیرد . این آزمون امتحان نهایی دوره است و توسط اساتیدی که در سال تحصیلی MAT 5141 و MAT 5142 را تدریس می کنند نمره گذاری می شود. درجه S (رضایت بخش) یا NS (راضی کننده نیست).

جزء / جزء درس: تحقیق / پژوهش

آزمون جامع MAT 9904: توپولوژی I / آزمون جامع: توپولوژی I

این آزمون محتوای دوره MAT 5151 را پوشش می دهد . این آزمون امتحان نهایی دوره است و توسط اساتیدی که در سال تحصیلی MAT 5551 و MAT 5552 را تدریس می کنند تصحیح می شود. دارای رتبه S (رضایت بخش) یا NS (غیر رضایت بخش) / این آزمون محتوای دوره MAT 5151 را پوشش می دهد . این آزمون امتحان نهایی دوره است و توسط اساتیدی که در سال تحصیلی MAT 5151 و MAT 5152 را تدریس می کنند نمره گذاری می شود. درجه S (رضایت بخش) یا NS (راضی کننده نیست).

جزء / جزء درس: تحقیق / پژوهش

آزمون جامع MAT 9905: توپولوژی II / آزمون جامع: توپولوژی II

این آزمون محتوای دوره MAT 5152 را پوشش می دهد . این آزمون امتحان نهایی دوره است و توسط اساتیدی که در سال تحصیلی MAT 5151 و MAT 5152 را تدریس می کنند، علامت گذاری می شود. دارای رتبه S (رضایت بخش) یا NS (غیر رضایت بخش). / این آزمون محتوای درس MAT 5152 را در بر می گیرد . این آزمون امتحان نهایی دوره است و توسط اساتیدی که در سال تحصیلی MAT 5151 و MAT 5152 را تدریس می کنند نمره گذاری می شود. درجه S (رضایت بخش) یا NS (راضی کننده نیست).

جزء / جزء درس: تحقیق / پژوهش

آزمون جامع MAT 9906: معادلات دیفرانسیل I / آزمون جامع: معادلات دیفرانسیل I

این آزمون محتوای دوره MAT 5131 را پوشش می دهد . این آزمون امتحان نهایی دوره است و توسط اساتیدی که در سال تحصیلی MAT 5131 و MAT 5133 را تدریس می کنند، علامت گذاری می شود. دارای رتبه S (رضایت بخش) یا NS (غیر رضایت بخش). / این آزمون محتوای درس MAT 5131 را در بر می گیرد . این آزمون امتحان نهایی دوره است و توسط اساتیدی که در سال تحصیلی MAT 5131 و MAT 5133 را تدریس می کنند نمره گذاری می شود. درجه S (رضایت بخش) یا NS (راضی کننده نیست).

جزء / جزء درس: تحقیق / پژوهش

آزمون جامع MAT 9907: معادلات دیفرانسیل II / آزمون جامع: معادلات دیفرانسیل II

این آزمون شامل محتوای دوره MAT5133 می باشد. این آزمون امتحان نهایی دوره است و توسط اساتیدی که در سال تحصیلی MAT 5131 و MAT 5133 را تدریس می کنند، علامت گذاری می شود. دارای رتبه S (رضایت بخش) یا NS (غیر رضایت بخش). / این آزمون محتوای درس MAT 5133 را در بر می گیرد . این آزمون امتحان نهایی دوره است و توسط اساتیدی که در سال تحصیلی MAT 5131 و MAT 5133 را تدریس می کنند نمره گذاری می شود. درجه S (رضایت بخش) یا NS (راضی کننده نیست).

جزء / جزء درس: تحقیق / پژوهش

آزمون جامع MAT 9908: ریاضیات گسسته I / آزمون جامع: ریاضیات گسسته I

این آزمون محتوای دوره MAT5505 را پوشش می دهد. این آزمون امتحان نهایی دوره است و توسط معلمانی که در سال تحصیلی MAT 5105 و MAT 5107 را تدریس می کنند تصحیح می شود. دارای رتبه S (رضایت بخش) یا NS (غیر رضایت بخش). / این آزمون محتوای درس MAT 5105 را در بر می گیرد . این آزمون امتحان نهایی دوره است و توسط اساتیدی که در سال تحصیلی MAT 5105 و MAT 5107 را تدریس می کنند نمره گذاری می شود. درجه S (رضایت بخش) یا NS (راضی کننده نیست).

جزء / جزء درس: تحقیق / پژوهش

آزمون جامع MAT 9909: ریاضیات گسسته II / آزمون جامع: ریاضیات گسسته II

این آزمون محتوای دوره MAT5107 را پوشش می دهد. این آزمون امتحان نهایی دوره است و توسط اساتیدی که در سال تحصیلی MAT5105 و MAT5107 را تدریس می کنند تصحیح می شود. رتبه بندی S (رضایت بخش) و NS (راضی کننده نیست). / این آزمون محتوای درس MAT 5107 را در بر می گیرد . این آزمون امتحان نهایی دوره است و توسط اساتیدی که در سال تحصیلی MAT 5105 و MAT 5107 را تدریس می کنند نمره گذاری می شود. درجه S (رضایت بخش) یا NS (راضی کننده نیست).

جزء / جزء درس: تحقیق / پژوهش

آزمون جامع MAT 9910: تئوری احتمال I / آزمون جامع: تئوری احتمال I

این آزمون محتوای دوره MAT5170 را پوشش می دهد. این آزمون امتحان نهایی دوره است و توسط اساتیدی که در سال تحصیلی MAT 5170 و MAT5171 را تدریس می کنند تصحیح می شود. رتبه بندی S (رضایت بخش) و NS (راضی کننده نیست). / این آزمون محتوای درس MAT 5170 را در بر می گیرد . این آزمون امتحان نهایی دوره است و توسط اساتیدی که در سال تحصیلی MAT 5170 و MAT 5171 را تدریس می کنند نمره گذاری می شود. درجه S (رضایت بخش) یا NS (راضی کننده نیست).

جزء / جزء درس: تحقیق / پژوهش

آزمون جامع MAT 9911: نظریه احتمال II / آزمون جامع: نظریه احتمال II

این آزمون محتوای MAT5571 ترش را پوشش می دهد. این آزمون امتحان نهایی دوره است و توسط اساتیدی که در سال تحصیلی MAT5170 و MAT5171 تدریس می کنند تصحیح می شود. دارای رتبه S (رضایت بخش) یا NS (غیر رضایت بخش). / این آزمون محتوای درس MAT 5171 را در بر می گیرد . این آزمون امتحان نهایی دوره است و توسط اساتیدی که در سال تحصیلی MAT 5170 و MAT 5171 را تدریس می کنند نمره گذاری می شود. درجه S (رضایت بخش) یا NS (راضی کننده نیست).

جزء / جزء درس: تحقیق / پژوهش

آزمون جامع MAT 9912: آمار ریاضی I / آزمون جامع: آمار ریاضی I

این آزمون محتوای دوره MAT5190 را پوشش می دهد. این آزمون امتحان نهایی دوره است و توسط اساتیدی که در سال تحصیلی MAT5190 و MAT5191 تدریس می کنند تصحیح می شود. دارای رتبه S (رضایت بخش) یا NS (راضی کننده نیست).. / این آزمون محتوای دوره MAT 5190 را پوشش می دهد . این آزمون امتحان نهایی دوره است و توسط اساتیدی که در سال تحصیلی MAT 5190 و MAT 5191 را تدریس می کنند نمره گذاری می شود. درجه S (رضایت بخش) یا NS (راضی کننده نیست).

جزء / جزء درس: تحقیق / پژوهش

آزمون جامع MAT 9913: آمار و ریاضیات II / آزمون جامع: آمار ریاضی II

این آزمون محتوای دوره MAT5191 را پوشش می دهد. این آزمون امتحان نهایی دوره است و توسط اساتیدی که در سال تحصیلی MAT5190 و MAT5191 تدریس می کنند تصحیح می شود. دارای رتبه S (رضایت بخش) یا NS (غیر رضایت بخش). / این آزمون محتوای درس MAT 5191 را در بر می گیرد . این آزمون امتحان نهایی دوره است و توسط اساتیدی که در سال تحصیلی MAT 5190 و MAT 5191 را تدریس می کنند نمره گذاری می شود. درجه S (رضایت بخش) یا NS (راضی کننده نیست).

جزء / جزء درس: تحقیق / پژوهش

آزمون جامع پیشرفته MAT 9998

برنامه درسی برای آزمون جامع پیشرفته توسط کمیته مشاوره پایان نامه (CCT) تعیین می شود. برنامه درسی باید حداقل شش ماه قبل از تاریخ امتحان در اختیار دانشجو قرار گیرد. برنامه درسی باید حاوی فرم، محتوا و انتظارات برای آزمون جامع پیشرفته باشد. آزمون جامع پیشرفته می تواند کتبی و/یا شفاهی باشد. دارای رتبه S (رضایت بخش) یا NS (غیر رضایت بخش). / برنامه درسی آزمون جامع پیشرفته توسط کمیته مشاوره پایان نامه (TAC) تجویز می شود. برنامه درسی باید حداقل شش ماه قبل از تاریخ امتحان به دانش آموز داده شود. برنامه درسی باید فرم، محتوا و انتظارات آزمون جامع پیشرفته را ارائه دهد. آزمون جامع پیشرفته می تواند کتبی و/یا شفاهی باشد. درجه S (رضایت بخش) یا NS (راضی کننده نیست).

جزء / جزء درس: تحقیق / پژوهش

منبع

https://catalogue.uottawa.ca/en/courses/mat/

+ نوشته شده در چهارشنبه بیست و چهارم اسفند ۱۴۰۱ ساعت 18:39 توسط علی رضا نقش نیلچی |

14-برنامه ها و دوره ها دانشکده ریاضی در دانشگاه اوتاوا

MAT 5158 Lie Groups I (3 اعتبار)

این دوره معادل ریاضی 6104 در دانشگاه کارلتون است.

جزء: سخنرانی

MAT 5165 تئوری خودکار I (3 اعتبار)

این دوره معادل ریاضی 5605 در دانشگاه کارلتون است.

جزء: سخنرانی

MAT 5167 زبان های رسمی و تجزیه و تحلیل نحوی (3 اعتبار)

این دوره معادل MATH/COMP 5807 در دانشگاه کارلتون است.

جزء: سخنرانی

MAT 5168 Homology (3 اعتبار)

این دوره معادل ریاضی 5202 در دانشگاه کارلتون است.

جزء: سخنرانی

MAT 5170 نظریه احتمال I (3 واحد)

فضاهای احتمالی، متغیرهای تصادفی، انتظارات ریاضی به عنوان یک انتگرال، توزیع‌های مشترک، اندازه‌گیری مستقل و محصول، توزیع‌ها و بسط اندازه‌گیری‌های احتمال، لم‌های Borel-Cantelli، مفاهیم همگرایی، دنباله‌ای از متغیرهای تصادفی مستقل و همسان تعریف شده‌اند. این دوره معادل STAT 5308 در دانشگاه کارلتون است.

جزء: سخنرانی

پیش نیازها: MAT 3125 و MAT 3172 (MATH 3001، MATH 3002 و MATH 3500).

MAT 5171 نظریه احتمال II (3 اعتبار)

قوانین اعداد بزرگ، توابع مشخصه، قضیه حد مرکزی، احتمال و انتظار شرطی، خواص ابتدایی و قضایای همگرایی مارتینگل ها، مقدمه ای بر حرکت براونی. این دوره معادل ریاضی 5709 در دانشگاه کارلتون است.

جزء: سخنرانی

پیش نیاز: MAT 5170 (STAT 5708).

فرآیند تصادفی MAT 5172: فصل های انتخاب شده (3 اعتبار)

این دوره معادل STAT 5108 در دانشگاه کارلتون است.

جزء: سخنرانی

استنتاج آماری MAT 5176 (3 اعتبار)

آزمون‌های معناداری خالص؛ قوی ترین تست های یکنواخت بدون سوگیری و بدون واریانس؛ مقایسه مجانبی آزمون ها؛ فاصله اطمینان؛ تئوری نمونه بزرگ و آزمون‌های مجذور کای. استنتاج احتمال؛ استنتاج بیز؛ استنتاج تجربی بیزی؛ القای امانی و ساختاری؛ روش های نمونه گیری تکراری این دوره معادل STAT 5107 در دانشگاه کارلتون است.

جزء: سخنرانی

پیش نیازها: MAT 4170 یا معادل آن و MAT 5191 .

تجزیه و تحلیل چند متغیره نرمال MAT 5177 (3 اعتبار)

این دوره معادل STAT 5500 در دانشگاه کارلتون است.

جزء: سخنرانی

MAT 5180 آنالیز عددی I برای معادلات دیفرانسیل (3 واحد)

حسابی اعداد ممیز شناور; حل عددی معادلات دیفرانسیل معمولی. روش تفاضل محدود برای معادلات دیفرانسیل جزئی. ثبات، ثبات و همگرایی: تحلیل فون نویمان، شرط کورانت-فریدریش-لوی، قضیه لاکس. روش اجزای محدود: مسائل مرزی و معادلات دیفرانسیل جزئی بیضی. روش های طیفی و شبه طیفی.

جزء: سخنرانی

MAT 5590 آمار ریاضی I (3 واحد)

تئوری تصمیم گیری آماری; توابع احتمال؛ کفایت؛ قضیه فاکتورسازی; خانواده های نمایی؛ برآوردگرهای UMVU; تابع اطلاعات فیشر؛ حد پایین Cramer-Rao؛ حداکثر احتمال و تخمین لحظه؛ تخمین نقطه ثابت و قوی؛ خواص مجانبی؛ تخمین نقطه بیزی این دوره معادل STAT 5600 در دانشگاه کارلتون است.

جزء: سخنرانی

پیش نیاز: MAT 3172 , MAT 3375 . دوره های MAT 5775 ، MAT 5190 را نمی توان برای اعتبار ترکیب کرد.

MAT 5591 آمار ریاضی II (3 واحد)

فواصل و محورهای اعتماد؛ فواصل بیزی؛ آزمون های بهینه و نظریه نیمن-پیرسون; تست های احتمال و نمره رائو؛ آزمون اهمیت؛ تست تناسب؛ نظریه مبتنی بر نمونه های بزرگ و کاربردهای حداکثر احتمال و برآورد قوی. این دوره معادل STAT 5101 در دانشگاه کارلتون است.

جزء: سخنرانی

پیش نیاز: MAT 5590 .

مدل‌های خطی MAT 5193 (3 اعتبار)

تئوری مدل های خطی رتبه های غیر جامع: توابع قابل تخمین، بهترین برآوردگرهای بی طرف خطی، تأیید فرضیه ها، مناطق اطمینان. طبقه بندی چند بعدی؛ تحلیل کوواریانس؛ مدل های مولفه های واریانس؛ روش حداکثر احتمال؛ روش MINQUE، ANOVA. موضوعات متفرقه این دوره معادل STAT 5103 در دانشگاه کارلتون است.

جزء: سخنرانی

پیش نیاز MAT 5593

طراحی آزمایشات MAT 5195 (3 اعتبار)

مروری بر نظریه مدل خطی. متعامد بودن؛ بلوک های کامل با تصادفی سازی کامل، طرح های تقسیم شده. پلان های مربع لاتین; نظریه تصادفی؛ طرح های بلوک ناقص؛ آزمایشات فاکتوریل؛ نظریه تصادفی سازی؛ اثرات مخدوش کننده و تکثیر کسری. روش سطح پاسخ. موضوعات متفرقه

جزء: سخنرانی

تجزیه و تحلیل چند متغیره MAT 5196 (3 اعتبار)

این دوره با هدف دادن فرصت به دانش آموز برای انجام تحقیقات ریاضی در زمینه یک پروژه با همکاری یک سازمان حامی در بخش دولتی یا خصوصی است. شامل سمینارهایی در مورد موضوعات مرتبط با پروژه دانش آموز است. نمره نهایی S (رضایت‌بخش) یا NS (راضی‌کننده نیست) توسط استاد مسئول دوره با مشورت استاد راهنما، بر اساس محتوای ریاضی و بر اساس ارائه شفاهی و کتبی نتایج تعیین می‌شود. این دوره معادل STAT 5109 در دانشگاه کارلتون است.

جزء: سخنرانی

پیش نیاز: مجوز از موسسه.

MAT 5197 Stochastic Optimization (3 اعتبار)

این دوره معادل STAT 5601 در دانشگاه کارلتون است.

جزء: سخنرانی

پیش نیاز: STAT 3106 یا MAT 4371 .

مدل‌های تصادفی MAT 5198 (3 اعتبار)

این دوره معادل ریاضی 5701 در دانشگاه کارلتون است.

جزء: سخنرانی

MAT 5309 تجزیه و تحلیل هارمونیک روی گروه ها (3 اعتبار)

این دوره معادل ریاضی 6002 در دانشگاه کارلتون است.

جزء: سخنرانی

توپولوژی MAT 5312: فصل های منتخب (3 اعتبار)

این دوره معادل ریاضی 6201 در دانشگاه کارلتون است.

جزء: سخنرانی

مباحث MAT 5313 در احتمال و آمار (3 واحد)

این دوره معادل ریاضی 6507 در دانشگاه کارلتون است.

جزء: سخنرانی

MAT 5714 مسائل تئوری و آمار (3 واحد)

این دوره معادل ریاضی 6508 در دانشگاه کارلتون است.

جزء: سخنرانی

برنامه ریزی نظرسنجی MAT 5315 (3 اعتبار)

جزء: سخنرانی

تجزیه و تحلیل MAT 5326: فصل های منتخب (3 اعتبار)

این دوره معادل ریاضی 6008 در دانشگاه کارلتون است.

جزء: سخنرانی

MAT 5327 جبر - فصل های انتخاب شده: مقدمه ای بر هندسه جبری (3 واحد)

این دوره معادل ریاضی 6101 در دانشگاه کارلتون است.

جزء: سخنرانی

تجزیه و تحلیل MAT 5328: فصل های منتخب (3 اعتبار)

این دوره معادل ریاضی 6008 در دانشگاه کارلتون است.

جزء: سخنرانی

تجزیه و تحلیل MAT 5329: فصل های منتخب (3 اعتبار)

این دوره معادل ریاضی 6009 در دانشگاه کارلتون است.

جزء: سخنرانی

تجزیه و تحلیل MAT 5330: فصل های منتخب (3 اعتبار)

این دوره معادل ریاضی 6102 در دانشگاه کارلتون است.

جزء: سخنرانی

تجزیه و تحلیل MAT 5331: فصل های منتخب (3 اعتبار)

این دوره معادل ریاضی 6103 در دانشگاه کارلتون است.

جزء: سخنرانی

MAT 5361 Mathematical Logic: فصل های منتخب (3 اعتبار)

این دوره معادل ریاضی 6806 در دانشگاه کارلتون است.

جزء: سخنرانی

MAT 5375 مقدمه ای بر آمار ریاضی (3 واحد)

استنباط آماری; توزیع آمار کلاسیک و قضایای حد مرکزی مرتبط. تخمین پارامتریک; آمار کافی؛ برآوردگر کارآمد؛ پارادایم نیمن-پیرسون، آزمون های نسبت درستنمایی؛ روش های پارامتریک و ناپارامتریک برای مقایسه دو نمونه. طراحی آزمایش ها، تجزیه و تحلیل داده های طبقه بندی شده، مدل های خطی تعمیم یافته، نظریه تصمیم گیری و استنتاج بیزین. این درس برای دانشجویان آمار کاربردی ضروری است. این دوره معادل STAT 5610 در دانشگاه کارلتون است.

جزء: سخنرانی

دوره های MAT 5775 ، MAT 5590 را نمی توان برای اعتبار ترکیب کرد.

سمینار / سمینار MAT 5990 (3 واحد / 3 واحد)

این دوره معادل ریاضی 5900 در دانشگاه کارلتون است. / این دوره معادل ریاضی 5900 در دانشگاه کارلتون می باشد.

جریان / جزء دوره: سخنرانی / خواندن

سمینار کارشناسی ارشد MAT 5990S / سمینار کارشناسی ارشد (3 واحد / 3 واحد)

جریان / جزء دوره: سخنرانی / خواندن

سمینار / سمینار MAT 5990T (3 واحد / 3 واحد)

جریان / جزء دوره: سخنرانی / خواندن

MAT 5991 Directed Studies / Directed Studies (3 واحد / 3 واحد)

این دوره معادل ریاضی 5901 در دانشگاه کارلتون است. / این درس معادل ریاضی 5901 در دانشگاه کارلتون است.

جزء / جزء درس: تحقیق / پژوهش

سمینار MAT 5992 در آمار زیستی (3 واحد / 3 واحد)

دانش آموزان به صورت گروهی بر روی تجزیه و تحلیل داده های تجربی یا طرح های آزمایشی کار می کنند. مشارکت آزمایشگران در این تیم ها تشویق می شود. تیم های دانشجویی نتایج خود را در سمینار ارائه می کنند و گزارش کتبی مختصری از کار خود تهیه می کنند.

جریان / جزء دوره: سخنرانی / خواندن

MAT 5996 کارآموزی پژوهشی / کارآموزی پژوهشی (3 واحد / 3 واحد)

این دوره با هدف دادن فرصت به دانش آموز برای انجام تحقیقات ریاضی در زمینه یک پروژه با همکاری یک سازمان حامی در بخش دولتی یا خصوصی است. شامل سمینارهایی در مورد موضوعات مرتبط با پروژه دانش آموز است. نمره نهایی S (رضایت‌بخش) یا NS (راضی‌کننده نیست)، توسط استاد مسئول دوره با مشورت استاد راهنما و بر اساس محتوای ریاضی و ارائه شفاهی و کتبی نتایج تعیین می‌شود. / دوره پروژه محور که به دانشجویان این فرصت را می دهد تا در ریاضیات کاربردی به عنوان یک پروژه مشارکتی با حامیان دولتی یا صنعتی تحقیق کنند. کار پروژه و سمینار در موضوعات مرتبط.

جریان / جزء دوره: سخنرانی / خواندن

سمینار / سمینار MAT 6990 (3 واحد / 3 واحد)

این دوره معادل ریاضی 6900 در دانشگاه کارلتون است. / این دوره معادل ریاضی 6900 در دانشگاه کارلتون می باشد.

جریان / جزء دوره: سخنرانی / خواندن

MAT 6991 Directed Studies / Directed Studies (3 واحد / 3 واحد)

این دوره معادل ریاضی 6901 در دانشگاه کارلتون است. / این درس معادل ریاضی 6901 در دانشگاه کارلتون است.

جزء / جزء درس: تحقیق / پژوهش

پروژه MAT 6997 در ریاضیات و آمار / پروژه در ریاضیات و آمار (6 واحد / 6 واحد)

پروژه در ریاضیات و آمار توسط یک استاد تایید شده توسط مدیر تحصیلات تکمیلی و منجر به نوشتن یک گزارش عمیق (حدود 30-40 صفحه) می شود. رتبه S (رضایت بخش) یا NS (غیر رضایت بخش) توسط مدیر پروژه و استاد دیگری که توسط مدیر تحصیلات تکمیلی در ریاضیات و آمار منصوب شده است. پروژه به طور معمول در یک جلسه تکمیل می شود. این دوره معادل ریاضی 5910 در دانشگاه کارلتون است. / پروژه در ریاضیات و آمار با نظارت استاد مورد تایید مدیر تحصیلات تکمیلی و منجر به نگارش گزارش عمیق (حدود 30-40 صفحه). درجه S (رضایت بخش) یا NS (غیر رضایت بخش) توسط استاد راهنما و توسط استاد دیگری که توسط مدیر تحصیلات تکمیلی در ریاضیات و آمار منصوب می شود. پروژه به طور معمول در یک جلسه تکمیل می شود. این دوره معادل ریاضی 5910 در دانشگاه کارلتون است.

جزء / جزء درس: تحقیق / پژوهش

مجوز اداره الزامی است.

+ نوشته شده در چهارشنبه بیست و چهارم اسفند ۱۴۰۱ ساعت 18:38 توسط علی رضا نقش نیلچی |

13-برنامه ها و دوره ها دانشکده ریاضی در دانشگاه اوتاوا

تئوری بازی‌های MAT 5324 (3 واحد)

این درس معادل ریاضی 5607 در دانشگاه کارلتون است.

جزء درس: خواندن

مباحث MAT 5325 در علم اطلاعات و سیستم ها (3 واحد)

این دوره معادل ریاضی 5802 در دانشگاه کارلتون است.

جزء درس: خواندن

مباحث مربوط به تجزیه و تحلیل MAT 5326 (3 واحد)

این دوره معادل ریاضی 6008 در دانشگاه کارلتون است.

جزء درس: خواندن

مباحث MAT 5327 در جبر (3 واحد)

این دوره معادل ریاضی 6101 در دانشگاه کارلتون است.

جزء درس: خواندن

مباحث مربوط به تجزیه و تحلیل MAT 5328 (3 واحد)

این دوره معادل ریاضی 6008 در دانشگاه کارلتون است.

جزء درس: خواندن

موضوعات در تجزیه و تحلیل MAT 5329 (3 واحد)

این دوره معادل ریاضی 6009 در دانشگاه کارلتون است.

جزء درس: خواندن

مباحث MAT 5330 در جبر (3 واحد)

این دوره معادل ریاضی 6102 در دانشگاه کارلتون است.

جزء درس: خواندن

مباحث MAT 5331 در جبر (3 واحد)

این دوره معادل ریاضی 6103 در دانشگاه کارلتون است.

جزء درس: خواندن

محاسبات کوانتومی MAT 5341 (3 واحد)

فضای بیت کوانتومی؛ در هم تنیدگی. قابل مشاهده در مکانیک کوانتومی ماتریس چگالی و تجزیه اشمیت. رمزنگاری کوانتومی دروازه های منطقی کلاسیک و کوانتومی تبدیل فوریه کوانتومی الگوریتم کوانتومی شور برای فاکتورسازی اعداد صحیح. این درس معادل ریاضی 5821 در دانشگاه کارلتون است.

جزء درس: خواندن

MAT 5343 جنبه های ریاضی موجک ها و پردازش سیگنال دیجیتال (3 واحد)

روش های فشرده سازی بدون تلفات تبدیل فوریه گسسته و روش های فشرده سازی مبتنی بر فوریه. JPEG و MPEG. تجزیه و تحلیل موجک. فیلترهای دیجیتال و تبدیل موجک گسسته. موجک Daubechie. فشرده سازی موجک. این دوره معادل ریاضی 5822 در دانشگاه کارلتون است.

جزء درس: خواندن

پیش نیاز: جبر خطی و سری فوریه

مباحث MAT 5361 در منطق ریاضی (3 واحد)

این دوره معادل ریاضی 6806 در دانشگاه کارلتون است.

جزء درس: خواندن

MAT 5375 مقدمه ای بر آمار ریاضی (3 واحد)

قضایای حد؛ توزیع های نمونه تخمین پارامتریک; مفاهیم کفایت و کارایی؛ پارادایم نیمن-پیرسون، آزمون های نسبت درستنمایی؛ روش های پارامتری و ناپارامتریک برای مقایسه های دو نمونه ای. مفاهیم طراحی تجربی، تجزیه و تحلیل داده های طبقه بندی شده، مدل خطی عمومی، نظریه تصمیم گیری و استنتاج بیزی. این درس برای دانشجویان در آمار کاربردی ضروری است. این دوره معادل STAT 5610 در دانشگاه کارلتون است.

جزء درس: خواندن

دوره های MAT 5190 ، MAT 5375 را نمی توان برای واحدها ترکیب کرد.

MAT 5105 ریاضیات گسسته کاربردی I: نظریه گراف (3 واحد)

مسیرها و چرخه ها، درختان، اتصال، مسیرهای اویلری و چرخه های همیلتونی، رنگ آمیزی لبه ها، مجموعه ها و دسته های مستقل، رنگ آمیزی رئوس، نمودارهای مسطح، نمودارهای جهت دار. موضوعات انتخاب شده از موضوعات زیر: نظریه گراف جبری، نظریه گراف توپولوژیکی، نمودارهای تصادفی. این دوره معادل ریاضی 5818 در دانشگاه کارلتون است.

جزء: سخنرانی

بهینه سازی ترکیبی MAT 5106 (3 اعتبار)

نظریه جریان و موضوعات مرتبط موضوعات زیر از جمله موارد زیر پوشش داده خواهد شد: مسیرهای حداقل، درختان مولد حداقل هزینه، جریان های حداکثر هزینه، جریان های حداقل هزینه. جفت شدن بهینه در نمودارهای دو بخشی این دوره معادل ریاضی 5808 در دانشگاه کارلتون است.

جزء: سخنرانی

MAT 5107 ریاضیات گسسته کاربردی II: شمارش ترکیبی (3 واحد)

توابع مولد معمولی و نمایی؛ فرمول های محصول؛ جایگشت ها نت برگ; درختان؛ شاخص چرخه; روش WZ وارونگی لاگرانژ؛ تجزیه و تحلیل تکینگی توابع مولد و رفتار مجانبی آنها موضوعات انتخاب شده از موضوعات زیر: نمودارهای تصادفی، ساختارهای ترکیبی تصادفی، توابع فرا هندسی. این درس معادل ریاضی 5819 در دانشگاه کارلتون است.

جزء: سخنرانی

MAT 5121 مقدمه ای بر فضاهای هیلبرت (3 اعتبار)

این دوره معادل ریاضی 5009 در دانشگاه کارلتون است.

جزء: سخنرانی

MAT 5122 Banach Algebras (3 اعتبار)

این دوره معادل ریاضی 5003 در دانشگاه کارلتون است.

جزء: سخنرانی

MAT 5125 Real Analysis I (3 اعتبار)

اندازه گیری و ادغام، اندازه گیری و انتگرال گیری لبگ بر روی R، قضیه فوبینی، قضیه لبگ-رادون-نیکودیم، تداوم و مشتق مطلق، فضاهای Lp. فصل های منتخب مانند نظریه استون-دانیل. این دوره معادل ریاضی 5007 در دانشگاه کارلتون است.

جزء: سخنرانی

پیش نیاز: MAT 3125 (MATH 3001 و MATH 3002).

MAT 5126 Real Analysis II (3 اعتبار)

فضاهای باناخ و هیلبرت، عملگرهای خطی محدود، فضاهای دوگانه. فصل‌های انتخاب شده از میان موارد زیر: توپولوژی‌های ضعیف، قضیه آلاوغلو، عملگرهای فشرده، حساب دیفرانسیل در فضاهای Banach، قضایای نمایش Riesz. این دوره معادل ریاضی 5008 در دانشگاه کارلتون است.

جزء: سخنرانی

پیش نیاز MAT 5126

تجزیه و تحلیل پیچیده MAT 5127 (3 اعتبار)

این دوره معادل ریاضی 5005 در دانشگاه کارلتون است.

جزء: سخنرانی

MAT 5131 معادلات دیفرانسیل معمولی I (3 واحد)

این دوره معادل ریاضی 5405 در دانشگاه کارلتون است.

جزء: سخنرانی

MAT 5133 معادلات دیفرانسیل جزئی I (3 اعتبار)

این درس معادل ریاضی 5406 در دانشگاه کارلتون است.

جزء: سخنرانی

پیش نیاز: یک دوره سطح متوسط در معادلات دیفرانسیل معمولی مانند MAT 3130 Dynamical Systems یا معادل آن، یا مجوز مدرسه یا گروه.

معادلات دیفرانسیل MAT 5134: فصل های انتخاب شده (3 اعتبار)

این درس معادل ریاضی 5407 در دانشگاه کارلتون است.

جزء: سخنرانی

MAT 5141 جبر I: حلقه ها و ماژول ها (3 اعتبار)

ماژول ها و حلقه های نوتری و آرتینی. مجموعه های جبری، آرمان های آنها، قضیه پایه هیلبرت، آرمان های رادیکال، هیلبرت نولستلنساتز. محل قرارگیری حلقه ها و ماژول ها. حاصل ضرب تانسور ماژول ها و جبرها. حلقه ها و مدول های نیمه ساده، لم شور، قضیه چگالی جاکوبسون، قضیه آرتین-ودربرن. دنباله های دقیق کوتاه، ماژول های رایگان، ماژول های تصویری، ماژول های تزریقی، ماژول های مسطح. این دوره معادل ریاضی 5107 در دانشگاه کارلتون است.

جزء: سخنرانی

MAT 5142 جبر II: گروه ها و نظریه گالوا (3 اعتبار)

کنش های گروهی، فرمول کلاس، قضایای سایلو، سری مرکزی، ترکیب و مشتق، قضیه جردن-هولدر، بسط میدان ها و چندجمله ای های حداقل، بسته شدن جبری، پسوندهای قابل تفکیک، یکپارچگی، گروه های گالوا، قضیه بنیادی نظریه گالویس، میدان های محدود، پسوندهای سیکلوتومیک، قضیه اساسی جبر، پسوندهای متعالی. این دوره معادل ریاضی 5109 در دانشگاه کارلتون است.

جزء: سخنرانی

MAT 5143 Lie Algebra (3 اعتبار)

این دوره معادل ریاضی 5104 در دانشگاه کارلتون است.

جزء: سخنرانی

MAT 5144 جبر جابجایی (3 اعتبار)

طیف اولیه یک حلقه جابجایی (به عنوان فضای توپولوژیکی)؛ محل حلقه ها و ماژول ها؛ حاصل ضرب تانسور ماژول ها و جبرها. قضیه صفر هیلبرت و پیامدهای جبرهای محدود تولید شده در یک میدان. ابعاد Krull یک حلقه؛ قضایای وابستگی انتگرال، بالا رفتن و پایین رفتن. لم عادی سازی نوتر و نظریه بعد در جبرهای تولید شده محدود در یک میدان. حلقه‌های نوتری و قضیه «پایه» هیلبرت. مقدمه‌ای بر انواع جبری وابسته و شکل‌های آنها.

جزء: سخنرانی

نظریه گروه MAT 5145 (3 اعتبار)

این دوره معادل ریاضی 5106 در دانشگاه کارلتون است.

جزء: سخنرانی

حلقه ها و ماژول های MAT 5146 (3 اعتبار)

این دوره معادل ریاضی 5103 در دانشگاه کارلتون است.

جزء: سخنرانی

MAT 5147 جبر همسانی و نظریه مقوله (3 اعتبار)

این دوره معادل ریاضی 5108 در دانشگاه کارلتون است.

جزء: سخنرانی

MAT 5148 نمایندگی گروه ها و برنامه ها (3 واحد)

جزء: سخنرانی

MAT 5149 هندسه جبری (3 اعتبار)

برخی مفاهیم جبر جابجایی، قضیه صفر هیلبرت، مجموعه های جبری، توپولوژی زاریسکی. منیفولدهای Affine و Projective بر روی یک میدان بسته جبری. توابع منظم و کاربردهای منطقی. موضوعات انتخاب شده از: رابطه بین انواع پیچیده جبری و انواع تحلیلی پیچیده. ژانرها تقسیم کننده ها؛ بسته نرم افزاری مستقیم؛ قضایای ریمان-روخ و بزوت.

جزء: سخنرانی

پیش نیاز: MAT 3143

MAT 5151 توپولوژی I (3 اعتبار)

فضاهای توپولوژیکی؛ توپولوژی محصول و توپولوژی ضریب. بدیهیات شمارش پذیری و بدیهیات جداسازی. فضاهای فشرده و متصل؛ هموتوپی، گروه بنیادی; همگرایی فیلترها و توالی های تعمیم یافته این دوره معادل ریاضی 5205 در دانشگاه کارلتون است.

جزء: سخنرانی

پیش نیاز: MAT 3153 (MATH 3001).

MAT 5152 Topology II (3 اعتبار)

پوشش ها، همسانی (اصولات آیلنبرگ-استینرود)، کاربردها، ساخت نظریه همسانی. این دوره معادل ریاضی 5206 در دانشگاه کارلتون است.

جزء: سخنرانی

پیش نیازها: MAT 3143 و MAT 5151 (MATH 3100 و MATH 5205).

انواع دیفرانسیل MAT 5155 (3 اعتبار)

این دوره معادل ریاضی 5208 در دانشگاه کارلتون است.

جزء: سخنرانی

+ نوشته شده در چهارشنبه بیست و چهارم اسفند ۱۴۰۱ ساعت 18:36 توسط علی رضا نقش نیلچی |

12-برنامه ها و دوره ها دانشکده ریاضی در دانشگاه اوتاوا

تجزیه و تحلیل تصادفی MAT 5173 (3 واحد)

حرکت براونی، مارتینگل های پیوسته و ادغام تصادفی. این دوره معادل STAT 5604 در دانشگاه کارلتون است.

جزء درس: خواندن

عملکرد شبکه MAT 5174 (3 واحد)

این دوره بر روی تکنیک های پیشرفته در ارزیابی عملکرد شبکه های پیچیده بزرگ تمرکز خواهد کرد. موضوعات ممکن است شامل نظریه صف کلاسیک و تجزیه و تحلیل شبیه سازی باشد. مدل های شبکه های بسته؛ سیستم های از دست دادن و تاخیر؛ مسدود کردن احتمالات این دوره معادل STAT 5704 در دانشگاه کارلتون است.

جزء درس: خواندن

پیش نیاز: آشنایی با فرآیندهای احتمالی و تصادفی و نوبت دهی یا اجازه مربی.

استنتاج آماری قوی MAT 5175 (3 واحد)

این دوره معادل STAT 5106 در دانشگاه کارلتون است.

جزء درس: خواندن

استنتاج آماری پیشرفته MAT 5176 (3 واحد)

آزمون اهمیت خالص؛ یکنواخت قوی ترین تست های بی طرفانه و ثابت. مقایسه مجانبی آزمون ها؛ فاصله اطمینان؛ تئوری نمونه بزرگ نسبت درستنمایی و آزمون کای اسکوئر. استنتاج احتمال؛ استنتاج بیزی موضوعاتی مانند استنتاج تجربی بیز، استنتاج باوری و ساختاری، روش های نمونه گیری مجدد. این دوره معادل STAT 5107 در دانشگاه کارلتون است.

جزء درس: خواندن

نظریه نرمال چند متغیره MAT 5177 (3 واحد)

این دوره معادل STAT 5500 در دانشگاه کارلتون است.

جزء درس: خواندن

MAT 5180 آنالیز عددی برای معادلات دیفرانسیل (3 واحد)

محاسبات با اشاره شناور؛ حل عددی معادلات دیفرانسیل معمولی. روش های تفاضل محدود برای معادلات دیفرانسیل جزئی. ثبات، ثبات و همگرایی: تحلیل فون نویمان، شرط کورانت-فریدریش-لوی، قضیه لاکس. روش های اجزای محدود: مسائل ارزش مرزی و معادلات دیفرانسیل جزئی بیضوی. روش های طیفی و شبه طیفی این دوره معادل ریاضی 5806 در دانشگاه کارلتون است.

جزء درس: خواندن

MAT 5181 داده کاوی I (3 واحد)

تجسم و کشف دانش در مجموعه داده های عظیم؛ یادگیری بدون نظارت: الگوریتم های خوشه بندی. کاهش ابعاد؛ یادگیری تحت نظارت: تشخیص الگو، تکنیک های هموارسازی، طبقه بندی. از نرم افزارهای کامپیوتری استفاده خواهد شد. این دوره معادل STAT 5703 در دانشگاه کارلتون است.

جزء درس: خواندن

MAT 5182 آمار کاربردی و محاسباتی مدرن (3 اعتبار)

نمونه‌برداری مجدد و روش‌های فشرده کامپیوتری: بوت استرپ، jackknife با برنامه‌های کاربردی برای تخمین سوگیری، تخمین واریانس، فواصل اطمینان، و تحلیل رگرسیون. روش های هموارسازی در تخمین منحنی. طبقه‌بندی آماری و تشخیص الگو: روش‌های شمارش خطا، طبقه‌بندی‌کننده‌های بهینه، تخمین‌های بوت استرپ از بایاس خطای طبقه‌بندی اشتباه. این دوره معادل STAT 5702 در دانشگاه کارلتون است.

جزء درس: خواندن

MAT 5185 روشهای مجانبی ریاضیات کاربردی (3 واحد)

سری مجانبی: خواص، تطبیق، کاربرد در معادلات دیفرانسیل خطی و غیرخطی. بسط مجانبی انتگرالها: روشهای ابتدایی، روشهای لاپلاس، فاز ثابت و شیب دارترین نزول، لمای واتسون، لمای ریمان-لبگ. روش های اغتشاش: اغتشاش منظم و منفرد برای معادلات دیفرانسیل، تحلیل مقیاس چندگانه، نظریه لایه مرزی، نظریه WKB. این دوره معادل ریاضی 5408 در دانشگاه کارلتون است.

جزء درس: خواندن

مباحث ریاضی کاربردی MAT 5187 (3 واحد)

این دوره معادل ریاضی 5403 در دانشگاه کارلتون است.

جزء درس: خواندن

MAT 5190 آمار ریاضی I (3 واحد)

تئوری تصمیم گیری آماری; توابع احتمال؛ کفایت؛ قضیه فاکتورسازی; خانواده های نمایی؛ برآوردگرهای UMVU؛ اطلاعات فیشر؛ کران پایین کرامر-رائو; حداکثر احتمال و تخمین لحظه؛ تخمین نقطه ثابت و قوی خواص مجانبی؛ تخمین نقطه بیزی این دوره معادل STAT 5600 در دانشگاه کارلتون است.

جزء درس: خواندن

پیش نیاز: MAT 3172 , MAT 3375 . دوره های MAT 5190 ، MAT 5375 را نمی توان برای واحدها ترکیب کرد.

MAT 5191 آمار ریاضی II (3 واحد)

فواصل و محورهای اعتماد؛ فواصل بیزی؛ آزمون های بهینه و نظریه نیمن-پیرسون; آزمون های نسبت احتمال و امتیاز؛ آزمون اهمیت؛ تست مناسب بودن؛ تئوری نمونه بزرگ و کاربردها برای حداکثر احتمال و برآورد قوی. این دوره معادل STAT 5101 در دانشگاه کارلتون است.

جزء درس: خواندن

پیش نیاز: MAT 5190 .

نظریه و روش نمونه گیری MAT 5192 (3 واحد)

نمونه گیری احتمال نابرابر با و بدون جایگزینی. نظریه یکپارچه خطاهای استاندارد؛ رویکرد پیش بینی؛ تخمین نسبت و رگرسیون؛ لایه بندی و طرح های بهینه؛ نمونه گیری خوشه ای چند مرحله ای; نمونه برداری دوگانه؛ زمینه های تحصیلی؛ پس از طبقه بندی؛ بدون پاسخ؛ خطاهای اندازه گیری مطالب مرتبط. این دوره معادل STAT 5102 در دانشگاه کارلتون است.

جزء درس: خواندن

مدل های خطی MAT 5193 (3 واحد)

تئوری مدل های خطی با رتبه کامل: توابع قابل تخمین، بهترین برآوردگرهای خطی بی طرفانه، آزمون فرضیه، مناطق اطمینان. طبقه بندی چند طرفه؛ تحلیل کوواریانس؛ مدل‌های مؤلفه‌های واریانس: برآورد حداکثر احتمال، روش‌های MINQUE، ANOVA. موضوعات متفرقه این دوره معادل STAT 5103 در دانشگاه کارلتون است.

جزء درس: خواندن

پیش نیاز: MAT 4175 (MATH 4500) یا MAT 5190 (STAT 5600).

MAT 5194 فرآیندهای تصادفی و تجزیه و تحلیل سری زمانی (3 واحد)

این دوره معادل STAT 5104 در دانشگاه کارلتون است.

جزء درس: خواندن

طراحی آزمایشات MAT 5195 (3 واحد)

مروری بر نظریه مدل خطی. متعامد بودن؛ طرح‌های بلوک تصادفی و طرح‌های خرد شده؛ طرح های مربع لاتین; نظریه تصادفی سازی؛ طرح های بلوک ناقص؛ آزمایشات فاکتوریل؛ همانندسازی مخدوش کننده و کسری؛ روش شناسی سطح پاسخ موضوعات متفرقه این دوره معادل STAT 5105 در دانشگاه کارلتون است.

جزء درس: خواندن

پیش نیازها: MAT 3375 و MAT 3376 یا MAT 5190 (STAT 3505 و STAT 4500 یا STAT 5600).

تجزیه و تحلیل چند متغیره MAT 5196 (3 واحد)

این دوره معادل STAT 5109 در دانشگاه کارلتون است.

جزء درس: خواندن

بهینه سازی تصادفی MAT 5197 (3 واحد)

موضوعات انتخاب شده از برنامه نویسی پویا تصادفی، فرآیندهای تصمیم مارکوف، نظریه جستجو، توقف بهینه. این دوره معادل STAT 5601 در دانشگاه کارلتون است.

جزء درس: خواندن

پیش نیاز: STAT 3106 یا MAT 4371 .

مدل‌های تصادفی MAT 5198 (3 واحد)

سیستم‌های مارکوف، شبکه‌های تصادفی، شبکه‌های صف، فرآیندهای فضایی، روش‌های تقریب در فرآیندهای تصادفی و تئوری صف. برنامه های کاربردی برای مدل سازی و تحلیل سیستم های ارتباطی کامپیوتری و سایر شبکه های توزیع شده. این دوره معادل ریاضی 5701 در دانشگاه کارلتون است.

جزء درس: خواندن

مباحث ریاضی ترکیبی MAT 5301 (3 واحد)

این دوره معادل ریاضی 5609 در دانشگاه کارلتون است.

جزء درس: خواندن

بهینه سازی خطی MAT 5303 (3 واحد)

این دوره معادل ریاضی 5801 در دانشگاه کارلتون است.

جزء درس: خواندن

بهینه سازی غیرخطی MAT 5304 (3 واحد)

این دوره معادل ریاضی 5803 در دانشگاه کارلتون است.

جزء درس: خواندن

موضوعات تحقیق در عملیات MAT 5307 (3 واحد)

این دوره معادل ریاضی 5804 در دانشگاه کارلتون است.

جزء درس: خواندن

مباحث MAT 5308 در طراحی الگوریتم (3 واحد)

این دوره معادل ریاضی 5805 در دانشگاه کارلتون است.

جزء درس: خواندن

MAT 5309 تجزیه و تحلیل هارمونیک روی گروه ها (3 واحد)

این دوره معادل ریاضی 6002 در دانشگاه کارلتون است.

جزء درس: خواندن

موضوعات توپولوژی MAT 5312 (3 واحد)

این دوره معادل ریاضی 6201 در دانشگاه کارلتون است.

جزء درس: خواندن

مباحث MAT 5313 در احتمال و آمار (3 واحد)

این دوره معادل ریاضی 6507 در دانشگاه کارلتون است.

جزء درس: خواندن

مباحث MAT 5314 در احتمال و آمار (3 واحد)

این دوره معادل ریاضی 6508 در دانشگاه کارلتون است.

جزء درس: خواندن

MAT 5315 طراحی پیشرفته نظرسنجی (3 واحد)

جزء درس: خواندن

MAT 5317 تجزیه و تحلیل داده های طبقه بندی شده (3 واحد)

تجزیه و تحلیل جداول یک طرفه و دو طرفه تاریخ اسمی. جداول چند بعدی احتمالی، مدل های ورود به سیستم خطی. تست های تقارن، همگنی حاشیه ای در جداول مربع. جداول ناقص؛ جداول با دسته بندی های مرتب شده؛ حاشیه های ثابت، مدل های لجستیک با پاسخ باینری. اقدامات انجمن و توافق؛ کاربردهای بیولوژیکی این دوره معادل STAT 5602 در دانشگاه کارلتون است.

جزء درس: خواندن

MAT 5318 قابلیت اطمینان و تجزیه و تحلیل بقا (3 واحد)

این دوره معادل STAT 5603 در دانشگاه کارلتون است.

جزء درس: خواندن

مباحث MAT 5319 در احتمال و آمار (3 واحد)

این دوره معادل ریاضی 6507 در دانشگاه کارلتون است.

جزء درس: خواندن

+ نوشته شده در چهارشنبه بیست و چهارم اسفند ۱۴۰۱ ساعت 18:34 توسط علی رضا نقش نیلچی |

11-برنامه ها و دوره ها دانشکده ریاضی در دانشگاه اوتاوا

MAT 5142 جبر II: گروه ها و نظریه گالوا (3 واحد)

کنش های گروهی، معادله کلاس، قضایای سایلو، سری مرکزی، ترکیب و مشتق شده، قضیه جردن-هولدر، پسوند میدان و چندجمله ای های حداقل، بسته شدن جبری، پسوندهای قابل تفکیک، پسوند حلقه انتگرال، گروه های گالوا، قضیه بنیادی نظریه گالوا، میدان های محدود، سیکلوتومیک بسط میدان، قضیه اساسی جبر، بسط های ماورایی. این دوره معادل ریاضی 5109 در دانشگاه کارلتون است.

جزء درس: خواندن

MAT 5143 Lie Algebra (3 واحد)

این دوره معادل ریاضی 5104 در دانشگاه کارلتون است.

جزء درس: خواندن

MAT 5144 جبر جابجایی (3 واحد)

طیف اولیه یک حلقه جابجایی (به عنوان فضای توپولوژیکی)؛ محلی سازی حلقه ها و ماژول ها؛ حاصل ضرب تانسور ماژول ها و جبرها. Nullstellensatz هیلبرت و پیامدهای جبرهای محدود تولید شده. ابعاد Krull یک حلقه؛ وابستگی یکپارچه، بالا رفتن، پایین رفتن. Noether هنجارسازی لم و نظریه بعد برای جبرهای محدود تولید شده در یک میدان. حلقه های نوتر و قضیه پایه هیلبرت. مقدمه‌ای بر انواع جبری وابسته و شکل‌های آنها. این دوره معادل ریاضی 5001 در دانشگاه کارلتون است.

جزء درس: خواندن

نظریه گروه MAT 5145 (3 اعتبار)

این دوره معادل ریاضی 5106 در دانشگاه کارلتون است.

جزء درس: خواندن

حلقه ها و ماژول های MAT 5146 (3 واحد)

این دوره معادل ریاضی 5103 در دانشگاه کارلتون است.

جزء درس: خواندن

MAT 5147 جبر همسانی و نظریه مقوله (3 واحد)

این دوره معادل ریاضی 5108 در دانشگاه کارلتون است.

جزء درس: خواندن

MAT 5148 Groups Representations and Applications (3 واحد)

این دوره معادل ریاضی 5102 در دانشگاه کارلتون است.

جزء درس: خواندن

MAT 5149 هندسه جبری (3 واحد)

مروری کوتاه بر جبر جابجایی، Nullstellensatz هیلبرت، مجموعه‌های جبری و توپولوژی زاریسکی. انواع آفین و تصویری در زمینه های بسته جبری. توابع منظم و نقشه های منطقی. موضوعات اضافی انتخاب شده از: رابطه انواع بر روی اعداد مختلط به منیفولدهای تحلیلی مختلط، جنس، مقسوم‌کننده‌ها، دسته‌های خط، قضیه ریمان-روش، قضیه بزو. این دوره معادل ریاضی 5002 در دانشگاه کارلتون است.

جزء درس: خواندن

مباحث هندسه MAT 5150 (3 واحد)

این دوره معادل ریاضی 5201 در دانشگاه کارلتون است.

جزء درس: خواندن

MAT 5151 توپولوژی I (3 واحد)

فضاهای توپولوژیکی، توپولوژی های محصول و شناسایی، بدیهیات شمارش پذیری و جداسازی، فشردگی، اتصال، همتوپی، گروه بنیادی، همگرایی خالص و فیلتر. این دوره معادل ریاضی 5205 در دانشگاه کارلتون است.

جزء درس: خواندن

MAT 5152 Topology II (3 واحد)

پوشش فضاها، همسانی از طریق بدیهیات Eilenberg-Steenrod، کاربردها، ساخت یک تابع همسانی. این دوره معادل ریاضی 5206 در دانشگاه کارلتون است.

جزء درس: خواندن

پیش نیازها: MAT 3143 و MAT 5151 (MATH 3100 و MATH 5205).

منیفولدهای متفاوت MAT 5155 (3 واحد)

این دوره معادل ریاضی 5208 در دانشگاه کارلتون است.

جزء درس: خواندن

MAT 5158 Lie Groups (3 واحد)

این دوره معادل ریاضی 6104 در دانشگاه کارلتون است.

جزء درس: خواندن

رمزنگاری ریاضی MAT 5160 (3 واحد)

تجزیه و تحلیل روش های رمزنگاری مورد استفاده در احراز هویت و حفاظت از داده ها، با توجه خاص به ریاضیات اساسی، به عنوان مثال هندسه جبری، نظریه اعداد، و میدان های محدود. موضوعات پیشرفته در رمزنگاری کلید عمومی: RSA و فاکتورسازی اعداد صحیح، دیفی-هلمن، لگاریتم های گسسته، منحنی های بیضوی. موضوعات در تحقیقات جاری این دوره معادل ریاضی 5300 در دانشگاه کارلتون است.

جزء درس: خواندن

پیش نیاز: جبر ممتاز در مقطع کارشناسی شامل نظریه گروه و رشته های محدود.

منطق ریاضی MAT 5161 (3 واحد)

یک دوره کارشناسی ارشد در منطق ریاضی. منطق گزاره ای و محمولی، نظریه اثبات، بریدگی گنتزن، کامل بودن، فشردگی، مدل های هنکین، نظریه مدل، محاسبات و غیرقابل تصمیم گیری. موضوعات ویژه (مجاز زمان) بسته به علایق مربی و مخاطب. این دوره معادل ریاضی 5301 در دانشگاه کارلتون است.

جزء درس: خواندن

پیش نیاز: ممتاز جبر، تجزیه و تحلیل و توپولوژی (یا اجازه استاد).

MAT 5162 مبانی ریاضی علوم کامپیوتر (3 واحد)

مبانی زبان های تابعی، محاسبات لامبدا (تایپ شده، چند شکلی تایپ شده، بدون تایپ)، ایزومورفیسم کری هاوارد، اثبات ها به عنوان برنامه، نظریه نرمال سازی و بازنویسی، معناشناسی عملیاتی، تخصیص نوع، مقدمه ای بر معناشناسی معنایی برنامه ها، برنامه نویسی نقطه ثابت. موضوعات انتخاب شده از: معناشناسی معنایی برای محاسبات لامبدا، مدل های زبان های برنامه نویسی، نظریه پیچیدگی و منطق محاسبات، مدل های سیستم های همزمان و توزیع شده و غیره. این دوره معادل ریاضی 6807 در دانشگاه کارلتون است.

جزء درس: خواندن

پیش نیاز: در مقطع کارشناسی جبر و توپولوژی یا تجزیه و تحلیل را کسب کند. آشنایی با منطق مفید است.

نظریه اعداد تحلیلی MAT 5163 (3 واحد)

این دوره معادل ریاضی 5305 در دانشگاه کارلتون است.

جزء درس: خواندن

MAT 5164 نظریه اعداد جبری (3 واحد)

این درس معادل ریاضی 5306 در دانشگاه کارلتون است.

جزء درس: خواندن

MAT 5165 Theory of Automata (3 واحد)

این دوره معادل ریاضی 5605 در دانشگاه کارلتون است.

جزء درس: خواندن

MAT 5167 رسمی تجزیه و تحلیل زبان و نحو (3 اعتبار)

این دوره معادل MATH/COMP 5807 در دانشگاه کارلتون است.

جزء درس: خواندن

نظریه همسانی MAT 5168 (3 واحد)

این دوره معادل ریاضی 5202 در دانشگاه کارلتون است.

جزء درس: خواندن

MAT 5169 مبانی هندسه (3 واحد)

این دوره معادل ریاضی 5207 در دانشگاه کارلتون است.

جزء درس: خواندن

MAT 5170 نظریه احتمال I (3 واحد)

فضاهای احتمال، متغیرهای تصادفی، مقادیر مورد انتظار به عنوان انتگرال، توزیع مشترک، معیارهای مستقل و محصول، توابع توزیع تجمعی و بسط اندازه‌گیری‌های احتمال، لم‌های Borel-Cantelli، مفاهیم همگرایی، دنباله‌های مستقل توزیع شده یکسان متغیرهای تصادفی. این دوره معادل STAT 5708 در دانشگاه کارلتون است.

جزء درس: خواندن

پیش نیازها: MAT 3125 و MAT 3172 (MATH 3001، MATH 3002 و MATH 3500).

MAT 5171 نظریه احتمال II (3 واحد)

قوانین اعداد بزرگ، توابع مشخصه، قضیه حد مرکزی، احتمالات و انتظارات شرطی، خواص اساسی و قضایای همگرایی برای مارتینگل ها، مقدمه ای بر حرکت براونی. این دوره معادل ریاضی 5709 در دانشگاه کارلتون است.

جزء درس: خواندن

پیش نیاز: MAT 5170 (STAT 5708).

موضوعات MAT 5172 در فرآیندهای تصادفی (3 واحد)

این دوره معادل STAT 5108 در دانشگاه کارلتون است.

جزء درس: خواندن

+ نوشته شده در چهارشنبه بیست و چهارم اسفند ۱۴۰۱ ساعت 18:33 توسط علی رضا نقش نیلچی |

10-برنامه ها و دوره ها دانشکده ریاضی در دانشگاه اوتاوا

نظریه نمایش MAT 4343 (3 اعتبار)

نظریه بازنمایی گروه ها و جبرها: کاراکترها، نمایش های تقلیل ناپذیر، نمایش های القایی، عملگرهای درهم تنیده.

جزء: سخنرانی

پیش نیازها: MAT 3141 یا MAT 3543 .

نظریه گراف MAT 4348 (3 اعتبار)

زنجیره ها و چرخه ها، درختان، اتصال، مسیرهای اویلری و چرخه های همیلتونی، رنگ آمیزی لبه ها، مجموعه ها و دسته های پایدار، رنگ آمیزی رئوس، نمودارهای مسطح، نمودارهای جهت دار.

جزء: سخنرانی

پیش نیازها: ( MAT 2748 یا MAT 3748 )، ( MAT 2541 یا MAT 2543 ).

نظریه ترکیبی MAT 4349 (3 اعتبار)

اصل گنجاندن -- طرد، تولید توابع و تقسیم اعداد صحیح، نظریه شمارش پولیا، مربع لاتین، سیستم های سه گانه اشتاینر، صفحات بلوکی، هندسه های محدود، مجموعه های جزئی مرتب شده و شبکه ها.

جزء: سخنرانی

پیش نیازها: MAT 2348 , MAT 2543 , MAT 2541 .

احتمال کاربردی MAT 4371 (3 اعتبار)

مقدمه ای بر فرآیندهای تصادفی از دیدگاه فرآیندهای مارکوف. بررسی مبانی احتمال، قضایای حدی و شرطی. فرآیند پواسون قضایای حدی برای فرآیندهای احیا کننده زمان گسسته و پیوسته فرآیند مارکوف. فرآیندهای مارکوف پنهان در فضای حالت محدود. برنامه های کاربردی انتخاب شده از: پردازش سیگنال، صف بندی، اقتصاد، امور مالی و علم اکچوئری.

جزء: سخنرانی

پیش نیازها: MAT 2771 , ( MAT 2541 یا MAT 2742 ).

MAT 4372 ریاضیات مالی (3 واحد)

بررسی انتظارات مشروط و مقدمه ای بر مارتینگال، زمان توقف و پاکت اسنل. نرخ بهره و ارزش فعلی، ارزش گذاری گزینه زمانی گسسته. بازنگری توزیع نرمال چند متغیره با کاربرد در نظریه پورتفولیو مارکویتز مقدمه ای بر حرکت براونی و فرمول بلک اسکولز برای گزینه های اروپایی.

جزء: سخنرانی

پیش نیاز: MAT 2375 , MAT 3572

MAT 4373 یادگیری ماشین و آمار (3 اعتبار)

تجزیه و تحلیل متمایز، تجزیه و تحلیل اجزای اصلی، ماشین‌های بردار پشتیبان. بازتولید کرنل فضاهای هیلبرت و روش های هسته. شبکه های عصبی؛ نظریه VC، یادگیری PAC. موضوعات اضافی مانند: مدل سازی بیزی، یادگیری چندگانه، تقویت.

جزء: سخنرانی

پیش نیاز: MAT 2122 , MAT 2771 , MAT 2775 , MAT 3373 .

حساب آماری مدرن MAT 4374 (3 اعتبار)

شبیه سازی، روش رد و نمونه گیری ترجیحی. برنامه های کاربردی برای زنجیره های مارکوف مونت کارلو. نمونه برداری مجدد و سایر روش های عددی مانند بوت استرپ و جک نایف با کاربردها. روش های هموارسازی برای تخمین توابع.

جزء: سخنرانی

پیش نیازها: MAT 3572 , ( MAT 3775 یا MAT 3778 ).

روش های آمار چند بعدی MAT 4375 (3 اعتبار)

توزیع نرمال چند بعدی: خواص، تخمین، آزمون فرضیه. موضوعات انتخاب شده از موارد زیر: رگرسیون چند بعدی، تحلیل واریانس و کوواریانس، تمایز با اشکال خطی، تحلیل عاملی، همبستگی متعارف. تجزیه و تحلیل داده ها با استفاده از نرم افزارهای آماری.

جزء: سخنرانی

پیش نیازها: ( MAT 2541 یا MAT 2742 )، ( MAT 3375 یا MAT 3378 ).

MAT 4376 فصل های منتخب در آمار (3 اعتبار)

فصل های منتخب در آمار.

جزء: سخنرانی

پیش نیاز: MAT 2375 (بسته به موضوع دوره ممکن است پیش نیازهای اضافی اعمال شود).

MAT 4377 فصل های منتخب در احتمال کاربردی (3 اعتبار)

فصل های منتخب در احتمالات.

جزء: سخنرانی

پیش نیاز: MAT 2371 (بسته به موضوع دوره ممکن است پیش نیازهای اضافی اعمال شود).

MAT 4378 تجزیه و تحلیل داده های طبقه بندی شده در آمار زیستی (3 اعتبار)

جداول احتمالی چند عاملی مدل های خطی تعمیم یافته برای داده های باینری و طبقه بندی شده رگرسیون لجستیک: استنتاج و اعتبارسنجی مدل ها. مدل های لاگ خطی و لاجیت برای جداول فرکانس. نمونه هایی از علوم زیستی در کلاس از نرم افزارهای آماری استفاده خواهد شد.

جزء: سخنرانی

پیش نیاز: MAT 3375 .

MAT 4387 تئوری و عمل بهینه سازی (3 واحد)

مسائل بهینه سازی، برنامه ریزی غیرخطی، بهینه سازی بدون قید، تحدب و اجبار، قضایای وجود، روش نیوتن و روش گرادیان، بهینه سازی با قیود، روش گرادیان با پیش بینی، روابط کوهن تاکر، دوگانگی، روش اوزاوا. برنامه ریزی خطی، روش سیمپلکس.

جزء: سخنرانی

پیش نیازها: ( MAT 2724 یا MAT 2784 )، (MAT 2521 یا (MAT 2520, MAT 2722 ) یا ( MAT 2522 , MAT 2525 ).

MAT 4799 فصل های منتخب در ریاضیات (3 واحد)

روی موضوعات پیشرفته کار کنید.

جزء: سخنرانی

پیش نیاز: 24 واحد دروس MAT در سطح 3000 یا بالاتر.

پروژه تحقیقاتی کارشناسی MAT 4900 (3 واحد / 3 واحد)

دانشجو یک پروژه تحقیقاتی یک ترم را زیر نظر یک یا چند نفر از اعضای گروه انجام خواهد داد. دانشجو گزارشی از تحقیقات خود می نویسد و سمیناری را در مورد موضوع پروژه و مشارکت خود ارائه می دهد. این دوره برای دانشجویان علاقه مند به ادامه تحصیلات عالی طراحی شده است. / دانشجو پروژه یک ترم تحصیلی را که زیر نظر یک یا چند نفر از اعضای هیأت علمی در گروه انجام می شود، انجام خواهد داد. دانشجو گزارشی می نویسد و سمیناری در مورد برخی از جنبه های تحقیق و مشارکت خود ارائه می دهد. این دوره برای دانشجویان علاقه مند به ادامه تحصیل در مقطع کارشناسی ارشد در نظر گرفته شده است.

جزء / جزء درس: تحقیق / پژوهش

پیش نیاز: دانش آموز باید در سال چهارم در یک برنامه ممتاز در ریاضیات یا آمار باشد، معدل حداقل 7.0 داشته باشد و از گروه مجوز بگیرد. / پیش نیازها: دانشجو باید در سال چهارم یک برنامه افتخاری در ریاضیات یا آمار با حداقل CGPA 7.0 باشد و مجوز دپارتمان را دریافت کند.

سمینار / سمینار MAT 4992 (3 واحد / 3 واحد)

ارائه توسط دانش آموزان در مورد موضوعات منتخب. / ارائه دانشجویی موضوعات منتخب.

جریان / جزء دوره: سخنرانی / خواندن

پیش نیازها: (9 اعتبار از MAT 3520 , MAT 3521 , MAT 3541, MAT 3543 ) یا (9 اعتبار از MAT 3120 , MAT 3521 , MAT 3543 , MAT 3741 ). / پیش نیازها: (9 اعتبار از MAT 3120 , MAT 3121 , MAT 3141 , MAT 3143 ) یا (9 اعتبار از MAT 3120 , MAT 3121 , MAT 3143 , MAT 3341 ).

MAT 4995 موضوعات منتخب در ریاضیات / موضوعات ویژه در ریاضیات (3 واحد / 3 واحد)

روی موضوعات پیشرفته کار کنید. / انتخاب موضوعات پیشرفته.

جریان / جزء دوره: سخنرانی / خواندن

پیش نیاز: 12 واحد درسی در ریاضیات (MAT) در سطح 3000 یا بالاتر. بسته به موضوع دوره، پیش نیازهای اضافی ممکن است اعمال شود. / پیش نیاز: 12 واحد درسی در ریاضیات (MAT) در سطح 3000 به بالا. بسته به موضوع ممکن است پیش نیازهای اضافی اعمال شود

MAT 4996 موضوعات منتخب در ریاضیات کاربردی / موضوعات ویژه در ریاضیات کاربردی (3 واحد / 3 واحد)

مباحث عمیق ریاضیات کاربردی. / منتخب مباحث پیشرفته در ریاضیات کاربردی.

جریان / جزء دوره: سخنرانی / خواندن

پیش نیاز: تایید استاد.

MAT 5105 ریاضیات کاربردی گسسته I: Gra. تئوری (3 واحد)

مسیرها و چرخه ها، درختان، اتصال، تورهای اویلر و چرخه های همیلتون، رنگ آمیزی لبه ها، مجموعه ها و دسته های مستقل، رنگ آمیزی راس، نمودارهای مسطح، نمودارهای جهت دار. موضوعات انتخاب شده از یک یا چند حوزه زیر: نظریه گراف جبری، نظریه توپولوژیک، نمودارهای تصادفی. این دوره معادل ریاضی 5818 در دانشگاه کارلتون است.

جزء درس: خواندن

بهینه سازی ترکیبی MAT 5106 (3 واحد)

تئوری جریان شبکه و مطالب مرتبط موضوعات شامل کوتاه ترین مسیرها، حداقل درختان پوشا، حداکثر جریان، جریان حداقل هزینه خواهد بود. تطبیق بهینه در نمودارهای دوبخشی. این دوره معادل ریاضی 5808 در دانشگاه کارلتون است.

جزء درس: خواندن

MAT 5107 ریاضیات کاربردی گسسته II: شمارش ترکیبی (3 واحد)

توابع مولد معمولی و نمایی؛ فرمول های محصول؛ جایگشت ها نت برگ; درختان ریشه دار؛ چرخه شاخص؛ روش WZ وارونگی لاگرانژ؛ تجزیه و تحلیل تکینگی توابع مولد و مجانبی موضوعات انتخاب شده از یک یا چند حوزه زیر: نمودارهای تصادفی، ساختارهای ترکیبی تصادفی، توابع فراهندسی. این درس معادل ریاضی 5819 در دانشگاه کارلتون است.

جزء درس: خواندن

MAT 5121 Introduction to Hilbert Space (3 واحد)

این دوره معادل ریاضی 5009 در دانشگاه کارلتون است.

جزء درس: خواندن

MAT 5122 Banach Algebras (3 واحد)

این دوره معادل ریاضی 5003 در دانشگاه کارلتون است.

جزء درس: خواندن

MAT 5125 Real Analysis I (3 اعتبار)

اندازه گیری کلی و انتگرال، اندازه گیری و انتگرال لبگ روی R، قضیه فوبینی، قضیه لبگ-رادون-نیکودیم، تداوم و تمایز مطلق، Lp-فضاها. موضوعات منتخب مانند نظریه دانیل-استون. این دوره معادل ریاضی 5007 در دانشگاه کارلتون است.

جزء درس: خواندن

پیش نیاز: MAT 3125 (MATH 3001 و MATH 3002).

MAT 5126 Real Analysis II (3 واحد)

فضاهای باناخ و هیلبرت، عملگرهای خطی محدود، فضاهای دوگانه. موضوعات انتخاب شده از: توپولوژی های ضعیف و ضعیف، قضیه آلاوغلو، عملگرهای فشرده، حساب دیفرانسیل در فضاهای Banach، قضایای نمایش ریس. این دوره معادل ریاضی 5008 در دانشگاه کارلتون است.

جزء درس: خواندن

پیش نیاز: MAT 5125 (MATH 5007).

تجزیه و تحلیل مجتمع MAT 5127 (3 واحد)

این دوره معادل ریاضی 5005 در دانشگاه کارلتون است.

جزء درس: خواندن

MAT 5131 معادلات دیفرانسیل معمولی I (3 واحد)

یک یا دو سیستم خطی تخصصی، راه حل اساسی. سیستم های غیرخطی، وجود و یکتایی، جریان. تعادل، راه حل های تناوبی، پایداری منیفولدهای ثابت و نظریه هذلولی. موضوعات برگرفته شده، اما نه محدود به: اغتشاش و روش های مجانبی، اشکال عادی و دوشاخه ها، دینامیک جهانی. این دوره معادل ریاضی 5405 در دانشگاه کارلتون است.

جزء درس: خواندن

MAT 5133 معادلات دیفرانسیل جزئی I (3 واحد)

معادلات مرتبه اول، روش مشخصه ها، طبقه بندی معادلات مرتبه دوم، جداسازی متغیرها، توابع گرین. فضاهای Lp و Soboloev، توزیع ها، فرمول بندی تغییرات و جواب های ضعیف، قضیه لاکس-میلگرام، تقریب گالرکین. PD های سهموی معادلات موج، سیستم های هذلولی، PD های غیرخطی، معادلات انتشار واکنش، سیستم های دینامیکی بی بعدی، نظم. این درس معادل ریاضی 5406 در دانشگاه کارلتون است.

جزء درس: خواندن

مجوز اداره الزامی است.

مباحث MAT 5134 در معادلات دیفرانسیل (3 واحد)

این درس معادل ریاضی 5407 در دانشگاه کارلتون است.

جزء درس: خواندن

MAT 5141 جبر I: حلقه ها و ماژول ها (3 واحد)

ماژول ها و حلقه های نوتری و آرتینی. مجموعه‌های جبری، آرمان‌های در حال محو، قضیه پایه هیلبرت، آرمان‌های رادیکال، هیلبرت نولستلن‌ساتز. محلی سازی حلقه ها و ماژول ها. حاصل ضرب تانسور ماژول ها و جبرها. حلقه ها و مدول های نیمه ساده، لم شور، قضیه چگالی جاکوبسون، قضیه آرتین-ودربرن. دنباله های دقیق کوتاه، ماژول های رایگان، ماژول های تصویری، ماژول های تزریقی، ماژول های مسطح. این دوره معادل ریاضی 5107 در دانشگاه کارلتون است.

جزء درس:: خواندن

+ نوشته شده در چهارشنبه بیست و چهارم اسفند ۱۴۰۱ ساعت 18:31 توسط علی رضا نقش نیلچی |

9-برنامه ها و دوره ها دانشکده ریاضی در دانشگاه اوتاوا

نظریه گراف MAT 4348 (3 اعتبار)

مسیرها و چرخه ها، درختان، اتصال، تورهای اویلر و چرخه های همیلتون، رنگ آمیزی لبه ها، مجموعه ها و دسته های مستقل، رنگ آمیزی راس، نمودارهای مسطح، نمودارهای جهت دار.

جزء درس: خواندن

پیش نیازها: ( MAT 2348 یا MAT 3348 )، ( MAT 2141 or MAT 2143 ).

نظریه ترکیبی MAT 4349 (3 اعتبار)

اصل گنجاندن -- طرد، تولید توابع و پارتیشن های اعداد صحیح، نظریه شمارش پولیا، مربع های لاتین، سیستم های سه گانه اشتاینر، طرح های بلوک، هندسه های محدود، پوست ها و شبکه ها.

جزء درس: خواندن

پیش نیاز: MAT 2348 , MAT 2143 , MAT 2141 .

احتمال کاربردی MAT 4371 (3 واحد)

مقدمه ای بر فرآیندهای تصادفی، با تاکید بر فرآیندهای مارکوف. بررسی احتمالات پایه، قضایای حدی و شرطی. فرآیند ماهی قضایای حدی برای فرآیندهای احیا کننده فرآیندهای مارکوف زمان گسسته و زمان پیوسته. فرآیندهای مارکوف پنهان در فضاهای حالت محدود. برنامه های کاربردی انتخاب شده از پردازش سیگنال، تئوری صف، اقتصاد، امور مالی و علوم اکچوئری.

جزء درس: خواندن

پیش نیازها: MAT 2371 , ( MAT 2141 یا MAT 2342 ).

MAT 4372 ریاضیات مالی (3 واحد)

بررسی انتظارات مشروط و مقدمه ای بر مارتینگال، زمان توقف و پاکت اسنل. نرخ بهره و ارزش فعلی، قیمت گذاری گزینه زمانی گسسته. بررسی نرمال چند متغیره با کاربردهای نظریه پورتفولیو مارکویتز مقدمه ای بر حرکت براونی و فرمول بلک اسکولز برای گزینه های اروپایی.

جزء درس: خواندن

پیش نیاز: MAT 2375 , MAT 3172 .

یادگیری ماشین آماری MAT 4373 (3 واحد)

تجزیه و تحلیل متمایز، تجزیه و تحلیل اجزای اصلی، ماشین‌های بردار پشتیبان. بازتولید کرنل فضاهای هیلبرت و روش های هسته. شبکه های عصبی؛ نظریه VC; یادگیری CAP. موضوعات اضافی ممکن است شامل موارد زیر باشد: مدل سازی بیزی، یادگیری چندگانه، تقویت.

جزء درس: خواندن

پیش نیازها: MAT 2122 , MAT 2371 , MAT 2375 , MAT 3373 .

MAT 4374 آمار محاسباتی مدرن (3 اعتبار)

شبیه سازی شامل روش رد و نمونه گیری اهمیت. برنامه های کاربردی برای زنجیره های مونت کارلو مارکوف. روش‌های نمونه‌گیری مجدد مانند bootstrap و jackknife با کاربردها. روش های هموارسازی در تخمین منحنی.

جزء درس: خواندن

پیش نیازها: MAT 3172 , ( MAT 3375 یا MAT 3378 ).

روش‌های آماری چند متغیره MAT 4375 (3 واحد)

توزیع نرمال چند متغیره: خواص، تخمین، آزمایش. موضوعات انتخاب شده از رگرسیون چند متغیره، تحلیل واریانس و کوواریانس، تحلیل افتراق خطی، تحلیل مؤلفه و عامل، همبستگی متعارف. تجزیه و تحلیل داده ها با استفاده از بسته های نرم افزاری آماری.

جزء درس: خواندن

پیش نیازها: ( MAT 2141 یا MAT 2342 )، ( MAT 3375 یا MAT 3378 ).

موضوعات MAT 4376 در آمار (3 واحد)

موضوعات منتخب در آمار.

جزء درس: خواندن

پیش نیاز: MAT2375 (بسته به موضوع ممکن است پیش نیازهای اضافی اضافه شود).

مباحث احتمال کاربردی MAT 4377 (3 واحد)

مباحث در نظریه احتمال.

جزء درس: خواندن

پیش نیاز: MAT 2371 (بسته به موضوع ممکن است پیش نیازهای اضافی اعمال شود).

MAT 4378 تجزیه و تحلیل داده های طبقه بندی شده در آمار زیستی (3 واحد)

جداول احتمالی چند طرفه مدل های خطی تعمیم یافته برای داده های باینری و شمارش. رگرسیون لجستیک؛ استنباط و تایید مدل مدل های لاگ خطی و لاجیت برای جداول فرکانس چندراهی. برنامه های کاربردی برگرفته از علوم زیستی در این دوره از بسته های کامپیوتری آماری استفاده خواهد شد.

جزء درس: خواندن

پیش نیاز: MAT 3375 .

MAT 4387 Optimization: Theory and Practice (3 واحد)

مسائل بهینه سازی، برنامه ریزی غیرخطی، بهینه سازی نامحدود، تحدب و اجبار، نظریه وجود، شیب و روش های نیوتنی بهینه سازی مقید، روش گرادیان با طرح ریزی، روابط کوهن تاکر، دوگانگی، روش اوزاوا. برنامه ریزی خطی، روش سیمپلکس.

جزء درس: خواندن

پیش نیازها: (MAT 2120, MAT 2121) یا ( MAT 2122 , MAT 2125 ) یا ( MAT 2120, MAT 2322 ), ( MAT 2324 یا MAT 2384 ).

MAT 4399 مباحث ویژه در ریاضیات (3 واحد)

منتخب موضوعات پیشرفته

جزء درس: خواندن

پیش نیاز: 24 واحد در دوره های MAT در سطح 3000 به بالا.

MAT 4124 مقدمه ای بر تحلیل عملکردی (3 اعتبار)

معرفی فضاهای هیلبرت و باناخ با تاکید بر فضاهای هیلبرت. سری فوریه و تبدیل. عملگرهای خطی در فضاهای هیلبرت مقدمه ای بر تحلیل طیفی موضوعات انتخاب شده از: عملگرهای فشرده، عملگرهای نامحدود و غیره.

جزء: سخنرانی

پیش نیاز: MAT 3520 .

MAT 4125 Measurement and Integration I (3 اعتبار)

اندازه گیری و ادغام، اندازه گیری و انتگرال گیری لبگ بر روی R، قضیه فوبینی، قضیه لبگ-رادون-نیکودیم، تداوم و مشتق مطلق، فضاهای Lp.

جزء: سخنرانی

پیش نیاز: MAT 3520 .

MAT 4126 Measurement and Integration II (3 اعتبار)

فضاهای باناخ و فضاهای هیلبرت، عملگرهای خطی محدود، فضاهای دوگانه، موضوعات مکمل.

جزء: سخنرانی

پیش نیاز: MAT 4525 .

MAT 4130 مقدمه ای بر معادلات دیفرانسیل جزئی (3 واحد)

مدل سازی با معادلات دیفرانسیل جزئی (PDEs)، PDE های ابتدایی و روش جداسازی متغیرها، طبقه بندی PDE ها، PDE های خطی درجه یک و روش مشخصه ها، حداکثر اصول برای PDE های بیضوی و حل کلاسیک معادله لاپلاس، توابع گرین ، روش های تنوع. معادلات گرما و موج

جزء: سخنرانی

پیش نیازها: MAT 2522 , MAT 2525 , ( MAT 2541 or MAT 2742 ) , ( MAT 2724 or MAT 2784 ).

MAT 4141 Rings and Modules II (3 اعتبار)

ماژول ها و حلقه های نوتری و آرتینی. مجموعه‌های جبری، آرمان‌های آنها، قضیه پایه هیلبرت، آرمان‌های رادیکال، هیلبرت نولستلن‌ساتز. محل حلقه ها و ماژول ها حاصل ضرب تانسور ماژول ها و جبرها. حلقه ها و مدول های نیمه ساده، لم شور، قضیه چگالی جاکوبسون، قضیه آرتین-ودربرن. دنباله های دقیق کوتاه، ماژول های رایگان، ماژول های تصویری، ماژول های تزریقی، ماژول های مسطح.

جزء: سخنرانی

پیش نیازها: MAT 3141 یا MAT 3543 .

MAT 4142 مقدمه ای بر جبرهای دروغ (3 اعتبار)

ساختار جبرهای Lie با ابعاد محدود که قابل حل، nilpotent یا نیمه ساده هستند.

جزء: سخنرانی

پیش نیاز: MAT 3141 یا MAT 3543 .

MAT 4143 Groups and Galois Theory (3 اعتبار)

کنش های گروهی، فرمول کلاس، قضایای سایلو، سری مرکزی، ترکیب و مشتق، قضیه جردن-هولدر، امتداد میدان ها و چندجمله ای های حداقل، بسته جبری، پسوندهای قابل تفکیک، پسوند اعداد صحیح حلقه ها، گروه های گالوا، قضیه بنیادی نظریه گالوا، میدان های محدود ، پسوندهای سیکلوتومیک، قضیه اساسی جبر، پسوندهای متعالی.

جزء: سخنرانی

پیش نیاز: MAT 3541 یا MAT 3543 یا ( MAT 2541 , MAT 2543 , MAT 3743 ).

MAT 4144 مقدمه ای بر گروه های دروغ (3 اعتبار)

گروه های خطی، نقشه های نمایی، مطابقت دروغ، هممورفیسم ها و پوشش ها، زیر گروه های بسته، گروه های کلاسیک، زیرگروه های کارتن، گروه های بنیادی، انواع، فضاهای همگن، گروه های دروغ عمومی.

جزء: سخنرانی

پیش نیازها: MAT 2543 ، MAT 3520 ، (MAT 3541 یا MAT 3543 یا MAT 3741 ).

توپولوژی عمومی MAT 4153 (3 اعتبار)

فضاهای توپولوژیکی، توپولوژی محصول و توپولوژی ضریب، بدیهیات شمارش پذیری و بدیهیات جداسازی، فشردگی، متریزاسیون.

جزء: سخنرانی

پیش نیاز: MAT 3120 یا MAT 3553 .

MAT 4154 مقدمه ای بر هندسه جبری (3 اعتبار)

خلاصه جبر جابجایی، قضیه صفرهای هیلبرت، مجموعه های جبری، توپولوژی زاریسکی. منیفولدهای Affine و Projective بر روی یک میدان بسته جبری. توابع منظم و کاربردهای منطقی. موضوعات انتخاب شده از: رابطه بین انواع پیچیده جبری و انواع تحلیلی پیچیده، جنسیت، مقسوم‌عام، دسته‌های خط، قضیه ریمان-روخ، قضیه بزو.

جزء: سخنرانی

پیش نیاز: MAT 3543 .

MAT 4157 توپولوژی جبری I (3 اعتبار)

پوشش فضاها، همسانی از طریق بدیهیات آیلنبرگ-استینرود، کاربردها، ساخت یک تابع همسانی.

جزء: سخنرانی

پیش نیازها: MAT 3543 , ( MAT 3553 یا MAT 3520 ).

MAT 4158 توپولوژی جبری II (3 اعتبار)

فصول منتخب توپولوژی جبری.

جزء: سخنرانی

پیش نیاز: MAT 3120 , MAT 3543 .

مباحث MAT 4162 در منطق ریاضی (3 واحد)

انتخاب موضوعاتی مانند نظریه مدل، تحلیل غیر استاندارد، نظریه تابع بازگشتی، نظریه مجموعه ها یا فلسفه ریاضیات.

جزء: سخنرانی

پیش نیاز: MAT 3361 .

MAT 4167 فصل های منتخب: نظریه اعداد (3 اعتبار)

فصول منتخب در نظریه اعداد تحلیلی، نظریه اعداد جبری، تقریب دیوفانتین، اشکال مدولار یا هندسه حسابی.

جزء: سخنرانی

پیش نیاز: MAT 3543 .

MAT 4170 نظریه احتمال I (3 واحد)

فضاهای احتمالی، متغیرهای تصادفی، انتظارات ریاضی به‌عنوان یک انتگرال، قوانین مشترک، اندازه‌گیری استقلال و محصول، توزیع و گسترش اندازه‌گیری‌های احتمال، لم‌های بورل-کانتلی، مفاهیم همگرایی، دنباله‌ای از متغیرهای تصادفی مستقل و همسان تعریف شده‌اند.

جزء: سخنرانی

پیش نیاز: MAT 3520 , MAT 3572 .

MAT 4171 نظریه های احتمال II (3 اعتبار)

قوانین اعداد بزرگ، توابع مشخصه، قضیه حد مرکزی، احتمال و انتظار شرطی، موضوعات مکمل.

جزء: سخنرانی

پیش نیاز: MAT 4570 .

MAT 4175 مقدمه ای بر آمار ریاضی (3 واحد)

قضایای حدی توزیع های مربوط به نمونه گیری تخمین پارامتریک مفاهیم عملکرد و کارایی کافی لم نیمن-پیرسون، آزمون‌های مبتنی بر تابع تنوع. روش های پارامتریک و ناپارامتریک برای مقایسه دو نمونه. مفاهیم اساسی برای طراحی آزمایش، تجزیه و تحلیل جداول احتمالی، مدل خطی کلی، نظریه تصمیم گیری و استنتاج بیزی. قبلا MAT 3575.

جزء: سخنرانی

پیش نیازها: MAT 2775 ، (MAT 2521 یا MAT 2522 )، ( MAT 2541 یا MAT 2742 ).

تحلیل و کاربردهای تانسور MAT 4183 (3 اعتبار)

تحلیل تانسور و کاربردهای آن در هندسه ریمانی و نظریه نسبیت

جزء: سخنرانی

پیش نیازها: MAT 2522 , MAT 2525 , ( MAT 2541 or MAT 2742 ).

MAT 4199 موضوعات منتخب در ریاضیات (3 واحد)

روی موضوعات پیشرفته کار کنید.

جزء: سخنرانی

پیش نیاز: 12 واحد درسی در ریاضیات (MAT) در سطح 3000 یا بالاتر. بسته به موضوع دوره، پیش نیازهای اضافی ممکن است اعمال شود.

+ نوشته شده در چهارشنبه بیست و چهارم اسفند ۱۴۰۱ ساعت 18:29 توسط علی رضا نقش نیلچی |

8-برنامه ها و دوره ها دانشکده ریاضی در دانشگاه اوتاوا

MAT 4155 Elementary Manifold Theory (3 واحد)

منیفولدها، ساختارهای قابل تمایز، فضای مماس، میدان های برداری، اشکال دیفرانسیل، میدان های تانسور، متریک ریمانی.

جزء درس: خواندن

پیش نیاز: MAT 2141 , MAT 3120 .

MAT 4157 توپولوژی جبری I (3 واحد)

پوشش فضاها، همسانی از طریق بدیهیات Eilenberg-Steenrod، کاربردها، ساخت یک تابع همسانی.

جزء درس: خواندن

پیش نیازها: MAT 3143 ( MAT 3153 یا MAT 3120 ).

MAT 4158 توپولوژی جبری II (3 واحد)

مباحث توپولوژی جبری.

جزء درس: خواندن

پیش نیاز: MAT 3120 , MAT 3143 .

مباحث MAT 4162 در منطق ریاضی (3 واحد)

موضوعات منتخب، مانند: نظریه مدل، تحلیل غیر استاندارد، نظریه توابع بازگشتی، نظریه مجموعه های پیشرفته، فلسفه ریاضیات.

جزء درس: خواندن

پیش نیاز: MAT 3361 .

مباحث MAT 4167 در نظریه اعداد (3 واحد)

موضوعاتی از نظریه اعداد تحلیلی، نظریه اعداد جبری، تقریب دیوفانتین، اشکال مدولار یا هندسه حسابی.

جزء درس: خواندن

پیش نیاز: MAT 3143 .

MAT 4170 نظریه احتمال I (3 واحد)

فضاهای احتمال، متغیرهای تصادفی، مقادیر مورد انتظار به عنوان انتگرال، توزیع مشترک، معیارهای مستقل و محصول، توابع توزیع تجمعی و بسط معیارهای احتمال، لم های Borel-Cantelli، مفاهیم همگرایی، دنباله های مستقل و توزیع شده یکسان متغیرهای تصادفی.

جزء درس: خواندن

پیش نیاز: MAT 3120 , MAT 3172 .

MAT 4171 نظریه احتمال II (3 اعتبار)

قوانین اعداد بزرگ، توابع مشخصه، قضیه حد مرکزی، احتمال شرطی و انتظار، برخی موضوعات اضافی.

جزء درس: خواندن

پیش نیاز: MAT 4170 .

MAT 4175 مقدمه ای بر آمار ریاضی (3 واحد)

قضایای حدی توزیع های نمونه برداری تخمین پارامتریک مفاهیم کفایت و کارایی. پارادایم نیمن-پیرسون، آزمون های نسبت احتمال. روش های پارامتریک و ناپارامتریک برای مقایسه دو نمونه. مفاهیم طراحی تجربی، تجزیه و تحلیل داده های طبقه بندی شده، مدل خطی عمومی، نظریه تصمیم گیری و استنتاج بیزی. قبلا MAT 3175.

جزء درس: خواندن

پیش نیازها: MAT 2375 ، (MAT 2121 یا MAT 2122 )، ( MAT 2141 یا MAT 2342 ).

تحلیل و کاربرد تانسور MAT 4183 (3 واحد)

تحلیل تانسور با کاربرد در هندسه ریمانی و نظریه نسبیت

جزء درس: خواندن

پیش نیازها: MAT 2122 , MAT 2125 , ( MAT 2141 or MAT 2342 ).

MAT 4199 مباحث ویژه در ریاضیات (3 واحد)

منتخب موضوعات پیشرفته

جزء درس: خواندن

پیش نیاز: 12 واحد درسی در ریاضیات (MAT) در سطح 3000 یا بالاتر. بسته به موضوع ممکن است پیش نیازهای اضافی اعمال شود.

نظریه نمایش MAT 4343 (3 اعتبار)

نظریه بازنمایی گروه ها و جبرها: کاراکترها، نمایش های تقلیل ناپذیر، نمایش های القایی، عملگرهای درهم تنیده.

جزء درس: خواندن

پیش نیازها: MAT 3141 یا MAT 3143 .

+ نوشته شده در چهارشنبه بیست و چهارم اسفند ۱۴۰۱ ساعت 18:28 توسط علی رضا نقش نیلچی |

7-برنامه ها و دوره ها دانشکده ریاضی در دانشگاه اوتاوا

MAT 3172 مبانی احتمال (3 اعتبار)

ارائه نظریه احتمال بدون نظریه اندازه گیری. بردارهای تصادفی: استقلال، احتمال و انتظار شرطی، پیامدها. انواع حالت های همگرایی و استفاده از آنها در اثبات قضایای کلاسیک. مقدمه ای بر فرآیندهای تصادفی ساده مانند فرآیندهای پواسون یا انشعاب.

جزء: سخنرانی

پیش نیازها: MAT 2371 ، (MAT 2521 یا MAT 2522 )، ( MAT 2541 یا MAT 2742 ).

ریاضیات مهندسی MAT 3320 (3 واحد)

راه حل های سری معادلات دیفرانسیل. توابع لژاندر و بسل مسائل Sturm-Liouville، توابع متعامد. سری فوریه. معادلات دیفرانسیل جزئی: مقدمه و کاربردها

جزء: سخنرانی

پیش نیازها: (MAT 2521 یا MAT 2522 یا MAT 2722 )، ( MAT 2724 یا MAT 2784 ).

MAT 3341 جبر خطی کاربردی (3 اعتبار)

هنجارهای بردارها و ماتریس ها. شکل متعارف Schur، تجزیه QR و LU، تجزیه Cholesky، تجزیه مقدار منفرد، شبه معکوس، شکل جردن، قضیه Cayley-Hamilton، ماتریس و تحلیل نمایی ماتریس ها. تخمین مقدار ویژه و قضیه دیسک گرشگورین. فرم های درجه دوم، اصل رایلی و اصل مینی ماکس. این دوره شامل اثبات و کاربرد روش های محاسباتی است.

جزء: سخنرانی

پیش نیازها: ( MAT 1722 یا MAT 1725 )، ( MAT 2541 یا MAT 2742 ).

MAT 3343 جبر کاربردی (3 اعتبار)

نظریه گروه و نظریه میدان محدود. کدهای باینری: کدهای همینگ و کدهای BCH. فصول انتخابی جبر کاربردی

جزء: سخنرانی

پیش نیازها: ( MAT 2541 یا MAT 2742 )، ( MAT 2543 or MAT 2748 ).

MAT 3348 ریاضیات گسسته کاربردی (3 واحد)

درختان و کاربردهای آنها، کاربرد گراف ها، شبکه ها و جریان ها، تئوری کوپلینگ، مقدمه ای بر برنامه ریزی خطی.

جزء: سخنرانی

پیش نیازها: MAT 1741 , ( MAT 2748 یا CSI 2501 ).

MAT 3361 مقدمه ای بر منطق ریاضی (3 واحد)

رویکرد صوری به منطق و محمولات گزاره‌ای، نحو و معناشناسی، نظام‌های اثبات صوری، کامل و فشردگی. نظریه های رسمی و مدل های آنها موضوعات انتخاب شده از لیست زیر: منطق در علوم کامپیوتر، مبانی ریاضیات، نظریه مجموعه ها، نظریه محاسبات.

جزء: سخنرانی

پیش نیازها: MAT 2362 و یکی از MAT 2120، MAT 2125 ، MAT 2141 ، MAT 2143 ، MAT 2348 یا CSI 2101 .

روش‌های یادگیری ماشین MAT 3373 (3 اعتبار)

رگرسیون خطی و چند جمله ای چند متغیره، رگرسیون لجستیک، روش k نزدیکترین همسایه. روش های منظم سازی، استنتاج بیزی، طبقه بندی بیزی ساده لوحانه. اعتبار سنجی متقابل، تکنیک های بوت استرپ. درختان تصمیم تجزیه و تحلیل مؤلفه های اصلی پارتیشن بندی.

جزء: سخنرانی

پیش نیاز: MAT 1341 , (( MAT 2371 , MAT 2375 ) یا MAT 2377 ).

تجزیه و تحلیل رگرسیون MAT 3375 (3 اعتبار)

تئوری توزیع، آزمون فرضیه و تخمین برای تحلیل رگرسیون ساده، چندگانه و غیرخطی. مدل های خطی تعمیم یافته و رگرسیون پواسون. تجزیه و تحلیل داده ها با استفاده از نرم افزارهای آماری.

جزء: سخنرانی

پیش نیازها: MAT 1741 , MAT 2771 , ( MAT 2775 or MAT 2778 or MAT 2779 ).

MAT 3377 نمونه گیری و نظرسنجی (3 اعتبار)

مقدمه ای بر طراحی و تحلیل نظرسنجی نمونه گیری تصادفی ساده، طبقه ای، متناسب، پس طبقه ای، خوشه ای و چند سطحی. توسعه کامل تئوری؛ مثال ها. تجزیه و تحلیل داده ها با استفاده از نرم افزارهای آماری.

جزء: سخنرانی

پیش نیاز: MAT 2775 یا MAT 2777 یا MAT 2778 یا MAT 2779 .

MAT 3378 تجزیه و تحلیل طرح‌های آزمایش‌ها (3 اعتبار)

قوانین نمونه برداری برای طرح های آزمایشی طرح‌های آزمایشی: بلوک‌های تصادفی، کامل یا ناقص، مربع‌های لاتین، «قطعات تقسیم‌شده»، کسری. تحلیل سطحی تابع رگرسیون اندازه نمونه و محاسبه تابع توان. استنتاج همزمان. مدل های افکت های تصادفی تجزیه و تحلیل داده ها با استفاده از نرم افزارهای آماری.

جزء: سخنرانی

پیش نیازها: MAT 1741 , MAT 2771 , ( MAT 2775 or MAT 2778 or MAT 2779 ).

MAT 3379 Introduction to Time Series (3 اعتبار)

رویکرد زمانی: تجزیه مدل‌های روند، مدل‌های اتورگرسیو و میانگین متحرک (ARMA)، فرآیند غیر ثابت و فصلی، مدل‌های فضای حالت. رویکرد طیفی: رگرسیون با تاخیر، سیگنال‌های قطعی و مدل‌هایی با ضرایب تصادفی. نمونه هایی از سری زمانی مالی تجزیه و تحلیل مجموعه داده ها با استفاده از نرم افزارهای آماری.

جزء: سخنرانی

پیش نیازها: MAT 2771 , ( MAT 2775 یا MAT 2778 یا MAT 2779 ).

MAT 3380 مقدمه ای بر روش های عددی (3 واحد)

ریشه های معادلات غیرخطی (نقطه ثابت، نت وون، سکانس، دو بخش). شرطی سازی یک سیستم معادلات خطی. روش‌های تکراری برای سیستم‌های معادلات خطی و غیرخطی (گاوس-سیدل، گاوس-ژاکوبی، SOR؛ نقطه ثابت، نیوتن). درونیابی و تقریب چند جمله ای، تمایز عددی و یکپارچه سازی. روش های عددی برای معادلات دیفرانسیل. تجزیه و تحلیل خطا

جزء: سخنرانی

پیش نیازها: MAT 2522 , MAT 2525 , ( MAT 2541 or MAT 2742 ) , ( MAT 2724 or MAT 2784 ).

MAT 3395 مقدمه ای بر مدل سازی ریاضی (3 واحد)

مقدمه‌ای بر مدل‌سازی و روش‌های ریاضی مورد استفاده برای کاربردها. مدل‌های ریاضی از علوم کاربردی می‌آیند و از تکنیک‌های حساب دیفرانسیل، معادلات دیفرانسیل، جبر خطی و هندسه برداری استفاده می‌کنند.

جزء: سخنرانی

پیش نیازها: ( MAT 2541 یا MAT 2742 )، ( MAT 2522 or MAT 2722 )، ( MAT 2724 or MAT 2784 ).

MAT 4124 مقدمه ای بر تحلیل عملکردی (3 واحد)

مقدمه ای بر باناخ و با تاکید بر فضاهای هیلبرت. سری فوریه و تبدیل فوریه. عملگرهای خطی در فضاهای هیلبرت مقدمه ای بر نظریه طیفی. موضوعات منتخب از میان: عملگرهای فشرده، عملگرهای نامحدود و غیره.

جزء درس: خواندن

پیش نیاز: MAT 3120 .

MAT 4125 Measure and Integration I (3 واحد)

اندازه گیری کلی و انتگرال، اندازه گیری و انتگرال لبگ بر روی R، قضیه فوبینی، قضیه Lebesgue-Radon-Nikodym، تداوم و تمایز مطلق، Lp-فضاها.

جزء درس: خواندن

پیش نیاز: MAT 3120 .

MAT 4126 Measure and Integration II (3 اعتبار)

فضاهای Banach و Hilbert، عملگرهای خطی محدود، فضاهای دوگانه، برخی موضوعات اضافی.

جزء درس: خواندن

پیش نیاز: MAT 4125 .

MAT 4130 مقدمه ای بر معادلات دیفرانسیل جزئی (3 واحد)

مدل سازی با معادلات دیفرانسیل جزئی (PDEs)، PDE های ابتدایی و روش جداسازی متغیرها، طبقه بندی PDE ها، PDE های مرتبه اول خطی و روش مشخصه ها، حداکثر اصول برای معادلات بیضوی و حل کلاسیک معادله لاپلاس، توابع گرین، روش های تغییرات . معادلات گرما و موج

جزء درس: خواندن

پیش نیازها: MAT 2122 , MAT 2125 , ( MAT 2141 or MAT 2342 ) , ( MAT 2324 or MAT 2384 ).

حلقه ها و ماژول های II MAT 4141 (3 واحد)

جزء درس: خواندن

پیش نیازها: MAT 3141 یا MAT 3143 .

MAT 4142 مقدمه ای بر جبرهای دروغ (3 واحد)

ساختار جبرهای دروغ بعد محدود قابل حل، nilpotent و نیمه ساده.

جزء درس: خواندن

پیش نیاز: MAT 3141 یا MAT 3143 .

MAT 4143 Groups and Galois Theory (3 واحد)

جزء درس: خواندن

پیش نیاز: MAT 4141 یا MAT 3143 یا ( MAT 2141 and MAT 2143 and MAT 3343 ).

MAT 4144 Introduction to Lie Groups (3 واحد)

گروه های خطی: نقشه نمایی، مطابقت دروغ. هممورفیسم ها و پوشش ها. زیر گروه های بسته گروه های کلاسیک: زیر گروه های کارتن، گروه های بنیادی. منیفولدها. فضاهای همگن گروه های دروغ عمومی

جزء درس: خواندن

پیش نیازها: MAT 2143 ، MAT 3120 ، (MAT 3141 یا MAT 3143 یا MAT 3341 ).

توپولوژی عمومی MAT 4153 (3 واحد)

فضاهای توپولوژیکی، توپولوژی های محصول و شناسایی، بدیهیات شمارش پذیری و جداسازی، فشردگی، متریساسیون.

جزء درس: خواندن

پیش نیاز: MAT 3120 یا MAT 3153 .

MAT 4154 مقدمه ای بر هندسه جبری (3 واحد)

جزء درس: خواندن

پیش نیاز: MAT 3143 .

+ نوشته شده در چهارشنبه بیست و چهارم اسفند ۱۴۰۱ ساعت 18:27 توسط علی رضا نقش نیلچی |

7-برنامه ها و دوره ها دانشکده ریاضی در دانشگاه اوتاوا

حلقه ها و ماژول های MAT 3143 (3 واحد)

حلقه‌ها و ایده‌آل‌ها، قضایای هم‌مورفیسم و هم‌مورفیسم، حوزه‌های ایده‌آل اصلی و حلقه‌های عاملی، حلقه‌های چند جمله‌ای و ساخت میدان‌های محدود. ماژول ها، مجموع مستقیم و نابود کننده های ماژول ها، ماژول های رایگان، طبقه بندی ماژول ها بر روی یک PID.

جزء درس: خواندن

پیش نیاز: MAT 2141 , MAT 2143 .

MAT 3153 مقدمه ای بر توپولوژی (3 واحد)

مجموعه ها، عملکردها، مسئولیت پذیری. توپولوژی خط واقعی و فضای اقلیدسی، فشردگی و پیوستگی، توابع پیوسته. مقدمه ای بر روش های جبری در توپولوژی: همتوپی ها و تعداد سیم پیچی منحنی ها در صفحه، شاخص یک میدان برداری در صفحه یا طبقه بندی سطوح.

جزء درس: خواندن

پیش نیاز: (MAT 2120, MAT 2121) یا (MAT 2120, MAT 2322 ) یا ( MAT 2122 , MAT 2125 ).

MAT 3155 مقدمه ای بر هندسه دیفرانسیل. (3 واحد)

مقدمه ای بر هندسه ریمانی ابتدایی، کاربرد در منحنی ها و سطوح، موضوعات خاص انتخاب شده از هندسه و فیزیک.

جزء درس: خواندن

پیش نیازها: (MAT 2120, MAT 2121) یا ( MAT 2122 , MAT 2125 ) یا ( MAT 2120, MAT 2322 ), ( MAT 2141 یا MAT 2342 ).

MAT 3166 مقدمه ای بر نظریه اعداد (3 واحد)

موضوعات انتخاب شده از: دنباله فری، قضایای فرما- اویلر-ویلسون، باقی مانده های توان و ریشه های اولیه، معادلات دیوفانتین، کسرهای ادامه دار، اعداد جبری و ماورایی، توابع حسابی، توزیع اعداد اول.

جزء درس: خواندن

پیش نیاز: MAT 2143 یا MAT 2348 .

MAT 3172 مبانی احتمال (3 واحد)

مروری بر احتمال از دیدگاه نظری غیر اندازه گیری. بردارهای تصادفی؛ استقلال، انتظار و احتمال مشروط، پیامدها. انواع مختلفی از همگرایی که منجر به اثبات قضایای اصلی در نظریه احتمال کلاسیک می شود. مقدمه ای بر فرآیندهای تصادفی ساده مانند فرآیندهای پواسون و انشعاب.

جزء درس: خواندن

پیش نیازها: MAT 2371 ، (MAT 2121 یا MAT 2122 )، ( MAT 2141 یا MAT 2342 ).

MAT 3320 Mathematics for Engineers (3 واحد)

حل های سری معادلات دیفرانسیل معمولی. توابع لژاندر و بسل مسائل Sturm-Liouville، توابع متعامد. سری فوریه. معادلات دیفرانسیل جزئی: مقدمه و کاربردها

جزء درس: خواندن

پیش نیازها: (MAT 2121 یا MAT 2122 یا MAT 2322 )، ( MAT 2324 یا MAT 2384 ).

MAT 3341 جبر خطی کاربردی (3 واحد)

هنجارهای برداری و ماتریس. شکل متعارف Schur، QR، LU، Cholesky و تجزیه مقدار منفرد، معکوس های تعمیم یافته، فرم جردن، قضیه کیلی-همیلتون، تجزیه و تحلیل ماتریس و نمایی ماتریس ها، تخمین مقدار ویژه و قضیه دایره گرشگورین. فرم های درجه دوم، اصول رایلی و مینیما. این دوره شامل اثبات و کاربرد روش های محاسباتی است.

جزء درس: خواندن

پیش نیازها: ( MAT 1322 یا MAT 1325 )، ( MAT 2141 or MAT 2342 ).

MAT 3343 جبر کاربردی (3 واحد)

گروه ها و فیلدهای محدود؛ کدهای باینری: کدهای Hamming و BCH. سایر مباحث جبر کاربردی

جزء درس: خواندن

پیش نیازها: ( MAT 2141 یا MAT 2342 )، ( MAT 2143 or MAT 2348 ).

MAT 3348 ریاضیات گسسته کاربردی (3 واحد)

درختان و کاربردها، کاربردهای نمودارها، شبکه ها و جریان ها، تئوری تطبیق، مقدمه ای بر برنامه ریزی خطی.

جزء درس: خواندن

پیش نیازها: MAT 1341 , ( MAT 2348 or CSI 2101 ).

MAT 3361 مقدمه ای بر منطق ریاضی (3 واحد)

رویکردهای صوری به منطق گزاره ای و محمولی. نحو و معناشناسی. سیستم های اثبات رسمی کامل بودن و فشردگی. نظریه های رسمی و مدل های آنها موضوعات انتخاب شده از: منطق در علوم کامپیوتر، مبانی ریاضیات، نظریه مجموعه ها، نظریه محاسبات.

جزء درس: خواندن

پیش نیازها: MAT 2362 و یکی از MAT 2120، MAT 2125 ، MAT 2141 ، MAT 2143 ، MAT 2348 یا CSI 2101 .

MAT 3373 Methods of Machine Learning (3 واحد)

رگرسیون خطی و چند جمله‌ای چند متغیره، رگرسیون لجستیک، k نزدیک‌ترین همسایه‌ها. روش های منظم سازی، استنتاج بیزی، طبقه بندی ساده بیز. اعتبار سنجی متقابل، بوت استرپ. روش های درختی تجزیه و تحلیل اجزای اصلی خوشه بندی.

جزء درس: خواندن

پیش نیازها: MAT 1341 , (( MAT 2371 , MAT 2375 ) یا MAT 2377 ).

تجزیه و تحلیل رگرسیون MAT 3375 (3 واحد)

تئوری توزیع، آزمون فرضیه و تخمین رگرسیون ساده، چندگانه و غیرخطی. مدل های خطی تعمیم یافته، لجستیک و رگرسیون پواسون. تجزیه و تحلیل داده ها با استفاده از بسته های نرم افزاری آماری.

جزء درس: خواندن

پیش نیازها: MAT 1341 , MAT 2371 , ( MAT 2375 or MAT 2378 or MAT 2379 ).

MAT 3377 نمونه برداری و بررسی (3 واحد)

مقدمه ای بر طراحی و تحلیل نظرسنجی ها. نمونه گیری تصادفی ساده، طبقه ای، متناسب، پس طبقه ای، خوشه ای و چند مرحله ای. نمونه ها و توسعه کامل نظری. تجزیه و تحلیل داده ها با استفاده از بسته های نرم افزاری آماری.

جزء درس: خواندن

پیش نیاز: MAT 2375 یا MAT 2377 یا MAT 2378 یا MAT 2379 .

MAT 3378 تجزیه و تحلیل طرح های آزمایشی (3 واحد)

تئوری توزیع برای طرح های تجربی طرح‌های آزمایشی: طرح‌های بلوک کاملاً تصادفی، کامل و ناقص، طرح‌های مربع لاتین، طرح‌های اسپلیت پلات، کسری، فاکتوریل و سطح پاسخ. اندازه نمونه و تعیین توان استنتاج همزمان. مدل های مولفه های واریانس تجزیه و تحلیل داده ها با استفاده از بسته های نرم افزاری آماری.

جزء درس: خواندن

پیش نیازها: MAT 1341 , MAT 2371 , ( MAT 2375 or MAT 2378 or MAT 2379 ).

MAT 3379 مقدمه ای بر تحلیل سری های زمانی (3 واحد)

روش‌های حوزه زمان: بی‌روند، مدل‌های میانگین متحرک اتورگرسیو (ARMA)، غیر ایستایی و فصلی، روش‌شناسی فضای حالت. روش‌های حوزه فرکانس: مدل‌های رگرسیون تاخیری، ورودی قطعی و مدل‌های ضریب تصادفی. نمونه هایی از سری زمانی مالی داده های سری زمانی با استفاده از بسته های نرم افزاری تجزیه و تحلیل خواهند شد.

جزء درس: خواندن

پیش نیازها: MAT 2371 ، ( MAT 2375 یا MAT 2378 یا MAT 2379 ).

MAT 3380 مقدمه ای بر روش های عددی (3 واحد)

ریشه های معادلات غیر خطی (نقطه ثابت، نیوتن، مقطع، دو بخش). شماره وضعیت سیستم های خطی. روش های تکرار شونده برای سیستم های خطی و غیر خطی (گاوس-سیدل، گاوس-ژاکوبی، SOR؛ نقطه ثابت، نیوتن). درونیابی و تقریب چند جمله ای، تمایز عددی و یکپارچه سازی. روش های عددی برای معادلات دیفرانسیل. تجزیه و تحلیل خطا

جزء درس: خواندن

پیش نیازها: MAT 2122 , MAT 2125 , ( MAT 2141 or MAT 2342 ) , ( MAT 2324 or MAT 2384 ).

MAT 3395 مقدمه ای بر مدل های ریاضی (3 واحد)

مقدمه ای بر مدل سازی و تکنیک های ریاضی مورد استفاده در برنامه های کاربردی. مدل‌های ریاضی از حوزه‌های مختلف علوم کاربردی می‌آیند و از تکنیک‌هایی از حساب دیفرانسیل و انتگرال، معادلات دیفرانسیل، جبر خطی و هندسه برداری استفاده می‌کنند.

جزء درس: خواندن

پیش نیازها: ( MAT 2141 یا MAT 2342 )، ( MAT 2122 or MAT 2322 )، ( MAT 2324 or MAT 2384 ).

MAT 3500 تاریخچه ریاضیات I (3 واحد)

مروری بر توسعه تفکر ریاضی از دوران باستان (بابلی، مصری و یونانی) تا دوران مدرن.

جزء: سخنرانی

پیش نیاز: 12 واحد دروس MAT در سطح 2000 یا بالاتر.

MAT 3101 History of Mathematics II (3 واحد)

توسعه تاریخی ریاضیات از طریق چند موضوع مانند عدد، شانس، فضا، تقریب، انتزاع بی نهایت کوچک یا جبری.

جزء: سخنرانی

پیش نیاز: 12 واحد دروس MAT در سطح 2000 یا بالاتر.

تجزیه و تحلیل واقعی MAT 3120 (3 اعتبار)

فضاهای متریک، توابع پیوسته. فشردگی و اتصال. برنامه های کاربردی پیمانکاری قضیه تابع معکوس و قضیه تابع ضمنی. سری توابع: انواع همگرایی، سری توان، سری فوریه. مباحث مربوط به فضاهای تابعی مانند: قضیه تقریب وایرشتراس، فضاهای L¢2.

جزء: سخنرانی

پیش نیازها: ( MAT 2522 , MAT 2525 ) یا (MAT 2520, MAT 2521).

MAT 3121 توابع یک متغیر مختلط I (3 اعتبار)

اعداد مختلط. توابع تحلیلی ادغام، سری Laurent، محاسبه باقیمانده ها. برنامه های سازگار

جزء: سخنرانی

پیش نیازها: ( MAT 2522 , MAT 2525 ) یا (MAT 2520, MAT 2521). دوره های MAT 3521 ، MAT 3721 را نمی توان برای اعتبار ترکیب کرد.

MAT 3130 مقدمه ای بر سیستم های دینامیکی (3 اعتبار)

سیستم های معادلات دیفرانسیل خطی. مقدمه‌ای بر سیستم‌های غیرخطی: قضایای وجود و یکتایی، جریان، پایداری تعادل‌ها، انواع ثابت، مدارهای تناوبی، جریان‌های مسطح.

جزء: سخنرانی

پیش نیازها: (MAT 2520, MAT 2521) یا (MAT 2520, MAT 2722 ) یا ( MAT 2522 , MAT 2525 ), ( MAT 2541 یا MAT 2742 ), ( MAT 2724 یا MAT 2784 ).

حلقه ها و ماژول های MAT 3143 (3 اعتبار)

حلقه‌ها و ایده‌آل‌ها، قضایای هم‌مورفیسم و هم‌شکلی، حلقه‌های اصلی و حلقه‌های عاملی، حلقه‌های چندجمله‌ای و ساخت میدان‌های محدود. ماژول ها، مبالغ مستقیم و لغو کننده های ماژول ها، ماژول های رایگان، طبقه بندی ماژول ها در یک حلقه اصلی.

جزء: سخنرانی

پیش نیاز: MAT 2541 , MAT 2543 .

MAT 3153 مقدمه ای بر توپولوژی (3 اعتبار)

مجموعه ها، توابع، شمارش پذیری. توپولوژی خط واقعی و فضای اقلیدسی، مجموعه های فشرده و متصل، توابع پیوسته. مقدمه ای بر روش های جبری در توپولوژی: هموتوپی و ضریب پیوند منحنی ها در صفحه، شاخص یک میدان برداری در صفحه یا طبقه بندی سطوح.

جزء: سخنرانی

پیش نیاز: (MAT 2520, MAT 2521) یا (MAT 2520, MAT 2722 ) یا ( MAT 2522 , MAT 2525 ).

MAT 3155 مقدمه ای بر هندسه دیفرانسیل (3 اعتبار)

مقدمه ای بر تئوری ریمانی ابتدایی، کاربرد در منحنی ها و سطوح، مباحث ویژه از هندسه و فیزیک.

جزء: سخنرانی

پیش نیازها: (MAT 2520, MAT 2521) یا ( MAT 2522 , MAT 2525 ) یا ( MAT 2520, MAT 2722 ), ( MAT 2541 یا MAT 2742 ).

MAT 3166 مقدمه ای بر نظریه اعداد (3 واحد)

انتخاب موضوعات از میان موارد زیر: دنباله های فری، قضایای فرما، اویلر و ویلسون. باقیمانده های درجه دوم و بالاتر. ریشه های بدوی معادلات دیوفانتین کسرهای ادامه دار اعداد جبری و ماورایی. توابع حسابی توزیع اعداد اول

جزء: سخنرانی

پیش نیاز: MAT 2543 یا MAT 2748 .

+ نوشته شده در چهارشنبه بیست و چهارم اسفند ۱۴۰۱ ساعت 12:17 توسط علی رضا نقش نیلچی |

6-برنامه ها و دوره ها دانشکده ریاضی در دانشگاه اوتاوا

MAT 2141 جبر خطی تخصصی (3 اعتبار)

فضاهای برداری، مجموع مستقیم و مکمل زیرفضاها، نقشه های خطی، نمایش های ماتریسی نقشه های خطی، فضاهای دوگانه، نقشه های الحاقی، نقشه های چندخطی، تعیین کننده، محصولات اسکالر، پیش بینی های متعامد، الگوریتم گرم اشمیت. مقادیر ویژه و بردارها، قطری سازی ماتریس های متقارن. این دوره بر نمایش همه نتایج تاکید دارد.

جزء: گروه بحث، سخنرانی

پیش نیازها: MAT 1741 , ( MAT 1748 یا MAT 1762 یا MAT 2762 ).

MAT 2143 مقدمه ای بر نظریه گروه (3 واحد)

گروه ها: حساب مدول n، جایگشت، گروه های چرخه ای. کلاس های چپ و راست، قضیه لاگرانژ. زیر گروه های نرمال، هممورفیسم ها، گروه های بهره، قضایای هم شکلی. محصولات مستقیم و طبقه بندی گروه های آبلی از نوع محدود.

جزء: گروه بحث، سخنرانی

پیش نیازها: MAT 1741 , ( MAT 1748 یا MAT 1762 یا MAT 2762 ).

MAT 2322 حساب دیفرانسیل و انتگرال III برای مهندسین (3 واحد)

مازاد توابع چندین متغیر. انتگرال ها و برنامه های کاربردی متعدد. فیلدهای برداری و مشتقات آنها. منحنی ها. عملگرهای دیفرانسیل برداری انتگرال های منحنی. سطوح و سطح یکپارچه. قضیه استوکس، گاوس و غیره

جزء: سخنرانی

پیش نیازها: ( MAT 1722 یا MAT 1725 یا MAT 1732 )، ( MAT 1741 یا دوره جبر خطی CEGEP). دوره های MAT 2722 , MAT 2522 , MAT 2521 را نمی توان برای دریافت واحد با هم ترکیب کرد.

MAT 2324 معادلات دیفرانسیل و تبدیل لاپلاس (3 واحد)

مفاهیم کلی معادلات مرتبه اول معادلات دیفرانسیل خطی مرتبه بالاتر عملگرهای دیفرانسیل تبدیل لاپلاس. سیستم های معادلات دیفرانسیل. راه حل های سری در مجاورت یک نقطه معمولی.

جزء: سخنرانی

پیش نیازها: MAT 1741 ، ( MAT 1722 یا MAT 1725 یا MAT 1732 ). دوره های MAT 2724 ، MAT 2784 را نمی توان برای اعتبار ترکیب کرد.

MAT 2342 مقدمه ای بر جبر خطی کاربردی (3 اعتبار)

بررسی فضاهای برداری و جبر ماتریسی، حاصل ضرب نقطه ای، گرم اشمیت، برآمدگی های متعامد. مقادیر ویژه و بردارها، قطری سازی ماتریس های متقارن. تجزیه به مقادیر منفرد. کاربرد در سیستم های دینامیکی گسسته خطی، به حداقل رساندن اشکال درجه دوم و تقریب حداقل مربعات، تجزیه و تحلیل مؤلفه های اصلی. برنامه های کاربردی دیگر انتخاب شده از: برنامه ریزی خطی، دوگانگی و روش سیمپلکس. مقدمه ای بر میدان های محدود و نظریه کدگذاری

جزء: سخنرانی

پیش نیاز: MAT 1702 یا MAT 1741 .

MAT 2348 ریاضیات گسسته (3 واحد)

بررسی سریع مجموعه ها، توابع، روابط، عود، روش های شمارش اساسی. درمان عمیق روابط عود، کارکردهای ایجاد کننده و اصول گنجاندن - طرد. جنبه های نظریه گراف.

جزء: سخنرانی

پیش نیازها: MAT 1741 ، ( MAT 1748 یا MAT 1725 یا MAT 1762 یا MAT 2762 یا MAT 2541 ).

MAT 2355 مقدمه ای بر هندسه (3 اعتبار)

هندسه اقلیدسی و غیر اقلیدسی; هندسه های وابسته; هندسه تصویری دگرگونی ها و گروه های تبدیل.

جزء: سخنرانی

پیش نیاز: MAT 1702 یا MAT 1741 .

MAT 2362 مبانی ریاضیات (3 واحد)

مقدمه ای بر مفهوم برهان، نظریه مجموعه ها و مبانی ریاضیات. منطق گزاره ای، مقدمه ای بر منطق محمول و نظریه های بدیهی. تکنیک های اثبات (مستقیم، با تناقض، مورد به مورد، سازنده و غیر سازنده، تکرار). نظریه مجموعه های غیررسمی (توابع، روابط هم ارزی، روابط نظم). پارادوکس ها مقدمه ای بر نظریه مجموعه های بدیهی و کدگذاری ریاضی. اصل انتخاب، لم زورن. کاردینالیته مجموعه ها

جزء: گروه بحث، سخنرانی

پیش نیازها: ( MAT 1722 یا MAT 1725 )، ( MAT 1741 یا دوره جبر خطی CEGEP).

MAT 2371 مقدمه ای بر احتمال (3 اعتبار)

بدیهیات احتمال و پیامدهای آنها. احتمال و استقلال مشروط. متغیرهای تصادفی، توابع توزیع و چگالی، گشتاورها، توزیع های نمونه. قانون ضعیف اعداد بزرگ، مجموع متغیرهای تصادفی مستقل، تابع مولد گشتاور، مفاهیم همگرایی، قضیه حد مرکزی.

جزء: سخنرانی

پیش نیاز: MAT 1722 یا MAT 1725 یا MAT 1732 . دوره های MAT 2771 , MAT 2777 , ADM 2703 , ECO 3550 , HSS 2781 , PSY 2506 را نمی توان برای کسب امتیاز با هم ترکیب کرد.

MAT 2375 مقدمه ای بر آمار (3 اعتبار)

نظریه استنتاج آماری: تخمین نقطه و فاصله، آزمون فرضیه. کاربرد در مدل های معمولی مقدمه ای بر روش های ناپارامتریک

جزء: سخنرانی

پیش نیاز: MAT 2371 . دوره های MAT 2775 , MAT 2777 , MAT 2778 , MAT 2779 , ADM 2703 , ECO 3550 , HSS 2781 , PSY 2506 نمی توانند برای کسب امتیاز با هم ترکیب شوند.

MAT 2377 احتمال و آمار برای مهندسین (3 واحد)

معرفی مختصر موضوعات زیر: تحلیل ترکیبی، احتمالات و متغیرهای تصادفی، توابع چگالی و توزیع برای متغیرهای نوع گسسته یا پیوسته. انتظارات و واریانس ریاضی؛ توزیع نرمال، دو جمله ای و پواسون. تخمین و آزمون فرضیه ها؛ روش حداقل مربعات، همبستگی و رگرسیون. این نظریه با شبیه سازی نشان داده شده است. محتوای دوره عمدتاً به سمت آمار و روش های کنترل کیفیت برای مهندسان است. دوره های MAT 2777 , MAT 1771 , MAT 1772 , MAT 2771 , MAT 2775 , MAT 2778 , MAT 2779 , ADM 2703 , ECO 3550 , HSS 2781 ,PSY 2106 را نمی توان برای اعتبار ترکیب کرد.

جزء: سخنرانی

پیش نیاز: MAT 1720 یا MAT 1721 یا MAT 1727 یا MAT 1730 . دوره MAT 1722 یا MAT 1725 یا MAT 1732 همزمان با MAT 2777 است .

MAT 2379 مقدمه ای بر آمار زیستی (3 اعتبار)

آمار توصیفی از طریق نرم افزارهای آماری. مقدمه ای بر نظریه احتمال. چگالی معمولی قضیه حد مرکزی و تخمین آماری از طریق شبیه سازی. آزمون فرضیه، طراحی تجربی، مقایسه دو نمونه، تجزیه و تحلیل داده های طبقه ای و رگرسیون. نمونه های موجود در علوم زیستی توسط نرم افزارهای آماری تحلیل می شوند.

جزء: سخنرانی

پیش نیاز: MAT 1720 یا MAT 1721 یا MAT 1727 یا MAT 1730 . دوره های MAT 2379 , MAT 1371 , MAT 1372 , MAT 1373 , MAT 2375 , MAT 2377 , ADM 2303 , ECO 3150, HSS 2381 , PSY 2106 نمی توانند با هم ترکیب شوند.

MAT 2384 معادلات دیفرانسیل و روش های عددی (3 واحد)

مفاهیم کلی معادلات مرتبه اول معادلات دیفرانسیل خطی مرتبه بالاتر عملگرهای دیفرانسیل تبدیل لاپلاس. سیستم های معادلات دیفرانسیل. راه حل های سری در مجاورت یک نقطه معمولی. روش های عددی شامل تحلیل خطا، تفکیک و انتگرال گیری عددی و تفکیک عددی معادلات دیفرانسیل.

جزء: سخنرانی

پیش نیازها: MAT 1741 ، ( MAT 1722 یا MAT 1725 یا MAT 1732 ). دوره های MAT 2784 ، MAT 2724 را نمی توان برای اعتبار ترکیب کرد.

MAT 3100 تاریخچه ریاضیات I (3 واحد)

بررسی خطوط اصلی پیشرفت ریاضی از بابلی ها، مصری ها و یونانی ها تا دوران مدرن.

جزء درس: خواندن

پیش نیاز: 12 واحد در دوره های MAT در سطح 2000 به بالا.

MAT 3101 History of Mathematics II (3 واحد)

توسعه تاریخی ریاضیات از طریق چند موضوع اصلی مانند شمارش، فضا، تصادفی، تقریب، بی‌نهایت کوچک یا انتزاع جبری دیده می‌شود.

جزء درس: خواندن

پیش نیاز: 12 واحد در دوره های MAT در سطح 2000 به بالا.

MAT 3120 Real Analysis (3 واحد)

فضاهای متریک، توابع پیوسته. فشردگی و پیوستگی. نقشه برداری انقباض قضیه تابع معکوس و قضیه تابع ضمنی. مجموعه ای از توابع؛ حالت های همگرایی، سری توان، سری فوریه. موضوعات مربوط به فضاهای تابع مانند: تقریب وایرشتراس، فاصله L¢2.

جزء درس: خواندن

پیش نیازها: ( MAT 2122 , MAT 2125 ) یا (MAT 2120, MAT 2121).

MAT 3121 Complex Analysis I (3 واحد)

اعداد مختلط. توابع تحلیلی ادغام، سری Laurent، حساب باقیمانده. نگاشتهای منسجم

جزء درس: خواندن

پیش نیازها: ( MAT 2122 , MAT 2125 ) یا (MAT 2120, MAT 2121). دوره های MAT 3121 , MAT 3321 را نمی توان برای واحدها ترکیب کرد.

MAT 3130 Introduction to Dynamical Systems (3 واحد)

سیستم های معادلات دیفرانسیل خطی. مقدمه ای بر سیستم های غیر خطی قضایای وجود و یکتایی، جریان، ثبات تعادل ها، منیفولدهای ثابت، مدارهای تناوبی، جریان های مسطح.

جزء درس: خواندن

پیش نیازها: (MAT 2120, MAT 2121) یا (MAT 2120, MAT 2322 ) یا ( MAT 2122 , MAT 2125 ), ( MAT 2141 یا MAT 2342 ), ( MAT 2324 یا MAT 2384 ).

+ نوشته شده در چهارشنبه بیست و چهارم اسفند ۱۴۰۱ ساعت 12:15 توسط علی رضا نقش نیلچی |

5-برنامه ها و دوره ها دانشکده ریاضی در دانشگاه اوتاوا

MAT 2141 Honors Linear Algebra (3 واحد)

فضاهای برداری، مجموع مستقیم و مکمل زیرفضاها، نقشه های خطی، نمایش نقشه های خطی با ماتریس، فضاهای دوگانه، نگاشت های انتقالی، نگاشت های چند خطی، عوامل تعیین کننده، محصولات داخلی، پیش بینی های متعامد، الگوریتم گرام اشمیت. مقادیر ویژه و بردارهای ویژه، قطری سازی ماتریس های متقارن. تاکید این دوره بر اثبات تمامی نتایج است.

جزء درس: گروه بحث، سخنرانی

پیش نیازها: MAT1341، (MAT1348 یا MAT1362 یا MAT2362).

MAT 2143 مقدمه ای بر نظریه گروه (3 واحد)

گروه ها: مدول حسابی n، جایگشت، گروه های چرخه ای. Cosets و قضیه لاگرانژ. زیر گروه های نرمال، هممورفیسم ها، گروه های بهره، قضایای هم شکلی. محصولات مستقیم و قضیه ساختار گروه های آبلی محدود تولید شده

جزء درس: گروه بحث، سخنرانی

پیش نیازها: MAT 1341 , ( MAT 1348 or MAT 1362 or MAT 2362 ).

MAT 2322 Calculus III برای مهندسین (3 واحد)

مازاد توابع چندین متغیر. ادغام های متعدد و برنامه های کاربردی. فیلدهای برداری و مشتقات آنها. منحنی ها عملگرهای دیفرانسیل برداری انتگرال های خطی سطوح و انتگرال های سطحی. قضایای استوکس، گاوس و غیره

جزء درس: خواندن

پیش نیازها: ( MAT 1322 یا MAT 1325 یا MAT 1332 )، ( MAT 1341 یا CEGEP جبر خطی). دوره های MAT 2322 , MAT 2122 , MAT 2121 برای واحدها قابل ترکیب نیستند.

MAT 2324 معادلات دیفرانسیل معمولی و تبدیل لاپلاس (3 واحد)

مفاهیم کلی معادلات مرتبه اول معادلات دیفرانسیل خطی مرتبه بالاتر. عملگرهای دیفرانسیل لاپلاس تبدیل می شود. سیستم های معادلات دیفرانسیل. راه حل های سری در مورد نقاط معمولی.

جزء درس: خواندن

پیش نیازها: MAT 1341 , ( MAT 1322 or MAT 1325 or MAT 1332 ). دوره های MAT 2324 , MAT 2384 را نمی توان برای واحدها ترکیب کرد.

MAT 2342 مقدمه ای بر جبر خطی کاربردی (3 واحد)

بررسی فضاهای برداری و جبر ماتریسی، محصولات داخلی، گرم اشمیت، برآمدگی های متعامد. مقادیر ویژه و بردارهای ویژه، قطری سازی ماتریس های متقارن. تجزیه مقدار منفرد. کاربرد در سیستم های دینامیکی گسسته خطی، به حداقل رساندن اشکال درجه دوم و تقریب حداقل مربعات، تجزیه و تحلیل مؤلفه های اصلی. برنامه های کاربردی دیگر انتخاب شده از: برنامه ریزی خطی، دوگانگی و روش سیمپلکس. مقدمه ای بر میدان های محدود و نظریه کدگذاری

جزء درس: خواندن

پیش نیاز: MAT 1302 یا MAT 1341 .

MAT 2348 ریاضیات گسسته (3 واحد)

بررسی سریع مجموعه ها، توابع، روابط، استقراء، تکنیک های شمارش اولیه. درمان عمیق روابط عود، توابع مولد، و اصل شمول - طرد. جنبه های نظریه گراف.

جزء درس: خواندن

پیش نیازها: MAT 1341 ، ( MAT 1348 یا MAT 1325 یا MAT 1362 یا MAT 2362 یا MAT 2141 ).

MAT 2355 مقدمه ای بر هندسه (3 واحد)

هندسه اقلیدسی و غیر اقلیدسی; هندسه وابسته، هندسه تصویری. تحولات و گروه های تحول.

جزء درس: خواندن

پیش نیاز: MAT 1302 یا MAT 1341 .

MAT 2362 مبانی ریاضیات (3 واحد)

مقدمه ای بر برهان ها، نظریه مجموعه ها و مبانی ریاضیات. منطق گزاره ای، مقدمه ای بر منطق محمول و نظریه های بدیهی. براهین فنی (مستقیم، با تناقض، با موارد، سازنده و غیر سازنده، استقراء). نظریه مجموعه های غیررسمی (مجموعه ها، توابع، روابط هم ارزی، روابط نظم). پارادوکس ها مقدمه ای بر نظریه مجموعه های بدیهی و رمزگذاری ریاضیات. اصل انتخاب، لمای زورن. کاردینالیته مجموعه ها

جزء درس: گروه بحث، سخنرانی

پیش نیازها: ( MAT 1322 یا MAT 1325 )، ( MAT 1341 یا دوره جبر خطی CEGEP).

MAT 2371 مقدمه ای بر احتمال (3 واحد)

بدیهیات احتمال و پیامدهای آنها. احتمال و استقلال مشروط. متغیرهای تصادفی، توزیع ها و چگالی ها، گشتاورها، توزیع های نمونه گیری. قانون ضعیف اعداد بزرگ، مجموع متغیرهای تصادفی مستقل، توابع مولد گشتاور، مفاهیم همگرایی، قضیه حد مرکزی.

جزء درس: خواندن

پیش نیاز: MAT 1322 یا MAT 1325 یا MAT 1332 . دوره های MAT 2371 , MAT 2377 , ADM 2303 , ECO 3150 , HSS 2381 , PSY 2106 برای واحدها قابل ترکیب نیستند.

MAT 2375 مقدمه ای بر آمار (3 واحد)

نظریه استنتاج آماری; تخمین نقطه ای و فاصله ای، آزمون فرضیه ها. استنباط در مورد مدل های معمولی مقدمه ای بر روش های ناپارامتریک

جزء درس: خواندن

پیش نیاز: MAT 2371 . دوره های MAT 2375 , MAT 2377 , MAT 2378 , MAT 2379 , ADM 2303 , ECO 3150 , HSS 2381 , PSY 2106 برای واحدها قابل ترکیب نیستند.

MAT 2377 احتمال و آمار برای مهندسین (3 واحد)

بررسی مختصر از: تجزیه و تحلیل ترکیبی. احتمال و متغیرهای تصادفی؛ چگالی و توابع توزیع گسسته و پیوسته؛ انتظار و واریانس؛ توزیع نرمال (گاوسی)، دو جمله ای و پواسون. تخمین آماری و آزمون فرضیه. روش حداقل مربعات، همبستگی و رگرسیون. تاکید بر آمار و روش های کنترل کیفیت برای مهندسان است. دوره های MAT 2377 , MAT 1371 , MAT 1372 , MAT 2371 , MAT 2375 , MAT 2378 , MAT 2379 , ADM 2303 , ECO 3150 , HSS 2381 , PSY 6 برای واحد 2 قابل ترکیب نیستند.

جزء درس: خواندن

پیش نیاز: MAT 1320 یا MAT 1321 یا MAT 1327 یا MAT 1330 . دوره MAT 1322 یا MAT 1325 یا MAT 1332 شرط لازم برای MAT 2377 است .

MAT 2379 مقدمه ای بر آمار زیستی (3 واحد)

آمار توصیفی با استفاده از بسته نرم افزاری. بررسی مختصر احتمال توزیع نرمال قضیه حد مرکزی و تخمین آماری از طریق شبیه سازی نشان داده شده است. آزمون فرضیه، طراحی آزمایش‌ها، نمونه‌گیری زوجی، داده‌های طبقه‌بندی و رگرسیون. نمونه هایی از علوم زیستی با نرم افزارهای آماری تجزیه و تحلیل شدند.

جزء درس: خواندن

پیش نیاز: MAT 1320 یا MAT 1321 یا MAT 1327 یا MAT 1330 . دوره های MAT 2379 , MAT 1371 , MAT 1372 , MAT 1373 , MAT 2375 , MAT 2377 , ADM 2303 , ECO 3150, HSS 2381 , PSY 2106 برای واحدها قابل ترکیب نیستند.

MAT 2384 معادلات دیفرانسیل معمولی و روش های عددی (3 واحد)

مفاهیم کلی معادلات مرتبه اول معادلات دیفرانسیل خطی مرتبه بالاتر. عملگرهای دیفرانسیل لاپلاس تبدیل می شود. سیستم های معادلات دیفرانسیل. راه حل های سری در مورد نقاط معمولی. روش های عددی از جمله تجزیه و تحلیل خطا. تمایز عددی، ادغام و حل معادلات دیفرانسیل.

جزء درس: خواندن

پیش نیازها: MAT 1341 , ( MAT 1322 or MAT 1325 or MAT 1332 ). دوره های MAT 2384 , MAT 2324 را نمی توان برای واحدها ترکیب کرد.

MAT 2122 حساب دیفرانسیل چند متغیر (3 واحد)

مشتق به عنوان یک نقشه خطی، قضیه کلرو-شوارتز، قضیه تیلور، قضیه تابع ضمنی، قضیه ارزش شدید، نقاط بحرانی، ضریب لاگرانژ، انتگرال دو و سه، فوبینی، مختصات کروی و استوانه ای، تغییر متغیرها. انتگرال های منحنی، قضیه گرین، سطوح و انتگرال های پارامتریک، قضیه دورانی و استوک، وجود پتانسیل ها، واگرایی و قضیه گاوس. برنامه ها

جزء: گروه بحث، سخنرانی

پیش نیازها: ( MAT 1725 یا MAT 1722 )، ( MAT 1741 یا دوره جبر خطی CEGEP با دوره MAT 1741 همزمان ). دوره های MAT 2122 و MAT 2722 را نمی توان برای اعتبار ترکیب کرد.

MAT 2125 Elements of Real Analysis (3 اعتبار)

ویژگی های کامل بودن اصلاح شده اعداد حقیقی، supremum و infimum، کران های بالا و پایین. توپولوژی R¢n. تداوم یکنواخت فشردگی، قضیه هاینه بورل. انتگرال ریمان، قضیه اساسی حساب دیفرانسیل و انتگرال، انتگرال های نامناسب. توالی و سری توابع، همگرایی یکنواخت، سری فوریه.

جزء: گروه بحث، سخنرانی

پیش نیاز: MAT 1725 یا MAT 2522 یا ( MAT 1722 and one of MAT 1748 , MAT 1762 , MAT 2762 ).

+ نوشته شده در چهارشنبه بیست و چهارم اسفند ۱۴۰۱ ساعت 12:14 توسط علی رضا نقش نیلچی |

4-برنامه ها و دوره ها دانشکده ریاضی در دانشگاه اوتاوا

MAT 1330 حساب دیفرانسیل و انتگرال برای علوم زیستی I (3 واحد)

مشتقات: قواعد حاصل و ضریب، مشتق توابع مرکب، مشتق توابع نمایی، توابع لگاریتمی و توابع مثلثاتی پایه، مشتقات مرتبه بالاتر، نمودار توابع. کاربردهای مشتق در علوم زیستی. سیستم های دینامیکی گسسته، نقاط تعادل، پایداری، نمودار به شکل تار عنکبوت. انتگرال ها: انتگرال های معین و نامعین، قضیه اساسی حساب دیفرانسیل و انتگرال، انتگرال های اولیه، روش های انتگرال گیری با جانشینی و با قطعات. کاربردهای انتگرال در علوم زیستی.

جزء: گروه بحث، سخنرانی

پیش نیاز: MAT 1339 یا Ontario Mathematics 4U (MCV4U) یا معادل آن. دوره های MAT 1700 , MAT 1708 , MAT 1720 , MAT 1721 , MAT 1727 , MAT 1729 , MAT 1730 را نمی توان برای کسب امتیاز با هم ترکیب کرد.

MAT 1332 حساب دیفرانسیل و انتگرال برای علوم زیستی II (3 واحد)

انتگرال: انتگرال عددی، انتگرال نامناسب. مقدمه ای بر معادلات دیفرانسیل، تکنیک های حل معادلات دیفرانسیل ساده، حل عددی معادلات دیفرانسیل و مدل سازی علوم زیستی با استفاده از معادلات دیفرانسیل. مقدمه ای بر جبر خطی: ماتریس ها و جبر با ماتریس ها، تعیین کننده ها، مقادیر و بردارهای ویژه (در دو و سه بعدی). توابع چندین متغیر: نمایش های گرافیکی، مشتقات جزئی. سیستم های معادلات دیفرانسیل: نقاط تعادل، پایداری، پرتره های فاز و تجزیه و تحلیل جهانی. برای اطلاع شما، این دوره در درجه اول برای دانش آموزانی که در برنامه های علوم زیستی ثبت نام کرده اند در نظر گرفته شده است. لطفا الزامات برنامه خود را بررسی کنید.

جزء: گروه بحث، سخنرانی

پیش نیاز: MAT 1730 یا MAT 1727 . دوره های MAT 1732 , MAT 1703 , MAT 1722 , MAT 1725 را نمی توان برای کسب امتیاز با هم ترکیب کرد.

MAT 1739 مقدمه ای بر حساب و بردار (3 واحد)

سرعت تغییر لحظه ای به عنوان حد، مشتقات چند جمله ای با استفاده از حد، مشتقات حاصل، توابع مرکب، مشتقات توابع گویا، مثلثاتی، لگاریتمی و رادیکال. کاربردها: حداکثر، حداقل، و نمایش های گرافیکی. نقاط تقعر و عطف، مشتق دوم. بهینه سازی در مدل هایی که دارای توابع چند جمله ای، گویا و نمایی هستند. بردارهای دو و سه بعدی. اشکال دکارتی، قطبی و هندسی. عملیات جبری روی بردارها، حاصل ضرب اسکالر، حاصلضرب برداری. کاربردها برای پیش بینی ها، مساحت متوازی الاضلاع، حجم متوازی الاضلاع. معادلات صفحات و خطوط به صورت پارامتریک اسکالر و برداری، در فضای دو بعدی و سه بعدی. تقاطع خطوط و صفحات. حل حداکثر سه معادله خطی با سه مجهول با حذف یا جایگزینی. تفسیر هندسی راه حل ها MAT 1739 یک دوره ارتقاء است. می توان آن را به این صورت دنبال کرد یا برای برآوردن شرایط پذیرش. در هر صورت، نمی توان آن را برای اعتبارات برای اهداف مورد نیاز برنامه حفظ کرد. رتبه بندی S/NS.

جزء: سخنرانی، گروه بحث

پیش نیاز: Ontario Mathematics 4U Advanced Functions (MHF4U) یا MAT 1318 یا معادل آن. دوره های MAT 1739 ، ریاضیات 4U انتاریو و بردارها (MCV4U) را نمی توان برای اعتبار ترکیب کرد.

MAT 1341 مقدمه ای بر جبر خطی (3 اعتبار)

بررسی اعداد مختلط قضیه اساسی جبر. بررسی محصول و پیش بینی های اسکالر و برداری. مقدمه ای بر فضاهای برداری، استقلال خطی، مبانی. فضاهای عملکردی حل سیستم های معادلات خطی، جبر ماتریس ها، تعیین کننده ها، مقادیر و بردارهای ویژه. روش گرام اشمیت و پیش بینی های متعامد. تبدیل های خطی، هسته های آنها، تصاویر آنها و ماتریس های مرتبط با آنها. کاربردها (به عنوان مثال در هندسه، شبکه ها، معادلات دیفرانسیل).

جزء: گروه بحث، سخنرانی

پیش نیاز: MAT1339 یا Ontario Mathematics 4U (MCV4U) یا معادل آن. دوره های MAT1302، MAT1341 را نمی توان برای کسب واحد با هم ترکیب کرد.

MAT 1748 ریاضیات گسسته برای علوم کامپیوتر (3 واحد)

مقدمه ای بر ساختارهای گسسته به عنوان پایه علم کامپیوتر. منطق پیشنهادات ساختارهای بنیادی: توابع، روابط، مجموعه ها. اصول اولیه شمارش: آرگومان شمارش، اصل کشو، جایگشت ها و ترکیب ها. مقدمه ای بر ساختارهای یک نمایش ریاضی: مستقیم، توسط پوچ، مورد به مورد، با عود. عناصر نظریه گراف: ایزومورفیسم، درختان چرخه، نمودارهای جهت دار. نمونه ها عمدتا در زمینه علوم کامپیوتر انتخاب خواهند شد.

جزء: سخنرانی، گروه بحث

پیش نیاز: MAT 1718 /Math. ویژگی‌های پیشرفته Ontario 4U (MHF4U) یا معادل آن. این دوره را نمی توان برای دانش آموزی که قبلاً برای MAT 2348 امتیاز دریافت کرده است، اعتبار داد . دوره‌های MAT 1748 ، MAT 1762 را نمی‌توان برای کسب امتیاز با هم ترکیب کرد.

MAT 1762 استدلال و برهان ریاضی (3 اعتبار)

عناصر منطق، نظریه مجموعه ها، توابع، روابط هم ارزی و کاردینالیته. تکنیک های اثبات مفاهیم با استفاده از مجموعه اعداد صحیح طبیعی، اعداد صحیح مدول n، اعداد گویا، واقعی و مختلط معرفی می شوند. کاوش خط واقعی: کامل بودن، برتری، پیامدها و محدودیت ها. برخی از مفاهیم با مثال هایی از هندسه، جبر و نظریه اعداد نشان داده خواهد شد.

جزء: گروه بحث، سخنرانی

پیش نیاز: MAT 1339 یا Ontario Mathematics 4U Computation and Vectors (MCV4U) یا معادل آن. دوره های MAT 1762 و MAT 1748 را نمی توان برای اعتبار ترکیب کرد.

آمار توصیفی MAT 1371 (3 واحد)

عناصر آمار توصیفی: هیستوگرام و نمودار باکس ویسکر. میانگین نمونه و انحراف معیار؛ احتمالات ابتدایی؛ قانون عادی؛ تخمین آماری و آزمون فرضیه. همبستگی و رگرسیون نمونه ها با نرم افزار آماری تجزیه و تحلیل شدند.

جزء: گروه بحث، سخنرانی

دوره‌های MAT1371، MAT2371، MAT2377، MAT2379 را نمی‌توان برای کسب اعتبار ترکیب کرد. این دوره نمی تواند برای واحدهای یک برنامه دانشکده علوم یا فنی حساب شود.

MAT 1372 عناصر احتمال و استنتاج آماری (3 واحد)

توزیع ها قانون اعداد بزرگ و قضیه حد مرکزی. نمونه برداری. کاربردهای احتمالات آزمون هایی با توزیع نرمال، t و مجذور کای. همبستگی و رگرسیون.

جزء: آزمایشگاه، سخنرانی

پیش نیاز: MAT 1371 . دوره های MAT 1372 , MAT 2771 , MAT 2777 , MAT 2779 را نمی توان برای کسب واحد با هم ترکیب کرد. این دوره نمی تواند برای واحدهای یک برنامه دانشکده علوم حساب شود.

تجزیه و تحلیل داده های کامپیوتری MAT 1373 (3 اعتبار)

مقدمه ای بر نرم افزارهای کامپیوتری آماری. آمار توصیفی و تحلیل داده های کامپیوتری. توزیع ها و کاربردهای آزمون های پارامتریک و ناپارامتریک استاندارد با شبیه سازی با نرم افزار تفسیر می شوند.

جزء: سخنرانی

دوره های MAT 1773 , MAT 2771 , MAT 2777 , MAT 2779 را نمی توان برای کسب واحد با هم ترکیب کرد. این دوره نمی تواند برای واحدهای یک برنامه دانشکده علوم حساب شود.

MAT 1374 Probability and Games of Chance: Poker 101 (3 اعتبار)

مقدمه‌ای بر تئوری احتمالات، نظریه بازی‌ها و مبانی ریاضی بازی‌های شانسی که با کاربرد آنها در بازی‌های پوکر مانند تگزاس هولدم نشان داده شده است. جنبه های اجتماعی بازی

جزء: سخنرانی

این درس نمی تواند به عنوان یک درس انتخابی در علوم برای دانشجویان دانشکده علوم استفاده شود.

MAT 1795 The Beauty of Mathematics (3 واحد)

موضوعات منتخب از ریاضیات جدید و باستان. محتوای دوره از سالی به سال دیگر متفاوت است. موضوعات ممکن شامل، اما محدود به این موارد نیست: هندسه کلاسیک، نظریه اعداد، نظریه آشوب و ریاضیات برای معلمان در کلاس ابتدایی. برای درس سال جاری با دپارتمان ریاضیات و آمار تماس بگیرید.

جزء: سخنرانی

پیش نیاز: این درس نمی تواند به عنوان یک رشته انتخابی در رشته علوم برای دانشجویان دانشکده علوم محسوب شود.

حساب دیفرانسیل و انتگرال چند متغیره MAT 2122 (3 واحد)

مشتقات به عنوان نقشه های خطی، قانون زنجیره ای. قضیه Clairaut-Schwarz. قضیه تیلور. قضیه تابع ضمنی نقاط افراطی، بحرانی. ضرب کننده های لاگرانژ انتگرال دو و سه گانه، قضیه فوبینی، مختصات قطبی، کروی و استوانه ای. تغییر متغیرها انتگرال های خط، قضیه گرین. سطوح پارامتری و انتگرال های سطحی. قضیه کرل و استوکس، وجود پتانسیل ها. واگرایی و قضیه گاوس. برنامه ها

جزء درس: گروه بحث، سخنرانی

پیش نیازها: ( MAT 1325 یا MAT 1322 )، ( MAT 1341 یا جبر خطی CEGEP با MAT 1341 به عنوان شرط اصلی). دوره های MAT 2122 , MAT 2322 را نمی توان برای واحدها ترکیب کرد.

MAT 2125 Elementary Real Analysis (3 اعتبار)

بررسی خصوصیات کامل بودن اعداد حقیقی. Supremum و Infimum, lim sup, lim inf. توپولوژی R¢n. تداوم یکنواخت فشردگی، هاینه بورل. انتگرال ریمان، قضیه اساسی حساب دیفرانسیل و انتگرال، انتگرال های نامناسب. توالی و سری توابع، همگرایی یکنواخت. سری فوریه.

جزء درس: گروه بحث، سخنرانی

پیش نیازها: MAT1325 یا MAT2122 یا (MAT1322 و یکی از MAT1348، MAT1362، MAT2362).

+ نوشته شده در چهارشنبه بیست و چهارم اسفند ۱۴۰۱ ساعت 12:13 توسط علی رضا نقش نیلچی |

3-برنامه ها و دوره ها دانشکده ریاضی در دانشگاه اوتاوا

MAT 1302 Mathematical Methods II (3 واحد)

حل سیستم های معادلات خطی. جبر ماتریس ها عوامل تعیین کننده اعداد مختلط، قضیه اساسی جبر. مقادیر ویژه و بردارهای ماتریس های واقعی. مقدمه ای بر فضاهای برداری، استقلال خطی، مبانی. برنامه ها پیش نیاز: یکی از دوره های زیر: ریاضیات انتاریو 4U یا ریاضیات مدیریت داده ها (MDM 4U) یا توابع پیشرفته (MHF4U)، MAT 1318 ، MAT 1339 یا یک دوره معادل. دوره های MAT 1702 و MAT 1741 را نمی توان برای اعتبار ترکیب کرد. این دوره عمدتاً برای دانشجویان دانشکده مدیریت و دانشکده علوم اجتماعی در نظر گرفته شده است.

جزء: گروه بحث، سخنرانی

پیش نیاز: ریاضیات انتاریو 4U یا ریاضیات مدیریت داده (MDM 4U) یا توابع پیشرفته (MHF4U)، MAT 1318 ، MAT 1339 یا یک دوره معادل. دوره های MAT 1702 و MAT 1741 را نمی توان برای اعتبار ترکیب کرد.

MAT 1303 Mathematical Methods III (3 واحد)

سکانس، سریال، سریال کامل، سریال تیلور. معادلات تفاضل محدود: حل کلی معادلات خطی با ضرایب ثابت. تعمیق روشهای یکپارچه سازی انتگرال های نامناسب مشتقات توابع مرکب چندین متغیر. گرادیان، مشتق در یک جهت، صفحه مماس. مشتقات جزئی مرتبه بالاتر. افراط و تفریط با یا بدون محدودیت. انتگرال دوگانه

جزء: سخنرانی

پیش نیاز: MAT 1700 یا MAT 1729 . MAT 1702 همزمان با MAT 1703 است . دوره های MAT 1703 , MAT 1722 , MAT 1725 , MAT 1732 را نمی توان برای کسب امتیاز با هم ترکیب کرد.

MAT 1708 مقدمه ای بر حساب دیفرانسیل و انتگرال (3 واحد)

بررسی توابع ابتدایی، مقدمه‌ای بر حدود، سری‌های هندسی، مقدمه‌ای بر حساب دیفرانسیل و انتگرال توابع یک متغیر، کاربردهای مشتق و انتگرال، تقریب خطی، کاربرد در مسائل بهینه‌سازی. دانش آموزانی که قبلاً مشتقات و قوانین اشتقاق را مطالعه کرده اند باید در MAT 1300 ثبت نام کنند . این دوره عمدتاً مختص دانشجویان دانشکده هنر و دانشکده علوم اجتماعی می باشد. دانشجویانی که MCV4U، MAT 1739 یا معادل آن را تکمیل کرده‌اند ، قویاً تشویق می‌شوند که به جای MAT 1708 در MAT 1700 ثبت‌نام کنند .

جزء: گروه بحث، سخنرانی

پیش نیاز: یکی از دوره های زیر: توابع پیشرفته (MHF4U) یا MAT 1718 یا معادل آن. دوره های MAT 1708، MAT 1700، MAT 1720، MAT 1721 ، MAT 1727 ، MAT 1729 ، MAT 1730 را نمی توان برای کسب امتیاز با هم ترکیب کرد.

توابع MAT 1318 (3 اعتبار)

توابع چند جمله ای و گویا: فاکتورسازی، قضیه باقیمانده، خانواده های چندجمله ای با توابع چند جمله ای مشخص، زوج و فرد. لگاریتم و نمایی پایه های مختلف، قوانین آنها. توابع مثلثاتی: اندازه گیری بر حسب رادیان، مقادیر ضرایب مثلثاتی اصلی، فرمول زوایای مرکب، هویت های مثلثاتی. حل معادلات و نابرابری های مربوط به مقادیر مطلق، توابع چند جمله ای، گویا، نمایی و لگاریتمی. نمودارهای آنها عملیات روی توابع: جمع و ضرب نقطه، ترکیب. توابع معکوس میانگین و سرعت تغییر لحظه ای، تقریب نرخ لحظه ای تغییر، سکنت ها و مماس ها بر نمودارها. کاربردها برای مطالعه منحنی ها، ماکزیمم ها و حداقل های توابع. MAT 1718 یک دوره ارتقاء است. می توان آن را به این صورت دنبال کرد یا برای برآوردن شرایط پذیرش. در هر صورت، نمی توان آن را برای اعتبارات برای اهداف مورد نیاز برنامه حفظ کرد. رتبه بندی S/NS.

جزء: سخنرانی

پیش نیاز: توابع ریاضی درجه 11 انتاریو (MCR3U) یا معادل آن. دوره های MAT 1718 ، انتاریو ریاضیات 4U پیشرفته (MHF4U) را نمی توان برای اعتبار ترکیب کرد.

حساب دیفرانسیل و انتگرال I MAT 1720 (3 واحد)

تعریف شهودی حد؛ تداوم؛ بیان قضیه ارزش میانی مروری کوتاه بر فرمول های اساسی مشتق: محصولات، نمایی، و توابع مثلثاتی. مشتقات ضرایب توابع، لگاریتم و توابع مثلثاتی معکوس. تقریب عددی مشتقات با اختلاف محدود. مطالعات توابع با استفاده از مشتقات اول و دوم. گزاره های قضایای کرانه های رسیده و افزایش های محدود. قانون بیمارستان مشتق ضمنی، نرخ های مرتبط، بهینه سازی، تقریب خطی، روش نیوتن. انتگرال معین و قضیه اساسی. ابتدایی توابع ابتدایی، روشهای ادغام (ادغام با قطعات، جایگزینی، کسری جزئی). ادغام دیجیتال: نقطه میانی، ذوزنقه و فرمول های سیمپسون. تجزیه و تحلیل خطا

جزء: گروه بحث، سخنرانی

پیش نیاز: MAT 1339 یا Ontario Mathematics 4U Computation and Vectors (MCV4U) یا معادل آن. دوره های MAT 1700 , MAT 1708 , MAT 1720 , MAT 1721 , MAT 1727 , MAT 1729 , MAT 1730 نمی توانند برای کسب اعتبار ترکیب شوند.

MAT 1721 حساب دیفرانسیل و انتگرال I (3 واحد)

نرخ آنی تغییر و تعریف حد. تداوم؛ بیان قضیه ارزش میانی مشتقات چند جمله ای با استفاده از حد، مشتقات حاصل، توابع مرکب، مشتقات توابع گویا، مثلثاتی و رادیکال، نمایی. مشتقات ضرایب توابع، لگاریتم و توابع مثلثاتی معکوس. تقریب عددی مشتقات با اختلاف محدود. مطالعات توابع با استفاده از مشتقات اول و دوم. برنامه های کاربردی: حداکثر، حداقل، و نمایش های گرافیکی. نقاط تقعر و عطف، مشتق دوم. گزاره های قضایای کرانه های رسیده و افزایش های محدود. قانون بیمارستان مشتق ضمنی، نرخ های مرتبط، بهینه سازی، تقریب خطی، روش نیوتن. من' انتگرال معین و قضیه اساسی. ابتدایی توابع ابتدایی، روشهای ادغام (ادغام با قطعات، جایگزینی، کسری جزئی). ادغام عددی: نقطه میانی، ذوزنقه و فرمول سیمپسون. تجزیه و تحلیل خطا

جزء: گروه بحث، سخنرانی

پیش نیاز: MAT 1318 یا Ontario Advanced Functions 4U (MHF4U) یا معادل آن. دوره های MAT 1721 , MAT 1720 , MAT 1700 , MAT 1708 , MAT 1729 , MAT 1727 , MAT 1730 نمی توانند برای کسب امتیاز ترکیب شوند.

MAT 1722 حساب دیفرانسیل و انتگرال II (3 اعتبار)

انتگرال های نامناسب کاربردهای انتگرال معادلات دیفرانسیل قابل تفکیک روش اویلر برای معادلات دیفرانسیل. سوئیت و سریال. فرمول تیلور و سری تیلور. توابع دو و سه متغیر. مشتقات جزئی، مشتقات زنجیره ای، مشتقات جهتی، صفحات مماس و خطوط عادی.

جزء: گروه بحث، سخنرانی

پیش نیاز: MAT 1720 یا MAT 1721 . دوره های MAT 1722 , MAT 1703 , MAT 1725 , MAT 1732 را نمی توان برای کسب امتیاز با هم ترکیب کرد.

MAT 1725 حساب دیفرانسیل و انتگرال II و مقدمه ای بر تحلیل ریاضی (3 واحد)

این دوره دوم در حساب دیفرانسیل و انتگرال به نفع شهود هندسی و فیزیکی است و در عین حال مفاهیم اساسی تجزیه و تحلیل ریاضی را در نظر می گیرد. تجدید نظر در نابرابری ها دنباله ها. اصل کامل بودن اعداد حقیقی. تداوم. ارائه قضایای مقادیر میانی، حداکثر، افزایش های محدود، تیلور و اثبات برخی از آنها. منحنی ها و سطوح استاندارد در R¢2 و R¢3. توابع 2 و 3 متغیر. مشتقات جزئی، مشتقات جهت دار، مشتق به صورت نقشه خطی دیده می شود. صفحات مماس و خطوط معمولی.

جزء: گروه بحث، سخنرانی

پیش نیاز: MAT 1720 یا MAT 1721 . دوره های MAT 1725 , MAT 1703 , MAT 1722 , MAT 1732 را نمی توان برای کسب امتیاز با هم ترکیب کرد. این دوره برای دانشجویان علاقه مند به دنبال کردن دوره های پیشرفته در ریاضیات است.

MAT 1727 حساب دیفرانسیل و انتگرال برای علوم زیستی I (3 واحد)

نرخ آنی تغییر و تعریف حد. تداوم مشتقات چند جمله ای با استفاده از حد، قواعد حاصلضرب و ضریب، مشتق توابع مرکب، مشتق توابع نمایی، توابع لگاریتمی و توابع مثلثاتی پایه، مشتقات مرتبه بالاتر، نمودار توابع. کاربردهای مشتق در علوم زیستی. سیستم های دینامیکی گسسته، نقاط تعادل، پایداری، نمودار به شکل تار عنکبوت. انتگرال ها: انتگرال های معین و نامعین، قضیه اساسی حساب دیفرانسیل و انتگرال، انتگرال های اولیه، روش های انتگرال گیری با جانشینی و با قطعات. کاربردهای انتگرال در علوم زیستی.

جزء: گروه بحث، سخنرانی

پیش نیاز: MAT 1318 یا Ontario Advanced Functions 4U (MHF4U) یا معادل آن. دوره های MAT 1727 , MAT 1730 , MAT 1700 , MAT 1708 , MAT 1720 , MAT 1721 , MAT 1729 را نمی توان برای کسب امتیاز با هم ترکیب کرد.

MAT 1729 Mathematical Methods I (3 واحد)

نرخ آنی تغییر و تعریف حد. تداوم مشتقات چند جمله ای با استفاده از حد، مشتقات حاصل، توابع مرکب، مشتقات توابع گویا، و رادیکال ها، نمایی. مشتقات ضرایب توابع، لگاریتم. مطالعات توابع با استفاده از مشتقات اول و دوم. برنامه های کاربردی: حداکثر، حداقل، و نمایش های گرافیکی. نقاط تقعر و عطف، مشتق دوم. مشتق ضمنی، نرخ های مرتبط، بهینه سازی. سری هندسی. حساب انتگرالی توابع یک متغیر و کاربردها. توابع چندین متغیر مشتقات جزئی.

جزء: گروه بحث، سخنرانی

پیش نیاز: MAT 1318 یا Ontario Advanced Functions 4U (MHF4U) یا معادل آن. دوره های MAT 1729 , MAT 1720 , MAT 1721 , MAT 1700 , MAT 1708 , MAT 1727 , MAT 1730 را نمی توان برای کسب امتیاز با هم ترکیب کرد.

+ نوشته شده در چهارشنبه بیست و چهارم اسفند ۱۴۰۱ ساعت 12:12 توسط علی رضا نقش نیلچی |

2-برنامه ها و دوره ها دانشکده ریاضی در دانشگاه اوتاوا

حساب دیفرانسیل و انتگرال MAT 1332 برای علوم زیستی II (3 واحد)

انتگرال: یکپارچه سازی عددی. انتگرال های نامناسب مقدمه ای بر معادلات دیفرانسیل: چند تکنیک برای حل معادلات دیفرانسیل ساده، حل عددی معادلات دیفرانسیل و مدل ها در علوم زیستی با استفاده از معادلات دیفرانسیل. مقدمه ای بر جبر خطی: ماتریس ها و جبر ماتریسی، تعیین کننده ها، مقادیر ویژه و بردارهای ویژه (در دو یا سه بعدی). توابع چندین متغیر: نمایش های گرافیکی، مشتقات جزئی. سیستم های معادلات دیفرانسیل: نقاط تعادل، پایداری، پرتره فاز و تحلیل جهانی.

جزء درس: گروه بحث، سخنرانی

پیش نیاز: MAT 1330 یا MAT 1327. دوره های MAT 1332 , MAT 1303 , MAT 1322 , MAT 1325 برای واحدها قابل ترکیب نیستند. این دوره در درجه اول برای دانش آموزانی است که در یک برنامه علوم زیستی ثبت نام کرده اند. لطفاً الزامات برنامه خود را تأیید کنید.

MAT 1339 مقدمه ای بر حساب و بردار (3 واحد)

سرعت تغییر لحظه ای به عنوان حد، مشتقات چند جمله ای با استفاده از حد، مشتقات حاصل، قاعده زنجیره ای، مشتقات توابع گویا، مثلثاتی، نمایی، لگاریتمی و رادیکال. برنامه های کاربردی برای یافتن ماکزیمم و مینیمم و ترسیم نمودار. مقعر و نقاط عطف، مشتق دوم. بهینه سازی در مدل های شامل توابع چند جمله ای، گویا و نمایی. وکتورهای دو بعدی و سه بعدی. اشکال دکارتی، قطبی و هندسی. عملیات جبری بردارها، حاصل ضرب نقطه ای، ضربدری. کاربردها برای برجستگی ها، مساحت متوازی الاضلاع، حجم متوازی الاضلاع. فرم پارامتریک اسکالر و برداری معادلات خطوط و صفحات دو و سه بعدی. تقاطع خطوط و صفحات. حل حداکثر سه معادله در سه مجهول با حذف یا جایگزینی. تفسیر هندسی راه حل ها پیش نیاز: عملکردهای Ontario 4U (MHF4U) یا MAT1318 یا معادل آن. دوره های MAT1339، Ontario 4U Calculus and Vectors (MCV4U) یا هر معادل دیگری را نمی توان برای واحدها ترکیب کرد. MAT1339 ممکن است برای اهداف ارتقاء یا به عنوان یک شرط پذیرش گرفته شود در همه موارد، واحدهای این دوره به عنوان بخشی از الزامات برنامه به حساب نمی آیند. طرح درجه بندی S/NS.

جزء درس: گروه بحث، سخنرانی

پیش نیاز: عملکردهای Ontario 4U (MHF4U) یا MAT 1318 یا معادل آن. دروس MAT 1339 ، Ontario 4U Calculus and Vectors (MCV4U) یا هر معادل دیگری را نمی توان برای واحدها ترکیب کرد.

MAT 1341 مقدمه ای بر جبر خطی (3 واحد)

بررسی اعداد مختلط قضیه اساسی جبر. بررسی محصولات برداری و اسکالر، پیش بینی ها. مقدمه ای بر فضاهای برداری، استقلال خطی، مبانی. فضاهای عملکردی حل سیستم های معادلات خطی، جبر ماتریسی، تعیین کننده ها، مقادیر ویژه و بردارهای ویژه. گرام اشمیت، پیش بینی های متعامد. تبدیل های خطی، هسته و تصویر، ماتریس های استاندارد آنها. برنامه های کاربردی (مانند هندسه، شبکه ها، معادلات دیفرانسیل)

جزء درس: گروه بحث، سخنرانی

پیش نیاز: MAT1339 یا Ontario 4U Calculus and Vectors (MCV4U)، یا معادل آن. دوره های MAT1341، MAT1302 را نمی توان برای واحدها ترکیب کرد.

MAT 1348 ریاضیات گسسته برای محاسبات (3 واحد)

مقدمه ای بر ساختارهای گسسته به عنوان پایه ای برای محاسبات منطق گزاره ای ساختارهای بنیادی: توابع، روابط، مجموعه ها. مبانی شمارش: آرگومان های شمارش، اصل چاله کبوتر، جایگشت ها و ترکیب ها. مقدمه بر برهان: مستقیم، با تناقض، با موارد، استقراء. موضوعات در نظریه گراف: ایزومورفیسم، چرخه ها، درختان، نمودارهای جهت دار. در صورت امکان برنامه های کاربردی از محاسبات و فناوری اطلاعات گنجانده خواهد شد.

جزء درس: گروه بحث، سخنرانی

پیش نیاز: MAT 1318 یا Ontario 4U Advanced Functions (MHF4U) یا معادل آن. این درس توسط هیچ دانشجویی که قبلاً واحد MAT 2348 را دریافت کرده است نمی تواند برای واحدها شرکت کند . دروس MAT 1348 ، MAT 1362 برای واحدها قابل ترکیب نیستند.

MAT 1362 استدلال و اثبات ریاضی (3 واحد)

عناصر منطق، نظریه مجموعه ها، توابع، روابط هم ارزی و کاردینالیته. شواهد فنی مفاهیم با استفاده از مجموعه ای از اعداد صحیح، اعداد صحیح مدول n، اعداد گویا، واقعی و مختلط معرفی می شوند. کاوش خط واقعی: کامل بودن، برتری، توالی ها و محدودیت ها. برخی از مفاهیم با مثال هایی از هندسه، جبر و نظریه اعداد نشان داده می شود.

جزء درس: گروه بحث، سخنرانی

پیش نیاز: MAT 1339 یا Ontario 4U Calculus and Vectors (MCV4U) یا معادل آن. MAT 1362 ، MAT 1348 را نمی توان برای واحدها ترکیب کرد.

آمار توصیفی MAT 1371 (3 واحد)

موضوعات از آمار توصیفی: هیستوگرام و نمودار جعبه. میانگین و انحراف معیار مشاهده شده؛ احتمال ابتدایی؛ گچ معمولی؛ تخمین آماری و آزمون فرضیه. همبستگی و رگرسیون نمونه ها با نرم افزار آماری تجزیه و تحلیل شدند.

جزء درس: گروه بحث، سخنرانی

دوره های MAT1371، MAT2371، MAT2377، MAT2379 را نمی توان برای واحدها ترکیب کرد. این درس نمی تواند برای واحد در هیچ برنامه ای در دانشکده علوم یا فنی باشد.

MAT 1372 عناصر احتمال و استنتاج آماری (3 واحد)

توزیع های احتمال قانون اعداد بزرگ و قضیه حد مرکزی نمونه برداری. کاربردهای احتمال آزمایش با توزیع های نرمال، t و مجذور کای. همبستگی و رگرسیون.

جزء درس: آزمایشگاه، خواندن

پیش نیاز: MAT 1371 . دوره های MAT 1372 , MAT 2371 , MAT 2377 , MAT 2379 برای واحدها قابل ترکیب نیستند. این درس در هیچ برنامه ای در دانشکده علوم نمی تواند واحد باشد.

MAT 1373 تجزیه و تحلیل داده ها توسط کامپیوتر (3 واحد)

مقدمه ای بر یک بسته آماری در کامپیوتر. آمار توصیفی و تجزیه و تحلیل داده ها توسط کامپیوتر. توزیع ها و کاربردهای آزمون های پارامتری و ناپارامتریک استاندارد با استفاده از تابع شبیه سازی یک بسته آماری بررسی می شود.

جزء درس: خواندن

دوره های MAT 1373 , MAT 2371 , MAT 2377 , MAT 2379 برای واحدها قابل ترکیب نیستند. این درس در هیچ برنامه ای در دانشکده علوم نمی تواند واحد باشد.

MAT 1374 احتمالات و بازی های شانسی: پوکر 101 (3 واحد)

مقدمه‌ای بر تئوری احتمالات اولیه، نظریه بازی‌ها و زیربنای ریاضی بازی‌های شانسی که از طریق کاربردهای آنها در بازی‌های پوکر مانند تگزاس هولدم نشان داده شده است. جنبه های اجتماعی بازی

جزء درس: خواندن

این درس نمی تواند به عنوان یک رشته انتخابی علمی برای دانشجویان دانشکده علوم محسوب شود.

MAT 1395 The Beauty of Mathematics (3 واحد)

موضوعات منتخب از ریاضیات جدید و باستان. محتوای دوره از سال به سال متفاوت است. مضامین انتخاب شده ممکن است شامل هندسه کلاسیک، نظریه اعداد، نظریه آشوب و ریاضیات برای معلمان مدارس ابتدایی باشد، اما محدود به آنها نیست. برای پیشنهاد سال جاری به بخش ریاضیات و آمار مراجعه کنید.

جزء درس: خواندن

پیش نیاز: این درس نمی تواند به عنوان یک درس انتخابی برای دانشجویان دانشکده علوم محسوب شود.

MAT 1700 Mathematical Methods I (3 واحد)

بررسی توابع ابتدایی مرزها سری هندسی. حساب دیفرانسیل و انتگرال توابع یک متغیر و کاربردها. توابع چندین متغیر مشتقات جزئی.

جزء: گروه بحث، سخنرانی

پیش نیاز: حساب دیفرانسیل و انتگرال و بردار (MCV4U) یا MAT 1739 . دوره های MAT 1700 , MAT 1708 , MAT 1720 , MAT 1730 را نمی توان برای کسب امتیاز با هم ترکیب کرد. این دوره در درجه اول برای دانشجویان دانشکده مدیریت در نظر گرفته شده است.

+ نوشته شده در چهارشنبه بیست و چهارم اسفند ۱۴۰۱ ساعت 12:10 توسط علی رضا نقش نیلچی |

1-برنامه ها و دوره ها دانشکده ریاضی در دانشگاه اوتاوا

MAT 1300 Mathematical Methods I (3 واحد)

بررسی توابع ابتدایی محدودیت ها. سری هندسی. حساب دیفرانسیل و انتگرال در یک متغیر با کاربردها. توابع چندین متغیر مشتقات جزئی.

جزء درس: گروه بحث، سخنرانی

پیش نیاز: یکی از حساب و بردار (MCV4U) یا MAT 1339 . دوره های MAT 1300 , MAT 1308 , MAT 1320 , MAT 1330 برای واحدها قابل ترکیب نیستند. این دوره در درجه اول برای دانشجویان دانشکده مدیریت در نظر گرفته شده است.

MAT 1302 Mathematical Methods II (3 واحد)

حل سیستم های معادلات خطی. جبر ماتریسی. تعیین کننده ها اعداد مختلط، قضیه اساسی جبر. مقادیر ویژه و بردارهای ویژه ماتریس های واقعی. مقدمه ای بر فضاهای برداری، استقلال خطی، مبانی. برنامه ها این دوره عمدتاً برای دانشجویان دانشکده مدیریت و دانشکده علوم اجتماعی در نظر گرفته شده است.

جزء درس: گروه بحث، سخنرانی

پیش نیازها: یکی از ریاضیات مدیریت داده انتاریو 4U (MDM 4U)، توابع پیشرفته انتاریو 4U (MHF4U)، MAT1318، MAT1339 یا معادل آن. دوره های MAT1302، MAT1341 را نمی توان برای واحدها ترکیب کرد.

MAT 1303 Mathematical Methods III (3 واحد)

سکانس، سریال، سریال قدرت، سریال تیلور. معادلات تفاضلی: حل کلی معادلات خطی با ضرایب ثابت. تکنیک های اضافی ادغام انتگرال های نامناسب قانون زنجیره ای برای توابع چندین متغیر. گرادیان، مشتق جهت، صفحه مماس. مشتقات جزئی مرتبه بالاتر. افراطی با یا بدون محدودیت.

جزء درس: خواندن

پیش نیاز: MAT 1300 یا MAT 1329 . MAT 1302 لازمه MAT 1303 است . دوره های MAT 1303 , MAT 1322 , MAT 1325 , MAT 1332 برای واحدها قابل ترکیب نیستند.

MAT 1308 مقدمه ای بر حساب دیفرانسیل و انتگرال (3 واحد)

بررسی توابع ابتدایی مقدمه ای بر محدودیت ها سری هندسی. مقدمه ای بر حساب دیفرانسیل و انتگرال در یک متغیر با کاربردها. تقریب های خطی، برنامه های کاربردی برای بهینه سازی. دانش آموزانی که قبلاً قوانین مشتق و تمایز را مطالعه کرده اند باید به جای آن از MAT 1300 استفاده کنند . این دوره در درجه اول برای دانشجویان دانشکده های هنر و علوم اجتماعی محفوظ است. به دانش‌آموزانی که MCV4U، MAT1339 یا معادل آن را دریافت کرده‌اند، قویاً توصیه می‌شود در عوض برای MAT1300 ثبت نام کنند.

جزء درس: گروه بحث، سخنرانی

پیش نیاز: یکی از توابع پیشرفته (MHF4U) یا MAT 1318 یا معادل آن. دوره MAT 1308 , MAT 1300 , MAT 1320 , MAT 1321 , MAT 1327 , MAT 1329 , MAT 1330 برای واحدها قابل ترکیب نیستند.

توابع MAT 1318 (3 واحد)

توابع چند جمله ای و گویا: فاکتورگیری، قضیه باقیمانده، خانواده های چند جمله ای با توابع چند جمله ای مشخص، فرد و زوج. لگاریتم و نمایی به مبانی مختلف، قوانین آنها. توابع مثلثاتی: اندازه گیری رادیانی، مقادیر نسبت های مثلثاتی اولیه، فرمول های زاویه مرکب، هویت های مثلثاتی. حل معادلات و نامساوی شامل مقادیر مطلق، توابع چند جمله ای، گویا، لگاریتمی، نمایی و مثلثاتی. نمودارهای آنها عملیات روی توابع: جمع و ضرب نقطه ای، ترکیب. توابع معکوس میانگین و نرخ آنی تغییر، نرخ تقریبی تغییر لحظه ای، تقسیمات و مماس بر نمودارها. برنامه های کاربردی برای ترسیم نمودار و یافتن ماکزیمم و مینیمم توابع. استفاده از توابع برای مدل‌سازی، درون‌یابی و برون‌یابی داده‌ها. MAT1318 ممکن است برای اهداف ارتقاء به عنوان یک شرط پذیرش در نظر گرفته شود. در همه موارد، واحدهای این دوره به عنوان بخشی از الزامات برنامه به حساب نمی آیند. طرح درجه بندی S/NS.

جزء درس: خواندن

پیش نیاز: توابع درجه 11 انتاریو (MCR3U) یا معادل آن. دوره های MAT 1318 ، Ontario 4U Advanced Functions (MHF4U) یا هر معادل دیگری را نمی توان برای واحدها ترکیب کرد.

MAT 1320 Calculus I (3 واحد)

تعریف شهودی محدودیت ها؛ تداوم، بیان قضیه ارزش میانی. بررسی سریع فرمول های مشتق پایه: محصولات، قانون زنجیره، نمایی، و توابع مثلثاتی. مشتقات ضریب، لگاریتم، توابع مثلثاتی معکوس. تقریب تفاضل محدود مشتقات. تجزیه و تحلیل توابع از طریق مشتقات اول و دوم. گزاره های قضایای ارزش افراطی و میانگین. قانون L'Hospital. تمایز ضمنی، نرخ های مرتبط، بهینه سازی، تقریب خطی، روش نیوتن. انتگرال معین و قضیه اساسی حساب دیفرانسیل و انتگرال. ضد مشتقات توابع ابتدایی، تکنیک های ادغام (ادغام با قطعات، جایگزینی، کسر جزئی). ادغام عددی: نقطه میانی، قانون ذوزنقه ای و قانون سیمپسون. تجزیه و تحلیل خطا

جزء درس: گروه بحث، سخنرانی

پیش نیاز: یکی از MAT 1339 ، حساب و بردارهای Ontario 4U (MCV4U) یا معادل آن. دوره های MAT 1300 , MAT 1308 , MAT 1320 , MAT 1321 , MAT 1327 , MAT 1329 , MAT 1330 برای واحدها قابل ترکیب نیستند.

MAT 1321 Intensive Calculus I (3 واحد)

نرخ آنی تغییر و تعریف حدود. تداوم، بیان قضیه ارزش میانی. مشتقات چند جمله ای با استفاده از حد، مشتقات حاصل، قاعده زنجیره ای، مشتقات توابع گویا، مثلثاتی، نمایی و رادیکال. مشتقات ضریب، لگاریتم، توابع مثلثاتی معکوس. تقریب تفاضل محدود مشتقات. تجزیه و تحلیل توابع از طریق مشتقات اول و دوم. کاربردهایی برای یافتن ماکزیمم و مینیمم. تقعر و نقاط عطف، و ترسیم نمودار. گزاره های قضایای ارزش افراطی و میانگین. قانون L'Hospital. تمایز ضمنی، نرخ های مرتبط، بهینه سازی، تقریب خطی، روش نیوتن. انتگرال معین و قضیه اساسی حساب دیفرانسیل و انتگرال. ضد مشتقات توابع ابتدایی، تکنیک های ادغام (ادغام با قطعات، جایگزینی، کسر جزئی). ادغام عددی: نقطه میانی، قانون ذوزنقه ای و قانون سیمپسون. تجزیه و تحلیل خطا

جزء درس: گروه بحث، سخنرانی

پیش نیاز: یکی از MAT 1318 ، Ontario 4U Advanced Functions (MHF4U) یا معادل آن. دروس MAT 1321 , MAT 1320 , MAT 1300 , MAT 1308 , MAT 1329 , MAT 1327 , MAT 1330 برای واحدها قابل ترکیب نیستند. پیش نیاز MAT1321

MAT 1322 Calculus II (3 واحد)

انتگرال های نامناسب کاربردهای انتگرال معادلات دیفرانسیل قابل تفکیک روش اویلر برای معادلات دیفرانسیل. سکانس، سریال. فرمول و سری تیلور. توابع دو و سه متغیر. مشتقات جزئی، قانون زنجیره، مشتقات جهت، صفحات مماس و خطوط عادی.

جزء درس: گروه بحث، سخنرانی

پیش نیاز: MAT 1320 یا MAT 1321 . دوره های MAT 1322 , MAT 1303 , MAT 1332 , MAT 1325 برای واحدها قابل ترکیب نیستند.

MAT 1325 Calculus II و مقدمه ای بر تجزیه و تحلیل (3 واحد)

دوره دوم در حساب دیفرانسیل و انتگرال با تاکید بر شهود هندسی و فیزیکی که در آن به مبانی مفهومی حساب دیفرانسیل و انتگرال-تحلیل نیز توجه شده است. بررسی نابرابری ها دنباله ها اصل کامل بودن اعداد حقیقی. تداوم. برهان برخی از: قضایای مقدار متوسط و افراطی، قضیه ارزش متوسط. قضیه تیلور. منحنی ها و سطوح استاندارد در 2 و 3 فاصله. بردارهای مماس، صفحات و نرمال ها. مشتقات جزئی، مشتقات جهت دار، مشتقات به صورت نقشه های خطی.

جزء درس: گروه بحث، سخنرانی

پیش نیاز: MAT 1320 یا MAT 1321 . دوره های MAT 1325 , MAT 1303 , MAT 1322 , MAT 1332 برای واحدها قابل ترکیب نیستند. این دوره در درجه اول برای دانش آموزانی است که علاقه مند به دنبال کردن دوره های پیشرفته در ریاضیات هستند.

محاسبات فشرده MAT 1327 برای علوم زیستی I (3 واحد)

نرخ آنی تغییر و تعریف حدود. تداوم مشتقات چند جمله‌ای با استفاده از حد، قواعد حاصل و ضریب، قانون زنجیره، مشتق توابع نمایی، لگاریتمی و مثلثاتی پایه، مشتقات بالاتر، ترسیم منحنی. کاربردهای مشتق در علوم زیستی. سیستم های دینامیکی گسسته: نقاط تعادل، پایداری، تار عنکبوت. انتگرال ها: انتگرال های نامعین و معین، قضیه اساسی حساب دیفرانسیل و انتگرال، پاد مشتق، جایگزینی، انتگرال گیری توسط قطعات. کاربردهای انتگرال در علوم زیستی.

جزء درس: گروه بحث، سخنرانی

پیش نیاز: یکی از MAT 1318 ، Ontario 4U Advanced Functions (MHF4U) یا معادل آن. دوره های MAT 1327 , MAT 1330 , MAT 1300 , MAT 1308 , MAT 1320 , MAT 1321 , MAT 1329 برای واحدها قابل ترکیب نیستند.

MAT 1329 Intensive Mathematical Methods I (3 واحد)

نرخ آنی تغییر و تعریف حدود. تداوم مشتقات چند جمله ای با استفاده از حد، مشتقات حاصل، قاعده زنجیره ای، مشتقات توابع گویا، نمایی و رادیکال. مشتقات ضریب، لگاریتم. تجزیه و تحلیل توابع از طریق مشتقات اول و دوم. کاربردهایی برای یافتن ماکزیمم و مینیمم. تقعر و نقاط عطف، و ترسیم نمودار. تمایز ضمنی، نرخ های مرتبط، بهینه سازی. سری هندسی. حساب انتگرال در یک متغیر با برنامه های کاربردی. توابع چندین متغیر مشتقات جزئی.

جزء درس: گروه بحث، سخنرانی

پیش نیاز: یکی از MAT 1318 ، Ontario 4U Advanced Functions (MHF4U) یا معادل آن. دوره های MAT 1329 , MAT 1320 , MAT 1321 , MAT 1300 , MAT 1308 , MAT 1327 , MAT 1330 برای واحدها قابل ترکیب نیستند.

حساب دیفرانسیل و انتگرال MAT 1330 برای علوم زیستی I (3 واحد)

مشتقات: قواعد حاصل و ضریب، قانون زنجیره، مشتق توابع نمایی، لگاریتمی و مثلثاتی پایه، مشتقات بالاتر، ترسیم منحنی. کاربردهای مشتق در علوم زیستی. سیستم های دینامیکی گسسته: نقاط تعادل، پایداری، تار عنکبوت. انتگرال ها: انتگرال های نامعین و معین، قضیه اساسی حساب دیفرانسیل و انتگرال، پاد مشتق، جایگزینی، انتگرال گیری توسط قطعات. کاربردهای انتگرال در علوم زیستی.

جزء درس: گروه بحث، سخنرانی

پیش نیاز: یکی از MAT 1339 ، حساب و بردارهای Ontario 4U (MCV4U) یا معادل آن. دوره های MAT 1300 , MAT 1308 , MAT 1320 , MAT 1321 , MAT 1327 , MAT 1329 , MAT1330 برای واحدها قابل ترکیب نیستند.نا

+ نوشته شده در چهارشنبه بیست و چهارم اسفند ۱۴۰۱ ساعت 12:5 توسط علی رضا نقش نیلچی |

دکتر جواد بهبودیان

نام: جواد بهبودیان (Javad Behboodian)

تاریخ تولد: دوم فروردین ۱۳۱۰

درگذشت: دوازدهم فروردین ۱۳۹۹
محل تولد: شیراز

ملیت: ایرانی

شهرت: ریاضیات، آمار

مختصری از بیوگرافی دکتر جواد بهبودیان

دکتر جواد بهبودیان در سال 1310 در شیراز متولد شد و تحصیلات ابتدایی و دبیرستان خود را در مدارس ابن سینای شیراز، سلطانی شیراز و دارالفنون تهران به اتمام رسانید.

ایشان تحصیلات دانشگاهی خود را در رشته ریاضی آغاز و در سال 1333 لیسانس ریاضی خود را از دانشکده علوم دانشگاه تهران و در همین سال لیسانس آموزش ریاضی را از دانشسرایعالی دانشگاه تهران اخذ نمود. سپس در سالهای 1337-1333 در دبیرستانهای شیراز به عنوان دبیر ریاضی مشغول شد.

دکتر بهبودیان برای ادامه تحصیل در دوره های بالاتر در سال 1337 به عنوان بورسیه راهی کشور آمریکا شد و دوره کارشناسی ارشد آمار ریاضی را در دانشگاه میشیگان در سال 1340 با موفقیت به پایان رسانید و در سال 1343 موفق به کسب درجه دکتری آمار ریاضی در همان دانشگاه شد. او فعالیت آموزشی خود را در سال 1343 با مرتبه استادیاری در بخش ریاضی سابق دانشگاه شیراز آغاز نمود و در سال 1347 به مرتبه دانشیاری ارتقاء یافت و با کسب امتیاز های پژوهشی و آموزشی لازم در سال 1351 به درجه استادی دانشکده ادبیات و علوم سابق دانشگاه شیراز دست یافت. او تمام مدت در دانشگاه شیراز در مقطع کارشناسی و تحصیلات تکمیلی به آمموزش و پژوهش مشغول بوده است. گفتنی است که دکتر بهبودیان در سال 1350 دانشیار مدعو دانشگاه کرولینای شمالی آمریکا، در سال 1355 استاد مدعو دانشگاه اتانفورد آمریکا و در سال 1367 استاد مدعو دانشگاه لون بلژیک بود. ایشان دروس آمار، احتمال و ریاضی را در مقطع مختلف تحصیلی تدریسنمود و دارای مقاله هاییدر مجله های خارجی و ایرانی در زمینه آمار ریاضی، آموزش ریاضی به زبانهای انگلیسی و فارسی می باشد. همچنین چندین پایان نامه کارشناسی ارشد و دکترا را راهنمایی کرده و چند طرحپژوهشی را در دانشگاه شیراز به پایان رسانیده است.

دکتر بهبودیان ضمن انجام فعالیتهای آموزشی و پژوهشی به تألیف کتاب نیز توجه خاصی داشته است. کتابهای ایشان به شرح زیراند:

-- آمار ناپارامتری، چاپ پنجم با تجدید نظر کلی 1387، دانشگاه شیراز.
-- آمار و احتمال مقدماتی، چاپ سی و چهارم با تجدید نظر کلی 1388، آستان قدس.
-- آمار ریاضی، چاپ چهارم 1388، انتشارات امیر کبیر.
-- تصمیم آماری 1374، دانشگاه شیراز.
-- رگرسیون، چاپ پنجم با تجدید نظر کلی 1384، دانشگاه پیام نور.
-- روشهای ناپارامتری آمار 1377، دانشگاه پیام نور.
-- مثلث خیام- پاسکال (تألیف بهبودیان، بیات، تیموری) 1384، دانشگاه صنعتی شریف.

ایشان در هیأت تحریریه مجله های اندیشه آماری انجمن آمار ایران، بولتن انجمن ریاضی ایران و گلچین ریاضی دانشگاه شیراز همکاری داشته اند. در حال حاضر عضو هیأت تحریریه مجله علوم و فنون ایران (JIST, A)، مجله پژوهشی انجمن آمار ایران (JIRSS)، مجله علوم دانشگاه شهید چمران اهواز، مجله گستره ریاضی(JMEX) دانشگاه آزاد اسلامی شیراز می باشند. در ضمن Reviewer انجمن ریاضی آمریکا هم هستند.

از فعالیتهای ایشان در سمت اجرایی می توان از ریاست بخش ریاضی در سالهای 1349-1346، ریاست بخش ریاضی و آمار در سالهای 1353-1350، ریاست دانشکده ادبیات و علوم سابق در سالهای 1354-1353 و ریاست بخش آمار در سالهای 1377-1374 نام برد.

دکتر بهبودیان عضو انجمن ریاضی ایران، انجمن آمار ایران و از پایه گذاران این دو انجمن می باشد. او در سالهای 75-74 دبیر انجمن آمار بوده است. ایشان عضو فرهنگستان علوم جمهوری اسلامی ایران، انجمن ریاضی آمریکا (AMS)، مجمع ریاضی آمریکا (ASA)، انجمن آمار آمریکا (MAA)، مؤسسه آمار ریاضی آمریکا (IMS) و انجمن آمار کشور های اسلامی نیز می باشند.

وی دبیر نخستین کنفرانس ریاضی ایران در دانشگاه شیراز در فروردین 1349، دبیر علمی نخستین کنفرانس آمار ایران در دانشگاه صنعتی اصفهان در 1370 و دبیر علمی کنگره حاتم نی ریز در 1378 در نی ریز بوده اند.

دکتر بهبودیان از مهر ماه 1382 استاد تمام وقت دانشگاه آزاد اسلامی واحد شیراز و مدیر گروه کارشناسی ارشد ریاضی این دانشگاه بود. او دارای یک پسر و یک دختر می‌باشد که هر دو دارای تحصیلات دانشگاهی و همسر و فرزند می‌باشند. بهترین افتخار نامبرده، به گفته او، دانشجویان سابق او می باشند که در ایران و خارج به مقامهای علمی و دانشگاهی نائل شده اند.

$دکتر جواد بهبودیان -- دانشگاه جهرم، همایش آمار$

دکتر جواد بهبودیان -- دانشگاه جهرم، همایش آمار (2013)

مدارک دانشگاهی
لیسانس ریاضی: گروه ریاضی دانشگاه تهران، تهران 1333
لیسانس آموزش ریاضی: دانشسرایعالی تهران: تهران 1333
کارشناسی ارشد آمار ریاضی: بخش ریاضی دانشگاه میشیگان آمریکا (شهر آن آربر) 1340
دکترای آمار ریاضی: بخش ریاضی دانشگاه میشیگان آمریکا (شهر آن آربر) 1343
گواهینامه پژوهش و ارزیابی: دانشگاه شیکاگو آمریکا، تابستان 1352.

عناوین آموزشی
دبیر ریاضی دبیرستانهای شیراز 1337-1333
استادیار بخش ریاضی دانشگاه شیراز 1347-1343
دانشیار بخش ریاضی و آمار دانشگاه شیراز 1351-1347
استاد بخش ریاضی و آمار دانشگاه شیراز 1352
استادمان (Professor Emeritus ) بخش آمار دانشگاه شیراز 1380 (باز نشسته)
استاد گروه ریاضی کارشناسی ارشد دانشگاه آزاد اسلامی شیراز از 1382

دروس تدریس شده
ریاضی عمومی، آمار و احتمال مقدماتی، احتمال، آمار ریاضی، آمار ناپارامتری، رگرسیون، آشنائی با نظریه تصمیم، استنباط آماری، آنالیز چند متغیره، استنباط آماری پیشرفته، آنالیز حقیقی، نظریه اندازه ، نظریه احتمال، استنباط پیشرفته، نمونه های بزرگ، آمار پیشرفته، آمار بیز پیشرفته.

عضویت در انجمن های علمی و فرهنگستان
انجمن آمار آمریکا (ASA)، انجمن ریاضی آمریکا (AMS)، مجمع ریاضی آمریکا (MAA)، انجمن ریاضی ایران، انجمن آمار ایران، مؤسسه آمار آمریکا (IMS)، انجمن آمار کشور های اسلامی، عضو فرهنگستان علوم جمهوری اسلامی ایران.

کتابهای تألیفی به زبان فارسی

- آمار ناپارامتری، چاپ پنجم با تجدید نظر کلی 1387، دانشگاه شیراز.
- آمار و احتمال مقدماتی، چاپ سی و چهارم با تجدید نظر کلی 1388، آستان قدس.
- آمار ریاضی، چاپ چهارم 1388، انتشارات امیر کبیر.
- تصمیم آماری 1374، دانشگاه شیراز.
- رگرسیون، چاپ پنجم با تجدید نظر کلی 1384، دانشگاه پیام نور.
- روشهای ناپارامتری آمار 1377، دانشگاه پیام نور.
- مثلث خیام- پاسکال (تألیف بهبودیان، بیات، تیموری) 1384، دانشگاه صنعتی شریف.

راهنمائی پایان نامه‌ها
کارشناسی ارشد بیش از 50 – دکترا بیش از 10 (در گذشته و حال در دانشگاه آزاد اسلامی و دانشگاه شیراز).

عضو هیأت تحریریه مجلات علمی در گذشته
بولتن انجمن ریاضی ایران، اندیشه آماری انجمن آمار ایران، علوم و فنون دانشگاه شیراز، گلچین ریاضی دانشگاه شیراز.

عضو هیأت تحریریه مجلات علمی در زمان حال
علوم و فنون دانشگاه شیراز (IJST,A)، مجله پژوهشی انجمن آمار ایران (JIRSS)، مجله علوم دانشگاه شهید چمران اهواز، مجله گستره ریاضی دانشگاه آزاد اسلامی شیراز (JMEX) انجمن ریاضی آمریکا، مؤسسه آمار ریاضی آمریکا (IMS).

سمت‌های اجرائی در گذشته

رئیس بخش ریاضی دانشکده ادبیات و علوم سابق 1349-1346
رئیس بخش ریاضی و آمار دانشکده ادبیات و علوم سابق 1353-1350
رئیس دانشکده ادبیات و علوم سابق 1354-1353
رئیس بخش آمار دانشکده علوم 1377-1374

سمتهای اجرائی در زمان حال
مدیر گروه کارشناسی ارشد ریاضی دانشگاه آزاد اسلامی شیراز از 1383.

کنفرانس‌ها

دبیر نخستین کنفرانس ریاضی ایران در دانشگاه شیراز، فروردین 1349
دبیر علمی نخستین کنفرانس آمار ایران در دانشگاه صنعتی اصفهان، شهریور 1370
دبیر علمی کنگره حاتم نی ریزی، ریاضیدان ایرانی در نی ریز ، آبان 1378

فرصتهای مطالعاتی
دانشیار مدعو بخش آمار دانشگاه کارولینای شمالی آمریکا، 1351-1350
استاد مدعو بخش آمار دانشگاه استانفورد آمریکا، 1356-1355
استاد مدعو بخش ریاضی دانشگاه کاتولیک لون بلژیک، 1368-1367

مقاله های علمی به زبان فارسی و انگلیسی

این مقاله‌ها در مجله‌های ریاضی یا آمار فارسی و انگلیسی چاپ شده اند. در ضمن برخی در سمینارها و کنفرانس‌ها ارائه شده‌اند:

C. V. JAVAD BEHBOODIAN

Current Academic Position

Professor Emeritus if Statistics, Since 2001.

Professor of Mathematics and Statics of Shiraz
Islamic Azad University, Since 2003.

Previous Academic Positions
Shiraz High Schools Mathematic Teacher, 1954-1958
Assistant Professor of Mathematics, 1965-1968
Associate Professor of Mathematics and Statistics, 1969-1974
Professor of Mathematics and Statistics, 1975-2007

Prrvious Administrative Positions
Chairman of the Department of Mathematics 1967-1969
Chairman of the Department of Mathematics and Statistics 1995-1997
Dean of the College of Arts and Sciences, 1974-1975
Chairman of the Departments of Statics, 1995-1997

Current Administrative Position

Chairman of the Graduate Department of Mathematics,

At Shiraz Islamic Azad University, Since 2003.

Degrees

B.S. College of Sciences Tehran University, 1954(Math)
B.A. Teacher Training College, Tehran University, 1954 (Math Educ.)
M.S. University of Michigan, Ann Arbor, 1961 (Math. Stat.)
PhD University of Michigan, Ann Aebor, 1965 (Math. Stat.)
Certificate (Summer Graduate Study) University of Chicago, 1973 (Research of Evaluation).

Position in Conferences

Organizer of the first Iranian Mathematics Confrrence, Shiraz University 1969.
Scientific Secretary of the first Iranian Statistical Cinference, Isfahan Industrial University 1991.
Scientific Socratary of the Congress of Hatam Nirizi (Iranian Mathematician), Niriz, Fars, 1999.

Courses Taught
High school Mathematics, General Mathematics, General Probability and Statistics, Statistical inference (MS and PhD level), Measure and Probability Theory, Decision Theory, Advinced Bayesian Statistics, Mulvariate Analysis, Nonparametric Statistics, Regression Analysis.

Visiting Other Universities
1- visiting Associate Professor, University of N.C., Dept. of Stat. , Chapel Hill, N. C. , USA. (Fulbright visitor Researcher), 1970-1971.
2- Visiting Professor, Stuonford University, Dept. of stat., Stanford, California, USA (Teaching and Research), 1975-1976.
3- Visiting Professor, University of Levren, Dept. of Math., Levren, Belgian (Research Professor), 1987-1988.

Membership in Societies

Iranian mathematical Society.
Iranian Statistical Society.
American Statistical Association(ASA)
American Mathematical Society(AMS)
Mathematical Association of America(MAA)
Institute of Mathematical statistics(IMS)
Membership in Editional Boards:

Iranian Journal of Science and Technology(IJST)
Journal of Iranian Statistical Society (JIRSS)
Journal of Sciences of Ahvaz Shahid Chamran Univ.
Reviewer of Math Review.
Journal of Mathematica Extension(JMEX)

مآخذ...

آشنائی با اساتید دانشگاه شیراز، روابط عمومی دانشگاه شیراز، 1376.

منبع

https://www.ihoosh.ir/article/61689/%D8%B2%D9%86%D8%AF%DA%AF%DB%8C%D9%86%D8%A7%D9%85%D9%87-%D8%B1%DB%8C%D8%A7%D8%B6%DB%8C%D8%AF%D8%A7%D9%86%D8%A7%D9%86-%D8%AF%DA%A9%D8%AA%D8%B1-%D8%AC%D9%88%D8%A7%D8%AF-%D8%A8%D9%87%D8%A8%D9%88%D8%AF%DB%8C%D8%A7%D9%86

+ نوشته شده در سه شنبه بیست و سوم اسفند ۱۴۰۱ ساعت 19:36 توسط علی رضا نقش نیلچی |

پروفسور علی‌اکبر عالِم‌زاده

فهرست

نهفتن

بخش آغازین
زندگی
آثار
تغییر وضعیت زیربخش‌های آثار
- تألیفات
- ترجمه‌ها
منابع

علی‌اکبر عالم‌زاده

افزودن زبان‌ها

از ویکی‌پدیا، دانشنامهٔ آزاد

علی‌اکبر عالم‌زاده
زادهٔ	۸ خرداد ۱۳۲۲ مشهد، ایران
درگذشت	۱۰ مرداد ۱۴۰۱ (۷۹ سال) تهران، ایران
ملیت	ایرانی
شناخته‌شده برای	ترجمه
جایزه(ها)	کتاب سال جمهوری اسلامی ایران [۱]
پیشینه علمی
شاخه(ها)	ریاضیات
محل کار	دانشگاه خوارزمی، مؤسسه ریاضیات

علی‌اکبر عالِم‌زاده (۸ خرداد ۱۳۲۲ – ١٠ مرداد ١۴٠١) ریاضی‌دان، مترجم، استاد دانشگاه ایرانی بود که بیش از ۵۰ جلد کتاب در حوزهٔ ریاضیات به فارسی ترجمه کرده‌است. کتاب اصول آنالیز ریاضی با ترجمهٔ وی در سال ۱۳۶۲ به عنوان کتاب سال جمهوری اسلامی ایران و کتاب جبر مجرد با ترجمهٔ وی در سال ۱۳۷۶ به عنوان کتاب برگزیده سال انتخاب شد.[۱][۲]

زندگی[ویرایش]

علی‌اکبر عالم‌زاده در سال ۱۳۲۲ در شهر مشهد به دنیا آمد. در سال ۱۳۴۴ مدرک کارشناسی ریاضی خود را از دانشگاه فردوسی مشهد دریافت کرد. در سال ۱۳۴۷ دورهٔ کارشناسی ارشد ریاضی (مدرسی ریاضیات) را در دانشگاه خوارزمی تهران (مؤسسهٔ ریاضیات) با موفقیت به پایان رساند و از آن هنگام به تدریس ریاضیات در دانشگاه خوارزمی پرداخت تا آنکه در سال ۱۳۵۰ برای اتمام تحصیلات به انگلستان اعزام شد. وی در سال ۱۳۵۳ موفق به اخذ درجهٔ دکترا از دانشگاه ساوث‌همپتون شد و سپس به ایران بازگشت و بار دیگر در دانشگاه خوارزمی به تدریس پرداخت. تا آنکه مجدداً برای دورهٔ یک سالهٔ فوق دکترا به دانشگاه لیدز انگلستان رفت و پس از پایان دورهٔ مذکور به ایران مراجعت نمود. از آن زمان تاکنون علاوه بر تدریس در دانشگاه، به ترجمهٔ کتب ریاضی مبادرت ورزیده‌است.[۱][۳]

آثار[ویرایش]

تألیفات[ویرایش]

مبانی هندسه، تهران: انتشارات علمی و فنی، ۱۳۷۸
زبان حال ریاضی‌دان، تهران: مؤسسه نشر علوم نوین، ۱۳۷۴
حل مسائل حساب دیفرانسیل و انتگرال با هندسهٔ تحلیلی ریچارد ا. سیلورمن «کتاب عام»، تهران: ققنوس، ۱۳۸۴ [در سه جلد]

ترجمه‌ها[ویرایش]

اصول آنالیز ریاضی، والتر رودین، تهران: علمی و فنی، [کتاب سال جمهوری اسلامی ایران در سال ۱۳۶۲]
آنالیز ریاضی، نوشتهٔ تام. م. اپوستل، انتشارات دانشگاه صنعتی شریف
مباحثی در جبر، ی. ن. هراشتاین، ۱۳۵۹
حساب دیفرانسیل و انتگرال و هندسهٔ تحلیلی جدید، ریچارد ا. سیلورمن، علمی و فنی، ۱۳۶۳ [در سه جلد]
حساب دیفرانسیل و انتگرال با هندسهٔ تحلیلی (کتاب عام)، ریچارد ا. سیلورمن، ققنوس، ۱۳۷۱ [در سه جلد]
جبر مجرد، آی. ان. هراشتاین، تهران: مؤسسه انتشارات علمی دانشگاه صنعتی شریف، ۱۳۸۱
حساب دبفرانسیل و انتگرال و هندسهٔ تحلیلی، آر. ای. آدامز، [در دو جلد]
نظریه و مسائل جبرخطی، سیمور لیپ‌شوتس، [با همکاری دکتر مصطفی شاهزمانیان]
معادلات دیفرانسیل، سی. ری وایلی، تهران: مؤسسه نشر علوم نوین، [با همکاری مجید محمدزاده]
جبر، توماس دبلیو. هانگرفورد، انتشارات پژوهش، [با همکاری دکتر حسین ذاکری]
معادلات دیفرانسیل جزئی برای علوم مهندسی، استانلی ج. فارلو، مؤسسه نشر علوم نوین، ۱۳۷۰ [با همکاری مجید محمدزاده]
حساب دیفرانسیل و انتگرال با هندسه تحلیلی، لویی لیتهلد، نشر نوین، [در سه جلد]
جبر مجرد، دبورا سی آرانگو، مؤسسه علمی–فرهنگی نص، ۱۳۸۱
حساب دیفرانسیل و انتگرال و هندسه تحلیلی جدید، جرج بی. توماس و راس ال. فینی، انتشارات ققنوس، [در سه جلد، با همکاری داریوش بهمردی]
نظریهٔ تحلیلی اعداد، تام م. اپوستل، نشر منصوری، [در دو جلد، با همکاری علی‌اکبر رحیم‌زاده]
آشنایی با جبر مجرد، دبلیو. کیت نیکلسون، سیمای دانش، ۱۳۸۰
آنالیز عددی، ریچارد ال. بوردن و ج. دوگلاس فیرز و آلبرت سی. رینولدز، ققنوس، [با همکاری دکتر اسماعیل بابلیان و محمدرضا امیدوار]
آنالیز عددی کاربردی، کورتیس اف. جرالد و پاتریک او. ویتلی، آییژ، ۱۳۸۶
نظریه و مسائل حساب دیفرانسیل و انتگرال، فرانک آیرس، فارابی، ۱۳۷۲ [با همکاری دکتر غلامرضا زباندان]
حساب دیفرانسیل و انتگرال با هندسهٔ تحلیلی، روبرت الیس و دنی گولیک، پژوهش، ۱۳۷۳ [در سه جلد]
مسائل حساب دیفرانسیل و انتگرال و هندسه تحلیلی، جرج بی. توماس، مؤسسه نشر علوم نوین، ۱۳۷۲ [در سه جلد]
حساب دیفرانسیل و انتگرال با هندسهٔ تحلیلی، رولاند ای. لارسن و رابرت پی. هوستتلر و بروس اچ. ادواردز، اتحاد، ۱۳۷۲ [در سه جلد]
حساب برداری، جرالد ای. مارسدن و آنتونی ج. ترومبا، مؤسسه نشر علوم نوین، [با همکاری حسین محمدداودی]
آنالیز تابعی، والتر رودین، مؤسسه نشر علوم نوین، ۱۳۸۲
معادلات دیفرانسیل معمولی، ا. آی. کیزلف و ام. ال. کرازنف و جی. آی. ماکارنو، نور، ۱۳۶۳ [با همکاری حسین دوستی]
آنالیز حقیقی و مختلط، والتر رودین، مبتکران، ۱۳۷۶
حساب دیفرانسیل و انتگرال، تام. م. اپوستل، مرکز نشر دانشگاهی، ۱۳۶۰ [جلد اول با همکاری علیرضا ذکائی، مهدی رضائی دلفی، فرخ فیروزان]
حساب دیفرانسیل و انتگرال، تام. م. اپوستل، انتشارات کتابفروشی دهخدا [جلد دوم]
جبر خطی مقدماتی، برنارد کلمن، علوی، ۱۳۶۶ [با همکاری روانشاد دکتر مسعود فرزان]
هندسهٔ دیفرانسیل، آبراهام گوئتس، علوی، ۱۳۶۶ [با همکاری علی استادباشی‌زاده]
مسائل و تمرینات در ریاضیات عالی، پی. ای. دانکو و ا. جی. پوپوف و تی. یا. کوزف نیکووا، مؤسسه نشر علوم نوین، ۱۳۷۰ [در دو جلد با همکاری علی استادباشی‌زاده]
حساب دیفرانسیل و انتگرال، سی. هنری ادواردز و دیوید ای. پنی، جنگل، ۱۳۸۷ [در دو جلد]
نظریه و مسائل آنالیز ریاضی، مورای آر. اشپیگل، جنگل، ۱۳۸۵
احتمال، سیمور لیپ‌شوتس و مارک لیپسون، جنگل، ۱۳۸۴
ریاضیات گسسته، سیمور لیپ‌شوتس، اسحاق
اصول آنالیز حقیقی، کارلامبوس دی. علی‌پرانتز و اون بورکین‌شاو، تهران: آینده دیگر، ۱۳۸۶
مسائل حل شده در آنالیز حقیقی، کارلامبوس دی. علی‌پرانتز و اون بورکین‌شاو، تهران: آینده دیگر، ۱۳۸۷
نخستین درس در فرایندهای تصادفی، ساموئل کارلین و هووارد ام. تیلور، مؤسسه نشر علوم نوین، ۱۳۷۳ [با همکاری دکتر عین‌الله پاشا]
نظریه و مسایل متغیرهای مختلط، مورای آر. اشپیگل، تهران: آییژ، ۱۳۸۶

منبع

https://fa.wikipedia.org/wiki/%D8%B9%D9%84%DB%8C%E2%80%8C%D8%A7%DA%A9%D8%A8%D8%B1_%D8%B9%D8%A7%D9%84%D9%85%E2%80%8C%D8%B2%D8%A7%D8%AF%D9%87

+ نوشته شده در سه شنبه نهم اسفند ۱۴۰۱ ساعت 11:51 توسط علی رضا نقش نیلچی |

امید علی شهنی كرم‌زاده

زندگینامه ریاضیدانان: امید علی شهنی كرم‌زاده

پروفسور امید علی شهنی كرم‌زاده

نام: امید علی شهنی کرمزاده
تولد: 1324 - مسجد سلیمان - ایران
ملیت: ایرانی

مرتبه علمی: استاد (1362)

امیدعلی شهنی کرم‌زاده ریاضیدان ایرانی است. پروفسور کرم زاده در سال ۱۳۲۴ در شهر مسجدسلیمان متولد شد. وی به خاطر تلاش برای عمومی کردن علم ریاضی، موفق به کسب جایزه ترویج علم ایران گردید. کرم زاده در سال ۱۳۸۴ بعنوان چهره ماندگار کشور معرفی شد.

دوران تحصیل
شهنی کرم‌زاده در سال ۱۳۴۸ در رشته ریاضیات محض از دانشگاه تهران، مدرک کارشناسی خود را گرفت. سپس در دانشگاه اکستر بریتانیا مشغول به تحصیل گشت. وی مدارک کارشناسی ارشد و دکترای خود را به ترتیب در سال‌های ۱۳۵۰ و ۱۳۵۳ در رشته جبر اخذ نمود. در ۲۷ سالگی مفتخر به اخذ دکترای ریاضی از این کشور شد و بلافاصله در دانشگاه جندی شاپور اهواز مشغول به کار شد. از او تاکنون مقالات بسیاری حاوی ریاضی اصیل در مجلات خارجی، به چاپ رسیده‌است.

پروفسور کرم‌زاده، علاوه بر شرکت در کنفرانس‌های ریاضی خارج از کشور و ایراد سخنرانی در چندین المپیاد جهانی ریاضی، در چندین دوره نیز به عنوان سرپرست تیم اعزامی ایران در المپیاد جهانی ریاضی حضور داشته‌است. کرم‌زاده در سال ۱۳۵۳ به عنوان عضو فعال انجمن ریاضی آمریکا (AMS) شروع به فعالیت کرد، که کماکان نیز با این انجمن، در حال همکاری می‌باشد. وی از سال ۱۳۵۴ تا ۱۳۵۸ به عنوان رئیس دانشکده علوم ریاضی و کامپیوتر دانشگاه جندی شاپور اهواز (چمران) مشغول به فعالیت بود.

تحصیلات:
دیپلم: مسجد سلیمان (ریاضی 1343)
كارشناسی: دانشگاه تهران (ریاضی 1348)
كارشناسی ارشد: دانشگاه اکستر انگلستان (ریاضی 1350)
دكترا: دانشگاه اکستر انگلستان (ریاضی 1353)

عضویت در مجامع علمی

انجمن ریاضی ایران،

انجمن ریاضی آمریكا،

انجمن ریاضی انگلستان،
انجمن ریاضی ژاپن

اتحادیه ریاضی معلمان آمریكا.

برخی از فعالیت های علمی و طرح ها
تعداد مقالات چاپ شده در مجلات علمی پژوهشی داخلی : 20 مقاله
تعداد مقالات چاپ شده در مجلات علمی بین المللی: 30 مقاله

تعداد مقالات ارائه شده در مجامع علمی ملی: 15 مقاله

تعداد مقالات ارائه شده در مجامع علمی بین المللی : 10 مقاله

مسؤولیت های اجرایی:

مدیر گروه ریاضی از سال 1354 تا 1356
رئیس دانشکدة علوم ریاضی از 1356 تا 1358
مدیر گروه ریاضی از 1365 تا 1380
رئیس دانشکده علوم ریاضی از 1380 تا1386
عضو هیأت ممیزه دانشگاه شهید چمران
عضو شورای دانشگاه شهید چمران
عضو كمیته پژوهشی دانشگاه شهید چمران
عضو تیم سرپرستی دانش آموزان المپیاد ریاضی به مدت 14 سال از سال 1367
در چندین دوره متوالی عضو و سرپرست كمیته برگزاری ریاضی دانشجویی
عضو هیأت تحریریه مجلات نشر ریاضی
ولتن انجمن ریاضی ایران
مجله علوم دانشگاه تربیت معلم
مجله ریاضی دانشكده علوم دانشگاه تهران
مجله علوم دانشگاه شهید چمران.

جوایز و مدال ها:
جایزه ویژه ترویج علوم در سال 1383 توسط انجمن ترویج علم ایران

چهره ماندگار کشور در سال 1384

کتاب ها:

-- آشنایی با نظریه حلقه ها

ناشر: دانشگاه شهید چمران اهواز (منصور معتمدی: نویسنده اول، نصراله امامی: ویراستارادبی، امیدعلی شهنی كرم زاده : ویراستارعلمی.)

-- نتایج باورنكردنی در ریاضیات

ناشر: دانشگاه شهید چمران اهواز (امیدعلی شهنی كرم زاده: نویسنده اول، ممتحن: همكار.)

مقالات:

-- No_Solf injectvity of stongly regular rings کنفرانس: گارگاه جبر جابجایی

-- Krull dimension versus Noetherion کنفرانس: همایش ماهانه انجمن ریاضی

-- The key methods and results in mathematics سی و یكمین كنفرانس ریاضی ایران (شهریورماه)

-- On C(X) modulo its socle Int. Conf. کنفرانس: On Applicable General Topology

-- تولد و رشد (C(x كنفرانس جبر

-- بند كلاسیك كرول همایش جبر در اكستر انگلستان

-- در مورد سوالی از ماتلیس كنگره بین المللی ریاضیدانان دانشگاه برلین
-- درباره خارج قسمت حلقه توابع پیوسته روی ساكل كنفرانس بین المللی توپولوژی كاربردی
-- چگونه قضیه بسازیم! کنفرانس: اولین كنفرانس آموزش ریاضی
-- عكس نتایج را باید عكس گذشتگان دریابیم اولین كنفرانس بهینه‌سازی و كاربردهای آن، دانشگاه فردوسی مشهد
-- اثبات‌های فراموش‌نشدنی كنفرانس آموزش ریاضی و بزرگداشت پرویز شهریاری (اردیبهشت‌ماه)، دانشگاه كرمان
-- On an essential concept in ring theory سی و ششمین كنفرانس بین‌المللی ریاضی (شهریورماه)، دانشگاه یزد
-- كنگره بین المللی ریاضی دانان دانشگاه هلسینكی فنلاند

پایان نامه ها (به عنوان استاد راهنما و استاد مشاور)

-- بعد كرول كلاسیك روی زیرمدول‌های اول یك مدول (راهنما - كارشناسی ارشد - دانشجو: ابراهیم بیگدلی(

-- ایدال‌های شبه اول و محدب در (C(X (راهنما - كارشناسی ارشد - دانشجو: اكرم حیدری)

-- نقاط بریدگی و فضاهای نقاط بریدگی (راهنما - كارشناسی ارشد - دانشجو: امین طلا بیگی)

-- همریختی‌های متناهی در حلقه توابع پیوسته (راهنما - كارشناسی ارشد - دانشجو: میترا فتحی)

-- فضاهای بلمبرگ و تعمیم آنها )مشاور - کارشناسی ارشد - دانشجو: زینب صداقت جو)

-- مدول توابع روی حلقه‌های توابع پیوست (راهنما - كارشناسی ارشد - دانشجو: طاهره مروج)

-- اجتماع ایدال های اول مینیمال در حلقه توابع پیوسته روی فضاهای فشرده (مشاور - كارشناسی ارشد - دانشجو: نسرین قنواتی)

-- حلقه‌های ضعیف خوش تركیب و تقریباً خوش تركیب (مشاور - كارشناسی ارشد - دانشجو: محمد توحیدی)

-- ایدآل محدب CX (مشاور - كارشناسی ارشد - دانشجو: علیرضا الفتی)

-- C(X)به پیمانه ی ساكل (مشاور - كارشناسی ارشد - دانشجو: پریسا حقیقت زاده)

-- توابعی كه متمم - صفرمجموعه ها را به متمم- صفر مجموعه ها تصویر می كنند. (راهنما - كارشناسی ارشد - دانشجو: وفا مجیدی)

-- بعد كرول روی مدول های دوطرفه (مشاور - كارشناسی ارشد - دانشجو: سیده زهرا مرعشی زاده)

-- حلقه های نویتری با ساكل اساسی (راهنما - كارشناسی ارشد - دانشجو: مریم شیرعلی)

-- مدول های بالابرنده روی حلقه های تام راست (مشاور - كارشناسی ارشد - دانشجو: مهرنوش بایمانی)

-- بعد كرول توپولوژیكی (مشاور - كارشناسی ارشد - دانشجو: اكرم نوروزی)

-- بررسی قانون ایدال اول در حلقه های تعویض پذیر (راهنما - كارشناسی ارشد - دانشجو: زهرا اسماعیلیان)

-- رده بندی حلقه تعویض ﭘذیر با تعداد متناهی زیرحلقه یكدار (مشاور - كارشناسی ارشد - دانشجو: اكرم قاسمی)

-- رده بندی توسیع های مینیمال حلقه های تعویض پذیر (مشاور - كارشناسی ارشد - دانشجو: مینا خواجه پور)

-- اعضای ایدال های اول مینیمال در حلقه های تعویض ناپذیر (راهنما - كارشناسی ارشد - دانشجو: مریم محمدیان)

-- یكتایی تجزیه به ایدال ها در حلقه های تعویض پذیر نوتری كاهش یافته (راهنما - كارشناسی ارشد - دانشجو: حمیده ممبینی)

-- بررسی متناهی بودن زنجیرها از حلقه های میانی (مشاور - كارشناسی ارشد - دانشجو: پروانه مهدی زاده كوزری)

-- بررسی حوزه های تجزیه یكتا (راهنما - كارشناسی ارشد - دانشجو: طیبه طاهری)

-- مدولهای poor-پروژكتیو (مشاور - كارشناسی ارشد - دانشجو: سعاد رحمتی پور)

-- تعمیم تجزیه ایدال ها به ایدال های متباین (مشاور - كارشناسی ارشد - دانشجو: زینب‌السادات مرعشی‌زاده)

-- توسیع های حلقه های تعویض پذیر (راهنما - كارشناسی ارشد - دانشجو: مصطفی راه‌نورد)

-- مجموع مستقیم مدول های ریكارت (مشاور - كارشناسی ارشد - دانشجو: فرشته مطاعی)

-- بررسی نقش تولید مثال توسط دانش آموزان در بهبود یادگیری ریاضی و مهارت های حل مسئله (مشاور - كارشناسی ارشد - دانشجو: ثریا حیدری ارجلو)

-- اثبات و استدلال ریاضی و جایگاه آن در ریاضیات مدرسه ای (مشاور - كارشناسی ارشد - دانشجو: فاطمه حویزاوی)

-- اثبات بی كلام (راهنما - كارشناسی ارشد - دانشجو: زینب حریزاوی)

-- ویژگی های اعداد حقیقی (راهنما - كارشناسی ارشد - دانشجو: فاطمه صادقی)

-- زیر حلقه ها و زیر حلقه های ماكسیمال حلقه های صفر بعدی (راهنما - كارشناسی ارشد - دانشجو: كاوه موسی وند)

-- توصیف حلقه های مشهوربه VNL (ون نیومن موضعی) (راهنما - كارشناسی ارشد - دانشجو: مجتبی حیدری)

-- بعد تام و دوآل بعد تام مدول ها (راهنما - دكترا - دانشجو: مریم داودیان)

-- بازشناختP -فضاها (راهنما - دكترا - دانشجو: سوسن افروز)

-- فضاهایλ -فشرده (راهنما - دكترا - دانشجو: محمدعلی سیاوشی)

-- حلقه های خارج قسمتی زیر حلقه های شمارا تابعیC(X) (راهنما - دكترا - دانشجو: امیر ویسی)

-- حلقه ‏های خود-انژكتیو راست كه در آن‏ها هر عضو مجموع دو عضو یكال است. (راهنما - كارشناسی ارشد - دانشجو: الهام فرازمند)

-- انژكتیو نسبی روی زیرمدول های بسته (راهنما - كارشناسی ارشد - دانشجو: اعظم مظفری خواه)

-- تاثیر نرم افزار بر یادگیری مطالب ریاضیات (هندسه) (راهنما - كارشناسی ارشد - دانشجو: سیدمصطفی حمیدی)

-- انتقال بعضی خواص جبری بین حلقه و زیر حلقه ماكسیمال (راهنما - دكترا - دانشجو: علی نمازی)

-- برخی از خواص ایدآل توابع پیوسته با پشتیبان شبه فشرده (راهنما - كارشناسی ارشد - دانشجو: اکرم السادات مرعشی)

-- حلقه توابع پیوسته و فضای ایدال های ماكزیمال آنها (راهنما - كارشناسی ارشد - دانشجو: مطهره شیرعلی)

-- پیوند بین جبر و هندسه (راهنما - كارشناسی ارشد - دانشجو: مهشید مرادی شلال)

-- راه‌هایی كه حوزه صحیح خارج قسمتیCX بتواند یك حوزه صحیح ارزه باشد )راهنما - كارشناسی ارشد - دانشجو: سمیه سلطان پور)

-- زیرمدول‌های اساسی (راهنما - دكترا - دانشجو: مجتبی قیراطی)

-- زیرمدول‌های C(x) x… x C(x) و اید‌آل‌های متناهی اولر توابع مشتق‌پذیر (راهنما - كارشناسی ارشد - دانشجو: عیسی اسلامی‌دونچالی)

-- ایدال‌هاو z-ایدال‌های حلقه‌ی CX (راهنما - دكترا - دانشجو: منیره پیمان)

-- بازگشت به مثلث (راهنما - كارشناسی ارشد - دانشجو: سعید كمال وندیان)

-- مرتب‌های ماكسیمال شامل یك حلقه‌ی ایدال‌ساز (راهنما - كارشناسی ارشد - دانشجو: مریم اسكندری نیا)

-- مدول‌ها و زیرمدول‌های اول كلاسیك Classical Prime Modules and Prime Submodules (راهنما - دكترا - دانشجو: محمود بهبودی)

-- مدول‌هایM -انژكتیو و M اید‌ال‌های اول (راهنما - كارشناسی ارشد - دانشجو: بهرام احمدی)

-- مدول‌های تماماً اول و زیر مدول‌های اول Fully Prime Modules and Prime Submodules (راهنما - دكترا - دانشجو: هاشم كوهی)

-- یك توزیع مینیمال از حلقه C(X) (راهنما - كارشناسی ارشد - دانشجو: حمیدرضا صاحبی)

-- شمارش‌پذیری بعد نویتری مدول‌ها (راهنما - كارشناسی ارشد - دانشجو: نسرین شیرعلی)

-- خواص نسبی توپولوژی و فضاهای توپولوژی (راهنما - كارشناسی ارشد - دانشجو: امیر نیكو)

-- الف-o-انژكتیو (راهنما - كارشناسی ارشد - دانشجو: احسان ممتحن)

-- یك توپولوژی زاریسكی برای مدول ها (راهنما - كارشناسی ارشد - دانشجو: مریم زینالی)

-- مدول های دد كیند (راهنما - كارشناسی ارشد - دانشجو: سیاوش شریفی)

-- زیر جبر به طور موضعی شمارای حلقه ی توابع پیوسته (راهنما - دكترا - دانشجو: سمیه سلطان پور)

-- سوپر ساكل حلقه توابع پیوسته (راهنما - دكترا - دانشجو: سحر قاسم زاده قزوینی)

-- فضاهای مدول های زاریسكی روی حلقه های دلخواه (راهنما - كارشناسی ارشد - دانشجو: شیدا كریمی)

-- انقباض ساكل در حلقه های توابع پیوسته (راهنما - كارشناسی ارشد - دانشجو: هاجر امیری)

-- ارزیاب ها روی مدول (راهنما - كارشناسی ارشد - دانشجو: سهیلا شمخی زاده)

-- محاسبه پایه گروبنر (راهنما - دكترا - دانشجو: امید غیورنجف آباد)

-- زیر مدول‌های قویاً كوچك (راهنما - كارشناسی ارشد - دانشجو: مریم انصاریان)

-- توسیع‌های مدول‌های قویا‌˝‌بزرگ (راهنما - كارشناسی ارشد - دانشجو: سارا سلطان پور)

-- بعد تك زنجیری مدول ها (راهنما - كارشناسی ارشد - دانشجو: مجتبی یوسفی قلعه گژدمی)

-- زیر مدول های قویاچگال (راهنما – دكترا - دانشجو: ابراهیم قشقایی)

-- بررسی ایده‌آل‌های وابسته به G ایدالها (راهنما - كارشناسی ارشد – دانشجو: علیرضا علیزاده‌ مقدم)

-- مباحثی در حلقه های تركیب (راهنما - كارشناسی ارشد - دانشجو: ابراهیم قشقایی)

-- انطباق cs-حلقه های ناتكین بر حلقه های –ppبسته (راهنما - كارشناسی ارشد - دانشجو: پروانه مهدی پور)

-- بررسی و مطالعه ی نامساوی حسابی – هندسی (راهنما - كارشناسی ارشد - دانشجو: مریم شهرستانی)

-- روش مور در توپولوژی و كاربرد آن در هندسه (راهنما - كارشناسی ارشد - دانشجو: سیدغلامرضا حسینی)

-- تعمیم ایدال ها و زیر مدول های اولیه (راهنما - كارشناسی ارشد - دانشجو: علی زیدی عبدیان)

-- مدول ریكات (راهنما - كارشناسی ارشد - دانشجو: زینب یوسفی)

-- برهان خلف در ریاضی و كاربرد آن در مساله معروف دو نیمساز (راهنما - كارشناسی ارشد - دانشجو: حدا زیرانی ناو)

-- بررسی هسته توابع پیوسته مثبت برروی شبه میدان ها (مشاور - كارشناسی ارشد - دانشجو: فاطمه افلاطونی)

منبع

https://www.ihoosh.ir/article/71919/%D8%B2%D9%86%D8%AF%DA%AF%DB%8C%D9%86%D8%A7%D9%85%D9%87-%D8%B1%DB%8C%D8%A7%D8%B6%DB%8C%D8%AF%D8%A7%D9%86%D8%A7%D9%86-%D8%A7%D9%85%DB%8C%D8%AF-%D8%B9%D9%84%DB%8C-%D8%B4%D9%87%D9%86%DB%8C-%D9%83%D8%B1%D9%85%E2%80%8C%D8%B2%D8%A7%D8%AF%D9%87

+ نوشته شده در دوشنبه هشتم اسفند ۱۴۰۱ ساعت 0:16 توسط علی رضا نقش نیلچی |

4-فضای اقلیدسی

ساختار آفین [ ویرایش ]

مقاله اصلی: فضای آفین

برخی از خصوصیات اساسی فضاهای اقلیدسی تنها به این حقیقیت بستگی دارد که فضای اقلیدسی یک فضای وابسته است . به آنها ویژگی های آفین گفته می شود و شامل مفاهیم خطوط، فضاهای فرعی و موازی است که در بخش های بعدی به تفصیل توضیح داده می شود.

فضاهای فرعی [ ویرایش ]

نوشتار اصلی: تخت (هندسه)

بگذارید E یک فضای اقلیدسی باشد و ${\overright arrow {E}}$ فضای برداری همبند با آن

یک زیرفضای مسطح ، اقلیدسی یا زیرفضای وابسته E زیرمجموعه F از E است به طوری که

${\overrightarrow {F}}=\left\{{\overrightarrow {PQ}}\mid P\in F,Q\in F\right\}$

همانطور که فضای برداری همبند F یک زیرفضای خطی (زیرزفضای برداری) از. ${\overright arrow {E}}.$ یک زیرفضای اقلیدسی F یک فضای اقلیدسی با $\overrightarrow F$ به عنوان فضای برداری همبند. این زیرفضای خطی $\overrightarrow F$ جهت F نیز نامیده می شود .

اگر P نقطه ای از F باشد ،

$F=\left\{P+v\mid v\in {\overright arrow {F}}\right\}.$

برعکس، اگر P نقطه ای از E و باشد ${\overright arrow {V}}$ زیر فضای خطی است، ${\overright arrow {E}},$ سپس

$P+V=\left\{P+v\mid v\in V\right\}$

یک زیر فضای اقلیدسی جهت است ${\overright arrow {V}}$ . (فضای برداری همبند این زیرفضا است ${\overright arrow {V}}$ .)

فضای برداری اقلیدسی ${\overright arrow {E}}$ (یعنی یک فضای اقلیدسی که برابر است با ${\overright arrow {E}}$ ) دارای دو نوع زیرفضا است: زیرفضاهای اقلیدسی و زیرفضاهای خطی آن. زیرفضاهای خطی زیرفضاهای اقلیدسی هستند و یک زیرفضای اقلیدسی یک زیرفضای خطی است اگر و فقط اگر حاوی بردار صفر باشد.

خطوط و بخش ها [ ویرایش ]

در یک فضای اقلیدسی، یک خط یک زیرفضای اقلیدسی از بعد یک است. از آنجایی که یک فضای برداری با بعد یک توسط هر بردار غیر صفر پوشیده شده است، یک خط مجموعه ای از فرم است

$\left\{P+\lambda {\overrightarrow {PQ}}\mid \lambda \in \mathbb {R} \right\},$

که در آن P و Q دو نقطه متمایز از فضای اقلیدسی به عنوان بخشی از خط هستند.

نتیجه این است که دقیقاً یک خط وجود دارد که از دو نقطه متمایز (شامل) می گذرد. این بدان معناست که دو خط مجزا حداکثر در یک نقطه قطع می شوند.

یک نمایش متقارن تر از خط عبوری از P و Q است

$\left\{O+(1-\lambda ){\overrightarrow {OP}}+\lambda {\overrightarrow {OQ}}\mid \lambda \in \mathbb {R} \right\},$

جایی که O یک نقطه دلخواه است (لازم نیست در خط).

در فضای برداری اقلیدسی، بردار صفر معمولاً برای O انتخاب می شود . این اجازه می دهد تا فرمول قبلی را ساده کنید

$\left\{(1-\lambda )P+\lambda Q\mid \lambda \in \mathbb {R} \right\}.$

یک قرارداد استاندارد اجازه استفاده از این فرمول را در هر فضای اقلیدسی می دهد، به فضای آفین § ترکیبات آفین و barycenter مراجعه کنید .

پاره خط ، یا به سادگی پاره ، که به نقاط P و Q می پیوندد ، زیرمجموعه نقاطی است که 0 ≤ ≤ ≤ 1 در فرمول های قبلی است. PQ یا QP نشان داده می شود . به این معنا که

$PQ=QP=\left\{P+\lambda {\overrightarrow {PQ}}\mid 0\leq \lambda \leq 1\right\}.$

موازی سازی [ ویرایش ]

دو فضای فرعی S و T با ابعاد یکسان در فضای اقلیدسی اگر جهت یکسانی داشته باشند (یعنی فضای برداری همبند یکسان) موازی هستند. [a] به طور معادل، اگر بردار ترجمه v وجود داشته باشد که یکی را به دیگری ترسیم کند، موازی هستند:

$T=S+v.$

با توجه به یک نقطه P و یک زیرفضای S ، دقیقاً یک زیر فضای وجود دارد که حاوی P و موازی با S است ، که $P+{\overright arrow {S}}.$ در موردی که S یک خط است (زیرزفضای بعد یک)، این ویژگی بدیهیات Playfair است .

نتیجه این است که در یک صفحه اقلیدسی، دو خط یا در یک نقطه به هم می رسند یا موازی هستند.

مفهوم زیرفضاهای موازی به زیرفضاهای با ابعاد مختلف تعمیم داده شده است: اگر جهت یکی از آنها در جهت دیگری باشد، دو زیرفضا موازی هستند.

ساختار متریک [ ویرایش ]

فضای برداری ${\overright arrow {E}}$ همبند با فضای اقلیدسی E یک فضای ضرب درونی است . این به معنای یک فرم دوخطی متقارن است

${\begin{aligned}{\overrightarrow {E}}\times {\overrightarrow {E}}&\to \mathbb {R} \\(x,y)&\mapsto \langle x,y\rangle \end{تراز شده}}$

که قطعی مثبت است (یعنی $\langle x,x\rangle$ همیشه برای x ≠ 0 مثبت است ).

حاصلضرب درونی فضای اقلیدسی اغلب حاصل ضرب نقطه ای نامیده می شود و x ⋅ y نشان داده می شود . این به ویژه زمانی است که یک سیستم مختصات دکارتی انتخاب شده باشد، زیرا در این مورد، حاصل ضرب داخلی دو بردار حاصل ضرب نقطه بردار مختصات آنها است . به همین دلیل و به دلایل تاریخی، نماد نقطه بیشتر از نماد براکت برای حاصل ضرب داخلی فضاهای اقلیدسی استفاده می شود. این مقاله این استفاده را دنبال خواهد کرد. به این معنا که $\langle x,y\rangle$ در ادامه این مقاله x ⋅ y نشان داده می شود .

نرم اقلیدسی بردار x است

$\|x\|={\sqrt {x\cdot x}}.$

حاصل ضرب درونی و نرم امکان بیان و اثبات خواص متریک و توپولوژیکی هندسه اقلیدسی را فراهم می کند . زیربخش بعدی اساسی ترین آنها را شرح می دهد. در این بخش‌ها، E یک فضای اقلیدسی دلخواه را نشان می‌دهد و ${\overright arrow {E}}$ فضای برداری ترجمه آن را نشان می دهد.

فاصله و طول [ ویرایش ]

نوشتار اصلی: فاصله اقلیدسی

فاصله (به طور دقیق تر فاصله اقلیدسی ) بین دو نقطه از فضای اقلیدسی، نرم بردار ترجمه است که یک نقطه را به نقطه دیگر نگاشت می کند . به این معنا که

$d(P,Q)={\Bigl \|}{\overrightarrow {PQ}}{\vphantom {\frac {|}{}}}{\Bigr \|}.$

طول یک قطعه PQ فاصله d ( P , Q ) بین نقاط انتهایی آن P و Q است . اغلب نشان داده می شود|پس| $|PQ|$ .

فاصله یک متریک است ، زیرا قطعی مثبت، متقارن است و نابرابری مثلث را برآورده می کند.

$d(P,Q)\leq d(P,R)+d(R,Q).$

علاوه بر این، تساوی درست است اگر و تنها در صورتی که یک نقطه R متعلق به بخش PQ باشد . این نابرابری به این معنی است که طول هر یال یک مثلث کوچکتر از مجموع طول یال های دیگر است. این خاستگاه اصطلاح نابرابری مثلثی است .

با فاصله اقلیدسی، هر فضای اقلیدسی یک فضای متریک کامل است .

متعامد بودن [ ویرایش ]

نوشتارهای اصلی: عمود و متعامد

دو بردار غیر صفر u و v از ${\overright arrow {E}}$ (فضای برداری همبند فضای اقلیدسی E ) عمود یا متعامد هستند اگر حاصل ضرب درونی آنها صفر باشد:

$u\cdot v=0$

دو زیرفضای خطی از ${\overright arrow {E}}$ اگر هر بردار غیر صفر بردار اول عمود بر هر بردار غیر صفر بردار دوم باشد متعامد هستند. این بدان معناست که تقاطع زیرفضاهای خطی به بردار صفر کاهش می یابد.

دو خط و به طور کلی دو زیرفضای اقلیدسی (یک خط را می توان به عنوان یک زیرفضای اقلیدسی در نظر گرفت.) متعامد هستند اگر جهت آنها (فضاهای برداری همبند زیرفضاهای اقلیدسی) متعامد باشند. دو خط متعامد را که قطع می کنند عمود می گویند .

دو بخش AB و AC که نقطه پایانی مشترک A دارند عمود هستند یا زاویه قائمه تشکیل می دهند اگر بردارها ${\overright arrow {AB}}$ و ${\overright arrow {AC}}$ متعامد هستند.

اگر AB و AC یک زاویه قائمه تشکیل دهند، یک زاویه دارد

$|BC|^{2}=|AB|^{2}+|AC|^{2}.$

این قضیه فیثاغورث است . اثبات آن در این زمینه آسان است، زیرا با بیان این موضوع بر حسب حاصلضرب درونی، با استفاده از دوخطی بودن و تقارن حاصلضرب داخلی، می توان گفت:

${\begin{aligned}|BC|^{2}&={\overrightarrow {BC}}\cdot {\overrightarrow {BC}}\\&=\left({\overrightarrow {BA}}+{ \overrightarrow {AC}}\right)\cdot \left({\overrightarrow {BA}}+{\overrightarrow {AC}}\right)\\&={\overrightarrow {BA}}\cdot {\overrightarrow {BA }}+{\overrightarrow {AC}}\cdot {\overrightarrow {AC}}-2{\overrightarrow {AB}}\cdot {\overrightarrow {AC}}\\&={\overrightarrow {AB}}\cdot {\overrightarrow {AB}}+{\overrightarrow {AC}}\cdot {\overrightarrow {AC}}\\&=|AB|^{2}+|AC|^{2}.\end{تراز شده}}$

${\overrightarrow {AB}}\cdot {\overrightarrow {AC}}=0$ از آنجایی که این دو بردار متعامد هستند استفاده می شود.

زاویه [ ویرایش ]

نوشتار اصلی: زاویه

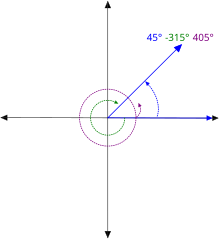
زوایای مثبت و منفی در صفحه جهت دار

زاویه θ (غیر جهت‌دار) بین دو بردار غیرصفر x و y در ${\overright arrow {E}}$ است

$\theta =\arccos \left({\frac {x\cdot y}{\left\|x\right\|\left\|y\right\|}}\right)$

که در آن arccos مقدار اصلی تابع آرکوزین است . با نابرابری کوشی-شوارتز ، استدلال آرکوزین در بازه [-1، 1] است . بنابراین θ حقیقی است و 0 ≤ θ ≤ π (یا 0 ≤ θ ≤ 180 اگر زاویه ها بر حسب درجه اندازه گیری شوند).

زاویه ها در خط اقلیدسی مفید نیستند، زیرا می توانند فقط 0 یا π باشند .

در یک صفحه اقلیدسی جهت دار ، می توان زاویه جهت دو بردار را تعریف کرد. سپس زاویه جهت دو بردار x و y مخالف زاویه جهت y و x است . در این حالت، زاویه دو بردار می تواند هر مقدار مدول یک مضرب صحیح 2 π داشته باشد . به طور خاص، یک زاویه بازتابی π < θ < 2 π برابر با زاویه منفی - π < θ - 2 π <0 است .

زاویه دو بردار اگر در اعداد مثبت ضرب شوند تغییر نمی کند. به طور دقیق تر، اگر x و y دو بردار باشند و λ و μ اعداد حقیقی باشند، آنگاه

$\operatorname {angle} (\lambda x,\mu y)={\begin{cases}\operatorname {angle} (x,y)\qquad \qquad {\text{if }}\lambda {\text { و }}\mu {\text{ علامت یکسانی دارند}}\\\pi -\operatorname {angle} (x,y)\qquad {\text{در غیر این صورت}}.\end{موارد}}$

اگر A ، B و C سه نقطه در فضای اقلیدسی باشند، زاویه قطعات AB و AC زاویه بردارها است. ${\overright arrow {AB}}$ ${\overrightarrow {AC}}.$ از آنجایی که ضرب بردارها در اعداد مثبت زاویه را تغییر نمی دهد، می توان زاویه دو نیم خط با نقطه اولیه A را تعریف کرد: زاویه پاره های AB و AC است که در آن B و C نقاط دلخواه هستند، یک روی هر نیم خط اگرچه کمتر مورد استفاده قرار می گیرد، می توان به طور مشابه زاویه پاره ها یا نیم خطوطی را که نقطه اولیه مشترکی ندارند تعریف کرد.

زاویه دو خط به صورت زیر تعریف می شود. اگر θ زاویه دو پاره، یکی روی هر خط باشد، زاویه هر دو پاره دیگر، یکی در هر خط، θ یا π - θ است . یکی از این زوایا در بازه [0, π /2] و دیگری در [ π /2, π ] است . زاویه غیر جهت‌دار دو خط، در بازه [0, π /2] است . در یک صفحه اقلیدسی گرا، زاویه جهت دو خط متعلق به بازه [- π /2، π/2] است..

مختصات دکارتی [ ویرایش ]

همچنین ببینید: سیستم مختصات دکارتی

هر فضای برداری اقلیدسی دارای یک مبنای متعامد است (در واقع، بی نهایت در بعد بالاتر از یک، و دو در بعد یک)، که یک مبنای است. $(e_{1},\dots,e_{n})$ بردارهای واحد ( $\|e_{i}\|=1$ ) که متعامد جفتی هستند ( $e_{i}\cdot e_{j}=0$ برای i ≠ j ). به طور دقیق تر، با توجه به هر مبنایی $(b_{1},\dots,b_{n})،$ فرآیند گرم اشمیت یک مبنای متعارف را محاسبه می کند به طوری که برای هر i ، گستره های خطی(ه1،…،همن) $(e_{1},\dots,e_{i})$ و $(b_{1},\dots,b_{i})$ برابر هستند. [7]

با توجه به فضای اقلیدسی E ، یک قاب دکارتی مجموعه ای از داده های متشکل از یک مبنای متعارف از، ${\overright arrow {E}},$ و نقطه ای از E که مبدأ نامیده می شود و اغلب به او نشان داده می شود . یک قاب دکارتی $(O,e_{1},\dots,e_{n})$ امکان تعریف مختصات دکارتی برای هر دو E و ${\overright arrow {E}}$ به روش زیر.

مختصات دکارتی بردار v از ${\overright arrow {E}}$ ضرایب v بر اساس متعارف هستند. $e_{1},\dots,e_{n}.$ برای مثال مختصات دکارتی یک بردار $v$ بر اساس متعارف(ه1،ه2،ه3) $(e_{1},e_{2},e_{3})$ (که ممکن است به عنوان نامگذاری شود $(x,y,z)$ به عنوان یک قرارداد) در یک فضای اقلیدسی 3 بعدی است $(\alpha _{1},\alpha _{2},\alpha _{3})$ اگر $v=\alpha _{1}e_{1}+\alpha _{2}e_{2}+\alpha _{3}e_{3}$ . از آنجایی که مبنای متعارف است، ضریب i-امین است $\alpha _{i}$ برابر حاصلضرب نقطه است $v\cdot e_{i}.$

مختصات دکارتی نقطه P از E مختصات دکارتی بردار هستند ${\overrightarrow {OP}}.$

سایر مختصات [ ویرایش ]

مختصات کج سه بعدی

مقاله اصلی: سیستم مختصات

از آنجایی که فضای اقلیدسی یک فضای آفین است ، می توان یک قاب آفین را روی آن در نظر گرفت که همان قاب اقلیدسی است، با این تفاوت که نیازی نیست که اساس متعامد باشد. این مختصات وابسته را تعریف می‌کند که گاهی مختصات کج نامیده می‌شود تا تاکید شود بردارهای پایه متعامد زوجی نیستند.

یک مبنای وابسته به فضای اقلیدسی با بعد n مجموعه ای از n + 1 نقطه است که در یک ابرصفحه وجود ندارد. یک پایه وابسته مختصات باری مرکزی را برای هر نقطه تعریف می کند.

بسیاری از سیستم های مختصات دیگر را می توان بر روی فضای اقلیدسی E با بعد n به روش زیر تعریف کرد. فرض کنید f یک همومورفیسم (یا اغلب یک دیفئومورفیسم ) از یک زیرمجموعه باز متراکم از E به یک زیر مجموعه باز از. $\mathbb{R} ^{n}.$ مختصات یک نقطه x از E اجزای f ( x ) هستند . سیستم مختصات قطبی (بعد 2) و سیستم مختصات کروی و استوانه ای (بعد 3) به این ترتیب تعریف می شوند.

برای نقاطی که خارج از دامنه f هستند، مختصات ممکن است گاهی اوقات به عنوان حد مختصات نقاط همسایه تعریف شوند، اما این مختصات ممکن است به طور یکتا تعریف نشده باشند و ممکن است در همسایگی نقطه پیوسته نباشند. به عنوان مثال، برای سیستم مختصات کروی، طول جغرافیایی در قطب تعریف نشده است، و در ضد نصف النهار ، طول جغرافیایی به طور ناپیوسته از -180 درجه تا +180 درجه عبور می کند.

این روش برای تعریف مختصات به راحتی به سایر ساختارهای ریاضی و به ویژه به منیفولدها گسترش می یابد .

ایزومتریک [ ویرایش ]

ایزومتریکی بین دو فضای متریک یک بهی ک و پوشا است که فاصله را حفظ می کند، یعنی [ b]

$d(f(x),f(y))=d(x,y).$

در مورد فضای برداری اقلیدسی، ایزومتری که مبدأ را به مبدأ ترسیم می کند، نرم را حفظ می کند.

$\|f(x)\|=\|x\|,$

زیرا نرم یک بردار فاصله آن از بردار صفر است. همچنین ضرب داخلی را حفظ می کند

$f(x)\cdot f(y)=x\cdot y,$

از آنجا که

$x\cdot y={\frac {1}{2}}\left(\|x+y\|^{2}-\|x\|^{2}-\|y\|^{ 2}\راست).$

ایزومتریک فضاهای برداری اقلیدسی یک ایزومورفیسم خطی است . [ج] [8]

یک ایزومتری $f\colon E\to F$ فضاهای اقلیدسی ایزومتری را تعریف می کند:→ ${\overrightarrow {f}}\colon {\overrightarrow {E}}\to {\overrightarrow {F}}$ فضاهای برداری اقلیدسی همبند. این بدان معناست که دو فضای اقلیدسی ایزومتریک دارای ابعاد یکسانی هستند. برعکس، اگر E و F فضاهای اقلیدسی باشند ، O ∈ E , O ∈ F و:→ ${\overrightarrow {f}}\colon {\overrightarrow {E}}\to {\overrightarrow {F}}$ یک ایزومتریک است، سپس نقشه $f\colon E\to F$ تعریف شده بوسیله ی

$f(P)=O'+{\overrightarrow {f}}\left({\overrightarrow {OP}}\right)$

ایزومتری از فضاهای اقلیدسی است.

از نتایج قبلی چنین برمی‌آید که ایزومتریکی از فضاهای اقلیدسی خطوط را به خطوط، و به طور کلی‌تر زیرفضاهای اقلیدسی را به زیرفضاهای اقلیدسی با همان بعد، ترسیم می‌کند، و اینکه محدودیت ایزومتریک در این زیرفضاها، ایزومتریک‌های این زیرفضاها هستند.

ایزومتریک با نمونه های اولیه [ ویرایش ]

اگر E یک فضای اقلیدسی است، فضای برداری همبند با آن ${\overright arrow {E}}$ را می توان به عنوان فضای اقلیدسی در نظر گرفت. هر نقطه O ∈ E ایزومتریک فضاهای اقلیدسی را تعریف می کند

$P\mapsto {\overrightarrow {OP}},$

که O را به بردار صفر نگاشت می کند و هویت نقشه خطی همبند را دارد. ایزومتریک معکوس نقشه است

$v\mapsto O+v.$

یک قاب اقلیدسی $(O,e_{1},\dots,e_{n})$ امکان تعریف نقشه را فراهم می کند

${\begin{aligned}E&\to \mathbb {R} ^{n}\\P&\mapsto \left(e_{1}\cdot {\overright arrow {OP}},\dots ,e_{n} \cdot {\overrightarrow {OP}}\right),\end{aligned}}$

که ایزومتری از فضاهای اقلیدسی است. ایزومتریک معکوس است

${\begin{aligned}\mathbb {R} ^{n}&\to E\\(x_{1}\dots,x_{n})&\mapsto \left(O+x_{1}e_ {1}+\dots +x_{n}e_{n}\right).\end{تراز شده}}$

این بدان معنی است که تا یک هم شکلی، دقیقاً یک فضای اقلیدسی از یک بعد معین وجود دارد.

این توجیهی است که بسیاری از نویسندگان درباره آن صحبت می کنند $\mathbb {R} ^{n}$ به عنوان فضای اقلیدسی بعد n .

گروه اقلیدسی [ ویرایش ]

مقالات اصلی: گروه اقلیدسی و تبدیل صلب

ایزومتری از فضای اقلیدسی به خود را ایزومتریک اقلیدسی ، تبدیل اقلیدسی یا تبدیل صلب می نامند . دگرگونی های صلب فضای اقلیدسی یک گروه (تحت ترکیب ) را تشکیل می دهد که گروه اقلیدسی نامیده می شود و اغلب با E( n ) ISO( n ) نشان داده می شود .

ساده ترین تبدیل های اقلیدسی ترجمه ها هستند

$P\to P+v.$

آنها با بردارها مطابقت دوگانه دارند. این دلیلی است برای نامیدن فضای ترجمه ها فضای برداری همبند با فضای اقلیدسی. ترجمه ها یک زیر گروه عادی از گروه اقلیدسی را تشکیل می دهند.

ایزومتریک اقلیدسی f فضای اقلیدسی E یک ایزومتری خطی را تعریف می کند. ${\overright arrow {f}}$ فضای برداری همبند (منظور از ایزومتری خطی ، ایزومتری است که یک نقشه خطی نیز هست ) به صورت زیر: نشان دادن بردار با ${\overrightarrow {PQ}}$ ، اگر O یک نقطه دلخواه از E باشد ، یکی دارد

${\overrightarrow {f}}({\overrightarrow {OP}})=f(P)-f(O).$

اثبات اینکه این یک نقشه خطی است که به انتخاب O بستگی ندارد، ساده است.

نقشه $f\to {\overright arrow {f}}$ یک هممورفیسم گروهی از گروه اقلیدسی به گروه ایزومتریک های خطی است که به آن گروه متعامد می گویند . هسته این هممورفیسم گروه ترجمه است که نشان می دهد زیرگروه عادی از گروه اقلیدسی است.

ایزومتریک هایی که نقطه معین P را ثابت می کنند، زیر گروه تثبیت کننده گروه اقلیدسی را نسبت به P تشکیل می دهند . محدودیت این تثبیت کننده هممورفیسم گروه فوق یک هم شکلی است. بنابراین ایزومتریک هایی که نقطه معین را ثابت می کنند، گروهی هم شکل با گروه متعامد تشکیل می دهند.

فرض کنید P یک نقطه، f یک ایزومتری، و t ترجمه ای باشد که P را به f ( P ) نشان می دهد . ایزومتری $g=t^{-1}\circ f$ P را رفع می کند . بنابراین $f=t\circ g,$ و گروه اقلیدسی ضرب نیمه مستقیم گروه ترجمه و گروه متعامد است.

گروه متعامد ویژه زیرگروه عادی گروه متعامد است که دستی را حفظ می کند . زیر گروهی از شاخص دو از گروه متعامد است . تصویر معکوس آن توسط گروه هممورفیسم $f\to {\overright arrow {f}}$ یک زیرگروه عادی از شاخص دو از گروه اقلیدسی است که گروه اقلیدسی ویژه یا گروه جابجایی نامیده می شود . عناصر آن را حرکات صلب یا جابجایی می نامند .

حرکات صلب شامل هویت ، ترجمه، چرخش (حرکات صلب که حداقل یک نقطه را ثابت می کنند) و همچنین حرکات پیچی می باشد .

نمونه‌های معمولی از تبدیل‌های صلب که حرکات صلب نیستند، بازتاب‌ها هستند، که تبدیل‌های صلب هستند که یک ابر صفحه را ثابت می‌کنند و هویت نیستند. آنها همچنین دگرگونی هایی هستند که شامل تغییر علامت یک مختصات در چارچوب اقلیدسی می شوند.

از آنجایی که گروه اقلیدسی ویژه زیر گروهی از شاخص دو از گروه اقلیدسی است، با توجه به بازتاب r ، هر تبدیل صلب که حرکت صلب نیست حاصل ضرب r و حرکت صلب است. بازتاب لغزشی نمونه ای از تبدیل صلب است که یک حرکت صلب یا بازتاب نیست.

تمام گروه هایی که در این بخش در نظر گرفته شده اند، گروه های دروغ و گروه های جبری هستند .

توپولوژی [ ویرایش ]

مقاله اصلی: فضای n حقیقی § خواص توپولوژیکی

فاصله اقلیدسی فضای اقلیدسی را به یک فضای متریک و در نتیجه فضای توپولوژیکی تبدیل می کند . این توپولوژی را توپولوژی اقلیدسی می نامند . در شرایطی که، $\mathbb {R} ^{n}،$ این توپولوژی همچنین توپولوژی ضرب است .

مجموعه های باز زیرمجموعه هایی هستند که شامل یک توپ باز در اطراف هر یک از نقاط خود هستند. به عبارت دیگر، توپ های باز پایه توپولوژی را تشکیل می دهند .

بعد توپولوژیکی فضای اقلیدسی برابر با بعد آن است. این بدان معناست که فضاهای اقلیدسی با ابعاد مختلف همومورف نیستند . علاوه بر این، قضیه تغییرناپذیری دامنه بیان می‌کند که زیرمجموعه‌ای از فضای اقلیدسی باز است (برای توپولوژی زیرفضا ) اگر و تنها در صورتی که به زیرمجموعه باز فضای اقلیدسی با همان بعد همومورف باشد.

فضاهای اقلیدسی کامل و به صورت محلی فشرده هستند . یعنی یک زیرمجموعه بسته از فضای اقلیدسی اگر محدود باشد (یعنی در یک توپ موجود باشد) فشرده است. به طور خاص، توپ های بسته فشرده هستند.

تعاریف بدیهی [ ویرایش ]

تعریف فضاهای اقلیدسی که در این مقاله توضیح داده شده است اساساً با تعریف اقلیدس متفاوت است . در واقع، اقلیدس به طور رسمی فضا را تعریف نکرد، زیرا تصور می شد که این فضا توصیفی از جهان فیزیکی است که مستقل از ذهن انسان وجود دارد. نیاز به یک تعریف رسمی تنها در پایان قرن نوزدهم، با معرفی هندسه های غیر اقلیدسی ظاهر شد .

دو رویکرد متفاوت استفاده شده است. فلیکس کلاین پیشنهاد کرد که هندسه ها را از طریق تقارن آنها تعریف کنیم . ارائه فضاهای اقلیدسی ارائه شده در این مقاله، اساساً از برنامه ارلانگن او با تأکید بر گروه های ترجمه و ایزومتریک صادر شده است.

از سوی دیگر، دیوید هیلبرت مجموعه ای از بدیهیات را با الهام از فرضیات اقلیدس پیشنهاد کرد . آنها به هندسه مصنوعی تعلق دارند، زیرا هیچ تعریفی از اعداد حقیقی ندارند . بعدها جی دی بیرکوف و آلفرد تارسکی مجموعه های ساده تری از بدیهیات را پیشنهاد کردند که از اعداد حقیقی استفاده می کنند (به بدیهیات بیرکوف و بدیهیات تارسکی مراجعه کنید ).

امیل آرتین در جبر هندسی ثابت کرده است که همه این تعاریف از فضای اقلیدسی معادل هستند. [9] اثبات اینکه همه تعاریف فضاهای اقلیدسی اصول هیلبرت را برآورده می‌کنند و آنهایی که شامل اعداد حقیقی (از جمله تعریف فوق) هستند، تقریباً آسان است. بخش دشوار اثبات آرتین به شرح زیر است. در بدیهیات هیلبرت، همخوانی یک رابطه هم ارزی در بخش ها است. بنابراین می توان طول یک قطعه را به عنوان کلاس هم ارزی آن تعریف کرد. بنابراین باید ثابت کرد که این طول دارای ویژگیهایی است که اعداد حقیقی غیرمنفی را مشخص می کنند. آرتین این را با بدیهیاتی معادل بدیهیات هیلبرت ثابت کرد.

استفاده [ ویرایش ]

از زمان یونان باستان ، فضای اقلیدسی برای مدل سازی اشکال در دنیای فیزیکی استفاده می شد. بنابراین در بسیاری از علوم مانند فیزیک , مکانیک , و ستاره شناسی استفاده می شود . همچنین به طور گسترده در تمام زمینه های فنی که مربوط به اشکال، شکل، مکان و موقعیت هستند، مانند معماری ، ژئودزی ، توپوگرافی ، ناوبری ، طراحی صنعتی یا نقشه کشی فنی استفاده می شود .

فضای ابعاد بالاتر از سه در چندین نظریه مدرن فیزیک رخ می دهد. بعد بالاتر را ببینید . آنها همچنین در فضاهای پیکربندی سیستم های فیزیکی رخ می دهند .

علاوه بر هندسه اقلیدسی ، فضاهای اقلیدسی نیز به طور گسترده در سایر زمینه های ریاضیات استفاده می شود. فضاهای مماس منیفولدهای دیفرانسیل پذیر ، فضاهای برداری اقلیدسی هستند. به طور کلی، منیفولد فضایی است که به صورت محلی با فضاهای اقلیدسی تقریب می شود. بیشتر هندسه های غیر اقلیدسی را می توان با یک منیفولد مدل کرد و در فضای اقلیدسی با ابعاد بالاتر جاسازی کرد . به عنوان مثال، یک فضای بیضوی را می توان با یک بیضی مدل کرد . در فضای اقلیدسی نمایش اشیایی ریاضی که ماهیت هندسی پیشینی ندارند معمول است. یک مثال در میان بسیاری، نمایش معمولی است نمودارها _

سایر فضاهای هندسی [ ویرایش ]

از زمان معرفی هندسه‌های غیراقلیدسی در پایان قرن نوزدهم ، فضاهای زیادی در نظر گرفته شده‌اند که می‌توان در مورد آن‌ها استدلال هندسی را مانند فضاهای اقلیدسی انجام داد. به طور کلی، آنها برخی از ویژگی ها را با فضاهای اقلیدسی به اشتراک می گذارند، اما ممکن است ویژگیهایی نیز داشته باشند که می توانند نسبتاً عجیب به نظر برسند. برخی از این فضاها از هندسه اقلیدسی برای تعریف خود استفاده می کنند یا می توانند به عنوان زیرفضاهای فضای اقلیدسی با ابعاد بالاتر مدل شوند. هنگامی که چنین فضایی با بدیهیات هندسی تعریف می شود ، جاسازی فضا در فضای اقلیدسی یک راه استاندارد برای اثبات سازگاری تعریف آن است، یا به طور دقیق تر برای اثبات سازگاری نظریه آن، اگر هندسه اقلیدسی سازگار است (که قابل اثبات نیست).

فضای آفین [ ویرایش ]

مقاله اصلی: فضای آفین

فضای اقلیدسی فضایی وابسته به متریک است . فضاهای آفین کاربردهای بسیار دیگری در ریاضیات دارند. به طور خاص، همانطور که آنها در هر زمینه تعریف می شوند ، امکان انجام هندسه را در زمینه های دیگر فراهم می کنند.

به محض در نظر گرفتن سؤالات غیر خطی، به طور کلی مفید است که فضاهای وابسته را روی اعداد مختلط به عنوان بسط فضاهای اقلیدسی در نظر بگیریم. برای مثال، یک دایره و یک خط همیشه دارای دو نقطه تقاطع (احتمالاً متمایز نیستند) در فضای ترکیبی مختلط هستند. بنابراین، بیشتر هندسه جبری در فضاهای وابسته مختلط و فضاهای وابسته بر روی میدان‌های بسته جبری ساخته می‌شود . بنابراین اشکالی که در هندسه جبری در این فضاهای نزدیک مورد مطالعه قرار می گیرند، انواع جبری آفین نامیده می شوند .

فضاهای وابسته روی اعداد گویا و به طور کلی بر روی فیلدهای اعداد جبری پیوندی بین هندسه (جبری) و نظریه اعداد ایجاد می کنند . به عنوان مثال، آخرین قضیه فرما را می توان بیان کرد: "یک منحنی فرما با درجه بالاتر از دو، هیچ نقطه ای در صفحه وابستگی بر روی منطقی ها ندارد."

هندسه در فضاهای وابسته در یک میدان محدود نیز به طور گسترده مورد مطالعه قرار گرفته است. به عنوان مثال، منحنی های بیضوی بر روی میدان های محدود به طور گسترده در رمزنگاری استفاده می شود .

فضای تصویری [ ویرایش ]

نوشتار اصلی: فضای تصویری

در اصل، فضاهای تصویری با افزودن « نقاط در بی‌نهایت » به فضاهای اقلیدسی، و به‌طور کلی به فضاهای وابسته، معرفی شده‌اند تا ادعای «دو خط همسطح دقیقاً در یک نقطه به هم می‌رسند» درست باشد. فضای تصویری با فضاهای اقلیدسی و وابسته در خاصیت همسانگرد بودن اشتراک دارد، یعنی هیچ خاصیتی از فضا وجود ندارد که امکان تمایز بین دو نقطه یا دو خط را فراهم کند. بنابراین، معمولاً از یک تعریف همسانگرد تر استفاده می شود که شامل تعریف فضای تصویری به عنوان مجموعه خطوط برداری در یک فضای برداری با ابعاد یک دیگر است.

در مورد فضاهای وابسته، فضاهای تصویری بر روی هر میدانی تعریف می شوند و فضاهای اساسی هندسه جبری هستند .

هندسه های غیر اقلیدسی [ ویرایش ]

نوشتار اصلی: هندسه نااقلیدسی

هندسه نااقلیدسی معمولاً به فضاهای هندسی اطلاق می شود که در آن فرض موازی نادرست است. آنها شامل هندسه بیضوی ، که در آن مجموع زوایای یک مثلث بیش از 180 درجه است، و هندسه هذلولی ، که در آن این مجموع کمتر از 180 درجه است. معرفی آنها در نیمه دوم قرن نوزدهم و اثبات سازگاری نظریه آنها ( اگر هندسه اقلیدسی متناقض نباشد) یکی از پارادوکس هایی است که منشأ بحران اساسی در ریاضیات ابتدای قرن بیستم است. انگیزه نظام‌سازی نظریه‌های بدیهی در ریاضیات را برانگیخت.

فضاهای منحنی [ ویرایش ]

مقالات اصلی: منیفولد و منیفولد ریمانی

منیفولد فضایی است که در مجاورت هر نقطه شبیه فضای اقلیدسی است. از نظر فنی، منیفولد یک فضای توپولوژیکی است ، به طوری که هر نقطه دارای یک همسایگی است که به زیر مجموعه باز فضای اقلیدسی همومورف است. منیفولدها را می‌توان با افزایش درجه این "شباهت" به منیفولدهای توپولوژیکی ، منیفولدهای متمایز ، منیفولدهای صاف و منیفولدهای تحلیلی طبقه‌بندی کرد . با این حال، هیچ یک از این نوع «شباهت ها» به فاصله ها و زاویه ها، حتی تقریباً، احترام نمی گذارند.

فواصل و زوایا را می توان بر روی یک منیفولد صاف با ارائه یک متریک اقلیدسی متغییر بر روی فضاهای مماس در نقاط منیفولد تعریف کرد (این فضاهای مماس فضاهای برداری اقلیدسی هستند). این منجر به منیفولد ریمانی می شود . به طور کلی، خطوط مستقیم در منیفولد ریمانی وجود ندارند، اما نقش آنها توسط ژئودزیک ها ، که "کوتاه ترین مسیرها" بین دو نقطه هستند، ایفا می شود. این اجازه می دهد تا فواصل را که در امتداد ژئودزیک ها اندازه گیری می شوند، و زوایای بین ژئودزیک ها، که زاویه مماس آنها در فضای مماس در محل تقاطع آنها است، تعیین کنیم. بنابراین، منیفولدهای ریمانی به صورت محلی مانند فضای اقلیدسی که خم شده است رفتار می کنند.

فضاهای اقلیدسی به طور پیش پا افتاده ای منیفولدهای ریمانی هستند. نمونه ای که این خوب را نشان می دهد، سطح یک کره است . در این حالت ژئودزیک ها کمان های دایره ای بزرگ هستند که در زمینه جهت یابی به آن ها ارتودوم می گویند . به طور کلی، فضاهای هندسه های غیر اقلیدسی را می توان به صورت منیفولدهای ریمانی درک کرد.

فضای شبه اقلیدسی [ ویرایش ]

حاصل ضرب درونی یک فضای برداری حقیقی یک فرم دوخطی قطعی مثبت است و بنابراین با یک فرم درجه دوم قطعی مثبت مشخص می شود . یک فضای شبه اقلیدسی یک فضای وابسته با یک فضای برداری حقیقی همبند با یک فرم درجه دوم غیر منحط است (که ممکن است نامعین باشد ).

یک مثال اساسی از چنین فضایی، فضای مینکوفسکی است که فضا-زمان نسبیت خاص اینشتین است . این یک فضای چهار بعدی است که متریک با فرم درجه دوم تعریف می شود

$x^{2}+y^{2}+z^{2}-t^{2}،$

که در آن آخرین مختصات ( t ) زمانی است و سه مختصات دیگر ( x , y , z ) مکانی هستند.

برای در نظر گرفتن گرانش ، نسبیت عام از یک منیفولد شبه ریمانی استفاده می کند که دارای فضاهای مینکوفسکی به عنوان فضاهای مماس است . انحنای این منیفولد در یک نقطه تابعی از مقدار میدان گرانشی در این نقطه است.

همچنین ببینید [ ویرایش ]

پورتال ریاضی

فضای هیلبرت ، تعمیم به بعد بی نهایت، مورد استفاده در تحلیل عملکردی

پاورقی ها [ ویرایش ]

^ ممکن است به زمینه یا نویسنده بستگی داشته باشد که آیا یک زیرفضا با خودش موازی است یا خیر
^ اگر شرط یک به یک و پوشا بودن حذف شود، تابعی که فاصله را حفظ می کند، لزوماً تزریقی است و ایزومتری از دامنه آن تا تصویر آن است.
^ اثبات: باید آن را ثابت کرد $f(\lambda x+\mu y)-\lambda f(x)-\mu f(y)=0$ . برای آن کافی است ثابت کنیم که مربع نرم سمت چپ صفر است. با استفاده از دوخطی بودن حاصلضرب داخلی، این نرم مربع را می توان به یک ترکیب خطی از، $\|f(x)\|^{2}،$ $\|f(y)\|^{2}،$ و $f(x)\cdot f(y).$ از آنجایی که f یک ایزومتری است، این ترکیب خطی از $\|x\|^{2}،\|y\|^{2}،$ و $x\cdot y,$ که به صفر ساده می شود.

منبع

https://en.wikipedia.org/wiki/Euclidean_space

+ نوشته شده در چهارشنبه سوم اسفند ۱۴۰۱ ساعت 18:51 توسط علی رضا نقش نیلچی |

3-فضای اقلیدسی

تعریف فنی [ ویرایش ]

آفضای برداری اقلیدسی یک فضای حاصلضرب داخلی با ابعاد محدودبر رو یا عداد حقیقی. [6]

یک فضای اقلیدسی یک فضای نزدیک بر روی حقیقی است به طوری که فضای برداری مرتبط یک فضای برداری اقلیدسی است. فضاهای اقلیدسی را گاهی فضاهای همبسته اقلیدسی می نامند تا آنها را از فضاهای برداری اقلیدسی متمایز کند. [6]

اگر E یک فضای اقلیدسی باشد، فضای برداری مرتبط با آن (فضای برداری اقلیدسی) اغلب نشان داده می شود. ${\overright arrow {E}}.$ بعد فضای اقلیدسی، بعد فضای برداری مرتبط با آن است.

عناصر E نقطه نامیده می شوند و معمولا با حروف بزرگ نشان داده می شوند. عناصر از ${\overright arrow {E}}$ بردارهای اقلیدسی یا بردارهای آزاد نامیده می شوند . آنها را ترجمه نیز می نامند ، اگرچه، به بیان درست، ترجمه تبدیل هندسی است که حاصل عمل یک بردار اقلیدسی در فضای اقلیدسی است.

عمل ترجمه v روی نقطه P نقطه ای را ایجاد می کند که P + v نشان داده می شود . این عمل راضی می کند

$P+(v+w)=(P+v)+w.$

نکته: + دوم در سمت چپ یک جمع برداری است. all other + نشان دهنده عمل یک بردار روی یک نقطه است. این نماد مبهم نیست، زیرا برای تمایز بین دو معنای + کافی است به ماهیت استدلال سمت چپ آن نگاه کنیم.

این حقیقیت که عمل آزاد و متعدی است به این معنی است که برای هر جفت نقطه ( P , Q ) دقیقا یک بردار جابجایی v وجود دارد به طوری که P + v = Q . این بردار v را Q - P یا نشان می دهندپس→. ${\overrightarrow {PQ}}.$

همانطور که قبلا توضیح داده شد، برخی از خصوصیات اساسی فضاهای اقلیدسی ناشی از ساختار فضای نزدیک است. آنها در § ساختار Affine و زیربخش های آن توضیح داده شده اند. خواص حاصل از ضرب داخلی در § ساختار متریک و زیربخش های آن توضیح داده شده است.

نمونه های اولیه [ ویرایش ]

برای هر فضای برداری، جمع آزادانه و گذرا روی خود فضای برداری عمل می کند. بنابراین یک فضای برداری اقلیدسی را می توان به عنوان یک فضای اقلیدسی مشاهده کرد که خود را به عنوان فضای برداری مرتبط دارد.

یک مورد معمولی از فضای برداری اقلیدسی است $\mathbb {R} ^{n}$ به عنوان یک فضای برداری مجهز به ضرب نقطه به عنوان یک ضرب داخلی مشاهده می شود . اهمیت این مثال خاص از فضای اقلیدسی در این حقیقیت است که هر فضای اقلیدسی نسبت به آن هم شکل است . به طور دقیق‌تر، با توجه به فضای اقلیدسی E با بعد n ، انتخاب نقطه‌ای به نام مبدا و مبنای متعارف ${\overright arrow {E}}$ ایزومورفیسم فضاهای اقلیدسی از E تا را تعریف می کند. $\mathbb{R} ^{n}.$

از آنجایی که هر فضای اقلیدسی با بعد n نسبت به آن هم شکل است، فضای اقلیدسی $\mathbb {R} ^{n}$ گاهی اوقات فضای استاندارد اقلیدسی با بعد n نامیده می شود . [5]

+ نوشته شده در چهارشنبه سوم اسفند ۱۴۰۱ ساعت 18:50 توسط علی رضا نقش نیلچی |

2-فضای اقلیدسی

تعریف [ ویرایش ]

تاریخچه تعریف [ ویرایش ]

فضای اقلیدسی توسط یونانیان باستان به عنوان انتزاعی از فضای فیزیکی ما معرفی شد . نوآوری بزرگ آنها، که در عناصر اقلیدس ظاهر شد ، ساختن و اثبات تمام هندسه با شروع از چند ویژگی بسیار اساسی بود که از دنیای فیزیکی انتزاع شده است و به دلیل فقدان ابزارهای اساسی تر، نمی توان آنها را از نظر ریاضی اثبات کرد. این ویژگی‌ها در زبان امروزی ، اصل‌ها یا بدیهیات نامیده می‌شوند . این روش برای تعریف فضای اقلیدسی هنوز تحت عنوان هندسه مصنوعی استفاده می شود .

در سال 1637، رنه دکارت مختصات دکارتی را معرفی کرد و نشان داد که این امکان کاهش مسائل هندسی را به محاسبات جبری با اعداد فراهم می کند. این کاهش هندسه به جبر یک تغییر عمده در دیدگاه بود، زیرا تا آن زمان اعداد حقیقی بر حسب طول و فواصل تعریف می شدند.

هندسه اقلیدسی تا قرن نوزدهم در فضاهایی با ابعاد بیش از سه به کار نمی رفت. لودویگ شلافلی هندسه اقلیدسی را به فضاهایی با بعد n تعمیم داد ، با استفاده از هر دو روش مصنوعی و جبری، و تمام چند توپ های منظم (مشابه های با ابعاد بالاتر جامدات افلاطونی ) را که در فضاهای اقلیدسی با هر بعد وجود دارند، کشف کرد. [4]

علیرغم استفاده گسترده از رویکرد دکارت که هندسه تحلیلی نامیده می شد ، تعریف فضای اقلیدسی تا پایان قرن نوزدهم بدون تغییر باقی ماند. معرفی فضاهای برداری انتزاعی امکان استفاده از آنها را در تعریف فضاهای اقلیدسی با یک تعریف صرفا جبری فراهم کرد. نشان داده شده است که این تعریف جدید از نظر بدیهیات هندسی معادل تعریف کلاسیک است. این تعریف جبری است که امروزه بیشتر برای معرفی فضاهای اقلیدسی استفاده می شود.

انگیزه تعریف مدرن [ ویرایش ]

تعریف [ ویرایش ]

تاریخچه تعریف [ ویرایش ]

انگیزه تعریف مدرن [ ویرایش ]

یکی از راه‌هایی که می‌توان صفحه اقلیدسی را در نظر گرفت، مجموعه‌ای از نقاط است که روابط خاصی را برآورده می‌کنند، که بر حسب فاصله و زاویه قابل بیان است. به عنوان مثال، دو عملیات اساسی (که به آنها حرکت گفته می شود ) در فضا وجود دارد . یکی ترجمه است که به معنای جابجایی صفحه است به طوری که هر نقطه در یک جهت و به همان فاصله جابجا شود. دیگری چرخش حول یک نقطه ثابت در صفحه است که در آن تمام نقاط صفحه از یک زاویه به دور آن نقطه ثابت می چرخند. یکی از اصول اولیه هندسه اقلیدسی این است که دو شکل (معمولاً به عنوان زیرمجموعه در نظر گرفته می شوند ) از صفحه باید معادل ( همسان) در نظر گرفته شوند.) اگر بتوان یکی را با توالی ترجمه، چرخش و بازتاب به دیگری تبدیل کرد (به زیر مراجعه کنید ).

برای اینکه همه اینها از نظر ریاضی دقیق شود، این نظریه باید به وضوح آنچه فضای اقلیدسی است و مفاهیم مربوط به فاصله، زاویه، ترجمه و چرخش را تعریف کند. حتی زمانی که در تئوری های فیزیکی استفاده می شود ، فضای اقلیدسی انتزاعی است که از مکان های فیزیکی حقیقی، چارچوب های مرجع خاص ، ابزار اندازه گیری و غیره جدا شده است. یک تعریف کاملاً ریاضی از فضای اقلیدسی نیز سوالات مربوط به واحدهای طول و سایر ابعاد فیزیکی را نادیده می گیرد : فاصله در یک فضای "ریاضی" یک عدد است ، نه چیزی که در اینچ یا متر بیان می شود.

روش استاندارد برای تعریف ریاضی فضای اقلیدسی، همانطور که در ادامه این مقاله انجام شد، به عنوان مجموعه ای از نقاط است که یک فضای برداری حقیقی بر روی آنها عمل می کند ، فضای ترجمه ها که مجهز به یک ضرب درونی است . [1] عمل ترجمه ها فضا را به یک فضای همبند تبدیل می کند و این امکان تعریف خطوط، سطوح، فضاهای فرعی، بعد و موازی را فراهم می کند . ضرب داخلی امکان تعیین فاصله و زاویه را فراهم می کند.

مجموعه $\mathbb {R} ^{n}$ از n- درایه از اعداد حقیقی مجهز به حاصل ضرب نقطه ای یک فضای اقلیدسی با بعد n است . برعکس، انتخاب نقطه‌ای به نام مبدأ و مبنای متعارف فضای ترجمه‌ها معادل تعریف یک هم‌شکل بین فضای اقلیدسی با بعد n و $\mathbb {R} ^{n}$ به عنوان فضای اقلیدسی دیده می شود.

نتیجه این است که هر چیزی که در مورد فضای اقلیدسی می توان گفت می توان در مورد آن نیز گفت. $\mathbb{R} ^{n}.$ بنابراین، بسیاری از نویسندگان، به ویژه در سطح ابتدایی، تماس می گیرند $\mathbb {R} ^{n}$ فضای استاندارد اقلیدسی بعد n ، [5] یا به سادگی فضای اقلیدسی بعد n .

دلیلی برای ارائه چنین تعریف انتزاعی از فضاهای اقلیدسی و کار با آن به جای $\mathbb {R} ^{n}$ این است که اغلب ترجیح داده می شود که به شیوه ای بدون مختصات و بدون مبدا کار شود (یعنی بدون انتخاب یک مبنا ترجیحی و یک مبدا ترجیحی). دلیل دیگر این است که هیچ مبدأ و مبنایی در جهان فیزیکی وجود ندارد.

یکی از راه‌هایی که می‌توان صفحه اقلیدسی را در نظر گرفت، مجموعه‌ای از نقاط است که روابط خاصی را برآورده می‌کنند، که بر حسب فاصله و زاویه قابل بیان است. به عنوان مثال، دو عملیات اساسی (که به آنها حرکت گفته می شود ) در هواپیما وجود دارد . یکی ترجمه است که به معنای جابجایی صفحه است به طوری که هر نقطه در یک جهت و به همان فاصله جابجا شود. دیگری چرخش حول یک نقطه ثابت در صفحه است که در آن تمام نقاط صفحه از یک زاویه به دور آن نقطه ثابت می چرخند. یکی از اصول اولیه هندسه اقلیدسی این است که دو شکل (معمولاً به عنوان زیرمجموعه در نظر گرفته می شوند ) از صفحه باید معادل ( همسان) در نظر گرفته شوند.) اگر بتوان یکی را با توالی ترجمه، چرخش و بازتاب به دیگری تبدیل کرد (به زیر مراجعه کنید ).

+ نوشته شده در چهارشنبه سوم اسفند ۱۴۰۱ ساعت 18:48 توسط علی رضا نقش نیلچی |

1-فضای اقلیدسی

یک نقطه در فضای سه بعدی اقلیدسی را می توان با سه مختصات قرار داد.

فضای اقلیدسی فضای اساسی هندسه است که برای نمایش فضای فیزیکی در نظر گرفته شده است . در اصل، یعنی در عناصر اقلیدس ، فضای سه بعدی هندسه اقلیدسی بود ، اما در ریاضیات مدرن فضاهای اقلیدسی با هر بعد عدد صحیح مثبت وجود دارد ، [1] از جمله فضای سه بعدی و صفحه اقلیدسی (بعد دو). ). واجد شرایط اقلیدسی برای تشخیص فضاهای اقلیدسی از سایر فضاهایی که بعداً در فیزیک و ریاضیات مدرن مورد توجه قرار گرفتند استفاده می شود.

هندسه‌شناسان یونان باستان فضای اقلیدسی را برای مدل‌سازی فضای فیزیکی معرفی کردند. کار آنها توسط ریاضیدان یونانی باستان اقلیدس در عناصر خود [2] جمع آوری شد ، با نوآوری بزرگ اثبات تمام ویژگی های فضا به عنوان قضایا ، با شروع از چند ویژگی اساسی، به نام فرض ها ، که یا به عنوان بدیهی در نظر گرفته شدند (برای به عنوان مثال، دقیقاً یک خط مستقیم وجود دارد که از دو نقطه می گذرد، یا اثبات آن غیرممکن به نظر می رسید ( مقاله موازی ).

پس از معرفی هندسه های غیراقلیدسی در پایان قرن نوزدهم ، فرضیه های قدیمی برای تعریف فضاهای اقلیدسی از طریق نظریه بدیهی دوباره رسمیت یافتند . تعریف دیگری از فضاهای اقلیدسی با استفاده از فضاهای برداری و جبر خطی معادل تعریف بدیهی نشان داده شده است. این تعریف است که بیشتر در ریاضیات مدرن استفاده می شود و در این مقاله به تفصیل شرح داده شده است. [3] در تمام تعاریف، فضاهای اقلیدسی از نقاطی تشکیل شده‌اند که تنها با ویژگی‌هایی که برای تشکیل فضای اقلیدسی باید داشته باشند، مشخص می‌شوند.

اساساً در هر بعد فقط یک فضای اقلیدسی وجود دارد. یعنی تمام فضاهای اقلیدسی در یک بعد معین هم شکل هستند . بنابراین، در بسیاری از موارد، می توان با یک فضای اقلیدسی خاص کار کرد که عموماً فضای n حقیقی است . ، $\mathbb {R} ^{n},$ مجهز به ضرب نقطه . ایزومورفیسم از فضای اقلیدسی به $\mathbb {R} ^{n}$ به هر نقطه یک n - اعداد حقیقی مرتبط می کند که آن نقطه را در فضای اقلیدسی قرار می دهند و مختصات دکارتی آن نقطه نامیده می شوند.

+ نوشته شده در چهارشنبه سوم اسفند ۱۴۰۱ ساعت 18:44 توسط علی رضا نقش نیلچی |

امضای متریک

مقاله

از ویکیپدیا، دانشنامه آزاد

در ریاضیات ، امضای ( v ، p ، r ) یک تانسور متریک g (یا معادل آن، یک فرم درجه دوم حقیقی که به عنوان یک فرم دوخطی متقارن حقیقی در یک فضای برداری با بعد محدود تصور می شود ) عدد (با کثرت شمارش) از مقادیر ویژه مثبت، منفی و صفر ماتریس متقارن حقیقی g ab تانسور متریک با توجه به یک مبنا . در فیزیک نسبیتی ، v نشان دهنده زمان یا بعد مجازی و p برای بعد فضا و فیزیکی است. از طرف دیگر، می توان آن را به عنوان ابعاد یک زیرفضای مثبت و صفر حداکثر تعریف کرد . بر اساس قانون اینرسی سیلوستر، این اعداد به انتخاب مبنا بستگی ندارند و بنابراین می توان از آنها برای طبقه بندی متریک استفاده کرد. امضا اغلب با یک جفت اعداد صحیح ( v ، p ) نشان داده می شود که دلالت بر r = 0، یا به عنوان یک لیست صریح از نشانه های مقادیر ویژه مانند (+، -، -، -) یا (-، +، +، +) است. به ترتیب برای امضاهای (1، 3، 0) و (3، 1، 0) . [1]

اگر v و p هر دو غیر صفر باشند، امضا نامشخص یا مختلط است و اگر r غیر صفر باشد، منحط است. یک متریک ریمانی یک متریک با امضای قطعی مثبت ( v , 0) است . یک متریک لورنتسی یک متریک با امضا ( p ، 1) ، یا (1، p ) است .

مفهوم دیگری از امضای یک تانسور متریک غیرمنحط وجود دارد که توسط یک عدد منفرد s تعریف شده به صورت ( v - p ) ارائه می‌شود ، که در آن v و p مانند بالا هستند، که معادل تعریف بالا است وقتی بعد n = v + p داده شود . یا ضمنی به عنوان مثال، s = 1 − 3 = −2 برای (+، −، −، −) و بازتاب آن s' = − s = +2 برای (-، +، +، +) است .

تعریف [ ویرایش ]

امضای یک تانسور متریک به عنوان امضای فرم درجه دوم مربوطه تعریف می شود . [2] این تعداد ( v , p , r ) مقادیر ویژه مثبت، منفی و صفر هر ماتریس (یعنی در هر مبنایی برای فضای برداری زیرین) است که شکل را نشان می‌دهد، که با تعدد جبری آنها شمرده می‌شود . معمولاً r = 0 مورد نیاز است، که مانند این است که بگوییم یک تانسور متریک باید غیرمنحط باشد، یعنی هیچ بردار غیرصفری به همه بردارها متعامد نیست.

طبق قانون اینرسی سیلوستر، اعداد ( v ، p ، r ) مستقل از مبنا هستند.

خواص [ ویرایش ]

امضا و ابعاد [ ویرایش ]

با قضیه طیفی، یک ماتریس متقارن n × n بر روی حقیقی ها همیشه قابل قطر است و بنابراین دقیقاً n مقدار ویژه حقیقی دارد (با تعدد جبری شمرده می شود ). بنابراین v + p = n = dim( V ) .

قانون اینرسی سیلوستر: استقلال انتخاب پایه و وجود مبنای متعارف [ ویرایش ]

با توجه به قانون اینرسی سیلوستر ، امضای حاصل ضرب اسکالر (معروف به شکل دوخطی متقارن حقیقی)، g به انتخاب مبنا بستگی ندارد. علاوه بر این، برای هر متریک g امضا ( v , p , r ) مبنایی وجود دارد که g ab = +1 برای a = b = 1، ...، v ، g ab = -1 برای a = b = v + 1، ...، v + p و g ab= 0 در غیر این صورت. نتیجه می شود که یک ایزومتریک ( V 1 , g 1 ) → ( V 2 , g 2 ) وجود دارد اگر و فقط اگر امضاهای g 1 و g 2 برابر باشند. به همین ترتیب امضا برای دو ماتریس متجانس برابر است و یک ماتریس را تا همخوانی طبقه بندی می کند. به طور معادل، امضا در مدارهای گروه خطی عمومی GL( V ) در فضای تانسورهای متقارن رتبه 2 S 2 V * ثابت است و هر مدار را طبقه بندی می کند.

تفسیر هندسی شاخص ها [ ویرایش ]

عدد v (درمقابل p ) حداکثر بعد یک زیرفضای برداری است که حاصلضرب اسکالر g مثبت-معین (مثلاً منفی-معین) است و r بعد رادیکال حاصلضرب اسکالر g یا صفر است. زیرفضای ماتریس متقارن g ab حاصلضرب اسکالر . بنابراین یک ضرب اسکالر غیر منحط دارای امضا ( v , p , 0) با v + p = n است . دوگانگی از موارد خاص ( v ,p , 0) مربوط به دو مقدار ویژه اسکالر است که می توانند با انعکاس متقابل به یکدیگر تبدیل شوند.

مثالها [ ویرایش ]

ماتریس ها [ ویرایش ]

امضای ماتریس هویت n × n ( n ، 0، 0) است . امضای یک ماتریس مورب تعداد اعداد مثبت، منفی و صفر در قطر اصلی آن است .

ماتریس های زیر هر دو امضای یکسانی دارند (1، 1، 0) ، بنابراین به دلیل قانون اینرسی سیلوستر با هم همخوانی دارند :

$\begin{pmatrix} 1 & 0 \\ 0 & -1 \end{pmatrix}, \quad \begin{pmatrix} 0 & 1 \\ 1 & 0 \end{pmatrix}.$

ضرب اسکالر [ ویرایش ]

ضرب اسکالر استاندارد تعریف شده در $\mathbb {R} ^{n}$ دارای امضاهای n بعدی ( v , p , r ) است که در آن v + p = n و رتبه r = 0 است .

در فیزیک، فضای مینکوفسکی یک منیفولد فضازمان استآر4 $\R^4$ با v = 1 و p = 3 مبنا، و دارای یک ضرب اسکالر است که توسط هر دو تعریف شده است ${\بررسی {g}}$ ماتریس:

${\check {g}}={\begin{pmatrix}-1&0&0&0\\0&1&0&0\\0&0&1&0\\0&0&0&1\end{pmatrix}}$

که امضا دارد $(1،3،0)^{-}$ و به عنوان فضای برتر یا فضا مانند شناخته می شود. یا امضای آینه ای $(1،3،0)^{+}$ ، معروف به مجازی برتری یا زمان مانند با $\ کلاه g$ ماتریس

${\hat {g}}={\begin{pmatrix}1&0&0&0\\0&-1&0&0\\0&0&-1&0\\0&0&0&-1\end{pmatrix}}=-{\بررسی {g}}$

نحوه محاسبه امضا [ ویرایش ]

روش هایی برای محاسبه امضای یک ماتریس وجود دارد.

برای هر ماتریس متقارن n × n غیر منحط ، آن را مورب قرار دهید (یا تمام مقادیر ویژه آن را بیابید) و تعداد علائم مثبت و منفی را بشمارید.
برای یک ماتریس متقارن، چند جمله‌ای مشخصه دارای تمام ریشه‌های حقیقی است که نشانه‌های آن‌ها ممکن است در برخی موارد کاملاً توسط قانون نشانه‌های دکارت تعیین شود .
الگوریتم لاگرانژ راهی را برای محاسبه یک مبنای متعامد ، و بنابراین محاسبه یک ماتریس مورب متجانس (بنابراین، با همان امضا) به دیگری ارائه می دهد: امضای یک ماتریس مورب تعداد عناصر مثبت، منفی و صفر در قطر آن است. .
با توجه به معیار ژاکوبی، یک ماتریس متقارن مثبت-معین است اگر و تنها در صورتی که همه عوامل تعیین کننده جزئی اصلی آن مثبت باشند.

امضا در فیزیک [ ویرایش ]

در ریاضیات، قرارداد معمول برای هر منیفولد ریمانی استفاده از یک تانسور متریک مثبت-معین است (به این معنی که پس از قطری‌سازی، عناصر روی قطر همگی مثبت هستند).

در فیزیک نظری ، فضازمان با یک منیفولد شبه ریمانی مدل‌سازی می‌شود . امضا تعداد کاراکترهای زمان مانند یا فضا مانند را در فضازمان به معنایی که توسط نسبیت خاص تعریف شده است، شمارش می کند : همانطور که در فیزیک ذرات استفاده می شود ، متریک دارای یک مقدار ویژه در زیرفضای زمان مانند است و مقدار ویژه آینه ای آن در فضای فرعی دارد. فضای فرعی فضا مانند در مورد خاص متریک مینکوفسکی ،

$ds^2 = c^2 dt^2 - dx^2 - dy^2 - dz^2$ ،

امضای متریک است $(1،3،0)^{+}$ یا (+، -، -، -) اگر مقدار ویژه آن در جهت زمانی تعریف شده باشد، یا $(1،3،0)^{-}$ یا (-، +، +، +) اگر مقدار ویژه در سه جهت فضایی x ، y و z تعریف شده باشد . (گاهی اوقات از قرارداد علامت مخالف استفاده می شود، اما با علامتی که در اینجا داده شده است ، مستقیماً زمان مناسب را اندازه گیری می کند .)

تغییر امضا [ ویرایش ]

اگر یک متریک در همه جا منظم باشد، امضای متریک ثابت است. با این حال، اگر معیارهایی را مجاز بدانیم که در برخی از ابرسطوح ها منحط یا ناپیوسته هستند، امضای متریک ممکن است در این سطوح تغییر کند. [3] چنین معیارهای تغییر امضا ممکن است در کیهان‌شناسی و گرانش کوانتومی کاربرد داشته باشد .

همچنین ببینید [ ویرایش ]

منبع

https://en.wikipedia.org/wiki/Metric_signature

+ نوشته شده در چهارشنبه سوم اسفند ۱۴۰۱ ساعت 18:29 توسط علی رضا نقش نیلچی |

تعامل کوارتیک

از ویکیپدیا، دانشنامه آزاد

در تئوری میدان کوانتومی ، برهمکنش کوارتیک نوعی برهمکنش خود در یک میدان اسکالر است . انواع دیگری از برهمکنش های کوارتیک را می توان تحت عنوان برهمکنش های چهار فرمیونی یافت . یک میدان اسکالر آزاد کلاسیک $\varphi$ معادله کلاین-گوردون را برآورده می کند . اگر یک میدان اسکالر مشخص شود $\varphi$ ، یک برهمکنش کوارتیک با افزودن یک عبارت انرژی پتانسیل نشان داده می شود $({\lambda }/{4!})\varphi ^{4}$ به چگالی لاگرانژی . ثابت جفت شدن $\لامبدا$ در فضازمان 4 بعدی بی بعد است .

این مقاله از $(+،-،-،-)$ امضای متریک برای فضای مینکوفسکی

لاگرانژی برای یک میدان اسکالر حقیقی [ ویرایش ]

چگالی لاگرانژی برای یک میدان اسکالر حقیقی با اندرکنش کوارتیک است

${\mathcal {L}}(\varphi )={\frac {1}{2}}[\partial ^{\mu }\varphi \partial _{\mu }\varphi -m^{2} \varphi ^{2}]-{\frac {\lambda }{4!}}\varphi ^{4}.$

این لاگرانژ دارای یک نقشه تقارن جهانی Z 2 است $\varphi \to -\varphi$ .

لاگرانژی برای یک میدان اسکالر مختلط[ ویرایش ]

لاگرانژی برای یک میدان اسکالر مختلط می تواند به صورت زیر ایجاد شود. برای دو میدان اسکالر $\varphi _{1}$ و $\varphi _{2}$ لاگرانژی فرم دارد

${\mathcal {L}}(\varphi _{1},\varphi _{2})={\frac {1}{2}}[\partial _{\mu }\varphi _{1}\partial ^ {\mu }\varphi _{1}-m^{2}\varphi _{1}^{2}]+{\frac {1}{2}}[\partial _{\mu }\varphi _{ 2}\partial ^{\mu }\varphi _{2}-m^{2}\varphi _{2}^{2}]-{\frac {1}{4}}\lambda (\varphi _{ 1}^{2}+\varphi _{2}^{2})^{2}،$

که می توان به طور خلاصه تر نوشت و یک میدان اسکالر مختلط را معرفی کرد $\phi$ که تعریف میشود

$\phi \equiv {\frac {1}{{\sqrt {2}}}}(\varphi _{1}+i\varphi _{2})،$

$\phi ^{*}\equiv {\frac {1}{{\sqrt {2}}}}(\varphi _{1}-i\varphi _{2}).$

بیان شده بر حسب این میدان اسکالر مختلط، لاگرانژی فوق می شود

${\mathcal {L}}(\phi )=\جزئی ^{\mu }\phi ^{*}\partial _{\mu }\phi -m^{2}\phi ^{*}\phi -\ لامبدا (\phi ^{*}\phi )^{2}،$

که در نتیجه معادل مدل SO(2) میدان های اسکالر حقیقی است $\varphi _{1}،\varphi _{2}$ ، همانطور که با گسترش میدان مختلط قابل مشاهده است $\phi$ در قسمت های حقیقی و مختلط

با $ن$ میدان های اسکالر حقیقی ، می توانیم یک داشته باشیم $\varphi ^{4}$ مدلی با تقارن جهانی SO(N) که توسط لاگرانژی ارائه شده است

${\mathcal {L}}(\varphi _{1},...,\varphi _{N})={\frac {1}{2}}[\partial ^{\mu }\varphi _{a }\partial _{\mu }\varphi _{a}-m^{2}\varphi _{a}\varphi _{a}]-{\frac {1}{4}}\lambda (\varphi _ {a}\varphi _{a})^{2},\quad a=1,...,N.$

بسط میدان مختلط در بخشهای حقیقی و مختلط نشان می دهد که معادل مدل SO(2) میدانهای اسکالر حقیقی است.

در تمام مدل های بالا، ثابت جفت $\لامبدا$ باید مثبت باشد، زیرا در غیر این صورت پتانسیل پایین تر خواهد بود و خلاء پایداری وجود نخواهد داشت. همچنین، انتگرال مسیر فاینمن که در زیر مورد بحث قرار می‌گیرد، نامشخص خواهد بود. در 4 بعد $\phi ^{4}$ نظریه ها دارای یک قطب لاندو هستند . این بدان معناست که بدون یک برش در مقیاس انرژی بالا، عادی سازی مجدد این نظریه را بی اهمیت جلوه می دهد .

را $\phi ^{4}$ مدل متعلق به کلاس گریفیتز-سیمون( Griffiths-Simon) است، [1] به این معنی که می‌توان آن را به عنوان حد ضعیف مدل Ising در نوع خاصی از گراف نیز نمایش داد. بی اهمیت بودن هر دو $\phi ^{4}$ مدل و مدل Ising در $d\geq 4$ را می توان از طریق یک نمایش گرافیکی به نام بسط جریان تصادفی نشان داد. [2]

کوانتیزاسیون انتگرال فاینمن [ ویرایش ]

مقاله اصلی: فرمول انتگرال مسیر

بسط نمودار فاینمن را می توان از فرمول انتگرال مسیر فاینمن نیز بدست آورد . [3] مقادیر انتظار خلاء مرتب‌شده زمانی چندجمله‌ای‌ها در φ، که به توابع گرین n-ذره‌ای معروف هستند، با ادغام در تمام زمینه‌های ممکن ساخته می‌شوند، که با مقدار انتظار خلاء بدون میدانهای خارجی نرمال می‌شوند.

$\langle\Omega|\mathcal{T}\{{\phi}(x_1)\cdots {\phi}(x_n)\}|\Omega\rangle=\frac{\int \mathcal{D}\phi \phi (x_1)\cdots \phi(x_n) e^{i\int d^4x \left({1\over 2}\partial^\mu \phi \partial_\mu \phi -{m^2 \over 2} \phi^2-{\lambda\over 4!}\phi^4\right)}}{\int \mathcal{D}\phi e^{i\int d^4x \left({1\over 2} \partial^\mu \phi \partial_\mu \phi -{m^2 \over 2}\phi^2-{\lambda\over 4!}\phi^4\right)}}.$

همه این توابع گرین را می توان با بسط نمایی در J ( x )φ( x ) در تابع مولد به دست آورد.

$Z[J] =\int \mathcal{D}\phi e^{i\int d^4x \left({1\over 2}\partial^\mu \phi \partial_\mu \phi -{m^2 \over 2}\phi^2-{\lambda\over 4!}\phi^4+J\phi\right)} = Z[0] \sum_{n=0}^{\infty} \frac{1 }{n!} \langle\Omega|\mathcal{T}\{{\phi}(x_1)\cdots {\phi}(x_n)\}|\Omega\rangle.$

یک چرخش Wick ممکن است برای مختلط کردن زمان اعمال شود. با تغییر امضا به (++++) سپس یک انتگرال مکانیک آماری φ4 در فضای اقلیدسی 4 بعدی به دست می‌آید .

$Z[J]=\int \mathcal{D}\phi e^{-\int d^4x \left({1\over 2}(\nabla\phi)^2+{m^2 \بیش از 2}\ phi^2+{\lambda\over 4!}\phi^4+J\phi\right)}.$

به طور معمول، این برای پراکندگی ذرات با گشتاور ثابت اعمال می شود، در این صورت، تبدیل فوریه مفید است و به جای آن

${\tilde {Z}}[{\tilde {J}}]=\int {\mathcal {D}}{\tilde {\phi }}e^{-\int d^{4}p\ چپ ({1 \ بیش از 2}(p^{2}+m^{2}){\tilde {\phi }}^{2}-{\tilde {J}}{\tilde {\phi }}+ {\lambda \over 4!}{\int {d^{4}p_{1} \over (2\pi )^{4}}{d^{4}p_{2} \over (2\pi ) ^{4}}{d^{4}p_{3} \over (2\pi )^{4}}\delta (p-p_{1}-p_{2}-p_{3}){\tilde {\phi }}(p){\tilde {\phi }}(p_{1}){\tilde {\phi }}(p_{2}){\tilde {\phi }}(p_{3}) }\درست)}.$

جایی که $\delta (x)$ تابع دلتای دیراک است .

ترفند استاندارد برای ارزیابی این انتگرال عملکردی این است که آن را به عنوان حاصل ضرب عوامل نمایی، به صورت شماتیک، بنویسیم.

${\tilde {Z}}[{\tilde {J}}]=\int {\mathcal {D}}{\tilde {\phi }}\prod _{p}\left[e^{- (p^{2}+m^{2}){\tilde {\phi }}^{2}/2}e^{-\lambda /4!\int {d^{4}p_{1} \ بیش از (2\pi )^{4}}{d^{4}p_{2} \over (2\pi )^{4}}{d^{4}p_{3} \over (2\pi ) ^{4}}\delta (p-p_{1}-p_{2}-p_{3}){\tilde {\phi }}(p){\tilde {\phi }}(p_{1}) {\tilde {\phi }}(p_{2}){\tilde {\phi }}(p_{3})}e^{{\tilde {J}}{\tilde {\phi }}}\right ].$

دو عامل نمایی دوم را می توان به صورت سری توانی بسط داد و ترکیبات این بسط را می توان به صورت گرافیکی نشان داد. انتگرال با λ = 0 را می توان به عنوان حاصلضرب بی نهایت انتگرال ابتدایی گاوسی در نظر گرفت و نتیجه را می توان به صورت مجموع نمودارهای فاینمن بیان کرد که با استفاده از قوانین فاینمن زیر محاسبه می شود:

هر میدان $\tilde{\phi}(p)$ در نقطه n تابع اقلیدسی گرین با یک خط خارجی (نیم لبه) در نمودار نشان داده می شود و با تکانه p همراه است .
هر رأس با یک عامل -λ نشان داده می شود .
در یک مرتبه معین λk ، تمام نمودارهای دارای n خط خارجی و k راس به گونه ای ساخته می شوند که گشتاور جریان در هر راس صفر باشد. هر خط داخلی با ضریب 1/( q 2 + m 2 ) نشان داده می شود، که در آن q تکانه ای است که از آن خط عبور می کند.
هر لحظه بدون محدودیت روی همه مقادیر ادغام می شود.
نتیجه با یک ضریب تقارن تقسیم می‌شود، که تعداد راه‌هایی است که خطوط و رئوس نمودار را می‌توان بدون تغییر اتصال آن دوباره مرتب کرد.
نمودارهای حاوی "حباب های خلاء"، زیرگراف های متصل بدون خطوط خارجی را درج نکنید.

آخرین قانون تأثیر تقسیم بر را در نظر می گیرد $\tilde{Z}[0]$ . قوانین فاینمن فضای مینکوفسکی مشابه هستند، با این تفاوت که هر رأس با نشان داده می شود $-i\lambda$ در حالی که هر خط داخلی با ضریب i /( q 2 - m 2 + i ε ) نشان داده می شود، که در آن عبارت ε نشان دهنده چرخش کوچک Wick است که برای همگرایی انتگرال گاوسی فضای مینکوفسکی لازم است.

عادی سازی مجدد [ ویرایش ]

مقاله اصلی: عادی سازی مجدد

انتگرال‌های روی لحظه‌ای نامحدود، که «انتگرال‌های حلقه» نامیده می‌شوند، در نمودارهای فاینمن معمولاً واگرا می‌شوند. این معمولاً با نرمال‌سازی مجدد انجام می‌شود، که رویه‌ای برای افزودن عبارات متضاد به لاگرانژی است، به‌گونه‌ای که نمودارهای ساخته‌شده از لاگرانژی و متقابل‌های اصلی متناهی باشند. [4] یک مقیاس عادی سازی مجدد باید در این فرآیند معرفی شود و ثابت جفت و جرم به آن وابسته می شوند. این وابستگی است که به قطب لاندو که قبلاً ذکر شد منتهی می شود و مستلزم آن است که برش محدود نگه داشته شود. متناوباً، اگر اجازه داده شود که برش تا بی نهایت برود، قطب لاندو را می توان تنها در صورتی اجتناب کرد که جفت مجدد نرمال شده به صفر برسد و این نظریه را ارائه می کند.پیش پا افتاده . [5]

شکست خود به خودی تقارن [ ویرایش ]

نوشتار اصلی: شکستن تقارن خود به خود

یک ویژگی جالب می تواند رخ دهد اگر m 2 منفی شود، اما λ همچنان مثبت باشد. در این حالت، خلاء از دو حالت کم انرژی تشکیل شده است که هر یک به طور خود به خود تقارن جهانی Z 2 نظریه اصلی را می شکند. این منجر به ظهور حالت های جمعی جالبی مانند دیوارهای دامنه می شود . در نظریه O (2)، خلاء روی یک دایره قرار می گیرد و انتخاب یکی به طور خود به خود تقارن O (2) را می شکند. تقارن شکسته پیوسته منجر به بوزون گلدستون می شود . این نوع شکستن تقارن خود به خودی جزء اساسی مکانیسم هیگز است . [6]

شکست خود به خودی تقارن های گسسته [ ویرایش ]

ساده‌ترین سیستم نسبیتی که در آن می‌توانیم شکست تقارن خود به خود را ببینیم، سیستمی با یک میدان اسکالر واحد است. $\varphi$ با لاگرانژی

${\mathcal {L}}(\varphi )={\frac {1}{2}}(\partial \varphi )^{2}+{\frac {1}{2}}\mu ^{2}\ varphi ^{2}-{\frac {1}{4}}\lambda \varphi ^{4}\equiv {\frac {1}{2}}(\partial \varphi )^{2}-V(\ وارفی)،$

جایی که $\mu ^{2}>0$ و

$V(\varphi )\equiv -{\frac {1}{2}}\mu ^{2}\varphi ^{2}+{\frac {1}{4}}\lambda \varphi ^{4}.$

به حداقل رساندن پتانسیل با توجه به $\varphi$ منجر به

$V'(\varphi _{0})=0\Longleftrightarrow \varphi _{0}^{2}\equiv v^{2}={\frac {\mu ^{2}}{\lambda }}.$

اکنون میدان را پیرامون این حداقل نوشته گسترش می دهیم

$\varphi (x)=v+\sigma (x)،$

و در لاگرانژی جایگزین می کنیم

${\mathcal {L}}(\varphi )=\underbrace {-{\frac {\mu ^{4}}{4\lambda }}}_{{{\text{ثابت غیر مهم}}}}+\underbrace {{\frac {1}{2}}[(\partial \sigma )^{2}-({\sqrt {2}}\mu )^{2}\sigma ^{2}]}_{{{ \text{میدان اسکالر عظیم}}}}+\underbrace {(-\lambda v\sigma ^{3}-{\frac {\lambda }{4}}\sigma ^{4})}_{{{\ متن{تعاملات با خود}}}}.$

جایی که ما متوجه می شویم که اسکالر $\سیگما$ اکنون یک اصطلاح جمعی مثبت دارد.

تفکر بر حسب مقادیر انتظار خلاء به ما امکان می‌دهد بفهمیم که وقتی تقارن خود به خود شکسته می‌شود چه اتفاقی می‌افتد. لاگرانژی اصلی تحت عنوان ثابت بود $Z_{2}$ تقارن $\varphi \rightarrow -\varphi$ . از آنجا که

$\langle \Omega |\varphi |\Omega \rangle =\pm {\sqrt {{\frac {6\mu ^{2}}{\lambda }}}}$

هر دو حداقل هستند، باید دو خلاء متفاوت وجود داشته باشد: $|\Omega _{\pm }\rangle$ با

$\langle \Omega _{\pm }|\varphi |\Omega _{\pm }\rangle =\pm {\sqrt {{\frac {6\mu ^{2}}{\lambda }}}}.$

از آنجا که $Z_{2}$ تقارن می گیرد $\varphi \rightarrow -\varphi$ ، باید طول بکش $|\Omega _{+}\rangle \فلش راست چپ |\Omega _{-}\rangle$ همچنین. دو خلاء ممکن برای این نظریه معادل هستند، اما باید یکی را انتخاب کرد. اگرچه به نظر می رسد که در لاگرانژی جدید $Z_{2}$ تقارن ناپدید شده است، هنوز وجود دارد، اما اکنون مانند آن عمل می کند . $\sigma \rightarrow -\sigma -2v.$ این یک ویژگی کلی تقارن های خود به خود شکسته است: خلاء آنها را می شکند، اما آنها در واقع در لاگرانژ شکسته نمی شوند، فقط پنهان هستند و اغلب فقط به صورت غیر خطی درک می شوند. [7]

راه حل های دقیق [ ویرایش ]

مجموعه ای از راه حل های کلاسیک دقیق برای معادله حرکت نظریه وجود دارد که به شکل نوشته شده است.

$\partial ^{2}\varphi +\mu _{0}^{2}\varphi +\lambda \varphi ^{3}=0$

که می توان برای بی توده ها نوشت، $\mu _{0}=0$ مورد به عنوان [8]

$\varphi (x)=\pm \mu \left({\frac {2}{\lambda }}\right)^{1 \over 4}{\rm {sn}}(p\cdot x+\ تتا، من)$

باسn $\,{\rm {sn\!}}$ یک تابع بیضوی ژاکوبی و $\,\mu ,\theta$ دو ثابت ادغام، به شرطی که رابطه پراکندگی زیر برقرار باشد

$p^{2}=\mu ^{2}\left({\frac {\lambda }{2}}\right)^{{1 \over 2}}.$

نکته جالب این است که ما با یک معادله بدون جرم شروع کردیم، اما راه حل دقیق موجی را با رابطه پراکندگی مناسب برای حل عظیم توصیف می کند. وقتی جرم جرم صفر نباشد یک می شود

$\varphi (x)=\pm {\sqrt {{\frac {2\mu ^{4}}{\mu _{0}^{2}+{\sqrt {\mu _{0}^{4} +2\lambda \mu ^{4}}}}}}}{{\rm {sn}}}\left(p\cdot x+\theta ,{\sqrt {{\frac {-\mu _{0} ^{2}+{\sqrt {\mu _{0}^{4}+2\lambda \mu ^{4}}}}{-\mu _{0}^{2}-{\sqrt {\ mu _{0}^{4}+2\lambda \mu ^{4}}}}}}}\راست)$

اکنون رابطه پراکندگی است

$p^{2}=\mu _{0}^{2}+{\frac {\lambda \mu ^{4}}{\mu _{0}^{2}+{\sqrt {\mu _{ 0}^{4}+2\lambda \mu ^{4}}}}}.$

در نهایت، برای مورد شکست تقارن، یکی دارد

$\varphi (x)=\pm v\cdot {{\rm {dn}}}(p\cdot x+\theta,i)،$

بودن $v={\sqrt {{\frac {2\mu _{0}^{2}}{3\lambda }}}}$ و رابطه پراکندگی زیر برقرار است

$p^{2}={\frac {\lambda v^{2}}{2}}.$

این راه حل های موجی جالب هستند، با وجود اینکه با معادله ای با علامت جرم اشتباه شروع کردیم، رابطه پراکندگی رابطه درستی دارد. علاوه بر این، عملکرد ژاکوبیدn $\,{{\rm {dn}}}\!$ هیچ صفر

از ویکیپدیا، دانشنامه آزاد

این مقاله از $(+،-،-،-)$ امضای متریک برای فضای مینکوفسکی

لاگرانژی برای یک میدان اسکالر حقیقی [ ویرایش ]

چگالی لاگرانژی برای یک میدان اسکالر حقیقی با اندرکنش کوارتیک است

${\mathcal {L}}(\varphi )={\frac {1}{2}}[\partial ^{\mu }\varphi \partial _{\mu }\varphi -m^{2} \varphi ^{2}]-{\frac {\lambda }{4!}}\varphi ^{4}.$

این لاگرانژ دارای یک نقشه تقارن جهانی Z 2 است $\varphi \to -\varphi$ .

لاگرانژی برای یک میدان اسکالر مختلط[ ویرایش ]

که می توان به طور خلاصه تر نوشت و یک میدان اسکالر مختلط را معرفی کرد $\phi$ که تعریف میشود

$\phi \equiv {\frac {1}{{\sqrt {2}}}}(\varphi _{1}+i\varphi _{2})،$

$\phi ^{*}\equiv {\frac {1}{{\sqrt {2}}}}(\varphi _{1}-i\varphi _{2}).$

بیان شده بر حسب این میدان اسکالر مختلط، لاگرانژی فوق می شود

${\mathcal {L}}(\phi )=\جزئی ^{\mu }\phi ^{*}\partial _{\mu }\phi -m^{2}\phi ^{*}\phi -\ لامبدا (\phi ^{*}\phi )^{2}،$

بسط میدان مختلط در بخشهای حقیقی و مختلط نشان می دهد که معادل مدل SO(2) میدانهای اسکالر حقیقی است.

کوانتیزاسیون انتگرال فاینمن [ ویرایش ]

مقاله اصلی: فرمول انتگرال مسیر

همه این توابع گرین را می توان با بسط نمایی در J ( x )φ( x ) در تابع مولد به دست آورد.

$Z[J]=\int \mathcal{D}\phi e^{-\int d^4x \left({1\over 2}(\nabla\phi)^2+{m^2 \بیش از 2}\ phi^2+{\lambda\over 4!}\phi^4+J\phi\right)}.$

به طور معمول، این برای پراکندگی ذرات با گشتاور ثابت اعمال می شود، در این صورت، تبدیل فوریه مفید است و به جای آن

جایی که $\delta (x)$ تابع دلتای دیراک است .

هر فیلد $\tilde{\phi}(p)$ در نقطه n تابع اقلیدسی گرین با یک خط خارجی (نیم لبه) در نمودار نشان داده می شود و با تکانه p همراه است .
هر رأس با یک عامل -λ نشان داده می شود .
در یک مرتبه معین λk ، تمام نمودارهای دارای n خط خارجی و k راس به گونه ای ساخته می شوند که گشتاور جریان در هر راس صفر باشد. هر خط داخلی با ضریب 1/( q 2 + m 2 ) نشان داده می شود، که در آن q تکانه ای است که از آن خط عبور می کند.
هر لحظه بدون محدودیت روی همه مقادیر ادغام می شود.
نتیجه با یک ضریب تقارن تقسیم می‌شود، که تعداد راه‌هایی است که خطوط و رئوس نمودار را می‌توان بدون تغییر اتصال آن دوباره مرتب کرد.
نمودارهای حاوی "حباب های خلاء"، زیرگراف های متصل بدون خطوط خارجی را درج نکنید.

عادی سازی مجدد [ ویرایش ]

مقاله اصلی: عادی سازی مجدد

شکست خود به خودی تقارن [ ویرایش ]

نوشتار اصلی: شکستن تقارن خود به خود

شکست خود به خودی تقارن های گسسته [ ویرایش ]

${\mathcal {L}}(\varphi )={\frac {1}{2}}(\partial \varphi )^{2}+{\frac {1}{2}}\mu ^{2}\ varphi ^{2}-{\frac {1}{4}}\lambda \varphi ^{4}\equiv {\frac {1}{2}}(\partial \varphi )^{2}-V(\ وارفی)،$

جایی که $\mu ^{2}>0$ و

$V(\varphi )\equiv -{\frac {1}{2}}\mu ^{2}\varphi ^{2}+{\frac {1}{4}}\lambda \varphi ^{4}.$

به حداقل رساندن پتانسیل با توجه به $\varphi$ منجر به

$V'(\varphi _{0})=0\Longleftrightarrow \varphi _{0}^{2}\equiv v^{2}={\frac {\mu ^{2}}{\lambda }}.$

اکنون میدان را پیرامون این حداقل نوشته گسترش می دهیم

$\varphi (x)=v+\sigma (x)،$

و در لاگرانژی جایگزین می کنیم

جایی که ما متوجه می شویم که اسکالر $\سیگما$ اکنون یک اصطلاح جمعی مثبت دارد.

$\langle \Omega |\varphi |\Omega \rangle =\pm {\sqrt {{\frac {6\mu ^{2}}{\lambda }}}}$

هر دو حداقل هستند، باید دو خلاء متفاوت وجود داشته باشد: $|\Omega _{\pm }\rangle$ با

$\langle \Omega _{\pm }|\varphi |\Omega _{\pm }\rangle =\pm {\sqrt {{\frac {6\mu ^{2}}{\lambda }}}}.$

راه حل های دقیق [ ویرایش ]

مجموعه ای از راه حل های کلاسیک دقیق برای معادله حرکت نظریه وجود دارد که به شکل نوشته شده است.

$\partial ^{2}\varphi +\mu _{0}^{2}\varphi +\lambda \varphi ^{3}=0$

که می توان برای بی توده ها نوشت، $\mu _{0}=0$ مورد به عنوان [8]

$\varphi (x)=\pm \mu \left({\frac {2}{\lambda }}\right)^{1 \over 4}{\rm {sn}}(p\cdot x+\ تتا، من)$

باسn $\,{\rm {sn\!}}$ یک تابع بیضوی ژاکوبی و $\,\mu ,\theta$ دو ثابت ادغام، به شرطی که رابطه پراکندگی زیر برقرار باشد

$p^{2}=\mu ^{2}\left({\frac {\lambda }{2}}\right)^{{1 \over 2}}.$

اکنون رابطه پراکندگی است

$p^{2}=\mu _{0}^{2}+{\frac {\lambda \mu ^{4}}{\mu _{0}^{2}+{\sqrt {\mu _{ 0}^{4}+2\lambda \mu ^{4}}}}}.$

در نهایت، برای مورد شکست تقارن، یکی دارد

$\varphi (x)=\pm v\cdot {{\rm {dn}}}(p\cdot x+\theta,i)،$

بودن $v={\sqrt {{\frac {2\mu _{0}^{2}}{3\lambda }}}}$ و رابطه پراکندگی زیر برقرار است

$p^{2}={\frac {\lambda v^{2}}{2}}.$

این راه حل های موجی جالب هستند، با وجود اینکه با معادله ای با علامت جرم اشتباه شروع کردیم، رابطه پراکندگی رابطه درستی دارد. علاوه بر این، عملکرد ژاکوبی $\,{{\rm {dn}}}\!$ هیچ صفر واقعی ندارد و بنابراین میدان هرگز صفر نیست، بلکه حول یک مقدار ثابت مشخص حرکت می کند که در ابتدا برای توصیف شکست خود به خودی تقارن انتخاب شده است.

اگر توجه داشته باشیم که راه حل را می توان در فرم جستجو کرد، اثبات منحصر به فرد بودن می تواند ارائه شود $\varphi =\varphi (\xi)$ بودن $\xi =p\cdot x$ . سپس، معادله دیفرانسیل جزئی تبدیل به یک معادله دیفرانسیل معمولی می شود که تابع بیضوی ژاکوبی را با $پ$ ارضای رابطه پراکندگی مناسب

همچنین ببینید [ ویرایش ]

ندارد و بنابراین میدان هرگز صفر نیست، بلکه حول یک مقدار ثابت مشخص حرکت می کند که در ابتدا برای توصیف شکست خود به خودی تقارن انتخاب شده است.

همچنین ببینید [ ویرایش ]

منبع

https://en.wikipedia.org/wiki/Quartic_interaction

+ نوشته شده در سه شنبه دوم اسفند ۱۴۰۱ ساعت 7:55 توسط علی رضا نقش نیلچی |

پتانسیل کلمن-واینبرگ

مدل کلمن-واینبرگ الکترودینامیک کوانتومی یک میدان اسکالر را در چهار بعدی نشان می‌دهد . لاگرانژی برای مدل است

$L=-{\frac {1}{4}}(F_{\mu \nu })^{2}+|D_{\mu }\phi |^{2}-m^{2}| \phi |^{2}-{\frac {\lambda }{6}}|\phi |^{4}$

جایی که میدان اسکالر پیچیده است، $F_{{\mu \nu }}=\جزئی _{\mu }A_{\nu }-\جزئی _{\nu }A_{\mu }$ تانسور میدان الکترومغناطیسی است و $D_{\mu }=\partial _{\mu }-\mathrm {i} (e/\hbar c)A_{\mu }$ مشتق کوواریانت حاوی بار الکتریکیه $ه$ از میدان الکترومغناطیسی

فرض کن که $\لامبدا$ غیر منفی است سپس اگر عبارت جرمی تاکیونیک باشد، $m^{2}<0$ شکست خود به خودی از تقارن سنج در انرژی های پایین وجود دارد که نوعی از مکانیسم هیگز است . از طرف دیگر، اگر مجذور جرم مثبت باشد، $m^{2}>0$ انتظار خلاء میدان $\phi$ صفر است. در سطح کلاسیک دومی نیز صادق است اگر $m^{2}=0$ . با این حال، همانطور که توسط سیدنی کلمن و اریک واینبرگ نشان داده شد ، حتی اگر جرم مجدد نرمال شده صفر باشد، باز هم تقارن خود به خود به دلیل اصلاحات تابشی شکسته می شود (این یک مقیاس جرم را به یک نظریه کلاسیک همسو معرفی می کند - مدل دارای یک ناهنجاری منسجم است ).

همین امر می تواند در سایر نظریه های گیج نیز اتفاق بیفتد. در فاز شکسته نوسانات میدان اسکالر $\phi$ خود را به‌عنوان یک بوزون هیگز نورانی طبیعی نشان می‌دهند ، در واقع حتی برای توضیح شکست تقارن ضعیف الکتریکی در مدل حداقلی بسیار سبک‌تر از بوزون‌های برداری . مدل های غیرمینیمالی وجود دارند که سناریوهای واقعی تری ارائه می دهند. همچنین تغییرات این مکانیسم برای تقارن های فرضی خود به خود شکسته از جمله ابرتقارن پیشنهاد شد .

به همین ترتیب ممکن است بتوان گفت که مدل دارای یک انتقال فاز مرتبه اول به عنوان تابعی از $m^{2}$ . این مدل آنالوگ چهار بعدی نظریه سه بعدی گینزبورگ-لاندو است که برای توضیح خواص ابررساناها در نزدیکی انتقال فاز استفاده می شود .

نسخه سه‌بعدی مدل کلمن-واینبرگ، انتقال فاز ابررسانا را کنترل می‌کند که می‌تواند هم مرتبه اول و هم مرتبه دوم باشد، بسته به نسبت پارامتر گینزبورگ-لاندو. $\kappa \equiv \lambda /e^{2}$ ، با یک نقطه سه بحرانی نزدیک است $\kappa =1/{\sqrt 2}$ که نوع I را از ابررسانایی نوع II جدا می کند . از لحاظ تاریخی، ترتیب انتقال فاز ابررسانا برای مدت طولانی مورد بحث بود زیرا فاصله دمایی که در آن نوسانات بزرگ هستند ( فاصله گینزبورگ ) بسیار کوچک است. این سوال در نهایت در سال 1982 حل شد. [1] اگر پارامتر Ginzburg-Landau� $\کاپا$ که ابررساناهای نوع I و نوع II را متمایز می کند ( اینجا را نیز ببینید ) به اندازه کافی بزرگ است، نوسانات گرداب مهم می شود که انتقال به مرتبه دوم را هدایت می کند. نقطه سه‌گانه تقریباً در آن نهفته است $\kappa =0.76/{\sqrt {2}}$ ، یعنی کمی کمتر از مقدار $\kappa =1/{\sqrt {2}}$ جایی که نوع I به ابررسانای نوع II تبدیل می شود . این پیش بینی در سال 2002 توسط شبیه سازی کامپیوتری مونت کارلو تایید شد . [2]

ادبیات [ ویرایش ]

S. Coleman و E. Weinberg (1973). "اصلاحات تشعشعی به عنوان منشأ شکست تقارن خود به خود". بررسی فیزیکی D. 7 (6): 1888-1910. arXiv : hep-th/0507214 . Bibcode : 1973PhRvD...7.1888C . doi : 10.1103/PhysRevD.7.1888 . S2CID 6898114 .
LD Landau (1937). "در تئوری انتقال فاز. II". Zhurnal Eksperimental'noi i Teoreticheskoi Fiziki . 7 : 627.
VL Ginzburg و LD Landau (1950). "درباره نظریه ابررسانایی". Zhurnal Eksperimental'noi i Teoreticheskoi Fiziki . 20 : 113-137. doi : 10.1007/978-3-540-68008-6_4 . شابک 978-3-540-68004-8.
M.Tinkham (2004). مقدمه ای بر ابررسانایی Dover Books on Physics (ویرایش دوم). دوور . شابک 0-486-43503-2.

همچنین ببینید [ ویرایش ]

تعامل کوارتیک

منابع

https://en.wikipedia.org/wiki/Coleman%E2%80%93Weinberg_potential

+ نوشته شده در سه شنبه دوم اسفند ۱۴۰۱ ساعت 7:38 توسط علی رضا نقش نیلچی |

شکست خود به خودی تقارن

از ویکیپدیا، دانشنامه آزاد

نظریه میدان کوانتومی
نمودار فاینمن
تاریخ
نشان می دهد زمینه
نشان می دهد تقارن ها
نشان می دهد ابزار
نشان می دهد معادلات
نشان می دهد مدل استاندارد
نشان می دهد نظریه های ناقص
نشان می دهد دانشمندان
v تی ه

مکانیک آماری

ترمودینامیک نظریه جنبشی
نشان می دهد آمار ذرات
نشان می دهد مجموعه های ترمودینامیکی
نشان می دهد مدل ها
نشان می دهد پتانسیل ها
نشان می دهد دانشمندان
v تی ه

شکست خود به خودی تقارن یک فرآیند خودبه‌خودی شکستن تقارن است که در آن یک سیستم فیزیکی در حالت متقارن خود به خود به حالت نامتقارن ختم می‌شود. [1] [2] [3] به طور خاص، می‌تواند سیستم‌هایی را توصیف کند که معادلات حرکت یا لاگرانژ از تقارن پیروی می‌کنند، اما راه‌حل‌های خلاء کم‌انرژی همان تقارن را نشان نمی‌دهند . هنگامی که سیستم به یکی از آن راه حل های خلاء می رود، تقارن برای آشفتگی های اطراف آن خلاء شکسته می شود، حتی اگر کل لاگرانژ این تقارن را حفظ کند.

نمای کلی [ ویرایش ]

طبق تعریف، شکست تقارن خود به خودی مستلزم وجود قوانین فیزیکی (مثلاً مکانیک کوانتومی ) است که تحت یک تبدیل تقارن (مانند انتقال یا چرخش) ثابت هستند، به طوری که هر جفت پیامدهایی که فقط بر اساس آن تبدیل متفاوت هستند، توزیع احتمال یکسانی دارند. به عنوان مثال اگر اندازه گیری های یک قابل مشاهده در هر دو موقعیت مختلف دارای توزیع احتمال یکسان باشند، قابل مشاهده دارای تقارن انتقالی است.

شکست خود به خودی تقارن زمانی رخ می دهد که این رابطه از بین برود، در حالی که قوانین فیزیکی زیربنایی متقارن باقی می مانند.

برعکس، در شکست تقارن صریح ، اگر دو نتیجه در نظر گرفته شود، توزیع احتمالات یک جفت پیامد می تواند متفاوت باشد. به عنوان مثال در یک میدان الکتریکی، نیروهای وارد بر یک ذره باردار در جهات مختلف متفاوت است، بنابراین تقارن دورانی به صراحت توسط میدان الکتریکی که این تقارن را ندارد، شکسته می‌شود.

فازهای ماده، مانند بلورها، آهنرباها و ابررساناهای معمولی، و همچنین انتقال فاز ساده را می توان با شکست تقارن خود به خود توصیف کرد. استثناهای قابل توجه شامل فازهای توپولوژیکی ماده مانند اثر هال کوانتومی کسری است .

به طور معمول، زمانی که شکست تقارن خود به خود رخ می دهد، ویژگی های قابل مشاهده سیستم به روش های مختلف تغییر می کند. به عنوان مثال، چگالی، تراکم پذیری، ضریب انبساط حرارتی و گرمای ویژه زمانی که یک مایع به جامد تبدیل می شود، انتظار می رود که تغییر کند.

مثالها [ ویرایش ]

پتانسیل سومبررو [ ویرایش ]

همچنین نگاه کنید به: پتانسیل کلمن-واینبرگ

یک گنبد متقارن رو به بالا را در نظر بگیرید که یک فرورفتگی در پایین آن می چرخد. اگر توپی در اوج گنبد قرار گیرد، سیستم نسبت به چرخش حول محور مرکزی متقارن است. اما توپ ممکن است به طور خود به خود این تقارن را با فرود آمدن گنبد به داخل فرورفته، نقطه ای با کمترین انرژی، بشکند . پس از آن، توپ در نقطه ای ثابت در محیط استراحت می کند. گنبد و توپ تقارن فردی خود را حفظ می کنند، اما سیستم اینطور نیست. [4]

نمودار تابع پتانسیل "سومبررو" گلدستون $V(\phi)$ .

در ساده‌ترین مدل نسبیتی ایده‌آل‌شده، تقارن خود به خود شکسته از طریق یک نظریه میدان اسکالر گویا خلاصه می‌شود . لاگرانژ مربوط به یک میدان اسکالر $\phi$ که اساسا نحوه رفتار یک سیستم را دیکته می کند، می تواند به دو اصطلاح جنبشی و بالقوه تقسیم شود،

${\mathcal {L}}=\جزئی ^{\mu }\phi \partial _{\mu }\phi -V(\phi ).$

( 1 )

در این اصطلاح بالقوه است $V(\phi)$ که شکستن تقارن باعث می شود. نمونه ای از یک پتانسیل، ناشی از جفری گلدستون [5] در نمودار سمت چپ نشان داده شده است.

$V(\phi )=-5|\phi |^{2}+|\phi |^{4}\,$ .

( 2 )

این پتانسیل دارای تعداد نامتناهی از حداقل های ممکن (حالت خلاء) است که توسط

$\phi ={\sqrt {5/2}}e^{i\theta }$ .

( 3 )

برای هر θ واقعی بین 0 و 2 π . این سیستم همچنین دارای یک حالت خلاء ناپایدار مربوط به Φ = 0 است . این حالت دارای تقارن U(1) است . با این حال، هنگامی که سیستم در یک وضعیت خلاء پایدار خاص قرار می‌گیرد (معادل انتخابی از θ )، به نظر می‌رسد که این تقارن از بین رفته یا "خود به خودی شکسته شده است".

در واقع، هر انتخاب دیگری از θ دقیقاً انرژی مشابهی خواهد داشت، و معادلات تعیین‌کننده به تقارن احترام می‌گذارند، اما حالت پایه (خلاء) تئوری تقارن را می‌شکند، که دلالت بر وجود یک بوزون بدون جرم Nambu-Goldstone ، حالت در حال اجرا دارد. دور دایره در حداقل این پتانسیل، و نشان می دهد که حافظه ای از تقارن اولیه در لاگرانژ وجود دارد. [6] [7]

نمونه های دیگر [ ویرایش ]

برای مواد فرومغناطیسی ، قوانین زیربنایی تحت چرخش های فضایی ثابت هستند. در اینجا، پارامتر ترتیب مغناطیسی است که چگالی دوقطبی مغناطیسی را اندازه گیری می کند. بالاتر از دمای کوری ، پارامتر ترتیب صفر است، که از نظر فضایی ثابت است، و تقارن شکسته نمی شود. با این حال، در زیر دمای کوری، مغناطش یک مقدار ثابت ناپدیدکننده به دست می‌آورد، که به جهت خاصی اشاره می‌کند (در شرایط ایده‌آل که تعادل کامل داریم؛ در غیر این صورت، تقارن انتقالی نیز شکسته می‌شود). تقارن‌های چرخشی باقی‌مانده که جهت این بردار را ثابت می‌گذارند، بر خلاف چرخش‌های دیگر که انجام نمی‌دهند و در نتیجه خود به خود شکسته می‌شوند، ناگسستنی می‌مانند.
قوانینی که یک جامد را توصیف می کنند در گروه کامل اقلیدسی ثابت هستند ، اما خود جامد به طور خود به خود این گروه را به یک گروه فضایی تجزیه می کند . جابجایی و جهت گیری پارامترهای ترتیب هستند.
نسبیت عام دارای تقارن لورنتس است، اما در مدل‌های کیهانی FRW ، میدان میانگین 4 سرعت که با میانگین‌گیری از سرعت کهکشان‌ها تعریف می‌شود (کهکشان‌ها مانند ذرات گاز در مقیاس کیهان‌شناختی عمل می‌کنند) به عنوان یک پارامتر نظمی عمل می‌کند که این تقارن را می‌شکند. نظرات مشابهی را می توان در مورد پس زمینه مایکروویو کیهانی بیان کرد.
برای مدل الکتروضعیف ، همانطور که قبلا توضیح داده شد، یک جزء از میدان هیگز پارامتر ترتیبی را فراهم می کند که تقارن گیج الکتروضعیف را به تقارن گیج الکترومغناطیسی می شکند. مانند مثال فرومغناطیسی، یک انتقال فاز در دمای الکتریکی ضعیف وجود دارد. همین اظهار نظر درباره عدم تمایل ما به توجه به تقارن های شکسته نشان می دهد که چرا اینقدر طول کشید تا ما یکپارچگی ضعیف الکتریکی را کشف کنیم.
در ابررساناها، یک میدان جمعی ماده متراکم ψ وجود دارد که به عنوان پارامتر ترتیبی که تقارن گیج الکترومغناطیسی را می شکند، عمل می کند.
یک میله پلاستیکی استوانه ای نازک بردارید و دو سر آن را به هم فشار دهید. قبل از کمانش، سیستم تحت چرخش متقارن است و بنابراین به طور مشهود به صورت استوانه ای متقارن است. اما پس از کمانش، متفاوت و نامتقارن به نظر می رسد. با این وجود، ویژگی‌های تقارن استوانه‌ای هنوز وجود دارد: با نادیده گرفتن اصطکاک، چرخش آزادانه میله به اطراف نیرویی لازم نیست، حالت پایه در زمان جابه‌جا می‌شود، و بر خلاف نوسانات شعاعی در جهت سگک این حالت چرخشی عملاً بوزون مورد نیاز Nambu-Goldstone است .
یک لایه یکنواخت از سیال را روی یک صفحه افقی بی نهایت در نظر بگیرید. این سیستم تمام تقارن های صفحه اقلیدسی را دارد. اما حالا سطح زیرین را به طور یکنواخت گرم کنید تا خیلی داغتر از سطح بالایی شود. هنگامی که گرادیان دما به اندازه کافی بزرگ شود، سلول های همرفت تشکیل می شوند و تقارن اقلیدسی را می شکنند.
مهره ای را روی حلقه دایره ای در نظر بگیرید که به قطر عمودی چرخانده شده است . همانطور که سرعت چرخش به تدریج از حالت سکون افزایش می یابد، مهره در ابتدا در نقطه تعادل اولیه خود در پایین حلقه باقی می ماند (به طور شهودی پایدار، پایین ترین پتانسیل گرانشی ). در یک سرعت چرخشی بحرانی معین، این نقطه ناپایدار می شود و مهره به یکی از دو تعادل جدید ایجاد شده دیگر، در فاصله مساوی از مرکز، می پرد. در ابتدا، سیستم از نظر قطر متقارن است، اما پس از عبور از سرعت بحرانی، مهره به یکی از دو نقطه تعادل جدید ختم می‌شود و در نتیجه تقارن را می‌شکند.

شکست خود به خودی تقارن نشان داده شده است : در سطوح انرژی بالا ( سمت چپ )، توپ در مرکز قرار می گیرد و نتیجه متقارن است. در سطوح انرژی پایین تر ( سمت راست )، "قوانین" کلی متقارن باقی می مانند، اما "سومبررو" متقارن یک نتیجه نامتقارن را اعمال می کند، زیرا در نهایت توپ باید در نقطه ای تصادفی در پایین قرار گیرد، "خود به خود" و نه همه موارد دیگر.

آزمایش دو بالن نمونه ای از شکست تقارن خود به خودی است که هر دو بادکنک در ابتدا تا حداکثر فشار محلی باد می شوند. هنگامی که مقداری هوا از یک بالن به بالون دیگر جریان می یابد، فشار در هر دو بالن کاهش می یابد و سیستم را در حالت نامتقارن پایدارتر می کند.

در فیزیک ذرات [ ویرایش ]

در فیزیک ذرات ، ذرات حامل نیرو معمولاً با معادلات میدانی با تقارن سنج مشخص می شوند . معادلات آنها پیش بینی می کند که اندازه گیری های خاصی در هر نقطه از میدان یکسان خواهد بود. برای مثال، معادلات میدانی ممکن است پیش‌بینی کنند که جرم دو کوارک ثابت است. حل معادلات برای یافتن جرم هر کوارک ممکن است دو جواب بدهد. در یک محلول، کوارک A سنگین‌تر از کوارک B است. در محلول دوم، کوارک B به همان میزان از کوارک A سنگین‌تر است . تقارن معادلات توسط تک تک جواب ها منعکس نمی شود، بلکه توسط طیف راه حل ها منعکس می شود.

یک اندازه‌گیری واقعی تنها یک راه‌حل را منعکس می‌کند، که نشان‌دهنده شکست در تقارن نظریه اساسی است. "پنهان" اصطلاحی بهتر از "شکسته" است، زیرا تقارن همیشه در این معادلات وجود دارد. این پدیده شکست تقارن خود به خودی (SSB) نامیده می شود زیرا هیچ چیز (که ما از آن می دانیم) تقارن را در معادلات نمی شکند. [8] : 194-195 به دلیل ماهیت شکستن تقارن خود به خود، بخش های مختلف کیهان اولیه تقارن را در جهات مختلف می شکند و منجر به نقص های توپولوژیکی می شود ، مانند دیوارهای حوزه دو بعدی، رشته های کیهانی یک بعدی ، صفر بعدی. تک قطبی و/یابافت ها ، بسته به گروه هموتوپی مربوطه و پویایی نظریه. به عنوان مثال، شکست تقارن هیگز ممکن است رشته های کیهانی اولیه را به عنوان یک محصول فرعی ایجاد کرده باشد. تقارن GUT فرضی به طور کلی تک قطبی ایجاد می کند و مشکلاتی را برای GUT ایجاد می کند مگر اینکه تک قطبی ها (همراه با دیواره های دامنه GUT) از طریق تورم کیهانی از جهان قابل مشاهده ما خارج شوند . [9]

تقارن کایرال [ ویرایش ]

مقاله اصلی: شکستن تقارن کایرال

شکست تقارن کایرال نمونه ای از شکست تقارن خود به خودی است که بر تقارن کایرال برهمکنش های قوی در فیزیک ذرات تأثیر می گذارد. این ویژگی کرومودینامیک کوانتومی است ، نظریه میدان کوانتومی که این برهمکنش‌ها را توصیف می‌کند، و مسئول بخش عمده جرم (بیش از 99٪) نوکلئون‌ها و در نتیجه تمام مواد رایج است، زیرا کوارک‌های محدود به نور را به 100 تبدیل می‌کند. باریون ها سنگین ترند . بوزون های تقریبی Nambu-Goldstone در این فرآیند شکست تقارن خود به خود ، پیون هستند، که جرم آن مرتبه ای سبک تر از جرم نوکلئون ها است. این به عنوان نمونه اولیه و عنصر مهم مکانیسم هیگز زیربنای شکست تقارن ضعیف الکتریکی عمل کرد.

مکانیسم هیگز [ ویرایش ]

مقاله‌های اصلی: مکانیسم هیگز و تعامل یوکاوا

نیروهای قوی، ضعیف و الکترومغناطیسی همه را می توان به عنوان ناشی از تقارن سنج درک کرد که در توصیف تقارن یک افزونگی است. مکانیسم هیگز ، شکست تقارن خود به خودی تقارن سنج، جزء مهمی در درک ابررسانایی فلزات و منشاء جرم ذرات در مدل استاندارد فیزیک ذرات است. اصطلاح "شکستن تقارن خود به خود" در اینجا به عنوان قضیه الیتزور اشتباه است.بیان می کند که تقارن سنج محلی هرگز نمی تواند خود به خود شکسته شود. در عوض، پس از تثبیت گیج، تقارن سراسری (یا افزونگی) را می توان به روشی که به طور رسمی شبیه شکستن تقارن خود به خودی است، شکست. یکی از پیامدهای مهم تمایز بین تقارن های واقعی و تقارن سنج این است که نامبو-گلدستون بدون جرم ناشی از شکستن خود به خود تقارن گیج در توصیف میدان برداری سنج جذب می شود و حالت های میدان برداری عظیمی را ارائه می دهد، مانند حالت پلاسما در یک ابررسانا یا حالت هیگز مشاهده شده در فیزیک ذرات.

در مدل استاندارد فیزیک ذرات، شکستن تقارن خود به خودی تقارن سنج SU(2) × U(1) مرتبط با نیروی الکترو ضعیف، جرم هایی را برای چندین ذره ایجاد می کند و نیروهای الکترومغناطیسی و ضعیف را از هم جدا می کند. بوزون های W و Z ذرات بنیادی هستند که واسطه برهمکنش ضعیف هستند ، در حالی که فوتون واسطه برهمکنش الکترومغناطیسی است . در انرژی های بسیار بیشتر از 100 گیگا ولت، همه این ذرات به شیوه ای مشابه رفتار می کنند. نظریه وینبرگ -سالم پیش‌بینی می‌کند که در انرژی‌های پایین‌تر، این تقارن شکسته می‌شود تا فوتون و بوزون‌های عظیم W و Z پدیدار شوند. [10] علاوه بر این، فرمیون ها به طور مداوم توده ایجاد می کنند.

بدون شکستن تقارن خود به خود، مدل استاندارد برهمکنش ذرات بنیادی به وجود تعدادی ذره نیاز دارد. با این حال، برخی از ذرات ( بوزون‌های W و Z ) بدون جرم پیش‌بینی می‌شوند، در حالی که در واقعیت مشاهده می‌شود که جرم دارند. برای غلبه بر این، شکست تقارن خود به خودی توسط مکانیسم هیگز تقویت می شود تا به این ذرات جرم بدهد. همچنین نشان دهنده وجود ذره جدیدی به نام بوزون هیگز است که در سال 2012 شناسایی شد.

ابررسانایی فلزات یک آنالوگ ماده متراکم از پدیده هیگز است که در آن چگالشی از جفت الکترون های کوپر به طور خود به خود تقارن گیج U(1) مرتبط با نور و الکترومغناطیس را می شکند.

شکست تقارن دینامیکی [ ویرایش ]

شکست تقارن دینامیکی (DSB) شکل خاصی از شکست تقارن خود به خودی است که در آن حالت پایه سیستم در مقایسه با توصیف نظری آن (یعنی لاگرانژی ) خواص تقارن را کاهش داده است.

شکست دینامیکی یک تقارن سراسری یک شکست خود به خودی تقارن است که نه در سطح درخت (کلاسیک) (یعنی در سطح عمل لخت)، بلکه به دلیل اصلاحات کوانتومی (یعنی در سطح عمل مؤثر) اتفاق می‌افتد . .

شکست دینامیکی تقارن سنج ظریف تر است. در شکست تقارن سنج خود به خودی معمولی، یک ذره هیگز ناپایدار در نظریه وجود دارد که خلاء را به فاز شکسته تقارن سوق می دهد. (به عنوان مثال، برهمکنش ضعیف الکترونی را ببینید.) با این حال، در شکست تقارن گیج دینامیکی، هیچ ذره هیگز ناپایداری در تئوری عمل نمی کند، اما حالت های محدود خود سیستم، میدان های ناپایداری را فراهم می کند که انتقال فاز را ارائه می دهد. برای مثال، باردین، هیل و لیندنر مقاله ای منتشر کردند که تلاش می کند مکانیسم هیگز معمولی را در مدل استاندارد جایگزین کند.توسط یک DSB که توسط یک حالت محدود از کوارک‌های ضد بالا هدایت می‌شود. (این مدل‌ها، که در آنها یک ذره ترکیبی نقش بوزون هیگز را بازی می‌کند، اغلب به عنوان «مدل‌های هیگز مرکب» نامیده می‌شوند.) [11] شکست دینامیکی تقارن سنج اغلب به دلیل ایجاد یک میعانات فرمیونی است - به عنوان مثال، میعانات کوارکی که به شکست دینامیکی تقارن کایرال در کرومودینامیک کوانتومی متصل است . ابررسانایی مرسوم نمونه‌ای پارادایماتیک از سمت ماده متراکم است، جایی که جاذبه‌های با واسطه فونون، الکترون‌ها را به جفت متصل می‌کنند و سپس متراکم می‌شوند و در نتیجه تقارن سنج الکترومغناطیسی را می‌شکنند.

در فیزیک ماده متراکم [ ویرایش ]

اکثر مراحل ماده را می توان از طریق عدسی شکستن تقارن خود به خود درک کرد. برای مثال، کریستال‌ها آرایه‌های تناوبی از اتم‌ها هستند که در همه ترجمه‌ها ثابت نیستند (فقط در زیر مجموعه کوچکی از ترجمه‌ها توسط یک بردار شبکه). آهنرباها دارای قطب شمال و جنوب هستند که در جهت خاصی جهت گیری شده اند و تقارن چرخشی را می شکند . علاوه بر این مثال‌ها، مجموعه کاملی از فازهای متقارن‌شکن دیگر ماده وجود دارد - از جمله فازهای نماتیکی کریستال‌های مایع، امواج با چگالی بار و اسپین، ابرسیال‌ها و بسیاری دیگر.

چندین نمونه شناخته شده از ماده وجود دارد که نمی توان آنها را با شکست تقارن خود به خود توصیف کرد، از جمله: فازهای مرتب شده از نظر توپولوژیکی ماده، مانند مایعات هال کوانتومی کسری ، و مایعات اسپین . این حالت ها هیچ تقارنی را نمی شکند، بلکه فازهای متمایز ماده هستند. برخلاف مورد شکست تقارن خود به خود، چارچوب کلی برای توصیف چنین حالت هایی وجود ندارد. [12]

تقارن پیوسته [ ویرایش ]

فرومغناطیس سیستم متعارفی است که به طور خود به خود تقارن پیوسته اسپین ها را در زیر دمای کوری و در h = 0 می شکند ، جایی که h میدان مغناطیسی خارجی است. در زیر دمای کوری ، انرژی سیستم تحت وارونگی مغناطش m ( x ) ثابت است به طوری که m ( x ) = - m ( -x ) . تقارن به طور خود به خود به صورت h → 0 شکسته می شود که همیلتونی تحت تبدیل وارونگی ثابت می شود، اما مقدار انتظار ثابت نیست.

فازهای خودبخودی با تقارن شکسته شده ماده با یک پارامتر مرتبه مشخص می شوند که کمیتی را که تقارن مورد بررسی را می شکند، توصیف می کند. به عنوان مثال، در یک آهنربا، پارامتر ترتیب مغناطش محلی است.

شکست خود به خودی یک تقارن پیوسته ناگزیر با حالت‌های بدون شکاف (به این معنی که این حالت‌ها برای برانگیختن انرژی هزینه ندارند) همراه است. به عنوان مثال، حالت‌های ارتعاشی در یک کریستال، به نام فونون‌ها، با نوسانات آهسته چگالی اتم‌های کریستال مرتبط هستند. حالت گلدستون مرتبط برای آهنرباها امواج نوسانی اسپینی هستند که به عنوان امواج اسپین شناخته می شوند. برای حالت های شکستن تقارن، که پارامتر ترتیب آنها یک کمیت حفظ شده نیست، حالت های Nambu-Goldstone معمولاً بدون جرم هستند و با سرعت ثابت منتشر می شوند.

یک قضیه مهم، به دلیل مرمین و واگنر، بیان می‌کند که در دمای محدود، نوسانات گرمایی فعال شده حالت‌های Nambu-Goldstone نظم دوربرد را از بین می‌برند و از شکسته شدن تقارن خود به خود در سیستم‌های یک‌بعدی و دو بعدی جلوگیری می‌کنند. به طور مشابه، نوسانات کوانتومی پارامتر نظم از شکستن بیشتر انواع تقارن پیوسته در سیستم های یک بعدی حتی در دمای صفر جلوگیری می کند. (یک استثناء مهم فرومغناطیس ها هستند که پارامتر ترتیب آنها، مغناطش، یک کمیت کاملاً حفظ شده است و هیچ گونه نوسانات کوانتومی ندارد.)

سایر سیستم‌های برهمکنش دوربرد، مانند سطوح منحنی استوانه‌ای که از طریق پتانسیل کولمب یا پتانسیل یوکاوا در تعامل هستند ، نشان داده شده است که تقارن انتقالی و چرخشی را می‌شکنند. [13] نشان داده شد، در حضور یک همیلتونی متقارن، و در حد حجم نامتناهی، سیستم به طور خود به خود یک پیکربندی کایرال را اتخاذ می کند - یعنی تقارن صفحه آینه را می شکند .

تعمیم و استفاده فنی [ ویرایش ]

برای اینکه تقارن خود به خود شکسته شود، باید سیستمی وجود داشته باشد که در آن چندین نتیجه به یک اندازه محتمل باشد. بنابراین سیستم به عنوان یک کل با توجه به این نتایج متقارن است. با این حال، اگر سیستم نمونه برداری شود (یعنی اگر سیستم واقعاً مورد استفاده قرار گیرد یا به هر طریقی با آن تعامل داشته باشد)، یک نتیجه خاص باید رخ دهد. اگرچه سیستم به عنوان یک کل متقارن است، اما هرگز با این تقارن مواجه نمی شود، بلکه فقط در یک حالت نامتقارن خاص است. از این رو، گفته می شود که تقارن به طور خود به خود در آن نظریه شکسته شده است. با این وجود، این واقعیت که هر پیامد به یک اندازه محتمل است، بازتابی از تقارن زیربنایی است، که بنابراین اغلب «تقارن پنهان» نامیده می‌شود و پیامدهای رسمی مهمی دارد. (مقاله مربوط به بوزون گلدستون را ببینید .)

وقتی یک نظریه با توجه به یک گروه تقارن متقارن است ، اما مستلزم آن است که یک عنصر از گروه متمایز باشد، در این صورت تقارن خود به خود شکسته شده است. این نظریه نباید دیکته کند که کدام عضو متمایز است، فقط آن یکی است . از این نقطه به بعد، نظریه را می توان به گونه ای تلقی کرد که گویی این عنصر در واقع متمایز است، با این شرط که هر نتیجه ای که از این طریق به دست می آید باید با در نظر گرفتن میانگین هر یک از عناصر گروه که عنصر متمایز است، متقارن شود.

مفهوم مهم در نظریه های فیزیک پارامتر ترتیب است . اگر میدانی (اغلب یک فیلد پس‌زمینه) وجود داشته باشد که مقدار انتظاری را به دست آورد (نه لزوماً مقدار انتظار خلاء ) که تحت تقارن مورد نظر ثابت نیست، می‌گوییم که سیستم در فاز مرتب شده است و تقارن خود به خود است. شکسته شده. این به این دلیل است که سایر زیرسیستم‌ها با پارامتر مرتبه تعامل دارند، که یک «قاب مرجع» را برای اندازه‌گیری مشخص می‌کند. در آن حالت، حالت خلاء از تقارن اولیه تبعیت نمی کند (که آن را ثابت نگه می دارد، در حالت ویگنر که به صورت خطی تحقق یافته است.که در آن یک سینگل خواهد بود)، و در عوض تحت تقارن (پنهان) تغییر می کند، که اکنون در حالت (غیرخطی) Nambu–Goldstone اجرا می شود . به طور معمول، در غیاب مکانیسم هیگز، بوزون های گلدستون بدون جرم به وجود می آیند.

گروه تقارن می تواند گسسته باشد، مانند گروه فضایی یک کریستال، یا پیوسته (به عنوان مثال، یک گروه دروغ )، مانند تقارن چرخشی فضا. با این حال، اگر سیستم فقط شامل یک بعد فضایی منفرد باشد، آنگاه فقط تقارن های گسسته ممکن است در حالت خلاء نظریه کوانتومی کامل شکسته شوند ، اگرچه یک راه حل کلاسیک ممکن است تقارن پیوسته را بشکند.

جایزه نوبل [ ویرایش ]

در 7 اکتبر 2008، آکادمی سلطنتی علوم سوئد جایزه نوبل فیزیک سال 2008 را به سه دانشمند به دلیل کارشان در شکستن تقارن فیزیک زیر اتمی اعطا کرد. یوچیرو نامبو ، از دانشگاه شیکاگو ، نیمی از جایزه را برای کشف مکانیسم تقارن شکسته خود به خودی در زمینه برهمکنش های قوی، به ویژه شکست تقارن کایرال ، به دست آورد . فیزیکدانان ماکوتو کوبایاشی و توشیهیده ماسکاوا ، از دانشگاه کیوتو ، نیمی دیگر از جایزه را برای کشف منشا شکست صریح تقارن CP در برهمکنش های ضعیف به اشتراک گذاشتند. [14]این منشا در نهایت به مکانیسم هیگز وابسته است، اما، تا کنون به عنوان یک ویژگی "درست" جفت های هیگز شناخته شده است، نه یک پدیده تقارن خود به خود شکسته.

همچنین ببینید [ ویرایش ]

یادداشت ها [ ویرایش ]

^ Note that (as in fundamental Higgs driven spontaneous gauge symmetry breaking) the term "symmetry breaking" is a misnomer when applied to gauge symmetries.

منبع

https://en.wikipedia.org/wiki/Spontaneous_symmetry_breaking

+ نوشته شده در دوشنبه یکم اسفند ۱۴۰۱ ساعت 2:13 توسط علی رضا نقش نیلچی |

نقطه عطف

از ویکیپدیا، دانشنامه آزاد

این مقاله شامل فهرستی از مراجع عمومی است ، اما فاقد استنادهای درون خطی متناظر کافی است . لطفا با معرفی نقل قول های دقیق تر به بهبود این مقاله کمک کنید. ( جولای 2013 ) ( نحوه و زمان حذف این پیام الگو را بیاموزید )

نمودار y = x 3 با نقطه عطف در (0,0)، که همچنین یک نقطه ثابت است .

ریشه ها ، نقاط ثابت ، نقطه عطف و تقعر یک چند جمله ای مکعبی x ^3 − 3 × ^2 − 144 x + 432 (خط سیاه) و مشتقات اول و دوم آن (قرمز و آبی).

در حساب دیفرانسیل و هندسه دیفرانسیل ، نقطه عطف ، خم شدن ، یا عطف (انگلیسی انگلیسی: inflexion ) نقطه‌ای از منحنی صفحه صاف است که در آن انحنا علامت تغییر می‌کند. به طور خاص، در مورد نمودار یک تابع ، این نقطه ای است که در آن تابع از مقعر (مقعر به سمت پایین) به محدب (مقعر به سمت بالا) یا بالعکس تغییر می کند.

برای نمودار تابعی از کلاس C 2 تمایزپذیری ( f ، اولین مشتق آن f' ، و مشتق دوم آن f'' ، وجود دارند و پیوسته هستند)، از شرط f'' = 0 نیز می توان برای یافتن یک نقطه عطف استفاده کرد. از آنجایی که برای تغییر f'' از مقدار مثبت (مقعر رو به بالا) به یک مقدار منفی (مقعر رو به پایین) یک نقطه f' ' = 0 باید ارسال شود یا برعکس، زیرا f'' پیوسته است. نقطه عطف منحنی جایی است که f'' = 0 و علامت آن در نقطه تغییر می کند (از مثبت به منفی یا از منفی به مثبت). [1]نقطه ای که مشتق دوم ناپدید می شود اما علامت آن تغییر نمی کند، گاهی اوقات نقطه موج یا نقطه موج می گویند .

در هندسه جبری یک نقطه عطف به طور کلی تر تعریف می شود، به عنوان یک نقطه منظم که در آن مماس با منحنی به ترتیب حداقل 3 برخورد می کند، و یک نقطه موج دار یا هایپرفلکس به عنوان نقطه ای که مماس با منحنی به ترتیب حداقل 4 ملاقات می کند، تعریف می شود. .

تعریف [ ویرایش ]

نقاط عطف در هندسه دیفرانسیل نقاطی از منحنی هستند که انحنا علامت خود را تغییر می دهد. [2] [3]

به عنوان مثال، نمودار تابع متمایز دارای یک نقطه عطف در ( x , f ( x )) است اگر و فقط در صورتی که اولین مشتق f' دارای یک انتها مجزا در x باشد . (این با گفتن اینکه f یک اکسترموم دارد یکسان نیست ). یعنی در برخی از همسایگی ها، x تنها نقطه ای است که در آن f' یک حداقل یا حداکثر (محلی) دارد. اگر تمام افراط های f منزوی باشند ، نقطه عطف نقطه ای از نمودار f است که در آن نقطه عطفمماس از منحنی عبور می کند.

نقطه عطف سقوط نقطه عطفی است که در آن مشتق در دو طرف نقطه منفی است. به عبارت دیگر، یک نقطه عطف است که تابع در نزدیکی آن در حال کاهش است. نقطه افزایش عطف نقطه ای است که مشتق در هر دو طرف نقطه مثبت است. به عبارت دیگر، یک نقطه عطف است که تابع در نزدیکی آن در حال افزایش است.

برای یک منحنی صاف که توسط معادلات پارامتری به دست می‌آید ، یک نقطه یک نقطه عطف است اگر انحنای علامت‌دار آن از مثبت به منفی یا از منفی به مثبت تغییر کند، یعنی علامت تغییر کند .

برای یک منحنی صاف که نمودار یک تابع دو برابر قابل تمایز است، نقطه عطف نقطه ای از نمودار است که در آن مشتق دوم یک صفر مجزا دارد و علامت آن را تغییر می دهد.

در هندسه جبری ، یک نقطه غیر مفرد یک منحنی جبری نقطه عطف است اگر و فقط اگر عدد تقاطع خط مماس و منحنی (در نقطه مماس) بیشتر از 2 باشد. انگیزه اصلی این تعریف متفاوت، این است که در غیر این صورت مجموعه نقاط عطف یک منحنی یک مجموعه جبری نخواهد بود . در واقع، مجموعه نقاط عطف یک منحنی جبری مسطح دقیقاً نقاط غیرمفرد آن هستند که صفرهای تعیین کننده هسین تکمیل تصویری آن هستند .

نمودار f ( x ) = sin(2 x ) از - π /4 تا 5 π /4; مشتق دوم f″ ( x ) = –4sin(2 x ) است ، و علامت آن برعکس علامت f است . مماس آبی است که در آن منحنی محدب است (بالاتر از مماس خودش )، سبز در جایی که مقعر است (زیر مماس آن)، و قرمز در نقاط عطف است: 0، π /2 و π.

شرط لازم اما نه کافی [ ویرایش ]

برای یک تابع f ، اگر مشتق دوم آن f″ ( x ) در x 0 وجود داشته باشد و x 0 یک نقطه عطف برای f باشد ، آنگاه f″ ( x 0 ) = 0 ، اما این شرط برای داشتن یک نقطه عطف کافی نیست. ، حتی اگر مشتقاتی از هر مرتبه ای وجود داشته باشد. در این مورد، به مشتق غیرصفری پایین‌ترین مرتبه (بالاتر از دوم) نیز نیاز است تا از مرتبه فرد (سوم، پنجم و غیره) باشد. اگر مشتق غیرصفر پایین‌ترین مرتبه از مرتبه زوج باشد، نقطه یک نقطه عطف نیست، بلکه یک نقطه موجی است.. با این حال، در هندسه جبری، هم نقاط عطف و هم نقاط موج دار معمولاً نقاط عطف نامیده می شوند . مثالی از یک نقطه موج دار x = 0 برای تابع f است که با f ( x ) = x 4 داده می شود .

در اظهارات قبلی، فرض می‌شود که f مشتق غیر صفر مرتبه بالاتری در x دارد که لزوماً اینطور نیست. اگر اینطور باشد، شرطی که اولین مشتق غیرصفر دارای نظم فرد باشد، نشان می‌دهد که علامت f ' ( x ) در دو طرف x در همسایگی x یکسان است . اگر این علامت مثبت باشد ، نقطه یک نقطه عطف صعودی است . اگر منفی باشد ، نقطه یک نقطه عطف سقوط است .

نقاط عطف شرایط کافی:

شرط وجود کافی برای یک نقطه عطف در حالتی که f ( x ) k بار به طور پیوسته در یک همسایگی مشخص از یک نقطه x 0 با k فرد و k ≥ 3 قابل تفکیک باشد ، این است که f ( n ) ( x 0 ) = 0 برای n = 2، ...، k − 1 و f ( k ) ( x 0 ) ≠ 0 . سپس f ( x ) دارای نقطه عطف در استx 0 .
یکی دیگر از شرایط وجود کافی کلی تر، مستلزم آن است که f″ ( x 0 + ε ) و f″ ( x 0 - ε ) دارای علائم متضاد در همسایگی x 0 باشند ( برونشتاین و سمندیایف 2004، ص 231).

دسته بندی نقاط عطف [ ویرایش ]

y = x^ 4 – x دارای مشتق دوم صفر در نقطه (0,0) است، اما نقطه عطف نیست زیرا مشتق چهارم اولین مشتق غیر صفر درجه بالاتر است (مشتق سوم نیز صفر است).

نقاط عطف را نیز می توان بر اساس صفر یا غیرصفر بودن f ' ( x ) دسته بندی کرد .

اگر f ' ( x ) صفر باشد، نقطه یک نقطه عطف ثابت است
اگر f ' ( x ) صفر نباشد، نقطه یک نقطه عطف غیر ثابت است

یک نقطه عطف ثابت یک اکسترومم موضعی نیست . به طور کلی، در زمینه توابع چندین متغیر واقعی ، یک نقطه ثابت که یک انتها محلی نیست، نقطه زین نامیده می شود .

یک مثال از یک نقطه عطف ثابت، نقطه (0، 0) در نمودار y = x 3 است . مماس محور x است که نمودار را در این نقطه قطع می کند.

یک مثال از یک نقطه عطف غیر ثابت، نقطه (0، 0) در نمودار y = x 3 + ax ، برای هر غیر صفر a است . مماس در مبدا خط y = ax است که نمودار را در این نقطه قطع می کند.

توابع با ناپیوستگی [ ویرایش ]

برخی از توابع بدون داشتن نقاط عطف، تقعر را تغییر می دهند. در عوض، آنها می توانند تقعر را در اطراف مجانب یا ناپیوستگی های عمودی تغییر دهند. به عنوان مثال، تابعایکس↦1ایکس $x\mapsto {\frac {1}{x}}$ برای x منفی مقعر و برای x مثبت محدب است ، اما نقطه عطف ندارد زیرا 0 در دامنه تابع نیست.

توابع دارای نقاط عطف که مشتق دوم آنها ناپدید نمی شود [ ویرایش ]

برخی از توابع پیوسته دارای یک نقطه عطف هستند، حتی اگر مشتق دوم هرگز 0 نباشد. برای مثال، تابع ریشه مکعب وقتی x منفی است به سمت بالا مقعر است، و وقتی x مثبت است به سمت پایین مقعر است، اما هیچ مشتقی از هر مرتبه ای در مبدا ندارد.

همچنین ببینید [ ویرایش ]

نقطه بحرانی (ریاضی)
آستانه اکولوژیکی
پیکربندی هس توسط نه نقطه عطف یک منحنی بیضی شکل گرفته است
Ogee ، یک فرم معماری با نقطه عطف
راس (منحنی) ، حداقل یا حداکثر محلی انحنا

منبع

https://en.wikipedia.org/wiki/Inflection_point

+ نوشته شده در دوشنبه یکم اسفند ۱۴۰۱ ساعت 2:8 توسط علی رضا نقش نیلچی |

شکستن تقارن

از ویکیپدیا، دانشنامه آزاد

پنهان شدناین مقاله دارای مشکلات متعددی است. لطفاً به بهبود آن کمک کنید یا درباره این مسائل در صفحه بحث بحث کنید . ( با نحوه و زمان حذف این پیام های الگو آشنا شوید )

این مقاله نیاز به توجه یک متخصص فیزیک دارد . مشکل خاص این است: کمبود. مانند یک فرهنگ لغت شکستن تقارن را مورد بحث قرار می دهد، بدون اینکه بگوید چرا تقریباً در هر زمینه ای از فیزیک بسیار مهم است. حتی قضیه نوتر را در اینجا یا در صفحات فرعی مورد بحث قرار نمی دهد . ( مه 2014 )

این مقاله برای تأیید نیاز به نقل قول های اضافی دارد . ( اکتبر 2021 )

برای کاربردهای دیگر، شکستن تقارن (ابهام‌زدایی) را ببینید .

یک توپ در ابتدا در بالای تپه مرکزی (C) قرار دارد. این موقعیت یک تعادل ناپایدار است: یک اغتشاش بسیار کوچک باعث سقوط آن به یکی از دو چاه پایدار چپ (L) یا راست (R) می شود. حتی اگر تپه متقارن باشد و دلیلی برای سقوط توپ در دو طرف وجود نداشته باشد، حالت نهایی مشاهده شده متقارن نیست.

در فیزیک ، شکستن تقارن پدیده‌ای است که در آن نوسانات (بی نهایت) کوچکی که روی سیستمی که از نقطه بحرانی عبور می‌کند ، با تعیین اینکه کدام شاخه از یک انشعاب انتخاب می‌شود، سرنوشت سیستم را تعیین می‌کند. برای یک ناظر خارجی که از نوسانات (یا " نویز ") آگاه نیست، انتخاب دلخواه به نظر می رسد. این فرآیند را «شکستن تقارن » می‌نامند، زیرا چنین انتقال‌هایی معمولاً سیستم را از حالت متقارن اما بی‌نظم به یک یا چند حالت معین می‌آورند. این پدیده بخشی از اکثر نظریه های همه چیز است. تصور می شود شکستن تقارن نقش عمده ای در شکل گیری الگو ایفا می کند .

در مقاله علمی خود در سال 1972 با عنوان "بیشتر متفاوت است" [1] برنده جایزه نوبل P.W. اندرسون از ایده شکست تقارن استفاده کرد تا نشان دهد که حتی اگر تقارن درست باشد، برعکس آن، ساخت گرایی، که این ایده است که دانشمندان به راحتی می توانند پدیده های پیچیده را با توجه به نظریه هایی که اجزای آنها را توصیف می کنند، پیش بینی کنند، درست نیست.

شکست تقارن را می توان به دو نوع تقسیم کرد، شکست تقارن صریح و شکست تقارن خود به خودی ، که مشخصه آن این است که آیا معادلات حرکت ثابت نمی ماند یا حالت پایه ثابت نمی شود.

شکستن تقارن صریح [ ویرایش ]

نوشتار اصلی: شکستن تقارن صریح

در شکست تقارن صریح، معادلات حرکتی که یک سیستم را توصیف می‌کنند، تحت تقارن شکسته متغیر هستند. در مکانیک هامیلتونی یا مکانیک لاگرانژی ، این زمانی اتفاق می‌افتد که حداقل یک عبارت در همیلتونی (یا لاگرانژی) وجود داشته باشد که به صراحت تقارن داده شده را بشکند.

در محیط همیلتونی، این اغلب زمانی مورد مطالعه قرار می گیرد که بتوان همیلتونی را نوشتاچ=اچ0+اچبین المللی $H=H_{0}+H_{\text{int}}$ .

اینجااچ0 $H_{0}$ یک "همیلتونی پایه" است که دارای تقارن آشکار است. به طور واضح تر، تحت عمل یک گروه (دروغ) متقارن است جی $جی$ . اغلب این هامیلتونی قابل ادغام است.

رااچبین المللی $H_{\text{int}}$ یک آشفتگی یا تعامل همیلتونی است. این تحت عمل ثابت نیستجی $جی$ . اغلب با یک پارامتر کوچک و آشفته متناسب است.

شکست خود به خودی تقارن [ ویرایش ]

نوشتار اصلی: شکستن تقارن خود به خود

در شکست تقارن خود به خود، معادلات حرکت سیستم ثابت است، اما سیستم اینطور نیست. این به این دلیل است که پس‌زمینه ( فضا-زمان ) سیستم، خلأ آن ، غیر تغییرناپذیر است. چنین شکست تقارنی با یک پارامتر سفارشی پارامتر می شود . یک مورد خاص از این نوع شکستن تقارن شکستن تقارن دینامیکی است .

در محیط لاگرانژی نظریه میدان کوانتومی، لاگرانژی $L$ تابعی از میدان های کوانتومی است که تحت عمل یک گروه تقارن ثابت استجی $جی$ . با این حال، پیکربندی حالت پایه (مقدار انتظار خلاء) فیلدها ممکن است در زیر ثابت نباشدجی $جی$ ، اما در عوض تا حدی تقارن را به یک زیر گروه می شکنداچ $اچ$ ازجی $جی$ . این شکست خود به خودی تقارن است .

خارج از تقارن سنج، شکست خود به خودی تقارن با انتقال فاز همراه است . به عنوان مثال در مدل Ising ، زمانی که دمای سیستم به زیر دمای بحرانی می‌رسدز2 $\mathbb {Z} _{2}$ تقارن خلاء شکسته شده است و یک انتقال فاز از سیستم را می دهد.

در چارچوب تقارن گیج، شکستن تقارن خود به خود مکانیزمی است که با آن میدان‌های گیج می‌توانند جرمی را به‌دست آورند، علی‌رغم اینکه گیج تغییر ناپذیری اعمال می‌کند که چنین میدان‌هایی بدون جرم باشند. این به این دلیل است که شکست تقارن خود به خودی تقارن سنج، عدم تغییر گیج را می شکند و به میدان های گیج اجازه می دهد تا عظیم باشند. همچنین، در این زمینه، استفاده از "شکستن تقارن"، در حالی که استاندارد است، یک نام اشتباه است، زیرا "تقارن" گیج در واقع یک تقارن نیست، بلکه یک افزونگی در توصیف سیستم است. از نظر ریاضی، این افزونگی یک انتخاب بی‌اهمیت است ، که تا حدودی شبیه به افزونگی ناشی از انتخاب مبنا است.

مثالها [ ویرایش ]

شکست تقارن می تواند هر یک از سناریوهای زیر را پوشش دهد: [2]

شکستن تقارن دقیق قوانین اساسی فیزیک با تشکیل ظاهرا تصادفی برخی ساختارها.
وضعیتی در فیزیک که در آن یک حالت حداقل انرژی تقارن کمتری نسبت به خود سیستم دارد.
موقعیت‌هایی که وضعیت واقعی سیستم، تقارن‌های اساسی دینامیک را منعکس نمی‌کند، زیرا حالت متقارن آشکار ناپایدار است (پایداری به قیمت عدم تقارن محلی به دست می‌آید ).
موقعیت‌هایی که معادلات یک نظریه ممکن است دارای تقارن‌های خاصی باشند، اگرچه راه‌حل‌های آنها ممکن است نداشته باشند (تقارن‌ها "پنهان" هستند).

یکی از اولین موارد تقارن شکسته که در متون فیزیک مورد بحث قرار گرفته است مربوط به شکلی است که توسط یک جسم چرخان یکنواخت از سیال تراکم ناپذیر در تعادل گرانشی و هیدرواستاتیکی به دست آمده است . ژاکوبی [3] و کمی بعد لیوویل ، [4]در سال 1834، زمانی که انرژی جنبشی در مقایسه با انرژی گرانشی جسم دوار از مقدار بحرانی معینی فراتر رفت، یک بیضی سه محوری یک راه حل تعادلی برای این مشکل بود. تقارن محوری ارائه شده توسط کروی های مک لورین در این نقطه انشعاب شکسته شده است. علاوه بر این، در بالای این نقطه انشعاب، و برای تکانه زاویه ای ثابت، راه حل هایی که انرژی جنبشی را به حداقل می رساند، بیضی های ژاکوبی متقارن غیر محوری به جای کروی های ماکلورین هستند .

همچنین ببینید [ ویرایش ]

منابع

https://en.wikipedia.org/wiki/Symmetry_breaking

+ نوشته شده در دوشنبه یکم اسفند ۱۴۰۱ ساعت 2:6 توسط علی رضا نقش نیلچی |

مطالب قدیمی‌تر