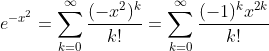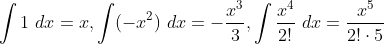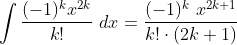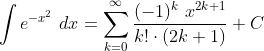این مقاله شامل فهرستی از مراجع عمومی است ، اما فاقد استنادهای درون خطی متناظر کافی است . لطفا با معرفی نقل قول های دقیق تر به بهبود این مقاله کمک کنید. ( ژانویه 2015 ) ( نحوه و زمان حذف این پیام الگو را بیاموزید )

(مختصات x) دایره های قرمز نقاط ثابت هستند . مربع های آبی نقطه عطف هستند .
نقطه بحرانی اصطلاحی است که در بسیاری از شاخه های ریاضیات استفاده می شود .
وقتی با توابع یک متغیر حقیقی سروکار داریم ، نقطه بحرانی نقطهای در دامنه تابع است که در آن تابع یا مشتق پذیر نیست یا مشتق آن برابر با صفر است. [1] به طور مشابه، هنگام برخورد با متغیرهای مختلط ، یک نقطه بحرانی نقطهای در دامنه تابع است که در آن یا هولومورفیک نیست یا مشتق آن برابر با صفر است. [2] [3] به همین ترتیب، برای تابعی از چندین متغیر حقیقی ، یک نقطه بحرانی مقداری در دامنه آن است که در آن گرادیان تعریف نشده یا برابر با صفر است. [4]
مقدار تابع در یک نقطه بحرانی یک مقدار بحرانی است . [5]
این نوع از تعریف به نقشه های مشتق پذیر بین گسترش می یابد

به طور خاص، اگر C یک منحنی مسطح باشد که با یک معادله ضمنی f ( x , y ) = 0 تعریف شده است ، نقاط بحرانی طرح ریزی بر روی محور x ، موازی با محور y ، نقاطی هستند که مماس بر C هستند. موازی با محور y هستند ، این نقاطی است که در آن
به عبارت دیگر، نقاط بحرانی نقاطی هستند که قضیه تابع ضمنی در آنها کاربرد ندارد.
مفهوم نقطه بحرانی اجازه توصیف ریاضی یک پدیده نجومی را می دهد که قبل از زمان کوپرنیک توضیح داده نشده بود . نقطه ثابت در مدار یک سیاره، نقطه ای از مسیر سیاره در کره آسمانی است ، جایی که به نظر می رسد حرکت سیاره قبل از شروع مجدد در جهت دیگر متوقف می شود. این به دلیل نقطه بحرانی پرتاب مدار به دایره دایره البروج رخ می دهد .
نقطه بحرانی یک تابع متغیر واحد [ ویرایش ]
نقطه بحرانی یک تابع از یک متغیر حقیقی منفرد ، f ( x ) ، مقدار x 0 در دامنه f است که در آن f مشتق پذیر نیست یا مشتق آن 0 است (یعنی
توجه کنید که چگونه برای یک تابع متمایز ، نقطه بحرانی همان نقطه ثابت است .
اگرچه به راحتی در نمودار (که یک منحنی است) قابل مشاهده است، مفهوم نقطه بحرانی یک تابع نباید با مفهوم نقطه بحرانی، در برخی جهت، یک منحنی اشتباه گرفته شود (برای تعریف دقیق به زیر مراجعه کنید ) . اگر g ( x , y ) یک تابع متمایز از دو متغیر باشد، آنگاه g ( x , y ) = 0 معادله ضمنی یک منحنی است . یک نقطه بحرانی چنین منحنی، برای طرح ریزی موازی با محور y (نقشه ( x , y ) → x )، نقطه ای از منحنی است که در آن.
از این تعاریف نتیجه می شود که یک تابع متمایز f ( x ) دارای یک نقطه بحرانی x 0 با مقدار بحرانی y 0 است ، اگر و فقط اگر ( x 0 , y 0 ) نقطه بحرانی نمودار آن برای طرح ریزی موازی x باشد. محور، با همان مقدار بحرانی y 0 . اگر f در x 0 به دلیل موازی شدن مماس با محور y مشتق پذیر نباشد ، x 0 دوباره نقطه بحرانی f است ، اما اکنون ( x 0 , y 0 ) نقطه بحرانی نمودار آن برای طرح ریزی است. موازی با محور y
به عنوان مثال، نقاط بحرانی دایره واحد معادله

مثالها [ ویرایش ]
- کارکرد
در همه جا با مشتق مشتق پذیر است
این تابع دارای یک نقطه بحرانی منحصر به فرد −1 است، زیرا عدد یکتایی x 0 برای آن است2.
این نقطه حداقل جهانی f است . مقدار بحرانی مربوطه است.
نمودار f یک سهمی مقعر به سمت بالا است، نقطه بحرانی آبسیس راس است که در آن خط مماس افقی است، و مقدار بحرانی مربوط به راس است و ممکن است با تقاطع این خط مماس و خط مماس نشان داده شود. محور y .
- کارکرد
برای همه x تعریف شده و برای x ≠ 0 با مشتق قابل تفکیک است
از آنجایی که f در x = 0 و قابل تفکیک نیست
در غیر این صورت، آن نقطه بحرانی منحصر به فرد است. نمودار تابع f در این نقطه یک کاسپ با مماس عمودی دارد . مقدار بحرانی مربوطه است.
- تابع مقدار مطلق
در همه جا مشتق پذیر است به جز در نقطه بحرانی x = 0 ، جایی که یک نقطه حداقل جهانی با مقدار بحرانی 0 دارد.
- کارکرد
نقاط بحرانی ندارد نقطه x = 0 یک نقطه بحرانی نیست زیرا در دامنه تابع گنجانده نشده است.
مکان نقاط بحرانی [ ویرایش ]
طبق قضیه گاوس-لوکاس ، تمام نقاط بحرانی یک تابع چند جمله ای در صفحه مختلط در داخل بدنه محدب ریشه های تابع قرار دارند. بنابراین برای یک تابع چند جمله ای با ریشه های حقیقی، تمام نقاط بحرانی حقیقی هستند و بین بزرگترین و کوچکترین ریشه ها قرار دارند.
حدس سندوف بیان میکند که اگر همه ریشههای یک تابع در دیسک واحد در صفحه مختلط قرار گیرند، حداقل یک نقطه بحرانی در فاصله واحد از هر ریشه معین وجود دارد.
نقاط بحرانی یک منحنی ضمنی [ ویرایش ]
همچنین ببینید: منحنی جبری
نقاط بحرانی نقش مهمی در مطالعه منحنی های سطحی تعریف شده توسط معادلات ضمنی ایفا می کنند ، به ویژه برای ترسیم آنها و تعیین توپولوژی آنها . مفهوم نقطه بحرانی که در این بخش استفاده می شود، ممکن است متفاوت از قسمت قبلی به نظر برسد. در واقع این تخصص به یک مورد ساده از مفهوم کلی نقطه بحرانی است که در زیر آورده شده است .
بنابراین، منحنی C را در نظر می گیریم که با یک معادله ضمنی تعریف شده است




نقطه C برای آن حیاتی است 


این بدان معناست که این تعریف یک مورد خاص از تعریف کلی یک نقطه بحرانی است که در زیر آورده شده است .
تعریف نقطه بحرانی برای


برخی از نویسندگان نقاط بحرانی C را به عنوان نقاطی که برای هر یک از آنها حیاتی هستند تعریف می کنند


و بنابراین راه حل های هر یک از سیستم های معادلات هستند که نقاط بحرانی را مشخص می کنند. با این تعریف کلی تر، نقاط بحرانی برای
استفاده از تمایز [ ویرایش ]
وقتی منحنی C جبری است، یعنی زمانی که با یک چند جملهای دو متغیره f تعریف میشود ، آنگاه ممیز ابزار مفیدی برای محاسبه نقاط بحرانی است.
در اینجا ما فقط طرح را در نظر می گیریم

اجازه دهید دیسک

به طور دقیق تر، یک ریشه ساده ازدیسک

یک ریشه چندگانه تمایز یا به چندین نقطه بحرانی یا مجانب عطف که دارای ارزش بحرانی یکسان هستند، یا به یک نقطه بحرانی که همچنین یک نقطه عطف است، یا به یک نقطه منفرد مطابقت دارد.
چندین متغیر [ ویرایش ]
برای تابعی از چندین متغیر حقیقی ، یک نقطه P (که مجموعه ای از مقادیر برای متغیرهای ورودی است که به عنوان یک نقطه در نظر گرفته می شود.آر
یک نقطه بحرانی (جایی که تابع قابل تفکیک است) ممکن است یک حداکثر محلی ، یک حداقل محلی یا یک نقطه زینتی باشد . اگر تابع حداقل دو بار به طور پیوسته مشتق پذیر باشد، موارد مختلف را می توان با در نظر گرفتن مقادیر ویژه ماتریس هسین مشتقات دوم متمایز کرد.
یک نقطه بحرانی که در آن ماتریس هسین غیرمفرد است، گفته میشود که غیرمنحط است و نشانههای مقادیر ویژه هسین، رفتار محلی تابع را تعیین میکنند. در مورد تابعی از یک متغیر منفرد، هسین به سادگی دومین مشتق است که به عنوان یک ماتریس 1×1 در نظر گرفته میشود، که اگر و فقط اگر صفر نباشد غیرمفرد است. در این حالت، یک نقطه بحرانی غیر انحطاط، بسته به علامت مشتق دوم، یک ماکزیمم محلی یا یک مینیمم محلی است که برای حداقل محلی مثبت و برای حداکثر محلی منفی است. اگر مشتق دوم صفر باشد، نقطه بحرانی به طور کلی یک نقطه عطف است ، اما ممکن است یک نقطه موجی نیز باشد ، که ممکن است حداقل محلی یا حداکثر محلی باشد.
برای تابعی از n متغیر، تعداد مقادیر ویژه منفی ماتریس هسین در یک نقطه بحرانی را شاخص نقطه بحرانی می نامند. یک نقطه بحرانی غیر منحط یک حداکثر محلی است اگر و فقط اگر شاخص n باشد ، یا به طور معادل، اگر ماتریس هسین منفی قطعی باشد . اگر شاخص صفر باشد، یک حداقل محلی است، یا اگر ماتریس هسین مثبت قطعی باشد . برای سایر مقادیر شاخص، یک نقطه بحرانی غیر انحطاط یک نقطه زینی است ، یعنی نقطه ای که در برخی جهات حداکثر و در برخی دیگر حداقل است.
کاربرد بهینه سازی [ ویرایش ]
مقاله اصلی: بهینه سازی ریاضی
بر اساس قضیه فرما ، همه ماکزیمم ها و مینیمم های محلی یک تابع پیوسته در نقاط بحرانی رخ می دهند. بنابراین، برای یافتن ماکزیمم و مینیمم محلی یک تابع قابل تفکیک، از نظر تئوری، محاسبه صفرهای گرادیان و مقادیر ویژه ماتریس هسین در این صفرها کافی است. این نیاز به حل یک سیستم معادلات دارد که می تواند کار دشواری باشد. الگوریتمهای عددی معمول برای یافتن اکسترمهای محلی بسیار کارآمدتر هستند، اما نمیتوانند تأیید کنند که همه اکستریمها پیدا شدهاند. به ویژه، در بهینه سازی جهانی ، این روش ها نمی توانند تأیید کنند که خروجی واقعاً بهینه جهانی است.
هنگامی که تابع کمینه سازی یک چند جمله ای چند متغیره است ، نقاط بحرانی و مقادیر بحرانی راه حل های یک سیستم معادلات چند جمله ای هستند و الگوریتم های مدرن برای حل چنین سیستم هایی روش های تایید شده رقابتی را برای یافتن حداقل جهانی ارائه می دهند.
نقطه بحرانی یک نقشه مشتق پذیر [ ویرایش ]
با توجه به یک نقشه متمایز 

برخی از نویسندگان [7] تعریف کمی متفاوت ارائه می دهند: نقطه بحرانی f یک نقطه از است
این تعاریف به نقشه های دیفرانسیل بین منیفولدهای قابل تفکیک به روش زیر گسترش می یابد. اجازه دهید:





کاربرد در توپولوژی [ ویرایش ]
نقاط بحرانی برای مطالعه توپولوژی منیفولدها و انواع جبری حقیقی اساسی هستند . [5] به ویژه، آنها ابزار اساسی برای نظریه مورس و نظریه فاجعه هستند هستند .
پیوند بین نقاط بحرانی و توپولوژی در حال حاضر در سطح پایین تری از انتزاع ظاهر می شود. به عنوان مثال، اجازه دهید





در مورد انواع جبری حقیقی، این مشاهدات مرتبط با قضیه بزو به ما اجازه میدهد تا تعداد اجزای متصل را با تابعی از درجات چندجملهای که تنوع را تعریف میکنند، محدود کنیم.
همچنین ببینید [ ویرایش ]
- نقطه مفرد یک منحنی
- نظریه تکینگی
- قضیه گاوس-لوکاس
https://en.wikipedia.org/wiki/Critical_point_%28mathematics%29
از ویکیپدیا، دانشنامه آزاد
نباید با نیم نرم یا pseudonorm اشتباه گرفته شود .
در جبر خطی ، تحلیل تابعی و حوزههای مرتبط ریاضیات ، یک شبههنجار از این نظر شبیه به یک هنجار است که بدیهیات هنجار را برآورده میکند، با این تفاوت که نابرابری مثلث با جایگزین میشود.

تعریف [ ویرایش ]
شبه نرم [1] در فضای برداری


- غیر منفی بودن :پ≥0;
- همگنی مطلق :
برای همه
و همه اسکالرهاس;
- قعی وجود دارد
به طوری که
برای همه.
- اگر
سپس این نابرابری به نابرابری مثلث کاهش می یابد . از این نظر است که این شرط نابرابری مثلث معمولی را تعمیم می دهد.
- اگر
آشبه هنجار [1] یک شبه نیمهنجار است که موارد زیر را نیز برآورده میکند:
- مثبت قطعی /نقطه جدا کننده : اگر
راضی می کند
سپس.
یک جفت


ضرب کننده
اینفیموم همه ارزش هایک


یک هنجار (به ترتیب، یک نیم نرم ) فقط یک شبه هنجار (به ترتیب، یک شبه نیمهنجار) است که ضریب آن برابر است با1.
توپولوژی [ ویرایش ]
اگر





هر فضای برداری توپولوژیکی شبه نرمدار قابل شبه سنجی است .
یک فضای شبه هنجاری کامل a نامیده می شودفضای شبه باناخ . هرفضای باناخ یک فضای شبه باناخ است، البته نه برعکس.
تعاریف مرتبط [ ویرایش ]
همچنین ببینید: جبر باناخ
یک فضای شبه نورمی



جبر شبه هنجاری کاملَ Aمیده می شودشبه جبر باناخ .
خصوصیات [ ویرایش ]
فضای برداری توپولوژیکی (TVS) یک فضای شبههنجاری است اگر و تنها در صورتی که یک همسایگی محدود از مبدأ داشته باشد. [2]
مثالها [ ویرایش ]
از آنجایی که هر هنجاری یک شبه هنجار است، هر فضای هنجاری نیز یک فضای شبه هنجاری است.

را


![{\displaystyle L^{p}([0,1])}](https://wikimedia.org/api/rest_v1/media/math/render/svg/d53d55ccc06ce5cc9ec3bede2be3e7933c206ee3)
![{\displaystyle L^{p}([0,1])}](https://wikimedia.org/api/rest_v1/media/math/render/svg/d53d55ccc06ce5cc9ec3bede2be3e7933c206ee3)
![{\displaystyle L^{p}([0,1])}](https://wikimedia.org/api/rest_v1/media/math/render/svg/d53d55ccc06ce5cc9ec3bede2be3e7933c206ee3)

![{\displaystyle L^{p}([0,1])}](https://wikimedia.org/api/rest_v1/media/math/render/svg/d53d55ccc06ce5cc9ec3bede2be3e7933c206ee3)
همچنین ببینید [ ویرایش ]
- فضای برداری توپولوژیکی قابل اندازه گیری - فضای برداری توپولوژیکی که توپولوژی آن را می توان با متریک تعریف کرد
- هنجار (ریاضیات) - طول در یک فضای برداری
- نیم نرم - تابع غیرمنفی-حقیقی در فضای برداری حقیقی یا مختلط که نابرابری مثلث را برآورده می کند و کاملاً همگن است.
- فضای برداری توپولوژیکی - فضای برداری با مفهوم نزدیکی
منابع [ ویرایش ]
- ^ a bپرش به بالا: Kalton 1986 ، صفحات 297-324.
- ^ a bپرش به بالا: Wilansky 2013 ، ص. 55.
- آل، چارلز ای. رابرت لوون (2001). راهنمای تاریخچه توپولوژی عمومی . اسپرینگر _ شابک 0-7923-6970-X.
- کانوی، جان بی (1990). دوره ای در تحلیل عملکردی . اسپرینگر _ شابک 0-387-97245-5.
- Kalton, N. (1986). "توابع چندگانه ساب هارمونیک در فضاهای شبه باناخ" (PDF) . Studia Mathematica . موسسه ریاضیات، آکادمی علوم لهستان. 84 (3): 297-324. doi : 10.4064/sm-84-3-297-324 . ISSN 0039-3223 .
- نیکولاسکی، نیکولا کاپیتونوویچ (1992). تحلیل تابعی I: تحلیل تابعی خطی . دایره المعارف علوم ریاضی. جلد 19. اسپرینگر . شابک 3-540-50584-9.
- رودین، والتر (1991). تحلیل عملکردی . سری بین المللی در ریاضیات محض و کاربردی. جلد 8 (ویرایش دوم). نیویورک، نیویورک: McGraw-Hill Science/Engineering/Math . شابک 978-0-07-054236-5. OCLC 21163277 .
- سوارتز، چارلز (1992). مقدمه ای بر تحلیل عملکردی . CRC را فشار دهید . شابک 0-8247-8643-2.
- ویلانسکی، آلبرت (2013). روش های مدرن در فضاهای برداری توپولوژیکی . Mineola، نیویورک: Dover Publications, Inc. ISBN 978-0-486-49353-4. OCLC 849801114 .
https://en.wikipedia.org/wiki/Quasinorm
مجموعه بسته
از ویکیپدیا، دانشنامه زاد
این مقاله در مورد مکمل یک مجموعه باز است . برای مجموعه ای که تحت یک عملیات بسته شده است، به بسته شدن (ریاضیات) مراجعه کنید . برای کاربردهای دیگر، بسته (ابهامزدایی) را ببینید .
در هندسه , توپولوژی و شاخه های مرتبط ریاضیات , مجموعه بسته مجموعه ای است که مکمل ن یک مجموعه باز است . [1] [2] در یک فضای توپولوژیکی ، یک مجموعه بسته را می توان به عنوان مجموعه ای تعریف کرد که شامل تمام نقاط حد خود است . در یک فضای متریک کامل ، مجموعه بسته مجموعه ای است که تحت عملیات حد بسته می شود . این نباید با منیفولد بسته اشتباه گرفته شود .
تعاریف معادل [ ویرایش ]
طبق تعریف، یک زیر مجموعه 













یک توصیف جایگزین از مجموعه های بسته از طریق توالی ها و شبکه ها در دسترس است . یک زیر مجموعه 





















یک زیر مجموعه بسته است اگر و تنها در صورتی که حاوی هر نقطه نزدیک به ن باشد.
از نظر همگرایی خالص، یک امتیاز





























مجموعه های بسته همچنین می توانند برای توصیف توابع پیوسته استفاده شوند : نقشه:












اطلاعات بیشتر درباره مجموعه های بسته [ ویرایش ]
مفهوم مجموعه بسته در بالا بر حسب مجموعه های باز تعریف شده است ، مفهومی که برای فضاهای توپولوژیکی و همچنین برای سایر فضاهایی که ساختارهای توپولوژیکی را حمل میکنند، مانند فضاهای متریک ، منیفولدهای قابل تمایز ، فضاهای یکنواخت و فضاهای گیج معنا دارد .
بسته بودن یک مجموعه بستگی به فضایی دارد که در ن تعبیه شده است. با این حال، فضاهای جمع و جور هاوسدورف « کاملاً بسته » هستند ، به این معنا که، اگر فضای هاسدورف فشرده را تعبیه کنید.



علاوه بر این، هر زیر مجموعه بسته از یک فضای فشرده فشرده است، و هر زیرفضای فشرده از یک فضای هاسدورف بسته است.
مجموعه های بسته نیز توصیف مفیدی از فشردگی ارائه می دهند: فضای توپولوژیکی

فضای توپولوژیکی 





خواص [ ویرایش ]
همچنین ببینید: بدیهیات بسته شدن کوراتوفسکی
یک مجموعه بسته دارای مرز خاص خود است . به عبارت دیگر، اگر شما "خارج" یک مجموعه بسته هستید، ممکن است مقدار کمی را در هر جهتی حرکت دهید و همچنان خارج از مجموعه بمانید. توجه داشته باشید که اگر مرز مجموعه تهی باشد، به عنوان مثال در فضای متریک اعداد گویا، برای مجموعه اعدادی که مربع نها کوچکتر است، این نیز صادق است.2.
- هر اشتراک از هر خانواده از مجموعه های بسته بسته است (این شامل اشتراک های بی نهایت مجموعه بسته است)
- اتحاد مجموعه های بسته بسیار محدود بسته است.
- مجموعه تهی بسته است.
- کل مجموعه بسته است.
در واقع، اگر مجموعه ای داده شود












مجموعه هایی که می توانند به عنوان اتحاد تعداد زیادی مجموعه بسته قابل شمارش ساخته شوند ، مجموعه F σ نشان داده می شوند . این مجموعه ها نیازی به بسته شدن ندارند.
مثالها [ ویرایش ]
- فاصله بسته
اعداد واقعی بسته است. ( برای توضیح نماد مجموعه براکت و پرانتز به فاصله (ریاضیات) مراجعه کنید.)
- فاصله واحد
در فضای متریک اعداد حقیقی و مجموعه بسته شده است
از اعداد گویا بین
و1
(شامل) در فضای اعداد گویا بسته است اما
در اعداد واقعی بسته نشده است.
- برخی از مجموعه ها نه باز هستند و نه بسته، به عنوان مثال بازه نیمه باز
در اعداد واقعی
- برخی از مجموعه ها هم باز و هم بسته هستند و به نها مجموعه های کلوپن می گویند .
- پرتو
بسته است.
- مجموعه کانتور یک مجموعه بسته غیرمعمول است به این معنا که کاملاً از نقاط مرزی تشکیل شده است و هیچ جا متراکم نیست.
- نقاط Singleton (و در نتیجه مجموعه های محدود) در فضاهای T 1 و فضاهای هاسدورف بسته می شوند .
- مجموعه اعداد صحیح ز
یک مجموعه بسته نامحدود و نامحدود در اعداد حقیقی است.
- اگر:
تابعی بین فضاهای توپولوژیکی است
پیوسته است اگر و فقط در صورتی که پیش تصویر مجموعه های بسته وارد شود
در بسته هستند.
همچنین ببینید [ ویرایش ]
- مجموعه Clopen - زیر مجموعه ای که هم باز و هم بسته است
- نقشه بسته – تابعی که زیر مجموعه های باز (بهعنوان بسته) را به زیر مجموعه های باز (بهعنوان بسته) ارسال میکند.
- منطقه بسته - زیر مجموعه باز متصل از یک فضای توپولوژیکی
- مجموعه باز - زیر مجموعه اصلی یک فضای توپولوژیکی
- همسایگی - مجموعه باز حاوی یک نقطه مشخص
- منطقه (ریاضیات) - زیر مجموعه باز متصل یک فضای توپولوژیکی
- ست بسته معمولی
از ویکیپدیا، دانشنامه آزاد
در تجزیه و تحلیل هارمونیک در ریاضیات ، تابعی از نوسان میانگین محدود ، که به عنوان تابع BMO نیز شناخته میشود ، تابعی با مقدار واقعی است که نوسان میانگین آن محدود (محدود) است. فضای توابع نوسان میانگین محدود ( BMO )، فضای تابعی است که به تعبیر دقیق، همان نقشی را در نظریه فضاهای هاردی Hp ایفا می کند که فضای L∞ توابع محدود شده اساسا در نظریه L ایفا می کند. p -spaces : به نام فضای John–Nirenberg نیز نامیده می شود ، به نام فریتز جان و لوئیس نیرنبرگ که برای اولین بار آن را معرفی و مطالعه کردند.
یادداشت تاریخی [ ویرایش ]
به گفته نیرنبرگ (1985 ، ص 703 و ص 707)، [1] فضای توابع نوسان میانگین محدود توسط جان (1961 ، صفحات 410-411) در ارتباط با مطالعات خود در مورد نگاشت از یک مجموعه محدود معرفی شد. Ω متعلق به Rn به Rn و مشکلات مربوطه ناشی از تئوری الاستیسیته ، دقیقاً از مفهوم کرنش الاستیک : نماد اصلی در مقاله ای که توسط جان و نیرنبرگ (1961) از نزدیک معرفی شد ، [2] که در آن چندین ویژگی از این فضاهای تابع ثابت شد. گام مهم بعدی در توسعه این نظریه اثبات دوگانگی بین BMO و فضای هاردی H 1 توسط چارلز ففرمن [3] بود، در مقاله یادداشت شده Fefferman & Stein 1972 : اثبات سازنده این نتیجه، معرفی روش های جدید. و شروع توسعه بیشتر این نظریه توسط آکیهیتو اوچیاما ارائه شد . [4]
تعریف [ ویرایش ]
تعریف 1. میانگین نوسان یک تابع قابل انتگرال محلی u بر روی یک ابر مکعب [5] Q در Rn به عنوان مقدار انتگرال زیر تعریف می شود :

- | س | حجم Q است ، یعنی اندازه گیری Lebesgue آن
- u Q میانگین مقدار u در مکعب Q است ، یعنی
تعریف 2. یک تابع BMO یک تابع محلی قابل ادغام u است که میانگین نوسان فوق العاده آن که بر مجموعه تمام مکعب های Q موجود در R n گرفته شده است محدود است.
تبصره 1 . بالاترین نوسان میانگین، هنجار BMO از u نامیده می شود . [6] و با || نشان داده می شود u || BMO (و در برخی موارد با || u || ∗ نیز مشخص می شود ).
تبصره 2 . استفاده از مکعبهای Q در Rn بهعنوان حوزههای ادغامی که بر روی آنها نوسان میانگین محاسبه میشود، اجباری نیست: ویگرینک (2001) به جای آن از توپها استفاده میکند و همانطور که استاین (1993، ص 140) اشاره کرد ، در انجام این کار کاملاً عمل میکند. تعریف معادلی از توابع نوسان میانگین محدود به وجود می آید.
نشانه گذاری [ ویرایش ]
- نماد جهانی مورد استفاده برای مجموعه توابع BMO در یک دامنه معین Ω BMO ( Ω ) است : وقتی Ω = Rn ، BMO ( Rn ) به سادگی به عنوان BMO نشان داده می شود .
- هنجار BMO یک تابع BMO معین u با || نشان داده می شود u || BMO : در برخی موارد به صورت || نیز مشخص می شود u || ∗ .
ویژگی های اساسی [ ویرایش ]
توابع BMO به صورت محلی قابل ادغام p هستند [ ویرایش ]
توابع BMO به صورت محلی L p هستند اگر 0 < p <∞، اما لازم نیست به صورت محلی محدود شوند. در واقع، با استفاده از نابرابری جان-نیرنبرگ، میتوانیم آن را ثابت کنیم
BMO یک فضای Banach است [ ویرایش ]
توابع ثابت دارای نوسان میانگین صفر هستند، بنابراین توابع متفاوت برای ثابت c > 0 می توانند مقدار نرمال BMO یکسانی داشته باشند حتی اگر تفاوت آنها تقریباً در همه جا صفر نباشد . بنابراین تابع || u || BMO به درستی یک هنجار در فضای ضریب توابع BMO است و فضای توابع ثابت در دامنه در نظر گرفته شده را مدول می کند .
میانگین مکعب های مجاور قابل مقایسه هستند [ ویرایش ]
همانطور که از نام آن پیداست، میانگین یا میانگین یک تابع در BMO هنگام محاسبه آن بر روی مکعب های نزدیک به یکدیگر در موقعیت و مقیاس، نوسان زیادی ندارد. به طور دقیق، اگر Q و R مکعب های دوتایی هستند به گونه ای که مرزهای آنها با هم تماس داشته باشد و طول ضلع Q کمتر از نصف طول ضلع R نباشد (و بالعکس)
که در آن C > 0 مقداری ثابت جهانی است. این ویژگی در واقع معادل f است که در BMO است، یعنی اگر f یک تابع انتگرال پذیر محلی باشد به طوری که | f R − f Q | ≤ C برای همه مکعبهای دوتایی Q و R مجاور به معنایی که در بالا توضیح داده شد و f در BMO دوتایی است (که در آن برتری فقط بر مکعبهای دوتایی Q گرفته میشود )، سپس f در BMO است. [7]
BMO فضای برداری دوگانه H 1 است [ ویرایش ]
ففرمن (1971) نشان داد که فضای BMO دو برابر H 1 است ، فضای هاردی با p = 1 است . [8] جفت شدن بین f∈ H 1 و g ∈ BMO توسط
اگرچه در تعریف این انتگرال کمی دقت لازم است، زیرا به طور کلی مطلقاً همگرا نیست.
نابرابری جان-نیرنبرگ [ ویرایش ]
نابرابری جان -نیرنبرگ تخمینی است که نشان میدهد یک تابع نوسان میانگین کراندار تا چه حد ممکن است از میانگین خود به میزان معینی منحرف شود.
بیانیه [ ویرایش ]
برای هر



برعکس، اگر این نابرابری روی همه مکعبهایی با مقداری C ثابت به جای || برقرار باشد f || BMO ، سپس f در BMO با هنجار حداکثر یک بار ثابت C است .
نتیجه: فاصله در BMO تا L ∞ [ ویرایش ]
نابرابری جان-نیرنبرگ در واقع می تواند اطلاعات بیشتری نسبت به هنجار BMO یک تابع بدهد. برای یک تابع محلی ادغام پذیر f ، اجازه دهید A ( f ) A > 0 غیر رسمی باشد که برای آن
نابرابری جان-نیرنبرگ نشان میدهد که A ( f ) ≤ C|| f || BMO برای مقداری ثابت جهانی C. با این حال، برای یک تابع L ∞ ، نابرابری بالا برای همه A > 0 برقرار خواهد بود. به عبارت دیگر، اگر f در L ∞ باشد، A ( f ) = 0 است . از این رو ثابت A ( f ) راهی برای اندازه گیری فاصله یک تابع در BMO از زیرفضای L ∞ به ما می دهد . این عبارت را می توان دقیق تر بیان کرد: [9] یک ثابت C وجود دارد که فقط به بعد n بستگی دارد ، به طوری که برای هر تابع f ∈ BMO( Rn ) نابرابری دو طرفه زیر برقرار است.
تعمیم ها و پسوندها [ ویرایش ]
فضاهای BMOH و BMOA [ ویرایش ]
هنگامی که بعد فضای محیط 1 باشد، فضای BMO را می توان به عنوان یک زیرفضای خطی از توابع هارمونیک روی دیسک واحد مشاهده کرد و نقش اصلی را در نظریه فضاهای هاردی ایفا می کند : با استفاده از تعریف 2 ، می توان آن را تعریف کرد. فضای BMO( T ) روی دایره واحد به عنوان فضای توابع f : T → R به طوری که
یعنی به گونه ای که میانگین نوسان آن بر روی هر کمان I دایره واحد [10] محدود باشد. در اینجا مانند قبل f I مقدار میانگین f روی قوس I است.
تعریف 3. یک تابع تحلیلی روی دیسک واحد به BMO هارمونیک یا در فضای BMOH تعلق دارد اگر و فقط اگر انتگرال پواسون یک تابع BMO( T ) باشد . بنابراین، BMOH فضای تمام توابع u با شکل زیر است:
مجهز به هنجار:
زیرفضای توابع تحلیلی متعلق به BMOH را فضای تحلیلی BMO یا فضای BMOA می نامند .
BMOA به عنوان فضای دوگانه H 1 ( D ) [ ویرایش ]
چارلز ففرمن در کار اصلی خود ثابت کرد که فضای BMO واقعی دوگانه به فضای هاردی با ارزش واقعی در نیمه فضای بالایی است. [11] در تئوری تحلیل مختلط و هارمونیک بر روی واحد. دیسک، نتیجهاش به صورت زیر بیان میشود. [12] فرض کنید H p ( D ) فضای هاردی تحلیلی روی دیسک واحد باشد . برای p = 1، ( H 1 )* را با BMOA با جفت کردن f ∈ H 1 ( D ) شناسایی میکنیم. و g ∈ BMOA با استفاده از تبدیل ضد خطی Tg
توجه داشته باشید که اگرچه حد همیشه برای یک تابع H1 f وجود دارد و Tg عنصری از فضای دوگانه ( H1 )* است، از آنجایی که تبدیل ضد خطی است ، ما ایزومورفیسم ایزومتریک بین ( H1 ) نداریم . * و BMOA. با این حال، اگر فضایی از توابع مزدوج BMOA را در نظر بگیریم، می توان ایزومتری را به دست آورد .
فضای VMO [ ویرایش ]
فضای VMO توابع نوسان میانگین ناپدید شدن، بسته شدن در BMO توابع پیوسته ای است که در بی نهایت ناپدید می شوند. همچنین میتوان آن را بهعنوان فضای توابعی تعریف کرد که «نوسانهای میانگین» آنها روی مکعبهای Q نه تنها محدود است، بلکه بهطور یکنواخت به صفر گرایش دارند زیرا شعاع مکعب Q به 0 یا ∞ متمایل میشود. فضای VMO نوعی آنالوگ فضای هاردی از فضای توابع پیوسته است که در بی نهایت ناپدید می شوند، و به ویژه فضای هاردی با ارزش واقعی H 1 دوگانه VMO است. [13]
ارتباط با تبدیل هیلبرت [ ویرایش ]
یک تابع محلی ادغام پذیر f در R BMO است اگر و فقط اگر بتوان آن را به صورت نوشتاری کرد
که در آن f i ∈ L ∞ ، α یک ثابت و H تبدیل هیلبرت است .
سپس هنجار BMO معادل infimum از است
به طور مشابه f VMO است اگر و فقط در صورتی که بتوان آن را به شکل بالا با توابع پیوسته یکنواخت با f i در R نشان داد . [14]
فضای دوتایی BMO [ ویرایش ]
اجازه دهید Δ مجموعه ای از مکعب های دوتایی را در R n نشان دهد . BMO دوتایی فضایی که BMO d نوشته میشود فضای توابعی است که همان نابرابری را برای توابع BMO برآورده میکند، فقط که برتری روی همه مکعبهای دوتایی است. این برتری گاهی با ||•|| نشان داده می شود BMO d .
این فضا به درستی حاوی BMO است. به طور خاص، تابع log( x ) χ [0،∞) تابعی است که در BMO دوتایی است اما در BMO نیست. اما اگر تابع f به گونه ای باشد که || f (•− x )|| BMO d ≤ C برای همه x در Rn برای برخی C > 0، سپس با یک سوم ترفند f نیز در BMO است . در مورد BMO روی T n به جای R n ، تابع f به گونه ای است که || f (•− x )|| BMO d ≤ C برای n+1 x انتخاب مناسب ، سپس f نیز در BMO است. این بدان معناست که BMO( Tn ) تقاطع n+1 ترجمه BMO دوتایی است. با دوگانگی ، H 1 ( Tn ) مجموع n +1 ترجمه H 1 دوتایی است . [15]
اگرچه BMO دوتایی یک کلاس بسیار محدودتر از BMO است، بسیاری از قضایا که برای BMO صادق هستند، برای BMO دوتایی بسیار سادهتر اثبات میشوند، و در برخی موارد میتوان قضایای BMO اصلی را با اثبات آنها ابتدا در حالت دوتایی خاص بازیابی کرد. [16]
مثالها [ ویرایش ]
نمونه هایی از توابع BMO شامل موارد زیر است:
- همه توابع محدود (قابل اندازه گیری). اگر f در L ∞ باشد ، آنگاه || f || BMO ≤ 2||f|| ∞ : [17] با این حال، عکس آن همانطور که در مثال زیر نشان می دهد درست نیست.
- تابع log(| P |) برای هر چند جمله ای P که به طور یکسان صفر نیست: به ویژه، این برای | P ( x )| = | x |. [17]
- اگر w یک وزن A ∞ باشد ، log( w ) BMO است. برعکس، اگر f BMO باشد، e δf یک وزن A ∞ برای δ>0 به اندازه کافی کوچک است: این واقعیت نتیجه نابرابری جان-نیرنبرگ است . [18]
https://en.wikipedia.org/wiki/Bounded_mean_oscillation
از ویکیپدیا، دانشنامه آزاد
برای فضای شوارتز یک گروه لی نیمه ساده، فضای شوارتز هاریش-چاندرا را ببینید . برای فضای شوارتز یک گروه آبلی فشرده محلی، تابع شوارتز-بروهات را ببینید .
در ریاضیات ، فضای شوارتز


یک تابع گاوسی دو بعدی نمونه ای از یک تابع به سرعت در حال کاهش است.
فضای شوارتز به افتخار ریاضیدان فرانسوی لوران شوارتز نامگذاری شده است .
تعریف [ ویرایش ]
اجازه دهید











برای قرار دادن زبان مشترک در این تعریف، می توان یک تابع به سرعت در حال کاهش را اساساً یک تابع f ( x ) در نظر گرفت ، به طوری که f ( x ) ، f ′( x ) ، f “( x ) و ... همه در همه جا وجود دارند. R و به عنوان x → ± سریعتر از هر توان متقابل x به صفر برود . به طور خاص، S ( Rn , C ) زیر فضایی از فضای تابع C ( Rn , C ) از توابع هموار از Rn به C است .
نمونه هایی از توابع در فضای شوارتز [ ویرایش ]
- اگر α یک چند شاخص باشد و a یک عدد حقیقی مثبت باشد ، پس
- هر تابع صاف f با پشتیبانی فشرده در S ( R n ) است. این واضح است زیرا هر مشتق f پیوسته است و در حمایت از f پشتیبانی می شود ، بنابراین ( xα D β ) f دارای حداکثر در Rn با قضیه مقدار شدید است .
- از آنجا که فضای شوارتز یک فضای برداری است، هر چند جمله ای
می تواند در یک ضریب ضرب شود
برای
یک ثابت حقیقی، برای دادن عنصری از فضای شوارتز. به طور خاص، تعبیه چند جملهای در فضای شوارتز وجود دارد.
خواص [ ویرایش ]
خواص تحلیلی [ ویرایش ]
- از قاعده لایب نیتس چنین می شود که S ( Rn ) نیز تحت ضرب نقطه ای بسته است :
اگر f , g ∈ 𝒮( R n ) آنگاه حاصل ضرب fg ∈ 𝒮( R n ) است .
- تبدیل فوریه یک ایزومورفیسم خطی F:𝒮( Rn ) → 𝒮( Rn ) است .
- اگر f ∈ 𝒮( R ) آنگاه f به طور یکنواخت روی R پیوسته است .
- 𝒮( R n ) یک محدب محلی متمایز Fréchet Schwartz بر روی اعداد مختلط است .
- هم 𝒮( R n ) و هم فضای دوگانه قوی آن نیز عبارتند از:
- فضاهای محدب محلی هاسدورف کامل ،
- فضاهای مونتل هسته ای ،
مشخص است که در فضای دوگانه هر فضای مونتل، یک دنباله در توپولوژی دوگانه قوی همگرا می شود اگر و فقط اگر در توپولوژی ضعیف* همگرا شود ، [1]
- فضاهای فرابورنولوژیک ،
- فضاهای مکی بشکه ای بازتابی .
رابطه فضاهای شوارتز با دیگر فضاهای برداری توپولوژیکی [ ویرایش ]
- اگر 1 ≤ p ≤ ، آنگاه 𝒮( R n ) ⊂ L p ( R n ) .
- اگر 1≤ p < ، آنگاه 𝒮 ( Rn ) در L p ( Rn ) متراکم است .
- فضای تمام توابع دست انداز ، C
ج( R n ) در 𝒮( R n ) گنجانده شده است .
همچنین ببینید [ ویرایش ]
- عملکرد ضربه
- تابع شوارتز-بروهات
- فضای هسته ای
منابع [ ویرایش ]
- ^ Trèves 2006 ، صفحات 351-359.
https://en.wikipedia.org/wiki/Schwartz_space
ز ویکیپدیا، دانشنامه آزاد
برای فضای شوارتز یک گروه لی نیمه ساده، فضای شوارتز هاریش-چاندرا را ببینید . برای فضای شوارتز یک گروه آبلی فشرده محلی، تابع شوارتز-بروهات را ببینید .
در ریاضیات ، فضای شوارتز


یک تابع گاوسی دو بعدی نمونه ای از یک تابع به سرعت در حال کاهش است.
فضای شوارتز به افتخار ریاضیدان فرانسوی لوران شوارتز نامگذاری شده است .
تعریف [ ویرایش ]
اجازه دهید











برای قرار دادن زبان مشترک در این تعریف، می توان یک تابع به سرعت در حال کاهش را اساساً یک تابع f ( x ) در نظر گرفت ، به طوری که f ( x ) ، f ′( x ) ، f “( x ) و ... همه در همه جا وجود دارند. R و به عنوان x → ± سریعتر از هر توان متقابل x به صفر بروید . به طور خاص، S ( Rn , C ) زیر فضایی از فضای تابع C ( Rn , C ) از توابع صاف از Rn به C است .
نمونه هایی از توابع در فضای شوارتز [ ویرایش ]
- اگر α یک چند شاخص باشد و a یک عدد حقیقی مثبت باشد ، پس
- هر تابع صاف f با پشتیبانی فشرده در S ( R n ) است. این واضح است زیرا هر مشتق f پیوسته است و در حمایت از f پشتیبانی می شود ، بنابراین ( xα D β ) f دارای حداکثر در Rn با قضیه مقدار شدید است .
- از آنجا که فضای شوارتز یک فضای برداری است، هر چند جمله ای
می تواند در یک ضریب ضرب شوده-آایکس2
برای
یک ثابت حقیقی، برای دادن عنصری از فضای شوارتز. به طور خاص، تعبیه چند جملهای در فضای شوارتز وجود دارد.
خواص [ ویرایش ]
خواص تحلیلی [ ویرایش ]
- از قاعده لایب نیتس چنین می شود که S ( Rn ) نیز تحت ضرب نقطه ای بسته است :
اگر f , g ∈ 𝒮( R n ) آنگاه حاصل ضرب fg ∈ 𝒮( R n ) است .
- تبدیل فوریه یک ایزومورفیسم خطی F:𝒮( Rn ) → 𝒮( Rn ) است .
- اگر f ∈ 𝒮( R ) آنگاه f به طور یکنواخت روی R پیوسته است .
- 𝒮( R n ) یک محدب محلی متمایز فریچت شوارتز بر روی اعداد مختلط است .
- هم 𝒮( R n ) و هم فضای دوگانه قوی آن نیز عبارتند از:
- فضاهای محدب محلی هاسدورف کامل ،
- فضاهای مونتل هسته ای ،
مشخص است که در فضای دوگانه هر فضای مونتل، یک دنباله در توپولوژی دوگانه قوی همگرا می شود اگر و فقط اگر در توپولوژی ضعیف* همگرا شود ، [1]
- فضاهای فرابورنولوژیک ،
- فضاهای مکی بشکه ای بازتابی .
رابطه فضاهای شوارتز با دیگر فضاهای برداری توپولوژیکی [ ویرایش ]
- اگر 1 ≤ p ≤ ، آنگاه 𝒮( R n ) ⊂ L p ( R n ) .
- اگر 1≤ p < ، آنگاه 𝒮 ( Rn ) در L p ( Rn ) متراکم است .
- فضای تمام توابع دست انداز ، C
ج( R n ) در 𝒮( R n ) گنجانده شده است .
همچنین ببینید [ ویرایش ]
- عملکرد ضربه
- تابع شوارتز-بروهات
- فضای هسته ای
منابع [ ویرایش ]
- ^ Trèves 2006 ، صفحات 351-359.
https://en.wikipedia.org/wiki/Schwartz_space
ویکی پدیا، دانشنامه آزاد
در ریاضیات ، نابرابری مارتینگل دوب ، که به نام نابرابری زیرمارتینگل کولموگروف نیز شناخته می شود ، نتیجه مطالعه فرآیندهای تصادفی است . این یک محدودیت در احتمال اینکه یک زیرمارتینگیل از هر مقدار داده شده در یک بازه زمانی معین فراتر رود، می دهد. همانطور که از نام آن پیداست، نتیجه معمولاً در موردی داده میشود که فرآیند یک مارتینگل باشد ، اما نتیجه برای زیر مارتینگلها نیز معتبر است.
این نابرابری به دلیل ریاضیدان آمریکایی جوزف ال دوب است .
بیانیه نابرابری [ ویرایش ]
تنظیم نابرابری دوب یک زیرمارتینگیل نسبت به فیلتر فضای احتمال زیرین است. اندازه گیری احتمال در فضای نمونه مارتینگل با P نشان داده می شود . مقدار مورد انتظار متناظر یک متغیر تصادفی X ، همانطور که توسط انتگرال لبگ تعریف شده است، با E[ X ] نشان داده می شود .
به طور غیررسمی، نابرابری دوب بیان میکند که مقدار مورد انتظار فرآیند در زمان نهایی، احتمال اینکه یک مسیر نمونه از قبل به بالاتر از مقدار خاصی برسد را کنترل میکند. از آنجایی که اثبات از استدلال بسیار مستقیم استفاده می کند، بر خلاف بسیاری از قضایای دیگر در مورد فرآیندهای تصادفی، به هیچ فرض محدود کننده ای در مورد فیلترسازی اساسی یا خود فرآیند نیاز ندارد. در تنظیم زمان پیوسته، پیوستگی راست (یا پیوستگی چپ) مسیرهای نمونه مورد نیاز است، اما فقط به این دلیل که بدانیم مقدار فوقالعاده یک مسیر نمونه با مقدار فوقالعاده یک زیرمجموعه زمانهای متراکم قابل شمارش دلخواه برابر است.
زمان گسسته [ ویرایش ]
اجازه دهید X 1 ، ...، X n یک زیر مارتینگال زمان گسسته نسبت به یک فیلتر باشد.
نابرابری زیرمارتینگیل [ توضیح لازم است ] این را می گوید
برای هر عدد مثبت C اثبات بر این واقعیت تئوری مجموعه متکی است که رویداد تعریف شده توسط max( Xi ) > C ممکن است به عنوان اتحادیه متفرقه رویدادهای E i که توسط Xi > C و Xj ≤ C برای همه j < i تعریف شده است، تجزیه شود . سپس
با استفاده از خاصیت زیرمارتینگیل برای آخرین نابرابری و این واقعیت که
که واضح تر از نتیجه بیان شده است. با استفاده از این واقعیت ابتدایی که X n ≤ max( X n , 0) , نابرابری زیرمارتینگیل داده شده به دست می آید.
در این اثبات، ویژگی زیرمارتینگیل یک بار به همراه تعریف انتظار شرطی استفاده می شود . [1] همچنین میتوان این اثبات را به زبان فرآیندهای تصادفی بیان کرد تا نتیجهای از این قضیه قدرتمند باشد که یک زیر مارتینگال متوقف شده خود یک زیرمارتینگل است. [2] در این تنظیمات، حداقل شاخص i که در اثبات فوق ظاهر میشود، به عنوان زمان توقف تفسیر میشود .
زمان پیوسته [ ویرایش ]
حال اجازه دهید X t یک زیرمارتینگیل باشد که با بازه [0,T] از اعداد واقعی، نسبت به فیلتر Ft فضای احتمال زیرین نمایه شده است، که به این صورت است :
برای همه s < t . نابرابری زیرمارتینگیل [ توضیحات لازم ] می گوید که اگر مسیرهای نمونه مارتینگل تقریباً مطمئناً راست-پیوسته باشند، پس
برای هر عدد مثبت C این نتیجه نتیجه زمان گسسته فوق است که با نوشتن به دست آمده است
که در آن Q 1 ⊂ Q 2 ⊂ ⋅⋅⋅ هر دنباله ای از مجموعه های متناهی است که اتحاد آن مجموعه همه اعداد گویا باشد. برابری اول نتیجه فرض راست تداوم است، در حالی که برابری دوم صرفاً نظری مجموعه است. نابرابری زمان گسسته برای گفتن آن اعمال می شود
برای هر i ، و این به حدی می رسد که نابرابری زیرمارتینگیل را به دست می دهد. [3] این گذر از زمان گسسته به زمان پیوسته بسیار منعطف است، زیرا فقط به داشتن یک زیرمجموعه متراکم قابل شمارش از [0,T] نیاز دارد، که میتواند به طور خودکار از یک توالی فزاینده از مجموعههای محدود ساخته شود. به این ترتیب، نابرابری زیرمارتینگیل حتی برای مجموعههای شاخص کلیتر، که لازم نیست فواصل یا اعداد طبیعی باشند، برقرار است . [4]
نابرابری های بیشتر [ ویرایش ]
نابرابریهای زیرمارتینگیل بیشتری نیز به دلیل دوب وجود دارد. حال اجازه دهید X t یک مارتینگل یا یک زیرمارتینگیل مثبت باشد. اگر مجموعه شاخص غیرقابل شمارش باشد، (مانند بالا) فرض کنید که مسیرهای نمونه راست-پیوسته هستند. در این سناریوها، نابرابری جنسن دلالت بر این دارد که | X t | p یک زیرمارتینگل برای هر عدد p ≥ 1 است ، مشروط بر اینکه این متغیرهای تصادفی جدید همگی دارای انتگرال محدود باشند. سپس نابرابری زیرمارتینگیل برای گفتن اینکه [5] قابل اعمال است.
برای هر عدد مثبت C در اینجا T زمان نهایی است ، یعنی بزرگترین مقدار مجموعه شاخص. علاوه بر این یکی دارد
اگر p بزرگتر از یک باشد. این که گاهی اوقات به عنوان حداکثر نابرابری دوب شناخته می شود ، نتیجه مستقیم ترکیب نمایش کیک لایه با نابرابری زیرمارتینگیل و نابرابری هلدر است . [6]
علاوه بر نابرابری فوق، وجود دارد [7]
نابرابری های مرتبط [ ویرایش ]
نابرابری دوب برای مارتینگل های گسسته زمان دلالت بر نابرابری کلموگروف دارد : اگر X 1 , X 2 , ... دنباله ای از متغیرهای تصادفی مستقل با ارزش واقعی باشد که هر کدام دارای میانگین صفر هستند، واضح است که
بنابراین S n = X 1 + ... + X n یک مارتینگل است. توجه داشته باشید که نابرابری جنسن دلالت بر این دارد که |S n | اگر S n یک مارتینگل باشد یک زیرمارتینگل غیرمنفی است. بنابراین، با گرفتن p = 2 در نابرابری مارتینگل دوب،
که دقیقاً بیانیه نابرابری کولموگروف است. [8]
کاربرد: حرکت براونی [ ویرایش ]
فرض کنید B حرکت براونی یک بعدی متعارف را نشان دهد . سپس [9]
اثبات دقیقاً به شرح زیر است: از آنجایی که تابع نمایی به طور یکنواخت در حال افزایش است، برای هر λ غیر منفی،
با نابرابری دوب، و از آنجایی که نمایی حرکت براونی یک زیر مارتینگال مثبت است،
از آنجایی که سمت چپ به λ بستگی ندارد ، λ را برای به حداقل رساندن سمت راست انتخاب کنید: λ = C / T نابرابری مورد نظر را نشان می دهد.
منابع
https://en.wikipedia.org/wiki/دوب%27s_martingale_inequality
از ویکیپدیا، دانشنامه آزاد
در تحلیل واقعی و تئوری اندازه گیری ، قضیه همگرایی ویتالی ، که به نام ریاضیدان ایتالیایی جوزپه ویتالی نامگذاری شده است ، تعمیم قضیه همگرایی غالب معروف هانری لبگ است . این توصیفی از همگرایی در L p از نظر همگرایی در اندازه گیری و شرایط مربوط به انتگرال یکنواخت است .
تعاریف اولیه [ ویرایش ]
اجازه دهید
![{\displaystyle \mu :{\mathcal {A}}\to [0,\infty ]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/4998756e4cf75020b264007108ec2d50f0842e08)





- مجموعه ای از توابع
یکنواخت انتگرال پذیر نامیده می شود اگر
، یعنی
.
- مجموعه ای از توابع
گفته می شود که دارای انتگرال های یکنواخت مطلقاً پیوسته است اگر
، یعنی
. این تعریف گاهی اوقات به عنوان تعریفی از انتگرال یکنواخت استفاده می شود. با این حال، با تعریف انتگرال یکنواخت ارائه شده در بالا متفاوت است.
چه زمانی



مورد اندازه گیری محدود [ ویرایش ]
اجازه دهید




و
همگرا می شود
که در
;
- توالی توابع
همگرا می شود
-اندازه گیری به
و
به طور یکنواخت قابل ادغام است.
برای اثبات، به تک نگاری بوگاچف "نظریه اندازه گیری، جلد اول" مراجعه کنید. [1]
مورد اندازه گیری بی نهایت [ ویرایش ]
اجازه دهید






- توالی توابع
همگرا می شود
-اندازه گیری به
;
دارای انتگرالهای کاملاً پیوسته یکنواخت است.
- برای هر
، وجود دارد
به طوری که
و
چه زمانی


برعکس قضیه [ ویرایش ]
اجازه دهید








چه زمانی

برای اثبات، به تک نگاری بوگاچف "نظریه اندازه گیری، جلد اول" مراجعه کنید. [1]
https://en.wikipedia.org/wiki/Vitali_convergence_theorem
از ویکی پدیا، دانشنامه آزاد
در ریاضیات، انتگرال یکنواخت یک مفهوم مهم در آنالیز حقیقی ، آنالیز تابعی و تئوری اندازه گیری است و نقشی حیاتی در نظریه مارتینگال ایفا می کند .
تعریف نظری اندازه گیری [ ویرایش ]
انتگرال یکنواخت، بسط مفهوم خانواده ای از توابع است که در آنها تسلط دارند
تعریف الف: فرض کنید




هر زمان که
تعریف A برای فضاهای اندازه گیری بی نهایت محدود کننده است. تعریف کلی تر [3] از انتگرال یکنواخت که در فضاهای اندازه گیری کلی به خوبی کار می کند توسط GA Hunt معرفی شد .
تعریف H: فرض کنید

جایی که
برای فضاهای اندازه گیری محدود، نتیجه زیر [4] از تعریف H به دست می آید:
قضیه 1: اگر

بسیاری از کتاب های درسی احتمال، قضیه 1 را به عنوان تعریف انتگرال یکنواخت در فضاهای احتمال ارائه می کنند. زمانی که فضا

قضیه 2: فرض کنید








به ویژه، هم ارزی تعاریف A و H برای معیارهای محدود بلافاصله از قضیه 2 به دست می آید. برای این مورد، عبارت در تعریف A با گرفتن به دست می آید
تعریف احتمال [ ویرایش ]
در تئوری احتمال، تعریف A یا عبارت قضیه 1 اغلب به عنوان تعاریف انتگرال یکنواخت با استفاده از انتظار نمادگذاری متغیرهای تصادفی ارائه می شود.، [5] [6] [7] یعنی،
1. یک کلاس
- محدود وجود دارد
به طوری که برای هر
که در
،
و
- برای هر
وجود دارد
به طوری که برای هر قابل اندازه گیری
به طوری که
و هر
که در
،
.
یا به طور متناوب
2. یک کلاس





سفتی و انتگرال یکنواخت [ ویرایش ]
یکی از پیامدهای انتگرال یکنواخت یک کلاس





با این حال، این بدان معنا نیست که خانواده 

پیوسگی مطلق یکنواخت [ ویرایش ]
مفهوم دیگری از یکنواختی وجود دارد که کمی متفاوت از انتگرال یکنواخت است که در نظریه احتمالات و اندازه گیری نیز کاربردهای زیادی دارد و برای داشتن انتگرال محدود به متغیرهای تصادفی نیاز ندارد [9]
تعریف: فرض کنید(




![{\displaystyle E[|X|I_{A}]<\varepsilon }](https://wikimedia.org/api/rest_v1/media/math/render/svg/e66a7b637eb75ac43d6b73033d07eda01732400b)

اگر اندازه گیری محدود باشد و اتم نداشته باشد، معادل انتگرال یکنواخت است.
اصطلاح «پیوستگی مطلق یکنواخت» استاندارد نیست، [ نیازمند منبع ] اما توسط برخی نویسندگان استفاده می شود. [10] [11]
نتایج مرتبط [ ویرایش ]
نتایج زیر برای تعریف احتمالی کاربرد دارد. [12]
- تعریف 1 را می توان با در نظر گرفتن محدودیت ها بازنویسی کرد
- یک دنباله غیر UI. فرض کنید
، و تعریف کنید
،در غیر این صورت.
به وضوح
، و در واقع ،
برای همه n . با این حال،
و در مقایسه با تعریف 1، مشاهده می شود که پیوستگی به طور یکنواخت انتگرال پذیر نیست.
پیوستگیغیر UI از RV ها. مساحت زیر نوار همیشه برابر با 1 است،
- با استفاده از تعریف 2 در مثال بالا، می توان دریافت که بند اول به این صورت برآورده شده است.1
هنجار همه
هستند یعنی محدود شده اند. اما بند دوم آنطور که گفته شد برقرار نیست
مثبت، یک فاصله وجود دارد
با اندازه کمتر از
و
برای همه
.
- اگر
یک متغیر تصادفی UI است ، با تقسیم
و با محدود کردن هر یک از این دو، می توان دید که یک متغیر تصادفی یکنواخت انتگرال پذیر همیشه در محدود می شود1
.
- اگر دنباله ای از متغیرهای تصادفی باشد
تحت سلطه یک انتگرال پذیر، غیر منفی است
: یعنی برای همه ω و n ،
سپس کلاس
از متغیرهای تصادفی
به طور یکنواخت انتگرال پذیر است.
- کلاسی از متغیرهای تصادفی محدود شده در
(
) به طور یکنواخت انتگرال پذیر است.
قضایای مربوط [ ویرایش ]
در ادامه از چارچوب احتمالی استفاده می کنیم، اما صرف نظر از متناهی اندازه گیری، با اضافه کردن شرط کرانه در زیر مجموعه انتخاب شده1()
- قضیه دانفورد - پتیس [13] [14]یک کلاس [ توضیح لازم ] از متغیرهای تصادفی
اگر و تنها در صورتی که برای توپولوژی ضعیف نسبتا فشرده باشد، به طور یکنواخت انتگرال پذیر است
. [ توضیحات لازم است ] [ نیازمند منبع ]
- قضیه د لا واله پوسین [15] [16]خانواده
اگر و تنها در صورتی که تابع محدب فزاینده غیر منفی وجود داشته باشد، به طور یکنواخت انتگرال پذیر است
به طوری که
ارتباط با همگرایی متغیرهای تصادفی [ ویرایش ]
مقاله اصلی: همگرایی متغیرهای تصادفی
یک 



https://en.wikipedia.org/wiki/Uniform_integrability
از ویکیپدیا، دانشنامه آزاد
در تئوری اندازه گیری ، قضیه همگرایی مسلط لبگ شرایط کافی را فراهم می کند که تحت آن تقریباً در همه جا همگرایی دنباله ای از توابع متضمن همگرایی در هنجار L 1 است . قدرت و کاربرد آن دو مزیت نظری اولیه انتگرال لبگ نسبت به انتگرال ریمان است .
علاوه بر ظاهر مکرر آن در تجزیه و تحلیل ریاضی و معادلات دیفرانسیل جزئی، به طور گسترده ای در نظریه احتمال استفاده می شود ، زیرا شرایط کافی برای همگرایی مقادیر مورد انتظار متغیرهای تصادفی را فراهم می کند .
بیانیه [ ویرایش ]
قضیه همگرایی غالب لبگ. [1] اجازه دهید



برای همه اعداد n در مجموعه شاخص دنباله و همه نقاط
که همچنین دلالت دارد
نکته 1. عبارت " g قابل انتگرال است" به معنای آن تابع قابل اندازه گیری است
نکته 2. همگرایی دنباله و غلبه توسط


تبصره 3. اگر

تبصره 4. در حالی که
![[0,1]](https://wikimedia.org/api/rest_v1/media/math/render/svg/738f7d23bb2d9642bab520020873cccbef49768d)


اثبات [ ویرایش ]
بدون از دست دادن کلیت ، می توان فرض کرد که f حقیقی است، زیرا می توان f را به بخش های حقیقی و موهومی آن تقسیم کرد (به یاد داشته باشید که دنباله ای از اعداد مختلط همگرا می شوند اگر و فقط اگر همتایان حقیقی و موهومی آن همگرا شوند) و نابرابری مثلث را اعمال کنید. در پایان.
قضیه همگرایی غالب لبگ یک مورد خاص از قضیه فاتو-لبگ است . با این حال، در زیر یک دلیل مستقیم وجود دارد که از لم فاتو به عنوان ابزار ضروری استفاده می کند.
از آنجایی که f حد نقطهای دنباله ( fn ) توابع قابل اندازهگیری است که تحت تسلط g هستند ، همچنین قابل اندازهگیری و تحت تسلط g است ، بنابراین انتگرالپذیر است. علاوه بر این، (اینها بعدا مورد نیاز خواهند بود)،
برای همه n و
دومی از اینها به طور پیش پا افتاده درست است (با همان تعریف f ). با استفاده از خطی بودن و یکنواختی انتگرال لبگ
توسط لم معکوس Fatou (در اینجا است که ما از این حقیقیت استفاده می کنیم که | f − f n | در بالا توسط یک تابع انتگرال پذیر محدود شده است)
که دلالت بر این دارد که حد وجود دارد و ناپدید می شود
در نهایت، از آن زمان
ما آن را داریم
حال این قضیه دنبال می شود.
اگر مفروضات فقط μ-تقریباً در همه جا برقرار باشند، پس یک مجموعه μ-تهی N ∈ Σ وجود دارد به طوری که توابع f n 1 S \ N مفروضات را در همه جای S برآورده می کنند . سپس تابع f ( x ) که به عنوان حد نقطهای f n ( x ) برای x ∈ S \ N و با f ( x ) = 0 برای x ∈ N تعریف شده است، قابل اندازهگیری است و حد نقطهای این دنباله تابع تغییر یافته است. مقادیر این انتگرالها تحت تأثیر این تغییرات انتگرالهای این مجموعه تهی N قرار نمیگیرند ، بنابراین قضیه همچنان پابرجاست.
DCT پابرجاست حتی اگر f n از نظر اندازه به f همگرا شود (اندازه محدود) و تابع غالب تقریباً در همه جا غیر منفی است.
بحث در مورد مفروضات [ ویرایش ]
این فرض که توالی تحت سلطه مقداری g قابل انتگرال است را نمی توان نادیده گرفت. این را می توان به صورت زیر مشاهده کرد: f n ( x ) = n را برای x در بازه ( 0, 1/ n ] تعریف کنید و در غیر این صورت f n ( x ) = 0 را تعریف کنید . = sup n f n توجه کنید
با واگرایی سری هارمونیک . از این رو، یکنواختی انتگرال لبگ به ما می گوید که هیچ تابع انتگرال پذیری وجود ندارد که بر دنباله در [0،1] مسلط باشد. یک محاسبه مستقیم نشان می دهد که انتگرال و محدودیت نقطه ای برای این دنباله جابجا نمی شوند:
زیرا حد نقطه ای دنباله تابع صفر است . توجه داشته باشید که دنباله ( fn ) حتی به طور یکنواخت انتگرالپذیر نیست ، بنابراین قضیه همگرایی Vitali نیز قابل اجرا نیست.
قضیه همگرایی محدود [ ویرایش ]
یکی از پیامدهای قضیه همگرایی غالب، قضیه همگرایی محدود است ، که بیان میکند که اگر ( fn ) دنبالهای از توابع قابل اندازهگیری با مقدار مختلط محدود یکنواخت است که به صورت نقطهای در فضای اندازهگیری محدود ( S , Σ, μ) همگرا میشود (یعنی یک که در آن μ( S ) متناهی است) به یک تابع f ، سپس حد f یک تابع انتگرال پذیر است و
نکته: همگرایی نقطهای و مرز یکنواخت دنباله را میتوان برای حفظ تنها μ- تقریباً در همه جا آرام کرد ، مشروط بر اینکه فضای اندازهگیری ( S ، Σ، μ) کامل باشد یا f بهعنوان یک تابع قابل اندازهگیری انتخاب شود که μ-تقریباً در همه جا موافق است. μ- تقریباً در همه جا حد نقطه ای موجود است.
اثبات [ ویرایش ]
از آنجایی که دنباله به طور یکنواخت محدود است، یک عدد حقیقی M وجود دارد به طوری که | f n ( x )| ≤ M برای همه x ∈ S و برای همه n . g ( x ) = M را برای تمام x ∈ S تعریف کنید . سپس توالی تحت تسلط g است . علاوه بر این، g انتگرالپذیر است زیرا یک تابع ثابت در مجموعه ای از اندازه گیری های محدود است. بنابراین، نتیجه از قضیه همگرایی غالب به دست می آید.
اگر مفروضات فقط μ-تقریباً در همه جا برقرار باشند، پس یک مجموعه μ-تهی N ∈ Σ وجود دارد به طوری که توابع f n 1 S \ N مفروضات را در همه جای S برآورده می کنند .
همگرایی غالب در فضاهای L p (نتیجه) [ ویرایش ]
اجازه دهید




دنباله را فرض کنید






سپس همه





ایده اثبات: قضیه اصلی را به دنباله تابع اعمال کنید

برنامه های افزودنی [ ویرایش ]
قضیه همگرایی غالب برای توابع قابل اندازهگیری با مقادیر در فضای باناخ نیز اعمال میشود ، با اینکه تابع غالب همچنان غیرمنفی و انتگرالپذیر است. فرض همگرایی تقریباً در همه جا می تواند تضعیف شود و فقط نیاز به همگرایی در اندازه باشد .
قضیه همگرایی غالب در مورد انتظارات مشروط نیز کاربرد دارد. [2]
همچنین ببینید [ ویرایش ]
- همگرایی متغیرهای تصادفی ، همگرایی در میانگین
- قضیه همگرایی یکنواخت (نیازی به تسلط تابع انتگرال پذیر نیست، بلکه یکنواختی دنباله را در نظر می گیرد)
- لم شفه
- یکپارچگی یکنواخت
- قضیه همگرایی ویتالی (تعمیم قضیه همگرایی غالب لبگ)
یادداشت ها
منبع
https://en.wikipedia.org/wiki/Dominated_convergence_theorem
از ویکیپدیا، دانشنامه آزاد
در ریاضیات ، به طور خاص در حساب دیفرانسیل و انتگرال چند متغیره ، قضیه تابع ضمنی [a] ابزاری است که به روابط اجازه می دهد تا به توابع چندین متغیر حقیقی تبدیل شوند . این کار را با نمایش رابطه به عنوان نمودار یک تابع انجام می دهد . ممکن است یک تابع واحد وجود نداشته باشد که نمودار آن بتواند کل رابطه را نشان دهد، اما ممکن است چنین تابعی در محدودیت دامنه رابطه وجود داشته باشد. قضیه تابع ضمنی شرط کافی برای اطمینان از وجود چنین تابعی را می دهد.
به طور دقیق تر، با توجه به سیستمی از m معادلات f i ( x 1 , ..., x n , y 1 , ..., y m ) = 0, i = 1, ..., m (اغلب به اختصار F ( x , y ) = 0 )، این قضیه بیان می کند که، تحت شرایط ملایم در مشتقات جزئی (با توجه به هر y i ) در یک نقطه، m متغیرهای y i توابع مشتق پذیر x j در برخی موارد هستند.همسایگی نقطه از آنجایی که این توابع به طور کلی نمی توانند به صورت بسته بیان شوند ، آنها به طور ضمنی توسط معادلات تعریف می شوند و این انگیزه نام قضیه است. [1]
به عبارت دیگر، در شرایط ملایم در مشتقات جزئی، مجموعه صفرهای یک سیستم معادلات به صورت محلی نمودار یک تابع است.
تاریخچه [ ویرایش ]
آگوستین-لوئیس کوشی (1789-1857) اولین شکل دقیق قضیه تابع ضمنی است. اولیس دینی (1845-1918) نسخه متغیر حقیقی قضیه تابع ضمنی را به بافت توابع هر تعداد متغیر حقیقی تعمیم داد. [2]
مثال اول [ ویرایش ]
دایره واحد را می توان به عنوان منحنی سطح f ( x , y ) = 1 تابع f ( x , y ) = x 2 + y 2 تعیین کرد. در اطراف نقطه A، y را می توان به عنوان یک تابع y ( x ) بیان کرد. در این مثال می توان این تابع را به صورت واضح نوشت;
اگر تابع f ( x , y ) = x 2 + y 2 را تعریف کنیم ، آنگاه معادله f ( x , y ) = 1 دایره واحد را به عنوان مجموعه سطح {( x , y ) | f ( x , y ) = 1} . هیچ راهی برای نمایش دایره واحد به عنوان نمودار تابعی از یک متغیر y = g ( x ) وجود ندارد زیرا برای هر انتخاب x ∈ (-1, 1)، دو گزینه از y وجود دارد ، یعنی
با این حال، می توان بخشی از دایره را به عنوان نمودار یک تابع از یک متغیر نشان داد. اگر اجازه دهیم

هدف از قضیه تابع ضمنی این است که به ما بگوید که توابعی مانند g 1 ( x ) و g 2 ( x ) تقریبا همیشه وجود دارند، حتی در شرایطی که نمی توانیم فرمول های صریح را بنویسیم. این تضمین می کند که g 1 ( x ) و g 2 ( x ) مشتق پذیر هستند و حتی در شرایطی که فرمولی برای f ( x , y ) نداریم کار می کند .
تعاریف [ ویرایش ]
اجازه دهید








همانطور که در بالا ذکر شد، این ممکن است همیشه امکان پذیر نباشد. بنابراین ما یک نکته را رفع می کنیم












برای بیان قضیه تابع ضمنی، به ماتریس ژاکوبین نیاز داریم



جایی که







بیان قضیه [ ویرایش ]
اجازه دهید





![{\displaystyle J_{f,\mathbf {y} }(\mathbf {a} ,\mathbf {b} )=\left[{\frac {\partial f_{i}}{\partial y_{j}}} (\mathbf {a} ,\mathbf {b} )\right]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/23fa28aac64bb9a2ec05d198291b291cfc040c4e)





![{\displaystyle J_{f,\mathbf {x} }(\mathbf {a} ,\mathbf {b} )=\left[{\frac {\partial f_{i}}{\partial x_{j}}} (\mathbf {a}،\mathbf {b})\راست]،}](https://wikimedia.org/api/rest_v1/media/math/render/svg/5dca6d13ba18d76dd877c869803e9575ca7f91b3)


مشتقات بالاتر [ ویرایش ]
اگر علاوه بر این،





اثبات مورد دو بعدی [ ویرایش ]
فرض کنید


قضیه - اگر




اثبات از آنجایی که F مشتق پذیر است، دیفرانسیل F را از طریق مشتقات جزئی می نویسیم:
از آنجایی که ما محدود به حرکت در منحنی هستیمداف=0





اکنون ما به دنبال راه حلی برای این ODE در یک بازه باز در اطراف نقطه هستیم

از این می دانیم که

مثال دایره [ ویرایش ]
اجازه دهید به مثال دایره واحد برگردیم . در این مورد n = m = 1 و
بنابراین، در اینجا، Y در بیان قضیه فقط عدد 2 b است. نقشه خطی تعریف شده توسط آن معکوس است اگر و فقط اگر b ≠ 0 باشد. با قضیه تابع ضمنی می بینیم که می توانیم به صورت محلی دایره را به شکل y = g ( x ) برای تمام نقاطی که y ≠ 0 بنویسیم . همانطور که قبلا ذکر شد برای (±1، 0) با مشکل مواجه می شویم. قضیه تابع ضمنی را میتوان با نوشتن x بهعنوان تابعی از y ، به این دو نقطه نیز اعمال کرد، یعنی:

مشتق ضمنی y نسبت به x و مشتق x نسبت به y را می توان با تمایز کامل تابع ضمنی یافت.


کاربرد: تغییر مختصات [ ویرایش ]
فرض کنید یک فضای m بعدی داریم که با مجموعه ای از مختصات پارامتر شده است










![{\displaystyle (Df)(a,b)=\left[{\begin{matrix}-1&\cdots &0\\\vdots &\ddots &\vdots \\0&\cdots &-1\end{matrix}} \left|{\begin{matrix}{\frac {\partial h_{1}}{\partial x_{1}}}(b)&\cdots &{\frac {\partial h_{1}}{\partial x_{m}}}(b)\\\vdots &\ddots &\vdots \\{\frac {\partial h_{m}}{\partial x_{1}}}(b)&\cdots &{\ frac {\partial h_{m}}{\partial x_{m}}}(b)\\\end{matrix}}\right.\right]=[-I_{m}|J].}](https://wikimedia.org/api/rest_v1/media/math/render/svg/1ecb08835787c4ce30095f49de340414e7202bdc)


مثال: مختصات قطبی [ ویرایش ]
به عنوان یک کاربرد ساده از موارد فوق، صفحه را در نظر بگیرید که توسط مختصات قطبی ( R , θ ) پارامتر شده است. ما می توانیم با تعریف توابع x ( R , θ ) = R cos( θ ) و y ( R , θ ) = R sin( θ ) به یک سیستم مختصات جدید ( مختصات دکارتی ) برویم . این امر با توجه به هر نقطه ( R , θ ) امکان یافتن مختصات دکارتی متناظر ( x ,y ) . چه زمانی می توانیم به عقب برگردیم و دکارتی را به مختصات قطبی تبدیل کنیم؟ در مثال قبلی کافی است که det J ≠ 0 با

کلیات [ ویرایش ]
نسخه باناخ space [ ویرایش ]
بر اساس قضیه تابع معکوس در فضاهای باناخ ، می توان قضیه تابع ضمنی را به نگاشتهای با ارزش فضایی باناخ گسترش داد. [5] [6]
اجازه دهید X ، Y ، Z فضاهای باناخ باشند . اجازه دهید نگاشت f : X × Y → Z به طور پیوسته Fréchet متمایزپذیر باشد. اگر



توابع ضمنی از توابع غیر مشتق پذیر [ ویرایش ]
اشکال مختلفی از قضیه تابع ضمنی برای مواردی وجود دارد که تابع f مشتق پذیر نباشد. استاندارد است که یکنواختی شدید محلی در یک بعد کافی است. [7] شکل کلی تر زیر توسط کوماگای بر اساس مشاهدات جیتورنتروم اثبات شد. [8] [9]
یک تابع پیوسته را در نظر بگیرید








همچنین ببینید [ ویرایش ]
- قضیه تابع معکوس
- قضیه رتبه ثابت : هم قضیه تابع ضمنی و هم قضیه تابع معکوس را می توان به عنوان موارد خاصی از قضیه رتبه ثابت دید.
منبع
https://en.wikipedia.org/wiki/Implicit_function_theorem
توزیع ها، تک بعدی [ ویرایش ]
تبدیل فوریه در این جدول را می توان در Erdélyi (1954) یا Kammler (2000 ، ضمیمه) یافت.
| عملکرد | تبدیل فوریه فرکانس واحد، معمولی | تبدیل فوریه فرکانس واحد، زاویه ای | تبدیل فوریه فرکانس غیر واحدی و زاویه ای | ملاحظات | |
|---|---|---|---|---|---|
 |  |  |  | ||
| 301 |  |  |  |  | توزیع δ ( ξ ) نشان دهنده تابع دلتای دیراک است . |
| 302 |  |  |  |  | قانون دوگانه 301. |
| 303 |  |  |  |  | این از 103 و 301 به دست می آید. |
| 304 |  |  |  |  | این از قوانین 101 و 303 با استفاده از فرمول اویلر نتیجه می گیرد : |
| 305 |  |  |  |  | این از 101 و 303 استفاده می شود |
| 306 |  |  |  |  | این از 101 و 207 استفاده می شود |
| 307 |  |  |  |  | این از 101 و 207 استفاده می شود |
| 308 |  |  |  |  | در اینجا n یک عدد طبیعی و δ ( n ) ( ξ ) n امین مشتق توزیع تابع دلتای دیراک است. این قانون از قوانین 107 و 301 ناشی می شود. با ترکیب این قانون با 101، می توانیم همه چند جمله ای ها را تبدیل کنیم . |
 |  |  |  | دوگانه قانون 308. δ ( n ) ( ξ ) N امین مشتق توزیع تابع دلتای دیراک است. این قانون از 106 و 302 پیروی می کند. | |
| 309 |  |  |  |  | در اینجا sgn( ξ ) تابع علامت است . توجه داشته باشید که1/ایکستوزیع نیست هنگام آزمایش در برابر توابع شوارتز ، استفاده از مقدار اصلی کوشی ضروری است . این قانون در مطالعه تبدیل هیلبرت مفید است . |
| 310 |  |  |  |  | 1/x nتوزیع همگنی است که توسط مشتق توزیعی تعریف می شود |
| 311 |  |  |  |  | این فرمول برای 0 > α > -1 معتبر است . برای α > 0 برخی از اصطلاحات مفرد در مبدأ به وجود می آیند که می توان آنها را با تمایز 318 پیدا کرد. اگر Re α > -1 ، آنگاه | x | α یک تابع قابل ادغام محلی است و بنابراین یک توزیع معتدل است. تابع α ↦ | x | α یک تابع هولومورفیک از نیم صفحه سمت راست تا فضای توزیعهای معتدل است. این یک بسط مرومورفیک منحصربهفرد را به یک توزیع معتدل میپذیرد که با علامت | نیز مشخص میشود x | α برای α ≠ -1، -3، ... (نگاه کنید بهتوزیع همگن .) |
 |  |  |  | مورد ویژه 311. | |
| 312 |  |  |  |  | قانون دوگانه 309. این بار تبدیل فوریه باید به عنوان یک مقدار اصلی کوشی در نظر گرفته شود . |
| 313 |  |  |  |  | تابع u ( x ) تابع مرحله واحد Heaviside است . این از قوانین 101، 301 و 312 ناشی می شود. |
| 314 |  |  |  |  | این تابع به عنوان تابع شانه دیراک شناخته می شود. این نتیجه را می توان از 302 و 102 به دست آورد، همراه با این واقعیت که به عنوان توزیع |
| 315 |  |  |  |  | تابع J 0 ( x ) تابع بسل مرتبه صفر از نوع اول است. |
| 316 |  |  |  |  | این یک تعمیم 315 است. تابع J n ( x ) تابع بسل مرتبه n از نوع اول است. تابع T n ( x ) چند جمله ای چبیشف از نوع اول است . |
| 317 |  |  |  |  | γ ثابت اویلر- ماسکرونی است . استفاده از انتگرال قسمت محدود هنگام آزمایش ضروری است1/| ξ |،1/| ω |،1/| ν |در برابر توابع شوارتز جزئیات این ممکن است ضریب تابع دلتا را تغییر دهد. |
| 318 |  |  |  |  | این فرمول برای 1 > α > 0 معتبر است . از تمایز برای استخراج فرمول برای توان های بالاتر استفاده کنید. u تابع Heaviside است. |
منبع
https://en.wikipedia.org/wiki/Fourier_transform
جداول تبدیل فوریه مهم [ ویرایش ]
جداول زیر برخی از تبدیل های فوریه به شکل بسته را ثبت می کنند. برای توابع f ( x ) ، g ( x ) و h ( x ) تبدیل فوریه خود را به ترتیب با f̂ ، ĝ و ĥ نشان می دهند. فقط سه قرارداد متداول گنجانده شده است. توجه به این نکته ممکن است مفید باشد که مدخل 105 رابطه ای بین تبدیل فوریه یک تابع و تابع اصلی به دست می دهد که می تواند به عنوان ارتباط بین تبدیل فوریه و معکوس آن دیده شود.
روابط عملکردی، تک بعدی [ ویرایش ]
تبدیل فوریه در این جدول را می توان در Erdélyi (1954) یا Kammler (2000 ، ضمیمه) یافت.
| عملکرد | تبدیل فوریه فرکانس واحد، معمولی | تبدیل فوریه فرکانس واحد، زاویه ای | تبدیل فوریه فرکانس غیر واحدی و زاویه ای | ملاحظات | |
|---|---|---|---|---|---|
 |  |  |  | تعریف | |
| 101 |  |  |  |  | خطی بودن |
| 102 |  |  |  |  | تغییر در حوزه زمانی |
| 103 |  |  |  |  | تغییر در حوزه فرکانس، دوتایی 102 |
| 104 |  |  |  |  | مقیاس بندی در حوزه زمان اگر | یک | بزرگ است، سپس f ( ax ) در اطراف 0 متمرکز شده است و پخش می شود و صاف می شود. |
| 105 |  |  |  |  | ثنویت. در اینجا f̂ باید با استفاده از همان روش ستون تبدیل فوریه محاسبه شود. نتایج حاصل از تعویض متغیرهای "ساختگی" x و ξ یا ω یا ν . |
| 106 |  |  |  |  | زیرا f تابع شوارتز است |
| 107 |  |  |  |  | این دوگانه 106 است |
| 108 |  |  |  |  | نماد f ∗ g نشان دهنده انحراف f و g است - این قاعده قضیه کانولوشن است |
| 109 |  |  |  |  | این دوگانه 108 است |
| 110 | برای f ( x ) کاملا واقعی |  |  |  | تقارن هرمیتی z مزدوج مختلط را نشان می دهد . |
| 111 | برای f ( x ) کاملا واقعی و زوج | f̂ ( ξ ) , f̂ ( ω ) و f̂ ( ν ) توابع زوج کاملا واقعی. | |||
| 112 | برای f ( x ) کاملا واقعی و فرد | f̂ ( ξ ) , f̂ ( ω ) و f̂ ( ν ) توابع فرد کاملاً خیالی هستند . | |||
| 113 | برای f ( x ) کاملاً خیالی |  |  |  | z مزدوج مختلطرا نشان می دهد. |
| 114 |  |  |  |  | صرف مختلط ، تعمیم 110 و 113 |
| 115 |  |  |  |  | این از قوانین 101 و 103 با استفاده از فرمول اویلر نتیجه می گیرد : |
| 116 |  |  |  |  | این از 101 و 103 با استفاده از فرمول اویلر به دست می آید : |
توابع ادغامپذیر مربع، تک بعدی [ ویرایش ]
تبدیل فوریه در این جدول را می توان در Campbell & Foster (1948) ، Erdélyi (1954) یا Kammler (2000 ، ضمیمه) یافت.
| عملکرد | تبدیل فوریه فرکانس واحد، معمولی | تبدیل فوریه فرکانس واحد، زاویه ای | تبدیل فوریه فرکانس غیر واحدی و زاویه ای | ملاحظات | |
|---|---|---|---|---|---|
 |  |  |  | ||
| 201 |  |  |  |  | پالس مستطیلی و تابع sinc نرمال شده که در اینجا به صورت sinc( x ) = تعریف می شودگناه (π x )/π x |
| 202 |  |  |  |  | قانون دوگانه 201. تابع مستطیل شکل یک فیلتر پایین گذر ایده آل است و تابع sinc پاسخ ضربه غیر علّی چنین فیلتری است. تابع sinc در اینجا به صورت sinc( x ) = تعریف می شود sin (π x )/π x |
| 203 |  |  |  |  | تابع tri( x ) تابع مثلثی است |
| 204 |  |  |  |  | قانون دوگانه 203. |
| 205 |  |  |  |  | تابع u ( x ) تابع مرحله واحد Heaviside و a > 0 است. |
| 206 |  |  |  |  | این نشان میدهد که برای تبدیلهای فوریه واحد، تابع گاوسی e - αx 2 تبدیل فوریه خودش برای انتخابی از α است. برای انتگرال پذیری آن باید Re( α ) > 0 داشته باشیم . |
| 207 |  |  |  |  | این به عنوان سینوسی فاز دوم پیچیده یا تابع "چیپ" شناخته می شود. [53] |
| 208 |  |  |  |  | برای Re( a ) > 0 . یعنی تبدیل فوریه یک تابع نمایی در حال فروپاشی دو طرفه یک تابع لورنتسی است . |
| 209 |  |  |  |  | سکانت هایپربولیک تبدیل فوریه خودش است |
| 210 |  |  |  |  | H n چند جمله ای مرتبهn هرمیت است . اگر a = 1 باشد، توابع گاوس-هرمیت، توابع ویژه عملگر تبدیل فوریه هستند. برای اشتقاق، به چند جمله ای هرمیت مراجعه کنید . فرمول برای n = 0 به 206 کاهش می یابد . |
قضیه پلانچرل و قضیه پارسوال [ ویرایش ]
فرض کنید f ( x ) و g ( x ) انتگرال پذیر باشند و f̂ ( ξ ) و ĝ ( ξ ) تبدیل فوریه آنها باشند. اگر f ( x ) و g ( x ) نیز مربع انتگرال پذیر باشند ، فرمول پارسوال به شرح زیر است: [17]
که در آن نوار نشان دهنده صرف پیچیده است .
قضیه پلانچرل که از مطالب فوق نتیجه می گیرد بیان می کند که [18]
قضیه پلانچرل این امکان را فراهم میکند که تبدیل فوریه را با استدلال پیوستگی به یک عملگر واحد در L 2 ( R ) بسط دهیم . در L 1 ( R ) ∩ L 2 ( R ) ، این پسوند با تبدیل فوریه اصلی تعریف شده در L 1 ( R ) مطابقت دارد ، بنابراین دامنه تبدیل فوریه به L 1 ( R ) + L 2 ( R ) بزرگ می شود (و در نتیجه به L p ( R )برای 1 ≤ p ≤ 2 ). قضیه پلانچرل در علوم این تعبیر را دارد که تبدیل فوریه انرژی کمیت اصلی را حفظ می کند. اصطلاحات این فرمول ها کاملاً استاندارد نیست. قضیه پارسوال فقط برای سری فوریه اثبات شد و اولین بار توسط لیاپانوف اثبات شد. اما فرمول پارسوال برای تبدیل فوریه نیز منطقی است، و بنابراین حتی اگر در زمینه تبدیل فوریه توسط پلانچرل ثابت شد، هنوز هم اغلب به عنوان فرمول پارسوال، یا رابطه پارسوال، یا حتی قضیه پارسوال از آن یاد می شود.
دوگانگی Pontryagin را برای فرمول بندی کلی این مفهوم در زمینه گروه های آبلی فشرده محلی ببینید.
فرمول جمع پواسون [ ویرایش ]
مقاله اصلی: فرمول جمع پواسون
فرمول جمع پواسون (PSF) معادله ای است که ضرایب سری فوریه جمع تناوبی یک تابع را به مقادیر تبدیل فوریه پیوسته تابع مرتبط می کند. فرمول جمع پواسون می گوید که برای توابع به اندازه کافی منظم f ،
دارای انواع مختلفی از اشکال مفید است که با استفاده از خواص مقیاسپذیری و تغییر زمان تبدیل فوریه از شکل اصلی به دست میآیند. این فرمول در مهندسی، فیزیک و نظریه اعداد کاربرد دارد. دو دامنه فرکانس فرمول جمع پواسون استاندارد تبدیل فوریه گسسته زمان نیز نامیده می شود .
جمع پواسون به طور کلی با فیزیک محیط های تناوبی مانند هدایت گرما روی یک دایره مرتبط است. جواب اصلی معادله گرما روی یک دایره تابع تتا نامیده می شود . در تئوری اعداد برای اثبات ویژگیهای تبدیل توابع تتا استفاده میشود، که معلوم میشود یک نوع شکل مدولار است ، و به طور کلی به نظریه اشکال اتومورفیک متصل است، جایی که در یک طرف فرمول ردیابی سلبرگ ظاهر میشود .
تمایز [ ویرایش ]
فرض کنید f ( x ) یک تابع کاملاً متمایز پیوسته است و هم f و هم مشتق آن f' قابل انتگرال هستند. سپس تبدیل فوریه مشتق به دست می آید
به طور کلی تر، تبدیل فوریه n امین مشتق f ( n ) با استفاده از
با اعمال تبدیل فوریه و استفاده از این فرمول ها می توان برخی از معادلات دیفرانسیل معمولی را به معادلات جبری تبدیل کرد که حل آنها بسیار آسان تر است. این فرمولها همچنین قاعده کلی را ایجاد میکنند که " f ( x ) صاف است اگر و فقط اگر f̂ ( ξ ) به سرعت به 0 برای | ξ | ∞ ∞ بیفتد ." با استفاده از قوانین مشابه برای تبدیل فوریه معکوس، میتوان گفت: " f ( x ) به سرعت به 0 میافتد برای | x | ∞ اگر و فقط اگر f̂ ( ξ )صاف است."
قضیه کانولوشن [ ویرایش ]
مقاله اصلی: قضیه کانولوشن
تبدیل فوریه بین کانولوشن و ضرب توابع ترجمه می شود. اگر f ( x ) و g ( x ) به ترتیب با تبدیل های فوریه f̂ ( ξ ) و ĝ ( ξ ) توابع انتگرال پذیر باشند، تبدیل فوریه کانولوشن از حاصلضرب تبدیل های فوریه f̂ ( ξ ) و ĝ ( به دست می آید. ξ ) (در سایر قراردادها برای تعریف تبدیل فوریه ممکن است یک عامل ثابت ظاهر شود).
این بدان معنی است که اگر:
که در آن ∗ عملیات پیچیدگی را نشان می دهد، سپس:
در تئوری سیستم خطی زمان ثابت (LTI) ، معمولاً g ( x ) به عنوان پاسخ ضربه یک سیستم LTI با ورودی f ( x ) و خروجی h ( x ) تفسیر میشود ، زیرا تکانه واحد را جایگزین f ( x ) میکنیم. h ( x ) = g ( x ) را به دست می دهد . در این حالت ĝ ( ξ ) نشان دهنده پاسخ فرکانسی سیستم است.
برعکس، اگر f ( x ) را بتوان به عنوان حاصلضرب دو تابع مربعی انتگرال پذیر p ( x ) و q ( x ) تجزیه کرد ، آنگاه تبدیل فوریه f ( x ) با کانولوشن تبدیل های فوریه مربوطه p̂ ( ξ ) به دست می آید. ) و q̂ ( ξ ) .
قضیه همبستگی متقابل [ ویرایش ]
مقاله اصلی: همبستگی متقابل
به روشی مشابه، می توان نشان داد که اگر h ( x ) همبستگی متقابل f ( x ) و g ( x ) باشد :
سپس تبدیل فوریه h ( x ) برابر است با:
به عنوان یک مورد خاص، خودهمبستگی تابع f ( x ) به صورت زیر است:
برای کدام
توابع ویژه [ ویرایش ]
یکی از انتخاب های مهم یک پایه متعارف برای L 2 ( R ) توسط توابع Hermite ارائه شده است.
که در آن He n ( x ) چندجملهای هرمیت " احتمالگرا" هستند که به صورت تعریف میشوند.
تحت این قرارداد برای تبدیل فوریه، ما آن را داریم

به عبارت دیگر، توابع هرمیت یک سیستم متعارف کامل از توابع ویژه برای تبدیل فوریه در L 2 ( R ) را تشکیل می دهند. [14] با این حال، این انتخاب از توابع ویژه منحصر به فرد نیست. تنها چهار مقدار ویژه مختلف از تبدیل فوریه وجود دارد (±1 و ± i ) و هر ترکیب خطی از توابع ویژه با مقدار ویژه یکسان تابع ویژه دیگری را به دست می دهد. در نتیجه، می توان L 2 ( R ) را به صورت مجموع مستقیم چهار فضای H 0 , H 1 , H تجزیه کرد.2 و H 3 که در آن تبدیل فوریه روی He k به سادگی با ضرب در i k عمل می کند.
از آنجایی که مجموعه کامل توابع هرمیت وضوح هویت را ارائه میکند، تبدیل فوریه را میتوان با چنین مجموع عباراتی که با مقادیر ویژه بالا وزن شدهاند، نشان داد و این مجموع را میتوان به صراحت جمع کرد. این رویکرد برای تعریف تبدیل فوریه اولین بار توسط نوربرت وینر انجام شد . [19] در میان ویژگیهای دیگر، توابع هرمیت بهطور تصاعدی در حوزههای فرکانس و زمان کاهش مییابند، و بنابراین از آنها برای تعریف تعمیم تبدیل فوریه، یعنی تبدیل فوریه کسری مورد استفاده در تحلیل زمان-فرکانس استفاده میشود. [20] در فیزیک ، این تبدیل توسط ادوارد کاندون معرفی شد . [21]
ارتباط با گروه هایزنبرگ [ ویرایش ]
گروه هایزنبرگ گروه خاصی از عملگرهای واحد در فضای هیلبرت L 2 ( R ) از توابع مجتمع مربعی با ارزش f روی خط واقعی است که توسط ترجمه های ( T y f ) ( x ) = f ( x + y ) ایجاد می شود. و ضرب در e 2π ixξ , ( M ξ f ) ( x ) = e 2π ixξ f (x ) . این اپراتورها مانند جابجایی (گروهی) آنها رفت و آمد نمی کنند
ضرب در ثابت (مستقل از x ) e 2π iyξ ∈ U (1) ( گروه دایره اعداد مختلط مدول واحد). به عنوان یک گروه انتزاعی، گروه هایزنبرگ گروه سه بعدی سه بعدی Lie ( x , ξ , z ) ∈ R 2 × U (1) با قانون گروه است.
گروه هایزنبرگ را با H 1 نشان دهید . روش بالا نه تنها ساختار گروه، بلکه یک نمایش واحد استاندارد از H1 را در فضای هیلبرت توصیف می کند، که ما آن را با ρ نشان می دهیم : H1 → B ( L2 ( R ) ) . اتومورفیسم خطی R 2 را تعریف کنید
به طوری که J 2 = − I . این J را می توان به یک اتومورفیسم منحصر به فرد H 1 گسترش داد :
طبق قضیه استون-فون نویمان ، نمایش های واحد ρ و ρ ∘j به طور واحد معادل هستند، بنابراین یک درهم تنیده منحصر به فرد W ∈ U ( L 2 ( R ) ) وجود دارد که
این عملگر W تبدیل فوریه است.
بسیاری از خصوصیات استاندارد تبدیل فوریه پیامدهای فوری این چارچوب کلی تر هستند. [22] برای مثال، مربع تبدیل فوریه، W 2 ، یک درهم تنیده مرتبط با J 2 = − I است، و بنابراین داریم ( W 2 f ) ( x ) = f (- x ) بازتابی از تابع اصلی f .
دامنه پیچیده [ ویرایش ]
انتگرال برای تبدیل فوریه
می توان مقادیر مختلط آرگومان ξ را مطالعه کرد. بسته به ویژگیهای f ، این ممکن است اصلاً از محور واقعی همگرا نشود، یا ممکن است به یک تابع تحلیلی پیچیده برای همه مقادیر ξ = σ + iτ یا چیزی در بین آن همگرا شود. [23]
قضیه پیلی-وینر می گوید که f صاف است (یعنی n - بار برای همه اعداد صحیح مثبت n قابل تمایز است ) و به طور فشرده پشتیبانی می شود اگر و فقط اگر f̂ ( σ + iτ ) یک تابع هولومورفیک باشد که برای آن ثابت a > 0 وجود داشته باشد. که برای هر عدد صحیح n ≥ 0 ،
برای مقداری C ثابت (در این مورد، f روی [− a , a ] پشتیبانی میشود .) این را میتوان با گفتن اینکه f̂ یک تابع کامل است که به سرعت در σ کاهش مییابد (برای τ ثابت ) و رشد نمایی در τ (به طور یکنواخت در σ ) کاهش مییابد. ). [24]
(اگر f صاف نباشد، اما فقط L 2 باشد، گزاره همچنان با n = 0 برقرار است. [25] ) فضای چنین توابعی از یک متغیر مختلط ، فضای Paley-Wiener نامیده می شود. این قضیه به گروه های دروغ نیمه ساده تعمیم داده شده است . [26]
اگر f روی نیم خط t ≥ 0 پشتیبانی شود ، آنگاه f را «علت» می گویند زیرا تابع پاسخ ضربه ای یک فیلتر قابل تحقق فیزیکی باید این ویژگی را داشته باشد، زیرا هیچ اثری نمی تواند مقدم بر علت آن باشد. پیلی و وینر نشان دادند که پس از آن ، f به یک تابع هولومورفیک در نیم صفحه پایین پیچیده τ < 0 گسترش مییابد که وقتی τ به سمت بینهایت میرود ، به صفر میرود. [27] عکس آن نادرست است و مشخص نیست که چگونه تبدیل فوریه یک تابع علی را مشخص کنیم. [28]
تبدیل لاپلاس [ ویرایش ]
همچنین ببینید: تبدیل لاپلاس § تبدیل فوریه
تبدیل فوریه f̂ ( ξ ) مربوط به تبدیل لاپلاس F ( s ) است که برای حل معادلات دیفرانسیل و تحلیل فیلترها نیز استفاده می شود .
ممکن است اتفاق بیفتد که تابع f که انتگرال فوریه آن به هیچ وجه روی محور واقعی همگرا نمی شود، با این حال تبدیل فوریه پیچیده ای در ناحیه ای از صفحه مختلط تعریف شده است .
به عنوان مثال، اگر f ( t ) دارای رشد نمایی باشد، به عنوان مثال،
برای برخی از ثابت های C ، a ≥ 0 ، سپس [29]
همگرا برای همه 2π τ < - a ، تبدیل لاپلاس دو طرفه f است.
نسخه معمول تر ("یک طرفه") تبدیل لاپلاس است
اگر f نیز علی و تحلیلی باشد، آنگاه:
از دیدگاهی دیگر، شاید کلاسیکتر، تبدیل لاپلاس از نظر شکل شامل یک عبارت تنظیمکننده نمایی اضافی است که به آن اجازه میدهد خارج از خط خیالی جایی که تبدیل فوریه تعریف میشود، همگرا شود. به این ترتیب، میتواند برای سریها و انتگرالهای بهطور نمایی واگرا همگرا شود، در حالی که تجزیه فوریه اصلی نمیتواند، امکان تجزیه و تحلیل سیستمهای دارای عناصر واگرا یا بحرانی را فراهم میکند. دو نمونه خاص از پردازش سیگنال خطی، ساخت شبکههای فیلتر همهگذر از فیلترهای حساس و کاهشدهنده از طریق لغو دقیق قطب صفر در دایره واحد است. چنین طرحهایی در پردازش صوتی رایج هستند، جایی که پاسخ فاز بسیار غیرخطی مانند Reverb جستجو میشود.
علاوه بر این، زمانی که پاسخهای پالسمانند تمدید شده برای کار پردازش سیگنال جستجو میشوند، سادهترین راه برای تولید آنها داشتن یک مدار است که یک پاسخ زمانی واگرا تولید میکند، و سپس لغو واگرایی آن از طریق پاسخ متضاد و جبرانی تاخیری. در آنجا، فقط مدار تأخیر در بین، توصیف فوریه کلاسیک را می پذیرد که بسیار مهم است. هر دو مدار کناری ناپایدار هستند و تجزیه فوریه همگرا را قبول ندارند. با این حال، آنها یک توصیف دامنه لاپلاس را میپذیرند، با نیمصفحههای همگرایی یکسان در صفحه مختلط (یا در مورد گسسته، صفحه Z)، که در آن اثرات آنها لغو میشود.
در ریاضیات مدرن، تبدیل لاپلاس به طور معمول تحت روش های فوریه قرار می گیرد. هر دوی آنها با ایده بسیار کلی تر و انتزاعی تر تحلیل هارمونیک جمع می شوند.
منبع
https://en.wikipedia.org/wiki/Fourier_transform
تبدیل فوریه برای توابعی که خارج از یک بازه صفر هستند [ ویرایش ]
ارتباط نزدیکی بین تعریف سری فوریه و تبدیل فوریه برای توابع f که خارج از یک بازه صفر هستند وجود دارد. برای چنین تابعی میتوانیم سری فوریه آن را در هر بازهای که شامل نقاطی باشد که f صفر نیست محاسبه کنیم. تبدیل فوریه نیز برای چنین تابعی تعریف شده است. با افزایش طول بازهای که در آن سری فوریه را محاسبه میکنیم، ضرایب سری فوریه شبیه تبدیل فوریه و مجموع سری فوریه f شبیه تبدیل فوریه معکوس میشوند. به طور دقیق تر، فرض کنید T به اندازه کافی بزرگ است که بازه [T/2،T/2-] شامل بازهای است که f صفر نیست. سپس ضریب سری c n به صورت زیر بدست می آید:
از مقایسه این با تعریف تبدیل فوریه، چنین است که:
زیرا f ( x ) در خارج از [- صفر استتی/2،تی/2] . بنابراین، ضرایب فوریه برابر با مقادیر تبدیل فوریه نمونه برداری شده در شبکه ای از عرض است.1/تیضرب در عرض شبکه1/تی.
تحت شرایط مناسب، سری فوریه f برابر با تابع f خواهد بود. به عبارت دیگر، f را می توان نوشت:
که در آن آخرین مجموع به سادگی اولین مجموع است که با استفاده از تعاریف ξ n = بازنویسی شده استn/تیو Δ ξ =n + 1/تی-n/تی=1/تی.
این جمع دوم یک مجموع ریمان است. با اجازه دادن به T → ∞ به انتگرال تبدیل فوریه معکوس همانطور که در بالا بیان شد همگرا می شود. در شرایط مناسب، این استدلال ممکن است دقیق شود. [13]
مثال [ ویرایش ]
شکلهای زیر یک تصویر بصری ارائه میدهند که چگونه تبدیل فوریه، وجود فرکانس در یک تابع خاص را اندازهگیری میکند. تابع نشان داده شده f ( t ) = cos(6π t ) e -π t 2 در 3 هرتز نوسان می کند (اگر t ثانیه را اندازه گیری کند) و به سرعت به 0 میل می کند. (فاکتور دوم در این معادله یک تابع پوششی است که سینوسی پیوسته را شکل می دهد. شکل کلی آن یک تابع گاوسی است ). این تابع به طور ویژه برای داشتن یک تبدیل فوریه حقیقی انتخاب شده است که می تواند به راحتی ترسیم شود. تصویر اول شامل نمودار آن است. به منظور محاسبه

وضعیت کلی ممکن است کمی پیچیدهتر از این باشد، اما از نظر روحی، تبدیل فوریه نشان میدهد که چقدر از یک فرکانس فردی در تابع f ( t ) وجود دارد.
منبع
https://en.wikipedia.org/wiki/Fourier_transform#math_Eq.2
تاریخچه [ ویرایش ]
مقالات اصلی: تحلیل فوریه § تاریخچه و سری فوریه § تاریخ
در سال 1822، فوریه ادعا کرد (نگاه کنید به جوزف فوریه § تئوری تحلیلی گرما ) که هر تابع، خواه پیوسته یا ناپیوسته، می تواند به یک سری سینوس بسط یابد. [10] آن کار مهم توسط دیگران تصحیح و گسترش یافت تا پایه و اساس اشکال مختلف تبدیل فوریه را که از آن زمان استفاده شده است، فراهم کند.
مقدمه [ ویرایش ]
همچنین ببینید: تحلیل فوریه و سری فوریه
تابع f (قرمز) ابتدا به سری فوریه آن تبدیل می شود : مجموع امواج سینوسی (به رنگ آبی). سپس این سینوسی ها در سراسر طیف فرکانس پخش می شوند و به صورت پیک ( توابع دلتای دیراک ) در حوزه فرکانس نشان داده می شوند. نمایش دامنه فرکانس تابع ( f̂ ) مجموعه ای از این پیک ها است.
اگرچه سری فوریه می تواند شکل موج های تناوبی را به عنوان مجموع سینوسی های مرتبط با هارمونیک نشان دهد، سری فوریه نمی تواند شکل موج های غیر تناوبی را نشان دهد. با این حال، تبدیل فوریه قادر است شکل موج های غیر تناوبی را نیز نمایش دهد. این امر با اعمال یک فرآیند محدود کننده برای طولانی کردن دوره هر شکل موج تا بی نهایت و سپس در نظر گرفتن آن به عنوان یک شکل موج دوره ای به دست می آید. [11]
در مطالعه سری فوریه، ضرایب فوریه نشان دهنده دامنه هر سینوسی مرتبط با هماهنگی موجود در سری فوریه تابع تناوبی f است. به طور مشابه، تبدیل فوریه دامنه و فاز هر سینوسی موجود در تابع (احتمالاً غیر تناوبی) f را نشان میدهد .
تبدیل فوریه از یک انتگرال (یا "جمع پیوسته") استفاده می کند که از ویژگی های سینوس و کسینوس برای بازیابی دامنه و فاز هر سینوسی در یک سری فوریه استفاده می کند. تبدیل فوریه معکوس این امواج را با استفاده از یک انتگرال مشابه برای بازتولید تابع اصلی دوباره ترکیب می کند.
استفاده از سینوسی های مختلط برای نمایش سینوس های حقیقی [ ویرایش ]
همچنین ببینید: فرکانس منفی § ساده سازی تبدیل فوریه
برای ساده کردن ریاضی، مطلوب است که سری فوریه را به صورت مجموع نمایی های مختلط بنویسیم (به سری فوریه § شکل نمایی مراجعه کنید ). هر سینوسی مختلط نمایی یا مختلط فرکانس ξ را می توان با استفاده از فرمول اویلر به عنوان مجموع موج کسینوس فرکانس ξ برای مولفه حقیقی به اضافه یک موج سینوسی همچنین فرکانس ξ برای مؤلفه موهومی بیان کرد:
بیان سینوس های حقیقی به صورت سینوسی های مختلط، ضرایب فوریه را ضروری می کند


نشان دادن نمایی مختلط در سه بعدی. مؤلفه حقیقی یک موج کسینوس است. جزء موهومی یک موج سینوسی است. آنها با هم یک مارپیچ را تشکیل می دهند. نفی فرکانس را می توان به عنوان تغییر دستی مارپیچ درک کرد . چرخش با جهت مخالف اما با همان تعداد چرخش در ثانیه.
این نمایی های مختلط ممکن است فرکانس منفی داشته باشند . برای مثال، هر دو سینوسی مختلط e 2π iξx و e -2π iξx یک چرخه را در هر واحد x کامل می کنند، اما اولی نشان دهنده فرکانس مثبت است در حالی که دومی نشان دهنده فرکانس منفی است. فرکانس مثبت را می توان به عنوان چرخش در خلاف جهت عقربه های ساعت در مورد صفحه مختلط درک کرد در حالی که فرکانس منفی را می توان به عنوان چرخش در جهت عقربه های ساعت در مورد صفحه مختلط درک کرد. هنگامی که سینوسی های مختلط به عنوان یک مارپیچ در سه بعدی تفسیر می شوند (با بعد سوم که جزء موهومی است)، نفی فرکانس به سادگی حالت دستی مارپیچ را تغییر می دهد.. [12]
امواج حقیقی سینوسی و کسینوس را می توان از نمایش نمایی مختلط سینوسی ها بازیابی کرد. به عنوان مثال، نتیجه ای از فرمول اویلر اجازه می دهد تا امواج کسینوس و سینوسی را به عنوان بخش حقیقی یا موهومی یک سینوسی مختلط یا به عنوان مجموع وزنی دو سینوسی مختلط با فرکانس مخالف بیان کنیم:
در نتیجه، یک شکل کلی از هر سینوسی حقیقی (با فرکانس ξ ، تغییر فاز θ و دامنه A ) را می توان به صورت مجموع دو سینوسی مختلط با فرکانس مخالف ( ξ و - ξ ) اما قدر مساوی بیان کرد.آ/2) و با تغییر فاز θ که در هر دو ضرایب مختلط آنها تعبیه شده است:
از این رو، هر سینوسی حقیقی (و سیگنال حقیقی) را می توان متشکل از یک فرکانس مثبت و منفی در نظر گرفت که اجزای موهومی آن خنثی می شوند اما اجزای حقیقی آن به طور مساوی در تشکیل سیگنال حقیقی مشارکت دارند.
برای اجتناب از استفاده از اعداد مختلط و فرکانس های منفی، تبدیل های سینوسی و کسینوس با هم می توانند به عنوان شکل جایگزین معادل تبدیل فوریه استفاده شوند.
منبع
https://en.wikipedia.org/wiki/Fourier_transform

از ویکیپدیا، دانشنامه آزاد
در ریاضیات ، قضیه فوکس ، که به نام لازاروس فوکس نامگذاری شده است، بیان میکند که یک معادله دیفرانسیل مرتبه دوم شکل
دارای یک راه حل قابل بیان توسط یک سری فربنیوس تعمیم یافته زمانی که





برای برخی از s حقیقی مثبت راه حل اول است.، یا
برای برخی از r حقیقی مثبت راه حل دوم است.، که در آن y 0 راه حل اول است.
شعاع همگرایی آن حداقل به اندازه حداقل شعاع همگرایی 

همچنین ببینید [ ویرایش ]
منبع
https://en.wikipedia.org/wiki/Fuchs%27_theorem
فانوس شوارتز با



یکی از ظرافتهای مساحت سطح، در مقایسه با طول قوس منحنیها، این است که سطح را نمیتوان به سادگی بهعنوان محدودهای از اشکال چندوجهی که به یک سطح صاف معین تقریب میکنند، تعریف کرد. هرمان شوارتز نشان داد که در حال حاضر برای استوانه، انتخاب های مختلف تقریبی سطوح مسطح می تواند به مقادیر محدود کننده متفاوتی از ناحیه منجر شود. این مثال به عنوان فانوس شوارتز شناخته می شود . [2] [3]
رویکردهای مختلفی برای تعریف کلی سطح در اواخر قرن نوزدهم و اوایل قرن بیستم توسط هنری لبسگو و هرمان مینکوفسکی ارائه شد. در حالی که برای سطوح صاف تکه ای یک مفهوم طبیعی منحصر به فرد از مساحت سطح وجود دارد، اگر سطحی بسیار نامنظم یا ناهموار باشد، ممکن است به هیچ وجه نتوان منطقه ای را به آن اختصاص داد. یک مثال معمولی با سطحی با سنبله هایی که به صورت متراکم در سراسر آن پخش شده اند، ارائه می شود. بسیاری از سطوح از این نوع در مطالعه فراکتال ها رخ می دهد . بسط مفهوم مساحت که تا حدی عملکرد آن را انجام می دهد و ممکن است حتی برای سطوح بسیار نامنظم تعریف شود در تئوری اندازه گیری هندسی مورد مطالعه قرار می گیرد . یک مثال خاص از چنین پسوندی است محتوای سطح مینکوفسکی
فرمول های رایج [ ویرایش ]
همچنین ببینید: فهرست فرمول ها در هندسه ابتدایی
| شکل | معادله | متغیرها |
|---|---|---|
| مکعب |  | s = طول ضلع |
| مکعبی |  | ℓ = طول، b = عرض، h = ارتفاع |
| منشور مثلثی |  | b = طول پایه مثلث، h = ارتفاع مثلث، l = فاصله بین پایه های مثلثی، p , q , r = اضلاع مثلث |
| همه منشورها |  | B = مساحت یک پایه، P = محیط یک پایه، h = ارتفاع |
| کره |  | r = شعاع کره، d = قطر |
| نیمکره |  | r = شعاع نیمکره |
| پوسته نیمکره ای |  | R = شعاع خارجی نیمکره. r = شعاع داخلی نیمکره. |
| لون کروی |  | r = شعاع کره، θ = زاویه دو وجهی |
| توروس |  | r = شعاع کوچک (شعاع لوله)، R = شعاع بزرگ (فاصله از مرکز لوله تا مرکز چنبره) |
| سیلندر بسته |  | r = شعاع پایه دایره ای، h = ارتفاع استوانه |
| سطح منحنی یک مخروط |  |  s = ارتفاع مایل مخروط، |
| سطح کامل یک مخروط |  | s = ارتفاع مایل مخروط، r = شعاع پایه دایره ای، |
| هرم |  | B = مساحت پایه، P = محیط پایه، L = ارتفاع مایل |
| هرم مربع |  | b = طول پایه، s = ارتفاع مایل، h = ارتفاع عمودی |
| هرم مستطیلی |  | ℓ = طول، b = عرض، h = ارتفاع |
| چهار وجهی |  | a = طول ضلع |
| سطح انقلاب |  | |
| سطح پارامتریک |  |  = معادله برداری پارامتریک سطح = معادله برداری پارامتریک سطح
|
نسبت سطح یک کره و استوانه با شعاع و ارتفاع یکسان [ ویرایش ]
مخروط، کره و استوانه ای به شعاع r و ارتفاع h .
از فرمول های داده شده در زیر می توان برای نشان دادن اینکه مساحت سطح یک کره و استوانه با شعاع و ارتفاع یکسان به نسبت 2: 3 به شرح زیر استفاده می شود.
بگذارید شعاع r و ارتفاع h باشد (که برای کره 2 r است).
کشف این نسبت به ارشمیدس نسبت داده شده است . [4]
منبع
https://en.wikipedia.org/wiki/Surface_area
از ویکیپدیا، دانشنامه آزاد
این مقاله در مورد بخش خط است. برای استخوان، شعاع (استخوان) را ببینید. برای کاربردهای دیگر، شعاع (ابهامزدایی) را ببینید .
دایره با محیط C به رنگ سیاه، قطر D به رنگ آبی، شعاع R به رنگ قرمز، و مرکز یا مبدا O به رنگ سبز.
در هندسه کلاسیک ، شعاع دایره یا کره هر یک از پاره خط ها از مرکز آن تا محیط آن است و در استفاده مدرن تر، طول آنها نیز می باشد. این نام از کلمه لاتین radius گرفته شده است که به معنای پرتو و همچنین پره چرخ ارابه است. [1] جمع شعاع می تواند شعاع (از جمع لاتین) یا شعاع جمع انگلیسی معمولی باشد. [2] مخفف معمولی و نام متغیر ریاضی شعاع R یا r است. با گسترش، قطر D به عنوان دو برابر شعاع تعریف می شود: [3]
اگر جسمی مرکز نداشته باشد، این اصطلاح ممکن است به شعاع محیطی ، شعاع دایره محدود یا کره محصور آن اشاره کند. در هر صورت، شعاع ممکن است بیش از نصف قطر باشد، که معمولاً به عنوان حداکثر فاصله بین هر دو نقطه از شکل تعریف می شود. شعاع یک شکل هندسی معمولاً شعاع بزرگترین دایره یا کره موجود در آن است. شعاع داخلی یک حلقه، لوله یا دیگر جسم توخالی، شعاع حفره آن است.
برای چند ضلعی های منظم ، شعاع همان شعاع محیطی آن است. [4] شعاع چند ضلعی منتظم را آپوتم نیز میگویند . در تئوری گراف ، شعاع یک گراف حداقل در تمام رئوس u حداکثر فاصله از u تا هر رأس دیگر گراف است. [5]
شعاع دایره با محیط ( محیط ) C برابر است
فهرست
فرمول [ ویرایش ]
برای بسیاری از اشکال هندسی، شعاع رابطه کاملاً مشخصی با سایر معیارهای شکل دارد.
حلقه ها [ ویرایش ]
همچنین ببینید: مساحت دایره
شعاع دایره ای با مساحت A برابر است
شعاع دایره ای که از سه نقطه غیر خطی P 1 , P 2 , P 3 می گذرد با
که در آن θ زاویه
∠ P 1 P 2 P 3
است. این فرمول از قانون سینوس ها استفاده می کند . اگر سه نقطه با مختصات آنها ( x 1 , y 1 ) , ( x 2 , y 2 ) و ( x 3 , y 3 ) داده شوند، شعاع را می توان به صورت بیان کرد.
چند ضلعی های منظم [ ویرایش ]
همچنین ببینید: دایره محدود
| n | R n |
|---|---|
| 3 | 0.577 350... |
| 4 | 0.707 106... |
| 5 | 0.850 650... |
| 6 | 1.0 |
| 7 | 1.152 382... |
| 8 | 1.306 562... |
| 9 | 1.461 902... |
| 10 | 1.618 033... |
برای مثال یک مربع ( n =4)
شعاع r یک چندضلعی منتظم با n ضلع به طول s با r = R n s به دست می آید که در آن
هایپرمکعب [ ویرایش ]
شعاع یک ابر مکعب d بعدی با ضلع s است
استفاده در سیستم های مختصات [ ویرایش ]
مختصات قطبی [ ویرایش ]
نوشتار اصلی: سیستم مختصات قطبی
سیستم مختصات قطبی یک سیستم مختصات دو بعدی است که در آن هر نقطه از یک صفحه با فاصله از یک نقطه ثابت و یک زاویه از یک جهت ثابت تعیین می شود.
نقطه ثابت (مشابه با مبدأ سیستم دکارتی ) قطب نامیده می شود و پرتوی از قطب در جهت ثابت محور قطبی است . فاصله از قطب را مختصات شعاعی یا شعاع می گویند و زاویه را مختصات زاویه ای ، زاویه قطبی یا آزیموت می نامند . [6]
مختصات استوانه ای [ ویرایش ]
نوشتار اصلی: سیستم مختصات استوانهای
در سیستم مختصات استوانه ای، یک محور مرجع انتخابی و یک صفحه مرجع انتخابی عمود بر آن محور وجود دارد. مبدأ سیستم نقطهای است که هر سه مختصات را میتوان صفر داد. این محل تقاطع بین صفحه مرجع و محور است.
این محور را بهطور متفاوتی محور استوانهای یا طولی مینامند تا آن را از محور قطبی متمایز کند ، که پرتویی است که در صفحه مرجع قرار دارد و از مبدا شروع میشود و در جهت مرجع قرار میگیرد.
فاصله از محور ممکن است فاصله شعاعی یا شعاع نامیده شود ، در حالی که مختصات زاویه ای گاهی اوقات به عنوان موقعیت زاویه ای یا به عنوان آزیموت نامیده می شود . شعاع و آزیموت با هم مختصات قطبی نامیده می شوند ، زیرا با یک سیستم مختصات قطبی دوبعدی در صفحه از طریق نقطه، موازی با صفحه مرجع مطابقت دارند. مختصات سوم ممکن است ارتفاع یا ارتفاع (اگر صفحه مرجع افقی در نظر گرفته شود)، موقعیت طولی ، [7] یا موقعیت محوری نامیده می شود . [8]
مختصات کروی [ ویرایش ]
نوشتار اصلی: سیستم مختصات کروی
در یک سیستم مختصات کروی، شعاع فاصله یک نقطه از یک مبدأ ثابت را توصیف می کند. موقعیت آن اگر بیشتر با زاویه قطبی اندازه گیری شده بین جهت شعاعی و جهت اوج ثابت، و زاویه آزیموت، زاویه بین برآمدگی متعامد جهت شعاعی بر روی صفحه مرجعی که از مبدا می گذرد و متعامد به نقطه اوج است، تعریف شود. و یک جهت مرجع ثابت در آن صفحه.
همچنین مشاهده کنید [ ویرایش ]
منبع
https://en.wikipedia.org/wiki/Radius


در حساب دیفرانسیل و انتگرال ، قانون زنجیره ای مشتق یک "تابع تابع" را توصیف می کند: ترکیب دو تابع، که در آن خروجی z تابعی از یک متغیر میانی y است که به نوبه خود تابعی از متغیر ورودی x است.
فرض کنید y به عنوان تابع 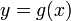 و z به عنوان تابع داده شده است
و z به عنوان تابع داده شده است 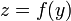 . میزان تغییر z بر حسب y توسط مشتق داده می شود
. میزان تغییر z بر حسب y توسط مشتق داده می شود 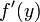 و نرخی که در آن y بر حسب x تغییر می کند توسط مشتق داده می شود
و نرخی که در آن y بر حسب x تغییر می کند توسط مشتق داده می شود 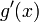 . بنابراین نرخی که z بر حسب x تغییر میکند، حاصلضرب است
. بنابراین نرخی که z بر حسب x تغییر میکند، حاصلضرب است 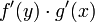 ، و با جایگزین
، و با جایگزین 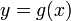 کردن آن، قانون زنجیره را داریم
کردن آن، قانون زنجیره را داریم
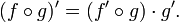
برای تبدیل آن به نماد سنتی ( لایبنیتس )، توجه میکنیم
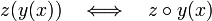
و
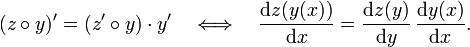 .
.
در شکل یادگاری عبارت اخیر است
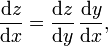
به خاطر سپردن آن آسان است، زیرا گویی d y در صورت و مخرج سمت راست لغو می شود.
[ ویرایش ]حساب چند متغیره
گسترش قانون زنجیره به توابع چند متغیره ممکن است با در نظر گرفتن مشتق به عنوان یک تقریب خطی برای یک تابع متمایز به دست آید.
حالا اجازه دهید 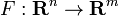 و
و 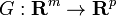 تابع هایی با F دارای مشتق D F در
تابع هایی با F دارای مشتق D F در 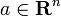 و G دارای مشتق D G در
و G دارای مشتق D G در 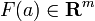 . بنابراین D F یک نقشه خطی از
. بنابراین D F یک نقشه خطی از 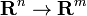 و D G یک نقشه خطی از
و D G یک نقشه خطی از 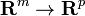 . سپس
. سپس 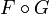 در
در 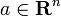 با مشتق قابل تمایز است
با مشتق قابل تمایز است
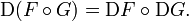
منبع
https://www.theochem.ru.nl/~pwormer/Knowino/knowino.org/wiki/Chain_rule.html
ویژگی های مشخصه [ ویرایش ]
کسینوس هایپربولیک [ ویرایش ]
می توان نشان داد که مساحت زیر منحنی کسینوس هذلولی (در یک بازه محدود) همیشه برابر با طول قوس مربوط به آن بازه است: [15]
مماس هایپربولیک[ ویرایش ]
مماس هذلولی جواب (یکتا) معادله دیفرانسیل f ′ = 1 − f 2 است که f (0) = 0 دارد. [16] [17]
روابط مفید [ ویرایش ]
توابع هذلولی بسیاری از هویت ها را برآورده می کنند که همه آنها از نظر شکل شبیه به هویت های مثلثاتی هستند . در واقع، قانون آزبورن [18] بیان می کند که می توان هر هویت مثلثاتی را برای تبدیل کرد




توابع زوج و فرد:
از این رو:
بنابراین، cosh x و sech x توابع زوج هستند . بقیه توابع فرد هستند .
سینوس و کسینوس هایپربولیک:
که آخرین آنها شبیه به هویت مثلثاتی فیثاغورثی است .
یکی هم دارد
برای توابع دیگر
مجموع آرگومان ها [ ویرایش ]
به ویژه
همچنین:
فرمول های تفریق [ ویرایش ]
همچنین: [19]
فرمول های نیم آرگومان [ ویرایش ]
که در آن sgn تابع علامت است .
اگر x ≠ 0 ، سپس [20]
فرمول های مربعی [ ویرایش ]
نابرابری ها [ ویرایش ]
نابرابری زیر در آمار مفید است: 
این را می توان با مقایسه ترم به ترم سری تیلور دو تابع ثابت کرد.
توابع معکوس به عنوان لگاریتم [ ویرایش ]
مقاله اصلی: تابع هذلولی معکوس
"منحنی هیپربولیک" به اینجا هدایت می شود. برای منحنی هندسی، Hyperbola را ببینید .
در ریاضیات , توابع هذلولی مشابه توابع مثلثاتی معمولی هستند , اما با استفاده از هذلولی به جای دایره تعریف می شوند . همانطور که نقاط (cost ، sin t ) دایره ای با شعاع واحد تشکیل می دهند ، نقاط (cosh t ، sinh t ) نیمه سمت راست هذلولی واحد را تشکیل می دهند. همچنین، به طور مشابه، مشتقات sin( t ) و cos( t ) cos( t ) هستند .و –sin( t ) ، مشتقات sinh( t ) و cosh( t ) cosh( t ) و +sinh( t ) هستند .
توابع هذلولی در محاسبات زوایا و فواصل در هندسه هذلولی رخ می دهند . آنها همچنین در راه حل های بسیاری از معادلات دیفرانسیل خطی (مانند معادله تعریف یک خطی )، معادلات مکعبی ، و معادله لاپلاس در مختصات دکارتی رخ می دهند. معادلات لاپلاس در بسیاری از زمینه های فیزیک از جمله نظریه الکترومغناطیسی ، انتقال حرارت ، دینامیک سیالات و نسبیت خاص مهم هستند.
توابع هذلولی اساسی عبارتند از: [1]
- سینوس هذلولی "sinh" ( / ˈ s ɪ ŋ , ˈ s ɪ n tʃ , ˈ ʃ aɪ n / )، [2]
- کسینوس هذلولی "cosh" ( / ˈ k ɒ ʃ , ˈ k oʊ ʃ / )، [3]
که از آن مشتق شده است: [4]
- تانژانت هذلولی "tanh" ( / ˈ t æ ŋ , ˈ t æ n tʃ , ˈ θ æ n / )، [5]
- کسکانت هذلولی "csch" یا "cosech" ( / ˈ k oʊ s ɛ tʃ , ˈ k oʊ ʃ ɛ k / [3] )
- سکانت هذلولی "sech" ( / ˈ s ɛ tʃ , ˈ ʃ ɛ k / )، [6]
- هذلولی همتنژانت "coth" ( / ˈ k ɒ θ , ˈ k oʊ θ / )، [7] [8]
مربوط به توابع مثلثاتی مشتق شده است.
توابع هذلولی معکوس عبارتند از:
- سینوس هذلولی منطقه "arsinh" (همچنین به "sinh -1 "، "asinh" یا گاهی اوقات "arcsinh" نشان داده می شود) [9] [10] [11]
- کسینوس هذلولی ناحیه "arcosh" (همچنین به "cosh -1 "، "acosh" یا گاهی اوقات "arccosh" نشان داده می شود)
- و غیره
پرتویی از هذلولی واحد x 2 − y 2 = 1 در نقطه (cosh a , sinh a ) , جایی که a دو برابر مساحت بین پرتو، هذلولی و محور x است. برای نقاط روی هذلولی زیر محور x ، ناحیه منفی در نظر گرفته می شود ( نسخه متحرک با مقایسه با توابع مثلثاتی (دایره ای) را ببینید).
توابع هذلولی یک متغیر حقیقی به نام زاویه هذلولی می گیرند . اندازه یک زاویه هذلولی دو برابر مساحت بخش هذلولی آن است . توابع هذلولی ممکن است برحسب پایه های یک مثلث قائم الزاویه که این بخش را پوشش می دهد، تعریف شوند.
در تحلیل مختلط ، توابع هذلولی به عنوان بخش های مختلط سینوس و کسینوس به وجود می آیند. سینوس هیپربولیک و کسینوس هذلولی توابع کامل هستند . در نتیجه، سایر توابع هذلولی در کل صفحه مختلط مرومورفیک هستند.
بر اساس قضیه لیندمان – وایرشتراس ، توابع هذلولی برای هر مقدار جبری غیرصفری متغیر، یک مقدار ماورایی دارند . [12]
توابع هیپربولیک در دهه 1760 به طور مستقل توسط وینچنزو ریکاتی و یوهان هاینریش لامبرت معرفی شدند. [13] Riccati از Sc. و رونوشت ( sinus/cosinus circulare ) اشاره به توابع حلقوی و Sh. و چ. ( سینوس/کوسینوس هیپربولیکو ) برای اشاره به توابع هذلولی. لامبرت این نام ها را پذیرفت، اما اختصارات را به نام هایی که امروزه استفاده می شود تغییر داد. [14] اختصارات sh , ch , th , cth نیز در حال حاضر بسته به ترجیح شخصی استفاده می شود.
فهرست
- 1نشانه گذاری
- 2تعاریف
- 2.1تعاریف نمایی
- 2.2تعاریف معادلات دیفرانسیل
- 2.3تعاریف مختلط مثلثاتی
- 3ویژگی های مشخص کننده
- 3.1کسینوس هیپربولیک
- 3.2تانژانت هیپربولیک
- 4روابط مفید
- 4.1مجموع استدلال ها
- 4.2فرمول های تفریق
- 4.3فرمول های نیم متغیر
- 4.4فرمول های مربعی
- 4.5نابرابری ها
- 5توابع معکوس به عنوان لگاریتم
- 6مشتقات
- 7مشتقات دوم
- 8انتگرال های استاندارد
- 9عبارات سری تیلور
- 10ضربهای نامتناهی و کسرهای ادامه دار
- 11مقایسه با توابع دایره ای
- 12رابطه با تابع نمایی
- 13توابع هذلولی برای اعداد مختلط
- 14همچنین ببینید
- 15منابع
- 16لینک های خارجی
نشانه گذاری [ ویرایش ]
مقاله اصلی: توابع مثلثاتی § نمادگذاری
تعاریف [ ویرایش ]
سین ، کوش و تن
csch ، sech و coth
روش های معادل مختلفی برای تعریف توابع هذلولی وجود دارد.
تعاریف نمایی [ ویرایش ]
sinh x نصف اختلاف e x و e - x است
cosh x میانگین e x و e - x است _
از نظر تابع نمایی : [1] [4]
- سینوس هیپربولیک: قسمت فرد تابع نمایی، یعنی
- کسینوس هیپربولیک: قسمت زوج تابع نمایی، یعنی
- مماس هیپربولیک:
- کتانژانت هیپربولیک: برای x ≠ 0 ،
- سکانس هیپربولیک:
- کسکانت هذلولی: برای x ≠ 0 ،
تعاریف معادلات دیفرانسیل [ ویرایش ]
توابع هذلولی را می توان به عنوان جواب معادلات دیفرانسیل تعریف کرد : سینوس و کسینوس هذلولی حل ( s , c ) یک سیستم هستند.



sinh( x ) و cosh( x ) نیز راهحل منحصربهفرد معادله f ″( x ) = f ( x ) هستند، به طوری که f (0) = 1 ، f ′(0) = 0 برای کسینوس هذلولی، و f (0) = 0 ، f ′(0) = 1 برای سینوس هذلولی.
تعاریف مختلط توابع مثلثاتی [ ویرایش ]
توابع هذلولی نیز ممکن است از توابع مثلثاتی با متغیر های مختلط استنتاج شوند:
- سینوس هیپربولیک: [1]
- کسینوس هیپربولیک: [1]
- تانژانت هیپربولیک:
- کتانژانت هیپربولیک:
- سکانس هیپربولیک:
- کسکانت هیپربولیک:
جایی که i واحد موهومی با i 2 = −1 است.
تعاریف فوق به تعاریف نمایی از طریق فرمول اویلر مرتبط هستند (به § توابع هیپربولیک برای اعداد مختلط زیر مراجعه کنید).
از آنجا که
![]()
انتگرال آن دارای نمایش سری قدرت است
![]()
بیایید حد نسبت های مطلق این سری را پیدا کنیم:
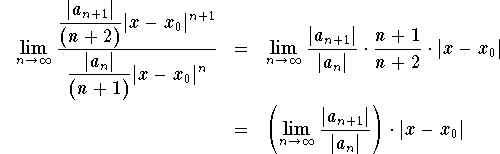
اما توجه داشته باشید که این دقیقاً همان عبارتی است که هنگام محاسبه حد نسبتهای مطلق سری تیلور از f ( x ) به آن برخورد می کنیم. بنابراین هر دو سری شعاع همگرایی یکسانی دارند!
سری تیلور و چند جمله ای ها
سری تیلور چند جمله ای چیست؟
سری تیلور با مرکز ![]() یک چند جمله ای خود چند جمله ای است! (این را با چند جمله ای مورد علاقه خود بررسی کنید و از فرمول سری تیلور با مرکز استفاده
یک چند جمله ای خود چند جمله ای است! (این را با چند جمله ای مورد علاقه خود بررسی کنید و از فرمول سری تیلور با مرکز استفاده ![]() کنید!)
کنید!)
اگر مرکز 0 نباشد چه؟ سپس شخص واقعاً چند جمله ای را بازنویسی می کند و ![]() به جای استفاده از آن
به جای استفاده از آن ![]() به عنوان "بلوک های سازنده" آن استفاده می کند.
به عنوان "بلوک های سازنده" آن استفاده می کند.
در اینجا یک مثال آورده شده است: سری تیلور را با مرکز ![]() چند جمله ای
چند جمله ای ![]() پیدا کنید. بیایید مشتقات آن را بگیریم و وصل کنیم
پیدا کنید. بیایید مشتقات آن را بگیریم و وصل کنیم ![]() :
:
![]() بنابراین p (-1)=1+3+5=9.
بنابراین p (-1)=1+3+5=9.
p '( x )=2 x -3، بنابراین p '(-1)=-2-3=-5.
p ''( x )=2، بنابراین p ''(-1)=2.
تمام مشتقات بالاتر 0 هستند، بنابراین سری تیلور خاتمه می یابد!
با استفاده از فرمول ما به دست می آوریم:
![]()
از این رو، فهمیدن اینکه یک تابع دارای سری پایانی تیلور است، سخت نیست، اگر و فقط اگر تابع چند جمله ای باشد.
ضرب سری تیلور در چند جمله ای
بیایید سعی کنیم بسط سری تیلور ![]() با مرکز را پیدا کنیم
با مرکز را پیدا کنیم ![]() .
.
برای پیدا کردن سری تیلور برای ![]() ، از آن استفاده کنید
، از آن استفاده کنید 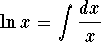 . شما بسط را بدست می آورید:
. شما بسط را بدست می آورید:
![]()
همانطور که در مثال بالا می توانیم بازنویسی کنیم
![]()
سپس هر دو عبارت را ضرب می کنیم:

بدون وارد شدن به جزئیات فنی: اگر اولین عبارت های این سری را بنویسید، می توانید قدرت های مربوط به ( x -1) را با هم ترکیب کنید تا شروع سری تیلور را برای f ( x ) بدست آورید:
![]()
خودت آن را امتحان کن!
تقریباً چندان پیچیده نیست: نمایش سری تیلور را با مرکز ![]() برای
برای ![]() پیدا کنید.
پیدا کنید.
منبع
http://www.sosmath.com/calculus/tayser/tayser05/tayser05.html

میتوانیم این سریها را طوری ضرب کنیم که انگار سریهای متناهی هستند. ما ضرایب را جمع آوری می کنیم:
جمله ثابت 1 است .
ترم درجه اول 1 + 1 = 2 است.
ترم درجه دوم 1 + 1 + 1/2 = 5/2 است.
ترم درجه سوم 1 + 1 + 1/2 + 1/6 = 8/3 است
ترم درجه چهارم 1 + 1 + 1/2 + 1/6 + 1/24 = 65/24 است.
ما میتوانیم این فرآیند را بهطور نامحدود ادامه دهیم، یا بهتر است از رایانه برای تولید شرایط استفاده کنیم.
سریال است
5 8 65
1 + x + x 2 + x 3 + x 4 + ...
2 3 24
تقسیم بندی سری های قدرت
فرض کنید میخواهیم نمایش سری توانی را در مخرج ضرب کنیم و ضرایب را برابر کنیم: (c 0 + c 1 x + c 2 x 2 + ...)(1 + x + x 2 /2 + x 3 /6 + x 4 /24 + ...) = (x - x 3 /3 + x 5 /5- x 7/7 + ...)
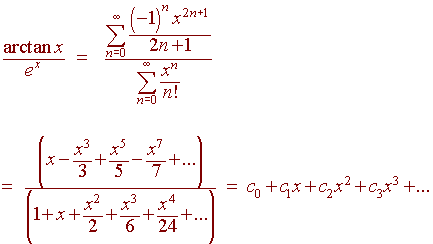
ضریب ثابت به ما c 0 = 0 می دهد .
عبارت درجه اول به ما c 0 + c 1 = 1 می دهد. بنابراین c 1 = 1 .
جمله درجه دوم 1 + c 2 = 0 به ما می دهد . بنابراین c 2 = -1 .
عبارت درجه سوم 1/2 - 1 + c 3 = -1/3 به ما می دهد . بنابراین c 3 = 1 - 1/2 - 1/3 = 1/6 .
و غیره
منبع
https://ltcconline.net/greenl/courses/107/Series/taylrser.htm
مشخصات وب
 در این وبلاگ به ریاضیات و کاربردهای آن و تحقیقات در آنها پرداخته می شود. مطالب در این وبلاگ ترجمه سطحی و اولیه است و کامل نیست.در صورتی سوال یا نظری در زمینه ریاضیات دارید مطرح نمایید .در صورت امکان به آن می پردازم. من دوست دارم برای یافتن پاسخ به سوالات و حل پروژه های علمی با دیگران همکاری نمایم.در صورتی که شما هم بامن هم عقیده هستید با من تماس بگیرید.
در این وبلاگ به ریاضیات و کاربردهای آن و تحقیقات در آنها پرداخته می شود. مطالب در این وبلاگ ترجمه سطحی و اولیه است و کامل نیست.در صورتی سوال یا نظری در زمینه ریاضیات دارید مطرح نمایید .در صورت امکان به آن می پردازم. من دوست دارم برای یافتن پاسخ به سوالات و حل پروژه های علمی با دیگران همکاری نمایم.در صورتی که شما هم بامن هم عقیده هستید با من تماس بگیرید.09132003030
موضوعات وب
- نظریه طیف گراف
- پرواز
- هندسه
- هسته ای
- ترکببات
- نمایش گروه
- سیستم های دینامیکی
- نظریه کد گذاری
- ریاضی فازی
- جبر پیشرفته
- توپولوژی
- معادلات دیفرانسیل
- مقاله ها
- سیستم عصبی
- آنالیز عددی
- آنالیزریاضی و آنالیز حقیقی
- توابع مختلط و کاربردها
- نظریه اعداد
- برنامه ریزی خطی و غیر خطی
- حل عددی معادلات دیفرانسیل
- نظریه مجموعه ها
- جبرخطی و جبرخطی عددی
- اقتصاد
- تاریخ ریاضی
- انسان شناسی وفلسفه ریاضی
- توپولوژی جبری
- هندسه جبری
- هندسه ریمانی و هندسه هذلوی
- بازی
- نقشه برداری دریایی
- گراف
- آمار غیرپارامتری
- نجوم
- منیفولد دیفرانسیل
- نظریه گروه
- نظریه حلقه
- نظریه مدول ها
- آمار و احتمال
- ریاضی 2
- فیزیک -ریاضی
- تحقیق
- ریاضی مهندسی
- درس ترمودینامیک و مکانیک آماری
- مکانیک تحلیلی
- برق یا فیزیک 2
- فیزیک مدرن
- کوانتم
- نسبیت
پیوندها
پیوندهای روزانه
آرشیو وب
- دی ۱۴۰۴
- آذر ۱۴۰۴
- آبان ۱۴۰۴
- شهریور ۱۴۰۴
- مرداد ۱۴۰۴
- خرداد ۱۴۰۴
- اردیبهشت ۱۴۰۴
- بهمن ۱۴۰۳
- دی ۱۴۰۳
- آذر ۱۴۰۳
- آبان ۱۴۰۳
- مهر ۱۴۰۳
- خرداد ۱۴۰۳
- اردیبهشت ۱۴۰۳
- فروردین ۱۴۰۳
- اسفند ۱۴۰۲
- بهمن ۱۴۰۲
- دی ۱۴۰۲
- آذر ۱۴۰۲
- آبان ۱۴۰۲
- مهر ۱۴۰۲
- تیر ۱۴۰۲
- خرداد ۱۴۰۲
- اردیبهشت ۱۴۰۲
- فروردین ۱۴۰۲
- اسفند ۱۴۰۱
- بهمن ۱۴۰۱
- دی ۱۴۰۱
- آبان ۱۴۰۱
- مهر ۱۴۰۱
- شهریور ۱۴۰۱
- مرداد ۱۴۰۱
- تیر ۱۴۰۱
- خرداد ۱۴۰۱
- اردیبهشت ۱۴۰۱
- فروردین ۱۴۰۱
- آرشيو



























![{\displaystyle X_{i}\leq \operatorname {E} [X_{i+1}\mid {\mathcal {F}}_{i}].}](https://wikimedia.org/api/rest_v1/media/math/render/svg/4699e423b741373bfd93b333c7dd88e46ff13514)
![{\displaystyle P\left[\max _{1\leq i\leq n}X_{i}\geq C\right]\leq {\frac {\operatorname {E} [{\textrm {max}}(X_ {n}،0)]}{C}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/17c8d5ccc2985893a662756c26e3caa7dfa02052)
![{\displaystyle CP(E_{i})=\int _{E_{i}}C\,dP\leq \int _{E_{i}}X_{i}\,dP\leq \int _{E_{ i}}{\text{E}}[X_{n}\mid {\mathcal {F}}_{i}]\,dP=\int _{E_{i}}X_{n}\,dP, }](https://wikimedia.org/api/rest_v1/media/math/render/svg/97a75b25386bc4449937c187622406f2c0e9b803)

![{\displaystyle X_{s}\leq \operatorname {E} [X_{t}\mid {\mathcal {F}}_{s}].}](https://wikimedia.org/api/rest_v1/media/math/render/svg/c355b118cbb95b7bb59228b1a9f9662bbbb710c8)
![{\displaystyle P\left[\sup _{0\leq t\leq T}X_{t}\geq C\right]\leq {\frac {\operatorname {E} [{\textrm {max}}(X_ {T}،0)]}{C}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/2dd96eb822d3f1ddc7778fcc16870c47332f98e9)
![{\displaystyle \sup _{0\leq t\leq T}X_{t}=\sup\{X_{t}:t\in [0,T]\cap \mathbb {Q} \}=\lim _ {i\to \infty }\sup\{X_{t}:t\in [0,T]\cap Q_{i}\}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/1b22f85961131d65cf6a4de9aef731daf2dbc613)
![{\displaystyle P\left[\sup _{t\in [0,T]\cap Q_{i}}X_{t}\geq C\right]\leq {\frac {\operatorname {E} [{\ textrm {max}}(X_{T},0)]}{C}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/69b26135c5adbe62fd19e2745a0c2baec763ee73)
![{\displaystyle {\text{P}}[\sup _{t}|X_{t}|\geq C]\leq {\frac {{\text{E}}[|X_{T}|^{p }]}{C^{p}}}.}](https://wikimedia.org/api/rest_v1/media/math/render/svg/1334ecc9cb89a5da3e64abddb6368f6ce2d69888)
![{\displaystyle {\text{E}}[|X_{T}|^{p}]\leq {\text{E}}\left[\sup _{0\leq s\leq T}|X_{s }|^{p}\right]\leq \left({\frac {p}{p-1}}\right)^{p}{\text{E}}[|X_{T}|^{p }]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/83f6b727f90d23c0e6147bfb725decfb19b9d8e1)
![{\displaystyle {\text{E}}\left|\sup _{0\leq s\leq T}X_{s}\right|\leq {\frac {e}{e-1}}\left(1 +{\text{E}}[\max\{|X_{T}|\log |X_{T}|,0\}]\راست)}](https://wikimedia.org/api/rest_v1/media/math/render/svg/19bf464ce9280a449652acc69d55d24ef81e54f1)
![{\displaystyle {\begin{aligned}\operatorname {E} \left[X_{1}+\cdots +X_{n}+X_{n+1}\mid X_{1},\ldots ,X_{n} \right]&=X_{1}+\cdots +X_{n}+\operatorname {E} \left[X_{n+1}\mid X_{1},\ldots ,X_{n}\right]\ \&=X_{1}+\cdots +X_{n}،\end{تراز شده}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/e4e1758a5a9aecf9a8a2f4924f6fab0c2c7da1d0)
![{\displaystyle P\left[\max _{1\leq i\leq n}\left|S_{i}\right|\geq \lambda \right]\leq {\frac {\operatorname {E} \left[ S_{n}^{2}\right]}{\lambda ^{2}}}،}](https://wikimedia.org/api/rest_v1/media/math/render/svg/901d68d85b1dcfde0b0eeb740ac56f7e03ee2aa1)
![{\displaystyle P\left[\sup _{0\leq t\leq T}B_{t}\geq C\right]\leq \exp \left(-{\frac {C^{2}}{2T} }\درست).}](https://wikimedia.org/api/rest_v1/media/math/render/svg/73d503050f20b58c26523ec27f525f5c4d23bfdf)

![{\displaystyle {\begin{aligned}P\left[\sup _{0\leq t\leq T}B_{t}\geq C\right]&=P\left[\sup _{0\leq t\ leq T}\exp(\lambda B_{t})\geq \exp(\lambda C)\right]\\[8pt]&\leq {\frac {\operatorname {E} [\exp(\lambda B_{ T})]}{\exp(\lambda C)}}\\[8pt]&=\exp \left({\tfrac {1}{2}}\lambda ^{2}T-\lambda C\راست )&&\operatorname {E} \left[\exp(\lambda B_{t})\right]=\exp \left({\tfrac {1}{2}}\lambda ^{2}t\right)\ پایان{تراز شده}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/a7adc5f4ced3ecbe70772469ff09afc03f99ca28)




















![\int_0^1 h(x)\,dx \ge \int_{\frac{1}{m}}^1{h(x)\,dx} = \sum_{n=1}^{m-1} \int_{\left(\frac{1}{n+1},\frac{1}{n}\right]}{h(x)\,dx} \ge \sum_{n=1}^{m -1} \int_{\left(\frac{1}{n+1},\frac{1}{n}\right]}{n\,dx}=\sum_{n=1}^{m- 1} \frac{1}{n+1} \to \infty \qquad \text{as }m\to\infty](https://wikimedia.org/api/rest_v1/media/math/render/svg/6ce44a95f776d71b7c2ad5e232e8787195a5d949)





![{\displaystyle (Df)(\mathbf {a} ,\mathbf {b} )=\left[{\begin{matrix}{\frac {\partial f_{1}}{\partial x_{1}}}( \mathbf {a} ,\mathbf {b} )&\cdots &{\frac {\partial f_{1}}{\partial x_{n}}}(\mathbf {a} ,\mathbf {b} )\ \\vdots &\ddots &\vdots \\{\frac {\partial f_{m}}{\partial x_{1}}}(\mathbf {a} ,\mathbf {b} )&\cdots &{\ frac {\partial f_{m}}{\partial x_{n}}}(\mathbf {a} ,\mathbf {b} )\end{matrix}}\right|\left.{\begin{matrix} \frac {\partial f_{1}}{\partial y_{1}}}(\mathbf {a} ,\mathbf {b} )&\cdots &{\frac {\partial f_{1}}{\partial y_{m}}}(\mathbf {a} ,\mathbf {b} )\\\vdots &\ddots &\vdots \\{\frac {\partial f_{m}}{\partial y_{1}} }(\mathbf {a} ,\mathbf {b} )&\cdots &{\frac {\partial f_{m}}{\partial y_{m}}}(\mathbf {a} ,\mathbf {b} )\\\پایان{ماتریس}}\راست]=[X|Y]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/fbcfcdca6f88f8a6d7d0264d4bfab73bd2ff795f)
![{\displaystyle \left[{\frac {\partial g_{i}}{\partial x_{j}}}(\mathbf {x})\right]_{m\times n}=-\left[J_{ f,\mathbf {y} }(\mathbf {x} ,g(\mathbf {x} ))\right]_{m\times m}^{-1}\,\left[J_{f,\mathbf {x} }(\mathbf {x} ,g(\mathbf {x} ))\right]_{m\times n}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/f91c52a4f75b5a475156d03f4e2d12175e5be8bb)
















![{\displaystyle \psi _{n}(x)={\frac {\sqrt[{4}]{2}}{\sqrt {n!}}}e^{-\pi x^{2}}\ mathrm {He} _{n}\left(2x{\sqrt {\pi }}\right)}](https://wikimedia.org/api/rest_v1/media/math/render/svg/a9121f54a3fdbb0eedecf2aef5a379bdfae414b7)















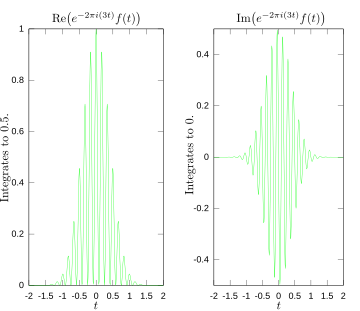
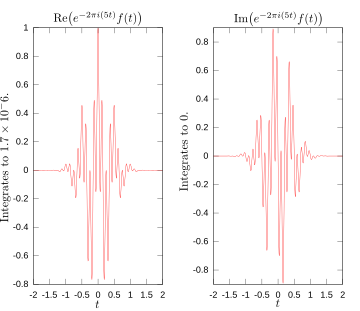










 = مشتق جزئی از
= مشتق جزئی از
 = مشتق جزئی از
= مشتق جزئی از







![{\displaystyle r={\frac {\sqrt {[(x_{2}-x_{1})^{2}+(y_{2}-y_{1})^{2}][(x_{2) }-x_{3})^{2}+(y_{2}-y_{3})^{2}][(x_{3}-x_{1})^{2}+(y_{3} -y_{1})^{2}]}}{2|x_{1}y_{2}+x_{2}y_{3}+x_{3}y_{1}-x_{1}y_{3 }-x_{2}y_{1}-x_{3}y_{2}|}}.}](https://wikimedia.org/api/rest_v1/media/math/render/svg/caffb954e8c39a26dcc5e4ad4f66494edd313008)
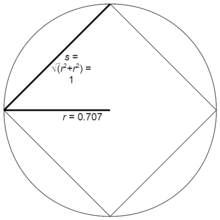







![{\displaystyle {\begin{aligned}\sinh(x+y)&=\sinh x\cosh y+\cosh x\sinh y\\\cosh(x+y)&=\cosh x\cosh y+\sinh x \sinh y\\[6px]\tanh(x+y)&={\frac {\tanh x+\tanh y}{1+\tanh x\tanh y}}\\\end{تراز شده}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/8a343fcb86c5fa15cceb217f4e92410c70a6e200)




![{\displaystyle {\begin{aligned}\sinh \left({\frac {x}{2}}\right)&={\frac {\sinh x}{\sqrt {2(\cosh x+1)} }}&&=\operatorname {sgn} x\,{\sqrt {\frac {\cosh x-1}{2}}}\\[6px]\cosh \left({\frac {x}{2}} \right)&={\sqrt {\frac {\cosh x+1}{2}}}\\[6px]\tanh \left({\frac {x}{2}}\right)&={\ frac {\sinh x}{\cosh x+1}}&&=\operatorname {sgn} x\,{\sqrt {\frac {\cosh x-1}{\cosh x+1}}}={\frac {e^{x}-1}{e^{x}+1}}\end{تراز شده}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/412a4ffd109486f684e515634b33447b13444954)