توسط علی رضا نقش نیلچی
| دوشنبه هفتم آبان ۱۴۰۳ | 6:44
دعوت به رمزگذاری
مشکلات
در ادبیات مدرن رمزنگاری - برای نشان دادن مشکلات و روشهای اساسی - دو شخصیت ساختگی به نامهای آلیس و باب معرفی شدهاند که اکنون بهطور سنتی به قهرمانهای کنش تبدیل شدهاند. منشأ آنها به وضوح به دلیل شخصیت سازی حروف A و B است که در زبان رسمی محققان استفاده می شود. این واقعیت که دو نماد به شخصیتهایی تبدیل شدهاند که اکنون متون چهرهای به آنها اختصاص میدهند - و با مقداری بیشرمانه، حتی یک شخصیت، هرچند جنینی، شاید فراتر از بازی، به این معنی باشد که این ماده خود را به یک کاربرد فوری وامی دارد. و زمینهای را میطلبد که در آن مدعیان یا گهگاهی متحدان یک مسابقه را بتوان مستقیماً و نه به طور انتزاعی شناخت.
به عنوان مثال: آلیس و باب یک بحث دارند و تمام دارایی های مشترک را تقسیم می کنند. برای برخی از اشیا انتخاب آسان است، در حالی که برای برخی دیگر یک قرعه کشی لازم است تا تصمیم بگیرد که آن را به چه کسی اختصاص دهد. اما این دو قصد ملاقات ندارند (یا اکنون کیلومترها از هم فاصله دارند) و می خواهند قرعه کشی را از طریق تلفن انجام دهند. کدام یک از این دو به اندازه کافی سخاوتمند - و قابل اعتماد - خواهد بود که به دیگری اجازه دهد سکه کلاسیک را برگرداند و نتیجه قرعه کشی را به او بگوید؟
وضعیت حساس است، خطر برافروختن مجدد اختلافات و بدتر شدن روابط را در پی دارد، اما... نگران نباشید: هر دو می توانند روی روشی توافق کنند که احتمال پنجاه درصدی (یعنی یک تساوی منصفانه) را برای هر یک از آنها تضمین کند، بدون نیاز به اعتماد به دیگری، فقط داشتن حداقل دانش از پیچیدگی محاسباتی برخی از عملیات های حسابی روی اعداد صحیح. آلیس و باب خوشبختانه روی این موضوع آماده شده اند و مشکل حل شده است.
مشکل دیگر در عوض این است که آلیس و باب مشتاق تبادل پیام هستند - مهم نیست چه ماهیتی دارد، حتی اگر همه موافق باشند که آنها مهربان هستند. اما سرنوشت آنها، افسوس، در این مورد نیز این است که در فاصله زیادی قرار داشته باشند و به همین دلیل می خواهند روی کلیدی به توافق برسند که محتوای واقعی پیام ها را رمزگذاری کند : فرض کنید چارلی، خواستگاری که آلیس آن را رد کرده است. ، در غیر این صورت می توانند از آن برای ایجاد مشکل در روابط خود استفاده کنند. در اینجا نیز جای نگرانی نیست: باب در یک دوره رمزنگاری کلید عمومی شرکت کرده است و به طور واضح به آلیس توضیح می دهد که چگونه می توانند ادامه دهند. چارلی پیام را قطع می کند و متوجه می شود که نمی تواند برنامه پارازیت خود را اجرا کند. او نیز همین دوره را در زمینه رمزنگاری دنبال کرده است و برای او واضح است که حتی اگر ارتباطات آنها را رهگیری کند، نمی تواند کلید رمزگذاری را که آلیس و باب قصد دارند برای تبادل پیام به توافق برسند، یاد بگیرد.
قبل از اینکه یک رشته علمی باشد، رمزنگاری یک عمل، مجموعه ای از قوانین، روش ها و ابزارها بود. تقریباً به یک هنر تبدیل شده بود: هنر تبادل پیام بدون درک محتوای واقعی، حتی اگر رهگیری شود. رشته ای با جایگاهی مبهم، مرزی با جادو و باطنی. در این زمینه، آلیس و باب هنوز متولد نشده اند. ما با مشکلات جاسوسی سر و کار داریم، دشمنانی که مشتاقند اطلاعاتی را که با متحدانمان رد و بدل می کنیم به دست آورند تا از آن به ضرر خود استفاده کنند.
واضح است که منشأ باستانی است و نه تنها به نیازهای تجاری، بلکه بیش از هر چیز دیپلماتیک و نظامی مرتبط است. مشخص است که در بسیاری از موارد سرنوشت درگیری ها با این توانایی برای شناخت از قبل حرکات حریف تعیین شده است. سپس ظهور شبکه های ارتباطی دیجیتال که به طور منظم در زندگی روزمره مورد استفاده قرار می گیرد، نیازهای جدیدی را برای امنیت و حفاظت از حریم خصوصی می طلبد . و ریاضیات - به ویژه نظریه اعداد - ماهیت رمزنگاری را تغییر داد، آن را از هاله رمز و راز آن رها کرد و آن را از یک هنر به یک علم تبدیل کرد.
اما دو مشکل قبلی مربوط به آلیس و باب چه وجه اشتراکی با این موضوع قدیمی دارند: قرعهکشی که از طریق تلفن انجام میشود یا تعویض یک کلید رمزگذاری زیر بینی شخصی که آن را رهگیری میکند، اما کسی که هرگز قادر به انجام آن نیست. از آن استفاده کنم؟ واقعیت این است که وقتی ریاضیات با رسمی شدن آن در بخشی درگیر می شود، یک سری مسائل ظاهراً متفاوت و غیر مرتبط را نیز آشکار می کند که در عوض یک وحدت تعریف شده و اغلب عمیق را نشان می دهد.
و این همان چیزی است که اخیراً اتفاق افتاده است: مشکل فقط در (1) رمزگذاری یا رمزگشایی یک پیام نیست ، بلکه در "تأیید کردن" آن است، یعنی: (2) شناسایی فرستنده پیام و (3) درک آیا پیام دست نخورده است یا در حین انتقال دستکاری شده است . اما همچنین: (4) توافق با کسی در مورد یک قطعه داده که مخفی نگه داشته شود ، حتی اگر از یک کانال انتقال ناامن استفاده کنید. (5) به طور تصادفی تصمیم بگیرید، با شانس موفقیت برابر در مقایسه با یک همکار غیرقابل اعتماد . (6) بدون اینکه منبع یا راز آن را فاش کنید، آگاه سازید که علم خاصی دارید .
اولین مشکل ذکر شده، امنیت انتقال است که فیلم های جنگی و جاسوسی متعددی ما را به آن عادت کرده اند. دوم این است که از صحت فرستنده ; در این مورد، علاوه بر بازی دوگانه جاسوسی، لازم است مشکلات مدرن تراکنش های اقتصادی از راه دور را به خاطر بسپاریم: دستگاه خودپرداز یا به اصطلاح امضای دیجیتال که به ما امکان می دهد حتی از طریق ایمیل نیز شناسایی شویم. سومین مشکل ذکر شده مربوط به یکپارچگی پیام است . این تله ای است که پیشینه های معروفی دارد: رومئو به مانتوا پناه می برد و از پرستار مورد اعتماد خود (به اصطلاح!) خبر دروغ مرگ ژولیت را دریافت می کند. مشکلات (4) قرعه کشی از راه دور و (5) تعویض کلید مواردی هستند که قبلاً آلیس و باب را در حال کار در آنها دیده ایم و راه حل آنها بعداً آشکار خواهد شد. آخرین مشکل لیست شده به اصطلاح به دانش صفر می پردازد: چگونه می توانیم تضمین کنیم که اطلاعاتی داریم بدون اینکه جنبه های اساسی آن آشکار شود؟ به عنوان مثال، چگونه نیکولو فونتانا، تارتالیای معروف، در قرن شانزدهم اعلام کرد که فرمول حل رادیکال های معادلات درجه سوم را بدون اینکه مجبور باشد آن را برای جامعه ریاضی آشکار کند (حداقل تا زمانی که موفق به انجام این کار شود) کشف کرده است. )؟ در این مورد، مشکل دشوار نیست: فقط باید نشان دهید که می دانید چگونه ریشه برخی از معادلات پیشنهاد شده توسط دیگران را محاسبه کنید. هر کسی به راحتی می تواند درستی پاسخ را تأیید کند و پس از چند اجرا از این دست خود را متقاعد کند که هرکسی که ریشه معادلات را پیدا کرده است، لزوماً باید یک روش مطمئن داشته باشد، یک فرمول دقیقاً: تأیید اینکه آیا یک عدد معین یک ریشه است یا خیر، یک عملیات است. بسیار ساده تر از یافتن آن، حداقل برای کسانی که فرمول آن را نمی دانند. اما در عوض به این فکر کنید که اختراعی ساخته اید که برای ثبت اختراع آن درخواست بودجه می کنید: یک نگاه به پروژه برای درک ایده کافی است و می فهمید که ایده همه چیز است. در همان زمان، شما می خواهید وام دهنده شما مطمئن باشد که مکانیسم کار می کند. اعتماد کنیم یا نه؟ کدام مسیر را دنبال کنیم؟
واضح است که در این مسیر مشکلات چند برابر می شود. برای اکثر آنها، عمل راه حل های تجربی، خاص و متفاوت از مورد به مورد پیدا کرده است. ریاضیات سعی می کند همه این مسائل را به عنوان موارد خاصی از یک مسئله واحد و اساسی ببیند.
انسانها ابتدا کلماتی را خلق کردند تا یکدیگر را درک کنند و سپس - شاید توبه کنند - رمزنگاری را اختراع کردند تا فقط برای برخی خود را بفهمند. اما در این راه، علاوه بر جلب کنجکاوی غالباً علاقه مند طردشدگان، مجبور بودند به دنیایی از اسرار پناه ببرند تا با چند نفر در میان بگذارند. نسخه جدید و مدرن رمزنگاری، چیزی که رمزنگاری کلید عمومی نامیده میشود ، به نظر میرسد از میل جهانی ریاضیدانان به رفتار یکسان با همه، کنجکاو و با اعتماد به نفس، و حذف حتی کوچکترین اشتراکگذاری راز از ارتباطات خصوصی ما، زاده شده است. با چه موفقیتی خواهیم دید.
با این حال، قبل از پرداختن به ایدهها و روشهای اساسی، خوب است که یک مشاهده اصلی داشته باشیم: در مسئله کلاسیک انتقال پیام ، از آلیس تا باب، با تلاش شخصی مانند چارلی برای رمزگشایی محتوای واقعی - مشکلی که به آن کمک میکند. خود را برای گنجاندن همه چیزهای دیگر که تبدیل به جنبه ها یا تخصص های خاصی می شوند در خود گنجانده است - معمولاً رفتار مشروع به کسانی که سعی در برقراری ارتباط دارند اختصاص می دهد، در حالی که استراق سمع به مثابه فردی که بی جهت به "کسب و کار خود" نمی پردازد، با دیدی منفی تلقی می شود. ". هیچ چیز در مورد این فعالیت نمی تواند دور از واقعیت باشد: برای مثال، مشخص است که یکی از معروف ترین موارد استفاده از تکنیک های رمزنگاری در طول جنگ جهانی دوم رخ داد، زمانی که سرویس مخفی انگلیس با کمک ضروری آلن تورینگ ( 1912-1954)، در اوایل سال 1942 موفق به رمزگشایی ماشین رمز انیگما شد که توسط فرماندهی آلمانی استفاده می شد. و این واقعیت برای سرنوشت جنگ تعیین کننده بود (حتی اگر ماشین دیگری به نام T-52 در تمام طول جنگ فعال بماند).
با این روحیه عینی است که رمزنگاران و حتی بیشتر از آن ریاضیدانان خود را به در نظر گرفتن روش های خود وامی دارند: تاریخ رمزنگاری مملو از حرکات و حرکات متقابل است، نوعی رقابت بین کسانی که همیشه روش های رمزگذاری جدید را ابداع می کنند و کسانی که بی وقفه روش های رمزگذاری را پیدا می کنند. روشی برای رمزگشایی سیستم جدید نیز.
کسانی که رمزگذاری می کنند و کسانی که رمزگشایی می کنند باید در یک سطح در نظر گرفته شوند. اینها دو روش متفاوت از یک پدیده هستند، مانند دو بخش که اندازه گیری آنها علائم متفاوتی دارد، فقط به این دلیل که جهت مثبت خط مستقیم در یک جهت انتخاب شده است تا جهت دیگر. ملاحظات اخلاقی رفتار به زمینه دیگری تعلق دارد.
اطلاعات مختصر و جذاب در مورد رویدادهای تاریخی و ایده های مدرن فعالیت رمزنگاری از نقطه نظر فنی در Sgarro [1] و Berardi, Beutelspacher [2] موجود است. درمان گستردهتر، اما همچنان به شیوهای قانعکننده روایت میشود، برخورد سینگ [3] است. هرکسی که بخواهد مشکل را از نقطه نظر تأثیر آن بر توسعه سیستم های ارتباطی دیجیتال - و در نتیجه عمدتاً با توجه به مشکلات اجتماعی و حقوقی - طرح ریزی کند، می تواند با Giustozzi، Monti و Zimuel [4] مشورت کند.
کلید رمزگذاری
اگرچه ممکن است متناقض به نظر برسد، همه موافق هستند که برای تجهیز خود به روشی برای انتقال پیام های محرمانه در طول یک کانال قابل رهگیری، لازم است قبلاً یک کانال امن در دسترس باشد که از طریق آن A و B بتوانند کلیدی را مبادله کنند. یکی برای رمزگذاری پیام ها و دیگری برای رمزگشایی خدمت می کند.
واقعیت این است که این کانال امن نمی تواند برای انتقال عادی استفاده شود، اما شاید در شرایط استثنایی ایجاد شود که تکرار آن دشوار است. به عنوان مثال، در استعاره جاسوسی که به خوبی برای این موقعیت ها مناسب است، A و B با یکدیگر ملاقات می کنند و مستقیماً در مورد کلیدی که بعداً استفاده خواهند کرد توافق می کنند. بسه کانال امنی که با نزدیکی آنها و امکان برقراری ارتباط صوتی ارائه می شود هرگز تکرار نخواهد شد، اما کلید تضمین محرمانه بودن ارتباطات آینده آنها در امتداد کانال دیگری و معمول تر است که - آنها به خوبی می دانند - به طور سیستماتیک توسط رقیب C رهگیری می شود. .
نقش اساسی کلید رمزگذاری حتی در دوره ای مدون شد که در آن فعالیت رمزنگاری که همیشه در زمینه نظامی به طور گسترده مورد استفاده قرار می گرفت به نوعی حداکثر استفاده رسید. فیلولوژیست هلندی ژان گیوم کرکخوف (1835-1903)، در کار خود La cryptographie militaire در سال 1883، مشاهده می کند که امنیت یک سیستم رمزنگاری تنها به محرمانه بودن کلید بستگی دارد.
به عبارت دیگر، بدون بحث پذیرفته می شود که یک رهگیر احتمالی از پیام های رمزگذاری شده و همچنین از سیستم رمزگذاری استفاده شده آگاه می شود: چیزی که او نباید بداند کلید است. امنیت انتقال به محرمانه بودن آن بستگی دارد و بالعکس: رهگیر فقط باید کلید را بداند تا بتواند همه پیام ها را رمزگشایی کند.
پس مشکل از دید کسانی که می خواهند پیام های محرمانه رد و بدل کنند چیست؟ واضح است که قبل از هر چیز کلید سیستم رمزنگاری باید برای چند نفر شناخته شود، کسانی که ارسال می کنند و کسانی که دریافت می کنند و احتمالاً هیچ کس دیگری، زیرا - همانطور که می دانیم - رهگیرها ظلم های کمی دارند. و سپس لازمه سادگی را با هم ترکیب کنید - بتوانید آن را به خاطر بسپارید بدون اینکه اسنادی را در اطراف آن بنویسید که امکان یافتن آن وجود دارد و برای سهولت استفاده - همراه با نوعی پیچیدگی که اجازه نمی دهد به راحتی آن را ردیابی کنید. با بررسی تعداد معینی از پیام های رمزگذاری شده. بیایید بگوییم که مشکلات کلید رمزنگاری به اشتراک گذاری آن بین چندین موضوع و رابطه متعادل بین سادگی و پیچیدگی استفاده است.
کمی تاریخچه
به گفته سوتونیوس ویتا سزاروم ، یکی از قدیمیترین سیستمهای رمزی به ژولیوس سزار برمیگردد و در جنگ او علیه گولها مورد استفاده قرار میگرفت. مشخص است که قبلاً از سیستمهای دیگر، اغلب بسیار اصلی نیز استفاده شده بود، اما این یکی از Cesare شاید اولین موردی باشد که گاه به گاه نیست: یک روش، یک سیستم را پیشنهاد میکند، با کلیدهای مختلف قابل تکرار است.
این ایده در حقیقت آنقدر ساده است که زیرکی گول ها را ارج نمی نهد، اما ما آن را برای راحتی توضیح فرض می کنیم: پس از مرتب کردن حروف به ترتیب الفبایی کلاسیک، دایره ای در نظر گرفته شده - بنابراین، با حرف a به دنبال z - هر حرف به همان میزان به سمت راست منتقل می شود. بنابراین، اگر ترجمه از دو حرف باشد، a تبدیل به c، b تبدیل به d ... و به همین ترتیب، تا زمانی که z تبدیل به b شود مانند طرح زیر که در آن هر حرف متن ساده بالای حرف رمزگذاری شده مربوطه قرار میگیرد :
abcdefghilmnopqrstuvz
cdefghilmnopqrstuvzab
سپس تمام حروف موجود در پیام به طور منظم به حروف رمز مربوطه تغییر می کنند. این رمز سزار (یا ترجمه) است و اطلاعات اساسی کلید در این مورد فقط با کمیتی که ارزش ترجمه را مشخص می کند داده می شود: آشکارا در مجموع 21 کلید رمزگذاری مجزا وجود دارد - یکی از آنها بی اهمیت است. هویت
معیار سادگی مطمئناً برآورده می شود. شاید خیلی زیاد. و فکر کردن به حرکت از یک ترجمه به یک قرابت، برای افزایش کمی تعداد رمزها بدون اینکه سیستم را غیر عملی کند، دشوار نیست. این بدان معنی است که به جای فرمولی مانند:
n'=n+k
جایی که n نشان دهنده موقعیت حرفی است که باید رمزگذاری شود، n' موقعیت حرف رمزگذاری شده مربوطه (n, n' =1, 2, ... , 21) و k کلید است، یک عبارت از نوع خواهد بود. استفاده می شود:
n'=an+b
در این مورد ، کلید توسط جفت اعداد صحیح مرتب شده (a, b) داده می شود که هر دو از 21 تجاوز نمی کنند . لازم است که اجازه دهید GCD(a,21)=1 باشد ، یعنی عدد صحیح a هیچ مقسوم علیه مشترکی با 21 نداشته باشد (همانطور که می گویند: a و 21 باید برای یکدیگر اول باشند ). محاسبه (تمرین!) تعداد رمزهای مشابه که متمایز هستند آسان است: 252 است که یکی از آنها هنوز هویت است.
تعداد رمزها بیشتر از قبل است، اما هنوز خیلی کم است که نمیتوان با حمله رمزگشاهای ماهر روبرو شد. یک استراتژی می تواند این باشد که به جای استفاده از یک فرمول ساده مانند ترجمه یا قرابت، هر گونه جایگشتی را برای تعیین حروف رمزگذاری شده فرض کنیم. 21 جایگشت احتمالی وجود دارد! و این عددی است که دارای 20 رقم اعشاری است و هر رمزی را از خطر شکسته شدن در اثر تلاش محافظت می کند. اما خوب نیست. زیرا هر کسی که ارسال میکند و دریافت میکند باید جایگشت حروفی را که انتخاب کردهاند، به زیان پنهان کاری، در جایی ثبت کند: کلید رمزنگاری با اطلاعاتی که به خاطر سپردن و استفاده ساده باشد داده نمیشود، بلکه خود کل جایگشت است.
بنابراین مشکلی که پیش میآید این است: چگونه با استفاده از یک مکانیسم ساده برای به خاطر سپردن، یک جایگشت از حروف الفبا ایجاد کنیم؟ در عمل این مشکل باعث ایجاد ایده کلمات کلیدی شده است . در این مرحله، از زمان سزار، ما قبلاً به رنسانس رسیدهایم، زمانی که تکنیکهای رمزنگاری - مرتبط با رشد تجارت و تماسهای دیپلماتیک بین دولتها - از یک دوره تاریک احیا شدند.
پس از برداشتن یک کلمه بدون تکرار، حروف آن به عنوان اولین جایگشت مورد استفاده قرار می گیرد و از یک مکان خاص شروع می شود. حروف دیگر رمز در ادامه فهرست شدهاند و از حروفی که قبلاً استفاده شدهاند صرفنظر میکنند. به عنوان مثال، با استفاده از کلمه کلیدی hello که از حرف d شروع می شود، یعنی از جایگاه چهارم، جایگشت زیر به دست می آید:
abcdefghilmnopqrstuvz
tuzsalvebcdfghimnopqr
در این مورد، کلید رمزنگاری به جفت کاهش می یابد (سلام، 4). اما داستان به اینجا ختم نمی شود: یک رمزگشا با دانش خوبی از آمار، برخی جداول و تعداد کافی پیام رمزگذاری شده که A و B رد و بدل کرده اند، می تواند به سرعت کلید را ردیابی کند. طبیعتاً، او میداند که حروف مختلف الفبا با چه فراوانی در متون همسانی که میخواهد رمزگشایی کند - چه حروف عاشقانه یا پیامهای نظامی - ظاهر میشوند و به زودی، برای مثال، حروف صدادار و صامتهای خاص را بیشتر تشخیص خواهد داد. از حروف دیگر استفاده می شود. همه با ابهام زیاد، اما فقط برای لحظه. او آزمایشها، حدسها، تلاشهای کم و بیش انگیزهای را انجام میدهد تا زمانی که کلمهای با معنای کامل پیدا کند یا دورهای را که رمزگذاری انجام میشود تشخیص دهد: اساساً طول کلمه کلیدی.
در این مرحله انجام شده است. از اینجا یک گام کوتاه برای شکستن کل رمز است.
چگونه می توان فرکانس های آماری را لغو کرد و از تکرارهای دوره ای اجتناب کرد؟ به راحتی می توان تشخیص داد که تجزیه و تحلیل فرکانس با این واقعیت امکان پذیر است که رمز جایگزین تک الفبایی است ، یعنی هر حرف همیشه با همان حرف در طول انتقال کل پیام رمزگذاری می شود. این اشکال را می توان با جابجایی به رمزهای جایگزین چند الفبایی حل کرد ، برای مثال با استفاده از صد علامت مختلف، از هر ماهیت، برای رمزگذاری 21 حرف متن ساده. برای مثال، اگر بدانیم که در پیامهایی که به آن علاقه داریم، حرف a به طور متوسط ده بار از صد مورد اتفاق میافتد، کافی است از ده علامت مختلف برای رمزگذاری آن استفاده کنیم. نگران نباشید: لازم نیست بین متن ساده و الفبای رمزگذاری شده تناظر یک به یک وجود داشته باشد، بلکه فقط باید یکسان باشد: عبور از متن رمزگذاری شده به متن ساده. به این ترتیب، حرف a یک بار به یک صورت و یک بار به روش دیگر به ده روش مختلف رمزگذاری می شود و بسامد آن عملاً لغو می شود: اما هرکس پیام را دریافت کند و سیستم رمزگذاری را بشناسد، در هر صورت قادر است تا ده مورد را تشخیص دهد. نمادهای مختلف باید به عنوان a تفسیر شوند.
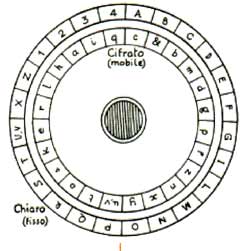
رمز دیسک
با این حال، واضح است که مشکل فقط تا حدی حل شده است زیرا در تناوب مداوم بین جستجوی سادگی سیستم و امنیت آن، این روش فرستنده و گیرنده را ملزم می کند تا خود را به یک جدول چشمگیر برای مشورت با هر یک مجهز کنند. زمان و این واقعیت ضمن ارائه اطلاعات مفید در برخی موارد، با نیاز به محرمانه بودن کلید منافات دارد.
با این حال، گام بعدی که در قرن پانزدهم توسط برخی از محققان رنسانس شناسایی شد و به صراحت توسط هنرمند و ریاضیدان بزرگ لئون باتیستا آلبرتی (1406-1472) پیشنهاد شد، تعیین کننده است: او در اثر خود Modus scribendi in ziferas در سال 1466، چند الفبایی را معرفی می کند. جایگزینی که انجام آن آسان است و چرخههایی را که در رمزگذاری رخ میدهد و بنابراین درک دورههای رمز را بسیار دشوارتر میکند. این ایده تا دوران مدرن به طور قابل ملاحظه ای بدون تغییر باقی خواهد ماند.
برای این منظور باید خود را به رمز پویا مجهز کرد : هر حرف از متن ساده بسته به موقعیت آن در خود متن، هر از گاهی به طور متفاوت رمزگذاری می شود. آلبرتی، به عنوان سازنده ماهری که بود، مکانیزم عملی را نیز ابداع کرده بود، مجهز به دو نسخه الفبا بر روی دو دیسک که میتوانستند نسبت به یکدیگر بچرخند و بنابراین از طرق مختلف با یکدیگر مکاتبه کنند. : پس از رمزگذاری یک حرف از پیام، یک چرخش ساده از یک یا چند بریدگی به شما امکان می دهد مکاتبات را برای حرف بعدی که باید رمزگذاری شود تغییر دهید. برای استفاده از آن توسط شخص دریافت کننده پیام، دانستن نقطه تطابق اولیه دیسک ها و تعداد بریدگی هایی که باید بعد از هر عملیات رمزگذاری بچرخند، کافی است. این کلید سیستم رمزگذاری ایجاد شده توسط لئون باتیستا آلبرتی است. این ایده مربوط به تناظر پویا بین حروف الفبا که در طول پیام متغیر بود، توسط دیپلمات فرانسوی بلز دو ویژنر (1523-1596) در قرن بعد محقق شد و مورد استفاده قرار گرفت و در اثر او Traité des chiffres ou گسترده شد. secrètes maniéres d'escrire of 1586: رمزهای به دست آمده، که عملاً تا دهه 1900 فعال بودند، همگی نام او را گرفتند: رمزهای ویژنر.
در این رمزها، تناظر پویا با استفاده از یک کلمه متعارف ترکیب می شود تا به عنوان کلیدی استفاده شود که دیگر نیازی به انتخاب بدون تکرار ندارد، که به نظر می رسد اولین رسمی سازی آن در رساله De furtivis literarum notos، vulgo وجود دارد. de ziferis ، نوشته شده در سال 1563 توسط دانشمند و فیلسوف Giovan Battista della Porta.
ایده این است که از حروف کلمه کلیدی استفاده شود که تا زمانی که لازم است در متن ساده به طور مداوم تکرار شود تا رمزی (از نوع سزار ) مورد استفاده در آن لحظه را نشان دهد. در اصل، حرفی که باید رمزگذاری شود و حرف متناظر کلمه کلیدی بهعنوان نوعی مختصات مسطح استفاده میشود که با آن حرف رمزگذاری شده را در چارچوبی شناسایی میکنیم - یک تابلو ، همانطور که امروز در ریاضیات میگوییم - که شامل تمام سزار ممکن است. رمزها
به عنوان مثال، کلمه hello را دوباره به عنوان کلید انتخاب کنید و فرض کنید می خواهید پیام را منتقل کنید:
ریاضیات بخون و همیشه خوشحال خواهی بود.
عملیات به شرح زیر است:
1. هر حرف از پیام ساده مطابق با یک حرف کلید قرار می گیرد که در صورت لزوم مطابق با حروف آن تکرار می شود:
ریاضی بخون
سلام سلام
سلام علیکم همیشه
شاد سلام سلام سلام سلام سلام
2. حرف کلید نشان می دهد که از کدام رمز برای حرف متن ساده مربوطه استفاده شود، با مراجعه به جدول زیر، که شامل تمام رمزهای سزار به شیوه ای منظم است :

3. برای رمزگذاری پیام، از حروف کلمه کلیدی برای شناسایی رمز استفاده می شود: بنابراین، برای حرف اول s ، خطی که با s همان hello شروع می شود استفاده می شود و n مشخص می شود . برای حرف t ساده بعدی، رمز رمزی است که با a در hello شروع می شود و بنابراین حتی پس از رمزگذاری t باقی می ماند. اکنون از l کلمه کلیدی برای رمزگذاری u و تبدیل آن به g و غیره استفاده می کنیم . پیام رمزگذاری شده شکل می گیرد...
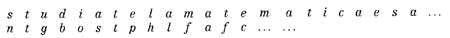
تو ادامه بده برای درک بهتر استفاده از رمز پویا، مشاهده کنید که چگونه از این قطعه کوچک به نظر می رسد که حرف e بار اول با p و دفعه بعد با c رمزگذاری شده است . برعکس، حرف f مخفف m و t به دلیل این واقعیت است که این حروف موقعیتهای مختلفی را در پیام متنی معمولی اشغال میکنند.
بدیهی است که با تغییر کلمه کلیدی، تعداد نامحدودی از رمزها از این طریق به دست می آید. و اگر کلید به اندازه کافی طولانی باشد - و محدودیتی که در آن حروف تکراری وجود ندارد دیگر مورد نیاز نیست - دوره سیستم رمزگذاری به نسبت طولانی است. با این حال، ما نباید روش های آمار و یا توانایی و سرسختی رمزگشاها را دست کم بگیریم: برای دانستن تعداد کافی از پیام های رمزگذاری شده، در طول زمان روش هایی برای یافتن دوره سیستم رمزگذاری و از اینجا به صورت تجربی ایجاد شده است. راه، کلید را ردیابی کنید.
این نتایج، ناگفته نماند که در زمینه نظامی به دست آمده است. معماران اصلی افسر پروس فریدریش ویلهلم کاسیکی (1805-1881) و بعدها ژنرال آمریکایی ویلیام فردریک فریدمن (1891-1969) بودند. ایده اتخاذ شده توسط کاسیسکی مبتنی بر تجزیه و تحلیل تکرار گروههایی از حروف است که در رابطه مستقیم با طول کلمه کلیدی قرار میگیرند: این امکان را فراهم میکند که رمز به اجزای تک الفبایی خود تقسیم شود، که رمزگشایی آنها سادهتر است. کار فریدمن در عوض بر این احتمال تمرکز دارد که هر دو حرف در یک متن رمزی در واقع با یک حرف متن ساده مطابقت دارند. شرح مختصری از این روش ها، بدون پیچیدگی های فنی بیش از حد، را می توان در متن چابک Berardi و Beutelspacher [2] یافت. بنابراین ما به سپیده دم دهه 1900 رسیدیم، زمانی که دستگاه های الکترومکانیکی برای پردازش مقادیر روزافزون داده هایی که به عملیات رمزگشایی متصل بودند و در نتیجه برای عملیات دوگانه تنظیم دقیق سیستم رمزگذاری آماده بودند. .
ماشین های رمزگذاری
دوره ابزارهای رمزگذاری و رمزگشایی ابتدا سیستم های مکانیکی و سپس الکتریکی و الکترونیکی را به عنوان پیامد تکامل خود مفهوم ارتباطات دید. مقاله شانون در سال 1949 [5] نشانه ورود قطعی رمزنگاری به حوزه نظریه اطلاعات است. عصر رمزگذاری خودکار است . ما قبلاً به ماشین رمز انیگما
اشاره کردهایم ، مجموعهای که قبلاً در دهه 1920 برای اهداف تجاری طراحی شده بود و سپس به عنوان استانداردی برای ارتباطات محرمانه توسط فرماندهی آلمان در طول جنگ جهانی دوم اقتباس شد. این دستگاه از تعداد معینی دیسک دوار (سه عدد در پیچیده ترین نسخه ها) تشکیل شده بود که هر کدام از آنها الفبا را با استفاده از مدارهای الکتریکی پیچیده رمزگذاری می کردند. علاوه بر این، برای پیچیدگی بیشتر، این روتورها با توجه به کلیدی که به صورت رمزگذاری شده نیز ارسال می شد، روز به روز به روشی متفاوت به یکدیگر متصل می شدند. پس از هر حرف ارسال شده، آنها تحت یک چرخش قرار گرفتند.
مجموعه ای از روش ها برای رمزگشایی مفید بودند، از جمله روش هایی که از طریق به دست آوردن اطلاعات از طریق جاسوسی سنتی و همچنین آمار، مطالعه ساختارهای جبری و ترکیبی، بررسی عادات فرستنده های آلمانی و عبارات عامیانه، تجزیه و تحلیل مقادیر زیادی از داده ها با استفاده از دیگر ماشینهای الکترومکانیکی مخصوص ساخته شده ( بمبهای معروف ، بهاصطلاح تیک تاک کلاسیکشان). برای سهولت بیشتر در کار و صرفه جویی آشکار در ابزار، انیگما از یک بازتابنده استفاده کرد که به لطف آن از کلیدهای یکسان و عملیات های مشابه هم برای رمزگذاری و هم برای رمزگشایی استفاده می شد: متن ساده روی صفحه کلید تایپ می شود و دستگاه به طور مناسب مرتب می شود. با توجه به کلید، متن کدگذاری شده روی صفحه نمایش خوانده می شود. برعکس، اگر متن کد شده را تایپ کنید، متن ساده را مستقیماً می خوانید. سیستم رمزنگاری برگشت پذیر است و این ویژگی ساختاری عناصر اساسی را برای رمزگشایی فراهم می کند.
داستان جذاب این ماشین، اصول ساخت آن و اینکه چگونه گروهی از ریاضیدانان، فیلسوفان و معمدانان که توسط فرماندهی انگلیسی در پارک بلتی جمع شده بودند، توانستند آن را حداقل در برخی از جنبه های آن، به ویژه برای جنگ در دریا رمزگشایی کنند. آنها به خوبی در زندگینامه آلن تورینگ نوشته اندرو هاجز t6 و در تاریخ رمزنگاری سینگ [3] آمده است.
سایر ماشینها و سیستمهای دیگر بخشی از تاریخ رمزنگاری قرن بیستم هستند. بهترین سیستم شناخته شده که برای طولانی ترین مدت در برابر حملات رمزگشایی مقاومت کرده است، سیستمی است که به طور رسمی در سال 1977 توسط دولت ایالات متحده تأسیس شد، DES ( استاندارد رمزگذاری داده ها )، یک رمز تک الفبایی که امنیت آن بر روی کلید 56 بیتی (که 8 بیت کنترل هستند)، در سال 1998 شکسته شد. این اولین سیستم رمزگذاری تجاری است که به عنوان یک استاندارد توسط یک نهاد نظارتی ایجاد شد تا از گسترش سیستم های رمزگذاری ناسازگار با یکدیگر جلوگیری شود.
DES یک سری تبدیلات ابتدایی را انجام می دهد که چندین بار بر روی بسته های ساختاری مناسب متن تکرار می شود تا بیت هایی را که آن را تشکیل می دهند تحت یک تغییر کلی قرار دهد که اساساً به کلید انتخاب شده وابسته است: الگوریتم ها عمومی می شوند. کلید - با رعایت دقیقترین اصل کرکهوف - تنها دادهای است که کاربر تنظیم میکند.
جنبه مهم این است که رمزگذاری می تواند در زمان واقعی با یک کامپیوتر با قدرت متوسط انجام شود. علاوه بر این، سیستم متقارن است به این معنا که، مانند همه سیستمهایی که تا این لحظه مثال زده شده، از کلید مستقیماً برای رمزگشایی استفاده میشود. یک
عدد 56 بیتی حاوی مقدار زیادی اطلاعات است: شما 7، 2 x 10 16 کلید مختلف دارید. با این حال، از اولین ظهور، به نظر محققان برای مقابله با منابعی که به طور قابل پیش بینی در آینده توسعه خواهند یافت، کوتاه تر از آن به نظر می رسید. و همانطور که انتظار می رفت، این دلیل اصلی رمزگشایی آن بود، اگرچه این امر نیازمند قدرت هزاران رایانه بود که به طور همزمان کار می کردند، هماهنگ شده از طریق اینترنت .
در واقع، در زمینه ماشینهای محاسباتی بزرگی است که به مسائل رمزنگاری اختصاص داده شده است که در دهه 1900 این آگاهی به وجود آمد که برای داشتن یک رمز کامل ، یعنی رمزی که نمیتوان آن را شکست، کلید باید به این صورت باشد. اطلاعات زیادی به عنوان کلید پیام های ممکن. یک پارادوکس ظاهری، که با این حال، تنها مفهوم کلید رمزنگاری را به جلو می برد. به عنوان مثال رمز Vernam است که به نام مهندس ارتباطات راه دور گیلبرت ورنام (1890-1960) نامگذاری شده است که در آن کلید یک مولد اعداد تصادفی است. تعجب آور نیست که هر کلید را می توان به صورت عددی کدگذاری کرد: واضح است که با این سطح از پیشرفت و شروع روش های دیجیتال، می توان به خوبی فکر کرد که پیام نیز چیزی جز یک عدد نیست که در تعداد معینی کدگذاری شده است. از بیت ها . مشکل واقعی که باقی می ماند مشکل کلید است: تولید، حفاظت و انتقال آن.
به این ترتیب، با هر استفاده جدید، کلید همیشه جدید است. هرگز از انتقالی به انتقال دیگر تکرار نمیشود و در واقع، پس از استفاده حذف میشود (آمریکاییها از پد یکبار مصرف صحبت میکنند تا تاکید بر استفاده غیرقابل تکرار از کلید داشته باشند) اما راز واقعی اکنون در راه متمرکز شده است. که تولید می شود.
| اولین رمزی که توسط Vernam در سال 1917 طراحی شد شامل دستگاهی است که قادر به اجرای انحصاری یا V، مدت به ترم، سیگنال های دوتایی بر روی دو نوار است. در یک نوار متنی وجود دارد که باید رمزگذاری شود، در دیگری کلید: در نتیجه، در هر موقعیت خروجی ، 1 به دست می آید اگر و فقط اگر دو موقعیت متناظر روی نوارها متفاوت باشند: 0 و 1 یا 1. و 0. ابتکار روش در این واقعیت نهفته است که ناتوانی عملیات "a V -"، که در آن a یک متغیر باینری است: |
aV(aVb)=b
برگشت پذیری سیستم را تضمین می کند.
اما برای نشان دادن معنای استفاده از کلید یکبار مصرف لزوماً یک محیط تکنولوژیکی بسیار پیچیده ضروری نیست: برای مثال، به این فکر کنید که با همکار خود ثابت کنید که کلید انتقال پیام های رمزگذاری شده توسط نسخه خاصی از کمدی الهی داده شده است. . شما رمزگذاری à la Vigenère را با استفاده از تمام حروف متوالی کار دانته به عنوان کلید انجام می دهید: " nelmezzodelcammindinostravita...... " با این قرارداد که برای پیام بعدی کلید از جایی شروع می شود که در پیام قبلی متوقف شده است. بدیهی است که سیستم هیچ دوره ای ندارد: رمزگذاری هرگز به همان شکل تکرار نمی شود. اما ماشینی که با آزمون و خطا پیش می رفت، مطمئناً دیر یا زود می تواند پیام های شما را رمزگشایی کند و شاید همه آیات کمدی الهی را بازنویسی کند !
در این مرحله از توسعه، ما به ایدهای نیاز داریم که مفهوم کلید رمزنگاری را با امکانات بسیار زیادی ارائه کند و در عین حال آن را از نیاز به اشتراک گذاری بین چندین طرف، حتی بین فرستنده و گیرنده، رها کند. مدیریت کلیدها، که اغلب دست و پا گیر هستند، تولید آنها، ارسال آنها به گیرندگان، نیازهای امنیتی... این نقطه حیاتی واقعی سیستم های رمزگذاری است. و این همان چیزی است که از ایده کلید عمومی ، در مقابل استفاده خصوصی، شخصی و مخفیانه از کلید، پیشرفت زیادی دریافت کرد. کلیدی که میتوانید با هر کسی که میخواهد پیامی را رمزگذاری کند و برای شما ارسال کند، ارتباط برقرار کنید، اما برای رمزگشایی که فقط شما میدانید چگونه آن را انجام دهید مفید نیست.
تبادل کلید
آلیس و باب را از سر می گیریم که با مشکل مبادله کلیدی برای استفاده برای ارتباطات شخصی خود دست و پنجه نرم می کنند، اما از کنجکاوی چارلی در امان هستند. آنها امکان ملاقات ندارند اما ماشین هایی با ظرفیت محاسباتی و ارتباطی خوب دارند، علیرغم اینکه می دانند ایمیل هایشان مرتباً رهگیری می شود. آنها به این ترتیب پیش خواهند رفت: با تلفن - که توسط چارلی حسود نیز شنود می شود - یک عدد صحیح مثبت n را ثابت می کنند . سپس هر یک از آنها به تنهایی، بدون اینکه آن را برای کسی فاش کند، دیگری را انتخاب میکند: آلیس a را درست میکند و باب b را درست میکند ، آلیس به باب مقدار n a را میگوید و باب ارزش n b را به او میگوید (و چارلی به همه چیز گوش میدهد). اکنون آلیس n ab را صرفاً با بالا بردن مقداری که باب به او ابلاغ کرده است را به توان مخفی خود a محاسبه می کند و به طور مشابه باب همان مقدار را با افزایش na به توان b که فقط او می داند محاسبه می کند. این همه (در ویژگی جابجایی محصول):
(n a ) b = (n b ) a = n ab
و هر دوی آنها این شماره را می دانند که به عنوان کلید رمزنگاری آنها عمل می کند. چارلی ناامید n a و n b را جداگانه می داند اما a و b را نمی داند که باید دو لگاریتم پایه n محاسبه کند . این مشکل اوست، زیرا آلیس و باب اعداد ( n، a و b ) را به اندازه کافی بالا انتخاب کردند تا سیستمهای محاسباتی چارلی را خارج از این امکان قرار دهند، در اصل ساده اما در عمل بسیار وقتگیر.
میدانیم که موضوع کجاست: محاسبه نمایی، حتی با یک سیستم کم یا قدرتمند، میتواند به راحتی انجام شود در حالی که معکوس آن، لگاریتم، میتواند به منابع محاسباتی نیاز داشته باشد که از نظر زمان غیرقابل تحمل هستند.
این ایده ای است که در دهه 70 بوجود آمد و سپس در Diffie and Hellman [7] منتشر شد: ارائه یک تابع - معکوس بله، در غیر این صورت رمزگشایی ممکن نیست، اما به یک معنا به راحتی محاسبه می شود و بسیار دشوار است. محاسبه معکوس طولانی یا عملاً غیرممکن است - تابعی که در اصطلاحات آنگلوساکسون در حال حاضر مرسوم است، به آن trapdoor می گویند .
سقوط آسان است، در حالی که صعود به عقب عملاً غیرممکن است (مگر اینکه یک مسیر مخفی بدانید).
یکی از این توابع، در واقع توابعی که در گستردهترین پیادهسازیهای سیستمهای رمزنگاری مورد استفاده قرار میگیرد، با حاصل ضرب اعداد صحیح به دست میآید: در حالی که این یک عملیات آسان برای انجام حتی بین اعداد با ارقام زیاد است (به شرطی که محاسبه در دسترس داشته باشید. ابزارهای بسیار قدرتمند)، عملیات معکوس که تجزیه به عوامل است می تواند به طور غیرقابل تحمل طولانی باشد. تخمین های مربوط به فاکتورسازی تعدادی از چند صد رقم اعشار، علیرغم داشتن مدرن ترین سیستم های محاسبه سریع موجود، هنوز بر حسب میلیون ها سال اندازه گیری می شوند. این یک مسئله تئوری اعداد است که از نظر محاسباتی غیرقابل حل به نظر می رسد.
کلید عمومی
اولین کاربرد برای مشکل انتقال رمزگذاری شده پیام ها، یعنی مشکل اصلی رمزنگاری، بر اساس مشاهده - پیش پا افتاده اما تعیین کننده - است که کلید رمزگذاری کانال ارتباطی را متقارن می کند. از A به B منتقل میشود، اما این فرآیند همچنین میتواند بدون تغییر رمز یا کلید معکوس شود: احتمالاً، اگر رمز برگشتپذیر نباشد، همه عملیاتها باید معکوس شوند.
تقارن کانال - این جزء ساختاری فرآیند ارتباط - در عمل با یک تابع رمز ترفند تغییر میکند: کانال نامتقارن میشود. رمزگذاری فقط در یک جهت امکان پذیر است و خود فرستنده - که دستورالعمل های رمزگذاری را دارد - قادر به رمزگشایی پیام ها نیست.
اکنون دو کلید متمایز وجود دارد: یکی برای رمزگذاری، که برای همه کسانی که می خواهند پیام رمزگذاری شده ارسال کنند، به طور عمومی شناخته شده است، و دیگری برای رمزگشایی که توسط گیرنده پیام ها کاملاً مخفی نگه داشته می شود. بدیهی است که کلیدها به یکدیگر وابسته هستند - در غیر این صورت پیام ها هرگز نمی توانند رمزگشایی شوند - اما دانش یکی برای ردیابی دیگری کافی نیست... مگر اینکه شما رازی را بدانید: یک تابع ترفند.
مشکل اشتراک گذاری کلید رمزنگاری کاملاً حل شده است و سادگی رمزگذاری به دشواری شدید رمزگشایی مرتبط است. این همه به عملکرد ترفند بستگی دارد!
سیستم RSA
این سیستم، چند سال پس از ایده توابع ترفند ، در Rivest، Shamir و Adleman [8] ظاهر میشود و دقیقاً بر اساس دشواری یافتن منابع محاسباتی کافی برای تجزیه به عوامل اول اعداد صحیح است که دارای ارقام متعدد هستند.
الگوریتمی که برای اجرای عملی پیشنهاد شده است، از پیچیدگی محاسباتی برخی از فرآیندهای تئوری اعداد، مربوط به محاسبات مدولار (که در کادر مقابل بحث شده است، که نتایجی را که به الگوریتم اجازه عملکرد میدهد، نیز توضیح میدهد) بهرهبرداری میکند.
شایان توجه است که این نتایج، که همه خلاصه شده و به طور کامل در Disquisitiones Arithmeticae گاوس (1801) بیان شدهاند، اساساً برای اویلر و در برخی موارد برای فرما در قرن هفدهم شناخته شده بود. به نظر می رسد به کارگیری این نتایج، که در دوره ای یافت می شود که چشم انداز محاسبه سریع حتی از دور قابل تصور نبود، نمونه خارق العاده ای از ثمربخشی تفکر ریاضی و عقلانیتی است که در تحقیق این بزرگان ذاتی است. ارقام ریاضی
بیایید با توضیح ایده پشت سیستم رمزنگاری کلید عمومی شروع کنیم و مشاهده کنیم که برخی از عملیات که ممکن است در نگاه اول در مقایسه با زمان محاسبه بسیار گران به نظر برسند، در عوض به راحتی قابل محاسبه هستند: این مورد، برای مثال، نمایی و بزرگترین مقسومکننده مشترک است. از دو عدد - حتی بسیار بزرگ - و همچنین محاسبه مدول باقیمانده n. جالب است بدانید که این سادگی، علیرغم انواعی که در طول زمان ایجاد شده اند، اساساً توسط یک نتیجه کلاسیک دیگر با اهمیت بسیار ارائه شده است: الگوریتم تقسیمات متوالی یا الگوریتم اقلیدسی که ریشه و منطق آن در عناصر اقلیدس است. و در مسائل مورد بحث در قرن 3 قبل از میلاد (برای مشکلات پیچیدگی محاسباتی در مورد عملیات مختلف می توان به عنوان مثال Salomaa [9] یا Ferragine و Luccio [10] مراجعه کرد).
همه چیز برای راه اندازی سیستم آماده است: هر کسی که قصد دارد گیرنده پیام های محرمانه شود - فرض کنید باب است - کلید خود را تعمیر کرده و عمومی می کند، به طوری که هر کسی که می خواهد یک پیام رمزگذاری شده برای او ارسال کند (نه تنها آلیس، بلکه همچنین دیگران) می داند چگونه رفتار کند. برای این منظور، باب باید برخی از انتخاب ها و برخی عملیات مقدماتی را انجام دهد: توجه به این نکته که امنیت رمز به کیفیت این انتخاب ها بستگی دارد، اضافی است.
با این حال، در اینجا ارزش پرداختن به این جزئیات را ندارد، بلکه تلاش برای روشن کردن روش در اصول آن است (کسانی که برای دانستن این جزئیات بی تاب هستند باید با Koeblitz [11]، Salomaa [9] یا Ferragine و Luccio [10] مشورت کنند. ).
باب یک جفت از اعداد ( e, n ) را با این شرط انتخاب می کند که e و φ(n) ضریب اول مشترک نداشته باشند:
GCD(e, φ(n)) = 1
گفتیم که این انتخاب حتی در محاسبه مشکل ایجاد نمی کند. اگر دو عدد e و n کاملاً بزرگ باشند و همانطور که مشاهده شد بهترین کار این است که معیارهای مناسب برای افزایش استحکام سیستم رعایت شود. این جفت ( e, n ) کلید عمومی باب است که او آن را در دسترس همه قرار می دهد، اما مراقب باشید... باب هیچ اشاره ای به مقدار φ( n ) - حتی به آلیس - نخواهد کرد، زیرا این راز اوست. ، کلید شخصی او که به او امکان رمزگشایی پیام ها را می دهد.
در واقع، باب با استفاده از φ( n )، عدد d را محاسبه می کند که همخوانی درجه اول را حل می کند:
e*x≡1 (mod φ(n))
این عدد d (mod φ( n )) است که مستقیماً برای رمزگشایی پیام ها استفاده می کند. شرط اول بودن e و φ( n ) برای یکدیگر تضمین می کند که همخوانی قبلی یک راه حل منحصر به فرد را تا مدول همخوانی φ( n ) می پذیرد.
اکنون هر کسی توانایی ارسال یک پیام محرمانه را برای باب دارد و او آماده است تا آن را رمزگشایی کند. این روش به این صورت انجام می شود: برای مثال آلیس می خواهد پیام m را (که قبلاً به طور مناسب با یک عدد کدگذاری شده است) ارسال کند. برای این کار، m را به توان e ببرید و مدول باقیمانده n عدد به دست آمده را محاسبه کنید. او دقیقاً از اطلاعاتی که باب به همه اطلاع داده بود - کلید عمومی خود ( e, n ) - برای دریافت پیام رمزگذاری شده c استفاده کرد :
c≡m e (mod n)
چگونه باب می تواند پیام را بازسازی کند، یعنی از c به m برگردد ، و چرا هیچ کس دیگری که c را رهگیری می کند و کلید عمومی باب را می داند قادر به انجام همین کار نیست؟ برای باب آسان است، زیرا او φ(n) را می داند و d را محاسبه کرده است . او فقط باید پیام رمزگذاری شده c را به توان مخفی d برساند . در واقع، همانطور که پیدا شد، ed = kφ(n)+1 مربوط به مقداری عدد صحیح k است و بنابراین داریم:
c d ≡(m e ) d ≡m ed ≡m kφ(n)+1 ≡(m φ(n) ) k *m ≡m(mod n)
که در آن از ویژگی پایداری رابطه همخوانی با توجه به حاصلضرب و قضیه اویلر-فرمات استفاده کردیم: m φ(n) ≡1 (mod n).
رازی که فقط به باب اجازه می دهد پیام را رمزگشایی کند چیست؟ واضح است که در توان d قرار دارد که از کلید رمزگذاری e استفاده می کند و آن را معکوس می کند (مدول φ(n)) . و d با دانستن φ(n) به دست می آید: همانطور که گفتیم این راز واقعی است زیرا محاسبه φ(n) به اندازه تجزیه n به عوامل پیچیده است. وقتی باب کلید عمومی خود را انتخاب کرد، آینده نگری داشت که n را به عنوان حاصلضرب اعداد اول خاص انتخاب کند و بنابراین، به لطف خاصیت ضربی φ اویلر، محاسبه φ(n) برای او بسیار آسان است. در این فرآیند، ویژگیهای اساسی حساب مدولار و φ اویلر شناسایی خواهند شد.
استراتژی بهینه باب دقیقاً این است که n را به عنوان حاصل ضرب تنها دو عدد اول، به اندازه کافی بزرگ و نه خیلی نزدیک به یکدیگر انتخاب کند. به این ترتیب n = p*q با p و q اول است و داریم:
φ(n)=(p - 1)*(q - 1)
بنابراین، همه چیز بر اساس فاکتورسازی اول است. این واقعیت همچنین نشاندهنده «نقطه ضعف» سیستم رمزنگاری است: امنیت مبتنی بر «ناآگاهی» ما از بسیاری از پدیدههای مربوط به اعداد اول است. اگر و زمانی که تحقیقات ریاضی موفق به حل مسائل توزیع اعداد اول شود و روشی کارآمد برای فاکتورگیری بیابد، روش فوراً کارایی خود را از دست خواهد داد... و ما باید به توابع ترفند جدیدی روی بیاوریم.
بار دیگر، همانطور که اغلب اتفاق می افتد، پیشرفت فنی مستقیماً تابع دانش نظری است.
امضای دیجیتال
مشکل اصالت فرستنده اهمیت فزاینده ای پیدا می کند زیرا عملیات های بیشتر و بیشتری با ماهیت و اهمیت مختلف به صورت الکترونیکی انجام می شود. امضای دیجیتال در حال تبدیل شدن به یک ابزار قانونی در بسیاری از کشورها است.
اصل آن چیست؟ در واقع، با «معکوس کردن» اصل انتقال رمزگذاری شده با یک کلید عمومی به دست می آید. بنابراین، بیایید فرض کنیم که باب - همیشه او - می خواهد پیام را منتقل کند، اما این بار، جنبه مهم در رازداری m نهفته است - که همه باید بدانند - بلکه در این است که خود را با قطعیت توسط گیرنده شناسایی کند . این در نهایت عملکردی است که توسط امضای ما انجام میشود: فقط ما میتوانیم آن را انجام دهیم و در نتیجه همه میتوانند تشخیص دهند که یک سند از طرف ما آمده است.
به عنوان مثال، باب از طریق ایمیل از خارج به بانک خود می نویسد تا مقداری اعتبار را دریافت کند: شناسایی باید ایمن باشد. البته باب کلید عمومی خود را دارد ( e, n ) که همه میدانند و به تنهایی توان d را نیز محاسبه کرده است که به او امکان رمزگشایی پیامها را میدهد. با مسلح شدن به این داده ها، باب جفت ( m, m d ) را به عنوان پیامی به بانک خود می فرستد و با اطمینان شناسایی می شود زیرا با محاسبه ای مشابه آنچه که انجام شده است، بلافاصله این اتفاق می افتد:
m≡(m d ) e (mod n)
به عبارت دیگر، شخصی که پیام رمزگذاری شده md را ارسال کرده و اعلام می کند که پیام m به صورت متن واضح است ، فقط می تواند باب باشد. به دو واقعیت توجه کنید: اول اینکه باب صرفاً با اعلام نمایش d
امضا نمیکند ، که مجبور نیست فاش کند و برای تشخیص آن کافی نیست. و سپس، در نتیجه این واقعیت اول، هیچ "امضایی" جدا از اسناد وجود ندارد، که در جایی سپرده شده و در صورت لزوم برای مقایسه شناخته می شود: هر امضایی متناظر با یک سند است، با آن و فقط با آن زندگی می کند. حتی اگر باب کلید عمومی خود را انتخاب نکرده باشد، کسی می تواند آن را برای او انجام دهد. به عنوان مثال، فرض کنید که او مشتری یک موسسه اعتباری است که هنگام برداشت پول از یک دستگاه خودکار باید او را بشناسد. واضح است که مؤسسه باید به باب و سایر مشتریان کارتی با داده های مغناطیسی آنها ارائه دهد و کد شخصی را در اختیار آنها بگذارد که امکان شناسایی آسان را فراهم می کند. اما، از سوی دیگر، به همان اندازه روشن است که نگهداری اطلاعات مربوط به مشتریان و کدهای شخصی آنها در جایی، به عنوان مثال در یک پایگاه داده که امنیت آن باید دائماً نظارت شود، چقدر خطرناک است. سیستم امضای دیجیتال به مؤسسه اجازه میدهد تا برای هر مشتری کلید عمومی خود ( e, n ) را محاسبه کند، ضریب ویژه d را محاسبه کند ، آن را به طرف علاقهمند ارسال کند - مهم نیست که کلید را به آنها اطلاع دهد ( e, n ) - و سپس .. d را از فایل های خود حذف کنید. همچنین میتوان تشخیص را تنها با استفاده از ( e, n ) انجام داد، که میتوان آن را نیز در نمایش گذاشت و در دسترس همه قرار داد. محرمانه بودن سیستم مصادف با محرمانه بودن d است ، که فقط طرف ذینفع می داند: به نظر می رسد این آینده کدهای مخفی، کلیدهای عمومی و محاسبات در انتظار همه ما است.
قرعه کشی آلیس و باب
آنچه باید مورد بررسی قرار گیرد روشی است که در آن دو مدعی می توانند قرعه کشی را انجام دهند، بدون اینکه امکان ملاقات برای بررسی درستی انجام تمام عملیات ها وجود داشته باشد. این مشکل مستقیماً به رویههای رمزنگاری - انتقال و اعتبارسنجی پیامهای محرمانه - مربوط نمیشود، بلکه بر اساس همان اصل کلید عمومی است ، یعنی امکان انجام عملیاتی که معکوس آن برای محاسبه فوری قابل دسترسی نیست، مگر اینکه مقداری وجود داشته باشد. اطلاعات اضافی
در این حالت، آلیس و باب متقابلاً یک تابع ترفند f را انتخاب می کنند. بنابراین، آلیس، برای مثال، مقدار x آرگومان را ثابت میکند، f (x) را محاسبه میکند و به باب پیشنهاد میکند که به طور تصادفی خاصیتی از x را انتخاب کند که احتمال درستی آن 50٪ است: برای مثال، وقتی x یک عدد کامل است، از او می خواهد بگوید زوج است یا فرد. واضح است که برای باب ردیابی از f (x) تا x غیرممکن است: اگر او درست حدس بزند، پیروزی در تساوی متعلق به اوست، در غیر این صورت از آن آلیس است و خود باب می تواند به راحتی خود را در این مورد متقاعد کند. انتخاب تصادفی و منصفانه بود، همانطور که در قرعه کشی لازم بود.
معمولاً حتی برای رویه ای از این نوع جالب ترین توابع از نظریه اعداد گرفته می شود. در اینجا یکی است که از یک ویژگی غیر پیش پا افتاده استفاده می کند: مانند انتخاب کلید عمومی، آلیس دو عدد اول بسیار بزرگ p و q را ثابت می کند و حاصلضرب آنها n=p*q را محاسبه می کند . او ارزش n را به باب می گوید، اما نه فاکتورگیری را که طبق معمول راز اوست. به نوبه خود، باب نیز یک عدد صحیح u را بین 1 و n/2 انتخاب می کند ، u 2 (mod n) را محاسبه می کند و این عدد را به آلیس می رساند. آلیس به راحتی می تواند دو ریشه مربع u 2 را که در بازه (1,n/2) قرار گرفته اند پیدا کند زیرا او فاکتورگیری n را می داند و اگر مقدار u انتخاب شده توسط باب را حدس بزند، برنده قرعه کشی خواهد شد: زیرا این دقیقاً 50٪ شانس برنده شدن دارد. بنابراین آلیس انتخاب خود را به باب اعلام می کند، که تنها در صورتی می تواند موافقت کند که آلیس به درستی حدس زده باشد، زیرا در غیر این صورت از او خواسته می شود که بگوید جذر دیگر u 2 چیست ... اما او قادر به محاسبه آن نیست.
نتیجه گیری
اکنون واضح است که رمزنگاری - که به لطف نیازهای تجاری، دیپلماتیک و نظامی تکامل یافته است، اخیراً دنیای جاسوسان و ژنرال ها را رها کرده است (یا بهتر بگوییم دامنه عمل خود را گسترش داده است) و شامل عملیات هایی می شود که هر روز توسط همه انجام می شود. حوزه خصوصی و شخصی از این طریق بر مشکلاتی با ارزش اجتماعی و سیاسی تأثیر گذاشته است، دارای اهمیت اقتصادی و قانونی است، حریم خصوصی ما، آزادی بیان و محرمانه بودن ارتباطات ما را شامل می شود. این دیگر فقط یک واقعیت "فنی" نیست که در یک دنیای مهم کاربرد پیدا می کند، بلکه محدود و به علاوه برای آگاهی ما بیگانه است. نیاز به گرهگشایی این شبکه از برنامهها، تمایز پشتیبانی فنی از عملکرد، بهرهبرداری از کاربرد عملی و ارزش ایدهآل آن، یک کار بسیار پیچیده است زیرا موضوع به سرعت تکامل مییابد، دائماً همگام با انتشار روشهای محاسبه سریع و ارتباطات دیجیتال: در این رابطه شایسته است به کتاب گیوستوزی، مونتی و زیموئل [4] برای خواننده ایتالیایی اشاره شود. از سوی دیگر، پیچیدگی شدید مسائل مربوط به این واقعیت منعکس می شود که امروزه رمزنگاری خود را در تقاطع عملی و مفهومی رشته های علمی متعدد می بیند: حتی مشکل صرف پرداختن به واقعیت فنی ناب، صرف نظر از کاربردهای انجام شده. از آن، ما را وادار می کند تا با گشت و گذار در زمینه ماشین های محاسبه و نظریه اطلاعات، به روشی غیر پیش پا افتاده به نظریه الگوریتم ها و پیچیدگی محاسباتی روی آوریم : مجموعه ای از موضوعات بسیار مدرن، که در برخی موارد هنوز به دنبال رسمی بودن خود هستند. ساختار، با تأثیرات عمیق و متنوع بر یکدیگر، که از طریق آن وسعت مهارت های لازم تقویت می شود.
در مورد ریاضیات، امروزه به نظر می رسد نظریه اعداد موضوعی است که برای یافتن توابع ترفند و یافتن استراتژی های پیچیده الگوریتمی مناسب است. اما رمزنگاری همچنین به طور گسترده به تکنیکهای آماری و روشهای حساب احتمالات، ساختارهای جبری و اخیراً هندسه جبری نیز میپردازد.
همانطور که مشاهده می شود، در پوشش مدرن رمزنگاری کلید عمومی، یک زمینه تحقیقاتی با علاقه نظری بزرگ است که مستقیماً با ارزش برنامه ها مرتبط است، در واقع اغلب بلافاصله توسط نیازهای آنها دیکته می شود.
اما شایان ذکر است که منطقه زمانی سیستم های رمزنگاری کاملاً آزاد نیست. به دلایل امنیتی، برنامههای رمزگذاری در نظر گرفته شده برای برنامههای غیرنظامی تحت کنترل هستند و با برخی پیچشهای خندهدار، با «سلاحهای جنگی» با هدف ممنوعیت صادرات آنها برابر میشوند: این داستان واقعی است که فیل زیمرمن، نویسنده کتاب به آن پرداخته است. نرم افزار PGP ( Pretty Good Privacy ) و مدافع متقاعد شده حق شخصی برای حفظ حریم خصوصی است که برنامه آن را دیگر نمی توان آزادانه از اینترنت دانلود کرد.
و بنابراین، به نوعی، رمزنگاری به اجبار به حوزه مشکلات نظامی، تحت پوشش محرمانه، "پس زده می شود".
https://matematica.unibocconi.eu/articoli/invito-alla-crittografia
و
و
و

![{\displaystyle [a,b]_{+}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/c7289995fc78776166741f2a036fbcfb0e632c02)
![{\displaystyle [a,b]_{-}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/59120bf940c61971319243298b88ebb28f752588)

![{\displaystyle \operatorname {ad} _{A}(B)=[A,B]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/8a40684049019f333e05818bcd1ce5b48f839561)

![{\textstyle e^{A}Be^{-A}\ =\ B+[A,B]+{\frac {1}{2!}}[A,[A,B]]+{\frac {1 {3!}}[A,[A,[A,B]]]+\cdots \ =\ e^{\operatorname {ad} _{A}}(B).}](https://wikimedia.org/api/rest_v1/media/math/render/svg/5e4b0b44677de183969e936bb4cede2bf5515ad4)



![{\displaystyle \operatorname {ad} _{x}\operatorname {ad} _{y}(z)=[x,[y,z]\,]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/8c27f6b58b814f258e43d4529f26e9ec0523b58a)
![{\displaystyle \operatorname {ad} _{x}^{2}\!(z)\ =\ \operatorname {ad} _{x}\!(\operatorname {ad} _{x}\!(z) )\ =\ [x،[x،z]\،].}](https://wikimedia.org/api/rest_v1/media/math/render/svg/856ad01497c91a4c78ba471c5ba199d82744c717)











![{\displaystyle x^{y}=x[x,y].}](https://wikimedia.org/api/rest_v1/media/math/render/svg/dbfda5e3214a078a56860ef1d958532efd6ecc6c)
![{\displaystyle [y,x]=[x,y]^{-1}.}](https://wikimedia.org/api/rest_v1/media/math/render/svg/59c8c7dabf4a3f20a3f9a04a295468426eb22009)
![{\displaystyle [xz,y]=[x,y]^{z}\cdot [z,y].}](https://wikimedia.org/api/rest_v1/media/math/render/svg/51d505bd20b4dfad61942e780f9019f2342a28df)
![{\displaystyle \left[x^{-1},y\right]=[y,x]^{x^{-1}}.}](https://wikimedia.org/api/rest_v1/media/math/render/svg/5ec4802d72362fa5f8b6f440bee17b73b8f9ff48)
![{\displaystyle \left[\left[x,y\right],z^{x}\right]\cdot \left[[z,x],y^{z}\right]\cdot \چپ[[y ,z],x^{y}\right]=1.}](https://wikimedia.org/api/rest_v1/media/math/render/svg/969627eb5e4b01b893d68ba8cb5aefb6fb9dcb4e)
![{\displaystyle (xy)^{2}=x^{2}y^{2}[y,x][[y,x],y].}](https://wikimedia.org/api/rest_v1/media/math/render/svg/9c75b2bcc9c723ec68c6e482e9e1e002b02082d3)
![{\displaystyle (xy)^{n}=x^{n}y^{n}[y,x]^{\binom {n}{2}}.}](https://wikimedia.org/api/rest_v1/media/math/render/svg/128ae0855aada1e122d118d63c2bfa18a08eb603)
![{\displaystyle [a,b]=ab-ba.}](https://wikimedia.org/api/rest_v1/media/math/render/svg/c73ba7fbd6260acd540051cc2c6f9131ff0d7f8e)

![{\displaystyle [A+B,C]=[A,C]+[B,C]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/b3f1c95436e1c9c40871bc7a3704072ae067dc10)
![{\displaystyle [A,A]=0}](https://wikimedia.org/api/rest_v1/media/math/render/svg/7c816c8f8631ef069ad0b1aee64ed996ad8309ed)
![{\displaystyle [A,B]=-[B,A]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/37b04a066443e96c0b27d4b14f7f5d51c7b2b0c3)
![{\displaystyle [A,[B,C]]+[B,[C,A]]+[C,[A,B]]=0}](https://wikimedia.org/api/rest_v1/media/math/render/svg/046dbc0d4387302c8d321afb443e35bc1890fcac)
![{\displaystyle [A,BC]=[A,B]C+B[A,C]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/1c7c96785faa7d6e5ecc7d8ada53830b24338c60)
![{\displaystyle [A,BCD]=[A,B]CD+B[A,C]D+BC[A,D]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/aa03949d714777910e992c14aeed34adf42d9766)
![{\displaystyle [A,BCDE]=[A,B]CDE+B[A,C]DE+BC[A,D]E+BCD[A,E]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/8b79c370dc9984ff5e2720b3e06c6153af7ba572)
![{\displaystyle [AB,C]=A[B,C]+[A,C]B}](https://wikimedia.org/api/rest_v1/media/math/render/svg/71ba3177011b65b292d8dc39dd2e3391f29b0a07)
![{\displaystyle [ABC,D]=AB[C,D]+A[B,D]C+[A,D]BC}](https://wikimedia.org/api/rest_v1/media/math/render/svg/b9e755fd1fe3c26c40e007256c6976b9612e5d9b)
![{\displaystyle [ABCD,E]=ABC[D,E]+AB[C,E]D+A[B,E]CD+[A,E]BCD}](https://wikimedia.org/api/rest_v1/media/math/render/svg/4e00b8c22f5a63ff3dbbcf8a74f0d01f43994afa)
![{\displaystyle [A,B+C]=[A,B]+[A,C]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/7f50e382d516600cfe9f7a34376ebe694bb62177)
![{\displaystyle [A+B,C+D]=[A,C]+[A,D]+[B,C]+[B,D]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/2e47836a02ce95e65488370410a80446b1ae636c)
![{\displaystyle [AB,CD]=A[B,C]D+[A,C]BD+CA[B,D]+C[A,D]B=A[B,C]D+AC[B, D]+[A,C]DB+C[A,D]B}](https://wikimedia.org/api/rest_v1/media/math/render/svg/a8b90ee684250322ac794d8cb193d75c8c1d4db3)
![{\displaystyle [[A,C],[B,D]]=[[[A,B],C],D]+[[[B,C],D],A]+[[[C, D],A],B]+[[[D,A],B],C]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/33e847e641c8d2810846e666be23d2512b08eb2f)
![{\displaystyle [A^{N},B^{M}]=\sum _{n=0}^{N-1}\sum _{m=0}^{M-1}A^{n} B^{m}[A,B]B^{Nn-1}A^{Mm-1}=\sum _{n=0}^{N-1}\sum _{m=0}^{M-1}B^{n}A^{m}[A,B]A^{Nn-1}B^{Mm-1}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/b2a8a7436d26ef75d1023a36ffa1c561597c8506)
![{\displaystyle [AB,C]_{\pm }=A[B,C]_{-}+[A,C]_{\pm }B}](https://wikimedia.org/api/rest_v1/media/math/render/svg/187aaec93ded1a30cd6ad33d9e323c786d4a39fd)
![{\displaystyle [AB,CD]_{\pm }=A[B,C]_{-}D+AC[B,D]_{-}+[A,C]_{-}DB+C[ A,D]_{\pm }B}](https://wikimedia.org/api/rest_v1/media/math/render/svg/2abfd9c204056463779a2541fa7f5bc02930bf9a)
![{\displaystyle [[A,B],[C,D]]=[[[B,C]_{+},A]_{+},D]-[[[B,D]_{+} ,A]_{+},C]+[[[A,D]_{+},B]_{+},C]-[[A,C]_{+},B]_{+ },D]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/6c14c4def5d057ec857052e280d0c27658c3796d)
![{\displaystyle \left[A,[B,C]_{\pm }\right]+\left[B,[C,A]_{\pm }\right]+\left[C,[A,B ]_{\pm }\right]=0}](https://wikimedia.org/api/rest_v1/media/math/render/svg/7fa38c6ec51fd44c85b6a7dd7820d8ebaee4f2cf)
![{\displaystyle [A,BC]_{\pm }=[A,B]_{-}C+B[A,C]_{\pm }=[A,B]_{\pm }C\mp B[A,C]_{-}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/cee7d373e2721aa7ec3c50a8f645785d7da7b804)
![{\displaystyle [A,BC]=[A,B]_{\pm }C\mp B[A,C]_{\pm }}](https://wikimedia.org/api/rest_v1/media/math/render/svg/2f480a46e5c19fea0ae860621b38e69606a71239)
![{\displaystyle e^{A}e^{B}e^{-A}e^{-B}=\exp \!\left([A,B]+{\frac {1}{2!}} [A{+}B,[A,B]]+{\frac {1}{3!}}\left({\frac {1}{2}}[A,[B,[B,A]]]+[A{+}B,[A{+}B,[A,B]]]\right)+\cdots \right )](https://wikimedia.org/api/rest_v1/media/math/render/svg/f104655d91482ecf24b550407ef28112b27bd564)
![{\displaystyle [\omega ,\eta ]_{gr}:=\omega \eta -(-1)^{\deg \omega \deg \eta }\eta \omega .}](https://wikimedia.org/api/rest_v1/media/math/render/svg/4a31537974b529c2386b07f032b0452d7ab70e81)
![{\displaystyle \operatorname {ad} _{x}(y)=[x,y]=xy-yx.}](https://wikimedia.org/api/rest_v1/media/math/render/svg/06e06c88110f66faa14de2b3fba0644b13e96429)

![{\displaystyle \mathrm {ad} _{x}[y,z]\ =\ [\mathrm {ad} _{x}\!(y),z]\,+\,[y,\mathrm {ad} } _{x}\!(z)].}](https://wikimedia.org/api/rest_v1/media/math/render/svg/97e49b2f65e16c28bbcad712a40e4bf680ebf909)
![{\displaystyle \operatorname {ad} _{[x,y]}=\left[\operatorname {ad} _{x},\operatorname {ad} _{y}\right].}](https://wikimedia.org/api/rest_v1/media/math/render/svg/3c43069feeed684198e360f083c3c004bf3cb2f2)




 و
و یا عدد صحیح است یا
یا عدد صحیح است یا برای
برای  . در اینجا، شرایط
. در اینجا، شرایط  به این معنی که هیچ رابطه ای از فرم وجود ندارد
به این معنی که هیچ رابطه ای از فرم وجود ندارد برای هر عدد صحیح
برای هر عدد صحیح  باید تحمیل شود.
باید تحمیل شود. جایی که
جایی که  یک گروه کوکستر با مولد است
یک گروه کوکستر با مولد است  سیستم کوکستر نامیده می شود . توجه داشته باشید که به طور کل
سیستم کوکستر نامیده می شود . توجه داشته باشید که به طور کل  به طور منحصر به فرد توسط تعیین نمی شود
به طور منحصر به فرد توسط تعیین نمی شود و
و هم شکل هستند اما سیستم های کوکستر معادل نیستند، زیرا اولی دارای 3 مولد و دومی دارای 1 + 3 = 4 مولد است (برای توضیح این نماد به زیر مراجعه کنید).
هم شکل هستند اما سیستم های کوکستر معادل نیستند، زیرا اولی دارای 3 مولد و دومی دارای 1 + 3 = 4 مولد است (برای توضیح این نماد به زیر مراجعه کنید). برای همه
برای همه ; به این ترتیب مولدها دگرگونی هستند .
; به این ترتیب مولدها دگرگونی هستند . ، سپس مولدها
، سپس مولدها و
و رفت و آمد این امر با مشاهده آن نتیجه می گیرد
رفت و آمد این امر با مشاهده آن نتیجه می گیرد ،
،
 .
. ، بنابراین
، بنابراین . یعنی کموتاتور از
. یعنی کموتاتور از برای
برای ،
،
 .
. و
و مزدوج هستند : در واقع
مزدوج هستند : در واقع .
. ماتریس متقارن با ورودی ها
ماتریس متقارن با ورودی ها . در واقع، هر ماتریس متقارن با ورودی های مورب منحصراً 1 و ورودی های غیر مورب در مجموعه
. در واقع، هر ماتریس متقارن با ورودی های مورب منحصراً 1 و ورودی های غیر مورب در مجموعه یک ماتریس کوکستر است.
یک ماتریس کوکستر است. اگر و فقط اگر مجاور هستند
اگر و فقط اگر مجاور هستند .
. یا بزرگتر
یا بزرگتر ، مربوط به
، مربوط به با ورودی ها
با ورودی ها ، اما عناصر اصلاح شده اند و متناسب با حاصلضرب نقطه مولدهای زوجی هستند. ماتریس شلافلی مفید است زیرا مقادیر ویژه آن تعیین می کند که آیا گروه کوکستر از نوع محدود (همه مثبت)، نوع آفین (همه غیر منفی، حداقل یک صفر) یا نوع نامعین (در غیر این صورت) است. نوع نامشخص گاهی اوقات بیشتر تقسیم می شود، به عنوان مثال به گروه های هذلولی و دیگر گروه های کوکستر. با این حال، چندین تعاریف غیر معادل برای گروه های کوکستر هذلولی وجود دارد.
، اما عناصر اصلاح شده اند و متناسب با حاصلضرب نقطه مولدهای زوجی هستند. ماتریس شلافلی مفید است زیرا مقادیر ویژه آن تعیین می کند که آیا گروه کوکستر از نوع محدود (همه مثبت)، نوع آفین (همه غیر منفی، حداقل یک صفر) یا نوع نامعین (در غیر این صورت) است. نوع نامشخص گاهی اوقات بیشتر تقسیم می شود، به عنوان مثال به گروه های هذلولی و دیگر گروه های کوکستر. با این حال، چندین تعاریف غیر معادل برای گروه های کوکستر هذلولی وجود دارد. و
و از A -mod، و دو زیرمجموعه
از A -mod، و دو زیرمجموعه و
و از B -mod، سپس
از B -mod، سپس یک جفت پیچشی در A -mod است (یعنیتی
یک جفت پیچشی در A -mod است (یعنیتی و
و حداکثر زیرمجموعه با ویژگی هستند
حداکثر زیرمجموعه با ویژگی هستند ; این بدان معناست که هر M در A -mod یک دنباله دقیق کوتاه طبیعی را می پذیرد
; این بدان معناست که هر M در A -mod یک دنباله دقیق کوتاه طبیعی را می پذیرد  با U در
با U در ،یک جفت پیچشی در B -mod است. علاوه بر این، محدودیتهای تابعهای F و G معادلهای معکوس بین آنها ایجاد میکنندتی
،یک جفت پیچشی در B -mod است. علاوه بر این، محدودیتهای تابعهای F و G معادلهای معکوس بین آنها ایجاد میکنندتی ، در حالی که محدودیت های F' و G' معادل های معکوس بین
، در حالی که محدودیت های F' و G' معادل های معکوس بین . (توجه داشته باشید که این معادلات ترتیب جفت های پیچشی را تغییر می دهند
. (توجه داشته باشید که این معادلات ترتیب جفت های پیچشی را تغییر می دهند و=مد-ب
و=مد-ب .
. که در آن T i مجموع مستقیم متناهی از مجموع مستقیم T هستند .
که در آن T i مجموع مستقیم متناهی از مجموع مستقیم T هستند .

 ).
). که در آن V یکانی است و D قطری است و یکانی.
که در آن V یکانی است و D قطری است و یکانی. . به این معنا که،
. به این معنا که، روی دایره یکانی صفحه مختلط خواهد بود.
روی دایره یکانی صفحه مختلط خواهد بود. یکانی است
یکانی است یکانی است
یکانی است .
. با توجه به ضرب داخلی معمولی. به عبارت دیگر،
با توجه به ضرب داخلی معمولی. به عبارت دیگر، .
. .
. برای همه
برای همه  ، جایی که
، جایی که .
.

 با
با  گروه یکانی ویژه SU(2) نامیده می شود.
گروه یکانی ویژه SU(2) نامیده می شود.
 و ه ،
و ه ، بالا و زوایای
بالا و زوایای  می تواند هر مقداری را بگیرد.
می تواند هر مقداری را بگیرد. و ،
و ، فاکتورسازی زیر را دارد:
فاکتورسازی زیر را دارد:

![{\displaystyle {\begin{aligned}J_{1}=J^{23}=-J^{32}&=i{\begin{pmatrix}0&0&0&0\\0&0&0&0\\0&0&0&-1\\0&0&1&0\end{ pmatrix}}،&K_{1}=J^{01}=-J^{10}&=i{\begin{pmatrix}0&1&0&0\\1&0&0&0\\0&0&0&0\\0&0&0&0\end{pmatrix}}،\\[ 8pt]J_{2}=J^{31}=-J^{13}&=i{\begin{pmatrix}0&0&0&0\\0&0&0&1\\0&0&0&0\\0&-1&0&0\end{pmatrix}}،&K_{2 }=J^{02}=-J^{20}&=i{\begin{pmatrix}0&0&1&0\\0&0&0&0\\1&0&0&0\\0&0&0&0\end{pmatrix}}،\\[8pt]J_{3}= J^{12}=-J^{21}&=i{\begin{pmatrix}0&0&0&0\\0&0&-1&0\\0&1&0&0\\0&0&0&0\end{pmatrix}}،&K_{3}=J^{03} =-J^{30}&=i{\begin{pmatrix}0&0&0&1\\0&0&0&0\\0&0&0&0\\1&0&0&0\end{pmatrix}}.\\[8pt]\end{تراز شده}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/de40244c815ee6f36581ba60f61f0b7298340202)
 عبارتند از:
عبارتند از: ![{\displaystyle \left[J^{\mu \nu },J^{\rho \sigma }\right]=i\left(\eta ^{\sigma \mu }J^{\rho \nu }+\ eta ^{\nu \sigma }J^{\mu \rho }-\eta ^{\rho \mu }J^{\sigma \nu }-\eta ^{\nu \rho }J^{\mu \ سیگما }\راست).}](https://wikimedia.org/api/rest_v1/media/math/render/svg/10c8bd479de1483b9b8780f8bdca6683a9d68253)
![{\displaystyle \left[J_{i},J_{j}\right]=i\epsilon _{ijk}J_{k},\quad \left[J_{i},K_{j}\right]=i \epsilon _{ijk}K_{k},\quad \left[K_{i},K_{j}\right]=-i\epsilon _{ijk}J_{k}.}](https://wikimedia.org/api/rest_v1/media/math/render/svg/98fc929a703f98001573ea442bf785c5a4e4cc01)
 به ترتیب متقارن و متعامد.
به ترتیب متقارن و متعامد.
 در عبارت کلی
در عبارت کلی ![{\displaystyle {\begin{aligned}\pi _{\left({\frac {1}{2}},0\right)}(J_{i})&={\frac {1}{2}} \left(\sigma _{i}\otimes 1_{(1)}+1_{(2)}\otimes J_{i}^{(0)}\right)={\frac {1}{2}} \sigma _{i}\\\pi _{\left({\frac {1}{2}},0\right)}(K_{i})&={\frac {-i}{2}} \left(1_{(2)}\otimes J_{i}^{(0)}-\sigma _{i}\otimes 1_{(1)}\right)={\frac {i}{2}} \sigma _{i}\\[6pt]\pi _{\left(0,{\frac {1}{2}}\right)}(J_{i})&={\frac {1}{2 }}\left(J_{i}^{(0)}\times 1_{(2)}+1_{(1)}\otimes \sigma _{i}\right)={\frac {1}{2 }}\sigma _{i}\\\pi _{\left(0,{\frac {1}{2}}\right)}(K_{i})&={\frac {-i}{2 }}\left(1_{(1)}\otimes \sigma _{i}-J_{i}^{(0)}\otimes 1_{(2)}\right)={\frac {-i}{ 2}}\sigma _{i}\end{تراز شده}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/82e5dc00c0687f8d08d2c1c26e6a83814b0751c4)
 مجموع مستقیم آنها به عنوان نمایش شکل می گیرد،
مجموع مستقیم آنها به عنوان نمایش شکل می گیرد، ![{\displaystyle {\begin{aligned}\pi _{\left({\frac {1}{2}},0\right)\oplus \left(0,{\frac {1}{2}}\right )}\left(J_{i}\right)&={\frac {1}{2}}{\begin{pmatrix}\sigma _{i}&0\\0&\sigma _{i}\end{pmatrix }}\\[8pt]\pi _{\left({\frac {1}{2}},0\right)\oplus \left(0,{\frac {1}{2}}\right)} \left(K_{i}\right)&={\frac {i}{2}}{\begin{pmatrix}\sigma _{i}&0\\0&-\sigma _{i}\end{pmatrix} }\end{تراز شده}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/d02cad0b53887c76ad70cf8ddcf6808d14dafc1f)
 این عنصر بر روی عناصر 4 جزئی (Ψ L , Ψ R ) از ( V L ⊕ V R ) که
این عنصر بر روی عناصر 4 جزئی (Ψ L , Ψ R ) از ( V L ⊕ V R ) که 
 و
و ( جبر مختلط لی درک می شود) از نظریه نمایش گروه چرخش شناخته شده است و توسط
( جبر مختلط لی درک می شود) از نظریه نمایش گروه چرخش شناخته شده است و توسط  که در آن برچسبهای j 0 و j 1 حذف شدهاند زیرا برای همه بردارهای پایه در نمایش یکسان هستند.
که در آن برچسبهای j 0 و j 1 حذف شدهاند زیرا برای همه بردارهای پایه در نمایش یکسان هستند.![{\displaystyle [J_{i},K_{j}]=i\epsilon _{ijk}K_{k},}](https://wikimedia.org/api/rest_v1/media/math/render/svg/c77785f2bee4f038b023a457545a28ba4dff05fe) سه گانه ( Ki ، Ki ، Ki ) ≡ K یک
سه گانه ( Ki ، Ki ، Ki ) ≡ K یک 

![{\displaystyle [K_{\pm },K_{3}]=\pm J_{\pm },\quad [K_{+},K_{-}]=-2J_{3}.}](https://wikimedia.org/api/rest_v1/media/math/render/svg/cd13abefc97b740b51aee963a620d78ac52af5d0)
 جایی که
جایی که

 منجر به
منجر به  که β j زاویه B j روی شکل قطبی است. برای | B j | ≠ 0 دنبال می شود
که β j زاویه B j روی شکل قطبی است. برای | B j | ≠ 0 دنبال می شود و
و بر اساس قرارداد انتخاب شده است. دو مورد احتمالی وجود دارد:
بر اساس قرارداد انتخاب شده است. دو مورد احتمالی وجود دارد:


![{\displaystyle {\begin{aligned}(\Pi (R)f)(\theta (x),\varphi (x))&=\sum _{l=1}^{\infty }\sum _{m ,=-l}^{l}\sum _{m'=-l}^{l}D_{mm'}^{(l)}(R)f_{lm'}Y_{m}^{l} \left(\theta \left(R^{-1}x\right),\varphi \left(R^{-1}x\right)\right),\\[5pt]&R\in \mathrm {SO } (3)، x\in \mathbb {S} ^{2}،\end{تراز شده}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/4cb5445bb988d965183c70659ffb38fd943e2830)
 .
.
 و تا یک علامت منحصر به فرد هستند (از آنجایی که ±Π f همان f را می دهد )، بنابراین
و تا یک علامت منحصر به فرد هستند (از آنجایی که ±Π f همان f را می دهد )، بنابراین



 بر روی توانای حل های معادله دیفرانسیل ریمان برای تعریف γ ′ استفاده شده است.
بر روی توانای حل های معادله دیفرانسیل ریمان برای تعریف γ ′ استفاده شده است.

=P[u(\Lambda )(z)]،}](https://wikimedia.org/api/rest_v1/media/math/render/svg/5a37158f83f2322b2ebd757dfaaa5dc60f875264)
=P\left\{{\begin{matrix}\eta &\zeta &\theta &\\\alpha &\beta &\gamma &\;u \\\alpha '&\beta '&\gamma '&\end{matrix}}\right\},}](https://wikimedia.org/api/rest_v1/media/math/render/svg/bf2ced3db6ae6e119edbf996ab6a84470e92844d)

 این نظریه در
این نظریه در  از آنجایی که نمایش های یک بعدی B با نمایش های ماتریس های مورب مطابقت دارد، با ورودی های مختلط غیرصفر z و z -1 ، بنابراین شکل را دارند.
از آنجایی که نمایش های یک بعدی B با نمایش های ماتریس های مورب مطابقت دارد، با ورودی های مختلط غیرصفر z و z -1 ، بنابراین شکل را دارند. برای k یک عدد صحیح، ν حقیقی و با z = re iθ . نمایش ها
برای k یک عدد صحیح، ν حقیقی و با z = re iθ . نمایش ها  که با
که با  سری اصلی را می توان به طور مستقیم بر روی تعریف کرد
سری اصلی را می توان به طور مستقیم بر روی تعریف کرد با فرمول
با فرمول 
 G را می توان بر روی مجموع مستقیم جبری زیرفضاهای تقلیل ناپذیر K به طور صریح محاسبه کرد و می توان مستقیماً تأیید کرد که زیرفضای کم بعدی این مجموع مستقیم را به عنوان یک
G را می توان بر روی مجموع مستقیم جبری زیرفضاهای تقلیل ناپذیر K به طور صریح محاسبه کرد و می توان مستقیماً تأیید کرد که زیرفضای کم بعدی این مجموع مستقیم را به عنوان یک با عمل ارائه شده توسط
با عمل ارائه شده توسط 
 فقط سری اصلی مورد نیاز است. این بلافاصله تجزیه در زیرنمایش ها را به همراه دارد
فقط سری اصلی مورد نیاز است. این بلافاصله تجزیه در زیرنمایش ها را به همراه دارد نماینده منظم چپ گروه لورنتس، و
نماینده منظم چپ گروه لورنتس، و نمایش منظم در فضای هذلولی سه بعدی. (اولی فقط شامل نمایش های سری اصلی با k زوج و دومی فقط آنهایی با k = 0 است.)
نمایش منظم در فضای هذلولی سه بعدی. (اولی فقط شامل نمایش های سری اصلی با k زوج و دومی فقط آنهایی با k = 0 است.)
 تعریف شده بوسیله ی
تعریف شده بوسیله ی
 جایی که
جایی که و نقشه U بر روی C c ( G ) توسط
و نقشه U بر روی C c ( G ) توسط به یک واحد از
به یک واحد از

 نشان دهنده
نشان دهنده  و
و و
و سپس
سپس 
 با یک قضیه
با یک قضیه  مجموع محدودی از کانولوشن توابع مشابه است، فرمول وارونگی برای چنین f برقرار است. می توان آن را به کلاس های بسیار گسترده تری از توابع که شرایط تمایز پذیری ملایم را برآورده می کنند، گسترش داد.
مجموع محدودی از کانولوشن توابع مشابه است، فرمول وارونگی برای چنین f برقرار است. می توان آن را به کلاس های بسیار گسترده تری از توابع که شرایط تمایز پذیری ملایم را برآورده می کنند، گسترش داد.  یک نمایش است که در آن نوار نشان دهنده صرف مختلط ورودی در ماتریس های نماینده است. این نتیجه از آن است که صرف مختلط با جمع و ضرب جابجا می شود.
یک نمایش است که در آن نوار نشان دهنده صرف مختلط ورودی در ماتریس های نماینده است. این نتیجه از آن است که صرف مختلط با جمع و ضرب جابجا می شود.  را می توان به صورت یکتا به صورت π = π + + π − نوشت ، که در آن
را می توان به صورت یکتا به صورت π = π + + π − نوشت ، که در آن  با
با هولومورفیک (خطی مختلط) و
هولومورفیک (خطی مختلط) و ضد هولومورفیک (خطی مزدوج). برای
ضد هولومورفیک (خطی مزدوج). برای از آنجا که
از آنجا که هولومورفیک است،
هولومورفیک است، ضد هولومورفیک است. بررسی مستقیم عبارات صریح برای
ضد هولومورفیک است. بررسی مستقیم عبارات صریح برای و
و در رابطه
در رابطه  مانند
مانند
 که در آن دستور نمایش های گروه از exp( X ) = exp( X ) پیروی می کند . نتیجه می شود که نمایش های تقلیل ناپذیر ( m , n ) نمایندگان ماتریس حقیقی دارند اگر و فقط اگر m = n باشد. نمایشهای تقلیلپذیر در فرم ( m , n ) ⊕ ( n , m ) نیز ماتریسهای حقیقی دارند.
که در آن دستور نمایش های گروه از exp( X ) = exp( X ) پیروی می کند . نتیجه می شود که نمایش های تقلیل ناپذیر ( m , n ) نمایندگان ماتریس حقیقی دارند اگر و فقط اگر m = n باشد. نمایشهای تقلیلپذیر در فرم ( m , n ) ⊕ ( n , m ) نیز ماتریسهای حقیقی دارند.
 سپس یک نمایندگی مرتبط از وجود دارد
سپس یک نمایندگی مرتبط از وجود دارد![{\displaystyle \pi (X)(A)=[\pi (X),A],\qquad A\in \operatorname {End} (V),\ X\in {\mathfrak {g}}.}](https://wikimedia.org/api/rest_v1/media/math/render/svg/14dda900425ebf02a5b31fc163f92f8bf94317ed)

 و اگر عمل محدود به
و اگر عمل محدود به سپس دو نمایش فوق به ترتیب نمایش
سپس دو نمایش فوق به ترتیب نمایش  یا
یا که پیچیدگی آن است
که پیچیدگی آن است تولید شده توسط ماتریس های گاما به صورت مجموع مستقیم
تولید شده توسط ماتریس های گاما به صورت مجموع مستقیم ![{\displaystyle {\mathcal {Cl}}_{3,1}(\mathbb {R} )=(0,0)\oplus \left({\frac {1}{2}},{\frac {1 {2}}\right)\oplus [(1,0)\oplus (0,1)]\oplus \left({\frac {1}{2}},{\frac {1}{2}} \right)_{p}\plus (0,0)_{p},}](https://wikimedia.org/api/rest_v1/media/math/render/svg/34cc8aa2566982bb75078b36648a4edb1dbceaee)
 دو نقش دارد [
دو نقش دارد [ ![{\displaystyle \sigma ^{\mu \nu }=-{\frac {i}{4}}\left[\gamma ^{\mu },\gamma ^{\nu }\right],}](https://wikimedia.org/api/rest_v1/media/math/render/svg/d98c87892b2963661a67eb08538b8d9151b11463)
 ماتریس های گاما هستند، سیگماها، که تنها 6 تای آنها به دلیل ضد تقارن براکت غیر صفر هستند، فضای نمایش تانسور را در بر می گیرند. علاوه بر این، آنها روابط کموتاسیون جبر لی لورنتس را دارند،
ماتریس های گاما هستند، سیگماها، که تنها 6 تای آنها به دلیل ضد تقارن براکت غیر صفر هستند، فضای نمایش تانسور را در بر می گیرند. علاوه بر این، آنها روابط کموتاسیون جبر لی لورنتس را دارند، ![{\displaystyle \left[\sigma ^{\mu \nu },\sigma ^{\rho \tau }\right]=i\left(\eta ^{\tau \mu }\sigma ^{\rho \nu }+\eta ^{\nu \tau }\sigma ^{\mu \rho }-\eta ^{\rho \mu }\sigma ^{\tau \nu }-\eta ^{\nu \rho }\ سیگما ^{\mu \tau }\right)}](https://wikimedia.org/api/rest_v1/media/math/render/svg/bfb242b95f2e9074e8f90d7ece473e6806c0cfc0)
 آن را به فضایی از بیسپینورها تبدیل می کند.
آن را به فضایی از بیسپینورها تبدیل می کند. و گروه پوانکاره این نمایش ها به طور کلی غیر قابل تقلیل نیستند.
و گروه پوانکاره این نمایش ها به طور کلی غیر قابل تقلیل نیستند.
 g ∈ SO(3; 1) + . اگر قرار است P در Π گنجانده شود ، سازگاری با
g ∈ SO(3; 1) + . اگر قرار است P در Π گنجانده شود ، سازگاری با 


 داده شده توسط
داده شده توسط
 (با m بعد ماتریس ها).
(با m بعد ماتریس ها). 
 ولی
ولی مرکز است
مرکز است مرکز هر جبر لی نیمه ساده بی اهمیت است
مرکز هر جبر لی نیمه ساده بی اهمیت است 

 یک نمایش غیر قابل کاهش با بیشترین وزن μ 0 است، پس
یک نمایش غیر قابل کاهش با بیشترین وزن μ 0 است، پس دارای بالاترین وزن w 0 ⋅ (- μ ) است.
دارای بالاترین وزن w 0 ⋅ (- μ ) است.  سیستم ریشه از
سیستم ریشه از در شکل سمت راست نشان داده شده است.
در شکل سمت راست نشان داده شده است.  جایی که
جایی که انعکاس در صفحه متعامد به γ است زیرا γ در تمام ریشه ها محدوده است.
انعکاس در صفحه متعامد به γ است زیرا γ در تمام ریشه ها محدوده است. 
 که در
که در همگن درجه μ در
همگن درجه μ در و همگن درجه ν در
و همگن درجه ν در
![{\displaystyle (\phi _{\mu ,\nu }(g)P){\begin{pmatrix}z_{1}\\z_{2}\\\end{pmatrix}}=\left[\phi _ {\mu ,\nu }{\begin{pmatrix}a&b\\c&d\\\end{pmatrix}}P\right]{\begin{pmatrix}z_{1}\\z_{2}\\\end{ pmatrix}}=P\left({\begin{pmatrix}a&b\\c&d\\\end{pmatrix}}^{-1}{\begin{pmatrix}z_{1}\\z_{2}\\\ end{pmatrix}}\right),\quad P\in \mathbf {P} _{\mu ,\nu }^{2}.}](https://wikimedia.org/api/rest_v1/media/math/render/svg/ca7903362ecb0e4277fcddaf15e7aa8b1500745e)


 ) از محصولات تانسوری نمایش های خطی مختلط تقلیل ناپذیر π m = μ و π n = ν از
) از محصولات تانسوری نمایش های خطی مختلط تقلیل ناپذیر π m = μ و π n = ν از
 در جایی که R + مجموعه ریشه های مثبت است، ρ بالاترین وزن، و δ نصف مجموع ریشه های مثبت است. ضرب درونی
در جایی که R + مجموعه ریشه های مثبت است، ρ بالاترین وزن، و δ نصف مجموع ریشه های مثبت است. ضرب درونی جبر لی است
جبر لی است زیر
زیر  از طریق این محصول درونی با عناصر شناسایی می شوند
از طریق این محصول درونی با عناصر شناسایی می شوند برای
برای
![{\displaystyle [\sigma _{i},\sigma _{j}]=2i\epsilon _{ijk}\sigma _{k}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/d006f76499cbbb5daebd5742f0cbc47fdf858002)
![{\displaystyle [j_{i},j_{j}]=i\epsilon _{ijk}j_{k},\quad [j_{i},k_{j}]=i\epsilon _{ijk}k_{ k}،\quad [k_{i}،k_{j}]=-i\epsilon _{ijk}j_{k}،}](https://wikimedia.org/api/rest_v1/media/math/render/svg/13c1be39aeae2de2e3782dfdc6733ef54b59054c)



 نگاشت نمایی است، p نقشه پوششی از است
نگاشت نمایی است، p نقشه پوششی از است روی SO(3; 1) + و σ ایزومورفیسم جبر لی القا شده توسط آن است. نقشه های Π، π و دو ف نشان دهنده هستند. تصویر فقط تا حدی درست است که Π تصویری باشد.
روی SO(3; 1) + و σ ایزومورفیسم جبر لی القا شده توسط آن است. نقشه های Π، π و دو ف نشان دهنده هستند. تصویر فقط تا حدی درست است که Π تصویری باشد. روی نیست.
روی نیست. 
 به طوری که q = exp( Q ) .
به طوری که q = exp( Q ) . 
![{\displaystyle {\begin{aligned}&\exp(-X)\exp(i\pi H)\\{}={}&\exp \left({\begin{pmatrix}0&-1\\0&0\ \\end{pmatrix}}\right)\exp \left(i\pi {\begin{pmatrix}1&0\\0&-1\\\end{pmatrix}}\right)\\[6pt]{}={ }&{\begin{pmatrix}1&-1\\0&1\\\end{pmatrix}}{\begin{pmatrix}-1&0\\0&-1\\\end{pmatrix}}\\[6pt]{} ={}&{\begin{pmatrix}-1&1\\0&-1\\\end{pmatrix}}\\{}={}&q.\end{تراز شده}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/aa5ed329487377223ecbe27aec02e128db475c77)
 نمایندگی ها آنها را می توان (و معمولاً) از ابتدا یادداشت کرد. نمایشهای گروه
نمایندگی ها آنها را می توان (و معمولاً) از ابتدا یادداشت کرد. نمایشهای گروه 
 می توان در فضای چند جمله ای
می توان در فضای چند جمله ای 

![{\displaystyle (\phi _{n}(g)P){\begin{pmatrix}z_{1}\\z_{2}\\\end{pmatrix}}=\left[\phi _{n}{ \begin{pmatrix}a&b\\c&d\\\end{pmatrix}}P\right]{\begin{pmatrix}z_{1}\\z_{2}\\\end{pmatrix}}=P\left( {\begin{pmatrix}a&b\\c&d\\\end{pmatrix}}^{-1}{\begin{pmatrix}z_{1}\\z_{2}\\\end{pmatrix}}\right) ,\qquad P\in \mathbf {P} _{n}^{2}.}](https://wikimedia.org/api/rest_v1/media/math/render/svg/e12ababe179e733686c8f409b7e7da5e43a6cff8)

 ، این نمایش ها به جبرهای لی ماتریسی تبدیل می شوند.
، این نمایش ها به جبرهای لی ماتریسی تبدیل می شوند.
 برای برخی از فضای برداری V یک نمایش است، یک نمایش Π از مولفه متصل G توسط تعریف می شود
برای برخی از فضای برداری V یک نمایش است، یک نمایش Π از مولفه متصل G توسط تعریف می شود
 با این حال، در حالت کلی، به عنوان مثال برای
با این حال، در حالت کلی، به عنوان مثال برای سوژه ای است . یکی از راههای نشان دادن این موضوع استفاده از ایزومورفیسم است
سوژه ای است . یکی از راههای نشان دادن این موضوع استفاده از ایزومورفیسم است دومی
دومی  (به مقاله مرتبط مراجعه کنید). نقشه ضریب با نشان داده می شود
(به مقاله مرتبط مراجعه کنید). نقشه ضریب با نشان داده می شود نقشه
نقشه روی است.
روی است. 
 سوژه ای است.
سوژه ای است.  برای پیدا کردن اینکه exp برای مؤلفه متصل گروه لورنتس است.
برای پیدا کردن اینکه exp برای مؤلفه متصل گروه لورنتس است. ممکن است منحصراً به صورت
ممکن است منحصراً به صورت 
![{\displaystyle {\begin{aligned}h&={\begin{pmatrix}c&a-ib\\a+ib&-c\end{pmatrix}}&&(a,b,c)\in \mathbb {R} ^{ 3}\\[4pt]u&={\begin{pmatrix}d+ie&f+ig\\-f+ig&d-ie\end{pmatrix}}&&(d,e,f,g)\in \mathbb {R } ^{4}{\text{ موضوع }}d^{2}+e^{2}+f^{2}+g^{2}=1.\end{تراز شده}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/6cb1ad35e53e354d0b06eed2365f239c54a77e74)
 )
)
 جایی که
جایی که بنابراین از نظر توپولوژیکی،
بنابراین از نظر توپولوژیکی، 
 ممکن است جایگزین شود
ممکن است جایگزین شود ) که یک مسیر از u به
) که یک مسیر از u به  یک حلقه در است
یک حلقه در است از آنجایی که u و - u نقاط پادپای هستند و به یک نقطه قابل انقباض نیست. اما یک مسیر از u به - u ، از آنجا دوباره به u ، یک حلقه به داخل
از آنجایی که u و - u نقاط پادپای هستند و به یک نقطه قابل انقباض نیست. اما یک مسیر از u به - u ، از آنجا دوباره به u ، یک حلقه به داخل نقشه پوشش است) در
نقشه پوشش است) در![{\displaystyle \left[\Pi (\Lambda _{1})\Pi (\Lambda _{2})\Pi ^{-1}(\Lambda _{1}\Lambda _{2})\راست] ^{2}=1\پیکان راست \Pi (\Lambda _{1}\Lambda _{2})=\pm \Pi (\Lambda _{1})\Pi (\Lambda _{2})،\quad \Lambda _{1}،\Lambda _{2}\in \mathrm {SO} (3;1)،}](https://wikimedia.org/api/rest_v1/media/math/render/svg/f0fac0a1e3fbcdd611c896fd10167559110cb8a1)

 از جبر لی
از جبر لی

![{\displaystyle \left[A_{i},A_{j}\right]=i\varepsilon _{ijk}A_{k},\quad \left[B_{i},B_{j}\right]=i \varepsilon _{ijk}B_{k},\quad \left[A_{i},B_{j}\right]=0,}](https://wikimedia.org/api/rest_v1/media/math/render/svg/7571771f330e56636c4a6312d4faf3d24f3adfbe)
 و
و به ترتیب دهانه
به ترتیب دهانه ![{\displaystyle {\begin{aligned}{\mathfrak {so}}(3;1)\hookrightarrow {\mathfrak {so}}(3;1)_{\mathbb {C} }&\cong \mathbf {A } _{\mathbb {C} }\oplus \mathbf {B} _{\mathbb {C} }\cong {\mathfrak {su}}(2)_{\mathbb {C} }\oplus {\mathfrak { su}}(2)_{\mathbb {C} }\\[5pt]&\cong {\mathfrak {sl}}(2,\mathbb {C})\oplus {\mathfrak {sl}}(2, = {\mathfrak {sl}}(2,\mathbb {C} )_{\mathbb {C} }\hookleftarrow {\mathfrak {sl}}(2,\mathbb {C})،\end{تراز شده}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/10e3df986a30ae93db371438a9b2ebbd754c3116)



 این شامل زیرگروه فشرده SU(2) × SU(2) با جبر لی است
این شامل زیرگروه فشرده SU(2) × SU(2) با جبر لی است دومی یک فرم واقعی فشرده است
دومی یک فرم واقعی فشرده است


 -نمایش های خطی
-نمایش های خطی  -نمایش های خطی از
-نمایش های خطی از به دست آمده از طریق ایزومورفیسم ها در
به دست آمده از طریق ایزومورفیسم ها در  جایی که
جایی که نمایش های مختلط خطی تقلیل ناپذیر هستند
نمایش های مختلط خطی تقلیل ناپذیر هستند بازنمودهای مزدوج مختلط آنها. (برچسبگذاری معمولاً در ادبیات ریاضیات 0، 1، 2، ... است، اما اعداد نیمه صحیح در اینجا برای مطابقت با برچسبگذاری انتخاب میشوند.(3،1)}
بازنمودهای مزدوج مختلط آنها. (برچسبگذاری معمولاً در ادبیات ریاضیات 0، 1، 2، ... است، اما اعداد نیمه صحیح در اینجا برای مطابقت با برچسبگذاری انتخاب میشوند.(3،1)} جبر لی است.) در اینجا حاصل ضرب تانسور به معنای قبلی
جبر لی است.) در اینجا حاصل ضرب تانسور به معنای قبلی  و با محدودیت، کسانی که از
و با محدودیت، کسانی که از که در آن V یک فضای برداری با بعد محدود است. اینها، تا یک
که در آن V یک فضای برداری با بعد محدود است. اینها، تا یک 

 نمایشهای تقلیلناپذیر (2 n + 1) بعدی
نمایشهای تقلیلناپذیر (2 n + 1) بعدی 
 جایی که δ
جایی که δ
 از گروه کامل لورنتس O(3; 1) با استفاده از
از گروه کامل لورنتس O(3; 1) با استفاده از  به طور مستقل توسط برگمن و
به طور مستقل توسط برگمن و ![{\displaystyle \psi '^{\alpha }(x)=D{[\Lambda ]^{\alpha }}_{\beta }\psi ^{\beta }\left(\Lambda ^{-1}x \درست)،}](https://wikimedia.org/api/rest_v1/media/math/render/svg/14a5e6e7000d878ba0b269ab4b2ad9b9f953da69)
![{\displaystyle \Psi ^{\alpha }(x)\to \Psi '^{\alpha }(x)=U[\Lambda ,a]\Psi ^{\alpha }(x)U^{-1} \left[\Lambda ,a\right]=D{\left[\Lambda ^{-1}\right]^{\alpha }}_{\beta }\Psi ^{\beta }(\Lambda x+a )}](https://wikimedia.org/api/rest_v1/media/math/render/svg/d93a2b81a646f5e49ad3aa6f97e989e0b8f656b9)

![{\displaystyle a^{\dagger }(\mathbf {p} ,\sigma )\rightarrow a'^{\dagger }\left(\mathbf {p} ,\sigma \right)=U[\Lambda ]a^ {\ dagger }(\mathbf {p} ,\sigma )U\left[\Lambda ^{-1}\right]=a^{\dagger }(\Lambda \mathbf {p},\rho )D^{ (s)}{\left[R(\Lambda ,\mathbf {p} )^{-1}\right]^{\rho }}_{\sigma },}](https://wikimedia.org/api/rest_v1/media/math/render/svg/a4a1538d6ec6f9dc40cc6c892f5928854569708f)

![{\displaystyle {D[\Lambda ]^{\alpha }}_{\alpha '}u^{\alpha '}(\mathbf {p} ,\lambda )={D^{(s)}[R( \Lambda ,\mathbf {p} )]^{\lambda '}}_{\lambda }u^{\alpha }\left(\Lambda \mathbf {p} ,\lambda '\right),}](https://wikimedia.org/api/rest_v1/media/math/render/svg/94355cf17a76e10990f64a36a8727f10f286aaa2)

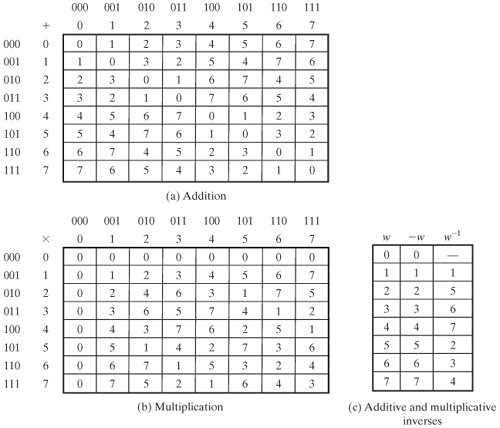
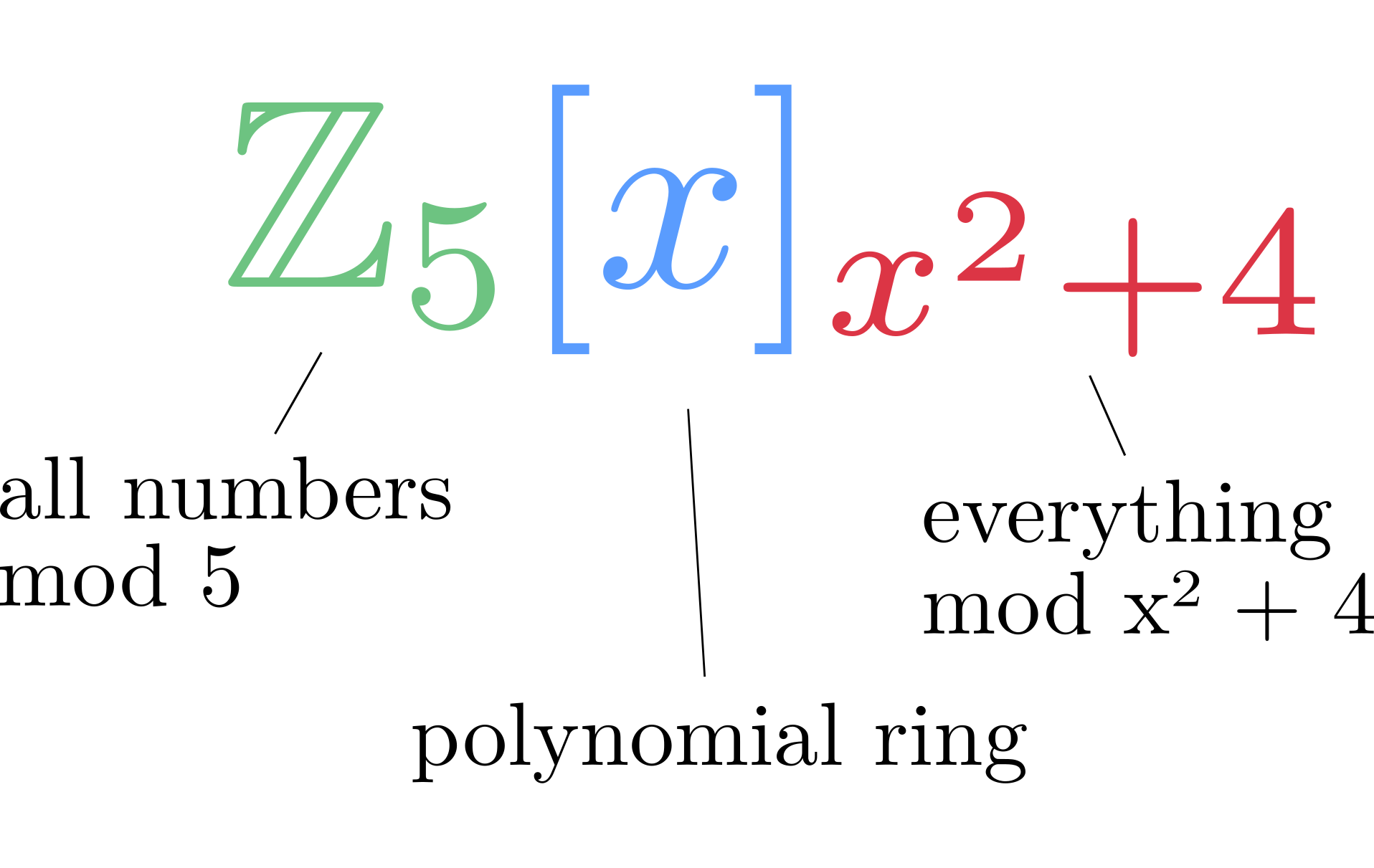
 ،
، ، یا
، یا .
.  برای شاخه های مختلف ریاضیات اساسی است (به
برای شاخه های مختلف ریاضیات اساسی است (به 
 ، زیرا 0 = { a }. )
، زیرا 0 = { a }. )


 ، ما داریم
، ما داریم
 ، مجموعه ای شامل تمام اعداد صحیح قابل تقسیم بر n ، که در آن
، مجموعه ای شامل تمام اعداد صحیح قابل تقسیم بر n ، که در آن مجموعه
مجموعه  (که همانطور که قبلا ذکر شد با حلقه هم شکل است
(که همانطور که قبلا ذکر شد با حلقه هم شکل است یک
یک  با n عنصر، اما اینطور نیست
با n عنصر، اما اینطور نیست  . این شامل
. این شامل (که در
(که در  .
. :
:  :
:

 (یعنی باقیمانده
(یعنی باقیمانده وقتی تقسیم بر
وقتی تقسیم بر ).
).





 برای
برای - با استفاده از
- با استفاده از 





 بر روی
بر روی  یک میدان جبری بسته است، سپس حلقه ماتریس دارای ورودی هایی از است
یک میدان جبری بسته است، سپس حلقه ماتریس دارای ورودی هایی از است جایی که
جایی که  اعداد صحیح مثبت هستند و
اعداد صحیح مثبت هستند و  جبر است
جبر است  ماتریس های بیش از k .
ماتریس های بیش از k . قابل حل است اگر ...
قابل حل است اگر ... که هر کدام در
که هر کدام در  آن
آن  آبلی
آبلی  که هر کدام
که هر کدام  و هر کدام
و هر کدام  آن
آن  و
و ![G^{(i+1)} = [G^{(i)}، G^{(i)}]](https://groupprops.subwiki.org/w/images/math/6/1/8/61821731652d94617999581509cf6397.png)
 یک
یک  گروههای قابل حل هستند . سپس
گروههای قابل حل هستند . سپس  یک
یک  قابل حل باشند،
قابل حل باشند،  نیز قابل حل است.
نیز قابل حل است. همه زیرگروه های
همه زیرگروه های  قابل حل است.
قابل حل است. و
و  ، پس قابل حل است اگر و فقط اگر باشد. علاوه بر این، اگر چنین است، طول مشتق شده برابر است با طول مشتق شده از , مگر اینکه یکی از گروه ها جزئی و دیگری آبلی غیر جزئی باشد.
، پس قابل حل است اگر و فقط اگر باشد. علاوه بر این، اگر چنین است، طول مشتق شده برابر است با طول مشتق شده از , مگر اینکه یکی از گروه ها جزئی و دیگری آبلی غیر جزئی باشد. 




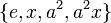 ،
، 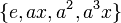


 یا
یا  )
) ; مانند حلقه تولید شده توسط مقادیر کاراکتر
; مانند حلقه تولید شده توسط مقادیر کاراکتر (بنابراین، این یک
(بنابراین، این یک 

 (سایز 1)
(سایز 1) (سایز 2)
(سایز 2) (سایز 2)
(سایز 2) (سایز 2)
(سایز 2) -هسته
-هسته -هسته
-هسته -هسته
-هسته نه صفر است و نه
نه صفر است و نه  مدول
مدول  . این را با مورد فرد مقایسه کنید
. این را با مورد فرد مقایسه کنید  ، درجه
، درجه
 و مرتبه
و مرتبه
 به عنصر چرخش مرتبه چهار و مولد دوم به عنصر انعکاس
به عنصر چرخش مرتبه چهار و مولد دوم به عنصر انعکاس درجه دو نگاشت می شود.
درجه دو نگاشت می شود. گروه دور ای مرتبه چهار را تعریف کنید (با استفاده از
گروه دور ای مرتبه چهار را تعریف کنید (با استفاده از  ،
،  حتی:
حتی: .
.  :
: 
 تعداد زیرگروه ها است
تعداد زیرگروه ها است  ، که در آن
، که در آن  تابع شمارش مقسوم علیه و
تابع شمارش مقسوم علیه و  تابع مجموع مقسوم علیه است. ساختار زیر گروه گروه دو وجهی را ببینید
تابع مجموع مقسوم علیه است. ساختار زیر گروه گروه دو وجهی را ببینید 


 و رفت و
و رفت و  آمد نکنید
آمد نکنید ، که طبیعی است، اما
، که طبیعی است، اما  طبیعی نیست
طبیعی نیست





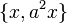

 -- یکی از
-- یکی از 

 -- یکی از
-- یکی از 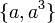


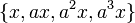

 و
و  : نظم حاصلضرب دستورات
: نظم حاصلضرب دستورات 
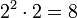
 دارای توانی برابر با
دارای توانی برابر با  .
. در این وبلاگ به ریاضیات و کاربردهای آن و تحقیقات در آنها پرداخته می شود. مطالب در این وبلاگ ترجمه سطحی و اولیه است و کامل نیست.در صورتی سوال یا نظری در زمینه ریاضیات دارید مطرح نمایید .در صورت امکان به آن می پردازم. من دوست دارم برای یافتن پاسخ به سوالات و حل پروژه های علمی با دیگران همکاری نمایم.در صورتی که شما هم بامن هم عقیده هستید با من تماس بگیرید.
در این وبلاگ به ریاضیات و کاربردهای آن و تحقیقات در آنها پرداخته می شود. مطالب در این وبلاگ ترجمه سطحی و اولیه است و کامل نیست.در صورتی سوال یا نظری در زمینه ریاضیات دارید مطرح نمایید .در صورت امکان به آن می پردازم. من دوست دارم برای یافتن پاسخ به سوالات و حل پروژه های علمی با دیگران همکاری نمایم.در صورتی که شما هم بامن هم عقیده هستید با من تماس بگیرید.