توسط علی رضا نقش نیلچی
| سه شنبه بیستم دی ۱۴۰۱ | 15:19
گاز ایده آل (فرآیند برگشت پذیر) [ ویرایش ]
مقاله اصلی: فرآیند آدیاباتیک برگشت پذیر
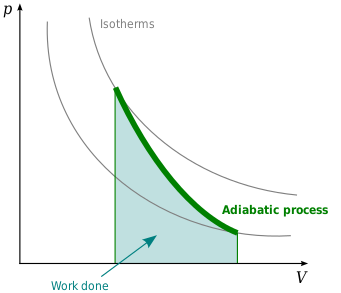
برای یک ماده ساده، در طی یک فرآیند آدیاباتیک که در آن حجم افزایش می یابد، انرژی داخلی ماده کار باید کاهش یابد.
معادله ریاضی برای یک گاز ایده آل که تحت یک فرآیند برگشت پذیر (یعنی بدون تولید آنتروپی) آدیاباتیک قرار می گیرد را می توان با معادله فرآیند پلی تروپیک نشان داد [3]

که در آن P فشار، V حجم، و γ شاخص آدیاباتیک یا نسبت ظرفیت گرمایی است که به صورت تعریف شده است.

در اینجا C P گرمای ویژه برای فشار ثابت، C V گرمای ویژه برای حجم ثابت، و f تعداد درجات آزادی است (3 برای یک گاز تک اتمی، 5 برای یک گاز دو اتمی یا یک گاز از مولکول های خطی مانند دی اکسید کربن).
برای گاز ایده آل تک اتمی γ =5/3و برای یک گاز دو اتمی (مانند نیتروژن و اکسیژن ، اجزای اصلی هوا)، γ =7/5. [11] توجه داشته باشید که فرمول فوق فقط برای گازهای ایده آل کلاسیک (یعنی گازهای بسیار بالاتر از دمای صفر مطلق) و نه گازهای بوز-انیشتین یا فرمی قابل استفاده است .
همچنین می توان از قانون گاز ایده آل برای بازنویسی رابطه فوق بین P و V به صورت [3] استفاده کرد.


که در آن T دمای مطلق یا ترمودینامیکی است.
نمونه ای از فشرده سازی آدیاباتیک [ ویرایش ]
کورس تراکم در یک موتور بنزینی می تواند به عنوان نمونه ای از تراکم آدیاباتیک استفاده شود. مفروضات مدل عبارتند از: حجم غیر فشرده سیلندر یک لیتر است (1 لیتر = 1000 سانتی متر 3 = 0.001 متر مکعب ) . گاز درون هوا است که فقط از نیتروژن و اکسیژن مولکولی تشکیل شده است (بنابراین یک گاز دو اتمی با 5 درجه آزادی و بنابراین γ =7/5) نسبت تراکم موتور 10:1 است (یعنی حجم 1 لیتری گاز فشرده نشده توسط پیستون به 0.1 لیتر کاهش می یابد). و گاز فشرده نشده تقریباً در دما و فشار اتاق است (دمای گرم اتاق ~ 27 درجه سانتیگراد یا 300 کلوین و فشار 1 بار = 100 کیلو پاسکال، یعنی فشار معمولی اتمسفر سطح دریا).

بنابراین ثابت آدیاباتیک برای این مثال حدود 6.31 Pam 4.2 است.
اکنون گاز به حجم 0.1 لیتر (0.0001 متر مکعب ) فشرده می شود ، که فرض می کنیم آنقدر سریع اتفاق می افتد که هیچ گرمایی وارد یا خارج از گاز از دیواره ها نمی شود. ثابت آدیاباتیک ثابت می ماند، اما فشار حاصل ناشناخته است

اکنون می توانیم فشار نهایی را حل کنیم [12]

یا 25.1 بار. این افزایش فشار بیش از یک نسبت تراکم ساده 10:1 است که نشان می دهد. این به این دلیل است که گاز نه تنها فشرده می شود، بلکه کار انجام شده برای فشرده سازی گاز انرژی داخلی آن را نیز افزایش می دهد، که خود را با افزایش دمای گاز و افزایش فشار بیشتر از مقداری که از یک محاسبه ساده 10 حاصل می شود نشان می دهد. برابر فشار اولیه
ما می توانیم دمای گاز فشرده در سیلندر موتور را نیز با استفاده از قانون گاز ایده آل، PV = nRT حل کنیم ( n مقدار گاز بر حسب مول و R ثابت گاز برای آن گاز است). شرایط اولیه ما 100 کیلو پاسکال فشار، 1 لیتر حجم و 300 K دما است، ثابت تجربی ما ( nR ) این است:

می دانیم که گاز فشرده دارای V = 0.1 L و P = است2.51 × 10 6 Pa ، بنابراین می توانیم دما را حل کنیم:

این دمای نهایی 753 کلوین یا 479 درجه سانتیگراد یا 896 درجه فارنهایت است که بسیار بالاتر از نقطه اشتعال بسیاری از سوختها است. به همین دلیل است که یک موتور با تراکم بالا به سوختهایی نیاز دارد که بهطور خاص فرموله شده باشند تا خود اشتعال نشوند (که باعث کوبش موتور در هنگام کار در این شرایط دما و فشار میشود) یا اینکه یک سوپرشارژر با یک خنککننده اینترکولر برای افزایش فشار اما با فشار پایینتر نیاز دارد. افزایش دما مفید خواهد بود. یک موتور دیزل در شرایط شدیدتر کار می کند، با نسبت تراکم 16:1 یا بیشتر معمولی است، تا دمای گاز بسیار بالایی را فراهم کند، که احتراق فوری سوخت تزریق شده را تضمین می کند.
انبساط آزاد آدیاباتیک یک گاز [ ویرایش ]
همچنین ببینید: گسترش رایگان
برای انبساط آزاد آدیاباتیک یک گاز ایده آل، گاز در یک ظرف عایق قرار می گیرد و سپس اجازه می دهد در خلاء منبسط شود. از آنجایی که هیچ فشار خارجی برای انبساط گاز وجود ندارد، کار انجام شده توسط یا روی سیستم صفر است. از آنجایی که این فرآیند شامل هیچ گونه انتقال حرارت یا کاری نمی شود، قانون اول ترمودینامیک نشان می دهد که تغییر انرژی خالص داخلی سیستم صفر است. برای یک گاز ایده آل، دما ثابت می ماند زیرا انرژی داخلی در آن حالت فقط به دما بستگی دارد. از آنجایی که در دمای ثابت، آنتروپی متناسب با حجم است، آنتروپی در این حالت افزایش مییابد، بنابراین این فرآیند غیرقابل برگشت است.
استخراج رابطه P – V برای گرمایش و سرمایش آدیاباتیک [ ویرایش ]
تعریف فرآیند آدیاباتیک این است که انتقال حرارت به سیستم صفر است، δQ = 0 . سپس طبق قانون اول ترمودینامیک،

| | ( a1 ) |
که در آن dU تغییر در انرژی داخلی سیستم و δW کاری است که توسط سیستم انجام می شود. هر کاری ( δW ) انجام شده باید با هزینه انرژی داخلی U انجام شود ، زیرا هیچ گرمایی δQ از محیط اطراف تامین نمی شود. کار فشار-حجم δW انجام شده توسط سیستم به صورت تعریف می شود

| | ( a2 ) |
با این حال، P در طول یک فرآیند آدیاباتیک ثابت نمی ماند، بلکه همراه با V تغییر می کند.
لازم است بدانیم که چگونه مقادیر dP و dV به یکدیگر مرتبط می شوند که فرآیند آدیاباتیک ادامه می یابد. برای یک گاز ایده آل (قانون گاز ایده آل PV = nRT را به یاد بیاورید ) انرژی داخلی با داده می شود

| | ( a3 ) |
که در آن α تعداد درجات آزادی تقسیم بر 2 است، R ثابت گاز جهانی و n تعداد مول های سیستم (ثابت) است.
معادله افتراق (a3) نتیجه می دهد

| | ( a4 ) |
معادله (a4) اغلب به صورت dU = nC V dT بیان می شود زیرا C V = αR .
حال معادلات (a2) و (a4) را با معادله (a1) جایگزین کنید تا به دست آید

Factorize - P dV :

و هر دو طرف را بر PV تقسیم کنید :

پس از ادغام سمت چپ و راست از V 0 به V و از P 0 به P و تغییر اضلاع به ترتیب،

هر دو طرف را نشان دهید، جایگزین کنیدα + 1/αبا γ ، نسبت ظرفیت گرمایی

و برای به دست آوردن علامت منفی را حذف کنید

از این رو،

و


| | ( b1 ) |
در عین حال، کار انجام شده توسط تغییرات فشار-حجم در نتیجه این فرآیند، برابر است

| | ( b2 ) |
از آنجایی که ما نیاز داریم که فرآیند آدیاباتیک باشد، معادله زیر باید درست باشد

| | ( b3 ) |
با اشتقاق قبلی،

| | ( b4 ) |
بازآرایی (b4) می دهد

جایگزین کردن این به (b2) می دهد

با ادغام عبارت کار را به دست می آوریم،

جایگزینی γ =α + 1/αدر ترم دوم،

تنظیم مجدد،

با استفاده از قانون گاز ایده آل و با فرض یک مقدار مولی ثابت (همانطور که اغلب در موارد عملی اتفاق می افتد)،

با فرمول پیوسته،

یا

جایگزینی W به عبارت قبلی ،

جایگزینی این عبارت و (b1) در (b3) به دست می آید

ساده سازی،



اشتقاق فرمول گسسته و بیان کار [ ویرایش ]
تغییر انرژی داخلی یک سیستم که از حالت 1 به حالت 2 اندازه گیری می شود برابر است با
در عین حال، کار انجام شده توسط تغییرات فشار-حجم در نتیجه این فرآیند، برابر است

| | ( c2 ) |
از آنجایی که ما نیاز داریم که فرآیند آدیاباتیک باشد، معادله زیر باید درست باشد

| | ( c3 ) |
با اشتقاق قبلی،

| | ( ج4 ) |
بازآرایی (c4) می دهد

جایگزین کردن این به (c2) می دهد

با ادغام عبارت کار را به دست می آوریم،

جایگزینی γ =α + 1/αدر ترم دوم،

تنظیم مجدد،

با استفاده از قانون گاز ایده آل و با فرض یک مقدار مولی ثابت (همانطور که اغلب در موارد عملی اتفاق می افتد)،

با فرمول پیوسته،

یا

جایگزینی W به عبارت قبلی ،

جایگزینی این عبارت و (c1) در (c3) به دست می آید

ساده سازی،



ترسیم نمودار adiabats [ ویرایش ]
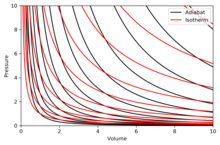
آدیابات منحنی آنتروپی ثابت در یک نمودار است. برخی از خواص آدیابات ها در نمودار P - V نشان داده شده است. این ویژگیها را میتوان از رفتار کلاسیک گازهای ایدهآل خواند، به جز در منطقهای که PV کوچک میشود (دمای پایین)، که در آن اثرات کوانتومی مهم میشوند.
- هر adiabat به طور مجانبی هم به محور V و هم به محور P نزدیک می شود (درست مانند ایزوترم ها ).
- هر adiabat هر ایزوترم را دقیقاً یک بار قطع می کند.
- آدیابات شبیه ایزوترم به نظر می رسد، با این تفاوت که در حین انبساط، آدیابات فشار بیشتری نسبت به ایزوترم از دست می دهد، بنابراین شیب تندتری (عمودی تر) دارد.
- اگر ایزوترم ها به سمت شمال شرقی (45 درجه) مقعر باشند، آدیابات ها به سمت شرق شمال شرقی (31 درجه) مقعر هستند.
- اگر آدیابات ها و ایزوترم ها به ترتیب در فواصل منظم آنتروپی و دما نمودار شوند (مانند ارتفاع روی نقشه کانتور)، آنگاه با حرکت چشم به سمت محورها (به سمت جنوب غربی)، تراکم ایزوترم ها ثابت می ماند، اما می بیند که تراکم آدیابات ها رشد می کند. استثنا بسیار نزدیک به صفر مطلق است، جایی که چگالی آدیابات ها به شدت کاهش می یابد و نادر می شوند ( به قضیه نرنست مراجعه کنید ). [ توضیح لازم است ]
نمودار سمت راست یک نمودار P – V با برهم نهی آدیابات ها و ایزوترم ها است:
ایزوترم ها منحنی های قرمز و آدیابات ها منحنی های سیاه هستند.
آدیابات ها ایزنتروپیک هستند.
حجم، محور افقی و فشار، محور عمودی است.
ریشه شناسی [ ویرایش ]
اصطلاح آدیاباتیک ( / ˌ æ d i ə ˈ b æ t ɪ k / ) انگلیسی سازی از واژه یونانی ἀδιάβατος «صعب العبور» (که توسط گزنفون رودها استفاده می شود) است. در مفهوم ترمودینامیکی توسط رانکین (1866)، [13] [14] و توسط ماکسول در سال 1871 (به صراحت این اصطلاح را به رانکین نسبت می دهد) استفاده می شود. [15] ریشه ریشهشناسی در اینجا به عدم امکان انتقال انرژی به عنوان گرما و انتقال ماده از طریق دیوار مربوط میشود.
لغت یونانی ἀδιάβατος از خصوصیات ἀ- ("نه") و διαβατός، "قابل عبور"، به نوبه خود از διά ("از طریق") و βαῖνειν ("راه رفتن، رفتن، آمدن") تشکیل شده است. [16]
اهمیت مفهومی در نظریه ترمودینامیکی [ ویرایش ]
فرآیند آدیاباتیک از روزهای اولیه برای ترمودینامیک مهم بوده است. در کار ژول مهم بود زیرا راهی برای ارتباط تقریبا مستقیم مقادیر گرما و کار فراهم می کرد.
انرژی می تواند وارد یا خروج از یک سیستم ترمودینامیکی محصور شده توسط دیوارهایی شود که از انتقال جرم فقط به عنوان گرما یا کار جلوگیری می کند. بنابراین، یک مقدار کار در چنین سیستمی می تواند تقریباً مستقیماً به مقدار معادل گرما در یک چرخه دو اندام مرتبط باشد. اندام اول یک فرآیند کار آدیاباتیک ایزوکوریک است که انرژی داخلی سیستم را افزایش می دهد . دوم، انتقال حرارت ایزوکوریک و بدون کار که سیستم را به حالت اولیه خود باز می گرداند. بر این اساس، رانکین به جای کمیت کالریمتری، مقدار گرما را در واحدهای کار اندازه گیری کرد. [17] در سال 1854، رانکین از کمیتی استفاده کرد که آن را "تابع ترمودینامیکی" نامید که بعدها آنتروپی نامیده شد، و در آن زمان او همچنین درباره "منحنی عدم انتقال گرما" نوشت [18].که بعدها آن را منحنی آدیاباتیک نامید. [13] چرخه کارنو علاوه بر دو اندام همدما، دو اندام آدیاباتیک نیز دارد.
برای مبانی ترمودینامیک، اهمیت مفهومی این مورد توسط برایان، [19] توسط کاراتئودوری [1] و بورن مورد تاکید قرار گرفت. [20] دلیل آن این است که کالریسنجی نوعی دما را پیشفرض میگیرد که قبلاً قبل از بیانیه قانون اول ترمودینامیک تعریف شده است، مانند یکی بر اساس مقیاسهای تجربی. چنین پیش فرضی شامل تمایز بین دمای تجربی و دمای مطلق است. در عوض، تعریف دمای مطلق ترمودینامیکی بهتر است تا زمانی که قانون دوم به عنوان مبنای مفهومی در دسترس باشد، باقی بماند. [21]
در قرن هجدهم، قانون بقای انرژی هنوز به طور کامل تدوین یا تثبیت نشده بود و ماهیت گرما مورد بحث قرار گرفت. یک رویکرد برای این مشکلات این بود که گرما را که با کالریمتری اندازه گیری می شد، به عنوان یک ماده اولیه که از نظر کمیت حفظ می شود، در نظر گرفت. در اواسط قرن نوزدهم، به عنوان نوعی انرژی شناخته شد و قانون بقای انرژی نیز از این طریق به رسمیت شناخته شد. دیدگاهی که در نهایت خود را تثبیت کرد و در حال حاضر درست تلقی می شود، این است که قانون بقای انرژی یک اصل بدیهی است و گرما باید به عنوان پیامد آن تحلیل شود. در این نور، گرما نمی تواند جزئی از انرژی کل یک جسم واحد باشد زیرا یک متغیر حالت نیستبلکه متغیری است که انتقال بین دو جسم را توصیف می کند. فرآیند آدیاباتیک مهم است زیرا جزء منطقی این دیدگاه فعلی است. [21]
کاربردهای متفاوت کلمه آدیاباتیک [ ویرایش ]
این مقاله از دیدگاه ترمودینامیک ماکروسکوپی نوشته شده است و در این مقاله از واژه آدیاباتیک به روش سنتی ترمودینامیک معرفی شده توسط رانکین استفاده شده است. در مقاله حاضر اشاره شده است که برای مثال، اگر فشرده سازی یک گاز سریع باشد، در این صورت زمان کمی برای انتقال حرارت وجود دارد، حتی زمانی که گاز توسط یک دیواره مشخص جداسازی نشده باشد. به این معنا، گاهی اوقات به طور تقریبی یا ضعیف گفته میشود که فشردهسازی سریع یک گاز آدیاباتیک است ، اگرچه اغلب از ایزنتروپیک فاصله دارد، حتی زمانی که گاز بهصورت آدیاباتیک توسط یک دیواره مشخص جدا نشده باشد.
با این حال، مکانیک کوانتومی و مکانیک آماری کوانتومی ، کلمه آدیاباتیک را به معنای بسیار متفاوتی به کار میبرند ، معنایی که در برخی مواقع تقریباً مخالف مفهوم ترمودینامیکی کلاسیک به نظر میرسد. در تئوری کوانتومی، کلمه آدیاباتیک می تواند به معنای چیزی نزدیک به ایزنتروپیک، یا شاید نزدیک به شبه استاتیک باشد، اما کاربرد این کلمه بین این دو رشته بسیار متفاوت است.
از یک سو، در نظریه کوانتومی، اگر یک عنصر اغتشاشگر کار فشاری تقریباً بی نهایت آهسته (یعنی شبه استاتیک) انجام شود، گفته می شود که به صورت آدیاباتیک انجام شده است . ایده این است که شکل توابع ویژه به آرامی و پیوسته تغییر می کند، به طوری که هیچ پرش کوانتومی ایجاد نمی شود و تغییر عملاً برگشت پذیر است. در حالی که اعداد اشغال بدون تغییر هستند، با این وجود تغییراتی در سطوح انرژی یک به یک متناظر، قبل و بعد از فشرده سازی، حالت های ویژه وجود دارد. بنابراین یک عنصر مزاحم کار بدون انتقال حرارت و بدون ایجاد تغییرات تصادفی در سیستم انجام شده است. مثلا مکس بورنمی نویسد: "در واقع، معمولاً این حالت "آدیاباتیک" است که باید با آن انجام دهیم: یعنی حالت محدود کننده ای که در آن نیروی خارجی (یا واکنش اجزای سیستم بر روی یکدیگر) بسیار آهسته عمل می کند. در این مورد، به یک تقریب بسیار بالا

یعنی هیچ احتمالی برای انتقال وجود ندارد و سیستم در حالت اولیه پس از قطع اغتشاش قرار دارد. بنابراین، چنین آشفتگی آهسته، همانطور که به طور کلاسیک است، برگشت پذیر است.» [22]
از سوی دیگر، در نظریه کوانتومی، اگر یک عنصر اغتشاشگر کار فشاری به سرعت انجام شود، اعداد اشغال و انرژی حالات ویژه را متناسب با انتگرال لحظه گذار و مطابق با نظریه اغتشاش وابسته به زمان تغییر میدهد. شکل عملکردی خود حالت های ویژه را مختل می کند. در آن نظریه به چنین تغییر سریعی گفته میشود که آدیاباتیک نیست و کلمهی مخالف دیاباتیک برای آن به کار میرود.
تحقیقات اخیر [23] نشان می دهد که توان جذب شده از اغتشاش با نرخ این انتقال های غیر آدیاباتیک مطابقت دارد. این مربوط به فرآیند کلاسیک انتقال انرژی به شکل گرما است، اما با مقیاسهای زمانی نسبی معکوس در مورد کوانتومی. فرآیندهای آدیاباتیک کوانتومی در مقیاسهای زمانی نسبتاً طولانی رخ میدهند، در حالی که فرآیندهای آدیاباتیک کلاسیک در مقیاسهای زمانی نسبتاً کوتاه رخ میدهند. همچنین باید توجه داشت که مفهوم "گرما" (با اشاره به کمیت انرژی حرارتیانتقال داده می شود) در سطح کوانتومی تجزیه می شود و شکل خاص انرژی (معمولاً الکترومغناطیسی) باید به جای آن در نظر گرفته شود. جذب ناچیز یا ناچیز انرژی ناشی از اغتشاش در یک فرآیند کوانتومی آدیاباتیک، توجیه خوبی برای شناسایی آن به عنوان آنالوگ کوانتومی فرآیندهای آدیاباتیک در ترمودینامیک کلاسیک و استفاده مجدد از این واژه فراهم میکند.
علاوه بر این، در ترمودینامیک اتمسفر، فرآیند دیاباتیک فرآیندی است که در آن گرما مبادله می شود. [24]
در ترمودینامیک کلاسیک، چنین تغییر سریعی همچنان آدیاباتیک نامیده می شود، زیرا سیستم از نظر آدیاباتیک ایزوله است و هیچ انتقال انرژی به عنوان گرما وجود ندارد. برگشت ناپذیری شدید تغییر، به دلیل ویسکوزیته یا تولید آنتروپی دیگر ، بر این کاربرد کلاسیک تأثیری ندارد.
بنابراین برای یک توده گاز، در ترمودینامیک ماکروسکوپی، کلمات به قدری استفاده میشوند که گاهی اوقات فشردهسازی بهطور ضعیف یا تقریباً آدیاباتیک است، اگر آنقدر سریع باشد که از انتقال حرارت جلوگیری کند، حتی اگر سیستم از نظر آدیاباتیک ایزوله نباشد. اما در تئوری آماری کوانتومی، فشردهسازی در صورتی که سریع باشد، آدیاباتیک نامیده نمیشود، حتی اگر سیستم به معنای کلاسیک ترمودینامیکی آن از نظر آدیاباتیک جدا شده باشد. همانطور که در بالا ذکر شد، کلمات در دو رشته متفاوت استفاده می شوند.
همچنین ببینید [ ویرایش ]
مباحث مربوط به فیزیک
فرآیندهای ترمودینامیکی مرتبط





 ) واحدها از نظر ریاضی، توزیع نرمال به
) واحدها از نظر ریاضی، توزیع نرمال به 
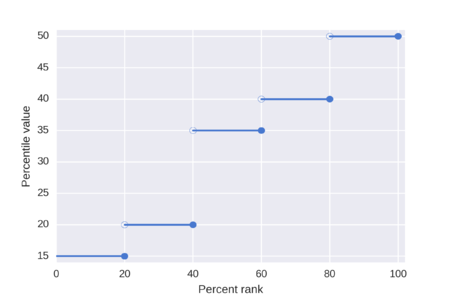
 یک لیست از N مقادیر مرتب شده (مرتب شده از حداقل به بزرگترین) کوچکترین مقدار در لیست است به طوری که بیش از P درصد داده ها به شدت کمتر از مقدار و حداقل P درصد داده ها کمتر یا مساوی باشد. به آن ارزش این ابتدا با محاسبه رتبه ترتیبی و سپس گرفتن مقدار از لیست مرتب شده مطابق با آن رتبه به دست می آید. رتبه
یک لیست از N مقادیر مرتب شده (مرتب شده از حداقل به بزرگترین) کوچکترین مقدار در لیست است به طوری که بیش از P درصد داده ها به شدت کمتر از مقدار و حداقل P درصد داده ها کمتر یا مساوی باشد. به آن ارزش این ابتدا با محاسبه رتبه ترتیبی و سپس گرفتن مقدار از لیست مرتب شده مطابق با آن رتبه به دست می آید. رتبه 

 . این به سادگی توسط انجام می شود
. این به سادگی توسط انجام می شود![{\displaystyle v(x)=v_{\lfloor x\rfloor }+(x{\bmod {1}})(v_{\lfloor x\rfloor +1}-v_{\lfloor x\rfloor })،\ برای همه x\in [1,N]:v(i)=v_{i}{\text{, for }}i=1,2,\ldots ,N,}](https://wikimedia.org/api/rest_v1/media/math/render/svg/eeae87405f0184fabff114665b843cbb94a3abbc)
 از
از  از
از  ،
، تعریف نشده است، نیازی به این نیست زیرا در ضرب می شود
تعریف نشده است، نیازی به این نیست زیرا در ضرب می شود .) همانطور که می بینیم،
.) همانطور که می بینیم،  و ثابتی که تابعی از اندازه نمونه
و ثابتی که تابعی از اندازه نمونه 
 ، مربوط به
، مربوط به  :
:

![[0,1]](https://wikimedia.org/api/rest_v1/media/math/render/svg/738f7d23bb2d9642bab520020873cccbef49768d) محدوده
محدوده  باید نتیجه ای در محدوده تولید کند یا مجبور به تولید شود
باید نتیجه ای در محدوده تولید کند یا مجبور به تولید شود![[1,N]](https://wikimedia.org/api/rest_v1/media/math/render/svg/d6fc7b14276a914ff6cbdf59b806eb601020f473) ، که ممکن است به معنای عدم وجود مکاتبات یک به یک در منطقه وسیع تر باشد. یکی از نویسنده ها انتخابی را پیشنهاد کرده است
، که ممکن است به معنای عدم وجود مکاتبات یک به یک در منطقه وسیع تر باشد. یکی از نویسنده ها انتخابی را پیشنهاد کرده است  جایی که
جایی که 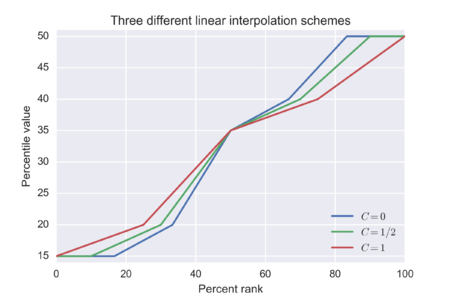
![{\displaystyle x=f(p)={\begin{cases}Np+{\frac {1}{2}},\forall p\in \left[p_{1},p_{N}\right],\ \1،\برای همه p\in \چپ[0,p_{1}\راست]،\\N،\برای همه p\in \چپ[p_{N},1\راست].\پایان{موارد}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/b7800366b8eeac526ee3fc22b45ed5dfd1550e62)
![p_{i}={\frac {1}{N}}\left(i-{\frac {1}{2}}\right),i\in [1,N]\cap \mathbb {N}](https://wikimedia.org/api/rest_v1/media/math/render/svg/69e7a4bfdbaf07f8b5e36ccd021ff966f5e540d3)



![x=f(p,N)=p(N-1)+1{\text{, }}p\in [0,1]](https://wikimedia.org/api/rest_v1/media/math/render/svg/e25ef7db919bca75354f8af45d7208a1c5a626b2)
![\بنابراین p={\frac {x-1}{N-1}}{\text{, }}x\in [1,N].](https://wikimedia.org/api/rest_v1/media/math/render/svg/0a4c15310db22c92a626068484739e320bace185)
 رابطه یک به یک است برای
رابطه یک به یک است برای![p\in [0,1]](https://wikimedia.org/api/rest_v1/media/math/render/svg/33c3a52aa7b2d00227e85c641cca67e85583c43c) ، تنها یکی از سه نوع دارای این ویژگی است. از این رو پسوند "INC"، برای شامل ، در تابع اکسل.
، تنها یکی از سه نوع دارای این ویژگی است. از این رو پسوند "INC"، برای شامل ، در تابع اکسل. ، در حالی که نسخه "INC"، نوع دوم، اینطور نیست. در واقع هر عددی کوچکتر از
، در حالی که نسخه "INC"، نوع دوم، اینطور نیست. در واقع هر عددی کوچکتر از نیز مستثنی است و باعث خطا می شود.)
نیز مستثنی است و باعث خطا می شود.)![{\displaystyle x=f(p,N)={\begin{cases}1{\text{, }}p\in \left[0,{\frac {1}{N+1}}\right]\ \p(N+1){\text{, }}p\in \left({\frac {1}{N+1}},{\frac {N}{N+1}}\راست)\\ N{\text{, }}p\in \left[{\frac {N}{N+1}},1\right]\end{cases}}.}](https://wikimedia.org/api/rest_v1/media/math/render/svg/e7bef62b06df2ee9322c8ac5b1d10b43c07176f6)

 به ترتیب با مقادیر نمونه مرتب شده N ما مرتبط است. اجازه دهید
به ترتیب با مقادیر نمونه مرتب شده N ما مرتبط است. اجازه دهید
 چه زمانی
چه زمانی ،
، برای ژنرال
برای ژنرال ،
،


 مقدار انرژی است که سیستم با گرم کردن به دست می آورد،
مقدار انرژی است که سیستم با گرم کردن به دست می آورد،
 تغییر در آنتروپی است. علامت برابر به یک
تغییر در آنتروپی است. علامت برابر به یک 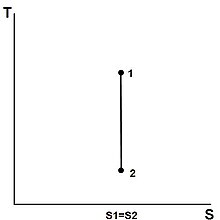
 یا
یا .
. 



 آنتالپی خاص در حالت خروج برای فرآیند واقعی است،
آنتالپی خاص در حالت خروج برای فرآیند واقعی است، آنتالپی خاص در حالت خروج برای فرآیند ایزنتروپیک است.
آنتالپی خاص در حالت خروج برای فرآیند ایزنتروپیک است.



 ) از رابطه زیر بدست می آید
) از رابطه زیر بدست می آید
 ، و غیره
، و غیره تمام فرآیندهای برگشت پذیر آدیاباتیک ایزنتروپیک هستند. این منجر به دو مشاهدات مهم می شود:
تمام فرآیندهای برگشت پذیر آدیاباتیک ایزنتروپیک هستند. این منجر به دو مشاهدات مهم می شود:

 ، و
، و
 و
و ، سپس
، سپس


 ثابت است از این رو با ادغام معادله فوق، با فرض یک گاز کامل کالری، به دست می آوریم
ثابت است از این رو با ادغام معادله فوق، با فرض یک گاز کامل کالری، به دست می آوریم

 ،
،
 اما nR = خود ثابت است، بنابراین
اما nR = خود ثابت است، بنابراین .)
.)
 (در هر خال)،
(در هر خال)، و
و


 یا
یا




















 = فشار،
= فشار، ،
، = دما،
= دما، = جرم،
= جرم، = ثابت گاز برای گاز خاص =
= ثابت گاز برای گاز خاص = ،
، = ثابت گاز جهانی،
= ثابت گاز جهانی، = وزن مولکولی گاز مخصوص،
= وزن مولکولی گاز مخصوص، = تراکم،
= تراکم، = گرمای ویژه در فشار ثابت،
= گرمای ویژه در فشار ثابت، = گرمای ویژه در حجم ثابت.
= گرمای ویژه در حجم ثابت.









































 پس باید این باشد
پس باید این باشد
 ،
، .
.


















 پتانسیل
پتانسیل  تعداد ذرات در سیستم، و
تعداد ذرات در سیستم، و تعداد انواع ذرات در سیستم است.
تعداد انواع ذرات در سیستم است. ، یک
، یک  کار ترمودینامیکی کمتر،
کار ترمودینامیکی کمتر،  ، توسط سیستم بر روی محیط اطراف خود انجام می شود.
، توسط سیستم بر روی محیط اطراف خود انجام می شود.  .
. ،
،

 جایی که
جایی که جایی که
جایی که جایی که
جایی که


 و ضرایب دیفرانسیل متغیر طبیعی
و ضرایب دیفرانسیل متغیر طبیعی فقط متغیرهای منفرد هستند
فقط متغیرهای منفرد هستند

 زیرا T یک متغیر طبیعی برای آنتالپی H نیست.
زیرا T یک متغیر طبیعی برای آنتالپی H نیست. به طوری که
به طوری که برای یک
برای یک 




 جایی که
جایی که





















 به طوری که
به طوری که
 . آنتروپی شانون (در
. آنتروپی شانون (در  و اگر آنتروپی با واحد اندازه گیری شود
و اگر آنتروپی با واحد اندازه گیری شود در هر nat، سپس آنتروپی با:
در هر nat، سپس آنتروپی با:
 ).
).
 در دمای معینی وارد سیستم می شود
در دمای معینی وارد سیستم می شود 

 و
و به طوری که دومی به طور آدیاباتیک از اولی قابل دسترسی است اما بالعکس نیست. تعریف آنتروپی حالت های مرجع به ترتیب 0 و 1 آنتروپی یک حالت
به طوری که دومی به طور آدیاباتیک از اولی قابل دسترسی است اما بالعکس نیست. تعریف آنتروپی حالت های مرجع به ترتیب 0 و 1 آنتروپی یک حالت به عنوان بزرگترین عدد تعریف می شود
به عنوان بزرگترین عدد تعریف می شود به طوری که
به طوری که ، در ایالت
، در ایالت


 ) و کار، یعنی
) و کار، یعنی (
(  (کار فشار-حجم)، در سراسر مرزهای سیستم، به طور کلی باعث تغییر در آنتروپی سیستم می شود. انتقال به عنوان گرما مستلزم انتقال آنتروپی است
(کار فشار-حجم)، در سراسر مرزهای سیستم، به طور کلی باعث تغییر در آنتروپی سیستم می شود. انتقال به عنوان گرما مستلزم انتقال آنتروپی است ، جایی که
، جایی که در یک
در یک  ، یعنی میزان تغییر
، یعنی میزان تغییر از آنتروپی کمیت گسترده
از آنتروپی کمیت گسترده
 نرخ خالص جریان آنتروپی ناشی از جریان جرم به داخل و خارج از سیستم است (که در آن
نرخ خالص جریان آنتروپی ناشی از جریان جرم به داخل و خارج از سیستم است (که در آن آنتروپی در واحد جرم است).
آنتروپی در واحد جرم است). نرخ جریان آنتروپی ناشی از جریان گرما در سراسر مرز سیستم است.
نرخ جریان آنتروپی ناشی از جریان گرما در سراسر مرز سیستم است. نرخ
نرخ  جایی که
جایی که جریان گرما است و
جریان گرما است و درجه حرارت در است
درجه حرارت در است پورت جریان گرما به سیستم.
پورت جریان گرما به سیستم. هرگز یک کمیت شناخته شده نیست، بلکه همیشه بر اساس عبارت بالا مشتق شده است. بنابراین، نسخه سیستم باز قانون دوم به طور مناسب تر به عنوان "معادله تولید آنتروپی" توصیف می شود زیرا مشخص می کند که
هرگز یک کمیت شناخته شده نیست، بلکه همیشه بر اساس عبارت بالا مشتق شده است. بنابراین، نسخه سیستم باز قانون دوم به طور مناسب تر به عنوان "معادله تولید آنتروپی" توصیف می شود زیرا مشخص می کند که ، با صفر برای فرآیندهای برگشت پذیر یا بزرگتر از صفر برای فرآیندهای برگشت ناپذیر.
، با صفر برای فرآیندهای برگشت پذیر یا بزرگتر از صفر برای فرآیندهای برگشت ناپذیر. و فشار
و فشار تا یک جلد نهایی
تا یک جلد نهایی
 مقدار گاز (به
مقدار گاز (به  تا دمای نهایی
تا دمای نهایی






 اندازه گیری تغییر آنتروپی را معرفی می کند،
اندازه گیری تغییر آنتروپی را معرفی می کند، . تغییر آنتروپی جهت را توصیف می کند و مقدار تغییرات ساده مانند انتقال حرارت بین سیستم ها را - همیشه از گرمتر به سردتر به طور خود به خود - کمیت می دهد.
. تغییر آنتروپی جهت را توصیف می کند و مقدار تغییرات ساده مانند انتقال حرارت بین سیستم ها را - همیشه از گرمتر به سردتر به طور خود به خود - کمیت می دهد. آنتروپی مولی استاندارد هر عنصر یا ترکیب را تشکیل می دهد، نشانگر مقدار انرژی ذخیره شده توسط یک ماده در298 K.
آنتروپی مولی استاندارد هر عنصر یا ترکیب را تشکیل می دهد، نشانگر مقدار انرژی ذخیره شده توسط یک ماده در298 K.  . این عبارت از طریق برخی مراحل به معادله
. این عبارت از طریق برخی مراحل به معادله  [تغییر انرژی آزاد گیبس سیستم]
[تغییر انرژی آزاد گیبس سیستم] [تغییر آنتالپی]
[تغییر آنتالپی] [تغییر آنتروپی].
[تغییر آنتروپی]. 


 ماتریس
ماتریس 



 ) و در ترمودینامیک کلاسیک (
) و در ترمودینامیک کلاسیک ( همراه با
همراه با  .
.  جذب بی نهایت گرما
جذب بی نهایت گرما به صورت برگشت پذیر، توسط داده می شود
به صورت برگشت پذیر، توسط داده می شود . به طور واضح تر، یک انرژی
. به طور واضح تر، یک انرژی در دسترس نیست برای انجام کار مفید، که در آن
در دسترس نیست برای انجام کار مفید، که در آن دمای سردترین مخزن در دسترس یا سینک حرارتی خارج از سیستم است. برای بحث بیشتر،
دمای سردترین مخزن در دسترس یا سینک حرارتی خارج از سیستم است. برای بحث بیشتر،  . این به معنای انتگرال خط است
. این به معنای انتگرال خط است
 سیستم (بدون احتساب محیط اطراف) به خوبی به عنوان گرما تعریف شده است
سیستم (بدون احتساب محیط اطراف) به خوبی به عنوان گرما تعریف شده است به سیستم تقسیم بر دمای سیستم منتقل می شود
به سیستم تقسیم بر دمای سیستم منتقل می شود
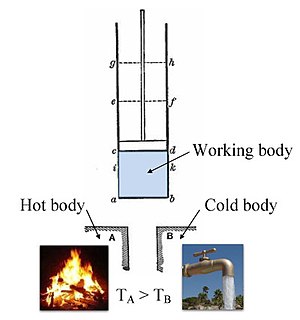
 گرمای موتور از مخزن داغ است و
گرمای موتور از مخزن داغ است و  گرما به مخزن سرد موتور است. برای به دست آوردن راندمان کارنو که 1 - T C / T H است (عددی کمتر از یک)، کلوین مجبور شد نسبت خروجی کار به گرمای جذب شده در طول انبساط همدما را با کمک معادله کارنو-کلاپیرون ارزیابی کند. که حاوی یک تابع ناشناخته به نام تابع کارنو بود. این احتمال که تابع کارنو می تواند دمایی باشد که از نقطه صفر دما اندازه گیری می شود توسط
گرما به مخزن سرد موتور است. برای به دست آوردن راندمان کارنو که 1 - T C / T H است (عددی کمتر از یک)، کلوین مجبور شد نسبت خروجی کار به گرمای جذب شده در طول انبساط همدما را با کمک معادله کارنو-کلاپیرون ارزیابی کند. که حاوی یک تابع ناشناخته به نام تابع کارنو بود. این احتمال که تابع کارنو می تواند دمایی باشد که از نقطه صفر دما اندازه گیری می شود توسط 


 هنگامی که از معادله (
هنگامی که از معادله (  یا
یا با در نظر گرفتن قرارداد علامت گرما که در آن QH > 0 گرمایی است که از مخزن داغ است و توسط موتور جذب می شود و Q C < 0 گرمای تلف شده ای است که از موتور به مخزن سرد منتقل می شود. بنابراین، گرمای بیشتری نسبت به چرخه کارنو به مخزن سرد داده می شود. نابرابری فوق
با در نظر گرفتن قرارداد علامت گرما که در آن QH > 0 گرمایی است که از مخزن داغ است و توسط موتور جذب می شود و Q C < 0 گرمای تلف شده ای است که از موتور به مخزن سرد منتقل می شود. بنابراین، گرمای بیشتری نسبت به چرخه کارنو به مخزن سرد داده می شود. نابرابری فوق اگر مجدداً تغییر آنتروپی یک مخزن حرارتی را با ΔS r,i = - Q i / T i نشان دهیم ، برای i به عنوان H (مخزن گرم) یا C (مخزن سرد)، با در نظر گرفتن قرارداد سیگنال فوق الذکر پس از آن گرمای موتور
اگر مجدداً تغییر آنتروپی یک مخزن حرارتی را با ΔS r,i = - Q i / T i نشان دهیم ، برای i به عنوان H (مخزن گرم) یا C (مخزن سرد)، با در نظر گرفتن قرارداد سیگنال فوق الذکر پس از آن گرمای موتور یا
یا




 . رابطه است
. رابطه است .
. .
.



![{\displaystyle \mathbf {j} (\mathbf {r} ,t)=\int _{-\infty }^{t}\left[\int _{V}\sigma (\mathbf {r} -\mathbf {r} ',tt')\;\mathbf {E} (\mathbf {r} ',t')\;{\text{d}}^{3}\mathbf {r} '\,\right] {\text{d}}t'\,}](https://wikimedia.org/api/rest_v1/media/math/render/svg/9f355663d9723ac3e30a18de988a86cdb0ef34a9)










 در این وبلاگ به ریاضیات و کاربردهای آن و تحقیقات در آنها پرداخته می شود. مطالب در این وبلاگ ترجمه سطحی و اولیه است و کامل نیست.در صورتی سوال یا نظری در زمینه ریاضیات دارید مطرح نمایید .در صورت امکان به آن می پردازم. من دوست دارم برای یافتن پاسخ به سوالات و حل پروژه های علمی با دیگران همکاری نمایم.در صورتی که شما هم بامن هم عقیده هستید با من تماس بگیرید.
در این وبلاگ به ریاضیات و کاربردهای آن و تحقیقات در آنها پرداخته می شود. مطالب در این وبلاگ ترجمه سطحی و اولیه است و کامل نیست.در صورتی سوال یا نظری در زمینه ریاضیات دارید مطرح نمایید .در صورت امکان به آن می پردازم. من دوست دارم برای یافتن پاسخ به سوالات و حل پروژه های علمی با دیگران همکاری نمایم.در صورتی که شما هم بامن هم عقیده هستید با من تماس بگیرید.