کموتاتور (جابجا گر)
ن مقاله در مورد مفهوم ریاضی است. برای بخش الکتریکی، کموتاتور (الکتریکی) را ببینید . برای رابطه بین موجودات مزدوج متعارف ، به رابطه کموتاسیون متعارف مراجعه کنید . برای کاربردهای دیگر، Commutation را ببینید .
در ریاضیات , جابجایی نشان می دهد که تا چه حد یک عملیات باینری معین از جابجایی ناموفق است . در تئوری گروه و تئوری حلقه از تعاریف مختلفی استفاده می شود .
نظریه گروه
[ ویرایش ]
جابجا گر دو عنصر g و h از گروه G عنصر است
[ g ، h ] = g ^-1 h ^-1 gh .
این عنصر برابر با هویت گروه است اگر و فقط اگر g و h رفت و آمد کنند (یعنی اگر و فقط اگر gh = hg ).
مجموعه تمام کموتاتورهای یک گروه به طور کلی تحت عملیات گروه بسته نیست، اما زیرگروه G تولید شده توسط همه جابجا گر ها بسته است و گروه مشتق شده یا زیرگروه جابجا گر G نامیده می شود . جابجا گرها برای تعریف گروه های nilpotent و قابل حل و بزرگترین گروه ضریب آبلی استفاده می شوند .
از تعریف کموتاتور فوق در سراسر این مقاله استفاده شده است، اما بسیاری از نظریه پردازان گروه، کموتاتور را به این صورت تعریف می کنند.
[ g ، h ] = ghg ^-1 h^ -1 . [ 1 ] [ 2 ]
با استفاده از تعریف اول، این می تواند به صورت [ g^ -1 ، h^ -1 ] بیان شود .
هویت (نظریه گروهی)
[ ویرایش ]
هویت های کموتاتور ابزار مهمی در نظریه گروه هستند . [ 3 ] عبارت a x نشان دهنده مزدوج a با x است که به صورت x -1 ax تعریف شده است .
و
و
و
![{\displaystyle x^{y}=x[x,y].}](https://wikimedia.org/api/rest_v1/media/math/render/svg/dbfda5e3214a078a56860ef1d958532efd6ecc6c)
![{\displaystyle [y,x]=[x,y]^{-1}.}](https://wikimedia.org/api/rest_v1/media/math/render/svg/59c8c7dabf4a3f20a3f9a04a295468426eb22009)
![{\displaystyle [xz,y]=[x,y]^{z}\cdot [z,y].}](https://wikimedia.org/api/rest_v1/media/math/render/svg/51d505bd20b4dfad61942e780f9019f2342a28df)
![{\displaystyle \left[x^{-1},y\right]=[y,x]^{x^{-1}}.}](https://wikimedia.org/api/rest_v1/media/math/render/svg/5ec4802d72362fa5f8b6f440bee17b73b8f9ff48)
![{\displaystyle \left[\left[x,y\right],z^{x}\right]\cdot \left[[z,x],y^{z}\right]\cdot \چپ[[y ,z],x^{y}\right]=1.}](https://wikimedia.org/api/rest_v1/media/math/render/svg/969627eb5e4b01b893d68ba8cb5aefb6fb9dcb4e)
هویت (5) پس از فیلیپ هال و ارنست ویت به نام هویت هال ویت نیز شناخته می شود . این یک آنالوگ نظری گروهی از هویت ژاکوبی برای کموتاتور نظری حلقه است (به بخش بعدی مراجعه کنید).
NB، تعریف فوق از مزدوج a توسط x توسط برخی از نظریه پردازان گروه استفاده می شود. [ 4 ] بسیاری از نظریه پردازان گروه دیگر مزدوج a توسط x را به عنوان xax -1 تعریف می کنند . [ 5 ] این اغلب نوشته می شودxالف
بسیاری از هویت ها که زیرگروه های خاصی مدول واقعی هستند نیز استفاده می شوند. اینها می توانند به ویژه در مطالعه گروه های قابل حل و گروه های nilpotent مفید باشند . به عنوان مثال، در هر گروهی، توان های دوم به خوبی رفتار می کنند:
![{\displaystyle (xy)^{2}=x^{2}y^{2}[y,x][[y,x],y].}](https://wikimedia.org/api/rest_v1/media/math/render/svg/9c75b2bcc9c723ec68c6e482e9e1e002b02082d3)
اگر زیر گروه مشتق شده مرکزی باشد، پس
![{\displaystyle (xy)^{n}=x^{n}y^{n}[y,x]^{\binom {n}{2}}.}](https://wikimedia.org/api/rest_v1/media/math/render/svg/128ae0855aada1e122d118d63c2bfa18a08eb603)
نظریه حلقه
[ ویرایش ]
حلقه ها اغلب از تقسیم پشتیبانی نمی کنند. بنابراین، جابجا گردو عنصر a و b از یک حلقه (یا هر جبر انجمنی ) به طور متفاوت با
![{\displaystyle [a,b]=ab-ba.}](https://wikimedia.org/api/rest_v1/media/math/render/svg/c73ba7fbd6260acd540051cc2c6f9131ff0d7f8e)
کموتاتور صفر است اگر و فقط اگر a و b جابجا شوند. در جبر خطی ، اگر دو شکل درونی یک فضا با ماتریس های رفت و آمد بر حسب یک مبنا نشان داده شوند، آنگاه بر حسب هر مبنا به این شکل نمایش داده می شوند. با استفاده از کموتاتور به عنوان یک براکت لی ، هر جبر انجمنی را می توان به جبر لی تبدیل کرد .
ضد جابجا گر دو عنصر a و b یک حلقه یا جبر انجمنی با تعریف می شود
گاهی اوقات
![{\displaystyle [a,b]_{+}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/c7289995fc78776166741f2a036fbcfb0e632c02)
![{\displaystyle [a,b]_{-}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/59120bf940c61971319243298b88ebb28f752588)
جابجا گردو عملگر که در فضای هیلبرت عمل میکنند ، یک مفهوم مرکزی در مکانیک کوانتومی است ، زیرا نشان میدهد که چقدر دو قابل مشاهده توصیفشده توسط این عملگرها میتوانند به طور همزمان اندازهگیری شوند. اصل عدم قطعیت به موجب رابطه رابرتسون- شرودینگر در نهایت یک قضیه در مورد چنین تغییردهندههایی است . [ 7 ] در فضای فاز ، جابجا گرهای معادل ضربهای ستاره تابعی براکتهای مویال نامیده میشوند و کاملاً با ساختارهای کموتاتور فضایی هیلبرت که ذکر شد همشکل هستند.
هویت (نظریه حلقه)
[ ویرایش ]
کموتاتور دارای ویژگی های زیر است:
هویت های لی-جبر
[ ویرایش ]
![{\displaystyle [A+B,C]=[A,C]+[B,C]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/b3f1c95436e1c9c40871bc7a3704072ae067dc10)
![{\displaystyle [A,A]=0}](https://wikimedia.org/api/rest_v1/media/math/render/svg/7c816c8f8631ef069ad0b1aee64ed996ad8309ed)
![{\displaystyle [A,B]=-[B,A]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/37b04a066443e96c0b27d4b14f7f5d51c7b2b0c3)
![{\displaystyle [A,[B,C]]+[B,[C,A]]+[C,[A,B]]=0}](https://wikimedia.org/api/rest_v1/media/math/render/svg/046dbc0d4387302c8d321afb443e35bc1890fcac)
رابطه (3) ضد جابجا گر نامیده می شود ، در حالی که (4) هویت ژاکوبی است .
هویت های اضافی
[ ویرایش ]
![{\displaystyle [A,BC]=[A,B]C+B[A,C]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/1c7c96785faa7d6e5ecc7d8ada53830b24338c60)
![{\displaystyle [A,BCD]=[A,B]CD+B[A,C]D+BC[A,D]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/aa03949d714777910e992c14aeed34adf42d9766)
![{\displaystyle [A,BCDE]=[A,B]CDE+B[A,C]DE+BC[A,D]E+BCD[A,E]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/8b79c370dc9984ff5e2720b3e06c6153af7ba572)
![{\displaystyle [AB,C]=A[B,C]+[A,C]B}](https://wikimedia.org/api/rest_v1/media/math/render/svg/71ba3177011b65b292d8dc39dd2e3391f29b0a07)
![{\displaystyle [ABC,D]=AB[C,D]+A[B,D]C+[A,D]BC}](https://wikimedia.org/api/rest_v1/media/math/render/svg/b9e755fd1fe3c26c40e007256c6976b9612e5d9b)
![{\displaystyle [ABCD,E]=ABC[D,E]+AB[C,E]D+A[B,E]CD+[A,E]BCD}](https://wikimedia.org/api/rest_v1/media/math/render/svg/4e00b8c22f5a63ff3dbbcf8a74f0d01f43994afa)
![{\displaystyle [A,B+C]=[A,B]+[A,C]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/7f50e382d516600cfe9f7a34376ebe694bb62177)
![{\displaystyle [A+B,C+D]=[A,C]+[A,D]+[B,C]+[B,D]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/2e47836a02ce95e65488370410a80446b1ae636c)
![{\displaystyle [AB,CD]=A[B,C]D+[A,C]BD+CA[B,D]+C[A,D]B=A[B,C]D+AC[B, D]+[A,C]DB+C[A,D]B}](https://wikimedia.org/api/rest_v1/media/math/render/svg/a8b90ee684250322ac794d8cb193d75c8c1d4db3)
![{\displaystyle [[A,C],[B,D]]=[[[A,B],C],D]+[[[B,C],D],A]+[[[C, D],A],B]+[[[D,A],B],C]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/33e847e641c8d2810846e666be23d2512b08eb2f)
اگر A یک عنصر ثابت از یک حلقه R باشد ، هویت (1) را می توان به عنوان یک قانون لایب نیتس برای نقشه تفسیر کرد.
![{\displaystyle \operatorname {ad} _{A}(B)=[A,B]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/8a40684049019f333e05818bcd1ce5b48f839561)
به عبارت دیگر، نقشه آگهی A یک مشتق بر روی حلقه R تعریف می کند . هویت های (2)، (3) قوانین لایب نیتس را برای بیش از دو عامل نشان می دهند و برای هر اشتقاقی معتبر هستند. هویت های (4) - (6) را می توان به عنوان قوانین لایب نیتس نیز تفسیر کرد. هویت های (7)، (8) Z - دوخطی بودن را بیان می کنند .
از هویت (9)، می توان دریافت که جابجایی قدرت های عدد صحیح عناصر حلقه عبارت است از:
![{\displaystyle [A^{N},B^{M}]=\sum _{n=0}^{N-1}\sum _{m=0}^{M-1}A^{n} B^{m}[A,B]B^{Nn-1}A^{Mm-1}=\sum _{n=0}^{N-1}\sum _{m=0}^{M-1}B^{n}A^{m}[A,B]A^{Nn-1}B^{Mm-1}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/b2a8a7436d26ef75d1023a36ffa1c561597c8506)
برخی از هویتهای فوق را میتوان با استفاده از نماد ± زیرمجموعه بالا به آنتیکموتاتور تعمیم داد. [ 8 ] به عنوان مثال:
![{\displaystyle [AB,C]_{\pm }=A[B,C]_{-}+[A,C]_{\pm }B}](https://wikimedia.org/api/rest_v1/media/math/render/svg/187aaec93ded1a30cd6ad33d9e323c786d4a39fd)
![{\displaystyle [AB,CD]_{\pm }=A[B,C]_{-}D+AC[B,D]_{-}+[A,C]_{-}DB+C[ A,D]_{\pm }B}](https://wikimedia.org/api/rest_v1/media/math/render/svg/2abfd9c204056463779a2541fa7f5bc02930bf9a)
![{\displaystyle [[A,B],[C,D]]=[[[B,C]_{+},A]_{+},D]-[[[B,D]_{+} ,A]_{+},C]+[[[A,D]_{+},B]_{+},C]-[[A,C]_{+},B]_{+ },D]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/6c14c4def5d057ec857052e280d0c27658c3796d)
![{\displaystyle \left[A,[B,C]_{\pm }\right]+\left[B,[C,A]_{\pm }\right]+\left[C,[A,B ]_{\pm }\right]=0}](https://wikimedia.org/api/rest_v1/media/math/render/svg/7fa38c6ec51fd44c85b6a7dd7820d8ebaee4f2cf)
![{\displaystyle [A,BC]_{\pm }=[A,B]_{-}C+B[A,C]_{\pm }=[A,B]_{\pm }C\mp B[A,C]_{-}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/cee7d373e2721aa7ec3c50a8f645785d7da7b804)
![{\displaystyle [A,BC]=[A,B]_{\pm }C\mp B[A,C]_{\pm }}](https://wikimedia.org/api/rest_v1/media/math/render/svg/2f480a46e5c19fea0ae860621b38e69606a71239)
هویت های نمایی
[ ویرایش ]
حلقه یا جبری را در نظر بگیرید که در آن نمایی است هالف=انقضا(الف)=1+الف+12!الف2+⋯
در چنین حلقهای، لم هادامارد که برای کموتاتورهای تودرتو اعمال میشود، به دست میدهد:
![{\textstyle e^{A}Be^{-A}\ =\ B+[A,B]+{\frac {1}{2!}}[A,[A,B]]+{\frac {1 {3!}}[A,[A,[A,B]]]+\cdots \ =\ e^{\operatorname {ad} _{A}}(B).}](https://wikimedia.org/api/rest_v1/media/math/render/svg/5e4b0b44677de183969e936bb4cede2bf5515ad4)
یک بسط مشابه، تغییردهنده گروهی عبارات را بیان می کند
![{\displaystyle e^{A}e^{B}e^{-A}e^{-B}=\exp \!\left([A,B]+{\frac {1}{2!}} [A{+}B,[A,B]]+{\frac {1}{3!}}\left({\frac {1}{2}}[A,[B,[B,A]]]+[A{+}B,[A{+}B,[A,B]]]\right)+\cdots \right )](https://wikimedia.org/api/rest_v1/media/math/render/svg/f104655d91482ecf24b550407ef28112b27bd564)
حلقه ها و جبرهای درجه بندی شده
[ ویرایش ]
هنگامی که با جبرهای درجه بندی شده سروکار داریم ، کموتاتور معمولا با جابجایی درجه بندی شده جایگزین می شود که در اجزای همگن به صورت تعریف می شود.
![{\displaystyle [\omega ,\eta ]_{gr}:=\omega \eta -(-1)^{\deg \omega \deg \eta }\eta \omega .}](https://wikimedia.org/api/rest_v1/media/math/render/svg/4a31537974b529c2386b07f032b0452d7ab70e81)
اشتقاق الحاقی
[ ویرایش ]
به خصوص اگر یکی با چند جابجا گر در یک حلقه R سر و کار داشته باشد ، نماد دیگری مفید خواهد بود. برای یک عنصر
![{\displaystyle \operatorname {ad} _{x}(y)=[x,y]=xy-yx.}](https://wikimedia.org/api/rest_v1/media/math/render/svg/06e06c88110f66faa14de2b3fba0644b13e96429)
این نگاشت یک مشتق بر روی حلقه R است :
با هویت ژاکوبی ، آن نیز اشتقاقی بر عملیات کموتاسیون است:
![{\displaystyle \mathrm {ad} _{x}[y,z]\ =\ [\mathrm {ad} _{x}\!(y),z]\,+\,[y,\mathrm {ad} } _{x}\!(z)].}](https://wikimedia.org/api/rest_v1/media/math/render/svg/97e49b2f65e16c28bbcad712a40e4bf680ebf909)
به عنوان مثال، با نوشتن چنین نگاشت هایی، به دست می آوریم
![{\displaystyle \operatorname {ad} _{x}\operatorname {ad} _{y}(z)=[x,[y,z]\,]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/8c27f6b58b814f258e43d4529f26e9ec0523b58a)
![{\displaystyle \operatorname {ad} _{x}^{2}\!(z)\ =\ \operatorname {ad} _{x}\!(\operatorname {ad} _{x}\!(z) )\ =\ [x،[x،z]\،].}](https://wikimedia.org/api/rest_v1/media/math/render/svg/856ad01497c91a4c78ba471c5ba199d82744c717)
![{\displaystyle \operatorname {ad} _{[x,y]}=\left[\operatorname {ad} _{x},\operatorname {ad} _{y}\right].}](https://wikimedia.org/api/rest_v1/media/math/render/svg/3c43069feeed684198e360f083c3c004bf3cb2f2)
در مقابل، همیشه هممورفیسم حلقه نیست : معمولا 
قانون مولد لایب نیتس
[ ویرایش ]
قانون کلی لایب نیتس ، که مشتقات مکرر یک محصول را بسط می دهد، می تواند به صورت انتزاعی با استفاده از نمایش الحاقی نوشته شود:
جایگزین کردن
همچنین ببینید
[ ویرایش ]
- ضد جابجا گر
- همکار
- فرمول بیکر-کمپبل-هاسدورف
- رابطه کموتاسیون متعارف
- مرکزی ساز با نام مستعار
- اشتقاق (جبر انتزاعی)
- براکت مویال
- مشتق پینچرل
- براکت پواسون
- کموتاتور سه تایی
- لم سه زیر گروه
https://en.wikipedia.org/wiki/Commutator
, بنابراین با ![{\displaystyle {\mathcal {K}}_{C}=\left[{\mathcal {K}}_{\mathbb {P} ^{2}}+{\mathcal {O}}(d)\راست ]_{\vert C}={\mathcal {O}}(d-3)_{\vert C}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/6e72412d378cbcdf6ddc2dfe5759602c314627ae)
توسط مکان ناپدید شدن یک بخش داده می شود
دارای جنس هندسی
تعداد تکینگی ها در صورت شمارش صحیح است.
ممکن است به عنوان یک عدد مختلط تعریف شود
مشروط به شرایط
اگر
و
، جایی که
حلقه همدلی گرا تام است. 
یک 
برای برخی
این تیره را تیره بیضوی می نامند.
از این نظر یک جنس نیست، زیرا در مورد همدلی ها ثابت نیست.
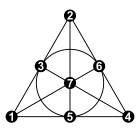
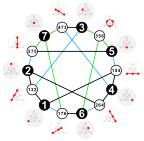
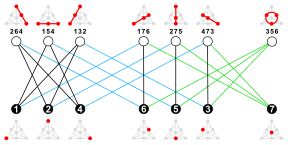
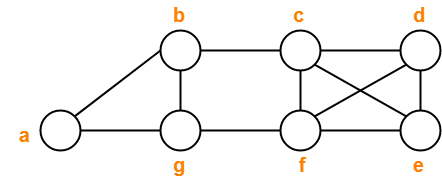
. این تنها نمودار با این چند جمله ای مشخص است که آن را به نموداری تبدیل می کند که توسط طیف آن تعیین می شود.
.
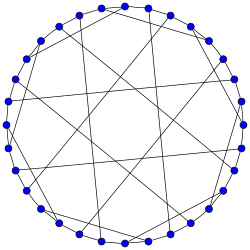
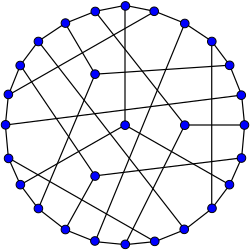
. این تنها گراف با این چند جمله ای مشخص است که آن را به گرافی تبدیل می کند که توسط طیف آن تعیین می شود.
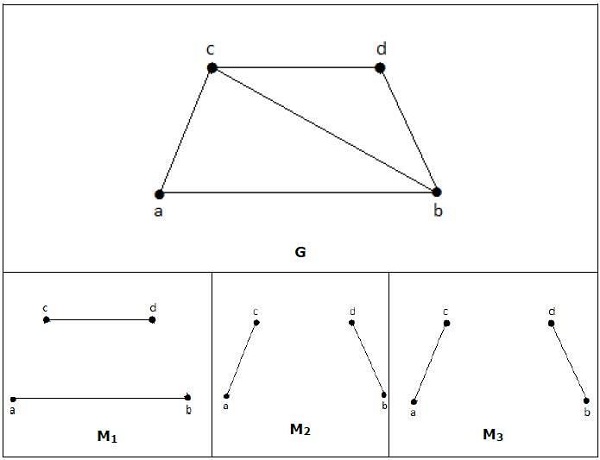
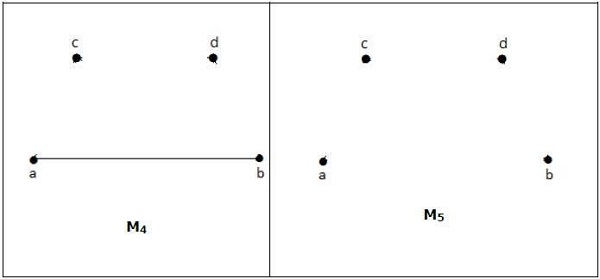
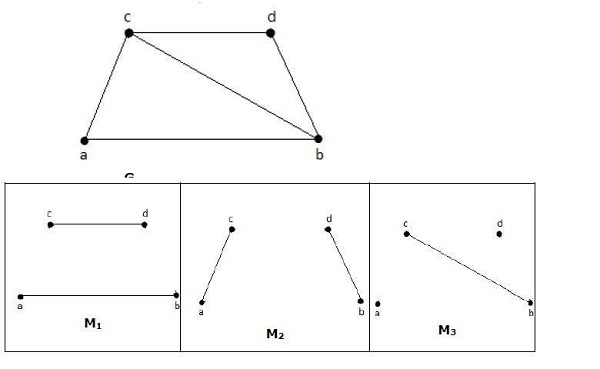
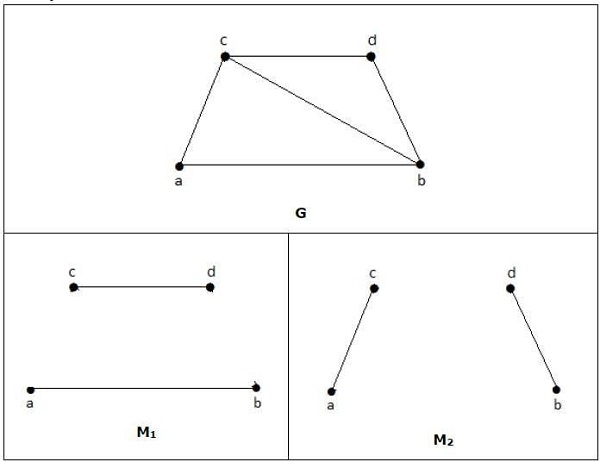
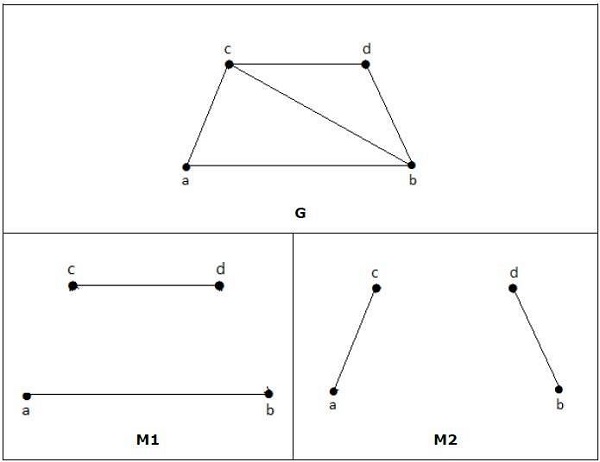
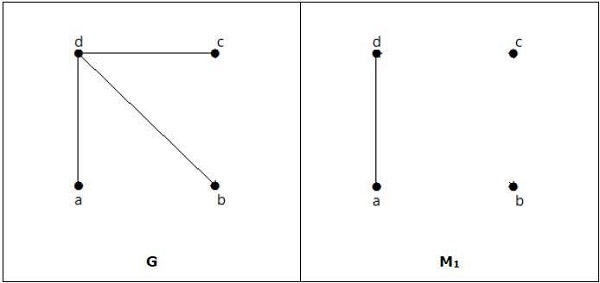
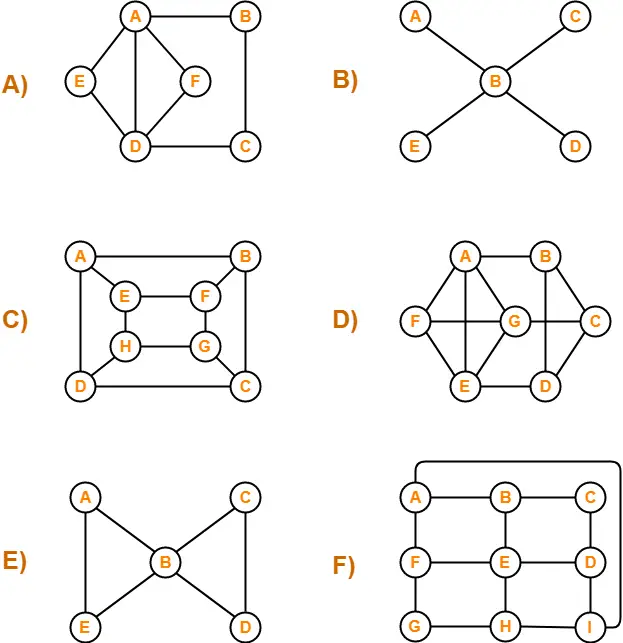
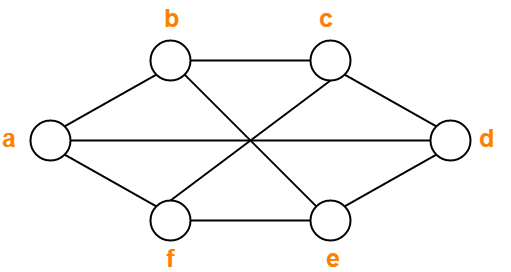
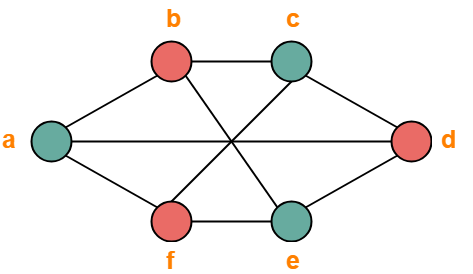
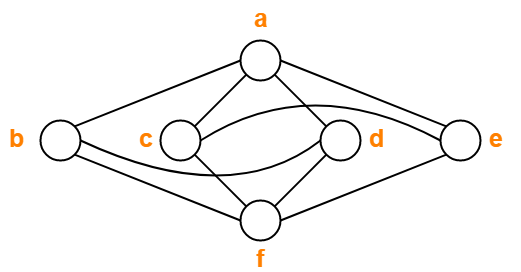
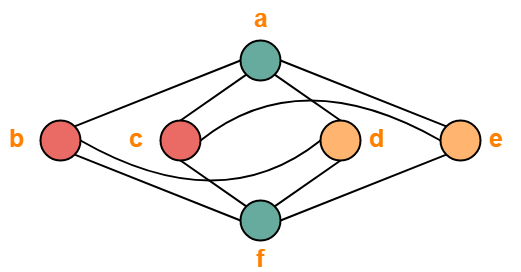
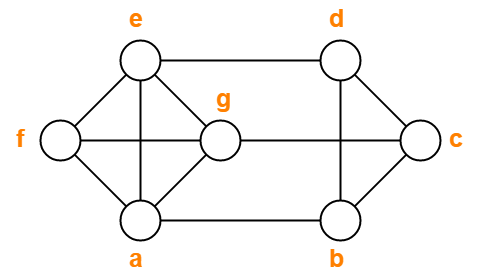
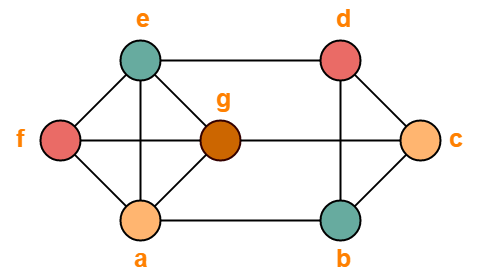
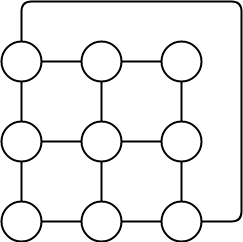
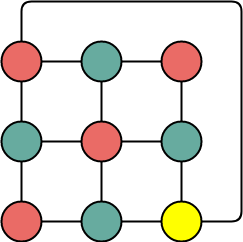
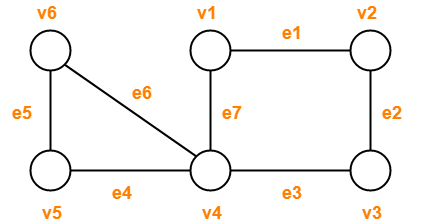
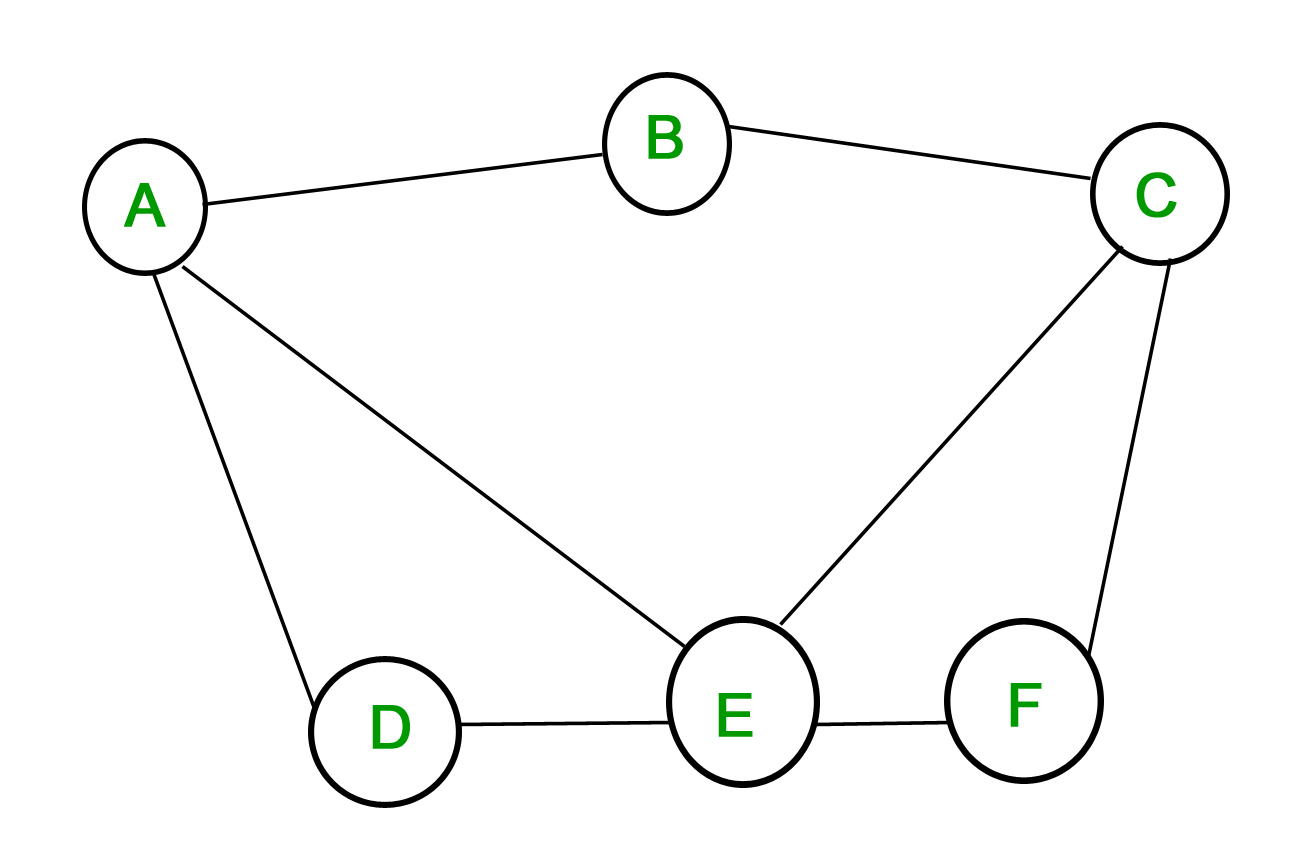
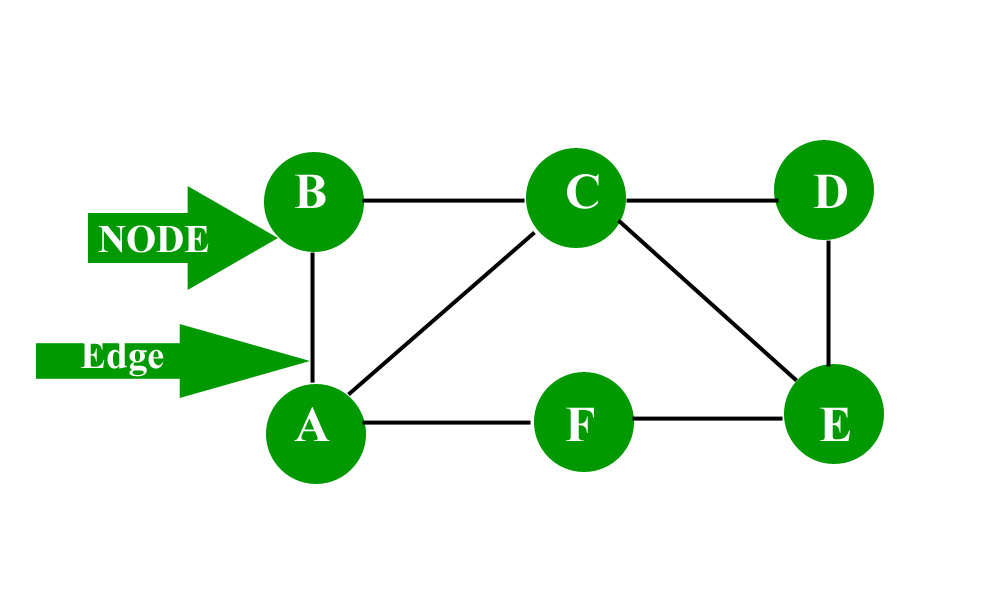
معمولاً دو تصویر از نمودارها به ما داده نمی شود، اما در عوض توضیح مختصری از این که چه رئوسی به یکدیگر متصل هستند، داده می شود. این توسط یا و 
.svg?uselang=fa)
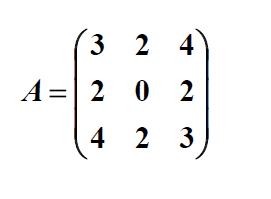
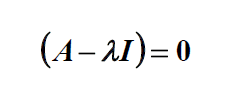
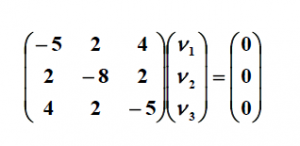
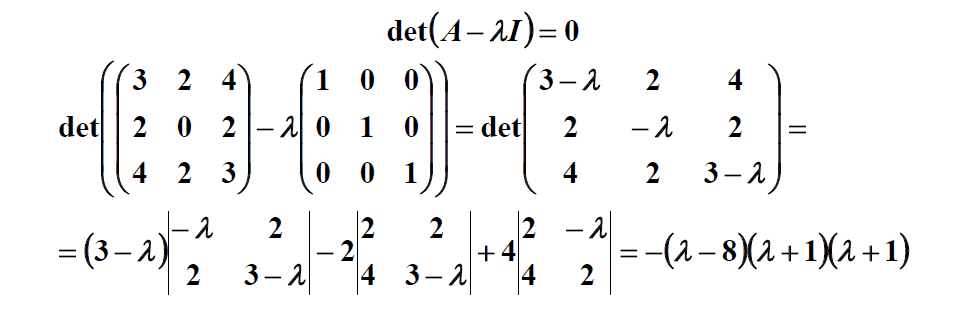
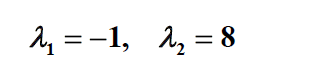
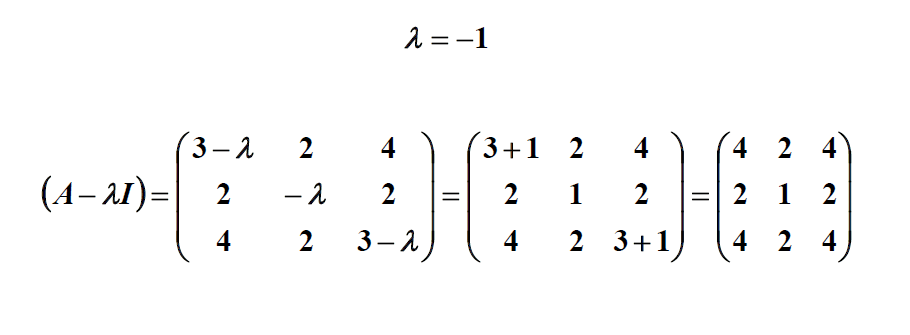
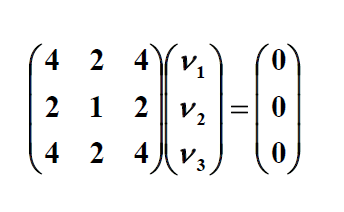
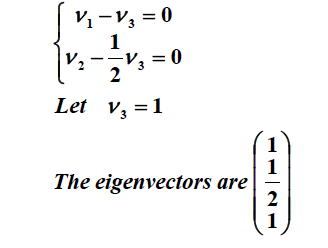
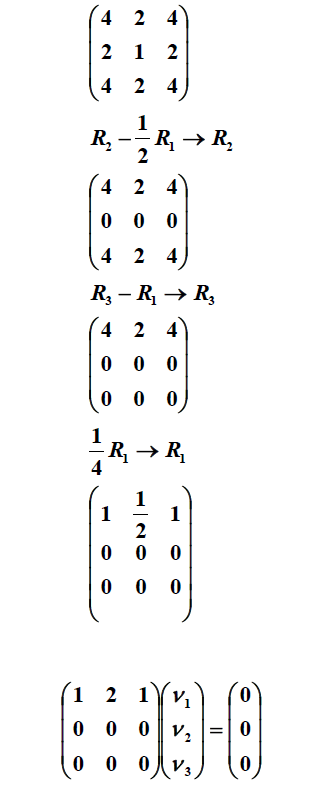
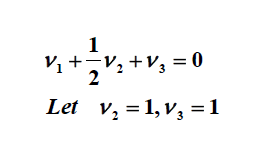
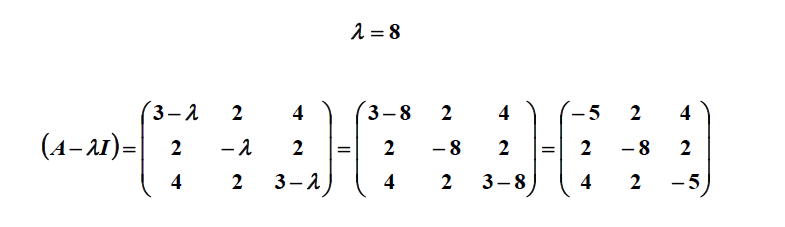
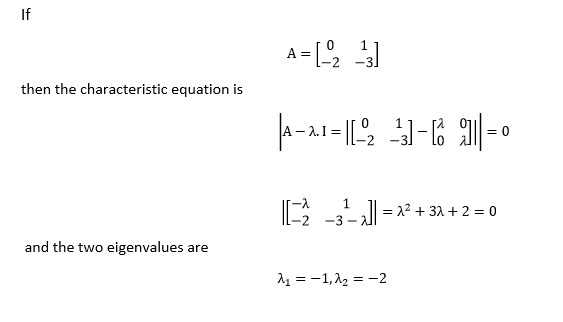
با 
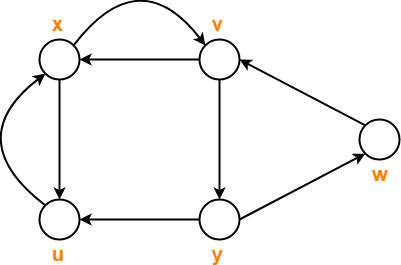
، گرافی است که رأسهای آن نظیر 
است.
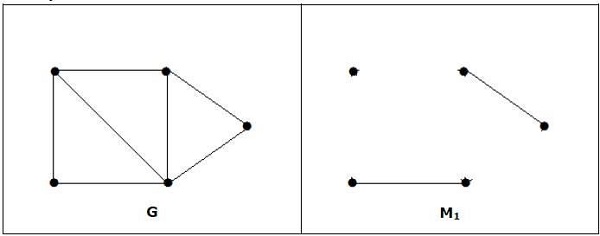
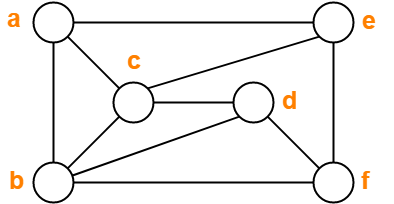
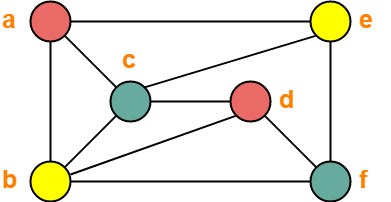
نمونه ای از نمودار دو مکعبی است
. 
نمودار مکعب -ترکس؟
در این وبلاگ به ریاضیات و کاربردهای آن و تحقیقات در آنها پرداخته می شود. مطالب در این وبلاگ ترجمه سطحی و اولیه است و کامل نیست.در صورتی سوال یا نظری در زمینه ریاضیات دارید مطرح نمایید .در صورت امکان به آن می پردازم. من دوست دارم برای یافتن پاسخ به سوالات و حل پروژه های علمی با دیگران همکاری نمایم.در صورتی که شما هم بامن هم عقیده هستید با من تماس بگیرید.