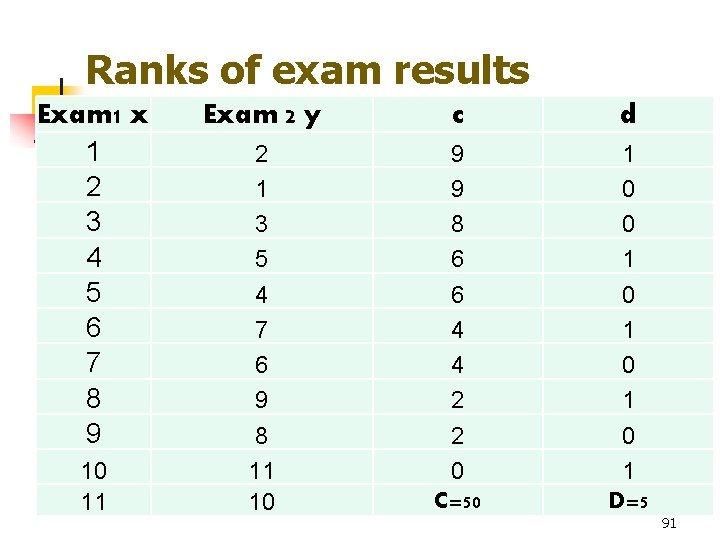
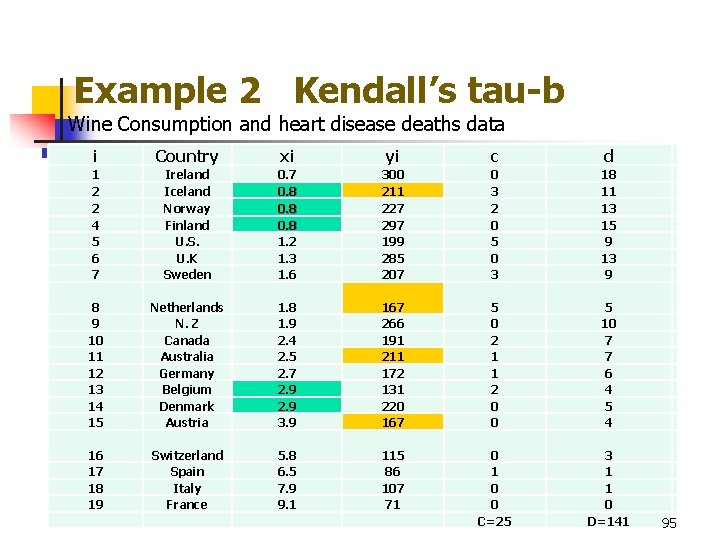
روش «شپیلکین»؛ چگونه ریاضیات تقلب در انتخابات روسیه را لو میدهد؟

نگارش از عکس: آسوشیتد پرس
تاریخ انتشار ۱۹/۰۳/۲۰۲۴ - ۲۰:۳۴
همرسانی این مطلب نظرها
انتخاب مجدد ولادیمیر پوتین با بیش از ۸۷ درصد آرا با انتقادهای گستردهای در خارج از روسیه مواجه شده است. در داخل این کشور نیز شماری از رسانههای مخالفان در صحت آرا تردید کردهاند.
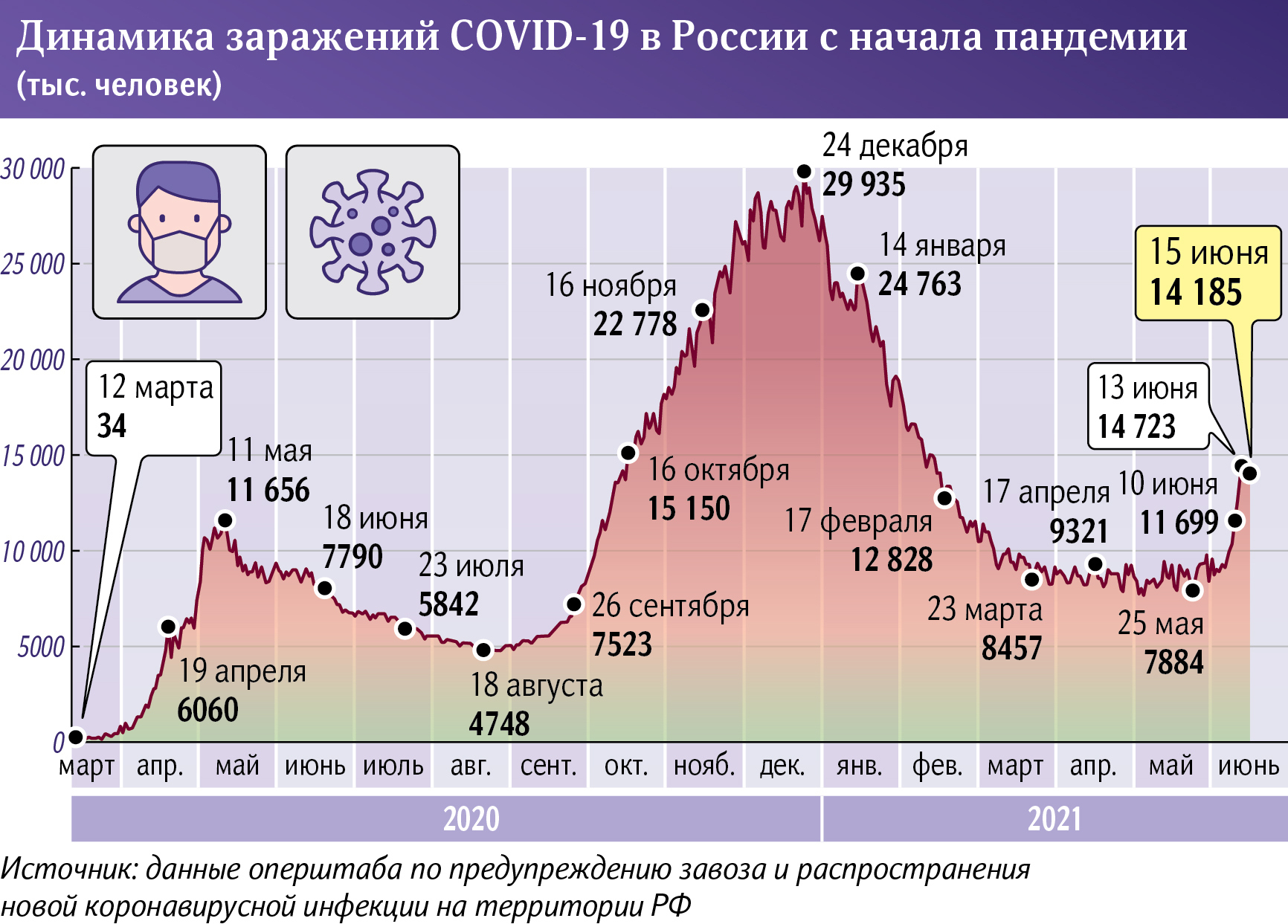
در اولین برآوردهای رسانههای مستقل روسیه در مورد میزان تقلب در انتخابات ریاستجمهوری روسیه، که از روز جمعه ۱۵ تا یکشنبه ۱۷ مارس برگزار شد، تعداد برگههای رای جعلی ۲۰ تا ۳۰ میلیون عدد تخمین زده شده است.
مدوزا، سایت روزنامهنگاری تحقیقی روسی، در مطلبی نوشته است «حدود ۲۲ میلیون برگه رای رسماً به نفع ولادیمیر پوتین جعل شده است». «نوایا گازتا اروپا»، یک رسانه دیگر اپوزیسیون روسیه، به این نتیجه رسیده که تقلب حتی گستردهتری وجود داشته است. بر اساس برآورد آنها، ۳۱.۶ میلیون برگه رای به نفع ولادیمیر پوتین جعل شده است.
متیو وایمن، کارشناس مسائل سیاسی روسیه در دانشگاه کیل بریتانیا، در این باره میگوید سه تخمین انجامشده «تقلب در مقیاسی بیسابقه در تاریخ انتخابات روسیه» را نشان میدهند.
این سه برآورد، نقطه مشترک دیگری هم دارند: همه آنها از الگوریتم یکسانی برای کشف بهترین تخمین ممکن از تعداد آرای نادرست به نفع ولادیمیر پوتین استفاده میکنند.
این روش که «متد شپیلکین» نام دارد، به نام سرگئی شپیلکین متخصص آمار که حدود ده سال پیش آن را برای اولین بار توسعه داد، نامگذاری شده است.
کار او در تجزیه و تحلیل انتخابات در روسیه، که در سال ۲۰۰۷ آغاز شد، تا کنون برایش چندین جایزه معتبر را به همراه آورده است. در عین حال اما دشمنان قدرتمندی را نیز برایش درست کرده و نامش از فوریه سال پیش در فهرست «عوامل خارجی» دولت روسیه ثبت شده است.
دیمیتری کوگان، آماردان مستقر در استونی که با سرگئی شپیلکین و دیگران برای توسعه ابزاری برای تجزیه و تحلیل نتایج انتخابات کار کرده است، میگوید روش او «روشی ساده برای ارزیابی کمی تقلب در انتخابات در روسیه ارائه میدهد، در حالی که بیشتر رویکردهای دیگر عمدتاً برای تشخیص وجود یا عدم وجود تقلب استفاده میشود.»
روش شپیلکین «بر اساس میزان مشارکت در هر شعبه رایگیری» است و هدف این است که مشخص شود در کدام حوزههای رایگیری مشارکت بهطور غیرعادی بالا به نظر میرسد.

ولادیمیر پوتین رئیس جمهور روسیه عکس: آسوشیتد پرس
این تئوری میگوید نسبت آرای هر نامزد بسته به میزان مشارکت تغییر نمیکند (یا فقط به صورت جزئی تغییر میکند). الکساندر شن، ریاضیدان و آماردان در دانشگاه علوم کامپیوتر مونپلیه، میگوید در جایی که نرخ مشارکت منفجر میشود، «ما متوجه شدیم که این تکامل متناسب توزیع آرا به طور کامل ناپدید میشود و ولادیمیر پوتین ذینفع اصلی آرای اضافی است.»
برای تعیین کمیت تقلب، کافی است آرای ولادیمیر پوتین را با نتایجی که اگر توزیع آرا «صادقانه» انجام میشد، مقایسه کنیم. تفاوت دو درصد، تصوری از میزان دستکاری نتایج به نفع او و یا مطابق آنچه مخالفان میگویند «بازی پر کردن برگه رای و نوشتن نام ولادیمیر پوتین»، به دست میدهد.
روش شپیلکین با این حال محدودیتهایی نیز دارد. مثل اینکه باید حتما چند شعبه رایگیری موجود باشد که کارشناسان به طور منطقی مطمئن باشند در آنها تقلبی صورت نگرفته است.
همچنین اگر متقلبان روشهای ظریفتری را برای جعل نتایج استفاده میکردند، به عنوان مثال با برداشتن رای یکی از نامزدها و اضافه کردن آنها به نفع ولادیمیر پوتین، روش شپیلکین دیگر جواب نمیداد. آقای کوگان میگوید: «این واقعیت که مقامات همچنان از ابتداییترین روشها برای تقلب استفاده میکنند، نشان میدهد که برای آنها متوجه شدن بقیه اهمیتی ندارد.»
متیو وایمن میگوید این تخمینها همچنین «یک سلاح سیاسی مهم» هستند، چرا که اجازه میدهند «روایت رسمی روسیه مبنی بر اینکه نرخ مشارکت بالا بوده و رای در حمایت از پوتین نشان میدهد که کشور متحد است، به چالش کشیده شوند.»
جف هاون نیز میگوید: «این کلیشه وجود دارد که طبق آن روسها به طور طبیعی به شخصیتهای اقتدارگرا رای میدهند. نشان دادن اینکه ارقام چگونه بزرگنمایی شدهاند، راهی برای اثبات این است که واقعیت بسیار ظریفتر است.»
https://parsi.euronews.com/2024/03/19/the-shpilkin-method-or-how-math-reveals-electoral-fraud-in-russia





















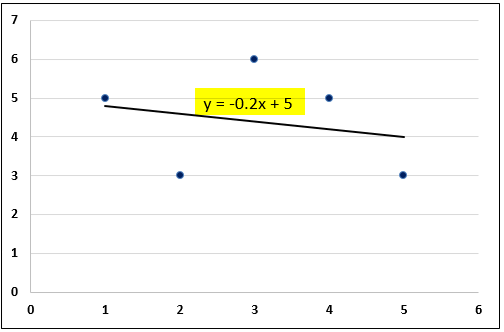
 ، جایی که y i یک پسوند فنری اندازه گیری شده است.
، جایی که y i یک پسوند فنری اندازه گیری شده است.  و بنابراین ممکن است یک مدل تجربی برای مشاهدات خود مشخص کنیم،
و بنابراین ممکن است یک مدل تجربی برای مشاهدات خود مشخص کنیم،


 ، معمولا با تخمین زده می شود
، معمولا با تخمین زده می شود![{\displaystyle \operatorname {var} ({\hat {\beta }}_{j})=\sigma ^{2}\left(\left[X^{\mathsf {T}}X\right]^{ -1}\right)_{jj}\approx {\hat {\sigma }}^{2}C_{jj}،}](https://wikimedia.org/api/rest_v1/media/math/render/svg/d85cf89d392a9c191ff1fe3429654bd748a02b2b)



 بستگی به ارزش دارد
بستگی به ارزش دارد که باعث می شود نمودار باقیمانده یک اثر "فن کردن" به سمت بزرگتر ایجاد کند
که باعث می شود نمودار باقیمانده یک اثر "فن کردن" به سمت بزرگتر ایجاد کند برابر است.
برابر است.  ،
،  اضافه شده، کجا
اضافه شده، کجا یک ثابت است (این شکل
یک ثابت است (این شکل  ،
،  اضافه شده است.) در زمینه
اضافه شده است.) در زمینه  , i = 1, …, n , جایی که
, i = 1, …, n , جایی که یک
یک  یک
یک  ، که در آن m پارامترهای قابل تنظیم در بردار نگهداری می شوند
، که در آن m پارامترهای قابل تنظیم در بردار نگهداری می شوند . هدف یافتن مقادیر پارامتر برای مدلی است که "بهترین" با داده ها مطابقت دارد.
. هدف یافتن مقادیر پارامتر برای مدلی است که "بهترین" با داده ها مطابقت دارد. 

 ارزش های. نوسانات تصادفی در مورد
ارزش های. نوسانات تصادفی در مورد نشان می دهد که یک مدل خطی مناسب است.
نشان می دهد که یک مدل خطی مناسب است. :
: 
 و شیب به عنوان
و شیب به عنوان ، تابع مدل توسط داده می شود
، تابع مدل توسط داده می شود .
.  مناسب است.
مناسب است.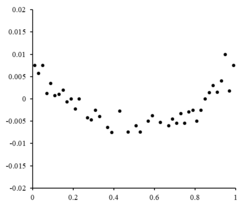
 برای داده ها مناسب خواهد بود. باقی مانده برای یک مدل سهموی را می توان از طریق محاسبه کردta
برای داده ها مناسب خواهد بود. باقی مانده برای یک مدل سهموی را می توان از طریق محاسبه کردta  .
. 
 ، معادلات گرادیان تبدیل می شود
، معادلات گرادیان تبدیل می شود

 تابعی از
تابعی از و قرار دادن متغیرهای مستقل و وابسته در ماتریس
و قرار دادن متغیرهای مستقل و وابسته در ماتریس و
و به ترتیب می توانیم حداقل مربعات را به صورت زیر محاسبه کنیم. توجه داشته باشید که
به ترتیب می توانیم حداقل مربعات را به صورت زیر محاسبه کنیم. توجه داشته باشید که مجموعه ای از تمام داده ها است.
مجموعه ای از تمام داده ها است. 



 که هدف را به حداقل می رساند. اکثر الگوریتم ها شامل انتخاب مقادیر اولیه برای پارامترها هستند. سپس، پارامترها به صورت مکرر پالایش می شوند، یعنی مقادیر با تقریب متوالی به دست می آیند:
که هدف را به حداقل می رساند. اکثر الگوریتم ها شامل انتخاب مقادیر اولیه برای پارامترها هستند. سپس، پارامترها به صورت مکرر پالایش می شوند، یعنی مقادیر با تقریب متوالی به دست می آیند:
 بردار شیفت نامیده می شود. در برخی از الگوریتمهای متداول، در هر تکرار ممکن است مدل با تقریب به یک بسط
بردار شیفت نامیده می شود. در برخی از الگوریتمهای متداول، در هر تکرار ممکن است مدل با تقریب به یک بسط  :
:

 ، معادله گرادیان صفر تنظیم شده و برای آن حل می شود
، معادله گرادیان صفر تنظیم شده و برای آن حل می شود


 این مدل ممکن است یک خط مستقیم، یک سهمی یا هر ترکیب خطی دیگری از توابع را نشان دهد. در NLLSQ (حداقل مربعات غیرخطی) پارامترها به عنوان توابع ظاهر می شوند، مانند
این مدل ممکن است یک خط مستقیم، یک سهمی یا هر ترکیب خطی دیگری از توابع را نشان دهد. در NLLSQ (حداقل مربعات غیرخطی) پارامترها به عنوان توابع ظاهر می شوند، مانند و غیره اگر مشتقات
و غیره اگر مشتقات یا ثابت هستند یا فقط به مقادیر متغیر مستقل بستگی دارند، مدل در پارامترها خطی است. در غیر این صورت مدل غیر خطی است.
یا ثابت هستند یا فقط به مقادیر متغیر مستقل بستگی دارند، مدل در پارامترها خطی است. در غیر این صورت مدل غیر خطی است.


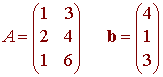
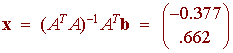
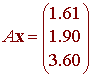
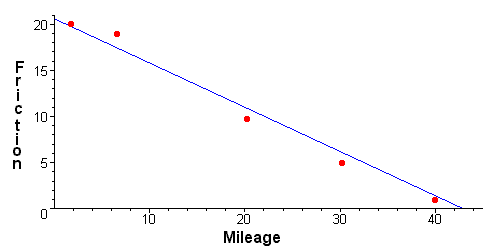
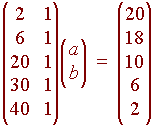
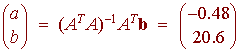
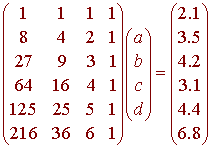
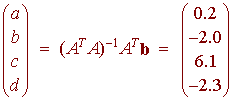
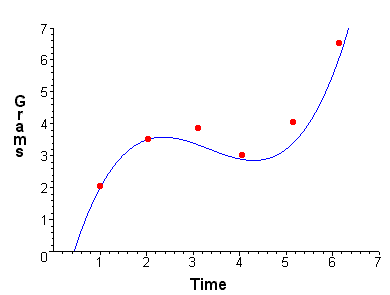




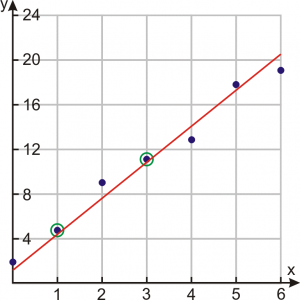

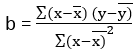
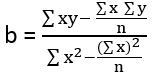
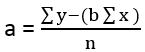
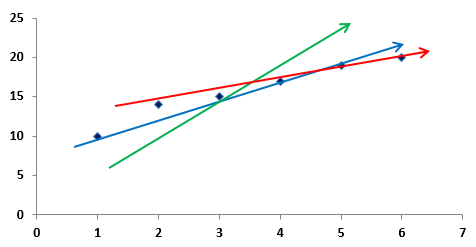
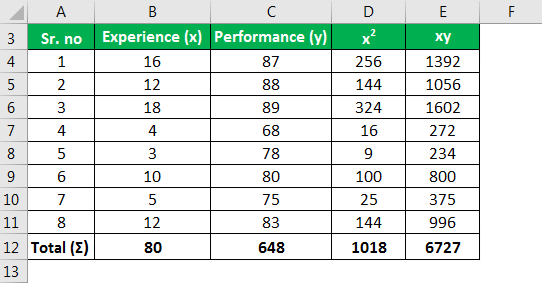
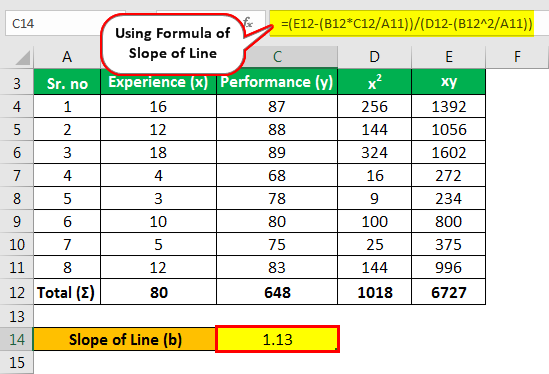
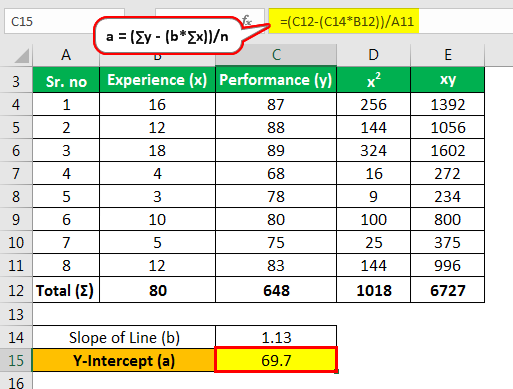
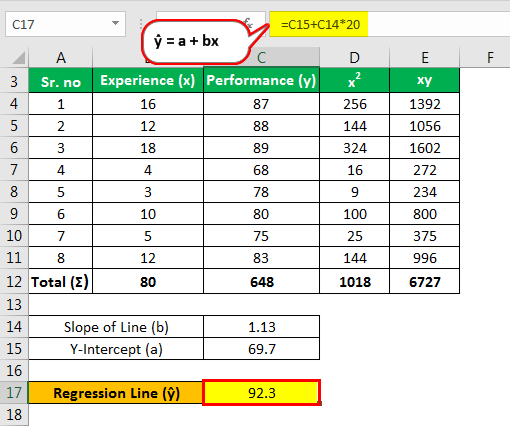
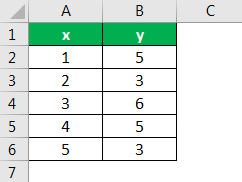
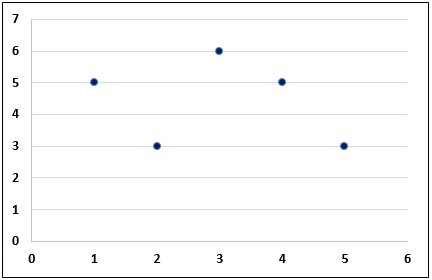
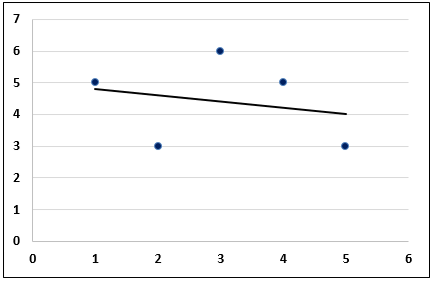
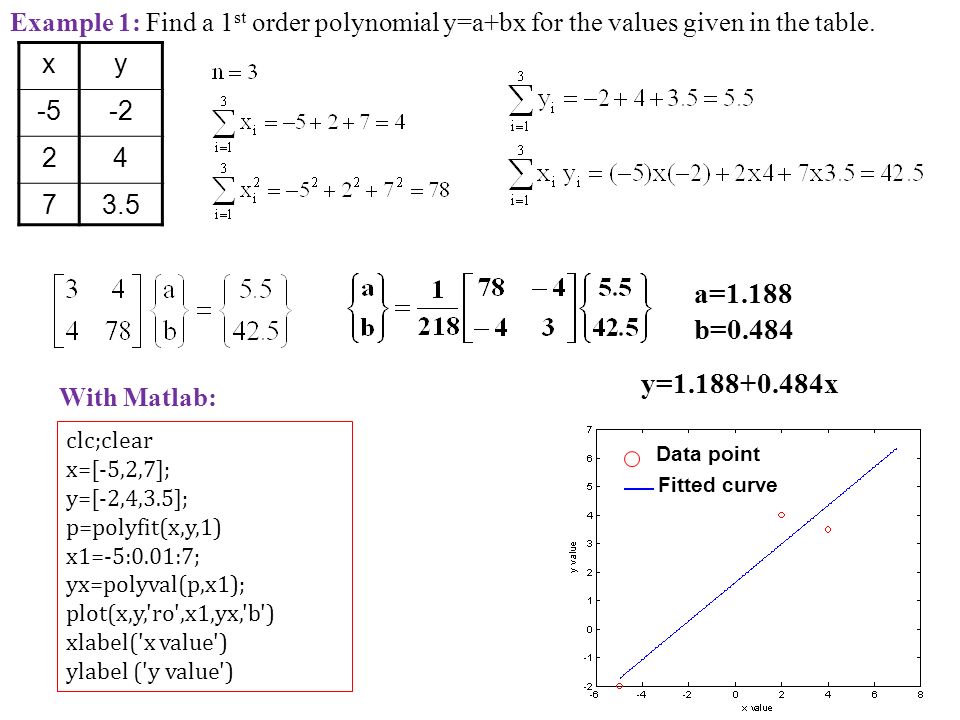
 https://slideplayer.com/slide/9440910/
https://slideplayer.com/slide/9440910/





 :
:






 دنباله ای از متغیرهای تصادفی با ارزش واقعی و کاملا ثابت است
دنباله ای از متغیرهای تصادفی با ارزش واقعی و کاملا ثابت است برای همه
برای همه ،
، ![{\displaystyle g:[0,1]\to \mathbb {R} }](https://wikimedia.org/api/rest_v1/media/math/render/svg/26aef45c20ce13e8d53e79e068df9b5804c5c170) ، و
، و . ساختن
. ساختن
 کاملاً همگرا است،
کاملاً همگرا است، ، و
، و سپس
سپس مانند
مانند جایی که
جایی که .
. و
و  در توزیع همگرا می شود
در توزیع همگرا می شود مانند
مانند همچنین در توزیع همگرا می شود
همچنین در توزیع همگرا می شود باید مستقل باشند، اما لزوماً به طور یکسان توزیع نشده باشند. این قضیه همچنین مستلزم آن متغیرهای تصادفی است
باید مستقل باشند، اما لزوماً به طور یکسان توزیع نشده باشند. این قضیه همچنین مستلزم آن متغیرهای تصادفی است
 ، و اینکه سرعت رشد این لحظات با شرایط لیاپانوف که در زیر ارائه شده است محدود می شود.
، و اینکه سرعت رشد این لحظات با شرایط لیاپانوف که در زیر ارائه شده است محدود می شود. دنباله ای از متغیرهای تصادفی مستقل است که هر کدام دارای مقدار مورد انتظار محدود هستند
دنباله ای از متغیرهای تصادفی مستقل است که هر کدام دارای مقدار مورد انتظار محدود هستند و واریانس
و واریانس  . تعريف كردن
. تعريف كردن
 ، وضعیت لیاپانوف
، وضعیت لیاپانوف![{\displaystyle \lim _{n\to \infty }\;{\frac {1}{s_{n}^{2+\delta }}}\,\sum _{i=1}^{n}\ mathbb {E} \left[\left|X_{i}-\mu _{i}\right|^{2+\delta }\right]=0}](https://wikimedia.org/api/rest_v1/media/math/render/svg/94a9702c705f509d1e7c582a0e9fcf5415d667aa)
 در توزیع به یک متغیر تصادفی عادی استاندارد همگرا می شود، به عنوان
در توزیع به یک متغیر تصادفی عادی استاندارد همگرا می شود، به عنوان تا بی نهایت می رود:
تا بی نهایت می رود:
 .
.
![{\displaystyle \lim _{n\to \infty }{\frac {1}{s_{n}^{2}}}\sum _{i=1}^{n}\mathbb {E} \left[ (X_{i}-\mu _{i})^{2}\cdot \mathbf {1} _{\left\{X_{i}:\left|X_{i}-\mu _{i}\ راست|>\varepsilon s_{n}\right\}}\right]=0}](https://wikimedia.org/api/rest_v1/media/math/render/svg/919a24fda71d1e6997e391b8445e633e0a756beb)
 تابع
تابع 
 .
. یک
یک  ، با بردار میانگین
، با بردار میانگین![{\textstyle {\boldsymbol {\mu }}=\mathbb {E} [\mathbf {X} _{i}]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/6244dc64b15d110166d68121979554959b73c907) و
و  (در میان اجزای بردار)، و این بردارهای تصادفی مستقل و به طور یکسان توزیع شده اند. جمع بندی این بردارها به صورت مؤلفه ای انجام می شود. قضیه حد مرکزی چند بعدی بیان می کند که وقتی مقیاس بندی می شود، مجموع به یک
(در میان اجزای بردار)، و این بردارهای تصادفی مستقل و به طور یکسان توزیع شده اند. جمع بندی این بردارها به صورت مؤلفه ای انجام می شود. قضیه حد مرکزی چند بعدی بیان می کند که وقتی مقیاس بندی می شود، مجموع به یک 
![{\displaystyle {\begin{bmatrix}X_{1(1)}\\\vdots \\X_{1(k)}\end{bmatrix}}+{\begin{bmatrix}X_{2(1)}\ \\vdots \\X_{2(k)}\end{bmatrix}}+\cdots +{\begin{bmatrix}X_{n(1)}\\\vdots \\X_{n(k)}\end {bmatrix}}={\begin{bmatrix}\sum _{i=1}^{n}\left[X_{i(1)}\right]\\\vdots \\\sum _{i=1} ^{n}\left[X_{i(k)}\right]\end{bmatrix}}=\sum _{i=1}^{n}\mathbf {X} _{i}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/e0aec2e3895f5d517973d01b48f22a9ae94296cc)

![{\displaystyle {\frac {1}{\sqrt {n}}}\sum _{i=1}^{n}\left[\mathbf {X} _{i}-\mathbb {E} \left( X_{i}\right)\right]={\frac {1}{\sqrt {n}}}\sum _{i=1}^{n}(\mathbf {X} _{i}-{\ boldsymbol {\mu }})={\sqrt {n}}\left({\overline {\mathbf {X} }}_{n}-{\boldsymbol {\mu }}\راست)~.}](https://wikimedia.org/api/rest_v1/media/math/render/svg/04cd4a073edaf3e3a0ddb8fdabe603e016be039f)

 برابر است با
برابر است با
 مستقل باش
مستقل باش  -بردارهای تصادفی با ارزش که هر کدام دارای میانگین صفر هستند. نوشتن
-بردارهای تصادفی با ارزش که هر کدام دارای میانگین صفر هستند. نوشتن و فرض کنید
و فرض کنید ![{\displaystyle \Sigma =\operatorname {Cov} [S]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/6bbdd46ff8928b02fc4e37a7fc14c51ceaf58b40) معکوس پذیر است اجازه دهید
معکوس پذیر است اجازه دهید یک باشد
یک باشد  گاوسی بعدی با میانگین و ماتریس کوواریانس مشابه
گاوسی بعدی با میانگین و ماتریس کوواریانس مشابه  ،
،![{\displaystyle \left|\mathbb {P} [S\in U]-\mathbb {P} [Z\in U]\right|\leq C\,d^{1/4}\gamma ~,}](https://wikimedia.org/api/rest_v1/media/math/render/svg/6c26c26cb1dedbb0db401fd2ebfb479ec45fb4cc)
 یک ثابت جهانی است،
یک ثابت جهانی است، ![{\displaystyle \gamma =\sum _{i=1}^{n}\mathbb {E} \left[\left\|\Sigma ^{-1/2}X_{i}\right\|_{2 }^{3}\right]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/84812af63e8f6578d530dae6334daab92c838f1e) ، و
، و نشان دهنده هنجار اقلیدسی در
نشان دهنده هنجار اقلیدسی در لازم است.
لازم است. 


 . فرض کنید ما به
. فرض کنید ما به 
 . قضیه حد مرکزی کلاسیک اندازه و شکل توزیعی نوسانات تصادفی حول عدد قطعی را توصیف می کند.
. قضیه حد مرکزی کلاسیک اندازه و شکل توزیعی نوسانات تصادفی حول عدد قطعی را توصیف می کند. و حد آن
و حد آن ( یعنی
( یعنی )
) . سودمندی قضیه این است که توزیع
. سودمندی قضیه این است که توزیع![{\textstyle \mathbb {E} [X_{i}]=\mu }](https://wikimedia.org/api/rest_v1/media/math/render/svg/72ca6904a07544cb510973b19c644024f7e15a4a) و
و ![{\textstyle \operatorname {Var} [X_{i}]=\sigma ^{2}<\infty }](https://wikimedia.org/api/rest_v1/media/math/render/svg/448bb57a7caae2db8c4c5bf94d9672bfe71fb9b2) . سپس به عنوان
. سپس به عنوان :
: 
 ، همگرایی در توزیع به این معنی است که
، همگرایی در توزیع به این معنی است که  ،
،![{\displaystyle \lim _{n\to \infty }\mathbb {P} \left[{\sqrt {n}}({\bar {X}}_{n}-\mu )\leq z\right] =\lim _{n\to \infty }\mathbb {P} \left[{\frac {{\sqrt {n}}({\bar {X}}_{n}-\mu )}{\sigma }}\leq {\frac {z}{\sigma }}\right]=\Phi \left({\frac {z}{\sigma }}\right),}](https://wikimedia.org/api/rest_v1/media/math/render/svg/defd4cf70972fa6a76a8570fee6551f4cb7d70b8)
 cdf معمولی استاندارد است که در آن ارزیابی شده است
cdf معمولی استاندارد است که در آن ارزیابی شده است![{\displaystyle \lim _{n\to \infty }\;\sup _{z\in \mathbb {R} }\;\left|\mathbb {P} \left[{\sqrt {n}}({ \bar {X}}_{n}-\mu )\leq z\right]-\Phi \left({\frac {z}{\sigma }}\right)\right|=0~,}](https://wikimedia.org/api/rest_v1/media/math/render/svg/835addcb3ec37594d1e9a6a78c0373a5e7b2eddc)
 نشان دهنده حداقل کران بالایی (یا
نشان دهنده حداقل کران بالایی (یا 









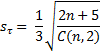



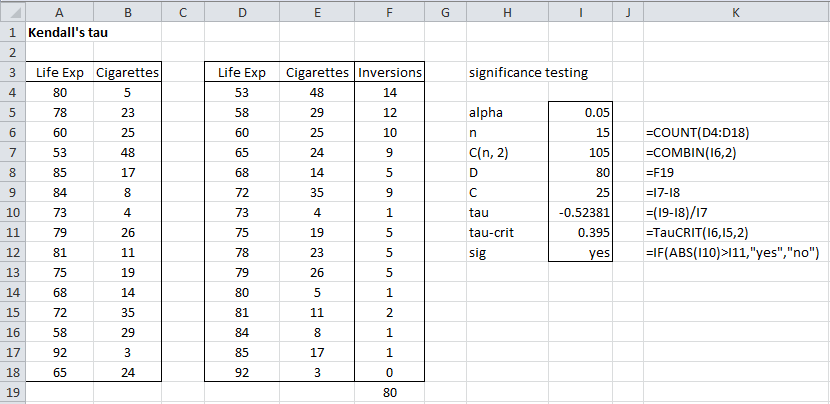

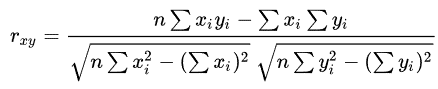
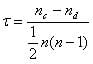
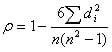





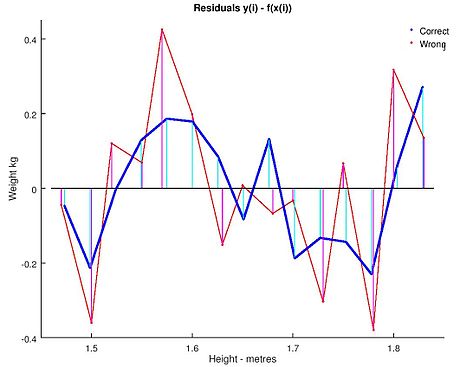
 جایی که
جایی که شعاع فاصله جسم با یکی از اجسام است. در معادله پارامترها
شعاع فاصله جسم با یکی از اجسام است. در معادله پارامترها و
و  برای تعیین مسیر مدار استفاده می شود. ما داده های زیر را اندازه گیری کرده ایم.
برای تعیین مسیر مدار استفاده می شود. ما داده های زیر را اندازه گیری کرده ایم. (در درجه)
(در درجه) . اکنون می توانیم از این فرم برای نمایش داده های مشاهده ای خود استفاده کنیم:
. اکنون می توانیم از این فرم برای نمایش داده های مشاهده ای خود استفاده کنیم: جایی که
جایی که  و
و  و
و  توسط ستون اول ضریب ساخته می شود
توسط ستون اول ضریب ساخته می شود  مقادیر مربوطه است
مقادیر مربوطه است بنابراین
بنابراین و
و 

 و
و
 به طور معمول توزیع می شود ، با میانگین و واریانس همانطور که قبلا داده شد:
به طور معمول توزیع می شود ، با میانگین و واریانس همانطور که قبلا داده شد: 

 در y خطی است ، به این معنی که ترکیبی خطی از متغیرهای وابسته y i را نشان می دهد . وزن های این ترکیب خطی توابع رگرسیون X هستند و به طور کلی نابرابر هستند. مشاهدات با وزن زیاد را تأثیرگذار می نامند زیرا تأثیر بارزتری بر ارزش برآوردگر دارند.
در y خطی است ، به این معنی که ترکیبی خطی از متغیرهای وابسته y i را نشان می دهد . وزن های این ترکیب خطی توابع رگرسیون X هستند و به طور کلی نابرابر هستند. مشاهدات با وزن زیاد را تأثیرگذار می نامند زیرا تأثیر بارزتری بر ارزش برآوردگر دارند.


 و تخمین
و تخمین از نظر عددی با مانده و تخمین OLS برای β 2 در رگرسیون زیر یکسان خواهد بود :
از نظر عددی با مانده و تخمین OLS برای β 2 در رگرسیون زیر یکسان خواهد بود : 




![{\ displaystyle {\ start {تراز شده} {\ کلاه {\ بتا}} & = {\ frac {\ sum {x_ {i} y_ {i}} - {\ frac {1} {n}} \ sum {x_ {i}} \ sum {y_ {i}}} {\ sum {x_ {i} ^ {2}} - {\ frac {1} {n}} (\ sum {x_ {i}}) ^ {2 }}} = {\ frac {\ operatorname {Cov} [x، y]} {\ operatorname {Var} [x]}} \\ {\ hat {\ alpha}} & = {\ overline {y}} - {\ hat {\ beta}} \، {\ overline {x}} \، \ end {تراز شده}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/817c4939058094674f0ef2787ef175b5c7170c07)

 و
و  به ستونی از ماتریس داده اشاره دارد.)
به ستونی از ماتریس داده اشاره دارد.)

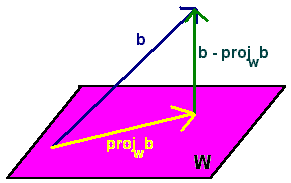
 متعامد به است
متعامد به است  برابر است با صفر برای هر بردار انطباق ، v . این بدان معنی است که
برابر است با صفر برای هر بردار انطباق ، v . این بدان معنی است که کوتاهترین بردارهای ممکن است
کوتاهترین بردارهای ممکن است ، یعنی واریانس باقیمانده حداقل ممکن است. این در سمت راست نشان داده شده است.
، یعنی واریانس باقیمانده حداقل ممکن است. این در سمت راست نشان داده شده است. و یک ماتریس K با این فرض که یک ماتریس
و یک ماتریس K با این فرض که یک ماتریس![[X \ K]](https://wikimedia.org/api/rest_v1/media/math/render/svg/b0c7583e31f8e4111806d1612b81b39d3f76af01) غیر مفرد است و K T X = 0 (
غیر مفرد است و K T X = 0 ( 


![\ mathrm {E} {\ big [} \، x_ {i} (y_ {i} -x_ {i} ^ {T} \ beta) \، {\ big]} = 0.](https://wikimedia.org/api/rest_v1/media/math/render/svg/cb1a1f1cb2be7e80f44761892bf788fe2b2af548)

 ، فقط ستون های دیگر حاوی داده های واقعی هستند ، بنابراین در اینجا
، فقط ستون های دیگر حاوی داده های واقعی هستند ، بنابراین در اینجا 




 توسط رگرسیون ها به عنوان
توسط رگرسیون ها به عنوان  بردار ضریب حداقل مربعات است
بردار ضریب حداقل مربعات است 

 ، که می تواند با فرمول صریح ارائه شود:
، که می تواند با فرمول صریح ارائه شود: 



 ، برآورد MLE برای σ 2 است . این دو برآوردگر در نمونه های بزرگ کاملاً شبیه به هم هستند. برآوردگر اول همیشه
، برآورد MLE برای σ 2 است . این دو برآوردگر در نمونه های بزرگ کاملاً شبیه به هم هستند. برآوردگر اول همیشه 


 ، یک تابع خطی از گیرنده ها است:
، یک تابع خطی از گیرنده ها است:



 نقاط (گرد به بزرگترین عدد صحیح بعدی) که مقادیر متغیرهای توضیحی آنها نزدیکترین نقطه به نقطه ارزیابی پاسخ است.
نقاط (گرد به بزرگترین عدد صحیح بعدی) که مقادیر متغیرهای توضیحی آنها نزدیکترین نقطه به نقطه ارزیابی پاسخ است.  و 1 ، با
و 1 ، با  نشانگر درجه چند جمله ای محلی است.
نشانگر درجه چند جمله ای محلی است.
 روی فضای مورد نظر
روی فضای مورد نظر که به دو پارامتر بستگی دارد ،
که به دو پارامتر بستگی دارد ،  . فرض کنید که فرضیه خطی بر اساس است
. فرض کنید که فرضیه خطی بر اساس است به
به  مانند
مانند ، و عملکرد زیان زیر را در نظر بگیرید
، و عملکرد زیان زیر را در نظر بگیرید
 ماتریس واقعی ضرایب ،
ماتریس واقعی ضرایب ،  و زیرنویس i بردارهای ورودی و خروجی مجموعه آموزشی را برمی شمارد. از آنجا که
و زیرنویس i بردارهای ورودی و خروجی مجموعه آموزشی را برمی شمارد. از آنجا که یک متریک است ، یک ماتریس متقارن ، مثبت و مشخص است و به همین ترتیب ، یک ماتریس متقارن دیگری نیز وجود دارد
یک متریک است ، یک ماتریس متقارن ، مثبت و مشخص است و به همین ترتیب ، یک ماتریس متقارن دیگری نیز وجود دارد  به طوری که
به طوری که  . عملکرد زیان فوق را می توان با مشاهده آن به یک ردیف مرتب کرد
. عملکرد زیان فوق را می توان با مشاهده آن به یک ردیف مرتب کرد . با چیدمان بردارها
. با چیدمان بردارها به ستون های
به ستون های ماتریس
ماتریس ماتریس
ماتریس به ترتیب می توان تابع زیان فوق را به صورت زیر نوشت:
به ترتیب می توان تابع زیان فوق را به صورت زیر نوشت:
 مورب مربع است
مورب مربع است  ماتریسی که ورودی های آن است
ماتریسی که ورودی های آن است  تمایز با توجه به
تمایز با توجه به
 تابع ضرر غیر منفرد است
تابع ضرر غیر منفرد است به حداقل خود در
به حداقل خود در

 در این وبلاگ به ریاضیات و کاربردهای آن و تحقیقات در آنها پرداخته می شود. مطالب در این وبلاگ ترجمه سطحی و اولیه است و کامل نیست.در صورتی سوال یا نظری در زمینه ریاضیات دارید مطرح نمایید .در صورت امکان به آن می پردازم. من دوست دارم برای یافتن پاسخ به سوالات و حل پروژه های علمی با دیگران همکاری نمایم.در صورتی که شما هم بامن هم عقیده هستید با من تماس بگیرید.
در این وبلاگ به ریاضیات و کاربردهای آن و تحقیقات در آنها پرداخته می شود. مطالب در این وبلاگ ترجمه سطحی و اولیه است و کامل نیست.در صورتی سوال یا نظری در زمینه ریاضیات دارید مطرح نمایید .در صورت امکان به آن می پردازم. من دوست دارم برای یافتن پاسخ به سوالات و حل پروژه های علمی با دیگران همکاری نمایم.در صورتی که شما هم بامن هم عقیده هستید با من تماس بگیرید.