1-گروه دو وجهی:D8
فهرست |
این مقاله در مورد یک گروه خاص است ، یعنی یک گروه منحصر به فرد تا ایزومورفیسم . مشاهده اطلاعات خاص (مانند تئوری نمایش خطی، ساختار زیر گروه) در مورد این گروه
مشاهده لیست کاملی از گروه های خاص (این یک لیست بسیار بزرگ است!) [نمایش بیشتر]
تعریف
تعریف با ارائه
گروه دو وجهی  ، که گاهی اوقات نامیده می شود
، که گاهی اوقات نامیده می شود  ، همچنین به نام گروه دو وجهی درجه هشت یا گروه دو وجهی درجه چهار (از آنجایی که عملکرد طبیعی آن بر روی چهار عنصر است)، یا گاهی اوقات گروه اکتیو ، با ارائه زیر ، با
، همچنین به نام گروه دو وجهی درجه هشت یا گروه دو وجهی درجه چهار (از آنجایی که عملکرد طبیعی آن بر روی چهار عنصر است)، یا گاهی اوقات گروه اکتیو ، با ارائه زیر ، با  نشان دادن همانی ، تعریف می شود. عنصر:
نشان دادن همانی ، تعریف می شود. عنصر:

در اینجا، عنصر  را چرخش یا مولد قطعه دور ای می نامند و
را چرخش یا مولد قطعه دور ای می نامند و  به آن انعکاس می گویند .
به آن انعکاس می گویند .
آیا در مورد ارائه به طور کلی یا این یکی به طور خاص گیج شده اید؟ اگر با این چیزها تازه کار هستید، ساخت گروه دو وجهی:D8 را از ارائه آن بررسی کنید. نظریه پردازان پیچیده گروه باید به سادگی به یاد بیاورند که ارائه ضرب نیمه مستقیم، اتحاد غیرمستقیم ارائه ها به علاوه عمل توسط روابط صرف است.
تعریف هندسی
گروه دو وجهی  (همچنین نامیده می شود
(همچنین نامیده می شود  ) به عنوان گروهی از تمام تقارن های مربع (4 ضلعی منظم) تعریف می شود. این یک زیرگروه دورای دارد که شامل چرخشها است (که زیرگروه دورای ایجاد شده
) به عنوان گروهی از تمام تقارن های مربع (4 ضلعی منظم) تعریف می شود. این یک زیرگروه دورای دارد که شامل چرخشها است (که زیرگروه دورای ایجاد شده  توسط
توسط
تعریف به عنوان یک گروه جایگشت
اطلاعات بیشتر: D8 در S4
این گروه (تا ایزومورفیسم) زیر گروه گروه متقارن است  که توسط:
که توسط:

 این را می توان با در نظر گرفتن رئوس مربع و در نظر گرفتن عنصری از
این را می توان با در نظر گرفتن رئوس مربع و در نظر گرفتن عنصری از  نظر عملکرد القایی آن بر رئوس، به تعریف هندسی مرتبط کرد . این به ارائه از طریق تنظیمات
نظر عملکرد القایی آن بر رئوس، به تعریف هندسی مرتبط کرد . این به ارائه از طریق تنظیمات  و
و  .
.
جدول ضرب
در اینجا،  عنصر همانی را نشان می دهد،
عنصر همانی را نشان می دهد،  عنصری از مرتبه 4 است، و
عنصری از مرتبه 4 است، و  عنصری از درجه دو است که برابر نیست
عنصری از درجه دو است که برابر نیست  ، مانند ارائه بالا.
، مانند ارائه بالا.
عنصر ردیف در سمت چپ و عنصر ستون در سمت راست ضرب می شود.
| عنصر |  |  |  |  |  | 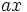 | 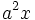 |  |
|---|---|---|---|---|---|---|---|---|
 |  |  |  |  |  | 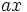 | 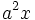 |  |
 |  |  |  |  | 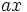 | 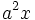 |  |  |
 |  |  |  |  | 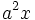 |  |  | 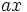 |
 |  |  |  |  |  |  | 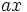 | 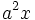 |
 |  |  | 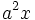 | 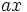 |  |  |  |  |
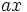 | 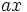 |  |  | 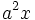 |  |  |  |  |
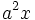 | 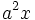 | 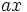 |  |  |  |  |  |  |
 |  | 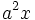 | 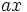 |  |  |  |  |  |
تعاریف دیگر
گروه دو وجهی را می توان به روش های زیر توصیف کرد:
- گروه دو وجهی مرتبه هشت.
- گروه دو وجهی تعمیم یافته مربوط به گروه دور ای مرتبه چهار .
- هولومورف گروه دور ای مرتبه چهار .
- ضرب اکلیل خارجی گروه دور ای درجه دو با گروه دور ای درجه دو، از طریق عمل منظم عمل می کند.
- زیر گروه
 - Sylow از گروه متقارن در چهار حرف .
- Sylow از گروه متقارن در چهار حرف . - زیر گروه
 - Sylow از گروه متقارن در پنج حرف .
- Sylow از گروه متقارن در پنج حرف . - زیر گروه
 - Sylow از گروه متناوب در شش حرف .
- Sylow از گروه متناوب در شش حرف . - گروه ماتریس واحد مثلثی درجه سه روی
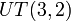 میدان :F2 ،
میدان :F2 ،  - زیرگروه Sylow از PSL(3،2) .
- زیرگروه Sylow از PSL(3،2) . - گروه فوقالعاده ترتیب
 و نوع «+».
و نوع «+».
موقعیت در طبقه بندی ها
| نوع طبقه بندی | نام در آن طبقه بندی |
|---|---|
| شناسه GAP | (8،3) یعنی سومین گروه از مرتبه 8 |
| سالن-شماره ارشد | (8،4)، یعنی 4 در میان گروه های مرتبه 8 |
| نماد تالار - ارشد | 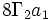 |
عناصر
اطلاعات بیشتر: ساختار عنصر گروه دو وجهی: D8
در زیر، همه عناصر را فهرست میکنیم، همچنین تفسیر هر عنصر را در زیر شرح هندسی گروه دو وجهی به عنوان تقارنهای یک 4 ضلعی، و برای نمایش جایگشت مربوطه ارائه میکنیم (به D8 در S4 مراجعه کنید ). توجه داشته باشید که برای کنوانسیون های مختلف، می توان مکاتبات متفاوتی را به دست آورد، بنابراین ممکن است با سایر مکاتبات در جاهای دیگر مطابقت نداشته باشد. توجه داشته باشید که توضیحات زیر، قرارداد عمل چپ را برای توابع و قرارداد مربوطه را برای ترکیب فرض میکند، و از این رو، برخی از ورودیها ممکن است در صورت اتخاذ کنوانسیون عمل درست، متفاوت شوند. :
عنصر از نظر  و و | توضیحات هندسی | جایگشت در رئوس | ترتیب عنصر |
|---|---|---|---|
 (عنصر همانی) (عنصر همانی) | هیچ کاری نمی کند، یعنی مربع را ثابت می گذارد |  | 1 |
 | چرخش با زاویه  (یعنی (یعنی  ) در خلاف جهت عقربه های ساعت ) در خلاف جهت عقربه های ساعت |  | 4 |
 | چرخش بر اساس زاویه  (یعنی )، که نیم دور (یعنی )، که نیم دور نیز نامیده می شود نیز نامیده می شود |  | 2 |
 | چرخش با زاویه 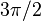 (یعنی (یعنی  ) در خلاف جهت عقربه های ساعت، یا معادل آن، توسط ) در خلاف جهت عقربه های ساعت، یا معادل آن، توسط  (یعنی، (یعنی،  ) در جهت عقربه های ساعت ) در جهت عقربه های ساعت |  | 4 |
 | بازتابی در مورد رئوس اتصال مورب "2" و "4" |  | 2 |
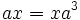 | انعکاس خطی که نقاط میانی اضلاع مخالف "14" و "23" را به هم وصل می کند |  | 2 |
 | انعکاس در مورد رئوس اتصال مورب "1" و "3" |  | 2 |
 | انعکاس خطی که نقاط میانی اضلاع مخالف "12" و "34" را به هم وصل می کند |  | 2 |
 در این وبلاگ به ریاضیات و کاربردهای آن و تحقیقات در آنها پرداخته می شود. مطالب در این وبلاگ ترجمه سطحی و اولیه است و کامل نیست.در صورتی سوال یا نظری در زمینه ریاضیات دارید مطرح نمایید .در صورت امکان به آن می پردازم. من دوست دارم برای یافتن پاسخ به سوالات و حل پروژه های علمی با دیگران همکاری نمایم.در صورتی که شما هم بامن هم عقیده هستید با من تماس بگیرید.
در این وبلاگ به ریاضیات و کاربردهای آن و تحقیقات در آنها پرداخته می شود. مطالب در این وبلاگ ترجمه سطحی و اولیه است و کامل نیست.در صورتی سوال یا نظری در زمینه ریاضیات دارید مطرح نمایید .در صورت امکان به آن می پردازم. من دوست دارم برای یافتن پاسخ به سوالات و حل پروژه های علمی با دیگران همکاری نمایم.در صورتی که شما هم بامن هم عقیده هستید با من تماس بگیرید.