از قضیه استفاده کنیم که به ما می‌گوید حلقهF [ x ]m ( x )رایک میدان است اگر و فقط اگرm ( x )تحویل ناپذیر است این به طور کلی آسان نیست - اگر درجهm ( x )بالا است، این کار به مقدار زیادی کار دستی نیاز دارد
خوشبختانه، معمولاً از ما خواسته می شود که این را با آن نشان دهیمm ( x )دارای درجه 2 یا 3. در این مورد، می توانیم از نتیجه 5.29 (یک چند جمله ای) استفاده کنیم.m ( x )درجه 2 یا 3 در یک میدان تحویل ناپذیر است اگر و فقط اگر ریشه نداشته باشد).

همه مقادیر ممکن را وارد می کنیم یعنی به آن ارزیابی می شود

A=Z5​[x]/(x^2+4​)

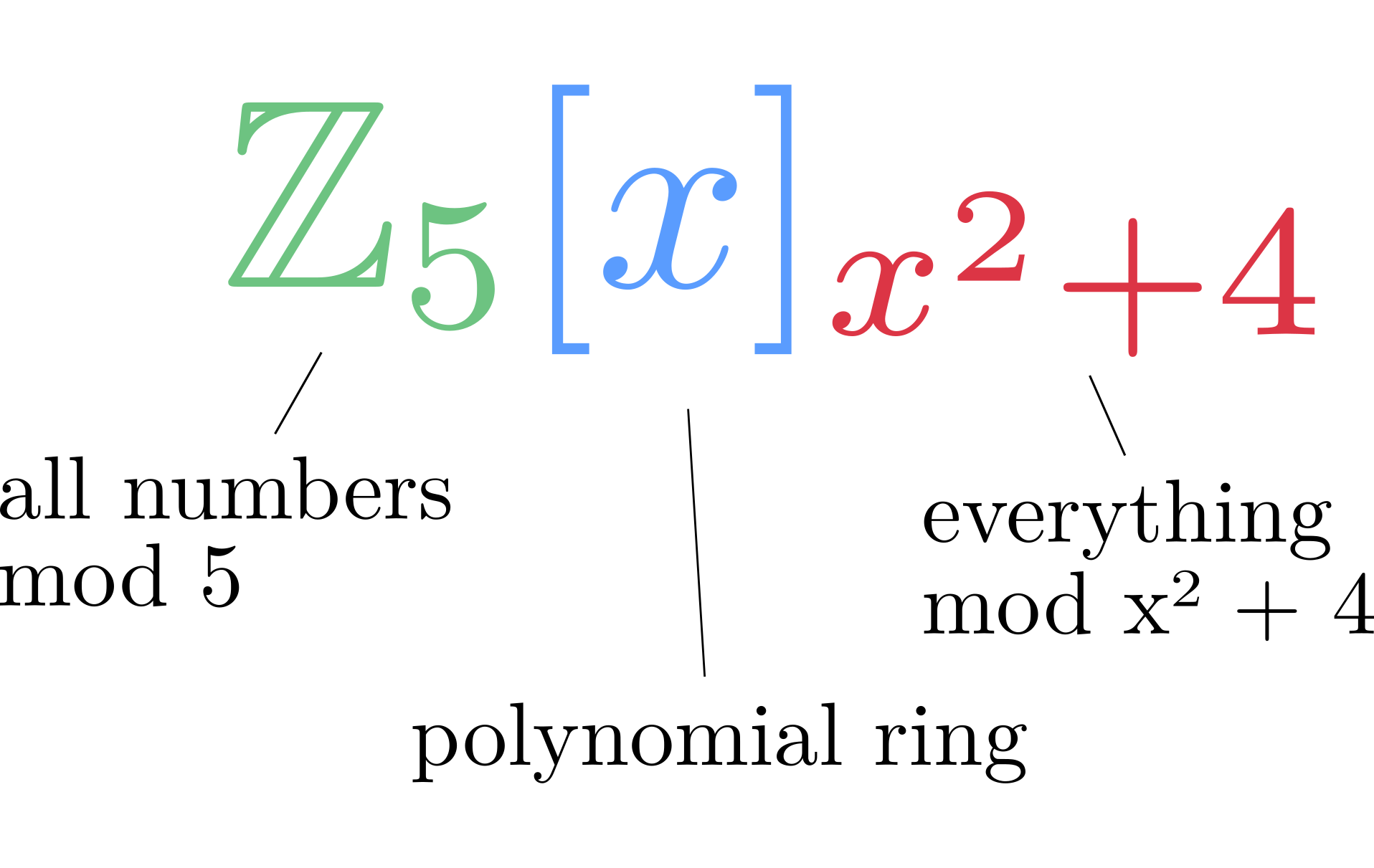
Polynomial ring explanation

m(0)=0^2+4=4

m(1)=1^2+4=0

m(2)=2^2+4=3

m(3)=3^2+4=3

m(4)=4^2+4=0

بنابراین

x^2+4=(x−1)(x−4)=(x+4)(x+1)

بنابراین میدان نیست

منبع

https://xyquadrat.ch/2020/12/19/is-polynomial-ring-field/