ضرب اسکالر کلیفورد [ ویرایش ]
وقتی مشخصه 2 نباشد، شکل درجه دوم Q روی V را می توان به شکل درجه دوم روی تمام Cl( V , Q ) (که با Q نیز نشان دادیم ) گسترش داد. یک تعریف مستقل از مبنا از یکی از این پسوندها است
که در آن 〈 a 〉 0 قسمت اسکالر a (قسمت درجه-0 در درجه بندی Z ) را نشان می دهد. می توان آن را نشان داد
که در آن v i عناصر V هستند - این هویت برای عناصر دلخواه Cl( V , Q ) صادق نیست .
شکل دوخطی متقارن مرتبط بر روی Cl( V , Q ) توسط داده می شود
می توان بررسی کرد که وقتی به V متناهی می شود، به شکل دوخطی اصلی کاهش می یابد . شکل دو خطی روی تمام کلر ( V , Q ) غیر دژنره است اگر و فقط اگر روی V غیر دژنره باشد.
عملگر ضرب کليفورد چپ (به ترتيب راست) در جابجايي a t عنصر a ، ضميمه ضرب کليفورد چپ (به ترتيب راست) در a نسبت به اين حاصلضرب داخلي است. به این معنا که،
و
ساختار جبرهای کلیفورد [ ویرایش ]
در این بخش فرض می کنیم که مشخصه 2 نیست، فضای برداری V بعد متناهی است و شکل دو خطی متقارن Q غیر منحط است.
جبر ساده مرکزی روی K یک جبر ماتریسی روی یک جبر تقسیم (بعد متناهی) با مرکز K است. به عنوان مثال، جبرهای ساده مرکزی بر روی حقیقی ها، جبرهای ماتریسی بر روی حقیقی ها یا چهارتایی ها هستند.
- اگر V بعد زوج داشته باشد ، Cl( V ، Q ) یک جبر ساده مرکزی روی K است.
- اگر V بعد زوج داشته باشد، زیر جبر زوج Cl [0] ( V , Q ) یک جبر ساده مرکزی بر روی یک بسط درجه دوم K یا مجموع دو جبر ساده مرکزی هم شکل بر K است.
- اگر V بعد فرد داشته باشد، Cl( V ، Q ) یک جبر ساده مرکزی بر روی یک بسط درجه دوم K یا مجموع دو جبر ساده مرکزی هم شکل بر K است.
- اگر V بعد فرد داشته باشد، آنگاه زیر جبر زوج Cl [0] ( V , Q ) یک جبر ساده مرکزی روی K است.
ساختار جبرهای کلیفورد را می توان با استفاده از نتیجه زیر به صراحت کار کرد. فرض کنید که U دارای بعد زوج و یک فرم دوخطی غیرمفرد با d متمایز است، و فرض کنید که V فضای برداری دیگری با شکل درجه دوم است. جبر کلیفورد U + V با حاصل ضرب تانسور جبرهای کلیفورد U و (-1) dim( U )/2 dV هم شکل است، که فضای V با شکل درجه دوم آن ضرب در (-1) dim( U ) است. )/2 د . بیش از حقیقیات، این به ویژه دلالت بر آن دارد
از این فرمول ها می توان برای یافتن ساختار تمام جبرهای کلیفورد حقیقی و جبرهای مختلط کلیفورد استفاده کرد. طبقه بندی جبرهای کلیفورد را ببینید .
قابل توجه است که کلاس هم ارزی موریتا یک جبر کلیفورد (نظریه نمایش آن: کلاس هم ارزی دسته مدول ها روی آن) فقط به امضای ( p - q ) mod 8 بستگی دارد . این یک شکل جبری از تناوب بوت است.
گروه لیپشیتز [ ویرایش ]
کلاس گروههای لیپشیتز (با نام مستعار [15] گروههای کلیفورد یا گروههای کلیفورد–لیپسشیتز) توسط رودولف لیپشیتز کشف شد . [16]
در این بخش فرض می کنیم که V بعد متناهی است و شکل درجه دوم Q غیر منحط است .
یک عمل بر روی عناصر جبر کلیفورد توسط گروه واحدهای آن ممکن است بر حسب یک صرف پیچ خورده تعریف شود: صرف پیچ خورده توسط x نقشه های y ↦ α ( x ) y x -1 را نشان می دهد ، که در آن α چرخش اصلی تعریف شده در بالا است.
گروه لیپ شیتز Γ به عنوان مجموعه ای از عناصر معکوس x تعریف می شود که مجموعه بردارها را تحت این عمل تثبیت می کند، [17] به این معنی که برای همه v در V داریم:
این فرمول همچنین یک عمل از گروه لیپ شیتز را در فضای برداری V تعریف می کند که شکل درجه دوم Q را حفظ می کند و بنابراین یک هم شکلی از گروه لیپ شیتز به گروه متعامد می دهد. گروه لیپ شیتز شامل تمام عناصر r از V است که برای آنها Q ( r ) در K معکوس است ، و این عناصر با بازتاب های مربوطه روی V عمل می کنند که v را به v می رساند - (〈 r , v 〉 + 〈 v , r 〉) r / س ( ر ). (در مشخصه 2 اینها را برش های متعامد می نامند تا بازتاب.)
اگر V یک فضای برداری حقیقی با ابعاد متناهی با فرم درجه دوم غیر منحط باشد، گروه لیپ شیتز با توجه به شکل (توسط قضیه Cartan-Dieudonné ) روی گروه متعامد V نگاشت می شود و هسته از عناصر غیر صفر تشکیل شده است. میدان K . این منجر به توالی های دقیق می شود
در زمینه های دیگر یا با فرم های نامشخص، نقشه به طور کلی روی آن نیست و شکست توسط هنجار اسپینور ثبت می شود.
هنجار اسپینور [ ویرایش ]
اطلاعات بیشتر: هنجار اسپینور § گروه های همومولوژی و متعامد گالوا
در مشخصه دلخواه، هنجار اسپینور Q در گروه لیپ شیتز توسط تعریف می شود
این یک هممورفیسم از گروه لیپ شیتز به گروه K × از عناصر غیر صفر K است. زمانی که V با زیرفضای جبر کلیفورد شناسایی می شود، با شکل درجه دوم Q از V مطابقت دارد. چندین نویسنده هنجار اسپینور را کمی متفاوت تعریف می کنند، به طوری که با ضریب 1-، 2 یا 2- در Γ1 با هنجار اینجا متفاوت است . تفاوت در مشخصه غیر از 2 خیلی مهم نیست.
عناصر غیرصفر K در گروه ( K × ) 2 مربع از عناصر غیر صفر میدان K ، هنجار اسپینور دارند . بنابراین وقتی V بعد متناهی و غیر منفرد است، یک نقشه القایی از گروه متعامد V به گروه K × /( K × ) 2 دریافت می کنیم که هنجار اسپینور نیز نامیده می شود. هنجار اسپینور بازتاب در مورد r ⊥ ، برای هر بردار r ، دارای تصویر Q ( r ) در K × /( K × ) 2 است.، و این ویژگی به طور منحصر به فرد آن را در گروه متعامد تعریف می کند. این توالی های دقیق را نشان می دهد:
توجه داشته باشید که در مشخصه 2 گروه {±1} فقط یک عنصر دارد.
از نقطه نظر همشکلی گالوا گروههای جبری ، هنجار اسپینور یک هممورفیسم پیوندی در همشکلی است. نوشتن μ 2 برای گروه جبری ریشه های مربع 1 (در یک میدان مشخصه نه 2 تقریباً مشابه یک گروه دو عنصری با عمل گالوای بی اهمیت است)، دنباله دقیق کوتاه
یک توالی دقیق طولانی در همومولوژی به دست می دهد که آغاز می شود
0مین گروه همشناسی گالوا از یک گروه جبری با ضرایب K فقط گروهی از نقاط با ارزش K است: H 0 ( G ؛ K ) = G ( K ) و H 1 (μ2 ؛ K ) ≅ K × /( K × ) 2 ، که دنباله قبلی را بازیابی می کند
که در آن هنجار اسپینور هممورفیسم اتصال H 0 (O V ؛ K ) → H 1 (μ 2 ؛ K ) است.
گروه های چرخش و پین [ ویرایش ]
اطلاعات بیشتر: اسپین group ، پین group و اسپینor
در این بخش فرض می کنیم که V بعد متناهی و شکل دوخطی آن غیر منفرد است.
گروه پین پین V ( K ) زیرگروه گروه لیپ شیتز Γ از عناصر اسپینور هنجار 1 است ، و به طور مشابه گروه اسپین V ( K ) زیرگروه عناصر دیکسون ثابت 0 در پین V ( K ) است. وقتی مشخصه 2 نباشد ، اینها عناصر تعیین کننده 1 هستند. گروه اسپین معمولاً دارای اندیس 2 در گروه پین است.
از بخش قبل به یاد بیاورید که یک هم شکلی از گروه لیپ شیتز بر روی گروه متعامد وجود دارد. ما گروه متعامد ویژه را تصویر Γ 0 تعریف می کنیم . اگر K مشخصه 2 را نداشته باشد ، این فقط گروهی از عناصر گروه متعامد تعیین کننده 1 است. اگر K مشخصه 2 داشته باشد ، تمام عناصر گروه متعامد دارای تعیین کننده 1 هستند و گروه متعامد ویژه مجموعه عناصر دیکسون ثابت 0 است.
یک هم شکلی از گروه پین به گروه متعامد وجود دارد. تصویر از عناصر اسپینور هنجار 1 ∈ K × /( K × ) 2 تشکیل شده است. هسته از عناصر +1 و −1 تشکیل شده است و دارای مرتبه 2 است مگر اینکه K دارای مشخصه 2 باشد. به طور مشابه یک هم شکلی از گروه اسپین به گروه متعامد ویژه V وجود دارد.
در حالت متداول که V یک فضای قطعی مثبت یا منفی روی حقیقیات است، گروه اسپین روی گروه متعامد خاص نگاشت می شود و زمانی که V حداقل بعد 3 داشته باشد، به سادگی متصل می شود. بعلاوه هسته این هممورفیسم از 1 و -1 تشکیل شده است. بنابراین در این مورد گروه اسپین، اسپین( n ) یک پوشش دوتایی از SO( n ) است. لطفاً توجه داشته باشید که اتصال ساده گروه اسپین به طور کلی درست نیست: اگر V R p باشد ، q برای p و q هر دو حداقل2 سپس گروه اسپین به سادگی متصل نمی شود. در این مورد گروه جبری اسپین p , q به سادگی به عنوان یک گروه جبری متصل می شود، حتی اگر گروهی از نقاط با ارزش حقیقی آن اسپین p , q ( R ) به سادگی متصل نیست. این یک نکته نسبتاً ظریف است که نویسندگان حداقل یک کتاب استاندارد را در مورد گروه های چرخشی کاملاً گیج کرده است. [ کدام؟ ]
اسپینورها [ ویرایش ]
جبرهای کلیفورد Cl p , q ( C ) با p + q = 2 n زوج، جبرهای ماتریسی هستند که نمایش مختلط ای از بعد 2 n دارند. با متناهی کردن به گروه پین p ، q ( R ) یک نمایش مختلط از گروه پین با همان بعد به دست میآوریم که نمایش اسپین نامیده میشود . اگر این را به گروه اسپین اسپین p ، q ( R ) متناهی کنیم، آنگاه به صورت مجموع دو نمایش نیمه اسپین تقسیم می شود.(یا نمایشهای ویل ) با ابعاد 2 n -1 .
اگر p + q = 2 n + 1 فرد باشد، جبر کلیفورد Cl p , q ( C ) مجموع دو جبر ماتریسی است که هر کدام نمایشی از بعد 2 n دارند و اینها نیز هر دو نمایش پین هستند. گروه پین p , q ( R ) . با متناهییت به گروه اسپین اسپین p , q ( R ) اینها هم شکل می شوند، بنابراین گروه اسپین یک نمایش اسپینور مختلط با بعد 2 n دارد.
به طور کلیتر، گروههای اسپینور و گروههای پین در هر زمینه، نمایشهای مشابهی دارند که ساختار دقیق آن به ساختار جبرهای کلیفورد مربوطه بستگی دارد : هرگاه جبر کلیفورد دارای عاملی باشد که جبر ماتریسی بر روی برخی جبر تقسیمبندی است، نمایش متناظری از جبر کلیفورد را دریافت میکنیم. گروه پین و اسپین بر روی آن جبر تقسیم. برای مثال هایی در مورد حقیقی ها به مقاله اسپینورها مراجعه کنید.
اسپینورهای حقیقی [ ویرایش ]
اطلاعات بیشتر: اسپینor
برای توصیف بازنمایی های اسپین حقیقی، باید بدانیم که گروه اسپین چگونه در جبر کلیفورد خود قرار دارد. گروه پین ، پین p ، q مجموعه ای از عناصر معکوس در Cl p ، q است که می تواند به عنوان حاصل ضرب بردارهای واحد نوشته شود:
در مقایسه با تحقق های عینی بالا از جبرهای کلیفورد، گروه پین با ضربات بازتاب های دلخواه بسیاری مطابقت دارد: این پوششی از گروه متعامد O( p , q ) است. گروه اسپین متشکل از عناصر پین p , q است که حاصل تعداد زوج بردار واحد هستند. بنابراین توسط قضیه Cartan-Dieudonné اسپین پوششی از گروه چرخش های مناسب SO( p , q ) است.
فرض کنید α : Cl → Cl اتومورفیسمی باشد که با نگاشت v ↦ − v بر روی بردارهای خالص عمل می کند. سپس به طور خاص، اسپین p ، q زیرگروه پین p است، q عناصر آن توسط α ثابت میشوند . اجازه دهید
(اینها دقیقاً عناصر درجه زوج در Cl p , q هستند.) سپس گروه اسپین در Cl قرار دارد.[0]
p ، q.
نمایشهای تقلیلناپذیر Cl p , q به نمایش گروه پین متناهی میشوند. برعکس، از آنجایی که گروه پین توسط بردارهای واحد تولید میشود، تمام نمایشهای تقلیلناپذیر آن به این صورت القا میشوند. بنابراین این دو نمایش بر هم منطبق هستند. به همین دلایل، نمایشهای تقلیلناپذیر اسپین با نمایشهای تقلیلناپذیر Cl منطبق است.[0]
p ، q.
برای طبقهبندی نمایشهای پین، فقط باید به طبقهبندی جبرهای کلیفورد مراجعه کرد. برای یافتن نمایشهای اسپین (که نمایشهایی از زیر جبر زوج هستند)، ابتدا میتوان از یکی از همشکلیها استفاده کرد (به بالا مراجعه کنید).
و یک نمایش اسپین در امضا ( p , q ) را به عنوان یک نمایش پین در امضا ( p , q -1) یا ( q , p -1) درک کنید.
برنامه های کاربردی [ ویرایش ]
هندسه دیفرانسیل [ ویرایش ]
یکی از کاربردهای اصلی جبر بیرونی در هندسه دیفرانسیل است که در آن برای تعریف دسته ای از اشکال دیفرانسیل بر روی یک منیفولد صاف استفاده می شود. در مورد منیفولد ریمانی ( شبه- ) فضاهای مماس مجهز به یک فرم درجه دوم طبیعی است که توسط متریک القا می شود . بنابراین، می توان یک بسته نرم افزاری کلیفورد را در قیاس با بسته خارجی تعریف کرد. این چند کاربرد مهم در هندسه ریمانی دارد . شاید مهم تر، پیوند به یک منیفولد اسپین ، مرتبط با آن باشدمنیفولدهای اسپینور باندل و اسپین c .
فیزیک [ ویرایش ]
جبرهای کلیفورد کاربردهای مهم متعددی در فیزیک دارند. فیزیکدانان معمولاً جبر کلیفورد را جبری میدانند که مبنای آن توسط ماتریسهای γ 0 , ..., γ 3 به نام ماتریس دیراک ایجاد میشود که این ویژگی را دارند.
که در آن η ماتریس شکل درجه دوم امضا (1، 3) (یا (3، 1) مربوط به دو انتخاب معادل امضای متریک است). اینها دقیقاً روابط تعیین کننده برای جبر کلیفورد Cl هستند
1،3( R ) که کمپلکسی آن Cl است
1،3( R ) C که بر اساس طبقه بندی جبرهای کلیفورد ، با جبر 4 × 4 ماتریس های مختلط Cl 4 ( C ) ≈ M 4 ( C ) هم شکل است. با این حال، بهتر است علامت Cl را حفظ کنید
1،3( R ) C ، از آنجایی که هر تبدیلی که شکل دوخطی را به شکل متعارف میگیرد ، تبدیل لورنتس فضای زمان زیرین نیست.
بنابراین جبر فضازمان کلیفورد که در فیزیک استفاده می شود ساختار بیشتری نسبت به Cl 4 ( C ) دارد. علاوه بر این دارای مجموعه ای از تبدیل های ترجیحی است - تبدیلات لورنتس. اینکه آیا برای شروع مختلطسازی ضروری است تا حدی به قراردادهای مورد استفاده بستگی دارد و تا حدی بستگی به مقداری دارد که شخص میخواهد مستقیماً در آن گنجانده شود، اما مختلطسازی اغلب در مکانیک کوانتومی ضروری است، جایی که نمایش چرخشی جبر دروغ ( 1، 3) در داخل آن نشسته است. جبر کلیفورد معمولاً به جبر کلیفورد مختلط نیاز دارد. برای مرجع، جبر دروغ چرخشی توسط داده شده است
این در کنوانسیون (3، 1) است، بنابراین در Cl
3،1( R ) C . [18]
ماتریس دیراک اولین بار توسط پل دیراک نوشته شد، زمانی که او سعی داشت معادله موج مرتبه اول نسبیتی برای الکترون بنویسد ، و یک هم ریختی صریح از جبر کلیفورد به جبر ماتریس های مختلط بدهد. از نتیجه برای تعریف معادله دیراک و معرفی عملگر دیراک استفاده شد. کل جبر کلیفورد در نظریه میدان کوانتومی به شکل دو خطی میدان دیراک نشان داده می شود .
استفاده از جبرهای کلیفورد برای توصیف نظریه کوانتومی در میان دیگران توسط ماریو شونبرگ ، [19] توسط دیوید هستن از نظر حساب هندسی ، توسط دیوید بوم و باسیل هیلی و همکارانش در قالب سلسله مراتبی از جبرهای کلیفورد ، و توسط الیو کونته و همکاران [20] [21]
بینایی کامپیوتر [ ویرایش ]
جبرهای کلیفورد در مسئله تشخیص و طبقه بندی کنش در بینایی کامپیوتر به کار گرفته شده است. رودریگز و همکاران [22] یک جاسازی کلیفورد را برای تعمیم فیلترهای MACH سنتی به ویدئو (حجم فضایی-زمانی سه بعدی) و دادههای با ارزش برداری مانند جریان نوری پیشنهاد میکند. داده های با ارزش برداری با استفاده از تبدیل فوریه کلیفورد تجزیه و تحلیل می شوند. بر اساس این بردارها، فیلترهای عمل در حوزه فوریه کلیفورد سنتز می شوند و با استفاده از همبستگی کلیفورد، شناسایی اقدامات انجام می شود. نویسندگان اثربخشی تعبیه کلیفورد را با تشخیص اقداماتی که معمولاً در فیلمهای بلند کلاسیک و تلویزیون پخش ورزشی انجام میشوند، نشان میدهند.
کلیات [ ویرایش ]
- در حالی که این مقاله بر جبر کلیفورد از یک فضای برداری بر روی یک میدان تمرکز دارد، این تعریف بدون تغییر به یک مدول در هر حلقه واحد، انجمنی و جابجایی گسترش مییابد. [3]
- جبرهای کلیفورد ممکن است به شکلی بالاتر از درجه دوم در یک فضای برداری تعمیم داده شوند. [23]
همچنین ببینید [ ویرایش ]
- جبر فضای فیزیکی ، APS
- ساخت و ساز کیلی-دیکسون
- طبقه بندی جبرهای کلیفورد
- تحلیل کلیفورد
- مدول کلیفورد
- ساختار چرخش مختلط
- اپراتور دیراک
- جبر بیرونی
- هویت فیرز
- ماتریس های گاما
- جبر کلیفورد تعمیم یافته
- جبر هندسی
- ماتریس های گاما با ابعاد بالاتر
- عدد فوق مختلط
- اکتونیون
- Paravector
- کواترنیون
- گروه چرخش
- ساختار چرخش
- اسپینور
- بسته نرم افزاری اسپینور
منبع
https://en.wikipedia.org/wiki/Clifford_algebra
ضد اتومورفیسم [ ویرایش ]
علاوه بر اتومورفیسم α ، دو ضد اتومورفیسم وجود دارد که نقش مهمی در تجزیه و تحلیل جبرهای کلیفورد دارند. به یاد بیاورید که جبر تانسور T ( V ) دارای یک ضدخودمورفیسم است که ترتیب را در همه حاصل از بردارها معکوس می کند:
از آنجایی که IQ ایدهآل تحت این معکوس ثابت است، این عملیات به یک ضد اتومورفیسم Cl( V , Q ) نزول میکند که عمل انتقال یا معکوس نامیده میشود که با xt نشان داده میشود . انتقال یک ضد اتومورفیسم است: ( xy ) t = y t x t . عملیات جابجایی از درجه بندی Z 2 استفاده نمی کند، بنابراین ما یک ضد اتومورفیسم دوم را با ترکیب α و ترانهاده تعریف می کنیم. ما این عملیات را صرف کلیفورد می گوییم
از بین دو ضد اتومورفیسم، جابجایی اساسیتر است. [14]
توجه داشته باشید که همه این عملیاتها به صورت چرخشی هستند . می توان نشان داد که روی عناصری که در درجه بندی Z خالص هستند به صورت 1± عمل می کنند . در واقع، هر سه عملیات فقط به مدول درجه 4 بستگی دارند. یعنی اگر x با درجه k خالص باشد، پس
که در آن علائم توسط جدول زیر آورده شده است:
| k mod 4 | 0 | 1 | 2 | 3 | … |
|---|---|---|---|---|---|
 | + | - | + | - | (-1) k |
 | + | + | - | - | (-1) k ( k - 1)/2 |
 | + | - | - | + | (-1) k ( k + 1)/2 |
مثال: در ابعاد کوچک [ ویرایش ]
بگذارید K هر میدان مشخصه باشد نه 2 .
ابعاد 1 [ ویرایش ]
برای کم نور V = 1 ، اگر Q دارای دیاگ مورب ( a ) باشد، یعنی یک بردار غیرصفر x وجود دارد به طوری که Q ( x ) = a ، آنگاه Cl( V , Q ) جبر-ایزومورف به جبر K است . تولید شده توسط یک عنصر x که x^ 2 = a را برآورده می کند ، جبر درجه دوم K [ X ] / ( X^2 - a ) .
به طور خاص، اگر a = 0 (یعنی Q شکل درجه دوم صفر است) آنگاه Cl( V , Q ) جبر-ایزومورف به جبر اعداد دوگانه روی K است.
اگر a یک مربع غیر صفر در K باشد، آنگاه Cl( V , Q ) ≃ K ⊕ K .
در غیر این صورت، Cl( V , Q ) با پسوند میدان درجه دوم K ( √ a ) از K هم شکل است.
ابعاد 2 [ ویرایش ]
برای dim V = 2 ، اگر Q دارای دیاگ مورب ( a , b ) با غیر صفر a و b باشد (که اگر Q غیر منحط باشد همیشه وجود دارد )، آنگاه Cl( V , Q ) با جبر K ایجاد شده هم شکل است. توسط عناصر x و y که x 2 = a ، y 2 = b و xy = - yx را برآورده می کند.
بنابراین Cl( V , Q ) با جبر چهارتایی (تعمیم یافته) ( a , b ) K هم شکل است. زمانی که a = b = -1 ، ربعهای همیلتون را بازیابی میکنیم ، زیرا H = (-1، -1 ) R.
به عنوان یک مورد خاص، اگر مقداری x در V Q ( x ) = 1 را برآورده کند ، آنگاه Cl( V , Q ) ≃ M 2 ( K ) .
خواص [ ویرایش ]
ارتباط با جبر بیرونی [ ویرایش ]
با توجه به فضای برداری V ، می توان جبر خارجی ⋀ V را ساخت که تعریف آن مستقل از هر شکل درجه دوم روی V است. معلوم می شود که اگر K مشخصه 2 را نداشته باشد، یک هم ریختی طبیعی بین ⋀ V و Cl( V , Q ) وجود دارد که به عنوان فضاهای برداری در نظر گرفته می شوند (و یک هم شکلی در مشخصه دو وجود دارد که ممکن است طبیعی نباشد). این یک هم ریختی جبر است اگر و فقط اگر Q = 0 باشد. بنابراین می توان جبر کلیفورد را در نظر گرفت Cl( V , Q) به عنوان غنی سازی (یا دقیق تر، کوانتیزه کردن، رجوع کنید به مقدمه) جبر بیرونی در V با ضربی که به Q بستگی دارد (هنوز می توان محصول بیرونی را مستقل از Q تعریف کرد ).
ساده ترین راه برای ایجاد ایزومورفیسم این است که یک مبنای متعامد { e 1 , ... , e n } را برای V انتخاب کنید و آن را به پایه ای برای Cl( V , Q ) همانطور که در بالا توضیح داده شد گسترش دهید . نقشه Cl( V , Q ) → ⋀ V توسط
توجه داشته باشید که این فقط در صورتی کار می کند که مبنای { e 1 , ..., e n } متعامد باشد. می توان نشان داد که این نقشه مستقل از انتخاب مبنای متعامد است و بنابراین یک هم ریختی طبیعی به دست می دهد.
اگر مشخصه K 0 باشد ، می توان ایزومورفیسم را با ضد تقارن نیز تعیین کرد. توابع f k را تعریف کنید : V × ⋯ × V → Cl( V , Q ) توسط
که در آن مجموع بر گروه متقارن روی k عناصر، S k گرفته می شود. از آنجایی که f k متناوب است ، یک نقشه خطی منحصر به فرد را القا می کند ⋀ k V → Cl( V , Q ) . مجموع مستقیم این نقشه ها یک نقشه خطی بین ⋀ V و Cl( V , Q ) به دست می دهد. این نقشه را می توان یک هم ریختی خطی نشان داد و طبیعی است.
یک راه مختلط تر برای مشاهده رابطه، ساختن یک فیلتراسیون روی Cl( V , Q ) است. به یاد بیاورید که جبر تانسوری T ( V ) دارای فیلتراسیون طبیعی است: F 0 ⊂ F 1 ⊂ F 2 ⊂ ⋯ ، که در آن F k شامل مجموع تانسورها با مرتبه ≤ k است. با پیشبینی آن به جبر کلیفورد، یک فیلتر روی Cl( V , Q ) ایجاد میشود . جبر درجه بندی شده مرتبط
به طور طبیعی نسبت به جبر بیرونی هم شکل است ⋀ V. از آنجایی که جبر درجه بندی شده مربوط به یک جبر فیلتر شده همیشه با جبر فیلتر شده به عنوان فضاهای برداری فیلتر شده هم شکل است (با انتخاب مکمل های F k در F k + 1 برای همه k )، این یک هم شکلی (اگرچه نه طبیعی) در هر یک ارائه می دهد. مشخصه، حتی دو.
درجه بندی [ ویرایش ]
در ادامه فرض کنید که مشخصه 2 نباشد. [10]
جبرهای کلیفورد جبرهای درجه بندی Z 2 ( همچنین به عنوان ابرجبر شناخته می شوند ) هستند. در واقع، نقشه خطی روی V که با v ↦ − v ( بازتاب از طریق مبدأ ) تعریف شده است، شکل درجه دوم Q را حفظ می کند و بنابراین با خاصیت جهانی جبرهای کلیفورد به یک خودمورفیسم جبری گسترش می یابد.
از آنجایی که α یک چرخش است (یعنی مربع با هویت است )، می توان Cl( V ، Q ) را به فضاهای ویژه مثبت و منفی α تجزیه کرد.
جایی که
از آنجایی که α یک اتومورفیسم است، چنین است که:
که در آن بالانویس های پرانتزی مدول 2 خوانده می شوند. این به Cl( V , Q ) ساختار یک جبر با درجه بندی Z 2 می دهد . زیرفضای Cl [0] ( V , Q ) زیر جبری از Cl( V , Q ) را تشکیل می دهد که زیر جبر زوج نامیده می شود . زیرفضای Cl [1] ( V , Q ) قسمت فرد Cl( V , Q ) نامیده می شود .(این یک زیر جبر نیست). این درجه بندی Z 2 نقش مهمی در تحلیل و کاربرد جبرهای کلیفورد ایفا می کند. خودمورفیسم α را انحلال اصلی یا گرید می نامند . عناصری که در این درجه بندی Z 2 خالص هستند به سادگی زوج یا فرد هستند.
تذکر . در مشخصه not 2 فضای برداری زیرین Cl( V , Q ) یک درجه بندی N و یک درجه بندی Z را از هم شکلی متعارف با فضای برداری زیرین جبر بیرونی ⋀ V به ارث می برد . [11] توجه به این نکته مهم است که این فقط یک درجه بندی فضای برداری است . یعنی ضرب کلیفورد به N -grading یا Z- grading احترام نمی گذارد، فقط به Z 2 -grading احترام می گذارد: برای مثال اگر Q ( v ) ≠ 0 ، سپس v ∈ Cl .1 ( V , Q ) , اما v 2 ∈ Cl 0 ( V , Q ) , نه در Cl 2 ( V , Q ) . خوشبختانه، درجه بندی ها به روش طبیعی مرتبط هستند: Z 2 ≅ N / 2 N ≅ Z / 2 Z . علاوه بر این، جبر کلیفورد دارای فیلتر Z است:
درجه یک عدد کلیفورد معمولاً به درجه در درجه N اشاره دارد.
زیر جبر زوج Cl [0] ( V , Q ) جبر کلیفورد خود با جبر کلیفورد هم شکل است. [12] [13] اگر V مجموع مستقیم متعامد یک بردار a با هنجار غیرصفر Q ( a ) و یک زیرفضای U باشد، در آن صورت Cl [0] ( V , Q ) با Cl( U , - Q ( a ) هم شکل است. ) Q ) ، جایی که − Q (الف ) Q شکل Q است که به U متناهی شده و در - Q ( a ) ضرب می شود. به ویژه در مورد حقیقیات، این نشان می دهد که:
در حالت قطعی منفی، این یک شامل Cl 0، n -1 ( R ) ⊂ Cl 0، n ( R ) می دهد، که دنباله را گسترش می دهد.
R ⊂ C ⊂ H ⊂ H ⊕ H ⊂ ⋯
به همین ترتیب، در حالت مختلط، می توان نشان داد که زیر جبر زوج Cl n ( C ) نسبت به Cl n -1 ( C ) هم شکل است.
مثالها: ساختن کواترنیونها و کواترنیونهای دوگانه [ ویرایش ]
کواترنیون ها [ ویرایش ]
در این بخش، کواترنیون های همیلتون به عنوان جبر فرعی زوج جبر کلیفورد Cl 0,3 ( R ) ساخته شده است.
بگذارید فضای برداری V فضای سه بعدی حقیقی R 3 باشد و شکل درجه دوم Q منفی متریک اقلیدسی معمول باشد. سپس برای v , w در R 3 شکل دوخطی (یا حاصل ضرب اسکالر) داریم.
اکنون حاصلضرب کلیفورد بردارهای v و w را معرفی کنید
این فرمول از علامت منفی استفاده می کند، بنابراین مطابقت با کواترنیون ها به راحتی نشان داده می شود.
مجموعه ای از بردارهای واحد متعامد R 3 را به صورت e 1 ، e 2 و e 3 نشان دهید، سپس حاصلضرب کلیفورد روابط را به دست می دهد.
و
عنصر کلی جبر کلیفورد Cl 0,3 ( R ) توسط
ترکیب خطی عناصر درجه زوج Cl 0,3 ( R ) زیر جبر زوج Cl را تعریف می کند.[0]
0,3( R ) با عنصر کلی
عناصر پایه را می توان با عناصر پایه چهارگانه i , j , k as شناسایی کرد
که نشان می دهد که زیر جبر زوج Cl[0]
0,3( R ) جبر کواترنیونی حقیقی همیلتون است .
برای دیدن این، محاسبه کنید
و
سرانجام،
ربعات دوگانه [ ویرایش ]
در این بخش، کواترنیونهای دوگانه بهعنوان جبر زوج کلیفورد فضای چهاربعدی حقیقی با فرم درجه دوم منحط ساخته میشوند. [8] [9]
اجازه دهید فضای برداری V فضای چهار بعدی حقیقی R4 باشد ، و اجازه دهید شکل درجه دوم Q یک شکل منحط باشد که از متریک اقلیدسی در R3 به دست آمده است . برای v ، w در R 4 فرم دوخطی منحط را معرفی می کند
این محصول اسکالر منحط اندازهگیری فاصله را در R4 روی ابر صفحه R3 انجام میدهد .
حاصلضرب کلیفورد بردارهای v و w با استفاده از
توجه داشته باشید که علامت منفی برای ساده کردن مطابقت با کواترنیون ها معرفی شده است.
مجموعه ای از بردارهای واحد متعامد متقابل R 4 را به صورت e 1 , e 2 , e 3 و e 4 نشان دهید، سپس حاصلضرب کلیفورد روابط را به دست می دهد.
و
عنصر کلی جبر کلیفورد Cl( R 4 , d ) دارای 16 جزء است. ترکیب خطی عناصر درجه زوج، زیر جبر زوج Cl را تعریف می کند[0]
( R 4 , d ) با عنصر کلی
عناصر پایه را می توان با عناصر پایه چهارگانه i ، j ، k و واحد دوگانه ε به عنوان شناسایی کرد.
این مکاتبات Cl را فراهم می کند[0]
0،3،1( R ) با جبر چهارگانه دوگانه .
برای دیدن این، محاسبه کنید
و
مبادلات e 1 و e 4 علامت های متناوب را به تعداد دفعات زوج نشان می دهند و نشان می دهد که ε واحد دوتایی با عناصر پایه چهارتایی i , j و k حرکت می کند.
مثالها: جبرهای حقیقی و مختلط کلیفورد [ ویرایش ]
مهمترین جبرهای کلیفورد آنهایی هستند که بر روی فضاهای برداری حقیقی و مختلط مجهز به اشکال درجه دوم غیرمنحط هستند .
هر یک از جبرهای Cl p , q ( R ) و Cl n ( C ) با A یا A ⊕ A هم شکل هستند که در آن A یک حلقه ماتریس کامل با ورودی های R ، C یا H است. برای طبقه بندی کامل این جبرها طبقه بندی جبرهای کلیفورد را ببینید .
اعداد حقیقی [ ویرایش ]
نوشتار اصلی: جبر هندسی
جبرهای کلیفورد گاهی اوقات به عنوان جبرهای هندسی نیز شناخته می شوند که اغلب بر روی اعداد حقیقی هستند.
هر شکل درجه دوم غیر منحط در یک فضای بردار حقیقی با ابعاد متناهی معادل شکل مورب استاندارد است:
که در آن n = p + q بعد فضای برداری است. جفت اعداد صحیح ( p , q ) را امضای شکل درجه دوم می نامند . فضای برداری حقیقی با این شکل درجه دوم اغلب R p , q نشان داده می شود . جبر کلیفورد در R p , q را Cl p , q ( R ) نشان می دهند. نماد Cl n ( R ) به معنای Cl n ,0 ( R ) یا Cl 0, n (ر ) بسته به اینکه نویسنده فضاهای مثبت-معین یا منفی-معین را ترجیح می دهد.
یک مبنای استاندارد { e 1 , ..., e n } برای R p , q از n = p + q بردار متعامد متقابل تشکیل شده است که p آن مربع به +1 و q از کدام مربع به 1- است. بنابراین، جبر Cl p , q ( R ) دارای بردارهای p است که مربع آن به 1+ و q بردارهای آن مربع به 1- است.
چند مورد با ابعاد پایین عبارتند از:
- Cl 0,0 ( R ) به طور طبیعی با R هم شکل است زیرا هیچ بردار غیر صفر وجود ندارد.
- Cl 0,1 ( R ) یک جبر دوبعدی است که توسط e 1 ایجاد می شود و مربع آن برابر 1 است و جبری-ایزومورف به C است، میدان اعداد مختلط .
- Cl 0,2 ( R ) یک جبر چهار بعدی است که با {1, e 1 , e 2 , e 1 e 2 } پوشانده شده است. سه عنصر آخر همگی مربع به 1- و ضد جابجایی هستند، و بنابراین جبر نسبت به چهارتایی H هم شکل است.
- Cl 0,3 ( R ) یک جبر 8 بعدی ایزومورف به مجموع مستقیم H ⊕ H است .
اعداد مختلط [ ویرایش ]
همچنین می توان جبرهای کلیفورد را بر روی فضاهای برداری مختلط مطالعه کرد. هر فرم درجه دوم غیر منحط در فضای برداری مختلط با بعد n معادل فرم مورب استاندارد است.
بنابراین، برای هر بعد n ، تا ایزومورفیسم تنها یک جبر کلیفورد از یک فضای برداری مختلط با فرم درجه دوم غیر منحط وجود دارد. جبر کلیفورد را در C n با شکل درجه دوم استاندارد با Cl n ( C ) نشان خواهیم داد.
برای چند مورد اول شخص متوجه می شود که
- Cl 0 ( C ) ≅ C ، اعداد مختلط
- Cl 1 ( C ) ≅ C ⊕ C ، اعداد دو مختلط
- Cl 2 ( C ) ≅ M 2 ( C ) ، دو کواترنیون ها
که در آن M n ( C ) نشان دهنده جبر n × n ماتریس روی C است.
مبانی و ابعاد [ ویرایش ]
از آنجایی که V به شکل درجه دوم Q مجهز شده است ، در مشخصه نه برابر 2 ، پایه هایی برای V وجود دارد که متعامد هستند . یک پایه متعامد برای یک فرم دوخطی متقارن است
برای
هویت بنیادی کلیفورد دلالت بر این دارد که برای یک مبنای متعامد
برای
این کار دستکاری بردارهای پایه متعامد را بسیار ساده می کند. یک محصول داده شده است
اگر بعد V روی K n باشد و { e 1 , ..., e n } یک مبنای متعامد از ( V , Q ) باشد ، آنگاه Cl( V , Q ) با یک پایه بر روی K آزاد است.
حاصلضرب خالی ( k = 0 ) به عنوان عنصر هویت ضربی تعریف می شود . برای هر مقدار k n عنصر پایه وجود دارد، بنابراین بعد کل جبر کلیفورد برابر است
مقدمه و ویژگی های اساسی [ ویرایش ]
جبر کلیفورد یک جبر انجمنی واحد است که شامل و توسط فضای برداری V بر روی یک میدان K ، که در آن V به شکل درجه دوم Q مجهز شده است و توسط آن ایجاد می شود . جبر کلیفورد Cl( V , Q ) "آزادترین" جبر انجمنی واحدی است که توسط V با شرط [4] تولید می شود.
که در آن حاصلضرب سمت چپ جبر است و عدد 1 هویت ضربی آن است . ایده «آزادترین» یا «عمومی ترین» جبر بودن موضوع این هویت را می توان به طور رسمی از طریق مفهوم یک ویژگی جهانی بیان کرد ، همانطور که در زیر انجام می شود .
در جایی که V یک فضای برداری واقعی با ابعاد محدود است و Q غیر منحط است ، Cl( V ، Q ) ممکن است با برچسب Cl p , q ( R ) شناسایی شود ، که نشان میدهد V مبنای متعامد با عناصر p با ei 2 = دارد . +1 ، q با e i 2 = −1 ، و جایی که Rنشان می دهد که این جبر کلیفورد بیش از واقعیات است. یعنی ضرایب عناصر جبر اعداد واقعی هستند. این اساس را می توان با مورب متعامد یافت .
جبر آزاد تولید شده توسط V ممکن است به صورت جبر تانسور ⨁ n ≥0 V ⊗ ⋯ ⊗ V نوشته شود، یعنی مجموع حاصلضرب تانسور n کپی از V روی تمام n ، و بنابراین جبر کلیفورد ضریب خواهد بود. این جبر تانسور توسط ایده آل دو طرفه ایجاد شده توسط عناصر شکل v ⊗ v − Q ( v )1 برای همه عناصر v ∈ V. حاصل ضرب القا شده توسط حاصل ضرب تانسور در جبر ضریب با استفاده از کنار هم (مثلاً uv ) نوشته می شود. ارتباط آن از تداعی حاصلضرب تانسور ناشی می شود.
جبر کلیفورد دارای یک زیرفضای متمایز V است که تصویر نقشه جاسازی شده است. چنین فضای فرعی به طور کلی نمی تواند به طور منحصر به فرد تعیین شود تنها با توجه به جبر K- هم شکل به جبر کلیفورد .
اگر مشخصه میدان زمین K 2 نباشد ، می توان هویت بنیادی بالا را به شکل بازنویسی کرد.
جایی که
شکل دوخطی متقارن مرتبط با Q از طریق هویت قطبی است .
اشکال درجه دوم و جبرهای کلیفورد در مشخصه 2 یک مورد استثنایی را تشکیل می دهند. به طور خاص، اگر char( K ) = 2 باشد، این درست نیست که یک فرم درجه دوم به طور منحصر به فرد یک فرم دوخطی متقارن را تعیین می کند که Q ( v ) = 〈 v ، v 〉 را برآورده می کند، و نه اینکه هر شکل درجه دوم مبنای متعامد را قبول دارد . بسیاری از عبارات این مقاله شامل این شرط است که مشخصه 2 نیست و در صورت حذف این شرط نادرست است.
به عنوان کوانتیزه کردن جبر بیرونی [ ویرایش ]
جبرهای کلیفورد ارتباط نزدیکی با جبرهای بیرونی دارند. در واقع، اگر Q = 0 باشد، جبر کلیفورد Cl( V , Q ) فقط جبر بیرونی ⋀ V است. برای Q غیرصفر ، یک هم ریختی خطی متعارف بین ⋀ V و Cl( V , Q ) وجود دارد که هرگاه میدان زمین K مشخصه دو را نداشته باشد. یعنی به طور طبیعی هم شکل هستندبه عنوان فضاهای برداری، اما با ضرب های مختلف (در مورد مشخصه دو، آنها هنوز به عنوان فضاهای برداری هم شکل هستند، نه به طور طبیعی). ضرب کلیفورد همراه با زیرفضای متمایز کاملاً غنی تر از محصول بیرونی است زیرا از اطلاعات اضافی ارائه شده توسط Q استفاده می کند.
جبر کلیفورد یک جبر فیلتر شده است ، جبر درجه بندی شده مربوط به جبر بیرونی است.
به طور دقیقتر، جبرهای کلیفورد را میتوان بهعنوان کوانتیزهسازیهای جبر بیرونی (ر.ک. گروه کوانتومی ) در نظر گرفت، به همان شکلی که جبر ویل کوانتیزهسازی جبر متقارن است .
جبرهای ویل و جبرهای کلیفورد ساختار دیگری از جبر * را میپذیرند و میتوان آنها را بهعنوان جملههای زوج و فرد یک ابرجبر متحد کرد ، همانطور که در جبرهای CCR و CAR بحث شده است.
مالکیت جهانی و ساخت و ساز [ ویرایش ]
فرض کنید V یک فضای برداری روی یک فیلد K باشد، و اجازه دهید Q : V → K یک شکل درجه دوم روی V باشد. در بیشتر موارد مورد علاقه فیلد K یا میدان اعداد حقیقی R یا میدان اعداد مختلط C یا یک میدان متناهی است .
جبر کلیفورد Cl( V , Q ) یک جفت ( A , i ) است، [5] [6] که در آن A یک جبر انجمنی واحد بر K است و i یک نقشه خطی i است : V → Cl( V ، Q ) رضایت بخش است . i ( v ) 2 = Q ( v )1 برای همه v در V ، با موارد زیر تعریف می شودخاصیت جهانی : با توجه به هر جبر انجمنی واحد A روی K و هر نقشه خطی j : V → A به گونه ای که
(در جایی که 1 A نشان دهنده هویت ضربی A است)، یک هم شکل جبری منحصر به فرد f وجود دارد : Cl( V , Q ) → A به طوری که نمودار زیر تغییر می کند (یعنی به گونه ای که f ∘ i = j ) :
شکل درجه دوم Q را می توان با یک فرم دوخطی ( نه لزوما متقارن ) جایگزین کرد . _ _
وقتی مشخصه فیلد 2 نباشد ، ممکن است با چیزی که در آن صورت یک نیاز معادل است جایگزین شود.
که در آن شکل دو خطی ممکن است به متقارن بودن بدون از دست دادن کلیت محدود شود.
جبر کلیفورد همانطور که در بالا توضیح داده شد همیشه وجود دارد و می تواند به صورت زیر ساخته شود: با کلی ترین جبری که حاوی V است، یعنی جبر تانسور T ( V ) شروع کنید و سپس با گرفتن یک ضریب مناسب، هویت بنیادی را اعمال کنید . در مورد ما میخواهیم IQ ایدهآل دو طرفه را در T ( V ) که توسط همه عناصر شکل ایجاد میشود در نظر بگیریم.
برای همه
محصول حلقه ای که توسط این ضریب به ارث می رسد گاهی اوقات به عنوان محصول کلیفورد [7] نامیده می شود تا آن را از محصول بیرونی و محصول اسکالر متمایز کند.
سپس ساده است که نشان دهیم Cl( V , Q ) حاوی V است و خاصیت جهانی فوق را برآورده می کند، به طوری که Cl تا یک ایزومورفیسم منحصر به فرد منحصر به فرد است. بنابراین از "کلیفورد" جبر Cl( V , Q ) صحبت می شود. همچنین از این ساختار نتیجه می شود که i تزریقی است . معمولاً i را رها می کنیم و V را به عنوان زیرفضای خطی Cl( V , Q ) در نظر می گیریم .
توصیف جهانی جبر کلیفورد نشان میدهد که ساخت کل ( V , Q ) ماهیت کارکردی دارد . یعنی کلر را میتوان بهعنوان تابعی از دسته فضاهای برداری با فرمهای درجه دوم (که مورفیسم آنها نقشههای خطی با حفظ شکل درجه دوم هستند) تا دسته جبرهای انجمنی در نظر گرفت. ویژگی جهانی تضمین می کند که نقشه های خطی بین فضاهای برداری (با حفظ شکل درجه دوم) به طور منحصر به فردی به هم شکلی های جبر بین جبرهای کلیفورد مرتبط گسترش می یابد.
این مقاله در مورد جبر کلیفورد (متعامد) است. برای جبر ساده کلیفورد، جبر ویل را ببینید .
| ساختار جبری ← نظریه حلقه نظریه حلقه |
|---|
 |
| نشان می دهد مفاهیم اساسی |
| نشان می دهد |
| پنهان شدنحلقه های غیر جابجایی • کموتاتور جبر کلیفورد جبر اپراتور |
در ریاضیات ، جبر کلیفورد [a] جبری است که توسط یک فضای برداری با شکل درجه دوم ایجاد می شود و یک جبر انجمنی واحد است . آنها به عنوان جبرهای K ، اعداد حقیقی ، اعداد مختلط ، چهارتایی و چندین سیستم اعداد ابرمختلط دیگر را تعمیم می دهند . [1] [2] نظریه جبرهای کلیفورد ارتباط نزدیکی با نظریه اشکال درجه دوم و تبدیلهای متعامد دارد .. جبرهای کلیفورد کاربردهای مهمی در زمینه های مختلف از جمله هندسه ، فیزیک نظری و پردازش تصویر دیجیتال دارند. نام آنها از نام ریاضیدان انگلیسی ویلیام کینگدون کلیفورد گرفته شده است.
آشناترین جبرهای کلیفورد، جبرهای کلیفورد متعامد ، به عنوان جبرهای کلیفورد ( شبه ) ریمانی نیز شناخته می شوند، که از جبرهای کلیفورد متمایز است. [3]
فهرست
- 1مقدمه و خواص اساسی
- 2مالکیت جهانی و ساخت و ساز
- 3مبنا و بعد
- 4مثال: جبرهای واقعی و پیچیده کلیفورد
- 5مثال: ساختن کواترنیون و کواترنیون دوگانه
- 6مثال: در ابعاد کوچک
- 7خواص
- 8ساختار جبرهای کلیفورد
- 9گروه لیپ شیتز
- 10گروه های اسپین و پین
- 11اسپینورها
- 12برنامه های کاربردی
- 13تعمیم ها
- 14همچنین ببینید
- 15یادداشت
- 16منابع
- 17بیشتر خواندن
- 18لینک های خارجی
از ویکیپدیا، دانشنامه آزاد
در محاسبات کوانتومی و تئوری اطلاعات کوانتومی ، دروازه های کلیفورد عناصر گروه کلیفورد هستند ، مجموعه ای از تبدیل های ریاضی که بر جایگشت عملگرهای پائولی تأثیر می گذارد . این مفهوم توسط دانیل گوتسمن معرفی شد و به نام ریاضیدان ویلیام کینگدون کلیفورد نامگذاری شده است . [1] مدارهای کوانتومی که فقط از گیت های کلیفورد تشکیل شده اند را می توان به طور موثر با یک کامپیوتر کلاسیک به دلیل قضیه گوتسمن-کنیل شبیه سازی کرد .
فهرست
گروه کلیفورد [ ویرایش ]
تعریف [ ویرایش ]
ماتریس های پائولی ،
مبنایی را برای عملگرهای چگالی یک کیوبیت منفرد و همچنین برای واحدهایی که می توان برای آنها اعمال کرد، فراهم می کند. برای{\displaystyle n}
گروه کلیفورد به عنوان گروهی از واحدهایی که گروه پائولی را عادی می کنند تعریف می شود:
برخی از نویسندگان گروه کلیفورد را به عنوان گروه ضریب تعریف می کنند 


معلوم می شود [3] که گروه بهره














ژنراتورها [ ویرایش ]
گروه کلیفورد توسط سه گیت هادامار ، S و CNOT تولید می شود. [4] از آنجایی که همه ماتریسهای پائولی را میتوان از دروازههای فاز S و هادامارد ساخت، هر دروازه پائولی نیز بهطور بیاهمیت عنصری از گروه کلیفورد است.
این







دروازه هادامارد [ ویرایش ]
دروازه هادامارد
عضو گروه کلیفورد به عنوان 

دروازه اس [ ویرایش ]
دروازه فاز
یک دروازه کلیفورد است به عنوان

دروازه CNOT [ ویرایش ]
گیت CNOT برای دو کیوبیت اعمال می شود. بین

 | CNOT CNOT CNOT |
|---|---|
 |  |
 |  |
 |  |
 |  |
ویژگی ها و برنامه ها [ ویرایش ]
ترتیب دروازه های کلیفورد و دروازه های پائولی را می توان تعویض کرد. برای مثال، این را می توان با در نظر گرفتن عملگر زیر روی 2 کیوبیت نشان داد

ما آن را میدانیم: 

بنابراین A معادل است

شبیه سازی [ ویرایش ]
قضیه Gottesman–Knill بیان میکند که یک مدار کوانتومی با استفاده از عناصر زیر میتواند به طور موثر در یک کامپیوتر کلاسیک شبیهسازی شود:
- آماده سازی کیوبیت ها در حالت های پایه محاسباتی،
- دروازه های کلیفورد و
- اندازه گیری در مبنای محاسباتی
قضیه Gottesman–Knill نشان میدهد که حتی برخی از حالتهای بسیار درهمتنیده را میتوان به طور موثر شبیهسازی کرد. چندین نوع مهم از الگوریتمهای کوانتومی فقط از گیتهای کلیفورد استفاده میکنند که مهمترین آنها الگوریتمهای استاندارد برای تقطیر درهم تنیدگی و تصحیح خطای کوانتومی است .
ساخت مجموعه ای جهانی از دروازه های کوانتومی [ ویرایش ]
دروازه های کلیفورد یک مجموعه جهانی از دروازه های کوانتومی را تشکیل نمی دهند زیرا همه دروازه ها اعضای گروه کلیفورد نیستند و برخی از دروازه ها را نمی توان به طور دلخواه با مجموعه ای محدود از عملیات تقریب زد. به عنوان مثال، گیت تغییر فاز (که از لحاظ تاریخی به آن معروف است
![{\displaystyle T={\begin{bmatrix}1&0\\0&e^{i{\frac {\pi }{4}}}\end{bmatrix}}={\sqrt {S}}={\sqrt[{ 4}]{Z}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/13e0c3923c7a9e3d6242de77aee06aac27c77d71)
برای نشان دادن اینکه

با این حال، گروه کلیفورد، هنگامی که با
همچنین ببینید [ ویرایش ]
منبع
https://en.wikipedia.org/wiki/Clifford_gates
جدول 4.7 محاسبه معکوس ضربی ( x 7 + x + 1) mod ( x 8 + x 4 + x 3 + x + 1) را نشان می دهد. نتیجه این است که ( x 7 + x + 1) 1 = ( x 7 ). یعنی ( x 7 + x + 1) ( x 7 )
|
ملاحظات محاسباتی
یک چند جمله ای f ( x ) در GF( 2n )
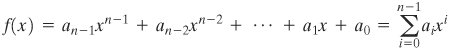
را می توان به طور منحصر به فرد با n ضرایب باینری آن ( a n 1 a n 2 ... a 0 ) نشان داد. بنابراین، هر چند جمله ای در GF( 2n ) را می توان با یک عدد n بیتی نشان داد.
[صفحه 125]
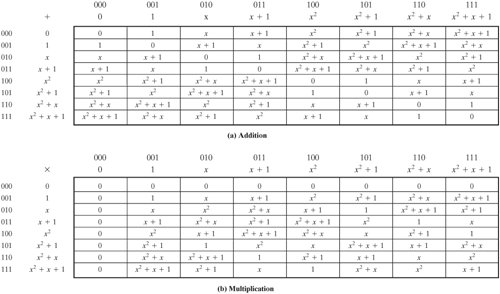
جداول 4.5 و 4.6 جداول جمع و ضرب را برای GF(2 3 ) مدول m ( x ) = ( x 3 + x + 1) نشان می دهد. جدول 4.5 از نمایش باینری و جدول 4.6 از نمایش چند جمله ای استفاده می کند. |
اضافه شدن
دیدیم که جمع چندجمله ای ها با جمع ضرایب متناظر انجام می شود و در مورد چندجمله ای های بیش از Z 2 جمع فقط عمل XOR است. بنابراین، جمع دو چند جمله ای در GF( 2n ) مربوط به عملیات XOR بیتی است.
دو چند جمله ای را در GF(2 8 ) از مثال قبلی ما در نظر بگیرید: f ( x ) = x 6 + x 4 + x 2 + x + 1 و g ( x ) = x 7 + x + 1.
|
ضرب
هیچ عملیات XOR ساده ای وجود ندارد که ضرب را در GF(2 n ) انجام دهد، با این حال، یک تکنیک نسبتاً ساده و به راحتی قابل پیاده سازی در دسترس است. ما این تکنیک را با ارجاع به GF(2 8 ) با استفاده از m ( x ) = x 8 + x 4 + x 3 + x + 1 مورد بحث قرار خواهیم داد، که میدان محدود مورد استفاده در AES است. این تکنیک به راحتی به GF( 2n ) تعمیم می یابد.
این تکنیک بر اساس مشاهده است که
معادله 4-8
![]()
[صفحه 126]
یک لحظه فکر باید شما را متقاعد کند که معادله (4.8) درست است. اگر نه، آن را تقسیم کنید. به طور کلی، در GF(2 n ) با یک چند جمله ای درجه n ام p ( x )، x n mod p ( x ) = [ p ( x ) x n ] داریم.
حال، چند جمله ای را در GF(2 8 ) در نظر بگیرید که به شکل f ( x ) = b 7 x 7 + b 6 x 6 + b 5 x 5 + b 4 x 4 + b 3 x 3 + b 2 x 2 است. + b 1 x + b 0 . اگر در x ضرب کنیم، داریم
معادله 4-9
![]()
اگر b 7 = 0، نتیجه یک چند جمله ای با درجه کمتر از 8 است که در حال حاضر به شکل کاهش یافته است و نیازی به محاسبه بیشتر نیست. اگر b 7 = 1، مدول کاهش m ( x ) با استفاده از رابطه (4.8) به دست می آید:
x x f ( x ) = ( b 6 x 7 + b 5 x 6 + b 4 x 5 + b 3 x 4 + b 2 x 3 +
b 1 x 2 + b 0 x ) + ( x 4 + x 3 + x + 1)
نتیجه می شود که ضرب در x (یعنی 00000010) می تواند به صورت یک شیفت چپ 1 بیتی و به دنبال آن یک XOR بیتی شرطی با (00011011) پیاده سازی شود که نشان دهنده ( x 4 + x 3 + x + 1) است. به طور خلاصه،
معادله 4-10
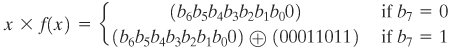
ضرب در توان بالاتر x را می توان با اعمال مکرر معادله (4.10) به دست آورد. با افزودن نتایج میانی، ضرب در هر ثابت در GF(2 8 ) میتوان به دست آورد.
در مثال قبلی نشان دادیم که برای f ( x ) = x 6 + x 4 + x 2 + x + 1، g ( x ) = x 7 + x + 1، و m ( x ) = x 8 + x 4 + x 3 + x + 1، f ( x ) x g ( x ) mod m ( x ) = x 7+ x 6 + 1. با انجام مجدد این کار در حساب باینری، باید (01010111) x (10000011) را محاسبه کنیم. ابتدا نتایج حاصل از ضرب در توان های x را تعیین می کنیم : (01010111) x (00000001) = (10101110) (01010111) x (00000100) = (01011100) (01010111) x (00001000) = (10001110) (01010111) x (00010000) = (00011100) (01010111) x (00100000) = (00001110) (01010111) x (01000000) = (00011100) (01010111) x (10000000) = (00111000) بنابراین، (01010111) x (10000011) = (01010111) x [(00000001) x (00000010) x (10000000)] = (01010111) که معادل x 7 + x 6 + 1 است. |
[صفحه 127]
استفاده از ژنراتور
یک تکنیک معادل برای تعریف یک میدان محدود به شکل GF( 2n ) با استفاده از همان چند جملهای تقلیلناپذیر، گاهی راحتتر است. برای شروع، ما به دو تعریف نیاز داریم: یک مولد g از یک میدان محدود F مرتبه q (شامل عناصر q ) عنصری است که اولین قدرتهای q 1 آن تمام عناصر غیر صفر F را تولید می کند. یعنی عناصر F از 0 تشکیل شده است. , g 0 , g 1 ,..., g q 2 . یک فیلد F را در نظر بگیرید که با یک چند جمله ای f ( x ) تعریف شده است. عنصر b موجود در F ریشه نامیده می شوداز چند جمله ای اگر f ( b ) = 0 باشد. در نهایت، می توان نشان داد که یک ریشه g از یک چند جمله ای تقلیل ناپذیر، مولد میدان متناهی است که روی آن چند جمله ای تعریف شده است.
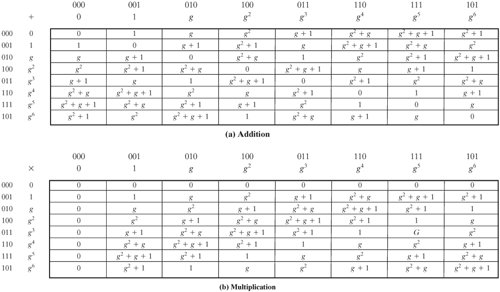
اجازه دهید میدان محدود GF(23) را در نظر بگیریم ، که بر روی چند جمله ای تقلیل ناپذیر x 3 + x + 1 تعریف شده است، که قبلاً بحث شد. بنابراین، مولد g باید f ( x ) = g 3 + g + 1 = 0 را برآورده کند. همانطور که قبلاً بحث شد، به خاطر داشته باشید که ما نیازی به یافتن یک راه حل عددی برای این برابری نداریم. بلکه با حساب چند جمله ای سروکار داریم که در آن محاسبات بر روی ضرایب مدول 2 انجام می شود. بنابراین، راه حل برابری قبلی g 3 = g 1 = g است.+ 1. اکنون نشان می دهیم که g در واقع همه چند جمله ای های درجه کمتر از 3 را تولید می کند. موارد زیر را داریم: g 4 = g ( g 3 ) = g ( g + 1) = g 2 + g g 5 = g ( g 4 ) = g ( g 2 + g ) = g 3 + g 2 = g 2 + g + 1 g 6 = g ( g 5 ) = g ( g 2 + g + 1 ) = g 3 + g 2 + g = g 2 + g + g + 1 = g 2 + 1 g 7 = g ( g 6 ) = g ( g 2 + 1) = g 3 + g = g + g + 1 = 1 = g 0 می بینیم که توان های g همه چند جمله ای های غیر صفر را در GF(2 3 ) تولید می کنند. همچنین، باید واضح باشد که g k = g k mod 7 برای هر عدد صحیح k . جدول 4.8 نمایش توان و همچنین نمایش های چند جمله ای و باینری را نشان می دهد.
این نمایش قدرت ضرب را آسان می کند. برای ضرب در نماد قدرت، نماهای مدول 7 را اضافه کنید. به عنوان مثال، g 4 x g 6 = g (10 mod 7) = g 3 = g + 1. همین نتیجه با استفاده از حساب چند جمله ای به دست می آید، به صورت زیر: g داریم 4 = g 2 + g و g 6 = g 2 + 1. سپس، ( g 2 + g ) x ( g 2 + 1) = g 4 + g 3+ g 2 + 1. سپس باید ( g 4 + g 3 + g 2 + 1) mod ( g 3 + g + 1) را با تقسیم تعیین کنیم: [صفحه 129]
نتیجه g + 1 را دریافت می کنیم که با نتیجه به دست آمده با استفاده از نمایش قدرت مطابقت دارد. جدول 4.9 جداول جمع و ضرب را برای GF(2 3 ) با استفاده از نمایش توان نشان می دهد. توجه داشته باشید که این نتایج یکسان با نمایش چند جمله ای (جدول 4.6) با تعویض برخی از سطرها و ستون ها به دست می دهد.
جدول 4.9. GF(2 3 ) محاسبات با استفاده از مولد برای چند جمله ای ( x 3 + x + 1) (این مورد در نسخه چاپی صفحه 128 نمایش داده شده است)
|
به طور کلی، برای GF( 2n ) با چند جمله ای تقلیل ناپذیر f ( x )، g n = f ( x ) g n را تعیین کنید. سپس تمام توان های g را از g n +1 تا g 2 n 2 محاسبه کنید. عناصر میدان با توان های g از تا g 2 n 2 به اضافه مقدار 0 مطابقت دارد. برای ضرب دو عنصر در میدان، از برابری g k = g k mod استفاده کنید (2n 1)برای هر عدد صحیحk.
خلاصه
در این بخش نحوه ساخت یک میدان محدود از مرتبه 2 n را نشان دادیم . به طور خاص، ما GF(2 n ) را با ویژگی های زیر تعریف کردیم:
GF(2 n ) از 2 n عنصر تشکیل شده است.
عملیات باینری + و x بر روی مجموعه تعریف می شوند. عملیات جمع، تفریق، ضرب و تقسیم را می توان بدون خروج از مجموعه انجام داد. هر عنصر از مجموعه غیر از 0 دارای یک معکوس ضرب است.
ما نشان دادیم که عناصر GF( 2n ) را می توان به عنوان مجموعه ای از همه چند جمله ای های درجه n 1 یا کمتر با ضرایب باینری تعریف کرد. هر چند جمله ای از این قبیل را می توان با یک مقدار n بیت منحصر به فرد نشان داد. حساب به عنوان مدول حسابی چند جمله ای چند جمله ای غیر قابل تقلیل درجه n تعریف می شود. همچنین دیدهایم که تعریف معادل یک میدان محدود GF( 2n ) از یک مولد استفاده میکند و حساب با استفاده از توانهای مولد تعریف میشود.
https://flylib.com/books/en/3.190.1.50/1/
[صفحه 121]
برای p = 3 و n = 2، چند جمله ای های 3 2 = 9 در مجموعه عبارتند از | ||
0 | ایکس | 2 x |
1 | x + 1 | 2 x + 1 |
2 | x + 2 | 2 x + 2 |
برای p = 2 و n = 3، 2 3 = 8 چند جمله ای های مجموعه هستند | ||
0 | x + 1 | x 2 + x |
1 | x 2 | x 2 + x + 1 |
ایکس | x 2 + 1 | |
با تعریف مناسب عملیات حسابی، هر مجموعه S یک میدان محدود است. این تعریف شامل عناصر زیر است:
[صفحه 122]
حساب از قواعد معمولی حساب چند جمله ای با استفاده از قواعد اساسی جبر پیروی می کند، با دو اصلاح زیر.
محاسبات روی ضرایب با مدول p انجام می شود . یعنی از قوانین حساب برای میدان محدود Z p استفاده می کنیم.
اگر ضرب منجر به یک چند جمله ای با درجه بزرگتر از n 1 شود، آنگاه چند جمله ای با مقداری چند جمله ای تقلیل ناپذیر m ( x ) درجه n کاهش می یابد . یعنی بر m ( x ) تقسیم می کنیم و باقی مانده را نگه می داریم. برای یک چند جمله ای f ( x )، باقیمانده به صورت r ( x ) = f ( x ) mod m ( x ) بیان می شود.
استاندارد رمزگذاری پیشرفته (AES) از حساب در میدان محدود GF(2 8 ) با چند جمله ای تقلیل ناپذیر m ( x ) = x 8 + x 4 x 3 + x + 1 استفاده می کند. دو چند جمله ای f ( x ) = x را در نظر بگیرید. 6 + x 4 + x 2 + x + 1 و g ( x ) = x 7 + x + 1. سپس f ( x ) + g ( x ) = x 6 + x 4 x 2 + x + 1 + x 7 + x + 1 f ( x ) x g ( x ) = x 13 + x 11 + x 9 + x 8 + x 7 + x 7 + x 5 + x 3 + x 2 + x + x 6 + x 4 + x 2 + x + 1 = x 13 + x 11 + x 9 + x 8 + x 6 + x 5 + x 4 + x 3 + 1
بنابراین، f ( x ) x g ( x ) mod m ( x ) = x 7 + x 6 + 1. |
مانند محاسبات مدولار معمولی، ما مفهوم مجموعه ای از باقیمانده ها را در محاسبات چند جمله ای مدولار داریم . مجموعه ای از باقیمانده های مدول m ( x )، یک چند جمله ای درجه n ، از pn عنصر تشکیل شده است . هر یک از این عناصر با یکی از p n چند جمله ای درجه m < n نشان داده می شود.
کلاس باقیمانده [ x + 1]، مدول m ( x )، از همه چند جمله ای های a ( x ) تشکیل شده است به طوری که a ( x ) |
می توان نشان داد که مجموعه همه چند جمله ای ها با مدول n ام درجه چند جمله ای m ( x ) بدیهیات شکل 4.1 را برآورده می کند و بنابراین یک میدان محدود را تشکیل می دهد. علاوه بر این، تمام میدان های محدود یک مرتبه معین هم شکل هستند. یعنی هر دو ساختار میدان محدود از یک مرتبه معین ساختار یکسانی دارند، اما نمایش یا برچسبهای عناصر ممکن است متفاوت باشد.
[صفحه 123]
برای ساختن میدان محدود GF(2 3 )، باید یک چند جملهای تقلیلناپذیر درجه 3 انتخاب کنیم. تنها دو چند جملهای از این قبیل وجود دارد: ( x3 + x 2 + 1 ) و ( x3 + x + 1 ). با استفاده از دومی، جدول 4.6 جداول جمع و ضرب را برای GF(2 3 ) نشان می دهد. توجه داشته باشید که این مجموعه جداول ساختاری مشابه با جدول 4.5 دارد. بنابراین، ما موفق شده ایم راهی برای تعریف یک فیلد مرتبه 2 3 پیدا کنیم.
جدول 4.6. مدول حسابی چند جمله ای ( x 3 + x + 1) (این مورد در نسخه چاپی صفحه 124 نمایش داده شده است)
|
پیدا کردن معکوس ضربی
همانطور که الگوریتم اقلیدسی را می توان برای یافتن بزرگترین مقسوم علیه مشترک دو چند جمله ای تطبیق داد، الگوریتم اقلیدسی توسعه یافته را نیز می توان برای یافتن معکوس ضربی یک چند جمله ای تطبیق داد. به طور خاص، اگر درجه b ( x ) کمتر از درجه m ( x ) و gcd[ m ( x )، b ( x )] باشد ، الگوریتم معکوس ضربی b ( x ) مدول m ( x ) را پیدا خواهد کرد. = 1. اگر m ( x ) یک چند جملهای تقلیلناپذیر باشد، هیچ عاملی جز خودش یا 1 ندارد، به طوری که gcd[ m( x )، b ( x )] = 1. الگوریتم به شرح زیر است:
EXTENDED EUCLID[ m ( x ), b ( x )]
1. [A1( x ), A2( x ), A3( x )]  [1, 0, x )]; [B1( x )، B2( x )، B3( x )]
[1, 0, x )]; [B1( x )، B2( x )، B3( x )]  [0، 1، x )]
2.
اگر B3( x ) = 0 A3( x ) = gcd[ m ( x )، b ( x ) را برگردانید . ]؛ بدون معکوس 3.
اگر B3( x ) = 1 بازگشت B3( x ) = gcd[ m ( x )، b ( x )]; B2( x ) = b ( x ) 1 mod m ( x )
4. Q(x) = ضریب A3( x )/B3( x )
5. [T1( x )، T2( x )، T3( x ) ]
[0، 1، x )]
2.
اگر B3( x ) = 0 A3( x ) = gcd[ m ( x )، b ( x ) را برگردانید . ]؛ بدون معکوس 3.
اگر B3( x ) = 1 بازگشت B3( x ) = gcd[ m ( x )، b ( x )]; B2( x ) = b ( x ) 1 mod m ( x )
4. Q(x) = ضریب A3( x )/B3( x )
5. [T1( x )، T2( x )، T3( x ) ]  [A1( x )B1( x )، A2( x ) Q( x )B2( x )، A3( x ) QB3( x )]
6. [A1( x )، A2( x )، A3( x )]
[A1( x )B1( x )، A2( x ) Q( x )B2( x )، A3( x ) QB3( x )]
6. [A1( x )، A2( x )، A3( x )]  [B1( x )، B3( x )]
7. [B1( x )، B2( x )، B3( x )]
[B1( x )، B3( x )]
7. [B1( x )، B2( x )، B3( x )]  [T1( x )، T3( x )]
8. goto 2
[T1( x )، T3( x )]
8. goto 2
رم GF(2n)
[صفحه 119 (ادامه)] 4.6. فیلدهای محدود فرم GF(2 n )قبلاً در این فصل اشاره کردیم که ترتیب یک میدان محدود باید به شکل p n باشد که در آن p یک عدد اول و n یک عدد صحیح مثبت است. در بخش 4.4، ما به حالت خاص فیلدهای محدود با ترتیب p نگاه کردیم . ما دریافتیم که با استفاده از محاسبات مدولار در Z p ، همه بدیهیات یک فیلد (شکل 4.1) برآورده می شوند. برای چند جمله ای های بیش از p n ، با n > 1، عملیات مدول p n میدانی تولید نمی کند. در این بخش، ما نشان میدهیم که چه ساختاری بدیهیات یک میدان را در مجموعهای با عناصر p n برآورده میکند و روی GF( 2n ) تمرکز میکنیم. انگیزه تقریباً همه الگوریتمهای رمزگذاری، اعم از متقارن و کلید عمومی، شامل عملیات حسابی روی اعداد صحیح هستند. اگر یکی از عملیاتی که در الگوریتم استفاده می شود تقسیم است، باید به صورت حسابی تعریف شده روی یک فیلد کار کنیم. برای راحتی و کارایی پیادهسازی، ما همچنین میخواهیم با اعداد صحیحی کار کنیم که دقیقاً در تعداد معینی از بیتها قرار میگیرند، بدون الگوهای بیت تلف شده. یعنی ما می خواهیم با اعداد صحیح در محدوده 0 تا 2 n 1 کار کنیم که در یک کلمه n بیتی قرار می گیرند.
همانطور که مثال قبل اشاره می کند، اگر قرار باشد از تمام عملیات های حسابی استفاده شود، و بخواهیم طیف کاملی از اعداد صحیح را در n بیت نمایش دهیم، مدول حسابی کار نخواهد کرد. به طور معادل، مجموعه اعداد صحیح مدول 2 n ، برای n > 1، یک فیلد نیست. علاوه بر این، حتی اگر الگوریتم رمزگذاری فقط از جمع و ضرب استفاده کند، اما از تقسیم استفاده نمی کند، استفاده از مجموعه Z 2 n مشکوک است، همانطور که مثال زیر نشان می دهد. [صفحه 120]
به طور شهودی، به نظر میرسد که الگوریتمی که اعداد صحیح را بهطور ناهموار بر روی خودشان نگاشت میکند، ممکن است از نظر رمزنگاری ضعیفتر از الگوریتمی باشد که یک نقشهبرداری یکنواخت ارائه میدهد. بنابراین، میدان های محدود فرم GF( 2n ) برای الگوریتم های رمزنگاری جذاب هستند. به طور خلاصه، ما به دنبال مجموعه ای متشکل از 2 n عنصر، همراه با تعریف جمع و ضرب بر روی مجموعه ای هستیم که یک فیلد را تعریف می کند. ما می توانیم یک عدد صحیح منحصر به فرد در محدوده 0 تا 2 n 1 به هر عنصر مجموعه اختصاص دهیم. به خاطر داشته باشید که ما از محاسبات مدولار استفاده نخواهیم کرد، زیرا دیدیم که این منجر به یک فیلد نمی شود. در عوض، نشان خواهیم داد که چگونه محاسبات چند جمله ای وسیله ای را برای ساخت میدان مورد نظر فراهم می کند. حسابی چند جمله ای مدولار مجموعه S همه چند جمله ای های درجه n 1 یا کمتر را در میدان Z p در نظر بگیرید. بنابراین، هر چند جمله ای شکلی دارد
که در آن هر a i مقداری در مجموعه {0, 1,..., p 1} می گیرد. در مجموع p n چند جمله ای مختلف در S وجود دارد. |
از قضیه استفاده کنیم که به ما میگوید حلقهF [ x ]m ( x )رایک میدان است اگر و فقط اگرm ( x )تحویل ناپذیر است این به طور کلی آسان نیست - اگر درجهm ( x )بالا است، این کار به مقدار زیادی کار دستی نیاز دارد
خوشبختانه، معمولاً از ما خواسته می شود که این را با آن نشان دهیمm ( x )دارای درجه 2 یا 3. در این مورد، می توانیم از نتیجه 5.29 (یک چند جمله ای) استفاده کنیم.m ( x )درجه 2 یا 3 در یک میدان تحویل ناپذیر است اگر و فقط اگر ریشه نداشته باشد).
همه مقادیر ممکن را وارد می کنیم یعنی به آن ارزیابی می شود
A=Z5[x]/(x^2+4)
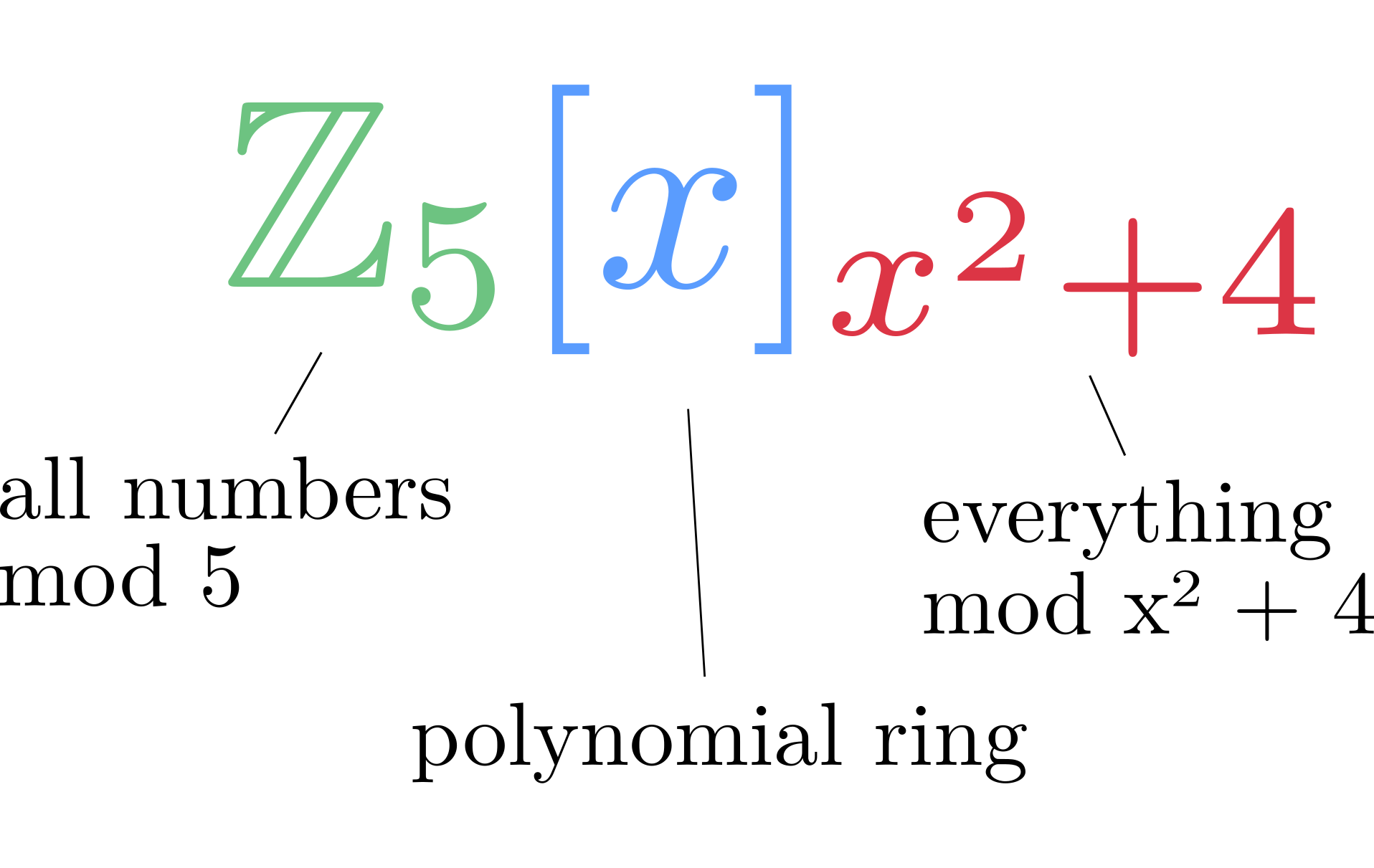
m(0)=0^2+4=4
m(1)=1^2+4=0
m(2)=2^2+4=3
m(3)=3^2+4=3
m(4)=4^2+4=0
بنابراین
x^2+4=(x−1)(x−4)=(x+4)(x+1)
بنابراین میدان نیست
منبع
https://xyquadrat.ch/2020/12/19/is-polynomial-ring-field/
کلاس های همخوانی[ ویرایش ]
مانند هر رابطه تطابقی، مدول همخوانی n یک رابطه هم ارزی است و کلاس هم ارزی عدد صحیح a که با a n نشان داده می شود مجموعه {... , a − 2 n , a − n , a , a + n است. a + 2 n , ... }. این مجموعه که از تمام اعداد صحیح متجانس با یک مدول n تشکیل شده است، کلاس همخوانی ، کلاس باقیمانده یا به سادگی باقی مانده نامیده می شود.از عدد صحیح a پیمانه n . هنگامی که مدول n از متن شناخته می شود، آن باقیمانده نیز ممکن است [ a ] نشان داده شود .
سیستم های باقی مانده [ ویرایش ]
هر کلاس باقیمانده مدول n ممکن است توسط هر یک از اعضای آن نمایش داده شود، اگرچه ما معمولاً هر کلاس باقیمانده را با کوچکترین عدد صحیح غیر منفی که به آن کلاس تعلق دارد نشان می دهیم [2] (زیرا این باقیمانده مناسبی است که از تقسیم حاصل می شود). هر دو عضو از کلاس های باقیمانده مختلف مدول n، مدول n ناهمخوان هستند . علاوه بر این، هر عدد صحیح متعلق به یک و تنها یک کلاس باقیمانده پیمانه n است. [3]
مجموعه اعداد صحیح {0, 1, 2, ..., n − 1 } را کمترین سیستم باقیمانده پیمانه n می نامند . به هر مجموعه ای از n عدد صحیح که هیچ دوتای آن ها مدول n متجانس نیستند ، سیستم باقیمانده کامل مدول n نامیده می شود .
سیستم کمترین باقیمانده یک سیستم باقیمانده کامل است و یک سیستم باقیمانده کامل به سادگی مجموعهای است که دقیقاً شامل یک نماینده از هر کلاس باقیمانده مدول n است. [4] به عنوان مثال. کمترین مقدار باقیمانده سیستم مدول 4 {0، 1، 2، 3} است. برخی دیگر از سیستم های باقیمانده کامل مدول 4 عبارتند از:
- {1، 2، 3، 4}
- {13، 14، 15، 16}
- {−2، −1، 0، 1}
- {−13، 4، 17، 18}
- {−5، 0، 6، 21}
- {27، 32، 37، 42}
برخی از مجموعه هایی که مدول 4 سیستم باقیمانده کامل نیستند عبارتند از:
- {−5، 0، 6، 22}، زیرا 6 با 22 مدول 4 همخوانی دارد.
- {5، 15}، زیرا یک مدول سیستم باقیمانده کامل 4 باید دقیقاً 4 کلاس باقیمانده ناهمخوان داشته باشد.
سیستم های باقیمانده کاهش یافته [ ویرایش ]
مقاله اصلی: سیستم باقیمانده کاهش یافته
با توجه به تابع اویلر φ( n ) , هر مجموعه ای از اعداد صحیح φ( n ) که نسبتاً اول با n هستند و تحت مدول n متقابلاً ناهمخوان هستند، مدول سیستم باقیمانده کاهش یافته n نامیده می شود . [5] مجموعه {5،15} از بالا، برای مثال، نمونهای از مدول 4 سیستم باقیمانده کاهشیافته است.
مدول n اعداد صحیح [ ویرایش ]
مجموعه تمام طبقات همخوانی اعداد صحیح برای مدول n حلقه اعداد صحیح مدول n نامیده می شود ، [6] و نشان داده می شود.




مجموعه برای n > 0 به صورت زیر تعریف می شود:
(وقتی n = 0 ،

جمع، تفریق و ضرب را بر روی تعریف می کنیم
تأیید اینکه این یک تعریف مناسب است، از ویژگی های ارائه شده قبل استفاده می کند.
به این ترتیب،

همانطور که در حساب برای ساعت 24 ساعته.
ما از علامت گذاری استفاده می کنیم





این نیز می تواند از گروه ساخته شود

به جای حذف حالت خاص n = 0 ، استفاده از آن مفیدتر است

حلقه اعداد صحیح مدول n یک میدان متناهی است اگر و فقط اگر n اول باشد (این تضمین می کند که هر عنصر غیر صفر دارای یک معکوس ضربی است ). اگر


زیر گروه ضربی اعداد صحیح پیمانه n با نشان داده می شود


بسط اعداد واقعی [ ویرایش ]
همچنین ببینید: عملیات ماژول
این بخش خالی است شما می توانید با اضافه کردن به آن کمک کنید . ( ژوئیه 2022 ) |
برنامه های کاربردی [ ویرایش ]
در ریاضیات نظری، حساب مدولار یکی از پایههای نظریه اعداد است که تقریباً بر همه جنبههای مطالعه آن تأثیر میگذارد، و همچنین در نظریه گروه ، نظریه حلقه ، نظریه گره و جبر انتزاعی بهطور گسترده استفاده میشود . در ریاضیات کاربردی، در جبر کامپیوتر ، رمزنگاری ، علوم کامپیوتر ، شیمی و هنرهای تجسمی و موسیقی استفاده می شود.
یک کاربرد بسیار عملی، محاسبه جمعهای چک در شناسههای شماره سریال است. به عنوان مثال، شماره کتاب استاندارد بینالمللی (ISBN) از مدول 11 (برای شابک 10 رقمی) یا مدول 10 (برای ISBN 13 رقمی) برای تشخیص خطا استفاده میکند. به همین ترتیب، برای مثال، شماره حساب های بانکی بین المللی (IBAN) از محاسبات مدول 97 برای تشخیص خطاهای ورودی کاربر در شماره حساب های بانکی استفاده می کند. در شیمی، آخرین رقم شماره ثبت CAS (یک شماره شناسایی منحصر به فرد برای هر ترکیب شیمیایی) یک رقم چک است.که با گرفتن آخرین رقم از دو قسمت اول شماره رجیستری CAS برابر 1، رقم قبلی ضربدر 2، رقم قبلی ضربدر 3 و غیره، جمع کردن همه اینها و محاسبه مجموع مدول 10 محاسبه می شود.
در رمزنگاری، محاسبات مدولار مستقیماً زیربنای سیستمهای کلید عمومی مانند RSA و Diffie-Hellman است و زمینههای محدودی را فراهم میکند که زیربنای منحنیهای بیضوی قرار دارند و در انواع الگوریتمهای کلید متقارن از جمله استاندارد رمزگذاری پیشرفته ( AES)، الگوریتم رمزگذاری بینالمللی داده استفاده میشود. IDEA)، و RC4 . RSA و Diffie-Hellman از توان مدولار استفاده می کنند.
در جبر کامپیوتری، معمولاً از محاسبات مدولار برای محدود کردن اندازه ضرایب صحیح در محاسبات و دادههای میانی استفاده میشود. از آن در فاکتورسازی چند جمله ای استفاده می شود ، مسئله ای که همه الگوریتم های کارآمد شناخته شده برای آن از محاسبات مدولار استفاده می کنند. این توسط کارآمدترین پیاده سازی های چند جمله ای بزرگترین مقسوم علیه مشترک ، جبر خطی دقیق و الگوریتم های پایه گروبنر بر روی اعداد صحیح و اعداد گویا استفاده می شود. همانطور که در Fidonet در دهه 1980 ارسال شد و در Rosetta Code بایگانی شد ، از محاسبات مدولار برای رد فرضیه مجموع توان های اویلر در میکروکامپیوتر QL Sinclair استفاده شد. با استفاده از تنها یک چهارم دقت اعداد صحیح مورد استفاده توسط یک ابررایانه CDC 6600 برای رد آن دو دهه قبل از طریق جستجوی brute force . [9]
در علوم کامپیوتر، محاسبات مدولار اغلب در عملیات بیتی و سایر عملیاتهایی که شامل ساختارهای داده چرخهای با عرض ثابت هستند، به کار میرود . عملیات مدول ، همانطور که در بسیاری از زبان های برنامه نویسی و ماشین حساب ها پیاده سازی می شود ، یک کاربرد از محاسبات مدولار است که اغلب در این زمینه استفاده می شود. عملگر منطقی XOR 2 بیت، مدول 2 را جمع می کند.
در موسیقی، مدول حسابی 12 برای در نظر گرفتن سیستم خلق و خوی مساوی دوازده تنی ، که در آن اکتاو و هم ارزی هماهنگ رخ می دهد، استفاده می شود (یعنی زیر و بمی ها در نسبت 1:2 یا 2:1 معادل هستند، و C- شار برابر است. همان D- Flat در نظر گرفته می شود ).
روش بیرون ریختن نه ها ، بررسی سریع محاسبات حسابی اعشاری انجام شده با دست را ارائه می دهد. این بر اساس مدول حسابی مدولار 9 است، و به طور خاص بر روی خاصیت حیاتی که 10 ≡ 1 (mod 9) است.
مدول حسابی 7 در الگوریتم هایی استفاده می شود که روز هفته را برای یک تاریخ معین تعیین می کند. به طور خاص، تطابق زلر و الگوریتم روز قیامت به شدت از محاسبات مدولو-7 استفاده می کنند.
به طور کلی تر، حساب مدولار در رشته هایی مانند حقوق (مثلاً تقسیم بندی )، اقتصاد (مثلاً نظریه بازی ) و سایر حوزه های علوم اجتماعی کاربرد دارد، که در آن تقسیم و تخصیص متناسب منابع، بخش مرکزی تحلیل را ایفا می کند.
پیچیدگی محاسباتی [ ویرایش ]
از آنجایی که محاسبات مدولار دارای چنین طیف وسیعی از کاربردها است، مهم است که بدانیم حل یک سیستم همخوانی چقدر سخت است. یک سیستم خطی از همخوانی ها را می توان در زمان چند جمله ای با شکلی از حذف گاوسی حل کرد. برای جزئیات بیشتر به قضیه همخوانی خطی مراجعه کنید . الگوریتمهایی مانند کاهش مونتگومری نیز وجود دارند که به عملیاتهای ساده حسابی مانند ضرب و مدول توان n اجازه میدهند تا به طور موثر بر روی اعداد بزرگ انجام شوند.
برخی از عملیات، مانند یافتن یک لگاریتم گسسته یا یک تطابق درجه دوم ، به نظر می رسد به سختی فاکتورسازی اعداد صحیح هستند و بنابراین نقطه شروعی برای الگوریتم های رمزنگاری و رمزگذاری هستند. این مشکلات ممکن است NP-intermediate باشند.
حل یک سیستم معادلات حسابی مدولار غیر خطی NP-complete است. [10]
نمونه های پیاده سازی [ ویرایش ]
| این بخش احتمالاً حاوی تحقیقات اصلی است . لطفاً با تأیید ادعاهای مطرح شده و افزودن نقلقولهای درون خطی ، آن را بهبود ببخشید . اظهاراتی که فقط شامل تحقیقات اصلی است باید حذف شوند. ( مه 2020 ) ( با نحوه و زمان حذف این پیام الگو آشنا شوید ) |
در زیر سه تابع C نسبتاً سریع وجود دارد، دو تابع برای انجام ضرب مدولار و یکی برای توان مدولار در اعداد صحیح بدون علامت بزرگتر از 63 بیت، بدون سرریز عملیات گذرا.
روشی الگوریتمی برای محاسبه
uint64_t mul_mod ( uint64_t a , uint64_t b , uint64_t m ) {
اگر ( ! (( a | b ) & ( 0xFFFFFFFFULL << 32 )) ) a * b % m ;
uint64_t d = 0 , mp2 = m >> 1 ;
int i ;
if ( a >= m ) a %= m ;
اگر ( b >= m ) b %= m ;
برای ( i = 0 ; i < 64 ; ++ i ) {
d = ( d > mp2 ) ? ( d << 1 ) - m : d << 1 ;
اگر ( a & 0x800000000000000ULL ) d += b ;
اگر ( d >= m ) d -= m ;
a <<= 1 ;
}
بازگشت d ;
}
در معماریهای رایانهای که در آن یک قالب دقیق گسترده با حداقل 64 بیت مانتیس موجود است (مانند نوع طولانی دوتایی اکثر کامپایلرهای x86 C)، روال زیر [ توضیحات لازم است ] ، با استفاده از ترفندی که توسط سختافزار، شناور است. ضرب نقطه منجر به مهمترین بیتهای حاصل در نگهداری میشود، در حالی که ضرب اعداد صحیح باعث میشود کمترین بیتهای مهم حفظ شوند: [ نیازمند منبع ]
uint64_t mul_mod ( uint64_t a , uint64_t b , uint64_t m ) {
x طولانی دوبل ;
uint64_t c ;
int64_t r ;
if ( a >= m ) a %= m ;
اگر ( b >= m ) b %= m ;
x = a ;
c = x * b / m ;
r = ( int64_t )( a * b - c * m ) % ( int64_t ) m ;
برگردانید r < 0 ? r + m : r ;
}
در زیر یک تابع C برای انجام توان مدولار وجود دارد که از تابع mul_mod پیاده سازی شده در بالا استفاده می کند.
روشی الگوریتمی برای محاسبه
uint64_t pow_mod ( uint64_t a , uint64_t b , uint64_t m ) {
uint64_t r = m == 1 ? 0 : 1 ;
در حالی که ( b > 0 ) {
if ( b & 1 ) r = mul_mod ( r , a , m );
b = b >> 1 ;
a = mul_mod ( a , a , m );
}
بازگشت r ;
}
با این حال، برای اینکه همه روال های بالا کار کنند، m نباید از 63 بیت تجاوز کند.
همچنین ببینید [ ویرایش ]
- حلقه بولی
- بافر دایره ای
- بخش (ریاضی)
- میدان محدود
- نماد افسانه
- توان مدولار
- مدول (ریاضیات)
- گروه ضربی از اعداد صحیح پیمانه n
- دوره پیزانو (دنباله های فیبوناچی مدول n )
- ریشه اولیه پیمانه n
- متقابل درجه دوم
- باقیمانده درجه دوم
- بازسازی منطقی (ریاضیات)
- سیستم باقیمانده کاهش یافته
- حسابی شماره سریال (مورد خاصی از محاسبات مدولار)
- جبر بولی دو عنصری
- موضوعات مربوط به نظریه گروه در پشت محاسبات مدولار:
- سایر قضایای مهم مربوط به محاسبات مدولار:
- قضیه کارمایکل
- قضیه باقی مانده چینی
- قضیه اویلر
- قضیه کوچک فرما (مورد خاص قضیه اویلر)
- قضیه لاگرانژ
- Thue's lemma
منبع
https://en.wikipedia.org/wiki/Modular_arithmetic
از ویکیپدیا، دانشنامه آزاد
این مقاله در مورد نماد (mod n ) است. برای عملیات باینری mod( a,n ) به عملیات مدولو مراجعه کنید .
زمان سنجی در این ساعت از مدول حسابی 12 استفاده می کند. با افزودن 4 ساعت به ساعت 9 ساعت 1 به دست می آید، زیرا 13 با 1 مدول 12 مطابقت دارد.
در ریاضیات ، محاسبات مدولار یک سیستم حسابی برای اعداد صحیح است ، که در آن اعداد با رسیدن به مقدار معینی که مدول نامیده میشود، در اطراف خود قرار میگیرند. رویکرد مدرن به حساب مدولار توسط کارل فردریش گاوس در کتاب Disquisitiones Arithmeticae که در سال 1801 منتشر شد، توسعه یافت.
یک کاربرد آشنا از محاسبات مدولار در ساعت 12 ساعته است که در آن روز به دو دوره 12 ساعته تقسیم می شود. اگر الان ساعت 7:00 است، 8 ساعت بعد ساعت 3:00 خواهد بود. جمع ساده منجر به 7 + 8 = 15 می شود ، اما ساعت ها هر 12 ساعت به دور خود می پیچند. از آنجایی که عدد ساعت با رسیدن به 12 از صفر شروع می شود، این مدول حسابی 12 است. از نظر تعریف زیر، 15 مطابق با 3 مدول 12 است، بنابراین "15:00" در ساعت 24 ساعته "3" نمایش داده می شود. :00 اینچ در یک ساعت 12 ساعته.
فهرست
- 1تجانس
- 2خواص
- 3کلاس های همخوانی
- 4سیستم های باقی مانده
- 5اعداد صحیح modulo n
- 6گسترش به اعداد واقعی
- 7برنامه های کاربردی
- 8پیچیدگی محاسباتی
- 9نمونه اجراها
- 10همچنین ببینید
- 11یادداشت
- 12منابع
- 13لینک های خارجی
همخوانی [ ویرایش ]
با توجه به یک عدد صحیح n > 1 که مدول نامیده می شود ، به دو عدد صحیح a و b گفته می شود که مدول n متجانس هستند، اگر n مقسوم علیه تفاوت آنها باشد (یعنی اگر یک عدد صحیح k وجود داشته باشد به طوری که a - b = kn باشد ). .
مدول همگامی n یک رابطه هم ارزی است، به این معنی که یک رابطه هم ارزی است که با عملیات جمع ، تفریق و ضرب سازگار است . مدول همخوانی n نشان داده می شود:
پرانتز به این معنی است که (mod n ) برای کل معادله اعمال می شود، نه فقط در سمت راست (اینجا، b ). این نماد نباید با علامت b mod n (بدون پرانتز) که به عملیات مدول اشاره دارد، اشتباه گرفته شود . در واقع، b mod n عدد صحیح منحصر به فرد a را نشان می دهد به طوری که 0 ≤ a < n و


رابطه تطابق ممکن است به صورت بازنویسی شود
رابطه آن را با تقسیم اقلیدسی به صراحت نشان می دهد . با این حال، b در اینجا لازم نیست باقیمانده تقسیم a بر n باشد. در عوض، چیزی که عبارت a ≡ b (mod n ) بیان می کند این است که a و b وقتی بر n تقسیم می شوند باقیمانده یکسانی دارند . به این معنا که،
که در آن 0 ≤ r < n باقیمانده مشترک است. با کم کردن این دو عبارت، رابطه قبلی را بازیابی می کنیم:
با تنظیم k = p − q .
مثالها [ ویرایش ]
در مدول 12 می توان ادعا کرد که:
زیرا 38 − 14 = 24 ، که مضرب 12 است. راه دیگر برای بیان این است که بگوییم هر دو 38 و 14 با تقسیم بر 12 باقیمانده 2 مشابهی دارند.
تعریف همخوانی در مورد مقادیر منفی نیز صدق می کند. مثلا:
خواص [ ویرایش ]
رابطه هم ارزی تمام شرایط یک رابطه هم ارزی را برآورده می کند :
- بازتاب: a ≡ a (mod n )
- تقارن: a ≡ b (mod n ) اگر b ≡ a (mod n ) برای همه a , b و n .
- گذرا: اگر a ≡ b (mod n ) و b ≡ c (mod n ) , آنگاه a ≡ c ( mod n )
اگر a 1 ≡ b 1 (mod n ) و a 2 ≡ b 2 (mod n ) و یا a ≡ b (mod n ) ، آنگاه: [1]
- a + k ≡ b + k (mod n ) برای هر عدد صحیح k (سازگاری با ترجمه)
- ka ≡ kb (mod n ) برای هر عدد صحیح k (سازگاری با مقیاس بندی)
- ka ≡ kb (mod kn ) برای هر عدد صحیح k
- a 1 + a 2 ≡ b 1 + b 2 (mod n ) (سازگاری با جمع)
- a 1 – a 2 ≡ b 1 – b 2 (mod n ) (سازگاری با تفریق)
- a 1 a 2 ≡ b 1 b 2 (mod n ) (سازگاری با ضرب)
- a k ≡ b k (mod n ) برای هر عدد صحیح غیر منفی k (سازگاری با توان)
- p ( a ) ≡ p ( b ) (mod n ) ، برای هر چند جملهای p ( x ) با ضرایب صحیح (سازگاری با ارزیابی چند جملهای)
اگر a ≡ b (mod n ) ، آنگاه به طور کلی نادرست است که k a ≡ k b (mod n ) . با این حال، موارد زیر صادق است:
- اگر c ≡ d (mod φ ( n ))، که در آن φ تابع تایانت اویلر است ، a c ≡ a d ( mod n ) —به شرطی که a همزمان با n باشد .
برای لغو شرایط رایج، قوانین زیر را داریم:
- اگر a + k ≡ b + k (mod n ) ، جایی که k هر عدد صحیحی است، a ≡ b (mod n )
- اگر ka ≡ kb (mod n ) و k با n همزمان اول باشد ، a ≡ b (mod n )
- اگر ka ≡ kb (mod kn ) و k ≠ 0 , آنگاه a ≡ b (mod n )
معکوس ضربی مدولار با قوانین زیر تعریف می شود:
- وجود: یک عدد صحیح با -1 وجود دارد به طوری که aa -1 ≡ 1 (mod n ) اگر و فقط اگر a هم اول با n باشد وجود دارد. این عدد صحیح a –1 ، معکوس ضربی مدولار یک مدول n نامیده می شود .
- اگر a ≡ b (mod n ) و a –1 وجود داشته باشد، a –1 ≡ b –1 (mod n ) (سازگاری با معکوس ضربی، و اگر a = b ، مدول یکتایی n ) وجود دارد.
- اگر ax ≡ b (mod n ) و a همزمان با n باشد ، آنگاه راه حل این همخوانی خطی با x ≡ a -1 b (mod n ) به دست می آید.
معکوس ضربی x ≡ a –1 (mod n ) را می توان با حل معادله بزوت به طور موثر محاسبه کرد. 

به طور خاص، اگر p یک عدد اول باشد، a برای هر a همآغاز با p است به طوری که 0 < a < p ; بنابراین یک معکوس ضربی برای همه a وجود دارد که با مدول صفر p مطابقت ندارد.
برخی از ویژگی های پیشرفته تر روابط همخوانی به شرح زیر است:
- قضیه کوچک فرما : اگر p اول باشد و a را تقسیم نکند ، a p – 1 ≡ 1 (mod p ) .
- قضیه اویلر : اگر a و n هم اول باشند، آنگاه a φ ( n ) ≡ 1 ( mod n ) که φ تابع اویلر است.
- یک نتیجه ساده از قضیه کوچک فرما این است که اگر p اول باشد، a −1 ≡ a p− 2 (mod p ) معکوس ضربی 0 < a < p است. به طور کلی تر، از قضیه اویلر، اگر a و n هم اول باشند، a −1 ≡ a φ ( n ) − 1 (mod n ) .
- نتیجه ساده دیگر این است که اگر a ≡ b (mod φ ( n ))، که در آن φ تابع تاینت اویلر است، آنگاه k a ≡ k b (mod n ) ارائه شده k با n همخوان است .
- قضیه ویلسون : p اول است اگر و فقط اگر ( p − 1)! ≡ −1 (mod p ) .
- قضیه باقیمانده چینی : برای هر a , b و هم اول m , n , یک x یکتا (mod mn ) وجود دارد به طوری که x ≡ a (mod m ) و x ≡ b ( mod n ) . در واقع، x ≡ bm n –1 m + an m –1 n (mod mn ) که در آن m n -1 معکوس m استمدول n و n m -1 معکوس n مدول m است.
- قضیه لاگرانژ : همخوانی f ( x ) ≡ 0 (mod p ) , که در آن p اول است و f ( x ) = a 0 x n + ... + a n چند جمله ای با ضرایب صحیح است به طوری که a 0 ≠ 0 ( mod p ) ، حداکثر n ریشه دارد.
- مدول ریشه اولیه n : یک عدد g یک مدول ریشه ابتدایی n است اگر برای هر عدد صحیح یک هم اول به n یک عدد صحیح k وجود داشته باشد به طوری که g k ≡ a (mod n ) باشد. یک مدول ریشه اولیه n وجود دارد اگر و فقط اگر n برابر با 2، 4، pk یا 2 pk باشد ، که در آن p یک عدد اول فرد و k یک عدد صحیح مثبت است. اگر یک مدول ریشه اولیه n وجود داشته باشد، دقیقاً وجود داردφ ( φ ( n )) چنین ریشه های ابتدایی، که در آن φ تابع اویلر است.
- باقیمانده درجه دوم : یک عدد صحیح a یک مدول باقیمانده درجه دوم n است، اگر یک عدد صحیح x وجود داشته باشد به طوری که x 2 ≡ a (mod n ) وجود داشته باشد. معیار اویلر بیان می کند که اگر p یک عدد اول فرد باشد و a مضرب p نباشد ، a یک مدول باقیمانده درجه دوم p است اگر و فقط اگر
تابع تولید [ ویرایش | ویرایش منبع ]
یک تابع مولد برای چند جمله ای لاگر است
چند جمله ای های مرتبط لاگر [ ویرایش | ویرایش منبع ]
برخی از چند جمله ای های لاگر مرتبط هستند
چند جمله ای های لاگر مرتبط (تعمیم شده) با چند جمله ای های معمولی لاگر آویزان می شوند
با یکدیگر. فرمول رودریگز شما این است
چند جمله ای های لاگر مرتبط معادله لاگر را برآورده می کند
اولین چند جمله ای های لاگر اختصاص داده شده عبارتند از:
برای محاسبه می توان از فرمول بازگشتی استفاده کرد
استفاده کنید.
اپراتور اشتورم-لیوویل است
و با تابع وزن
چند جمله ای های مرتبط لاگر را می توان به صورت انتگرال مسیر بیان کرد :
وجود دارد
تحلیل مجانبی [ ویرایش | ویرایش منبع ]
اتم هیدروژن [ ویرایش | ویرایش منبع ]
چند جمله ای های لاگر در مکانیک کوانتومی در حل معادله شرودینگر برای اتم هیدروژن یا در حالت کلی برای پتانسیل کولن کاربرد دارند. [3] با استفاده از چند جملهای لاگر اختصاص داده شده، بخش شعاعی تابع موج را میتوان به صورت نوشتاری
(ثابت عادی سازی



داده شده، با عدد کوانتومی اصلی 






پیوندهای وب [ ویرایش | ویرایش منبع ]
- Eric W. Weiststein : Laguerre Polynomial . در: MathWorld (انگلیسی).
- چند جمله ای های لاگر ( یادگاری 29 فوریه 2016 در آرشیو اینترنت ). در: ipf.uni-stuttgart.de.
- توابع لاگرئن در: stellarcom.org.
- توابع موج شعاعی، چند جمله ای لاگر. در: physik.uni-ul
منبع
https://de.wikipedia.org/wiki/Laguerre-Polynome
چند جملهای لاگر (به نام ادموند لاگر ) چند جملهای خاص در بازه هستند.![[0،\infty]](https://wikimedia.org/api/rest_v1/media/math/render/svg/52088d5605716e18068a460dec118214954a68e9)
فهرست
- 1معادله دیفرانسیل و چند جمله ای ها
- 2خواص
- 3چند جمله ای های لاگر مرتبط
- 4تحلیل مجانبی
- 5اتم هیدروژن
- 6لینک های وب
- 7ارجاعات و یادداشت های فردی
معادله دیفرانسیل و چند جمله ای [ ویرایش | ویرایش منبع ]
معادله دیفرانسیل لاگر [ ویرایش | ویرایش منبع ]
معادله دیفرانسیل لاگر

یک معادله دیفرانسیل خطی معمولی مرتبه دوم برای
این یک مورد خاص از معادله دیفرانسیل اشتورم-لیوویل است
اولین چند جمله ای ها [ ویرایش | ویرایش منبع ]
پنج چند جمله ای اول لاگر
پنج چند جمله ای اول لاگر هستند
تعریفی که معمولاً در فیزیک استفاده می شود این است که چند جمله ای های لاگر در یک ضریب ضرب می شوند.
خواص [ ویرایش | ویرایش منبع ]
فرمول های بازگشتی [ ویرایش | ویرایش منبع ]
چند جمله ای لاگر
با استفاده از فرمول بازگشتی زیر محاسبه می شود
فرمول های بازگشتی زیر نیز اعمال می شوند:



یک فرمول صریح برای چند جمله ای های لاگر است

مثال
به چند جمله ای تبدیل می شود


برای به دست آوردن این چند جمله ای باید از چند جمله ای استفاده کرد

بنابراین چند جمله ای است
فرمول رودریگز [ ویرایش | ویرایش منبع ]
که
و
چند جمله ای لاگر از معادله اول با استفاده از قانون محصول برای مشتقات بالاتر و هویت ها محاسبه می شود.{


معادله دوم چند جمله ای لاگر را با قضیه دو جمله ای و هویت می دهد
انتگرال کانتور زیر را ارزیابی کنید.
1منحنی است که مبدا را به
در امتداد یک خط مستقیم
2
کانتور را پارامتر کنید. منحنی ما به خصوص ساده است:و
بنابراین کانتور خود را به صورت زیر می نویسیم.
3
محاسبه دzدتی. نتایج ما را با انتگرال جایگزین کنید.
4
ارزیابی کنید.5
همان انتگرال را ارزیابی کنید، اما کجاγمنحنی است که مبدا را به
در امتداد
. پارامتر ما تغییر می کند
و
- ما در اینجا نشان دادیم که برای توابع غیر تحلیلی مانند
انتگرال کانتور به مسیر انتخاب شده بستگی دارد. ما میتوانیم نشان دهیم که این تابع با بررسی اینکه آیا بخشهای واقعی و خیالی معادلات کوشی-ریمان را برآورده میکنند، غیر تحلیلی است. مانند
و
این برای نشان دادن غیر تحلیلی بودن کافی است.
قسمت3
قضیه اساسی انتگرال های کانتور
1
تعمیم قضیه اساسی حساب دیفرانسیل و انتگرال. از آنجایی که به انتگرال های کانتور مربوط می شود، این قضیه برای محاسبه آسان مقدار انتگرال های کانتور تا زمانی که بتوانیم یک پاد مشتق پیدا کنیم استفاده می شود. اثبات این قضیه مشابه تمام قضیه های بنیادی دیگر برهان های حساب دیفرانسیل و انتگرال است، اما برای اختصار آن را در اینجا بیان نمی کنیم.- تابع را فرض کنید
آنتی مشتق دارد
به طوری که
از طریق یک دامنه
و اجازه دهید
یک کانتور در
جایی که
و
نقطه شروع و پایان هستند
به ترتیب. سپس
مستقل از مسیر برای همه مسیرهای پیوسته است
با طول محدود، و مقدار آن توسط
- تابع را فرض کنید
2
انتگرال زیر را با پارامترسازی مستقیم ارزیابی کنید.این نیم دایره در خلاف جهت عقربه های ساعت از
به
3
پارامترسازی کنیدγ،پیدا کردندzدتی،
و ارزیابی کنید.
4
همان انتگرال را با استفاده از قضیه اساسی انتگرال های کانتور ارزیابی کنید. با این حال، در این روش،در انتگرال یک مشکل ارائه می دهد. از آنجایی که ما می دانیم
وجود تابع لگاریتمی نشاندهنده یک برش شاخه است که نمیتوانیم آن را ادغام کنیم. خوشبختانه، ما می توانیم برش شاخه خود را به گونه ای انتخاب کنیم که کانتور ما در دامنه ما به خوبی مشخص شود. شاخه اصلی لگاریتم، که در آن برش شاخه از اعداد حقیقی غیرمثبت تشکیل شده است، در این مورد کار می کند، زیرا کانتور ما به دور آن برش شاخه می رود. تا زمانی که تشخیص دهیم لگاریتم اصلی یک آرگومان تعریف شده دارد
بقیه مراحل محاسبات ساده هستند.
- برای شاخه اصلی لگاریتم، می بینیم که
و
https://www.wikihow.com/Calculate-Contour-Integrals
چند جملهای لژاندر ( پس از آدرین-ماری لژاندر )، که توابع کروی ناحیهای نیز نامیده میشوند، چند جملهای خاص هستند که روی بازه ![[-1،1]](https://wikimedia.org/api/rest_v1/media/math/render/svg/51e3b7f14a6f70e614728c583409a0b9a8b9de01)
فهرست
معادله دیفرانسیل و چند جمله ای [ ویرایش | ویرایش منبع ]
معادله دیفرانسیل لژاندر [ ویرایش | ویرایش منبع ]
معادله دیفرانسیل لژاندر
همچنین می توان به صورت یک معادله دیفرانسیل خطی معمولی مرتبه دوم در فرم نوشت
برای![x \ در [-1,1]](https://wikimedia.org/api/rest_v1/media/math/render/svg/1f9d0dda56ce3e01e14570ac9aef0021c6125722)

این یک مورد خاص از معادله دیفرانسیل Sturm-Liouville است
جواب کلی این معادله دیفرانسیل است
با دو تابع مستقل خطی



علاوه بر این، یک معادله دیفرانسیل لژاندر تعمیم یافته وجود دارد که راه حل های آن چند جمله ای های لژاندر مرتبط نامیده می شوند .
اولین چند جمله ای ها [ ویرایش | ویرایش منبع ]
شش چند جمله ای اول لژاندر
اولین چند جمله ای های لژاندر عبارتند از:
که
با براکت گاوس
که

![{\mathbb Q}[x]](https://wikimedia.org/api/rest_v1/media/math/render/svg/da33ddef34ad0c677b6eb7e042f574ee0e7553f7)
ساخت چند جمله ای های متعامد [ ویرایش | ویرایش منبع ]
برای یک فاصله زمانی![I = [a,b]](https://wikimedia.org/api/rest_v1/media/math/render/svg/6d6214bb3ce7f00e496c0706edd1464ac60b73b5)


![P_n\in\R[X]](https://wikimedia.org/api/rest_v1/media/math/render/svg/ee840442661e2d073eadbb276082fbb8b4b361e9)
برای همه

برای فاصله![I = [-1,1]](https://wikimedia.org/api/rest_v1/media/math/render/svg/7edb704e6cad4f0d3828511af70f70be8861ccab)



خواص [ ویرایش | ویرایش منبع ]
فرمول رودریگز [ ویرایش | ویرایش منبع ]
فرمول رودریگز را می توان با فرمول فا دی برونو ارزیابی کرد و دوباره شکل صریح آن را به دست آورد.
نمایش انتگرالی [ ویرایش | ویرایش منبع ]
برای همه
فرمول های بازگشتی [ ویرایش | ویرایش منبع ]
فرمول های بازگشتی زیر برای چند جمله ای های لژاندر اعمال می شود:
اولین فرمول بازگشتی را می توان با استفاده از جایگزینی نوشت
با اعمال قانون اشتقاق برای عبارات از نوع


شرایط اولیه هستند
در
سیستم کامل متعامد [ ویرایش | ویرایش منبع ]
فضای هیلبرت را در نظر بگیرید![V:= L^2([-1,1]؛ \R)](https://wikimedia.org/api/rest_v1/media/math/render/svg/8fb95919b12ba38e52bb364a5093cc0b0364657d)
![[-1،1]](https://wikimedia.org/api/rest_v1/media/math/render/svg/51e3b7f14a6f70e614728c583409a0b9a8b9de01)

خانواده


اعمال می شود

به موجب آن


با ضرایب انبساط
در ادبیات فیزیکی یا فنی، کامل بودن اغلب به عنوان یک معادله توزیع به صورت زیر نوشته می شود :

به موجب آن






- متعامد بودن:
برای
.
- کامل بودن:
برای همه
(به معنای
-همگرایی).
ریشه ها [ ویرایش | ویرایش منبع ]

![I = [-1,1]](https://wikimedia.org/api/rest_v1/media/math/render/svg/7edb704e6cad4f0d3828511af70f70be8861ccab)






تعیین ریشههای چندجملهای لژاندر یک کار متداول در ریاضیات عددی است ، زیرا آنها نقش اصلی را در مربعسازی گاوس-لژاندر یا بسط توابع «دلخواه» بر حسب چندجملهای ذکر شده در «سیستم کامل متعامد» بازی میکنند. جداول زیادی برای این کار وجود دارد، اما استفاده از آنها اغلب با ناراحتی همراه است، زیرا تعداد زیادی جداول با دقت مناسب باید برای یک واکنش انعطاف پذیر در دسترس باشد. هنگام جستجوی صفرها، آگاهی از فاصله زمانی تنها ارزش محدودی در انتخاب یک شروع تکرار دارد، به خصوص که دانش صفرهای چند جمله ای دیگر نیز مورد نیاز است. یکی با افزایش



مثلا












با چنین مقدار اولیه و دو "فرمول بازگشتی" اول ، هم مقدار تابع و هم مشتق آن را می توان در یک محاسبه تعیین کرد. با استفاده از روش نیوتن ، همه به جز دو صفر بیرونی را می توان با همگرایی بیشتر از درجه دوم یافت، زیرا صفرها در مجاورت نقاط عطف قرار دارند. دو صفر بیرونی "فقط" به صورت درجه دوم همگرا می شوند، i. اچ. فاصله اولیه تا صفر



تخمین داده شده بخشی از یک الگوریتم بسیار کوتاه است که تمام ریشه های یک چند جمله ای لژاندر و همچنین وزن های مناسب برای ربع گاوس-لژاندر را ارائه می دهد.
خصوصیات عمومی [ ویرایش | ویرایش منبع ]
برای هر
![x \ در [-1,1]](https://wikimedia.org/api/rest_v1/media/math/render/svg/1f9d0dda56ce3e01e14570ac9aef0021c6125722)
تابع تولید [ ویرایش | ویرایش منبع ]
برای همه


سری پاور در سمت راست دارای برای
کارکرد

اصطلاحی که اغلب در فیزیک وجود دارد

توابع لژاندر نوع دوم [ ویرایش | ویرایش منبع ]
پنج تابع اول لژاندر از نوع دوم
فرمول های بازگشتی چند جمله ای های لژاندر برای توابع لژاندر نوع دوم نیز اعمال می شود، به طوری که می توان آنها را به طور تکراری با مشخص کردن مورد اول تعیین کرد:
در اینجا، شاخه اصلی باید برای لگاریتم استفاده شود ، که تکینگی ها را حذف می کند

حوزه های کاربردی [ ویرایش | ویرایش منبع ]
از جمله چند جمله ای لژاندر برای شبیه سازی کره های کروی، به عنوان مثال برای تعیین زاویه تیلور در مخروط تیلور ، که اساس هندسه در الکتروریسی است، استفاده می شود.
پیوندهای وب [ ویرایش | ویرایش منبع ]
- Eric W. Weiststein : Legendre Polynomial . در: MathWorld (انگلیسی).
- JB Calvert: Legendre Polynomials . (انگلیسی)
منبع
https://de.wikipedia.org/wiki/Legendre-Polynom#Legendresche_Differentialgleichung
از ویکیپدیا، دانشنامه آزاد
این مقاله در مورد توپولوژی جبری است . برای واژه زنجیره در نظریه نظم ، به زنجیره (نظریه نظم) مراجعه کنید.در توپولوژی جبری , یک زنجیره k ترکیب خطی رسمی از سلولهای k در یک مجموعه سلولی است . در کمپلکس های ساده (به ترتیب، کمپلکس های مکعبی )، k -chains ترکیبی از k -simplices (به ترتیب، k - cubes)، [1] [2] [3] هستند اما لزوماً به هم متصل نیستند. زنجیر در همسانی استفاده می شود . عناصر یک گروه همسانی کلاس های هم ارزی زنجیره ها هستند.
فهرست
تعریف [ ویرایش ]
برای یک مجتمع ساده 



جایی که



ادغام در زنجیره ها [ ویرایش ]
ادغام در زنجیره ها با در نظر گرفتن ترکیب خطی انتگرال ها بر روی ساده های زنجیره با ضرایب (که معمولاً اعداد صحیح هستند) تعریف می شود. مجموعه ای از زنجیره های k یک گروه را تشکیل می دهد و دنباله این گروه ها را مجموعه زنجیره ای می نامند .
عملگر مرزی روی زنجیره ها [ ویرایش ]
مرز منحنی چند ضلعی ترکیبی خطی از گره های آن است. در این مورد، ترکیبی خطی از A 1 تا A 6 . با فرض اینکه بخش ها همگی از چپ به راست جهت گیری شده اند (به ترتیب افزایش از A k به A k +1 )، مرز A 6 − A 1 است.
یک منحنی چند ضلعی بسته، با فرض جهت گیری ثابت، دارای مرز صفر است.
مرز یک زنجیره ترکیب خطی مرزهای ساده در زنجیره است. مرز یک k -chain یک ( k -1)- زنجیره است. توجه داشته باشید که مرز یک سیمپلکس یک سیمپلکس نیست، بلکه یک زنجیره با ضرایب 1 یا -1 است - بنابراین زنجیره ها بسته شدن ساده ها در زیر عملگر مرزی هستند.
مثال 1: مرز یک مسیر ، تفاوت صوری نقاط انتهایی آن است: این یک مجموع تلسکوپی است . برای نشان دادن، اگر 1-زنجیره


![t_{1}=[v_{1}، v_{2}]\،](https://wikimedia.org/api/rest_v1/media/math/render/svg/424b79b7bc911752e98a646e5bd73e87722bb646)
![t_{2}=[v_{2}، v_{3}]\،](https://wikimedia.org/api/rest_v1/media/math/render/svg/855f9af385ecc3370babbbe1fa6422a689392273)
![t_{3}=[v_{3}، v_{4}]\،](https://wikimedia.org/api/rest_v1/media/math/render/svg/d424e8189297d85bb84da732b4415c48d0fe964e)
مثال 2: مرز مثلث مجموع صوری لبه های آن با علائمی است که به گونه ای مرتب شده اند که پیمایش مرز را در خلاف جهت عقربه های ساعت انجام دهند.
یک زنجیره زمانی چرخه نامیده می شود که مرز آن صفر باشد. به زنجیره ای که مرز یک زنجیره دیگر است، مرز می گویند . مرزها چرخه هستند، بنابراین زنجیره ها یک مجموعه زنجیره ای را تشکیل می دهند که گروه های همسانی آن (مرزهای مدول چرخه) گروه های همسانی ساده نامیده می شوند.
مثال 3: صفحه سوراخ شده در مبدا دارای گروه 1-همسانی غیر اساسی است زیرا دایره واحد یک چرخه است، اما یک مرز نیست.
در هندسه دیفرانسیل ، دوگانگی بین عملگر مرزی روی زنجیره ها و مشتق بیرونی با قضیه کلی استوکس بیان می شود .
https://en.wikipedia.org/wiki/Chain_(algebraic_topology)
از ویکیپدیا، دانشنامه آزاد
![]()
جستجوی زنجیره در ویکیواژه، فرهنگ لغت رایگان.
زنجیر مجموعهای از پیوندهای متصل است که معمولاً از فلز ساخته میشوند.
زنجیره همچنین ممکن است به موارد زیر اشاره داشته باشد:
فهرست
- 1لوازم جانبی و پوشاک
- 2مکان ها
- 3افراد با نام
- 4هنر، سرگرمی و رسانه
- 5تجارت و اقتصاد
- 6ریاضیات
- 7مکانیک، مهندسی و ادوات
- 8علوم پایه
- 9دنباله ها
- 10اندازه گیری
- 11استفاده های دیگر
- 12همچنین ببینید
لوازم جانبی و پوشاک [ ویرایش ]
- پست زنجیره ای ، نوعی زره ساخته شده از حلقه های زنجیره ای به هم پیوسته
- گردنبند یا زنجیر گردن، نوعی زیورآلات است که به دور گردن بسته می شود
مکان ها [ ویرایش ]
- پل زنجیره ای (بوداپست) ، یک پل معلق که بر روی رودخانه دانوب بین بودا و پست قرار دارد.
- پل زنجیره ای (رودخانه پوتوماک) ، پلی بر روی رودخانه پوتوماک در آبشار کوچک در واشنگتن دی سی
- چینز (سایت زمین شناسی) ، سایت زمین شناسی در فلات شمال غربی Exmoor، سامرست، انگلستان
- پل یونیون (توید) (یا "پل زنجیره ای")، پلی در نورثامبرلند
افراد با نام [ ویرایش ]
- ارنست چین (1906-1979)، شیمیدان برنده جایزه نوبل که به دلیل جداسازی پنی سیلین مشهور است.
- جان تی چین جونیور (متولد 1934) ژنرال بازنشسته نیروی هوایی ایالات متحده
هنر، سرگرمی، و رسانه [ ویرایش ]
فیلم و تلویزیون [ ویرایش ]
- زنجیر (فیلم) فیلمی محصول سال ۲۰۰۴ به نویسندگی و کارگردانی جم کوهن است
- زنجیر ، فیلم کوتاهی با بازی کشتیگیر TNA ، کرت آنگل
- Chains ( Blackadder ) ، قسمتی از سریال کمدی بریتانیایی Blackadder II در سال 1986
- زنجیر عشق (سریال تلویزیونی) ، نمایش بازی دوستیابی آمریکایی که از یک سریال تلویزیونی هلندی اقتباس شده است
ادبیات [ ویرایش ]
- زنجیر (رمان) ، رمانی تاریخی-تخیلی از لوری هالس اندرسون محصول 2008.
- زنجیر (نمایشنامه) ، نمایشنامه ای محصول 1909 توسط الیزابت بیکر
- زنجیر (نمایشنامه) ، نمایشنامه ای محصول سال 1992 توسط پرل کلیج
موسیقی [ ویرایش ]
- Chain (باند) ، یک گروه موسیقی راک بلوز استرالیایی که از دهه 1960 تا به امروز فعال است
آلبوم ها [ ویرایش ]
- زنجیره (Bonnie Pink EP) ، 2008
- زنجیره (آلبوم KAT-TUN) ، 2012
- زنجیره (آلبوم پل هیگ) ، 1989
- زنجیره (آلبوم پیلون) ، 1990
آهنگ ها [ ویرایش ]
- "زنجیره" (آهنگ DLT) ، 1996
- "زنجیره" (آهنگ نیک جوناس) ، 2014
- "Chains" (آهنگ پتی بدون عشق) ، 1990
- "Chains" (آهنگ کوکی ها) ، 1962، توسط گروه Beatles
- زنجیر (آهنگ تینا آرنا) 1994
- "زنجیره" (آهنگ آشر) ، 2015
- "زنجیره"، آهنگ شیکاگو از آلبوم 1982 شیکاگو 16
- "زنجیره"، آهنگی از Fire Theft از آلبوم خود در سال 2003
تجارت و اقتصاد [ ویرایش ]
- زنجیره (املاک و مستغلات) ، گروهی از خریداران/فروشندگان که به هم مرتبط هستند
- سلسله فرماندهی ، خط اقتدار و مسئولیت که در امتداد آن دستورات صادر می شود
- فروشگاه زنجیره ای ، یک فروشگاه خرده فروشی که دارای یک نام تجاری و مدیریت مرکزی است
- دلارهای زنجیر شده، برای بیان مقادیر واقعی دلار که در طول زمان برای تورم تنظیم شده است، استفاده می شود
- زنجیره سینما یا زنجیره فیلم
- زنجیره سرد ، یک زنجیره تامین با کنترل دما
- زنجیره ای فست فود
- هتل های زنجیره ای
- رستوران زنجیره ای
- زنجیره تامین ، یک سیستم هماهنگ از سازمانها، افراد، فعالیتها، اطلاعات و منابع درگیر در انتقال یک محصول یا خدمات از عرضهکننده به مشتری.
- زنجیره ارزش ، یک مفهوم مدیریت برای اولین بار توسط مایکل پورتر توصیف شد
ریاضیات [ ویرایش ]
- زنجیره (مجموعه مرتب شده) ، یک مجموعه کاملاً مرتب، معمولاً زیر مجموعه ای از یک مجموعه جزئی مرتب شده معین
- زنجیره (توپولوژی جبری) ، یک ترکیب خطی رسمی از k -simplices
- زنجیره ساده (توپولوژی) ، مجموعه ای از مجموعه های باز متصل که دو نقطه را به هم متصل می کنند
- مجموعه زنجیره ای ، تعمیم ساختار توپولوژی جبری به جبر همسانی
- قانون زنجیره ای ، ابزاری برای تمایز در حساب
- دنباله زنجیره ، اعداد در مطالعه ریاضی کسرهای ادامه دار
- نماد پیکان زنجیره ای کانوی ، راهی برای بیان توان با استفاده از فلش ها
- زنجیره جردن ، دنباله ای از بردارهای ویژه تعمیم یافته مستقل خطی با رتبه نزولی
- زنجیره مارکوف ، یک فرآیند تصادفی زمان گسسته با ویژگی مارکوف
- شبه کمان ، که در دل خود مفهوم یک زنجیره را دارد
مکانیک، مهندسی و ادوات [ ویرایش ]
- زنجیر پیوند میله (زنجیره بلوک)، یک زنجیر محرک مکانیکی
- زنجیر دوچرخه ، زنجیر غلتکی که نیرو را از پدالها به چرخ محرک دوچرخه منتقل میکند.
- بافر و جفت زنجیر ، یک دستگاه راه آهن
- چرخشی (یا "زنجیره")، شکل یک کابل انعطاف پذیر آویزان است که در انتهای آن حمایت می شود و توسط یک نیروی گرانشی یکنواخت بر روی آن اثر می گذارد.
- Chain Home و Chain Home Low ، یک سیستم RDF (رادار) اولیه بریتانیا در دوران جنگ جهانی دوم
- ابزار زنجیر ، وسیله مکانیکی کوچکی است که برای "شکستن" زنجیر دوچرخه استفاده می شود به گونه ای که بتوان آن را با همان ابزار ترمیم کرد.
- زنجیره نقاله ، زنجیره ای که اقلام را در سیستم های نوار نقاله زنجیره ای منتقل می کند
- زنجیر محرک ، راهی برای انتقال نیروی مکانیکی از مکانی به مکان دیگر
- زنجیر غلتکی که بیشتر برای انتقال نیروی مکانیکی استفاده می شود
- زنجیره خود روان کننده ، برای از بین بردن نیاز به روغن کاری بیشتر
- زنجیر برف یا زنجیر چرخ ، دستگاههایی که روی لاستیکهای وسایل نقلیه نصب میشوند تا حداکثر کشش را ایجاد کنند
- زنجیر تایم ، بخشی از یک موتور احتراق داخلی
علم [ ویرایش ]
شیمی [ ویرایش ]
- واکنش زنجیره ای ، دنباله ای از واکنش ها که در آن یک محصول واکنش پذیر یا محصول فرعی باعث واکنش های اضافی می شود
- زنجیره ایده آل ، یک مدل ریاضی از تاشو پلیمری
- زنجیره پلیمری ، ساختار یک پلیمر
- زنجیره کرم مانند (یا زنجیره نیمه انعطاف پذیر)، مدلی در فیزیک پلیمر که برای توصیف رفتار پلیمرهای نیمه انعطاف پذیر استفاده می شود.
کاربردهای دیگر در علم [ ویرایش ]
- زنجیره انتقال الکترون ، دنباله ای از واکنش های شیمیایی که باعث انتقال الکترون از طریق غشاء می شود.
- زنجیره غذایی ، فهرست سلسله مراتبی یا بازگشتی از شکارچیان و طعمه ها
دنباله ها [ ویرایش ]
ویژگی های زمین شناسی [ ویرایش ]
- مجمع الجزایر ، زنجیره ای از جزایر
- زنجیره دهانه ، خطی از دهانه ها بر روی سطح یک جسم نجومی
- رشته کوه ، زنجیره ای از تپه ها یا کوه ها
سکانس های دیگر [ ویرایش ]
- پل زنجیره ای
- زنجیره ای، سیاره ای ، زنجیره ای از کره ها که به عنوان زمینه های تکامل در کیهان شناسی الهیات عمل می کنند
- خدمه زنجیر (زنجیره های فوتبال)، به طول 10 یارد، برای تعیین نقطه برای رسیدن به اولین سقوط
- گروه اراذل و اوباش
- نامه زنجیره ای ، پیامی که سعی می کند گیرنده را وادار کند تا تعدادی کپی از پیام تهیه کند و سپس آنها را به یک یا چند گیرنده جدید ارسال کند.
- سلسله اتفاقات
- زنجیره فکر ، یک فرآیند فکری پیوسته که در آن ایده ها یکی از دیگری را دنبال می کنند
- سیگار کشیدن زنجیره ای ، عادت به سیگار کشیدن مداوم
- دوخت زنجیره ای ، در خیاطی و گلدوزی، یک سری دوخت حلقه دار که یک زنجیره را تشکیل می دهند.
- زنجیر زنی، تکنیکی از تحلیل رفتاری کاربردی برای آموزش وظایف پیچیده با تقسیم آنها به مراحل ساده تر
- زنجیر دیزی (ابهامزدایی) ، معانی مختلف
- زنجیره رودخانه هادسون ، یکی از چندین زنجیره مورد استفاده در محاصره رودخانه هادسون
- زنجیره انسانی (سیاست) ، نوعی اعتراض
- زنجیره دلالت، در نشانه شناسی، نظام درهم تنیده ای از دال ها
اندازه گیری [ ویرایش ]
- زنجیر (واحد) ، واحد طول
- زنجیره گانتر ، واحد اندازه گیری
- زنجیره ای شدن مترو شهر نیویورک ، تعیین مکان در امتداد خطوط راه آهن
کاربردهای دیگر [ ویرایش ]
- زنجیره (کاست) ، کاست پرورش دهنده و ماهیگیری که در شرق اوتار پرادش، هند یافت می شود.
- زنجیر (دریانوردی) ، سکوهای کوچک در کنارههای کشتیها
- بند (بودیسم) (زنجیره ذهنی)، یک دلبستگی ذهنی عمیقاً ریشهدار که مانع از دستیابی فرد به رهایی از رنج میشود.
همچنین ببینید [ ویرایش ]
- زنجیر (ابهامزدایی)
- زنجیره ای از برکه ها (ابهام زدایی)
- زنجیر شده (ابهام زدایی)
- سریال (ابهامزدایی)
- زنجیره (ابهامزدایی)
- چان (ابهامزدایی)
منبع
https://en.wikipedia.org/wiki/Chain_(disambiguation)
مشخصات وب
 در این وبلاگ به ریاضیات و کاربردهای آن و تحقیقات در آنها پرداخته می شود. مطالب در این وبلاگ ترجمه سطحی و اولیه است و کامل نیست.در صورتی سوال یا نظری در زمینه ریاضیات دارید مطرح نمایید .در صورت امکان به آن می پردازم. من دوست دارم برای یافتن پاسخ به سوالات و حل پروژه های علمی با دیگران همکاری نمایم.در صورتی که شما هم بامن هم عقیده هستید با من تماس بگیرید.
در این وبلاگ به ریاضیات و کاربردهای آن و تحقیقات در آنها پرداخته می شود. مطالب در این وبلاگ ترجمه سطحی و اولیه است و کامل نیست.در صورتی سوال یا نظری در زمینه ریاضیات دارید مطرح نمایید .در صورت امکان به آن می پردازم. من دوست دارم برای یافتن پاسخ به سوالات و حل پروژه های علمی با دیگران همکاری نمایم.در صورتی که شما هم بامن هم عقیده هستید با من تماس بگیرید.09132003030
موضوعات وب
- نظریه طیف گراف
- پرواز
- هندسه
- هسته ای
- ترکببات
- نمایش گروه
- سیستم های دینامیکی
- نظریه کد گذاری
- ریاضی فازی
- جبر پیشرفته
- توپولوژی
- معادلات دیفرانسیل
- مقاله ها
- سیستم عصبی
- آنالیز عددی
- آنالیزریاضی و آنالیز حقیقی
- توابع مختلط و کاربردها
- نظریه اعداد
- برنامه ریزی خطی و غیر خطی
- حل عددی معادلات دیفرانسیل
- نظریه مجموعه ها
- جبرخطی و جبرخطی عددی
- اقتصاد
- تاریخ ریاضی
- انسان شناسی وفلسفه ریاضی
- توپولوژی جبری
- هندسه جبری
- هندسه ریمانی و هندسه هذلوی
- بازی
- نقشه برداری دریایی
- گراف
- آمار غیرپارامتری
- نجوم
- منیفولد دیفرانسیل
- نظریه گروه
- نظریه حلقه
- نظریه مدول ها
- آمار و احتمال
- ریاضی 2
- فیزیک -ریاضی
- تحقیق
- ریاضی مهندسی
- درس ترمودینامیک و مکانیک آماری
- مکانیک تحلیلی
- برق یا فیزیک 2
- فیزیک مدرن
- کوانتم
- نسبیت
پیوندها
پیوندهای روزانه
آرشیو وب
- اسفند ۱۴۰۴
- بهمن ۱۴۰۴
- دی ۱۴۰۴
- آذر ۱۴۰۴
- آبان ۱۴۰۴
- شهریور ۱۴۰۴
- مرداد ۱۴۰۴
- خرداد ۱۴۰۴
- اردیبهشت ۱۴۰۴
- بهمن ۱۴۰۳
- دی ۱۴۰۳
- آذر ۱۴۰۳
- آبان ۱۴۰۳
- مهر ۱۴۰۳
- خرداد ۱۴۰۳
- اردیبهشت ۱۴۰۳
- فروردین ۱۴۰۳
- اسفند ۱۴۰۲
- بهمن ۱۴۰۲
- دی ۱۴۰۲
- آذر ۱۴۰۲
- آبان ۱۴۰۲
- مهر ۱۴۰۲
- تیر ۱۴۰۲
- خرداد ۱۴۰۲
- اردیبهشت ۱۴۰۲
- فروردین ۱۴۰۲
- اسفند ۱۴۰۱
- بهمن ۱۴۰۱
- دی ۱۴۰۱
- آبان ۱۴۰۱
- مهر ۱۴۰۱
- شهریور ۱۴۰۱
- مرداد ۱۴۰۱
- تیر ۱۴۰۱
- خرداد ۱۴۰۱
- آرشيو

















![{\displaystyle \operatorname {Cl} _{p,q}^{[0]}=\{x\in \operatorname {Cl} _{p,q}\mid \alpha (x)=x\}.}](https://wikimedia.org/api/rest_v1/media/math/render/svg/0e214b8b455c0610747a107adad00e2c3573ca61)
![{\displaystyle \operatorname {Cl} _{p,q}^{[0]}\approx \operatorname {Cl} _{p,q-1},{\text{ for }}q>0}](https://wikimedia.org/api/rest_v1/media/math/render/svg/4add0c62afed4cf6f1c8d379c39b3f15e6f031d1)
![{\displaystyle \operatorname {Cl} _{p,q}^{[0]}\approx \operatorname {Cl} _{q,p-1},{\text{ for }}p>0}](https://wikimedia.org/api/rest_v1/media/math/render/svg/79f190bb97289dfe3a50eb02e74e3cffe2663246)

![{\displaystyle {\begin{aligned}\sigma ^{\mu \nu }&=-{\frac {i}{4}}\left[\gamma ^{\mu },\,\gamma ^{\nu }\right],\\\left[\sigma ^{\mu \nu },\,\sigma ^{\rho \tau }\right]&=i\left(\eta ^{\tau \mu }\ سیگما ^{\rho \nu }+\eta ^{\nu \tau }\sigma ^{\mu \rho }-\eta ^{\rho \mu }\sigma ^{\tau \nu }-\eta ^ {\nu \rho }\sigma ^{\mu \tau }\right).\end{تراز شده}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/9b5881264248f2f1787c4d1d2c4de84dd1678754)







![{\displaystyle \operatorname {Cl} (V,Q)=\operatorname {Cl} ^{[0]}(V,Q)\oplus \operatorname {Cl} ^{[1]}(V,Q)}](https://wikimedia.org/api/rest_v1/media/math/render/svg/34698bf037377a2edaee78a3dd92e84f286c2065)
![{\displaystyle \operatorname {Cl} ^{[i]}(V,Q)=\left\{x\in \operatorname {Cl} (V,Q)\mid \alpha (x)=(-1)^ {i}x\right\}.}](https://wikimedia.org/api/rest_v1/media/math/render/svg/b6902ed1e7c0361df4271000a56e7b76c029990e)
![{\displaystyle \operatorname {Cl} ^{[i]}(V,Q)\operatorname {Cl} ^{[j]}(V,Q)=\operatorname {Cl} ^{[i+j]}( V,Q)}](https://wikimedia.org/api/rest_v1/media/math/render/svg/23cb5e567bcf36cd16a56b991facede0ba9d69c9)

![{\displaystyle \operatorname {Cl} _{p,q}^{[0]}(\mathbf {R} )\cong {\begin{cases}\operatorname {Cl} _{p,q-1}(\ mathbf {R} )&q>0\\\نام اپراتور {Cl} _{q,p-1}(\mathbf {R})&p>0\end{موارد}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/55a73e10c8b20fb6d947e7f9a0b81288e3b7408c)







































![{\displaystyle TX{T^{\dagger }}=\left[{\begin{array}{*{20}{c}}1&0\\0&{e^{i{\frac {\pi }{4} }}}\end{array}}\right]\left[{\begin{array}{*{20}{c}}0&1\\1&0\end{array}}\right]\left[{\begin{ array}{*{20}{c}}1&0\\0&{e^{-i{\frac {\pi }{4}}}}\end{array}}\right]=\left[{\begin {array}{*{20}{c}}0&{e^{-i{\frac {\pi }{4}}}}\\{e^{i{\frac {\pi }{4}} }}&0\end{آرایه}}\right]\نه \در {{\mathbf {P} }_{1}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/b650351031619893c1884699e081375f03aa2215)
 1 (mod ( x 4 + x 3 + x + 1)).
1 (mod ( x 4 + x 3 + x + 1)). (10000011)
(10000011) (00011011) = (01000111)
(00011011) = (01000111)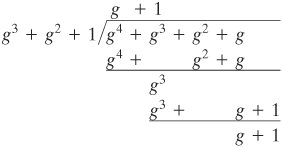
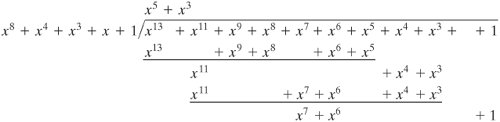
 ( m ( x )). به طور معادل، کلاس باقیمانده [ x + 1] شامل همه چند جمله ای های a ( x ) است که برابری a ( x ) mod m ( x ) = x + 1 را برآورده می کند.
( m ( x )). به طور معادل، کلاس باقیمانده [ x + 1] شامل همه چند جمله ای های a ( x ) است که برابری a ( x ) mod m ( x ) = x + 1 را برآورده می کند.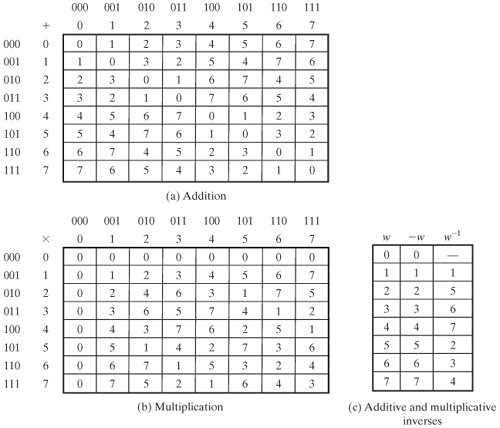






















![L_{2}^{k}(x)={\frac {1}{2}}\,\left[x^{2}-2\,(k+2)\,x+(k+1)( k+2)\راست]](https://wikimedia.org/api/rest_v1/media/math/render/svg/ae15ad7b67ff44bbd7e3003468ef214b46a99f37)
![{\displaystyle L_{3}^{k}(x)={\frac {1}{6}}\,\left[-x^{3}+3\,(k+3)\,x^{ 2}-3\,(k+2)\,(k+3)\,x+(k+1)\,(k+2)\,(k+3)\راست]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/3908ce0eabd5a11f1e577eff87d3829369bfddc5)






![{\displaystyle \Psi _{n,l,m}(r,\vartheta ,\varphi )={\sqrt {\frac {4\,(nl-1)!}{(n+l)!\;n \,(na_{0}/Z)^{3}}}}\left[{\frac {2r}{na_{0}/Z}}\right]^{l}\exp {\left\{- {\frac {r}{na_{0}/Z}}\right\}}\;L_{nl-1}^{2l+1}\left({\frac {2r}{na_{0}/Z }}\right)\;Y_{l,m}(\vartheta ,\varphi )}](https://wikimedia.org/api/rest_v1/media/math/render/svg/45c656de94c4f217677df1ae610d165293d61938)
































![{\displaystyle {\frac {\mathrm {d} }{\mathrm {d} x}}\left[\left(1-x^{2}\right)\,y'(x)\right]+n (n+1)\,y(x)=0}](https://wikimedia.org/api/rest_v1/media/math/render/svg/1d8d5660d19479dff340689f286576cb5d0aaf67)

































![{\begin{aligned}\partial _{1}c&=\partial _{1}(t_{1}+t_{2}+t_{3})\\&=\partial _{1}(t_{1 })+\جزئی _{1}(t_{2})+\جزئی _{1}(t_{3})\\&=\جزئی _{1}([v_{1},v_{2}] )+\جزئی _{1}([v_{2}، v_{3}])+\جزئی _{1}([v_{3}،v_{4}])\\&=([v_{2 }]-[v_{1}])+([v_{3}]-[v_{2}])+([v_{4}]-[v_{3}])\\&=[v_{4 }]-[v_{1}].\end{تراز شده}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/be8134591887754d91b8d72e5ce50bda7abb465c)