توسط علی رضا نقش نیلچی
| دوشنبه بیست و چهارم آبان ۱۴۰۰ | 19:13
از ویکیپدیا، دانشنامه آزاد
پرش به ناوبریپرش به جستجو
دیسک پوانکاره با خطوط موازی هذلولی

مدل دیسک پوانکاره از کاشی کاری سه ضلعی کوتاه شده .
در هندسه، مدل دیسک پوانکاره ، که به آن مدل دیسک منسجم نیز میگویند، مدلی از هندسه هذلولی دو بعدی است که در آن نقاط هندسه در داخل دیسک واحد قرار دارند و خطوط مستقیم شامل تمام کمانهای دایرهای موجود در آن دیسک است. که بر روی مرز دیسک متعامد هستند ، به اضافه تمام قطرهای دیسک.
گروه ایزومتریک های حفظ جهت گیری مدل دیسک توسط گروه واحد ویژه SU(1,1) داده شده است .
همراه با مدل کلاین و مدل نیمه فضای پوانکاره ، توسط یوجنیو بلترامی پیشنهاد شد که از این مدل ها برای نشان دادن اینکه هندسه هذلولی با هندسه اقلیدسی همخوانی دارد، استفاده کرد . این نام به افتخار هانری پوانکاره گرفته شده است ، زیرا کشف مجدد این نمایش چهارده سال بعد بیشتر از اثر اصلی بلترامی شناخته شد. [1]
مدل توپ پوانکاره مدل مشابه است 3 یا N هندسه هذلولی بعدی که در آن نقطه از هندسه در می N بعدی واحد توپ .
فهرست

دیسک پوانکاره با 3 خط مستقیم فوق موازی (هذلولی).
خطوط مستقیم هذلولی شامل تمام کمانهای دایرههای اقلیدسی است که در داخل دیسک قرار دارند و با مرز دیسک متعامد هستند ، به اضافه تمام قطرهای دیسک.
قطب نما و ساخت و ساز مستقیم [ ویرایش ]
خط هذلولی منحصر به فرد از طریق دو نقطه P و Q که روی قطر دایره مرزی نیستند را می توان به صورت زیر ساخت :
- اجازه دهید P' وارونگی در دایره مرزی نقطه P باشد
- بگذارید Q' وارونگی در دایره مرزی نقطه Q باشد
- بگذارید M نقطه وسط قطعه PP باشد
- بگذارید N نقطه وسط قطعه QQ باشد
- رسم خط m تا M عمود بر قطعه PP'
- رسم خط n تا N عمود بر بخش QQ'
- اجازه دهید C جایی باشد که خط m و خط n قطع می شوند.
- دایره c را با مرکز C و عبور از P (و Q) رسم کنید.
- قسمتی از دایره c که داخل دیسک است خط هذلولی است.
اگر P و Q روی قطر دایره مرزی باشند، آن قطر خط هذلولی است.
راه دیگر این است:
- بگذارید M نقطه وسط قطعه PQ باشد
- خط m تا M را عمود بر قطعه PQ رسم کنید
- اجازه دهید P' وارونگی در دایره مرزی نقطه P باشد
- اجازه دهید N نقطه وسط قطعه PP باشد
- رسم خط n تا N عمود بر بخش PP'
- اجازه دهید C جایی باشد که خط m و خط n قطع می شوند.
- دایره c را با مرکز C و عبور از P (و Q) رسم کنید.
- قسمتی از دایره c که داخل دیسک است خط هذلولی است.
فاصله ها در این مدل معیارهای Cayley-Klein هستند . با توجه به دو نقطه مجزا ص و س در داخل دیسک، خط هذلولی منحصر به فرد اتصال آنها قطع مرز در دو نقطه ایده آل ، و ب ، آنها برچسب به طوری که نقاط هستند، به منظور، ، ص ، س ، ب و | ق | > | ap | و | pb | > | qb | .
فاصله هذلولی بین p و q پس از آن است .
.
میله های عمودی نشان دهنده طول اقلیدسی پاره خطی است که نقاط بین آنها را در مدل به هم متصل می کند (نه در امتداد کمان دایره)، ln لگاریتم طبیعی است .

جایی که و
و  فاصله p مربوط به q تا مرکز دیسک است،
فاصله p مربوط به q تا مرکز دیسک است، فاصله بین ص و س ،
فاصله بین ص و س ، شعاع دایره مرزی دیسک و
شعاع دایره مرزی دیسک و  است تابع وارون هذلولوی از کسینوس هایپربولیک .
است تابع وارون هذلولوی از کسینوس هایپربولیک .
هنگامی که دیسک مورد استفاده دیسک واحد باز باشد و یکی از نقاط مبدا باشد و فاصله اقلیدسی بین نقاط r باشد، فاصله هذلولی برابر است با:  جایی که
جایی که  است تابع وارون هذلولوی از تانژانت هایپربولیک .
است تابع وارون هذلولوی از تانژانت هایپربولیک .
هنگامی که دیسک استفاده می شود دیسک واحد باز و نقطه است بین مبدا و نقطه قرار دارد
بین مبدا و نقطه قرار دارد  (یعنی دو نقطه در یک شعاع هستند، زاویه قطبی یکسانی دارند و
(یعنی دو نقطه در یک شعاع هستند، زاویه قطبی یکسانی دارند و ، فاصله هذلولی آنها است
، فاصله هذلولی آنها است . این به فرمول قبلی کاهش می یابد اگر
. این به فرمول قبلی کاهش می یابد اگر .
.
دایره (مجموعه ای از تمام نقاط در یک هواپیما که در یک فاصله معین از یک نقطه داده شده، مرکز آن) یک دایره را به طور کامل در داخل دیسک لمس کردن و یا متقاطع مرز آن است. مرکز هذلولی دایره در مدل به طور کلی با مرکز اقلیدسی دایره مطابقت ندارد، اما آنها در همان شعاع دایره مرزی هستند.
ابر چرخه ها [ ویرایش ]
hypercycle (مجموعه ای از تمام نقاط در یک هواپیما که در یک طرف و در یک فاصله معین از یک خط داده شده، محور خود هستند) قوس دایره اقلیدسی یا وتر دایره مرز این است که از فاصله دایره مرزی در یک غیر حق زاویه . محور آن خط هذلولی است که در دو نقطه ایده آل مشترک است . این منحنی با فاصله همسان نیز شناخته می شود.
طالع بینی [ ویرایش ]
horocycle (یک منحنی که طبیعی و یا عمود بر ژئودزیک همگی مجانبی در همان جهت)، یک دایره در داخل دیسک که از لمس دایره حاشیه قرص است. نقطه ای که دایره مرزی را لمس می کند، بخشی از چرخه طالع بینی نیست. این یک نقطه ایده آل است و مرکز هذلولی هوروسیکلت است.
خلاصه اقلیدسی [ ویرایش ]
دایره اقلیدسی:
- که به طور کامل در داخل دیسک است یک دایره هذلولی است .
(زمانی که مرکز دیسک داخل دایره نباشد، مرکز اقلیدسی همیشه به مرکز دیسک نزدیکتر از مرکز هذلولی است، یعنی  دارای.)
دارای.)
- که داخل دیسک است و مرز را لمس می کند، یک هوروسیکل است .
- که مرز را به صورت متعامد قطع می کند یک خط هذلولی است . و
- که مرز را به صورت غیر متعامد قطع می کند یک ابر چرخه است .
وتر اقلیدسی دایره مرزی:
- که از مرکز می گذرد یک خط هذلولی است. و
- که از مرکز نمی گذرد یک هایپرسیکل است.
متریک و انحنا [ ویرایش ]

نمای مدل « توپ » پوانکاره از لانه زنبوری منتظم هذلولی ، {3،5،3}
اگر u و v دو بردار در فضای برداری n بعدی واقعی R n با هنجار اقلیدسی معمولی باشند، که هر دو هنجار کمتر از 1 دارند، ممکن است یک متغیر ایزومتریک را با

جایی که  نشان دهنده هنجار اقلیدسی معمول است. سپس تابع فاصله است
نشان دهنده هنجار اقلیدسی معمول است. سپس تابع فاصله است

چنین تابع فاصله ای برای هر دو بردار هنجار کمتر از یک تعریف می شود و مجموعه این بردارها را به فضای متریک تبدیل می کند که مدلی از فضای هذلولی با انحنای ثابت -1 است. این مدل دارای خاصیت همسانی است که زاویه بین دو منحنی متقاطع در فضای هذلولی با زاویه مدل یکسان است.
مرتبط تانسور متریک از مدل دیسک پوانکاره داده شده است [2]

که در آن x i مختصات دکارتی فضای اقلیدسی محیطی است. ژئودزیک از مدل دیسک محافل عمود بر حوزه مرز S N -1 .
یک قاب متعارف با توجه به این متریک ریمانی توسط

با قاب دوگانه 1-فرم

در دو بعد [ ویرایش ]
مقاله اصلی: متریک پوانکاره
در دو بعد، با توجه به این قاب ها و اتصال Levi-Civita، فرم های اتصال توسط ماتریس متقارن متقارن 1 شکل منحصر به فرد ارائه شده است.  که بدون پیچش است، یعنی معادله ماتریس را برآورده می کند
که بدون پیچش است، یعنی معادله ماتریس را برآورده می کند  . حل این معادله برای
. حل این معادله برای بازده - محصول
بازده - محصول

که در آن ماتریس انحنا قرار دارد

بنابراین، انحنای دیسک هیپربولیک است

ارتباط با مدل های دیگر هندسه هذلولی [ ویرایش ]
همچنین ببینید: هندسه هایپربولیک § اتصال بین مدل ها

مدل دیسک پوانکاره (خط P )، و روابط آنها با مدل های دیگر
ارتباط با مدل دیسک کلاین [ ویرایش ]
مدل کلاین دیسک (همچنین به عنوان مدل بلترامی-کلین شناخته می شود) و مدل دیسک پوانکاره هر دو مدل که پروژه طیف هواپیما اغراقی در یک هستند دیسک . این دو مدل از طریق یک طرح ریزی روی یا از مدل نیمکره به هم مرتبط هستند . مدل دیسک کلاین یک پیش بینی املایی به مدل نیمکره است در حالی که مدل دیسک پوانکاره یک طرح ریزی استریوگرافی است .
مزیت مدل دیسک کلاین این است که خطوط در این مدل آکوردهای مستقیم اقلیدسی هستند . اشکال آن این است که مدل دیسک کلاین است منسجم (دایره و زاویه ها تحریف شده).
هنگامی که خطوط یکسان در هر دو مدل بر روی یک دیسک نمایش داده می شود، هر دو خط از دو نقطه ایده آل مشابه عبور می کنند . (نقاط ایده آل در همان نقطه باقی می مانند) همچنین قطب وتر در مدل دیسک کلاین مرکز دایره ای است که در مدل دیسک پوانکاره حاوی قوس است.
یک نقطه ( x , y ) در مدل دیسک پوانکاره به نگاشت می شود در مدل کلاین
در مدل کلاین
یک نقطه ( x , y ) در مدل کلاین به{ در مدل دیسک پوانکاره
در مدل دیسک پوانکاره
برای امتیاز ایده آل  و فرمول ها تبدیل می شوند
و فرمول ها تبدیل می شوند  بنابراین نقاط ثابت هستند.
بنابراین نقاط ثابت هستند.
اگر  یک بردار هنجار کوچکتر از یک است که نقطه ای از مدل دیسک پوانکاره را نشان می دهد، سپس نقطه متناظر مدل دیسک کلاین با:
یک بردار هنجار کوچکتر از یک است که نقطه ای از مدل دیسک پوانکاره را نشان می دهد، سپس نقطه متناظر مدل دیسک کلاین با:

برعکس، از یک بردار  هنجار کمتر از یک نشان دهنده نقطه ای از مدل بلترامی-کلاین است، نقطه متناظر مدل دیسک پوانکاره به صورت زیر به دست می آید:
هنجار کمتر از یک نشان دهنده نقطه ای از مدل بلترامی-کلاین است، نقطه متناظر مدل دیسک پوانکاره به صورت زیر به دست می آید:

رابطه با مدل نیم صفحه پوانکاره [ ویرایش ]
همچنین نگاه کنید به: تبدیل Cayley § Conformal map
مدل دیسک پوانکاره و مدل نیم صفحه پوانکاره هر دو به نام هانری پوانکاره نامگذاری شده اند .
اگر  بردار هنجار کوچکتر از یک است که نقطه ای از مدل دیسک پوانکاره را نشان می دهد، سپس نقطه متناظر مدل نیم صفحه به صورت زیر به دست می آید:
بردار هنجار کوچکتر از یک است که نقطه ای از مدل دیسک پوانکاره را نشان می دهد، سپس نقطه متناظر مدل نیم صفحه به صورت زیر به دست می آید:

یک نقطه (x,y) در مدل دیسک به در مدل نیمه هواپیما [3]
در مدل نیمه هواپیما [3]
یک نقطه (x,y) در مدل نیم صفحه به نگاشت می شود در مدل دیسک
در مدل دیسک
ارتباط با مدل هایپربولوئید [ ویرایش ]

مدل hyperboloid می تواند به عنوان تی معادله نشان 2 = X 1 2 + X 2 2 1، تی> 1. می توان از آن برای ساخت یک مدل دیسک پوانکاره به عنوان یک طرح مشاهده شده از (t=-1, x 1 =0, x 2 =0) استفاده کرد و نیمه هایپربولوئید بالایی را روی دیسک واحد در t=0 نمایش داد. ژئودزیک قرمز در مدل دیسک پوانکاره به ژئودزیک قهوهای روی هیپربولوئید سبز نشان میدهد.

انیمیشن یک کاشی کاری هذلولی جزئی {7،3} از هایپربولوئید که در چشم انداز پوانکر چرخیده است.
مدل دیسک پوانکاره و همچنین مدل کلاین به صورت تصویری به مدل هایپربولوئید مربوط می شوند . اگر یک نقطه [ t , x 1 , ..., x n ] در صفحه بالای هیپربولوئید مدل هایپربولوئید داشته باشیم، بدین ترتیب یک نقطه در مدل هایپربولوئید تعریف می کنیم، ممکن است آن را بر روی صفحه t = 0 قرار دهیم. تقاطع آن با یک خط کشیده شده از [-1، 0، ...، 0]. نتیجه نقطه متناظر مدل دیسک پوانکاره است.
برای مختصات دکارتی ( t , x i ) در هیپربولوئید و ( y i ) در صفحه، فرمول های تبدیل عبارتند از:


فرمول های نمایش استریوگرافیک بین کره و صفحه را مقایسه کنید.
ساختارهای هندسه تحلیلی در صفحه هذلولی [ ویرایش ]
ساختار اصلی هندسه تحلیلی یافتن خطی از دو نقطه داده شده است. در مدل دیسک پوانکاره، خطوط در صفحه توسط بخشهایی از دایرههایی که معادلات شکلی دارند، تعریف میشوند.

که شکل کلی یک دایره متعامد به دایره واحد یا بر اساس قطر است. با توجه به دو نقطه u و v در دیسک که روی قطر قرار ندارند، می توانیم دایره این شکل را که از هر دو نقطه می گذرد حل کنیم و به دست آوریم.
![{\displaystyle {\begin{aligned}x^{2}+y^{2}&{}+{\frac {v_{1}(u_{2}^{2}+v_{2}^{2} +1)-v_{2}(u_{1}^{2}+v_{1}^{2}+1)}{u_{1}v_{2}-u_{2}v_{1}}} x\\[8pt]&{}+{\frac {u_{2}(u_{1}^{2}+v_{1}^{2}+1)-u_{1}(u_{2}^ {2}+v_{2}^{2}+1)}{u_{1}v_{2}-u_{2}v_{1}}}y+1=0\,.\end{تراز شده}} }](https://wikimedia.org/api/rest_v1/media/math/render/svg/f65eb0e73ee28b703a59b3fdfcc8eb28facd52a6)
اگر نقاط u و v نقاطی در مرز دیسک هستند که در نقاط انتهایی قطر قرار ندارند، موارد فوق ساده می شود

میتوانیم زاویه بین قوس دایرهای را که نقاط انتهایی آن ( نقاط ایدهآل ) با بردارهای واحد u و v داده شدهاند ، و کمانی که نقاط انتهایی آن s و t هستند را با استفاده از یک فرمول محاسبه کنیم. از آنجایی که نقاط ایده آل در مدل کلاین و مدل دیسک پوانکاره یکسان است، فرمول ها برای هر مدل یکسان است.
اگر خطوط هر دو مدل دارای قطر باشند، به طوری که v = − u و t = − s ، آنگاه ما فقط زاویه بین دو بردار واحد را پیدا می کنیم و فرمول زاویه θ است.

اگر v = - u اما t = - s نباشد ، فرمول بر حسب حاصلضرب گوه تبدیل می شود ( )
)

جایی که



اگر هر دو آکورد قطر نباشند، فرمول کلی به دست می آید

جایی که



با استفاده از هویت بینه-کوشی و این واقعیت که این بردار واحد ما ممکن است بالاتر از عبارت صرفا از نظر بازنویسی هستند محصول از نقطه ، به عنوان



تحقق هنری [ ویرایش ]

کاشی کاری هذلولی مثلثی (6،4،2) که الهام بخش MC Escher بود
همچنین ببینید: MC Escher و Circle Limit III
MC Escher مفهوم نمایش بی نهایت را در یک صفحه دو بعدی بررسی کرد. بحث و گفتگو با HSM Coxeter ریاضیدان کانادایی در حدود سال 1956 باعث الهام بخش علاقه اشر به تسلسل های هذلولی شد ، که کاشی کاری های منظم صفحه هایپربولیک هستند. حکاکیهای چوبی اشر Circle Limit I–IV این مفهوم را بین سالهای 1958 و 1960 نشان میدهد، آخرین مورد، Circle Limit IV: Heaven and Hell در سال 1960 است. [4] به گفته برونو ارنست، بهترین آنها Circle Limit III است .
همچنین ببینید [ ویرایش ]
منابع
https://en.wikipedia.org/wiki/Poincar%C3%A9_disk_model







 :
:

 ، که می توان آن را به صورت پارامتری نشان داد:
، که می توان آن را به صورت پارامتری نشان داد:
 جایی که
جایی که  واحد طول قوس از نقطه است
واحد طول قوس از نقطه است  به نقطه
به نقطه  بر
بر 


 ، می توانیم ارزیابی کنیم
، می توانیم ارزیابی کنیم  ، و به دلیل
، و به دلیل ،
، .
. 
 محدود به نابرابری های زیر:
محدود به نابرابری های زیر:



 . اگر
. اگر یک میدان برداری سه بعدی است، سپس واگرایی از
یک میدان برداری سه بعدی است، سپس واگرایی از  .
.


![{\displaystyle {\begin{aligned}I&=\iiint _{V}\nabla \cdot \mathbf {F} \,\mathrm {d} V\\[6pt]&=\iiint _{V}\left( {\frac {\partial \mathbf {F_{x}} }{\partial x}}+{\frac {\partial \mathbf {F_{y}} }{\partial y}}+{\frac {\partial \mathbf {F_{z}} }{\partial z}}\right)\mathrm {d} V\\[6pt]&=\iiint _{V}(4x+4y+4z)\,\mathrm {d } V\\[6pt]&=\int _{0}^{3}\int _{-2}^{2}\int _{0}^{2\pi }(4x+4y+4z)\ ,\mathrm {d} V\end{تراز شده}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/d474d797d9611bde7396b5ad3c477fc3954e40fb)
![{\displaystyle {\begin{aligned}\int _{0}^{3}\int _{-2}^{2}\int _{0}^{2\pi }(4x+4y+4z)\ ,\mathrm {d} V&=\int _{-2}^{2}\int _{0}^{2\pi }(12y+12z+18)\,\mathrm {d} y\,\mathrm {d} z\\[6pt]&=\int _{0}^{2\pi }24(2z+3)\,\mathrm {d} z\\[6pt]&=48\pi (2\ pi +3)\end{تراز شده}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/620b3ddd2e22372f036668159bdb83c2be45446e)







 .
.
 ضریب H با
ضریب H با 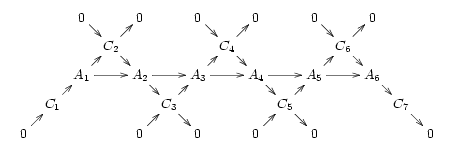
 و جفت نهایی مورفیسم
و جفت نهایی مورفیسم  . اگر شیئی وجود دارد
. اگر شیئی وجود دارد و مورفیسم
و مورفیسم  به طوری که }
به طوری که } دقیق است، سپس دقت
دقیق است، سپس دقت  تضمین شده است. مجدداً مقوله گروهها را مثال میزنیم، این واقعیت که im( f ) هسته برخی هممورفیسمها در H است، نشان میدهد که آن یک
تضمین شده است. مجدداً مقوله گروهها را مثال میزنیم، این واقعیت که im( f ) هسته برخی هممورفیسمها در H است، نشان میدهد که آن یک 


 .
.
 و
و  فاصله p مربوط به q تا مرکز دیسک است،
فاصله p مربوط به q تا مرکز دیسک است، فاصله بین ص و س ،
فاصله بین ص و س ، شعاع دایره مرزی دیسک و
شعاع دایره مرزی دیسک و  است
است  جایی که
جایی که  است
است  بین مبدا و نقطه قرار دارد
بین مبدا و نقطه قرار دارد  (یعنی دو نقطه در یک شعاع هستند، زاویه قطبی یکسانی دارند و
(یعنی دو نقطه در یک شعاع هستند، زاویه قطبی یکسانی دارند و ، فاصله هذلولی آنها است
، فاصله هذلولی آنها است . این به فرمول قبلی کاهش می یابد اگر
. این به فرمول قبلی کاهش می یابد اگر .
. دارای.)
دارای.)

 نشان دهنده هنجار اقلیدسی معمول است. سپس تابع فاصله است
نشان دهنده هنجار اقلیدسی معمول است. سپس تابع فاصله است



 که بدون پیچش است، یعنی معادله ماتریس را برآورده می کند
که بدون پیچش است، یعنی معادله ماتریس را برآورده می کند  . حل این معادله برای
. حل این معادله برای



 در مدل کلاین
در مدل کلاین در مدل دیسک پوانکاره
در مدل دیسک پوانکاره و فرمول ها تبدیل می شوند
و فرمول ها تبدیل می شوند  بنابراین نقاط ثابت هستند.
بنابراین نقاط ثابت هستند. یک بردار هنجار کوچکتر از یک است که نقطه ای از مدل دیسک پوانکاره را نشان می دهد، سپس نقطه متناظر مدل دیسک کلاین با:
یک بردار هنجار کوچکتر از یک است که نقطه ای از مدل دیسک پوانکاره را نشان می دهد، سپس نقطه متناظر مدل دیسک کلاین با:


 در مدل نیمه هواپیما
در مدل نیمه هواپیما  در مدل دیسک
در مدل دیسک




![{\displaystyle {\begin{aligned}x^{2}+y^{2}&{}+{\frac {v_{1}(u_{2}^{2}+v_{2}^{2} +1)-v_{2}(u_{1}^{2}+v_{1}^{2}+1)}{u_{1}v_{2}-u_{2}v_{1}}} x\\[8pt]&{}+{\frac {u_{2}(u_{1}^{2}+v_{1}^{2}+1)-u_{1}(u_{2}^ {2}+v_{2}^{2}+1)}{u_{1}v_{2}-u_{2}v_{1}}}y+1=0\,.\end{تراز شده}} }](https://wikimedia.org/api/rest_v1/media/math/render/svg/f65eb0e73ee28b703a59b3fdfcc8eb28facd52a6)


 )
)












 تمام اجسام محدب مسطح را می توان بر حسب
تمام اجسام محدب مسطح را می توان بر حسب 



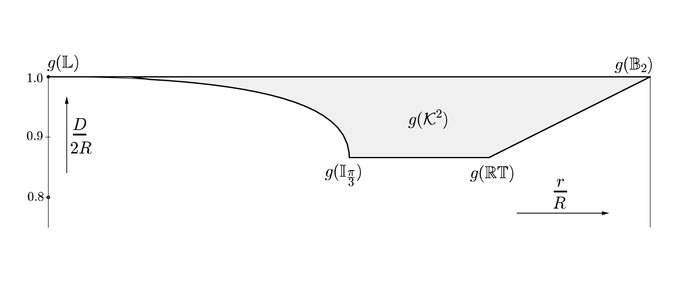
 نشان دهنده بخش خط است،
نشان دهنده بخش خط است،  مثلث متساوی الاضلاع،
مثلث متساوی الاضلاع، 
 دایره واحد
دایره واحد


 که در آن artanh است
که در آن artanh است 
 :
:  :
: 










 . صفحه هذلولی به عنوان بردارهای x با ‖ x ‖ = 1 و x 0 مثبت ("م timلفه زمانی") در این فضا تعبیه شده است . سپس فاصله ذاتی (در تعبیه شده) بین نقاط u و v توسط داده می شود
. صفحه هذلولی به عنوان بردارهای x با ‖ x ‖ = 1 و x 0 مثبت ("م timلفه زمانی") در این فضا تعبیه شده است . سپس فاصله ذاتی (در تعبیه شده) بین نقاط u و v توسط داده می شود







 روی فضا
روی فضا  نقاط مربوط به
نقاط مربوط به  نقاط مربوطه را در
نقاط مربوطه را در  روی فضا
روی فضا  نقاط مربوطه را در
نقاط مربوطه را در  نقاط مربوط به مدل
نقاط مربوط به مدل  نقاط مربوط به
نقاط مربوط به  ، معیار داده شده توسط
، معیار داده شده توسط  .
.
 .
. ، جایی که
، جایی که  است
است 

 ، اگرچه می توان با انتخاب یک دایره به اندازه کافی کوچک خودسرانه آن را بست.
، اگرچه می توان با انتخاب یک دایره به اندازه کافی کوچک خودسرانه آن را بست.



 و طول آن در طول این چرخه چرخه.
و طول آن در طول این چرخه چرخه. 
 .
.


 . نتیجه فیثاغورث در حد مثلث های کوچک بازیابی می شود.
. نتیجه فیثاغورث در حد مثلث های کوچک بازیابی می شود. (جایی که r روی کره است)
(جایی که r روی کره است)  گفته می شود که مدول یا هنجار z یکی است (همیلتون آن را تنسور z می نامید). اما از آنجا که r در یک کره در 3 فضا قرار دارد ، exp (θ r) در کیه ای در 4 فضا قرار دارد که اکنون
گفته می شود که مدول یا هنجار z یکی است (همیلتون آن را تنسور z می نامید). اما از آنجا که r در یک کره در 3 فضا قرار دارد ، exp (θ r) در کیه ای در 4 فضا قرار دارد که اکنون  با t در
با t در 
 به 1 است . برای نسخه دلخواه
به 1 است . برای نسخه دلخواه  جایی که
جایی که  یا
یا  برای یک
برای یک 

 هنجار معمولي اقليدسي است. ما همچنین تعریف می کنیم
هنجار معمولي اقليدسي است. ما همچنین تعریف می کنیم

 یکی از پنج
یکی از پنج  شکل انجمنی
شکل انجمنی  پس از آن یک شکل 4 همسان موازی ، فرم همبستگی است. این اشکال
پس از آن یک شکل 4 همسان موازی ، فرم همبستگی است. این اشکال  یا.
یا.  بیش از حد و معمولاً ادامه دارد
بیش از حد و معمولاً ادامه دارد
 همچنین تعریف شده واقعی است: به کمک
همچنین تعریف شده واقعی است: به کمک  از زمان هماهنگ
از زمان هماهنگ  ظهور.
ظهور. که امروزه بیشتر در
که امروزه بیشتر در  انتخاب شد دومی نیز در فیزیک ذرات مورد استفاده قرار می گیرد
انتخاب شد دومی نیز در فیزیک ذرات مورد استفاده قرار می گیرد  فهمیدن:
فهمیدن:
 ولی،
ولی،
 )
) آیا می توانند
آیا می توانند  می توان با معیارهای مثبت و اقلیدسی مثبت استفاده کرد و هنوز امضای صحیح مینکوفسکی را دریافت می کنید
می توان با معیارهای مثبت و اقلیدسی مثبت استفاده کرد و هنوز امضای صحیح مینکوفسکی را دریافت می کنید
 را می توان به سه کلاس تقسیم کرد:
را می توان به سه کلاس تقسیم کرد: از هر بعد اینها هستند
از هر بعد اینها هستند

 . در یک پایه مناسب
. در یک پایه مناسب ،
، ، ویژگی اویلر
، ویژگی اویلر  است
است ،
، . در مورد
. در مورد 
 فرمول را داریم
فرمول را داریم
 ، حداقل اگر ما با استفاده از جریمه کافی
، حداقل اگر ما با استفاده از جریمه کافی  است
است 


 تابع
تابع


 مشخصه اویلر مداری.
مشخصه اویلر مداری. فراوان است ، پس از آن چند جمله ای هیلبرت درجه اول را می دهد
فراوان است ، پس از آن چند جمله ای هیلبرت درجه اول را می دهد تعبیه به فضای پروژکتور. به عنوان مثال ، پوسته معمولی
تعبیه به فضای پروژکتور. به عنوان مثال ، پوسته معمولی دارای مدرک است
دارای مدرک است ، که یک بسته نرم افزاری کافی برای جنس می دهد
، که یک بسته نرم افزاری کافی برای جنس می دهد 
 سپس فرمول ریمان-روخ می خواند
سپس فرمول ریمان-روخ می خواند
 چند جمله ای هیلبرت
چند جمله ای هیلبرت



 ، از آنجا که درجه آن برای همه منفی است
، از آنجا که درجه آن برای همه منفی است  . به خصوص،
. به خصوص، تعبیه به
تعبیه به  جایی که
جایی که  از آنجا که
از آنجا که . این در ساخت
. این در ساخت 
 ) رضایت بخش
) رضایت بخش نابرابری زیر را شامل می شود:
نابرابری زیر را شامل می شود: 
 ابعاد فضای بخشهای جهانی
ابعاد فضای بخشهای جهانی  مربوط به D ( به عنوان جداکننده
مربوط به D ( به عنوان جداکننده  ، و به همین ترتیب
، و به همین ترتیب . اما دوگانگی Serre برای انواع پروژکتور غیر مفرد در مورد خاص از یک منحنی بیانگر آن است
. اما دوگانگی Serre برای انواع پروژکتور غیر مفرد در مورد خاص از یک منحنی بیانگر آن است دوگانه ایزومورفیک است
دوگانه ایزومورفیک است . بنابراین ، دست چپ با
. بنابراین ، دست چپ با  با تعریف برای اثبات قضیه برای تقسیم کننده عمومی ، می توان با اضافه کردن امتیازات یک به یک به تقسیم کننده ادامه داد و اطمینان حاصل کرد که مشخصه اویلر بر این اساس به سمت راست تغییر می یابد.
با تعریف برای اثبات قضیه برای تقسیم کننده عمومی ، می توان با اضافه کردن امتیازات یک به یک به تقسیم کننده ادامه داد و اطمینان حاصل کرد که مشخصه اویلر بر این اساس به سمت راست تغییر می یابد. مدت به عنوان یک بعد از اولین
مدت به عنوان یک بعد از اولین 
 یک
یک  ، مجموعه اعداد پیچیده علاوه بر این ،
، مجموعه اعداد پیچیده علاوه بر این ،  تعداد دسته های ریمان تعداد دسته های آن است. به عنوان مثال نوع سطح ریمان نشان داده شده در سمت راست سه است. به طور دقیق تر ، جنس به عنوان نیمی از اولین
تعداد دسته های ریمان تعداد دسته های آن است. به عنوان مثال نوع سطح ریمان نشان داده شده در سمت راست سه است. به طور دقیق تر ، جنس به عنوان نیمی از اولین  با ضرایب پیچیده این جنس سطوح فشرده ریمان را
با ضرایب پیچیده این جنس سطوح فشرده ریمان را  یک عنصر از
یک عنصر از  منجر به یک تقسیم کننده می شود
منجر به یک تقسیم کننده می شود  که تعریف میشود
که تعریف میشود
 مجموعه همه صفرها و قطبها است
مجموعه همه صفرها و قطبها است  از رابطه زیر بدست می آید
از رابطه زیر بدست می آید
 نشان دهنده درجه (گاهی اوقات به نام index) نیز تقسیم کننده است
نشان دهنده درجه (گاهی اوقات به نام index) نیز تقسیم کننده است بر روی سطح ، به طوری که تمام ضرایب
بر روی سطح ، به طوری که تمام ضرایب  غیر منفی هستند به طور شهودی ، ما می توانیم از این نظر به عنوان تمام عملکردهای مرومورفیک استفاده کنیم که قطبها در هر نقطه بدتر از ضریب مربوطه در
غیر منفی هستند به طور شهودی ، ما می توانیم از این نظر به عنوان تمام عملکردهای مرومورفیک استفاده کنیم که قطبها در هر نقطه بدتر از ضریب مربوطه در منفی است ، پس ما به آن نیاز داریم
منفی است ، پس ما به آن نیاز داریم 

 در قضیه به ویژه ، تا زمانی که
در قضیه به ویژه ، تا زمانی که ، مدت تصحیح 0 است ، به این ترتیب
، مدت تصحیح 0 است ، به این ترتیب

 . برای
. برای بنابراین ، توابع باید
بنابراین ، توابع باید  . به طور کلی ، دنباله
. به طور کلی ، دنباله دنباله ای در حال افزایش است
دنباله ای در حال افزایش است
 در یک نسخه از
در یک نسخه از از نظر ریمان به شکلی مرومورف گسترش می یابد: از آن زمان دارای یک قطب مضاعف است
از نظر ریمان به شکلی مرومورف گسترش می یابد: از آن زمان دارای یک قطب مضاعف است
 (جایی که
(جایی که 
 ، مانند یک
، مانند یک  ، جایی که
، جایی که  یک
یک  ) جنس آن یکی است: اولین گروه همسان شناسی مفرد آن به طور آزاد توسط دو حلقه تولید می شود ، همانطور که در تصویر سمت راست نشان داده شده است. مختصات پیچیده استاندارد
) جنس آن یکی است: اولین گروه همسان شناسی مفرد آن به طور آزاد توسط دو حلقه تولید می شود ، همانطور که در تصویر سمت راست نشان داده شده است. مختصات پیچیده استاندارد ،
، ، همانطور که در بالا ذکر شد برای
، همانطور که در بالا ذکر شد برای با
با درجه
درجه کاملاً منفی است ، به طوری که اصطلاح تصحیح 0 است. توالی ابعاد را می توان از نظریه
کاملاً منفی است ، به طوری که اصطلاح تصحیح 0 است. توالی ابعاد را می توان از نظریه  ، دنباله ای که در بالا ذکر شد
، دنباله ای که در بالا ذکر شد همیشه درست است که در بیشتر نقاط دنباله شروع می شود
همیشه درست است که در بیشتر نقاط دنباله شروع می شود  مواردی که در توالیهای دیگر وجود دارد و نقاط نهایی زیادی دارند (به
مواردی که در توالیهای دیگر وجود دارد و نقاط نهایی زیادی دارند (به  فضای بخش های هولومورف L را نشان می دهد . این فضا متناهی خواهد بود. ابعاد آن مشخص شده است
فضای بخش های هولومورف L را نشان می دهد . این فضا متناهی خواهد بود. ابعاد آن مشخص شده است . اجازه دهید K دلالت
. اجازه دهید K دلالت 
 از آنجا که تنها عملکردهای هولومورفیک روی X ثابت ها هستند. درجه L صفر است ، و
از آنجا که تنها عملکردهای هولومورفیک روی X ثابت ها هستند. درجه L صفر است ، و بسته نرم افزاری بی اهمیت است. بدین ترتیب،
بسته نرم افزاری بی اهمیت است. بدین ترتیب،
 ، اثبات این است که وجود دارد گرم هولومورفیک یک اشکال.
، اثبات این است که وجود دارد گرم هولومورفیک یک اشکال. می دهد
می دهد

 .
.
 .
. 



 . این از
. این از 




 متعلق به شبکه Z + τ Z یک
متعلق به شبکه Z + τ Z یک 
![\ displaystyle [\ wp '(z)] ^ {2} = 4 [\ wp (z)] ^ {3} -g_ {2} \ wp (z) -g_ {3} ،}](https://wikimedia.org/api/rest_v1/media/math/render/svg/d094adcb0b3a44c6e5cbdc747eef133ab81f4d67)
 یا صریحاً
یا صریحاً
 ،
،  ،
،  و
و . همچنین توجه داشته باشید که برخی از نویسندگان ژاکوبین به عنوان تعریف
. همچنین توجه داشته باشید که برخی از نویسندگان ژاکوبین به عنوان تعریف  . در اینجا ما در حال تصویب کنوانسیون هستیم که بردار شیب
. در اینجا ما در حال تصویب کنوانسیون هستیم که بردار شیب یک وکتور ستون است. تخصص بیشتر ، هنگامی که
یک وکتور ستون است. تخصص بیشتر ، هنگامی که  یک مانیفولد ریمانی باشید و بگذارید
یک مانیفولد ریمانی باشید و بگذارید  یک نقشه متفاوت باشد. سپس یکی ممکن است در نظر
یک نقشه متفاوت باشد. سپس یکی ممکن است در نظر 
 است
است  توسط
توسط
 متریک ریمانی نخواهد بود
متریک ریمانی نخواهد بود  از آنجایی که مثبت نیست ، قطعی است. به عنوان مثال ، اگر
از آنجایی که مثبت نیست ، قطعی است. به عنوان مثال ، اگر برای هر یک تزریقی است
برای هر یک تزریقی است 
 این یک غوطه وری است ، و بنابراین پوشش جهانی هر منیفولد ریمانی به طور خودکار یک معیار ریمانی را به ارث می برد. به طور کلی ، اما با همان اصل ، هر فضای پوشش یک مانیفولد ریمانی یک معیار ریمانی را به ارث می برد.
این یک غوطه وری است ، و بنابراین پوشش جهانی هر منیفولد ریمانی به طور خودکار یک معیار ریمانی را به ارث می برد. به طور کلی ، اما با همان اصل ، هر فضای پوشش یک مانیفولد ریمانی یک معیار ریمانی را به ارث می برد. دو منیفولد ریمانی باشید و
دو منیفولد ریمانی باشید و  با ساختار صاف
با ساختار صاف  بر
بر  که می تواند از چند طریق توصیف شود.
که می تواند از چند طریق توصیف شود. ممکن است فرد تعریف کند
ممکن است فرد تعریف کند
 یک نمودار مختصات صاف باشد
یک نمودار مختصات صاف باشد  و اجازه دهید
و اجازه دهید یک نمودار مختصات صاف باشد
یک نمودار مختصات صاف باشد  سپس
سپس  نمودار مختصات صاف است
نمودار مختصات صاف است  برای راحتی اجازه دهید
برای راحتی اجازه دهید مجموعه متقارن مثبت مثبت را مشخص کنید
مجموعه متقارن مثبت مثبت را مشخص کنید ماتریس های واقعی بیان مختصات از
ماتریس های واقعی بیان مختصات از و بیانگر مختصات از
و بیانگر مختصات از سپس نمایندگی مختصات محلی از
سپس نمایندگی مختصات محلی از  داده شده توسط
داده شده توسط
 به عنوان ضرب n برابر تعریف کنید
به عنوان ضرب n برابر تعریف کنید  اگر یکی به هر نسخه از آن را می دهد
اگر یکی به هر نسخه از آن را می دهد  با توجه به معیار استاندارد ریمانی آن ،
با توجه به معیار استاندارد ریمانی آن ،  بعنوان یک زیرمنفرد تعبیه شده (همانطور که در بالا) وجود دارد ، می توان متریک محصول Riemannian را در نظر گرفت
بعنوان یک زیرمنفرد تعبیه شده (همانطور که در بالا) وجود دارد ، می توان متریک محصول Riemannian را در نظر گرفت به آن یک
به آن یک  و
و  دو معیار ریمانی باشید
دو معیار ریمانی باشید  سپس ، برای هر شماره
سپس ، برای هر شماره![\ displaystyle \ lambda \ in [0،1] ،}](https://wikimedia.org/api/rest_v1/media/math/render/svg/7eef2d5921c69ea9eb6377fe22579a12eda4c93e)

 و
و  یک معیار دیگر ریمانی است.
یک معیار دیگر ریمانی است.

 بازگشت آن در امتداد φ β است .
بازگشت آن در امتداد φ β است .![{\ displaystyle \ gamma: [a، b] \ to M](https://wikimedia.org/api/rest_v1/media/math/render/svg/b5c2d8d0dd04be91ac24d40469cc8b8ad0c7057d) متفاوت است ، سپس به هریک اختصاص می دهد
متفاوت است ، سپس به هریک اختصاص می دهد  یک بردار
یک بردار  در فضای بردار
در فضای بردار اندازه آن با هنجار قابل اندازه گیری است
اندازه آن با هنجار قابل اندازه گیری است  بنابراین
بنابراین یک تابع غیر منفی را در فاصله تعریف می کند
یک تابع غیر منفی را در فاصله تعریف می کند  طول به عنوان انتگرال این عملکرد تعریف شده است. با این حال ، همانطور که در اینجا ارائه می شود ، هیچ دلیلی وجود ندارد که انتظار داشته باشیم این عملکرد یکپارچه شود. معمولاً فرض کنید که g به صورت مداوم و
طول به عنوان انتگرال این عملکرد تعریف شده است. با این حال ، همانطور که در اینجا ارائه می شود ، هیچ دلیلی وجود ندارد که انتظار داشته باشیم این عملکرد یکپارچه شود. معمولاً فرض کنید که g به صورت مداوم و به طور مداوم متمایز می شود ، به طوری که تابعی که باید یکپارچه باشد غیر منعطف و پیوسته است ، و از این رو طول
به طور مداوم متمایز می شود ، به طوری که تابعی که باید یکپارچه باشد غیر منعطف و پیوسته است ، و از این رو طول 

 توسط
توسط
 خاصیت تقارن آن
خاصیت تقارن آن  خاصیت انعکاس آن
خاصیت انعکاس آن  و نابرابری مثلث
و نابرابری مثلث اگرچه برخی از عوارض فنی جزئی نیز وجود دارد (مانند تأیید اینکه هر دو نقطه با یک مسیر متمایز به هم متصل می شوند). فهم آن اساسی تر است
اگرچه برخی از عوارض فنی جزئی نیز وجود دارد (مانند تأیید اینکه هر دو نقطه با یک مسیر متمایز به هم متصل می شوند). فهم آن اساسی تر است تضمین می کند
تضمین می کند و از این رو
و از این رو  همه بدیهیات یک متریک را برآورده می کند.
همه بدیهیات یک متریک را برآورده می کند.
 همزمان با ساختار فضای توپولوژیکی اصلی است
همزمان با ساختار فضای توپولوژیکی اصلی است  غیر قابل تشخیص است و حتی تعیین موقعیت یا ماهیت این نقاط حتی در موارد به ظاهر ساده مانند زمان
غیر قابل تشخیص است و حتی تعیین موقعیت یا ماهیت این نقاط حتی در موارد به ظاهر ساده مانند زمان نسبت به این ساختار فضای متریک ، فرد می گوید یک مسیر
نسبت به این ساختار فضای متریک ، فرد می گوید یک مسیر![{\ displaystyle c: [a، b] \ to M](https://wikimedia.org/api/rest_v1/media/math/render/svg/57801bc98b672c06d66583417b5114f2a36d2e6d) یک واحد سرعت است
یک واحد سرعت است ![{\ displaystyle t_ {0} \ in [a، b]](https://wikimedia.org/api/rest_v1/media/math/render/svg/25c9abe498a595aa49b749c92b744e127800c140) یک فاصله وجود دارد
یک فاصله وجود دارد![sub \ نمایشگر J \ زیر مجموعه [a، b]](https://wikimedia.org/api/rest_v1/media/math/render/svg/ad23fd9e4daa0124313d437a8bc46c3cc6328f26) که شامل
که شامل و از این قبیل
و از این قبیل
 برای همه
برای همه  سپس یکی به طور خودکار
سپس یکی به طور خودکار  با استفاده از نابرابری مثلث در تقریب جمع ریمان از انتگرال که طول را تعیین می کند
با استفاده از نابرابری مثلث در تقریب جمع ریمان از انتگرال که طول را تعیین می کند  بنابراین وضعیت ژئودزیکی با سرعت واحد همانطور که در بالا آورده شد نیاز است
بنابراین وضعیت ژئودزیکی با سرعت واحد همانطور که در بالا آورده شد نیاز است  و
و  تا حد ممکن از یکدیگر دور باشند. واقعیت این است که ما فقط برای منحنی به دنبال به صورت محلی کشش خود را بیرون می توسط دو مثال اول داده شده در زیر منعکس شده؛ شکل جهانی
تا حد ممکن از یکدیگر دور باشند. واقعیت این است که ما فقط برای منحنی به دنبال به صورت محلی کشش خود را بیرون می توسط دو مثال اول داده شده در زیر منعکس شده؛ شکل جهانی از رابطه زیر بدست می آید
از رابطه زیر بدست می آید به یاد بیاورید
به یاد بیاورید از منحنی
از منحنی  با متریک استاندارد ریمانی آن ، پس از آن یک مسیر واحد سرعت در امتداد یک دایره استوایی یک هندسه خواهد بود. یک مسیر واحد سرعت در امتداد سایر حلقه های عرض جغرافیایی نخواهد بود.
با متریک استاندارد ریمانی آن ، پس از آن یک مسیر واحد سرعت در امتداد یک دایره استوایی یک هندسه خواهد بود. یک مسیر واحد سرعت در امتداد سایر حلقه های عرض جغرافیایی نخواهد بود. با معیار استاندارد ریمانی سپس یک خط واحد سرعت مانند
با معیار استاندارد ریمانی سپس یک خط واحد سرعت مانند یک ژئودزیک اما منحنی است
یک ژئودزیک اما منحنی است  یک ژئودزیکی با سرعت واحد وجود دارد
یک ژئودزیکی با سرعت واحد وجود دارد  به
به  به طوری که
به طوری که برای همه
برای همه ![{\ displaystyle s ، t \ in [a، b].](https://wikimedia.org/api/rest_v1/media/math/render/svg/38794ff3a511c6ed891dbedcb49711717fc05739)
 به دنباله ای از منحنی های واحد سرعت متمایز متمایز متمایز از واحد
به دنباله ای از منحنی های واحد سرعت متمایز متمایز متمایز از واحد  حد فرعی حاصل از ژئودزیک مورد نظر است.
حد فرعی حاصل از ژئودزیک مورد نظر است. با معیار استاندارد ریمانی آن ، و یکی طول می کشد
با معیار استاندارد ریمانی آن ، و یکی طول می کشد و
و هیچ ژئودزیکی با سرعت واحد از یک به دیگری وجود ندارد.
هیچ ژئودزیکی با سرعت واحد از یک به دیگری وجود ندارد.
![\ displaystyle M = {\ Big \ {} {\ text functions توابع پیوسته}} f: [0،1] \ به \ mathbb {R} {\ text {با} \ sup _ {x \ در [0 ، 1]} | f (x) | \ leq 1 \ بزرگ \}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/d32b59479d6be03329ff60e3145988a75c35c2bb)
![\ displaystyle d (f، g) = \ sup _ {x \ in [0،1]} | f (x) -g (x) |.}](https://wikimedia.org/api/rest_v1/media/math/render/svg/d4968cb9f2028481e49bb5c4a09a337ae1840ce7)
 مهم است که این متریک از ساختار ریمانی ناشی شود.
مهم است که این متریک از ساختار ریمانی ناشی شود. (از طرف دیگر ، این نمادین گاه برای
(از طرف دیگر ، این نمادین گاه برای  بین
بین  است تعبیه توپولوژیکی اگر
است تعبیه توپولوژیکی اگر (جایی که
(جایی که  یک
یک  یک نقشه صاف باشید سپس
یک نقشه صاف باشید سپس یک محله وجود دارد
یک محله وجود دارد  به طوری که
به طوری که  تعبیه شده است.)
تعبیه شده است.) . علاقه در اینجا به چه میزان است
. علاقه در اینجا به چه میزان است از
از کافی است ، و بهترین مرز خطی ممکن است. به عنوان مثال
کافی است ، و بهترین مرز خطی ممکن است. به عنوان مثال  همانطور که صریحاً توسط
همانطور که صریحاً توسط  چنین باشد که
چنین باشد که و
و در هر نقطه
در هر نقطه  .
. و
و . شرط دوم ، تقریباً بیان شده ، می گوید که f ( X ) به مرز Y مماس نیست .
. شرط دوم ، تقریباً بیان شده ، می گوید که f ( X ) به مرز Y مماس نیست . ما داریم
ما داریم
 σ- هستند
σ- هستند 
 و
و  ما داریم
ما داریم  ،
، و
و  اگر
اگر 
 . در تئوری مدل نیز مفهوم قوی تری از
. در تئوری مدل نیز مفهوم قوی تری از 
 است
است  از
از  ) اگر
) اگر
 .
. است، چه از بعد حداکثر است
است، چه از بعد حداکثر است به گونه ای که
به گونه ای که  می تواند به صورت خطی در داخل جاسازی شود
می تواند به صورت خطی در داخل جاسازی شود ![\ displaystyle h \ colon [-1،1] \ to (-1،1)](https://wikimedia.org/api/rest_v1/media/math/render/svg/ba1591adb5a4700221b75086a48fc5d979ad5e2a) یک عملکرد صاف
یک عملکرد صاف  . سپس کره ای با متریک
. سپس کره ای با متریک
 سطح زول است.
سطح زول است. یک خانواده یک پارامتر از عوامل ساختاری وجود دارد
یک خانواده یک پارامتر از عوامل ساختاری وجود دارد  به طوری که
به طوری که یک سطح صفر و
یک سطح صفر و  .
.





































































![\ displaystyle K = - {\ beta ^ {2} \ over ((s- \ alpha) ^ {2} + \ beta ^ {2}) ^ 2}}، \، \، K_ {m} = - {r [(s- \ alpha) ^ {2} + \ beta ^ {2})] + \ beta _ {t} (s- \ alpha) + \ beta \ alpha _ {t} \ over [(s- \ alpha) ^ {2} + \ beta ^ {2}] ^ {\ frac {3} {2}}}.}](https://wikimedia.org/api/rest_v1/media/math/render/svg/ff1ab2130e1d570ae5585c216637fb7661847192)












 ،
، .
. . برای مشخص کردن مشتقات کواریانس کافی است که مشتق کواریانس هر زمینه بردار پایه را مشخص کنید
. برای مشخص کردن مشتقات کواریانس کافی است که مشتق کواریانس هر زمینه بردار پایه را مشخص کنید در امتداد
در امتداد .
.
 مؤلفه های ارتباط با توجه به سیستم مختصات محلی هستند. در نظریه منیفولدهای ریمانیان و شبه ریمانی ، مؤلفه های اتصال Levi-Civita با توجه به سیستم مختصات محلی به عنوان
مؤلفه های ارتباط با توجه به سیستم مختصات محلی هستند. در نظریه منیفولدهای ریمانیان و شبه ریمانی ، مؤلفه های اتصال Levi-Civita با توجه به سیستم مختصات محلی به عنوان  و
و ما گرفتیم
ما گرفتیم



 .
. با این عبارت آورده شده است:
با این عبارت آورده شده است:
 برای هر شاخص بالایی
برای هر شاخص بالایی  و
و  برای هر شاخص پایین
برای هر شاخص پایین  .
.
 چگالی مقیاس (از وزن 1+) است ، بنابراین دریافت می کنیم:
چگالی مقیاس (از وزن 1+) است ، بنابراین دریافت می کنیم:
 ، تمایز کواریان به سادگی تمایز جزئی است:
، تمایز کواریان به سادگی تمایز جزئی است:
 ، ما داریم:
، ما داریم:
 ، ما داریم:
، ما داریم:
 ، ما داریم:
، ما داریم:
 ، ما داریم:
، ما داریم:
 ، ما داریم:
، ما داریم:

 . نشان می دهد که:
. نشان می دهد که:
 است
است 

 .
.
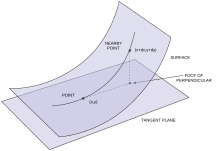
 بلکه به خود بردار v نیز بستگی دارد
بلکه به خود بردار v نیز بستگی دارد .
.
 یک میدان تانسور
یک میدان تانسور  در یک نقطه
در یک نقطه  در یک منیفولد:
در یک منیفولد:
 یک میدان بردار در امتداد منحنی است
یک میدان بردار در امتداد منحنی است از بین می رود و سپس منحنی ژئودزیک مشتق کواریان نامیده می شود. اگر مشتق هموردا است
از بین می رود و سپس منحنی ژئودزیک مشتق کواریان نامیده می شود. اگر مشتق هموردا است  از طریق نقشه
از طریق نقشه  به طوری که فضای مماس در
به طوری که فضای مماس در  توسط بردارها پوشانده شده است
توسط بردارها پوشانده شده است
 با متریک موجود در M سازگار است :
با متریک موجود در M سازگار است :
 ، یک نفر دارد
، یک نفر دارد .
. .
. ، همچنین نوشته شده است
، همچنین نوشته شده است ، به عنوان پیش بینی متعامد مشتق معمول روی فضای مماس تعریف شده است:
، به عنوان پیش بینی متعامد مشتق معمول روی فضای مماس تعریف شده است:
 فضای مماس متعامد است ، می توان معادلات عادی را حل کرد:
فضای مماس متعامد است ، می توان معادلات عادی را حل کرد: .
.



 ، که نشان دهنده قسمت
، که نشان دهنده قسمت ![\ displaystyle \ phi: [- 1،1] \ to M](https://wikimedia.org/api/rest_v1/media/math/render/svg/7e5d89fc45414df51e7c7100dd8a5034886d0f05) به طوری که
به طوری که  و
و ، و مشتق کواریانس از f در p تعریف شده است
، و مشتق کواریانس از f در p تعریف شده است![{\ displaystyle \ left (\ nabla _ {\ mathbf {v}} f \ Right) _ {p} = \ left (f \ circ \ phi \ Right) '\ چپ (0 \ راست) = \ lim _ {t \ به 0} t ^ {- 1} \ left (f \ left [\ phi \ left (T \ Right) \ Right] -f \ left [p \ Right] \ Right).}](https://wikimedia.org/api/rest_v1/media/math/render/svg/46a0a2fbe4bfe716387d68d4468d99ccd9dce830)
 تابعی است که با هر نقطه p در دامنه مشترک f و v مقیاس همراه است
تابعی است که با هر نقطه p در دامنه مشترک f و v مقیاس همراه است در نقطه p در یک منیفولد صاف یک بردار مماس اختصاص می دهد
در نقطه p در یک منیفولد صاف یک بردار مماس اختصاص می دهد به هر جفت
به هر جفت  ، متشکل از یک بردار tangent v در p و زمینه بردار u در محله ای از p تعریف شده است ، به گونه ای که خواص زیر را در خود نگه می دارد (برای هر بردار v ، x و y در p ، زمینه های بردار u و w در یک محله از p تعریف می شود ، مقادیر مقیاس g و h در p و عملکرد مقیاس f تعریف شده در یک محله از p ):
، متشکل از یک بردار tangent v در p و زمینه بردار u در محله ای از p تعریف شده است ، به گونه ای که خواص زیر را در خود نگه می دارد (برای هر بردار v ، x و y در p ، زمینه های بردار u و w در یک محله از p تعریف می شود ، مقادیر مقیاس g و h در p و عملکرد مقیاس f تعریف شده در یک محله از p ): خطی است
خطی است  بنابراین
بنابراین
 بنابراین:
بنابراین:![\ displaystyle \ left (\ nabla _ {\ mathbf {v}} \ left [\ mathbf {u} + \ mathbf {w} \ Right] \ Right) _ {p} = \ چپ (\ nabla _ {\ mathbf {v}} \ mathbf {u} \ Right) _ {p} + \ left (\ nabla _ {\ mathbf {v}} \ mathbf {w} \ Right) _ {p}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/f5b778432f3325c9ea994ac1c4e9ccdd347033fe)
![\ displaystyle \ left (\ nabla _ {\ mathbf {v}} \ left [f \ mathbf {u} \ Right] \ Right) _ {p} = f (p) \ سمت چپ (\ nabla _ {\ mathbf v}} \ mathbf {u}) _ {p} + (\ nabla _ {\ mathbf {v}} f \ Right) _ {p} \ mathbf {u} _ {p}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/3c53045366df9ce75d7334db9d378a1ae88d5f0e) .
. نشانگر فیلد برداری است که مقدار آن در هر نقطه از p دامنه ، بردار مماس است
نشانگر فیلد برداری است که مقدار آن در هر نقطه از p دامنه ، بردار مماس است تعریف شده در یک محله از P ، مشتق کواریانس آن است
تعریف شده در یک محله از P ، مشتق کواریانس آن است به روشی تعریف شده است تا عملكرد حاصل با انقباض تنشور و قاعده محصول سازگار باشد. به این معنا که،
به روشی تعریف شده است تا عملكرد حاصل با انقباض تنشور و قاعده محصول سازگار باشد. به این معنا که،![{\ displaystyle \ left (\ nabla _ {\ mathbf {v}} \ alpha \ Right) _ {p} \ چپ (\ mathbf {u} _ {p} \ Right) = \ nabla _ {\ mathbf {v } \ left [\ alpha \ left (\ mathbf {u} \ Right) \ Right] _ {p} - \ alpha _ {p} \ left [\ left (\ nabla _ {\ mathbf {v}} \ mathbf شما} \ درست) _ {پ} \ درست].}](https://wikimedia.org/api/rest_v1/media/math/render/svg/f99f0886345bebb1123ad6cb5d6810b8795e3a36)
 و
و در محله ای از نقطه p :
در محله ای از نقطه p :
 از همان ارزش
از همان ارزش

 ، که به عنوان ورودی های آن در نظر گرفته می شود: (1) یک بردار ، u ، در نقطه P تعریف شود ، و (2) یک
، که به عنوان ورودی های آن در نظر گرفته می شود: (1) یک بردار ، u ، در نقطه P تعریف شود ، و (2) یک  ، همچنین در نقطه P . تفاوت اصلی از مشتقات جهت دار معمول در این است که
، همچنین در نقطه P . تفاوت اصلی از مشتقات جهت دار معمول در این است که ، جایی که
، جایی که و
و  بردارهای مماس واحد برای مختصات قطبی ، که به عنوان پایه ای برای تجزیه یک بردار از نظر
بردارهای مماس واحد برای مختصات قطبی ، که به عنوان پایه ای برای تجزیه یک بردار از نظر  و
و  ، که ما به طور خلاصه همانند آنها را نمایندگی خواهیم کرد
، که ما به طور خلاصه همانند آنها را نمایندگی خواهیم کرد  و
و  به ترتیب و همیشه شاخص خود را فرض کنید
به ترتیب و همیشه شاخص خود را فرض کنید  از 1 تا 3 اجرا می شود. ما فرض خواهیم کرد که این سیستم های مختصات در فضای سه بعدی اقلیدسی تعبیه شده اند. مختصات
از 1 تا 3 اجرا می شود. ما فرض خواهیم کرد که این سیستم های مختصات در فضای سه بعدی اقلیدسی تعبیه شده اند. مختصات  برای
برای
 برای
برای

 برای
برای
 برای
برای 


 برای
برای  ،که در آن
،که در آن ردیف و
ردیف و  ستون
ستون















![\ mathcal {E} _ {ijk = \ left [\ mathbf {b} _i، \ mathbf {b} _j، \ mathbf {b} _k \ right] = (\ mathbf {b} _i \ times \ mathbf {b _j) \ cdot \ mathbf {b} _k ~؛ ~~ \ mathcal {E} ^ {ijk} = \ left [\ mathbf {b} ^ i، \ mathbf {b} ^ j، \ mathbf {b} ^ k \ درست]](https://wikimedia.org/api/rest_v1/media/math/render/svg/0ff8cee95f0d851c6e17855f9efa90baacfcb500)



 نشان داده می شود که
نشان داده می شود که 


![\ mathbf {u} \ times \ mathbf {v} = [(\ mathbf {b} _m \ times \ mathbf {b} _n) \ cdot \ mathbf {b} _s] ~ u ^ m ~ v ^ n ~ \ mathbf b} ^ s = \ mathcal {E} _ {smn} ~ u ^ m ~ v ^ n \ mathbf {b} ^ s](https://wikimedia.org/api/rest_v1/media/math/render/svg/316c491176058cfffb31f3f6878d44eda4f0653e)
 است
است 
 یک بردار پایه دکارتی است. از این رو،
یک بردار پایه دکارتی است. از این رو،
![\ fill {تراز} \ mathbf {b} _m \ بار \ mathbf {b} _n & = \ frac {\ جزئی \ mathbf {x}} {\ جزئی q ^ m} \ بار \ frac {\ جزئی \ mathbf {x } {\ جزئی q ^ n} = \ frac {\ جزئی (x_p ~ \ mathbf {e} _p)} {\ جزئی q ^ m} \ بار \ frac {\ جزئی (x_q ~ \ mathbf {e} _q) } {\ جزئی q ^ n} \\ [8pt] & = \ frac {\ partial x_p} {\ partial q ^ m} ~ \ frac {\ جزئی x_q} {\ جزئی q ^ n} ~ \ mathbf {e _p \ times \ mathbf {e} _q = \ varepsilon_ {ipq} ~ \ frac {\ جزئی x_p} {\ جزئی q ^ m} ~ \ frac {\ جزئی x_q} {\ جزئی q ^ n} ~ \ mathbf {e _i \ end {تراز کردن}](https://wikimedia.org/api/rest_v1/media/math/render/svg/6e260f052daf21c2aafe16c46c40d01f2471495d)


![\ fill {تراز} \ mathbf {u} \ بار \ mathbf {v} & = \ varepsilon_ {ijk} ~ \ hat {u} _j ~ \ hat v} _k ~ \ mathbf {e} _i = \ varepsilon_ {ijk } ~ \ frac {\ جزئی x_j} {\ جزئی q ^ m} ~ \ frac {\ جزئی x_k} {\ جزئی q ^ n} ~ \ frac {\ جزئی جزئی x_i} {\ جزئی q ^ s} ~ u ^ m ~ v ^ n ~ \ mathbf {b} ^ s \\ [8pt] & = [(\ mathbf {b} _m \ Times \ mathbf {b} _n) \ cdot \ mathbf {b} _s] ~ u ^ m v ^ n ~ \ mathbf {b} ^ s = \ mathcal {E} _ {smn} ~ u ^ m ~ v ^ n \ mathbf {b} ^ s \ end {تراز](https://wikimedia.org/api/rest_v1/media/math/render/svg/d9663d103d89692c7e93cc2b5041d56e275ef20a)
 تعریف شده توسط
تعریف شده توسط 
 می تواند در مختصات منحنی به صورت بیان شود
می تواند در مختصات منحنی به صورت بیان شود
 می تواند در مختصات منحنی به صورت بیان شود
می تواند در مختصات منحنی به صورت بیان شود

 یک تانسور مرتبه دوم است ، سپس تعیین کننده توسط رابطه تعریف می شود
یک تانسور مرتبه دوم است ، سپس تعیین کننده توسط رابطه تعریف می شود![\ left [\ boldsymbol S} \ cdot \ mathbf {u}، \ boldsymbol {S} \ cdot \ mathbf {v}، \ boldsymbol S} \ cdot \ mathbf {w} \ Right] = \ det \ boldsymbol S} \ چپ [\ mathbf {u} ، \ mathbf {v} ، \ mathbf {w} \ Right]](https://wikimedia.org/api/rest_v1/media/math/render/svg/3d45df1a660b1f145e06b8f8b86f04d8d69fcf2c)
 بردارهای دلخواه و
بردارهای دلخواه و![\ left [\ mathbf {u}، \ mathbf {v}، \ mathbf {w} \ Right]: = \ mathbf {u} \ cdot (\ mathbf {v} \ بار \ mathbf {W}).](https://wikimedia.org/api/rest_v1/media/math/render/svg/11e2a58fd353028bb79dda5a46e874563e9ab21a)


![\ mathbf {b} ^ i = \ boldsymbol {F} ^ {- \ rm {T}} \ cdot \ mathbf {e} ^ i ~؛ ~~ g ^ {ij} = [\ boldsymbol {F} ^ {- \ rm {1}} \ cdot \ boldsymbol {F} ^ {- \ rm {T}}] _ {ij} ~؛ ~~ g_ {ij} = [g ^ {ij}] ^ {- 1} = [ \ boldsymbol {F} ^ {\ rm {T}} \ cdot \ boldsymbol {F}] _ {ij](https://wikimedia.org/api/rest_v1/media/math/render/svg/cdacfeb6f24e52d94cc79c806e68ff60f013a72f)
 جاکوبین تحول باشید. سپس ، از تعریف تعیین کننده ،
جاکوبین تحول باشید. سپس ، از تعریف تعیین کننده ،![\ left [\ mathbf {b} _1، \ mathbf {b} _2، \ mathbf {b} _3 \ Right] = \ det \ boldsymbol {F} \ left [\ mathbf {e} _1، \ mathbf {e} _2 ، \ mathbf {e} _3 \ Right].](https://wikimedia.org/api/rest_v1/media/math/render/svg/27fb40b2c4c5aff231420ea55a9fa2087acb5869)
![\ left [\ mathbf {e} _1، \ mathbf {e} _2، \ mathbf {e} _3 \ Right] = 1](https://wikimedia.org/api/rest_v1/media/math/render/svg/9acb2516827df5a7fa7b889b38161ea0c7edcd29)
![J = \ det \ boldsymbol {F} = \ left [\ mathbf {b} _1، \ mathbf {b} _2، \ mathbf {b} _3 \ Right] = \ mathbf {b _1 \ cdot (\ mathbf {b _2 \ بار \ mathbf {b} _3)](https://wikimedia.org/api/rest_v1/media/math/render/svg/c246b146b59a610afbd5f727ed1d99ddd6dba4cb)
![\ displaystyle g: = \ det [g_ {ij}]](https://wikimedia.org/api/rest_v1/media/math/render/svg/862e1ae368f9114d096d6a73ea9b1c0e1dfe3863)
![g = \ det [\ boldsymbol {F} ^ {\ rm {T}}] \ cdot \ det [\ boldsymbol {F}] = J \ cdot J = J ^ 2](https://wikimedia.org/api/rest_v1/media/math/render/svg/18f8d6db9ee13068f9021b8025f691bfdc225f1e)
![\ det [g ^ {ij}] = \ cfrac {1 {{J ^ 2](https://wikimedia.org/api/rest_v1/media/math/render/svg/5ddad469d755523d50e3eaad1cb5076f61f754e3)
![[g ^ {ij}] = [g_ {ij}] ^ {- 1}](https://wikimedia.org/api/rest_v1/media/math/render/svg/3c4a027ea5efffa5271d721a669f1ead309ccec8) ،
،









 در این وبلاگ به ریاضیات و کاربردهای آن و تحقیقات در آنها پرداخته می شود. مطالب در این وبلاگ ترجمه سطحی و اولیه است و کامل نیست.در صورتی سوال یا نظری در زمینه ریاضیات دارید مطرح نمایید .در صورت امکان به آن می پردازم. من دوست دارم برای یافتن پاسخ به سوالات و حل پروژه های علمی با دیگران همکاری نمایم.در صورتی که شما هم بامن هم عقیده هستید با من تماس بگیرید.
در این وبلاگ به ریاضیات و کاربردهای آن و تحقیقات در آنها پرداخته می شود. مطالب در این وبلاگ ترجمه سطحی و اولیه است و کامل نیست.در صورتی سوال یا نظری در زمینه ریاضیات دارید مطرح نمایید .در صورت امکان به آن می پردازم. من دوست دارم برای یافتن پاسخ به سوالات و حل پروژه های علمی با دیگران همکاری نمایم.در صورتی که شما هم بامن هم عقیده هستید با من تماس بگیرید.