1-تقسیم بر صفر
از ویکیپدیا، دانشنامه آزاد
برای دیگر کاربردها، تقسیم بر صفر (ابهامزدایی) را ببینید .
| این مقاله شامل فهرستی از مراجع عمومی است ، اما فاقد استنادهای درون خطی متناظر کافی است. لطفا با معرفی نقل قول های دقیق تر به بهبود این مقاله کمک کنید. ( آوریل 2016 ) ( نحوه و زمان حذف این پیام الگو را بیاموزید ) |
. وقتی x از سمت راست به 0 نزدیک می شود، y به بی نهایت نزدیک می شود. وقتی x از سمت چپ به 0 نزدیک می شود، y به بی نهایت منفی نزدیک می شود.
در ریاضیات ، تقسیم بر صفر ، تقسیمی است که در آن مخرج (مخرج) صفر است . چنین تقسیمی را می توان به طور رسمی به صورت بیان کرد
ساختارهای ریاضی وجود دارد که در آنهاآ
در محاسبات ، یک خطای برنامه ممکن است در نتیجه تلاش برای تقسیم بر صفر ایجاد شود. بسته به محیط برنامه نویسی و نوع عدد (مثلاً ممیز شناور ، عدد صحیح ) که بر صفر تقسیم می شود، ممکن است توسط استاندارد ممیز شناور IEEE 754 بی نهایت مثبت یا منفی ایجاد کند، یک استثنا ایجاد کند، یک پیام خطا ایجاد کند، برنامه برای خاتمه، منجر به یک مقدار خاص غیر عددی ، [2] یا خرابی .
محاسبات ابتدایی [ ویرایش ]
هنگامی که تقسیم در سطح ریاضی ابتدایی توضیح داده می شود، اغلب به عنوان تقسیم مجموعه ای از اشیاء به قسمت های مساوی در نظر گرفته می شود. به عنوان مثال، داشتن ده کوکی را در نظر بگیرید، و این کوکی ها باید به طور مساوی بین پنج نفر در یک میز توزیع شوند. هر فرد دریافت می کرد
بنابراین، برای تقسیم بر صفر، وقتی 10 کوکی به طور مساوی بین 0 نفر در یک میز توزیع می شود، تعداد کوکی هایی که هر فرد دریافت می کند چقدر است؟ کلمات خاصی را می توان در سوال مشخص کرد تا مشکل را برجسته کند. مشکل این سوال «چه زمانی» است. هیچ راهی برای توزیع 10 کوکی برای هیچ کس وجود ندارد. از این رو،
اگر مثلاً 5 کوکی و 2 نفر وجود دارد، مشکل در "توزیع یکنواخت" است. در هر پارتیشن عدد صحیح از 5 چیز به 2 قسمت، یا یکی از قسمت های پارتیشن دارای عناصر بیشتری نسبت به دیگری خواهد بود یا یک باقیمانده وجود خواهد داشت (نوشته شده به صورت5/2= 2 r1). یا مشکل 5 کوکی و 2 نفر را می توان با نصف کردن یک کوکی حل کرد که ایده کسری را معرفی می کند (5/2= 2+1/2) . از طرف دیگر مشکل 5 کوکی و 0 نفر را به هیچ وجه نمی توان حل کرد که معنای "تقسیم" را حفظ کند.
در جبر ابتدایی ، روش دیگری برای نگریستن به تقسیم بر صفر این است که همیشه می توان تقسیم را با استفاده از ضرب بررسی کرد. با در نظرگرفتن10/0مثال بالا، تنظیم x =10/0، اگر x برابر ده تقسیم بر صفر باشد، x ضربدر صفر برابر با ده است، اما x وجود ندارد که وقتی در صفر ضرب می شود، ده (یا هر عددی غیر از صفر) را به دست دهد. اگر به جای x =10/0، x =0/0، سپس هر x این سوال را برآورده می کند که "چه عدد x ضرب در صفر، صفر می دهد؟"
تلاش های اولیه [ ویرایش ]
Brāhmasphuṭasiddhānta برهماگوپتا ( حدود ۵۹۸–۶۶۸ ) قدیمی ترین متنی است که صفر را به تنهایی به عنوان یک عدد در نظر می گیرد و عملیات های مربوط به صفر را تعریف می کند. [3] نویسنده نمی تواند تقسیم بر صفر را در متون خود توضیح دهد: تعریف او به راحتی می تواند به پوچ های جبری منجر شود. به گفته براهماگوپتا،
عدد مثبت یا منفی وقتی بر صفر تقسیم شود کسری است که مخرج آن صفر است. صفر تقسیم بر یک عدد منفی یا مثبت یا صفر است یا به صورت کسری با عدد صفر و مقدار متناهی به عنوان مخرج بیان می شود. صفر تقسیم بر صفر صفر است.
در سال 830، ماهاویرا تلاش کرد اشتباهی را که براهماگوپتا در کتابش گانیتا سارا سامگراها مرتکب شده بود تصحیح کند : «عددی وقتی بر صفر تقسیم میشود بدون تغییر میماند». [3]
جبر [ ویرایش ]
چهار عمل اصلی - جمع، تفریق، ضرب و تقسیم - که برای اعداد صحیح (اعداد صحیح مثبت) اعمال میشود، با برخی محدودیتها، در محاسبات ابتدایی به عنوان چارچوبی برای پشتیبانی از گسترش قلمرو اعداد مورد استفاده قرار میگیرند. به عنوان مثال، برای اینکه بتوان یک عدد کامل را از عدد دیگر تفریق کرد، قلمرو اعداد باید به کل مجموعه اعداد صحیح گسترش داده شود تا اعداد صحیح منفی را در بر گیرد. به طور مشابه، برای پشتیبانی از تقسیم هر عدد صحیح بر هر عدد دیگر، قلمرو اعداد باید به اعداد گویا گسترش یابد .. در طول این گسترش تدریجی سیستم اعداد، مراقبت می شود تا اطمینان حاصل شود که "عملیات توسعه یافته"، زمانی که برای اعداد قدیمی اعمال می شود، نتایج متفاوتی ایجاد نمی کند. به زبان ساده، از آنجایی که تقسیم بر صفر هیچ معنایی ندارد ( تعریف نشده است ) در تنظیم اعداد کامل، با گسترش تنظیمات به اعداد واقعی یا حتی مختلط ، این درست باقی میماند .
همانطور که قلمرو اعدادی که این عملیات را می توان برای آنها اعمال کرد گسترش می یابد، تغییراتی در نحوه مشاهده عملیات نیز وجود دارد. به عنوان مثال، در قلمرو اعداد صحیح، تفریق دیگر یک عملیات اساسی در نظر گرفته نمی شود، زیرا می توان آن را با جمع اعداد علامت دار جایگزین کرد. [4] به همین ترتیب، هنگامی که قلمرو اعداد گسترش می یابد تا اعداد گویا را نیز در بر گیرد، تقسیم با ضرب در اعداد گویا معین جایگزین می شود. با توجه به این تغییر دیدگاه، سؤال «چرا نمیتوانیم بر صفر تقسیم کنیم؟» به «چرا یک عدد گویا نمیتواند مخرج صفر داشته باشد؟» میشود. پاسخ به این سوال تجدید نظر شده دقیقا مستلزم بررسی دقیق تعریف اعداد گویا است.
در رویکرد مدرن برای ساخت میدان اعداد حقیقی، اعداد گویا به عنوان یک گام میانی در توسعه ظاهر می شوند که بر اساس نظریه مجموعه ها بنا شده است. ابتدا، اعداد طبیعی (شامل صفر) بر اساس مبانی بدیهی مانند سیستم بدیهی Peano ایجاد میشوند و سپس به حلقه اعداد صحیح بسط مییابند . مرحله بعدی تعریف اعداد گویا است با در نظر گرفتن اینکه این کار باید تنها با استفاده از مجموعه ها و عملیاتی که قبلاً ایجاد شده اند انجام شود، یعنی جمع، ضرب و اعداد صحیح. با شروع مجموعه ای از جفت های مرتب شده از اعداد صحیح، {( a , b )} با b ≠ 0 ، یک رابطه باینری تعریف کنید.در این مجموعه توسط ( a , b ) ≃ ( c , d ) اگر و فقط اگر ad = bc باشد. این رابطه به عنوان یک رابطه هم ارزی نشان داده می شود و کلاس های هم ارزی آن به عنوان اعداد گویا تعریف می شوند. در اثبات صوری است که این رابطه یک رابطه هم ارزی است که شرط صفر نبودن مختصات دوم مورد نیاز است (برای تأیید گذر ). [5] [6] [7]
توضیح فوق ممکن است برای بسیاری از اهداف بسیار انتزاعی و فنی باشد، اما اگر وجود و ویژگیهای اعداد گویا را، همانطور که معمولاً در ریاضیات ابتدایی انجام میشود، فرض کنیم، «دلیل» مجاز نبودن تقسیم بر صفر از دید پنهان میماند. با این وجود، می توان یک توجیه (غیر دقیق) در این زمینه ارائه داد.
از خصوصیات سیستم اعدادی که استفاده می کنیم (یعنی اعداد صحیح، گویا، واقعی و غیره) نتیجه می شود، اگر b ≠ 0 باشد، a = b × c است. فرض کنید که آ/0یک عدد c است، پس باید a = 0 × c = 0 باشد. با این حال، عدد منفرد c باید با معادله 0 = 0 × c تعیین شود ، اما هر عددی این معادله را برآورده می کند، بنابراین ما نمی توانیم یک مقدار عددی به آن اختصاص دهیم.0/0. [8]
تقسیم به عنوان معکوس ضرب [ ویرایش ]
مفهومی که تقسیم را در جبر توضیح می دهد این است که آن معکوس ضرب است. به عنوان مثال، [9]
بیان
به طور کلی، یک مقدار را نمی توان به کسری که مخرج آن 0 است نسبت داد، بنابراین مقدار آن تعریف نشده باقی می ماند.
) می تواند برای تشخیص عدد از حرف استفاده شود (بیشتر در محاسبات، ناوبری و در ارتش استفاده می شود). به نظر می رسد رقم 0 با یک نقطه در مرکز به عنوان یک گزینه در نمایشگرهای 
معادل هستند:
برای 
به طوری که 
. سمت چپ این معادله را می توان به عنوان تفاوت محدوده های 
اپراتور 
. 
این نام قابل انعطاف پذیری ریاضی آن است ، که بیشتر به ![{\ displaystyle {\ start {تراز شده} u_ {a} (t) & = u_ {m} (t) \ cdot \ cos (\ امگا t + \ phi) + i \ cdot u_ {m} (t) \ cdot \ sin (\ امگا t + \ phi) \\ & = u_ {m} (t) \ cdot \ چپ [\ cos (\ امگا t + \ phi) + i \ cdot \ sin (\ امگا t + \ phi) \ راست] \ \ & = u_ {m} (t) \ cdot e ^ {i (\ امگا t + \ phi)}. \ ، \ پایان {تراز شده}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/37242f9ff59dbd2d9ed8ce281605c7bb9ebf0465)
برای 
:
دو چالش برای اجرای عملی به عنوان تجمع ارائه می دهد:
مورد نیاز است. خروجی مربوطه متعاقباً توسط به تأخیر می افتد
هنگام ایجاد قسمت خیالی یک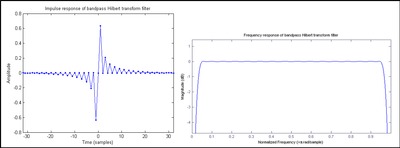 
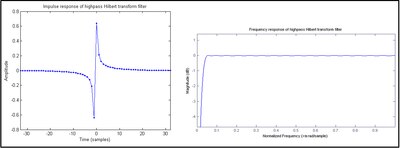
![تو [n]](https://wikimedia.org/api/rest_v1/media/math/render/svg/e6f1362207606428a09d907db25527859eab6ac3)
، با 
، و تبدیل گسسته هیلبرت![{\ hat {u}} [n]](https://wikimedia.org/api/rest_v1/media/math/render/svg/b9374254c890a695913751d90f0248bf30260a26)
، DTFT از
![{\ displaystyle {\ start {تراز شده} {\ کلاه {u}} [n] & = {\ scriptstyle \ mathrm {DTFT} ^ {- 1}} (U (\ omega)) \ * \ {\ scriptstyle \ mathrm {DTFT} ^ {- 1}} (- i \ cdot \ operatorname {sgn} (\ امگا)) \\ & = u [n] \ * \ {\ frac {1} {2 \ pi}} \ int _ {- \ pi} ^ {\ pi} (- i \ cdot \ operatorname {sgn} (\ omega)) \ cdot e ^ {i \ omega n} \، \ mathrm {d} \ omega \\ & = u [ n] \ * \ \ underbrace {{\ frac {1} {2 \ pi}} \ left [\ int _ {- \ pi} ^ {0} i \ cdot e ^ {i \ omega n} \، \ mathrm {d} \ امگا - \ int _ {0} ^ {\ pi} i \ cdot e ^ {i \ omega n} \، \ mathrm {d} \ امگا \ راست]} _ {h [n]} ، \ پایان {تراز شده}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/6ce04b3a6fd925320ecd65d574152eebc3a24c87)
![{\ displaystyle h [n] \ \ triangleq \ {\ start {cases} 0، & {\ text {for}} n {\ text {even}} \\ {\ frac {2} {\ pi n}} & {\ text {for}} n {\ text {odd}} ، \ end {موارد}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/759a9546ab3c3371675c11e7f41bbac4aea1f4e5)
![تو [n] ،](https://wikimedia.org/api/rest_v1/media/math/render/svg/db24ca554e6645bd66aa851b6dbc45543a906f0c)
برای ایجاد یک ![{\ displaystyle h_ {N} [n] \ \ triangleq \ sum _ {m = - \ infty} ^ {\ infty} h [n-mN]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/68c941a14a6807d0a23edf0c67e9c4123f9b7527)
![{\ displaystyle {\ scriptstyle \ mathrm {DFT}} \ چپ (تو [n] \ راست)}](https://wikimedia.org/api/rest_v1/media/math/render/svg/3a227c2caa955761fadeef6c6dd73c5da296539c)
با نمونه هایی از توزیع ![{\ displaystyle h [n]،}](https://wikimedia.org/api/rest_v1/media/math/render/svg/d95e01506ee85989abead7eebfa72ae91f5e61e6)
نشان داده شده توسط ![{\ tilde {h}} [n] ،](https://wikimedia.org/api/rest_v1/media/math/render/svg/ab116fb3573ead55e7b305a3e064b893a3839520)
جایگزین کردن ![{\ displaystyle {\ scriptstyle \ mathrm {DFT}} \ چپ ({\ tilde {h}} [n] \ سمت راست)}](https://wikimedia.org/api/rest_v1/media/math/render/svg/19307ee7a40ed0fb1475787a0133b0ce5075f8e3)
برای نمونه های ![{\ displaystyle {\ tilde {h}} _ {N} [n] \ \ triangleq \ sum _ {m = - \ infty} ^ {\ infty} {\ tilde {h}} [n-mN].}](https://wikimedia.org/api/rest_v1/media/math/render/svg/7b18bc36f1a8ea3d2128983fe3ec612f0397eb2a)
![{\ displaystyle {\ tilde {h}} [n]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/df0a3a5c199d8c1d0527bf16b60cf63058b6e119)
است
توالی خروجی شامل 
خروجی های
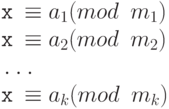
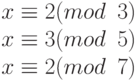
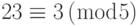
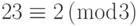
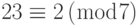
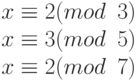
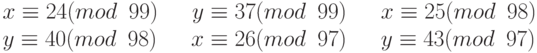
پس 
پس 
یا
پس 
پس 
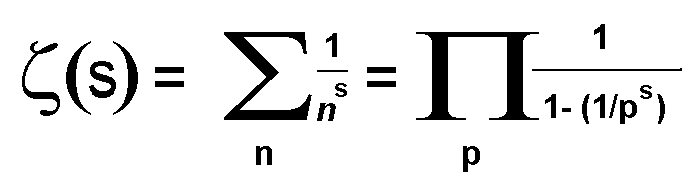
![{\displaystyle {\begin{aligned}{\mathcal {F}}\left\{\mathbf {x} \right\}[m]&=\sum \limits _{k=1}^{n}x_{k}\cdot e^{{-2\pi i}{\frac {mk}{n}}},\mathbf {x} =\left\{\gcd(k,n)\right\}\quad {\text{for}}\,k\in \left\{1\dots n\right\}\\\varphi (n)&={\mathcal {F}}\left\{\mathbf {x} \right\}[1]=\sum \limits _{k=1}^{n}\gcd(k,n)e^{{-2\pi i}{\frac {k}{n}}}.\end{aligned}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/3eb6e9b0bca4db124c0da54548202dfffecdcb87)
در این وبلاگ به ریاضیات و کاربردهای آن و تحقیقات در آنها پرداخته می شود. مطالب در این وبلاگ ترجمه سطحی و اولیه است و کامل نیست.در صورتی سوال یا نظری در زمینه ریاضیات دارید مطرح نمایید .در صورت امکان به آن می پردازم. من دوست دارم برای یافتن پاسخ به سوالات و حل پروژه های علمی با دیگران همکاری نمایم.در صورتی که شما هم بامن هم عقیده هستید با من تماس بگیرید.