نگاشت همدیس
از ویکیپدیا، دانشنامه آزاد
برای دیگر کاربردها، Conformal (ابهامزدایی) را ببینید .

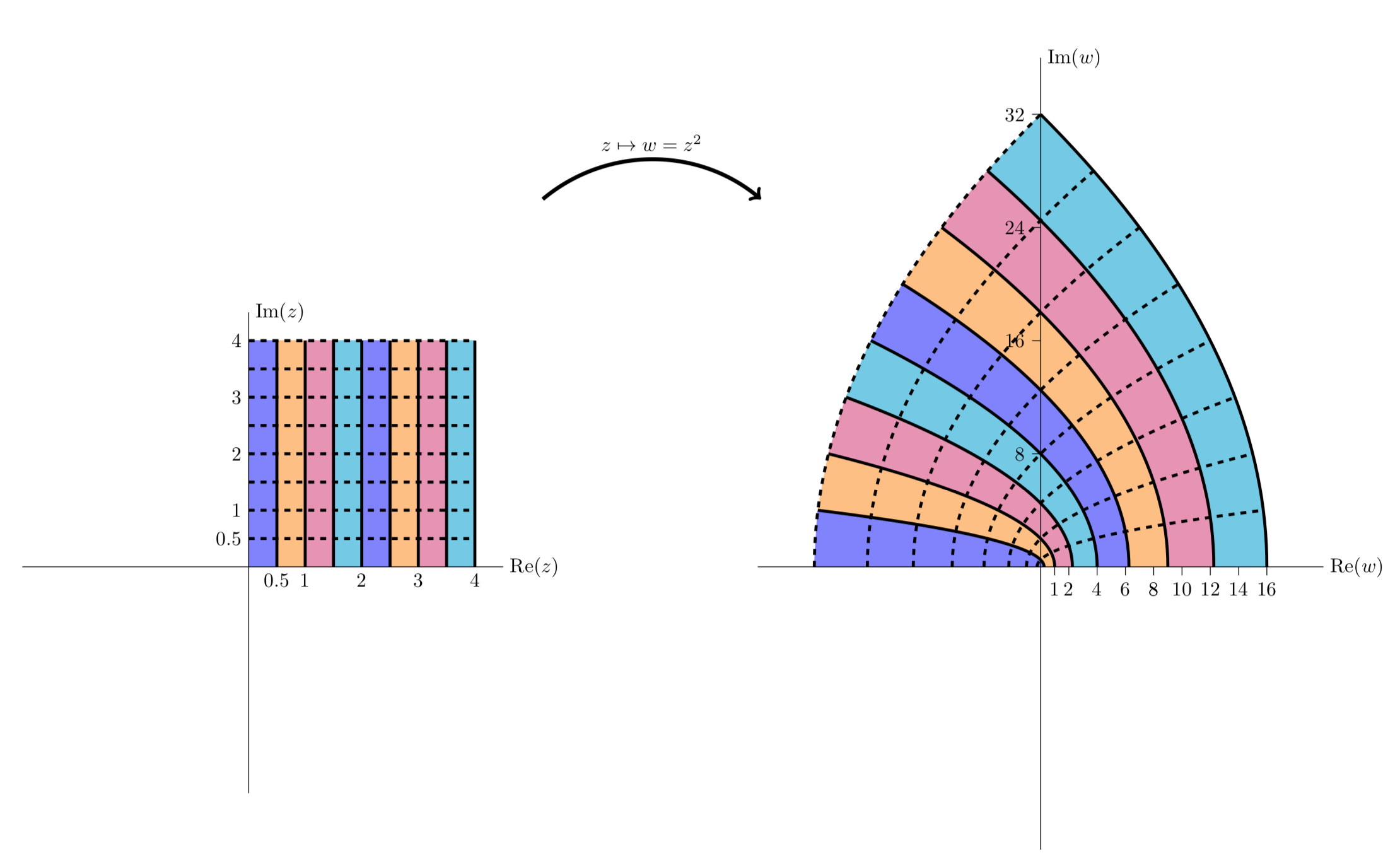
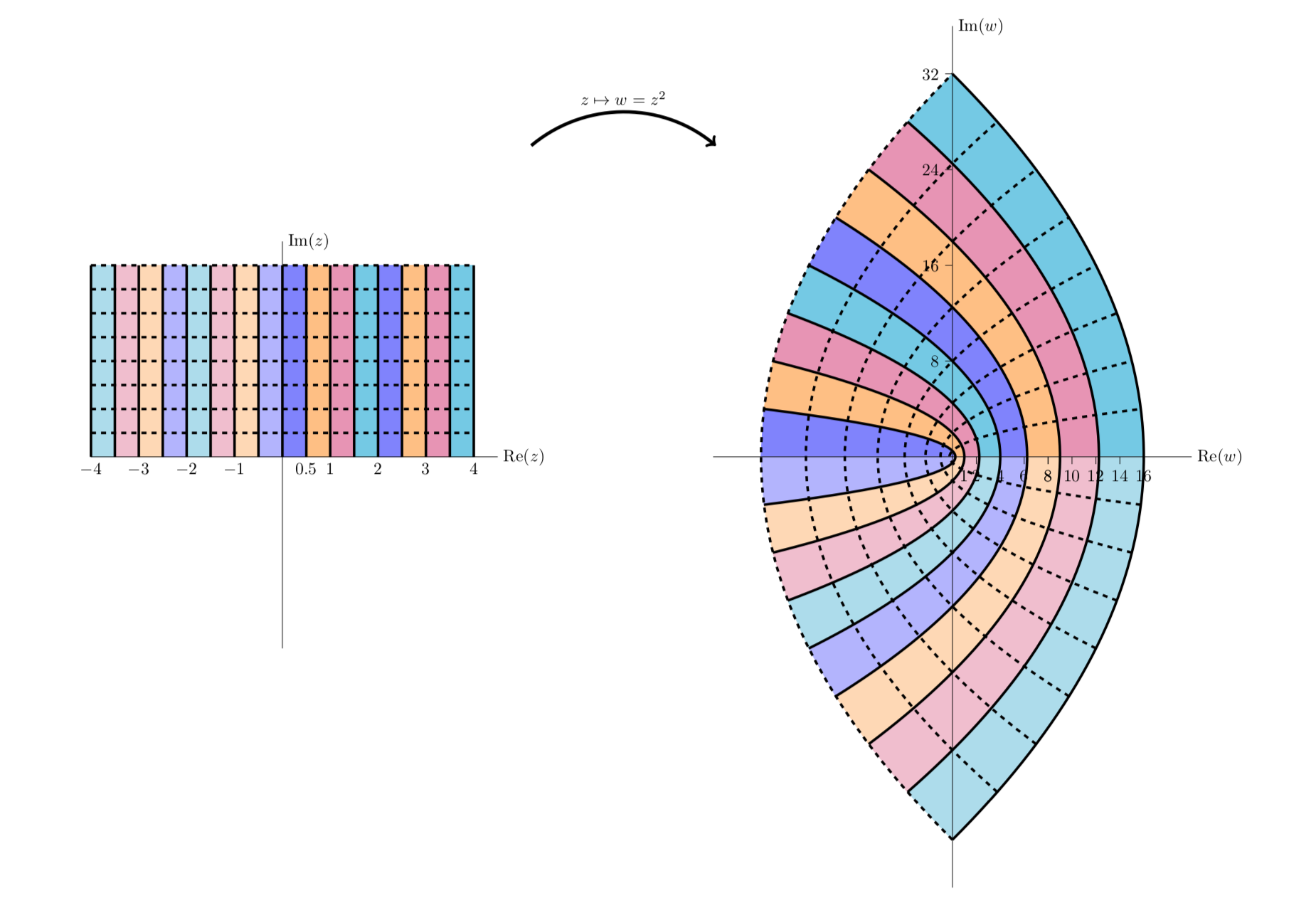
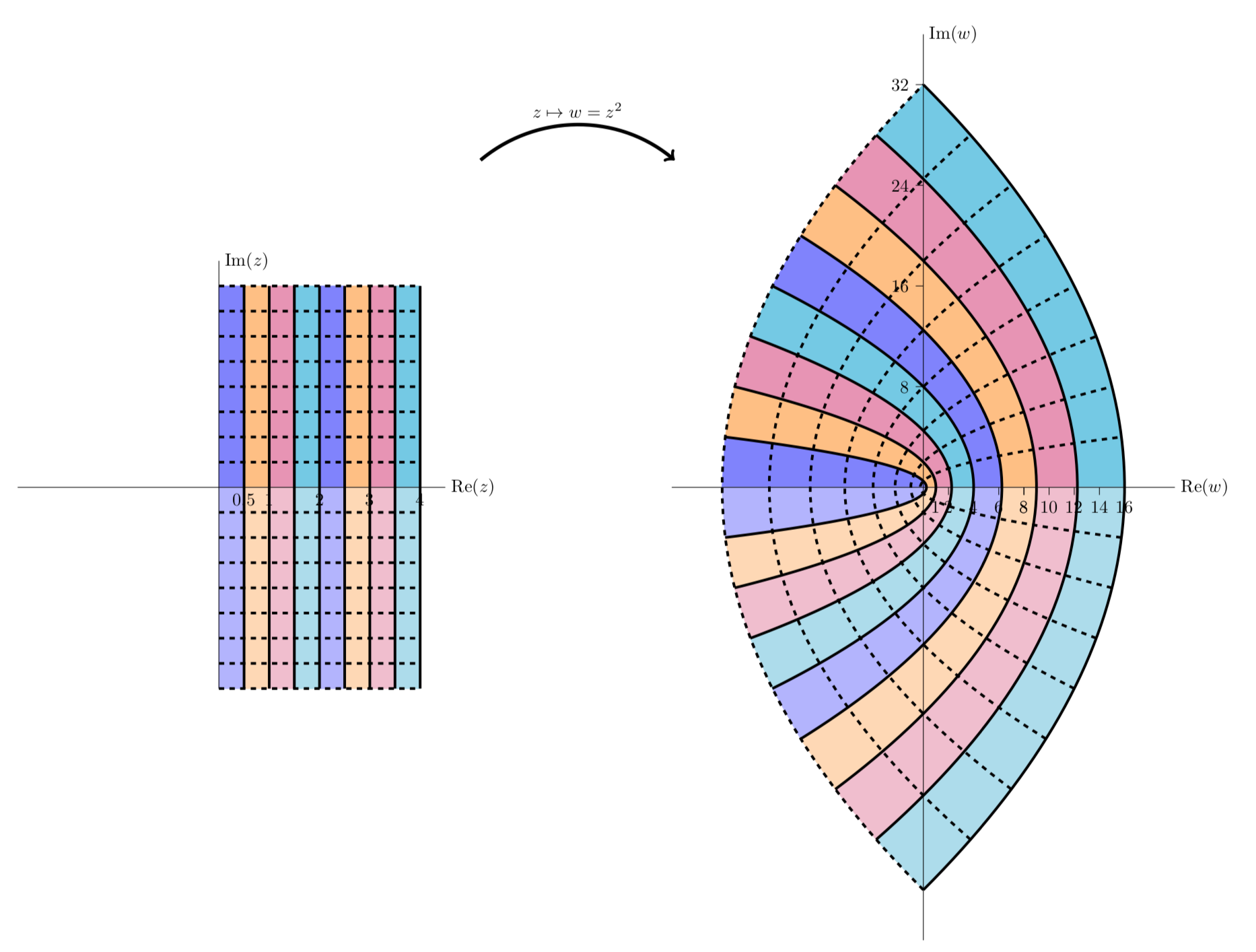
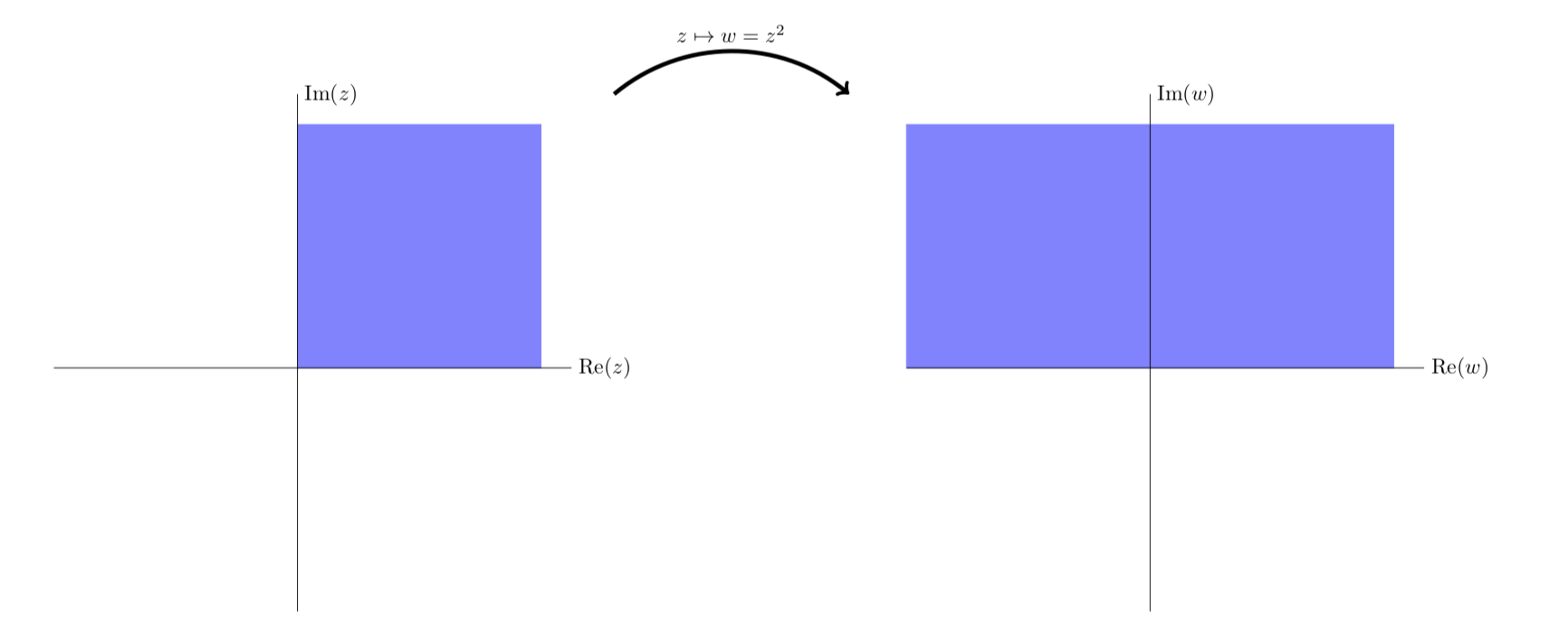
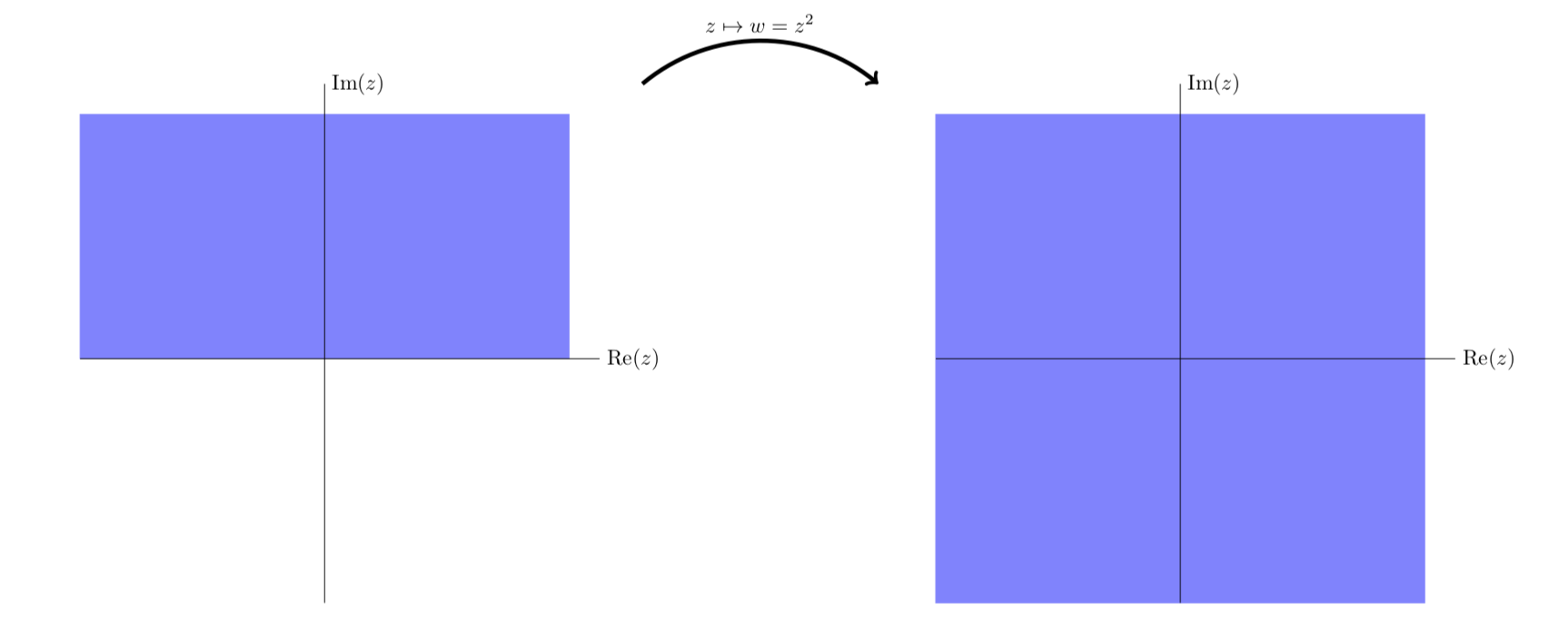
یک شبکه مستطیل شکل (بالا) و تصویر آن در زیر یک نگاشت همدیس (پایین). دیده می شود که
(پایین). دیده می شود که جفت خطوطی را که در 90 درجه متقاطع هستند تا جفت منحنی هایی که هنوز در 90 درجه متقاطع هستند، ترسیم می کند.
جفت خطوطی را که در 90 درجه متقاطع هستند تا جفت منحنی هایی که هنوز در 90 درجه متقاطع هستند، ترسیم می کند.
در ریاضیات ، نگاشت همدیس تابعی است که به صورت محلی زاویه ها را حفظ می کند، اما لزوما طول ها را حفظ نمی کند.
رسمی تر، اجازه دهید و
و زیر مجموعه های باز باشد
زیر مجموعه های باز باشد . یک تابع
. یک تابع در یک نقطه همدیس (یا حفظ زاویه ) نامیده می شود
در یک نقطه همدیس (یا حفظ زاویه ) نامیده می شود اگر زوایای بین منحنی های هدایت شده را حفظ کند
اگر زوایای بین منحنی های هدایت شده را حفظ کند ، و همچنین حفظ جهت گیری. نگاشتهای همدیس هم زوایای و هم اشکال شکلهای بینهایت کوچک را حفظ میکنند، اما لزوماً اندازه یا انحنای آنها را حفظ نمیکنند .
، و همچنین حفظ جهت گیری. نگاشتهای همدیس هم زوایای و هم اشکال شکلهای بینهایت کوچک را حفظ میکنند، اما لزوماً اندازه یا انحنای آنها را حفظ نمیکنند .
ویژگی همدیس را می توان بر حسب ماتریس مشتق ژاکوبین یک تبدیل مختصات توصیف کرد. زمانی که ژاکوبین در هر نقطه یک عدد اسکالر مثبت ضربدر یک ماتریس چرخش ( متعامد با یک تعیین کننده) باشد، تبدیل مطابق است. برخی از نویسندگان انطباق را شامل نگاشتهای جهتگیری معکوس میکنند که ژاکوبینها را میتوان به صورت هر عدد اسکالر ضربدر هر ماتریس متعامد نوشت. [1]
برای نگاشتها در دو بعد، نگاشتهای همدیس (حفظ جهت گیری) دقیقاً توابع تحلیلی مختلط معکوس محلی هستند. در ابعاد سه و بالاتر، قضیه لیوویل به شدت نگاشتهای همدیس را به چند نوع محدود می کند.
مفهوم انطباق به شیوه ای طبیعی به نگاشت های بین منیفولدهای ریمانی یا نیمه ریمانی تعمیم می یابد.
فهرست
نگاشت های همدیس در دو بعدی [ ویرایش ]
اگر زیر مجموعه ای باز از صفحه مختلط است
زیر مجموعه ای باز از صفحه مختلط است ، سپس یک تابع
، سپس یک تابع  منطبق است اگر و فقط اگر هولومورفیک باشد و مشتق آن در همه جا غیر صفر باشد
منطبق است اگر و فقط اگر هولومورفیک باشد و مشتق آن در همه جا غیر صفر باشد . اگر
. اگر ضد هولومورفیک است ( مزوج با یک تابع هولومورفیک)، زوایا را حفظ می کند اما جهت آنها را معکوس می کند .
ضد هولومورفیک است ( مزوج با یک تابع هولومورفیک)، زوایا را حفظ می کند اما جهت آنها را معکوس می کند .
در ادبیات، تعریف دیگری از conformal وجود دارد: نگاشت برداری که در یک مجموعه باز در هواپیما یک به یک و هولومورفیک است. قضیه نگاشت باز تابع معکوس (تعریف شده در تصویر از
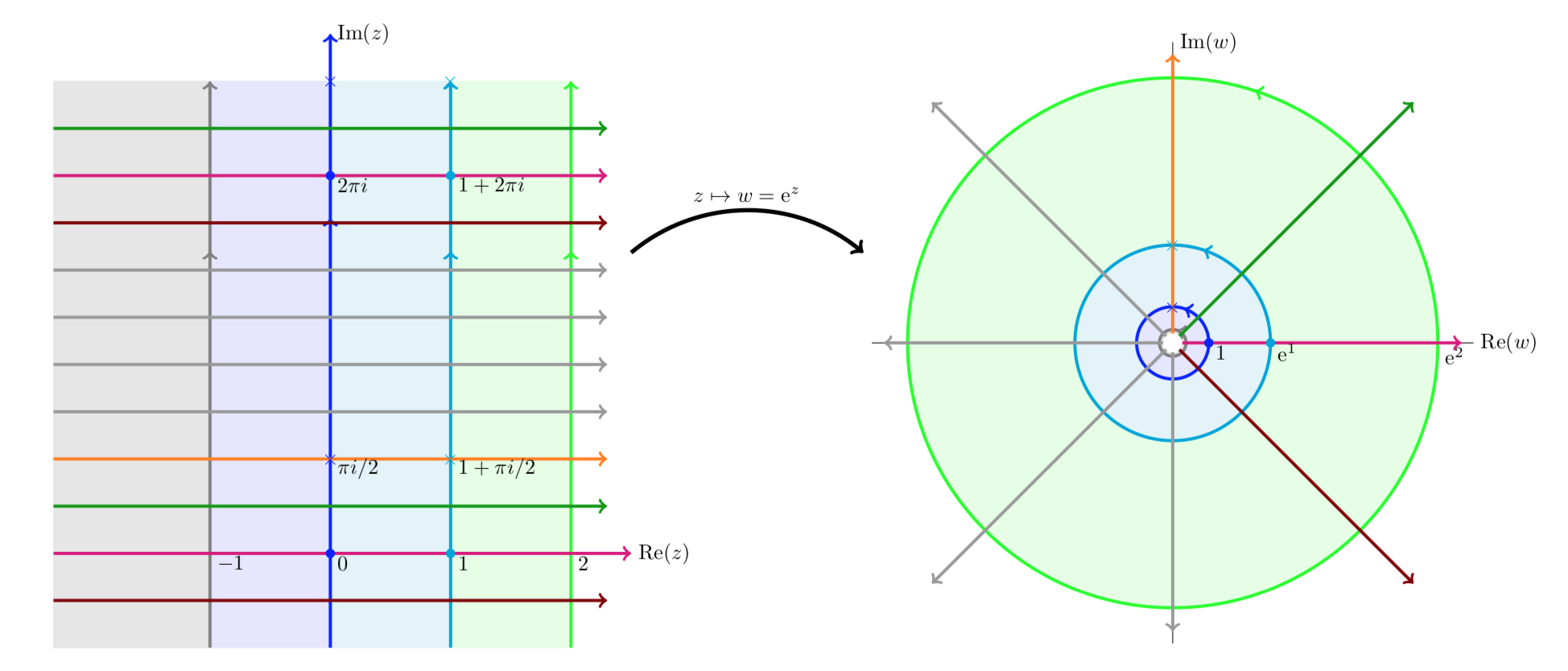
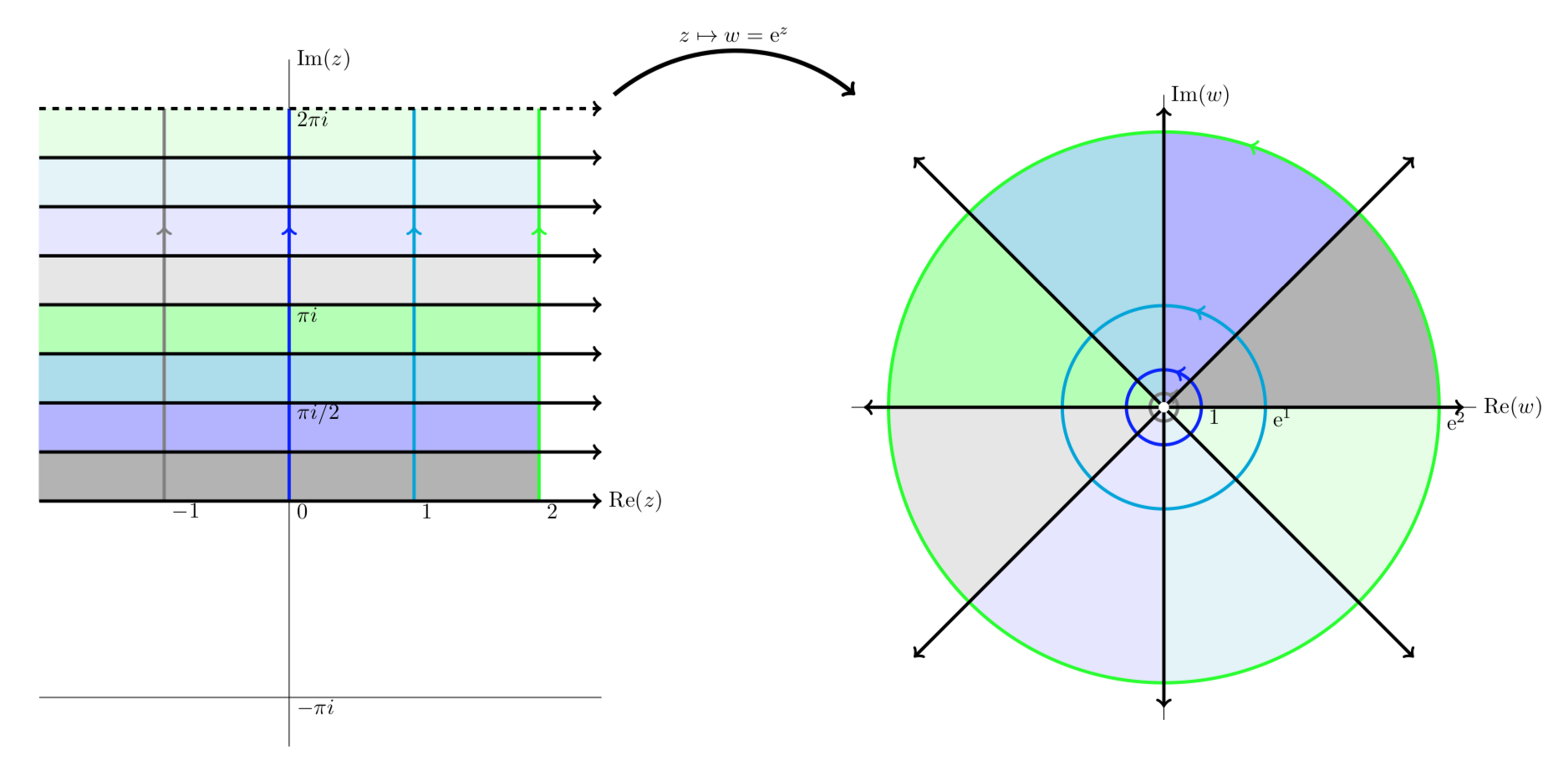
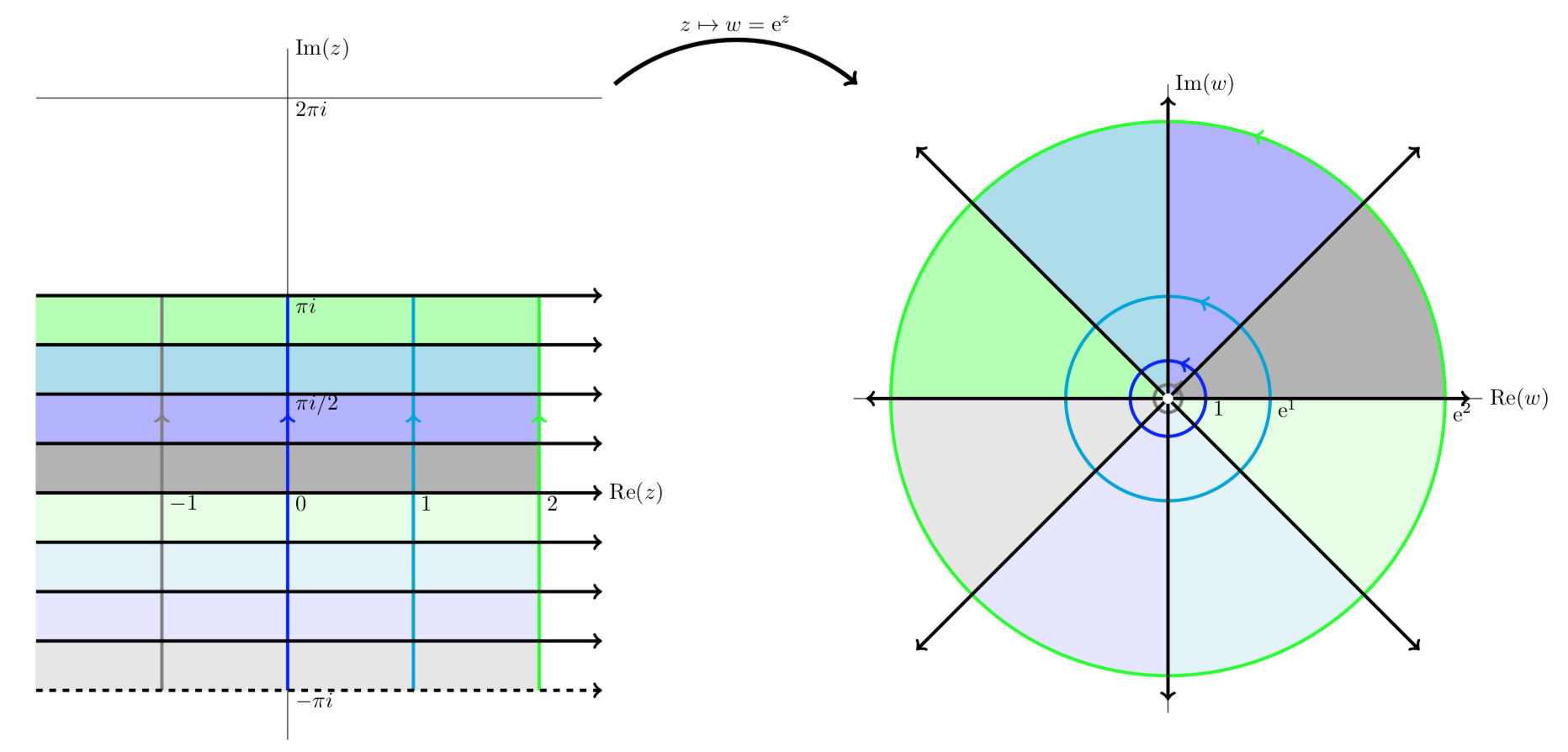
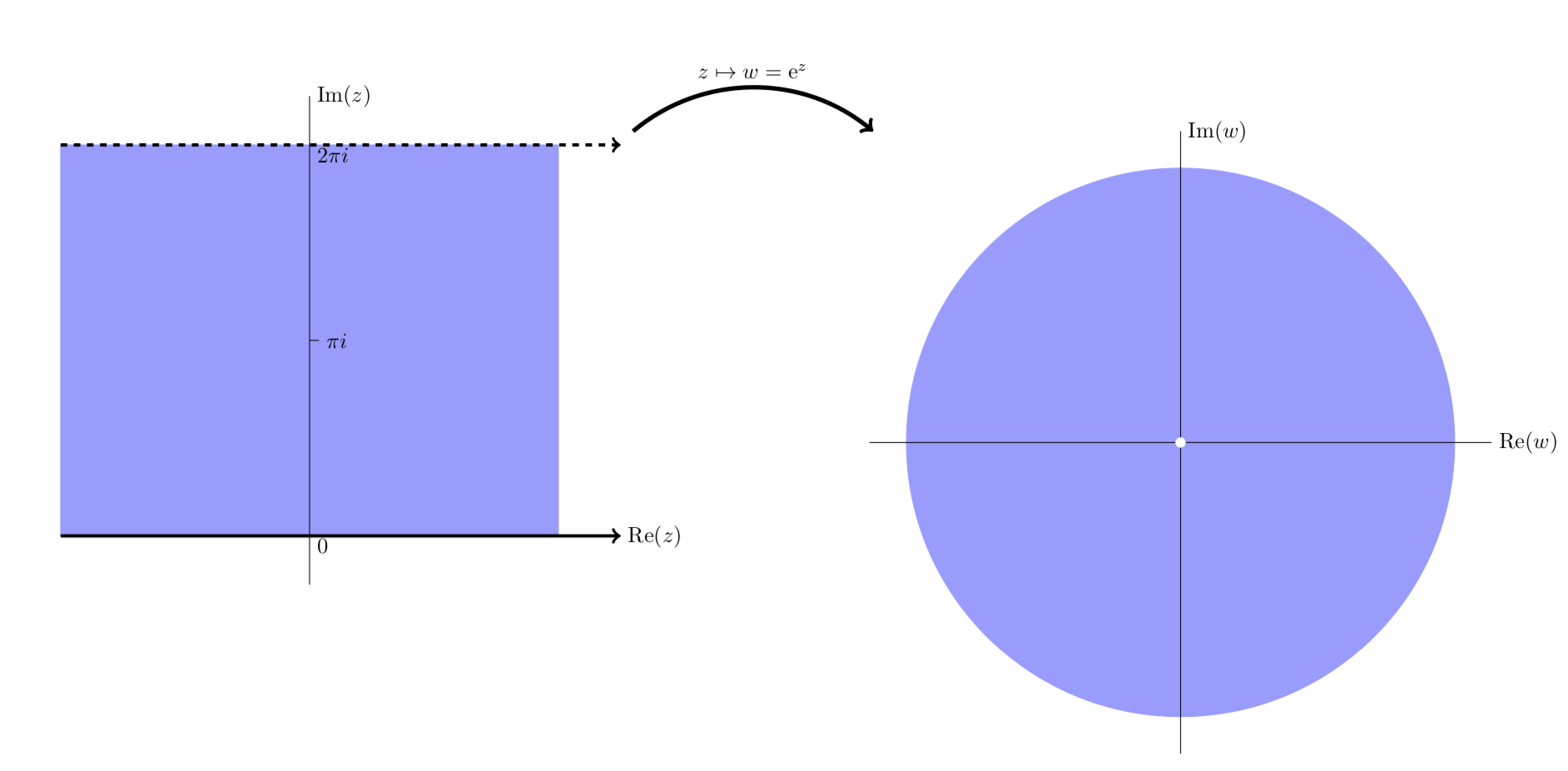
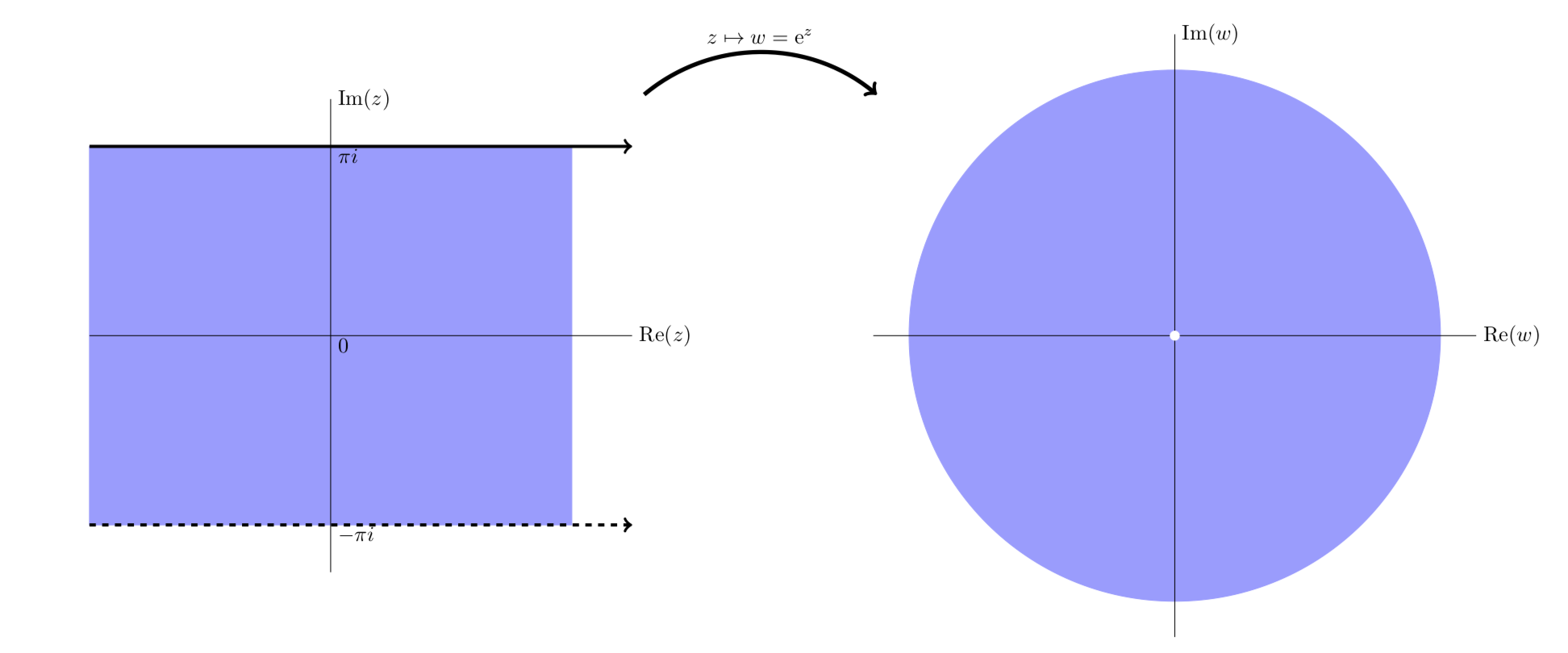
که در یک مجموعه باز در هواپیما یک به یک و هولومورفیک است. قضیه نگاشت باز تابع معکوس (تعریف شده در تصویر از ) هولومورفیک بودن. بنابراین، بر اساس این تعریف، یک نگاشت مطابق است اگر و تنها در صورتی که باهولومورفیک باشد. دو تعریف برای نگاشت های همدیس معادل نیستند. یک به یک و هولومورفیک بودن به معنای داشتن مشتق غیر صفر است. با این حال، تابع نمایی یک تابع هولومورف با مشتق غیر صفر است، اما یک به یک نیست زیرا تناوبی است. [2]
) هولومورفیک بودن. بنابراین، بر اساس این تعریف، یک نگاشت مطابق است اگر و تنها در صورتی که باهولومورفیک باشد. دو تعریف برای نگاشت های همدیس معادل نیستند. یک به یک و هولومورفیک بودن به معنای داشتن مشتق غیر صفر است. با این حال، تابع نمایی یک تابع هولومورف با مشتق غیر صفر است، اما یک به یک نیست زیرا تناوبی است. [2]
قضیه نگاشت ریمان ، یکی از نتایج عمیق تجزیه و تحلیل مختلط ، بیان می کند که هر باز غیر خالی به سادگی به زیر مجموعه مناسب متصل می شود. یک نگاشت همدیس دوطرفه را به دیسک واحد باز میپذیرد
یک نگاشت همدیس دوطرفه را به دیسک واحد باز میپذیرد .
.
نگاشت های همدیس جهانی در کره ریمان [ ویرایش ]
یک نگاشت از کره ریمان بر روی خودش، اگر و فقط اگر تبدیل موبیوس باشد، مطابقت دارد .
مزدوج مختلط تبدیل موبیوس زاویه ها را حفظ می کند، اما جهت را معکوس می کند. به عنوان مثال، وارونگی دایره .
نگاشت های همدیس در سه بعدی یا بیشتر [ ویرایش ]
هندسه ریمانی [ ویرایش ]
همچنین ببینید: هندسه همدیس
در هندسه ریمانی ، دو معیار ریمانی  و
و روی یک منیفولد صاف
روی یک منیفولد صاف اگر به صورت هم ارز نامیده می شوند
اگر به صورت هم ارز نامیده می شوند برای برخی عملکرد مثبت
برای برخی عملکرد مثبت بر
بر . کارکرد
. کارکرد عامل همدیس نامیده می شود .
عامل همدیس نامیده می شود .
تفاوت بین دو منیفولد ریمانی در صورتی که متریک عقب نشینی شده به طور همدیس با متریک اصلی معادل باشد، نگاشت همدیس نامیده می شود. به عنوان مثال، طرح ریزی استریوگرافیک یک کره بر روی صفحه که با یک نقطه در بی نهایت تقویت شده است، یک نگاشت مطابق است.
همچنین می توان یک ساختار همدیس را بر روی یک منیفولد صاف به عنوان یک کلاس از معیارهای ریمانی معادل همسان تعریف کرد.
فضای اقلیدسی [ ویرایش ]
یک قضیه کلاسیک جوزف لیوویل نشان می دهد که نگاشت های همدیس در ابعاد بالاتر بسیار کمتر از دو بعدی است. هر نگاشت همدیس از یک زیرمجموعه باز فضای اقلیدسی به همان فضای اقلیدسی با بعد سه یا بیشتر را می توان از سه نوع تبدیل تشکیل داد: یک همسانی ، یک ایزومتریک ، و یک تبدیل همدیس خاص .
برنامه های کاربردی [ ویرایش ]
نگاشت کشی [ ویرایش ]
مقاله اصلی: پیشبینی نگاشت همدیس
در کارتوگرافی ، چندین طرح نگاشت نامگذاری شده ، از جمله پیشبینی مرکاتور و پیشبینی استریوگرافی ، مطابق هستند. آنها مخصوصاً برای استفاده در ناوبری دریایی مفید هستند زیرا خاصیت منحصر به فرد آن در نمایش هر مسیر تحمل ثابت به عنوان یک قطعه مستقیم است. چنین مسیری که به نام رومب (یا از نظر ریاضی لوکسودروم) شناخته می شود در ناوبری دریایی ترجیح داده می شود زیرا کشتی ها می توانند در جهت ثابت قطب نما حرکت کنند.
فیزیک و مهندسی [ ویرایش ]
نگاشتهای همدیس برای حل مسائل در مهندسی و فیزیک بسیار مقدارمند هستند که می توانند بر حسب توابع یک متغیر مختلط بیان شوند و در عین حال هندسه های نامناسبی را نشان می دهند. با انتخاب یک نگاشت برداری مناسب، تحلیلگر می تواند هندسه نامناسب را به هندسه بسیار راحت تر تبدیل کند. برای مثال، ممکن است کسی بخواهد میدان الکتریکی را محاسبه کند، ، ناشی از بار نقطه ای واقع در نزدیکی گوشه دو صفحه رسانا که با یک زاویه مشخص از هم جدا شده اند (که در آن
، ناشی از بار نقطه ای واقع در نزدیکی گوشه دو صفحه رسانا که با یک زاویه مشخص از هم جدا شده اند (که در آن مختصات مختلط یک نقطه در 2 فاصله است). حل این مشکل به خودی خود به شکل بسته کاملاً ناشیانه است. با این حال، با استفاده از یک نگاشت همدیس بسیار ساده، زاویه نامناسب به یکی از دقیقاً نگاشت می شود.
مختصات مختلط یک نقطه در 2 فاصله است). حل این مشکل به خودی خود به شکل بسته کاملاً ناشیانه است. با این حال، با استفاده از یک نگاشت همدیس بسیار ساده، زاویه نامناسب به یکی از دقیقاً نگاشت می شود. رادیان یعنی گوشه دو صفحه به یک خط مستقیم تبدیل می شود. در این حوزه جدید، حل مشکل (محاسبه میدان الکتریکی تحت تاثیر یک بار نقطه ای واقع در نزدیکی دیوار رسانا) بسیار آسان است. راه حل در این حوزه به دست می آید،
رادیان یعنی گوشه دو صفحه به یک خط مستقیم تبدیل می شود. در این حوزه جدید، حل مشکل (محاسبه میدان الکتریکی تحت تاثیر یک بار نقطه ای واقع در نزدیکی دیوار رسانا) بسیار آسان است. راه حل در این حوزه به دست می آید، ، و سپس با توجه به آن به دامنه اصلی برگردید
، و سپس با توجه به آن به دامنه اصلی برگردید به عنوان یک تابع به دست آمد ( یعنی ترکیب
به عنوان یک تابع به دست آمد ( یعنی ترکیب و
و ) از
) از ، از کجا
، از کجا را می توان به عنوان مشاهده کرد
را می توان به عنوان مشاهده کرد ، که تابعی از
، که تابعی از ، اساس مختصات اصلی. توجه داشته باشید که این برنامه مغایرتی با این واقعیت نیست که نگاشتهای همنوع زاویهها را حفظ میکنند، آنها این کار را فقط برای نقاطی در داخل دامنه خود انجام میدهند و نه در مرز. مثال دیگر استفاده از تکنیک نگاشت conformal برای حل مسئله مقدار مرزی ریزش مایع در مخازن است. [3]
، اساس مختصات اصلی. توجه داشته باشید که این برنامه مغایرتی با این واقعیت نیست که نگاشتهای همنوع زاویهها را حفظ میکنند، آنها این کار را فقط برای نقاطی در داخل دامنه خود انجام میدهند و نه در مرز. مثال دیگر استفاده از تکنیک نگاشت conformal برای حل مسئله مقدار مرزی ریزش مایع در مخازن است. [3]
اگر تابعی هارمونیک باشد (یعنی معادله لاپلاس را برآورده کند  ) روی یک دامنه صفحه (که دو بعدی است)، و از طریق یک نگاشت همدیس به دامنه صفحه دیگری تبدیل می شود، تبدیل نیز هارمونیک است. به همین دلیل، هر تابعی که با یک پتانسیل تعریف میشود، میتواند توسط یک نگاشت همدیس تبدیل شود و همچنان توسط یک پتانسیل کنترل شود. مثالهایی در فیزیک از معادلات تعریف شده توسط یک پتانسیل شامل میدان الکترومغناطیسی ، میدان گرانشی ، و در دینامیک سیالات ، جریان پتانسیل است که تقریبی برای جریان سیال با فرض چگالی ثابت، ویسکوزیته صفر ، و جریان غیر چرخشی است .. یکی از نمونههای کاربرد دینامیکی سیال از یک نگاشت همنقل، تبدیل Joukowsky است .
) روی یک دامنه صفحه (که دو بعدی است)، و از طریق یک نگاشت همدیس به دامنه صفحه دیگری تبدیل می شود، تبدیل نیز هارمونیک است. به همین دلیل، هر تابعی که با یک پتانسیل تعریف میشود، میتواند توسط یک نگاشت همدیس تبدیل شود و همچنان توسط یک پتانسیل کنترل شود. مثالهایی در فیزیک از معادلات تعریف شده توسط یک پتانسیل شامل میدان الکترومغناطیسی ، میدان گرانشی ، و در دینامیک سیالات ، جریان پتانسیل است که تقریبی برای جریان سیال با فرض چگالی ثابت، ویسکوزیته صفر ، و جریان غیر چرخشی است .. یکی از نمونههای کاربرد دینامیکی سیال از یک نگاشت همنقل، تبدیل Joukowsky است .
نگاشتهای همدیس در حل معادلات دیفرانسیل جزئی غیرخطی در برخی از هندسههای خاص نیز مقدارمند هستند. چنین راه حل های تحلیلی یک بررسی مفید در مورد دقت شبیه سازی عددی معادله حاکم ارائه می دهد. به عنوان مثال، در مورد جریان سطح آزاد بسیار چسبناک در اطراف یک دیوار نیمه نامتناهی، دامنه را می توان به یک نیم صفحه نگاشت کرد که در آن راه حل یک بعدی است و محاسبه آن ساده است. [4]
برای سیستمهای گسسته، نوری و یانگ راهی برای تبدیل مکان ریشه سیستمهای گسسته به منبع ریشه پیوسته از طریق یک نگاشت همشکل شناخته شده در هندسه (با نام مستعار نگاشت وارونه ) ارائه کردند. [5]
معادلات ماکسول [ ویرایش ]
مقاله اصلی: تبدیل موج کروی
گروه بزرگی از نگاشتهای همدیس برای حل معادلات ماکسول توسط Ebenezer Cunningham (1908) و Harry Bateman (1910) شناسایی شدند. آموزش آنها در دانشگاه کمبریج به آنها امکان استفاده از روش بارهای تصویری و روش های مرتبط با تصاویر برای کره ها و وارونگی را داده بود. همانطور که توسط اندرو وارویک (2003) استادان تئوری بیان شده است : [6]
هر راه حل چهار بعدی را می توان در یک ابر کره چهار بعدی با شعاع کاذب معکوس کرد. به منظور تولید یک راه حل جدید
به منظور تولید یک راه حل جدید
وارویک این «قضیه نسبیت جدید» را بهعنوان پاسخ کمبریج به انیشتین برجسته میکند، و بر اساس تمرینهایی با استفاده از روش وارونگی، مانند آنچه در کتاب درسی جیمز هاپوود جین ، نظریه ریاضی الکتریسیته و مغناطیس یافت میشود، پایهگذاری شده است.
نسبیت عام [ ویرایش ]
در نسبیت عام ، نگاشت های همدیس ساده ترین و در نتیجه رایج ترین نوع تبدیل های علی هستند. از نظر فیزیکی، اینها جهانهای مختلفی را توصیف میکنند که در آنها همه رویدادها و فعل و انفعالات یکسان هنوز (به طور علّی) ممکن است، اما یک نیروی اضافی جدید برای تأثیرگذاری این امر ضروری است (یعنی تکرار همه مسیرهای یکسان باعث انحراف از حرکت ژئودزیکی میشود ، زیرا متریک تانسور متفاوت است). این اغلب برای تلاش برای ایجاد مدلهایی برای توسعه فراتر از انحنای تکینگی استفاده می شود ، به عنوان مثال برای اجازه دادن به توصیف جهان حتی قبل از انفجار بزرگ .
همچنین مشاهده کنید [ ویرایش ]
منابع
https://en.wikipedia.org/wiki/Conformal_map
محلی را حفظ میکند. یک تابع تحلیلی در هر نقطه ای که مشتق غیر صفر داشته باشد همدیس است . برعکس، هر نگاشت همشکل از یک متغیر پیچیده که مشتقات جزئی پیوسته دارد، تحلیلی است. نگاشت همدیس در تحلیلی مختلط همچنین در بسیاری از زمینههای فیزیک و مهندسی بسیار مهم است.
همراه با خطوط متناظر آنها پس از تبدیل نشان داده شده است. مون و اسپنسر (1988) و کرانتز (1999، صفحات 183-194) جداول نگاشتهای همسان را ارائه دادند.
و در و در صفحه مختلط باشد ،
و
، منسجم است
(کرانتز 1999، ص 80). علاوه بر این، if
یک تابع تحلیلی است به طوری که
یک چند جمله ای در
(گرین و کرانتز 1997؛ کرانتز 1999، ص 80) است.
، بخش های حقیقی و موهومی باید
معادلات کوشی-ریمان و معادله لاپلاس را برآورده کنند، بنابراین به طور خودکار یک پتانسیل اسکالر و به اصطلاح تابع جریان ارائه می کنند. اگر بتوان یک مشکل فیزیکی پیدا کرد که راه حل برای آن معتبر است، راه حلی را به دست می آوریم - که ممکن است به طور مستقیم به دست آوردن آن بسیار دشوار باشد - با کار معکوس.
،
،
تشکیل شده است و تابع بالقوه برای دو بار خط باردار موازی مخالف است (Feynman et al. 1989, §7-5; Lamb 1945, p. 69).
،
میدان را نزدیک لبه یک صفحه نازک می دهد (Feynman et al. 1989, §7-5).
،
،
میدان را در نزدیکی بیرون یک گوشه مستطیل شکل می دهد (Feynman et al. 1989, §7-5).
،











 (پایین). دیده می شود که
(پایین). دیده می شود که
 و
و زیر مجموعه های باز باشد
زیر مجموعه های باز باشد . یک تابع
. یک تابع در یک نقطه همدیس (یا حفظ زاویه ) نامیده می شود
در یک نقطه همدیس (یا حفظ زاویه ) نامیده می شود اگر زوایای بین
اگر زوایای بین  ، و همچنین حفظ جهت گیری. نگاشتهای همدیس هم زوایای و هم اشکال شکلهای بینهایت کوچک را حفظ میکنند، اما لزوماً اندازه یا
، و همچنین حفظ جهت گیری. نگاشتهای همدیس هم زوایای و هم اشکال شکلهای بینهایت کوچک را حفظ میکنند، اما لزوماً اندازه یا  ، سپس یک
، سپس یک  منطبق است
منطبق است  و
و روی یک منیفولد صاف
روی یک منیفولد صاف اگر به صورت هم ارز نامیده می شوند
اگر به صورت هم ارز نامیده می شوند برای برخی عملکرد مثبت
برای برخی عملکرد مثبت بر
بر ، ناشی از بار نقطه ای واقع در نزدیکی گوشه دو صفحه رسانا که با یک زاویه مشخص از هم جدا شده اند (که در آن
، ناشی از بار نقطه ای واقع در نزدیکی گوشه دو صفحه رسانا که با یک زاویه مشخص از هم جدا شده اند (که در آن مختصات مختلط یک نقطه در 2 فاصله است). حل این مشکل به خودی خود به شکل بسته کاملاً ناشیانه است. با این حال، با استفاده از یک نگاشت همدیس بسیار ساده، زاویه نامناسب به یکی از دقیقاً نگاشت می شود.
مختصات مختلط یک نقطه در 2 فاصله است). حل این مشکل به خودی خود به شکل بسته کاملاً ناشیانه است. با این حال، با استفاده از یک نگاشت همدیس بسیار ساده، زاویه نامناسب به یکی از دقیقاً نگاشت می شود. رادیان یعنی گوشه دو صفحه به یک خط مستقیم تبدیل می شود. در این حوزه جدید، حل مشکل (محاسبه میدان الکتریکی تحت تاثیر یک بار نقطه ای واقع در نزدیکی دیوار رسانا) بسیار آسان است. راه حل در این حوزه به دست می آید،
رادیان یعنی گوشه دو صفحه به یک خط مستقیم تبدیل می شود. در این حوزه جدید، حل مشکل (محاسبه میدان الکتریکی تحت تاثیر یک بار نقطه ای واقع در نزدیکی دیوار رسانا) بسیار آسان است. راه حل در این حوزه به دست می آید، ، و سپس با توجه به آن به دامنه اصلی برگردید
، و سپس با توجه به آن به دامنه اصلی برگردید به عنوان یک تابع به دست آمد ( یعنی
به عنوان یک تابع به دست آمد ( یعنی  و
و ، که تابعی از
، که تابعی از ) روی یک دامنه صفحه (که دو بعدی است)، و از طریق یک نگاشت همدیس به دامنه صفحه دیگری تبدیل می شود، تبدیل نیز هارمونیک است. به همین دلیل، هر تابعی که با یک
) روی یک دامنه صفحه (که دو بعدی است)، و از طریق یک نگاشت همدیس به دامنه صفحه دیگری تبدیل می شود، تبدیل نیز هارمونیک است. به همین دلیل، هر تابعی که با یک  به منظور تولید یک راه حل جدید
به منظور تولید یک راه حل جدید














































 در این وبلاگ به ریاضیات و کاربردهای آن و تحقیقات در آنها پرداخته می شود. مطالب در این وبلاگ ترجمه سطحی و اولیه است و کامل نیست.در صورتی سوال یا نظری در زمینه ریاضیات دارید مطرح نمایید .در صورت امکان به آن می پردازم. من دوست دارم برای یافتن پاسخ به سوالات و حل پروژه های علمی با دیگران همکاری نمایم.در صورتی که شما هم بامن هم عقیده هستید با من تماس بگیرید.
در این وبلاگ به ریاضیات و کاربردهای آن و تحقیقات در آنها پرداخته می شود. مطالب در این وبلاگ ترجمه سطحی و اولیه است و کامل نیست.در صورتی سوال یا نظری در زمینه ریاضیات دارید مطرح نمایید .در صورت امکان به آن می پردازم. من دوست دارم برای یافتن پاسخ به سوالات و حل پروژه های علمی با دیگران همکاری نمایم.در صورتی که شما هم بامن هم عقیده هستید با من تماس بگیرید.