توسط علی رضا نقش نیلچی
| دوشنبه هشتم اردیبهشت ۱۳۹۹ | 16:31
احمد طاهر آذر ، 1 ، 2  کریستوس ولوس ، 3
کریستوس ولوس ، 3
 نیکولاوس ا. گرودیموس ، 4 جورج س. تامبراس ، 4
نیکولاوس ا. گرودیموس ، 4 جورج س. تامبراس ، 4 ویتن تان فام ، 5
ویتن تان فام ، 5 احمد جی. رادوان ، 2 ، 6
احمد جی. رادوان ، 2 ، 6 سانداراپندیان ویدیاناتان ، 7 عادل اواناس ، 8 و
سانداراپندیان ویدیاناتان ، 7 عادل اواناس ، 8 و  عیسی م.موز -پچکو 9
عیسی م.موز -پچکو 9
سردبیر دانشگاهی: کارلوس گرششنون
دریافت21 اکتبر 2016
اصلاح شده در12 دسامبر 2016
پذیرفته شده22 دسامبر 2016
منتشر شده02 فوریه 2017
چکیده
چند سیستم خاص آشوب آور بدون نقاط تعادل ناپایدار اخیراً مورد بررسی قرار گرفته است. شایان ذکر است که این سیستم های خاص با سیستم های هرج و مرج عادی متفاوت هستند زیرا نمی توان ملاک کلاسیک شیلنیکوف را برای اثبات هرج و مرج چنین سیستم هایی استفاده کرد. یک سیستم آشوب آور غیر عادی و بدون تعادل در این کار ارائه شده است. ما خصوصیات دینامیکی و همگام سازی سیستم جدید را کشف می کنیم. علاوه بر این ، تحقق فیزیکی سیستم بدون تعادل نیز برای نشان دادن امکان سنجی آن اجرا شده است.
1. معرفی
در دهه های گذشته مقدار زیادی از ادبیات در مورد سیستم های هرج و مرج منتشر شده است ، به عنوان مثال سیستم لورنز [ 1 ] ، سیستم راسلر [ 2 ] ، سیستم چن و یوتا [ 3 ] ، جریانهای ساده هرج و مرج [ 4 ، 5 ] ، سیستم هرج و مرج یادبود. با جاذبه های قلبی شکل [ 6 ] ، مدار آشوب آور مبتنی بر memristor [ 7 ، 8 ] ، نوسان سازهای مبتنی بر MOS- ترانزیستورها [ 9 ، 10 ] ، طرح های آنالوگ دیجیتال مخلوط [ 11 ] ، تحقق کاملاً دیجیتالی سیستم های آشوب آور [ 12 ، 13 ] یا نوسان ساز الکترومکانیکی [ 14] پیچیدگی سیستم های آشوب آور در برنامه های مختلف مهندسی از رمزگذاری تصویر پاتولوژیک رنگ نامتقارن استفاده شده است [ 15 ، 16 ] ، کنترل و همگام سازی [ 17 ، 18 ] ، یک طرح ارتباطات ویدئویی هرج و مرج از طریق انتقال از راه دور WAN [ 19 ] ، و رمزگذاری تصویر با بهمن جلوه های [ 20 ] به طرح رمزگذاری صوتی [ 21 ] و غیره.
اکنون از مطالعات مختلف به خوبی مشخص شده است كه نقاط تعادل نقش مهمی در فهم ما از هرج و مرج در سیستمهای غیرخطی دارند [ 22 - 24 ]. به طور کلی ، سیستم های هرج و مرج متعارف از تعادل ناپایدار برخوردار هستند و ما می توانیم با معیار Shilnikov هرج و مرج را در چنین سیستمهایی تأیید کنیم [ 25 ، 26 ]. با این حال ، تحقیقات اخیر به طور مداوم نشان داده اند که رفتار پر هرج و مرج را می توان در سیستم های سه بعدی (سه بعدی) بدون تعادل مشاهده کرد [ 27 ].
مطالعه سیستم های بدون تعادل دارای سابقه ای طولانی است و مدل های مختلف الکترومکانیکی با چرخش و مدارهای الکتریکی با فضای فاز استوانه ای را شرح می دهد. یکی از اولین نمونه های مشابه توسط آرنولد سامرفلد در سال 1902 توضیح داده شده است [ 28 ] ، با مطالعه نوسانات ناشی از موتور با وزنی نامتعادل و کشف ضبط رزونانس ، که "اثر سامرفلد" نامیده می شود. این پدیده نشانگر عدم موفقیت سیستم مکانیکی چرخشی است که به دلیل تعامل رزونانس آن با قسمت دیگری از سیستم ، توسط یک روتور محدود گشتاور به سرعت چرخش مورد نظر می چرخد [ 29 ، 30 ]. چند دهه بعد ، در سالهای 1984-85 ، نوسه [ 31 ] و هوور [ 32 ]] این مطالعه را با سیستم دینامیکی پیشنهادی خود بدون تعادل و تغییرات مختلف آن هدایت کرده اند ، جایی که می توان نوسانات آشفتگی پنهان را پیدا کرد [ 4 ، 33 - 36 ].
روال جستجوی سیستماتیک توسط جعفری و همکاران توسعه یافته است. برای تعیین جریانهای درجه دوم ساده و بدون تعادل [ 24 ، 27 ]. وانگ و چن هنگام مطالعه یک سیستم پر هرج و مرج با هر تعداد تعادل ، سیستم جدیدی را بدون تعادل یافتند [ 24 ]. وی با استفاده از یک ثابت در سیستم Sprott D ، ویژگیهای دینامیکی یک سیستم هرج و مرج بدون تعادل را کشف کرد [ 37 ]. جاذبه های چندگانه در یک سیستم سه بعدی با نقطه عدم تعادل در [ 38 ] گزارش شده است. Akgul و همکاران. یک ژنراتور عدد تصادفی با یک سیستم هرج و مرج سه بعدی و بدون تعادل طراحی کرد [ 39 ]. علاوه بر این، 4D سیستم بدون تعادل با hyperchaos در ارائه شده [ 40 - 42] جالب است بدانیم که سیستم های هرج و مرج و بدون تعادل "جاذبه های پنهان" را نشان می دهند [ 43 - 46 ]. علاقه زیادی به کشف جاذبه های پنهان شده است زیرا نمی توان با استفاده از روشهای رایج محاسباتی بومی سازی شد [ 47 - 52 ].
این مطالعه با بررسی یک سیستم آشوب آور جدید و بدون تعادل ، به تحقیقات در مورد سیستم های دارای جاذبه های پنهان کمک می کند. در بخش بعدی توضیحات و پویایی سیستم بدون تعادل ارائه شده است. هماهنگ سازی دو سیستم آشوب آور جدید و بدون تعادل در بخش 3 مورد مطالعه قرار می گیرد . سیستم نظری توسط یک مدار الکترونیکی مطابق گزارش بخش 4 تحقق یافته است . سرانجام ، اظهارات نتیجه گیری در آخرین بخش آورده شده است.
2. توضیحات و دینامیک سیستم بدون تعادل
جعفری و همکاران. رویکردی مؤثر برای بررسی سیستمهای بالقوه بدون تعادل ارائه داده است [ 27 ]. نویسنده مدل کلی ساخته شده و اعمال معمول جستجو سیستماتیک برای به دست آوردن هفده ساده جریان با تعادل [ 27 ]. با انگیزه سیستم های جعفری و همکاران ، در این کار یک شکل کلی را به شرح زیر در نظر می گیریم:که در آن سه حالت از شکل کلی هستند ، و ، در حالی که نه پارامترها ( ) با . یک غیرخطی مطلق در ( 1 ) گنجانده شده است زیرا این یک اصطلاح بالقوه برای طراحی سیستم های غیرخطی با ویژگی های خاص است [ 53 ، 54 ].
برای پیدا کردن تعادل سیستم ( 1 ) ، سه معادله زیر را حل می کنیم:با جایگزینی ( 2 ) ، ( 3 ) به ( 4 ) ، داریمبه راحتی می توان تأیید کرد که معادله متناقض استبه عبارت دیگر ، در این حالت مدل کلی ( 1 ) تعادلی ندارد.
با استفاده از یک روش جستجوی منظم [ 27 ] به ( 1 ) ، یک سیستم سه بعدی ساده به شکل زیر بدست می آید:که در آن سه حالت هستند ، و در حالی که دو پارامتر مثبت هستند . با توجه به شرط ( 6 ) ، اثبات اینكه هیچ تعادلی در سیستم جدید وجود ندارد ( 7 ) امری بی اهمیت است .
جالب است که سیستم ( 7 ) می تواند سیگنال های هرج و مرج ایجاد کند اگرچه عدم وجود تعادل وجود دارد. برای ، و شرایط اولیه ، سیستم ( 7 ) تولید رفتار آشفته همانطور که در شکل نشان داده شده است 1 . همانطور که در شکل 1 مشاهده می شود ، شکل موجهای هرج و مرج و طیف های پهنای باند نشان دهنده هرج و مرج بودن سیستم هستند ( 7 ). علاوه بر این ، پرتره های فاز پر هرج و مرج سیستم ( 7 ) در شکل 2 نشان داده شده است . محاسبه توان لیاپانوف و ابعاد کاپلان نیویورک از سیستم بدون تعادل ( 7 ) هستند ، ، ، و ، به ترتیب. به عبارت دیگر ، سیستم (7 ) دارای جاذبه های پنهانی است که برای طیف گسترده ای از فرآیندهای علمی و مهندسی بسیار مهم است [ 55 - 58 ]. در کار ما ، الگوریتم مشهور ولف و همکاران. [ 59 ] برای محاسبه نمایندگان لیاپونف استفاده شده است. زمان محاسبه 10000 است. خاطرنشان می شود ، با توجه به مقادیر متفاوت از مأمورین محدود محلی لیپونوف و بعد لیپونوف برای نقاط مختلف ، حداکثر ابعاد محدود محلی محلی لیاپونوف در شبکه نقطه باید در نظر گرفته شود [ 60 - 62 ].

(آ)

(ب)

(ج)

(د)

(ه)

(ح)

(آ)
(ب)
(ج)
(د)
(ه)
(ح)
شکل 1
شکل موج آشفته و طیف فرکانس تولید شده از سیستم ( 7 ): (الف) سری زمانی ، (ب) طیف دامنه تک طرفه ، (ج) سری زمانی ، (د) طیف دامنه تک طرفه ، (ه) سری زمانی و (f) طیف دامنه یک طرفه از .

(آ)

(ب)

(ج)

(د)

(آ)
(ب)
(ج)
(د)
شکل 2
چهار نمایش از جذب پر هرج و مرج در سیستم بدون تعادل ( 7 ) در یک هواپیما، (ب) هواپیما، (ج) هواپیما، و (د) فضا برای ، و شرایط اولیه .
دینامیک سیستم بدون تعادل با تغییر مقدار پارامتر bifurcation در دامنه 0.2 تا 0.36 مورد بررسی قرار گرفته است. نمودارهای 3 و 4 نمودار bifurcation و نمودار نمایانگرهای حداکثر Lyapunov (MLEs) سیستم بدون تعادل را نشان می دهد. همانطور که از شکل 3 و 4 مشاهده می شود ، سیستم ( 7 ) نوسانات دوره ای را برای آنها نشان می دهد . به عنوان مثال ، نوسانات دوره ای مختلف سیستم ( 7 ) در شکل 5 نشان داده شده است . برایرفتارهای پیچیده ای از سیستم مشاهده می شود. علاوه بر این ، به راحتی می توان حضور یک مسیر دوبرابر دوره به هرج و مرج را هنگام افزایش ارزش پارامتر بررسی کرد .

شکل 3
نمودار شکاف سیستم بدون تعادل ( 7 ) برای و .

شکل 4
حداکثر محرک های لیاپانوف سیستم بدون تعادل ( 7 ) برای تغییر مقدار پارامتر از 0.2 به 0.36.

(آ)

(ب)

(ج)

(د)

(آ)
(ب)
(ج)
(د)
شکل 5
چهار نمایش از چرخه های محدود در سیستم بدون تعادل ( 7 ) در (الف) نوسانات دوره -1 ( ) ، (ب) نوسان پریود-2 ( ) ، (ج) نوسانات دوره -4 ( ) و (د) دوره- 8 نوسان ( ) برای شرایط اولیه و .
3. هماهنگ سازی دو سیستم یکسان و بدون تعادل
دهه گذشته شاهد توسعه سریع برنامه های هماهنگ سازی برای سیستم های آشوب آور بیشمار بوده زیرا هماهنگ سازی نقش اساسی در برنامه های کاربردی دارد [ 63 - 67 ]. بنابراین ، هنگام بررسی یک سیستم آشوب آور جدید ، باید توانایی همگام سازی آن را در نظر گرفت. در این بخش ، هماهنگ سازی دو سیستم جدید بدون تعادل (سیستم های کارشناسی ارشد و برده) را از طریق یک کنترل کننده تطبیقی بررسی می کنیم که به عنوان یک رویکرد مؤثر گزارش شده است [ 68 - 70 ].
در اینجا سیستم استاد بدون تعادل توسط ارائه شده استجایی که سه متغیر حالت وجود دارد ، و پارامترهای سیستم ناشناخته ، . سیستم برده بدون تعادل توسط داده می شودکه در آن ، و متغیرهای سیستم هستند و یک کنترل تطبیقی است. با محاسبه تفاوت بین سیستم برده و سیستم مستر ، خطاهای حالت به صورت تعریف می شونددر نتیجه دینامیک خطای حالت توسط محاسبه می شودخطای تخمین پارامتر به عنوان نشان داده می شود جایی که تخمین پارامتر ناشناخته ( ) است . با تمایز ( 12 ) ، می گیریم
ما یک کنترل تطبیقی را برای همگام سازی سیستم برده بدون تعادل ( 9 ) با سیستم کارشناسی ارشد ( 8 ) و بدون تعادل به شرح زیر طراحی می کنیم:در کنترل تطبیقی ( 14 )، سه مقدار ثابت افزایش مثبت ، و در حالی که قانون به روز رسانی پارامتر با ساخته
به راحتی می توان تأیید کرد که سیستم برده ( 9 ) و سیستم کارشناسی ارشد ( 8 ) در هنگام استفاده از کنترل تطبیقی پیشنهادی هماهنگ شده اند ( 14 ). ما با استفاده از عملکرد انتخاب شده Lyapunov این نتیجه را اثبات می کنیم:از ( 16 ) ، ما این تفاوت را دارند :با ترکیب ( 8 ) ، ( 9 ) و ( 14 ) ، دینامیک خطای همگام سازی به دست می آیدسرانجام ، با جایگزینی ( 13 ) و ( 18 ) به ( 17 ) ، تمایز عملکرد Lyapunov را می توان به عنوان ساده تربدیهی است که تمایز یک عملکرد نیمه منفی است. بنابراین، با توجه به لم Barbalat است [ 71 ]، ما ، و نمایی به عنوان . در نتیجه ، هماهنگی بین سیستم برده ( 9 ) و سیستم کارشناسی ارشد ( 8 ) تأیید می شود.
برای تأیید محاسبه طرح همگام سازی ، نمونه ای را در نظر می گیریم که مقادیر پارامتر سیستم master و سیستم برده به عنوان ثابت می شوندحالات اولیه سیستم کارشناسی ارشد فرض می شوددر حالی که حالت های اولیه سیستم برده به عنوان انتخاب می شوندما را ثابت افزایش مثبت که ، ، و و مجموعه ای از شرایط اولیه برآورد پارامتر، این است که،ساعت-تاریخ خطاهای هماهنگ سازی ، ، در شکل گزارش 6 . علاوه بر این ، سری زمانی استاد و سیستم های برده در شکل 7 نشان داده شده است . از نمودارهای 6 و 7 مشاهده مستقیم همگام سازی سیستم برده و سیستم مستر ساده است.

شکل 6
تاریخچه زمان خطاهای همگام سازی بین سیستم برده بدون تعادل ( 9 ) و سیستم کارشناسی ارشد بدون تعادل ( 8 ).

(آ)

(ب)

(ج)

(آ)
(ب)
(ج)
شکل 7
سری زمانی سیستم مستر (آبی جامد) و سیستم های برده (قرمز قرمز): (الف) و ، (ب) و ، و (ج) و .
4- تحقق سیستم پیشنهادی بدون تعادل
موضوع تحقق مدلهای آشفته نظری به دلیل کاربردهای عملی توجه جدی خود را به خود جلب کرده است [ 65 ، 72 - 76 ]. بنابراین ، یک مدار الکترونیکی برای تحقق سیستم پیشنهادی بدون تعادل ( 7 ) در این بخش معرفی شده است. ما سه متغیر حالت سیستم را بدون تعادل ( 7 ) ذخیره کردیم ، یعنی ، و ، برای دریافت سیگنال های به اندازه کافی بزرگتر در مدار الکترونیکی خود. بنابراین ، سیستم بدون تعادل ( 7 ) به سیستم معادل زیر تبدیل می شود:
شکل 8 شماتیک مدار را برای تحقق سیستم نشان می دهد ( 24 ). همانطور که در شکل 8 نشان داده شده است ، سه یکپارچه سازنده ( ) با تقویت کننده های عملیاتی وجود دارد. مدار غیرخطی مطلق ( ) بر اساس دو تقویت کننده عملیاتی ( ) و دو دیود ( ) است. با اعمال قوانین مدار Kirchhoff در مدار طراحی شده ، معادله پیرامون زیر حاصل می شود:متغیرهای ، و در ( 25 ) متناظر با ولتاژ در خروجی از سه انتگرال ( ، و ) بود. به راحتی می توان تأیید کرد که سیستم ( 25 ) معادل سیستم بدون تعادل ( 24 ) با عادی سازی آن است . به منظور به دست آوردن و ، قطعات الکترونیکی به عنوان kΩ ، kΩ ، kΩ ، nF و . منبع تغذیه کلیه دستگاه های فعال می باشد. اجرای مدار روی تخته نرد در شکل 9 نشان داده شده است . ما سیگنال ها را در مدار واقعی با استفاده از اسیلوسکوپ اندازه گیری کرده ایم. نتایج تجربی در شکل 10 گزارش شده است که با نتایج عددی در شکل 2 توافق خوبی دارند .

شکل 8
شماتیک مدار شامل 16 مقاومت ، هفت تقویت کننده عملیاتی ، دو ضرب آنالوگ ، دو دیود و سه خازن.

شکل 9
تحقق فیزیکی سیستم نظری با استفاده از مؤلفه های الکترونیکی مشترک.

(آ)

(ب)

(ج)

(آ)
(ب)
(ج)
شکل 10
جذب جاذب مدار مدار طراحی شده در (a) هواپیما ، (ب) هواپیما ، و (ج) هواپیما.
5. نتیجه گیری ها
مطالعه حاضر یک سیستم اضافی و بدون تعادل ارائه می دهد که اخیراً مورد توجه جامعه پژوهش قرار گرفته است. دینامیک سیستم پیشنهادی توسط ابزارهای عددی و اجرای فیزیکی مورد مطالعه قرار می گیرد. جالب است كه این سیستم علی رغم عدم وجود تعادل ، می تواند سیگنال های هرج و مرج ایجاد كند. این سیستم با استفاده از اجزای رایج الکترونیکی به راحتی تحقق می یابد. بنابراین ، جالب خواهد بود که کاربرد عملی سیستم جدید را ارزیابی کنید. مطالعات بیشتر مربوط به برنامه های کاربردی ممکن در زمان واقعی سیستم در آثار آینده ما مورد بررسی قرار خواهد گرفت.
علاقه های رقابتی
نویسندگان اظهار داشتند که هیچگونه تضاد منافعی با انتشار این مقاله وجود ندارد.
تشکرها
نویسندگان ، پروفسور GuanRong Chen ، دانشکده مهندسی الکترونیک ، دانشگاه شهر هنگ کنگ ، را به دلیل ارائه منابع مفید بسیاری تصدیق می کنند.
منابع
https://www.hindawi.com/journals/complexity/2017/7871467/














![{\displaystyle {\begin{aligned}|R_{N}(z)|&\leq {\frac {|B_{2N}|}{2N(2N-1)|z|^{2N-1}}} \times {\begin{cases}1&{\text{ if }}\left|\arg z\right|\leq {\frac {\pi }{4}},\\\left|\csc(\arg z )\right|&{\text{ if }}{\frac {\pi }{4}}<\left|\arg z\right|<{\frac {\pi }{2}},\\\sec ^{2N}\left({\tfrac {\arg z}{2}}\right)&{\text{ if }}\left|\arg z\right|<\pi ,\end{cases}}\ \[6pt]\left|{\widetilde {R}}_{N}(z)\right|&\leq \left({\frac {\left|a_{N}\right|}{|z|^ {N}}}+{\frac {\left|a_{N+1}\right|}{|z|^{N+1}}}\right)\times {\begin{cases}1&{\text { if }}\left|\arg z\right|\leq {\frac {\pi }{4}},\\\left|\csc(2\arg z)\right|&{\text{ if } }{\frac {\pi }{4}}<\left|\arg z\right|<{\frac {\pi }{2}}.\end{موارد}}\end{تراز شده}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/49a2ef6c072d31d6b521b5e9094485cb362a6e3a)














![{\displaystyle n!\sim [{\rm {constant}}]\cdot n^{n+{\frac {1}{2}}}e^{-n}.}](https://wikimedia.org/api/rest_v1/media/math/render/svg/9a51109a2de3b04535d0b8065ec095be411bab47)
















 . مقاله حاضر در مورد مفهوم ترمودینامیکی است، نه در مورد مفهوم نظریه جنبشی.
. مقاله حاضر در مورد مفهوم ترمودینامیکی است، نه در مورد مفهوم نظریه جنبشی.









 . پیش بینی های استریوگرافی نقشه ها را به دور دایره ها می کشد و مرز دایره ای نوار را حفظ می کند. نتیجه ، تعبیه صاف نوار Möbius به R 3 با لبه دایره ای و بدون تقاطع خود است.
. پیش بینی های استریوگرافی نقشه ها را به دور دایره ها می کشد و مرز دایره ای نوار را حفظ می کند. نتیجه ، تعبیه صاف نوار Möbius به R 3 با لبه دایره ای و بدون تقاطع خود است.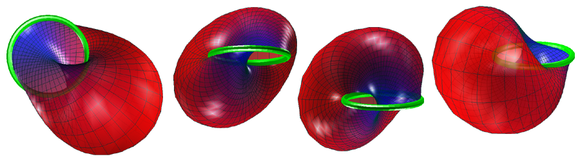
 مجموعه است
مجموعه است  پوسته پوسته شدن مدول یعنی یک نکته در
پوسته پوسته شدن مدول یعنی یک نکته در![\ displaystyle [A: B] = \ {(\ lambda A، \ lambda B): \ lambda \ in \ mathbf {R} \ setminus \ {0 \} \}.](https://wikimedia.org/api/rest_v1/media/math/render/svg/1703ee596b1a95aff033e95cb094f748509b4960)
![{\ نمایشگر [A: B]](https://wikimedia.org/api/rest_v1/media/math/render/svg/33dede24122dab634ef6f1bd8655cfed1922ce0a) با
با  یک نماینده منحصر به فرد دارد که مختصات دوم آن 1 است
یک نماینده منحصر به فرد دارد که مختصات دوم آن 1 است  . این نقاط کپی از خط اقلیدسی را تشکیل می دهند
. این نقاط کپی از خط اقلیدسی را تشکیل می دهند . با این حال ، کلاس هم ارزی از
. با این حال ، کلاس هم ارزی از![{\ نمایشگر [1: 0]](https://wikimedia.org/api/rest_v1/media/math/render/svg/2c9d83f60abcf946cc50d3cb984fecd2df57977b) چنین نماینده ای ندارد این نکته اضافی مانند بی نهایت نامعلوم رفتار می کند
چنین نماینده ای ندارد این نکته اضافی مانند بی نهایت نامعلوم رفتار می کند . مزیت
. مزیت و
و  . این مورد برای گروه Mbibius است.
. این مورد برای گروه Mbibius است.![\ displaystyle M = \ {((x، y)، [A: B]) \ in \ mathbf {R} ^ {2} \ Times \ mathbf {RP} ^ {1}: Ax = By \.](https://wikimedia.org/api/rest_v1/media/math/render/svg/0b404d0e84ae1eda5eab105bc8e3922a87937efc)
 از جانب
از جانب (یا در واقع هر خط) ، پس از آن زیر مجموعه می تواند در فضای اقلیدسی تعبیه شود
(یا در واقع هر خط) ، پس از آن زیر مجموعه می تواند در فضای اقلیدسی تعبیه شود  . حذف این خط مجموعه را می دهد
. حذف این خط مجموعه را می دهد![{\ displaystyle {\ شروع {تراز شده} M '& = \ {((x ، y) ، [A: B]) \ in \ mathbf {R} ^ {2} \ Times \ mathbf {RP} ^ {1} : Ax = By، \ B \ neq 0 \} \\ & = \ {(x، y، m) \ in \ mathbf {R} ^ {3}: mx = y \}، \ end {تراز شده}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/bcf3b7938d9e36db364fc7a559a516d0e9a9cb9c)
 .
.![\ displaystyle N = \ {((x، y)، [A: B]) \ in \ mathbf {R} ^ {2} \ Times \ mathbf {RP} ^ {1}: Ax = By، \ x ^ 2} + y ^ {2} \ leq 1 \}.](https://wikimedia.org/api/rest_v1/media/math/render/svg/c6b2f6cc02685f04099ed246d0abef0d90983481)
 . هندسه از
. هندسه از مجموعه راه حل یک معادله است
مجموعه راه حل یک معادله است  . چه موقع مجموعه راه حل تغییر نمی کند
. چه موقع مجموعه راه حل تغییر نمی کند نجات می یابد ، بنابراین خط فقط به کلاس هم ارزی بستگی دارد
نجات می یابد ، بنابراین خط فقط به کلاس هم ارزی بستگی دارد  که در
که در ، از طریق منشاء ، به طور خاص ، خط تعریف شده توسط آن ، در یک خط منحصر به فرد قرار دارد
، از طریق منشاء ، به طور خاص ، خط تعریف شده توسط آن ، در یک خط منحصر به فرد قرار دارد ![{\ displaystyle [-y: x]](https://wikimedia.org/api/rest_v1/media/math/render/svg/86fd60d8c2287388ac6c39f3768881a5b1791661) . نکته
. نکته اما ، در هر خط از خاستگاه نهفته است. برای این نقطه ، معادله
اما ، در هر خط از خاستگاه نهفته است. برای این نقطه ، معادله انحطاط به
انحطاط به . این همیشه درست است ، بنابراین هر
. این همیشه درست است ، بنابراین هر بر
بر  که در
که در ![\ displaystyle P = ((1،0) ، [0: 1])}](https://wikimedia.org/api/rest_v1/media/math/render/svg/82494e67b7475f512a85350bff1a409dbfff6e3e) . نیم دایره خلاف جهت عقربه ساعت را بکشید تا مسیری به وجود بیاید
. نیم دایره خلاف جهت عقربه ساعت را بکشید تا مسیری به وجود بیاید![\ displaystyle \ gamma (t) = ((\ \ cos (2 \ pi t))، \ sin (2 \ pi t))، [- \ sin (2 \ pi t)، \ cos (2 \ pi t)] )}](https://wikimedia.org/api/rest_v1/media/math/render/svg/8e4fca428e81158af73db9be51c049bcaae2550c) . مسیر متوقف می شود
. مسیر متوقف می شود ، که در آن نقطه می دهد
، که در آن نقطه می دهد ![\ displaystyle Q = ((- 1،0) ، [0: 1])}](https://wikimedia.org/api/rest_v1/media/math/render/svg/70844f757d63a3ab25862cb0d874d64120901951) . بجز
. بجز و
و  ، هر نقطه از مسیر از طریق منشا در یک خط متفاوت قرار دارد. از این رو
، هر نقطه از مسیر از طریق منشا در یک خط متفاوت قرار دارد. از این رو یک بار به دور دایره مرکزی سفر می کند
یک بار به دور دایره مرکزی سفر می کند 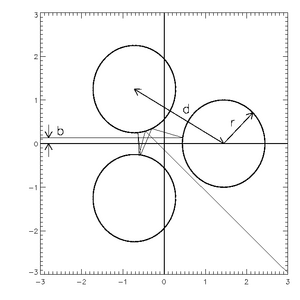


 ، به شرح زیر است:
، به شرح زیر است:
 روکش شده است مسیر طول، ها ، معادل زمان فروپاشی است، T ، ارائه ما در مقیاس (ثابت) سرعت مناسب. توجه داشته باشید که میزان پوسیدگی نمایی خاصیتی از پراکندگی هرج و مرج ناشی از فشار خون است. دستگاه های پراکندگی غیر فشار خون ممکن است دارای پوسیدگی حسابی باشند.
روکش شده است مسیر طول، ها ، معادل زمان فروپاشی است، T ، ارائه ما در مقیاس (ثابت) سرعت مناسب. توجه داشته باشید که میزان پوسیدگی نمایی خاصیتی از پراکندگی هرج و مرج ناشی از فشار خون است. دستگاه های پراکندگی غیر فشار خون ممکن است دارای پوسیدگی حسابی باشند. 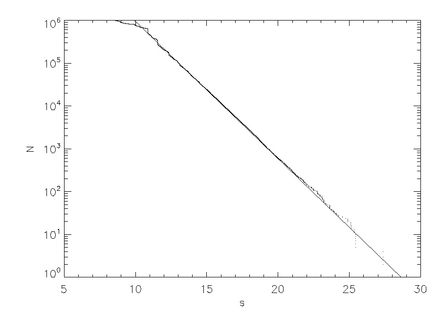



![\ theta \ in [- \ pi، \ pi]](https://wikimedia.org/api/rest_v1/media/math/render/svg/fb953905c1f4461b83fe73f5a00e751727ddd73b) ، نمایانگر زاویه اطراف دیسک در بازگشت و دوم ،
، نمایانگر زاویه اطراف دیسک در بازگشت و دوم ، ![\ phi \ in [- \ pi / 2، \ pi / 2]](https://wikimedia.org/api/rest_v1/media/math/render/svg/cde2ad5af060b602ccfcf027c34dfd11642cb703) ، نمایانگر زاویه برخورد / بازگشت به نسبت دیسک. زیرمجموعه ای از این دو متغیر ، به نام
، نمایانگر زاویه برخورد / بازگشت به نسبت دیسک. زیرمجموعه ای از این دو متغیر ، به نام 

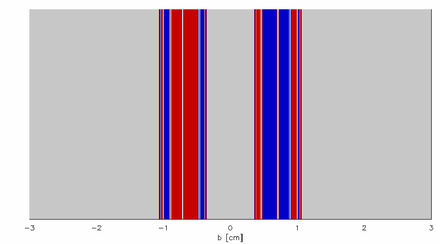
 ، و شمارش تعداد دفعات بازگشت تعداد دیسک ها از دیسک ها ، یعنی کسری عدم قطعیت. توجه داشته باشید که حتی اگر سیستم دو بعدی باشد ، یک پارامتر تأثیر یکسان برای اندازه گیری ابعاد فراکتال منیفولد پایدار کافی است. این در شکل 10 نشان داده شده است ، که حوضه های جذب را به عنوان تابعی از یک پارامتر تأثیر دوگانه نشان می دهد ،
، و شمارش تعداد دفعات بازگشت تعداد دیسک ها از دیسک ها ، یعنی کسری عدم قطعیت. توجه داشته باشید که حتی اگر سیستم دو بعدی باشد ، یک پارامتر تأثیر یکسان برای اندازه گیری ابعاد فراکتال منیفولد پایدار کافی است. این در شکل 10 نشان داده شده است ، که حوضه های جذب را به عنوان تابعی از یک پارامتر تأثیر دوگانه نشان می دهد ، و
و . منیفولد پایدار ، که در مرزهای بین حوضه ها دیده می شود ، در طول تنها یک بعد فراکتال است.
. منیفولد پایدار ، که در مرزهای بین حوضه ها دیده می شود ، در طول تنها یک بعد فراکتال است.
 بنابراین
بنابراین  . مجموعه ثابت ، تقاطع
. مجموعه ثابت ، تقاطع 


 و آن را به
و آن را به 

![{\ displaystyle \ psi _ {n + 1} ({\ vec {r}}، t) = \ int K ({\ vec {r}} - {\ vec {r}} ^ {،}، t) f [\ psi _ {n} ({\ vec {r}} ^ {،} ، t)] d {\ vec {r}} ^ {،}](https://wikimedia.org/api/rest_v1/media/math/render/svg/dbad9689ef6e3759ba8c806bbf568a7d3ff90518) ،
، مبدل به عنوان عملکرد سبز یک سیستم بدنی مرتبط مشتق شده است.
مبدل به عنوان عملکرد سبز یک سیستم بدنی مرتبط مشتق شده است. ![\ displaystyle f [\ psi _ {n ({\ vec {r} t ، t)]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/9fa3ba17d6e2b56466d57d8b60a2e46ec4925b90) ممکن است به طور یکسان نقشه لجستیک باشد
ممکن است به طور یکسان نقشه لجستیک باشد![\ displaystyle \ psi \ rightarrow G \ psi [1- \ tanh (\ psi)]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/fec62ff5ebcf9fac8e71b101d6d2da0ef37f2df2) و یا
و یا ![\ displaystyle f [\ psi] = \ psi ^ {2}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/331a4c25ef04f99d8d77f2be74bf1fa8a4ec21b2) یا
یا  ممکن است خدمت کند هنگامی که مشکلات انتشار موج از راه دور است
ممکن است خدمت کند هنگامی که مشکلات انتشار موج از راه دور است با طول موج
با طول موج  هسته محسوب می شوند
هسته محسوب می شوند  ممکن است یک شکل از عملکرد سبز برای
ممکن است یک شکل از عملکرد سبز برای ![\ displaystyle K ({\ vec {r}} - {\ vec {r}} ^ {،}، L) = {\ frac {ik \ exp [ikL]} {2 \ pi L}} \ exp [ \ frac {ik | \ vec {r}} - {\ vec {r}} ^ {،} | ^ {2}} {2L}}]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/634f66d2d768bec45cbd9d5b17fea78dd2d2ef88) .
.
 است:
است:

 ، و همه خازن ها به اندازه مساوی هستند. فرکانس غالب است
، و همه خازن ها به اندازه مساوی هستند. فرکانس غالب است . خروجی
. خروجی 
![[x ، y]](https://wikimedia.org/api/rest_v1/media/math/render/svg/1b7bd6292c6023626c6358bfd3943a031b27d663) عبور از نقشه لجستیک. اولین تکرار (آبی) شرط اولیه است که در اصل یک دایره را تشکیل می دهد. انیمیشن اولین و ششمین تکرار شرایط اولیه دایره ای را نشان می دهد. مشاهده می شود که با پیشرفت در تکرارها ، اختلاط اتفاق می افتد. تکرار ششم نشان می دهد که نقاط تقریباً کاملاً در فضای فاز پراکنده اند. اگر در تکرارها بیشتر پیشرفت کنیم ، اختلاط می توانست یکدست و غیرقابل برگشت باشد. نقشه لجستیک دارای معادله است
عبور از نقشه لجستیک. اولین تکرار (آبی) شرط اولیه است که در اصل یک دایره را تشکیل می دهد. انیمیشن اولین و ششمین تکرار شرایط اولیه دایره ای را نشان می دهد. مشاهده می شود که با پیشرفت در تکرارها ، اختلاط اتفاق می افتد. تکرار ششم نشان می دهد که نقاط تقریباً کاملاً در فضای فاز پراکنده اند. اگر در تکرارها بیشتر پیشرفت کنیم ، اختلاط می توانست یکدست و غیرقابل برگشت باشد. نقشه لجستیک دارای معادله است . برای گسترش فضای حالت نقشه لجستیک به دو بعد ، حالت دوم ،
. برای گسترش فضای حالت نقشه لجستیک به دو بعد ، حالت دوم ، اگر
اگر  و
و  در غیر این صورت.
در غیر این صورت.
 گفته می شود که در صورت وجود هر جفت
گفته می شود که در صورت وجود هر جفت  ، وجود دارد
، وجود دارد به طوری که
به طوری که . تغییر پذیری توپولوژیکی یک نسخه ضعیف از
. تغییر پذیری توپولوژیکی یک نسخه ضعیف از 



 ،
،
 ، جایی که
، جایی که 
 تغییر دینامیک از به طور منظم به یک پر هرج و مرج
تغییر دینامیک از به طور منظم به یک پر هرج و مرج 
 زمان است ، و
زمان است ، و  ،
،  ،
،  سیستم وجود داشته باشد
سیستم وجود داشته باشد 


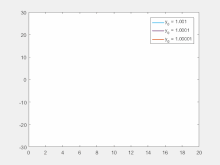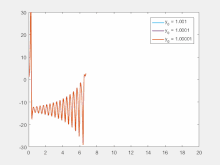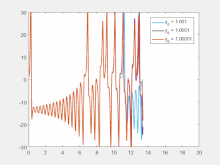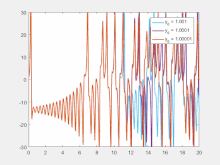
 ، این دو مسیر با نرخ مشخص شده توسط یکدیگر متفاوت می شوند
، این دو مسیر با نرخ مشخص شده توسط یکدیگر متفاوت می شوند
 نماینده لیاپونوف است. میزان جدایی به جهت گیری بردار جدایی اولیه بستگی دارد ، بنابراین طیف کاملی از مأمورین لیاپونف می توانند وجود داشته باشند. تعداد نمایندگان لیاپونف برابر است با تعدادی از ابعاد فضای فاز ، اگرچه مرجع است که فقط به بزرگترین مراجعه کنید. به عنوان مثال ، حداکثر نماینده Lyapunov (MLE) اغلب مورد استفاده قرار می گیرد ، زیرا پیش بینی کلی سیستم را تعیین می کند. معمولاً یک MLE مثبت به عنوان نشانه ای از هرج و مرج بودن سیستم در نظر گرفته می شود.
نماینده لیاپونوف است. میزان جدایی به جهت گیری بردار جدایی اولیه بستگی دارد ، بنابراین طیف کاملی از مأمورین لیاپونف می توانند وجود داشته باشند. تعداد نمایندگان لیاپونف برابر است با تعدادی از ابعاد فضای فاز ، اگرچه مرجع است که فقط به بزرگترین مراجعه کنید. به عنوان مثال ، حداکثر نماینده Lyapunov (MLE) اغلب مورد استفاده قرار می گیرد ، زیرا پیش بینی کلی سیستم را تعیین می کند. معمولاً یک MLE مثبت به عنوان نشانه ای از هرج و مرج بودن سیستم در نظر گرفته می شود. 
 آنتروپی
آنتروپی مقدار دیفرانسیل
مقدار دیفرانسیل 

 انرژی آزاد می کند
انرژی آزاد می کند


 از همیلتون واقعی.
از همیلتون واقعی. مربوط به ω است
مربوط به ω است
 غالباً منجر به ناپایداری عددی می شود و منجر به محدودیت اندازه زمان حرکت می شود
غالباً منجر به ناپایداری عددی می شود و منجر به محدودیت اندازه زمان حرکت می شود

























 یک
یک  به شکل پارامتری نوشته شده است
به شکل پارامتری نوشته شده است 
 ، که یک نقشه متفاوت است ، و
، که یک نقشه متفاوت است ، و  - نقشه برداری هویت از فضا
- نقشه برداری هویت از فضا  این به شکل یک
این به شکل یک  هویت دارد
هویت دارد  .
. این نتیجه می گیرد که عملکرد
این نتیجه می گیرد که عملکرد  یک تابع متفاوت از زمان است ؛ نمودار آن در یک فضای فاز طولانی قرار دارد
یک تابع متفاوت از زمان است ؛ نمودار آن در یک فضای فاز طولانی قرار دارد  و مسیر خطی (منحنی) سیستم دینامیکی نامیده می شود. طرح آن بر روی فضا{\ نمایشگر X}
و مسیر خطی (منحنی) سیستم دینامیکی نامیده می شود. طرح آن بر روی فضا{\ نمایشگر X} و برخی از قانون توصیف حرکت از نقاط فضای فاز با زمان. بسیاری از لحظات زمان
و برخی از قانون توصیف حرکت از نقاط فضای فاز با زمان. بسیاری از لحظات زمان . سپس مسیر نقطه
. سپس مسیر نقطه راه حل معادله دیفرانسیل خودمختار خواهد بود
راه حل معادله دیفرانسیل خودمختار خواهد بود  با شرایط اولیه
با شرایط اولیه  . سیستم پویا تعریف شده از این روش ، جریان فاز برای یک معادله دیفرانسیل مستقل نامیده می شود.
. سیستم پویا تعریف شده از این روش ، جریان فاز برای یک معادله دیفرانسیل مستقل نامیده می شود. - برخی نقشه برداری از مجموعه
- برخی نقشه برداری از مجموعه  . در واقع ، ما فرض می کنیم که یک نکته دلخواه است
. در واقع ، ما فرض می کنیم که یک نکته دلخواه است به نقطه می رود
به نقطه می رود  . سپس در زمان
. سپس در زمان این نکته به این نکته خواهد رسید
این نکته به این نکته خواهد رسید  و غیره
و غیره برگشت پذیر ، تکرار معکوس را نیز می توان تعریف کرد
برگشت پذیر ، تکرار معکوس را نیز می توان تعریف کرد  ،
، و غیره. بنابراین ، ما سیستمی را با نمونه های زمانی زیادی به دست می آوریم
و غیره. بنابراین ، ما سیستمی را با نمونه های زمانی زیادی به دست می آوریم  .
.
 کجا
کجا  - سرعت نقطه
- سرعت نقطه  - زاویه ای که موقعیت نقطه را روی دایره واحد تنظیم می کند. نمایش دو برابر
- زاویه ای که موقعیت نقطه را روی دایره واحد تنظیم می کند. نمایش دو برابر ، یک سیستم پویا را با زمان گسسته تعریف می کند ، فضای فاز آن یک دایره است.
، یک سیستم پویا را با زمان گسسته تعریف می کند ، فضای فاز آن یک دایره است.

 در این وبلاگ به ریاضیات و کاربردهای آن و تحقیقات در آنها پرداخته می شود. مطالب در این وبلاگ ترجمه سطحی و اولیه است و کامل نیست.در صورتی سوال یا نظری در زمینه ریاضیات دارید مطرح نمایید .در صورت امکان به آن می پردازم. من دوست دارم برای یافتن پاسخ به سوالات و حل پروژه های علمی با دیگران همکاری نمایم.در صورتی که شما هم بامن هم عقیده هستید با من تماس بگیرید.
در این وبلاگ به ریاضیات و کاربردهای آن و تحقیقات در آنها پرداخته می شود. مطالب در این وبلاگ ترجمه سطحی و اولیه است و کامل نیست.در صورتی سوال یا نظری در زمینه ریاضیات دارید مطرح نمایید .در صورت امکان به آن می پردازم. من دوست دارم برای یافتن پاسخ به سوالات و حل پروژه های علمی با دیگران همکاری نمایم.در صورتی که شما هم بامن هم عقیده هستید با من تماس بگیرید.