اشتقاق هندسی بصری
بیانیه
با توجه به عملکرد 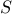 :
:
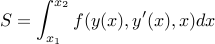
اویلر لاگرانژ می گوید که تابع 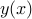 در یک نقطه ثابت تابعی
در یک نقطه ثابت تابعی 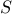 از:
از:
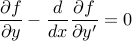
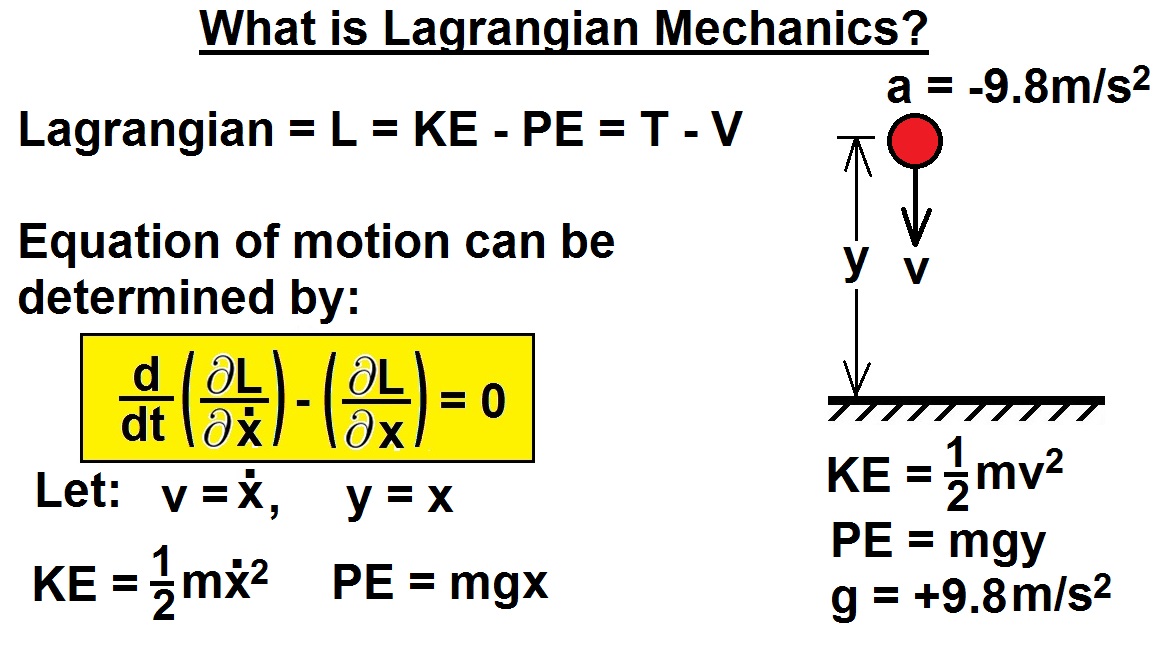
کجا 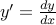 .
.
این نتیجه اغلب با استفاده از ادغام توسط قطعات ثابت می شود - اما معادله یک شرایط محلی را بیان می کند و باید با استفاده از استدلال محلی قابل استخراج باشد.
ما یک مشتق جایگزین را در زیر بررسی خواهیم کرد.
مثال انگیزشی
سیستمهای فیزیکی در تعادل پایدار به پیکربندی حرکت میکنند که به صورت محلی انرژی بالقوه آنها را به حداقل میرساند. به عنوان مثال، زنجیره ای را در نظر بگیرید که روی دو قرقره قرار دارد (در ارتفاع 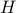 ، با فاصله از هم جدا شده اند
، با فاصله از هم جدا شده اند 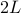 )، که زنجیر اضافی روی زمین قرار دارد.
)، که زنجیر اضافی روی زمین قرار دارد.
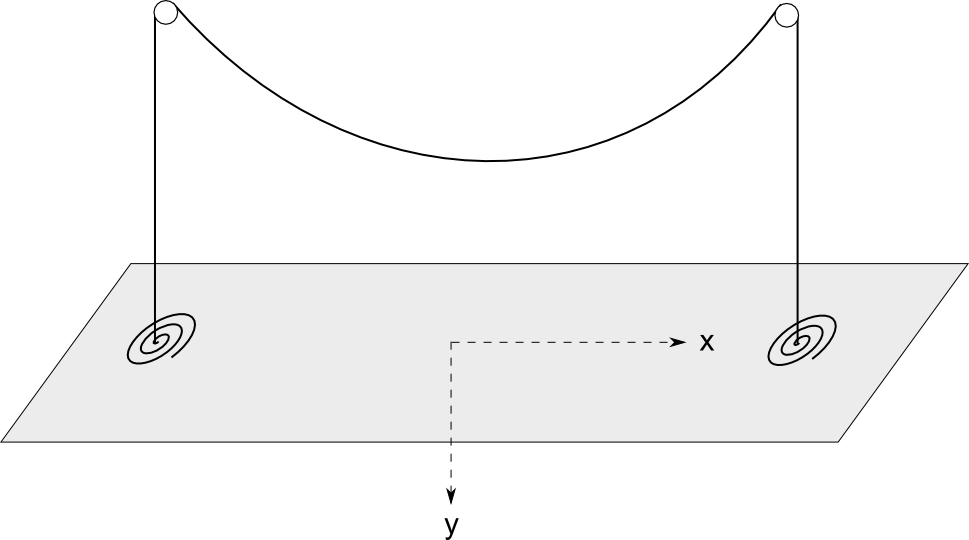 |
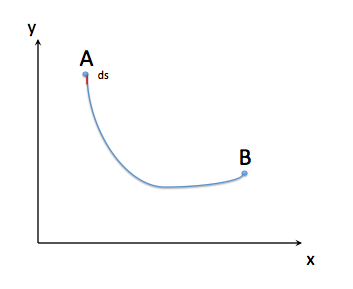
زنجیر بین دو قرقره شکلی به خود می گیرد که انرژی پتانسیل گرانشی آن را به حداقل می رساند. فضا جالب است: اگر زنجیر کشیده باشد، بالاتر از سطح زمین خواهد بود و انرژی بالایی دارد. اگر زنجیر خیلی آویزان باشد، زنجیر زیادی را از زمین بیرون می کشد و انرژی بالایی دارد. در این بین شکل بهینه است.
انرژی پتانسیل یک شکل معین از زنجیره 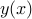 بین قرقره ها برابر است با:
بین قرقره ها برابر است با:
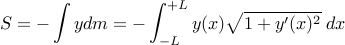
ما فقط در امتداد بخش بین قرقره ها یکپارچه شده ایم، زیرا می توانیم  در سطح زمین تعریف کنیم و ثابت ها (انرژی زنجیر آویزان خارج از قرقره ها) و عوامل ثابت (
در سطح زمین تعریف کنیم و ثابت ها (انرژی زنجیر آویزان خارج از قرقره ها) و عوامل ثابت ( 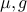 ) را نادیده بگیریم.
) را نادیده بگیریم.
اکنون می خواهیم تابعی را 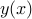 که حداقل می کند
که حداقل می کند 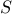 (با توجه به شرایط مرزی
(با توجه به شرایط مرزی 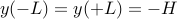 ) پیدا کنیم.
) پیدا کنیم.
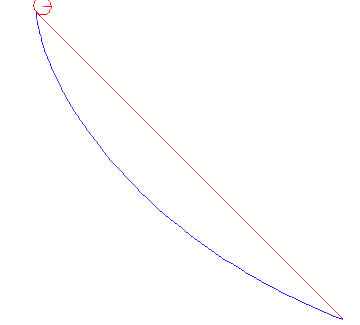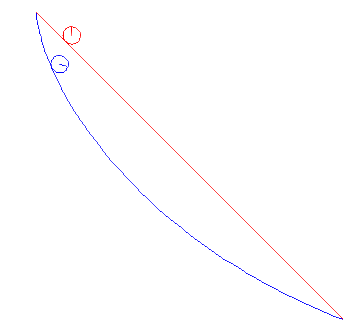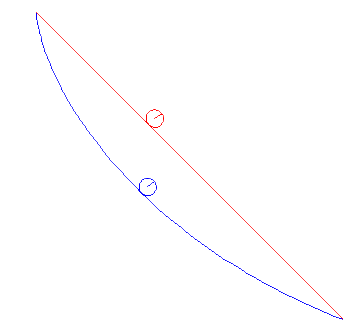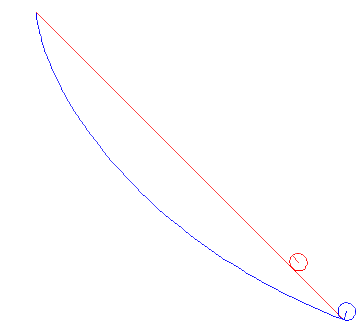
مشتق هندسی
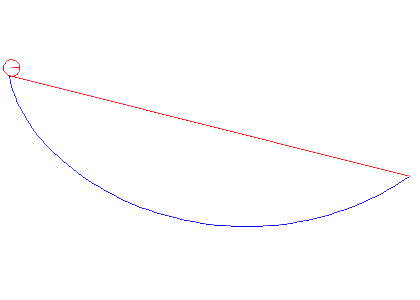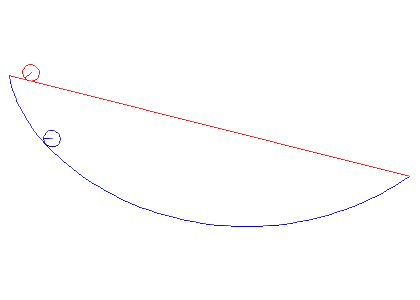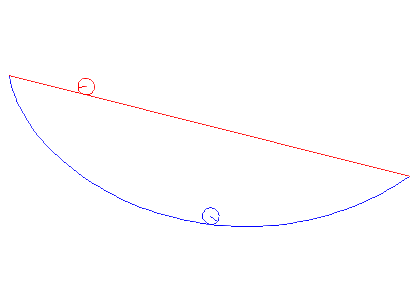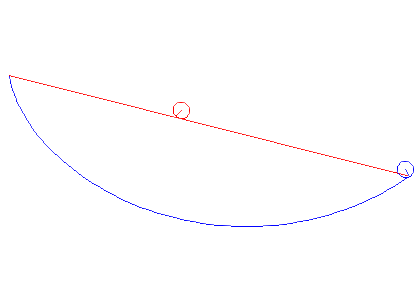
برای 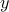 اینکه یک نقطه ثابت باشد
اینکه یک نقطه ثابت باشد 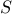 ، اغتشاشات کوچک در تابع
، اغتشاشات کوچک در تابع 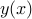 نباید مقدار
نباید مقدار 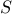 (به مرتبه اول) را تغییر دهد. بنابراین یک بخش بینهایت کوچک از
(به مرتبه اول) را تغییر دهد. بنابراین یک بخش بینهایت کوچک از 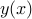 (خاکستری) را در اطراف گسسته در نظر
(خاکستری) را در اطراف گسسته در نظر 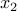 بگیرید. اغتشاش
بگیرید. اغتشاش 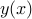 در
در 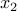 یک مقدار
یک مقدار 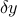 (تغییر از آبی –> قرمز) را در نظر خواهیم گرفت و تأثیر آن را بر
(تغییر از آبی –> قرمز) را در نظر خواهیم گرفت و تأثیر آن را بر 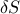 روی
روی 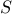 .
.
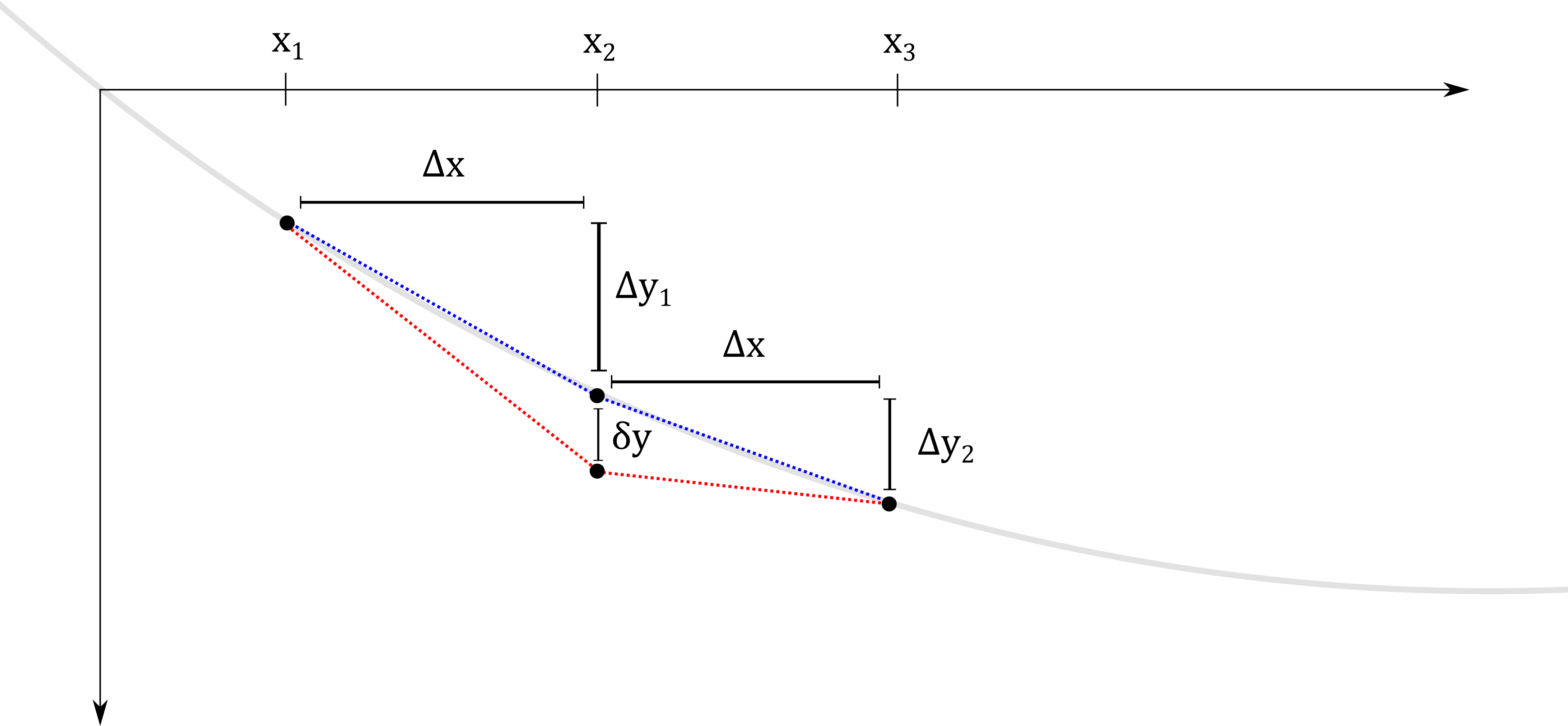 |
به خاطر آوردن: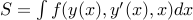
برهم زدن این نقطه 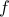 به دو صورت تأثیر می گذارد:
به دو صورت تأثیر می گذارد:
این مقدار در را تغییر می
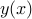 دهد
دهد 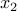 .
.این مشتقات
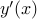 اطراف را تغییر می دهد
اطراف را تغییر می دهد 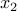 .
.
سهم اول به سادگی این است:
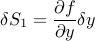
سهم دوم در دو بخش است: افزایش مشتق در سمت چپ، و کاهش مشتق در سمت راست. بر اساس شکل (قبل از اغتشاش) داریم:
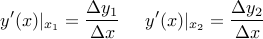
و بعد از اغتشاش:
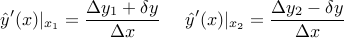
بنابراین تغییر در مشتقات به صورت زیر است:
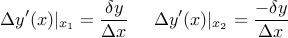
این مقدار تحت تأثیر قرار می  گیرد:
گیرد:
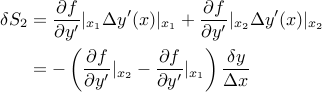
از آنجایی 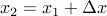 که می توانیم بنویسیم:
که می توانیم بنویسیم:
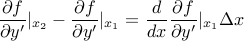
بنابراین در نهایت، اثر تغییر مشتقات عبارت است از:
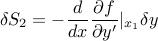
و اثر خالص برهم زدن نقطه این است:
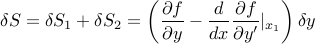
بنابراین به وضوح، نیاز 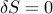 به اغتشاشات کوچک
به اغتشاشات کوچک 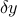 در هر نقطه از تابع، معادله اویلر-لاگرانژ را نشان می دهد:
در هر نقطه از تابع، معادله اویلر-لاگرانژ را نشان می دهد:
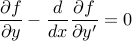
و اکنون هر دو اصطلاح معنی دارند:
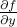 : مقدار اغتشاشات کوچک
: مقدار اغتشاشات کوچک 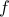 با تغییر مستقیم مقدار تاثیر می گذارد
با تغییر مستقیم مقدار تاثیر می گذارد 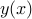 .
.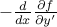 : اغتشاشات مقدار خالص
: اغتشاشات مقدار خالص 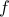 با تغییر مشتقات
با تغییر مشتقات 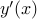 در همسایگی
در همسایگی 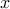 . (مشتق به سمت چپ افزایش مییابد، و به سمت راست کاهش مییابد - بنابراین اثر خالص بستگی به این دارد که چگونه
. (مشتق به سمت چپ افزایش مییابد، و به سمت راست کاهش مییابد - بنابراین اثر خالص بستگی به این دارد که چگونه 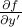 در طول بازه تغییر میکند
در طول بازه تغییر میکند 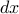 ).
).
در یک نقطه ثابت، این اثرات دقیقا باید لغو شوند.
نظرات نهایی
برای کاملتر شدن، راهحل مثال را استخراج میکنیم و آن را به یک زنجیره با طول ثابت تعمیم میدهیم .
راه حل
در این مورد:
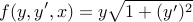
با اعمال مستقیم اویلر-لاگرانژ، متوجه می شویم:
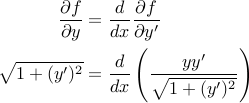
ما میتوانیم این را حل کنیم، اما روش سادهتر استفاده از یک قضیه است:
Thm : اگر 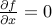 ، پس ثابت
، پس ثابت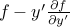 است .
است .
اثبات :
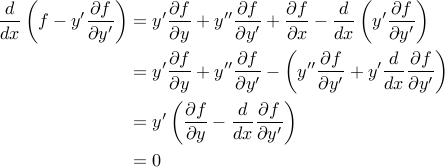
جایی که آخرین مرحله اعمال شکل اصلی معادله اویلر-لاگرانژ است.
از آنجایی که خاص ما 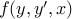 مستقل از است
مستقل از است 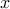 ، می توانیم این قضیه را اعمال کنیم:
، می توانیم این قضیه را اعمال کنیم:
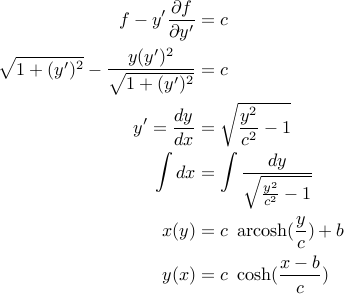
برای ثابت 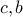 هایی که برای برآوردن شرایط مرزی انتخاب می شوند. این منحنی آشنا را به ما می دهد .
هایی که برای برآوردن شرایط مرزی انتخاب می شوند. این منحنی آشنا را به ما می دهد .
افزونه
ما می دانیم که اگر یک زنجیره با طول ثابت بین دو نقطه انتهایی ثابت آویزان کنیم، خط لوله نیز شکلی است که به وجود می آید. این تصادفی نیست.
مشکل زنجیره طول ثابت یک مشکل کمینه سازی محدود است، با همان عملکرد انرژی پتانسیل 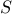 ، اما محدودیت اضافی که طول قوس
، اما محدودیت اضافی که طول قوس 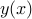 آن مقداری ثابت مشخص است.
آن مقداری ثابت مشخص است.
مشکلات محدود را با 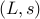 فاصله جداسازی و طول قوس زنجیره مشخص کنید.
فاصله جداسازی و طول قوس زنجیره مشخص کنید.
و مشکلات نامحدود توسط 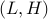 - فاصله و ارتفاع جداسازی.
- فاصله و ارتفاع جداسازی.
ما نشان خواهیم داد که راه حل این مشکل نیز با نشان دادن اینکه:
قضیه : برای یک مسئله مقید معین 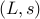 ، یک مسئله غیرمحدود متناظر وجود دارد
، یک مسئله غیرمحدود متناظر وجود دارد 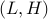 که شامل مسئله مقید به عنوان یک مسئله فرعی است. بنابراین مشکل محدود نیز باید یک سلسله مراتبی باشد.
که شامل مسئله مقید به عنوان یک مسئله فرعی است. بنابراین مشکل محدود نیز باید یک سلسله مراتبی باشد.
لم : برای هر 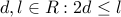 , ما همیشه می توانیم پیکربندی نامحدودی پیدا کنیم
, ما همیشه می توانیم پیکربندی نامحدودی پیدا کنیم 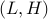 به طوری که طول زنجیره بین
به طوری که طول زنجیره بین 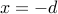 و
و 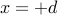 دقیقاً
دقیقاً 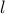 باشد .
باشد .
اثبات : به خانواده راه حل های بدون محدودیتی که پیدا کردیم مراجعه کنید. با انتخاب متمرکز مختصات،  و خانواده شکل می گیرد:
و خانواده شکل می گیرد:
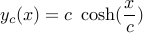
شرط مرزی 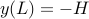 پارامتر را تعیین می کند
پارامتر را تعیین می کند  . در حال حاضر، به وضوح طول قوس بین
. در حال حاضر، به وضوح طول قوس بین 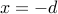 و
و 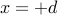 یک تابع کاهشی یکنواخت است
یک تابع کاهشی یکنواخت است  ، با افراط در
، با افراط در 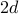 و
و 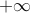 . (به عنوان مثال، برای
. (به عنوان مثال، برای 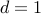 ، معلوم می شود که طول قوس است
، معلوم می شود که طول قوس است  )
)
بنابراین، هر مقدار 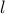 در این محدوده برای برخی قابل دستیابی است
در این محدوده برای برخی قابل دستیابی است 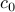 - و علاوه بر این، مقداری وجود دارد
- و علاوه بر این، مقداری وجود دارد 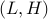 که باعث این امر می شود
که باعث این امر می شود  (به ویژه،
(به ویژه، 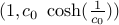 آثار).
آثار).
نتیجه : اکنون، با توجه به یک مسئله محدود 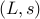 ، یک مسئله غیرمحدود بسازید به
، یک مسئله غیرمحدود بسازید به 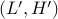 طوری که طول زنجیره بین
طوری که طول زنجیره بین 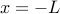 و
و 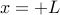 دقیقاً
دقیقاً  باشد. (که Lemma تضمین می کند که ما قادر به انجام آن هستیم). در این بازه، مسئله نامحدود با مسئله محدود یکسان است: طول قوس
باشد. (که Lemma تضمین می کند که ما قادر به انجام آن هستیم). در این بازه، مسئله نامحدود با مسئله محدود یکسان است: طول قوس  و نقاط پایانی که با
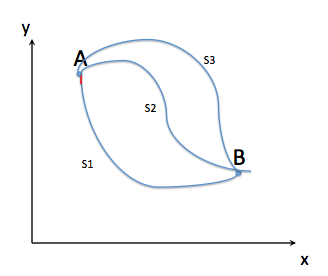
و نقاط پایانی که با 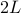 . اگر راه حل بهینه یک موقعیت (مثلا A) انرژی پتانسیل کمتری (در طول دهانه) نسبت به دیگری (B) داشته باشد، B می تواند شکل A را در طول دهانه به خود بگیرد، بدون اینکه هیچ محدودیتی را نقض کند، اما انرژی کمتری را در پی داشته باشد. تضاد بهینه، بنابراین هر دو مسئله باید راهحلهای یکسانی در طول بازه داشته باشند - و راهحل بهینه محدود نیز یک راهحل است.
. اگر راه حل بهینه یک موقعیت (مثلا A) انرژی پتانسیل کمتری (در طول دهانه) نسبت به دیگری (B) داشته باشد، B می تواند شکل A را در طول دهانه به خود بگیرد، بدون اینکه هیچ محدودیتی را نقض کند، اما انرژی کمتری را در پی داشته باشد. تضاد بهینه، بنابراین هر دو مسئله باید راهحلهای یکسانی در طول بازه داشته باشند - و راهحل بهینه محدود نیز یک راهحل است.
بنابراین ما همچنین راه حل مشکل محدود را استخراج کرده ایم. (بدون نیاز به ضریب لاگرانژ!)
منبع
https://preetum.nakkiran.org/lagrange.html




![C^{1}([a,b])](https://wikimedia.org/api/rest_v1/media/math/render/svg/b4d44d2584dad0d92346326d4eff220968446993) با شرایط مرزی
با شرایط مرزی و
و ، با تقریب منحنی منحنی با یک خط چند ضلعی با
، با تقریب منحنی منحنی با یک خط چند ضلعی با بخش ها و عبور از حد مجاز با افزایش خودسرانه تعداد بخش ها.
بخش ها و عبور از حد مجاز با افزایش خودسرانه تعداد بخش ها.![[الف، ب]](https://wikimedia.org/api/rest_v1/media/math/render/svg/9c4b788fc5c637e26ee98b45f89a5c08c85f7935) به
به و اجازه دهید
و اجازه دهید . به جای یک عملکرد صاف
. به جای یک عملکرد صاف خط چند ضلعی را با رئوس در نظر می گیریم
خط چند ضلعی را با رئوس در نظر می گیریم ، جایی که
، جایی که و
و . بر این اساس، تابع ما به یک تابع واقعی تبدیل می شود
. بر این اساس، تابع ما به یک تابع واقعی تبدیل می شود متغیرهای داده شده توسط
متغیرهای داده شده توسط
 مربوط به نقاطی است که در آن
مربوط به نقاطی است که در آن

 می دهد
می دهد![{\displaystyle {\frac {\partial J}{\partial y_{m}\Delta t}}=L_{y}\left(t_{m},y_{m},{\frac {y_{m+1 }-y_{m}}{\Delta t}}\right)-{\frac {1}{\Delta t}}\left[L_{y'}\left(t_{m},y_{m}, {\frac {y_{m+1}-y_{m}}{\Delta t}}\right)-L_{y'}\left(t_{m-1},y_{m-1},{\ frac {y_{m}-y_{m-1}}{\Delta t}}\right)\right],}](https://wikimedia.org/api/rest_v1/media/math/render/svg/009f74c389cb1aa937dea080441a3a99371492ca) و حد را به عنوان
و حد را به عنوان از سمت راست این عبارت بازده
از سمت راست این عبارت بازده
 از عملکردی
از عملکردی . یک شرط ضروری برای داشتن یک تابع متمایز بر روی یک تابع این است که مشتق تابعی آن در آن تابع ناپدید شود، که با آخرین معادله به دست میآید.
. یک شرط ضروری برای داشتن یک تابع متمایز بر روی یک تابع این است که مشتق تابعی آن در آن تابع ناپدید شود، که با آخرین معادله به دست میآید.


![{\displaystyle I[f]=\int _{x_{0}}^{x_{1}}{\mathcal {L}}(x,f,f',f'',\dots ,f^{( k)})~\mathrm {d} x~;~~f':={\cfrac {\mathrm {d} f}{\mathrm {d} x}}،~f'':={\cfrac { \mathrm {d} ^{2}f}{\mathrm {d} x^{2}}},~f^{(k)}:={\cfrac {\mathrm {d} ^{k}f} {\mathrm {d} x^{k}}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/e0225dddd92f86184bf165d4b5e4a58844f9049d)

 مشتقات (یعنی برای همه
مشتقات (یعنی برای همه ). مقادیر نقطه پایانی بالاترین مشتق
). مقادیر نقطه پایانی بالاترین مشتق انعطاف پذیر باقی بماند
انعطاف پذیر باقی بماند ) از یک متغیر مستقل منفرد (
) از یک متغیر مستقل منفرد ( ) که یک افراطی از عملکردی را تعریف می کنند
) که یک افراطی از عملکردی را تعریف می کنند![{\displaystyle I[f_{1},f_{2},\dots ,f_{m}]=\int _{x_{0}}^{x_{1}}{\mathcal {L}}(x, f_{1},f_{2},\dots,f_{m},f_{1}',f_{2}',\dots ,f_{m}')~\mathrm {d} x~;~~ f_{i}':={\cfrac {\mathrm {d} f_{i}}{\mathrm {d} x}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/f781ed0b37670be01ea7542d64eeef89d72a87c1)

 پس مقداری سطح است
پس مقداری سطح است![{\displaystyle I[f]=\int _{\Omega }{\mathcal {L}}(x_{1},\dots ,x_{n},f,f_{1},\dots ,f_{n} )\,\mathrm {d} \mathbf {x} \,\!~;~~f_{j}:={\cfrac {\partial f}{\partial x_{j}}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/e42836df9987f316a4141697b98757b87c6d08f1)


![{\displaystyle I[f_{1},f_{2},\dots ,f_{m}]=\int _{\Omega }{\mathcal {L}}(x_{1},\dots ,x_{n },f_{1},\dots ,f_{m},f_{1,1},\dots ,f_{1,n},\dots ,f_{m,1},\dots ,f_{m,n })\,\mathrm {d} \mathbf {x} \,\!~;~~f_{i,j}:={\cfrac {\partial f_{i}}{\partial x_{j}}} }](https://wikimedia.org/api/rest_v1/media/math/render/svg/80dedbd5d62ca4f9353f7a954124655f21e6266a)

![{\displaystyle {\begin{aligned}I[f]&=\int _{\Omega }{\mathcal {L}}(x_{1},x_{2},f,f_{1},f_{2 },f_{11},f_{12},f_{22},\dots ,f_{22\dots 2})\,\mathrm {d} \mathbf {x} \\&\qquad \quad f_{i }:={\cfrac {\partial f}{\partial x_{i}}}\;,\quad f_{ij}:={\cfrac {\partial ^{2}f}{\partial x_{i} \ x_{j}}}\;،\;\;\dots \end{تراز شده}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/c96618e8ff2b1fe9a72186bc017b213b567bb9e9)


 شاخص هایی هستند که تعداد متغیرها را در بر می گیرند، یعنی در اینجا آنها از 1 به 2 می روند.
شاخص هایی هستند که تعداد متغیرها را در بر می گیرند، یعنی در اینجا آنها از 1 به 2 می روند. برای مثال، به منظور جلوگیری از شمارش مشتق جزئی یکسان چندین بار
برای مثال، به منظور جلوگیری از شمارش مشتق جزئی یکسان چندین بار فقط یک بار در معادله قبلی ظاهر می شود.
فقط یک بار در معادله قبلی ظاهر می شود.![{\displaystyle {\begin{aligned}I[f_{1},\ldots ,f_{p}]&=\int _{\Omega }{\mathcal {L}}(x_{1},\ldots ,x_ {m};f_{1},\ldots,f_{p};f_{1,1},\ldots ,f_{p,m};f_{1,11},\ldots ,f_{p,mm} ;\ldots ;f_{p,1\ldots 1},\ldots,f_{p,m\ldots m})\,\mathrm {d} \mathbf {x} \\&\qquad \quad f_{i, \mu }:={\cfrac {\partial f_{i}}{\partial x_{\mu }}}\;,\quad f_{i,\mu _{1}\mu _{2}}:= {\cfrac {\partial ^{2}f_{i}}{\partial x_{\mu _{1}}\partial x_{\mu _{2}}}}\;,\;\;\dots \ پایان{تراز شده}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/52eecfa9f667cb99c73faf1e7335ea31eaf8dfef)

 چندین بار، درست مانند بخش فرعی قبلی. این را می توان به صورت فشرده تر بیان کرد
چندین بار، درست مانند بخش فرعی قبلی. این را می توان به صورت فشرده تر بیان کرد
 یک
یک ![C^{\infty }([a,b])](https://wikimedia.org/api/rest_v1/media/math/render/svg/659892a168b4498e587161258ca400db12561727) فضای
فضای ![f:[a,b]\ به M](https://wikimedia.org/api/rest_v1/media/math/render/svg/712c3e0984c28a1648af02d818a9a4fdec0141f0) . سپس، برای عملکرد
. سپس، برای عملکرد![S:C^{\infty }([a,b])\to \mathbb {R}](https://wikimedia.org/api/rest_v1/media/math/render/svg/7b5308c04282486e61284e50d918731f5d065af6) از فرم
از فرم![S[f]=\int _{a}^{b}(L\circ {\dot {f}})(t)\,\mathrm {d} t](https://wikimedia.org/api/rest_v1/media/math/render/svg/aa07716cf37832981db890147592174562074312)
 عبارت لاگرانژی است
عبارت لاگرانژی است معادل این جمله است که برای همه
معادل این جمله است که برای همه![t\in [a,b]](https://wikimedia.org/api/rest_v1/media/math/render/svg/b7f3050ace6dc0dd95250c418528da28eb477ffe) ، هر یک از مختصات فریم
، هر یک از مختصات فریم  از یک محله از
از یک محله از موارد زیر را به دست می دهد
موارد زیر را به دست می دهد معادلات:
معادلات:
 یک سیستم مکانیکی با
یک سیستم مکانیکی با فضای
فضای  لاگرانژی ، یعنی یک تابع با ارزش واقعی صاف به طوری که
لاگرانژی ، یعنی یک تابع با ارزش واقعی صاف به طوری که و
و هست یک
هست یک جایی که
جایی که بسته نرم افزاری
بسته نرم افزاری 
 مجموعه مسیرهای هموار باشد
مجموعه مسیرهای هموار باشد![{\displaystyle {\boldsymbol {q}}:[a,b]\to X}](https://wikimedia.org/api/rest_v1/media/math/render/svg/de52d438b2b841e73128afa9266346c8cc9e5643) برای کدام
برای کدام و
و عمل
عمل  از طریق تعریف شده است
از طریق تعریف شده است![{\displaystyle S[{\boldsymbol {q}}]=\int _{a}^{b}L(t,{\boldsymbol {q}}(t),{\dot {\boldsymbol {q}}} (t))\,dt.}](https://wikimedia.org/api/rest_v1/media/math/render/svg/c55e2d8b07c21a94752a392681498fb673aa04de)
 یک
یک  اگر و تنها اگر
اگر و تنها اگر
 مشتق زمانی است
مشتق زمانی است
 که شرایط مرزی را برآورده می کند
که شرایط مرزی را برآورده می کند ،
، ، و عملکردی را افراط می کند
، و عملکردی را افراط می کند
 دو بار به طور مداوم قابل تمایز است.
دو بار به طور مداوم قابل تمایز است.  نتیجه چنین آشفتگی باشد
نتیجه چنین آشفتگی باشد از
از کوچک است و
کوچک است و یک تابع متمایز رضایت بخش است
یک تابع متمایز رضایت بخش است . سپس تعریف کنید
. سپس تعریف کنید جایی که
جایی که .
. با توجه به ε .
با توجه به ε .

 .
.![{\displaystyle {\frac {\mathrm {d} J_{\varepsilon }}{\mathrm {d} \varepsilon }}=\int _{a}^{b}\left[\eta (x){\frac {\partial L_{\varepsilon }}{\partial g_{\varepsilon }}}+\eta '(x){\frac {\partial L_{\varepsilon }}{\partial g_{\varepsilon }'}}\ ,\right]\,\mathrm {d} x\,.}](https://wikimedia.org/api/rest_v1/media/math/render/svg/7e1c8262442eecf2eb54ab0b41ad9b6163d61f36)
![{\displaystyle \left.{\frac {\mathrm {d} J_{\varepsilon }}{\mathrm {d} \varepsilon }}\right|_{\varepsilon =0}=\int _{a}^{ b}\left[\eta (x){\frac {\partial L}{\partial f}}+\eta '(x){\frac {\partial L}{\partial f'}}\,\right ]\,\mathrm {d} x=0\ .}](https://wikimedia.org/api/rest_v1/media/math/render/svg/4ba853fceefd4a3c3baa01517dff4dfa7adf7f2d)
![{\displaystyle \int _{a}^{b}\left[{\frac {\partial L}{\partial f}}}-{\frac {\mathrm {d} }{\mathrm {d} x}} {\frac {\partial L}{\partial f'}}\right]\eta (x)\,\mathrm {d} x+\left[\eta (x){\frac {\partial L}{\partial f'}}\right]_{a}^{b}=0\ .}](https://wikimedia.org/api/rest_v1/media/math/render/svg/2d61f8ff39c124c2fbc6d71baaa1a96c07fc298a)
![{\displaystyle \int _{a}^{b}\left[{\frac {\partial L}{\partial f}}}-{\frac {\mathrm {d} }{\mathrm {d} x}} {\frac {\partial L}{\partial f'}}\right]\eta (x)\,\mathrm {d} x=0\,.}](https://wikimedia.org/api/rest_v1/media/math/render/svg/43f962c2602a7455a8aea5f0a8f7550c74a10296)

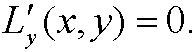
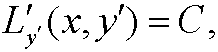
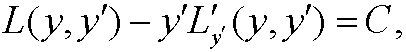
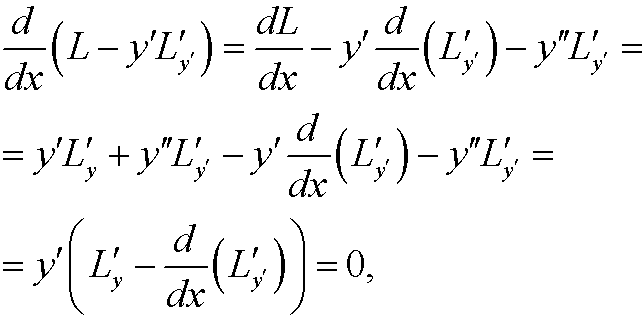
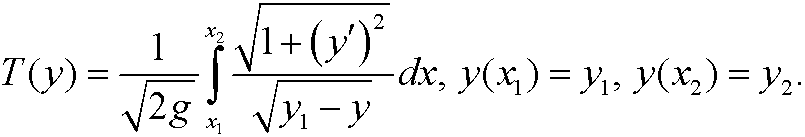
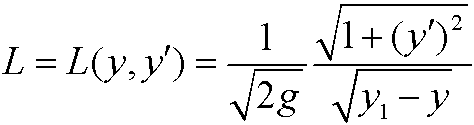
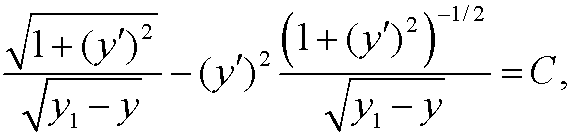
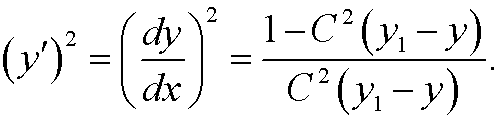
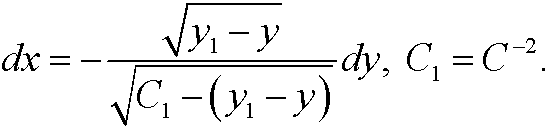
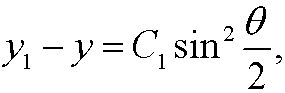
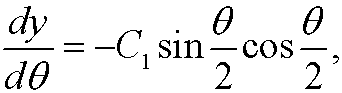
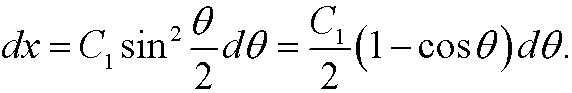
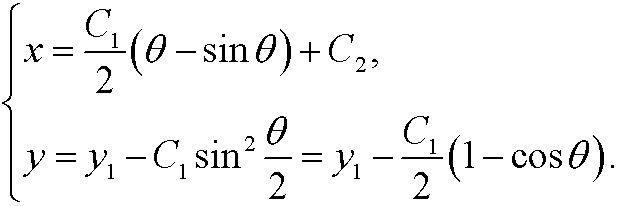


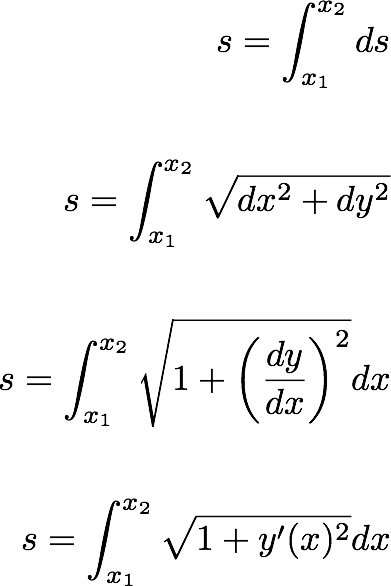
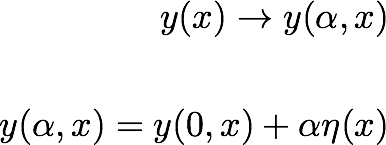
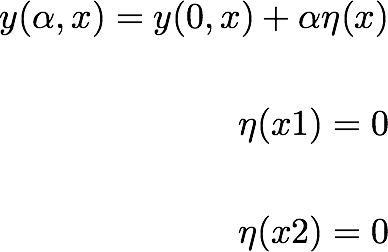
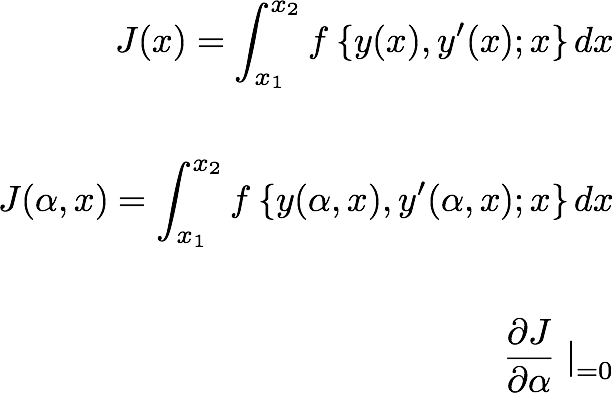
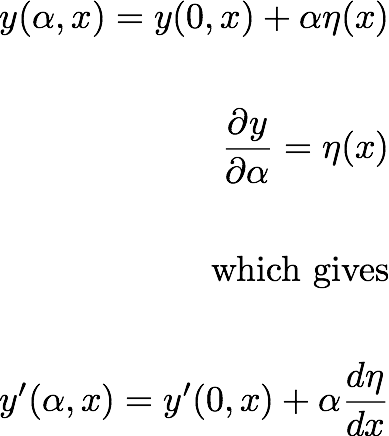
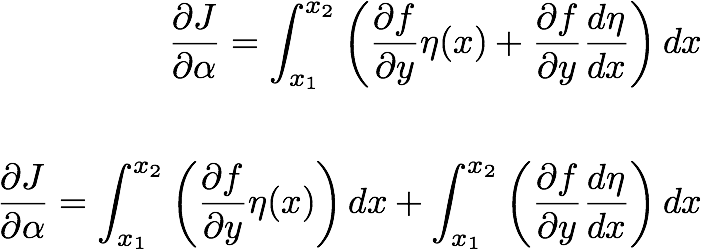
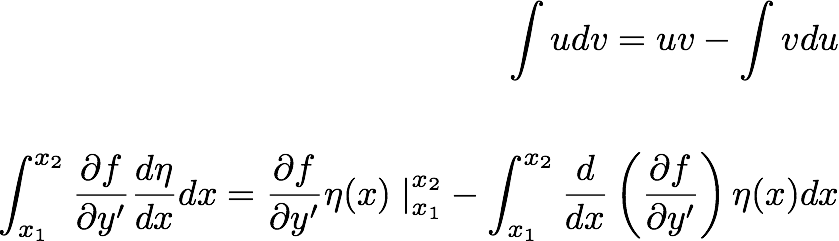
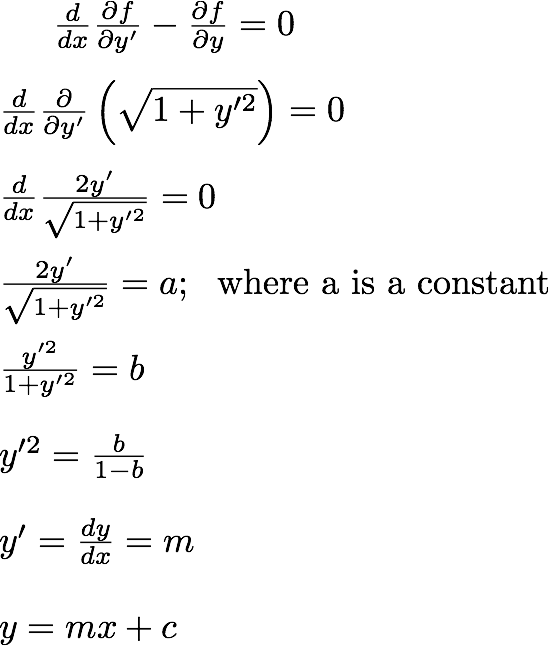




 و
و .
.


 این سری برای هر مقدار
این سری برای هر مقدار 
 n امین
n امین  n امین
n امین 



 و
و
 این می دهد
این می دهد برای
برای 
 بنابراین:
بنابراین:
 (
( برای مماس و کوتانژانت هذلولی).
برای مماس و کوتانژانت هذلولی).











 با شرایط اولیه
با شرایط اولیه شرایط اولیه روح را منحصر به فرد می کند، بدون هیچ جفت کارکردی
شرایط اولیه روح را منحصر به فرد می کند، بدون هیچ جفت کارکردی راه حل خواهد بود
راه حل خواهد بود






 ،
، ،
، یا
یا به یک هویت هذلولی، با بسط کامل آن بر حسب قدرت های انتگرال سینوس ها و کسینوس ها، تغییر سینوس به سینه و کسینوس به کوش، و تغییر علامت هر عبارت حاوی حاصل ضرب دو سین.
به یک هویت هذلولی، با بسط کامل آن بر حسب قدرت های انتگرال سینوس ها و کسینوس ها، تغییر سینوس به سینه و کسینوس به کوش، و تغییر علامت هر عبارت حاوی حاصل ضرب دو سین.




![{\displaystyle {\begin{aligned}\sinh(x+y)&=\sinh x\cosh y+\cosh x\sinh y\\\cosh(x+y)&=\cosh x\cosh y+\sinh x \sinh y\\[6px]\tanh(x+y)&={\frac {\tanh x+\tanh y}{1+\tanh x\tanh y}}\\\end{تراز شده}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/8a343fcb86c5fa15cceb217f4e92410c70a6e200)




![{\displaystyle {\begin{aligned}\sinh \left({\frac {x}{2}}\right)&={\frac {\sinh x}{\sqrt {2(\cosh x+1)} }}&&=\operatorname {sgn} x\,{\sqrt {\frac {\cosh x-1}{2}}}\\[6px]\cosh \left({\frac {x}{2}} \right)&={\sqrt {\frac {\cosh x+1}{2}}}\\[6px]\tanh \left({\frac {x}{2}}\right)&={\ frac {\sinh x}{\cosh x+1}}&&=\operatorname {sgn} x\,{\sqrt {\frac {\cosh x-1}{\cosh x+1}}}={\frac {e^{x}-1}{e^{x}+1}}\end{تراز شده}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/412a4ffd109486f684e515634b33447b13444954)




















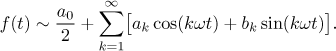


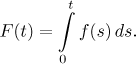
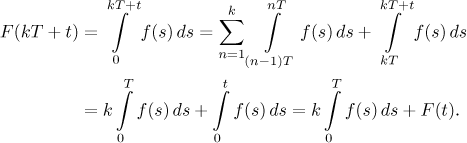
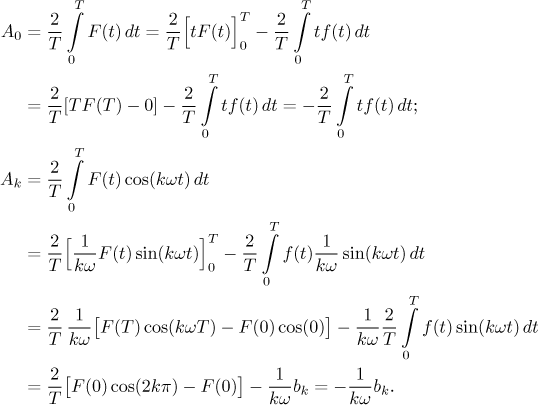

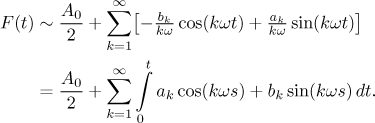


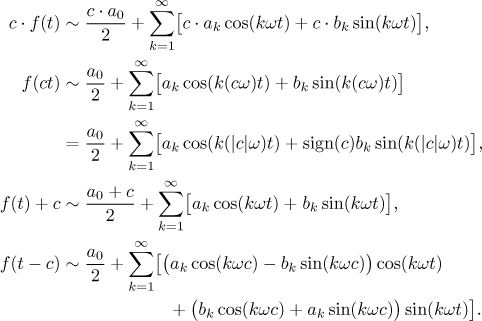
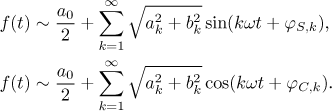
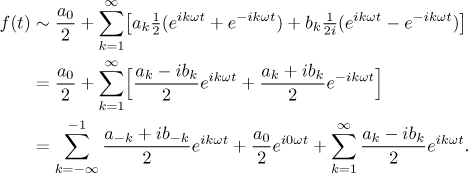
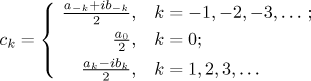
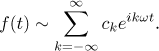
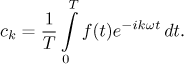

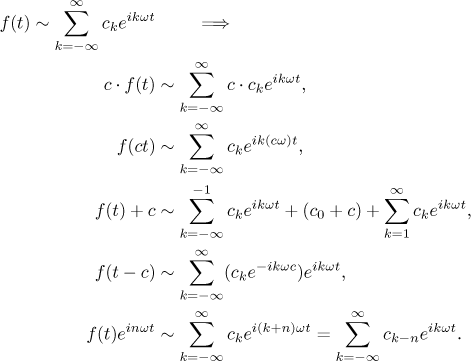










 .
.
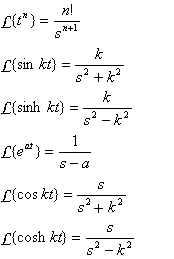











 در این وبلاگ به ریاضیات و کاربردهای آن و تحقیقات در آنها پرداخته می شود. مطالب در این وبلاگ ترجمه سطحی و اولیه است و کامل نیست.در صورتی سوال یا نظری در زمینه ریاضیات دارید مطرح نمایید .در صورت امکان به آن می پردازم. من دوست دارم برای یافتن پاسخ به سوالات و حل پروژه های علمی با دیگران همکاری نمایم.در صورتی که شما هم بامن هم عقیده هستید با من تماس بگیرید.
در این وبلاگ به ریاضیات و کاربردهای آن و تحقیقات در آنها پرداخته می شود. مطالب در این وبلاگ ترجمه سطحی و اولیه است و کامل نیست.در صورتی سوال یا نظری در زمینه ریاضیات دارید مطرح نمایید .در صورت امکان به آن می پردازم. من دوست دارم برای یافتن پاسخ به سوالات و حل پروژه های علمی با دیگران همکاری نمایم.در صورتی که شما هم بامن هم عقیده هستید با من تماس بگیرید.