1-گروه متناوب: A5
این مقاله در مورد یک گروه خاص است ، یعنی یک گروه منحصر به فرد تا ایزومورفیسم . مشاهده اطلاعات خاص (مانند تئوری نمایش خطی، ساختار زیر گروه) در مورد این گروه
مشاهده لیست کاملی از گروه های خاص (این یک لیست بسیار بزرگ است!) [نمایش بیشتر]
فهرست |
تعریف
گروه متناوب که به آن  نشان داده می شود و گروه متناوب درجه پنج
نشان داده می شود و گروه متناوب درجه پنج نامیده می شود، به روش های زیر تعریف می شود:
نامیده می شود، به روش های زیر تعریف می شود:
- این گروه جایگشت های زوج (یعنی گروه متناوب ) در پنج عنصر است.
- این گروه فون دایک است (گاهی اوقات گروه مثلث نامیده می شود ، اگرچه دومی معنای کمی متفاوت دارد) با پارامترها
 (گاهی اوقات به مرتبه معکوس به عنوان نوشته می شود
(گاهی اوقات به مرتبه معکوس به عنوان نوشته می شود  ).
). - این گروه ایکوس وجهی است ، یعنی گروهی از تقارن های حفظ جهت گیری ایکو وجهی منظم (یا معادل آن دوازده وجهی منظم).
 به این صورت مشاهده می شود، یا نشان داده می شود
به این صورت مشاهده می شود، یا نشان داده می شود  . اطلاعات بیشتر: طبقه بندی زیرگروه های محدود SO(3,R) ، نظریه نمایش خطی گروه متناوب:A5
. اطلاعات بیشتر: طبقه بندی زیرگروه های محدود SO(3,R) ، نظریه نمایش خطی گروه متناوب:A5 - این گروه خطی ویژه تصویری درجه دو در میدان چهار عنصر است، یعنی
 . همچنین گروه خطی ویژه درجه دو در میدان چهار عنصر است ، یعنی،
. همچنین گروه خطی ویژه درجه دو در میدان چهار عنصر است ، یعنی،  . همچنین گروه خطی عمومی تصویری درجه دو در میدان چهار عنصر ، یعنی،
. همچنین گروه خطی عمومی تصویری درجه دو در میدان چهار عنصر ، یعنی،  است.
است. - این گروه خطی ویژه تصویری درجه دو در میدان پنج عنصر ، یعنی،
 است.
است.
معادل سازی تعاریف
- هم ارزی تعاریف داخل (4) با ایزومورفیسم بین گروه های خطی زمانی که همریختی توان درجه دوگانه است، داده می شود .
- PGL(2،4) با A5 یکری است: معادل (1) و (4)
- PSL(2,5) با A5 هم شکل است: معادل (1) و (5)
نکته مهم: این صفحه در نوع خود به عنوان یک گروه انتزاعی متمرکز است. برای کسب اطلاعات بیشتر در مورد این گروه به عنوان زیرگروه شاخص دو در داخل گروه متقارن: S5 ، به A5 در S5 مراجعه کنید .
توابع حسابی
آیا می خواهید مقادیر تابع حسابی را با سایر گروه های هم تراز مقایسه و مقایسه کنید ؟ گروه های توابع #حساب 60 را بررسی کنید
توابع حسابی پایه
توابع حسابی ماهیت شمارشی
| عملکرد | مقدار | توضیح |
|---|---|---|
| تعداد زیر گروه ها | 59 | ساختار زیر گروه گروه متناوب: A5 |
| تعداد کلاس های مزدوج | 5 | به عنوان  : (2 * (تعداد پارتیشن های خود مزدوج از 5)) + (تعداد جفت های مزدوج پارتیشن های غیر خود مزدوج 5) = : (2 * (تعداد پارتیشن های خود مزدوج از 5)) + (تعداد جفت های مزدوج پارتیشن های غیر خود مزدوج 5) =  (بیشتر اینجا ) (بیشتر اینجا )As  , , 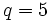 : :  ( در اینجا بیشتر ) ( در اینجا بیشتر )As  , ,  (زوج): (زوج):  (اطلاعات بیشتر در اینجا ) (اطلاعات بیشتر در اینجا )برای اطلاعات بیشتر به ساختار عناصر گروه متناوب مراجعه کنید:A5#تعداد کلاسهای مزدوج |
| تعداد کلاس های مزدوج زیر گروه ها | 9 | ساختار زیر گروه گروه متناوب: A5 |
خواص گروهی
خواص اساسی
| ویژگی | راضی | توضیح | اظهار نظر |
|---|---|---|---|
| گروه آبلیان | خیر |  ، ،  رفت و آمد نکنید رفت و آمد نکنید |  غیر آبلی است، غیر آبلی است،  . . |
| گروه nilpotent | خیر | بدون مرکز : مرکز بدیهی است |  غیر نیرومند است غیر نیرومند است  ، ، |
| گروه متاسیکلیک | خیر | ساده و غیر آبلی |  متاسیکلیک نیست متاسیکلیک نیست  ، ، |
| گروه فوق حل پذیر | خیر | ساده و غیر آبلی |  فوق حل پذیر نیست فوق حل پذیر نیست  ، ، |
| گروه قابل حل | خیر |  قابل حل نیست قابل حل نیست  ، ، | |
| گروه ساده | آره | کوچکترین گروه غیرآبلی ساده |
سایر خواص
| ویژگی | راضی | توضیح | اظهار نظر |
|---|---|---|---|
| گروه تی | آره | ساده و غیر آبلی | |
| گروه بازنمایی منطقی | خیر | ||
| گروه منطقی | خیر | ||
| گروه دوسوگرا | آره | همچنین طبقه بندی گروه های متناوب دوسوگرا را ببینید | |
| گروه کامل | خیر | صرف با جایگشت های فرد  ، اتومورفیسم های بیرونی را می دهد ، اتومورفیسم های بیرونی را می دهد | |
| گروه کامل | آره | از آن نتیجه می شود که یک گروه غیرآبلی ساده است . | |
| شور-گروه بدیهی | خیر | ضرب کننده شور گروه دوری ای است :Z2 . | |
| گروه N | آره | طبقه بندی گروه های متناوب که گروه های N هستند را ببینید |  یک گروه N است فقط برای یک گروه N است فقط برای  . . |
+ نوشته شده در سه شنبه بیست و هشتم دی ۱۴۰۰ ساعت 17:39 توسط علی رضا نقش نیلچی
|

 ،
، 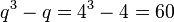
 ،
،  .
. :
: 
 فرد:
فرد:  ( بدون
( بدون  ): به
): به 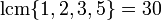

 (فرد):
(فرد):
 .
. در این وبلاگ به ریاضیات و کاربردهای آن و تحقیقات در آنها پرداخته می شود. مطالب در این وبلاگ ترجمه سطحی و اولیه است و کامل نیست.در صورتی سوال یا نظری در زمینه ریاضیات دارید مطرح نمایید .در صورت امکان به آن می پردازم. من دوست دارم برای یافتن پاسخ به سوالات و حل پروژه های علمی با دیگران همکاری نمایم.در صورتی که شما هم بامن هم عقیده هستید با من تماس بگیرید.
در این وبلاگ به ریاضیات و کاربردهای آن و تحقیقات در آنها پرداخته می شود. مطالب در این وبلاگ ترجمه سطحی و اولیه است و کامل نیست.در صورتی سوال یا نظری در زمینه ریاضیات دارید مطرح نمایید .در صورت امکان به آن می پردازم. من دوست دارم برای یافتن پاسخ به سوالات و حل پروژه های علمی با دیگران همکاری نمایم.در صورتی که شما هم بامن هم عقیده هستید با من تماس بگیرید.