توسط علی رضا نقش نیلچی
| جمعه هجدهم شهریور ۱۴۰۱ | 20:1
5 - محدودیت های ریاضیات قبل از برخی از پارادایم های زیستی
ما به تازگی با پژواک های متعدد – گاهی بسیار نزدیک – بین تمایلات جنسی و ریاضیات مواجه شده ایم. این نوع مقایسه در فرانسه بین سالهای 1970 تا 1990 در لحظه تأثیر روانکاو ژاک لاکان به طور گسترده مورد استفاده قرار گرفت. دومی انسان را به عنوان یک «موضوع» میدانست که آن را زیرلایه ناخودآگاه زبان میدانست که خود را در سرکوب، لغزش و حتی در آنچه او «اقدامها» میخواند نشان میدهد. سپس با استاد و چند تن از شاگردانش، موضوع لاکانی از طریق رویدادهای توپولوژیکی، مانند روبان های موبیوس (یکی دیگر از تأثیرات برش)، پارگی ها، بطری های کلاین و به ویژه طرح تصویری دسارگ، شکل گرفت و مورد بررسی قرار گرفت.که لبه های آن در بی نهایت به هم می پیوندند. در پلان تصویری، لاکان نموداری به نام Schéma R خود ایجاد کرد، که یک شکل چهارتایی را به صورت مورب برش میداد، بنابراین « Imaginaire » را در گوشه بالا سمت چپ، « Symbolique» را در گوشه پایین سمت راست قرار داد، در حالی که Réel فیگوری شده بود. توسط یک باند هچری که سمت چپ مورب را در Lacan، Les Ecrits دنبال میکند و مورب را در Lavendhomme Lieux du Sujet، 2002 فرا میگیرد.
از سوی دیگر، هر چیزی که در ریاضیات میتوانست صفر و بینهایت را بالا ببرد، یا پارادوکسهای منطقی بدیهیسازی (مثلاً پارادوکس تارسکی برای زبان، و گودل برای حساب) در «موضوع لاکانی» مورد احترام قرار گرفت. نقص هستیشناختی آن و کارکرد آن یک «مورد خالی» معرفتشناختی پوچ، بهطور آشناتر، میل برآورده نشده افلاطونی آن . در این شور و شعف نواندیشی که توسط سارتر در دهه 1940 دوباره فعال شد، اعداد سورئال کانوی که از بریدگی عمودی بین دو مجموعه خالی و شنا در یک بینهایت ابتدایی چندگانه ناشی میشوند، توسط آلن بدیو در کتاب Le Nombre et 1990 مورد بازدید قرار گرفتند. les nombres و توسط René Lavendhomme در سال 2002 Lieux du sujet .
فرصت خوبی برای تاکید بر این مقایسه است که انسان شناسیدر اینجا بین جنسیت و ریاضیات ماهیت بسیار متفاوتی با ماهیت لکانی وجود دارد. از نظر انسانزایی، ریاضیات - اجازه دهید یک بار دیگر به یاد بیاوریم - نظریه کلی نمایهسازیهای خالص و عمل مطلق شاخصهای خالص (تخلیهشده و غیراصولی) است. به این ترتیب، به طور ایده آل برای فیزیک، علم رویدادهای قابل نمایه سازی خالص در جهان، قابل استفاده است. و به این ترتیب نامفهوم است که ریاضیات با جنسیت خویشاوندی دارد، جایی که شاخصسازیها به شکل اندامهای همبسته، شیبهای همپیوسته، حرکتهای بینهایت (نیولتوان) نوازششان، در برانگیختگی پراکنده شیارها و گرماها فراوانند. مرز متجاوزانه ارگاسم بین کارکردهای قابل توصیف و حضور - غیاب - ظاهری غیرقابل توصیف. همه اینها بیشتر نوشته شده، همزمان، در ریاضیات، زمانی که در رابطه جنسی ریتمیک تر است، جایی که ریتم از دو جهت افراطی است. الف) اولاً، هر شریک دیگر نباید ریتم خود را بهعنوان یک مجموعه «بسته» توپولوژیکی تضمین کند، بلکه باید از دریافت آن از طرف دیگری به عنوان یک مجموعه «باز» توپولوژیکی با توجه به ویژگیهای آناتومیکی-فیزیولوژیکی و ریاضی دستهبندی رضایت داشته باشد. dual'، از دیاد، ممکن است یک دیاد سه گانه باشد. (ب) دوم، درونذهنی ریتمیک زوج (واقعی یا خیالی) نه تنها به کارکردهای بیاهمیت مربوط میشود، بلکه به همپوشانی تمایز اولیه انسانزای جهانی مربوط میشود: کارکرد/حضور-نبود-اختصاصی. مجموعه باز با توجه به خصوصیات تشریحی-فیزیولوژیکی و ریاضی دسته "دوگانه"، از دیاد، ممکن است یک دیاد سه گانه باشد. (ب) دوم، درونذهنی ریتمیک زوج (واقعی یا خیالی) نه تنها به کارکردهای بیاهمیت مربوط میشود، بلکه به همپوشانی تمایز اولیه انسانزای جهانی مربوط میشود: کارکرد/حضور-نبود-اختصاصی. مجموعه باز با توجه به خصوصیات تشریحی-فیزیولوژیکی و ریاضی دسته "دوگانه"، از دیاد، ممکن است یک دیاد سه گانه باشد. (ب) دوم، درونذهنی ریتمیک زوج (واقعی یا خیالی) نه تنها به کارکردهای بیاهمیت مربوط میشود، بلکه به همپوشانی تمایز اولیه انسانزای جهانی مربوط میشود: کارکرد/حضور-نبود-اختصاصی.
با این حال، برای درک کافی تلاقی بین ریاضیات و تمایلات جنسی که تا کنون بر آن اصرار داشتهایم، هنوز لازم است که سه حد اولی را در رویکردهای دوم تشخیص دهیم. (1) ناتوانی ریاضیات توپولوژیکی، سمپلتیک و حتی مقوله ای برای درک تشکیلات (Gestaltung) از طریق توالی (دوباره) بیوشیمی اخیر و تشکیلات (Gestaltung) از طریق (دوباره) توالی توسط اتصالات عصبی و شکاف های فیزیولوژی عصبی امروزی. . (2) به ویژه، ناتوانی ریاضی در توصیف "شانس تکامل" همانطور که توسط GT Eble درک شده است (رجوع کنید به زیر). (3) در نهایت، سکندری ریاضی قبل ازرویدادی به این صورت که در نهایت کیهان به عنوان رویداد نهایی و "اصلی" رویدادها خواهد بود. بنابراین صرفاً واقعی است، نه فنی.
با این حال، این سه جنبه در جنسیت هومینوئید تعیین کننده هستند، که عبارتند از: (الف) بهره برداری و تحقق بخشیدن به ظاهری ترین (دوباره) DNA که اکنون در پروتئومیکس (1997) به صورت جفت مورد مطالعه قرار گرفته است، و در غیر این صورت قوی ترین پیامدهای عصبی بین عملکردها و حضور - غیبت - ظاهری در ارگاسم دوجنسی. (ب) پیشرفته ترین تجربه شانس تکاملی در مقابل شانس احتمالی و آماری . (ایبل). (ج) چرا که نه، رویداد کلیدی یک رویداد-جهان.
5A. ریاضی در مقابل (دوباره) توالی به عنوان یک رویداد غیر قابل پیش بینی
یک روز، نویسنده متن حاضر در حال مرور یک Atlas de Cytologie دهه 1970 بود.زمانی که رنه لاوندوم ظاهر شد، به دلیل تصاویر سیاه و سفیدش، بسیار شیوا بود. این سوال مطرح شد: ریاضیدان در این مورد چه می تواند بگوید؟ پاسخ حتی صریح بود: هیچی. یک اطلس سیتولوژی نماها را در داخل سلول ها سازماندهی می کند، از این رو این اندامک ها که از سال 1939 آنها را "ساختارهای فوق العاده" می نامیم زیرا آنها را نمی توان با میکروسکوپ معمولی دید. مطمئناً، مطابق با پروتیمیکهای اخیر، چنین تصاویری اجازه نمیدهد پروتئینهایی که اندامکها را تشکیل میدهند، و حتی کمتر آمینواسیدهایی که پروتئینها را از طریق توالییابی دینامیکی و توالییابی مجددشان (با اطاعت از رابطهای بیوشیمیایی قوی و ضعیف) تشکیل میدهند. با این حال، اشکال (گشتالت) که ساده لوحانه میتوانیم ببینیم، آنقدر نامحتمل و مشخص هستند که وقتی از نحوه شکلگیری آنها اطلاع داریم (Gestaltung)، ما به وضوح می توانیم آنها را تصور کنیم، توهم ایجاد کنیم. در نگاه اول، بازدیدکننده من احساس کرده بود که دیگر در زمین شناخته شده نیست. این فراتر از ریاضیات بود، حداقل او.
روزی دیگر، رنه لاوندوم در حالی که نویسنده در حال بررسی یک شماره از مجله "La Recherche" بود که در آن تصویری از مغز انیشتین در کاسه آن وجود داشت، با تمام عجیب و غریبش در مسیرهای زمانی سمت چپ و رله هایی که مربوط به فضایی هستند، ظاهر شد. حتی بازنمایی های مکانی-زمانی، اجازه دهید بگوییم چهار بعدی. رنه لاوندوم حتی به تصویر نگاه نکرد. وقتی برای شام نشستیم، او اعتراف کرد که در کودکی از کمد افتاده است. این موضوع آنقدر روی مغز او تأثیر گذاشت که پزشک خانواده آرزو کرد والدینش زنده نمی ماند. از نظر بیوگرافی، این می تواند دافعه او را قبل از تماشای نورون های مغزی توضیح دهد. با این حال، در همان شماره 'La Recherche'، یک ریاضیدان دیگر به طعنه در مورد همان موضوع صحبت کرد.
با این حال، از سال 1950، ریاضیدانان از تلاش خود برای مدل سازی این رویداد به عنوان یک رویداد دریغ نکرده اند. در پاسخ به این سوال که "این تحول درست است یا نادرست؟" تئوری مقولهها، در فصل خود درباره بستهها (théorie des faisceaux)، دعوت میکند اکنون اضافه کنیم: «کجا؟» و وقتی که.' با نشان دادن این نکته در بخش دوم Dominique Bourn Schize et Guise ، رنه لاوندوم هیستری Studien über فروید را در پرتو این نوع منطق محلی بازخوانی کرد.. در یک راه، او نشان داد که چهار بیمار آنجا که توسط فروید توصیف میشود، همه در چندین «مکان» (محل) گفتمانهایی هستند که ناسازگار هستند، و در نتیجه با توجه به ظرفیتشان در شناسایی این مکانها، سریع، تدریجی یا هرگز درمان نشدهاند. ، سپس در نهایت مهاجرت از آنها. مشکلات مکان منطقی ناطق در هر نوع گفتمانی و منطق جهان های گفتمانی اساسی است. رنه که قبلاً در آگوست 2002 بسیار بیمار بود، چندین پیش نویس از متنی با عنوان: A partir des quatre (univers de) discours را به نویسنده منتقل کرد.از لاکان، که در آن با ظرافت نسبتاً معجزه آسایی چهار مکان گفتاری از هر گفتمان فلسفی (حتی علمی) توصیف شده است: (1) le discours du Maitre، (2) le discours de l'Universitaire، (3) le discours de l'Hystérique. ، (4) le discours de l'Analyste، که همگی به روشنگری نظریه مقوله ها به عنوان یک نظریه توپوس ، به معنای جهان گفتمان ها پاسخ می دهند.
با این وجود، صفحه پایانی Lieux du sujet به محض اینکه در سال 2001، مانعی برای هر مدلسازی ریاضی این رویداد بهعنوان چنین رویدادی بود، بود. در واقع، ما در آنجا می خوانیم: "پیشنهادی که می تواند کاوش باشد و من آن را به عنوان اکتسابی در نظر نمی گیرم، دیدن " اشیاء" مقوله ای صرفاً به عنوان اعداد صحیح، و " فلش های " طبقه بندی است.به عنوان متقاطع" (به معنای نظریه توپولوژیکی گره ها، که نویسنده قبلاً توجه ریاضیدان را به آن جلب کرده بود). برای تعیین اشیاء رویدادهای تکاملی، مانند اسیدهای آمینه که پروتئینها را تشکیل میدهند، یا همچنان در مورد یادگیری از طریق (دوباره) اتصالات و (دوبار) برشهای عصبی. در آنجا این رویداد تنها شامل جابجایی عناصر خنثی در دنباله نیست، بلکه شامل عناصر پر از پتانسیل های شیمیایی چند عاملیمانند پیوندهای کووالانسی، یونی، هیدروژنی، آبگریز، بدون اشاره به فعل و انفعالات واندروال. در واقعیت عینی، آیا «اشیاء» واقعی به اندازه تیرها «تیرانداز» نیستند؟ در واقع، در این پیشنهاد نهایی، به نظر می رسد که ریاضیدان خسته هیچ توهمی در رویکرد خود نداشته است. در متن قاطع تر دیگری در مورد توپولوژی، او قبلاً به پایان رسیده بود: "ما نقشه ای از جهان نداریم".
5B. ریاضیات در مقابل شانس تکاملی
در سال 1999، جی تی ایبل در مقاله مهم خود در مورد ماهیت دوگانه شانس در زیست شناسی تکاملی و دیرین زیست شناسی ("Paleobiology 25") شایستگی زیادی داشت که از زمان انتخاب طبیعی داروین ، و به ویژه از زمان تعادل نقطه گذاری شده گولد و الدرج ، این مفهوم را مشاهده کرد. "شانس" دو واقعیت بسیار متفاوت را پوشش می دهد: یک شانس احتمالی (آماری) و یک شانس تکاملی محسوس. او دومی را به طور گسترده در موارد متعدد توسعه میدهد، اما ما در اینجا به دو مورد مورد علاقه خود بسنده میکنیم: (الف) توالیبندی (دوباره) آمینو آمیدهای تشکیلدهنده پروتئینها و (ب) اکسپشنهای بیشمار بدن زاویهای همو در رقص، موسیقی، تصاویر، مواد مخدر، آموزش.
سپس، ما باید اندازه گیری کنیم که ریاضیدان تا چه حد از آخرین حس «شانس» ناراحت است. برای اطمینان، اجازه دهید به F. William Lawvere که قبلاً توسط ما به عنوان یک ریاضیدان ذهن انسان شناسی با آن برخورد کرده ایم، رجوع کنیم. یک مفهوم طبقه بندی شده باید او را در مورد ویژگی رویدادها (ونیر، سابق) مورد توجه قرار می داد. در واقع، اگر نظریه مقولات یک «ساختارگرایی دگرگونیها» ( Lavendhomme ) است، احتمالاً نقطه اصلی آن در کنار هم بودن است ، جایی که دیگر بحث حرکت از حالتی به حالت دیگر در یک مقوله نیست، بلکه در نظر گرفتن برخی موارد است. «کارگزاران» دگرگونیها را از یک مقوله به دسته دیگر نمایه میکنند، سپس به «تحولات طبیعی» (آیلنبرگ و مک کین) از هویت به معادل اشاره میکنند.(Lawvere)، یا پیش پا افتاده تر به نوعی انعکاس آینه ای (Lavenhomme). این دومی موقعیتی است که همان، بدون توقف همان، دیگر واقعاً همان نیست، بلکه نوآوری می کند - چه از دسته C به دسته D حرکت کنیم، چه برعکس (به این معنی که ما از "ضمیمه در مورد" صحبت خواهیم کرد. راست" و "ضمیمه در سمت چپ"). در این موقعیت، همان بر اساس برخی از "منفیات هگلی" (Lavendhomme) برخی از جنبه های دیگری را در بر می گیرد. به شرطی که به "وضعیت ریاضی" احترام بگذارد، به این معنی که، برای هر A از دسته C و برای هر B از Dدسته، برخی از نمودارها رفت و آمد دارند. آیا مظهر آن دگرگونیهای طبیعی (یعنی بدون شرایط اولیه بیش از حد) که موضوع اولیه آیلنبرگ و مک کین بود، زمانی که شروع به کار روی چیزی کردند که در ابتدا «چیز» نامیده میشدند، وجود نداشت، و این - یک روز خوب - آنها جسارت معرفتشناختی و هستیشناختی را داشتند که در ادای احترام به ارسطو «مقولههایی» بخوانند؟
شاید. اما لاور به شکلی سازشآمیز، با توسعه نظریهی الحاق خود، شروع به استناد به مفهوم کلاسیک دیالکتیک کرد. اکنون، شانس تکاملی ابله - که به طور قاطعانه "رویداد" را بر اساس جهان انسان زایی 3 افتتاح می کند - با هر نوع دیالکتیکی به طور اساسی از بین می رود. در واقع دیالکتیک هگلی – و بیش از همهانگلسین، که لاور فراموش نمیکند - تلاش نهایی WORLD 2 برای بازیابی احتمالی احتمالی تاریخ به شکلی از ضرورت در مقیاس بزرگ و متوسط بوده است. به اندازه ای که «قدرت حق را بنیان گذارد» (هگل). برعکس، شانس تکاملی کنونی هرگونه توجیه و ضرورت را در هر نظمی، هر چند بد یا خوب فرض میشود، از بین میبرد. رنه لاواندهوم به طور غریزی از اطمینان لاور در مورد الحاقی مبهوت شد . به طور عجیبی (به طور علامتی؟)، در شروع ریاضیات مفهومی خود ، لاور اعلام کرد که از بخش کمکی صرف نظر خواهد کرد.
بیایید ناراحتی ریاضیدان قبل از «شانس تکاملی» را بدون یادآوری رنه تام، که قبلاً برای روشنکنندهترین توپولوژی دیفرانسیل هفت فاجعه ابتدایی، یادآور شدیم، پشت سر نگذاریم. در یک جلسه رسمی در آکادمی علوم در پاریس، او از مخاطبان خود دعوت کرد که از این پس هر گونه تحقیق در مورد بیوشیمی را که او توضیح داد، نتایج آن از نظر ریاضی قابل بازنمایی، قابل درک و توصیف نیست، کنار بگذارند!
5C. ریاضیات در برابر کل کیهان به عنوان رویدادی تکاملی و «آگهی ماجراجو». شگفتی تحسین برانگیز
در عشق استیون جی گولد به داروین، ما ظرفیت داروین را مییابیم که زندگی را به عنوان یک پدیده جهانی غولپیکر با آخرین اصل ساده و منحصربهفرد علّی درک کند : تغییرات بیپایان همراه با انتخاب .با تغییر محیط «تعادل نقطهگذاری شده» گولدیا الدرژین مشتاق همان درک وحدتگرایانه است، اگرچه دو ویژگی گونهها را در نظر میگیرد که هنوز در دوره داروین نامشخص بودند: (الف) پایداری آنها در دورههای طولانی، گاهی اوقات سه یا چهار میلیون سال. (ب) این واقعیت که گونهها فقط میتوانند در حاشیه گروههای یک گونه تکامل یابند، در نتیجه گونهای دیگر به وجود میآید که در تماس با گونه اصلی یا با آن زندگی میکند یا آن را حذف میکند یا با نفوذ کمکم آن را تغییر میدهد. این در اصطلاح «تعادل نقطهگذاری شده» پیشنهاد میشود (اولین ایده توسط الدگریج و اصطلاح توسط گولد بود).
سپس میبینیم که برای Anthropogénie - که پیشنهاد میکند پیدایش همو را در سیارهاش درک کند و همچنین سؤالاتی در مورد عادات متعالی کیهانی که هومو لحظهای از آن است، میپرسد، شانس تکاملی داروینی یا گولدی از بین میرود. به طور ریشه ای با همه کیهان شناسی ها و کیهان شناسی های سنتی. تا سال گذشته، هومو فقط از طریق مدلسازی یا پلاستیسیته (حکاکی) هر شکلگیری (Gestaltung) را تصور میکرد. بین سالهای 1900 و 2000، تشکیلهای بوسیله توالییابی (دوباره) دینامیکی (چه آمینو اسیدها یا اتصالات عصبی برشها) به طور اساسی با مدلسازی و شکلپذیری شکسته شدند. آنها جدیدترین و نگران کننده ترین کشف معرفت شناختی و هستی شناختی هومو هستند . از نظر حدس و گمان، بلکه از نظر عملی. اگر همه چیز در جهان نتیجه یک عمل الگوسازی باشد، وجود عبارت است از اطاعت (به عنوان یک فرشته) یا نافرمانی (به عنوان یک شیطان، شیطان) از اصل الگوسازی، مهم نیست که این اصل متحرک (یاوه، الله، دیوس) باشد. یا بی جان (Great Axiom, Reason, Man-yu). در نقطه مقابل، یک جهان از شانس تکاملی را نه میتوان اطاعت کرد و نه میتوان نافرمانی کرد، زیرا در فیزیک، زیستشناسی، تکنیک و نشانهشناسی آن به طور مادرزادی و در نهایت غیرقابل پیشبینی است. این فقط می تواند مبهوت و از این رو به دلیل خودانگیختگی خود، که در این موقعیت حس دقیق منبع (اسپون) خود را می گیرد، نفرت انگیز یا تحسین برانگیز باشد. و تمایلات جنسی، که رادیکالترین تجربهی تسلسلهای بیولوژیکی و بین مغزی با شگفتیشان است.
6. تمرینات قبل از ارگاسم، پارا ارگاسم و پس از ارگاسم
جنسیت در وجود انسان - و احتمالاً در جهان هستی - بسیار اساسی است که نشانهشناس و تکنسین هومو ایجاد کرده است - در کنار شیارها و گرماهایی که از زمان شامپانزه بونوبو ثابت شده است - معادلها، اعلامیهها، سوغاتیها و کنایههای بیشماری از آن. در روزمره ترین زندگی اش به ویژه همانطور که برای ریاضیات دیدیم، کیهان شناسی های علمی نمی توانند او را به طور کامل حفظ کنند، بنابراین از کیهان شناسی (هنری، ریتمیک) استفاده می کنند.
(Anthropogénies locales، Cosmogonies contemporaines، 1، Cosmogonie et cosmologie)
6A. هنرهای اجدادی
قبل از اینکه به سراغ کیهانشناسیهای جنسی (دوباره) توالییابی معاصر برویم، اجازه دهید با چند یادآوری اجدادی شروع کنیم. برای پریمات زاویه دار، خانه دوگون عملکردهای خانه داری خود را با زوایای مشخص تقسیم می کند "مانند اندام های مردی که به پهلو خوابیده و تولید مثل می کند" (گریوله). در غارهای پارینه سنگی و معابد بیشماری هیپوژال که در آن نافهای سهموی، بیضوی و هذلولی حکومت میکنند، تصاویر غالب فرجهای صریح در شووه، و ضمنی در تلاقی راهروهای لاسکو هستند. در همه جا، به ویژه در بورنئو شرقی (پیش از دوران نوسنگی)، سازماندهی دستهای آغشته به این امکان را میدهد که تطبیق و نقشهبرداری (فر. کاربرد) در خدمت اصول ریاضیات و تمایلات جنسی باشد. قاببندی ربعبندیشده دوران نوسنگی، کل اروپای قدیم ماریجا گیمبوتاس را با شکلهای پیوندی که کاملاً هندسی هستند، پوشش میدهد. در مصر، تحت هندسهها و تقویمهای اهرام، قدرت امپراتوریهای اولیه حق مشترک با محارم است. پاپیروس هریس 500 اظهارات ما را در مورد ترشح هورمونی نوازش هولوزومی و جذابیت شکاف عمودی وسط اصلی اعلام می کند: "عشق به تو در تمام بدنم نفوذ می کند / مثل شراب که در آب می آمیزد" ، "در قلعه من" عزیزم / در وسط ساختمان ایستاده / دو طرف باز است». اگر فرج غول پیکر تاج محل را به طور کلی عالی ترین بنای همو می دانند، به این دلیل است که تمام معماران آسیایی که آن را در اطراف بدن یک شاهزاده خانم عزیز مرده در هنگام زایمان ساخته اند آن را از یک برش عمودی مرکزی تا دو بال پخ شده (chanfrainées) در لب های فرج به یک راه حل منحصر به فرد در هنر مغول سازماندهی کرده اند. در مقایسه با برش بین دو مجموعه خالی که دارای اعداد سورئال کانوی هستند. ماتریس های الله، ماتریکس، ماتریکس، قرآن را تکرار می کند).
در یک کلام، حتی در کیهانشناسیهای ریتمیک، ریاضیات کیهانشناختی بیتوجه نمیماند. انتخاب پرسپکتیو، یکی از مؤلفه های ریاضی نقاشی، عاملی رایج برای تعیین شهوانی است. به عنوان مثال، دو دیدگاه متفاوت ژاپن و چین، بیشتر توپولوژیک، و برعکس دیدگاه غربی همگرا، هندسی تر، سه معرفت شناسی و هستی شناسی همبستگی جنسی را از نظر مکانی و زمانی تعیین کردند. L'Origne du Monde کوربه را نمی توان بدون نقطه ملاقات خطوط محو شده در پشت سطح، متقارن از نقطه تلاقی خطوط فضول قبل از سطح تصور کرد.
6B. کیهانشناسیهای (دوباره) توالییابی معاصر
در کنار تمام این شکلگیریهای اجدادی از طریق پلاستیسیته یا مدلسازی، کشف سازندهای بیوشیمیایی از طریق (دوباره) توالییابی (آمینو و عصبی) حداقل از سال 1970 باید جهانبینیهای انقلابی را برانگیخت. آنقدر انقلابی است که Anthropogénie برای یک بخش کامل از آنها صحبت می کند: Cosmogonies contemporaines . (Anthropogénies locales، Cosmogonies contemporaines)
بدیهی است که اولین راهاندازی در موسیقی رخ داده است ، هنری (دوباره) ترتیبدهنده فی نفسه، و هنری که ظاهراً ریاضی است . موسیقی را نزد استیو رایش آموخت، اما موسیقی محبوب در کابارههای شیکاگو را بهزودی از طریق رادیو تحت عنوان «موسیقی تکراری» جهانی کرد. به طور مشخص، هنگامی که بیوشیمیدانهای Dresler و Potter در سال 1991 در کشف آنزیمها (کتابخانه Sc. Am.) تلاش کردند معرفتشناسیها و هستیشناسیهای جدیدی را که توسط توالییابیهای (دوباره) آمیخته شدهاند، موضوعبندی کنند، فریاد زدند: « چیزی موسیقیایی وجود دارد.در این راستا، ژست رقص منابع مشابهی داشت و رقص رزاها که توسط تیری دی می فیلمبرداری شده بود، به زودی از روح موسیقی جدید پیروی می کرد.
از سوی دیگر، زمانی که نقاشی میشلین لو ، از سال 1980 تا 2000، «شکلگیری زنده» (گشتالتون) را بهعنوان توالیهای پویا (دوباره) - عصبی در ابتدا («من منظره مغزی را نقاشی میکنم»)، سپس آمینو (آمینو) را انتخاب کرد. "این مستلزم منطق جدیدی است") - به سختی به این موضوع پرداخته شده بود مگر در الفبای ها و اعداد جاسپر جان (1955) و آلباتروس استلا (1970) و در نهایت از نظر موضوعی در گزاره های 1970 دیوید لیپسیک .
معماریبه دلیل انبوه مواد آن (که آزمایشهای خطرناک را از بین میبرد)، قبل از ارائه روح بدیع، یعنی زیستگاه متوالی در آثار فرانک گهری، ساها حدید و تعداد انگشت شماری دیگر، باید منتظر دهه 2000 بود. یک کار بسیار دشوار هنگام یادآوری این موضوع که پستاندار انساننما که ده ماه قمری را در رحم سپری کرده است، همیشه از زیستگاه خود انتظار دارد که چیزی ایمن، تثبیتکننده، شبه باستانی داشته باشد، نه اینکه از احساس «دژا لا» و «دژاوو» جلوگیری کند. همان چیزی که او از معماریهای «مدرن» و پسمدرنِ شکلپذیرِ مجدد دهههای شصت و هفتاد ناامید شده بود، و «معماری آنی» را دنبال میکرد که مطابق میل آنی قابل اصلاح بود (در دهه 1970، Grataloup سوئیسی خانه هایی را در مواد قابل تغییر (مانند پلاستیک های Dupont de Nemours) پیشنهاد کرده بود که با استفاده از یک خانه ساده، ساکنان می توانند در آخرین میل خود دگرگون شوند. برای یک پستاندار، این آخرین میل او نبود؟ خوشبختانه، همان طور که خانه های گهری نشان داده اند، یک میل متوالی، آنی نیست.
6C. فضایل عکاسی
با این حال، از سال 1980، عکاسی ، هنری که به اندازه کافی مقرون به صرفه بود تا کاوشهای مخاطرهآمیز را مجاز کند، به پیر رادیسک، یک عکاس برجسته کیهانشناس، اجازه داد تا از شانس تکاملی Ebles et Gould بر روی عکاسیترین اشیاء، پوست ، بازدید کند . در این مناسبت زمینشناسی پوست، پوست صورتهای جفت ( زوجها )، شکم زبر آفریقایی ( لاکی )، شکم صاف آسیایی ( ماریلو )، درختان ( والدزنن )، دکورهای اپرا (la Monnaie) ظاهر شد. ), از اجرام آسمانی ( Heavenly Bodies) جایی که هنرمند لنتیگو را بر روی زنان برهنه در «همراهی» طبقهای با صورتهای فلکی ستارهای آسمان ترسیم میکند، مطابقت میدهد. شانس تکاملی که نزدیکترین و دورترین توپولوژی عمومی و دیفرانسیل را در آنجا مخلوط می کند. (Anthropogénies locales. Cosmogonies contemporaines 3. Photo analogique: Corps célestes (Pierre Radisic)
اخیراً، پیر رادیسیچ تصویری تولید کرد که ممکن است آن را خواجوراهو معاصر بنامیم و به اندازه کافی مطالعه حاضر ما را نشان می دهد. این موضوع از زمان فیلمهای پورناسکیپ (در واقع «Eroscape») که توسط جالوت در سال 2006 ویرایش شد برای او آشنا بود ، اما در جایی که عکاسی آنالوگ بود و از منابع سنتی نصب استفاده میکرد. این بار، رویکرد دیجیتال بود، و بنابراین میتوان از ویژگیهای نوشتار ریاضی استفاده کرد ، که میتواند تا حد زیادی چند جهته باشد. و از سوی دیگر کیفیت خاصی از رنگ سفید را بدست آورید، این مقدار کمی خالی، که توسط مک کی هنگام اختراع نمو کوچولو در سال 1905 پس از Dreams of Rarebit Fiend به دست آمد.. در عكاسي ديجيتال، رنگ سفيد حتي با غيرقابل تحمل بودن كاغذ حساس به نور تقويت مي شود. (Anthropogénies locales، Cosmogonies contemporaines 7، Bande dessinée : Le blanc d'annulation (McCay)
پی یر رادیسک با استفاده از دیجیتالی بودن اکنون موفق شد دو بدنی را که قبلاً در فیلم های پورن مناظر خود به شکل ارگاستیک درآورده بود، به عمومیت یک رویداد جهان ارتقا دهد.، بنابراین از امر حتی به امر متعالی می گذرد. رادیسیچ قبلاً توسط شخصیت مرسوم نماهایش تشویق شده بود که بیشتر به میکل آنژ (آخرین داوری) نزدیک است تا لئوناردو (نبرد آنگیاری). به شرطی که تنها چیزی که در بدن ها باقی می ماند دقیقاً قسمت های همبند آنها بود. از این رو با سرکوب سرها، که همیشه «بیانگر» باقی میمانند (نه ماورایی). برای این محدوده، عکاس اجساد را با خطوط آنامورفیک جنین شناسی هندسی آنها در دارسی تامپسون بیان کرد. در نهایت، او این اجسام را در ستونها یا خطوط بدون قاببندی یا بستن آنها قرار داد، به طوری که همه چیز هنوز به «مجموعههای باز» فضای توپولوژیکی صرف تعلق دارد. تصور کردن خود جهان تکاملی به عنوان رویداد و ماجراجویی، در اولین و آخرین دستاورد بیوشیمیایی و بین مغزی خود، در جفت جنسی و ارگاسمیک. هدف نهایی، ممکن است، هر شگفتی متافیزیکی (سابق) و تحسین (ad-) باشد.

پیر رادیسیچ، خواجوراهو

خواجوراهو. نمای معبد کاندیریا
با این حال، هر تمرین هنری محدودیت هایی دارد. عکاسی دیجیتال مستلزم تسلط عکاس است که او را از ارسال مقدماتی و تصادفی به طبیعت عکاسی آنالوگ منع میکند، تسلیم آن چنان پر رونق است که توانسته است نور موسمی را روی کوپلینگهای خاجوراهو سکولار هندی یا نور انتهایی استیگلیتز ثبت کند. بر روی بدن همسرش اوکیف (در) جاودانه شد. تسلیم شدنی که از اعتصاب به اعتصاب، نقاش میشلین لو در ژست رنگ - صفت - تطابق - ژست "شکل بندی های ویوانتس" خود مجسم کرده است. و آن را به وضوح در صداهای متوالی استیو رایش می شنویم. در حالت ایدهآل، تجربه کامل جهان را میتوان با نگاهی به Kahajurâho آن برنارد و پیر رادیسیچ، اما با پسزمینه میشلین لو به دست آورد.، همانطور که چشمان ما درنگ می کنند و به سمت چاپ یکی از برهنه های اوکیف استیگلیتز می روند . تلهیم استیو رایش زمینه موسیقی را فراهم می کند.
باغ های اطراف خانه توسط فرانک گری طراحی می شود.
6D. بهترین استراحتگاه ادبیات
با این حال، زبان، از آنجا که می تواند از همه چیز و از خود صحبت کند، و حتی محدودیت های آن را بیان کند، احتمالاً در اینجا مثل همیشه، در مورد موضوع فعلی ریاضیات و جنسیت، حرف آخر را می زند. و ما یک بار دیگر به افتتاح رنه لاوندوم می رویم. این بار در شعرهایش آلف . در سال 1980، در مقاله ای از "Litura"، ریاضیدان مکمل بودن نوشتن و خواندن ریاضی را که چند جهتی ، چپ/راست، بالا/پایین است، و نوشتن و خواندن زبانی که به اندازه زبان خطی هستند ، بیان کرده بود.
اما برای گستره یک نوشتار ریاضی-ادبی، صرف نوشتن کافی نبود. در سال 1877، مالارمه 200 صفحه Les mots anglais را نوشت. به گفته او، با آن، او «علمی بدیع» را ایجاد کرد که از زمان سوسور هرگز مورد توجه زبانشناسی ساختارگرا قرار نگرفت. در سال 1997، آلف ، به طور خلاصه تر، همان رویکرد واجی مالارمی را برای زبان فرانسه، یک زبان آوازی، ساخت. لاوندوم، ریاضیدانی که نسبت به موسیقی ناشنوا بود، گوش بدیعی برای واج شناسی داشت، از این رو، او غزل رمبو را - یک اختراع داوطلبانه ذهنی و نوجوانانه - به l' Aleph revisité عینی یا حداقل عینی تبدیل کرد.(Anthropogénies locales، Linguistique 1، Phonosémie et parti existentiel des langues)

رنه لاوندوم آلف
اکنون بیایید واجی زبان و نوشتار ریاضی-ادبی چند جهته را با هم ترکیب کنیم تا زوجی عاشق عاری از گرما را با کلماتی که به شکل مگن دیوید کنار هم قرار گرفته اند، که دو مثلث آن بدون واسطه در کنار هم قرار گرفته اند و فقط در نوک آن لمس می شوند، به تصویر بکشیم. : مبهم / دراگ / پاس /لاس /// پیست / تریست /فیل / ویل:

رنه لاوندوم آلف
روزی که شاعر آلفس را در دست داشت، نویسنده از او پرسید که آیا شعری هست که بهویژه نیت او را برآورده کند؟ او بدون معطلی به صفحه 24-25 در بخش با عنوان ساختار اشاره کرد. این صفحه دوتایی در واقع دو صفحه بود که فقط یک صفحه را تشکیل میدادند، بنابراین همزمانی و چند جهتی بودن شعری و ریاضی را چندبرابر میکردند، مانند Un coup de Dés jamais n'abolira le Hasard توسط Mallarmé . این بار زوج عاشق گرمای او را پس گرفته بودند.
























![{\displaystyle \chi _{[0,1]}(|\mathbf {x} |)\left(1-|\mathbf {x} |^{2}\راست)^{\delta }}](https://wikimedia.org/api/rest_v1/media/math/render/svg/c1f3e6c1f52f0ee9366c40ee6f67c65f11dbd03a)
















 Re( α ) > 0
Re( α ) > 0



































































































































































































 ممکن است هم برای یک تابع و هم برای تبدیل فوریه استفاده شود که این دو تنها با
ممکن است هم برای یک تابع و هم برای تبدیل فوریه استفاده شود که این دو تنها با  به دلیل استدلال تکانه به تبدیل فوریه اشاره دارد، در حالی که
به دلیل استدلال تکانه به تبدیل فوریه اشاره دارد، در حالی که به دلیل آرگومان موقعیتی به تابع اصلی اشاره می کند. اگرچه تایلدها ممکن است مانند در استفاده شوند
به دلیل آرگومان موقعیتی به تابع اصلی اشاره می کند. اگرچه تایلدها ممکن است مانند در استفاده شوند برای نشان دادن تبدیل فوریه، تیلدها همچنین ممکن است برای نشان دادن تغییر یک کمیت با شکل
برای نشان دادن تبدیل فوریه، تیلدها همچنین ممکن است برای نشان دادن تغییر یک کمیت با شکل  ، پس باید مراقب بود.
، پس باید مراقب بود.







































={1 \over {\sqrt {2\,\pi }}}\int \limits _{-\ infty }\limits ^{+\infty }f(x)\,{\exp(-i\,x_{\{\kappa \}}\,\omega _{\{\kappa \}}) \over { \sqrt {1+\kappa ^{2}\,x^{2}}}}\,dx}](https://wikimedia.org/api/rest_v1/media/math/render/svg/7386e6169be16e8cfb043eae8edd238c1275d0a7)
 یک عدد κ است و
یک عدد κ است و شاخص آنتروپیک است که با
شاخص آنتروپیک است که با  مورد محدود کننده این تبدیل یک رفتار لگ دورهای مجانبی را تحمیل میکند (یا فاز ک-تغییر شده توسط دفرمینه
مورد محدود کننده این تبدیل یک رفتار لگ دورهای مجانبی را تحمیل میکند (یا فاز ک-تغییر شده توسط دفرمینه ) و یک عامل میرایی به دنبال یک رفتار موجک مانند (
) و یک عامل میرایی به دنبال یک رفتار موجک مانند ( ).
).
 جایی که
جایی که برای
برای .
. برای هر
برای هر ، است
، است خود در مورد نمایش گروه محدود، جدول کاراکترهای گروه
خود در مورد نمایش گروه محدود، جدول کاراکترهای گروه  و حاصلضرب داخلی بین دو تابع کلاس (همه توابع تابع کلاس هستند زیرا
و حاصلضرب داخلی بین دو تابع کلاس (همه توابع تابع کلاس هستند زیرا  به عنوان ... تعریف شده است
به عنوان ... تعریف شده است با فاکتور نرمال کننده
با فاکتور نرمال کننده . تسلسل و توالی
. تسلسل و توالی مبنای متعارف فضای توابع کلاس است
مبنای متعارف فضای توابع کلاس است .
. را می توان به عنوان دهانه بیان کرد
را می توان به عنوان دهانه بیان کرد (
( irreps های
irreps های  . به طور مشابه برای
. به طور مشابه برای و
و ،
، . پونتریاژین دوگانه
. پونتریاژین دوگانه است
است و برای
و برای تبدیل فوریه آن برای است
تبدیل فوریه آن برای است .
.



 ، در این صورت حاصل ضرب نقطه ای تبدیل به انقباض
، در این صورت حاصل ضرب نقطه ای تبدیل به انقباض 

 .
.





















![{\displaystyle \psi _{n}(x)={\frac {\sqrt[{4}]{2}}{\sqrt {n!}}}e^{-\pi x^{2}}\ mathrm {He} _{n}\left(2x{\sqrt {\pi }}\right)}](https://wikimedia.org/api/rest_v1/media/math/render/svg/a9121f54a3fdbb0eedecf2aef5a379bdfae414b7)

 .
.









 بنابراین، گسترش تبدیل فوریه به حوزه مختلط به این معنی است که تبدیل لاپلاس را به عنوان یک مورد خاص در مورد توابع علی - اما با تغییر متغیر
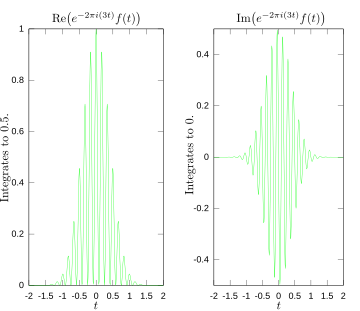
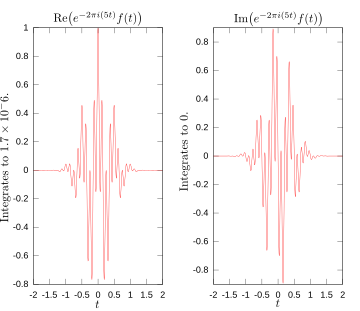
بنابراین، گسترش تبدیل فوریه به حوزه مختلط به این معنی است که تبدیل لاپلاس را به عنوان یک مورد خاص در مورد توابع علی - اما با تغییر متغیر  ما باید e - 2π i (3 t ) f ( t ) را انتگرالگیری کنیم . تصویر دوم نمودار قسمت های حقیقی و موهومی این تابع را نشان می دهد. بخش حقیقی انتگرال تقریبا همیشه مثبت است، زیرا وقتی f ( t ) منفی است، قسمت حقیقی e - 2π i (3 t ) نیز منفی است. از آنجایی که آنها با سرعت یکسانی نوسان می کنند، وقتی f ( t ) مثبت است، بخش حقیقی e - 2π i (3 t ) نیز مثبت است.. نتیجه این است که وقتی بخش حقیقی انتگرال را انتگرالگیری میکنید، عدد نسبتاً زیادی به دست میآید (در این مورد1/2). از سوی دیگر، هنگامی که شما سعی می کنید فرکانس را اندازه گیری کنید که وجود ندارد، مانند موردی که ما به آن نگاه می کنیم
ما باید e - 2π i (3 t ) f ( t ) را انتگرالگیری کنیم . تصویر دوم نمودار قسمت های حقیقی و موهومی این تابع را نشان می دهد. بخش حقیقی انتگرال تقریبا همیشه مثبت است، زیرا وقتی f ( t ) منفی است، قسمت حقیقی e - 2π i (3 t ) نیز منفی است. از آنجایی که آنها با سرعت یکسانی نوسان می کنند، وقتی f ( t ) مثبت است، بخش حقیقی e - 2π i (3 t ) نیز مثبت است.. نتیجه این است که وقتی بخش حقیقی انتگرال را انتگرالگیری میکنید، عدد نسبتاً زیادی به دست میآید (در این مورد1/2). از سوی دیگر، هنگامی که شما سعی می کنید فرکانس را اندازه گیری کنید که وجود ندارد، مانند موردی که ما به آن نگاه می کنیم ، می بینید که هر دو جزء حقیقی و موهومی این تابع به سرعت بین مقادیر مثبت و منفی تغییر می کنند، همانطور که در تصویر سوم ترسیم شده است. بنابراین، در این حالت، انتگرال به اندازه کافی سریع نوسان می کند به طوری که انتگرال بسیار کوچک است و مقدار تبدیل فوریه برای آن فرکانس تقریباً صفر است.
، می بینید که هر دو جزء حقیقی و موهومی این تابع به سرعت بین مقادیر مثبت و منفی تغییر می کنند، همانطور که در تصویر سوم ترسیم شده است. بنابراین، در این حالت، انتگرال به اندازه کافی سریع نوسان می کند به طوری که انتگرال بسیار کوچک است و مقدار تبدیل فوریه برای آن فرکانس تقریباً صفر است.







 ، سپس
، سپس .
. ، سپس
، سپس .
.
 . در واقع، نشان دادن عملگر تبدیل فوریه با
. در واقع، نشان دادن عملگر تبدیل فوریه با ، بنابراین
، بنابراین ، سپس برای توابع مناسب، دو بار اعمال تبدیل فوریه به سادگی تابع را برمیگرداند:
، سپس برای توابع مناسب، دو بار اعمال تبدیل فوریه به سادگی تابع را برمیگرداند: ، که می توان آن را به "عکوس زمان" تعبیر کرد. از آنجایی که زمان معکوس دو دوره ای است، اعمال این دو بار نتیجه می دهدf)=f}
، که می توان آن را به "عکوس زمان" تعبیر کرد. از آنجایی که زمان معکوس دو دوره ای است، اعمال این دو بار نتیجه می دهدf)=f} بنابراین عملگر تبدیل فوریه چهار دوره ای است و به همین ترتیب تبدیل فوریه معکوس را می توان با سه بار اعمال تبدیل فوریه به دست آورد:
بنابراین عملگر تبدیل فوریه چهار دوره ای است و به همین ترتیب تبدیل فوریه معکوس را می توان با سه بار اعمال تبدیل فوریه به دست آورد: . به ویژه تبدیل فوریه معکوس پذیر است (تحت شرایط مناسب).
. به ویژه تبدیل فوریه معکوس پذیر است (تحت شرایط مناسب). به طوری که
به طوری که ، ما داریم:
، ما داریم:
 شکل تبدیل فوریه بر حسب فرکانس معمولی ξ باشد.
شکل تبدیل فوریه بر حسب فرکانس معمولی ξ باشد. ، فرم جایگزین
، فرم جایگزین (که
(که 
 در فرمول وارونگی مربوطه خود
در فرمول وارونگی مربوطه خود
 (که
(که  در تعریف آن
در تعریف آن

 به عنوان یک فرکانس منفی، زیرا جزء طیفی مربوطه است
به عنوان یک فرکانس منفی، زیرا جزء طیفی مربوطه است اما بسیاری از هویتهای مربوط به تبدیل فوریه در آن قراردادها معتبر باقی میمانند، مشروط بر اینکه تمام عباراتی که به صراحت شامل i میشوند آن را با - i جایگزین کرده باشند . برای اضافه کردن سردرگمی بیشتر، توجه داشته باشید که از آنجایی که
اما بسیاری از هویتهای مربوط به تبدیل فوریه در آن قراردادها معتبر باقی میمانند، مشروط بر اینکه تمام عباراتی که به صراحت شامل i میشوند آن را با - i جایگزین کرده باشند . برای اضافه کردن سردرگمی بیشتر، توجه داشته باشید که از آنجایی که 










 مختلط باشد، اما دارای مزیت نمایش فشرده تمام اطلاعات لازم در مورد هر فرکانس است. تعبیر معمول این عدد مختلط این است که
مختلط باشد، اما دارای مزیت نمایش فشرده تمام اطلاعات لازم در مورد هر فرکانس است. تعبیر معمول این عدد مختلط این است که (
(  (
( 











 .
. 
 در فرکانس
در فرکانس با عدد مختلط داده می شود
با عدد مختلط داده می شود . ارزیابی
. ارزیابی  بجای
بجای ، متغیر تبدیل نشان دهنده
، متغیر تبدیل نشان دهنده 
 بنابراین می توان آن را به موارد زیر کاهش داد:
بنابراین می توان آن را به موارد زیر کاهش داد:
 در این زمینه غیر ضروری هستند.
در این زمینه غیر ضروری هستند.

 .
.










 در شکل بالا:
در شکل بالا: جایی که Nm 3 نشان دهنده درجه یا روابط مرد سوم و غیره است.
جایی که Nm 3 نشان دهنده درجه یا روابط مرد سوم و غیره است.
 و اکنون، می توانیم Nm / Nw را پیدا کنیم :
و اکنون، می توانیم Nm / Nw را پیدا کنیم :






























 در این وبلاگ به ریاضیات و کاربردهای آن و تحقیقات در آنها پرداخته می شود. مطالب در این وبلاگ ترجمه سطحی و اولیه است و کامل نیست.در صورتی سوال یا نظری در زمینه ریاضیات دارید مطرح نمایید .در صورت امکان به آن می پردازم. من دوست دارم برای یافتن پاسخ به سوالات و حل پروژه های علمی با دیگران همکاری نمایم.در صورتی که شما هم بامن هم عقیده هستید با من تماس بگیرید.
در این وبلاگ به ریاضیات و کاربردهای آن و تحقیقات در آنها پرداخته می شود. مطالب در این وبلاگ ترجمه سطحی و اولیه است و کامل نیست.در صورتی سوال یا نظری در زمینه ریاضیات دارید مطرح نمایید .در صورت امکان به آن می پردازم. من دوست دارم برای یافتن پاسخ به سوالات و حل پروژه های علمی با دیگران همکاری نمایم.در صورتی که شما هم بامن هم عقیده هستید با من تماس بگیرید.