برنامه های کاربردی [ ویرایش ]
ضرب خارجی در زمینه های مختلف کاربرد دارد. به عنوان مثال، در هندسه محاسباتی، فیزیک و مهندسی استفاده می شود. فهرست غیر جامعی از نمونه ها در زیر آمده است.
هندسه محاسباتی [ ویرایش ]
حاصل ضرب در محاسبه فاصله دو خط اریب (خط نه در یک صفحه) از یکدیگر در فضای سه بعدی ظاهر می شود.
ضرب خارجی می تواند برای محاسبه نرمال یک مثلث یا چندضلعی استفاده شود، عملیاتی که اغلب در گرافیک کامپیوتری انجام می شود . به عنوان مثال، سیم پیچی یک چند ضلعی (در جهت عقربه های ساعت یا خلاف جهت عقربه های ساعت) در مورد یک نقطه در چند ضلعی را می توان با مثلث کردن چند ضلعی (مانند پره زدن یک چرخ) و جمع کردن زوایای (بین پره ها) با استفاده از ضرب خارجی برای پیگیری وضعیت محاسبه کرد. نشانه هر زاویه
در هندسه محاسباتی صفحه ، از ضرب خارجی برای تعیین علامت زاویه تند تعریف شده توسط سه نقطه استفاده می شود .



که طول علامت ضرب ضربدر دو بردار است.
در سیستم مختصات "راست دست"، اگر نتیجه 0 باشد، نقاط هم خط هستند . اگر مثبت باشد، سه نقطه یک زاویه چرخش مثبت به اطراف را تشکیل می دهند



ضرب خارجی در محاسبه حجم یک چند وجهی مانند چهار وجهی یا متوازی الاضلاع استفاده می شود .
تکانه و گشتاور زاویه ای [ ویرایش ]
تکانه زاویه ای L یک ذره در یک مبدأ معین به صورت زیر تعریف می شود:
جایی که r بردار موقعیت ذره نسبت به مبدا است، p تکانه خطی ذره است.
به همین ترتیب، ممان M نیروی F B اعمال شده در نقطه B در اطراف نقطه A به صورت زیر داده می شود:
در مکانیک به گشتاور نیرو نیز گشتاور می گویند و به صورت می نویسند
از آنجایی که موقعیت r ، تکانه خطی p و نیروی F همگی بردارهای حقیقی هستند ، هر دو حرکت زاویه ای L و گشتاور نیروی M شبه بردار یا بردار محوری هستند .
بدنه صلب [ ویرایش ]
ضرب خارجی اغلب در توصیف حرکات صلب ظاهر می شود. دو نقطه P و Q در یک جسم صلب را می توان به صورت زیر مرتبط کرد:
جایی که


از موقعیت


نیروی لورنتس [ ویرایش ]
همچنین ببینید: نیروی لورنتس
ضرب خارجی برای توصیف نیروی لورنتس تجربه شده توسط بار الکتریکی متحرک q e استفاده می شود :
از آنجایی که سرعت v ، نیروی F و میدان الکتریکی E همگی بردارهای حقیقی هستند ، میدان مغناطیسی B یک شبه بردار است .
دیگر [ ویرایش ]
در محاسبات برداری , از ضرب ضربدری برای تعریف فرمول عملگر بردار curl استفاده می شود .
ترفند بازنویسی یک ضرب خارجی بر حسب ضرب ماتریس اغلب در هندسه اپی قطبی و چند نمای ظاهر می شود، به ویژه در هنگام استخراج محدودیت های تطبیق.
به عنوان یک ضرب خارجی [ ویرایش ]
ضرب خارجی در رابطه با ضرب خارجی. در قرمز بردار واحد متعامد و دو بردار واحد "موازی" هستند.
ضرب خارجی را می توان بر اساس ضرب خارجی تعریف کرد. می توان آن را به یک ضرب خارجی در ابعادی غیر از سه بعدی تعمیم داد . [19] این تعمیم یک تفسیر هندسی طبیعی از ضرب خارجی را امکان پذیر می کند. ، تقریباً به همان روشی که یک بردار یک عنصر خط جهتدار است. با توجه به دو بردار a و b ، می توان دو بردار a ∧ b را به صورت متوازی الاضلاع جهت دار که توسط a و b پوشانده شده است، مشاهده کرد . حاصل ضرب خارجی با گرفتن ستاره هاج از دو بردار a ∧ b ، نگاشت 2 بردار به بردارها به دست می آید:
این را می توان به عنوان عنصر چند بعدی جهت دار "عمود" بر دوبردار در نظر گرفت. در فضای d بعدی، ستاره هاج یک بردار k را به بردار ( d–k ) می برد. بنابراین تنها در ابعاد d = 3 نتیجه یک عنصر از بعد یک (3-2 = 1)، یعنی یک بردار است. به عنوان مثال، در ابعاد d = 4، حاصل ضرب خارجی دو بردار دارای بعد 4-2 = 2 است که یک دو بردار را به دست می دهد. بنابراین، فقط در سه بعد، ضرب خارجی ساختار جبری را برای ضرب بردارها تعریف می کند.
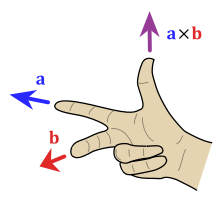
دستی [ ویرایش ]
![]()
این بخش احتمالاً حاوی تحقیقات اصلی است . لطفاً با تأیید ادعاهای مطرح شده و افزودن نقلقولهای درون خطی آن را بهبود ببخشید . اظهاراتی که فقط شامل تحقیقات اصلی است باید حذف شوند. ( سپتامبر 2021 ) ( با نحوه و زمان حذف این پیام الگو آشنا شوید )
سازگاری [ ویرایش ]
هنگامی که قوانین فیزیک به صورت معادله نوشته می شوند، می توان یک انتخاب دلخواه از سیستم مختصات، از جمله دستی، انجام داد. باید مراقب بود که هرگز معادله ای را یادداشت نکنید که در آن دو طرف تحت تمام تغییراتی که باید در نظر گرفته شوند، یکسان رفتار نمی کنند. برای مثال، اگر یک طرف معادله حاصل ضرب خارجی دو بردار قطبی باشد ، باید در نظر گرفت که نتیجه یک بردار محوری است . بنابراین، برای ثبات، طرف دیگر نیز باید یک بردار محوری باشد. [ نیاز به نقل از ] به طور کلی، نتیجه حاصل از حاصل ضرب ممکن است یک بردار قطبی یا یک بردار محوری باشد، بسته به نوع عملوندهای آن (بردارهای قطبی یا بردارهای محوری). یعنی بردارهای قطبی و بردارهای محوری به روشهای زیر تحت استفاده از ضرب خارجی به هم مرتبط هستند:
- بردار قطبی × بردار قطبی = بردار محوری
- بردار محوری × بردار محوری = بردار محوری
- بردار قطبی × بردار محوری = بردار قطبی
- بردار محوری × بردار قطبی = بردار قطبی
یا به صورت نمادین
- قطبی × قطبی = محوری
- محوری × محوری = محوری
- قطبی × محوری = قطبی
- محوری × قطبی = قطبی
از آنجا که حاصلضرب خارجی نیز ممکن است یک بردار قطبی باشد، ممکن است با تبدیل تصویر آینه ای تغییر جهت ندهد. با توجه به روابط فوق، اگر یکی از عملوندها بردار قطبی و دیگری بردار محوری باشد (مثلا حاصل ضرب خارجی دو بردار قطبی) این اتفاق می افتد. به عنوان مثال، یک ضرب سه گانه برداری که شامل سه بردار قطبی است، یک بردار قطبی است.
یک رویکرد بدون دست با استفاده از جبر خارجی امکان پذیر است.
پارادوکس مبنای متعارف [ ویرایش ]
بگذارید ( i ، j ، k ) یک مبنای متعارف باشد. بردارهای i ، j و k به جهت فضا بستگی ندارند. آنها حتی می توانند در غیاب هر جهتی تعریف شوند. بنابراین آنها نمی توانند بردارهای محوری باشند. اما اگر i و j بردارهای قطبی باشند، k یک بردار محوری برای i × j = k یا
j × i = k است . این یک پارادوکس است.
"محوری" و "قطبی" معیارهای فیزیکی برای بردارهای فیزیکی هستند. یعنی بردارهایی که مقادیر فیزیکی مانند سرعت یا میدان مغناطیسی را نشان می دهند. بردارهای i ، j و k بردارهای ریاضی هستند، نه محوری و نه قطبی. در ریاضیات حاصلضرب دو بردار بردار است. هیچ تناقضی وجود ندارد.
کلیات [ ویرایش ]
راه های مختلفی برای تعمیم ضرب خارجی به ابعاد بالاتر وجود دارد.
جبر لی [ ویرایش ]
نوشتار اصلی: جبر لی
حاصل ضرب خارجی را می توان به عنوان یکی از ساده ترین ضربات Lie مشاهده کرد، و بنابراین توسط جبرهای Lie تعمیم داده می شود ، که به عنوان ضربات باینری بدیهی شده اند که اصول چندخطی، تقارن کجی و اتحاد ژاکوبی را برآورده می کنند. جبرهای لی بسیاری وجود دارد و مطالعه آنها یک رشته اصلی ریاضیات است که نظریه لی نامیده می شود .
به عنوان مثال، جبر هایزنبرگ ساختار جبر لی دیگری را ارائه می دهد

کواترنیون ها [ ویرایش ]
اطلاعات بیشتر: کواترنیون ها و چرخش فضایی
ضرب خارجی را نیز می توان بر حسب کواترنیون ها توصیف کرد . به طور کلی، اگر یک بردار [ a 1 , a 2 , a 3 ] به صورت چهارتایی
a 1 i + a 2 j + a 3 k نمایش داده شود ، حاصل ضرب خارجی دو بردار را می توان با در نظر گرفتن حاصل ضرب آنها به عنوان چهارتایی و حذف آن به دست آورد. بخش حقیقی نتیجه قسمت حقیقی منفی حاصل ضرب نقطه ای دو بردار خواهد بود.
Octonions [ ویرایش ]
همچنین ببینید: ضرب خارجی هفت بعدی و Octonion
حاصل ضرب خارجی برای بردارهای 7 بعدی را می توان به همین روش با استفاده از اکتیون ها به جای کواترنیون ها به دست آورد. عدم وجود ضربات خارجی با ارزش برداری غیرمعمول دو بردار در ابعاد دیگر به نتیجه قضیه هورویتز مربوط می شود که تنها جبرهای تقسیم هنجاری جبرهایی با ابعاد 1، 2، 4 و 8 هستند.
ضرب خارجی [ ویرایش ]
مقالات اصلی: جبر خارجی و مقایسه جبر برداری و جبر هندسی § ضربات خارجی و خارجی
در بعد کلی، هیچ آنالوگ مستقیمی از ضرب خارجی باینری وجود ندارد که به طور خاص یک بردار را ایجاد کند. با این حال، ضرب خارجی وجود دارد که خواص مشابهی دارد، با این تفاوت که حاصلضرب خارجی دو بردار به جای یک بردار معمولی، اکنون یک بردار 2 است. همانطور که در بالا ذکر شد، ضرب خارجی را می توان به عنوان ضرب خارجی در سه بعدی با استفاده از عملگر ستاره Hodge برای نگاشت 2 بردار به بردار تفسیر کرد. دوگانه هاج از ضرب خارجی یک بردار ( n -2) را به دست می دهد که یک تعمیم طبیعی از ضرب خارجی در هر تعداد ابعاد است.
ضرب خارجی و حاصل نقطه می توانند (از طریق جمع) ترکیب شوند تا حاصل ضرب هندسی در جبر هندسی را تشکیل دهند.
ضرب خارجی [ ویرایش ]
همانطور که در بالا ذکر شد، ضرب خارجی را می توان در سه بعدی به عنوان Hodge dual ضرب خارجی تفسیر کرد. در هر n بعد محدود، هاج دوگانه حاصلضرب خارجی n - 1 بردار یک بردار است. بنابراین، به جای یک عملیات دودویی، در ابعاد محدود دلخواه، حاصل ضرب خارجی به عنوان دوگانه هاج حاصلضرب خارجی برخی از بردارهای n -1 داده شده تعمیم مییابد. این تعمیم ضرب خارجی نامیده می شود . [20]
ضرب جابجاگر [ ویرایش ]
مقالات اصلی: جبر هندسی § امتداد ضربات داخلی و خارجی ، ضرب خارجی § ضرب خارجی و دستی ، و ضرب خارجی § جبر لی
تفسیر فضای برداری سه بعدی جبر به عنوان زیر جبر 2 بردار (نه 1 بردار) جبر هندسی سه بعدی، که در آن 





جایی که
ضرب جابجاگر را می توان به چند بردار دلخواه در سه بعد تعمیم داد، که منجر به یک چند برداری متشکل از عناصر درجه 1 (1-بردار/ بردار واقعی ) و 2 (2-بردار/شبه بردار) می شود. در حالی که حاصلضرب جابجاگر دو بردار 1 در واقع با حاصلضرب خارجی یکسان است و یک 2 بردار به دست میدهد، جابجاگر یک بردار و یک بردار 2 بردار واقعی را به دست میدهد که در عوض با انقباضات چپ و راست در جبر هندسی حاصلضرب جابجاگر دو بردار 2 برابری ندارد، به همین دلیل است که حاصلضرب جابجاگر در وهله اول برای 2 بردار تعریف می شود. علاوه بر این، حاصلضرب سه گانه جابجاگر سه بردار 2 برابری با حاصلضرب سه گانه برداری همان سه شبه بردار در جبر برداری است. با این حال، حاصلضرب سه گانه جابجاگر سه بردار 1 در جبر هندسی در عوض منفی حاصلضرب سه گانه برداری همان سه بردار واقعی در جبر برداری است.
تعمیم به ابعاد بالاتر توسط همان حاصلضرب جابجاگر 2-بردار در جبرهای هندسی با ابعاد بالاتر ارائه می شود، اما بردارهای 2 دیگر شبه بردار نیستند. همانطور که حاصلضرب تعویض/تقاطع 2-بردارها در سه بعدی با ساده ترین جبر Lie مطابقت دارد ، جبرهای فرعی 2-بردار جبر هندسی با ابعاد بالاتر مجهز به حاصلضرب جابجاگر نیز با جبرهای Lie مطابقت دارند. [22] همچنین مانند سه بعد، ضرب جابجاگر را می توان به چند بردار دلخواه تعمیم داد.
جبر چند خطی [ ویرایش ]
در زمینه جبر چند خطی ، حاصل ضرب خارجی را می توان به عنوان تانسور (1،2) (یک تانسور مختلط ، به ویژه یک نقشه دوخطی ) مشاهده کرد که از فرم حجمی 3 بعدی ، [یادداشت 2] a (0،3 ) به دست آمده است. )-تانسور، با بالا بردن شاخص .
در جزئیات، فرم حجمی 3 بعدی یک ضرب را تعریف می کند




با ترجمه جبر بالا به هندسه، تابع "حجم متوازی الاضلاع تعریف شده توسط


به همین ترتیب، در ابعاد بالاتر میتوان ضربات خارجی تعمیمیافته را با بالا بردن شاخصهای شکل حجمی n- بعدی تعریف کرد.
تانسور، که به عنوان ورودی می گیرد
بردارها، و به عنوان خروجی 1 بردار – an می دهد
ضرب با ارزش برداری ary یا
-تانسور، که به عنوان ورودی 2 بردار می گیرد و تانسور متقارن اریب رتبه n - 2 را به عنوان خروجی می دهد - یک حاصلضرب دوتایی با مقادیر تانسور رتبه n - 2 . می توان تعریف هم کرد
تانسورهای دیگر k .
این ضربات همگی چند خطی و متقارن هستند و می توان آنها را بر حسب دترمینان و برابری تعریف کرد .
این




- عمود بر ابر صفحه تعریف شده توسط،
- قدر حجم متوازی الاضلاع تعریف شده توسط،
که می توان آن را به عنوان دترمینان G محاسبه کرد
- جهت گیری به طوری که
مثبت گرا است
این ضرب متناوب چند خطی منحصر به فرد است که به ارزیابی میرسد

در مختصات می توان یک فرمول برای این ارائه داد
این فرمول از نظر ساختار با فرمول دترمینان برای ضرب خارجی نرمال در R3 یکسان است با این تفاوت که ردیف بردارهای پایه آخرین ردیف در دترمینان است نه ردیف اول. دلیل این امر اطمینان از این است که بردارهای مرتب شده
( v 1 , ..., v n -1 , Λn –1 i=0v i )
دارای جهت گیری مثبت با توجه به ( e 1 ، ...، e n ). اگر n فرد باشد، این اصلاح مقدار را بدون تغییر باقی می گذارد، بنابراین این قرارداد با تعریف معمولی ضرب باینری مطابقت دارد. در صورتی که n زوج باشد، تمایز باید حفظ شود. این
![{\displaystyle [v_{1},\ldots ,v_{n}]:=\bigwedge _{i=0}^{n}v_{i}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/a3ded7786514805c536cc7c4063b827b634303f2)
و بنابراین به R n+1 ساختاری از جبر n-Lie می دهد (به گزاره 1 از [23] مراجعه کنید ).
تاریخچه [ ویرایش ]
در سال 1773، جوزف-لوئیس لاگرانژ از فرم اجزای هر دو نقطه و خارجی استفاده کرد تا چهار وجهی را در سه بعدی مطالعه کند. [24] [یادداشت 3]
در سال 1843، ویلیام روآن همیلتون ضرب کواترنیون و به همراه آن اصطلاحات بردار و اسکالار را معرفی کرد . با توجه به دو ربع [0, u ] و [0, v ] ، که در آن u و v بردارهایی در R 3 هستند ، حاصلضرب کواترنیون آنها را می توان به صورت [− u ⋅ v ، u × v ] خلاصه کرد . جیمز کلرک ماکسول از ابزارهای کواترنیون همیلتون برای توسعه معادلات الکترومغناطیس معروف خود استفاده کرد و به همین دلیل و دلایل دیگر، کواترنیون ها برای مدتی بخشی ضروری از آموزش فیزیک بودند.
در سال 1844، هرمان گراسمن جبر هندسی را منتشر کرد که به بعد دو یا سه وابسته نیست. گراسمن چندین ضرب را توسعه داد، از جمله یک ضرب خارجی که توسط [uv] نشان داده شد . [25] ( همچنین رجوع کنید به: جبر خارجی . )
در سال 1853، آگوستین-لوئیس کوشی ، یکی از معاصران گراسمن، مقاله ای در مورد کلیدهای جبری منتشر کرد که برای حل معادلات استفاده می شد و خواص ضربی مشابه حاصل ضرب داشت. [26] [27]
در سال 1878، ویلیام کینگدون کلیفورد اصول دینامیک را منتشر کرد که در آن اصطلاح ضرب برداری تایید شده است. در کتاب، این حاصل ضرب دو بردار به اندازه مساحت متوازی الاضلاع که دو ضلع آن هستند، و جهت عمود بر صفحه آنها تعریف شده است. [28] ( همچنین نگاه کنید به: جبر کلیفورد . )
در یادداشت های سخنرانی در سال 1881، گیبز ضرب خارجی را توسط
در سال 1908، Cesare Burali-Forti و Roberto Marcolongo نماد حاصلضرب برداری u ∧ v را معرفی کردند . [25] این در فرانسه و مناطق دیگر تا به امروز به عنوان نماد استفاده می شود×
همچنین ببینید [ ویرایش ]
- ضرب دکارتی - ضرب دو مجموعه
- جبر هندسی: سیستم های دوار
- ضربات خارجی چندگانه - ضرباتی که بیش از سه بردار را شامل می شوند
- ضرب بردارها
- ضرب چهارگانه
- × (نماد)
https://en.wikipedia.org/wiki/Cross_product










![{\displaystyle [x,y]=z,[x,z]=[y,z]=0.}](https://wikimedia.org/api/rest_v1/media/math/render/svg/bf27588f0b4586bd6a22e7e3d7c9d8513219e3ea)



![{\displaystyle [[x_{1},\ldots,x_{n}],y_{2},\ldots,y_{n}]=\sum _{i=1}^{n}[x_{1 },\ldots,x_{i-1},[x_{i},y_{2},\ldots,y_{n}],x_{i+1},\ldots ,x_{n},}](https://wikimedia.org/api/rest_v1/media/math/render/svg/8cec8eccbfa6d7d839058f46452d3339623469e9)













![{\displaystyle {\begin{aligned}\mathbf {a} \times \mathbf {b} =[\mathbf {a} ]_{\times }\mathbf {b} &={\begin{bmatrix}\,0& \!-a_{3}&\,\,a_{2}\\\,\,a_{3}&0&\!-a_{1}\\-a_{2}&\,\,a_{1} &\,0\end{bmatrix}}{\begin{bmatrix}b_{1}\\b_{2}\\b_{3}\end{bmatrix}}\\\mathbf {a} \times \mathbf { b} ={[\mathbf {b} ]_{\times }}^{\mathrm {\!\!T} }\mathbf {a} &={\begin{bmatrix}\,0&\,\,b_ {3}&\!-b_{2}\\-b_{3}&0&\,\,b_{1}\\\,\,b_{2}&\!-b_{1}&\,0\ end{bmatrix}}{\begin{bmatrix}a_{1}\\a_{2}\\a_{3}\end{bmatrix}}،\end{تراز شده}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/77eaf3e139944a22bc3543de85a65d2d280547c6)
![{\displaystyle [\mathbf {a} ]_{\times }{\stackrel {\rm {def}}{=}}{\begin{bmatrix}\,\,0&\!-a_{3}&\, \,\,a_{2}\\\,\,\,a_{3}&0&\!-a_{1}\\\!-a_{2}&\,\,a_{1}&\,\ ,0\end{bmatrix}}.}](https://wikimedia.org/api/rest_v1/media/math/render/svg/614cc7fd18f2f2e212803822f31acb2505c98c89)
![{\displaystyle [\mathbf {a} ]_{\times ,i}=\mathbf {a} \times \mathbf {{\hat {e}}_{i}} ,\;i\in \{1, 2،3\}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/74baaa1f6814e02fb133911b2bbab966485a3806)
![{\displaystyle [\mathbf {a} ]_{\times }=\sum _{i=1}^{3}\left(\mathbf {a} \times \mathbf {{\hat {e}}_{ i}} \right)\otimes \mathbf {{\hat {e}}_{i}}،}](https://wikimedia.org/api/rest_v1/media/math/render/svg/fb0381c1581881a166e2f4e9cefe0b236265eefd)
 اپراتور ضرب خارجی است .
اپراتور ضرب خارجی است .
![{\displaystyle [\mathbf {a} ]_{\times }=\mathbf {d} \mathbf {c} ^{\mathrm {T} }-\mathbf {c} \mathbf {d} ^{\mathrm { T}}.}](https://wikimedia.org/api/rest_v1/media/math/render/svg/d7bebe8181aeb49a3e8987339594fd7de7c454a9)

![{\displaystyle [\mathbf {a} ]_{\times }={\begin{bmatrix}0&c_{2}d_{1}-c_{1}d_{2}&c_{3}d_{1}-c_{ 1}d_{3}\\c_{1}d_{2}-c_{2}d_{1}&0&c_{3}d_{2}-c_{2}d_{3}\\c_{1}d_{ 3}-c_{3}d_{1}&c_{2}d_{3}-c_{3}d_{2}&0\end{bmatrix}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/3ff95aa2908dc95252f1a28c8a9167458c98c993)



![{\displaystyle [\mathbf {a} ]_{\times }\,\mathbf {a} =\mathbf {0} }](https://wikimedia.org/api/rest_v1/media/math/render/svg/6e918b623a3b34134199284e350a5a06f8fe0305)
![{\displaystyle \mathbf {a} ^{\mathrm {T} }\,[\mathbf {a} ]_{\times }=\mathbf {0} }](https://wikimedia.org/api/rest_v1/media/math/render/svg/3cd1a98ffd5ab228553c458345bb26af8422bb43)
![{\displaystyle \mathbf {b} ^{\mathrm {T} }\,[\mathbf {a} ]_{\times }\,\mathbf {b} =0.}](https://wikimedia.org/api/rest_v1/media/math/render/svg/c23cfb35b83ca69742e7da1381a7477a18d04e4d)

 با اجزای برداری مطابقت دارد. این توصیف ضرب خارجی اغلب با استفاده از قرارداد جمع انیشتین به صورت فشرده تر بیان می شود
با اجزای برداری مطابقت دارد. این توصیف ضرب خارجی اغلب با استفاده از قرارداد جمع انیشتین به صورت فشرده تر بیان می شود
 ( نماد لوی-سیویتا ). در آن صورت، این نمایش شکل دیگری از نمایش متقارن متقارن حاصلضرب خارجی است:
( نماد لوی-سیویتا ). در آن صورت، این نمایش شکل دیگری از نمایش متقارن متقارن حاصلضرب خارجی است:![{\displaystyle [\varepsilon _{ijk}a^{j}]=[\mathbf {a} ]_{\times }.}](https://wikimedia.org/api/rest_v1/media/math/render/svg/063b837f18afcf9a012a49f73f4b4c2e350e99e9)







 ما به سادگی آن را رها می کنیم
ما به سادگی آن را رها می کنیم و
و از فرمول، و دو جزء بعدی را پایین بیاورید:
از فرمول، و دو جزء بعدی را پایین بیاورید:
 دو عنصر بعدی باید به دور ماتریس بپیچند تا بعد از مولفه z، جزء x بیاید. برای وضوح، هنگام انجام این عملیات برای
دو عنصر بعدی باید به دور ماتریس بپیچند تا بعد از مولفه z، جزء x بیاید. برای وضوح، هنگام انجام این عملیات برای  دو جزء بعدی باید x و y در نظر گرفته شوند.
دو جزء بعدی باید x و y در نظر گرفته شوند.












 ، جایی که
، جایی که یک ماتریس چرخشی است با
یک ماتریس چرخشی است با .
.
 یک ماتریس 3 در 3 است و
یک ماتریس 3 در 3 است و انتقال معکوس و است
انتقال معکوس و است ماتریس کوفاکتور است. به راحتی می توان مشاهده کرد که چگونه این فرمول به فرمول قبلی کاهش می یابد
ماتریس کوفاکتور است. به راحتی می توان مشاهده کرد که چگونه این فرمول به فرمول قبلی کاهش می یابد ، رابطه زیر صادق است:
، رابطه زیر صادق است:








 با فرمول تانسوری داده می شود
با فرمول تانسوری داده می شود جایی که
جایی که تانسور کوواریانت لوی-سیویتا است (موقعیت شاخص ها را یادداشت می کنیم). که با فرمول ذاتی داده شده در اینجا مطابقت دارد .
تانسور کوواریانت لوی-سیویتا است (موقعیت شاخص ها را یادداشت می کنیم). که با فرمول ذاتی داده شده در اینجا مطابقت دارد . جایی که
جایی که نماد لوی- سویتا است (که یک شبه تانسور است). این فرمولی است که برای فیزیک روزمره استفاده می شود، اما فقط برای این انتخاب خاص پایه کار می کند.
نماد لوی- سویتا است (که یک شبه تانسور است). این فرمولی است که برای فیزیک روزمره استفاده می شود، اما فقط برای این انتخاب خاص پایه کار می کند. جایی که
جایی که نشان می دهد که آیا اساس جهت گیری یکسان با فضا دارد یا خیر.
نشان می دهد که آیا اساس جهت گیری یکسان با فضا دارد یا خیر.







 است (که در اینجا نام برده شده است).) و با نماد
است (که در اینجا نام برده شده است).) و با نماد 












 ،
، .
. به طوری که یک یادگاری آشناتر "BAC - CAB" به دست می آید، مانند "پشت کابین".
به طوری که یک یادگاری آشناتر "BAC - CAB" به دست می آید، مانند "پشت کابین".



 .
. جزئی از
جزئی از  از رابطه زیر بدست می آید:
از رابطه زیر بدست می آید:
 و
و اجزای
اجزای 
 [5]
[5]
![{\displaystyle \mathbf {a} \cdot [\mathbf {b} \times \mathbf {c} ]=\varepsilon _{ijk}a^{i}b^{j}c^{k}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/1f5abca130937a2012b0f42bf0a587074f8f08d6)
![{\displaystyle (\mathbf {a} \times [\mathbf {b} \times \mathbf {c} ])_{i}=\varepsilon _{ijk}a^{j}\varepsilon ^{k\ell m }b_{\ell }c_{m}=\varepsilon _{ijk}\varepsilon ^{k\ell m}a^{j}b_{\ell }c_{m},}](https://wikimedia.org/api/rest_v1/media/math/render/svg/d4b9001d4ed44c60bef2063869e9f9f04f79a66f)
 -امین جزء بردار حاصل. این را می توان با انجام یک انقباض بر روی نمادهای لوی-سویتا ساده کرد .
-امین جزء بردار حاصل. این را می توان با انجام یک انقباض بر روی نمادهای لوی-سویتا ساده کرد . جایی که
جایی که تابع دلتای کرونکر است (
تابع دلتای کرونکر است ( چه زمانی
چه زمانی و
و چه زمانی
چه زمانی  ) و
) و تابع دلتای کرونکر تعمیم یافته است . ما میتوانیم این اتحاد را با تشخیص این شاخص مشخص کنیم
تابع دلتای کرونکر تعمیم یافته است . ما میتوانیم این اتحاد را با تشخیص این شاخص مشخص کنیم  صرفا خروج خلاصه خواهد شد
صرفا خروج خلاصه خواهد شد . در ترم اول تعمیر می کنیم
. در ترم اول تعمیر می کنیم و بنابراین
و بنابراین . به همین ترتیب در ترم دوم اصلاح می کنیممن
. به همین ترتیب در ترم دوم اصلاح می کنیممن و بنابراین
و بنابراین .
.![{\displaystyle (\mathbf {a} \times [\mathbf {b} \times \mathbf {c} ])_{i}=(\delta _{i}^{\ell }\delta _{j}^ {m}-\delta _{i}^{m}\delta _{j}^{\ell })a^{j}b_{\ell }c_{m}=a^{j}b_{i} c_{j}-a^{j}b_{j}c_{i}=b_{i}(\mathbf {a} \cdot \mathbf {c} )-c_{i}(\mathbf {a} \cdot \mathbf {b} )\,.}](https://wikimedia.org/api/rest_v1/media/math/render/svg/bf362b74fdd08b44a8d0da1a117b4cad3d07b7b9)
 در سراسر سطح پارامتریک تعریف شده است
در سراسر سطح پارامتریک تعریف شده است :
: . بردار واحد نرمال
. بردار واحد نرمال به سطح داده شده توسط
به سطح داده شده توسط بنابراین انتگرال
بنابراین انتگرال یک ضرب سه گانه اسکالر است.
یک ضرب سه گانه اسکالر است.














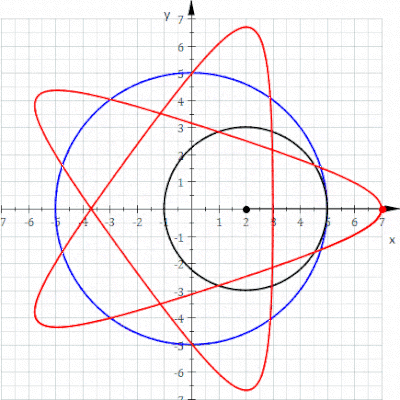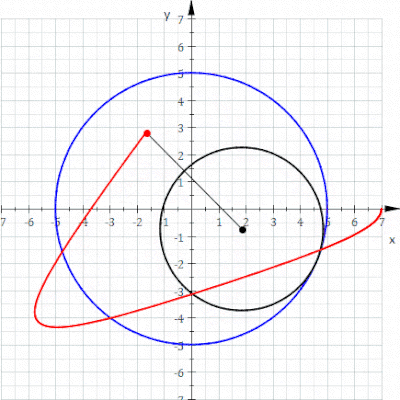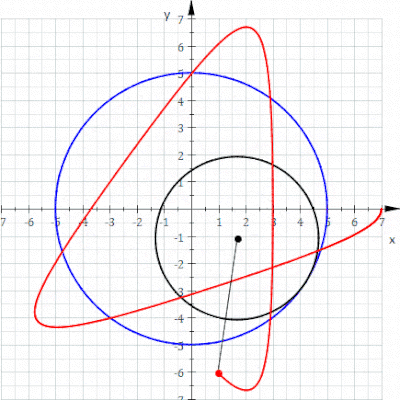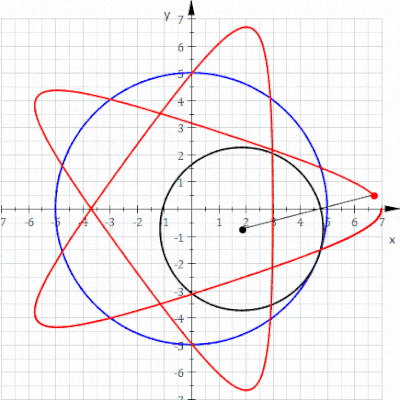

 (که در آن
(که در آن 
 (نگاه کنید
(نگاه کنید 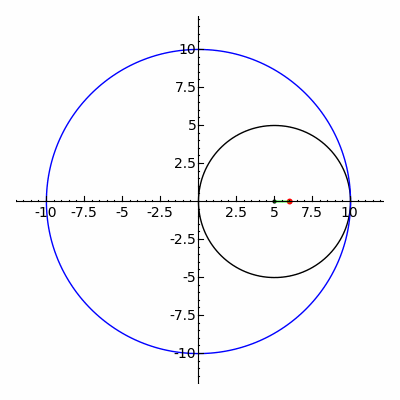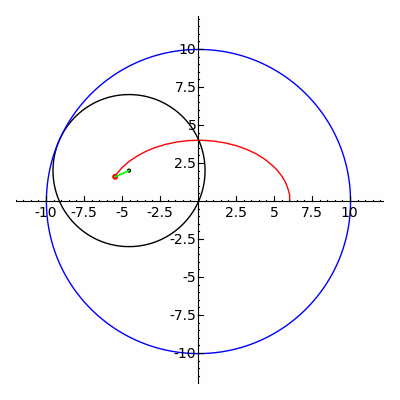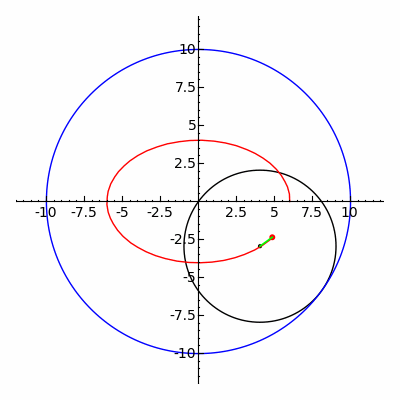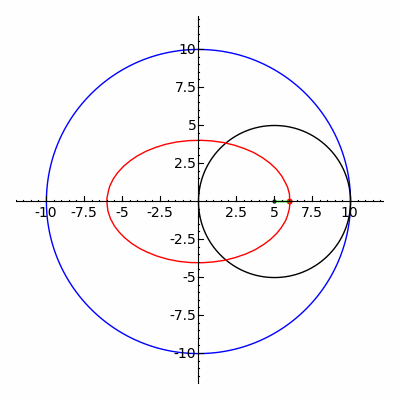

 دو
دو  و ثابت
و ثابت منحنی ها، به گونه ای که
منحنی ها، به گونه ای که ،
، ، و
، و برای همه
برای همه . رولت مولد
. رولت مولد مانند
مانند




 می توان آنها را برای بیان راه حل ها به صورت [10] مرتب کرد.
می توان آنها را برای بیان راه حل ها به صورت [10] مرتب کرد.









 خط
خط
 دایره
دایره


 خط
خط
 دایره
دایره
 این فرآیند ضمنی سازی نامیده می شود . اگر بتوان یکی از این معادلات را برای t حل کرد ، عبارت به دست آمده را می توان با معادله دیگر جایگزین کرد تا معادله ای فقط شامل x و y به دست آید : حل
این فرآیند ضمنی سازی نامیده می شود . اگر بتوان یکی از این معادلات را برای t حل کرد ، عبارت به دست آمده را می توان با معادله دیگر جایگزین کرد تا معادله ای فقط شامل x و y به دست آید : حل بدست آوردن
بدست آوردن  و با استفاده از این در
و با استفاده از این در معادله صریح را می دهد
معادله صریح را می دهد در حالی که موارد پیچیده تر یک معادله ضمنی از فرم را به دست می دهند
در حالی که موارد پیچیده تر یک معادله ضمنی از فرم را به دست می دهند


 و
و ما گرفتیم
ما گرفتیم و بنابراین
و بنابراین




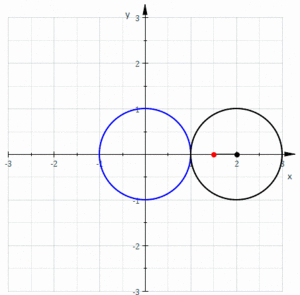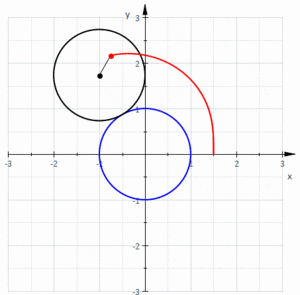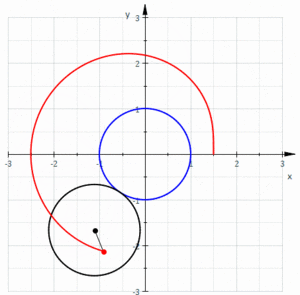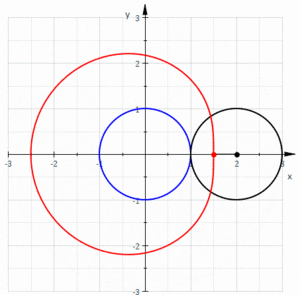


 و
و برای به دست آوردن
برای به دست آوردن 




 ، یعنی
، یعنی ،
، .
. ، معادله قطبی است
، معادله قطبی است

 ، شکل تروکوئید مرکزی معادله می شود
، شکل تروکوئید مرکزی معادله می شود

 ، لیماسون یک منحنی بسته ساده است. با این حال، مبدا معادله دکارتی ارائه شده در بالا را برآورده می کند، بنابراین نمودار این معادله دارای یک
، لیماسون یک منحنی بسته ساده است. با این حال، مبدا معادله دکارتی ارائه شده در بالا را برآورده می کند، بنابراین نمودار این معادله دارای یک  ، ناحیه محدود شده توسط منحنی محدب است و چه زمانی
، ناحیه محدود شده توسط منحنی محدب است و چه زمانی ، منحنی دارای یک فرورفتگی است که توسط دو
، منحنی دارای یک فرورفتگی است که توسط دو  ، نکته
، نکته نقطه
نقطه  نسبت به کاهش یافته استآ
نسبت به کاهش یافته استآ ، تورفتگی بیشتر می شود تا زمانی که، درب=آ
، تورفتگی بیشتر می شود تا زمانی که، درب=آ ، منحنی به یک کاردیوئید تبدیل می شود و تورفتگی به یک
، منحنی به یک کاردیوئید تبدیل می شود و تورفتگی به یک  ، کاسپ به یک حلقه داخلی منبسط می شود و منحنی در مبدا از خود عبور می کند. مانندب
، کاسپ به یک حلقه داخلی منبسط می شود و منحنی در مبدا از خود عبور می کند. مانندب است
است . چه زمانی
. چه زمانی این مساحت محصور شده توسط حلقه داخلی را دو بار می شمارد. در این حالت منحنی در زاویه از مبدا عبور می کند
این مساحت محصور شده توسط حلقه داخلی را دو بار می شمارد. در این حالت منحنی در زاویه از مبدا عبور می کند ، ناحیه محصور شده توسط حلقه داخلی است
، ناحیه محصور شده توسط حلقه داخلی است



 دایره ای باشد که مرکز آن نباشدپ
دایره ای باشد که مرکز آن نباشدپ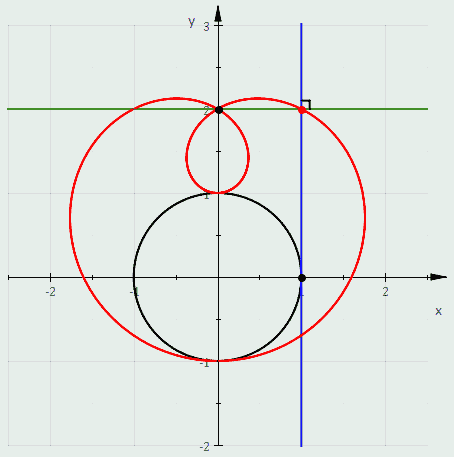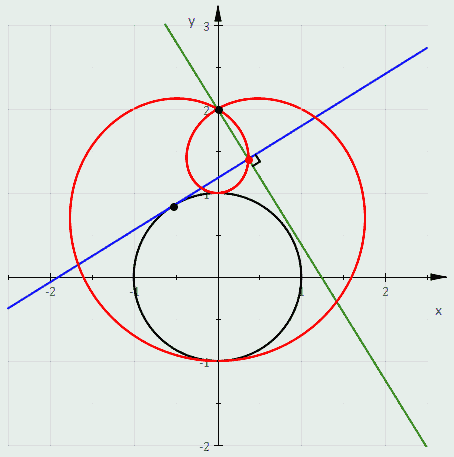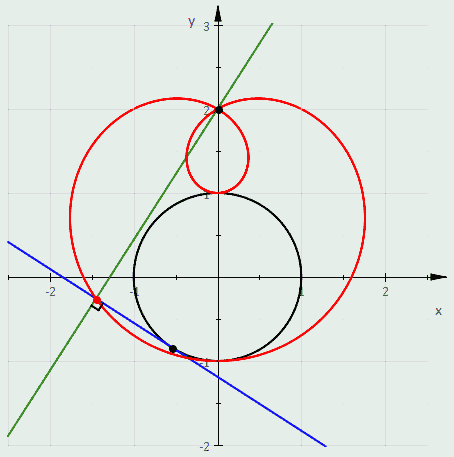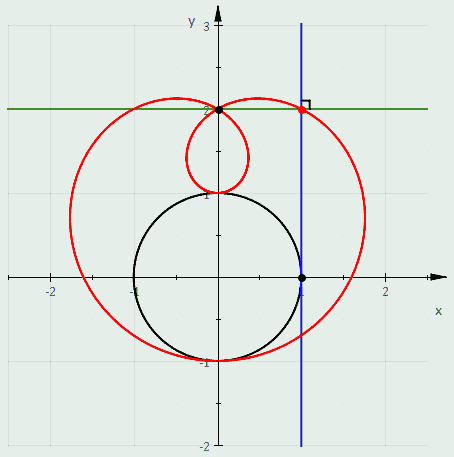
 معادله قطبی دارد
معادله قطبی دارد
 و روی مبدا تمرکز کنید. بنابراین یک لیماسون را می توان به عنوان معکوس مخروطی که در آن مرکز وارونگی یکی از کانون ها است، تعریف کرد. اگر مخروطی سهمی باشد، معکوس آن یک کاردیوئید است، اگر مخروطی هذلولی باشد، لیماسون مربوطه یک حلقه داخلی خواهد داشت، و اگر مخروطی بیضی باشد، لیماسون مربوطه هیچ حلقه ای نخواهد داشت.
و روی مبدا تمرکز کنید. بنابراین یک لیماسون را می توان به عنوان معکوس مخروطی که در آن مرکز وارونگی یکی از کانون ها است، تعریف کرد. اگر مخروطی سهمی باشد، معکوس آن یک کاردیوئید است، اگر مخروطی هذلولی باشد، لیماسون مربوطه یک حلقه داخلی خواهد داشت، و اگر مخروطی بیضی باشد، لیماسون مربوطه هیچ حلقه ای نخواهد داشت.

 و شعاع
و شعاع  ، زاویه چرخش دایره کوچک است
، زاویه چرخش دایره کوچک است و اشاره کنید
و اشاره کنید نقطه شروع (نمودار را ببینید) سپس نمایش پارامتری را دریافت می کنید :
نقطه شروع (نمودار را ببینید) سپس نمایش پارامتری را دریافت می کنید :

 دایره واحد را به نفروئید ترسیم می کند [3]
دایره واحد را به نفروئید ترسیم می کند [3] (منشا) با یک زاویه
(منشا) با یک زاویه را می توان با ضرب نقطه انجام داد
را می توان با ضرب نقطه انجام داد . از این رو
. از این رو اطراف نقطه
اطراف نقطه توسط زاویه
توسط زاویه ،
، اطراف نقطه
اطراف نقطه .
. نفروئید توسط چرخش نقطه ایجاد می شود2آ
نفروئید توسط چرخش نقطه ایجاد می شود2آ .
.
 استفاده شده. توابع مثلثاتی را ببینید .)
استفاده شده. توابع مثلثاتی را ببینید .) و
و به معادله
به معادله





 و
و




 .
.![{\displaystyle A=2\cdot {\tfrac {1}{2}}|\int _{0}^{\pi [x{\dot {y}}-y{\dot {x}}]\ ;d\varphi |=\cdots =24a^{2}\int _{0}^{\pi }\sin ^{2}\varphi \;d\varphi =12\pi a^{2}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/de13ba263785d0122ca3e5cefc4e65addd140efa) .
.

 یک دایره و
یک دایره و نقاط یک قطرد12
نقاط یک قطرد12 ، سپس پاکت مداد دایره ای که نقاط میانی روی آنها قرار دارد
، سپس پاکت مداد دایره ای که نقاط میانی روی آنها قرار دارد با نقطه میانی
با نقطه میانی

 راه حل سیستم است
راه حل سیستم است و از این رو یک نقطه از پاکت مداد دایره.
و از این رو یک نقطه از پاکت مداد دایره.

 نقاط (نمودار را ببینید) و آنها را به طور متوالی شماره گذاری کنید.
نقاط (نمودار را ببینید) و آنها را به طور متوالی شماره گذاری کنید. . (یعنی: نقطه دوم با سرعت سه برابر حرکت می کند.)
. (یعنی: نقطه دوم با سرعت سه برابر حرکت می کند.) . به منظور ساده نگه داشتن محاسبات، اثبات برای نفروئید با کاسپ در محور y ارائه شده است. معادله مماس : برای نفروئید با نمایش پارامتریک
. به منظور ساده نگه داشتن محاسبات، اثبات برای نفروئید با کاسپ در محور y ارائه شده است. معادله مماس : برای نفروئید با نمایش پارامتریک :
: ، در ابتدا.
، در ابتدا. است:
است:
 فرد به کاسپ نفروئید می رسد، جایی که هیچ تانژانتی وجود ندارد. برای
فرد به کاسپ نفروئید می رسد، جایی که هیچ تانژانتی وجود ندارد. برای  می توان تقسیم بر
می توان تقسیم بر بدست آوردن
بدست آوردن
 : معادله وتر حاوی دو نقطه
: معادله وتر حاوی دو نقطه است:
است:
 آکورد تا حدی منحط می شود. برای
آکورد تا حدی منحط می شود. برای می توان تقسیم بر
می توان تقسیم بر و معادله وتر را بدست می آورد:
و معادله وتر را بدست می آورد:
 متفاوت تعریف شده اند
متفاوت تعریف شده اند  پارامتر دایره ای است که آکوردهای آن مشخص می شود)، برای=
پارامتر دایره ای است که آکوردهای آن مشخص می شود)، برای= یکی همین خط را می گیرد. از این رو هر وتر از دایره بالا مماس بر نفروئید و است
یکی همین خط را می گیرد. از این رو هر وتر از دایره بالا مماس بر نفروئید و است


 دارای وکتور نرمال
دارای وکتور نرمال  . پرتو منعکس شده دارای بردار نرمال است (نمودار را ببینید
. پرتو منعکس شده دارای بردار نرمال است (نمودار را ببینید و حاوی نقطه دایره است
و حاوی نقطه دایره است 
 (بالا را ببین).
(بالا را ببین).

 با شعاع انحنا
با شعاع انحنا تکامل نشان می دهد
تکامل نشان می دهد
 واحد مناسب جهت گیری معمولی است.
واحد مناسب جهت گیری معمولی است.
 (به بخش بالا مراجعه کنید)
(به بخش بالا مراجعه کنید) (س. بخش خصوصیات متریک). از این رو تکامل دارای این نمایش است:
(س. بخش خصوصیات متریک). از این رو تکامل دارای این نمایش است:



 (نمودار را ببینید).
(نمودار را ببینید).


 .
.

 . پارامترسازی بالا دلالت بر منطقی بودن منحنی دارد که به معنای داشتن
. پارامترسازی بالا دلالت بر منطقی بودن منحنی دارد که به معنای داشتن 

 که در آن دوباره a شعاع دایره نورد است. بنابراین مساحت دلتوئید دو برابر دایره غلتان است.
که در آن دوباره a شعاع دایره نورد است. بنابراین مساحت دلتوئید دو برابر دایره غلتان است. 







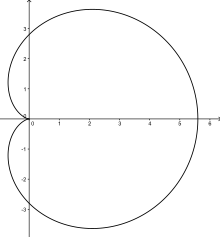

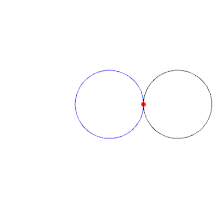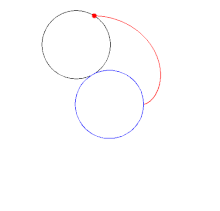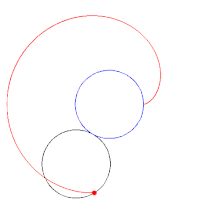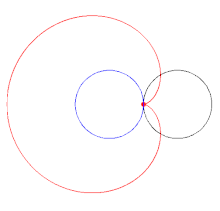





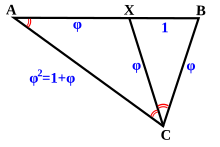
 و راس میانی دارای زاویه داخلی است
و راس میانی دارای زاویه داخلی است . این خاصیت عجیب دارد که تمام خطوطی که از راس میانی می گذرند محیط آن را نصف می کنند. [3]
. این خاصیت عجیب دارد که تمام خطوطی که از راس میانی می گذرند محیط آن را نصف می کنند. [3] ،
، ، و
، و در فاصله زمانی
در فاصله زمانی![{\displaystyle [0,2\pi ]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/348d40bf3f8b7e1c00c4346440d7e2e4f0cc9b91) زوایای داخلی یک مثلث دایره ای (بدون خودتقاطع) را تشکیل دهند اگر و فقط اگر از سیستم نابرابری ها تبعیت کنند.
زوایای داخلی یک مثلث دایره ای (بدون خودتقاطع) را تشکیل دهند اگر و فقط اگر از سیستم نابرابری ها تبعیت کنند.

 . زوایای پایه هر کدام 72 درجه است.
. زوایای پایه هر کدام 72 درجه است.








 از
از 





 .
. .
. .
. .
.

![{\displaystyle {\begin{aligned}f({\sqrt {2}})&={\sqrt {2}}-2<0,\\f(2)&=4>0,\\f'( x)&>0،\forall x\in [{\sqrt {2}},2].\end{تراز شده}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/66e4afeff8b2655b441e6111d842ff62bb27fcc3)

![{\displaystyle x={1 \over 3}{\Bigg (}1+{\sqrt[{3}]{-23+3i{\sqrt {237}} \over 4}}+{\sqrt[{3 }]{-23-3i{\sqrt {237}} \over 4}}{\Bigg )}.}](https://wikimedia.org/api/rest_v1/media/math/render/svg/823bc02ed3a453a10f81d062a8caaeaf450096b5)

 .
. 
![{\displaystyle {\begin{aligned}\alpha &=re^{i\varphi }=r(\cos \varphi +i\sin \varphi )={\frac {-23+3i{\sqrt {237}} }{4}}،\\r&={\frac {1}{4}}{\sqrt {(-23)^{2}+9\cdot 237}}={\frac {1}{4}} {\sqrt {2\cdot 11^{3}}}={\Bigg (}{\sqrt {\frac {11}{2}}}{\Bigg )}^{3},\\\cos \varphi &=-{\frac {23}{4}}{\frac {1}{r}}=-{\frac {23\cdot 2{\sqrt {2}}}{4\cdot 11{\sqrt { 11}}}}=-{\frac {23}{11{\sqrt {22}}}}،\\{\sqrt[{3}]{\alpha }}&={\sqrt[{3}] {r}}e^{\frac {i\varphi }{3}}={\sqrt[{3}]{r}}{\Big (}\cos {\Big (}{\frac {\varphi } {3}}{\Big )}+i\sin {\Big (}{\frac {\varphi }{3}}{\Big )}{\Big )}،\\{\sqrt[{3}] {\alpha }}+{\sqrt[{3}]{\bar {\alpha }}}&=2{\sqrt[{3}]{r}}\cos {\Big (}{\frac {\ varphi }{3}}{\Big )}={\sqrt {22}}\cos \!{\bigg (}{1 \over 3}\cos ^{-1}\!\!{\bigg (} \!-{23 \over 11{\sqrt {22}}}{\bigg )}{\bigg )},\\x&={\frac {1}{3}}{\bigg (}1+{\ sqrt[{3}]{\alpha }}+{\sqrt[{3}]{\bar {\alpha }}}{\bigg )}={1 \over 3}{\bigg (}1+{\ sqrt {22}}\cos \!{\bigg (}{1 \over 3}\cos ^{-1}\!\!{\bigg (}\!-{23 \over 11{\sqrt {22} }}{\bigg )}{\bigg )}{\bigg )}.\end{aligned}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/e29491473aa1576936006ec8df2184968a3a5724)

 یک شیف روی X است ، سپس یک شیف مربوطه وجود دارد
یک شیف روی X است ، سپس یک شیف مربوطه وجود دارد در X an . این ارتباط یک شی تحلیلی با یک شیء جبری یک تابع است . قضیه نمونه اولیه مربوط به X و X an می گوید که برای هر دو نوار منسجم
در X an . این ارتباط یک شی تحلیلی با یک شیء جبری یک تابع است . قضیه نمونه اولیه مربوط به X و X an می گوید که برای هر دو نوار منسجم  در X ، هممورفیسم طبیعی:
در X ، هممورفیسم طبیعی:
 شیف ساختار نوع جبری X و است
شیف ساختار نوع جبری X و است شیف ساختار گونه تحلیلی X an است . به عبارت دیگر، مقوله نوارهای منسجم در واریته جبری X معادل دسته نوارهای منسجم تحلیلی در واریته تحلیلی X an است و معادل آن بر روی اشیاء با نگاشت به دست می آید.
شیف ساختار گونه تحلیلی X an است . به عبارت دیگر، مقوله نوارهای منسجم در واریته جبری X معادل دسته نوارهای منسجم تحلیلی در واریته تحلیلی X an است و معادل آن بر روی اشیاء با نگاشت به دست می آید.
 طرحی از نوع محدود بر روی C باشد . سپس یک فضای توپولوژیکی X an وجود دارد که به عنوان یک مجموعه از نقاط بسته X با یک نقشه پیوسته گنجاندن λ X : X an → X تشکیل شده است . توپولوژی X an "توپولوژی مختلط" نامیده می شود (و بسیار متفاوت از توپولوژی زیرفضا است).
طرحی از نوع محدود بر روی C باشد . سپس یک فضای توپولوژیکی X an وجود دارد که به عنوان یک مجموعه از نقاط بسته X با یک نقشه پیوسته گنجاندن λ X : X an → X تشکیل شده است . توپولوژی X an "توپولوژی مختلط" نامیده می شود (و بسیار متفاوت از توپولوژی زیرفضا است). روی X طوری که
روی X طوری که یک فضای حلقه ای است و λ X : X an → X به نقشه فضاهای حلقه ای تبدیل می شود. فضا
یک فضای حلقه ای است و λ X : X an → X به نقشه فضاهای حلقه ای تبدیل می شود. فضا برای هر چند دیسک U یک ضریب مناسب از فضای توابع هولومورفیک روی U است .
برای هر چند دیسک U یک ضریب مناسب از فضای توابع هولومورفیک روی U است . بر روی X an (به نام شیف تحلیلی) و نقشه ای از قرقره های
بر روی X an (به نام شیف تحلیلی) و نقشه ای از قرقره های .
.  . مکاتبات
. مکاتبات یک تابع دقیق از دسته شیف ها تعریف می کند
یک تابع دقیق از دسته شیف ها تعریف می کند تزریقی است اگر f مناسب باشد، این نقشه یک هم ریختی است. یکی همچنین دارای ایزومورفیسم تمام نوارهای تصویر مستقیم بالاتر است
تزریقی است اگر f مناسب باشد، این نقشه یک هم ریختی است. یکی همچنین دارای ایزومورفیسم تمام نوارهای تصویر مستقیم بالاتر است در این مورد. [13]
در این مورد. [13] دو نوار جبری منسجم روی
دو نوار جبری منسجم روی یک نقشه از قفسه های استn
یک نقشه از قفسه های استn با
با . اگر
. اگر یک سلف تحلیلی منسجم از
یک سلف تحلیلی منسجم از .
.





 توسط مکان ناپدید شدن یک بخش داده می شود
توسط مکان ناپدید شدن یک بخش داده می شود دارای جنس هندسی
دارای جنس هندسی
 تعداد تکینگی ها در صورت شمارش صحیح است.
تعداد تکینگی ها در صورت شمارش صحیح است. مشروط به شرایط
مشروط به شرایط

 اگر
اگر و
و

 ، جایی که
، جایی که یک
یک  برای برخی
برای برخی این تیره را تیره بیضوی می نامند.
این تیره را تیره بیضوی می نامند. از این نظر یک جنس نیست، زیرا در مورد همدلی ها ثابت نیست.
از این نظر یک جنس نیست، زیرا در مورد همدلی ها ثابت نیست.
















































 در این وبلاگ به ریاضیات و کاربردهای آن و تحقیقات در آنها پرداخته می شود. مطالب در این وبلاگ ترجمه سطحی و اولیه است و کامل نیست.در صورتی سوال یا نظری در زمینه ریاضیات دارید مطرح نمایید .در صورت امکان به آن می پردازم. من دوست دارم برای یافتن پاسخ به سوالات و حل پروژه های علمی با دیگران همکاری نمایم.در صورتی که شما هم بامن هم عقیده هستید با من تماس بگیرید.
در این وبلاگ به ریاضیات و کاربردهای آن و تحقیقات در آنها پرداخته می شود. مطالب در این وبلاگ ترجمه سطحی و اولیه است و کامل نیست.در صورتی سوال یا نظری در زمینه ریاضیات دارید مطرح نمایید .در صورت امکان به آن می پردازم. من دوست دارم برای یافتن پاسخ به سوالات و حل پروژه های علمی با دیگران همکاری نمایم.در صورتی که شما هم بامن هم عقیده هستید با من تماس بگیرید.