اشتقاق ریشه ها [ ویرایش ]
این بخش چندین روش برای استخراج فرمول کاردانو را دوباره گروه بندی می کند.
روش کاردانو [ ویرایش ]
این روش به دلیل Scipione del Ferro و Tartaglia است، اما به افتخار جرولامو کاردانو که اولین بار آن را در کتاب آرس ماگنا خود (1545) منتشر کرد، نامگذاری شده است.
این روش برای یک مکعب فشرده t 3 + pt + q = 0 اعمال می شود. ایده این است که دو متغیر u و v را به گونهای معرفی کنیم که u + v = t و آن را در مکعب کاهش یافته جایگزین کنیم.
در این مرحله کاردانو شرط 3 uv + p = 0 را اعمال کرد. این سومین عبارت را در برابری قبلی حذف می کند و منجر به سیستم معادلات می شود
با دانستن مجموع و حاصل ضرب u 3 و v 3 ، نتیجه می گیریم که آنها دو راه حل معادله درجه دوم هستند .
بنابراین
ممیز این معادله است
بنابراین (بدون از دست دادن کلیت در انتخاب u یا v):
به عنوان u + v = t ، مجموع ریشه های مکعب این راه حل ها یک ریشه معادله است. به این معنا که
ریشه معادله است. این فرمول کاردانو است.
این به خوبی کار می کند زمانی که

ریشه های دیگر معادله را می توان با تغییر ریشه مکعب یا به طور معادل با ضرب ریشه مکعب در هر یک از دو ریشه مکعبی اولیه واحد به دست آورد.
تعویض ویتا [ ویرایش ]
جایگزینی ویتا روشی است که توسط فرانسوا ویت (Vieta نام لاتین اوست) در متنی که پس از مرگش در سال 1615 منتشر شد، معرفی شد که مستقیماً فرمول دوم روش کاردانو را ارائه میکند و از مشکل محاسبه دو ریشه مکعبی مختلف اجتناب میکند. [34]
با شروع از t 3 + pt + q = 0 ، جایگزینی ویتا t = w - است.پ/3 وات. [35]
جایگزینی t = w -پ/3 واتمکعب افسرده را به
با ضرب در w 3 ، یک معادله درجه دوم در w 3 بدست می آید :
اجازه دهید
هر ریشه غیر صفر این معادله درجه دوم باشد. اگر w 1 ، w 2 و w 3 سه ریشه مکعبی W باشند، آنگاه ریشه های مکعب فرورفته اصلی w 1 - هستند.پ/3 و 1، w 2 −پ/3 و 2و w 3 −پ/3 و 3. ریشه دیگر معادله درجه دوم است
روش لاگرانژ [ ویرایش ]
در مقاله خود Réflexions sur la résolution algébrique des équations («اندیشه هایی در مورد حل جبری معادلات»)، [36] ژوزف لوئیس لاگرانژ روش جدیدی را برای حل معادلات درجه پایین به روشی یکنواخت معرفی کرد، با این امید که بتواند تعمیم دهد. آن را برای درجات بالاتر این روش برای معادلات مکعب و کوارتیک به خوبی جواب می دهد ، اما لاگرانژ موفق به اعمال آن در معادله پنج نفری نشد، زیرا به حل یک چند جمله ای حلال درجه حداقل شش نیاز دارد. [37] [38] [39] به جز اینکه هیچ کس قبلاً موفق به حل مشکل نشده بود، این اولین نشانه عدم وجود فرمول جبری برای درجات 5 و بالاتر بود. این بعدها به عنوان قضیه آبل-روفینی ثابت شد. با این وجود، روشهای مدرن برای حل معادلات پنجاهی قابل حل، عمدتاً مبتنی بر روش لاگرانژ هستند. [39]
در مورد معادلات مکعبی، روش لاگرانژ همان جواب کاردانو را می دهد. روش لاگرانژ را می توان مستقیماً برای معادله مکعبی عمومی ax 3 + bx 2 + cx + d = 0 به کار برد، اما محاسبه با معادله مکعبی کاهش یافته، t 3 + pt + q = 0 ساده تر است .
ایده اصلی لاگرانژ کار با تبدیل فوریه گسسته ریشه ها به جای خود ریشه ها بود. به طور دقیق تر، اجازه دهید ξ یک ریشه سوم ابتدایی وحدت باشد، یعنی عددی به گونه ای که ξ 3 = 1 و ξ 2 + ξ + 1 = 0 (هنگام کار در فضای اعداد مختلط ،
تبدیل فوریه گسسته ریشه ها باشد. اگر s 0 ، s 1 و s 2 شناخته شده باشند، ممکن است ریشه ها با تبدیل فوریه معکوس که شامل معکوس کردن این تبدیل خطی است، از آنها بازیابی شوند. به این معنا که،
با فرمول ویتا ، s 0 در مورد یک مکعب افسرده صفر است و -ب/آبرای مکعب عمومی بنابراین، فقط s 1 و s 2 باید محاسبه شوند. آنها توابع متقارن ریشه نیستند (مبادله x 1 و x 2 نیز s 1 و s 2 )، اما برخی از توابع متقارن ساده s 1 و s 2 نیز در ریشه های معادله مکعبی متقارن هستند که باید حل شوند. بنابراین، این توابع متقارن را می توان بر حسب ضرایب (معلوم) مکعب اصلی بیان کرد، و این اجازه می دهد تا در نهایت s i را بیان کنیم.به عنوان ریشه های یک چند جمله ای با ضرایب شناخته شده. این برای هر درجه به خوبی جواب میدهد، اما در درجات بالاتر از چهار، چند جملهای بهدستآمده که دارای s i بهعنوان ریشه است، درجهای بالاتر از چند جملهای اولیه دارد، و بنابراین برای حل مفید نیست. این دلیلی است که روش لاگرانژ در درجات پنج و بالاتر شکست می خورد.
در مورد یک معادله مکعبی،






در مورد مکعب افسرده، یکی دارد





محاسبه S و P [ ویرایش ]
یک محاسبه ساده با استفاده از روابط ξ 3 = 1 و ξ 2 + ξ + 1 = 0 به دست می دهد
این نشان می دهد که P و S توابع متقارن ریشه ها هستند. با استفاده از هویت های نیوتن ، بیان آن ها بر حسب توابع متقارن ابتدایی ریشه ها ساده است.
با e 1 = 0 ، e 2 = p و e 3 = − q در مورد مکعب فرورفته، و e 1 = −ب/آ، e 2 =ج/آو e 3 = -د/آ، در حالت کلی.
برنامه های کاربردی [ ویرایش ]
معادلات مکعبی در زمینه های مختلف دیگر بوجود می آیند.
در ریاضیات [ ویرایش ]
- سه برش زاویه و دو برابر کردن مکعب دو مسئله باستانی هندسه هستند که ثابت شده است که با ساختن راسته و قطب نما قابل حل نیستند، زیرا معادل حل یک معادله مکعبی هستند.
- قضیه ماردن بیان می کند که کانون های بیضی اشتاینر هر مثلثی را می توان با استفاده از تابع مکعبی که ریشه های آن مختصات در صفحه مختلط سه رأس مثلث است، پیدا کرد. ریشه های اولین مشتق این مکعب مختصات مختلط آن کانون ها است.
- مساحت یک هفت ضلعی منتظم را می توان بر حسب ریشه یک مکعب بیان کرد. علاوه بر این، نسبت های مورب بلند به ضلع، ضلع به مورب کوتاه، و منفی مورب کوتاه به مورب بلند، همگی یک معادله مکعبی خاص را برآورده می کنند. علاوه بر این، نسبت شعاع به شعاع محیطی یک مثلث هفت ضلعی یکی از جواب های یک معادله مکعبی است. مقادیر توابع مثلثاتی زوایای مربوط به
معادلات مکعب را برآورده می کند.
- با توجه به کسینوس (یا تابع مثلثاتی دیگر) یک زاویه دلخواه، کسینوس یک سوم آن زاویه یکی از ریشه های یک مکعب است.
- حل معادله کوارتیک کلی به حل مکعب حلال آن متکی است .
- مقادیر ویژه یک ماتریس 3×3 ریشه های یک چند جمله ای مکعبی است که چند جمله ای مشخصه ماتریس است.
- معادله مشخصه ضرایب ثابت مرتبه سوم یا معادله دیفرانسیل خطی کوشی-اویلر (ضرایب متغیر همبعدی) یا معادله تفاوت یک معادله مکعبی است.
- نقاط تقاطع منحنی بزیه مکعبی و خط مستقیم را می توان با استفاده از معادله مکعبی مستقیم که منحنی بزیه را نشان می دهد محاسبه کرد.
- نقاط بحرانی یک تابع کوارتیک با حل یک معادله مکعبی (مجموعه مشتق برابر با صفر) پیدا می شود.
- نقاط عطف یک تابع پنجاهی ، حل یک معادله مکعبی است (مجموعه مشتق دوم برابر با صفر).
در سایر علوم [ ویرایش ]
- در شیمی تجزیه ، معادله شارلو ، که می تواند برای یافتن pH محلول های بافر استفاده شود ، می تواند با استفاده از یک معادله مکعبی حل شود.
- در ترمودینامیک ، معادلات حالت (که فشار، حجم و دمای یک ماده را به هم مرتبط میکند) حجم آن مکعب است.
- معادلات سینماتیکی شامل نرخ های شتاب خطی مکعبی هستند.
- سرعت امواج لرزه ای ریلی حل معادله مکعب موج ریلی است.
- سرعت حالت پایدار یک وسیله نقلیه که روی یک شیب با اصطکاک هوا حرکت می کند برای یک توان ورودی معین با یک معادله مکعبی فشرده حل می شود.
منبع
https://en.wikipedia.org/wiki/Cubic_equation





![{\displaystyle u={\sqrt[{3}]{-{\frac {q}{2}}+{\sqrt {{\frac {q^{2}}{4}}+{\frac {p ^{3}}{27}}}}}.}](https://wikimedia.org/api/rest_v1/media/math/render/svg/9d5bf9eaebfd5896d4f8dde09d59ff00381d33a9)
![{\displaystyle v={\sqrt[{3}]{-{\frac {q}{2}}-{\sqrt {{\frac {q^{2}}{4}}+{\frac {p ^{3}}{27}}}}}.}](https://wikimedia.org/api/rest_v1/media/math/render/svg/0a7232f72d8ec7b6cee76973ccfc6189a981b1dd)
![{\displaystyle t={\sqrt[{3}]{-{q \over 2}+{\sqrt {{q^{2} \over 4}+{p^{3} \over 27}}}} }+{\sqrt[{3}]{-{q \over 2}-{\sqrt {{q^{2} \over 4}+{p^{3} \over 27}}}}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/5d62f2e04f38bbf3c00fc86f15fe1a717fa25d82)








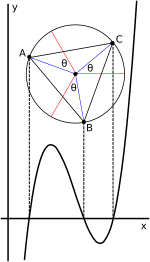

 یک زاویه در دایره واحد است. گرفتن1/3این زاویه مربوط به گرفتن یک ریشه مکعبی از یک عدد مختلط است. اضافه کردن - k2 π/3برای k = 1، 2 دیگر ریشه های مکعبی را پیدا می کند. و ضرب کسینوس این زوایای حاصل در
یک زاویه در دایره واحد است. گرفتن1/3این زاویه مربوط به گرفتن یک ریشه مکعبی از یک عدد مختلط است. اضافه کردن - k2 π/3برای k = 1، 2 دیگر ریشه های مکعبی را پیدا می کند. و ضرب کسینوس این زوایای حاصل در برای مقیاس تصحیح می کند.
برای مقیاس تصحیح می کند.

 تغییر علامت در صورت رد و بدل شدن دو ریشه،
تغییر علامت در صورت رد و بدل شدن دو ریشه،
![{\displaystyle t_{k}=2\,{\sqrt {-{\frac {p}{3}}}}\,\cos \left[\,{\frac {1}{3}}\arccos \ چپ ({\frac {3q}{2p}}{\sqrt {\frac {-3}{p}}}\,\right)-{\frac {2\pi k}{3}}\,\right ]\qquad {\text{برای }}k=0،1،2.}](https://wikimedia.org/api/rest_v1/media/math/render/svg/1852f999463435d82a62acdf648b210b1794be56)
 ). در غیر این صورت، هنوز درست است، اما زمانی که فقط یک ریشه واقعی وجود دارد، کسینوسهای مختلط و آرکوزینها را شامل میشود، و زمانی که p = 0 باشد، بی معنی است (تقسیم بر صفر) .
). در غیر این صورت، هنوز درست است، اما زمانی که فقط یک ریشه واقعی وجود دارد، کسینوسهای مختلط و آرکوزینها را شامل میشود، و زمانی که p = 0 باشد، بی معنی است (تقسیم بر صفر) .
 و معادله را بر تقسیم کنید
و معادله را بر تقسیم کنید این می دهد
این می دهد

![{\displaystyle t_{k}=2\,{\sqrt {-{\frac {p}{3}}}}\,\cos \left[{\frac {1}{3}}\arccos \left( {\frac {3q}{2p}}{\sqrt {\frac {-3}{p}}}\right)-{\frac {2\pi k}{3}}\right]\qquad {\text {برای }}k=0،1،2.}](https://wikimedia.org/api/rest_v1/media/math/render/svg/a702d0b6878463d3444d0ae34beee3fb9ea2d1c3)
![{\displaystyle {\begin{aligned}t_{0}&=-2{\frac {|q|}{q}}{\sqrt {-{\frac {p}{3}}}}\cosh \left [{\frac {1}{3}}\operatorname {arcosh} \left({\frac {-3|q|}{2p}}{\sqrt {\frac {-3}{p}}}\راست )\right]\qquad {\text{if }}~4p^{3}+27q^{2}>0~{\text{ and }}~p<0,\\t_{0}&=-2 {\sqrt {\frac {p}{3}}}\sinh \left[{\frac {1}{3}}\operatorname {arsinh} \left({\frac {3q}{2p}}{\sqrt {\frac {3}{p}}}\right)\right]\qquad {\text{if }}~p>0.\end{aligned}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/c4db866023eccccd6a208cdff730a2614478b136)


![{\displaystyle {\sqrt[{3}]{-{\frac {q}{2}}+{\sqrt {{\frac {q^{2}}{4}}+{\frac {p^{ 3}}{27}}}}}}+{\sqrt[{3}]{-{\frac {q}{2}}-{\sqrt {{\frac {q^{2}}{4} }+{\frac {p^{3}}{27}}}}}}.}](https://wikimedia.org/api/rest_v1/media/math/render/svg/56ea527f89e3bdb66eca0e1c1a5bb4a5512358df)
 و مکعب دیگر ریشه توسط
و مکعب دیگر ریشه توسط
 و
و![{\displaystyle {\sqrt[{3}]{{~}^{~}}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/24d9ec8c0118de0d1a1c4002b6edfa9a90209ddf) به عنوان نشان دهنده
به عنوان نشان دهنده ![{\displaystyle C-{\frac {p}{3C}}\quad {\text{with}}\quad C={\sqrt[{3}]{-{\frac {q}{2}}+{ \sqrt {{\frac {q^{2}}{4}}+{\frac {p^{3}}{27}}}}}}.}](https://wikimedia.org/api/rest_v1/media/math/render/svg/c87abe575ce3101b7076ebb7dd0b960d85195d3f)

 و زمانی که چند جمله ای مکعبی
و زمانی که چند جمله ای مکعبی 

 و
و را می توان به عنوان
را می توان به عنوان ![{\displaystyle C={\sqrt[{3}]{\frac {\Delta _{1}\pm {\sqrt {\Delta _{1}^{2}-4\Delta _{0}^{3 }}}}{2}}}،}](https://wikimedia.org/api/rest_v1/media/math/render/svg/57102b328503b04914d43ce3ab469e53c6fad58d)
 سپس علامت دیگر باید به جای آن انتخاب شود. اگر هر دو گزینه C = 0 را به دست آورند ، یعنی اگر
سپس علامت دیگر باید به جای آن انتخاب شود. اگر هر دو گزینه C = 0 را به دست آورند ، یعنی اگر یک کسری0/0در فرمول های زیر رخ می دهد که باید برابر با صفر تفسیر شوند (به انتهای این بخش مراجعه کنید). سپس، یکی از ریشه ها است
یک کسری0/0در فرمول های زیر رخ می دهد که باید برابر با صفر تفسیر شوند (به انتهای این بخش مراجعه کنید). سپس، یکی از ریشه ها است

 به این معنی که چند جمله ای مکعبی را می توان به صورت فاکتور گرفت
به این معنی که چند جمله ای مکعبی را می توان به صورت فاکتور گرفت یک محاسبه ساده اجازه می دهد تا تأیید شود که وجود این فاکتورگیری معادل است
یک محاسبه ساده اجازه می دهد تا تأیید شود که وجود این فاکتورگیری معادل است




 معادله اصلی مربوط به ریشه است
معادله اصلی مربوط به ریشه است معادله کاهش یافته توسط روابط
معادله کاهش یافته توسط روابط
 .
. سپس ممیز است
سپس ممیز است

 است
است
 و متمایز مکعب کاهش یافته مربوطه. با استفاده از فرمول مربوط به مکعب عمومی و مکعب کاهش یافته مرتبط، به این معنی است که تفکیک مکعب عمومی را می توان به صورت نوشتاری
و متمایز مکعب کاهش یافته مربوطه. با استفاده از فرمول مربوط به مکعب عمومی و مکعب کاهش یافته مرتبط، به این معنی است که تفکیک مکعب عمومی را می توان به صورت نوشتاری
 صفر نیست، دو حالت وجود دارد:
صفر نیست، دو حالت وجود دارد: مکعب دارای سه
مکعب دارای سه 



 صفر است اگر
صفر است اگر اگر p نیز صفر باشد، p = q = 0 ، و 0 یک ریشه سه برابری مکعب است. اگر
اگر p نیز صفر باشد، p = q = 0 ، و 0 یک ریشه سه برابری مکعب است. اگر و p ≠ 0 ، سپس مکعب یک ریشه ساده دارد
و p ≠ 0 ، سپس مکعب یک ریشه ساده دارد


 پس صفر است
پس صفر است مکعب یک ریشه سه گانه دارد
مکعب یک ریشه سه گانه دارد

 مکعب یک ریشه دوتایی دارد
مکعب یک ریشه دوتایی دارد






 و ریشه های دیگر ریشه های عامل دیگر هستند که با
و ریشه های دیگر ریشه های عامل دیگر هستند که با 


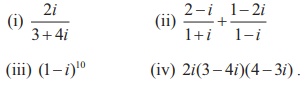
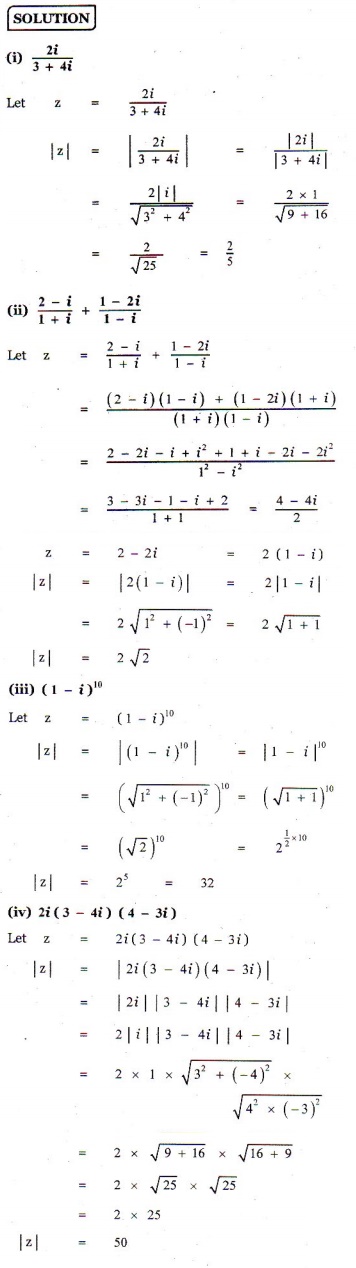


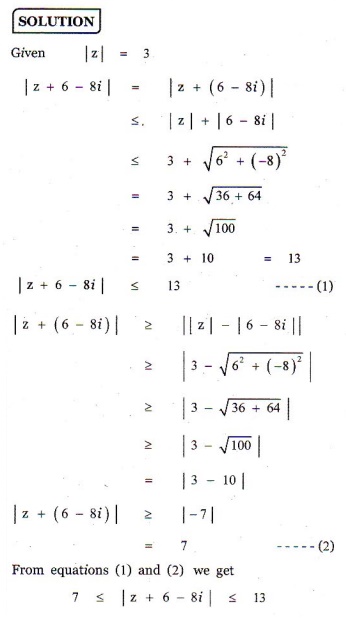






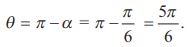

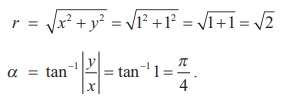
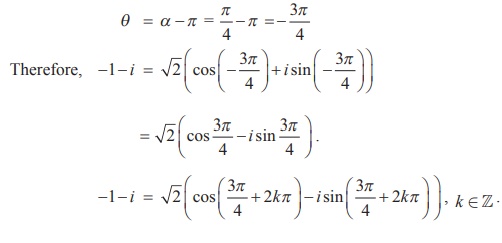
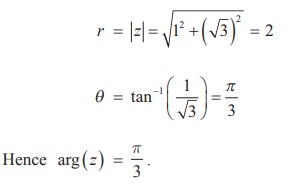
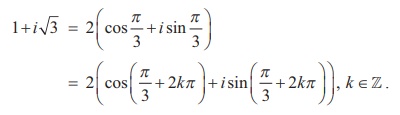

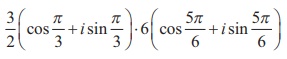
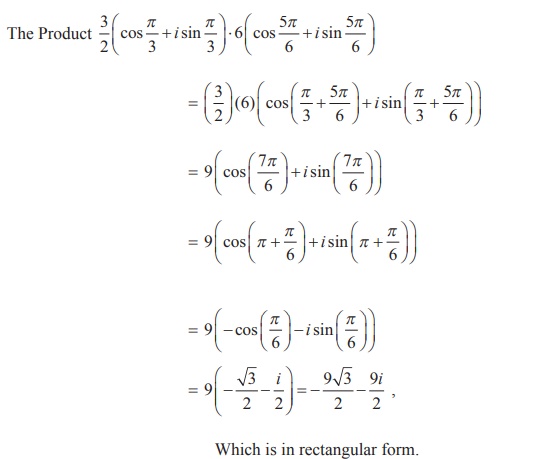
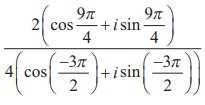
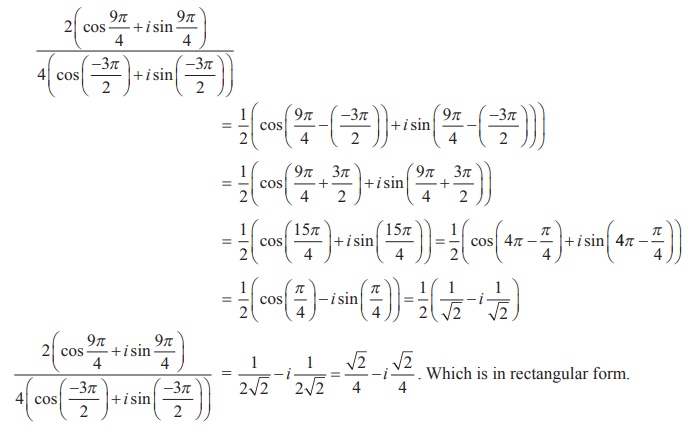
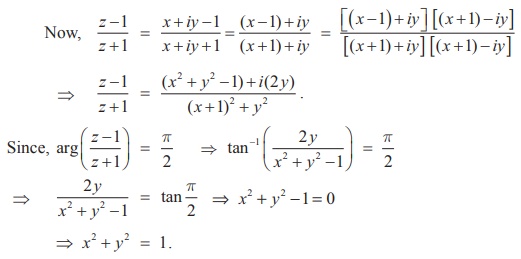

 و
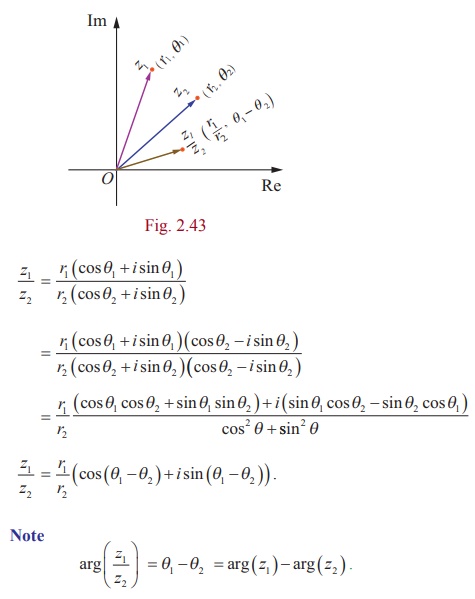
و ، فرمول د موآور این را بیان می کند
، فرمول د موآور این را بیان می کند یا معادل آن
یا معادل آن در این مثال، به راحتی می توان با ضرب سمت چپ، صحت معادله را بررسی کرد.
در این مثال، به راحتی می توان با ضرب سمت چپ، صحت معادله را بررسی کرد. که رابطه اساسی بین توابع مثلثاتی و تابع نمایی مختلط برقرار می کند.
که رابطه اساسی بین توابع مثلثاتی و تابع نمایی مختلط برقرار می کند.
 در حالی که سمت راست برابر است با
در حالی که سمت راست برابر است با












 اگر n یک
اگر n یک 










![{\displaystyle {\sqrt[{3}]{Q}}={\sqrt[{3}]{2}}(\cos \theta +\varepsilon \sin \theta )\qquad {\mbox{for }} \theta ={\frac {\pi }{9}},{\frac {7\pi }{9}},{\frac {13\pi }{9}}.}](https://wikimedia.org/api/rest_v1/media/math/render/svg/d01ac20f4cc5be35fb0488a9321a3069e9ef06b2)
 . سپس
. سپس . این حقیقیت (اگرچه می توان آن را به همان روشی که برای اعداد مختلط ثابت کرد) نتیجه مستقیم این حقیقت است که فضای ماتریس های نوع
. این حقیقیت (اگرچه می توان آن را به همان روشی که برای اعداد مختلط ثابت کرد) نتیجه مستقیم این حقیقت است که فضای ماتریس های نوع نسبت به
نسبت به 

 به شکل s + bi بنویسید .
به شکل s + bi بنویسید .
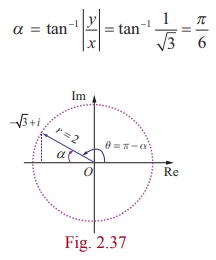
 و sin α = ½، α باید در ربع اول و α = 30 درجه باشد. از این رو،
و sin α = ½، α باید در ربع اول و α = 30 درجه باشد. از این رو،
 به شکل a + bi بنویسید .
به شکل a + bi بنویسید .
 و sin
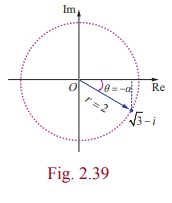
و sin  ، α باید در ربع چهارم باشد و α = 315 درجه باشد. از این رو،
، α باید در ربع چهارم باشد و α = 315 درجه باشد. از این رو،



 که به صورت مثلثاتی بیان شده اند کدامند؟
که به صورت مثلثاتی بیان شده اند کدامند؟
 و sin α = ½، α در ربع اول و α = 30 درجه است. بنابراین، از آنجایی که سینوس و کسینوس تناوبی هستند،
و sin α = ½، α در ربع اول و α = 30 درجه است. بنابراین، از آنجایی که سینوس و کسینوس تناوبی هستند،



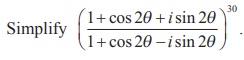
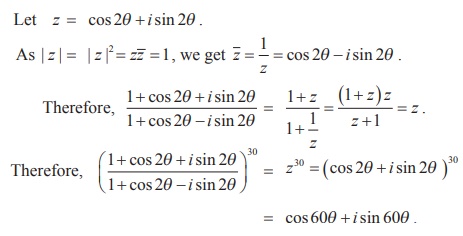

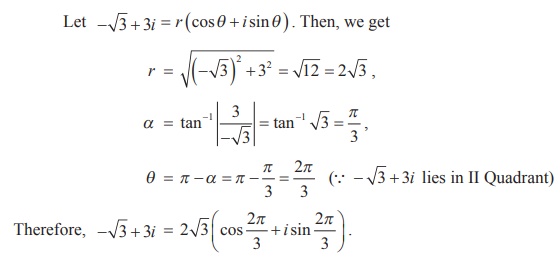
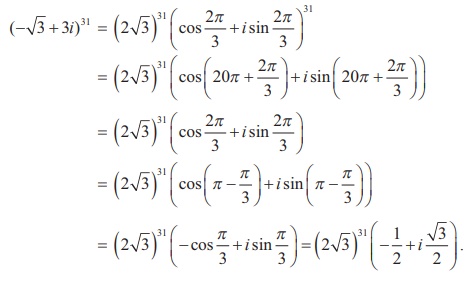
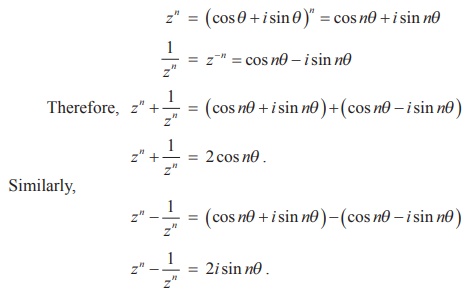
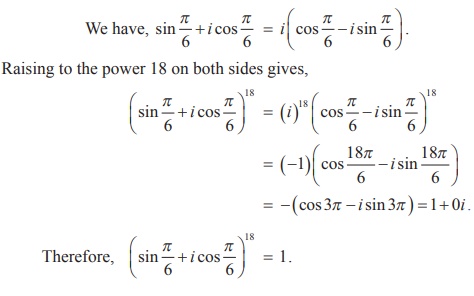





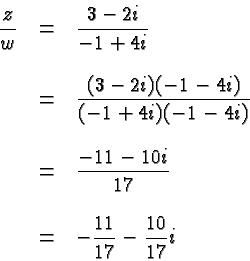













 عبارات پیچیده را ساده کنید:
عبارات پیچیده را ساده کنید:
 قدر مطلق یک عدد مختلط را بیابید:
قدر مطلق یک عدد مختلط را بیابید:
 مجموع، تفاضل و حاصل ضرب اعداد مختلط x و y را بیابید :
مجموع، تفاضل و حاصل ضرب اعداد مختلط x و y را بیابید :
 ضریب اعداد مختلط را بیابید:
ضریب اعداد مختلط را بیابید:
 یک عدد مختلط را به شکل مثلثاتی بنویسید:
یک عدد مختلط را به شکل مثلثاتی بنویسید:
 یک عدد مختلط را به شکل جبری بنویسید:
یک عدد مختلط را به شکل جبری بنویسید:
 توان یک عدد مختلط را پیدا کنید:
توان یک عدد مختلط را پیدا کنید:
 حل معادلات مختلط:
حل معادلات مختلط:










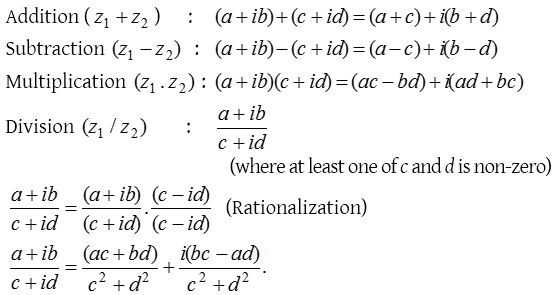


 در این وبلاگ به ریاضیات و کاربردهای آن و تحقیقات در آنها پرداخته می شود. مطالب در این وبلاگ ترجمه سطحی و اولیه است و کامل نیست.در صورتی سوال یا نظری در زمینه ریاضیات دارید مطرح نمایید .در صورت امکان به آن می پردازم. من دوست دارم برای یافتن پاسخ به سوالات و حل پروژه های علمی با دیگران همکاری نمایم.در صورتی که شما هم بامن هم عقیده هستید با من تماس بگیرید.
در این وبلاگ به ریاضیات و کاربردهای آن و تحقیقات در آنها پرداخته می شود. مطالب در این وبلاگ ترجمه سطحی و اولیه است و کامل نیست.در صورتی سوال یا نظری در زمینه ریاضیات دارید مطرح نمایید .در صورت امکان به آن می پردازم. من دوست دارم برای یافتن پاسخ به سوالات و حل پروژه های علمی با دیگران همکاری نمایم.در صورتی که شما هم بامن هم عقیده هستید با من تماس بگیرید.