از ویکیپدیا، دانشنامه آزاد
| این مقاله ممکن است برای اکثر خوانندگان برای درک آن بسیار فنی باشد . لطفاً بدون حذف جزئیات فنی، به بهبود آن کمک کنید تا برای افراد غیر متخصص قابل درک باشد . ( سپتامبر 2018 ) ( نحوه و زمان حذف این پیام الگو را بیاموزید ) |
"رویداد فاجعه بار" به اینجا هدایت می شود. برای دیگر کاربردها، فاجعه را ببینید ببینید .
در ریاضیات , نظریه فاجعه شاخه ای از نظریه انشعاب در مطالعه سیستم های دینامیکی است . همچنین یک مورد خاص خاص از نظریه تکینگی عمومی تر است عمومی تر در هندسه .
نظریه انشعاب پدیدههایی را که با تغییرات ناگهانی در رفتار ناشی از تغییرات کوچک در شرایط مشخص میشوند، مطالعه و طبقهبندی میکند و تجزیه و تحلیل میکند که چگونه ماهیت کیفی جوابهای معادله به پارامترهایی که در معادله ظاهر میشوند بستگی دارد. این ممکن است منجر به تغییرات ناگهانی و چشمگیر شود، برای مثال زمان و اندازه غیرقابل پیش بینی غیرقابل پیش بینی یک زمین لغزش .
نظریه فاجعه با کار ریاضیدان فرانسوی رنه تام در دهه 1960 سرچشمه گرفت و به دلیل تلاش های کریستوفر زیمن در دهه 1970 بسیار محبوب شد. این مورد خاص را در نظر می گیرد که در آن تعادل پایدار بلندمدت می تواند به عنوان حداقل یک تابع بالقوه صاف و کاملاً تعریف شده شناسایی شود ( تابع لیاپانوف). تغییرات کوچک در پارامترهای خاصی از یک سیستم غیرخطی می تواند باعث ظاهر یا ناپدید شدن تعادل و یا تغییر از جذب به دفع کننده و بالعکس شود و منجر به تغییرات بزرگ و ناگهانی در رفتار سیستم شود. با این حال، بررسی در یک فضای پارامتر بزرگتر، تئوری فاجعه نشان می دهد که چنین نقاط انشعاب تمایل دارند به عنوان بخشی از ساختارهای هندسی کیفی به خوبی تعریف شده رخ دهند.
در اواخر دهه 1970، کاربردهای تئوری فاجعه در حوزه های خارج از محدوده آن، به ویژه در زیست شناسی و علوم اجتماعی مورد انتقاد قرار گرفت. [1] [2] Zahler و Sussmann، در مقالهای در سال 1977 در Nature ، به چنین کاربردهایی اشاره کردند که "با استدلال نادرست، فرضیات دور از ذهن، پیامدهای نادرست و ادعاهای اغراق آمیز مشخص می شوند". [3] در نتیجه، نظریه فاجعه در کاربردها کمتر محبوب شده است. [4]
فجایع ابتدایی [ ویرایش ]
نظریه فاجعه نقاط بحرانی منحط تابع پتانسیل را تجزیه و تحلیل می کند - نقاطی که نه فقط مشتق اول، بلکه یک یا چند مشتق بالاتر تابع بالقوه نیز صفر هستند. اینها را میکروب هندسه فاجعه می نامند . انحطاط این نقاط بحرانی را می توان با گسترش عملکرد بالقوه به عنوان یک سری تیلور آشکار کرد . در اختلالات کوچک پارامترها
هنگامی که نقاط انحطاط صرفا تصادفی نیستند، بلکه از نظر ساختاری پایدار هستند ، نقاط انحطاط به عنوان مراکز سازماندهی برای ساختارهای هندسی خاص با انحطاط پایینتر، با ویژگیهای حیاتی در فضای پارامتر اطرافشان وجود دارند. اگر تابع پتانسیل به دو یا کمتر متغیر فعال و چهار یا کمتر پارامتر فعال بستگی داشته باشد، آنگاه تنها هفت ساختار عمومی برای این هندسههای انشعاب وجود دارد، با فرمهای استاندارد متناظر که سری تیلور در اطراف میکروبهای فاجعه را میتوان با دیفئومورفیسم تبدیل کرد . یک تبدیل صاف که عکس آن نیز صاف است). [ نیاز به نقل از ] این هفت نوع اساسی اکنون با نام هایی که تام به آنها داده است، ارائه شده است.
توابع بالقوه یک متغیر فعال [ ویرایش ]
نظریه فاجعه سیستم های دینامیکی را مطالعه می کند که تکامل [5] یک متغیر حالت را توصیف می کندایکس

در معادله فوق،�



فولد فاجعه [ ویرایش ]
فولد فاجعه، با سطح
یک جفت اکسترمای پایدار و ناپایدار در یک انشعاب چین ناپدید می شوند
هنگامی که a < 0 است ، پتانسیل V دو انتها دارد - یکی پایدار و دیگری ناپایدار. اگر پارامتر a به آرامی افزایش یابد، سیستم می تواند حداقل نقطه پایدار را دنبال کند. اما در a = 0 اکسترمای پایدار و ناپایدار به هم می رسند و نابود می شوند. این نقطه انشعاب است. در > 0 دیگر راه حل پایداری وجود ندارد. اگر یک سیستم فیزیکی از طریق یک انشعاب چین دنبال شود، بنابراین متوجه میشویم که با رسیدن به 0، پایداری a < 0 ناگهان از بین میرود و سیستم یک انتقال ناگهانی به یک رفتار جدید و بسیار متفاوت انجام میدهد. این مقدار انشعاب پارامتر a گاهی اوقات " نقطه اوج " نامیده می شود.
فاجعه کاسپ [ ویرایش ]
فاجعه کاسپ، با سطح
هندسه کاسپ زمانی بسیار متداول است که اگر پارامتر دوم، b به فضای کنترل اضافه شود، چه اتفاقی برای انشعاب چین می افتد . با تغییر پارامترها، میبینیم که اکنون یک منحنی (آبی) از نقاط در فضای ( a ، b ) وجود دارد که در آن ثبات از بین میرود، جایی که راهحل پایدار ناگهان به یک نتیجه جایگزین میرود.
اما در هندسه کاسپ، منحنی انشعاب به خودش حلقه میزند و شاخه دومی را ایجاد میکند که خود این محلول جایگزین ثبات خود را از دست میدهد و به مجموعه راهحل اصلی پرش میکند. بنابراین، با افزایش مکرر b و سپس کاهش آن، میتوان حلقههای پسماند را مشاهده کرد، زیرا سیستم به طور متناوب از یک راهحل پیروی میکند، به راهحل دیگر میپرد، دیگری را به عقب دنبال میکند و سپس به اولین راهحل بازمیگردد.
با این حال، این تنها در منطقه فضای پارامتر a < 0 امکان پذیر است . با افزایش a ، حلقههای پسماند کوچکتر و کوچکتر میشوند، تا زمانی که بالای a = 0 به طور کلی ناپدید شوند (فاجعه کاسپ)، و تنها یک راهحل پایدار وجود دارد.
همچنین میتوان در نظر گرفت که اگر b را ثابت نگه داریم و a را تغییر دهیم، چه اتفاقی میافتد . در حالت متقارن b = 0 ، یک انشعاب چنگال را با کاهش a مشاهده میکنیم، که یک محلول پایدار به طور ناگهانی به دو محلول پایدار و یک محلول ناپایدار با عبور سیستم فیزیکی به یک <0 از نقطه کاسپ (0,0) تقسیم میشود. (نمونه ای از شکستن تقارن خود به خود ). دور از نقطه اوج، هیچ تغییر ناگهانی در یک راه حل فیزیکی وجود ندارد: هنگام عبور از منحنی دوشاخه های چین، تنها چیزی که اتفاق می افتد این است که یک راه حل دوم جایگزین در دسترس است.
یک پیشنهاد معروف این است که می توان از فاجعه کاسپ برای مدل سازی رفتار یک سگ استرس استفاده کرد که ممکن است با گاو شدن یا عصبانی شدن پاسخ دهد. [6] پیشنهاد این است که در استرس متوسط ( a > 0 )، سگ یک انتقال آرام از پاسخ از گاو به عصبانی را نشان می دهد، بسته به اینکه چگونه تحریک می شود. اما سطوح استرس بالاتر مربوط به حرکت به منطقه است ( a < 0 ). سپس، اگر سگ شروع به گاو زدن کند، همچنان که بیشتر و بیشتر تحریک میشود، گاو باقی میماند، تا زمانی که به نقطه چین برسد، زمانی که ناگهان و بطور ناپیوسته به حالت عصبانیت میرسد. هنگامی که در حالت "عصبانی" قرار می گیرد، حتی اگر پارامتر تحریک مستقیم به میزان قابل توجهی کاهش یابد، عصبانی باقی می ماند.
یک سیستم مکانیکی ساده، "ماشین فاجعه زیمن"، به خوبی یک فاجعه کاسپ را نشان می دهد. در این دستگاه، تغییرات صاف در موقعیت انتهای فنر می تواند باعث تغییرات ناگهانی در موقعیت چرخشی چرخ متصل شود. [7]
شکست فاجعه بار یک سیستم پیچیده با افزونگی موازی را می توان بر اساس رابطه بین تنش های محلی و خارجی ارزیابی کرد. مدل مکانیک شکست ساختاری مشابه رفتار فاجعه کاسپ است. این مدل توانایی ذخیره یک سیستم پیچیده را پیشبینی میکند.
کاربردهای دیگر شامل انتقال الکترون کره بیرونی است که اغلب در سیستمهای شیمیایی و بیولوژیکی با آن مواجه میشود، [8] مدلسازی دینامیک هستههای تراکم ابر در جو، [9] و مدلسازی قیمتهای املاک و مستغلات. [10]
انشعاب های چین و هندسه کاسپ تا حد زیادی مهم ترین پیامدهای عملی تئوری فاجعه هستند. آنها الگوهایی هستند که بارها و بارها در فیزیک، مهندسی و مدل سازی ریاضی تکرار می شوند. آنها رویدادهای عدسی گرانشی قوی را تولید می کنند و یکی از روش های مورد استفاده برای تشخیص سیاهچاله ها و ماده تاریک جهان را از طریق پدیده عدسی گرانشی که تصاویر متعددی از اختروش های دور ایجاد می کند، در اختیار ستاره شناسان قرار می دهند . [11]
هندسه های فاجعه ساده باقی مانده در مقایسه بسیار تخصصی هستند و فقط برای ارزش کنجکاوی در اینجا ارائه شده اند.
فاجعه دم چلچله [ ویرایش ]
فاجعه دم چلچله، با سطح
سطح فاجعه دم چلچله
فضای پارامتر کنترل سه بعدی است. مجموعه انشعاب در فضای پارامتر از سه سطح انشعاب چینی تشکیل شده است که در دو خط انشعاب کاسپ به هم می رسند که به نوبه خود در یک نقطه انشعاب دم چلچله به هم می رسند.
با عبور پارامترها از سطح انشعاب های چین، یک حداقل و یک حداکثر تابع پتانسیل ناپدید می شوند. در انشعاب های کاسپ، دو حداقل و یک حداکثر با یک حداقل جایگزین می شوند. فراتر از آنها، دوشاخه های چین ناپدید می شوند. در نقطه دم چلچله دو مینیمم و دو ماکزیمم همگی در یک مقدار x به هم می رسند . برای مقادیر a > 0 ، فراتر از دم چلچله ای، بسته به مقادیر b و c ، یا یک جفت حداکثر-حداقل وجود دارد یا اصلاً هیچ یک وجود ندارد . دو تا از سطوح انشعاب های چین خورده، و دو خط انشعاب های کاسپ جایی که برای < 0 به هم می رسندبنابراین در نقطه دم چلچله ناپدید می شوند و تنها یک سطح از دوشاخه های چین باقی مانده است. آخرین نقاشی سالوادور دالی ، دم پرستو ، بر اساس این فاجعه ساخته شده است.
فاجعه پروانه [ ویرایش ]
فاجعه پروانه، با سطح
بسته به مقادیر پارامتر، تابع پتانسیل ممکن است سه، دو یا یک مینیمم محلی متفاوت داشته باشد که توسط مکان های انشعاب چین از هم جدا شده اند. در نقطه پروانه، 3 سطح مختلف انشعاب چین، 2 سطح انشعاب کاسپ، و خطوط انشعاب دم چلچله همگی به هم می رسند و ناپدید می شوند، و زمانی که 0 > یک ساختار کاسپ باقی می ماند .
توابع بالقوه دو متغیر فعال [ ویرایش ]
سطحی با ناف هذلولی و سطح کانونی آن. فاجعه هذلولی ناف فقط قسمت بالایی این تصویر است.
سطحی با ناف بیضی شکل و سطح کانونی آن. فاجعه ناف بیضوی فقط قسمت بالایی این تصویر است.
فاجعه های ناف نمونه هایی از فاجعه های کورانک 2 هستند. آنها را می توان در اپتیک در سطوح کانونی مشاهده کرد که توسط نور منعکس شده از یک سطح به صورت سه بعدی ایجاد می شود و ارتباط نزدیکی با هندسه سطوح تقریباً کروی دارند: نقطه نافی . تام پیشنهاد کرد که فاجعه ناف هذلولی شکستن یک موج را مدلسازی می کند و ناف بیضوی ایجاد ساختارهای مو مانند را مدل می کند.
فاجعه ناف هذلولی [ ویرایش ]
فاجعه ناف بیضوی [ ویرایش ]
فاجعه ناف سهموی [ ویرایش ]
نماد آرنولد [ ویرایش ]
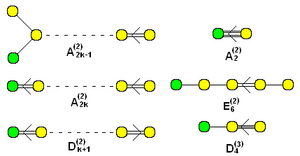
ولادیمیر آرنولد به دلیل ارتباط عمیق با گروه های ساده Lie به فاجعه ها طبقه بندی ADE داد . [ نیازمند منبع ]
- A 0 - یک نقطه غیر مفرد:
.
- الف 1 - یک اکسترمم موضعی، یا حداقل پایدار یا حداکثر ناپایدار
.
- الف 2 - تاشو
- الف 3 - کاسپ
- الف 4 - دم چلچله
- الف 5 - پروانه
- A k - نماینده یک دنباله نامتناهی از یک متغیر است
- D 4 - - ناف بیضوی
- D 4 + - ناف هذلولی
- د 5 - ناف سهمی
- D k - نماینده یک دنباله بی نهایت از اشکال ناف بیشتر
- E 6 - ناف نمادین
- E 7
- E 8
در نظریه تکینگی اشیایی وجود دارند که با اکثر گروههای ساده Lie مطابقت دارند.























 ، اگر غیر صفر باشد، شرایط زیر معادل هستند:
، اگر غیر صفر باشد، شرایط زیر معادل هستند:![{\mathfrak g}=[{\mathfrak g}،{\mathfrak g}]](https://wikimedia.org/api/rest_v1/media/math/render/svg/333cc17f062c6ef61f6bb26e09a4eda3d1116ef5) . به طور خاص، هر جبر لی نیمه ساده خطی یک جبر فرعی از است
. به طور خاص، هر جبر لی نیمه ساده خطی یک جبر فرعی از است ,
,  تزریقی است علاوه بر این، تصویر
تزریقی است علاوه بر این، تصویر  از
از  یک یکریختی است.
یک یکریختی است. ![{\displaystyle {\mathfrak {g}}/[{\mathfrak {g}}،{\mathfrak {g}}]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/483af7f49dfeb78dacd52249b9a6c04a91a9664a) نیمه ساده و آبلی است).
نیمه ساده و آبلی است).  برای هر پسوند فیلد نیمه ساده استاف⊃ک
برای هر پسوند فیلد نیمه ساده استاف⊃ک .
. 
 یک عملگر نیمه ساده (به عبارت دیگر پوچتوان) است.
یک عملگر نیمه ساده (به عبارت دیگر پوچتوان) است.  ، سپس تجزیه انتزاعی جردن بیان می کند که x را می توان به صورت منحصر به فرد نوشت:
، سپس تجزیه انتزاعی جردن بیان می کند که x را می توان به صورت منحصر به فرد نوشت:
 نیمه ساده است،
نیمه ساده است، پوچتوان است و
پوچتوان است و![{\displaystyle [s,n]=0}](https://wikimedia.org/api/rest_v1/media/math/render/svg/d07b8da250f1af66474583a1c6a2b583571eeb22) .
.  با x رفت و آمد می کند ، سپس با هر دو رفت و آمد می کند
با x رفت و آمد می کند ، سپس با هر دو رفت و آمد می کند همچنین.
همچنین.
 از
از ،
،

 از
از![{\displaystyle {\mathfrak {g}}_{\alpha }=\{x\in {\mathfrak {g}}|[h,x]=\alpha (h)x\,{\text{ برای همه } }h\in {\mathfrak {h}}\}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/9fa7d22607d30bbf4e1209d5cbcac9906a0e44e1) .
.
 و تجزیه وجود دارد (به عنوان یک
و تجزیه وجود دارد (به عنوان یک
 مجموعه ای از همه تابع های خطی غیر صفر است
مجموعه ای از همه تابع های خطی غیر صفر است . علاوه بر این، برای هر یک،
. علاوه بر این، برای هر یک، ،
،![{\displaystyle [{\mathfrak {g}}_{\alpha },{\mathfrak {g}}_{\beta }]\subseteq {\mathfrak {g}}_{\alpha +\beta }}](https://wikimedia.org/api/rest_v1/media/math/render/svg/424f39d8174b6699d28e5cab065b64851e628930) ، که برابری اگر است
، که برابری اگر است .
.![{\displaystyle [{\mathfrak {g}}_{\alpha },{\mathfrak {g}}_{-\alpha }]\oplus {\mathfrak {g}}_{-\alpha }\oplus {\ mathfrak {g}}_{\alpha }\simeq {\mathfrak {sl}}_{2}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/edf52deacb0d5efa28767c6917c82ca2920412f4) به عنوان جبر لی
به عنوان جبر لی ; به خصوص،
; به خصوص، .
. ; به عبارت دیگر،
; به عبارت دیگر، .
. متعامد با یکدیگر هستند اگر
متعامد با یکدیگر هستند اگر
 .)
.)
![{\displaystyle [e_{\alpha },f_{\alpha }]=h_{\alpha },[h_{\alpha },e_{\alpha }]=2e_{\alpha },[h_{\alpha }, f_{\alpha }]=-2f_{\alpha }}](https://wikimedia.org/api/rest_v1/media/math/render/svg/ce1ee98a2761028cb881bbb2dbd1f3ca6ae350f6) ; به عنوان مثال،،ه،
; به عنوان مثال،،ه، مطابق با اساس استاندارد از2
مطابق با اساس استاندارد از2 (از زمانی که اگر
(از زمانی که اگر ، سپس
، سپس در مرکز قرار دارد که صفر است.) علاوه بر این، از نظریه نمایش2
در مرکز قرار دارد که صفر است.) علاوه بر این، از نظریه نمایش2
 ).
). یک عدد صحیح است.
یک عدد صحیح است. دارای خواص
دارای خواص  و (2) مجموعه نقطه ثابت است
و (2) مجموعه نقطه ثابت است ، که به این معنی است
، که به این معنی است از
از
 و غیره. سپس3ل
و غیره. سپس3ل عناصر،من،من
عناصر،من،من (به نام مولدهای Chevalley ) تولید می کنند
(به نام مولدهای Chevalley ) تولید می کنند ،
،![{\displaystyle [h_{i},h_{j}]=0,}](https://wikimedia.org/api/rest_v1/media/math/render/svg/1609195c508362f0f7c9eafa6823994031bed0e6)
![{\displaystyle [e_{i},f_{i}]=h_{i},[e_{i},f_{j}]=0,i\neq j,}](https://wikimedia.org/api/rest_v1/media/math/render/svg/80ae0e126c47b8b23320418ebfcc7b2891f7820f)
![{\displaystyle [h_{i},e_{j}]=a_{ij}e_{j},[h_{i},f_{j}]=-a_{ij}f_{j},}](https://wikimedia.org/api/rest_v1/media/math/render/svg/2c45ac70c58df861756d2c3d8a4f427f9d6a403e)
 .
.![{\displaystyle [a_{ij}]_{1\leq i,j\leq l}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/e97673c49e8e3928eb710b3e7a2a919192ba0d1b)
 تولید شده توسطس
تولید شده توسطس و زیر جبر کارتن
و زیر جبر کارتن توسط
توسط ،
، نشان دهنده ماتریس مورب با
نشان دهنده ماتریس مورب با در مورب سپس تجزیه توسط داده می شود
در مورب سپس تجزیه توسط داده می شود

 که در
که در با مبنای استاندارد (ماتریسی)، معنی
با مبنای استاندارد (ماتریسی)، معنی - ردیف و
- ردیف و ستون -ام. این تجزیه از
ستون -ام. این تجزیه از
 تجزیه است
تجزیه است

 تجزیه است
تجزیه است

 (یا به طور کلی یک میدان بسته از نظر جبری با مشخصه صفر) توسط سیستم ریشه مرتبط با جبرهای فرعی کارتان طبقه بندی می شوند و سیستم های ریشه نیز به نوبه خود با نمودارهای دینکین طبقه بندی می شوند. نمونه هایی از جبرهای لی نیمه ساده،
(یا به طور کلی یک میدان بسته از نظر جبری با مشخصه صفر) توسط سیستم ریشه مرتبط با جبرهای فرعی کارتان طبقه بندی می شوند و سیستم های ریشه نیز به نوبه خود با نمودارهای دینکین طبقه بندی می شوند. نمونه هایی از جبرهای لی نیمه ساده،  +1
+1 ,
,  س2+1
س2+1 ، جبر لی متعامد
، جبر لی متعامد  سپ2
سپ2 ,
,  س2
س2 ،
،  ).
). خانواده مورد نیاز است زیرا
خانواده مورد نیاز است زیرا تک بعدی و جابجایی است و بنابراین نیمه ساده نیست.
تک بعدی و جابجایی است و بنابراین نیمه ساده نیست.
 . این چهار خانواده به همراه پنج استثنا (
. این چهار خانواده به همراه پنج استثنا ( 
 برای A n
برای A n  برای B n
برای B n  برای C n و
برای C n و برای D n . اگر کسی شروع به شماره گذاری کمتر کند، شمارش اضافی است، و بین جبرهای ساده لی هم
برای D n . اگر کسی شروع به شماره گذاری کمتر کند، شمارش اضافی است، و بین جبرهای ساده لی هم  جایی که
جایی که اگر ترکیبی خطی از ریشه های ساده با ضرایب صحیح غیر منفی باشد. فرض کنید
اگر ترکیبی خطی از ریشه های ساده با ضرایب صحیح غیر منفی باشد. فرض کنید ، که حداکثر زیر جبر قابل حل است
، که حداکثر زیر جبر قابل حل است -بردار
-بردار  ،
،  ، یک ساده وجود دارد
، یک ساده وجود دارد داشتن
داشتن به عنوان بالاترین وزن آن و (2) دو ماژول ساده با بالاترین وزن یکسان معادل هستند. به طور خلاصه، یک دوگانگی بین وجود دارد∗
به عنوان بالاترین وزن آن و (2) دو ماژول ساده با بالاترین وزن یکسان معادل هستند. به طور خلاصه، یک دوگانگی بین وجود دارد∗ ، منظور ما مخروط محدب است
، منظور ما مخروط محدب است جایی که∈[،-]
جایی که∈[،-]![{\displaystyle h_{\alpha }\in [{\mathfrak {g}}_{\alpha },{\mathfrak {g}}_{-\alpha }]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/223bf51f6caca4dd5f5fc26db27097f7c6b62d7a) یک بردار منحصر به فرد است به طوری که()=2
یک بردار منحصر به فرد است به طوری که()=2 . سپس این معیار چنین است:
. سپس این معیار چنین است:  اگر و فقط اگر، برای هر ریشه مثبت>0
اگر و فقط اگر، برای هر ریشه مثبت>0 یک عدد صحیح است و
یک عدد صحیح است و  .
. پیچیدگی آن (که باز هم نیمه ساده است). جبر لی حقیقی
پیچیدگی آن (که باز هم نیمه ساده است). جبر لی حقیقی . اگر شکل حقیقی روی آن منفی-معین باشد، فرم فشرده نامیده می شود. این لزوما جبر لی یک گروه لی فشرده است (از این رو، نام).
. اگر شکل حقیقی روی آن منفی-معین باشد، فرم فشرده نامیده می شود. این لزوما جبر لی یک گروه لی فشرده است (از این رو، نام). یک زیر فضای آبلی حداکثر. می توان نشان داد (به عنوان مثال، از حقیقیت
یک زیر فضای آبلی حداکثر. می توان نشان داد (به عنوان مثال، از حقیقیت زیر
زیر 
 به ارزش حقیقی استمن
به ارزش حقیقی استمن ; بنابراین، می توان با یک تابع حقیقی-خطی در فضای برداری حقیقی شناسایی کردمن
; بنابراین، می توان با یک تابع حقیقی-خطی در فضای برداری حقیقی شناسایی کردمن و بگیر
و بگیر . فرض کنید
. فرض کنید تابع خطی روی باشد
تابع خطی روی باشد برای
برای . سپس برای هر کدام
. سپس برای هر کدام ،
،![{\displaystyle [H,E_{ij}]=(e_{i}(H)-e_{j}(H))E_{ij}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/5d0e94dae98707390b3506002c4ee5e7c9c60472)
 ماتریسی است که دارای 1 در است
ماتریسی است که دارای 1 در است نقطه -ام و صفر در جای دیگر. از این رو، هر ریشه
نقطه -ام و صفر در جای دیگر. از این رو، هر ریشه و تجزیه فضای ریشه، تجزیه ماتریس ها است:
و تجزیه فضای ریشه، تجزیه ماتریس ها است: 
 و فرض کنید
و فرض کنید تجزیه فضای ویژه باشد
تجزیه فضای ویژه باشد به ترتیب فضاهای ویژه 1 و -1 هستند. به عنوان مثال، اگر
به ترتیب فضاهای ویژه 1 و -1 هستند. به عنوان مثال، اگر و
و .
. یک زیرفضای آبلی حداکثر باشد. اکنون،
یک زیرفضای آبلی حداکثر باشد. اکنون، متشکل از ماتریس های متقارن (با توجه به یک ضرب داخلی مناسب) و در نتیجه عملگرها در
متشکل از ماتریس های متقارن (با توجه به یک ضرب داخلی مناسب) و در نتیجه عملگرها در با مقادیر ویژه حقیقی به طور همزمان قابل قطریابی هستند. با تکرار آرگومان های فیلد پایه بسته جبری، تجزیه به دست می آید (به نام تجزیه فضای ریشه محدود ):
با مقادیر ویژه حقیقی به طور همزمان قابل قطریابی هستند. با تکرار آرگومان های فیلد پایه بسته جبری، تجزیه به دست می آید (به نام تجزیه فضای ریشه محدود ): 
 برای هر تابع خطی
برای هر تابع خطی ،
، .
. هر دو ریشه هستند).
هر دو ریشه هستند). ، سپس
، سپس ، ما آن را می بینیم
، ما آن را می بینیم رتبه دارد
رتبه دارد در این مورد ممکن است به عنوان ماتریس در نظر گرفته شود
در این مورد ممکن است به عنوان ماتریس در نظر گرفته شود با
با ، جایی که
، جایی که یک ماتریس مورب با ورودی های مورب است
یک ماتریس مورب با ورودی های مورب است ، پس داریم
، پس داریم![{\displaystyle [H,E_{i,j}]=(\lambda _{i}-\lambda _{j})E_{i,j}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/1094c5c1adc449497dcd14365d1010526dea7da5) .
. تابع های خطی هستند
تابع های خطی هستند داده شده توسط
داده شده توسط .
. در فضای
در فضای
 نیمه ساده است و
نیمه ساده است و تقلیل دهنده است. بسیاری از خصوصیات جبرهای لی نیمه ساده فقط به کاهش پذیری بستگی دارد.
تقلیل دهنده است. بسیاری از خصوصیات جبرهای لی نیمه ساده فقط به کاهش پذیری بستگی دارد. تقارن یک
تقارن یک  ، تشکیل شده توسط
، تشکیل شده توسط با افزودن یک بعد اضافی به جبر حلقه و اصلاح یک جابجایی به روشی غیر پیش پا افتاده به دست می آید که فیزیکدانان آن را
با افزودن یک بعد اضافی به جبر حلقه و اصلاح یک جابجایی به روشی غیر پیش پا افتاده به دست می آید که فیزیکدانان آن را  شامل
شامل![{\displaystyle {\mathfrak {g}}\otimes \mathbb {\mathbb {C} } [t,t^{-1}]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/5ffdf6ad5fdfdf601af98210f181594d5f7349b1) ، با مرکز تک بعدی.
، با مرکز تک بعدی. به عنوان یک فضای برداری،
به عنوان یک فضای برداری،![{\displaystyle {\widehat {\mathfrak {g}}}={\mathfrak {g}}\otimes \mathbb {\mathbb {C} } [t,t^{-1}]\oplus \mathbb {\mathbb {C} } c,}](https://wikimedia.org/api/rest_v1/media/math/render/svg/635a8df249d1af8333a3d01c61a53cebfcb48c66)
![{\displaystyle \mathbb {\mathbb {C} } [t,t^{-1}]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/24d3c75900023b6d276e960dc13a9858bb2efd13) فضای برداری مختلط
فضای برداری مختلط ![[a\otimes t^n+\alpha c, b\otime t^m+\beta c]=[a,b]\otimes t^{n+m}+\langle a|b\rangle n\delta_{m+ n,0}ج](https://wikimedia.org/api/rest_v1/media/math/render/svg/845b805b2d30f8eff9530c514eb2faf8a76f651c)
 و
و ، جایی که
، جایی که![[الف، ب]](https://wikimedia.org/api/rest_v1/media/math/render/svg/9c4b788fc5c637e26ee98b45f89a5c08c85f7935) براکت لی در جبر لی است
براکت لی در جبر لی است



 . در این مورد نیز باید n عنصر مرکزی دیگر برای n ژنراتور آبلی اضافه کرد.
. در این مورد نیز باید n عنصر مرکزی دیگر برای n ژنراتور آبلی اضافه کرد. . معرفی نماد،
. معرفی نماد، ، می توان تلاش کرد تا مبنای کارتان-ویل را گسترش دهد
، می توان تلاش کرد تا مبنای کارتان-ویل را گسترش دهد برای
برای ، با
، با تشکیل یک زیر جبر آبلی
تشکیل یک زیر جبر آبلی وآد(ج)
وآد(ج) بر
بر هستند
هستند و
و به ترتیب و مستقل از
به ترتیب و مستقل از برای.
برای.
 برای فرم کیلینگ در
برای فرم کیلینگ در برای فرم کیلینگ در جبر وابسته به Kac-Moody،
برای فرم کیلینگ در جبر وابسته به Kac-Moody،

 که در آن تنها آخرین معادله با عدم تغییر ثابت نمی شود و در عوض بر اساس قرارداد انتخاب می شود. قابل توجه، محدودیت از
که در آن تنها آخرین معادله با عدم تغییر ثابت نمی شود و در عوض بر اساس قرارداد انتخاب می شود. قابل توجه، محدودیت از زیرفضا یک فرم دوخطی با امضا می دهد
زیرفضا یک فرم دوخطی با امضا می دهد .
. . تعریف کردن
. تعریف کردن ، این را می توان بازنویسی کرد
، این را می توان بازنویسی کرد
 سپس
سپس غیر معمول است زیرا طول آن صفر است:
غیر معمول است زیرا طول آن صفر است: جایی که
جایی که شکل دوخطی روی ریشه ها است که توسط فرم کیلینگ ایجاد می شود.
شکل دوخطی روی ریشه ها است که توسط فرم کیلینگ ایجاد می شود. جایی که
جایی که جهت ها، بنابراین
جهت ها، بنابراین گاهی اوقات "مختصات مخروط نور" روی رشته نامیده می شوند.
گاهی اوقات "مختصات مخروط نور" روی رشته نامیده می شوند.  با
با جهت زمان مانند در امتداد
جهت زمان مانند در امتداد  جهت فضایی
جهت فضایی . سپس
. سپس مبنایی برای جبر حلقه مربوطه است و
مبنایی برای جبر حلقه مربوطه است و مبنایی برای جبر لی نزدیک است
مبنایی برای جبر لی نزدیک است ، نشان داده شده است
، نشان داده شده است جایی که
جایی که نمایش مختلط با پایه است
نمایش مختلط با پایه است و عمل را تعریف کنید
و عمل را تعریف کنید توسط (با
توسط (با )
)

 توسط اپراتور ترجمه ارائه شده است
توسط اپراتور ترجمه ارائه شده است در جبر رأس
در جبر رأس روابط کموتاسیون رضایت بخش
روابط کموتاسیون رضایت بخش![{\displaystyle [a_{m},a_{n}]=m\delta _{m+n,0}c}](https://wikimedia.org/api/rest_v1/media/math/render/svg/c77443aa2217c5741d18b680615ab0606a548ac2) را می توان به عنوان جبر لی قرابتی درک کرد
را می توان به عنوان جبر لی قرابتی درک کرد .
.

 روی فلان
روی فلان  همراه با یک
همراه با یک ![{\displaystyle [\,\cdot \,,\cdot \,]:{\mathfrak {g}}\times {\mathfrak {g}}\to {\mathfrak {g}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/6296f764a7944984cdc7eaa85de74a9566993bdd) براکت لی نامیده می شود که بدیهیات زیر را برآورده می کند:
براکت لی نامیده می شود که بدیهیات زیر را برآورده می کند: ![{\displaystyle [ax+by,z]=a[x,z]+b[y,z],}](https://wikimedia.org/api/rest_v1/media/math/render/svg/f568240b82f64c1f483ced15389429ad34a18bde)
![{\displaystyle [z,ax+by]=a[z,x]+b[z,y]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/6e8fe7285a34bcfbd5e9412bc16bf857d443864a)
 ،ب
،ب که در
که در ،
، که در
که در![[x,x]=0\](https://wikimedia.org/api/rest_v1/media/math/render/svg/07b140cc32f46dd51382217a0fe40d7941d248b0)
![{\displaystyle [x,[y,z]]+[y,[z,x]]+[z,[x,y]]=0\ }](https://wikimedia.org/api/rest_v1/media/math/render/svg/24d0a47764d6b33c7ede3e20eabb0d9b85004387)
![[x+y، x+y]](https://wikimedia.org/api/rest_v1/media/math/render/svg/b5c0808f3e1cacefc5287673604694a416f91361) و استفاده از جایگزینی نشان می دهد که
و استفاده از جایگزینی نشان می دهد که ![[x,y]+[y,x]=0\](https://wikimedia.org/api/rest_v1/media/math/render/svg/55d2a80df91d0e16cfa14924cfc729627f3234af) برای همه عناصر
برای همه عناصر ![{\displaystyle [x,y]=-[y,x],\ }](https://wikimedia.org/api/rest_v1/media/math/render/svg/c392773a54647318dc10eaadf3f60e84760a8980)
![{\displaystyle [x,x]=-[x,x].}](https://wikimedia.org/api/rest_v1/media/math/render/svg/820feb4fccd7dfcac452743bc926a4d2a234d640)
 . اگر جبر لی با یک
. اگر جبر لی با یک  .
.![[[x,y],z]](https://wikimedia.org/api/rest_v1/media/math/render/svg/5d1355c94372444268d5200cf3079e4b2e8c5510) لازم نیست برابر
لازم نیست برابر![[x،[y،z]]](https://wikimedia.org/api/rest_v1/media/math/render/svg/99c3a3b210ab676378107460425cdcd01b90d839) . با این حال،
. با این حال،  که در زیر براکت لی بسته شده است. یک ایده آل
که در زیر براکت لی بسته شده است. یک ایده آل  یک زیر جبر است که شرط قوی تر را برآورده می کند:
یک زیر جبر است که شرط قوی تر را برآورده می کند: ![{\displaystyle [{\mathfrak {g}},{\mathfrak {i}}]\subseteq {\mathfrak {i}}.}](https://wikimedia.org/api/rest_v1/media/math/render/svg/8242a1cf36864dc503b45192ace093a8a3bfae85)
![{\displaystyle \phi :{\mathfrak {g}}\to {\mathfrak {g'}},\quad \phi ([x,y])=[\phi (x),\phi (y)]\ {\text{برای همه}}\ x,y\ در {\mathfrak {g}}.}](https://wikimedia.org/api/rest_v1/media/math/render/svg/22e91ebab9c2aaf52ae7c5bd89f5d986038fd27b)
 در آن جبر عاملی یا جبر نسبی ساخته می شود
در آن جبر عاملی یا جبر نسبی ساخته می شود  و
و  اگر براکت آنها ناپدید شد رفت و آمد کنید:
اگر براکت آنها ناپدید شد رفت و آمد کنید:![{\displaystyle [x,y]=0}](https://wikimedia.org/api/rest_v1/media/math/render/svg/0bb3ac5611c95c794cec85401f417c5e0146185d) .
. مجموعه ای از عناصر در رفت و آمد با
مجموعه ای از عناصر در رفت و آمد با : به این معنا که، برای همه }
: به این معنا که، برای همه }![{\displaystyle {\mathfrak {z}}_{\mathfrak {g}}(S)=\{x\in {\mathfrak {g}}\ \mid \ [x,s]=0\ {\text{ برای همه }}ها در S\}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/beef7ab1fd4087d8f3c02729e51a1642e8467411) . متمرکز کننده از
. متمرکز کننده از . به طور مشابه، برای یک زیرفضای S ، زیرجبر
. به طور مشابه، برای یک زیرفضای S ، زیرجبر ![{\displaystyle {\mathfrak {n}}_{\mathfrak {g}}(S)=\{x\in {\mathfrak {g}}\ \mid \ [x,s]\in S\ {\text {برای همه}}\ s\در S\}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/1054639612ed3d9a3b8c1c4fbe652f15e3769355) .
.  بزرگترین زیر جبر است به طوری که
بزرگترین زیر جبر است به طوری که ، جابجاگر دو عنصر
، جابجاگر دو عنصر
 :
:
 ، که
، که ![[x,y]](https://wikimedia.org/api/rest_v1/media/math/render/svg/1b7bd6292c6023626c6358bfd3943a031b27d663) .
.  با عملیات براکت که توسط
با عملیات براکت که توسط ![{\displaystyle [x,y]=x\times y.}](https://wikimedia.org/api/rest_v1/media/math/render/svg/07242b4e095b05677a80bd7d7fde5f2fb3d76233) از آنجایی که این چولگی متقارن است
از آنجایی که این چولگی متقارن است و به جای تداعی، همانی ژاکوبی را ارضا می کند:
و به جای تداعی، همانی ژاکوبی را ارضا می کند:
 ممکن است به صورت یک چرخش بینهایت کوچک حول محور تصویر شود
ممکن است به صورت یک چرخش بینهایت کوچک حول محور تصویر شود ، با سرعتی برابر با اندازه
، با سرعتی برابر با اندازه![{\displaystyle [x,x]=x\times x=0}](https://wikimedia.org/api/rest_v1/media/math/render/svg/288c71f1e200894aee3e95818f3cf34f95b02eb6) .
.![{\displaystyle {\begin{aligned}\left[{\begin{bmatrix}a&b\\c&d\end{bmatrix}},{\begin{bmatrix}x&0\\0&y\end{bmatrix}}\right]&= {\begin{bmatrix}ax&by\\cx&dy\\\end{bmatrix}}-{\begin{bmatrix}ax&bx\\cy&dy\\\end{bmatrix}}\\&={\begin{bmatrix}0&b(yx )\\c(xy)&0\end{bmatrix}}\end{تراز شده}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/cc37131e7b2936b517ffb58fb811bcafb28b17d1)
 یک خرده جبر است، اما ایده آل نیست. در واقع، هر زیرفضای خطی تک بعدی یک جبر لی دارای ساختار جبر القایی است که به طور کلی ایده آل نیست. برای هر جبر لی ساده، همه جبرهای لی آبلی هرگز نمی توانند ایده آل باشند.
یک خرده جبر است، اما ایده آل نیست. در واقع، هر زیرفضای خطی تک بعدی یک جبر لی دارای ساختار جبر القایی است که به طور کلی ایده آل نیست. برای هر جبر لی ساده، همه جبرهای لی آبلی هرگز نمی توانند ایده آل باشند. و"
و" ،
،  متشکل از تمام جفت ها(،")،∈، "∈"
متشکل از تمام جفت ها(،")،∈، "∈" ، با عمل
، با عمل![{\displaystyle [(x,x'),(y,y')]=([x,y],[x',y'])،}](https://wikimedia.org/api/rest_v1/media/math/render/svg/00719cf5b8674e4be63e88fdd9403e9122d3a3ac)
 رفت و آمد با یکدیگر:.
رفت و آمد با یکدیگر:.![{\displaystyle [(x,0),(0,x')]=0.}](https://wikimedia.org/api/rest_v1/media/math/render/svg/fe813c102ddf8d403025225b2661eb68f25e0ad5)
 تقسیم می کند (یعنی بخشی را می پذیرد)، سپس
تقسیم می کند (یعنی بخشی را می پذیرد)، سپس .
.  که از
که از ![\delta ([x,y])=[\delta (x),y]+[x,\delta (y)]](https://wikimedia.org/api/rest_v1/media/math/render/svg/f87aef094b6b41ea9f7592abc397e6c714b87f7d)
 تعریف شده بوسیله
تعریف شده بوسیله ![{\displaystyle \mathrm {ad} _{x}(y):=[x,y]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/883a92018bbd927d508c0901ce8c4b5f2ac35dd8) . (این اشتقاقی در نتیجه همانی ژاکوبی است.) اشتقاق های بیرونی مشتقاتی هستند که از نمایش الحاقی جبر لی به دست نمی آیند. اگر
. (این اشتقاقی در نتیجه همانی ژاکوبی است.) اشتقاق های بیرونی مشتقاتی هستند که از نمایش الحاقی جبر لی به دست نمی آیند. اگر ، که زیر جبر لی از
، که زیر جبر لی از ; براکت جابجاگر است. مشتقات درونی یک زیر جبر لی ازDهr
; براکت جابجاگر است. مشتقات درونی یک زیر جبر لی ازDهr نمایندگی الحاقی
نمایندگی الحاقی از
از![{\displaystyle [x,i]\subset {\mathfrak {i}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/46b7aec174483dca01d46a3bc8e6d517b212423f) برای هرچی∈
برای هرچی∈ . برای جبر لی
. برای جبر لی ماتریس های مثلثی بالایی در
ماتریس های مثلثی بالایی در ، ایده الی دارد
، ایده الی دارد از ماتریس های مثلثی کاملاً بالایی (که در آن تنها عناصر غیرصفر بالای قطر ماتریس هستند). به عنوان مثال، جابجایی عناصر درب3
از ماتریس های مثلثی کاملاً بالایی (که در آن تنها عناصر غیرصفر بالای قطر ماتریس هستند). به عنوان مثال، جابجایی عناصر درب3 و3
و3 می دهد
می دهد![{\displaystyle {\begin{aligned}\left[{\begin{bmatrix}a&b&c\\0&d&e\\0&0&f\end{bmatrix}},{\begin{bmatrix}0&x&y\\0&0&z\\0&0&0\end{bmatrix} }\right]&={\begin{bmatrix}0&ax&ay+bz\\0&0&dz\\0&0&0\end{bmatrix}}-{\begin{bmatrix}0&dx&ex+yf\\0&0&fz\\0&0&0\end{bmatrix}}\ \&={\begin{bmatrix}0&(ad)x&(af)y-ex+bz\\0&0&(df)z\\0&0&0\end{bmatrix}}\end{تراز شده}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/68bbdd3d32fcb2dad0155719589956dd2aedaa47)
 .
. جبر لی تبدیل های خطی و⊆
جبر لی تبدیل های خطی و⊆ یک جبر لی. سپس
یک جبر لی. سپس جبر لی تقسیم شده است. شکل
جبر لی تقسیم شده است. شکل  تعریف شده است
تعریف شده است
 به عنوان ... تعریف شده است
به عنوان ... تعریف شده است
 مورفیسم همانی است. هم ارز،
مورفیسم همانی است. هم ارز،
 در رده فضاهای برداری همراه با
در رده فضاهای برداری همراه با ![[\cdot ,\cdot ]:A\otime A\right arrow A](https://wikimedia.org/api/rest_v1/media/math/render/svg/764006b09d12d3b9888095f97316a5e6f62927a1)
![{\displaystyle [\cdot ,\cdot ]\circ (\mathrm {id} +\tau )=0,}](https://wikimedia.org/api/rest_v1/media/math/render/svg/f226e135fda085b9cbfcd06be5297da26c6721cd)
![{\displaystyle [\cdot,\cdot]\circ ([\cdot,\cdot ]\otimes \mathrm {id})\circ (\mathrm {id} +\sigma +\sigma ^{2})=0. }](https://wikimedia.org/api/rest_v1/media/math/render/svg/56c5898590051c9eb3d726a05dec1fd49d89d2a2)
 ، ممکن است یک براکت لی توسط
، ممکن است یک براکت لی توسط ![[x,y]=xy-yx](https://wikimedia.org/api/rest_v1/media/math/render/svg/42b4220c8122ebd2a21c517ca80639581679cfa6) . با این براکت،آ
. با این براکت،آ![{\displaystyle (A,[\,\cdot \,,\cdot \,])}](https://wikimedia.org/api/rest_v1/media/math/render/svg/6c29f35b8690763357e300cf4ce9f7726bfc01c6) . هر جبر لی را می توان در جبری که از یک جبر انجمنی به این شکل ناشی می شود، جاسازی کرد.
. هر جبر لی را می توان در جبری که از یک جبر انجمنی به این شکل ناشی می شود، جاسازی کرد.  ، مثال قبلی دقیقاً جبر لی از n × n ماتریس است که نشان داده شده استل(،)
، مثال قبلی دقیقاً جبر لی از n × n ماتریس است که نشان داده شده استل(،) یا
یا ،
، ![{\displaystyle [X,Y]=XY-YX}](https://wikimedia.org/api/rest_v1/media/math/render/svg/838f73010b4f791eeaf245317fb4b6e07c45d741) جایی که مجاورت نشان دهنده ضرب ماتریس است. این جبر لی از
جایی که مجاورت نشان دهنده ضرب ماتریس است. این جبر لی از  ، جبر لی
، جبر لی  .
.  ، جبر لی از
، جبر لی از  ، که در آن ضرب G ضرب ماتریسی است. جبر لی مربوطه
، که در آن ضرب G ضرب ماتریسی است. جبر لی مربوطه : این شامل مشتقاتی از منحنی های ص در G در همانی است:
: این شامل مشتقاتی از منحنی های ص در G در همانی است:
 تعریف شده بوسیله یانقضا
تعریف شده بوسیله یانقضا ، که برای هر ماتریس همگرا می شود
، که برای هر ماتریس همگرا می شود .
. ، متشکل از همه n × n ماتریس با تعیین کننده 1. جبر لی آنسل(سی)
، متشکل از همه n × n ماتریس با تعیین کننده 1. جبر لی آنسل(سی) و جبر لی آنسل(آر)
و جبر لی آنسل(آر) .
. متشکل از n × n ماتریس واحد (راضی کننده∗=-1
متشکل از n × n ماتریس واحد (راضی کننده∗=-1 ). جبر لی آن استتو
). جبر لی آن استتو ).
). ، متشکل از ماتریس های متعامد یک تعیین کننده حقیقی (آتی=آ-1
، متشکل از ماتریس های متعامد یک تعیین کننده حقیقی (آتی=آ-1 ). جبر لی آن استس
). جبر لی آن استس متشکل از ماتریس های متقارن چول حقیقی (تی=-
متشکل از ماتریس های متقارن چول حقیقی (تی=- ). گروه کامل متعامدO
). گروه کامل متعامدO ، بدون شرط یک تعیین کننده، شاملاسO
، بدون شرط یک تعیین کننده، شاملاسO![{\displaystyle \left[x,y\right]=y}](https://wikimedia.org/api/rest_v1/media/math/render/svg/0fd758fcdf3bcdff0d2add99e8bfa2d6be7b1c6c) .
. 

 ، می بینیم که عناصر گروه لی حاصل ماتریس های مثلثی بالایی 2×2 با قطر واحد پایین هستند:
، می بینیم که عناصر گروه لی حاصل ماتریس های مثلثی بالایی 2×2 با قطر واحد پایین هستند:
 یک جبر لی سه بعدی است که توسط عناصر x ، y و z با براکت های لی تولید می شود.
یک جبر لی سه بعدی است که توسط عناصر x ، y و z با براکت های لی تولید می شود.![{\displaystyle [x,y]=z,\quad [x,z]=0,\quad [y,z]=0}](https://wikimedia.org/api/rest_v1/media/math/render/svg/4360eb6f88b60ae723e133e389c76b208658a816) .
.

 از گروه SO(3) توسط سه ماتریس پوشیده شده است
از گروه SO(3) توسط سه ماتریس پوشیده شده است 
![{\displaystyle [F_{1},F_{2}]=F_{3},}](https://wikimedia.org/api/rest_v1/media/math/render/svg/1d357a07d3fb64786da9f02bb9ad5f0a5027c3bf)
![{\displaystyle [F_{2},F_{3}]=F_{1},}](https://wikimedia.org/api/rest_v1/media/math/render/svg/356514684addccaaccc0b2872fa1521294d21727)
![{\displaystyle [F_{3},F_{1}]=F_{2}.}](https://wikimedia.org/api/rest_v1/media/math/render/svg/37b8356e46a3dcb952c873b955d8c2b92a6b8d20)
 با براکت لی داده شده توسط
با براکت لی داده شده توسط ![L_{[X,Y]}f=L_{X}(L_{Y}f)-L_{Y}(L_{X}f).\,](https://wikimedia.org/api/rest_v1/media/math/render/svg/b2744f4fa1f6829787912d0f27fd27fe5047422d)


![\operatorname {ad} (x)(y)=[x,y]](https://wikimedia.org/api/rest_v1/media/math/render/svg/883d113b6039d5f39214bec543d5198c7a16aa6b) ; این یک نمایش در فضای برداری است
; این یک نمایش در فضای برداری است یا
یا  ، و همه به شکل هستند،
، و همه به شکل هستند، به معنی n بعدی با براکت لی ساده.
به معنی n بعدی با براکت لی ساده.![{\mathfrak {g}}>[{\mathfrak {g}}،{\mathfrak {g}}]>[[{\mathfrak {g}}،{\mathfrak {g}}]،{\mathfrak {g }}]>[[[{\mathfrak {g}}،{\mathfrak {g}}]،{\mathfrak {g}}]،{\mathfrak {g}}]>\cdots](https://wikimedia.org/api/rest_v1/media/math/render/svg/0fbc7736bc5f43a440623e77833ea7de0cfa99fe)
![\operatorname {ad} (u):{\mathfrak {g}}\to {\mathfrak {g}},\quad \operatorname {ad} (u)v=[u,v]](https://wikimedia.org/api/rest_v1/media/math/render/svg/9e1b5c04d185bd495cc049795d628ba972f21ba9)
![{\mathfrak {g}}>[{\mathfrak {g}}،{\mathfrak {g}}]>[[{\mathfrak {g}}،{\mathfrak {g}}]،[{\mathfrak { g}}،{\mathfrak {g}}]]>[[[{\mathfrak {g}}،{\mathfrak {g}}]،[{\mathfrak {g}}،{\mathfrak {g}} ]]،[[{\mathfrak {g}}،{\mathfrak {g}}]،[{\mathfrak {g}}،{\mathfrak {g}}]]]>\cdots](https://wikimedia.org/api/rest_v1/media/math/render/svg/55be9f812e367366f54c391ec9559604163654ab)

![K({\mathfrak {g}}،[{\mathfrak {g}}،{\mathfrak {g}}])=0.](https://wikimedia.org/api/rest_v1/media/math/render/svg/0ecced3d594ff22f930666328433047354c990ea)

 با جبر لی
با جبر لی هم شکل است
هم شکل است دو شکل حقیقی دارد
دو شکل حقیقی دارد و
و .
.  یک
یک ![[\cdot،\cdot]](https://wikimedia.org/api/rest_v1/media/math/render/svg/28dd4c22d60192519c1c12cf645b040f368db9e9) که دارای خواص زیر است:
که دارای خواص زیر است:![[x+y,z]=[x,z]+[y,z],\quad [z,x+y]=[z,x]+[z,y]](https://wikimedia.org/api/rest_v1/media/math/render/svg/165b1dcd70eaf2436d298c473319328d0e72abda)
![[x,[y,z]]+[y,[z,x]]+[z,[x,y]]=0\چهارم](https://wikimedia.org/api/rest_v1/media/math/render/svg/c5140846419cb8d565520cb9aa5778495f05ef04)
![[x,x]=0\چهارم](https://wikimedia.org/api/rest_v1/media/math/render/svg/73f16254787dd7a9c55e04cdcd793322b28dde0e)
![{\displaystyle [x,y]=xy-yx.}](https://wikimedia.org/api/rest_v1/media/math/render/svg/adaa95a59e9814f5965d79550c54297626db87a9)
![{\displaystyle [x,y]=x^{-1}y^{-1}xy}](https://wikimedia.org/api/rest_v1/media/math/render/svg/c399517540666ad126816d1e0a58f9ee49685f0f) عملیات جابجاگر، و اجازه دهید
عملیات جابجاگر، و اجازه دهید سریال
سریال ![{\displaystyle [G_{i}،G_{j}]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/150f820d7588613c24f71d2c3d5fa7428b220c85) موجود است در
موجود است در برای هر
برای هر . سپس
. سپس
![{\displaystyle [xG_{i},yG_{j}]=[x,y]G_{i+j}\ }](https://wikimedia.org/api/rest_v1/media/math/render/svg/90fc5fb8eb2c05175b634364277504622dae858b)
 ; اغلب،
; اغلب، 











 : چرخش حول محور Z
: چرخش حول محور Z : چرخش حول محور X جدید
: چرخش حول محور X جدید با
با 

 یک کواترنیون واحد نیست، پس فرم همگن هنوز مضربی اسکالر از یک ماتریس چرخشی است، در حالی که شکل ناهمگن به طور کلی دیگر یک ماتریس متعامد نیست. به همین دلیل است که در کار عددی برای جلوگیری از اعوجاج، شکل همگن ترجیح داده می شود.
یک کواترنیون واحد نیست، پس فرم همگن هنوز مضربی اسکالر از یک ماتریس چرخشی است، در حالی که شکل ناهمگن به طور کلی دیگر یک ماتریس متعامد نیست. به همین دلیل است که در کار عددی برای جلوگیری از اعوجاج، شکل همگن ترجیح داده می شود.





 و بردار
و بردار به طوری که3
به طوری که3 .
. توسط یک کواترنیون�
توسط یک کواترنیون� تعریف
تعریف 
 یک کواترنیون حاوی بردار تعبیه شده است
یک کواترنیون حاوی بردار تعبیه شده است یک
یک  بردار چرخشی است"
بردار چرخشی است" . در پیاده سازی های محاسباتی این به دو ضرب کواترنیونی نیاز دارد. یک رویکرد جایگزین استفاده از جفت روابط است
. در پیاده سازی های محاسباتی این به دو ضرب کواترنیونی نیاز دارد. یک رویکرد جایگزین استفاده از جفت روابط است


 که
که

 اعمال شده است. با بهره برداری بعدی از اموالی که�
اعمال شده است. با بهره برداری بعدی از اموالی که� یک
یک  ، همراه با هویت برداری استاندارد
، همراه با هویت برداری استاندارد




 یک کواترنیون مانند یک بردار رفتار می کند
یک کواترنیون مانند یک بردار رفتار می کند



 کواترنیون حاصل است،
کواترنیون حاصل است، حاصلضرب متقاطع برداری است (بردار)،
حاصلضرب متقاطع برداری است (بردار)، ضرب اسکالر برداری (یک اسکالر) است.
ضرب اسکالر برداری (یک اسکالر) است.

 یک بردار واحد (محور چرخش) باشد و اجازه دهید
یک بردار واحد (محور چرخش) باشد و اجازه دهید . هدف ما نشان دادن آن است
. هدف ما نشان دادن آن است
 )، ما داریم
)، ما داریم![{\displaystyle {\begin{aligned}{\vec {v}}'&={\vec {v}}\cos ^{2}{\frac {\alpha }{2}}+\left({\vec {u}}{\vec {v}}-{\vec {v}}{\vec {u}}\right)\sin {\frac {\alpha }{2}}\cos {\frac {\alpha }{2}}-{\vec {u}}{\vec {v}}{\vec {u}}\sin ^{2}{\frac {\alpha }{2}}\\[6pt]& ={\vec {v}}\cos ^{2}{\frac {\alpha }{2}}+2\left({\vec {u}}\times {\vec {v}}\right)\ sin {\frac {\alpha }{2}}\cos {\frac {\alpha }{2}}-\left(\left({\vec {u}}\times {\vec {v}}\right )-\left({\vec {u}}\cdot {\vec {v}}\right)\right){\vec {u}}\sin ^{2}{\frac {\alpha }{2} }\\[6pt]&={\vec {v}}\cos ^{2}{\frac {\alpha }{2}}+2\left({\vec {u}}\times {\vec { v}}\right)\sin {\frac {\alpha }{2}}\cos {\frac {\alpha }{2}}-\left(\left({\vec {u}}\times {\ vec {v}}\right){\vec {u}}-\left({\vec {u}}\cdot {\vec {v}}\right){\vec {u}}\right)\sin ^{2}{\frac {\alpha }{2}}\\[6pt]&={\vec {v}}\cos ^{2}{\frac {\alpha }{2}}+2\left({\vec {u}}\times {\vec {v}}\right)\ sin {\frac {\alpha }{2}}\cos {\frac {\alpha }{2}}-\left(\left(\left({\vec {u}}\times {\vec {v} }\right)\times {\vec {u}}-\left({\vec {u}}\times {\vec {v}}\right)\cdot {\vec {u}}\right)-\ چپ ({\vec {u}}\cdot {\vec {v}}\right){\vec {u}}\right)\sin ^{2}{\frac {\alpha }{2}}\\ [6pt]&={\vec {v}}\cos ^{2}{\frac {\alpha }{2}}+2\left({\vec {u}}\times {\vec {v}} \right)\sin {\frac {\alpha }{2}}\cos {\frac {\alpha }{2}}-\left(\left({\vec {v}}-\left({\vec {u}}\cdot {\vec {v}}\right){\vec {u}}\right)-0-\left({\vec {u}}\cdot {\vec {v}}\right ){\vec {u}}\right)\sin ^{2}{\frac {\alpha }{2}}\\[6pt]&={\vec {v}}\cos ^{2}{\frac {\alpha }{2}}+2\left({\vec {u}}\times {\vec {v}}\right)\ sin {\frac {\alpha }{2}}\cos {\frac {\alpha }{2}}-\left({\vec {v}}-2{\vec {u}}\left({\ vec {u}}\cdot {\vec {v}}\right)\right)\sin ^{2}{\frac {\alpha }{2}}\\[6pt]&={\vec {v} }\cos ^{2}{\frac {\alpha }{2}}+2\left({\vec {u}}\times {\vec {v}}\right)\sin {\frac {\alpha }{2}}\cos {\frac {\alpha }{2}}-{\vec {v}}\sin ^{2}{\frac {\alpha }{2}}+2{\vec {u }}\left({\vec {u}}\cdot {\vec {v}}\right)\sin ^{2}{\frac {\alpha }{2}}\\[6pt]&={\ vec {v}}\left(\cos ^{2}{\frac {\alpha }{2}}-\sin ^{2}{\frac {\alpha }{2}}\right)+\left( {\vec {u}}\times {\vec {v}}\right)\left(2\sin {\frac {\alpha }{2}}\cos {\frac {\alpha }{2}}\ راست)+{\vec {u}}\left({\vec {u}}\cdot {\vec {v}}\right)\left(2\sin ^{2}{\frac {\alpha }{ 2}}\راست)\\[6pt]\end{تراز شده}}}={\vec {v}}\left(\cos ^{2}{\frac {\alpha }{2}}-\sin ^{2}{\frac {\alpha }{2}}\right)+ \left({\vec {u}}\times {\vec {v}}\right)\left(2\sin {\frac {\alpha }{2}}\cos {\frac {\alpha }{2 }}\right)+{\vec {u}}\left({\vec {u}}\cdot {\vec {v}}\right)\left(2\sin ^{2}{\frac {\ آلفا {2}}\راست)\\[6pt]\end{تراز شده}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/211d8613a1a8f990e93433cd4bd10937a2197eca)
![{\displaystyle {\begin{aligned}{\vec {v}}'&={\vec {v}}\left(\cos ^{2}{\frac {\alpha }{2}}-\sin ^ {2}{\frac {\alpha }{2}}\right)+\left({\vec {u}}\times {\vec {v}}\right)\left(2\sin {\frac { \alpha }{2}}\cos {\frac {\alpha }{2}}\right)+{\vec {u}}\left({\vec {u}}\cdot {\vec {v}} \right)\left(2\sin ^{2}{\frac {\alpha }{2}}\right)\\[6pt]&={\vec {v}}\cos \alpha +\left({ \vec {u}}\times {\vec {v}}\right)\sin \alpha +{\vec {u}}\left({\vec {u}}\cdot {\vec {v}}\ راست)\left(1-\cos \alpha \right)\\[6pt]&={\vec {v}}\cos \alpha +\left({\vec {u}}\times {\vec {v }}\right)\sin \alpha +{\vec {u}}\left({\vec {u}}\cdot {\vec {v}}\right)-{\vec {u}}\left( {\vec {u}}\cdot {\vec {v}}\right)\cos \alpha \\[6pt]&=\left({\vec {v}}-{\vec {u}}\left({\vec {u}}\cdot {\vec {v}}\right)\right)\cos \alpha +\ چپ({\vec {u}}\times {\vec {v}}\right)\sin \alpha +{\vec {u}}\left({\vec {u}}\cdot {\vec {v }}\right)\\[6pt]&={\vec {v}}_{\bot }\cos \alpha +\left({\vec {u}}\times {\vec {v}}\right )\sin \alpha +{\vec {v}}_{\|}\end{تراز شده}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/48bf26328d7a60ea06272e628ae4514076e0659a)
 و→"
و→" اجزای v → (به ترتیب عمود و موازی u → ) هستند. این
اجزای v → (به ترتیب عمود و موازی u → ) هستند. این 


 در حالی که تعریف همیلتون این است
در حالی که تعریف همیلتون این است . این کنوانسیون همچنین به عنوان "کنوانسیون JPL" برای استفاده از آن در برخی از بخشهای
. این کنوانسیون همچنین به عنوان "کنوانسیون JPL" برای استفاده از آن در برخی از بخشهای 
![{\displaystyle {\begin{aligned}\mathbf {p} '_{\text{alt}}={}&(\mathbf {v} \otimes \mathbf {v} +q_{r}^{2}\ mathbf {I} \mathbin {\color {red}\mathbf {-} } 2q_{r}[\mathbf {v} ]_{\times }+[\mathbf {v} ]_{\times ^{2 })\mathbf {p} &{\text{(قرارداد جایگزین، استفاده ممنوع!)}}\\=&\ (\mathbf {I} \mathbin {\color {red}\mathbf {-} } 2q_{r [\mathbf {v} ]_{\times }+2[\mathbf {v} ]_{\times }^{2})\mathbf {p} &\end{تراز شده}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/3750c56481e794e3fa99936110fba444b5c23188)
![{\displaystyle {\begin{aligned}\mathbf {R} _{alt}&=\mathbf {I} \mathbin {\color {red}\mathbf {-} } 2q_{r}[\mathbf {v} ] _{\times }+2[\mathbf {v} ]_{\times }^{2}\qquad {\text{(کنوانسیون جایگزین، استفاده ممنوع!)}}\\&={\begin{bmatrix}1 -2s(q_{j}^{2}+q_{k}^{2})&2(q_{i}q_{j}+q_{k}q_{r})&2(q_{i}q_{k }-q_{j}q_{r})\\2(q_{i}q_{j}-q_{k}q_{r})&1-2s(q_{i}^{2}+q_{k} ^{2})&2(q_{j}q_{k}+q_{i}q_{r})\\2(q_{i}q_{k}+q_{j}q_{r})&2(q_ {j}q_{k}-q_{i}q_{r})&1-2s(q_{i}^{2}+q_{j}^{2})\end{bmatrix}}\end{تراز شده} }}](https://wikimedia.org/api/rest_v1/media/math/render/svg/d28f0e656b8b25de89fbb55b260e7761dd7d38cf)

 . نمایش کواترنیونی این چرخش به صورت زیر ارائه می شود:
. نمایش کواترنیونی این چرخش به صورت زیر ارائه می شود:
 مزدوج کواترنیون است
مزدوج کواترنیون است




 . این فقط به 15 ضرب و 15 جمع برای ارزیابی نیاز دارد (یا 18 ضرب و 12 جمع اگر ضریب 2 از طریق ضرب انجام شود). به علامت کواترنیون اعمال می شود. این نتیجه همان فرمول کم کارآمد اما فشردهتر ضرب کواترنیون است
. این فقط به 15 ضرب و 15 جمع برای ارزیابی نیاز دارد (یا 18 ضرب و 12 جمع اگر ضریب 2 از طریق ضرب انجام شود). به علامت کواترنیون اعمال می شود. این نتیجه همان فرمول کم کارآمد اما فشردهتر ضرب کواترنیون است .
.
 ، دو ماتریس باید رفت و آمد داشته باشند. بنابراین، دو زیر گروه رفت و آمد
، دو ماتریس باید رفت و آمد داشته باشند. بنابراین، دو زیر گروه رفت و آمد ![{\displaystyle {\begin{aligned}\mathbf {z} _{\rm {l}}{\vec {v}}\mathbf {z} _{\rm {r}}&={\begin{pmatrix} 1&-dt_{ab}&-dt_{ac}&-dt_{ad}\\dt_{ab}&1&-dt_{bc}&-dt_{bd}\\dt_{ac}&dt_{bc}&1&-dt_{ cd}\\dt_{ad}&dt_{bd}&dt_{cd}&1\end{pmatrix}}{\begin{pmatrix}w\\x\\y\\z\end{pmatrix}}\\[3pt] \mathbf {z} _{\rm {l}}&=1+{dt_{ab}+dt_{cd} \over 2}i+{dt_{ac}-dt_{bd} \over 2}j+{dt_{ ad}+dt_{bc} \over 2}k\\[3pt]\mathbf {z} _{\rm {r}}&=1+{dt_{ab}-dt_{cd} \over 2}i+{ dt_{ac}+dt_{bd} \over 2}j+{dt_{ad}-dt_{bc} \over 2}k\end{تراز شده}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/d357c8e70a12570ad6275ed837bedb837306d11e)

 حول محوری که بردار داده می شود
حول محوری که بردار داده می شود توسط زاویه
توسط زاویه .
.![{\displaystyle {\begin{aligned}(a_{x},a_{y},a_{z})={}&{\frac {(q_{i},q_{j},q_{k})} {\sqrt {q_{i}^{2}+q_{j}^{2}+q_{k}^{2}}}}\\[2pt]\theta =2\operatorname {atan2} &\left ({\sqrt {q_{i}^{2}+q_{j}^{2}+q_{k}^{2}}},\,q_{r}\right),\end{تراز شده}} }](https://wikimedia.org/api/rest_v1/media/math/render/svg/bc1d62fe7285e7371d40e848e6bdfca990367d8d)
 متقاطع
متقاطع  حول این محور کواترنیون مرتبط توسط
حول این محور کواترنیون مرتبط توسط





 از ضرب منبسط شده، بردار را که محور چرخش است، چند برابر ثابت ترک می کند. زمانی که باید بردار محور را عادی کرد
از ضرب منبسط شده، بردار را که محور چرخش است، چند برابر ثابت ترک می کند. زمانی که باید بردار محور را عادی کرد است
است جایی که بردار نزدیک است
جایی که بردار نزدیک است

 یا
یا .
.![{\displaystyle {\begin{aligned}{\frac {\partial \mathbf {p'} }{\partial \mathbf {q} }}\equiv \left[{\frac {\partial \mathbf {p'} } {\partial q_{0}}},{\frac {\partial \mathbf {p'} }{\partial q_{x}}},{\frac {\partial \mathbf {p'} }{\partial q_ {y}}}،{\frac {\partial \mathbf {p'} }{\partial q_{z}}}\right]=\left[\mathbf {pq} -(\mathbf {pq} )^{ *},(\mathbf {pqi} )^{*}-\mathbf {pqi} ,(\mathbf {pqj} )^{*}-\mathbf {pqj} ,(\mathbf {pqk} )^{*} -\mathbf {pqk} \راست].\end{تراز شده}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/559fc109c72845625b201ccfa99036aa226cc204)
 که نشان دهنده محور اویلر است با کواترنیون داده می شود
که نشان دهنده محور اویلر است با کواترنیون داده می شود ،
،  و
و .
.![[0,2\pi]](https://wikimedia.org/api/rest_v1/media/math/render/svg/348d40bf3f8b7e1c00c4346440d7e2e4f0cc9b91) .
.
 ) با زاویه ای از
) با زاویه ای از

 در فضای سه بعدی، به عنوان یک ربع با مختصات حقیقی برابر با صفر، با ارزیابی صیغه
در فضای سه بعدی، به عنوان یک ربع با مختصات حقیقی برابر با صفر، با ارزیابی صیغه 
 ، یک چرخش فیزیکی در موردتو→
، یک چرخش فیزیکی در موردتو→ توسط2-
توسط2- هر دو به جهت گیری نهایی یکسانی با مسیرهای مجزا از طریق جهت گیری های میانی دست می یابند. با وارد کردن آن بردارها و زوایا در فرمول q بالا، متوجه میشویم که اگر q نشاندهنده اولین چرخش باشد، - q نشاندهنده چرخش دوم است. این یک اثبات هندسی است که صیغه کردن توسط q و - q باید همان ماتریس تبدیل چرخشی را ایجاد کند. این حقیقیت از نظر جبری با توجه به اینکه صیغه در q درجه دوم است تأیید می شود ، بنابراین علامت q لغو می شود و بر نتیجه تأثیر نمی گذارد. (نگاه کنید به
هر دو به جهت گیری نهایی یکسانی با مسیرهای مجزا از طریق جهت گیری های میانی دست می یابند. با وارد کردن آن بردارها و زوایا در فرمول q بالا، متوجه میشویم که اگر q نشاندهنده اولین چرخش باشد، - q نشاندهنده چرخش دوم است. این یک اثبات هندسی است که صیغه کردن توسط q و - q باید همان ماتریس تبدیل چرخشی را ایجاد کند. این حقیقیت از نظر جبری با توجه به اینکه صیغه در q درجه دوم است تأیید می شود ، بنابراین علامت q لغو می شود و بر نتیجه تأثیر نمی گذارد. (نگاه کنید به  ، هر دو q و - q یک مختصات حقیقی برابر با صفر خواهند داشت. در غیر این صورت، یک قسمت حقیقی مثبت خواهد داشت که نشان دهنده چرخش با زاویه کمتر از
، هر دو q و - q یک مختصات حقیقی برابر با صفر خواهند داشت. در غیر این صورت، یک قسمت حقیقی مثبت خواهد داشت که نشان دهنده چرخش با زاویه کمتر از و دیگری یک قسمت حقیقی منفی خواهد داشت که نشان دهنده چرخش با زاویه ای بزرگتر از
و دیگری یک قسمت حقیقی منفی خواهد داشت که نشان دهنده چرخش با زاویه ای بزرگتر از
 ،
، . مربع چرخش کواترنیون چرخش دو برابر زاویه حول یک محور است. به طور کلی q n چرخشی n برابر زاویه حول همان محور q است. این را می توان به n حقیقی دلخواه تعمیم داد که امکان درونیابی صاف بین جهت گیری های فضایی را فراهم می کند. رجوع به
. مربع چرخش کواترنیون چرخش دو برابر زاویه حول یک محور است. به طور کلی q n چرخشی n برابر زاویه حول همان محور q است. این را می توان به n حقیقی دلخواه تعمیم داد که امکان درونیابی صاف بین جهت گیری های فضایی را فراهم می کند. رجوع به 

 ، با زاویه چرخش 120 درجه یا2 π/3
، با زاویه چرخش 120 درجه یا2 π/3 






 ، جایی کهآر
، جایی کهآر ماتریس
ماتریس 
 و اگر یک کواترنیون واحد باشد،
و اگر یک کواترنیون واحد باشد، .
. ،
، مانند
مانند و
و ، جایی که
، جایی که ، معادله ما تبدیل می شود
، معادله ما تبدیل می شود . با استفاده از فرمول ضرب دو چهارتایی که به صورت قطعات اسکالر و برداری بیان می شوند،
. با استفاده از فرمول ضرب دو چهارتایی که به صورت قطعات اسکالر و برداری بیان می شوند،
![{\displaystyle {\begin{aligned}(0,\ \mathbf {p} ')=&((q_{r},\ \mathbf {v})(0,\ \mathbf {p} ))s(q_ {r},\ -\mathbf {v} )\\=&(q_{r}0-\mathbf {v} \cdot \mathbf {p} ,\ q_{r}\mathbf {p} +0\mathbf {v} +\mathbf {v} \times \mathbf {p} )s(q_{r},\ -\mathbf {v} )\\=&s(-\mathbf {v} \cdot \mathbf {p} ,\ q_{r}\mathbf {p} +\mathbf {v} \times \mathbf {p} )(q_{r},\ -\mathbf {v} )\\=&s(-\mathbf {v} \cdot \mathbf {p} q_{r}-(q_{r}\mathbf {p} +\mathbf {v} \times \mathbf {p} )\cdot (-\mathbf {v}),\ (- \mathbf {v} \cdot \mathbf {p} )(-\mathbf {v})+q_{r}(q_{r}\mathbf {p} +\mathbf {v} \times \mathbf {p}) +(q_{r}\mathbf {p} +\mathbf {v} \times \mathbf {p} )\times (-\mathbf {v} ))\\=&s\left(-\mathbf {v} \ cdot \mathbf {p} q_{r}+q_{r}\mathbf {v} \cdot \mathbf {p}،\ \mathbf {v} \left(\mathbf {v} \cdot \mathbf {p} \right)+q_{r}^{2}\mathbf {p} +q_{r}\mathbf {v} \times \mathbf {p} +\mathbf {v} \times \left(q_{r}\mathbf {p} +\mathbf {v} \times \mathbf {p} \right)\right)\\=&\ چپ (0,\ s\left(\mathbf {v} \otimes \mathbf {v} +q_{r}^{2}\mathbf {I} +2q_{r}[\mathbf {v} ]_{\times }+[\mathbf {v} ]_{\times }^{2}\right)\mathbf {p} \right),\end{تراز شده}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/791f3ce917350217ce39c6d61647940686c183f3)

![{\displaystyle [\mathbf {v} ]_{\times }}](https://wikimedia.org/api/rest_v1/media/math/render/svg/eb8c75c76fcc67f0d13e3298d0b6de20a0c1254e) ماتریس تبدیلی است که وقتی از سمت راست با یک بردار ضرب می شودتو
ماتریس تبدیلی است که وقتی از سمت راست با یک بردار ضرب می شودتو
 .
. ، می توانیم شناسایی کنیم
، می توانیم شناسایی کنیم ![{\displaystyle s\left(\mathbf {v} \otimes \mathbf {v} +q_{r}^{2}\mathbf {I} +2q_{r}[\mathbf {v} ]_{\times } +[\mathbf {v} ]_{\times }^{2}\right)}](https://wikimedia.org/api/rest_v1/media/math/render/svg/af9cc39b5fe69b350b9203c4f82dabeb799e0e3d) ، که پس از گسترش باید عبارتی را که به شکل ماتریس در بالا نوشته شده است، بیان کند.
، که پس از گسترش باید عبارتی را که به شکل ماتریس در بالا نوشته شده است، بیان کند.

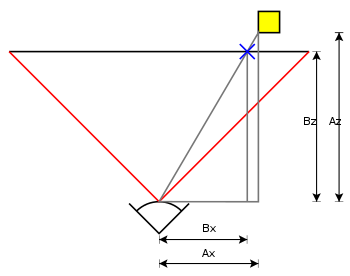
 – موقعیت سه بعدی نقطه A که قرار است پیش بینی شود.
– موقعیت سه بعدی نقطه A که قرار است پیش بینی شود. - موقعیت سه بعدی نقطه C که نشان دهنده دوربین است.
- موقعیت سه بعدی نقطه C که نشان دهنده دوربین است. -
-  - موقعیت
- موقعیت  - طرح ریزی دو بعدی ازآ.
- طرح ریزی دو بعدی ازآ.
 و
و بردار سه بعدی〈1،2،0〉
بردار سه بعدی〈1،2،0〉 به بردار دوبعدی پیش بینی می شود〈1،2〉
به بردار دوبعدی پیش بینی می شود〈1،2〉 .
. به عنوان موقعیت نقطه A نسبت به
به عنوان موقعیت نقطه A نسبت به  با توجه به سیستم مختصات اولیه این با
با توجه به سیستم مختصات اولیه این با  از جانبآ
از جانبآ به نتیجه این تبدیل اغلب a نامیده می شودتبدیل دوربین ، و می تواند به صورت زیر بیان شود، چرخش را بر حسب چرخش در موردx، yوzمی کند (این محاسبات فرض می کنند که محورها به عنوان یک
به نتیجه این تبدیل اغلب a نامیده می شودتبدیل دوربین ، و می تواند به صورت زیر بیان شود، چرخش را بر حسب چرخش در موردx، yوzمی کند (این محاسبات فرض می کنند که محورها به عنوان یک
 ، سپس ماتریس ها خارج می شوند (به عنوان هویت)، و این به یک تغییر ساده کاهش می یابد:.
، سپس ماتریس ها خارج می شوند (به عنوان هویت)، و این به یک تغییر ساده کاهش می یابد:.
 و غیره و به اختصار
و غیره و به اختصار به
به و
و به
به
![{\displaystyle {\begin{aligned}\mathbf {b} _{x}&={\frac {\mathbf {e} _{z}}{\mathbf {d} _{z}}}\mathbf {d } _{x}+\mathbf {e} _{x}،\\[5pt]\mathbf {b} _{y}&={\frac {\mathbf {e} _{z}}{\mathbf { d} _{z}}}\mathbf {d} _{y}+\mathbf {e} _{y}.\end{تراز شده}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/f002d3d4ed5e51f66a9e80bad596258adb82ed25)


 ، مستقیماً به میدان دید مربوط می شود که در آن
، مستقیماً به میدان دید مربوط می شود که در آن زاویه دید است (توجه: این فرض را بر این می گذارد که نقاط (-1،-1) و (1،1) را در گوشه های سطح دید خود ترسیم کنید)
زاویه دید است (توجه: این فرض را بر این می گذارد که نقاط (-1،-1) و (1،1) را در گوشه های سطح دید خود ترسیم کنید)
 اندازه نمایشگر است،،
اندازه نمایشگر است،، اندازه سطح ضبط (
اندازه سطح ضبط (  فاصله سطح ضبط تا
فاصله سطح ضبط تا  فاصله، از نقطه 3 بعدی در حال نمایش، تا مردمک ورودی است.
فاصله، از نقطه 3 بعدی در حال نمایش، تا مردمک ورودی است. با یک عمق ثابت متوسط جایگزین می شود
با یک عمق ثابت متوسط جایگزین می شود ،
، ![{\displaystyle {\begin{aligned}&P_{x}={\frac {X}{Z_{\text{ave}}}}\\[5pt]&P_{y}={\frac {Y}{Z_{ \text{ave}}}}\end{تراز شده}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/0d66248cfb79bcde6f7e7d136e18c3a7498b4ddd)
 .
.
 ضرب مختصات نقطه در:
ضرب مختصات نقطه در:
 مختصات صفحه نمایش x است
مختصات صفحه نمایش x است مختصات مدل x است
مختصات مدل x است فاصله
فاصله  فاصله موضوع است.
فاصله موضوع است.
 ،
، روی نقطه 2 بعدی
روی نقطه 2 بعدی ،
، با استفاده از یک طرح املایی موازی با محور y (که در آن y مثبت نشان دهنده جهت رو به جلو - نمای نمایه)، معادلات زیر را می توان استفاده کرد:
با استفاده از یک طرح املایی موازی با محور y (که در آن y مثبت نشان دهنده جهت رو به جلو - نمای نمایه)، معادلات زیر را می توان استفاده کرد:


















 که در آن
که در آن جزء طولی p در امتداد n است که توسط حاصل
جزء طولی p در امتداد n است که توسط حاصل  جزء عرضی p نسبت به n است و
جزء عرضی p نسبت به n است و
 با بررسی ماتریس چرخش به صورت تحلیلی.
با بررسی ماتریس چرخش به صورت تحلیلی. -axis) را می توان به صورت زیر بدست آورد:
-axis) را می توان به صورت زیر بدست آورد:

![{\displaystyle {\begin{aligned}\mathbf {A} _{X}&={\begin{bmatrix}1&0&0\\0&\cos \phi &-\sin \phi \\0&\sin \phi &\cos \phi \end{bmatrix}}\\[5px]\mathbf {A} _{Y}&={\begin{bmatrix}\cos \theta &0&\sin \theta \\0&1&0\\-\sin \theta &0& \cos \theta \end{bmatrix}}\\[5px]\mathbf {A} _{Z}&={\begin{bmatrix}\cos \psi &-\sin \psi &0\\\sin \psi & \cos \psi &0\\0&0&1\end{bmatrix}}\end{تراز شده}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/d396db64b528dcfaed8795003f033d534ae5de87)

 .
.
![{\displaystyle \mathbf {A} =\mathbf {I} _{3}\cos \theta +(1-\cos \theta ){\hat {\mathbf {e} }}{\hat {\mathbf {e } }}^{\mathsf {T}}+\left[{\hat {\mathbf {e} }}\right]_{\times }\sin \theta }](https://wikimedia.org/api/rest_v1/media/math/render/svg/c1e2785f256aa4d31f2f9fd0eda8a4290dcc1940)
![{\displaystyle \left[{\hat {\mathbf {e} }}\right]_{\times }={\begin{bmatrix}0&-e_{3}&e_{2}\\e_{3}&0&- e_{1}\\-e_{2}&e_{1}&0\end{bmatrix}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/7543a05032b732bedc3c2a829bccdaa4a1767a08)

 از ماتریس چرخش A به شرح زیر است:
از ماتریس چرخش A به شرح زیر است:

 جایی که
جایی که که می دهد
که می دهد











 از عبارت نهایی به دست آمده برای کواترنیون ها:
از عبارت نهایی به دست آمده برای کواترنیون ها:


![{\displaystyle [{\boldsymbol {\omega }}]_{\times }={\begin{bmatrix}0&-\omega _{z}&\omega _{y}\\\omega _{z}&0&- \omega _{x}\\-\omega _{y}&\omega _{x}&0\end{bmatrix}}={\frac {\mathrm {d} \mathbf {A} }{\mathrm {d } t}}\mathbf {A} ^{\mathsf {T}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/e77acfcca1f8dcc42a510d9c87e84bc9cac1fee2)

![{\displaystyle {\frac {\mathrm {d} \mathbf {r} }{\mathrm {d} t}}={\boldsymbol {\omega }}(t)\times \mathbf {r} (t)= [{\boldsymbol {\omega }}]_{\times }\mathbf {r} (t)}](https://wikimedia.org/api/rest_v1/media/math/render/svg/1ff9424c8647883330a8b9d739cb95a0e06f1c7c) (به
(به ![{\displaystyle {\frac {\mathrm {d} \mathbf {A} }{\mathrm {d} t}}\mathbf {A} ^{\mathsf {T}}(t)\mathbf {r} (t )=[{\boldsymbol {\omega }}]_{\times }\mathbf {r} (t)}](https://wikimedia.org/api/rest_v1/media/math/render/svg/c74108f541116e51a7ffb72a6f88465b229b727d)
![{\displaystyle {\frac {\mathrm {d} \mathbf {A} }{\mathrm {d} t}}\mathbf {A} ^{\mathsf {T}}(t)=[{\boldsymbol {\ امگا }}]_{\ بار }}](https://wikimedia.org/api/rest_v1/media/math/render/svg/5501f9dda072f6fd0085a041dc04e2208e7f7a32)
 جایی که
جایی که مزدوج (معکوس) از است
مزدوج (معکوس) از است .
.


 جایی که
جایی که
 (برعکس کردن ترتیب بردارها درب
(برعکس کردن ترتیب بردارها درب



 و اینکه − v̂x̂v̂ بازتاب x در مورد صفحه عمود بر v̂ است یک تفسیر هندسی به عملیات چرخش می دهد: چرخش اجزایی را که موازی با v هستند حفظ می کند و فقط آنهایی را که عمود هستند تغییر می دهد. سپس شرایط محاسبه می شود:
و اینکه − v̂x̂v̂ بازتاب x در مورد صفحه عمود بر v̂ است یک تفسیر هندسی به عملیات چرخش می دهد: چرخش اجزایی را که موازی با v هستند حفظ می کند و فقط آنهایی را که عمود هستند تغییر می دهد. سپس شرایط محاسبه می شود:







 که در آن محور یک بردار واحد است که جهت محور روتور را مشخص می کند. از مبدا، در هر جهت، همان محور چرخش است، با مقیاس زاویه معادل فاصله از مبدا. از هر نقطه دیگری در فضا، به طور مشابه همان بردار جهت اعمال شده نسبت به جهت نشان داده شده توسط نقطه شروع به جای مبدا، همان تغییر را در اطراف همان محورهایی اعمال می کند که بردار واحد مشخص می کند. اینزاویه∗محور
که در آن محور یک بردار واحد است که جهت محور روتور را مشخص می کند. از مبدا، در هر جهت، همان محور چرخش است، با مقیاس زاویه معادل فاصله از مبدا. از هر نقطه دیگری در فضا، به طور مشابه همان بردار جهت اعمال شده نسبت به جهت نشان داده شده توسط نقطه شروع به جای مبدا، همان تغییر را در اطراف همان محورهایی اعمال می کند که بردار واحد مشخص می کند. اینزاویه∗محور مقیاس گذاری هر نقطه یک مختصات منحصر به فرد در نماد Angle-Angle-Angle می دهد. تفاوت بین دو مختصات بلافاصله یک محور چرخش و زاویه بین دو جهت را ایجاد می کند.
مقیاس گذاری هر نقطه یک مختصات منحصر به فرد در نماد Angle-Angle-Angle می دهد. تفاوت بین دو مختصات بلافاصله یک محور چرخش و زاویه بین دو جهت را ایجاد می کند. تبرها این چرخش ها ممکن است به سادگی اضافه و کم شوند، به خصوص زمانی که فریم های در حال چرخش مانند زنجیره های IK به یکدیگر ثابت می شوند. تفاوت بین دو شی که در یک چارچوب مرجع قرار دارند به سادگی با کم کردن جهت آنها پیدا می شود. چرخش هایی که از منابع خارجی اعمال می شوند، یا از منابعی نسبت به چرخش فعلی هستند، هنوز نیاز به ضرب دارند، استفاده از فرمول رودریگز ارائه شده است.
تبرها این چرخش ها ممکن است به سادگی اضافه و کم شوند، به خصوص زمانی که فریم های در حال چرخش مانند زنجیره های IK به یکدیگر ثابت می شوند. تفاوت بین دو شی که در یک چارچوب مرجع قرار دارند به سادگی با کم کردن جهت آنها پیدا می شود. چرخش هایی که از منابع خارجی اعمال می شوند، یا از منابعی نسبت به چرخش فعلی هستند، هنوز نیاز به ضرب دارند، استفاده از فرمول رودریگز ارائه شده است.




![{\displaystyle {Q}=[{X}،{Y}،{Z}]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/cc821ccb9da7c1120e95a8253301474e3ae7b2a1) ،
،

![{\displaystyle {A}=[X,Y,Z]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/b732043aabcf7a1d454138c502433313f8e32bb0)
 ، و"
، و"![{\displaystyle [x,y,z]={\frac {A}{\|A\|}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/7becd9c40f0aec3b4d3762fd18f06833957010c4)



 حول
حول  .
. .
.
 و یک بردار چرخشی دیگر
و یک بردار چرخشی دیگر برای چرخاندن قاب به اطراف
برای چرخاندن قاب به اطراف









 نشان دهنده سه محور است. اینها میتوانند بهعنوان خلاصهنویسی برای چرخاندن چرخش به دور با استفاده از «چرخش یک بردار چرخشی» بالا استفاده شوند. این عبارات به بهترین شکل به عنوان قطعات کد نمایش داده می شوند.
نشان دهنده سه محور است. اینها میتوانند بهعنوان خلاصهنویسی برای چرخاندن چرخش به دور با استفاده از «چرخش یک بردار چرخشی» بالا استفاده شوند. این عبارات به بهترین شکل به عنوان قطعات کد نمایش داده می شوند.
![{\displaystyle {\text{x-axis}}=\left[x=cn_{x}^{2}+c_{1},\;y=cn_{x}n_{y}+sn_{z}، \;z=cn_{x}n_{z}-sn_{y}\right]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/f2d5d60e7e381e1f0ebc934f68aee30c3fc56f06)
![{\displaystyle {\text{y-axis}}=\left[x=cn_{y}n_{x}-sn_{z},\;y=cn_{y}^{2}+c_{1}، \;z=cn_{y}n_{z}+sn_{x}\right]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/ea4b603b0e87094cfb7487811077cc18530a606d)
![{\displaystyle {\text{z-axis}}=\left[x=cn_{z}n_{x}+sn_{y},\;y=cn_{z}n_{y}-sn_{x}، \;z=cn_{z}^{2}+c_{1}\right]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/57b034a19855bc69fd1cce3daf8d67de13379c21)








 "بالا" است. اگر یک محور دیگر اصلی در نظر گرفته شود، مختصات را می توان به سادگی تعویض کرد.
"بالا" است. اگر یک محور دیگر اصلی در نظر گرفته شود، مختصات را می توان به سادگی تعویض کرد.
 اگر زاویه 0 باشد، کار انجام شده است، نتیجه با
اگر زاویه 0 باشد، کار انجام شده است، نتیجه با
 برخی از مقادیر موقت؛ این مقادیر فقط به جزئی ارجاع داده می شوند...
برخی از مقادیر موقت؛ این مقادیر فقط به جزئی ارجاع داده می شوند... از نرمال پیش بینی شده در محور Y به عنوان زاویه چرخش استفاده کنید...
از نرمال پیش بینی شده در محور Y به عنوان زاویه چرخش استفاده کنید...


 و سپس از پایه برای ثبت تبدیل کواترنیون استفاده کنید...
و سپس از پایه برای ثبت تبدیل کواترنیون استفاده کنید... این زاویه است
این زاویه است این ضربات جزئی در زیر استفاده می شوند ...
این ضربات جزئی در زیر استفاده می شوند ... محاسبه بردار چرخش نرمال شده (محور چرخش)...
محاسبه بردار چرخش نرمال شده (محور چرخش)...

![{\displaystyle {a}=[{X}،{Y}،{Z}]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/fa710dbd1ad69bcb2ba16caf65d0ab0f6c4fa297) عادی شده است. اگر 0 چرخش وجود دارد، نتیجه را با
عادی شده است. اگر 0 چرخش وجود دارد، نتیجه را با



 سپس ترکیب چرخش R B با R A ، چرخش R C = R B R A است، با محور چرخش و زاویه که توسط حاصل ضرب ربعها تعریف میشود.
سپس ترکیب چرخش R B با R A ، چرخش R C = R B R A است، با محور چرخش و زاویه که توسط حاصل ضرب ربعها تعریف میشود. به این معنا که
به این معنا که

 و ارزیابی کنید
و ارزیابی کنید
 اجزای آن را می توان بر حسب اجزای یک کواترنیون واحد بیان کرد که نشان دهنده همان چرخش است.
اجزای آن را می توان بر حسب اجزای یک کواترنیون واحد بیان کرد که نشان دهنده همان چرخش است.
 نسبت به طرح کواترنیون اصلی q . با مقایسه مولفه ها به آن می رسیم
نسبت به طرح کواترنیون اصلی q . با مقایسه مولفه ها به آن می رسیم قابل ذکر است، اگر یکی از این بردارها در داخل واحد 3 کره قرار داشته باشد، دیگری در خارج خواهد بود.
قابل ذکر است، اگر یکی از این بردارها در داخل واحد 3 کره قرار داشته باشد، دیگری در خارج خواهد بود. و زاویه توسط θ اسکالر .
و زاویه توسط θ اسکالر .




 و جایی که { i , j , k }
و جایی که { i , j , k } 

 ما میتوانیم این را با پارامترهای کواترنیون به روشی مختصر نشان دهیم:
ما میتوانیم این را با پارامترهای کواترنیون به روشی مختصر نشان دهیم:
 ،
، و
و ، که پایه چرخشی را تشکیل می دهند که هر کدام از 3 مختصات تشکیل شده است که در مجموع 9 پارامتر را به دست می دهند.
، که پایه چرخشی را تشکیل می دهند که هر کدام از 3 مختصات تشکیل شده است که در مجموع 9 پارامتر را به دست می دهند.
 جایی که i
جایی که i که راه دیگری برای بیان آن است
که راه دیگری برای بیان آن است
 (به ترتیب توجه کنید، زیرا بردار در حال چرخش از سمت راست ضرب می شود).
(به ترتیب توجه کنید، زیرا بردار در حال چرخش از سمت راست ضرب می شود).




 (یا
(یا







 ما داریم
ما داریم
 طرح دوگانه یک بردار واحد است،
طرح دوگانه یک بردار واحد است،

 ، ابتدا آن را بر روی صفحه تعریف شده توسط محور z و خط گره ها پخش می کند. همانطور که زاویه بین صفحات است
، ابتدا آن را بر روی صفحه تعریف شده توسط محور z و خط گره ها پخش می کند. همانطور که زاویه بین صفحات است
 ، این منجر به:
، این منجر به:







 ما داریم
ما داریم








 (به
(به 











 .
. 























 ،
،  پارامتر کردناس2
پارامتر کردناس2 ، فضای محورهای چرخشی.
، فضای محورهای چرخشی.![{\displaystyle \mathbf {R} =[\cos(\theta /2)-Iu\sin(\theta /2)]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/ccaf9643d65a54a5bd1b4d962d07f605c9c67648) جایی که
جایی که
 شبه اسکالر (سه بردار درآر3
شبه اسکالر (سه بردار درآر3






 ممان های اینرسی اصلی جسم را نشان می دهیم، و ما فرض می کنیم
ممان های اینرسی اصلی جسم را نشان می دهیم، و ما فرض می کنیم  . سرعت های زاویه ای اطراف سه محور اصلی جسم هستند
. سرعت های زاویه ای اطراف سه محور اصلی جسم هستند و مشتقات زمانی آنها با نشان داده می شود
و مشتقات زمانی آنها با نشان داده می شود .
. . برای تعیین ماهیت تعادل، سرعت های زاویه ای اولیه کوچک را در امتداد دو محور دیگر فرض کنید. در نتیجه با توجه به رابطه (1)
. برای تعیین ماهیت تعادل، سرعت های زاویه ای اولیه کوچک را در امتداد دو محور دیگر فرض کنید. در نتیجه با توجه به رابطه (1)  خیلی کوچیکه. بنابراین، وابستگی زمانی از
خیلی کوچیکه. بنابراین، وابستگی زمانی از ممکن است مورد غفلت قرار گیرد.
ممکن است مورد غفلت قرار گیرد. از معادله (3)،
از معادله (3)،
 و
و .
. مخالف است و بنابراین چرخش حول این محور برای جسم پایدار است.
مخالف است و بنابراین چرخش حول این محور برای جسم پایدار است. نیز پایدار است.
نیز پایدار است. این بار
این بار خیلی کوچیکه. بنابراین، وابستگی زمانی از
خیلی کوچیکه. بنابراین، وابستگی زمانی از  ممکن است مورد غفلت قرار گیرد.
ممکن است مورد غفلت قرار گیرد.
 مخالف نیست ( و بنابراین رشد خواهد کرد) و بنابراین چرخش حول محور دوم ناپایدار است . بنابراین، حتی یک اختلال کوچک در امتداد محورهای دیگر باعث میشود که شیء به سمت چرخش حرکت کند.
مخالف نیست ( و بنابراین رشد خواهد کرد) و بنابراین چرخش حول محور دوم ناپایدار است . بنابراین، حتی یک اختلال کوچک در امتداد محورهای دیگر باعث میشود که شیء به سمت چرخش حرکت کند.

 .
.















 اگر ماتریس
اگر ماتریس  دارای یک
دارای یک 



 .
. 8
8 و.
و. .
.
 .
.


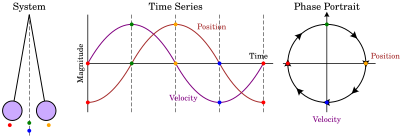
 جابجایی در زمان است،
جابجایی در زمان است، ˙
˙ اولین
اولین  دومین مشتق زمانی است،
دومین مشتق زمانی است، یعنی
یعنی  ،
، ،
،
 ثابت داده می شود.
ثابت داده می شود. ) از نظر فیزیکی، به عنوان مثال، یک
) از نظر فیزیکی، به عنوان مثال، یک  معادله دافینگ یک
معادله دافینگ یک  سیستم بدون نیروی محرکه است و
سیستم بدون نیروی محرکه است و
 فنر را فنر سخت کننده می نامند . برعکس، برای
فنر را فنر سخت کننده می نامند . برعکس، برای این یک فنر نرم کننده است (هنوز با
این یک فنر نرم کننده است (هنوز با و
و با فرض اینکه
با فرض اینکه جایی که ،
جایی که ، 23،
23، و .
و .
 با توجه به
با توجه به این نشان می دهد که راه حل های معادله دافینگ اجباری و میرا را می توان بر حسب سه پارامتر توصیف کرد.،
این نشان می دهد که راه حل های معادله دافینگ اجباری و میرا را می توان بر حسب سه پارامتر توصیف کرد.،
 و
و و
و ).
). اصطلاح، که اصطلاح دافینگ نیز نامیده می شود، می تواند کوچک باشد و سیستم به عنوان یک نوسان ساز هارمونیک ساده
اصطلاح، که اصطلاح دافینگ نیز نامیده می شود، می تواند کوچک باشد و سیستم به عنوان یک نوسان ساز هارمونیک ساده  ) و بدون رانده (
) و بدون رانده ( با
با![{\displaystyle {\begin{aligned}&{\dot {x}}\left({\ddot {x}}+\alpha x+\beta x^{3}\right)=0\\&\Rightarrow {\ frac {\mathrm {d} }{\mathrm {d} t}}\left[{\tfrac {1}{2}}\left({\dot {x}}\right)^{2}+{\ tfrac {1}{2}}\alpha x^{2}+{\tfrac {1}{4}}\beta x^{4}\right]=0\\&\Rightarrow {\tfrac {1}{ 2}}\left({\dot {x}}\right)^{2}+{\tfrac {1}{2}}\alpha x^{2}+{\tfrac {1}{4}}\ بتا x^{4}=H،\end{تراز شده}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/13f43121c8a0043599ca08ec3f0e54a8f6d4da31)
 و˙
و˙
 در H نشان می دهد که سیستم
در H نشان می دهد که سیستم 
 با
با
 و ،
و ،
![{\displaystyle {\begin{aligned}&{\dot {x}}\left({\ddot {x}}+\delta {\dot {x}}+\alpha x+\beta x^{3}\right )=0\\&\پیکان راست {\frac {\mathrm {d} }{\mathrm {d} t}}\left[{\tfrac {1}{2}}\left({\dot {x}} \right)^{2}+{\tfrac {1}{2}}\alpha x^{2}+{\tfrac {1}{4}}\beta x^{4}\right]=-\delta \,\left({\dot {x}}\right)^{2}\\&\Rightarrow {\frac {\mathrm {d} H}{\mathrm {d} t}}=-\delta \, \left({\dot {x}}\right)^{2}\leq 0,\end{تراز شده}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/6436cc695579e043d6e00909e791ec4d6fa8d004)
 برای میرایی بدون فشار دادن به نوسان ساز دافینگ میرا شده به (یکی از)
برای میرایی بدون فشار دادن به نوسان ساز دافینگ میرا شده به (یکی از)  اگر
اگر اگر
اگر و
و و
و

 به عنوان تابعی از
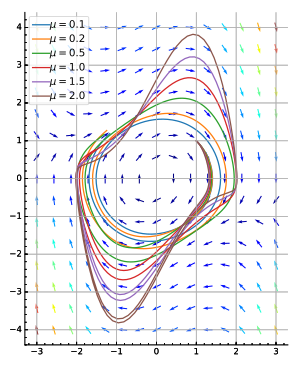
به عنوان تابعی از برای معادله دافینگ، با
برای معادله دافینگ، با و میرایی
و میرایی قسمت های چین خورده پاسخ فرکانسی ناپایدار هستند.
قسمت های چین خورده پاسخ فرکانسی ناپایدار هستند. 
 ) در
) در  برای یک نوسان ساز خطی با
برای یک نوسان ساز خطی با![{\displaystyle \left[\left(\omega ^{2}-\alpha -{\frac {3}{4}}\beta z^{2}\right)^{2}+\left(\delta \ omega \right)^{2}\right]\,z^{2}=\gamma ^{2}.}](https://wikimedia.org/api/rest_v1/media/math/render/svg/4e5ae6346cccac097a7185eb1a6087b099094ddc)

 ،.
،. و
و ) پاسخ فرکانس به سمت فرکانس بالا و به سمت فرکانس پایین برای نوسان ساز فنر نرم کننده (
) پاسخ فرکانس به سمت فرکانس بالا و به سمت فرکانس پایین برای نوسان ساز فنر نرم کننده ( ). سمت آویزان پایینی ناپایدار است - یعنی قسمت های خط چین در شکل های پاسخ فرکانسی - و نمی توان برای مدت زمان طولانی متوجه شد. در نتیجه، پدیده پرش خود را نشان می دهد:
). سمت آویزان پایینی ناپایدار است - یعنی قسمت های خط چین در شکل های پاسخ فرکانسی - و نمی توان برای مدت زمان طولانی متوجه شد. در نتیجه، پدیده پرش خود را نشان می دهد:











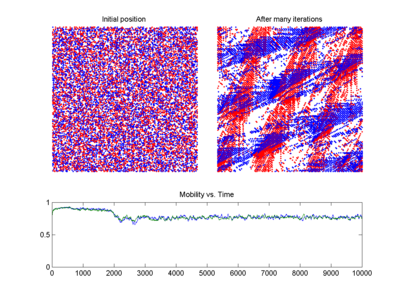
 سایر پارامترها دارای مقادیر زیر هستند:
سایر پارامترها دارای مقادیر زیر هستند:

 و
و شرایط اولیه هستند(0)=1
شرایط اولیه هستند(0)=1 و˙(0)=0.
و˙(0)=0. نقاط قرمز در پرتره های فازی در برخی مواقع وجود دارندتی
نقاط قرمز در پرتره های فازی در برخی مواقع وجود دارندتی



 در این وبلاگ به ریاضیات و کاربردهای آن و تحقیقات در آنها پرداخته می شود. مطالب در این وبلاگ ترجمه سطحی و اولیه است و کامل نیست.در صورتی سوال یا نظری در زمینه ریاضیات دارید مطرح نمایید .در صورت امکان به آن می پردازم. من دوست دارم برای یافتن پاسخ به سوالات و حل پروژه های علمی با دیگران همکاری نمایم.در صورتی که شما هم بامن هم عقیده هستید با من تماس بگیرید.
در این وبلاگ به ریاضیات و کاربردهای آن و تحقیقات در آنها پرداخته می شود. مطالب در این وبلاگ ترجمه سطحی و اولیه است و کامل نیست.در صورتی سوال یا نظری در زمینه ریاضیات دارید مطرح نمایید .در صورت امکان به آن می پردازم. من دوست دارم برای یافتن پاسخ به سوالات و حل پروژه های علمی با دیگران همکاری نمایم.در صورتی که شما هم بامن هم عقیده هستید با من تماس بگیرید.