تجسم
مقاله اصلی: خط میدان
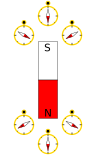
تجسم میدان های مغناطیسی
سمت چپ: جهت خطوط میدان مغناطیسی که با براده های آهنی پاشیده شده روی کاغذی که در بالای آهنربا قرار گرفته است نشان داده می شود.
سمت راست: سوزن های قطب نما در جهت میدان مغناطیسی محلی، به سمت قطب جنوب آهنربا و دور از قطب شمال آن قرار دارند.
میدان را می توان با مجموعه ای از خطوط میدان مغناطیسی ، که جهت میدان را در هر نقطه دنبال می کنند، تجسم کرد. خطوط را می توان با اندازه گیری قدرت و جهت میدان مغناطیسی در تعداد زیادی نقطه (یا در هر نقطه از فضا) ساخت. سپس، هر مکان را با یک فلش (به نام بردار ) که در جهت میدان مغناطیسی محلی با قدر آن متناسب با شدت میدان مغناطیسی است، علامت بزنید. با اتصال این فلش ها مجموعه ای از خطوط میدان مغناطیسی تشکیل می شود. جهت میدان مغناطیسی در هر نقطه موازی با جهت خطوط میدان مجاور است و چگالی محلی خطوط میدان را می توان متناسب با قدرت آن در نظر گرفت. خطوط میدان مغناطیسی مانند خطوط جریانی در جریان سیال هستند ، از این نظر که نشان دهنده توزیع پیوسته هستند و وضوح متفاوت خطوط بیشتر یا کمتر را نشان می دهد.
مزیت استفاده از خطوط میدان مغناطیسی به عنوان نمایش این است که بسیاری از قوانین مغناطیس (و الکترومغناطیس) را می توان به طور کامل و مختصر با استفاده از مفاهیم ساده ای مانند "تعداد" خطوط میدان در یک سطح بیان کرد. این مفاهیم را می توان به سرعت به شکل ریاضی خود "ترجمه" کرد. به عنوان مثال، تعداد خطوط میدانی که از یک سطح معین عبور می کنند، انتگرال سطح میدان مغناطیسی است. [ 10 ] : 237
پدیده های مختلف خطوط میدان مغناطیسی را به گونه ای نمایش می دهند که گویی خطوط میدان پدیده های فیزیکی هستند. به عنوان مثال، براده های آهن که در یک میدان مغناطیسی قرار می گیرند خطوطی را تشکیل می دهند که مطابق با "خطوط میدان" هستند. [ یادداشت 5 ] "خطوط" میدان مغناطیسی نیز به صورت بصری در شفق های قطبی نمایش داده می شوند ، که در آن فعل و انفعالات دوقطبی ذرات پلاسما رگه های قابل مشاهده ای از نور را ایجاد می کنند که با جهت محلی میدان مغناطیسی زمین همسو می شوند.
خطوط میدان می تواند به عنوان یک ابزار کیفی برای تجسم نیروهای مغناطیسی استفاده شود. در مواد فرومغناطیسی مانند آهن و در پلاسما، نیروهای مغناطیسی را می توان با تصور اینکه خطوط میدان یک کشش (مانند یک نوار لاستیکی) در طول خود و فشاری عمود بر طول آنها بر خطوط میدان مجاور اعمال می کنند، درک کرد. "بر خلاف" قطب های آهنربا جذب می شوند زیرا آنها توسط خطوط میدان زیادی به هم مرتبط هستند. قطب های "مانند" دفع می شوند زیرا خطوط میدان آنها به هم نمی رسند، اما به موازات یکدیگر قرار می گیرند و روی یکدیگر فشار می آورند.
میدان مغناطیسی آهنرباهای دائمی
نوشتار اصلی: ممان مغناطیسی § مدل ها
آهنرباهای دائمی اجسامی هستند که میدان های مغناطیسی پایدار خود را تولید می کنند. آنها از مواد فرومغناطیسی مانند آهن و نیکل ساخته شده اند که مغناطیسی شده اند و دارای قطب شمال و جنوب هستند.
میدان مغناطیسی آهنرباهای دائمی می تواند بسیار پیچیده باشد، به خصوص در نزدیکی آهنربا. میدان مغناطیسی یک آهنربای مستقیم کوچک [ یادداشت 6 ] با قدرت آهنربا (که گشتاور دوقطبی مغناطیسی آن m نامیده می شود ) متناسب است. معادلات بی اهمیت هستند و به فاصله از آهنربا و جهت آهنربا بستگی دارند. برای آهنرباهای ساده، m در جهت خطی است که از جنوب به قطب شمال آهنربا کشیده شده است. چرخاندن یک آهنربای میله ای معادل چرخش m آن در 180 درجه است.
میدان مغناطیسی آهنرباهای بزرگتر را می توان با مدلسازی آنها به عنوان مجموعه ای از تعداد زیادی آهنربای کوچک به نام دوقطبی بدست آورد . میدان مغناطیسی تولید شده توسط آهنربا، میدان مغناطیسی خالص این دوقطبی است. هر نیروی خالص وارد بر آهنربا در نتیجه جمع کردن نیروهای وارد بر دو قطبی منفرد است.
دو مدل ساده شده برای ماهیت این دوقطبی ها وجود دارد: مدل قطب مغناطیسی و مدل حلقه آمپرین . این دو مدل دو میدان مغناطیسی متفاوت H و B تولید می کنند . با این حال، در خارج از یک ماده، این دو یکسان هستند (به یک ثابت ضربی) به طوری که در بسیاری از موارد می توان تمایز را نادیده گرفت. این به ویژه در مورد میدان های مغناطیسی، مانند میدان های ناشی از جریان های الکتریکی که توسط مواد مغناطیسی ایجاد نمی شوند، صادق است.
یک مدل واقعی مغناطیس از هر یک از این مدل ها پیچیده تر است. هیچ یک از مدل ها به طور کامل توضیح نمی دهد که چرا مواد مغناطیسی هستند. مدل تک قطبی پشتیبانی آزمایشی ندارد. مدل حلقه آمپرین مقداری، اما نه تمام گشتاور مغناطیسی یک ماده را توضیح می دهد. این مدل پیشبینی میکند که حرکت الکترونها در یک اتم به گشتاور دوقطبی مغناطیسی مداری آن الکترونها متصل است و این گشتاورهای مداری به مغناطیس مشاهده شده در سطح ماکروسکوپی کمک میکنند. با این حال، حرکت الکترونها کلاسیک نیست، و گشتاور مغناطیسی اسپین الکترونها (که توسط هیچیک از مدلها توضیح داده نشده است) نیز سهم قابلتوجهی در گشتاور کل آهنرباها دارد.
مدل قطب مغناطیسی
همچنین ببینید: تک قطبی مغناطیسی
مدل قطب مغناطیسی: دو قطب مخالف، شمال (+) و جنوب (-)، که با فاصله d از هم جدا شده اند، یک میدان H (خطوط) ایجاد می کنند.
از نظر تاریخی، کتاب های درسی فیزیک اولیه، نیرو و گشتاور بین دو آهنربا را به دلیل دفع یا جذب یکدیگر توسط قطب های مغناطیسی به همان شیوه ای که نیروی کولن بین بارهای الکتریکی ایجاد می کند، مدل می کردند. در سطح میکروسکوپی، این مدل با شواهد تجربی در تضاد است و مدل قطبی مغناطیس دیگر روش معمولی برای معرفی این مفهوم نیست. [ 11 ] : 258 با این حال، به دلیل سادگی ریاضی، هنوز هم گاهی اوقات به عنوان یک مدل ماکروسکوپی برای فرومغناطیس استفاده می شود. [ 17 ]
در این مدل، یک میدان H مغناطیسی توسط بارهای مغناطیسی ساختگی که بر روی سطح هر قطب پخش می شود، تولید می شود . این بارهای مغناطیسی در واقع مربوط به میدان مغناطیسی M هستند . بنابراین، میدان H مشابه میدان الکتریکی E است که با بار الکتریکی مثبت شروع می شود و با بار الکتریکی منفی به پایان می رسد. بنابراین، در نزدیکی قطب شمال، تمام خطوط میدان H به سمت قطب شمال (چه در داخل آهنربا یا خارج) قرار دارند، در حالی که در نزدیکی قطب جنوب، همه خطوط میدان H به سمت قطب جنوب (چه در داخل آهنربا یا خارج) قرار دارند. همچنین، یک قطب شمال نیرویی را در جهت میدان H احساس می کند در حالی که نیروی وارد بر قطب جنوب مخالف میدان H است .
در مدل قطب مغناطیسی، دوقطبی مغناطیسی ابتدایی m توسط دو قطب مغناطیسی مخالف با قدرت قطب q m که توسط یک بردار فاصله کوچک d از هم جدا شده اند، تشکیل می شود ، به طوری که m = q m d . مدل قطب مغناطیسی میدان H را در داخل و خارج مواد مغناطیسی به درستی پیشبینی میکند، به ویژه این واقعیت که H در مقابل میدان مغناطیسی M درون یک آهنربای دائمی است.
از آنجایی که این مدل مبتنی بر ایده ساختگی چگالی بار مغناطیسی است ، مدل قطب دارای محدودیتهایی است. قطب های مغناطیسی نمی توانند جدا از یکدیگر مانند بارهای الکتریکی وجود داشته باشند، اما همیشه به صورت جفت شمال-جنوب هستند. اگر یک جسم مغناطیسی به نصف تقسیم شود، یک قطب جدید روی سطح هر قطعه ظاهر می شود، بنابراین هر یک دارای یک جفت قطب مکمل است. مدل قطب مغناطیسی مغناطیس تولید شده توسط جریان های الکتریکی و همچنین ارتباط ذاتی بین تکانه زاویه ای و مغناطیس را در نظر نمی گیرد .
مدل قطبی معمولاً بار مغناطیسی را به عنوان یک انتزاع ریاضی به جای یک ویژگی فیزیکی ذرات در نظر می گیرد. با این حال، یک تک قطبی مغناطیسی یک ذره فرضی (یا طبقه ای از ذرات) است که از نظر فیزیکی فقط یک قطب مغناطیسی (یک قطب شمال یا یک قطب جنوب) دارد. به عبارت دیگر، دارای یک "بار مغناطیسی" مشابه بار الکتریکی است. خطوط میدان مغناطیسی روی تک قطبی های مغناطیسی شروع یا خاتمه می یابند، بنابراین اگر وجود داشته باشند، استثناهایی برای این قاعده قائل می شوند که خطوط میدان مغناطیسی نه شروع می شوند و نه پایان. برخی از نظریه ها (مانند نظریه های متحد بزرگ ) وجود تک قطبی های مغناطیسی را پیش بینی کرده اند، اما تاکنون هیچ کدام مشاهده نشده است.
مدل حلقه آمپرین
مقاله اصلی: دوقطبی مغناطیسی
همچنین ببینید: گشتاور مغناطیسی اسپین و میکرومغناطیس
مدل حلقه آمپرین
یک حلقه جریان (حلقه) که در صفحه x می رود و در نقطه بیرون می آید، یک فیلد B (خطوط) تولید می کند. همانطور که شعاع حلقه جاری کوچک می شود، میدان های تولید شده با یک "دوقطبی مغناطیسی استاتیک" انتزاعی یکسان می شوند (که با یک فلش به سمت راست نشان داده می شود).
در مدل توسعه یافته توسط آمپر ، دوقطبی مغناطیسی ابتدایی که همه آهنرباها را تشکیل می دهد، یک حلقه آمپری به اندازه کافی کوچک با جریان I و ناحیه حلقه A است . ممان دوقطبی این حلقه m = IA است .
این دوقطبی های مغناطیسی یک میدان B مغناطیسی تولید می کنند .
میدان مغناطیسی یک دوقطبی مغناطیسی در شکل نشان داده شده است. از بیرون، دوقطبی مغناطیسی ایده آل با دوقطبی الکتریکی ایده آل با همان قدرت یکسان است. برخلاف دوقطبی الکتریکی، یک دوقطبی مغناطیسی به درستی به عنوان یک حلقه جریان با جریان I و مساحت a مدلسازی میشود . چنین حلقه جریان دارای گشتاور مغناطیسی است،
تعامل با آهنربا
نیروی بین آهنرباها
مقاله اصلی: نیروی بین آهنرباها
تعیین نیروی بین دو آهنربای کوچک بسیار پیچیده است زیرا به قدرت و جهت هر دو آهنربا و فاصله و جهت آنها نسبت به یکدیگر بستگی دارد. این نیرو به ویژه به چرخش آهنرباها در اثر گشتاور مغناطیسی حساس است. نیروی وارد بر هر آهنربا به گشتاور مغناطیسی آن و میدان مغناطیسی [ یادداشت 7 ] دیگری بستگی دارد.
برای درک نیروی بین آهنرباها، بررسی مدل قطب مغناطیسی ارائه شده در بالا مفید است. در این مدل، میدان H یک آهنربا هر دو قطب آهنربای دوم را فشار داده و می کشد. اگر این میدان H در هر دو قطب آهنربای دوم یکسان باشد، هیچ نیروی خالصی روی آن آهنربا وجود ندارد زیرا نیرو برای قطب های مخالف مخالف است. با این حال، اگر میدان مغناطیسی آهنربای اول غیر یکنواخت باشد (مانند H نزدیک یکی از قطب های آن)، هر قطب آهنربای دوم میدان متفاوتی را می بیند و تحت نیروی متفاوتی قرار می گیرد. این تفاوت در دو نیرو، آهنربا را در جهت افزایش میدان مغناطیسی حرکت می دهد و همچنین ممکن است باعث ایجاد گشتاور خالص شود.
این یک مثال خاص از یک قانون کلی است که آهنرباها به مناطقی با میدان مغناطیسی بالاتر جذب می شوند (یا بسته به جهت آهنربا دفع می شوند). هر میدان مغناطیسی غیر یکنواخت، خواه ناشی از آهنرباهای دائمی یا جریان های الکتریکی باشد، به این ترتیب به یک آهنربای کوچک نیرو وارد می کند.
جزئیات مدل حلقه آمپرین متفاوت و پیچیده تر است، اما نتیجه یکسانی را به همراه دارد: اینکه دوقطبی های مغناطیسی به مناطقی با میدان مغناطیسی بالاتر جذب/دفع می شوند. از نظر ریاضی، نیروی وارد بر آهنربای کوچکی که دارای گشتاور مغناطیسی m در اثر میدان مغناطیسی B است عبارت است از: [ 19 ] : معادله. 11.42
که در آن گرادیان ∇ تغییر کمیت m · B در واحد فاصله و جهت حداکثر افزایش m · B است . حاصل ضرب نقطه m · B = mB cos ( θ ) , که در آن m و B نشان دهنده بزرگی بردارهای m و B هستند و θ زاویه بین آنهاست. اگر m در همان جهت B باشد ، حاصل ضرب نقطهای مثبت است و گرادیان نقطهای «سربالایی» است که آهنربا را به مناطقی با میدان B بالاتر میکشد (بهطور دقیقتر m · B بزرگتر ). این معادله صرفاً فقط برای آهنرباهایی با اندازه صفر معتبر است، اما اغلب تقریب خوبی برای آهنرباهای نه چندان بزرگ است. نیروی مغناطیسی روی آهنرباهای بزرگتر با تقسیم آنها به مناطق کوچکتر تعیین می شود که هر یک دارای m خاص خود هستند و سپس نیروهای وارد بر هر یک از این مناطق بسیار کوچک جمع می شوند .























 که در آن
که در آن 
 یک
یک  چیزی را تشکیل می دهد که مبنای حرکت نامیده می شود . این «مبنا» مبنایی به معنای معمول ریاضی نیست. برای یک چیز، از آنجایی که توابع عادی نیستند، در عوض به یک تابع دلتا بهنجار می شوند ،
چیزی را تشکیل می دهد که مبنای حرکت نامیده می شود . این «مبنا» مبنایی به معنای معمول ریاضی نیست. برای یک چیز، از آنجایی که توابع عادی نیستند، در عوض به یک تابع دلتا بهنجار می شوند ، 
 جایی که
جایی که  زیرا اگر ذره اندازه گیری شود، 100% احتمال دارد که در جایی باشد .
زیرا اگر ذره اندازه گیری شود، 100% احتمال دارد که در جایی باشد . و اعداد کوانتومی مغناطیسی m l و m s . الکترونها در یک لایه فرعی از یک اتم (مانند s، p، d یا f) با مقادیری از
و اعداد کوانتومی مغناطیسی m l و m s . الکترونها در یک لایه فرعی از یک اتم (مانند s، p، d یا f) با مقادیری از به
به از جمله صفر. [ 3 ] بنابراین زیر پوسته های s، p، d و f هر کدام شامل 1، 3، 5 و 7 اوربیتال هستند. هر یک از این اوربیتال ها می توانند حداکثر دو الکترون (با اسپین های مخالف) را در خود جای دهند که اساس جدول تناوبی را تشکیل می دهند .
از جمله صفر. [ 3 ] بنابراین زیر پوسته های s، p، d و f هر کدام شامل 1، 3، 5 و 7 اوربیتال هستند. هر یک از این اوربیتال ها می توانند حداکثر دو الکترون (با اسپین های مخالف) را در خود جای دهند که اساس جدول تناوبی را تشکیل می دهند .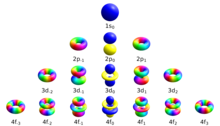
 از چپ به راست به ترتیب صعودی این
از چپ به راست به ترتیب صعودی این وابستگی مولفه آزیموتال را می توان به عنوان یک گرادیان رنگ تکراری مشاهده کرد
وابستگی مولفه آزیموتال را می توان به عنوان یک گرادیان رنگ تکراری مشاهده کرد بار حول محور عمودی
بار حول محور عمودی ،
، حالت کوانتومی کامل یک الکترون را در یک اتم مشخص کنید که تابع موج یا مدار آن نامیده می شود. معادله شرودینگر برای تابع موج یک اتم با یک الکترون یک معادله دیفرانسیل جزئی قابل تفکیک است . (این مورد برای اتم هلیوم خنثی یا اتم های دیگر با الکترون های متقابل متقابل نیست ، که به روش های پیچیده تری برای حل نیاز دارند [ 4 ] ). شعاع، زاویه همپوشانی (یا قطبی) و آزیموت: [ 5 ]
حالت کوانتومی کامل یک الکترون را در یک اتم مشخص کنید که تابع موج یا مدار آن نامیده می شود. معادله شرودینگر برای تابع موج یک اتم با یک الکترون یک معادله دیفرانسیل جزئی قابل تفکیک است . (این مورد برای اتم هلیوم خنثی یا اتم های دیگر با الکترون های متقابل متقابل نیست ، که به روش های پیچیده تری برای حل نیاز دارند [ 4 ] ). شعاع، زاویه همپوشانی (یا قطبی) و آزیموت: [ 5 ]
 در قالب قابل حل است
در قالب قابل حل است  . زیرا مقادیر زاویه آزیموت
. زیرا مقادیر زاویه آزیموت با 2 تفاوت دارد
با 2 تفاوت دارد رادیان (360 درجه) نشان دهنده همان موقعیت در فضا و قدر کلی استاف
رادیان (360 درجه) نشان دهنده همان موقعیت در فضا و قدر کلی استاف باید به مضرب عدد صحیح کوانتیزه شود
باید به مضرب عدد صحیح کوانتیزه شود ، تولید یک توان مختلط :
، تولید یک توان مختلط : . [ 6 ] این اعداد صحیح اعداد کوانتومی مغناطیسی هستند. همان ثابت در معادله colatitude ظاهر می شود، جایی که مقادیر بزرگتر از
. [ 6 ] این اعداد صحیح اعداد کوانتومی مغناطیسی هستند. همان ثابت در معادله colatitude ظاهر می شود، جایی که مقادیر بزرگتر از تمایل به کاهش قدر،
تمایل به کاهش قدر، و ارزش های
و ارزش های






 و
و . حتی برای ارزش های افراطی
. حتی برای ارزش های افراطی - مولفه این بردار کمتر از قدر کل آن است.
- مولفه این بردار کمتر از قدر کل آن است. ، بزرگی تکانه زاویه ای در
، بزرگی تکانه زاویه ای در .
. ، که قدر آن به عدد کوانتومی آزیموتال زیر پوسته آن مربوط می شودتوسط معادله:
، که قدر آن به عدد کوانتومی آزیموتال زیر پوسته آن مربوط می شودتوسط معادله: ،
، ثابت پلانک کاهش یافته است . توجه داشته باشید که این
ثابت پلانک کاهش یافته است . توجه داشته باشید که این بر
بر و تقریبی است
و تقریبی است برای بالا
برای بالا
 . رنگ ها فاز تابع موج را نشان می دهند.
. رنگ ها فاز تابع موج را نشان می دهند.





 با فرکانس ضرب در ثابت پلانک داده می شود
با فرکانس ضرب در ثابت پلانک داده می شود :
:












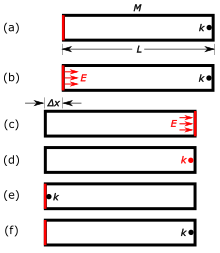
 و طول
و طول ،
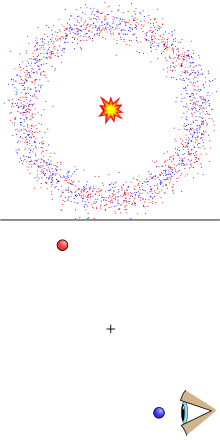
،  از چپ به راست تشعشع دارای تکانه است
از چپ به راست تشعشع دارای تکانه است از آنجایی که تکانه کل سیستم صفر است، سیلندر با سرعتی پس میزند
از آنجایی که تکانه کل سیستم صفر است، سیلندر با سرعتی پس میزند
 (با فرض
(با فرض ، سیلندر را پس از طی مسافتی متوقف می کند
، سیلندر را پس از طی مسافتی متوقف می کند

 در حین انتقال انرژی از راست به چپ نمی تواند بدون جرم باشد. اگر انرژی
در حین انتقال انرژی از راست به چپ نمی تواند بدون جرم باشد. اگر انرژی تناقض از بین می رود
تناقض از بین می رود 





 .
.![{\displaystyle [c_{i}^{A}]،[c_{j}^{B}]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/a2b47f980dac5bc92f73609aef7a6280f2f2be7f)









 .
. .
.




![{\displaystyle \rho =\sum _{i}w_{i}\left[\sum _{j}{\bar {c}}_{ij}(|\alpha _{ij}\rangle \otimes |\ بتا _{ij}\rangle )\right]\left[\sum _{k}c_{ik}(\langle \alpha _{ik}|\otimes \langle \beta _{ik}|)\right]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/cbf2f7c56adc4e273d3e3c73ee6a66e190c3f35c)





 .
.






 .
. یک کانال در تصویر هایزنبرگ و
یک کانال در تصویر هایزنبرگ و یک کانال ایده آل انتخاب شده باشید برای امکانپذیر ساختن مقایسه، باید ف را از طریق دستگاههای مناسب رمزگذاری و رمزگشایی کنیم، یعنی ترکیب را در نظر بگیریم.
یک کانال ایده آل انتخاب شده باشید برای امکانپذیر ساختن مقایسه، باید ف را از طریق دستگاههای مناسب رمزگذاری و رمزگشایی کنیم، یعنی ترکیب را در نظر بگیریم.


 عملیات n ورودی تحت عملیات را توصیف می کند
عملیات n ورودی تحت عملیات را توصیف می کند به طور مستقل و همتای مکانیکی کوانتومی
به طور مستقل و همتای مکانیکی کوانتومی  .
.
 با توجه به
با توجه به که
که و
و ، داریم
، داریم
 را می توان به عنوان نمایانگر پیامی متشکل از احتمالاً بی نهایت کلمه در نظر گرفت. شرط supremum حد در تعریف می گوید که، در حد، با فراخوانی کانال حداکثر r برابر طول یک کلمه، می توان به انتقال وفادار دست یافت. همچنین می توان گفت r تعداد حروفی است که در هر فراخوانی کانال می توانند بدون خطا ارسال شوند.
را می توان به عنوان نمایانگر پیامی متشکل از احتمالاً بی نهایت کلمه در نظر گرفت. شرط supremum حد در تعریف می گوید که، در حد، با فراخوانی کانال حداکثر r برابر طول یک کلمه، می توان به انتقال وفادار دست یافت. همچنین می توان گفت r تعداد حروفی است که در هر فراخوانی کانال می توانند بدون خطا ارسال شوند. بالاترین نرخ های قابل دستیابی است.
بالاترین نرخ های قابل دستیابی است.









 که
که  .
. فضاهای حالت (
فضاهای حالت (  خانواده عملگرها را نشان خواهد داد
خانواده عملگرها را نشان خواهد داد در
در  بین
بین 
 برای همه n
برای همه n ، که عمل را توصیف می کند
، که عمل را توصیف می کند به عنوان یک نقشه بین فضاهای هیلبرت، الحاق آن را بدست می آوریم
به عنوان یک نقشه بین فضاهای هیلبرت، الحاق آن را بدست می آوریم
 . از نظر فیزیکی، این بدان معنی است که در تصویر هایزنبرگ، مشاهده ناچیز پس از اعمال کانال، بی اهمیت باقی می ماند.
. از نظر فیزیکی، این بدان معنی است که در تصویر هایزنبرگ، مشاهده ناچیز پس از اعمال کانال، بی اهمیت باقی می ماند.





 هنوز جبر C* است. یک عنصر
هنوز جبر C* است. یک عنصر یک جبر C*
یک جبر C* اگر مثبت نامیده می شود
اگر مثبت نامیده می شود برای برخی
برای برخی . مثبت بودن یک نقشه بر این اساس تعریف می شود. این توصیف عموماً پذیرفته نشده است. ابزار
. مثبت بودن یک نقشه بر این اساس تعریف می شود. این توصیف عموماً پذیرفته نشده است. ابزار 
 ) منجر به حالت چند بدنی متفاوتی نمی شود.
) منجر به حالت چند بدنی متفاوتی نمی شود. و ذره 2 در حالت
و ذره 2 در حالت ، حالت دارد
، حالت دارد به علامت
به علامت  . این دو حالت نباید یک تفاوت قابل اندازه گیری داشته باشند، بنابراین باید بردار یکسان باشند، تا
. این دو حالت نباید یک تفاوت قابل اندازه گیری داشته باشند، بنابراین باید بردار یکسان باشند، تا 
 فاکتور فاز است. در فضای
فاکتور فاز است. در فضای  یا-1
یا-1 . بنابراین،
. بنابراین، 



 هریک از افراد آبلیان یکسان با آمارهای فردیα
هریک از افراد آبلیان یکسان با آمارهای فردیα ( یعنی سیستم یک فاز را انتخاب می کندهمنα
( یعنی سیستم یک فاز را انتخاب می کندهمنα هنگامی که دو فرد منفرد تحت مبادله آدیاباتیک در خلاف جهت عقربههای ساعت قرار میگیرند) همه با هم ترکیب میشوند، با هم آماری دارند .ن2α
هنگامی که دو فرد منفرد تحت مبادله آدیاباتیک در خلاف جهت عقربههای ساعت قرار میگیرند) همه با هم ترکیب میشوند، با هم آماری دارند .ن2α . این را میتوان با توجه به این نکته مشاهده کرد که با چرخش خلاف جهت عقربههای ساعت دو آنیون مرکب در اطراف یکدیگر، ن2
. این را میتوان با توجه به این نکته مشاهده کرد که با چرخش خلاف جهت عقربههای ساعت دو آنیون مرکب در اطراف یکدیگر، ن2 جفت آنیون انفرادی (یکی در هر انیون مرکب اول، یکی در هرییون مرکب دوم) که هر کدام یک فاز دارند .همنα
جفت آنیون انفرادی (یکی در هر انیون مرکب اول، یکی در هرییون مرکب دوم) که هر کدام یک فاز دارند .همنα

 در جبر هندسی از فرمول زیر استفاده می شود: [ 15 ] : 50-51
در جبر هندسی از فرمول زیر استفاده می شود: [ 15 ] : 50-51  ،
، زاویه چرخش است، و
زاویه چرخش است، و دوبردار نرمال شده است که صفحه چرخش را نشان می دهد به طوری که
دوبردار نرمال شده است که صفحه چرخش را نشان می دهد به طوری که .
. ، بنابراین فرمول اویلر اعمال می شود، [ 2 ] : 401 که چرخش را می دهد
، بنابراین فرمول اویلر اعمال می شود، [ 2 ] : 401 که چرخش را می دهد .
. بنابراین یک "چرخش در طول زمان" از معادله مشابه برای اعداد مختلط تقسیم می شود :
بنابراین یک "چرخش در طول زمان" از معادله مشابه برای اعداد مختلط تقسیم می شود : .
. با ضرب با شبه مقیاس تبدیل می شود تا عنصر دوگانه آن را تشکیل دهد
با ضرب با شبه مقیاس تبدیل می شود تا عنصر دوگانه آن را تشکیل دهد . [ 12 ] : 114 چرخش دوگانه عنصر فضا-زمان را تبدیل می کند
. [ 12 ] : 114 چرخش دوگانه عنصر فضا-زمان را تبدیل می کند از طریق زاویه
از طریق زاویه با شبه اسکالر
با شبه اسکالر است: [ 1 ] : 13
است: [ 1 ] : 13 
 به r∗
به r∗ : [ 1 ] : 13 [ 16 ]
: [ 1 ] : 13 [ 16 ]
 بازگشت است
بازگشت است  :
:
 : [ 18 ]
: [ 18 ]

 میدان های الکتریکی و مغناطیسی معمولی هستند و
میدان های الکتریکی و مغناطیسی معمولی هستند و شبه STA است. [ 2 ] : 230 متناوباً، در حال گسترش
شبه STA است. [ 2 ] : 230 متناوباً، در حال گسترش
 و
و میدانها از آن بازیابی می شوند
میدانها از آن بازیابی می شوند
 اصطلاح یک چارچوب مرجع معین را نشان میدهد، و به این ترتیب، استفاده از چارچوبهای مرجع مختلف، منجر به میدانهای نسبی ظاهراً متفاوتی میشود، دقیقاً مانند نسبیت خاص استاندارد. [ 2 ] : 233
اصطلاح یک چارچوب مرجع معین را نشان میدهد، و به این ترتیب، استفاده از چارچوبهای مرجع مختلف، منجر به میدانهای نسبی ظاهراً متفاوتی میشود، دقیقاً مانند نسبیت خاص استاندارد. [ 2 ] : 233 
 توسط [ 22 ] : 26 داده شده است
توسط [ 22 ] : 26 داده شده است
 اجزای چگالی جریان سه بعدی کلاسیک هستند. هنگامی که این مقادیر را به این ترتیب ترکیب می کنیم، به ویژه مشخص می شود که چگالی بار کلاسیک چیزی نیست جز جریانی که در جهت زمانی داده شده توسط
اجزای چگالی جریان سه بعدی کلاسیک هستند. هنگامی که این مقادیر را به این ترتیب ترکیب می کنیم، به ویژه مشخص می شود که چگالی بار کلاسیک چیزی نیست جز جریانی که در جهت زمانی داده شده توسط
 ، می توان دستکاری زیر را انجام داد: [ 23 ] : 231
، می توان دستکاری زیر را انجام داد: [ 23 ] : 231 ![{\displaystyle {\begin{aligned}\nabla \cdot \left[\nabla F\right]&=\nabla \cdot \left[\mu _{0}cJ\right]\\0&=\nabla \cdot J .\end{تراز شده}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/fddaae634e913589d397263ea660f33dbef138b9)

 ، مشابه چهار پتانسیل الکترومغناطیسی در حساب تانسور است. در STA به این صورت تعریف می شود
، مشابه چهار پتانسیل الکترومغناطیسی در حساب تانسور است. در STA به این صورت تعریف می شود
 اجزای پتانسیل مغناطیسی هستند. همانطور که تعریف شد، این میدان دارای واحدهای SI وبر در هر متر است (V⋅s⋅m -1 ).
اجزای پتانسیل مغناطیسی هستند. همانطور که تعریف شد، این میدان دارای واحدهای SI وبر در هر متر است (V⋅s⋅m -1 ).
 ، پتانسیل داده شده توسط
، پتانسیل داده شده توسط

 برای سادهترین مشکل معین به عنوان ثابت کردن سنج شناخته میشود . با این حال، در الکترودینامیک نسبیتی، شرط لورنز اغلب تحمیل می شود، جایی که
برای سادهترین مشکل معین به عنوان ثابت کردن سنج شناخته میشود . با این حال، در الکترودینامیک نسبیتی، شرط لورنز اغلب تحمیل می شود، جایی که . [ 2 ] : 231
. [ 2 ] : 231 




 .
. ، همان معادله حرکتی که در بالا برای میدان پتانسیل وجود دارد
، همان معادله حرکتی که در بالا برای میدان پتانسیل وجود دارد
 ماتریس های پائولی هستند (با نماد "کلاه" نشان دهنده آن است
ماتریس های پائولی هستند (با نماد "کلاه" نشان دهنده آن است یک عملگر ماتریسی است و نه عنصری در جبر هندسی)، و
یک عملگر ماتریسی است و نه عنصری در جبر هندسی)، و شرودینگر همیلتونی است.
شرودینگر همیلتونی است. به نمایندگی STA
به نمایندگی STA با استفاده از عناصر،σ1،σ2،
با استفاده از عناصر،σ1،σ2، ، از زیر جبر فضازمان با درجه زوج و شبه مقیاس
، از زیر جبر فضازمان با درجه زوج و شبه مقیاس : [ 2 ] : 37 [ 27 ] : 270، 271
: [ 2 ] : 37 [ 27 ] : 270، 271 

 یک چند بردار زوج جبر هندسی است و شرودینگر همیلتونی
یک چند بردار زوج جبر هندسی است و شرودینگر همیلتونی  یک بردار ثابت انتخابی دلخواه است. یک چرخش ثابت می تواند هر بردار ثابت انتخابی جایگزینی را ایجاد کند"
یک بردار ثابت انتخابی دلخواه است. یک چرخش ثابت می تواند هر بردار ثابت انتخابی جایگزینی را ایجاد کند" . [ 28 ] : 30
. [ 28 ] : 30  ، یک ضرب برداری (هندسی) وجود دارد
، یک ضرب برداری (هندسی) وجود دارد  ، ضرب درونی (نقطه ای).
، ضرب درونی (نقطه ای).  و ضرب بیرونی (خارجی، گوه ای).
و ضرب بیرونی (خارجی، گوه ای).  . حاصل ضرب برداری مجموع حاصلضرب درونی و بیرونی است: [ 1 ] : 6
. حاصل ضرب برداری مجموع حاصلضرب درونی و بیرونی است: [ 1 ] : 6 
 و
و اگر حاصل ضرب داخلی آنها صفر باشد متعامد هستند. بردارها
اگر حاصل ضرب داخلی آنها صفر باشد متعامد هستند. بردارها و 3 بردار فضایی
و 3 بردار فضایی . جمله های غیر صفر تانسور متریک مینکوفسکی عبارت های قطر هستند،
. جمله های غیر صفر تانسور متریک مینکوفسکی عبارت های قطر هستند، . برای
. برای :
:
 ، چهار بردار
، چهار بردار ، شش دو بردار
، شش دو بردار , چهار شبه بردار ( سه بردار )
, چهار شبه بردار ( سه بردار ) و یک شبه اسکالر
و یک شبه اسکالر  با
با . [ 1 ] : 11 شبه اسکالر با تمام عناصر STA درجه زوج جابجا می کند ، اما با همه عناصر STA درجه فرد ضد جابجا می کند . [ 4 ] : 6
. [ 1 ] : 11 شبه اسکالر با تمام عناصر STA درجه زوج جابجا می کند ، اما با همه عناصر STA درجه فرد ضد جابجا می کند . [ 4 ] : 6 

 به عنوان
به عنوان و دو بردارهای
و دو بردارهای  به عنوان
به عنوان . [ 1 ] : 22 [ 2 ] : 37 ماتریس های پائولی
. [ 1 ] : 22 [ 2 ] : 37 ماتریس های پائولی ، یک نمایش ماتریسی برای هستندσ1،σ2،σ3
، یک نمایش ماتریسی برای هستندσ1،σ2،σ3 . [ 2 ] : 37 برای هر جفتی از
. [ 2 ] : 37 برای هر جفتی از و ضرب خارجی غیر صفر عبارتند از: [ 2 ] : 37 [ 1 ] : 16
و ضرب خارجی غیر صفر عبارتند از: [ 2 ] : 37 [ 1 ] : 16 
 . [ 6 ] : 2 یک مثال است
. [ 6 ] : 2 یک مثال است . بردارهای تهی مماس بر مخروط نور (مخروط پوچ) هستند. [ 6 ] : 4 یک عنصر
. بردارهای تهی مماس بر مخروط نور (مخروط پوچ) هستند. [ 6 ] : 4 یک عنصر . [ 7 ] : 103 دو ناتوان
. [ 7 ] : 103 دو ناتوان  و
و ناتوان متعامد هستند اگر
ناتوان متعامد هستند اگر . [ 7 ] : 103 مثالی از یک جفت ناتوان متعامد است
. [ 7 ] : 103 مثالی از یک جفت ناتوان متعامد است و
و با
با . مقسومکنندههای صفر مناسب، عناصر غیرصفری هستند که حاصلضرب آنها صفر است، مانند بردارهای تهی یا غیر توانای متعامد. [ 8 ] : 191 جبر تقسیم جبری است که شامل عناصر معکوس (مقابل) ضربی برای هر عنصر است، اما این در صورتی رخ می دهد که مقسوم علیه های صفر مناسب وجود نداشته باشد و تنها ناتوان آن 1 باشد. [ 7 ] : 103 [ 9 ] : 211 [ a ] تنها جبرهای تقسیم انجمنی اعداد حقیقی، اعداد مختلط و رباعی ها [ 10 ] : 366 از آنجایی که STA یک جبر تقسیم نیست، برخی از عناصر STA ممکن است فاقد معکوس باشند. با این حال، تقسیم بر بردار غیر تهی
. مقسومکنندههای صفر مناسب، عناصر غیرصفری هستند که حاصلضرب آنها صفر است، مانند بردارهای تهی یا غیر توانای متعامد. [ 8 ] : 191 جبر تقسیم جبری است که شامل عناصر معکوس (مقابل) ضربی برای هر عنصر است، اما این در صورتی رخ می دهد که مقسوم علیه های صفر مناسب وجود نداشته باشد و تنها ناتوان آن 1 باشد. [ 7 ] : 103 [ 9 ] : 211 [ a ] تنها جبرهای تقسیم انجمنی اعداد حقیقی، اعداد مختلط و رباعی ها [ 10 ] : 366 از آنجایی که STA یک جبر تقسیم نیست، برخی از عناصر STA ممکن است فاقد معکوس باشند. با این حال، تقسیم بر بردار غیر تهی ممکن است با ضرب در معکوس آن، که به صورت تعریف شده است
ممکن است با ضرب در معکوس آن، که به صورت تعریف شده است  . [ 11 ] : 14
. [ 11 ] : 14  ارضای این معادلات: [ 1 ] : 63
ارضای این معادلات: [ 1 ] : 63 
 ، اما
، اما .
.





 ، این جزئی ها هستند
، این جزئی ها هستند



 عامل لورنتس است
عامل لورنتس است
 ما داریم
ما داریم
 [ 1 ] : 22-24
[ 1 ] : 22-24  مربع به وحدت، آنها به عنوان یک پایه فضایی خدمت می کنند. با استفاده از نماد ماتریس پائولی ، اینها نوشته شده اند
مربع به وحدت، آنها به عنوان یک پایه فضایی خدمت می کنند. با استفاده از نماد ماتریس پائولی ، اینها نوشته شده اند . بردارهای فضایی در STA با خط پررنگ مشخص می شوند. سپس با
. بردارهای فضایی در STA با خط پررنگ مشخص می شوند. سپس با و
و ،
، و برعکس آن
و برعکس آن عبارتند از:
عبارتند از:
 و
و باید استفاده شود.
باید استفاده شود. )
)





 با شکل استاندارد
با شکل استاندارد 
 اجزای که در آن
اجزای که در آن یا
یا .
. 

 که
که اسپین ذره ν است
اسپین ذره ν است  برای ذره ای که اسپین را نشان نمی دهد.
برای ذره ای که اسپین را نشان نمی دهد. متعلق به یک فضای مختلط قابل تفکیک هیلبرت
متعلق به یک فضای مختلط قابل تفکیک هیلبرت  همیشه می توان به صورت منحصر به فرد به عنوان یک ترکیب خطی از عناصر یک مبنای متعارف بیان کرد
همیشه می توان به صورت منحصر به فرد به عنوان یک ترکیب خطی از عناصر یک مبنای متعارف بیان کرد
 و عناصر پایه
و عناصر پایه . در این مورد، شرایط نرمال سازی ترجمه می شود
. در این مورد، شرایط نرمال سازی ترجمه می شود
 ، یعنی حالت های ویژه یک قابل مشاهده. به طور خاص، اگر قابل مشاهده گفته شده در حالت نرمال اندازه گیری شود
، یعنی حالت های ویژه یک قابل مشاهده. به طور خاص، اگر قابل مشاهده گفته شده در حالت نرمال اندازه گیری شود
 . [ 5 ] : 22
. [ 5 ] : 22 
 تابع چگالی احتمال برای یافتن یک ذره در یک موقعیت معین است. این مثالها بر تمایز در خصوصیات بین حالت و امر قابل مشاهده تأکید دارند. یعنی در حالی که
تابع چگالی احتمال برای یافتن یک ذره در یک موقعیت معین است. این مثالها بر تمایز در خصوصیات بین حالت و امر قابل مشاهده تأکید دارند. یعنی در حالی که حالت محدود اگر و فقط اگر برای هر نامیده می شود
حالت محدود اگر و فقط اگر برای هر نامیده می شود یک مجموعه جمع و جور وجود دارد
یک مجموعه جمع و جور وجود دارد  به گونه ای که
به گونه ای که برای همه
برای همه  . [ 9 ] انتگرال نشان دهنده احتمال یافتن یک ذره در یک منطقه محدود است.
. [ 9 ] انتگرال نشان دهنده احتمال یافتن یک ذره در یک منطقه محدود است. در هر زمان
در هر زمان . اگر احتمال خودسرانه نزدیک به
. اگر احتمال خودسرانه نزدیک به و
و دو کت مربوط به حالات کوانتومی، کت هستند
دو کت مربوط به حالات کوانتومی، کت هستند همچنین یک حالت کوانتومی از همان سیستم است. هر دو
همچنین یک حالت کوانتومی از همان سیستم است. هر دو و
و می تواند اعداد مختلط باشد. دامنه نسبی و فاز نسبی آنها بر حالت کوانتومی حاصل تأثیر می گذارد.
می تواند اعداد مختلط باشد. دامنه نسبی و فاز نسبی آنها بر حالت کوانتومی حاصل تأثیر می گذارد.
 و استخراج عوامل مشترک به دست می دهد:هم
و استخراج عوامل مشترک به دست می دهد:هم
 با حالت درهم بر روی آن، قسمت
با حالت درهم بر روی آن، قسمت  برای ناظر غیر قابل دسترس است. [ 3 ] : 2-22 حالت قطعه
برای ناظر غیر قابل دسترس است. [ 3 ] : 2-22 حالت قطعه  سپس به عنوان ردی جزئی بیان می شود
سپس به عنوان ردی جزئی بیان می شود برای فضای هیلبرت به اندازه کافی بزرگ
برای فضای هیلبرت به اندازه کافی بزرگ 
 ماتریس چگالی را می توان راهی برای استفاده از فرمالیسم تک ذره ای برای توصیف رفتار بسیاری از ذرات مشابه با دادن توزیع احتمال (یا مجموعه) حالت هایی در نظر گرفت که این ذرات را می توان در آنها یافت.
ماتریس چگالی را می توان راهی برای استفاده از فرمالیسم تک ذره ای برای توصیف رفتار بسیاری از ذرات مشابه با دادن توزیع احتمال (یا مجموعه) حالت هایی در نظر گرفت که این ذرات را می توان در آنها یافت.
 برای عملگر A به ترتیب ignkt و ignvalus هستند و " tr " نشان دهنده ردیابی است. [ 3 ] : 73 توجه به این نکته مهم است که دو نوع میانگین گیری در حال وقوع است، یکی (بیش از
برای عملگر A به ترتیب ignkt و ignvalus هستند و " tr " نشان دهنده ردیابی است. [ 3 ] : 73 توجه به این نکته مهم است که دو نوع میانگین گیری در حال وقوع است، یکی (بیش از ، و دیگری (بیش از
، و دیگری (بیش از ) بودن یک میانگین آماری (گفته نامنسجم ) با احتمالات p s که کوانتوم در آن حالت ها باشد.
) بودن یک میانگین آماری (گفته نامنسجم ) با احتمالات p s که کوانتوم در آن حالت ها باشد. مختصات فضایی یک الکترون آماده سازی یک سیستم با اندازه گیری مجموعه کاملی از قابل مشاهده های سازگار یک حالت کوانتومی خالص ایجاد می کند . معمولتر، آمادهسازی ناقص یک حالت کوانتومی مختلط ایجاد میکند . جواب های تابع موج
مختصات فضایی یک الکترون آماده سازی یک سیستم با اندازه گیری مجموعه کاملی از قابل مشاهده های سازگار یک حالت کوانتومی خالص ایجاد می کند . معمولتر، آمادهسازی ناقص یک حالت کوانتومی مختلط ایجاد میکند . جواب های تابع موج 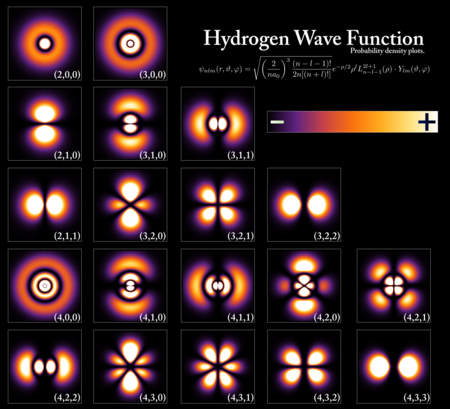
 ، با طول یک; یعنی با،
، با طول یک; یعنی با، که
که و
و مقادیر
مقادیر 



















![{\displaystyle {\begin{aligned}{\hat {H}}&=\sum _{n=1}^{N}{\hat {T}}_{n}+{\hat {V}}\ \[6pt]&=\sum _{n=1}^{N}{\frac {\mathbf {\hat {p}} _{n}\cdot \mathbf {\hat {p}} _{n} {2m_{n}}}+V(\mathbf {r} _{1},\mathbf {r} _{2},\ldots ,\mathbf {r} _{N},t)\\[6pt ]&=-{\frac {\hbar ^{2}}{2}}\sum _{n=1}^{N}{\frac {1}{m_{n}}}\nabla _{n} ^{2}+V(\mathbf {r} _{1},\mathbf {r} _{2},\ldots ,\mathbf {r} _{N},t)\end{تراز شده}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/926b8fdf3d6b254223215b88e0bdb7f0298d46ef)


![{\displaystyle {\begin{aligned}{\hat {H}}&=-{\frac {\hbar ^{2}}{2}}\sum _{i=1}^{N}{\frac { 1}{m_{i}}}\nabla _{i}^{2}+\sum _{i=1}^{N}V_{i}\\[6pt]&=\sum _{i=1 }^{N}\left(-{\frac {\hbar ^{2}}{2m_{i}}}\nabla _{i}^{2}+V_{i}\right)\\[6pt] &=\sum _{i=1}^{N}{\hat {H}}_{i}\end{تراز شده}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/bb87996553b25d30463ff8555445506dbf44bbe6)
 در این وبلاگ به ریاضیات و کاربردهای آن و تحقیقات در آنها پرداخته می شود. مطالب در این وبلاگ ترجمه سطحی و اولیه است و کامل نیست.در صورتی سوال یا نظری در زمینه ریاضیات دارید مطرح نمایید .در صورت امکان به آن می پردازم. من دوست دارم برای یافتن پاسخ به سوالات و حل پروژه های علمی با دیگران همکاری نمایم.در صورتی که شما هم بامن هم عقیده هستید با من تماس بگیرید.
در این وبلاگ به ریاضیات و کاربردهای آن و تحقیقات در آنها پرداخته می شود. مطالب در این وبلاگ ترجمه سطحی و اولیه است و کامل نیست.در صورتی سوال یا نظری در زمینه ریاضیات دارید مطرح نمایید .در صورت امکان به آن می پردازم. من دوست دارم برای یافتن پاسخ به سوالات و حل پروژه های علمی با دیگران همکاری نمایم.در صورتی که شما هم بامن هم عقیده هستید با من تماس بگیرید.