این یک بازبینی در انتظار این صفحه است. ممکن است با آخرین ویرایش پذیرفته شده که در 21 دسامبر 2010 پذیرفته شد متفاوت باشد .


فهرست |
متن زیر که در دست ساخت است، مقدمه ای بر مکانیک کوانتومی برای افراد غیرمجاز است. برای توضیحات فنی بیشتر، مکانیک کوانتومی/پیشرفته را ببینید .
مکانیک کوانتومی (از کلمه لاتین quantus ، "چقدر") نظریه ای در فیزیک است که رفتار ماده و انرژی را در مقیاس های بسیار کوچک توضیح می دهد و پیش بینی می کند - رفتاری که اغلب غیرعادی و گاهی بسیار غیر شهودی است، زیرا عمیقا در در تضاد با عقایدی که اکثر مردم درباره نحوه عملکرد دنیای فیزیکی دارند. شاید مهمترین عنصر سازنده در انقلاب فیزیک (دوره 1900-1925) باشد که محدودیت های فیزیک کلاسیک را از بین برد و فیزیک امروز را ایجاد کرد.
مکانیک کوانتومی، و درک موجودات کوانتومی ( یعنی چیزهایی که تحت قوانین مکانیک کوانتومی عمل میکنند) که ارائه میکند، ابزاری کاملاً ضروری در ایجاد بسیاری از فناوری مدرن امروزی بوده است. به طور خاص، کل حوزه الکترونیک نیمه هادی از اصول مکانیک کوانتومی استفاده می کند - و بدون الکترونیک نیمه هادی، دستگاه های الکترونیکی کوچک و ارزان تولید انبوه امروزی (مانند رایانه ها، تلفن های همراه و دوربین ها) کاملاً غیرممکن خواهد بود. همچنین لیزر و ابزارهای تشخیص پزشکی مانند MRI(تصویربرداری رزونانس مغناطیسی) بدون دانش مکانیک کوانتومی نمیتوانست وجود داشته باشد. شیمی مدرن (و از طریق آن، بیوشیمی) به طور فزاینده ای بر اصول مکانیک کوانتومی تکیه می کند تا درک خود را از برهم کنش مولکولی بیشتر کند.
مکانیک کوانتومی بسیار مهم است و نه تنها به خاطر فناوری که به ما داده است. آنچه دانشمندانی که مکانیک کوانتومی را کشف کردند این بود که بسیاری از اصول بنیادی فرضی که زیربنای چگونگی عملکرد واقعیت هستند (مثلاً علیت، موقعیت [1] ) اصلاً اساسی نیستند. به بیان ساده، «قواعد» در مقیاس بزرگی که در آن واقعیت فیزیکی را تجربه می کنیم، مطلق به نظر می رسند، اما وقتی واقعیت در مقیاس های بسیار کوچک بررسی می شود، وجود ندارند.
توضیح این است که «قواعد» که ما به عنوان حاکم بر رفتار واقعیت درک می کنیم، اغلب تنها به دلیل مصنوعات آماری در مقیاس بزرگ هستند. برای تشبیهی از این جنبه خاص، اگر نتیجه یک میلیون بار ورق زدن یک سکه را مشاهده کنید، ممکن است این تصور (نادرست) به دست بیاید که هر بار که یک سکه را چند بار ورق بزند، دقیقاً نصف زمانی است که دریافت می کند. دم و نیم سر البته این درست نیست اگر سکه فقط چند بار ورق بخورد: یک سکه را چهار بار بچرخانید، و به طور متوسط، یک هشتم مواقع یک چهره یکسان را نشان می دهد که هر چهار بار را نشان می دهد. [2]
این حقایق بسیار ضد شهودی در مورد نحوه عملکرد دنیای فیزیکی است که به مشکلاتی که اکثر مردم در اولین برخورد با مکانیک کوانتومی دارند کمک می کند. در واقع، گفته شده است که تنها فیزیکدانانی که مکانیک کوانتومی آنها را آزار نمی دهد، آنهایی هستند که به آن فکر نکرده اند. در انجام این اکتشافات، کاشفان مکانیک کوانتومی درک ما از ماهیت واقعیت را عمیقا تحت تأثیر قرار داده اند.
[ ویرایش ]یافته ها و پیش بینی های اصلی
از جمله یافته ها و پیش بینی های اصلی مکانیک کوانتومی عبارتند از:
- نور، و تمام تشعشعات الکترومغناطیسی ، در یک جریان پیوسته انرژی منتشر نمیشوند، بلکه در واحدهای بسیار کوچک با اندازههای از پیش تعیینشده، به نام کوانتا - که این نظریه نام خود را از آن گرفته است، منتشر میشود.
- یک رابطه ثابت بین طول موج یک کوانتوم نور و مقدار انرژی موجود در آن وجود دارد .
- نه تنها نور، بلکه انرژی و تعدادی دیگر از مواد اساسی (مانند بار الکتریکی) نیز کوانتیزه می شوند ، یعنی به طور بی نهایت قابل تقسیم نیستند. در واقع، عموماً تصور میشود که خود فضا و زمان نیز کوانتیزه میشوند، اگرچه جزئیات هنوز مبهم هستند. [3]
- فیزیک کلاسیک معتقد است که نور از امواج تشکیل شده است، به عنوان مثال، اغتشاشات در حال حرکت در میدان الکترومغناطیسی ، اما نور همچنین (به طور متناقض) به نظر می رسد که دارای ویژگی های ذرات است، یعنی موجوداتی که اندازه و شکل ثابتی دارند. به همین دلیل است که کوانتوم های امواج الکترومغناطیسی را فوتون - یعنی ذرات سبک - با استفاده از انتهایی که به طور سنتی برای ذرات در نظر گرفته شده است، می نامند.
- نه تنها چیزهایی که معمولاً به عنوان امواج در نظر گرفته می شوند دارای جنبه های ذره مانند هستند، بلکه چیزهایی که معمولاً به عنوان ذرات در نظر گرفته می شوند (مثلاً الکترون ها ) نیز جنبه های موج مانند دارند. این دوگانگی موج-ذره اکنون به عنوان یک جنبه ذاتی همه موجودات کوانتومی دیده می شود. [4]
- این سؤال را ایجاد می کند: به هر حال یک ذره چیست؟ این مدل ساده لوحانه، که چیزی شبیه به یک توپ کوچک است، به وضوح - بار دیگر - نتیجه این فرض نادرست است که جهان در سطح کوانتومی همان چیزی است که در سطح واقعیتی که ما تجربه می کنیم، بسیار کوچکتر است.
- بسیاری از فرآیندها در سطح کوانتومی فقط به ظاهر قطعی هستند. به عنوان مثال، در حالی که رفتار آنها، زمانی که به تعداد زیاد اندازهگیری میشود، از قوانینی پیروی میکند (مانند مثال ما در مورد چرخاندن سکه)، رویدادهای فردی قابل پیشبینی نیستند. به عنوان مثال، با توجه به مقدار زیادی از یک عنصر رادیواکتیو ، می توان به طور دقیق پیش بینی کرد که چه تعداد از آن اتم ها در یک زمان خاص تجزیه می شوند. با این حال، پیشبینی اینکه آیا و چه زمانی اتم خاصی تجزیه میشود، غیرممکن است .
- مکانیک کوانتومی همچنین نشان میدهد که برای بسیاری از ویژگیهای یک موجود کوانتومی (مثلاً اسپین آن )، آن ویژگی تا زمانی که اندازهگیری نشود، مقدار ثابت و معینی ندارد . به عبارت دیگر، آن صفت (یا به طور دقیق، ارزش آن) به نوعی تا زمانی که اندازه گیری نشود وجود ندارد. این نکته خاص از دهه 1920 منبع بحث های زیادی بوده است که تا به امروز ادامه دارد.
- یک ذره نمی تواند موقعیت کاملاً مشخص و به طور همزمان سرعت مشخصی داشته باشد. این یکی از جنبه های اصل عدم قطعیت معروف هایزنبرگ است . این اصل بیان میکند که جفت خاصی از ویژگیهای فیزیکی (مانند موقعیت/سرعت یا زمان/انرژی) نمیتوانند همزمان مقادیر کاملاً مشخصی داشته باشند. علاوه بر این، انجام یک اندازه گیری بر روی یک سیستم کوانتومی به طور اجتناب ناپذیری روی سیستم تأثیر می گذارد. اندازه گیری یک مشخصه یک موجود کوانتومی ذاتاً بر مقادیر سایر ویژگی های آن موجودیت تأثیر می گذارد. این به دلیل عدم وجود ظرافت ساده در طراحی آزمایش ها نیست ، بلکه یک ویژگی اساسی همه موجودات کوانتومی است.
[ ویرایش ]سوالات باز
اگرچه بسیاری از مکانیک کوانتومی در حال حاضر بسیار بهتر درک شده است که زمانی که برای اولین بار کشف شده بود، تعدادی از مسائل وجود دارد که هنوز نامشخص است و موضوع بحث های زیادی در میان دانشمندان است.
[ ویرایش ]سوال "گربه شرودینگر".
این احتمالاً بزرگترین سؤال باز در تمام مکانیک کوانتومی است. نام خود را از آزمایش فکری اروین شرودینگر ، یکی از نظریه پردازان کلیدی در توسعه مکانیک کوانتومی، در سال 1935 گرفته است .
اساساً، مشکل این است که خود مکانیک کوانتومی هیچ خط مرزی بین «دنیای کوانتومی»، سطح مقیاسی که در آن قوانین عجیب مکانیک کوانتومی اعمال میشود، و «جهان کلان»، سطح مقیاس جهانی که ما در آن اعمال میشود، نمیکشد. جایی نیست که بتوان گفت «اینجا قوانین دنیای کوانتومی محو میشوند و قوانین جهان «عادی» حاکم میشوند. تا آنجایی که به مکانیک کوانتومی مربوط می شود، هر سیستمی با هر اندازه ای را می توان با قوانین مکانیک کوانتومی توصیف کرد - و این می تواند به موقعیت هایی منجر شود که به نظر می رسد بی معنی هستند، نکته ای که به شدت توسط شرودینگر مطرح شده است.
بیشتر فرمولبندیهای مکانیک کوانتومی بهگونهای عمل میکنند که گویی یک سیستم کوانتومی حالت قطعی ندارد مگر اینکه به نحوی اندازهگیری شود (به خودی خود هنوز چیزی در حد یک نقطه اختلاف است). در این دیدگاه، اگر یک اتم رادیواکتیو منفرد جدا شود، قواعد مکانیک کوانتومی نشان میدهد که تا زمانی که اتم مشاهده نشود، حالت «واپاشی» یا «تجزیه نشده» مشخصی ندارد. بلکه در حالتی نامشخص است که در آن هر دو در یک زمان است. شرودینگر این مفهوم را همراه با این مشاهدات قرار داد که مکانیک کوانتومی را می توان در هر اندازه ای برای سیستمی به کار برد تا گربه مشکل ساز او را تولید کند.
او یک جعبه بسته حاوی یک گربه، یک ویال سم، یک اتم رادیواکتیو منفرد و مکانیزمی برای تشخیص پوسیدگی اتم و رهاسازی سم را تصور کرد. کل مجموعه سیستمی است که خود را می توان با قوانین مکانیک کوانتومی توصیف کرد - یعنی تا زمانی که آن را مشاهده کنیم، با باز کردن آن برای اینکه ببینیم گربه مرده است یا زنده است، حالت قطعی ندارد. اتم نه پوسیده است و نه پوسیده، سم نه آزاد می شود نه آزاد نشده، و گربه... نه مرده است و نه زنده.
این "به وضوح" بی معنی است - گربه ها یا مرده اند یا زنده هستند، نه به نحوی مرموز هر دو در یک زمان. با این حال، به نظر میرسد هیچ اشکالی در کاربرد نظریه کوانتومی وجود ندارد که پیشبینی میکند گربه همزمان مرده و هم زنده است. از آنجایی که مکانیک کوانتومی یکی از موفقترین تئوریهای علمی در تمام دوران است، زیرا پیشبینیهای (اغلب عجیب و غریب) آن همیشه در زمان آزمایش دقیق بودهاند، این بسیار نگرانکننده است. علاوه بر آن، البته، مکانیک کوانتومی مملو از انواع چیزهای «غیر ممکن» دیگر است، بنابراین هیچ کس حاضر نیست مشکل گربه را به عنوان «غیر ممکن» بنویسد.
برای مشکلتر شدن اوضاع، در سالهای اخیر آزمایشهایی انجام شده است که اجسام ماکروسکوپی (حلقههای ابررسانا) را نشان میدهند که به گونهای رفتار میکنند که گویی اجسام کوانتومی هستند. به عبارت دیگر، هنگامی که حلقه تغییر حالت می دهد (مثلاً تغییر در جریان الکتریکی در اطراف حلقه)، کل حلقه دقیقاً در همان لحظه تغییر حالت می دهد. [6]
بنابراین امکان رفتار کوانتومی عجیب و غریب در مقیاس های بزرگ - از جمله گربه هایی که به طور همزمان مرده و زنده هستند - کاملاً غیرممکن نیست. با این حال، از زمانی که این سوال برای اولین بار مطرح شد، اکثر فیزیکدانان باور نکرده اند که گربه در واقع در آن حالت میانی قرار دارد. اکثریت موافقند که "به نحوی" اتم "مشاهده" می شود و یا فروپاشی می کند یا فروپاشی نمی کند. کاری که هیچ کس نمی تواند انجام دهد این است که توضیح دهد که چگونه - از نظر فیزیک - این واقعاً اتفاق می افتد.
در چندین دهه از زمانی که شرودینگر در ابتدا مسئله خود را مطرح کرد، فیزیکدانان به شدت در مورد آن بحث کردند، اما اکنون پاسخی نزدیکتر یا واضح تر از زمانی که او برای اولین بار مطرح کرد وجود ندارد. نظریه ها و توضیحات (رقابتی) زیادی ارائه شده است، اما هیچ کدام ثابت نشده است، یا حتی حمایت گسترده ای به دست نیاورده است.
[ ویرایش ]محل در مقابل واقعیت
به بیان دقیق، قضیه بل، و آزمایشهای حاصل از آن، تنها به این معنی است که ما باید یک جنبه از مدل «کلاسیک» واقعیت را کنار بگذاریم.
این بخش در حال توسعه است
[ ویرایش ]کشف مکانیک کوانتومی
این بخش در حال توسعه است
- مروری بر فیزیک کلاسیک (یعنی انرژی پیوسته، فضا، زمان)
- اولین سرنخ ها
- منحنی بدنه مشکی
- انتشار عکس
- رادیواکتیویته، اگرچه این عمدتاً فیزیک هسته ای است
- اولین قدم ها
- معادله پلانک/ثابت
- انیشتین 1905
- مدل اتم کوانتیزه بور
- شکوه کامل
- د بروگلی
- هایزنبرگ
- شرودینگر
- احتمال تولد
- "پارادوکس" EPR
- قضیه بل
[ ویرایش ]برخی از اثرات غیرعادی مکانیک کوانتومی
مکانیک کوانتومی اثرات بسیار غیرعادی و باور کردنی ندارد. این بخش تعدادی از آنها را فهرست می کند.
این بخش در حال توسعه است
- مثال پلاریزاسیون 3 فیلتر (افراد می توانند خودشان این یکی را امتحان کنند): 2 فیلتر در 90 درجه نسبت به یکدیگر، هیچ نوری از آن عبور نمی کند. یک فیلتر سوم بین آنها اضافه کنید، در 45 درجه، اکنون مقداری نور عبور می کند
- همه چیزهای عجیب و غریب دو شکاف
- فوتون هایی که در یک زمان ساطع می شوند هنوز الگوهای تداخلی ایجاد می کنند
- وقتی نگاه می کنید ببینید از کدام شکاف عبور می کنند، الگوهای تداخل از بین می روند
- ابر سیال ها
- ابررسانایی
- حلقه های رسانای ماکروسکوپی به عنوان اجسام کوانتومی عمل می کنند
- قضیه بل و آزمایشهای مبتنی بر آن نشان دادهاند که ماهیت فضا و علیت با آنچه ما (و انیشتین ) میدانیم بسیار متفاوت است. به نظر میرسد دو ذره که در یک رویداد کوانتومی ایجاد شدهاند، ارتباط آنی اسرارآمیزی دارند، مهم نیست که بعداً چقدر از هم دور میشوند. یک ذره فوراً می داند که چه زمانی تغییر مهم برای ذره دیگر اتفاق می افتد. پیامدها و امکانات تکنولوژیکی این کشف نسبتاً اخیر هنوز در حال کشف است.
- یکی از پیامدهای این قضیه، تلهپورتاسیون کوانتومی است - شما میتوانید حالت کوانتومی را از یک مکان به مکان دیگر بدون هیچ گونه تماس فیزیکی بین آنها انتقال دهید، علاوه بر انتقال برخی اطلاعات (بنابراین نمیتوانید در این فرآیند از سرعت نور تجاوز کنید). یک واقعیت جالب این است که حالت کوانتومی در وهله اول باید از بین برود - حالت های کوانتومی دلخواه را نمی توان شبیه سازی کرد.
منبع
https://www.theochem.ru.nl/~pwormer/Knowino/knowino.org/wiki/Quantum_mechanics.html

![[l_x، l_y] = i l_z \،](https://www.theochem.ru.nl/~pwormer/Knowino/knowino.org/w/images/math/4/f/d/4fd29a72f0c2276ae712251415757d03.png)
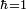 ).
).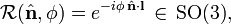
 نشان دهنده چرخش حول بردار واحد
نشان دهنده چرخش حول بردار واحد 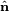 بر روی زاویه φ و l ≡ ( l x , l y , l z ) است. در مثال اتم دو الکترون بالا، ما l را به عنوان تکانه زاویه ای مداری یک الکترون ملاقات کردیم.
بر روی زاویه φ و l ≡ ( l x , l y , l z ) است. در مثال اتم دو الکترون بالا، ما l را به عنوان تکانه زاویه ای مداری یک الکترون ملاقات کردیم.![[H, l_x] = [H, l_y] = [H, l_z] = 0 \Longftrightarrow [H, \mathcal{R}(\hat{\mathbf{n}}, \phi)] = 0, \quad \ forall\، \hat{\mathbf{n}}\;\;\hbox{and}\;\; \ forall \phi.](https://www.theochem.ru.nl/~pwormer/Knowino/knowino.org/w/images/math/5/5/4/554e4a25c762fe02eff697a7ca9ec783.png)
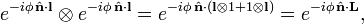
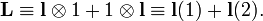
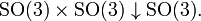
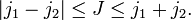
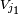 + 1 است ، فضای ویژه j 2 (1) با مقدار ویژه j 1 ( j 1 + 1)، برای بحث در این مورد به
+ 1 است ، فضای ویژه j 2 (1) با مقدار ویژه j 1 ( j 1 + 1)، برای بحث در این مورد به 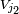 + 1 بعدی است ، فضای ویژه j 2 (2) با مقدار ویژه j 2 (j 2 + 1). شرایط مثلثی بیان می کند که فضای حاصلضرب تانسور به صورت مجموع مستقیم متعامد فضاهای ویژه J 2 تجزیه می شود.
+ 1 بعدی است ، فضای ویژه j 2 (2) با مقدار ویژه j 2 (j 2 + 1). شرایط مثلثی بیان می کند که فضای حاصلضرب تانسور به صورت مجموع مستقیم متعامد فضاهای ویژه J 2 تجزیه می شود.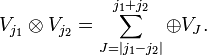
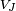 با عدد کوانتومی خاص J فقط یک بار رخ می دهد (به شرطی که J در محدوده باشد، در غیر این صورت رخ نمی دهد)، به عبارت دیگر تعدد J در فضای حاصلضرب تانسور با j ثابت 1 و j 2 صفر یا یک است.
با عدد کوانتومی خاص J فقط یک بار رخ می دهد (به شرطی که J در محدوده باشد، در غیر این صورت رخ نمی دهد)، به عبارت دیگر تعدد J در فضای حاصلضرب تانسور با j ثابت 1 و j 2 صفر یا یک است. 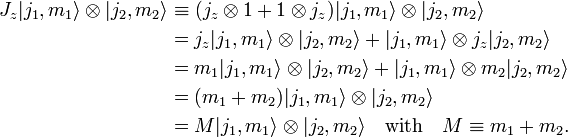
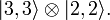
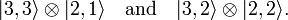


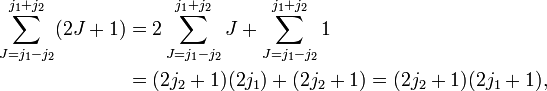
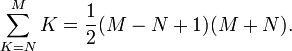
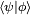
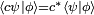
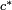
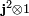 و
و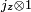
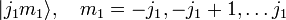
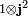 و
و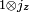
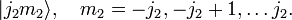
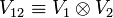 دارای یک پایه (2 j 1 + 1) (2 j 2 + 1) ابعادی غیر جفت نشده است .
دارای یک پایه (2 j 1 + 1) (2 j 2 + 1) ابعادی غیر جفت نشده است .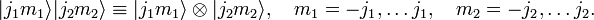
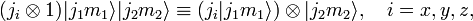
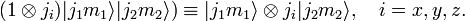
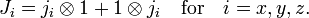
![[J_k،J_l] = i \sum_{m=x,y,z} \epsilon_{klm}J_m \,](https://www.theochem.ru.nl/~pwormer/Knowino/knowino.org/w/images/math/d/e/4/de47f892f12c64173c693d8f3359700e.png)
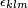 است . از این رو حالت های ویژه تکانه زاویه ای کل وجود دارد
است . از این رو حالت های ویژه تکانه زاویه ای کل وجود دارد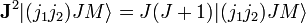
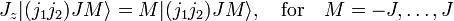
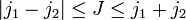
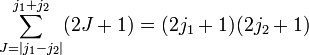
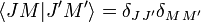
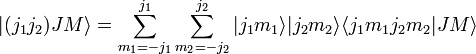
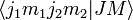 می نامند .
می نامند .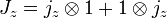
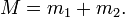
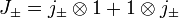
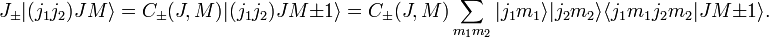
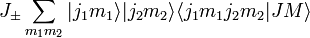
![=\sum_{m_1m_2}\left[ C_\pm(j_1,m_1)|j_1 m_1\pm 1\rangle |j_2m_2\rangle +C_\pm(j_2,m_2)|j_1 m_1\rangle |j_2 m_2\pm 1\ rangle \right] \langle j_1 m_1 j_2 m_2|JM\rangle](https://www.theochem.ru.nl/~pwormer/Knowino/knowino.org/w/images/math/f/7/2/f72f39f117c39ff919f50038f032e9ad.png)
![= \sum_{m_1m_2} |j_1m_1\rangle|j_2m_2\rangle \left[ C_\pm(j_1,m_1\mp 1) \langle j_1 {m_1\mp 1} j_2 m_2|JM\rangle +C_\pm(j_2, m_2\mp 1) \langle j_1 m_1 j_2 {m_2\mp 1}|JM\rangle \راست].](https://www.theochem.ru.nl/~pwormer/Knowino/knowino.org/w/images/math/8/2/9/82948bed290f30fb23cd3f95f09501d7.png)
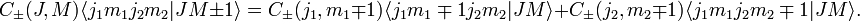

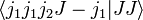 واقعی و مثبت در نظر گرفته می شود. با آخرین معادله تمام ضرایب کلبش-گوردان دیگر را
واقعی و مثبت در نظر گرفته می شود. با آخرین معادله تمام ضرایب کلبش-گوردان دیگر را 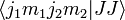 می توان یافت. عادی سازی با این شرط ثابت می شود که مجموع مربع ها که مطابق با هنجار حالت است
می توان یافت. عادی سازی با این شرط ثابت می شود که مجموع مربع ها که مطابق با هنجار حالت است 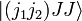 باید یک باشد.
باید یک باشد.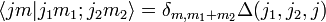
![\times \sum_t (-1)^t {\textstyle \frac{ \left[(2j+1) (j_1 +m_1 )! (j_1 -m_1)! (j_2 +m_2 )! (j_2 -m_2 )! (j+m)! (jm)! \right]^{\frac{1}{2}}}{t! (j_1 +j_2 -jt)! (j_1 -m_1 -t)! (j_2 +m_2 -t)! (j-j_2 +m_1 +t)! (j-j_1 -m_2 +t)!} }](https://www.theochem.ru.nl/~pwormer/Knowino/knowino.org/w/images/math/7/9/6/796ba37405d2c8667a5959d5af11a971.png)
![\Delta (j_1 ,j_2 ,j) \equiv \left[ \frac{ (j_1 +j_2 -j)! (j_1 -j_2 +j)! (-j_1 +j_2 +j)!} { (j_1 +j_2 +j+1)!}\right]^{{\frac{1}{2}}}،](https://www.theochem.ru.nl/~pwormer/Knowino/knowino.org/w/images/math/1/9/0/1901a2a3f0d1af384b5a7c2bceef71ce.png)
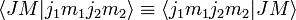
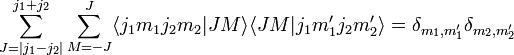
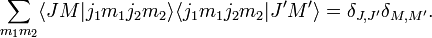
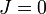 کلبش-گوردان ضرایب توسط
کلبش-گوردان ضرایب توسط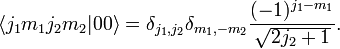
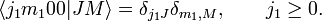
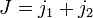 و
و 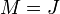 ما داریم
ما داریم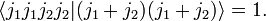
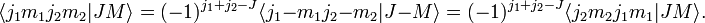
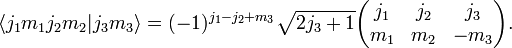
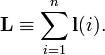
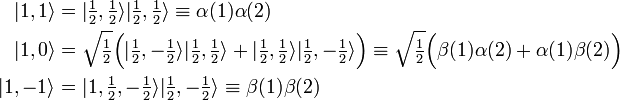
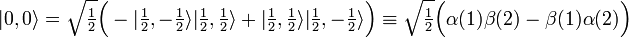
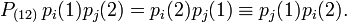
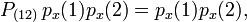
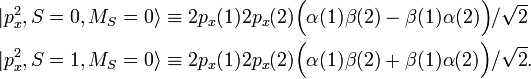
![\scriptstyle \mathcal{A} = [ (1) - (12) ]/2](https://www.theochem.ru.nl/~pwormer/Knowino/knowino.org/w/images/math/4/c/8/4c885922fbf58fc65ed32b54eca39c36.png) به دست می آیند ، که در آن (12) فضای همزمان و مختصات اسپین الکترون 1 و 2 را جابجا می کند و (1) عملگر هویت است (هیچ کاری انجام نمی دهد).
به دست می آیند ، که در آن (12) فضای همزمان و مختصات اسپین الکترون 1 و 2 را جابجا می کند و (1) عملگر هویت است (هیچ کاری انجام نمی دهد).![\begin{align} 2\mathcal{A} |p_x^2، S=0، M_S = 0\rangle &= 2p_x(1) 2p_x(2) \Big( \alpha(1)\beta(2) - \ beta(1)\alpha(2)\Big)/\sqrt{2} \\ & - 2p_x(2) 2p_x(1) \Big(\alpha(2)\beta(1)- \beta(2)\ alpha(1)\Big)/\sqrt{2} \\ &= 2 \left[ 2p_x(1) 2p_x(2) \Big( \alpha(1)\beta(2) - \\beta(1)\alpha (2)\Big)/\sqrt{2}\right]. \\ \پایان{تراز}](https://www.theochem.ru.nl/~pwormer/Knowino/knowino.org/w/images/math/4/9/3/4932b95abec37fccb37442aafee7f3d5.png)
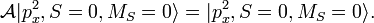
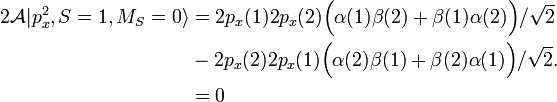
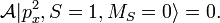
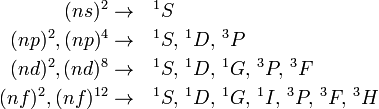

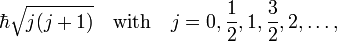
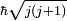 . در وهله دوم، طرح ریزی آن بر روی یک محور در فضا (محور کوانتیزاسیون، معمولاً به عنوان محور z در نظر گرفته می شود ) کوانتیزه می شود، فقط می تواند مقادیر را بگیرد.
. در وهله دوم، طرح ریزی آن بر روی یک محور در فضا (محور کوانتیزاسیون، معمولاً به عنوان محور z در نظر گرفته می شود ) کوانتیزه می شود، فقط می تواند مقادیر را بگیرد.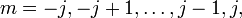
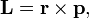
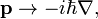
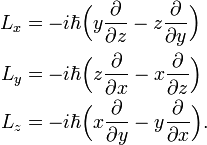
![[L_x,\,L_y] = i \hbar L_z, \quad [L_z,\,L_x] = i \hbar L_y, \quad [L_y,\,L_z] = i \hbar L_x.](https://www.theochem.ru.nl/~pwormer/Knowino/knowino.org/w/images/math/7/9/2/79239fbe386b8127382a6ff523f3274f.png)
![[A,\,B] \equiv AB - BA .](https://www.theochem.ru.nl/~pwormer/Knowino/knowino.org/w/images/math/3/7/b/37b01bb330b4d0aad5381872d240b193.png)
![\begin{align} \big[L_x,\, L_y\big] =& -\hbar^2\left[ \Big( y \frac{\partial}{\partial z} - z \frac{\partial}{ \partial y}\Big) \Big( z \frac{\partial}{\partial x} - x \frac{\partial}{\partial z}\Big) - \Big( z \frac{\partial}{ \جزئی x} - x \frac{\partial}{\partial z}\Big)\Big( y \frac{\partial}{\partial z} - z \frac{\partial}{\partial y}\Big ) \right] \\ =& -\hbar^2\left[ y \frac{\partial}{\partial x} - x \frac{\partial}{\partial y} \right] = i \hbar \left [-i\hbar \Big( x \frac{\partial}{\partial y} - y \frac{\partial}{\partial x} \Big)\right] = i\hbar L_z, \\ \end{ تراز کردن}](https://www.theochem.ru.nl/~pwormer/Knowino/knowino.org/w/images/math/a/3/e/a3e7555ecdbb93f8f5be3ace86d65081.png)
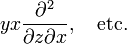
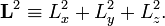
![[\mathbf{L}^2,\,L_k] = 0 \quad \hbox{for}\quad k=x,y,z,](https://www.theochem.ru.nl/~pwormer/Knowino/knowino.org/w/images/math/5/a/e/5ae39d319bf0b34a2b7511d948f7f745.png)
![L^2 = - \hbar^2 \left[ \frac{1}{\sin\theta} \frac{\partial}{\partial\theta} \sin\theta \frac{\partial}{\partial \theta } + \frac{1}{\sin^2\theta} \frac{\partial^2}{\partial\varphi^2}\right]،](https://www.theochem.ru.nl/~pwormer/Knowino/knowino.org/w/images/math/4/0/1/401dbaf67d4cf99eeb0d509fbd80675f.png)
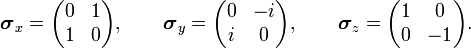
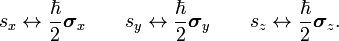
![[s_x,\,s_y] \فلش راست چپ \frac{\hbar^2}{4}[\boldsymbol{\sigma}_x\boldsymbol{\sigma}_y -\boldsymbol{\sigma}_y\boldsymbol{\sigma}_x ] = \frac{i\hbar^2}{2} \begin{pmatrix} 1 & 0 \\ 0 & -1 \\ \end{pmatrix} \فلش راست چپ i \hbar s_z.](https://www.theochem.ru.nl/~pwormer/Knowino/knowino.org/w/images/math/0/5/8/05833562b1b2b9add2ceb95a19ef8c41.png)
![[s_x,\,s_y] = i \hbar s_z, \quad [s_z,\,s_x] = i \hbar s_y, \quad [s_y,\,s_z] = i \hbar s_x,](https://www.theochem.ru.nl/~pwormer/Knowino/knowino.org/w/images/math/7/1/8/718d38546aae6331526c7bb889499e06.png)
![[j_k,j_l] = i \hbar\sum_{m=x,y,z} \varepsilon_{klm}j_m, \quad k, l, m = x,y,z,](https://www.theochem.ru.nl/~pwormer/Knowino/knowino.org/w/images/math/c/5/0/c503e6e00deacc630e342cfe81143668.png)
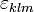 نماد
نماد 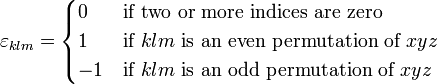
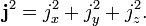
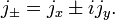
![[\mathbf{j}^2,\, j_k] = 0 \quad \mathrm{for}\;\; k = x، y، z.](https://www.theochem.ru.nl/~pwormer/Knowino/knowino.org/w/images/math/0/2/b/02bde432be406ca23afb9697859f6afa.png)

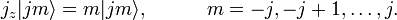
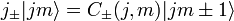
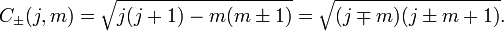
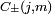 انتخابی که در اینجا انجام شده مطابق با کنوانسیون فاز کاندون و شورتلی است. حالات تکانه زاویه ای باید متعامد باشند (زیرا مقادیر ویژه آنها نسبت به عملگر هرمیتی متمایز است) و نرمال شده فرض می شود.
انتخابی که در اینجا انجام شده مطابق با کنوانسیون فاز کاندون و شورتلی است. حالات تکانه زاویه ای باید متعامد باشند (زیرا مقادیر ویژه آنها نسبت به عملگر هرمیتی متمایز است) و نرمال شده فرض می شود.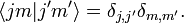
![[\mathbf{j}^2,\, j_\pm] = [\mathbf{j}^2,\, j_z]= 0,\qquad [j_z,\,j_\pm] = \pm j_\pm, \qquad j_-j_+ = \mathbf{j}^2 - j_z(j_z+1).](https://www.theochem.ru.nl/~pwormer/Knowino/knowino.org/w/images/math/9/9/1/991cc3adf6675cecb1529e9f55014951.png)
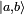 با آن پیدا کنیم
با آن پیدا کنیم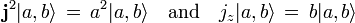 .
.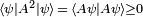 و از آنجایی که یک مقدار ویژه نوع خاصی از مقدار انتظاری است - یعنی یک مقدار با توجه به یک بردار ویژه - نتیجه میشود که j 2 فقط مقادیر ویژه واقعی غیرمنفی دارد. بنابراین مقدار ویژه آن را به صورت مربع عدد a 2 می نویسیم .
و از آنجایی که یک مقدار ویژه نوع خاصی از مقدار انتظاری است - یعنی یک مقدار با توجه به یک بردار ویژه - نتیجه میشود که j 2 فقط مقادیر ویژه واقعی غیرمنفی دارد. بنابراین مقدار ویژه آن را به صورت مربع عدد a 2 می نویسیم .![\scriptstyle [j^2, j_{\pm}]=0](https://www.theochem.ru.nl/~pwormer/Knowino/knowino.org/w/images/math/2/8/5/2850bc59ba014a61d9563819898cc4d7.png) و
و ![\scriptstyle [j_z, j_\pm] = \pm j_{\pm}](https://www.theochem.ru.nl/~pwormer/Knowino/knowino.org/w/images/math/b/1/9/b19bd3f892a072ac34ac135c03645457.png) ، متوجه می شویم که
، متوجه می شویم که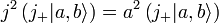
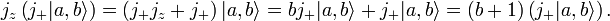
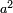 و یک بردار ویژه j z با مقدار ویژه b + 1 به دست می دهد، به طوری که
و یک بردار ویژه j z با مقدار ویژه b + 1 به دست می دهد، به طوری که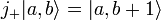
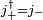 کت
کت 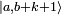 با هنجار به دست می آوریم
با هنجار به دست می آوریم![\begin{align} \langle a+b+k+1 | a+b+k+1 \rangle &= \langle a,b+k|j_-j_+|a,b+k \rangle = \langle a,b+k|\mathbf{j}^2- j_z( j_z+1) |a,b+k \rangle \\ &=[a^2-(b+k)(b+k+1)] \langle a,b+k | a,b+k\rangle. \پایان{تراز}](https://www.theochem.ru.nl/~pwormer/Knowino/knowino.org/w/images/math/8/2/4/82443a119f2cc7933fd5c7ecfcfb469c.png)
 ، در حالی که دقیقا
، در حالی که دقیقا 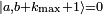 . برای آن مقدار k ، a 2 = ( b + k max ) ( b+ k max + 1).
. برای آن مقدار k ، a 2 = ( b + k max ) ( b+ k max + 1). با
با 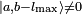 و a 2 = ( b - l max ) ( b - l max - 1) به دست می دهد.
و a 2 = ( b - l max ) ( b - l max - 1) به دست می دهد.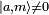 مشخص می شود . وقتی m انتگرال باشد عدد j انتگرال است و وقتی m نیمه انتگرال است نیمه انتگرال است. توجه داشته باشید که a 2 = j ( j + 1).
مشخص می شود . وقتی m انتگرال باشد عدد j انتگرال است و وقتی m نیمه انتگرال است نیمه انتگرال است. توجه داشته باشید که a 2 = j ( j + 1).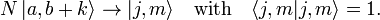
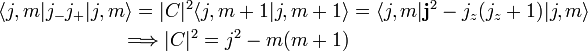
![{\displaystyle [N,X]=cX,}](https://wikimedia.org/api/rest_v1/media/math/render/svg/34981a0271e7d802e40809d41f08742a922a9e38) برای برخی از cاسکالر . اگر
برای برخی از cاسکالر . اگر یک حالت ویژه از N با معادله مقدار ویژه است،
یک حالت ویژه از N با معادله مقدار ویژه است، سپس عملگر X عمل می کند
سپس عملگر X عمل می کند![{\displaystyle {\begin{تراز شده}NX|n\rangle &=(XN+[N,X])|n\rangle \\&=XN|n\rangle +[N,X]|n\rangle \\& =Xn|n\rangle +cX|n\rangle \\&=(n+c)X|n\rangle .\end{تراز شده}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/6eaf3806c2784f9cf5f57319df09bc3ff695e511)
 یک حالت ویژه از N با مقدار ویژه n + c یا صفر است. عملگر X اگر c واقعی و مثبت باشد عملگر افزایش دهنده N است و اگر c واقعی و منفی باشد عملگر کاهنده برای N است.
یک حالت ویژه از N با مقدار ویژه n + c یا صفر است. عملگر X اگر c واقعی و مثبت باشد عملگر افزایش دهنده N است و اگر c واقعی و منفی باشد عملگر کاهنده برای N است.![{\displaystyle [N,X^{\dagger }]=-cX^{\dagger }.}](https://wikimedia.org/api/rest_v1/media/math/render/svg/e3395ea77248bdf9d4afb58dfd5fc4b2adb3ddf4)

 جایی که i واحد خیالی است .
جایی که i واحد خیالی است .![{\displaystyle [J_{i},J_{j}]=i\hbar \epsilon _{ijk}J_{k},}](https://wikimedia.org/api/rest_v1/media/math/render/svg/452ea8c532b6bf78f44018b1ec58cddcb9b610e8) که در آن ε ijk نماد Levi-Civita است و هر یک از i ، j و k می توانند هر یک از مقادیر x ، y و z را بگیرند .
که در آن ε ijk نماد Levi-Civita است و هر یک از i ، j و k می توانند هر یک از مقادیر x ، y و z را بگیرند .![{\displaystyle \left[J_{z},J_{\pm }\right]=\pm \hbar J_{\pm },}](https://wikimedia.org/api/rest_v1/media/math/render/svg/c17698b4dd2452ca516a2e67791fd193793ae0ef)
![{\displaystyle \left[J_{+},J_{-}\right]=2\hbar J_{z}.}](https://wikimedia.org/api/rest_v1/media/math/render/svg/d542739b7f035b0a0976f0bca47cf8ef62f8bebc) (از نظر فنی، این جبر لی است
(از نظر فنی، این جبر لی است ).
).![{\displaystyle {\begin{aligned}J_{z}J_{\pm }|j\,m\rangle &=\left(J_{\pm }J_{z}+\left[J_{z},J_{ \pm }\right]\right)|j\,m\rangle \\&=\left(J_{\pm }J_{z}\pm \hbar J_{\pm }\right)|j\,m\ rangle \\&=\hbar \left(m\pm 1\right)J_{\pm }|j\,m\rangle .\end{تراز شده}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/9995b65fceba587cb374c3170a3db3d0adc88af3)

 مقداری اسکالر ضربدر است
مقداری اسکالر ضربدر است ،
،

 )
)

![{\displaystyle J_{-}J_{+}=(J_{x}-iJ_{y})(J_{x}+iJ_{y})=J_{x}^{2}+J_{y}^{ 2}+i[J_{x}،J_{y}]=J^{2}-J_{z}^{2}-\hbar J_{z}،}](https://wikimedia.org/api/rest_v1/media/math/render/svg/180f780cd664922bdfbfd3d56b32f036050ad439)
![{\displaystyle J_{+}J_{-}=(J_{x}+iJ_{y})(J_{x}-iJ_{y})=J_{x}^{2}+J_{y}^{ 2}-i[J_{x}،J_{y}]=J^{2}-J_{z}^{2}+\hbar J_{z}.}](https://wikimedia.org/api/rest_v1/media/math/render/svg/5803012b929c6f9dd7bac574a71ad2c2bc6f2779)




 )، یک نفر دارد
)، یک نفر دارد

 جایی که من چرخش هسته ای هستم.
جایی که من چرخش هسته ای هستم.


 جایی که→
جایی که→ تکانه زاویه ای است،پ→
تکانه زاویه ای است،پ→ تکانه خطی است،
تکانه خطی است، جرم کاهش یافته سیستم است،ه
جرم کاهش یافته سیستم است،ه شارژ الکترونیکی است وز
شارژ الکترونیکی است وز عدد اتمی هسته است. مشابه عملگرهای نردبانی تکانه زاویه ای، یکی دارد
عدد اتمی هسته است. مشابه عملگرهای نردبانی تکانه زاویه ای، یکی دارد و
و .
.![{\displaystyle [A_{\pm },L_{z}]=\mp {\boldsymbol {i}}\hbar A_{\mp }}](https://wikimedia.org/api/rest_v1/media/math/render/svg/07f0fe3a400a6139a7980d27bdcbdf0e47c526c8) و
و![{\displaystyle [A_{\pm },L^{2}]=\mp 2\hbar ^{2}A_{\pm }-2\hbar A_{\pm }L_{z}\pm 2\hbar A_ {z}L_{\pm }}](https://wikimedia.org/api/rest_v1/media/math/render/svg/22368e378a634ef2eb9de857490aa715e54aaf5e) . از این رو،
. از این رو، و
و بنابراین
بنابراین که "؟" یک عدد کوانتومی نوپا را نشان می دهد که از بحث بیرون می آید.
که "؟" یک عدد کوانتومی نوپا را نشان می دهد که از بحث بیرون می آید. و پائولی معادله III:
و پائولی معادله III: و با معادله شروع می شود
و با معادله شروع می شود و در حال گسترش، به دست می آید (با فرض
و در حال گسترش، به دست می آید (با فرض حداکثر مقدار عدد کوانتومی تکانه زاویه ای همخوان با سایر شرایط است)
حداکثر مقدار عدد کوانتومی تکانه زاویه ای همخوان با سایر شرایط است) که منجر به فرمول Rydberg می شود :
که منجر به فرمول Rydberg می شود : دلالت بر آن دارد
دلالت بر آن دارد ، جایی که
، جایی که عدد کوانتومی سنتی است.
عدد کوانتومی سنتی است.![{\displaystyle H=1/(2\mu )[p_{r}^{2}+(1/r^{2})L^{2}]+V(r)}](https://wikimedia.org/api/rest_v1/media/math/render/svg/8b548e07b8bd41a88c5b0e058d0f4008470a44c8) جایی که
جایی که وپ
وپ تکانه شعاعی است
تکانه شعاعی است که واقعی و خود مزدوج است.
که واقعی و خود مزدوج است. یک بردار ویژه از همیلتونی است که〉
یک بردار ویژه از همیلتونی است که〉 تکانه زاویه ای است و
تکانه زاویه ای است و و ممکن است همیلتونی را به عنوان برچسب گذاری کنیم
و ممکن است همیلتونی را به عنوان برچسب گذاری کنیم 
![{\displaystyle H=1/(2\mu )[p_{r}^{2}+(1/r^{2})l(l+1)\hbar ^{2}]+V(r)}](https://wikimedia.org/api/rest_v1/media/math/render/svg/4f44e6fffc25849cce5761206adcaa86d84e2612)
 مانند
مانند
 برای اسکالرها
برای اسکالرها و
و . بردار
. بردار ممکن است به دو صورت مختلف ارزیابی شود
ممکن است به دو صورت مختلف ارزیابی شود که می توان آن را دوباره تنظیم کرد
که می توان آن را دوباره تنظیم کرد}](https://wikimedia.org/api/rest_v1/media/math/render/svg/c789ff51cddc8b558ddea6278b9eaee4f7fc7c4d) نشان دادن
نشان دادن  یک حالت ویژه از
یک حالت ویژه از با ارزش ویژه
با ارزش ویژه ا
ا سپس"=
سپس"= و حالت
و حالت با
با معادله ای مناسب برای
معادله ای مناسب برای با
با اگر انرژی منفی باشد یک کران بالایی برای عملگر نردبان وجود دارد (بنابراین〉
اگر انرژی منفی باشد یک کران بالایی برای عملگر نردبان وجود دارد (بنابراین〉 برای برخی
برای برخی سپس از معادله ( 1 )
سپس از معادله ( 1 ) و
و

 با
با و
و سپس
سپس و در ادامه این،
و در ادامه این، در حال حاضر همیلتونین فقط سطوح انرژی مثبت دارد که از آن مشخص است
در حال حاضر همیلتونین فقط سطوح انرژی مثبت دارد که از آن مشخص است

 و سپس
و سپس این در حال کاهش در انرژی استℏ
این در حال کاهش در انرژی استℏ مگر اینکه برای مقداری از
مگر اینکه برای مقداری از . شناسایی این مقدار به عنوان
. شناسایی این مقدار به عنوان
 به طوری که
به طوری که دادن رابطه بازگشتی در
دادن رابطه بازگشتی در با حل
با حل
 و عملگرهای کاهش دهنده را اعمال کنید
و عملگرهای کاهش دهنده را اعمال کنید :
: دادن دنباله،
دادن دنباله، با همان انرژی اما با
با همان انرژی اما با [14]
[14] باید یک مضرب نیمه صحیح غیر منفی ħ باشد .
باید یک مضرب نیمه صحیح غیر منفی ħ باشد .
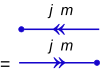







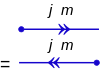


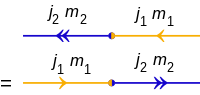

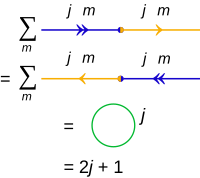






 ، و
، و .
.


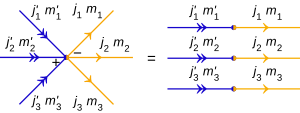

 .
.
 .
. ، مجموعه ایالت ها را در نظر بگیرید
، مجموعه ایالت ها را در نظر بگیرید برای همه ممکن
برای همه ممکن و
و ، یعنی مجموعه حالت هایی که از چرخش حالت شروع به هر شکل ممکن به وجود می آیند. گستره خطی آن مجموعه یک فضای برداری است ، و بنابراین شیوه ای که عملگرهای چرخشی یک حالت را به حالت دیگر نشان می دهند، نمایشی از گروه عملگرهای چرخش است.
، یعنی مجموعه حالت هایی که از چرخش حالت شروع به هر شکل ممکن به وجود می آیند. گستره خطی آن مجموعه یک فضای برداری است ، و بنابراین شیوه ای که عملگرهای چرخشی یک حالت را به حالت دیگر نشان می دهند، نمایشی از گروه عملگرهای چرخش است.
 .
. که در آن R یک عملگر چرخشی است . به عنوان یک نتیجه،
که در آن R یک عملگر چرخشی است . به عنوان یک نتیجه،![{\displaystyle [H,R]=0}](https://wikimedia.org/api/rest_v1/media/math/render/svg/55ca790f49501a692d19581c1e02757584a8a859) ، و سپس
، و سپس![[H,\mathbf {J} ]=\mathbf {0}](https://wikimedia.org/api/rest_v1/media/math/render/svg/316d3c62d119440ee1b4fd5bfbce4e40e6263a07) به دلیل رابطه بین J و R. با قضیه Ehrenfest ، نتیجه می شود که J حفظ شده است.
به دلیل رابطه بین J و R. با قضیه Ehrenfest ، نتیجه می شود که J حفظ شده است. ). از طرف دیگر، H ممکن است همیلتونی همه ذرات و میدانهای جهان باشد، و سپس H همیشه از نظر چرخشی ثابت است ، زیرا قوانین اساسی فیزیک جهان بدون توجه به جهتگیری یکسان هستند. این مبنایی است برای اینکه بگوییم پایستگی تکانه زاویه ای یک اصل کلی فیزیک است.
). از طرف دیگر، H ممکن است همیلتونی همه ذرات و میدانهای جهان باشد، و سپس H همیشه از نظر چرخشی ثابت است ، زیرا قوانین اساسی فیزیک جهان بدون توجه به جهتگیری یکسان هستند. این مبنایی است برای اینکه بگوییم پایستگی تکانه زاویه ای یک اصل کلی فیزیک است. همه مقادیر معینی دارند و از سوی دیگر میگویند
همه مقادیر معینی دارند و از سوی دیگر میگویند  همه مقادیر مشخصی دارند، زیرا چهار مورد آخر معمولاً حفظ می شوند (ثابت حرکت). روش رفت و برگشت بین این پایه ها استفاده از ضرایب کلبش-گوردان است .
همه مقادیر مشخصی دارند، زیرا چهار مورد آخر معمولاً حفظ می شوند (ثابت حرکت). روش رفت و برگشت بین این پایه ها استفاده از ضرایب کلبش-گوردان است . :
:
 .
.

 ، موارد زیر را بدست می آوریم
، موارد زیر را بدست می آوریم جایی که
جایی که هارمونیک های کروی هستند . [28]
هارمونیک های کروی هستند . [28] همراه با
همراه با وجی
وجی مجموعه کاملی از مشاهده پذیرهای رفت و آمد را تشکیل می دهند. علاوه بر این، آنها به آن نیاز داشتندΓ
مجموعه کاملی از مشاهده پذیرهای رفت و آمد را تشکیل می دهند. علاوه بر این، آنها به آن نیاز داشتندΓ و
و . [13] اشتقاق فعلی با در نظر نگرفتن مجموعه ساده شده استΓ
. [13] اشتقاق فعلی با در نظر نگرفتن مجموعه ساده شده استΓ .
. (چرخش 360 درجه عملگر همانی است)، این در مکانیک کوانتومی فرض نمی شود، و معلوم می شود که اغلب درست نیست: زمانی که عدد کوانتومی تکانه زاویه ای کل یک عدد نیم صحیح است (1/2، 3/2). ، و غیره.)،
(چرخش 360 درجه عملگر همانی است)، این در مکانیک کوانتومی فرض نمی شود، و معلوم می شود که اغلب درست نیست: زمانی که عدد کوانتومی تکانه زاویه ای کل یک عدد نیم صحیح است (1/2، 3/2). ، و غیره.)، و هنگامی که یک عدد صحیح است،
و هنگامی که یک عدد صحیح است، . [6] از نظر ریاضی، ساختار چرخشها در جهان SO(3) نیست ، گروه چرخشهای سهبعدی در مکانیک کلاسیک. در عوض، SU(2) است که برای چرخش های کوچک با SO(3) یکسان است، اما در جایی که چرخش 360 درجه از نظر ریاضی از چرخش 0 درجه متمایز می شود. (اما چرخش 720 درجه همان چرخش 0 درجه است.) [6]
. [6] از نظر ریاضی، ساختار چرخشها در جهان SO(3) نیست ، گروه چرخشهای سهبعدی در مکانیک کلاسیک. در عوض، SU(2) است که برای چرخش های کوچک با SO(3) یکسان است، اما در جایی که چرخش 360 درجه از نظر ریاضی از چرخش 0 درجه متمایز می شود. (اما چرخش 720 درجه همان چرخش 0 درجه است.) [6] در همه شرایط، زیرا چرخش 360 درجه یک پیکربندی فضایی مانند عدم چرخش است. (این با چرخش 360 درجه حالت داخلی (اسپین) ذره متفاوت است، که ممکن است مانند عدم چرخش باشد یا نباشد.) به عبارت دیگر،
در همه شرایط، زیرا چرخش 360 درجه یک پیکربندی فضایی مانند عدم چرخش است. (این با چرخش 360 درجه حالت داخلی (اسپین) ذره متفاوت است، که ممکن است مانند عدم چرخش باشد یا نباشد.) به عبارت دیگر، اپراتورها ساختار SO(3) را دارند ، در حالی که
اپراتورها ساختار SO(3) را دارند ، در حالی که و؛ داخلی
و؛ داخلی ساختار SU(2) را حمل می کند .
ساختار SU(2) را حمل می کند . ، یکی یک حالت ویژه را انتخاب می کند
، یکی یک حالت ویژه را انتخاب می کند و قرعه کشی می کند
و قرعه کشی می کند یعنی اعداد کوانتومی تکانه زاویهای مداری فقط میتوانند اعداد صحیح باشند، نه نیمه صحیح.
یعنی اعداد کوانتومی تکانه زاویهای مداری فقط میتوانند اعداد صحیح باشند، نه نیمه صحیح. یک عملگر چرخشی باشد که هر حالت کوانتومی را حول محور بچرخاند
یک عملگر چرخشی باشد که هر حالت کوانتومی را حول محور بچرخاند ، اپراتور
، اپراتور در مورد محور
در مورد محور
 ; در نتیجه [6]
; در نتیجه [6] جایی که exp نمایی ماتریسی است .
جایی که exp نمایی ماتریسی است .

 حالت داخلی (اسپین) همه ذرات را بدون حرکت دادن هیچ ذره یا میدانی در فضا می چرخاند. رابطه J = L + S از:
حالت داخلی (اسپین) همه ذرات را بدون حرکت دادن هیچ ذره یا میدانی در فضا می چرخاند. رابطه J = L + S از:

 ، و
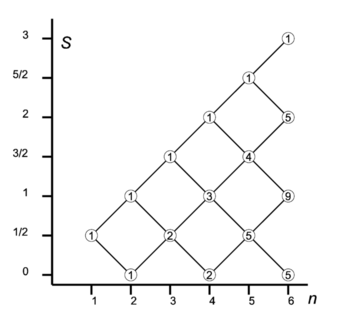
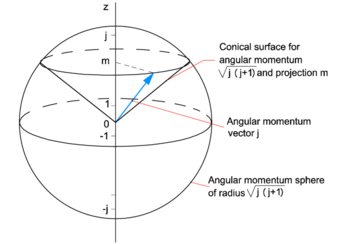
، و برای پنج مخروط از پایین به بالا. از آنجا که
برای پنج مخروط از پایین به بالا. از آنجا که ، بردارها همه با طول نشان داده شده اند
، بردارها همه با طول نشان داده شده اند . حلقه ها نشان دهنده این واقعیت است که
. حلقه ها نشان دهنده این واقعیت است که با قطعیت شناخته شده است، اما
با قطعیت شناخته شده است، اما و
و  ناشناخته هستند؛ بنابراین هر بردار کلاسیک با طول و مولفه z مناسب رسم می شود و مخروط را تشکیل می دهد. مقدار مورد انتظار تکانه زاویه ای برای یک مجموعه معین از سیستم ها در حالت کوانتومی مشخص شده توسط
ناشناخته هستند؛ بنابراین هر بردار کلاسیک با طول و مولفه z مناسب رسم می شود و مخروط را تشکیل می دهد. مقدار مورد انتظار تکانه زاویه ای برای یک مجموعه معین از سیستم ها در حالت کوانتومی مشخص شده توسط و
و می تواند جایی در این مخروط باشد در حالی که نمی توان آن را برای یک سیستم واحد تعریف کرد (از آنجا که اجزای
می تواند جایی در این مخروط باشد در حالی که نمی توان آن را برای یک سیستم واحد تعریف کرد (از آنجا که اجزای با یکدیگر رفت و آمد نکنید).
با یکدیگر رفت و آمد نکنید). تقریباً 100000000 است، اساساً فرقی نمیکند که مقدار دقیق یک عدد صحیح باشد مانند 100000000 یا 100000001 یا یک عدد غیر صحیح مانند 100000000.2 - مراحل گسسته در حال حاضر برای اندازهگیری بسیار کوچک هستند.
تقریباً 100000000 است، اساساً فرقی نمیکند که مقدار دقیق یک عدد صحیح باشد مانند 100000000 یا 100000001 یا یک عدد غیر صحیح مانند 100000000.2 - مراحل گسسته در حال حاضر برای اندازهگیری بسیار کوچک هستند. به این صورت تعریف می شوند:
به این صورت تعریف می شوند:
 یک حالت ویژه همزمان از
یک حالت ویژه همزمان از ، می توان ثابت کرد که هر یک از حالا
، می توان ثابت کرد که هر یک از حالا و
و یا صفر است یا یک حالت ویژه همزمان از
یا صفر است یا یک حالت ویژه همزمان از به ترتیب. در صورتی که استفاده از عملگر نردبان حالتی با مقدار برای را ایجاد کند، نتیجه صفر است
به ترتیب. در صورتی که استفاده از عملگر نردبان حالتی با مقدار برای را ایجاد کند، نتیجه صفر است  یک تابع حالت برای سیستم با مقدار ویژه باشد"
یک تابع حالت برای سیستم با مقدار ویژه باشد" برای
برای برای
برای به دست آمده است،
به دست آمده است، اعمال هر دو طرف معادله بالا به
اعمال هر دو طرف معادله بالا به از آنجا که
از آنجا که  منفی نیست و
منفی نیست و . بدین ترتیب"
. بدین ترتیب"![{\displaystyle [J_{y},J_{z}]=i\hbar J_{x},\;\;[J_{z},J_{x}]=i\hbar J_{y}.}](https://wikimedia.org/api/rest_v1/media/math/render/svg/7eeb3ba71de968e573852eb052632b0e3b111eb0) آنها را می توان برای به دست آوردن دو معادله ترکیب کرد که با استفاده از آنها با هم نوشته می شوند±
آنها را می توان برای به دست آوردن دو معادله ترکیب کرد که با استفاده از آنها با هم نوشته می شوند± نشانه های زیر،
نشانه های زیر، جایی که یکی از معادلات از+
جایی که یکی از معادلات از+ نشانه ها و دیگری استفاده می کند-
نشانه ها و دیگری استفاده می کند- نشانه ها اعمال هر دو طرف بالا به
نشانه ها اعمال هر دو طرف بالا به موارد فوق نشان می دهد که
موارد فوق نشان می دهد که دو تابع ویژه از
دو تابع ویژه از ، مگر اینکه یکی از توابع صفر باشد که در این صورت یک تابع ویژه نیست. برای توابعی که صفر نیستند،
، مگر اینکه یکی از توابع صفر باشد که در این صورت یک تابع ویژه نیست. برای توابعی که صفر نیستند، توابع ویژه بیشتر از
توابع ویژه بیشتر از تا زمانی که بزرگی مقدار ویژه حاصله باشد"
تا زمانی که بزرگی مقدار ویژه حاصله باشد" . از آنجایی که مقادیر ویژه از
. از آنجایی که مقادیر ویژه از کمترین مقدار ویژه باشد و
کمترین مقدار ویژه باشد و بالاترین باشد سپس
بالاترین باشد سپس و
و از آنجایی که هیچ حالتی وجود ندارد که مقدار ویژه از
از آنجایی که هیچ حالتی وجود ندارد که مقدار ویژه از یا
یا . با استفاده از
. با استفاده از به معادله اول،
به معادله اول، به دوم، و با استفاده از
به دوم، و با استفاده از ، می توان نشان داد که
، می توان نشان داد که و
و کم کردن معادله اول از دومی و تنظیم مجدد
کم کردن معادله اول از دومی و تنظیم مجدد از آنجا که
از آنجا که ، عامل دوم منفی است. سپس فاکتور اول باید صفر باشد و بنابراین
، عامل دوم منفی است. سپس فاکتور اول باید صفر باشد و بنابراین .
. ناشی از کاربرد پی در
ناشی از کاربرد پی در  یا
یا که مقدار ویژه را کاهش یا افزایش می دهند
که مقدار ویژه را کاهش یا افزایش می دهند اجازه دهید
اجازه دهید جایی که
جایی که سپس با استفاده از
سپس با استفاده از و
و و مقادیر ویژه مجاز ازجی
و مقادیر ویژه مجاز ازجی بیان کننده
بیان کننده ، و جایگزین کردن
، و جایگزین کردن 
 و
و روابط جابجاکر مشابهی دارند
روابط جابجاکر مشابهی دارند برای
برای با ارزش ویژه"
با ارزش ویژه" ،
، حل کردن برای
حل کردن برای جایی که
جایی که مستقل از
مستقل از به
به حل برای مقدار ویژه"
حل برای مقدار ویژه" جایی که
جایی که یک عدد صحیح است. [16] از مطالب فوق و رابطه ℓ=-ℓ،(-ℓ+1)،…،(ℓ-1)،ℓ
یک عدد صحیح است. [16] از مطالب فوق و رابطه ℓ=-ℓ،(-ℓ+1)،…،(ℓ-1)،ℓ  ، نتیجه می شود که
، نتیجه می شود که باید تک ارزشی باشد. توابع موج نیمه صحیح دو مقدار ممکن، چگالی احتمال تک مقداری دارند. [18] این توسط Pauli در سال 1939 به رسمیت شناخته شد (به نقل از Japaridze و همکاران [19] ).
باید تک ارزشی باشد. توابع موج نیمه صحیح دو مقدار ممکن، چگالی احتمال تک مقداری دارند. [18] این توسط Pauli در سال 1939 به رسمیت شناخته شد (به نقل از Japaridze و همکاران [19] ). و
و . [20] [21] اینها در زیر عملگرهای نردبانی رفتار خوبی ندارند، اما مشخص شده است که در توصیف ذرات کوانتومی صلب مفید هستند [22]
. [20] [21] اینها در زیر عملگرهای نردبانی رفتار خوبی ندارند، اما مشخص شده است که در توصیف ذرات کوانتومی صلب مفید هستند [22] تعریف اپراتورهای جدید
تعریف اپراتورهای جدید


 و
و همه رفت و آمد می کنند
همه رفت و آمد می کنند
 ، ما پیدا می کنیم
، ما پیدا می کنیم
 باید یک عدد صحیح باشد که از آن
باید یک عدد صحیح باشد که از آن
![{\displaystyle \left[L^{2},L_{x}\right]=\left[L^{2},L_{y}\right]=\left[L^{2},L_{z} \right]=0.}](https://wikimedia.org/api/rest_v1/media/math/render/svg/7c0c210fa104686bbd31f2c99fb1eb18b85ea724)
![{\displaystyle {\begin{aligned}\left[L^{2},L_{x}\right]&=\left[L_{x}^{2},L_{x}\right]+\left[ L_{y}^{2},L_{x}\right]+\left[L_{z}^{2},L_{x}\right]\\&=L_{y}\چپ[L_{y },L_{x}\right]+\left[L_{y},L_{x}\right]L_{y}+L_{z}\left[L_{z},L_{x}\right]+ \left[L_{z},L_{x}\right]L_{z}\\&=L_{y}\left(-i\hbar L_{z}\right)+\left(-i\hbar L_ {z}\right)L_{y}+L_{z}\left(i\hbar L_{y}\right)+\left(i\hbar L_{y}\right)L_{z}\\&= 0\end{تراز شده}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/24d5af5109980d5e987b42d7caa0e948f0ea882c)
 جایی که
جایی که  جزء اپراتور تکانه زاویه ای کلاسیک است و
جزء اپراتور تکانه زاویه ای کلاسیک است و براکت پواسون است . [9]
براکت پواسون است . [9]![{\displaystyle {\begin{aligned}\left[S^{2},S_{i}\right]&=0,\\\left[J^{2},J_{i}\right]&=0 .\end{تراز شده}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/d71b39708852fc42ae08ec9462f022e53eb0caea)
 جایی که
جایی که انحراف معیار در مقادیر اندازه گیری شده X و است
انحراف معیار در مقادیر اندازه گیری شده X و است نشان دهنده مقدار انتظاری X است . اگر x، y، z دوباره مرتب شوند، یا اگر L با J یا S جایگزین شود، این نابرابری نیز صادق است .
نشان دهنده مقدار انتظاری X است . اگر x، y، z دوباره مرتب شوند، یا اگر L با J یا S جایگزین شود، این نابرابری نیز صادق است . .
. ،
،
 ،
،
 .
.
 ،
،

 ،
،
 گاهی اوقات عدد کوانتومی طرح ریزی اسپین نامیده می شود .
گاهی اوقات عدد کوانتومی طرح ریزی اسپین نامیده می شود . .
. ،
،
 ،
،
 گاهی اوقات عدد کوانتومی طرح تکانه زاویه ای کل نامیده می شود .
گاهی اوقات عدد کوانتومی طرح تکانه زاویه ای کل نامیده می شود . .
.

 . همتایان مکانیکی کوانتومی این اجسام رابطه مشابهی دارند:
. همتایان مکانیکی کوانتومی این اجسام رابطه مشابهی دارند: که در آن L x ، L y ، L z سه عملگر مختلف مکانیکی کوانتومی هستند.
که در آن L x ، L y ، L z سه عملگر مختلف مکانیکی کوانتومی هستند. که در آن ∇ عملگر دیفرانسیل برداری، del است .
که در آن ∇ عملگر دیفرانسیل برداری، del است . . اسپین اغلب به صورت ذره ای به تصویر کشیده می شود که به معنای واقعی کلمه حول یک محور می چرخد، اما این تنها یک استعاره است: نزدیک ترین آنالوگ کلاسیک بر اساس گردش موج است. [2] همه ذرات بنیادی یک اسپین مشخص دارند ( بوزون های اسکالر دارای اسپین صفر هستند). برای مثال، الکترونها همیشه �اسپین ۱/۲� دارند در حالی که فوتونها همیشه �اسپین ۱� دارند (جزئیات زیر ).
. اسپین اغلب به صورت ذره ای به تصویر کشیده می شود که به معنای واقعی کلمه حول یک محور می چرخد، اما این تنها یک استعاره است: نزدیک ترین آنالوگ کلاسیک بر اساس گردش موج است. [2] همه ذرات بنیادی یک اسپین مشخص دارند ( بوزون های اسکالر دارای اسپین صفر هستند). برای مثال، الکترونها همیشه �اسپین ۱/۲� دارند در حالی که فوتونها همیشه �اسپین ۱� دارند (جزئیات زیر ).
![{\displaystyle \left[L_{x},L_{y}\right]=i\hbar L_{z},\;\;\left[L_{y},L_{z}\right]=i\hbar L_{x},\;\;\left[L_{z},L_{x}\right]=i\hbar L_{y},}](https://wikimedia.org/api/rest_v1/media/math/render/svg/0c070d006eef73e6fc20120f0c21d5f712a1f2cc)
![{\displaystyle [X,Y]\Equiv XY-YX.}](https://wikimedia.org/api/rest_v1/media/math/render/svg/47f2a7c6c66824aa3a4f94481eb03b62fcc6ae35)
![{\displaystyle \left[L_{l},L_{m}\right]=i\hbar \sum _{n=1}^{3}\varepsilon _{lmn}L_{n},}](https://wikimedia.org/api/rest_v1/media/math/render/svg/5e64c60e6e08cbe0e00541179ae374ee3e31277d) که در آن l ، m ، n شاخص های مؤلفه هستند (1 برای x ، 2 برای y، 3 برای z)، و εlmn نشان دهنده نماد Levi - Civita است .
که در آن l ، m ، n شاخص های مؤلفه هستند (1 برای x ، 2 برای y، 3 برای z)، و εlmn نشان دهنده نماد Levi - Civita است .
![{\displaystyle [x_{l},p_{m}]=i\hbar \delta _{lm}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/2363420037b45b6869e104533de2bcb5720054da) ، جایی که δlm دلتای کرونکر است .
، جایی که δlm دلتای کرونکر است . که در آن L n جزء عملگر تکانه زاویه ای کلاسیک است و
که در آن L n جزء عملگر تکانه زاویه ای کلاسیک است و![{\displaystyle \left[S_{l},S_{m}\right]=i\hbar \sum _{n=1}^{3}\varepsilon _{lmn}S_{n},\quad \left[ J_{l},J_{m}\right]=i\hbar \sum _{n=1}^{3}\varepsilon _{lmn}J_{n}.}](https://wikimedia.org/api/rest_v1/media/math/render/svg/da92689505e62437b32d72efefa443aded9680a6)
 یابنابراین(3)
یابنابراین(3) به ترتیب در نماد ریاضی)، یعنی جبر لی مرتبط با چرخش در سه بعدی. همین امر در مورد J و S نیز صادق است . دلیل آن در زیر مورد بحث قرار گرفته است . این روابط جابجاکر برای اندازه گیری و عدم قطعیت مرتبط هستند، همانطور که در ادامه بیشتر مورد بحث قرار می گیرد.
به ترتیب در نماد ریاضی)، یعنی جبر لی مرتبط با چرخش در سه بعدی. همین امر در مورد J و S نیز صادق است . دلیل آن در زیر مورد بحث قرار گرفته است . این روابط جابجاکر برای اندازه گیری و عدم قطعیت مرتبط هستند، همانطور که در ادامه بیشتر مورد بحث قرار می گیرد.


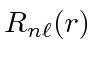
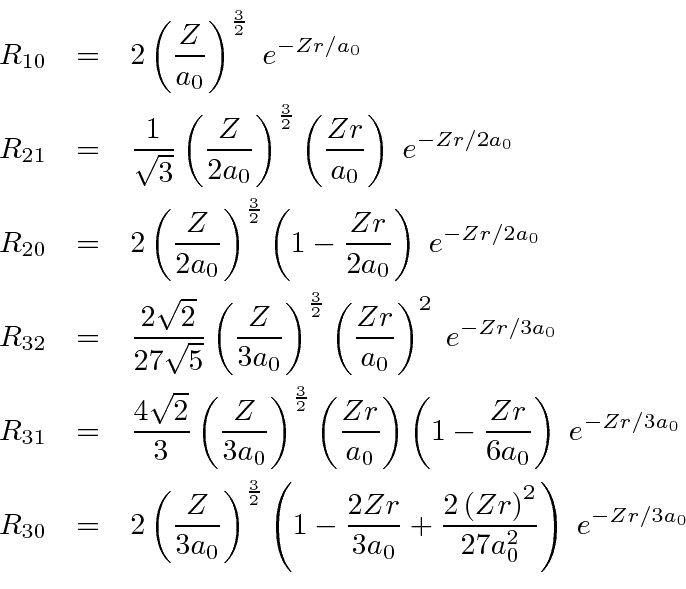
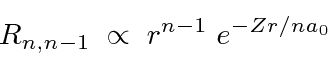
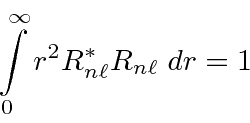
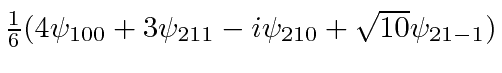
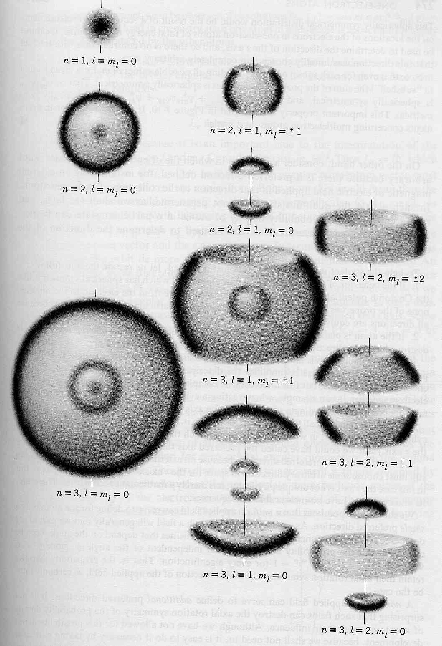
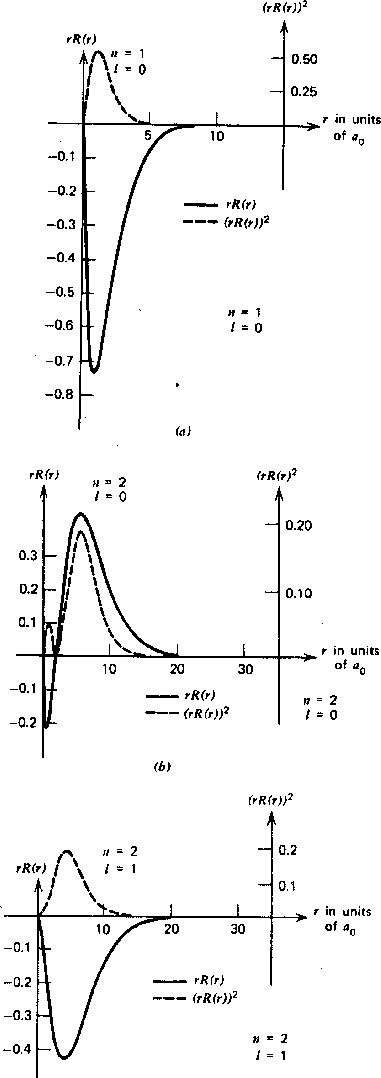
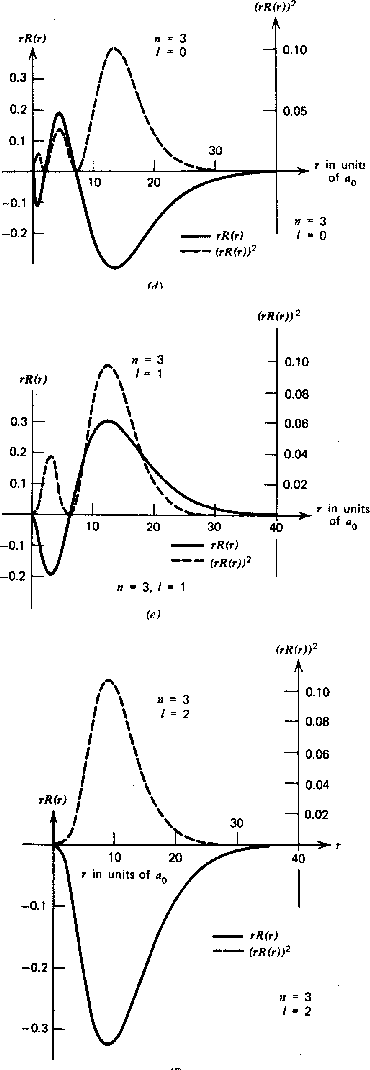
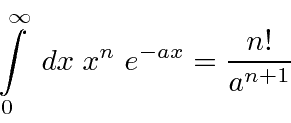
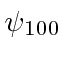
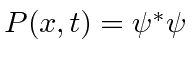
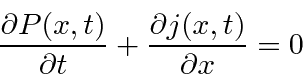
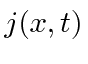
![\begin{displaymath}\bgroup\color{black} j(x,t)={\hbar\over 2mi} \left[\psi^*{\pa... ...r\partial x}-{\ partial\psi^*\over\partial x}\psi\right] \egroup\end{displaymath}](https://quantummechanics.ucsd.edu/ph130a/130_notes/img1065.png)
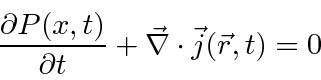
![\bgroup\color{black}$\displaystyle \vec{j}(\vec{r},t)={\hbar\over 2mi} \left[\ps... ...bla}\psi(\vec {r},t)-\psi(\vec{r},t)\vec{\nabla}\psi^*(\vec{r},t)\right] $\egroup](https://quantummechanics.ucsd.edu/ph130a/130_notes/img1069.png)







 (معادل 1)
(معادل 1)
 (معادل 2)
(معادل 2)
 (معادل 3)
(معادل 3) (معادل 4)
(معادل 4) (معادل 5)
(معادل 5) (معادل 6)
(معادل 6) (معادل 7)
(معادل 7) (معادل 8) بخش زمانی
(معادل 8) بخش زمانی (معادل 9) بخش فضایی
(معادل 9) بخش فضایی (معادل 12)
(معادل 12) (معادل 13)
(معادل 13) (معادل 14)
(معادل 14)
 در یک بعد،
در یک بعد، در دو بعد و
در دو بعد و در سه بعدی اگر دو ذره وجود دارد، باید مجموع انرژی جنبشی هر ذره را بنویسید. به عنوان مثال، کل انرژی جنبشی یک ذره با جرم m 1 و یک ذره با جرم m 2 در یک بعد برابر است با
در سه بعدی اگر دو ذره وجود دارد، باید مجموع انرژی جنبشی هر ذره را بنویسید. به عنوان مثال، کل انرژی جنبشی یک ذره با جرم m 1 و یک ذره با جرم m 2 در یک بعد برابر است با . انرژی جنبشی یک سیستم را به صورت سه بعدی حاوی یک الکترون و یک پروتون بنویسید.
. انرژی جنبشی یک سیستم را به صورت سه بعدی حاوی یک الکترون و یک پروتون بنویسید. ، محاسبه
، محاسبه و
و . اکنون مشتقات جزئی دوم را محاسبه کنید
. اکنون مشتقات جزئی دوم را محاسبه کنید و
و .
.


 چرخش دیراک برای تبدیل به عنوان
چرخش دیراک برای تبدیل به عنوان




![{\displaystyle \sigma ^{\mu \nu }={\frac {i}{2}}[\gamma ^{\mu },\gamma ^{\nu }]~.}](https://wikimedia.org/api/rest_v1/media/math/render/svg/c9e2271999698158d61e356297a43e9821fab684)
 از
از 




 ژنراتور
ژنراتور
 تبدیل لورنتس باشد. معادله دیراک است
تبدیل لورنتس باشد. معادله دیراک است












![{\displaystyle \sigma ^{\mu \nu }={\frac {i}{2}}[\gamma ^{\mu },\gamma ^{\nu }]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/2c0ba5e0514cff9eae8b231e09932002b04cb89d)

 در امتداد فیبر دسته اسپین.) واینبرگ استدلال های بیشتری برای تفسیر فیزیکی این موارد به عنوان تکانه زاویه ای کلی و ذاتی ارائه می دهد.
در امتداد فیبر دسته اسپین.) واینبرگ استدلال های بیشتری برای تفسیر فیزیکی این موارد به عنوان تکانه زاویه ای کلی و ذاتی ارائه می دهد. 






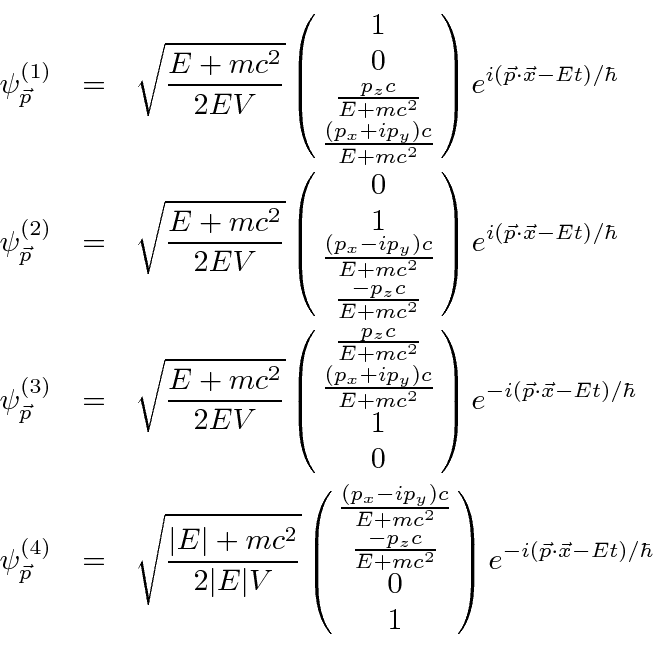
 نشان می دهد که تمام اجزای تابع موج به صورت جداگانه رابطه نسبیتی انرژی - تکانه را برآورده می کنند. بنابراین معادله جستجو شده که هم در مکان و هم در زمان مرتبه اول است
نشان می دهد که تمام اجزای تابع موج به صورت جداگانه رابطه نسبیتی انرژی - تکانه را برآورده می کنند. بنابراین معادله جستجو شده که هم در مکان و هم در زمان مرتبه اول است








 (
( "d-slash" تلفظ می شود)،
"d-slash" تلفظ می شود)، 



















 تعریف شده در فضای زمان تخت (
تعریف شده در فضای زمان تخت (  . بیان آن همچنین حاوی
. بیان آن همچنین حاوی  به عنوان جرم و همچنین سایر ثابت های فیزیکی تفسیر می شود.
به عنوان جرم و همچنین سایر ثابت های فیزیکی تفسیر می شود. ، معادله دیراک پس از آن است
، معادله دیراک پس از آن است

 ماتریس های پیچیده
ماتریس های پیچیده  ) که روابط تعیین کننده ضد تعویض را برآورده می کند:
) که روابط تعیین کننده ضد تعویض را برآورده می کند:
 عنصر متریک مینکوفسکی و شاخص ها است
عنصر متریک مینکوفسکی و شاخص ها است بر روی 0،1،2 و 3 اجرا کنید. این ماتریسها را میتوان بهصراحت تحت یک انتخاب نمایش محقق کرد. دو انتخاب رایج، نمایندگی دیراک است
بر روی 0،1،2 و 3 اجرا کنید. این ماتریسها را میتوان بهصراحت تحت یک انتخاب نمایش محقق کرد. دو انتخاب رایج، نمایندگی دیراک است

 یکسان هستند، اما
یکسان هستند، اما 


 به عنوان ... تعریف شده است
به عنوان ... تعریف شده است
 ) که
) که
 :
:
 : نوشته شده به روش معمول بر حسب عمل چپ مشتق، داریم
: نوشته شده به روش معمول بر حسب عمل چپ مشتق، داریم
 به معادله دیراک می دهد
به معادله دیراک می دهد



 تقارن برای استخراج جریان ذخیره شده
تقارن برای استخراج جریان ذخیره شده

 تقارن که می فرستد
تقارن که می فرستد
 برای بی نهایت کوچک بودن، در مرتبه اول کار می کنیم
برای بی نهایت کوچک بودن، در مرتبه اول کار می کنیم مقررات. از بحث قبلی بلافاصله شاهد تغییر صریح در لاگرانژی به دلیل
مقررات. از بحث قبلی بلافاصله شاهد تغییر صریح در لاگرانژی به دلیل
 .
. پس راضی هستند
پس راضی هستند






 جایی که
جایی که
 :
:
 بردار
بردار ، با
، با
 و
و ماتریس هرمیتی ریشه مربع است.
ماتریس هرمیتی ریشه مربع است.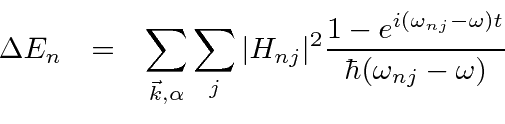
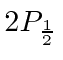
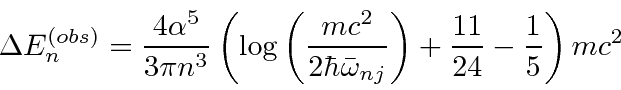
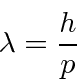
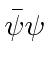

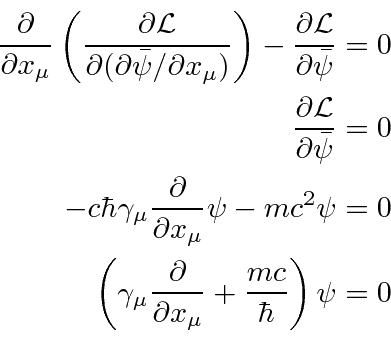
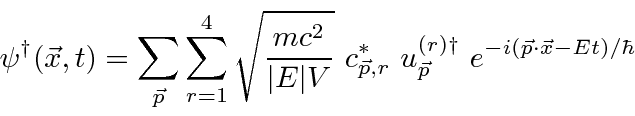
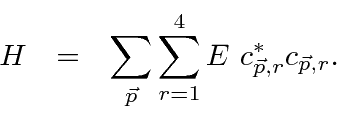
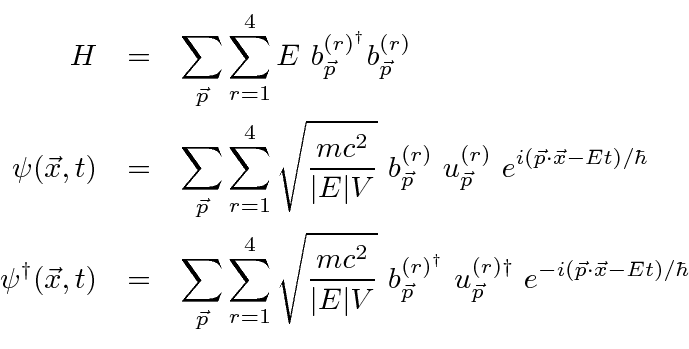
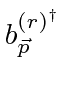
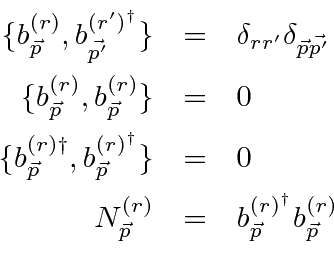
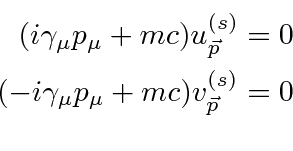
![\begin{displaymath}\bgroup\color{black} H={1\over 2m}\left(\vec{\sigma}\cdot[\ve... ...{e\over c}\vec{A }(\vec{r},t)]\right)^2-e\phi(\vec{r},t) \egroup\end{displaymath}](https://quantummechanics.ucsd.edu/ph130a/130_notes/img482.png)
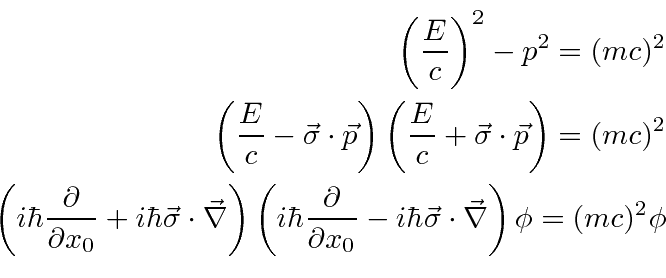
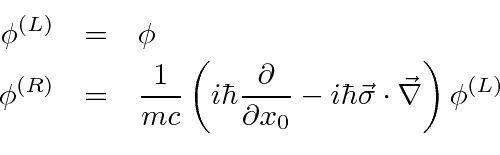
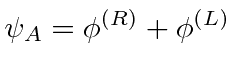
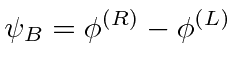
![\begin{eqnarray*} \pmatrix{-i\hbar{\partial\over\partial x_0} & -i\hbar\vec{\sig... ...] =\hbar\left[\gamma_\mu{ \جزئی\ بیش از x_\mu}\راست] \\ \پایان{eqnarray*}](https://quantummechanics.ucsd.edu/ph130a/130_notes/img489.png)
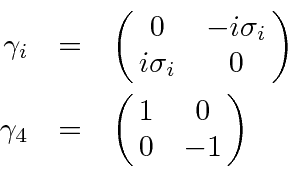
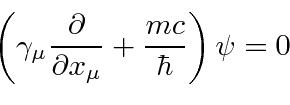
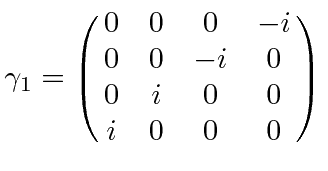
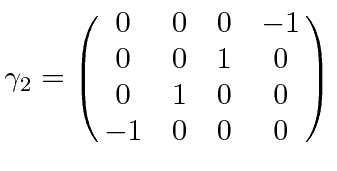
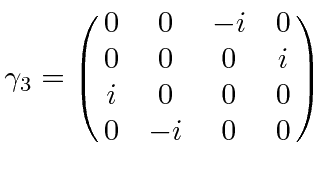
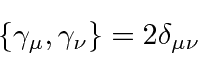
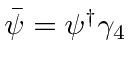
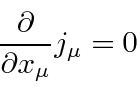
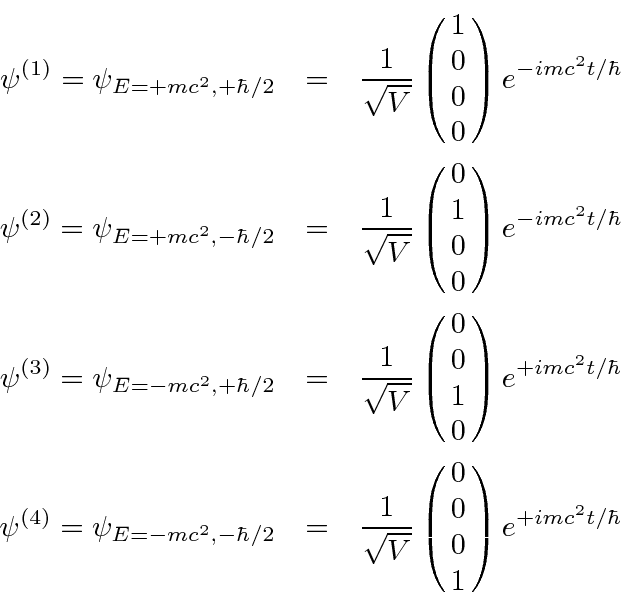
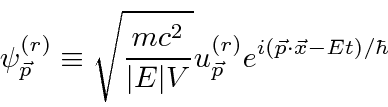
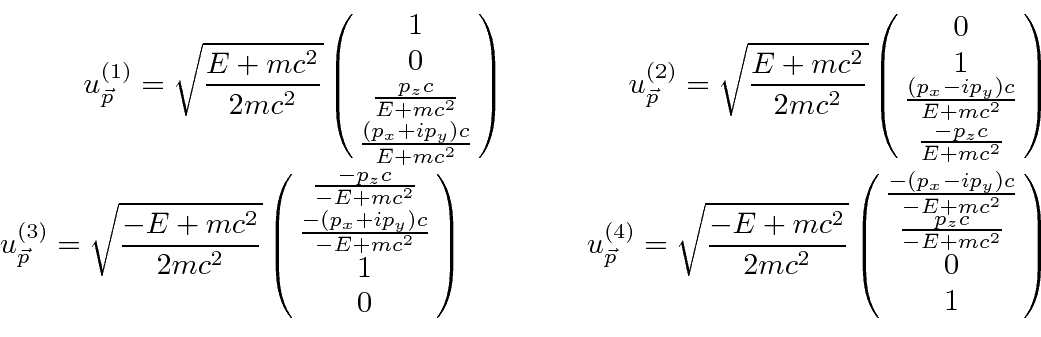
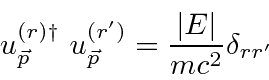
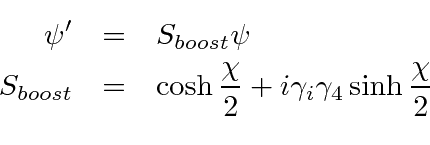
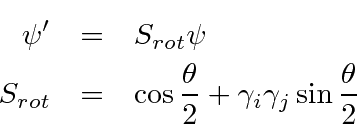
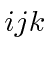
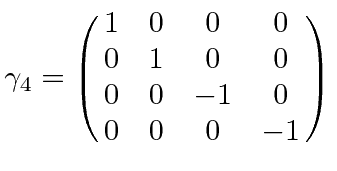
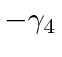
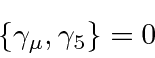
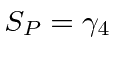
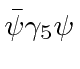
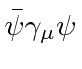
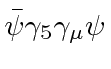
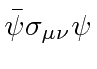
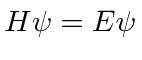
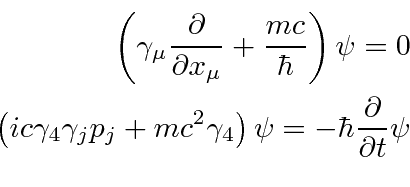
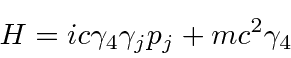
![\begin{displaymath}\bgroup\color{black} [H,L_z]=ic\gamma_4[\gamma_jp_j,xp_y-yp_x]=\hbar c\gamma_4(\gamma_1p_y-\gamma_2 p_x) \egroup\gmath}{display](https://quantummechanics.ucsd.edu/ph130a/130_notes/img539.png)
![\begin{displaymath}\bgroup\color{black} {[H,S_z]}=\hbar c\gamma_4[\gamma_2p_x-\gamma_1p_y] \egroup\end{displaymath}](https://quantummechanics.ucsd.edu/ph130a/130_notes/img540.png)
![\begin{eqnarray*}[H,J_z]=[H,L_z]+[H,S_z]=\hbar c\gamma_4(\gamma_1p_y-\gamma_2 p_x)+\hbar c\gamma_4[\gamma_2p_x-\gamma_1p_y] =0 \\ \end{eqnarray*}](https://quantummechanics.ucsd.edu/ph130a/130_notes/img541.png)
![\begin{displaymath}\bgroup\color{black} [H,\vec{S}\cdot\vec{p}]=[H,\vec{S}]\cdot\vec{p}=0 \egroup\ پایان{نمایش}](https://quantummechanics.ucsd.edu/ph130a/130_notes/img542.png)
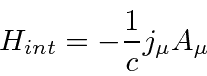
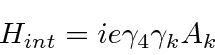
![\begin{eqnarray*} \langle v_k\rangle&=&\sum\limits_{\vec{p}}\sum\limits_{r=1}^4\... ...mma_k u^{(r') }_{\vec{p}} e^{2i\vert E\vert t/\hbar}\right] \\ \end{eqnarray*}](https://quantummechanics.ucsd.edu/ph130a/130_notes/img546.png)
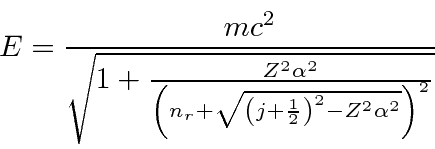
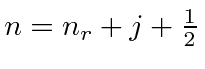
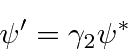
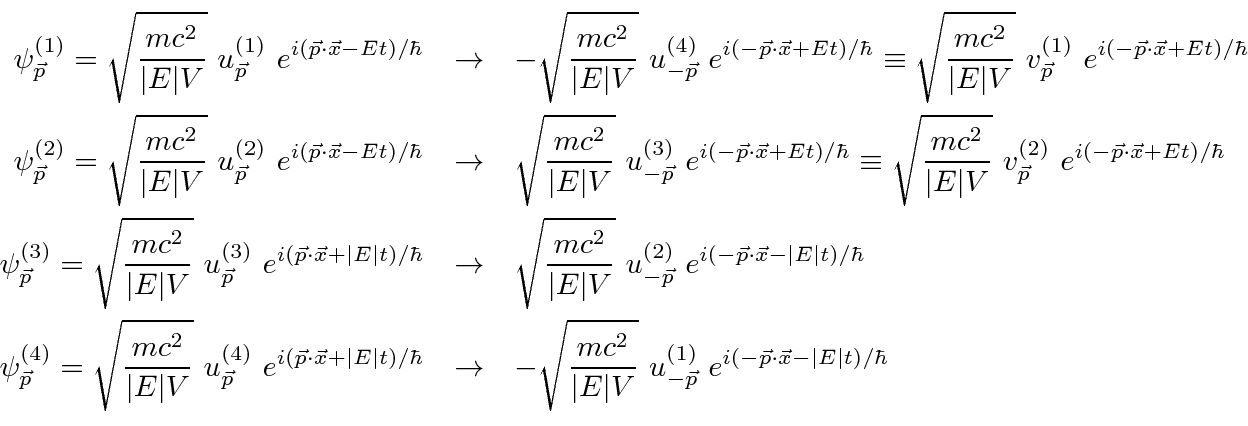
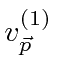
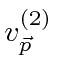
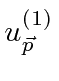
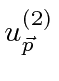

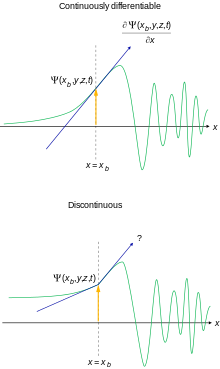

 در حالت | α , ω 〉 است
در حالت | α , ω 〉 است


 در این وبلاگ به ریاضیات و کاربردهای آن و تحقیقات در آنها پرداخته می شود. مطالب در این وبلاگ ترجمه سطحی و اولیه است و کامل نیست.در صورتی سوال یا نظری در زمینه ریاضیات دارید مطرح نمایید .در صورت امکان به آن می پردازم. من دوست دارم برای یافتن پاسخ به سوالات و حل پروژه های علمی با دیگران همکاری نمایم.در صورتی که شما هم بامن هم عقیده هستید با من تماس بگیرید.
در این وبلاگ به ریاضیات و کاربردهای آن و تحقیقات در آنها پرداخته می شود. مطالب در این وبلاگ ترجمه سطحی و اولیه است و کامل نیست.در صورتی سوال یا نظری در زمینه ریاضیات دارید مطرح نمایید .در صورت امکان به آن می پردازم. من دوست دارم برای یافتن پاسخ به سوالات و حل پروژه های علمی با دیگران همکاری نمایم.در صورتی که شما هم بامن هم عقیده هستید با من تماس بگیرید.