از ویکیپدیا، دانشنامه آزاد

یک کلاغ سیاه
غیر
کلاغ غیر سیاه و سفید
پارادوکس کلاغ نشان می دهد که هر دوی این تصاویر شواهدی را بر فرض سیاه بودن همه کلاغ ها ارائه می دهند.
تناقض کلاغ سیاه ، همچنین به عنوان شناخته شده تناقض همپل ، کلاغ همپل ، یا به ندرت تناقض پرنده شناسی داخلی ، [1] است تناقض ناشی از درخواست از آنچه به منزله شواهد برای یک بیانیه. مشاهده اجسامی که نه سیاه هستند و نه زاغ ، ممکن است به طور رسمی احتمال سیاه بودن همه زاغها را افزایش دهند ، هرچند که از نظر شهودی ، این مشاهدات بی ارتباط هستند.
این مسئله توسط منطق کارل گوستاو همپل در دهه 1940 برای نشان دادن تناقض بین منطق استقرایی و شهود مطرح شد . [2]
فهرست
پارادوکس [ ویرایش ]
همپل پارادوکس را بر اساس فرضیه توصیف می کند : [3] [4]
(1) همه زاغ ها سیاه هستند . به صورت ضمنی ، این را می توان به صورت زیر بیان کرد: اگر چیزی کلاغ است ، پس سیاه است.
از طریق تقابل ، این بیانیه است معادل به:
(2) اگر چیزی سیاه نیست ، پس زاغ نیست.
در همه شرایطی که (2) درست است ، (1) نیز صادق است - و همینطور ، در همه شرایطی که (2) نادرست است (یعنی اگر دنیایی تصور شود که در آن چیزی که سیاه نبود ، اما زاغ بود ، وجود داشته است) ، (1) نیز نادرست است.
با توجه به یک عبارت کلی مانند همه زاغ ها سیاه هستند ، یک فرم از همان عبارت که به نمونه قابل مشاهده خاصی از طبقه عمومی اشاره می کند ، معمولاً شواهدی برای آن بیانیه کلی تلقی می شود. مثلا،
(3) کلاغ حیوان خانگی من سیاه است.
شواهدی است که این فرضیه را تایید می کند که همه زاغ ها سیاه هستند .
این پارادوکس زمانی بوجود می آید که همین فرایند روی گزاره (2) اعمال شود. با مشاهده یک سیب سبز ، می توانید موارد زیر را مشاهده کنید:
(4) این سیب سبز سیاه نیست و زاغ نیست.
با همین استدلال ، این گزاره شواهدی است که (2) اگر چیزی سیاه نباشد ، پس زاغ نیست. اما از آنجا که (همانطور که در بالا گفته شد) این عبارت از نظر منطقی معادل (1) همه زاغ ها سیاه هستند ، بنابراین مشاهده می شود که دیدن یک سیب سبز شواهدی است که تصور می کند که همه زاغ ها سیاه هستند. این نتیجه گیری متناقض به نظر می رسد زیرا نشان می دهد که با نگاه کردن به یک سیب اطلاعاتی در مورد زاغها به دست آمده است.
قطعنامه های پیشنهادی [ ویرایش ]
معیار نیکود می گوید که فقط مشاهدات زاغها باید بر دیدگاه افراد در مورد سیاه بودن همه کلاغها تأثیر بگذارد. مشاهده موارد بیشتر از کلاغهای سیاه باید دیدگاه را پشتیبانی کند ، مشاهده کلاغهای سفید یا رنگی باید با آن مغایرت داشته باشد و مشاهدات غیر کلاغها نباید هیچ تاثیری داشته باشد. [5]
شرط هم ارز بودن همپل بیان می کند که وقتی یک گزاره ، X ، شواهدی را به نفع گزاره دیگر Y ارائه می کند ، X نیز شواهدی را به نفع هر گزاره ای که منطقاً معادل Y باشد ، ارائه می دهد. [6]
در واقع ، مجموعه کلاغ ها محدود هستند. مجموعه چیزهای غیر سیاه یا بی نهایت است یا فراتر از شمارش بشر. برای تأیید عبارت "همه کلاغها سیاه هستند" ، لازم است همه زاغها را مشاهده کنید. این کار دشوار اما شدنی است. برای تأیید این جمله "همه چیزهای سیاه و سفید غیر کلاغ هستند" ، لازم است همه چیزهای غیر سیاه را بررسی کنیم. ممکن نیست. مشاهده یک کلاغ سیاه می تواند به عنوان یک مقدار محدود از شواهد تأییدی در نظر گرفته شود ، اما مشاهده یک غیر زاغ غیر سیاه ، مقدار بی شماری از شواهد خواهد بود.
این تناقض نشان می دهد که معیار نیکود و شرط هم ارز بودن همپل با یکدیگر سازگار نیستند. قطعنامه پارادوکس باید حداقل یکی از موارد زیر را رد کند: [7]
- موارد منفی بدون تأثیر (! PC) ،
- شرط معادل (EC) ، یا ،
- تأیید اعتبار توسط موارد مثبت (NC).
یک قطعنامه رضایت بخش نیز باید توضیح دهد که چرا به نظر ساده لوحانه یک پارادوکس وجود دارد. راه حل هایی که نتیجه گیری متناقض را می پذیرند می توانند این کار را با ارائه گزاره ای که از نظر شهودی ما اشتباه می دانیم اما به راحتی با (PC) اشتباه گرفته می شود ، انجام دهند ، در حالی که راه حل هایی که (EC) یا (NC) را رد می کنند باید گزاره ای را ارائه دهند که ما به طور شهودی می دانیم درست است اما به راحتی با (EC) یا (NC) اشتباه گرفته می شود.
پذیرش افراد غیر زاغ به عنوان مرتبط [ ویرایش ]
اگرچه این نتیجه گیری از پارادوکس ضد شهودی به نظر می رسد ، برخی از رویکردها می پذیرند که مشاهدات (رنگین) زاغ ها در واقع می تواند شواهدی معتبر در حمایت از فرضیه های مربوط به (سیاهی جهانی) کلاغ ها باشد.
قطعنامه همپل [ ویرایش ]
خود همپل نتیجه متناقض را پذیرفت و استدلال کرد که دلیل این که نتیجه نتیجه متناقض به نظر می رسد این است که ما اطلاعات قبلی را در اختیار داریم که بدون آن مشاهده یک غیر زاغ غیر سیاه می تواند در واقع شواهدی در مورد سیاه بودن همه کلاغ ها ارائه دهد.
او این موضوع را با مثال کلی سازی "همه نمک های سدیم زرد می سوزند" نشان می دهد و از ما می خواهد که مشاهده ای را که در هنگام نگه داشتن شخصی قطعه ای از یخ خالص در شعله بی رنگ که زرد نمی شود ، در دست بگیریم: [3] : 19– 20
این نتیجه می تواند این ادعا را تأیید کند که "هرچه زرد نمی سوزد ، نمک سدیم نیست" ، و در نتیجه ، به واسطه شرط معادل سازی ، فرمول اصلی را تأیید می کند. چرا این ما را به عنوان پارادوکسیک تحت تأثیر قرار می دهد؟ دلیل این امر هنگامی مشخص می شود که ما وضعیت قبلی را با موردی مقایسه کنیم که در آن جسمی که ساختار شیمیایی آن هنوز برای ما ناشناخته است در شعله نگه داشته شده و زرد نمی شود و در تجزیه و تحلیل بعدی مشخص می شود که فاقد سدیم است. نمک. این نتیجه ، بدون شک باید توافق کنیم ، همان چیزی است که بر اساس فرضیه انتظار می رفت ... بنابراین داده های بدست آمده در اینجا شواهدی را برای فرضیه تأیید می کند. ... در موارد به ظاهر متناقض تأیید ، ما اغلب در مورد رابطه شواهد داده شده قضاوت نمی کنیم ، تنها به فرضیه H ... ما به طور ضمنی مقایسه H را با مجموعه ای از شواهد که شامل E است به همراه مقدار اضافی اطلاعاتی که تصادفاً در اختیار داریم ، معرفی می کنیم. در تصویر ما ، این اطلاعات شامل دانش (1) است که ماده مورد استفاده در آزمایش یخ است و (2) اینکه یخ حاوی نمک سدیم نیست. اگر این اطلاعات اضافی را همانطور که داده شد فرض کنیم ، مطمئناً نتیجه آزمایش نمی تواند به فرضیه مورد بررسی هیچگونه قوت ببخشد. اما اگر مراقب باشیم از این اشاره ضمنی به دانش اضافی اجتناب کنیم ... تناقضات ناپدید می شوند. این اطلاعات شامل دانش (1) است که ماده مورد استفاده در آزمایش یخ است و (2) اینکه یخ حاوی نمک سدیم نیست. اگر این اطلاعات اضافی را همانطور که داده شد فرض کنیم ، مطمئناً نتیجه آزمایش نمی تواند به فرضیه مورد بررسی هیچگونه قوت ببخشد. اما اگر مراقب باشیم از این اشاره ضمنی به دانش اضافی اجتناب کنیم ... تناقضات ناپدید می شوند. این اطلاعات شامل دانش (1) است که ماده مورد استفاده در آزمایش یخ است و (2) اینکه یخ حاوی نمک سدیم نیست. اگر این اطلاعات اضافی را همانطور که داده شد فرض کنیم ، مطمئناً نتیجه آزمایش نمی تواند به فرضیه مورد بررسی هیچگونه قوت ببخشد. اما اگر مراقب باشیم از این اشاره ضمنی به دانش اضافی اجتناب کنیم ... تناقضات ناپدید می شوند.
راه حل استاندارد بیزی [ ویرایش ]
یکی از رایج ترین قطعنامه های پیشنهادی این است که این نتیجه را بپذیرید که مشاهده سیب سبز شواهدی از سیاه بودن همه زاغ ها را ارائه می دهد ، اما این استدلال که مقدار تأیید ارائه شده بسیار کم است ، به دلیل اختلاف زیاد بین تعداد زاغ ها و تعداد اجسام غیر سیاه بر اساس این قطعنامه ، نتیجه گیری متناقض به نظر می رسد زیرا ما به طور شهودی میزان شواهد ارائه شده از مشاهده سیب سبز را صفر برآورد می کنیم ، در حالی که در واقع غیر صفر است اما بسیار کوچک است.
ارائه IJ Good از این استدلال در 1960 [8] شاید مشهورترین باشد ، و انواع استدلال از آن زمان رایج بوده است ، [9] اگرچه در 1958 ارائه شده بود [10] و اشکال اولیه استدلال ظاهر شد در اوایل سال 1940. [11]
استدلال گود شامل محاسبه وزن شواهد ارائه شده توسط مشاهده یک کلاغ سیاه یا کفش سفید به نفع این فرضیه است که تمام زاغهای موجود در مجموعه اشیا سیاه هستند. وزن شواهد لگاریتم عامل بیز است ، که در این مورد به سادگی عاملی است که شانس فرضیه در هنگام مشاهده تغییر می کند. استدلال به شرح زیر است:
... فرض کنید که وجود دارد  اشیایی که ممکن است در هر لحظه دیده شوند ، که از آن جمله است
اشیایی که ممکن است در هر لحظه دیده شوند ، که از آن جمله است  زاغ هستند و
زاغ هستند و  سیاه هستند ، و این
سیاه هستند ، و این  اشیاء هر کدام احتمالاتی دارند
اشیاء هر کدام احتمالاتی دارند  از دیده شدن اجازه دهید
از دیده شدن اجازه دهید فرضیه ای باشد که وجود دارد
فرضیه ای باشد که وجود دارد  کلاغهای سیاه پوست ، و فرض کنید که فرضیه ها
کلاغهای سیاه پوست ، و فرض کنید که فرضیه ها در ابتدا قابل تعادل هستند سپس ، اگر تصادفاً یک کلاغ سیاه ببینیم ، عامل بیز به نفع
در ابتدا قابل تعادل هستند سپس ، اگر تصادفاً یک کلاغ سیاه ببینیم ، عامل بیز به نفع است
است

یعنی اگر تعداد زاغهای موجود زیاد شناخته شود حدود 2 عدد. اما اگر ما یک کفش سفید می بینیم تنها عامل آن است


و این تنها از حدود وحدت فراتر می رود  اگر
اگر  بزرگ است در مقایسه با
بزرگ است در مقایسه با  به بنابراین وزن شواهد ارائه شده از رویت یک کفش سفید مثبت است ، اما اگر تعداد زاغ ها در مقایسه با تعداد اجسام غیر سیاه مشخص باشد ، اندک است. [12]
به بنابراین وزن شواهد ارائه شده از رویت یک کفش سفید مثبت است ، اما اگر تعداد زاغ ها در مقایسه با تعداد اجسام غیر سیاه مشخص باشد ، اندک است. [12]
بسیاری از طرفداران این قطعنامه و انواع آن طرفدار احتمال بیزی بوده اند و امروزه آن را معمولاً راه حل بیزی می نامند ، اگرچه ، همانطور که چیاره [13] مشاهده می کند ، "چیزی به نام راه حل بیزی وجود ندارد. "راه حل" های مختلفی که بیزی ها با استفاده از تکنیک های بیزی ارائه کرده اند. " رویکردهای قابل توجه با استفاده از تکنیک های بیزی (که برخی از آنها PC را می پذیرند و در عوض NC را رد می کنند) شامل Earman ، [14] Eells ، [15] گیبسون ، [16] Hosiasson-Lindenbaum ، [11] Howson and Urbach ، [17] Mackie ، [ 18] و هینتیکا ، [19]او ادعا می کند که رویکرد وی "بیشتر بیزی است تا به اصطلاح" راه حل بیزی "از همان پارادوکس". رویکردهای بیزی که از نظریه استنباط استقرایی کارناپ استفاده می کنند عبارتند از هومبورگ ، [20] ماهر ، [7] و فیتلسون و هاثورن. [9] وراناس [21] اصطلاح "راه حل استاندارد بیزی" را برای جلوگیری از سردرگمی معرفی کرد.
روش کارناپ [ ویرایش ]
ماهر [7] نتیجه متناقض را می پذیرد و آن را اصلاح می کند:
یک غیر زاغ (با هر رنگی) تأیید می کند که همه کلاغ ها سیاه هستند زیرا
(i) اطلاعاتی که این شیء زاغ نیست این احتمال را حذف می کند که این شیء یک مثال کلی برای تعمیم باشد و
(II) این احتمال را که اجسام مشاهده نشده زاغ باشند ، کاهش می دهد ، در نتیجه احتمال اینکه آنها به عنوان مثال های متضاد برای تعمیم باشند ، کاهش می یابد.
برای رسیدن به (ii) ، او به نظریه احتمال استقرایی کارناپ متوسل می شود ، که (از دیدگاه بیزی) راهی برای تعیین احتمالات قبلی است که به طور طبیعی استقرا را اجرا می کند. طبق نظریه کارناپ ، احتمال خلفی ، ، آن شی ،
، آن شی ،  ، دارای محمول خواهد بود ،
، دارای محمول خواهد بود ،  ، پس از شواهد
، پس از شواهد  مشاهده شده است ، عبارت است از:
مشاهده شده است ، عبارت است از:

جایی که  احتمال اولیه آن است که
احتمال اولیه آن است که  دارای محمول است
دارای محمول است  ؛
؛  تعداد اجسامی است که مورد بررسی قرار گرفته اند (طبق شواهد موجود
تعداد اجسامی است که مورد بررسی قرار گرفته اند (طبق شواهد موجود  )؛
)؛  تعداد اشیاء مورد بررسی است که معلوم شد دارای محمول هستند
تعداد اشیاء مورد بررسی است که معلوم شد دارای محمول هستند ، و
، و  ثابت است که مقاومت در برابر تعمیم را اندازه گیری می کند.
ثابت است که مقاومت در برابر تعمیم را اندازه گیری می کند.
اگر نزدیک به صفر است ،
نزدیک به صفر است ،  پس از مشاهده یک شیء که مشخص شد محمول است بسیار نزدیک به یک خواهد بود
پس از مشاهده یک شیء که مشخص شد محمول است بسیار نزدیک به یک خواهد بود  ، در حالی که اگر
، در حالی که اگر  بسیار بزرگتر از
بسیار بزرگتر از  ،
،  بسیار نزدیک خواهد بود
بسیار نزدیک خواهد بود  صرف نظر از کسری از اجسام مشاهده شده که دارای محمول بودند
صرف نظر از کسری از اجسام مشاهده شده که دارای محمول بودند  به با استفاده از این رویکرد Carnapian ، ماهر گزاره ای را که ما به طور شهودی (و درست) می دانیم اشتباه است ، اما به راحتی با نتیجه متناقض اشتباه می گیرد ، مشخص می کند. گزاره مورد بحث این است که مشاهده غیر زاغ ها به ما رنگ کلاغ ها را می گوید. در حالی که این به طور شهودی نادرست است و همچنین بر اساس نظریه القایی Carnap نادرست است ، مشاهده غیر زاغ ها (طبق همان نظریه) باعث می شود که ما تخمین خود را از تعداد کل زاغها کاهش دهیم ، و در نتیجه تعداد تخمینی نمونه های احتمالی را به این قانون که همه زاغ ها سیاه هستند.
به با استفاده از این رویکرد Carnapian ، ماهر گزاره ای را که ما به طور شهودی (و درست) می دانیم اشتباه است ، اما به راحتی با نتیجه متناقض اشتباه می گیرد ، مشخص می کند. گزاره مورد بحث این است که مشاهده غیر زاغ ها به ما رنگ کلاغ ها را می گوید. در حالی که این به طور شهودی نادرست است و همچنین بر اساس نظریه القایی Carnap نادرست است ، مشاهده غیر زاغ ها (طبق همان نظریه) باعث می شود که ما تخمین خود را از تعداد کل زاغها کاهش دهیم ، و در نتیجه تعداد تخمینی نمونه های احتمالی را به این قانون که همه زاغ ها سیاه هستند.
از این رو ، از دیدگاه بیزی-کارناپی ، مشاهده غیر زاغ چیزی در مورد رنگ زاغ به ما نمی گوید ، اما در مورد شیوع زاغ ها به ما می گوید و با کاهش "همه زاغ ها سیاه هستند" پشتیبانی می کند. برآورد تعداد زاغ هایی که ممکن است سیاه نباشند.
نقش دانش پیشینه [ ویرایش ]
بیشتر بحث پارادوکس به طور کلی و رویکرد بیزی به طور خاص بر ارتباط دانش پیشینه متمرکز شده است. به طرز شگفت انگیزی ، ماهر [7] نشان می دهد که برای یک دسته بزرگ از پیکربندی های احتمالی دانش پیش زمینه ، مشاهده یک غیر زاغ سیاه نادر دقیقاً به همان میزان تأیید مشاهده یک زاغ سیاه است. پیکربندی دانش پیش زمینه ای که او در نظر می گیرد ، مواردی است که توسط یک مثال نمونه ارائه شده است ، یعنی گزاره ای که یک رابطه استاز گزاره های اتمی ، که هر کدام یک محمول واحد را به یک فرد واحد نسبت می دهند ، بدون این که دو گزاره اتمی شامل یک فرد باشند. بنابراین ، گزاره ای از شکل "A یک کلاغ سیاه است و B یک کفش سفید است" را می توان با درنظر گرفتن "کلاغ سیاه" و "کفش سفید" به عنوان نمونه پیشنهادی در نظر گرفت.
به نظر می رسد که اثبات ماهر با نتیجه استدلال بیزی در تضاد است ، این بود که مشاهده یک سیاه زاغ غیر سیاه ، شواهد بسیار کمتری نسبت به مشاهده یک زاغ سیاه دارد. دلیل آن این است که دانش پیشین که Good و دیگران استفاده می کنند نمی تواند در قالب یک مثال پیشنهادی بیان شود - به ویژه ، انواع روش استاندارد بیزی اغلب تصور می کنند (همانطور که Good در استدلال ذکر شده در بالا انجام داد) که تعداد کل کلاغها ، اجسام غیر سیاه و/یا تعداد کل اجسام ، مقادیر مشخصی هستند. ماهر اظهار می دارد ، "دلیل این که ما فکر می کنیم چیزهای غیرسیاهی بیشتر از زاغ ها وجود دارد این است که در مورد مواردی که تا به امروز مشاهده کرده ایم صادق بوده است. شواهدی از این دست را می توان با یک مثال نمونه نشان داد. اما ... هر نمونه پیشنهادی به عنوان شواهد زمینه ای ،
فیتلسون و هاوثورن [9] شرایطی را بررسی کردند که تحت آن مشاهده یک غیر زاغ سیاه رنگ شواهد کمتری نسبت به مشاهده یک زاغ سیاه نشان می دهد. آنها نشان می دهند که اگر یک شیء است که به طور تصادفی انتخاب شده است ،
یک شیء است که به طور تصادفی انتخاب شده است ،  این گزاره است که شیء سیاه است و
این گزاره است که شیء سیاه است و  این گزاره است که شیء یک زاغ است ، پس شرط:
این گزاره است که شیء یک زاغ است ، پس شرط:

برای مشاهده یک زاغ غیر سیاه سیاه شواهد کمتری نسبت به مشاهده یک زاغ سیاه وجود دارد. در اینجا ، خطی بر گزاره ، نفی منطقی آن گزاره را نشان می دهد.
این شرط به ما نمی گوید تفاوت بین شواهد ارائه شده چقدر زیاد است ، اما محاسبه بعدی در همان مقاله نشان می دهد که وزن شواهد ارائه شده توسط یک کلاغ سیاه بیشتر از چیزی است که توسط یک سیاه زاغ غیرسیاه ارائه شده است. به این مقدار برابر است با مقدار اطلاعات اضافی (در بیت ، اگر پایه لگاریتم 2 باشد) که با توجه به این فرضیه که همه زاغ ها سیاه نیستند ، هنگامی که یک زاغ با رنگ ناشناخته سیاه تشخیص داده می شود ، ارائه می شود.
به این مقدار برابر است با مقدار اطلاعات اضافی (در بیت ، اگر پایه لگاریتم 2 باشد) که با توجه به این فرضیه که همه زاغ ها سیاه نیستند ، هنگامی که یک زاغ با رنگ ناشناخته سیاه تشخیص داده می شود ، ارائه می شود.
فیتلسون و هاثورن [9] توضیح می دهند که:
تحت شرایط عادی،  ممکن است جایی در حدود 0.9 یا 0.95 باشد. بنابراین
ممکن است جایی در حدود 0.9 یا 0.95 باشد. بنابراین جایی در حدود 1.11 یا 1.05 است. بنابراین ، ممکن است به نظر برسد که یک نمونه واحد از یک کلاغ سیاه از حمایت بیشتر از یک زاغ غیر سیاه جلوگیری نمی کند. با این حال ، در شرایط قابل قبول می توان نشان داد که دنباله ای از
جایی در حدود 1.11 یا 1.05 است. بنابراین ، ممکن است به نظر برسد که یک نمونه واحد از یک کلاغ سیاه از حمایت بیشتر از یک زاغ غیر سیاه جلوگیری نمی کند. با این حال ، در شرایط قابل قبول می توان نشان داد که دنباله ای از موارد (یعنی n کلاغ سیاه ، در مقایسه با n غیر کلاغ غیر سیاه) نسبت نسبت های احتمال را به ترتیب
موارد (یعنی n کلاغ سیاه ، در مقایسه با n غیر کلاغ غیر سیاه) نسبت نسبت های احتمال را به ترتیب  ، که به طور قابل توجهی برای بزرگ منفجر می شود
، که به طور قابل توجهی برای بزرگ منفجر می شود  به
به
نویسندگان خاطرنشان می کنند که تجزیه و تحلیل آنها کاملاً با این فرض مطابقت دارد که یک زاغ غیر سیاه سیاه مقدار بسیار کمی شواهد ارائه می دهد ، اگرچه آنها سعی در اثبات آن ندارند. آنها فقط تفاوت بین میزان شواهدی که یک کلاغ سیاه ارائه می دهد و میزان شواهدی که یک زاغ غیر سیاه سیاه ارائه می دهد را محاسبه می کنند.
رد بحث استقرا از موارد مثبت [ ویرایش ]
برخی از رویکردها برای حل پارادوکس بر مرحله استقرایی تمرکز می کنند. آنها اختلاف دارند که آیا مشاهده یک نمونه خاص (مانند یک زاغ سیاه) شواهدی است که لزوماً اعتماد به فرضیه کلی را افزایش می دهد (مانند اینکه کلاغ ها همیشه سیاه هستند).
شاه ماهی قرمز [ ویرایش ]
خوب [22] نمونه ای از دانش پیش زمینه را ارائه می دهد که در آن مشاهده یک کلاغ سیاه احتمال سیاه بودن همه زاغ ها را کاهش می دهد:
فرض کنید ما می دانیم که در یکی از دو جهان هستیم ، و فرضیه ، H ، در نظر گرفته شده این است که تمام زاغهای جهان ما سیاه هستند. ما از قبل می دانیم که در یک جهان صد زاغ سیاه وجود دارد ، هیچ کلاغی سیاه و یک میلیون پرنده دیگر وجود ندارد. و اینکه در جهان دیگر هزار کلاغ سیاه ، یک کلاغ سفید و یک میلیون پرنده دیگر وجود دارد. یک پرنده به طور مساوی به طور تصادفی از بین همه پرندگان جهان ما انتخاب شده است. معلوم می شود یک زاغ سیاه است. این شواهد محکمی است ... ما در جهان دوم هستیم ، جایی که همه کلاغها سیاه نیستند.
گود نتیجه می گیرد که کفش سفید یک " شاه ماهی قرمز " است: گاهی اوقات حتی یک زاغ سیاه می تواند شواهدی بر خلاف این فرضیه که همه کلاغ ها سیاه هستند ، ارائه دهد ، بنابراین این واقعیت که مشاهده یک کفش سفید می تواند از آن حمایت کند ، تعجب آور نیست و ارزش توجه ندارد. به به گفته گود ، معیار نیکود نادرست است و بنابراین نتیجه متناقض به دنبال ندارد.
همپل این را به عنوان راه حلی برای تناقض نپذیرفت و اصرار داشت که گزاره "c یک زاغ است و سیاه است" باید "به تنهایی و بدون اشاره به اطلاعات دیگر" مورد توجه قرار گیرد و اشاره کرد که "... بخش 5.2 (ب) مقاله من در ذهن ... که ظاهر پارادوکسیکال در مواردی مانند کفش سفید تا حدی ناشی از عدم رعایت این حداکثر است. " [23]
س Theالی که مطرح می شود این است که آیا پارادوکس را باید در شرایطی که هیچ اطلاعات پیش زمینه ای وجود ندارد (همانطور که همپل نشان می دهد) ، یا در زمینه اطلاعات پیش زمینه ای که در مورد زاغها و اشیاء سیاه در اختیار داریم ، یا در مورد همه تنظیمات احتمالی اطلاعات پس زمینه
خوب نشان داده بود که برای برخی از تنظیمات دانش پیشین ، معیار نیکود نادرست است (به شرطی که ما مایل باشیم "حمایت استقرایی" را با "افزایش احتمال" برابر کنیم - به زیر مراجعه کنید). این احتمال وجود داشت که با توجه به پیکربندی واقعی دانش ما ، که بسیار متفاوت از مثال گود است ، معیار نیکود همچنان صادق باشد و بنابراین ما همچنان می توانیم به نتیجه متناقض برسیم. از طرف دیگر ، همپل تأکید می کند که دانش قبلی ما شاه ماهی قرمز است و ما باید القاء را با توجه به شرایط نادانی کامل در نظر بگیریم.
بچه خوب [ ویرایش ]
ماهر در قطعنامه پیشنهادی خود به طور ضمنی از این واقعیت استفاده کرده است که گزاره "همه زاغ ها سیاه هستند" بسیار محتمل است زمانی که به احتمال زیاد هیچ کلاغی وجود ندارد. گود قبلاً از این حقیقت برای پاسخ به اصرار همپل استفاده کرده بود که معیار نیکود را باید در غیاب اطلاعات پیشین درک کرد: [24]
... تصور کنید یک نوزاد تازه متولد شده باهوش دارای مدارهای عصبی داخلی است که او را قادر می سازد با منطق رسمی ، نحو انگلیسی و احتمال ذهنی برخورد کند. او ممکن است پس از تعریف دقیق یک زاغ استدلال کند که احتمال وجود کلاغ وجود ندارد و بنابراین بسیار محتمل است که همه زاغ ها سیاه باشند ، یعنی درست است. وی در ادامه می گوید: "از طرف دیگر ، اگر کلاغ وجود داشته باشد ، احتمال اینکه رنگ آنها متنوع باشد وجود دارد. بنابراین ، اگر بخواهم کشف کنم که حتی یک زاغ سیاه نیز وجود دارد ، به آن فکر می کنم
درست است. وی در ادامه می گوید: "از طرف دیگر ، اگر کلاغ وجود داشته باشد ، احتمال اینکه رنگ آنها متنوع باشد وجود دارد. بنابراین ، اگر بخواهم کشف کنم که حتی یک زاغ سیاه نیز وجود دارد ، به آن فکر می کنم احتمال آن کمتر از ابتدا باشد. '
احتمال آن کمتر از ابتدا باشد. '
به گفته گود ، این امر به همان اندازه نزدیک است که می توان انتظار داشت به شرایط جهل کامل برسیم ، و به نظر می رسد که شرایط نیکود هنوز نادرست است. ماهر استدلال گود را با استفاده از نظریه القایی کارناپ برای رسمی شدن این تصور که اگر یک زاغ وجود داشته باشد ، به احتمال زیاد تعداد زیادی وجود دارد ، دقیق تر کرد. [25]
استدلال ماهر یک جهان دقیقاً از دو شیء را در نظر می گیرد ، که هر یک بسیار زاغ نیست (یک در هزار شانس) و به طور منطقی بعید است که سیاه باشد (یک از ده شانس). با استفاده از فرمول Carnap برای استقراء ، او متوجه می شود که احتمال سیاه بودن همه کلاغها از 0.9985 به 0.8995 کاهش می یابد هنگامی که مشخص می شود یکی از دو شیء یک کلاغ سیاه است.
ماهر نتیجه می گیرد که نه تنها نتیجه گیری متناقض درست است ، بلکه معیار نیکود در غیاب دانش پیشین نادرست است (به جز این که تعداد اجسام جهان دو است و احتمال زاغها کمتر از چیزهای سیاه است).
محمولات ممتاز [ ویرایش ]
کواین [26] استدلال کرد که راه حل پارادوکس در تشخیص این است که برخی از محمولات ، که او آنها را انواع طبیعی نامید ، از نظر استقراء دارای موقعیت ممتازی هستند. این را می توان با مثال نلسون گودمن از گرای محمول نشان دادبه اگر یک شیء قبل از (به عنوان مثال) 2021 آبی باشد و بعد از آن سبز باشد ، گره است. واضح است که ما انتظار داریم اجسامی که قبل از سال 2021 آبی بودند بعد از آن آبی باقی بمانند ، اما ما انتظار نداریم که اجسامی که قبل از سال 2021 به شکل خاکستری در آمده بودند بعد از 2021 آبی باشند ، زیرا پس از سال 2021 آنها سبز خواهند بود. توضیح کواین این است که "آبی" نوعی طبیعی است. یک محمول ممتاز که می توانیم برای استقراء از آن استفاده کنیم ، در حالی که "grue" یک نوع طبیعی نیست و استفاده از استقرا با آن منجر به خطا می شود.
این نشان می دهد که می توان پارادوکس را حل کرد-معیار نیکود برای انواع طبیعی مانند "آبی" و "سیاه" صادق است ، اما برای محمولات مصنوعی مصنوعی ، مانند "گرو" یا "غیر زاغ" نادرست است. بر اساس این قطعنامه ، پارادوکس بوجود می آید ، زیرا ما به طور ضمنی معیار نیکود را در مورد همه محمولات در حالی که در واقع فقط برای انواع طبیعی صدق می کند تفسیر می کنیم.
رویکرد دیگر ، که بر محمولات خاص نسبت به سایرین دلخواه است ، توسط هینتیکا اتخاذ شد. [19] هینتیکا با انگیزه یافتن رویکرد بیزی در مورد پارادوکس که از دانش در مورد فراوانی نسبی زاغها و چیزهای سیاه استفاده نمی کند ، استفاده کرد . به گفته وی ، استدلال های مربوط به فرکانس های نسبی همیشه نمی تواند بی ربطی شواهد متشکل از مشاهدات اجسام نوع A را به منظور آشنایی با اشیاء از نوع A نشان دهد.
استدلال او را می توان با بازنویسی پارادوکس با استفاده از محمولاتی غیر از "زاغ" و "سیاه" نشان داد. به عنوان مثال ، "همه مردان قد بلند هستند" معادل "همه افراد کوتاه قد زن هستند" ، و بنابراین مشاهده این که یک فرد تصادفی انتخاب شده یک زن کوتاه قد است ، باید شواهدی مبنی بر قد بلند همه مردان ارائه دهد. علیرغم این واقعیت که ما دانش قبلی نداریم تا نشان دهیم تعداد مردان به طور چشمگیری کمتر از افراد کوتاه قد است ، ما همچنان خود را متمایل به رد این نتیجه می دانیم. مثال هینتیکا این است: "... به نظر می رسد یک تعمیم مانند" هیچ اجسام مادی بی نهایت بخش پذیر نیستند "، بدون توجه به آنچه در مورد فرکانس های نسبی موجودات مادی و غیر مادی در جهان گفتمان خود تصور می کند ، کاملاً تحت تأثیر سوالات مربوط به موجودات غیر مادی قرار نمی گیرد. "
راه حل او این است که نظمی را در مجموعه محمولات وارد کند. هنگامی که سیستم منطقی مجهز به این نظم است ، می توان دامنه یک تعمیم مانند "همه زاغ ها سیاه هستند" را محدود کرد تا فقط برای زاغ ها اعمال شود و نه برای چیزهای غیر سیاه ، زیرا امتیازات نظم بر زاغ ها بر غیر -چیزهای سیاه به قول خودش:
"اگر ما فرض کنیم که محدودیت کلی" همه کلاغها سیاه هستند "را می توان به کلاغها محدود کرد ، این بدان معناست که ما اطلاعات خارجی داریم که می توانیم در مورد وضعیت واقعی به آنها اعتماد کنیم. پارادوکس از این واقعیت ناشی می شود این اطلاعات ، که دیدگاه خودجوش ما را نسبت به وضعیت رنگ آمیزی می کند ، در درمان معمول موقعیت استقرایی گنجانده نشده است. " [19]
رد شرایط معادل سازی همپل [ ویرایش ]
برخی از رویکردها برای حل پارادوکس شرط هم ارز بودن همپل را رد می کنند. به این معنا که آنها ممکن است شواهدی مبنی بر این که همه اشیاء غیر سیاه سیاه زاغ نیستند ، در نظر نگیرند تا لزوماً از عبارات معادل منطقی مانند همه زاغ ها سیاه باشند .
تأیید انتخابی [ ویرایش ]
شفلر و گودمن [27] رویکردی را در مورد پارادوکسی که شامل نظر کارل پوپر مبنی بر این است که فرضیه های علمی هرگز به طور واقعی تأیید نمی شوند ، بلکه فقط جعلی هستند ، در پیش گرفتند.
این رویکرد با ذکر این نکته آغاز می شود که مشاهده یک کلاغ سیاه ثابت نمی کند که "همه کلاغ ها سیاه هستند" ، اما فرضیه مخالف "هیچ کلاغی سیاه نیست" را جعل می کند. از سوی دیگر ، یک غیر کلاغ غیر سیاه ، هم با "همه کلاغ ها سیاه هستند" و هم با "بدون کلاغ سیاه نیست" سازگار است. به قول نویسندگان:
... بیانیه ای که همه کلاغ های سیاه و سفید است نه تنها راضی شده توسط شواهدی از یک کلاغ سیاه سیاه و سفید است اما علاقه به چنین شواهد، از disconfirms کلاغ سیاه سیاه بیانیه خلاف که همه کلاغ سیاه و سفید نیست، یعنی ارضا انکار آن است. به بیان دیگر ، یک کلاغ سیاه این فرضیه را تأیید می کند که همه زاغ ها سیاه هستند نه این که: به این ترتیب به طور انتخابی تایید می شود که همه کلاغ ها سیاه هستند .
تأیید انتخابی شرط معادل سازی را نقض می کند زیرا یک کلاغ سیاه به طور انتخابی تأیید می کند "همه زاغ ها سیاه هستند" اما نه "همه چیزهای غیر سیاه" غیر کلاغ هستند ".
القای احتمالی یا غیر احتمالی [ ویرایش ]
مفهوم تأیید انتخابی شفلر و گودمن نمونه ای از تفسیر "ارائه شواهد به نفع ..." است که با "افزایش احتمال ..." مطابقت ندارد. این باید ویژگی کلی همه قطعنامه هایی باشد که شرط معادل سازی ، زیرا گزاره های معادل منطقی باید همیشه احتمال یکسانی داشته باشند.
مشاهده یک زاغ سیاه نمی تواند احتمال گزاره "همه زاغ ها سیاه هستند" را افزایش دهد بدون این که دقیقاً همان تغییری را در احتمال "همه چیزهای غیر سیاه" زاغ نداشته باشند "ایجاد کند. اگر یک مشاهده به طور استقرایی از اولی پشتیبانی می کند اما دومی را پشتیبانی نمی کند ، پس "پشتیبانی استقرایی" باید به چیزی غیر از تغییرات احتمالات گزاره ها اشاره کند. یک خلأ احتمالی این است که "همه" را به عنوان "تقریباً همه" تفسیر کنیم-"تقریباً همه زاغ ها سیاه هستند" معادل "تقریباً همه چیزهای غیر سیاه غیر زاغ نیستند" ، و این گزاره ها می توانند احتمالات بسیار متفاوتی داشته باشند. [28]
این س questionال گسترده تری از رابطه نظریه احتمال با استدلال استقرایی ایجاد می کند. کارل پوپر استدلال کرد که نظریه احتمال به تنهایی نمی تواند القاء را در نظر بگیرد. بحث او شامل تقسیم یک فرضیه است ، ، به قسمتی که با شواهد به صورت قیاسی استناد می شود ،
، به قسمتی که با شواهد به صورت قیاسی استناد می شود ،  ، و بخش دیگری این میتواند با دو راه انجام شود.
، و بخش دیگری این میتواند با دو راه انجام شود.
ابتدا ، تقسیم بندی را در نظر بگیرید: [29]

جایی که  ،
،  و
و  احتمالاً مستقل هستند:
احتمالاً مستقل هستند:  و غیره شرطی که برای امکان چنین شکاف H و E ضروری است این است
و غیره شرطی که برای امکان چنین شکاف H و E ضروری است این است ، یعنی آن
، یعنی آن به احتمال زیاد توسط پشتیبانی می شود
به احتمال زیاد توسط پشتیبانی می شود  به
به
مشاهده پوپر این است که بخشی ،  ، از
، از  که از طرف پشتیبانی دریافت می کند
که از طرف پشتیبانی دریافت می کند  در واقع به صورت قیاسی از
در واقع به صورت قیاسی از  ، در حالی که بخشی از
، در حالی که بخشی از  که به صورت قیاسی از آن پیروی نمی کند
که به صورت قیاسی از آن پیروی نمی کند  هیچ حمایتی از طرف دریافت نمی کند
هیچ حمایتی از طرف دریافت نمی کند  - به این معنا که،
- به این معنا که،  به
به
دوم ، تقسیم: [30]

جدا می کند  به
به  ، که همانطور که پوپر می گوید ، "منطقاً قوی ترین بخش آن است
، که همانطور که پوپر می گوید ، "منطقاً قوی ترین بخش آن است  (یا از محتوای
(یا از محتوای  ) که از [قیاسی] ناشی می شود
) که از [قیاسی] ناشی می شود  "، و
"، و  ، که به گفته وی ، "شامل همه موارد است
، که به گفته وی ، "شامل همه موارد است  که فراتر می رود
که فراتر می رود  ". او ادامه می دهد:
". او ادامه می دهد:
میکند  ، در این مورد ، هر گونه پشتیبانی از عامل را ارائه دهید
، در این مورد ، هر گونه پشتیبانی از عامل را ارائه دهید  ، که در حضور
، که در حضور  برای بدست آوردن به تنهایی مورد نیاز است
برای بدست آوردن به تنهایی مورد نیاز است  ؟ پاسخ این است: نه. هرگز اینطور نیست. در واقع،
؟ پاسخ این است: نه. هرگز اینطور نیست. در واقع، پشتیبانی می کند
پشتیبانی می کند  مگر اینکه هیچ کدام
مگر اینکه هیچ کدام  یا
یا  (که امکاناتی هستند که مورد علاقه نیستند). ...
(که امکاناتی هستند که مورد علاقه نیستند). ...
این نتیجه برای تفسیر استقرایی حساب احتمال کاملاً مخرب است. همه پشتوانه های احتمالی صرفاً قیاسی هستند: آن قسمتی از فرضیه که به صورت قیاسی مستند به شواهد نمی شود ، همیشه با شواهد قویاً پشتیبانی می شود ... چیزی به نام پشتیبانی احتمالی وجود دارد. حتی ممکن است چیزی به عنوان حمایت استقرایی وجود داشته باشد (اگرچه ما به سختی چنین تصور می کنیم). اما محاسبه احتمال نشان می دهد که حمایت احتمالی نمی تواند پشتیبان استقرایی باشد.
منبع
https://en.wikipedia.org/wiki/Raven_paradox





 برای هر طرح خود الحاقی E در Q .
برای هر طرح خود الحاقی E در Q .





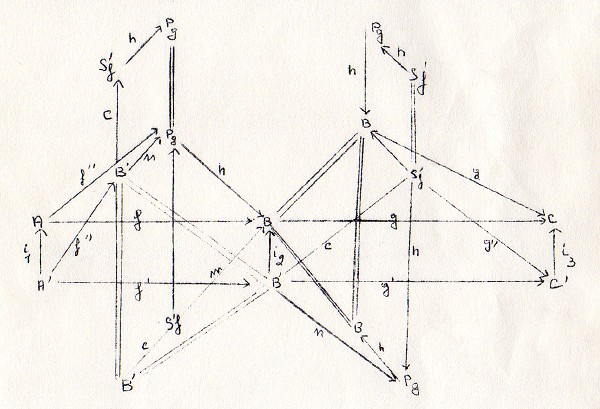
 در شکل بالا:
در شکل بالا: جایی که Nm 3 نشان دهنده درجه یا روابط مرد سوم و غیره است.
جایی که Nm 3 نشان دهنده درجه یا روابط مرد سوم و غیره است.
 و اکنون، می توانیم Nm / Nw را پیدا کنیم :
و اکنون، می توانیم Nm / Nw را پیدا کنیم :

















 بر هر دو
بر هر دو  و
و  ، اثبات به شرح زیر است:
، اثبات به شرح زیر است:








 برای نادرست وجود ندارد Y . این را می توان به عنوان نوعی
برای نادرست وجود ندارد Y . این را می توان به عنوان نوعی  باید تابع implication را با دو پارامتر یعنی عبارت lambda نشان دهد
باید تابع implication را با دو پارامتر یعنی عبارت lambda نشان دهد  باید معادل
باید معادل  به
به می توان با تعریف یک تابع lambda اثبات کرد
می توان با تعریف یک تابع lambda اثبات کرد  ، و
، و  ، جایی که
، جایی که نشان دهنده
نشان دهنده  با تعریف
با تعریف بنابراین ، منطق منطقی
بنابراین ، منطق منطقی 
 ترجمه می شود به
ترجمه می شود به  در منطق ترکیبی ، کجا
در منطق ترکیبی ، کجا


 که معادله را برآورده می کند
که معادله را برآورده می کند  ، اما در غیر این صورت نامعتبر است. این هسته اصلی مشکلی است که
، اما در غیر این صورت نامعتبر است. این هسته اصلی مشکلی است که 
 فقط می تواند نمایندگی کند
فقط می تواند نمایندگی کند  به با این حال ، هیچ راه مناسبی برای محدود کردن انتزاع lambda به یک مقدار یا اطمینان از وجود مقدار وجود ندارد.
به با این حال ، هیچ راه مناسبی برای محدود کردن انتزاع lambda به یک مقدار یا اطمینان از وجود مقدار وجود ندارد.
 در محدوده
در محدوده  به ترتیب
به ترتیب 


 به مقدارسنج جهانی
به مقدارسنج جهانی  ، که نمونه ای از تناقض است
، که نمونه ای از تناقض است  به از آنجا که این جمله برای آن مقدار خاص نادرست است ، کل عبارت جهانی نادرست است. از آنجا که بند وجودی با یک عملوند اشتباه همراه است ، کل جمله نادرست است. راه دیگر برای نشان دادن این امر نفی کل جمله و رسیدن به یک
به از آنجا که این جمله برای آن مقدار خاص نادرست است ، کل عبارت جهانی نادرست است. از آنجا که بند وجودی با یک عملوند اشتباه همراه است ، کل جمله نادرست است. راه دیگر برای نشان دادن این امر نفی کل جمله و رسیدن به یک 


 از همه P ها Q هستند ،
از همه P ها Q هستند ،  ، در حالی که آزمون "همه غیر Q" غیر P هستند "نیاز به ارجاع به برخی از گزینه های آماری فرم دارد
، در حالی که آزمون "همه غیر Q" غیر P هستند "نیاز به ارجاع به برخی از گزینه های آماری فرم دارد  بدون آزمایش داروی ضد آن
بدون آزمایش داروی ضد آن 


 سپس
سپس  " می توان معنی آن را درک کرد "
" می توان معنی آن را درک کرد " "
" ،
،  ، به معنی "نامعین" یا "نامناسب" وقتی
، به معنی "نامعین" یا "نامناسب" وقتی سپس
سپس  پس زاغ است
پس زاغ است 
 برای اجسام مختلف مستقل هستند
برای اجسام مختلف مستقل هستند  و غیره سپس تعداد تخمینی کلاغها 50 نفر است. تعداد تخمین زده شده از چیزهای سیاه 50 است. تعداد تخمین زده شده از کلاغهای سیاه 25 عدد و تعداد تخمین زده شده از زاغهای سیاهپوست (مثالهای فرضیات) 25 عدد است.
و غیره سپس تعداد تخمینی کلاغها 50 نفر است. تعداد تخمین زده شده از چیزهای سیاه 50 است. تعداد تخمین زده شده از کلاغهای سیاه 25 عدد و تعداد تخمین زده شده از زاغهای سیاهپوست (مثالهای فرضیات) 25 عدد است. : "همه کلاغها سیاه هستند" و
: "همه کلاغها سیاه هستند" و  : "همه چیزهای سیاه و سفید غیر روغنی هستند" به دلیل پیش فرض های وجودی متفاوت آنها کاملاً معادل نیستند . علاوه بر این ، اگرچه
: "همه چیزهای سیاه و سفید غیر روغنی هستند" به دلیل پیش فرض های وجودی متفاوت آنها کاملاً معادل نیستند . علاوه بر این ، اگرچه

 از دیده شدن اجازه دهید
از دیده شدن اجازه دهید فرضیه ای باشد که وجود دارد
فرضیه ای باشد که وجود دارد  کلاغهای سیاه پوست ، و فرض کنید که فرضیه ها
کلاغهای سیاه پوست ، و فرض کنید که فرضیه ها در ابتدا قابل تعادل هستند سپس ، اگر تصادفاً یک کلاغ سیاه ببینیم ، عامل بیز به نفع
در ابتدا قابل تعادل هستند سپس ، اگر تصادفاً یک کلاغ سیاه ببینیم ، عامل بیز به نفع است
است


 اگر
اگر  بزرگ است در مقایسه با
بزرگ است در مقایسه با  ، آن شی ،
، آن شی ،  ، پس از شواهد
، پس از شواهد  مشاهده شده است ، عبارت است از:
مشاهده شده است ، عبارت است از:
 احتمال اولیه آن است که
احتمال اولیه آن است که  تعداد اجسامی است که مورد بررسی قرار گرفته اند (طبق شواهد موجود
تعداد اجسامی است که مورد بررسی قرار گرفته اند (طبق شواهد موجود  تعداد اشیاء مورد بررسی است که معلوم شد دارای محمول هستند
تعداد اشیاء مورد بررسی است که معلوم شد دارای محمول هستند ثابت است که مقاومت در برابر تعمیم را اندازه گیری می کند.
ثابت است که مقاومت در برابر تعمیم را اندازه گیری می کند. این گزاره است که شیء سیاه است و
این گزاره است که شیء سیاه است و  این گزاره است که شیء یک زاغ است ، پس شرط:
این گزاره است که شیء یک زاغ است ، پس شرط:
 به این مقدار برابر است با مقدار اطلاعات اضافی (در بیت ، اگر پایه لگاریتم 2 باشد) که با توجه به این فرضیه که همه زاغ ها سیاه نیستند ، هنگامی که یک زاغ با رنگ ناشناخته سیاه تشخیص داده می شود ، ارائه می شود.
به این مقدار برابر است با مقدار اطلاعات اضافی (در بیت ، اگر پایه لگاریتم 2 باشد) که با توجه به این فرضیه که همه زاغ ها سیاه نیستند ، هنگامی که یک زاغ با رنگ ناشناخته سیاه تشخیص داده می شود ، ارائه می شود. ممکن است جایی در حدود 0.9 یا 0.95 باشد. بنابراین
ممکن است جایی در حدود 0.9 یا 0.95 باشد. بنابراین جایی در حدود 1.11 یا 1.05 است. بنابراین ، ممکن است به نظر برسد که یک نمونه واحد از یک کلاغ سیاه از حمایت بیشتر از یک زاغ غیر سیاه جلوگیری نمی کند. با این حال ، در شرایط قابل قبول می توان نشان داد که دنباله ای از
جایی در حدود 1.11 یا 1.05 است. بنابراین ، ممکن است به نظر برسد که یک نمونه واحد از یک کلاغ سیاه از حمایت بیشتر از یک زاغ غیر سیاه جلوگیری نمی کند. با این حال ، در شرایط قابل قبول می توان نشان داد که دنباله ای از ، که به طور قابل توجهی برای بزرگ منفجر می شود
، که به طور قابل توجهی برای بزرگ منفجر می شود 
 احتمالاً مستقل هستند:
احتمالاً مستقل هستند:  و غیره شرطی که برای امکان چنین شکاف H و E ضروری است این است
و غیره شرطی که برای امکان چنین شکاف H و E ضروری است این است ، یعنی آن
، یعنی آن به
به
 ، که همانطور که پوپر می گوید ، "منطقاً قوی ترین بخش آن است
، که همانطور که پوپر می گوید ، "منطقاً قوی ترین بخش آن است  ، که به گفته وی ، "شامل همه موارد است
، که به گفته وی ، "شامل همه موارد است  یا
یا  (که امکاناتی هستند که مورد علاقه نیستند). ...
(که امکاناتی هستند که مورد علاقه نیستند). ... درست است مگر اینکه
درست است مگر اینکه  درست است و
درست است و  دروغ است اگر شرطهای
دروغ است اگر شرطهای 



 از جانب
از جانب  ، برای هرچی
، برای هرچی ![\ وجود دارد x \ در P. \ [D (x) \ rightarrow \ forall y \ in P. \ D (y)]. \،](https://wikimedia.org/api/rest_v1/media/math/render/svg/75c1fa1b93071f47570b0dcd24706d0ea68577d8)
 درست است هرگاه A نادرست باشد ، یعنی هر گزاره ای از یک گزاره غلط
درست است هرگاه A نادرست باشد ، یعنی هر گزاره ای از یک گزاره غلط ![\ وجود دارد x \ در P. \ [D (x) \ rightarrow \ forall y \ in P. \ D (y)] \،](https://wikimedia.org/api/rest_v1/media/math/render/svg/db18168b2ba4e5820c506d949ff69bbf96d43806)






 در این وبلاگ به ریاضیات و کاربردهای آن و تحقیقات در آنها پرداخته می شود. مطالب در این وبلاگ ترجمه سطحی و اولیه است و کامل نیست.در صورتی سوال یا نظری در زمینه ریاضیات دارید مطرح نمایید .در صورت امکان به آن می پردازم. من دوست دارم برای یافتن پاسخ به سوالات و حل پروژه های علمی با دیگران همکاری نمایم.در صورتی که شما هم بامن هم عقیده هستید با من تماس بگیرید.
در این وبلاگ به ریاضیات و کاربردهای آن و تحقیقات در آنها پرداخته می شود. مطالب در این وبلاگ ترجمه سطحی و اولیه است و کامل نیست.در صورتی سوال یا نظری در زمینه ریاضیات دارید مطرح نمایید .در صورت امکان به آن می پردازم. من دوست دارم برای یافتن پاسخ به سوالات و حل پروژه های علمی با دیگران همکاری نمایم.در صورتی که شما هم بامن هم عقیده هستید با من تماس بگیرید.