ابزار
از ویکیپدیا، دانشنامه آزاد
| ترمودینامیک |
|---|
 موتور حرارتی کلاسیک کارنو |
| نشان می دهد شاخه ها |
| نشان می دهد |
| نشان می دهد |
| نشان می دهد |
| نشان می دهد |
| نشان می دهد |
| نشان می دهد |
نشان می دهد
|
| نشان می دهد دانشمندان |
| نشان می دهد دیگر |
چرخه کارنو یک چرخه ترمودینامیکی ایده آل است که توسط فیزیکدان فرانسوی سادی کارنو در سال 1824 پیشنهاد شد و توسط دیگران در دهه های 1830 و 1840 گسترش یافت. با قضیه کارنو ، حد بالایی را برای بازده هر موتور ترمودینامیکی کلاسیک در طول تبدیل گرما به کار ، یا برعکس، کارایی یک سیستم تبرید در ایجاد اختلاف دما از طریق اعمال کار بر روی سیستم، فراهم میکند.
در چرخه کارنو، یک سیستم یا موتور انرژی را به شکل گرما بین دو مخزن حرارتی در دماها منتقل می کند.





| ویدیوهای خارجی | |
|---|---|
مراحل [ ویرایش ]
چرخه کارنو به عنوان یک چرخه ترمودینامیکی ایده آل که توسط موتور حرارتی کارنو انجام می شود ، شامل مراحل زیر است:
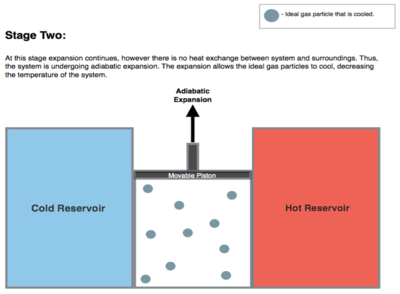
انبساط همدما . گرما (به عنوان یک انرژی) به طور برگشت پذیر از مخزن دمای داغ در دمای ثابت TH به گاز در دمای بینهایت کمتر از TH منتقل می شود (تا امکان انتقال گرما به گاز بدون تغییر عملاً دمای گاز بنابراین اضافه یا جذب گرمای همدما فراهم شود ). در طی این مرحله (1 تا 2 در شکل 1 ، A تا B در شکل 2 )، گاز از نظر حرارتی با مخزن دمای داغ در تماس است (در حالی که از نظر حرارتی از مخزن دمای سرد جدا شده است) و گاز اجازه انبساط داده و کار را انجام می دهد. روی محیط اطراف با فشار دادن گاز پیستون به سمت بالا (شکل مرحله 1، سمت راست). اگرچه فشار از نقاط 1 تا 2 کاهش می یابد (شکل 1) دمای گاز در طول فرآیند تغییر نمی کند زیرا گرمای منتقل شده از مخزن دمای داغ به گاز دقیقاً برای انجام کار بر روی محیط اطراف توسط گاز استفاده می شود. بدون تغییر انرژی داخلی گاز (بدون تغییر دمای گاز برای یک گاز ایده آل). گرمای QH > 0 از مخزن دمای داغ جذب می شود و در نتیجه آنتروپی افزایش می یابد .
گاز بر حسب مقدار
.
انبساط ایزنتروپیک ( آدیاباتیک برگشت پذیر ) گاز (خروجی کار ایسنتروپیک). برای این مرحله (2 تا 3 در شکل 1 ، B تا C در شکل 2 ) گاز موتور از نظر حرارتی از مخازن سرد و گرم عایق می شود، بنابراین آنها نه گرما را دریافت می کنند و نه از دست می دهند، یک فرآیند " آدیاباتیک ". گاز با کاهش فشار خود به انبساط ادامه می دهد، کار روی محیط اطراف انجام می دهد (بالا بردن پیستون؛ مرحله 2 شکل، سمت راست)، و مقداری از انرژی داخلی را از دست می دهد که برابر با کار انجام شده است. انبساط گاز بدون ورودی گرما باعث سرد شدن گاز به دمای "سرد" می شود (با از دست دادن انرژی داخلی خود) که بی نهایت بالاتر از دمای مخزن سرد T C است . آنتروپی بدون تغییر باقی میماند زیرا هیچ گرمایی Q بین سیستم (گاز) و محیط اطراف آن منتقل نمیشود، بنابراین یک فرآیند ایزنتروپیک، به معنی عدم تغییر آنتروپی در فرآیند).
فشرده سازی ایزوترمال. گرما به طور برگشت پذیر به مخزن دمای پایین در دمای ثابت T C (دفع حرارت همدما) منتقل می شود. در این مرحله (3 تا 4 در شکل 1 ، C تا D در شکل 2 )، گاز موتور در تماس حرارتی با مخزن سرد در دمای T C (در حالی که از نظر حرارتی از مخزن دمای داغ جدا شده است) و دمای گاز است. بی نهایت بالاتر از این دما است (برای انتقال حرارت از گاز به مخزن سرد بدون تغییر عملا دمای گاز). محیط اطراف روی گاز کار می کند و پیستون را به پایین فشار می دهد (شکل مرحله 3، سمت راست). مقداری از انرژی که توسط گاز حاصل از این کار به دست میآید دقیقاً به عنوان انرژی گرمایی QC < 0 (منفی خروج از سیستم، طبق قرارداد جهانی در ترمودینامیک) به مخزن سرد منتقل میشود ، بنابراین آنتروپی سیستم کاهش مییابد. میزان
. [1]
زیرا فشردگی همدما باعث کاهش تعدد گاز می شود.
فشرده سازی ایزنتروپیک. (4 به 1 در شکل 1 ، D تا A در شکل 2 ) یک بار دیگر گاز موجود در موتور از مخازن سرد و گرم عایق حرارتی می شود، و موتور بدون اصطکاک فرض می شود و فرآیند به اندازه کافی کند است، بنابراین برگشت پذیر است. در طی این مرحله، محیط اطراف روی گاز کار می کند، پیستون را بیشتر به سمت پایین فشار می دهد (مرحله 4 شکل، سمت راست)، انرژی داخلی آن را افزایش می دهد، آن را فشرده می کند و باعث می شود که دمای آن به دمای بی نهایت کمتر از TH برگردد . به کار اضافه شده به سیستم، اما آنتروپی بدون تغییر باقی می ماند. در این مرحله گاز در همان حالت ابتدای مرحله 1 قرار دارد.
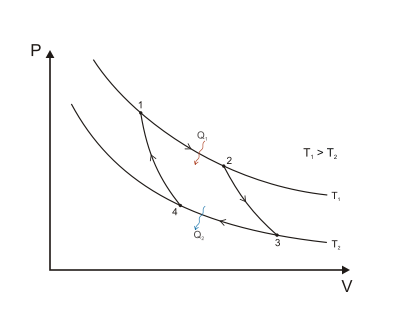
شکل 1 : چرخه کارنو که بر روی یک نمودار PV برای نشان دادن کار انجام شده نشان داده شده است. 1-به-2 (انبساط همدما)، 2-به-3 (انبساط ایسنتروپیک)، 3-به-4 (فشرده سازی همدما)، 4-به-1 (فشرده سازی ایسنتروپیک).
در این حالت، از آنجایی که یک چرخه ترمودینامیکی برگشت پذیر است (بدون تغییر خالص در سیستم و محیط اطراف آن در هر سیکل) [2] [1]

این درست است به عنوان


نمودار فشار-حجم [ ویرایش ]
هنگامی که یک چرخه کارنو بر روی نمودار فشار-حجم ترسیم می شود ( شکل 1 )، مراحل همدما از خطوط همدما برای سیال عامل پیروی می کنند، مراحل آدیاباتیک بین ایزوترم ها حرکت می کنند و ناحیه محدود شده توسط مسیر چرخه کامل، کل کار را نشان می دهد. را می توان در یک چرخه انجام داد. از نقطه 1 تا 2 و نقطه 3 تا 4 دما ثابت است (فرایند همدما). انتقال حرارت از نقطه 4 به 1 و نقطه 2 به 3 برابر با صفر است (فرایند آدیاباتیک).
خواص و اهمیت [ ویرایش ]
نمودار دما – آنتروپی [ ویرایش ]
مقاله اصلی: نمودار دما – آنتروپی
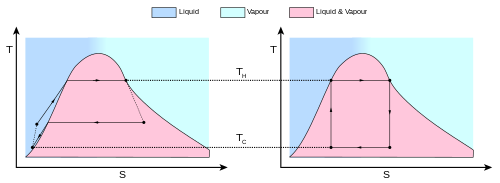
شکل 2 : یک چرخه کارنو به عنوان یک چرخه ترمودینامیکی ایده آل که توسط یک موتور حرارتی کارنو انجام می شود ، که بر روی نمودار TS (دما آنتروپی T-S) نشان داده شده است. چرخه بین یک مخزن گرم در دمای T H و یک مخزن سرد در دمای T C انجام می شود . محور عمودی دمای سیستم و محور افقی آنتروپی سیستم است. A-to-B (انبساط همدما)، B-to-C (انبساط ایسنتروپیک)، C-to-D (فشرده سازی همدما)، D-to-A (فشرده سازی ایسنتروپیک).
شکل 3 : یک چرخه ترمودینامیکی تعمیم یافته که بین یک مخزن داغ در دمای TH و یک مخزن سرد در دمای TC انجام می شود . طبق قانون دوم ترمودینامیک ، چرخه نمی تواند در خارج از باند دما از TC تا TH گسترش یابد . منطقه به رنگ قرمز، | Q C |، مقدار انرژی مبادله شده بین سیستم و مخزن سرد است. مساحت سفید W مقدار انرژی کاری است که سیستم با محیط اطرافش مبادله می کند. مقدار حرارت مبادله شده با مخزن داغ مجموع این دو است. اگر سیستم مانند یک موتور رفتار کند، فرآیند در جهت عقربههای ساعت در اطراف حلقه حرکت میکند و اگر مانند یک یخچال رفتار کند در خلاف جهت عقربههای ساعت حرکت میکند. بازده به چرخه، نسبت ناحیه سفید (کار) تقسیم بر مجموع نواحی سفید و قرمز (گرمای جذب شده از مخزن داغ) است. Q C (انرژی از دست رفته به مخزن سرد) را می توان به عنوان یک تفریق مستقیم یا به صورت مجموع یک کمیت منفی بیان کرد که می تواند به قراردادهای مختلفی منجر شود.
رفتار موتور یا یخچال کارنو با استفاده از نمودار دما- آنتروپی ( نمودار T - S ) که در آن حالت ترمودینامیکی با نقطه ای از نمودار با آنتروپی ( S ) به عنوان محور افقی و دما مشخص می شود، بهتر درک می شود. T ) به عنوان محور عمودی ( شکل 2 ). برای یک سیستم بسته ساده (تجزیه و تحلیل جرم کنترل)، هر نقطه در نمودار نشان دهنده وضعیت خاصی از سیستم است. یک فرآیند ترمودینامیکی با یک منحنی نشان داده می شود که حالت اولیه (A) و حالت نهایی (B) را به هم متصل می کند. مساحت زیر منحنی عبارت است از:
| ( 1 ) |
که مقدار گرمای منتقل شده در فرآیند است. اگر فرآیند سیستم را به سمت آنتروپی بیشتر سوق دهد، سطح زیر منحنی مقدار گرمای جذب شده توسط سیستم در آن فرآیند است. در غیر این صورت، مقدار گرمایی است که از سیستم خارج می شود یا از آن خارج می شود. برای هر فرآیند چرخه ای، یک بخش بالایی از چرخه و یک بخش پایین تر وجود دارد. در نمودارهای T - S برای یک چرخه جهت عقربه های ساعت، ناحیه زیر قسمت بالایی انرژی جذب شده توسط سیستم در طول چرخه خواهد بود، در حالی که ناحیه زیر قسمت پایین انرژی حذف شده از سیستم در طول چرخه خواهد بود. سپس مساحت داخل چرخه تفاوت بین این دو (انرژی گرمای خالص جذب شده) است، اما از آنجایی که انرژی داخلی سیستم باید به مقدار اولیه خود بازگشته باشد، این تفاوت باید مقدار کار انجام شده توسط سیستم در هر چرخه باشد. . با مراجعه به شکل 1 ، از نظر ریاضی، برای یک فرآیند برگشت پذیر، ممکن است مقدار کار انجام شده در یک فرآیند چرخه ای را به صورت زیر بنویسیم:
| ( 2 ) |
از آنجایی که dU یک دیفرانسیل دقیق است ، انتگرال آن بر روی هر حلقه بسته صفر است و نتیجه آن این است که سطح داخل حلقه در نمودار T - S برابر است با کل کار انجام شده توسط سیستم بر روی محیط اطراف اگر حلقه باشد. در جهت عقربههای ساعت پیمایش میشود، و (ب) برابر است با کل کار انجام شده بر روی سیستم توسط محیط اطراف هنگامی که حلقه در جهت خلاف جهت عقربههای ساعت پیمایش میشود.
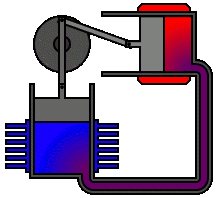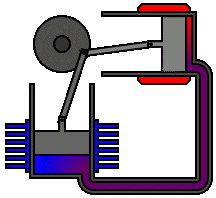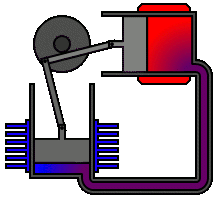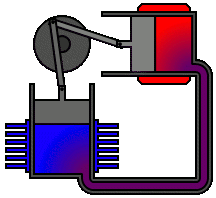
شکل 4 : چرخه کارنو که بین یک مخزن گرم در دمای TH و یک مخزن سرد در دمای TC انجام می شود .
چرخه کارنو [ ویرایش ]
شکل 5 : تجسم یک چرخه کارنو
ارزیابی انتگرال فوق به ویژه برای یک چرخه کارنو ساده است. مقدار انرژی منتقل شده به عنوان کار است
مقدار کل گرمای منتقل شده از مخزن گرم به سیستم (در انبساط همدما) خواهد بود.

به دلیل حفظ انرژی، گرمای خالص منتقل شده،س
کارایی
| ( 3 ) |
جایی که
- W کار انجام شده توسط سیستم است (انرژی خروجی از سیستم به عنوان کار)،
<0 گرمای گرفته شده از سیستم (انرژی گرمایی خروجی از سیستم) است.
> 0 گرمای وارد شده به سیستم (انرژی گرمایی ورودی به سیستم) است.
دمای مطلق مخزن سرد است و
دمای مطلق مخزن گرم است.
حداکثر آنتروپی سیستم است
حداقل آنتروپی سیستم است
بیان با دما




این تعریف راندمان کار موتور حرارتی کارنو به عنوان کسری از کار انجام شده توسط سیستم به انرژی حرارتی دریافتی سیستم از مخزن داغ در هر سیکل است. این انرژی حرارتی آغازگر چرخه است.
چرخه کارنو معکوس [ ویرایش ]
یک چرخه موتور حرارتی کارنو که شرح داده شد یک چرخه کاملاً برگشت پذیر است. یعنی تمام فرآیندهای تشکیل دهنده آن را می توان معکوس کرد که در این صورت تبدیل به پمپ حرارتی و چرخه تبرید کارنو می شود . این بار، چرخه دقیقاً یکسان می ماند با این تفاوت که جهت هر گونه فعل و انفعالات حرارتی و کاری معکوس می شود. گرما از مخزن با دمای پایین جذب میشود، گرما به مخزن با دمای بالا دفع میشود و برای انجام همه اینها یک ورودی کاری لازم است. نمودار P - V چرخه معکوس کارنو مانند چرخه موتور حرارتی کارنو است با این تفاوت که جهت فرآیندها معکوس است. [3]
قضیه کارنو [ ویرایش ]
مقاله اصلی: قضیه کارنو (ترمودینامیک)
از نمودار بالا می توان دریافت که برای هر چرخه ای که بین دماها کار می کند

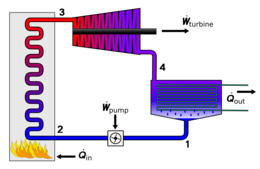
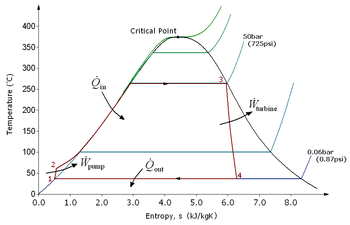
شکل 6 : یک موتور واقعی (سمت چپ) در مقایسه با چرخه کارنو (راست). آنتروپی یک ماده واقعی با دما تغییر می کند. این تغییر با منحنی در نمودار T - S نشان داده می شود . برای این شکل، منحنی یک تعادل بخار-مایع را نشان می دهد ( به چرخه رانکین مراجعه کنید ). سیستم های برگشت ناپذیر و تلفات انرژی (مثلاً کار در اثر اصطکاک و تلفات حرارتی) مانع از تحقق ایده آل در هر مرحله می شود.
قضیه کارنو بیانیه رسمی این واقعیت است: هیچ موتوری که بین دو مخزن حرارتی کار می کند نمی تواند کارآمدتر از موتور کارنو بین همان مخازن باشد. بنابراین، معادله 3 حداکثر بازده ممکن را برای هر موتوری با استفاده از دماهای مربوطه نشان می دهد. نتیجهای از قضیه کارنو بیان میکند که: همه موتورهای برگشتپذیر که بین مخازن حرارتی یکسانی کار میکنند به یک اندازه کارآمد هستند. تنظیم مجدد سمت راست معادله شکل سادهتری از معادله را به دست میدهد، یعنی اینکه حداکثر بازده نظری یک موتور حرارتی برابر است با اختلاف دمای بین مخزن سرد و گرم تقسیم بر دمای مطلق مخزن گرم. . با نگاهی به این فرمول یک واقعیت جالب آشکار می شود: کاهش دمای مخزن سرد تاثیر بیشتری بر بازده سقف یک موتور حرارتی خواهد داشت تا اینکه دمای مخزن داغ را به همان میزان افزایش دهد. در دنیای واقعی، دستیابی به این امر ممکن است دشوار باشد زیرا مخزن سرد اغلب دمای محیط موجود است.
به عبارت دیگر، حداکثر بازده در صورتی به دست می آید که آنتروپی در هر چرخه تغییر نکند. تغییر آنتروپی در هر چرخه ایجاد می شود، برای مثال، اگر اصطکاک وجود داشته باشد که منجر به اتلاف کار به گرما شود. در این صورت، چرخه برگشت پذیر نیست و قضیه کلازیوس به جای برابری تبدیل به نابرابری می شود. در غیر این صورت، از آنجایی که آنتروپی یک تابع حالت است ، تخلیه گرمای مورد نیاز به محیط برای دفع آنتروپی اضافی منجر به کاهش (حداقل) راندمان می شود. بنابراین معادله 3 کارایی هر موتور حرارتی برگشت پذیر را نشان می دهد .
در موتورهای حرارتی مزوسکوپی، کار در هر چرخه عملیات به طور کلی به دلیل نویز حرارتی در نوسان است. اگر چرخه به صورت شبه ایستا انجام شود، نوسانات حتی در مقیاس مزو مقیاس ناپدید می شوند. [4] با این حال، اگر چرخه سریعتر از زمان استراحت محیط کار انجام شود، نوسانات کار اجتناب ناپذیر است. با این وجود، هنگامی که نوسانات کار و گرما شمارش می شود، یک برابری دقیق میانگین نمایی کار انجام شده توسط هر موتور حرارتی را به انتقال حرارت از حمام حرارتی گرمتر مرتبط می کند. [5]
کارایی موتورهای حرارتی واقعی [ ویرایش ]
همچنین ببینید: موتور حرارتی § راندمان
کارنو متوجه شد که در واقعیت، ساخت یک موتور ترمودینامیکی برگشت پذیر امکان پذیر نیست . بنابراین، موتورهای حرارتی واقعی حتی کمتر از آنچه در معادله 3 نشان داده شده است، کارآمد هستند . علاوه بر این، موتورهای واقعی که در امتداد سبک چرخه کارنو (انبساط همدما / انبساط ایزوتروپیک / تراکم همدما / تراکم ایزنتروپیک) کار می کنند نادر هستند. با این وجود، معادله 3 برای تعیین حداکثر بازدهی که میتوان برای مجموعه معینی از مخازن حرارتی انتظار داشت، بسیار مفید است.
اگرچه چرخه کارنو یک ایده آل سازی است، اما رابطه 3 به عنوان بیان کارایی کارنو هنوز مفید است. دمای متوسط را در نظر بگیرید ،

برای چرخه کارنو یا معادل آن، مقدار متوسط 〈 T H 〉 برابر با بالاترین دمای موجود، یعنی T H و 〈 T C 〉 کمترین، یعنی T C خواهد بود . برای سایر چرخههای ترمودینامیکی کمتر کارآمد، 〈 T H 〉 کمتر از T H و 〈 T C 〉 بالاتر از T C خواهد بود . به عنوان مثال، این می تواند نشان دهد که چرا یک گرم کننده یا احیاء کننده می تواند بازده حرارتی نیروگاه های بخار را بهبود بخشد و چرا راندمان حرارتی نیروگاه های سیکل ترکیبی (که دارای توربین های گازی هستند که در دماهای بالاتر کار می کنند) از بخار معمولی فراتر می رود. گیاهان اولین نمونه اولیه موتور دیزل بر اساس اصول چرخه کارنو بود.
به عنوان یک ساختار ماکروسکوپی [ ویرایش ]
مقاله اصلی: موتور حرارتی کارنو § به عنوان یک ساختار ماکروسکوپی
موتور حرارتی کارنو ، در نهایت، یک ساختار نظری است که بر اساس یک سیستم ترمودینامیکی ایده آل است . در سطح عملی در مقیاس انسانی، چرخه کارنو یک مدل با ارزش است، مانند پیشرفت در توسعه موتور دیزل . با این حال، در مقیاس ماکروسکوپی، محدودیتهای اعمال شده توسط مفروضات مدل، غیرعملی بودن و در نهایت ناتوانی در انجام هر کاری را ثابت میکند . [6] به این ترتیب، طبق قضیه کارنو ، موتور کارنو ممکن است به عنوان حد نظری موتورهای حرارتی در مقیاس ماکروسکوپی در نظر گرفته شود تا هر وسیله عملی که میتوان ساخت. [7]
همچنین ببینید [ ویرایش ]
منبع
https://en.wikipedia.org/wiki/Carnot_cycle














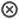
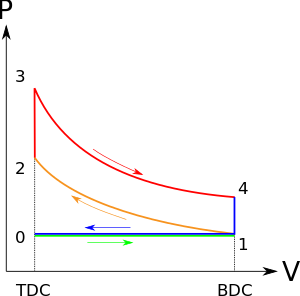
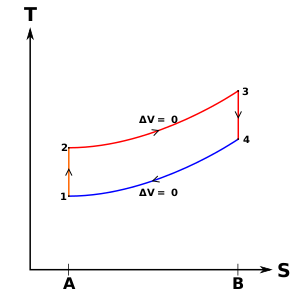

 "نسبت انفجار" نامیده می شود.
"نسبت انفجار" نامیده می شود. "نسبت انبساط ایسنتروپیک" نامیده می شود. (برای چرخه اتو همان نسبت تراکم است
"نسبت انبساط ایسنتروپیک" نامیده می شود. (برای چرخه اتو همان نسبت تراکم است ). از نظر مکانیکی، این انبساط مخلوط گاز داغ در سیلندر است که به عنوان ضربه انبساط (قدرت) شناخته می شود.
). از نظر مکانیکی، این انبساط مخلوط گاز داغ در سیلندر است که به عنوان ضربه انبساط (قدرت) شناخته می شود.
 انرژی از 1-2-3 و به سیستم اضافه می شود
انرژی از 1-2-3 و به سیستم اضافه می شود انرژی از سیستم 3-4-1 حذف می شود. از نظر کار و حرارت اضافه شده به سیستم
انرژی از سیستم 3-4-1 حذف می شود. از نظر کار و حرارت اضافه شده به سیستم
























 (به
(به 



 نسبت گرمای ویژه است
نسبت گرمای ویژه است




 نسبت تراکم است
نسبت تراکم است :
:

 برای هوا 1.4 است، افزایش در
برای هوا 1.4 است، افزایش در



 به
به در نمودار زیر). این یک مدل ریاضی ایدهآل است: دیزلهای فیزیکی واقعی در این دوره افزایش فشار دارند، اما نسبت به چرخه اتو کمتر مشخص است. در مقابل، چرخه اتوی ایده آل موتور بنزینی به یک فرآیند حجم ثابت در طول آن فاز تقریب می زند.
در نمودار زیر). این یک مدل ریاضی ایدهآل است: دیزلهای فیزیکی واقعی در این دوره افزایش فشار دارند، اما نسبت به چرخه اتو کمتر مشخص است. در مقابل، چرخه اتوی ایده آل موتور بنزینی به یک فرآیند حجم ثابت در طول آن فاز تقریب می زند.
 فشار و V حجم یا
فشار و V حجم یا اگر فرآیند بر اساس جرم واحد قرار گیرد، حجم خاص است. چرخه دیزل ایده آل گاز ایده آل را در نظر می گیرد و شیمی احتراق ، اگزوز و فرآیندهای شارژ مجدد را نادیده می گیرد و به سادگی چهار فرآیند متمایز را دنبال می کند:
اگر فرآیند بر اساس جرم واحد قرار گیرد، حجم خاص است. چرخه دیزل ایده آل گاز ایده آل را در نظر می گیرد و شیمی احتراق ، اگزوز و فرآیندهای شارژ مجدد را نادیده می گیرد و به سادگی چهار فرآیند متمایز را دنبال می کند: ، اما طبق تعریف (ایسنتروپیک) هیچ انرژی به صورت گرما به داخل یا خارج سیستم منتقل نمی شود. در طی فرآیند فشار ثابت (قرمز، ایزوباریک )، انرژی به صورت گرما وارد سیستم می شود
، اما طبق تعریف (ایسنتروپیک) هیچ انرژی به صورت گرما به داخل یا خارج سیستم منتقل نمی شود. در طی فرآیند فشار ثابت (قرمز، ایزوباریک )، انرژی به صورت گرما وارد سیستم می شود . در طی فرآیندهای ایزنتروپیک بالا (زرد)، انرژی به شکل به خارج از سیستم منتقل می شود
. در طی فرآیندهای ایزنتروپیک بالا (زرد)، انرژی به شکل به خارج از سیستم منتقل می شود ، اما طبق تعریف (ایسنتروپیک) هیچ انرژی به صورت گرما به داخل یا خارج سیستم منتقل نمی شود. در طول فرآیند حجم ثابت (سبز، ایزوکوریک )، مقداری از انرژی به عنوان گرما از طریق فرآیند کاهش فشار مناسب از سیستم خارج می شود.
، اما طبق تعریف (ایسنتروپیک) هیچ انرژی به صورت گرما به داخل یا خارج سیستم منتقل نمی شود. در طول فرآیند حجم ثابت (سبز، ایزوکوریک )، مقداری از انرژی به عنوان گرما از طریق فرآیند کاهش فشار مناسب از سیستم خارج می شود. . کاری که از سیستم خارج می شود برابر است با کاری که وارد سیستم می شود به اضافه تفاوت بین گرمای اضافه شده به سیستم و حرارتی که از سیستم خارج می شود. به عبارت دیگر، سود خالص کار برابر است با تفاوت بین گرمای اضافه شده به سیستم و گرمایی که از سیستم خارج می شود.
. کاری که از سیستم خارج می شود برابر است با کاری که وارد سیستم می شود به اضافه تفاوت بین گرمای اضافه شده به سیستم و حرارتی که از سیستم خارج می شود. به عبارت دیگر، سود خالص کار برابر است با تفاوت بین گرمای اضافه شده به سیستم و گرمایی که از سیستم خارج می شود.
 بازده حرارتی است
بازده حرارتی است نسبت برش است
نسبت برش است (نسبت بین حجم پایان و شروع برای فاز احتراق)
(نسبت بین حجم پایان و شروع برای فاز احتراق)




 را می توان به دمای شعله سوخت مورد استفاده تقریب زد. دمای شعله را می توان به دمای شعله آدیاباتیک سوخت با نسبت هوا به سوخت و فشار تراکم مربوطه تقریب زد.
را می توان به دمای شعله سوخت مورد استفاده تقریب زد. دمای شعله را می توان به دمای شعله آدیاباتیک سوخت با نسبت هوا به سوخت و فشار تراکم مربوطه تقریب زد. .
.  را می توان به دمای هوای ورودی تقریب زد.
را می توان به دمای هوای ورودی تقریب زد.











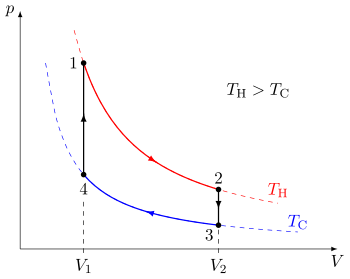
 ، جایی که
، جایی که



























 ، سپس
، سپس
 بردار با اجزا است
بردار با اجزا است ،
، ، و
، و
 بردار با مختصات مختلط است:
بردار با مختصات مختلط است:![{\displaystyle \mathbf {a} =[{\frac {1}{2}}({\frac {1}{\lambda }}-\lambda ),-{\frac {i}{2}}({ \frac {1}{\lambda }}+\lambda ),1].}](https://wikimedia.org/api/rest_v1/media/math/render/svg/9d5d338cb35165858d91d7076b25277522143951)

 به عنوان پارامترهای حقیقی در نامگذاری این تابع مولد به نام هرگلوتز ، ما از Courant & Hilbert 1962 ، §VII.7 پیروی میکنیم که یادداشتهای منتشر نشده او را برای کشف آن اعتبار میدانند.
به عنوان پارامترهای حقیقی در نامگذاری این تابع مولد به نام هرگلوتز ، ما از Courant & Hilbert 1962 ، §VII.7 پیروی میکنیم که یادداشتهای منتشر نشده او را برای کشف آن اعتبار میدانند. ، به طوری که
، به طوری که آنالوگ عملگر هارمونیک جامد است
آنالوگ عملگر هارمونیک جامد است ، [16] یک تابع تولید کننده برای مجموعه استاندارد شده ای از عملگرهای تانسور کروی بدست می آید .
، [16] یک تابع تولید کننده برای مجموعه استاندارد شده ای از عملگرهای تانسور کروی بدست می آید .
 's تبدیل تحت چرخش ها (به زیر مراجعه کنید) به همان شیوه ای است
's تبدیل تحت چرخش ها (به زیر مراجعه کنید) به همان شیوه ای است 's، که به نوبه خود تضمین می کند که آنها عملگرهای تانسور کروی هستند
's، که به نوبه خود تضمین می کند که آنها عملگرهای تانسور کروی هستند ، با
، با و
و با رعایت تمام خصوصیات این عملگرها، مانند قضیه ترکیب کلبش-گوردان و قضیه ویگنر-اکارت . علاوه بر این، آنها یک مجموعه استاندارد شده با مقیاس یا عادی سازی ثابت هستند.
با رعایت تمام خصوصیات این عملگرها، مانند قضیه ترکیب کلبش-گوردان و قضیه ویگنر-اکارت . علاوه بر این، آنها یک مجموعه استاندارد شده با مقیاس یا عادی سازی ثابت هستند. و دیگری از
و دیگری از و
و ، به شرح زیر (فاز کاندون – شورتلی):
، به شرح زیر (فاز کاندون – شورتلی):![{\displaystyle r^{\ell }\,{\begin{pmatrix}Y_{\ell }^{m}\\Y_{\ell }^{-m}\end{pmatrix}}=\left[{\ frac {2\ell +1}{4\pi }}\right]^{1/2}{\bar {\Pi }}_{\ell }^{m}(z){\begin{pmatrix}\ چپ(-1\راست)^{m}(A_{m}+iB_{m})\\(A_{m}-iB_{m})\end{pmatrix}}،\qquad m>0.}](https://wikimedia.org/api/rest_v1/media/math/render/svg/066f9cfa96f2c4550337a93bf73d61517362c834) و برای m = 0 :
و برای m = 0 : اینجا
اینجا
 و
و![{\displaystyle {\bar {\Pi }}_{\ell }^{m}(z)=\left[{\frac {(\ell -m)!}{(\ell +m)!}}\ راست]^{1/2}\sum _{k=0}^{\left\lطبقه (\ell -m)/2\right\rfloor }(-1)^{k}2^{-\ell } {\binom {\ell }{k}}{\binom {2\ell -2k}{\ell }}{\frac {(\ell -2k)!}{(\ell -2k-m)!}} \;r^{2k}\;z^{\ell -2k-m}.}](https://wikimedia.org/api/rest_v1/media/math/render/svg/7e4c8fef579a7f234ae71d6ed82da1013e72c592) برای
برای این کاهش می یابد
این کاهش می یابد
 اساساً چند جمله ای لژاندر مرتبط است
اساساً چند جمله ای لژاندر مرتبط است ، و عوامل
، و عوامل اساسا هستند
اساسا هستند .
. ، و
، و که به صراحت در بالا ذکر شده است، به دست می آوریم:
که به صراحت در بالا ذکر شده است، به دست می آوریم:![{\displaystyle Y_{3}^{1}=-{\frac {1}{r^{3}}}\left[{\tfrac {7}{4\pi }}\cdot {\tfrac {3} {16}}\right]^{1/2}\left(5z^{2}-r^{2}\right)\left(x+iy\right)=-\left[{\tfrac {7} {4\pi }}\cdot {\tfrac {3}{16}}\right]^{1/2}\left(5\cos ^{2}\theta -1\right)\left(\sin \ تتا e^{i\varphi }\right)}](https://wikimedia.org/api/rest_v1/media/math/render/svg/ed582e41ffef571704b11f0ad0dee2d0c0f40858)
![{\displaystyle Y_{4}^{-2}={\frac {1}{r^{4}}}\left[{\tfrac {9}{4\pi }}\cdot {\tfrac {5} {32}}\right]^{1/2}\left(7z^{2}-r^{2}\right)\left(x-iy\right)^{2}=\left[{\tfrac {9}{4\pi }}\cdot {\tfrac {5}{32}}\right]^{1/2}\left(7\cos ^{2}\theta -1\right)\left( \sin ^{2}\theta e^{-2i\varphi }\right)}](https://wikimedia.org/api/rest_v1/media/math/render/svg/4bcad8b6882705b752928a0c469aa0ef2f9e306f) ممکن است تأیید شود که این با عملکرد فهرست شده در اینجا و اینجا مطابقت دارد .
ممکن است تأیید شود که این با عملکرد فهرست شده در اینجا و اینجا مطابقت دارد . فقطآمتر
فقطآمتر شرایط (کسینوس) گنجانده شده است، و برای
شرایط (کسینوس) گنجانده شده است، و برای فقط
فقط اصطلاحات (سینوس ها) شامل می شوند:
اصطلاحات (سینوس ها) شامل می شوند:

 ، و
، و تعریف نشده است، همه هارمونیک های کروی به جز آنهایی که با
تعریف نشده است، همه هارمونیک های کروی به جز آنهایی که با
 . سپس، همانطور که از بسیاری جهات می توان دید (شاید به سادگی از تابع تولید هرگلوتز)، با
. سپس، همانطور که از بسیاری جهات می توان دید (شاید به سادگی از تابع تولید هرگلوتز)، با
 به
به . بیانیه برابری هارمونیک های کروی پس از آن است
. بیانیه برابری هارمونیک های کروی پس از آن است (این را می توان به صورت زیر مشاهده کرد: چند جمله ای های لژاندر (-1) + m را به دست می دهند و از تابع نمایی (-1) m داریم ، با هم برای هارمونیک های کروی برابری (-1) .)
(این را می توان به صورت زیر مشاهده کرد: چند جمله ای های لژاندر (-1) + m را به دست می دهند و از تابع نمایی (-1) m داریم ، با هم برای هارمونیک های کروی برابری (-1) .)
 در مورد مبدایی که بردار واحد را ارسال می کند
در مورد مبدایی که بردار واحد را ارسال می کند . تحت این عملیات، هارمونیک کروی درجه
. تحت این عملیات، هارمونیک کروی درجه و سفارش دهیدمتر
و سفارش دهیدمتر تبدیل به یک ترکیب خطی از هارمونیک های کروی با همان درجه می شود. به این معنا که،
تبدیل به یک ترکیب خطی از هارمونیک های کروی با همان درجه می شود. به این معنا که، جایی که
جایی که یک ماتریس از نظم است
یک ماتریس از نظم است که به چرخش بستگی دارد
که به چرخش بستگی دارد![{\displaystyle Y_{\ell }^{m}({\mathbf {r} }')=\sum _{m'=-\ell }^{\ell [D_{mm'}^{(\ell )}({\mathcal {R}})]^{*}Y_{\ell }^{m'}({\mathbf {r} })،}](https://wikimedia.org/api/rest_v1/media/math/render/svg/d90f021b19abdcb67fe194dea9981c6473be594a) جایی که
جایی که مزدوج مختلط یک عنصر از ماتریس D ویگنر است . به ویژه زمانی که"
مزدوج مختلط یک عنصر از ماتریس D ویگنر است . به ویژه زمانی که" با چرخش آزیموت ما هویت را بدست می آوریم،
با چرخش آزیموت ما هویت را بدست می آوریم،
 . در کره واحداس2
. در کره واحداس2 ، هر تابع قابل انتگرالگیری مربع:
، هر تابع قابل انتگرالگیری مربع: بنابراین می توان به عنوان یک ترکیب خطی از این موارد گسترش داد:
بنابراین می توان به عنوان یک ترکیب خطی از این موارد گسترش داد:


 همچنین می تواند از نظر هارمونیک های حقیقی گسترش یابد
همچنین می تواند از نظر هارمونیک های حقیقی گسترش یابد در بالا به عنوان جمع
در بالا به عنوان جمع
 . مزایای بسط از نظر توابع هارمونیک حقیقی
. مزایای بسط از نظر توابع هارمونیک حقیقی این است که برای توابع حقیقی است
این است که برای توابع حقیقی است تضمین شده است که حقیقی هستند، در حالی که ضرایب آنها
تضمین شده است که حقیقی هستند، در حالی که ضرایب آنها در گسترش آنها از نظر
در گسترش آنها از نظر ) آن خاصیت را ندارند.
) آن خاصیت را ندارند.
 جایی که
جایی که



 سپس f در فضای سوبولف H s ( S 2 ) است . به طور خاص، قضیه تعبیه سوبولف نشان می دهد که f بی نهایت قابل تمایز است به شرطی که
سپس f در فضای سوبولف H s ( S 2 ) است . به طور خاص، قضیه تعبیه سوبولف نشان می دهد که f بی نهایت قابل تمایز است به شرطی که برای همه s .
برای همه s . و("،"،")
و("،"،") ، به ترتیب، زاویه
، به ترتیب، زاویه که در آن نقش توابع مثلثاتی که در سمت راست ظاهر می شوند توسط هارمونیک های کروی و نقش سمت چپ توسط چند جمله ای های لژاندر ایفا می شود .
که در آن نقش توابع مثلثاتی که در سمت راست ظاهر می شوند توسط هارمونیک های کروی و نقش سمت چپ توسط چند جمله ای های لژاندر ایفا می شود .

 ، درجه هارمونیک ناحیه ای مربوط به بردار واحد x ، به صورت [21] تجزیه می شود.
، درجه هارمونیک ناحیه ای مربوط به بردار واحد x ، به صورت [21] تجزیه می شود.
 به عنوان مضرب ثابت چند جمله ای Gegenbauer مناسب داده می شود :
به عنوان مضرب ثابت چند جمله ای Gegenbauer مناسب داده می شود :
 که در آن ω n -1 حجم ( n -1) -کره است.
که در آن ω n -1 حجم ( n -1) -کره است. بسیاری از اصطلاحات در این مجموع به طور پیش پا افتاده صفر هستند. ارزش هایج
بسیاری از اصطلاحات در این مجموع به طور پیش پا افتاده صفر هستند. ارزش هایج و
و
![{\displaystyle \Re [Y_{\ell m}]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/fe4514a0a6a49a33432a4bf36efe1f6fa05cb3dc) برابر است با 0 در امتداد دایره های بزرگی که از قطب ها می گذرند و در امتداد دایره های − m با عرض جغرافیایی مساوی. تابع هر بار که از یکی از این خطوط عبور می کند علامت تغییر می دهد.
برابر است با 0 در امتداد دایره های بزرگی که از قطب ها می گذرند و در امتداد دایره های − m با عرض جغرافیایی مساوی. تابع هر بار که از یکی از این خطوط عبور می کند علامت تغییر می دهد.
![{\displaystyle \Re [Y_{\ell }^{m}]=0}](https://wikimedia.org/api/rest_v1/media/math/render/svg/26617636b368a6d09ed57405f1fb8652eb51e617) ، یا به جای آن کجاℑ[]=0
، یا به جای آن کجاℑ[]=0![{\displaystyle \Im [Y_{\ell }^{m}]=0}](https://wikimedia.org/api/rest_v1/media/math/render/svg/2b2fb51f4ee139b5891db76afaa139113a04982d) . خطوط گره ای از
. خطوط گره ای از و
و


 . هارمونیک های کروی را می توان به فضای اقلیدسی با ابعاد بالاتر تعمیم دادآر
. هارمونیک های کروی را می توان به فضای اقلیدسی با ابعاد بالاتر تعمیم دادآر به شرح زیر منجر به توابع می شوداس-1→سی
به شرح زیر منجر به توابع می شوداس-1→سی . [24] اجازه دهید P فضای چندجملهای همگن با مقدار مختلط درجه را در n متغیر حقیقی نشان دهد که در اینجا به عنوان تابع در نظر گرفته میشود.آر→سی
. [24] اجازه دهید P فضای چندجملهای همگن با مقدار مختلط درجه را در n متغیر حقیقی نشان دهد که در اینجا به عنوان تابع در نظر گرفته میشود.آر→سی . یعنی یک p چند جمله ای در P است به شرطی که برای هر حقیقی باشد∈آر
. یعنی یک p چند جمله ای در P است به شرطی که برای هر حقیقی باشد∈آر ، یک نفر دارد
، یک نفر دارد
 این هارمونیک های کروی جامد (منظم) هستند . اجازه دهید H نشان دهنده فضای توابع در کره واحد باشد
این هارمونیک های کروی جامد (منظم) هستند . اجازه دهید H نشان دهنده فضای توابع در کره واحد باشد با محدودیت از A به دست می آید
با محدودیت از A به دست می آید
 از توابع پیوسته دراس-1
از توابع پیوسته دراس-1 با توجه به توپولوژی یکنواخت ، توسط قضیه استون-وایرشتراس . در نتیجه، مجموع این فضاها در فضای L 2 ( Sn - 1 ) از توابع انتگرال پذیر مربع روی کره نیز متراکم است. بنابراین هر تابع مربع ادغام پذیر در کره به طور منحصر به فردی به یک سری هارمونیک کروی تجزیه می شود، جایی که این سری به معنای L 2 همگرا می شود .
با توجه به توپولوژی یکنواخت ، توسط قضیه استون-وایرشتراس . در نتیجه، مجموع این فضاها در فضای L 2 ( Sn - 1 ) از توابع انتگرال پذیر مربع روی کره نیز متراکم است. بنابراین هر تابع مربع ادغام پذیر در کره به طور منحصر به فردی به یک سری هارمونیک کروی تجزیه می شود، جایی که این سری به معنای L 2 همگرا می شود . اثبات دیگری می دهد که فضاهای H به صورت زوجی متعامد و در L 2 کامل هستند ( Sn - 1 ) .
اثبات دیگری می دهد که فضاهای H به صورت زوجی متعامد و در L 2 کامل هستند ( Sn - 1 ) .
 جایی که شاخص ها راضی کننده | 1 | ≤ 2 ≤ ⋯ ≤ n -1 و مقدار ویژه - n -1 ( n -1 + n -2) است . عملکردهای موجود در محصول بر حسب تابع Legendre تعریف می شوند
جایی که شاخص ها راضی کننده | 1 | ≤ 2 ≤ ⋯ ≤ n -1 و مقدار ویژه - n -1 ( n -1 + n -2) است . عملکردهای موجود در محصول بر حسب تابع Legendre تعریف می شوند
 برای ψ یک هارمونیک کروی و ρ یک چرخش. نمایش H نمایشی غیر قابل تقلیل از SO(3) است . [27]
برای ψ یک هارمونیک کروی و ρ یک چرخش. نمایش H نمایشی غیر قابل تقلیل از SO(3) است . [27] متقارن بر روی شاخص ها، به طور منحصر به فرد توسط نیاز تعیین می شود
متقارن بر روی شاخص ها، به طور منحصر به فرد توسط نیاز تعیین می شود شرطی که ψ هارمونیک باشد معادل این ادعا است که تانسور
شرطی که ψ هارمونیک باشد معادل این ادعا است که تانسور 

 . [6] همانطور که در مقدمه پیشنهاد شد، این دیدگاه احتمالاً منشأ اصطلاح "هارمونیک کروی" است (یعنی محدودیت در کره یک تابع هارمونیک ).
. [6] همانطور که در مقدمه پیشنهاد شد، این دیدگاه احتمالاً منشأ اصطلاح "هارمونیک کروی" است (یعنی محدودیت در کره یک تابع هارمونیک ). در ادبیات مکانیک کوانتومی معمولاً به عنوان فاز کاندون -شورتلی شناخته می شود. در جامعه مکانیک کوانتومی، استفاده از این فاکتور فاز در تعریف چندجملهای لژاندر مرتبط ، یا اضافه کردن آن به تعریف توابع هارمونیک کروی، معمول است . در تعریف توابع هارمونیک کروی نیازی به استفاده از فاز Condon-Shortley وجود ندارد، اما گنجاندن آن می تواند برخی از عملیات مکانیکی کوانتومی، به ویژه کاربرد عملگرهای بالا بردن و پایین آوردن را ساده کند . جوامع ژئودزی [12] و مغناطیسی هرگز فاکتور فاز کاندون-شورتلی را در تعاریف خود از توابع هارمونیک کروی و همچنین در تعاریف چند جمله ای های لژاندر مرتبط نمی گنجانند. [13]
در ادبیات مکانیک کوانتومی معمولاً به عنوان فاز کاندون -شورتلی شناخته می شود. در جامعه مکانیک کوانتومی، استفاده از این فاکتور فاز در تعریف چندجملهای لژاندر مرتبط ، یا اضافه کردن آن به تعریف توابع هارمونیک کروی، معمول است . در تعریف توابع هارمونیک کروی نیازی به استفاده از فاز Condon-Shortley وجود ندارد، اما گنجاندن آن می تواند برخی از عملیات مکانیکی کوانتومی، به ویژه کاربرد عملگرهای بالا بردن و پایین آوردن را ساده کند . جوامع ژئودزی [12] و مغناطیسی هرگز فاکتور فاز کاندون-شورتلی را در تعاریف خود از توابع هارمونیک کروی و همچنین در تعاریف چند جمله ای های لژاندر مرتبط نمی گنجانند. [13]![{\displaystyle {\begin{aligned}Y_{\ell m}&={\begin{cases}{\dfrac {i}{\sqrt {2}}}\left(Y_{\ell }^{m}- (-1)^{m}\,Y_{\ell }^{-m}\right)&{\text{if}}\ m<0\\Y_{\ell }^{0}&{\text {if}}\ m=0\\{\dfrac {1}{\sqrt {2}}}\left(Y_{\ell }^{-m}+(-1)^{m}\,Y_{ \بلا }^{m}\right)&{\text{if}}\ m>0.\end{cases}}\\&={\begin{cases}{\dfrac {i}{\sqrt {2 }}}\left(Y_{\ell }^{-|m|}-(-1)^{m}\,Y_{\ell }^{|m|}\راست)&{\text{if} }\ m<0\\Y_{\ell }^{0}&{\text{if}}\ m=0\\{\dfrac {1}{\sqrt {2}}}\left(Y_{\ ell }^{-|m|}+(-1)^{m}\,Y_{\ell }^{|m|}\right)&{\text{if}}\ m>0.\end{ case}}\\&={\begin{cases}{\sqrt {2}}\,(-1)^{m}\,\Im [{Y_{\ell }^{|m|}}]& {\text{if}}\ m<0\\Y_{\ell }^{0}&{\text{if}}\ m=0\\{\sqrt {2}}\,(-1)^ {m}\,\Re [{Y_{\ell }^{m}}]&{\text{if}}\ m>0.\end{cases}}\end{تراز شده}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/281f6a87023810f7fa9a80d46805c8ad18597fe8)
![{\displaystyle Y_{\ell }^{m}={\begin{cases}{\dfrac {1}{\sqrt {2}}}\left(Y_{\ell |m|}-iY_{\ell , -|m|}\right)&{\text{if}}\ m<0\\[4pt]Y_{\ell 0}&{\text{if}}\ m=0\\[4pt]{\ dfrac {(-1)^{m}}{\sqrt {2}}}\left(Y_{\ell |m|}+iY_{\ell ,-|m|}\right)&{\text{if }}\ m>0.\end{موارد}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/27971bab040e0ab0b2533f34865c0a6225cb12d2)
![{\displaystyle Y_{\ell m}={\begin{cases}\left(-1\right)^{m}{\sqrt {2}}{\sqrt {{\dfrac {2\ell +1}{ 4\pi }}{\dfrac {(\ell -|m|)!}{(\ell +|m|)!}}}}\;P_{\ell }^{|m|}(\cos \ تتا )\ \sin(|m|\varphi )&{\text{if }}m<0\\[4pt]{\sqrt {\dfrac {2\ell +1}{4\pi }}}\ P_ {\ell }^{m}(\cos \theta )&{\text{if }}m=0\\[4pt]\left(-1\right)^{m}{\sqrt {2}}{ \sqrt {{\dfrac {2\ell +1}{4\pi }}{\dfrac {(\ell -m)!}{(\ell +m)!}}}}\;P_{\ell } ^{m}(\cos \theta )\ \cos(m\varphi )&{\text{if }}m>0\,.\end{cases}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/20ccbde100d451bfe2fff46127a1e31705c95351)
 ، که با خروجی معادلات بالا مطابقت دارد.
، که با خروجی معادلات بالا مطابقت دارد. ) برای محورهای مختلط و ترکیبی هستند، اما نسخه های حقیقی اساساً فقط x ، y و z هستند .
) برای محورهای مختلط و ترکیبی هستند، اما نسخه های حقیقی اساساً فقط x ، y و z هستند . معلوم می شود که
معلوم می شود که مبنای فضای چندجمله ای های هارمونیک و همگن درجه است
مبنای فضای چندجمله ای های هارمونیک و همگن درجه است و یک فرمول صریح برای
و یک فرمول صریح برای
 نتیجه می شود که
نتیجه می شود که
 اما ممکن است به صورت انتزاعی تر در پایه کت کروی متعارف کامل بیان شود .
اما ممکن است به صورت انتزاعی تر در پایه کت کروی متعارف کامل بیان شود . . به طور خاص، ما می گوییم که یک تابع چند جمله ای (با ارزش مختلط).
. به طور خاص، ما می گوییم که یک تابع چند جمله ای (با ارزش مختلط). درجه همگن است
درجه همگن است
 . ما این را می گوییم
. ما این را می گوییم جایی کهΔ
جایی کهΔ لاپلاسی است . سپس برای هر کدام
لاپلاسی است . سپس برای هر کدام
 فقط فضای 3 بعدی تمام توابع خطی است
فقط فضای 3 بعدی تمام توابع خطی است ، ما یک فضای 5 بعدی داریم:
، ما یک فضای 5 بعدی داریم:
 فرمول
فرمول
 . این چند جمله ای به راحتی هارمونیک دیده می شود. اگر بنویسیم
. این چند جمله ای به راحتی هارمونیک دیده می شود. اگر بنویسیم ، ما بدست می آوریم
، ما بدست می آوریم که می توان آن را بازنویسی کرد
که می توان آن را بازنویسی کرد پس از استفاده از فرمول چند جمله ای لژاندر مرتبط پ
پس از استفاده از فرمول چند جمله ای لژاندر مرتبط پ ، ممکن است این را به عنوان فرمول هارمونیک کروی تشخیص دهیم.
، ممکن است این را به عنوان فرمول هارمونیک کروی تشخیص دهیم. [7] (به بخش زیر در مورد موارد خاص هارمونیک های کروی مراجعه کنید.)
[7] (به بخش زیر در مورد موارد خاص هارمونیک های کروی مراجعه کنید.)
 . در سراسر بخش، ما از قرارداد استاندارد استفاده می کنیممتر>0
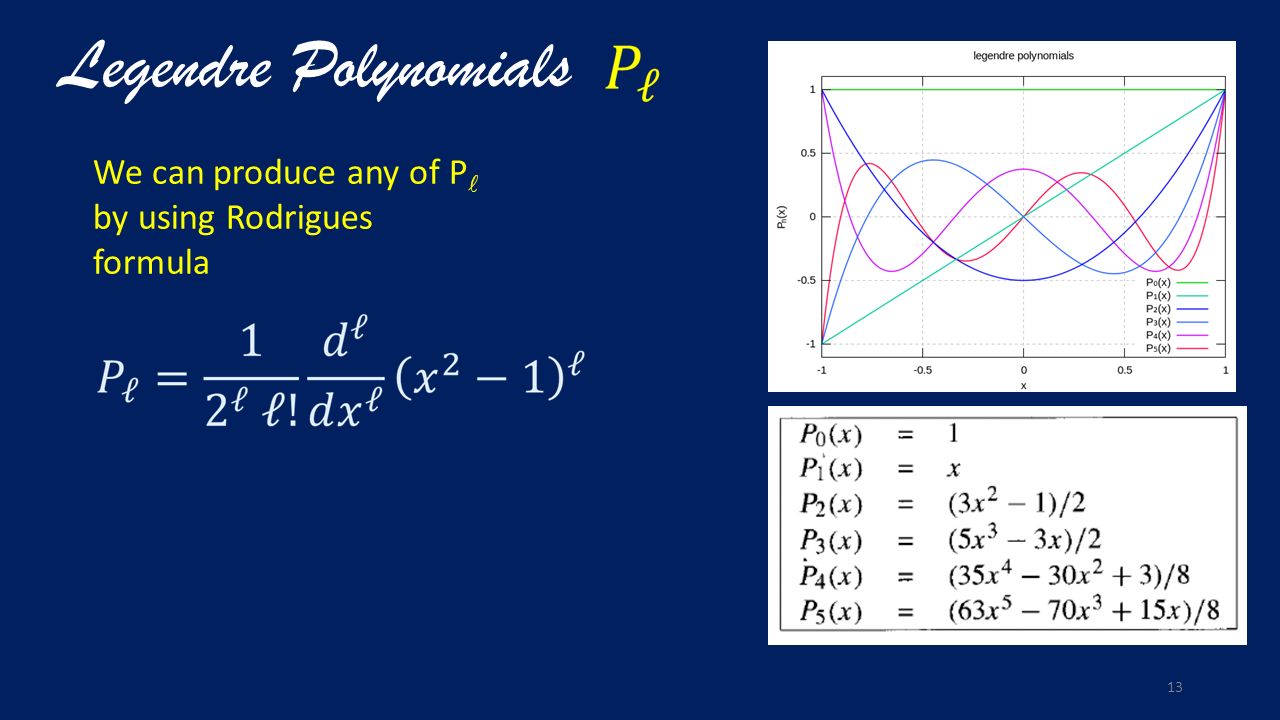
. در سراسر بخش، ما از قرارداد استاندارد استفاده می کنیممتر>0 که نرمال سازی طبیعی با فرمول رودریگز است.
که نرمال سازی طبیعی با فرمول رودریگز است.
 با
با و=
و= در فضای مختلط از
در فضای مختلط از به
به با رنگ های ایجاد شده با تابع Mathematica 13.1 ComplexPlot3D
با رنگ های ایجاد شده با تابع Mathematica 13.1 ComplexPlot3D

 چند جمله ای های لژاندر بدون فاز کاندون-شورتلی (برای جلوگیری از دوبار شمارش فاز) هستند.
چند جمله ای های لژاندر بدون فاز کاندون-شورتلی (برای جلوگیری از دوبار شمارش فاز) هستند.







 در نقطه x مرتبط با مجموعه ای از جرم های نقطه m i واقع در نقاط x i توسط داده شد
در نقطه x مرتبط با مجموعه ای از جرم های نقطه m i واقع در نقاط x i توسط داده شد

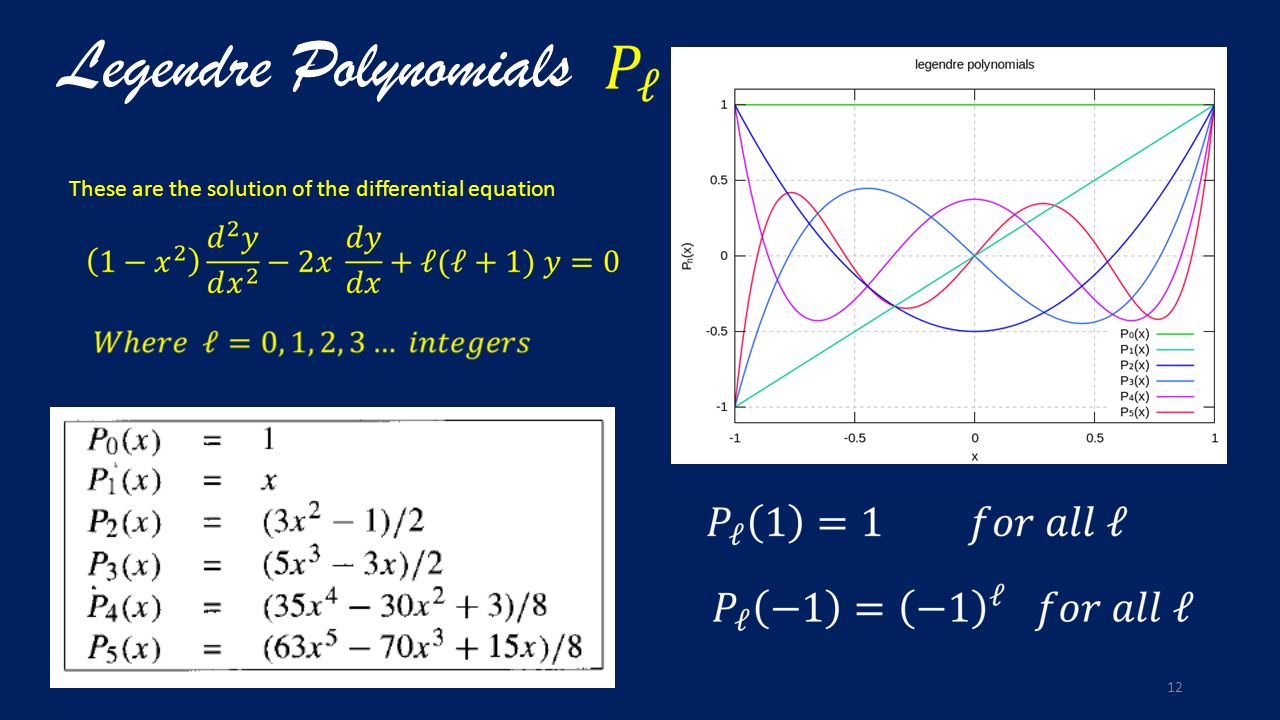
![{\displaystyle P_{i}:[-1,1]\to \mathbb {R} }](https://wikimedia.org/api/rest_v1/media/math/render/svg/a9beeaf69d50f479b69391bbaade7008fc0e1f16) چند جمله ای های لژاندر هستند و می توان آنها را به عنوان حالت خاصی از هارمونیک های کروی به دست آورد. پس از آن، لاپلاس در خاطرات خود در سال 1782، این ضرایب را با استفاده از مختصات کروی برای نشان دادن زاویه γ بین x 1 و x بررسی کرد . ( برای تجزیه و تحلیل دقیق تر به کاربردهای چند جمله ای لژاندر در فیزیک مراجعه کنید.)
چند جمله ای های لژاندر هستند و می توان آنها را به عنوان حالت خاصی از هارمونیک های کروی به دست آورد. پس از آن، لاپلاس در خاطرات خود در سال 1782، این ضرایب را با استفاده از مختصات کروی برای نشان دادن زاویه γ بین x 1 و x بررسی کرد . ( برای تجزیه و تحلیل دقیق تر به کاربردهای چند جمله ای لژاندر در فیزیک مراجعه کنید.)


 .
. که از معادله لاپلاس پیروی می کنند. اگر کسی از همگنی برای استخراج یک عامل وابستگی شعاعی استفاده کند، ارتباط با مختصات کروی بلافاصله ایجاد می شود.
که از معادله لاپلاس پیروی می کنند. اگر کسی از همگنی برای استخراج یک عامل وابستگی شعاعی استفاده کند، ارتباط با مختصات کروی بلافاصله ایجاد می شود. از چند جمله ای درجه فوق الذکر
از چند جمله ای درجه فوق الذکر به عنوان هارمونیک های کروی لاپلاس شناخته می شوند، زیرا اولین بار توسط پیر سیمون د لاپلاس در سال 1782 معرفی شدند .
به عنوان هارمونیک های کروی لاپلاس شناخته می شوند، زیرا اولین بار توسط پیر سیمون د لاپلاس در سال 1782 معرفی شدند . تعریف کردنم:
تعریف کردنم: ، ماتریس پواسون به صورت تعریف شده است
، ماتریس پواسون به صورت تعریف شده است ، جایی که
، جایی که ماتریس سمپلتیکی است که تحت همان قراردادها برای مرتب کردن مجموعه مختصات استفاده می شود. از تعریف بر می آید که:
ماتریس سمپلتیکی است که تحت همان قراردادها برای مرتب کردن مجموعه مختصات استفاده می شود. از تعریف بر می آید که:![{\displaystyle {\mathcal {P}}_{ij}(\varepsilon )=[MJM^{T}]_{ij}=\sum _{k=1}^{N}\left({\frac { \partial \varepsilon _{i}}{\partial \eta _{k}}}{\frac {\partial \varepsilon _{j}}{\partial \eta _{N+k}}}-{\frac {\partial \varepsilon _{i}}{\partial \eta _{N+k}}}{\frac {\partial \varepsilon _{j}}{\partial \eta _{k}}}\right) =\sum _{k=1}^{N}\left({\frac {\partial \varepsilon _{i}}{\partial q_{k}}}{\frac {\partial \varepsilon _{j} }{\partial p_{k}}}-{\frac {\partial \varepsilon _{i}}{\partial p_{k}}}{\frac {\partial \varepsilon _{j}}{\partial q_ {k}}}\right)=\{\varepsilon _{i}،\varepsilon _{j}\}_{\eta }.}](https://wikimedia.org/api/rest_v1/media/math/render/svg/1a15e99967eb4d344ec57733457bae103ff0ffc0)

 به عنوان ماتریس لاگرانژ شناخته می شود و عناصر آن با براکت های لاگرانژ مطابقت دارد . آخرین اتحاد را نیز می توان به صورت زیر بیان کرد:
به عنوان ماتریس لاگرانژ شناخته می شود و عناصر آن با براکت های لاگرانژ مطابقت دارد . آخرین اتحاد را نیز می توان به صورت زیر بیان کرد:![{\displaystyle \sum _{k=1}^{2N}\{\eta _{i}،\eta _{k}\}[\eta _{k}،\eta _{j}]=-\ دلتا _{ij}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/cc66924f661f0d8deef403c52a795fd322ebcfe7)
 ، که مستقیماً منجر به وضعیت علامتی می شود:
، که مستقیماً منجر به وضعیت علامتی می شود: . [1]
. [1] ثابت حرکت است این به این معنی است که اگر
ثابت حرکت است این به این معنی است که اگر یک مسیر یا راه حل برای معادلات حرکت همیلتون است ، پس
یک مسیر یا راه حل برای معادلات حرکت همیلتون است ، پس در طول آن مسیر سپس
در طول آن مسیر سپس
 به صراحت به زمان بستگی ندارد. این معادله به معادله لیوویل معروف است . محتوای قضیه لیوویل این است که تکامل زمانی یک اندازه گیری توسط تابع توزیع داده می شود
به صراحت به زمان بستگی ندارد. این معادله به معادله لیوویل معروف است . محتوای قضیه لیوویل این است که تکامل زمانی یک اندازه گیری توسط تابع توزیع داده می شود  ناپدید می شود (
ناپدید می شود ( )، سپس
)، سپس ثابت های مستقل حرکت باید در چرخش متقابل باشند ، جایی که
ثابت های مستقل حرکت باید در چرخش متقابل باشند ، جایی که و
و صراحتاً مستقل از زمان هستند
صراحتاً مستقل از زمان هستند  ) ثابت های حرکت، براکت پواسون آنها نیز همینطور است
) ثابت های حرکت، براکت پواسون آنها نیز همینطور است . با این حال، این همیشه نتیجه مفیدی را ارائه نمی دهد، زیرا تعداد ثابت های حرکتی ممکن محدود است
. با این حال، این همیشه نتیجه مفیدی را ارائه نمی دهد، زیرا تعداد ثابت های حرکتی ممکن محدود است  برای یک سیستم با
برای یک سیستم با منیفولد نمادین باشد ، یعنی منیفولد مجهز به یک شکل نمادین : یک 2 شکل
منیفولد نمادین باشد ، یعنی منیفولد مجهز به یک شکل نمادین : یک 2 شکل  که هر دو بسته است (یعنی مشتق بیرونی آن
که هر دو بسته است (یعنی مشتق بیرونی آن  ناپدید می شود) و غیر منحط . به عنوان مثال، در درمان فوق، مصرف کنید
ناپدید می شود) و غیر منحط . به عنوان مثال، در درمان فوق، مصرف کنید و بگیر
و بگیر
 ضرب داخلی یا عملیات انقباض تعریف شده توسط
ضرب داخلی یا عملیات انقباض تعریف شده توسط ، پس عدم انحطاط برابر است با گفتن این که برای هر یک شکل
، پس عدم انحطاط برابر است با گفتن این که برای هر یک شکل به طوری که
به طوری که . متناوبا، از سوی دیگر،
. متناوبا، از سوی دیگر، . سپس اگر
. سپس اگر یک عملکرد صاف است
یک عملکرد صاف است را می توان تعریف کرد
را می توان تعریف کرد . دیدن آن آسان است
. دیدن آن آسان است
 on ( M , ω ) یک عملیات دوخطی روی توابع متمایز است که توسط تعریف شده است
on ( M , ω ) یک عملیات دوخطی روی توابع متمایز است که توسط تعریف شده است ; براکت پواسون دو تابع روی M خود تابعی از M است . براکت پواسون ضد متقارن است زیرا:
; براکت پواسون دو تابع روی M خود تابعی از M است . براکت پواسون ضد متقارن است زیرا:

 مشتق لی (کاملا معادل) تابع f را نشان می دهد .
مشتق لی (کاملا معادل) تابع f را نشان می دهد . ارضای شرایط مرز
ارضای شرایط مرز و معادله دیفرانسیل مرتبه اول
و معادله دیفرانسیل مرتبه اول
 ; وقتی این درست باشد، Ω α را یک میدان برداری سمپلتیک می نامند . یادآوری اتحاد کارتن
; وقتی این درست باشد، Ω α را یک میدان برداری سمپلتیک می نامند . یادآوری اتحاد کارتن  و d ω = 0 ، نتیجه می شود که
و d ω = 0 ، نتیجه می شود که . بنابراین، Ω α یک میدان برداری نمادین است اگر و فقط اگر α یک شکل بسته باشد . از آنجا که
. بنابراین، Ω α یک میدان برداری نمادین است اگر و فقط اگر α یک شکل بسته باشد . از آنجا که ، نتیجه می شود که هر میدان برداری هامیلتونی X f یک میدان برداری ساده است و جریان همیلتونی متشکل از تبدیلات متعارف است. از (1) بالا، تحت جریان همیلتونی X H ،
، نتیجه می شود که هر میدان برداری هامیلتونی X f یک میدان برداری ساده است و جریان همیلتونی متشکل از تبدیلات متعارف است. از (1) بالا، تحت جریان همیلتونی X H ،
 و
و معادلات همیلتون برای تکامل زمانی سیستم بلافاصله از این فرمول پیروی می کند.
معادلات همیلتون برای تکامل زمانی سیستم بلافاصله از این فرمول پیروی می کند.

![{\displaystyle {\mathcal {L}}_{v}\iota _{w}\omega =\iota _{{\mathcal {L}}_{v}w}\omega +\iota _{w}{ \mathcal {L}}_{v}\omega =\iota _{[v,w]}\omega +\iota _{w}{\mathcal {L}}_{v}\omega .}](https://wikimedia.org/api/rest_v1/media/math/render/svg/cc16f7218b3ca566bce6637f9565b15efb57f3a7)
 ، اتحاد کارتن و این واقعیت که
، اتحاد کارتن و این واقعیت که یک فرم بسته است،
یک فرم بسته است،![{\displaystyle \iota _{[v,w]}\omega ={\mathcal {L}}_{v}\iota _{w}\omega =d(\iota _{v}\iota _{w} \omega )+\iota _{v}d(\iota _{w}\omega )=d(\iota _{v}\iota _{w}\omega )=d(\omega (w,v)) .}](https://wikimedia.org/api/rest_v1/media/math/render/svg/0f795101df10dd21f0716cc78d27b5a5307ce8ce)
![{\displaystyle [v,w]=X_{\omega (w,v)}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/abac09ab89da06328cafade8dcab9a2f568bf89d) ، به طوری که
، به طوری که![{\displaystyle [X_{f},X_{g}]=X_{\omega (X_{g},X_{f})}=-X_{\omega (X_{f},X_{g})}= -X_{\{f،g\}}.}](https://wikimedia.org/api/rest_v1/media/math/render/svg/7db4169c89959ab5dd91ff7676d4832e497bb088)
 از اتحاد متناظر برای براکت لی فیلدهای برداری به دست می آید، اما این فقط تا یک تابع ثابت محلی صادق است. با این حال، برای اثبات اتحاد ژاکوبی برای براکت پواسون، کافی است نشان دهیم که:
از اتحاد متناظر برای براکت لی فیلدهای برداری به دست می آید، اما این فقط تا یک تابع ثابت محلی صادق است. با این حال، برای اثبات اتحاد ژاکوبی برای براکت پواسون، کافی است نشان دهیم که:![{\displaystyle \operatorname {ad} _{\{g,f\}}=\operatorname {ad} _{-\{f,g\}}=[\operatorname {ad} _{f},\operatorname { تبلیغ} _{g}]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/3add2e4111344e6a7b5f99af35f629b1892fb378) جایی که اپراتور
جایی که اپراتور در توابع صاف در M با تعریف شده است
در توابع صاف در M با تعریف شده است  و براکت در سمت راست جابجایی اپراتورها است،
و براکت در سمت راست جابجایی اپراتورها است،![{\displaystyle [\operatorname {A} ,\,\operatorname {B} ]\;=\;\operatorname {A} \operatorname {B} -\operatorname {B} \operatorname {A} }](https://wikimedia.org/api/rest_v1/media/math/render/svg/d7f97f3ece87400d2b60f4bff90b63e785f72198) . توسط (1) ، اپراتور
. توسط (1) ، اپراتور در فضای پیکربندی، اجازه دهید
در فضای پیکربندی، اجازه دهید حرکت مزدوج آن باشد . نگاشت حرکت مزدوج یک جبر دروغ ضد هم شکلی از براکت لی تا براکت پواسون است:
حرکت مزدوج آن باشد . نگاشت حرکت مزدوج یک جبر دروغ ضد هم شکلی از براکت لی تا براکت پواسون است:![{\displaystyle \{P_{X},P_{Y}\}=-P_{[X,Y]}.}](https://wikimedia.org/api/rest_v1/media/math/render/svg/1b807235723849825479543549bdc6d709f120bf)
 در فضای پیکربندی به عنوان
در فضای پیکربندی به عنوان جایی که
جایی که چارچوب مختصات محلی است. حرکت مزدوج به
چارچوب مختصات محلی است. حرکت مزدوج به
 توابع تکانه با مختصات مزدوج هستند. یکی پس از آن، برای یک نقطه
توابع تکانه با مختصات مزدوج هستند. یکی پس از آن، برای یک نقطه در فضای فاز ،
در فضای فاز ،![{\displaystyle {\begin{aligned}\{P_{X},P_{Y}\}(q,p)&=\sum _{i}\sum _{j}\left\{X^{i} (q)\;p_{i}،Y^{j}(q)\;p_{j}\right\}\\&=\sum _{ij}p_{i}Y^{j}(q) {\frac {\partial X^{i}}{\partial q^{j}}}-p_{j}X^{i}(q){\frac {\partial Y^{j}}{\partial q^{i}}}\\&=-\sum _{i}p_{i}\;[X,Y]^{i}(q)\\&=-P_{[X,Y]}( q,p).\end{تراز شده}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/0ba5433f5ac6a3170d8f796bd25cd1ec64a47f0b)
 به معنای
به معنای متغیرهای مستقل: تکانه
متغیرهای مستقل: تکانه ; موقعیت،
; موقعیت، ; و زمان،
; و زمان،


 و
و به عنوان یکی از مختصات تکانه متعارف جدید.
به عنوان یکی از مختصات تکانه متعارف جدید. تابع دیگری است که به فضا و زمان فاز بستگی دارد. قوانین زیر برای هر سه تابع صادق است
تابع دیگری است که به فضا و زمان فاز بستگی دارد. قوانین زیر برای هر سه تابع صادق است فضا و زمان فاز:
فضا و زمان فاز:


 در فضای فاز ثابت است (اما ممکن است به زمان بستگی داشته باشد).
در فضای فاز ثابت است (اما ممکن است به زمان بستگی داشته باشد). برای هرچی
برای هرچی در فضای فاز ، با توجه به دو تابع
در فضای فاز ، با توجه به دو تابع و
و ، [یادداشت 1] براکت پواسون شکل می گیرد
، [یادداشت 1] براکت پواسون شکل می گیرد
 جایی که
جایی که دلتای کرونکر است .
دلتای کرونکر است . تابعی در مسیر منیفولد راه حل است. سپس از قانون زنجیره چند متغیره ،
تابعی در مسیر منیفولد راه حل است. سپس از قانون زنجیره چند متغیره ،
 و
و برای حل معادلات همیلتون . به این معنا که،
برای حل معادلات همیلتون . به این معنا که،

 می تواند به عنوان مختصات براکت عمل کند. براکت های پواسون متغیرهای متعارفی هستند .
می تواند به عنوان مختصات براکت عمل کند. براکت های پواسون متغیرهای متعارفی هستند .
 ، گاهی اوقات به عنوان Liouvillian شناخته می شود (به قضیه لیوویل (همیلتونی) مراجعه کنید ).
، گاهی اوقات به عنوان Liouvillian شناخته می شود (به قضیه لیوویل (همیلتونی) مراجعه کنید ).
 ثابت کیهانی است ،آر
ثابت کیهانی است ،آر به عمل اینشتین-هیلبرت معروف است . تانسور ریمان تانسور نیروی جزر و مدی است و از نمادهای کریستوفل و مشتقات نمادهای کریستوفل ساخته شده است که ارتباط متریک را در فضازمان تعریف می کند. خود میدان گرانشی از نظر تاریخی به تانسور متریک نسبت داده می شد. دیدگاه مدرن این است که ارتباط "بنیادی تر" است. این به دلیل درک این است که می توان اتصالات را با پیچش غیر صفر نوشت . اینها متریک را بدون تغییر یک بیت هندسه تغییر می دهند. در مورد "جهت واقعی گرانش" (مثلاً روی سطح زمین، به سمت پایین است)، این از تانسور ریمان می آید: این چیزی است که "میدان نیروی گرانشی" را توصیف می کند که اجسام متحرک احساس می کنند و واکنش نشان می دهند. به. (این عبارت آخر باید واجد شرایط باشد: فی نفسه "میدان نیرو" وجود ندارد ؛ اجسام متحرک از ژئودزیک ها در منیفولد توصیف شده توسط اتصال پیروی می کنند. آنها در یک " خط مستقیم " حرکت می کنند.)
به عمل اینشتین-هیلبرت معروف است . تانسور ریمان تانسور نیروی جزر و مدی است و از نمادهای کریستوفل و مشتقات نمادهای کریستوفل ساخته شده است که ارتباط متریک را در فضازمان تعریف می کند. خود میدان گرانشی از نظر تاریخی به تانسور متریک نسبت داده می شد. دیدگاه مدرن این است که ارتباط "بنیادی تر" است. این به دلیل درک این است که می توان اتصالات را با پیچش غیر صفر نوشت . اینها متریک را بدون تغییر یک بیت هندسه تغییر می دهند. در مورد "جهت واقعی گرانش" (مثلاً روی سطح زمین، به سمت پایین است)، این از تانسور ریمان می آید: این چیزی است که "میدان نیروی گرانشی" را توصیف می کند که اجسام متحرک احساس می کنند و واکنش نشان می دهند. به. (این عبارت آخر باید واجد شرایط باشد: فی نفسه "میدان نیرو" وجود ندارد ؛ اجسام متحرک از ژئودزیک ها در منیفولد توصیف شده توسط اتصال پیروی می کنند. آنها در یک " خط مستقیم " حرکت می کنند.) به عنوان میدان، معادلات میدان انیشتین را به دست می آوریم
به عنوان میدان، معادلات میدان انیشتین را به دست می آوریم

 جایی که
جایی که . این باعث می شود مختصات انتگرال مستقل باشد، زیرا ریشه تعیین متریک معادل دترمینان ژاکوبین است . علامت منفی نتیجه امضای متریک است (تعیین کننده به خودی خود منفی است). [5] این نمونهای از فرم حجمی است که قبلاً مورد بحث قرار گرفت و در فضازمان غیر مسطح آشکار میشود.
. این باعث می شود مختصات انتگرال مستقل باشد، زیرا ریشه تعیین متریک معادل دترمینان ژاکوبین است . علامت منفی نتیجه امضای متریک است (تعیین کننده به خودی خود منفی است). [5] این نمونهای از فرم حجمی است که قبلاً مورد بحث قرار گرفت و در فضازمان غیر مسطح آشکار میشود. . لاگرانژی است
. لاگرانژی است
 . ما می توانیم معادلات میدان انیشتین را در حضور میدان EM با استفاده از این لاگرانژی تولید کنیم. تانسور انرژی - تکانه است
. ما می توانیم معادلات میدان انیشتین را در حضور میدان EM با استفاده از این لاگرانژی تولید کنیم. تانسور انرژی - تکانه است



 جایی که
جایی که مشتق کوواریانت است . برای فضای آزاد، می توانیم تانسور فعلی را برابر با صفر قرار دهیم،
مشتق کوواریانت است . برای فضای آزاد، می توانیم تانسور فعلی را برابر با صفر قرار دهیم، . حل معادلات انیشتین و ماکسول حول یک توزیع جرم کروی متقارن در فضای آزاد منجر به سیاهچاله باردار رایسنر-نوردستروم با عنصر خط تعیین کننده (نوشته شده در واحدهای طبیعی و با بار Q ) می شود: [5]
. حل معادلات انیشتین و ماکسول حول یک توزیع جرم کروی متقارن در فضای آزاد منجر به سیاهچاله باردار رایسنر-نوردستروم با عنصر خط تعیین کننده (نوشته شده در واحدهای طبیعی و با بار Q ) می شود: [5]
 چهار گرادیان را ببینید . μ شاخصی است که مقادیر 0 (برای مختصات زمانی) و 1، 2، 3 (برای مختصات مکانی) را می گیرد، بنابراین به طور دقیق فقط یک مشتق یا مختصات وجود دارد . به طور کلی، تمام مشتقات مکانی و زمانی در چگالی لاگرانژی ظاهر می شوند، به عنوان مثال در مختصات دکارتی، چگالی لاگرانژی به شکل کامل است:
چهار گرادیان را ببینید . μ شاخصی است که مقادیر 0 (برای مختصات زمانی) و 1، 2، 3 (برای مختصات مکانی) را می گیرد، بنابراین به طور دقیق فقط یک مشتق یا مختصات وجود دارد . به طور کلی، تمام مشتقات مکانی و زمانی در چگالی لاگرانژی ظاهر می شوند، به عنوان مثال در مختصات دکارتی، چگالی لاگرانژی به شکل کامل است: در اینجا ما همان چیزی را می نویسیم، اما از ∇ برای مخفف کردن تمام مشتقات فضایی به عنوان بردار استفاده می کنیم.
در اینجا ما همان چیزی را می نویسیم، اما از ∇ برای مخفف کردن تمام مشتقات فضایی به عنوان بردار استفاده می کنیم. را می توان نوشت (با استفاده از واحدهای طبیعی c = ε 0 = 1 ) به صورت
را می توان نوشت (با استفاده از واحدهای طبیعی c = ε 0 = 1 ) به صورت![{\displaystyle {\mathcal {S}}[\mathbf {A} ]=-\int _{\mathcal {M}}\left({\frac {1}{2}}\,\mathbf {F} \ wedge \ast \mathbf {F} -\mathbf {A} \wedge \ast \mathbf {J} \راست).}](https://wikimedia.org/api/rest_v1/media/math/render/svg/8de2c4985590ad977943d0feb4ddf40ea55dd83c)

 زیرا F یک شکل دقیق است .
زیرا F یک شکل دقیق است . هر چند مورد کلی مورد توجه عموم است. در همه موارد، نیازی به انجام هیچ گونه کوانتیزه ای نیست. اگرچه معادلات یانگ-میلز از نظر تاریخی ریشه در نظریه میدان کوانتومی دارند، معادلات فوق کاملا کلاسیک هستند. [2] [3]
هر چند مورد کلی مورد توجه عموم است. در همه موارد، نیازی به انجام هیچ گونه کوانتیزه ای نیست. اگرچه معادلات یانگ-میلز از نظر تاریخی ریشه در نظریه میدان کوانتومی دارند، معادلات فوق کاملا کلاسیک هستند. [2] [3]![{\displaystyle {\mathcal {S}}[\mathbf {A} ]=\int _{\mathcal {M}}\mathrm {tr} \left(\mathbf {A} \wedge d\mathbf {A} + {\frac {2}{3}}\mathbf {A} \wedge \mathbf {A} \wedge \mathbf {A} \راست).}](https://wikimedia.org/api/rest_v1/media/math/render/svg/09f106f7abb66f2f598299bd4ca2b6ab4cb66e21)
 جایی که
جایی که بخشی از یک بسته بردار با فیبر است
بخشی از یک بسته بردار با فیبر است . را
. را قدرت میدانی آن است. معادلات اویلر -لاگرانژ برای تابع گینزبورگ-لاندو معادلات یانگ-میلز هستند.
قدرت میدانی آن است. معادلات اویلر -لاگرانژ برای تابع گینزبورگ-لاندو معادلات یانگ-میلز هستند.
 جایی که
جایی که عملگر ستاره هاج است ، یعنی تانسور کاملاً ضد متقارن. این معادلات ارتباط نزدیکی با معادلات یانگ – میلز – هیگز دارند . لاگرانژی دیگر در نظریه سایبرگ-ویتن یافت می شود .
عملگر ستاره هاج است ، یعنی تانسور کاملاً ضد متقارن. این معادلات ارتباط نزدیکی با معادلات یانگ – میلز – هیگز دارند . لاگرانژی دیگر در نظریه سایبرگ-ویتن یافت می شود . جایی که
جایی که الحاق دیراک آن است و
الحاق دیراک آن است و نماد اسلش فاینمن برای است
نماد اسلش فاینمن برای است . در نظریه کلاسیک نیازی به تمرکز بر اسپینورهای دیراک نیست. اسپینورهای ویل پایه کلی تری را ارائه می دهند. آنها را می توان مستقیماً از جبر کلیفورد فضازمان ساخت . کارهای ساختمانی در هر تعداد ابعاد، [3] و اسپینورهای دیراک به عنوان یک مورد خاص ظاهر می شوند. اسپینورهای ویل این مزیت اضافی را دارند که میتوانند در یک ویلبین برای متریک در منیفولد ریمانی استفاده شوند . این مفهوم ساختار چرخشی را امکانپذیر میسازد ، که، به طور کلی، راهی برای فرمولبندی اسپینورها به طور مداوم در یک فضازمان منحنی است.
. در نظریه کلاسیک نیازی به تمرکز بر اسپینورهای دیراک نیست. اسپینورهای ویل پایه کلی تری را ارائه می دهند. آنها را می توان مستقیماً از جبر کلیفورد فضازمان ساخت . کارهای ساختمانی در هر تعداد ابعاد، [3] و اسپینورهای دیراک به عنوان یک مورد خاص ظاهر می شوند. اسپینورهای ویل این مزیت اضافی را دارند که میتوانند در یک ویلبین برای متریک در منیفولد ریمانی استفاده شوند . این مفهوم ساختار چرخشی را امکانپذیر میسازد ، که، به طور کلی، راهی برای فرمولبندی اسپینورها به طور مداوم در یک فضازمان منحنی است.
 تانسور الکترومغناطیسی است ، D مشتق کوواریانس سنج است ، و/
تانسور الکترومغناطیسی است ، D مشتق کوواریانس سنج است ، و/ نماد فاینمن برای است
نماد فاینمن برای است با
با جایی که
جایی که چهار پتانسیل الکترومغناطیسی است . اگرچه کلمه "کوانتوم" در بالا آمده است، اما این یک مصنوع تاریخی است. تعریف میدان دیراک به هیچوجه نیاز به کمیتسازی ندارد، میتوان آن را بهعنوان یک میدان کاملاً کلاسیک از اسپینورهای ضد رفتوآمد ویل نوشت که از اصول اولیه جبر کلیفورد ساخته شده است . [3] فرمول کلاسیک کامل گیج ثابت در Bleecker ارائه شده است. [2]
چهار پتانسیل الکترومغناطیسی است . اگرچه کلمه "کوانتوم" در بالا آمده است، اما این یک مصنوع تاریخی است. تعریف میدان دیراک به هیچوجه نیاز به کمیتسازی ندارد، میتوان آن را بهعنوان یک میدان کاملاً کلاسیک از اسپینورهای ضد رفتوآمد ویل نوشت که از اصول اولیه جبر کلیفورد ساخته شده است . [3] فرمول کلاسیک کامل گیج ثابت در Bleecker ارائه شده است. [2]
 تانسور قدرت میدان گلوئون است . همانطور که در مورد الکترودینامیک بالا، ظاهر کلمه "کوانتوم" در بالا فقط توسعه تاریخی آن را تایید می کند. لاگرانژی و تغییر ناپذیری گیج آن را می توان به شیوه ای کاملا کلاسیک فرموله کرد و با آن رفتار کرد. [2] [3]
تانسور قدرت میدان گلوئون است . همانطور که در مورد الکترودینامیک بالا، ظاهر کلمه "کوانتوم" در بالا فقط توسعه تاریخی آن را تایید می کند. لاگرانژی و تغییر ناپذیری گیج آن را می توان به شیوه ای کاملا کلاسیک فرموله کرد و با آن رفتار کرد. [2] [3] با عبارتهایی که شامل چگالی بار پیوسته ρ در A·s·m -3 و چگالی جریان هستند جایگزین میشوند.
با عبارتهایی که شامل چگالی بار پیوسته ρ در A·s·m -3 و چگالی جریان هستند جایگزین میشوند. در A·m −2 . چگالی لاگرانژی حاصل برای میدان الکترومغناطیسی به صورت زیر است:
در A·m −2 . چگالی لاگرانژی حاصل برای میدان الکترومغناطیسی به صورت زیر است:

 ، ما گرفتیم
، ما گرفتیم
 در واقع حاصل ضرب درونی دو چهار بردار است . ما چگالی بار را در بردار 4 فعلی و پتانسیل را در بردار 4 بالقوه بسته بندی می کنیم. این دو بردار جدید هستند
در واقع حاصل ضرب درونی دو چهار بردار است . ما چگالی بار را در بردار 4 فعلی و پتانسیل را در بردار 4 بالقوه بسته بندی می کنیم. این دو بردار جدید هستند
 علاوه بر این، میتوانیم میدانهای E و B را در آنچه به عنوان تانسور الکترومغناطیسی شناخته میشود، بسته بندی کنیم
علاوه بر این، میتوانیم میدانهای E و B را در آنچه به عنوان تانسور الکترومغناطیسی شناخته میشود، بسته بندی کنیم  . ما این تانسور را به صورت تعریف می کنیم
. ما این تانسور را به صورت تعریف می کنیم اصطلاحی که ما به دنبال آن هستیم معلوم می شود
اصطلاحی که ما به دنبال آن هستیم معلوم می شود



 دارای واحدهای J·m −3 است . در اینجا عبارت اندرکنش شامل یک چگالی جرم پیوسته ρ در kg·m -3 است . این امر ضروری است زیرا استفاده از یک منبع نقطه ای برای یک میدان منجر به مشکلات ریاضی می شود.
دارای واحدهای J·m −3 است . در اینجا عبارت اندرکنش شامل یک چگالی جرم پیوسته ρ در kg·m -3 است . این امر ضروری است زیرا استفاده از یک منبع نقطه ای برای یک میدان منجر به مشکلات ریاضی می شود. ، با
، با ارائه یک اصطلاح جنبشی، و تعامل
ارائه یک اصطلاح جنبشی، و تعامل اصطلاح بالقوه همچنین نظریه گرانش نوردستروم را ببینید که چگونه می توان آن را برای مقابله با تغییرات در طول زمان اصلاح کرد. این شکل در مثال بعدی نظریه میدان اسکالر تکرار شده است.
اصطلاح بالقوه همچنین نظریه گرانش نوردستروم را ببینید که چگونه می توان آن را برای مقابله با تغییرات در طول زمان اصلاح کرد. این شکل در مثال بعدی نظریه میدان اسکالر تکرار شده است.


 را می توان به صورت نوشتاری
را می توان به صورت نوشتاری
 برای عبارت جنبشی یک ذره نقطه آزاد که به صورت نوشته شده است
برای عبارت جنبشی یک ذره نقطه آزاد که به صورت نوشته شده است . نظریه اسکالر تعمیم تئوری میدان یک ذره است که در یک پتانسیل حرکت می کند. وقتی که
. نظریه اسکالر تعمیم تئوری میدان یک ذره است که در یک پتانسیل حرکت می کند. وقتی که جایی که
جایی که دیفرانسیل است . یک عبارت معادل است
دیفرانسیل است . یک عبارت معادل است
 متریک ریمانی در منیفولد میدان. یعنی زمین ها
متریک ریمانی در منیفولد میدان. یعنی زمین ها فقط مختصات محلی در نمودار مختصات منیفولد هستند. سومین شکل رایج این است
فقط مختصات محلی در نمودار مختصات منیفولد هستند. سومین شکل رایج این است
 و
و ، گروه لی SU(N) . این گروه را می توان با هر گروه Lie یا، به طور کلی، با یک فضای متقارن جایگزین کرد . ردیابی فقط شکل کشتار در پنهان است. فرم Killing یک فرم درجه دوم را در منیفولد میدان ارائه میکند، سپس لاگرانژی فقط عقبنشینی این فرم است. متناوبا، لاگرانژ را می توان به عنوان عقب نشینی فرم مورر-کارتان به فضازمان پایه نیز دید.
، گروه لی SU(N) . این گروه را می توان با هر گروه Lie یا، به طور کلی، با یک فضای متقارن جایگزین کرد . ردیابی فقط شکل کشتار در پنهان است. فرم Killing یک فرم درجه دوم را در منیفولد میدان ارائه میکند، سپس لاگرانژی فقط عقبنشینی این فرم است. متناوبا، لاگرانژ را می توان به عنوان عقب نشینی فرم مورر-کارتان به فضازمان پایه نیز دید. به طوری که معادلات حرکت با استفاده از یک اصل عمل به دست می آید که به صورت زیر نوشته می شود:
به طوری که معادلات حرکت با استفاده از یک اصل عمل به دست می آید که به صورت زیر نوشته می شود:
 ، تابعی از متغیرهای وابسته است
، تابعی از متغیرهای وابسته است ، مشتقات آنها و خود s
، مشتقات آنها و خود s![{\displaystyle {\mathcal {S}}\left[\varphi _{i}\right]=\int {{\mathcal {L}}\left(\varphi _{i}(s),\left\{ {\frac {\partial \varphi _{i}(s)}{\partial s^{\alpha }}}\right\},\{s^{\alpha }\}\right)\,\mathrm { d} ^{n}s}،}](https://wikimedia.org/api/rest_v1/media/math/render/svg/3b611482dbb4372e4099dbd2a0d1d85398e33625)
 ; و s = { s α } مجموعه n متغیر مستقل سیستم از جمله متغیر زمان را نشان می دهد و با α = 1، 2، 3، ...، n نمایه می شود . حروف خوشنویسی،
; و s = { s α } مجموعه n متغیر مستقل سیستم از جمله متغیر زمان را نشان می دهد و با α = 1، 2، 3، ...، n نمایه می شود . حروف خوشنویسی، فرم حجم تابع میدان است ، یعنی اندازه دامنه تابع میدان.
فرم حجم تابع میدان است ، یعنی اندازه دامنه تابع میدان.

 ، سپس منیفولد میدان است
، سپس منیفولد میدان است . اگر میدان یک میدان برداری حقیقی باشد ، منیفولد میدان به هم شکل است
. اگر میدان یک میدان برداری حقیقی باشد ، منیفولد میدان به هم شکل است
![{\displaystyle {\mathcal {S}}[\varphi ]=\int {\mathcal {L}}(\varphi ,{\boldsymbol {\nabla }}\varphi ,\partial \varphi /\partial t,\mathbf {x} ,t)\,\mathrm {d} ^{3}\mathbf {x} \,\mathrm {d} t.}](https://wikimedia.org/api/rest_v1/media/math/render/svg/d3d560ca7f50accea120979fd0a8fff5707979f6)

 . این تضمین می کند که عمل تحت تبدیل مختصات کلی ثابت است. در ادبیات ریاضی، فضا-زمان یک منیفولد ریمانی در نظر گرفته می شود م
. این تضمین می کند که عمل تحت تبدیل مختصات کلی ثابت است. در ادبیات ریاضی، فضا-زمان یک منیفولد ریمانی در نظر گرفته می شود م
 ضرب خارجی است و
ضرب خارجی است و جذر تعیین کننده است
جذر تعیین کننده است از تانسور متریک
از تانسور متریک  و بنابراین معمولاً هنگام بحث از نظریه میدان در فضازمان مسطح حذف می شود. به همین ترتیب، استفاده از نمادهای ضرب خارجی ای بینش بیشتری را در مورد مفهوم معمولی حجم در حساب چند متغیره ارائه نمی دهد، و بنابراین این نمادها نیز به همین ترتیب حذف می شوند. برخی از کتاب های درسی قدیمی تر، به عنوان مثال، لاندو و لیفشیتز می نویسند-
و بنابراین معمولاً هنگام بحث از نظریه میدان در فضازمان مسطح حذف می شود. به همین ترتیب، استفاده از نمادهای ضرب خارجی ای بینش بیشتری را در مورد مفهوم معمولی حجم در حساب چند متغیره ارائه نمی دهد، و بنابراین این نمادها نیز به همین ترتیب حذف می شوند. برخی از کتاب های درسی قدیمی تر، به عنوان مثال، لاندو و لیفشیتز می نویسند- برای فرم حجم، از آنجایی که علامت منهای برای تانسورهای متریک با امضا (+---) یا (-+++) مناسب است (زیرا در هر صورت، تعیین کننده منفی است). هنگام بحث در مورد نظریه میدان در منیفولدهای کلی ریمانی، فرم حجمی معمولاً با علامت اختصاری نوشته می شود.
برای فرم حجم، از آنجایی که علامت منهای برای تانسورهای متریک با امضا (+---) یا (-+++) مناسب است (زیرا در هر صورت، تعیین کننده منفی است). هنگام بحث در مورد نظریه میدان در منیفولدهای کلی ریمانی، فرم حجمی معمولاً با علامت اختصاری نوشته می شود. جایی که
جایی که ستاره هاج است . به این معنا که،
ستاره هاج است . به این معنا که،

 مکرر دیده می شود. گمراه نشوید: فرم حجمی به طور ضمنی در انتگرال بالا وجود دارد، حتی اگر به صراحت نوشته نشده باشد.
مکرر دیده می شود. گمراه نشوید: فرم حجمی به طور ضمنی در انتگرال بالا وجود دارد، حتی اگر به صراحت نوشته نشده باشد.





![1/(h_1h_2h_3)partial/(partialu_i)((h_1h_2h_3)/(h_i^2)partial/(partialu_i)) =(g(u_(i+1)،u_(i+2)))/(h_1h_2h_3)جزئی /(partialu_i)[f_i(u_i)partial/(partialu_i)] =1/(h_i^2f_i)partial/(partialu_i)(f_ipartial/(partialu_i))](https://mathworld.wolfram.com/images/equations/StaeckelDeterminant/NumberedEquation3.svg)






















 در این وبلاگ به ریاضیات و کاربردهای آن و تحقیقات در آنها پرداخته می شود. مطالب در این وبلاگ ترجمه سطحی و اولیه است و کامل نیست.در صورتی سوال یا نظری در زمینه ریاضیات دارید مطرح نمایید .در صورت امکان به آن می پردازم. من دوست دارم برای یافتن پاسخ به سوالات و حل پروژه های علمی با دیگران همکاری نمایم.در صورتی که شما هم بامن هم عقیده هستید با من تماس بگیرید.
در این وبلاگ به ریاضیات و کاربردهای آن و تحقیقات در آنها پرداخته می شود. مطالب در این وبلاگ ترجمه سطحی و اولیه است و کامل نیست.در صورتی سوال یا نظری در زمینه ریاضیات دارید مطرح نمایید .در صورت امکان به آن می پردازم. من دوست دارم برای یافتن پاسخ به سوالات و حل پروژه های علمی با دیگران همکاری نمایم.در صورتی که شما هم بامن هم عقیده هستید با من تماس بگیرید.