ریاضیات | نظریه مجموعه ها

قضیه

از ویکیپدیا، دانشنامه آزاد

نباید با Teorema , Theorema یا Theory اشتباه گرفت .

قضیه فیثاغورث حداقل 370 اثبات شناخته شده دارد. [1]

در ریاضیات ، قضیه عبارتی است که ثابت شده یا قابل اثبات است. [a] [2] [ 3] اثبات یک قضیه یک استدلال منطقی است که از قواعد استنتاج یک سیستم قیاسی استفاده می کند تا ثابت کند که قضیه نتیجه منطقی بدیهیات و قضایای قبلاً اثبات شده است.

در ریاضیات رایج، بدیهیات و قواعد استنتاج معمولاً به صورت ضمنی رها می‌شوند، و در این مورد، آنها تقریباً همیشه همان نظریه مجموعه‌های زرملو-فرانکل با اصل انتخاب (ZFC) یا یک نظریه کم‌قدرت‌تر هستند، مانند حساب پیانو . [ب] به طور کلی، ادعایی که صریحاً قضیه نامیده می‌شود، نتیجه اثبات شده‌ای است که پیامد فوری سایر قضایای شناخته شده نیست. علاوه بر این، بسیاری از نویسندگان تنها مهم ترین نتایج را به عنوان قضایا واجد شرایط می دانند و از اصطلاحات لم ، گزاره و نتیجه برای قضایای کم اهمیت استفاده می کنند.

در منطق ریاضی ، مفاهیم قضایا و برهان ها به منظور امکان استدلال ریاضی درباره آنها رسمیت یافته است. در این زمینه، گزاره‌ها به فرمول‌های خوش‌تشکیل برخی از زبان‌های رسمی تبدیل می‌شوند . یک نظریه شامل برخی از گزاره های پایه به نام بدیهیات ، و برخی از قواعد استنتاج (که گاهی در بدیهیات گنجانده می شود) است. قضایای نظریه گزاره هایی هستند که با استفاده از قواعد استنباط می توان از بدیهیات استخراج کرد. [ج] این رسمی‌سازی منجر به نظریه اثبات شد ، که امکان اثبات قضایای کلی در مورد قضایا و برهان‌ها را فراهم می‌کند. به‌ویژه، قضایای ناتمامی گودل نشان می‌دهد که هر نظریه ثابتی که شامل اعداد طبیعی است، گزاره‌های درستی درباره اعداد طبیعی دارد که قضایای نظریه نیستند (یعنی نمی‌توان آنها را در داخل نظریه اثبات کرد).

از آنجایی که بدیهیات غالباً انتزاعی از خصوصیات جهان فیزیکی هستند ، ممکن است قضایا بیانگر مقداری حقیقت در نظر گرفته شوند، اما برخلاف تصور قانون علمی که تجربی است ، توجیه صدق یک قضیه صرفاً قیاسی است . [6] [7]

قضیه و حقیقت [ ویرایش ]

تا پایان قرن نوزدهم و بحران بنیادی ریاضیات ، همه نظریه‌های ریاضی از چند ویژگی اساسی ساخته می‌شدند که بدیهی تلقی می‌شدند. به عنوان مثال، حقایقی که هر عدد طبیعی یک جانشین دارد، و اینکه دقیقاً یک خط وجود دارد که از دو نقطه مشخص می گذرد. این خصوصیات اساسی که کاملاً مشهود در نظر گرفته می شدند، اصول یا بدیهیات نامیده می شدند . برای مثال فرضیه های اقلیدس . همه قضایا با استفاده ضمنی یا صریح از این خصوصیات اساسی اثبات می‌شدند و به دلیل شواهد این ویژگی‌های اساسی، یک قضیه ثابت شده به عنوان حقیقت قطعی تلقی می‌شد، مگر اینکه اشتباهی در اثبات وجود داشته باشد. به عنوان مثال، مجموع زوایای داخلی یک مثلث برابر با 180 درجه است و این به عنوان یک واقعیت غیرقابل تردید در نظر گرفته شد.

یکی از جنبه های بحران بنیادی ریاضیات کشف هندسه های غیر اقلیدسی بود که به هیچ تناقضی منجر نمی شود، اگرچه در چنین هندسه هایی مجموع زوایای یک مثلث با 180 درجه متفاوت است. بنابراین، بسته به اینکه فرض پنجم اقلیدس فرض شود یا رد شود، خاصیت "مجموع زوایای یک مثلث برابر با 180 درجه است" صادق است یا نادرست. به طور مشابه، استفاده از ویژگی‌های اساسی «بدیهی» مجموعه‌ها منجر به تناقض پارادوکس راسل می‌شود . این با تشریح قوانینی که برای دستکاری مجموعه ها مجاز است حل شده است.

این بحران با بازنگری مجدد مبانی ریاضیات برای دقیق تر کردن آنها حل شده است . در این مبانی جدید، یک قضیه فرمول خوبی از یک نظریه ریاضی است که از بدیهیات و قواعد استنتاج نظریه قابل اثبات است . بنابراین، قضیه فوق در مورد مجموع زوایای مثلث به این صورت می شود: بر اساس بدیهیات و قواعد استنتاج هندسه اقلیدسی ، مجموع زوایای داخلی مثلث برابر با 180 درجه است . به طور مشابه، پارادوکس راسل ناپدید می شود زیرا در یک نظریه مجموعه بدیهی شده، مجموعه همه مجموعه ها را نمی توان با یک فرمول خوب بیان کرد. به‌طور دقیق‌تر، اگر بتوان مجموعه همه مجموعه‌ها را با یک فرمول خوب بیان کرد، این نشان می‌دهد که این نظریه ناسازگار است و هر ادعای خوب شکل‌گرفته و همچنین نفی آن، یک قضیه است.

در این زمینه، اعتبار یک قضیه تنها به صحت اثبات آن بستگی دارد. مستقل از حقیقت یا حتی اهمیت بدیهیات است. این بدان معنا نیست که اهمیت بدیهیات جالب نیست، بلکه فقط به این معنی است که اعتبار یک قضیه مستقل از اهمیت بدیهیات است. این استقلال ممکن است با اجازه دادن به استفاده از نتایج برخی حوزه‌های ریاضی در حوزه‌های ظاهراً نامرتبط مفید باشد.

یک پیامد مهم این طرز تفکر در مورد ریاضیات این است که اجازه می دهد تا نظریه ها و قضایای ریاضی را به عنوان اشیاء ریاضی تعریف کنیم و قضایا را در مورد آنها اثبات کنیم. به عنوان مثال قضایای ناتمامی گودل هستند . به طور خاص، ادعاهای کاملاً شکل‌گیری شده‌ای وجود دارد که می‌توان ثابت کرد که قضیه‌ای از نظریه محیط نیستند، اگرچه می‌توان آنها را در یک نظریه گسترده‌تر اثبات کرد. به عنوان مثال قضیه گودشتاین است که می توان آن را در حساب Peano بیان کرد ، اما ثابت شده است که در حساب Peano قابل اثبات نیست. با این حال، در برخی از نظریه‌های عمومی‌تر، مانند نظریه مجموعه‌های زرملو-فرانکل، قابل اثبات است .

ملاحظات معرفتی [ ویرایش ]

بسیاری از قضایای ریاضی گزاره‌های شرطی هستند که برهان‌های آنها از شرایطی که به عنوان فرضیه یا مقدمات شناخته می‌شوند، نتیجه‌گیری می‌کنند . در پرتو تفسیر برهان به عنوان توجیه حقیقت، نتیجه اغلب به عنوان پیامد ضروری فرضیه ها در نظر گرفته می شود. یعنی اینکه نتیجه در صورت درست بودن فرضیه‌ها صادق است - بدون هیچ فرضی دیگری. با این حال، مشروط می تواند در سیستم های قیاسی خاص ، بسته به معانی اختصاص داده شده به قواعد اشتقاق و نماد شرطی (مثلاً منطق غیر کلاسیک ) متفاوت تفسیر شود.

اگرچه قضایا را می توان به شکل کاملاً نمادین نوشت (مثلاً به عنوان گزاره هایی در حساب گزاره ای )، آنها اغلب به طور غیر رسمی در یک زبان طبیعی مانند انگلیسی برای خوانایی بهتر بیان می شوند. همین امر در مورد براهین نیز صدق می‌کند، که اغلب به‌عنوان استدلال‌های غیررسمی سازمان‌یافته و واضح بیان می‌شوند که قصد دارند خوانندگان را به صحت بیان قضیه بدون تردید متقاعد کنند و اصولاً می‌توان از آن‌ها یک اثبات نمادین رسمی ساخت.

علاوه بر خوانایی بهتر، بررسی استدلال‌های غیررسمی معمولاً آسان‌تر از استدلال‌های صرفاً نمادین است - در واقع، بسیاری از ریاضیدانان ترجیح می‌دهند برهانی را بیان کنند که نه تنها اعتبار یک قضیه را نشان می‌دهد، بلکه به نوعی توضیح می‌دهد که چرا واضح است. درست است، واقعی. در برخی موارد، حتی ممکن است بتوان یک قضیه را با استفاده از تصویر به عنوان اثبات آن اثبات کرد.

از آنجایی که قضایا در هسته ریاضیات قرار دارند، در زیبایی شناسی آن نیز نقش اساسی دارند . قضایا اغلب به‌عنوان «بی‌اهمیت» یا «مشکل» یا «عمیق» یا حتی «زیبا» توصیف می‌شوند. این قضاوت های ذهنی نه تنها از فردی به فرد دیگر، بلکه با زمان و فرهنگ نیز متفاوت است: به عنوان مثال، به عنوان یک دلیل به دست می آید، ساده شده یا بهتر درک می شود، قضیه ای که زمانی دشوار بود ممکن است بی اهمیت شود. [8] از سوی دیگر، یک قضیه عمیق ممکن است به سادگی بیان شود، اما اثبات آن ممکن است شامل ارتباطات شگفت‌انگیز و ظریف بین حوزه‌های متفاوت ریاضیات باشد. آخرین قضیه فرما یک مثال شناخته شده از چنین قضیه ای است. [9]

گزارش غیررسمی قضایا [ ویرایش ]

از نظر منطقی ، بسیاری از قضایا به شکل شرطی اندیکاتور هستند : اگر A، پس B. چنین قضیه ای B را اثبات نمی کند - فقط B نتیجه ضروری A است .در این مورد، A فرضیه قضیه («فرضیه» در اینجا به معنای چیزی بسیار متفاوت از حدس است ) و B نتیجه‌گیری قضیه نامیده می‌شود . این دو با هم (بدون اثبات) گزاره یا گزاره قضیه نامیده می شوند (مثلاً " اگر A، آنگاه B " گزاره است ). به طور متناوب، A و B را می توان به ترتیب مقدم و نتیجه نیز نامید . [10] قضیه "اگر n یک عدد طبیعی زوج است ، پس n / 2 یک عدد طبیعی است" یک مثال معمولی است که در آن فرضیه " n یک عدد طبیعی زوج است" و نتیجه گیری " n / 2 است " همچنین یک عدد طبیعی".

برای اینکه یک قضیه ثابت شود، در اصل باید به عنوان یک گزاره دقیق و صوری قابل بیان باشد. با این حال، قضایا معمولاً به‌جای شکلی کاملاً نمادین به زبان طبیعی بیان می‌شوند – با این پیش‌فرض که می‌توان یک گزاره رسمی را از حالت غیررسمی استخراج کرد.

در ریاضیات رایج است که تعدادی از فرضیه ها را در یک زبان مشخص انتخاب می کنند و اعلام می کنند که این نظریه شامل تمام گزاره های قابل اثبات از این فرضیه ها است. این فرضیه ها اساس نظریه را تشکیل می دهند و بدیهیات یا فرضیه ها نامیده می شوند. رشته ریاضیات معروف به نظریه اثبات ، زبان های رسمی، بدیهیات و ساختار برهان ها را مطالعه می کند.

یک نقشه مسطح با پنج رنگ به طوری که هیچ دو منطقه با یک رنگ به هم نمی رسند. در واقع می توان آن را به این روش تنها با چهار رنگ رنگ آمیزی کرد. قضیه چهار رنگ بیان می کند که چنین رنگ آمیزی برای هر نقشه مسطحی امکان پذیر است، اما هر اثبات شناخته شده شامل یک جستجوی محاسباتی است که برای بررسی دستی بسیار طولانی است.

برخی از قضایا « بی‌اهمیت » هستند، به این معنا که از تعاریف، بدیهیات و قضایای دیگر به‌طریق آشکاری تبعیت می‌کنند و حاوی هیچ بینش شگفت‌انگیزی نیستند. از سوی دیگر، برخی ممکن است "عمیق" نامیده شوند، زیرا اثبات آنها ممکن است طولانی و دشوار باشد، شامل حوزه هایی از ریاضیات باشد که به طور سطحی از بیان خود قضیه متمایز است، یا ارتباطات شگفت انگیزی را بین حوزه های متفاوت ریاضیات نشان دهد. [11] یک قضیه ممکن است ساده باشد و در عین حال عمیق باشد. یک مثال عالی آخرین قضیه فرما است ، [9] و بسیاری از نمونه های دیگر از قضایای ساده اما عمیق در نظریه اعداد و ترکیبات ، در میان حوزه های دیگر وجود دارد .

قضایای دیگر دلیل شناخته شده ای دارند که نمی توان به راحتی آن را نوشت. بارزترین مثال ها قضیه چهار رنگ و حدس کپلر است . هر دوی این قضیه ها تنها با تقلیل آنها به یک جستجوی محاسباتی که سپس توسط یک برنامه کامپیوتری تأیید می شود، به درستی شناخته می شوند. در ابتدا، بسیاری از ریاضیدانان این شکل از اثبات را نپذیرفتند، اما به طور گسترده ای پذیرفته شده است. دورون زیلبرگر ، ریاضیدان، حتی تا آنجا پیش رفته است که ادعا می کند اینها احتمالاً تنها نتایج بی اهمیتی هستند که ریاضیدانان تا به حال ثابت کرده اند. [12] بسیاری از قضایای ریاضی را می توان به محاسبات ساده تر کاهش داد، از جمله هویت های چند جمله ای، هویت های مثلثاتی [13] و هویت های فرا هندسی. [14] [ صفحه مورد نیاز ]

ارتباط با نظریه های علمی [ ویرایش ]

در این بخش هیچ منبعی ذکر نشده است . لطفاً با افزودن نقل قول به منابع معتبر به بهبود این بخش کمک کنید . اطلاعات بدون مرجع ممکن است مشکل ایجاد کرده و پاک شوند . ( فوریه 2018 ) ( نحوه و زمان حذف این پیام الگو را بیاموزید )

قضایا در ریاضیات و نظریه ها در علم از نظر معرفت شناسی تفاوت اساسی دارند . یک نظریه علمی قابل اثبات نیست. ویژگی اصلی آن این است که ابطال پذیر است ، یعنی پیش بینی هایی در مورد جهان طبیعی انجام می دهد که با آزمایش ها قابل آزمایش هستند . هر گونه اختلاف بین پیش‌بینی و آزمایش، نادرستی نظریه علمی را نشان می‌دهد، یا حداقل دقت یا دامنه اعتبار آن را محدود می‌کند. از سوی دیگر، قضایای ریاضی، گزاره‌های صوری کاملاً انتزاعی هستند: اثبات یک قضیه نمی‌تواند شامل آزمایش‌ها یا شواهد تجربی دیگر باشد، به همان شیوه‌ای که چنین شواهدی برای حمایت از نظریه‌های علمی استفاده می‌شود. [6]

حدس کولاتز : یک راه برای نشان دادن پیچیدگی آن، گسترش تکرار از اعداد طبیعی به اعداد مختلط است. نتیجه یک فراکتال است که (براساس جهانی بودن ) شبیه مجموعه ماندلبروت است .

با این وجود، درجاتی از تجربه گرایی و جمع آوری داده ها در کشف قضایای ریاضی دخیل است. با ایجاد یک الگو، گاهی اوقات با استفاده از یک رایانه قدرتمند، ریاضیدانان ممکن است ایده ای در مورد آنچه باید اثبات کنند، و در برخی موارد حتی برنامه ای برای چگونگی شروع به انجام اثبات داشته باشند. همچنین می‌توان یک مثال متقابل پیدا کرد و بنابراین عدم امکان اثبات برای گزاره‌ای که بیان شد، و احتمالاً اشکال محدودی از گزاره اصلی را پیشنهاد کرد که ممکن است برهان‌های امکان‌پذیر داشته باشند.

برای مثال، هم حدس کولاتز و هم فرضیه ریمان مسائل حل نشده شناخته شده ای هستند. آنها به طور گسترده از طریق بررسی های تجربی مورد مطالعه قرار گرفته اند، اما اثبات نشده باقی می مانند. حدس Collatz برای مقادیر شروع تا حدود 2.88 × 10 18 تأیید شده است . فرضیه ریمان تأیید شده است که برای 10 تریلیون صفر اول غیر پیش پا افتاده تابع زتا صادق است . اگرچه اکثر ریاضیدانان می توانند این فرض را تحمل کنند که حدس و فرضیه درست است، هیچ یک از این گزاره ها اثبات شده تلقی نمی شوند.

چنین شواهدی دلیل نمی شود. به عنوان مثال، حدس مرتنز عبارتی است درباره اعداد طبیعی که اکنون نادرست بودن آن شناخته شده است، اما هیچ مثال متقابل صریحی (یعنی یک عدد طبیعی n که تابع مرتنز M ( n ) برابر یا بیشتر از جذر n باشد ) وجود ندارد. شناخته شده: همه اعداد کمتر از 10 14 دارای خاصیت مرتنز هستند و کوچکترین عددی که این خاصیت را ندارد تنها کمتر از نمایی 10 40 × 1.59 است که تقریباً 10 به توان 4.3 × 10 39 است . از آنجایی که تعداد ذرات جهان به طور کلی کمتر از 10 به توان 100 در نظر گرفته می شود (یک گوگول )، هیچ امیدی به یافتن یک مثال متقابل صریح با جستجوی جامع وجود ندارد .

کلمه "نظریه" در ریاضیات نیز وجود دارد تا مجموعه ای از بدیهیات، تعاریف و قضایای ریاضی را نشان دهد، مثلاً در نظریه گروه (به نظریه ریاضی مراجعه کنید ). در علم، به‌ویژه فیزیک، و مهندسی نیز «قضیه‌هایی» وجود دارد، اما آنها اغلب اظهارات و برهانی دارند که در آن مفروضات فیزیکی و شهود نقش مهمی دارند. بدیهیات فیزیکی که چنین «قضیه‌هایی» بر آن‌ها مبتنی است، خود قابل ابطال هستند.

اصطلاحات [ ویرایش ]

تعدادی اصطلاح مختلف برای گزاره های ریاضی وجود دارد. این عبارات بیانگر نقشی است که عبارات در یک موضوع خاص بازی می کنند. تمایز بین اصطلاحات مختلف گاهی اوقات کاملاً دلخواه است و استفاده از برخی اصطلاحات در طول زمان تکامل یافته است.

بدیهیات یا فرضیه یک فرض اساسی در مورد موضوع مطالعه است که بدون اثبات پذیرفته می شود. مفهوم مرتبط ، تعریفی است که معنای یک کلمه یا عبارت را بر حسب مفاهیم شناخته شده می دهد. هندسه کلاسیک بین بدیهیات که گزاره های کلی هستند تشخیص می دهد. و فرضیه ها، که گزاره هایی در مورد اجسام هندسی هستند. [15] از نظر تاریخی، بدیهیات به عنوان " بدیهی " تلقی می شدند. امروزه آنها صرفاً درست فرض می شوند.
حدس عبارت است از گزاره اثبات نشده ای که اعتقاد بر این است که درست باشد. حدس ها معمولاً در انظار عمومی ساخته می شوند و به نام سازنده آنها نامگذاری می شوند (مثلاً حدس گلدباخ و حدس کولاتز ). اصطلاح فرضیه نیز به این معنا به کار می رود (مثلاً فرضیه ریمان ) که نباید با «فرضیه» به عنوان مقدمه برهان اشتباه گرفته شود. اصطلاحات دیگری نیز در مواردی استفاده می‌شوند، برای مثال مشکل زمانی که افراد مطمئن نیستند که آیا این گفته باید درست باشد یا خیر. آخرین قضیه فرما از نظر تاریخی یک قضیه نامیده می شد، اگرچه برای قرن ها فقط یک حدس بود.
قضیه عبارتی است که صحت آن بر اساس بدیهیات و قضایای دیگر ثابت شده است.
گزاره، قضیه ای است با اهمیت کمتر، یا قضیه ای است که آنقدر ابتدایی یا بلافاصله بدیهی تلقی می شود که ممکن است بدون اثبات بیان شود. این را نباید با "گزاره" همانطور که در منطق گزاره ای استفاده می شود اشتباه گرفت . در هندسه کلاسیک، اصطلاح «گزاره» به گونه‌ای متفاوت به کار می‌رفت: در « عناصر اقلیدس » ( حدود 300 پیش از میلاد )، همه قضایا و ساختارهای هندسی بدون توجه به اهمیتشان «گزاره‌ها» نامیده می‌شدند.
لم یک «گزاره جانبی» است - گزاره ای با کاربرد کمی خارج از کاربرد آن در یک اثبات خاص. با گذشت زمان ممکن است یک لم اهمیت پیدا کند و به عنوان یک قضیه در نظر گرفته شود ، اگرچه اصطلاح "لم" معمولاً به عنوان بخشی از نام آن حفظ می شود (مثلا لم گاوس ، لم زورن و لم اساسی ).
نتیجه ، گزاره‌ای است که بلافاصله از یک قضیه یا بدیهیات دیگر، با اثبات کمی یا بدون نیاز به آن، پیروی می‌کند. [16] نتیجه ممکن است بیان مجدد یک قضیه به شکل ساده‌تر یا برای یک مورد خاص باشد : برای مثال، قضیه "همه زوایای داخلی مستطیل قائم الزاویه هستند " نتیجه ای دارد که "همه زوایای داخلی در یک مستطیل مربع ، زوایای قائم هستند " - مربع حالت خاصی از مستطیل است.
تعمیم یک قضیه، قضیه ای است با یک گزاره مشابه اما دامنه وسیع تری که از آن می توان قضیه اصلی را به عنوان یک مورد خاص ( نتیجه ) استنتاج کرد . [d]

اصطلاحات دیگری نیز ممکن است به دلایل تاریخی یا عرفی استفاده شوند، به عنوان مثال:

هویت ، قضیه‌ای است که برابری بین دو عبارت را بیان می‌کند، که برای هر ارزشی در قلمرو آن (مثلاً هویت بزو و هویت واندرموند ) وجود دارد.
یک قاعده قضیه ای است که یک فرمول مفید را ایجاد می کند (مثلا قانون بیز و قانون کرامر ).
یک قانون یا اصل قضیه ای است با کاربرد گسترده (مثلا قانون اعداد بزرگ ، قانون کسینوس ، قانون صفر-یک کلموگروف ، اصل هارناک ، اصل حداقل کران بالا ، و اصل چاله کبوتر ). [e]

چند قضیه معروف حتی نام‌های خاص‌تری دارند، برای مثال، الگوریتم تقسیم ، فرمول اویلر ، و پارادوکس Banach–Tarski .

طرح بندی [ ویرایش ]

یک قضیه و اثبات آن معمولاً به صورت زیر بیان می شود:

قضیه (نام شخصی که آن را ثابت کرده به همراه سال کشف یا انتشار اثبات)

بیان قضیه (گاهی اوقات گزاره نامیده می شود )

اثبات

شرح برهان

پایان

پایان اثبات ممکن است با حروف QED ( quod erat demonstrandum ) یا با یکی از علائم سنگ قبر ، مانند "□" یا "∎"، به معنای "پایان اثبات" که توسط پل هالموس پس از استفاده از آنها در مجلات برای نشان دادن پایان یک مقاله. [17]

سبک دقیق به نویسنده یا انتشارات بستگی دارد. بسیاری از نشریات دستورالعمل ها یا ماکروهایی را برای حروفچینی به سبک خانه ارائه می کنند .

معمولاً قبل از یک قضیه تعاریفی وجود دارد که معنای دقیق اصطلاحات به کار رفته در قضیه را توصیف می کند. همچنین معمول است که قبل از یک قضیه تعدادی گزاره یا لم وجود داشته باشد که سپس در اثبات استفاده می شود. با این حال، لم ها گاهی در اثبات یک قضیه گنجانده می شوند، یا با برهان های تودرتو، یا با براهین آنها پس از اثبات قضیه ارائه می شوند.

پیامدهای یک قضیه یا بین قضیه و اثبات ارائه می شود یا مستقیماً بعد از اثبات. گاهی اوقات، پیامدها برای خود دلایلی دارند که دلیل تبعیت آنها از قضیه را توضیح می دهد.

لور [ ویرایش ]

تخمین زده شده است که هر سال بیش از یک چهارم میلیون قضیه اثبات می شود. [18]

قصیده معروف "ریاضیدان وسیله ای برای تبدیل قهوه به قضایا است" احتمالاً به خاطر آلفرد رنی است ، اگرچه اغلب به همکار رنی، پل اردوس (و رنی ممکن است به اردوس فکر می کرد) که مشهور بود نسبت داده می شود. برای قضایای زیادی که تولید کرد، تعداد همکاری‌هایش و نوشیدن قهوه‌اش. [19]

طبقه بندی گروه های ساده محدود توسط برخی به عنوان طولانی ترین اثبات یک قضیه در نظر گرفته می شود. این شامل ده ها هزار صفحه در 500 مقاله مجله توسط حدود 100 نویسنده است. اعتقاد بر این است که این مقالات با هم یک اثبات کامل را ارائه می دهند، و چندین پروژه در حال انجام امیدوارند که این اثبات را کوتاه و ساده کنند. [20] قضیه دیگری از این نوع قضیه چهار رنگ است که اثبات تولید شده توسط رایانه برای انسان طولانی تر از آن است که بتواند آن را بخواند. این یکی از طولانی ترین برهان های شناخته شده یک قضیه است که بیانیه آن را می توان به راحتی توسط یک فرد غیر روحانی فهمید. [ نیازمند منبع ]

قضایا در منطق [ ویرایش ]

در منطق ریاضی ، نظریه رسمی مجموعه ای از جملات در یک زبان رسمی است . جمله یک فرمول خوب و بدون متغیر آزاد است. جمله ای که عضو یک نظریه است یکی از قضایای آن است و نظریه مجموعه قضایای آن است. معمولاً یک نظریه تحت رابطه نتیجه منطقی بسته است . برخی از حساب ها یک نظریه را تعریف می کنند که تحت رابطه پیامد معنایی بسته شود (⊨ $\مدل ها$ ، در حالی که دیگران آن را تحت پیامد نحوی یا رابطه مشتق پذیری بسته تعریف می کنند (⊢ $\vdash$ ). [21] [22] [23] [24] [25] [26] [27] [28] [29] [30]

این نمودار موجودیت های نحوی را نشان می دهد که می توانند از زبان های رسمی ساخته شوند . نمادها و رشته های نمادها ممکن است به طور کلی به فرمول های مزخرف و به خوبی شکل گرفته تقسیم شوند . یک زبان رسمی را می توان با مجموعه فرمول های خوش فرم آن یکسان تصور کرد. مجموعه فرمول های به خوبی شکل گرفته ممکن است به طور کلی به قضایا و غیر قضایا تقسیم شوند.

برای اینکه یک نظریه تحت یک رابطه مشتق پذیری بسته شود، باید با یک سیستم قیاسی مرتبط باشد که نحوه استخراج قضایا را مشخص کند. سیستم قیاسی ممکن است به صراحت بیان شود، یا ممکن است از متن روشن باشد. بسته شدن مجموعه خالی تحت رابطه نتیجه منطقی مجموعه ای را به دست می دهد که فقط شامل آن جملاتی است که قضایای سیستم قیاسی هستند.

در معنای وسیعی که این اصطلاح در منطق به کار می رود، لازم نیست یک قضیه درست باشد، زیرا نظریه ای که آن را در بر می گیرد ممکن است نسبت به معنایی معین، یا نسبت به تفسیر استاندارد زبان زیربنایی نامطلوب باشد. نظریه ای که ناسازگار است همه جملات را به عنوان قضیه دارد.

تعریف قضایا به عنوان جملات یک زبان رسمی در نظریه اثبات مفید است ، که شاخه ای از ریاضیات است که ساختار برهان های صوری و ساختار فرمول های قابل اثبات را مطالعه می کند. همچنین در نظریه مدل که به رابطه بین نظریه های رسمی و ساختارهایی می پردازد که قادر به ارائه یک معناشناسی برای آنها از طریق تفسیر است، اهمیت دارد .

اگرچه قضایا ممکن است جملات تفسیر نشده باشند، اما در عمل ریاضیدانان بیشتر به معانی جملات، یعنی به گزاره هایی که بیان می کنند، علاقه مند هستند. آنچه قضایای صوری را مفید و جالب می کند این است که ممکن است آنها را به عنوان گزاره های صادق و اشتقاقات آنها را دلیلی بر صدق آنها تفسیر کرد. قضیه ای که تفسیر آن یک گزاره درست در مورد یک نظام صوری است (بر خلاف درون یک نظام صوری) فرا قضیه نامیده می شود .

برخی از قضایای مهم در منطق ریاضی عبارتند از:

نحو و معناشناسی [ ویرایش ]

مقالات اصلی: نحو (منطق) و معنای رسمی (منطق)

مفهوم یک قضیه صوری اساساً نحوی است، برخلاف مفهوم یک قضیه صادق که معرف معناشناسی است . سیستم های قیاسی مختلف بسته به پیش فرض های قواعد اشتقاق (یعنی باور ، توجیه یا سایر روش ها ) می توانند تفاسیر دیگری ارائه دهند. استحکام یک سیستم رسمی بستگی به این دارد که آیا همه قضایای آن نیز معتبر هستند یا خیر . روایی فرمولی است که تحت هر تفسیر ممکن صادق است (مثلاً در منطق گزاره‌ای کلاسیک، اعتبارها توتولوژی هستند ). یک سیستم رسمی زمانی از نظر معنایی کامل در نظر گرفته می شود که تمام قضایای آن نیز توتولوژی باشند.

تفسیر یک قضیه صوری [ ویرایش ]

نوشتار اصلی: تفسیر (منطق)

قضایا و نظریه ها [ ویرایش ]

مقالات اصلی: تئوری و نظریه (منطق ریاضی)

https://en.wikipedia.org/wiki/Theorem

+ نوشته شده در چهارشنبه ششم دی ۱۴۰۲ ساعت 19:52 توسط علی رضا نقش نیلچی |

1-تقسیم بر صفر

از ویکیپدیا، دانشنامه آزاد

برای دیگر کاربردها، تقسیم بر صفر (ابهام‌زدایی) را ببینید .

این مقاله شامل فهرستی از مراجع عمومی است ، اما فاقد استنادهای درون خطی متناظر کافی است. لطفا با معرفی نقل قول های دقیق تر به بهبود این مقاله کمک کنید. ( آوریل 2016 ) ( نحوه و زمان حذف این پیام الگو را بیاموزید )

. وقتی x از سمت راست به 0 نزدیک می شود، y به بی نهایت نزدیک می شود. وقتی x از سمت چپ به 0 نزدیک می شود، y به بی نهایت منفی نزدیک می شود.

در ریاضیات ، تقسیم بر صفر ، تقسیمی است که در آن مخرج (مخرج) صفر است . چنین تقسیمی را می توان به طور رسمی به صورت بیان کرد ${\textstyle {\tfrac {a}{0}}}$ ، که در آن a سود سهام (عدد) است. در محاسبات معمولی ، این عبارت معنی ندارد، زیرا هیچ عددی وجود ندارد که وقتی در 0 ضرب شود ، یک (با فرضآ ${\textstyle a\neq 0}$ ) بنابراین، تقسیم بر صفر تعریف نشده است . از آنجایی که هر عددی که در صفر ضرب شود صفر است، عبارت ${\tfrac {0}{0}}$ همچنین تعریف نشده است. وقتی به صورت حد باشد ، شکلی نامعین است . از نظر تاریخی، یکی از اولین ارجاعات ثبت شده به عدم امکان ریاضی اختصاص یک مقدار بهآ ${\textstyle {\tfrac {a}{0}}}$ در نقد فیلسوف انگلیسی-ایرلندی جورج برکلی از حساب بی نهایت کوچک در سال 1734 در تحلیلگر ("اشباح مقادیر از دست رفته") آمده است. [1]

ساختارهای ریاضی وجود دارد که در آنهاآ ${\textstyle {\tfrac {a}{0}}}$ برای برخی مانند کره ریمان ( مدلی از صفحه پیچیده توسعه یافته ) و خط واقعی توسعه یافته پروجکتیو تعریف شده است . با این حال، چنین ساختارهایی تمام قاعده های معمولی حسابی را برآورده نمی کنند ( اصولات میدان ).

در محاسبات ، یک خطای برنامه ممکن است در نتیجه تلاش برای تقسیم بر صفر ایجاد شود. بسته به محیط برنامه نویسی و نوع عدد (مثلاً ممیز شناور ، عدد صحیح ) که بر صفر تقسیم می شود، ممکن است توسط استاندارد ممیز شناور IEEE 754 بی نهایت مثبت یا منفی ایجاد کند، یک استثنا ایجاد کند، یک پیام خطا ایجاد کند، برنامه برای خاتمه، منجر به یک مقدار خاص غیر عددی ، [2] یا خرابی .

محاسبات ابتدایی [ ویرایش ]

هنگامی که تقسیم در سطح ریاضی ابتدایی توضیح داده می شود، اغلب به عنوان تقسیم مجموعه ای از اشیاء به قسمت های مساوی در نظر گرفته می شود. به عنوان مثال، داشتن ده کوکی را در نظر بگیرید، و این کوکی ها باید به طور مساوی بین پنج نفر در یک میز توزیع شوند. هر فرد دریافت می کرد ${\tfrac {10}{5}}=2$ بیسکویت ها. به طور مشابه، اگر ده کوکی وجود داشته باشد و فقط یک نفر سر میز باشد، آن شخص دریافت خواهد کرد ${\tfrac {10}{1}}=10$ بیسکویت ها.

بنابراین، برای تقسیم بر صفر، وقتی 10 کوکی به طور مساوی بین 0 نفر در یک میز توزیع می شود، تعداد کوکی هایی که هر فرد دریافت می کند چقدر است؟ کلمات خاصی را می توان در سوال مشخص کرد تا مشکل را برجسته کند. مشکل این سوال «چه زمانی» است. هیچ راهی برای توزیع 10 کوکی برای هیچ کس وجود ندارد. از این رو، ${\tfrac {10}{0}}$ - حداقل در محاسبات ابتدایی - گفته می شود که یا بی معنی است یا تعریف نشده است.

اگر مثلاً 5 کوکی و 2 نفر وجود دارد، مشکل در "توزیع یکنواخت" است. در هر پارتیشن عدد صحیح از 5 چیز به 2 قسمت، یا یکی از قسمت های پارتیشن دارای عناصر بیشتری نسبت به دیگری خواهد بود یا یک باقیمانده وجود خواهد داشت (نوشته شده به صورت5/2= 2 r1). یا مشکل 5 کوکی و 2 نفر را می توان با نصف کردن یک کوکی حل کرد که ایده کسری را معرفی می کند (5/2= 2+1/2) . از طرف دیگر مشکل 5 کوکی و 0 نفر را به هیچ وجه نمی توان حل کرد که معنای "تقسیم" را حفظ کند.

در جبر ابتدایی ، روش دیگری برای نگریستن به تقسیم بر صفر این است که همیشه می توان تقسیم را با استفاده از ضرب بررسی کرد. با در نظرگرفتن10/0مثال بالا، تنظیم x =10/0، اگر x برابر ده تقسیم بر صفر باشد، x ضربدر صفر برابر با ده است، اما x وجود ندارد که وقتی در صفر ضرب می شود، ده (یا هر عددی غیر از صفر) را به دست دهد. اگر به جای x =10/0، x =0/0، سپس هر x این سوال را برآورده می کند که "چه عدد x ضرب در صفر، صفر می دهد؟"

تلاش های اولیه [ ویرایش ]

Brāhmasphuṭasiddhānta برهماگوپتا ( حدود ۵۹۸–۶۶۸ ) قدیمی ترین متنی است که صفر را به تنهایی به عنوان یک عدد در نظر می گیرد و عملیات های مربوط به صفر را تعریف می کند. [3] نویسنده نمی تواند تقسیم بر صفر را در متون خود توضیح دهد: تعریف او به راحتی می تواند به پوچ های جبری منجر شود. به گفته براهماگوپتا،

عدد مثبت یا منفی وقتی بر صفر تقسیم شود کسری است که مخرج آن صفر است. صفر تقسیم بر یک عدد منفی یا مثبت یا صفر است یا به صورت کسری با عدد صفر و مقدار متناهی به عنوان مخرج بیان می شود. صفر تقسیم بر صفر صفر است.

در سال 830، ماهاویرا تلاش کرد اشتباهی را که براهماگوپتا در کتابش گانیتا سارا سامگراها مرتکب شده بود تصحیح کند : «عددی وقتی بر صفر تقسیم می‌شود بدون تغییر می‌ماند». [3]

جبر [ ویرایش ]

چهار عمل اصلی - جمع، تفریق، ضرب و تقسیم - که برای اعداد صحیح (اعداد صحیح مثبت) اعمال می‌شود، با برخی محدودیت‌ها، در محاسبات ابتدایی به عنوان چارچوبی برای پشتیبانی از گسترش قلمرو اعداد مورد استفاده قرار می‌گیرند. به عنوان مثال، برای اینکه بتوان یک عدد کامل را از عدد دیگر تفریق کرد، قلمرو اعداد باید به کل مجموعه اعداد صحیح گسترش داده شود تا اعداد صحیح منفی را در بر گیرد. به طور مشابه، برای پشتیبانی از تقسیم هر عدد صحیح بر هر عدد دیگر، قلمرو اعداد باید به اعداد گویا گسترش یابد .. در طول این گسترش تدریجی سیستم اعداد، مراقبت می شود تا اطمینان حاصل شود که "عملیات توسعه یافته"، زمانی که برای اعداد قدیمی اعمال می شود، نتایج متفاوتی ایجاد نمی کند. به زبان ساده، از آنجایی که تقسیم بر صفر هیچ معنایی ندارد ( تعریف نشده است ) در تنظیم اعداد کامل، با گسترش تنظیمات به اعداد واقعی یا حتی مختلط ، این درست باقی می‌ماند .

همانطور که قلمرو اعدادی که این عملیات را می توان برای آنها اعمال کرد گسترش می یابد، تغییراتی در نحوه مشاهده عملیات نیز وجود دارد. به عنوان مثال، در قلمرو اعداد صحیح، تفریق دیگر یک عملیات اساسی در نظر گرفته نمی شود، زیرا می توان آن را با جمع اعداد علامت دار جایگزین کرد. [4] به همین ترتیب، هنگامی که قلمرو اعداد گسترش می یابد تا اعداد گویا را نیز در بر گیرد، تقسیم با ضرب در اعداد گویا معین جایگزین می شود. با توجه به این تغییر دیدگاه، سؤال «چرا نمی‌توانیم بر صفر تقسیم کنیم؟» به «چرا یک عدد گویا نمی‌تواند مخرج صفر داشته باشد؟» می‌شود. پاسخ به این سوال تجدید نظر شده دقیقا مستلزم بررسی دقیق تعریف اعداد گویا است.

در رویکرد مدرن برای ساخت میدان اعداد حقیقی، اعداد گویا به عنوان یک گام میانی در توسعه ظاهر می شوند که بر اساس نظریه مجموعه ها بنا شده است. ابتدا، اعداد طبیعی (شامل صفر) بر اساس مبانی بدیهی مانند سیستم بدیهی Peano ایجاد می‌شوند و سپس به حلقه اعداد صحیح بسط می‌یابند . مرحله بعدی تعریف اعداد گویا است با در نظر گرفتن اینکه این کار باید تنها با استفاده از مجموعه ها و عملیاتی که قبلاً ایجاد شده اند انجام شود، یعنی جمع، ضرب و اعداد صحیح. با شروع مجموعه ای از جفت های مرتب شده از اعداد صحیح، {( a , b )} با b ≠ 0 ، یک رابطه باینری تعریف کنید.در این مجموعه توسط ( a , b ) ≃ ( c , d ) اگر و فقط اگر ad = bc باشد. این رابطه به عنوان یک رابطه هم ارزی نشان داده می شود و کلاس های هم ارزی آن به عنوان اعداد گویا تعریف می شوند. در اثبات صوری است که این رابطه یک رابطه هم ارزی است که شرط صفر نبودن مختصات دوم مورد نیاز است (برای تأیید گذر ). [5] [6] [7]

توضیح فوق ممکن است برای بسیاری از اهداف بسیار انتزاعی و فنی باشد، اما اگر وجود و ویژگی‌های اعداد گویا را، همانطور که معمولاً در ریاضیات ابتدایی انجام می‌شود، فرض کنیم، «دلیل» مجاز نبودن تقسیم بر صفر از دید پنهان می‌ماند. با این وجود، می توان یک توجیه (غیر دقیق) در این زمینه ارائه داد.

از خصوصیات سیستم اعدادی که استفاده می کنیم (یعنی اعداد صحیح، گویا، واقعی و غیره) نتیجه می شود، اگر b ≠ 0 باشد، a = b × c است. فرض کنید که آ/0یک عدد c است، پس باید a = 0 × c = 0 باشد. با این حال، عدد منفرد c باید با معادله 0 = 0 × c تعیین شود ، اما هر عددی این معادله را برآورده می کند، بنابراین ما نمی توانیم یک مقدار عددی به آن اختصاص دهیم.0/0. [8]

تقسیم به عنوان معکوس ضرب [ ویرایش ]

مفهومی که تقسیم را در جبر توضیح می دهد این است که آن معکوس ضرب است. به عنوان مثال، [9]

${\frac {6}{3}}=2$ زیرا 2 مقداری است که مقدار مجهول در آن وجود دارد

$?\times 3=6$ درست است. اما بیان

${\frac {6}{0}}=\,x$ نیاز به یافتن مقداری برای کمیت مجهول در آن دارد

$x\times 0=6.$ اما هر عددی که در 0 ضرب شود 0 است و بنابراین هیچ عددی وجود ندارد که معادله را حل کند.

بیان

${\frac {0}{0}}=\,x$ نیاز به یافتن مقداری برای کمیت مجهول در آن دارد

$x\times 0=0.$ باز هم، هر عددی که در 0 ضرب شود 0 است و بنابراین این بار هر عدد معادله را حل می کند به جای اینکه یک عدد وجود داشته باشد که بتوان آن را به عنوان مقدار در نظر گرفت.0/0.

به طور کلی، یک مقدار را نمی توان به کسری که مخرج آن 0 است نسبت داد، بنابراین مقدار آن تعریف نشده باقی می ماند.

+ نوشته شده در سه شنبه یازدهم بهمن ۱۴۰۱ ساعت 8:36 توسط علی رضا نقش نیلچی |

ادامه صفر

فیزیک

مقدار صفر برای بسیاری از کمیت های فیزیکی نقش ویژه ای دارد. برای برخی از کمیت ها، سطح صفر به طور طبیعی از تمام سطوح دیگر متمایز می شود، در حالی که برای برخی دیگر کم و بیش خودسرانه انتخاب می شود. به عنوان مثال، برای دمای مطلق (همانطور که بر حسب کلوین اندازه گیری می شود )، صفر کمترین مقدار ممکن است ( دمای منفی تعریف شده است، اما سیستم های دمای منفی در واقع سردتر نیستند). این برخلاف دماهای مثلاً در مقیاس سلسیوس است که در آن صفر به طور دلخواه در نقطه انجماد آب تعریف می شود. اندازه گیری شدت صدا بر حسب دسی بل یا فون، سطح صفر به طور دلخواه در یک مقدار مرجع تنظیم می شود - به عنوان مثال، در یک مقدار برای آستانه شنوایی. در فیزیک ، انرژی نقطه صفر کمترین انرژی ممکنی است که یک سیستم فیزیکی مکانیک کوانتومی ممکن است داشته باشد و انرژی حالت پایه سیستم است.

علم شیمی

صفر به عنوان عدد اتمی عنصر نظری تترنوترون پیشنهاد شده است. نشان داده شده است که خوشه ای متشکل از چهار نوترون ممکن است به اندازه کافی پایدار باشد که به تنهایی یک اتم در نظر گرفته شود. این عنصر بدون پروتون و بدون بار در هسته آن ایجاد می کند.

در اوایل سال 1926، آندریاس فون آنتروفوف اصطلاح نوترونیوم را برای شکل حدسی ماده متشکل از نوترون‌های بدون پروتون ابداع کرد و آن را به عنوان عنصر شیمیایی عدد اتمی صفر در سر نسخه جدید خود از جدول تناوبی قرار داد. سپس به عنوان یک گاز نجیب در وسط چندین نمایش مارپیچی از سیستم تناوبی برای طبقه بندی عناصر شیمیایی قرار گرفت.

علوم کامپیوتر

رایج ترین روش در طول تاریخ بشر شروع به شمارش در یک بوده است و این تمرین در زبان های برنامه نویسی کامپیوتری کلاسیک اولیه مانند Fortran و COBOL است. با این حال، در اواخر دهه 1950 LISP شماره‌گذاری مبتنی بر صفر را برای آرایه‌ها معرفی کرد در حالی که Algol 58 پایه‌گذاری کاملاً انعطاف‌پذیر را برای زیرنویس‌های آرایه معرفی کرد (که هر عدد صحیح مثبت، منفی یا صفر را به عنوان پایه برای زیرنویس‌های آرایه مجاز می‌کرد)، و بیشتر زبان‌های برنامه‌نویسی بعدی یکی یا دیگری را اتخاذ کردند. از این سمت ها به عنوان مثال، عناصر یک آرایه با شروع از 0 در C شماره گذاری می شوند ، به طوری که برای یک آرایه nموارد دنباله ای از شاخص های آرایه از 0 تا n -1 اجرا می شود .

ممکن است بین نمایه سازی مبتنی بر 0 و 1 سردرگمی وجود داشته باشد. به عنوان مثال، JDBC جاوا پارامترهای 1 را ایندکس می کند، اگرچه خود جاوا از نمایه سازی مبتنی بر 0 استفاده می کند. [62]

در پایگاه داده ها ممکن است یک فیلد مقدار نداشته باشد. سپس گفته می شود که مقدار صفر دارد . [63] برای فیلدهای عددی مقدار صفر نیست. برای فیلدهای متنی این نه خالی است و نه رشته خالی. وجود مقادیر تهی به منطق سه مقداری منجر می شود . دیگر یک شرط درست یا نادرست نیست، اما می تواند نامشخص باشد. هر محاسباتی از جمله مقدار تهی یک نتیجه صفر را ارائه می دهد. [64]

اشاره گر تهی یک اشاره گر در یک برنامه کامپیوتری است که به هیچ شی یا تابعی اشاره نمی کند. در C، ثابت عدد صحیح 0 در زمان کامپایل زمانی که در یک زمینه اشاره گر ظاهر می شود، به اشاره گر تهی تبدیل می شود، و بنابراین 0 یک راه استاندارد برای ارجاع به اشاره گر تهی در کد است. با این حال، نمایش داخلی نشانگر تهی ممکن است هر الگوی بیتی باشد (احتمالا مقادیر متفاوت برای انواع داده های مختلف). [ نیازمند منبع ]

در ریاضیات 0- و 0+ معادل 0 است. هر دو -0 و +0 دقیقاً یک عدد را نشان می دهند، یعنی هیچ "صفر مثبت" یا "صفر منفی" متمایز از صفر وجود ندارد. با این حال، در برخی از نمایش‌های اعداد علامت‌دار سخت‌افزاری کامپیوتر ، صفر دارای دو نمایش مجزا است، یکی مثبت که با اعداد مثبت و دیگری منفی با اعداد منفی گروه‌بندی شده است. این نوع نمایش دوگانه با علامت صفر شناخته می‌شود که شکل اخیر گاهی اوقات صفر منفی نامیده می‌شود. این نمایش‌ها شامل بزرگی علامت‌گذاری شده و نمایش‌های اعداد صحیح باینری مکمل (اما نه فرم باینری مکمل این دو مورد استفاده در اکثر رایانه‌های مدرن) و بیشتر ممیز شناور است.نمایش اعداد (مانند فرمت های ممیز شناور IEEE 754 و IBM S/390 ).

در باینری، 0 نشان دهنده مقدار "خاموش" است، که به معنای عدم جریان الکتریسیته است. [65]

صفر مقدار false در بسیاری از زبان های برنامه نویسی است.

دوره یونیکس (تاریخ و زمان مرتبط با مهر زمانی صفر) از نیمه شب قبل از اول ژانویه 1970 آغاز می شود. [66] [67] [68]

دوره کلاسیک Mac OS و دوره Palm OS (تاریخ و زمان مرتبط با مهر زمانی صفر) از نیمه شب قبل از اول ژانویه 1904 آغاز می شود. [69]

بسیاری از APIها و سیستم‌عامل‌هایی که به برنامه‌ها نیاز دارند یک مقدار صحیح را به عنوان وضعیت خروج برگردانند، معمولاً از صفر برای نشان دادن موفقیت و مقادیر غیر صفر برای نشان دادن خطا یا شرایط هشدار خاص استفاده می‌کنند.

برنامه نویسان اغلب از یک صفر بریده برای جلوگیری از اشتباه گرفتن با حرف " O " استفاده می کنند. [70]

سایر زمینه ها

در جانورشناسی تطبیقی و علوم شناختی ، تشخیص اینکه برخی از حیوانات آگاهی از مفهوم صفر را نشان می‌دهند به این نتیجه می‌رسد که قابلیت انتزاع عددی در اوایل تکامل گونه‌ها پدید آمده است. [71]
در تلفن، فشردن 0 اغلب برای شماره گیری از شبکه شرکت یا شهر یا منطقه دیگر و 00 برای شماره گیری خارج از کشور استفاده می شود . در برخی کشورها، با شماره گیری 0 تماسی برای کمک اپراتور ایجاد می شود .
دی وی دی هایی که می توانند در هر منطقه ای پخش شوند، گاهی اوقات به عنوان " منطقه 0 " شناخته می شوند.
چرخ های رولت معمولاً دارای یک فضای "0" (و گاهی اوقات همچنین یک فضای "00") هستند که حضور آن هنگام محاسبه بازده نادیده گرفته می شود (در نتیجه به خانه اجازه می دهد در دراز مدت برنده شود).
در فرمول یک ، اگر قهرمان جهان در سال بعد از پیروزی خود در مسابقه عنوان، دیگر در فرمول یک شرکت نکند، 0 به یکی از رانندگان تیمی داده می شود که قهرمان فعلی با آن عنوان را به دست آورد. این اتفاق در سال‌های 1993 و 1994 با رانندگی دیمون هیل با ماشین 0 رخ داد، زیرا قهرمان جهان ( به ترتیب نایجل منسل و آلن پروست ) در مسابقات قهرمانی رقابت نکردند.
در سیستم بزرگراه های بین ایالتی ایالات متحده ، در اکثر ایالت ها خروجی ها بر اساس نزدیک ترین نقطه مایل از پایانه غربی یا جنوبی بزرگراه در داخل آن ایالت شماره گذاری می شوند. تعدادی که کمتر از نیم مایل (800 متر) از مرزهای ایالت در آن جهت فاصله دارند به عنوان خروجی 0 شماره گذاری می شوند.

نمادها و نمادها

مقاله اصلی: نمادهای صفر

رقم عددی مدرن 0 معمولا به صورت دایره یا بیضی نوشته می شود. به طور سنتی، بسیاری از حروف چاپی، حرف بزرگ O را گردتر از رقم باریک‌تر و بیضوی 0 می‌کردند . برخی از مدل ها حتی کلید جداگانه ای برای رقم 0 نداشتند. این تمایز در نمایشگرهای کاراکتر مدرن برجسته شد . [72]

یک صفر بریده شده (0/ $0\!\!\!{/}$ ) می تواند برای تشخیص عدد از حرف استفاده شود (بیشتر در محاسبات، ناوبری و در ارتش استفاده می شود). به نظر می رسد رقم 0 با یک نقطه در مرکز به عنوان یک گزینه در نمایشگرهای IBM 3270 منشاء گرفته است و با برخی از حروف چاپی رایانه ای مدرن مانند Andalé Mono و در برخی از سیستم های رزرو خطوط هوایی ادامه یافته است. یک تغییر از یک نوار عمودی کوتاه به جای نقطه استفاده می کند. برخی از فونت‌های طراحی‌شده برای استفاده با رایانه‌ها، یکی از جفت‌های بزرگ-O-رقم-0 را گردتر و دیگری را زاویه‌دارتر (نزدیک‌تر به یک مستطیل) کردند. تمایز بیشتر در حروف جعلی-ممانعت کننده به کار رفته در پلاک خودروهای آلمانی استبا برش دادن رقم 0 در سمت راست بالا. در برخی از سیستم ها، حرف O یا عدد 0 یا هر دو، برای جلوگیری از سردرگمی از استفاده حذف می شوند.

برچسب سال

مقاله اصلی: سال صفر

در عصر تقویم قبل از میلاد ، سال 1 قبل از میلاد اولین سال قبل از 1 پس از میلاد است. سال صفر وجود ندارد. در مقابل، در شماره گذاری سال های نجومی ، سال 1 قبل از میلاد با شماره 0، سال 2 قبل از میلاد −1 شماره گذاری می شود و غیره. [73]

همچنین ببینید

https://en.wikipedia.org/wiki/0

+ نوشته شده در سه شنبه یازدهم بهمن ۱۴۰۱ ساعت 8:33 توسط علی رضا نقش نیلچی |

صفر

"صفر" و "هیچ" به اینجا هدایت می شوند. برای کاربردهای دیگر، 0 (ابهام‌زدایی) و صفر (ابهام‌زدایی) را ببینید . برای آلبوم موسیقی، Naught (آلبوم) را ببینید.

این مقاله در مورد عدد و رقم 0 است. نباید با حرف O یا علامت O که برای نشان دادن تایید استفاده می شود اشتباه گرفته شود.

به دلایل فنی ، "0#" به اینجا هدایت می شود. برای مفهوم در نظریه مجموعه ها، به Zero sharp مراجعه کنید .

این مقاله برای تأیید نیاز به نقل قول های اضافی دارد . لطفاً با افزودن نقل قول به منابع معتبر به بهبود این مقاله کمک کنید . اطلاعات بدون مرجع ممکن است مشکل ایجاد کرده و پاک شوند. یافتن منابع: "0" - اخبار · روزنامه ها · کتاب ها · محقق · JSTOR
( ژوئیه 2022 ) ( با نحوه و زمان حذف این پیام الگو آشنا شوید )

← -1

1 →

−1 0 1 2 3 4 5 6 7 8 9 →

← 0 10 20 30 40 50 60 70 80 90 →

اصلی

0، صفر، "اوه" ( / oʊ / ) ، هیچ، هیچ، صفر

صفر، هیچ، 0

0 2

0 3

0 6

0 8

0 12

0 16

عربی ، کردی ، فارسی ، سندی ، اردو

零، 〇

០

๐

🧦

0 ( صفر ) عددی است که یک کمیت خالی را نشان می دهد . در نمادهای ارزش مکانی مانند سیستم اعداد هندو-عربی ، 0 نیز به عنوان یک رقم عددی نگهدارنده مکان عمل می کند ، که با ضرب ارقام سمت چپ 0 در ریشه ، معمولاً در 10 ، کار می کند. به عنوان یک عدد، 0 نقش اصلی را در ریاضیات به عنوان هویت جمعی اعداد صحیح ، اعداد حقیقی و دیگر ساختارهای جبری ایفا می کند .

نام های رایج برای عدد 0 در انگلیسی صفر ، naught ، naught ( / n ɔː t / ) ، nil است. در زمینه هایی که حداقل یک رقم مجاور آن را از حرف O متمایز می کند ، گاهی اوقات عدد به صورت oh یا o تلفظ می شود ( / oʊ / ). اصطلاحات غیررسمی یا عامیانه برای 0 شامل zilch و zip است. از نظر تاریخی، باید ، چیزی ( / ɔː t / )، ورمز ، نیز استفاده شده است.

علم اشتقاق لغات

مقاله‌های اصلی: نام‌هایی برای عدد 0 و نام‌هایی برای عدد 0 به زبان انگلیسی

کلمه zero از طریق فرانسوی zéro از زبان ایتالیایی zero به زبان انگلیسی آمده است ، انقباض شکل ونیزی zevero زبان ایتالیایی zefiro از طریق ṣafira یا ṣifr . [1] در زمان جاهلیت کلمه صفر (عربی صفر ) به معنای خالی بود. [2] وقتی سیفر برای ترجمه śūnya ( سنسکریت : शून्य ) از هند استفاده شد، به معنای صفر تکامل یافت . [2] اولین استفاده شناخته شده انگلیسی از صفر در سال 1598 بود .

فیبوناچی ریاضیدان ایتالیایی (حدود 1170-1250)، که در شمال آفریقا بزرگ شد و به عنوان معرفی کننده سیستم اعشاری به اروپا شناخته شد، از اصطلاح zephyrum استفاده کرد . این در ایتالیایی به zefiro تبدیل شد و سپس در ونیزی به صفر رسید. کلمه ایتالیایی zefiro از قبل وجود داشته است (به معنی باد غربی از زبان لاتین و یونانی zephyrus ) و ممکن است هنگام رونویسی عربی ṣifr بر املای آن تأثیر گذاشته باشد. [4]

استفاده مدرن

بسته به زمینه، ممکن است کلمات مختلفی برای عدد صفر یا مفهوم صفر استفاده شود. برای مفهوم ساده کمبود، اغلب از کلمات "هیچ" و "هیچ" استفاده می شود. گاهی از کلمه «هیچ» یا «هیچ» استفاده می شود.

اغلب در زمینه خواندن یک رشته ارقام، مانند شماره تلفن ، آدرس خیابان ، شماره کارت اعتباری ، زمان سربازی ، یا سال، "اوه" نامیده می شود (مثلاً کد منطقه 201 "دو اوه یک" تلفظ می شود. سالی مانند 1907 اغلب "نوزده و هفت" تلفظ می شود). وجود ارقام دیگر، که نشان می دهد رشته فقط شامل اعداد است، از اشتباه گرفتن با حرف O جلوگیری می کند. به همین دلیل، سیستم هایی که شامل رشته هایی با حروف و اعداد هستند (مثلا کد پستی کانادا ) ممکن است استفاده از حرف O را ممنوع کنند.

کلمات عامیانه برای صفر شامل "زیپ"، "زیلچ"، "نادا" و "خراش" است. [5]

"نیل" برای بسیاری از ورزش ها در انگلیسی بریتانیایی استفاده می شود . بسیاری از ورزش‌ها کلمات خاصی برای نمره صفر دارند، مانند " عشق " در تنیس - از فرانسوی l'œuf ، "تخم مرغ" - و " اردک " در کریکت ، کوتاه کردن "تخم مرغ اردک". "تخم غاز" یکی دیگر از اصطلاحات عامیانه عمومی است که برای صفر استفاده می شود. [5]

تاریخ

خاور نزدیک باستان

nfr

قلب با نای
زیبا، دلپذیر، خوب

اعداد مصر باستان از پایه 10 بودند. [6] آنها از هیروگلیف برای ارقام استفاده می کردند و موقعیتی نبودند . در سال 1770 قبل از میلاد، مصریان نماد صفر در متون حسابداری داشتند. نماد nfr به معنی زیبا نیز برای نشان دادن سطح پایه در نقشه های مقبره ها و اهرام استفاده می شد و فاصله ها نسبت به خط پایه در بالا یا پایین این خط اندازه گیری می شد. [7]

در اواسط هزاره دوم قبل از میلاد ، ریاضیات بابلی دارای یک سیستم عددی موقعیتی پایه 60 پیچیده بود. فقدان یک مقدار موقعیتی (یا صفر) با فاصله بین اعداد جنسی کوچک نشان داده شد. در لوحی که در کیش کشف شد (مرتبط به 700 سال قبل از میلاد)، کاتب بیل بن آپلو از سه قلاب به عنوان یک مکان نگهدار در همان سیستم بابلی استفاده کرد. [8] تا سال 300 قبل از میلاد، یک نماد نقطه گذاری (دو گوه مایل) به عنوان این مکان نگهدار انتخاب شد. [9] [10]

مکان نگهدار بابلی یک صفر واقعی نبود زیرا به تنهایی استفاده نمی شد و همچنین در انتهای یک عدد استفاده نمی شد. بنابراین اعدادی مانند 2 و 120 (60×2)، 3 و 180 (3×60)، 4 و 240 (4×60) یکسان به نظر می‌رسند، زیرا اعداد بزرگ‌تر فاقد یک مکان‌گردان نهایی جنسیتی هستند. فقط زمینه می تواند آنها را متمایز کند. [ نیازمند منبع ]

آمریکای پیش از کلمبیا

مایا عدد صفر

تقویم Long Count Mesoamerican که در جنوب مرکزی مکزیک و آمریکای مرکزی ایجاد شد، نیاز به استفاده از صفر به عنوان یک مکان نگهدار در سیستم اعداد موقعیتی ویژسیمال (پایه-20) خود داشت. بسیاری از گلیف های مختلف، از جمله quatrefoil جزئی به عنوان نماد صفر برای این تاریخ های Long Count استفاده می شد، که قدیمی ترین آنها (در Stela 2 در Chiapa de Corzo، Chiapas ) دارای تاریخ 36 قبل از میلاد است. [آ]

از آنجایی که هشت تاریخ اولیه Long Count در خارج از سرزمین مایا ظاهر می شود، [11] عموماً اعتقاد بر این است که استفاده از صفر در قاره آمریکا قبل از مایاها بوده و احتمالاً اختراع اولمک ها بوده است. [12] بسیاری از قدیمی‌ترین تاریخ‌های Long Count در قلب اولمک یافت شدند، اگرچه تمدن اولمک در قرن چهارم قبل از میلاد ، چندین قرن قبل از اولین تاریخ‌های شناخته شده Long Count به پایان رسید.

اگرچه صفر جزء لاینفک اعداد مایا شد، با یک " شکل صدفی " متفاوت و خالی مانند لاک پشت که برای بسیاری از تصویرهای عدد "صفر" استفاده می شود، فرض بر این است که بر سیستم های اعداد دنیای قدیم تأثیری نداشته است.

Quipu ، یک دستگاه بند ناف گره‌دار، که در امپراتوری اینکاها و جوامع پیشین آن در منطقه آند برای ثبت حسابداری و سایر داده‌های دیجیتال استفاده می‌شد، در یک سیستم موقعیتی پایه ده کدگذاری می‌شود. صفر با عدم وجود گره در موقعیت مناسب نشان داده می شود.

دوران باستان کلاسیک

یونانیان باستان هیچ نمادی برای صفر نداشتند (μηδέν، تلفظ می شود "midén")، و برای آن از مکان نما استفاده نمی کردند . [13] به گفته چارلز سیف ، ریاضیدان ، یونانیان باستان پس از 500 سال قبل از میلاد شروع به استفاده از علامت صفر بابلی برای کار خود در نجوم کردند که آن را با حرف یونانی کوچک ό ( όμικρον ) یا omicron نشان می داد. [14] با این حال، پس از استفاده از مکان‌گردان صفر بابلی برای محاسبات نجومی، معمولاً اعداد را به اعداد یونانی برمی‌گردانند . [14] به نظر می رسید یونانی ها با استفاده از صفر به عنوان عدد مخالفت فلسفی داشتند. [14] برخی دیگر از محققان، پذیرش جزئی صفر بابلی را در یونان به تاریخ بعدی می‌دهند، به طوری که دانشمند آندریاس نیدر تاریخ آن را پس از 400 سال قبل از میلاد و رابرت کاپلان ریاضیدان آن را پس از فتوحات اسکندر تعیین کرده است. [15] [16]

یونانیان در مورد وضعیت صفر به عنوان یک عدد مطمئن نبودند. برخی از آنها از خود می پرسیدند: «چطور نمی شود بودن؟»، منجر به استدلال های فلسفی و در قرون وسطی ، در مورد ماهیت و وجود صفر و خلاء شد. پارادوکس های Zeno of Elea تا حد زیادی به تفسیر نامشخص صفر بستگی دارد. [17]

نمونه ای از نماد یونانی اولیه برای صفر (گوشه سمت راست پایین) از پاپیروس قرن دوم

تا سال 150 پس از میلاد، بطلمیوس ، تحت تأثیر هیپارخوس و بابلی ها، از نمادی برای صفر استفاده می کرد.-درجه) [18] [19] در کار خود در مورد نجوم ریاضی به نام Syntaxis Mathematica ، همچنین به عنوان Almagest شناخته می شود . [20] این صفر هلنیستی شاید اولین مورد استفاده مستند از یک عدد به نمایندگی از صفر در جهان قدیم بود. [21] بطلمیوس بارها از آن در Almagest خود (VI.8) برای بزرگی خورشید گرفتگی و ماه گرفتگی استفاده کرد. نشان دهنده ارزش هر دو رقم و دقیقه استغوطه ور شدن در اولین و آخرین تماس اعداد به طور پیوسته از 0 تا 12 تا 0 تغییر می کردند، زیرا ماه از روی خورشید عبور می کرد (یک پالس مثلثی)، که در آن دوازده رقم قطر زاویه ای خورشید بود. دقیقه غوطه وری از 0 " 0" تا 31 " 20" تا 0 " 0" جدول بندی شد، جایی که 0 " 0" از نماد به عنوان مکان نگهدار در دو موقعیت از سیستم اعداد موقعیتی جنسی کوچک خود استفاده می کرد، [ b] در حالی که ترکیب به معنای یک بود. زاویه صفر دقیقه غوطه وری نیز یک تابع پیوسته بود1/1231 " 20" √ d(24−d) (نبض مثلثی با اضلاع محدب )، که d تابع رقمی و 31 " 20" مجموع شعاع دیسک‌های خورشید و ماه بود. [22] نماد بطلمیوس یک مکان نگهدار و همچنین عددی بود که توسط دو تابع ریاضی پیوسته، یکی در داخل دیگری استفاده می شد، بنابراین به معنای صفر بود، نه هیچ.

اولین استفاده از صفر در محاسبه عید پاک جولیان قبل از 311 بعد از میلاد ، در اولین مدخل در جدول عهدنامه ها که در یک سند اتیوپی برای سال های 311 تا 369 پس از میلاد محفوظ است، با استفاده از کلمه Geez برای "هیچ" رخ داده است. (ترجمه انگلیسی در جاهای دیگر «0» است) در کنار اعداد Geez (بر اساس اعداد یونانی)، که از جدولی معادل منتشر شده توسط کلیسای اسکندریه به یونانی قرون وسطی ترجمه شده است. [23] این استفاده در سال 525 بعد از میلاد در جدولی معادل تکرار شد که توسط Dionysius Exiguus از طریق لاتین nulla یا "none" ترجمه شده بود .اعداد رومی . [24] وقتی تقسیم صفر به عنوان باقیمانده تولید شد، nihil به معنای "هیچ" استفاده می شد. این صفرهای قرون وسطایی توسط تمام ماشین حساب های قرون وسطایی آینده عید پاک استفاده می شد. "N" اولیه به عنوان نماد صفر در جدول اعداد رومی توسط Bede - یا همکارانش - در حدود سال 725 پس از میلاد استفاده شد. [25]

چین

این تصویری از صفر است که در میله های شمارش چینی بیان شده است، بر اساس مثال ارائه شده توسط تاریخچه ریاضیات . یک فضای خالی برای نشان دادن صفر استفاده می شود. [26]

Sūnzĭ Suanjing ، با تاریخ ناشناخته، اما تخمین زده می شود که مربوط به قرن 1 تا 5 پس از میلاد باشد، و سوابق ژاپنی مربوط به قرن 18، توصیف می کند که چگونه قرن . سیستم میله‌های شمارش چینی قرن چهارم قبل از میلاد ، فرد را قادر می‌سازد تا محاسبات اعشاری را انجام دهد. همانطور که در Suanjing Xiahou Yang (425–468 بعد از میلاد) اشاره شد که بیان می‌کند که برای ضرب یا تقسیم یک عدد بر 10، 100، 1000 یا 10000، تنها کاری که شخص باید انجام دهد، با میله‌های روی صفحه شمارش، حرکت دادن آنها به جلو است. یا به عقب، با 1، 2، 3، یا 4 مکان، [27] بر اساس تاریخچه ریاضیات ، میله ها "نمایش اعشاری یک عدد، با یک فضای خالی که نشان دهنده صفر است." [26]سیستم میله شمارش یک سیستم نشانه گذاری موقعیتی در نظر گرفته می شود. [28]

در سال 690 پس از میلاد، امپراتور Wǔ شخصیت‌های زتیانی را معرفی کرد که یکی از آنها "〇" بود. در اصل به معنای "ستاره" است، پس از آن [ چه زمانی؟ ] به نمایش صفر رسید.

در آن زمان صفر به عنوان یک عدد تلقی نمی شد، بلکه به عنوان یک "موقعیت خالی" تلقی می شد. [29] رساله ریاضی 1247 Qín Jiǔsháo در نه بخش قدیمی ترین متن ریاضی چینی بازمانده با استفاده از نماد گرد برای صفر است. [30] نویسندگان چینی با ایده اعداد منفی توسط سلسله هان (قرن دوم پس از میلاد) آشنا بودند، همانطور که در نه فصل در مورد هنر ریاضی دیده می شود . [31]

+ نوشته شده در سه شنبه یازدهم بهمن ۱۴۰۱ ساعت 8:24 توسط علی رضا نقش نیلچی |

اسامی عدد 0 در انگلیسی

از ویکیپدیا، دانشنامه آزاد

" صفر " نام معمولی برای عدد 0 در انگلیسی است. در انگلیسی بریتانیایی "nought" نیز استفاده می شود. در انگلیسی آمریکایی "naught" گاهی اوقات برای صفر استفاده می شود، اما (مانند انگلیسی بریتانیایی) "naught" اغلب به عنوان یک کلمه قدیمی برای هیچ استفاده می شود. "نیل"، "عشق" و "اردک" توسط ورزش های مختلف برای امتیازات صفر استفاده می شود.

نیاز به حفظ تمایز صریح بین رقم صفر و حرف O ، [a] وجود دارد که، زیرا هر دو معمولاً در املای انگلیسی (و در واقع اکثر املای هایی که از خط لاتین و اعداد عربی استفاده می کنند ) با دایره یا بیضی ساده نشان داده می شوند . سابقه چند قرنی دارند که اغلب با هم مخلوط می شوند. با این حال، در زبان انگلیسی گفتاری، عدد 0 اغلب به عنوان حرف " o " (" اوه ") خوانده می شود. مثلاً هنگام دیکته کردن شماره تلفن، سری ارقام "1070" ممکن است به صورت "یک صفر هفت صفر" یا "یک اوه هفت اوه" گفته شود، اگرچه حرف "O" روی صفحه کلید تلفن در واقع با رقم 6 مطابقت دارد.

در زمینه های خاص، صفر و هیچ چیز قابل تعویض نیستند، همانطور که "تهی" است. اصطلاحات ورزشی گاهی اوقات به عنوان اصطلاحات عامیانه برای صفر استفاده می شوند، مانند "nada"، "zilch" و "zip".

"صفر" و "رمز" [ ویرایش ]

"صفر" و "شيفر" هر دو نامي براي عدد 0 هستند، اما استفاده از "cipher" براي عدد نادر است و امروزه فقط در زبان انگليسي ادبي است. [1] دوتایی هستند ، به این معنی که از راه های مختلف وارد زبان شده اند اما ریشه ریشه شناسی یکسانی دارند که عربی « صفر » است. از طریق ایتالیایی، این به "zefiro" و از آنجا به "صفر" در انگلیسی مدرن، پرتغالی، فرانسوی، کاتالان، رومانیایی و ایتالیایی ("cero" در اسپانیایی) تبدیل شد. اما از طریق اسپانیایی به « cifra » و از آن‌جا به « cifre » در فرانسوی باستان ، «cifră» در رومانیایی و «cipher» در انگلیسی مدرن تبدیل شد (و «

"صفر" بیشتر در ریاضیات و علوم استفاده می شود، در حالی که "رمز" فقط در سبک ادبی استفاده می شود. هر دو معانی دیگری نیز دارند . ممکن است فردی به عنوان یک «رمز اجتماعی» نامیده شود، اما برای مثال، نام او را «آقای صفر» بگذارد. [2]

HW Fowler در بحث خود در مورد "naught" و "nought" در کاربرد مدرن انگلیسی (به زیر مراجعه کنید)، از "cipher" برای نامگذاری عدد 0 استفاده می کند . [3]

«هیچ» و «هیچ» در مقابل «باید» و «هیچ چیز» [ ویرایش ]

در انگلیسی، "nought" و "naught" به معنای صفر یا هیچ هستند، در حالی که "ought" و "aught" (اولی به معنای اسمی آن) به طور دقیق به معنای "همه" یا "هر چیزی" هستند و نامی برای عدد 0 نیستند. با این وجود، آنها گاهی اوقات به این صورت در انگلیسی آمریکایی استفاده می شوند . به عنوان مثال، "aught" به عنوان یک مکان نگهدار برای صفر در تلفظ اعداد سال تقویمی. این عمل سپس در تلفظ اصطلاحات مشتق شده نیز مجدداً به کار می رود، مانند زمانی که کالیبر تفنگ 0.30-06 Springfield (معرفی شده در سال 1906) بر این اساس با نام "Thirty-aught-6" نامیده می شود.

کلمات "nought" و "naught" انواع املایی هستند. به گفته اچ دبلیو فاولر ، آن‌ها آنطور که تصور می‌شود تصادفی مدرن نیستند، بلکه از انگلیسی قدیم به این شکل نشات گرفته‌اند. در انگلیسی بریتانیایی تمایزی بین این دو وجود دارد، اما این تمایز جهانی نیست. این تمایز این است که "هیچ" در درجه اول در معنای واقعی حسابی استفاده می شود، جایی که عدد 0 به طور مستقیم معنی می شود، در حالی که "هیچ" در معانی شعری و بلاغی استفاده می شود، جایی که "هیچ" به همان اندازه می تواند جایگزین شود. بنابراین نام بازی رومیزی « noughts & crosses » است، در حالی که عبارات بلاغی عبارتند از: «بی‌نیاز»، «به‌هیچ‌وجه گذاشتن»، و « کلمه مناسب در زمان مناسب ، "هیچ" را به عنوان "قدیمی" برچسب گذاری می کند. [3] [4]

در حالی که انگلیسی بریتانیایی این تمایز را ایجاد می کند، در انگلیسی آمریکایی ، املای "naught" برای هر دو معنای تحت اللفظی و بلاغی / شاعرانه ترجیح داده می شود. [4]

«naught» و «nought» به ترتیب از انگلیسی باستانی « nāwiht » و « nōwiht » می آیند که هر دو به معنای « هیچ » هستند. آنها ترکیبات no- ("نه") و wiht ("چیز") هستند. [4] [5] [6]

کلمات "aught" و "ought" (این دومی به معنای اسمی آن) به طور مشابه از انگلیسی قدیم " āwiht " و " ōwiht " آمده اند که به طور مشابه ترکیبات a ("ever") و wiht هستند . معانی آنها متضاد "هیچ" و "هیچ" است - آنها به معنای " هر چیزی " یا " همه " هستند. (فاولر اشاره می کند که "همه" یک باستان گرایی است، و "همه" اکنون در عباراتی مانند "برای همه (آنچه) می دانم" استفاده می شود، جایی که زمانی آنها "برای هر چیزی (آنچه) می دانم" بودند.) [4] [7] [8]

با این حال، "aught" و "باید" نیز گاهی اوقات به عنوان نام برای 0 استفاده می شود، در تضاد با معانی دقیق آنها. دلیل این امر، بازنگری است که به موجب آن «هیچ» و «هیچ» به‌عنوان «باید» و «چیز» اشتباه شنیده شده است. [2] [4]

ساموئل جانسون فکر می کرد که از آنجایی که "هیچ" به طور کلی برای "هر چیزی" در ترجیح "باید" استفاده می شود، بنابراین "هیچ" نیز باید برای "هیچ" در ترجیح "هیچ" استفاده شود. با این حال، او مشاهده کرد که «عرف در استفاده از «هیچ» برای «بد» و «هیچ» برای «هیچ» به طور برگشت‌ناپذیری غالب شده است. در حالی که این تمایز در زمان او وجود داشت، در انگلیسی مدرن، همانطور که توسط فاولر و ریدرز دایجست در بالا مشاهده شد، امروزه وجود ندارد. با این حال، معنای "naught" به معنای "بد" هنوز در کلمه " شیطان " که صرفاً اسم "naught" به اضافه پسوند صفت " -y " است حفظ شده است. این هرگز املای "بذل" نبوده است.

کلمات "owt" و "nowt" در انگلیسی شمالی استفاده می شود . به عنوان مثال، اگر فعلاً باید این کار را انجام دهید، اگر کاری را بیهوده انجام می دهید، آن را برای خودتان انجام دهید. [9]

کلمه aught برای 0 در یک سری از یک یا چند برای اندازه های بزرگتر از 1 به کار می رود. برای سیم سنج آمریکایی ، بزرگترین گیج ها 1/0، 2/0، 3/0، و 4/0 نوشته می شوند و تلفظ می شوند. یک aught، "دو aught"، و غیره. قطر گلوله های شات 0، 00، و 000 "تک aught"، "دبل aught"، و "سه تایی" تلفظ می شود. نام های دهه با صفر اول (مثلاً 1900 تا 1909) به صورت "aught" یا "nought" تلفظ می شدند. این منجر به این می شود که سال 1904 ('04) به عنوان "[نوزده] نه چهار" یا "[نوزده] نه چهار" صحبت شود. تلفظ قابل قبول دیگر «[نوزده] آه چهار» است.

نام دهه [ ویرایش ]

همچنین نگاه کنید به: Aughts

در حالی که "s2000s" برای توصیف دهه متشکل از سال های 2000-2009 در تمام کشورهای انگلیسی زبان استفاده شده است، برخی تفاوت های ملی در استفاده از اصطلاحات دیگر وجود دارد.

در 1 ژانویه 2000، بی‌بی‌سی افراد بدخواه (برگرفته از «nought» [10] کلمه‌ای که در بسیاری از کشورهای انگلیسی‌زبان برای صفر استفاده می‌شود)، به‌عنوان نام بالقوه برای دهه جدید فهرست کرد. [11] این یک نام رایج برای دهه در بریتانیا [12] [13] [14] [15] [16] و استرالیا، [17] [18] و همچنین برخی دیگر از کشورهای انگلیسی زبان تبدیل شده است. با این حال، این به توصیف جهانی تبدیل نشده است، زیرا همانطور که داگلاس کوپلند در اوایل دهه اشاره کرد، "[Noughties] کار نخواهد کرد زیرا در آمریکا کلمه "nought" هرگز برای صفر استفاده نمی شود، هرگز هرگز." [19]

مجله موسیقی و سبک زندگی آمریکایی وایرد «Naughties» را ترجیح داد، که آنها ادعا می‌کنند اولین بار توسط گروه هنری Foomedia در سال 1999 پیشنهاد شد . ستون The Straight Dope . [21]

ورزش [ ویرایش ]

همچنین ببینید: اردک (کریکت)

در امتیازات رویدادهای ورزشی، به ویژه تنیس و فوتبال انجمنی ، عدد 0 دارای نام های بسیار تخصصی "عشق" و " نیل " است. این می تواند برای خبرخوانان رادیو و تلویزیون مشکل ایجاد کند، زیرا خواننده باید بداند که از چه نامی استفاده کند، در حالی که امتیاز اغلب به صورت رقم "0" در فیلمنامه نوشته می شود. (مک لیش به خوانندگان توصیه می کند که در صورت لزوم عدد را روی فیلمنامه با کلمات بنویسند.) [22] در کریکت ، گفته می شود که ضربه زنی که بدون گل بیرون است، " اردک " را زده است، اما از "اردک" استفاده نمی شود. به عنوان مترادف صفر به همان صورت که "عشق" یا "نفر" عبارتند از:و معمولاً در قرائت رسمی جدول امتیازات یک تیم استفاده نمی شود.

هیچ منشا قطعی برای نام امتیاز تنیس برای 0، "عشق" وجود ندارد. این اولین بار در زبان انگلیسی رخ داده است، منشا نسبتاً اخیر دارد و در زبان های دیگر استفاده نمی شود. رایج‌ترین فرضیه‌ای که باور می‌شود این است که از انگلیسی‌زبانان مشتق شده است که به اشتباه صدای فرانسوی l'œuf ("تخم مرغ") را می‌شنوند، که نام نمره صفر در زبان فرانسه است، زیرا نماد صفر در جدول امتیازات استفاده می‌شود. نماد صفر بیضی شکل بود که از نظر بصری شبیه تخم مرغ بود. [23] [24] در استفاده از "اردک" به عنوان نام امتیاز صفر توسط یک خفاش کننده در کریکت، پشتیبانی مماسی برای این وجود دارد، که نام آن از نام کامل "تخم مرغابی" برای آن امتیاز گرفته شده است. کریکت باز زیر[26]

و هنگامی که یازده در برابر یازده قرار می گیرند،
و برای بدست آوردن استادی سخت می جنگند،
کسی که امتیاز را بالاتر می برد در آسمان هفتم است، کسی که تخمی
می گذارد ، در ورطه ای از درد.
- MK Brodie (1865) [27]

نام مربوط به "تخم مرغابی" در کریکت "تخم مرغ غاز" در بیسبال است، نامی که منشأ آن شرحی است در نیویورک تایمز 1886 که در آن روزنامه نگار بیان می کند که "بازیکنان نیویورک 9 نفر را به مردان بوستون هدیه کردند. تخم غاز ناخوشایند، یعنی نه نمره صفر. [25]

با این حال، فرضیه l'œuf مشکلات متعددی دارد، از جمله مهم ترین آنها این است که در تنیس زمین امتیاز روی صفحه امتیاز قرار نمی گیرد و شواهد کمی وجود دارد که فرانسوی ها همیشه از l'œuf به عنوان نام امتیاز صفر استفاده کرده اند. در وهله اول، این نام به اندازه این فرضیه که "عشق" از آن گرفته شده است، حکایتی است. ( به عنوان مثال، ژاکوب برنولی در نامه ای به دوست خود ، از à اما برای توصیف امتیاز صفر تا صفر اولیه در تنیس زمینی استفاده کرد که در انگلیسی به معنای «عشق همه» است.) برخی از فرضیه های جایگزین مشکلات مشابهی دارند. به عنوان مثال: این ادعا که "عشق" از اسکاتلندی ها می آیدکلمه "luff" به معنی "هیچ" در اولین مانع قرار می گیرد، زیرا هیچ مدرک معتبری وجود ندارد که در وهله اول چنین کلمه ای در اسکاتلندی وجود داشته باشد. [25] [28]

با توجه به فرهنگ لغت انگلیسی آکسفورد، اولین استفاده از کلمه "عشق" در انگلیسی به معنای "صفر" برای تعریف نحوه انجام یک بازی بود، نه امتیاز در خود بازی. بازی‌های قمار را می‌توان برای سهام (پول) یا "برای عشق (بازی)"، به عنوان مثال، برای شرط بندی صفر انجام داد. اولین کاربرد ثبت شده ای که در OED نقل شد در سال 1678 بود. تغییر معنی از "نمره صفر" به "نمره صفر" یک جهش مفهومی عظیم نیست و اولین استفاده ثبت شده از کلمه "عشق" به معنای "بدون امتیاز" است. " توسط هویل در سال 1742 است . [29]

رادیو بی بی سی 5 زنده نسخه های اسپین آف تلفن فوتبال خود را در 6-0-6 (" 6-oh-six ") با تمرکز بر کریکت و تنیس با نام های "6-Duck-6" و "6-Love" پخش کرده است. -6 اینچ به ترتیب در ماه های تابستان در خارج از فصل فوتبال.

نام دیگری برای 0 که در ورزش استفاده می شود " nil " است. این از کلمه لاتین " nihil " گرفته شده است که به معنای "هیچ" است. اگرچه در انگلیسی بریتانیایی رایج است، اما در نتایج فوتبال و موارد مشابه، در انگلیسی ایالات متحده به ندرت استفاده می شود. انگلیسی "nil" یک زبان عامیانه نیست و در زمینه های رسمی از جمله اصطلاحات تخصصی فنی (مثلاً "nil by mouth") و نتایج رای گیری رخ می دهد. [30] [31] [32]

"O" ("اوه") [ ویرایش ]

در زبان انگلیسی گفتاری، عدد 0 اغلب به صورت حرف " o " خوانده می شود که اغلب oh نوشته می شود. این امر به ویژه زمانی اتفاق می افتد که این رقم در لیستی از ارقام دیگر قرار گیرد. در حالی که می توان گفت که "یک میلیون در پایه ده به صورت یک و شش صفر بیان می شود"، سری ارقام "1070" را می توان به صورت "یک صفر هفت صفر" یا "یک اوه هفت اوه" خواند. این به ویژه در مورد شماره های تلفن صادق است (به عنوان مثال 867-5309 ، که می توان آن را به عنوان "هشت-شش-هفت-پنج-سه-اوه-نه" گفت). مثال دیگر، نام جیمز باند ، 007 است، که همیشه به عنوان "double-o هفت" خوانده می شود، نه "double-07". [33] [34] [35]

حرف "o" ("oh") همچنین در انگلیسی گفتاری به عنوان نام عدد 0 هنگام گفتن زمان در ساعت 24 ساعته استفاده می شود ، به ویژه در انگلیسی که توسط نیروهای نظامی بریتانیا و آمریکا استفاده می شود. بنابراین 16:05 "شانزده و پنج" و 08:30 "اوه هشت و سی" است. [36]

استفاده از O به عنوان یک عدد می تواند منجر به سردرگمی مانند سیستم گروه خونی ABO شود . خون می تواند حاوی آنتی ژن A (نوع A)، آنتی ژن B (نوع B)، هر دو (نوع AB) یا هیچ (نوع O) باشد. از آنجایی که "O" نشان دهنده کمبود آنتی ژن است، برای انگلیسی زبانان می تواند معنی دارتر باشد که عدد "oh" (صفر) را نشان دهد. اما «گروه خونی O» به درستی با حرف O نوشته می شود نه با عدد 0. [37]

پوچ [ ویرایش ]

در زمینه های خاص، صفر و هیچ چیز قابل تعویض نیستند، همانطور که "تهی" است. با این حال، در ریاضیات و بسیاری از رشته های علمی، تمایز ایجاد می شود (به null مراجعه کنید ). عدد 0 با صفر نشان داده می شود در حالی که null نمایشی از یک مجموعه خالی {} است. از این رو در علوم کامپیوتر ، صفر نشان دهنده نتیجه یک محاسبات ریاضی مانند 2-2 است، در حالی که تهی برای یک حالت تعریف نشده استفاده می شود (به عنوان مثال، یک مکان حافظه که به طور صریح مقداردهی اولیه نشده است).

زبان عامیانه [ ویرایش ]

اصطلاحات ورزشی ( نگاه کنید به بالا ) گاهی اوقات به عنوان اصطلاحات عامیانه برای صفر استفاده می شود، مانند " nada "، " zilch " و " zip ".

"زیلچ" یک اصطلاح عامیانه برای صفر است و همچنین می تواند به معنای "هیچ" باشد. منشا این اصطلاح ناشناخته است. [38]

همچنین ببینید [ ویرایش ]

نام های عدد 0 در زبان های مختلف.

+ نوشته شده در سه شنبه یازدهم بهمن ۱۴۰۱ ساعت 8:17 توسط علی رضا نقش نیلچی |

قضیه هاوسدورف (یا پارادوکس )

قضیه هاوسدورف (یا پارادوکس ) - گزاره ای که در نظریه مجموعه ها در مورد وجود زیر مجموعه قابل شمارش اثبات شده است $تی$ کره دو بعدی $S ^ {2}$ ، علاوه بر این ${\ bar S} ^ {2} = S ^ {2} \ setminus T$ که می تواند به عنوان اتحادیه ای از سه مجموعه جدا از هم نشان داده شود $آ$ ، $ب$ و $ج$ ، همسو با یکدیگر و کثرت از $B \ جام C$ ... اولین بار [1] در سال 1914 توسط فلیکس هاوسدورف منتشر شد . این قضیه (و همچنین پارادوکس دو برابر شدن توپ بر اساس ایده های آن ) ناسازگاری نمایش های نظری مجموعه با عمل هندسی معمولی را نشان می دهد (استدلال ، به ویژه ، دو نسخه ${\ bar S} ^ {2}$ می تواند به شش قطعه تقسیم شود و از سه نسخه ساخته شود ${\ bar S} ^ {2}$ ) بنابراین ، گاهی اوقات "پارادوکس" نامیده می شود.

اثبات قضیه از بدیهیات انتخابی استفاده اساسی می کند . جایگزینی این بدیهی با برخی موارد جایگزین ، به شما امکان می دهد نفی قضیه هاوسدورف را اثبات کنید (یعنی عدم امکان تقسیم مربوط به کره).

از این قضیه نتیجه می شود که در یک کره دو بعدی هیچ اندازه گیری نهایی برای همه زیر مجموعه ها و گرفتن مقادیر مساوی در مجموعه های همخوان (یعنی با توجه به حرکت کره) ثابت نیست.

گاهی اوقات "پارادوکس هاوسدورف" به عنوان قضیه دیگری قابل اثبات است که در همان مقاله مورد بررسی اثبات شده است. این قضیه مثالی شبیه به مجموعه ویتالی ارائه می دهد . او ادعا می کند که یک قطعه واحد می تواند به تعداد قابل شماری تقسیم شود و فقط با استفاده از شیفت ، قطعه ای به طول دو را تشکیل دهد. این نشان می دهد این است که هیچ وجود دارد اندازه گیری در خط است که در تمام زیر مجموعه های تعریف شده و ثابت با توجه به ترجمه است. با این وجود ، می توان برای تمام زیرمجموعه های محدود هواپیما (و همچنین خط مستقیم) اندازه گیری کاملاً افزودنی تعریف کرد ، به گونه ای که مجموعه های متقارن قیچی دارای اندازه مساوی باشند.

محتوا

ایده اثبات [ ویرایش | ویرایش کد ]

در اینجا نسخه ساده قضیه را اثبات می کنیم. یعنی ، ما وجود کاشی کاری کره را با مجموعه ای از نقاط قابل شمارش سوراخ شده ثابت خواهیم کرد (ما آن را می نامیم ${\ bar S} ^ {2}$ ) به سه قطعه متناوب جفتی $آ$ ، $ب$ و $ج$ به طوری که $B \ جام C$ همخوان با زیرمجموعه $آ$ ... مانند قضیه هاوسدورف ، این عبارت نشان می دهد که در یک کره دو بعدی تعریف "منطقه" غیرممکن است که ارزش آن برای هر زیرمجموعه وجود داشته باشد و در حین حرکت بدون تغییر باقی بماند .

اثبات به سه مرحله زیر تقسیم می شود:

یک پارتیشن خاص از برخی گروه ها با دو ژنراتور پیدا کنید $\ گاما$ به سه زیر مجموعه
ما یک عمل ایزومتریک رایگان از این گروه در ساخت ${\ bar S} ^ {2}$ ...
با استفاده از پارتیشن بندی $\ گاما$ و بدیهیات انتخابی به منظور تولید پارتیشن دلخواه کره.

مرحله 1 [ ویرایش | ویرایش کد ]

کیلی ارل از گروه $\ گاما$ ، و زیرمجموعه ها ${{\ mathbb A}} ، \؛ {{\ mathbb B}}$ و ${{\ mathbb C}}$ به ترتیب با قرمز ، آبی و سبز مشخص شده است.

یک گروه را در نظر بگیرید $\ گاما$ با دو ژنراتور $آ$ و $ب$ و نسبت ها $a ^ {2} = 1$ و $b ^ {3} = 1$ (به عبارت دیگر، $\ Gamma = {{\ mathbb Z}} _ {2} * {{\ mathbb Z}} _ {3}$ جایی که $*$ محصول رایگان گروهها را نشان می دهد ). گروه $\ گاما$ شامل یک کلمه خالی است که ما آن را نشان می دهیم $یکی$ (این واحد گروه ماست) و کلمات پایانی سه شخصیت $b ، \؛ b ^ {{- 1}}$ و $آ$ به طوری که $ب$ و $ب ^ {{- 1}}$ متناوب با $آ$ ... بنابراین ، تمام عناصر (به جز یکی) را می توان بصورت منحصر به فرد به صورت زیر نشان داد $ab ^ {{\ pm 1}} ab ^ {{\ pm 1}} \ نقاط b ^ {{\ pm 1}} a$ یا $b ^ {{\ pm 1}} ab ^ {{\ pm 1}} a \ ldots b ^ {{\ pm 1}} a$ یا $ab ^ {{\ pm 1}} ab ^ {{\ pm 1}} \ ldots ab ^ {{\ pm 1}}$ یا $b ^ {{\ pm 1}} ab ^ {{\ pm 1}} a \ ldots ab ^ {{\ pm 1}}$ ...

گروه $\ گاما$ می تواند به شرح زیر تجزیه شود: اجازه دهید ${{\ mathbb A}}$ بسیاری از کلمات با شروع وجود دارد $ب$ ، ${{\ mathbb B}}$ بسیاری از کلمات با شروع وجود دارد $ب ^ {{- 1}}$ و ${{\ mathbb C}}$ مجموعه ای از همه عناصر دیگر وجود خواهد داشت $\ گاما$ ... روشن است که

$\ Gamma = {{\ mathbb A}} \ cup {{\ mathbb B}} \ cup {{\ mathbb C}} ،$

یعنی ما گروه خود را تقسیم کردیم $\ گاما$ به سه زیرمجموعه جداگانه همچنین

${{\ mathbb A}} = b {{\ mathbb C}} ،$

${{\ mathbb B}} = b ^ {{- 1}} {{\ mathbb C}} ،$

${{\ mathbb A}} \ جام {{\ mathbb B}} \ زیرمجموعه {{\ mathbb A}} \ جام {{\ mathbb B}} \ جام \ {1 ، \؛ a \} = a {{\ mathbb C}}.$

مرحله 2 [ ویرایش | ویرایش کد ]

به راحتی می توان نشان داد که نمایندگی وجود دارد $\ گاما$ با چرخش کره به گونه ای که عمل حاصله به جز تعداد قابل شمارش امتیاز ، در کل کره آزاد باشد. بیایید این مجموعه قابل شمارش را از حوزه خارج کنیم و باقیمانده را فراخوانی کنیم ${\ bar S} ^ {2}$ ... (در واقع ، اگر دو چرخش کره را از زاویه بگیرید $\ پی$ و $2 \ pi / 3$ موقعیت کلی و مقایسه آنها با ژنراتورها $آ$ و $ب$ ، سپس عمل القا شده $\ گاما$ این شرط را برآورده خواهد کرد).

مرحله 3 [ ویرایش | ویرایش کد ]

مجموعه را در نظر بگیرید $ایکس$ حاوی یک عنصر از هر مدار $\ گاما$ در ${\ bar S} ^ {2}$ (بیان موجودیت این مجموعه بر اساس بدیهیات انتخاب است ). سپس کره "تراشه" ما ${\ bar S} ^ {2}$ به عنوان اتحادیه ای از مجموعه های جداگانه زیر نشان داده شده است:

${\ bar S} ^ {2} = A \ cup B \ cup C ،$

جایی که

$A = {{\ mathbb A}} X ، \؛ B = {{\ mathbb B}} X ، \؛ C = {{\ mathbb C}} X.$

با استفاده از همان روش مرحله 1 ، به دست می آوریم:

$A = bC ،$

$B = b ^ {{- 1}} C ،$

$A \ cup B \ زیر مجموعه aC ،$

و از $آ$ و $ب$ isometries هستند ، $آ$ ، $ب$ و $ج$ همخوان ، و $A \ جام B$ همخوان با زیرمجموعه $ج$ ...

منبع

https://ru.wikipedia.org/wiki/%D0%A2%D0%B5%D0%BE%D1%80%D0%B5%D0%BC%D0%B0_%D0%A5%D0%B0%D1%83%D1%81%D0%B4%D0%BE%D1%80%D1%84%D0%B0

+ نوشته شده در یکشنبه بیست و هفتم تیر ۱۴۰۰ ساعت 19:52 توسط علی رضا نقش نیلچی |

ادامه پارادوکس باناخ-تارسکی

بدست آوردن بی نهایت توپ از یک [ ویرایش ]

با استفاده از پارادوکس باناخ-تارسکی، می توان برای هر عدد صحیح n ≥ 3 و k ≥ 1 ، k از یک توپ در فضای n اقلیدسی تهیه کرد ، یعنی یک توپ را می توان به k قطعات تقسیم کرد تا هر یک آنها برابر با یک توپ از همان اندازه اصلی است. با استفاده از این واقعیت که گروه آزاد F 2 از درجه 2 یک زیر گروه آزاد از رتبه قابل شمارش نامحدود را قبول می کند ، اثبات مشابهی نشان می دهد که کره واحد S n -1 را می توان به تعداد قابل شماری زیادی تقسیم کرد ، که هر کدام به طور مساوی قابل تجزیه هستند (با دو قطعات) به S n -1 با استفاده از چرخش با استفاده از خواص تحلیلی گروه چرخشی SO ( n ) ، که یک گروه Lie تحلیلی متصل است ، می توان بیشتر ثابت کرد که کره S n -1 می تواند به تعداد قطعات واقعی تقسیم شود (یعن $2 ^ {\ aleph _ {0}}$ قطعه) ، به طوری که هر قطعه با دو قطعه برابر با S n -1 با استفاده از چرخش قابل تجزیه است . این نتایج سپس به واحد توپی محروم از مبدا گسترش می یابد. مقاله ای از والری چورکین در سال 2010 اثبات جدیدی از نسخه پیوسته تناقض باناخ-تارسکی ارائه می دهد. [13]

تناقض فون نویمان در صفحه اقلیدسی [ ویرایش ]

مقاله اصلی: تناقض فون نویمان

در صفحه اقلیدسی ، دو شکل که با توجه به گروه حرکات اقلیدسی برابر تجزیه می شوند ، لزوماً از یک ناحیه هستند و بنابراین ، تجزیه متناقض مربع یا دیسک از نوع باناخ-تارسکی که فقط از همگرایی های اقلیدسی استفاده می کند ، غیرممکن است. یک توضیح مفهومی از تمایز بین موارد مسطح و بعدی بالاتر توسط جان فون نویمان داده شده است : بر خلاف گروه SO (3) چرخش ها در سه بعد ، گروه E (2) از حرکت های اقلیدسی صفحه قابل حل است ، که حاکی از وجود یک اقدام متناهی-افزودنی در E (2) و R 2که تحت ترجمه و چرخش ثابت نیست و تجزیه متناقض مجموعه های غیر قابل اغماض را رد می کند. فون نویمان سپس س followingال زیر را مطرح كرد: آیا اگر یك گروه بزرگتر از معادلات مجاز باشد ، آیا می توان چنین تجزیه متناقضی را ایجاد كرد؟

واضح است که اگر یکی شباهت ها را اجازه دهد ، هر دو مربع موجود در صفحه حتی بدون تقسیم بیشتر نیز معادل می شوند. این انگیزه محدود توجه فرد به گروه SA 2 از تبدیل آفین منطقه حفظ . از آنجا که منطقه حفظ شده است ، هر تجزیه متناقض مربع با توجه به این گروه به همان دلایل تجزیه یک توپ باناخ-تارسکی ضد تصور خواهد بود. در حقیقت ، گروه SA 2 شامل یک گروه فرعی خاص SL (2 ، R ) به عنوان یک زیر گروه است که به نوبه خود شامل گروه آزاد F 2 استبا دو ژنراتور به عنوان یک زیر گروه. این قابل قبول است که اثبات پارادوکس باناخ-تارسکی را می توان در صفحه تقلید کرد. مشکل اصلی در اینجاست که مربع واحد تحت عملکرد گروه خطی SL (2 ، R ) ثابت نیست ، بنابراین نمی توان به راحتی یک تجزیه متناقض را از گروه به مربع انتقال داد ، همانطور که در مرحله سوم اثبات فوق پارادوکس باناخ-تارسکی. علاوه بر این ، نقاط ثابت گروه دشواری هایی را به همراه دارد (به عنوان مثال ، منشا origin تحت تمام تحولات خطی ثابت است). به همین دلیل فون نویمان از گروه بزرگتر SA 2 استفاده کرداز جمله ترجمه ها ، و او تجزیه متناقضی از مربع واحد با توجه به گروه بزرگ ساخته شده (در سال 1929). با استفاده از روش باناخ-تارسکی ، پارادوکس مربع را می توان به شرح زیر تقویت کرد:

هر دو زیرمجموعه محدود هواپیمای اقلیدسی با فضای داخلی غیر خالی با توجه به نقشه های شبه حفظ منطقه مساوی هستند.

همانطور که فون نویمان یادداشت می کند: [14]

"Infibgedessen gibt es bereits in der Ebene kein nichtnegatives additive Maß (wo das Einheitsquadrat das Maß 1 hat)، das gegenüber allen Abbildungen von A 2 بدون تغییر."

"مطابق با این ، در حال حاضر در هواپیما هیچ اندازه گیری افزودنی غیر منفی وجود ندارد (که واحد مربع اندازه آن 1 باشد) ، که با توجه به تمام تحولات متعلق به A 2 [گروه حفظ منطقه تحولات آفرین]. "

برای توضیح بیشتر ، این س ofال که آیا معیار افزودنی محدودی (که تحت برخی از تغییرات خاص حفظ می شود) وجود دارد یا خیر ، به این بستگی دارد که چه تغییراتی مجاز است. اندازه گیری باناخ از مجموعه های در هواپیما، است که توسط انتقال و چرخش حفظ شده است، توسط تحولات غیر ایزومتریک حفظ نمی حتی زمانی که هیچ حفظ مساحت چند ضلعی. نقاط صفحه (غیر از مبدا) را می توان به دو مجموعه متراکم تقسیم کرد که ممکن است A و B نامیده شوند . اگر نقاط A یک چند ضلعی معین با یک تغییر شکل خاص با حفظ منطقه و نقاط B توسط دیگری تبدیل شوند ، هر دو مجموعه می توانند به زیر مجموعه های A تبدیل شونددر دو چند ضلعی جدید نشان می دهد. چند ضلعی های جدید همان مساحت چند ضلعی قدیمی را دارند ، اما دو مجموعه تبدیل شده نمی توانند همان اندازه قبلی را داشته باشند (از آنجا که آنها فقط بخشی از نقاط A را شامل می شوند) ، و بنابراین هیچ اندازه ای وجود ندارد که "کار کند".

گروه گروه های جدا شده توسط فون نویمان در جریان مطالعه پدیده باناخ - تارسکی برای بسیاری از زمینه های ریاضیات بسیار مهم است: این گروه ها گروه های قابل قبول یا گروه هایی با میانگین ثابت هستند و شامل تمام گروه های محدود و همه قابل حل هستند . به طور کلی ، تجزیه های متناقض هنگامی بوجود می آیند که گروه مورد استفاده برای معادل سازی در تعریف تجزیه برابر قابل قبول نباشد .

پیشرفت اخیر [ ویرایش ]

2000: مقاله ون نویمان امکان تجزیه متناقض فضای داخلی مربع را با توجه به گروه خطی SL (2 ، R ) باز گذاشت (واگن ، سوال 7.4). در سال 2000 ، میکلوس لاچکوویچ ثابت کرد که چنین تجزیه ای وجود دارد. [15] به طور دقیق تر ، اجازه دهید A خانواده تمام زیر مجموعه های هواپیما با فضای داخلی غیر خالی و با فاصله مثبت از مبدا باشد ، و B خانواده تمام مجموعه های مسطح با خاصیتی که اتحادیه بسیاری از آنها ترجمه می کند تحت برخی از عناصر SL (2 ، R ) حاوی محله سوراخ شده از مبدا است. سپس تمام مجموعه های خانواده A SL هستند (2 ،R ) -equidecomposable، و به همین ترتیب برای مجموعه در B . از این رو می توان گفت که هر دو خانواده از مجموعه های متناقضی تشکیل شده اند.
2003: مدتها بود که شناخته شده بود که هواپیمای کامل با توجه به SA 2 متناقض است و حداقل تعداد قطعات با 4 برابر خواهد بود به شرط وجود زیرگروه رایگان تغییر مکان محلی SA 2 . در سال 2003 Kenzi Satô چنین زیرگروهی را ساخت و تأیید کرد که چهار قطعه کافی است. [16]
2011: کاغذ Laczkovich است [17] در سمت چپ باز امکان اگر یک گروه رایگان F از تکهای خطی تحولات اقدام بر روی دیسک سوراخ وجود دارد D \ {0،0} بدون نقطه ثابت شده است. Grzegorz Tomkowicz چنین گروهی را ساخت ، [18] نشان داد که سیستم همخوانی A ≈ B ≈ C ≈ B U C را می توان با استفاده از F و D تحقق بخشید {0/0}.
2017: مدتهاست که شناخته شده است که در هواپیمای هذلولی H 2 یک مجموعه E وجود دارد که یک سوم ، چهارم و ... و یک است $2 ^ {\ aleph _ {0}}$ قسمت هفتم H 2 . نیاز توسط isometries گرایش های حفاظت از راضی بود H 2 . نتایج مشابهی توسط جان فرانک آدامز [19] و یان میسیلسکی [20] بدست آمد که نشان داد واحد کره S 2 شامل یک مجموعه E است که نیم ، یک سوم ، یک چهارم و ... و یک $2 ^ {\ aleph _ {0}}$ قسمت هفتم S 2 . Grzegorz Tomkowicz [21] نشان داد كه ساخت و سازهای آدامز و مایسیلسكی را می توان برای بدست آوردن یك مجموعه E از H 2 با همان خصوصیات S 2 تعمیم داد .
2017: تناقض فون نویمان مربوط به هواپیمای اقلیدسی است ، اما در عین حال فضاهای کلاسیک دیگری نیز وجود دارد که پارادوکس ها در آنها امکان پذیر است. به عنوان مثال ، می توان س askال کرد که آیا یک پارادوکس Banach – Tarski در صفحه هذلولی H 2 وجود دارد ؟ این را Jan Mycielski و Grzegorz Tomkowicz نشان دادند. [22] [23] تومکوویچ [24] همچنین ثابت کرد که بسیاری از پارادوکس های کلاسیک نتیجه آسان یک نتیجه نظری نمودار و این واقعیت است که گروه های مورد نظر به اندازه کافی غنی هستند.
2018: در سال 1984 ، Jan Mycielski و Stan Wagon [25] تجزیه متناقضی از هواپیمای هذلولی H 2 را که از مجموعه های بورل استفاده می کند ، ساختند . پارادوکس بستگی به وجود یک درستی ناپیوسته زیر گروه از گروه از isometries از H 2 . پارادوکس مشابهی توسط Grzegorz Tomkowicz [26] بدست آمده است که یک زیرگروه G کاملاً ناپیوسته G از گروه وابسته SA (3 ، Z ) را ساخت. وجود چنین گروهی وجود زیرمجموعه E از Z 3 را نشان می دهد به طوری که برای هر F محدود از Z 3 یک عنصر g از G وجود دارد به طوری که ${\ displaystyle g (E) = E \ مثلث F}$ ، جایی که ${\ displaystyle E \ ، \ مثلث \ ، F}$ تفاوت متقارن E و F را نشان می دهد .
2019: پارادوکس باناخ-تارسکی از قطعات کاملاً تکراری استفاده می کند. در مورد تعداد زیادی از قطعات ، هر دو مجموعه با فضای داخلی غیر خالی با استفاده از ترجمه به طور مساوی قابل تجزیه هستند. اما اجازه می دهد تنها قطعه اندازه گیری لبسگو بدست: اگر A و B زیرمجموعه از R N با فضای داخلی غیر خالی، و سپس آنها را اندازه لبگ برابر اگر و تنها اگر آنها قابل شمارش equidecomposable با استفاده از لبسگو قطعه اندازه گیری هستند. Jan Mycielski و Grzegorz Tomkowicz [27] این نتیجه را به گروه های Lie بعدی محدود و دومین گروه های توپولوژیکی محلی فشرده قابل شمارش که کاملاً از هم جدا شده اند و یا دارای تعداد زیادی از اجزای متصل هستند ، گسترش دادند.

منبع

https://en.wikipedia.org/wiki/Banach%E2%80%93Tarski_paradox

+ نوشته شده در یکشنبه بیست و هفتم تیر ۱۴۰۰ ساعت 18:55 توسط علی رضا نقش نیلچی |

پارادوکس باناخ-تارسکی

"آیا می توان یک توپ را به تعداد محدودی از مجموعه نقاط تجزیه کرد و دوباره به دو توپ یکسان با توپ اصلی مونتاژ کرد؟"

پارادوکس باناخ-تارسکی است قضیه در مجموعه ای نظری هندسه ، که بیان موارد زیر است: با توجه به جامد توپ در فضای 3 بعدی، وجود دارد وجود دارد تجزیه توپ را به یک تعداد متناهی از متلاشی شدن زیر مجموعه ، که پس از آن می توانید قرار داده می شود تماس با هم به روشی متفاوت برای بدست آوردن دو کپی یکسان از توپ اصلی. در واقع ، فرآیند مونتاژ فقط شامل حرکت قطعات به اطراف و چرخش آنها بدون تغییر شکل آنها است. با این حال ، قطعات خود به معنای معمول "جامد" نیستند ، بلکه پراکندگی بی نهایت نقاط هستند. بازسازی می تواند با پنج قطعه کار کند. [1]

شکل قویتر قضیه به این معناست که با توجه به هر دو جسم جامد "معقول" (مانند یک توپ کوچک و یک توپ بزرگ) ، قطعات بریده شده هر یک را می توان دوباره در دیگری جمع کرد. این امر اغلب به صورت غیررسمی عنوان می شود: "یک نخود می تواند خرد شود و دوباره در خورشید جمع شود" و " پارادوکس نخود و خورشید " نامیده می شود.

دلیل اینکه پارادوکس قضیه Banach – Tarski نامیده می شود این است که با شهود اساسی هندسی در تضاد است. "دو برابر شدن توپ" را با تقسیم آن به قطعات و حرکت آنها را در اطراف با چرخش و ترجمه ، بدون هیچ گونه کشش، خم شدن، و یا اضافه کردن نقاط جدید، به نظر می رسد غیر ممکن است، از آنجا که همه این عملیات باید ، به طور مستقیم صحبت کردن، برای حفظ حجم. این شهود که چنین عملیاتی حجم ها را حفظ می کند از نظر ریاضیات پوچ نیست و حتی در تعریف رسمی جلدها نیز گنجانده شده است. اما این در اینجا قابل اجرا نیست زیرا در این حالت تعریف حجم زیرمجموعه های در نظر گرفته شده غیرممکن است. جمع آوری مجدد آنها یک حجم را تولید می کند ، که اتفاقاً متفاوت از حجم در آغاز است.

برخلاف بیشتر قضیه ها در هندسه ، اثبات این نتیجه به انتخاب بدیهیات برای نظریه مجموعه ها به روشی حیاتی بستگی دارد. این را می توان با استفاده از بدیهی انتخاب اثبات کرد ، که امکان ساخت مجموعه های غیر قابل اندازه گیری را فراهم می کند ، یعنی مجموعه ای از نقاط که به معنای عادی حجم ندارند و ساخت آنها به تعداد بی شماری از انتخاب ها نیاز دارد. [2]

در سال 2005 نشان داده شد که قطعات موجود در تجزیه می توانند به گونه ای انتخاب شوند که بتوانند به طور مداوم به محل خود منتقل شوند بدون اینکه به یکدیگر برخورد کنند. [3]

همانطور که به طور مستقل توسط لروی [4] و سیمپسون اثبات شده است ، [5] پارادوکس Banach – Tarski اگر فردی به جای فضاهای توپولوژیکی با محلی کار کند ، حجم را نقض نمی کند. در این محیط انتزاعی ، می توان زیر فضایی را بدون نقطه داشت اما همچنان غیر خالی بود. قسمتهای تجزیه متناقض به معنای محلهای متقاطع بسیار هستند ، به حدی که باید به برخی از این تقاطعها جرم مثبت داده شود. اجازه می دهد تا این توده پنهان در نظر گرفته شود ، تئوری محلی ها اجازه می دهد تا همه زیرمجموعه ها (و حتی همه زیرمقیاس ها) فضای اقلیدسی به طور رضایت بخشی اندازه گیری شوند.

فهرست

نشریه باناخ و تارسکی [ ویرایش ]

در یک مقاله در سال 1924 منتشر شده است، [6] استفان Banach و تارسکی داد ساخت چنین تجزیه متناقض ، بر اساس کار قبلی توسط جوزپه ویتالی مربوط به فاصله واحد و در تجزیه متناقض از حوزه های فلیکس هاسدورف ، و مورد بحث تعداد سوالات مرتبط در مورد تجزیه زیر مجموعه های فضاهای اقلیدسی در ابعاد مختلف. آنها بیان کلی تر زیر را ثابت کردند ، شکل قوی پارادوکس Banach – Tarski :

با توجه به هر دو زیرمجموعه محدود A و B یک فضای اقلیدسی حداقل در سه بعد ، که هر دو دارای فضای غیرخالی هستند ، پارتیشن های A و B به تعداد محدودی از زیرمجموعه های جداگانه وجود دارد ، ${\ displaystyle B = B_ {1} \ cup \ cdots \ cup B_ {k}}$ (برای بعضی از k عدد صحیح ) ، بدین ترتیب که برای هر (عدد صحیح) i بین 1 تا k ، مجموعه های A i و B i همخوان هستند .

حال بگذارید A توپ اصلی باشد و B اتحادیه دو نسخه ترجمه شده از توپ اصلی باشد. سپس گزاره به این معنی است که شما می توانید توپ اصلی A را به تعداد مشخصی از قطعات تقسیم کنید و سپس این قطعات را بچرخانید و ترجمه کنید به گونه ای که نتیجه آن کل مجموعه B باشد که شامل دو نسخه از A است .

شکل قوی تناقض Banach – Tarski در ابعاد یک و دو نادرست است ، اما Banach و Tarski نشان دادند که اگر تعداد زیادی از زیرمجموعه ها مجاز باشند ، جمله مشابه درست باقی می ماند . تفاوت بین ابعاد 1 و 2 از یک سو، و 3 و بالاتر در سوی دیگر، با توجه به ساختار غنی تر از گروه E ( N ) از حرکات اقلیدسی در 3 ابعاد. برای n = 1 ، 2 گروه قابل حل است ، اما برای n ≥ 3 شامل یک گروه آزاد با دو مولد است. جان فون نویمان خواص گروه معادلاتی را که تجزیه متناقض را امکان پذیر می کند مطالعه کرد و مفهوم گروه های قابل تطبیق را معرفی کرد . وی همچنین نوعی تناقض را در صفحه پیدا کرد که از تغییرات آفرین با حفظ منطقه به جای همگرایی های معمول استفاده می کند.

تارسکی ثابت کرد که گروه های قابل قبول دقیقاً همان گروه هایی هستند که هیچ تجزیه متناقضی برای آنها وجود ندارد. از آنجا که در پارادوکس Banach – Tarski فقط به زیرگروه های رایگان نیاز است ، این منجر به حدس و گمان طولانی مدت فون نویمان شد که در سال 1980 رد شد.

منبع

https://en.wikipedia.org/wiki/Banach%E2%80%93Tarski_paradox

+ نوشته شده در یکشنبه بیست و هفتم تیر ۱۴۰۰ ساعت 18:44 توسط علی رضا نقش نیلچی |

عدد اصلی

یک تابع زیستی ، f : X → Y ، از مجموعه X به مجموعه Y نشان می دهد که مجموعه ها کاردینالیته یکسانی دارند ، در این حالت برابر با کاردینال شماره 4 است.

آلف نول ، کوچکترین کاردینال بیکران

در ریاضیات ، اعداد کاردینال یا به طور خلاصه کاردینال ها ، تعمیم اعداد طبیعی است که برای اندازه گیری کاردینالیته (اندازه) مجموعه ها استفاده می شود . اصلی بودن یک مجموعه محدود یک عدد طبیعی است: تعداد عناصر موجود در مجموعه. ترامتناهی اعداد کاردینال، اغلب نشان داده می شود با استفاده از نماد عبری{\ displaystyle \ aleph} $\ آلف$ ( aleph ) به دنبال یک زیرنویس ، [1] اندازه مجموعه های بی نهایت را توصیف می کند .

کاردینالیته از نظر توابع ذهنی تعریف می شود . دو مجموعه دارای کاردینالیته یکسانی هستند ، و فقط در صورت وجود مکاتبه یک به یک (عنصر انتخاب) بین عناصر این دو مجموعه. در مورد مجموعه های متناسب ، این با مفهوم شهودی اندازه مطابقت دارد. در مورد مجموعه های بی نهایت ، رفتار پیچیده تر است. یک قضیه بنیادی ناشی از گئورگ کانتور نشان می دهد که این امکان وجود دارد که مجموعه های نامحدود دارای کاردینالیته های مختلف باشند ، و به ویژه کاردینالیته مجموعه اعداد واقعی بیشتر از کاردینگی مجموعه اعداد طبیعی است . همچنین برای زیر مجموعه مناسب نیز امکان پذیر است از یک مجموعه بی نهایت دارای کاردینالیته مشابه مجموعه اصلی است - اتفاقی که نمی تواند با زیر مجموعه های مناسب مجموعه های محدود رخ دهد.

یک دنباله منتقل شده از اعداد اصلی وجود دارد:

$0،1،2،3 ، \ ldots ، n ، \ ldots ؛ \ aleph _ {0} ، \ aleph _ {1} ، \ aleph _ {2} ، \ ldots ، \ aleph _ {\ alpha} ، \ ldots . \$

این توالی با اعداد طبیعی شامل صفر (کاردینالهای متناهی) شروع می شود ، که پس از آنها اعداد آلف (کاردینالهای بی نهایت مجموعه های منظم ) دنبال می شوند. اعداد آلف توسط اعداد ترتیبی نمایه می شوند . با فرض بدیهی انتخابی ، این توالی نا محدود شامل هر عدد اصلی است. اگر کسی آن بدیهی را رد کند ، با وجود کاردینالهای بی نهایت اضافی که الف نیستند ، وضعیت پیچیده تر است.

کاردینالیته به عنوان بخشی از تئوری مجموعه به خاطر خود مورد مطالعه قرار می گیرد . همچنین ابزاری است که در شاخه های ریاضیات از جمله تئوری مدل ، ترکیبی ، جبر انتزاعی و تحلیل ریاضی مورد استفاده قرار می گیرد . در تئوری دسته بندی ، اعداد اصلی اسکلتی از دسته مجموعه ها را تشکیل می دهند .

فهرست

تاریخچه [ ویرایش ]

مفهوم کاردینالیته ، همانطور که اکنون فهمیده شد ، توسط گئورگ کانتور ، مبدع نظریه مجموعه ها ، در 1874-1884 تدوین شد. از کاردینالیت می توان برای مقایسه جنبه ای از مجموعه های محدود استفاده کرد. به عنوان مثال ، مجموعه های {1،2،3} و {4،5،6} برابر نیستند ، اما دارای کاردینیت یکسان هستند ، یعنی سه. این است که با وجود یک تاسیس پوشا و یکبهیک (یعنی یک تناظر یک به یک) بین دو مجموعه، مانند مکاتبات {1 → 4، 2 → 5، 3 → 6}.

کانتور مفهوم انتخاب خود را در مجموعه های بی نهایت [2] به کار برد (به عنوان مثال مجموعه اعداد طبیعی N = {0 ، 1 ، 2 ، 3 ، ...}). بنابراین ، او تمام مجموعه هایی را که دارای یک انتخاب با N هستند ، نامگذاری می کند (قابل شمارش بی نهایت) ، که همه دارای تعداد اصلی یکسان هستند. این شماره اصلی نامیده می شود{\ displaystyle \ aleph _ {0}} $\ aleph _ {0}$ ، الف تهی . او اعداد اصلی این مجموعه های نامحدود را اعداد کاردینال نامحدود نامید .

کانتور ثابت کرد که هر زیرمجموعه نامحدودی از N دارای کاردینیت مشابه N است ، حتی اگر این به نظر می رسد مغایر با شهود است. وی همچنین ثابت کرد که مجموعه تمام جفتهای مرتب شده اعداد طبیعی قابل انکار است. این بدان معنی است که مجموعه تمام اعداد منطقی نیز قابل محاسبه است ، زیرا هر منطقی را می توان با یک جفت عدد صحیح نشان داد. او بعداً ثابت کرد که مجموعه تمام اعداد جبری واقعی نیز قابل انکار است. هر عدد جبری واقعی z ممکن است به عنوان یک توالی محدود از اعداد صحیح رمزگذاری شود ، که ضرایبی در معادله چند جمله ای است که یک راه حل برای آن است ، یعنی n-tuple مرتب شده ( a 0 ،a 1 ، ...، a n )، a i ∈ Z همراه با یک جفت منطقی ( b 0 ، b 1 ) به گونه ای که z ریشه منحصر به فرد چند جمله ای با ضرایب است ( a 0 ، a 1 ، ... ، a n ) که در فاصله ( b 0 ، b 1 ) قرار دارد.

کانتور در مقاله خود در سال 1874 " درباره ویژگی مجموعه ای از تمام اعداد واقعی جبری " ، با نشان دادن این که مجموعه ای از اعداد واقعی بیشتر از N است ، ثابت کرد که اعداد اصلی با مرتبه بالاتر وجود دارد . اثبات وی از استدلالی با فاصله های تو در تو استفاده می کرد ، اما در مقاله ای در سال 1891 ، او با استفاده از استدلال مورب مبتکرانه اما ساده تر ، همان نتیجه را ثابت کرد . به شماره کاردینال جدید مجموعه اعداد واقعی ، کاردینالیت پیوستار گفته می شود و کانتور از این علامت استفاده می کند ${\ mathfrak {c}}$ برای این.

کانتور همچنین بخش بزرگی از نظریه عمومی اعداد اصلی را ایجاد کرد. او ثابت کرد که کوچکترین عدد اساسی ترانسفینیت وجود دارد ( $\ aleph _ {0}$ ، Aleph-null) ، و این که برای هر شماره کاردینال یک کاردینال بزرگتر بعدی وجود دارد

${\ displaystyle (\ aleph _ {1} ، \ aleph _ {2} ، \ aleph _ {3} ، \ ldots).}$

فرضیه پیوستگی او گزاره ای است که ${\ mathfrak {c}}$ مثل این هست که $\ آلف _ {1}$ . مشخص شده است که این فرضیه مستقل از بدیهیات استاندارد نظریه مجموعه ریاضی است. نه می تواند از مفروضات استاندارد اثبات شود و نه رد شود.

انگیزه [ ویرایش ]

در استفاده غیررسمی ، یک عدد اصلی همان چیزی است که به طور معمول به عنوان شماره شمارش گفته می شود ، به شرطی که 0 در آن گنجانده شود: 0 ، 1 ، 2 ، .... آنها ممکن است با اعداد طبیعی که با 0 شروع می شوند مشخص شوند. دقیقاً همان چیزی که می توان به طور رسمی به عنوان اعداد اساسی محدود تعریف کرد . کاردینالهای بی نهایت فقط در ریاضیات و منطق سطح بالاتر اتفاق می افتد .

به طور رسمی ، یک عدد غیر صفر را می توان برای دو منظور استفاده کرد: توصیف اندازه یک مجموعه ، یا توصیف موقعیت یک عنصر در یک دنباله. برای مجموعه ها و دنباله های محدود به راحتی می توان فهمید که این دو مفهوم با هم منطبق هستند ، زیرا برای هر عددی که یک موقعیت را در یک دنباله توصیف می کند ، می توان مجموعه ای را ساخت که دارای اندازه دقیق باشد. به عنوان مثال ، 3 موقعیت "c" را در دنباله <"a" ، "b" ، "c" ، "d" ، ...> توصیف می کند ، و ما می توانیم مجموعه {a ، b ، c} را بسازیم که دارای 3 عنصر است.

با این حال ، هنگام کار با مجموعه های بی نهایت ، تشخیص این دو ضروری است ، زیرا این دو مفهوم در واقع برای مجموعه های بی نهایت متفاوت هستند. در نظر گرفتن جنبه موقعیت منجر به اعداد ترتیبی می شود ، در حالی که جنبه اندازه توسط اعداد اصلی که در اینجا توضیح داده می شوند ، تعمیم می یابد.

شهود تعریف رسمی کاردینال ساخت مفهومی از اندازه نسبی یا "بزرگ" بودن یک مجموعه است ، بدون اشاره به نوع اعضای آن. برای مجموعه های محدود این آسان است. یکی به سادگی تعداد عناصر یک مجموعه را محاسبه می کند. برای مقایسه اندازه مجموعه های بزرگتر ، لازم است که تصورات تصفیه شده بیشتری را جلب کنید.

مجموعه ای Y حداقل به عنوان بزرگ به عنوان یک مجموعه ای است X اگر یک وجود دارد تزریقی نقشه برداری از عناصر X به عناصر Y . با یک نقشه نگارشی ، هر عنصر از مجموعه X با یک عنصر منحصر به فرد از مجموعه Y مشخص می شود . این به راحتی توسط یک مثال قابل درک است. فرض کنید مجموعه های X = {1،2،3} و Y = {a، b، c، d} را داریم ، سپس با استفاده از این مفهوم اندازه ، مشاهده خواهیم کرد که یک نقشه برداری وجود دارد:

1 →

2 → ب

3 → ج

که تزریقی است و از این رو نتیجه می گیریم که Y دارای کاردینالیته بزرگتر یا مساوی X است . عنصر d هیچگونه نقشه برداری از عنصر را ندارد ، اما این مورد مجاز است زیرا ما فقط به نقشه برداری تزریقی نیاز داریم و لزوماً به یک نقشه نگارشی و بر روی آن نیاز نداریم . مزیت این مفهوم این است که می توان آن را به مجموعه های بی نهایت گسترش داد.

سپس می توانیم این رابطه را به یک رابطه سبک برابری گسترش دهیم. گفته می شود دو مجموعه X و Y در صورت وجود تجانس بین X و Y ، کاردینالیت یکسانی دارند . توسط قضیه شرودر-برنشتاین ، این معادل است که وجود دارد هر دو یک نگاشت تزریقی از X به Y ، و یک نگاشت تزریقی از Y به X . سپس می نویسیم | X | = | Y |. عدد اصلی X خود اغلب به عنوان کمترین ترتیب a تعریف می شودبا | a | = | X |. [3] این کار انتساب کاردینال فون نویمان است . برای منطقی بودن این تعریف ، باید ثابت شود که هر مجموعه دارای کاردیتالیتی مشابه برخی از ترتیب های معمول است. این عبارت یک اصل منظم است . با این وجود می توان در مورد کاردینالیته نسبی مجموعه ها بدون اختصاص صریح اسامی به اشیا discuss بحث کرد.

مثال کلاسیک مورد استفاده ، پارادوکس بی نهایت هتل است که پارادوکس هتل بزرگ هتل هیلبرت نیز نامیده می شود . فرض کنید یک مهمانخانه دار در هتلی با تعداد بی نهایت اتاق وجود دارد. هتل پر است ، و سپس یک مهمان تازه وارد می شود. می توان با دعوت از میهمان که در اتاق 1 بود به اتاق 2 ، از مهمان در اتاق 2 به اتاق 3 و غیره جا داد تا مهمان اضافی جا بیفتد و اتاق 1 را خالی بگذارید. ما می توانیم به وضوح بخشی از این نقشه برداری را بنویسیم:

1 → 2

2 → 3

3 → 4

...

n → n + 1

...

با این انتساب ، می توانیم ببینیم که مجموعه {1،2،3 ، ...} دارای کاردینالیته مشابه مجموعه {2،3،4 ، ...} است ، زیرا یک انتخاب بین اولی و دومی نشان داده شده است این انگیزه تعریف یک مجموعه نامحدود است که مجموعه ای است که دارای زیر مجموعه ای مناسب از همان کاردینالیته باشد (به عنوان مثال ، یک مجموعه Dedekind - بی نهایت ). در این حالت {2،3،4 ، ...} زیرمجموعه مناسبی از {1،2،3 ، ...} است.

هنگام بررسی این اشیا large بزرگ ، ممکن است بخواهیم ببینیم که آیا مفهوم ترتیب شمارش با کاردینال تعریف شده در بالا برای این مجموعه های بی نهایت منطبق است یا خیر. این اتفاق می افتد که اینطور نیست با در نظر گرفتن مثال فوق می توان دریافت که اگر برخی از اشیا "" یکی بزرگتر از بی نهایت "وجود داشته باشند ، پس باید همان کارهدی همان مجموعه بی نهایت باشد که ما با آن شروع کردیم. ممکن است که به استفاده از یک مفهوم رسمی مختلف برای تعداد، نام ordinals ، بر اساس ایده های شمارش و توجه به هر یک از شماره به نوبه خود، و ما کشف کنند که مفاهیم کاردینالیتی و ordinality هستند واگرا زمانی که ما حرکت در خارج از اعداد محدود است.

می توان ثابت کرد که کاردینگی اعداد واقعی بیشتر از اعداد طبیعی است که قبلاً توصیف شد. این را می توان با استفاده از استدلال مورب کانتور تجسم کرد . س classicالات کلاسیک کاردینالیته (به عنوان مثال فرضیه پیوستار ) مربوط به کشف این است که آیا برخی از کاردینال ها بین برخی از جفت کاردینال های نامحدود دیگر وجود دارد یا خیر. در دوره های اخیر ریاضیدانان خصوصیات کاردینال های بزرگتر و بزرگتر را توصیف کرده اند.

از آنجا که کاردینالیته در ریاضیات چنین مفهومی رایج است ، از نامهای مختلفی استفاده می شود. از یکنواختی کاردینالیته گاهی اوقات به عنوان برابری قدرت ، برابری و تعادل شناخته می شود . بنابراین گفته می شود که دو مجموعه با کاردینالیته یکسان ، به ترتیب ، توانا ، متعادل یا برابر هستند .

تعریف رسمی [ ویرایش ]

به طور رسمی ، با فرض بدیهی بودن انتخاب ، کاردینالیته یک مجموعه X کمترین عدد ترتیبی α است به طوری که بین X و α یک انتخاب وجود دارد . این تعریف به انتساب کاردینال فون نویمان معروف است . اگر بدیهی انتخاب انتخاب نشود ، روش دیگری لازم است. قدیمی ترین تعریف از اصلی بودن یک مجموعه X (ضمنی در Cantor و صریح در Frege و Principia Mathematica ) به عنوان کلاس [ X ] تمام مجموعه هایی است که برابر با X هستند . این در ZFC یا سایر سیستم های مرتبط با تئوری مجموعه بدیهی کار نمی کند زیرا اگرX خالی نیست ، این مجموعه خیلی بزرگ است که نمی تواند مجموعه شود. در واقع، برای X ≠ ∅ است تزریق از جهان را به [وجود دارد X ] توسط نقشه برداری مجموعه متر به { متر } × X ، و این کار را با اصل موضوع محدودیت اندازه ، [ X ] یک کلاس مناسب است. این تعریف اما در تئوری نوع و در New Foundations و سیستم های مرتبط کارساز است . با این حال ، اگر ما از این کلاس به کسانی که با X برابر هستند و دارای کمترین رتبه هستند ، محدود شویم ، آنگاه کار خواهد کرد (این یک ترفند ناشی از دانا اسکات است : [4] کار می کند زیرا مجموعه اشیا with با هر درجه مشخص یک مجموعه است).

به طور رسمی ، ترتیب بین اعداد اصلی به شرح زیر تعریف می شود: | X | | Y | به این معنی است که از X به Y یک عملکرد تزریقی وجود دارد . کانتور-برنشتاین شرودر قضیه آمده است که اگر | X | | Y | و | Y | | X | سپس | X | = | Y |. اصل موضوع انتخاب معادل این گزاره است که با توجه به دو مجموعه X و Y ، یا | X | | Y | یا | Y | | X |.[5] [6]

یک مجموعه X در صورت وجود زیر مجموعه مناسب Y از X با |. ، Dedekind-infinite است X | = | Y | ، و Dedekind- محدود اگر چنین زیرمجموعه ای وجود نداشته باشد. محدود کاردینالها فقط می اعداد طبیعی ، به این معنا که یک مجموعه X محدود است اگر و تنها اگر | X | = | n | = n برای تعداد طبیعی n . هر مجموعه دیگری بی نهایت است .

با فرض بدیهی بودن انتخاب ، می توان اثبات کرد که مفاهیم Dedekind با مفاهیم استاندارد مطابقت دارند. همچنین می توان اثبات کرد که کاردینال{\ displaystyle \ aleph _ {0}} $\ aleph _ {0}$ ( aleph null یا aleph-0 ، جایی که aleph اولین حرف در الفبای عبری است ، نشان داده شده است{\ displaystyle \ aleph} $\ آلف$ ) از مجموعه اعداد طبیعی کوچکترین کاردینال بی نهایت است (یعنی هر مجموعه بی نهایت دارای زیر مجموعه ای از کاردینالیته است {\ displaystyle \ aleph _ {0}} $\ aleph _ {0}$ ) کاردینال بزرگتر بعدی با نشان داده می شود{\ displaystyle \ aleph _ {1}} $\ آلف _ {1}$ ، و غیره [1] برای هر ترتیب ترتیبی α ، یک عدد اصلی وجود دارد{\ displaystyle \ aleph _ {\ alpha} ،} $\ aleph _ {\ alpha} ،$ و این لیست تمام اعداد اصلی نامحدود را از بین می برد.

حساب کاردینال [ ویرایش ]

ما می توانیم بر روی اعداد اصلی عملکردهای حسابی تعریف کنیم که عملکردهای عادی را برای اعداد طبیعی تعمیم می دهند. می توان نشان داد که برای کاردینال های محدود ، این عملیات با عملیات معمول برای اعداد طبیعی همزمان است. بعلاوه ، این عملیات خصوصیات زیادی با حساب معمولی دارند.

کاردینال جانشین [ ویرایش ]

اطلاعات بیشتر: کاردینال جانشین

اگر بدیهی انتخاب وجود داشته باشد ، پس هر کاردینال κ یک جانشین دارد که با κ + مشخص می شود ، [1] جایی که κ + > κ است و هیچ کاردینال بین κ و جانشین آن وجود ندارد. (بدون بدیهی بودن انتخاب ، با استفاده از قضیه هارتوگز می توان نشان داد که برای هر شماره کاردینال κ حداقل کاردینال κ + وجود دارد به گونه ای که

$\ kappa ^ {+} \ nleq \ kappa.$ ) برای کاردینالهای متناهی ، جانشین به سادگی κ + 1 است. برای کاردینالهای بی نهایت ، کاردینال جانشین با ترتیب جانشین متفاوت است .

اضافه کردن کاردینال [ ویرایش ]

اگر X و Y هستند متلاشی شدن ، علاوه بر این توسط داده اتحادیه از X و Y . اگر دو مجموعه در حال حاضر مجزا نیست، پس آنها را می توان با مجموعه متلاشی شدن از کاردینالیتی مشابه جایگزین (به عنوان مثال، جایگزین X توسط X × {0} و Y توسط Y × {1}).

$| X | + | Y | = | X \ جام Y |.$

صفر یک هویت افزودنی κ + 0 = 0 + κ = κ است .

جمع به صورت تداعی کننده ( κ + μ ) + ν = κ + ( μ + ν ) است.

علاوه بر این خاصیت جابجایی κ + μ = μ + κ .

علاوه بر این در هر دو استدلال کاهش نمی یابد:

$(\ kappa \ leq \ mu) \ rightarrow ((\ kappa + \ nu \ leq \ mu + \ nu) {\ mbox {and}} (\ nu + \ kappa \ leq \ nu + \ mu)).$

با فرض بدیهی بودن انتخاب ، جمع اعداد اساسی نامحدود آسان است. اگر κ یا μ بی نهایت باشد ، پس

$\ kappa + \ mu = \ max \ {\ kappa، \ mu \} \ ،.$

تفریق [ ویرایش ]

با فرض بدیهی انتخابی و با توجه به یک کاردینال σ بی نهایت و یک کاردینال μ ، یک کاردینال κ وجود دارد به طوری که μ + κ = σ فقط و فقط اگر μ ≤ σ. اگر و فقط اگر μ <σ باشد منحصر به فرد خواهد بود (و برابر با σ).

ضرب کاردینال [ ویرایش ]

محصول کاردینال ها از محصول دکارتی حاصل می شود .

$| X | \ cdot | Y | = | X \ بار Y |$

κ · 0 = 0 · κ = 0.

κ · μ = 0 → ( κ = 0 یا μ = 0).

یکی هویت ضرب κ · 1 = 1 · κ = κ .

ضرب تداعی کننده است ( κ · μ ) · ν = κ · ( μ · ν ).

ضرب جابجایی κ · μ = μ · κ است .

ضرب در هر دو استدلال کاهش نمی یابد: κ ≤ μ → ( κ · ν ≤ μ · ν و ν · κ ≤ ν · μ ).

ضرب در جمع توزیع می کند : κ · ( μ + ν ) = κ · μ + κ · ν و ( μ + ν ) · κ = μ · κ + ν · κ .

با فرض بدیهی بودن انتخاب ، ضرب اعداد اصلی نامحدود نیز آسان است. اگر κ یا μ بی نهایت باشد و هر دو غیر صفر باشند ، پس

$\ kappa \ cdot \ mu = \ max \ {\ kappa، \ mu \}.$

بخش [ ویرایش ]

با فرض بدیهی انتخاب و با توجه به یک کاردینال π نامحدود و یک کاردینال غیر صفر μ ، یک کاردینال κ وجود دارد به طوری که μ · κ = π فقط و فقط اگر μ ≤ π . فقط و فقط اگر μ < π . منحصر به فرد خواهد بود (و برابر با π ) .

نمایش کاردینال [ ویرایش ]

بیان توسط

${\ displaystyle | X | ^ {| Y |} = \ چپ | X ^ {Y} \ راست | ،}$

که در آن X Y مجموعه تمام توابع از Y تا X است . [1]

κ 0 = 1 (به ویژه 0 0 = 1) ، عملکرد خالی را ببینید .

اگر 1 ≤ μ، 0 μ = 0.

1 μ = 1

κ 1 = κ

κ μ + ν = κ μ · κ ν .

κ μ · ν = ( κ μ ) ν .

( κ · μ ) ν = κ ν · μ ν .

بیان در هر دو استدلال کاهش نمی یابد:

(1 ≤ ν و κ ≤ μ ) → ( ν κ ≤ ν μ ) و

( کاپا ≤ میکرون ) → ( کاپا ν ≤ میکرون ν ).

2 | X | و کاردینال است مجموعه توانی از مجموعه X و استدلال مورب کانتور نشان می دهد که 2 | X | > | X | برای هر مجموعه ای X . این ثابت می کند که هیچ بزرگترین کاردینال وجود ندارد (زیرا برای هر کاردینال κ ، ما همیشه می توانیم یک کاردینال بزرگتر 2 κ پیدا کنیم ). در واقع ، کلاس کاردینال ها یک کلاس مناسب است . (این اثبات در برخی از نظریه های مجموعه ، به ویژه بنیادهای جدید ، ناموفق است).

تمام گزاره های باقی مانده در این بخش بدیهی انتخاب را در نظر می گیرند:

اگر κ و μ هر دو محدود و بزرگتر از 1، و ν بی نهایت است، پس از آن κ ν = μ ν .

اگر κ نامحدود و μ محدود و غیر صفر باشد ، پس κ μ = κ .

اگر 2 ≤ κ و 1 ≤ μ و حداقل یکی از آنها بی نهایت است ، پس:

حداکثر (κ، 2 μ ) ≤ κ μ ≤ حداکثر (2 κ ، 2 μ ).

با استفاده از قضیه König ، می توان κ <κ cf (κ) و κ نهایی بودن κ است.

ریشه ها [ ویرایش ]

با فرض بدیهی انتخابی و با توجه به یک کاردینال نامحدود κ و یک کاردینال محدود μ بزرگتر از 0 ، کاردینال ν راضی کننده است {\ displaystyle \ nu ^ {\ mu} = \ kappa} ${\ displaystyle \ nu ^ {\ mu} = \ kappa}$ خواهد بود { kappa} $\ کاپا$ .

لگاریتم [ ویرایش ]

با فرض بدیهی انتخاب و با توجه به یک کاردینال بی نهایت و یک کاردینال محدود μ بزرگتر از 1 ، ممکن است یک کاردینال λ رضایت بخش باشد یا نباشد ${\ displaystyle \ mu ^ {\ lambda} = \ kappa}$ . با این حال ، اگر چنین کاردینال وجود داشته باشد ، نامحدود و کمتر از κ است ، و هر کاردینالیته محدود ν بزرگتر از 1 نیز راضی خواهد کرد ${\ displaystyle \ nu ^ {\ lambda} = \ kappa}$ .

لگاریتم یک شماره کاردینال نامحدود κ به عنوان کمترین عدد μ μ تعریف می شود به طوری که κ ≤ 2 μ . لگاریتم های کاردینال نامحدود در برخی از زمینه های ریاضیات مفید هستند ، به عنوان مثال در مطالعه تغییرات اساسی در فضاهای توپولوژیک ، اگرچه آنها فاقد برخی از خصوصیات لگاریتم های اعداد واقعی مثبت هستند. [7] [8] [9]

فرضیه پیوستار [ ویرایش ]

فرضیه زنجیره (CH) می گوید که هیچ کاردینالها وجود دارد به شدت بین{\ displaystyle \ aleph _ {0}} $\ aleph _ {0}$ و {\ displaystyle 2 ^ {\ aleph _ {0}}.} $2 ^ {\ aleph _ {0}}.$ شماره اصلی اخیر نیز اغلب با نشان داده می شود {\ displaystyle {\ mathfrak {c}}} ${\ mathfrak {c}}$ ؛ این اصلیت پیوستار است (مجموعه اعداد واقعی ). در این مورد{\ displaystyle 2 ^ {\ aleph _ {0}} = \ aleph _ {1}.} $2 ^ {\ aleph _ {0}} = \ aleph _ {1}.$ [1] فرضیه تعمیم زنجیره (GCH) می گوید که برای هر مجموعه ای بی نهایت X ، هیچ کاردینالها وجود دارد به شدت بین | X | و 2 | X | . فرضیه پیوستار مستقل از بدیهیات معمول نظریه مجموعه است ، بدیهیات زرملو-فراینکل همراه با بدیهیات انتخابی ( ZFC ).

همچنین به [ ویرایش ] مراجعه کنید

پورتال ریاضیات

منبع

https://en.wikipedia.org/wiki/Cardinal_number

+ نوشته شده در یکشنبه نهم آذر ۱۳۹۹ ساعت 22:55 توسط علی رضا نقش نیلچی |

با یک رابطه هم ارز ضریب می شود

پرش به ناوبری پرش به جستجو

این مقاله درباره تعمیم نظریه مقوله است که در تئوری طرح استفاده می شود . برای معنای مشترک ، به کلاس معادل سازی مراجعه کنید .

در ریاضیات ، با توجه به یک رده C ، ضریب یک شی X X با یک رابطه هم ارز ${\ displaystyle f: R \ به X \ بار X}$ یک هم ارزی برای جفت نقشه است

${\ displaystyle R \ {\ overset {f} {\ to}} \ X \ times X \ {\ overset {\ operatorname {pr} _ {i}} {\ to}} \ X، \ \ i = 1، 2 ،}$

جایی که R یک جسم در C است و " f یک رابطه معادل است" به این معنی است که ، برای هر شی T در C ، تصویر (که یک مجموعه است ) از $f: R (T) = \ operatorname {Mor} (T، R) \ به X (T) \ بار X (T)$ یک رابطه هم ارزی است . این است که، یک بازتابی ، متقارن و متعدی ارتباط .

مورد اصلی در عمل این است که C مقوله همه طرحها در برخی از طرحهای S باشد. اما این مفهوم انعطاف پذیر است و همچنین می توان C را به عنوان دسته میله ها در نظر گرفت .

فهرست

مثالها [ ویرایش ]

بگذارید X یک مجموعه باشد و رابطه معادلاتی را در آن در نظر بگیرید. بگذارید Q مجموعه ای از همه کلاسهای هم ارزی در X باشد. سپس نقشه $q: X \ به Q$ که یک عنصر x را به کلاس هم ارزی که x به آن تعلق دارد می فرستد ، یک ضریب است.
در مثال بالا، Q است زیر مجموعه از مجموعه قدرت H از X . در هندسه جبری ، می توان H را با یک طرح هیلبرت جایگزین کرد یا اتحادیه جدا از طرح های هیلبرت را جایگزین کرد . در حقیقت ، Grothendieck یک طرح پیکارد نسبی از یک طرح مسطح X [1] به عنوان ضریب Q (از طرح Z با تقسیم کننده های موثر موثر بر X ) ساخت که یک طرح بسته از یک طرح Hilbert H است . نقشه ضریب $q: Z \ به Q$ سپس می توان آن را به عنوان نسبی از نقشه هابیل در نظر گرفت .

همچنین به [ ویرایش ] مراجعه کنید

ضریب دسته ای ، یک مورد خاص

یادداشت ها [ ویرایش ]

^ همچنین لازم است الیاف هندسی را یکپارچه فرض کنیم. مثال مامفورد نشان می دهد که "انتگرال" قابل حذف نیست.

منابع [ ویرایش ]

https://en.wikipedia.org/wiki/Quotient_by_an_equivalence_relation

+ نوشته شده در پنجشنبه هشتم آبان ۱۳۹۹ ساعت 9:15 توسط علی رضا نقش نیلچی |

رابطه هم ارزی جزئی

در ریاضیات ، یک رابطه هم ارز جزئی (که اغلب به اختصار PER خلاصه می شود ، در ادبیات قدیمی نیز رابطه معادل محدود نامیده می شود ) $R$ روی یک مجموعه $ایکس$ یک رابطه باینری است که متقارن و انتقالی است . به عبارت دیگر ، این برای همه مناسب است

$a ، b ، c \ در X$ که:

اگر $aRb$ ، سپس $سینه بند$ (تقارن)
اگر $aRb$ و $bRc$ ، سپس $aRc$ (انتقال پذیری)

اگر $R$ همچنین بازتابی ، پس از آن $R$ یک رابطه هم ارزی است .

فهرست

ویژگی ها و برنامه ها [ ویرایش ]

در نظریه مجموعه ها ، یک رابطه $R$ روی یک مجموعه

$ایکس$ PER

است اگر ، و فقط اگر ، $R$ یک رابطه هم ارز در زیر مجموعه است

$Y = \ {x \ در X | x \ ، R \ ، x \} \ subseteq X$ . با ساخت و ساز ، $R$ بازتابنده است $بله$ و بنابراین یک رابطه معادل در

$بله$ . در حقیقت، $R$ می تواند فقط در عناصر نگه دارد $بله$ : اگر $xRy$ ، سپس $yRx$ با تقارن ، بنابراین $xRx$ و $yYy$ با انتقال ، یعنی ${\ displaystyle x، y \ in Y}$ . با این حال ، مجموعه ای داده شده است $ایکس$ و یک زیر مجموعه $Y \ subseteq X$ ، یک رابطه هم ارز در $بله$ لازم نیست PER روشن باشید $ایکس$ ؛ به عنوان مثال ، با در نظر گرفتن مجموعه

${\ displaystyle E = \ {a، b، c، d \}}$ ، رابطه بیش از $E$ با مجموعه مشخص می شود ${\ displaystyle R = \ {a، b، c \} ^ {2} \ cup \ {(d، a) \}}$ یک رابطه معادل در است $\ {a ، b ، c \}$ اما PER روشن نیست $E$ از آنجا که نه متقارن است [یادداشت 1] و نه انتقالی [یادداشت 2] در $E$ .

هر رابطه هم ارز جزئی ، یک رابطه عملکردی است ، اما عکس این مسئله برقرار نیست.

هر رابطه معادل جزئی یک رابطه اقلیدسی درست است . برعکس این صدق نمی کند: به عنوان مثال ، xRy در اعداد طبیعی ، تعریف شده با 0 ≤ x ≤ y +1 ≤ 2 ، درست اقلیدسی است ، اما نه متقارن است (از آنجا که به عنوان مثال 2 R 1 ، اما نه 1 R 2) و نه انتقالی (از آنجا که به عنوان مثال 2 R 1 و 1 R 0 ، اما نه 2 R 0). به همین ترتیب ، هر رابطه معادل بخشی یک رابطه اقلیدسی چپ است ، اما برعکس نیست. هر رابطه معادل جزئی شبه انعکاسی است ، [1] در نتیجه اقلیدسی بودن.

در تنظیمات نظریه غیر مجموعه [ ویرایش ]

در تئوری نوع ، ریاضیات سازنده و کاربردهای آنها در علوم رایانه ، ساخت آنالوگ زیر مجموعه ها اغلب مشکل ساز است [2] - بنابراین در این زمینه ها PER بیشتر استفاده می شود ، به ویژه برای تعریف مجموعه های کوچک ، که بعضی اوقات به آنها مجموعه های جزئی گفته می شود. تشکیل یک مجموعه مقدماتی جزئی از یک نوع و یک PER مشابه تشکیل زیرمجموعه ها و ضریب ها در ریاضیات نظری مجموعه ای کلاسیک است.

مفهوم جبری همخوانی را می توان به معادلات جزئی نیز تعمیم داد ، و مفهوم زیر همرنگی ، یعنی یک رابطه همجنس که متقارن و انتقالی است ، اما لزوماً انعکاسی نیست ، حاصل می شود. [3]

مثالها [ ویرایش ]

یک مثال ساده از PER که رابطه هم ارزی نیست ، رابطه خالی است $R = \ emptyset$ ، اگر $ایکس$ خالی نیست

هسته توابع جزئی [ ویرایش ]

اگر $f$ یک تابع جزئی روی یک مجموعه است $آ$ ، سپس رابطه $\ تقریبا$ تعریف شده بوسیله ی $x \ تقریبا y$ اگر $f$ در تعریف شده است

$ایکس$ $f$ در تعریف شده است $y$ $f (x) = f (y)$

یک رابطه هم ارزی جزئی است ، زیرا کاملاً متقارن و انتقالی است.

اگر $f$ بنابراین بر روی برخی از عناصر تعریف نشده است $\ تقریبا$ یک رابطه هم ارزی نیست. از آنجا که اگر بازتابنده نیست $f (x)$ پس تعریف نشده است $x \ not \ تقریبا x$ - در واقع ، برای چنین $ایکس$ وجود ندارد $y \ در A$ به طوری که $x \ تقریبا y$ . بلافاصله نتیجه می شود که بزرگترین زیرمجموعه از $آ$ که در آن $\ تقریبا$ یک رابطه معادل است دقیقاً زیرمجموعه ای است که در آن قرار دارد $f$ تعریف شده است.

توابع مربوط به روابط معادل سازی [ ویرایش ]

بگذارید X و Y مجموعه های مجهز به روابط هم ارزی (یا PER) باشند، $\ تقریبی _ {X} ، \ تقریبی _ {Y}$ . برای $f ، g: X \ به Y$ ، تعريف كردن $f \ تقریبا g$ به معنی:

$\ forall x_ {0} \؛ x_ {1} ، \ quad x_ {0} \ تقریبی _ {X} x_ {1} \ Rightarrow f (x_ {0}) \ تقریبی _ {Y} g (x_ {1} )$

سپس $f \ تقریبی f$ به این معنی است که f یک عملکرد کاملاً مشخص از ضریب ها را القا می کند $X / \ تقریبی _ {X} \؛ \ به \؛ Y / \ تقریبی _ {Y}$ . بنابراین ، $\ تقریبا$ ایده تعریف تعریف شده بر روی ضریب ها و دو تابع القا کننده عملکرد یکسان را در ضریب گرفته می شود.

برابری مقادیر نقطه شناور IEEE [ ویرایش ]

استاندارد IEEE 754: 2008 شناور نقطه "EQ" را برای مقادیر نقطه شناور تعریف می کند. این محمول متقارن و انتقالی است ، اما به دلیل وجود مقادیر NaN که برای خود EQ نیستند ، بازتابنده نیست .

یادداشت ها [ ویرایش ]

${\ displaystyle dRa}$ ، اما نه ${\ displaystyle aRd}$
${\ displaystyle dRa}$ و ${\ displaystyle aRb}$ ، اما نه ${\ displaystyle dRb}$

منابع

https://en.wikipedia.org/wiki/Partial_equivalence_relation

+ نوشته شده در پنجشنبه هشتم آبان ۱۳۹۹ ساعت 9:12 توسط علی رضا نقش نیلچی |

کلاس معادل سازی

این مقاله در مورد معادل سازی در ریاضیات است. برای معادل سازی در موسیقی ، به کلاس معادل سازی (موسیقی) مراجعه کنید .

همرنگی نمونه ای از رابطه هم ارزی است. دو مثلث سمت چپ همخوان هستند ، در حالی که مثلث سوم و چهارم با هر مثلث دیگری که در اینجا نشان داده شده سازگار نیستند. بنابراین ، دو مثلث اول در یک کلاس معادل هستند ، در حالی که مثلث سوم و چهارم هر کدام در کلاس معادل خود هستند.

در ریاضیات ، وقتی عناصر بعضی از مجموعه های S مفهوم معادل سازی دارند (به صورت رابطه معادل سازی رسمی شده) بر روی آنها تعریف شده است ، بنابراین می توان به طور طبیعی مجموعه S را به کلاس های معادل تقسیم کرد . این کلاسهای معادل سازی به گونه ای ساخته شده اند که عناصر a و b متعلق به همان کلاس معادلاتی باشند ، و فقط اگر ، معادل باشند.

به طور رسمی ، با توجه به یک مجموعه S و یک رابطه معادل ~ در S ، کلاس هم ارزی یک عنصر a در S ، نشان داده شده با $[آ]$ ، [1] [2] مجموعه است [3]

${\ displaystyle \ {x \ in S \ mid x \ sim a \}}$

عناصر معادل a . این ممکن است به اثبات رسیده، از خواص تعریف روابط هم ارزی، که کلاسهای هم ارزی به صورت یک پارتیشن از S . این پارتیشن-مجموعه ای از هم ارزی کلاس های است که گاهی اوقات به نام مجموعه ای بهره یا فضای خارج قسمت از S توسط ~ ، و توسط نشان داده می شود S / ~ .

هنگامی که مجموعه S تا حدودی ساختار (مانند عملیات گروه یا یک توپولوژی ) و رابطه هم ارزی ~ سازگار با این ساختار است، مجموعه ای خارج قسمت اغلب یک ساختار مشابه از مجموعه پدر و مادر خود به ارث می برد. به عنوان مثال می توان به فضاهای ضریب در جبر خطی ، فضاهای ضریب در توپولوژی ، گروه های ضریب ، فضاهای همگن ، حلقه های بهره ، مونوئیدهای ضریب و دسته های ضریب اشاره کرد .

فهرست

مثالها [ ویرایش ]

اگر X مجموعه ای از تمام اتومبیل است، و ~ است رابطه هم ارزی "است همان رنگ به عنوان"، و سپس یک کلاس هم ارزی خاص را از تمام اتومبیل های سبز تشکیل، و X / ~ می تواند به طور طبیعی با مجموعه ای از تمام رنگ خودرو شناسایی .
اجازه دهید X شود مجموعه ای از مستطیل در یک هواپیما، و ~ رابطه هم ارزی "دارای همان منطقه به عنوان"، و سپس برای هر عدد حقیقی مثبت ، وجود خواهد داشت یک کلاس هم ارزی تمام مستطیل که منطقه . [4]
در نظر بگیرید پیمانه 2 رابطه هم ارزی در مجموعه ای از اعداد صحیح ، ℤ ، به طوری که X ~ Y اگر و تنها اگر تفاوت آنها X - Y یک IS تعداد حتی . این رابطه باعث ایجاد دقیقاً دو کلاس معادل سازی می شود: یک کلاس از همه اعداد زوج تشکیل شده و کلاس دیگر از همه اعداد فرد تشکیل شده است. با استفاده از براکت های مربعی در اطراف یک عضو کلاس برای نشان دادن یک کلاس هم ارز تحت این رابطه ، [7] ، [9] و [1] همه نشان دهنده همان عنصر ℤ / هستند . [5]
اجازه دهید X شود مجموعه ای از زوج مرتب از اعداد صحیح ( ، ب ) با غیر صفر ب ، و تعریف یک رابطه هم ارزی ~ در X به طوری که ( ، ب ) ~ ( ج ، د ) اگر و تنها اگر آگهی = قبل از میلاد ، سپس کلاس معادل جفت ( a ، b ) را می توان با عدد منطقی a / b شناسایی کرد، و می توان از این رابطه هم ارزی و کلاسهای هم ارزی آن تعریف رسمی از مجموعه اعداد گویا ارائه داد. [6] همان ساخت را می توان به حوزه کسرهای هر حوزه انتگرال تعمیم داد .
اگر X شامل تمام خطوط در، می گویند، یک فضای اقلیدسی ، و L ~ M بدان معنی است که L و M می خطوط موازی ، سپس مجموعه ای از خطوط که موازی به هر شکل دیگر یک کلاس هم ارزی، تا زمانی که یک خط است موازی با خودش در نظر گرفته شده است . در این وضعیت ، هر کلاس معادل یک نقطه را در بی نهایت تعیین می کند .

علامت گذاری و تعریف رسمی [ ویرایش ]

رابطه هم ارزی در یک مجموعه X است رابطه دودویی ~ در X رضایت سه ویژگی: [7] [8]

a ~ a برای همه a در X ( انعکاس پذیری ) ،
~ ب دلالت ب ~ برای همهو ب در X ( تقارن )،
اگر a ~ b و b ~ c سپس a ~ c برای همه a ، b و c در X (قابلیت انتقال ).

کلاس هم ارزی از یک عنصر نشان داده است [ ] و یا [ ] ~ ، [1] و به عنوان مجموعه ای تعریف شده ${\ displaystyle \ {x \ in X \ mid a \ sim x \}}$ از عناصر هستند که به مربوط توسط ~ . [3] کلمه "کلاس" در اصطلاح "کلاس معادل سازی" به کلاسهایی که در تئوری مجموعه تعریف شده است اشاره نمی کند ، با این حال کلاسهای معادل سازی اغلب به عنوان کلاسهای مناسب ظاهر می شوند .

مجموعه ای از تمام کلاسهای هم ارزی در X با توجه به یک رابطه هم ارزی R به عنوان نشان داده X / R ، است و به نام X پیمانه R (یا مجموعه ای بهره از X توسط R ). [9] نقشه پوشا $x \ mapsto [x]$ از X بر روی X / R ، که هر عنصر را به کلاس هم ارزی خود ترسیم می کند ، استنباط متعارف یا نقشه پیش بینی متعارف نامیده می شود .

وقتی عنصری انتخاب می شود (غالباً ضمنی) در هر کلاس معادل سازی ، این یک نقشه صحیح را به نام بخش تعریف می کند . اگر این بخش توسط نشان داده می شود بازدید کنندگان ، یکی است [ بازدید کنندگان ( ج )] = ج برای هر کلاس هم ارزی ج . عنصر بازدید کنندگان ( ج ) است که به نام نماینده از ج . با انتخاب مناسب بخش ، هر عنصر از یک کلاس ممکن است به عنوان نماینده کلاس انتخاب شود.

بعضی اوقات ، بخشی وجود دارد که "طبیعی" تر از بخش دیگر است. در این مورد، نمایندگان نامیده می شوند متعارف نمایندگان . به عنوان مثال ، در محاسبات مدولار ، رابطه هم ارزی را در اعداد صحیح تعریف شده به شرح زیر در نظر بگیرید: a ~ b اگر a - b مضربی از یک عدد صحیح مثبت داده شده n باشد ( مدول نامیده می شود ). هر کلاس شامل یک عدد صحیح غیر منفی منحصر به فرد کوچکتر از n است و این اعداد صحیح نمایندگان متعارف هستند. این کلاس و نماینده آن کم و بیش مشخص می شوند ، همانطور که این واقعیت را نشان می دهد که یک مدولاسیون است N یا ممکن است کلاس، و یا نماینده متعارف آن (که نشان دهنده باقی مانده از تقسیم ازتوسط N ).

خصوصیات [ ویرایش ]

هر عنصر x از X عضوی از کلاس معادل سازی [ x ] است . هر دو کلاس هم ارزی [ x ] و [ y ] یا برابر هستند یا از هم جدا هستند . بنابراین ، مجموعه تمام کلاس های هم ارزی X یک پارتیشن از X تشکیل می دهد : هر عنصر X به یک و فقط یک کلاس معادل تعلق دارد. [10] و برعکس ، هر پارتیشن X از یک رابطه معادل از این طریق بدست می آید ، که طبق آن x ~ y اگر و فقط اگرx و y مربوط به همان مجموعه پارتیشن هستند. [11]

از خصوصیات یک رابطه هم ارز نتیجه می گیرد که

x ~ y اگر و فقط اگر [ x ] = [ y ] باشد.

به عبارت دیگر ، اگر ~ یک رابطه معادل در مجموعه X باشد ، و x و y دو عنصر X هستند ، این عبارات معادل هستند:

$x \ سیم y$
$[x] = [سال]$
$[x] \ cap [y] \ neq \ emptyset.$

نمایش گرافیکی [ ویرایش ]

نمودار مثال معادل سازی با 7 کلاس

یک نمودار بدون جهت ممکن است به هر رابطه متقارنی در یک مجموعه X مرتبط باشد ، جایی که رئوس عناصر X هستند ، و دو راس s و t اگر و فقط اگر s ~ t باشد به هم متصل می شوند. از جمله این نمودارها نمودار روابط هم ارزی است. آنها مشخص به عنوان نمودار به طوری که اجزای متصل هستند دار و دسته . [12]

عوام [ ویرایش ]

اگر ~ یک رابطه معادل بر X باشد ، و

P ( x )

ویژگی عناصر X است به طوری که هر زمان

x ~ y ، P ( x )

اگر P ( y ) درست باشد ، P ( x ) درست است ، آنگاه گفته می شود که ویژگی P ثابت از ~ ، و یا به خوبی تعریف شده تحت رابطه ~ .

یک مورد خاص مکرر زمانی اتفاق می افتد که f تابعی از X به مجموعه دیگر Y باشد . اگر

F ( X 1 ) = F ( X 2 )

هر زمان که X 1 ~ X 2 ، پس از آن F گفته می شود تغییر ناپذیر کلاس تحت ~ ، و یا به سادگی تحت ناوردا ~ . این اتفاق می افتد ، مثلاً در تئوری شخصیت گروههای محدود. برخی از نویسندگان استفاده از "سازگار با ~ " یا فقط "جهات ~ " به جای "ثابت تحت ~ ".

هر تابع F : X → Y به خودی خود یک رابطه هم ارزی در تعریف X که بر طبق آن X 1 ~ X 2 اگر و تنها اگر

F ( X 1 ) = F ( X 2 ) .

کلاس هم ارزی X مجموعه ای از تمام عناصر در است X که به نقشه برداری F ( X ) یعنی طبقه [ X ] است تصویر معکوس از F ( X ). این رابطه هم ارزی به عنوان شناخته شده هسته از F .

به طور کلی ، یک تابع ممکن است آرگومان های معادل (تحت یک رابطه هم ارزی ~ X روی X ) را با مقادیر معادل ترسیم کند (تحت یک رابطه هم ارزی ~ Y روی Y ). چنین تابع است morphism از مجموعه مجهز به یک رابطه هم ارزی.

فضای کم در توپولوژی [ ویرایش ]

در توپولوژی ، یک فضای خارج قسمت است فضای توپولوژیک تشکیل شده بر روی مجموعه ای از کلاس هم ارزی یک رابطه هم ارزی در یک فضای توپولوژیک، با استفاده از توپولوژی فضای اصلی برای ایجاد توپولوژی بر روی مجموعه ای از کلاس هم ارزی است.

در جبر انتزاعی ، روابط همخوانی در مجموعه اساسی جبر به جبر این امکان را می دهد که جبر را در طبقات هم ارزی رابطه ، که جبر ضریب نامیده می شود ، القا کند . در جبر خطی ، فضای ضریب فضایی برشی است که با گرفتن یک گروه ضریب تشکیل می شود ، جایی که همومورفیسم ضریب یک نقشه خطی است . با گسترش، در جبر، فضای مدت بهره ممکن است برای استفاده از ماژول های خارج قسمت ، حلقه خارج قسمت ، گروه خارج قسمت، یا هر جبر ضریب. با این حال ، استفاده از این اصطلاح برای موارد عمومی تر ، اغلب می تواند به صورت قیاس با مدار یک عمل گروهی باشد.

مدارهای یک کنش گروهی روی یک مجموعه را می توان فضای فاکتور کنش روی مجموعه نامید ، به ویژه هنگامی که مدارهای کنش گروه ، کیهان های مناسب یک زیر گروه از یک گروه باشند ، که از عملکرد زیرگروه در ناشی می شوند گروه را با ترجمه های چپ یا به ترتیب کیهان های چپ را به عنوان مدارهای تحت ترجمه راست قرار دهید.

یک زیر گروه عادی از یک گروه توپولوژیکی ، که با عمل ترجمه بر روی گروه عمل می کند ، فضای کمی در حواس توپولوژی ، جبر انتزاعی و اقدامات گروهی به طور همزمان است.

اگرچه این اصطلاح را می توان برای مجموعه کلاسهای معادل سازی هر رابطه هم ارزی استفاده کرد ، اما احتمالاً با ساختار بیشتر ، هدف استفاده از این اصطلاح به طور کلی مقایسه آن نوع رابطه هم ارزی در مجموعه X است ، یا به یک رابطه هم ارزی که ساختار خاصی را القا می کند. مجموعه کلاسهای معادل سازی از ساختاری از همان نوع در X یا به مدارهای یک عمل گروهی. هم حس ساختاری که توسط یک رابطه هم ارزی حفظ شده است ، و هم مطالعه تغییر ناپذیرها تحت اقدامات گروهی ، منجر به تعریف تغییرات ناپایدار روابط هم ارزی می شود که در بالا آورده شد.

همچنین به [ ویرایش ] مراجعه کنید

تقسیم معادل ، روشی برای ابداع مجموعه های آزمایشی در تست نرم افزار بر اساس تقسیم ورودی های احتمالی برنامه به کلاس های هم ارزی با توجه به رفتار برنامه بر روی آن ورودی ها
فضای همگن ، فضای کمی گروه های دروغ
رابطه هم ارزی جزئی
با یک رابطه هم ارز ضریب می شود
عرضی (ترکیبی)

یادداشت ها

+ نوشته شده در پنجشنبه هشتم آبان ۱۳۹۹ ساعت 8:58 توسط علی رضا نقش نیلچی |

کلاس معادل سازی

${\ displaystyle \ {x \ in S \ mid x \ sim a \}}$

فهرست

مثالها [ ویرایش ]

اگر X مجموعه ای از تمام اتومبیل است، و ~ است رابطه هم ارزی "است همان رنگ به عنوان"، و سپس یک کلاس هم ارزی خاص را از تمام اتومبیل های سبز تشکیل، و X / ~ می تواند به طور طبیعی با مجموعه ای از تمام رنگ خودرو شناسایی .
اجازه دهید X شود مجموعه ای از مستطیل در یک هواپیما، و ~ رابطه هم ارزی "دارای همان منطقه به عنوان"، و سپس برای هر عدد حقیقی مثبت ، وجود خواهد داشت یک کلاس هم ارزی تمام مستطیل که منطقه . [4]
در نظر بگیرید پیمانه 2 رابطه هم ارزی در مجموعه ای از اعداد صحیح ، ℤ ، به طوری که X ~ Y اگر و تنها اگر تفاوت آنها X - Y یک IS تعداد حتی . این رابطه باعث ایجاد دقیقاً دو کلاس معادل سازی می شود: یک کلاس از همه اعداد زوج تشکیل شده و کلاس دیگر از همه اعداد فرد تشکیل شده است. با استفاده از براکت های مربعی در اطراف یک عضو کلاس برای نشان دادن یک کلاس هم ارز تحت این رابطه ، [7] ، [9] و [1] همه نشان دهنده همان عنصر ℤ / هستند . [5]
اجازه دهید X شود مجموعه ای از زوج مرتب از اعداد صحیح ( ، ب ) با غیر صفر ب ، و تعریف یک رابطه هم ارزی ~ در X به طوری که ( ، ب ) ~ ( ج ، د ) اگر و تنها اگر آگهی = قبل از میلاد ، سپس کلاس معادل جفت ( a ، b ) را می توان با عدد منطقی a / b شناسایی کرد، و می توان از این رابطه هم ارزی و کلاسهای هم ارزی آن تعریف رسمی از مجموعه اعداد گویا ارائه داد. [6] همان ساخت را می توان به حوزه کسرهای هر حوزه انتگرال تعمیم داد .
اگر X شامل تمام خطوط در، می گویند، یک فضای اقلیدسی ، و L ~ M بدان معنی است که L و M می خطوط موازی ، سپس مجموعه ای از خطوط که موازی به هر شکل دیگر یک کلاس هم ارزی، تا زمانی که یک خط است موازی با خودش در نظر گرفته شده است . در این وضعیت ، هر کلاس معادل یک نقطه را در بی نهایت تعیین می کند .

علامت گذاری و تعریف رسمی [ ویرایش ]

رابطه هم ارزی در یک مجموعه X است رابطه دودویی ~ در X رضایت سه ویژگی: [7] [8]

a ~ a برای همه a در X ( انعکاس پذیری ) ،
~ ب دلالت ب ~ برای همهو ب در X ( تقارن )،
اگر a ~ b و b ~ c سپس a ~ c برای همه a ، b و c در X (قابلیت انتقال ).

خصوصیات [ ویرایش ]

از خصوصیات یک رابطه هم ارز نتیجه می گیرد که

x ~ y اگر و فقط اگر [ x ] = [ y ] باشد.

به عبارت دیگر ، اگر ~ یک رابطه معادل در مجموعه X باشد ، و x و y دو عنصر X هستند ، این عبارات معادل هستند:

$x \ سیم y$
$[x] = [سال]$
$[x] \ cap [y] \ neq \ emptyset.$

نمایش گرافیکی [ ویرایش ]

نمودار مثال معادل سازی با 7 کلاس

عوام [ ویرایش ]

اگر ~ یک رابطه معادل بر X باشد ، و

P ( x )

ویژگی عناصر X است به طوری که هر زمان

x ~ y ، P ( x )

اگر P ( y ) درست باشد ، P ( x ) درست است ، آنگاه گفته می شود که ویژگی P ثابت از ~ ، و یا به خوبی تعریف شده تحت رابطه ~ .

یک مورد خاص مکرر زمانی اتفاق می افتد که f تابعی از X به مجموعه دیگر Y باشد . اگر

F ( X 1 ) = F ( X 2 )

هر تابع F : X → Y به خودی خود یک رابطه هم ارزی در تعریف X که بر طبق آن X 1 ~ X 2 اگر و تنها اگر

F ( X 1 ) = F ( X 2 ) .

فضای کم در توپولوژی [ ویرایش ]

همچنین به [ ویرایش ] مراجعه کنید

تقسیم معادل ، روشی برای ابداع مجموعه های آزمایشی در تست نرم افزار بر اساس تقسیم ورودی های احتمالی برنامه به کلاس های هم ارزی با توجه به رفتار برنامه بر روی آن ورودی ها
فضای همگن ، فضای کمی گروه های دروغ
رابطه هم ارزی جزئی
با یک رابطه هم ارز ضریب می شود
عرضی (ترکیبی)

یادداشت ها

+ نوشته شده در پنجشنبه هشتم آبان ۱۳۹۹ ساعت 8:58 توسط علی رضا نقش نیلچی |

پوچی

پوچی چیزی است که بسیار است غیر منطقی ، بنابراین به عنوان به احمقانه و یا گرفته شده است به طور جدی ، و یا دولت بودن است. "پوچ" یک صفت است که برای توصیف پوچی استفاده می شود ، به عنوان مثال ، "تایلر و پسران از پوچی وضعیت خندیدند." [1] آن را از لاتین مشتق شده برهان به معنی " از لحن "، از این رو غیر منطقی است. [2] ساردوس لاتین به معنی " ناشنوا " است و دلالت بر حماقت دارد . [1] پوچی با جدیت در استدلال در تضاد است. [3]در استفاده عمومی ، پوچی ممکن است مترادف با تمسخر و مزخرفات باشد . در کاربردهای تخصصی ، پوچی با استدلال بد یا افراط در استدلال به افراط و تفریط مرتبط است. مسخره بودن با افراط و تفریط های غیرمجاز ، خنده و تمسخر مرتبط است. و مزخرفات مربوط به عدم معناداری است . پوچ گرایی مفهومی در فلسفه است که به مفهوم پوچی مربوط می شود.

فهرست

تاریخچه [ ویرایش ]

پوچ در طول تاریخ غرب در مورد احمق و استدلال بسیار ضعیف برای شکل گیری عقیده استفاده شده است. [4]

یونان باستان

در آریستوفان ، 5 قرن قبل از میلاد کمدی زنبورهای ، شخصیت خود Philocleon به "پوچ" از دست پند ، نظر گرفته می شود فانتزی غیر معقول، و درست نیست. [5]

افلاطون غالباً از "پوچگی" برای توصیف استدلال بسیار ضعیف ، یا نتیجه گیری از اتخاذ موضعی باطل و استدلال به یک نتیجه گیری غلط ، به نام "پوچگی" استفاده می کرد (استدلال توسط reductio ad absurdum). افلاطون خود را به عنوان عدم استدلال پوچ علیه خود در پارمنیدس توصیف می کند . [6] در گورگیا ، افلاطون به عنوان "پوچ اجتناب ناپذیر" به عنوان نتیجه استدلال از یک فرض نادرست اشاره می کند. [7]

ارسطو پوچ پوچ غیرعقلانی را در استدلال با تجربی با استفاده از احتمال اصلاح کرد ، "پس از معرفی غیرمنطقی و هوایی از احتمال تحریک به آن ، ما باید آن را علیرغم پوچ بودن بپذیریم. [8] او ادعا کرد که پوچ بودن در استدلال با حجاب است. زبان جذاب در شعر ، "همانطور که هست ، پوچی با جذابیت شاعرانه ای که شاعر روی آن سرمایه گذاری می کند ، پوشیده شده است ... اما در شعر حماسه پوچی بی توجه می ماند". [8]

دوره رنسانس و اوایل دوره مدرن

میشل دو مونتاژ ، پدر مقاله و شک و تردید مدرن ، با بیان اینكه روند كاهش حماقت احمقانه است و پوچ ایجاد می كند ، گفت: "هر كوتاهی كه از كتاب خوب است ، ابزاری احمقانه است ... پوچی نیست [...] نباید از خودش درمان شود ... دلیل ، می تواند منطقی باشد. " [9]

فرانسیس بیکن ، مروج اولیه تجربی و روش علمی ، اظهار داشت که پوچ بودن یک مؤلفه ضروری پیشرفت علمی است و نباید همیشه از آن خندید. وی ادامه داد: روشهای جدید و جسورانه تفکر و فرضیه های جسورانه غالباً منجر به پوچی می شوند ، "زیرا اگر پوچی موضوع خنده باشد ، به شما شک می کنید ، اما جسارت بزرگ به ندرت بدون مقداری پوچ است." [10]

رویکرد به پوچی [ ویرایش ]

بلاغت [ ویرایش ]

پوچی وقتی بوجود می آید که گفتار شخصی از عقل سلیم فاصله بگیرد ، بیش از حد شعر است ، یا وقتی شخص قادر به دفاع از خود با گفتار و عقل نیست. در کتاب بلاغت ارسطو ، ارسطو درباره موقعیت هایی که در آن پوچ به کار می رود و چگونگی تأثیر آن در استفاده از اقناع شخص تأثیر می گذارد ، بحث می کند. ایده مرد ناتوانی در ترغیب کسی به قول خود پوچ است. [11] به گفته ارسطو ، یک سخنرانی نباید بیش از حد شاعرانه باشد زیرا پوچ و بی مزه بودن را به یک گفتار وارد می کند. هرگونه اطلاعات غیر ضروری در مورد پرونده غیر منطقی است و گفتار را نامشخص می کند. اگر سخنرانی بیش از حد نامشخص شود؛ توجیه پرونده آنها غیرمجاز است و این بحث را پوچ می کند. [12]

فلسفه [ ویرایش ]

اطلاعات بیشتر: پوچ گرایی

این غیر منطقی است که در دنیای غافل بدون هدف یا معنا به دنبال هدف یا معنا باشید یا ثروت بیش از حد را در مواجهه با مرگ مشخص جمع کنید. پوچ پوستی در فلسفه اگزیستانسیالیستی و وابسته به آن برای توصیف تلاش های بی معنی پوچ برای تلاش برای یافتن چنین معنایی یا هدف در دنیایی عینی و غافلگیر ، فلسفی معروف به پوچ گرایی استفاده می شود . [ نیاز به استناد ]

توماس نگل در مقاله خود با عنوان The Absurd ، پوچگی دائمی زندگی بشر را مورد تحلیل قرار داد. پوچی در زندگی وقتی آشکار می شود که زندگی ما را جدی می گیرد ، آشکار می شود ، در حالی که همزمان درک می کنیم که در هر کاری که انجام می دهیم ، داوری خاصی وجود دارد. او پیشنهاد می کند که هرگز جستجو برای پوچ را متوقف نکنید. علاوه بر این ، او پیشنهاد می کند که در میان پوچی ، طعنه طلبانه جستجو کنید. [ نیاز به استناد ]

فلسفه زبان

اطلاعات بیشتر: تناقض مور

GE Moore ، فیلسوف تحلیلی انگلیسی ، به عنوان پارادوکس زبان از جمله های پوچ سطحی چنین استناد کرد: "من سه شنبه گذشته به تصاویر رفتم اما آن را باور نمی کنم". آنها می توانند درست و منطقی سازگار باشند و در مورد بررسی بیشتر هدف زبانی کاربر متناقض نباشند. ویتگنشتاین مشاهده می کند که در بعضی شرایط غیرمعمول پوچ پوستی در چنین اظهاراتی از بین می رود ، زیرا مواردی وجود دارد که "باران می بارد اما من اعتقاد ندارم که" بتواند حس کند ، یعنی آنچه به نظر می رسد پوچ است مزخرف نیست. [13]

علامت گذاری با استدلال سالم

مفسران پزشکی روشها و استدلال را در داروهای جایگزین و مکمل و داروی یکپارچه مورد انتقاد قرار داده اند که این یا پوچ بودن یا بین شواهد و پوچ بودن است. آنها اظهار داشتند كه غالباً مردم را با اصطلاحات خوشبينانه ، مانند عبارات "طب جايگزين" و "طب مکمل" ، گمراه مي سازد و خواهان مشخص نمودن بين شواهد علمي معتبر و روش شناسي علمي و پوچي هستند. [14] [15]

پوچی در ادبیات [ ویرایش ]

فهرست هابز از پوچی

توماس هابز پوچی را از خطاها ، از جمله خطاهای اساسی زبانی متمایز می کند ، هنگامی که یک کلمه به سادگی برای اشاره به چیزهایی وجود دارد که نام آن را ندارد. به گفته آلوزیوس مارتینیچ : "آنچه هابز نگران آن است پوچی است. فقط انسانها می توانند یک پوچی را در آغوش بگیرند ، زیرا فقط انسانها زبان دارند و فیلسوفان نسبت به دیگران مستعد آن هستند." [16]هابز نوشت: "كلماتی كه به غیر از صدا چیزی را تصور نمی كنیم ، آنهایی هستند كه پوچ ، ناچیز و مزخرف می نامیم." ؛ یا از یک موضوع آزاد ؛ یک اراده آزاد ؛ یا هر آزاد ، اما عاری از مانع مخالفت ، من نباید بگویم که او خطایی داشته است ، بلکه این که سخنان وی بدون معنا بوده است ، یعنی پوچ است ». [17] وی هفت نوع پوچی را تفکیک کرد. در زیر خلاصه ای از مارتینیچ ، بر اساس آنچه که او توصیف می کند "شرح بالغ" هابز است که در "De Corpore" یافت شده است . 5. ، که همه از نمونه هایی استفاده می کنند که می توان در ارسطویی یا فلسفه دانشمند یافت ، و همه بازتاب "هابز" است.هاروی »این به" جدول پوچی پوچ "هابز معروف است.

"ترکیب نام جسمی با نام تصادف." به عنوان مثال ، "وجود یک موجود است" یا "یک هستی وجود است". این پوچ ها طبق نظر هابز ، نمونه ای از فلسفه دانشمندان است.
"ترکیب نام جسمی با نام فانتزم." به عنوان مثال ، "یک روح یک بدن است".
"ترکیب نام بدن با نام یک نام." به عنوان مثال ، "یک امر جهانی یک چیز است".
"ترکیب نام تصادف با نام فانتزی." به عنوان مثال ، "رنگ به نظر می رسد برای یک درک کننده".
"ترکیب نام تصادف با نام یک نام." به عنوان مثال ، "یک تعریف ، جوهر یک چیز است".
"ترکیب نام فانتزی با نام یک نام." به عنوان مثال ، "ایده ی مرد جهانی است".
"ترکیب نام یک چیز با نام یک عمل گفتار." برای مثال ، "بعضی موجودات به خودی خود موجودات هستند ".

به گفته مارتینیچ ، گیلبرت رایل در مورد انواع مسئله مورد بحث قرار گرفته است که هابز تحت عنوان " خطای دسته " به پوچی گفته می شود.

گرچه امروزه كاربردهای رایج "پوچگی" را مترادف با " مسخره بودن " می داند ، اما هابز دو مفهوم را به عنوان یكدیگر مورد بحث قرار داد ، در آن پوچی به نظر می رسد كه مربوط به استدلال نامعتبر است ، [16] [17] در حالی كه مسخره بودن با خنده ارتباط دارد. ، برتری و ناهنجاری . [18] [19] [20]

تئاتر پوچ

تئاتر پوچی یادآور شد سورئالیست جنبش نشان دادن نقوش از پوچانگاری.

"تئاتر باید یک تماشای خونین و غیر انسانی باشد که برای تمرین (تحریک دقیق) تماشاگران سرکوب شده جنایی و شهوانی تماشاگر طراحی شده است.
- آنتونین آرادو ، تئاتر و دوبل آن

الهیات [ ویرایش ]

"من معتقدم چون پوچ است"
- ترتولیان

پوچ گرایی به عنوان پایه ای برای برخی از استدلال های کلامی در مورد شکل گیری اعتقاد و ایمان ذکر شده است ، از جمله در فیدئولوژی ، یک نظریه معرفت شناختی مبنی بر اینکه عقل و ایمان ممکن است با یکدیگر خصمانه باشند. جمله " Credo quia absurdum " ("من معتقدم که پوچ است") به ترتولیان از د کارن کریستی منتسب شده است ، همانطور که فیلسوف ولتر ترجمه کرده است . [21] براساس كلیسای جدید ظهور ، آنچه ترتولیان در DCC 5 گفت: "[...] پسر خدا درگذشت ؛ به هر حال باید باور شود ، زیرا پوچ است." [22]

در قرن پانزدهم میلادی ، مکتب شناس اسپانیایی Tostatus ، آنچه که فکر می کرد کاهش پوچ استدلال در برابر یک کره کروی با استفاده از جزم ، استعمال می کند ، ادعا می کند که یک کره کروی به معنای وجود پادگان ها است . وی استدلال كرد كه این امر غیرممكن خواهد بود زیرا مستلزم این است كه مسیح دو بار ظاهر شود یا ساكنان پادتنها برای همیشه لعنت شوند ، كه وی ادعا كرد پوچی است. [ نیاز به استناد ]

پوچی می تواند به هر یک از عزم های دینی دقیق اشاره کند که چیزی را به نقض عقل سلیم سوق دهد. به عنوان مثال ، اصطلاحات مذهبی انعطاف ناپذیر ، گاهی اوقات به معنای اصرار غیر منطقی بر رعایت کلمات یا قوانین دقیق ، به جای هدف یا روح ، اصطلاحاً فارسیسم خوانده می شود . [23] [24] [25]

اندرو ویل پوچی ها را با "تضاد مسطح با کتاب مقدس" و "بدعت ها" گروه بندی کرد. [26]

نگرش به پوچی [ ویرایش ]

روانشناسی [ ویرایش ]

روانشناسان چگونگی سازگاری انسان با پوچ های مداوم زندگی را مطالعه می کنند. [27] در تبلیغات ، وجود یا عدم وجود یک تصویر پوچ برای تعدیل نگرش منفی نسبت به محصولات و افزایش شناخت محصول پیدا شد. [28]

طنز [ ویرایش ]

اطلاعات بیشتر: تئوری طنز و طنز پوچ گرایی

"من چیزی نمی توانم ببینم" - آلیس در سرزمین عجایب
"من ، شما باید چشم های خوب داشته باشید" - گربه چشایر

پوچ پوستی در طنز به کار می رود تا مردم بخندند یا یک نکته پیچیده را بیان کنند. یک نمونه ، " Jabberwocky " لوئیس کارول ، شعری از آیه مزخرف است که در اصل به عنوان بخشی از رمان پوچ گرایانه وی از طریق شیشه در حال جستجو ، و آنچه آلیس در آنجا یافت (1872) به نمایش درآمد. کارول منطق دان و تقلید بود منطق با استفاده از منطق و معکوس روش منطقی است. [29] خورخه لوئیس بورخس رمان نویس آرژانتینی در داستان های کوتاه خود از پوچ پوشی ها برای بیان امتیاز استفاده کرد. [30] فرانتس کافکا را مسخ نظر گرفته شده است پوچی توسط برخی از. [31]

پوچی در رشته های مختلف [ ویرایش ]

قانونی [ ویرایش ]

دکترین پوچی یک نظریه حقوقی در دادگاه های آمریکا است. [32] : 234–239 یک نوع پوچی ، معروف به " خطای جستجوی " ، هنگامی رخ می دهد که تصحیح متنی ساده برای اصلاح یک خطای آشکار روحانی ، مانند یک کلمه اشتباه انجام شود. [32] : 234–235 نوع دیگری از پوچی ، به نام "پوچی ارزیابی" ، هنگامی بوجود می آید که یک قانون قانونی ، با وجود هجی و دستور زبان مناسب ، "هیچ معنای اساسی ندارد". نمونه ای از این آیین نامه ای است که به اشتباه برای برنده شدن به جای از دست دادن طرف برای پرداخت حق وکالت معقول طرف مقابل فراهم کرده است. [32] :آموزه گرایی و رسیدن به هدف بیشتر ، هدف اصلی این آموزه را با دو اصل محدود نمی کند: "... پوچی و بی عدالتی در اجرای ماده برای این پرونده چنان هیجان انگیز است ، که تمام بشریت بدون تردید در رد این اتحاد متحد خواهند شد. برنامه " [33] و پوچ باید اصلاح شود" ... با تغییر متن به روشهای نسبتاً ساده ". [34] [32] : 237–239 این دکترین مطابق نمونه هایی از عقل سلیم تاریخی است. [35]

"عقل سلیم انسان قضاوت ذکر شده توسط پوفندورف [sic. Puffendorf] را تأیید می کند ، که قانون بولونیا که تصویب می کند" هر کس خون را در خیابان ها می کشد با حداکثر مجازات مجازات می شود "، به جراح که باز کرد گسترش نمی یابد. رهنمودهای شخصی که در خیابان به تناسب سقوط کرده است. همان عقل سلیم حکم ، استناد شده توسط Plowden را می پذیرد ، که اساسنامه اول ادوارد دوم ، که تصویب می کند زندانی که زندان را می شکند ، باید مقصر باشد. نه به زندانی که وقتی آتش آتش می زند بیرون می آید - "زیرا او را نباید آویزان کرد زیرا او نمی ماند تا بسوزد." [36]

منطق و علوم رایانه [ ویرایش ]

برهان خلف

Reductio ad absurdum ، کاهش به پوچ ، روشی برای اثبات در مباحث ، منطق و ریاضیات است ، از این رو با فرض اینکه یک گزاره صحیح است ، منجر به پوچی می شود. یک گزاره صحیح فرض شده است و این برای استنباط گزاره معروف به غلط استفاده می شود ، بنابراین گزاره اصلی باید نادرست بوده است. این یک سبک استدلال در جدالها است ، به موجب آن با فرض و استدلال برای دستیابی به چیزی که شناخته می شود به عنوان نادرست یا نقض عقل سلیم باشد ، موضع گیری باطل یا "پوچ" نشان داده می شود. از افلاطون برای استدلال در برابر سایر مواضع فلسفی استفاده می شود. [37] در منطق تحولات مدل ، از محدودیت پوچ استفاده می شود . [38]

در منطق ثابت است

"ثابت پوچ" ، که اغلب با نماد مشخص می شود ، در منطق رسمی استفاده می شود. [39] این نشان دهنده مفهوم falsum ، گزاره منطقی ابتدایی است که توسط "غلط" ثابت در چندین زبان برنامه نویسی مشخص شده است .

منطق را حاکم کنید

قاعده پوچی یک قاعده در منطق است ، همانگونه که پاتریک سوپس در منطق ، روش و فلسفه علم به کار می برد: مجموعه مقالات . [40]

منبع

https://en.wikipedia.org/wiki/Absurdity

+ نوشته شده در جمعه بیست و ششم اردیبهشت ۱۳۹۹ ساعت 3:11 توسط علی رضا نقش نیلچی |

پارادوکسهای تئوری مجموعه

این مقاله حاوی بحث در مورد پارادوكسهای تئوری مجموعه است . مانند اکثر پارادوکسهای ریاضی ، آنها معمولاً نتایج ریاضیاتی غافلگیرکننده و ضد شهود را آشکار می کنند ، و نه تناقضات منطقی واقعی در نظریه مجموعه های بدیهی مدرن .

فهرست

مبانی [ ویرایش ]

شماره کاردینال [ ویرایش ]

نظریه مجموعه همانطور که توسط جورج کانتور تصور می شود وجود مجموعه های نامتناهی را فرض می کند. از آنجا که این فرض از اصول اولیه قابل اثبات نیست ، بدیهی است از بی نهایت ، که تئوری وجود مجموعه N از اعداد طبیعی را اثبات می کند ، در تئوری مجموعه بدیهی وارد شده است . هر مجموعه نامتناهی که با شماره های طبیعی قابل شمارش است ، به همان اندازه N (کاردینالیت) با N است و گفته می شود که قابل شمارش است. نمونه هایی از مجموعه های بی حد و حصر بی شماری عبارتند از اعداد طبیعی ، عدد یکسان ، اعداد اصلی و همچنین همه اعداد منطقی ، یعنی کسری. این مجموعه ها مشترکاً با شماره کاردینال | ن| =\ displaystyle \ aleph _ {0}} $\ aleph _ {0$ (همه چیز) ، عددی بزرگتر از هر عدد طبیعی.

شماره کاردینال را می توان به شرح زیر تعریف کرد. دو مجموعه را تعیین کنید تا اندازه یکسان با هم داشته باشند: بین این دو مجموعه یک تجلی وجود دارد (مکاتبات یک به یک بین عناصر). سپس به صورت تعریف ، یک عدد کاردینال کلاس است که از کلیه مجموعه ها در یک اندازه تشکیل شده است. داشتن یک اندازه یک رابطه هم ارزی است و عدد کاردینال کلاس های هم ارزی هستند .

شماره های معمولی [ ویرایش ]

علاوه بر کاردینالیتی ، که اندازه یک مجموعه را توصیف می کند ، مجموعه های مرتب شده نیز موضوع تئوری مجموعه را تشکیل می دهند. اصل موضوع انتخاب تضمین می کند که هر مجموعه می توان مرتب و منظم ، به این معنی که کل سفارش را می توان در عناصر آن تحمیل به طوری که هر زیر مجموعه غیر خالی دارای یک عنصر اول با توجه به آن منظور. ترتیب یک مجموعه مرتب با یک عدد معمولی شرح داده شده است . به عنوان مثال ، 3 عدد ترتیب مجموعه {0 ، 1 ، 2} با ترتیب معمول 0 <1 <2 است. و ω تعداد عادی مجموعه ای از همه اعداد طبیعی است که به روش معمول سفارش داده می شوند. با غفلت از سفارش ، ما با شماره کاردینال | ن | = | ω | = \ displaystyle \ aleph _ {0}} $\ aleph _ {0$ .

اعداد معمولی را می توان با همان روشی که برای اعداد کاردینال استفاده می شود تعریف کرد. تعریف دو مجموعه به خوبی دستور داد تا از نوع همان نظم توسط: وجود دارد وجود دارد پوشا و یکبهیک بین دو مجموعه احترام به سفارش: عناصر کوچکتر به عناصر کوچکتر نقشه برداری. سپس به طور تعریف ، یک عدد مرتب ، کلاس است که از کلیه مجموعه های مرتب از همان نوع مرتبه تشکیل شده است. داشتن یک نوع مرتبه یک رابطه هم ارزی در کلاس مجموعه های مرتب است و اعداد مرتب کلاس های هم ارزی هستند.

دو مجموعه از نوع مرتبه‌ای یکسان ، کاردینالیت یکسانی دارند. این مکالمه به طور کلی برای مجموعه های نامحدود صحیح نیست: می توان ترتیبهای مختلف خوبی را به مجموعه اعداد طبیعی تحمیل کرد که باعث ایجاد تعداد ترتیب های مختلف می شود.

یک نظم طبیعی روی احکام وجود دارد ، که این خود یک نظم خوب است. با توجه به هر دستورالعمل α ، می توان مجموعه همه دستورالعمل ها را کمتر از α در نظر گرفت. به نظر می رسد که این مجموعه دارای شماره ترتیب α باشد. این مشاهدات برای به راه های مختلف معرفی ordinals، که در آن یک ترتیبی استفاده شده است برابر دانسته با مجموعه ای از تمام ordinals کوچکتر است. بنابراین ، این شکل از تعداد ترتیب ، نماینده متعارف از شکل قبلی کلاس هم ارزی است.

مجموعه های برق [ ویرایش ]

با تشکیل کلیه زیر مجموعه های مجموعه S (تمام گزینه های ممکن از عناصر آن) ، مجموعه قدرت P ( S ) را بدست می آوریم . جورج کانتور ثابت کرد که مجموعه قدرت همیشه بزرگتر از مجموعه است ، یعنی | P ( S ) | > | S | یک مورد خاص از قضیه کانتور ثابت می کند که مجموعه ای از همه اعداد واقعی R را نمی توان با شماره های طبیعی شمرد. R غیرقابل شمارش است: | ر | > | ن |

متناقضات مجموعه بی نهایت [ ویرایش ]

تئوری مجموعه به جای تکیه بر توصیفهای مبهم مانند "آنچه قابل بزرگنمایی نیست" یا "افزایش بدون محدودیت" است ، تعاریفی را برای اصطلاح نامتناهی ارائه می دهد تا معنای نامشخصی به عباراتی مانند "مجموعه همه اعداد طبیعی بی نهایت باشد" ارائه کند. . همانطور که برای مجموعه های محدود ، این تئوری تعاریف دیگری را ارائه می دهد که به ما امکان می دهد دو مجموعه بی نهایت را با هم مقایسه کنیم که آیا یک مجموعه "بزرگتر از" ، "کوچکتر از" یا "اندازه مشابه" است. اما هر شهود نسبت به اندازه مجموعه های محدود به اندازه مجموعه های نامتناهی اعمال نمی شود و منجر به نتایج ظاهرا متناقض مختلفی در مورد شمارش ، اندازه ، اندازه و ترتیب می شود.

متناقض های شمارش [ ویرایش ]

قبل از معرفی تئوری مجموعه ، مفهوم اندازه یک مجموعه مشکل ساز بوده است. این مورد توسط گالیله گالیله و برنارد بولزانو از جمله دیگران مورد بحث قرار گرفته است . آیا اندازه گیری تعداد اعداد طبیعی به اندازه مربع اعداد طبیعی با استفاده از روش شمارش است؟

پاسخ مثبت است، چرا که برای هر عدد طبیعی N یک عدد مربع وجود دارد N 2 و به همین ترتیب راه دیگری در اطراف.
جواب این است: نه ، زیرا مربع ها زیر مجموعه ای مناسب از طبیعت هستند: هر مربع یک عدد طبیعی است اما تعداد طبیعی نیز وجود دارد ، مانند 2 ، که مربع هایی با اعداد طبیعی نیستند.

با تعریف مفهوم اندازه یک مجموعه از نظر کاردینگی آن ، می توان موضوع را حل کرد. از آنجا که یک وجود دارد پوشا و یکبهیک بین دو مجموعه درگیر، این زیر در واقع به طور مستقیم از تعریف از کاردینالیتی یک مجموعه.

برای اطلاعات بیشتر در مورد پارادوکس های شمارش ، به متن پارادوکس هیلبرت از هتل گراند مراجعه کنید .

Je le vois، mais je ne crois pas [ ویرایش ]

"من آن را ببینید اما من باور نمی کنم،" کانتور به نوشته ریچارد ددکیند است: پس از اثبات این است که مجموعه ای از نقاط از یک مربع است که کاردینالیتی همان است که از نقاط روی یک لبه مربع کاردینالیتی زنجیره .

این نشان می دهد که "اندازه" مجموعه ها که به تنهایی توسط کاردینالیتی تعریف شده اند ، تنها روش مفید مقایسه مجموعه ها نیست. تئوری اندازه گیری تئوری ظریف تر اندازه ای را ارائه می دهد که با شهود ما مطابقت دارد که طول و مساحت اندازه های ناسازگار اندازه هستند.

شواهد نشان می دهد كه كانتور كاملاً به نتیجه خود اطمینان دارد و اظهار نظر وی به ددكیند به جای دغدغه های آن موقع در مورد صحت اثبات اثبات او در مورد آن است. [1] با این وجود، اظهار کانتور را نیز در خدمت به خوبی برای بیان تعجب است که بسیاری از ریاضیدانان پس از او در اولین مواجهه با یک نتیجه این است که پس از ضد شهودی را تجربه کرده اند.

متناقضات مرتب سازی [ ویرایش ]

در سال 1904 ارنست زرملو با استفاده از بدیهیات انتخاب (که به همین دلیل معرفی شد) ثابت کرد که هر مجموعه می تواند به خوبی مرتب شود. در سال 1963 ، پل جی کوهن نشان داد كه در زرملو-فرنكل نظریه تنظیم شده بدون محور انتخاب ، اثبات وجود نظم و ترتیب درست از اعداد واقعی امكان پذیر نیست.

با این حال ، توانایی مرتب سازی هر مجموعه اجازه می دهد تا ساختهای خاصی انجام شود که پارادوکسیک خوانده می شوند. یک مثال ، پارادوکس Banach-Tarski است ، قضیه ای که عموماً غیرعقل تلقی می شود. بیان می کند که می توان توپ یک شعاع ثابت را به تعداد محدودی از قطعات تجزیه کرد و سپس با ترجمه و چرخش معمولی (بدون مقیاس) آن قطعات را جابجا و مجدداً جمع کرد تا دو نسخه از یک نسخه اصلی بدست آید. ساخت این قطعات نیاز به بدیهیات انتخاب دارد؛ قطعات مناطق ساده توپ نیستند ، اما زیر مجموعه های پیچیده ای هستند .

متناقضات Supertask [ ویرایش ]

مقاله اصلی: supertask

در تئوری مجموعه ، مجموعه ای نامتناهی توسط برخی از مراحل ریاضی مانند "اضافه کردن یک عنصر" ایجاد نمی شود که بعداً "تعداد نامحدودی بار" انجام می شود. در عوض ، گفته می شود که مجموعه نامتناهی خاصی (مانند مجموعه تمام اعداد طبیعی ) از قبل ، "توسط فیات" ، به عنوان یک فرض یا بدیهی وجود دارد. با توجه به این مجموعه نامتناهی ، دیگر مجموعه های نامتناهی نیز به عنوان یک نتیجه منطقی اثبات می شوند. اما هنوز هم یک سوال فلسفی طبیعی برای تامل در مورد برخی اعمال جسمی است که در واقع پس از تعداد نامحدودی از مراحل گسسته تکمیل می شود. و تفسیر این سؤال با استفاده از نظریه مجموعه ، پارادوكسهای ابر كار را ایجاد می كند.

خاطرات Tristram Shandy [ ویرایش ]

Tristram Shandy ، قهرمان رمانی از لورنس استرن ، زندگی نامه خود را چنان با وجدان می نویسد که یک سال طول می کشد تا وقایع یک روز را پیش ببرد. اگر فانی باشد ، هرگز نمی تواند خاتمه یابد. اما اگر او برای همیشه زندگی می کرد ، هیچ بخشی از دفتر خاطرات وی نانوشته باقی می ماند ، زیرا برای هر روز از زندگی خود سالی اختصاص داده شده به توضیحات آن روز مطابقت دارد.

پارادوکس Ross-Littlewood [ ویرایش ]

مقاله اصلی: پارادوكس راس - لوتوود

نسخه افزایش یافته این نوع پارادوکس پایان بی نهایت از راه دور را به زمان محدود تغییر می دهد. یک مخزن عظیم را با توپ هایی که با شماره های 1 تا 10 ذکر شده پر کنید و شماره توپ را از بین ببرید. سپس توپ های موجود در شماره های 11 تا 20 را اضافه کنید و شماره را خاموش کنید. 2. همچنان به تعداد توپ های شماره 10 n - 9 تا 10 n اضافه کنید و برای حذف شماره توپ n برای همه اعداد طبیعی n = 3 ، 4 ، 5 ، .... بگذارید معامله اول نیم ساعت به طول انجامد ، اجازه دهید معاملات دوم چهارم ساعت یک ساعت و غیره انجام شود تا همه معاملات پس از آن تمام شوند یک ساعت. بدیهی است که مجموعه توپ های موجود در مخزن بدون محدودیت افزایش می یابد. با این وجود ، پس از یک ساعت مخزن خالی است زیرا برای هر توپ زمان حذف مشخص است.

پارادوکس با اهمیت توالی حذف بیشتر افزایش می یابد. اگر توپ ها در ترتیب 1 ، 2 ، 3 ، ... حذف نشوند ، اما در ترتیب 1 ، 11 ، 21 ، ... بعد از یک ساعت بی نهایت تعداد زیادی از توپ ها در مخزن جمع می شوند ، اگرچه همان مقدار مواد قبلی را دارد. منتقل شده

متناقضات اثبات و قطعی بودن [ ویرایش ]

تئوری مجموعه ساده لوحی به دلیل مفید بودن در حل سوالات مربوط به مجموعه های بینهایت ، دارای نقص های مهلک است. به طور خاص ، طعمه پارادوكسهای منطقی مانند مواردی كه در معرض پارادوكس راسل قرار دارد ، است . با کشف این پارادوکس ها ، مشخص شد که همه مجموعه هایی که می توانند به زبان تئوری مجموعه ساده لوحانه توصیف شوند ، می توانند بدون ایجاد تضاد وجود داشته باشند. در قرن بیستم ، تصویری از این پارادوکس ها در توسعه ابیاتومیزاسیون های مختلف نظریه های مجموعه مانند ZFC و NBG در کاربردهای رایج مشاهده شد. با این حال ، شکاف بین زبان بسیار رسمی و نمادین استاین نظریه ها و استفاده غیررسمی معمولی از زبان ریاضی منجر به شرایط مختلف متناقض می شود ، همچنین این سوال فلسفی دقیقاً چیست که چنین سیستمهای رسمی در واقع پیشنهاد می کنند که در مورد آن صحبت شوند.

پارادوكسهای اولیه: مجموعه همه مجموعه ها [ ویرایش ]

مقاله اصلی: پارادوکس راسل

در سال 1897 ریاضیدان ایتالیایی Cesare Burali-Forti فهمید که هیچ مجموعه ای وجود ندارد که شامل تمام اعداد ترتیبی باشد. همانطور که هر عدد مرتب توسط مجموعه ای از اعداد کوچکتر نظم تعریف می شود ، مجموعه ای مرتب Ω از همه عدد ترتیبی (در صورت وجود) متناسب با تعریف است و خود یک ترمینال است. از طرف دیگر ، هیچ شماره نظمی نمی تواند خود را در خود جای دهد ، بنابراین Ω نمی تواند یک دستورالعمل باشد. بنابراین ، مجموعه ای از همه شماره های ترتیب نمی تواند وجود داشته باشد.

در اواخر قرن نوزدهم ، کانتور از عدم وجود مجموعه کلیه شماره های کاردینال و مجموعه کلیه اعداد ترتیبی آگاهی داشت. وی در نامه هایی به دیوید هیلبرت و ریچارد ددکیند در مورد مجموعه های متناقض نوشت ، که عناصر آن را نمی توان همه در کنار هم فکر کرد ، و او از این نتیجه استفاده کرد تا ثابت کند که هر مجموعه ثابت دارای شماره کاردینال است.

پس از همه اینها ، نسخه پارادوکس "مجموعه همه مجموعه ها" که توسط Bertrand Russell در سال 1903 تصور شد ، به یک بحران جدی در تئوری مجموعه منجر شد. راسل تشخیص داد که عبارت x = x برای هر مجموعه صحیح است و بنابراین مجموعه همه مجموعه ها توسط { x | x = x . در سال 1906 او چندین مجموعه پارادوكس ساخت ، كه معروف ترین آنها مجموعه كل مجموعه هایی است كه خود در خود ندارند. راسل خودش این ایده انتزاعی را با استفاده از تصاویر بسیار مشخص توضیح داد. یک نمونه ، معروف به پارادوکس باربر ، می گوید: آرایشگر مردی که همه را تراشیده و فقط مردانی که خود را تراشیده نمی کنند ، مجبور است خود را اصلاح کند ، در صورتی که خود را تراشیده ندهد.

شباهت های نزدیکی بین پارادوکس راسل در نظریه مجموعه و پارادوکس Grelling-Nelson وجود دارد که نشان دهنده پارادوکس در زبان طبیعی است.

متناقضات با تغییر زبان [ ویرایش ]

پارادوكس كونيگ [ ويرايش ]

در سال 1905 ، جولیوس كونیگ ، ریاضیدان مجارستانی پارادوكس را براساس این واقعیت منتشر كرد كه فقط تعداد زیادی تعاریف محدود وجود دارد. اگر اعداد واقعی را به عنوان یک مجموعه مرتب تصور کنیم ، آن اعداد واقعی که می توانند به صورت نهایی تعریف شوند ، یک زیر مجموعه هستند. از این رو در این نظم خوب باید یک شماره واقعی اول وجود داشته باشد که به طور قطعی قابل تعریف نباشد. این تناقض آمیز است ، زیرا این عدد واقعی به طور خلاصه با جمله آخر تعریف شده است. این منجر به تضاد در نظریه مجموعه ساده لوحی می شود .

از این پارادوکس در نظریه مجموعه بدیهی اجتناب می شود. اگرچه امکان ارائه گزاره در مورد مجموعه به عنوان مجموعه وجود دارد ، اما توسط سیستم کدهای معروف به شماره های گودل ، هیچ فرمول وجود ندارد\ displaystyle \ phi (a، x) $\ phi (a، x)$ به زبان تئوری مجموعه که دقیقاً در زمانی که a وجود دارد کد برای توصیف محدود مجموعه است و این توضیحات توضیحی واقعی از مجموعه x است . این نتیجه به عنوان قضیه غیرقابل توصیف تارسکی شناخته شده است . این مربوط به یک کلاس گسترده ای از سیستم های رسمی است ، از جمله کلیه axiomatizations معمول مورد مطالعه تئوری مجموعه.

پارادوکس ریچارد [ ویرایش ]

مقاله اصلی: پارادوکس ریچارد

در همان سال ، ژول ریچارد ، ریاضیدان فرانسوی از نوعی از روش مورب کانتور استفاده کرد تا تضاد دیگری را در تئوری مجموعه ساده لوح بدست آورد. مجموعه A را از همه بزرگنمایی کلمات در نظر بگیرید. مجموعه E از تمام تعاریف محدود از اعداد واقعی زیر مجموعه ای از A است . همانطور که A قابل شمارش است ، E نیز چنین است . اجازه دهید ص شود N هفتم اعشاری از N امین عدد واقعی تعریف شده توسط مجموعه E ؛ ما به صورت یک عدد N داشتن صفر برای بخش جدایی ناپذیر و ص + 1 برای N امین اعشاری اگر Pاست یا نه به 8 یا 9 و مساوی اگر P برابر است با 8 یا 9. این تعداد N است مجموعه تعریف نشده E دلیل آن را از هر عدد حقیقی متناهی تعریف از متفاوت، یعنی N امین عدد توسط N هفتم رقمی اما N با تعداد محدودی از کلمات در این پاراگراف تعریف شده است. بنابراین باید در مجموعه E باشد. این یک تناقض است.

مانند پارادوكس كنیگ ، این پارادوكس در نظریه مجموعه بدیهیات قابل رسمی نیست زیرا به این توانایی نیاز دارد كه بفهمد آیا توصیف برای یك مجموعه خاص صدق می كند (یا معادل آن اینكه بگوییم آیا فرمول در واقع تعریف یك مجموعه است یا خیر).

پارادوکس Löwenheim و Skolem [ ویرایش ]

مقاله اصلی: پارادوکس Skolem

براساس کار ریاضیدان آلمانی ، لئوپولد لوونهایم (1915) ، ثورالف اسکولم ، منطق نروژی ، در سال 1922 نشان داد که هر تئوری سازگار برای حساب های محمول مرتبه اول ، نظریه نظریه مجموعه ، دارای الگویی بسیار محکم است . با این حال ، قضیه کانتور ثابت می کند که مجموعه های بی شماری وجود دارد. ریشه این پارادوکس به ظاهر این است که همیشه قابل شمارش یا عدم محاسبه یک مجموعه مطلق نیستاما می تواند بستگی به مدلی داشته باشد که در آن قلبی بودن اندازه گیری می شود. این امکان وجود دارد که یک مجموعه در یک مدل از تئوری مجموعه غیرقابل شمارش باشد اما در یک مدل بزرگتر قابل شمارش است (زیرا اجزای تعیین کننده پاسخگویی در مدل بزرگتر هستند اما مدل کوچکتر نیستند).

منبع

https://en.wikipedia.org/wiki/Paradoxes_of_set_theory

+ نوشته شده در جمعه بیست و ششم اردیبهشت ۱۳۹۹ ساعت 3:7 توسط علی رضا نقش نیلچی |

استوو تودورویویچ

پرش به پیمایش پرش به جستجو

استوو تودورویویچ

استوو تودورویویچ 1984.

حقایق اصلی
تولد	1955 Ubovića Brdo ( بوسنی و هرزگوین )
ملیت	صرب
مناطق	ریاضیات
کارگردان پایان نامه	Đuro Kurepa
دانشجویان دکتری	نتایج و اثبات استقلال در نظریه مجموعه های ترکیبی (1979)
تمایزات	جایزه اول BMS در 1980 و 1982 جایزه CRM-Fields-PIMS در سال 2012 جایزه شونفیلد در سال 2013 گویندگان جوایز گودل در سال 2016
محل	http://www.math.toronto.edu/stevo/

تغییر

ها Stevo Todorčević یک ریاضیدان کانادا-فرانسه-صربی، یکی از بزرگترین منطق دانان جهان و رهبر جهان در نظریه مجموعه ها و برنامه های خود را به ریاضیات محض است 1 . وی دارای صندلی تحقیق کانادا در ریاضیات در دانشگاه تورنتو 2 و مدیر ارشد پژوهش در مرکز ملی تحقیقات علمی (CNRS) در پاریس 3 است .

خلاصه

دوران کودکی و آموزش و پرورش [ ویرایش | تغییر کد ]

تودورویویچ در اوبوویچا برودو ، بوسنی و هرزگوین به دنیا آمد ، جایی که تا سال دوم دبستان زندگی می کرد. پس از آن ، خانواده وی به Banatsko Novo Selo نقل مکان کردند و در آنجا مدرسه ابتدایی 4 را به پایان رساند . او "اورو پردیچ" را نوشت 5دبیرستان در پانشنو. وی استعداد و علاقه خود را به ریاضیات در سال های سوم و چهارم دبیرستان نشان داد. پس از پایان دوره دبیرستان ، او در دانشکده علوم دانشگاه بلگراد ثبت نام کرد و در آنجا به تحصیل ریاضیات خالص پرداخت. وی در حین تحصیل در مقطع کارشناسی ، دوره های پیشرفته ریاضیات را در Đuro Kurepa گذراند. در سال 1978 ، او به مدرسه فارغ التحصیل رفت. Kurepa پایان نامه کارشناسی ارشد Todor Todević را به اندازه کافی تأیید کرد که به عنوان یک پایان نامه دکتری پذیرفته شود. صرف نظر از این ، Todorčević پایان نامه دکترای خود را در سال 1979 با Kurepa به عنوان نظر خود نوشت. كورپا در سخنرانی خود كه قبل از دفاع شفاهی پایان نامه دکترا بود ، تأكید كرد كه ویقادر به یافتن خوانندگان خارجی رساله دکتری استو در یوگسلاوی نبود ، قادر به درک و ارزیابی کار استوو و روی آوردن به دو استاد از انگلیس بود. كورپا اضافه كرد كه استعداد استوو يك معجزه بود و استوو با استعدادترين 40 دانشجوي دكترا بود.دانشجویانی که در گذشته از آنها مشاوره کرده است6 .

شغل [ ویرایش | تغییر کد ]

خلاصه [ ویرایش | تغییر کد ]

طبق مرکز تحقیقات ریاضی ، انستیتوی فیلدز و انستیتوی علوم ریاضی اقیانوس آرام 7، کارهای او به دلیل اصالت و درخشش فنی شناخته شده است. وی برای کشف و کار خود در مورد کارکردهای rho به ICM 1998 در برلین دعوت شد.او سهم عمده ای در مطالعه فضاهای S و L در توپولوژی داشت ، اثبات نظریه طبقه بندی قابل توجهی برای روابط گذرا در اولین مقطع غیر قابل شمارش ، یک مطالعه عمیق از زیر مجموعه های فشرده توابع کلاس 1 از Baire ، Fremlin ، Talagrand و دیگران را در تئوری فضایی Banach انجام داد. با P. Larson ، او حل مسئله اندازه گیری قدیمی فشرده Katetov را به پایان رساند. از برجسته ترین دستاوردهای اخیر Todorčević (و هم نویسندگان) سهم عمده ای در مشکلات فون نویمان و مهارام با جبرهای بولی ،

علاوه بر این 8 ، Todorcevic برای روش های جانبی طولانی خود در ensemblais نظری مجبور، اختراع و توسعه از پیاده روی در ordinals و ویژگی های آنها، و پژوهش های دیگر که در پیوند بین champes ریاضیات مختلف شناخته شده است.

کار ریاضی [ ویرایش | تغییر کد ]

این بخش خالی ، کافی و کامل و ناقص نیست. کمک شما خوش آمدید! چگونه آن را انجام دهیم؟

اولین کمک شناخته شده Todorčević در تئوری مجموعه در پایان نامه کارشناسی ارشد خود در سال 1978 داده شد. Todorčević دکترای خود را در سال 1979 از دانشگاه بلگراد با Đuro Kurepa به عنوان مشاور و کیت Devlin به عنوان خواننده خارجی به دست آورد. دابلین در دفاع حضور داشت. وی Todorčević را تشویق به بازدید از بیت المقدس کرد و در آنجا در سحرون شله در سخنرانی های اجباری 9 شرکت کرد .

در ژوئیه-آگوست 1980 Todor Todević در مدرسه شش هفته ای به نام Settop در تورنتو برگزار شد. در این کنفرانس ، تادورویویچ با ابراهیم وجود درختان سفت و سخت Aronszajn و قوام آن را اثبات کرد\ displaystyle MA + \ neg CH $\ displaystyle MA + \ neg CH$ + یک فضای اول وجود دارد {\ displaystyle S $S$ قابل شمارش. {\ نمایشگر CH} ${\ نمایشگر CH}$ مخفف مخفف Hypotesis Continuum 10 است .

وی در دهه 1980 نمایشی کلی از کار روی درختان از منظر ترکیبی و نظریه تنظیم ارائه داد و این کار را با بررسی امکانات منسجم برای انواع مختلف درختان ادامه داد و به دنبال یافتن نتایج درختان روی چندین کاردینال یا با انواع زیر درختان مورد نیاز یا ممنوع. ظرافت از ارائه آن به مخاطبان بزرگ برای این کار جذب 11 .

با توجه به محاسبه نمره در سال 1980 ، تودورویویچ نتیجه شگفت انگیز از نمره مربع را برای فناوری بی نظیر و معرفی شده ای که نتایج آن هنوز آشکار می شود ، اثبات کرد و نشان داد که پیشرفت مناسب برای روابط منفی جعبه براکت مربع 11 .

Todorčević از سال 1983 تا 1985 یک عضو پژوهش Miller در برکلی بود. در سال 1985/6 وی عضو انستیتوی مطالعات پیشرفته بود.

کار مشورتی [ ویرایش | تغییر کد ]

یکی از دانشجویان دکترا دانشجوی او ، الیاس فراه ، جایزه کیف 1997 را برای دکترا دریافت کرد. پایان نامه ها. دکترا در ماه ژوئن سال 1997 در دانشگاه تورنتو دریافت کرده بود 12 . یکی دیگر از دانشجویان دکترا تودورچویچ ، جاستین تاچ مور ، در سال 2006 در وین اتریش برنده جایزه "مسابقه دانشمندان جوان" شد. مسابقه بخشی از "افق حقیقت» جشن سده از گودل در سال 2006 بود 13 .

قیمت [ ویرایش | تغییر کد ]

Todorčević برنده است

جایزه اول انجمن ریاضی بالکان برای سالهای 1980 و 1982 14 ،
جایزه CRM-Fields-PIMS 2012 در علوم ریاضی 7 ،
جایزه Shoenfield برای 2013 15 و
بیست و هفتمین کنفرانس سالانه گودل 2016 انجمن منطق نمادین 16 .

ادامه نوشته

+ نوشته شده در پنجشنبه هفدهم مرداد ۱۳۹۸ ساعت 8:47 توسط علی رضا نقش نیلچی |

استوو تودورویویچ

پرش به پیمایش پرش به جستجو

استوو تودورویویچ

استوو تودورویویچ 1984.

حقایق اصلی
تولد	1955 Ubovića Brdo ( بوسنی و هرزگوین )
ملیت	صرب
مناطق	ریاضیات
کارگردان پایان نامه	Đuro Kurepa
دانشجویان دکتری	نتایج و اثبات استقلال در نظریه مجموعه های ترکیبی (1979)
تمایزات	جایزه اول BMS در 1980 و 1982 جایزه CRM-Fields-PIMS در سال 2012 جایزه شونفیلد در سال 2013 گویندگان جوایز گودل در سال 2016
محل	http://www.math.toronto.edu/stevo/

تغییر

خلاصه

دوران کودکی و آموزش و پرورش [ ویرایش | تغییر کد ]

شغل [ ویرایش | تغییر کد ]

خلاصه [ ویرایش | تغییر کد ]

کار ریاضی [ ویرایش | تغییر کد ]

این بخش خالی ، کافی و کامل و ناقص نیست. کمک شما خوش آمدید! چگونه آن را انجام دهیم؟

Todorčević از سال 1983 تا 1985 یک عضو پژوهش Miller در برکلی بود. در سال 1985/6 وی عضو انستیتوی مطالعات پیشرفته بود.

کار مشورتی [ ویرایش | تغییر کد ]

قیمت [ ویرایش | تغییر کد ]

Todorčević برنده است

جایزه اول انجمن ریاضی بالکان برای سالهای 1980 و 1982 14 ،
جایزه CRM-Fields-PIMS 2012 در علوم ریاضی 7 ،
جایزه Shoenfield برای 2013 15 و
بیست و هفتمین کنفرانس سالانه گودل 2016 انجمن منطق نمادین 16 .

ادامه نوشته

+ نوشته شده در پنجشنبه هفدهم مرداد ۱۳۹۸ ساعت 8:46 توسط علی رضا نقش نیلچی |

کورت گودل

از ویکیپدیا، دانشنامه آزاد

(تغییر مسیر از گودل )

"Gödel" تغییر مسیر داده است. برای زبان برنامه نویسی، به Gödel (زبان برنامه نویسی) مراجعه کنید . برای استفاده های دیگر، نگاه کنید به Godel (ابهام) .

کورت گودل

بدنیا آمدن	کورت فریدریش گودل 28 آوریل 1906 Brünn، اتریش-مجارستان (در حال حاضر برنو ، جمهوری چک )
فوت کرد	14 ژانویه 1978 (71 ساله) پرینستون ، نیوجرسی، ایالات متحده
شهروندی	چکسلواک، اتریش، ایالات متحده
آلما مادر	دانشگاه وین
شناخته شده برای	قضایای ناتمامیت گودل ، جهان constructible ،گودل قضیه کامل ، نظریه ω-سازگار ، قوام فرضیه زنجیره با ZFC ، گودل متریک ، اثبات هستی شناختی گودل ، منطق گودل-دامت ، استدلال تیرکمان بچه گانه
همسر (ها)	آدل نیمبورسکی (ازدواج 1938)
جوایز	جایزه آلبرت انیشتین (1951) مدال ملی علوم (1974) ForMemRS (1968) [1] همکار آکادمی بریتانیا [ نیازمند منبع ]
حرفه علمی
زمینه های	ریاضیات ، منطق ریاضی
موسسات	موسسه مطالعات پیشرفته
پایان نامه	Über die Vollständigkeit des Logikkalküls (در تکمیل محاسبات منطق) (1929)
مشاور دکترا	هانس هان
امضا

کورت گودل فردریش ( / ɡ ɜːr د əl / ؛ [2] آلمانی: [kʊɐ̯t ɡøːdl̩] ( گوش دادن ) ؛ 1906 آوریل 28 - ژانویه 14، 1978) بود اتریش-مجارستان متولد اتریش، و بعد از آمریکا، منطقدان ، ریاضیدان و فیلسوف . گودل در کنار ارسطو ، آلفرد تارسکی و گوتلوب فرگه به عنوان یکی از مهمترین منطق های تاریخ شناخته می شد؛ گودل تأثیر زیادی بر تفکر علمی و فلسفی در قرن بیستم داشت؛ زمانی که دیگران مانند برتراند راسل، [3] آلفرد نورث وایتهد ، [3] و دیوید هیلبرت تجزیه و تحلیل شد استفاده از منطق و نظریه مجموعهها به درک مبانی ریاضیات پیشگام گئورگ کانتور .

گودل دو قضیه ناقص خود را در سال 1931 منتشر کرد، زمانی که او 25 ساله بود، یک سال پس از پایان دکترای خود در دانشگاه وین .اولین قضیه ناقص بیان می کند که برای هر یک از سیستم های اصلی بازگشتی خودمختار، به اندازه کافی برای توصیف ریاضی اعداد طبیعی (به عنوان مثال ریاضی Peano )، گزاره های واقعی در مورد naturals وجود دارد که نمی تواند از axioms ثابت شود . برای اثبات این قضیه، گودل یک تکنیک را که در حال حاضر به عنوان شماره گودل شناخته می شود، توسعه داده است ، که عبارات رسمی را به عنوان اعداد طبیعی کپی می کند.

او همچنین نشان داد که نه اصل محوری و نه فرضیه پیوسته از اصول پذیرفته شده از نظریه مجموعه ، قابل قبول نیست، در حالی که این اصطلاحات سازگار هستند. نتیجه اولیه، درب را برای ریاضیدانان در نظر گرفت تا مبنای انتخاب در اثبات خود را فرض کنند. وی با تبیین ارتباط بین منطق کلاسیک ، منطق شهودی و منطق مدال ، سهم مهمی را در تئوری اثبات کرد .

فهرست

زندگی زودهنگام و آموزش [ ویرایش ]

دوران کودکی [ ویرایش ]

گودل 1906 آوریل 28، در Brünn، متولد شد اتریش-مجارستان (در حال حاضر برنو ، جمهوری چک ) به خانواده آلمانی از رودولف گودل (1874-1929)، مدیر یک کارخانه نساجی، و ماریان گودل ( موسوم به Handschuh، 1879- 1966) [4] در طول زندگی خود، گودل نزدیک به مادرش باقی خواهد ماند؛ مکاتبات آنها مکرر و گسترده بود. [5] در زمان تولدش، شهر دارای یک اکثریت آلمانی بودکه والدینش را شامل می شد. [6]پدرش کاتولیک بود و مادرش پروتستان بود و بچه ها پروتستان بودند. اجداد کورت گودل اغلب در زندگی فرهنگی برنن فعال بودند. به عنوان مثال، پدربزرگش جوزف گودل یک خواننده معروف آن زمان بود و برای چندین ساله یک عضو از Brünner Männergesangverein (اتحادیه Choral Men Brünn) بود. [7]

گودل به طور خودکار در 12 سالگی تبدیل به یک شهروند چکوسلواک شد زمانی که امپراطوری اتریش-مجارستان در پایان جنگ جهانی اول شکست خورد . (با توجه به همکلاسی خود Klepetař ، مانند بسیاری از ساکنان عمدتا آلمانی Sudetenländer ، "گودل در نظر گرفته خود همیشه اتریش و در تبعید در چکسلواکی". [8] او تصمیم گرفت تا تبدیل شدن به یک اتریشی شهروند در سن 23.[ نیازمند منبع ] هنگامی که آلمان ضمیمه گوتل در سال 1938 به طور خودکار شهروند آلمانی در سن 32 سالگی شد. پس از جنگ جهانی دوم (1948)، در سن 42 سالگی، او یک شهروند آمریکایی شد[9] .

در خانواده اش، جوان کورت به علت کنجکاوی ناخوشایند او به عنوان آقای ووروم ("آقای چرا") شناخته شد. به گفته برادرش رودلف، در سن شش یا هفت کرت از تب روماتیسمی رنج می برد ؛ او به طور کامل بهبود یافت، اما برای بقیه عمر او متقاعد شد که قلب او آسیب دائمی رنج می برد. گودل در سن چهار سالگی از "قسمت های مکرر سلامت ضعیف" رنج می برد که برای تمام عمر خود ادامه می یابد. [10]

گودل با حضور در Evangelische Volksschule ، یک مدرسه لوتری در Brünn 1912-1916، و در ثبت نام کرده بود آلمان Staats-Realgymnasium 1916-1924، عالی با درجه ممتاز در همه افراد خود را، به خصوص در ریاضیات، زبان و مذهب است. اگر چه کورت اولین بار در زبان ها پیشرفت کرد، اما بعدها بیشتر علاقه مند به تاریخ و ریاضیات شد. علاقه او به ریاضیات زمانی افزایش یافت که در سال 1920 برادر بزرگترش رودلف (متولد 1902) به وین رفت تا به دانشکده پزشکی دانشگاه وین برود . در نوجوانان، کورت مورد مطالعه قرار Gabelsberger مختصر ، گوته را نظریه رنگ و انتقادات اسحاق نیوتن، و نوشته های امانوئل کانت .

تحصیل در وین [ ویرایش ]

گودل در سن 18 سالگی به برادرش در وین پیوست و وارد دانشگاه وین شد. در آن زمان، او قبلا در سطح ریاضیات دانشگاهی تسلط داشت. [11] گرچه ابتدا قصد مطالعه فیزیک نظری داشت ، او همچنین در دوره های ریاضی و فلسفه حضور یافت. در طی این زمان، او ایده های واقع گرایی ریاضی را به دست آورد . او به نام Metaphysche Anfangsgründe der Naturwissenschaft کانت و در دایره وین با موریتس شلیک ، هانس هان و رودلف کارناب شرکت کرد . گودل سپس نظریه اعداد را مورد مطالعه قرار داد ، اما زمانی که او در یک سمینار اجرا شدموریتس شلیک که کتاب برانت راسل را « مقدمه ای بر فلسفه ریاضی » خواند ، علاقه مند به منطق ریاضی شد . بر طبق گوئدل، منطق ریاضی "علمی قبل از همه چیز بود که شامل ایده ها و اصولی است که همه علوم را در بر می گیرد". [12]

حضور در سخنرانی دیوید هیلبرت در بولونیا در مورد تکمیل و سازگاری سیستم های ریاضی ممکن است دوره زندگی گودل را تعیین کند. در سال 1928، هیلبرت و ویلهلم آکرمن منتشر شده DER Grundzüge theoretischen LOGIK ( اصول منطق ریاضی )، مقدمه ای بر منطق مرتبه اول که در آن مشکل کامل مطرح شد: آیا بدیهیات از یک سیستم رسمی برای استخراج هر بیانیه این است که درست به اندازه کافی در همه مدل های سیستم

این مشکل موضوعی بود که گودل برای کار دکترای خود انتخاب کرد. در سال 1929، در سن 23 سالگی، پایان نامه دکترای خود را تحت نظارت Hans Hahn تکمیل کرد . در آن، قضیه تکمیل نامتقارن خود را در مورد محاسبات پیش فرض مرتبه اول ایجاد کرد . او دکترای خود را در سال 1930 اهدا کرد و پایان نامه وی (همراه با برخی کارهای اضافی) توسط آکادمی علوم وین منتشر شد .

شغل [ ویرایش ]

تئوری ناقص [ ویرایش ]

دستاوردهای کرت گودل در منطق مدرن منحصر به فرد و برجسته است - در حقیقت این بیشتر از یک بنای تاریخی است، که نقطه عطفی است که در فضا و زمان قابل مشاهده است. ... موضوع منطق قطعا ماهیت و امکانات خود را با موفقیت گودل تغییر داده است.
- جان فون نیومن [13]

گودل در سال 1930 در دومین کنفرانس معرفتشناسی علوم دقیق در کنیگزبرگ 5-7 سپتامبر شرکت کرد. در اینجا او قضیه ناقص خود را تحویل داد . [14]

گودل قضیه ناتمام خود را در Uncerche Formale Sätze der Principia Mathematica und verwandter Systeme منتشر کرد (به زبان انگلیسی به نام " Proforms of Undecidable Principia Mathematica and related Systems "). در این مقاله، او برای هر سیستمی محاسبه کننده محوری که به اندازه کافی قدرتمند برای توصیف ریاضی اعداد طبیعی(به عنوان مثال، آئینهای Peano یا نظریه Zermelo-Fraenkel مجموعه با اصل محرک ) ثابت کرد، ثابت کرد که:

اگر یک (رسمی منطقی یا برهان) سیستم است سازگار ، نمی توان آن را کامل .
قوام بدیهیات می توانید در داخل خود نمی شود ثابت سیستم .

این قضیه به نیم قرن تلاشها پایان داد، شروع به کار فرگه و به پایان رساندن در Principia Mathematica و فرمالیسم هیلبرت ، برای پیدا کردن مجموعه ای از عبارات کافی برای همه ریاضیات.

در نهایت، ایده اصلی در قلب تئوری ناقص، نسبتا ساده است. گودل اساسا یک فرمول را ساخت که ادعا می کند که در یک سیستم رسمی داده شده قابل اثبات نیست. اگر این قابل اثبات بود، نادرست خواهد بود. بنابراین همیشه حداقل یک بیانیه درست، غیر قابل اثبات وجود دارد. به این معنا که برای هر computably شمارش مجموعه ای از بدیهیات برای حساب (که شده است، مجموعه ای است که می تواند در اصل باید توسط یک کامپیوتر ایده آل با منابع نامحدود چاپ)، یک فرمول است که درست است از حساب وجود دارد، اما است که قابل اثبات در نمی این سیستم. با این حال، برای ساخت این دقیق، گودل نیاز به تولید یک روش برای رمز کردن (به عنوان اعداد طبیعی) اظهارات، اثبات و مفهوم تحمل پذیری؛ او این کار را با استفاده از فرآیند شناخته شده به عنوان شماره گودل انجام داد .

در مقاله دو صفحه ای خود، Zum intuitionistischen Aussagenkalkül (1932)، گودل ارزش محدود ارزش منطق شهودی را رد کرد . در اثبات، او به روشنی از آنچه که بعدها به عنوانمنطق فازی Gödel-Dummett (یا منطق فازی Gödel ) شناخته می شود استفاده می شود.

اواسط دهه 1930: کار بیشتر و دیدار ایالات متحده [ ویرایش ]

گودل خود به دست آورده توانبخشی در وین در سال 1932، و در سال 1933 او شد Privatdozent به (مدرس دانشگاه، پرداخت نشده) وجود دارد. در سال 1933، آدولف هیتلر در آلمان قدرت گرفت و در سال های بعد نازی ها در اثر نفوذ در اتریش و بین ریاضیدانان وین رو به افزایش گذاشتند. در ژوئن 1936، موریتس شلیک ، که سمینار او علاقه مند گودل را به منطق آورده بود، توسط یکی از دانش آموزان سابق خود، یوهان نلببک ، ترور شد . این باعث "بحران شدید عصبی" در گودل شد. [15] وی علائم پارنویید، از جمله ترس از مسمومیت را بوجود آورد و چندین ماه در یک دستگاه بهداشتی برای بیماری های عصبی صرف کرد. [16]

در سال 1933، گودل برای اولین بار به ایالات متحده سفر کرد، جایی که او با البرت اینشتین ملاقات کرد ، که به یک دوست خوب تبدیل شد. [17] او به نشست سالانه انجمن ریاضی آمریکا رسید . در طول این سال، گودل ایده های محاسباتی و توابع بازگشتی را به نقطه ای رساند که او توانست سخنرانی در مورد توابع بازگشتی عمومی و مفهوم حقیقت را ارائه کند. این کار در نظریه شماره، با استفاده از شماره Gödel توسعه داده شد .

در سال 1934، گودل در مقطع کارشناسی در موسسه مطالعات پیشرفته (IAS) در پرینستون ، نیوجرسی، با عنوان « گزاره های غیرقابل پیش بینی سیستم های رسمی ریاضی»سخنرانی کرد . استیون کلین ، که تازه رشته دکترای خود را در پرینستون تکمیل کرده بود، یادداشت های این سخنرانی ها را منتشر کرد.

گودل دوباره در پاییز 1935 از IAS بازدید کرد. مسافرت و کار سخت او را خسته کرده بود و سال بعد او برای اولین بار از یک قسمت افسردگی بهبودیافت. او در سال 1937 به تدریس بازگشت. در طی این زمان، او بر اثبات ثبات مبانی انتخاب و فرضیه پیوسته کار کرد . او ادامه داد تا نشان دهد که این فرضیه ها نمیتوانند از سیستم مشترک عالئم نظریه مجموعه محروم شوند.

او با آدل نیمبورسکی (Porkert، 1899-1981) که بیش از 10 سال است که در 20 سپتامبر 1938 شناخته شده بود، ازدواج کرد. ارتباط آنها با والدینش مخالف بود، زیرا او رقصنده طلاق گرفته بود، شش سال بزرگتر از او بود.

درنتیجه او برای سفر دیگری به ایالات متحده رفت و پاییز سال 1938 را در IAS گذراند و انتشار هماهنگی مبانی انتخاب و فرضیه تعمیم عمومی را با مفاهیم نظریه مجموعه، [18]کلاسیک ریاضیات مدرن . در این کار او جهان سازنده را معرفی کرد ، یک مدل نظریه مجموعه ای که در آن تنها مجموعه هایی وجود دارند که می توانند از مجموعه های ساده تر ساخته شوند. گودل نشان داد که هر دو مبنای انتخاب (AC) و فرضیه پیوندی تعمیم یافته (GCH) در جهان سازنده صحت دارند و بنابراین باید با axiom Zermelo-Fraenkel سازگار باشدبرای نظریه مجموعه (ZF). این نتیجه عواقب قابل توجهی را برای کار ریاضیدانان به ارمغان می آورد، به این معنی که آنها می توانند اصل محوری را در هنگام اثبات قضیه هان Banach فرض کنند . پل کوهن بعد مدل ZF را ساخت که در آن AC و GCH غلط هستند؛ با هم این اثبات ها به این معنی است که AC و GCH مستقل از axioms ZF برای نظریه مجموعه است.

Godel بهار 1939 در دانشگاه نوتردام سپری کرد . [19]

پرینستون، انیشتین، شهروندی ایالات متحده [ ویرایش ]

پس از انشلوس در 12 مارس 1938، اتریش بخشی از آلمان نازی شد . آلمان عنوان " Privatdozent " را لغو کرد ، بنابراین گودل مجبور شد جای دیگری را تحت نظم جدید درخواست کند. ارتباط سابق وی با اعضای یهودی دایان وین، به ویژه با هان، علیه او محسوب می شود. دانشگاه وین تقاضای خود را کاهش داد.

اوضاع اوباما هنگامی که ارتش آلمان او را برای ارتش آماده کرد، تشدید شد. جنگ جهانی دوم در سپتامبر 1939 آغاز شد. پیش از این، گودل و همسرش وین را برای پرینستون ترک کرد . برای جلوگیری از مشکل حمل و نقل آتلانتیک، Gödels راه آهن Trans-Siberian را به اقیانوس آرام برد، از ژاپن به سانفرانسیسکو رفت (که در تاریخ 4 مارس 1940 به آن رسید)، سپس از طریق قطار به پرینستون عبور کرد. گودل موقعیتی را در موسسه مطالعات پیشرفته (IAS) پذیرفته است که قبلا در طول 1933-34 به آن سفر کرده بود. [20]

آلبرت اینشتین در این زمان در پرینستون زندگی می کرد. گودل و انیشتین یک دوستی قوی ایجاد کردند و شناخته شده بودند که با هم به مؤسسه مطالعات پیشرفته و با هم ملاقات می کردند. ماهیت مکالمات آنها رمز و راز دیگر اعضای موسسه بود. اقتصاددان Oscar Morgenstern می گوید که در انتهای زندگی اش، اینشتین اعتقاد داشت که «کار خودش بیشتر به معنای زیاد نیست، که تنها به مؤسسه می آید ... برای داشتن امتیاز دادن به خانه با Gödel». [21]

گودل و همسرش آدل، در تابستان 1942 در آبی هیل، مین ، در آبی هیل Inn در بالای خلیج قرار گرفتند. گودل صرفا در تعطیلات نبود اما تابستان بسیار کارآمد داشت. با استفاده از Heft 15 [جلد 15] آثار باقیمانده Arbeitshefte هنوز منتشر نشده گودل ، جان واتسون جونیور، گمان می کند که گودل اثبات استقلال مبانی انتخاب را از نظر تئوری نوعی، یک شکل ضعیف از نظریه مجموعه، کشف کرد. در حالی که در آبی هیل در سال 1942 است. دوست نزدیک گودل هائو وانگ از این حدس می گوید، یادآور می شود که نوت بوک های آبی هیل گودل شامل درمان گسترده ای برای این مشکل است.

در 5 دسامبر 1947، اینشتین و مورگنسترن با گودل به امتحان شهروندی ایالات متحده رفتند، جایی که آنها به عنوان شاهدان عمل کردند. گودل به آنها اطمینان داده بود که ناسازگاری در قانون اساسی ایالات متحده کشف کرده است که می تواند به ایالات متحده اجازه دهد که تبدیل به یک دیکتاتوری شود. انیشتین و مورگنسترن نگران رفتارهای غیرواقعی دوست خود می تواند به درخواست او آسیب برساند. قاضی فیلیپ فورمن ، که اینشتین را می شناخت و دادرسی در مورد شهروندی خود را انجام داد، قاضی شد. همه چیز به آرامی ادامه یافت تا زمانی که فورمن اتفاق می افتاد که از گودل سوال کند که آیا او فکر می کند دیکتاتوری مانند رژیم نازیمی تواند در ایالات متحده اتفاق می افتد Gödel سپس شروع به توضیح کشف خود را به Forman. فورمن فهمید چه اتفاقی افتاده است، گودل را خرد کرده و دادرسی را به سؤالات دیگر و نتیجه گیری معمول منتقل می کند. [22] [23]

گودل عضو دائمی موسسه مطالعات پیشرفته در پرینستون در سال 1946 شد. در این مدت او نشر را متوقف کرد، هرچند او ادامه داد. او پروفسور کامل در موسسه در سال 1953 و استاد افتخاری در سال 1976 شد. [24]

در طول سال های بسیاری در موسسه، منافع گودل به فلسفه و فیزیک تبدیل شده است. در سال 1949، او نشان داد که وجود راه حل هایی شامل منحنی های زمانبندی بسته به معادلات میدان انیشتین درنسبیت عام است . [25] او گفته است که این توضیح را به انیشتین به عنوان یک حضور برای او 70 روز تولد داده است. [26] او "چرخهای جهان" اجازه می دهد زمان سفر به گذشته و باعث انیشتین تردید در مورد نظریه خود است. راه حل های او به عنوان متریک Gödel (راه حل دقیق معادله میدان انیشتین ) شناخته شده است.

او مطالعه آثار گاتفریید لایبنیتس را مورد مطالعه و تحسین قرار داد اما معتقد بود که توطئه خصمانه برخی از آثار لایبنیتس را سرکوب کرده است. [27] به میزان کم او امانوئل کانت و ادموند هوسرل را مطالعه کرد . در اوایل دهه ی 1970، گودل در میان دوستانش، توضیح نسخه ی لایبنیتس از اثبات هستی شناختی آنسلم کانتربری را درباره وجود خداوند، منتشر کرد. این در حال حاضر به عنوان اثبات هستی شناسی گودل شناخته شده است .

جوایز و افتخارات [ ویرایش ]

گودل (با جولیان اشینگر ) اولین جایزه آلبرت انیشتین در سال 1951 و مدال ملی علوم در سال 1974 اهدا شد. [28] گدل در سال 1968 به عنوان عضو خارجی انجمن سلطنتی (ForMemRS) انتخاب شد . [1] او عضو هیئت مدیره ICM در سال 1950 در کمبریج، ماساچوست بود. [29] گودل جایزه ، جوایزی برای مقالات برجسته در حوزه علوم کامپیوتر نظری، بعد از او نام.

قبرستان کورت و آدل گودل در پرینستون، نیوجرسی، گورستان

زندگی و مرگ بعدی [ ویرایش ]

بعدا در زندگی او، گودل دوره های بی ثباتی ذهنی و بیماری را متحمل شد. او دچار وسواس ترس از مسموم شدن بود ؛ او تنها غذا را می خورد که همسرش، آدل، برای او آماده شده بود. اوایل سال 1977، او به مدت شش ماه بستری شد و دیگر نمی توانست غذای همسرش را تهیه کند. در غیبت او، حاضر به خوردن غذا، و در نهایت گرسنگی به مرگ. [30] وقتی که او درگذشت، 29 کیلوگرم (65 پوند) وزن کرد. گواهی مرگ او گزارش داده است که او از سوء تغذیه و ناامیدی ناشی از اختلال شخصیت در بیمارستان پرینستون در 14 ژانویه 1978 درگذشت . [31] او در گورستان پرینستون دفن شد . مرگ آدل در سال 1981 ادامه یافت.

زندگی شخصی [ ویرایش ]

دیدگاههای مذهبی [ ویرایش ]

گودل یک مظهر متقاعد کننده بود ، در سنت مسیحی. [32] او تصور کرد که خدا شخصا بود.

او معتقد است که در یک زندگی پس از مرگ، اظهار داشت: "البته این فرض می کند که روابط بسیاری وجود دارد که امروزه علم و حکمت را دریافت نکرده اند. هیچکدام از آنها را نمی دانم، اما من از این [زندگی پس از مرگ] مستقل از هر الهیات متقاعد شده ام." امروزه امروزه می توان با استدلال خالص درک کرد که "کاملا با واقعیت های شناخته شده سازگار است." "اگر جهان منطقی ساخته شود و معنی داشته باشد، باید چنین چیزی [به عنوان یک زندگی پس از مرگ] باشد". [33]

پاسخ گمشده به یک پرسشنامه، گودل دین خود را به عنوان "متولد لوتری" (اما نه عضو انجمن مذهبی) توصیف کرد. اعتقاد من ، به جای لایبنیتس به جای اسپینوزا ، تئیستی و نه متعصبانه است . "[34] به طور کلی توصیف دین ها، گودل می گوید: "مذاهب در اکثر موارد بد است اما دین نمی باشد". [35] به گفته همسرش آدل، "گودل، اگر چه او به کلیسا رفت، مذهبی بود و هر روز یکشنبه صبح کتاب مقدس را در رختخواب خواند"، [36] در حالی که از اسلام، او گفت: "من دوست دارم اسلام: این است یک ایده سازگارانه (یا پیوسته) از دین و ذهن باز است. " [37]

میراث [ ویرایش ]

انجمن کرت گودل ، که در سال 1987 تاسیس شد، به افتخار او نامگذاری شد. این سازمان بین المللی برای ارتقای تحقیق در حوزه منطق، فلسفه و تاریخ ریاضیات است . دانشگاه وین میزبان مرکز تحقیقات گودل کورت برای منطق ریاضی. انجمن منطق نمادین هر سال دعوت کرده است کورت گودل مدرس سالانه از سال 1990. یادداشت های فلسفی گودل در ویرایش مرکز تحقیقات گودل کورت است که در واقع فرهنگستان برلین-براندنبورگ علوم و علوم انسانی در آلمان است.

پنج جلد از آثار جمع شده گودل منتشر شده است. دو مورد اول شامل انتشارات گودل است. سوم شامل نوشته های منتشر نشده از گودل Nachlass ، و این دو نهایی شامل مکاتبات.

یک زندگینامه گودل توسط جان Dawson در سال 2005 منتشر شد: معضلات منطقی: زندگی و کار کورت گودل ( AK Peters ، Wellesley MA، ISBN 1-56881-256-6 ). گودل همچنین یکی از چهار ریاضیدانان است که در سال 2008 مستند " بی بی سی " تحت عنوان " Knowledge of Danger " توسط دیوید ملونه مورد بررسی قرار گرفت . [38]

داگلاس هافستادتر یک کتاب محبوب در سال 1979 به نام گدل، اسر، باخ را برای جشن گرفتن کار و ایده های گودل، همراه با هنرمندان MC Escher و آهنگساز یوهان سباستین باخ نوشت . این کتاب تا حدی به بررسی این واقعیت است که قضیه ناقص گودل را می توان به هر سیستم محاسباتی کامل تورینگ که شامل مغز انسان می شود، اعمال می کند .

کتابشناسی

ادامه نوشته

+ نوشته شده در یکشنبه شانزدهم تیر ۱۳۹۸ ساعت 0:12 توسط علی رضا نقش نیلچی |

پارادوکسهای Zeno

مقاله اصلی: پارادوکسهای زنو

پارادوکسهای Zeno بیش از دو هزار سال است که فیلسوفان، ریاضیدانان و فیزیکدانان را به فریب دادن، به چالش کشیدن، تحت تاثیر قرار دادن، الهام، خشم و فلاکت قرار داده اند. معروف ترین آئین ها علیه حرکت است که ارسطو در کتاب فیزیک ، کتاب VI آن را شرح داده است. [21]

آشیل و لاک پشت
دوگانگی
فلش
ردیف در حال حرکت

+ نوشته شده در جمعه چهاردهم تیر ۱۳۹۸ ساعت 14:2 توسط علی رضا نقش نیلچی |

القاء ترانسفینیت

اصل القای کامل نه تنها برای اظهارات در مورد اعداد طبیعی درست است، بلکه برای اظهارات در مورد عناصر هر مجموعه معتبر ، یعنی مجموعه ای با یک رابطه نامنظم است که حاوی هیچ زنجیره نزولی بی نهایت نیست . هر مجموعه ای از اعداد سرچشمه ، پایه ای است که شامل مجموعه ای از اعداد طبیعی است.

یک مجموعه معتبر کاربردی را می توان به صورت یک گام فرموله کرد:

نشان می دهد که اگر جمله ای برای همه m < n نگه داشته شود ، همان عبارت نیز برای n وجود دارد .

این شکل القایی، هنگامی که به مجموعه ای از ordinals (که به شکل طبقه ای مرتب شده و از این رو به خوبی تاسیس شده است)، القاء ترانسفینیت نامیده می شود . این یک تکنیک اثبات مهم درنظریه مجموعه ، توپولوژی و دیگر زمینه ها است.

اثبات های القاء ترانسفینیت معمولا سه مورد را تشخیص می دهند:

هنگامی که n حداقل عنصر است، یعنی عنصر کوچکتر از n وجود ندارد ؛
زمانی که n دارای پیشینی مستقیم است، یعنی مجموعه ای از عناصر کوچکتر از n دارای بزرگترین عنصر است؛
زمانی که n دارای پیشینی مستقیم نیست، یعنی n یک ترتیب نامحدود است .

به طور جدی لازم نیست که در الگوریتم transfinite برای اثبات یک پرونده پایه لازم باشد، زیرا این یک نمونه خاص خالی از گزاره است که اگر P برای تمام n < m درست باشد ، P درست از m است . به طور خلاصه درست است به این دلیل که هیچ مقادیر n < m وجود ندارد که می تواند بعنوان نمونه های مخالف استفاده شود. بنابراین موارد خاص موارد خاصی از پرونده عمومی است.

همبستگی با اصل خوب نظم[ ویرایش ]

اصل القای ریاضی معمولا به عنوان عاملی از اعداد طبیعی بیان می شود؛ اصول اساسی Peano را ببینید . با این حال، می توان آن را از اصل به خوبی مرتبه ثابت کرد . در واقع، فرض کنید:

مجموعه ای از اعداد طبیعی مرتب شده است .
هر عدد طبیعی یا 0، یا n + 1 برای برخی عدد طبیعی n است .
برای هر عدد طبیعی n ، n + 1 بیشتر از n است .

برای بدست آوردن القایی ساده از این عبارات، باید نشان داد که اگر (P ( n بعضی قضیه پیش بینی شده از n است که:

(P (0نگه می دارد و
هرگاه (P ( m درست باشد، (P ( m + 1 هم درست است

سپس (P ( n برای تمام n نگه می دارد .

اثبات اجازه دهید S مجموعه ای از اعداد طبیعی است که برای آن (P ( m نادرست است. بگذارید ببینیم چه اتفاقی می افتد اگر کسی ادعا کند که S غیرقابل است. سفارش خوب به ما می گوید که Sحداقل عنصر دارد، می گویند n . علاوه بر این، از آنجا که (P (0 درست است، N است 0. نیست از آنجا که هر عدد طبیعی است یا 0 یا برخی متر + 1 ، برخی از عدد طبیعی وجود دارد متر به طوری که متر + 1 = N . اکنون m کمتر از n است و n حداقل عنصر S است. به این معنی است که m در S نیست و بنابراین( P ( m درست است. این بدان معنی است که (P ( m + 1 درست است؛ به عبارت دیگر (P ( n درست است. این یک تناقض است، از آنجا که n در S بود . بنابراین S خالی است.

همچنین می توان ثابت کرد که القاء، با توجه به معیارهای دیگر، به این نتیجه می رسد که اصل مرتب سازي.

اثبات فرض کنید یک مجموعه غیر خالی وجود دارد، S ، از naturals که دارای حداقل عنصر است. فرض کنید (P ( n فرضیه ای است که n در S نیست . سپس (P (0درست است، زیرا اگر اشتباه باشد، 0 کوچکترین عنصر S است . علاوه بر این فرض کنید (P (1)، P (2)، ...، P ( n همه درست هستند. سپس اگر (P ( n +1نادرست است n +1 در S باشد ، بنابراین یک عنصر حداقل در S است ، یک تناقض است. بنابراین (P ( n+1 درست است بنابراین، توسط axiom القایی،( P ( n برای همه n نگه می دارد ، بنابراین S خالی است، یک تضاد.

ادامه نوشته

+ نوشته شده در جمعه بیست و چهارم اسفند ۱۳۹۷ ساعت 13:25 توسط علی رضا نقش نیلچی |

اصل القایی

اصل استقرا (با روش اشتباه گرفته شود القایی ) است بیانیه ای در مورد اعداد طبیعی در ریاضیات می یابد استفاده گسترده درتظاهرات تا ثابت کند که یک ویژگی خاص برای تمام اعداد صحیح، معتبر است. ایده بصری در پایه آن «اثر دومینو» است: برای اینکه تمام کاشیهای دومینو در کنار یک ردیف قرار بگیرند، دو شرایط کافی است:

اصل القاء این ایده را به موردی که ردیف از کاشی های بی پایان تشکیل شده است گسترش می دهد.

اجازه دهید کارت اول سقوط کند
که هر کارت به گونه ای قرار می گیرد که کاهش می یابد که کارت بعدی سقوط می کند.

بیانیه رسمی [ ویرایش | ویرایش wikitesto ]

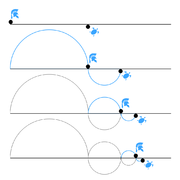
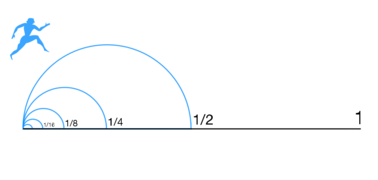
${displaystyle (forall P) [P (0) land (forall k in Mathbb {N}) (P (k) Rightarrow P (k + 1))] Rightarrow (Ø¨Ø±Ø§Û n ÛØ§ \ t Mathbb {N}) [P (n)]}$

ادامه نوشته

+ نوشته شده در جمعه بیست و چهارم اسفند ۱۳۹۷ ساعت 12:37 توسط علی رضا نقش نیلچی |

آموزش ریاضی

قضیه و حقیقت [ ویرایش ]

ملاحظات معرفتی [ ویرایش ]

گزارش غیررسمی قضایا [ ویرایش ]

ارتباط با نظریه های علمی [ ویرایش ]

اصطلاحات [ ویرایش ]

طرح بندی [ ویرایش ]

لور [ ویرایش ]

قضایا در منطق [ ویرایش ]

نحو و معناشناسی [ ویرایش ]

تفسیر یک قضیه صوری [ ویرایش ]

قضایا و نظریه ها [ ویرایش ]

محاسبات ابتدایی [ ویرایش ]

تلاش های اولیه [ ویرایش ]

جبر [ ویرایش ]

تقسیم به عنوان معکوس ضرب [ ویرایش ]

فیزیک

علم شیمی

علوم کامپیوتر

سایر زمینه ها

نمادها و نمادها

برچسب سال

همچنین ببینید

علم اشتقاق لغات

استفاده مدرن

تاریخ

خاور نزدیک باستان

آمریکای پیش از کلمبیا

دوران باستان کلاسیک

چین

"صفر" و "رمز" [ ویرایش ]

«هیچ» و «هیچ» در مقابل «باید» و «هیچ چیز» [ ویرایش ]

نام دهه [ ویرایش ]

ورزش [ ویرایش ]

"O" ("اوه") [ ویرایش ]

پوچ [ ویرایش ]

زبان عامیانه [ ویرایش ]

همچنین ببینید [ ویرایش ]

محتوا

ایده اثبات [ ویرایش | ویرایش کد ]

مرحله 1 [ ویرایش | ویرایش کد ]

مرحله 2 [ ویرایش | ویرایش کد ]

مرحله 3 [ ویرایش | ویرایش کد ]

بدست آوردن بی نهایت توپ از یک [ ویرایش ]

تناقض فون نویمان در صفحه اقلیدسی [ ویرایش ]

پیشرفت اخیر [ ویرایش ]

فهرست

نشریه باناخ و تارسکی [ ویرایش ]

فهرست

تاریخچه [ ویرایش ]

انگیزه [ ویرایش ]

تعریف رسمی [ ویرایش ]

حساب کاردینال [ ویرایش ]

کاردینال جانشین [ ویرایش ]

اضافه کردن کاردینال [ ویرایش ]

ضرب کاردینال [ ویرایش ]

نمایش کاردینال [ ویرایش ]

فرضیه پیوستار [ ویرایش ]

همچنین به [ ویرایش ] مراجعه کنید

منبع

فهرست

مثالها [ ویرایش ]

همچنین به [ ویرایش ] مراجعه کنید

یادداشت ها [ ویرایش ]

منابع [ ویرایش ]

فهرست

ویژگی ها و برنامه ها [ ویرایش ]

در تنظیمات نظریه غیر مجموعه [ ویرایش ]

مثالها [ ویرایش ]

هسته توابع جزئی [ ویرایش ]

توابع مربوط به روابط معادل سازی [ ویرایش ]

برابری مقادیر نقطه شناور IEEE [ ویرایش ]

یادداشت ها [ ویرایش ]

منابع

فهرست

تاریخچه [ ویرایش ]

رویکرد به پوچی [ ویرایش ]

بلاغت [ ویرایش ]

فلسفه [ ویرایش ]

الهیات [ ویرایش ]