گروه کواترنیون
گروه کواترنیون
این مقاله در مورد یک گروه خاص است ، یعنی یک گروه منحصر به فرد تا ایزومورفیسم . مشاهده اطلاعات خاص (مانند تئوری نمایش خطی، ساختار زیر گروه) در مورد این گروه
مشاهده لیست کاملی از گروه های خاص (این یک لیست بسیار بزرگ است!) [نمایش بیشتر]
فهرست
تعریف
تعریف با ارائه
گروه کواترنیون ارائه زیر را دارد :
هویت نشان داده می شود
، عنصر مشترک
نشان داده می شود
، و عناصر
به ترتیب نشان داده
می شوند.
آیا در مورد ارائه به طور کلی یا این یکی به طور خاص گیج شده اید؟ اگر با این چیزها تازه کار هستید، ساخت گروه کواترنیون را از ارائه آن بررسی کنید. نظریه پردازان گروه پیچیده می توانند معادل سازی ارائه های گروه دو حلقه ای را بخوانندتعاریف کلامی
گروه کواترنیون گروهی با هشت عنصر است که به یکی از روش های زیر قابل توصیف است:
- این گروه شامل هشت عنصر است
که در آن 1 عنصر هویت است،
و همه عناصر دیگر از ریشه مربع هستند
، به طوری که
و بیشتر،
(روابط باقی مانده را می توان از اینها استنباط کرد).
- این گروه دو حلقه ای با پارامتر 2 است، یعنی
.
- این گروه فیبوناچی
است.
جدول ضرب
در جدول زیر عنصر ردیف در سمت چپ و عنصر ستون در سمت راست ضرب شده است.
عنصر
موقعیت در طبقه بندی ها
نوع طبقه بندی نام در آن طبقه بندی شناسه GAP (8،4) یعنی چهارمین گروه از مرتبه 8 سالن-شماره ارشد 5 در میان گروه های مرتبه 8 نماد تالار - ارشد عناصر
اطلاعات بیشتر: ساختار عنصری گروه کواترنیونی
ساختار کلاس مزدوجی
کلاس مزدوجی اندازه کلاس مزدوجی ترتیب عناصر در کلاس مزدوجی متمرکز کننده عنصر اول کلاس 1 1 کل گروه 1 2 کل گروه 2 4 ، مثل
2 4 -- مثل
2 4 -- مثل
ساختار کلاس اتومورفیسم
کلاس هم ارزی (مدار) تحت عمل اتومورفیسم ها اندازه کلاس هم ارزی (مدار) تعداد کلاس های مزدوج در آن اندازه هر کلاس مزدوجی ترتیب عناصر 1 1 1 1 1 1 1 2 6 3 2 4
+ نوشته شده در سه شنبه بیست و هشتم دی ۱۴۰۰ ساعت 16:59 توسط علی رضا نقش نیلچی
|





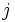









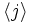



 در این وبلاگ به ریاضیات و کاربردهای آن و تحقیقات در آنها پرداخته می شود. مطالب در این وبلاگ ترجمه سطحی و اولیه است و کامل نیست.در صورتی سوال یا نظری در زمینه ریاضیات دارید مطرح نمایید .در صورت امکان به آن می پردازم. من دوست دارم برای یافتن پاسخ به سوالات و حل پروژه های علمی با دیگران همکاری نمایم.در صورتی که شما هم بامن هم عقیده هستید با من تماس بگیرید.
در این وبلاگ به ریاضیات و کاربردهای آن و تحقیقات در آنها پرداخته می شود. مطالب در این وبلاگ ترجمه سطحی و اولیه است و کامل نیست.در صورتی سوال یا نظری در زمینه ریاضیات دارید مطرح نمایید .در صورت امکان به آن می پردازم. من دوست دارم برای یافتن پاسخ به سوالات و حل پروژه های علمی با دیگران همکاری نمایم.در صورتی که شما هم بامن هم عقیده هستید با من تماس بگیرید.