راه حل های سه بعدی معادله لاپلاس
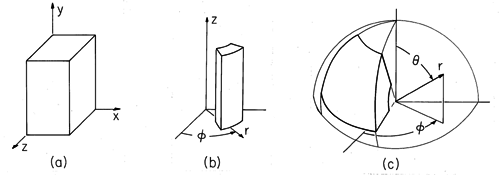
مرزهای طبیعی احاطه کننده حجم هایی که معادله پواسون باید در آنها برآورده شود در شکل 5.10.1 برای سه سیستم مختصات استاندارد نشان داده شده است. به طور کلی، توزیع پتانسیل در داخل حجم با توزیع پتانسیل دلخواه بر روی سطوح مرزی مطلوب است.
شکل 5.10.1 حجم های تعریف شده توسط مرزهای طبیعی در مختصات (الف) دکارتی، (ب) استوانه ای، و (ج) کروی.
اولین مورد در نظر گرفته شده در این بخش، گسترش راه حل های ضرب دو بعدی مختصات دکارتی و بسط های مودال معرفی شده در Secs است. 5.4 و 5.5 تا سه بعدی. با توجه به توزیع پتانسیل دلخواه بر روی یکی از شش سطح جعبه نشان داده شده در شکل 5.10.1، و با توجه به اینکه پنج سطح دیگر در پتانسیل صفر هستند، جواب معادله لاپلاس در داخل چیست؟ در صورت لزوم، می توان از برهم نهی شش راه حل برای برآوردن شرایط دلخواه در هر شش مرز استفاده کرد.
برای استفاده از رویکرد مودال یکسان در پیکربندی هایی که مرزها برای سایر سیستم های مختصات دکارتی طبیعی هستند، برای مثال استوانه ای و کروی نشان داده شده در شکل 5.10.1، اساساً از همان بسط ایده های اساسی که قبلاً نشان داده شده است استفاده می شود. با این حال، راه حل های ضرب شامل عملکردهای کمتر آشنا هستند. برای کسانی که راهحلهای دو بعدی، نحوه استفاده از آنها برای برآوردن شرایط مرزی دلخواه و نحوه گسترش آنها به پیکربندی مختصات دکارتی سهبعدی را میدانند، ادبیات ذکر شده در این بخش باید دسترسی آماده به آنچه برای بهرهبرداری از راهحلها لازم است را فراهم کند. سیستم های مختصات جدید علاوه بر سه سیستم مختصات استاندارد، بسیاری دیگر وجود دارند که معادله لاپلاس راهحلهای ضرب را میپذیرد. بخش آخر این بخش به عنوان مقدمه ای بر این سیستم های مختصات و راه حل های ضرب مرتبط در نظر گرفته شده است.
راه حل های ضرب مختصات دکارتی
در سه بعدی معادله لاپلاس است
ما به دنبال راهحلهایی میگردیم که بهعنوان ضربی از تابع x به تنهایی، X(x) ، تابعی از y به تنهایی، Y(y) و تابعی از z به تنهایی، Z(z) قابل بیان هستند .
با معرفی (2) به (1) و تقسیم
بر
تابع x به تنهایی، به یکی از y و یکی از z به تنهایی، صفر را به دست می دهد. از آنجایی که x، y ، و z متغیرهای مستقل هستند، مجموع صفر تنها در صورتی امکان پذیر است که هر یک از این سه «تابع» در واقع برابر با یک ثابت باشند. مجموع این ثابت ها باید صفر باشد.
توجه داشته باشید که اگر دو مورد از این سه ثابت جداسازی مثبت باشد، لازم است که سومی منفی باشد. ما این را با نوشتن (4) بر این اساس پیش بینی کردیم. راه حل های (4) هستند
جایی که
البته، نقشهای مختصات را میتوان عوض کرد، بنابراین جهت x یا z را میتوان وابستگی نمایی در نظر گرفت. از این راهحلها مشخص میشود که پتانسیل نمیتواند تناوبی یا نمایی در وابستگیهایش به هر سه مختصات باشد و همچنان راهحلی برای معادله لاپلاس باشد. در نگارش (6) با در نظر گرفتن X و Z به عنوان تناوبی، محدودیتهای پتانسیل را در صفحات ثابت y برآورده کردهایم .
بسط مودال در مختصات دکارتی
می توان ثابت ها و جواب ها را از (6) انتخاب کرد تا شرایط مرزی پتانسیل صفر در پنج مرز از شش مرز برقرار شود. با مختصات همانطور که در شکل 5.10.1a نشان داده شده است، توابع سینوسی برای X و Z برای اطمینان از پتانسیل صفر در صفحات x = 0 و z = 0 استفاده می شود . برای صفر کردن پتانسیل در صفحات x = a و z = w لازم است که
حل این معادلات مقدار ویژه k x = m
/a، k z = n
/w را به دست می دهد و از این رو
که در آن m و n اعداد صحیح هستند.
برای ایجاد پتانسیل صفر در مرز پنجم، بگوییم که در آن y = 0 ، تابع سینوس هذلولی برای نشان دادن وابستگی y استفاده می شود . بنابراین، مجموعهای از راهحلها که هر کدام یک شرط بالقوه صفر در پنج مرز را دارند، هستند
کجا با توجه به (5)
اینها را می توان برای برآوردن یک محدودیت پتانسیل دلخواه در مرز "آخرین"، جایی که y = b استفاده کرد . مثال زیر که Sec را گسترش می دهد. 5.5، این مفهوم را نشان می دهد.
مثال 5.10.1. تضعیف کننده خازنی در سه بعدی
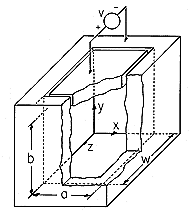
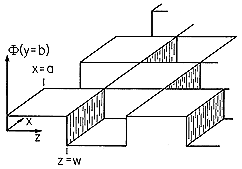
در تضعیف کننده مثال 5.5.1، توزیع میدان دو بعدی تقریب خوبی است زیرا یک بعد مقطعی در مقایسه با دیگری کوچک است. در شکل 5.5.5، a \ll w . اگر ابعاد مقطع a و w قابل مقایسه باشند، همانطور که در شکل 5.10.2 نشان داده شده است، میدان را می توان با برهم نهی مودال ارائه شده توسط (9) نشان داد.
شکل 5.10.2 ناحیه محدود شده با پتانسیل صفر در x = 0، x = a، z = 0، z = w و y = 0 . الکترود صفحه y = b را برای داشتن v پتانسیل محدود می کند .
در پنج صفحه x = 0، x = a، y = 0، z = 0 و z = w پتانسیل صفر است. در صفحه y = b ، توسط یک الکترود متصل به یک منبع ولتاژ، به v محدود شده است .
ارزیابی (10) در سطح الکترود باید v را بدهد .
ضرایب A mn با بهره برداری از متعامد بودن توابع ویژه تعیین می شود. به این معنا که،
جایی که
مراحلی که اکنون به بیانی برای هر ضریب معین A mn منجر میشوند ، بسط طبیعی آنهایی هستند که در Sec استفاده میشوند. 5.5. هر دو طرف (11) در تابع ویژه X i Z j ضرب می شوند و سپس هر دو طرف روی سطح در y = b ادغام می شوند .
به دلیل فرم ضرب هر عبارت، ادغام ها را می توان روی x و z به طور جداگانه انجام داد. با توجه به شرایط متعامد، (12)، تنها جمله غیر صفر در سمت راست در جمع m = i و n = j آمده است . این امکان حل معادله ضریب A ij را فراهم می کند . سپس با جایگزینی i
m و j \rightarrow n به دست می آوریم
انتگرال را می توان برای هر توزیع معینی از پتانسیل انجام داد. در این موقعیت خاص، پتانسیل سطح در y = b یکنواخت است. بنابراین، ادغام می دهد
پتانسیل مورد نظر که شرایط مرزی را در هر شش سطح برآورده می کند، با (10) و (15) داده می شود. توجه داشته باشید که عبارت اول در راه حلی که پیدا کردیم با عبارت اول در نمایش میدان دو بعدی یکسان نیست (5.5.9). مهم نیست نسبت a به w چقدر باشد ، اولین عبارت در جواب سه بعدی یک وابستگی سینوسی به z دارد ، در حالی که عبارت دوبعدی هیچ وابستگی به z ندارد .
برای تضعیف کننده خازنی شکل 5.5.5، چه سیگنال خروجی با این نمایش سه بعدی پیش بینی می شود؟ از (10) و (15) شارژ الکترود خروجی است
جایی که
با v = V sin
t ، در می یابیم که v o = V o cos
t در کجا
با استفاده از (16)، نتیجه می شود که دامنه ولتاژ خروجی است
جایی که ولتاژ نرمال شده است
و
این عبارت می تواند برای جایگزینی نمودار شکل 5.5.5 استفاده شود. در اینجا ما پیش بینی های دو بعدی و سه بعدی ولتاژ خروجی را با در نظر گرفتن (18) در حد b
a مقایسه می کنیم . در این حد، سینوس هذلولی تحت تسلط یکی از نمایی های آن قرار می گیرد و اولین جمله در این سری به دست می دهد.
در حد a/w \ll 1 ، وابستگی به فاصله بین الکترودهای ورودی و خروجی بیان شده توسط سمت راست با مدل دو بعدی یکسان می شود (5.5.15). با این حال، U ' = (8/
2 )U بدون در نظر گرفتن a/w .
این مثال مختصات دکارتی سهبعدی نشان میدهد که چگونه از خاصیت متعامد بودن راهحل ضرب برای ارائه پتانسیلی که روی پنج مرز صفر است در حالی که هر توزیع دلخواه را در مرز ششم فرض میکنیم، استفاده میشود. در این سطح ششم، پتانسیل شکل می گیرد
جایی که
توابع دو بعدی F mn برای نشان دادن شرایط مرزی "آخرین" استفاده شده است. این سری فوریه دو بعدی جایگزین سری فوریه تک بعدی Sec. 5.5 (5.5.17). در مثال، تابع موج مربعی دو بعدی نشان داده شده در شکل 5.10.3 را نشان می دهد. توجه داشته باشید که این تابع همانطور که باید در امتداد x = 0 ، x = a و z = 0، z = w به صفر می رسد. با عبور از هر یک از این خطوط "گرهی" علامت تغییر می کند، اما محدوده خارج از مستطیل اصلی هیچ علاقه فیزیکی ندارد، و از این رو رفتار خارج از آن محدوده بر اعتبار راه حل اعمال شده در مثال تأثیر نمی گذارد. از آنجایی که تابع نمایش داده شده در هر دو x و y فرد است ، می توان آن را فقط با توابع سینوسی نشان داد.
شکل 5.10.3 تابع موج مربعی دو بعدی که برای نشان دادن پتانسیل الکترود برای سیستم شکل 5.10.2 در صفحه y = b استفاده می شود .
هجوم ما به بسط های مودال سه بعدی، مفهوم متعامد بودن توابع را با توجه به یک فاصله یک بعدی تا قائم مقامی توابع با توجه به بخش دوبعدی یک صفحه گسترش می دهد. ما قادریم ضرایب V mn را در (20) تعیین کنیم زیرا این ضرایب برای تناسب با پتانسیل تجویز شده در سطح "ششم" ساخته شده است، زیرا اصطلاحات در سری متعامد هستند به این معنا که
در سایر سیستم های مختصات، یک رابطه متعامد مشابه برای راه حل های ضرب ارزیابی شده در یکی از سطوح تعریف شده توسط یک مختصات طبیعی ثابت وجود دارد. به طور کلی، یک تابع وزنی، توابع ویژه را در انتگرال انتگرال سطحی که مشابه (21) است، ضرب می کند.
به جز برخی موارد خاص، این تا جایی است که در بررسی راه حل های ضرب سه بعدی معادله لاپلاس پیش خواهیم رفت. در ادامه این بخش، ارجاعاتی به ادبیات برای راه حل های استوانه ای، کروی و سایر سیستم های مختصات داده شده است.
بسط مودال در سایر مختصات
یک حجم کلی که دارای مرزهای طبیعی در مختصات استوانه ای است در شکل 5.10.1b نشان داده شده است. راه حل های ضرب معادله لاپلاس شکل می گیرند
مختصات قطبی Sec. 5.7 یک مورد خاص است که در آن Z(z) یک ثابت است.
معادلات دیفرانسیل معمولی، مشابه (4) و (5) که F(
) و Z(z) را تعیین می کنند ، دارای ضرایب ثابت هستند و از این رو راه حل ها به ترتیب سینوس ها و کسینوس های m
و kz هستند . وابستگی شعاعی توسط یک معادله دیفرانسیل معمولی پیش بینی می شود که مانند (5.7.5)، دارای ضرایب متغیر در فضا است. متأسفانه، با وابستگی z ، راه حل ها به سادگی چند جمله ای نیستند. در عوض، آنها توابع بسل از مرتبه m و آرگومان kr هستند . همانطور که برای حل های ضرب معادله لاپلاس اعمال می شود، این توابع در متون فیلدهای استاندارد [1-4] توضیح داده شده اند . توابع بسل و مرتبط با آن در متون و رساله های ریاضیات توسعه یافته اند [5-8] .
همانطور که در دو و اکنون سه بعدی نشان داده شده است، راه حل یک توزیع پتانسیل دلخواه بر روی مرزها را می توان به عنوان برهم نهی راه حل هایی که هر کدام دارای پتانسیل مورد نظر در یک مرز و پتانسیل صفر در بقیه هستند، نوشت. خلاصه شده در جدول 5.10.1 اشکال به دست آمده توسط محلول ضرب، (22)، در نشان دادن پتانسیل برای توزیع دلخواه در سطح مشخص شده است. برای مثال، اگر پتانسیل روی سطح ثابت r تحمیل شود ، وابستگی شعاعی توسط توابع نظم حقیقی و استدلال مختلط بسل به دست میآید. آنچه برای نمایش
در سطح ثابت r لازم است، توابعی هستند که در
و z تناوبی هستند ، بنابراین انتظار داریم که این توابع بسل وابستگی نمایی مانند به r داشته باشند .
جدول 5.10.1 شکل راه حل های معادله LAPLACE در مختصات کلیندریکال هنگامی که پتانسیل در سطح داده شده محدود شده است و سایرین در پتانسیل صفر هستند
سطح
ثابتR(r)F()Z(z)
rتوابع نظم حقیقی بسل و استدلال مختلط (توابع بسل اصلاح شده)توابع مثلثاتی آرگومان حقیقیتوابع مثلثاتی آرگومان حقیقی
کارکردهای نظم مختلط بسل و استدلال مختلطتوابع مثلثاتی استدلال مختلطتوابع مثلثاتی آرگومان حقیقی
zتوابع نظم حقیقی و استدلال حقیقی بسلتوابع مثلثاتی آرگومان حقیقیتوابع مثلثاتی استدلال مختلط
در مختصات کروی، محلول های ضرب شکل می گیرند
از راه حل های مختصات استوانه ای، می توان حدس زد که توابع جدیدی برای توصیف R(r) مورد نیاز است . در واقع، اینها چند جمله ای ساده هستند. وابستگی
با یک معادله ضریب ثابت پیشبینی میشود و از این رو با توابع مثلثاتی آشنا نشان داده میشود. اما این
وابستگی توسط توابع لژاندر توصیف شده است. برخلاف توابع بسل که با سری های چند جمله ای نامتناهی توصیف می شوند، توابع لژاندر چند جمله ای های محدودی در cos (
) هستند . در رابطه با معادله لاپلاس، جواب ها در متون فیلدها خلاصه می شوند [1-4] . به عنوان راه حل برای معادلات دیفرانسیل معمولی، چند جمله ای های لژاندر در متون ریاضی ارائه شده اند [5،7] .
نام سایر سیستمهای مختصات سطوحی را نشان میدهد که با تنظیم یکی از متغیرها برابر با ثابت هستند: مختصات استوانهای بیضوی و مختصات کروی پرولات نمونههایی هستند که در آنها معادله لاپلاس قابل تفکیک است [2] . اولین قدم در بهره برداری از این سیستم های جدید، نوشتن عملگرهای لاپلاسین و سایر عملگرهای دیفرانسیل بر حسب آن مختصات است. این نیز در مراجع داده شده توضیح داده شده است.
5.11
خلاصه
در این فصل دو موضوع وجود دارد. اول، تقسیم یک راه حل برای معادله دیفرانسیل جزئی به یک بخش خاص است که برای متعادل کردن "درایو" در معادله دیفرانسیل طراحی شده است، و یک بخش همگن، که برای برآورده کردن راه حل کل با شرایط مرزی استفاده می شود. این فصل معادله پواسون را حل می کند. "درایو" به دلیل چگالی بار حجمی است و شرایط مرزی بر حسب پتانسیل های تعیین شده بیان می شود. در فصلهای بعدی، رویکرد مورد استفاده در اینجا برای مسائل ارزش مرزی که موقعیتهای فیزیکی مختلف را نشان میدهند، اعمال خواهد شد. معادلات دیفرانسیل و شرایط مرزی متفاوت خواهند بود، اما به دلیل خطی بودن آنها، می توان از همان رویکرد استفاده کرد.
دوم موضوع راهحلهای حاصل معادله لاپلاس است که بهدلیل متعامد بودن آنها میتوانند برای برآوردن شرایط مرزی دلخواه روی هم قرار گیرند. محور این بیانیه را می توان تا پایان ثانیه قدردانی کرد. 5.5. در پیکربندی در نظر گرفته شده در آن بخش، پتانسیل در تمام مرزهای دکارتی طبیعی یک منطقه محصور به جز یکی صفر است. نشان داده شده است که راهحلهای محصول را میتوان برای برآوردن یک شرط بالقوه دلخواه در مرز "آخرین" روی هم قرار داد. با ساختن مرز "آخرین" هر یک از مرزها و در صورت نیاز، روی هم قرار دادن راه حل های سری به تعداد مرزها، می توان شرایط دلخواه را در همه مرزها برآورده کرد. بخش مختصات قطبی این فرصت را میدهد که این ایدهها را به سیستمهایی که مختصات قابل تعویض نیستند تعمیم دهیم، در حالی که بخش راهحلهای دکارتی سهبعدی تعمیم معمولی به سه بعد را نشان میدهد.
در فصول بعدی، نیاز مکرر به حل معادله لاپلاس وجود خواهد داشت. برای این منظور، اغلب از سه دسته راه حل استفاده می شود: راه حل های دکارتی جدول 5.4.1، مختصات قطبی جدول 5.7.1، و سه راه حل مختصات کروی از Sec. 5.9. در فصل 10، که در آن پدیده های انتشار مغناطیسی معرفی شده اند و در فصل. در شکل 13، جایی که امواج الکترومغناطیسی توضیح داده شده است، کاربرد این ایده ها برای انتشار و معادلات هلمهولتز نشان داده شده است.
- M. Zahn، نظریه میدان الکترومغناطیسی: رویکرد حل مسئله ، جان وایلی و پسران، نیویورک (1979).
- پی. مون و دی اسپنسر، نظریه میدانی برای مهندسان ، ون نوستراند، پرینستون، نیوجرسی (1961).
- S. Ramo، JR Whinnery، و T. Van Duzer، میدانها و امواج در ارتباطات الکترونیک ، جان وایلی و پسران، نیویورک (1967).
- JR Melcher، Continuum Electromechanics ، MIT Press، کمبریج، ماساچوست (1981).
- FB Hildebrand, Advanced Calculus for Applications , Prentice-Hall, Inc, Englewood Cliffs, NJ (1962).
- GN Watson، A Treatise on Theory of Bessel Functions ، انتشارات دانشگاه کمبریج، لندن EC4. (1944).
- PM Morse and H. Feshbach, Methods of Theoretical Physics , McGraw-Hill Book Co., NY (1953).
- NW McLachlan، توابع بسل برای مهندسین ، انتشارات دانشگاه آکسفورد، لندن EC4 (1941).
https://web.mit.edu/6.013_book/www/chapter5/5.10.html
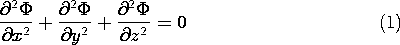

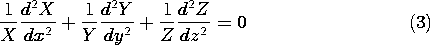
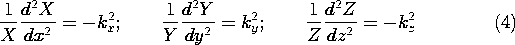

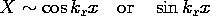
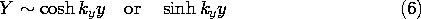

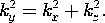
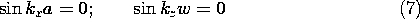
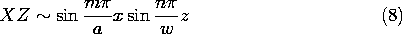
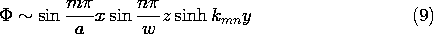
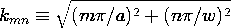
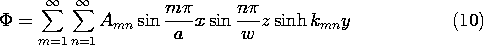
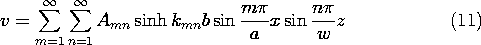
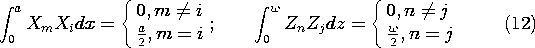
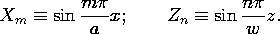
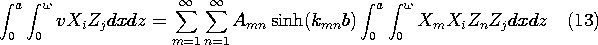
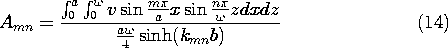
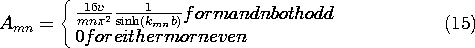
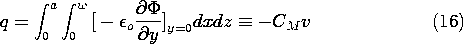
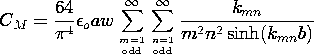

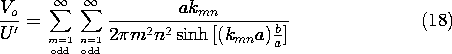
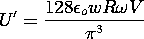
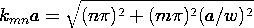
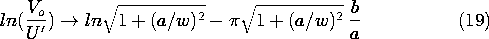

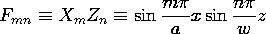
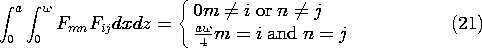


 در این وبلاگ به ریاضیات و کاربردهای آن و تحقیقات در آنها پرداخته می شود. مطالب در این وبلاگ ترجمه سطحی و اولیه است و کامل نیست.در صورتی سوال یا نظری در زمینه ریاضیات دارید مطرح نمایید .در صورت امکان به آن می پردازم. من دوست دارم برای یافتن پاسخ به سوالات و حل پروژه های علمی با دیگران همکاری نمایم.در صورتی که شما هم بامن هم عقیده هستید با من تماس بگیرید.
در این وبلاگ به ریاضیات و کاربردهای آن و تحقیقات در آنها پرداخته می شود. مطالب در این وبلاگ ترجمه سطحی و اولیه است و کامل نیست.در صورتی سوال یا نظری در زمینه ریاضیات دارید مطرح نمایید .در صورت امکان به آن می پردازم. من دوست دارم برای یافتن پاسخ به سوالات و حل پروژه های علمی با دیگران همکاری نمایم.در صورتی که شما هم بامن هم عقیده هستید با من تماس بگیرید.