3-تبدیل فوریه

تبدیل فوریه برای توابعی که خارج از یک بازه صفر هستند [ ویرایش ]

ارتباط نزدیکی بین تعریف سری فوریه و تبدیل فوریه برای توابع f که خارج از یک بازه صفر هستند وجود دارد. برای چنین تابعی می‌توانیم سری فوریه آن را در هر بازه‌ای که شامل نقاطی باشد که f صفر نیست محاسبه کنیم. تبدیل فوریه نیز برای چنین تابعی تعریف شده است. با افزایش طول بازه‌ای که در آن سری فوریه را محاسبه می‌کنیم، ضرایب سری فوریه شبیه تبدیل فوریه و مجموع سری فوریه f شبیه تبدیل فوریه معکوس می‌شوند. به طور دقیق تر، فرض کنید T به اندازه کافی بزرگ است که بازه [T/2،T/2-] شامل بازه‌ای است که f صفر نیست. سپس ضریب سری c n به صورت زیر بدست می آید:

$c_{n}={\frac {1}{T}}\int _{-{\frac {T}{2}}}^{\frac {T}{2}}f(x)\ ,e^{-2\pi i\left({\frac {n}{T}}\right)x}\,dx.$

از مقایسه این با تعریف تبدیل فوریه، چنین است که:

$c_{n}={\frac {1}{T}}{\hat {f}}\left({\frac {n}{T}}\right)$

زیرا f ( x ) در خارج از [- صفر استتی/2،تی/2] . بنابراین، ضرایب فوریه برابر با مقادیر تبدیل فوریه نمونه برداری شده در شبکه ای از عرض است.1/تیضرب در عرض شبکه1/تی.

تحت شرایط مناسب، سری فوریه f برابر با تابع f خواهد بود. به عبارت دیگر، f را می توان نوشت:

$f(x)=\sum _{n=-\infty }^{\infty }c_{n}\,e^{2\pi i\left({\frac {n}{T}}\ راست)x}=\sum _{n=-\infty }^{\infty }{\hat {f}}(\xi _{n})\ e^{2\pi i\xi _{n}x }\Delta \xi ,$

که در آن آخرین مجموع به سادگی اولین مجموع است که با استفاده از تعاریف ξ n = بازنویسی شده استn/تیو Δ ξ =n + 1/تی-n/تی=1/تی.

این جمع دوم یک مجموع ریمان است. با اجازه دادن به T → ∞ به انتگرال تبدیل فوریه معکوس همانطور که در بالا بیان شد همگرا می شود. در شرایط مناسب، این استدلال ممکن است دقیق شود. [13]

مثال [ ویرایش ]

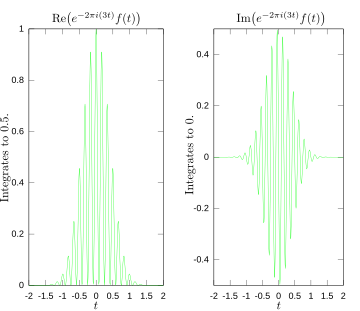
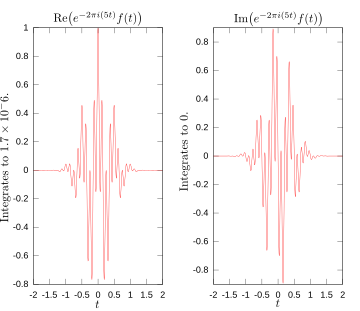
شکل‌های زیر یک تصویر بصری ارائه می‌دهند که چگونه تبدیل فوریه، وجود فرکانس در یک تابع خاص را اندازه‌گیری می‌کند. تابع نشان داده شده f ( t ) = cos(6π t ) e -π t 2 در 3 هرتز نوسان می کند (اگر t ثانیه را اندازه گیری کند) و به سرعت به 0 میل می کند. (فاکتور دوم در این معادله یک تابع پوششی است که سینوسی پیوسته را شکل می دهد. شکل کلی آن یک تابع گاوسی است ). این تابع به طور ویژه برای داشتن یک تبدیل فوریه حقیقی انتخاب شده است که می تواند به راحتی ترسیم شود. تصویر اول شامل نمودار آن است. به منظور محاسبه ${\hat {f}}(3)$ ما باید e - 2π i (3 t ) f ( t ) را ادغام کنیم . تصویر دوم نمودار قسمت های حقیقی و موهومی این تابع را نشان می دهد. بخش حقیقی انتگرال تقریبا همیشه مثبت است، زیرا وقتی f ( t ) منفی است، قسمت حقیقی e - 2π i (3 t ) نیز منفی است. از آنجایی که آنها با سرعت یکسانی نوسان می کنند، وقتی f ( t ) مثبت است، بخش حقیقی e - 2π i (3 t ) نیز مثبت است.. نتیجه این است که وقتی بخش حقیقی انتگرال را ادغام می‌کنید، عدد نسبتاً زیادی به دست می‌آید (در این مورد1/2). از سوی دیگر، هنگامی که شما سعی می کنید فرکانس را اندازه گیری کنید که وجود ندارد، مانند موردی که ما به آن نگاه می کنیم ${\hat {f}}(5)$ ، می بینید که هر دو جزء حقیقی و موهومی این تابع به سرعت بین مقادیر مثبت و منفی تغییر می کنند، همانطور که در تصویر سوم ترسیم شده است. بنابراین، در این حالت، انتگرال به اندازه کافی سریع نوسان می کند به طوری که انتگرال بسیار کوچک است و مقدار تبدیل فوریه برای آن فرکانس تقریباً صفر است.