بسط تیلور sinx ,x=p/2

توسط علی رضا نقش نیلچی | پنجشنبه یکم اردیبهشت ۱۴۰۱ | 18:28

بسط تیلور sinx ,x=p

توسط علی رضا نقش نیلچی | پنجشنبه یکم اردیبهشت ۱۴۰۱ | 16:53

بسط تیلور e^3x در 5=x

توسط علی رضا نقش نیلچی | پنجشنبه یکم اردیبهشت ۱۴۰۱ | 16:49

بسط تیلور سینوس

توسط علی رضا نقش نیلچی | پنجشنبه یکم اردیبهشت ۱۴۰۱ | 16:24

جملات سری تیلور f(x)=ln(2x) در 3=x

توسط علی رضا نقش نیلچی | پنجشنبه یکم اردیبهشت ۱۴۰۱ | 14:22

چهار ترم اول سری تیلور

building terms of the taylor polynomial

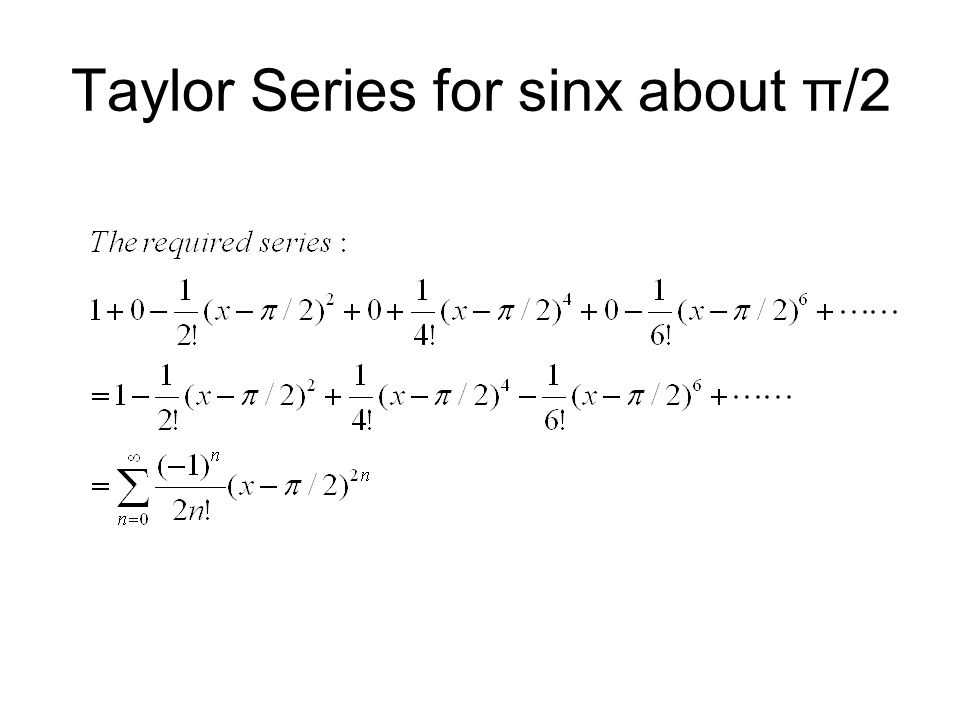
منبع

https://www.kristakingmath.com/blog/radius-interval-of-convergence-taylor-series

4-سری تیلور

توسط علی رضا نقش نیلچی | پنجشنبه یکم اردیبهشت ۱۴۰۱ | 13:13

محاسبه سری تیلور [ ویرایش ]

چندین روش برای محاسبه سری تیلور از تعداد زیادی توابع وجود دارد. می توان سعی کرد از تعریف سری تیلور استفاده کرد، اگرچه این اغلب مستلزم تعمیم شکل ضرایب بر اساس یک الگوی آشکار است. به‌علاوه، می‌توان از دستکاری‌هایی مانند جایگزینی، ضرب یا تقسیم، جمع یا تفریق سری‌های استاندارد تیلور برای ساخت سری تیلور یک تابع استفاده کرد، زیرا سری تیلور سری‌های توانی است. در برخی موارد، می توان سری تیلور را با اعمال مکرر ادغام توسط قطعات استخراج کرد. استفاده از سیستم های جبر رایانه ای برای محاسبه سری های تیلور بسیار راحت است .

مثال اول [ ویرایش ]

به منظور محاسبه چند جمله ای ماکلورین درجه 7 برای تابع

$f(x)=\ln(\cos x),\quad x\in \left(-{\frac {\pi }{2}},{\frac {\pi }{2}}\right )$ ،

می توان ابتدا تابع را به صورت بازنویسی کرد

$f(x)=\ln {\bigl (}1+(\cos x-1){\bigr )}\!$ .

سری تیلور برای لگاریتم طبیعی است (با استفاده از نماد O بزرگ )

$\ln(1+x)=x-{\frac {x^{2}}{2}}+{\frac {x^{3}}{3}}+{O}\left(x ^{4}\راست)\!$

و برای تابع کسینوس

$\cos x-1=-{\frac {x^{2}}{2}}+{\frac {x^{4}}{24}}-{\frac {x^{6}} {720}}+{O}\left(x^{8}\right)\!$ .

بسط سری دوم دارای یک جمله ثابت صفر است که ما را قادر می سازد سری دوم را با سری اول جایگزین کنیم و با استفاده از علامت O بزرگ به راحتی از عبارت های مرتبه بالاتر از درجه 7 حذف کنیم :

${\begin{aligned}f(x)&=\ln {\bigl (}1+(\cos x-1){\bigr )}\\&=(\cos x-1)-{\ tfrac {1}{2}}(\cos x-1)^{2}+{\tfrac {1}{3}}(\cos x-1)^{3}+{O}\left((\ cos x-1)^{4}\right)\\&=\left(-{\frac {x^{2}}{2}}+{\frac {x^{4}}{24}}- {\frac {x^{6}}{720}}+{O}\left(x^{8}\right)\right)-{\frac {1}{2}}\left(-{\frac {x^{2}}{2}}+{\frac {x^{4}}{24}}+{O}\left(x^{6}\right)\right)^{2}+{ \frac {1}{3}}\left(-{\frac {x^{2}}{2}}+O\left(x^{4}\right)\right)^{3}+{O }\left(x^{8}\right)\\&=-{\frac {x^{2}}{2}}+{\frac {x^{4}}{24}}-{\frac {x^{6}}{720}}-{\frac {x^{4}}{8}}+{\frac {x^{6}}{48}}-{\frac {x^{6 }}{24}}+O\left(x^{8}\right)\\&=-{\frac {x^{2}}{2}}-{\frac {x^{4}}{ 12}}-{\frac {x^{6}}{45}}+O\left(x^{8}\right).\end{تراز شده}}\!$

از آنجایی که کسینوس یک تابع زوج است، ضرایب برای تمام توان های فرد x , x 3 , x 5 , x 7 , ... باید صفر باشد.

مثال دوم [ ویرایش ]

فرض کنید می خواهیم سری تیلور در 0 تابع باشد

$g(x)={\frac {e^{x}}{\cos x}}.\!$

ما برای تابع نمایی داریم

$e^{x}=\sum _{n=0}^{\infty }{\frac {x^{n}}{n!}}=1+x+{\frac {x^{2} {2!}}+{\frac {x^{3}}{3!}}+{\frac {x^{4}}{4!}}+\cdots \!$

و مانند مثال اول،

$\cos x=1-{\frac {x^{2}}{2!}}+{\frac {x^{4}}{4!}}-\cdots \!$

فرض کنید سری قدرت است

${\frac {e^{x}}{\cos x}}=c_{0}+c_{1}x+c_{2}x^{2}+c_{3}x^{3} +\cdots \!$

سپس ضرب با مخرج و جایگزینی سری کسینوس حاصل می شود

${\begin{aligned}e^{x}&=\left(c_{0}+c_{1}x+c_{2}x^{2}+c_{3}x^{3}+ \cdots \right)\cos x\\&=\left(c_{0}+c_{1}x+c_{2}x^{2}+c_{3}x^{3}+c_{4} x^{4}+\cdots \right)\left(1-{\frac {x^{2}}{2!}}+{\frac {x^{4}}{4!}}-\cdots \right)\\&=c_{0}-{\frac {c_{0}}{2}}x^{2}+{\frac {c_{0}}{4!}}x^{4} +c_{1}x-{\frac {c_{1}}{2}}x^{3}+{\frac {c_{1}}{4!}}x^{5}+c_{2} x^{2}-{\frac {c_{2}}{2}}x^{4}+{\frac {c_{2}}{4!}}x^{6}+c_{3}x ^{3}-{\frac {c_{3}}{2}}x^{5}+{\frac {c_{3}}{4!}}x^{7}+c_{4}x^ {4}+\cdots \end{aligned}}\!$

جمع آوری شرایط تا مرتبه چهارم بازده

$e^{x}=c_{0}+c_{1}x+\left(c_{2}-{\frac {c_{0}}{2}}\right)x^{2}+\ چپ(c_{3}-{\frac {c_{1}}{2}}\right)x^{3}+\left(c_{4}-{\frac {c_{2}}{2}} +{\frac {c_{0}}{4!}}\right)x^{4}+\cdots \!$

ارزش های $ج_{i}$ می توان با مقایسه ضرایب با عبارت بالا برای یافت $e^{x}$ ، بازده:

${\frac {e^{x}}{\cos x}}=1+x+x^{2}+{\frac {2x^{3}}{3}}+{\frac {x ^{4}}{2}}+\cdots .\!$

مثال سوم [ ویرایش ]

در اینجا ما از روشی به نام "گسترش غیر مستقیم" برای گسترش تابع داده شده استفاده می کنیم. این روش از بسط تیلور شناخته شده تابع نمایی استفاده می کند. برای بسط (1 + x ) e x به عنوان یک سری تیلور در x ، از سری شناخته شده تیلور تابع e x استفاده می کنیم :

$e^{x}=\sum _{n=0}^{\infty }{\frac {x^{n}}{n!}}=1+x+{\frac {x^{2} }{2!}}+{\frac {x^{3}}{3!}}+{\frac {x^{4}}{4!}}+\cdots .$

بدین ترتیب،

${\begin{aligned}(1+x)e^{x}&=e^{x}+xe^{x}=\sum _{n=0}^{\infty }{\frac { x^{n}}{n!}}+\sum _{n=0}^{\infty }{\frac {x^{n+1}}{n!}}=1+\sum _{n =1}^{\infty }{\frac {x^{n}}{n!}}+\sum _{n=0}^{\infty }{\frac {x^{n+1}}{ n!}}\\&=1+\sum _{n=1}^{\infty }{\frac {x^{n}}{n!}}+\sum _{n=1}^{\ infty }{\frac {x^{n}}{(n-1)!}}=1+\sum _{n=1}^{\infty }\left({\frac {1}{n!} }+{\frac {1}{(n-1)!}}\right)x^{n}\\&=1+\sum _{n=1}^{\infty }{\frac {n+ 1}{n!}}x^{n}\\&=\sum _{n=0}^{\infty }{\frac {n+1}{n!}}x^{n}.\end {هم راستا}}$

مجموعه تیلور به عنوان تعاریف [ ویرایش ]

به طور کلاسیک، توابع جبری با یک معادله جبری تعریف می شوند، و توابع ماورایی (از جمله آنهایی که در بالا مورد بحث قرار گرفت) با ویژگی هایی مانند یک معادله دیفرانسیل تعریف می شوند. به عنوان مثال، تابع نمایی تابعی است که در همه جا با مشتق خود برابر است و در مبدا مقدار 1 را در نظر می گیرد. با این حال، می توان به همان اندازه یک تابع تحلیلی را با سری تیلور آن تعریف کرد.

سری تیلور برای تعریف توابع و " عملگرها " در حوزه های مختلف ریاضیات استفاده می شود. به ویژه، این امر در مناطقی که تعاریف کلاسیک توابع شکسته می شوند صادق است. به عنوان مثال، با استفاده از سری تیلور، می‌توان توابع تحلیلی را به مجموعه‌ای از ماتریس‌ها و عملگرها، مانند لگاریتم ماتریس نمایی یا ماتریس تعمیم داد .

در زمینه های دیگر، مانند تجزیه و تحلیل رسمی، راحت تر است که به طور مستقیم با خود سری های قدرت کار کنید. بنابراین می توان راه حل یک معادله دیفرانسیل را به عنوان یک سری توانی تعریف کرد که امیدواریم ثابت شود سری تیلور راه حل مورد نظر است.

سری تیلور در چندین متغیر [ ویرایش ]

سری تیلور همچنین ممکن است به توابع بیش از یک متغیر با [13] [14] تعمیم داده شود.

${\begin{aligned}T(x_{1},\ldots,x_{d})&=\sum _{n_{1}=0}^{\infty }\cdots \sum _{n_{ d}=0}^{\infty }{\frac {(x_{1}-a_{1})^{n_{1}}\cdots (x_{d}-a_{d})^{n_{d }}}{n_{1}!\cdots n_{d}!}}\,\left({\frac {\partial ^{n_{1}+\cdots +n_{d}}f}{\partial x_ {1}^{n_{1}}\cdots \partial x_{d}^{n_{d}}}}\right)(a_{1},\ldots ,a_{d})\\&=f( a_{1},\ldots ,a_{d})+\sum _{j=1}^{d}{\frac {\partial f(a_{1},\ldots ,a_{d})}{\ x_{j}}}(x_{j}-a_{j})+{\frac {1}{2!}}\sum _{j=1}^{d}\sum _{k=1} ^{d}{\frac {\partial ^{2}f(a_{1},\ldots ,a_{d})}{\partial x_{j}\partial x_{k}}}(x_{j} -a_{j})(x_{k}-a_{k})\\&\qquad \qquad +{\frac {1}{3!}}\sum _{j=1}^{d}\sum _{k=1}^{d}\sum _{l=1}^{d}{\frac {\partial ^{3}f(a_{1},\ldots ,a_{d})}{\ x_{j}\جزئی x_{k}\جزئی x_{l}}}(x_{j}-a_{j})(x_{k}-a_{k})(x_{l}-a_{l })+\cdots \end{تراز شده}}$

به عنوان مثال، برای یک تابع $f(x,y)$ که به دو متغیر x و y بستگی دارد ، سری تیلور به مرتبه دوم در مورد نقطه ( a , b ) است.

$f(a,b)+(xa)f_{x}(a,b)+(yb)f_{y}(a,b)+{\frac {1}{2!}}{\Big (}(xa)^{2}f_{xx}(a,b)+2(xa)(yb)f_{xy}(a,b)+(yb)^{2}f_{yy}(a, ب){\بزرگ)}$

که در آن زیرنویس ها مشتقات جزئی مربوطه را نشان می دهند .

یک بسط مرتبه دوم سری تیلور از یک تابع با مقدار اسکالر بیش از یک متغیر را می توان به صورت فشرده نوشت:

$T(\mathbf {x})=f(\mathbf {a})+(\mathbf {x} -\mathbf {a})^{\mathsf {T}}Df(\mathbf {a}) +{\frac {1}{2!}}(\mathbf {x} -\mathbf {a} )^{\mathsf {T}}\left\{D^{2}f(\mathbf {a}) \right\}(\mathbf {x} -\mathbf {a} )+\cdots ,$

که در آن D f ( a ) گرادیان f است که با x = a ارزیابی می شود و D 2 f ( a ) ماتریس هسین است . با اعمال نماد چند شاخص ، سری تیلور برای چندین متغیر تبدیل می شود

${\displaystyle T(\mathbf {x} )=\sum _{|\alpha |\geq 0}{\frac {(\mathbf {x} -\mathbf {a})^{\alpha }}{\alpha !}}\left({\mathrm {\partial } ^{\alpha }}f\right)(\mathbf {a})$

که باید به عنوان یک نسخه اختصاری چند شاخصه از معادله اول این پاراگراف، با تشبیه کامل به حالت تک متغیر درک شود.

مثال [ ویرایش ]

تقریب مرتبه دوم سری تیلور (به رنگ نارنجی) تابع f ( x , y ) = e x ln(1 + y ) در اطراف مبدا.

به منظور محاسبه بسط سری تیلور مرتبه دوم حول نقطه ( a , b ) = (0, 0) تابع

$f(x,y)=e^{x}\ln(1+y),$

ابتدا تمام مشتقات جزئی لازم را محاسبه می کند:

${\begin{aligned}f_{x}&=e^{x}\ln(1+y)\\[6pt]f_{y}&={\frac {e^{x}}{1 +y}}\\[6pt]f_{xx}&=e^{x}\ln(1+y)\\[6pt]f_{yy}&=-{\frac {e^{x}}{ (1+y)^{2}}}\\[6pt]f_{xy}&=f_{yx}={\frac {e^{x}}{1+y}}.\end{تراز شده}}$

ارزیابی این مشتقات در مبدا، ضرایب تیلور را به دست می دهد

${\begin{aligned}f_{x}(0,0)&=0\\f_{y}(0,0)&=1\\f_{xx}(0,0)&=0\ \f_{yy}(0,0)&=-1\\f_{xy}(0,0)&=f_{yx}(0,0)=1.\end{تراز شده}}$

جایگزینی این مقادیر به فرمول کلی

${\begin{aligned}T(x,y)=&f(a,b)+(xa)f_{x}(a,b)+(yb)f_{y}(a,b)\\ &{}+{\frac {1}{2!}}\left((xa)^{2}f_{xx}(a,b)+2(xa)(yb)f_{xy}(a,b )+(yb)^{2}f_{yy}(a,b)\right)+\cdots \end{تراز شده}}$

تولید می کند

${\begin{aligned}T(x,y)&=0+0(x-0)+1(y-0)+{\frac {1}{2}}{\Big (}0( x-0)^{2}+2(x-0)(y-0)+(-1)(y-0)^{2}{\Big )}+\cdots \\&=y+xy- {\frac {y^{2}}{2}}+\cdots \end{aligned}}$

از آنجایی که ln(1 + y ) در | y | < 1 ، ما داریم

$e^{x}\ln(1+y)=y+xy-{\frac {y^{2}}{2}}+\cdots ,\qquad |y|<1.$

مقایسه با سری فوریه [ ویرایش ]

نوشتار اصلی: سری فوریه

سری فوریه مثلثاتی فرد را قادر می سازد تا یک تابع تناوبی (یا تابعی که در بازه بسته [ a , b ] تعریف شده است ) را به عنوان مجموع نامتناهی از توابع مثلثاتی ( سینوس ها و کسینوس ها ) بیان کند. از این نظر، سری فوریه مشابه سری تیلور است، زیرا دومی به فرد اجازه می دهد تا یک تابع را به عنوان مجموع بی نهایت توان بیان کند . با این وجود، این دو سریال در چندین موضوع مرتبط با یکدیگر تفاوت دارند:

برش های محدود سری تیلور از f ( x ) در مورد نقطه x = a همگی دقیقاً برابر با f در a هستند. در مقابل، سری فوریه با ادغام در یک بازه کامل محاسبه می‌شود، بنابراین به طور کلی چنین نقطه‌ای وجود ندارد که تمام برش‌های محدود سری دقیق باشند.
محاسبه سری تیلور به دانش تابع در یک همسایگی کوچک دلخواه یک نقطه نیاز دارد، در حالی که محاسبه سری فوریه مستلزم دانستن تابع در کل بازه دامنه آن است . به تعبیری می توان گفت که سریال تیلور «محلی» و سری فوریه «جهانی» است.
سری تیلور برای تابعی تعریف می شود که مشتقات بی نهایت زیادی در یک نقطه دارد، در حالی که سری فوریه برای هر تابع انتگرال پذیر تعریف می شود . به طور خاص، این تابع هیچ جا قابل تمایز نیست. (به عنوان مثال، f ( x ) می تواند یک تابع وایرشتراس باشد .)
همگرایی هر دو سری خواص بسیار متفاوتی دارد. حتی اگر سری تیلور دارای شعاع همگرایی مثبت باشد، ممکن است سری حاصل با تابع منطبق نباشد. اما اگر تابع تحلیلی باشد، سری به صورت نقطه ای به تابع همگرا می شود، و به طور یکنواخت در هر زیر مجموعه فشرده بازه همگرایی . در مورد سری فوریه، اگر تابع مربع انتگرال پذیر باشد، سری در میانگین درجه دوم همگرا می شود ، اما الزامات اضافی برای اطمینان از همگرایی نقطه ای یا یکنواخت مورد نیاز است (به عنوان مثال، اگر تابع تناوبی و از کلاس C 1 باشد، پس همگرایی لباس فرم).
در نهایت، در عمل می‌خواهیم تابع را با تعداد محدودی از جمله‌ها، مثلاً با چند جمله‌ای تیلور یا مجموع جزئی سری مثلثاتی، تقریب بزنیم. در مورد سری تیلور، خطا در همسایگی نقطه ای که محاسبه می شود بسیار کوچک است، در حالی که ممکن است در یک نقطه دور بسیار بزرگ باشد. در مورد سری فوریه، خطا در امتداد دامنه تابع توزیع می شود.

همچنین مشاهده کنید [ ویرایش ]

منبع

https://en.wikipedia.org/wiki/Taylor_series

3-سری تیلور

توسط علی رضا نقش نیلچی | پنجشنبه یکم اردیبهشت ۱۴۰۱ | 13:9

خطای تقریب و همگرایی [ ویرایش ]

مقاله اصلی: قضیه تیلور

تابع سینوس (آبی) با چند جمله ای تیلور درجه 7 (صورتی) برای یک دوره کامل در مرکز مبدأ تقریباً تقریب دارد.

چند جمله ای های تیلور برای ln(1 + x ) فقط تقریب های دقیقی را در محدوده -1 < x≤ 1 ارائه می دهند. برای x > 1 ، چند جمله ای های تیلور با درجه بالاتر تقریب بدتری ارائه می دهند.

تقریب های تیلور برای ln(1 + x ) (سیاه). برای x > 1 ، تقریب ها واگرا می شوند.

تصویر سمت راست تقریب دقیق sin x در اطراف نقطه x = 0 است. منحنی صورتی یک چند جمله ای درجه هفت است:

$\sin \left(x\right)\approx x-{\frac {x^{3}}{3!}}+{\frac {x^{5}}{5!}}-{\frac {x ^{7}}{7!}}.\!$

خطا در این تقریب بیشتر از | نیست x | 9/9 ! . برای یک چرخه کامل در مرکز مبدا ( -π < x < π ) خطا کمتر از 0.08215 است. به طور خاص، برای -1 < x < 1 ، خطا کمتر از 0.000003 است.

در مقابل، همچنین تصویری از تابع لگاریتم طبیعی ln(1 + x ) و برخی از چندجمله ای های تیلور آن در اطراف a = 0 نشان داده شده است. این تقریب ها فقط در ناحیه -1 < x ≤ 1 به تابع همگرا می شوند . در خارج از این منطقه، چند جمله ای های درجه بالاتر تیلور، تقریب بدتری برای تابع هستند.

خطایی که در تقریب یک تابع با چند جمله ای تیلور درجه n آن رخ می دهد باقیمانده یا باقیمانده نامیده می شود و با تابع Rn ( x ) نشان داده می شود . از قضیه تیلور می توان برای به دست آوردن حدی در اندازه باقیمانده استفاده کرد.

به طور کلی، سری های تیلور به هیچ وجه نیازی به همگرایی ندارند. و در واقع مجموعه توابع با سری تیلور همگرا مجموعه ای ناچیز در فضای فریشه از توابع صاف است . و حتی اگر سری تیلور یک تابع f همگرا شود، نیازی نیست حد آن به طور کلی برابر با مقدار تابع f ( x ) باشد. به عنوان مثال، تابع

$f(x)={\begin{cases}e^{-1/x^{2}}&{\text{if }}x\neq 0\\[3mu]0&{\text{if } }x=0\end{موارد}}$

بی نهایت در x = 0 قابل تمایز است و تمام مشتقات آن صفر است. در نتیجه، سری تیلور از f ( x ) حدود x = 0 به طور یکسان صفر است. با این حال، f ( x ) تابع صفر نیست، بنابراین با سری تیلور آن در اطراف مبدا برابر نیست. بنابراین، f ( x ) مثالی از یک تابع صاف غیر تحلیلی است .

در تجزیه و تحلیل واقعی ، این مثال نشان می دهد که توابع بی نهایت قابل تمایز f ( x ) وجود دارد که سری تیلور آنها با f ( x ) برابر نیستند ، حتی اگر همگرا شوند. در مقابل، توابع هولومورف مورد مطالعه در تحلیل پیچیده همیشه دارای یک سری تیلور همگرا هستند، و حتی سری تیلور از توابع مرومورفیک ، که ممکن است دارای تکینگی باشند، هرگز به مقداری متفاوت از خود تابع همگرا نمی شوند. با این حال، تابع مختلط e −1/ z 2 به 0 نزدیک نمی‌شوددر امتداد محور فرضی به 0 نزدیک می شود، بنابراین در صفحه مختلط پیوسته نیست و سری تیلور آن در 0 تعریف نشده است.

به طور کلی‌تر، هر دنباله‌ای از اعداد حقیقی یا مختلط می‌تواند به‌عنوان ضرایبی در سری تیلور از یک تابع بی‌نهایت متمایز تعریف‌شده بر روی خط واقعی ظاهر شود که نتیجه لم بورل است . در نتیجه، شعاع همگرایی یک سری تیلور می تواند صفر باشد. حتی توابع بی نهایت قابل تمایز نیز بر روی خط واقعی تعریف شده اند که سری های تیلور در همه جا شعاع همگرایی 0 دارند. [8]

یک تابع را نمی توان به عنوان یک سری تیلور با محوریت تکینگی نوشت . در این موارد، اگر قدرت های منفی متغیر x را نیز مجاز بدانیم، اغلب می توان به یک بسط سری دست یافت . سری Laurent را ببینید . برای مثال، f ( x ) = e −1/ x 2 را می توان به صورت سری Laurent نوشت.

تعمیم [ ویرایش ]

با این حال، یک تعمیم [9] [10] از سری تیلور وجود دارد که با استفاده از حساب تفاوت‌های محدود ، به مقدار خود تابع برای هر تابع پیوسته محدود در (0,∞) همگرا می‌شود . به طور خاص، با توجه به Einar Hille ، یک قضیه زیر را دارد که برای هر t > 0 ،

$\lim _{h\to 0^{+}}\sum _{n=0}^{\infty }{\frac {t^{n}}{n!}}{\frac {\Delta _{h }^{n}f(a)}{h^{n}}}=f(a+t).$

اینجا Δn
ساعتn امین عملگر تفاضل محدود با اندازه گام h است. این سری دقیقاً سری تیلور است، با این تفاوت که به جای تمایز، تفاوت‌های تقسیم شده ظاهر می‌شود: این سری از نظر رسمی شبیه به سری‌های نیوتن است . وقتی تابع f در a تحلیلی است ، عبارت‌های سری با عبارت‌های سری تیلور همگرا می‌شوند و از این نظر سری معمول تیلور را تعمیم می‌دهند.

به طور کلی، برای هر دنباله نامتناهی a i ، هویت سری توانی زیر برقرار است:

$\sum _{n=0}^{\infty }{\frac {u^{n}}{n!}}\Delta ^{n}a_{i}=e^{-u}\sum _{j =0}^{\infty }{\frac {u^{j}}{j!}}a_{i+j}.$

بنابراین به طور خاص،

$f(a+t)=\lim _{h\to 0^{+}}e^{-t/h}\sum _{j=0}^{\infty }f(a+jh){\frac {(t/h)^{j}}{j!}}.$

سری سمت راست مقدار انتظاری f ( a + X ) است، که در آن X یک متغیر تصادفی توزیع شده توسط پواسون است که مقدار jh را با احتمال e - t / h می گیرد .( t / h ) j/ج !. از این رو،

$f(a+t)=\lim _{h\to 0^{+}}\int _{-\infty }^{\infty }f(a+x)dP_{t/h,h} (ایکس).$

قانون اعداد بزرگ نشان می دهد که هویت وجود دارد. [11]

فهرستی از سری مکلورن از برخی توابع رایج [ ویرایش ]

همچنین ببینید: لیست سری های ریاضی

چندین بسط مهم سری مکلورن دنبال می شود. [12] همه این بسط ها برای آرگومان های پیچیده x معتبر هستند .

تابع نمایی [ ویرایش ]

تابع نمایی e x (به رنگ آبی)، و مجموع اولین جمله های n + 1 سری تیلور آن در 0 (به رنگ قرمز).

تابع نمایی $e^{x}$ (با پایه e ) دارای سری مکلورن است

$e^{x}=\sum _{n=0}^{\infty }{\frac {x^{n}}{n!}}=1+x+{\frac {x^{2} }{2!}}+{\frac {x^{3}}{3!}}+\cdots$ .

برای همه x همگرا می شود .

لگاریتم طبیعی [ ویرایش ]

نوشتار اصلی: سری مرکاتور

لگاریتم طبیعی (با پایه e ) دارای سری مکلورن است

${\begin{aligned}\ln(1-x)&=-\sum _{n=1}^{\infty }{\frac {x^{n}}{n}}=-x- {\frac {x^{2}}{2}}-{\frac {x^{3}}{3}}-\cdots ,\\\ln(1+x)&=\sum _{n= 1}^{\infty }(-1)^{n+1}{\frac {x^{n}}{n}}=x-{\frac {x^{2}}{2}}+{ \frac {x^{3}}{3}}-\cdots .\end{تراز شده}}$

آنها برای همگرا می شوند $|x|<1$ . (علاوه بر این، سری برای ln(1 - x ) برای x = -1 همگرا می شود ، و سری برای ln(1 + x ) برای x = 1 همگرا می شود .)

سری هندسی [ ویرایش ]

سری هندسی و مشتقات آن دارای سری مکلورن هستند

${\begin{aligned}{\frac {1}{1-x}}&=\sum _{n=0}^{\infty }x^{n}\\{\frac {1}{ (1-x)^{2}}}&=\sum _{n=1}^{\infty }nx^{n-1}\\{\frac {1}{(1-x)^{3 }}}&=\sum _{n=2}^{\infty }{\frac {(n-1)n}{2}}x^{n-2}.\end{تراز شده}}$

همه همگرا هستند برای $|x|<1$ . اینها موارد خاصی از سری دوجمله ای هستند که در بخش بعدی آورده شده است.

سری دو جمله ای [ ویرایش ]

سری دوجمله ای سری توان است

$(1+x)^{\alpha }=\sum _{n=0}^{\infty }{\binom {\alpha }{n}}x^{n}$

که ضرایب آن ضرایب دوجمله ای تعمیم یافته است

${\binom {\alpha }{n}}=\prod _{k=1}^{n}{\frac {\alpha -k+1}{k}}={\frac {\alpha ( \alpha -1)\cdots (\alpha -n+1)}{n!}}.$

(اگر n = 0 باشد، این حاصلضرب یک محصول خالی است و مقدار 1 دارد.) برای همگرا می شود $|x|<1$ برای هر عدد واقعی یا مختلط α .

وقتی α = -1 ، این اساساً سری هندسی نامتناهی است که در بخش قبل ذکر شد. موارد خاص α =1/2و α = -1/2تابع جذر و معکوس آن را بدهید :

${\begin{aligned}(1+x)^{\frac {1}{2}}&=1+{\tfrac {1}{2}}x-{\tfrac {1}{8} }x^{2}+{\tfrac {1}{16}}x^{3}-{\tfrac {5}{128}}x^{4}+{\tfrac {7}{256}}x ^{5}-\cdots &&=\sum _{n=0}^{\infty }{\frac {(-1)^{n-1}(2n)!}{4^{n}(n! )^{2}(2n-1)}}x^{n}،\\(1+x)^{-{\frac {1}{2}}}&=1-{\tfrac {1}{ 2}}x+{\tfrac {3}{8}}x^{2}-{\tfrac {5}{16}}x^{3}+{\tfrac {35}{128}}x^{4 }-{\tfrac {63}{256}}x^{5}+\cdots &&=\sum _{n=0}^{\infty }{\frac {(-1)^{n}(2n) !}{4^{n}(n!)^{2}}}x^{n}.\end{تراز شده}}$

هنگامی که فقط عبارت خطی حفظ می شود، این به تقریب دو جمله ای ساده می شود .

توابع مثلثاتی [ ویرایش ]

توابع مثلثاتی معمول و معکوس آنها دارای سری مکلورن زیر هستند:

${\begin{aligned}\sin x&=\sum _{n=0}^{\infty }{\frac {(-1)^{n}}{(2n+1)!}}x^ {2n+1}&&=x-{\frac {x^{3}}{3!}}+{\frac {x^{5}}{5!}}-\cdots &&{\text{برای همه }}x\\[6pt]\cos x&=\sum _{n=0}^{\infty }{\frac {(-1)^{n}}{(2n)!}}x^{2n} &&=1-{\frac {x^{2}}{2!}}+{\frac {x^{4}}{4!}}-\cdots &&{\text{برای همه }}x\\ [6pt]\tan x&=\sum _{n=1}^{\infty }{\frac {B_{2n}(-4)^{n}\left(1-4^{n}\right)} {(2n)!}}x^{2n-1}&&=x+{\frac {x^{3}}{3}}+{\frac {2x^{5}}{15}}+\cdots && {\text{for }}|x|<{\frac {\pi }{2}}\\[6pt]\sec x&=\sum _{n=0}^{\infty }{\frac {(- 1)^{n}E_{2n}}{(2n)!}}x^{2n}&&=1+{\frac {x^{2}}{2}}+{\frac {5x^{4 }}{24}}+\cdots &&{\text{for }}|x|<{\frac {\pi }{2}}\\[6pt]\arcsin x&=\sum _{n=0}^ {\infty }{\frac {(2n)!}{4^{n}(n!)^{2}(2n+1)}}x^{2n+1}&&=x+{\frac {x^{3}}{6}}+{\frac {3x^{5}}{40}}+\cdots &&{\text{برای }}|x|\leq 1\\ [6pt]\arccos x&={\frac {\pi }{2}}-\arcsin x\\&={\frac {\pi }{2}}-\sum _{n=0}^{\infty }{\frac {(2n)!}{4^{n}(n!)^{2}(2n+1)}}x^{2n+1}&&={\frac {\pi }{2} }-x-{\frac {x^{3}}{6}}-{\frac {3x^{5}}{40}}-\cdots &&{\text{برای }}|x|\leq 1 \\[6pt]\arctan x&=\sum _{n=0}^{\infty }{\frac {(-1)^{n}}{2n+1}}x^{2n+1}&&= x-{\frac {x^{3}}{3}}+{\frac {x^{5}}{5}}-\cdots &&{\text{for }}|x|\leq 1,\ x\neq \pm i\end{تراز شده}}}=\sum _{n=0}^{\infty }{\frac {(-1)^{n}}{2n+1}}x^{2n+1}&&=x-{\frac {x^ {3}}{3}}+{\frac {x^{5}}{5}}-\cdots &&{\text{for }}|x|\leq 1,\ x\neq \pm i\end {هم راستا}}}=\sum _{n=0}^{\infty }{\frac {(-1)^{n}}{2n+1}}x^{2n+1}&&=x-{\frac {x^ {3}}{3}}+{\frac {x^{5}}{5}}-\cdots &&{\text{for }}|x|\leq 1,\ x\neq \pm i\end {هم راستا}}$

همه زوایا بر حسب رادیان بیان می شوند . اعداد B k که در بسط های tan x ظاهر می شوند اعداد برنولی هستند . E k در بسط sec x اعداد اویلر هستند .

توابع هذلولی [ ویرایش ]

توابع هذلولی دارای سری مکلورن هستند که نزدیک به سری برای توابع مثلثاتی مربوطه هستند:

${\begin{aligned}\sinh x&=\sum _{n=0}^{\infty }{\frac {x^{2n+1}}{(2n+1)!}}&&=x+ {\frac {x^{3}}{3!}}+{\frac {x^{5}}{5!}}+\cdots &&{\text{برای همه }}x\\[6pt]\ cosh x&=\sum _{n=0}^{\infty }{\frac {x^{2n}}{(2n)!}}&&=1+{\frac {x^{2}}{2! }}+{\frac {x^{4}}{4!}}+\cdots &&{\text{برای همه }}x\\[6pt]\tanh x&=\sum _{n=1}^{ \infty }{\frac {B_{2n}4^{n}\left(4^{n}-1\right)}{(2n)!}}x^{2n-1}&&=x-{\ frac {x^{3}}{3}}+{\frac {2x^{5}}{15}}-{\frac {17x^{7}}{315}}+\cdots &&{\text{ برای }}|x|<{\frac {\pi }{2}}\\[6pt]\operatorname {arsinh} x&=\sum _{n=0}^{\infty }{\frac {(-1) )^{n}(2n)!}{4^{n}(n!)^{2}(2n+1)}}x^{2n+1}&&=x-{\frac {x^{3 }}{6}}+{\frac {3x^{5}}{40}}-\cdots &&{\text{for }}|x|\leq 1\\[6pt]\operatorname {artanh} x&= \sum _{n=0}^{\infty }{\frac {x^{2n+1}}{2n+1}}&&=x+{\frac {x^{3}}{3}}+{\frac {x^{5}}{5}}+\cdots &&{\text{برای }}|x|\leq 1,\ x\neq \pm 1\end{تراز شده}}$

اعداد B k که در سری برای tanh x ظاهر می شوند اعداد برنولی هستند .

1-سری تیلور

توسط علی رضا نقش نیلچی | پنجشنبه یکم اردیبهشت ۱۴۰۱ | 12:56

سری تیلور

از ویکیپدیا، دانشنامه آزاد

اپراتور شیفت

با افزایش درجه چند جمله ای تیلور، به تابع صحیح نزدیک می شود. این تصویر sin x و تقریب های تیلور آن را با چند جمله ای های درجه 1 ، 3 ، 5 ، 7 ، 9 ، 11 و 13 در x = 0 نشان می دهد.

بخشی از مجموعه مقالات در مورد

حساب دیفرانسیل و انتگرال

نشان دادن

دیفرانسیل

نشان دادن

انتگرال

پنهان شدن

سلسله

تست های همگرایی
هندسی ( حساب هندسی ) هارمونیک متناوب قدرت دو جمله ای تیلور
حد جمع (آزمون ترم) نسبت ریشه انتگرال مقایسه مستقیم مقایسه محدود سری متناوب تراکم کوشی دیریکله هابیل

نشان دادن

بردار

نشان دادن

چند متغیره

نشان دادن

تخصصی

نشان دادن

متفرقه

در ریاضیات ، سری تیلور یک تابع ، مجموع نامتناهی از عبارت‌هایی است که برحسب مشتقات تابع در یک نقطه بیان می‌شوند. برای اکثر توابع رایج، تابع و مجموع سری تیلور آن در نزدیکی این نقطه برابر است. سری های تیلور به نام بروک تیلور نامگذاری شده اند که آنها را در سال 1715 معرفی کرد. اگر 0 نقطه ای باشد که مشتقات در نظر گرفته می شوند، سری های تیلور به نام کالین مکلارین که از این مورد خاص از سری تیلور استفاده گسترده ای کرده است ، سری مکلارین نیز نامیده می شود. در اواسط 1700.

مجموع جزئی که توسط اولین جمله های n + 1 یک سری تیلور تشکیل می شود، چند جمله ای درجه n است که n امین چند جمله ای تیلور تابع نامیده می شود. چند جمله ای های تیلور تقریبی از یک تابع هستند که با افزایش n به طور کلی بهتر می شوند . قضیه تیلور برآوردهای کمی را در مورد خطای ایجاد شده با استفاده از چنین تقریبی ارائه می دهد. اگر سری تیلور یک تابع همگرا باشد ، مجموع آن حد دنباله نامتناهی است .از چند جمله ای های تیلور یک تابع ممکن است با مجموع سری تیلور خود متفاوت باشد، حتی اگر سری تیلور آن همگرا باشد. یک تابع در نقطه x تحلیلی است اگر برابر مجموع سری تیلور آن در یک بازه باز (یا دیسک باز در صفحه مختلط ) حاوی x باشد. این بدان معناست که تابع در هر نقطه از بازه (یا دیسک) تحلیلی است.

فهرست

تعریف [ ویرایش ]

سری تیلور یک تابع واقعی یا با مقادیر مختلط f ( x ) که در یک عدد واقعی یا مختلط a بی نهایت قابل تفکیک است سری توانی است .

$f(a)+{\frac {f'(a)}{1!}}(xa)+{\frac {f''(a)}{2!}}(xa)^{2} +{\frac {f'''(a)}{3!}}(xa)^{3}+\cdots ,$

کجا n ! فاکتوریل n را نشان می دهد . در نماد سیگما فشرده تر ، این می تواند به صورت نوشته شود

$\sum _{n=0}^{\infty }{\frac {f^{(n)}(a)}{n!}}(xa)^{n}،$

که در آن f ( n ) ( a ) نشان دهنده n امین مشتق f ارزیابی شده در نقطه a است. (مشتق مرتبه صفر f خود f و ( x - a ) 0 و 0! هر دو به 1 تعریف می شوند . )

زمانی که a = 0 باشد، سری نیز سری مکلارین نامیده می شود . [1]

بسط مکلورن sin,cos,sinh,cosh

توسط علی رضا نقش نیلچی | چهارشنبه هجدهم اسفند ۱۴۰۰ | 9:28

Solved You can use the series for e», sin z, cos z, sinh z, | Chegg.com

فرمول های معکوس مثلثاتی هیپربولیک بر حسب لگاریتم

توسط علی رضا نقش نیلچی | دوشنبه دوم اسفند ۱۴۰۰ | 9:46

What is Hyperbolic Function 15

اتحادهایی از تابع های مثلثاتی هیپربولیک

توسط علی رضا نقش نیلچی | دوشنبه دوم اسفند ۱۴۰۰ | 9:45

${\begin{aligned}\cosh(ix)&={\frac {1}{2}}\left(e^{ix}+e^{-ix}\right)=\cos x\\\sinh(ix)&={\frac {1}{2}}\left(e^{ix}-e^{-ix}\right)=i\sin x\\\cosh(x+iy)&=\cosh(x)\cos(y)+i\sinh(x)\sin(y)\\\sinh(x+iy)&=\sinh(x)\cos(y)+i\cosh(x)\sin(y)\\\tanh(ix)&=i\tan x\\\cosh x&=\cos(ix)\\\sinh x&=-i\sin(ix)\\\tanh x&=-i\tan(ix)\end{aligned}}$

ادامه مجموعه محدب 3

توسط علی رضا نقش نیلچی | پنجشنبه سیزدهم آبان ۱۴۰۰ | 22:1

غلاف های محدب مجموعات مینکوفسکی [ ویرایش ]

افزودن مینکوفسکی با توجه به عملیات گرفتن غلاف های محدب رفتار خوبی دارد، همانطور که در گزاره زیر نشان داده شده است:

بگذارید S 1 , S 2 زیر مجموعه های یک فضای برداری واقعی باشند، غلاف محدب مجموع مینکوفسکی آنها، مجموع مینکوفسکی غلاف محدب آنها است.

$\operatorname {Conv} (S_{1}+S_{2})=\operatorname {Conv} (S_{1})+\operatorname {Conv} (S_{2}).$

این نتیجه به طور کلی برای هر مجموعه متناهی از مجموعه های غیر خالی صادق است:

${\text{Conv}}\left(\sum _{n}S_{n}\right)=\sum _{n}{\text{Conv}}\left(S_{n}\right) .$

در اصطلاح ریاضی، عملیات جمع مینکوفسکی و تشکیل غلاف های محدب ، عملیات رفت و آمد هستند . [14] [15]

مینکوفسکی مجموع مجموعه های محدب [ ویرایش ]

مجموع مینکوفسکی دو مجموعه محدب فشرده جمع و جور است. مجموع یک مجموعه محدب فشرده و یک مجموعه محدب بسته بسته است. [16]

قضیه معروف زیر که توسط دیودونه در سال 1966 اثبات شد، شرط کافی برای بسته بودن اختلاف دو زیرمجموعه محدب بسته را می دهد. [17] از مفهوم مخروط رکود یک زیرمجموعه محدب غیر خالی S استفاده می کند که به صورت زیر تعریف می شود:

$\operatorname {rec} S=\left\{x\in X\,:\,x+S\subseteq S\right\},$

که در آن این مجموعه یک مخروط محدب حاوی $0\in X$ و رضایت بخش $S+\operatorname {rec} S=S$ . توجه داشته باشید که اگر S بسته و محدب است پس S} $\operatorname {rec} S$ بسته است و برای همه $s_{0}\in S$ ،

$\operatorname {rec} S=\bigcap _{t>0}t(S-s_{0}).$

قضیه (دییودونی). فرض کنید A و B زیر مجموعه‌های غیر خالی، بسته و محدب یک فضای برداری توپولوژیکی محدب موضعی باشند به طوری که $\operatorname {rec} A\cap \operatorname {rec} B$ یک زیرفضای خطی است. اگر A یا B به صورت موضعی فشرده باشد، A - B بسته است.

تعمیم و بسط برای تحدب [ ویرایش ]

مفهوم تحدب در فضای اقلیدسی ممکن است با اصلاح تعریف در برخی یا جنبه های دیگر تعمیم یابد. از نام رایج "تحدب تعمیم یافته" استفاده می شود، زیرا اشیاء حاصل خواص خاصی از مجموعه های محدب را حفظ می کنند.

مجموعه های ستاره ای محدب (ستاره ای شکل) [ ویرایش ]

مقاله اصلی: دامنه ستاره

فرض کنید C مجموعه ای در فضای برداری واقعی یا مختلط باشد. C است محدب ستاره (ستاره شکل) اگر یک وجود دارد X 0 در C به طوری که پاره خط از X 0 به هر نقطه Y در C در موجود C . بنابراین یک مجموعه محدب غیر خالی همیشه محدب ستاره است اما مجموعه ستاره محدب همیشه محدب نیست.

تحدب متعامد [ ویرایش ]

نوشتار اصلی: غلاف محدب متعامد

نمونه ای از تحدب تعمیم یافته، تحدب متعامد است . [18]

مجموعه ای S در فضای اقلیدسی است که به نام قائم محدب یا ارتو محدب ، اگر هر موازی بخش به هر یک از محورهای مختصات اتصال دو نقطه از S دروغ کاملا در S . به راحتی می توان ثابت کرد که اشتراک هر مجموعه ای از مجموعه های قائم محدب، ماشتراک است. برخی دیگر از ویژگی های مجموعه های محدب نیز معتبر هستند.

هندسه نااقلیدسی [ ویرایش ]

تعریف مجموعه محدب و غلاف محدب به طور طبیعی به هندسه‌هایی که اقلیدسی نیستند با تعریف مجموعه‌ای محدب ژئودزیکی که شامل ژئودزیک‌هایی است که هر دو نقطه از مجموعه را به هم می‌پیوندند، گسترش می‌یابد.

توپولوژی سفارش [ ویرایش ]

تحدب را می توان برای یک مجموعه کاملاً مرتب X که دارای توپولوژی نظم است گسترش داد . [19]

اجازه دهید Y ⊆ X . زیرفضای Y یک مجموعه محدب است اگر برای هر جفت نقطه a , b در Y به طوری که a ≤ b بازه [ a , b ] = { x ∈ X | a ≤ x ≤ b } در Y موجود است . این است که، Y محدب است اگر و تنها اگر برای همه ، ب در Y ، ≤ ب دلالت [a , b ] ⊆ Y .

یک مجموعه محدب به طور کلی متصل نیست : یک مثال متضاد توسط فضای فرعی {1،2،3} در Z ارائه شده است ، که هم محدب است و هم متصل نیست.

فضاهای تحدب [ ویرایش ]

اگر ویژگی های خاصی از تحدب به عنوان بدیهیات انتخاب شوند، ممکن است مفهوم تحدب به اشیاء دیگر تعمیم داده شود .

با توجه به مجموعه X ، یک تحدب بیش از X یک مجموعه است 𝒞 از زیرمجموعه از X رضایت بدیهیات زیر است: [8] [9] [20]

مجموعه خالی و X در 𝒞 هستند
اشتراک هر مجموعه ای از 𝒞 در 𝒞 است .
اتحاد یک زنجیره (با توجه به رابطه شمول ) از عناصر 𝒞 در 𝒞 است .

عناصر 𝒞 را مجموعه های محدب و جفت ( X , 𝒞 ) را فضای محدب می نامند . برای تحدب معمولی، دو بدیهیات اول برقرار است و مورد سوم بی اهمیت است.

برای تعریف جایگزینی از تحدب انتزاعی، که بیشتر برای هندسه گسسته مناسب است، به هندسه های محدب مرتبط با آنتی ماتروئیدها مراجعه کنید .

همچنین ببینید [ ویرایش ]

منبع

https://en.wikipedia.org/wiki/Convex_set

ادامه مجموعه محدب2

توسط علی رضا نقش نیلچی | پنجشنبه سیزدهم آبان ۱۴۰۰ | 21:56

سایر خواص [ ویرایش ]

اجازه دهید X یک فضای برداری توپولوژیکی و $C\subsetq X$ محدب باشد

$\operatorname {Cl} C$ و $\operatorname {Int} C$ هر دو محدب هستند (یعنی بسته شدن و باطن مجموعه های محدب محدب هستند).
$a\in \operatorname {Int} C$ و $b\in \operatorname {Cl} C$ سپس $[a,b[\,\subseteq \operatorname {Int} C$ (جایی که $[a,b[\,:=\left\{(1-r)a+rb:0\leq r<1\right\}$ ).
اگر سپس:
- $\operatorname {cl} \left(\operatorname {Int} C\right)=\operatorname {Cl} C$ ، و
- $\operatorname {Int} C=\operatorname {Int} \left(\operatorname {Cl} C\right)=C^{i}$ ، جایی که $C^{i}$ است داخلی جبری از C .

بدنه های محدب و مجموع مینکوفسکی [ ویرایش ]

بدنه محدب [ ویرایش ]

نوشتار اصلی: بدنه محدب

هر زیر مجموعه از فضای برداری است که در داخل کوچکترین مجموعه محدب (به نام موجود بدنه محدب از )، یعنی اشتراک از تمام مجموعه محدب حاوی . اپراتور Convx-Hull () Conv ویژگی های مشخصه یک عملگر بدنه را دارد :

گسترده : S ⊆ Conv( S ) ,
غیر کاهشی : S ⊆ T نشان می دهد که Conv( S ) ⊆ Conv( T ) و
idempotent : Conv(Conv( S )) = Conv( S ) .

این عملیات محدب بدنه برای مجموعه ای از مجموعه محدب مورد نیاز است به شکل یک شبکه ، که در آن " ملحق " عملیات بدنه محدب از اتحاد دو مجموعه محدب است

$\operatorname {Conv} (S)\vee \operatorname {Conv} (T)=\operatorname {Conv} (S\cup T)=\operatorname {Conv} {\bigl (}\operatorname {Conv} ( S)\cup \operatorname {Conv} (T){\bigr )}.$

محل اشتراک هر مجموعه ای از مجموعه های محدب خود محدب است، بنابراین زیر مجموعه های محدب یک فضای برداری (واقعی یا پیچیده) یک شبکه کامل را تشکیل می دهند .

افزودن مینکوفسکی [ ویرایش ]

مقاله اصلی: اضافه مینکوفسکی

اضافه کردن مجموعه مینکوفسکی مجموع از مربع Q 1 = [0،1] 2 و Q 2 = [1،2] 2 پرسش مربع است 1 + Q 2 = [1،3] 2 .

در یک فضای برداری واقعی، مجموع دو مجموعه (غیر خالی) مینکوفسکی ، S 1 و S 2 ، به عنوان مجموعه S 1 + S 2 تعریف می شود که با افزودن بردارها به صورت عنصر از مجموعه های جمع تشکیل می شود.

$S_{1}+S_{2}=\{x_{1}+x_{2}:x_{1}\in S_{1},x_{2}\in S_{2}\}.$

به طور کلی تر، مجموع مینکوفسکی از یک خانواده محدود از مجموعه های (غیر خالی) S n مجموعه ای است که از جمع عنصر بردارها تشکیل می شود.

$\sum _{n}S_{n}=\left\{\sum _{n}x_{n}:x_{n}\in S_{n}\راست\}.$

برای جمع مینکوفسکی، مجموعه صفر {0} که فقط حاوی بردار صفر 0 است اهمیت ویژه‌ای دارد : برای هر زیرمجموعه S غیر خالی یک فضای برداری

$S+\{0\}=S;$

در اصطلاحات جبری، {0} است عنصر هویت از مینکوفسکی علاوه بر (در مجموعه ای از مجموعه های غیر خالی). [13]

ادامه مجموعه محدب 1

توسط علی رضا نقش نیلچی | پنجشنبه سیزدهم آبان ۱۴۰۰ | 21:49

مجموعه غیر محدب

مجموعه ای است که محدب نیست است که به نام مجموعه غیر محدب . چند ضلعی است که یک چند ضلعی محدب است که گاهی اوقات به نام چند ضلعی مقعر ، [3] و برخی از منابع به طور کلی استفاده از اصطلاح مجموعه ای مقعر به معنی یک مجموعه غیر محدب، [4] اما اکثر مقامات منع این استفاده. [5] [6]

مکمل یک مجموعه محدب، مانند کتیبه از یک تابع مقعر است، گاهی به نام مجموعه محدب معکوس ، به خصوص در زمینه بهینه سازی ریاضی . [7]

خواص [ ویرایش ]

با توجه به r نقاط u 1 , ... , u r در یک مجموعه محدب S , و r اعداد غیر منفی λ 1 , ... , λ r به گونه ای که λ 1 + ... + λ r = 1 ، ترکیب وابسته

$\sum _{k=1}^{r}\lambda _{k}u_{k}$

متعلق به اس . از آنجایی که تعریف مجموعه محدب حالت r = 2 است ، این ویژگی مجموعه های محدب را مشخص می کند.

چنین ترکیبی آفین است به نام ترکیب محدب از تو 1 ، ...، تو تحقیق .

اشتراک ها و اجتماع ها [ ویرایش ]

مجموعه ای از زیر مجموعه های محدب یک فضای برداری، یک فضای وابسته یا یک فضای اقلیدسی دارای ویژگی های زیر است: [8] [9]

مجموعه تهی و کل فضای محدب.
محل اشتراک هر مجموعه ای از مجموعه های محدب محدب است.
اجتماع از دنباله ای از مجموعه محدب محدب است، اگر آنها به صورت یک زنجیره غیر کاهش برای گنجاندن. برای این ویژگی، محدودیت به زنجیره مهم است، به عنوان اتحاد دو مجموعه محدب لازم نیست محدب.

مجموعه های محدب بسته [ ویرایش ]

مجموعه های محدب بسته مجموعه های محدبی هستند که تمام نقاط حد خود را در بر می گیرند . آنها را می توان به عنوان اشتراک نیمه فضاهای بسته (مجموعه نقاطی در فضا که در یک طرف یک ابر صفحه قرار دارند ) مشخص کرد.

از آنچه گفته شد مشخص می شود که این گونه اشتراک ها محدب هستند و همچنین مجموعه های بسته خواهند بود. برای اثبات عکس آن، یعنی هر مجموعه محدب بسته ممکن است به عنوان چنین اشتراکی نشان داده شود، به قضیه ابرصفحه پشتیبان نیاز داریم به این شکل که برای یک مجموعه محدب بسته داده شده C و نقطه P خارج از آن، یک نیمه فضای بسته H وجود دارد که حاوی C و نه P است . قضیه ابرصفحه پشتیبان یک مورد خاص از قضیه هان-باناخ در تحلیل تابعی است .

مجموعه ها و مستطیل های محدب [ ویرایش ]

فرض کنید C یک جسم محدب در صفحه باشد (مجموعه محدبی که فضای داخلی آن خالی نیست). می‌توانیم یک مستطیل r را به‌گونه‌ای در C بنویسیم که یک نسخه همتز R از r حدود C باشد. نسبت همتای مثبت حداکثر 2 است و: [10]

${\tfrac {1}{2}}\cdot \operatorname {Area} (R)\leq \operatorname {Area} (C)\leq 2\cdot \operatorname {Area} (r)$

نمودارهای بلاشکه-سانتالو [ ویرایش ]

مجموعه ${\mathcal {K}}^{2}$ تمام اجسام محدب مسطح را می توان بر حسب قطر جسم محدب D ، شعاع r آن (بزرگترین دایره موجود در جسم محدب) و شعاع محیطی R (کوچکترین دایره حاوی جسم محدب) پارامتر کرد . در واقع، این مجموعه را می توان با مجموعه ای از نابرابری های ارائه شده توسط [11] [12] توصیف کرد.

$2r\leq D\leq 2R$

$R\leq {\frac {\sqrt {3}}{3}}D$

$r+R\leq D$

$D^{2}{\sqrt {4R^{2}-D^{2}}}\leq 2R(2R+{\sqrt {4R^{2}-D^{2}}})$

و می توان آن را به عنوان تصویر تابع g که یک جسم محدب را به نقطه R 2 ارائه شده توسط ( r / R ، D /2 R ) ترسیم می کند، تجسم کرد . تصویر این تابع یک نمودار ( r , D , R ) بلاشکه-سانتالو شناخته شده است. [12]

نمودار بلاشچک -سانتولو ( r , D , R ) برای اجسام محدب مسطح $\mathbb {L}$ نشان دهنده بخش خط است، $\mathbb {I} _{\frac {\pi }{3}}$ مثلث متساوی الاضلاع، $\mathbb {RT}$ مثلث Reuleaux و $\mathbb {B} _{2}$ دایره واحد

متناوبا، مجموعه ${\mathcal {K}}^{2}$ همچنین می توان با عرض آن (کمترین فاصله بین هر دو ابرصفحه پشتیبانی موازی مختلف)، محیط و مساحت آن پارامتر کرد. [11] [12]

منبع

https://en.wikipedia.org/wiki/Convex_set

مجموعه محدب

توسط علی رضا نقش نیلچی | پنجشنبه سیزدهم آبان ۱۴۰۰ | 21:39

از ویکیپدیا، دانشنامه آزاد

تصویر یک مجموعه محدب که تا حدودی شبیه یک دایره تغییر شکل یافته است. پاره خط، که در بالا به رنگ مشکی نشان داده شده است، که نقاط x و y را به هم می پیوندد، کاملاً درون مجموعه قرار دارد که به رنگ سبز نشان داده شده است. از آنجایی که این برای هر مکان احتمالی هر دو نقطه در مجموعه فوق صادق است، مجموعه محدب است.

تصویر یک مجموعه غیر محدب. با قسمت خط بالا که به موجب آن از سیاه به قرمز تغییر می کند، نشان داده شده است. توضیح اینکه چرا این مجموعه بالا، که با رنگ سبز نشان داده شده است، غیر محدب است.

در هندسه ، یک زیرمجموعه از فضای اقلیدسی ، یا به طور کلی، یک فضای وابسته بر روی واقعی ها ، محدب است اگر با توجه به هر دو نقطه در زیر مجموعه، زیرمجموعه شامل کل پاره خطی باشد که به آنها می پیوندد. به طور معادل، یک مجموعه محدب یا یک ناحیه محدب ، زیرمجموعه‌ای است که هر خط را به یک پاره خط (احتمالاً خالی) قطع می‌کند. [1] [2] به عنوان مثال، یک مکعب جامد یک مجموعه محدب است، اما هر چیزی که توخالی است یا دارای فرورفتگی است، مثلاً به شکل هلال ، محدب نیست.

مرز یک مجموعه محدب است که همیشه یک منحنی محدب . تقاطع از تمام مجموعه محدب که حاوی یک زیر مجموعه داده از فضای اقلیدسی است به نام بدنه محدب از . این کوچکترین مجموعه محدب حاوی A است .

تابع محدب است مقدار واقعی تابع در تعریف فاصله با ملکی که آن کتیبه (مجموعه ای از نقاط در بالا و یا نمودار تابع) مجموعه ای محدب است. کمینه سازی محدب زیرشاخه ای از بهینه سازی است که مسئله کمینه سازی توابع محدب را در مجموعه های محدب مطالعه می کند. شاخه ای از ریاضیات که به مطالعه خصوصیات مجموعه های محدب و توابع محدب اختصاص دارد، آنالیز محدب نامیده می شود .

مفهوم مجموعه محدب را می توان به شرح زیر تعمیم داد.

فهرست

تعاریف [ ویرایش ]

یک تابع محدب است اگر و تنها در صورتی که رونوشت آن ، ناحیه (به رنگ سبز) بالای نمودار آن (به رنگ آبی)، مجموعه ای محدب باشد.

فرض کنید S یک فضای برداری یا یک فضای وابسته روی اعداد واقعی ، یا، به طور کلی، روی برخی از فیلدهای مرتب شده باشد. این شامل فضاهای اقلیدسی است که فضاهای وابسته هستند. زیر مجموعه C از S است محدب اگر، برای همه X و Y در C از پاره خط اتصال X و Y در شامل C . این بدان معنی است که ترکیب افین (1 - t ) x + ty متعلق به استC ، برای همه x و y در C ، و t در بازه [0، 1] . این نشان می‌دهد که تحدب (ویژگی محدب بودن) تحت تبدیل‌های وابسته ثابت است . این همچنین به این معنی است که یک مجموعه محدب در یک فضای برداری توپولوژیکی واقعی یا پیچیده به مسیر متصل است ، بنابراین متصل است .

یک مجموعه C استبه شدت محدب اگر هر نقطه روی پاره خط اتصالXوY از نقاط پایانی است در داخلداخلیازC.

مجموعه ای C است کاملا محدب اگر آن محدب و متعادل کننده شده .

محدب زیر مجموعه از R (مجموعه ای از اعداد حقیقی) فواصل و نقاط هستند R . برخی از نمونه‌های زیرمجموعه‌های محدب صفحه اقلیدسی عبارتند از چندضلعی‌های منتظم جامد، مثلث‌های جامد، و تقاطع مثلث‌های جامد. چند نمونه از زیر مجموعه های محدب فضای سه بعدی اقلیدسی ، جامدات ارشمیدسی و جامدات افلاطونی هستند . polyhedra به کپلر Poinsot شده نمونه هایی از مجموعه غیر محدب.

منبع

https://en.wikipedia.org/wiki/Convex_set

مثال یک فضای که همبند است اما همبند مسیری نیست

توسط علی رضا نقش نیلچی | یکشنبه دوم آبان ۱۴۰۰ | 19:51

enter image description here

γ(t)=〈(1+1/t)cost,(1+1/t)sint〉

γ t،همراه با دایره واحد راهی وجود ندارد که نقطه ای را در منحنی با نقطه ای روی دایره وصل کند. با این حال ، فضا بستار مجموعه همبند γ( ( 1 ، ∞ ) )، است بنابراین همبند است.

منبع

https://math.stackexchange.com/questions/1735601/space-which-is-connected-but-not-path-connected

یک فضای که همبند است اما همبند مسیری نیست

توسط علی رضا نقش نیلچی | یکشنبه دوم آبان ۱۴۰۰ | 19:20

این تابع پیوسته است پس مجموعه همبند را به همبند می نگارد اما بین دو قسمت بالا مسیری نیست

متذکر می گردد که [1,0] همبند است!

قضیه بوشنر و قضیه گشتاور هاسدورف در نیمه گروه های توپولوژیکی پایه

توسط علی رضا نقش نیلچی | شنبه یکم آبان ۱۴۰۰ | 2:6

همومورفیسم ضعف پذیری ضعیف برخی از جبرهای Banach

مجله بین المللی تحلیل و برنامه های غیرخطیمقاله 19 ، دوره 9، شماره 1 ، پاییز و زمستان 2018 ، صفحه 235-245 اصل مقاله ( 410.28 K )نوع مقاله: مقاله پژوهشیشناسه دیجیتال (DOI): 10.22075/ijnaa.2018.1201.1276نویسندگانحمید صادقی ؛ محمود لشکری زادهگروه ریاضی، دانشکده علوم، دانشگاه اصفهان، اصفهان، ایرانتاریخ دریافت : 21 بهمن 1394 ، تاریخ بازنگری : 15 بهمن 1396 ، تاریخ پذیرش : 06 فروردین 1397 چکیدهدر این مقاله مفهوم جابجایی $\varphi$ را برای جبر Banach $A$ معرفی می کنیم، که در آن $\varphi$ یک هم شکلی پیوسته روی $A$ است و مفهوم $\varphi$-قابلیت پذیری ضعیف برای $\ را مطالعه می کنیم. جبرهای باناخ جایگزین varphi$. مثالی می‌زنیم تا نشان دهیم که کلاس جبرهای Banach $\varphi$-ضعیف‌پذیر بزرگ‌تر از جبرهای Banach جایگزینی ضعیف است. ما سازگاری ضعیف $\varphi$ جبرهای جابجایی Banach $\varphi$ را مشخص می کنیم و برخی از ویژگی های ارثی را اثبات می کنیم. علاوه بر این، ما برخی از نتایج موجود قبلی را در مورد جبرهای Banach جابجایی ضعیف تأیید می‌کنیم، برای جبرهای Banach $\varphi$-تغییرپذیر $\varphi$-ضعیف.کلیدواژه هاجبر Banach ؛ $varphi$-commutative ؛ $varphi$-اشتقاق ؛ $varphi$-قابلیت ضعیف

منبع

https://journals.semnan.ac.ir/article_3099.html

همومورفیسم ضعف پذیری ضعیف برخی از جبرهای Banach

توسط علی رضا نقش نیلچی | شنبه یکم آبان ۱۴۰۰ | 2:3

منبع

https://journals.semnan.ac.ir/article_3099.html

تنوع محدود

توسط علی رضا نقش نیلچی | دوشنبه بیست و نهم شهریور ۱۴۰۰ | 1:45

از ویکیپدیا، دانشنامه آزاد

در تجزیه و تحلیل ریاضی ، یک تابع از تغییرات محدود ، همچنین به عنوان تابع BV شناخته می شود ، یک تابع با ارزش واقعی است که تنوع کلی آن محدود (محدود) است: نمودار تابع دارای این ویژگی به معنای دقیق رفتار می کند. برای یک تابع پیوسته از یک متغیر بودن به معنای تنوع محدود که فاصله در امتداد جهت از Y محور ، غفلت از سهم حرکت در طول X محور ، سفر یک نقطهحرکت در امتداد نمودار مقدار محدودی دارد. برای یک تابع پیوسته از چندین متغیر ، معنای تعریف یکسان است ، با این تفاوت که مسیر پیوسته ای که باید در نظر گرفته شود نمی تواند کل نمودار تابع داده شده باشد (که در این مورد یک سطح فوقانی است) ، اما می تواند هر تقاطع از نمودار خود را با یک ابرصفحه (در مورد توابع دو متغیر، یک هواپیما ) موازی با ثابت X محور و به Y محور.

توابع تغییرات محدود دقیقاً همان کارکردهایی هستند که با توجه به آنها می توان انتگرال ریمان -استیلتس را از همه توابع پیوسته یافت.

ویژگی دیگر بیان می کند که توابع تغییرات محدود در یک فاصله فشرده دقیقاً همان f هستند که می توانند به عنوان تفاوت g - h نوشته شوند ، جایی که هم g و h یکنواخت محدود هستند . به طور خاص ، یک عملکرد BV ممکن است ناپیوستگی داشته باشد ، اما حداکثر تعداد زیادی از آنها.

در مورد چند متغیر، تابع F تعریف شده روی یک زیر مجموعه باز Ω از $\ mathbb {R} ^{n}$ گفته می شود که اگر مشتق توزیعی آن یک اندازه گیری رادون محدود با بردار باشد ، تغییرات محدودی دارد .

یکی از مهمترین جنبه های توابع تغییرات محدود این است که آنها جبری از توابع ناپیوسته را تشکیل می دهند که اولین مشتق آن تقریباً در همه جا وجود دارد : با توجه به این واقعیت ، آنها می توانند و مکرراً برای تعریف راه حل های کلی مسائل غیر خطی شامل عملکردها ، معمولی و معمولی مورد استفاده قرار می گیرند. معادلات دیفرانسیل جزئی در ریاضیات ، فیزیک و مهندسی .

ما زنجیره های زیر را برای توابع پیوسته در یک فاصله بسته و محدود خط واقعی داریم:

به طور مداوم مشتقپذیر ⊆ lipschits را مداوم ⊆ کاملا پیوسته ⊆ مستمر و تنوع محدود ⊆ مشتقپذیر تقریبا در همه جا

فهرست

ادامه انتگرال ناسره

توسط علی رضا نقش نیلچی | جمعه بیست و ششم دی ۱۳۹۹ | 0:20

جمع بودن [ ویرایش ]

یک انتگرال نامناسب ممکن است از این نظر متفاوت باشد که حد ممکن است تعریف کننده آن وجود نداشته باشد. در این حالت ، تعریفهای پیچیده تری از حد وجود دارد که می تواند یک مقدار همگرا برای انتگرال نامناسب تولید کند. اینها به نام summability روش.

یک روش جمع بندی که در تحلیل فوریه مشهور است ، روش جمع بندی سزارو است . انتگرال

${\ displaystyle \ int _ {0} ^ {\ infty} f (x) \، dx}$

اگر سزارو جمع شود (C ، α) اگر باشد

${\ displaystyle \ lim _ {\ lambda \ to \ infty} \ int _ {0} ^ {\ lambda} \ left (1 - {\ frac {x} {\ lambda}} \ right) ^ {\ alpha} f (x) \ ، dx}$

وجود دارد و متناهی است ( Titchmarsh 1948 ، §1.15). مقدار این حد ، در صورت وجود ، (C ، α) حاصل جمع انتگرال است.

انتگرال دقیقاً وقتی جمع شود که به عنوان یک انتگرال نامناسب باشد. با این حال ، انتگرال هایی وجود دارد که (C ، α) برای α> 0 جمع می شوند که به عنوان انتگرال نامناسب همگرا نمی شوند (به معنای ریمان یا لبسگ). یک مثال انتگرال است

${\ displaystyle \ int _ {0} ^ {\ infty} \ sin x \، dx}$

که به عنوان یک انتگرال نامناسب وجود ندارد ، اما (C ، α) برای هر α> 0. جمع می شود. این یک نسخه انتگرال از سری Grandi است .

انتگرال های نامناسب چند متغیره [ ویرایش ]

انتگرال نامناسب همچنین می تواند برای توابع چندین متغیر تعریف شود. بسته به اینکه شخص به یکپارچه سازی در یک دامنه نامحدود نیاز داشته باشد ، از جمله تعریف کمی متفاوت است $\ R ^ 2$ ، یا یک تابع را با تکین ها ادغام می کند ، مانند $f (x، y) = \ log (x ^ {2} + y ^ {2})$ .

انتگرال نامناسب در دامنه های دلخواه [ ویرایش ]

اگر ${\ displaystyle f: \ mathbb {R} ^ {n} \ به \ mathbb {R}}$ یک عملکرد غیر منفی است که ریمان در هر مکعب جمع و جور قابل جمع شدن است $[-a، a] ^ {n}$ ، برای $a> 0$ ، سپس انتگرال نامناسب $\ mathbb {R} ^ {n}$ به عنوان حد تعریف شده است

$\ lim _ {a \ to \ infty} \ int _ {[- a، a] ^ {n}} f،$

به شرط وجود

یک تابع در یک دامنه دلخواه $\ mathbb {R} ^ {n}$ به یک تابع گسترش می یابد ${\ tilde {f}}$ بر $\ mathbb {R} ^ {n}$ با صفر در خارج از A :

${\ tilde {f}} (x) = {\ start {موارد} f (x) & x \ در A \\ 0 & x \ not \ در A \ end {موارد}}$

انتگرال ریمان یک تابع بیش از یک دامنه محدود A به عنوان انتگرال تابع توسعه یافته تعریف می شود ${\ tilde {f}}$ روی مکعب $[-a، a] ^ {n}$ حاوی A :

$\ int _ {A} f = \ int _ {[- a، a] ^ {n}} {\ tilde {f}}.$

به طور کلی ، اگر A نامحدود باشد ، انتگرال نامناسب ریمان در یک دامنه دلخواه در $\ mathbb {R} ^ {n}$ به عنوان حد تعریف شده است:

$\ int _ {A} f = \ lim _ {a \ to \ infty} \ int _ {A \ cap [-a، a] ^ {n}} f = \ lim _ {a \ to \ infty} \ int _ {[- a ، a] ^ {n}} {\ tilde {f}}.$

انتگرال نامناسب با تکینگی ها [ ویرایش ]

اگر f یک تابع غیر منفی باشد که در دامنه A محدودیتی نداشته باشد ، انتگرال نامناسب f با کوتاه کردن f در برخی از برش های M ، یکپارچه سازی تابع حاصل و سپس گرفتن حد به عنوان M به سمت بی نهایت تعیین می شود. این برای $M> 0$ ، تنظیم $f_ {M} = \ min \ {f ، M \}$ . سپس تعریف کنید

$\ int _ {A} f = \ lim _ {M \ to \ infty} \ int _ {A} f_ {M}$

به شرط وجود این محدودیت.

عملکردهایی با مقادیر مثبت و منفی [ ویرایش ]

این تعاریف برای توابع غیر منفی کاربرد دارند. یک تابع عمومی تر f می تواند به عنوان تفاوت در قسمت مثبت آن تجزیه شود $f _ {+} = \ max \ {f ، 0 \}$ و قسمت منفی $f _ {-} = \ max \ {- f ، 0 \}$ ، بنابراین

$f = f _ {+} - f _ {-}$

با $f _ {+}$ و $f _ {-}$ هر دو عملکرد غیر منفی. تابع f اگر هر یک از آنها یک انتگرال نامناسب ریمان داشته باشد $f _ {+}$ و $f _ {-}$ یکی دارد ، در این صورت مقدار آن انتگرال نامناسب توسط تعریف می شود

$\ int _ {A} f = \ int _ {A} f _ {+} - \ int _ {A} f _ {-}.$

برای وجود در این مفهوم ، انتگرال نامناسب لزوماً کاملاً جمع می شود ، از آنجا که

$\ int _ {A} | f | = \ int _ {A} f _ {+} + \ int _ {A} f _ {-}.$ [1] [2]

https://en.wikipedia.org/wiki/Improper_integral

ادامه انتگرال ناسره

توسط علی رضا نقش نیلچی | جمعه بیست و ششم دی ۱۳۹۹ | 0:15

انواع انتگرال [ ویرایش ]

بیش از یک نظریه ادغام وجود دارد . از نظر حساب ، نظریه انتگرال ریمان معمولاً به عنوان نظریه پیش فرض در نظر گرفته می شود. در استفاده از انتگرال های نامناسب ، مهم است که کدام تئوری ادغام در بازی است.

برای انتگرال ریمان (یا انتگرال داربوکس ، که معادل آن است) ، یکپارچه سازی نادرست هم برای فواصل نامحدود لازم است (از آنجا که نمی توان این فواصل را به تعداد زیادی زیرقسمت با طول محدود تقسیم کرد) و هم برای توابع نامحدود با انتگرال محدود (از با فرض اینکه در بالا نامحدود باشد ، انتگرال فوقانی نامحدود خواهد بود ، اما انتگرال پایین متناهی خواهد بود).
انتگرال Lebesgue معاملات متفاوت با دامنه نا محدود و توابع بیکران، به طوری که اغلب یک انتگرال که تنها به عنوان یک انتگرال ریمان نامناسب وجود دارد به عنوان یک (مناسب) Lebesgue انتگرال مانند وجود داشته باشد، ${\ displaystyle \ int _ {1} ^ {\ infty} {\ frac {1} {x ^ {2}}} \، dx}$ . از طرف دیگر ، انتگرال هایی نیز وجود دارند که دارای یک انتگرال نامناسب ریمان هستند اما یک انتگرال (مناسب) Lebesgue ندارند ، مانند $\ int _ {0} ^ {\ infty} {\ frac {\ sin x} {x}} \، dx$ . نظریه Lebesgue این را کمبود نمی داند: از نظر تئوری اندازه گیری ،
${\ displaystyle \ int _ {0} ^ {\ infty} {\ frac {\ sin x} {x}} \، dx = \ infty - \ infty}$ و قابل تعریف راضی کننده نیست. در برخی از شرایط ، ممکن است استفاده از انتگرال های نامناسب Lebesgue همانطور که برای مثال در هنگام تعیین مقدار اصلی کوشی مناسب است . انتگرال Lebesgue با استفاده فراگیر از انتگرال ها در کل خط واقعی ، در درمان نظری تبدیل فوریه کم و بیش ضروری است .
برای انتگرال Henstock – Kurzweil ، ادغام نامناسب ضروری نیست ، و این به عنوان نقطه قوت تئوری تلقی می شود: این شامل تمام توابع قابل تلفیق و نامناسب ریمان Lebesgue است.

انتگرال نامناسب ریمان و انتگرال Lebesgue [ ویرایش ]

شکل 1

شکل 2

در برخی موارد ، انتگرال

${\ displaystyle \ int _ {a} ^ {c} f (x) \، dx}$

را می توان به عنوان یک انتگرال (به عنوان مثال یک انتگرال Lebesgue ) بدون اشاره به حد تعریف کرد

${\ displaystyle \ lim _ {b \ to c ^ {-}} \ int _ {a} ^ {b} f (x) \، dx}$

اما در غیر این صورت به راحتی قابل محاسبه نیست. این امر اغلب هنگامی اتفاق می افتد که تابع f از a به c یک مجانب عمودی در c داشته باشد ، یا اگر c = ∞ باشد (به شکل 1 و 2 مراجعه کنید). در چنین مواردی ، انتگرال نامناسب ریمان به شما امکان می دهد انتگرال Lebesgue از تابع را محاسبه کند. به طور خاص ، قضیه زیر وجود دارد ( Apostol 1974 ، قضیه 10.33):

اگر تابع f را ریمان انتگرال در [ ، ب ] برای هر ب ≥ و انتگرال جزئی

${\ displaystyle \ int _ {a} ^ {b} | f (x) | \، dx}$

به عنوان b → bound ، سپس انتگرال های نامناسب ریمان محدود می شوند

${\ displaystyle \ int _ {a} ^ {\ infty} f (x) \، dx، \ quad {\ mbox {and}} \ int _ {a} ^ {\ infty} | f (x) | \، dx}$

هر دو وجود دارند بعلاوه ، f Lebesgue قابل تجزیه در [ a ، ∞] است و انتگرال Lebesgue آن برابر است با انتگرال نامناسب ریمان.

به عنوان مثال ، انتگرال

$\ int _ {0} ^ {\ infty} {\ frac {dx} {1 + x ^ {2}}}$

می تواند جایگزین به عنوان انتگرال نامناسب تفسیر شود

$\ lim _ {{b \ to \ infty}} \ int _ {0} ^ {b} {\ frac {dx} {1 + x ^ {2}}} = \ lim _ {{b \ to \ infty} } \ arctan {b} = {\ frac {\ pi} {2}} ،$

یا ممکن است به جای آن به عنوان یک انتگرال Lebesgue در مجموعه (0 ، ∞) تفسیر شود . از آنجا که هر دو نوع این انتگرال با هم توافق دارند ، شخص آزاد است که روش اول را برای محاسبه مقدار انتگرال انتخاب کند ، حتی اگر در نهایت بخواهد آن را به عنوان یک انتگرال Lebesgue در نظر بگیرد. بنابراین انتگرال های نامناسب به وضوح ابزاری مفید برای بدست آوردن مقادیر واقعی انتگرال ها هستند.

با این حال ، در موارد دیگر ، یک انتگرال Lebesgue بین نقاط انتهایی محدود حتی ممکن است تعریف نشده باشد ، زیرا انتگرال قسمتهای مثبت و منفی f هر دو نامحدود هستند ، اما انتگرال نامناسب ریمان ممکن است هنوز وجود داشته باشد. چنین مواردی انتگرال "به درستی نامناسب" هستند ، به این معنی که مقادیر آنها را نمی توان تعریف کرد مگر در چنین محدوداتی. مثلا،

${\ displaystyle \ int _ {0} ^ {\ infty} {\ frac {\ sin (x)} {x}} \، dx}$

از آنجا که نمی توان به عنوان یک ماده انتزاعی Lebesgue تفسیر کرد

${\ displaystyle \ int _ {0} ^ {\ infty} \ left | {\ frac {\ sin (x)} {x}} \ right | \، dx = \ infty.}$

${\ displaystyle f (x) = {\ frac {\ sin (x)} {x}}}$ با این وجود بین هر دو نقطه محدود متناسب است و انتگرال آن بین 0 و usually معمولاً به عنوان حد انتگرال قابل درک است:

${\ displaystyle \ int _ {0} ^ {\ infty} {\ frac {\ sin (x)} {x}} \، dx = \ lim _ {b \ to \ infty} \ int _ {0} ^ { b} {\ frac {\ sin (x)} {x}} \، dx = {\ frac {\ pi} {2}}.}$

تکینگی ها [ ویرایش ]

می توان از یکتایی یک انتگرال نامناسب صحبت کرد ، یعنی آن نقاط از خط اعداد واقعی توسعه یافته که در آن از حد استفاده می شود.

ارزش اصلی کوشی [ ویرایش ]

مقاله اصلی: ارزش اصلی کوشی

تفاوت مقادیر دو حد را در نظر بگیرید:

${\ displaystyle \ lim _ {a \ to 0 ^ {+}} \ left (\ int _ {- 1} ^ {- a} {\ frac {dx} {x}} + \ int _ {a} ^ { 1} {\ frac {dx} {x}} \ راست) = 0 ،}$

${\ displaystyle \ lim _ {a \ to 0 ^ {+}} \ left (\ int _ {- 1} ^ {- a} {\ frac {dx} {x}} + \ int _ {2a} ^ { 1} {\ frac {dx} {x}} \ سمت راست) = - \ ln 2.}$

اولین مورد ، ارزش اصلی کوشی در اصطلاح تعریف بد تعریف شده است

${\ displaystyle \ int _ {- 1} ^ {1} {\ frac {dx} {x}} {\} \ سمت چپ ({\ mbox {که}} \ {\ mbox {می دهد}} \ - \ نامعتبر + \ ناکافی \ راست).}$

به همین ترتیب ، ما داریم

{\ displaystyle \ lim _ {a \ to \ infty} \ int _ {- a} ^ {a} {\ frac {2x \، dx} {x ^ {2} +1}} = 0،} ${\ displaystyle \ lim _ {a \ to \ infty} \ int _ {- a} ^ {a} {\ frac {2x \، dx} {x ^ {2} +1}} = 0،}$

ولی

{\ displaystyle \ lim _ {a \ to \ infty} \ int _ {- 2a} ^ {a} {\ frac {2x \، dx} {x ^ {2} +1}} = - \ ln 4.} ${\ displaystyle \ lim _ {a \ to \ infty} \ int _ {- 2a} ^ {a} {\ frac {2x \، dx} {x ^ {2} +1}} = - \ ln 4.}$

مورد اول ارزش اصلی عبارت غیرقابل تعریف است

{\ displaystyle \ int _ {- \ infty} ^ {\ infty} {\ frac {2x \، dx} {x ^ {2} +1}} {\} \ سمت چپ ({\ mbox {which}} \ { \ mbox {dide}} \ - \ infty + \ infty \ right).} ${\ displaystyle \ int _ {- \ infty} ^ {\ infty} {\ frac {2x \، dx} {x ^ {2} +1}} {\} \ سمت چپ ({\ mbox {which}} \ { \ mbox {dide}} \ - \ infty + \ infty \ right).}$

تمام محدودیت های فوق موارد شکل نامشخص ∞ - هستند.

این آسیب شناسی ها بر عملکردهای "تلفیق پذیر Lebesgue" تأثیر نمی گذارد ، یعنی عملکردهای انتگرال مقادیر مطلق آنها محدود است.

انتگرال ناسره

توسط علی رضا نقش نیلچی | جمعه بیست و ششم دی ۱۳۹۹ | 0:1

انتگرال نامناسب از نوع اول. انتگرال ممکن است لازم باشد در یک دامنه نامحدود تعریف شود.

جدایی ناپذیر ریمان از نوع دوم. یکپارچه ممکن است به دلیل وجود یک مجانب عمودی در عملکرد وجود نداشته باشد.

بخشی از یک سری مقالات در مورد

حساب

دیفرانسیل[نمایش]

انتگرال[پنهان شدن]

تعاریف
لیست انتگرال ها تبدیل یکپارچه
ضد اشتقاق انتگرال ( نامناسب ) جدایی ناپذیر ریمان ادغام Lebesgue ادغام کانتور انتگرال توابع معکوس
ادغام توسط
قطعات دیسک ها پوسته های استوانه ای تعویض ( مثلثات ، وایراسترس ، اولر ) فرمول اولر فراکسیون جزئی تغییر ترتیب فرمول های کاهش افتراق زیر علامت انتگرال

سلسله[نمایش]

بردار[نمایش]

چند متغیره[نمایش]

تخصصی[نمایش]

واژه نامه حساب[نمایش]

در تجزیه و تحلیل ریاضی ، یک جدایی ناپذیر نامناسب است حد از یک انتگرال معین به عنوان یک نقطه پایانی از فاصله (بازدید کنندگان) ادغام رویکردهای مشخص هم عدد حقیقی ، $- \ بی فایده$ ، یا در بعضی موارد با نزدیک شدن هر دو نقطه انتهایی. چنین انتگرال غالباً به صورت نمادین درست مانند یک انتگرال معین استاندارد ، در بعضی موارد با بی نهایت به عنوان حد ادغام نوشته می شود.

به طور خاص ، انتگرال نامناسب محدودیت فرم است:

${\ displaystyle \ lim _ {b \ to \ infty} \ int _ {a} ^ {b} f (x) \، dx، \ qquad \ lim _ {a \ to - \ infty} \ int _ {a} ^ {b} f (x) \، dx،}$

یا

${\ displaystyle \ lim _ {c \ to b ^ {-}} \ int _ {a} ^ {c} f (x) \، dx، \ quad \ lim _ {c \ to a ^ {+}} \ int _ {c} ^ {b} f (x) \، dx،}$

که در آن یکی در نقطه پایانی (یا گاهی هر دو) محدودیت می گیرد ( Apostol 1967 ، §10.23).

با سو abuse استفاده از علامت گذاری ، انتگرال های نامناسب غالباً به صورت نمادین درست مانند انتگرال های مشخص استاندارد نوشته می شوند ، شاید با بی نهایت بودن در بین مرزهای ادغام. وقتی انتگرال مشخص وجود دارد (به معنای انتگرال ریمان یا انتگرال پیشرفته تر لبسگ ) ، این ابهام حل می شود زیرا هم انتگرال مناسب و هم نادرست از نظر ارزش با هم منطبق می شوند.

غالباً فرد قادر است مقادیر را برای انتگرال های نامناسب محاسبه کند ، حتی اگر این تابع به معنای متداول قابل جمع نیست (به عنوان مثال یکپارچه ریمان ) به دلیل تکینگی در تابع یا بی نهایت بودن یکی از مرزهای ادغام است.

فهرست

مثالها [ ویرایش ]

تعریف اصلی انتگرال ریمان برای تابعی مانند این اعمال نمی شود $1 / {x ^ {2}}$ در فاصله [1 ، ∞) ، زیرا در این حالت دامنه ادغام نامحدود است . با این حال ، انتگرال ریمان را اغلب می توان با تداوم ، با تعریف انتگرال نامناسب در عوض به عنوان یک حد ، گسترش داد

${\ displaystyle \ int _ {1} ^ {\ infty} {\ frac {1} {x ^ {2}}} \، dx = \ lim _ {b \ to \ infty} \ int _ {1} ^ { b} {\ frac {1} {x ^ {2}}} \، dx = \ lim _ {b \ to \ infty} \ left (- {\ frac {1} {b}} + {\ frac {1 } {1}} \ راست) = 1.}$

تعریف محدود انتگرال ریمان نیز عملکرد را پوشش نمی دهد $1 / {\ sqrt {x}}$ روی فاصله [0 ، 1]. مسئله در اینجا این است که Integrand در حوزه ادغام نامحدود است (تعریف نیاز دارد که دامنه یکپارچه سازی و Integrand محدود شوند). با این حال ، انتگرال نامناسب اگر به عنوان حد محدود شناخته شود ، وجود دارد

${\ displaystyle \ int _ {0} ^ {1} {\ frac {1} {\ sqrt {x}}} \، dx = \ lim _ {a \ to 0 ^ {+}} \ int _ {a} ^ {1} {\ frac {1} {\ sqrt {x}}} \، dx = \ lim _ {a \ to 0 ^ {+}} (2-2 {\ sqrt {a}}) = 2. }$

انتگرال نامناسب
$\ int _ {0} ^ {\ infty} {\ frac {dx} {(x + 1) {\ sqrt {x}}}} = \ pi$
دارای فواصل نامحدود برای دامنه و دامنه است.

بعضی اوقات انتگرال ها ممکن است در جایی که نامناسب هستند ، دو تک داشته باشند. در نظر بگیرید، برای مثال، تابع 1 / (( X + 1) √ X ) یکپارچه از 0 تا ∞ (راست نشان داده شده). در کران پایین، به عنوان X می رود به 0 تابع می رود به ∞ ، و کران بالا است ∞ ، هر چند تابع را به 0. می رود بنابراین این انتگرال مضاعف نامناسب است. یکپارچه ، مثلاً از 1 تا 3 ، یک مقدار معمولی ریمان برای تولید نتیجه π / 6 کافی است. به ادغام از 1 تا ∞ ، مبلغ ریمان امکان پذیر نیست. با این حال ، هر مرز فوقانی محدود ، مثلاً t (با t > 1) بگویید) ، یک نتیجه کاملاً مشخص ، 2 ارکان ( √ t ) - π / 2 می دهد . این یک حد محدود دارد زیرا t به بی نهایت می رود ، یعنی π / 2. به طور مشابه ، انتگرال از 1/3 به 1 به یک مقدار ریمان نیز اجازه می دهد ، به طور تصادفی دوباره π / 6 تولید می کند . جایگزینی 1/3 با یک مقدار دلخواه مثبت بازدید کنندگان (با بازدید کنندگان <1 ) به همان اندازه بی خطر است، به π / 2 - 2 arctan ( √ بازدید کنندگان ) . این نیز یک حد محدود دارد زیرا s به صفر می رسد ، یعنی π / 2. با ترکیب حدود دو قطعه ، نتیجه این انتگرال نامناسب است

${\ displaystyle {\ start {تراز شده} \ int _ {0} ^ {\ ناکافی} {\ frac {dx} {(x + 1) {\ sqrt {x}}}} & {} = \ lim _ {s \ به 0 ^ {+}} \ int _ {s} ^ {1} {\ frac {dx} {(x + 1) {\ sqrt {x}}}} + \ lim _ {t \ to \ invyy} \ int _ {1} ^ {t} {\ frac {dx} {(x + 1) {\ sqrt {x}}}} \\ & {} = \ lim _ {s \ تا 0 ^ {+}} \ left ({\ frac {\ pi} {2}} - 2 \ arctan {\ sqrt {s}} \ right) + \ lim _ {t \ to \ infty} \ left (2 \ arctan {\ sqrt {t }} - {\ frac {\ pi} {2}} \ راست) \\ & {} = {\ frac {\ pi} {2}} + \ چپ (\ pi - {\ frac {\ pi} {2 }} \ راست) \\ & {} = \ pi. \ end {تراز شده}}}$

این روند موفقیت را تضمین نمی کند. ممکن است محدودیتی وجود نداشته باشد یا بی نهایت باشد. به عنوان مثال ، در فاصله محدود از 0 تا 1 ، انتگرال 1 / x همگرا نیست. و بیش از فاصله نامحدود از 1 تا ∞ انتگرال 1 / √ x همگرا نیست.

انتگرال نامناسب
$\ int _ {- 1} ^ {1} {\ frac {dx} {\ sqrt [{3}] {x ^ {2}}}} = 6$
همگرایی می کند ، از آنجا که هر دو حد چپ و راست وجود دارد ، اگرچه یکپارچه در نزدیکی یک نقطه داخلی محدود نیست.

همچنین ممکن است اتفاق بیفتد که یک انتگرال نزدیک به یک نقطه داخلی بدون محدودیت باشد ، در این صورت انتگرال باید در آن نقطه تقسیم شود. برای همگرایی یکپارچه به عنوان یک کل ، انتگرال های حد در هر دو طرف باید وجود داشته باشند و باید محدود شوند. مثلا:

${\ start {تراز شده} \ int _ {- 1} ^ {1} {\ frac {dx} {\ sqrt [{3}] {x ^ {2}}}} و {} = \ lim _ {s \ به 0} \ int _ {- 1} ^ {- s} {\ frac {dx} {\ sqrt [{3}] {x ^ {2}}}} + \ lim _ {t \ to 0} \ int _ {t} ^ {1} {\ frac {dx} {\ sqrt [{3}] {x ^ {2}}}} \\ & {} = \ lim _ {s \ به 0} 3 (1- {\ sqrt [{3}] {s}}) + \ lim _ {t \ تا 0} 3 (1 - {\ sqrt [{3}] {t}}) \\ & {} = 3 + 3 \ \ & {} = 6. \ end {تراز شده}}$

اما انتگرال مشابه

${\ displaystyle \ int _ {- 1} ^ {1} {\ frac {dx} {x}}}$

از این طریق نمی توان مقداری اختصاص داد ، زیرا انتگرال های بالا و زیر صفر به طور مستقل با هم جمع نمی شوند. (با این حال ، به ارزش اصلی کوشی مراجعه کنید .)

همگرایی انتگرال [ ویرایش ]

انتگرال نامناسب اگر حد مشخص کننده آن وجود داشته باشد همگرا می شود. بنابراین به عنوان مثال یکی می گوید که انتگرال نامناسب

${\ displaystyle \ lim _ {t \ to \ infty} \ int _ {a} ^ {t} f (x) \، dx}$

اگر انتگرالهای زیر حد برای همه t به اندازه کافی بزرگ وجود داشته باشد و برابر با L است و مقدار حد برابر با L است .

همچنین ممکن است یک انتگرال نامناسب تا بی نهایت دور شود. در این حالت ، می توان مقدار ∞ (یا -∞) را به انتگرال اختصاص داد. برای مثال

${\ displaystyle \ lim _ {b \ to \ infty} \ int _ {1} ^ {b} {\ frac {1} {x}} \، dx = \ infty.}$

با این حال ، انتگرال های نامناسب دیگر ممکن است به سادگی در هیچ جهت خاصی از هم جدا شوند ، مانند

${\ displaystyle \ lim _ {b \ to \ infty} \ int _ {1} ^ {b} x \ sin (x) \، dx،}$

که وجود ندارد ، حتی به عنوان یک عدد واقعی گسترش یافته . به این واگرایی در اثر نوسان گفته می شود.

محدودیت روش یکپارچه سازی نادرست این است که این محدودیت باید با توجه به یک نقطه انتهایی در یک زمان انجام شود. بنابراین ، به عنوان مثال ، انتگرال نامناسب فرم

${\ displaystyle \ int _ {- \ infty} ^ {\ infty} f (x) \، dx}$

با گرفتن دو حد جداگانه می توان تعریف کرد. شوخ طبع بودن

${\ displaystyle \ int _ {- \ infty} ^ {\ infty} f (x) \، dx = \ lim _ {a \ to - \ infty} \ lim _ {b \ to \ infty} \ int _ {a } ^ {b} f (x) \، dx}$

مشروط بر اینکه حد دو برابر محدود باشد. همچنین می تواند به عنوان یک جفت انتگرال مجزا و نامناسب از نوع اول تعریف شود:

${\ displaystyle \ lim _ {a \ to - \ infty} \ int _ {a} ^ {c} f (x) \، dx + \ lim _ {b \ to \ infty} \ int _ {c} ^ {b } f (x) \، dx}$

که در آن c هر نقطه مناسب برای شروع ادغام است. این تعریف همچنین درصورتی که یکی از این انتگرال ها نامحدود باشد یا هر دو در صورت داشتن علامت یکسان ، اعمال می شود.

مثالی از یک انتگرال نامناسب که در آن هر دو نقطه انتهایی نامحدود هستند ، انتگرال گاوسی است ${\ displaystyle \ int _ {- \ infty} ^ {\ infty} e ^ {- x ^ {2}} \، dx = {\ sqrt {\ pi}}}$ . مثالی که تا بی نهایت ارزیابی می کند این است ${\ displaystyle \ int _ {- \ infty} ^ {\ infty} e ^ {x} \، dx}$ . اما حتی نمی توان سایر انتگرال های دیگر از این دست را بدون ابهام تعریف کرد ، مانند ${\ displaystyle \ int _ {- \ infty} ^ {\ infty} x \، dx}$ ، از آنجا که حد دو برابر بی نهایت و روش دو انتگرال است

${\ displaystyle \ lim _ {a \ to - \ infty} \ int _ {a} ^ {c} x \، dx + \ lim _ {b \ to \ infty} \ int _ {c} ^ {b} x \ ، dx}$

بازده - محصول $\ بی ارزش - \ بی ارزش$ . در این حالت ، با این وجود می توان یک انتگرال نامناسب را به معنای مقدار اصلی کوشی تعریف کرد :

${\ displaystyle \ operatorname {pv} \ int _ {- \ infty} ^ {\ infty} x \، dx = \ lim _ {b \ to \ infty} \ int _ {- b} ^ {b} x \، dx = 0.}$

س questionsالاتی که فرد باید در تعیین انتگرال نامناسب به آنها بپردازد عبارتند از:

آیا محدودیت وجود دارد؟
آیا می توان حد را محاسبه کرد؟

سوال اول مسئله تحلیل ریاضی است . روش دوم را می توان با استفاده از تکنیک های حسابگری ، بلکه در برخی موارد با ادغام کانتور ، تبدیل فوریه و سایر روش های پیشرفته تر مورد توجه قرار داد.

ترکیب gof اگر f , g به ترتیب پیوسته و اندازه پذیر باشد پیوسته است

توسط علی رضا نقش نیلچی | سه شنبه بیست و سوم دی ۱۳۹۹ | 19:58

تابع ساده اندازه پذیر

توسط علی رضا نقش نیلچی | سه شنبه بیست و سوم دی ۱۳۹۹ | 19:22

معادله انتگرال ولترا

توسط علی رضا نقش نیلچی | دوشنبه بیست و دوم دی ۱۳۹۹ | 17:44

در ریاضیات ، معادلات انتگرال ولترا نوع خاصی از معادلات انتگرال است . [1] آنها به دو گروه تقسیم می شوند كه از آنها به عنوان نوع اول و دوم یاد می شود.

یک معادله خطی ولترا از نوع اول است

$f (t) = \ int _ {a} ^ {t} K (t، s) \، x (s) \، ds$

که در آن ƒ یک تابع داده شده است و x یک تابع ناشناخته است که باید برای آن حل شود. معادله خطی ولترا از نوع دوم است

$x (t) = f (t) + \ int _ {a} ^ {t} K (t، s) x (s) \، ds.$

در نظریه عملگر و در نظریه فردهلم ، عملگرهای مربوطه عملگرهای Volterra نامیده می شوند . یک روش مفید برای حل چنین معادلاتی ، روش تجزیه آدومی ، به دلیل جورج آدمیان است .

یک معادله انتگرال خطی ولترا یک معادله کانولوشن است اگر

$x (t) = f (t) + \ int _ {{t_ {0}}} ^ {t} K (ts) x (s) \، ds.$

کارکرد $ک$ در انتگرال هسته نامیده می شود . چنین معادلاتی را می توان با استفاده از تکنیک های تبدیل لاپلاس تحلیل و حل کرد .

معادلات انتگرال ولترا توسط ویتو ولترا معرفی شد و سپس توسط ترائیان لالسكو در تز خود در سال 1908 ، Sur les équations de Volterra ، تحت مدیریت امیل پیكارد مورد مطالعه قرار گرفت . در سال 1911 ، لالسكو اولین كتاب درباره معادلات انتگرال را نوشت.

معادلات جدایی ناپذیر ولترا از طریق معادله تجدید ، در دموگرافی ، مطالعه مواد ویسکوالاستیک و در علم عملگر کاربرد دارند . [2]

فهرست

تبدیل معادله ولترا از نوع اول به نوع دوم [ ویرایش ]

یک معادله ولترا خطی از نوع اول را همیشه می توان به یک معادله خطی ولترا از نوع دوم تقلیل داد ، با این فرض که ${\ displaystyle K (t، t) \ neq 0}$ . با استفاده از مشتق معادله نوع اول ولترا:

${\ displaystyle {df \ over {dt}} = \ int _ {a} ^ {t} {\ partial K \ over {\ partial t}} x (s) ds + K (t، t) x (t) }$ تقسیم از طریق ${\ displaystyle K (t، t)}$ بازده - محصول:

${\ displaystyle x (t) = {1 \ over {K (t، t)}} {df \ over {dt}} - \ int _ {a} ^ {t} {1 \ over {K (t، t )}} {\ جزئی K = بیش از {\ جزئی t}} x ds}$ تعریف کردن

${\ textstyle {\ widetilde {f}} (t) = {1 \ بیش از {K (t، t)}} {df \ بیش از {dt}}}$ و ${\ textstyle {\ widetilde {K}} (t، s) = - {1 \ over {K (t، t)}} {\ partial K \ over {\ partial t}}}$ تبدیل معادله نوع اول را به یک معادله خطی ولترا از نوع دوم کامل می کند.

راه حل عددی با استفاده از قانون ذوزنقه ای [ ویرایش ]

یک روش استاندارد برای محاسبه حل عددی یک معادله خطی ولترا از نوع دوم ، قانون ذوزنقه ای است که برای زیرفواصل هایی با فاصله یکسان $\ دلتا x$ از رابطه زیر بدست می آید:

${\ displaystyle \ int _ {a} ^ {b} f (x) dx \ تقریبی {\ Delta x \ over {2}} \ left [f (x_ {0}) + 2 \ sum _ {i = 1} ^ {n-1} f (x_ {i}) + f (x_ {n}) \ راست]}$ با فرض فاصله مساوی برای subinterval ها ، ممکن است م componentلفه انتگرال معادله Volterra با تقریب زیر:

${\ displaystyle \ int _ {a} ^ {t} K (t، s) x (s) ds \ تقریبی {\ Delta s \ over {2}} \ left [K (t، s_ {0}) x ( s_ {0}) + 2K (t، s_ {1}) x (s_ {1}) + \ cdots + 2K (t، s_ {n-1}) x (s_ {n-1}) + K (t ، s_ {n}) x (s_ {n}) \ راست]}$ تعریف کردن ${\ displaystyle x_ {i} = x (s_ {i})}$ ${\ displaystyle f_ {i} = f (t_ {i})}$ ، و ${\ displaystyle K_ {ij} = K (t_ {i}، s_ {j})}$ ، ما سیستم معادلات خطی را داریم:

${\ displaystyle {\ شروع {تراز شده} x_ {0} & = f_ {0} \\ x_ {1} & = f_ {1} + {\ Delta s \ بیش از {2}} \ چپ (K_ {10} x_ {0} + K_ {11} x_ {1} \ right) \\ x_ {2} & = f_ {2} + {\ Delta s \ over {2}} \ left (K_ {20} x_ {0} + 2K_ {21} x_ {1} + K_ {22} x_ {2} \ راست) \\ & \ vdots \\ x_ {n} & = f_ {n} + {\ Delta s \ بیش از {2}} \ سمت چپ (K_ {n0} x_ {0} + 2K_ {n1} x_ {1} + \ cdots + 2K_ {n، n-1} x_ {n-1} + K_ {nn} x_ {n} \ سمت راست) \ پایان {هم راستا}}}$ این معادل معادله ماتریس است:

${\ displaystyle x = f + Mx \ حاوی x = (IM) ^ {- 1} f}$ برای هسته های خوش رفتار ، قاعده ذوزنقه ای به خوبی کار می کند.

کاربرد: نظریه خرابی [ ویرایش ]

یکی از زمینه هایی که معادلات انتگرال ولترا در آن ظاهر می شود ، تئوری خرابی است ، مطالعه خطر ورشکستگی در علم محاسبات. هدف این است که کمی از بین ببرد ${\ displaystyle \ psi (u) = \ mathbb {P} [\ tau (u) <\ infty]}$ ، جایی که $تو$ مازاد اولیه است و ${\ displaystyle \ tau (u)}$ زمان خرابی است. در مدل کلاسیک نظریه خرابی ، وضعیت خالص نقدی $X _ {{t}}$ تابعی از مازاد اولیه ، درآمد حق بیمه بدست آمده با نرخ است $ج$ ، و ادعاهای خروجی $\ xi$ :

${\ displaystyle X_ {t} = u + ct- \ sum _ {i = 1} ^ {N_ {t}} \ xi _ {i} ، \ quad t \ geq 0}$ جایی که ${\ displaystyle N_ {t}}$ یک روند پواسون برای تعداد ادعاها با شدت است $\ لامبدا$ . در این شرایط ، احتمال خرابی را می توان با یک معادله انتگرال ولترا از فرم نشان داد [3] :

${\ displaystyle \ psi (u) = {\ lambda \ over {c}} \ int _ {u} ^ {\ infty} S (x) dx + {\ lambda \ over {c}} \ int _ {0} ^ {u} \ psi (ux) S (x) dx}$ جایی که $S (\ cdot)$ است تابع بقا از توزیع ادعا می کند.

همچنین به [ ویرایش ] مراجعه کنید

منابع

https://en.wikipedia.org/wiki/Volterra_integral_equation

سری توانی

توسط علی رضا نقش نیلچی | جمعه نوزدهم دی ۱۳۹۹ | 23:58

از ویکیپدیا، دانشنامه آزاد

برای سری نوت‌بوک‌ها، سری IBM ThinkPad Power را ببینید .

در ریاضیات ، یک سری توانی (در یک متغیر ) یک سری نامتناهی از فرم است

$\sum _{n=0}^{\infty }a_{n}\left(xc\right)^{n}=a_{0}+a_{1}(xc)+a_{2}( xc)^{2}+\dots$

که در آن a n نشان دهنده ضریب n ام و c یک ثابت است. سری های توانی در آنالیز ریاضی مفید هستند، جایی که به عنوان سری های تیلور از توابع بی نهایت متمایز به وجود می آیند . در واقع، قضیه بورل نشان می دهد که هر سری توانی، سری تیلور از برخی تابع صاف است.

در بسیاری از موقعیت‌ها، c ( مرکز سری) برابر با صفر است، به عنوان مثال زمانی که یک سری مکلورن را در نظر می‌گیریم . در چنین مواردی، سری پاور شکل ساده تری به خود می گیرد

$\sum _{n=0}^{\infty }a_{n}x^{n}=a_{0}+a_{1}x+a_{2}x^{2}+\dots .$

فراتر از نقش آنها در تحلیل ریاضی، سری های توان در ترکیبات به عنوان توابع مولد (نوعی سری توانی استاندارد ) و در مهندسی الکترونیک (تحت نام تبدیل Z ) نیز دیده می شوند. نماد اعشاری آشنا برای اعداد حقیقی را می‌توان به عنوان نمونه‌ای از سری توانی، با ضرایب صحیح ، اما با آرگومان x ثابت در 1/10 مشاهده کرد . در نظریه اعداد ، مفهوم اعداد p -adic نیز ارتباط نزدیکی با سری توانی دارد.

فهرست

مثالها [ ویرایش ]

تابع نمایی (به رنگ آبی) و مجموع n + 1 جمله اول سری توان مکلورن آن (به رنگ قرمز).

هر چند جمله‌ای را می‌توان به راحتی به عنوان یک سری توان در اطراف هر مرکز c بیان کرد، اگرچه تمام ضرایب به استثنای محدود، صفر خواهند بود زیرا یک سری توانی دارای بی‌نهایت اصطلاحات تعریف شده است. به عنوان مثال، چند جمله ای ${\textstyle f(x)=x^{2}+2x+3}$ را می توان به عنوان یک سری توانی در اطراف مرکز نوشت ${\textstyle c=0}$ مانند

$f(x)=3+2x+1x^{2}+0x^{3}+0x^{4}+\cdots$ یا اطراف مرکز ${\textstyle c=1}$ مانند

$f(x)=6+4(x-1)+1(x-1)^{2}+0(x-1)^{3}+0(x-1)^{4}+ \cdots$ یا در واقع در اطراف هر مرکز دیگری ج . [1] می‌توان سری‌های توانی را مانند «چندجمله‌های درجه بی‌نهایت» دید، اگرچه سری‌های توانی چند جمله‌ای نیستند.

فرمول سری هندسی

${\frac {1}{1-x}}=\sum _{n=0}^{\infty }x^{n}=1+x+x^{2}+x^{3} +\cdots،$ که برای ${\textstyle |x|<1}$ ، یکی از مهم ترین نمونه های سری توانی است، مانند فرمول تابع نمایی

$e^{x}=\sum _{n=0}^{\infty }{\frac {x^{n}}{n!}}=1+x+{\frac {x^{2} }{2!}}+{\frac {x^{3}}{3!}}+\cdots ,$ و فرمول سینوس

$\sin(x)=\sum _{n=0}^{\infty }{\frac {(-1)^{n}x^{2n+1}}{(2n+1)!} }=x-{\frac {x^{3}}{3!}}+{\frac {x^{5}}{5!}}-{\frac {x^{7}}{7!} }+\cdots ,$

برای همه x حقیقی معتبر است.

این سری های پاور نیز نمونه هایی از سری تیلور هستند .

در مجموعه توانها [ ویرایش ]

توانی های منفی در یک سری توانی مجاز نیستند. برای مثال، ${\textstyle 1+x^{-1}+x^{-2}+\cdots }$ به عنوان یک سری توانی در نظر گرفته نمی شود (اگرچه یک سری لرنت است ). به همین ترتیب، توان های کسری مانند ${\textstyle x^{\frac {1}{2}}}$ مجاز نیستند (اما سری Puiseux را ببینید ). ضرایب ${\textstyle a_{n}}$ مجاز به وابستگی نیستند ${\textstyle x}$ ، به عنوان مثال:

$\sin(x)x+\sin(2x)x^{2}+\sin(3x)x^{3}+\cdots$ سری پاور نیست

شعاع همگرایی [ ویرایش ]

یک سری توانی ${\textstyle \sum _{n=0}^{\infty }a_{n}(xc)^{n}}$ برای برخی از مقادیر متغیر x همگرا است که همیشه x = c را شامل می شود (مثلاً، $(xc)^{0}$ به عنوان ارزیابی می کند1 و مجموع سری به این ترتیب است $a_{0}$ برای x = c ). این سری ممکن است برای مقادیر دیگر x واگرا شود . اگر c تنها نقطه همگرایی نباشد، همیشه یک عدد r با 0 < r ≤ ∞ وجود دارد به طوری که هر زمان که | x – c | < r و هر زمان که | x – c | > r _ عدد r شعاع همگرایی سری توان نامیده می شود . به طور کلی به عنوان داده می شود

$r=\liminf _{n\to \infty }\left|a_{n}\right|^{-{\frac {1}{n}}}$ یا به طور معادل

$r^{-1}=\limsup _{n\to \infty }\left|a_{n}\right|^{\frac {1}{n}}$ (این قضیه کوشی-هادامارد است ؛ برای توضیح نماد ، حد برتر و حد پایین را ببینید). ارتباط

$r^{-1}=\lim _{n\to \infty }\left|{a_{n+1} \over a_{n}}\راست|$ در صورت وجود این محدودیت نیز راضی است.

مجموعه ای از اعداد مختلط به گونه ای که | x – c | < r دیسک همگرایی سری نامیده می شود . این سری کاملاً در داخل دیسک همگرایی خود همگرا می شود و به طور یکنواخت در هر زیر مجموعه فشرده از دیسک همگرایی همگرا می شود.

برای | x – c | = r ، هیچ بیانیه کلی در مورد همگرایی سری وجود ندارد. با این حال، قضیه آبل بیان می کند که اگر سری برای مقداری z همگرا باشد به طوری که | z – c | = r ، سپس مجموع سری برای x = z حد مجموع سری برای x = c + t ( z – c ) است که در آن t یک متغیر حقیقی کمتر از1 که تمایل دارد1 .

عملیات روی سری توانی[ ویرایش ]

جمع و تفریق [ ویرایش ]

هنگامی که دو تابع f و g به سری توانی در اطراف یک مرکز c تجزیه می شوند ، سری توان مجموع یا تفاضل توابع را می توان با جمع و تفریق مدتی به دست آورد. یعنی اگر

$f(x)=\sum _{n=0}^{\infty }a_{n}(xc)^{n}$ و

$g(x)=\sum _{n=0}^{\infty }b_{n}(xc)^{n}$ سپس

$f(x)\pm g(x)=\sum _{n=0}^{\infty }(a_{n}\pm b_{n})(xc)^{n}.$

این درست نیست که اگر دو سری توانی ${\textstyle \sum _{n=0}^{\infty }a_{n}x^{n}}$ و ${\textstyle \sum _{n=0}^{\infty }b_{n}x^{n}}$ پس شعاع همگرایی یکسانی دارند ${\textstyle \sum _{n=0}^{\infty }\left(a_{n}+b_{n}\right)x^{n}}$ این شعاع همگرایی را نیز دارد. اگر ${\textstyle a_{n}=(-1)^{n}}$ و ${\textstyle b_{n}=(-1)^{n+1}\left(1-{\frac {1}{3^{n}}}\راست)}$ ، سپس هر دو سری شعاع همگرایی یکسانی دارند اما سری ${\textstyle \sum _{n=0}^{\infty }\left(a_{n}+b_{n}\right)x^{n}=\sum _{n=0}^{\infty } {\frac {(-1)^{n}}{3^{n}}}x^{n}}$ دارای شعاع همگرایی 3 است.

مجموع دو سری توان، حداقل، شعاع همگرایی کوچکتر از دو شعاع همگرایی دو سری خواهد داشت (و ممکن است از هر کدام بیشتر باشد، همانطور که در مثال بالا مشاهده می شود). [2]

ضرب و تقسیم [ ویرایش ]

با همین تعاریف برای $f(x)$ و $g(x)$ سری توان محصول و ضریب توابع را می توان به صورت زیر بدست آورد:

${\begin{aligned}f(x)g(x)&=\left(\sum _{n=0}^{\infty }a_{n}(xc)^{n}\right)\ چپ(\sum _{n=0}^{\infty }b_{n}(xc)^{n}\right)\\&=\sum _{i=0}^{\infty }\sum _{ j=0}^{\infty }a_{i}b_{j}(xc)^{i+j}\\&=\sum _{n=0}^{\infty }\left(\sum _{ i=0}^{n}a_{i}b_{ni}\right)(xc)^{n}.\end{تراز شده}}$

تسلسل و توالی ${\textstyle m_{n}=\sum _{i=0}^{n}a_{i}b_{ni}}$ به عنوان پیچیدگی دنباله ها شناخته می شود $a_{n}$ و $b_{n}$ .

برای تقسیم، اگر یکی دنباله را تعریف کند $d_{n}$ توسط

${\frac {f(x)}{g(x)}}={\frac {\sum _{n=0}^{\infty }a_{n}(xc)^{n}}{ \sum _{n=0}^{\infty }b_{n}(xc)^{n}}}=\sum _{n=0}^{\infty }d_{n}(xc)^{n }$ سپس

$f(x)=\left(\sum _{n=0}^{\infty }b_{n}(xc)^{n}\right)\left(\sum _{n=0}^ {\infty }d_{n}(xc)^{n}\right)$ و می توان به صورت بازگشتی برای عبارت ها حل کرد $d_{n}$ با مقایسه ضرایب

با حل معادلات مربوطه، فرمول هایی بر اساس تعیین کننده های ماتریس های معینی از ضرایب به دست می آید. $f(x)$ و $g(x)$

$d_{0}={\frac {a_{0}}{b_{0}}}$

$d_{n}={\frac {1}{b_{0}^{n+1}}}{\begin{vmatrix}a_{n}&b_{1}&b_{2}&\cdots &b_{ n}\\a_{n-1}&b_{0}&b_{1}&\cdots &b_{n-1}\\a_{n-2}&0&b_{0}&\cdots &b_{n-2}\\ \vdots &\vdots &\vdots &\ddots &\vdots \\a_{0}&0&0&\cdots &b_{0}\end{vmatrix}}$

مشتق و انتگرال[ ویرایش ]

یک بار یک تابع $f(x)$ به عنوان یک سری توانی مانند بالا داده شده است، در داخل حوزه همگرایی قابل مشتق گیری است. با در نظر گرفتن هر اصطلاح به طور جداگانه، می توان آن را به راحتی مشتق و انتگرال گیری کرد:

${\begin{aligned}f'(x)&=\sum _{n=1}^{\infty }a_{n}n(xc)^{n-1}=\sum _{n= 0}^{\infty }a_{n+1}(n+1)(xc)^{n},\\\int f(x)\,dx&=\sum _{n=0}^{\infty }{\frac {a_{n}(xc)^{n+1}}{n+1}}+k=\sum _{n=1}^{\infty }{\frac {a_{n-1 }(xc)^{n}}{n}}+k.\end{aligned}}$

هر دوی این سری ها شعاع همگرایی مشابه سری اصلی دارند.

توابع تحلیلی [ ویرایش ]

مقاله اصلی: تابع تحلیلی

تابع f تعریف شده روی زیرمجموعه باز U از R یا C اگر به صورت محلی توسط یک سری توان همگرا داده شود، تحلیلی نامیده می شود. این بدان معناست که هر a ∈ U یک همسایگی باز V ⊆ U دارد، به طوری که یک سری توان با مرکز a وجود دارد که به ازای هر x ∈ V به f ( x ) همگرا می شود .

هر سری توانی با شعاع همگرایی مثبت، در داخل منطقه همگرایی خود تحلیلی است. همه توابع هولومورفیک مختلط-تحلیلی هستند. مجموع و حاصلضرب توابع تحلیلی و تا زمانی که مخرج غیر صفر باشد، ضرایب تحلیلی هستند.

اگر تابعی تحلیلی باشد، بی نهایت قابل تمایز است، اما در حالت حقیقی عکس آن به طور کلی صادق نیست. برای یک تابع تحلیلی، ضرایب a n را می توان به صورت محاسبه کرد

$a_{n}={\frac {f^{\left(n\right)}\left(c\right)}{n!}}$

جایی که $f^{(n)}(c)$ نشان دهنده n امین مشتق f در c و $f^{(0)}(c) = f(c)$ . این بدان معنی است که هر تابع تحلیلی به صورت محلی با سری تیلور خود نشان داده می شود .

شکل کلی یک تابع تحلیلی کاملاً با رفتار محلی آن به معنای زیر تعیین می شود: اگر f و g دو تابع تحلیلی هستند که روی یک مجموعه باز متصل U تعریف شده اند، و اگر یک عنصر c∈ U وجود داشته باشد به طوری که f ( n ) ( c ) = g ( n ) ( c ) برای همه n ≥ 0 , سپس f ( x ) = g ( x ) برای همه x ∈ U.

اگر یک سری توان با شعاع همگرایی r داده شود، می توان ادامه های تحلیلی سری را در نظر گرفت، یعنی توابع تحلیلی f که روی مجموعه های بزرگتر از { x | | x − c | < r } و با سری توانی داده شده در این مجموعه موافقت کنید. عدد r به معنای زیر حداکثر است: همیشه یک عدد مختلط x با | وجود دارد x − c | = r به گونه ای که هیچ ادامه تحلیلی سری را نمی توان در x تعریف کرد .

بسط سری توان تابع معکوس یک تابع تحلیلی را می توان با استفاده از قضیه وارونگی لاگرانژ تعیین کرد .

رفتار نزدیک به مرز [ ویرایش ]

مجموع یک سری توان با شعاع همگرایی مثبت یک تابع تحلیلی در هر نقطه از داخل دیسک همگرایی است. با این حال، رفتارهای متفاوتی می تواند در نقاطی در مرز آن دیسک رخ دهد. مثلا:

واگرایی در حالی که مجموع به یک تابع تحلیلی گسترش می یابد : ${\textstyle \sum _{n=0}^{\infty }z^{n}}$ دارای شعاع همگرایی برابر است $1$ و در هر نقطه از $|z|=1$ . با این وجود، مجموع در $|z|<1$ ${\textstyle {\frac {1}{1-z}}}$ ، که در هر نقطه از هواپیما به جز برای $z=1$ .
همگرا در برخی نقاط واگرا در برخی دیگر : ${\textstyle \sum _{n=1}^{\infty }(-1)^{n+1}{\frac {z^{n}}{n}}}$ شعاع همگرایی دارد $1$ . برای همگرا می شود $z=1$ ، در حالی که برای $z=-1$
همگرایی مطلق در هر نقطه از مرز : ${\textstyle \sum _{n=1}^{\infty }{\frac {z^{n}}{n^{2}}}}$ شعاع همگرایی دارد $1$ ، در حالی که به طور مطلق و یکنواخت در هر نقطه از همگرا می شود $|z|=1$ به دلیل استفاده از آزمون ام واشتراس با سری همگرای هایپر هارمونیک ${\textstyle \sum _{n=1}^{\infty }{\frac {1}{n^{2}}}}$ .
همگرا در بسته شدن دیسک همگرایی اما مجموع پیوسته نیست : سرپینسکی مثالی [3] از یک سری توان با شعاع همگرایی ارائه کرد. $1$ ، همگرا در تمام نقاط با $|z|=1$ ، اما مجموع یک تابع نامحدود و به ویژه ناپیوسته است. یک شرط کافی برای تداوم یک طرفه در یک نقطه مرزی توسط قضیه آبل ارائه شده است .

سری استاندارد توانی [ ویرایش ]

مقاله اصلی: سری استاندارد توانی

در جبر انتزاعی ، شخص تلاش می‌کند تا ماهیت سری‌های توانی را بدون محدود شدن به میدان‌های اعداد حقیقی و مختلط، و بدون نیاز به صحبت در مورد همگرایی، به تصویر بکشد. این منجر به مفهوم سری توان استاندارد می شود ، مفهومی که در ترکیبات جبری کاربرد زیادی دارد .

سری توانی در چندین متغیر [ ویرایش ]

بسط نظریه برای اهداف حساب چند متغیره ضروری است . یک سری توان در اینجا به عنوان یک سری نامتناهی از فرم تعریف می شود

$f(x_{1},\dots,x_{n})=\sum _{j_{1},\dots ,j_{n}=0}^{\infty }a_{j_{1}, \dots ,j_{n}}\prod _{k=1}^{n}(x_{k}-c_{k})^{j_{k}},$ که در آن j = ( j 1 ، …، jn) بردار اعداد طبیعی است، ضرایب a (j 1 , …, j n ) معمولاً اعداد حقیقی یا مختلط هستند و مرکز c = ( c 1 , …, c n ) و آرگومان x = ( x 1 , …, x n ) معمولا بردارهای حقیقی یا مختلط هستند. نماد $\ پی$ نماد حاصل ضرب است. در نماد چند شاخصی راحت تر ، این را می توان نوشت

$f(x)=\sum _{\alpha \in \mathbb {N} ^{n}}a_{\alpha }(xc)^{\alpha }.$ جایی که $\mathbb {N}$ مجموعه اعداد طبیعی است و غیره $\mathbb {N} ^{n}$ مجموعه ای از n مرتبه - چند تایی اعداد طبیعی است.

تئوری چنین سری هایی مختلط تر از سری های تک متغیری با مناطق همگرایی مختلط تر است. به عنوان مثال، سری توانی ${\textstyle \sum _{n=0}^{\infty }x_{1}^{n}x_{2}^{n}}$ در مجموعه کاملاً همگرا است $\{(x_{1},x_{2}):|x_{1}x_{2}|<1\}$ بین دو هذلولی (این نمونه ای از یک مجموعه log-convex است ، به این معنا که مجموعه نقاط $(\log |x_1|، \log |x_2|)$ ، جایی که $(x_{1}،x_{2})$ در ناحیه فوق قرار دارد، مجموعه ای محدب است. به طور کلی تر، می توان نشان داد که وقتی c=0، فضای داخلی ناحیه همگرایی مطلق همیشه یک مجموعه لگ محدب است به این معنا.) از طرف دیگر، در داخل این ناحیه همگرایی می توان متمایز و ادغام کرد. در زیر علامت سری، درست مانند یک سری توانی معمولی. [4]

سفارش یک سری توانی [ ویرایش ]

فرض کنید α یک شاخص چندگانه برای یک سری توانی f ( x 1 , x 2 , …, x n ) باشد. ترتیب سری توان f به عنوان حداقل مقدار تعریف شده است $r$ به طوری که α ≠ 0 با وجود دارد $r=|\alpha |=\alpha _{1}+\alpha _{2}+\cdots +\alpha _{n}$ ، یا $\کوچک$ اگر f ≡ 0. به ویژه، برای یک سری توانی f ( x ) در یک متغیر منفرد x ، مرتبه f کوچکترین توان x با ضریب غیر صفر است. این تعریف به راحتی به سری لرنت گسترش می یابد .

منبع

https://en.wikipedia.org/wiki/Power_series

شعاع همگرایی

توسط علی رضا نقش نیلچی | پنجشنبه هجدهم دی ۱۳۹۹ | 16:21

از ویکیپدیا، دانشنامه آزاد

پرش به ناوبری پرش به جستجو

در ریاضیات ، شعاع همگرایی یک سری قدرت ، شعاع بزرگترین دیسکی است که مجموعه در آن جمع می شود . یا یک عدد واقعی غیر منفی است یا $\ بی فایده$ . هنگامی که آن را مثبت است، این سری قدرت مطلقا همگرا و یکنواخت در مجموعه های جمع و جور در داخل دیسک باز شعاع به شعاع همگرایی برابر، و آن است سری تیلور از تابع تحلیلی است که به آن همگرا.

فهرست

تعریف [ ویرایش ]

برای یک سری قدرت ƒ تعریف می شود:

$f (z) = \ sum_ {n = 0} ^ \ کمبود c_n (za) ^ n ،$

جایی که،

a یک ثابت پیچیده است ، مرکز دیسک همگرایی ،

ج نفر است N هفتم ضریب پیچیده، و

z یک متغیر پیچیده است.

شعاع همگرایی r یک عدد واقعی غیر منفی است یا $\ بی فایده$ به گونه ای که سری اگر

$| za | <r \ ،$

و اگر واگرایی کند

$| za | > r. ،$

برخی ممکن است یک تعریف جایگزین را ترجیح دهند ، زیرا وجود واضح است:

${\ displaystyle r = \ sup \ left \ {| za | \ \ left | \ \ sum _ {n = 0} ^ {\ infty} c_ {n} (za) ^ {n} \ {\ text {converges} } \ راست. \ راست \}}$

در مرز ، یعنی جایی که | z - a | = r ، رفتار سری قدرت ممکن است پیچیده باشد و این سری ممکن است برای برخی از مقادیر z جمع شده و برای برخی دیگر واگرایی کند. شعاع همگرایی نامحدود است اگر مجموعه برای همه اعداد مختلط z جمع شود . [1]

یافتن شعاع همگرایی [ ویرایش ]

دو مورد پیش می آید. حالت اول نظری است: وقتی همه ضرایب را بدانید $c_ {n}$ سپس محدودیت های خاصی را در نظر می گیرید و شعاع دقیق همگرایی را پیدا می کنید. حالت دوم عملی است: هنگامی که شما یک حل مشکل مشکل را با استفاده از سری سری ایجاد می کنید ، معمولاً فقط یک تعداد محدود اصطلاحات را در یک سری قدرت می دانید ، از چند اصطلاح تا صد اصطلاح. در این حالت دوم ، برون یابی طرح ، شعاع همگرایی را تخمین می زند.

شعاع نظری [ ویرایش ]

شعاع همگرایی را می توان با استفاده از آزمون ریشه در اصطلاحات سری پیدا کرد. تست ریشه از عدد استفاده می کند

${\ displaystyle C = \ limsup _ {n \ rightarrow \ infty} {\ sqrt [{n}] {| c_ {n} (za) ^ {n} |}} = \ limsup _ {n \ rightarrow \ infty} \ چپ ({\ sqrt [{n}] {| c_ {n} |}} \ راست) | za |}$

"lim sup" نشان دهنده حد برتر است . آزمایش ریشه بیان می کند که این سری در صورت C <1 همگرایی می کند و در صورت C > 1 از هم جدا می شود. از این رو اگر فاصله فاصله از z تا مرکز a کمتر از این باشد ، سری قدرت همگرا می شود.

$r = \ frac {1} {\ limsup_ {n \ rightarrow \ infty} \ sqrt [n] {| c_n |}}$

و اگر فاصله از آن عدد بیشتر شود ، اختلاف می یابد. این عبارت قضیه کوشی - هادامارد است . توجه داشته باشید که r = 1/0 به عنوان شعاع بی نهایت تفسیر می شود ، به این معنی که ƒ یک تابع کامل است .

حد درگیر در آزمون نسبت معمولاً آسانتر محاسبه می شود و وقتی این حد وجود داشته باشد ، نشان می دهد که شعاع همگرایی محدود است.

${\ displaystyle r = \ lim _ {n \ rightarrow \ infty} \ left | {\ frac {c_ {n}} {c_ {n + 1}}} \ right |.}$

این به شرح زیر نشان داده شده است. آزمون نسبت می گوید اگر سری جمع شود

$\ lim_ {n \ to \ infty} \ frac {| c_ {n + 1} (za) ^ {n + 1} |} {| c_n (za) ^ n |} <1$

که برابر است با

$| z - a | <\ frac {1} {\ lim_ {n \ to \ infty} \ frac {| c_ {n + 1} |} {| c_n |}} = \ lim_ {n \ to \ infty} \ left | \ frac { c_n} {c_ {n + 1}} \ راست |.$

برآورد عملی شعاع در مورد ضرایب واقعی [ ویرایش ]

نمودارهای عملکرد $f (\ varepsilon) = \ frac {\ varepsilon (1+ \ varepsilon ^ 3)} {\ sqrt {1 + 2 \ varepsilon}}.$
خط سبز جامد یک مجانب خط مستقیم در نمودار Domb – Sykes [2] ، نمودار (b) است که محور عمودی را در −2 قطع می کند و دارای شیب 1+ است. بنابراین یک تکینگی در وجود دارد ${\ displaystyle \ varepsilon = -1 / 2}$ و بنابراین شعاع همگرایی است ${\ displaystyle r = 1/2.}$

معمولاً در کاربردهای علمی فقط تعداد محدودی از ضرایب وجود دارد $c_ {n}$ شناخته شده اند به طور معمول ، [ مبهم ] به عنوان $n$ افزایش می یابد ، این ضرایب به یک رفتار منظم تبدیل می شوند که با نزدیکترین تکین محدود کننده شعاع تعیین می شود. در این مورد ، دو تکنیک اصلی ساخته شده است ، بر این اساس که ضرایب یک سری تیلور تقریباً نمایی با نسبت هستند $1 / r$ جایی که r شعاع همگرایی است.

حالت اصلی زمانی است که ضرایب در نهایت یک علامت مشترک دارند یا یک علامت متناوب دارند. همانطور که قبلاً در مقاله اشاره شد ، در بسیاری از موارد این محدودیت وجود دارد ${\ displaystyle \ lim _ {n \ to \ infty} {{c_ {n}} / {c_ {n-1}}}}$ وجود دارد ، و در این مورد ${\ displaystyle {1} / {r} = \ lim _ {n \ to \ infty} {{c_ {n}} / {c_ {n-1}}}.}$ منفی $ر$ یعنی تکین محدود کننده همگرایی در محور منفی است. با رسم نمودار ، این حد را تخمین بزنید $c_ {n} / c _ {{n-1}}$ در مقابل $1 / n$ ، و به صورت گرافیکی برون یابی به $1 / n = 0$ (به طور موثر $n = \ بی ارزش است$ ) از طریق یک تناسب خطی. رهگیری با $1 / n = 0$ متقابل شعاع همگرایی را تخمین می زند ، $1 / r$ . این طرح را طرح Domb – Sykes می نامند .
مورد پیچیده تر هنگامی است که علائم ضرایب الگوی پیچیده تری دارند. مرسر و رابرتز روش زیر را پیشنهاد کردند. [3] توالی مرتبط را تعریف کنید

${\ displaystyle b_ {n} ^ {2} = {\ frac {c_ {n + 1} c_ {n-1} -c_ {n} ^ {2}} {c_ {n} c_ {n-2} - c_ {n-1} ^ {2}}} \ quad n = 3،4،5 ، \ ldot.}$

بسیاری از موارد شناخته شده را ترسیم کنید $b_ {n}$ در مقابل $1 / n$ ، و به صورت گرافیکی برون یابی به $1 / n = 0$ از طریق تناسب خطی. رهگیری با $1 / n = 0$ متقابل شعاع همگرایی را تخمین می زند ، $1 / r$ .

این روش همچنین دو ویژگی دیگر از همگرایی را محدود می کند که تکینگی را محدود می کند. فرض کنید نزدیکترین تکینگی درجه باشد $پ$ و دارای زاویه است ${\ displaystyle \ pm \ theta}$ به محور واقعی سپس شیب تناسب خطی داده شده در بالا می باشد ${\ displaystyle - (p + 1) / r}$ . علاوه بر این ، طرح ${\ displaystyle {\ frac {1} {2}} \ سمت چپ ({\ frac {c_ {n-1} b_ {n}} {c_ {n}}} + {\ frac {c_ {n + 1}} {c_ {n} b_ {n}}} \ راست)}$ در مقابل $1 / n ^ {2}$ ، و سپس یک برازش مناسب به صورت ${\ displaystyle 1 / n ^ {2} = 0}$ رهگیری در $\ cos \ theta$ .

شعاع همگرایی در تحلیل پیچیده [ ویرایش ]

با در نظر گرفتن یک متغیر پیچیده ، یک سری توان با شعاع مثبت همگرایی را می توان به یک تابع هولوومرفیک تبدیل کرد . شعاع همگرایی را می توان با قضیه زیر مشخص کرد:

شعاع همگرایی یک سری سری ƒ متمرکز بر یک نقطه a برابر است با فاصله از a تا نزدیکترین نقطه که نمی توان ƒ را به گونه ای تعریف کرد که آن را هولومورفیک کند.

مجموعه کلیه نقاطی که فاصله آنها با a کاملاً کمتر از شعاع همگرایی باشد دیسک همگرایی نامیده می شود .

نمودار توابع توضیح داده شده در متن: تقریب ها با رنگ آبی ، دایره همگرایی با رنگ سفید

نزدیکترین نقطه یعنی نزدیکترین نقطه در صفحه پیچیده ، لزوماً روی خط واقعی نیست ، حتی اگر مرکز و همه ضرایب واقعی باشند. به عنوان مثال ، عملکرد

${\ displaystyle f (z) = {\ frac {1} {1 + z ^ {2}}}}$

از آنجا که هیچ یک از ویژگی های خاص در خط واقعی است $1 + z ^ 2$ هیچ ریشه واقعی ندارد. سری تیلور آن در حدود 0 توسط

$\ sum_ {n = 0} ^ \ بی اعتبار (-1) ^ nz ^ {2n}.$

آزمون ریشه نشان می دهد که شعاع همگرایی آن 1 است. مطابق با این ، تابع ƒ ( z ) در ± i دارای یکتایی است که در فاصله 1 از 0 است.

برای اثبات این قضیه ، به تجزیه و تحلیل توابع هولومورفیک مراجعه کنید .

یک مثال ساده [ ویرایش ]

عملکرد محاوره ای مثلثات را می توان در یک سری توان گسترش داد:

${\ displaystyle \ arctan (z) = z - {\ frac {z ^ {3}} {3}} + {\ frac {z ^ {5}} {5}} - {\ frac {z ^ {7} } {7}} + \ cdots.}$

به راحتی می توانید آزمایش ریشه را در این حالت انجام دهید تا دریابید که شعاع همگرایی 1 است.

مثال پیچیده تر [ ویرایش ]

این سری قدرت را در نظر بگیرید:

${\ displaystyle {\ frac {z} {e ^ {z} -1}} = \ sum _ {n = 0} ^ {\ infty} {\ frac {B_ {n}} {n!}} z ^ { n}}$

که در آن اعداد گویا B N هستند اعداد برنولی . ممکن است تلاش برای استفاده از آزمون نسبت برای یافتن شعاع همگرایی این سری کار دشواری باشد. اما قضیه تحلیل پیچیده ای که در بالا بیان شد به سرعت مسئله را حل می کند. در z = 0 ، از آنجا که تکینگی قابل جدا شدن است ، هیچ تکینگی وجود ندارد . بنابراین تنها تکینگی های غیرقابل حذف در نقاط دیگر واقع می شوند که مخرج صفر است. ما حل می کنیم

$e ^ z-1 = 0 \ ،$

با یادآوری اینکه اگر z = x + iy و e iy = cos ( y ) + i sin ( y ) سپس

$e ^ z = e ^ xe ^ {iy} = e ^ x (\ cos (y) + i \ sin (y)) ، \ ،$

و سپس x و y را واقعی بگیرید. از آنجا که y واقعی است ، مقدار مطلق cos ( y ) + i sin ( y ) لزوماً 1 است. بنابراین ، مقدار مطلق e z می تواند 1 باشد فقط اگر e x 1 باشد. از آنجا که x واقعی است ، این فقط در صورت x = 0 اتفاق می افتد بنابراین z خالص خیالی است و cos ( y ) + i sin ( y ) = 1. از آنجا که y واقعی است ، این فقط در صورت cos ( y ) = 1 و sin ( y ) = 0 ، بنابراین y یک عدد صحیح از 2 π است . در نتیجه نقاط منفرد این تابع در رخ می دهد

z = یک عدد صحیح صفر غیر صفر از 2 π i .

تکینگی های نزدیک به 0 ، که مرکز گسترش سری قدرت است ، در π 2 π i است . فاصله از مرکز تا هر یک از این نقاط 2 π است ، بنابراین شعاع همگرایی 2 π است .

همگرایی در مرز [ ویرایش ]

اگر سری توان در اطراف نقطه a گسترش یافته و شعاع همگرایی r باشد ، مجموعه تمام نقاط z به گونه ای است که | z - a | = R است دایره به نام مرز از دیسک همگرایی. یک سری قدرت ممکن است در هر نقطه از مرز انحراف داشته باشد ، یا در بعضی نقاط واگرا شود و در نقاط دیگر همگرا شود ، یا در تمام نقاط مرز همگرا شود. بعلاوه ، حتی اگر سریال در هر جایی از مرز (حتی به طور یکنواخت) همگرا شود ، لزوماً کاملاً همگرا نمی شود.

مثال 1: سری توان برای تابع ƒ ( z ) = 1 / (1 - z ) ، در حدود z = 0 گسترش می یابد ، که به سادگی

$\ sum_ {n = 0} ^ \ کمبود z ^ n ،$

شعاع همگرایی 1 دارد و در هر نقطه از مرز واگرا می شود.

مثال 2: سری توان g ( z ) = −ln (1 - z ) ، در حدود z = 0 گسترش یافته است ، که

$\ sum_ {n = 1} ^ \ بی اعتبار \ frac {1} {n} z ^ n ،$

شعاع همگرایی 1 دارد ، و برای z = 1 واگرایی می کند اما برای تمام نقاط دیگر مرز همگرا است. تابع ƒ ( Z ) در مثال 1 است مشتق از گرم ( Z ) .

مثال 3: سری قدرت

${\ displaystyle \ sum _ {n = 1} ^ {\ infty} {\ frac {1} {n ^ {2}}} z ^ {n}}$

شعاع همگرایی 1 دارد و کاملاً در هر جایی از مرز همگرایی می کند. اگرh تابع ارائه شده توسط این مجموعه بر روی دیسک واحد، پس یک مشتق از است( h ( Z برابر استg ( Z ) / Z باG از مثال 2. به نظر می رسد که ساعت ( Z ) است dilogarithm تابع.

مثال 4: سری توانی

${\ displaystyle \ sum _ {i = 1} ^ {\ infty} a_ {i} z ^ {i} {\ text {where}} a_ {i} = {\ frac {(-1) ^ {n-1 }} {2 ^ {n} n}} {\ text {for}} n = \ lfloor \ log _ {2} (i) \ rfloor +1 {\ text {، عدد صحیح منحصر به فرد با}} 2 ^ {n -1} \ leq i <2 ^ {n} ،}$

شعاع همگرایی 1 دارد و به طور یکنواخت در کل مرز | z | = 1 ، اما کاملاً در مرز همگرا نیست . [4]

میزان همگرایی [ ویرایش ]

اگر عملکرد را گسترش دهیم

$f (x) = \ sin x = \ sum ^ {\ infin} _ {n = 0} \ frac {(- 1) ^ n} {(2n + 1)!} x ^ {2n + 1} = x - \ frac {x ^ 3} {3!} + \ frac {x ^ 5} {5!} - \ cdots \ text {برای همه} x$

در اطراف نقطه x = 0 ، متوجه می شویم که شعاع همگرایی این سری برابر است $\ scriptstyle \ ناکارآمد$ به این معنی که این مجموعه برای همه اعداد مختلط جمع می شود. با این حال ، در برنامه ها ، اغلب به دقت یک جواب عددی علاقه مند می شود . هم تعداد اصطلاحات و هم مقداری که قرار است سری ارزیابی شود ، در درستی جواب تأثیر دارد. به عنوان مثال ، اگر بخواهیم f (0.1) = sin (0.1) را دقیقاً تا پنج رقم اعشار محاسبه کنیم ، فقط به دو اصطلاح اول سری احتیاج داریم. با این حال ، اگر دقت یکسانی را برای x = 1 می خواهیم ، باید پنج اصطلاح اول سری را ارزیابی و جمع کنیم. برای f (10) ، یکی 18 اصطلاح اول سری را می طلبد ، و برای f (100) 141 اصطلاح اول را باید ارزیابی کنیم.

بنابراین برای این مقادیر خاص ، سریعترین همگرایی انبساط سری قدرت در مرکز است و هرچه فرد از مرکز همگرایی دور می شود ، سرعت همگرایی کاهش می یابد تا زمانی که به مرز برسید (در صورت وجود) و از آن عبور کنید ، در این صورت سریال متفاوت خواهد شد.

Abscissa همگرایی یک سری Dirichlet [ ویرایش ]

یک مفهوم مشابه ، خلاصه همگرایی یک سری دیریشله است

$\ sum_ {n = 1} ^ \ بی اعتبار {a_n \ over n ^ s}$

چنین همگرا سری اگر بخشی واقعی از بازدید کنندگان بیشتر از یک شماره خاص بسته به ضرایب است N : در بعد افقی همگرایی.

منبع

https://en.wikipedia.org/wiki/Radius_of_convergence

آزمایش ریشه کوشی

توسط علی رضا نقش نیلچی | پنجشنبه هجدهم دی ۱۳۹۹ | 13:33

بخشی از یک سری مقالات در مورد

آزمونهای همگرایی
هندسی ( محاسبات هندسی ) هارمونیک متناوب قدرت دو جمله ای تیلور
حد جمع (آزمون ترم) نسبت ریشه انتگرال مقایسه مستقیم مقایسه را محدود کنید سریالهای متناوب تراکم کوشی دیریشله هابیل

بردار[نمایش]

چند متغیره[نمایش]

تخصصی[نمایش]

واژه نامه حساب[نمایش]

در ریاضیات ، آزمون ریشه ملاک همگرایی ( آزمون همگرایی ) یک سری بی نهایت است . بستگی به کمیت دارد

$\ limsup_ {n \ rightarrow \ infty} \ sqrt [n] {| a_n |} ،$

جایی که $a_ {n}$ شرایط سریال است و بیان می کند که اگر این مقدار کمتر از یک باشد ، مجموعه کاملاً همگرایی می کند ، اما اگر بیشتر از یک باشد ، اختلاف می یابد. خصوصاً در ارتباط با سری های برق بسیار مفید است .

فهرست

توضیح آزمایش ریشه [ ویرایش ]

نمودار تصمیم گیری برای آزمون ریشه

آزمون ریشه ابتدا توسط آگوستین-لویی کوشی تهیه شد که آن را در کتاب خود Cours d'analyse (1821) منتشر کرد. [1] بنابراین ، گاهی اوقات به عنوان آزمایش ریشه کوشی یا آزمایش رادیکال کوشی شناخته می شود . برای یک سریال

$\ sum _ {n = 1} ^ {\ infty} a_ {n}.$

آزمون ریشه از عدد استفاده می کند

$C = \ limsup_ {n \ rightarrow \ infty} \ sqrt [n] {| a_n |} ،$

جایی که "lim sup" حد برتر را نشان می دهد ، احتمالاً ∞ +. [2] توجه داشته باشید که اگر

$\ lim_ {n \ rightarrow \ infty} \ sqrt [n] {| a_n |} ،$

همگرا می شود و آن را برابر با C می کند و ممکن است به جای آن در آزمون ریشه استفاده شود.

تست ریشه بیان می کند که:

اگر C <1 باشد ، این مجموعه کاملاً همگرایی می کند ،
اگر C > 1 باشد ، سری اختلاف می یابد ،
اگر C = 1 باشد و حد از بالا دقیقاً نزدیک شود ، سری اختلاف می یابد ،
در غیر این صورت آزمون بی نتیجه است (این مجموعه ممکن است از هم جدا شود ، کاملاً همگرایی کند یا به طور مشروط همگرا شود ).

تعدادی سری وجود دارد که C = 1 برای آنها جمع می شود ، به عنوان مثال $\ textstyle \ sum 1 / {n ^ 2}$ ، و موارد دیگری نیز وجود دارد که C = 1 و سری متفاوت است ، به عنوان مثال $\ textstyle \ sum 1 / n$ .

برنامه برای تغذیه سری [ ویرایش ]

این آزمون را می توان با یک سری قدرت استفاده کرد

$f (z) = \ sum_ {n = 0} ^ \ کمبود c_n (zp) ^ n$

که در آن ضرایب c n ، و مرکز p اعداد مختلط هستند و آرگومان z یک متغیر پیچیده است.

شرایط این سری پس از آن که توسط داده شود N = C N ( Z - ص ) N . سپس یکی آزمون ریشه را در a n مانند بالا اعمال می کند. توجه داشته باشید که گاهی اوقات یک سری مانند این را یک سری توان "اطراف p " می نامند ، زیرا شعاع همگرایی شعاع R بزرگترین فاصله یا دیسک با مرکز p است به طوری که این مجموعه برای تمام نقاط z دقیقاً در داخل کشور ( همگرایی در مرز فاصله یا دیسک معمولاً باید جداگانه بررسی شود). نتیجهاز آزمون ریشه اعمال شده برای چنین سری قدرت قضیه کوشی-هادامارد است : شعاع همگرایی دقیقاً $1 / \ limsup_ {n \ rightarrow \ infty} {\ sqrt [n] {| c_n |}} ،$ مراقبت از اینکه منظور ما واقعاً است ... اگر مخرج 0 باشد.

اثبات [ ویرایش ]

اثبات همگرایی یک سری Σ a n کاربرد آزمون مقایسه است . اگر برای همه n ≥ N ( N مقداری عدد طبیعی ثابت ) داشته باشیم $\ sqrt [n] {| a_n |} \ le k <1 ،$ سپس $| a_n | \ le k ^ n <1$ . از سری هندسی $\ sum_ {n = N} ^ \ بی اعتبار k ^ n$ همگرایی می کند $\ sum_ {n = N} ^ \ بی اعتبار | a_n |$ توسط آزمون مقایسه. از این رو Σ a n کاملاً همگراست.

اگر $\ sqrt [n] {| a_n |}> 1$ برای بسیاری از بی نهایت N ، پس از آن N نتواند به همگرا به 0، از این رو سری واگرا است.

اثبات نتیجه گیری : برای یک سری قدرت Σ a n = Σ c n ( z - p ) n ، با توجه به موارد فوق می بینیم که اگر N وجود داشته باشد ، مجموعه همگرایی می کند به طوری که برای همه n ≥ N ما

$\ sqrt [n] {| a_n |} = \ sqrt [n] {| c_n (z - p) ^ n |} <1 ،$

معادل با

$\ sqrt [n] {| c_n |} \ cdot | z - p | <1$

برای همه n ≥ N ، این بدان معنی است که برای همگرایی سریال باید داشته باشیم

$| z - p | <1 / \ sqrt [n] {| c_n |}$ برای همه به اندازه کافی بزرگ n . این معادل گفتن است

$| z - p | <1 / \ limsup_ {n \ rightarrow \ infty} {\ sqrt [n] {| c_n |}} ،$

بنابراین

$R \ le 1 / \ limsup_ {n \ rightarrow \ infty} {\ sqrt [n] {| c_n |}}.$ اکنون تنها مکان دیگری که امکان همگرایی وجود دارد ، زمان است

$\ sqrt [n] {| a_n |} = \ sqrt [n] {| c_n (z - p) ^ n |} = 1 ،$

(از آنجا که نقاط> 1 واگرایی می کنند) و این شعاع همگرایی را تغییر نخواهد داد زیرا این فقط نقاطی است که در مرز فاصله یا دیسک قرار دارند

$R = 1 / \ limsup_ {n \ rightarrow \ infty} {\ sqrt [n] {| c_n |}}.$

مثالها [ ویرایش ]

مثال 1:

${\ displaystyle \ sum _ {i = 1} ^ {\ infty} {\ frac {2 ^ {i}} {i ^ {9}}}}$

استفاده از آزمون ریشه و استفاده از این واقعیت که^ {1 / n} = 1،} ${\ displaystyle \ lim _ {n \ rightarrow \ infty} n ^ {1 / n} = 1،}$

${\ displaystyle C = {\ sqrt [{n}] {| {\ frac {2 ^ {n}} {n ^ {9}}} |}} = {\ frac {\ sqrt [{n}] {2 ^ {n}}} {\ sqrt [{n}] {n ^ {9}}}} = {\ frac {2} {(n ^ {1 / n}) ^ {9}}} = 2}$

از آنجا که ${\ displaystyle C = 2> 1 ،}$ سریال واگرا می شود. [3]

مثال 2:

${\ displaystyle 1 + 1 + 0.5 + 0.5 + 0.25 + 0.25 + 0.125 + 0.125 + ...}$

آزمون ریشه همگرایی را نشان می دهد زیرا

${\ displaystyle r = \ limsup _ {n \ to \ infty} {\ sqrt [{n}] {| a_ {n} |}} = \ limsup _ {n \ to \ infty} {\ sqrt [{n} ] {| .5 ^ {n} |}} =. 5 <1.}$

این مثال نشان می دهد که چگونه آزمون ریشه قویتر از آزمون نسبت است . اگر این نسبت برای این سری بی نتیجه باشد $n$ عجیب است بنابراین ${\ displaystyle a_ {n} = a_ {n + 1} =. 5 ^ {n}}$ (اگر نه اگر $n$ حتی است) ، زیرا

${\ displaystyle r = \ lim _ {n \ to \ infty} \ left | {\ frac {a_ {n + 1}} {a_ {n}}} \ right | = \ lim _ {n \ to \ infty} \ چپ | {\ frac {2 \ cdot .5 ^ {n}} {2 \ cdot .5 ^ {n}}} \ راست | = 1.}$

منبع

https://en.wikipedia.org/wiki/Root_test

ادامه آزمون نسبت

توسط علی رضا نقش نیلچی | پنجشنبه هجدهم دی ۱۳۹۹ | 13:25

$متر$ آزمون نسبت [ ویرایش ]

این آزمون امتداد مستقیم آزمون نسبت دوم است [7] [9] . برای ${\ displaystyle 0 \ leq k \ leq m-1،}$ و مثبت $a_ {n}$ تعریف کردن:

${\ displaystyle L_ {k} \ Equ \ lim _ {n \ rightarrow \ infty} {\ frac {a_ {mn + k}} {a_ {n}}}}$

${\ displaystyle L \ Equ \ max (L_ {0}، L_ {1}، \ ldots، L_ {m-1})}$

توسط $متر$ آزمون نسبت th ، این سری:

اگر همگرایی کنید ${\ displaystyle L <{\ frac {1} {m}}}$
واگرایی کنید اگر ${\ displaystyle L> {\ frac {1} {m}}}$
اگر ${\ displaystyle L = {\ frac {1} {m}}}$ پس آزمون بی نتیجه است.

اگر محدودیت های فوق وجود نداشته باشد ، ممکن است از محدوده های برتر و فرومایه استفاده شود. برای

${\ displaystyle 0 \ leq k \ leq m-1}$ تعریف کردن:

${\ displaystyle L_ {k} \ Equ \ limsup _ {n \ rightarrow \ infty} {\ frac {a_ {mn + k}} {a_ {n}}}}$
${\ displaystyle \ ell _ {k} \ Equ \ liminf _ {n \ rightarrow \ infty} {\ frac {a_ {mn + k}} {a_ {n}}}}$
${\ displaystyle L \ Equ \ max (L_ {0}، L_ {1}، \ ldots، L_ {m-1})}$		${\ displaystyle \ ell \ Equ \ min (\ ell _ {0}، \ ell _ {1}، \ ldots، \ ell _ {m-1})}$

سپس این مجموعه:

اگر همگرایی کنید ${\ displaystyle L <{\ frac {1} {m}}}$
واگرایی کنید اگر ${\ displaystyle \ ell> {\ frac {1} {m}}}$
اگر ${\ displaystyle \ ell \ leq {\ frac {1} {m}} \ leq L}$ ، پس آزمون بی نتیجه است.

دویچه $\ varphi$ آزمون -ratio [ ویرایش ]

این آزمون یک پسوند است $متر$ آزمون نسبت th [17] .

فرض کنید که توالی $a_ {n}$ یک توالی کاهش مثبت است.

اجازه دهید ${\ displaystyle \ varphi: \ mathbb {Z} ^ {+} \ به \ mathbb {Z} ^ {+}}$ به گونه ای باشد که ${\ displaystyle \ lim _ {n \ to \ infty} {\ frac {n} {\ varphi (n)}}}$ وجود دارد مشخص کن ${\ displaystyle \ alpha = \ lim _ {n \ to \ infty} {\ frac {n} {\ varphi (n)}}}$ ، و فرض کنید $0 <\ alpha <1$ .

همچنین فرض کنید که ${\ displaystyle \ lim _ {n \ to \ infty} {\ frac {a _ {\ varphi (n)}} {a_ {n}}} = L.}$

سپس این مجموعه:

اگر همگرایی کنید ${\ displaystyle L <\ alpha}$
واگرایی کنید اگر ${\ displaystyle \ ell> \ alpha}$
اگر ${\ displaystyle L = \ alpha}$ ، پس آزمون بی نتیجه است.

منبع

https://en.wikipedia.org/wiki/Ratio_test

مطالب جدید تر مطالب قدیمی تر

مشخصات وب

در این وبلاگ به ریاضیات و کاربردهای آن و تحقیقات در آنها پرداخته می شود. مطالب در این وبلاگ ترجمه سطحی و اولیه است و کامل نیست.در صورتی سوال یا نظری در زمینه ریاضیات دارید مطرح نمایید .در صورت امکان به آن می پردازم. من دوست دارم برای یافتن پاسخ به سوالات و حل پروژه های علمی با دیگران همکاری نمایم.در صورتی که شما هم بامن هم عقیده هستید با من تماس بگیرید.
09132003030

ریاضیات

آموزش ریاضی

بسط تیلور sinx ,x=p/2

بسط تیلور sinx ,x=p

بسط تیلور e^3x در 5=x

بسط تیلور سینوس

جملات سری تیلور f(x)=ln(2x) در 3=x

4-سری تیلور

محاسبه سری تیلور [ ویرایش ]

مثال اول [ ویرایش ]

مثال دوم [ ویرایش ]

مثال سوم [ ویرایش ]

مجموعه تیلور به عنوان تعاریف [ ویرایش ]

سری تیلور در چندین متغیر [ ویرایش ]

مثال [ ویرایش ]

مقایسه با سری فوریه [ ویرایش ]

همچنین مشاهده کنید [ ویرایش ]

3-سری تیلور

خطای تقریب و همگرایی [ ویرایش ]

تعمیم [ ویرایش ]

فهرستی از سری مکلورن از برخی توابع رایج [ ویرایش ]

تابع نمایی [ ویرایش ]

لگاریتم طبیعی [ ویرایش ]

سری هندسی [ ویرایش ]

سری دو جمله ای [ ویرایش ]

توابع مثلثاتی [ ویرایش ]

توابع هذلولی [ ویرایش ]

1-سری تیلور

سری تیلور

فهرست

تعریف [ ویرایش ]

بسط مکلورن sin,cos,sinh,cosh

فرمول های معکوس مثلثاتی هیپربولیک بر حسب لگاریتم

اتحادهایی از تابع های مثلثاتی هیپربولیک

ادامه مجموعه محدب 3

غلاف های محدب مجموعات مینکوفسکی [ ویرایش ]

مینکوفسکی مجموع مجموعه های محدب [ ویرایش ]

تعمیم و بسط برای تحدب [ ویرایش ]

مجموعه های ستاره ای محدب (ستاره ای شکل) [ ویرایش ]

تحدب متعامد [ ویرایش ]

هندسه نااقلیدسی [ ویرایش ]

توپولوژی سفارش [ ویرایش ]

فضاهای تحدب [ ویرایش ]

همچنین ببینید [ ویرایش ]

ادامه مجموعه محدب2

سایر خواص [ ویرایش ]

بدنه های محدب و مجموع مینکوفسکی [ ویرایش ]

بدنه محدب [ ویرایش ]

افزودن مینکوفسکی [ ویرایش ]

ادامه مجموعه محدب 1

مجموعه غیر محدب

خواص [ ویرایش ]

اشتراک ها و اجتماع ها [ ویرایش ]

مجموعه های محدب بسته [ ویرایش ]

مجموعه ها و مستطیل های محدب [ ویرایش ]

نمودارهای بلاشکه-سانتالو [ ویرایش ]

مجموعه محدب

فهرست

تعاریف [ ویرایش ]

مثال یک فضای که همبند است اما همبند مسیری نیست

یک فضای که همبند است اما همبند مسیری نیست

قضیه بوشنر و قضیه گشتاور هاسدورف در نیمه گروه های توپولوژیکی پایه

همومورفیسم ضعف پذیری ضعیف برخی از جبرهای Banach

همومورفیسم ضعف پذیری ضعیف برخی از جبرهای Banach

تنوع محدود

فهرست

ادامه انتگرال ناسره

جمع بودن [ ویرایش ]

انتگرال های نامناسب چند متغیره [ ویرایش ]

انتگرال نامناسب در دامنه های دلخواه [ ویرایش ]

انتگرال نامناسب با تکینگی ها [ ویرایش ]

عملکردهایی با مقادیر مثبت و منفی [ ویرایش ]

ادامه انتگرال ناسره

انواع انتگرال [ ویرایش ]

انتگرال نامناسب ریمان و انتگرال Lebesgue [ ویرایش ]

تکینگی ها [ ویرایش ]

ارزش اصلی کوشی [ ویرایش ]

انتگرال ناسره

فهرست

مثالها [ ویرایش ]

$متر$ آزمون نسبت [ ویرایش ]

دویچه $\ varphi$ آزمون -ratio [ ویرایش ]